Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T12:05:49.618Z Has data issue: false hasContentIssue false
  • English
  • Français

Spatial dynamics of a nonlocal model with periodic delay and competition

Part of: Applications - Dynamical systems and ergodic theory Parabolic equations and systems

Published online by Cambridge University Press:  06 January 2020

L. ZHANG ,
K. H. LIU ,
Y. J. LOU  and
Z. C. WANG Open the ORCID record for Z. C. WANG [Opens in a new window]
L. ZHANG
Affiliation:
School of Mathematics and Statistics, Lanzhou University, Lanzhou, Gansu730000, People’s Republic of China, emails: lz@lzu.edu.cn; wangzhch@lzu.edu.cn
K. H. LIU
Affiliation:
Department of Applied Mathematics, The Hong Kong Polytechnic University, Hung Hom, Kowloon, Hong Kong, People’s Republic of China, emails: katrina.liu@connect.polyu.hk; yijun.lou@polyu.edu.hk Faculty of Science, Jiangsu University, Zhenjiang, Jiangsu212000, People’s Republic of China email: liukaihui@ujs.edu.cn
Y. J. LOU
Affiliation:
Department of Applied Mathematics, The Hong Kong Polytechnic University, Hung Hom, Kowloon, Hong Kong, People’s Republic of China, emails: katrina.liu@connect.polyu.hk; yijun.lou@polyu.edu.hk
Z. C. WANG
Affiliation:
School of Mathematics and Statistics, Lanzhou University, Lanzhou, Gansu730000, People’s Republic of China, emails: lz@lzu.edu.cn; wangzhch@lzu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Each species is subject to various biotic and abiotic factors during growth. This paper formulates a deterministic model with the consideration of various factors regulating population growth such as age-dependent birth and death rates, spatial movements, seasonal variations, intra-specific competition and time-varying maturation simultaneously. The model takes the form of two coupled reaction–diffusion equations with time-dependent delays, which bring novel challenges to the theoretical analysis. Then, the model is analysed when competition among immatures is neglected, in which situation one equation for the adult population density is decoupled. The basic reproduction number 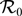$\mathcal{R}_0$ is defined and shown to determine the global attractivity of either the zero equilibrium (when 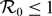$\mathcal{R}_0\leq 1$ ) or a positive periodic solution ( 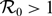$\mathcal{R}_0\gt1$ ) by using the dynamical system approach on an appropriate phase space. When the immature intra-specific competition is included and the immature diffusion rate is neglected, the model is neither cooperative nor reducible to a single equation. In this case, the threshold dynamics about the population extinction and uniform persistence are established by using the newly defined basic reproduction number 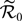$\widetilde{\mathcal{R}}_0$ as a threshold index. Furthermore, numerical simulations are implemented on the population growth of two different species for two different cases to validate the analytic results.

Keywords

Age structurediffusionseasonal effectsperiodic delayintra-specific competition

MSC classification

Primary: 35K57: Reaction-diffusion equations 37N25: Dynamical systems in biology
Secondary: 92D25: Population dynamics (general)
Type
Papers
Information
European Journal of Applied Mathematics , Volume 31 , Issue 6 , December 2020 , pp. 1070 - 1100
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

The work of YL and KL is supported in part by the Research Grants Council of Hong Kong (PolyU 153277/16P) and the Research Grants of Jiangsu University (4111190009). ZW and LZ are supported by NNSF of China (11371179 and 11701242) and the Fundamental Research Funds for the Central Universities (lzujbky-2017-ot09, lzujbky-2017-27 and lzujbky-2019-79).

References

Alto, B. W., Lounibos, L. P., Higgs, S. & Juliano, S. A. (2005) Larval competition differentially affects arbovirus infection in Aedes mosquitoes. Ecology 86(12), 3279–3288.CrossRefGoogle ScholarPubMed
Alto, B. W., Lounibos, L. P., Mores, C. N., & Reiskind, M. H. (2008) Larval competition alters susceptibility of adult Aedes mosquitoes to dengue infection. Proc. R. Soc. B 275(1633), 463–471.CrossRefGoogle ScholarPubMed
Altwegg, R. (2002) Trait-mediated indirect effects and complex life-cycles in two European frogs. Evol. Ecol. Res. 4(4), 519–536.Google Scholar
Brambell, F. W. R. (2010) The reproduction of the wild rabbit Oryctolagus cuniculus (L.). J. Zool. 114(1–2), 1–45.Google Scholar
Cantrell, R. S. & Cosner, C. (2004) Spatial Ecology via Reaction-Diffusion Equations. John Wiley & Sons, New York.CrossRefGoogle Scholar
Craig, L. E., Norris, D. E., Sanders, M. L., Glass, G. E. & Schwartz, B. S. (1996) Acquired resistance and antibody response of raccoons (Procyon lotor) to sequential feedings of Ixodes scapularis (Acari: Ixodidae). Vet. Parasitol. 63(3–4), 291–301.CrossRefGoogle Scholar
De Valdez, M. R. W. (2017) Mosquito species distribution across urban, suburban, and semi-rural residences in San Antonio, Texas. J. Vector Ecol. 42(1), 184.CrossRefGoogle ScholarPubMed
Dziminski, M. A. (2009) Intraspecific competition in the larvae of quacking frogs (Crinia georgiana). Copeia 2009(4), 724–726.Google Scholar
Ewing, D. A., Cobbold, C. A., Purse, B. V., Nunn, M. A. & White, S. M. (2016) Modelling the effect of temperature on the seasonal population dynamics of temperate mosquitoes. J. Theor. Biol. 400, 65–79.CrossRefGoogle ScholarPubMed
Fang, J., Gourley, S. A. & Lou, Y. (2016) Stage-structured models of intra-and inter-specific competition within age classes. J. Differ. Equ. 260(2), 1918–1953.Google Scholar
Friedman, A. (2008) Partial Differential Equations of Parabolic Type. Courier Dover Publications, New York.Google Scholar
Gaines, M. S. & McClenaghan, L. R Jr., (1980) Dispersal in small mammals. Ann. Rev. EcoL Syst. 11(1), 163–196.Google Scholar
Gourley, S. A. & Kuang, Y. (2003) Wavefronts and global stability in a time-delayed population model with stage structure. Proc. R. Soc. Lond. A 459(2034), 1563–1579.Google Scholar
Gourley, S. A., Liu, R. & Lou, Y. (2017) Intra-specific competition and insect larval development: A model with time-dependent delay. P. Roy. Soc. Edinb. A 147(2), 353–369.CrossRefGoogle Scholar
Gourley, S. A., Liu, R. & Wu, J. (2008) Spatiotemporal patterns of disease spread: Interaction of physiological structure, spatial movements, disease progression and human intervention. In: Structured Population Models in Biology and Epidemiology, vol. 1936. Springer, Berlin, pp. 165–208.CrossRefGoogle Scholar
Hale, J. K. (1988) Asymptotic Behavior of Dissipative Systems, vol. 25. American Mathematical Society.Google Scholar
Iannelli, M. (1995) Mathematical Theory of Age-Structured Population Dynamics. Giardini Editori e Stampatori, Pisa.Google Scholar
Ido, T., Alon, S., Ofer, O., Leon, B. & Yoel, M. (2013) Inter- and intra-specific density-dependent effects on life history and development strategies of larval mosquitoes. Plos One 8(3), e57875.Google Scholar
Jin, Y. & Zhao, X.-Q. (2009) Spatial dynamics of a nonlocal periodic reaction-diffusion model with stage structure. SIAM J. Math. Anal. 40(6), 2496–2516.CrossRefGoogle Scholar
Kontsiotis, V. J., Bakaloudis, D. E., Xofis, P., Konstantaras, N., Petrakis, N. & Tsiompanoudis, A. (2013) Modeling the distribution of wild rabbits (Oryctolagus cuniculus) on a Mediterranean island. Ecol. Res. 28(2), 317–325.CrossRefGoogle Scholar
Künkele, J. & Von Holst, D. (1996) Natal dispersal in the European wild rabbit. Anim. Behav. 51(5), 1047–1059.CrossRefGoogle Scholar
Lees, A. C. & Bell, D. J. (2008) A conservation paradox for the 21st century: The European wild rabbit Oryctolagus cuniculus, an invasive alien and an endangered native species. Mammal Rev. 38(4), 304–320.CrossRefGoogle Scholar
Legros, M., Lloyd, A. L., Huang, Y. & Gould, F. (2009) Density-dependent intraspecific competition in the larval stage of Aedes aegypti (Diptera: Culicidae): Revisiting the current paradigm. J. Med. Entomol. 46(3), 409–419.CrossRefGoogle ScholarPubMed
Levin, S. A. (1974) Dispersion and population interactions. Am. Nat. 108(960), 207–228.CrossRefGoogle Scholar
Li, J. & Brauer, F. (2008) Continuous-time age-structured models in population dynamics and epidemiology. In: Mathematical Epidemiology, Springer, Berlin, Heidelberg, pp. 205–227.CrossRefGoogle Scholar
Liang, X., Zhang, L. & Zhao, X.-Q. (2019) Basic reproduct ratios for periodic abstract functional differential equations (with application to a spatial model for Lyme disease). J. Dyn. Differ. Equ. 31, 1247–1278.Google Scholar
Liang, X. & Zhao, X.-Q. (2007) Asymptotic speeds of spread and traveling waves for monotone semiflows with applications. Commun. Pure Appl. Math. 60(1), 1–40.CrossRefGoogle Scholar
Liu, K., Lou, Y. & Wu, J. (2017) Analysis of an age structured model for tick populations subject to seasonal effects. J. Differ. Equ. 263(4), 2078–2112.CrossRefGoogle Scholar
Lou, Y. & Zhao, X.-Q. (2017) A theoretical approach to understanding population dynamics with seasonal developmental durations. J. Nonlinear Sci. 27(2), 573–603.Google Scholar
Martin, R. H. & Smith, H. L. (1990) Abstract functional-differential equations and reaction-diffusion systems. Trans. Am. Math. Soc. 321(1), 1–44.Google Scholar
Mcgrady, M. J., Ueta, M., Potapov, E. R., Utekhina, I., Masterov, V., Ladyguine, A., Zykov, V., Cibor, J., Fuller, M. & Seegar, W. S. (2003) Movements by juvenile and immature Steller’s Sea Eagles Haliaeetus pelagicus tracked by satellite. Ibis 145(2), 318–328.Google Scholar
Metz, J. A. J. & Diekmann, O. (1986) The Dynamics of Physiologically Structured Populations. Springer-Verlag, Berlin, Heidelberg.CrossRefGoogle Scholar
Nisbet, R. M. (1997) Delay-differential equations for structured populations. In: Structured-Population Models in Marine, Terrestrial, and Freshwater Systems. Springer, pp. 89–118.CrossRefGoogle Scholar
Ogden, N. H., Bigras-Poulin, M., O’Callaghan, C. J., Barker, I. K., Lindsay, L. R., Maarouf, A., Smoyer-Tomic, K. E., Waltner-Toews, D. & Charron, D. (2005) A dynamic population model to investigate effects of climate on geographic range and seasonality of the tick ixodes scapularis. Int. J. Parasitol. 35(4), 375–389.CrossRefGoogle ScholarPubMed
Reiskind, M. H. & Lounibos, L. P. (2009) Effects of intraspecific larval competition on adult longevity in the mosquitoes Aedes aegypti and Aedes albopictus. Med. Vet. Entomol. 23(1), 62–68.CrossRefGoogle ScholarPubMed
Silver, J. B. (2007) Mosquito Ecology: Field Sampling Methods. Springer Science & Business Media.Google Scholar
Simoy, M. I., Simoy, M. V. & Canziani, G. A. (2015) The effect of temperature on the population dynamics of Aedes aegypti. Ecol. Model. 314(5), 100–110.CrossRefGoogle Scholar
Smith, D. L., Perkins, T. A., Reiner, R. C., Barker, C. M., Niu, T., Chaves, L. F., Ellis, A. M., George, D. B., Menach, A. L. & Pulliam, J. R. C. (2014) Recasting the theory of mosquito-borne pathogen transmission dynamics and control. Trans. R. Soc. Trop. Med. Hyg. 108(4), 185–197.CrossRefGoogle ScholarPubMed
So, J. W.-H., Wu, J. & Zou, X. (2001) Structured population on two patches: Modelling dispersal and delay. J. Math. Biol. 43(1), 37–51.CrossRefGoogle Scholar
Thieme, H. R. & Zhao, X.-Q. (2003) Asymptotic speeds of spread and traveling waves for integral equations and delayed reaction–diffusion models. J. Differ. Equ. 195(2), 430–470.CrossRefGoogle Scholar
Wang, X. & Zou, X. (2018) Threshold dynamics of a temperature-dependent stage-structured mosquito population model with nested delays. Bull. Math. Biol. 80(7), 1962–1987.CrossRefGoogle ScholarPubMed
Webb, G. F. (1985) Theory of Nonlinear Age-Dependent Population Dynamics. Marcel Dekker, New York.Google Scholar
Willadsen, P. & Jongejan, F. (1999) Immunology of the tick–host interaction and the control of ticks and tick-borne diseases. Parasitol. Today 15(7), 258–262.CrossRefGoogle ScholarPubMed
Wilson, M. L., Litwin, T. S., Gavin, T. A., Capkanis, M. C., Maclean, D. C. & Spielman, A. (1990) Host-dependent differences in feeding and reproduction of Ixodes dammini (Acari: Ixodidae). J. Med. Entomol. 27(6), 945–954.Google Scholar
Wu, J. (1996) Theory and Applications of Partial Functional Differential Equations, vol. 119. Springer-Verlag, New York.CrossRefGoogle Scholar
Wu, X., Magpantay, F. M. G., Wu, J. & Zou, X. (2015) Stage-structured population systems with temporally periodic delay. Math. Methods Appl. Sci. 38(16), 3464–3481.Google Scholar
Xu, D. & Zhao, X.-Q. (2003) A nonlocal reaction-diffusion population model with stage structure. Canad. Appl. Math. Quart. 11(3), 303–319.Google Scholar
Xu, D. & Zhao, X.-Q. (2005) Dynamics in a periodic competitive model with stage structure. J. Math. Anal. Appl. 311(2), 417–438.Google Scholar
Yang, H., Boldrini, J., Fassoni, A., Lima, K., Freitas, L., Gomez, M., Andrade, V. & Freitas, A. (2014) Abiotic effects on population dynamics of mosquitoes and their influence on dengue transmission. In: Ecological Modelling Applied to Entomology, Springer, pp. 39–80.Google Scholar
Yi, T. & Zou, X. (2011) Global dynamics of a delay differential equation with spatial non-locality in an unbounded domain. J. Differ. Equ. 251(9), 2598–2611.Google Scholar
Zhang, L., Wang, Z.-C. & Zhao, X.-Q. (2015) Threshold dynamics of a time periodic reaction–diffusion epidemic model with latent period. J. Differ. Equ. 258(9), 3011–3036.CrossRefGoogle Scholar
Zhao, X.-Q. (2017) Basic reproduction ratios for periodic compartmental models with time delay. J. Dyn. Differ. Equ. 29, 67–82.CrossRefGoogle Scholar
Zhao, X.-Q. (2017) Dynamical Systems in Population Biology. Springer-Verlag, New York.CrossRefGoogle Scholar