Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T17:19:42.789Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral projections correlation structure for short-to-long range dependent processes

Part of: Markov processes Inference from stochastic processes Special classes of linear operators Stochastic processes Multivariate analysis

Published online by Cambridge University Press:  31 January 2020

P. PATIE Open the ORCID record for P. PATIE [Opens in a new window]  and
A. SRAPIONYAN Open the ORCID record for A. SRAPIONYAN [Opens in a new window]
P. PATIE
Affiliation:
School of Operations Research and Information Engineering, Cornell University, Ithaca, NY14853, USA email: pp396@orie.cornell.edu
A. SRAPIONYAN
Affiliation:
Center for Applied Mathematics, Cornell University, Ithaca, NY14853, USA email: as3348@cornell.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let X = (Xt)t≥0 be a stochastic process issued from 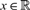$x \in \mathbb{R}$ that admits a marginal stationary measure v, i.e. vPtf = vf for all t ≥ 0, where 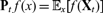$\textbf{P}_t\,f(x)= \mathbb{E}_x[f(\textbf{X}_t)]$ . In this paper, we introduce the (resp. biorthogonal) spectral projections correlation functions which are expressed in terms of projections.” Also, update first published online date, if available. into the eigenspaces of Pt (resp. and of its adjoint in the weighted Hilbert space L2 (v)). We obtain closed-form expressions involving eigenvalues, the condition number and/or the angle between the projections in the following different situations: when X = X with X = (Xt)t ≥ 0 being a Markov process, X is the subordination of X in the sense of Bochner, and X is a non-Markovian process which is obtained by time-changing X with an inverse of a subordinator. It turns out that these spectral projections correlation functions have different expressions with respect to these classes of processes which enables to identify substantial and deep properties about their dynamics. This interesting fact can be used to design original statistical tests to make inferences, for example, about the path properties of the process (presence of jumps), distance from symmetry (self-adjoint or non-self-adjoint) and short-to-long-range dependence. To reveal the usefulness of our results, we apply them to a class of non-self-adjoint Markov semigroups studied in Patie and Savov (to appear, Mem. Amer. Math. Soc., 179p), and then time-change by subordinators and their inverses.

Keywords

Spectral theoryspectral projectionscorrelation functionstime-changelong-range dependencepolynomial processesstatistical tests

MSC classification

Primary: 60G07: General theory of processes 47B40: Spectral operators, decomposable operators, well-bounded operators, etc. 62H20: Measures of association (correlation, canonical correlation, etc.)
Secondary: 62M02: Markov processes 62M07: Non-Markovian processes 60J55: Local time and additive functionals
Type
Papers
Information
European Journal of Applied Mathematics , Volume 32 , Issue 1 , February 2021 , pp. 1 - 31
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aït-Sahalia, Y. & Jacod, J. (2009) Testing for jumps in a discretely observed process. Ann. Statist. 37(1), 184–222.CrossRefGoogle Scholar
Aït-Sahalia, Y. & Jacod, J. (2011) Testing whether jumps have finite or infinite activity. Ann. Statist. 39(3), 1689–1719.CrossRefGoogle Scholar
Aletti, G., Leonenko, N. N. & Merzbach, E. (2018) Fractional Poisson fields and martingales. J. Stat. Phys. 170(4), 700–730.CrossRefGoogle Scholar
Baeumer, B. & Meerschaert, M. M. (2001) Stochastic solutions for fractional Cauchy problems. Fractional Calculus Appl. Anal. 4(4), 481–500.Google Scholar
Beigi, S. & Gohari, A. (2018) Φ-entropic measures of correlation. IEEE Trans. Inform. Theory 64(4, part 1), 2193–2211.CrossRefGoogle Scholar
Bhattacharjee, A. (2014) Distance correlation coefficient: an application with Bayesian approach in clinical data analysis. J. Mod. Appl. Stat. Methods 13(1), 23.CrossRefGoogle Scholar
Bingham, N. H., Goldie, C. M. & Teugels, J. L. (1989) Regular Variation, Vol. 27, Cambridge University Press, Cambridge.Google Scholar
Bochner, S. (1949) Diffusion equation and stochastic processes. Proc. Natl. Acad. Sci. U.S.A. 35(7), 368–370.CrossRefGoogle ScholarPubMed
Bochner, S. (2013) Harmonic Analysis and the Theory of Probability. Courier Corporation, Berkeley and Los Angeles.Google Scholar
Bryc, W., Dembo, A. & Kagan, A. (2004) On the maximum correlation coefficient. Theory Probab. Appl. 49(1), 191–197.Google Scholar
Chung, K. L. & Walsh, J. B. (2005) Markov Processes, Brownian Motion, and Time Symmetry, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], Vol. 249, 2nd ed., Springer, New York.CrossRefGoogle Scholar
Cox, J. C., Ingersoll, J. E. Jr., & Ross, S. A. (1985) An intertemporal general equilibrium model of asset prices. Econom. J. Econom. Soc. 53(2), 363–384.Google Scholar
Da Prato, G. (2006) An Introduction to Infinite-Dimensional Analysis, Springer Science & Business Media, Springer-Verlag, Berlin.CrossRefGoogle Scholar
Davies, E. B. (2000) Wild spectral behaviour of anharmonic oscillators. Bull. London Math. Soc. 32(4), 432–438.CrossRefGoogle Scholar
Dembo, A., Kagan, A. & Shepp, L. A. (2001) Remarks on the maximum correlation coefficient. Bernoulli 7(2), 343–350.CrossRefGoogle Scholar
Foss, S., Korshunov, D. & Zachary, S. (2013) An Introduction to Heavy-Tailed and Subexponential Distributions, Springer Series in Operations Research and Financial Engineering, 2nd ed., Springer, New York.CrossRefGoogle Scholar
Gebelein, H. (1941) Das statistische Problem der Korrelation als Variations-und Eigenwertproblem und sein Zusammenhang mit der Ausgleichsrechnung. ZAMM-J. Appl. Math. Mech./Zeitschrift für Angewandte Mathematik und Mechanik 21(6), 364–379.CrossRefGoogle Scholar
Gill, R. D., van der Laan, M. J. & Wellner, J. A. (1995) Inefficient Estimators of the Bivariate Survival Function for Three Models. Annales de l’IHP Probabilités et statistiques. Vol. 31. No. 3.Google Scholar
Hairer, M., Iyer, G., Koralov, L., Novikov, A. & Pajor-Gyulai, Z. (2018) A fractional kinetic process describing the intermediate time behaviour of cellular flows. Ann. Probab. 46(2), 897–955.CrossRefGoogle Scholar
Jang, P. A., Leth, L. R., Patie, P. & Srapionyan, A. (2018) Long-range dependence in volatility. An empirical study. Working Paper.Google Scholar
Jarrow, R. A., Patie, P., Srapionyan, A. & Zhao, Y. (2018) Risk-neutral pricing techniques and examples. https://www.researchgate.net/publication/328695749_Risk-neutral_pricing_techniques_and_examples.Google Scholar
Kochubei, A. N. (2011) General fractional calculus, evolution equations, and renewal processes. Integr. Equ. Oper. Theory 71(4), 583–600.CrossRefGoogle Scholar
Lancaster, H. O. (1957) Some properties of the bivariate normal distribution considered in the form of a contingency table. Biometrika 44(1/2), 289–292.CrossRefGoogle Scholar
Leonenko, N. N., Meerschaert, M. M., Schilling, R. L. & Sikorskii, A. (2014) Correlation structure of time-changed Lévy processes. Commun. Appl. Ind. Math. 6(1), e–483, 22.Google Scholar
Leonenko, N. N., Meerschaert, M. M. & Sikorskii, A. (2013) Correlation structure of fractional Pearson diffusions. Comput. Math. Appl. 66(5), 737–745.CrossRefGoogle ScholarPubMed
Leonenko, N. N., Meerschaert, M. M. & Sikorskii, A. (2013) Fractional Pearson diffusions. J. Math. Anal. Appl. 403(2), 532–546.CrossRefGoogle ScholarPubMed
Leonenko, N. N., Papić, I., Sikorskii, A. & Šuvak, N. (2017) Heavy-tailed fractional Pearson diffusions. Stoch. Process. Their Appl. 27(11), 3512–3335.CrossRefGoogle Scholar
Levakova, M., Tamborrino, M., Ditlevsen, S. & Lansky, P. (2015) A review of the methods for neuronal response latency estimation. Biosystems 136, 23–34.CrossRefGoogle ScholarPubMed
Meerschaert, M. M., Nane, E. & Vellaisamy, P. (2009) Fractional Cauchy problems on bounded domains. Ann. Probab. 37(3), 979–1007.CrossRefGoogle Scholar
Meerschaert, M. M. & Sikorskii, A. (2012) Stochastic Models for Fractional Calculus, De Gruyter Studies in Mathematics, Vol. 43, Walter de Gruyter & Co., Berlin.Google Scholar
Mijena, J. B. & Nane, E. (2014) Correlation structure of time-changed Pearson diffusions. Statist. Probab. Lett. 90, 68–77.CrossRefGoogle Scholar
Orsingher, E., Ricciuti, C. & Toaldo, B. (2018) On semi-Markov processes and their Kolmogorov’s integro-differential equations. J. Funct. Anal. 275(4), 830–868.CrossRefGoogle Scholar
Papadatos, N. & Xifara, T. (2013) A simple method for obtaining the maximal correlation coefficient and related characterizations. J. Multivariate Anal. 118, 102–114.CrossRefGoogle Scholar
Patie, P. & Savov, M. (2017) Cauchy problem of the non-self-adjoint Gauss-Laguerre semigroups and uniform bounds for generalized Laguerre polynomials. J. Spectr. Theory 7(3), 797–846.CrossRefGoogle Scholar
Patie, P. & Savov, M. (to appear) Spectral expansions of non-self-adjoint generalized Laguerre semigroups. Mem. Amer. Math. Soc. 179p.Google Scholar
Patie, P., Savov, M. & Zhao, Y. (to appear) Intertwining, excursion theory and Krein theory of strings for non-self-adjoint Markov semigroups. Ann. Probab. 51p. 47(5), 3231–3277.CrossRefGoogle Scholar
Patie, P. & Srapionyan, A. (2019) Self-similar Cauchy problems and generalized Mittag-Leffler functions. https://www.researchgate.net/publication/332655312_Self-similar_Cauchy_problems_and_generalized_Mittag-Leffler_functions.Google Scholar
Rényi, A. (1959) On measures of dependence. Acta Math. Acad. Sci. Hungar. 10, 441–451 (unbound insert).CrossRefGoogle Scholar
Samorodnitsky, G. (2016) Stochastic Processes and Long Range Dependence, Springer Series in Operations Research and Financial Engineering, Springer, Cham.CrossRefGoogle Scholar
Schilling, R. L., Song, R. & Vondraček, Z. (2012) Bernstein Functions: Theory and Applications, Vol. 37. Walter de Gruyter.CrossRefGoogle Scholar
Székely, G. J. & Rizzo, M. L. (2009) Brownian distance covariance. Ann. Appl. Stat. 3(4), 1303–1308.CrossRefGoogle Scholar
Székely, G. J., Rizzo, M. L. & Bakirov, N. K. (2007) Measuring and testing dependence by correlation of distances. Ann. Stat. 35(6), 2769–2794.CrossRefGoogle Scholar
Toaldo, B. (2015) Convolution-type derivatives, hitting-times of subordinators and time-changed C0-semigroups. Potential Anal. 42(1), 115–140.CrossRefGoogle Scholar
Yu, Y. On the maximal correlation coefficient. Statist. Probab. Lett. 78(9), 1072–1075 (2008).CrossRefGoogle Scholar