Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Adachi, Shinji
Shibata, Masataka
and
Watanabe, Tatsuya
2014.
Blow-up phenomena and asymptotic profiles of ground states of quasilinear elliptic equations withH1-supercritical nonlinearities.
Journal of Differential Equations,
Vol. 256,
Issue. 4,
p.
1492.
Chen, Jianqing
2014.
Multiple positive solutions to a class of modified nonlinear Schrödinger equations.
Journal of Mathematical Analysis and Applications,
Vol. 415,
Issue. 2,
p.
525.
Jeanjean, Louis
Luo, Tingjian
and
Wang, Zhi-Qiang
2015.
Multiple normalized solutions for quasi-linear Schrödinger equations.
Journal of Differential Equations,
Vol. 259,
Issue. 8,
p.
3894.
Adachi, Shinji
and
Watanabe, Tatsuya
2016.
Asymptotic uniqueness of ground states for a class of quasilinear Schrödinger equations with H1-supercritical exponent.
Journal of Differential Equations,
Vol. 260,
Issue. 3,
p.
3086.
ADACHI, Shinji
SHIBATA, Masataka
and
WATANABE, Tatsuya
2018.
A note on the uniqueness and the non-degeneracy of positive radial solutions for semilinear elliptic problems and its application.
Acta Mathematica Scientia,
Vol. 38,
Issue. 4,
p.
1121.
Zeng, Xiaoyu
and
Zhang, Yimin
2018.
Existence and Asymptotic Behavior for the Ground State of Quasilinear Elliptic Equations.
Advanced Nonlinear Studies,
Vol. 18,
Issue. 4,
p.
725.
Liu, Xiangqing
Liu, Jiaquan
and
Wang, Zhi-Qiang
2019.
Localized nodal solutions for quasilinear Schrödinger equations.
Journal of Differential Equations,
Vol. 267,
Issue. 12,
p.
7411.
Li, Houwang
and
Zou, Wenming
2023.
Quasilinear Schrödinger equations : ground
state and infinitely many normalized solutions.
Pacific Journal of Mathematics,
Vol. 322,
Issue. 1,
p.
99.

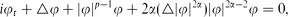
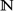 and odd
and odd 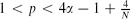 , the standing wave is stable, and when
, the standing wave is stable, and when 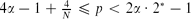 (where
(where 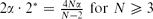 for
for 