INTRODUCTION
Corn (Zea mays L.) is a distichous plant (Paliwal et al., Reference Paliwal, Granados, Lafitte, Violic and Marathée2000) that arranges its leaves roughly in a plane, alternatingly on opposite sides of the stalk, especially if planted in rows. Peters and Woolley (Reference Peters and Woolley1959) first mentioned that if the seeds are arranged in a specific orientation at planting, plants would grow such that the leaves point preferentially into the space between the rows. Toler et al. (Reference Toler, Murdock, Stapleton and Wallace1999) found evidence similar to these observations, and described higher yields for plots with across-row-oriented leaf azimuths. Torres et al. (Reference Torres, Vossenkemper, Raun and Taylor2011) examined the effect of seed orientation on leaf azimuth distribution and showed that laying the seed flat, with embryo up or down and caryopsis attachment point across row, produced significantly higher yields than plots planted with randomly oriented seeds. They later concluded (Torres, Reference Torres2012) that this increase in yield resulted from greater light interception. Because all trials to date were hand-planted, it is not known how accurately the seeds must be oriented at planting to obtain the observed yield benefits, and how sensitive the effect is to variability in seed orientation. Other potential benefits of seed-oriented planting under investigation are that it will result in faster canopy closure, more effective weed suppression and reduced evaporation.
Maize growth models developed by researchers at the French National Institute for Agricultural Research (INRA) (Espana et al., Reference Espana, Baret, Aries, Chelle, Andrieu and Prevot1999; Fournier and Andrieu, Reference Fournier and Andrieu1999) provide a high-fidelity framework that allows astoundingly realistic computational analysis of maize plant canopies and lighting conditions. The models, however, assume uniform random distribution of the initial plant orientation. This model could be enhanced by incorporating a seed leaf azimuth distribution module based on initial seed orientation. This add-on module would allow a qualitative investigation of the effect of seed orientation accuracy on canopy development and light interception.
The objective of this research was to identify a probabilistic model for the correlation between seed orientation at planting and the resulting seed leaf azimuth distribution, which could be used in simulations of maize plots planted with oriented seeds.
MATERIALS AND METHODS
A seed-fixed reference system, as depicted in Figure 1, was defined. The origin was located at the approximate volumetric centre of the kernel, with the x-axis passing through the caryopsis attachment point, the z-axis in the direction of the embryo (in the figure out-of-plane) and the y-axis to complete a right-hand coordinate system.
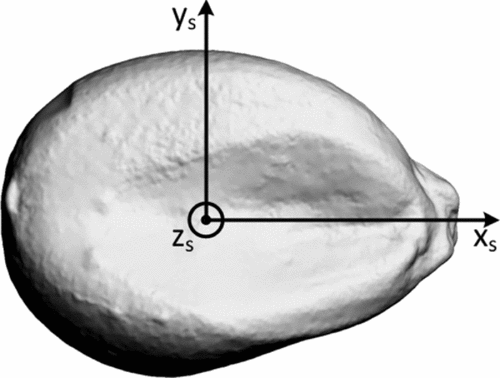
Figure 1. Definition of the seed-fixed reference system.
Four hybrids were chosen based on differing kernel shapes. The experiment included two Dekalb hybrids {DKC-6342, DKC-6346} and two Pioneer hybrids {P0902HR, P1162HR}, all of the grading ‘medium flat’, as shown in Figure 2. While the kernels of DKC-6342 are quite cuboid with distinct, parallel long sides and a well-defined caryopsis attachment point, those of P1162HR appear quite discoidal. The kernels of DKC-6346 and P0902HR lie somewhat in between these two extremes, with the kernels of P0902HR having more the streamlined shape of raindrops. These varying seed shapes were chosen based on future plans to mechanically orient the seeds during planting. As evident from Figure 2, it should also be noted that the shape variability among the randomly selected kernels of the same hybrid and the same grading is quite small.

Figure 2. Fifteen randomly selected kernels from four different hybrids.
The seeds were individually planted on potting soil about 2.5 to 3 cm deep in flower pots at the greenhouses at the Agronomy Farm at Oklahoma State University. Orientation for all seeds was ‘flat’ with the embryo either ‘up’ or ‘down’. For each trial, 40 seeds of each hybrid were planted in two replications. Pots were randomly oriented at in the greenhouse to avoid effects of light gradients and water was provided as needed to keep the soil sufficiently moist at all times.
Before covering the seed with soil, the orientation of each seed with respect to a reference line formed by markings on the flower pots (xp ) was recorded by digital imaging (Figure 3). The azimuth of the seed leaf was recorded at collar forming by the same method.

Figure 3. The seed's orientation in the pot's reference system.
Consistency in data collection was optimized by the use of a custom-built camera stand. The flower pot's drain hole was centred on a pin protruding from the centre of the base board, thus fixing all pots in the same location with respect to the camera's field of view. The camera was mounted above, facing straight down, thereby minimizing angular distortion in the images. The zoom on the camera was set such that the pot would fill the field of view. This image collection process proved to be repeatable and stable.
Seed and leaf azimuth angles in the images were determined by use of the graphics handling tool ‘Gimp’ (Gimp, 2013). Orientation angles were constrained to within ± π, with positive angles defined as counterclockwise with respect to xp . Because leaves tend to curve in three-dimensional space and are not necessarily symmetrical with respect to the rib, some judgment during leaf azimuth determination was involved. For consistency, the leaf azimuth was determined by setting the x-axis of the leaf, x l, such that it would connect the centre of the stalk with a point on the leaf rib about half the radius of the visible leaf from above.
Analysis of the same pictures by several operators showed that the measured seed orientations agreed to roughly +/− 1°, and the measured seed leaf orientations agreed to about +/− 1.8°. The initial seed azimuth with respect to the reference line on the pot was subtracted from the seed leaf azimuth with respect to the same line, to produce the seed leaf azimuth with respect to the seed.
Methods of circular statistics
Data in angular or directional form is widely encountered in various sciences. Our three-dimensional environment makes it frequently a natural choice to record data in terms of directions or angles. Often, three-dimensionality can be reduced to two dimensions by a simple rotation of the reference system such that the majority of the effect of interest is captured in a plane. Although such data is abundant, sound statistical methods for handling directional measurements started only developing in the late 1960s (Fisher, Reference Fisher1995).
As described by Mardia and Jupp (2000), ‘the sample space is typically a circle. . . so that standard methods for analysing univariate or multivariate measurement data cannot be used. Special directional methods are required which take into account the structure of these sample spaces’. The main issue with the application of methods intended for linear infinite spaces to circular data lies in the fact that on the line, 0° and 359° are 359° apart. On the circle these two measurements could equally be only 1° apart. The higher the concentration of the measurements, the smaller the error between the two classes of methods. After all, the ‘0°-direction’ in highly concentrated data can always be chosen such that ‘the circle can be cut open at the most convenient location’ (Fisher, Reference Fisher1995). In such cases, the mean, for example, from the linear domain closely agrees with the directional mean. As apparent from the data below, the data collected throughout this study is not highly concentrated and therefore mandated the application of circular statistical techniques.
The methods applied in the context of this research follow the elaborations in the three major references for circular statistics: Batschelet (1981), Fisher (Reference Fisher1995), and Mardia and Jupp (2000) have compiled exquisitely detailed guidelines for dealing with circular data. While in-depth treatment of the matter can be found in these references, a few of the key concepts are reviewed in the following.
Circular mean, variance and standard deviation
Each directional measurement can be regarded as a point on the unit circle. Therefore, the mean direction, or circular mean, is defined as the direction of the resultant vector R composed of the addition of the individual unit vectors.
The mean resultant length, Rm , is then defined as
where n is the number of measurements. Rm is bounded between 0 and 1 and is at the same time a measure for the concentration of the data. The closer Rm to 1 the more concentrated the data. Therefore, the sample circular variance Vs defined as
is a measure for the lack of concentration in the data.
The circular standard deviation on the other hand is not as one might expect simply the square root of Vs . Its particular, definition depends on the underlying probability distribution. The definition for the particular case of the von Mises distribution, as used throughout this work, is given by
where κ is the von Mises concentration parameter, discussed below.
The von mises distribution
The von Mises distribution is in the domain of circular data the analogue to the Normal distribution on the Real line and is based on a symmetric, unimodal probability model governed by the two parameters μ (mean direction) and κ (concentration parameter).
The probability density function of the von Mises distribution associated with an angular random variable θ is defined as
for 0 ≤ θ < 2π, 0 ≤ μ < 2π, and 0 ≤ κ < ∞. The function I 0 is the modified Bessel function of the first kind of order zero (Mardia and Jupp, 2000, p. 50). The larger κ, the more concentrated the data.
Estimates of the parameters μ and κ of a von Mises distribution are quite easily obtained. The circular mean of the data is already the maximum likelihood estimate of μ. The maximum likelihood estimate of the concentration parameter κ can then be written in dependence of the mean resultant length Rm (Fisher, Reference Fisher1995, p. 88). However, the accuracy of the estimate is sensitive with respect to sample size (especially for n < 15) and the estimated value of κ. Estimating κ may therefore be an iterative process that requires switching methods depending on the initial estimates of κ.
Goodness-of-fit of a probabilistic model can be checked visually by qq-plots, where the quantiles of the actual sample are compared to the quantiles of the hypothesized distribution. If the data points lie on the diagonal of the qq-plot, it is a good indication that the model is a good fit. The method applicable for the case of circular data is described in Fisher (Reference Fisher1995, p. 65f).
The U2-test for von Mises models is a more formal test for goodness-of-fit. The hypothesis that a given sample has been drawn from a von Mises distribution with estimated mean direction μ and concentration parameter κ is rejected if the computed value U2 exceeds a critical value, U2 crit. The critical values for U2 depend on the desired significance level and whether or not μ and/or κ are known a priori. Fisher (Reference Fisher1995) provides an appropriate table of U2 crit in the appendix.
Once candidate von Mises parameters have been computed, the test statistic En , defined as
can be used to check if the estimated mean direction μ is statistically different from a hypothetical mean direction μ 0. En is compared to the 100(1–0.5α)% point of the normal distribution. The hypothesis is rejected if En exceeds the critical value. Similarly, two concentration parameters κ 1 and κ 2 can be compared using the adapted F-test procedure for circular data described by Fisher (Reference Fisher1995, p. 131f). The critical value is taken from the F distribution. For example, comparing the estimates of κ 1 and κ 2 of two samples with n 1 and n 2 number of data points, respectively, the critical value for α = 0.05 would be F 1,(n1+n2–2)(P = 0.95). If the test statistic exceeds the critical value, the hypothesis that κ 1 and κ 2 are equal must be rejected.
RESULTS AND DISCUSSION
Emergence rate was approximately 98% for all hybrids: a total of 640 planted seeds produced 622 measureable plants.
Circular histograms
Circular histograms for all hybrids were computed. Figure 4 depicts the example for the hybrid DKC-6342. The bins in the histograms are 10° wide. The radial value indicates the fraction of recorded angular values per bin. Each of the histograms consists of roughly 80 data points.
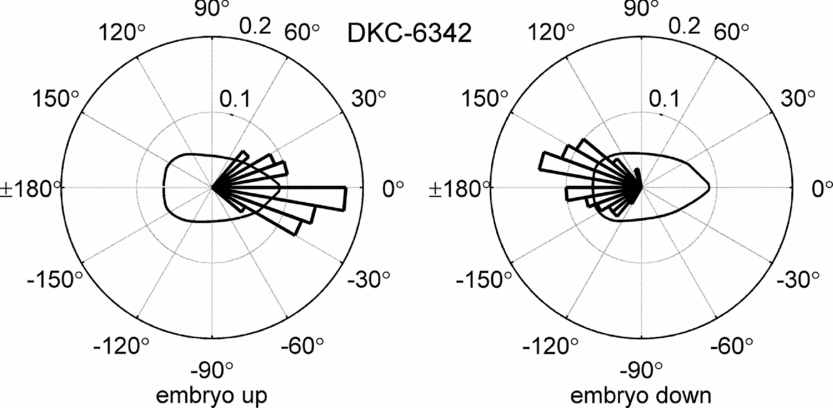
Figure 4. Circular histogram for the hybrid DKC-6342.
The histograms confirmed the findings by Torres et al. (Reference Torres, Vossenkemper, Raun and Taylor2011) that the seed orientation highly influences the seed leaf azimuth. However, it became immediately apparent that the orientation of the embryo also has a significant impact on the mean direction of the seed leaf azimuth. For embryo up, the mean direction of the seed leaf was roughly in the direction of the caryopsis attachment point, while for embryo down, it was roughly 180° offset. This effect was observable for all hybrids.
von mises parameter fitting
The von Mises parameters mean direction μ and concentration parameter κ were fitted to the data (Table 1). Without loss of generality, the data for orientations with embryo down were rotated by 180°, because the iterative fitting procedure may not converge properly if the angles are distributed around the linear discontinuity from −180° to +180°. The computed concentration parameter maintains its validity independently of the mean direction. The fitted mean direction for embryo down was afterwards transformed back into the original frame by a rotation of 180°.
Table 1. von Mises model parameters and goodness-of-fit tests for all treatments.
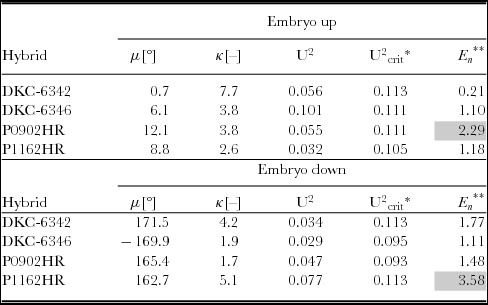
*α = 0.05, **α = 0.05 → En , crit = 1.96.
The parameter fitting indicated that the mean direction agrees with the intuitive estimates based on the circular histograms, in that the mean direction was roughly 0° for embryo up, and about 180° for embryo down, as measured from the xs -axis. The mean concentration parameter was about 4.5 for embryo up, and in the order of 3.2 for embryo down. This would indicate that the concentration parameters were generally higher for embryo up orientation. However, the formal comparison of the models as discussed below provided additional insight.
qq-plots and U2-test for goodness-of-fit assessment
qq-plots for each hybrid were computed for a visual assessment of the goodness-of-fit of the von Mises models. As evident from the qq-plot for the hybrid DKC-6342 as shown in Figure 5, the sample quantiles agreed well with the corresponding von Mises quantiles, thereby providing a first indication that the von Mises distribution was a suitable model for the correlation between seed and seed leaf azimuth.
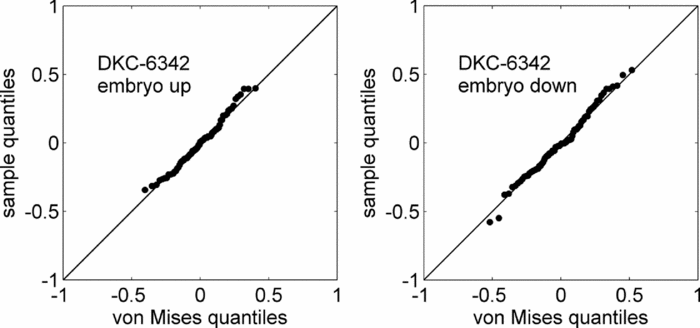
Figure 5. qq-plot for the hybrid DKC-6342.
The U2-test was applied to the models fitted above, and the results are summarized in Table 1. The hypothesis that the von Mises models were a good fit cannot be rejected for any of the models at a significance level of α = 0.05.
Relationship between mean seed leaf azimuth and seed coordinate system
The relationship between the seed coordinate frame and the mean seed leaf direction was at that point rather arbitrary, as exterior features such as the caryopsis attachment point, the location of the embryo or the apparent volumetric centre have been chosen to fix the reference frame to the seed, and the azimuths of the seed leaves have been measured and analysed with respect to that frame. The data in Table 1 suggest that the mean seed leaf direction was roughly in the direction of +xs for embryo up, and −xs for embryo down. The hypothesis, that the mean seed leaf azimuth was correlated with the arbitrarily chosen reference frame, was subjected to the E n-test described by Fisher (Reference Fisher1995). For example, for embryo up, the mean seed leaf azimuth is hypothesized to be 0°. The En-test checks if the fitted mean direction differs significantly from 0°. The results of this test are summarized in Table 1. For treatments {P0902HR, embryo down} and {P1162HR, embryo down}, the hypothesis that the mean direction was aligned with xs should be rejected. This observation could be attributable to the fact that the kernel shapes of P0902HR and P1162HR made it more difficult to locate xs , likely producing a higher measurement error during manual image analysis. For all other treatments, there was no evidence that the mean seed leaf direction differs from 0° for embryo up or from 180° for embryo down.
Comparison of the von mises concentration parameters
Applying the F-Test described above, the concentration parameters for embryo up and embryo down were compared across all combinations of hybrids. The results of the F-test for all combinations for a significance level of α = 0.05 are summarized in Table 2. The diagonal entries, which contain the comparison of embryo up and embryo down for one specific hybrid, show that only for P0902HR was the concentration parameter for embryo up and embryo down considered different. Furthermore, there was a significant difference in the concentration parameter between {DKC-6342, embryo up} and {DKC-6346, embryo down} and {P0902HR, embryo down}, as well as between {P0902HR, embryo up} and {DKC-6346, embryo down}. The F-test of comparison of embryo up with embryo down for the same hybrid did not confirm the visual impression given by the histograms. Except for P0902HR, the distributions for embryo up or embryo down could not be determined to be significantly different. This signifies that the seed leaf azimuth distribution model would be generally valid for both embryo up and embryo down for a given hybrid. However, a somewhat inconclusive picture is obtained from cross-comparison of one hybrid's embryo up/down model with that of another hybrid. Three out of twelve cross-comparisons require a rejection of the hypothesis that the models are equal, which was an indication that a general model applicable for all hybrids may not be justified.
Table 2. Cross-comparison of the concentration parameters for ‘embryo up’ and ‘embryo down’.
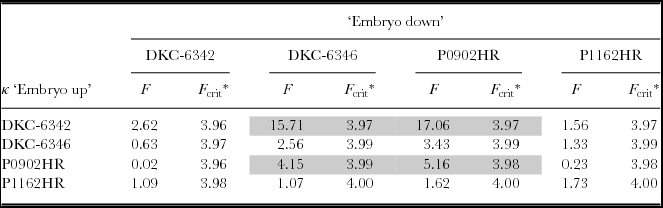
*α = 0.05.
Separate comparison of the concentration parameters for embryo up and embryo down provides further evidence that the seed leaf azimuth distribution models may be different across hybrids. As shown in Table 3, which contains the F-test results of the cross-comparison of the concentration parameters for embryo up, DKC-6342 and DKC-6346, as well as DKC-6342 and P1162HR, appeared to disagree on the concentration parameters.
Table 3. Comparison of the concentration parameters of the von Mises models.
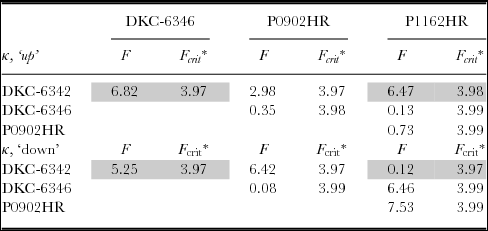
*α = 0.05.
The cross-comparison for embryo-down is summarized in Table 3, which suggests that only DKC-6346 and P0902HR and DKC-6342 and P1162HR agree on their concentration parameters. In summary, comparison of the concentration parameters therefore suggests that a single value was sufficient to describe the seed leaf azimuth distribution for embryo up or embryo down, but that the models in general must be considered different across hybrids.
Quasi-generalized model for plant growth simulation
Although a single model may not be suitable for all hybrids, a quasi-generalized model for simulation purposes can be formulated based on the findings discussed above. Considering the range of concentration parameters found, a model could take the form:
 \begin{equation}
\begin{array}{l@{\hspace*{8pt}}l}
& \mu = \{ 0,{\rm if}\;{\rm embryo}\;{\rm up}; \pi ,\;{\rm if}\;{\rm embryo}\;{\rm down} \} \\
\theta \sim vM(\mu ,\kappa )\\
& \kappa = (1.5,\,8) \\
\end{array}\end{equation}
\begin{equation}
\begin{array}{l@{\hspace*{8pt}}l}
& \mu = \{ 0,{\rm if}\;{\rm embryo}\;{\rm up}; \pi ,\;{\rm if}\;{\rm embryo}\;{\rm down} \} \\
\theta \sim vM(\mu ,\kappa )\\
& \kappa = (1.5,\,8) \\
\end{array}\end{equation}
Since the concentration parameter κ covers quite a large range, simulations with various values for κ could also be used to assess the sensitivity of canopy development and light interception with respect to κ.
CONCLUSIONS AND FUTURE WORK
The correlation between seed azimuth and seed leaf azimuth for seeds placed flat in the ground with embryo facing up or down can be described by a von Mises model, defined by a mean direction μ and a concentration parameter κ. The mean seed leaf direction depended on the initial orientation of the embryo. If the embryo faces upward, the mean seed leaf azimuth pointed in the direction of the caryopsis attachment point. If the embryo faces downward, the mean seed leaf azimuth was 180° offset. Although some deviations were observable, the mean directions across hybrids appeared not to differ from each other.
For the hybrids tested, the concentration parameters were calculated between 1.7 {P0902HR, embryo down} and 7.7 {DKC-6342, embryo up}. Although the concentration parameter for embryo up and embryo down for the hybrid P0902HR were calculated to be significantly different, it may be acceptable to conclude that the concentration parameters for embryo up and embryo down for one hybrid are the same. Formal comparison of the concentration parameters across hybrids showed that the hypothesis of equal concentration parameters across hybrids could not be accepted in general.
In the context of seed-oriented planting, the findings presented in this study signify that the azimuthal variability of the initial plant orientation follows at least the degree shown herein. Because the variability of seed leaf azimuths has to be considered a property of the plant, the variability of the initial plant orientation will never be less than what was discussed here even when the seeds can be perfectly aligned at planting. Moreover, the azimuthal variability of the seeds at planting may also be modelled by a von Mises distribution. The convolution of the two models – the variability due to planting and the variability inherent in the plant – may describe the total variability of the initial plant orientation. Simulations can now be used to assess the impact of planting orientation accuracy on canopy development and light interception. In reverse, the results may provide the long-sought insight into the planting orientation accuracy requirements, which are critical input for machinery development purposes.











