Distribution-based packet forwarding distance dissimilarity learning for topology characterizing in geographic routing

Abstract

We have previously shown that the geographic routing’s greedy packet forwarding distance (PFD), in dissimilarity values of its average measures, characterizes a mobile ad hoc network’s (MANET) topology by node size. In this article, we demonstrate a distribution-based analysis of the PFD measures that were generated by two representative greedy algorithms, namely GREEDY and ELLIPSOID. The result shows the potential of the distribution-based dissimilarity learning of the PFD in topology characterizing. Characterizing dynamic MANET topology supports context-aware performance optimization in position-based or geographic packet routing.

Introduction

The position-based or geographic routing protocols generate the greedy packet forwarding distance (PFD) feature (Kao et al., 2005); which, based on dissimilarity indices, characterizes a mobile ad hoc network’s (MANET) topology by node size (Kulin et al., 2021; Oladeji-Atanda & Mpoeleng, 2022). In multihop geographic routing, the greedy algorithm enables each intermediate network node to forward packets to a neighbor which is closer in Euclidean distance to a final destination (Kuruvila et al., 2004). Figure 1 illustrates a greedy forwarding at the node u, having transmission range r, which within its progress region would choose a neighbor, such as v, to be the next relay toward the destination d. The length measurement of the link between u and v thus forms the PFD. A node’s next-relay choice is also determined by the geometric computation peculiarity of its greedy algorithm. For example, as depicted in Figure 1, the GREEDY algorithm implements the metric $ \min \left\{\left|\overline{vd}\right|\right\} $ that chooses a neighbor having the minimum distance to the destination, whereas $ \min \left\{\left|\overline{uv}\right|+\left|\overline{vd}\right|\right\} $ describes the ELLIPSOID metric (Kao et al., 2005). By employing the ELLIPSOID and the GREEDY geographic packet forwarding metrics, Oladeji-Atanda and Mpoeleng (2022) have shown that the dissimilarities in the average values of the greedy PFD aid in characterizing MANET topology by node size. In this article, we demonstrate the potential of the geographic routing’s PFD distribution-based dissimilarity learning in MANET topology characterizing. The characterizing of topologies supports context-aware packet routing performance optimization in dynamic MANETs, such as the vehicular ad hoc networks (VANETs) and flying ad hoc networks (FANETs), where node size varies significantly (Medina et al., 2008; Silva et al., 2019).

Figure 1. A greedy packet forwarding.

Dissimilarity learning and topology characterizing

The positionings and associated links between the nodes describe the topology of a network, which may be characterized based on the dissimilarity indices of the elements’ statistical distribution. Cucka et al. (1997) showed that a network’s underlying topology or graph type could be distinguished by an exploration agent, to determine the most optimal exploitation method in path-search tasks of repetitive nature. In their demonstration with Delaunay and random graph types, the arc or link length averages and histogram distribution patterns differentiate the two. Kolaczyk and Csárdi (2020) showed a similar mode of characterizing social networks by the distribution patterns of the node degrees or neighbor links. In Schieber et al. (2017), the network-distance and the node-distance distributions are incorporated into the definition of a dissimilarity metric D(G, Gˊ) that quantifies graphs’ fluid flow capacity. The dissimilarity approach entails distinguishing between similar entities through pairwise comparison of their defining distance measures (Costa et al., 2020; Riesen & Bunke, 2010).

Methods

The greedy PFD elements that we analyze are based on the data obtained from the simulation experiment described in Oladeji-Atanda and Mpoeleng (2022). The elements were generated using the NS-3 network simulator and the Greedy Perimeter Stateless Routing routing protocol, and based on a VANET environment of 30, 50, 70, 90, and 110 node sizes (Silva et al., 2019). Other simulation parameters are the network area: 1,100 m²; nodal transmission range: 280 m; node speed: 0–15 m/s; simulation time: 200 s; and the packets type: 512 byte CBR/UDP. We illustrate greedy PFD distribution with the ELLIPSOID and GREEDY metrics due to their popularity in position-based routing protocol designs. We sort the metrics’ PFD performance collections into classes based on arbitrarily determined length delimitations. We then produce frequency distributions of the PFD elements in each class. Finally, we show that the derived charts depict dissimilarities, which a learning method can ascertain, in characterizing a MANET’s topology by node size.

Metrics of distance, classification, and dissimilarity indices

We specify metrics for the PFD element and its distribution classification. For two nodes u and v (Figure 1), the Euclidean distance between them in the two-dimensional plane is determined by

(1) $$ dist\left(u,v\right)\hskip0.35em =\hskip0.35em \sqrt{{\left({u}_x-{v}_x\right)}^2+{\left({u}_y-{v}_y\right)}^2}. $$

Note that position-based routing can be evaluated or performed in 2D or 3D (Medina et al., 2008; Silva et al., 2019). For the neighbors of a node u represented by the set $ N(u)t\hskip0.35em =\hskip0.35em \left\{{v}_1,\dots, {v}_n\right\}t $ at time t, its set of edges or links is described by

(2) $$ E(u)t\hskip0.35em =\hskip0.35em \left\{{e}_{u,{v}_i}(t)\;|\hskip0.24em dist\Big(u,{v}_i\Big)\hskip0.35em \le \hskip0.35em r,\hskip0.36em i\hskip0.35em =\hskip0.35em 1,\dots, |N(u)|\right\}. $$

Each link $ {e}_{u,{v}_i} $ has intrinsic values such as length, link duration, and so forth, associated with it. Our interest presently lies in the Euclidean “length” attribute of the greedy PFD, designated as $ {d}_{GF} $ (Oladeji-Atanda & Mpoeleng, 2022). Thus,

(3) $$ {d}_{GF}\left({e}_{u,{v}_i}(t)\right)\hskip0.35em =\hskip0.35em dist\left(u,{v}_i\right)(t). $$

In a packet routing session, the collection of the PFD elements is representable as

(4) $$ {D}_{GF}\hskip0.35em =\hskip0.35em \left\{{d}_{GF_i}(t)\hskip0.24em |\hskip0.24em i\hskip0.35em =\hskip0.35em 1,2,3,\dots, \left|{D}_{GF}\right|\right\} $$

For convenience, we do not continue showing the time t in our equations. Given a kth node size in a network, $ {D}_{GF}^k $ describes the relevant PFD collection, 1 ≤ k ≤ m, where m is the environment’s regular maximum. We can sort the elements in each $ {D}_{GF}^k $ into p subclasses based on the delimitations of the length l attribute. Let the set of the length delimitations be {l ₁, l ₂, …, l_p}, 0 < l ₁ < l ₂ < … < l_p, and l_p = r is the maximum nodal transmission range (Figure 1). Hence, we can sort the elements in each $ {D}_{GF}^k $ as follows:

$$ {D}_{GF}^{k1}\hskip0.35em =\hskip0.35em \left\{{d}_{GF_i}\;|\;{d}_{GF_i}>0\bigwedge {d}_{GF_i}\hskip0.35em \le \hskip0.35em {l}_1\right\}, $$

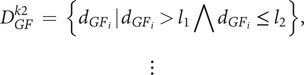$$ {D}_{GF}^{k2}\hskip0.35em =\hskip0.35em \left\{{d}_{GF_i}\;|\;{d}_{GF_i}>{l}_1\bigwedge {d}_{GF_i}\hskip0.35em \le \hskip0.35em {l}_2\right\},\\\vdots $$

(5) $$ {D}_{GF}^{kp}\hskip0.35em =\hskip0.35em \left\{{d}_{GF_i}\;|\hskip0.24em {d}_{GF_i}>{l}_{p-1}\bigwedge {d}_{GF_i}\hskip0.35em \le \hskip0.35em {l}_p\right\}. $$

We can then assign the number of PFD elements in each $ {D}_{GF}^{kj} $ (j = 1, …, p) to be the integer-valued occurrences count c^kj:

$$ {c}^{k1}\leftarrow \left|{D}_{GF}^{k1}\right|, $$

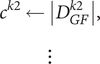$$ {c}^{k2}\leftarrow \left|{D}_{GF}^{k2}\right|,\\\vdots $$

(6) $$ {c}^{kp}\leftarrow \left|{D}_{GF}^{kp}\right|. $$

Thus, for the chart representing the kth node size of a network, we may plot the x,y-coordinates (l_j, c^kj) to display the relevant distribution. The c ^{kj(ELLIPSOID)} and c ^kj(GREEDY) charts representing ELLIPSOID and GREEDY forwarding outcomes can be plotted accordingly. Finally, a dissimilarity-learning method can perform intra- and inter-chart comparisons to differentiate between network node sizes k and k':

(7) $$ Diss\left({D}_{GF}^k,{D}_{GF}^{k\hbox{'}}\;\right)\hskip0.35em =\hskip0.35em x, $$

where the output, x ≥ 0, indicates the dissimilarity index value. We do not explicate the metric Diss(.) in this article, but we present distribution charts that illustrate the function in its expected outcomes. Example dissimilarity metrics and pattern recognition methods are described in Costa et al. (2020) and Schieber et al. (2017).

Results and discussion

As a result of our simulation experiment on neighbor choices of ELLIPSOID and GREEDY forwarding, we classify (as in equation (5)) the generated PFD elements by length delimitations of 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 120, 140, 160, 180, 200, 220, 240, 260, and 280 m. Then, we perform the occurrence count in each class (as in equation (6)) and plot the values as shown in Figures 2 and 3. Intra- and inter-chart comparisons show rich distinctions of the PFD frequency distributions for the ELLIPSOID and GREEDY forwarding methods. For instance, at the 110 node size, the ELLIPSOID’s cumulative occurrence count below 150 m PFD length measure is about 28,000 out of about 34,000 total, an approximate of 82%, whereas that of GREEDY is about 4,000 out of about 25,000, an approximate of 16%. Furthermore, across all the node sizes (i.e., Figure 2a–e), the 100-m PFD cumulative values for ELLIPSOID steadily increase from 43 to 76%, whereas that of GREEDY decreases from 18 to 6%. Similar trends are observable for the 200-m PFD limit, and so on.

Figure 2. (a–e) PFD occurrence count cumulative frequency distributions.

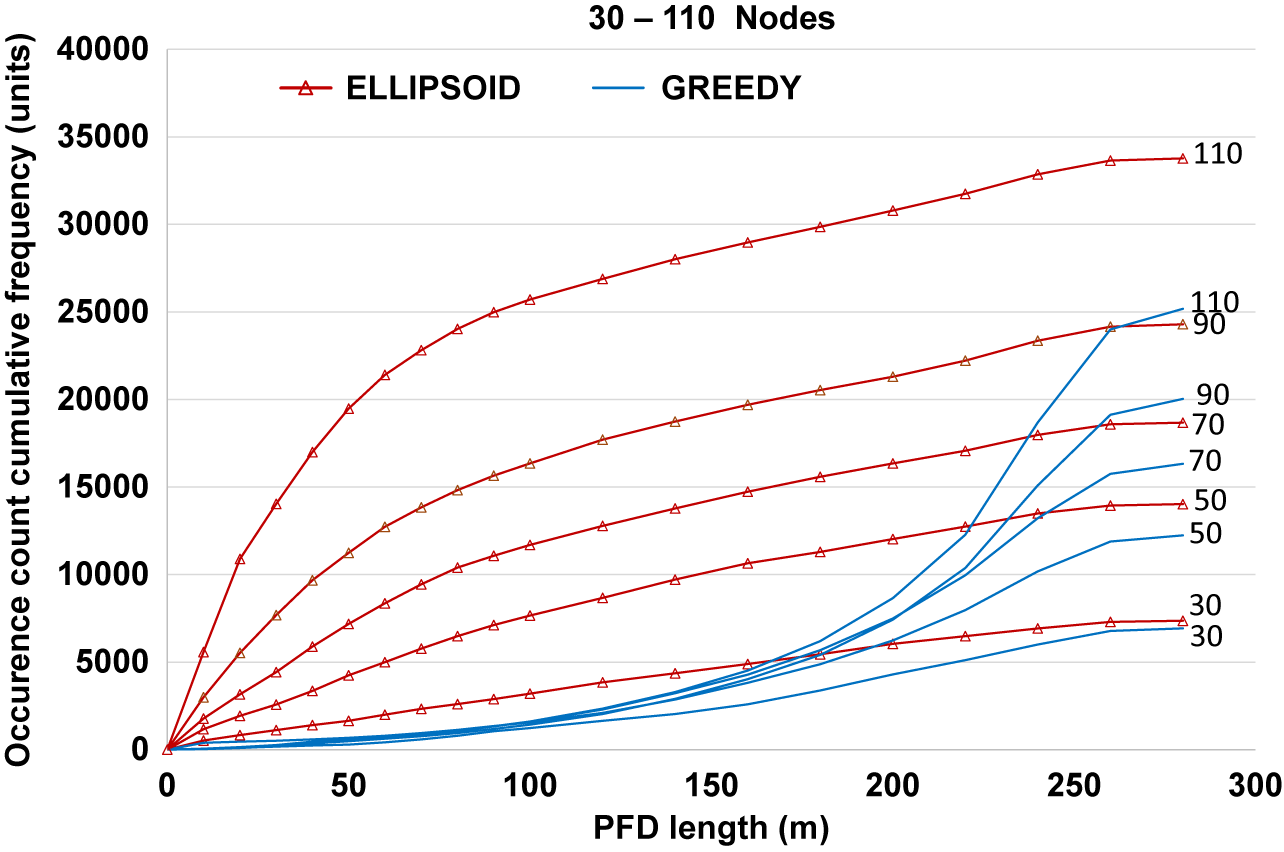
Figure 3. PFD occurrence count hierarchy of cumulative frequency distributions.

Figure 3 shows the charts of Figure 2a–e placed together. The ELLIPSOID charts show distinct hierarchies of the PFD distribution all through the 0–280 m classifications, whereas that of GREEDY is clear only from around 150 m upward. This implies that the ELLIPSOID’s PFD is more sensitive to node size variations, which recommends it to solely provide dissimilarity indices in a topology characterizing scheme. In general, both methods’ distinctive PFD outcomes are generalizable to other greedy metrics such as the Most Forward Routing and Compass Routing (Kao et al., 2005).

Conclusions

We have shown that a position-based or geographic routing protocol can perform dissimilarity learning of the greedy PFD distribution to characterize MANET topology by node size. The example next-relay neighbor choices of GREEDY and ELLIPSOID forwarding generated varied modes of the PFD, in length and proportion to network node size. The resultant distribution-based charts demonstrate an efficacious approach to PFD dissimilarity learning and topology characterizing. In dynamic environments, such as the VANET and the FANET, the characterizing of topologies is an aid in optimization tuning of a network’s parameters (Kulin et al., 2021), like variable-range transmission or topology control (Medina et al., 2008). Our investigation on PFD distribution involved a MANET with a uniform node speed of 0–15 m/s, whereas it will be necessary to also study the effect of different mobility rates. Moreover, some supervised learning applications should be involved in verifying the efficacy of the distribution-based dissimilarity learning of the PFD in topology characterizing.