Introduction
Developing perceptual and motor skills through extensive practice, that is, procedural learning is key to adapting to complex environmental stimuli (Simor et al., Reference Simor, Zavecz, Horváth, Éltető, Török, Pesthy, Gombos, Janacsek and Nemeth2019). It underlies several everyday behaviors and habits, such as language, social, and musical skills (Lieberman, Reference Lieberman2000; Romano Bergstrom et al., Reference Romano Bergstrom, Howard and Howard2012; Ullman, Reference Ullman2016). Procedural learning, among other cognitive mechanisms, requires recognizing and picking up probability-based regularities of the environment—a mechanism referred to as statistical learning (Armstrong et al., Reference Armstrong, Frost and Christiansen2017; Saffran et al., Reference Saffran, Aslin and Newport1996; Turk-Browne et al., Reference Turk-Browne, Scholl, Chun and Johnson2009). Although it has been widely researched for decades (Frost et al., Reference Frost, Armstrong and Christiansen2019), measuring statistical learning still faces difficulties. First, statistical learning tasks often require manual responses (see, e.g., Howard & Howard, Reference Howard and Howard1997; Nissen & Bullemer, Reference Nissen and Bullemer1987; Schlichting et al., Reference Schlichting, Guarino, Schapiro, Turk-Browne and Preston2017), which adds noise to the measurement (Vakil et al., Reference Vakil, Bloch and Cohen2017); moreover, manual responses are infeasible with special target groups like infants or Parkinson’s disease patients (Koch et al., Reference Koch, Sundqvist, Thornberg, Nyberg, Lum, Ullman, Barr, Rudner and Heimann2020; Vakil et al., Reference Vakil, Schwizer Ashkenazi, Nevet-Perez and Hassin-Baer2021b). Second, some of the widely used tasks do not allow to separate different mechanisms that contribute to procedural learning; thus, the measured performance does not solely reflect statistical learning (Nemethet al., Reference Nemeth, Janacsek and Fiser2013). A task that separates different aspects of procedural learning can contribute to more replicable and reliable findings. In this study, we aimed to develop the eye-tracking version of the widely used Alternating Serial Reaction Time (ASRT) task. Our version can overcome the above-mentioned difficulties: it minimizes required motor responses and can measure statistical learning separately from other mechanisms.
Using eye-tracking extends the potential scope of statistical learning research by providing information that mere manual reaction times (RTs) cannot. Tracking oculomotor responses enables us to catch predictive processing involved in statistical learning (Friston, Reference Friston2009) by measuring anticipatory eye movements. This way, we also can reveal the processes underlying participants’ mistakes (Tal & Vakil, Reference Tal and Vakil2020; Vakil et al., Reference Vakil, Schwizer Ashkenazi, Nevet-Perez and Hassin-Baer2021b). Moreover, in tasks requiring manual responses, learning involves inseparably both perceptual and motor components (Deroost & Soetens, Reference Deroost and Soetens2006), since participants typically both fixate on the appearing stimuli and press a corresponding button at the same time (Howard & Howard, Reference Howard and Howard1997). We can gain a closer insight into the ongoing perceptual/cognitive processes by minimizing the motor component of the learning: by using an oculomotor version.
Studies on procedural learning commonly use forced-choice RT tasks, such as the Serial Reaction Time (SRT) task (Nissen & Bullemer, Reference Nissen and Bullemer1987) or the ASRT task (Howard & Howard, Reference Howard and Howard1997). In both, target stimuli appear serially in one of the possible (usually four) locations, and participants are asked to press the key corresponding to the location of the target as fast as possible. Unknown to the participants, the order of the stimuli is not random but follows a specific structure. Both tasks can separate knowledge specific to this structure from a more general stimulus–response (S-R) mapping, indicated by faster responses regardless of the underlying structure of the task, henceforth referred to as general skill learning (Csabi et al., Reference Csabi, Varszegi-Schulz, Janacsek, Malecek and Nemeth2014; Vakil et al., Reference Vakil, Bloch and Cohen2017). The most significant difference between the SRT and ASRT tasks, however, lies in the transitional probabilities between consecutive elements. In the SRT task, appearing stimuli follow a predetermined order, that is, the transitional probability of consecutive elements is one. In the ASRT task, however, random elements alternate with pattern elements, that is, every second stimulus is random (Howard & Howard, Reference Howard and Howard1997; Nemeth et al., Reference Nemeth, Janacsek and Fiser2013). Due to this alternation, the transitional probability of consecutive elements is necessarily less than one.
This alternating structure of the ASRT task results in three important benefits. First, the underlying structure is more difficult to extract in the ASRT than in the SRT task, thus, participants hardly ever gain explicit knowledge (Janacsek et al., Reference Janacsek, Fiser and Nemeth2012; Nemeth et al., Reference Nemeth, Janacsek, Király, Londe, Németh, Fazekas, Adam and Csányi2013; Song et al., Reference Song, Howard and Howard2007; Vékony et al., Reference Vékony, Ambrus, Janacsek and Nemeth2021). This limits the possible learning mechanisms involved in the performance, resulting in a clearer, process-level measurement (see Farkas et al., Reference Farkas, Tóth-Fáber, Janacsek and Nemeth2021). Second, tracking the temporal dynamics of the learning process is unfeasible in the SRT task, as its pattern and random elements occur in separate blocks. In contrast, the alternation of random and pattern elements in the ASRT task enables us to measure the learning process continuously (Song et al., Reference Song, Howard and Howard2007). Third, and most importantly, while the measured learning on the SRT task does not solely depend on learning probability-based regularities, in the ASRT task, we can extract learning scores that reflect a purer measurement of statistical learning (Nemeth et al., Reference Nemeth, Janacsek and Fiser2013). These benefits merged with the advantages of using eye-tracking motivated us to develop an oculomotor version of the ASRT task.
Many previous studies have used the oculomotor version of the SRT task (Albouy et al., Reference Albouy, Ruby, Phillips, Luxen, Peigneux and Maquet2006; Bloch et al., Reference Bloch, Shaham, Vakil, Schwizer Ashkenazi and Zeilig2020; Kinder et al., Reference Kinder, Rolfs and Kliegl2008; Koch et al., Reference Koch, Sundqvist, Thornberg, Nyberg, Lum, Ullman, Barr, Rudner and Heimann2020; Lum, Reference Lum2020; Tal et al., Reference Tal, Bloch, Cohen-Dallal, Aviv, Schwizer Ashkenazi, Bar and Vakil2021; Tal & Vakil, Reference Tal and Vakil2020; Vakil et al., Reference Vakil, Bloch and Cohen2017; Vakil et al., Reference Vakil, Hayout, Maler and Schwizer Ashkenazi2021a), but to our knowledge, no study to date has developed the eye-tracking version of the ASRT task. Moreover, many of the above-mentioned eye-tracking-SRT studies have used a version where participants made both eye movements and manual responses (Lum, Reference Lum2020; Marcus et al., Reference Marcus, Karatekin and Markiewicz2006; Tal et al., Reference Tal, Bloch, Cohen-Dallal, Aviv, Schwizer Ashkenazi, Bar and Vakil2021; Tal & Vakil, Reference Tal and Vakil2020). Despite its benefits, no study to date has used an oculomotor version of the ASRT task. To fill this gap, we adapted the ASRT task to eye-tracking, using the oculomotor version that requires no manual responses.
Objective
We intended to develop a version of the ASRT task that (a) adequately measures statistical learning and general skill learning using oculomotor RT/learning-dependent anticipatory eye movements and (b) provides a robust and purer measurement of statistical learning than previous tasks.
Methods
Participants
Thirty-eight healthy young adults participated in our study. Due to the failure of the eye-tracker calibration, four participants were excluded; thus, we used the data of 34 participants (M age = 22.06 years, SD = 3.61 years, 29 females). Further, 10 participants were excluded from the analyses due to the outlier filtering for eye-tracking data quality (see Supplementary Materials Methods). Thus, our sample consisted of 24 participants (M age = 22.79 years, SD age = 4.02 years, M education = 14.83 years, SD education = 1.24 years, 20 females). Every participant provided informed consent to the procedure as approved by the research ethics committee of Eötvös Loránd University, Budapest, Hungary, and received course credits for their participation. The authors assert that all procedures contributing to this work comply with the ethical standards of the relevant national and institutional committees on human experimentation and with the Helsinki Declaration of 1975, as revised in 2008.
Task and procedure
We modified the ASRT task (Howard & Howard, Reference Howard and Howard1997) to measure statistical learning. Participants saw four empty circles—one in each corner of a 1,920 × 1,080 resolution screen, arranged in a square shape. One of them turned blue sequentially, indicating the activation of the stimulus. Participants were instructed to look at the active stimulus as fast as possible. After they fixated on it, the next stimulus appeared with a response–stimulus interval (RSI) of 500 ms. The stimulus presentation is described in the Supplementary Materials Methods.
Unbeknownst to the participants, the stimuli followed a predefined, alternating sequence. In this sequence, each first element belonged to a predetermined pattern (i.e., they always appeared in the same location), and each second appeared randomly in any of the four placeholders (e.g., 2-r-4-r-1-r-3-r, where numbers indicate one of the four circles on the screen, and “r” letters indicate a randomly selected circle out of the four). Because of this alternating structure, there were some chunks of three consecutive elements (triplets) that occurred with a higher probability. In the example provided above, 2-x-4, 4-x-1, 1-x-3, and 3-x-2 are high-probability triplets, because their last element can be both a pattern (when the “x” marks a random element) and a random element, occurring occasionally (where the “x” marks a pattern element). In contrast, the rest of the triplets occurred with lower probability: in the above example, for example, 2x1 or 4x3 were low-probability triplets, since they cannot be formed by the pattern. Due to this structure, high-probability triplets occurred with 62.5%, while low-probability triplets with 37.5% probability (for more details on the ASRT sequence structure, see Supplementary Materials Methods). Thus, the last elements of the high-probability triplets are more predictable than those of the low-probability triplets. Statistical learning is the performance difference on the last elements of high- and low-probability triplets: participants had learned the underlying statistical structure if they were faster and show more learning-dependent anticipations on the last elements of high-probability triplets than those of low-probability ones (see Figure 1).
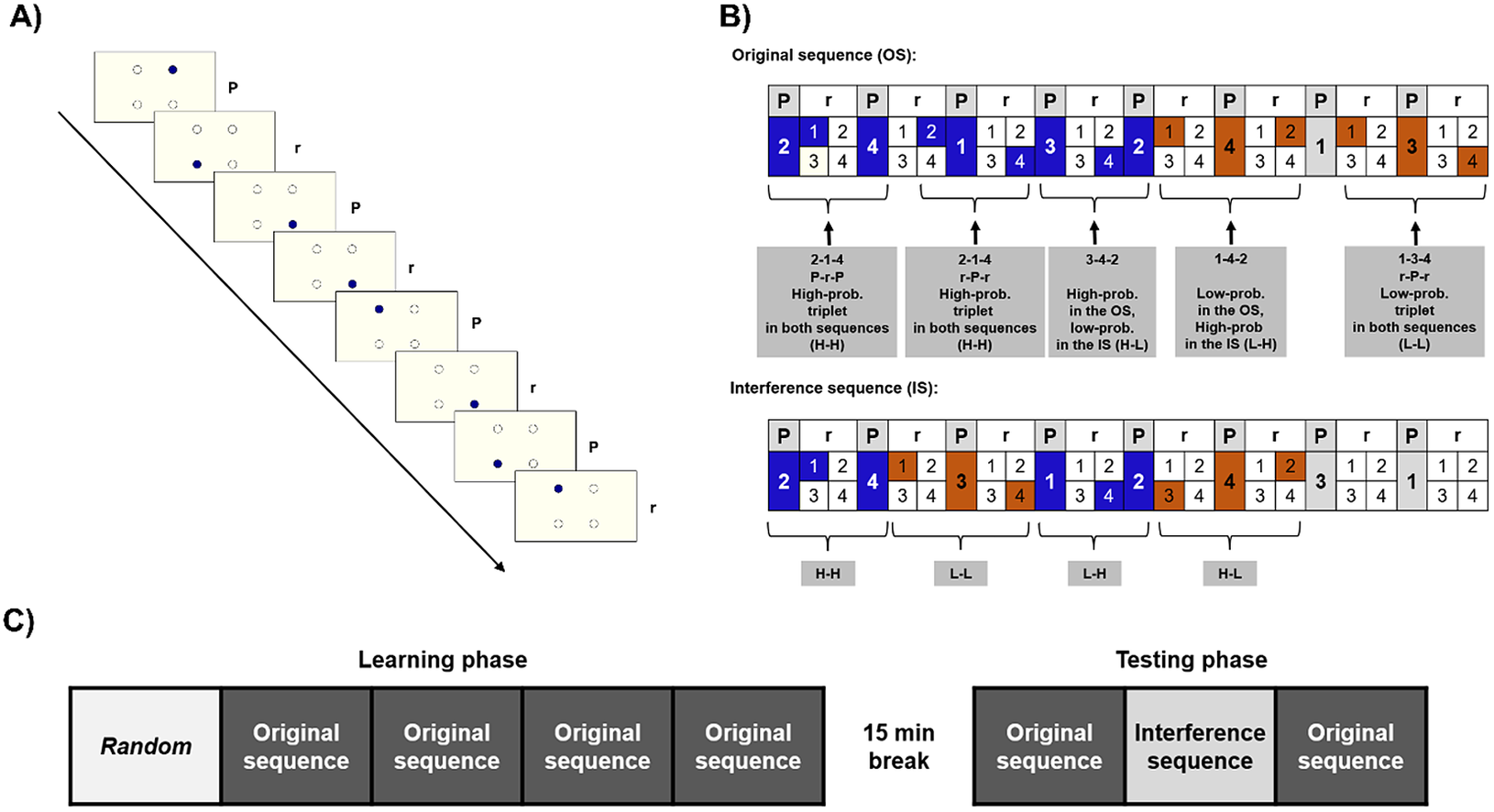
Figure 1. The task and design. (a) The active stimulus appeared in one of the four locations. Pattern and random stimuli alternated. (b) Examples for the original sequence (OS) and the interference sequence (IS). High-probability (High-prob.) triplets can be built up by two pattern (P) elements and one random (r), or by two random and one pattern element. Low-probability (Low-prob.) triplets can only be formed occasionally, by two random, and one pattern elements; thus, they occur less frequently. The OS and the IS partially overlapped: some triplets were high probability in both (HH), high in the OS, but low in the IS (H-L), low in the OS, but high in the IS (LH), and ones that were low in both (LL). (c) Study design. The first block consisted of randomized trials, then in the 2-5th epochs, participants practiced the OS. After a break of 15 min, they practiced the OS in the 6th epoch, then the previously unseen IS (seventh epoch), and in the eighth epoch, the OS returned.
The task was presented in blocks, each block contained 82 stimuli. Each block started with two random elements. Then an eight-element sequence was repeated 10 times. To avoid noise due to intra-individual variability, we merged five blocks into one unit of analysis called epoch. Furthermore, the task was divided into a Learning and a Testing phase, with a 15-min break between them. Before both phases, we calibrated the eye-tracker and tested the calibration using 20 random trials (see Supplementary Materials Methods for details). The Learning phase consisted of five epochs. In the first epoch, stimuli were generated randomly, by a uniform distribution. In the following four epochs, stimuli were generated based on one specific, randomly assigned 8-element sequence (henceforth referred to as original sequence [OS]), as defined above. The Testing phase consisted of three additional epochs (see Figure 1). Furthermore, we used a questionnaire and the Inclusion–Exclusion task (Destrebecqz & Cleeremans, Reference Destrebecqz and Cleeremans2001; Horváth et al., Reference Horváth, Török, Pesthy, Nemeth and Janacsek2020; Jacoby, Reference Jacoby1991) to access the level of explicit knowledge, see in the Supplementary Materials Methods.
In the Testing phase, we used the OS in the sixth and eighth epochs. However, in the seventh epoch, unknown to the participants, we used a different, previously unpracticed sequence to measure interference (interference sequence [IS]). The IS partially overlapped with the OS: two of the four pattern elements remained the same. For example, if the OS was 2-r-4-r-1-r-3-r, the IS could be 2-r-4-r-3-r-1-r, where the locations 2 and 4 remained unchanged, but the rest of the pattern differed. Consequently, four of the originally high-probability triplets remained high probability in the IS (“high-high” triplets: HH; in the example, 2-x-4 triplets). Twelve of the triplets that were high probability in the OS turned into low probability (“high-low”: HL; 4-x-1-, 1-x-3, and 3-x-2 in the example). Of the 48 originally low-probability triplets, 12 became high probability (“low-high”: LH; 4-x-3, 3-x-1, and 1-x-2 in the example) and 36 remained low probability in both sequences (“low-low”: LL, e.g., 2-x-3 in the example). See Figure 1 for examples.
Eye-tracking
Eye-tracker device
We used a Tobii Pro X3-120 eye-tracker to register the gaze positions (Tobii, Reference Tobii2017) at a sampling rate of 120 Hz. Its required subject-screen distance was 50–90 cm, optimally 65 cm. This distance in our study was M = 65.36 cm, SD = 4.15 cm. We used this ~65 cm to convert cm units to degrees of visual angle; all the angles reported are visual angles based on this measure. Under ideal conditions, the binocular accuracy of the device is ~0.4° and the precision value is 0.24°. Under nonideal conditions, the accuracy can vary between 0.4 and 1.0° and the precision can be ~0.23–0.52° (Tobii, Reference Tobii2017).
Software
To record eye-tracking data, we used the Tobii Pro Python SDK (Tobii Pro, Reference Tobii Pro2020), integrated into a Psychopy-based experiment script (Psychopy version: 3.2.3, Peirce et al., Reference Peirce, Gray, Simpson, MacAskill, Höchenberger, Sogo, Kastman and Lindeløv2019). The current oculomotor version is a modification of a previous, motor implementation of the ASRT task (Szegedi-Hallgató, Reference Szegedi-Hallgató2019). The script used in this study is available on GitHub (Project ET Zero Developers, 2021).
Gaze position estimation
We used the Tobii Pro Python SDK to obtain the recorded gaze data from the eye-tracker. This SDK returned the left and right eye data separately. We used a hybrid eye selection method, similar to Tobii’s “average” eye selection option (see Olsen, Reference Olsen2012), but optimized for minimizing the missing data: when data were available, we used the average of the position of both eyes, and the data of a single eye position when the other eye position was unavailable. When the position data were invalid for both eyes, we marked the sample as missing. We controlled for participants with accommodation issues by checking the registered eye-to-eye distances during fixations and excluded subjects with large differences between the gaze positions of the left and right eyes.
Fixation identification
Algorithm
Fixation identification was used only for calculating RTs, but not anticipatory eye movements (see later). We defined RT as the time interval between the appearance of a new stimulus and the start of the fixation on it. Responses were defined as valid if this fixation lasted 100 ms. To identify these fixations, we used the dispersion threshold identification algorithm, because this method is recommended for low-speed eye-tracking (<200 Hz, see SMI, 2017). We used the online version of this method, that is, we had a sliding window including the last recorded eye positions of the subject. We calculated the dispersion of the gaze direction, and the center of the fixation for each of these windows separately. To find whether fixation happened in the given window, the algorithm used two parameters: the dispersion threshold (DT) and the duration threshold (DuT). The main parameter was the maximum size of the area on the screen where the gaze direction can disperse within one fixation (i.e., the DT). We calculated the dispersion value (D) based on Salvucci and Goldberg (Reference Salvucci and Goldberg2000), see Supplementary Materials Methods for the formula. Fixations could be registered if the dispersion value was less than the DT. The second parameter was the minimum time interval indicating fixation, that is, the DuT—this equaled the size of the sliding window mentioned above (100 ms). We allowed inaccuracy in the eye positions using our third parameter, the size of the area of interest (AOI): We added square-shaped AOIs around all four stimuli placeholders (see Figure 2). Within each sliding window, we calculated the D, and if it was less than the DT, we identified a fixation. To determine whether the participant was looking at the active stimulus, we calculated the center of the fixation, and if it fell within the AOI, the response was registered, the active stimulus disappeared, and the next trial started.

Figure 2. AOIs used for (a) fixation identification and (b) anticipatory eye-movement calculation.
In addition, to fill the gaps of successive invalid data returned by the eye-tracker, we used linear interpolation included in the Tobii I-VT filter (see Olsen, Reference Olsen2012), which is based on the closest valid neighbors in both directions. The two main parameters of the interpolation are the maximum gap length (i.e., the maximum length of missing data that we still interpolate) and the maximum ratio of interpolated and registered data. Our parameters are shown in Table 1, and parameter selection is described in the Supplementary Materials Methods.
Table 1. Parameters of the algorithm used in fixation identification

Learning-dependent anticipation
Eye movements during the RSI were also recorded. It enabled us to record whether participants moved their eyes toward a placeholder after the active stimulus disappeared. Unlike some previous studies (e.g., Bloch et al., Reference Bloch, Shaham, Vakil, Schwizer Ashkenazi and Zeilig2020; Lum, Reference Lum2020; Tal et al., Reference Tal, Bloch, Cohen-Dallal, Aviv, Schwizer Ashkenazi, Bar and Vakil2021; Tal & Vakil, Reference Tal and Vakil2020; Vakil et al., Reference Vakil, Bloch and Cohen2017; Vakil et al., Reference Vakil, Hayout, Maler and Schwizer Ashkenazi2021a), we did not define anticipatory eye movements as fixations but rather as the last valid gaze position before the new stimulus appeared. Using this definition, we were able to identify anticipations shorter than the minimum length of fixations (100 ms, see above), and using the last, rather than the first gaze position enabled us to avoid carryover from the previous stimulus (as suggested in Tal et al., Reference Tal, Bloch, Cohen-Dallal, Aviv, Schwizer Ashkenazi, Bar and Vakil2021). Anticipating elements that correspond to high-probability triplets rather than to low-probability triplets (i.e., a high ratio of learning-dependent anticipations) means that the participants have acquired the statistical structure. Importantly, due to the statistical nature of the task, learning-dependent anticipations do not always mean accurate predictions, unlike in the eye-tracking SRT task with deterministic sequences (Vakil et al., Reference Vakil, Hayout, Maler and Schwizer Ashkenazi2021a; Reference Vakil, Schwizer Ashkenazi, Nevet-Perez and Hassin-Baer2021b).
We calculated the learning-dependent anticipation ratio by (a) identifying all anticipatory eye movements, (b) determining whether a given anticipatory eye movement was learning-dependent anticipation, and (c) calculating the ratio of learning-dependent anticipations compared to all anticipations. Since anticipatory eye movements were defined as occasions where the participant’s gaze moved away from the previous stimulus during the RSI, we divided the screen into four equal regions by the center lines. These four fields, each containing one of the possible placeholders, were the AOIs of the anticipatory eye movement calculation (see Figure 2). If the last detectable gaze did not fall within the AOI of the previous stimulus, the event was marked as anticipatory eye movement. If the location of the last gaze corresponded to a high-probability triplet (i.e., the participant’s eye settled in the AOI of a high-probability stimulus), we labeled it as learning-dependent anticipation. The ratio of the learning-dependent anticipations compared to all anticipations indicated statistical learning.
Participants showed anticipatory eye movements in 18.91% of all trials in our task overall. In 7.4% of all trials (i.e., 39.15% of the anticipatory eye movements), the anticipation corresponded to high-probability triplets; thus, they were learning-dependent anticipations. These ratios are much lower than those reported in SRT studies, where typically, most trials are anticipated (e.g., Vakil et al., Reference Vakil, Hayout, Maler and Schwizer Ashkenazi2021a). This might be because of the probabilistic nature of the ASRT task. Moreover, our participants might have changed their gaze direction less frequently than in previous studies with the SRT task, because repetitions can occur in the ASRT task—which cannot possibly happen in the deterministic SRT task. For the ratio of all anticipatory, and learning-dependent anticipatory eye movements separately in each epoch, see Figure 4 Panel a.
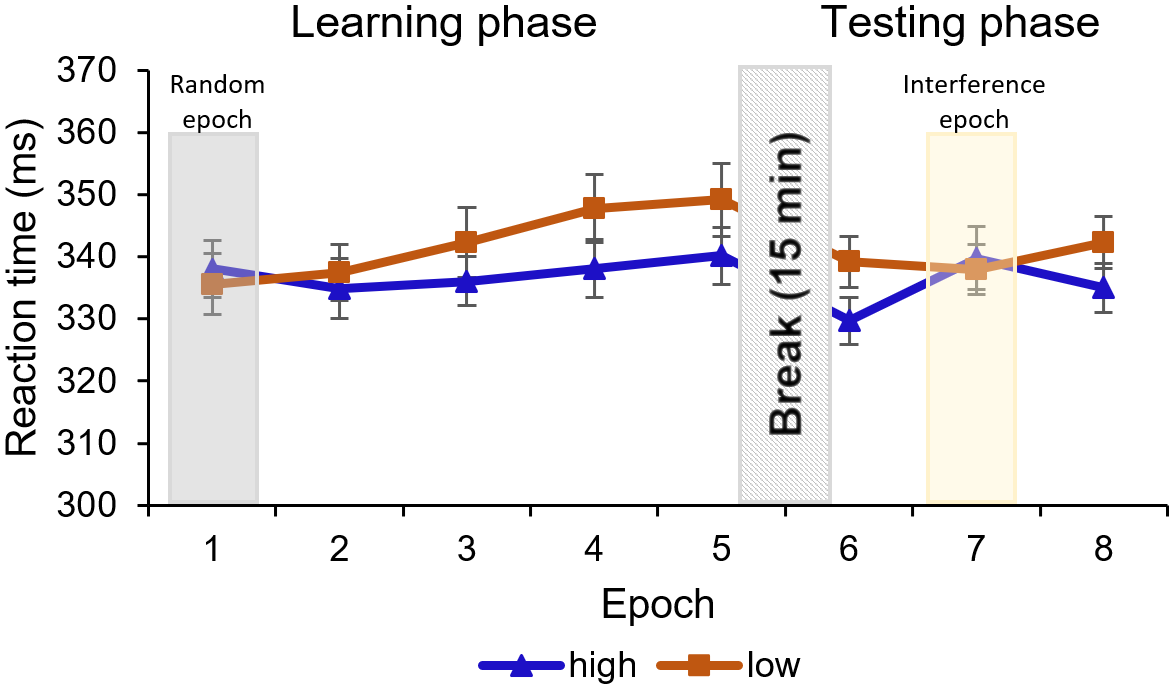
Figure 3. RTs are presented as a function of high-probability (blue line with triangle symbols) and low-probability (orange line with square symbol) triplets throughout the epochs of the Learning phase (1–5) and the Testing phase (6–8). Note that stimuli were presented randomly in the first epoch, and participants performed on an IS in the seventh epoch, instead of the OS used in the rest of the epochs (2–4th, sixth and eighth epochs). The difference between high- and low-probability triplets represents statistical learning. In the Learning phase, the difference between triplet types reached significance in the fourth and remained significant in the fifth epoch. In the Testing phase, the seventh, interference epoch has a temporal negative effect on the RT differences, but when the OS was presented (sixth and eighth epoch), the learning was significant again. Error bars represent the SEM.

Figure 4. (A) The ratio of all anticipatory eye movements (green line) and learning-dependent anticipatory eye movements (black line) compared to all trials, epochwise. Error bars represent the SEM. (B) Percentage of learning-dependent anticipation (solid line) compared to the chance level (dashed line) during the ASRT task. The first, randomized epoch shows the smallest value. In the Learning phase, anticipatory eye movements of the sequential epochs (2–5th) are determined by the original sequence to a higher extent than in the first (random) epoch. The interference epoch leads to a temporal decrease in the learning-dependent anticipation ratio. Error bars represent the SEM.
Statistical analysis
Statistical analyses were carried out using JASP 0.14.1 (JASP Team, 2017). First, we excluded trills (e.g., 2-1-2) and repetitions (e.g., 2-2). Participants show a preexisting tendency to react faster to these elements; thus, they can bias the RTs (Howard et al., Reference Howard, Howard, Japikse, DiYanni, Thompson and Somberg2004). Each element was categorized in a sliding window manner as the last element of a high- or a low-probability triplet (i.e., a given trial was the last element of a triplet, but it was also the middle and the first element of the two consecutive triplets, respectively), and we calculated for them separately and epoch-wise the (a) median RTs and (b) the ratio of learning-dependent anticipatory eye movements compared to all anticipatory eye movements.
We performed repeated-measures analyses of variance (ANOVAs) for the Learning and Testing phases. To evaluate the effect of epoch and trial type, we used post-hoc comparisons with Bonferroni correction. Greenhouse–Geisser epsilon (ε) correction was used if necessary. We calculated partial eta squared to measure effect sizes. The effect of the interference was further investigated by paired-samples t-tests or Wilcoxon tests (depending on whether the sample was normally distributed) comparing the RT of “HL” versus “LL” triplets and “LL” versus “LH” triplets in the interference (seventh) epoch. To show whether the data support the null hypothesis (H0), we additionally performed Bayesian paired-samples t-tests to calculate Bayes Factors (BF10) for relevant comparisons. BF10 between 1 and 3 means anecdotal evidence for H1, and values between 3 and 10 indicate substantial evidence for H1. Conversely, values between 0.33 and 1 indicate anecdotal evidence for H0, and values between 0.1 and 0.33 indicate substantial evidence for H0. Values around one do not support either hypothesis. The analysis of the Inclusion–Exclusion task is described in the Supplementary Materials Methods section.
Results
None of the participants reported explicit knowledge of the sequential structure of the ASRT task, for further details and the analysis of the Inclusion–Exclusion task, see Supplementary Materials Results. All data used in this article are available, see Zolnai et al. (Reference Zolnai, Dávid, Pesthy, Németh and Nemeth2021). Before the analysis described here, we filtered the eye-tracking data for outliers on data quality measures, see Supplementary Materials Methods section. We additionally performed every analysis without filtering, see Supplementary Tables S1 and S2.
Reaction time
Do the RTs show the effect of statistical learning?
We tested the progress of learning in the Learning phase (first five epochs) using a repeated-measures ANOVA on the RTs with the within-subject factors of TRIPLET (high versus low probability) and EPOCH (1–5). Note that we did not expect any learning in the first epoch, where participants were exposed to randomized stimuli; thus, they could not possibly acquire any statistical information. This epoch serves as a reference point showing the performance before learning.
The ANOVA showed a significant main effect of TRIPLET [F(1, 23) = 11.59, p = .002, η2p = .33]. Participants reacted slower to the low-probability triplets compared to high-probability triplets across the first five epochs, which shows that subjects learned the statistical differences between the displayed triplets. The EPOCH main effect was nonsignificant, [F(2.20, 50.68) = 3.01, p = .054, η2p = .12]; the gradual increasing of the RTs did not reach significance, indicating a lack of general skill learning. It is contradictory to the classic motor ASRT task, where the RT usually significantly decreases. The RT difference between high- and low-probability triplets changed throughout the task, that is, statistical learning was improving, as indicated by a significant TRIPLET × EPOCH interaction [F(4, 92) = 5.25, p < .001, η2p = .19]. As expected, the post-hoc test revealed no learning in the first, randomized epoch (pBonf > 0.99). The difference between the triplet types did not reach significance in the 2–3rd epochs either (pBonf ≥ .568), but it did in the 4–5th epochs (pBonf ≤ .016), meaning that significant learning could be shown from the 4th epoch on. For means and SEM, see Figure 3; for further details of the analysis, see Supplementary Table S1.
How does the IS affect statistical learning of the OS?
To test whether the knowledge acquired during the Learning phase was resistant to interference, we ran a repeated-measures ANOVA on RTs of the Testing phase, with TRIPLET (high/low probability) and EPOCH (6–8) as within-subject factors. The ANOVA showed a significant main effect of TRIPLET [F(1, 23) = 22.31, p < .001, η2 p = .49]: the RT was higher for low-probability triplets compared to high-probability triplets regardless of the epochs, in which difference mainly comes from the sixth and eighth epochs of the Testing phase, where we used the OS.
The EPOCH main effect was significant [F(1.60, 36.91) = 6.01, p = .009, η2p = .21]: the RT was faster in the sixth epoch than in the later epochs (pBonf ≤ .016), indicating a slowdown as the task progressed. The TRIPLET × EPOCH interaction reached significance [F(1.39, 31.93) = 5.80, p = .014, η2p = .20]: the post-hoc comparisons revealed that the RT difference between the low-probability and high-probability triplets remained significant in the sixth and the eighth epochs when participants were exposed to the OS (pBonf ≤ .033) but was not significant in the seventh (interference) epoch (pBonf > 0.99), which indicates that participants maintained their statistical learning performance despite being exposed to an IS (see Figure 3). For further details of the analysis, see Supplementary Table S1.
How do the OS and the IS interact inside the interference epoch?
To further investigate the effect of the IS, we compared RT within the interference epoch on different types of triplets (LL, HL, and LH as described in the Methods section). We found a significant difference between LL (M = 348.76, SD = 29.68) and HL (M = 339.99, SD = 25.44) triplet types [t(23) = −2.80, p = .010, d = −0.57, BF10 = 4.75], meaning that participants reacted faster on triplets that were high probability only in the OS compared to the ones that were low probability in both sequences, which shows that despite the interference, the acquired statistical structure of the OS still affected the RT. We also found significant difference between LL and LH (M = 335.64, SD = 19.03) triplet types [Z = 252.00, p = .003, rrb = .68, BF10 = 28.32], participants reacted to triplets that were high probability only in the IS compared to triplets that were low probability in both sequences. It indicates that the participants also learned the statistical structure of the IS. In summary, both sequences influenced the subject’s behavior during the interference epoch; thus, while the subjects learned the IS, they still remembered the OS.
Learning-dependent anticipatory eye movements
Does the learning-dependent anticipatory eye movement ratio show the effect of learning?
We tested the process of learning in the Learning phase by comparing the learning-dependent anticipation ratio in the different epochs, see Figure 4 Panel b. We used repeated-measures ANOVA for learning-dependent anticipation ratio with EPOCH as a within-subject factor. It revealed that the learning-dependent anticipations were more frequent in the later epochs, indicated by the significant EPOCH main effect [F(4, 92) = 14.76, p < .001, η2p = .39]. The post-hoc comparisons showed that learning-dependent anticipations show a faster learning curve than the RT data—participants make a significantly higher ratio of learning-dependent anticipatory eye movements after being exposed to a single epoch of the OS than in the first (randomized) epoch (pBonf < .001). However, learning did not develop further in the later epochs, as indicated by the lack of significance when comparing the 2–5th epochs (pBonf ≥ .098 in each comparison), meaning that learning plateaued in the second epoch (i.e., the first sequential epoch). For further details of the analysis, see Supplementary Table S2.
How does the interference epoch affect the learning-dependent anticipation ratio?
We tested the effect of the interference on the learning-dependent anticipation using a repeated-measures ANOVA on the learning-dependent anticipation ratio with EPOCH as a within-subject factor, which again showed a significant main effect [F(2, 46) = 14.47, p < .001, η2p = .39]. The post-hoc comparison showed a decreased learning-dependent anticipation ratio from the sixth epoch to the seventh (interference) epoch (pBonf < .001) and increased from the seventh to the eighth epoch (pBonf = .004)—participants anticipated high-probability triplets in the OS in a higher ratio than in the IS. There was no significant difference between the sixth and the eighth epochs (pBonf = .202), meaning that the interference did not significantly disrupt the learning-dependent anticipations of the OS (see Figure 4 Panel b).
Discussion
In our study, we aimed to develop the eye-tracking version of a statistical learning task (the ASRT task). We have shown that oculomotor RTs reflect robust, interference-resistant statistical learning, without any manual responses required. Moreover, we found that learning-dependent anticipatory eye movements indicated learning sooner than the RTs; thus, they might serve as a more sensitive index of the learning process. On the other hand, we found no general skill learning. For discussion of the Inclusion–Exclusion task, see Supplementary Materials Discussion.
Previous eye-tracking studies using the SRT task have also found that oculomotor RTs reflected learning (Albouy et al., Reference Albouy, Ruby, Phillips, Luxen, Peigneux and Maquet2006; Koch et al., Reference Koch, Sundqvist, Thornberg, Nyberg, Lum, Ullman, Barr, Rudner and Heimann2020; Marcus et al., Reference Marcus, Karatekin and Markiewicz2006; Vakil et al., Reference Vakil, Bloch and Cohen2017), which remained intact even after exposure to interference (Kinder et al., Reference Kinder, Rolfs and Kliegl2008; Vakil et al., Reference Vakil, Hayout, Maler and Schwizer Ashkenazi2021a). Our method, however, allows us to track the temporal dynamics of learning, unlike the oculomotor SRT task. This enabled us to show that participants also acquired the IS to some extent. Besides its methodological advantages, this result has theoretical importance: earlier studies claimed that if the performance does not return to baseline in the interference stage, it is due to a general skill learning (Vakil et al., Reference Vakil, Bloch and Cohen2017). Our study suggests that to a small extent, statistical learning of the IS can contribute to performance above baseline. Thus, our task provides a sensitive, nonmanual alternative to measure the dynamics of statistical learning.
Learning-dependent anticipatory eye movements indicated that participants predicted high-probability stimulus combinations more often than low-frequency combinations. Similar results were found on the SRT task (Vakil et al., Reference Vakil, Bloch and Cohen2017; Vakil et al., Reference Vakil, Hayout, Maler and Schwizer Ashkenazi2021a). Importantly, however, learning-dependent anticipatory eye movements appeared after as few as ~5 min of practice while learning on the RTs occurred only after ~15 min. These results imply that learning-dependent anticipations indicate robust learning as well as the RT; moreover, they might be an even more sensitive measure of implicit statistical learning. Interestingly, in contrast with previous oculomotor SRT (Kinder et al., Reference Kinder, Rolfs and Kliegl2008; Vakil et al., Reference Vakil, Hayout, Maler and Schwizer Ashkenazi2021a) or manual ASRT studies (Howard & Howard, Reference Howard and Howard1997), we found that average RTs did not decrease throughout the training, that is, we could not show general skill learning. We can speculate that this was due to a fatigue effect, considering our relatively long task. Alternatively, it can be due to the probability-based structure of our task: participants are likely to expect high-probability stimulus combinations even when low-probability ones occur (compare our results on learning-dependent anticipatory eye movements), which can result in a slowdown of the RTs. Another possibility is that general skill learning shown in previous studies is related to motor responses. A methodological explanation is that time passed since the last calibration drove the increase in the RTs; thus, for future studies, more frequent re-calibrations are advisable.
Conclusion
Our study is the first to demonstrate that statistical learning can be tracked and measured using an oculomotor version of the ASRT task. This version of the task is useful in both basic and clinical research. It allows us to minimize the motor component of the learning process; moreover, tracking anticipatory eye movements allow us insight into predictive processes. The smaller number of motion artifacts is also useful when using the paradigm combined with imaging techniques, such as magnetic resonance imaging and magnetoencephalography. Furthermore, our task enables the usage of the ASRT task on special target groups such as infants, or individuals with basal ganglia disorders (e.g., Parkinson’s disease, Huntington’s disease) or with cerebellum disorders (e.g., ataxia). To conclude, our study contributes to the field of implicit statistical learning by opening the possibility to apply the widely used ASRT task without manual responses required and gaining a highly fine-grained measure of the learning process.
Supplementary Materials
To view supplementary material for this article, please visit http://doi.org/10.1017/exp.2022.8.
Data availability statement
All data are available on the following link: https://osf.io/wu8a6/.
Funding statement
This work was supported by the National Brain Research Program (project NKFIH-OTKA K); Project no. 2017-1.2.1-NKP-2017-00002 has been implemented with the support provided by the Ministry of Innovation and Technology of Hungary from the National Research, Development and Innovation Fund, financed under the 128016 funding scheme; IDEXLYON Fellowship of the University of Lyon as part of the Programme Investissements d’Avenir (ANR-16-IDEX-0005) (to D.N).
Acknowledgments
The authors thank Teodóra Vékony and Eszter Tóth-Fáber for the helpful comments and suggestions on the manuscript.
Conflict of interest
The authors have no conflicts of interest to declare.
Authorship contributions
T.Z. wrote the task scripts, performed formal data analysis, designed the figures, and wrote and revised the manuscript. D.D. participated in the data collection, wrote, and revised the manuscript. O.P. performed formal data analysis, wrote and revised the manuscript, designed the figures, and supervised the data analyses. M.K. administered the project, supervised the data collection, and revised the manuscript. M.N. participated in the data collection and revised the manuscript. M.N. provided support for the eye-tracking and revised the manuscript. D.N. wrote and revised the manuscript, provided financial and theoretical support, and supervised the data analyses. All authors read and approved the final version of the manuscript.






Comments
Comments to the Author: Overall, this was a well conducted study. The inclusion of the control block of trials strengthened the results. The introduction (or perhaps methods) would be strengthened if a rationale could be provided for the outcome variable. The main outcome variable of interest is the number of anticipatory fixations. This differs from some past studies that have used saccadic latency or amplitude.
Also, some more details are required around the eye-tracking analysis. Which fixations were selected for analysis? For example, if a participant made multiple eye-movements to-and-from an AOI during the RSI period, which ones were analyzed. The first or the last? Could the authors also report the average number of anticipatory fixations, that were observed for each epoch. As I understand, each block comprised 82 trials, so it would be useful if descriptive statistics were reported around this, for example a sentence like “On average 70 out of a maximum of 82 anticipatory fixations were identified and submitted for analysis”. The idea here is to give the readers a sense of how much data was usable at the participant level. Could the authors also clarify the statement “If the direction of this movement corresponded to a…”. In this context, what does direction mean? Is it a fixation in the same quadrant as a high probability triplet?
Last, do check for minor typos (e.g., “one in each corner of a 1920 x 080..” – I think a 1 is missing).