Introduction
The goal of this note is to explain, favoring expedience over detail, how one can systematically obtain explicit numerical evidence in support of a B-SD-type conjecture for hypergeometric Calabi–Yau motives. For a Calabi–Yau threefold
![]() $ X/\unicode{x211A} $
with Hodge numbers
$ X/\unicode{x211A} $
with Hodge numbers
![]() $ {h}^{3,0}={h}^{0,3}=1,{h}^{2,1}={h}^{1,2}=a $
, Poincaré duality defines a non-degenerate alternating form on the third cohomology
$ {h}^{3,0}={h}^{0,3}=1,{h}^{2,1}={h}^{1,2}=a $
, Poincaré duality defines a non-degenerate alternating form on the third cohomology
![]() $ {H}^3(X) $
for any Weil cohomology theory. We view the collection of such cohomological realizations as arising from a so-called symplectic motive of rank
$ {H}^3(X) $
for any Weil cohomology theory. We view the collection of such cohomological realizations as arising from a so-called symplectic motive of rank
![]() $ 2+2a $
. We will focus on the case
$ 2+2a $
. We will focus on the case
![]() $ a=1 $
here; these motives, now colloquially called “(1,1,1,1)-motives,” are expected to exist in 1-parameter families (Golyshev & van Straten, Reference Golyshev and van Straten2023). Their typical Euler factors can be obtained as characteristic polynomials of the geometric
$ a=1 $
here; these motives, now colloquially called “(1,1,1,1)-motives,” are expected to exist in 1-parameter families (Golyshev & van Straten, Reference Golyshev and van Straten2023). Their typical Euler factors can be obtained as characteristic polynomials of the geometric
![]() $ p $
-Frobenius acting in the
$ p $
-Frobenius acting in the
![]() $ l $
-adic cohomology of
$ l $
-adic cohomology of
![]() $ X $
over the algebraic closure. They take the form
$ X $
over the algebraic closure. They take the form
with
![]() $ {\alpha}_p,{\beta}_p\in \unicode{x2124} $
.
$ {\alpha}_p,{\beta}_p\in \unicode{x2124} $
.
It is believed that the completed
![]() $ L $
-function
$ L $
-function
 $$ \Lambda (s)={\left(\frac{N}{\pi^4}\right)}^{s/2}\Gamma \left(\frac{s-1}{2}\right)\Gamma \left(\frac{s}{2}\right)\Gamma \left(\frac{s}{2}\right)\Gamma \left(\frac{s+1}{2}\right)L\left({H}^3(X),s\right), $$
$$ \Lambda (s)={\left(\frac{N}{\pi^4}\right)}^{s/2}\Gamma \left(\frac{s-1}{2}\right)\Gamma \left(\frac{s}{2}\right)\Gamma \left(\frac{s}{2}\right)\Gamma \left(\frac{s+1}{2}\right)L\left({H}^3(X),s\right), $$
is entire and satisfies
![]() $ \Lambda (s)=\pm \Lambda \left(4-s\right) $
, where
$ \Lambda (s)=\pm \Lambda \left(4-s\right) $
, where
![]() $ N $
is the conductor. The known meromorphicity and existence of a functional equation (Patrikis & Taylor, Reference Patrikis and Taylor2015) enable one in principle to study the leading coefficient of the Taylor series of
$ N $
is the conductor. The known meromorphicity and existence of a functional equation (Patrikis & Taylor, Reference Patrikis and Taylor2015) enable one in principle to study the leading coefficient of the Taylor series of
![]() $ L(s) $
along the lines suggested by the conjectures of Deligne (Reference Deligne1977) and Birch–Swinnerton–Dyer and Beĭlinson (Reference Beĭlinson1987), Bloch (Reference Bloch1980; Reference Bloch1983), Gillet and Soulé (Reference Gillet and Soulé1984). More broadly, if one is to think of these
$ L(s) $
along the lines suggested by the conjectures of Deligne (Reference Deligne1977) and Birch–Swinnerton–Dyer and Beĭlinson (Reference Beĭlinson1987), Bloch (Reference Bloch1980; Reference Bloch1983), Gillet and Soulé (Reference Gillet and Soulé1984). More broadly, if one is to think of these
![]() $ \left(\mathrm{1,1,1,1}\right) $
-motives as analogues of elliptic curves over
$ \left(\mathrm{1,1,1,1}\right) $
-motives as analogues of elliptic curves over
![]() $ \mathrm{\mathbb{Q}} $
two dimensions higher, a question arises of what standard motivic conjectures known to be true or confirmed numerically for elliptic curves survive in this new setup. The key and probably indispensable ingredient here will be a suitable automorphy theorem. Many believe, for instance, that a weight 3-paramodular newform (a Hecke-eigen (3,0)-regular form on the Siegel threefold parametrizing
$ \mathrm{\mathbb{Q}} $
two dimensions higher, a question arises of what standard motivic conjectures known to be true or confirmed numerically for elliptic curves survive in this new setup. The key and probably indispensable ingredient here will be a suitable automorphy theorem. Many believe, for instance, that a weight 3-paramodular newform (a Hecke-eigen (3,0)-regular form on the Siegel threefold parametrizing
![]() $ \left(1,N\right) $
-polarized abelian surfaces)
$ \left(1,N\right) $
-polarized abelian surfaces)
![]() $ {f}_M $
could be associated with such a motive
$ {f}_M $
could be associated with such a motive
![]() $ M $
of conductor
$ M $
of conductor
![]() $ N $
so that
$ N $
so that
![]() $ L\left({f}_M,s\right)=L\left(M,s\right) $
. With automorphy proven––in general, or for any given motive
$ L\left({f}_M,s\right)=L\left(M,s\right) $
. With automorphy proven––in general, or for any given motive
![]() $ M $
––one could try to proceed by relating the central
$ M $
––one could try to proceed by relating the central
![]() $ L $
-value (or the leading coefficient) at
$ L $
-value (or the leading coefficient) at
![]() $ s=2 $
obtained from an integral representation for the
$ s=2 $
obtained from an integral representation for the
![]() $ L $
-function to a certain Hodge-theoretic volume arising in a biextension of
$ L $
-function to a certain Hodge-theoretic volume arising in a biextension of
![]() $ M $
, an idea that can be traced back to Bloch’s early work (Bloch, Reference Bloch1980); see also (Bloch & Kato, Reference Bloch and Kato1990; Kontsevich & Zagier, Reference Kontsevich and Zagier2001; Scholl, Reference Scholl1991).
$ M $
, an idea that can be traced back to Bloch’s early work (Bloch, Reference Bloch1980); see also (Bloch & Kato, Reference Bloch and Kato1990; Kontsevich & Zagier, Reference Kontsevich and Zagier2001; Scholl, Reference Scholl1991).
In analytic rank
![]() $ 1 $
, one would seek a
$ 1 $
, one would seek a
![]() $ \mathrm{GSp}(4) $
-analog of the Gross–Zagier formula (Gross & Zagier, Reference Gross and Zagier1986) that might express
$ \mathrm{GSp}(4) $
-analog of the Gross–Zagier formula (Gross & Zagier, Reference Gross and Zagier1986) that might express
![]() $ {L}^{\mathrm{\prime}}(M,2) $
in terms of the height pairing between certain curves on the Siegel threefold parametrizing special abelian surfaces. Its proof, however, is expected to be very difficult and not to be found soon, so a numerical study is desirable as a second-best. Once the Dirichlet series of
$ {L}^{\mathrm{\prime}}(M,2) $
in terms of the height pairing between certain curves on the Siegel threefold parametrizing special abelian surfaces. Its proof, however, is expected to be very difficult and not to be found soon, so a numerical study is desirable as a second-best. Once the Dirichlet series of
![]() $ M $
and the shape of the functional equation are known, the technology described in Dokchitser(Reference Dokchitser2004) and implemented in Magma (Bosma et al., Reference Bosma, Cannon and Playoust1997), enables one (in principle) to compute the Taylor expansion of
$ M $
and the shape of the functional equation are known, the technology described in Dokchitser(Reference Dokchitser2004) and implemented in Magma (Bosma et al., Reference Bosma, Cannon and Playoust1997), enables one (in principle) to compute the Taylor expansion of
![]() $ L\left(M,s\right) $
to an arbitrary precision.
$ L\left(M,s\right) $
to an arbitrary precision.
The paper (Roberts & Villegas, Reference Roberts and Villegas2022) is an excellent introduction to hypergeometric motives and explains how to compute hypergeometric
![]() $ L $
-functions. The present note can be viewed by the reader as a companion paper. We show how a combination of two ideas specific to hypergeometric pencils enables one to write down closed formulas for the (archimedean) extension volumes and obtain evidence in support of B-SD. One is the principle that gamma structures (Golyshev & Mellit, Reference Golyshev and Mellit2014) give rise to Betti structures. The other says that the motive of the total space of a hypergeometric pencil can be used to provide every fiber with a biextension Hodge structure (Bloch et al., Reference Bloch, de Jong and Sertöz2023). The relevant biextension can be viewed as joining together two Katz’s extensions [20, 8.4.7, 8.4.9] going the opposite directions.
$ L $
-functions. The present note can be viewed by the reader as a companion paper. We show how a combination of two ideas specific to hypergeometric pencils enables one to write down closed formulas for the (archimedean) extension volumes and obtain evidence in support of B-SD. One is the principle that gamma structures (Golyshev & Mellit, Reference Golyshev and Mellit2014) give rise to Betti structures. The other says that the motive of the total space of a hypergeometric pencil can be used to provide every fiber with a biextension Hodge structure (Bloch et al., Reference Bloch, de Jong and Sertöz2023). The relevant biextension can be viewed as joining together two Katz’s extensions [20, 8.4.7, 8.4.9] going the opposite directions.
Hypergeometric (1,1,1,1)-families
The arithmetic of some of these hypergeometric families was studied by, for example, Dwork (Reference Dwork1969) and Schoen (Reference Schoen1986). The interest in families of
![]() $ \unicode{x211A} $
-Calabi–Yau motives with points of maximally unipotent monodromy surged in the wake of the discovery of mirror symmetry (Candelas et al., Reference Candelas, de la Ossa, Green and Parkes1991). The simplest are the
$ \unicode{x211A} $
-Calabi–Yau motives with points of maximally unipotent monodromy surged in the wake of the discovery of mirror symmetry (Candelas et al., Reference Candelas, de la Ossa, Green and Parkes1991). The simplest are the
![]() $ 14 $
hypergeometric families, which directly generalize the famous Dwork pencil (Doran & Morgan, Reference Doran and Morgan2006; Hofmann & van Straten, Reference Hofmann and van Straten2015). These (and certain “quadratic twists” of these, as we will see) are probably the most amenable to direct computation with the
$ 14 $
hypergeometric families, which directly generalize the famous Dwork pencil (Doran & Morgan, Reference Doran and Morgan2006; Hofmann & van Straten, Reference Hofmann and van Straten2015). These (and certain “quadratic twists” of these, as we will see) are probably the most amenable to direct computation with the
![]() $ l $
-adic and Betti-de Rham realizations.
$ l $
-adic and Betti-de Rham realizations.
N. Katz introduced implicitly the concept of a hypergeometric motivic sheaf in Reference Katz1990 by analyzing in detail hypergeometric differential equations, that is, scalar differential equations of the form
with
 $$ {L}_{\alpha, \beta }=\prod \limits_{i=1}^n\left(D-{\alpha}_i\right)-\lambda z\prod \limits_{j=1}^n\left(D-{\beta}_j\right),\hskip0.36em D=z\frac{d}{dz}, $$
$$ {L}_{\alpha, \beta }=\prod \limits_{i=1}^n\left(D-{\alpha}_i\right)-\lambda z\prod \limits_{j=1}^n\left(D-{\beta}_j\right),\hskip0.36em D=z\frac{d}{dz}, $$
and proving a theorem that states that an irreducible regular singular hypergeometric differential equation with rational indices (and
![]() $ \lambda \in \overline{\unicode{x211A}} $
) is motivic, i.e., arises in a piece of relative cohomology in a pencil of algebraic varieties defined over a number field. An analog of Katz’s theorem holds for tame hypergeometric
$ \lambda \in \overline{\unicode{x211A}} $
) is motivic, i.e., arises in a piece of relative cohomology in a pencil of algebraic varieties defined over a number field. An analog of Katz’s theorem holds for tame hypergeometric
![]() $ l $
-adic sheaves over
$ l $
-adic sheaves over
![]() $ {\mathbf{G}}_m/\overline{\unicode{x211A}} $
whose local inertiae act quasiunipotently. If one furthermore requires that the sets
$ {\mathbf{G}}_m/\overline{\unicode{x211A}} $
whose local inertiae act quasiunipotently. If one furthermore requires that the sets
![]() $ \exp \left(2\pi \mathrm{i}{\alpha}_i\right) $
’s and
$ \exp \left(2\pi \mathrm{i}{\alpha}_i\right) $
’s and
![]() $ \exp \left(2\pi \mathrm{i}{\beta}_j\right) $
’s are each
$ \exp \left(2\pi \mathrm{i}{\beta}_j\right) $
’s are each
![]() $ \mathrm{Gal}\left(\overline{\unicode{x211A}}/\unicode{x211A}\right) $
-stable and
$ \mathrm{Gal}\left(\overline{\unicode{x211A}}/\unicode{x211A}\right) $
-stable and
![]() $ \lambda \in \unicode{x211A} $
, a motivic construction can be defined over
$ \lambda \in \unicode{x211A} $
, a motivic construction can be defined over
![]() $ \unicode{x211A} $
, cf. (Beukers et al., Reference Beukers, Cohen and Mellit2015).
$ \unicode{x211A} $
, cf. (Beukers et al., Reference Beukers, Cohen and Mellit2015).
Gamma structures give rise to Betti structures
In order to refine hypergeometric
![]() $ D $
-modules to Hodge modules one needs to identify the
$ D $
-modules to Hodge modules one needs to identify the
![]() $ \unicode{x211A} $
-bases of the spaces of local solutions that represent the periods of relative
$ \unicode{x211A} $
-bases of the spaces of local solutions that represent the periods of relative
![]() $ \unicode{x211A} $
-de Rham forms along
$ \unicode{x211A} $
-de Rham forms along
![]() $ \unicode{x211A} $
-Betti cycles. Following Dwork, one can think of hypergeometric families as deformations of Fermat hypersurfaces (with their relatively simple motivic structures) obtained by introducing an extra monomial to the defining equation. From this perspective, it is clear that the leading expansion coefficients of
$ \unicode{x211A} $
-Betti cycles. Following Dwork, one can think of hypergeometric families as deformations of Fermat hypersurfaces (with their relatively simple motivic structures) obtained by introducing an extra monomial to the defining equation. From this perspective, it is clear that the leading expansion coefficients of
![]() $ \unicode{x211A} $
-Betti solutions of hypergeometric Hodge modules should be proportional to products of the values of the gamma function at rational arguments corresponding to the hypergeometric indices. A theorem on hypergeometric monodromy in Golyshev and Mellit (Reference Golyshev and Mellit2014) says, in particular, the following. Assume that (A1):
$ \unicode{x211A} $
-Betti solutions of hypergeometric Hodge modules should be proportional to products of the values of the gamma function at rational arguments corresponding to the hypergeometric indices. A theorem on hypergeometric monodromy in Golyshev and Mellit (Reference Golyshev and Mellit2014) says, in particular, the following. Assume that (A1):
• the sets
![]() $ \exp \left(2\pi \mathrm{i}{\alpha}_i\right) $
’s and
$ \exp \left(2\pi \mathrm{i}{\alpha}_i\right) $
’s and
![]() $ \exp \left(2\pi \mathrm{i}{\beta}_j\right) $
’s are each
$ \exp \left(2\pi \mathrm{i}{\beta}_j\right) $
’s are each
![]() $ \mathrm{Gal}\left(\overline{\unicode{x211A}}/\unicode{x211A}\right) $
-stable and
$ \mathrm{Gal}\left(\overline{\unicode{x211A}}/\unicode{x211A}\right) $
-stable and
![]() $ \lambda \in \unicode{x211A} $
$ \lambda \in \unicode{x211A} $
•
![]() $ {\alpha}_i\ne {\beta}_{i^{\prime }} \operatorname {mod}\ \unicode{x2124} $
for all
$ {\alpha}_i\ne {\beta}_{i^{\prime }} \operatorname {mod}\ \unicode{x2124} $
for all
![]() $ i,{i}^{\prime } $
$ i,{i}^{\prime } $
and, merely to make our statement simpler, that
•
![]() $ {\alpha}_i\ne {\alpha}_{i^{\prime }} \operatorname {mod}\ \unicode{x2124} $
for all
$ {\alpha}_i\ne {\alpha}_{i^{\prime }} \operatorname {mod}\ \unicode{x2124} $
for all
![]() $ i\ne {i}^{\prime } $
either.
$ i\ne {i}^{\prime } $
either.
Put
 $$ \boldsymbol{\Gamma} (s)={\boldsymbol{\Gamma}}_{\alpha, \beta }(s)=\prod \limits_{i=1}^n\Gamma {\left(s-{\alpha}_i+1\right)}^{-1}\prod \limits_{i=1}^n\Gamma {\left(-s+{\beta}_i+1\right)}^{-1}\left(s\in \unicode{x2102}\right), $$
$$ \boldsymbol{\Gamma} (s)={\boldsymbol{\Gamma}}_{\alpha, \beta }(s)=\prod \limits_{i=1}^n\Gamma {\left(s-{\alpha}_i+1\right)}^{-1}\prod \limits_{i=1}^n\Gamma {\left(-s+{\beta}_i+1\right)}^{-1}\left(s\in \unicode{x2102}\right), $$
and
![]() $ {\mathrm{A}}_i={e}^{2\pi \mathrm{i}{\alpha}_i},{\mathrm{B}}_j={e}^{2\pi \mathrm{i}{\beta}_j} $
. To simplify notation, assume until the end of this paragraph that
$ {\mathrm{A}}_i={e}^{2\pi \mathrm{i}{\alpha}_i},{\mathrm{B}}_j={e}^{2\pi \mathrm{i}{\beta}_j} $
. To simplify notation, assume until the end of this paragraph that
![]() $ \lambda ={\left(-1\right)}^n $
. In general,
$ \lambda ={\left(-1\right)}^n $
. In general,
![]() $ \left(\ast \right) $
comes with a gamma structure that is defined to be the set
$ \left(\ast \right) $
comes with a gamma structure that is defined to be the set
![]() $ \gamma =\left\{{\sum}_{s\in {s}_0+\unicode{x2124}}\boldsymbol{\Gamma} (s)\hskip0.1em {z}^s\hskip0.2em |\hskip0.2em {s}_0\in \unicode{x2102}\right\} $
of formal solutions to
$ \gamma =\left\{{\sum}_{s\in {s}_0+\unicode{x2124}}\boldsymbol{\Gamma} (s)\hskip0.1em {z}^s\hskip0.2em |\hskip0.2em {s}_0\in \unicode{x2102}\right\} $
of formal solutions to
![]() $ \left(\ast \right) $
and is meant to specialize to a Betti structure when the hypergeometric indices are rational. In particular, consider the basis of local solutions of
$ \left(\ast \right) $
and is meant to specialize to a Betti structure when the hypergeometric indices are rational. In particular, consider the basis of local solutions of
![]() $ \left(\ast \right) $
at
$ \left(\ast \right) $
at
![]() $ 0 $
given by
$ 0 $
given by
 $$ {S}_{{\mathrm{A}}_j}(z)=\sum \limits_{l=0}^{\infty}\boldsymbol{\Gamma} \left(l+{\alpha}_j\right)\hskip0.1em {z}^{l+{\alpha}_j}\in \gamma . $$
$$ {S}_{{\mathrm{A}}_j}(z)=\sum \limits_{l=0}^{\infty}\boldsymbol{\Gamma} \left(l+{\alpha}_j\right)\hskip0.1em {z}^{l+{\alpha}_j}\in \gamma . $$
Then the monodromy of
![]() $ \left(\ast \right) $
around
$ \left(\ast \right) $
around
![]() $ 0 $
is given by
$ 0 $
is given by
Denote by
![]() $ {\mathrm{V}}_{\mathrm{A}} $
the respective Vandermonde matrix
$ {\mathrm{V}}_{\mathrm{A}} $
the respective Vandermonde matrix
 $$ {\mathrm{V}}_{\mathrm{A}}=\left(\begin{array}{cccc}1& {\mathrm{A}}_1& \cdots & {\mathrm{A}}_1^{n-1}\\ {}1& {\mathrm{A}}_2& \cdots & {\mathrm{A}}_2^{n-1}\\ {}\vdots & \vdots & & \vdots \end{array}\right). $$
$$ {\mathrm{V}}_{\mathrm{A}}=\left(\begin{array}{cccc}1& {\mathrm{A}}_1& \cdots & {\mathrm{A}}_1^{n-1}\\ {}1& {\mathrm{A}}_2& \cdots & {\mathrm{A}}_2^{n-1}\\ {}\vdots & \vdots & & \vdots \end{array}\right). $$
The global monodromy of
![]() $ \hskip0.1em \left(\ast \right)\hskip0.1em $
in the basis
$ \hskip0.1em \left(\ast \right)\hskip0.1em $
in the basis
![]() $ {V}_{\mathrm{A}}^t{\left({S}_{{\mathrm{A}}_1}(z),\dots, {S}_{{\mathrm{A}}_n}(z)\right)}^t $
is shown in Golyshev and Mellit (Reference Golyshev and Mellit2014) to be in
$ {V}_{\mathrm{A}}^t{\left({S}_{{\mathrm{A}}_1}(z),\dots, {S}_{{\mathrm{A}}_n}(z)\right)}^t $
is shown in Golyshev and Mellit (Reference Golyshev and Mellit2014) to be in
![]() $ {\mathrm{GL}}_n\left(\unicode{x211A}\right) $
, and in fact defines a
$ {\mathrm{GL}}_n\left(\unicode{x211A}\right) $
, and in fact defines a
![]() $ \unicode{x211A} $
-local system that underlies a Hodge module.
$ \unicode{x211A} $
-local system that underlies a Hodge module.
To identify the Hodge filtration, we proceed as follows. For simplicity, let us further assume, as is the case with our hypergeometric
![]() $ \left(\mathrm{1,1,1,1}\right) $
-motives, that (A2):
$ \left(\mathrm{1,1,1,1}\right) $
-motives, that (A2):
•
![]() $ n $
is divisible by
$ n $
is divisible by
![]() $ 4 $
;
$ 4 $
;
• the sets
![]() $ \mathrm{A} $
’s and
$ \mathrm{A} $
’s and
![]() $ \mathrm{B} $
’s are maximally non-interlaced on the unit circle in the sense that it can be broken into two complementary sectors containing all
$ \mathrm{B} $
’s are maximally non-interlaced on the unit circle in the sense that it can be broken into two complementary sectors containing all
![]() $ \mathrm{A} $
’s resp.
$ \mathrm{A} $
’s resp.
![]() $ \mathrm{B} $
’s;
$ \mathrm{B} $
’s;
•
![]() $ \left\{{\alpha}_i\right\}\subset \left[\hskip0.1em 0,1\hskip0.1em \right),\{{\beta}_j\}\subset \left(-1,0\hskip0.1em \right]. $
$ \left\{{\alpha}_i\right\}\subset \left[\hskip0.1em 0,1\hskip0.1em \right),\{{\beta}_j\}\subset \left(-1,0\hskip0.1em \right]. $
To fix a scaling, set
![]() $ \lambda =\exp {\sum}_i\left(\psi \left(\overline{\alpha_i}\right)-\psi \left(\overline{\beta_i}\right)\right) $
, where
$ \lambda =\exp {\sum}_i\left(\psi \left(\overline{\alpha_i}\right)-\psi \left(\overline{\beta_i}\right)\right) $
, where
![]() $ \psi (x)=\frac{\Gamma^{\prime }(x)}{\Gamma (x)} $
and
$ \psi (x)=\frac{\Gamma^{\prime }(x)}{\Gamma (x)} $
and
![]() $ \overline{y} $
denotes the unique representative of the class
$ \overline{y} $
denotes the unique representative of the class
![]() $ \hskip0.1em y\hskip0.5em \operatorname{mod}\hskip0.5em \unicode{x2124} $
in
$ \hskip0.1em y\hskip0.5em \operatorname{mod}\hskip0.5em \unicode{x2124} $
in
![]() $ \left(0,1\right] $
:
$ \left(0,1\right] $
:
![]() $ \overline{y}=1-\left\{-y\right\} $
. It follows from the multiplication formula for the gamma function that
$ \overline{y}=1-\left\{-y\right\} $
. It follows from the multiplication formula for the gamma function that
![]() $ \lambda \in \unicode{x211A} $
. Let
$ \lambda \in \unicode{x211A} $
. Let
![]() $ \mathrm{univ}:U\to {\left({\mathbf{G}}_m\backslash \left\{{\lambda}^{-1}\right\}\right)}^{\mathrm{an}} $
denote the universal cover. Let
$ \mathrm{univ}:U\to {\left({\mathbf{G}}_m\backslash \left\{{\lambda}^{-1}\right\}\right)}^{\mathrm{an}} $
denote the universal cover. Let
![]() $ \mathcal{U} $
be the weight
$ \mathcal{U} $
be the weight
![]() $ 1-2n $
VHS whose underlying local system is constant with the fiber
$ 1-2n $
VHS whose underlying local system is constant with the fiber
![]() $ {\unicode{x211A}}^n $
, and the Hodge filtration is given as follows: consider the matrix
$ {\unicode{x211A}}^n $
, and the Hodge filtration is given as follows: consider the matrix
![]() $ {\Pi}_{\mathrm{A}}(z) $
whose
$ {\Pi}_{\mathrm{A}}(z) $
whose
![]() $ j $
th column is
$ j $
th column is
![]() $ {\left(z\frac{d}{dz}\right)}^j{V}_{\mathrm{A}}^t{\left({S}_{{\mathrm{A}}_1}\left(\lambda z\right),\dots, {S}_{{\mathrm{A}}_n}\left(\lambda z\right)\right)}^t $
, and let
$ {\left(z\frac{d}{dz}\right)}^j{V}_{\mathrm{A}}^t{\left({S}_{{\mathrm{A}}_1}\left(\lambda z\right),\dots, {S}_{{\mathrm{A}}_n}\left(\lambda z\right)\right)}^t $
, and let
![]() $ {\mathrm{Fil}}^{-n/2-j}\mathcal{U} $
be the span of rows
$ {\mathrm{Fil}}^{-n/2-j}\mathcal{U} $
be the span of rows
![]() $ 0,\dots, j $
in
$ 0,\dots, j $
in
![]() $ {\unicode{x211A}}^n\otimes \unicode{x2102} $
.
$ {\unicode{x211A}}^n\otimes \unicode{x2102} $
.
It is convenient to follow Deligne’s and Bloch’s convention and twist
![]() $ \mathcal{U} $
by
$ \mathcal{U} $
by
![]() $ \unicode{x211A}\left(1-n\right) $
: there exists a unique weight
$ \unicode{x211A}\left(1-n\right) $
: there exists a unique weight
![]() $ -1 $
hypergeometric VHS
$ -1 $
hypergeometric VHS
![]() $ \mathcal{V} $
on
$ \mathcal{V} $
on
![]() $ {\left({\mathbf{G}}_m\backslash \left\{{\lambda}^{-1}\right\}\right)}^{\mathrm{an}} $
such that
$ {\left({\mathbf{G}}_m\backslash \left\{{\lambda}^{-1}\right\}\right)}^{\mathrm{an}} $
such that
![]() $ \mathcal{U}\otimes \unicode{x211A}\left(1-n\right)={\mathrm{univ}}^{\ast}\mathcal{V} $
. Katz’s weight convention is the opposite of ours for
$ \mathcal{U}\otimes \unicode{x211A}\left(1-n\right)={\mathrm{univ}}^{\ast}\mathcal{V} $
. Katz’s weight convention is the opposite of ours for
![]() $ \mathcal{U} $
. For each
$ \mathcal{U} $
. For each
![]() $ {z}_0\ne {\lambda}^{-1} $
in
$ {z}_0\ne {\lambda}^{-1} $
in
![]() $ {\mathbf{G}}_m\left(\unicode{x211A}\right) $
, his theory of
$ {\mathbf{G}}_m\left(\unicode{x211A}\right) $
, his theory of
![]() $ l $
-adic hypergeometric sheaves enables one to construct naturally a weight
$ l $
-adic hypergeometric sheaves enables one to construct naturally a weight
![]() $ \left(2n-1\right) $
hypergeometric Galois representation
$ \left(2n-1\right) $
hypergeometric Galois representation
![]() $ {R}_{z_0} $
. Finally, Magma’s convention on hypergeometric motives is yet something different: there should exist a hypergeometric motive
$ {R}_{z_0} $
. Finally, Magma’s convention on hypergeometric motives is yet something different: there should exist a hypergeometric motive
![]() $ {M}_{z_0} $
of weight
$ {M}_{z_0} $
of weight
![]() $ n-1 $
such that
$ n-1 $
such that
![]() $ {R}_{z_0}={H}_{{\mathrm{e}}^{\prime}\mathrm{t}}\left({M}_{z_0}\otimes \unicode{x211A}\left(-n/2\right),{\unicode{x211A}}_l\right) $
and
$ {R}_{z_0}={H}_{{\mathrm{e}}^{\prime}\mathrm{t}}\left({M}_{z_0}\otimes \unicode{x211A}\left(-n/2\right),{\unicode{x211A}}_l\right) $
and
![]() $ {\mathcal{V}}_{z_0}={H}_{\mathrm{dR}}\left({M}_{z_0}\otimes \unicode{x211A}\left(n/2\right)\right) $
. Conceptually, these are all minor details that affect the computations in a trivial way.
$ {\mathcal{V}}_{z_0}={H}_{\mathrm{dR}}\left({M}_{z_0}\otimes \unicode{x211A}\left(n/2\right)\right) $
. Conceptually, these are all minor details that affect the computations in a trivial way.
Deligne’s conjecture
Evidence for Deligne’s conjecture for Calabi–Yau motives has been obtained in the last decade ((Roberts, Reference Robertsn.d.; Yang, Reference Yang2021), and unpublished computations by Candelas–de la Ossa–van Straten). With the assumptions made in the previous paragraph, it says that the value
![]() $ L\left({M}_{z_0},n/2\right) $
is proportional with a rational factor to a certain minor arising from the Betti to de Rham identification for
$ L\left({M}_{z_0},n/2\right) $
is proportional with a rational factor to a certain minor arising from the Betti to de Rham identification for
![]() $ {\mathcal{V}}_{z_0} $
, or equivalently, from the period matrix for the Hodge structure
$ {\mathcal{V}}_{z_0} $
, or equivalently, from the period matrix for the Hodge structure
![]() $ {\mathcal{V}}_{z_0}\otimes \unicode{x211A}\left(-1\right) $
. Concretely, one expects
$ {\mathcal{V}}_{z_0}\otimes \unicode{x211A}\left(-1\right) $
. Concretely, one expects
 $$ \frac{L\left({M}_{z_0},n/2\right)}{\det \hskip0.3em {\left(2\pi \mathrm{i}\right)}^n\operatorname{Re}\hskip0.3em {\Pi}_{\mathrm{A}}{\left({z}_0\right)}_{\left\{0,\dots, n/2-1\right\},\left\{0,\dots, n/2-1\right\}}}\in \unicode{x211A}, $$
$$ \frac{L\left({M}_{z_0},n/2\right)}{\det \hskip0.3em {\left(2\pi \mathrm{i}\right)}^n\operatorname{Re}\hskip0.3em {\Pi}_{\mathrm{A}}{\left({z}_0\right)}_{\left\{0,\dots, n/2-1\right\},\left\{0,\dots, n/2-1\right\}}}\in \unicode{x211A}, $$
where the subscript indicates the top-left quarter of the period matrix. Experimenting with the
![]() $ L $
-functions (as implemented in Magma) for the case
$ L $
-functions (as implemented in Magma) for the case
![]() $ n=4 $
corresponding to weight
$ n=4 $
corresponding to weight
![]() $ 3 $
Calabi–Yau motives, one checks the identity numerically for various different values of
$ 3 $
Calabi–Yau motives, one checks the identity numerically for various different values of
![]() $ {z}_0 $
for the
$ {z}_0 $
for the
![]() $ 7 $
out of the 14 MUM families that are non-resonant at
$ 7 $
out of the 14 MUM families that are non-resonant at
![]() $ z=0 $
(a hypergeometric differential equation is non-resonant at
$ z=0 $
(a hypergeometric differential equation is non-resonant at
![]() $ 0 $
resp.
$ 0 $
resp.
![]() $ \infty $
if the eigenvalues
$ \infty $
if the eigenvalues
![]() $ \mathrm{A} $
’s resp.
$ \mathrm{A} $
’s resp.
![]() $ \mathrm{B} $
’s of the local monodromy operator are distinct). Concretely, the
$ \mathrm{B} $
’s of the local monodromy operator are distinct). Concretely, the
![]() $ \alpha $
’s and
$ \alpha $
’s and
![]() $ \beta $
’s in the seven families are as in the left table below.
$ \beta $
’s in the seven families are as in the left table below.
The quadratic twist and the Birch–Swinnerton–Dyer period
Following a suggestion by Fernando Rodriguez Villegas, we twist the
![]() $ \alpha $
’s and
$ \alpha $
’s and
![]() $ \beta $
’s by shifting all the indices by
$ \beta $
’s by shifting all the indices by
![]() $ -\frac{1}{2} $
:
$ -\frac{1}{2} $
:
![]() $ \tilde{\alpha},\tilde{\beta} $
are, respectively, in the right table;
$ \tilde{\alpha},\tilde{\beta} $
are, respectively, in the right table;
![]() $ \tilde{\lambda} $
is now obtained from
$ \tilde{\lambda} $
is now obtained from
![]() $ \tilde{\alpha},\tilde{\beta} $
by the same rule as above.
$ \tilde{\alpha},\tilde{\beta} $
by the same rule as above.
 $$ {\displaystyle \begin{array}{ccc}1& \left[\frac{1}{12},\frac{5}{12},\frac{7}{12},\frac{11}{12}\right]& \left[\mathrm{0,0,0,0}\right]\\ {}2& \left[\frac{1}{10},\frac{3}{10},\frac{7}{10},\frac{9}{10}\right]& \left[\mathrm{0,0,0,0}\right]\\ {}3& \left[\frac{1}{8},\frac{3}{8},\frac{5}{8},\frac{7}{8}\right]& \left[\mathrm{0,0,0,0}\right]\\ {}4& \left[\frac{1}{6},\frac{1}{4},\frac{3}{4},\frac{5}{6}\right]& \left[\mathrm{0,0,0,0}\right]\\ {}5& \left[\frac{1}{6},\frac{1}{3},\frac{2}{3},\frac{5}{6}\right]& \left[\mathrm{0,0,0,0}\right]\\ {}6& \left[\frac{1}{5},\frac{2}{5},\frac{3}{5},\frac{4}{5}\right]& \left[\mathrm{0,0,0,0}\right]\\ {}7& \left[\frac{1}{4},\frac{1}{3},\frac{2}{3},\frac{3}{4}\right]& \left[\mathrm{0,0,0,0}\right].\end{array}}{\displaystyle \begin{array}{ccc}\tilde{1}& \left[-\frac{5}{12},-\frac{1}{12},\frac{1}{12},\frac{5}{12}\right]& \left[-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}\right]\\ {}\tilde{2}& \left[-\frac{2}{5},-\frac{1}{5},\frac{1}{5},\frac{2}{5}\right]& \left[-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}\right]\\ {}\tilde{3}& \left[-\frac{3}{8},-\frac{1}{8},\frac{1}{8},\frac{3}{8}\right]& \left[-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}\right]\\ {}\tilde{4}& \left[-\frac{1}{3},-\frac{1}{4},\frac{1}{4},\frac{1}{3}\right]& \left[-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}\right]\\ {}\tilde{5}& \left[-\frac{1}{3},-\frac{1}{6},\frac{1}{6},\frac{1}{3}\right]& \left[-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}\right]\\ {}\tilde{6}& \left[-\frac{3}{10},-\frac{1}{10},\frac{1}{10},\frac{3}{10}\right]& \left[-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}\right]\\ {}\tilde{7}& \left[-\frac{1}{4},-\frac{1}{6},\frac{1}{6},\frac{1}{4}\right]& \left[-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}\right].\end{array}} $$
$$ {\displaystyle \begin{array}{ccc}1& \left[\frac{1}{12},\frac{5}{12},\frac{7}{12},\frac{11}{12}\right]& \left[\mathrm{0,0,0,0}\right]\\ {}2& \left[\frac{1}{10},\frac{3}{10},\frac{7}{10},\frac{9}{10}\right]& \left[\mathrm{0,0,0,0}\right]\\ {}3& \left[\frac{1}{8},\frac{3}{8},\frac{5}{8},\frac{7}{8}\right]& \left[\mathrm{0,0,0,0}\right]\\ {}4& \left[\frac{1}{6},\frac{1}{4},\frac{3}{4},\frac{5}{6}\right]& \left[\mathrm{0,0,0,0}\right]\\ {}5& \left[\frac{1}{6},\frac{1}{3},\frac{2}{3},\frac{5}{6}\right]& \left[\mathrm{0,0,0,0}\right]\\ {}6& \left[\frac{1}{5},\frac{2}{5},\frac{3}{5},\frac{4}{5}\right]& \left[\mathrm{0,0,0,0}\right]\\ {}7& \left[\frac{1}{4},\frac{1}{3},\frac{2}{3},\frac{3}{4}\right]& \left[\mathrm{0,0,0,0}\right].\end{array}}{\displaystyle \begin{array}{ccc}\tilde{1}& \left[-\frac{5}{12},-\frac{1}{12},\frac{1}{12},\frac{5}{12}\right]& \left[-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}\right]\\ {}\tilde{2}& \left[-\frac{2}{5},-\frac{1}{5},\frac{1}{5},\frac{2}{5}\right]& \left[-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}\right]\\ {}\tilde{3}& \left[-\frac{3}{8},-\frac{1}{8},\frac{1}{8},\frac{3}{8}\right]& \left[-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}\right]\\ {}\tilde{4}& \left[-\frac{1}{3},-\frac{1}{4},\frac{1}{4},\frac{1}{3}\right]& \left[-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}\right]\\ {}\tilde{5}& \left[-\frac{1}{3},-\frac{1}{6},\frac{1}{6},\frac{1}{3}\right]& \left[-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}\right]\\ {}\tilde{6}& \left[-\frac{3}{10},-\frac{1}{10},\frac{1}{10},\frac{3}{10}\right]& \left[-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}\right]\\ {}\tilde{7}& \left[-\frac{1}{4},-\frac{1}{6},\frac{1}{6},\frac{1}{4}\right]& \left[-\frac{1}{2},-\frac{1}{2},-\frac{1}{2},-\frac{1}{2}\right].\end{array}} $$
Put
![]() $ {\tilde{\boldsymbol{\Gamma}}}_{\tilde{\alpha},\tilde{\beta}}(s)={\tilde{\lambda}}^{1/2}{\boldsymbol{\Gamma}}_{\tilde{\alpha},\tilde{\beta}}(s) $
. One has
$ {\tilde{\boldsymbol{\Gamma}}}_{\tilde{\alpha},\tilde{\beta}}(s)={\tilde{\lambda}}^{1/2}{\boldsymbol{\Gamma}}_{\tilde{\alpha},\tilde{\beta}}(s) $
. One has
![]() $ {\tilde{\boldsymbol{\Gamma}}}_{\tilde{\alpha},\tilde{\beta}}(s)={\tilde{\lambda}}^{1/2}\hskip0.1em {\boldsymbol{\Gamma}}_{\alpha, \beta}\left(s+1/2\right). $
All that has been said up to now about hypergeometric Hodge structures works identically for the seven families and the seven twists. However, we expect the twist to raise the “average” analytic rank in the family. Starting with an
$ {\tilde{\boldsymbol{\Gamma}}}_{\tilde{\alpha},\tilde{\beta}}(s)={\tilde{\lambda}}^{1/2}\hskip0.1em {\boldsymbol{\Gamma}}_{\alpha, \beta}\left(s+1/2\right). $
All that has been said up to now about hypergeometric Hodge structures works identically for the seven families and the seven twists. However, we expect the twist to raise the “average” analytic rank in the family. Starting with an
![]() $ {L}_{\tilde{\alpha},\tilde{\beta}} $
as above, we will construct a “biextension” variation of mixed Hodge structure formally in hypergeometric terms. Although it is not true in general that the product of two differential operators of motivic origin is again motivic, there are situations when one can construct mixed motivic variations formally.
$ {L}_{\tilde{\alpha},\tilde{\beta}} $
as above, we will construct a “biextension” variation of mixed Hodge structure formally in hypergeometric terms. Although it is not true in general that the product of two differential operators of motivic origin is again motivic, there are situations when one can construct mixed motivic variations formally.
Theorem
With the assumptions (A1) and (A2) made in 2 and 3, the differential equation
![]() $ {DL}_{\tilde{\alpha},\tilde{\beta}}\hskip0.5em DS(z)=0 $
is motivic, that is, underlies a VMHS of geometric origin.
$ {DL}_{\tilde{\alpha},\tilde{\beta}}\hskip0.5em DS(z)=0 $
is motivic, that is, underlies a VMHS of geometric origin.
Proof
The idea is that under certain conditions that hold in our case we can pass from the
![]() $ D $
-module corresponding to a differential operator
$ D $
-module corresponding to a differential operator
![]() $ L $
to the one corresponding to
$ L $
to the one corresponding to
![]() $ DLD $
by successively convoluting it with the star resp. the shriek extension of the “constant object”
$ DLD $
by successively convoluting it with the star resp. the shriek extension of the “constant object”
![]() $ \mathcal{O} $
on
$ \mathcal{O} $
on
![]() $ {\mathbf{G}}_{\mathbf{m}}-\left\{1\right\} $
to
$ {\mathbf{G}}_{\mathbf{m}}-\left\{1\right\} $
to
![]() $ {\mathbf{G}}_{\mathbf{m}} $
. The background is Katz (Reference Katz1990); all references in the proof are to this book. Denote
$ {\mathbf{G}}_{\mathbf{m}} $
. The background is Katz (Reference Katz1990); all references in the proof are to this book. Denote
![]() $ \partial =\frac{d}{dz},D=z\partial $
as above,
$ \partial =\frac{d}{dz},D=z\partial $
as above,
![]() $ \hskip0.1em \mathcal{D}={\mathcal{D}}_{{\mathbf{G}}_{\mathbf{m}}}=\unicode{x2102}\left[z,{z}^{-1},\partial \right],{\mathcal{D}}_{{\unicode{x1D538}}^11}=\unicode{x2102}\left[z,\partial \right]. $
Let
$ \hskip0.1em \mathcal{D}={\mathcal{D}}_{{\mathbf{G}}_{\mathbf{m}}}=\unicode{x2102}\left[z,{z}^{-1},\partial \right],{\mathcal{D}}_{{\unicode{x1D538}}^11}=\unicode{x2102}\left[z,\partial \right]. $
Let
![]() $ j $
be the open immersion
$ j $
be the open immersion
![]() $ {\mathbf{G}}_{\mathbf{m}}\hookrightarrow {\unicode{x1D538}}^11 $
, and let inv denote the inversion map on
$ {\mathbf{G}}_{\mathbf{m}}\hookrightarrow {\unicode{x1D538}}^11 $
, and let inv denote the inversion map on
![]() $ {\mathbf{G}}_{\mathbf{m}} $
. We denote the Fourier transform functor by FT.
$ {\mathbf{G}}_{\mathbf{m}} $
. We denote the Fourier transform functor by FT.
1. Katz’s lemma on indicial polynomials. [2.9.5] Write
![]() $ L $
as a polynomial in
$ L $
as a polynomial in
![]() $ z $
whose coefficients are in turn polynomials in
$ z $
whose coefficients are in turn polynomials in
![]() $ D $
:
$ D $
:
![]() $ L={\sum}_{k=0}^d{z}^k{P}_k(D) $
. Then:
$ L={\sum}_{k=0}^d{z}^k{P}_k(D) $
. Then:
![]() $ {P}_0(y) $
has no zeroes in
$ {P}_0(y) $
has no zeroes in
![]() $ {\unicode{x2124}}_{<0} $
iff
$ {\unicode{x2124}}_{<0} $
iff
![]() $ {P}_0(y) $
has no zeroes in
$ {P}_0(y) $
has no zeroes in
![]() $ {\unicode{x2124}}_{\ge 0} $
iff
$ {\unicode{x2124}}_{\ge 0} $
iff
2. The D-modules
![]() $ {F}_k={\mathcal{D}}_{{\unicode{x1D538}}^11}/{\mathcal{D}}_{{\unicode{x1D538}}^11}\left(D-k\right) $
with
$ {F}_k={\mathcal{D}}_{{\unicode{x1D538}}^11}/{\mathcal{D}}_{{\unicode{x1D538}}^11}\left(D-k\right) $
with
![]() $ k\in \unicode{x2124} $
. The lemma says that for
$ k\in \unicode{x2124} $
. The lemma says that for
![]() $ k\ge 0 $
, the D-module
$ k\ge 0 $
, the D-module
![]() $ {F}_k $
is isomorphic to
$ {F}_k $
is isomorphic to
![]() $ {j}_{!}\mathcal{O} $
; for
$ {j}_{!}\mathcal{O} $
; for
![]() $ k<0 $
, the D-module
$ k<0 $
, the D-module
![]() $ {F}_k $
is isomorphic to
$ {F}_k $
is isomorphic to
![]() $ {j}_{\ast}\mathcal{O} $
.
$ {j}_{\ast}\mathcal{O} $
.
We will need a version of this: put
![]() $ {E}_k=\mathcal{D}/\mathcal{D}\left(D-z\left(D-k\right)\right) $
with
$ {E}_k=\mathcal{D}/\mathcal{D}\left(D-z\left(D-k\right)\right) $
with
![]() $ k\in \unicode{x2124} $
. Denote by
$ k\in \unicode{x2124} $
. Denote by
![]() $ {j}^{\prime } $
the open immersion
$ {j}^{\prime } $
the open immersion
![]() $ {\mathbf{G}}_{\mathbf{m}}-\left\{1\right\}\hookrightarrow {\mathbf{G}}_{\mathbf{m}} $
. We claim that for
$ {\mathbf{G}}_{\mathbf{m}}-\left\{1\right\}\hookrightarrow {\mathbf{G}}_{\mathbf{m}} $
. We claim that for
![]() $ k\ge 0 $
, the D-module
$ k\ge 0 $
, the D-module
![]() $ {E}_k $
is
$ {E}_k $
is
![]() $ {j}_{!}^{\prime }{\mathcal{O}}_{{\mathbf{G}}_{\mathbf{m}}-\left\{1\right\}} $
. For
$ {j}_{!}^{\prime }{\mathcal{O}}_{{\mathbf{G}}_{\mathbf{m}}-\left\{1\right\}} $
. For
![]() $ k<0 $
, the D-module
$ k<0 $
, the D-module
![]() $ {E}_k $
is
$ {E}_k $
is
![]() $ {j}_{\ast}^{\prime }{\mathcal{O}}_{{\mathbf{G}}_{\mathbf{m}}-\left\{1\right\}} $
. Indeed, put
$ {j}_{\ast}^{\prime }{\mathcal{O}}_{{\mathbf{G}}_{\mathbf{m}}-\left\{1\right\}} $
. Indeed, put
![]() $ z=1+u $
, then
$ z=1+u $
, then
![]() $ D-z\left(D-k\right)=\left(1+u\right)\partial -\left(1+u\right)\left(1+u\right)\partial +\left(1+u\right)k=-\left(1+u\right)\left(u\partial -k\right) $
.
$ D-z\left(D-k\right)=\left(1+u\right)\partial -\left(1+u\right)\left(1+u\right)\partial +\left(1+u\right)k=-\left(1+u\right)\left(u\partial -k\right) $
.
3. Katz’s “key lemma.” [5.2.3] Let the convolution sign stand for convolution with no supports on
![]() $ {\mathbf{G}}_{\mathbf{m}} $
. For any holonomic module
$ {\mathbf{G}}_{\mathbf{m}} $
. For any holonomic module
![]() $ M $
on
$ M $
on
![]() $ {\mathbf{G}}_{\mathbf{m}} $
we have
$ {\mathbf{G}}_{\mathbf{m}} $
we have
and [5.2.3.1]
4. We define the star (resp. the shriek) Ur-object to be
resp.
Claim. The star Ur-object is
![]() $ {E}_0 $
. Proof (cf. [6.3.5]): use the key lemma with
$ {E}_0 $
. Proof (cf. [6.3.5]): use the key lemma with
![]() $ M=\mathcal{D}/\mathcal{D}\left(1- zD\right) $
. The LHS becomes
$ M=\mathcal{D}/\mathcal{D}\left(1- zD\right) $
. The LHS becomes
 $$ {\displaystyle \begin{array}{l}{j}^{\ast}\mathrm{FT}\left({\mathcal{D}}_{{\unicode{x1D538}}^11}/{\mathcal{D}}_{{\unicode{x1D538}}^11}\left(\left(D+1\right)+z\right)\right)\cong {j}^{\ast}\left({\mathcal{D}}_{{\unicode{x1D538}}^11}/{\mathcal{D}}_{{\unicode{x1D538}}^11}\mathrm{FT}\left(\left(D+1\right)+z\right)\right)\cong \\ {}\hskip21.9em {j}^{\ast}\left({\mathcal{D}}_{{\unicode{x1D538}}^11}/{\mathcal{D}}_{{\unicode{x1D538}}^11}\left(-D+\partial \right)\right)\cong \mathcal{D}/\mathcal{D}\left(D- zD\right).\end{array}} $$
$$ {\displaystyle \begin{array}{l}{j}^{\ast}\mathrm{FT}\left({\mathcal{D}}_{{\unicode{x1D538}}^11}/{\mathcal{D}}_{{\unicode{x1D538}}^11}\left(\left(D+1\right)+z\right)\right)\cong {j}^{\ast}\left({\mathcal{D}}_{{\unicode{x1D538}}^11}/{\mathcal{D}}_{{\unicode{x1D538}}^11}\mathrm{FT}\left(\left(D+1\right)+z\right)\right)\cong \\ {}\hskip21.9em {j}^{\ast}\left({\mathcal{D}}_{{\unicode{x1D538}}^11}/{\mathcal{D}}_{{\unicode{x1D538}}^11}\left(-D+\partial \right)\right)\cong \mathcal{D}/\mathcal{D}\left(D- zD\right).\end{array}} $$
5. Let
![]() $ H={P}_0(D)-{zP}_1(D) $
be an irreducible hypergeometric operator, so that the sets of roots
$ H={P}_0(D)-{zP}_1(D) $
be an irreducible hypergeometric operator, so that the sets of roots
![]() $ \operatorname{mod}\unicode{x2124} $
of
$ \operatorname{mod}\unicode{x2124} $
of
![]() $ {P}_0 $
and
$ {P}_0 $
and
![]() $ {P}_1 $
are disjoint. Assume further that
$ {P}_1 $
are disjoint. Assume further that
![]() $ {P}_1 $
has no integer roots and
$ {P}_1 $
has no integer roots and
![]() $ {P}_0 $
has no integer roots in
$ {P}_0 $
has no integer roots in
![]() $ {\unicode{x2124}}_{\ge 0} $
. We claim that
$ {\unicode{x2124}}_{\ge 0} $
. We claim that
Indeed, in order to convolute with
![]() $ {E}_0 $
one convolutes first with
$ {E}_0 $
one convolutes first with
![]() $ \mathcal{D}/\mathcal{D}\left(D-z\right) $
then with
$ \mathcal{D}/\mathcal{D}\left(D-z\right) $
then with
![]() $ \mathcal{D}/\mathcal{D}\left(1- zD\right)\cong {\left[z\mapsto -z\right]}_{\ast}\left(\mathcal{D}/\mathcal{D}\left(1+ zD\right)\right) $
. The result of the first convolution is simply
$ \mathcal{D}/\mathcal{D}\left(1- zD\right)\cong {\left[z\mapsto -z\right]}_{\ast}\left(\mathcal{D}/\mathcal{D}\left(1+ zD\right)\right) $
. The result of the first convolution is simply
![]() $ \mathcal{D}/\mathcal{D}\left(\left(D+1\right){P}_0(D)-{zP}_1(D)\right) $
as
$ \mathcal{D}/\mathcal{D}\left(\left(D+1\right){P}_0(D)-{zP}_1(D)\right) $
as
![]() $ {P}_1 $
has no integer roots, [5.3.1]. In order to convolute with
$ {P}_1 $
has no integer roots, [5.3.1]. In order to convolute with
![]() $ \mathcal{D}/\mathcal{D}\left(1+ zD\right) $
one now uses the second statement of the key lemma, obtaining
$ \mathcal{D}/\mathcal{D}\left(1+ zD\right) $
one now uses the second statement of the key lemma, obtaining
 $$ {\displaystyle \begin{array}{ll}{\mathrm{inv}}^{\ast}\left(\mathcal{D}/\mathcal{D}\left(-{DP}_0\left(-D-1\right)-\partial {P}_1\left(-D-1\right)\right)\right)& \cong {\mathrm{inv}}^{\ast}\left(\mathcal{D}/\mathcal{D}\left(-{zDP}_0\left(-D-1\right)-{DP}_1\left(-D-1\right)\right)\right)\\ {}& \cong \mathcal{D}/\mathcal{D}\left({DP}_0\left(D-1\right)+{zDP}_1\left(D-1\right)\right).\end{array}} $$
$$ {\displaystyle \begin{array}{ll}{\mathrm{inv}}^{\ast}\left(\mathcal{D}/\mathcal{D}\left(-{DP}_0\left(-D-1\right)-\partial {P}_1\left(-D-1\right)\right)\right)& \cong {\mathrm{inv}}^{\ast}\left(\mathcal{D}/\mathcal{D}\left(-{zDP}_0\left(-D-1\right)-{DP}_1\left(-D-1\right)\right)\right)\\ {}& \cong \mathcal{D}/\mathcal{D}\left({DP}_0\left(D-1\right)+{zDP}_1\left(D-1\right)\right).\end{array}} $$
Finally, the effect of
![]() $ {\left[z\mapsto -z\right]}_{\ast } $
is in simply changing the sign of
$ {\left[z\mapsto -z\right]}_{\ast } $
is in simply changing the sign of
![]() $ z $
.
$ z $
.
6. Let
![]() $ {}^{\vee } $
denote the “passing to adjoints” anti-automorphism sending
$ {}^{\vee } $
denote the “passing to adjoints” anti-automorphism sending
![]() $ t $
to
$ t $
to
![]() $ t $
and
$ t $
and
![]() $ \partial $
to
$ \partial $
to
![]() $ -\partial $
, so that the formal adjoint of
$ -\partial $
, so that the formal adjoint of
![]() $ \left({P}_0\left(D-1\right)-{zP}_1\left(D-1\right)\right)D $
is
$ \left({P}_0\left(D-1\right)-{zP}_1\left(D-1\right)\right)D $
is
![]() $ \left(-D-1\right)\left({P}_0\left(-D-2\right)-{P}_1\left(-D-2\right)z\right). $
Assume now that
$ \left(-D-1\right)\left({P}_0\left(-D-2\right)-{P}_1\left(-D-2\right)z\right). $
Assume now that
![]() $ {P}_0 $
has no integer roots. The previous consideration applies so convoluting with
$ {P}_0 $
has no integer roots. The previous consideration applies so convoluting with
![]() $ {E}_0 $
we get the
$ {E}_0 $
we get the
![]() $ \mathcal{D} $
-module corresponding to the operator
$ \mathcal{D} $
-module corresponding to the operator
Passing to adjoints again,
we arrive at the
![]() $ \mathcal{D} $
-module
$ \mathcal{D} $
-module
7. To finish the proof, take
![]() $ H $
to be the hypergeometric operator whose indices are
$ H $
to be the hypergeometric operator whose indices are
![]() $ \tilde{\alpha} $
’s and
$ \tilde{\alpha} $
’s and
![]() $ \tilde{\beta} $
’s shifted by
$ \tilde{\beta} $
’s shifted by
![]() $ -1 $
, and the position of the singularities are the same. By Katz,
$ -1 $
, and the position of the singularities are the same. By Katz,
![]() $ H $
is motivic. By the argument above, one can pass from the D-module
$ H $
is motivic. By the argument above, one can pass from the D-module
![]() $ \mathcal{D}/\mathcal{D}H $
to the D-module
$ \mathcal{D}/\mathcal{D}H $
to the D-module
![]() $ \mathcal{D}/\mathcal{D}\left({DL}_{\tilde{\alpha},\tilde{\beta}}D\right) $
by successively applying the motivic operations of convolution with the motivic object
$ \mathcal{D}/\mathcal{D}\left({DL}_{\tilde{\alpha},\tilde{\beta}}D\right) $
by successively applying the motivic operations of convolution with the motivic object
![]() $ {E}_{-1} $
and passage to duals. Hence,
$ {E}_{-1} $
and passage to duals. Hence,
![]() $ \mathcal{D}/\mathcal{D}\left({DL}_{\tilde{\alpha},\tilde{\beta}}D\right) $
is itself motivic, namely
$ \mathcal{D}/\mathcal{D}\left({DL}_{\tilde{\alpha},\tilde{\beta}}D\right) $
is itself motivic, namely
![]() $ \mathcal{D}/\mathcal{D}\left({DL}_{\tilde{\alpha},\tilde{\beta}}D\right)\simeq \left(\left(\mathcal{D}/\mathcal{D}{L}_{\tilde{\alpha},\tilde{\beta}}\right)\ast {j}_{!}\mathcal{O}\right)\ast {\hskip0.1em }_{!}{j}_{\ast}\mathcal{O} $
.
$ \mathcal{D}/\mathcal{D}\left({DL}_{\tilde{\alpha},\tilde{\beta}}D\right)\simeq \left(\left(\mathcal{D}/\mathcal{D}{L}_{\tilde{\alpha},\tilde{\beta}}\right)\ast {j}_{!}\mathcal{O}\right)\ast {\hskip0.1em }_{!}{j}_{\ast}\mathcal{O} $
.
■
We remark that all these considerations translate immediately into the
![]() $ l $
-adic setting. We stick with Hodge modules, but what we need here is a concrete description suitable for computation. The significance of the twist is that the variation of mixed Hodge structure in question is a biextension VHS (Hain, Reference Hain1990), that is, sits in a
$ l $
-adic setting. We stick with Hodge modules, but what we need here is a concrete description suitable for computation. The significance of the twist is that the variation of mixed Hodge structure in question is a biextension VHS (Hain, Reference Hain1990), that is, sits in a
![]() $ \unicode{x211A}(1)\hookrightarrow \mathcal{V}\twoheadrightarrow \unicode{x211A} $
; this would not be the case without the twist. Think of the fiber
$ \unicode{x211A}(1)\hookrightarrow \mathcal{V}\twoheadrightarrow \unicode{x211A} $
; this would not be the case without the twist. Think of the fiber
![]() $ \mathcal{V} $
at
$ \mathcal{V} $
at
![]() $ {z}_0\in \unicode{x211A} $
as realized in
$ {z}_0\in \unicode{x211A} $
as realized in
![]() $ {H}^3\left({X}_{z_0},\unicode{x211A}(2)\right) $
for a threefold
$ {H}^3\left({X}_{z_0},\unicode{x211A}(2)\right) $
for a threefold
![]() $ {X}_{z_0} $
. By specializing this VMHS we construct a non-trivial (in general) biextension of
$ {X}_{z_0} $
. By specializing this VMHS we construct a non-trivial (in general) biextension of
![]() $ {H}^3\left({X}_{z_0},\unicode{x211A}(2)\right) $
, and by relaxing the structure to a once-extension, a class in absolute Hodge cohomology
$ {H}^3\left({X}_{z_0},\unicode{x211A}(2)\right) $
, and by relaxing the structure to a once-extension, a class in absolute Hodge cohomology
![]() $ {H}_{\mathrm{Hodge}}^4\left({X}_{z_0},\mathrm{\mathbb{R}}(2)\right) $
. According to the Beilinson rank conjecture, this class signals the presence of a non-trivial class
$ {H}_{\mathrm{Hodge}}^4\left({X}_{z_0},\mathrm{\mathbb{R}}(2)\right) $
. According to the Beilinson rank conjecture, this class signals the presence of a non-trivial class
![]() $ {c}_{z_0} $
in
$ {c}_{z_0} $
in
![]() $ {\mathrm{CH}}_0^{(2)}\left({X}_{z_0}\right)\otimes \unicode{x211A} $
.
$ {\mathrm{CH}}_0^{(2)}\left({X}_{z_0}\right)\otimes \unicode{x211A} $
.
In the language of period matrices, in addition to the 4 pure periods
one introduces an extension solution
![]() $ {S}_1(z)={\sum}_{n=0}^{\infty }{\tilde{\boldsymbol{\Gamma}}}_{\tilde{\alpha},\tilde{\beta}}(n){z}^n $
so that
$ {S}_1(z)={\sum}_{n=0}^{\infty }{\tilde{\boldsymbol{\Gamma}}}_{\tilde{\alpha},\tilde{\beta}}(n){z}^n $
so that
![]() $ {DL}_{\tilde{\alpha},\tilde{\beta}}{S}_1\left(\tilde{\lambda}z\right)=0 $
and the (transposed) biextension period matrix
$ {DL}_{\tilde{\alpha},\tilde{\beta}}{S}_1\left(\tilde{\lambda}z\right)=0 $
and the (transposed) biextension period matrix
 $$ {\Pi}_{\overset{\sim }{\mathrm{A}}}^{\mathrm{biext}}(z)={\left(1,\frac{d}{dz}\dots, {\left(\frac{d}{dz}\right)}^5\right)}^t\hskip2pt \left(\int {S}_1(\lambda z)\frac{dz}{z},\int {\Phi}_1(z)\frac{dz}{z},\int {\Phi}_2(z)\frac{dz}{z},\int {\Phi}_3(z)\frac{dz}{z},\int {\Phi}_4(z)\frac{dz}{z},\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\right) $$
$$ {\Pi}_{\overset{\sim }{\mathrm{A}}}^{\mathrm{biext}}(z)={\left(1,\frac{d}{dz}\dots, {\left(\frac{d}{dz}\right)}^5\right)}^t\hskip2pt \left(\int {S}_1(\lambda z)\frac{dz}{z},\int {\Phi}_1(z)\frac{dz}{z},\int {\Phi}_2(z)\frac{dz}{z},\int {\Phi}_3(z)\frac{dz}{z},\int {\Phi}_4(z)\frac{dz}{z},\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\right) $$
with the choice of the constant terms in the
![]() $ 0 $
th row being
$ 0 $
th row being
A version of the Birch–Swinnerton–Dyer-type conjecture (Bloch, Reference Bloch1980; Kontsevich & Zagier, Reference Kontsevich and Zagier2001; Scholl, Reference Scholl1991) translates into the following statement. By analogy with the elliptic curve cases two dimensions lower, one expects that the archimedean component of the height of
![]() $ {c}_{z_0} $
is essentially the ratio of two minors of
$ {c}_{z_0} $
is essentially the ratio of two minors of
![]() $ \operatorname{Re}\hskip0.2em {\Pi}_{\tilde{\mathrm{A}}}^{\mathrm{biext}}\left({z}_0\right) $
:
$ \operatorname{Re}\hskip0.2em {\Pi}_{\tilde{\mathrm{A}}}^{\mathrm{biext}}\left({z}_0\right) $
:
 $$ {h}_{\mathrm{arch}}\left({c}_{z_0}\right)={\tilde{\boldsymbol{\Gamma}}}_{\tilde{\alpha},\tilde{\beta}}{(0)}^{-1}\cdot \frac{\hskip0.5em \det \operatorname{Re}{\Pi}_{\tilde{\mathrm{A}}}^{\mathrm{biext}}{\left({z}_0\right)}_{\left\{\mathrm{0,1,2}\right\},\left\{\mathrm{0,1,2}\right\}}}{\det \hskip0.2em \operatorname{Re}{\Pi}_{\tilde{\mathrm{A}}}^{\mathrm{biext}}{\left({z}_0\right)}_{\left\{1,2\right\},\left\{1,2\right\}}}. $$
$$ {h}_{\mathrm{arch}}\left({c}_{z_0}\right)={\tilde{\boldsymbol{\Gamma}}}_{\tilde{\alpha},\tilde{\beta}}{(0)}^{-1}\cdot \frac{\hskip0.5em \det \operatorname{Re}{\Pi}_{\tilde{\mathrm{A}}}^{\mathrm{biext}}{\left({z}_0\right)}_{\left\{\mathrm{0,1,2}\right\},\left\{\mathrm{0,1,2}\right\}}}{\det \hskip0.2em \operatorname{Re}{\Pi}_{\tilde{\mathrm{A}}}^{\mathrm{biext}}{\left({z}_0\right)}_{\left\{1,2\right\},\left\{1,2\right\}}}. $$
Assume, in addition, that the modulus
![]() $ {z}_0\in \unicode{x211A} $
is chosen so that there are no non-archimedean components of the height. Since the minor
$ {z}_0\in \unicode{x211A} $
is chosen so that there are no non-archimedean components of the height. Since the minor
![]() $ \det \operatorname{Re}{\Pi}_{\tilde{\mathrm{A}}}^{\mathrm{biext}}{\left({z}_0\right)}_{\left\{1,2\right\},\left\{1,2\right\}} $
occurring in the denominator is nothing else but the
$ \det \operatorname{Re}{\Pi}_{\tilde{\mathrm{A}}}^{\mathrm{biext}}{\left({z}_0\right)}_{\left\{1,2\right\},\left\{1,2\right\}} $
occurring in the denominator is nothing else but the
![]() $ {\tilde{\boldsymbol{\Gamma}}}_{\tilde{\alpha},\tilde{\beta}}{(0)}^{-2} $
-scaled Deligne period of
$ {\tilde{\boldsymbol{\Gamma}}}_{\tilde{\alpha},\tilde{\beta}}{(0)}^{-2} $
-scaled Deligne period of
![]() $ {M}_{z_0} $
, a version of B-SD for an analytic rank 1 motive
$ {M}_{z_0} $
, a version of B-SD for an analytic rank 1 motive
![]() $ {M}_{z_0} $
in a hypergeometric family as above would predict that
$ {M}_{z_0} $
in a hypergeometric family as above would predict that
 $$ r\left({z}_0\right):= \frac{L^{\prime}\left({M}_{z_0},2\right)}{{\tilde{\boldsymbol{\Gamma}}}_{\tilde{\alpha},\tilde{\beta}}{(0)}^{-3}\det \hskip0.2em \operatorname{Re}{\Pi}_{\tilde{\mathrm{A}}}^{\mathrm{biext}}{\left({z}_0\right)}_{\left\{\mathrm{0,1,2}\right\},\left\{\mathrm{0,1,2}\right\}}}\in {\unicode{x211A}}^{\ast }. $$
$$ r\left({z}_0\right):= \frac{L^{\prime}\left({M}_{z_0},2\right)}{{\tilde{\boldsymbol{\Gamma}}}_{\tilde{\alpha},\tilde{\beta}}{(0)}^{-3}\det \hskip0.2em \operatorname{Re}{\Pi}_{\tilde{\mathrm{A}}}^{\mathrm{biext}}{\left({z}_0\right)}_{\left\{\mathrm{0,1,2}\right\},\left\{\mathrm{0,1,2}\right\}}}\in {\unicode{x211A}}^{\ast }. $$
Examples
Consider the hypergeometric family
![]() $ \tilde{2} $
in the second table in 5. (so that
$ \tilde{2} $
in the second table in 5. (so that
![]() $ {\overset{\sim }{\boldsymbol{\Gamma}}}_{\overset{\sim }{\alpha },\overset{\sim }{\beta }}(0)=32\hskip0.1em {(2\pi \mathrm{i})}^{-4} $
). One finds numerically
$ {\overset{\sim }{\boldsymbol{\Gamma}}}_{\overset{\sim }{\alpha },\overset{\sim }{\beta }}(0)=32\hskip0.1em {(2\pi \mathrm{i})}^{-4} $
). One finds numerically
More:

Much of this can be generalized to higher-rank hypergeometrics or extended to cases involving certain higher regulators. The method can be extended to cases involving certain higher regulators as will be shown in a forthcoming paper with Matt Kerr. I thank Kilian Boenisch for checking the computations.
I thank the members of the International Groupe de Travail on differential equations in Paris for many helpful discussions, and Neil Dummigan and Emre Sertöz for comments and corrections. I thank the Max Planck Institute for Mathematics for its hospitality during my stay there in 2021.
I am deeply thankful to the Institut des Hautes Études Scientifiques for the extraordinary support it gave me in 2022.
Open peer review
To view the open peer review materials for this article, please visit http://doi.org/10.1017/exp.2023.15.
Funding statement
This research received no specific grant from any funding agency, commercial or not-for-profit sectors.
Competing interest
The author declares none.

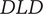
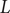
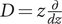
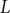
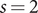

Comments
Please split the sentence “We show how a combination...” into two.