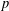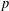Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
He, Xuhua
and
Kim, Ju-Lee
2019.
Jordan decompositions of cocenters of reductive 𝑝-adic groups.
Representation Theory of the American Mathematical Society,
Vol. 23,
Issue. 10,
p.
294.
He, Xuhua
2019.
Cocenter of p-adic groups, II: Induction map.
Advances in Mathematics,
Vol. 345,
Issue. ,
p.
972.
He, Xuhua
and
Nie, Sian
2020.
A geometric interpretation of Newton strata.
Selecta Mathematica,
Vol. 26,
Issue. 1,
Ganapathy, Radhika
and
He, Xuhua
2024.
Tits Groups of Iwahori-Weyl Groups and Presentations of Hecke Algebras.
Transformation Groups,
Vol. 29,
Issue. 4,
p.
1419.