Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T21:29:29.317Z Has data issue: false hasContentIssue false
  • English
  • Français

CONTINUITY OF UNIVERSALLY MEASURABLE HOMOMORPHISMS

Part of: Set theory Abstract harmonic analysis Topological and differentiable algebraic systems

Published online by Cambridge University Press:  13 August 2019

CHRISTIAN ROSENDAL
CHRISTIAN ROSENDAL*
Affiliation:
Department of Mathematics, Statistics, and Computer Science (M/C 249), University of Illinois at Chicago, 851 S. Morgan St., Chicago, IL 60607-7045, USA; rosendal.math@gmail.com

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Answering a longstanding problem originating in Christensen’s seminal work on Haar null sets [Math. Scand. 28 (1971), 124–128; Israel J. Math. 13 (1972), 255–260; Topology and Borel Structure. Descriptive Topology and Set Theory with Applications to Functional Analysis and Measure Theory, North-Holland Mathematics Studies, 10 (Notas de Matematica, No. 51). (North-Holland Publishing Co., Amsterdam–London; American Elsevier Publishing Co., Inc., New York, 1974), iii+133 pp], we show that a universally measurable homomorphism between Polish groups is automatically continuous. Using our general analysis of continuity of group homomorphisms, this result is used to calibrate the strength of the existence of a discontinuous homomorphism between Polish groups. In particular, it is shown that, modulo 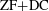$\text{ZF}+\text{DC}$, the existence of a discontinuous homomorphism between Polish groups implies that the Hamming graph on 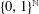$\{0,1\}^{\mathbb{N}}$ has finite chromatic number.

MSC classification

Primary: 03E15: Descriptive set theory
Secondary: 22A05: Structure of general topological groups 43A05: Measures on groups and semigroups, etc.
Type
Research Article
Information
Forum of Mathematics, Pi , Volume 7 , 2019 , e5
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2019

References

Banach, S., ‘Sur l’équation fonctionnelle f (x + y) = f (x) + f (y)’, Fund. Math. 1 (1920), 123–124.Google Scholar
Christensen, J. P. R., ‘Borel structures in groups and semigroups’, Math. Scand. 28 (1971), 124–128.Google Scholar
Christensen, J. P. R., ‘On sets of Haar measure zero in abelian Polish groups’, Israel J. Math. 13 (1972), 255–260 .Google Scholar
Christensen, J. P. R., Topology and Borel Structure. Descriptive Topology and Set Theory with Applications to Functional Analysis and Measure Theory, North-Holland Mathematics Studies, 10 (Notas de Matematica, No. 51). (North-Holland Publishing Co., Amsterdam–London; American Elsevier Publishing Co., Inc., New York, 1974), iii+133 pp.Google Scholar
van Dantzig, D., ‘Zur topologischen Algebra. III. Brouwersche und Cantorsche Gruppen’, Compos. Math. 3 (1936), 408–426. (German).Google Scholar
Elekes, M. and Nagy, D., ‘Haar null and Haar meager sets: a survey and new results’, Bull. Lond. Math. Soc., Preprint, 2016, arXiv:1606.06607, to appear.Google Scholar
Fischer, P. and Słodkowski, Z., ‘Christensen zero sets and measurable convex functions’, Proc. Amer. Math. Soc. 79(3) (1980), 449–453.Google Scholar
Fréchet, M., ‘Pri la funkcia ekvacio f (x + y) = f (x) + f (y)’, Enseign. Math. 15 (1913), 390–393.Google Scholar
Guran, I. Y., ‘Topological groups similar to Lindelöf groups’, Dokl. Akad. Nauk SSSR 256(6) (1981), 1305–1307. (in Russian).Google Scholar
Larson, P., ‘The filter dichotomy and medial limits’, J. Math. Log. 9(2) (2009), 159–165.Google Scholar
Larson, P. and Zapletal, J., ‘Discontinuous homomorphisms, selectors, and automorphisms of the complex field’, Proc. Amer. Math. Soc. 147 (2019), 1733–1737.Google Scholar
Meyer, P.-A., ‘Limites médiales, d’après Mokobodzki’, inSéminaire de Probabilités, VII (Univ. Strasbourg, année universitaire 1971–1972), Lecture Notes in Mathematics, 321 (Springer, Berlin, 1973), 198–204.Google Scholar
Mokobodzki, G., ‘Ultrafiltres rapides sur N. Construction d’une densité relative de deux potentiels comparables’, (French) 1969 Séminaire de Théorie du Potentiel, dirigé par M. Brelot, G. Choquet et J. Deny: 1967/68, Exp. 12 22 pp. Secrétariat mathématique, Paris.Google Scholar
Normann, D., ‘Martin’s axiom and medial functions’, Math. Scand. 38 (1976), 167–176.Google Scholar
di Prisco de Venanzi, C. A. and Todorčević, S., ‘Souslin partitions of products of finite sets’, Adv. Math. 176 (2003), 145–173.Google Scholar
Rosendal, C., ‘Universally measurable subgroups of countable index’, J. Symbolic Logic 75(3) (2010), 1081–1086.Google Scholar
Schwartz, L., ‘Sur le théorème du graphe fermé’, C. R. Acad. Sci. Paris Sér. A-B 263 (1966), A602–A605.Google Scholar
Sierpiński, W., ‘Sur un problème de M. Lusin’, Giornale di Matematiche di Battaglini (3) 7 (1917), 272–277.Google Scholar
Sierpiński, W., ‘Sur l’équation fonctionnelle f (x + y) = f (x) + f (y)’, Fund. Math. 1 (1920), 116–122.Google Scholar
Solecki, S., ‘Actions of non-compact and non-locally compact Polish groups’, J. Symbolic Logic 65 (2000), 1881–1894.Google Scholar
Solecki, S., ‘Amenability, free subgroups, and Haar null sets in non-locally compact groups’, Proc. Lond. Math. Soc. (3) 93(3) (2006), 693–722.Google Scholar
Steinhaus, H., ‘Sur les distances des points dans les ensembles de mesure positive’, Fund. Math. 1 (1920), 93–104.Google Scholar
Stroock, D. W., ‘On a theorem of Laurent Schwartz’, C. R. Acad. Sci. Paris, Sér. I 349 (2011), 5–6.Google Scholar
Uspenskiĭ, V. V., ‘On subgroups of minimal topological groups’, inTopology and its Applications Volume 155 (Issue 14), (15 August 2008), 1580–1606. Special Issue: Workshop on the Urysohn space.Google Scholar
Weil, A., L’intégration dans les Groupes Topologiques et ses Applications, Deuxième Édition, (Hermann, Paris, 1965).Google Scholar