Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T21:14:23.721Z Has data issue: false hasContentIssue false
  • English
  • Français

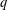EXISTENCE OF $q$-ANALOGS OF STEINER SYSTEMS

Part of: Finite geometry and special incidence structures

Published online by Cambridge University Press:  30 August 2016

MICHAEL BRAUN ,
TUVI ETZION ,
PATRIC R. J. ÖSTERGÅRD ,
ALEXANDER VARDY  and
ALFRED WASSERMANN
MICHAEL BRAUN
Affiliation:
Darmstadt University of Applied Sciences, Darmstadt, Germany; michael.braun@h-da.de
TUVI ETZION
Affiliation:
Technion, Haifa, Israel; etzion@cs.technion.ac.il
PATRIC R. J. ÖSTERGÅRD
Affiliation:
Aalto University, Aalto, Finland; patric.ostergard@aalto.fi
ALEXANDER VARDY
Affiliation:
University of California San Diego, La Jolla, California, USA Nanyang Technological University, Singapore; avardy@ucsd.edu
ALFRED WASSERMANN
Affiliation:
University of Bayreuth, Bayreuth, Germany; Alfred.Wassermann@uni-bayreuth.de

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

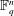Let $\mathbb{F}_{q}^{n}$ be a vector space of dimension $n$ over the finite field 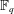$\mathbb{F}_{q}$. A 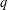$q$-analog of a Steiner system (also known as a 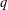$q$-Steiner system), denoted 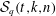${\mathcal{S}}_{q}(t,\!k,\!n)$, is a set 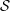${\mathcal{S}}$ of 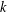$k$-dimensional subspaces of 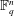$\mathbb{F}_{q}^{n}$ such that each $t$-dimensional subspace of 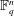$\mathbb{F}_{q}^{n}$ is contained in exactly one element of 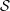${\mathcal{S}}$. Presently, 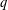$q$-Steiner systems are known only for 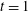$t\,=\,1\!$, and in the trivial cases $t\,=\,k$ and 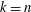$k\,=\,n$. In this paper, the first nontrivial 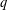$q$-Steiner systems with $t\,\geqslant \,2$ are constructed. Specifically, several nonisomorphic 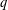$q$-Steiner systems 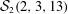${\mathcal{S}}_{2}(2,3,13)$ are found by requiring that their automorphism groups contain the normalizer of a Singer subgroup of 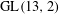$\text{GL}(13,2)$. This approach leads to an instance of the exact cover problem, which turns out to have many solutions.

MSC classification

Primary: 51E10: Steiner systems
Type
Research Article
Information
Forum of Mathematics, Pi , Volume 4 , 2016 , e7
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2016

References

Abel, R. J. R. and Buratti, M., ‘Difference families’, inHandbook of Combinatorial Designs, 2nd edn, (eds. Colbourn, C. J. and Dinitz, J. H.) (Chapman & Hall/CRC, Boca Raton, 2007), 392–410.Google Scholar
Abel, R. J. R. and Greig, M., ‘BIBDs with small block size’, inHandbook of Combinatorial Designs, 2nd edn, (eds. Colbourn, C. J. and Dinitz, J. H.) (Chapman & Hall/CRC, Boca Raton, 2007), 72–79.Google Scholar
Ahlswede, R., Aydinian, H. K. and Khachatrian, L. H., ‘On perfect codes and related concepts’, Des. Codes Cryptogr. 22 (2001), 221–237.CrossRefGoogle Scholar
Baer, R., Linear Algebra and Projective Geometry (Academic Press, New York, 1952).Google Scholar
Beth, T., Jungnickel, D. and Lenz, H., Design Theory, 2nd edn, Vol. I. (Cambridge University Press, Cambridge, 1999).Google Scholar
Beutelspacher, A., ‘Parallelismen in unendlichen projektiven Raumen endlicher Dimension’, Geom. Dedicata 7 (1978), 499–506.CrossRefGoogle Scholar
Braun, M., Kerber, A. and Laue, R., ‘Systematic construction of q-analogs of designs’, Des. Codes Cryptogr. 34 (2005), 55–70.CrossRefGoogle Scholar
Cameron, P., ‘Generalisation of Fisher’s inequality to fields with more than one element’, inCombinatorics, (eds. McDonough, T. P. and Mavron, V. C.) London Math. Soc. Lecture Note, 13 (Cambridge University Press, Cambridge, 1974), 9–13.CrossRefGoogle Scholar
Cameron, P., ‘Locally symmetric designs’, Geom. Dedicata 3 (1974), 65–76.CrossRefGoogle Scholar
Cayley, A., ‘On the triadic arrangements of seven and fifteen things’, Philos. Mag. 37 (1850), 50–53.Google Scholar
Cohn, H., ‘Projective geometry over F1 and the Gaussian binomial coefficients’, Amer. Math. Monthly 111 (2004), 487–495.Google Scholar
Colbourn, C. J. and Dinitz, J. H. (Eds.), Handbook of Combinatorial Designs, 2nd edn, (Chapman & Hall/CRC, Boca Raton, 2007).Google Scholar
Cossidente, A. and de Resmini, M. J., ‘Remarks on Singer cyclic groups and their normalizers’, Des. Codes Cryptogr. 32 (2004), 97–102.CrossRefGoogle Scholar
Delsarte, P., ‘Association schemes and t-designs in regular semilattices’, J. Combin. Theory Ser. A 20 (1976), 230–243.CrossRefGoogle Scholar
Dye, R. H., ‘Maximal subgroups of symplectic groups stabilizing spreads II’, J. Lond. Math. Soc. 40(2) (1989), 215–226.CrossRefGoogle Scholar
Etzion, T., ‘Covering of subspaces by subspaces’, Des. Codes Cryptogr. 72 (2014), 405–421.CrossRefGoogle Scholar
Etzion, T. and Vardy, A., ‘Error-correcting codes in projective space’, IEEE Trans. Inform. Theory 57 (2011), 1165–1173.CrossRefGoogle Scholar
Etzion, T. and Vardy, A., ‘On q-analogs for Steiner systems and covering designs’, Adv. Math. Commun. 5 (2011), 161–176.Google Scholar
Euler, L., ‘Consideratio quarumdam serierum quae singularibus proprietatibus sunt praeditae’, Novi Comment. Acad. Sci. Petropolitanae 3(1750–1751) 10–12. 86–108; Opera Omnia, Ser. I, vol. 14, B. G. Teubner, Leipzig, 1925, pp. 516–541.Google Scholar
Fazeli, A., Lovett, S. and Vardy, A., ‘Nontrivial t-designs over finite fields exist for all t ’, J. Combin. Theory Ser. A 127 (2014), 149–160.CrossRefGoogle Scholar
Goldman, J. R. and Rota, G.-C., ‘On the foundations of combinatorial theory IV: finite vector spaces and Eulerian generating functions’, Stud. Appl. Math. 49 (1970), 239–258.CrossRefGoogle Scholar
Greig, M., ‘Some balanced incomplete block design constructions’, Congr. Numer. 77 (1990), 121–134.Google Scholar
Hanani, H., ‘A class of three-designs’, J. Combin. Theory Ser. A 26 (1979), 1–19.CrossRefGoogle Scholar
Ho, T., Médard, M., Koetter, R., Karger, D., Effros, M., Shi, J. and Leong, B., ‘A random linear network coding approach to multicast’, IEEE Trans. Inform. Theory 52 (2006), 4413–4430.CrossRefGoogle Scholar
Huppert, B., Endliche Gruppen I (Springer, Berlin, 1967).CrossRefGoogle Scholar
Kantor, W. M., ‘Linear groups containing a Singer cycle’, J. Algebra 62 (1980), 232–234.CrossRefGoogle Scholar
Kaski, P. and Östergård, P. R. J., Classification Algorithms for Codes and Designs (Springer, Berlin, 2006).Google Scholar
Kaski, P. and Pottonen, O., ‘Libexact user guide, Version 1.0’, HIIT Technical Reports 2008-1, Helsinki Institute for Information Technology, 2008.Google Scholar
Keevash, P., ‘The existence of designs’, Preprint 2014, arXiv:1401.3665.Google Scholar
Kiermaier, M. and Laue, R., ‘Derived and residual subspace designs’, Adv. Math. Commun. 9 (2015), 105–115.CrossRefGoogle Scholar
Kirkman, T. P., ‘On a problem in combinations’, Cambridge Dublin Math. J. II (1847), 191–204.Google Scholar
Knuth, D. E., ‘Dancing links’, inMillennial Perspectives in Computer Science (eds. Davies, J., Roscoe, B. and Woodcock, J.) (Palgrave Macmillan, Basingstoke, 2000), 187–214.Google Scholar
Koelink, E. and van Assche, W., ‘Leonhard Euler and a q-analogue of the logarithm’, Proc. Amer. Math. Soc. 137 (2009), 1663–1676.CrossRefGoogle Scholar
Koetter, R. and Kschischang, F. R., ‘Coding for errors and erasures in random network coding’, IEEE Trans. Inform. Theory 54 (2008), 3579–3591.CrossRefGoogle Scholar
Kohnert, A. and Kurz, S., ‘Construction of large constant dimension codes with a prescribed minimum distance’, inMathematical Methods in Computer Science, (eds. Calmet, J., Geiselmann, W. and Müller-Quade, J.) Lecture Notes in Computer Science, 5393 (Springer, Berlin, 2008), 31–42.CrossRefGoogle Scholar
Kramer, E. and Mesner, D., ‘ t-designs on hypergraphs’, Discrete Math. 15 (1976), 263–296.CrossRefGoogle Scholar
Laue, R., ‘Eine konstruktive Version des Lemmas von Burnside’, Bayreuther Math. Schr. 28 (1989), 111–125.Google Scholar
van Lint, J. H. and Wilson, R. M., A Course in Combinatorics, 2nd edn (Cambridge University Press, Cambridge, 2001).CrossRefGoogle Scholar
Metsch, K., ‘Bose-Burton type theorems for finite projective, affine and polar spaces’, inSurveys in Combinatorics (eds. Lamb, J. D. and Preece, D. A.) London Math. Soc. Lecture Note, 267 (Cambridge University Press, Cambridge, 1999), 137–166.Google Scholar
Miyakawa, M., Munemasa, A. and Yoshiara, S., ‘On a class of small 2-designs over GF(q)’, J. Combin. Des. 3 (1995), 61–77.CrossRefGoogle Scholar
Plücker, J., System der analytischen Geometrie: auf neue Betrachtungsweisen gegründet, und insbesondere eine ausführliche Theorie der Curven dritter Ordnung enthaltend, (Duncker und Humblot, Berlin, 1835).Google Scholar
Ray-Chaudhuri, D. K. and Singhi, N. M., ‘ q-analogues of t-designs and their existence’, Linear Algebra Appl. 114/115 (1989), 57–68.CrossRefGoogle Scholar
Schmalz, B., ‘The t-designs with prescribed automorphism group, new simple 6-designs’, J. Combin. Des. 1 (1993), 125–170.CrossRefGoogle Scholar
Schwartz, M. and Etzion, T., ‘Codes and anticodes in the Grassmann graph’, J. Combin. Theory Ser. A 97 (2002), 27–42.CrossRefGoogle Scholar
Steiner, J., ‘Combinatorische Aufgabe’, J. reine angew. Math. 45 (1853), 181–182.Google Scholar
Suzuki, H., ‘2-designs over GF(2 m )’, Graphs Combin. 6 (1990), 293–296.CrossRefGoogle Scholar
Suzuki, H., ‘2-designs over GF(q)’, Graphs Combin. 8 (1992), 381–389.CrossRefGoogle Scholar
Teirlinck, L., ‘Non-trivial t-designs without repeated blocks exist for all t ’, Discrete Math. 65 (1987), 301–311.CrossRefGoogle Scholar
Thomas, S., ‘Designs over finite fields’, Geom. Dedicata 21 (1987), 237–242.Google Scholar
Thomas, S., ‘Designs and partial geometries over finite fields’, Geom. Dedicata 63 (1996), 247–253.CrossRefGoogle Scholar
Tits, J., ‘Sur les analogues algébriques des groupes semi-simples complexes’, inColloque d’Algébre Supèrieure, tenu á Bruxelles du 19 au 22 décembre 1956, Centre Belge de Recherches Mathématiques Établissements Ceuterick (Louvain, Paris, Librairie Gauthier-Villars, 1957), 261–289.Google Scholar
Wang, J., ‘Quotient sets and subset-subspace analogy’, Adv. Appl. Math. 23 (1999), 333–339.CrossRefGoogle Scholar
Wilson, R. M., ‘Cyclotomy and difference families in elementary abelian groups’, J. Number Theory 4 (1972), 17–47.CrossRefGoogle Scholar
Yeung, R. W., Information Theory and Network Coding (Springer, Berlin, 2008).Google Scholar
Supplementary material: File

Braun supplementary material

Braun supplementary material

Download Braun supplementary material(File)
File 43.3 KB