Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T14:06:17.831Z Has data issue: false hasContentIssue false
  • English
  • Français

GLOBAL NEARLY-PLANE-SYMMETRIC SOLUTIONS TO THE MEMBRANE EQUATION

Part of: Representations of solutions Hyperbolic equations and systems Partial differential equations Classical differential geometry

Published online by Cambridge University Press:  05 August 2020

LEONARDO ABBRESCIA  and
WILLIE WAI YEUNG WONG Open the ORCID record for WILLIE WAI YEUNG WONG [Opens in a new window]
LEONARDO ABBRESCIA
Affiliation:
Department of Mathematics, Michigan State University, East Lansing, Michigan, USA; leonardo@math.msu.edu
WILLIE WAI YEUNG WONG
Affiliation:
Department of Mathematics, Michigan State University, East Lansing, Michigan, USA; wongwwy@math.msu.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that any simple planar travelling wave solution to the membrane equation in spatial dimension 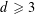$d\geqslant 3$ with bounded spatial extent is globally nonlinearly stable under sufficiently small compactly supported perturbations, where the smallness depends on the size of the support of the perturbation as well as on the initial travelling wave profile. The main novelty of the argument is the lack of higher order peeling in our vector-field-based method. In particular, the higher order energies (in fact, all energies at order $2$ or higher) are allowed to grow polynomially (but in a controlled way) in time. This is in contrast with classical global stability arguments, where only the ‘top’ order energies used in the bootstrap argument exhibit growth, and reflects the fact that the background travelling wave solution has ‘infinite energy’ and the coefficients of the perturbation equation are not asymptotically Lorentz invariant. Nonetheless, we can prove that the perturbation converges to zero in 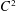$C^{2}$ by carefully analysing the nonlinear interactions and exposing a certain ‘vestigial’ null structure in the equations.

MSC classification

Primary: 35L72: Quasilinear second-order hyperbolic equations 35B35: Stability
Secondary: 35C07: Traveling wave solutions 53A10: Minimal surfaces, surfaces with prescribed mean curvature
Type
Differential Geometry and Geometric Analysis
Information
Forum of Mathematics, Pi , Volume 8 , 2020 , e13
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution-NonCommercial-ShareAlike licence (http://creativecommons.org/licenses/by-nc-sa/4.0/), which permits noncommercial re-use, distribution, and reproduction in any medium, provided the same Creative Commons licence is included and the original work is properly cited. The written permission of Cambridge University Press must be obtained for commercial re-use.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Allen, P., Andersson, L. and Isenberg, J., ‘Timelike minimal submanifolds of general co-dimension in Minkowski space time’, J. Hyperbolic Differ. Equ. 3(4) (2006), 691–700.CrossRefGoogle Scholar
Alinhac, S., ‘The null condition for quasilinear wave equations in two space dimensions. I’, Invent. Math. 145(3) (2001), 597–618.CrossRefGoogle Scholar
Alinhac, S., ‘The null condition for quasilinear wave equations in two space dimensions. II’, Amer. J. Math. 123(6) (2001), 1071–1101.CrossRefGoogle Scholar
Alinhac, S., ‘An example of blowup at infinity for a quasilinear wave equation’, Astérisque (284) (2003), 1–91. Autour de l’analyse microlocale.Google Scholar
Aurilia, A. and Christodoulou, D., ‘Theory of strings and membranes in an external field. I. General formulation’, J. Math. Phys. 20(7) (1979), 1446–1452.CrossRefGoogle Scholar
Brendle, S., ‘Hypersurfaces in Minkowski space with vanishing mean curvature’, Comm. Pure Appl. Math. 55(10) (2002), 1249–1279.CrossRefGoogle Scholar
Choquet-Bruhat, Y., ‘Maximal submanifolds and submanifolds with constant mean extrinsic curvature of a Lorentzian manifold’, Ann. Sc. Norm. Sup. Pisa Cl. Sci. (4) 3(3) (1976), 361–376.Google Scholar
Christodoulou, D., The Formation of Shocks in 3-dimensional Fluids, EMS Monographs in Mathematics (European Mathematical Society (EMS), Zürich, 2007).CrossRefGoogle Scholar
Deng, Y. and Pusateri, F., ‘On the global behavior of weak null quasilinear wave equations’, Comm. Pure Appl. Math. 73 (2020), 1035–1099.CrossRefGoogle Scholar
Donninger, R., Krieger, J., Szeftel, J. and Wong, W. W.-Y., ‘Codimension one stability of the catenoid under the vanishing mean curvature flow in Minkowski space’, Duke Math. J. 165 (2016), 723–791.CrossRefGoogle Scholar
Holzegel, G., Klainerman, S., Speck, J. R. and Wong, W. W.-Y., ‘Shock formation in small-data solutions to 3D quasilinear wave equations: an overview’, J. Hyperbolic Differ. Equ. 13(1) (2016), 1–105.CrossRefGoogle Scholar
Hoppe, J., ‘Relativistic membranes’, J. Phys. A 46(2) (2013), 023001, 30.Google Scholar
Jerrard, R., ‘Defects in semilinear wave equation and timelike minimal surfaces in Minkowski space’, Anal. PDE 4 (2011), 285–340.Google Scholar
Jerrard, R., Novaga, M. and Orlandi, G., ‘On the regularity of timelike extremal surfaces’, Commun. Contemp. Math. 17(1) (2015), 1450048.CrossRefGoogle Scholar
John, F., ‘Formation of singularities in one-dimensional nonlinear wave propagation’, Comm. Pure Appl. Math. 27 (1974), 377–405.CrossRefGoogle Scholar
Kibble, T., ‘Topology of cosmic domains and strings’, J. Phys. A 9 (1976), 1387–1398.CrossRefGoogle Scholar
Klainerman, S., ‘Global existence for nonlinear wave equations’, Comm. Pure Appl. Math. 33(1) (1980), 43–101.CrossRefGoogle Scholar
Klainerman, S., ‘Long-time behavior of solutions to nonlinear evolution equations’, Arch. Ration. Mech. Anal. 78(1) (1982), 73–98.CrossRefGoogle Scholar
Klainerman, S., ‘Long time behaviour of solutions to nonlinear wave equations’, inProceedings of the International Congress of Mathematicians, Vols 1, 2 (Warsaw, 1983) (PWN, Warsaw, 1984), 1209–1215.Google Scholar
Klainerman, S., ‘Global existence of small amplitude solutions to nonlinear Klein-Gordon equations in four space-time dimensions’, Comm. Pure Appl. Math. 38(5) (1985), 631–641.CrossRefGoogle Scholar
Lax, P. D., ‘Development of singularities of solutions of nonlinear hyperbolic partial differential equations’, J. Math. Phys. 5 (1964), 611–613.CrossRefGoogle Scholar
Lax, P. D., ‘Hyperbolic systems of conservation laws and the mathematical theory of shock waves’, inSociety for Industrial and Applied Mathematics, Philadelphia, PA, Conference Board of the Mathematical Sciences Regional Conference Series in Applied Mathematics, 11 (Society for Industrial and Applied Mathematics, Philadelphia, PA, 1973).Google Scholar
LeFloch, P. G. and Ma, Y., The Hyperboloidal Foliation Method, Series in Applied and Computational Mathematics, 2 (World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ, 2014).Google Scholar
Lindblad, H., ‘A remark on global existence for small initial data of the minimal surface equation in Minkowskian space time’, Proc. Amer. Math. Soc. 132(4) (2004), 1095–1102 (electronic).CrossRefGoogle Scholar
Lindblad, H., ‘Global solutions of quasilinear wave equations’, Amer. J. Math. 130(1) (2008), 115–157.CrossRefGoogle Scholar
Lindblad, H. and Rodnianski, I., ‘Global existence for the Einstein vacuum equations in wave coordinates’, Comm. Math. Phys. 256(1) (2005), 43–110.CrossRefGoogle Scholar
Liu, J. and Zhou, Y., ‘Uniqueness and stability of traveling waves to the time-like extremal hypersurface in Minkowski space’. Preprint, 2019, arXiv:1903.04129.Google Scholar
Luk, J. and Speck, J., ‘Shock formation in solutions to the 2D compressible Euler equations in the presence of non-zero vorticity’, Invent. Math. 214(1) (2018), 1–169.CrossRefGoogle Scholar
Milbredt, O., ‘The Cauchy problem for membranes’, PhD Thesis, Freien Universität Berlin, 2008.Google Scholar
Neu, J. C., ‘Kinks and the minimal surface equation in Minkowski space’, Physica D 43 (1990), 421–434.Google Scholar
Nguyen, L. and Tian, G., ‘On smoothness of timelike maximal cylinders in three-dimensional vacuum spacetimes’, Classical Quantum Gravity 30(16)165010 (2013).CrossRefGoogle Scholar
Shatah, J., ‘Space-time resonances’, Quart. Appl. Math. 68(1) (2010), 161–167.CrossRefGoogle Scholar
Sherman, J. and Morrison, W. J., ‘Adjustment of an inverse matrix corresponding to a change in one element of a given matrix’, Ann. Math. Stat. 21 (1950), 124–127.CrossRefGoogle Scholar
Sideris, T. C., ‘Global existence of harmonic maps in Minkowski space’, Comm. Pure Appl. Math. 42(1) (1989), 1–13.CrossRefGoogle Scholar
Speck, J., Shock Formation in Small-data Solutions to 3D Quasilinear Wave Equations, Mathematical Surveys and Monographs, 214 (American Mathematical Society, Providence, RI, 2016).CrossRefGoogle Scholar
Speck, J., Holzegel, G., Luk, J. and Wong, W. W.-Y., ‘Stable shock formation for nearly simple outgoing plane symmetric waves’, Ann. PDE 2 (2016), 10.CrossRefGoogle Scholar
Vilenkin, A. and Shellard, E. P. S., Cosmic Strings and Other Topological Defects, (Cambridge University Press, Cambridge, UK, 1994).Google Scholar
Wang, J. and Wei, C., ‘Global existence of smooth solution to relativistic membrane equation with large data’. Preprint, 2017, arXiv:1708.03839.Google Scholar
Wong, W. W.-Y., ‘Global existence for the minimal surface equation on ℝ1, 1’, Proc. Amer. Math. Soc., Ser. B 4 (2017), 47–52.CrossRefGoogle Scholar
Wong, W. W. Y., (2017), ‘Small data global existence and decay for two dimensional wave maps’. Preprint, 2017, arXiv:1712.07684 (Under review).Google Scholar
Wong, W. W. Y., ‘Singularities of axially symmetric time-like minimal submanifolds in Minkowski space’, J. Hyperbolic Differ. Equ. 15(1) (2018), 1–13.CrossRefGoogle Scholar