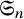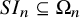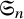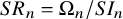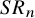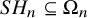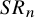1 Introduction
Let
![]() ${\mathbf {x}}_n = (x_1, \dots , x_n)$
be a list of n variables and let
${\mathbf {x}}_n = (x_1, \dots , x_n)$
be a list of n variables and let
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
be the polynomial ring in these variables over
${\mathbb {C}}[{\mathbf {x}}_n]$
be the polynomial ring in these variables over
![]() ${\mathbb {C}}$
. The symmetric group
${\mathbb {C}}$
. The symmetric group
![]() ${\mathfrak {S}}_n$
acts on
${\mathfrak {S}}_n$
acts on
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
by subscript permutation; the fixed subspace
${\mathbb {C}}[{\mathbf {x}}_n]$
by subscript permutation; the fixed subspace
![]() ${\mathbb {C}}[{\mathbf {x}}_n]^{{\mathfrak {S}}_n}$
is the algebra of symmetric polynomials. The coinvariant ideal
${\mathbb {C}}[{\mathbf {x}}_n]^{{\mathfrak {S}}_n}$
is the algebra of symmetric polynomials. The coinvariant ideal
![]() $I_n \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
is the ideal
$I_n \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
is the ideal
![]() $I_n := ( {\mathbb {C}}[{\mathbf {x}}_n]^{{\mathfrak {S}}_n}_+ )$
generated by the space
$I_n := ( {\mathbb {C}}[{\mathbf {x}}_n]^{{\mathfrak {S}}_n}_+ )$
generated by the space
![]() ${\mathbb {C}}[{\mathbf {x}}_n]^{{\mathfrak {S}}_n}_+$
of symmetric polynomials with vanishing constant term, and the coinvariant ring
${\mathbb {C}}[{\mathbf {x}}_n]^{{\mathfrak {S}}_n}_+$
of symmetric polynomials with vanishing constant term, and the coinvariant ring
![]() $R_n := {\mathbb {C}}[{\mathbf {x}}_n] / I_n$
is the quotient of
$R_n := {\mathbb {C}}[{\mathbf {x}}_n] / I_n$
is the quotient of
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
by
${\mathbb {C}}[{\mathbf {x}}_n]$
by
![]() $I_n$
.
$I_n$
.
The graded
![]() ${\mathfrak {S}}_n$
-module
${\mathfrak {S}}_n$
-module
![]() $R_n$
is among the most important objects in algebraic combinatorics. E. Artin proved [Reference Artin4] that the ‘sub-staircase monomials’
$R_n$
is among the most important objects in algebraic combinatorics. E. Artin proved [Reference Artin4] that the ‘sub-staircase monomials’
![]() $\{ x_1^{a_1} \cdots x_n^{a_n} \,:\, a_i < i \}$
descend to a basis of
$\{ x_1^{a_1} \cdots x_n^{a_n} \,:\, a_i < i \}$
descend to a basis of
![]() $R_n$
, so that
$R_n$
, so that
![]() $R_n$
has Hilbert series
$R_n$
has Hilbert series
where we use the standard q-number and q-factorial notation
Chevalley showed [Reference Chevalley10] that
![]() $R_n \cong {\mathbb {C}}[{\mathfrak {S}}_n]$
carries the regular representation of
$R_n \cong {\mathbb {C}}[{\mathfrak {S}}_n]$
carries the regular representation of
![]() ${\mathfrak {S}}_n$
as an ungraded
${\mathfrak {S}}_n$
as an ungraded
![]() ${\mathfrak {S}}_n$
-module, and Borel showed [Reference Borel8] that
${\mathfrak {S}}_n$
-module, and Borel showed [Reference Borel8] that
![]() $R_n = H^{\bullet }(\mathrm {Fl}(n))$
presents the cohomology of the type A complete flag variety.
$R_n = H^{\bullet }(\mathrm {Fl}(n))$
presents the cohomology of the type A complete flag variety.
Now let
![]() ${\mathbf {x}}_n = (x_1, \dots , x_n)$
and
${\mathbf {x}}_n = (x_1, \dots , x_n)$
and
![]() ${\mathbf {y}}_n = (y_1, \dots , y_n)$
be two sets of n commuting variables and consider the polynomial ring
${\mathbf {y}}_n = (y_1, \dots , y_n)$
be two sets of n commuting variables and consider the polynomial ring
![]() ${\mathbb {C}}[{\mathbf {x}}_n, {\mathbf {y}}_n]$
over these variables with the diagonal action of
${\mathbb {C}}[{\mathbf {x}}_n, {\mathbf {y}}_n]$
over these variables with the diagonal action of
![]() ${\mathfrak {S}}_n$
, viz.
${\mathfrak {S}}_n$
, viz.
Let
![]() $DI_n \subseteq {\mathbb {C}}[{\mathbf {x}}_n, {\mathbf {y}}_n]$
be the ideal generated by the
$DI_n \subseteq {\mathbb {C}}[{\mathbf {x}}_n, {\mathbf {y}}_n]$
be the ideal generated by the
![]() ${\mathfrak {S}}_n$
-invariants with vanishing constant term. Garsia and Haiman [Reference Garsia and Haiman12, Reference Haiman17] initiated the study of the diagonal coinvariant ring
${\mathfrak {S}}_n$
-invariants with vanishing constant term. Garsia and Haiman [Reference Garsia and Haiman12, Reference Haiman17] initiated the study of the diagonal coinvariant ring
The quotient
![]() $DR_n$
is a doubly-graded
$DR_n$
is a doubly-graded
![]() ${\mathfrak {S}}_n$
-module. Haiman used the algebraic geometry of Hilbert schemes to prove [Reference Haiman18] that
${\mathfrak {S}}_n$
-module. Haiman used the algebraic geometry of Hilbert schemes to prove [Reference Haiman18] that
![]() $\dim DR_n = (n+1)^{n-1}$
and that, as an ungraded
$\dim DR_n = (n+1)^{n-1}$
and that, as an ungraded
![]() ${\mathfrak {S}}_n$
-module, the space
${\mathfrak {S}}_n$
-module, the space
![]() $DR_n$
carries the sign-twisted permutation action of
$DR_n$
carries the sign-twisted permutation action of
![]() ${\mathfrak {S}}_n$
on size n parking functions. Carlsson and Oblomkov used the Lusztig-Smelt paving of affine Springer fibers to give [Reference Carlsson and Oblomkov9] a monomial basis of
${\mathfrak {S}}_n$
on size n parking functions. Carlsson and Oblomkov used the Lusztig-Smelt paving of affine Springer fibers to give [Reference Carlsson and Oblomkov9] a monomial basis of
![]() $DR_n$
, which restricts to Artin’s basis of
$DR_n$
, which restricts to Artin’s basis of
![]() $R_n$
when the y-variables are set to zero.
$R_n$
when the y-variables are set to zero.
Next, let
![]() ${\mathbf {x}}_n = (x_1, \dots , x_n)$
be a list of n commuting variables and let
${\mathbf {x}}_n = (x_1, \dots , x_n)$
be a list of n commuting variables and let
![]() $\mathbf {\theta }_n = (\theta _1, \dots , \theta _n)$
be a list of n anticommuting variables. The superspace ring of rank n is the tensor product
$\mathbf {\theta }_n = (\theta _1, \dots , \theta _n)$
be a list of n anticommuting variables. The superspace ring of rank n is the tensor product
of the polynomial ring in the x-variables and the exterior algebra over the
![]() $\theta $
-variables. This ring arises in physics, where the x-variables correspond to the states of bosons and the
$\theta $
-variables. This ring arises in physics, where the x-variables correspond to the states of bosons and the
![]() $\theta $
-variables correspond to the states of fermions; see, for example, [Reference Peskin and Schroeder28]. Accordingly, we shall refer to x-degree as bosonic degree and
$\theta $
-variables correspond to the states of fermions; see, for example, [Reference Peskin and Schroeder28]. Accordingly, we shall refer to x-degree as bosonic degree and
![]() $\theta $
-degree as fermionic degree. The ring
$\theta $
-degree as fermionic degree. The ring
![]() $\Omega _n$
also arises in differential geometry as the ring of polynomial-valued holomorphic differential forms on complex n-space (and we would write
$\Omega _n$
also arises in differential geometry as the ring of polynomial-valued holomorphic differential forms on complex n-space (and we would write
![]() $dx_i$
instead of
$dx_i$
instead of
![]() $\theta _i$
); this explains our use of
$\theta _i$
); this explains our use of
![]() $\Omega $
.
$\Omega $
.
The symmetric group
![]() ${\mathfrak {S}}_n$
acts diagonally on superspace by the rule
${\mathfrak {S}}_n$
acts diagonally on superspace by the rule
Once again, we denote by
![]() $(\Omega _n)^{{\mathfrak {S}}_n}_+$
the subalgebra of invariant polynomials with vanishing constant term and consider the quotient ring
$(\Omega _n)^{{\mathfrak {S}}_n}_+$
the subalgebra of invariant polynomials with vanishing constant term and consider the quotient ring
where the supercoinvariant ideal
![]() $SI_n \subseteq \Omega _n$
is given by
$SI_n \subseteq \Omega _n$
is given by
Like
![]() $DR_n$
, the quotient
$DR_n$
, the quotient
![]() $SR_n$
is a bigraded
$SR_n$
is a bigraded
![]() ${\mathfrak {S}}_n$
-module, this time with respect to bosonic and fermionic degree.
${\mathfrak {S}}_n$
-module, this time with respect to bosonic and fermionic degree.
The study of
![]() $SR_n$
was initiated by the Fields Institute Combinatorics GroupFootnote
1
in roughly 2018. This group conjectured that
$SR_n$
was initiated by the Fields Institute Combinatorics GroupFootnote
1
in roughly 2018. This group conjectured that
![]() $\dim SR_n$
is the ordered Bell number counting ordered set partitions of
$\dim SR_n$
is the ordered Bell number counting ordered set partitions of
![]() $[n] := \{1, \dots , n \}$
and that, as an ungraded
$[n] := \{1, \dots , n \}$
and that, as an ungraded
![]() ${\mathfrak {S}}_n$
-module, the quotient
${\mathfrak {S}}_n$
-module, the quotient
![]() $SR_n$
carries the permutation action of
$SR_n$
carries the permutation action of
![]() ${\mathfrak {S}}_n$
on these ordered set partitions, up to sign twist. Furthermore, this group conjectured that the doubly-graded
${\mathfrak {S}}_n$
on these ordered set partitions, up to sign twist. Furthermore, this group conjectured that the doubly-graded
![]() ${\mathfrak {S}}_n$
-structure of
${\mathfrak {S}}_n$
-structure of
![]() $SR_n$
was given by
$SR_n$
was given by
 $$ \begin{align} {\mathrm {grFrob}}(SR_n; q, z) = \sum_{k = 1}^n z^{n-k} \cdot \Delta^{\prime}_{e_{k-1}} e_n \mid_{t \rightarrow 0}, \end{align} $$
$$ \begin{align} {\mathrm {grFrob}}(SR_n; q, z) = \sum_{k = 1}^n z^{n-k} \cdot \Delta^{\prime}_{e_{k-1}} e_n \mid_{t \rightarrow 0}, \end{align} $$
where q tracks bosonic degree, z tracks fermionic degree,
![]() $e_n$
is the elementary symmetric function of degree n, and
$e_n$
is the elementary symmetric function of degree n, and
![]() $\Delta ^{\prime }_{e_{k-1}}$
is a primed delta operator acting on the ring
$\Delta ^{\prime }_{e_{k-1}}$
is a primed delta operator acting on the ring
![]() $\Lambda $
of symmetric functions; see [Reference Haglund, Remmel and Wilson14, Reference Zabrocki40] for more details. The identity (1.9) implies that the bigraded Hilbert series of
$\Lambda $
of symmetric functions; see [Reference Haglund, Remmel and Wilson14, Reference Zabrocki40] for more details. The identity (1.9) implies that the bigraded Hilbert series of
![]() $SR_n$
is given by
$SR_n$
is given by
 $$ \begin{align} {\mathrm {Hilb}}(SR_n; q, z) = \sum_{k = 1}^n z^{n-k} \cdot [k]!_q \cdot {\mathrm {Stir}}_q(n,k), \end{align} $$
$$ \begin{align} {\mathrm {Hilb}}(SR_n; q, z) = \sum_{k = 1}^n z^{n-k} \cdot [k]!_q \cdot {\mathrm {Stir}}_q(n,k), \end{align} $$
where the q-Stirling number
![]() ${\mathrm {Stir}}_q(n,k)$
is defined by the recursion
${\mathrm {Stir}}_q(n,k)$
is defined by the recursion
together with the initial condition
 $$ \begin{align} {\mathrm {Stir}}_q(0,k) = \begin{cases} 1 & k = 0 \\ 0 & \text{otherwise}. \end{cases} \end{align} $$
$$ \begin{align} {\mathrm {Stir}}_q(0,k) = \begin{cases} 1 & k = 0 \\ 0 & \text{otherwise}. \end{cases} \end{align} $$
Equation (1.10) was conjectured explicitly by Sagan and Swanson [Reference Sagan and Swanson33, Conj. 6.5].
The conjectures (1.9) and (1.10) were publicized at a BIRS meeting in January 2019. This resulted in great excitement. Haglund, Rhoades and Shimozono [Reference Haglund, Rhoades and Shimozono15] had introduced the quotient ring
and had proven [Reference Haglund, Rhoades and Shimozono16] that
Pawlowski and Rhoades [Reference Pawlowski and Rhoades27] introduced the moduli space
![]() $X_{n,k}$
of n-tuples of lines
$X_{n,k}$
of n-tuples of lines
![]() $(\ell _1, \dots , \ell _n)$
in
$(\ell _1, \dots , \ell _n)$
in
![]() ${\mathbb {C}}^k$
such that
${\mathbb {C}}^k$
such that
![]() $\ell _1 + \cdots + \ell _k = {\mathbb {C}}^k$
and proved the cohomology presentation
$\ell _1 + \cdots + \ell _k = {\mathbb {C}}^k$
and proved the cohomology presentation
The authors [Reference Rhoades and Wilson30] introduced the superspace Vandermonde
and showed that the subspace
![]() $V_{n,k} \subseteq \Omega _n$
obtained by starting with
$V_{n,k} \subseteq \Omega _n$
obtained by starting with
![]() $\delta _{n,k}$
and closing under the partial derivative operators
$\delta _{n,k}$
and closing under the partial derivative operators
![]() $\frac {\partial }{\partial x_i}$
and linearity carries a graded
$\frac {\partial }{\partial x_i}$
and linearity carries a graded
![]() ${\mathfrak {S}}_n$
-action with graded character
${\mathfrak {S}}_n$
-action with graded character
![]() $\Delta ^{\prime }_{e_{k-1}} e_n \mid _{t = 0}$
. Of all of these models, the supercoinvariant ring
$\Delta ^{\prime }_{e_{k-1}} e_n \mid _{t = 0}$
. Of all of these models, the supercoinvariant ring
![]() $SR_n$
has the most intrinsic invariant-theoretic definition which extends to arbitrary complex reflection groups
$SR_n$
has the most intrinsic invariant-theoretic definition which extends to arbitrary complex reflection groups
![]() $G \subseteq GL_n({\mathbb {C}})$
in the most obvious way.
$G \subseteq GL_n({\mathbb {C}})$
in the most obvious way.
Zabrocki extended the conjecture (1.9) in a different direction by introducing another set of commuting variables
![]() ${\mathbf {y}}_n = (y_1, \dots , y_n)$
and considering the triply-graded
${\mathbf {y}}_n = (y_1, \dots , y_n)$
and considering the triply-graded
![]() ${\mathfrak {S}}_n$
-module obtained by quotienting
${\mathfrak {S}}_n$
-module obtained by quotienting
![]() ${\mathbb {C}}[{\mathbf {x}}_n, {\mathbf {y}}_n] \otimes \wedge \{ \mathbf {\theta }_n \}$
by the ideal I generated by
${\mathbb {C}}[{\mathbf {x}}_n, {\mathbf {y}}_n] \otimes \wedge \{ \mathbf {\theta }_n \}$
by the ideal I generated by
![]() ${\mathfrak {S}}_n$
-invariants with vanishing constant term. Zabrocki conjectured [Reference Zabrocki40] that
${\mathfrak {S}}_n$
-invariants with vanishing constant term. Zabrocki conjectured [Reference Zabrocki40] that
 $$ \begin{align} {\mathrm {grFrob}} \left( {\mathbb {C}}[{\mathbf {x}}_n, {\mathbf {y}}_n] \otimes \wedge \{ \mathbf{\theta}_n \} / I; q, t, z \right) = \sum_{k = 1}^n z^{n-k} \cdot \Delta^{\prime}_{e_{k-1}} e_n, \end{align} $$
$$ \begin{align} {\mathrm {grFrob}} \left( {\mathbb {C}}[{\mathbf {x}}_n, {\mathbf {y}}_n] \otimes \wedge \{ \mathbf{\theta}_n \} / I; q, t, z \right) = \sum_{k = 1}^n z^{n-k} \cdot \Delta^{\prime}_{e_{k-1}} e_n, \end{align} $$
where q tracks x-degree, t tracks y-degree, and z tracks
![]() $\theta $
-degree. Observe that (1.17) reduces to (1.9) if the y-variables are set to zero, and Haiman’s theorem [Reference Haiman18] when the
$\theta $
-degree. Observe that (1.17) reduces to (1.9) if the y-variables are set to zero, and Haiman’s theorem [Reference Haiman18] when the
![]() $\theta $
-variables are set to zero. The conjecture (1.17) was the first predicted algebraic model for
$\theta $
-variables are set to zero. The conjecture (1.17) was the first predicted algebraic model for
![]() $\Delta ^{\prime }_{e_{k-1}} e_n$
; the authors [Reference Rhoades and Wilson30] gave a parallel conjectural model for
$\Delta ^{\prime }_{e_{k-1}} e_n$
; the authors [Reference Rhoades and Wilson30] gave a parallel conjectural model for
![]() $\Delta ^{\prime }_{e_{k-1}} e_n$
involving the superspace Vandermondes
$\Delta ^{\prime }_{e_{k-1}} e_n$
involving the superspace Vandermondes
![]() $\delta _{n,k}$
. The conjecture (1.17) was extended to two sets of bosonic variables and two sets of fermionic variables by D’Adderio, Iraci and Vanden Wyngaerd [Reference D’Adderio, Iraci and Vanden Wyngaerd11] using
$\delta _{n,k}$
. The conjecture (1.17) was extended to two sets of bosonic variables and two sets of fermionic variables by D’Adderio, Iraci and Vanden Wyngaerd [Reference D’Adderio, Iraci and Vanden Wyngaerd11] using
![]() $\Theta $
-operators on symmetric functions; the case of two sets of fermionic variables alone was solved by Iraci-Rhoades-Romero [Reference Iraci, Rhoades and Romero20] and Kim-Rhoades [Reference Kim and Rhoades22]; see [Reference Kim21, Reference Kim and Rhoades23] for a connection between this quotient and skein relations on set partitions. F. Bergeron has a substantial family [Reference Bergeron5, Reference Bergeron6, Reference Bergeron7] of conjectures on coinvariant quotients with multiple sets of bosonic and fermionic variables.
$\Theta $
-operators on symmetric functions; the case of two sets of fermionic variables alone was solved by Iraci-Rhoades-Romero [Reference Iraci, Rhoades and Romero20] and Kim-Rhoades [Reference Kim and Rhoades22]; see [Reference Kim21, Reference Kim and Rhoades23] for a connection between this quotient and skein relations on set partitions. F. Bergeron has a substantial family [Reference Bergeron5, Reference Bergeron6, Reference Bergeron7] of conjectures on coinvariant quotients with multiple sets of bosonic and fermionic variables.
Despite all of this activity, the equations (1.9) and (1.10) on the structure of
![]() $SR_n$
remained frustratingly conjectural. The methods that were used to successfully analyze objects like
$SR_n$
remained frustratingly conjectural. The methods that were used to successfully analyze objects like
![]() $R_{n,k}, X_{n,k}$
and
$R_{n,k}, X_{n,k}$
and
![]() $V_{n,k}$
have not yet been extended to study
$V_{n,k}$
have not yet been extended to study
![]() $SR_n$
. Swanson and Wallach [Reference Swanson and Wallach36, Reference Swanson and Wallach37] proved that the
$SR_n$
. Swanson and Wallach [Reference Swanson and Wallach36, Reference Swanson and Wallach37] proved that the
![]() ${\mathrm {sign}}$
-isotypic component of (1.9) is correct and that the fermionic degree
${\mathrm {sign}}$
-isotypic component of (1.9) is correct and that the fermionic degree
![]() $n-k$
piece of
$n-k$
piece of
![]() $SR_n$
has top bosonic degree
$SR_n$
has top bosonic degree
![]() $(n-k) \cdot (k-1) + {k \choose 2}$
as predicted by (1.10); this was the only significant progress on
$(n-k) \cdot (k-1) + {k \choose 2}$
as predicted by (1.10); this was the only significant progress on
![]() $SR_n$
. In fact, before this paper, even the dimension of
$SR_n$
. In fact, before this paper, even the dimension of
![]() $SR_n$
was unknown.
$SR_n$
was unknown.
In this paper, we will prove that the formula (1.10) calculates the bigraded Hilbert series of
![]() $SR_n$
(Theorem 5.3). We will also prove (Theorem 5.1) an ‘operator conjecture’ of Swanson and Wallach [Reference Swanson and Wallach37], which describes the harmonic space
$SR_n$
(Theorem 5.3). We will also prove (Theorem 5.1) an ‘operator conjecture’ of Swanson and Wallach [Reference Swanson and Wallach37], which describes the harmonic space
![]() $SH_n \subseteq \Omega _n$
attached to the supercoinvariant ring
$SH_n \subseteq \Omega _n$
attached to the supercoinvariant ring
![]() $SR_n$
using certain ‘higher Euler operators’ on
$SR_n$
using certain ‘higher Euler operators’ on
![]() $\Omega _n$
which act by polarization.Footnote
2
The space
$\Omega _n$
which act by polarization.Footnote
2
The space
![]() $SH_n$
is helpful for machine computations because
$SH_n$
is helpful for machine computations because
![]() $SH_n \cong SR_n$
as doubly-graded
$SH_n \cong SR_n$
as doubly-graded
![]() ${\mathfrak {S}}_n$
-modules, and yet members of
${\mathfrak {S}}_n$
-modules, and yet members of
![]() $SH_n$
are honest superspace elements
$SH_n$
are honest superspace elements
![]() $f \in \Omega _n$
rather than cosets
$f \in \Omega _n$
rather than cosets
![]() $f + SI_n \in SR_n$
. The
$f + SI_n \in SR_n$
. The
![]() ${\mathfrak {S}}_n$
-module structure of
${\mathfrak {S}}_n$
-module structure of
![]() $SR_n$
, ungraded or (bi)graded, remains open.
$SR_n$
, ungraded or (bi)graded, remains open.
We turn to a description of our methods. The analysis of
![]() $R_{n,k}$
and its variations relied on the remarkably well-behaved Gröbner theory of its defining ideal
$R_{n,k}$
and its variations relied on the remarkably well-behaved Gröbner theory of its defining ideal
![]() $(x_1^k, \dots , x_n^k, e_n, \dots , e_{n-k+1}) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
. This facilitated multiple provable combinatorial bases [Reference Gillespie and Rhoades13, Reference Haglund, Rhoades and Shimozono15, Reference Meyer26, Reference Pawlowski and Rhoades27] of
$(x_1^k, \dots , x_n^k, e_n, \dots , e_{n-k+1}) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
. This facilitated multiple provable combinatorial bases [Reference Gillespie and Rhoades13, Reference Haglund, Rhoades and Shimozono15, Reference Meyer26, Reference Pawlowski and Rhoades27] of
![]() $R_{n,k}$
from which its structure as a graded vector space or
$R_{n,k}$
from which its structure as a graded vector space or
![]() ${\mathfrak {S}}_n$
-module could be studied. There exists an extension of Gröbner theory to the superspace ring
${\mathfrak {S}}_n$
-module could be studied. There exists an extension of Gröbner theory to the superspace ring
![]() $\Omega _n$
, but the Gröbner theory of the supercoinvariant ideal
$\Omega _n$
, but the Gröbner theory of the supercoinvariant ideal
![]() $SI_n \subseteq \Omega _n$
has proven to be inscrutable. Combinatorially, this has translated into a failure of using straightening arguments to show that nice potential bases of
$SI_n \subseteq \Omega _n$
has proven to be inscrutable. Combinatorially, this has translated into a failure of using straightening arguments to show that nice potential bases of
![]() $SR_n$
span this quotient ring. Indeed, our approach does not prove the existence of any specific basis of
$SR_n$
span this quotient ring. Indeed, our approach does not prove the existence of any specific basis of
![]() $SR_n$
. For a potential road from our methods to an Artin-like basis of
$SR_n$
. For a potential road from our methods to an Artin-like basis of
![]() $SR_n$
conjectured by Sagan and Swanson [Reference Sagan and Swanson33, Conj. 6.7], see Theorem 5.4, Conjecture 5.5 and Proposition 5.7.
$SR_n$
conjectured by Sagan and Swanson [Reference Sagan and Swanson33, Conj. 6.7], see Theorem 5.4, Conjecture 5.5 and Proposition 5.7.
Since the direct analysis of
![]() $SR_n$
by means of a basis has proven elusive, we adopt an indirect approach that stands, in a nutshell, on the elimination of fermionic variables. This allows us to trade supercommutative algebra problems in
$SR_n$
by means of a basis has proven elusive, we adopt an indirect approach that stands, in a nutshell, on the elimination of fermionic variables. This allows us to trade supercommutative algebra problems in
![]() $\Omega _n$
for commutative algebra problems in
$\Omega _n$
for commutative algebra problems in
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
, for which more tools have been developed.
${\mathbb {C}}[{\mathbf {x}}_n]$
, for which more tools have been developed.
For a given subset
![]() $J \subseteq [n]$
, we use a miraculous identity (Lemma 3.3) involving partial derivatives of complete homogeneous symmetric polynomials to deduce the existence of a regular sequence
$J \subseteq [n]$
, we use a miraculous identity (Lemma 3.3) involving partial derivatives of complete homogeneous symmetric polynomials to deduce the existence of a regular sequence
![]() $p_{J,1}, \dots , p_{J,n} \in {\mathbb {C}}[{\mathbf {x}}_n]$
(Lemma 3.5) in
$p_{J,1}, \dots , p_{J,n} \in {\mathbb {C}}[{\mathbf {x}}_n]$
(Lemma 3.5) in
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
. These regular sequences are used to prove (Proposition 3.7) that the bigraded Hilbert series of
${\mathbb {C}}[{\mathbf {x}}_n]$
. These regular sequences are used to prove (Proposition 3.7) that the bigraded Hilbert series of
![]() $SR_n$
is bounded above by the expression (1.10).
$SR_n$
is bounded above by the expression (1.10).
Next, we introduce a family
![]() ${\mathfrak {D}}_J$
of combinatorially defined differential operators acting on
${\mathfrak {D}}_J$
of combinatorially defined differential operators acting on
![]() $\Omega _n$
, which are indexed by subsets
$\Omega _n$
, which are indexed by subsets
![]() $J \subseteq [n]$
. We prove (Lemma 4.8) that the
$J \subseteq [n]$
. We prove (Lemma 4.8) that the
![]() ${\mathfrak {D}}_J$
exhibit a triangularity property with respect to the Gale order on subsets
${\mathfrak {D}}_J$
exhibit a triangularity property with respect to the Gale order on subsets
![]() $J \subseteq [n]$
with leading term given by the polynomialFootnote
3
$J \subseteq [n]$
with leading term given by the polynomialFootnote
3
 $$ \begin{align} f_J := \prod_{j \in J} x_j \left( \prod_{i \,> \, j} (x_j - x_i) \right) \in {\mathbb {C}}[{\mathbf {x}}_n]. \end{align} $$
$$ \begin{align} f_J := \prod_{j \in J} x_j \left( \prod_{i \,> \, j} (x_j - x_i) \right) \in {\mathbb {C}}[{\mathbf {x}}_n]. \end{align} $$
This leads to a general recipe (Theorem 5.4) for constructing bases of
![]() $SR_n$
from bases of the various commutative quotient rings
$SR_n$
from bases of the various commutative quotient rings
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
by the colon ideals
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
by the colon ideals
By identifying
![]() $(I_n : f_J)$
with the ideal
$(I_n : f_J)$
with the ideal
![]() $(p_{J,1}, \dots , p_{J,n})$
cut out by the regular sequence in
$(p_{J,1}, \dots , p_{J,n})$
cut out by the regular sequence in
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
used to prove the upper bound on
${\mathbb {C}}[{\mathbf {x}}_n]$
used to prove the upper bound on
![]() ${\mathrm {Hilb}}(SR_n;q,z)$
(Theorem 4.12), we are able to prove both the operator theorem characterizing the superharmonic space
${\mathrm {Hilb}}(SR_n;q,z)$
(Theorem 4.12), we are able to prove both the operator theorem characterizing the superharmonic space
![]() $SH_n$
(Theorem 5.1) and the formula (1.10) for the bigraded Hilbert series of
$SH_n$
(Theorem 5.1) and the formula (1.10) for the bigraded Hilbert series of
![]() $SR_n$
(Theorem 5.3).
$SR_n$
(Theorem 5.3).
The rest of the paper is organized as follows. In Section 2
, we give background material on superspace and commutative algebra. In Section 3
, we bound the bigraded Hilbert series of
![]() $SR_n$
from above using regular sequences. In Section 4
, we introduce the differential operators
$SR_n$
from above using regular sequences. In Section 4
, we introduce the differential operators
![]() ${\mathfrak {D}}_J$
and relate them to the colon ideals
${\mathfrak {D}}_J$
and relate them to the colon ideals
![]() $(I_n : f_J)$
. In Section 5
, we prove our main results: the operator theorem and the Hilbert series of
$(I_n : f_J)$
. In Section 5
, we prove our main results: the operator theorem and the Hilbert series of
![]() $SR_n$
. We also present a conjecture for an Artin-like basis of
$SR_n$
. We also present a conjecture for an Artin-like basis of
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
and prove this conjecture in a special case. We close in Section 6
with some open problems.
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
and prove this conjecture in a special case. We close in Section 6
with some open problems.
2 Background
2.1 Superspace
As in the introduction, the superspace ring
![]() $\Omega _n = {\mathbb {C}}[{\mathbf {x}}_n] \otimes \wedge \{ \mathbf {\theta }_n \}$
is the tensor product of a symmetric algebra of rank n and an exterior algebra of rank n, both over
$\Omega _n = {\mathbb {C}}[{\mathbf {x}}_n] \otimes \wedge \{ \mathbf {\theta }_n \}$
is the tensor product of a symmetric algebra of rank n and an exterior algebra of rank n, both over
![]() ${\mathbb {C}}$
. A monomial in
${\mathbb {C}}$
. A monomial in
![]() $\Omega _n$
is a nonzero product of the generators
$\Omega _n$
is a nonzero product of the generators
![]() ${\mathbf {x}}_n = (x_1, \dots , x_n)$
and
${\mathbf {x}}_n = (x_1, \dots , x_n)$
and
![]() $\mathbf {\theta }_n = (\theta _1, \dots , \theta _n)$
. A bosonic monomial is a monomial that only involves the generators
$\mathbf {\theta }_n = (\theta _1, \dots , \theta _n)$
. A bosonic monomial is a monomial that only involves the generators
![]() ${\mathbf {x}}_n$
, whereas a fermionic monomial is a monomial that only involves the generators
${\mathbf {x}}_n$
, whereas a fermionic monomial is a monomial that only involves the generators
![]() $\mathbf {\theta }_n$
. For any subset
$\mathbf {\theta }_n$
. For any subset
![]() $J \subseteq [n]$
, we let
$J \subseteq [n]$
, we let
![]() $\theta _J$
be the product of the fermionic generators
$\theta _J$
be the product of the fermionic generators
![]() $\theta _j$
indexed by
$\theta _j$
indexed by
![]() $j \in J$
in increasing order; we have a direct sum decomposition
$j \in J$
in increasing order; we have a direct sum decomposition
The Gale order
![]() $\leq _{\mathrm {Gale}}$
on subsets
$\leq _{\mathrm {Gale}}$
on subsets
![]() $J \subseteq [n]$
of the same cardinality will be used heavily. This partial order is defined by
$J \subseteq [n]$
of the same cardinality will be used heavily. This partial order is defined by
This order will be used to compare fermionic monomials
![]() $\theta _J$
in the superspace ring
$\theta _J$
in the superspace ring
![]() $\Omega _n$
.
$\Omega _n$
.
The ring
![]() $\Omega _n$
may be identified with polynomial valued differential forms on
$\Omega _n$
may be identified with polynomial valued differential forms on
![]() ${\mathbb {C}}^n$
; as such, it carries a plethora of derivative operators. For
${\mathbb {C}}^n$
; as such, it carries a plethora of derivative operators. For
![]() $1 \leq i \leq n$
, let
$1 \leq i \leq n$
, let
![]() $\partial _i: {\mathbb {C}}[{\mathbf {x}}_n] \rightarrow {\mathbb {C}}[{\mathbf {x}}_n]$
be the usual partial differentiation with respect to
$\partial _i: {\mathbb {C}}[{\mathbf {x}}_n] \rightarrow {\mathbb {C}}[{\mathbf {x}}_n]$
be the usual partial differentiation with respect to
![]() $x_i$
. By acting on the first tensor factor of
$x_i$
. By acting on the first tensor factor of
![]() $\Omega _n = {\mathbb {C}}[{\mathbf {x}}_n] \otimes \wedge \{ \mathbf {\theta }_n \}$
, this extends to an action
$\Omega _n = {\mathbb {C}}[{\mathbf {x}}_n] \otimes \wedge \{ \mathbf {\theta }_n \}$
, this extends to an action
![]() $\partial _i: \Omega _n \rightarrow \Omega _n$
. For
$\partial _i: \Omega _n \rightarrow \Omega _n$
. For
![]() $1 \leq i \leq n$
, let
$1 \leq i \leq n$
, let
![]() $\partial ^{\theta }_i: \wedge \{ \mathbf {\theta }_n \} \rightarrow \wedge \{ \mathbf {\theta }_n \}$
be the contraction operator defined on fermionic monomials by
$\partial ^{\theta }_i: \wedge \{ \mathbf {\theta }_n \} \rightarrow \wedge \{ \mathbf {\theta }_n \}$
be the contraction operator defined on fermionic monomials by
 $$ \begin{align} \partial^\theta_i: \theta_{j_1} \cdots \theta_{j_r} = \begin{cases} (-1)^{s-1} \theta_{j_1} \cdots \widehat{\theta_{j_s}} \cdots \theta_{j_r} & \text{if}\ j_s = i\ \text{for some}\ s, \\ 0 & \text{otherwise} \end{cases} \end{align} $$
$$ \begin{align} \partial^\theta_i: \theta_{j_1} \cdots \theta_{j_r} = \begin{cases} (-1)^{s-1} \theta_{j_1} \cdots \widehat{\theta_{j_s}} \cdots \theta_{j_r} & \text{if}\ j_s = i\ \text{for some}\ s, \\ 0 & \text{otherwise} \end{cases} \end{align} $$
for any distinct indices
![]() $1 \leq j_1, \dots , j_r \leq n$
where
$1 \leq j_1, \dots , j_r \leq n$
where
![]() $\widehat {\cdot }$
denotes omission. By acting on the second tensor factor of
$\widehat {\cdot }$
denotes omission. By acting on the second tensor factor of
![]() $\Omega _n = {\mathbb {C}}[{\mathbf {x}}_n] \otimes \wedge \{ \mathbf {\theta }_n \}$
, we have a fermionic derivative operator
$\Omega _n = {\mathbb {C}}[{\mathbf {x}}_n] \otimes \wedge \{ \mathbf {\theta }_n \}$
, we have a fermionic derivative operator
![]() $\partial ^{\theta }_i: \Omega _n \rightarrow \Omega _n$
.
$\partial ^{\theta }_i: \Omega _n \rightarrow \Omega _n$
.
We let
![]() $d: \Omega _n \rightarrow \Omega _n$
be the Euler operator of differential geometry defined by
$d: \Omega _n \rightarrow \Omega _n$
be the Euler operator of differential geometry defined by
 $$ \begin{align} d: f \mapsto \sum_{i = 1}^n \partial_i f \cdot \theta_i \end{align} $$
$$ \begin{align} d: f \mapsto \sum_{i = 1}^n \partial_i f \cdot \theta_i \end{align} $$
for all
![]() $f \in \Omega _n$
. This operator lowers bosonic degree by 1 while raising fermionic degree by 1. We will need ‘higher’ versions
$f \in \Omega _n$
. This operator lowers bosonic degree by 1 while raising fermionic degree by 1. We will need ‘higher’ versions
![]() $d_j: \Omega _n \rightarrow \Omega _n$
$d_j: \Omega _n \rightarrow \Omega _n$
![]() $(j \geq 1)$
of these operators given by
$(j \geq 1)$
of these operators given by
 $$ \begin{align} d_j: f \mapsto \sum_{i = 1}^n \partial_i^j f \cdot \theta_i. \end{align} $$
$$ \begin{align} d_j: f \mapsto \sum_{i = 1}^n \partial_i^j f \cdot \theta_i. \end{align} $$
The operator
![]() $d_j$
decreases bosonic degree by j while raising fermionic degree by 1. We have
$d_j$
decreases bosonic degree by j while raising fermionic degree by 1. We have
![]() $d_1 = d$
. If
$d_1 = d$
. If
![]() $J = \{ j_1 < j_2 < \cdots \}$
is a set of positive integers, we write
$J = \{ j_1 < j_2 < \cdots \}$
is a set of positive integers, we write
for the corresponding product of higher Euler operators.
Considering bosonic and fermionic degree separately, superspace
![]() $\Omega _n$
admits a bigrading
$\Omega _n$
admits a bigrading
 $$ \begin{align} \Omega_n = \bigoplus_{i \geq 0} \bigoplus_{j = 0}^n (\Omega_n)_{i,j} \quad \text{ where } \quad (\Omega_n)_{i,j} = {\mathbb {C}}[{\mathbf {x}}_n]_i \otimes \wedge^j \{ \mathbf{\theta}_n \}. \end{align} $$
$$ \begin{align} \Omega_n = \bigoplus_{i \geq 0} \bigoplus_{j = 0}^n (\Omega_n)_{i,j} \quad \text{ where } \quad (\Omega_n)_{i,j} = {\mathbb {C}}[{\mathbf {x}}_n]_i \otimes \wedge^j \{ \mathbf{\theta}_n \}. \end{align} $$
The diagonal action of the symmetric group
![]() ${\mathfrak {S}}_n$
on
${\mathfrak {S}}_n$
on
![]() $\Omega _n$
preserves this bigrading. As in the introduction, we let
$\Omega _n$
preserves this bigrading. As in the introduction, we let
![]() $(\Omega _n)^{{\mathfrak {S}}_n}$
be the fixed subalgebra for this action.
$(\Omega _n)^{{\mathfrak {S}}_n}$
be the fixed subalgebra for this action.
Let
![]() $I \subseteq \Omega _n$
be a bihomogeneous ideal in superspace (such as
$I \subseteq \Omega _n$
be a bihomogeneous ideal in superspace (such as
![]() $SI_n$
). Analysis of the quotient ring
$SI_n$
). Analysis of the quotient ring
![]() $\Omega _n/I$
is often complicated by the fact that its elements
$\Omega _n/I$
is often complicated by the fact that its elements
![]() $f + I$
are cosets rather than superspace elements
$f + I$
are cosets rather than superspace elements
![]() $f \in \Omega _n$
. The theory of (superspace) harmonics is a powerful technique for replacing cosets with honest elements of superspace. We turn to a description of this method.
$f \in \Omega _n$
. The theory of (superspace) harmonics is a powerful technique for replacing cosets with honest elements of superspace. We turn to a description of this method.
The partial derivative operators
![]() $\partial _i, \partial ^\theta _i: \Omega _n \rightarrow \Omega _n$
satisfy the relations
$\partial _i, \partial ^\theta _i: \Omega _n \rightarrow \Omega _n$
satisfy the relations
for all
![]() $1 \leq i, j \leq n$
. Since these are the defining relations of
$1 \leq i, j \leq n$
. Since these are the defining relations of
![]() $\Omega _n$
, for any superspace element
$\Omega _n$
, for any superspace element
![]() $f = f(x_1, \dots , x_n, \theta _1, \dots , \theta _n) \in \Omega _n$
, we get an operator
$f = f(x_1, \dots , x_n, \theta _1, \dots , \theta _n) \in \Omega _n$
, we get an operator
by replacing each
![]() $x_i$
in f with the bosonic derivative
$x_i$
in f with the bosonic derivative
![]() $\partial _i$
and each
$\partial _i$
and each
![]() $\theta _i$
in f with the fermionic derivative
$\theta _i$
in f with the fermionic derivative
![]() $\partial ^{\theta }_i$
. This leads to an action of superspace on itself given by
$\partial ^{\theta }_i$
. This leads to an action of superspace on itself given by
The
![]() $\odot $
-action gives
$\odot $
-action gives
![]() $\Omega _n$
-module structure on
$\Omega _n$
-module structure on
![]() $\Omega _n$
.
$\Omega _n$
.
We use the
![]() $\odot $
-action to construct an inner product on
$\odot $
-action to construct an inner product on
![]() $\Omega _n$
as follows. Let
$\Omega _n$
as follows. Let
![]() $\overline {\cdot }: \Omega _n \rightarrow \Omega _n$
be the conjugate-linear involution that fixes all bosonic monomials, satisfies
$\overline {\cdot }: \Omega _n \rightarrow \Omega _n$
be the conjugate-linear involution that fixes all bosonic monomials, satisfies
![]() $\overline { \theta _{i_1} \cdots \theta _{i_r} } = \theta _{i_r} \cdots \theta _{i_1}$
for all fermionic monomials
$\overline { \theta _{i_1} \cdots \theta _{i_r} } = \theta _{i_r} \cdots \theta _{i_1}$
for all fermionic monomials
![]() $\theta _{i_1} \cdots \theta _{i_r}$
, and sends any scalar
$\theta _{i_1} \cdots \theta _{i_r}$
, and sends any scalar
![]() $c \in {\mathbb {C}}$
to its complex conjugate
$c \in {\mathbb {C}}$
to its complex conjugate
![]() $\overline {c}$
. The pairing
$\overline {c}$
. The pairing
is easily seen to be an inner product, with the monomials
![]() $\{ x_1^{a_1} \cdots x_n^{a_n} \cdot \theta _I \}$
forming an orthogonal (but not orthonormal) basis.
$\{ x_1^{a_1} \cdots x_n^{a_n} \cdot \theta _I \}$
forming an orthogonal (but not orthonormal) basis.
Now suppose
![]() $I \subseteq \Omega _n$
is a bihomogeneous ideal defined over
$I \subseteq \Omega _n$
is a bihomogeneous ideal defined over
![]() ${\mathbb {R}}$
(such as
${\mathbb {R}}$
(such as
![]() $SI_n$
). We have the equality
$SI_n$
). We have the equality
of subspaces of
![]() $\Omega _n$
, where
$\Omega _n$
, where
![]() $I^{\perp }$
is calculated with respect to the above inner product. The subspace
$I^{\perp }$
is calculated with respect to the above inner product. The subspace
![]() $I^{\perp } \subseteq \Omega _n$
is the harmonic space attached to I. We have a direct sum decomposition
$I^{\perp } \subseteq \Omega _n$
is the harmonic space attached to I. We have a direct sum decomposition
![]() $\Omega _n = I \oplus I^{\perp }$
and an isomorphism of bigraded vector spaces
$\Omega _n = I \oplus I^{\perp }$
and an isomorphism of bigraded vector spaces
![]() $\Omega _n/I \cong I^{\perp }$
. If I is
$\Omega _n/I \cong I^{\perp }$
. If I is
![]() ${\mathfrak {S}}_n$
-stable, the isomorphism
${\mathfrak {S}}_n$
-stable, the isomorphism
![]() $\Omega _n/I \cong I^{\perp }$
is also an isomorphism of bigraded
$\Omega _n/I \cong I^{\perp }$
is also an isomorphism of bigraded
![]() ${\mathfrak {S}}_n$
-modules. The harmonic model
${\mathfrak {S}}_n$
-modules. The harmonic model
![]() $I^{\perp }$
of
$I^{\perp }$
of
![]() $\Omega _n/I$
is useful because its members are honest superspace elements rather than cosets.
$\Omega _n/I$
is useful because its members are honest superspace elements rather than cosets.
We close this subsection with a combinatorial identity due to Sagan and Swanson that will be useful in our analysis of
![]() $SR_n$
. For a subset
$SR_n$
. For a subset
![]() $J \subseteq [n]$
, we define the J-staircase to be the sequence
$J \subseteq [n]$
, we define the J-staircase to be the sequence
![]() ${\mathrm {st}}(J) = ({\mathrm {st}}(J)_1, \dots , {\mathrm {st}}(J)_n)$
, where
${\mathrm {st}}(J) = ({\mathrm {st}}(J)_1, \dots , {\mathrm {st}}(J)_n)$
, where
 $$ \begin{align} {\mathrm{st}}(J)_1 := \begin{cases} 0 & 1 \in J \\ 1 & 1 \notin J \end{cases} \end{align} $$
$$ \begin{align} {\mathrm{st}}(J)_1 := \begin{cases} 0 & 1 \in J \\ 1 & 1 \notin J \end{cases} \end{align} $$
and
 $$ \begin{align} {\mathrm{st}}(J)_{i+1} := \begin{cases} {\mathrm{st}}(J)_i & i+1 \in J \\ {\mathrm{st}}(J)_i + 1 & i+1 \notin J. \end{cases} \end{align} $$
$$ \begin{align} {\mathrm{st}}(J)_{i+1} := \begin{cases} {\mathrm{st}}(J)_i & i+1 \in J \\ {\mathrm{st}}(J)_i + 1 & i+1 \notin J. \end{cases} \end{align} $$
For example, if
![]() $n = 7$
and
$n = 7$
and
![]() $J = \{ 3,5,6\}$
, we have
$J = \{ 3,5,6\}$
, we have
![]() ${\mathrm {st}}(J) = ({\mathrm {st}}(J)_1, \dots , {\mathrm {st}}(J)_7) = (1,2,2,3,3,3,4)$
. Observe that
${\mathrm {st}}(J) = ({\mathrm {st}}(J)_1, \dots , {\mathrm {st}}(J)_7) = (1,2,2,3,3,3,4)$
. Observe that
![]() ${\mathrm {st}}(\varnothing ) = (1, 2, \dots , n)$
is the usual staircase.
${\mathrm {st}}(\varnothing ) = (1, 2, \dots , n)$
is the usual staircase.
Lemma 2.1. (Sagan-Swanson [Reference Sagan and Swanson33])
We have the polynomial identity
 $$ \begin{align} \sum_{J \subseteq [n]} \left( \prod_{i = 1}^n [{\mathrm{st}}(J)_i]_q \right) \cdot z^{|J|} = \sum_{k = 1}^n z^{n-k} \cdot [k]!_q \cdot {\mathrm {Stir}}_q(n,k). \end{align} $$
$$ \begin{align} \sum_{J \subseteq [n]} \left( \prod_{i = 1}^n [{\mathrm{st}}(J)_i]_q \right) \cdot z^{|J|} = \sum_{k = 1}^n z^{n-k} \cdot [k]!_q \cdot {\mathrm {Stir}}_q(n,k). \end{align} $$
2.2 Commutative algebra
Our overarching strategy for analyzing
![]() $SR_n$
is to transfer problems involving the superspace ring
$SR_n$
is to transfer problems involving the superspace ring
![]() $\Omega _n$
to problems involving the better-understood polynomial ring
$\Omega _n$
to problems involving the better-understood polynomial ring
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
. We review the relevant notions from commutative algebra.
${\mathbb {C}}[{\mathbf {x}}_n]$
. We review the relevant notions from commutative algebra.
A commutative graded
![]() ${\mathbb {C}}$
-algebra
${\mathbb {C}}$
-algebra
![]() $A = \bigoplus _{i \geq 0} A_i$
is Artinian if A is a finite-dimensional
$A = \bigoplus _{i \geq 0} A_i$
is Artinian if A is a finite-dimensional
![]() ${\mathbb {C}}$
-vector space. The Hilbert series of A is
${\mathbb {C}}$
-vector space. The Hilbert series of A is
assuming each graded piece
![]() $A_i$
is finite-dimensional.
$A_i$
is finite-dimensional.
A sequence
![]() $f_1, \dots , f_n$
of n polynomials in
$f_1, \dots , f_n$
of n polynomials in
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
of homogeneous positive degrees is a regular sequence if, for each
${\mathbb {C}}[{\mathbf {x}}_n]$
of homogeneous positive degrees is a regular sequence if, for each
![]() $0 \leq i \leq n-1$
, we have a short exact sequence
$0 \leq i \leq n-1$
, we have a short exact sequence
where the first map is induced by multiplication by
![]() $f_{i+1}$
and the second map is the canonical projection. If the regular sequence
$f_{i+1}$
and the second map is the canonical projection. If the regular sequence
![]() $f_1, \dots , f_n$
consists of homogeneous polynomials, the quotient ring
$f_1, \dots , f_n$
consists of homogeneous polynomials, the quotient ring
![]() ${\mathbb {C}}[{\mathbf {x}}_n]/(f_1, \dots , f_n)$
is a finite-dimensional graded vector space with Hilbert series
${\mathbb {C}}[{\mathbf {x}}_n]/(f_1, \dots , f_n)$
is a finite-dimensional graded vector space with Hilbert series
An Artinian graded quotient
![]() ${\mathbb {C}}[{\mathbf {x}}_n]/{\mathfrak {a}}$
of
${\mathbb {C}}[{\mathbf {x}}_n]/{\mathfrak {a}}$
of
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
is a complete intersection if
${\mathbb {C}}[{\mathbf {x}}_n]$
is a complete intersection if
![]() ${\mathfrak {a}} = (f_1, \dots , f_n)$
for some length n regular sequence
${\mathfrak {a}} = (f_1, \dots , f_n)$
for some length n regular sequence
![]() $f_1, \dots , f_n \in {\mathbb {C}}[{\mathbf {x}}_n]$
of homogeneous polynomials.
$f_1, \dots , f_n \in {\mathbb {C}}[{\mathbf {x}}_n]$
of homogeneous polynomials.
The regularity of a sequence
![]() $f_1, \dots , f_n \in {\mathbb {C}}[{\mathbf {x}}_n]$
of polynomials of homogeneous positive degree can be interpreted in terms of the variety cut out by
$f_1, \dots , f_n \in {\mathbb {C}}[{\mathbf {x}}_n]$
of polynomials of homogeneous positive degree can be interpreted in terms of the variety cut out by
![]() $f_1, \dots , f_n$
. Given any set
$f_1, \dots , f_n$
. Given any set
![]() $S \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
of polynomials, write
$S \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
of polynomials, write
for the locus of points in
![]() ${\mathbb {C}}^n$
on which the polynomials in S vanish.
${\mathbb {C}}^n$
on which the polynomials in S vanish.
Lemma 2.2. Let
![]() $f_1, \dots , f_n \in {\mathbb {C}}[{\mathbf {x}}_n]$
be a list of n homogeneous polynomials in
$f_1, \dots , f_n \in {\mathbb {C}}[{\mathbf {x}}_n]$
be a list of n homogeneous polynomials in
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
of positive degree. The sequence
${\mathbb {C}}[{\mathbf {x}}_n]$
of positive degree. The sequence
![]() $f_1, \dots , f_n$
is a regular sequence if and only if the variety
$f_1, \dots , f_n$
is a regular sequence if and only if the variety
![]() ${\mathbf {V}}(f_1, \dots , f_n) \subseteq {\mathbb {C}}^n$
cut out by these polynomials consists of the origin
${\mathbf {V}}(f_1, \dots , f_n) \subseteq {\mathbb {C}}^n$
cut out by these polynomials consists of the origin
![]() $\{ 0 \}$
alone.
$\{ 0 \}$
alone.
Let
![]() ${\mathfrak {a}} \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
be an ideal and let
${\mathfrak {a}} \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
be an ideal and let
![]() $f \in {\mathbb {C}}[{\mathbf {x}}_n]$
be a polynomial. The colon ideal (or ideal quotient) is
$f \in {\mathbb {C}}[{\mathbf {x}}_n]$
be a polynomial. The colon ideal (or ideal quotient) is
It is not difficult to check that
![]() $({\mathfrak {a}} : f)$
is an ideal in
$({\mathfrak {a}} : f)$
is an ideal in
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
which contains
${\mathbb {C}}[{\mathbf {x}}_n]$
which contains
![]() ${\mathfrak {a}}$
, and that
${\mathfrak {a}}$
, and that
![]() $({\mathfrak {a}} : f) = {\mathbb {C}}[{\mathbf {x}}_n]$
if and only if
$({\mathfrak {a}} : f) = {\mathbb {C}}[{\mathbf {x}}_n]$
if and only if
![]() $f \in {\mathfrak {a}}$
.
$f \in {\mathfrak {a}}$
.
Colon ideals will play a crucial role in our work, and we will need a criterion for determining a generating set for them. Let
![]() $A = \bigoplus _{i = 0}^d A_i$
be a finite-dimensional graded
$A = \bigoplus _{i = 0}^d A_i$
be a finite-dimensional graded
![]() ${\mathbb {C}}$
-algebra with
${\mathbb {C}}$
-algebra with
![]() $A_d \neq 0$
. The algebra A is a Poincaré duality algebra if
$A_d \neq 0$
. The algebra A is a Poincaré duality algebra if
-
• its top component
 $A_d \cong {\mathbb {C}}$
is a 1-dimensional complex vector spaces, and
$A_d \cong {\mathbb {C}}$
is a 1-dimensional complex vector spaces, and -
• for any
 $0 \leq i \leq d$
, the multiplication map
$0 \leq i \leq d$
, the multiplication map
 $A_i \otimes A_{d-i} \longrightarrow A_d \cong {\mathbb {C}}$
is a perfect pairing.
$A_i \otimes A_{d-i} \longrightarrow A_d \cong {\mathbb {C}}$
is a perfect pairing.
If
![]() $A = \bigoplus _{i = 0}^d A_d$
is a Poincaré duality algebra with
$A = \bigoplus _{i = 0}^d A_d$
is a Poincaré duality algebra with
![]() $d \neq 0$
, the maximal degree d is called the socle degree of A. The following commutative algebra lemma will be remarkably useful to us.
$d \neq 0$
, the maximal degree d is called the socle degree of A. The following commutative algebra lemma will be remarkably useful to us.
Lemma 2.3. (Abe-Horiguchi-Masuda-Murai-Sato [Reference Abe, Horiguchi, Masuda, Murai and Sato2, Lem. 2.4])
Suppose
![]() ${\mathfrak {a}}, {\mathfrak {a}}' \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
are homogeneous ideals and
${\mathfrak {a}}, {\mathfrak {a}}' \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
are homogeneous ideals and
![]() $f \in {\mathbb {C}}[{\mathbf {x}}_n]$
is a homogeneous polynomial of degree k with
$f \in {\mathbb {C}}[{\mathbf {x}}_n]$
is a homogeneous polynomial of degree k with
![]() $f \notin {\mathfrak {a}}$
. Suppose
$f \notin {\mathfrak {a}}$
. Suppose
![]() ${\mathfrak {a}}' \subseteq ({\mathfrak {a}} : f)$
. If
${\mathfrak {a}}' \subseteq ({\mathfrak {a}} : f)$
. If
![]() ${\mathbb {C}}[{\mathbf {x}}_n]/{\mathfrak {a}}'$
is a Poincaré duality algebra of socle degree r and
${\mathbb {C}}[{\mathbf {x}}_n]/{\mathfrak {a}}'$
is a Poincaré duality algebra of socle degree r and
![]() ${\mathbb {C}}[{\mathbf {x}}_n]/{\mathfrak {a}}$
is a Poincaré duality algebra of socle degree
${\mathbb {C}}[{\mathbf {x}}_n]/{\mathfrak {a}}$
is a Poincaré duality algebra of socle degree
![]() $r + k$
, then
$r + k$
, then
![]() ${\mathfrak {a}}' = ({\mathfrak {a}} : f)$
.
${\mathfrak {a}}' = ({\mathfrak {a}} : f)$
.
We remark that [Reference Abe, Horiguchi, Masuda, Murai and Sato2, Lem. 2.4] was stated over the field
![]() ${\mathbb {R}}$
of real numbers, but its proof goes through without change for arbitrary fields.
${\mathbb {R}}$
of real numbers, but its proof goes through without change for arbitrary fields.
The polynomial ring
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
inherits a theory of harmonics from the superspace ring
${\mathbb {C}}[{\mathbf {x}}_n]$
inherits a theory of harmonics from the superspace ring
![]() $\Omega _n$
. Partial differentiation yields an action
$\Omega _n$
. Partial differentiation yields an action
![]() $\odot : {\mathbb {C}}[{\mathbf {x}}_n] \times {\mathbb {C}}[{\mathbf {x}}_n] \rightarrow {\mathbb {C}}[{\mathbf {x}}_n]$
of the polynomial ring
$\odot : {\mathbb {C}}[{\mathbf {x}}_n] \times {\mathbb {C}}[{\mathbf {x}}_n] \rightarrow {\mathbb {C}}[{\mathbf {x}}_n]$
of the polynomial ring
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
on itself, which gives rise to an inner product
${\mathbb {C}}[{\mathbf {x}}_n]$
on itself, which gives rise to an inner product
If
![]() $I \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
is a homogeneous ideal, we have a direct sum decomposition
$I \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
is a homogeneous ideal, we have a direct sum decomposition
![]() ${\mathbb {C}}[{\mathbf {x}}_n] = I \oplus I^{\perp }$
and an identification
${\mathbb {C}}[{\mathbf {x}}_n] = I \oplus I^{\perp }$
and an identification
of the harmonic space
![]() $I^{\perp }$
as a subspace of
$I^{\perp }$
as a subspace of
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
.
${\mathbb {C}}[{\mathbf {x}}_n]$
.
The harmonic theory of the classical coinvariant ideal
![]() $I_n \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
is given as follows. Let
$I_n \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
is given as follows. Let
![]() $\delta _n \in {\mathbb {C}}[{\mathbf {x}}_n]$
be the Vandermonde determinant
$\delta _n \in {\mathbb {C}}[{\mathbf {x}}_n]$
be the Vandermonde determinant
Then
![]() $I_n^{\perp }$
is a cyclic
$I_n^{\perp }$
is a cyclic
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
-module under the
${\mathbb {C}}[{\mathbf {x}}_n]$
-module under the
![]() $\odot $
-action generated by
$\odot $
-action generated by
![]() $\delta _n$
. In symbols, we have
$\delta _n$
. In symbols, we have
We write
![]() $H_n$
for the subspace
$H_n$
for the subspace
![]() $I_n^{\perp } = {\mathbb {C}}[{\mathbf {x}}_n] \odot \delta _n \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
; we have an isomorphism
$I_n^{\perp } = {\mathbb {C}}[{\mathbf {x}}_n] \odot \delta _n \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
; we have an isomorphism
![]() $R_n \cong H_n$
of graded
$R_n \cong H_n$
of graded
![]() ${\mathfrak {S}}_n$
-modules. The annihilator of
${\mathfrak {S}}_n$
-modules. The annihilator of
![]() $\delta _n$
under the
$\delta _n$
under the
![]() $\odot $
-action is precisely the coinvariant ideal
$\odot $
-action is precisely the coinvariant ideal
![]() $I_n$
:
$I_n$
:
3 Upper Bound
3.1 A regular sequence in
 ${\mathbb {C}}[{\mathbf {x}}_n]$
${\mathbb {C}}[{\mathbf {x}}_n]$
Our first lemma gives a general technique for constructing interesting elements of the supercoinvariant ideal
![]() $SI_n$
.
$SI_n$
.
Lemma 3.1. The supercoinvariant ideal
![]() $SI_n \subseteq \Omega _n$
contains the classical coinvariant ideal
$SI_n \subseteq \Omega _n$
contains the classical coinvariant ideal
![]() $I_n \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
and is closed under the action of the Euler operator
$I_n \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
and is closed under the action of the Euler operator
![]() $d: \Omega _n \rightarrow \Omega _n$
.
$d: \Omega _n \rightarrow \Omega _n$
.
Proof. The operator d commutes with the action of
![]() ${\mathfrak {S}}_n$
on
${\mathfrak {S}}_n$
on
![]() $\Omega _n$
, so the result follows from the Leibniz formula
$\Omega _n$
, so the result follows from the Leibniz formula
which holds for any bihomogeneous
![]() $f, g \in \Omega _n$
(the sign is
$f, g \in \Omega _n$
(the sign is
![]() $+$
if f has even fermionic degree and
$+$
if f has even fermionic degree and
![]() $-$
otherwise) and the relation
$-$
otherwise) and the relation
![]() $d \circ d = 0$
.
$d \circ d = 0$
.
Ideals in
![]() $\Omega _n$
that are closed under the action of d are called differential ideals. To the knowledge of the authors, the supercoinvariant ideal
$\Omega _n$
that are closed under the action of d are called differential ideals. To the knowledge of the authors, the supercoinvariant ideal
![]() $SI_n$
is the first differential ideal that has received significant attention in algebraic combinatorics.
$SI_n$
is the first differential ideal that has received significant attention in algebraic combinatorics.
The most important elements of
![]() $SI_n$
arising from Lemma 3.1 are as follows. Let
$SI_n$
arising from Lemma 3.1 are as follows. Let
![]() $h_r, e_r \in {\mathbb {C}}[{\mathbf {x}}_n]$
be the complete homogeneous and elementary symmetric polynomials
$h_r, e_r \in {\mathbb {C}}[{\mathbf {x}}_n]$
be the complete homogeneous and elementary symmetric polynomials
Here and throughout, if
![]() $S \subseteq [n]$
is an index set, we use
$S \subseteq [n]$
is an index set, we use
![]() $h_r(S)$
and
$h_r(S)$
and
![]() $e_r(S)$
to denote the complete homogeneous and elementary symmetric polynomials of degree r in the variables indexed by S. For example, we have
$e_r(S)$
to denote the complete homogeneous and elementary symmetric polynomials of degree r in the variables indexed by S. For example, we have
For any subset
![]() $S \subseteq [n]$
, it is well-known that
$S \subseteq [n]$
, it is well-known that
Indeed, (3.3) follows inductively from the identity
![]() $h_r(S \cup i) = x_i h_{r-1}(S \cup i) + h_r(S)$
, which holds whenever
$h_r(S \cup i) = x_i h_{r-1}(S \cup i) + h_r(S)$
, which holds whenever
![]() $i \notin S$
. By Lemma 3.1, we have
$i \notin S$
. By Lemma 3.1, we have
Elements of
![]() $SI_n$
of the form (3.3) and (3.4) are the only ones we will need.
$SI_n$
of the form (3.3) and (3.4) are the only ones we will need.
For any subset
![]() $J \subseteq [n]$
, we construct a sequence
$J \subseteq [n]$
, we construct a sequence
![]() $(q_{J,1}, q_{J,2}, \dots , q_{J,n})$
of superspace elements as follows. Given
$(q_{J,1}, q_{J,2}, \dots , q_{J,n})$
of superspace elements as follows. Given
![]() $J \subseteq [n]$
, the sequence
$J \subseteq [n]$
, the sequence
![]() $(q_{J,1}, q_{J,2}, \dots , q_{J,n})$
in
$(q_{J,1}, q_{J,2}, \dots , q_{J,n})$
in
![]() $\Omega _n$
is defined by
$\Omega _n$
is defined by
 $$ \begin{align} q_{J,i} := \begin{cases} h_i(\{i, i+1, \dots, n\}) \cdot \theta_J & i < \min(J) \\ dh_r(J \cup \{i+1, \dots, n\}) \cdot \theta_{J - \max(J \cap \{1, \dots, i\})} & i \geq \min(J), \end{cases} \end{align} $$
$$ \begin{align} q_{J,i} := \begin{cases} h_i(\{i, i+1, \dots, n\}) \cdot \theta_J & i < \min(J) \\ dh_r(J \cup \{i+1, \dots, n\}) \cdot \theta_{J - \max(J \cap \{1, \dots, i\})} & i \geq \min(J), \end{cases} \end{align} $$
where in the second branch
![]() $r = n - |J \cup \{i+1, \dots , n\}| + 1$
.
$r = n - |J \cup \{i+1, \dots , n\}| + 1$
.
The superspace elements
![]() $q_{J,i}$
may be visualized (and remembered) as follows. Consider a linear array of n boxes labeled
$q_{J,i}$
may be visualized (and remembered) as follows. Consider a linear array of n boxes labeled
![]() $1, \dots , n$
from left to right, where the boxes in positions
$1, \dots , n$
from left to right, where the boxes in positions
![]() $j \in J$
are decorated with a
$j \in J$
are decorated with a
![]() $\theta $
. We consider moving a pointer from left to right along this array. When
$\theta $
. We consider moving a pointer from left to right along this array. When
![]() $n = 7$
and
$n = 7$
and
![]() $J = \{3,5,6\}$
, the picture is shown in Figure 1.
$J = \{3,5,6\}$
, the picture is shown in Figure 1.
-
• When the pointer is at a position i which is strictly to the left of all of the
 $\theta $
decorations, the corresponding superspace element is
$\theta $
decorations, the corresponding superspace element is
 $q_{J,i} = h_i(\{i, i+1, \dots , n\}) \cdot \theta _J$
.
$q_{J,i} = h_i(\{i, i+1, \dots , n\}) \cdot \theta _J$
. -
• When the pointer is at a position i which is weakly to the right of at least one
 $\theta $
decoration, the corresponding superspace element is
$\theta $
decoration, the corresponding superspace element is
 $q_{J,i} = dh_r(J \cup \{i+1, \dots , n \}) \cdot \theta _{\overline {J}}$
, where
$q_{J,i} = dh_r(J \cup \{i+1, \dots , n \}) \cdot \theta _{\overline {J}}$
, where
 $\overline {J}$
consists of all elements of J except for the closest element
$\overline {J}$
consists of all elements of J except for the closest element
 $j \in J$
weakly to the right of the pointer and
$j \in J$
weakly to the right of the pointer and
 $r = n - |J \cup \{i+1, \dots , n\}| + 1$
is the minimal degree such that
$r = n - |J \cup \{i+1, \dots , n\}| + 1$
is the minimal degree such that
 $h_r(J \cup \{i+1, \dots , n\}) \in I_n$
lies in the classical coinvariant ideal.
$h_r(J \cup \{i+1, \dots , n\}) \in I_n$
lies in the classical coinvariant ideal.
In our example, we have
We record some basic observations about the polynomials
![]() $q_{J,i}$
.
$q_{J,i}$
.
Lemma 3.2. Let
![]() $J \subseteq [n]$
and let
$J \subseteq [n]$
and let
![]() $(q_{J,1}, q_{J,2}, \dots , q_{J,n})$
be the associated sequence of elements of
$(q_{J,1}, q_{J,2}, \dots , q_{J,n})$
be the associated sequence of elements of
![]() $\Omega _n$
. For any
$\Omega _n$
. For any
![]() $1 \leq i \leq n$
, the superspace element
$1 \leq i \leq n$
, the superspace element
![]() $q_{J,i}$
satisfies the following properties.
$q_{J,i}$
satisfies the following properties.
-
1. We have
 $q_{J,i} \in SI_n$
.
$q_{J,i} \in SI_n$
. -
2. The superspace element
 $q_{J,i}$
is bihomogeneous with fermionic degree
$q_{J,i}$
is bihomogeneous with fermionic degree
 $|J|$
and bosonic degree
$|J|$
and bosonic degree
 ${\mathrm {st}}(J)_i$
where
${\mathrm {st}}(J)_i$
where
 ${\mathrm {st}}(J) = ({\mathrm {st}}(J)_1, \dots , {\mathrm {st}}(J)_n)$
is the J-staircase.
${\mathrm {st}}(J) = ({\mathrm {st}}(J)_1, \dots , {\mathrm {st}}(J)_n)$
is the J-staircase. -
3. The element
 $q_{J,i}$
lies in the subspace
$q_{J,i}$
lies in the subspace
 $\bigoplus _{J \leq _{{\mathrm {Gale}}} K} {\mathbb {C}}[{\mathbf {x}}_n] \cdot \theta _K$
of
$\bigoplus _{J \leq _{{\mathrm {Gale}}} K} {\mathbb {C}}[{\mathbf {x}}_n] \cdot \theta _K$
of
 $\Omega _n$
spanned by monomials whose fermionic parts are greater than or equal to J in Gale order.
$\Omega _n$
spanned by monomials whose fermionic parts are greater than or equal to J in Gale order.
Proof. The memberships (3.3) and (3.4) and the construction of
![]() $q_{J,i}$
imply (1). Moving the pointer from
$q_{J,i}$
imply (1). Moving the pointer from
![]() $i-1$
to i does not change the bosonic degree of
$i-1$
to i does not change the bosonic degree of
![]() $q_{J,i}$
when the box i is decorated with a
$q_{J,i}$
when the box i is decorated with a
![]() $\theta $
, and increases the bosonic degree of
$\theta $
, and increases the bosonic degree of
![]() $q_{J,i}$
by 1 otherwise, so (2) also holds by construction. To see why (3) is true, observe that the only surviving fermionic monomials
$q_{J,i}$
by 1 otherwise, so (2) also holds by construction. To see why (3) is true, observe that the only surviving fermionic monomials
![]() $\theta _K$
in the expression
$\theta _K$
in the expression
 $$ \begin{align} dh_r(J \cup \{i+1, \dots, n\}) \cdot &\theta_{J - \max(J \cap \{1, \dots, i\})} = \nonumber\\ & \sum_{k \in J \cup \{i+1, \dots, n \}} \partial_k h_r(J \cup \{i+1, \dots, n\}) \cdot \theta_k \cdot \theta_{J - \max(J \cap \{1, \dots, i\})} \end{align} $$
$$ \begin{align} dh_r(J \cup \{i+1, \dots, n\}) \cdot &\theta_{J - \max(J \cap \{1, \dots, i\})} = \nonumber\\ & \sum_{k \in J \cup \{i+1, \dots, n \}} \partial_k h_r(J \cup \{i+1, \dots, n\}) \cdot \theta_k \cdot \theta_{J - \max(J \cap \{1, \dots, i\})} \end{align} $$
satisfy
![]() $J \leq _{\mathrm {Gale}} K$
.
$J \leq _{\mathrm {Gale}} K$
.

Figure 1 The pointer construction for the superspace elements
![]() $q_{J,i} \in \Omega _n$
and the polynomials
$q_{J,i} \in \Omega _n$
and the polynomials
![]() $p_{J,i} \in {\mathbb {C}}[{\mathbf {x}}_n]$
. Here,
$p_{J,i} \in {\mathbb {C}}[{\mathbf {x}}_n]$
. Here,
![]() $n = 7$
and
$n = 7$
and
![]() $J = \{3,5,6\}$
. Boxes whose positions in J are indicated with a
$J = \{3,5,6\}$
. Boxes whose positions in J are indicated with a
![]() $\theta $
. Shaded boxes indicate the set of bosonic variables involved at each stage; boxes with a
$\theta $
. Shaded boxes indicate the set of bosonic variables involved at each stage; boxes with a
![]() $\theta $
are always shaded. The degree of the h-polynomial in
$\theta $
are always shaded. The degree of the h-polynomial in
![]() $q_{J,i}$
and
$q_{J,i}$
and
![]() $p_{J,i}$
is the number of unshaded boxes, plus one. Once the pointer crosses the red line (i.e., reaches the minimum element of J), the definition of
$p_{J,i}$
is the number of unshaded boxes, plus one. Once the pointer crosses the red line (i.e., reaches the minimum element of J), the definition of
![]() $q_{J,i}$
and
$q_{J,i}$
and
![]() $p_{J,i}$
involves derivatives. The pointer points to shaded boxes to the left of the right line, and an unshaded box or
$p_{J,i}$
involves derivatives. The pointer points to shaded boxes to the left of the right line, and an unshaded box or
![]() $\theta $
box to the right of the red line. The
$\theta $
box to the right of the red line. The
![]() $\theta $
decoration with an
$\theta $
decoration with an
![]() $\times $
corresponds to an unused
$\times $
corresponds to an unused
![]() $\theta $
-variable
$\theta $
-variable
![]() $\theta _s$
in the case of
$\theta _s$
in the case of
![]() $q_{J,i}$
, or a partial derivative
$q_{J,i}$
, or a partial derivative
![]() $\partial _s$
in the case of
$\partial _s$
in the case of
![]() $p_{J,i}$
. The
$p_{J,i}$
. The
![]() $\times $
appears on the closest
$\times $
appears on the closest
![]() $\theta $
which is weakly to the left of the pointer.
$\theta $
which is weakly to the left of the pointer.
We will be interested in the projections of the
![]() $q_{J,i}$
to
$q_{J,i}$
to
![]() ${\mathbb {C}}[{\mathbf {x}}_n] \cdot \theta _J$
. To this end, define polynomials
${\mathbb {C}}[{\mathbf {x}}_n] \cdot \theta _J$
. To this end, define polynomials
![]() $(p_{J,1}, p_{J,2}, \dots , p_{J,n}) \in {\mathbb {C}}[{\mathbf {x}}_n]$
by the rule
$(p_{J,1}, p_{J,2}, \dots , p_{J,n}) \in {\mathbb {C}}[{\mathbf {x}}_n]$
by the rule
 $$ \begin{align} p_{J,i} = \begin{cases} h_i(i, i+1, \dots, n\}) & i < \min(J) \\ \partial_s( h_r(J \cup \{i+1, \dots, n\})) & s = \max(J \cap \{1, \dots, i\}), \end{cases} \end{align} $$
$$ \begin{align} p_{J,i} = \begin{cases} h_i(i, i+1, \dots, n\}) & i < \min(J) \\ \partial_s( h_r(J \cup \{i+1, \dots, n\})) & s = \max(J \cap \{1, \dots, i\}), \end{cases} \end{align} $$
where (as in the definition of
![]() $q_{J,i}$
) in the second branch
$q_{J,i}$
) in the second branch
![]() $r := n - |J \cup \{i+1, \dots , n\}| + 1$
. As with the superspace elements
$r := n - |J \cup \{i+1, \dots , n\}| + 1$
. As with the superspace elements
![]() $q_{J,i}$
, the polynomials
$q_{J,i}$
, the polynomials
![]() $p_{J,i}$
are easily visualized using the pointer construction. The index s on the partial derivative operator
$p_{J,i}$
are easily visualized using the pointer construction. The index s on the partial derivative operator
![]() $\partial _s$
is the maximal element of j weakly to the left of the pointer. As the pointer moves from left to right, the degree of the h-polynomial increases and its number of arguments decreases. When
$\partial _s$
is the maximal element of j weakly to the left of the pointer. As the pointer moves from left to right, the degree of the h-polynomial increases and its number of arguments decreases. When
![]() $n = 7$
and
$n = 7$
and
![]() $J = \{3,5,6\}$
, Figure 1 yields
$J = \{3,5,6\}$
, Figure 1 yields
By Lemma 3.2 (3), we have
for all subsets
![]() $J \subseteq [n]$
and
$J \subseteq [n]$
and
![]() $1 \leq i \leq n$
. The polynomials
$1 \leq i \leq n$
. The polynomials
![]() $p_{J,i} \in {\mathbb {C}}[{\mathbf {x}}_n]$
are the ‘Gale-leading terms’ of the
$p_{J,i} \in {\mathbb {C}}[{\mathbf {x}}_n]$
are the ‘Gale-leading terms’ of the
![]() $q_{J,i} \in \Omega _n$
and will give us access to the tools of classical commutative algebra in
$q_{J,i} \in \Omega _n$
and will give us access to the tools of classical commutative algebra in
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
. In particular, we will prove that
${\mathbb {C}}[{\mathbf {x}}_n]$
. In particular, we will prove that
![]() $p_{J,1}, \dots , p_{J,n}$
is a regular sequence in
$p_{J,1}, \dots , p_{J,n}$
is a regular sequence in
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
as long as
${\mathbb {C}}[{\mathbf {x}}_n]$
as long as
![]() $1 \notin J$
. Our first step in doing so is an identity involving partial derivatives of homogeneous symmetric polynomials in partial variable sets.
$1 \notin J$
. Our first step in doing so is an identity involving partial derivatives of homogeneous symmetric polynomials in partial variable sets.
Lemma 3.3. If
![]() $S \subseteq [n]$
is any subset with
$S \subseteq [n]$
is any subset with
![]() $a,b \in S$
and
$a,b \in S$
and
![]() $c \notin S$
, then
$c \notin S$
, then
for all
![]() $r> 1$
.
$r> 1$
.
In Lemma 3.3, we allow the possibility
![]() $a = b$
, in which case the claimed equation is trivial.
$a = b$
, in which case the claimed equation is trivial.
Proof. The RHS of Equation (3.9) may be expanded and regrouped to give
 $$ \begin{align} &\partial_b h_r(S) + (x_c - x_b) \partial_b h_{r-1}(S \cup c) - (x_c - x_a) \partial_a h_{r-1}(S \cup c) = \nonumber\\ &\quad \left[ \partial_b (h_r(S) + x_c h_{r-1}(S \cup c)) - \partial_a(x_c h_{r-1}(S \cup c)) \right] - [x_b \partial_b h_{r-1}(S \cup c)] + [x_a \partial_a h_{r-1}(S \cup c)]. \end{align} $$
$$ \begin{align} &\partial_b h_r(S) + (x_c - x_b) \partial_b h_{r-1}(S \cup c) - (x_c - x_a) \partial_a h_{r-1}(S \cup c) = \nonumber\\ &\quad \left[ \partial_b (h_r(S) + x_c h_{r-1}(S \cup c)) - \partial_a(x_c h_{r-1}(S \cup c)) \right] - [x_b \partial_b h_{r-1}(S \cup c)] + [x_a \partial_a h_{r-1}(S \cup c)]. \end{align} $$
Since
![]() $h_r(S) + x_c h_{r-1}(S \cup c) = h_r(S \cup c)$
, the expression in the first set of brackets
$h_r(S) + x_c h_{r-1}(S \cup c) = h_r(S \cup c)$
, the expression in the first set of brackets
![]() $[ \, \cdots ]$
on the RHS of Equation (3.10) equals
$[ \, \cdots ]$
on the RHS of Equation (3.10) equals
![]() $[\partial _b h_r(S \cup c) - \partial _a h_r(S \cup c) + \partial _a h_r(S)]$
, the expression in the second set of brackets equals
$[\partial _b h_r(S \cup c) - \partial _a h_r(S \cup c) + \partial _a h_r(S)]$
, the expression in the second set of brackets equals
![]() $[ \partial _b (x_b h_{r-1}(S \cup c)) - h_{r-1}(S \cup c) ]$
, and the expression in the third set of brackets equals
$[ \partial _b (x_b h_{r-1}(S \cup c)) - h_{r-1}(S \cup c) ]$
, and the expression in the third set of brackets equals
![]() $ [ \partial _a (x_a h_{r-1}(S \cup c)) - h_{r-1}(S \cup c)]$
. Plugging all this in yields
$ [ \partial _a (x_a h_{r-1}(S \cup c)) - h_{r-1}(S \cup c)]$
. Plugging all this in yields

with the indicated cancellations. After performing these cancellations, the RHS of Equation (3.11) may be regrouped as
 $$ \begin{align} [\partial_b h_r(S \cup c) - \partial_a h_r(S \cup c) + \partial_a h_r(S)] - [ \partial_b (x_b h_{r-1}(S \cup c))] + [ \partial_a (x_a h_{r-1}(S \cup c))] \nonumber\\ = \partial_a h_r(S) + \left\{ \partial_b (h_r(S \cup c) - x_b h_{r-1}(S \cup c)) \right\} - \left\{ \partial_a(h_r(S \cup c) - x_a h_{r-1}(S \cup c)) \right\}. \end{align} $$
$$ \begin{align} [\partial_b h_r(S \cup c) - \partial_a h_r(S \cup c) + \partial_a h_r(S)] - [ \partial_b (x_b h_{r-1}(S \cup c))] + [ \partial_a (x_a h_{r-1}(S \cup c))] \nonumber\\ = \partial_a h_r(S) + \left\{ \partial_b (h_r(S \cup c) - x_b h_{r-1}(S \cup c)) \right\} - \left\{ \partial_a(h_r(S \cup c) - x_a h_{r-1}(S \cup c)) \right\}. \end{align} $$
Since the expression
![]() $h_r(S \cup c) - x_b h_{r-1}(S \cup c) = h_r( (S \cup c) - b )$
is independent of
$h_r(S \cup c) - x_b h_{r-1}(S \cup c) = h_r( (S \cup c) - b )$
is independent of
![]() $x_b$
, the partial derivative
$x_b$
, the partial derivative
![]() $\partial _b$
in the first set of curly braces
$\partial _b$
in the first set of curly braces
![]() $\{ \, \cdots \}$
on the RHS of Equation (3.12) vanishes; the expression in the second set of curly braces vanishes for similar reasons. This completes the proof of Equation (3.9).
$\{ \, \cdots \}$
on the RHS of Equation (3.12) vanishes; the expression in the second set of curly braces vanishes for similar reasons. This completes the proof of Equation (3.9).
The polynomial identity in Lemma 3.3 is, to the authors, somewhat miraculous; it would be nice to have a conceptual understanding of ‘why’ it should be true. We use this identity to show that the ideal
![]() ${\mathcal {I}}_J$
generated by the polynomials
${\mathcal {I}}_J$
generated by the polynomials
![]() $p_{J,1}, \dots , p_{J,n} \in {\mathbb {C}}[{\mathbf {x}}_n]$
contains certain strategic partial derivatives.
$p_{J,1}, \dots , p_{J,n} \in {\mathbb {C}}[{\mathbf {x}}_n]$
contains certain strategic partial derivatives.
Lemma 3.4. Let
![]() $J \subseteq [n]$
and write
$J \subseteq [n]$
and write
![]() ${\mathcal {I}}_J = (p_{J,1}, \dots , p_{J,n}) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
for the ideal generated by
${\mathcal {I}}_J = (p_{J,1}, \dots , p_{J,n}) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
for the ideal generated by
![]() $p_{J,1}, \dots , p_{J,n}$
. For any index
$p_{J,1}, \dots , p_{J,n}$
. For any index
![]() $j \in J$
, we have
$j \in J$
, we have
![]() $\partial _j h_{n-|J|+1}(J) \in {\mathcal {I}}_J$
.
$\partial _j h_{n-|J|+1}(J) \in {\mathcal {I}}_J$
.
Proof. We prove the following claim, which is stronger than the lemma and amenable to induction.
Claim: The polynomials in question lie in the ideal
where
![]() $j_0 = \min (J)$
is the smallest element of J.
$j_0 = \min (J)$
is the smallest element of J.
The pointer construction makes it clear that the generators of
![]() ${\mathcal {I}}^{\prime }_J$
do not involve the variables
${\mathcal {I}}^{\prime }_J$
do not involve the variables
![]() $x_1, x_2, \dots , x_{j_0 - 1}$
and so lie in the polynomial ring
$x_1, x_2, \dots , x_{j_0 - 1}$
and so lie in the polynomial ring
![]() ${\mathbb {C}}[x_{j_0}, x_{j_0 + 1}, \dots , x_n]$
generated by the remaining variables. We prove the Claim by induction on the number
${\mathbb {C}}[x_{j_0}, x_{j_0 + 1}, \dots , x_n]$
generated by the remaining variables. We prove the Claim by induction on the number
![]() $n - j_0 + 1$
of variables in the ambient ring of
$n - j_0 + 1$
of variables in the ambient ring of
![]() ${\mathcal {I}}^{\prime }_J$
.
${\mathcal {I}}^{\prime }_J$
.
If
![]() $J = \{n-r+1, \dots , n-1, n\}$
is a terminal subset of
$J = \{n-r+1, \dots , n-1, n\}$
is a terminal subset of
![]() $[n]$
, the polynomials in the Claim are generators of the ideal
$[n]$
, the polynomials in the Claim are generators of the ideal
![]() ${\mathcal {I}}^{\prime }_J$
. Furthermore, for any subset
${\mathcal {I}}^{\prime }_J$
. Furthermore, for any subset
![]() $J \subseteq [n]$
, if
$J \subseteq [n]$
, if
![]() $j = \max (J)$
is the largest element of J, then
$j = \max (J)$
is the largest element of J, then
![]() $\partial _j h_{n-|J|+1}(J) = p_{J,n}$
is also a generator of
$\partial _j h_{n-|J|+1}(J) = p_{J,n}$
is also a generator of
![]() ${\mathcal {I}}^{\prime }_J$
.
${\mathcal {I}}^{\prime }_J$
.
By the above paragraph, we may assume that
![]() $j_0 = \min (J) \neq \max (J)$
and that there exists an element
$j_0 = \min (J) \neq \max (J)$
and that there exists an element
![]() $c \in [n] - J$
with
$c \in [n] - J$
with
![]() $c> j_0$
. Let
$c> j_0$
. Let
![]() $c_0 := \min \{ j_0 < c \leq n \,:\, c \notin J \}$
be the smallest such c and define
$c_0 := \min \{ j_0 < c \leq n \,:\, c \notin J \}$
be the smallest such c and define
![]() $S \subseteq [n]$
by
$S \subseteq [n]$
by
Observe that the elements
![]() $j_0, j_0 + 1, \dots , c_0 - 2, c_0 - 1$
of S lie in J. Let
$j_0, j_0 + 1, \dots , c_0 - 2, c_0 - 1$
of S lie in J. Let
![]() $r := n - |S| + 1$
. We apply Lemma 3.3 iteratively as follows.
$r := n - |S| + 1$
. We apply Lemma 3.3 iteratively as follows.
-
• Since
 $\partial _{c_0 - 1} h_r(S), \partial _{c_0 - 1} h_{r-1}(S \cup c_0), \partial _{c_0 - 2}(S \cup c_0) \in {\mathcal {I}}^{\prime }_J$
, Lemma 3.3 with
$\partial _{c_0 - 1} h_r(S), \partial _{c_0 - 1} h_{r-1}(S \cup c_0), \partial _{c_0 - 2}(S \cup c_0) \in {\mathcal {I}}^{\prime }_J$
, Lemma 3.3 with
 $a = c_0 - 2, b = c_0 - 1$
, and
$a = c_0 - 2, b = c_0 - 1$
, and
 $c = c_0$
implies
$c = c_0$
implies
 $\partial _{c_0 - 2} h_r(S) \in {\mathcal {I}}^{\prime }_J$
.
$\partial _{c_0 - 2} h_r(S) \in {\mathcal {I}}^{\prime }_J$
. -
• Since
 $\partial _{c_0 - 2} h_r(S), \partial _{c_0 - 2} h_{r-1}(S \cup c_0), \partial _{c_0 - 3}(S \cup c_0) \in {\mathcal {I}}^{\prime }_J$
, Lemma 3.3 with
$\partial _{c_0 - 2} h_r(S), \partial _{c_0 - 2} h_{r-1}(S \cup c_0), \partial _{c_0 - 3}(S \cup c_0) \in {\mathcal {I}}^{\prime }_J$
, Lemma 3.3 with
 $a = c_0 - 3, b = c_0 - 2,$
and
$a = c_0 - 3, b = c_0 - 2,$
and
 $c = c_0$
implies
$c = c_0$
implies
 $\partial _{c_0 - 3} h_r(S) \in {\mathcal {I}}^{\prime }_J$
.
$\partial _{c_0 - 3} h_r(S) \in {\mathcal {I}}^{\prime }_J$
. -
• Since
 $\partial _{c_0 - 3} h_r(S), \partial _{c_0 - 3} h_{r-1}(S \cup c_0), \partial _{c_0 - 4}(S \cup c_0) \in {\mathcal {I}}^{\prime }_J$
, Lemma 3.3 with
$\partial _{c_0 - 3} h_r(S), \partial _{c_0 - 3} h_{r-1}(S \cup c_0), \partial _{c_0 - 4}(S \cup c_0) \in {\mathcal {I}}^{\prime }_J$
, Lemma 3.3 with
 $a = c_0 - 3, b = c_0 - 2,$
and
$a = c_0 - 3, b = c_0 - 2,$
and
 $c = c_0$
implies
$c = c_0$
implies
 $\partial _{c_0 - 4} h_r(S) \in {\mathcal {I}}^{\prime }_J$
, and so on.
$\partial _{c_0 - 4} h_r(S) \in {\mathcal {I}}^{\prime }_J$
, and so on.
We see that the polynomials
lie in
![]() ${\mathcal {I}}^{\prime }_J$
so that
${\mathcal {I}}^{\prime }_J$
so that
as ideals in
![]() ${\mathbb {C}}[x_{j_0}, x_{j_0 + 1}, \dots , x_n]$
. But the generators on the ideal on the LHS of (3.16) do not involve the variable
${\mathbb {C}}[x_{j_0}, x_{j_0 + 1}, \dots , x_n]$
. But the generators on the ideal on the LHS of (3.16) do not involve the variable
![]() $x_{c_0}$
. In fact, if we consider the variable set
$x_{c_0}$
. In fact, if we consider the variable set
obtained from our old variable set
![]() $(x_{j_0}, x_{j_0 + 1}, \dots , x_n)$
by removing
$(x_{j_0}, x_{j_0 + 1}, \dots , x_n)$
by removing
![]() $x_{c_0}$
, then
$x_{c_0}$
, then
as ideals in
![]() ${\mathbb {C}}[{\mathbf {x}}]$
where
${\mathbb {C}}[{\mathbf {x}}]$
where
![]() $J' = (J - j_0) \cup c_0$
is the corresponding cyclic rotation of the set J. Since the variable set
$J' = (J - j_0) \cup c_0$
is the corresponding cyclic rotation of the set J. Since the variable set
![]() ${\mathbf {x}}$
contains fewer variables than the original set
${\mathbf {x}}$
contains fewer variables than the original set
![]() $\{ x_{j_0}, x_{j_0 + 1}, \dots , x_n \}$
, we are done by induction.
$\{ x_{j_0}, x_{j_0 + 1}, \dots , x_n \}$
, we are done by induction.
An example may help clarify Lemma 3.4 and its proof. Suppose
![]() $n = 7$
and
$n = 7$
and
![]() $J = \{3,5,6\}$
. We have
$J = \{3,5,6\}$
. We have
![]() ${\mathcal {I}}_J = (p_{J,1}, \dots , p_{J,7})$
, where
${\mathcal {I}}_J = (p_{J,1}, \dots , p_{J,7})$
, where
Our aim is to show that the ideal
![]() ${\mathcal {I}}_J$
contains the elements
${\mathcal {I}}_J$
contains the elements
To this end, we reason as follows.
-
• The element
 $\partial _6 h_5(356) = p_{J,7}$
is a generator of
$\partial _6 h_5(356) = p_{J,7}$
is a generator of
 ${\mathcal {I}}_J$
. This was one of the desired memberships.
${\mathcal {I}}_J$
. This was one of the desired memberships. -
• Since
 $\partial _3 h_3(34567) = p_{J,3}, \partial _3 h_4(3567) = p_{J,4},$
and
$\partial _3 h_3(34567) = p_{J,3}, \partial _3 h_4(3567) = p_{J,4},$
and
 $\partial _5 h_4(3567) = p_{J,5}$
are elements of
$\partial _5 h_4(3567) = p_{J,5}$
are elements of
 ${\mathcal {I}}_J$
, Lemma 3.3 with
${\mathcal {I}}_J$
, Lemma 3.3 with
 $S = \{3,5,6,7\}, a = 3, b = 5$
and
$S = \{3,5,6,7\}, a = 3, b = 5$
and
 $c = 4$
implies
$c = 4$
implies
 $\partial _3 h_4(3567) \in {\mathcal {I}}_J$
.
$\partial _3 h_4(3567) \in {\mathcal {I}}_J$
. -
• Since
 $\partial _3 h_4(3567), \partial _6 h_4(3567) = p_{J,6},$
and
$\partial _3 h_4(3567), \partial _6 h_4(3567) = p_{J,6},$
and
 $\partial _6 h_5(356)$
are elements of
$\partial _6 h_5(356)$
are elements of
 ${\mathcal {I}}_J$
, Lemma 3.3 with
${\mathcal {I}}_J$
, Lemma 3.3 with
 ${S = \{3,5,6\}, a = 3, b = 6}$
and
${S = \{3,5,6\}, a = 3, b = 6}$
and
 $c = 7$
implies
$c = 7$
implies
 $\partial _3 h_5(356) \in {\mathcal {I}}_J$
. This was one of the desired memberships.
$\partial _3 h_5(356) \in {\mathcal {I}}_J$
. This was one of the desired memberships. -
• Since
 $\partial _5 h_4(3567) = p_{J,5}, \partial _6 h_4(3567) = p_{J,6}, \partial _6 h_5(356) \in {\mathcal {I}}_J$
, Lemma 3.3 with
$\partial _5 h_4(3567) = p_{J,5}, \partial _6 h_4(3567) = p_{J,6}, \partial _6 h_5(356) \in {\mathcal {I}}_J$
, Lemma 3.3 with
 $S = \{3,5,6\}, a = 5, b = 6$
and
$S = \{3,5,6\}, a = 5, b = 6$
and
 $c = 7$
implies
$c = 7$
implies
 $\partial _5 h_5(356) \in {\mathcal {I}}_J$
. This was the remaining desired membership.
$\partial _5 h_5(356) \in {\mathcal {I}}_J$
. This was the remaining desired membership.
Observe that we did not use the generators
![]() $p_{J,1}, p_{J,2} \in {\mathcal {I}}_J$
to derive these memberships, so that in fact we showed membership in the smaller ideal
$p_{J,1}, p_{J,2} \in {\mathcal {I}}_J$
to derive these memberships, so that in fact we showed membership in the smaller ideal
Lemma 3.5. Let
![]() $J \subseteq [n]$
with
$J \subseteq [n]$
with
![]() ${\mathrm {st}}(J) = ({\mathrm {st}}(J)_1, \dots , {\mathrm {st}}(J)_n)$
. If
${\mathrm {st}}(J) = ({\mathrm {st}}(J)_1, \dots , {\mathrm {st}}(J)_n)$
. If
![]() $1 \notin J$
, the sequence of polynomials
$1 \notin J$
, the sequence of polynomials
![]() $p_{J,1}, \dots , p_{J,n}$
is a regular sequence in
$p_{J,1}, \dots , p_{J,n}$
is a regular sequence in
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
of homogeneous degrees
${\mathbb {C}}[{\mathbf {x}}_n]$
of homogeneous degrees
![]() ${\mathrm {st}}(J)_1, \dots , {\mathrm {st}}(J)_n$
.
${\mathrm {st}}(J)_1, \dots , {\mathrm {st}}(J)_n$
.
If
![]() $1 \in J$
, then
$1 \in J$
, then
![]() $p_{J,1} = \partial _1 h_1(x_1, \dots , x_n) = \partial _1 (x_1 + \cdots + x_n) = 1$
is a unit in
$p_{J,1} = \partial _1 h_1(x_1, \dots , x_n) = \partial _1 (x_1 + \cdots + x_n) = 1$
is a unit in
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
. Correspondingly, we have
${\mathbb {C}}[{\mathbf {x}}_n]$
. Correspondingly, we have
![]() ${\mathrm {st}}(J)_1 = 0$
. Since members of regular sequences are required to be of positive homogeneous degree, we must exclude this case from Lemma 3.5.
${\mathrm {st}}(J)_1 = 0$
. Since members of regular sequences are required to be of positive homogeneous degree, we must exclude this case from Lemma 3.5.
Proof. Since
![]() $1 \notin J$
, the sequence
$1 \notin J$
, the sequence
![]() ${\mathrm {st}}(J)$
has positive entries. The assertion on degrees is Lemma 3.2 (2). As in Lemma 3.4, let
${\mathrm {st}}(J)$
has positive entries. The assertion on degrees is Lemma 3.2 (2). As in Lemma 3.4, let
![]() ${\mathcal {I}}_J = ( p_{J,1}, \dots , p_{J,n} ) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
. By Lemma 2.2, it is enough to show that the variety
${\mathcal {I}}_J = ( p_{J,1}, \dots , p_{J,n} ) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
. By Lemma 2.2, it is enough to show that the variety
![]() ${\mathbf {V}}({\mathcal {I}}) \subseteq {\mathbb {C}}^n$
cut out by
${\mathbf {V}}({\mathcal {I}}) \subseteq {\mathbb {C}}^n$
cut out by
![]() ${\mathcal {I}}$
consists of
${\mathcal {I}}$
consists of
![]() $\{ 0 \}$
alone. We use elimination to focus on coordinates in
$\{ 0 \}$
alone. We use elimination to focus on coordinates in
![]() ${\mathbb {C}}^n$
indexed by J.
${\mathbb {C}}^n$
indexed by J.
Swanson and Wallach proved [Reference Swanson and Wallach37, Lem. 6.2] that that the polynomials
![]() $\partial _j h_{n-|J|+1}(J)$
for
$\partial _j h_{n-|J|+1}(J)$
for
![]() $j \in J$
have no common zero in
$j \in J$
have no common zero in
![]() ${\mathbb {C}}^J$
. By Lemma 3.4, for any locus point
${\mathbb {C}}^J$
. By Lemma 3.4, for any locus point
![]() $a = (a_1, \dots , a_n) \in {\mathbf {V}}({\mathcal {I}}_J)$
, we must have
$a = (a_1, \dots , a_n) \in {\mathbf {V}}({\mathcal {I}}_J)$
, we must have
![]() $a_j = 0$
for any
$a_j = 0$
for any
![]() $j \in J$
. Setting the variables
$j \in J$
. Setting the variables
![]() $\{x_j \,:\, j \in J \}$
to zero in the remaining polynomials
$\{x_j \,:\, j \in J \}$
to zero in the remaining polynomials
gives a sequence of positive degree homogeneous polynomials in
![]() ${\mathbb {C}}[x_i \,:\, i \notin J]$
which are easily seen to be triangular. We conclude that
${\mathbb {C}}[x_i \,:\, i \notin J]$
which are easily seen to be triangular. We conclude that
![]() $a_i = 0$
for
$a_i = 0$
for
![]() $i \notin J$
, so that
$i \notin J$
, so that
![]() $a = 0$
as required.
$a = 0$
as required.
Lemma 3.5 implies that the quotient ring
![]() ${\mathbb {C}}[{\mathbf {x}}_n]/(p_{J,1}, \dots , p_{J,n})$
has Hilbert series
${\mathbb {C}}[{\mathbf {x}}_n]/(p_{J,1}, \dots , p_{J,n})$
has Hilbert series
This formula remains true when
![]() $1 \in J$
, for then
$1 \in J$
, for then
![]() $p_{J,1} = 1$
and
$p_{J,1} = 1$
and
![]() ${\mathbb {C}}[{\mathbf {x}}_n]/(p_{J,1}, \dots , p_{J,n}) = 0$
. In particular, there exists a set
${\mathbb {C}}[{\mathbf {x}}_n]/(p_{J,1}, \dots , p_{J,n}) = 0$
. In particular, there exists a set
![]() ${\mathcal {B}}_n(J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
of homogeneous polynomials with degree generating function
${\mathcal {B}}_n(J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
of homogeneous polynomials with degree generating function
![]() $[{\mathrm {st}}(J)_1]_q \cdots [{\mathrm {st}}(J)_n]_q$
such that
$[{\mathrm {st}}(J)_1]_q \cdots [{\mathrm {st}}(J)_n]_q$
such that
![]() ${\mathcal {B}}_n(J)$
descends to a vector space basis of
${\mathcal {B}}_n(J)$
descends to a vector space basis of
![]() ${\mathbb {C}}[{\mathbf {x}}_n]/(p_{J,1}, \dots , p_{J,n})$
.
${\mathbb {C}}[{\mathbf {x}}_n]/(p_{J,1}, \dots , p_{J,n})$
.
3.2 An abstract straightening lemma
The proof of Lemma 3.5 relied on a a tricky induction in Lemma 3.4 and miraculous polynomial identity in Lemma 3.3. Our next result should persuade the reader that Lemma 3.5 was worth the effort.
Lemma 3.6. (Straightening)
Let
![]() $J \subseteq [n]$
with
$J \subseteq [n]$
with
![]() ${\mathrm {st}}(J) = ({\mathrm {st}}(J)_1, \dots , {\mathrm {st}}(J)_n)$
. There exists a finite set
${\mathrm {st}}(J) = ({\mathrm {st}}(J)_1, \dots , {\mathrm {st}}(J)_n)$
. There exists a finite set
![]() ${\mathcal {B}}_n(J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
of nonzero homogeneous polynomials with degree generating function
${\mathcal {B}}_n(J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
of nonzero homogeneous polynomials with degree generating function
such that for any polynomial
![]() $f \in {\mathbb {C}}[{\mathbf {x}}_n]$
, we have an expression of the form
$f \in {\mathbb {C}}[{\mathbf {x}}_n]$
, we have an expression of the form
 $$ \begin{align} f \cdot \theta_J = \left(\sum_{m\in {\mathcal{B}}_n(J)} c_{f,m} \cdot m \cdot \theta_J \right) + g + \Sigma, \end{align} $$
$$ \begin{align} f \cdot \theta_J = \left(\sum_{m\in {\mathcal{B}}_n(J)} c_{f,m} \cdot m \cdot \theta_J \right) + g + \Sigma, \end{align} $$
where
-
• the
 $c_{f,m} \in {\mathbb {C}}$
are constants which depend on f and m,
$c_{f,m} \in {\mathbb {C}}$
are constants which depend on f and m, -
• the element
 $g \in SI_n$
lies in the supercoinvariant ideal, and
$g \in SI_n$
lies in the supercoinvariant ideal, and -
• the ‘error term’
 $\Sigma $
lies in
$\Sigma $
lies in
 $\bigoplus _{J <_{{\mathrm {Gale}}} K} {\mathbb {C}}[{\mathbf {x}}_n] \cdot \theta _K$
.
$\bigoplus _{J <_{{\mathrm {Gale}}} K} {\mathbb {C}}[{\mathbf {x}}_n] \cdot \theta _K$
.
Proof. As explained after Lemma 3.5, there exists a set
![]() ${\mathcal {B}}_n(J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
of homogeneous polynomials with the given degree generating function which descends to a vector space basis of
${\mathcal {B}}_n(J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
of homogeneous polynomials with the given degree generating function which descends to a vector space basis of
![]() ${\mathbb {C}}[{\mathbf {x}}_n]/(p_{J,1}, \dots , p_{J,n})$
. We prove that
${\mathbb {C}}[{\mathbf {x}}_n]/(p_{J,1}, \dots , p_{J,n})$
. We prove that
![]() ${\mathcal {B}}_n(J)$
satisfies the conditions of the lemma.
${\mathcal {B}}_n(J)$
satisfies the conditions of the lemma.
The given polynomial
![]() $f \in {\mathbb {C}}[{\mathbf {x}}_n]$
may be written as
$f \in {\mathbb {C}}[{\mathbf {x}}_n]$
may be written as
 $$ \begin{align} f = \left( \sum_{m \in {\mathcal{B}}_n(J)} c_{f,m} \cdot m \right) + \sum_{j = 1}^n A_j \cdot p_{J,j} \end{align} $$
$$ \begin{align} f = \left( \sum_{m \in {\mathcal{B}}_n(J)} c_{f,m} \cdot m \right) + \sum_{j = 1}^n A_j \cdot p_{J,j} \end{align} $$
for some scalars
![]() $c_{f,m} \in {\mathbb {C}}$
and polynomials
$c_{f,m} \in {\mathbb {C}}$
and polynomials
![]() $A_j \in {\mathbb {C}}[{\mathbf {x}}_n]$
. Multiplying both sides of Equation (3.23) by
$A_j \in {\mathbb {C}}[{\mathbf {x}}_n]$
. Multiplying both sides of Equation (3.23) by
![]() $\theta _J$
yields
$\theta _J$
yields
 $$ \begin{align} f \cdot \theta_J = \left( \sum_{m \in {\mathcal{B}}_n(J)} c_{f,m} \cdot m \cdot \theta_J \right) + \sum_{j = 1}^n A_j \cdot p_{I,j} \cdot \theta_J. \end{align} $$
$$ \begin{align} f \cdot \theta_J = \left( \sum_{m \in {\mathcal{B}}_n(J)} c_{f,m} \cdot m \cdot \theta_J \right) + \sum_{j = 1}^n A_j \cdot p_{I,j} \cdot \theta_J. \end{align} $$
Equation (3.8) gives the relation
 $$ \begin{align} f \cdot \theta_J \equiv \left( \sum_{m \in {\mathcal{B}}_n(J)} c_{f,m} \cdot m \cdot \theta_J \right) + \sum_{j = 1}^n \pm A_j \cdot q_{J,j} \quad\mod \bigoplus_{J <_{\mathrm {Gale}} K} {\mathbb {C}}[{\mathbf {x}}_n] \cdot \theta_K \end{align} $$
$$ \begin{align} f \cdot \theta_J \equiv \left( \sum_{m \in {\mathcal{B}}_n(J)} c_{f,m} \cdot m \cdot \theta_J \right) + \sum_{j = 1}^n \pm A_j \cdot q_{J,j} \quad\mod \bigoplus_{J <_{\mathrm {Gale}} K} {\mathbb {C}}[{\mathbf {x}}_n] \cdot \theta_K \end{align} $$
modulo the linear subspace
![]() $\bigoplus _{J <_{\mathrm {Gale}} K} {\mathbb {C}}[{\mathbf {x}}_n] \cdot \theta _K$
of
$\bigoplus _{J <_{\mathrm {Gale}} K} {\mathbb {C}}[{\mathbf {x}}_n] \cdot \theta _K$
of
![]() $\Omega _n$
. Finally, Lemma 3.2 (1) implies the membership
$\Omega _n$
. Finally, Lemma 3.2 (1) implies the membership
![]() $g := \sum _{j = 1}^n \pm A_j \cdot q_{J,j} \in SI_n$
, which completes the proof.
$g := \sum _{j = 1}^n \pm A_j \cdot q_{J,j} \in SI_n$
, which completes the proof.
Lemma 3.6 implies that the set
![]() ${\mathcal {B}}_n \subseteq \Omega _n$
of superspace elements given by
${\mathcal {B}}_n \subseteq \Omega _n$
of superspace elements given by
descends to a spanning set in
![]() $SR_n$
. Indeed, if this were not the case, let
$SR_n$
. Indeed, if this were not the case, let
![]() $J \subseteq [n]$
be a Gale-maximal subset such that
$J \subseteq [n]$
be a Gale-maximal subset such that
![]() $f \cdot \theta _J \in \Omega _n$
does not lie in the span of
$f \cdot \theta _J \in \Omega _n$
does not lie in the span of
![]() ${\mathcal {B}}_n$
modulo
${\mathcal {B}}_n$
modulo
![]() $SI_n$
for some
$SI_n$
for some
![]() $f \in {\mathbb {C}}[{\mathbf {x}}_n]$
. Lemma 3.6 implies that
$f \in {\mathbb {C}}[{\mathbf {x}}_n]$
. Lemma 3.6 implies that
 $$ \begin{align} f \cdot \theta_J \equiv \left(\sum_{m\in {\mathcal{B}}_n(J)} c_{f,m} \cdot m \cdot \theta_J \right) + \Sigma \qquad \mod SI_n \end{align} $$
$$ \begin{align} f \cdot \theta_J \equiv \left(\sum_{m\in {\mathcal{B}}_n(J)} c_{f,m} \cdot m \cdot \theta_J \right) + \Sigma \qquad \mod SI_n \end{align} $$
for some constants
![]() $c_{f,m} \in {\mathbb {C}}$
where
$c_{f,m} \in {\mathbb {C}}$
where
![]() $\Sigma \in \bigoplus _{J <_{{\mathrm {Gale}}} K} {\mathbb {C}}[{\mathbf {x}}_n] \cdot \theta _K$
. The term in the parentheses certainly lies in the span of
$\Sigma \in \bigoplus _{J <_{{\mathrm {Gale}}} K} {\mathbb {C}}[{\mathbf {x}}_n] \cdot \theta _K$
. The term in the parentheses certainly lies in the span of
![]() ${\mathcal {B}}_n$
. The Gale-maximality of J implies that
${\mathcal {B}}_n$
. The Gale-maximality of J implies that
![]() $\Sigma $
lies in the span of
$\Sigma $
lies in the span of
![]() ${\mathcal {B}}_n$
, as well, giving a contradiction.
${\mathcal {B}}_n$
, as well, giving a contradiction.
The straightening result of Lemma 3.6 is rather abstract in that it does not give a formula for the polynomials in
![]() ${\mathcal {B}}_n(J)$
. While any generic set of polynomials of the appropriate degrees will do, the authors are unaware of an explicit formula for the set
${\mathcal {B}}_n(J)$
. While any generic set of polynomials of the appropriate degrees will do, the authors are unaware of an explicit formula for the set
![]() ${\mathcal {B}}_n(J)$
. In general, objects related to
${\mathcal {B}}_n(J)$
. In general, objects related to
![]() $SR_n$
have resisted analysis by Gröbner-theoretic techniques, which is reflected in the abstract statement of Lemma 3.6.
$SR_n$
have resisted analysis by Gröbner-theoretic techniques, which is reflected in the abstract statement of Lemma 3.6.
Lemma 3.6 implies an upper bound for the bigraded Hilbert series of
![]() $SR_n$
. Given two polynomials
$SR_n$
. Given two polynomials
![]() $f(q,z), g(q,z)$
in variables
$f(q,z), g(q,z)$
in variables
![]() $q, z$
, we write
$q, z$
, we write
![]() $f \leq g$
to mean that
$f \leq g$
to mean that
![]() $g - f$
is a polynomial in
$g - f$
is a polynomial in
![]() $q,z$
with nonnegative coefficients.
$q,z$
with nonnegative coefficients.
Proposition 3.7. The bigraded Hilbert series
![]() ${\mathrm {Hilb}}(SR_n;q,z)$
is bounded above by
${\mathrm {Hilb}}(SR_n;q,z)$
is bounded above by
 $$ \begin{align} {\mathrm {Hilb}}(SR_n;q,z) \leq \sum_{J \subseteq [n]} z^{|J|} \sum_{f \in {\mathcal{B}}_n(J)} q^{\deg(f)} = \sum_{k = 1}^n z^{n-k} \cdot [k]!_q \cdot {\mathrm {Stir}}_q(n,k). \end{align} $$
$$ \begin{align} {\mathrm {Hilb}}(SR_n;q,z) \leq \sum_{J \subseteq [n]} z^{|J|} \sum_{f \in {\mathcal{B}}_n(J)} q^{\deg(f)} = \sum_{k = 1}^n z^{n-k} \cdot [k]!_q \cdot {\mathrm {Stir}}_q(n,k). \end{align} $$
Proof. As explained above, Lemma 3.6 implies that
![]() ${\mathcal {B}}_n = \bigsqcup _{J \subseteq [n]} {\mathcal {B}}_n(J)$
descends to a spanning set of
${\mathcal {B}}_n = \bigsqcup _{J \subseteq [n]} {\mathcal {B}}_n(J)$
descends to a spanning set of
![]() $SR_n$
. Since
$SR_n$
. Since
![]() $\sum _{m \in {\mathcal {B}}_n(J)} q^{\deg (m)} = [{\mathrm {st}}(J)_1]_q \cdots [{\mathrm {st}}(J)_n]_q$
, the result follows from Lemma 2.1.
$\sum _{m \in {\mathcal {B}}_n(J)} q^{\deg (m)} = [{\mathrm {st}}(J)_1]_q \cdots [{\mathrm {st}}(J)_n]_q$
, the result follows from Lemma 2.1.
4 Differential operators and colon ideals
The straightening result of Lemma 3.6 led to the upper bound on the dimension of
![]() $SR_n$
in Proposition 3.7. Our next task is to bound this dimension from below. To this end, we define strategic differential operators
$SR_n$
in Proposition 3.7. Our next task is to bound this dimension from below. To this end, we define strategic differential operators
![]() ${\mathfrak {D}}_J$
whose action on
${\mathfrak {D}}_J$
whose action on
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
has Gale maximum term
${\mathbb {C}}[{\mathbf {x}}_n]$
has Gale maximum term
![]() $\theta _J$
. Analysis of this leading term will lead to finding a lower bound for quotient rings of the form
$\theta _J$
. Analysis of this leading term will lead to finding a lower bound for quotient rings of the form
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
, where
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
, where
![]() $I_n \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
is the classical coinvariant ideal and the
$I_n \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
is the classical coinvariant ideal and the
![]() $f_J \in {\mathbb {C}}[{\mathbf {x}}_n]$
are products of linear forms determined by
$f_J \in {\mathbb {C}}[{\mathbf {x}}_n]$
are products of linear forms determined by
![]() ${\mathfrak {D}}_J$
. It will turn out (Theorem 4.12) that
${\mathfrak {D}}_J$
. It will turn out (Theorem 4.12) that
![]() $(I_n : f_J)$
is generated by the regular sequence
$(I_n : f_J)$
is generated by the regular sequence
![]() $p_{J,1}, \dots , p_{J,n}$
of Lemma 3.5. Together with the triangularity property of the
$p_{J,1}, \dots , p_{J,n}$
of Lemma 3.5. Together with the triangularity property of the
![]() ${\mathfrak {D}}_J$
, this will lead to the required lower bound on
${\mathfrak {D}}_J$
, this will lead to the required lower bound on
![]() $SR_n$
.
$SR_n$
.
4.1 The differential operators
 ${\mathfrak {D}}_J$
${\mathfrak {D}}_J$
Let
![]() ${\mathcal {H}}$
be the
${\mathcal {H}}$
be the
![]() $n \times n$
matrix of complete homogeneous symmetric polynomials whose row i, column j entry is given by
$n \times n$
matrix of complete homogeneous symmetric polynomials whose row i, column j entry is given by
We have
![]() $h_0 = 1$
and interpret
$h_0 = 1$
and interpret
![]() $h_{j-i} = 0$
whenever
$h_{j-i} = 0$
whenever
![]() $i> j$
, so the matrix
$i> j$
, so the matrix
![]() ${\mathcal {H}}$
is lower triangular with 1’s on the diagonal. We use the matrix
${\mathcal {H}}$
is lower triangular with 1’s on the diagonal. We use the matrix
![]() ${\mathcal {H}}$
to define a family of differential operators as follows. Given a subset
${\mathcal {H}}$
to define a family of differential operators as follows. Given a subset
![]() $K \subseteq [n]$
, we introduce the ‘reversal’ notation
$K \subseteq [n]$
, we introduce the ‘reversal’ notation
Definition 4.1. For any subset
![]() $J \subseteq [n]$
, define a differential operator
$J \subseteq [n]$
, define a differential operator
![]() ${\mathfrak {D}}_J$
acting on
${\mathfrak {D}}_J$
acting on
![]() $\Omega _n$
by
$\Omega _n$
by
where
![]() $\Delta _{[n] - J, ([n] - I)^*}({\mathcal {H}}) \in {\mathbb {C}}[{\mathbf {x}}_n]$
is the minor of
$\Delta _{[n] - J, ([n] - I)^*}({\mathcal {H}}) \in {\mathbb {C}}[{\mathbf {x}}_n]$
is the minor of
![]() ${\mathcal {H}}$
with row set
${\mathcal {H}}$
with row set
![]() $[n] - J$
and column set
$[n] - J$
and column set
![]() $([n] - I)^*$
.
$([n] - I)^*$
.
Since the matrix
![]() ${\mathcal {H}}$
is lower triangular, the coefficient of
${\mathcal {H}}$
is lower triangular, the coefficient of
![]() $d_I$
in
$d_I$
in
![]() ${\mathfrak {D}}_J$
is zero unless we have
${\mathfrak {D}}_J$
is zero unless we have
![]() $I^* \leq _{\mathrm {Gale}} J$
in Gale order. As an example, when
$I^* \leq _{\mathrm {Gale}} J$
in Gale order. As an example, when
![]() $n = 3$
, the matrix
$n = 3$
, the matrix
![]() ${\mathcal {H}}$
is given by
${\mathcal {H}}$
is given by
 $$ \begin{align*} {\mathcal{H}} = \begin{pmatrix} 1 & 0 & 0 \\ x_2 + x_3 & 1 & 0 \\ x_3^2 & x_3 & 1 \end{pmatrix} \end{align*} $$
$$ \begin{align*} {\mathcal{H}} = \begin{pmatrix} 1 & 0 & 0 \\ x_2 + x_3 & 1 & 0 \\ x_3^2 & x_3 & 1 \end{pmatrix} \end{align*} $$
and we have the differential operators

acting on superspace elements
![]() $f \in \Omega _3$
where the indicated minors of
$f \in \Omega _3$
where the indicated minors of
![]() ${\mathcal {H}}$
vanish for support reasons. Applying the formula
${\mathcal {H}}$
vanish for support reasons. Applying the formula
![]() $d_i(f) = ( x_1^i \odot f ) \theta _1 + (x_2^i \odot f) \theta _2 + (x_3^i \odot f) \theta _3$
, these operators may be expressed in the more illuminating form
$d_i(f) = ( x_1^i \odot f ) \theta _1 + (x_2^i \odot f) \theta _2 + (x_3^i \odot f) \theta _3$
, these operators may be expressed in the more illuminating form
 $$ \begin{align*} {\mathfrak{D}}_{12}(f) &= ( x_1 (x_1 - x_2) (x_1 - x_3) x_2 (x_2 - x_3) ) \odot f \cdot \theta_1 \theta_2 \\ {\mathfrak{D}}_{13}(f) &= ( x_1^2 x_2^2 + x_1^2 x_2 x_3 - x_1 x_2^2 x_3 - x_1^3 x_3 ) \odot f \cdot \theta_1 \theta_2 - (x_1 (x_1 - x_2) (x_1 - x_3) x_3) \odot f \cdot \theta_1 \theta_3 \\ {\mathfrak{D}}_{23}(f) &= (x_1^2 x_2 - x_1 x_2^2) \odot f \cdot \theta_1 \theta_2 + (x_1^2 x_3 - x_1 x_3^2) \odot f \cdot \theta_1 \theta_3 + (x_2 (x_2 - x_3) x_3) \odot f \cdot \theta_2 \theta_3, \end{align*} $$
$$ \begin{align*} {\mathfrak{D}}_{12}(f) &= ( x_1 (x_1 - x_2) (x_1 - x_3) x_2 (x_2 - x_3) ) \odot f \cdot \theta_1 \theta_2 \\ {\mathfrak{D}}_{13}(f) &= ( x_1^2 x_2^2 + x_1^2 x_2 x_3 - x_1 x_2^2 x_3 - x_1^3 x_3 ) \odot f \cdot \theta_1 \theta_2 - (x_1 (x_1 - x_2) (x_1 - x_3) x_3) \odot f \cdot \theta_1 \theta_3 \\ {\mathfrak{D}}_{23}(f) &= (x_1^2 x_2 - x_1 x_2^2) \odot f \cdot \theta_1 \theta_2 + (x_1^2 x_3 - x_1 x_3^2) \odot f \cdot \theta_1 \theta_3 + (x_2 (x_2 - x_3) x_3) \odot f \cdot \theta_2 \theta_3, \end{align*} $$
which reveals a triangularity property with respect to the fermionic monomials
![]() $\theta _1 \theta _2, \theta _1 \theta _3$
and
$\theta _1 \theta _2, \theta _1 \theta _3$
and
![]() $\theta _2 \theta _3$
. Furthermore, the ‘leading coefficient’
$\theta _2 \theta _3$
. Furthermore, the ‘leading coefficient’
![]() $\theta _J$
involved in
$\theta _J$
involved in
![]() ${\mathfrak {D}}_J$
has the form
${\mathfrak {D}}_J$
has the form
![]() $f_J \odot (-)$
up to a sign where the polynomials
$f_J \odot (-)$
up to a sign where the polynomials
![]() $f_J$
were defined in the introduction. We will show that this is a general phenomenon. Our first lemma in this direction is a simple result on the application of the
$f_J$
were defined in the introduction. We will show that this is a general phenomenon. Our first lemma in this direction is a simple result on the application of the
![]() $d_I$
operator to polynomials in
$d_I$
operator to polynomials in
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
; its proof is left to the reader.
${\mathbb {C}}[{\mathbf {x}}_n]$
; its proof is left to the reader.
Lemma 4.2. Let
![]() $f \in {\mathbb {C}}[{\mathbf {x}}_n]$
be a polynomial and let
$f \in {\mathbb {C}}[{\mathbf {x}}_n]$
be a polynomial and let
![]() $I = \{ i_1 < \cdots < i_r \}$
and
$I = \{ i_1 < \cdots < i_r \}$
and
![]() $K = \{k_1 < \cdots < k_r \}$
be two subsets of
$K = \{k_1 < \cdots < k_r \}$
be two subsets of
![]() $[n]$
of the same size. The coefficient of
$[n]$
of the same size. The coefficient of
![]() $\theta _K$
in
$\theta _K$
in
![]() $d_I(f) \in \Omega _n$
is the determinant of partial derivatives
$d_I(f) \in \Omega _n$
is the determinant of partial derivatives
 $$ \begin{align} \begin{vmatrix} \partial_{k_1}^{i_1} f & & \cdots & & \partial_{k_1}^{i_r} f \\ & & & & \\ \vdots & & & & \vdots \\ & & & & \\ \partial_{k_r}^{i_1} f & & \cdots & & \partial_{k_r}^{i_r} f \\ \end{vmatrix}. \end{align} $$
$$ \begin{align} \begin{vmatrix} \partial_{k_1}^{i_1} f & & \cdots & & \partial_{k_1}^{i_r} f \\ & & & & \\ \vdots & & & & \vdots \\ & & & & \\ \partial_{k_r}^{i_1} f & & \cdots & & \partial_{k_r}^{i_r} f \\ \end{vmatrix}. \end{align} $$
Definition 4.1 and Lemma 4.2 motivate the following family of polynomials
![]() ${\mathfrak {F}}_{J,K} \in {\mathbb {C}}[{\mathbf {x}}_n]$
indexed by pairs of subsets
${\mathfrak {F}}_{J,K} \in {\mathbb {C}}[{\mathbf {x}}_n]$
indexed by pairs of subsets
![]() $J, K \subseteq [n]$
. The definition of the
$J, K \subseteq [n]$
. The definition of the
![]() ${\mathfrak {F}}_{J,K}$
also involves the matrix
${\mathfrak {F}}_{J,K}$
also involves the matrix
![]() ${\mathcal {H}}$
.
${\mathcal {H}}$
.
Definition 4.3. Let J and K be two subsets of
![]() $[n]$
of the same size. Define a polynomial
$[n]$
of the same size. Define a polynomial
![]() ${\mathfrak {F}}_{J,K} \in {\mathbb {C}}[{\mathbf {x}}_n]$
by
${\mathfrak {F}}_{J,K} \in {\mathbb {C}}[{\mathbf {x}}_n]$
by
where the row and column indices in the determinant
![]() $\left | x_k^i \right |{}_{k \in K, i \in I}$
are written in increasing order.
$\left | x_k^i \right |{}_{k \in K, i \in I}$
are written in increasing order.
The differential operators
![]() ${\mathfrak {D}}_J$
and the polynomials
${\mathfrak {D}}_J$
and the polynomials
![]() ${\mathfrak {F}}_{J,K}$
are related by
${\mathfrak {F}}_{J,K}$
are related by
for all
![]() $f \in {\mathbb {C}}[{\mathbf {x}}_n]$
.
$f \in {\mathbb {C}}[{\mathbf {x}}_n]$
.
Remark 4.4. The polynomial
![]() $\Delta _{[n] - J, ([n] - I)^*}({\mathcal {H}})$
appearing in Definition 4.3 is (up to variable reversal) a flagged skew Schur polynomial whose flagging parameter depends on J and whose shape depends on I and J, as may be seen from the Jacobi-Trudi formula. This is how the
$\Delta _{[n] - J, ([n] - I)^*}({\mathcal {H}})$
appearing in Definition 4.3 is (up to variable reversal) a flagged skew Schur polynomial whose flagging parameter depends on J and whose shape depends on I and J, as may be seen from the Jacobi-Trudi formula. This is how the
![]() ${\mathfrak {F}}_{J,K}$
were discovered, but their matrix minor formulation is more convenient for our purposes.
${\mathfrak {F}}_{J,K}$
were discovered, but their matrix minor formulation is more convenient for our purposes.
We aim to show that the
![]() ${\mathfrak {F}}_{J,K}$
are triangular with respect to Gale order. As a first step, we express
${\mathfrak {F}}_{J,K}$
are triangular with respect to Gale order. As a first step, we express
![]() ${\mathfrak {F}}_{J,K}$
as a single
${\mathfrak {F}}_{J,K}$
as a single
![]() $n \times n$
determinant.
$n \times n$
determinant.
Lemma 4.5. Let
![]() $J = \{ j_1 < \cdots < j_r \}$
and
$J = \{ j_1 < \cdots < j_r \}$
and
![]() $K = \{ k_1 < \cdots < k_r \}$
be two subsets of
$K = \{ k_1 < \cdots < k_r \}$
be two subsets of
![]() $[n]$
of the same size. Write
$[n]$
of the same size. Write
![]() $b(J) = (b(J)_1 < b(J)_2 < \cdots )$
for the entries in the complement
$b(J) = (b(J)_1 < b(J)_2 < \cdots )$
for the entries in the complement
![]() $[n] - J$
of the set J, written in increasing order. Define an
$[n] - J$
of the set J, written in increasing order. Define an
![]() $n \times n$
matrix
$n \times n$
matrix
![]() $A_{J,K}$
in block form
$A_{J,K}$
in block form
 $$ \begin{align} A_{J,K} = \begin{pmatrix} B_{J,K} \\ C_{J,K} \end{pmatrix}, \end{align} $$
$$ \begin{align} A_{J,K} = \begin{pmatrix} B_{J,K} \\ C_{J,K} \end{pmatrix}, \end{align} $$
where the top block
![]() $B_{J,K}$
has size
$B_{J,K}$
has size
![]() $r \times n$
and entries
$r \times n$
and entries
 $$ \begin{align} B_{J,K} = \begin{pmatrix} x_{k_1}^n & & \cdots & & x_{k_1}^1 \\ \vdots & & & & \vdots \\ x_{k_r}^n & & \cdots & & x_{k_r}^1 \\ \end{pmatrix} \end{align} $$
$$ \begin{align} B_{J,K} = \begin{pmatrix} x_{k_1}^n & & \cdots & & x_{k_1}^1 \\ \vdots & & & & \vdots \\ x_{k_r}^n & & \cdots & & x_{k_r}^1 \\ \end{pmatrix} \end{align} $$
and the bottom block
![]() $C_{J,K}$
has size
$C_{J,K}$
has size
![]() $(n-r) \times n$
and entries
$(n-r) \times n$
and entries
We have
![]() ${\mathfrak {F}}_{J,K} = \pm \det (A_{J,K})$
.
${\mathfrak {F}}_{J,K} = \pm \det (A_{J,K})$
.
Proof. The determinant
![]() $\det (A_{J,K})$
may be evaluated using the rule
$\det (A_{J,K})$
may be evaluated using the rule
 $$ \begin{align} \det(A_{J,K}) = \sum_{\substack{I \subseteq [n] \\ |I| = r}} (-1)^{\sum I - {r +1 \choose 2}} \cdot \Delta_I(B_{J,K}) \cdot \Delta_{[n]-I}(C_{J,K}), \end{align} $$
$$ \begin{align} \det(A_{J,K}) = \sum_{\substack{I \subseteq [n] \\ |I| = r}} (-1)^{\sum I - {r +1 \choose 2}} \cdot \Delta_I(B_{J,K}) \cdot \Delta_{[n]-I}(C_{J,K}), \end{align} $$
where
![]() $\Delta _I(B_{J,K})$
is the maximal minor of
$\Delta _I(B_{J,K})$
is the maximal minor of
![]() $B_{J,K}$
with column set I and
$B_{J,K}$
with column set I and
![]() $\Delta _{[n]-I}(C_{J,K})$
is the maximal minor of
$\Delta _{[n]-I}(C_{J,K})$
is the maximal minor of
![]() $C_{J,K}$
with complementary column set
$C_{J,K}$
with complementary column set
![]() $[n] - I$
. Now compare with the definition of
$[n] - I$
. Now compare with the definition of
![]() ${\mathfrak {F}}_{J,K}$
.
${\mathfrak {F}}_{J,K}$
.
To illustrate Lemma 4.5, we let
![]() $n = 5$
,
$n = 5$
,
![]() $J = \{1,3\}$
, and write
$J = \{1,3\}$
, and write
![]() $K = \{a,b\}$
for
$K = \{a,b\}$
for
![]() $1 \leq a < b \leq 5$
. Lemma (4.5) expresses
$1 \leq a < b \leq 5$
. Lemma (4.5) expresses
![]() ${\mathfrak {F}}_{J,K} = {\mathfrak {F}}_{13,ab}$
as the following
${\mathfrak {F}}_{J,K} = {\mathfrak {F}}_{13,ab}$
as the following
![]() $5 \times 5$
determinant:
$5 \times 5$
determinant:
 $$ \begin{align*} {\mathfrak{F}}_{13,ab} = \pm \begin{vmatrix} x_a^5 & x_a^4 & x_a^3 & x_a^2 & x_a^1 \\[2pt] x_b^5 & x_b^4 & x_b^3 & x_b^2 & x_b^1 \\[2pt] h_1(2345) & 1 & 0 & 0 & 0 \\[2pt] h_3(45) & h_2(45) & h_1(45) & 1 & 0 \\[2pt] h_4(5) & h_3(5) & h_2(5) & h_1(5) & 1 \end{vmatrix}. \end{align*} $$
$$ \begin{align*} {\mathfrak{F}}_{13,ab} = \pm \begin{vmatrix} x_a^5 & x_a^4 & x_a^3 & x_a^2 & x_a^1 \\[2pt] x_b^5 & x_b^4 & x_b^3 & x_b^2 & x_b^1 \\[2pt] h_1(2345) & 1 & 0 & 0 & 0 \\[2pt] h_3(45) & h_2(45) & h_1(45) & 1 & 0 \\[2pt] h_4(5) & h_3(5) & h_2(5) & h_1(5) & 1 \end{vmatrix}. \end{align*} $$
The determinant in Lemma 4.5 may be evaluated to give the desired triangularity relation for the polynomials
![]() ${\mathfrak {F}}_{J,K}$
. Lemma 4.5 will also imply that the
${\mathfrak {F}}_{J,K}$
. Lemma 4.5 will also imply that the
![]() ${\mathfrak {F}}_{J,J}$
are given the polynomials
${\mathfrak {F}}_{J,J}$
are given the polynomials
![]() $f_J \in {\mathbb {C}}[{\mathbf {x}}_n]$
appearing in the introduction. We reiterate their definition below.
$f_J \in {\mathbb {C}}[{\mathbf {x}}_n]$
appearing in the introduction. We reiterate their definition below.
Definition 4.6. For any subset
![]() $J \subseteq [n]$
, let
$J \subseteq [n]$
, let
![]() $f_J \in {\mathbb {C}}[{\mathbf {x}}_n]$
be the polynomial
$f_J \in {\mathbb {C}}[{\mathbf {x}}_n]$
be the polynomial
 $$ \begin{align} f_J := \prod_{j \in J} x_j \left( \prod_{i = j+1}^n (x_j - x_i) \right). \end{align} $$
$$ \begin{align} f_J := \prod_{j \in J} x_j \left( \prod_{i = j+1}^n (x_j - x_i) \right). \end{align} $$
Observe that the f-polynomial corresponding to a set J factors
![]() $f_J = \prod _{j \in J} f_{\{j\}}$
into f-polynomials corresponding to singletons contained in J. The polynomials
$f_J = \prod _{j \in J} f_{\{j\}}$
into f-polynomials corresponding to singletons contained in J. The polynomials
![]() $f_J \in {\mathbb {C}}[{\mathbf {x}}_n]$
will have deep ties to the supercoinvariant ring
$f_J \in {\mathbb {C}}[{\mathbf {x}}_n]$
will have deep ties to the supercoinvariant ring
![]() $SR_n$
. For later use, we record a criterion for when
$SR_n$
. For later use, we record a criterion for when
![]() $f_J$
lies in the classical coinvariant ideal
$f_J$
lies in the classical coinvariant ideal
![]() $I_n \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
.
$I_n \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
.
Lemma 4.7. Let
![]() $J \subseteq [n]$
. We have
$J \subseteq [n]$
. We have
![]() $f_J \in I_n$
if and only if
$f_J \in I_n$
if and only if
![]() $1 \in J$
.
$1 \in J$
.
Proof. Suppose
![]() $1 \in J$
, so that
$1 \in J$
, so that
![]() $f_{\{1\}} \mid f_J$
. We claim
$f_{\{1\}} \mid f_J$
. We claim
![]() $f_{\{1\}} = x_1 (x_1 - x_2) ( x_1 - x_3) \cdots (x_1 - x_n) \in I_n$
. Indeed, if t is a new variable, then modulo
$f_{\{1\}} = x_1 (x_1 - x_2) ( x_1 - x_3) \cdots (x_1 - x_n) \in I_n$
. Indeed, if t is a new variable, then modulo
![]() $I_n$
we have
$I_n$
we have
so that
and taking the coefficient of
![]() $t^d$
yields
$t^d$
yields
We conclude that
 $$ \begin{align} f_{\{1\}} = \sum_{d = 0}^{n-1} (-1)^d e_d(x_2, \dots, x_n) \cdot x_1^{n-d} \equiv n \cdot x_1^n \equiv 0 \quad\mod I_n, \end{align} $$
$$ \begin{align} f_{\{1\}} = \sum_{d = 0}^{n-1} (-1)^d e_d(x_2, \dots, x_n) \cdot x_1^{n-d} \equiv n \cdot x_1^n \equiv 0 \quad\mod I_n, \end{align} $$
where we used the fact that
![]() $x_1^n \in I_n$
.
$x_1^n \in I_n$
.
Now suppose
![]() $1 \notin J$
. Recall that
$1 \notin J$
. Recall that
![]() ${\mathrm {ann}}_{{\mathbb {C}}[{\mathbf {x}}_n]}(\delta _n) = I_n$
under the
${\mathrm {ann}}_{{\mathbb {C}}[{\mathbf {x}}_n]}(\delta _n) = I_n$
under the
![]() $\odot $
-action of
$\odot $
-action of
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
on itself. Therefore, to show that
${\mathbb {C}}[{\mathbf {x}}_n]$
on itself. Therefore, to show that
![]() $f_J \notin I_n$
, it is enough to show that
$f_J \notin I_n$
, it is enough to show that
![]() $f_J \odot \delta _n \neq 0$
. Since
$f_J \odot \delta _n \neq 0$
. Since
![]() $f_J = \prod _{j \in J} f_{\{j\}}$
, it suffices to show that
$f_J = \prod _{j \in J} f_{\{j\}}$
, it suffices to show that
![]() $f_J \odot \delta _n \neq 0$
when
$f_J \odot \delta _n \neq 0$
when
![]() $J = J_0 := \{2, 3, \dots , n \}$
is the maximal subset of
$J = J_0 := \{2, 3, \dots , n \}$
is the maximal subset of
![]() $[n]$
not containing
$[n]$
not containing
![]() $1$
. By definition, we have
$1$
. By definition, we have
so that the terms of
![]() $f_{J_0}$
are (up to a global sign) the terms of
$f_{J_0}$
are (up to a global sign) the terms of
![]() $\delta _n$
in which
$\delta _n$
in which
![]() $x_1$
does not appear. If we use
$x_1$
does not appear. If we use
![]() $\doteq $
to denote equality up to a nonzero scalar, we therefore have
$\doteq $
to denote equality up to a nonzero scalar, we therefore have
where we used the fact that both
![]() $f_{J_0}$
and
$f_{J_0}$
and
![]() $\delta _n$
are homogeneous of degree
$\delta _n$
are homogeneous of degree
![]() ${n \choose 2}$
and the fact that
${n \choose 2}$
and the fact that
![]() $f \odot f> 0$
for any homogeneous nonzero polynomial f.
$f \odot f> 0$
for any homogeneous nonzero polynomial f.
The determinant in Lemma 4.5 may be evaluated to give the desired triangularity relation for the polynomials
![]() ${\mathfrak {F}}_{J,K}$
. Lemma 4.5 will also imply that
${\mathfrak {F}}_{J,K}$
. Lemma 4.5 will also imply that
![]() ${\mathfrak {F}}_{J,J} = \pm f_J$
.
${\mathfrak {F}}_{J,J} = \pm f_J$
.
Lemma 4.8. We have
![]() ${\mathfrak {F}}_{J,K} = 0$
unless
${\mathfrak {F}}_{J,K} = 0$
unless
![]() $J \geq _{{\mathrm {Gale}}} K$
in Gale order. Furthermore, we have
$J \geq _{{\mathrm {Gale}}} K$
in Gale order. Furthermore, we have
Proof. We factor
![]() $\prod _{k \in K} x_k$
out of the upper block
$\prod _{k \in K} x_k$
out of the upper block
![]() $B_{J,K}$
of the determinant
$B_{J,K}$
of the determinant
![]() $\det (A_{J,K}) = \pm {\mathfrak {F}}_{J,K}$
in Lemma 4.5. Next, we apply column operations to eliminate the
$\det (A_{J,K}) = \pm {\mathfrak {F}}_{J,K}$
in Lemma 4.5. Next, we apply column operations to eliminate the
![]() $h_d(S)$
’s in the bottom portion
$h_d(S)$
’s in the bottom portion
![]() $C_{J,K}$
of this determinant.
$C_{J,K}$
of this determinant.
Specifically, we focus on each pivot 1 in
![]() $C_{J,K}$
from bottom to top. Working to the left from a given pivot 1, in row i of
$C_{J,K}$
from bottom to top. Working to the left from a given pivot 1, in row i of
![]() $C_{J,K}$
, we subtract
$C_{J,K}$
, we subtract
![]() $x_c$
times column j of
$x_c$
times column j of
![]() $A_{J,K}$
from column
$A_{J,K}$
from column
![]() $j-1$
, where
$j-1$
, where
![]() $x_c$
is a variable belonging to
$x_c$
is a variable belonging to
![]() $\{x_{b(J)_i}, \dots , x_n \} - \{ x_{b(J)_{i+1}}, \dots , x_n \}$
. Since
$\{x_{b(J)_i}, \dots , x_n \} - \{ x_{b(J)_{i+1}}, \dots , x_n \}$
. Since
![]() $h_d(S) = x_c h_{d-1}(S) + h_d(S - c)$
whenever
$h_d(S) = x_c h_{d-1}(S) + h_d(S - c)$
whenever
![]() $c \in S$
, this eliminates the
$c \in S$
, this eliminates the
![]() $h_d(S)$
’s from the bottom portion
$h_d(S)$
’s from the bottom portion
![]() $C_{J,K}$
of our determinant. After performing these operations, the determinant
$C_{J,K}$
of our determinant. After performing these operations, the determinant
![]() $\det (A_{J,K})$
is reduced to a single maximal minor of its (new) upper portion
$\det (A_{J,K})$
is reduced to a single maximal minor of its (new) upper portion
![]() $B_{J,K}$
, from which the result follows.
$B_{J,K}$
, from which the result follows.
To see how this works in our example
![]() $J = \{1,3\}$
and
$J = \{1,3\}$
and
![]() $K = \{a, b\}$
, we factor out
$K = \{a, b\}$
, we factor out
![]() $x_a x_b$
from the top two rows of our determinant to get
$x_a x_b$
from the top two rows of our determinant to get
 $$ \begin{align*} \begin{vmatrix} x_a^5 & x_a^4 & x_a^3 & x_a^2 & x_a^1 \\[2pt] x_b^5 & x_b^4 & x_b^3 & x_b^2 & x_b^1 \\[2pt] h_1(2345) & 1 & 0 & 0 & 0 \\[2pt] h_3(45) & h_2(45) & h_1(45) & 1 & 0 \\[2pt] h_4(5) & h_3(5) & h_2(5) & h_1(5) & 1 \end{vmatrix} = x_a x_b \begin{vmatrix} x_a^4 & x_a^3 & x_a^2 & x_a^1 & 1 \\[2pt] x_b^4 & x_b^3 & x_b^2 & x_b^1 & 1 \\[2pt] h_1(2345) & 1 & 0 & 0 & 0 \\[2pt] h_3(45) & h_2(45) & h_1(45) & 1 & 0 \\[2pt] h_4(5) & h_3(5) & h_2(5) & h_1(5) & 1 \end{vmatrix}. \end{align*} $$
$$ \begin{align*} \begin{vmatrix} x_a^5 & x_a^4 & x_a^3 & x_a^2 & x_a^1 \\[2pt] x_b^5 & x_b^4 & x_b^3 & x_b^2 & x_b^1 \\[2pt] h_1(2345) & 1 & 0 & 0 & 0 \\[2pt] h_3(45) & h_2(45) & h_1(45) & 1 & 0 \\[2pt] h_4(5) & h_3(5) & h_2(5) & h_1(5) & 1 \end{vmatrix} = x_a x_b \begin{vmatrix} x_a^4 & x_a^3 & x_a^2 & x_a^1 & 1 \\[2pt] x_b^4 & x_b^3 & x_b^2 & x_b^1 & 1 \\[2pt] h_1(2345) & 1 & 0 & 0 & 0 \\[2pt] h_3(45) & h_2(45) & h_1(45) & 1 & 0 \\[2pt] h_4(5) & h_3(5) & h_2(5) & h_1(5) & 1 \end{vmatrix}. \end{align*} $$
Our focus shifts to the bottom three rows. Since the bottom pivot 1 is in column 5, we subtract
![]() $x_5$
times each column from the previous column, resulting in
$x_5$
times each column from the previous column, resulting in
 $$ \begin{align*} x_a x_b \begin{vmatrix} x_a^4 & x_a^3 & x_a^2 & x_a^1 & 1 \\[2pt] x_b^4 & x_b^3 & x_b^2 & x_b^1 & 1 \\[2pt] h_1(2345) & 1 & 0 & 0 & 0 \\[2pt] h_3(45) & h_2(45) & h_1(45) & 1 & 0 \\[2pt] h_4(5) & h_3(5) & h_2(5) & h_1(5) & 1 \end{vmatrix} = x_a x_b \begin{vmatrix} x_a^4 - x_a^3 x_5 & x_a^3 - x_a^2 x_5 & x_a^2 - x_a x_5 & x_a^1 - x_5 & 1 \\[2pt] x_b^4 - x_b^3 x_5 & x_b^3 - x_b^2 x_5 & x_b^2 - x_b x_5 & x_b^1 - x_5 & 1 \\[2pt] h_1(234) & 1 & 0 & 0 & 0 \\[2pt] h_3(4) & h_2(4) & h_1(4) & 1 & 0 \\[2pt] 0 & 0 & 0 & 0 & 1 \end{vmatrix}. \end{align*} $$
$$ \begin{align*} x_a x_b \begin{vmatrix} x_a^4 & x_a^3 & x_a^2 & x_a^1 & 1 \\[2pt] x_b^4 & x_b^3 & x_b^2 & x_b^1 & 1 \\[2pt] h_1(2345) & 1 & 0 & 0 & 0 \\[2pt] h_3(45) & h_2(45) & h_1(45) & 1 & 0 \\[2pt] h_4(5) & h_3(5) & h_2(5) & h_1(5) & 1 \end{vmatrix} = x_a x_b \begin{vmatrix} x_a^4 - x_a^3 x_5 & x_a^3 - x_a^2 x_5 & x_a^2 - x_a x_5 & x_a^1 - x_5 & 1 \\[2pt] x_b^4 - x_b^3 x_5 & x_b^3 - x_b^2 x_5 & x_b^2 - x_b x_5 & x_b^1 - x_5 & 1 \\[2pt] h_1(234) & 1 & 0 & 0 & 0 \\[2pt] h_3(4) & h_2(4) & h_1(4) & 1 & 0 \\[2pt] 0 & 0 & 0 & 0 & 1 \end{vmatrix}. \end{align*} $$
This has the effect of eliminating the argument
![]() $x_5$
from the h’s. To eliminate the
$x_5$
from the h’s. To eliminate the
![]() $x_4$
’s from the arguments of the h’s, we focus on the pivot 1 in row 4, column 4. For each column before column 2, we subtract
$x_4$
’s from the arguments of the h’s, we focus on the pivot 1 in row 4, column 4. For each column before column 2, we subtract
![]() $x_4$
times the subsequent column. The result is
$x_4$
times the subsequent column. The result is
 $$ \begin{align*} x_a x_b \begin{vmatrix} x_a^4 - x_a^3 x_5 - x_a^3 x_4 + x_a^2 x_4 x_5 & x_a^3 - x_a^2 x_5 - x_a^2 x_4 + x_a x_4 x_5 & x_a^2 - x_a x_5 - x_a x_4 + x_4 x_5 & x_a^1 - x_5 & 1 \\[2pt] x_b^4 - x_b^3 x_5 - x_b^3 x_4 + x_b^2 x_4 x_5 & x_b^3 - x_b^2 x_5 - x_b^2 x_4 + x_b x_4 x_5 & x_b^2 - x_b x_5 - x_b x_4 + x_4 x_5 & x_b^1 - x_5 & 1 \\[2pt] h_1(23) & 1 & 0 & 0 & 0 \\[2pt] 0 & 0 & 0 & 1 & 0 \\[2pt] 0 & 0 & 0 & 0 & 1 \end{vmatrix}. \end{align*} $$
$$ \begin{align*} x_a x_b \begin{vmatrix} x_a^4 - x_a^3 x_5 - x_a^3 x_4 + x_a^2 x_4 x_5 & x_a^3 - x_a^2 x_5 - x_a^2 x_4 + x_a x_4 x_5 & x_a^2 - x_a x_5 - x_a x_4 + x_4 x_5 & x_a^1 - x_5 & 1 \\[2pt] x_b^4 - x_b^3 x_5 - x_b^3 x_4 + x_b^2 x_4 x_5 & x_b^3 - x_b^2 x_5 - x_b^2 x_4 + x_b x_4 x_5 & x_b^2 - x_b x_5 - x_b x_4 + x_4 x_5 & x_b^1 - x_5 & 1 \\[2pt] h_1(23) & 1 & 0 & 0 & 0 \\[2pt] 0 & 0 & 0 & 1 & 0 \\[2pt] 0 & 0 & 0 & 0 & 1 \end{vmatrix}. \end{align*} $$
The entries of this matrix are better written using elementary symmetric polynomials, viz.
 $$ \begin{align*} x_a x_b \begin{vmatrix} x_a^4 - x_a^3 e_1(45) + x_a^2 e_2(45) & x_a^3 - x_a^2 e_1(45) + x_a e_2(45) & x_a^2 - x_a e_1(45) + e_2(45) & x_a - e_1(5) & 1 \\[2pt] x_b^4 - x_b^3 e_1(45) + x_b^2 e_2(45) & x_b^3 - x_b^2 e_1(45) + x_b e_2(45) & x_b^2 - x_b e_1(45) + e_2(45) & x_b - e_1(5) & 1 \\[2pt] h_1(23) & 1 & 0 & 0 & 0 \\[2pt] 0 & 0 & 0 & 1 & 0 \\[2pt] 0 & 0 & 0 & 0 & 1 \end{vmatrix}. \end{align*} $$
$$ \begin{align*} x_a x_b \begin{vmatrix} x_a^4 - x_a^3 e_1(45) + x_a^2 e_2(45) & x_a^3 - x_a^2 e_1(45) + x_a e_2(45) & x_a^2 - x_a e_1(45) + e_2(45) & x_a - e_1(5) & 1 \\[2pt] x_b^4 - x_b^3 e_1(45) + x_b^2 e_2(45) & x_b^3 - x_b^2 e_1(45) + x_b e_2(45) & x_b^2 - x_b e_1(45) + e_2(45) & x_b - e_1(5) & 1 \\[2pt] h_1(23) & 1 & 0 & 0 & 0 \\[2pt] 0 & 0 & 0 & 1 & 0 \\[2pt] 0 & 0 & 0 & 0 & 1 \end{vmatrix}. \end{align*} $$
Continuing to pivot 1 in row 3, column 2, we multiply the second column by
![]() $- x_2 - x_3$
and add it to the first column. The result is
$- x_2 - x_3$
and add it to the first column. The result is
 $$ \begin{align*} x_a x_b \begin{vmatrix} x_a^4 - x_a^3 e_1(2345) + x_a^2 e_2(2345) - x_a e_3(2345) + e_4(2345) & x_a^3 - x_a^2 e_1(45) + x_a e_2(45) & x_a^2 - x_a e_1(45) + e_2(45) & x_a - e_1(5) & 1 \\[2pt] x_b^4 - x_b^3 e_1(2345) + x_b^2 e_2(2345) - x_b e_3(2345) + e_4(2345) & x_b^3 - x_b^2 e_1(45) + x_b e_2(45) & x_b^2 - x_b e_1(45) + e_2(45) & x_b - e_1(5) & 1 \\[2pt]0 & 1 & 0 & 0 & 0 \\[2pt] 0 & 0 & 0 & 1 & 0 \\[2pt] 0 & 0 & 0 & 0 & 1 \end{vmatrix}. \end{align*} $$
$$ \begin{align*} x_a x_b \begin{vmatrix} x_a^4 - x_a^3 e_1(2345) + x_a^2 e_2(2345) - x_a e_3(2345) + e_4(2345) & x_a^3 - x_a^2 e_1(45) + x_a e_2(45) & x_a^2 - x_a e_1(45) + e_2(45) & x_a - e_1(5) & 1 \\[2pt] x_b^4 - x_b^3 e_1(2345) + x_b^2 e_2(2345) - x_b e_3(2345) + e_4(2345) & x_b^3 - x_b^2 e_1(45) + x_b e_2(45) & x_b^2 - x_b e_1(45) + e_2(45) & x_b - e_1(5) & 1 \\[2pt]0 & 1 & 0 & 0 & 0 \\[2pt] 0 & 0 & 0 & 1 & 0 \\[2pt] 0 & 0 & 0 & 0 & 1 \end{vmatrix}. \end{align*} $$
which may be expressed as the smaller
![]() $2 \times 2$
determinant
$2 \times 2$
determinant
 $$ \begin{align*} x_a x_b \begin{vmatrix} x_a^4 - x_a^3 e_1(2345) + x_a^2 e_2(2345) - x_a e_3(2345) + e_4(2345) & x_a - e_1(5) \\[2pt] x_b^4 - x_b^3 e_1(2345) + x_b^2 e_2(2345) - x_b e_3(2345) + e_4(2345) & x_b - e_1(5) \end{vmatrix}. \end{align*} $$
$$ \begin{align*} x_a x_b \begin{vmatrix} x_a^4 - x_a^3 e_1(2345) + x_a^2 e_2(2345) - x_a e_3(2345) + e_4(2345) & x_a - e_1(5) \\[2pt] x_b^4 - x_b^3 e_1(2345) + x_b^2 e_2(2345) - x_b e_3(2345) + e_4(2345) & x_b - e_1(5) \end{vmatrix}. \end{align*} $$
The entries in this smaller determinant factor as
 $$ \begin{align*} x_a x_b \begin{vmatrix} (x_a - x_2)(x_a - x_3)(x_a - x_4)(x_a - x_5) & (x_a - x_5) \\[2pt] (x_b - x_2)(x_b - x_3)(x_b - x_4)(x_b - x_5) & (x_b - x_5) \\ \end{vmatrix}. \end{align*} $$
$$ \begin{align*} x_a x_b \begin{vmatrix} (x_a - x_2)(x_a - x_3)(x_a - x_4)(x_a - x_5) & (x_a - x_5) \\[2pt] (x_b - x_2)(x_b - x_3)(x_b - x_4)(x_b - x_5) & (x_b - x_5) \\ \end{vmatrix}. \end{align*} $$
For general
![]() $J = \{j_1 < \cdots < j_r \}$
and
$J = \{j_1 < \cdots < j_r \}$
and
![]() $K = \{k_1 < \cdots < k_r \}$
, this procedure yields the formula
$K = \{k_1 < \cdots < k_r \}$
, this procedure yields the formula
expressing
![]() ${\mathfrak {F}}_{J,K}$
as an
${\mathfrak {F}}_{J,K}$
as an
![]() $r \times r$
determinant times the variables indexed by K. If
$r \times r$
determinant times the variables indexed by K. If
![]() $k_p> j_q$
, the
$k_p> j_q$
, the
![]() $(p,q)$
-entry of the determinant in Equation (4.19) vanishes. If
$(p,q)$
-entry of the determinant in Equation (4.19) vanishes. If
![]() $J \not \leq _{\mathrm {Gale}} K$
, this determinant has the block form
$J \not \leq _{\mathrm {Gale}} K$
, this determinant has the block form
![]() $\begin {vmatrix} * & * \\ \mathbf {0} & * \end {vmatrix}$
where the southwest block of zeros intersects the main diagonal, so that
$\begin {vmatrix} * & * \\ \mathbf {0} & * \end {vmatrix}$
where the southwest block of zeros intersects the main diagonal, so that
![]() ${\mathfrak {F}}_{J,K} = 0$
. If
${\mathfrak {F}}_{J,K} = 0$
. If
![]() $J = K$
, the determinant in Equation (4.19) is upper triangular, and the product of diagonal entries is as described in the statement of the lemma.
$J = K$
, the determinant in Equation (4.19) is upper triangular, and the product of diagonal entries is as described in the statement of the lemma.
4.2 The colon ideal
 $(I_n : f_J)$
in
$(I_n : f_J)$
in
 ${\mathbb {C}}[{\mathbf {x}}_n]$
${\mathbb {C}}[{\mathbf {x}}_n]$
Thanks to Lemma 4.8, the differential operators
![]() ${\mathfrak {D}}_J$
exhibit useful triangularity with respect to the Gale order on fermionic monomials. In order to consider their fermionic leading term
${\mathfrak {D}}_J$
exhibit useful triangularity with respect to the Gale order on fermionic monomials. In order to consider their fermionic leading term
![]() $\theta _J$
, we will study the colon ideals
$\theta _J$
, we will study the colon ideals
where
![]() $I_n \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
is the classical coinvariant ideal.
$I_n \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
is the classical coinvariant ideal.
It will turn out (Theorem 4.12) that the ideal
![]() $(I_n : f_J)$
has two other equivalent definitions. As a first step to proving this, we introduce the following bigraded subspace of
$(I_n : f_J)$
has two other equivalent definitions. As a first step to proving this, we introduce the following bigraded subspace of
![]() $\Omega _n$
.
$\Omega _n$
.
Definition 4.9. Let
![]() $SH^{\prime }_n$
be the smallest linear subspace of
$SH^{\prime }_n$
be the smallest linear subspace of
![]() $\Omega _n$
which
$\Omega _n$
which
-
• contains the superspace Vandermonde
 $\delta _n$
,
$\delta _n$
, -
• is closed under all bosonic partial derivatives
 $\partial _1, \dots , \partial _n$
, and
$\partial _1, \dots , \partial _n$
, and -
• is closed under the action of the higher Euler operators
 $d_i$
for
$d_i$
for
 $i \geq 1$
.
$i \geq 1$
.
Swanson and Wallach showed [Reference Swanson and Wallach37] that
![]() $SH^{\prime }_n$
is annihilated by the supercoinvariant ideal
$SH^{\prime }_n$
is annihilated by the supercoinvariant ideal
![]() $SI_n \subseteq \Omega _n$
under the
$SI_n \subseteq \Omega _n$
under the
![]() $\odot $
-action, so that
$\odot $
-action, so that
![]() $SH^{\prime }_n \subseteq SH_n$
is a subset of the superharmonic space. We will show (Theorem 5.1) that in fact
$SH^{\prime }_n \subseteq SH_n$
is a subset of the superharmonic space. We will show (Theorem 5.1) that in fact
![]() $SH^{\prime }_n = SH_n$
. For now, we can use
$SH^{\prime }_n = SH_n$
. For now, we can use
![]() $SH^{\prime }_n$
and our triangularity results (Lemmas 3.2 and 4.8) to show that the polynomials
$SH^{\prime }_n$
and our triangularity results (Lemmas 3.2 and 4.8) to show that the polynomials
![]() $p_{J,1}, \dots , p_{J,n}$
from Section 3 lie in
$p_{J,1}, \dots , p_{J,n}$
from Section 3 lie in
![]() $(I_n : f_J)$
.
$(I_n : f_J)$
.
Lemma 4.10. Let
![]() $J \subseteq [n]$
. For any
$J \subseteq [n]$
. For any
![]() $1 \leq i \leq n$
, we have
$1 \leq i \leq n$
, we have
![]() $p_{J,i} \in (I_n : f_J)$
.
$p_{J,i} \in (I_n : f_J)$
.
Proof. Let
![]() $q_{J,i} \in SI_n$
be the supercoinvariant ideal element associated to
$q_{J,i} \in SI_n$
be the supercoinvariant ideal element associated to
![]() $p_{J,i}$
. By Lemma 3.2 (3), we have
$p_{J,i}$
. By Lemma 3.2 (3), we have
for some polynomials
![]() $A_L \in {\mathbb {C}}[{\mathbf {x}}_n]$
. However, Lemma 4.8 implies that
$A_L \in {\mathbb {C}}[{\mathbf {x}}_n]$
. However, Lemma 4.8 implies that
for some
![]() $B_K \in {\mathbb {C}}[{\mathbf {x}}_n]$
, where
$B_K \in {\mathbb {C}}[{\mathbf {x}}_n]$
, where
![]() $\doteq $
denotes equality up to a nonzero scalar. Since
$\doteq $
denotes equality up to a nonzero scalar. Since
![]() ${\mathfrak {D}}_J$
is a linear combination of
${\mathfrak {D}}_J$
is a linear combination of
![]() $d_I$
operators with coefficients in
$d_I$
operators with coefficients in
![]() $\partial _1, \dots , \partial _n$
, we have
$\partial _1, \dots , \partial _n$
, we have
where the
![]() $\subseteq $
is justified by the work of Swanson and Wallach [Reference Swanson and Wallach37]. Since
$\subseteq $
is justified by the work of Swanson and Wallach [Reference Swanson and Wallach37]. Since
![]() $SI_n$
annihilates
$SI_n$
annihilates
![]() $SH_n$
under the
$SH_n$
under the
![]() $\odot $
-action and
$\odot $
-action and
![]() $q_{J,i} \in SI_n$
, we have
$q_{J,i} \in SI_n$
, we have
The triangularity relations (4.21) and (4.22) force
Since
![]() ${\mathrm {ann}}_{{\mathbb {C}}[{\mathbf {x}}_n]}(\delta _n) = I_n$
, this implies that
${\mathrm {ann}}_{{\mathbb {C}}[{\mathbf {x}}_n]}(\delta _n) = I_n$
, this implies that
![]() $p_{J,i} \cdot f_J \in I_n$
, or equivalently,
$p_{J,i} \cdot f_J \in I_n$
, or equivalently,
![]() $p_{J,i} \in (I_n : f_J)$
.
$p_{J,i} \in (I_n : f_J)$
.
The colon ideals
![]() $(I_n : f_J)$
are connected to a class of permutations in
$(I_n : f_J)$
are connected to a class of permutations in
![]() ${\mathfrak {S}}_n$
. If
${\mathfrak {S}}_n$
. If
![]() $1 \leq j \leq n$
, a permutation
$1 \leq j \leq n$
, a permutation
![]() $w \in {\mathfrak {S}}_n$
is called j-resentful if
$w \in {\mathfrak {S}}_n$
is called j-resentful if
![]() $w(j) = n$
, or the value
$w(j) = n$
, or the value
![]() $w(j)+1$
appears among
$w(j)+1$
appears among
![]() ${w(j+1), w(j+2), \dots , w(n)}$
.Footnote
4
The permutation w is j-Nietzschean if it is not j-resentful.Footnote
5
${w(j+1), w(j+2), \dots , w(n)}$
.Footnote
4
The permutation w is j-Nietzschean if it is not j-resentful.Footnote
5
If
![]() $J \subseteq [n]$
is a subset, a permutation
$J \subseteq [n]$
is a subset, a permutation
![]() $w \in {\mathfrak {S}}_n$
is J-Nietzschean if it is j-Nietzschean for all
$w \in {\mathfrak {S}}_n$
is J-Nietzschean if it is j-Nietzschean for all
![]() $j \in J$
. We write
$j \in J$
. We write
for the set of all J-Nietszschean permutations in
![]() ${\mathfrak {S}}_n$
. Nietzschean permutations are counted by a simple product formula.
${\mathfrak {S}}_n$
. Nietzschean permutations are counted by a simple product formula.
Proposition 4.11. Let
![]() $J \subseteq [n]$
. The number of J-Nietzschean permutations in
$J \subseteq [n]$
. The number of J-Nietzschean permutations in
![]() ${\mathfrak {S}}_n$
is given by
${\mathfrak {S}}_n$
is given by
 $$ \begin{align} |{\mathfrak{N}}_J| = \prod_{i = 1}^n {\mathrm{st}}(J)_i, \end{align} $$
$$ \begin{align} |{\mathfrak{N}}_J| = \prod_{i = 1}^n {\mathrm{st}}(J)_i, \end{align} $$
where
![]() ${\mathrm {st}}(J) = ({\mathrm {st}}(J)_1, \dots , {\mathrm {st}}(J)_n)$
is the J-staircase.
${\mathrm {st}}(J) = ({\mathrm {st}}(J)_1, \dots , {\mathrm {st}}(J)_n)$
is the J-staircase.
Proof. We consider decomposing the one-line notation of permutations
![]() $w = [w(1), \dots , w(n)] \in {\mathfrak {S}}_n$
to the permutation
$w = [w(1), \dots , w(n)] \in {\mathfrak {S}}_n$
to the permutation
![]() $[1] \in {\mathfrak {S}}_1$
by iteratively removing the last letter
$[1] \in {\mathfrak {S}}_1$
by iteratively removing the last letter
![]() $w(n)$
and ‘standardizing’ to the unique order-isomorphic permutation in
$w(n)$
and ‘standardizing’ to the unique order-isomorphic permutation in
![]() ${\mathfrak {S}}_{n-1}$
. For example, the permutation
${\mathfrak {S}}_{n-1}$
. For example, the permutation
![]() $[6,3,5,1,4,7,2] \in {\mathfrak {S}}_7$
decomposes as follows:
$[6,3,5,1,4,7,2] \in {\mathfrak {S}}_7$
decomposes as follows:

Reversing this process, we can build up from
![]() $[1] \in {\mathfrak {S}}_1$
to a permutation in
$[1] \in {\mathfrak {S}}_1$
to a permutation in
![]() ${\mathfrak {S}}_n$
by appending a new letter to the end at each stage. In order for the resulting permutation
${\mathfrak {S}}_n$
by appending a new letter to the end at each stage. In order for the resulting permutation
![]() $w = [w(1), \dots , w(n)] \in {\mathfrak {S}}_n$
to be J-Nietzschean, suppose we have a permutation
$w = [w(1), \dots , w(n)] \in {\mathfrak {S}}_n$
to be J-Nietzschean, suppose we have a permutation
![]() $[v(1), \dots , v(k-1)] \in {\mathfrak {S}}_{k-1}$
at some intermediate stage and we want to build a permutation in
$[v(1), \dots , v(k-1)] \in {\mathfrak {S}}_{k-1}$
at some intermediate stage and we want to build a permutation in
![]() ${\mathfrak {S}}_{k}$
. We may append any of the numbers in
${\mathfrak {S}}_{k}$
. We may append any of the numbers in
![]() $\{1, \dots , k\}$
to
$\{1, \dots , k\}$
to
![]() $[v(1), \dots , v(k-1)]$
, except the following.
$[v(1), \dots , v(k-1)]$
, except the following.
-
• If
 $k \in J$
is a Nietzschean position, we cannot append k, since this would ultimately force
$k \in J$
is a Nietzschean position, we cannot append k, since this would ultimately force
 $w(k) = n$
or force an entry 1 larger than
$w(k) = n$
or force an entry 1 larger than
 $w(k)$
to appear among
$w(k)$
to appear among
 $w(k+1), \dots , w(n)$
, so that w would be k-resentful.
$w(k+1), \dots , w(n)$
, so that w would be k-resentful. -
• Whether or not k is a Nietzschean position, we cannot append a value
 $v(j) + 1$
for any Nietzschean position
$v(j) + 1$
for any Nietzschean position
 $j \in J$
satisfying
$j \in J$
satisfying
 $j < k$
, since this would ultimately force
$j < k$
, since this would ultimately force
 $w(j) + 1$
to appear among
$w(j) + 1$
to appear among
 $w(j+1), \dots , w(n)$
, so that w would be j-resentful. The value
$w(j+1), \dots , w(n)$
, so that w would be j-resentful. The value
 $v(j)$
at a Nietzschean position
$v(j)$
at a Nietzschean position
 $j < k$
inductively satisfies
$j < k$
inductively satisfies
 $v(j) < k-1$
.
$v(j) < k-1$
.
In general, the conditions above imply that the number of choices to append to
![]() $[v(1), \dots , v(k-1)]$
is
$[v(1), \dots , v(k-1)]$
is
which yields the claimed product formula.
We will see that
![]() $|{\mathfrak {N}}_J| = \dim {\mathbb {C}}[{\mathbf {x}}_n]/(I_n:f_J)$
, so J-Nietzschean permutations enumerate bases of
$|{\mathfrak {N}}_J| = \dim {\mathbb {C}}[{\mathbf {x}}_n]/(I_n:f_J)$
, so J-Nietzschean permutations enumerate bases of
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
. However, the connection between Nietzschean permutations and colon ideals goes deeper than this. To explain, we recall the powerful theory of orbit harmonics.
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
. However, the connection between Nietzschean permutations and colon ideals goes deeper than this. To explain, we recall the powerful theory of orbit harmonics.
For any subset
![]() $Z \subseteq {\mathbb {C}}^n$
, let
$Z \subseteq {\mathbb {C}}^n$
, let
![]() ${\mathbf {I}}(Z) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
be the ideal of polynomials which vanish on Z:
${\mathbf {I}}(Z) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
be the ideal of polynomials which vanish on Z:
The quotient ring
![]() ${\mathbb {C}}[Z] := {\mathbb {C}}[{\mathbf {x}}_n]/{\mathbf {I}}(Z)$
is the coordinate ring of Z and has a natural identification with the family of polynomial functions
${\mathbb {C}}[Z] := {\mathbb {C}}[{\mathbf {x}}_n]/{\mathbf {I}}(Z)$
is the coordinate ring of Z and has a natural identification with the family of polynomial functions
![]() $Z \longrightarrow {\mathbb {C}}$
. If we assume the locus
$Z \longrightarrow {\mathbb {C}}$
. If we assume the locus
![]() $Z \subseteq {\mathbb {C}}^n$
is finite (as we will from here on), by Lagrange interpolation any function
$Z \subseteq {\mathbb {C}}^n$
is finite (as we will from here on), by Lagrange interpolation any function
![]() $Z \longrightarrow {\mathbb {C}}$
is the restriction of a polynomial in
$Z \longrightarrow {\mathbb {C}}$
is the restriction of a polynomial in
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
, so we may identify
${\mathbb {C}}[{\mathbf {x}}_n]$
, so we may identify
![]() ${\mathbb {C}}[Z]$
with the vector space formal
${\mathbb {C}}[Z]$
with the vector space formal
![]() ${\mathbb {C}}$
-linear combinations of elements of Z.
${\mathbb {C}}$
-linear combinations of elements of Z.
The quotient ring
![]() ${\mathbb {C}}[Z] = {\mathbb {C}}[{\mathbf {x}}_n]/{\mathbf {I}}(Z)$
is almost never graded, but there is a way to produce a graded quotient of
${\mathbb {C}}[Z] = {\mathbb {C}}[{\mathbf {x}}_n]/{\mathbf {I}}(Z)$
is almost never graded, but there is a way to produce a graded quotient of
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
from
${\mathbb {C}}[{\mathbf {x}}_n]$
from
![]() ${\mathbf {I}}(Z)$
. For any nonzero polynomial
${\mathbf {I}}(Z)$
. For any nonzero polynomial
![]() $f \in {\mathbb {C}}[{\mathbf {x}}_n]$
, let
$f \in {\mathbb {C}}[{\mathbf {x}}_n]$
, let
![]() $\tau (f)$
be the highest degree homogeneous component of f. That is, if
$\tau (f)$
be the highest degree homogeneous component of f. That is, if
![]() $f = f_d + \cdots + f_1 + f_0$
where
$f = f_d + \cdots + f_1 + f_0$
where
![]() $f_i$
is homogeneous of degree i and
$f_i$
is homogeneous of degree i and
![]() $f_d \neq 0$
, we have
$f_d \neq 0$
, we have
![]() $\tau (f) = f_d$
. We define a new ideal
$\tau (f) = f_d$
. We define a new ideal
![]() ${\mathrm {gr}} \, {\mathbf {I}}(Z) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
by
${\mathrm {gr}} \, {\mathbf {I}}(Z) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
by
The ideal
![]() ${\mathrm {gr}} \, {\mathbf {I}}(Z)$
is homogeneous by construction. We have an isomorphism of vector spaces
${\mathrm {gr}} \, {\mathbf {I}}(Z)$
is homogeneous by construction. We have an isomorphism of vector spaces
where the latter quotient
![]() ${\mathbb {C}}[{\mathbf {x}}_n]/ {\mathrm {gr}} \, {\mathbf {I}}(Z)$
is a graded vector space. The Hilbert series of
${\mathbb {C}}[{\mathbf {x}}_n]/ {\mathrm {gr}} \, {\mathbf {I}}(Z)$
is a graded vector space. The Hilbert series of
![]() ${\mathbb {C}}[{\mathbf {x}}_n]/ {\mathrm {gr}} \, {\mathbf {I}}(Z)$
may be regarded as a q-enumerator of Z which depends in a subtle way on the embedding of Z inside
${\mathbb {C}}[{\mathbf {x}}_n]/ {\mathrm {gr}} \, {\mathbf {I}}(Z)$
may be regarded as a q-enumerator of Z which depends in a subtle way on the embedding of Z inside
![]() ${\mathbb {C}}^n$
.
${\mathbb {C}}^n$
.
As an example, if
![]() $Z = {\mathfrak {S}}_n$
is the set of points in
$Z = {\mathfrak {S}}_n$
is the set of points in
![]() ${\mathbb {C}}^n$
of the form
${\mathbb {C}}^n$
of the form
![]() $[w(1), \dots , w(n)]$
for
$[w(1), \dots , w(n)]$
for
![]() $w \in {\mathfrak {S}}_n$
, then
$w \in {\mathfrak {S}}_n$
, then
![]() ${\mathrm {gr}} \, {\mathbf {I}}({\mathfrak {S}}_n) = I_n$
is the classical coinvariant ideal and the coinvariant ring
${\mathrm {gr}} \, {\mathbf {I}}({\mathfrak {S}}_n) = I_n$
is the classical coinvariant ideal and the coinvariant ring
![]() $R_n = {\mathbb {C}}[{\mathbf {x}}_n]/I_n$
is obtained in this way. The following result states that the colon ideals
$R_n = {\mathbb {C}}[{\mathbf {x}}_n]/I_n$
is obtained in this way. The following result states that the colon ideals
![]() $(I_n : f_J)$
also arise via orbit harmonics.
$(I_n : f_J)$
also arise via orbit harmonics.
Theorem 4.12. For any subset
![]() $J \subseteq [n]$
, the following three ideals in
$J \subseteq [n]$
, the following three ideals in
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
are equal.
${\mathbb {C}}[{\mathbf {x}}_n]$
are equal.
-
1. The colon ideal
 $(I_n : f_J)$
.
$(I_n : f_J)$
. -
2. The ideal
 $(p_{J,1}, \dots , p_{J,n})$
generated by the homogeneous polynomials
$(p_{J,1}, \dots , p_{J,n})$
generated by the homogeneous polynomials
 $p_{J,1}, \dots , p_{J,n} \in {\mathbb {C}}[{\mathbf {x}}_n]$
.
$p_{J,1}, \dots , p_{J,n} \in {\mathbb {C}}[{\mathbf {x}}_n]$
. -
3. The homogeneous ideal
 ${\mathrm {gr}} \, {\mathbf {I}}({\mathfrak {N}}_J)$
attached to the locus
${\mathrm {gr}} \, {\mathbf {I}}({\mathfrak {N}}_J)$
attached to the locus
 ${\mathfrak {N}}_J \subseteq {\mathbb {C}}^n$
of J-Nietzschean permutations in
${\mathfrak {N}}_J \subseteq {\mathbb {C}}^n$
of J-Nietzschean permutations in
 ${\mathfrak {S}}_n$
. Here we consider
${\mathfrak {S}}_n$
. Here we consider
 ${\mathfrak {S}}_n \subseteq {\mathbb {C}}^n$
as the set of rearrangements of the specific point
${\mathfrak {S}}_n \subseteq {\mathbb {C}}^n$
as the set of rearrangements of the specific point
 $(1, 2, \dots , n) \in {\mathbb {C}}^n$
.
$(1, 2, \dots , n) \in {\mathbb {C}}^n$
.
If
![]() ${\mathcal {I}}_J \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
denotes this common ideal, the Hilbert series of
${\mathcal {I}}_J \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
denotes this common ideal, the Hilbert series of
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / {\mathcal {I}}_J$
is given by
${\mathbb {C}}[{\mathbf {x}}_n] / {\mathcal {I}}_J$
is given by
 $$ \begin{align} {\mathrm {Hilb}} \left( {\mathbb {C}}[{\mathbf {x}}_n] / {\mathcal{I}}_J; q \right) = \prod_{i = 1}^n [{\mathrm{st}}(J)_i]_q, \end{align} $$
$$ \begin{align} {\mathrm {Hilb}} \left( {\mathbb {C}}[{\mathbf {x}}_n] / {\mathcal{I}}_J; q \right) = \prod_{i = 1}^n [{\mathrm{st}}(J)_i]_q, \end{align} $$
where
![]() ${\mathrm {st}}(J) = ({\mathrm {st}}(J)_1, \dots , {\mathrm {st}}(J)_n)$
is the J-staircase.
${\mathrm {st}}(J) = ({\mathrm {st}}(J)_1, \dots , {\mathrm {st}}(J)_n)$
is the J-staircase.
Proof. Suppose
![]() $1 \in J$
. Lemma 4.7 states that
$1 \in J$
. Lemma 4.7 states that
![]() $f_J \in I_n$
, so that
$f_J \in I_n$
, so that
![]() $(I_n : f_J) = {\mathbb {C}}[{\mathbf {x}}_n]$
. Furthermore, we have
$(I_n : f_J) = {\mathbb {C}}[{\mathbf {x}}_n]$
. Furthermore, we have
![]() $p_{J,1} = \partial _1 h_1(x_1, \dots , x_n) = 1$
, so that
$p_{J,1} = \partial _1 h_1(x_1, \dots , x_n) = 1$
, so that
![]() $(p_{J,1}, \dots , p_{J,n}) = {\mathbb {C}}[{\mathbf {x}}_n]$
. Finally, since every permutation
$(p_{J,1}, \dots , p_{J,n}) = {\mathbb {C}}[{\mathbf {x}}_n]$
. Finally, since every permutation
![]() $w \in {\mathfrak {S}}_n$
is 1-resentful, we have
$w \in {\mathfrak {S}}_n$
is 1-resentful, we have
![]() ${\mathfrak {N}}_J = \varnothing $
so that
${\mathfrak {N}}_J = \varnothing $
so that
![]() ${\mathrm {gr}} \, {\mathbf {I}}({\mathfrak {N}}_J) = {\mathbb {C}}[{\mathbf {x}}_n]$
. Since
${\mathrm {gr}} \, {\mathbf {I}}({\mathfrak {N}}_J) = {\mathbb {C}}[{\mathbf {x}}_n]$
. Since
![]() ${\mathrm {st}}(J)_1 = 0$
, we are done in this case and assume that
${\mathrm {st}}(J)_1 = 0$
, we are done in this case and assume that
![]() $1 \notin J$
going forward.
$1 \notin J$
going forward.
Lemma 4.10 yields the containment of ideals
so that
![]() $(2) \subseteq (1)$
. We apply Lemma 2.3 with
$(2) \subseteq (1)$
. We apply Lemma 2.3 with
![]() ${\mathfrak {a}} = I_n, {\mathfrak {a}}' = (p_{J,1}, \dots , p_{J,n}),$
and
${\mathfrak {a}} = I_n, {\mathfrak {a}}' = (p_{J,1}, \dots , p_{J,n}),$
and
![]() $f = f_J$
. We check the conditions of this lemma.
$f = f_J$
. We check the conditions of this lemma.
-
• The ideal
 $I_n$
is generated by the regular sequence
$I_n$
is generated by the regular sequence
 $e_1, \dots , e_n \in {\mathbb {C}}[{\mathbf {x}}_n]$
. The Artinian quotient
$e_1, \dots , e_n \in {\mathbb {C}}[{\mathbf {x}}_n]$
. The Artinian quotient
 ${\mathbb {C}}[{\mathbf {x}}_n]/(e_1, \dots , e_n)$
is a complete intersection, and hence Gorenstein. Artinian Gorenstein graded quotients of
${\mathbb {C}}[{\mathbf {x}}_n]/(e_1, \dots , e_n)$
is a complete intersection, and hence Gorenstein. Artinian Gorenstein graded quotients of
 ${\mathbb {C}}[{\mathbf {x}}_n]$
are Poincaré duality algebras; see, for example, [Reference Maeno and Watanabe24, Prop. 2.1]. The socle degree of
${\mathbb {C}}[{\mathbf {x}}_n]$
are Poincaré duality algebras; see, for example, [Reference Maeno and Watanabe24, Prop. 2.1]. The socle degree of
 $I_n$
is
$I_n$
is
 ${n \choose 2}$
.Footnote
6
${n \choose 2}$
.Footnote
6
-
• Since
 $1 \notin J$
, Lemma 3.5 implies that
$1 \notin J$
, Lemma 3.5 implies that
 $p_{J,1}, \dots , p_{J,n}$
is a regular sequence, so that the quotient
$p_{J,1}, \dots , p_{J,n}$
is a regular sequence, so that the quotient
 ${\mathbb {C}}[{\mathbf {x}}_n] / (p_{J,1}, \dots , p_{J,n})$
is also a Poincaré duality algebra. The socle degree of this algebra is
${\mathbb {C}}[{\mathbf {x}}_n] / (p_{J,1}, \dots , p_{J,n})$
is also a Poincaré duality algebra. The socle degree of this algebra is
 $\deg p_{J,1} + \cdots + \deg p_{J,n} - n = {\mathrm {st}}(J)_1 + \cdots + {\mathrm {st}}(J)_n - n$
.
$\deg p_{J,1} + \cdots + \deg p_{J,n} - n = {\mathrm {st}}(J)_1 + \cdots + {\mathrm {st}}(J)_n - n$
. -
• Since
 $1 \notin J$
, Lemma 4.7 implies
$1 \notin J$
, Lemma 4.7 implies
 $f_J \notin I_n$
. Furthermore, the polynomial
$f_J \notin I_n$
. Furthermore, the polynomial
 $f_J$
has degree
$f_J$
has degree
 $\deg f_J = \sum _{i = 1}^n (i - {\mathrm {st}}(J)_i)$
.
$\deg f_J = \sum _{i = 1}^n (i - {\mathrm {st}}(J)_i)$
.
Since we have
 $$ \begin{align} {\mathrm{st}}(J)_1 + \cdots + {\mathrm{st}}(J)_n - n + \sum_{i = 1}^n (i - {\mathrm{st}}(J)_i) = {n \choose 2}, \end{align} $$
$$ \begin{align} {\mathrm{st}}(J)_1 + \cdots + {\mathrm{st}}(J)_n - n + \sum_{i = 1}^n (i - {\mathrm{st}}(J)_i) = {n \choose 2}, \end{align} $$
we may apply Lemma 2.3 to conclude
so that (1) = (2). This also implies that the claimed Hilbert series formula holds for
![]() ${\mathcal {I}}_J = (1)$
or
${\mathcal {I}}_J = (1)$
or
![]() $(2)$
.
$(2)$
.
For any radical ideals
![]() ${\mathcal {I}}, {\mathcal {J}} \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
, the colon ideal
${\mathcal {I}}, {\mathcal {J}} \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
, the colon ideal
![]() $({\mathcal {I}}:{\mathcal {J}}) = \{ f \in {\mathbb {C}}[{\mathbf {x}}_n] \,:\, f \cdot {\mathcal {J}} \subseteq {\mathcal {I}} \}$
has the interpretation
$({\mathcal {I}}:{\mathcal {J}}) = \{ f \in {\mathbb {C}}[{\mathbf {x}}_n] \,:\, f \cdot {\mathcal {J}} \subseteq {\mathcal {I}} \}$
has the interpretation
in terms of varieties in
![]() ${\mathbb {C}}^n$
, where the bar stands for Zariski closure. If
${\mathbb {C}}^n$
, where the bar stands for Zariski closure. If
![]() ${\mathbf {V}}({\mathcal {I}})$
is a finite locus of points, the bar can be removed.
${\mathbf {V}}({\mathcal {I}})$
is a finite locus of points, the bar can be removed.
Write
![]() ${\mathfrak {R}}_J := {\mathfrak {S}}_n - {\mathfrak {N}}_J$
for the resentful complement of the J-Nietzschean permutations in
${\mathfrak {R}}_J := {\mathfrak {S}}_n - {\mathfrak {N}}_J$
for the resentful complement of the J-Nietzschean permutations in
![]() ${\mathfrak {S}}_n$
. Recall that we take the specific embedding of
${\mathfrak {S}}_n$
. Recall that we take the specific embedding of
![]() ${\mathfrak {S}}_n \subset {\mathbb {C}}^n$
by taking all rearrangements of the coordinates of
${\mathfrak {S}}_n \subset {\mathbb {C}}^n$
by taking all rearrangements of the coordinates of
![]() $(1, 2, \dots , n) \in {\mathbb {C}}^n$
. This also embeds
$(1, 2, \dots , n) \in {\mathbb {C}}^n$
. This also embeds
![]() ${\mathfrak {R}}_J$
and
${\mathfrak {R}}_J$
and
![]() ${\mathfrak {N}}_J$
inside
${\mathfrak {N}}_J$
inside
![]() ${\mathbb {C}}^n$
.
${\mathbb {C}}^n$
.
The (inhomogeneous) polynomial
 $$ \begin{align} \tilde{f}_J := \prod_{j \in J} (x_j - n) \prod_{i> j} (x_j - x_i + 1) \end{align} $$
$$ \begin{align} \tilde{f}_J := \prod_{j \in J} (x_j - n) \prod_{i> j} (x_j - x_i + 1) \end{align} $$
vanishes on
![]() ${\mathfrak {R}}_J$
. In fact, we have
${\mathfrak {R}}_J$
. In fact, we have
where
![]() $\tilde {I}_n$
is the ‘deformed version’ of the classical coinvariant ideal
$\tilde {I}_n$
is the ‘deformed version’ of the classical coinvariant ideal
Since
![]() $\tilde {I}_n$
is radical and
$\tilde {I}_n$
is radical and
![]() $\tilde {f}_J$
has no repeated factors, the Nullstellensatz implies
$\tilde {f}_J$
has no repeated factors, the Nullstellensatz implies
where
![]() $\sqrt {\cdot }$
stands for the radical of an ideal. Taking associated graded ideals gives
$\sqrt {\cdot }$
stands for the radical of an ideal. Taking associated graded ideals gives
where the containment
![]() $\subseteq $
is justified by considering the leading term of a polynomial
$\subseteq $
is justified by considering the leading term of a polynomial
![]() $\tilde {g} \in {\mathbb {C}}[{\mathbf {x}}_n]$
such that
$\tilde {g} \in {\mathbb {C}}[{\mathbf {x}}_n]$
such that
![]() $\tilde {g} \cdot \tilde {f}_J \in \tilde {I}_n$
.
$\tilde {g} \cdot \tilde {f}_J \in \tilde {I}_n$
.
For arbitrary ideals
![]() ${\mathcal {I}}$
and polynomials f, the containment
${\mathcal {I}}$
and polynomials f, the containment
![]() ${\mathrm {gr}} \, ({\mathcal {I}} : f ) \subseteq ({\mathrm {gr}} \, {\mathcal {I}} : \tau (f) )$
can certainly be strict. However, in our setting, Proposition 4.11 and the fact that
${\mathrm {gr}} \, ({\mathcal {I}} : f ) \subseteq ({\mathrm {gr}} \, {\mathcal {I}} : \tau (f) )$
can certainly be strict. However, in our setting, Proposition 4.11 and the fact that
 $$ \begin{align} \dim {\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J) = \prod_{i = 1}^n {\mathrm{st}}(J)_i = |{\mathfrak{N}}_J| \end{align} $$
$$ \begin{align} \dim {\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J) = \prod_{i = 1}^n {\mathrm{st}}(J)_i = |{\mathfrak{N}}_J| \end{align} $$
imply
which forces
![]() ${\mathrm {gr}} \, {\mathbf {I}}({\mathfrak {N}}_J) = (I_n : f_J)$
so that (1) = (3) and the theorem is proved.
${\mathrm {gr}} \, {\mathbf {I}}({\mathfrak {N}}_J) = (I_n : f_J)$
so that (1) = (3) and the theorem is proved.
5 Operator theorem and Hilbert series
5.1 Operator theorem
We are ready to give our characterization of the harmonic space
![]() $SH_n = SI_n^{\perp } \subseteq \Omega _n$
. The following result was conjectured by Swanson and Wallach [Reference Swanson and Wallach37], and was previously conjectured by N. Bergeron, Li, Machacek, Sulzgruber and Zabrocki (unpublished).
$SH_n = SI_n^{\perp } \subseteq \Omega _n$
. The following result was conjectured by Swanson and Wallach [Reference Swanson and Wallach37], and was previously conjectured by N. Bergeron, Li, Machacek, Sulzgruber and Zabrocki (unpublished).
Theorem 5.1. (Operator Theorem)
The superharmonic space
![]() $SH_n \subseteq \Omega _n$
is generated as a
$SH_n \subseteq \Omega _n$
is generated as a
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
-module under the
${\mathbb {C}}[{\mathbf {x}}_n]$
-module under the
![]() $\odot $
-action by
$\odot $
-action by
![]() $d_I(\delta _n)$
for subsets
$d_I(\delta _n)$
for subsets
![]() $I \subseteq [n-1]$
. In symbols, we have
$I \subseteq [n-1]$
. In symbols, we have
The sum appearing in Theorem 5.1 is not direct. Since
![]() $d_i(\delta _n) = 0$
whenever
$d_i(\delta _n) = 0$
whenever
![]() $i> n$
and we have
$i> n$
and we have
![]() $d_i d_j = - d_j d_i$
, Theorem 5.1 may be rephrased as follows.
$d_i d_j = - d_j d_i$
, Theorem 5.1 may be rephrased as follows.
The superharmonic space
![]() $SH_n$
is the smallest linear subspace of
$SH_n$
is the smallest linear subspace of
![]() $\Omega _n$
which
$\Omega _n$
which
-
• contains the Vandermonde determinant
 $\delta _n$
,
$\delta _n$
, -
• is closed under the differentiation operators
 $\partial _1, \dots , \partial _n$
acting on the x-variables, and
$\partial _1, \dots , \partial _n$
acting on the x-variables, and -
• is closed under the higher derivative operators
 $d_i$
for
$d_i$
for
 $i \geq 1$
.
$i \geq 1$
.
Proof. Observe that the sum on the RHS of Equation (5.1) is the space
![]() $SH^{\prime }_n$
of Definition 4.9. As explained after Definition 4.9, Swanson and Wallach proved [Reference Swanson and Wallach37] that
$SH^{\prime }_n$
of Definition 4.9. As explained after Definition 4.9, Swanson and Wallach proved [Reference Swanson and Wallach37] that
![]() $SH^{\prime }_n \subseteq SH_n$
. Since
$SH^{\prime }_n \subseteq SH_n$
. Since
![]() $SR_n \cong SH_n$
, Corollary 3.7 gives an upper bound on the dimension of
$SR_n \cong SH_n$
, Corollary 3.7 gives an upper bound on the dimension of
![]() $SH_n$
. In order to show that this containment is an equality, we use the
$SH_n$
. In order to show that this containment is an equality, we use the
![]() ${\mathfrak {D}}_J$
operators and the colon ideals
${\mathfrak {D}}_J$
operators and the colon ideals
![]() $(I_n : f_J)$
to show that the dimension of
$(I_n : f_J)$
to show that the dimension of
![]() $SH^{\prime }_n$
is sufficiently large.
$SH^{\prime }_n$
is sufficiently large.
Let
![]() $J \subseteq [n]$
. Applying the differential operator
$J \subseteq [n]$
. Applying the differential operator
![]() ${\mathfrak {D}}_J$
to
${\mathfrak {D}}_J$
to
![]() $\delta _n$
yields an element
$\delta _n$
yields an element
![]() ${\mathfrak {D}}_J(\delta _n) \in SH^{\prime }_n$
. We use our lemmata to derive the following facts about the superspace element
${\mathfrak {D}}_J(\delta _n) \in SH^{\prime }_n$
. We use our lemmata to derive the following facts about the superspace element
![]() ${\mathfrak {D}}_J(\delta _n)$
.
${\mathfrak {D}}_J(\delta _n)$
.
-
• By Lemma 4.2 and the vanishing assertion of Lemma 4.8, the coefficient of
 $\theta _K$
in
$\theta _K$
in
 ${\mathfrak {D}}_J(\delta _n)$
is zero unless
${\mathfrak {D}}_J(\delta _n)$
is zero unless
 $K \leq _{{\mathrm {Gale}}} J$
.
$K \leq _{{\mathrm {Gale}}} J$
. -
• By Lemma 4.2 and the product formula in Lemma 4.8, the coefficient of
 $\theta _J$
in
$\theta _J$
in
 ${\mathfrak {D}}_J(\delta _n)$
is
${\mathfrak {D}}_J(\delta _n)$
is
 $\pm \, f_J \odot \delta _n $
.
$\pm \, f_J \odot \delta _n $
.
For any element
![]() $f \in \Omega _n$
, the annihilator
$f \in \Omega _n$
, the annihilator
is an ideal in the polynomial ring
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
. For any subset
${\mathbb {C}}[{\mathbf {x}}_n]$
. For any subset
![]() $J \subseteq [n]$
, we calculate
$J \subseteq [n]$
, we calculate
where we used the fact that the annihilator of the Vandermonde
![]() $\delta _n$
is the classical coinvariant ideal
$\delta _n$
is the classical coinvariant ideal
![]() $I_n$
. We claim that there exists a set
$I_n$
. We claim that there exists a set
![]() ${\mathcal {B}}_n(J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
of homogeneous polynomials such that
${\mathcal {B}}_n(J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
of homogeneous polynomials such that
-
• the set
 ${\mathcal {B}}_n(J)$
has degree generating function
${\mathcal {B}}_n(J)$
has degree generating function
 $\sum _{g \in {\mathcal {B}}(J)} q^{\deg (g)} = \prod _{i = 1}^n [{\mathrm {st}}(J)_i]_q$
and
$\sum _{g \in {\mathcal {B}}(J)} q^{\deg (g)} = \prod _{i = 1}^n [{\mathrm {st}}(J)_i]_q$
and -
• the set
 $\{ g \odot (f_J \odot \delta _n) \,:\, g \in {\mathcal {B}}_n(J) \}$
of polynomials in
$\{ g \odot (f_J \odot \delta _n) \,:\, g \in {\mathcal {B}}_n(J) \}$
of polynomials in
 ${\mathbb {C}}[{\mathbf {x}}_n]$
is linearly independent.
${\mathbb {C}}[{\mathbf {x}}_n]$
is linearly independent.
Indeed, Theorem 4.12 implies that there exists a set
![]() ${\mathcal {B}}_n(J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
of homogeneous polynomials with the given degree generating function which descends to a linearly independent subset of
${\mathcal {B}}_n(J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
of homogeneous polynomials with the given degree generating function which descends to a linearly independent subset of
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J )$
. Since
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J )$
. Since
![]() ${\mathrm {ann}}_{{\mathbb {C}}[{\mathbf {x}}_n]}(\delta _n) = I_n$
, for any such
${\mathrm {ann}}_{{\mathbb {C}}[{\mathbf {x}}_n]}(\delta _n) = I_n$
, for any such
![]() ${\mathcal {B}}_n(J)$
, the set of polynomials
${\mathcal {B}}_n(J)$
, the set of polynomials
![]() $\{ g \odot (f_J \odot \delta _n) \,:\, g \in {\mathcal {B}}_n(J) \}$
will be linearly independent in
$\{ g \odot (f_J \odot \delta _n) \,:\, g \in {\mathcal {B}}_n(J) \}$
will be linearly independent in
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
.
${\mathbb {C}}[{\mathbf {x}}_n]$
.
We combine our observations to prove the theorem. Suppose that some linear combination
 $$ \begin{align} \sum_{J \subseteq [n]} \sum_{g_J \in {\mathcal{B}}_n(J)} c_{J,g_J} (g_J \cdot \theta_J) \in \Omega_n \end{align} $$
$$ \begin{align} \sum_{J \subseteq [n]} \sum_{g_J \in {\mathcal{B}}_n(J)} c_{J,g_J} (g_J \cdot \theta_J) \in \Omega_n \end{align} $$
(where the
![]() $c_{J,g_J} \in {\mathbb {C}}$
are scalars) annihilates the space
$c_{J,g_J} \in {\mathbb {C}}$
are scalars) annihilates the space
![]() $SH^{\prime }_n$
as a differential operator:
$SH^{\prime }_n$
as a differential operator:
 $$ \begin{align} \left(\sum_{J \subseteq [n]} \sum_{g_J \in {\mathcal{B}}_n(J)} c_{J,g_J} (g_J \cdot \theta_J) \right) \odot SH^{\prime}_n = 0. \end{align} $$
$$ \begin{align} \left(\sum_{J \subseteq [n]} \sum_{g_J \in {\mathcal{B}}_n(J)} c_{J,g_J} (g_J \cdot \theta_J) \right) \odot SH^{\prime}_n = 0. \end{align} $$
By fermionic homogeneity, we may as well assume that
![]() $(\star )$
for all
$(\star )$
for all
![]() $J \subseteq [n]$
such that there is some
$J \subseteq [n]$
such that there is some
![]() $c_{J,g_J} \neq 0$
, the set J has a fixed size.
$c_{J,g_J} \neq 0$
, the set J has a fixed size.
In particular, for any
![]() $K \subseteq [n]$
, we have
$K \subseteq [n]$
, we have
 $$ \begin{align} \left(\sum_{J \subseteq [n]} \sum_{g_J \in {\mathcal{B}}_n(J)} c_{J,g_J} (g_J \cdot \theta_J) \right) \odot {\mathfrak{D}}_K(\delta_n) = 0. \end{align} $$
$$ \begin{align} \left(\sum_{J \subseteq [n]} \sum_{g_J \in {\mathcal{B}}_n(J)} c_{J,g_J} (g_J \cdot \theta_J) \right) \odot {\mathfrak{D}}_K(\delta_n) = 0. \end{align} $$
Working toward a contradiction, assume that at least one of the scalars
![]() $c_{J,g_J} \in {\mathbb {C}}$
is nonzero. Choose
$c_{J,g_J} \in {\mathbb {C}}$
is nonzero. Choose
![]() $J_0 \subseteq [n]$
minimal under the Gale order such that at least one
$J_0 \subseteq [n]$
minimal under the Gale order such that at least one
![]() $c_{J_0, g_{J_0}}$
is nonzero. Letting
$c_{J_0, g_{J_0}}$
is nonzero. Letting
![]() $K = J_0$
, we have
$K = J_0$
, we have
 $$ \begin{align} \!0 &= \left(\sum_{J \subseteq [n]} \sum_{g_J \in {\mathcal{B}}_n(J)} c_{J,g_J} ( g_J \cdot \theta_J) \right) \odot {\mathfrak{D}}_{J_0}(\delta_n)\qquad \qquad\qquad \end{align} $$
$$ \begin{align} \!0 &= \left(\sum_{J \subseteq [n]} \sum_{g_J \in {\mathcal{B}}_n(J)} c_{J,g_J} ( g_J \cdot \theta_J) \right) \odot {\mathfrak{D}}_{J_0}(\delta_n)\qquad \qquad\qquad \end{align} $$
 $$ \begin{align} &\doteq \left( \sum_{g_{J_0} \in {\mathcal{B}}_n(J_0)} c_{J_0,g_{J_0}} \cdot g_{J_0} \right) \odot \text{(coefficient of}\ \theta_{J_0}\ \text{in}\ {\mathfrak{D}}_{J_0}(\delta_n)) \end{align} $$
$$ \begin{align} &\doteq \left( \sum_{g_{J_0} \in {\mathcal{B}}_n(J_0)} c_{J_0,g_{J_0}} \cdot g_{J_0} \right) \odot \text{(coefficient of}\ \theta_{J_0}\ \text{in}\ {\mathfrak{D}}_{J_0}(\delta_n)) \end{align} $$
 $$ \begin{align} &\ = \sum_{g_{J_0} \in {\mathcal{B}}_n(J_0)} c_{J_0,g_{J_0}} \cdot g_{J_0} \odot \left[ \pm f_{J_0} \odot \delta_n \right],\qquad\qquad\qquad\qquad \end{align} $$
$$ \begin{align} &\ = \sum_{g_{J_0} \in {\mathcal{B}}_n(J_0)} c_{J_0,g_{J_0}} \cdot g_{J_0} \odot \left[ \pm f_{J_0} \odot \delta_n \right],\qquad\qquad\qquad\qquad \end{align} $$
where the second equality follows from the homogeneity assumption
![]() $(\star )$
and our Gale minimality assumption and
$(\star )$
and our Gale minimality assumption and
![]() $\doteq $
denotes equality up to a nonzero scalar. The linear independence of the set
$\doteq $
denotes equality up to a nonzero scalar. The linear independence of the set
![]() $\{ g_{J_0} \odot ( f_{J_0} \odot \delta _n ) \,:\, g_{J_0} \in {\mathcal {B}}_n(J_0) \}$
forces
$\{ g_{J_0} \odot ( f_{J_0} \odot \delta _n ) \,:\, g_{J_0} \in {\mathcal {B}}_n(J_0) \}$
forces
![]() $c_{J_0,g_{J_0}} = 0$
for all
$c_{J_0,g_{J_0}} = 0$
for all
![]() $g_{J_0} \in {\mathcal {B}}_n(J_0)$
, which is a contradiction.
$g_{J_0} \in {\mathcal {B}}_n(J_0)$
, which is a contradiction.
We have the chain of inequalities
where the first inequality comes from the last paragraph, the second inequality follows because
![]() ${SH^{\prime }_n \subseteq SH_n}$
, the equality holds because
${SH^{\prime }_n \subseteq SH_n}$
, the equality holds because
![]() $SH_n$
is the harmonic space to the quotient
$SH_n$
is the harmonic space to the quotient
![]() $SR_n$
, and the last inequality holds because of Corollary 3.7. These are all equalities, forcing
$SR_n$
, and the last inequality holds because of Corollary 3.7. These are all equalities, forcing
![]() $SH_n = SH^{\prime }_n$
.
$SH_n = SH^{\prime }_n$
.
5.2 Hilbert series
Our goal in this subsection is to calculate the Hilbert series of
![]() $SR_n$
and describe a method for producing bases of
$SR_n$
and describe a method for producing bases of
![]() $SR_n$
. The key to our approach is the following general linear independence criterion.
$SR_n$
. The key to our approach is the following general linear independence criterion.
Lemma 5.2. Suppose that for each
![]() $J \subseteq [n]$
, we have a set
$J \subseteq [n]$
, we have a set
![]() ${\mathcal {C}}_n(J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
of homogeneous polynomials such that
${\mathcal {C}}_n(J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
of homogeneous polynomials such that
![]() ${\mathcal {C}}_n(J)$
descends to a linearly independent subset of
${\mathcal {C}}_n(J)$
descends to a linearly independent subset of
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
. Then the set
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
. Then the set
![]() ${\mathcal {C}}_n \subseteq \Omega _n$
given by
${\mathcal {C}}_n \subseteq \Omega _n$
given by
descends to a linearly independent subset of
![]() $SR_n$
.
$SR_n$
.
The proof of Lemma 5.2 is quite similar to the proof of Theorem 5.1.
Proof. If not, we could find scalars
![]() $c_{J, g_J} \in {\mathbb {C}}$
not all zero so that
$c_{J, g_J} \in {\mathbb {C}}$
not all zero so that
 $$ \begin{align} \sum_{J \subseteq [n]} \sum_{g_J \in {\mathcal{C}}_n(J)} c_{J, g_J} (g_J \cdot \theta_J) = 0 \quad \text{in}\ SR_n \end{align} $$
$$ \begin{align} \sum_{J \subseteq [n]} \sum_{g_J \in {\mathcal{C}}_n(J)} c_{J, g_J} (g_J \cdot \theta_J) = 0 \quad \text{in}\ SR_n \end{align} $$
or equivalently,
 $$ \begin{align} \left( \sum_{J \subseteq [n]} \sum_{g_J \in {\mathcal{C}}_n(J)} c_{J, g_J} (g_J \cdot \theta_J) \right) \odot SH_n = 0. \end{align} $$
$$ \begin{align} \left( \sum_{J \subseteq [n]} \sum_{g_J \in {\mathcal{C}}_n(J)} c_{J, g_J} (g_J \cdot \theta_J) \right) \odot SH_n = 0. \end{align} $$
If we choose
![]() $J_0 \subseteq [n]$
to be Gale-minimal such that
$J_0 \subseteq [n]$
to be Gale-minimal such that
![]() $c_{J_0, g_{J_0}} \neq 0$
for some
$c_{J_0, g_{J_0}} \neq 0$
for some
![]() $g_{J_0} \in {\mathcal {C}}_n(J_0)$
, the relation
$g_{J_0} \in {\mathcal {C}}_n(J_0)$
, the relation
 $$ \begin{align} \left( \sum_{J \subseteq [n]} \sum_{g_J \in {\mathcal{C}}_n(J)} c_{J, g_J} (g_J \cdot \theta_J) \right) \odot {\mathfrak{D}}_{J_0} (\delta_n) = 0 \end{align} $$
$$ \begin{align} \left( \sum_{J \subseteq [n]} \sum_{g_J \in {\mathcal{C}}_n(J)} c_{J, g_J} (g_J \cdot \theta_J) \right) \odot {\mathfrak{D}}_{J_0} (\delta_n) = 0 \end{align} $$
implies (just as in the proof of Theorem 5.1) that
 $$ \begin{align} \sum_{g_{J_0} \in {\mathcal{C}}_n(J_0)} c_{J_0, g_{J_0}} \cdot g_{J_0} \odot (f_{J_0} \odot \delta_n) = 0, \end{align} $$
$$ \begin{align} \sum_{g_{J_0} \in {\mathcal{C}}_n(J_0)} c_{J_0, g_{J_0}} \cdot g_{J_0} \odot (f_{J_0} \odot \delta_n) = 0, \end{align} $$
which contradicts the linear independence of
![]() ${\mathcal {C}}_n(J_0)$
in
${\mathcal {C}}_n(J_0)$
in
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_{J_0})$
.
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_{J_0})$
.
We have all the tools necessary to calculate the Hilbert series of
![]() $SR_n$
. This proves a conjecture [Reference Sagan and Swanson33, Conj. 6.5] of Sagan and Swanson.
$SR_n$
. This proves a conjecture [Reference Sagan and Swanson33, Conj. 6.5] of Sagan and Swanson.
Theorem 5.3. The bigraded Hilbert series of
![]() $SR_n$
is
$SR_n$
is
 $$ \begin{align} {\mathrm {Hilb}}(SR_n;q,z) = \sum_{k = 1}^n z^{n-k} \cdot [k]!_q \cdot {\mathrm {Stir}}_q(n,k). \end{align} $$
$$ \begin{align} {\mathrm {Hilb}}(SR_n;q,z) = \sum_{k = 1}^n z^{n-k} \cdot [k]!_q \cdot {\mathrm {Stir}}_q(n,k). \end{align} $$
Proof. For all subsets
![]() $J \subseteq [n]$
, let
$J \subseteq [n]$
, let
![]() $B_n(J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
be a family of homogeneous polynomials which descends to a basis of
$B_n(J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
be a family of homogeneous polynomials which descends to a basis of
![]() ${\mathbb {C}}[{\mathbf {x}}_n]/(I_n : f_J)$
. By Theorem 4.12, the degree generating function for polynomials in
${\mathbb {C}}[{\mathbf {x}}_n]/(I_n : f_J)$
. By Theorem 4.12, the degree generating function for polynomials in
![]() ${\mathcal {B}}_n(J)$
is
${\mathcal {B}}_n(J)$
is
 $$ \begin{align} \sum_{g_J \in {\mathcal{B}}_n(J)} q^{\deg(g_J)} = [{\mathrm{st}}(J)_1]_q \cdots [{\mathrm{st}}(J)_n]_q. \end{align} $$
$$ \begin{align} \sum_{g_J \in {\mathcal{B}}_n(J)} q^{\deg(g_J)} = [{\mathrm{st}}(J)_1]_q \cdots [{\mathrm{st}}(J)_n]_q. \end{align} $$
Lemma 5.2 guarantees that
![]() ${\mathcal {B}}_n := \bigsqcup _{J \subseteq [n]} {\mathcal {B}}_n(J) \cdot \theta _J$
descends to a linearly independent subset of
${\mathcal {B}}_n := \bigsqcup _{J \subseteq [n]} {\mathcal {B}}_n(J) \cdot \theta _J$
descends to a linearly independent subset of
![]() $SR_n$
. However, Lemma 2.1 shows that
$SR_n$
. However, Lemma 2.1 shows that
 $$ \begin{align} &{\mathrm {Hilb}}(SR_n;q,z) \geq \sum_{J \subseteq [n]} \left( \sum_{g_J \in {\mathcal{B}}_n(J)} q^{\deg(g_J)} \right) \cdot z^{|J|} \nonumber\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad= \sum_{k = 1}^n z^{n-k} \cdot [k]!_q \cdot {\mathrm {Stir}}_q(n,k) \geq {\mathrm {Hilb}}(SR_n;q,z), \end{align} $$
$$ \begin{align} &{\mathrm {Hilb}}(SR_n;q,z) \geq \sum_{J \subseteq [n]} \left( \sum_{g_J \in {\mathcal{B}}_n(J)} q^{\deg(g_J)} \right) \cdot z^{|J|} \nonumber\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad= \sum_{k = 1}^n z^{n-k} \cdot [k]!_q \cdot {\mathrm {Stir}}_q(n,k) \geq {\mathrm {Hilb}}(SR_n;q,z), \end{align} $$
where the inequality is a consequence of Proposition 3.7. This forces the linearly independent subset
![]() ${\mathcal {B}}_n \subseteq SR_n$
to be a basis and the inequalities to be equalities.
${\mathcal {B}}_n \subseteq SR_n$
to be a basis and the inequalities to be equalities.
We present a recipe for building bases of
![]() $SR_n$
from bases of the various commutative quotients
$SR_n$
from bases of the various commutative quotients
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
. We also show how bases of the quotients
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
. We also show how bases of the quotients
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
induce bases of the superharmonic space
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
induce bases of the superharmonic space
![]() $SH_n$
. Since
$SH_n$
. Since
![]() $\Omega _n = SH_n \oplus SI_n$
, bases of
$\Omega _n = SH_n \oplus SI_n$
, bases of
![]() $SH_n$
automatically descend to bases of
$SH_n$
automatically descend to bases of
![]() $SR_n = \Omega _n / SI_n$
. Working in
$SR_n = \Omega _n / SI_n$
. Working in
![]() $SH_n$
can be useful for machine computations since we do not need to consider cosets
$SH_n$
can be useful for machine computations since we do not need to consider cosets
![]() $f + SI_n \in SR_n$
.
$f + SI_n \in SR_n$
.
Theorem 5.4. Suppose that, for every subset
![]() $J \subseteq [n]$
, we have a set
$J \subseteq [n]$
, we have a set
![]() ${\mathcal {B}}_n(J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
of polynomials. Let
${\mathcal {B}}_n(J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
of polynomials. Let
The following are equivalent.
-
1. For all
 $J \subseteq [n]$
, the set
$J \subseteq [n]$
, the set
 ${\mathcal {B}}_n(J)$
descends to a basis of the quotient ring
${\mathcal {B}}_n(J)$
descends to a basis of the quotient ring
 ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
.
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
. -
2. We have a basis of the superharmonic space
 $SH_n$
given by (5.20)
$SH_n$
given by (5.20) $$ \begin{align} \bigsqcup_{J \subseteq [n]} \left\{ (b_J \cdot \theta_J \odot {\mathfrak{D}}_J(\delta_n)) \odot {\mathfrak{D}}_J(\delta_n) \,:\, b_J \in {\mathcal{B}}_n(J) \right\}. \end{align} $$
$$ \begin{align} \bigsqcup_{J \subseteq [n]} \left\{ (b_J \cdot \theta_J \odot {\mathfrak{D}}_J(\delta_n)) \odot {\mathfrak{D}}_J(\delta_n) \,:\, b_J \in {\mathcal{B}}_n(J) \right\}. \end{align} $$
Either of (1) or (2) implies the following.
-
1. The set
 ${\mathcal {B}}_n$
descends to a basis of
${\mathcal {B}}_n$
descends to a basis of
 $SR_n$
.
$SR_n$
.
Proof. The proof of Theorem 5.3 shows that (1) implies (3), so it is enough to verify that (1) and (2) are equivalent.
We define a map
![]() $\Psi $
of vector spaces
$\Psi $
of vector spaces
by the formula
Since the coefficient of
![]() $\theta _J$
in
$\theta _J$
in
![]() ${\mathfrak {D}}_J(\delta _n)$
is
${\mathfrak {D}}_J(\delta _n)$
is
![]() $\pm (f_J \odot \delta _n)$
, we have
$\pm (f_J \odot \delta _n)$
, we have
so that
![]() $\Psi $
is well-defined.
$\Psi $
is well-defined.
We claim that
![]() $\Psi $
is a bijection. Theorems 4.12 and 5.3 imply that the domain and codomain of
$\Psi $
is a bijection. Theorems 4.12 and 5.3 imply that the domain and codomain of
![]() $\Psi $
have the same dimension, so it is enough to show that
$\Psi $
have the same dimension, so it is enough to show that
![]() $\Psi $
is a surjection. Indeed, Lemma 4.8 implies
$\Psi $
is a surjection. Indeed, Lemma 4.8 implies
![]() ${\mathfrak {D}}_J(\delta _n) = (f_J \odot \delta _n) \cdot \theta _J + \Sigma $
, where
${\mathfrak {D}}_J(\delta _n) = (f_J \odot \delta _n) \cdot \theta _J + \Sigma $
, where
![]() $\Sigma \in \bigoplus _{K <_{\mathrm {Gale}} J} {\mathbb {C}}[{\mathbf {x}}_n] \cdot \theta _K$
. As a consequence, we have
$\Sigma \in \bigoplus _{K <_{\mathrm {Gale}} J} {\mathbb {C}}[{\mathbf {x}}_n] \cdot \theta _K$
. As a consequence, we have
for each
![]() $J \subseteq [n]$
. However, Theorem 4.12 implies that
$J \subseteq [n]$
. However, Theorem 4.12 implies that
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
is Artinian Gorenstein with socle spanned by
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
is Artinian Gorenstein with socle spanned by
![]() $f_J \odot \delta _n$
. It follows that
$f_J \odot \delta _n$
. It follows that
as ideals in
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
. Working modulo the subspace
${\mathbb {C}}[{\mathbf {x}}_n]$
. Working modulo the subspace
![]() $\bigoplus _{K <_{\mathrm {Gale}} J} {\mathbb {C}}[{\mathbf {x}}_n] \cdot \theta _K$
, we have
$\bigoplus _{K <_{\mathrm {Gale}} J} {\mathbb {C}}[{\mathbf {x}}_n] \cdot \theta _K$
, we have
 $$ \begin{align} &\left[({\mathbb {C}}[{\mathbf {x}}_n] \cdot \theta_J) \odot {\mathfrak{D}}_J(\delta_n) \right] \odot {\mathfrak{D}}_J(\delta_n) = (I_n : f_J)^\perp \odot {\mathfrak{D}}_J(\delta_n) \nonumber\\[5pt] &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\equiv {\mathbb {C}}[{\mathbf {x}}_n] \odot {\mathfrak{D}}_J(\delta_n) \quad\mod \bigoplus_{K <_{\mathrm {Gale}} J} {\mathbb {C}}[{\mathbf {x}}_n] \cdot \theta_K. \end{align} $$
$$ \begin{align} &\left[({\mathbb {C}}[{\mathbf {x}}_n] \cdot \theta_J) \odot {\mathfrak{D}}_J(\delta_n) \right] \odot {\mathfrak{D}}_J(\delta_n) = (I_n : f_J)^\perp \odot {\mathfrak{D}}_J(\delta_n) \nonumber\\[5pt] &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\equiv {\mathbb {C}}[{\mathbf {x}}_n] \odot {\mathfrak{D}}_J(\delta_n) \quad\mod \bigoplus_{K <_{\mathrm {Gale}} J} {\mathbb {C}}[{\mathbf {x}}_n] \cdot \theta_K. \end{align} $$
The surjectivity of
![]() $\Psi $
follows from induction on Gale order and Theorem 5.1.
$\Psi $
follows from induction on Gale order and Theorem 5.1.
5.3 Superspace Artin monomials
Theorem 5.4 gives a recipe for finding bases
![]() ${\mathcal {B}}_n$
of
${\mathcal {B}}_n$
of
![]() $SR_n$
from bases
$SR_n$
from bases
![]() ${\mathcal {B}}_n(J)$
of the commutative quotients
${\mathcal {B}}_n(J)$
of the commutative quotients
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
. Although a generic set
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
. Although a generic set
![]() ${\mathcal {B}}_n(J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
of polynomials of the appropriate degrees will descend to a basis of
${\mathcal {B}}_n(J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
of polynomials of the appropriate degrees will descend to a basis of
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
, the complexity of the ideals
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
, the complexity of the ideals
![]() $(I_n : f_J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
has so far obstructed progress on finding non-generic bases
$(I_n : f_J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
has so far obstructed progress on finding non-generic bases
![]() ${\mathcal {B}}_n(J)$
of
${\mathcal {B}}_n(J)$
of
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
. We present a conjecture in this direction.
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
. We present a conjecture in this direction.
Define the set of J-Artin monomials by
That is, the set
![]() ${\mathcal {A}}_n(J)$
consists of monomials in
${\mathcal {A}}_n(J)$
consists of monomials in
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
whose exponent sequences fit below the J-staircase. We have
${\mathbb {C}}[{\mathbf {x}}_n]$
whose exponent sequences fit below the J-staircase. We have
![]() ${\mathcal {A}}_n(J) = \varnothing $
whenever
${\mathcal {A}}_n(J) = \varnothing $
whenever
![]() $1 \in J$
. If
$1 \in J$
. If
![]() $J = \varnothing $
, then
$J = \varnothing $
, then
![]() ${\mathcal {A}}_n(\varnothing ) = \{ x_1^{a_1} \cdots x_n^{a_n} \,:\, a_i < i \}$
was proven by E. Artin [Reference Artin4] to descend to a basis of
${\mathcal {A}}_n(\varnothing ) = \{ x_1^{a_1} \cdots x_n^{a_n} \,:\, a_i < i \}$
was proven by E. Artin [Reference Artin4] to descend to a basis of
![]() $R_n$
.
$R_n$
.
Conjecture 5.5. For any subset
![]() $J \subseteq [n]$
, the J-Artin monomials
$J \subseteq [n]$
, the J-Artin monomials
![]() ${\mathcal {A}}_n(J)$
descend to a basis of
${\mathcal {A}}_n(J)$
descend to a basis of
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
.
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
.
Artin’s result [Reference Artin4] proves Conjecture 5.5 when
![]() $J = \varnothing $
. By Theorem 5.4, if Conjecture 5.5 is true, then
$J = \varnothing $
. By Theorem 5.4, if Conjecture 5.5 is true, then
would descend to a basis for
![]() $SR_n$
. This would prove a conjecture [Reference Sagan and Swanson33, Conj. 6.7] of Sagan and Swanson.Footnote
7
Thanks to Theorem 4.12, for any given J it would suffice to prove that
$SR_n$
. This would prove a conjecture [Reference Sagan and Swanson33, Conj. 6.7] of Sagan and Swanson.Footnote
7
Thanks to Theorem 4.12, for any given J it would suffice to prove that
![]() ${\mathcal {A}}_n(J)$
is linearly independent in or spans
${\mathcal {A}}_n(J)$
is linearly independent in or spans
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
.
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
.
We will give evidence for Conjecture 5.5 by showing that it holds when
![]() $J = \{r+1, \dots , n-1, n\}$
is Gale-maximal. This requires a preparatory lemma on certain ideals
$J = \{r+1, \dots , n-1, n\}$
is Gale-maximal. This requires a preparatory lemma on certain ideals
![]() ${\mathcal {J}}_{r,p,n} \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
generated by partial derivatives of h-polynomials.
${\mathcal {J}}_{r,p,n} \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
generated by partial derivatives of h-polynomials.
Lemma 5.6. Let
![]() $r \geq 1$
, let
$r \geq 1$
, let
![]() $1 \leq p \leq n+1$
, and consider the ideal
$1 \leq p \leq n+1$
, and consider the ideal
generated by n partial derivatives of homogeneous symmetric polynomials in the full variable set
![]() ${\mathbf {x}}_n$
. The set of monomials
${\mathbf {x}}_n$
. The set of monomials
descends to a basis for
![]() ${\mathcal {J}}_{r,p,n}$
.
${\mathcal {J}}_{r,p,n}$
.
Lemma 5.6 says that
![]() ${\mathbb {C}}[{\mathbf {x}}_n]/{\mathcal {J}}_{r,p,n}$
shares the same monomial basis as the quotient by variable powers
${\mathbb {C}}[{\mathbf {x}}_n]/{\mathcal {J}}_{r,p,n}$
shares the same monomial basis as the quotient by variable powers
![]() ${\mathbb {C}}[{\mathbf {x}}_n]/(x_1^{r-1} ,\dots , x_{p-1}^{r-1}, x_p^r, \dots , x_n^r)$
. Since
${\mathbb {C}}[{\mathbf {x}}_n]/(x_1^{r-1} ,\dots , x_{p-1}^{r-1}, x_p^r, \dots , x_n^r)$
. Since
![]() ${\mathcal {J}}_{r,p,n}$
has inscrutable Gröbner theory, our proof of Lemma 5.6 relies on exact sequences. Harada, Horiguchi, Murai, Precup and Tymoczko used a similar style of argument to prove an analogous result [Reference Harada, Horiguchi, Murai, Precup and Tymoczko19, Thm. 7.1] on an Artin-like basis for the cohomology rings of regular nilpotent Hessenberg varieties.
${\mathcal {J}}_{r,p,n}$
has inscrutable Gröbner theory, our proof of Lemma 5.6 relies on exact sequences. Harada, Horiguchi, Murai, Precup and Tymoczko used a similar style of argument to prove an analogous result [Reference Harada, Horiguchi, Murai, Precup and Tymoczko19, Thm. 7.1] on an Artin-like basis for the cohomology rings of regular nilpotent Hessenberg varieties.
Proof. If
![]() $r = 1$
and
$r = 1$
and
![]() $p> 1$
, then
$p> 1$
, then
![]() $\partial _1 h_1 = \partial _1 (x_1 + \cdots + x_n) = 1 \in {\mathcal {J}}_{r,p,n}$
so that
$\partial _1 h_1 = \partial _1 (x_1 + \cdots + x_n) = 1 \in {\mathcal {J}}_{r,p,n}$
so that
![]() ${\mathcal {J}}_{r,p,n} = {\mathbb {C}}[{\mathbf {x}}_n]$
is the unit ideal. Since
${\mathcal {J}}_{r,p,n} = {\mathbb {C}}[{\mathbf {x}}_n]$
is the unit ideal. Since
![]() ${\mathcal {M}}_{1,p,n} = \varnothing $
, the result is true in this case. We assume that
${\mathcal {M}}_{1,p,n} = \varnothing $
, the result is true in this case. We assume that
![]() $r> 1$
or
$r> 1$
or
![]() $r = 1$
and
$r = 1$
and
![]() $p = 1$
going forward.
$p = 1$
going forward.
We leave it to the reader to verify the formula
where
![]() $C = r + n - p + 1$
. Since
$C = r + n - p + 1$
. Since
![]() $1 \leq p \leq n+1$
and
$1 \leq p \leq n+1$
and
![]() $r \geq 1$
, we have
$r \geq 1$
, we have
![]() $C> 0$
, and Equation (5.31) implies that
$C> 0$
, and Equation (5.31) implies that
In particular, if we let
![]() $S = [n] - \{p\}$
, we have
$S = [n] - \{p\}$
, we have
so that
![]() ${\mathcal {J}}_{r,p+1,n} \subseteq {\mathcal {J}}_{r,p,n}$
and
${\mathcal {J}}_{r,p+1,n} \subseteq {\mathcal {J}}_{r,p,n}$
and
![]() ${\mathbf {V}}({\mathcal {J}}_{r,p,n}) \subseteq {\mathbf {V}}({\mathcal {J}}_{r,p+1,n})$
. Swanson and Wallach [Reference Swanson and Wallach37, Lem. 6.2] showed that
${\mathbf {V}}({\mathcal {J}}_{r,p,n}) \subseteq {\mathbf {V}}({\mathcal {J}}_{r,p+1,n})$
. Swanson and Wallach [Reference Swanson and Wallach37, Lem. 6.2] showed that
![]() ${\mathbf {V}}({\mathcal {J}}_{r,n+1,n}) = \{0\}$
, so that
${\mathbf {V}}({\mathcal {J}}_{r,n+1,n}) = \{0\}$
, so that
![]() ${\mathbf {V}}({\mathcal {J}}_{r,p,n}) = \{0 \}$
(our assumptions on r and p guarantee that the generators of
${\mathbf {V}}({\mathcal {J}}_{r,p,n}) = \{0 \}$
(our assumptions on r and p guarantee that the generators of
![]() ${\mathcal {J}}_{r,p,n}$
have positive degree). Lemma 2.2 shows that the generating set of
${\mathcal {J}}_{r,p,n}$
have positive degree). Lemma 2.2 shows that the generating set of
![]() ${\mathcal {J}}_{r,p,n}$
is a regular sequence, so that
${\mathcal {J}}_{r,p,n}$
is a regular sequence, so that
The memberships (5.32) and (5.33) imply that
![]() $x_p \cdot \partial _p h_r \in {\mathcal {J}}_{r,p,n}$
, so that
$x_p \cdot \partial _p h_r \in {\mathcal {J}}_{r,p,n}$
, so that
![]() $x_p \cdot {\mathcal {J}}_{r,p+1,n} \subseteq {\mathcal {J}}_{r,p,n}$
. We therefore have an exact sequence
$x_p \cdot {\mathcal {J}}_{r,p+1,n} \subseteq {\mathcal {J}}_{r,p,n}$
. We therefore have an exact sequence
where the first map is induced by multiplication by
![]() $x_p$
and the second map is the canonical projection. The next step is to identify the target of the second map in this sequence in terms of a smaller variable set.
$x_p$
and the second map is the canonical projection. The next step is to identify the target of the second map in this sequence in terms of a smaller variable set.
Let
![]() $\bar {{\mathbf {x}}}_{n-1} = (x_1, \dots , x_{p-1}, x_{p+1}, \dots , x_n)$
be the variable set
$\bar {{\mathbf {x}}}_{n-1} = (x_1, \dots , x_{p-1}, x_{p+1}, \dots , x_n)$
be the variable set
![]() ${\mathbf {x}}_n$
with
${\mathbf {x}}_n$
with
![]() $x_p$
removed. Let
$x_p$
removed. Let
be the surjection defined by
![]() $\pi (x_i) = x_i$
for
$\pi (x_i) = x_i$
for
![]() $i \neq p$
and
$i \neq p$
and
![]() $\pi (x_p) = 0$
. Let
$\pi (x_p) = 0$
. Let
![]() $\bar {{\mathcal {J}}}_{r,p,n-1} \subseteq {\mathbb {C}}[\bar {{\mathbf {x}}}_{n-1}]$
be the ideal with the same generating set as
$\bar {{\mathcal {J}}}_{r,p,n-1} \subseteq {\mathbb {C}}[\bar {{\mathbf {x}}}_{n-1}]$
be the ideal with the same generating set as
![]() ${\mathcal {J}}_{r,p,n-1}$
, but in the variable set
${\mathcal {J}}_{r,p,n-1}$
, but in the variable set
![]() $\bar {{\mathbf {x}}}_{n-1}$
. Writing
$\bar {{\mathbf {x}}}_{n-1}$
. Writing
![]() $S = [n] - \{p\}$
, for any
$S = [n] - \{p\}$
, for any
![]() $d> 0$
and any
$d> 0$
and any
![]() $i \neq p$
, we have the evaluation
$i \neq p$
, we have the evaluation
 $$ \begin{align} &\pi: \partial_i h_d \mapsto \left[ \partial_i h_d \right]_{x_p \, \rightarrow \, 0} = \left[ \partial_i (x_p \cdot h_{d-1} + h_d(S)) \right]_{x_p \, \rightarrow \, 0} \nonumber \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad= \left[ x_p \cdot \partial_i ( h_{d-1} + h_d(S)) \right]_{x_p \, \rightarrow \, 0} = \partial_i h_d(S). \end{align} $$
$$ \begin{align} &\pi: \partial_i h_d \mapsto \left[ \partial_i h_d \right]_{x_p \, \rightarrow \, 0} = \left[ \partial_i (x_p \cdot h_{d-1} + h_d(S)) \right]_{x_p \, \rightarrow \, 0} \nonumber \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad= \left[ x_p \cdot \partial_i ( h_{d-1} + h_d(S)) \right]_{x_p \, \rightarrow \, 0} = \partial_i h_d(S). \end{align} $$
Furthermore, we have
Comparing the generators of
![]() ${\mathcal {J}}_{r,p,n}$
with those of
${\mathcal {J}}_{r,p,n}$
with those of
![]() $\bar {{\mathcal {J}}}_{r,p,n-1}$
and using
$\bar {{\mathcal {J}}}_{r,p,n-1}$
and using
![]() $h_r(S) \in \bar {{\mathcal {J}}}_{r,p,n-1}$
, we conclude that
$h_r(S) \in \bar {{\mathcal {J}}}_{r,p,n-1}$
, we conclude that
so that the exact sequence (5.35) induces a new exact sequence
 $$ \begin{align} \frac{{\mathbb {C}}[{\mathbf {x}}_n]}{{\mathcal{J}}_{r,p+1,n}} \xrightarrow{ \, \, \times \, x_p \, \,} \frac{{\mathbb {C}}[{\mathbf {x}}_n]}{{\mathcal{J}}_{r,p,n}} \xrightarrow{ \, \, \psi \, \, } \frac{{\mathbb {C}}[\bar{{\mathbf {x}}}_{n-1}]}{\bar{{\mathcal{J}}}_{r,p,n-1}} \rightarrow 0, \end{align} $$
$$ \begin{align} \frac{{\mathbb {C}}[{\mathbf {x}}_n]}{{\mathcal{J}}_{r,p+1,n}} \xrightarrow{ \, \, \times \, x_p \, \,} \frac{{\mathbb {C}}[{\mathbf {x}}_n]}{{\mathcal{J}}_{r,p,n}} \xrightarrow{ \, \, \psi \, \, } \frac{{\mathbb {C}}[\bar{{\mathbf {x}}}_{n-1}]}{\bar{{\mathcal{J}}}_{r,p,n-1}} \rightarrow 0, \end{align} $$
where the surjection
![]() $\psi $
is induced by
$\psi $
is induced by
![]() $\pi $
. The Hilbert series formula (5.34) implies that the dimensions of the vector spaces on either side of (5.40) add to the dimension of the vector space in the middle, so the first map in (5.40) is injective, and we have a short exact sequence
$\pi $
. The Hilbert series formula (5.34) implies that the dimensions of the vector spaces on either side of (5.40) add to the dimension of the vector space in the middle, so the first map in (5.40) is injective, and we have a short exact sequence
 $$ \begin{align} 0 \rightarrow \frac{{\mathbb {C}}[{\mathbf {x}}_n]}{{\mathcal{J}}_{r,p+1,n}} \xrightarrow{ \, \, \times \, x_p \, \,} \frac{{\mathbb {C}}[{\mathbf {x}}_n]}{{\mathcal{J}}_{r,p,n}} \xrightarrow{ \, \, \psi \, \, } \frac{{\mathbb {C}}[\bar{{\mathbf {x}}}_{n-1}]}{\bar{{\mathcal{J}}}_{r,p,n-1}} \rightarrow 0. \end{align} $$
$$ \begin{align} 0 \rightarrow \frac{{\mathbb {C}}[{\mathbf {x}}_n]}{{\mathcal{J}}_{r,p+1,n}} \xrightarrow{ \, \, \times \, x_p \, \,} \frac{{\mathbb {C}}[{\mathbf {x}}_n]}{{\mathcal{J}}_{r,p,n}} \xrightarrow{ \, \, \psi \, \, } \frac{{\mathbb {C}}[\bar{{\mathbf {x}}}_{n-1}]}{\bar{{\mathcal{J}}}_{r,p,n-1}} \rightarrow 0. \end{align} $$
By induction, we may assume that
![]() ${\mathcal {M}}_{r,p+1,n}$
descends to a basis of
${\mathcal {M}}_{r,p+1,n}$
descends to a basis of
![]() ${\mathbb {C}}[{\mathbf {x}}_n]/{\mathcal {J}}_{r,p+1,n}$
and that
${\mathbb {C}}[{\mathbf {x}}_n]/{\mathcal {J}}_{r,p+1,n}$
and that
descends to a basis of
![]() ${\mathbb {C}}[\bar {{\mathbf {x}}}_{n-1}]/\bar {{\mathcal {J}}}_{r,p,n-1}$
. The exactness of (5.41) and the observation
${\mathbb {C}}[\bar {{\mathbf {x}}}_{n-1}]/\bar {{\mathcal {J}}}_{r,p,n-1}$
. The exactness of (5.41) and the observation
guarantee that
![]() ${\mathcal {M}}_{r,p,n}$
descends to a basis for
${\mathcal {M}}_{r,p,n}$
descends to a basis for
![]() ${\mathbb {C}}[{\mathbf {x}}_n]/{\mathcal {J}}_{r,p,n}$
, which completes the proof.
${\mathbb {C}}[{\mathbf {x}}_n]/{\mathcal {J}}_{r,p,n}$
, which completes the proof.
Proposition 5.7. Conjecture 5.5 is true when
![]() $J = \{r+1, \dots , n-1,n\}$
is a Gale-maximal subset of
$J = \{r+1, \dots , n-1,n\}$
is a Gale-maximal subset of
![]() $[n]$
.
$[n]$
.
Proof. By Theorem 4.12, the generators of
![]() $(I_n : f_J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
are
$(I_n : f_J) \subseteq {\mathbb {C}}[{\mathbf {x}}_n]$
are
 $$ \begin{align} &h_1(x_1, \dots, x_n), \, \, h_2(x_1, \dots, x_n), \quad \dots \quad h_r(x_r, \dots, x_n), \nonumber\\ &\qquad\qquad\qquad\partial_{r+1} h_{r+1}(x_{r+1}, \dots, x_n), \, \, \partial_{r+2} h_{r+1}(x_{r+1}, \dots, x_n), \quad \dots \quad \partial_n h_{r+1}(x_{r+1}, \dots, x_n). \end{align} $$
$$ \begin{align} &h_1(x_1, \dots, x_n), \, \, h_2(x_1, \dots, x_n), \quad \dots \quad h_r(x_r, \dots, x_n), \nonumber\\ &\qquad\qquad\qquad\partial_{r+1} h_{r+1}(x_{r+1}, \dots, x_n), \, \, \partial_{r+2} h_{r+1}(x_{r+1}, \dots, x_n), \quad \dots \quad \partial_n h_{r+1}(x_{r+1}, \dots, x_n). \end{align} $$
Since
![]() $h_d(x_d, \dots , x_n) = x_d^d + \Sigma $
, where
$h_d(x_d, \dots , x_n) = x_d^d + \Sigma $
, where
![]() $\Sigma $
is a linear combination of terms which are
$\Sigma $
is a linear combination of terms which are
![]() $> x_d^d$
in lexicographial order, we see that
$> x_d^d$
in lexicographial order, we see that
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
is spanned by monomials of the form
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
is spanned by monomials of the form
![]() $x_1^{b_1} \cdots x_n^{b_n}$
where
$x_1^{b_1} \cdots x_n^{b_n}$
where
![]() $b_i < i$
for
$b_i < i$
for
![]() $i \leq r$
. The generators
$i \leq r$
. The generators
![]() $\partial _i h_{r+1}(x_{r+1}, \dots , x_n)$
of
$\partial _i h_{r+1}(x_{r+1}, \dots , x_n)$
of
![]() $(I_n : f_J)$
and Lemma 5.6 (applied over the set
$(I_n : f_J)$
and Lemma 5.6 (applied over the set
![]() $\{x_{r+1}, \dots , x_n \}$
of variables indexed by J) imply that
$\{x_{r+1}, \dots , x_n \}$
of variables indexed by J) imply that
![]() ${\mathcal {A}}_n(J)$
descends to a spanning set of
${\mathcal {A}}_n(J)$
descends to a spanning set of
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
. This spanning set must be a basis by Theorem 4.12.
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
. This spanning set must be a basis by Theorem 4.12.
Given Proposition 5.7, a natural strategy for proving Conjecture 5.5 would be to induct on the position of J in Gale order. The base case of J Gale-maximal is handled by Proposition 5.7. If
![]() $i \notin J$
and
$i \notin J$
and
![]() $i+1 \in J$
, we have
$i+1 \in J$
, we have
![]() $s_i \cdot J <_{\mathrm {Gale}} J$
, where
$s_i \cdot J <_{\mathrm {Gale}} J$
, where
![]() $s_i = (i,i+1)$
is the adjacent transposition in
$s_i = (i,i+1)$
is the adjacent transposition in
![]() ${\mathfrak {S}}_n$
. Furthermore, the property
${\mathfrak {S}}_n$
. Furthermore, the property
![]() $({\mathfrak {a}} : f g) = ( ({\mathfrak {a}} : f) : g)$
of colon ideals gives rise to a natural injection
$({\mathfrak {a}} : f g) = ( ({\mathfrak {a}} : f) : g)$
of colon ideals gives rise to a natural injection
where
![]() $\varphi (f) := (x_i - x_{i+1}) \times s_i \cdot f$
is defined by swapping the variables
$\varphi (f) := (x_i - x_{i+1}) \times s_i \cdot f$
is defined by swapping the variables
![]() $x_i \leftrightarrow x_{i+1}$
and multiplying by
$x_i \leftrightarrow x_{i+1}$
and multiplying by
![]() $x_i - x_{i+1}$
. Unfortunately, the map
$x_i - x_{i+1}$
. Unfortunately, the map
![]() $\varphi $
does not relate to the structure of monomials in
$\varphi $
does not relate to the structure of monomials in
![]() ${\mathcal {A}}_n(s_i \cdot J)$
and
${\mathcal {A}}_n(s_i \cdot J)$
and
![]() ${\mathcal {A}}_n(J)$
in an obvious way; this has made Conjecture 5.5 resistant to inductive attack.
${\mathcal {A}}_n(J)$
in an obvious way; this has made Conjecture 5.5 resistant to inductive attack.
6 Conclusion
The most glaring open problem of our work is to enhance the Hilbert series result of Theorem 5.3 and prove the Fields Conjecture 1.9 on the bigraded
![]() ${\mathfrak {S}}_n$
-structure of
${\mathfrak {S}}_n$
-structure of
![]() $SR_n$
. One way to achieve this would be to show that the composite linear map
$SR_n$
. One way to achieve this would be to show that the composite linear map
 $$ \begin{align} \varphi: \bigoplus_{k = 1}^n V_{n,k} \hookrightarrow \Omega_n \twoheadrightarrow SR_n \end{align} $$
$$ \begin{align} \varphi: \bigoplus_{k = 1}^n V_{n,k} \hookrightarrow \Omega_n \twoheadrightarrow SR_n \end{align} $$
is bijective, where
![]() $V_{n,k} \subseteq \Omega _n$
are the spaces constructed by the authors [Reference Rhoades and Wilson30] and described in the introduction. Thanks to Theorem 5.3 and [Reference Rhoades and Wilson30], we know that the domain and target of
$V_{n,k} \subseteq \Omega _n$
are the spaces constructed by the authors [Reference Rhoades and Wilson30] and described in the introduction. Thanks to Theorem 5.3 and [Reference Rhoades and Wilson30], we know that the domain and target of
![]() $\varphi $
have the same vector space dimension, so we are asking that
$\varphi $
have the same vector space dimension, so we are asking that
![]() $\varphi $
have a generic property. Unfortunately, much like in the case of Conjecture 5.5, proving that
$\varphi $
have a generic property. Unfortunately, much like in the case of Conjecture 5.5, proving that
![]() $\varphi $
satisfies this generic property has exhibited resistance to direct attack.
$\varphi $
satisfies this generic property has exhibited resistance to direct attack.
Various ideas in this paper have made appearances in the theory of Hessenberg varieties. Lemma 2.3 on the realization of colon ideals
![]() $({\mathfrak {a}} : f)$
by complete intersections was used by Abe, Horiguchi, Masuda, Murai and Sato [Reference Abe, Horiguchi, Masuda, Murai and Sato2] to relate the cohomology rings of Hessenberg varieties to derivation modules of hyperplane arrangements associated to down-closed sets in positive root posets. The polynomials
$({\mathfrak {a}} : f)$
by complete intersections was used by Abe, Horiguchi, Masuda, Murai and Sato [Reference Abe, Horiguchi, Masuda, Murai and Sato2] to relate the cohomology rings of Hessenberg varieties to derivation modules of hyperplane arrangements associated to down-closed sets in positive root posets. The polynomials
![]() $f_J \in {\mathbb {C}}[{\mathbf {x}}_n]$
appearing in this paper factor into products
$f_J \in {\mathbb {C}}[{\mathbf {x}}_n]$
appearing in this paper factor into products
![]() $\prod _{j \in J} f_{\{j\}}$
labeled by singletons. In turn, the polynomials
$\prod _{j \in J} f_{\{j\}}$
labeled by singletons. In turn, the polynomials
![]() $f_{\{j\}}$
labeled by singletons resemble members of a family
$f_{\{j\}}$
labeled by singletons resemble members of a family
![]() $f_{j,i} \in {\mathbb {C}}[{\mathbf {x}}_n]$
of polynomials appearing in the work of Abe, Harada, Horiguchi and Masuda [Reference Abe, Harada, Horiguchi and Masuda1]. The polynomials
$f_{j,i} \in {\mathbb {C}}[{\mathbf {x}}_n]$
of polynomials appearing in the work of Abe, Harada, Horiguchi and Masuda [Reference Abe, Harada, Horiguchi and Masuda1]. The polynomials
![]() $f_{j,i}$
were used to present the cohomology of regular nilpotent Hessenberg varieties using a GKM-style excision which bears combinatorial resemblance to removing J-resentful permutations from
$f_{j,i}$
were used to present the cohomology of regular nilpotent Hessenberg varieties using a GKM-style excision which bears combinatorial resemblance to removing J-resentful permutations from
![]() ${\mathfrak {S}}_n$
to arrive at J-Nietzschean permutations. An Artin-like basis of these cohomology rings was proven by Harada, Horiguchi, Murai, Precup and Tymoczko [Reference Harada, Horiguchi, Murai, Precup and Tymoczko19]; we use similar techniques in the proof of Lemma 5.6 to show in Proposition 5.7 that the Artin monomials attached to terminal subsets
${\mathfrak {S}}_n$
to arrive at J-Nietzschean permutations. An Artin-like basis of these cohomology rings was proven by Harada, Horiguchi, Murai, Precup and Tymoczko [Reference Harada, Horiguchi, Murai, Precup and Tymoczko19]; we use similar techniques in the proof of Lemma 5.6 to show in Proposition 5.7 that the Artin monomials attached to terminal subsets
![]() $J = \{ r, r+1, \dots , n \} \subseteq [n]$
descend to a basis of the quotient rings
$J = \{ r, r+1, \dots , n \} \subseteq [n]$
descend to a basis of the quotient rings
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
. Given these technical parallels, the authors suspect that there is a deeper connection between the supercoinvariant ring
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
. Given these technical parallels, the authors suspect that there is a deeper connection between the supercoinvariant ring
![]() $SR_n$
and Hessenberg theory. We present a conjecture in this direction as follows.
$SR_n$
and Hessenberg theory. We present a conjecture in this direction as follows.
Recall that a finite-dimensional graded
![]() ${\mathbb {C}}$
-algebra
${\mathbb {C}}$
-algebra
![]() $A = \bigoplus _{i = 0}^d A_i$
with
$A = \bigoplus _{i = 0}^d A_i$
with
![]() $A_d \neq 0$
satisfies Poincaré Duality if
$A_d \neq 0$
satisfies Poincaré Duality if
![]() $A_d \cong {\mathbb {C}}$
is 1-dimensional and if the multiplication
$A_d \cong {\mathbb {C}}$
is 1-dimensional and if the multiplication
![]() $A_i \otimes A_{d-i} \rightarrow A_d \cong {\mathbb {C}}$
is a perfect paring for all
$A_i \otimes A_{d-i} \rightarrow A_d \cong {\mathbb {C}}$
is a perfect paring for all
![]() $0 \leq i \leq d$
. If A satisfies Poincaré Duality, an element
$0 \leq i \leq d$
. If A satisfies Poincaré Duality, an element
![]() $\ell \in A_1$
of homogeneous degree 1 is a Lefschetz element if, for all
$\ell \in A_1$
of homogeneous degree 1 is a Lefschetz element if, for all
![]() $i < d/2$
, the map
$i < d/2$
, the map
of multiplication by
![]() $\ell ^{d - 2i}$
is a bijection. If a Lefschetz element
$\ell ^{d - 2i}$
is a bijection. If a Lefschetz element
![]() $\ell \in A_1$
exists, the algebra A is said to satisfy the Hard Lefschetz property.
$\ell \in A_1$
exists, the algebra A is said to satisfy the Hard Lefschetz property.
Algebras A which satisfy PD and HL arise naturally in geometry. If X is a smooth closed complex projective variety, its cohomology ring
![]() $A = H^{\bullet }(X)$
satisfies PD and HL (here we double the grading by setting
$A = H^{\bullet }(X)$
satisfies PD and HL (here we double the grading by setting
![]() $A_i := H^{2i}(X)$
). For example, the coinvariant ring
$A_i := H^{2i}(X)$
). For example, the coinvariant ring
![]() $R_n = {\mathbb {C}}[{\mathbf {x}}_n]/I_n = H^{\bullet }(\mathrm {Fl}(n))$
satisfies PD and HL. Maeno, Numata and Wachi proved [Reference Maeno, Numata and Wachi25] that a linear form
$R_n = {\mathbb {C}}[{\mathbf {x}}_n]/I_n = H^{\bullet }(\mathrm {Fl}(n))$
satisfies PD and HL. Maeno, Numata and Wachi proved [Reference Maeno, Numata and Wachi25] that a linear form
![]() $\ell = c_1 x_1 + \cdots + c_n x_n$
is a Lefschetz element of
$\ell = c_1 x_1 + \cdots + c_n x_n$
is a Lefschetz element of
![]() $R_n$
if and only if the coefficients
$R_n$
if and only if the coefficients
![]() $c_1, \dots , c_n \in {\mathbb {C}}$
are distinct.
$c_1, \dots , c_n \in {\mathbb {C}}$
are distinct.
Even if a variety X is not smooth, its cohomology ring
![]() $H^{\bullet }(X)$
can still satisfy PD and HL. Abe, Horiguchi, Masuda, Murai and Sato proved [Reference Abe, Horiguchi, Masuda, Murai and Sato2, Thm. 12.1] that
$H^{\bullet }(X)$
can still satisfy PD and HL. Abe, Horiguchi, Masuda, Murai and Sato proved [Reference Abe, Horiguchi, Masuda, Murai and Sato2, Thm. 12.1] that
![]() $H^{\bullet }(X)$
satisfies PD and HL when X is a regular nilpotent Hessenberg variety, despite the fact that these varieties are usually singular. Furthermore, a graded algebra
$H^{\bullet }(X)$
satisfies PD and HL when X is a regular nilpotent Hessenberg variety, despite the fact that these varieties are usually singular. Furthermore, a graded algebra
![]() $A = \bigoplus _{i = 0}^d A_i$
can still satisfy PD and HL, and so behave like the cohomology ring of a hypothetical smooth compact variety X. As we have seen, the quotients
$A = \bigoplus _{i = 0}^d A_i$
can still satisfy PD and HL, and so behave like the cohomology ring of a hypothetical smooth compact variety X. As we have seen, the quotients
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
satisfy PD since they are complete intersections. For the next conjecture, we adopt the convention that the zero ring
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
satisfy PD since they are complete intersections. For the next conjecture, we adopt the convention that the zero ring
![]() $0 = H^{\bullet }(\varnothing )$
satisfies HL.
$0 = H^{\bullet }(\varnothing )$
satisfies HL.
Conjecture 6.1. For any
![]() $J \subseteq [n]$
, the quotient ring
$J \subseteq [n]$
, the quotient ring
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
satisfies the Hard Lefschetz property.
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
satisfies the Hard Lefschetz property.
Conjecture 6.1 has been tested for
![]() $n \leq 7$
. Computational data suggests that the linear forms
$n \leq 7$
. Computational data suggests that the linear forms
![]() $\ell = c_1 x_1 + \cdots + c_n x_n$
continue to serve as Lefschetz elements, provided
$\ell = c_1 x_1 + \cdots + c_n x_n$
continue to serve as Lefschetz elements, provided
![]() $c_1, \dots , c_n \in {\mathbb {C}}$
are distinct. We suspect that the Hodge-Riemann relations hold for
$c_1, \dots , c_n \in {\mathbb {C}}$
are distinct. We suspect that the Hodge-Riemann relations hold for
![]() ${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
, as well (see [Reference Abe, Horiguchi, Masuda, Murai and Sato2, Sec. 12]).
${\mathbb {C}}[{\mathbf {x}}_n] / (I_n : f_J)$
, as well (see [Reference Abe, Horiguchi, Masuda, Murai and Sato2, Sec. 12]).
One of the most aesthetically pleasing aspects of
![]() $SR_n$
is its direct extension to general complex reflection groups. An element
$SR_n$
is its direct extension to general complex reflection groups. An element
![]() $g \in GL_n({\mathbb {C}})$
is a pseudoreflection if g is conjugate to a diagonal matrix of the form
$g \in GL_n({\mathbb {C}})$
is a pseudoreflection if g is conjugate to a diagonal matrix of the form
![]() $\mathrm {diag}(\zeta ,1,\dots ,1)$
, where
$\mathrm {diag}(\zeta ,1,\dots ,1)$
, where
![]() $\zeta \in {\mathbb {C}}^{\times }$
is a root-of-unity of finite order. A finite subgroup
$\zeta \in {\mathbb {C}}^{\times }$
is a root-of-unity of finite order. A finite subgroup
![]() $G \subseteq GL_n({\mathbb {C}})$
is a complex reflection group if G is generated by pseudoreflections.
$G \subseteq GL_n({\mathbb {C}})$
is a complex reflection group if G is generated by pseudoreflections.
The natural action of a complex reflection group
![]() $G \subseteq GL_n({\mathbb {C}})$
on
$G \subseteq GL_n({\mathbb {C}})$
on
![]() ${\mathbb {C}}^n$
induces actions of G on
${\mathbb {C}}^n$
induces actions of G on
![]() ${\mathbb {C}}[{\mathbf {x}}_n]$
and
${\mathbb {C}}[{\mathbf {x}}_n]$
and
![]() $\Omega _n$
by linear substitutions. Chevalley proved [Reference Chevalley10] that the invariant subring
$\Omega _n$
by linear substitutions. Chevalley proved [Reference Chevalley10] that the invariant subring
![]() ${\mathbb {C}}[{\mathbf {x}}_n]^G$
admits a set
${\mathbb {C}}[{\mathbf {x}}_n]^G$
admits a set
![]() $f_1, \dots , f_n$
of algebraically independent homogeneous generators of positive degrees, so that
$f_1, \dots , f_n$
of algebraically independent homogeneous generators of positive degrees, so that
![]() ${\mathbb {C}}[{\mathbf {x}}_n]^G = {\mathbb {C}}[f_1, \dots , f_n]$
is itself a polynomial ring. Although the
${\mathbb {C}}[{\mathbf {x}}_n]^G = {\mathbb {C}}[f_1, \dots , f_n]$
is itself a polynomial ring. Although the
![]() $f_i$
are not unique, their degrees
$f_i$
are not unique, their degrees
![]() $d_1, \dots , d_n$
are uniquely determined by G. Solomon [Reference Solomon34] proved that the superspace invariants
$d_1, \dots , d_n$
are uniquely determined by G. Solomon [Reference Solomon34] proved that the superspace invariants
![]() $(\Omega _n)^G$
are a free
$(\Omega _n)^G$
are a free
![]() ${\mathbb {C}}[{\mathbf {x}}_n]^G$
-module and described a basis for this module as follows.
${\mathbb {C}}[{\mathbf {x}}_n]^G$
-module and described a basis for this module as follows.
Theorem 6.2. (Solomon [Reference Solomon34])
Let
![]() $f_1, \dots , f_n \in {\mathbb {C}}[{\mathbf {x}}_n]^{{\mathfrak {S}}_n}$
be any list of algebraically independent homogeneous generators of
$f_1, \dots , f_n \in {\mathbb {C}}[{\mathbf {x}}_n]^{{\mathfrak {S}}_n}$
be any list of algebraically independent homogeneous generators of
![]() ${\mathbb {C}}[{\mathbf {x}}_n]^{{\mathfrak {S}}_n}$
. The space
${\mathbb {C}}[{\mathbf {x}}_n]^{{\mathfrak {S}}_n}$
. The space
![]() $(\Omega _n)^{{\mathfrak {S}}_n}$
is a free module over
$(\Omega _n)^{{\mathfrak {S}}_n}$
is a free module over
![]() ${\mathbb {C}}[{\mathbf {x}}_n]^{{\mathfrak {S}}_n}$
with basis
${\mathbb {C}}[{\mathbf {x}}_n]^{{\mathfrak {S}}_n}$
with basis
Solomon’s Theorem 6.2 describes the space
![]() $(\Omega _n)^G$
of G-invariants as a
$(\Omega _n)^G$
of G-invariants as a
![]() ${\mathbb {C}}[{\mathbf {x}}_n]^G$
-module. Any fundamental system of invariants
${\mathbb {C}}[{\mathbf {x}}_n]^G$
-module. Any fundamental system of invariants
![]() $f_1, \dots , f_n \in {\mathbb {C}}[{\mathbf {x}}_n]^G$
gives rise to a generating set for the G-supercoinvariant ideal
$f_1, \dots , f_n \in {\mathbb {C}}[{\mathbf {x}}_n]^G$
gives rise to a generating set for the G-supercoinvariant ideal
![]() $SI_G$
generated by
$SI_G$
generated by
![]() $(\Omega _n)^G_+$
. We have
$(\Omega _n)^G_+$
. We have
![]() $SI_G = (f_1, \dots , f_n, df_1, \dots , df_n)$
and may use this presentation to study the quotient
$SI_G = (f_1, \dots , f_n, df_1, \dots , df_n)$
and may use this presentation to study the quotient
![]() $SR_G := \Omega _n / SI_G$
as a bigraded G-module.
$SR_G := \Omega _n / SI_G$
as a bigraded G-module.
Solomon used Theorem 6.2 to give a uniform proof of the product formula
 $$ \begin{align} \sum_{g \in G} t^{\dim \mathrm{Fix}(g)} = (t + d_1 - 1) \cdots (t + d_n - 1), \end{align} $$
$$ \begin{align} \sum_{g \in G} t^{\dim \mathrm{Fix}(g)} = (t + d_1 - 1) \cdots (t + d_n - 1), \end{align} $$
where
![]() $\mathrm {Fix}(g) = \{ v \in {\mathbb {C}}^n \,:\, g \cdot v = v \}$
is the fixed subspace of
$\mathrm {Fix}(g) = \{ v \in {\mathbb {C}}^n \,:\, g \cdot v = v \}$
is the fixed subspace of
![]() ${\mathbb {C}}^n$
attached to g. In type A, this is equivalent to the factorization
${\mathbb {C}}^n$
attached to g. In type A, this is equivalent to the factorization
 $$ \begin{align} \sum_{k = 0}^n c(n,k) \cdot t^k = t (t+1) \cdots (t + n - 1), \end{align} $$
$$ \begin{align} \sum_{k = 0}^n c(n,k) \cdot t^k = t (t+1) \cdots (t + n - 1), \end{align} $$
where
![]() $c(n,k)$
is the Stirling number of the first kind counting permutations
$c(n,k)$
is the Stirling number of the first kind counting permutations
![]() $w \in {\mathfrak {S}}_n$
with k cycles. However, the algebra of
$w \in {\mathfrak {S}}_n$
with k cycles. However, the algebra of
![]() $SR_n = \Omega _n / SI_n$
is governed by ordered set partitions, which relate to Stirling numbers of the second kind.
$SR_n = \Omega _n / SI_n$
is governed by ordered set partitions, which relate to Stirling numbers of the second kind.
Ordered set partitions of
![]() $[n]$
are in bijective correspondence with faces in the type A Coxeter complex. All available data in types BCD suggest that the fermionic degree k piece of
$[n]$
are in bijective correspondence with faces in the type A Coxeter complex. All available data in types BCD suggest that the fermionic degree k piece of
![]() $SR_G := \Omega _n/SI_G$
has dimension equal to the number of codimension k faces in the corresponding Coxeter complex (in type A this is a consequence of Theorem 5.3). We also have agreement in type H
$SR_G := \Omega _n/SI_G$
has dimension equal to the number of codimension k faces in the corresponding Coxeter complex (in type A this is a consequence of Theorem 5.3). We also have agreement in type H
![]() $_3$
. However, in type F
$_3$
. However, in type F
![]() $_4$
, these quantities disagree. The bigraded Hilbert series of
$_4$
, these quantities disagree. The bigraded Hilbert series of
![]() $SR_{\mathrm {F}_4}$
is given by
$SR_{\mathrm {F}_4}$
is given by
 $$ \begin{align} &{\mathrm {Hilb}}(SR_{\mathrm{F}_4};q,z) = \nonumber\\ &\left( \begin{array}{c} 1 + 4q + 9 q^2 + 16 q^3 + 25 q^4 + 36 q^5 + 48 q^6 + 60 q^7 + 71 q^8 + 80 q^9 + 87 q^{10} + 92 q^{11} + 94 q^{12} + \\ 92 q^{13} + 87 q^{14} + 80 q^{15} + 71 q^{16} + 60 q^{17} + 48 q^{18} + 36 q^{19} + 25q^{20} + 16 q^{21} + 9 q^{22} 4 + q^{23} + q^{24} \end{array} \right) \cdot z^0 + \nonumber \\ &\left(\! \begin{array}{c} 4 + 15q + 32q^2 + 55q^3 + 84q^4 + 118q^5 +152 q^6 + 182 q^7 + 204 q^8 + 215 q^9 + 216 q^{10} + 207 q^{11} + \\ 188 q^{12} + 161 q^{13} + 132 q^{14} + 105 q^{15} + 80 q^{16} + 58 q^{17} + 40 q^{18} + 26 q^{19} + 16 q^{20} + 9 q^{21} + 4 q^{22} + q^{23} \end{array} \!\right) \cdot z^1 + \nonumber\\ &\left( \begin{array}{c} 6 + 20 q + 39 q^2 + 64 q^3 + 95 q^4 + 128 q^5 + 154 q^6 + 168 q^7 + 164 q^8 + 140 q^9 + \\ 122 q^{10} + 100 q^{11} + 75 q^{12} + 52 q^{13} + 34 q^{14} + 20 q^{15} + 10 q^{16} + 4 q^{17} + q^{18} \end{array} \right) \cdot z^2 \nonumber\\ + &\left( \begin{array}{c} 4 +10 q + 16 q^2 + 25 q^3 + 36 q^4 + 43 q^5 + \\ 44 q^6 + 36 q^7 + 16 q^8 + 9 q^9 + 4 q^{10} + q^{11} \end{array} \right) \cdot z^3 + z^4, \end{align} $$
$$ \begin{align} &{\mathrm {Hilb}}(SR_{\mathrm{F}_4};q,z) = \nonumber\\ &\left( \begin{array}{c} 1 + 4q + 9 q^2 + 16 q^3 + 25 q^4 + 36 q^5 + 48 q^6 + 60 q^7 + 71 q^8 + 80 q^9 + 87 q^{10} + 92 q^{11} + 94 q^{12} + \\ 92 q^{13} + 87 q^{14} + 80 q^{15} + 71 q^{16} + 60 q^{17} + 48 q^{18} + 36 q^{19} + 25q^{20} + 16 q^{21} + 9 q^{22} 4 + q^{23} + q^{24} \end{array} \right) \cdot z^0 + \nonumber \\ &\left(\! \begin{array}{c} 4 + 15q + 32q^2 + 55q^3 + 84q^4 + 118q^5 +152 q^6 + 182 q^7 + 204 q^8 + 215 q^9 + 216 q^{10} + 207 q^{11} + \\ 188 q^{12} + 161 q^{13} + 132 q^{14} + 105 q^{15} + 80 q^{16} + 58 q^{17} + 40 q^{18} + 26 q^{19} + 16 q^{20} + 9 q^{21} + 4 q^{22} + q^{23} \end{array} \!\right) \cdot z^1 + \nonumber\\ &\left( \begin{array}{c} 6 + 20 q + 39 q^2 + 64 q^3 + 95 q^4 + 128 q^5 + 154 q^6 + 168 q^7 + 164 q^8 + 140 q^9 + \\ 122 q^{10} + 100 q^{11} + 75 q^{12} + 52 q^{13} + 34 q^{14} + 20 q^{15} + 10 q^{16} + 4 q^{17} + q^{18} \end{array} \right) \cdot z^2 \nonumber\\ + &\left( \begin{array}{c} 4 +10 q + 16 q^2 + 25 q^3 + 36 q^4 + 43 q^5 + \\ 44 q^6 + 36 q^7 + 16 q^8 + 9 q^9 + 4 q^{10} + q^{11} \end{array} \right) \cdot z^3 + z^4, \end{align} $$
and this expression has
![]() $q \rightarrow 1$
specialization
$q \rightarrow 1$
specialization
This coefficient sequence is almost the same as the reversed f-vector
![]() $(1152, 2304, 1392, 240, 1)$
of the type F
$(1152, 2304, 1392, 240, 1)$
of the type F
![]() $_4$
Coxeter complex, but the coefficients of
$_4$
Coxeter complex, but the coefficients of
![]() $z^2$
and
$z^2$
and
![]() $z^3$
are too large by 4. Finding a precise invariant-theoretic description of the Hilbert series of
$z^3$
are too large by 4. Finding a precise invariant-theoretic description of the Hilbert series of
![]() $SR_G$
would likely be very interesting.
$SR_G$
would likely be very interesting.
Acknowledgments
The authors are grateful to François Bergeron, Nantel Bergeron, Sutanay Bhattacharya, Raymond Chou, Darij Grinberg, Jim Haglund, Daniël Kroes, Yasuhide Numata, Vic Reiner, Bruce Sagan, Josh Swanson, Nolan Wallach, Tianyi Yu and Mike Zabrocki for many helpful conversations. The authors are grateful to anonymous referees whose comments improved the exposition of this paper.
Funding statement
B. Rhoades was partially supported by NSF Grants DMS-1953781 and DMS-2246846. A. Wilson was partially supported by an AMS Simons PUI grant.
Competing interests
The authors have no competing interest to declare.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.