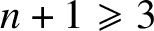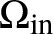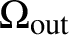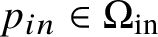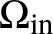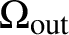Inverse problems for nonlinear hyperbolic equations with disjoint sources and receivers

Abstract

The article studies inverse problems of determining unknown coefficients in various semi-linear and quasi-linear wave equations given the knowledge of an associated source-to-solution map. We introduce a method to solve inverse problems for nonlinear equations using interaction of three waves that makes it possible to study the inverse problem in all globally hyperbolic spacetimes of the dimension $n+1\geqslant 3$ and with partial data. We consider the case when the set $\Omega _{\mathrm{in}}$ , where the sources are supported, and the set $\Omega _{\mathrm{out}}$ , where the observations are made, are separated. As model problems we study both a quasi-linear equation and a semi-linear wave equation and show in each case that it is possible to uniquely recover the background metric up to the natural obstructions for uniqueness that is governed by finite speed of propagation for the wave equation and a gauge corresponding to change of coordinates. The proof consists of two independent components. In the geometric part of the article we introduce a novel geometrical object, the three-to-one scattering relation. We show that this relation determines uniquely the topological, differential and conformal structures of the Lorentzian manifold in a causal diamond set that is the intersection of the future of the point $p_{in}\in \Omega _{\mathrm{in}}$ and the past of the point $p_{out}\in \Omega _{\mathrm{out}}$ . In the analytic part of the article we study multiple-fold linearisation of the nonlinear wave equation using Gaussian beams. We show that the source-to-solution map, corresponding to sources in $\Omega _{\mathrm{in}}$ and observations in $\Omega _{\mathrm{out}}$ , determines the three-to-one scattering relation. The methods developed in the article do not require any assumptions on the conjugate or cut points.

1 Introduction

Let $(M,g)$ be a smooth Lorentzian manifold of dimension $1+n$ with $n\geqslant 2$ and signature $(-,+,\ldots ,+)$ . Using the standard notations, for $p,q\in M$ we write $p \le q$ if there is a causal path on M from p to q or $p=q$ . Also, we write $p\ll q$ if there is a time-like path on M from p to q. Using these relations, we define the causal future past and future of a point $p\in M$ through

$$ \begin{align*}J^+(p) = \{x \in M: p \le x\}\quad \text{and} \quad J^-(p) = \{x \in M : x \le p\}.\end{align*} $$

The chronological future and past of p are defined analogously with the causal relation replaced by the chronological relation,

$$ \begin{align*}I^+(p)=\{x \in M: p \ll x\}\quad \text{and}\quad I^-(q) = \{x \in M : x \ll q\}.\end{align*} $$

We will make the standing assumption that $(M,g)$ is globally hyperbolic. Here, by global hyperbolicity we mean that $(M,g)$ is causal (i.e., no closed causal curve exists) and, additionally, if $p,q \in M$ with $p\le q$ , then $J^+(p)\cap J^-(q)$ is compact [1 3]. Global hyperbolicity implies that the relation $\le $ is closed while $\ll $ is open and consequently that $J^{\pm }$ is closed while $I^{\pm }$ is open. It also implies that there exists a global splitting in ‘time’ and ‘space’ in the sense that $(M,g)$ is isometric to $\mathbb R\times M_0$ with the metric taking the form

(1.1) $$ \begin{align} g=c(x^0,x')\left(-dx^0\otimes\,dx^0+g_0(x^0,x')\right), \quad \forall x^0 \in \mathbb R,\ x' \in M_0, \end{align} $$

where c is a smooth positive function and $g_0$ is a Riemannian metric on the n-dimensional manifold $M_0$ smoothly depending on the parameter $x^0$ . Moreover, each set $\{x^0\}\times M_0$ is a Cauchy hypersurface in M; that is, any inextendible causal curve intersects it exactly once. For the sake of brevity, we will sometimes identify points, functions and tensors over the manifold $(M,g)$ with their preimage in $\mathbb R\times M_0$ without explicitly writing the diffeomorphism.

In this article, we consider the inverse problems with partial data for semi-linear and quasi-linear wave equations, where the set $\Omega _{\mathrm{in}}$ , where the sources are supported, and the set ${\Omega _{\mathrm{out}}}$ , where the observations are made, may be separated. Motivated by applications, such problems can be called remote sensing problems. Similar problems with separated sources and measurements are encountered in radar imaging problems [3, 4, 18, 30] and seismic imaging [3 1, 32, 33, 88]. Recently, uniqueness results for inverse problems with separated sources and receivers have been obtained for the fractional powers of elliptic differential operators; see, for example, results in [34, 35] for the fractional Schrödinger operators and [6 6] for the nonlinear fractional Schrödinger equations. The study of the semi-linear model is carried out throughout the article as a simpler analytical model that clarifies the main methodology. A quasi-linear model is also considered to show the robustness of the method to various kinds of nonlinearities.

The main novelties of the article are that we develop a framework for inverse problems for nonlinear equations, where one uses interaction of only three waves. To this end, we formulate the concept of three-to-one scattering relation that is applicable for a wide class of nonlinear equations (see Theorem 1.3). This approach makes it possible to study the inverse problem in all dimensions $n+1\geqslant 3$ and the partial data problems with separated sources and observations.

1.1 The semi-linear model

Our main aim is to study quasi-linear equations, but to describe how the method works, we start our considerations with semi-linear equations. We consider the model setup

(1.2) $$ \begin{align} \begin{aligned} \begin{cases} \Box_{g}u+u^m=f\,\quad \text{on}\ (-\infty,T)\times M_0, \\ u=0 \quad \text{on}\ (-\infty,-T)\times M_0. \end{cases} \end{aligned} \end{align} $$

Here, $m\geqslant 3$ is an integer and $T>0$ is a parameter to be fixed later and the source f is real-valued and compactly supported in the set $(-T,T)\times M_0$ . The wave operator, $\Box _g$ , is defined in local coordinates $(x^0,\ldots ,x^n)$ by the expression

$$ \begin{align*}\Box_{g} u = -\sum_{j,k=0}^n\left|\det g\right|{}^{-\frac{1}{2}} \frac{\partial}{\partial x^j}( \left|\det g\right|{}^{\frac{1}{2}}g^{jk} \frac{\partial u}{\partial x^k}),\end{align*} $$

where $g^{jk}$ stands for the elements of the inverse of g. Note that we are using the $(x^0,x')$ -coordinate system on M that is given by (1.1).

1.2 The quasi-linear model

For the quasi-linear wave equation, we first consider a family of smooth real-valued symmetric tensors $G_z(x)=G(x,z){=(G_{jk}(x,z))_{j,k=0}^n}$ with $x \in M$ and $z \in \mathbb R$ satisfying

1. (i) $G(x,0)=g(x)$ and $\partial _z G(x,0)=0$ for all $x \in M$ .

2. (ii) The tensor $h(x)=\frac {1}{2}\partial ^2_z G(x,0)$ satisfies $\langle v,v\rangle _h\neq 0$ for all nonzero $v\in LM$ .

Here, $LM$ denotes the bundle of light-like vectors on M with respect to the metric g. We subsequently consider the equation

(1.3) $$ \begin{align} \begin{aligned} \begin{cases} \Box_{G_u}u=f\,\quad \text{on}\ (-\infty,T)\times M_0, \\ u=0 \quad \text{on}\ (-\infty,-T)\times M_0. \end{cases} \end{aligned} \end{align} $$

Here, the quasi-linear wave operator $\Box _{G_u}$ is defined in local coordinates $(x^0,\ldots ,x^n)$ through

$$ \begin{align*}\Box_{G_u}u = -\sum_{j,k=0}^n\left|\det G(x,{ u(x)})\right|{}^{-\frac{1}{2}} \frac{\partial}{\partial x^j} \bigg( \left|\det G(x,{ u(x)})\right|{}^{\frac{1}{2}}G^{jk}(x,{ u(x)}) \frac{\partial u}{\partial x^k}{ (x)}\bigg),\end{align*} $$

where $G^{jk}$ stands for elements of the inverse of G. We will assume that the source f in (1.3) is real-valued and compactly supported in $(-T,T)\times M_0$ .

Remark 1. The need to work with real-valued sources f in our quasi-linear model is physically motivated due to the fact that the solution u to equation (1.3) appears in the real-valued tensor $G(x,z)$ . This imposition is not necessary in the semi-linear model.

In Subsection 2.1 we show that each of the Cauchy problems (1.2)–(1.3) above admits a unique solution

$$ \begin{align*}u \in \mathcal C^2((-\infty,T)\times M_0),\quad \forall\, f \in \mathscr C_O,\end{align*} $$

where given any relatively compact open set $\mathcal O \subset (-T,T)\times M_0$ , we define

(1.4) $$ \begin{align} \mathscr C_{\mathcal O}=\{h \in H^{n+1}(\mathbb R\times M_0;\mathbb R)\,:\,\operatorname{\mathrm{supp}} h \subset \mathcal O,\quad \|h\|_{H^{n+1}(\mathbb R\times M_0)}\leqslant r_{\mathcal O}\}\end{align} $$

and $r_{\mathcal O}$ is a sufficiently small constant depending on $(M,g)$ , $\mathcal O$ and T.

1.3 Source-to-solution map and the remote sensing inverse problem

Our primary interest lies in the setting that the sources can be actively placed near a world line $\mu _{\mathrm{in}}$ and the corresponding unique small solution u will be be measured near another disjoint world line $\mu _{\mathrm{out}}$ corresponding to some observer. The main question is whether such experiments corresponding to the separated source and observation regions determine the structure of the background unperturbed media; that is, $(M,g)$ .

To state the inverse problem precisely, let us consider two disjoint time-like future-pointing smooth paths

$$ \begin{align*}\mu_{\text{in}}:[t_0^-,t_0^+]\to M \quad \text{and}\quad \mu_{\text{out}}:[s_0^-,s_0^+]\to M\end{align*} $$

and impose the conditions that

(1.5) $$ \begin{align} \mu_{\text{out}}(s_0^+)\notin I^+(\mu_{\text{in}}(t_0^+))\quad \text{and}\quad \mu_{\text{in}}(t_0^-) \notin J^-(\mu_{\text{out}}(s_0^-)). \end{align} $$

Next, let us consider the source and observation regions $\Omega _{\mathrm{in}}$ and $\Omega _{\mathrm{out}}$ as small neighbourhoods of $\mu _{\mathrm{in}}([t_0^-,t_0^+])$ and $\mu _{\mathrm{out}}([s_0^-,s_0^+])$ in M, respectively. These two open neighbourhoods will be precisely defined in Subsection 1.4. We will also make the standing assumption that

$$ \begin{align*}(\Omega_{\text{in}}, g_{|_{\Omega_{\text{in}}}}) \quad \text{and}\quad (\Omega_{\text{out}},g_{|_{\Omega_{\text{out}}}})\end{align*} $$

are a priori known as Lorentzian manifolds; that is, we are given local coordinates, the transition functions between the local charts and the metric tensors on these coordinate charts.

The partial data inverse problem with separated sources and observations (or the remote sensing problem) can now be formulated as follows. Is it possible to uniquely determine the unperturbed manifold $(M,g)$ (recall that $G(x,0)=g(x)$ ) by observing solutions to the nonlinear wave equations (1.2) or (1.3) in $\Omega _{\mathrm{out}}$ that arise from small sources placed in $\Omega _{\mathrm{in}}$ ? The inverse problems with partial data are widely encountered in applications. The partial data problems where the sources and observations are made only on a part of boundary have been a focus of research for inverse problems for linear elliptic equations [22, 2 3, 37, 4 7, 4 8, 49, 5 1, 5 6, 5 7, 59, 60, 6 2, 68, 7 2]. However, in most of these results it is assumed that the sets where the sources are supported and where the solutions are observed do intersect, with the notable exceptions in [4 8, 49, 5 6]. In particular, in inverse problems for hyperbolic equations it is essential that the sources, which are physically implemented by acoustic transducers, or by air guns or explosives in seismic imaging, are located far away from the sensors that observe the wave fields with a high precision. This is why the partial data problems are essential in applications. The partial data problems with separated sources and observations have been studied for linear hyperbolic equations, but the present results require convexity or other geometrical restrictions that guarantee the exact controllability of the system [5 8, 70]. Let us remark that we can also apply the results in this article in the case when $\Omega _{\mathrm{in}}$ and $\Omega _{\mathrm{out}}$ intersect.

To formulate the inverse problem precisely, we define the source-to-solution map $\mathscr L$ associated to the semi-linear Cauchy equation (1.2) through the expression

(1.6) $$ \begin{align} \mathscr L f= u\,|_{\Omega_{\text{out}}}, \quad \forall\, f \in \mathscr{C}_{\Omega_{\text{in}}}, \end{align} $$

where u is the unique small solution to (1.2) subject to the source f and the set $\mathscr C_{\Omega _{\mathrm{in}}}$ is as defined by (1.4). Analogously, we define the source-to-solution map $\mathscr N$ for the quasi-linear Cauchy equation (1.3) through the expression

(1.7) $$ \begin{align} \mathscr N f= u\,|_{\Omega_{\text{out}}}, \quad \forall \,f\in \mathscr{C}_{\Omega_{\text{in}}}, \end{align} $$

where u is the unique small solution to (1.3) subject to the source f.

Our inverse problem can now be restated as whether the manifold $(M,g)$ can be uniquely recovered given the source-to-solution map $\mathscr L$ or $\mathscr N$ . Recall that $g(x)=G(x,0)$ in the quasi-linear model.

Due to finite speed of propagation for the wave equation, the optimal region where one can recover the geometry is the causal diamond generated by the source region $\Omega _{\mathrm{in}}$ and $\Omega _{\mathrm{out}}$ that is defined through

(1.8) $$ \begin{align} \mathbb D_e=\left(\bigcup_{q \in \Omega_{\text{in}}} I^{+}(q)\right) \cap \left(\bigcup_{q \in \Omega_{\text{out}}} {I}^{-}(q)\right),\end{align} $$

given the knowledge of the source-to-solution map $\mathscr L$ or $\mathscr N$ . As we will see, we are able to recover the geometry in the slightly smaller set; that is, a causal diamond determined by the points $\mu _{\mathrm{in}}(t_0^-)$ and $\mu _{\mathrm{out}}(s_0^+)$ ,

(1.9) $$ \begin{align} \mathbb D= I^{+}(\mu_{\text{in}}(t_0^-)) \cap {I}^{-}(\mu_{\text{out}}(s_0^+)).\end{align} $$

1.4 Main results

Before stating the main results, let us define, in detail, the source and observation neighbourhoods of the two future-pointing time-like curves

$$ \begin{align*}\mu_{\text{in}}:[t_0^-,t_0^+]\to M \quad \text{and}\quad \mu_{\text{out}}:[s_0^-,s_0^+]\to M\end{align*} $$

satisfying (1.5). We begin by extending the time-like paths to slightly larger intervals

$$ \begin{align*}\mu_{\text{in}}:[t_1^-,t_1^+]\to M \quad \text{and}\quad \mu_{\text{out}}:[s_1^-,s_1^+]\to M\end{align*} $$

and proceed to define the source and observation regions as a foliation of time-like future-pointing paths near the paths $\mu _{\mathrm{in}}((t_1^-,t_1^+))$ and $\mu _{\mathrm{out}}((s_1^-,s_1^+))$ . To make this precise, we use Fermi coordinates near these paths.

Let $\{\alpha _{i}\}_{i=1}^n$ be an orthonormal basis for $\dot {\mu }_{\mathrm{in}}(t_1^-)^\perp $ and subsequently consider $\{e_{i}(t)\}_{i=1}^{n}$ to denote the parallel transport of $\{\alpha _i\}_{i=1}^n$ along $\mu _{\mathrm{in}}$ to the point $\mu _{\mathrm{in}}(t)$ . Let

$$ \begin{align*}F_{\text{in}}: (t_1^-,t_1^+) \times B(0,\delta) \to M\end{align*} $$

be defined through

$$ \begin{align*}F_{\text{in}}(t,y) = \exp_{\mu_{\text{in}}(t)}(\sum_{i=1}^n y^i e_{i}(t)).\end{align*} $$

Here, $B(0,\delta )$ is the ball of radius $\delta $ in $\mathbb R^n$ . For $\delta $ sufficiently small, the map $F_{\mathrm{in}}$ is a smooth diffeomorphism and the paths

$$ \begin{align*}\mu_a(t) = F_{\text{in}}(t,a) \quad a \in B(0,\delta)\end{align*} $$

are smooth time-like paths. We define $F_{\mathrm{out}}: (s_1^-,s_1^+)\times B(0,\delta )\to M$ analogously as above with $\mu _{\mathrm{in}}$ replaced by $\mu _{\mathrm{out}}$ . Finally, we define the source and observation regions through the expression

(1.10) $$ \begin{align} \begin{aligned} \Omega_{\text{in}}&= \{ F_{\text{in}}(t,y)\,:\, t \in (t_1^-,t_1^+),\quad y\in B(0,\delta)\}\\ \Omega_{\text{out}}&= \{ F_{\text{out}}(t,y)\,:\, t \in (s_1^-,s_1^+),\quad y \in B(0,\delta)\}. \end{aligned} \end{align} $$

We will impose that $\delta $ is small enough so that the following condition is satisfied. This can always be guaranteed in view of (1.5).

(1.11) $$ \begin{align} \Omega_{\text{in}} \cap J^{-}(F_{\text{out}}(\{s_1^-\}\times B(0,\delta))=\emptyset \quad \text{and}\quad \overline{\Omega_{\text{out}}}\cap J^+(\mu_{\text{in}}(t_1^+))=\emptyset. \end{align} $$

Our main result regarding the inverse problems for the semi-linear and quasi-linear models above can be stated as follows.

Theorem 1.1. Let $m \geqslant 3$ be an integer and $(M^{(1)},g^{(1)})$ , $(M^{(2)},g^{(2)})$ be smooth globally hyperbolic Lorentzian manifolds of dimension $1+n\geqslant 3$ . Let $G^{(j)}_z$ , $j=1,2$ , be a symmetric tensor on $M^{(j)}$ that satisfies conditions (i)–(ii) and recall that $g^{(j)}(x)=G^{(j)}(x,0)$ for all $x \in M^{(j)}$ . Let $\mu _{\mathrm{in}}^{(j)}:[t_0^-,t_0^+]\to M^{(j)}$ and $\mu _{\mathrm{out}}^{(j)}:[s_0^-,s_0^+]\to M^{(j)}$ be smooth time-like paths satisfying (1.5). For $j=1,2$ , let the source region $\Omega _{\mathrm{in}}^{(j)}$ and the observation region $\Omega ^{(j)}_{\mathrm{out}}$ be defined by (1.10). We assume that these neighbourhoods are sufficiently small so that (1.11) holds. Let $T>0$ be sufficiently large so that

$$ \begin{align*}\mathbb D_e^{(j)}\subset (-T,T)\times M^{(j)}_0\quad \text{for}\ j=1,2,\end{align*} $$

and also that there exists isometric diffeomorphisms

$$ \begin{align*}\Psi^k:(\Omega_{k}^{(1)},g^{(1)}|_{\Omega_{k}^{(1)}})\to (\Omega_{k}^{(2)},g^{(2)}|_{\Omega_{k}^{(2)}})\quad k \in \{\textit{in},{\textit{out}}\}.\end{align*} $$

Next, and for $j=1,2$ , we consider the source-to-solution maps $\mathscr L^{(j)}$ and $\mathscr N^{(j)}$ associated to (1.2)–(1.3) respectively and assume that one of the following statements hold:

1. (i) $\Psi ^{\text {in}}\circ (\mathscr L^{(1)}(f))= \mathscr L^{(2)}(f\circ (\Psi ^{\text {in}})^{-1})$ for all sources $f\in \mathscr C^{(1)}_{\Omega _{\mathrm{in}}^{(1)}}$ ,

or

1. (ii) $\Psi ^{\text {in}}\circ (\mathscr N^{(1)}(f))= \mathscr N^{(2)}(f\circ (\Psi ^{\text {in}})^{-1})$ for all sources $f\in \mathscr C^{(1)}_{\Omega _{\mathrm{in}}^{(1)}}$ ,

where the set $\mathscr C^{(1)}_{\Omega ^{(1)}_{\mathrm{in}}}$ is defined by (1.4) associated to $T>0$ and the manifold $(M^{(1)},g^{(1)})$ .

Then, under the hypotheses above, there exists a smooth diffeomorphism $\Psi :\mathbb D^{(1)} \to \mathbb D^{(2)}$ that is equal to $\Psi ^{\text {in}}$ on the set $\Omega ^{(1)}_{\mathrm{in}}\cap \mathbb D^{(1)}$ and equals $\Psi ^{\text {out}}$ on the set $\Omega ^{(1)}_{\mathrm{out}}\cap \mathbb D^{(1)}$ and such that

$$ \begin{align*}\Psi^*g^{(2)}=c\,g^{(1)}\quad \text{on}\ \mathbb D^{(1)},\end{align*} $$

for some smooth real-valued function $c=c(x)$ , $c:\mathbb D^{(1)}\to \mathbb R_+$ .

Moreover, in the case that statement (i) holds and if $(n,m)\neq (3,3)$ , we have $c\equiv 1$ on the causal diamond $\mathbb D^{(1)}$ .

Remark 2. Note that if $\mu _{\mathrm{out}}(s_1^+) \notin I^+(\mu _{\mathrm{in}}(t_1^-))$ , then $\mathbb D$ is the empty set and the content of the previous theorem is empty. Therefore, it is implicitly assumed in this article in addition to (1.5) that $\mu _{\mathrm{out}}(s_1^+) \in I^+(\mu _{\mathrm{in}}(t_1^-))$ . We also remark that the recovery of the conformal factor in the exceptional case $(n,m)=(3,3)$ is briefly addressed in the last section of the article.

Remark 3. Let us make a brief remark about the restriction $m\geqslant 3$ in our semi-linear model (1.2). Our methodology to prove Theorem 1.1 is based on the nonlinear interaction of three waves to reduce the inverse problem to a purely geometric problem, namely, the study of the three-to-one scattering relation that we will formulate in the next section. To analyse the interaction of the three waves, we use Gaussian beams. In the case $m\geqslant 3$ this interaction together with an application of Green’s identity leads, at a principal level, to the study of product of four Gaussian beams that is sufficient to obtain the three-to-one scattering relation. For this reason, the case $m=2$ lies outside the scope of the current article. In our quasi-linear model (1.3), the assumptions on the first and second derivatives of $G(x,z)$ at $z=0$ are also based on a similar observation.

1.5 Recovery of geometry from the three-to-one scattering relation

The proof of Theorem 1.1 will be divided into an analytical and a geometrical part, with Sections 2–5 covering the analytical part and Sections 6–7 covering the geometric part of the analysis. In the analysis part, we use the idea of multiple-fold linearisation of the wave equation first used in [64] together with the principle of propagation of singularities for the wave equation, resulting in a geometrical data on the set $\mathbb D$ , the three-to-one scattering relation, that we will next define.

Before formulation of the definition, we set some notations. We say that geodesics $\gamma _{v_{1}}$ and $\gamma _{v_2}$ are distinct if the maximal geodesics that are extensions of $\gamma _{v_{1}}$ and $\gamma _{v_{2}}$ do not coincide as subsets of M. Also, for $v=(x,\eta )\in L^+M$ , let $s(v)=\sup \{s>0:\ \gamma _{v}([0,s))\subset M\}$ and $\rho (v)=\sup \{s\in [0,s(v)]:\ \gamma _{v}(s)\not \in I^+(x)\}$ . As discussed in Subsection 6.3, $\gamma _v(\rho (v))$ is called the first cut point of $\gamma _v$ .

For $v=(x,\eta )\in L^+M$ , let $\overrightarrow {\;\gamma _{v}}=\gamma _{x,\eta }([0,s(x,\eta )))$ be the light-like geodesics that are maximally extended in M to the future from v. Also, let $\overleftarrow {\;\gamma _{v}}=\gamma _{x,-\eta }([0,s(x,-\eta )))$ be the geodesic that emanates from v to the past.

Next we consider a set $\operatorname {\mathrm {R}}\subset (L^+M)^4$ of 4-tuples of vectors $(v_0,v_1, v_2,v_3)$ and say that these vectors satisfy relation $\operatorname {\mathrm {R}}$ if $(v_0,v_1, v_2,v_3)\in \operatorname {\mathrm {R}}$ .

Definition 1.2. Let $\Omega _{\mathrm{in}}, \Omega _{\mathrm{out}} \subset M$ be open. We say that a relation $\operatorname {\mathrm {R}} \subset L^+ \Omega _{\mathrm{out}} \times (L^+ \Omega _{\mathrm{in}})^3$ is a three-to-one scattering relation if it has the following two properties:

1. (R1) If $(v_0,v_1, v_2,v_3) \in \operatorname {\mathrm {R}}$ , then there exists an intersection point $y \in \overleftarrow {\;\gamma _{v_0}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$ .

2. (R2) Let $(v_0,v_1,v_2,v_3)\in (L^+M)^4$ . Assume that $\gamma _{v_{j}}$ , $j=0,1,2,3$ , are distinct and there exists $y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}.$ Moreover, assume that $y=\gamma _{v_{0}}(s_0)$ with $s_0\in (-\rho (v_0),0]$ and $y=\gamma _{v_{j}}(s_j)$ for all $j=1,2,3$ , with $s_j\in [0,\rho (v_j))$ . Denote $\xi _j=\dot \gamma _{v_{j}}(s_j)$ for $j=0,1,2,3$ and assume that $\xi _0 \in \operatorname {\mathrm {span}}(\xi _1, \xi _2, \xi _3)$ . Then, it holds that $(v_{0},v_{1}, v_{2},v_{3}) \in \operatorname {\mathrm {R}}$ .

In other words, (R1) means that if $(v_0,v_1, v_2,v_3) \in \operatorname {\mathrm {R}}$ , then it is necessary that the future-pointing geodesics $\gamma _{v_1},\gamma _{v_2}$ and $\gamma _{v_3}$ must intersect at some point y and some future-pointing geodesic emanating from y arrives to $v_0$ . The condition (R2) means for $(v_0,v_1, v_2,v_3) \in \operatorname {\mathrm {R}}$ it is sufficient that the future-pointing geodesics $\gamma _{v_1},\gamma _{v_2}$ and $\gamma _{v_3}$ intersect at some point y before their first cut points and that the past-pointing null geodesic $\gamma _{v_0}$ arrives to the point y in the direction $\xi _0$ that is in the span of the velocity vectors of $\gamma _{v_1},\gamma _{v_2}$ and $\gamma _{v_3}$ at the point y and, finally, that the geodesic $\gamma _{v_0}([s_0,0])$ has no cut points. The relation $\operatorname {\mathrm {R}}$ is visualised in Figure 3.

Figure 1 Nonlinear interaction of three waves when $m=3$ and g is the Minkowski metric. The four figures are snapshots of the waves in the space $\mathbb R^3$ at different times, with time progressing from top to bottom. First figure from the top: Plane waves before interactions. Second figure: The 2-wave interactions (black line segments) appear but do not cause singularities that propagate in new directions. Third figure: The 3-wave interactions generate a new wave (blue cone). Fourth figure: The new wave propagates near the $x^1, x^2$ plane. By varying the directions of the incoming plane waves, a wave propagating near any plane can be generated. Note that, for general g, the picture may be more complicated due to caustics.

Figure 2 Schematic of the geometric setting. The time-like paths $\mu _{\mathrm{in}}$ and $\mu _{\mathrm{out}}$ are in green and their neighbourhoods $\Omega _{\mathrm{in}}$ and $\Omega _{\mathrm{\rm out}}$ are in orange. The set $\mathbb D$ is enclosed by the black rectangle. The set $I^+({ \mu _{\mathrm{\rm in}}(t_1^+)})$ is in light blue, and the set $J^-({ \mu _{\mathrm{out}}(s_1^+)})$ is in light red; cf. (1.5).

Figure 3 Three-to-one scattering relation $\operatorname {\mathrm {R}}$ in the $1+2$ -dimensional Minkowski space. The red vectors $v_1$ , $v_2$ and $v_3$ and the green vector $v_0$ satisfy $(v_0,v_1,v_2,v_3) \in \operatorname {\mathrm {R}}$ . The vector $\xi _0$ in Definition 1.2 is in blue and the vectors $\xi _1$ , $\xi _2$ and $\xi _3$ are in black. The latter three have the same base point with $\xi _0$ and are not labelled.

We emphasise that in Definition 1.2 there are no requirements for the 4-tuples $(v_0,v_1, v_2,v_3)$ for which the conditions in (R1) or (R2) are not valid. This has the important consequence that to verify that the source-to-solution map $\mathscr L$ or $\mathscr N$ determines a three-to-one scattering relation, we need to consider only those 4-tuples $(v_0,v_1, v_2,v_3)$ for which the geodesics $\gamma _{v_j}$ , $j=0,1,2,3$ do not intersect at the conjugate points and the structure of the multiple pairwise intersections of the geodesics is simple. This makes it possible to avoid technical geometrical difficulties encountered in several studies on inverse problems for linear and nonlinear differential equations; see, for example, [23, 24, 40, 64].

The following theorem states that the three-to-one scattering relation determines uniquely the topological, differential and conformal structure of the set $\mathbb D$ .

Theorem 1.3. Let $(M^{(1)},g^{(1)})$ , $(M^{(2)},g^{(2)})$ be smooth globally hyperbolic Lorentzian manifolds of dimension $1+n\geqslant 3$ . Let $\mu _{\mathrm{in}}^{(j)}:[t_0^-,t_0^+]\to M^{(j)}$ and $\mu _{\mathrm{out}}^{(j)}:[s_0^-,s_0^+]\to M^{(j)}$ be smooth time-like paths satisfying (1.5). For $j=1,2$ , let the source region $\Omega _{\mathrm{in}}^{(j)}$ and the observation region $\Omega ^{(j)}_{\mathrm{out}}$ be defined by (1.10). We assume that these neighbourhoods are sufficiently small so that (1.11) holds. Moreover, we assume that there are isometric diffeomorphisms

$$ \begin{align*}\Psi^k:(\Omega_{k}^{(1)},g^{(1)}|_{\Omega_{k}^{(1)}})\to (\Omega_{k}^{(2)},g^{(2)}|_{\Omega_{k}^{(2)}})\quad k \in \{{\textit{in}},{\textit{out}}\}.\end{align*} $$

Suppose next that there are relations $\operatorname {\mathrm {R}}^{(j)}\subset L^+\Omega _{out}^{(j)}\times (L^+\Omega _{in}^{(j)})^3$ , $j=1,2$ , that satisfy conditions (R1) and (R2) in Definition 1.2 for manifolds $(M^{(j)},g^{(j)})$ and that

(1.12) $$ \begin{align} \operatorname{\mathrm{R}}^{(2)}=\bigg\{(\Psi^{in}_*v_0,\Psi^{out}_*v_1,\Psi^{out}_*v_2,\Psi^{out}_*v_3)\ \bigg|\ (v_0,v_1,v_2,v_3)\in \operatorname{\mathrm{R}}^{(1)}\bigg\}. \end{align} $$

Then there exists a smooth diffeomorphism $\Psi :\mathbb D^{(1)} \to \mathbb D^{(2)}$ that is equal to $\Psi ^{\text {in}}$ on the set $\Omega ^{(1)}_{\mathrm{in}}\cap \mathbb D^{(1)}$ and equals $\Psi ^{\text {out}}$ on the set $\Omega ^{(1)}_{\mathrm{out}}\cap \mathbb D^{(1)}$ and such that

$$ \begin{align*}\Psi^*g^{(2)}=c\,g^{(1)}\quad \text{on}\ \mathbb D^{(1)},\end{align*} $$

for some smooth real-valued function $c=c(x)$ , $c:\mathbb D^{(1)}\to \mathbb R_+$ .

The motivation of Definition 1.2 and Theorem 1.3 is to provide a general framework that allows the results of this article to be applicable for other nonlinear hyperbolic equations similar to those studied in this article. Indeed, to consider some different kind of nonlinear hyperbolic equation (for example, such as $\square _g u+\|\nabla u\|_g^3=f$ in $\mathbb R^{1+n}$ ; see [92] for the case $n=3$ ) one can define that $(v_0,v_1, v_2,v_3)$ satisfies the relation $\operatorname {\mathrm {R}}_{sim}$ if three singular waves sent to directions $v_1,v_2$ and $v_3$ interact so that the interaction produces a wave whose wave front contains the covector corresponding to $v_0$ . Then to apply Theorem 1.3 one has to show that $\operatorname {\mathrm {R}}_{sim}$ satisfies conditions (R1) and (R2). We note that condition (R1) is natural as the second-order interaction of waves does not produce singularities that propagate to new directions; see [36, 64]. Condition (R2) is motivated by the general results for the interaction of three waves; see [7, 7 7, 83] and references therein. We emphasise that to verify condition (R2) one has to consider only geodesics that have no conjugate points and thus this condition can be verified without analysing interaction of waves near caustics.

1.6 Previous literature

The study of nonlinear wave equations is a fascinating topic in analysis with a rich literature. In contrast with the study of linear wave equations, there are numerous challenges in studying the existence, uniqueness and stability of solutions to such equations. These equations physically arise in the study of general relativity, such as the Einstein field equations. They also appear in the study of vibrating systems or the detection of perturbations arising in electronics, such as the telegraph equation or the study of semi-conductors; see, for instance, [15]. We mention in particular that the quasi-linear model (1.3) studied in this article is a model for studying Einstein’s equations in wave coordinates [7 5].

This article uses extensively the nonlinear interaction of three waves to solve the inverse problems. To analyse this, we use Gaussian beams. An alternative way to consider the nonlinear interaction is to use microlocal analysis and conormal singularities; see [36, 38, 7 8]. There are many results on such nonlinear interaction, starting with the studies of Bony [1 4], Melrose and Ritter [77] and Rauch and Reed [8 2]. However, these studies concern the direct problem and differ from the setting of this article in that they assumed that the geometrical setting of the interacting singularities and, in particular, the locations and types of caustics, is known a priori. In inverse problems we need to study waves on an unknown manifold, so we do not know the underlying geometry and, therefore, the location of the singularities of the waves. For example, the waves can have caustics that may even be of an unstable type.

Earlier, inverse problems for nonlinear hyperbolic equations with unknown metric have been studied using interaction of waves only in the (1+3)-dimensional case using interaction of four or more waves. Inverse problems for nonlinear scalar wave equations with a quadratic nonlinearity were studied in [64] using multiple-fold linearisation. Together with the phenomenon of propagation of singularities for the wave equation, the authors reduced the inverse problem for the wave equation to the study of light observation sets. This approach was extended in [19, 39, 5 2, 7 1]. In [63], the coupled Einstein and scalar field equations were studied. The result has been more recently strengthened in [7 3, 91] for the Einstein scalar field equations with general sources and for the Einstein–Maxwell equations. In particular, a technique to determine the conformal factor using the microlocal symbols of the observed waves was developed in [91].

Aside from the works mentioned above, the majority of works have been on inverse problems for semi-linear wave equations, with quadratic nonlinearities studied in [64], a general semi-linear term studied in [40, 7 3] and quadratic derivatives studied in [92]; see also [6 7] and references therein. All these works concern the $(1+3)$ -dimensional case. In recent works [16, 17, 29], the authors have also studied problems of recovering zeroth- and first-order terms for semi-linear wave equations with Minkowski metric. We note that three wave interactions were used in [16, 17] to determine the lower order terms in the equations and in modelling nonlinear elastic scattering from discontinuities [20, 2 1]. In [28, 6 9] similar multiple-fold linearisation methods were introduced to study inverse problems for elliptic nonlinear equations; see also [61].

All of the aforementioned works consider inverse problems for various types of nonlinear wave equations subject to small sources. The presence of a nonlinear term in the partial differential equation (PDE) is a strong tool in obtaining the uniqueness results. To discuss this feature in some detail, we note that the analogous inverse problem for the linear wave equation (see (2.1)) is still a major open problem. For this problem, much is known in the special setting that the coefficients of the metric are time-independent. We refer the reader to the work of Belishev and Kurylev in [1 2] that uses the boundary control method introduced in [10] to solve this problem and to [5, 50, 5 3, 6 5] for a state-of-the-art result in the application of the boundary control method and finally to [41] for the related scattering control method. The boundary control method is known to fail in the case of general time-dependent coefficients, since it uses the unique continuation principle of Tataru [89]. This principle is known to be false in the cases that the time dependence of coefficients is not real-analytic [1, 2]. We refer the reader to [25] for recovery of coefficients of a general linear wave equation under an analyticity assumption with respect to the time coordinate.

In the more challenging framework of general time-dependent coefficients and by using the alternative technique of studying the propagation of singularities for the wave equation, the inverse problem for the linear wave equation (see (2.1)) is reduced to the injectivity of the scattering relation on M; see the definition (5.1). The injectivity of the scattering relation is open unless the geometry of the manifold is static and an additional convex foliation codition is satisfied [86] on the spatial part of the manifold. In the studies of recovery of sub-principal coefficients for the linear wave equation, we refer the reader to the recent works [26, 27, 85] for recovery of zeroth- and first-order coefficients and to [87] for a reduction from the boundary data for the inverse problem associated to (2.1) to the study of geometrical transforms on M. This latter approach has been recently extended to general real principal type differential operators [80].

The main underlying principle in the presence of a nonlinearity is that linearisation of the equation near the trivial solution results in a nonlinear interaction of solutions to the linear wave equation producing much richer dynamics for propagation of singularities. Owing to this richer dynamics, and somewhat paradoxically, inverse problems for nonlinear wave equations have been solved in much more general geometrical contexts than their counterparts for the linear wave equations.

Let us now discuss some of the main novelties of the present work. Firstly, we consider threefold linearisation of the nonlinear equations (1.2)–(1.3) and can therefore analyse inverse problems using interaction of three waves instead of earlier works relying on interaction of four waves. This makes it possible to consider more general equations with simpler techniques. Due to the new techniques, we can consider inverse problems on Lorenzian manifolds with any dimension $n+1\ge 3$ . As a second novelty, we introduce a new concept, the three-to-one scattering relation that can be applied for many kinds of nonlinear equations and which we hope to be useful for other researchers in the field of inverse problems. Also, this makes it possible to consider inverse problems in the remote sensing setting that includes both forward- and back-scattering problems. Finally, we mention our quite general quasi-linear model problem (1.3) with an unknown nonlinearity in the leading order term. We successfully study this complicated model with the use of Gaussian beams and show that the source-to-solution map determines the three-to-one scattering relation.

1.7 Outline of the article

We begin with some preliminaries in Section 2, starting with Proposition 2.1 that shows that the forward problems (1.2)–(1.3) are well-posed. We also recall the technique of multiple-fold linearisation and apply it to the semi-linear and quasi-linear equations separately. This will relate the source-to-solution maps, $\mathscr L$ and $\mathscr N$ , to the study of products of solutions to the linear wave equation; see (2.6) and (2.10). In Section 3, we briefly recall the construction of the classical Gaussian beams for the linear wave equation. We also show that it is possible to explicitly construct real-valued sources supported in the source and observation regions that generate exact solutions to the linear wave equations that are close in a suitable sense to the real parts of Gaussian beams. In Section 5 we prove the main analytical theorems, showing that the source-to-solution maps lead to a three-to-one scattering relation; see Theorem 5.1–5.2. Combined with Theorem 1.3, this proves the first half of Theorem 1.1 on the recovery of the topological, differential and conformal structure of the casual diamond $\mathbb D$ .

The geometrical sections of the article are concerned with the study of a general three-to-one scattering relation $\operatorname {\mathrm {R}}$ on M and the proof of Theorem 1.3. In Section 6, we recall some technical lemmas on globally hyperbolic Lorentzian geometries. In Section 7, we prove Theorem 7.10, showing that it is possible to use the three-to-one scattering relation to construct the earliest arrivals on $\mathbb D$ . Combining this with the results of [64] leads to unique recovery of the topological, differential and conformal structure of $(\mathbb D, g|_{\mathbb D})$ that completes the proof of Theorem 1.3.

Finally, Section 8 is concerned with the proof of Theorem 1.1. The first half of the proof – that is, the recovery of the topological, differential and conformal structure of the manifold – follows immediately from combining Theorems 5.1–5.2 together with Theorem 1.3. The remainder of this section deals with the recovery of the conformal factor c on $\mathbb D$ .

2 Preliminaries

2.1 Forward problem

In this section, we record the following proposition about existence and uniqueness of solutions to (1.2)–(1.3) subject to suitable sources f. The local existence of solutions to semi-linear and quasi-linear wave equations is well-studied in the literature; see, for example, [4 5, 84, 90, 93].

Proposition 2.1. Given any open and bounded set $O \subset (-T,T)\times M_0$ , there exists a sufficiently small $r_O>0$ such that given any $f \in \mathscr C_O$ (with $\mathscr C_O$ as defined by (1.4)), each of the equations (1.2) or (1.3) admits a unique real-valued solution u in the energy space

$$ \begin{align*}u \in L^{\infty}(-T,T;H^{n+2}(M_0))\cap \mathcal C^{0,1}(-T,T;H^{n+1}(M_0))\cap \mathcal C^2((-T,T)\times M_0).\end{align*} $$

Moreover, the dependence of u to the source f is continuous.

The proof of this proposition in the semi-linear case (1.2) follows by minor modifications to [55]. In the quasi-linear case, the proof follows with minor modifications to the proof of [93, Theorem 6].

2.2 Multiple-fold linearisation

We will discuss the technique of multiple-fold linearisation of nonlinear equations that was first used in [64]. Before presenting the approach in our semi-linear and quasi-linear settings, we consider the linear wave equation on M,

(2.1) $$ \begin{align} \begin{aligned} \begin{cases} \Box_{g} u =f, &\text{on}\ M, \\ u=0, &\text{on}\ M\setminus J^+(\operatorname{\mathrm{supp}} f) \end{cases} \end{aligned} \end{align} $$

with real-valued sources $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$ . We also need to consider the wave equation with reversed causality; that is,

(2.2) $$ \begin{align} \begin{aligned} \begin{cases} \Box_{g} u =f, &\text{on}\ M, \\ u=0, &\text{on}\ M\setminus J^-(\operatorname{\mathrm{supp}} f) \end{cases} \end{aligned} \end{align} $$

with real-valued sources $f \in C^{\infty }_c(\Omega _{\mathrm{out}})$ .

2.2.1 m-Fold linearisation of the semi-linear equation (1.2)

Let $m\geqslant 3$ . We consider real-valued sources $f_0 \in C^{\infty }_c(\Omega _{\mathrm{out}})$ and $f_j \in C^{\infty }_c(\Omega _{\mathrm{in}})$ , $j=1,\ldots ,m$ . We denote by $u_j$ , $j=1,\ldots ,m$ the unique solution to (2.1) subject to source $f_j$ and denote by $u_0$ the unique solution to (2.2) subject to source $f_0$ . Let $\varepsilon =(\varepsilon _1,\ldots ,\varepsilon _m) \in \mathbb R^m$ be a small vector and define the source

$$ \begin{align*}f_\varepsilon{(x)}= \sum_{j=1}^m\varepsilon_j f_{j}{(x),\quad x\in M}.\end{align*} $$

Given $\varepsilon $ sufficiently close to the origin in $\mathbb R^m$ , we have $f_\epsilon \in \mathscr C_{\Omega _{\mathrm{in}}}$ . Let us define

(2.3) $$ \begin{align} w{(x)} = \frac{\partial^m}{\partial\varepsilon_1 \partial\varepsilon_2\ldots\partial\varepsilon_m}\,u_\varepsilon{(x)}\bigg |_{\varepsilon=0},\end{align} $$

where $u_\varepsilon $ is the unique small solution to (1.2) subject to the source $f_\varepsilon \in \mathscr C_{\Omega _{\mathrm{in}}}$ .

It is straightforward to see that the function w defined by (2.3) solves

(2.4) $$ \begin{align} \begin{aligned} \begin{cases} \Box_{g} w =-m! \,u_1\,u_2\,u_3\ldots u_m, &\text{on}\ M, \\ w=0, &\text{on}\ M\setminus J^+(\bigcup_{j=1}^m\operatorname{\mathrm{supp}} f_m). \end{cases} \end{aligned} \end{align} $$

Multiplying the latter equation with $u_0$ and using the Green’s identity,

(2.5) $$ \begin{align} \int_M w\,\Box_g u_0\,dV_g=\int_M u_0\,\Box_g w \,dV_g, \end{align} $$

we deduce that

(2.6) $$ \begin{align} \int_{\Omega_{\text{out}}} f_0 \frac{\partial^m}{\partial\varepsilon_1\ldots\partial\varepsilon_m} \mathscr L f_\varepsilon \bigg|_{\varepsilon=0}\,dV_g = -m!\,\int_M u_0\,u_1\ldots u_m\,dV_g. \end{align} $$

We emphasise that by global hyperbolicity, the integrand on the right-hand side is supported on the compact set

(2.7) $$ \begin{align} J^-(\operatorname{\mathrm{supp}} f_0)\cap\bigcup_{j=1}^m J^+(\operatorname{\mathrm{supp}} f_j)\subset \mathbb D_e \subset (-T,T)\times M_0,\end{align} $$

which makes the integral well-defined (see (1.8)). Note that the latter inclusion is due to the hypothesis of Theorem 1.1 on the size of T. We deduce from (2.6) that the source-to-solution map $\mathscr L$ for the semi-linear equation (1.2) determines the knowledge of integrals of products of m solutions to the linear wave equation (2.1) and a solution to (2.2).

2.2.2 Three-fold linearisation of the quasi-linear equation (1.3)

We consider sources $f_j \in C^{\infty }_c(\Omega _{\mathrm{in}})$ , $j=0,1,2,3$ and for each small vector $\varepsilon =(\varepsilon _1,\varepsilon _2,\varepsilon _3)\in \mathbb R^3$ consider the three-parameter family of sources

$$ \begin{align*}f_\varepsilon=\varepsilon_1f_1+\varepsilon_2f_2+\varepsilon_3f_3 .\end{align*} $$

Let $u_\varepsilon $ be the unique small solution to (1.3) subject to the source $f_\varepsilon \in \mathscr C_{\Omega _{\mathrm{in}}}$ . Recall that, by definition, $G(x,0)=g(x)$ , $\partial _z G(x,0)=0$ and $h(x)=\frac {1}{2} \frac {\partial ^2}{\partial z^2} G(x,0)$ . First, we note that the following identities hold in a neighbourhood of $z=0$ :

$$ \begin{align*}G_z^{jk}=g^{jk}-S^{jk}\,z^2+\mathcal O(|z|^3),\end{align*} $$

$$ \begin{align*}\left|\det G_z\right|=\left|\det g\right|\, (1+\operatorname{\mathrm{Tr}}(hg^{-1})z^2)+\mathcal O(|z|^3),\end{align*} $$

where $S^{jk}=\sum _{j',k'=0}^n g^{jj'}\,h_{j'k'}\,g^{k'k}.$ Using these identities in the expression for $\Box _{G_z}$ with z replaced with $u_\varepsilon $ , it follows that the function

(2.8) $$ \begin{align} w = \frac{\partial^3}{\partial\varepsilon_1 \partial\varepsilon_2\partial\varepsilon_3}\,u_\varepsilon \bigg |_{\varepsilon=0} \end{align} $$

solves the following equation on M:

(2.9) $$ \begin{align} &\Box_g w - \operatorname{\mathrm{Tr}}(hg^{-1}) u_1u_2f_3- \operatorname{\mathrm{Tr}}(hg^{-1}) u_2u_3f_1- \operatorname{\mathrm{Tr}}(hg^{-1}) u_3u_1f_2\nonumber\\ &\qquad\qquad-\sum_{j,k=0}^n\left| \det g\right|{}^{-\frac{1}{2}}\frac{\partial}{\partial x^j}(\left|\det g\right|{}^{\frac{1}{2}}\operatorname{\mathrm{Tr}}(hg^{-1})g^{jk}u_1u_2\frac{\partial u_3}{\partial x^k})\nonumber\\ &\qquad\qquad-\sum_{j,k=0}^n\left| \det g\right|{}^{-\frac{1}{2}}\frac{\partial}{\partial x^j}(\left|\det g\right|{}^{\frac{1}{2}}\operatorname{\mathrm{Tr}}(hg^{-1})g^{jk}u_2u_3\frac{\partial u_1}{\partial x^k})\nonumber\\ &\qquad\qquad-\sum_{j,k=0}^n\left| \det g\right|{}^{-\frac{1}{2}}\frac{\partial}{\partial x^j}(\left|\det g\right|{}^{\frac{1}{2}}\operatorname{\mathrm{Tr}}(hg^{-1})g^{jk}u_3u_1\frac{\partial u_2}{\partial x^k})\nonumber\\ &\qquad\qquad+2\sum_{j,k=0}^n\left| \det g\right|{}^{-\frac{1}{2}}\frac{\partial}{\partial x^j}(\left|\det g\right|{}^{\frac{1}{2}}S^{jk}u_1u_2\frac{\partial u_3}{\partial x^k})\nonumber\\ &\qquad\qquad+2\sum_{j,k=0}^n\left| \det g\right|{}^{-\frac{1}{2}}\frac{\partial}{\partial x^j}(\left|\det g\right|{}^{\frac{1}{2}}S^{jk}u_2u_3\frac{\partial u_1}{\partial x^k})\nonumber\\ &\qquad\qquad+2\sum_{j,k=0}^n\left| \det g\right|{}^{-\frac{1}{2}}\frac{\partial}{\partial x^j}(\left|\det g\right|{}^{\frac{1}{2}}S^{jk}u_3u_1\frac{\partial u_2}{\partial x^k})=0, \end{align} $$

subject to the initial conditions $w=0$ on $M\setminus J^+(\bigcup _{j=1}^3\operatorname {\mathrm {supp}} f_j)$ . Note that the knowledge of the source-to-solution map $\mathscr N$ determines $w|_{\Omega _{\mathrm{out}}}$ . Also,

$$ \begin{align*}\nabla^g u = \sum_{j,k=0}^ng^{jk}\frac{\partial u}{\partial x^j} \frac{\partial}{\partial x^k}\quad \forall\, u \in \mathcal C^{\infty}(M),\end{align*} $$

which implies that

$$ \begin{align*}\sum_{j,k=0}^n g^{jk}\frac{\partial u}{\partial x^j}\frac{\partial v}{\partial x^k}= \langle \nabla^g u,\nabla^g v \rangle_g\end{align*} $$

and

$$ \begin{align*}\sum_{j,k=0}^nS^{jk}\frac{\partial u}{\partial x^j}\frac{\partial v}{\partial x^k}= \langle \nabla^g u,\nabla^g v \rangle_h,\end{align*} $$

for all $u, v \in \mathcal C^{\infty }(M)$ . Therefore, recalling that

$$ \begin{align*}dV_g = \left|\det g\right|{}^{\frac{1}{2}}\, dx^0\wedge dx^1\wedge \ldots \wedge dx^n\end{align*} $$

and multiplying equation (2.9) with $u_0$ that solves (2.2) subject to a source $f_0\in \mathcal C^{\infty }_c(\Omega _{\mathrm{out}})$ followed by integrating by parts (analogously to (2.5)), we deduce that

(2.10) $$ \begin{align} &\int_{\Omega_{\text{out}}} f_0 \frac{\partial^3}{\partial\varepsilon_1\partial\varepsilon_2\partial\varepsilon_3} \mathscr N f_\varepsilon \bigg |_{\varepsilon=0}\,dV_g \nonumber\\ &\quad = 2\int_{M} \left(u_1u_2\langle \nabla^gu_3,\nabla^gu_0\rangle_h+u_2u_3\langle \nabla^gu_1,\nabla^gu_0\rangle_h+u_3u_1\langle \nabla^gu_2,\nabla^gu_0\rangle_h\right)\,dV_g\nonumber\\ &\qquad-\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})\left(u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_g+u_2u_3\langle \nabla^gu_1,\nabla^gu_0 \rangle_g+u_3u_1\langle \nabla^gu_2,\nabla^gu_0 \rangle_g\right)\,dV_g\nonumber\\ &\qquad+\int_M \operatorname{\mathrm{Tr}}(hg^{-1})\,u_0\left(u_1u_2f_3+u_2u_3f_1+u_3u_1f_2\right)\,dV_g. \end{align} $$

Analogous to (2.6), the integrands on the right-hand side expression are all supported on the compact set

$$ \begin{align*}J^-(\operatorname{\mathrm{supp}} f_0)\cap\bigcup_{j=1}^m J^+(\operatorname{\mathrm{supp}} f_j)\subset \mathbb D_e \subset (-T,T)\times M_0,\end{align*} $$

for T sufficiently large as stated in the hypothesis of Theorem 1.1.

3 Gaussian beams

Gaussian beams are approximate solutions to the linear wave equation

$$ \begin{align*}\Box_g u=0 \quad \text{on}\ (-T,T)\times M_0\end{align*} $$

that concentrate on a finite piece of a null geodesic $\gamma : [a,b] \to (-T,T)\times M_0$ , exhibiting a Gaussian profile of decay away from the segment of the geodesic. Here, we are considering an affine parametrisation of the null geodesic $\gamma $ ; that is,

(3.1) $$ \begin{align} \nabla^g_{\dot{\gamma}(s)}\dot{\gamma}(s)=0,\quad \langle \dot{\gamma}(s),\dot{\gamma}(s)\rangle_g=0\quad \forall\, s \in [a,b]. \end{align} $$

We will make the standing assumption that the end points $\gamma (a)$ and $\gamma (b)$ lie outside $(-T,T)\times M_0$ . Gaussian beams are a classical construction and go back to [6, 8 1]. They have been used in the context of inverse problems in many works; see, for example, [11, 26, 29, 54]. In order to recall the expression of Gaussian beams in local coordinates, we first briefly recall the well-known Fermi coordinates near a null geodesic.

Lemma 3.1 Fermi coordinates

Let $\hat \delta> 0$ , $a < b$ and let $\gamma : (a-\hat {\delta },b+\hat {\delta }) \to M$ be a null geodesic on M parametrised as given by (3.1) and whose end points lie outside $(-T,T)\,\times\, M_0$ . There exists a coordinate neighbourhood $(U,\psi )$ of $\gamma ([a,b])$ , with the coordinates denoted by $(y^0:=s,y^1,\ldots ,y^n)=(s,y')$ , such that

1. (i) $\psi (U)=(a-\delta ',b+\delta ') \times B(0,\delta ')$ where $B(0,\delta ')$ is the ball in $\mathbb {R}^{n}$ centred at the origin with radius $\delta '> 0$ .

2. (ii) $\psi (\gamma (s))=(s,\underbrace {0,\ldots ,0}_{n \hspace {1mm}\text {times}})$ .

Moreover, the metric tensor g satisfies in this coordinate system

(3.2) $$ \begin{align} g|_\gamma = 2ds\otimes dy^1+ \sum_{\alpha=2}^n \,dy^\alpha\otimes \,dy^\alpha \end{align} $$

and $\frac {\partial }{\partial y^i} g_{jk}|_\gamma = 0$ for $i,j,k=0,\ldots ,n$ . Here, $|_\gamma $ denotes the restriction on the curve $\gamma $ .

We refer the reader to [29, Section 4.1, Lemma 1] for a proof of this lemma. Using the Fermi coordinates discussed above, Gaussian beams can be written through the expressions

(3.3) $$ \begin{align} \mathcal U_\lambda(y) = e^{i\lambda \phi(y)} A_\lambda(y) \quad \text{for} \quad \lambda>0\end{align} $$

and

(3.4) $$ \begin{align} \mathcal U_\lambda(y) = e^{-i\lambda\bar{\phi}(y)}\bar{A}_\lambda(y) \quad \text{for}\quad\lambda<0.\end{align} $$

Here, $\bar {\cdot }$ stands for the complex conjugation and the phase function $\phi $ and the amplitude function $A_\lambda $ are given by the expressions

(3.5) $$ \begin{align} \begin{aligned} \phi(s,y') = \sum_{j=0}^{N} \phi_j(s,y')& \quad \text{and} \quad A_\lambda(s,y')= \chi(\frac{|y'|}{\delta'}) \sum_{j=0}^{N} \lambda^{-j}a_{j}(s,y'),\\ &a_j(s,y')=\sum_{k=0}^{N} a_{j,k}(s,y'), \end{aligned} \end{align} $$

where for each $j,k=0,\ldots ,N$ , $\phi _j$ is a complex-valued homogeneous polynomial of degree j in the variables $y^{1},\ldots , y^n$ and $a_{j,k}$ is a complex-valued homogeneous polynomial of degree k with respect to the variables $y^1,\ldots ,y^n$ and, finally, $\chi :\mathbb R\to \mathbb R$ is a nonnegative smooth function of compact support such that $\chi (t)=1$ for $|t| \leqslant \frac {1}{4}$ and $\chi (t)=0$ for $|t|\geqslant \frac {1}{2}$ .

The determination of the phase terms $\phi _j$ and amplitudes $a_j$ with $j=0,1,2,\ldots ,N$ is carried out by following the method of Wentzel–Kramers–Brillouin (WKB in short) in the semi-classical parameter $\lambda $ , based on the requirement that

(3.6) $$ \begin{align} \begin{aligned} &\frac{\partial^{|\alpha|}}{\partial y^{\prime\alpha}}\langle d\phi,d\phi\rangle_g=0 \quad \text{on}\ (a,b)\times\{y'=0\},\\ &\frac{\partial^{|\alpha|}}{\partial y^{\prime\alpha}}\left( 2\langle d\phi,da_j \rangle_g- (\Box_g\phi)a_j + i \Box_ga_{j-1}\right)=0\quad \text{on}\ (a,b)\times\{y'=0\}, \end{aligned}\end{align} $$

for all $j=0,1,\ldots ,N$ and all multi-indices $\alpha =(\alpha _1,\ldots ,\alpha _n) \in \{0,1,\ldots \}^n$ with $|\alpha |=\alpha _1+\ldots +\alpha _n\leqslant N$ .

We do not proceed to solve these equations here as this can be found in all the works mentioned above but instead summarise the main properties of Gaussian beams as follows:

1. (1) $\phi (s,0)=0$ .

2. (2) $\Im (\phi )(s,y') \geqslant C |y'|^2$ for all points $y \in (a,b)\times B(0,\delta ')$ .

3. (3) $\| \Box _{g} \mathcal U_\lambda \|_{H^k((-T,T)\times M_0)} \lesssim |\lambda |^{-K},$ where $K=\frac {N+1}{2}+\frac {n}{4}-k-2$ .

Here, $\Im $ stands for the imaginary part of a complex number and by the notation $A\lesssim B$ we mean that there exists a constant C independent of the parameter $\lambda $ such that $A \leqslant C B$ .

For the purposes of our analysis, we also need to recall the Fermi coordinate expressions for $\phi _1$ , $\phi _2$ and $a_{0,0}$ ; see (3.5). We recall from [29] that

(3.7) $$ \begin{align} \begin{aligned} \phi_0(s,y')=0,\quad \phi_1(s,y')&= y_1,\quad \phi_2(s,y')=\sum_{j,k=1}^n H_{jk}(s)y^jy^k,\\ \quad a_{0,0}(s)&=(\det Y(s))^{-\frac{1}{2}}. \end{aligned} \end{align} $$

The matrices H and Y are described as follows. The symmetric complex-valued matrix H solves the Riccati equation

(3.8) $$ \begin{align} \frac{d}{ds} H + HCH + D=0, \quad \forall s \in (a,b), \quad H(\hat{s}_0)=H_0,\quad \Im H_0>0, \end{align} $$

where C and D are the matrices defined through

(3.9) $$ \begin{align} \begin{cases} C_{11}= 0&\\ C_{jj}=2& \quad j=2,\ldots,n, \\ C_{jk}=0& \quad \text{otherwise,} \end{cases} \qquad \text{where}\ D_{jk}= \frac{1}{4} \frac{\partial^2 g^{11}}{\partial y^j \partial y^k}. \end{align} $$

We recall the following result from [5 3, Section 8] regarding solvability of the Riccati equation.

Lemma 3.2. Let $\hat {s}_0 \in (a,b)$ and let $H_0=Z_0Y_0^{-1}$ be a symmetric matrix with $\Im H_0> 0$ . The Riccati equation (3.8), together with the initial condition $H(\hat {s}_0) = H_0$ , has a unique solution $H(s)$ for all $s \in (a,b)$ . We have $\Im H>0$ and $H(s)=Z(s)Y^{-1}(s)$ , where the matrix-valued functions $Z(s),Y(s)$ solve the first-order linear system

$$ \begin{align*}\frac{d}{ds} Y = CZ\quad \text{and}\quad \frac{d}{ds} Z = -DY, \quad \text{subject to} \quad Y(\hat{s}_0)=Y_0,\quad Z(\hat{s}_0)=H_0.\end{align*} $$

Moreover, the matrix $Y(s)$ is nondegenerate on $(a,b)$ and there holds

$$ \begin{align*}\det(\Im H(s)) \cdot |\det(Y(s))|^2=\det(\Im(H_0)). \end{align*} $$

As for the remainder of the terms $\phi _j$ with $j\geqslant 3$ and the rest of the amplitude terms $a_{j,k}$ with $j,k$ not both simultaneously zero, we recall from [29] that they solve first-order ordinary differential equations (ODEs) along the null geodesic $\gamma $ and can be determined uniquely by fixing their values at some fixed point $\hat {s}_0 \in (a,b)$ .

4 Source terms that generate real parts of Gaussian beams

Let $v=(q,\xi ) \in L^+\Omega _{\mathrm{in}}$ or $v=(q,\xi ) \in L^+\Omega _{\mathrm{out}}$ , where $L^+\Omega _{\mathrm{in}}$ and $L^+\Omega _{\mathrm{out}}$ denote the bundle of future-pointing light-like vectors in $\Omega _{\mathrm{in}}$ and $\Omega _{\mathrm{out}}$ , respectively. We consider a Gaussian beam solution $\mathcal U_\lambda $ of order $N=\lceil \frac {3n}{2}\rceil +8$ as in the previous section, concentrating on a future-pointing null geodesic $\gamma _{q,\xi }:[a,b]\to M$ passing through q in the direction $\xi $ . Here $\gamma _{q,\xi }$ is parametrised as in (3.1) subject to

(4.1) $$ \begin{align} \gamma_{q,\xi}(0)=q \quad \text{and}\quad \dot{\gamma}_{q,\xi}(0)=\xi.\end{align} $$

As before, we assume that the end points of the null geodesic lie outside the set $(-T,T)\times M_0$ .

In this section, we would like to give a canonical way of constructing Gaussian beams followed by a canonical method of constructing real-valued sources that generate the real parts of these Gaussian beams. Recall that the construction of a Gaussian beam $\mathcal U_\lambda $ that concentrates on $\gamma _{q,\xi }$ has a large degree of freedom associated with the various initial data for the governing ODEs of the phase and amplitude terms in (3.5). The support of a Gaussian beam around a geodesic that is given by the parameter $\delta '$ is also another degree of freedom in the construction.

We start with fixing the choice of the phase terms $\phi _j$ with $j\geqslant 3$ and the amplitude terms $a_{j,k}$ with $j,k=0,1,\ldots ,N$ (and both indices not simultaneously zero), by assigning zero initial value for their respective ODEs along the null geodesic $\gamma _{q,\xi }$ at the point $q=\gamma _{q,\xi }(0)$ . Therefore, to complete the construction of the Gaussian beam $\mathcal U_\lambda $ , it suffices to fix a small parameter $\delta '>0$ and also to choose $Y(0)$ and $Z(0)$ in Lemma 3.2. This will then fix the remaining functions $\phi _2$ and $a_{0,0}$ in the Gaussian beam construction. To account for the latter two degrees of freedom in the construction, we introduce the notation $\iota =(Y(0),Z(0))\in \mathcal T$ where

(4.2) $$ \begin{align} \begin{aligned} \mathcal T = \{ (Y_0,Z_0)\in \mathbb C^{(1+n)^2}\times \mathbb C^{(1+n)^2}\,:\,& Z_0Y_0^{-1}\ \text{is symmetric} \\ &\text{and}\ \Im( Z_0Y_0^{-1})>0\}.\end{aligned}\end{align} $$

Using the notations above, we can explicitly determine (or identify) Gaussian beam functions

(4.3) $$ \begin{align} \mathcal U_\lambda=\mathcal U_{\lambda,v,\iota,\delta'},\end{align} $$

subject to each $\lambda \in \mathbb R$ that denotes the asymptotic parameter in the construction, a vector $v=(q,\xi ) \in L^+\Omega _{\mathrm{in}}$ or $v=(q,\xi ) \in L^+\Omega _{\mathrm{out}}$ that fixes the geodesic $\gamma _{v}$ , a small $\delta '>0$ that fixes the support around the geodesic and the choice of $\iota \in \mathcal T$ that fixes the initial values for the ODEs governing $\phi _2$ and $a_{0,0}$ . As discussed above, the rest of the terms in the Gaussian beam are fixed by setting the initial values for their ODEs to be zero at the point q. For the sake of brevity and where there is no confusion, we will hide these parameters in the notation $\mathcal U_\lambda $ .

Our aim in the remainder of this section is to construct a source $f\in \mathcal C^{\infty }_c(\Omega _{\mathrm{in}})$ such that the solution to the linear wave equation (2.1) with this source term is close to the real part of the complex-valued Gaussian beam $\mathcal U_\lambda $ , in a sense that will be made precise below. We then give an analogous construction of sources for $\Omega _{\mathrm{out}}$ .

Remark 4. Let us emphasise that the need to work with real-valued sources is due to the fact that in the case of the quasi-linear wave equation (1.3), the solution to the wave equation appears in the tensor $G(x,u)$ . Therefore, for the sake of physical motivations of our inverse problem, it is crucial to work with real-valued solutions to the wave equations (1.2)–(1.3).

To simplify the notations, we use the embedding of M into $\mathbb R \times M_0$ to define the $(x^0,x')$ -coordinates on M described in the introduction. Next, we write $q=(q_0,q')$ and define two function $\zeta _{\pm ,v,\delta '} \in \mathcal C^\infty (\mathbb R)$ such that

(4.4) $$ \begin{align} \zeta_{-,v,\delta'}(x^0)= \begin{cases} 0 & \text{if}\,\, x^0\leqslant q_0-\delta',\\ 1 & \text{if}\,\,x^0\geqslant q_0-\frac{\delta'}{2}. \end{cases} \end{align} $$

and

(4.5) $$ \begin{align} \zeta_{+,v,\delta'}(x^0) = \begin{cases} 0 & \text{if}\,\, x^0\geqslant q_0,\\ 1 & \text{if}\,\,x^0 \leqslant q_0-\frac{\delta'}{2}. \end{cases} \end{align} $$

We are now ready to define the source. Emphasising the dependence on $\lambda $ , $v=(q,\xi )$ , $\delta '$ and the initial values for ODEs of $Y(s)$ and $Z(s)$ at the point $s=0$ (see (4.1)) that is governed by $\iota \in \mathcal T$ , we write

(4.6) $$ \begin{align} f^{+}_{\lambda,v,\iota,\delta'} = \zeta_{+,v,\delta'} \Box_{g} (\zeta_{-,v,\delta'} \Re \,\mathcal U_\lambda) \in \mathcal C^{\infty}_c(\Omega_{\text{in}}), \end{align} $$

where $\Re $ denotes the real part of a complex number. We require the parameter $\delta '$ to be sufficiently small so that

$$ \begin{align*}\operatorname{\mathrm{supp}} f^{+}_{\lambda,v,\iota,\delta'} \subset \Omega_{\text{in}}.\end{align*} $$

Note that since $(\Omega _{\mathrm{in}},g|_{\Omega _{\mathrm{in}}})$ is assumed to be known (see the hypothesis of Theorem 1.1), $f_{\lambda ,v,\iota ,\delta '}^+$ will also be known. As $\zeta _{-,v,\delta '} = 1$ on the support of $1-\zeta _{+,v,\delta '}$ , it holds that

$$ \begin{align*}\Box_{g} (\zeta_{-,v,\delta'} \Re\, \mathcal U_\lambda) - f^+_{\lambda,v,\iota,\delta'} = (1-\zeta_{+,v,\delta'})\Box_{g} \Re \mathcal U_\lambda. \end{align*} $$

Now applying the property (3) of Gaussian beams in Section 3 with $k=\frac {n}{2}+2$ and the fact that $N=\lceil \frac {3n}{2}\rceil +8$ implies the bound

$$ \begin{align*}\|\Box_{g}(\zeta_{-,v,\delta'} \Re\, \mathcal U_\lambda) - f^+_{\lambda,v,\iota,\delta'} \|_{H^k((-T,T)\times M_0)} \lesssim |\lambda|^{-\frac{n+1}{2}}|\lambda|^{-1}. \end{align*} $$

We write $u^+_{\lambda ,v,\iota ,\delta '} = u$ where u is the solution of the linear wave equation (2.1) with the source $f = f^+_{\lambda ,v,\iota ,\delta '}$ . By combining the above estimate with the usual energy estimate for the wave equation and the Sobolev embedding of $\mathcal C^1((-T,T)\times M_0)$ in $H^{k}((-T,T)\times M_0)$ with $k=\frac {n}{2}+2$ , we obtain

(4.7) $$ \begin{align} \|\zeta_{-,v,\delta'} \Re\, \mathcal U_\lambda - u^+_{\lambda,v,\iota,\delta'} \|_{\mathcal C^1((-T,T)\times M_0)} \lesssim |\lambda|^{-\frac{n+1}{2}}|\lambda|^{-1}. \end{align} $$

Observe that while the Gaussian beam $\mathcal U_\lambda $ is supported near the geodesic $\gamma $ , the function $u^+_{\lambda ,v,\iota ,\delta '}$ is not supported near this geodesic anymore but nevertheless, as can be seen from the latter estimate, it is rather small away from the geodesic.

We will also need a test function corresponding to $v=(q,\xi ) \in L^+\Omega _{\mathrm{out}}$ whose construction differs from that of $f^+_{\lambda ,v,\iota ,\delta '}$ above only to the extent that the roles of $\zeta _{+,v,\delta '}$ and $\zeta _{-,v,\delta '}$ are reversed in (4.6). That is, we define

(4.8) $$ \begin{align} f_{\lambda,v,\iota,\delta'}^- = \zeta_{-,v,\delta'} \Box_{g} (\zeta_{+,v,\delta'}\Re\, \mathcal U_\lambda) \in \mathcal C^{\infty}_c(\Omega_{\text{out}}). \end{align} $$

Since $(\Omega _{\mathrm{out}},g|_{\Omega _{\mathrm{out}}})$ is assumed to be known, $f_{\lambda ,v,\delta '}^-$ will also be known, and the analogue of (4.7) reads

(4.9) $$ \begin{align} \|\zeta_{+,v,\delta'} \Re\, \mathcal U_\lambda - u^-_{\lambda,v,\iota,\delta'} \|_{\mathcal C^1((-T,T)\times M_0)} \lesssim |\lambda|^{-\frac{n+1}{2}}|\lambda|^{-1}, \end{align} $$

where $u^-_{\lambda ,v,\iota ,\delta '}=u$ is now defined as the solution to the linear wave equation with reversed causality

(4.10) $$ \begin{align} \begin{aligned} \begin{cases} \Box_{g} u = f, &\text{on}\ M, \\ u=0& \text{on}\ M\setminus J^-(\operatorname{\mathrm{supp}} f), \end{cases} \end{aligned} \end{align} $$

with the source $f=f_{\lambda ,v,\iota ,\delta '}^-$ .

Finally, and before closing the section, we record the following estimate for the compactly supported sources $f^{\pm }_{\lambda ,v,\iota ,\delta '}$ that follows from the definitions (4.6), (4.8) and property (3) of Gaussian beams in Section 3:

(4.11) $$ \begin{align} \|f^{\pm}_{\lambda,v,\iota,\delta'}\|_{L^2(M)} \lesssim |\lambda|^{1-\frac{n}{2}}. \end{align} $$

5 Reduction from the source-to-solution map to the three-to-one scattering relation

We begin by considering

$$ \begin{align*}v_{0}=(q_{0},\xi_{0}) \in L^+\Omega_{\text{out}}\quad \text{and}\quad v_1=(q_1,\xi_1) \in L^+\Omega_{\text{in}}\end{align*} $$

and require that the null geodesics $\gamma _{v_j}$ , $j=0,1,$ are distinct. Here, $L^{\pm }\Omega _{\mathrm{out}}$ and $L^{\pm }\Omega _{\mathrm{in}}$ denote the bundle of future- and past-pointing light-like vectors on $\Omega _{\mathrm{out}}$ and $\Omega _{\mathrm{in}}$ , respectively.

As mentioned above, we impose that $\gamma _{v_0}$ and $\gamma _{v_1}$ are not reparametrisations of the same curve. This condition can always be checked via the map $\mathscr L$ or $\mathscr N$ . To sketch this argument, we note that based on a simple first-order linearisation of the source-to-solution map – that is $\partial _{\varepsilon } \mathscr N(\varepsilon f)|_{\varepsilon =0}$ or $\partial _{\varepsilon } \mathscr L(\varepsilon f)|_{\varepsilon =0}$ – we can obtain the source-to-solution map $L^{\mathrm{lin}}_g$ associated to the linearised operator $\Box _{g}$ with sources in $\Omega _{\mathrm{in}}$ and receivers in $\Omega _{\mathrm{out}}$ . To be precise, $L^{\mathrm{lin}}_g: L^2(\Omega _{\mathrm{in}}) \to H^1(\Omega _{\mathrm{out}})$ is defined through the mapping

$$ \begin{align*}L^{\mathrm{lin}}_g f = u|_{\Omega_{\text{out}}}\quad \forall\, f \in L^2(\Omega_{\text{in}}),\end{align*} $$

where u is the unique solution to (2.1) subject to the source f.

Then, for example, based on the main result of [87], we can determine the scattering relation, $\Lambda _g$ for sources in $\Omega _{\mathrm{in}}$ and receivers in $\Omega _{\mathrm{out}}$ ; that is, the source-to-solution map $\mathscr L$ or $\mathscr N$ uniquely determines

(5.1) $$ \begin{align} \Lambda_g(v)= \{(\gamma_v(s),c\,\dot{\gamma}_v(s))\,:c\in \mathbb R\setminus \{0\},\,s>0,\quad \gamma_v(s)\in \Omega_{\text{out}}\}, \quad \forall \,v\in L^+\Omega_{\text{in}}. \end{align} $$

Using this scattering map, it is possible to determine if the two null geodesics $\gamma _{v_0}$ and $\gamma _{v_1}$ above are distinct or not. Indeed, to remove the possibility of identical null geodesics, we must have

(5.2) $$ \begin{align} v_0 \notin \Lambda_g(v_1).\end{align} $$

Having fixed $v_0\in L^+\Omega _{\mathrm{out}}$ , $v_1\in L^+\Omega _{\mathrm{in}}$ subject to the requirement (5.2), we proceed to define the test set $\Sigma _{v_0,v_1}$ as the set of all tuplets given by

(5.3) $$ \begin{align} \begin{aligned} \Sigma_{v_0,v_1}=\{(v_0,\kappa_0,\iota_{0},\ldots, v_3,\kappa_3, \iota_{3})\,:\, &v_2, v_3 \in L^+\Omega_{\text{in}}, \quad \kappa_j \in \mathbb R\setminus \{0\},\\ & \iota_j \in \mathcal T,\quad j=0,1,2,3,\} \end{aligned} \end{align} $$

where we recall that $\mathcal T$ is defined by (4.2). Note that $v_0$ and $v_1$ are a priori fixed and their inclusion in the tuplets $\sigma \in \Sigma _{v_0,v_1}$ is purely for aesthetic reasons.

Given any small $\delta '>0$ and $\sigma =(v_0,\kappa _0,\iota _{0},\ldots , v_3,\kappa _3, \iota _{3}) \in \Sigma _{v_0,v_1}$ , we consider the null geodesics $\gamma _{v_{j}}$ , $j=0,1,2,3$ , passing through $q_{j}$ in the directions $\xi _{j}$ and parametrisation as in (3.1). Recall that we are writing $v_j=(q_j,\xi _j)$ for $j=0,1,2,3$ . We also denote by $y^{(j)}$ the Fermi coordinates near $\gamma _{v_j}$ given by Lemma 3.1 and subsequently, following the notation (4.3), we construct for each $\lambda>0$ the Gaussian beams $\mathcal U_{\kappa _j\lambda }^{(j)}=\mathcal U_{\kappa _j\lambda ,v_j,\iota _j,\delta '}$ of order

(5.4) $$ \begin{align} N=\lceil\frac{3n}{2}\rceil+8 \end{align} $$

and the form

(5.5) $$ \begin{align} \mathcal U^{(j)}_{\kappa_j\lambda}(x)= \begin{cases} e^{i\kappa_j\lambda\phi^{(j)}(x)}A^{(j)}_{\kappa_j\lambda}(x) &\quad\text{if}\quad \kappa_j>0,\\ e^{i\kappa_j\lambda\bar{\phi}^{(j)}(x)}\bar{A}^{(j)}_{\kappa_j\lambda}(x)&\quad\text{if}\quad \kappa_j<0. \end{cases} \end{align} $$

We recall that the functions $\phi ^{(j)}, A^{(j)}_{\kappa _j\lambda }$ are exactly as in Section 3 with a support $\delta '$ around the null geodesic $\gamma _{v_j}$ (see (3.5)) and the initial conditions for all ODEs assigned at the points $q^{(j)}$ . As discussed in Section 4, we set the initial values for the phase terms $\phi ^{(j)}_k$ with $k=3,\ldots ,N$ and all $a^{(j)}_{k,l}$ with $k,l=0,1,\ldots ,N$ (and not both simultaneously zero) to be zero at the point $q_{j}$ . Finally, and to complete the construction of the Gaussian beams, we set

$$ \begin{align*}(Y^{(j)}(0),Z^{(j)}(0)) = \iota_j \in \mathcal T.\end{align*} $$

5.1 Reduction from the source-to-solution map $\mathscr L$ to the three-to-one scattering relation

Let $v_0 \in L^+\Omega _{\mathrm{out}}$ and $v_1\in L^+\Omega _{\mathrm{in}}$ subject to (5.2). We begin by considering an arbitrary element $\sigma =(v_0,\kappa _0,\iota _0,\ldots ,v_3,\kappa _3,\iota _3) \in \Sigma _{v_0,v_1}$ and also an arbitrary function $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$ . Let the source terms $f^+_{\kappa _j\lambda ,v_{j},\iota _j,\delta '}$ for $j=1,2,3$ and the test source $f_{\kappa _0\lambda ,v_0,\iota _0,\delta '}^-$ be defined as in Section 4 and define for each small vector $\varepsilon =(\varepsilon _1,\varepsilon _2,\varepsilon _3,\ldots ,\varepsilon _m) \in \mathbb R^m$ the source $F^{\mathrm{semi}}_{\varepsilon ,\lambda ,\sigma ,\delta ',f}$ given by the equation

(5.6) $$ \begin{align} F^{\mathrm{semi}}_{\varepsilon,\lambda,\sigma,\delta',f}= \begin{cases} \varepsilon_1\,f^+_{\kappa_1\lambda,v_1,\iota_1,\delta'}+\varepsilon_2\,f^+_{\kappa_2\lambda,v_2,\iota_2,\delta'}+\varepsilon_3\,f^+_{\kappa_3\lambda,v_3,\iota_3,\delta'} & \text{if}\,\, m=3,\\ \varepsilon_1\,f^+_{\kappa_1\lambda,v_1,\iota_1,\delta'}+\varepsilon_2\,f^+_{\kappa_2\lambda,v_2,\iota_2,\delta'}+\varepsilon_3\,f^+_{\kappa_3\lambda,v_3,\iota_3,\delta'}+\sum_{j=4}^m \varepsilon_j\,f, & \text{if}\,\, m\geqslant 4.\\ \end{cases} \end{align} $$

For a fixed $\lambda>0$ and small enough $\varepsilon _j$ , $j=1,2,3,\ldots ,m$ , it holds that $F^{\mathrm{semi}}_{\varepsilon ,\lambda ,\sigma ,\delta ',f} \in \mathscr C_{\Omega _{\mathrm{in}}}$ . We let $u^{\mathrm{semi}}_{\varepsilon ,\lambda ,\sigma ,\delta ',f}$ denote the unique small solution to (1.2) subject to this source term. Note that, in particular, there holds

$$ \begin{align*}\partial_{\varepsilon_j} u^{\mathrm{semi}}_{\varepsilon,\lambda,\sigma,\delta'}\bigg|_{\varepsilon = 0}=\begin{cases} u^+_{\kappa_j\lambda,v_{j},\iota_j,\delta'} & \text{if}\,\, j=1,2,3,\\ u_f & \text{if }\ m \geqslant 4\ \text{and}\ j=4,\ldots,m, \end{cases} \end{align*} $$

where $u_f$ is the unique solution to (2.1) subject to the source f and, as discussed in Section 4, $u^+_{\kappa _j\lambda ,v_{j},\iota _j,\delta '}$ is the unique solution to equation (2.1) subject to the source $f_{\kappa _j\lambda ,v_{j},\iota _j,\delta '}^+$ and is close, in the sense of the estimate (4.7), to the real part of the Gaussian beam solutions of forms (5.5) supported in a $\delta '$ -neighbourhood of the light ray $\gamma _{v_j}$ with $j=1,2,3$ .

Finally, we define for each small $\delta '>0$ , $\sigma \in \Sigma _{v_0,v_1}$ and $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$ the analytical data $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f}$ corresponding to the semi-linear equation (1.2) by the expression

(5.7) $$ \begin{align} \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}= \lim_{\lambda\to+\infty}\,\lambda^{\frac{n+1}{2}} \int_{\Omega_{\text{out}}}f_{\kappa_0\lambda,v_0,\iota_0,\delta'}^-\, \frac{\partial^m}{\partial\varepsilon_1\ldots\partial\varepsilon_m} u^{\mathrm{semi}}_{\varepsilon,\lambda,\sigma,\delta',f} \bigg |_{\varepsilon=0}\,dV_g, \end{align} $$

where we recall that $u^{\mathrm{semi}}_{\varepsilon ,\lambda ,\sigma ,\delta ',f}$ is the unique solution to (1.2) subject to the source $F^{\mathrm{semi}}_{\varepsilon ,\lambda ,\sigma ,\delta ',f}$ given by (5.6). Let us emphasise that the knowledge of the source-to-solution map, $\mathscr L$ , determines the analytical data $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f}$ . We have the following theorem.

Theorem 5.1. Let $v_0\in L^+\Omega _{\mathrm{out}}$ and $v_1\in L^+\Omega _{\mathrm{in}}$ be such that (5.2) holds. The following statements hold:

1. (i) If $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ^{\prime }_j,f} \neq 0$ for some $\sigma \in \Sigma _{v_0,v_1}$ and $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$ and a sequence $\{\delta ^{\prime }_j\}_{j=1}^{\infty }$ converging to zero, then there exists an intersection point $y \in \overleftarrow {\;\gamma _{v_0}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$ .

2. (ii) Let $v_2,v_3 \in L^+\Omega _{\mathrm{in}}$ . Assume that $\gamma _{v_{j}}$ , $j=0,1,2,3$ , are distinct and there exists a point $y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}.$ Moreover, assume that $y=\gamma _{v_{0}}(s_0)$ with $s_0\in (-\rho (v_0),0]$ and $y=\gamma _{v_{j}}(s_j)$ for all $j=1,2,3$ , with $s_j\in [0,\rho (v_j))$ . Denote $\xi _j=\dot \gamma _{v_{j}}(s_j)$ for $j=0,1,2,3$ and assume that $\xi _0 \in \operatorname {\mathrm {span}}(\xi _1, \xi _2, \xi _3)$ . Then, there exists $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$ , $\kappa _j \in \mathbb R\setminus \{0\}$ and $\iota _j \in \mathcal T$ , $j=0,1,2,3$ such that $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f}\neq 0$ for all $\delta '$ sufficiently small.

We will prove Theorem 5.1 in Subsection 5.3. Observe that as an immediate corollary of Theorem 5.1 it follows that the relation

$$ \begin{align*} \operatorname{\mathrm{R}}_{\text{semi-lin}} = \{&(v_{0},v_{1}, v_{2},v_{3})\in L^+ \Omega_{\text{out}} \times (L^+ \Omega_{\text{in}})^3: \gamma_{v_j}\text{s are pair-wise not identical,} \\& \text{there are}\ f \in C^{\infty}_c(\Omega_{\text{in}}), \kappa_j \in \mathbb R \setminus \{0\} \quad \text{and}\quad \iota_j \in \mathcal T, j=0,1,2,3, \\&\text{s.t for all small}\ \delta'>0, \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f} \ne 0\ \text{where}\ \sigma = (v_{0},\kappa_0,\iota_0,\dots, v_{3},\kappa_3,\iota_3) \}, \end{align*} $$

is a three-to-one scattering relation; that is, it satisfies (R1) and (R2) in Definition 1.2. Therefore, since the source-to-solution map $\mathscr L$ determines $\operatorname {\mathrm {R}}_{\mathrm{semi-lin}}$ , the first part of Theorem 1.1 – that is, the recovery of the topological, differential and conformal structure of $\mathbb D$ from the source-to-solution map $\mathscr L$ – follows immediately from combining Theorem 5.1 and Theorem 1.3.

5.2 Reduction from the source-to-solution map $\mathscr N$ to the three-to-one scattering relation

Analogous to the previous section, we begin by considering an arbitrary element $\sigma \in \Sigma _{v_0,v_1}$ . Next, we define the three-parameter family of sources $F^{\mathrm{quasi}}_{\varepsilon ,\lambda ,\sigma ,\delta '}$ with $\varepsilon = (\varepsilon _1, \varepsilon _2, \varepsilon _3)$ given by the equation

(5.8) $$ \begin{align} F^{\mathrm{quasi}}_{\varepsilon,\lambda,\sigma,\delta'}= \varepsilon_1\,f^+_{\kappa_1\lambda,v_1,\iota_1,\delta'}+\varepsilon_2\,f^+_{\kappa_2\lambda,v_2,\iota_2,\delta'}+\varepsilon_3\,f^+_{\kappa_3\lambda,v_3,\iota_3,\delta'}. \end{align} $$

For a fixed $\lambda>0$ and small enough $\varepsilon _j$ , $j=1,2,3$ , it holds that $F^{\mathrm{quasi}}_{\varepsilon ,\lambda ,\sigma ,\delta '} \in \mathscr C_{\Omega _{\mathrm{in}}}$ . We let $u^{\mathrm{quasi}}_{\varepsilon ,\lambda ,\sigma ,\delta '}$ denote the unique small solution to (1.3) subject to this source term. Note that

$$ \begin{align*}\partial_{\varepsilon_j} u^{\mathrm{quasi}}_{\varepsilon,\lambda,\sigma,\delta'}\bigg|_{\varepsilon = 0}=u^+_{\kappa_j\lambda,v_{j},\iota_j,\delta'}\quad \text{for}\ j=1,2,3,\end{align*} $$

where we recall from Section 4 that $u^+_{\kappa _j\lambda ,v_{j},\iota _j,\delta '}$ is the unique solution to equation (2.1) subject to the source $f_{\kappa _j\lambda ,v_{j},\iota _j,\delta '}^+$ and is close, in the sense of the estimate (4.7), to the real part of the Gaussian beam solutions of forms (5.5) supported in a $\delta '$ -neighbourhood of the light ray $\gamma _{v_j}$ with $j=1,2,3$ .

Finally, we define for each small $\delta '>0$ and $\sigma \in \Sigma _{v_0,v_1}$ the analytical data $\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta '}$ by the expression

(5.9) $$ \begin{align} \mathscr D^{\mathrm{quasi}}_{\sigma,\delta'}= \lim_{\lambda\to+\infty}\,\lambda^{\frac{n-3}{2}} \int_{\Omega_{\text{out}}}f_{\kappa_0\lambda,v_0,\iota_0,\delta'}^-\, \frac{\partial^3}{\partial\varepsilon_1\partial\varepsilon_2\partial\varepsilon_3} u^{\mathrm{quasi}}_{\varepsilon,\lambda,\sigma,\delta'} \bigg |_{\varepsilon=0}\,dV_g, \end{align} $$

where we recall that $u^{\mathrm{quasi}}_{\varepsilon ,\lambda ,\sigma ,\delta '}$ is the unique solution to (1.3) subject to the source $F^{\mathrm{quasi}}_{\varepsilon ,\lambda ,v,\delta '}$ given by (5.8). Let us emphasise that the knowledge of the source-to-solution map, $\mathscr N$ , determines the analytical data $\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta '}$ . Note also that the scaling in (5.9) differs from that of (5.7) as the asymptotic behavior of the corresponding integrands varies in the semi-linear and quasi-linear models. We have the following theorem.

Theorem 5.2. Let $v_0\in L^+\Omega _{\mathrm{out}}$ and $v_1\in L^+\Omega _{\mathrm{in}}$ be such that (5.2) holds. The following statements hold:

1. (i) If $\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta ^{\prime }_j} \neq 0$ for some $\sigma \in \Sigma _{v_0,v_1}$ and a sequence $\{\delta ^{\prime }_j\}_{j=1}^{\infty }$ converging to zero, then there exists an intersection point $y \in \overleftarrow {\;\gamma _{v_0}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$ .

2. (ii) Let $v_2,v_3 \in L^+\Omega _{\mathrm{in}}$ . Assume that $\gamma _{v_{j}}$ , $j=0,1,2,3$ , are distinct and there exists a point $y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}.$ Moreover, assume that $y=\gamma _{v_{0}}(s_0)$ with $s_0\in (-\rho (v_0),0]$ and $y=\gamma _{v_{j}}(s_j)$ for all $j=1,2,3$ , with $s_j\in [0,\rho (v_j))$ . Denote $\xi _j=\dot \gamma _{v_{j}}(s_j)$ for $j=0,1,2,3$ and assume that $\xi _0 \in \operatorname {\mathrm {span}}(\xi _1, \xi _2, \xi _3)$ . Then, there exists $\kappa _j \in \mathbb R\setminus \{0\}$ and $\iota _j \in \mathcal T$ , $j=0,1,2,3$ such that $\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta '}\neq 0$ for all $\delta '$ sufficiently small.

We prove Theorem 5.2 in Subsection 5.4. Observe that as an immediate corollary of Theorem 5.2 it follows that the relation

$$ \begin{align*} \operatorname{\mathrm{R}}_{\text{quasi-lin}} = \{&(v_{0},v_{1}, v_{2},v_{3})\in L^+ \Omega_{\text{out}} \times (L^+ \Omega_{\text{in}})^3: \gamma_{v_j}\text{s are pair-wise not identical,} \\& \text{there are}\ \kappa_j \in \mathbb R \setminus \{0\} \quad \text{and}\quad \iota_j \in \mathcal T, j=0,1,2,3, \\&\text{s.t for all small}\ \delta'>0, \mathscr D^{\mathrm{quasi}}_{\sigma,\delta'} \ne 0\ \text{where}\ \sigma = (v_{0},\kappa_0,\iota_0,\dots, v_{3},\kappa_3,\iota_3) \}, \end{align*} $$

is a three-to-one scattering relation; that is, it satisfies (R1) and (R2) in Definition 1.2. Therefore, since the source-to-solution map $\mathscr N$ determines $\operatorname {\mathrm {R}}_{\mathrm{quasi}}$ , the first part of Theorem 1.1 – that is, the recovery of the topological, differential and differential structure of $\mathbb D$ from the source-to-solution map $\mathscr N$ – follows immediately from combining Theorem 5.2 and Theorem 1.3.

5.3 Proof of Theorem 5.1

Note that by expression (2.6) in Subsection 2.2, the source-to-solution map $\mathscr L$ determines the knowledge of the expression

$$ \begin{align*}\mathcal I_{\lambda,\sigma,\delta',f}=\int_M u^{-}_{\kappa_0\lambda,v_0,\iota_0,\delta'} u^{+}_{\kappa_1\lambda,v_1,\iota_1,\delta'}u^{+}_{\kappa_2\lambda,v_2,\iota_2,\delta'} u^{+}_{\kappa_3\lambda,v_3,\iota_3,\delta'}\,u_f^{m-3}dV_g,\end{align*} $$

where we recall that the notations $u^{\pm }_{\kappa _j\lambda ,v_j,\iota _j,\delta '}$ are as defined in Section 5. Recall also that the function $u^{+}_{\kappa _j\lambda ,v_j,\iota _j,\delta '}$ , $j=1,2,3$ (respectively $u^-_{\kappa _0\lambda ,v_0,\iota _0,\delta '}$ ) is close in the sense of (4.7) (respectively (4.9)) to the Gaussian beams $\mathcal U_{\kappa _j\lambda }^{(j)}=\mathcal U_{\kappa _j\lambda ,v_j,\iota _j,\delta '}$ (respectively $\mathcal U_{\kappa _0\lambda }^{(0)}=\mathcal U_{\kappa _0\lambda ,v_0,\iota _0,\delta '}$ ). Finally, the function $u_f$ is the unique solution to (2.1) subject to the source $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$ . Note also that by (2.6), there holds

$$ \begin{align*}\mathscr D^{\mathrm{semi}}_{\sigma,\delta',f} = -m! \lim_{\lambda \to \infty}\lambda^{\frac{n+1}{2}} \mathcal I_{\lambda,\sigma,\delta',f}.\end{align*} $$

Next, we observe from the definitions (3.5) that the Gaussian beams $\mathcal U^{(j)}_{\kappa _j\lambda }$ , $j=0,1,2,3$ satisfy the uniform bounds

(5.10) $$ \begin{align} \|\mathcal U_{\kappa_j\lambda}^{(j)}\|_{L^{\infty}((-T,T)\times M_0)}\leqslant C_j,\end{align} $$

for some constants $C_j$ independent of $\lambda $ . Together with the estimates (4.7)–(4.9), it follows that

$$ \begin{align*}\lambda^{\frac{n+1}{2}}\mathcal I_{\lambda,\sigma,\delta',f}=\lambda^{\frac{n+1}{2}}\int_{M}\zeta_{+,v_0,\delta'}\Re\, \mathcal U_{\kappa_0\lambda}^{(0)}\left(\prod_{j=1}^3\zeta_{-,v_j,\delta'}\Re\, \mathcal U_{\kappa_j\lambda}^{(j)}\right)u_f^{m-3}\,dV_{g}+\mathcal O(\lambda^{-1}),\end{align*} $$

which implies that

(5.11) $$ \begin{align} \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}=-m! \lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\int_{M}\zeta_{+,v_0,\delta'}\Re\, \mathcal U_{\kappa_0\lambda}^{(0)}\left(\prod_{j=1}^3\zeta_{-,v_j,\delta'}\Re\, \mathcal U_{\kappa_j\lambda}^{(j)}\right)u_f^{m-3}\,dV_{g}. \end{align} $$

Note that given $\delta '>0$ sufficiently small, the latter integrand is supported on a compact subset of $\mathbb D_e$ (see (1.8)).

Before proving Theorem 5.1, we state the following lemma.

Lemma 5.3. Given any point p in M that lies on a null geodesic $\overrightarrow {\gamma _v}$ with $v \in L^+\Omega _{\mathrm{in}}$ , there exists a real-valued source $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$ such that the solution $u_f$ to (2.1) with source f satisfies

$$ \begin{align*}u_f(p)\neq 0.\end{align*} $$

Proof. Let $p=\gamma _v(s)$ for some $v=(q,\xi ) \in L^+\Omega _{\mathrm{in}}$ and some $s\geqslant 0$ . Let $y=(y^0,y^1,\ldots ,y^n)$ denote the Fermi coordinate system in a tubular neighbourhood of $\gamma $ and note that $p=(s,0)$ . We consider for each $\lambda>0$ , $\iota \in \mathcal T$ and $\delta '$ small the Gaussian beam $\mathcal U_\lambda $ of order $N=\lceil \frac {3n}{2}\rceil +8$ , near the geodesic $\gamma $ that is fixed by the choices $\lambda $ , $\delta '$ and $\iota $ (see Section 4). Next, consider the source $f=f^+_{\lambda ,v,\iota ,\delta '}$ and recall that the solution $u=u^+_{\lambda ,v,\iota ,\delta '}$ to equation (2.1) with source term f is asymptotically close to $\mathcal U_{\lambda }$ in the sense of (4.7). Together with the explicit expressions (3.5), we deduce that

$$ \begin{align*}u(p)=u(s,0)= a_{0,0}(s)+\mathcal O(\lambda^{-1}).\end{align*} $$

Recalling the expression for the principal amplitude term $a_{0,0}$ (see (3.7)), we deduce that there exists $\iota \in \mathcal T$ such that $a_{0,0}(s)=1$ . The claim follows trivially with this choice of $\iota $ and $\lambda $ sufficiently large.

5.3.1 Proof of statement (i) in Theorem 5.1

We assume that $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f} \neq 0$ for some $\sigma =(v_0,\kappa _0,\iota _0,\ldots ,v_3,\kappa _3,\iota _3)\in \Sigma _{v_0,v_1}$ and $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$ and a family of $\delta '$ s converging to zero. First, observe that the corresponding null geodesics $\gamma _{v_j}$ with $j=0,1,2,3$ must simultaneously intersect at least once on $\mathbb D_e$ , since otherwise the support of the amplitude functions $A^{(j)}_{\kappa _j\lambda }$ in the expression (5.11) become disjoint sets for all sufficiently small $\delta '$ . Subsequently, the integrand in (5.11) vanishes independent of the parameter $\lambda $ , implying that $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f}=0$ for all $\delta '$ small. Let $\mathcal A=\{y_1,\ldots ,y_N\}$ denote the set of intersection points of the four null geodesics $\gamma _{v_j}$ , $j=0,1,2,3$ on $\mathbb D_e$ . In terms of the set $\mathcal A$ , we observe that given $\delta '$ sufficiently small, the expression (5.11) reduces as follows:

(5.12) $$ \begin{align} \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}=-m! \lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\sum_{\ell=1}^N\int_{U_\ell}\zeta_{+,v_0,\delta'}\Re\, \mathcal U_{\kappa_0\lambda}^{(0)}\left(\prod_{j=1}^3\zeta_{-,v_j,\delta'}\Re\, \mathcal U_{\kappa_1\lambda}^{(j)}\right)u_f\,dV_{g},\end{align} $$

where $U_\ell $ , $\ell =1,\ldots ,N,$ is a small open neighbourhood of the point $y_\ell $ in $\mathbb D_e$ that depends on $\delta '$ .

To complete the proof of statement (i), we need to show that there is a point $y \in \mathcal A$ that satisfies the more restrictive casual condition $y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$ . It is straightforward to see that if $y_\ell \notin \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$ for some $\ell =1,\ldots ,N$ , then

$$ \begin{align*}\int_{U_\ell}\zeta_{+,v_0,\delta'}\Re\, \mathcal U_{\kappa_0\lambda}^{(0)}\left(\prod_{j=1}^3\zeta_{-,v_j,\delta'}\Re\, \mathcal U_{\kappa_1\lambda}^{(j)}\right)dV_{g}=0,\end{align*} $$

for all $\delta '$ sufficiently small. Indeed, this follows from the definitions of the cutoff functions $\zeta _{+,v_0,\delta '}$ and $\zeta _{-,v_j,\delta '}$ , $j=1,2,3$ ; see (4.4)–(4.5). Since $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f} \neq 0$ for a sequence $\{\delta ^{\prime }_k\}_{k=1}^{\infty }$ converging to zero by the hypothesis (i) of the theorem, it follows that there must exist a point $y \in \mathcal A$ such that $y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$ .

5.3.2 Proof of statement (ii) in Theorem 5.1

We are assuming here that

$$ \begin{align*}(v_0,v_1,v_2,v_3) \in L^+\Omega_{\text{out}} \times (L^+\Omega_{\text{in}})^3\end{align*} $$

satisfies the hypothesis of statement (ii) and want to prove that there exists a real-valued function $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$ and $\kappa_j \in \mathbb R\setminus \{0\} \mbox{ and } \iota_j \in \mathcal T $ with $j=0,1,2,3$ such that given

$$\begin{align*}\sigma=(v_0,\kappa_0,\iota_0,\ldots,v_3,\kappa_3,\iota_3),\end{align*}$$

and all $\delta '>0$ sufficiently small, there holds

$$ \begin{align*}\mathscr D^{\mathrm{semi}}_{\sigma,\delta',f} \neq 0.\end{align*} $$

Let us first emphasise that given the hypothesis of statement (ii), there is a unique point $y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$ . To show this, we give a proof by contradiction and suppose that there is another distinct point $\tilde {y} \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$ . If $\tilde y \le y$ , then there exists a broken path consisting of null geodesics that connects one of the points $\pi (v_j)$ , $j=1,2,3,$ to the point y. Together with [79, Proposition 10.46] we obtain that $\tau (\pi (v_j),y)>0$ , yielding a contradiction since $y=\gamma _{v_j}(s_j)$ with $s_j \in [0,\rho (v_j))$ . In the alternative case that $y \le \tilde {y}$ , there exists a broken path consisting of null geodesics that connects the point y to the point $\pi (v_0)$ . Together with [79, Proposition 10.46] we obtain that $\tau (y,\pi (v_0))>0$ , yielding a contradiction since $y=\gamma _{v_0}(s_0)$ with $s_0 \in (-\rho (v_0),0]$ .

Next, we observe that given $\delta '$ sufficiently small together with the fact that $y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$ , the expression (5.11) reduces as follows:

(5.13) $$ \begin{align} \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}=-m! \lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\int_{M}\left(\prod_{j=0}^3\Re\, \mathcal U_{\kappa_1\lambda}^{(j)}\right)\,u_f^{m-3}\,dV_{g}. \end{align} $$

We will use the method of stationary phase to analyse the product of the four Gaussian beams in (5.13). Let us begin by considering the unique point $y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$ . We choose the real-valued function $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$ such that $u_f(y) \neq 0$ . This is possible thanks to Lemma 5.3. Next, we choose the nonzero constants $\kappa _0,\ldots ,\kappa _3$ , so that

(5.14) $$ \begin{align} \sum_{j=0}^3 \kappa_j \dot{\gamma}_{v_j}(s_j)=0,\end{align} $$

where $\gamma _{v_j}(s_j)=y$ . Recall that these constants exist by our assumption that the tangents to $\gamma _{v_j}$ are linearly dependent at y. The constants $\kappa _j$ , $j=0,1,2,3$ can be chosen to be all nonzero, since any three pair-wise linearly independent null vectors are linearly independent (see Lemma 6.21 for the proof).

We consider the four families of Gaussian beams along the geodesics $\gamma _{v_j}$ , $j=0,1,2,3$ , as in (5.5). We choose the initial datum $\iota _j \in \mathcal T$ for the initial values $(Y^{(j)}(0),Z^{(j)}(0))$ governing ODEs of the matrices $Y^{(j)}(s)$ and $Z^{(j)}(s)$ , so that

(5.15) $$ \begin{align} Y^{(j)}(s_j)=I \quad \text{and}\quad Z^{(j)}(s_j) = i\, I,\end{align} $$

where we recall that $\gamma _{v_j}(s_j)=y$ . Note in particular that given this choice of $\iota _j \in \mathcal T$ , $j=0,1,2,3$ , there holds

(5.16) $$ \begin{align} a_{0,0}^{(j)}(y)= 1\quad \text{for}\ j=0,1,2,3.\end{align} $$

In the remainder of the proof, we show that given the function f and the tuplet $\sigma =(v_0,\kappa _0,\iota _0,\ldots ,v_3,\kappa _3,\iota _3)$ constructed as above and all $\delta '>0$ sufficiently small, there holds $ \mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f} \neq 0.$

It can be easily verified from the choice of the parametrisation (3.1), Lemma 3.1 and the expression for the phase function given by (3.7) that

(5.17) $$ \begin{align} \dot{\gamma}_{v_j}(s)=\nabla^g\phi^{(j)}|_{\gamma_{v_j}(s)}=\nabla^g\bar{\phi}^{(j)}|_{\gamma_{v_j}(s)}\quad \text{for}\ j=0,1,2,3. \end{align} $$

Let us define

(5.18) $$ \begin{align} S(x):= \Phi^{(0)}(x)+ \Phi^{(1)}(x)+ \Phi^{(2)}(x)+ \Phi^{(3)}(x),\end{align} $$

where

(5.19) $$ \begin{align} \Phi^{(j)}(x) = \begin{cases} \kappa_j\phi^{(j)}(x) &\quad\text{if}\quad \kappa_j>0,\\ \kappa_j\bar{\phi}^{(j)}(x)&\quad\text{if}\quad \kappa_j<0. \end{cases} \end{align} $$

We have the following lemma.

Lemma 5.4. Suppose that $y=\overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$ and that (5.14) holds. Let S be defined by (5.18) and denote by d an auxiliary Riemannian distance function on M. There holds

1. (i) $S(y)=0$ .

2. (ii) $\nabla ^{g}S(y)=0$ .

3. (iii) $\Im S(\tilde {y}) \geqslant a\, d(\tilde {y},y)^2$ for all points $\tilde {y}$ in a neighbourhood of y. Here $a>0$ is a constant.

We refer the reader to [29, Lemma 5] for the proof of this lemma.

Lemma 5.5. Suppose that $y=\overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$ and that (5.14) holds. Let S be defined by (5.18) and let $F \in \mathcal C^1(M)$ be compactly supported in a sufficiently small neighbourhood of the point y. There holds

$$ \begin{align*}\lim_{\lambda \to \infty}\lambda^{\frac{n+1}{2}} \int_M e^{i\lambda S(x)}F(x)\,dV_g = C_0\,F(y),\end{align*} $$

where $C_0 \in \mathbb C$ only depends on $(M,g)$ and $c_0=\Re \, C_0 \neq 0$ .

Proof. We fix a coordinate system $(x^0,\ldots ,x^n)$ in a small neighbourhood about the point y, so that $y=(0,\ldots ,0)$ . By Lemma 5.4, there holds

$$ \begin{align*}S(x) = \sum_{j,k=0}^n Q_{jk}x^jx^k + R(x),\end{align*} $$

where $|R(x)|=\mathcal O(|x|^3)$ and the matrix $Q=(Q_{jk})_{j,k=0}^n$ has a positive definite imaginary part. We assume that F is supported in a sufficiently small neighbourhood U of the point y, so that

$$ \begin{align*}\Im S(x) \geqslant \frac{1}{2}(\sum_{j,k=0}^n \Im Q_{jk}x^jx^k)\geqslant C|x|^2\quad \text{on}\ U,\end{align*} $$

for some $C>0$ that depends on $(M,g)$ . Next, we note that

$$ \begin{align*} \left|\int_{U} (F(x)-F(0)) e^{i\lambda S(x)}\,dV_g\right| &\leqslant \int_{U} |F(x)-F(0)| e^{-C\lambda|x|^2}\left|\det g\right|{}^{\frac{1}{2}}\,dx\\ &\leqslant \|F\|_{\mathcal C^1(M)} \int_U |x| e^{-C\lambda|x|^2}\left|\det g\right|{}^{\frac{1}{2}}\,dx\lesssim \lambda^{-\frac{n+1}{2}}\lambda^{-\frac{1}{2}}. \end{align*} $$

Therefore,

$$ \begin{align*} &\lim_{\lambda \to \infty}\lambda^{\frac{n+1}{2}} \int_M e^{i\lambda S(x)}F(x)\,dV_g= F(0)\left|\det g(0)\right|{}^{\frac{1}{2}}\lim_{\lambda\to\infty} \lambda^{\frac{n+1}{2}} \int_Ue^{i\lambda\sum_{j,k=0}^nQ_{jk}x^jx^k}\,dx\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad= C_0 F(y), \end{align*} $$

where we applied the method of stationary phase in the last step; see, for example, Theorem 7.7.5 in [42].

Let us now return to the expression (5.13) and note that it reduces as follows:

(5.20) $$ \begin{align} &\lim_{\lambda\to\infty}\lambda^{\frac{n+1}{2}}\mathcal I_{\lambda,\sigma,\delta',f}=\lim_{\lambda\to\infty}\lambda^{\frac{n+1}{2}}\int_{M}u_f^{m-3}\Re \,\mathcal U_{\kappa_0\lambda}^{(0)}\,\Re\, \mathcal U_{\kappa_1\lambda}^{(1)}\, \Re\, \mathcal U_{\kappa_2\lambda}^{(2)}\,\Re \,\mathcal U_{\kappa_3\lambda}^{(3)}\,dV_{g}\nonumber\\ &= \lim_{\lambda\to\infty}2^{-4}\lambda^{\frac{n+1}{2}}\sum_{\ell_0,\ell_1,\ell_2,\ell_3 =1,2}\int_{M}u_f^{m-3}\vartheta_{\ell_0}(\mathcal U_{\kappa_0\lambda}^{(0)})\vartheta_{\ell_1}(\mathcal U_{\kappa_1\lambda}^{(1)})\vartheta_{\ell_2}(\mathcal U_{\kappa_2\lambda}^{(2)})\vartheta_{\ell_3}(\mathcal U_{\kappa_3\lambda}^{(3)})\,dV_{g}, \end{align} $$

where

$$ \begin{align*}\vartheta_{1}(z)= z\quad \text{and} \quad\vartheta_2(z) = \bar{z},\quad \text{for all}\ z \in \mathbb C.\end{align*} $$

Lemma 5.6. Given $\sigma \in \Sigma _{v_0,v_1}$ , with $y=\overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$ , the choice of $\kappa _0,\ldots ,\kappa _3$ satisfying (5.14) and the initial data $\iota _0,\ldots \iota _3\in \mathcal T$ satisfying (5.15), there holds

$$ \begin{align*}\mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}=\lim_{\lambda\to \infty}2^{-3}\lambda^{\frac{n+1}{2}} \Re\left(\int_{M}u_f^{m-3}\,\mathcal U_{\kappa_0\lambda}^{(0)}\mathcal U_{\kappa_1\lambda}^{(1)}\mathcal U_{\kappa_2\lambda}^{(2)}\mathcal U_{\kappa_3\lambda}^{(3)}\,dV_{g}\right).\end{align*} $$

Proof. Observe that the summation in expression (5.20) contains 16 terms and we are claiming that only two terms here contribute in the limit as $\lambda $ approaches infinity, when $(\ell _0,\ell _1,\ell _2,\ell _3)\in \{(1,1,1,1),(2,2,2,2)\}$ . To see that the other terms do not contribute, we note that

(5.21) $$ \begin{align} \int_{M}u_f^{m-3}\prod_{j=0}^3\vartheta_{\ell_j}(\mathcal U_{\kappa_j\lambda}^{(j)})\,dV_{g}= \int_M u_f^{m-3}\,e^{i\lambda S_{\ell_0,\ell_1,\ell_2,\ell_3}}(\prod_{j=0}^3 \vartheta_{\ell_j}(B_{\kappa_j\lambda}^{(j)}))\,dV_g,\end{align} $$

where $S_{\ell _0,\ell _1,\ell _2,\ell _3}(x)= \sum _{j=0}^3\vartheta _{\ell _j}(\Phi ^{(j)}(x))$ and

(5.22) $$ \begin{align} B^{(j)}_{\kappa_j\lambda}(x) = \begin{cases} A^{(j)}_{\kappa_j \lambda}(x) &\quad\text{if}\quad \kappa_j>0,\\ \bar{A}^{(j)}_{\kappa_j\lambda}(x)&\quad\text{if}\quad \kappa_j<0. \end{cases} \end{align} $$

We observe that since y is the only point of the intersection between the four null geodesics $\gamma _{v_j}$ in $\mathbb D_e \subset (-T,T)\times M_0$ , the integral above is supported in a small neighbourhood of the point y. It is easy to verify that

$$ \begin{align*}S_{1,1,1,1}=S\quad \text{and}\quad S_{2,2,2,2}=\bar{S},\end{align*} $$

where S is as defined in (5.18). Thus, by Lemma 5.4, there holds

$$ \begin{align*}\nabla^g S_{\ell_0,\ell_1,\ell_2,\ell_3}(y)=0 \quad \text{for}\ (\ell_0,\ell_1,\ell_2,\ell_3)\in \{(1,1,1,1),(2,2,2,2)\}.\end{align*} $$

Moreover, using the identity (5.17) together with the fact that $\kappa _j$ , $j=0,1,2,3$ are all nonzero, we conclude that

$$ \begin{align*}\nabla^g S_{\ell_0,\ell_1,\ell_2,\ell_3}(y)\neq 0 \quad \text{for}\ (\ell_0,\ell_1,\ell_2,\ell_3)\notin \{(1,1,1,1),(2,2,2,2)\}.\end{align*} $$

This implies that for all $(\ell _0,\ell _1,\ell _2,\ell _3)\notin \{(1,1,1,1),(2,2,2,2)\}$ , the phase function $S_{\ell _0,\ell _1,\ell _2,\ell _3}$ appearing in (5.21) does not have a critical point near y. Thus, we can repeatedly use integration by parts to conclude that

$$ \begin{align*}\lim_{\lambda\to \infty}\int_M e^{i\lambda S_{\ell_0,\ell_1,\ell_2,\ell_3}}(\prod_{j=0}^3 \vartheta_{\ell_j}(B_{\kappa_j\lambda}^{(j)}))u_f^{m-3}\,dV_g= \mathcal O(\lambda^{-\infty}),\end{align*} $$

whenever $(\ell _0,\ell _1,\ell _2,\ell _3)\notin \{(1,1,1,1),(2,2,2,2)\}$ . By combining the above arguments, we obtain

$$ \begin{align*} &\mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}= 2^{-4}\lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\left(\int_{M}u_f^{m-3}\prod_{j=0}^3\mathcal U_{\kappa_j\lambda}^{(j)}\,dV_{g}+\int_{M}u_f^{m-3}\prod_{j=0}^3\overline{\mathcal U_{\kappa_j\lambda}^{(j)}}\,dV_{g}\right)\\ &\qquad\qquad\qquad\qquad\qquad\qquad=2^{-3}\lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\Re \int_{M}\left(\prod_{j=0}^3\mathcal U_{\kappa_j\lambda}^{(j)}\right)u_f^{m-3}\,dV_{g}.\end{align*} $$

Using Lemma 5.6, we conclude that the expression for $\mathscr D_{\sigma ,\delta '}$ reduces to

$$ \begin{align*}\mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}=2^{-3}\Re\left(\lim_{\lambda\to\infty}\lambda^{\frac{n+1}{2}}\int_M e^{i\lambda S(x)} u_f^{m-3}(x)\,B_{\kappa_0\lambda}^{(0)}(x)B_{\kappa_1\lambda}^{(1)}(x)B_{\kappa_2\lambda}^{(2)}(x)B_{\kappa_3\lambda}^{(3)}(x)\,dV_g\right).\end{align*} $$

Note that thanks to (5.16), there holds

(5.23) $$ \begin{align} B^{(j)}_{\kappa_j\lambda}(y)=1,\quad \text{for}\ j=0,1,2,3.\end{align} $$

We expand the amplitudes $a_{\kappa _j\lambda }^{(j)}$ in the expressions for $B^{(j)}_{\kappa _j \lambda }$ in terms of the functions $a_k^{(j)}$ as in (3.5) and apply Lemma 5.4 together with the method of stationary phase (see, e.g., Theorem 7.7.5 in [4 2]) to (5.13), term-wise after this expansion. Using the key hypothesis (5.23) together with Lemma 5.5, we conclude that

$$ \begin{align*}\mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}= c_{0}u_f(y), \end{align*} $$

where $c_0$ is a nonzero real constant as given by Lemma 5.5 and y is the unique intersection point given in hypothesis (ii) of the Theorem. Note that the application of Lemma 5.5 is justified here since the product of the four amplitude functions is supported in a small neighbourhood of y that depends on the parameter $\delta '$ and so the hypothesis of Lemma 5.5 is satisfied for $\delta '$ sufficiently small. Finally, since $u_f(y) \neq 0$ , it follows that $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f} \neq 0$ , thus completing the proof of Theorem 5.1.

5.4 Proof of Theorem 5.2

Applying the linearisation argument in Subsection 2.2, we deduce that the source-to-solution map $\mathscr N$ determines the knowledge of the expression

$$ \begin{align*} \tilde{\mathcal I}_{\lambda,\sigma,\delta'}&=\int_M \operatorname{\mathrm{Tr}}(hg^{-1})\,u_0\left(u_1u_2f_3+u_2u_3f_1+u_3u_1f_2\right)\,dV_g\\ &\quad+2\int_{M} \left(u_1u_2\langle \nabla^gu_3,\nabla^gu_0\rangle_h+u_2u_3\langle \nabla^gu_1,\nabla^gu_0\rangle_h+u_3u_1\langle \nabla^gu_2,\nabla^gu_0\rangle_h\right)\,dV_g\\ &\quad -\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})\left(u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_g+u_2u_3\langle \nabla^gu_1,\nabla^gu_0 \rangle_g+u_3u_1\langle \nabla^gu_2,\nabla^gu_0 \rangle_g\right)\,dV_g, \end{align*} $$

where $u_j= u^+_{\kappa _j\lambda ,v_j,\delta '}$ for $j=1,2,3$ and $u_0=u^-_{\kappa _0\lambda ,v_0,\iota _0,\delta '}$ . Also, $f_0=f^-_{\kappa _0\lambda ,v_0,\iota _0,\delta '}$ and $f_j=f^+_{\kappa _j\lambda ,v_j,\iota _j,\delta '}$ for $j=1,2,3$ . Note also that

$$ \begin{align*}\mathscr D_{\sigma,\delta'}= \lim_{\lambda\to\infty}\lambda^{\frac{n-3}{2}}\tilde{\mathcal I}_{\lambda,\sigma,\delta'}.\end{align*} $$

The proof of (i) in Theorem 5.2 is exactly as the proof of (i) in Theorem 5.1. To show (ii), we proceed as before by showing that if there is a point $y\in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$ that satisfies the hypothesis of statement (ii), then there exists $\kappa _j \in \mathbb R\setminus \{0\}$ and $\iota _j \in \mathcal T$ , such that $\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta '}\neq 0$ , for all $\delta '$ sufficiently small and $\sigma =(v_0,\kappa _0,\iota _0,\ldots ,v_3,\kappa _3,\iota _3)$ .

Observe that using the same argument as in the preceding section, we can show that there is a unique point in $\overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$ . Again, analogous to the previous section, we observe that since the tangent vectors to $\gamma _{v_j}$ , $j=1,2,3,$ are linearly dependent at the point y, there exist nonzero constants $\kappa _0,\kappa _1,\kappa _2,\kappa _3$ such that the linear dependence equation (5.14) holds at the point y. We also choose $\iota _j \in \mathcal T$ such that (5.15) holds at the point y and subsequently define the Gaussian beams along the geodesics $\gamma _{v_j}$ , $j=0,1,2,3$ , as in (5.5). Recall that due to the choice of initial conditions given by (5.15), the amplitude functions satisfy (5.16).

We proceed to show that given this choice of $\sigma $ , there holds $\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta '}\neq 0$ for all $\delta '$ small. This will be achieved by proving the following three estimates:

(5.24) $$ \begin{align} \lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}}\int_M \operatorname{\mathrm{Tr}}(hg^{-1})\,u_0\left(u_1u_2f_3+u_2u_3f_1+u_3u_1f_2\right)\,dV_g=0,\end{align} $$

and

(5.25) $$ \begin{align} \begin{aligned} \lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}}\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})(u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_g&+u_2u_3\langle \nabla^gu_1,\nabla^gu_0 \rangle_g\\ &+u_3u_1\langle \nabla^gu_2,\nabla^gu_0 \rangle_g)\,dV_g=0 \end{aligned} \end{align} $$

and, finally, that

(5.26) $$ \begin{align} &\lim_{\lambda\to \infty}\lambda^{\frac{n-3}{2}}\int_{M} (u_1u_2\langle \nabla^gu_3,\nabla^gu_0\rangle_h+u_2u_3\langle \nabla^gu_1,\nabla^gu_0\rangle_h\nonumber\\ &\qquad\qquad\qquad\qquad\qquad\qquad+u_3u_1\langle \nabla^gu_2,\nabla^gu_0\rangle_h)\,dV_g=c_0\,\kappa_0^2\,h(\dot{\gamma}^{(0)}(s_0),\dot{\gamma}^{(0)}(s_0)), \end{align} $$

where $c_0$ is a nonzero constant depending on the geometry $(M,g)$ . Note that by assumption (ii) on the family of metrics $G_z$ , h is nondegenerate on null vectors and therefore the right-hand side of the above expression is nonzero. Thus, it follows from the above three estimates that $\mathscr D^{\mathrm{quasi}}_{\sigma ,\delta '}$ is nonzero.

Let us begin by showing that (5.24) holds. Using the estimates (4.7)–(4.9) together with the uniform boundedness of Gaussian beams in $\lambda $ (see (5.10)) and the estimate (4.11), it follows that

$$ \begin{align*} &\left| \int_M \operatorname{\mathrm{Tr}}(hg^{-1})\,u_0\left(u_1u_2f_3+u_2u_3f_1+u_3u_1f_2\right)\,dV_g \right| \\ &\qquad\qquad\lesssim \|u_0\|_{\mathcal C(V)}(\|u_1\|_{\mathcal C(V)} \|u_2\|_{\mathcal C(V)}\|f_3\|_{\mathcal C(V)}+ \|u_2\|_{\mathcal C(V)} \|u_3\|_{\mathcal C(V)}\|f_1\|_{\mathcal C(V)}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad+\|u_3\|_{\mathcal C(V)} \|u_1\|_{\mathcal C(V)}\|f_2\|_{\mathcal C(V)}) \lesssim \lambda^{1-\frac{n}{2}}, \end{align*} $$

where $V=J^-(\operatorname {\mathrm {supp}} f_0) \cap \bigcup _{j=1}^3 J^+(\operatorname {\mathrm {supp}} f_j)$ is compact and lies inside $(-T,T)\times M_0$ by the hypothesis of Theorem 1.1.

Next, we show that (5.25) holds. We use again the estimates (4.7)–(4.9) together with the uniform boundedness of Gaussian beams in $\lambda $ (see (5.10)) to write

$$ \begin{align*} &\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})u_1u_2\langle du_3,du_0 \rangle_g\,dV_g\\ &\quad =2^{-4}\sum_{\ell_0,\ldots,\ell_3=1,2}\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})\vartheta_{\ell_j}(\mathcal U_{\kappa_1\lambda}^{(1)})\vartheta_{\ell_j}(\mathcal U_{\kappa_2\lambda}^{(2)})\langle \vartheta_{\ell_j}(\nabla^g\mathcal U_{\kappa_3\lambda}^{(3)}),\vartheta_{\ell_j}(\nabla^g\mathcal U_{\kappa_0\lambda}^{(0)}) \rangle_g\,dV_g\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad +\mathcal O(\lambda^{-1}\lambda^{-\frac{n-3}{2}}). \end{align*} $$

Here, recalling (5.17) and applying property (ii) in Lemma 5.4 together with a similar argument as in the proof of Lemma 5.6, we can show that as $\lambda $ approaches infinity, only two terms in the above sum contribute so that

$$ \begin{align*} &\lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}} \int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_g\,dV_g\\ &\qquad\qquad\qquad\qquad\qquad=2^{-3}\Re \left(\lim_{\lambda\to \infty}\lambda^{\frac{n-3}{2}}\int_M \operatorname{\mathrm{Tr}}(g^{-1}h) \mathcal U_{\kappa_1\lambda}^{(1)}\mathcal U_{\kappa_2\lambda}^{(2)}\langle \nabla^g\mathcal U_{\kappa_3\lambda}^{(3)},\nabla^g\mathcal U_{\kappa_0\lambda}^{(0)}\rangle_g\,dV_g\right). \end{align*} $$

Here, using the defining expressions (5.5) and (5.18) together with the uniform boundedness of Gaussian beams in the parameter $\lambda $ (see (5.10)), we write

$$ \begin{align*}\mathcal U_{\kappa_1\lambda}^{(1)}\mathcal U_{\kappa_2\lambda}^{(2)}\langle \nabla^g\mathcal U_{\kappa_3\lambda}^{(3)},\nabla^g\mathcal U_{\kappa_0\lambda}^{(0)}\rangle_g= e^{i\lambda S(x)}\left(-\lambda^2\langle \nabla^g\Phi^{(3)},\nabla^g\Phi^{(0)}\rangle_g\prod_{j=0}^3 B^{(j)}_{\kappa_j\lambda}+\mathcal O(\lambda)\right),\end{align*} $$

where $B^{(j)}_{\kappa _j\lambda }$ are defined as in (5.22). Using this identity, together with (5.16) and Lemma 5.5, we obtain that

$$ \begin{align*} &\lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}}\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_g\,dV_g\\ &\qquad\qquad\qquad= -2^{-3}\lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\Re\,\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})e^{i\lambda S}\langle \nabla^g\Phi^{(3)},\nabla^g\Phi^{(0)} \rangle_g\,dV_g\\ &\qquad\qquad\qquad\qquad\qquad\qquad =-2^{-3}c_0 \operatorname{\mathrm{Tr}}(g^{-1}(y)h(y))\langle \nabla^g\Phi^{(3)}(y),\nabla^g\Phi^{(0)}(y) \rangle_{g(y)}, \end{align*} $$

where we recall that $c_0\neq 0$ is as given by Lemma 5.5. Thus, adding the contributions from the other two terms in (5.25), we deduce that

$$ \begin{align*} & \lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}}\int_{M}\operatorname{\mathrm{Tr}}(hg^{-1})(u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_g+u_2u_3\langle \nabla^gu_1,\nabla^gu_0 \rangle_g\\ &\qquad\qquad\qquad\qquad\qquad\qquad +u_3u_1\langle \nabla^gu_2,\nabla^gu_0 \rangle_g)\,dV_g\\ &\qquad\qquad =-2^{-3}c_0\operatorname{\mathrm{Tr}}(g^{-1}(y)h(y))\left(\sum_{j=1}^3 \langle \nabla^g\Phi^{(j)}(y),\nabla^g\Phi^{(0)}(y)\rangle_{g(y)}\right)\\ &\qquad\qquad=-2^{-3}c_0\operatorname{\mathrm{Tr}}(g^{-1}(y)h(y))\,\langle \underbrace{\sum_{j=1}^3 \nabla^g\Phi^{(j)}(y)}_{-\nabla^g\Phi^{(0)}(y)},\nabla^g\Phi^{(0)}(y)\rangle_{g(y)} \\ &\qquad\qquad\qquad\qquad\qquad=2^{-3}c_0\operatorname{\mathrm{Tr}}(g^{-1}(y)h(y))\langle \nabla^g\Phi^{(0)}(y),\nabla^g\Phi^{(0)}(y)\rangle_{g(y)}=0, \end{align*} $$

where we used property (ii) in Lemma 5.4 to get the last step and there we applied (5.17) and the fact that $\gamma _{v_0}$ is a null geodesic.

Finally, we proceed to prove the remaining estimate (5.26). Note that analogous to the proof of (5.25), there holds

$$ \begin{align*} &\lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}} \int_{M}u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_h\,dV_g\\ &\qquad\qquad\qquad\qquad\qquad=2^{-3}\Re \left(\lim_{\lambda\to \infty}\lambda^{\frac{n-3}{2}}\int_M\mathcal U_{\kappa_1\lambda}^{(1)}\mathcal U_{\kappa_2\lambda}^{(2)}\langle \nabla^g\mathcal U_{\kappa_3\lambda}^{(3)},\nabla^g\mathcal U_{\kappa_0\lambda}^{(0)}\rangle_h\,dV_g\right). \end{align*} $$

Now, using the expression

$$ \begin{align*}\mathcal U_{\kappa_1\lambda}^{(1)}\mathcal U_{\kappa_2\lambda}^{(2)}\langle \nabla^g\mathcal U_{\kappa_3\lambda}^{(3)},\nabla^g\mathcal U_{\kappa_0\lambda}^{(0)}\rangle_g= e^{i\lambda S(x)}\left(-\lambda^2\langle \nabla^g\Phi^{(3)},\nabla^g\Phi^{(0)}\rangle_h\prod_{j=0}^3 B^{(j)}_{\kappa_j\lambda}+\mathcal O(\lambda)\right),\end{align*} $$

together with Lemma 5.5 and the key identity (5.16), we obtain

$$ \begin{align*} &\lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}}u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_h\,dV_g\\ &\qquad\qquad\qquad\qquad = -2^{-3}\lim_{\lambda\to \infty} \lambda^{\frac{n+1}{2}}\Re\,\int_{M}e^{i\lambda S}\langle \nabla^g\Phi^{(3)},\nabla^g\Phi^{(0)} \rangle_h\,dV_g\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad =-2^{-3}c_0 \langle \nabla^g\Phi^{(3)}(y),\nabla^g\Phi^{(0)}(y) \rangle_{h(y)}, \end{align*} $$

where we recall that $c_0\neq 0$ is as given by Lemma 5.5. Finally, adding the analogous contributions from the remaining two terms in (5.26), we obtain

$$ \begin{align*} &\lim_{\lambda\to \infty} \lambda^{\frac{n-3}{2}}\int_{M}(u_1u_2\langle \nabla^gu_3,\nabla^gu_0 \rangle_h+u_2u_3\langle \nabla^gu_1,\nabla^gu_0 \rangle_h\\ &\qquad\qquad +u_3u_1\langle \nabla^gu_2,\nabla^gu_0 \rangle_h)\,dV_g=-2^{-3}c_0\,\langle \sum_{j=1}^3\underbrace{\nabla^g\Phi^{(j)}(y)}_{-\nabla^g\Phi^{(0)}(y)},\nabla^g\Phi^{(0)}(y)\rangle_{h(y)}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad =2^{-3}c_0\langle \nabla^g\Phi^{(0)}(y),\nabla^g\Phi^{(0)}(y)\rangle_{h(y)}\neq 0, \end{align*} $$

where we used property (ii) in the definition of the tensor $G(x,z)$ in the last step. This concludes the proof of the Theorem 5.2.

6 On globally hyperbolic manifolds

We start the geometric part of our analysis. In this section, we give some geometric notations and results that will be used to prove Theorem 1.3. As before, we assume $(M,g)$ to be a globally hyperbolic Lorentzian manifold of dimension $1+n$ with $n \geqslant 2$ . We write $\le $ and $\ll $ for the causal and chronological relations on M and recall that the length L of a causal curve $\alpha :I\to M$ is given by

$$ \begin{align*}L(\alpha)=\int_I \sqrt{-g(\dot{\alpha}(s),\dot{\alpha}(s))}\,ds.\end{align*} $$

We write $\tau $ for the time separation function on $M \times M$ that is defined for each $p \le q$ via

$$ \begin{align*}\tau(p,q)=\sup\{L(\alpha)\,:\,\alpha\ \text{is a future-pointing curve from}\ p\ \text{to}\ q\}.\end{align*} $$

We define $\tau (p,q)=0$ if $p\le q$ does not hold. Recall that $\le $ is closed, $\ll $ is open and that $\tau $ is continuous; see, for example, [79, Lemmas 3 (p. 403), 21–22 (p. 412)]. Occasionally we will consider causal relations on a subset $\Omega \subset M$ , and we say that $x \le y$ in $\Omega $ if there is a causal future-pointing path from x to y, staying in $\Omega $ , or if $x = y$ . Analogously, $x \ll y$ in $\Omega $ if there is a time-like future-pointing path from x to y, staying in $\Omega $ .

The next shortcut argument (see [79, Prop. 46 (p. 294)]) will be very useful in what follows.

Lemma 6.1. If there is a future-pointing causal path from x to y on M that is not a null pregeodesic, then $x \ll y$ .

The above lemma implies that $x \ll y$ is equivalent with $\tau (x,y)> 0$ . On the other hand, if $x \le y$ and $\tau (x,y) = 0$ , then there is a null geodesic joining x and y and all causal paths joining x and y are null geodesics, up to reparametrisation. While $L(\gamma )$ vanishes for all null geodesics $\gamma $ , it may happen that $\tau (x,y)> 0$ for some points x and y joined by a null geodesic $\gamma $ . In this case we say that $\gamma $ is not optimising. In Subsection 6.2 we will recall the notion of cut function that tells when a null geodesic stops being optimising. Optimising null geodesics are discussed further in Subsection 6.3.

It should be emphasised that all technical complications in the geometric proof in the next section are related to cases where not all null geodesics are optimising. In fact, if all null geodesics are optimising, then Theorem 1.3 follows immediately from Lemma 7.3 and [64, Theorem 1.2] and many tools discussed in the present section are not needed.

To simplify the notations we often lift functions and relations from M to $TM$ by using the natural projection $\pi : TM \to M$ . For example, we write $v \le w$ if $\pi (v) \le \pi (w)$ and $\tau (v,w) =\tau (\pi (v), \pi (w))$ , for $v,w \in TM$ . The bundle of light-like vectors is denoted by $LM$ , and $L^+ M$ and $L^-M$ are the future and past-pointing subbundles. We define the causal bundle (with boundary)

$$ \begin{align*} C M = \{v \in TM : v\ \text{is causal}\} \end{align*} $$

and write again $C^+ M$ and $C^- M$ for the future- and past-pointing subbundles. When $K \subset M$ , we write $LK = \{(x,\xi ) \in LM : x \in K\}$ and use the analogous notation for other bundles as well.

We denote by $\gamma _{v} : (a,b) \to M$ the inextendible geodesic on M with the initial data $v \in CM$ and write

$$ \begin{align*} \beta_v : (a,b) \to TM, \quad \beta_{v}(s) = (\gamma_{v}(s),\dot\gamma_{v}(s)). \end{align*} $$

Then $\beta _v(0) = v$ and $a < 0 < b$ .

6.1 Compactness results

For $p, q \in M$ the causal future and past of p and q, respectively, are

$$ \begin{align*} J^+(p) = \{x \in M: p \le x\}, \quad J^-(q) = \{x \in M : x \le q\}. \end{align*} $$

The causal diamonds

(6.1) $$ \begin{align} J^+(p) \cap J^-(q) = \{ x \in M : p \le x \le q \} \end{align} $$

are compact. More generally, we write $J^\pm (S) = \bigcup _{x \in S} J^\pm (x)$ for a set $S \subset M$ . If $K_1, K_2 \subset M$ are compact, then $J^+(K_1) \cap J^-(K_2)$ is also compact. Indeed, writing $K = K_1 \cup K_2$ , this follows from $J^+(K) \cap J^-(K)$ being compact and both $J^+(K_1)$ and $J^-(K_2)$ being closed; see [4 6, Th. 2.1 and Prop. 2.3].

The fact that $(M,g)$ is not assumed to be geodesically complete causes some technical difficulties. We will typically handle these issues by working in a compact subset. We have the following variation of [9, Lem. 9.34].

Lemma 6.2. Let $K \subset M$ be compact and suppose that $v_j \to v$ in $C^+ K$ , $s_j \to s \geqslant 0$ in $\mathbb R$ and that $\gamma _{v_j}(s_j) \in K$ . Then the inextendible geodesic $\gamma _v : (a,b) \to M$ satisfies $b> s$ .

Proof. As K is compact, by passing to a subsequence, still denoted by $(v_j, s_j)$ , we may assume that $\gamma _{v_j}(s_j) \to x$ in K. Let $\tilde x \in M$ satisfy $x \ll \tilde x$ . To get a contradiction, suppose that $b \le s$ . Let $0 < t < b$ . Then $\gamma _v(t) = \lim _{j \to \infty } \gamma _{v_j}(t)$ and for large j it holds that $\gamma _{v_j}(t) \le \gamma _{v_j}(s_j) \ll \tilde x$ . As the relation $\le $ is closed, it follows that $\gamma _v(t) \le \tilde x$ for $0 < t < b$ . Now the future inextendible causal curve $\gamma _v(t)$ , $0 < t < b$ , never leaves the compact set $J^+(p) \cap J^-(q)$ where $p = \pi (v)$ and $q = \tilde x$ . This is a contradiction with [79, Lem. 13, p. 408].

Lemma 6.3. Let $K \subset M$ be compact. The exit function

$$ \begin{align*} R(v) = \sup \{ s \geqslant 0 : \gamma_{v}(s) \in K\}, \quad v \in C^+ K \end{align*} $$

is finite and upper semi-continuous.

Proof. Finiteness follows from [79, Lem. 13 (p. 408)]. Suppose that $v_j \to v$ in $C^+ K$ and that $t_j := R(v_j) \to t$ for some $t \geqslant 0$ . The upper semi-continuity $t \le R(v)$ follows from the convergence $\gamma _{v_{j}}(t_{j}) \to \gamma _v(t)$ in K, which again follows from Lemma 6.2.

Lemma 6.4. Suppose that $v_j \to v$ in $C^+M$ . If a sequence $s_j \geqslant 0$ , $j \in \mathbb N$ , satisfies $\gamma _{v_j}(s_j) \to y$ for some $y \in M$ , then $s_j$ converges.

Proof. We write $\pi (v) = x$ , $\pi (v_j) = x_j$ and $\gamma _{v_j}(s_j) = y_j$ . Let X and Y be bounded neighbourhoods of x and y, respectively, and write $K= J^+(\overline X) \cap J^-(\overline Y)$ . Then we have $x_j, y_j \in K$ for large j. Now Lemma 6.3 implies that $s_j < R(v_j) \le R(v) + 1$ for large j, where R is the exit function of K. Write $t^+ = \limsup _{j \to \infty } s_j$ and $t^- = \liminf _{j \to \infty } s_j$ . These are both finite. There are subsequences $s_{j_k}^\pm $ converging to $t^\pm $ and $\gamma _{v_{j_k}}(s_{j_k}^\pm ) \to \gamma _v(t^\pm ) = y$ . Now $t^- = t^+$ by global hyperbolicity.

The analogues of Lemmas 6.2–6.4 hold also for past-pointing vectors.

6.2 Cut function

The cut function is defined by

$$ \begin{align*} \rho(v) = \sup \{ s> 0 : \tau(v,\beta_{v}(s)) = 0 \}, \quad v \in L^+ M. \end{align*} $$

We define $\rho (v)$ also for $v \in L^- M$ by the above expression but with respect to the opposite time orientation. It follows from the definition of $\rho $ and Lemma 6.1 that if $\gamma _v(s)$ is well-defined for some $s> \rho (v)$ , then there is a time-like path from $\gamma _v(0)$ to $\gamma _v(s)$ . On the other hand, [9, Lem. 9.13] implies the following.

Lemma 6.5. Let $v \in L^+M$ and $s < \rho (v)$ . Then the geodesic segment along $\gamma _v$ is the only causal path from $\gamma _v(0)$ to $\gamma _v(s)$ up to a reparametrisation.

The following lemma is a variant of [9, Prop. 9.7].

Lemma 6.6. The cut function $\rho : L^+ M \to [0,\infty ]$ is lower semi-continuous.

Proof. Suppose that $v_j \to v$ in $L^+M$ and write $t_j = \rho (v_j)$ . We need to show that if $t_j \to t$ for some $t \geqslant 0$ then $t \geqslant \rho (v)$ . To get a contradiction, suppose that the opposite holds. Then there is $\delta> 0$ such that $t + \delta < \rho (v)$ . In particular, $\gamma _v(t+\delta )$ is well-defined, and this implies that $\gamma _{v_j}(t_j + \delta )$ is also well-defined for large j. Writing $x_j = \pi (v_j)$ and $y_j = \gamma _{v_j}(t_j + \delta )$ , there holds $\tau (x_j, y_j)> 0$ since $t_j + \delta> \rho (v_j)$ . We also write $(x,\xi ) = v$ and $y = \gamma _v(t + \delta )$ . Then $x_j \to x$ and $y_j \to y$ . Let X be a bounded neighbourhood of x and define $K= \overline X$ .

Let us choose an auxiliary Riemannian metric on M and denote by $SM$ the unit sphere bundle with respect to that metric. By [79, Prop. 19, p. 411] there is a time-like geodesic from $x_j$ to $y_j$ . We may reparametrise this geodesic to obtain time-like $\xi _j$ in $C^+_{x_j} K \cap S_{x_j} M$ and $s_j> 0$ satisfying $\gamma _{x_j,\xi _j}(s_j) = y_j$ . As $C^+ K \cap SM$ is compact, by passing to a subsequence, we may assume that $\xi _j \to \tilde \xi $ for some $\tilde \xi \in C^+_{x} K \cap S_x M$ . Lemma 6.4 implies that $s_j \to s$ for some $s \geqslant 0$ .

If there is no $c \in \mathbb R$ such that $\tilde \xi = c \xi $ , then there are two distinct causal geodesics from x to y. This is a contradiction in view of Lemma 6.5 since $x = \pi (v)$ , $y = \gamma _v(t+\delta )$ and $t + \delta < \rho (v)$ . Hence, there is $c \in \mathbb R$ such that $\tilde \xi = c \xi $ , and, in fact, $c> 0$ since $\xi , \tilde \xi \in C^+_{x} K$ and $\tilde \xi \in S_x M.$ Now $(x_j,c^{-1}\xi _j) \to v$ and $cs_j \to t + \delta $ . None of the points $\gamma _v(r)$ , $0 \le r \le t + \delta $ , is conjugate to x along $\gamma _v$ by [9, Th. 10.72], and the map $s \mapsto \gamma _v(s)$ is injective due to global hyperbolicity. Hence, there is a neighbourhood U of $[0, t+\delta ] v$ such that $\pi \times \exp $ is injective on U. But $t_j v_j, (x_j, s_j \xi _j) \in U$ for large j and both are mapped to $(x_j, y_j)$ . This is a contradiction since the former is light-like and the latter is time-like.

The following lemma is a variant of [9, Prop. 9.5].

Lemma 6.7. Let $v_j \to v$ in $L^+M$ and $\rho (v_j) \to t$ in $\mathbb R$ . Suppose that $\gamma _v(t)$ is well-defined. Then $\rho (v) = t$ .

Proof. Lower semi-continuity of $\rho $ implies that $\rho (v) \le t$ . To get a contradiction, suppose there is $\delta> 0$ such that $\rho (v) + \delta < t$ . Then $\rho (v) + \delta < \rho (v_j)$ for large j. We are led to the contradiction

$$ \begin{align*} \tau(v, \beta_{v}(\rho(v) + \delta)) = \lim_{j \to \infty} \tau(v_j, \beta_{v_j}(\rho(v) + \delta)) = 0. \end{align*} $$

The analogues of Lemmas 6.5–6.7 hold also for past-pointing vectors. Moreover, the cut function has the following symmetry.

Lemma 6.8. Let $v \in L^+M$ and suppose that $\gamma _v(\rho (v))$ is well-defined. Then

$$ \begin{align*} \rho(-\beta_v(\rho(v))) = \rho(v). \end{align*} $$

Proof. Write $w = -\beta _v(\rho (v))$ . To get a contradiction, suppose that $\rho (w) < s < \rho (v)$ . Then there is a past-pointing time-like path from $\gamma _w(0)$ to $\gamma _w(s)$ , a contradiction with $\tau (v,w) = 0$ . To get a contradiction, suppose that $\rho (v) < \rho (w)$ . For small $\epsilon> 0$ the vector $\tilde w = -\beta _v(\rho (v) + \epsilon )$ is well-defined. Moreover, lower semi-continuity of $\rho $ implies that $\rho (v) + \epsilon < \rho (\tilde w)$ for small enough $\epsilon> 0$ . Lemma 6.5 implies then that $\gamma _{\tilde w}$ is the only causal path from $\gamma _{\tilde w}(0)$ to $\gamma _{\tilde w}(\rho (v) + \epsilon ) = \pi (v)$ . Therefore, $\tau (v, \tilde w) = 0$ , a contradiction with the definition of $\tilde w$ .

The above lemma implies that if $\gamma _v(s)$ , with $s < 0$ , and $\gamma _v(\rho (v))$ are both well-defined, then there is a time-like path from $\gamma _v(s)$ to $\gamma _v(\rho (v))$ .

6.3 Optimising geodesics and earliest observation functions

Recall that a null geodesic $\gamma $ from x to y on M is not optimising if $\tau (x,y)> 0$ . In other words, if $\gamma = \gamma _v$ for some $v \in L^+M$ , then it is optimising from $x = \gamma _v(0)$ to $y = \gamma _v(s)$ if and only if $s \leqslant \rho (v)$ . In the case $s = \rho (v)$ there may be other optimising null geodesics from x to y, corresponding to different initial directions at x. One more simple, but nonetheless useful, observation is that if there is an optimising null geodesic from x to y, then all causal paths from x to y are optimising null geodesics. This follows from Lemma 6.1.

The results below will be applied to one of the paths $\mu _{\mathrm{in}}:[t_1^-,t_1^+]\to M$ and $\mu _{\mathrm{out}}:[s_1^-,s_1^+]\to M$ . However, to simplify the notations, we consider here a time-like future-pointing path $\mu : [-1,1] \to M$ . The paths $\mu _{\mathrm{in}}$ and $\mu _{\mathrm{out}}$ can be reparametrised so that they are of this form.

We define the earliest observation functions

$$ \begin{align*} f_\mu^+(x) &=\inf\{s\in(-1,1] : \tau(x,\mu(s))>0\ \text{or}\ s = 1 \}, \quad &x \in M,\\ f_\mu^-(x) &=\sup\{s\in[-1,1) : \tau(\mu(s),x)>0\ \text{or}\ s = -1 \}, \quad &x \in M. \end{align*} $$

We could also work with an alternative definition of $f_\mu ^+(x)$ omitting ‘or $s=1$ ’ above, with the understanding that the infimum of the empty set is $\infty $ . However, we prefer to follow [64] where the above choice was used. A convenient consequence of the choice is that both $f_\mu ^+$ and $f_\mu ^-$ are continuous on the whole M; see [64, Lemma 2.3 (iv)].

Lemma 6.9. Let $\mu : [-1,1] \to M$ be a time-like future-pointing path. Suppose that a point $x \le \mu (1)$ satisfies $x \not \le \mu (-1)$ ; in other words, $x \notin J^-(\mu (-1))$ . Then there is $s \in (-1, 1]$ such that either there is an optimising null geodesic from x to $\mu (s)$ or $x = \mu (s)$ . In both cases $s = f_\mu ^+(x)$ .

Proof. We set $s = f_\mu ^+(x)$ and $y = \mu (s)$ . If $s = 1$ , then $x \le y$ by the assumption $x \le \mu (1)$ . On the other hand, if $s < 1$ , then $x \le y$ also since the causal relation $\le $ is closed. Hence, there is a causal path from x to y or $x=y$ . It remains to show that in the former case there holds $\tau (x,y) = 0$ , since the path from x to y is then a null geodesic up to a reparametrisation by Lemma 6.1. There holds $s> -1$ since $x \not \le \mu (-1)$ . This again implies that $\tau (x,y) = 0$ .

A variation of the above proof gives the following.

Lemma 6.10. Let $\mu : [-1,1] \to M$ be a time-like future-pointing path. Suppose that $\mu (-1) \le x$ and $\mu (1) \not \le x$ . Then there is $s \in [-1, 1)$ such that there is an optimising null geodesic from $\mu (s)$ to x or $x = \mu (s)$ . In both cases $s = f_\mu ^-(x)$ .

Lemma 6.11. Let $\mu : [-1,1] \to M$ be a time-like future-pointing path, let $v \in L^+M$ and write $f(s) = f_\mu ^+(\gamma _v(s))$ . Suppose that $\mu $ and $\gamma _{v}$ do not intersect. Then

1. (1) f is increasing;

2. (2) if $-1 < f(s_0) < 1$ for some $s_0$ , then f is strictly increasing near $s_0$ ;

3. (3) if $f(s_0) = 1$ and $\gamma _v(s_0) < \mu (1)$ for some $s_0$ , then f is strictly increasing for $s < s_0$ near $s_0$ .

Proof. If there is $s> s_0$ such that $f(s) \leqslant f(s_0)$ and $f(s) < 1$ , then there is a causal path from $\gamma _v(s_0)$ to $\mu (f(s_0))$ via $\gamma _v(s)$ that is not a null pregeodesic and therefore $\tau (\gamma _v(s_0), \mu (f(s_0)))> 0$ by Lemma 6.1. If also $-1 < f(s_0)$ then there holds $\tau (\gamma _v(s_0), \mu (f(s_0))) = 0$ , a contradiction. This shows (2) and also that if $f(s_0) = 1$ then $f(s) = 1$ for $s> s_0$ .

If $f(s_0) = -1$ , then $f(s) = -1$ for $s < s_0$ . Indeed, there is a causal path from $\gamma _v(s)$ to $\mu (-1)$ via $\gamma _v(s_0)$ that is not a null pregeodesic. We have shown (1).

Let us now suppose that $f(s_0) = 1$ and there is a causal path from $\gamma _v(s_0)$ to $\mu (1)$ . Let $s < s_0$ be near $s_0$ . There is a causal path from $\gamma _v(s)$ to $\mu (1)$ via $\gamma _v(s_0)$ that is not a null pregeodesic and therefore $\tau (\gamma _v(s_0), \mu (1))> 0$ . But then also $\tau (\gamma _v(s_0), \mu (t))> 0$ for t close to 1 by continuity. This implies that $f(s) < 1$ and as also $-1 < f(s)$ by continuity, we see that (3) follows from (2).

We have the following variant of [64, Lemma 2.3(iv)].

Lemma 6.12. Let $\mu _a : [-1,1] \to M$ be a family of time-like future-pointing paths and suppose that $\mu _a(s) = (s, a)$ , $a \in U \subset \mathbb R^n$ , in some local coordinates. Suppose that $x_j \to x$ in M and $a_j \to a$ in U. Then $f_{\mu _{a_j}}^+(x_j) \to f_{\mu _a}^+(x)$ .

Proof. Let us consider first the case that $s:=f_{\mu _a}^+(x) < 1$ . Then $\tau (x, (s + \epsilon , a))> 0$ for any small $\epsilon> 0$ . Continuity of $\tau $ implies that $\tau (x_j, (s + \epsilon , a_j))> 0$ for large j. Hence, $\limsup _{j\to \infty }f_{\mu _{a_j}}^+(x_j) \leqslant s + \epsilon \to s$ as $\epsilon \to 0$ . Clearly, also $\limsup _{j\to \infty }f_{\mu _{a_j}}^+(x_j) \leqslant s$ in the case $s = 1$ .

To get a contradiction, suppose that $\tilde s := \liminf _{j\to \infty }f_{\mu _{a_j}}^+(x_j) < s$ . By passing to a subsequence, we may replace $\liminf $ by $\lim $ above. Moreover,

$$ \begin{align*} \tau(x_j, (s, a_j)) \geqslant \tau(x_j, (\tilde s, a_j)) + \tau((\tilde s, a_j), (s, a_j)), \end{align*} $$

and letting $j \to \infty $ , we obtain

$$ \begin{align*} \tau(x, (s, a)) \geqslant \tau((\tilde s, a), (s, a))> 0. \end{align*} $$

This is in contradiction with $s=f_{\mu _a}^+(x)$ since $s> \tilde s \geqslant -1$ .

6.4 Three shortcut arguments

We denote the image of a path $\mu : I \to M$ , with I an interval in $\mathbb R$ , by

$$ \begin{align*} \overline \mu = \mu(I) = \{\mu(s) : s \in I\} \end{align*} $$

and use also the shorthand notations

$$ \begin{align*} \overleftarrow{\;\gamma_v} = \{x \in \overline{\gamma_v} : x \le \pi(v) \}, \quad \overrightarrow{\gamma_v} = \{x \in \overline{\gamma_v} : x \ge \pi(v) \}. \end{align*} $$

We say that two geodesics $\gamma _v$ and $\gamma _w$ are distinct if $\overline {\gamma _v} \ne \overline {\gamma _w}$ .

Lemma 6.13. Let $x_1, x_2, y \in M$ and $v_1, v_2, w \in L^+ M$ . Suppose that $\gamma _{v_j}$ is optimising from $x_j$ to y for $j=1,2$ and that $\gamma _{v_1}$ , $\gamma _{v_2}$ and $\gamma _{w}$ are all distinct. Suppose, furthermore, that $y_j \in \overline {\gamma _{v_j}} \cap \overline {\gamma _{w}}$ satisfy $x_j < y_j$ for both $j=1,2$ . Then either $y=y_1=y_2$ or at least one of $y_1$ , $y_2$ satisfies $y < y_j$ .

Proof. As $y_j, y \in \overline {\gamma _{v_j}}$ , there holds either $y < y_j$ or $y_j \le y$ . We suppose that $y_j \le y$ for both $j=1,2$ and show that $y=y_1=y_2$ .

To get a contradiction, suppose that $y_1 < y_2$ . The path from $x_1$ to y obtained by first following $\gamma _{v_1}$ from $x_1$ to $y_1$ , then $\gamma _{w}$ from $y_1$ to $y_2$ and finally $\gamma _{v_2}$ from $y_2$ to y is not a null pregeodesic since $\gamma _{v_1}$ and $\gamma _w$ are distinct and $x_1 < y_1 < y_2$ . But Lemma 6.1 implies that $x_1 \ll y$ , a contradiction with $\gamma _{v_1}$ being optimising from $x_1$ to y. By symmetry, $y_2 < y_1$ also leads to a contradiction.

We have shown that $y_1 = y_2$ . To get a contradiction, suppose that $y_1 < y$ . The path obtained by first following $\gamma _{v_1}$ from $x_1$ to $y_1$ and then $\gamma _{v_2}$ from $y_1$ to y is not a null pregeodesic, leading again to the contradiction $x_1 \ll y$ .

Lemma 6.14. Let $v \in L^+ M$ , let $K \subset M$ be compact and let $x \in \overline {\gamma _v}$ satisfy $x < \pi (v)$ . Then there is a neighbourhood $\mathcal U \subset L^+ M$ of v such that for all $w \in \mathcal U$ it holds that if there are $y \in \overrightarrow {\gamma _{w}} \cap K$ and $z \in \overrightarrow {\gamma _{v}} \cap K$ satisfying $y < z$ and two distinct geodesics from y to z, then $\gamma _v$ is not optimising from x to z.

Proof. Suppose that there are $\{w_j\}_{j=1}^{\infty }\subset L^+M$ with $\lim _{j\to \infty }w_j=v$ and

$$ \begin{align*} y_j \in \overrightarrow{\gamma_{w_j}} \cap K, \quad z_j \in \overrightarrow{\gamma_{v}} \cap K, \end{align*} $$

satisfying $y_j < z_j$ and two distinct geodesics from $y_j$ to $z_j$ . Due to compactness, we may pass to a subsequence and assume without loss of generality that $y_j \to y$ and $z_j \to z$ for some $y, z \in K$ . Now $w_j \to v$ and $y_j \to y$ imply that $y \in \overrightarrow {\gamma _{v}}$ .

We show first that the points y and z must be distinct. To get a contradiction, suppose that $y=z$ . As M is globally hyperbolic, y has an arbitrarily small neighbourhood U such that no causal path that leaves U ever returns to U. Thus, for large j the two distinct causal geodesics from $y_j$ to $z_j$ are contained in U. But when U is small, it is contained in a convex neighbourhood of y; see, for example, [79, Prop. 7 (p. 130)], a contradiction.

As $y_j < z_j$ , the relation $\le $ is closed and $y \ne z$ , we have $y < z$ . Denote by $\eta _j$ the direction of a geodesic from $y_j$ to $z_j$ , normalised with respect to some auxiliary Riemannian metric. Due to compactness, we may pass to a subsequence and assume without loss of generality that $\eta _j \to \eta $ .

If $\eta $ is not tangent to $\gamma _v$ at y, then the causal path given by $\gamma _v$ from $x < \pi (v) \le y$ to y and by $\gamma _{y,\eta }$ from $y < z$ to z is not a null pregeodesic. Hence, $\gamma _v$ is not optimising from x to z as required.

Let us now suppose that $\eta $ is tangent to $\gamma _v$ at y. We write $z_j = \gamma _{y, \eta _j}(s_j)$ . Lemma 6.4 implies that $s_j \to s$ for some $s \geqslant 0$ and therefore $z = \gamma _{y, \eta }(s)$ . Moreover, $\rho (y,\eta _j) \leqslant s_j$ by Lemma 6.5, and by passing once again to a subsequence we may assume that $\rho (y,\eta _j) \to t$ for some $t \leqslant s$ . Now $\gamma _{y,\eta }(t)$ is well-defined and Lemma 6.7 implies that $\rho (y,\eta ) = t$ . Finally, Lemma 6.8 implies that $\gamma _v$ is not optimising from x to $z = \gamma _{y, \eta }(s)$ .

Lemma 6.15. Let $v \in L^+ M$ , let $K \subset M$ be compact and let $x \in \overline {\gamma _v}$ satisfy $x < \pi (v)$ . Let $\mu _a : [-1,1] \to M$ be a family of time-like and future-pointing paths and suppose that $\mu _a(s) = (s, a)$ , $a \in U \subset \mathbb R^n$ , in some local coordinates. Suppose, furthermore, that $\overline {\gamma _v} \cap \overline {\mu _0} = \emptyset $ and $f_{\mu _0}^+(x)> -1$ . Then there are neighbourhoods $\mathcal U \subset L^+ M$ of v and $U' \subset U$ of the origin in $\mathbb R^n$ such that for all $w \in \mathcal U$ and all $a \in U'$ it holds that if there are $y \in \overrightarrow {\gamma _{v}} \cap K$ and $z \in \overrightarrow {\gamma _{w}} \cap K$ satisfying $y < z$ and two distinct geodesics from y to z, then $f_{\mu _a}^+(z) \geqslant f_{\mu _a}^+(\gamma _v(t))$ whenever $\gamma _v$ is optimising from x to $\gamma _v(t)$ .

Proof. Let $\xi \in L_x^+ M$ satisfy $\overline {\gamma _{x,\xi }} = \overline {\gamma _v}$ . To get a contradiction, suppose that there are

$$ \begin{align*} w_j \in L^+ M,\quad a_j \in U,\quad y_j \in \overrightarrow{\gamma_{v}} \cap K, \quad z_j \in \overrightarrow{\gamma_{w_j}} \cap K, \quad t_j \in (0, \rho(x,\xi)], \end{align*} $$

and two distinct geodesics from $y_j$ to $z_j$ , satisfying $w_j \to v$ , $a_j \to 0$ , $y_j < z_j$ and

(6.2) $$ \begin{align} f_{\mu_{a_j}}^+(z_j) < f_{\mu_{a_j}}^+(\gamma_v(t_j)). \end{align} $$

Due to compactness, we may pass to a subsequence and assume without loss of generality that $y_j \to y$ and $z_j \to z$ for some $y, z \in K$ . Now $w_j \to v$ and $z_j \to z$ imply that $z \in \overrightarrow {\gamma _{v}}$ . As in the proof of Lemma 6.14, we see that $\gamma _v$ is not optimising from $x < y$ to z. In particular, $z = \gamma _{x,\xi }(s)$ for some $s> \rho (x,\xi )$ .

It follows from (6.2) that $f_{\mu _{a_j}}^+(z_j) < 1$ and therefore $z_j < \mu _{a_j}(1)$ . As the relation $\le $ is closed, we have $z \le \mu _0(1)$ and, in fact, $z < \mu _0(1)$ as $\overline {\gamma _v} \cap \overline {\mu _0} = \emptyset $ . Using the assumptions $\overline {\gamma _v} \cap \overline {\mu _0} = \emptyset $ and $f_{\mu _0}^+(x)> -1$ , Lemma 6.11 implies that the function $t \mapsto f_{\mu _0}^+(\gamma _{x,\xi }(t))$ is strictly increasing for $t < s$ near s. Hence,

$$ \begin{align*} f_{\mu_0}^+(\gamma_{x,\xi}(\rho(x,\xi))) < f_{\mu_0}^+(\gamma_{x,\xi}(s)) = f^+_{\mu_0}(z). \end{align*} $$

Moreover,

$$ \begin{align*} f_{\mu_{a_j}}^+(z_j) \leqslant f_{\mu_{a_j}}^+(\gamma_{x,\xi}(t_j)) \leqslant f_{\mu_{a_j}}^+(\gamma_{x,\xi}(\rho(x,\xi))), \end{align*} $$

and letting $j \to \infty $ leads to the contradiction $f_{\mu _0}^+(z)<f_{\mu _0}^+(z)$ .

6.5 Flowout from a point

Consider the following set given by the flowout along null rays from a point $x \in M$

(6.3) $$ \begin{align} C(x) &= \{\beta_{x,\xi}(1) : \xi \in L_x^+ M \}\subset TM. \end{align} $$

It is easy to see that $C(x)$ is a smooth submanifold of dimension n in $TM$ .

Lemma 6.16. Let $\mathcal F \subset M$ be finite and nonempty, write $C = \bigcup _{x \in \mathcal F} \overline {C(x)}$ and let $v \in C$ . Then there is a neighbourhood $V \subset L^+M$ of v such that any $w \in C \cap V$ satisfies $\overleftarrow {\;\gamma _v} \cap \overleftarrow {\;\gamma _w} \cap \mathcal F \ne \emptyset $ .

Proof. Write $K=J^+(\mathcal F) \cap J^-(\mathcal F)$ and let R be the corresponding exit function. There are a neighbourhood $W_0 \subset L^+M$ of v and $\epsilon> 0$ such that $\gamma _w(s)$ is well-defined for $w \in W_0$ and $s \in I$ where $I = [-R(-v)-\epsilon , 0]$ . As R is upper semi-continuous, there is a neighbourhood $W_1 \subset W_0$ of v such that $R(-w) \leqslant R(-v) + \epsilon $ for all $w \in \overline W_1$ . We may assume that $W_1$ is bounded. Choose an auxiliary Riemannian metric on M and denote by d the distance function with respect to this metric. Define the function

$$ \begin{align*} h : \overline W_1 \times I \to \mathbb R, \quad h(w,s) = d(\gamma_w(s), \mathcal F \setminus \overleftarrow{\;\gamma_v}). \end{align*} $$

Then h is uniformly continuous and there is $c> 0$ such that $h(v,s)> c$ for all $s \in I$ . Hence, there is a neighbourhood $W_2 \subset W_1$ of v such that $h(w,s)> 0$ for all $w \in W_2$ and $s \in I$ . Now $w \in C \cap W_2$ satisfies $\overleftarrow {\;\gamma _w} \cap (\mathcal F \setminus \overleftarrow {\;\gamma _v}) = \emptyset $ . Therefore, $w \in C$ implies that $\overleftarrow {\;\gamma _w} \cap (\mathcal F \cap \overleftarrow {\;\gamma _v}) \ne \emptyset $ .

6.6 Earliest observation sets

We define the set of earliest observations $E(x)$ of null rays from $x \in M$ to $\Omega \subset M$ by

(6.4) $$ \begin{align} E(x) &= \{ v \in \overline{C(x)} : \pi(v) \in \Omega\ \text{and there is no}\ \tilde v \in \overline{C(x)}\ \text{s.t.}\ \tilde v \ll v \}. \end{align} $$

The sets $E(x)$ and $C(x)$ are illustrated in Figure 4. We will assume that $\Omega $ has the following form in some local coordinates $F:U\subset \mathbb R^{1+n}\to M$ ,

1. (F) $\Omega = F((-1,1) \times B(0,\delta ))$ for a small $\delta>0$ and that the paths $s\mapsto (s,a)$ are time-like and future-pointing for all $s\in (-1,1)$ and $a \in B(0,\delta )$ .

Note that the abstract condition (F) is satisfied, for example, for the set $\Omega =\Omega _{\mathrm{out}}$ and $\Omega =\Omega _{\mathrm{in}}$ given by (1.10).

Figure 4 Geometric setting of Lemma 7.3 in the $1+2$ -dimensional Minkowski space. The time axis is vertical. Set $\Omega _{\mathrm{out}}$ is the orange solid cylinder, projection $\pi (C(y))$ is the light blue cone, and $\pi (E(y))$ is drawn in dark blue. Point y is in blue, points $x_1, x_2$ are in black and vectors $v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$ are in red. Geodesics $\gamma _{v_1}$ and $\gamma _{v_2}$ are the black lines.

Lemma 6.17. Let an open set $\Omega \subset M$ satisfy (F) and let a point $x \in M$ satisfy $x \notin J^-(F(\{-1\}\times B(0,\delta )))$ . Then

(6.5) $$ \begin{align} E(x) = \{\beta_{x,\xi}(s) : \xi \in L_x^+ M,\ 0 \leqslant s \leqslant \rho(x,\xi),\ \gamma_{x,\xi}(s) \in \Omega\}. \end{align} $$

Proof. Denote by $E_0$ the right-hand side of (6.5), let $v \in E_0$ and write $y=\pi (v)$ . If $x=y$ , then clearly $v \in E(x)$ . Let us now consider the case that there are $\xi \in L_x^+ M$ and $0 < s\leqslant \rho (x,\xi )$ such that $v=\beta _{x,\xi }(s)$ . Clearly, $v\in C(x)$ and $\gamma _{x,\xi }$ is optimising from x to y. To get a contradiction, suppose that $v\notin E(x)$ . Then there exists $\tilde v\in C(x)$ such that $\tilde v \ll v$ , and writing $\tilde y = \pi (\tilde v)$ we are led to the contradiction $x \le \tilde y \ll y$ with $\gamma _{x,\xi }$ being optimising from x to y. This shows that $v \in E(x)$ .

On the other hand, let $v\in E(x)$ and $y=\pi (v)$ . If $x=y$ , then clearly $v \in E_0$ . Let us now consider the case that there are are $\xi \in L_x^+ M$ and $r> 0$ such that $v=\beta _{x,\xi }(r)$ . Working in the local coordinates (F), there is $(s_0,a) \in (-1,1) \times B(0,\delta )$ such that $y = F(s_0,a)$ . We define $\mu _a : [-1,1] \to M$ by $\mu _a(s) = F(s,a)$ . Now $x < y \le \mu _a(1)$ and we assumed also $x \not \le \mu _a(-1)$ . Lemma 6.9 implies then that $x \in \overline {\mu _a}$ or there is an optimising geodesic from x to $\mu _a(s_1)$ for some $s_1 \in (-1,1]$ . The former case is not possible, since $x < y$ and $x,y \in \overline {\mu _a}$ imply $x \ll y$ , and this is a contradiction with $v \in E(x)$ . Hence, there is an optimising geodesic $\tilde \gamma $ from x to $\mu _a(s_1)$ for some $s_1 \in (-1,1]$ . We have $s_0 = s_1$ since $s_0 < s_1$ is a contradiction with $\tilde \gamma $ being optimising, and $s_0> s_1$ is a contradiction with $v \in E(x)$ . Hence, $\tilde \gamma $ is optimising from x to y, and so is $\gamma _{x,\xi }$ . Moreover, $\gamma _{x,\xi }$ being optimising from x to $y = \pi (v)$ implies that $v \in E_0$ .

Lemma 6.18. Let $\Omega \subset M$ and $x \in M$ be as in Lemma 6.17. Then

(6.6) $$ \begin{align} E(x) = \{(y,\eta) \in L^+ \Omega :\ \text{there is}\ \epsilon> 0\ \text{such that}\ \gamma_{y,\eta}(s) \in \pi(E(x))& \\\notag\text{for all}\ s \in [0, \epsilon]\ \text{or for all}\ s \in [-\epsilon,0]&\}. \end{align} $$

Proof. Denote by $E_0$ the right-hand side of (6.6) and let $(y,\eta ) \in E(x)$ . If $x = y$ , then $\gamma _{y,\eta }(s) \in \pi (E(x))$ for $s \geqslant 0$ close to zero, since $\Omega $ is open and (6.5) holds. Analogously, if $x \ne y$ , then $\gamma _{y,\eta }(s) \in \pi (E(x))$ for $s \leqslant 0$ close to zero. Hence, $E(x) \subset E_0$ .

We show that $(y,\eta ) \in E_0$ implies $(y,\eta ) \in E(x)$ only in the case that there is $\epsilon> 0$ such that $\gamma _{y,\eta }(s) \in \pi (E(x))$ for all $s \in [-\epsilon ,0]$ . The other case is analogous. We write $\tilde y = \gamma _{y,\eta }(-\epsilon )$ . Then (6.5) implies that $\tau (x,y) = 0$ and that there is $\xi \in L^+_x M$ such that $\tilde y = \gamma _{x,\xi }(s)$ for some $s \in (0,\rho (x,\xi )]$ . The path from x to y along $\gamma _{x,\xi }$ from x to $\tilde y$ and along $\gamma _{y,\eta }$ from $\tilde y$ to y is a null pregeodesic since $\tau (x,y) = 0$ . Therefore, $(y,\eta ) = \beta _{x,\xi }(r)$ for some $r \in (0,\rho (x,\xi )]$ and $(y,\eta ) \in E(x)$ .

Lemma 6.19. Let $\Omega \subset M$ and $x \in M$ be as in Lemma 6.17. Suppose that a set $C \subset \Omega $ satisfies $\pi (E(x)) \subset C \subset J^+(x)$ . Then

(6.7) $$ \begin{align} \pi(E(x)) &= \{y \in C : \text{ there is no}\ \tilde y \in C\ \text{s.t.}\ \tilde y \ll y\ \text{in}\ \Omega \}. \end{align} $$

Proof. Denote by $E_0$ the right-hand side of (6.7) and let $y \in \pi (E(x))$ . If $x = y$ , then there is no $\tilde y \in C$ such that $\tilde y \ll y$ since $x \le \tilde y$ by the assumption $C \subset J^+(x)$ . Hence, $y \in E_0$ . Suppose now that $y \ne x$ . By Lemma 6.17 there are $\xi \in L_x^+ M$ and $0 < s\leqslant \rho (x,\xi )$ such that $y=\gamma _{x,\xi }(s)$ . Moreover, $y \in C$ and $\gamma _{x,\xi }$ is optimising from x to y. To get a contradiction, suppose that there exists $\tilde y\in C$ such that $\tilde y \ll y$ . As $C \subset J^+(x)$ , we are led to the contradiction $x \le \tilde y \ll y$ with $\gamma _{x,\xi }$ being optimising from x to y. This shows that $y \in E_0$ .

Let $y \in E_0$ . If $x = y$ , then $y \in \pi (E(x))$ . Let us now assume that $x \ne y$ . In the local coordinates (F) we may write $y = F(s_0,a)$ for some $(s_0,a) \in (-1,1) \times B(0,\delta )$ and define the path $\mu _a(s) = F(s,a)$ . There holds $x < y \le \mu _a(1)$ since $C \subset J^+(x)$ . As in the proof of Lemma 6.17, there is an optimising geodesic $\tilde \gamma $ from x to $\tilde y := F(s_1, a)$ for some $s_1 \in (-1,1]$ . Lemma 6.17 implies that $\tilde y \in \pi (E(x))$ . Now $s_0 < s_1$ is a contradiction with $\tilde \gamma $ being optimising since $x \le y \ll \tilde y$ in this case, and $s_0> s_1$ is a contradiction with $y \in E_0$ since $\tilde y \in \pi (E(x)) \subset C$ and $\tilde y \ll y$ in this case. Therefore, $s_0 = s_1$ and $y = \tilde y \in \pi (E(x))$ .

Lemma 6.20. Let $\Omega \subset M$ , $x \in M$ and $C \subset \Omega $ be as in Lemma 6.19. Then the path $\mu _a : [-1,1] \to M$ , defined by $\mu _a(s) = F(s,a)$ with $a \in B(0,\delta )$ in the local coordinates (F), satisfies

(6.8) $$ \begin{align} f_{\mu_a}^+(x) &= \inf \{s \in [-1,1] : F(s,a) \in C\ \text{or}\ s=1\}. \end{align} $$

Proof. Suppose for the moment that $x \le F(1,a)$ . We write $s_0$ and $s_1$ for the left- and right-hand sides of (6.8), respectively. Lemma 6.9 implies that $s_0> -1$ and that either $x = F(s_0, a)$ or there is an optimising geodesic from x to $F(s_0, a)$ .

Case $x = F(s_0, a)$ and $s_0 < 1$ . Then $x \in \Omega $ and $x \in \pi (E(x)) \subset C$ . Now $s_1 \leqslant s_0$ and $s_1 < s_0$ is a contradiction with $C \subset J^+(x)$ . Hence, $s_0 = s_1$ in this case.

Case $x = F(s_0, a)$ and $s_0 = 1$ . Then $J^+(x) \cap \Omega = \emptyset $ and also $s_1 = 1$ .

Case that $s_0 < 1$ and there is an optimising geodesic $\gamma $ from x to $y_0 := F(s_0, a)$ . As $\gamma $ is optimising from x to $y_0$ , Lemma 6.17 implies that $y_0 \in \pi (E(x)) \subset C$ . Hence, $s_1 \leqslant s_0$ . Moreover, $y_1 := F(s_1, a) \in \overline C$ and $x \le y_1$ since $C \subset J^+(x)$ and the causal relation $\le $ is closed. Finally, $s_1 < s_0$ leads to the contradiction $x \le y_1 \ll y_0$ with $\gamma $ being optimising from x to $y_0$ .

Case that there is an optimising geodesic $\gamma $ from x to $F(1, a)$ or $x \not \le F(1,a)$ . Then $x \not \le F(s,a)$ for all $-1 < s < 1$ . In other words, $F(s, a) \notin J^+(x)$ for all $-1 < s < 1$ , and $s_0 = s_1 = 1$ .

6.7 On the span of three light-like vectors

We start with a simple lemma about the linear span of two light-like vectors on Lorentzian manifolds.

Lemma 6.21. Let y be a point on a Lorentzian manifold $(M,g)$ of dimension $1+n$ with $n \geqslant 2$ . Let $\xi _1,\xi _2,\xi _3 \in T_y M\setminus 0$ be light-like vectors such that they are not all multiples of each other. Then,

$$ \begin{align*}c_1\xi_1+c_2\xi_2+c_3\xi_3=0 \implies c_1=c_2=c_3=0.\end{align*} $$

Proof. It suffices to work in the normal coordinate system at the point y where the metric evaluated at the point y is the Minkowski metric. After scaling and without loss of generality, we can write $\xi _j= (1,\xi ^{\prime }_j)$ , $j=1,2,3$ for vectors $\xi ^{\prime }_j \in \mathbb R^{n}$ that satisfy $|\xi ^{\prime }_j|=1$ . Thus, it follows that

$$ \begin{align*}c_1+c_2+c_3=0,\quad \text{and}\quad c_1\xi^{\prime}_1+c_2\xi^{\prime}_2+c_3\xi^{\prime}_3=0.\end{align*} $$

Two of the numbers $c_1,c_2,c_3$ must be nonpositive or nonnegative. Without loss of generality, we assume $c_1$ and $c_2$ have this property, namely, $c_1,c_2 \geqslant 0$ or $c_1,c_2 \leqslant 0$ . Then, the previous identity implies that

$$ \begin{align*}|c_1\xi^{\prime}_1+c_2\xi^{\prime}_2|=|c_3\xi^{\prime}_3|=|c_3|=|c_1+c_2|=|c_1|+|c_2|=|c_1\xi^{\prime}_1|+|c_2\xi^{\prime}_2|.\end{align*} $$

Since the vectors $\xi ^{\prime }_1$ , $\xi ^{\prime }_2$ are not multiples of each other, it follows that $c_1=c_2=0$ and, subsequently, that $c_3=0$ .

Next, we consider the linear span of three light-like vectors. The following lemma is taken from [16, Lemma 1].

Lemma 6.22. Let y be a point on a Lorentzian manifold $(M,g)$ of dimension $1+n$ with $n \geqslant 2$ . Let $\xi _1, \eta \in T_y M \setminus 0$ be light-like. In any neighbourhood of $\xi _1$ in $T_y M$ , there exist two light-like vectors $\xi _2, \xi _3$ such that $\eta $ is in $\operatorname {\mathrm {span}}(\xi _1, \xi _2, \xi _3)$ .

We will also need a variation of the above lemma as follows.

Lemma 6.23. Let $x \in M$ , $\xi _0, \xi _1 \in L^+_x M$ and let $U \subset L^+_x M$ be a neighbourhood of $\xi _1$ . Suppose that $\xi _0 \notin \operatorname {\mathrm {span}}(\xi _1)$ . There is a neighbourhood $V \subset T_x M$ of $\xi _0$ and $\xi _2 \in U$ such that for any $\eta \in V$ there is $\xi _3 \in U$ such that $\eta \in \operatorname {\mathrm {span}}(\xi _1,\xi _2,\xi _3)$ and $\eta \notin \operatorname {\mathrm {span}}(\xi _j)$ , $j=1,2,3$ .

Proof. We choose normal coordinates centred at y. Then g is the Minkowski metric on the fibre $T_y M = \mathbb R^{1+n}$ . The statement is invariant with respect to nonvanishing rescaling of $\xi _0$ and $\xi _1$ , and we assume without loss of generality that $\xi _j = (1,\xi _j')$ with $\xi _j'$ a unit vector in $\mathbb R^n$ , $j=0,1$ . We choose an orthonormal basis $e_1,\dots ,e_n$ of $\mathbb R^n$ such that $e_1 = \xi _1'$ and $\xi _0' \in \operatorname {\mathrm {span}}(e_1,e_2)$ . Then in this basis it holds for some $a,b \in \mathbb R$ that

(6.9) $$ \begin{align} \xi_1 = (1,1,0,\underbrace{0,\dots,0}_{n-2\ \text{times}}), \quad \xi_0 = (1, a, b, \underbrace{0,\dots,0}_{n-2\ \text{times}}). \end{align} $$

Choose a small enough $r> 0$ so that both vectors

$$ \begin{align*} \xi_+ = (1, \sqrt{1-r^2}, r, \underbrace{0,\dots,0}_{n-2\ \text{times}}), \quad \xi_- = (1, \sqrt{1-r^2}, -r, \underbrace{0,\dots,0}_{n-2\ \text{times}}), \end{align*} $$

are in U and $\xi _0 \notin \operatorname {\mathrm {span}}(\xi _\pm )$ . We set $\xi _2 = \xi _+$ .

Let $\delta = (\delta _0, \delta _1, \delta _2) \in \mathbb R^3$ and $\epsilon \in \mathbb R^{n-2}$ be close to the respective origins. Consider the following perturbation of $\xi _0$ :

$$ \begin{align*} \eta = (1 + \delta_0, a + \delta_1, b + \delta_2, \epsilon) \end{align*} $$

and $\xi _3$ of the form

$$ \begin{align*} \xi_3 = (1, \sqrt{1-r^2 - c^2 |\epsilon|^2}, -r, c\epsilon), \end{align*} $$

where $c \in \mathbb R$ . The system $c_1 \xi _1 + c_2 \xi _2 + c_3 \xi _3 = \eta $ for $c_1, c_2, c_3 \in \mathbb R$ reads in matrix form

$$ \begin{align*} \begin{pmatrix} 1 & 1 & 1 & 1 +\delta_0 \\ 1 & \sqrt{1-r^2} & \sqrt{1-r^2 - c^2 |\epsilon|^2} & a + \delta_1 \\ 0 & r & -r & b + \delta_2 \\ 0 & 0 & c\epsilon & \epsilon \\ \end{pmatrix} \end{align*} $$

and two steps of the Gaussian elimination algorithm reduces this to

$$ \begin{align*} \begin{pmatrix} 1 & 1 & 1 & 1 +\delta_0 \\ 0 & 1 & w & z \\ 0 & 0 & x & y \\ 0 & 0 & c\epsilon & \epsilon \\ \end{pmatrix} \end{align*} $$

where the specific form of $y = y(\delta ,\epsilon )$ , $z = z(\delta ,\epsilon )$ and $w=w(c,\epsilon )$ is not important to us, and

$$ \begin{align*} x = x(c,\epsilon) = \frac{r}{\sqrt{1-r^2}-1} \left(2-\sqrt{1-r^2}-\sqrt{1-r^2-c^2|\epsilon|^2}\right). \end{align*} $$

As $x \ne 0$ , the above system has a solution if and only if

(6.10) $$ \begin{align} x(c,\epsilon)-cy(\delta,\epsilon) = 0. \end{align} $$

To get a contradiction, suppose that $y(0,0) = 0$ . Then $\xi _0 \in \operatorname {\mathrm {span}}(\xi _1, \xi _2)$ , and as $\xi _0, \xi _1$ and $\xi _2$ are all light-like, Lemma 6.21 applies to show that $\xi _0 \in \operatorname {\mathrm {span}}(\xi _1)$ or $\xi _0 \in \operatorname {\mathrm {span}}(\xi _2)$ . But $\xi _0 \notin \operatorname {\mathrm {span}}(\xi _j)$ for both $j=1,2$ , a contradiction.

We write $F(c,\delta ,\epsilon )$ for the left-hand side of (6.10) and $y_0 = y(0,0)$ and $x_0 = x(c,0)$ , the latter being independent from c. Setting $c_0 = x_0 / y_0$ , we see that $F(c_0, 0, 0) = 0$ and $\partial _c F(c_0, 0, 0) = -y_0 \ne 0$ . By the implicit function theorem there is a neighbourhood $V_0 \subset \mathbb R^{3+(n-2)}$ of the origin and a smooth map $h : V_0 \to \mathbb R$ such that $h(0,0) = c_0$ and $F(h(\delta , \epsilon ), \delta , \epsilon ) = 0$ for all $(\delta , \epsilon ) \in V_0$ . As $\xi _3 = \xi _-$ when $\epsilon = 0$ , by making $V_0$ smaller if necessary, we have that $\xi _3$ , with $c=h(\delta , \epsilon )$ , is in U for all $(\delta , \epsilon ) \in V_0$ .

By making $V_0$ smaller if necessary, we can also guarantee that $\eta \notin \operatorname {\mathrm {span}}(\xi _j)$ for $j=1,2,3$ , since $\xi _0 \notin \operatorname {\mathrm {span}}(\xi _j)$ , $j=1,2$ and $\xi _0 \notin \operatorname {\mathrm {span}}(\xi _-)$ .

7 Recovery of earliest observation sets and proof of Theorem 1.3

The aim of this section is to prove Theorem 1.3. As in the hypothesis of the theorem, we consider time-like paths $\mu _{\mathrm{in}}:[t_0^-,t_0^+]\to M$ and $\mu _{\mathrm{out}}:[s_0^-,s_0^+]\to M$ and define the source and observe regions $\Omega _{\mathrm{in}}$ and $\Omega _{\mathrm{out}}$ by (1.10). Recall that the extensions $\mu _{\mathrm{in}} : (t_1^-,t_1^+)\to M$ and $\mu _{\mathrm{out}}:(s_1^-,s_1^+)\to M$ are contained in $\Omega _{\mathrm{in}}$ and $\Omega _{\mathrm{out}}$ , respectively. We will assume as in the hypothesis of the theorem that $\delta $ is sufficiently small so that (1.11) holds.

Remark 5. Throughout the remainder of the article and without loss of generality, we will assume that $s_1^\pm = \pm 1$ and that $t_1^\pm =\pm 1$ . With this convenient choice of notation, we have

$$ \begin{align*}\Omega_{\text{in}}=F_{\text{in}}((-1,1)\times B(0,\delta)),\quad \text{and} \quad \Omega_{\text{out}}=F_{\text{out}}((-1,1)\times B(0,\delta)),\end{align*} $$

and therefore the abstract foliation condition (F), which was studied in the previous section, holds for these sets.

We recall from Definition 1.2 that $\operatorname {\mathrm {R}} \in L^+ \Omega _{\mathrm{out}} \times (L^+ \Omega _{\mathrm{in}})^3$ is a three-to-one scattering relation if it has the following two properties:

1. (R1) If $(v_0,v_1, v_2,v_3) \in \operatorname {\mathrm {R}}$ , then there is $y \in \overleftarrow {\;\gamma _{v_0}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}$ .

2. (R2) Assume that $\gamma _{v_{j}}$ , $j=0,1,2,3$ , are distinct and there exists $y \in \overleftarrow {\;\gamma _{v_{0}}} \cap \bigcap _{j=1}^3 \overrightarrow {\gamma _{v_{j}}}.$ Moreover, assume that $y=\gamma _{v_{0}}(s_0)$ with $s_0\in (-\rho (v_0),0]$ and $y=\gamma _{v_{j}}(s_j)$ for all $j=1,2,3$ , with $s_j\in [0,\rho (v_j))$ . Denote $\xi _j=\dot \gamma _{v_{j}}(s_j)$ for $j=0,1,2,3$ and assume that $\xi _0 \in \operatorname {\mathrm {span}}(\xi _1, \xi _2, \xi _3)$ . Then, it holds that $(v_{0},v_{1}, v_{2},v_{3}) \in \operatorname {\mathrm {R}}$ .

7.1 Lower and upper bounds for conical pieces

We define a conical piece associated to a three-to-one scattering relation $\operatorname {\mathrm {R}}$ and $v_{1}, v_{2} \in L^+\Omega _{\mathrm{in}}$ by

$$ \begin{align*} \operatorname{\mathrm{CP}}(v_{1}, v_{2}) &= \{ v_{0} \in L^+\Omega_{\text{out}} : \text{ there is}\ v_{3} \in L^+\Omega_{\text{in}}\ \text{such that} (v_{0},v_{1}, v_{2},v_{3}) \in \operatorname{\mathrm{R}} \}. \end{align*} $$

Lemma 7.1. Let $v_{1} \in L^+ \Omega _{\mathrm{in}}$ , $v_{0} \in L^+ \Omega _{\mathrm{out}}$ and write $\pi (v_{1}) = x$ and $\pi (v_{0}) = z$ . Suppose that $\gamma _{v_{1}}$ is optimising from x to a point y in M and that $\gamma _{v_{0}}$ is optimising from y to z. Suppose furthermore that $\gamma _{v_{1}}$ and $\gamma _{v_{0}}$ do not intersect at x or at z. Then there is a vector $v_{2} \in L^+ \Omega _{\mathrm{in}}$ , arbitrarily close to $v_{1}$ and a set $C \subset \operatorname {\mathrm {CP}}(v_{1}, v_{2})$ such that C is a neighbourhood of $v_{0}$ in $C(y)$ .

Proof. Let $s_{j} \in \mathbb R$ satisfy $\gamma _{v_{j}}(-s_j) = y$ , $j=0,1$ and write $\xi _j = \dot \gamma _{v_{j}}(-s_j)$ . As $\gamma _{v_{1}}$ is optimising from x to y and $\gamma _{v_{0}}$ is optimising from y to z, these two geodesics do not intersect at any point $\tilde y \ne y$ satisfying $x < \tilde y < z$ . We have also assumed that they do not intersect at x or z. Hence, there is such a neighbourhood $V_0 \subset L_y^+ M$ of $\xi _0$ that y is the unique point satisfying $y \in \overleftarrow {\;\gamma _{\tilde v_{0}}} \cap \overrightarrow {\gamma _{v_{1}}}$ where $\tilde v_{0} = \beta _{y,\eta }(s_0)$ and $\eta \in V_0$ .

Observe that $\xi _0 \notin \operatorname {\mathrm {span}}(\xi _1)$ since $\gamma _{v_{1}}$ and $\gamma _{v_{0}}$ do not intersect at x. Let $U \subset L_y^+ M$ be a neighbourhood of $\xi _1$ such that $\gamma _{y,\xi }(s_1) \in \Omega _{\mathrm{in}}$ for all $\xi \in U$ . By Lemma 6.23 there is a neighbourhood $V \subset V_0$ of $\xi _0$ and $\xi _2 \in U$ such that for any $\eta \in V$ there is $\xi _3 \in U$ such that $\eta \in \operatorname {\mathrm {span}}(\xi _1,\xi _2,\xi _3)$ and $\eta \notin \operatorname {\mathrm {span}}(\xi _j)$ , $j=1,2,3$ . Writing $v_{j} = \beta _{y,\xi _j}(s_j)$ , $j=2,3$ , we have $(\tilde v_{0}, v_{1}, v_{2}, v_{3}) \in \operatorname {\mathrm {R}}$ for $\eta \in V$ , due to (R2). To conclude, we use the fact that the image of V under the map $\eta \mapsto \beta _{y, \eta }(s_0)$ is a smooth submanifold of dimension n in $T M$ .

Lemma 7.2. Let $v_{1}, v_{2} \in L^+\Omega _{\mathrm{in}}$ satisfy $\overline {\gamma _{v_{1}}} \ne \overline {\gamma _{v_{2}}}$ . We write

(7.1) $$ \begin{align} K = J^+(\overline{\Omega_{\text{in}}}) \cap J^-(\overline{\Omega_{\text{out}}}). \end{align} $$

Then the set $\mathcal F = \overrightarrow {\gamma _{v_{1}}} \cap \overrightarrow {\gamma _{v_{2}}} \cap K$ is finite and

$$ \begin{align*} \operatorname{\mathrm{CP}}(v_{1}, v_{2}) \subset \bigcup_{x \in \mathcal F} \overline{C(x)}. \end{align*} $$

Proof. Observe that K is compact since both $\Omega _{\mathrm{in}}$ and $\Omega _{\mathrm{out}}$ are bounded. If $\mathcal F$ is not finite, then it has an accumulation point, and using Lemma 6.4 we obtain the contradiction $\overline {\gamma _{v_{1}}} = \overline {\gamma _{v_{2}}}$ . The second claim follows immediately from (R1).

7.2 Relating earliest observation sets to a three-to-one scattering relation

Recall that the observation set $\Omega _{\mathrm{out}}$ satisfies (F) and take $\Omega = \Omega _{\mathrm{out}}$ and $F = F_{\mathrm{out}}$ in the definition (6.4) of the earliest observation sets $E(y)$ , $y \in M$ . We will next relate $E(y)$ to a set constructed from $\operatorname {\mathrm {R}}$ . To this end, define the set $E(v,w)$ for $v,w \in L^+\Omega _{\mathrm{in}}$ as follows: let $C(v,w)$ be the closure in $T \Omega _{\mathrm{out}}$ of the union $\bigcup _{C \in \mathcal C(v,w)} C$ where

$$ \begin{align*} \mathcal C(v,w) = \{ C : & C \subset T\Omega_{\text{out}}\ \text{is a smooth manifold of dimension}\ n\ \text{s.t.} \\& C \subset \operatorname{\mathrm{CP}}(v,\tilde v) \cap \operatorname{\mathrm{CP}}(w,\tilde w)\ \text{for some}\ \tilde v, \tilde w \in L^+\Omega_{\text{in}} \\&\text{ satisfying}\ \overline{\gamma_v} \ne \overline{\gamma_{\tilde v}}\ \text{and}\ \overline{\gamma_w} \ne \overline{\gamma_{\tilde w}} \}, \end{align*} $$

then we set

$$ \begin{align*} \tilde E(v,w) &= \{ u \in C(v,w) : \text{ there is no}\ \tilde u \in C(v,w)\ \text{s.t.}\ \tilde u \ll u\ \text{in}\ \Omega_{\text{out}}\} \end{align*} $$

and

$$ \begin{align*} E(v,w) = \{(z,\zeta) :\ \text{there is}\ \epsilon> 0\ \text{such that}\ \gamma_{z,\zeta}(s) \in \pi(\tilde E(v,w))& \\ \text{for all}\ s \in [0, \epsilon]\ \text{or for all}\ s \in [-\epsilon,0]&\}. \end{align*} $$

The following lemma describes the basic idea that we will use to construct earliest observation sets given a three-to-one scattering relation $\operatorname {\mathrm {R}}$ . The geometric setting of the lemma is shown in Figure 4.

Lemma 7.3. Let $v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$ and suppose that there are $x_j < \pi (v_j)$ such that $\gamma _{v_j}$ is optimising from $x_j$ to a point $y \in \overrightarrow {\gamma _{v_1}} \cap \overrightarrow {\gamma _{v_2}}$ for $j=1,2$ . Suppose furthermore that $\overline {\gamma _{v_1}} \ne \overline {\gamma _{v_2}}$ and that $y \notin J^-(F_{\mathrm{out}}(\{-1\}\times B(0,\delta )))$ . Then $E(y) \subset C(v_1,v_2)$ , $\pi (C(v_1, v_2)) \subset J^+(y)$ and $E(y) = E(v_1, v_2)$ .

Proof. Let $u \in E(y)$ . We will show that $u \in C(v_1,v_2)$ . Note that $\gamma _{u}$ is optimising from y to $z := \pi (u)$ by Lemma 6.17. Suppose for the moment that neither $\gamma _{v_1}$ nor $\gamma _{v_2}$ intersects $\gamma _u$ at z. As $\gamma _{v_j}$ is optimising from $x_j$ to y, the geodesics $\gamma _u$ and $\gamma _{v_j}$ cannot intersect at $\pi (v_j)$ , and Lemma 7.1 implies that there are $\tilde v_j \in L^+ \Omega _{\mathrm{in}}$ and $C_j \subset \operatorname {\mathrm {CP}}(v_j, \tilde v_j)$ such that $C_j$ is a neighbourhood of u in $C(y)$ . As $C(y)$ is a smooth manifold of dimension n, the intersection $C_1 \cap C_2$ is a smooth manifold of dimension n containing u. Hence, $u \in C(v_1,v_2)$ .

Let us now consider the case that $\gamma _{v_1}$ or $\gamma _{v_2}$ intersects $\gamma _u$ at z. Choose $\eta \in L_y^+ M$ and $t> 0$ so that $\overline {\gamma _{y,\eta }} = \overline {\gamma _u}$ and $\gamma _{y,\eta }(t) = z$ . We have $t \leqslant \rho (y,\eta )$ and there are $\eta _k \in L_y^+ M$ and $0 < t_k < \rho (y,\eta _k)$ such that writing $u_k = \beta _{y,\eta _k}(t_k)$ and $z_k = \pi (u_k)$ there holds $u_k \to u$ and neither $\gamma _{v_1}$ nor $\gamma _{v_2}$ intersects $\gamma _{u_k}$ at $z_k$ . The argument above implies that $u_k \in C(v_1,v_2)$ . As $C(v_1,v_2)$ is closed, also $u \in C(v_1,v_2)$ .

Let $u \in C(v_1, v_2)$ . We will show that $\pi (u) \in J^+(y)$ . Consider first the case that $u \in C$ for some $C \in \mathcal C(v_1,v_2)$ and $\overline {\gamma _{v_j}} \ne \overline {\gamma _{u}}$ for $j=1,2$ . Then there are $y_j \in \overleftarrow {\;\gamma _{u}} \cap \overrightarrow {\gamma _{v_j}}$ . As $x_j < \pi (v_j) \le y_j$ , Lemma 6.13 implies that either $y=y_1=y_2$ or at least one of $y_1$ and $y_2$ satisfies $y < y_j$ . In both cases $y \le \pi (u)$ ; that is, $\pi (u) \in J^+(y)$ . Consider now the case that there is sequence $u_k$ , $k \in \mathbb N$ , such that $u_k \in C_k$ for some $C_k \in \mathcal C(v_1,v_2)$ and $u_k \to u$ . The sequence $u_k$ can be chosen so that $\overline {\gamma _{v_j}} \ne \overline {\gamma _{u_k}}$ also for $j=1,2$ and $k=1,2,\dots $ . We obtain $y \le \pi (u)$ also in this case since the relation $\le $ is closed.

We have shown, in particular, that $\pi (E(y)) \subset \pi (C(v_1,v_2)) \subset J^+(y)$ . Lemma 6.19 implies now that $\pi (\tilde E(v_1,v_2)) = \pi (E(y))$ . Finally, $E(y) = E(v_1, v_2)$ follows immediately from Lemma 6.18.

7.3 Local test for optimality before intersection

In Lemma 7.3 the geodesic $\gamma _{v_1}$ needs to be optimising from $x_1$ to y. We will give a construction that allows us to distinguis the optimising and nonoptimising but close to optimising cases, given $\operatorname {\mathrm {R}}$ . We begin with an auxiliary lemma.

Lemma 7.4. Let $v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$ and let $u_1 \in C \in \mathcal C(v_1, v_2)$ . Then there is $u_2 \in C$ such that $\overline {\gamma _{u_1}} \ne \overline {\gamma _{u_2}}$ and $\overleftarrow {\;\gamma _{u_1}} \cap \overleftarrow {\;\gamma _{u_2}} \cap \overrightarrow {\gamma _{v_j}} \ne \emptyset $ for both $j=1,2$ .

Proof. As C is a smooth manifold of dimension n there is $u_2$ satisfying $\overline {\gamma _{u_1}} \ne \overline {\gamma _{u_2}}$ in any neighbourhood of $u_1$ in C. Lemma 7.2 implies that for some $\tilde v_1 \in L^+ \Omega _{\mathrm{in}}$ and finite $\mathcal F \subset \overrightarrow {\gamma _{v_1}}$ there holds

$$ \begin{align*} C \subset \operatorname{\mathrm{CP}}(v_1, \tilde v_1) \subset \bigcup_{x \in \mathcal F} \overline{C(x)}. \end{align*} $$

Then Lemma 6.16 implies that $\mathcal F \cap \overleftarrow {\;\gamma _{u_1}} \cap \overleftarrow {\;\gamma _{u_2}}\ne \emptyset $ when $u_2 \in C$ is close enough to $u_1$ . The proof that $\overleftarrow {\;\gamma _{u_1}} \cap \overleftarrow {\;\gamma _{u_2}} \cap \overrightarrow {\gamma _{v_2}} \ne \emptyset $ is analogous.

Lemma 7.5. Let $v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$ and $x_1 \in M$ be as in Lemma 7.3. Then there do not exist $\tilde v_1, \tilde v_2 \in L^+ \Omega _{\mathrm{in}}$ and nonempty $C \in \mathcal C(\tilde v_1, \tilde v_2)$ such that $C \subset E(v_1, v_2)$ and $x_1 \ll \tilde x_1$ for some $\tilde x_1 \in \overleftarrow {\;\gamma _{\tilde v_1}}$ .

Proof. To get a contradiction, we suppose that there are $\tilde v_1, \tilde v_2 \in L^+ \Omega _{\mathrm{in}}$ and nonempty $C \in \mathcal C(\tilde v_1, \tilde v_2)$ such that $C \subset E(v_1, v_2)$ and $x_1 \ll \tilde x_1$ for some $\tilde x_1 \in \overleftarrow {\;\gamma _{\tilde v_1}}$ . By Lemma 7.4 there are $u_1, u_2 \in C$ and $\tilde y \in M$ such that $\overline {\gamma _{u_1}} \ne \overline {\gamma _{u_2}}$ and $\tilde y \in \overleftarrow {\;\gamma _{u_1}} \cap \overleftarrow {\;\gamma _{u_2}} \cap \overrightarrow {\gamma _{\tilde v_1}}$ . Lemma 7.3 gives $E(v_1, v_2) = E(y)$ , and as $C \subset E(v_1, v_2)$ , there holds $y \in \overleftarrow {\;\gamma _{u_1}} \cap \overleftarrow {\;\gamma _{u_2}} \cap \overrightarrow {\gamma _{v_1}}$ . As $y, \tilde y \in \overline {\gamma _{u_1}}$ , we have $\tilde y \le y$ or $y < \tilde y$ .

Case $y < \tilde y$ . The causal path from y to $\pi (u_1)$ , given by $\gamma _{u_2}$ from y to $\tilde y$ and $\gamma _{u_1}$ from $\tilde y$ to $\pi (u_1)$ , is not a null pregeodesic. This is a contradiction with $u_1 \in E(y)$ .

Case $\tilde y \le y$ . There is a causal path from $x_1$ to $\tilde x_1$ , and there is a causal path from $\tilde x_1$ to y given by $\gamma _{\tilde v_1}$ from $\tilde x_1$ to $\tilde y$ and by $\gamma _{u_1}$ from $\tilde y$ to y. Therefore, there is a causal path from $x_1$ to y via $\tilde x_1$ and $x_1 \ll \tilde x_1$ , a contradiction with $\gamma _v$ being optimising from $x_1$ to y.

Lemma 7.6. Let $v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$ and $x_1, y \in M$ be as in Lemma 7.3, and let

$$ \begin{align*}\mu_{\text{in}} : [-1,1] \to \Omega_{\text{in}}\end{align*} $$

be a time-like and future-pointing path. Suppose that $\mu _{\mathrm{in}}(s) \in \overline {\gamma _{v_1}}$ for some $s \in [-1,1)$ and $\mu _{\mathrm{in}}(s) \ll y$ . Suppose furthermore that $\mu _{\mathrm{in}}(1) \not \le y$ and $E(v_1, v_2) \ne \emptyset $ . Then there are $\tilde v_1, \tilde v_2 \in L^+ \Omega _{\mathrm{in}}$ and nonempty $C \in \mathcal C(\tilde v_1, \tilde v_2)$ such that $C \subset E(v_1, v_2)$ and $\mu _{\mathrm{in}}(\tilde s) \in \overleftarrow {\;\gamma _{\tilde v_1}}$ for some $\tilde s> s$ .

Proof. By Lemma 7.3 we have $E(v_1, v_2) = E(y)$ . As $E(y)$ is a nonempty manifold with (nonsmooth) boundary, there is $u \in E(y)$ such that $E(y)$ is a smooth manifold near u. Then $\gamma _u$ is optimising from y to $z:=\pi (u)$ and also slightly past z.

By Lemma 6.10 there is $\tilde s \in (s,1)$ such that either there is an optimising geodesic from $\mu _{\mathrm{in}}(\tilde s)$ to y or $y = \mu _{\mathrm{in}}(\tilde s)$ .

Let us consider the former case first. Choose $\tilde v_1$ in the tangent bundle of that geodesic so that $\tilde x:=\pi (\tilde v_1) \in \Omega _{\mathrm{in}}$ and $\mu _{\mathrm{in}}(\tilde s) < \tilde x < y$ . By Lemma 7.1 there are $\tilde v_2 \in L^+ \Omega _{\mathrm{in}}$ and $C \subset \operatorname {\mathrm {CP}}(\tilde v_{1}, \tilde v_{2})$ such that C is a neighbourhood of u in $C(y)$ . But $C(y) \subset E(y)$ near u.

Let us now suppose that $y = \mu _{\mathrm{in}}(\tilde s)$ . Choose $\xi _0, \xi _1 \in L^+_y M$ such that $\overline {\gamma _{y,\xi _0}} = \overline {\gamma _{u}}$ and $\overline {\gamma _{y,\xi _1}} \ne \overline {\gamma _{u}}$ . By Lemma 6.23 there is a neighbourhood $V \subset L_y^+ M$ of $\xi _0$ and $\xi _2 \in L_y^+ M$ such that for any $\eta \in V$ there is $\xi _3 \in L_y^+ M$ such that $\eta \in \operatorname {\mathrm {span}}(\xi _1,\xi _2,\xi _3)$ and $\eta \notin \operatorname {\mathrm {span}}(\xi _j)$ , $j=1,2,3$ . We write $\tilde v_j = (y, \xi _j)$ , $j=1,2$ . Observe that y is the only point in $\overleftarrow {\;\gamma _{\tilde u}} \cap \overrightarrow {\gamma _{\tilde v_1}}$ for $\tilde u$ close to u since $\gamma _u$ is optimising from y to a point past $\pi (u)$ . As in the proof of Lemma 7.1, we see that there is $C \subset \operatorname {\mathrm {CP}}(\tilde v_1, \tilde v_2)$ such that C is a neighbourhood of u in $C(y)$ .

7.4 Global recovery

Let $\mu _a$ be as in Lemma 6.20, with $\Omega =\Omega _{\mathrm{out}}$ , and define for $v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$ ,

$$ \begin{align*} f_a(v_1,v_2) = \inf \{s \in [-1,1] : \mu_a(s) \in \pi(C(v_1,v_2))\ \text{or}\ s=1\}. \end{align*} $$

Figure 5 illustrates the function $f_a(v_1, v_2)$ .

Figure 5 Function $f_0(v_1, v_2)$ in the $1+2$ -dimensional Minkowski space. Left. The time-like path $\mu _0 = \mu _{\mathrm{out}}$ is the green line segment, and the point $z=\mu _0(f_0(v_1,v_2))$ is also green. The thick blue line segment is the optimising geodesic from y to z. It is contained in the cone $\pi (C(y))$ . The time axis is vertical, and the sets $\Omega _{\mathrm{out}}$ , $\pi (C(y))$ , $\pi (E(y))$ , as well as the points $y, x_1, x_2$ , vectors $v_1, v_2$ and geodesics $\gamma _{v_1}, \gamma _{v_2}$ , are as in Figure 4. Right. Inequality $f_0(v_1,v_2) \le f_0(v_1, w_2)$ as in Lemma 7.8. The vector $w_2$ is dashed red and the points $z=\mu _0(f_0(v_1,v_2))$ and $\tilde z=\mu _0(f_0(v_1,w_2))$ are green. The points $y, x_1, x_2$ , vectors $v_1, v_2$ , geodesics $\gamma _{v_1}, \gamma _{v_2}$ and path $\mu _0$ are as on the left.

Lemma 7.7. Let $v_1, v_2 \in L^+ \Omega _{\mathrm{in}}$ and $y \in M$ be as in Lemma 7.3. Then

$$ \begin{align*}f_a(v_1,v_2) = f_{\mu_a}^+(y).\end{align*} $$

Proof. Follows immediately from Lemmas 6.20 and 7.3.

Lemma 7.8. Let $v_1 \in L^+ \Omega _{\mathrm{in}}$ and let $x_1 \in \overline {\gamma _{v_1}}$ satisfy $x_1 < \pi (v_1)$ . Suppose that $\overline {\gamma _{v_1}} \cap \overline {\mu _0} = \emptyset $ and $f_{\mu _0}^+(x_1)> -1$ . Then there is a neighbourhood $\mathcal U \subset L^+ \Omega _{\mathrm{in}}$ of $v_1$ such that all $v_2 \in L^+ \Omega _{\mathrm{in}}$ and $w_2 \in \mathcal U$ satisfy the following. If there is $x_2 < \pi (v_2)$ such that $\gamma _{v_j}$ is optimising from $x_j$ to a point $y \in \overrightarrow {\gamma _{v_1}} \cap \overrightarrow {\gamma _{v_2}}$ for $j=1,2$ , $\overline {\gamma _{v_1}} \ne \overline {\gamma _{v_2}}$ , $y \notin J^-(F_{\mathrm{out}}(\{-1\}\times B(0,\delta )))$ and $\overrightarrow {\gamma _{w_2}} \cap \overrightarrow {\gamma _{v_1}} \cap J^-(y) = \emptyset $ , then $f_0(v_1,v_2) \leqslant f_0(v_1,w_2)$ .

Proof. Let $\mathcal U$ be small enough so that it is contained in the two neighbourhoods given by Lemmas 6.14 and 6.15. When applying Lemmas 6.14 and 6.15 we take $v = v_1$ , $x = x_1$ and $K = J^+(\overline {\Omega _{\mathrm{in}}}) \cap J^-(\overline {\Omega _{\mathrm{out}}})$ . Moreover, let $U'$ be as in Lemma 6.15.

Let $w_2 \in \mathcal U$ , $C \in \mathcal C(v_1,w_2)$ and let $u_1 \in C$ satisfy $\pi (u) \in \overline {\mu _a}$ for $a \in U'$ . We write $\pi (u_1) = F_{\mathrm{out}}(s, a)$ for some $s \in [-1,1]$ and begin by showing that

(7.2) $$ \begin{align} f_a(v_1,v_2) \leqslant s. \end{align} $$

By Lemma 7.4 there are $u_2 \in C$ , satisfying $\overline {\gamma _{u_1}} \ne \overline {\gamma _{u_2}}$ , and

$$ \begin{align*} y_1 \in \overleftarrow{\;\gamma_{u_1}} \cap \overleftarrow{\;\gamma_{u_2}} \cap \overrightarrow{\gamma_{v_1}}, \quad y_2 \in \overleftarrow{\;\gamma_{u_1}} \cap \overleftarrow{\;\gamma_{u_2}} \cap \overrightarrow{\gamma_{w_2}}. \end{align*} $$

Case $y_1 = y_2$ . Now $\overrightarrow {\gamma _{w_2}} \cap \overrightarrow {\gamma _{v_1}} \cap J^-(y) = \emptyset $ implies $y < y_1$ . Hence, by Lemma 7.7

$$ \begin{align*} f_a(v_1, v_2) = f_{\mu_a}^+(y) \leqslant f_{\mu_a}^+(y_1) \leqslant s. \end{align*} $$

Case $y_2 < y_1$ . It follows from Lemma 6.14 that the geodesic $\gamma _{v_1}$ is not optimising from $x_1$ to $y_1$ . Therefore, $y < y_1$ . As above, this implies $f_a(v_1,v_2) \leqslant s$ .

Case $y_1 < y_2$ . Lemma 6.15 implies

$$ \begin{align*} f_a(v_1, v_2) = f_{\mu_a}^+(y) \leqslant f_{\mu_a}^+(y_2) \leqslant s. \end{align*} $$

We have shown (7.2).

Let $u \in C(v_1,w_2)$ satisfy $\pi (u) = F_{\mathrm{out}}(s,0)$ for some $s \in [-1,1]$ . Then there are $C_j \in \mathcal C(v_1,w_2)$ , $u_j \in C_j$ , $s_j \in (-1,1)$ and $a_j \in U'$ such that $\pi (u_j) = F(s_j, a_j)$ and $u_j \to u$ . Now (7.2) implies $f_{a_j}(v_1, v_2) \leqslant s_j$ , and letting $j \to \infty $ , we obtain $f_0(v_1, v_2) \leqslant s$ .

Lemma 7.9. Let $v_1 \in L^+ \Omega _{\mathrm{in}}$ and let $x_1 \in \overline {\gamma _{v_1}}$ satisfy $x_1 < \pi (v_1)$ . Suppose that $\gamma _{v_1}$ is optimising from $x_1$ to a point y. Then there is a neighbourhood $\mathcal U \subset L^+ \Omega _{\mathrm{in}}$ of $v_1$ such that all $v_2 \in \mathcal U$ satisfy the following. If there is $\tilde y \in \overrightarrow {\gamma _{v_2}} \cap \overrightarrow {\gamma _{v_1}} \cap J^-(y)$ , then there is $x_2 < \pi (v_2)$ such that $\gamma _{v_2}$ is optimising from $x_2$ to $\tilde y$ .

Proof. To get a contradiction, suppose that there are sequences $L^+M\ni v_j \to v_1$ and

$$ \begin{align*} \tilde y_j \in \overrightarrow{\gamma_{v_j}} \cap \overrightarrow{\gamma_{v_1}} \cap J^-(y) \end{align*} $$

such that for all $x \in \overline {\gamma _{v_j}}$ there holds: if $x < \pi (v_j)$ then $x \ll \tilde y_j$ . Due to compactness of $J^+(\pi (v_1)) \cap J^-(y)$ , we may assume that $\tilde y_j \to \tilde y$ for some $\tilde y \in M$ . Then $\tilde y \in \overrightarrow {\gamma _{v_1}}$ and $\tilde y \le y$ . We choose $\eta _j \in L_{\tilde y_j}^- M$ and $r_j \geqslant 0$ so that $\overline {\gamma _{\tilde y_j, \eta _j}} = \overline {\gamma _{v_j}}$ , $\gamma _{\tilde y_j, \eta _j}(r_j) = \pi (v_j)$ and so that $\eta _j \to \eta $ and $r_j \to r$ for some $\eta \in L_y^- M$ and $r \geqslant 0$ . Then $\rho (\tilde y_j, \eta _j) \leqslant r_j$ and $\gamma _{\tilde y,\eta }(r) = \pi (v_1)$ . Lemma 6.7 implies that $\rho (\tilde y,\eta ) \leqslant r$ . But this is a contradiction with $\gamma _{v_1}$ being optimising from $x_1 < \pi (v_1)$ to y since $\tilde y \le y$ .

We are now ready to prove the main theorem in this section, which shows that the earliest arrivals can be reconstructed from the relation $\operatorname {\mathrm {R}}$ . Figure 6 outlines the geometric setting of the theorem.

Figure 6 Schematic of the geometric setting of Theorem 7.10. The time-like paths $\mu _{\mathrm{in}}$ and $\mu _0$ in green. Vectors $v_1$ , $\tilde v_1$ and $v_2$ are in red. Points $x = \mu _{\mathrm{in}}(s)$ and $\tilde x = \mu _{\mathrm{in}}(\tilde s)$ are in black and point $z = \mu _0(f_0(v_1,v_2))$ is in green. Here $f_0(v_1, v_2) \ge f_{\mathrm{crit}}(v_1)$ . Observe that this case cannot arise in the Minkowski space.

Theorem 7.10. Let $s \in [-1,1)$ and let $v_1 \in L^+ \Omega _{\mathrm{in}}$ satisfy

$$ \begin{align*} \mu_{\text{in}}(s) \in \overline{\gamma_{v_1}}, \quad \mu_{\text{in}}(s) < \pi(v_1), \quad \overline{\gamma_{v_1}} \cap \overline{\mu_0} = \emptyset. \end{align*} $$

Suppose also that $\mu _{\mathrm{in}}(s)$ and $\pi (v_1)$ are close enough so that $\gamma _{v_1}$ is optimising from $\mu _{\mathrm{in}}(s)$ to a point beyond $\pi (v_1)$ . Then there is a neighbourhood $\mathcal U \subset L^+ \Omega _{\mathrm{in}}$ of $v_1$ such that for all neighbourhoods $\mathcal U' \subset \mathcal U$ of $v_1$ there holds

(7.3) $$ \begin{align} &\{E(v_1, v_2) : v_2 \in \mathcal U', f_0(v_1,v_2) \leqslant f_{\text{crit}}\ \text{and}\ f_0(v_1, v_2) < 1\} \\\notag&\qquad= \{E(y) : y=\gamma_{v_1}(r), 0\leqslant r \leqslant \rho(v_1)\ \text{and}\ f_{\mu_0}^+(y) < 1\}, \end{align} $$

where $f_{\mathrm{crit}} = \inf \{ f_0(v_1, v_2) : v_2 \in \mathcal W \}$ and

$$ \begin{align*} \mathcal W=\{ v_2 \in \mathcal U' : \ &\overline{\gamma_{v_1}} \ne \overline{\gamma_{v_2}}\ \text{and there are}\ \tilde v_1, \tilde v_2 \in L^+ \Omega_{\text{in}} \\& \text{and nonempty}\ C \in \mathcal C(\tilde v_1, \tilde v_2)\ \text{such that} \\& C \subset E(v_1, v_2)\ \text{and}\ \mu_{\text{in}}(\tilde s) \in \overleftarrow{\;\gamma_{\tilde v_1}}\ \text{for some}\ \tilde s> s\}. \end{align*} $$

Proof. Write $x_1 = \mu _{\mathrm{in}}(s)$ and observe that $f^+_{\mu _0}(x_1)> -1$ since

(7.4) $$ \begin{align} \Omega_{\text{in}} \cap J^-(F_{\text{out}}(\{-1\}\times B(0,\delta))) = \emptyset. \end{align} $$

Let $\mathcal U$ be small enough so that it is contained in the two neighbourhoods given by Lemmas 7.8 and 7.9.

Denote the left-hand side of (7.3) by $\mathcal E$ . Let $y \in \overrightarrow {\gamma _{v_1}}$ and suppose that $\gamma _{v_1}$ is optimising from $x_1$ to a point beyond y and that $f_{\mu _0}^+(y) < 1$ . We will show that $E(y) \in \mathcal E$ . Lower semi-continuity of $\rho $ implies that there is $v_2 \in \mathcal U'$ and $x_2 < \pi (v_2)$ such that $\gamma _{v_2}$ is optimising from $x_2$ to y and $\overline {\gamma _{v_1}} \ne \overline {\gamma _{v_2}}$ . Moreover, (7.4) implies that $y \notin J^-(F_{\mathrm{out}}(\{-1\}\times B(0,\delta )))$ . Now Lemmas 7.3 and 7.7 give $E(v_1, v_2) = E(y)$ and $f_0(v_1, v_2) = f_{\mu _0}^+(y)$ . Hence, $E(y) \in \mathcal E$ follows after we show that $f_0(v_1,v_2) \leqslant f_{\mathrm{crit}}$ .

Let $w_2 \in \mathcal U'$ satisfy $\overline {\gamma _{v_1}} \ne \overline {\gamma _{w_2}}$ . If $\overrightarrow {\gamma _{w_2}} \cap \overrightarrow {\gamma _{v_1}} \cap J^-(y) = \emptyset $ , then $f_0(v_1,v_2) \leqslant f_0(v_1,w_2)$ by Lemma 7.8. On the other hand, if $\overrightarrow {\gamma _{w_2}} \cap \overrightarrow {\gamma _{v_1}} \cap J^-(y) \ne \emptyset $ , then Lemmas 7.9 and 7.5 imply that $w_2 \notin \mathcal W$ . Hence, $f_0(v_1,v_2) \leqslant f_{\mathrm{crit}}$ .

We turn to the opposite inclusion and suppose that $v_2 \in \mathcal U'$ , $f_0(v_1,v_2) \leqslant f_{\mathrm{crit}}$ and $f_0(v_1, v_2) < 1$ . To get a contradiction, suppose that there does not exist $y \in \overrightarrow {\gamma _{v_1}} \cap \overrightarrow {\gamma _{v_2}}$ such that $\gamma _{v_1}$ is optimising from $x_1$ to y. This implies that there is also $\tilde x_1 \in \overline {\gamma _{v_1}}$ such that $x_1 < \tilde x_1 < \pi (v_1)$ and there does not exist $y \in \overrightarrow {\gamma _{v_1}} \cap \overrightarrow {\gamma _{v_2}}$ such that $\gamma _{v_1}$ is optimising from $\tilde x_1$ to y. Consider a point $\tilde y \in \overline {\gamma _{v_1}}$ such that $\gamma _{v_1}$ is optimising from $\tilde x_1$ to $\tilde y$ and $\pi (v_1) < \tilde y$ . Then there are $w_2 \in \mathcal U'$ and $\tilde x_2 < \pi (w_2)$ such that $\gamma _{w_2}$ is optimising from $\tilde x_2$ to $\tilde y$ and $\overline {\gamma _{v_1}} \ne \overline {\gamma _{w_2}}$ . Note that $\overrightarrow {\gamma _{v_2}} \cap \overrightarrow {\gamma _{v_1}} \cap J^-(\tilde y) = \emptyset $ as there does not exist $y \in \overrightarrow {\gamma _{v_1}} \cap \overrightarrow {\gamma _{v_2}}$ such that $\gamma _{v_1}$ is optimising from $\tilde x_1$ to y. Lemmas 7.7 and 7.8 imply that

(7.5) $$ \begin{align} f_{\mu_0}^+(\tilde y) = f_0(v_1,w_2) \leqslant f_0(v_1,v_2). \end{align} $$

We will now consider two cases.

Case that there is $y \in \overline {\gamma _{v_1}}$ such that $x_1 \ll y$ and $y \in J^-(\overline {\Omega _{\mathrm{out}}})$ . Then the point $\tilde y$ can be chosen so that $x_1 \ll \tilde y$ . Observe that $f_0(v_1, v_2) < 1$ implies $E(v_1, v_2) \ne \emptyset $ . Moreover, $\overline {\Omega _{\mathrm{out}}} \cap J^+(\mu _{\mathrm{in}}(1)) = \emptyset $ implies that $\mu _{\mathrm{in}}(1) \not \le y$ . Lemma 7.6 gives $w_2 \in \mathcal W$ . Therefore,

$$ \begin{align*} f_0(v_1,v_2) \leqslant f_{\text{crit}} \leqslant f_{\mu_0}^+(\tilde y) = f_0(v_1,w_2) \leqslant f_0(v_1,v_2). \end{align*} $$

But here $\tilde y \in \overline {\gamma _{v_1}}$ can be any point satisfying $\pi (v_1) < \tilde y$ , $\tau (\tilde x_1, \tilde y) = 0$ and $\tau (x_1, \tilde y)> 0$ . In particular, there is an open interval of numbers $r> 0$ such that

$$ \begin{align*} f_{\mu_0}^+(\gamma_{v_1}(r)) = f_0(v_1,v_2). \end{align*} $$

Taking into account the assumption that $f_0(v_1,v_2) < 1$ , Lemma 6.11 implies that $f_0(v_1,v_2) = -1$ . But $f^+_{\mu _0}(x_1)> -1$ and $f^+_{\mu _0}$ is increasing along $\gamma _{v_1}$ , a contradiction.

Case that there does not exist $y \in \overline {\gamma _{v_1}}$ such that $x_1 \ll y$ and $y \in J^-(\overline {\Omega _{\mathrm{out}}})$ . By Lemma 6.3 the point $\tilde y \in \overline {\gamma _{v_1}}$ can be chosen so that $\tilde y$ is not in the interior of the set K in (7.1). Then $f_{\mu _0}^+(\tilde y) = 1$ and (7.5) gives a contradiction with $f_0(v_1, v_2) < 1$ .

There is $y \in \overrightarrow {\gamma _{v_1}} \cap \overrightarrow {\gamma _{v_2}}$ such that $\gamma _{v_1}$ is optimising from $x_1$ to y. Lemma 7.9 implies that there is $x_2 < \pi (v_2)$ such that $\gamma _{v_2}$ is optimising from $x_2$ to y. Now Lemmas 7.3 and 7.7 give $E(v_1, v_2) = E(y)$ and $f_0(v_1, v_2) = f_{\mu _0}^+(y)$ , and $E(v_1, v_2)$ is in the set on the right-hand side of (7.3).

We are now ready to complete the proof of Theorem 1.3. Recall that $\pi :TM\to M$ is the map to the base point of the vector. Writing $U=\Omega _{\mathrm{out}}$ , we have

$$ \begin{align*} \mathcal E_U(y)=\pi(E(y)), \end{align*} $$

where the notation $\mathcal E_U(y)$ stands for the earliest light observation set of a point y with respect to the observation set U; see [64]. Roughly speaking, the set $\mathcal E_U(y)$ corresponds to the first observations made in the set U when there is a point source at y that sends light to all directions. Letting $v_1 \in L^+ \Omega _{\mathrm{in}}$ in Theorem 7.10 converge to a vector $v \in L_x^+ M$ , with $x=\mu _{\mathrm{in}}(s)$ for some $s\in (-1,1)$ , we see that the relation $\operatorname {\mathrm {R}}$ determines the set

$$ \begin{align*} \{E(y): \ y=\gamma_{v}(r),\ 0\leqslant r \leqslant \rho(v),\ E(y)\cap \mu_0([-1,1)) \ne \emptyset\} \end{align*} $$

for all such v. Here $E(y)\cap \mu _0([-1,1)) \ne \emptyset $ is equivalent with $f_{\mu _0}^+(y) < 1$ .

Recalling the normalisation in Remark 5, we define

$$ \begin{align*} \tilde{\mathbb D} = I^+(\mu_{\text{in}}(-1)) \cap I^-(\mu_{\text{out}}(1)). \end{align*} $$

Then the causal diamond $\mathbb D$ defined by (1.9) is contained in this larger diamond $\tilde {\mathbb D}$ . We see that the relation $\operatorname {\mathrm {R}}$ uniquely determines the set

$$ \begin{align*} E(\tilde{\mathbb D})= \{E(y)\subset T\Omega_{\text{out}}: &y=\gamma_{v}(r),\ v \in L^+_{\mu_{\text{in}}(s)} M,\ s\in (-1,1),\ r\in [0,\rho(v)],\ \\ &E(y)\cap \mu_0([-1,1)) \ne \emptyset \}. \end{align*} $$

Here $\mu _0 = \mu _{\mathrm{out}}$ . Thus, R determines

$$ \begin{align*} \mathcal E_U(\tilde{\mathbb D}) :=\{\mathcal E_U(y):\ y\in \tilde{\mathbb D}\}=\{\pi(S):\ S \in E(\tilde{\mathbb D})\}. \end{align*} $$

This reduces the proof of Theorem 1.3 to the inverse problem with passive measurements studied in [64]. By [64, Theorem 1.2], the set $\mathcal E_U(\tilde {\mathbb D})$ determines the topological, differential and conformal structures of the smaller diamond $\mathbb D$ . This proves Theorem 1.3. $\square $

8 Proof of Theorem 1.1

This section is concerned with the proof of Theorem 1.1. The first claim in the theorem, namely, determining the conformal, topological and differential structure of the manifold $(M,g)$ from either of the source-to-solution maps $\mathscr L$ or $\mathscr N$ , follows from Theorems 5.1–5.2 and Theorem 1.3. To see this, we begin by defining the relations

$$ \begin{align*} \operatorname{\mathrm{R}}_{\text{semi-lin}} = \{&(v_{0},v_{1}, v_{2},v_{3})\in L^+ \Omega_{\text{out}} \times (L^+ \Omega_{\text{in}})^3: \gamma_{v_j}\text{s are pair-wise not identical,} \\& \text{there are}\ f \in C^{\infty}_c(\Omega_{\text{in}}), \kappa_j \in \mathbb R \setminus \{0\} \quad \text{and}\quad \iota_j \in \mathcal T, j=0,1,2,3, \\&\text{s.t for all small}\ \delta'>0, \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f} \ne 0\ \text{where}\ \sigma = (v_{0},\kappa_0,\iota_0,\dots, v_{3},\kappa_3,\iota_3) \} \end{align*} $$

and

$$ \begin{align*} \operatorname{\mathrm{R}}_{\text{quasi-lin}} = \{&(v_{0},v_{1}, v_{2},v_{3})\in L^+ \Omega_{\text{out}} \times (L^+ \Omega_{\text{in}})^3: \gamma_{v_j}\text{s are pair-wise not identical,} \\& \text{there are}\ \kappa_j \in \mathbb R \setminus \{0\} \quad \text{and}\quad \iota_j \in \mathcal T, j=0,1,2,3, \\&\text{s.t for all small}\ \delta'>0, \mathscr D^{\mathrm{quasi}}_{\sigma,\delta'} \ne 0\ \text{where}\ \sigma = (v_{0},\kappa_0,\iota_0,\dots, v_{3},\kappa_3,\iota_3) \}. \end{align*} $$

It follows as a consequence of Theorems 5.1–5.2 that the source-to-solution map $\mathscr L$ (respectively $\mathscr N$ ) determines $\operatorname {\mathrm {R}}_{\mathrm{semi-lin}}$ (respectively $\operatorname {\mathrm {R}}_{\mathrm{quasi-lin}}$ ) and that the latter relations are both examples of three-to-one scattering relations; that is, they both satisfy conditions (R1) and (R2). We can therefore apply Theorem 1.3 to uniquely determine the topological, differential and conformal structure of the manifold $(M,g)$ on $\mathbb D$ from either of the source-to-solution maps $\mathscr L$ or $\mathscr N$ .

In the remainder of this section, we complete the proof of Theorem 1.1 by showing that in the case of the semi-linear equation (1.2) and if $(n,m)\neq 3$ , the conformal factor can also be determined uniquely. We will follow the ideas set out in [91]. Here, there will be some modifications as we are using Gaussian beams. The exceptional case $(n,m)=(3,3)$ will require an alternative approach that will be briefly discussed at the end of this section.

To set the idea in motion, we write $g=c\hat {g}$ for the metric on $\mathbb D$ , where $\hat {g}$ is known and $c>0$ is a smooth unknown function. Naturally, we will think of the metrics g and $\hat {g}$ as metrics on the manifold M that are conformal to each other only on the set $\mathbb D$ . Let us consider the Gaussian beams $\mathcal U_\lambda $ described in Section 3. Our aim here is to show that the values of the phase function $\phi $ restricted to the set $\mathbb D$ are independent of the conformal factor, while the principal part of the amplitude function, $a_{0,0}$ , restricted to the set $\mathbb D$ is given by

(8.1) $$ \begin{align} a_{0,0}=c^{-\frac{n-1}{4}}\hat{a}_{0,0}, \end{align} $$

where $\hat {a}_{0,0}$ is independent of the conformal factor. Showing that $\phi $ is independent of the conformal factor is trivial since the equation (3.6) for the phase function is conformally invariant.

To show (8.1), we start by recalling that the wave operator changes under conformal scalings of the metric according to the expression

(8.2) $$ \begin{align} \Box_{c\hat g} u = c^{-\frac{n+3}{4}} (\Box_{\hat{g}} + q_c) (c^{\frac{n-1}{4}}u)\quad \text{on}\ \mathbb D, \end{align} $$

where $q_c= -c^{\frac {1-n}{4}}\Box _{\hat {g}}(c^{\frac {n-1}{4}})$ .

We now return to the construction of Gaussian beams associated to the operator $\Box _g$ on M and note that due to the scaling property above on the set $\mathbb D$ , there is a one-to-one correspondence between Gaussian beams for $\Box _g$ and $\Box _{\hat {g}}+q_c$ . Here, by a Gaussian beam for $\Box _{\hat g} +q_c$ , we mean an ansatz

$$ \begin{align*}\hat{\mathcal U}_\lambda = e^{i\lambda \hat{\phi}} \hat{A}_{\lambda} \quad \text{for}\ \lambda>0\end{align*} $$

and

$$ \begin{align*}\hat{\mathcal U}_\lambda = \overline{e^{i\lambda \hat{\phi}}\hat{A}_{\lambda}} \quad \text{for}\ \lambda<0,\end{align*} $$

where we are using Fermi coordinates $(\hat {s},\hat {y}')$ near $\gamma $ with respect to the metric $\hat {g}$ and define the phase, $\hat {\phi }$ , and amplitude, $\hat {A}_{\lambda }$ , analogously to (3.5). Here, because of the presence of the zeroth-order term $q_c$ , the governing equations for construction of the phase and amplitude terms read as follows:

(8.3) $$ \begin{align} \begin{aligned} &\frac{\partial^{|\alpha|}}{\partial \hat{y}^{\prime\alpha}}\langle d\hat{\phi},d\hat{\phi}\rangle_{\hat g}=0 \quad \text{on}\ (\hat{a},\hat{b})\times\{\hat{y}'=0\},\\ &\frac{\partial^{|\alpha|}}{\partial \hat{y}^{\prime\alpha}}\left( 2\langle d\hat{\phi},d\hat{a}_j \rangle_{\hat g}- (\Box_{\hat g}\hat{\phi})\hat{a}_j + i (\Box_{\hat g}+q_c)\hat{a}_{j-1}\right)=0\quad \text{on}\ (\hat{a},\hat{b})\times\{\hat{y}'=0\}, \end{aligned}\end{align} $$

for all $j=0,1,\ldots ,N$ and all multi-indices $\alpha =(\alpha _1,\ldots ,\alpha _n) \in \{0,1,\ldots \}^n$ with $|\alpha |=\alpha _1+\ldots +\alpha _n\leqslant N$ . Thus, by setting $j=0$ in (8.3), it follows that at each point $y \in \mathbb D$ , $\hat {a}_{0,0}(y)$ is independent of the conformal factor c. To summarise, the principal part of the amplitude $a_{0,0}$ for the Gaussian beams $\mathcal U_\lambda $ on the set $\mathbb D$ must be given by (8.1) for some $\hat {a}_{0,0}$ that arises from solving (8.3) and is only dependent on the conformal class of the metric on $\mathbb D$ .

We now return to the task of showing that the conformal factor c can be uniquely determined at every point $y \in \mathbb D$ . Applying arguments similar to the proof of [29, Lemma 4], we can show that there exists a null geodesic $\gamma _{v_0}$ for some $v_0 \in L^{-}\Omega _{\mathrm{out}}$ passing through y and a null geodesic $\gamma _{v_1}$ with $v_1 \in L^+\Omega _{\mathrm{in}}$ passing through y, such that $\gamma _{v_0}$ and $\gamma _{v_1}$ have a single intersection point on the set $\mathbb D$ . Note that this property can be checked via the knowledge of the topological, differential and conformal structure of the manifold since null vectors are conformally invariant.

We now consider two null geodesics $\gamma _{v_2}$ and $\gamma _{v_3}$ in a small neighbourhood of $\gamma _{v_1}$ passing through y and such that

$$ \begin{align*}\{ \dot{\gamma}_{v_0}(s_0), \dot{\gamma}_{v_1}(s_1),\dot{\gamma}_{v_2}(s_2),\dot{\gamma}_{v_3}(s_3)\}\end{align*} $$

forms a linearly dependent set. Here, $\gamma _{v_j}(s_j)=y$ for $j=0,1,2,3$ . We emphasise that the existence of such null geodesics is guaranteed by Lemma 6.22. Now given any choice $v_0,\ldots ,v_3$ as above, we pick $\iota _j \in \mathcal T_{v_j}$ such that the amplitude term $a_{0,0}^{(j)}$ is real-valued and nonzero at the point y. We note from (8.1) that this condition can also be checked via just the conformal structure of $\mathbb D$ . Finally, we set $\kappa _0=1$ and let $\kappa _1,\kappa _2,\kappa _3\in \mathbb R\setminus \{0\}$ be arbitrary. We then consider $\sigma \in \Sigma _{v_0,v_1}$ given by $v_j$ , $\iota _j$ and $\kappa _j$ with $j=0,1,2,3$ constructed as above. As discussed, the choice $\sigma $ can be determined by just knowning the topological, differential and conformal structure of $\mathbb D$ .

Note that although $\kappa _0=1$ is fixed and $v_j$ , $\iota _j$ are also fixed for $j=0,1,2,3$ , we are free to vary $\kappa _1$ , $\kappa _2$ and $\kappa _3$ and also an arbitrary real-valued source term $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$ . For each choice of f and each nonzero $\kappa _1,\kappa _2,\kappa _3$ , we proceed to compute $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f}$ . Following the steps of the proof in Theorem 5.1 and in view of the linear dependence of $\{\dot {\gamma }_{v_j}(s_j)\}_{j=0}^3$ and the fact that $a^{(j)}_{0,0}(y)$ are all real-valued, we conclude that if $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f} \neq 0$ for some choice of $\kappa _1$ , $\kappa _2$ and $\kappa _3$ and some function $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$ , then there holds

(8.4) $$ \begin{align} \sum_{j=0}^3 \kappa_j \dot{\gamma}_{v_j}(s_j)=0.\end{align} $$

We fix $\sigma $ corresponding to such a choice of $\kappa _1$ , $\kappa _2$ and $\kappa _3$ and proceed to explicitly find the value of $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta '}$ showing that it determines c. Indeed, by retracing the proof of Theorem 5.1, using the fact that $dV_{g}=c^{\frac {n+1}{2}}dV_{\hat g}$ , together with fact that the values of the phase functions $\phi ^{(j)}$ , $j=0,1,2,3$ are independent of the conformal factor and that $a_{0,0}^{(j)}$ is real-valued at y and (8.1) holds, we obtain

(8.5) $$ \begin{align} \mathscr D^{\mathrm{semi}}_{\sigma,\delta',f}= C \,c(y)^{\frac{n+1}{2}} \,(c(y)^{-\frac{n-1}{4}})^4u_f(y)^{m-3}= C c(y)^{-\frac{n-3}{2}}u_f^{m-3}(y),\end{align} $$

where C is a constant that only depends on the conformal class in a neighbourhood of y.

The preceding analysis shows that given each $f \in C^{\infty }_c(\Omega _{\mathrm{in}})$ , we can recover the value of $c(y)^{-\frac {n-3}{2}}u_f^{m-3}(y)$ at each point $y \in \mathbb D$ . This can be simplified further by using sources f that generate real parts of Gaussian beams and such that they have (asymptotically) prescribed values at each point $y \in \mathbb D$ as in Lemma 5.3. Indeed, owing to equations (8.2)–(8.3), we can repeat the argument in the proof of Lemma 5.3 to construct explicit sources $f_\lambda \in C^{\infty }_c(\Omega _{\mathrm{in}})$ only depending on the conformal class $\hat {g}$ on $\mathbb D$ such that

$$ \begin{align*}u_{f_\lambda}(y)= c(y)^{-\frac{n-1}{4}}+\mathcal O(\lambda^{-1}),\end{align*} $$

where $\lambda>0$ is a large parameter. Combining this with (8.5) and taking a limit as $\lambda \to \infty $ , we conclude that the knowledge of the source-to-solution map $\mathscr L$ determines uniquely the values

$$ \begin{align*}c(y)^{-\frac{n-3}{2}} \,c(y)^{-\frac{(n-1)(m-3)}{4}},\end{align*} $$

at each point $y \in \mathbb D$ . Thus, it follows that c can be determined uniquely on the set $\mathbb D$ , unless $(n,m)=(3,3)$ .

We remark that in the case $(n,m)=(3,3)$ this simple approach does not yield any information. To treat this case, one needs to look further in the asymptotic expansion of $\mathcal I_{\lambda ,\sigma ,\delta ',f}$ (see Subsection 5.3) with respect to the parameter $\lambda $ than just the principal behavior that is captured by $\mathscr D^{\mathrm{semi}}_{\sigma ,\delta ',f}$ . This will also require explicitly evaluating the subprincipal term $a_{1,0}$ in the expression for the Gaussian beams (see (3.5)). As one of the main novelties of this article is the generalisation to arbitrary dimensions and also for the sake of brevity, we omit this analysis in this article. Note also that the paper [91] already deals with the particular case $n=3$ , although there the authors use a four-wave interaction.

Before closing the section, we also remark that in the case of the quasi-linear source-to-solution map $\mathscr N$ , this approach entangles information about the tensors h and the conformal factor c at the point y and additional efforts may be needed to uniquely reconstruct the conformal factor.