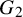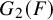1 Introduction
Let F be a non-archimedean local field of characteristic
![]() $0$
and residue characteristic p. Let
$0$
and residue characteristic p. Let
![]() $W_F$
be the Weil group of F and let
$W_F$
be the Weil group of F and let
![]() $WD_F = W_F \times \mathrm {SL}_2({\mathbb C})$
be the Weil-Deligne group. For a connected reductive group G over F, which we assume to be split for simplicity, Langlands conjectured that there is a surjective finite-to-one map from the set
$WD_F = W_F \times \mathrm {SL}_2({\mathbb C})$
be the Weil-Deligne group. For a connected reductive group G over F, which we assume to be split for simplicity, Langlands conjectured that there is a surjective finite-to-one map from the set
![]() $\mathrm {Irr}(G)$
of (equivalence classes of) irreducible smooth representations of
$\mathrm {Irr}(G)$
of (equivalence classes of) irreducible smooth representations of
![]() $G(F)$
to the set
$G(F)$
to the set
![]() $\Phi (G)$
of (equivalence classes of) L-parameters
$\Phi (G)$
of (equivalence classes of) L-parameters
where
![]() $G^{\vee }$
is the Langlands dual group of G and the homomorphisms are taken up to
$G^{\vee }$
is the Langlands dual group of G and the homomorphisms are taken up to
![]() $G^{\vee }$
-conjugacy. This leads to a partition of the set of equivalence classes of irreducible representations of
$G^{\vee }$
-conjugacy. This leads to a partition of the set of equivalence classes of irreducible representations of
![]() $G(F)$
into a disjoint union of finite subsets, which are the fibers of the map and are called L-packets. Moreover, one would like to characterize the map
$G(F)$
into a disjoint union of finite subsets, which are the fibers of the map and are called L-packets. Moreover, one would like to characterize the map
by requiring that it satisfies a number of natural conditions and to have a refined parametrization of its fibers.
This local Langland conjecture (LLC) has now been proved for
![]() $\mathrm {GL}_n$
by Harris-Taylor [Reference Harris and TaylorHT] and Henniart [Reference HenniartHe] where the map
$\mathrm {GL}_n$
by Harris-Taylor [Reference Harris and TaylorHT] and Henniart [Reference HenniartHe] where the map
![]() $\mathcal {L}$
is a bijection. Building upon this, the LLC has now been shown for the quasi-split classical groups (i.e. symplectic, special orthogonal and unitary groups) by the work of Arthur [Reference ArthurA], Moeglin and Mok [Reference MokM], as a consequence of the theory of twisted endoscopy using the stable twisted trace formula of
$\mathcal {L}$
is a bijection. Building upon this, the LLC has now been shown for the quasi-split classical groups (i.e. symplectic, special orthogonal and unitary groups) by the work of Arthur [Reference ArthurA], Moeglin and Mok [Reference MokM], as a consequence of the theory of twisted endoscopy using the stable twisted trace formula of
![]() $\mathrm {GL}_n$
, and extended to pure inner forms by various authors by various means (see for example [Reference Kaletha, Minguez, Shin and WhiteKMSW, Reference Moeglin and RenardMR, Reference Chen and ZouCZ1, Reference Chen and ZouCZ2]). It has also been shown for the group
$\mathrm {GL}_n$
, and extended to pure inner forms by various authors by various means (see for example [Reference Kaletha, Minguez, Shin and WhiteKMSW, Reference Moeglin and RenardMR, Reference Chen and ZouCZ1, Reference Chen and ZouCZ2]). It has also been shown for the group
![]() $\mathrm {GSp}(4)$
and its inner forms in [Reference Gan and TakedaGT] and [Reference Gan and TantonoGTW] using theta correspondence as the main tool. For general G, the recent work of Fargues-Scholze [Reference Fargues and ScholzeFS] gives a general geometric construction of a semisimplified LLC (which is a priori weaker than the full LLC). In another direction, for general tamely ramified groups, the work of Kaletha [Reference KalethaK1, Reference KalethaK2] constructs an LLC for supercuspidal L-packets.
$\mathrm {GSp}(4)$
and its inner forms in [Reference Gan and TakedaGT] and [Reference Gan and TantonoGTW] using theta correspondence as the main tool. For general G, the recent work of Fargues-Scholze [Reference Fargues and ScholzeFS] gives a general geometric construction of a semisimplified LLC (which is a priori weaker than the full LLC). In another direction, for general tamely ramified groups, the work of Kaletha [Reference KalethaK1, Reference KalethaK2] constructs an LLC for supercuspidal L-packets.
1.1 The main result
The purpose of this paper is to establish the local Langlands conjecture for the split exceptional group
![]() $G = G_2$
. More precisely, we prove:
$G = G_2$
. More precisely, we prove:
Main Theorem
There is a natural surjective map
with finite fibers satisfying the following properties:
-
(i)
 $\pi \in \mathrm {Irr}(G_2)$
is square-integrable (or a discrete series representation) if and only if
$\pi \in \mathrm {Irr}(G_2)$
is square-integrable (or a discrete series representation) if and only if
 $\mathcal {L}(\pi )$
does not factor through a proper Levi subgroup of
$\mathcal {L}(\pi )$
does not factor through a proper Levi subgroup of
 $G_2^{\vee }= G_2({\mathbb C})$
.
$G_2^{\vee }= G_2({\mathbb C})$
. -
(ii)
 $\pi \in \mathrm {Irr}(G_2)$
is tempered if and only if
$\pi \in \mathrm {Irr}(G_2)$
is tempered if and only if
 $\mathcal {L}(\pi )(W_F)$
is bounded in
$\mathcal {L}(\pi )(W_F)$
is bounded in
 $G_2^{\vee }= G_2({\mathbb C})$
. More precisely, if
$G_2^{\vee }= G_2({\mathbb C})$
. More precisely, if
 $\pi $
is contained in an induced representation
$\pi $
is contained in an induced representation
 $\mathrm {Ind}_P^{G_2} \tau $
, with
$\mathrm {Ind}_P^{G_2} \tau $
, with
 $P =MN$
a parabolic subgroup and
$P =MN$
a parabolic subgroup and
 $\tau $
a unitary discrete series representation of its Levi factor M, then
$\tau $
a unitary discrete series representation of its Levi factor M, then
 $\mathcal {L}(\pi )$
is the composite of the L-parameter of
$\mathcal {L}(\pi )$
is the composite of the L-parameter of
 $\tau $
with the natural inclusion
$\tau $
with the natural inclusion
 $M^{\vee } \hookrightarrow G_2^{\vee }= G_2({\mathbb C})$
, Here, note that the Levi subgroup M is either
$M^{\vee } \hookrightarrow G_2^{\vee }= G_2({\mathbb C})$
, Here, note that the Levi subgroup M is either
 $\mathrm {GL}_2$
or
$\mathrm {GL}_2$
or
 $\mathrm {GL}_1^2$
, for which the LLC is known.
$\mathrm {GL}_1^2$
, for which the LLC is known. -
(iii) If
 $\pi \in \mathrm {Irr}(G_2)$
is nontempered, so that
$\pi \in \mathrm {Irr}(G_2)$
is nontempered, so that
 $\pi $
is the unique Langlands quotient of a standard module
$\pi $
is the unique Langlands quotient of a standard module
 $\mathrm {Ind}_P^{G_2} \tau $
induced from a proper parabolic subgroup
$\mathrm {Ind}_P^{G_2} \tau $
induced from a proper parabolic subgroup
 $P = MN$
, then
$P = MN$
, then
 $\mathcal {L}(\pi )$
is the composite of the L-parameter of
$\mathcal {L}(\pi )$
is the composite of the L-parameter of
 $\tau $
with the natural inclusion
$\tau $
with the natural inclusion
 $M^{\vee } \hookrightarrow G_2^{\vee }= G_2({\mathbb C})$
.
$M^{\vee } \hookrightarrow G_2^{\vee }= G_2({\mathbb C})$
. -
(iv) The map
 $\mathcal {L}$
features in the following two commutative diagrams:
$\mathcal {L}$
features in the following two commutative diagrams:-
(a)

-
(b)

In these diagrams, the symbol L refers to the known LLC for
 $\mathrm {PD}^{\times }$
and
$\mathrm {PD}^{\times }$
and
 $\mathrm {Sp_6}$
and the maps on the right hand columns of the diagrams are induced by the natural maps of dual groups For the left hand columns in the two diagrams, the symbol
$\mathrm {Sp_6}$
and the maps on the right hand columns of the diagrams are induced by the natural maps of dual groups For the left hand columns in the two diagrams, the symbol
 $\theta $
refers to an appropriate theta correspondence (to be explained below) and rest refers to the restriction of representations, with the notation
$\theta $
refers to an appropriate theta correspondence (to be explained below) and rest refers to the restriction of representations, with the notation
 $ \mathrm {Irr}(\mathrm {Sp_6})_{/\mathrm {PGSp_6}}$
denoting the set of
$ \mathrm {Irr}(\mathrm {Sp_6})_{/\mathrm {PGSp_6}}$
denoting the set of
 $\mathrm {PGSp_6}(F)$
-orbits on
$\mathrm {PGSp_6}(F)$
-orbits on
 $\mathrm {Irr}(\mathrm {Sp_6})$
. Moreover,
$\mathrm {Irr}(\mathrm {Sp_6})$
. Moreover,
 $\mathrm {Irr}(G_2) = \mathrm {Irr}^{\heartsuit }(G_2) \sqcup \mathrm {Irr}^{\spadesuit }(G_2)$
is a decomposition of
$\mathrm {Irr}(G_2) = \mathrm {Irr}^{\heartsuit }(G_2) \sqcup \mathrm {Irr}^{\spadesuit }(G_2)$
is a decomposition of
 $\mathrm {Irr}(G_2)$
into the disjoint union of two subsets (see Theorem 1.1 below).
$\mathrm {Irr}(G_2)$
into the disjoint union of two subsets (see Theorem 1.1 below).
-
-
(v) The map
 $\mathcal {L}$
is uniquely characterized by the properties (i), (ii), (iii) and (iv).
$\mathcal {L}$
is uniquely characterized by the properties (i), (ii), (iii) and (iv). -
(vi) The map
 $\mathcal {L}$
also features in the following commutative diagram: Here,
$\mathcal {L}$
also features in the following commutative diagram: Here,
 $\mathrm {Irr}_{gen, ds}(\bullet )$
refers to the subset of generic discrete series representations in
$\mathrm {Irr}_{gen, ds}(\bullet )$
refers to the subset of generic discrete series representations in
 $\mathrm {Irr}(\bullet )$
, the left hand column of the diagram is induced by the relevant maps of dual groups mentioned in (iv) above and
$\mathrm {Irr}(\bullet )$
, the left hand column of the diagram is induced by the relevant maps of dual groups mentioned in (iv) above and
 ${\mathrm {spin}}_*$
refers to a certain spin lifting whose construction will be explained in §4.
${\mathrm {spin}}_*$
refers to a certain spin lifting whose construction will be explained in §4.
-
(vii) For each
 $\phi \in \Phi (G_2)$
, the fiber of
$\phi \in \Phi (G_2)$
, the fiber of
 $\mathcal {L}$
over
$\mathcal {L}$
over
 $\phi $
is in natural bijection with
$\phi $
is in natural bijection with
 $\mathrm {Irr} S_{\phi }$
, where when
$\mathrm {Irr} S_{\phi }$
, where when $$\begin{align*}S_{\phi} = \pi_0(Z_{G_2({\mathbb C})}(\phi)),\end{align*}$$
$$\begin{align*}S_{\phi} = \pi_0(Z_{G_2({\mathbb C})}(\phi)),\end{align*}$$
 $p \ne 3$
. When
$p \ne 3$
. When
 $p=3$
, this is still true unless perhaps for
$p=3$
, this is still true unless perhaps for
 $\phi \in \iota ^{\prime }_*(\Phi _{ds}(\mathrm {PGL}_3))$
. Moreover, for tempered
$\phi \in \iota ^{\prime }_*(\Phi _{ds}(\mathrm {PGL}_3))$
. Moreover, for tempered
 $\phi $
, the trivial character of
$\phi $
, the trivial character of
 $S_{\phi }$
corresponds to the unique generic element in
$S_{\phi }$
corresponds to the unique generic element in
 $\mathcal {L}^{-1}(\phi )$
.
$\mathcal {L}^{-1}(\phi )$
.
-
(viii) The LLC for
 $G_2$
satisfies the following global-local compatibility. Suppose that
$G_2$
satisfies the following global-local compatibility. Suppose that
 $\Pi $
is a globally generic regular algebraic cuspidal automorphic representation of
$\Pi $
is a globally generic regular algebraic cuspidal automorphic representation of
 $G_2$
over a totally real number field k with a Steinberg local component. Suppose that is a Galois representation associated to
$G_2$
over a totally real number field k with a Steinberg local component. Suppose that is a Galois representation associated to $$\begin{align*}\rho_{\Pi}: \mathrm{Gal}(\overline{k}/k) \longrightarrow \mathrm{GL}_7(\overline{{\mathbb Q}}_l)\end{align*}$$
$$\begin{align*}\rho_{\Pi}: \mathrm{Gal}(\overline{k}/k) \longrightarrow \mathrm{GL}_7(\overline{{\mathbb Q}}_l)\end{align*}$$
 $\Pi $
, in the sense that for almost all places v,
$\Pi $
, in the sense that for almost all places v,
 $\rho _{\Pi }(\mathrm {Frob}_v)_{ss}$
is conjugate to the Satake parameter
$\rho _{\Pi }(\mathrm {Frob}_v)_{ss}$
is conjugate to the Satake parameter
 $s_{\Pi _v} \in G_2(\overline {{\mathbb Q}}_l)$
. Then
$s_{\Pi _v} \in G_2(\overline {{\mathbb Q}}_l)$
. Then
 $\rho _{\Pi }$
factors through
$\rho _{\Pi }$
factors through
 $G_2(\overline {{\mathbb Q}}_l)$
(uniquely up to
$G_2(\overline {{\mathbb Q}}_l)$
(uniquely up to
 $G_2(\overline {{\mathbb Q}}_l)$
-conjugation) and for each finite place v, the restriction of
$G_2(\overline {{\mathbb Q}}_l)$
-conjugation) and for each finite place v, the restriction of
 $\rho _{\Pi }$
to the local Galois group
$\rho _{\Pi }$
to the local Galois group
 $\mathrm { Gal}(\overline {k}_v/k_v)$
corresponds to the local L-parameter
$\mathrm { Gal}(\overline {k}_v/k_v)$
corresponds to the local L-parameter
 $\mathcal {L}(\Pi _v)$
.
$\mathcal {L}(\Pi _v)$
.
-
(ix) Fix a nontrivial additive character
 $\psi : F \rightarrow {\mathbb C}^{\times }$
. In [Reference Gan and SavinGS24], we have developed a theory of
$\psi : F \rightarrow {\mathbb C}^{\times }$
. In [Reference Gan and SavinGS24], we have developed a theory of
 $\gamma $
-factors
$\gamma $
-factors
 $\gamma (s, \pi \times \tau ,\psi )$
for every
$\gamma (s, \pi \times \tau ,\psi )$
for every
 $\pi \in \mathrm {Irr}(G_2)$
and
$\pi \in \mathrm {Irr}(G_2)$
and
 $\tau \in \mathrm {Irr}(\mathrm {GL}_r)$
. Then where
$\tau \in \mathrm {Irr}(\mathrm {GL}_r)$
. Then where $$\begin{align*}\gamma(s, \pi \times \tau, \psi) = \gamma(s, \mathrm{std} \circ \mathcal{L}(\pi)) \otimes \phi_{\tau}, \psi) \end{align*}$$
$$\begin{align*}\gamma(s, \pi \times \tau, \psi) = \gamma(s, \mathrm{std} \circ \mathcal{L}(\pi)) \otimes \phi_{\tau}, \psi) \end{align*}$$
 $\phi _{\tau }: WD_F \longrightarrow \mathrm {GL}_r({\mathbb C})$
is the L-parameters of
$\phi _{\tau }: WD_F \longrightarrow \mathrm {GL}_r({\mathbb C})$
is the L-parameters of
 $\tau $
and
$\tau $
and
 $\mathrm {std}: G_2({\mathbb C}) \hookrightarrow \mathrm {GL}_7({\mathbb C})$
.
$\mathrm {std}: G_2({\mathbb C}) \hookrightarrow \mathrm {GL}_7({\mathbb C})$
.
-
(x) The map
 $\mathcal {L}$
is also uniquely characterized by the properties (i), (ii), (iii) and (ix).
$\mathcal {L}$
is also uniquely characterized by the properties (i), (ii), (iii) and (ix).
1.2 Construction of
 $\mathcal {L}$
$\mathcal {L}$
Let us make a few remarks regarding the undefined notation in (iv) and (vi) of the Main Theorem above and give a brief sketch of the main ideas used in the construction of
![]() $\mathcal {L}$
. The starting point of our work is the local theta correspondences furnished by the following dual pairs:
$\mathcal {L}$
. The starting point of our work is the local theta correspondences furnished by the following dual pairs:
 $$\begin{align*}\begin{cases} \mathrm{PD}^{\times} \times G_2 \subset E_6^{D} \\ G_2 \times \mathrm{PGSp_6} \subset E_7 \end{cases} \end{align*}$$
$$\begin{align*}\begin{cases} \mathrm{PD}^{\times} \times G_2 \subset E_6^{D} \\ G_2 \times \mathrm{PGSp_6} \subset E_7 \end{cases} \end{align*}$$
where the exceptional groups of type E are of adjoint type and D denotes a cubic division F-algebra, so that
![]() $\mathrm {PD}^{\times }$
is the unique inner form of
$\mathrm {PD}^{\times }$
is the unique inner form of
![]() $\mathrm {PGL}_3$
. One can thus consider the restriction of the minimal representation of E to the relevant dual pair and obtain a local theta correspondence. In particular, for a representation
$\mathrm {PGL}_3$
. One can thus consider the restriction of the minimal representation of E to the relevant dual pair and obtain a local theta correspondence. In particular, for a representation
![]() $\pi $
of one member of a dual pair, one has a big theta lift
$\pi $
of one member of a dual pair, one has a big theta lift
![]() $\Theta (\pi )$
on the other member of the dual pair, and its maximal semisimple quotient
$\Theta (\pi )$
on the other member of the dual pair, and its maximal semisimple quotient
![]() $\theta (\pi )$
. In [Reference Gan and SavinGS23], the following theorem was shown:
$\theta (\pi )$
. In [Reference Gan and SavinGS23], the following theorem was shown:
Theorem 1.1.
(i) (Howe duality) The Howe duality theorem holds for the above dual pairs, i.e.
![]() $\Theta (\pi )$
has finite length and its maximal semisimple quotient
$\Theta (\pi )$
has finite length and its maximal semisimple quotient
![]() $\theta (\pi )$
is irreducible or zero.
$\theta (\pi )$
is irreducible or zero.
(ii) (Theta dichotomy) Let
![]() $\pi \in \mathrm {Irr}(G_2)$
. Then
$\pi \in \mathrm {Irr}(G_2)$
. Then
![]() $\pi $
has nonzero theta lift to exactly one of
$\pi $
has nonzero theta lift to exactly one of
![]() $\mathrm {PD}^{\times }$
or
$\mathrm {PD}^{\times }$
or
![]() $\mathrm {PGSp}_6$
.
$\mathrm {PGSp}_6$
.
In view of the above dichotomy theorem, one has a decomposition
where
![]() $\mathrm {Irr}^{\heartsuit }(G_2)$
consists of those irreducible representations which participate in theta correspondence with
$\mathrm {Irr}^{\heartsuit }(G_2)$
consists of those irreducible representations which participate in theta correspondence with
![]() $\mathrm {PGSp_6}$
and
$\mathrm {PGSp_6}$
and
![]() $\mathrm {Irr}^{\spadesuit }(G_2)$
consists of those which participate in theta correspondence with
$\mathrm {Irr}^{\spadesuit }(G_2)$
consists of those which participate in theta correspondence with
![]() $\mathrm {PD}^{\times }$
. This explains the left hand sides of the two commutative diagrams in (iv) of the Main Theorem.
$\mathrm {PD}^{\times }$
. This explains the left hand sides of the two commutative diagrams in (iv) of the Main Theorem.
We can now sketch how one can define the map
![]() $\mathcal {L}: \mathrm {Irr}(G_2) \longrightarrow \Phi (G_2)$
. Suppose that
$\mathcal {L}: \mathrm {Irr}(G_2) \longrightarrow \Phi (G_2)$
. Suppose that
![]() $\pi \in \mathrm {Irr}(G_2)$
, then we define its L-parameter
$\pi \in \mathrm {Irr}(G_2)$
, then we define its L-parameter
![]() $\phi _{\pi }:= \mathcal {L}(\pi )$
as follows:
$\phi _{\pi }:= \mathcal {L}(\pi )$
as follows:
-
• if
 $\pi \in \mathrm {Irr}^{\spadesuit }(G_2)$
, say
$\pi \in \mathrm {Irr}^{\spadesuit }(G_2)$
, say
 $\theta _D(\pi ) = \tau _D \in \mathrm {Irr}(\mathrm {PD}^{\times })$
, consider the Jacquet-Langlands lift
$\theta _D(\pi ) = \tau _D \in \mathrm {Irr}(\mathrm {PD}^{\times })$
, consider the Jacquet-Langlands lift
 $\tau $
of
$\tau $
of
 $\tau _D$
to
$\tau _D$
to
 $\mathrm {PGL}_3$
with L-parameter
$\mathrm {PGL}_3$
with L-parameter
 $\phi _{\tau }$
. Then we set where
$\phi _{\tau }$
. Then we set where $$\begin{align*}\phi_{\pi} = \iota' \circ \phi_{\tau}: WD_F \longrightarrow \mathrm{SL}_3({\mathbb C}) \subset G_2({\mathbb C}). \end{align*}$$
$$\begin{align*}\phi_{\pi} = \iota' \circ \phi_{\tau}: WD_F \longrightarrow \mathrm{SL}_3({\mathbb C}) \subset G_2({\mathbb C}). \end{align*}$$
 $\iota ': \mathrm {SL}_3({\mathbb C}) \hookrightarrow G_2({\mathbb C})$
is the natural inclusion.
$\iota ': \mathrm {SL}_3({\mathbb C}) \hookrightarrow G_2({\mathbb C})$
is the natural inclusion.
-
• if
 $\pi \in \mathrm {Irr}^{\heartsuit }(G_2)$
, say
$\pi \in \mathrm {Irr}^{\heartsuit }(G_2)$
, say
 $\theta (\pi ) = \sigma \in \mathrm {Irr}(\mathrm {PGSp_6})$
, then gives rise to an L-parameter (à la Arthur)
$\theta (\pi ) = \sigma \in \mathrm {Irr}(\mathrm {PGSp_6})$
, then gives rise to an L-parameter (à la Arthur) $$\begin{align*}\mathrm{rest}(\sigma)\in \mathrm{Irr}(\mathrm{Sp_6}(F))_{/ \mathrm{PGSp_6}(F)}, \end{align*}$$
At this point, one needs to show that
$$\begin{align*}\mathrm{rest}(\sigma)\in \mathrm{Irr}(\mathrm{Sp_6}(F))_{/ \mathrm{PGSp_6}(F)}, \end{align*}$$
At this point, one needs to show that $$\begin{align*}\phi_{\mathrm{rest}(\sigma)}: WD_F \longrightarrow \mathrm{SO}_7({\mathbb C}).\end{align*}$$
$$\begin{align*}\phi_{\mathrm{rest}(\sigma)}: WD_F \longrightarrow \mathrm{SO}_7({\mathbb C}).\end{align*}$$
 $\phi _{\mathrm {rest}(\sigma )}$
factors through
$\phi _{\mathrm {rest}(\sigma )}$
factors through
 $G_2({\mathbb C})$
, uniquely up to
$G_2({\mathbb C})$
, uniquely up to
 $G_2({\mathbb C})$
-conjugacy. We shall achieve this by a global argument, using various globalization results which are given in Appendices A and B (i.e. §9 and §11), the construction of Galois representations associated to cohomological cuspidal representations of
$G_2({\mathbb C})$
-conjugacy. We shall achieve this by a global argument, using various globalization results which are given in Appendices A and B (i.e. §9 and §11), the construction of Galois representations associated to cohomological cuspidal representations of
 $\mathrm {GL}_7$
and the group theoretic results of Chenevier [Reference ChenevierC] and Greiss [Reference GriessGr95]. After this, we set
$\mathrm {GL}_7$
and the group theoretic results of Chenevier [Reference ChenevierC] and Greiss [Reference GriessGr95]. After this, we set
 $\phi _{\pi } := \phi _{\mathrm {rest}(\theta (\pi ))}$
as a map valued in
$\phi _{\pi } := \phi _{\mathrm {rest}(\theta (\pi ))}$
as a map valued in
 $G_2({\mathbb C})$
, well-defined up to
$G_2({\mathbb C})$
, well-defined up to
 $G_2({\mathbb C})$
-conjugacy.
$G_2({\mathbb C})$
-conjugacy.
In other words, using the theta correspondence and theta dichotomy, we deduce the LLC for
![]() $G_2$
from the known LLC for
$G_2$
from the known LLC for
![]() $\mathrm {PD}^{\times }$
and
$\mathrm {PD}^{\times }$
and
![]() $\mathrm {Sp_6}$
. Moreover, by construction, one has the commutative diagrams in (iv), and the various results alluded to above give the characterization of
$\mathrm {Sp_6}$
. Moreover, by construction, one has the commutative diagrams in (iv), and the various results alluded to above give the characterization of
![]() $\mathcal {L}$
in (v).
$\mathcal {L}$
in (v).
1.3 Fibers of
 $\mathcal {L}$
$\mathcal {L}$
Parametrizing the fibers of
![]() $\mathcal {L}$
(i.e. showing (vii) of the Main Theorem) is the most delicate part of this paper which requires key new ideas. In constructing the map
$\mathcal {L}$
(i.e. showing (vii) of the Main Theorem) is the most delicate part of this paper which requires key new ideas. In constructing the map
![]() $\mathcal {L}$
, we had only needed to appeal to the LLC for
$\mathcal {L}$
, we had only needed to appeal to the LLC for
![]() $\mathrm {Sp_6}$
. To explicate the fibers of
$\mathrm {Sp_6}$
. To explicate the fibers of
![]() $\mathcal {L}$
(for example, to show that
$\mathcal {L}$
(for example, to show that
![]() $\mathcal {L}$
is surjective), it would help greatly if the LLC for
$\mathcal {L}$
is surjective), it would help greatly if the LLC for
![]() $\mathrm {PGSp_6}$
is known. Of course, the requirement of compatibility of restriction with the LLC of
$\mathrm {PGSp_6}$
is known. Of course, the requirement of compatibility of restriction with the LLC of
![]() $\mathrm {Sp}_{2n}$
places severe constraints on the LLC for
$\mathrm {Sp}_{2n}$
places severe constraints on the LLC for
![]() $\mathrm {PGSp}_{2n}$
, but there is an inherent “quadratic ambiguity” on both the representation theoretic and Galois theoretic sides that the LLC for
$\mathrm {PGSp}_{2n}$
, but there is an inherent “quadratic ambiguity” on both the representation theoretic and Galois theoretic sides that the LLC for
![]() $\mathrm {Sp}_{2n}$
cannot resolve. We circumvent the lack of the full LLC for
$\mathrm {Sp}_{2n}$
cannot resolve. We circumvent the lack of the full LLC for
![]() $\mathrm {PGSp_6}$
by making crucial use of the following inputs:
$\mathrm {PGSp_6}$
by making crucial use of the following inputs:
-
• In his thesis and subsequent work [Reference XuXu1, Reference XuXu2], Bin Xu has resolved the quadratic ambiguities on the representation theoretic side, defining a partition of
 $\mathrm {Irr}(\mathrm {PGSp}_{2n})$
into candidate local L-packets and establishing Arthur’s multiplicity formula in the global setting based on these local partitions. We will summarize his results that we need in §7;
$\mathrm {Irr}(\mathrm {PGSp}_{2n})$
into candidate local L-packets and establishing Arthur’s multiplicity formula in the global setting based on these local partitions. We will summarize his results that we need in §7; -
• We make use of results of Kret and Shin [Reference Kret and ShinKS] who gave a construction of Galois representations valued in
 $\mathrm {GSpin}_{2n+1}({\mathbb C})$
associated to certain cuspidal automorphic representations of
$\mathrm {GSpin}_{2n+1}({\mathbb C})$
associated to certain cuspidal automorphic representations of
 $\mathrm {GSp}_{2n}$
. This is summarized in §5;
$\mathrm {GSp}_{2n}$
. This is summarized in §5; -
• By a combination of the similitude classical theta lifting from
 $\mathrm {PGSp_6}$
to
$\mathrm {PGSp_6}$
to
 $\mathrm {PGSO}_8$
and the theory of triality on
$\mathrm {PGSO}_8$
and the theory of triality on
 $\mathrm {PGSO}_8$
, we construct on the representation theoretic side a Spin lifting which should be associated to the map of dual groups
$\mathrm {PGSO}_8$
, we construct on the representation theoretic side a Spin lifting which should be associated to the map of dual groups $$\begin{align*}{\mathrm{spin}}_*: \mathrm{Irr}(\mathrm{PGSp_6}) \longrightarrow \mathrm{Irr}(\mathrm{SO}_8) \longrightarrow \mathrm{Irr}( \mathrm{GL}_8) \end{align*}$$
given by the spin representation of
$$\begin{align*}{\mathrm{spin}}_*: \mathrm{Irr}(\mathrm{PGSp_6}) \longrightarrow \mathrm{Irr}(\mathrm{SO}_8) \longrightarrow \mathrm{Irr}( \mathrm{GL}_8) \end{align*}$$
given by the spin representation of $$\begin{align*}{\mathrm{spin}}: \mathrm{Spin}_7({\mathbb C}) \longrightarrow \mathrm{SO}_8({\mathbb C}) \longrightarrow \mathrm{GL}_8({\mathbb C}) \end{align*}$$
$$\begin{align*}{\mathrm{spin}}: \mathrm{Spin}_7({\mathbb C}) \longrightarrow \mathrm{SO}_8({\mathbb C}) \longrightarrow \mathrm{GL}_8({\mathbb C}) \end{align*}$$
 $\mathrm {Spin}_7({\mathbb C})$
; this is given in §4.
$\mathrm {Spin}_7({\mathbb C})$
; this is given in §4.
The combination of these various inputs to understand the fibers of
![]() $\mathcal {L}$
requires an execution too delicate to explain in the introduction. An outcome of this is the commutative diagram in (vi) of the Main Theorem, which plays a key role in the proof of (vii).
$\mathcal {L}$
requires an execution too delicate to explain in the introduction. An outcome of this is the commutative diagram in (vi) of the Main Theorem, which plays a key role in the proof of (vii).
This exploitation of triality to produce the Spin lifting is certainly one of the main innovations of this paper; it will be discussed in greater detail in §4. The idea can be pushed further to yield a weak LLC for
![]() $\mathrm {PGSp_6}$
; this is carried out in Appendix C of this paper. Such applications of triality in the global setting were first obtained in the paper [Reference Chenevier and GanCG2] of G. Chenevier and the first author.
$\mathrm {PGSp_6}$
; this is carried out in Appendix C of this paper. Such applications of triality in the global setting were first obtained in the paper [Reference Chenevier and GanCG2] of G. Chenevier and the first author.
1.4 Prior work, related literature and further remarks
We conclude this introduction by mentioning some prior work towards the LLC for
![]() $G_2$
and their relevance to the current paper:
$G_2$
and their relevance to the current paper:
-
• In [Reference Savin and WeissmanSW], the second author and M. Weissman showed that an irreducible generic supercuspidal representation of
 $G_2$
has nonzero theta lift to a generic supercuspidal representation of exactly one of
$G_2$
has nonzero theta lift to a generic supercuspidal representation of exactly one of
 $\mathrm {PGL}_3$
or
$\mathrm {PGL}_3$
or
 $\mathrm {PGSp_6}$
; this is a precursor of the dichotomy theorem of [Reference Gan and SavinGS23] mentioned above.
$\mathrm {PGSp_6}$
; this is a precursor of the dichotomy theorem of [Reference Gan and SavinGS23] mentioned above. -
• In [Reference Harris, Khare and ThorneHKT], Harris-Khare-Thorne constructed a bijection
where the LHS refers to the set of irreducible generic supercuspidal representations, whereas the RHS refers to supercuspidal L-parameters, i.e. discrete L-parameters $$\begin{align*}\mathrm{Irr}_{sc, gen}(G_2(F)) \longleftrightarrow \Phi_{sc}(G_2) \end{align*}$$
$$\begin{align*}\mathrm{Irr}_{sc, gen}(G_2(F)) \longleftrightarrow \Phi_{sc}(G_2) \end{align*}$$
 $W_F \longrightarrow G_2({\mathbb C})$
trivial on the Deligne
$W_F \longrightarrow G_2({\mathbb C})$
trivial on the Deligne
 $\mathrm {SL}_2$
. In doing this, they made use of the results of Savin-Weissman [Reference Savin and WeissmanSW], Chenevier [Reference ChenevierC] and Hundley-Liu [Reference Hundley and LiuHL] (on an automorphic descent from
$\mathrm {SL}_2$
. In doing this, they made use of the results of Savin-Weissman [Reference Savin and WeissmanSW], Chenevier [Reference ChenevierC] and Hundley-Liu [Reference Hundley and LiuHL] (on an automorphic descent from
 $\mathrm {GL}_7$
to
$\mathrm {GL}_7$
to
 $G_2$
). In addition, they made crucial use of potential modularity results from the theory of Galois representations. For this paper, we shall not make use of the results of [Reference Harris, Khare and ThorneHKT]. Rather, we shall reprove their result by different means in the course of the proof of the Main Theorem. More precisely, we do not appeal to automorphic descent [Reference Hundley and LiuHL] or potentially modularity results, but exploit the theory of triality and [Reference Savin and WeissmanSW].
$G_2$
). In addition, they made crucial use of potential modularity results from the theory of Galois representations. For this paper, we shall not make use of the results of [Reference Harris, Khare and ThorneHKT]. Rather, we shall reprove their result by different means in the course of the proof of the Main Theorem. More precisely, we do not appeal to automorphic descent [Reference Hundley and LiuHL] or potentially modularity results, but exploit the theory of triality and [Reference Savin and WeissmanSW].
-
• In [Reference Aubert, Moussaoui and SolleveldAMS], Aubert-Moussaoui-Solleveld defined the notion of cuspidal support for enhanced L-parameters and formulated the conjecture [Reference Aubert, Moussaoui and SolleveldAMS, Conj. 7.8] that the LLC map should be compatible with the cuspidal support maps on both sides. In a recent preprint [Reference Aubert and XuAX], Aubert-Xu explored the implications of [Reference Aubert, Moussaoui and SolleveldAMS, Conj. 7.8] (which is formulated as [Reference Aubert and XuAX, Property 2.3.14]) for the LLC of
 $G_2$
. For
$G_2$
. For
 $p \ne 2 $
or
$p \ne 2 $
or
 $3$
, they took Kaletha’s construction of the LLC for supercuspidal L-packets as a starting point and tried to use the usual desiderata of the LLC and [Reference Aubert, Moussaoui and SolleveldAMS, Conj. 7.8] as guiding principles to extend it to non-supercuspidal representations, as well as the remaining (singular) supercuspidal ones.
$3$
, they took Kaletha’s construction of the LLC for supercuspidal L-packets as a starting point and tried to use the usual desiderata of the LLC and [Reference Aubert, Moussaoui and SolleveldAMS, Conj. 7.8] as guiding principles to extend it to non-supercuspidal representations, as well as the remaining (singular) supercuspidal ones.More precisely, for non-supercuspidal representations of
 $G_2$
, they used essentially the same process as [Reference Gan and SavinGS23, §3.5] to define the LLC and then verify that this is consistent with [Reference Aubert, Moussaoui and SolleveldAMS, Conj. 7.8]. An interesting aspect of their work is the use of [Reference Aubert, Moussaoui and SolleveldAMS, Conj. 7.8] to limit the possible options for the enhanced L-parameters of singular supercuspidal representations. This places nontrivial constraints on the possible enhanced L-parameters, but is ultimately not sufficient for them to obtain a definitive LLC map for
$G_2$
, they used essentially the same process as [Reference Gan and SavinGS23, §3.5] to define the LLC and then verify that this is consistent with [Reference Aubert, Moussaoui and SolleveldAMS, Conj. 7.8]. An interesting aspect of their work is the use of [Reference Aubert, Moussaoui and SolleveldAMS, Conj. 7.8] to limit the possible options for the enhanced L-parameters of singular supercuspidal representations. This places nontrivial constraints on the possible enhanced L-parameters, but is ultimately not sufficient for them to obtain a definitive LLC map for
 $G_2$
.
$G_2$
.From our point of view, the association of (enhanced) L-parameters to non-supercuspidal representations of
 $G_2$
is completely dictated by the usual desiderata of the LLC, as we explained in [Reference Gan and SavinGS23, §3.5]. Hence, for us, the main point in constructing the LLC for
$G_2$
is completely dictated by the usual desiderata of the LLC, as we explained in [Reference Gan and SavinGS23, §3.5]. Hence, for us, the main point in constructing the LLC for
 $G_2$
is to take care of the supercuspidal representations, especially the non-generic ones. In particular, we do not use the results of Kaletha [Reference KalethaK1, Reference KalethaK2] in this paper. It will of course be interesting to see if the LLC supplied by our Main Theorem agrees with the supercuspidal L-packets constructed by Kaletha [Reference KalethaK1, Reference KalethaK2] in the case of
$G_2$
is to take care of the supercuspidal representations, especially the non-generic ones. In particular, we do not use the results of Kaletha [Reference KalethaK1, Reference KalethaK2] in this paper. It will of course be interesting to see if the LLC supplied by our Main Theorem agrees with the supercuspidal L-packets constructed by Kaletha [Reference KalethaK1, Reference KalethaK2] in the case of
 $G_2$
.
$G_2$
. -
• Likewise, it will be interesting to verify the compatibility of our LLC map with the semisimple one defined by Fargues-Scholze [Reference Fargues and ScholzeFS]. Currently, besides the case of
 $\mathrm {GL}_n$
and related groups, such compatibility results are known for
$\mathrm {GL}_n$
and related groups, such compatibility results are known for
 $\mathrm {GSp}_4$
and odd unitary groups. The proofs proceed by global means, using Shimura varieties and Arthur multiplicity formula. Both these ingredients are not available in the setting of
$\mathrm {GSp}_4$
and odd unitary groups. The proofs proceed by global means, using Shimura varieties and Arthur multiplicity formula. Both these ingredients are not available in the setting of
 $G_2$
.
$G_2$
. -
• We have given two independent characterizations of
 $\mathcal {L}$
in (v) and (x) of the Main Theorem. The characterization of
$\mathcal {L}$
in (v) and (x) of the Main Theorem. The characterization of
 $\mathcal {L}$
in (v) via the commutative diagrams in (iv) is of an extrinsic nature, involving transfers of representations to other groups. One may complain that this is not-so-satisfactory. On the other hand, the construction and characterization of the LLC for classical groups G by twisted endoscopic transfer to
$\mathcal {L}$
in (v) via the commutative diagrams in (iv) is of an extrinsic nature, involving transfers of representations to other groups. One may complain that this is not-so-satisfactory. On the other hand, the construction and characterization of the LLC for classical groups G by twisted endoscopic transfer to
 $\mathrm {GL}_n$
in the work of Arthur [Reference ArthurA] is in the same spirit as our characterization in (v). Namely, the LLC map
$\mathrm {GL}_n$
in the work of Arthur [Reference ArthurA] is in the same spirit as our characterization in (v). Namely, the LLC map
 $\mathcal {L}_G$
for a classical G is the unique map for which one has a commutative diagram: where t stands for the twisted endoscopic transfer and
$\mathcal {L}_G$
for a classical G is the unique map for which one has a commutative diagram: where t stands for the twisted endoscopic transfer and
 $\mathrm {std}: G^{\vee } \rightarrow \mathrm {GL}_n({\mathbb C})$
is the standard representation.
$\mathrm {std}: G^{\vee } \rightarrow \mathrm {GL}_n({\mathbb C})$
is the standard representation.
The characterization by gamma factors of pairs in (x) is more intrinsic and closer in spirit to the characterization of the LLC for
 $\mathrm {GL}_n$
. Such a characterization is perhaps more useful for applications to number theory. since it is more closely connected with L-functions.
$\mathrm {GL}_n$
. Such a characterization is perhaps more useful for applications to number theory. since it is more closely connected with L-functions. -
• We do not address the issues of stability and endoscopic character identities for our L-packets in this paper. This is obviously a natural problem to consider. One should be able to show these using a combination of theta correspondence and the stable trace formula, along the lines of [Reference Chan and GanCG] for the LLC of
 $\mathrm {GSp}_4$
.
$\mathrm {GSp}_4$
. -
• In Appendix C (i.e. §12), we show how the exploitation of the principle of triality and the results of Kret-Shin allow one to construct a weak LLC map for
 $\mathrm {PGSp_6}$
. We also explain how this refines the results of Bin Xu [Reference XuXu2] for similitude classical groups in the limited context of
$\mathrm {PGSp_6}$
. We also explain how this refines the results of Bin Xu [Reference XuXu2] for similitude classical groups in the limited context of
 $\mathrm {PGSp_6}$
.
$\mathrm {PGSp_6}$
.
2 Theta Dichotomy
We begin by recalling in greater detail the main results of [Reference Gan and SavinGS23] that were briefly alluded to in the introduction.
2.1 Theta correspondences
In [Reference Gan and SavinGS23], we studied the local theta correspondence for the following dual pairs:

where D denotes a cubic division F-algebra. More precisely, one has the dual pairs
 $$\begin{align*}\begin{cases} (\mathrm{PGL}_3 \rtimes {\mathbb Z}/2{\mathbb Z}) \times G_2 \subset E_6 \rtimes {\mathbb Z}/2{\mathbb Z} \\ \mathrm{PD}^{\times} \times G_2 \subset E_6^{D} \\ G_2 \times \mathrm{PGSp_6} \subset E_7 \end{cases} \end{align*}$$
$$\begin{align*}\begin{cases} (\mathrm{PGL}_3 \rtimes {\mathbb Z}/2{\mathbb Z}) \times G_2 \subset E_6 \rtimes {\mathbb Z}/2{\mathbb Z} \\ \mathrm{PD}^{\times} \times G_2 \subset E_6^{D} \\ G_2 \times \mathrm{PGSp_6} \subset E_7 \end{cases} \end{align*}$$
where the exceptional groups of type E are of adjoint type. One can thus consider the restriction of the minimal representation of E to the relevant dual pair and obtain a local theta correspondence. In particular, for a representation
![]() $\pi $
of one member of a dual pair, one has a big theta lift
$\pi $
of one member of a dual pair, one has a big theta lift
![]() $\Theta (\pi )$
on the other member of the dual pair, and its maximal semisimple quotient
$\Theta (\pi )$
on the other member of the dual pair, and its maximal semisimple quotient
![]() $\theta (\pi )$
. In [Reference Gan and SavinGS23], the following theorem was shown:
$\theta (\pi )$
. In [Reference Gan and SavinGS23], the following theorem was shown:
Theorem 2.1.
(i) (Howe duality) The Howe duality theorem holds for the above dual pairs, i.e.
![]() $\Theta (\pi )$
has finite length and its maximal semisimple quotient
$\Theta (\pi )$
has finite length and its maximal semisimple quotient
![]() $\theta (\pi )$
is irreducible or zero.
$\theta (\pi )$
is irreducible or zero.
(ii) (Theta dichotomy) Let
![]() $\pi \in \mathrm {Irr}(G_2)$
. Then
$\pi \in \mathrm {Irr}(G_2)$
. Then
![]() $\pi $
has nonzero theta lift to exactly one of
$\pi $
has nonzero theta lift to exactly one of
![]() $\mathrm {PD}^{\times }$
or
$\mathrm {PD}^{\times }$
or
![]() $\mathrm {PGSp}_6$
. In particular, one has a decomposition:
$\mathrm {PGSp}_6$
. In particular, one has a decomposition:
where
![]() $\mathrm {Irr}^{\heartsuit }(G_2)$
consists of those irreducible representations which participate in theta correspondence with
$\mathrm {Irr}^{\heartsuit }(G_2)$
consists of those irreducible representations which participate in theta correspondence with
![]() $\mathrm {PGSp_6}$
and
$\mathrm {PGSp_6}$
and
![]() $\mathrm {Irr}^{\spadesuit }(G_2)$
consists of those which participate in theta correspondence with
$\mathrm {Irr}^{\spadesuit }(G_2)$
consists of those which participate in theta correspondence with
![]() $\mathrm {PD}^{\times }$
.
$\mathrm {PD}^{\times }$
.
(iii) More precisely, one has:
-
(a) the theta correspondence for
 $\mathrm {PD}^{\times } \times G_2$
defines an injective map which is bijective if
$\mathrm {PD}^{\times } \times G_2$
defines an injective map which is bijective if $$\begin{align*}\theta_{D} : \mathrm{Irr}^{\spadesuit}(G_2) \hookrightarrow \mathrm{Irr}(\mathrm{PD}^{\times}), \end{align*}$$
$$\begin{align*}\theta_{D} : \mathrm{Irr}^{\spadesuit}(G_2) \hookrightarrow \mathrm{Irr}(\mathrm{PD}^{\times}), \end{align*}$$
 $p\ne 3$
. Moreover,
$p\ne 3$
. Moreover,
 $\mathrm {Irr}^{\spadesuit }(G_2)$
is contained in the subset
$\mathrm {Irr}^{\spadesuit }(G_2)$
is contained in the subset
 $\mathrm {Irr}_{ds}(G_2)$
of discrete series representations.
$\mathrm {Irr}_{ds}(G_2)$
of discrete series representations.
-
(b) the theta correspondence for
 $G_2 \times \mathrm {PGSp_6}$
defines an injection The map
$G_2 \times \mathrm {PGSp_6}$
defines an injection The map $$\begin{align*}\theta: \mathrm{Irr}^{\heartsuit}(G_2) \hookrightarrow \mathrm{Irr} (\mathrm{PGSp_6}). \end{align*}$$
$$\begin{align*}\theta: \mathrm{Irr}^{\heartsuit}(G_2) \hookrightarrow \mathrm{Irr} (\mathrm{PGSp_6}). \end{align*}$$
 $\theta $
carries tempered representations to tempered representations.
$\theta $
carries tempered representations to tempered representations.
-
(c) the theta correspondence for
 $(\mathrm {PGL}_3\rtimes {\mathbb Z}/2{\mathbb Z}) \times G_2$
defines an injective map where
$(\mathrm {PGL}_3\rtimes {\mathbb Z}/2{\mathbb Z}) \times G_2$
defines an injective map where $$\begin{align*}\theta_{M_3} : \mathrm{Irr}^{\clubsuit}(G_2) \hookrightarrow \mathrm{Irr} (\mathrm{PGL}_3 \rtimes {\mathbb Z}/2{\mathbb Z}), \end{align*}$$
$$\begin{align*}\theta_{M_3} : \mathrm{Irr}^{\clubsuit}(G_2) \hookrightarrow \mathrm{Irr} (\mathrm{PGL}_3 \rtimes {\mathbb Z}/2{\mathbb Z}), \end{align*}$$
 $\mathrm {Irr}^{\clubsuit }(G_2) \subset \mathrm {Irr}^{\heartsuit }(G_2)$
is the subset of representations which participates in theta correspondence with
$\mathrm {Irr}^{\clubsuit }(G_2) \subset \mathrm {Irr}^{\heartsuit }(G_2)$
is the subset of representations which participates in theta correspondence with
 $\mathrm {PGL}_3 \rtimes {\mathbb Z}/2{\mathbb Z}$
. The map
$\mathrm {PGL}_3 \rtimes {\mathbb Z}/2{\mathbb Z}$
. The map
 $\theta _{M_3}$
respects tempered (resp. discrete series) representations. Moreover, its image has been completely determined.
$\theta _{M_3}$
respects tempered (resp. discrete series) representations. Moreover, its image has been completely determined.
By Theorem 2.1(iii), as a refinement of the decomposition of
![]() $\mathrm {Irr}(G_2)$
in Theorem 2.1(i), one has a further decomposition
$\mathrm {Irr}(G_2)$
in Theorem 2.1(i), one has a further decomposition
where
![]() $\mathrm {Irr}^{\clubsuit }(G_2)$
consists of those representations which participate in theta correspondence with
$\mathrm {Irr}^{\clubsuit }(G_2)$
consists of those representations which participate in theta correspondence with
![]() $\mathrm {PGL}_3\rtimes {\mathbb Z}/2{\mathbb Z}$
and
$\mathrm {PGL}_3\rtimes {\mathbb Z}/2{\mathbb Z}$
and
![]() $ \mathrm {Irr}^{\diamondsuit }(G_2)$
consists of those which participate exclusively in the theta correspondence with
$ \mathrm {Irr}^{\diamondsuit }(G_2)$
consists of those which participate exclusively in the theta correspondence with
![]() $\mathrm {PGSp_6}$
. Further, we have a trichotomy result for discrete series representations:
$\mathrm {PGSp_6}$
. Further, we have a trichotomy result for discrete series representations:
Proposition 2.3. Each irreducible discrete series representation of
![]() $G_2$
has a nonzero discrete series theta lift to exactly one of
$G_2$
has a nonzero discrete series theta lift to exactly one of
![]() $\mathrm {PD}^{\times }$
,
$\mathrm {PD}^{\times }$
,
![]() $\mathrm {PGL}_3 \rtimes {\mathbb Z}/2{\mathbb Z}$
or
$\mathrm {PGL}_3 \rtimes {\mathbb Z}/2{\mathbb Z}$
or
![]() $\mathrm {PGSp_6}$
. Setting
$\mathrm {PGSp_6}$
. Setting
![]() $\mathrm {Irr}^{\bullet }_{ds}(G_2) = \mathrm {Irr}_{ds}(G_2) \cap \mathrm {Irr}^{\bullet }(G_2)$
, this trichotomy is given by the disjoint union
$\mathrm {Irr}^{\bullet }_{ds}(G_2) = \mathrm {Irr}_{ds}(G_2) \cap \mathrm {Irr}^{\bullet }(G_2)$
, this trichotomy is given by the disjoint union
In fact, the results of [Reference Gan and SavinGS23] give a precise determination of the maps
![]() $\theta _{M_3}$
and
$\theta _{M_3}$
and
![]() $\theta $
on nonsupercuspidal (in particular nontempered) representations. These precise results are too intricate to recall here; we refer the reader to [Reference Gan and SavinGS23].
$\theta $
on nonsupercuspidal (in particular nontempered) representations. These precise results are too intricate to recall here; we refer the reader to [Reference Gan and SavinGS23].
2.2 Maps of L-parameters
The above dichotomy results on the representation theory side is reflected to some extent by analogous results on the side of L-parameters. Recall the natural morphisms of Langlands dual groups
which induce natural maps
Moreover, the outer automorphism of
![]() $\mathrm {SL}_3({\mathbb C})$
induces an action of
$\mathrm {SL}_3({\mathbb C})$
induces an action of
![]() ${\mathbb Z}/2{\mathbb Z}$
on
${\mathbb Z}/2{\mathbb Z}$
on
![]() $\Phi (\mathrm {PGL}_3)$
. We note:
$\Phi (\mathrm {PGL}_3)$
. We note:
Lemma 2.4.
(i) The map
![]() $\iota ^{\prime }_*$
gives an injection
$\iota ^{\prime }_*$
gives an injection
whose image we denote by
![]() $\Phi ^{\spadesuit \clubsuit }(G_2)$
. It restricts to an injection
$\Phi ^{\spadesuit \clubsuit }(G_2)$
. It restricts to an injection
and the image of
![]() $\Phi _{ds}(\mathrm {PGL}_3)$
is characterized as those
$\Phi _{ds}(\mathrm {PGL}_3)$
is characterized as those
![]() $\phi \in \Phi _{ds}(G_2)$
such that the local L-factor
$\phi \in \Phi _{ds}(G_2)$
such that the local L-factor
![]() $L(s, \mathrm {std} \circ \iota \circ \phi )$
has a pole at
$L(s, \mathrm {std} \circ \iota \circ \phi )$
has a pole at
![]() $s=0$
.
$s=0$
.
Moreover, for
![]() $\phi \in \Phi _{ds}(\mathrm {PGL}_3)$
with component group
$\phi \in \Phi _{ds}(\mathrm {PGL}_3)$
with component group
![]() $S_{\phi } = \mu _3$
, one has
$S_{\phi } = \mu _3$
, one has
 $$\begin{align*}S_{\iota^{\prime}_*(\phi)} = \begin{cases} \mu_3 \text{ if } \phi\ \text{is not self-dual;} \\ S_3 \text{ if } \phi\ \text{is self-dual.} \end{cases} \end{align*}$$
$$\begin{align*}S_{\iota^{\prime}_*(\phi)} = \begin{cases} \mu_3 \text{ if } \phi\ \text{is not self-dual;} \\ S_3 \text{ if } \phi\ \text{is self-dual.} \end{cases} \end{align*}$$
(ii) The map
![]() $\iota _*$
gives an injection
$\iota _*$
gives an injection
which restricts to an injection
The image of
![]() $\Phi ^{\diamondsuit }_{ds}(G_2)$
is characterized as those
$\Phi ^{\diamondsuit }_{ds}(G_2)$
is characterized as those
![]() $\phi ' \in \Phi _{ds}(\mathrm {PGSp_6})$
such that the local L-factor
$\phi ' \in \Phi _{ds}(\mathrm {PGSp_6})$
such that the local L-factor
![]() $L(s, {\mathrm {spin}} \circ \phi ')$
has a pole at
$L(s, {\mathrm {spin}} \circ \phi ')$
has a pole at
![]() $s=0$
. Moreover, for
$s=0$
. Moreover, for
![]() $\phi \in \Phi ^{\diamondsuit }_{ds}( G_2)$
with component group
$\phi \in \Phi ^{\diamondsuit }_{ds}( G_2)$
with component group
![]() $S_{\phi }$
, one has
$S_{\phi }$
, one has
where
![]() $Z(\mathrm {Spin}_7) \cong \mu _2$
is the center of
$Z(\mathrm {Spin}_7) \cong \mu _2$
is the center of
![]() $\mathrm {Spin}_7({\mathbb C})$
.
$\mathrm {Spin}_7({\mathbb C})$
.
(iii) The map
is injective and restricts to an injection
Proof. (i) If
![]() $\phi _1, \phi _2 \in \Phi (\mathrm {PGL}_3)$
are conjugate in
$\phi _1, \phi _2 \in \Phi (\mathrm {PGL}_3)$
are conjugate in
![]() $G_2(\mathbb C)$
, then the following semi-simple representations are isomorphic:
$G_2(\mathbb C)$
, then the following semi-simple representations are isomorphic:
We need to show that this isomorphism implies
![]() $\phi _1\cong \phi _2$
or
$\phi _1\cong \phi _2$
or
![]() $\phi _1\cong \phi _2^{\vee }$
. This is obvious if
$\phi _1\cong \phi _2^{\vee }$
. This is obvious if
![]() $\phi _1$
is irreducible. If
$\phi _1$
is irreducible. If
![]() $\phi _1$
contains an irreducible two dimensional summand, then that summand must be contained in
$\phi _1$
contains an irreducible two dimensional summand, then that summand must be contained in
![]() $\phi _2$
or
$\phi _2$
or
![]() $\phi _2^{\vee }$
. Assume that it is contained in
$\phi _2^{\vee }$
. Assume that it is contained in
![]() $\phi _2$
. The one-dimensional summand of
$\phi _2$
. The one-dimensional summand of
![]() $\phi _1$
is the determinant inverse of the two-dimensional summand, hence it is also contained in
$\phi _1$
is the determinant inverse of the two-dimensional summand, hence it is also contained in
![]() $\phi _2$
and thus
$\phi _2$
and thus
![]() $\phi _1\cong \phi _2$
. We leave the case of three summands as an exercise. Assume
$\phi _1\cong \phi _2$
. We leave the case of three summands as an exercise. Assume
![]() $\phi \in \Phi _{ds}(\mathrm {PGL}_3)$
. Then the centralizer of
$\phi \in \Phi _{ds}(\mathrm {PGL}_3)$
. Then the centralizer of
![]() $\phi $
in
$\phi $
in
![]() $\mathrm {SL}_3(\mathbb C)$
is
$\mathrm {SL}_3(\mathbb C)$
is
![]() $\mu _3$
. The stabilizer in
$\mu _3$
. The stabilizer in
![]() $G_2(\mathbb C)$
of
$G_2(\mathbb C)$
of
![]() $1\subset 1+ \phi + \phi ^{\vee }$
is
$1\subset 1+ \phi + \phi ^{\vee }$
is
![]() $\mathrm {SL}_3(\mathbb C) \rtimes {\mathbb Z}/2{\mathbb Z}$
. It follows that the centralizer of
$\mathrm {SL}_3(\mathbb C) \rtimes {\mathbb Z}/2{\mathbb Z}$
. It follows that the centralizer of
![]() $\phi $
in
$\phi $
in
![]() $G_2(\mathbb C)$
is either
$G_2(\mathbb C)$
is either
![]() $\mu _3$
or
$\mu _3$
or
![]() $S_3$
, depending on whether
$S_3$
, depending on whether
![]() $\phi \not \cong \phi ^{\vee }$
or
$\phi \not \cong \phi ^{\vee }$
or
![]() $\phi \cong \phi ^{\vee }$
respectively.
$\phi \cong \phi ^{\vee }$
respectively.
For (ii) and (iii), we refer the reader to [Reference Gross and SavinGrS2, Chapter 4, Section 1].
3 Definition of
 $\mathcal {L}$
$\mathcal {L}$
In this section, we will define the LLC map
using the results of the previous section and establish some initial properties of
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
3.1 First definition of
 $\mathcal {L}$
$\mathcal {L}$
We shall give two slightly different constructions of the map
![]() $\mathcal {L}$
.
$\mathcal {L}$
.
For the first construction (which was sketched in the introduction), we make use of the decomposition
introduced in Theorem 2.1(i). First consider
![]() $\pi \in \mathrm {Irr}^{\spadesuit }(G_2) \subset \mathrm {Irr}_{ds}(G_2)$
, and set
$\pi \in \mathrm {Irr}^{\spadesuit }(G_2) \subset \mathrm {Irr}_{ds}(G_2)$
, and set
![]() $\tau = \theta _D(\pi )$
for a unique
$\tau = \theta _D(\pi )$
for a unique
![]() $\tau \in \mathrm {Irr}(\mathrm {PD}^{\times })$
. By the Jacquet-Langlands correspondence and the LLC for
$\tau \in \mathrm {Irr}(\mathrm {PD}^{\times })$
. By the Jacquet-Langlands correspondence and the LLC for
![]() $\mathrm {PGL}_3$
, one has a discrete L-parameter
$\mathrm {PGL}_3$
, one has a discrete L-parameter
Composing this with the natural inclusion
we set
which is an element of
![]() $\Phi _{ds}(G_2)$
by Lemma 2.4(i).
$\Phi _{ds}(G_2)$
by Lemma 2.4(i).
For
![]() $\pi \in \mathrm {Irr}^{\heartsuit }(G_2)$
, let
$\pi \in \mathrm {Irr}^{\heartsuit }(G_2)$
, let
![]() $\sigma = \theta (\pi ) \in \mathrm {Irr}(\mathrm {PGSp_6})$
and consider its restriction
$\sigma = \theta (\pi ) \in \mathrm {Irr}(\mathrm {PGSp_6})$
and consider its restriction
By the LLC for
![]() $\mathrm {Sp_6}$
,
$\mathrm {Sp_6}$
,
![]() $\mathrm {rest}(\sigma )$
gives rise to an L-parameter
$\mathrm {rest}(\sigma )$
gives rise to an L-parameter
In view of Lemma 2.4, it remains to verify:
Proposition 3.1. For
![]() $\pi \in \mathrm {Irr}^{\heartsuit }(G_2)$
, with
$\pi \in \mathrm {Irr}^{\heartsuit }(G_2)$
, with
![]() $\sigma = \theta (\pi ) \in \mathrm {Irr}(\mathrm {PGSp_6})$
,
$\sigma = \theta (\pi ) \in \mathrm {Irr}(\mathrm {PGSp_6})$
,
so that it gives rise to a uniquely determined element
![]() $\mathcal {L}(\pi ) \in \Phi (G_2)$
by Lemma 2.4(iii).
$\mathcal {L}(\pi ) \in \Phi (G_2)$
by Lemma 2.4(iii).
We shall verify this in §3.3 by global means.
3.2 Second definition of
 $\mathcal {L}$
$\mathcal {L}$
Our second construction is closely related to the first and is based on the more refined decomposition
in (2.2).
For
![]() $\pi \in \mathrm {Irr}^{\spadesuit }(G_2)$
or
$\pi \in \mathrm {Irr}^{\spadesuit }(G_2)$
or
![]() $\mathrm {Irr}^{\diamondsuit }(G_2) \subset \mathrm {Irr}^{\heartsuit }(G_2)$
, the definition of
$\mathrm {Irr}^{\diamondsuit }(G_2) \subset \mathrm {Irr}^{\heartsuit }(G_2)$
, the definition of
![]() $\mathcal {L}(\pi )$
is as in the first construction above. Thus, the difference only arises for those
$\mathcal {L}(\pi )$
is as in the first construction above. Thus, the difference only arises for those
![]() $\pi \in \mathrm {Irr}^{\clubsuit }(G_2) \subset \mathrm {Irr}^{\heartsuit }(G_2)$
. Such a
$\pi \in \mathrm {Irr}^{\clubsuit }(G_2) \subset \mathrm {Irr}^{\heartsuit }(G_2)$
. Such a
![]() $\pi $
has nonzero theta lift to a unique
$\pi $
has nonzero theta lift to a unique
![]() $\tilde {\tau } \in \mathrm {Irr}(\mathrm {PGL}_3 \rtimes {\mathbb Z}/2{\mathbb Z})$
. Restricting
$\tilde {\tau } \in \mathrm {Irr}(\mathrm {PGL}_3 \rtimes {\mathbb Z}/2{\mathbb Z})$
. Restricting
![]() $\tilde {\tau }$
to
$\tilde {\tau }$
to
![]() $\mathrm {PGL}_3$
gives a well-defined element
$\mathrm {PGL}_3$
gives a well-defined element
and thus an L-parameter
which is well-defined up to the outer automorphism action. By Lemma 2.4, we may set
There is of course a need to reconcile the two definitions for
![]() $\pi \in \mathrm {Irr}^{\clubsuit }(G_2)$
. This follows readily from the explicit theta correspondences computed in [Reference Gan and SavinGS23, Thm. 8.2, Thm. 8.5, Thm. 15.1 and Thm. 15.2].
$\pi \in \mathrm {Irr}^{\clubsuit }(G_2)$
. This follows readily from the explicit theta correspondences computed in [Reference Gan and SavinGS23, Thm. 8.2, Thm. 8.5, Thm. 15.1 and Thm. 15.2].
3.3 Proof of Proposition 3.1
To complete the construction of
![]() $\mathcal {L}$
, it remains to verify Proposition 3.1. For a non-supercuspidal representation
$\mathcal {L}$
, it remains to verify Proposition 3.1. For a non-supercuspidal representation
![]() $\pi \in \mathrm {Irr}^{\heartsuit }(G_2)$
, we have determined in [Reference Gan and SavinGS23, Thm. 15.1, Thm 15.2 and Thm. 15.3] the representation
$\pi \in \mathrm {Irr}^{\heartsuit }(G_2)$
, we have determined in [Reference Gan and SavinGS23, Thm. 15.1, Thm 15.2 and Thm. 15.3] the representation
![]() $\theta (\pi ) \in \mathrm {Irr}(\mathrm {PGSp_6})$
explicitly. From this, Proposition 3.1 follows readily. Indeed, the results of [Reference Gan and SavinGS23] shows that
$\theta (\pi ) \in \mathrm {Irr}(\mathrm {PGSp_6})$
explicitly. From this, Proposition 3.1 follows readily. Indeed, the results of [Reference Gan and SavinGS23] shows that
![]() $\mathcal {L}(\pi ) \in \Phi (G_2)$
is given precisely by the discussion in [Reference Gan and SavinGS23, §3.5].
$\mathcal {L}(\pi ) \in \Phi (G_2)$
is given precisely by the discussion in [Reference Gan and SavinGS23, §3.5].
It remains to treat supercuspidal
![]() $\pi \in \mathrm {Irr}^{\heartsuit }(G_2)$
. We shall use a global argument.
$\pi \in \mathrm {Irr}^{\heartsuit }(G_2)$
. We shall use a global argument.
Let k be a totally real number field with a place w such that
![]() $k_w \cong F$
. Let
$k_w \cong F$
. Let
![]() $\mathbb {O}$
be a totally definite octonion algebra over F with automorphism group
$\mathbb {O}$
be a totally definite octonion algebra over F with automorphism group
![]() $G = \mathrm {Aut}(\mathbb {O})$
. Then
$G = \mathrm {Aut}(\mathbb {O})$
. Then
![]() $G_v$
is anisotropic at all archimedean places v and
$G_v$
is anisotropic at all archimedean places v and
![]() $G_v$
is the split
$G_v$
is the split
![]() $G_2$
at all finite places v. By Proposition 10.5 and Corollary 10.6 in Appendix A, we can find a cuspidal automorphic representation
$G_2$
at all finite places v. By Proposition 10.5 and Corollary 10.6 in Appendix A, we can find a cuspidal automorphic representation
![]() $\Pi = \otimes _v \Pi _v$
of G so that
$\Pi = \otimes _v \Pi _v$
of G so that
-
•
 $\Pi _w \cong \pi $
;
$\Pi _w \cong \pi $
; -
•
 $\Pi _{\infty }$
has sufficiently regular infinitesimal character at each archimedean place
$\Pi _{\infty }$
has sufficiently regular infinitesimal character at each archimedean place
 $\infty $
;
$\infty $
; -
•
 $\Pi _u \cong $
the Steinberg representation
$\Pi _u \cong $
the Steinberg representation
 $\mathrm {St}$
at some finite place
$\mathrm {St}$
at some finite place
 $u \ne w$
.
$u \ne w$
. -
•
 $\Pi $
has nonzero cuspidal global theta lift
$\Pi $
has nonzero cuspidal global theta lift
 $\Sigma := \theta (\Pi )$
to the split group
$\Sigma := \theta (\Pi )$
to the split group
 $\mathrm {PGSp_6}$
over k.
$\mathrm {PGSp_6}$
over k.
Here, in the last bullet point, we are considering the dual pair
![]() $G \times \mathrm {PGSp_6}$
in the k-rank 3 form of
$G \times \mathrm {PGSp_6}$
in the k-rank 3 form of
![]() $E_7$
(commonly denoted by
$E_7$
(commonly denoted by
![]() $E_{7,3}$
); this global theta correspondence was studied in [Reference Gross and SavinGrS2].
$E_{7,3}$
); this global theta correspondence was studied in [Reference Gross and SavinGrS2].
Now the nonzero cuspidal representation
![]() $\theta (\Pi ) =: \Sigma = \otimes _v \Sigma _v$
of
$\theta (\Pi ) =: \Sigma = \otimes _v \Sigma _v$
of
![]() $\mathrm {PGSp_6}$
satisfies:
$\mathrm {PGSp_6}$
satisfies:
-
•
 $\Sigma _w$
is the representation
$\Sigma _w$
is the representation
 $\theta (\pi )$
of
$\theta (\pi )$
of
 $\mathrm {PGSp_6}(k_w)$
.
$\mathrm {PGSp_6}(k_w)$
. -
•
 $\Sigma _{\infty }$
is a holomorphic discrete series with sufficiently regular infinitesimal character for every archimedean place
$\Sigma _{\infty }$
is a holomorphic discrete series with sufficiently regular infinitesimal character for every archimedean place
 $\infty $
.
$\infty $
. -
•
 $\Sigma _u$
is the Steinberg representation of
$\Sigma _u$
is the Steinberg representation of
 $\mathrm {PGSp_6}(k_u)$
.
$\mathrm {PGSp_6}(k_u)$
.
By Arthur [Reference ArthurA], the restriction of
![]() $\Sigma $
to
$\Sigma $
to
![]() $\mathrm {Sp_6}$
has a cuspidal transfer
$\mathrm {Sp_6}$
has a cuspidal transfer
![]() $\mathcal {A}(\mathrm {rest}(\Sigma ))$
to
$\mathcal {A}(\mathrm {rest}(\Sigma ))$
to
![]() $\mathrm {GL}_7$
(because of the Steinberg local component at u) which is regular algebraic at all real places. Now at each finite place v, it follows by local-global compatibility of the transfer from classical groups to
$\mathrm {GL}_7$
(because of the Steinberg local component at u) which is regular algebraic at all real places. Now at each finite place v, it follows by local-global compatibility of the transfer from classical groups to
![]() $\mathrm {GL}_N$
that the local L-parameter of
$\mathrm {GL}_N$
that the local L-parameter of
![]() $\mathcal {A}(\mathrm { rest}(\Sigma ))_v$
is the local L-parameter of
$\mathcal {A}(\mathrm { rest}(\Sigma ))_v$
is the local L-parameter of
![]() $\mathrm {rest}(\Sigma _v)$
. Moreover, by a result of Chenevier [Reference ChenevierC, Thm. E], at all finite places v, the local L-parameter of
$\mathrm {rest}(\Sigma _v)$
. Moreover, by a result of Chenevier [Reference ChenevierC, Thm. E], at all finite places v, the local L-parameter of
![]() $\mathcal {A}(\mathrm {rest}(\Sigma ))_v$
factors through
$\mathcal {A}(\mathrm {rest}(\Sigma ))_v$
factors through
![]() $G_2({\mathbb C})$
, uniquely up to
$G_2({\mathbb C})$
, uniquely up to
![]() $G_2$
-conjugacy. Hence, the local L-parameter of
$G_2$
-conjugacy. Hence, the local L-parameter of
![]() $\mathrm {rest}(\Sigma _w) = \mathrm {rest}(\theta (\pi ))$
takes value in
$\mathrm {rest}(\Sigma _w) = \mathrm {rest}(\theta (\pi ))$
takes value in
![]() $G_2({\mathbb C}) \subset \mathrm {SO}_7({\mathbb C})$
, as desired.
$G_2({\mathbb C}) \subset \mathrm {SO}_7({\mathbb C})$
, as desired.
We have thus completed the proof of Proposition 3.1.
3.4 Initial properties
The definition of
![]() $\mathcal {L}$
given above and the results of [Reference Gan and SavinGS23] allow us to read off some initial properties of
$\mathcal {L}$
given above and the results of [Reference Gan and SavinGS23] allow us to read off some initial properties of
![]() $\mathcal {L}$
readily. We highlight some of these here:
$\mathcal {L}$
readily. We highlight some of these here:
-
• (Nontempered representations) As mentioned above, the results of [Reference Gan and SavinGS23, Thm. 15.1] show that our definition of
 $\mathcal {L}$
gives the Langlands parametrization of nontempered representations discussed in [Reference Gan and SavinGS23, §3.5] (based on the consideration of usual desiderata). In particular,
$\mathcal {L}$
gives the Langlands parametrization of nontempered representations discussed in [Reference Gan and SavinGS23, §3.5] (based on the consideration of usual desiderata). In particular,
 $\mathcal {L}$
gives a bijection where the subscript “nt” stands for “nontempered”. In particular, nontempered L-packets of
$\mathcal {L}$
gives a bijection where the subscript “nt” stands for “nontempered”. In particular, nontempered L-packets of $$\begin{align*}\mathcal{L}: \mathrm{Irr}_{nt}(G_2) \longleftrightarrow \Phi_{nt}(G_2) \end{align*}$$
$$\begin{align*}\mathcal{L}: \mathrm{Irr}_{nt}(G_2) \longleftrightarrow \Phi_{nt}(G_2) \end{align*}$$
 $G_2$
are singletons.
$G_2$
are singletons.
-
• (Tempered representations) The results of [Reference Gan and SavinGS23, Thm 15.2, 15.3] imply that one has a commutative diagram

-
• (Tempered but non-discrete series) One has a surjection
such that the fiber over $$\begin{align*}\mathcal{L}: \mathrm{Irr}_t(G_2) \smallsetminus \mathrm{Irr}_{ds}(G_2) \twoheadrightarrow \Phi_t(G_2) \smallsetminus \Phi_{ds}(G_2) \end{align*}$$
$$\begin{align*}\mathcal{L}: \mathrm{Irr}_t(G_2) \smallsetminus \mathrm{Irr}_{ds}(G_2) \twoheadrightarrow \Phi_t(G_2) \smallsetminus \Phi_{ds}(G_2) \end{align*}$$
 $\phi $
has size
$\phi $
has size
 $1$
or
$1$
or
 $2$
, according to whether
$2$
, according to whether
 $|S_{\phi }| =1$
or
$|S_{\phi }| =1$
or
 $2$
. The fiber
$2$
. The fiber
 $\mathcal {L}^{-1}(\phi )$
has a unique generic representation, and we attach it to the trivial character of
$\mathcal {L}^{-1}(\phi )$
has a unique generic representation, and we attach it to the trivial character of
 $S_{\phi }$
.
$S_{\phi }$
.
-
• (Summary) In summary, we have established items (i), (ii) and (iii) of the Main Theorem. Moreover, the commutativity of the two diagrams in (iv) of the Main Theorem follows by the construction of
 $\mathcal {L}$
, as does the characterization of
$\mathcal {L}$
, as does the characterization of
 $\mathcal {L}$
given in (v) of the Main Theorem. Furthermore, we have also demonstrated (vii) of the Main Theorem for non-discrete-series parameters
$\mathcal {L}$
given in (v) of the Main Theorem. Furthermore, we have also demonstrated (vii) of the Main Theorem for non-discrete-series parameters
 $\phi $
(for all p).
$\phi $
(for all p). -
• (Compatibility with global Langlands)
We can also show (viii) of the Main Theorem. In the context of (viii) in the Main Theorem, the global theta lift
 $\Sigma $
of
$\Sigma $
of
 $\Pi $
to
$\Pi $
to
 $\mathrm {PGSp_6}$
is globally generic, regular algebraic and cuspidal with a Steinberg local component. Moreover, the transfer of
$\mathrm {PGSp_6}$
is globally generic, regular algebraic and cuspidal with a Steinberg local component. Moreover, the transfer of
 $\mathrm {rest}(\Sigma )$
to
$\mathrm {rest}(\Sigma )$
to
 $\mathrm {GL}_7$
is a regular algebraic cuspidal automorphic representation
$\mathrm {GL}_7$
is a regular algebraic cuspidal automorphic representation
 $\mathcal {A}(\mathrm {rest}(\Sigma ))$
(with cuspidality a consequence of the Steinberg local component). Hence, the Galois representation
$\mathcal {A}(\mathrm {rest}(\Sigma ))$
(with cuspidality a consequence of the Steinberg local component). Hence, the Galois representation
 $\rho _{\Pi }$
is associated with
$\rho _{\Pi }$
is associated with
 $\mathcal {A}(\mathrm {rest}(\Sigma ))$
. By [Reference ChenevierC, Thm. 6.4],
$\mathcal {A}(\mathrm {rest}(\Sigma ))$
. By [Reference ChenevierC, Thm. 6.4],
 $\rho _{\Pi }$
takes value in
$\rho _{\Pi }$
takes value in
 $G_2(\overline {{\mathbb Q}}_l)$
(after conjugation). By local-global compatibility [Reference Taylor and YoshidaTY, Reference CaraianiCa], the local Galois representation
$G_2(\overline {{\mathbb Q}}_l)$
(after conjugation). By local-global compatibility [Reference Taylor and YoshidaTY, Reference CaraianiCa], the local Galois representation
 $\rho _{\Pi , v}$
at each finite place v corresponds to the local L-parameter of
$\rho _{\Pi , v}$
at each finite place v corresponds to the local L-parameter of
 $\mathrm {rest}(\Sigma _v)$
. But by the construction of
$\mathrm {rest}(\Sigma _v)$
. But by the construction of
 $\mathcal {L}$
, the local L-parameter of
$\mathcal {L}$
, the local L-parameter of
 $\mathrm {rest}(\Sigma _v)$
is
$\mathrm {rest}(\Sigma _v)$
is
 $\mathrm {std} \circ \iota \circ \mathcal {L}(\Pi _v)$
. This establishes (viii).
$\mathrm {std} \circ \iota \circ \mathcal {L}(\Pi _v)$
. This establishes (viii). -
• (Preservation of
 $\gamma $
-factors) We now show (ix) of the Main Theorem. Let us first briefly recall the definition of the relevant
$\gamma $
-factors) We now show (ix) of the Main Theorem. Let us first briefly recall the definition of the relevant
 $\gamma $
-factors given in [Reference Gan and SavinGS24]. The results of [Reference Gan and SavinGS23] can be summarized as the construction of a map which is given in the following commutative diagram:
$\gamma $
-factors given in [Reference Gan and SavinGS24]. The results of [Reference Gan and SavinGS23] can be summarized as the construction of a map which is given in the following commutative diagram: $$\begin{align*}\mathrm{Lif} : \mathrm{Irr}(G_2) \longrightarrow \mathrm{Irr}(\mathrm{GL}_7) \end{align*}$$
Here,
$$\begin{align*}\mathrm{Lif} : \mathrm{Irr}(G_2) \longrightarrow \mathrm{Irr}(\mathrm{GL}_7) \end{align*}$$
Here,
-
– the two
 $\theta $
’s refer to the local theta correspondence;
$\theta $
’s refer to the local theta correspondence; -
– JL refers to the Jacquet-Langlands transfer;
-
– rest refers to the restriction of representations;
-
– Art refers to the functorial transfer of irreducible representations from
 $\mathrm {Sp_6}$
to
$\mathrm {Sp_6}$
to
 $\mathrm {GL}_7$
established by Arthur;
$\mathrm {GL}_7$
established by Arthur; -
–
 $\boxplus : \mathrm {Irr}_{ds}(\mathrm {PGL}_3) \longrightarrow \mathrm {Irr}(\mathrm {GL}_7)$
is the map
$\boxplus : \mathrm {Irr}_{ds}(\mathrm {PGL}_3) \longrightarrow \mathrm {Irr}(\mathrm {GL}_7)$
is the map  $$\begin{align*}\tau \mapsto \tau \times 1 \times \tau^{\vee}. \end{align*}$$
$$\begin{align*}\tau \mapsto \tau \times 1 \times \tau^{\vee}. \end{align*}$$
With the above preparation, we can now define the local
 $\gamma $
-factors. Fix a nontrivial additive character
$\gamma $
-factors. Fix a nontrivial additive character
 $\psi : F \rightarrow {\mathbb C}^{\times }$
. For
$\psi : F \rightarrow {\mathbb C}^{\times }$
. For
 $\pi \in \mathrm {Irr}(G_2)$
and
$\pi \in \mathrm {Irr}(G_2)$
and
 $\tau \in \mathrm {Irr}(\mathrm {GL}_r)$
, set where the
$\tau \in \mathrm {Irr}(\mathrm {GL}_r)$
, set where the $$\begin{align*}\gamma(s, \pi \times \tau,\psi) := \gamma(s, \mathrm{Lif}(\pi) \times \tau, \psi). \end{align*}$$
$$\begin{align*}\gamma(s, \pi \times \tau,\psi) := \gamma(s, \mathrm{Lif}(\pi) \times \tau, \psi). \end{align*}$$
 $\gamma $
-factor on the RHS is the Rankin-Selberg
$\gamma $
-factor on the RHS is the Rankin-Selberg
 $\gamma $
-factor defined by Jacquet-Piatetski-Shapiro-Shalika and Shahidi [Reference Gelbart and ShahidiGeSh].
$\gamma $
-factor defined by Jacquet-Piatetski-Shapiro-Shalika and Shahidi [Reference Gelbart and ShahidiGeSh].
Let
 $\phi _{\pi }: WD_F \longrightarrow G_2({\mathbb C})$
and
$\phi _{\pi }: WD_F \longrightarrow G_2({\mathbb C})$
and
 $\phi _{\tau }: WD_F \longrightarrow \mathrm {GL}_r({\mathbb C})$
be the L-parameters of
$\phi _{\tau }: WD_F \longrightarrow \mathrm {GL}_r({\mathbb C})$
be the L-parameters of
 $\pi $
and
$\pi $
and
 $\tau $
respectively and recall that
$\tau $
respectively and recall that
 $\mathrm {std}: G_2({\mathbb C}) \longrightarrow \mathrm {GL}_7({\mathbb C})$
is the standard degree 7 irreducible representation of
$\mathrm {std}: G_2({\mathbb C}) \longrightarrow \mathrm {GL}_7({\mathbb C})$
is the standard degree 7 irreducible representation of
 $G_2({\mathbb C})$
. Then it follows from the construction of the LLC for
$G_2({\mathbb C})$
. Then it follows from the construction of the LLC for
 $G_2$
and the definition of the relevant
$G_2$
and the definition of the relevant
 $\gamma $
-factors that one has: using the fact that the LLC for
$\gamma $
-factors that one has: using the fact that the LLC for $$\begin{align*}\gamma(s, \pi \times \tau, \psi) = \gamma(s, (\mathrm{std} \circ \phi_{\pi}) \otimes \phi_{\tau}, \psi), \end{align*}$$
$$\begin{align*}\gamma(s, \pi \times \tau, \psi) = \gamma(s, (\mathrm{std} \circ \phi_{\pi}) \otimes \phi_{\tau}, \psi), \end{align*}$$
 $\mathrm {GL}_r$
respects the Rankin-Selberg
$\mathrm {GL}_r$
respects the Rankin-Selberg
 $\gamma $
-factors. In other words, (ix) follows.
$\gamma $
-factors. In other words, (ix) follows.
The reader will no doubt complain that our definition of the
 $\gamma $
-factor makes the statement (ix) almost a formality, which would not be inaccurate description. However, the main result of [Reference Gan and SavinGS24] states that the family of invariants
$\gamma $
-factor makes the statement (ix) almost a formality, which would not be inaccurate description. However, the main result of [Reference Gan and SavinGS24] states that the family of invariants
 $\gamma (s, \pi \times \tau ,\psi )$
can be characterized by a (usual) list of properties which is independent of the LLC, including multiplicativity and the global functional equations (for certain cuspidal representations). This characterization of the
$\gamma (s, \pi \times \tau ,\psi )$
can be characterized by a (usual) list of properties which is independent of the LLC, including multiplicativity and the global functional equations (for certain cuspidal representations). This characterization of the
 $\gamma $
-factors shows that the definition given in [Reference Gan and SavinGS24] (and recalled above) is the only possible candidate, and it is this which gives non-trivial content to the statement (ix).
$\gamma $
-factors shows that the definition given in [Reference Gan and SavinGS24] (and recalled above) is the only possible candidate, and it is this which gives non-trivial content to the statement (ix).Finally, the characterization of
 $\mathcal {L}$
by (ix) asserted in (x) follows from the standard argument that the preservation of
$\mathcal {L}$
by (ix) asserted in (x) follows from the standard argument that the preservation of
 $\gamma $
-factors of pairs allows one to determine the 7-dimensional representation
$\gamma $
-factors of pairs allows one to determine the 7-dimensional representation
 $\mathrm { std} \circ \phi _{\pi }$
uniquely (for tempered
$\mathrm { std} \circ \phi _{\pi }$
uniquely (for tempered
 $\pi $
). Since
$\pi $
). Since
 $\mathrm {GL}_7({\mathbb C})$
-conjugacy of
$\mathrm {GL}_7({\mathbb C})$
-conjugacy of
 $G_2({\mathbb C})$
-valued L-parameters implies
$G_2({\mathbb C})$
-valued L-parameters implies
 $G_2({\mathbb C})$
-conjugacy (as we have exploited in the construction of
$G_2({\mathbb C})$
-conjugacy (as we have exploited in the construction of
 $\mathcal {L}$
), it follows that
$\mathcal {L}$
), it follows that
 $\phi _{\pi }$
is uniquely characterized up to
$\phi _{\pi }$
is uniquely characterized up to
 $G_2({\mathbb C})$
-conjugacy,
$G_2({\mathbb C})$
-conjugacy, -
3.5 The packets for
 $\Phi _{ds}^{\spadesuit \clubsuit }(G_2)$
$\Phi _{ds}^{\spadesuit \clubsuit }(G_2)$
By the above discussion, it remains to understand the map
on discrete series representations. In fact, by construction,
![]() $\mathcal {L}$
restricts to give:
$\mathcal {L}$
restricts to give:
and
The results of [Reference Gan and SavinGS23, §7 and §8] allow us to understand the fibers of the map
![]() $\mathcal {L}^{\spadesuit \clubsuit }$
quite precisely.
$\mathcal {L}^{\spadesuit \clubsuit }$
quite precisely.
Proposition 3.2. The map
![]() $\mathcal {L}^{\spadesuit \clubsuit }$
is surjective. Moreover, for
$\mathcal {L}^{\spadesuit \clubsuit }$
is surjective. Moreover, for
![]() $\phi \in \Phi ^{\spadesuit \clubsuit }_{ds}(G_2)$
, the fiber
$\phi \in \Phi ^{\spadesuit \clubsuit }_{ds}(G_2)$
, the fiber
![]() $\mathcal {L}^{-1}(\phi )$
contains a unique generic element (belonging to
$\mathcal {L}^{-1}(\phi )$
contains a unique generic element (belonging to
![]() $\mathrm {Irr}_{ds}^{\clubsuit }(G_2)$
). Further, for
$\mathrm {Irr}_{ds}^{\clubsuit }(G_2)$
). Further, for
![]() $p \ne 3$
, one has a natural bijection
$p \ne 3$
, one has a natural bijection
such that the unique generic element corresponds to the trivial character of
![]() $S_{\phi }$
. For
$S_{\phi }$
. For
![]() $p= 3$
, we only know that there is an injection
$p= 3$
, we only know that there is an injection
![]() $ \mathcal {L}^{-1}(\phi ) \hookrightarrow \mathrm {Irr} (S_{\phi })$
in general, though this injection is bijective when
$ \mathcal {L}^{-1}(\phi ) \hookrightarrow \mathrm {Irr} (S_{\phi })$
in general, though this injection is bijective when
![]() $\phi |_{\mathrm {SL}_2}$
is the subregular
$\phi |_{\mathrm {SL}_2}$
is the subregular
![]() $\mathrm {SL}_2$
in
$\mathrm {SL}_2$
in
![]() $G_2({\mathbb C})$
.
$G_2({\mathbb C})$
.
Proof. As almost all statements of the proposition follow from [Reference Gan and SavinGS23, §7 and §8], we will focus on the main new information here: the natural bijection
when
![]() $p \ne 3$
. To obtain this, we need to set things up rather carefully.
$p \ne 3$
. To obtain this, we need to set things up rather carefully.
Let
![]() $M_3$
be the F-algebra of
$M_3$
be the F-algebra of
![]() $3 \times 3$
-matrices, with associated Jordan algebra
$3 \times 3$
-matrices, with associated Jordan algebra
![]() $M_3^+$
. The automorphism group
$M_3^+$
. The automorphism group
![]() $\mathrm {Aut}(M_3^+)$
of
$\mathrm {Aut}(M_3^+)$
of
![]() $M_3^+$
is a disconnected group whose identity component is
$M_3^+$
is a disconnected group whose identity component is
![]() $H = \mathrm {PGL}_3$
, with Langlands dual group
$H = \mathrm {PGL}_3$
, with Langlands dual group
![]() $H^{\vee }= \mathrm {SL}_3({\mathbb C})$
. Note that
$H^{\vee }= \mathrm {SL}_3({\mathbb C})$
. Note that
![]() $H^1(F, H) = H^1(F, \mathrm {PGL}_3)$
classifies the isomorphism classes of central simple F-algebras of degree
$H^1(F, H) = H^1(F, \mathrm {PGL}_3)$
classifies the isomorphism classes of central simple F-algebras of degree
![]() $3$
, with the distinguished point corresponding to
$3$
, with the distinguished point corresponding to
![]() $M_3$
. Moreover, the invariant map gives a bijection:
$M_3$
. Moreover, the invariant map gives a bijection:
For each nontrivial
![]() $j \in {\mathbb Z}/3{\mathbb Z}$
, the associated central simple algebra
$j \in {\mathbb Z}/3{\mathbb Z}$
, the associated central simple algebra
![]() $D_j$
is a cubic division algebra. Moreover,
$D_j$
is a cubic division algebra. Moreover,
![]() $D_1$
and
$D_1$
and
![]() $D_2$
are opposite of each other, so that the inverse map
$D_2$
are opposite of each other, so that the inverse map
![]() $x \mapsto x^{-1}$
gives a canonical isomorphism of multiplicative groups
$x \mapsto x^{-1}$
gives a canonical isomorphism of multiplicative groups
![]() $i: D_1^{\times } \cong D_2^{\times }$
.
$i: D_1^{\times } \cong D_2^{\times }$
.
Suppose that
![]() $\tau $
is a discrete series representation of
$\tau $
is a discrete series representation of
![]() $\mathrm {PGL}_3$
. Then for
$\mathrm {PGL}_3$
. Then for
![]() $j \in {\mathbb Z}/3{\mathbb Z}$
, one has a Jacquet-Langlands transfer
$j \in {\mathbb Z}/3{\mathbb Z}$
, one has a Jacquet-Langlands transfer
![]() $JL_{D_j}(\tau )$
of
$JL_{D_j}(\tau )$
of
![]() $\tau $
to
$\tau $
to
![]() $D_j^{\times }$
. Via the isomorphism
$D_j^{\times }$
. Via the isomorphism
![]() $i: D_1^{\times } \cong D_2^{\times }$
, we may compare
$i: D_1^{\times } \cong D_2^{\times }$
, we may compare
![]() $JL_{D_1}(\tau )$
and
$JL_{D_1}(\tau )$
and
![]() $JL_{D_2}(\tau )$
. One has
$JL_{D_2}(\tau )$
. One has
Consider now
![]() $[\phi ] \in \Phi _{ds}^{\spadesuit \clubsuit }(G_2)$
, which is a
$[\phi ] \in \Phi _{ds}^{\spadesuit \clubsuit }(G_2)$
, which is a
![]() $G_2$
-conjugacy class of homomorphisms
$G_2$
-conjugacy class of homomorphisms
![]() $\phi : WD_F \longrightarrow G_2({\mathbb C})$
. One has a projective system (relative to
$\phi : WD_F \longrightarrow G_2({\mathbb C})$
. One has a projective system (relative to
![]() $G_2$
-conjugacy) of centralizer subgroups
$G_2$
-conjugacy) of centralizer subgroups
![]() $Z_{G_2}(\phi )$
which are finite of order
$Z_{G_2}(\phi )$
which are finite of order
![]() $3$
, and thus identified with the component groups
$3$
, and thus identified with the component groups
![]() $S_{\phi }$
. We denote this projective system of local component groups by
$S_{\phi }$
. We denote this projective system of local component groups by
![]() $S_{[\phi ]}$
and set
$S_{[\phi ]}$
and set
![]() $C_{[\phi ]} = Z_{G_2}(S_{[\phi ]})$
: this is a projective system of subgroups of
$C_{[\phi ]} = Z_{G_2}(S_{[\phi ]})$
: this is a projective system of subgroups of
![]() $G_2({\mathbb C})$
which are simply-connected of type
$G_2({\mathbb C})$
which are simply-connected of type
![]() $A_2$
. We fix a projective system (relative to
$A_2$
. We fix a projective system (relative to
![]() $G_2$
-conjugacy) of isomorphisms
$G_2$
-conjugacy) of isomorphisms
Note that there are basically two inner automorphism classes of such projective systems of isomorphisms, exchanged by an outer automorphism of
![]() $\mathrm {SL}_3({\mathbb C})$
.
$\mathrm {SL}_3({\mathbb C})$
.
By virtue of
![]() $i_{[\phi ]}$
, one has:
$i_{[\phi ]}$
, one has:
-
(a)
 $[\phi ]$
gives rise to a well-defined
$[\phi ]$
gives rise to a well-defined
 $\mathrm {SL}_3({\mathbb C})$
-conjugacy classes of maps i.e. a discrete series L-parameter of
$\mathrm {SL}_3({\mathbb C})$
-conjugacy classes of maps i.e. a discrete series L-parameter of $$\begin{align*}[\rho]: WD_F \longrightarrow \mathrm{SL}_3({\mathbb C}), \end{align*}$$
$$\begin{align*}[\rho]: WD_F \longrightarrow \mathrm{SL}_3({\mathbb C}), \end{align*}$$
 $H = \mathrm {PGL}_3$
, so that Let
$H = \mathrm {PGL}_3$
, so that Let $$\begin{align*}[\phi] = i_{[\phi]} \circ [\rho]. \end{align*}$$
$$\begin{align*}[\phi] = i_{[\phi]} \circ [\rho]. \end{align*}$$
 $\tau _{\rho }$
be the discrete series representation of
$\tau _{\rho }$
be the discrete series representation of
 $\mathrm {PGL}_3$
with L-parameter
$\mathrm {PGL}_3$
with L-parameter
 $\rho $
.
$\rho $
.
-
(b) One also has a projective system of isomorphism
inducing a projection system of bijections: $$\begin{align*}i_{[\phi]} : Z(H^{\vee}) = Z(\mathrm{SL}_3({\mathbb C})) \longrightarrow S_{[\phi]} = Z(C_{[\phi]}) \end{align*}$$
Hence, an element
$$\begin{align*}i_{[\phi]} : Z(H^{\vee}) = Z(\mathrm{SL}_3({\mathbb C})) \longrightarrow S_{[\phi]} = Z(C_{[\phi]}) \end{align*}$$
Hence, an element
 $\eta \in \mathrm {Irr}(S_{[\phi ]})$
gives rise to a central simple algebra
$\eta \in \mathrm {Irr}(S_{[\phi ]})$
gives rise to a central simple algebra
 $D_{j(\eta )}$
of degree
$D_{j(\eta )}$
of degree
 $3$
, determined by its invariant
$3$
, determined by its invariant
 $j(\eta ) \in {\mathbb Z}/3{\mathbb Z}$
.
$j(\eta ) \in {\mathbb Z}/3{\mathbb Z}$
.
-
(c) By combining (a) and (b), one sees that
 $\eta \in \mathrm {Irr}(S_{[\phi ]})$
gives rise to a representation
$\eta \in \mathrm {Irr}(S_{[\phi ]})$
gives rise to a representation  $$\begin{align*}\tau_{\phi, \eta} = JL_{D_{j(\eta)}}(\tau_{\rho}) \in \mathrm{Irr}(PD_{j(\eta)}^{\times}). \end{align*}$$
$$\begin{align*}\tau_{\phi, \eta} = JL_{D_{j(\eta)}}(\tau_{\rho}) \in \mathrm{Irr}(PD_{j(\eta)}^{\times}). \end{align*}$$
Now the central simple algebra
![]() $D_{j(\eta )}$
, or rather its associated Jordan algebra
$D_{j(\eta )}$
, or rather its associated Jordan algebra
![]() $D_{j(\eta )}^+$
gives rise to a local theta correspondence for the dual pair
$D_{j(\eta )}^+$
gives rise to a local theta correspondence for the dual pair
This is the local theta correspondence used in the definition of
![]() $\theta _{D}$
and
$\theta _{D}$
and
![]() $\theta _{M_3}$
in the Main Theorem. Observe that
$\theta _{M_3}$
in the Main Theorem. Observe that
![]() $D_{j(\eta )}^+ \cong D_{-j(\eta )}^+$
and we have canonical (up to inner automorphisms) isomorphisms
$D_{j(\eta )}^+ \cong D_{-j(\eta )}^+$
and we have canonical (up to inner automorphisms) isomorphisms
where the composite
![]() $i : PD_{j(\eta )}^{\times } \rightarrow PD_{-j(\eta )}^{\times }$
is given by
$i : PD_{j(\eta )}^{\times } \rightarrow PD_{-j(\eta )}^{\times }$
is given by
![]() $i(x)=x^{-1}$
(up to inner automorphisms). Hence one can define a representation
$i(x)=x^{-1}$
(up to inner automorphisms). Hence one can define a representation
where for the last isomorphism we used the fact that
![]() $i^* ( JL_{D_{j(\eta )}}(\tau _{\rho }))= JL_{D_{-j(\eta )}}(\tau _{\rho }^{\vee })$
as observed earlier. When
$i^* ( JL_{D_{j(\eta )}}(\tau _{\rho }))= JL_{D_{-j(\eta )}}(\tau _{\rho }^{\vee })$
as observed earlier. When
![]() $p \ne 3$
, we have seen in [Reference Gan and SavinGS23] that
$p \ne 3$
, we have seen in [Reference Gan and SavinGS23] that
![]() $\pi _{\eta }$
is nonzero irreducible. When
$\pi _{\eta }$
is nonzero irreducible. When
![]() $p =3$
, we only know this nonvanishing when
$p =3$
, we only know this nonvanishing when
![]() $\eta $
is trivial or if
$\eta $
is trivial or if
![]() $\phi $
gives the subregular
$\phi $
gives the subregular
![]() $\mathrm {SL}_2$
when restricted to the Deligne
$\mathrm {SL}_2$
when restricted to the Deligne
![]() $\mathrm {SL}_2$
.
$\mathrm {SL}_2$
.
It is clear from the construction of
![]() $\mathcal {L}$
that one has
$\mathcal {L}$
that one has
This gives the natural parametrization of the fibers of
![]() $\mathcal {L}^{\spadesuit \clubsuit }$
in the proposition.
$\mathcal {L}^{\spadesuit \clubsuit }$
in the proposition.
Note that this parametrization does not depend on the choice of the projective system of isomorphism
![]() $i_{[\phi ]}$
. Indeed, there are 2 such choices as noted above, but changing the choice replaces
$i_{[\phi ]}$
. Indeed, there are 2 such choices as noted above, but changing the choice replaces
![]() $\rho $
by
$\rho $
by
![]() $\rho ^{\vee }$
in (a) above (and hence
$\rho ^{\vee }$
in (a) above (and hence
![]() $\tau _{\rho }$
by
$\tau _{\rho }$
by
![]() $\tau _{\rho }^{\vee }$
) and j by
$\tau _{\rho }^{\vee }$
) and j by
![]() $-j$
in (b). Hence, under this new regime,
$-j$
in (b). Hence, under this new regime,
![]() $\eta \in \mathrm {Irr}(S_{[\phi ]})$
is associated by the same process to
$\eta \in \mathrm {Irr}(S_{[\phi ]})$
is associated by the same process to
as asserted.
After the above proposition, we see that to prove the Main Theorem, it remains to analyze the map
For example, a first key question to address is whether this map is surjective. Before addressing such questions, let us describe in the following two sections some ingredients we shall use.
4 Triality and Spin Lifting
In this section, we explain how the principle of triality, together with the theory of theta correspondence, can be used to construct a candidate Spin functorial lifting
This also explains the diagram in (vi) of the Main Theorem.
4.1 Triality and Spin representations
We begin with a brief discussion of the phenomenon of triality. Recall that there are 3 different maps over F:
where the groups
![]() $\mathrm {SO}_8$
and
$\mathrm {SO}_8$
and
![]() $\mathrm {PGSO}_8$
are split. These three morphisms are non-conjugate under
$\mathrm {PGSO}_8$
are split. These three morphisms are non-conjugate under
![]() $\mathrm {PGSO}_8$
but are cyclically permuted by an order 3 outer automorphism of
$\mathrm {PGSO}_8$
but are cyclically permuted by an order 3 outer automorphism of
![]() $\mathrm {PGSO}_8$
(the triality automorphism). Moreover, they induce corresponding morphisms
$\mathrm {PGSO}_8$
(the triality automorphism). Moreover, they induce corresponding morphisms
on the dual side. Without loss of generality, let us fix
and call it the “standard
![]() $\mathrm {SO}_8$
”. Then
$\mathrm {SO}_8$
”. Then
![]() $f_1^{\vee } = \mathrm {std}: \mathrm {Spin}_8({\mathbb C}) \longrightarrow \mathrm {SO}_8({\mathbb C})$
will be called the standard representation of
$f_1^{\vee } = \mathrm {std}: \mathrm {Spin}_8({\mathbb C}) \longrightarrow \mathrm {SO}_8({\mathbb C})$
will be called the standard representation of
![]() $\mathrm {Spin}_8({\mathbb C})$
. On the other hand,
$\mathrm {Spin}_8({\mathbb C})$
. On the other hand,
![]() $f_2^{\vee }$
and
$f_2^{\vee }$
and
![]() $f_3^{\vee }$
will be called the half-spin representations of
$f_3^{\vee }$
will be called the half-spin representations of
![]() $\mathrm {Spin}_8({\mathbb C})$
.
$\mathrm {Spin}_8({\mathbb C})$
.
Consider now the standard embedding

Then as representations of
![]() $\mathrm {Spin}_7({\mathbb C})$
, one has:
$\mathrm {Spin}_7({\mathbb C})$
, one has:
Thus, one has a very useful and convenient description of the Spin representation of
![]() $\mathrm {Spin}_7({\mathbb C})$
.
$\mathrm {Spin}_7({\mathbb C})$
.
4.2 Implication
We observe some implications in representation theory.
For an irreducible generic representation
![]() $\sigma $
of
$\sigma $
of
![]() $\mathrm {PGSp_6}$
, and
$\mathrm {PGSp_6}$
, and
![]() $\sigma ^{\flat } \in \mathrm {Irr}(\mathrm {Sp_6})$
contained in the restriction
$\sigma ^{\flat } \in \mathrm {Irr}(\mathrm {Sp_6})$
contained in the restriction
![]() $\mathrm {rest}(\sigma )$
, one may consider the usual (isometry) theta lift of
$\mathrm {rest}(\sigma )$
, one may consider the usual (isometry) theta lift of
![]() $\sigma ^{\flat }$
from
$\sigma ^{\flat }$
from
![]() $\mathrm {Sp_6}$
to
$\mathrm {Sp_6}$
to
![]() $\mathrm {SO}_8$
, as well as the similitude theta lift of
$\mathrm {SO}_8$
, as well as the similitude theta lift of
![]() $\sigma $
to
$\sigma $
to
![]() $\mathrm {PGSO}_8$
. Both these theta lifts are nonzero and one has the following compatibility:
$\mathrm {PGSO}_8$
. Both these theta lifts are nonzero and one has the following compatibility:
If the L-parameter of
![]() $\sigma ^{\flat }$
is
$\sigma ^{\flat }$
is
![]() $\phi ^{\flat }$
, then the L-parameter of any irreducible constituent of
$\phi ^{\flat }$
, then the L-parameter of any irreducible constituent of
![]() $f_1^*(\theta (\sigma ))$
is
$f_1^*(\theta (\sigma ))$
is
![]() $\phi ^{\flat } \oplus 1$
.
$\phi ^{\flat } \oplus 1$
.
On the other hand, if one considers
![]() $f_2^*(\theta (\sigma ))$
instead, one potentially gets a very different representation of
$f_2^*(\theta (\sigma ))$
instead, one potentially gets a very different representation of
![]() $\mathrm {SO}_8$
with a very different L-parameter. Indeed, consider the special case when
$\mathrm {SO}_8$
with a very different L-parameter. Indeed, consider the special case when
![]() $\sigma $
is unramified with Satake parameter
$\sigma $
is unramified with Satake parameter
![]() $s \in \mathrm {Spin}_7({\mathbb C})$
. Then one can show that
$s \in \mathrm {Spin}_7({\mathbb C})$
. Then one can show that
![]() $\theta (\sigma )$
is unramified with Satake parameter
$\theta (\sigma )$
is unramified with Satake parameter
![]() $i(s) \in \mathrm {Spin}_8({\mathbb C})$
. Thus, the Satake parameter for
$i(s) \in \mathrm {Spin}_8({\mathbb C})$
. Thus, the Satake parameter for
![]() $f_1^*(\theta (\sigma ))$
is
$f_1^*(\theta (\sigma ))$
is
![]() $f_1^{\vee }(i(s)) = 1 \oplus s \in \mathrm {SO}_8({\mathbb C})$
(as we noted above), whereas that of
$f_1^{\vee }(i(s)) = 1 \oplus s \in \mathrm {SO}_8({\mathbb C})$
(as we noted above), whereas that of
![]() $f_2^*(\theta (\sigma ))$
is
$f_2^*(\theta (\sigma ))$
is
This suggests that the map on generic representations of
![]() $\mathrm {PGSp_6}$
given by
$\mathrm {PGSp_6}$
given by
is nothing but the Langlands functorial lifting corresponding to the spin representation
after one composes the above with the functorial lifting
provided by Cogdell-Kim-Piatetski-Shapiro-Shahidi [Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPSS]) or Arthur [Reference ArthurA].
4.3 Spin lifting
Motivated by the above, we can now define the Spin lifting
by
Observe that the above construction can be carried out globally as well. Namely, if
![]() $\Sigma $
is a globally generic cuspidal automorphic representation of
$\Sigma $
is a globally generic cuspidal automorphic representation of
![]() $\mathrm {PGSp_6}$
over a number field k, then the global theta lift
$\mathrm {PGSp_6}$
over a number field k, then the global theta lift
![]() $\theta (\Sigma )$
on
$\theta (\Sigma )$
on
![]() $\mathrm {PGSO}_8$
is globally generic and thus nonzero. Suppose further that
$\mathrm {PGSO}_8$
is globally generic and thus nonzero. Suppose further that
![]() $\theta (\Sigma )$
is cuspidal. Then
$\theta (\Sigma )$
is cuspidal. Then
![]() $f_2^*(\theta (\Sigma ))$
gives rise to a submodule of globally generic cusp forms on
$f_2^*(\theta (\Sigma ))$
gives rise to a submodule of globally generic cusp forms on
![]() $\mathrm {SO}_8$
, all of whose summands are weak spin lifting of
$\mathrm {SO}_8$
, all of whose summands are weak spin lifting of
![]() $\Sigma $
. Its transfer
$\Sigma $
. Its transfer
![]() $\mathcal {A} \left ( f_2^*(\theta (\Sigma )) \right )$
to
$\mathcal {A} \left ( f_2^*(\theta (\Sigma )) \right )$
to
![]() $\mathrm {GL}_8$
(à la Cogdell-Kim-Piatetski-Shapiro-Shahidi [Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPSS]) is then an isobaric automorphic representation of
$\mathrm {GL}_8$
(à la Cogdell-Kim-Piatetski-Shapiro-Shahidi [Reference Cogdell, Kim, Piatetski-Shapiro and ShahidiCKPSS]) is then an isobaric automorphic representation of
![]() $\mathrm {GL}_8$
(of orthogonal type): this is the global analog of the local construction above. Moreover, for each place v, one has:
$\mathrm {GL}_8$
(of orthogonal type): this is the global analog of the local construction above. Moreover, for each place v, one has:
4.4 A key property
We shall now show a key property of our local spin lifting
![]() ${\mathrm {spin}}_*$
.
${\mathrm {spin}}_*$
.
Proposition 4.1. Let
![]() $\sigma $
be an irreducible generic discrete series representation of
$\sigma $
be an irreducible generic discrete series representation of
![]() $\mathrm {PGSp_6}(F)$
and set
$\mathrm {PGSp_6}(F)$
and set
![]() $\tau = {\mathrm {spin}}_*(\sigma ) \in \mathrm {Irr}(\mathrm {GL}_8)$
. Then the following holds:
$\tau = {\mathrm {spin}}_*(\sigma ) \in \mathrm {Irr}(\mathrm {GL}_8)$
. Then the following holds:
-
(i) For the
 $\gamma $
-factors provided by the Langlands-Shahidi theory, for any non-trivial character
$\gamma $
-factors provided by the Langlands-Shahidi theory, for any non-trivial character $$\begin{align*}\gamma(s, \sigma, \mathrm{spin}, \psi) = \gamma(s, {\mathrm{spin}}_*(\sigma), \mathrm{std},\psi), \end{align*}$$
$$\begin{align*}\gamma(s, \sigma, \mathrm{spin}, \psi) = \gamma(s, {\mathrm{spin}}_*(\sigma), \mathrm{std},\psi), \end{align*}$$
 $\psi $
of F.
$\psi $
of F.
-
(ii) Let
 $\chi $
be a quadratic character of
$\chi $
be a quadratic character of
 $F^{\times }$
. Then
$F^{\times }$
. Then  $$\begin{align*}{\mathrm{spin}}_*(\sigma \otimes \chi) = {\mathrm{spin}}_*(\sigma) \otimes \chi. \end{align*}$$
$$\begin{align*}{\mathrm{spin}}_*(\sigma \otimes \chi) = {\mathrm{spin}}_*(\sigma) \otimes \chi. \end{align*}$$
Proof. We shall prove this via a classical global to local argument. Choose a totally complex number field k with some finite set
![]() $T \sqcup \{ u,w\}$
of finite places (with T nonempty) such that
$T \sqcup \{ u,w\}$
of finite places (with T nonempty) such that
![]() $k_u\cong k_w \cong F \cong k_v$
for all
$k_u\cong k_w \cong F \cong k_v$
for all
![]() $v\in T$
. By the globalization result in Proposition 10.7 of Appendix A, there exists a globally generic cuspidal automorphic representation
$v\in T$
. By the globalization result in Proposition 10.7 of Appendix A, there exists a globally generic cuspidal automorphic representation
![]() $\Sigma $
such that
$\Sigma $
such that
-
•
 $\Sigma _v\cong \sigma $
for all
$\Sigma _v\cong \sigma $
for all
 $v \in T$
;
$v \in T$
; -
•
 $\Sigma _u$
is the Steinberg representation
$\Sigma _u$
is the Steinberg representation
 $\mathrm {St}$
;
$\mathrm {St}$
; -
•
 $\Sigma _{w}$
is a generic supercuspidal representation
$\Sigma _{w}$
is a generic supercuspidal representation
 $\delta $
;
$\delta $
; -
•
 $\Sigma _v$
is a spherical representation at all other finite places v.
$\Sigma _v$
is a spherical representation at all other finite places v.
Fix a global additive character
![]() $\Psi $
of
$\Psi $
of
![]() $k \backslash \mathbb {A}_k$
with
$k \backslash \mathbb {A}_k$
with
![]() $\Psi _u=\Psi _w = \psi =\Psi _v$
for all
$\Psi _u=\Psi _w = \psi =\Psi _v$
for all
![]() $v \in T$
. For a sufficiently large set S of places, containing
$v \in T$
. For a sufficiently large set S of places, containing
![]() $T \sqcup \{u,w\}$
and all archimedean places, we have a global functional equation
$T \sqcup \{u,w\}$
and all archimedean places, we have a global functional equation
where
![]() $L^S$
denotes the partial L-function. Since
$L^S$
denotes the partial L-function. Since
![]() $\Sigma $
is generic, its theta lift
$\Sigma $
is generic, its theta lift
![]() $\theta (\Sigma )$
to
$\theta (\Sigma )$
to
![]() $\mathrm {PGSO}_8$
is non-zero and generic. Moreover, since
$\mathrm {PGSO}_8$
is non-zero and generic. Moreover, since
![]() $\Sigma _u$
is the Steinberg representation, its theta lift to
$\Sigma _u$
is the Steinberg representation, its theta lift to
![]() $\mathrm {PGSO}_6$
(the smaller group in the Rallis-Witt tower) is 0. Hence
$\mathrm {PGSO}_6$
(the smaller group in the Rallis-Witt tower) is 0. Hence
![]() $\theta (\Sigma )$
is cuspidal.
$\theta (\Sigma )$
is cuspidal.
By the global analog of the Spin lifting discussed in the previous subsection, we have an isobaric generic automorphic representation
on
![]() $\mathrm {GL}_8$
. Likewise, we have the global functional equation
$\mathrm {GL}_8$
. Likewise, we have the global functional equation
Next, by the theta correspondence of unramified representations, observe that
Moreover, one can readily check that
Indeed, the local components at finite places outside of
![]() $T \sqcup \{ u,w\}$
are generic principal series representations and hence their spin lifts and
$T \sqcup \{ u,w\}$
are generic principal series representations and hence their spin lifts and
![]() $\gamma $
-factors are easily computable. For complex groups, the theta correspondence is explicitly known, [Reference Adams and BarbaschAB] (observe here that
$\gamma $
-factors are easily computable. For complex groups, the theta correspondence is explicitly known, [Reference Adams and BarbaschAB] (observe here that
![]() $\mathrm {PGSp_6}(\mathbb C)=\mathrm {Sp_6}(\mathbb C)/\mu _2$
so the usual theta correspondence is already a correspondence for similitude groups), so that one can check the identities at complex places. Hence, we deduce that
$\mathrm {PGSp_6}(\mathbb C)=\mathrm {Sp_6}(\mathbb C)/\mu _2$
so the usual theta correspondence is already a correspondence for similitude groups), so that one can check the identities at complex places. Hence, we deduce that
This gives the identity for representations of
![]() $G_2(F)$
:
$G_2(F)$
:
Since we can vary the size of T, by considering the quotient of two such identities (say with
![]() $|T| = 1$
and
$|T| = 1$
and
![]() $2$
respectively), we deduce that
$2$
respectively), we deduce that
as desired. This proves (i).
For (ii), globalize
![]() $\chi $
to a quadratic Hecke character
$\chi $
to a quadratic Hecke character
![]() $\mathcal {\chi }$
of
$\mathcal {\chi }$
of
![]() $\mathbb {A}_k^{\times }$
. By examining places outside S, one checks readily that
$\mathbb {A}_k^{\times }$
. By examining places outside S, one checks readily that
![]() ${\mathrm {spin}}_*(\Sigma \otimes \mathcal {\chi })$
and
${\mathrm {spin}}_*(\Sigma \otimes \mathcal {\chi })$
and
![]() ${\mathrm {spin}}_*(\Sigma ) \otimes \mathcal {\chi }$
are nearly equivalent. By the strong multiplicity one theorem for
${\mathrm {spin}}_*(\Sigma ) \otimes \mathcal {\chi }$
are nearly equivalent. By the strong multiplicity one theorem for
![]() $\mathrm {GL}_8$
, it follows that
$\mathrm {GL}_8$
, it follows that
![]() ${\mathrm {spin}}_*(\sigma \otimes \chi ) \cong {\mathrm {spin}}_*(\sigma )\otimes \chi $
, as desired.
${\mathrm {spin}}_*(\sigma \otimes \chi ) \cong {\mathrm {spin}}_*(\sigma )\otimes \chi $
, as desired.
5 Results of Kret-Shin
In this section, we briefly recall a special case of some recent results of Kret-Shin relevant for our applications. By combining the Spin lifting of the previous section and the results of Kret-Shin recalled here, we shall prove (vi) of the Main Theorem.
5.1 Results of Kret-Shin
Assume that
![]() $\Sigma $
is a cuspidal automorphic representation of
$\Sigma $
is a cuspidal automorphic representation of
![]() $\mathrm {PGSp_6}$
over a totally real number field k such that
$\mathrm {PGSp_6}$
over a totally real number field k such that
-
•
 $\Sigma _{\infty }$
is a sufficiently regular generic discrete series representation at each archimedean place
$\Sigma _{\infty }$
is a sufficiently regular generic discrete series representation at each archimedean place
 $\infty $
;
$\infty $
; -
•
 $\Sigma _u$
is the Steinberg representation for some finite place u of k.
$\Sigma _u$
is the Steinberg representation for some finite place u of k.
Then Kret-Shin [Reference Kret and ShinKS, Thm. Reference ArthurA] constructed a global Galois representation
satisfying:
-
• for almost all places v,
 $\rho _{\Sigma }(\mathrm {Frob}_v)_{ss}$
is conjugate to the Satake parameter
$\rho _{\Sigma }(\mathrm {Frob}_v)_{ss}$
is conjugate to the Satake parameter
 $s_{\Sigma _v}$
in
$s_{\Sigma _v}$
in
 $\mathrm {Spin}_7(\overline {{\mathbb Q}}_l)$
;
$\mathrm {Spin}_7(\overline {{\mathbb Q}}_l)$
; -
•
 ${\mathrm {std}}\circ \rho _{\Sigma }$
is the Galois representation associated to the restriction
${\mathrm {std}}\circ \rho _{\Sigma }$
is the Galois representation associated to the restriction
 $\mathrm {rest}(\Sigma )$
of
$\mathrm {rest}(\Sigma )$
of
 $\Sigma $
to
$\Sigma $
to
 $\mathrm {Sp_6}$
.
$\mathrm {Sp_6}$
.
5.2 Spin lifting and Kret-Shin parameters
We shall apply the results of Kret-Shin to the following problem. Suppose that
![]() $\sigma $
is an irreducible generic discrete series representation of
$\sigma $
is an irreducible generic discrete series representation of
![]() $\mathrm {PGSp_6}$
. Then
$\mathrm {PGSp_6}$
. Then
![]() $\sigma $
determines a pair
$\sigma $
determines a pair
where
![]() $\phi ^{\flat }$
is the L-parameter of
$\phi ^{\flat }$
is the L-parameter of
![]() $\mathrm {rest}(\sigma )$
and
$\mathrm {rest}(\sigma )$
and
![]() $\phi ^{\#}$
is the L-parameter of the Spin lifting
$\phi ^{\#}$
is the L-parameter of the Spin lifting
![]() ${\mathrm {spin}}_*(\sigma )$
. On the other hand, one has the natural map
${\mathrm {spin}}_*(\sigma )$
. On the other hand, one has the natural map
and it is natural to ask if there exists
![]() $\phi \in \Phi (\mathrm {PGSp_6})$
such that
$\phi \in \Phi (\mathrm {PGSp_6})$
such that
Such a
![]() $\phi $
would be a natural candidate for an L-parameter of
$\phi $
would be a natural candidate for an L-parameter of
![]() $\sigma $
. The results of Kret-Shin allow us to show the existence of such a
$\sigma $
. The results of Kret-Shin allow us to show the existence of such a
![]() $\phi $
.
$\phi $
.
Proposition 5.1. Let
![]() $\sigma \in \mathrm {Irr}_{gen,ds}(\mathrm {PGSp_6})$
be an irreducible generic discrete series representation. Then there exists
$\sigma \in \mathrm {Irr}_{gen,ds}(\mathrm {PGSp_6})$
be an irreducible generic discrete series representation. Then there exists
![]() $\phi \in \Phi _{ds}(\mathrm {PGSp_6})$
such that
$\phi \in \Phi _{ds}(\mathrm {PGSp_6})$
such that
-
•
 $\mathrm {std}_*(\phi )$
is the L-parameter of
$\mathrm {std}_*(\phi )$
is the L-parameter of
 $\mathrm {rest}(\sigma )$
and
$\mathrm {rest}(\sigma )$
and -
•
 ${\mathrm {spin}}_*(\phi )$
is the L-parameter of
${\mathrm {spin}}_*(\phi )$
is the L-parameter of
 ${\mathrm {spin}}_*(\sigma )$
.
${\mathrm {spin}}_*(\sigma )$
.
Proof. Let k be a totally real number field with a place w such that
![]() $k_w \cong F$
and consider the group
$k_w \cong F$
and consider the group
![]() $\mathrm {PGSp_6}$
over k. By the globalization result in Proposition 10.7, we can find a globally generic cuspidal automorphic representation
$\mathrm {PGSp_6}$
over k. By the globalization result in Proposition 10.7, we can find a globally generic cuspidal automorphic representation
![]() $\Sigma $
such that
$\Sigma $
such that
-
•
 $\Sigma _w \cong \sigma $
;
$\Sigma _w \cong \sigma $
; -
•
 $\Sigma _u$
is the Steinberg representation for some finite place
$\Sigma _u$
is the Steinberg representation for some finite place
 $u \ne w$
;
$u \ne w$
; -
•
 $\Sigma _{v}$
is a generic supercuspidal representation at some other finite place
$\Sigma _{v}$
is a generic supercuspidal representation at some other finite place
 $v\neq w, u$
;
$v\neq w, u$
; -
•
 $\Sigma _{\infty }$
is a sufficiently regular generic discrete series representation for all archimedean places
$\Sigma _{\infty }$
is a sufficiently regular generic discrete series representation for all archimedean places
 $\infty $
.
$\infty $
.
Such a
![]() $\Sigma $
is L-algebraic in the sense of [Reference Buzzard and GeeBG].
$\Sigma $
is L-algebraic in the sense of [Reference Buzzard and GeeBG].
Now on one hand, one may consider the global Spin lifting
![]() ${\mathrm {spin}}_*(\Sigma )$
: this is an isobaric automorphic representation of
${\mathrm {spin}}_*(\Sigma )$
: this is an isobaric automorphic representation of
![]() $\mathrm {GL}_8$
which is L-algebraic in the sense of [Reference Buzzard and GeeBG]. On the other hand, by Kret-Shin [Reference Kret and ShinKS, Thm. Reference ArthurA], one can associate to
$\mathrm {GL}_8$
which is L-algebraic in the sense of [Reference Buzzard and GeeBG]. On the other hand, by Kret-Shin [Reference Kret and ShinKS, Thm. Reference ArthurA], one can associate to
![]() $\Sigma $
a
$\Sigma $
a
![]() $\mathrm {Spin}_7(\overline {{\mathbb Q}}_l)$
-valued Galois representation
$\mathrm {Spin}_7(\overline {{\mathbb Q}}_l)$
-valued Galois representation
![]() $\rho _{\Sigma }$
. Then the 8-dimensional representation
$\rho _{\Sigma }$
. Then the 8-dimensional representation
![]() ${\mathrm {spin}} \circ \rho _{\Sigma }$
is a Galois representation associated to
${\mathrm {spin}} \circ \rho _{\Sigma }$
is a Galois representation associated to
![]() ${\mathrm {spin}}_*(\Sigma )$
(by considering unramified places). Let
${\mathrm {spin}}_*(\Sigma )$
(by considering unramified places). Let
![]() $\phi $
be the local L-parameter corresponding to the local Galois representation deduced from
$\phi $
be the local L-parameter corresponding to the local Galois representation deduced from
![]() $\rho _{\Sigma }$
at the place w. Then by local-global compatibility [Reference Taylor and YoshidaTY, Reference CaraianiCa], one sees readily that
$\rho _{\Sigma }$
at the place w. Then by local-global compatibility [Reference Taylor and YoshidaTY, Reference CaraianiCa], one sees readily that
![]() $\phi $
satisfies the requisite conditions of the proposition.
$\phi $
satisfies the requisite conditions of the proposition.
For a given
![]() $\sigma \in \mathrm {Irr}_{gen,ds}(\mathrm {PGSp_6})$
, we will call a
$\sigma \in \mathrm {Irr}_{gen,ds}(\mathrm {PGSp_6})$
, we will call a
![]() $\phi $
which satisfies the conditions of Proposition 5.1 a Kret-Shin parameter of
$\phi $
which satisfies the conditions of Proposition 5.1 a Kret-Shin parameter of
![]() $\sigma $
. Unfortunately, it is not true that
$\sigma $
. Unfortunately, it is not true that
![]() $\sigma $
necessarily has a unique Kret-Shin parameter, because
$\sigma $
necessarily has a unique Kret-Shin parameter, because
![]() $\mathrm {Spin}_7({\mathbb C})$
is not acceptable [Reference Chenevier and GanCG1]. However, any two Kret-Shin parameters are related to each other via twisting by a quadratic character. The following says that in some cases, the Kret-Shin parameter is unique.
$\mathrm {Spin}_7({\mathbb C})$
is not acceptable [Reference Chenevier and GanCG1]. However, any two Kret-Shin parameters are related to each other via twisting by a quadratic character. The following says that in some cases, the Kret-Shin parameter is unique.
Proposition 5.2. Assume that
![]() $\sigma \in \mathrm {Irr}_{gen, ds}(\mathrm {PGSp_6})$
is the theta lift of a generic discrete series
$\sigma \in \mathrm {Irr}_{gen, ds}(\mathrm {PGSp_6})$
is the theta lift of a generic discrete series
![]() $\pi $
of
$\pi $
of
![]() $G_2$
. Then the Kret-Shin parameter of
$G_2$
. Then the Kret-Shin parameter of
![]() $\sigma $
is unique (as an element of
$\sigma $
is unique (as an element of
![]() $\Phi (\mathrm {PGSp_6})$
) and is given by
$\Phi (\mathrm {PGSp_6})$
) and is given by
![]() $\iota \circ \mathcal {L}(\pi )$
.
$\iota \circ \mathcal {L}(\pi )$
.
Proof. Let k be a number field as in the proof of Proposition 5.1 and consider the split group
![]() $G_2$
over k. By Proposition 10.7 and Lemma 10.8 in Appendix A, we can find a globally generic cuspidal representation
$G_2$
over k. By Proposition 10.7 and Lemma 10.8 in Appendix A, we can find a globally generic cuspidal representation
![]() $\Pi $
such that
$\Pi $
such that
![]() $\Pi _w = \pi $
and
$\Pi _w = \pi $
and
![]() $\Pi _u$
is the Steinberg representation for some finite place
$\Pi _u$
is the Steinberg representation for some finite place
![]() $u \ne w$
. The global theta lift of
$u \ne w$
. The global theta lift of
![]() $\Pi $
to
$\Pi $
to
![]() $\mathrm {PGSp_6}$
is then a nonzero globally generic cuspidal representation
$\mathrm {PGSp_6}$
is then a nonzero globally generic cuspidal representation
![]() $\Sigma $
of
$\Sigma $
of
![]() $\mathrm {PGSp_6}$
. As in the proof of Proposition 5.1, by considering the global Spin lifting of
$\mathrm {PGSp_6}$
. As in the proof of Proposition 5.1, by considering the global Spin lifting of
![]() $\Sigma $
to
$\Sigma $
to
![]() $\mathrm {GL}_8$
and looking at unramified places, we deduce by the strong multiplicity one theorem that
$\mathrm {GL}_8$
and looking at unramified places, we deduce by the strong multiplicity one theorem that
This implies that the L-parameter of
![]() ${\mathrm {spin}}_*(\sigma )$
is
${\mathrm {spin}}_*(\sigma )$
is
![]() $1 + \phi ^{\flat }$
. On the other hand, it is also the case that
$1 + \phi ^{\flat }$
. On the other hand, it is also the case that
Hence,
![]() $\iota \circ \mathcal {L}(\pi )$
is a Kret-Shin parameter for
$\iota \circ \mathcal {L}(\pi )$
is a Kret-Shin parameter for
![]() $\sigma $
.
$\sigma $
.
Suppose
![]() $\phi $
is another Kret-Shin parameter for
$\phi $
is another Kret-Shin parameter for
![]() $\sigma $
. Then
$\sigma $
. Then
![]() $\phi $
is a quadratic twist of
$\phi $
is a quadratic twist of
![]() $\iota \circ \mathcal {L}(\pi )$
and
$\iota \circ \mathcal {L}(\pi )$
and
![]() ${\mathrm {spin}} \circ \phi = 1 \oplus \phi ^{\flat }$
. It follows by [Reference Harris, Khare and ThorneHKT, Lemma 4.6] (which is a group theoretic result based on [Reference GriessGr95]) that
${\mathrm {spin}} \circ \phi = 1 \oplus \phi ^{\flat }$
. It follows by [Reference Harris, Khare and ThorneHKT, Lemma 4.6] (which is a group theoretic result based on [Reference GriessGr95]) that
![]() $\iota \circ \mathcal {L}(\pi )$
and
$\iota \circ \mathcal {L}(\pi )$
and
![]() $\phi $
are in fact conjugate in
$\phi $
are in fact conjugate in
![]() $\mathrm {Spin}_7({\mathbb C})$
, i.e
$\mathrm {Spin}_7({\mathbb C})$
, i.e
This completes the proof of the proposition.
Corollary 5.3. One has the commutative diagram in (vi) of the Main Theorem.
6 Surjectivity of
 $\mathcal {L}^{\diamondsuit }$
$\mathcal {L}^{\diamondsuit }$
Using the results of the previous two sections, we shall explain in this section how one can show the surjectivity of
The main result of this section is:
Proposition 6.1. Let
![]() $\phi : WD_F \rightarrow G_2({\mathbb C})$
be a discrete series parameter belonging to
$\phi : WD_F \rightarrow G_2({\mathbb C})$
be a discrete series parameter belonging to
![]() $\Phi _{ds}^{\diamondsuit }(G_2)$
. Then there exists a generic discrete series representation
$\Phi _{ds}^{\diamondsuit }(G_2)$
. Then there exists a generic discrete series representation
![]() $\pi $
of
$\pi $
of
![]() $G_2$
such that
$G_2$
such that
![]() $\mathcal {L}(\pi ) = \phi $
.
$\mathcal {L}(\pi ) = \phi $
.
Proof. If the L-parameter
![]() $\phi $
is nontrivial on the Deligne
$\phi $
is nontrivial on the Deligne
![]() $\mathrm {SL}_2$
in
$\mathrm {SL}_2$
in
![]() $WD_F = W_F \times \mathrm {SL}_2({\mathbb C})$
, then the discussion in [Reference Gan and SavinGS23, §3.5] gives us a candidate non-supercuspidal generic discrete series
$WD_F = W_F \times \mathrm {SL}_2({\mathbb C})$
, then the discussion in [Reference Gan and SavinGS23, §3.5] gives us a candidate non-supercuspidal generic discrete series
![]() $\pi \in \mathrm {Irr}(G_2)$
with L-parameter
$\pi \in \mathrm {Irr}(G_2)$
with L-parameter
![]() $\phi $
. The results on theta correspondence in [Reference Gan and SavinGS23] allow us to determine
$\phi $
. The results on theta correspondence in [Reference Gan and SavinGS23] allow us to determine
![]() $\theta (\pi ) \in \mathrm {Irr}(\mathrm {PGSp_6})$
explicitly, as a non-supercuspidal discrete series representation. Using the knowledge of the LLC for
$\theta (\pi ) \in \mathrm {Irr}(\mathrm {PGSp_6})$
explicitly, as a non-supercuspidal discrete series representation. Using the knowledge of the LLC for
![]() $\mathrm {Sp_6}$
(specifically the L-parameters of generic non-supercuspidal discrete series representations), one readily checks that
$\mathrm {Sp_6}$
(specifically the L-parameters of generic non-supercuspidal discrete series representations), one readily checks that
![]() $\mathcal {L}(\pi ) = \phi $
as desired.
$\mathcal {L}(\pi ) = \phi $
as desired.
Henceforth, we focus on the case when
![]() $\phi : W_F \longrightarrow G_2({\mathbb C})$
is trivial on the Deligne
$\phi : W_F \longrightarrow G_2({\mathbb C})$
is trivial on the Deligne
![]() $\mathrm {SL}_2$
. Then the L-parameter
$\mathrm {SL}_2$
. Then the L-parameter
![]() $\iota \circ \phi $
is a supercuspidal L-parameter of
$\iota \circ \phi $
is a supercuspidal L-parameter of
![]() $\mathrm {PGSp_6}(F)$
. Likewise,
$\mathrm {PGSp_6}(F)$
. Likewise,
![]() $\phi ^{\flat }:= \mathrm {std} \circ \iota \circ \phi $
is a supercuspidal L-parameter of
$\phi ^{\flat }:= \mathrm {std} \circ \iota \circ \phi $
is a supercuspidal L-parameter of
![]() $\mathrm {Sp_6}$
and its L-packet contains a unique generic supercuspidal representation
$\mathrm {Sp_6}$
and its L-packet contains a unique generic supercuspidal representation
![]() $\sigma ^{\flat }$
with trivial central character. Let
$\sigma ^{\flat }$
with trivial central character. Let
![]() $\sigma $
be any irreducible generic supercuspidal representation of
$\sigma $
be any irreducible generic supercuspidal representation of
![]() $\mathrm {PGSp_6}$
such that the restriction to
$\mathrm {PGSp_6}$
such that the restriction to
![]() $\mathrm {Sp_6}$
contains
$\mathrm {Sp_6}$
contains
![]() $\sigma ^{\flat }$
. The main issue is to show that we can pick
$\sigma ^{\flat }$
. The main issue is to show that we can pick
![]() $\sigma $
so that it has nonzero theta lift to
$\sigma $
so that it has nonzero theta lift to
![]() $G_2$
.
$G_2$
.
Let
![]() $\phi _{\sigma }$
be a Kret-Shin parameter of
$\phi _{\sigma }$
be a Kret-Shin parameter of
![]() $\sigma $
(as provided by Proposition 5.1). Then one has
$\sigma $
(as provided by Proposition 5.1). Then one has
so that there is a quadratic character
![]() $\chi $
such that
$\chi $
such that
![]() $\iota \circ \phi = \phi _{\sigma } \otimes \chi $
. But by Proposition 4.1(ii),
$\iota \circ \phi = \phi _{\sigma } \otimes \chi $
. But by Proposition 4.1(ii),
![]() $\phi _{\sigma } \otimes \chi $
is a Kret-Shin parameter for
$\phi _{\sigma } \otimes \chi $
is a Kret-Shin parameter for
![]() $\sigma \otimes \chi $
. Hence, after replacing
$\sigma \otimes \chi $
. Hence, after replacing
![]() $\sigma $
by
$\sigma $
by
![]() $\sigma \otimes \chi $
, we may assume that
$\sigma \otimes \chi $
, we may assume that
![]() $\iota \circ \phi $
is a Kret-Shin parameter for
$\iota \circ \phi $
is a Kret-Shin parameter for
![]() $\sigma $
. In particular, we have the following identities of local L-functions:
$\sigma $
. In particular, we have the following identities of local L-functions:
with the first equality holding by Proposition 4.1(i) and the second holding by Proposition 5.1 (and the property of the LLC for
![]() $\mathrm {GL}_8$
). Since
$\mathrm {GL}_8$
). Since
and thus fixes a line in the 8-dimensional representation, we see that
Now it follows by [Reference Savin and WeissmanSW, Prop. 4.6 and Thm. 5.3] that
![]() $\sigma $
has nonzero theta lift
$\sigma $
has nonzero theta lift
![]() $\pi $
on
$\pi $
on
![]() $G_2$
, so that
$G_2$
, so that
![]() $\theta (\pi ) = \sigma $
and
$\theta (\pi ) = \sigma $
and
![]() $\mathcal {L}(\pi ) = \phi $
. This completes the proof of the proposition.
$\mathcal {L}(\pi ) = \phi $
. This completes the proof of the proposition.
7 Results of Bin Xu
After the results of the previous sections, the remaining issue is the parametrization of the fibers of
![]() $\mathcal {L}^{\diamondsuit }$
over
$\mathcal {L}^{\diamondsuit }$
over
![]() $\Phi _{ds}^{\diamondsuit }(G_2)$
. For this, we shall appeal to recent results of Bin Xu [Reference XuXu1, Reference XuXu2, Reference XuXu3] who studied the problem of extending the LLC for the isometry groups
$\Phi _{ds}^{\diamondsuit }(G_2)$
. For this, we shall appeal to recent results of Bin Xu [Reference XuXu1, Reference XuXu2, Reference XuXu3] who studied the problem of extending the LLC for the isometry groups
![]() $\mathrm {Sp}_{2n}$
to the corresponding similitude groups
$\mathrm {Sp}_{2n}$
to the corresponding similitude groups
![]() $\mathrm {GSp}_{2n}$
, whose Langlands dual groups are
$\mathrm {GSp}_{2n}$
, whose Langlands dual groups are
![]() $\mathrm {GSpin}_{2n+1}({\mathbb C})$
. Let us briefly recall his results, specialized to the context of
$\mathrm {GSpin}_{2n+1}({\mathbb C})$
. Let us briefly recall his results, specialized to the context of
![]() $n =3$
.
$n =3$
.
Take an L-parameter
![]() $\phi ^{\flat }$
for
$\phi ^{\flat }$
for
![]() $\mathrm {Sp_6}$
with associated L-packet
$\mathrm {Sp_6}$
with associated L-packet
![]() $\Pi _{\phi ^{\flat }}$
. Suppose that the representations in
$\Pi _{\phi ^{\flat }}$
. Suppose that the representations in
![]() $\Pi _{\phi ^{\flat }}$
have trivial central character (i.e. that
$\Pi _{\phi ^{\flat }}$
have trivial central character (i.e. that
![]() $\phi ^{\flat }$
can be lifted to
$\phi ^{\flat }$
can be lifted to
![]() $\mathrm {Spin}_7({\mathbb C})$
). We consider the finite set
$\mathrm {Spin}_7({\mathbb C})$
). We consider the finite set
Observe that the group
![]() $\mathrm {Hom}(F^{\times }, \mu _2)$
of quadratic characters of
$\mathrm {Hom}(F^{\times }, \mu _2)$
of quadratic characters of
![]() $F^{\times }$
can be regarded as the group of quadratic characters of
$F^{\times }$
can be regarded as the group of quadratic characters of
![]() $\mathrm {PGSp_6}$
(by composition with the similitude map) and acts naturally on
$\mathrm {PGSp_6}$
(by composition with the similitude map) and acts naturally on
![]() $\tilde {\Pi }_{\phi ^{\flat }}$
by twisting.
$\tilde {\Pi }_{\phi ^{\flat }}$
by twisting.
On the other hand, consider the (finite) set
of lifts of
![]() $\phi $
to
$\phi $
to
![]() $\mathrm {Spin}_7({\mathbb C})$
. The group
$\mathrm {Spin}_7({\mathbb C})$
. The group
![]() $\mathrm {Hom}(W_F, \mu _2)$
of quadratic characters of
$\mathrm {Hom}(W_F, \mu _2)$
of quadratic characters of
![]() $W_F$
acts transitively on
$W_F$
acts transitively on
![]() $\tilde {\Phi }_{\phi ^{\flat }}$
by twisting. In particular, one has a canonical identification of component groups for any two elements of
$\tilde {\Phi }_{\phi ^{\flat }}$
by twisting. In particular, one has a canonical identification of component groups for any two elements of
![]() $\tilde {\Phi }_{\phi ^{\flat }}$
.
$\tilde {\Phi }_{\phi ^{\flat }}$
.
In [Reference XuXu1, Reference XuXu2], Xu has obtained a partition of
![]() $\tilde {\Pi }_{\phi ^{\flat }}$
into a disjoint union of finite subsets satisfying the following list of properties, which is a compilation of [Reference XuXu1, Prop. 6.27, Prop. 6.28 and Thm. 6.30], [Reference XuXu2, Prop. 4.4 and Thm. 4.6]) and [Reference XuXu3, Thm. 4.1]:
$\tilde {\Pi }_{\phi ^{\flat }}$
into a disjoint union of finite subsets satisfying the following list of properties, which is a compilation of [Reference XuXu1, Prop. 6.27, Prop. 6.28 and Thm. 6.30], [Reference XuXu2, Prop. 4.4 and Thm. 4.6]) and [Reference XuXu3, Thm. 4.1]:
-
(a) If
 $\tilde {\Pi }_{\phi ^{\flat }}^X \subset \tilde {\Pi }_{\phi ^{\flat }}$
denotes one such subset, then all others are of the form
$\tilde {\Pi }_{\phi ^{\flat }}^X \subset \tilde {\Pi }_{\phi ^{\flat }}$
denotes one such subset, then all others are of the form
 $\tilde {\Pi }_{\phi ^{\flat }}^X \otimes \chi $
for a quadratic character
$\tilde {\Pi }_{\phi ^{\flat }}^X \otimes \chi $
for a quadratic character
 $\chi $
. We will call any of these subsets a Xu’s packet.
$\chi $
. We will call any of these subsets a Xu’s packet. -
(b) The natural restriction of representations of
 $\mathrm {PGSp_6}$
to
$\mathrm {PGSp_6}$
to
 $\mathrm {Sp_6}$
defines a bijection
$\mathrm {Sp_6}$
defines a bijection  $$\begin{align*}\tilde{\Pi}_{\phi^{\flat}}^X \longrightarrow \Pi_{\phi^{\flat}} / _{\mathrm{PGSp_6}}. \end{align*}$$
$$\begin{align*}\tilde{\Pi}_{\phi^{\flat}}^X \longrightarrow \Pi_{\phi^{\flat}} / _{\mathrm{PGSp_6}}. \end{align*}$$
-
(c) There is a natural bijection
for any lift $$\begin{align*}\tilde{\Pi}^X_{\phi^{\flat}} \longleftrightarrow \mathrm{Irr} (S_{\phi}/ Z(\mathrm{Spin}_7)) \end{align*}$$
$$\begin{align*}\tilde{\Pi}^X_{\phi^{\flat}} \longleftrightarrow \mathrm{Irr} (S_{\phi}/ Z(\mathrm{Spin}_7)) \end{align*}$$
 $\phi \in \tilde {\Phi }_{\phi ^{\flat }}$
with component group
$\phi \in \tilde {\Phi }_{\phi ^{\flat }}$
with component group
 $S_{\phi }$
.
$S_{\phi }$
.
-
(d) With respect to the parametrization above, the set
 $\tilde {\Pi }^X_{\phi ,\nu }$
satisfies the stability properties and local character identities required by the theory of endoscopy.
$\tilde {\Pi }^X_{\phi ,\nu }$
satisfies the stability properties and local character identities required by the theory of endoscopy. -
(e) For any
 $\sigma \in \tilde {\Pi }^X_{\phi ^{\flat }}$
and any
$\sigma \in \tilde {\Pi }^X_{\phi ^{\flat }}$
and any
 $\phi \in \tilde {\Phi }_{\phi ^{\flat }}$
, the stabilizer of
$\phi \in \tilde {\Phi }_{\phi ^{\flat }}$
, the stabilizer of
 $\sigma $
in
$\sigma $
in
 $\mathrm {Hom}(F^{\times }, \mu _2)$
is equal to the stabilizer of
$\mathrm {Hom}(F^{\times }, \mu _2)$
is equal to the stabilizer of
 $\phi $
in
$\phi $
in
 $\mathrm {Hom}(W_F, \mu _2)$
(identified via local class field theory). In particular, and the two sets above are (noncanonically) isomorphic as homogeneous sets under
$\mathrm {Hom}(W_F, \mu _2)$
(identified via local class field theory). In particular, and the two sets above are (noncanonically) isomorphic as homogeneous sets under $$\begin{align*}\# \{ \text{Xu's packets} \subset \tilde{\Pi}_{\phi^{\flat}}\} = \# \tilde{\Phi}_{\phi^{\flat}} \end{align*}$$
$$\begin{align*}\# \{ \text{Xu's packets} \subset \tilde{\Pi}_{\phi^{\flat}}\} = \# \tilde{\Phi}_{\phi^{\flat}} \end{align*}$$
 $\mathrm {Hom}(F^{\times }, \mu _2) = \mathrm {Hom}(W_F, \mu _2)$
.
$\mathrm {Hom}(F^{\times }, \mu _2) = \mathrm {Hom}(W_F, \mu _2)$
.
-
(f) Globally, Xu used these local L-packets to describe the tempered part of the automorphic discrete spectrum of
 $\mathrm {PGSp_6}$
in the style of Arthur’s conjecture, in terms of an Arthur multiplicity formula.
$\mathrm {PGSp_6}$
in the style of Arthur’s conjecture, in terms of an Arthur multiplicity formula.
There is no doubt that Xu’s packet
![]() $\tilde {\Pi }^X_{\phi ^{\flat }}$
is an L-packet for
$\tilde {\Pi }^X_{\phi ^{\flat }}$
is an L-packet for
![]() $\mathrm {PGSp_6}$
and its L-parameter should be an element of
$\mathrm {PGSp_6}$
and its L-parameter should be an element of
![]() $\tilde {\Phi }_{\phi ^{\flat }}$
. Constructing an LLC for
$\tilde {\Phi }_{\phi ^{\flat }}$
. Constructing an LLC for
![]() $\mathrm {PGSp_6}$
compatible with the restriction of representations to
$\mathrm {PGSp_6}$
compatible with the restriction of representations to
![]() $\mathrm {Sp_6}$
amounts to constructing an equivariant bijection between the two homogeneous sets in (e) above. However, this problem was not resolved in [Reference XuXu1, Reference XuXu2, Reference XuXu3]. We shall see in §9 how this issue can be resolved if
$\mathrm {Sp_6}$
amounts to constructing an equivariant bijection between the two homogeneous sets in (e) above. However, this problem was not resolved in [Reference XuXu1, Reference XuXu2, Reference XuXu3]. We shall see in §9 how this issue can be resolved if
![]() $\phi ^{\flat }$
takes value in
$\phi ^{\flat }$
takes value in
![]() $G_2({\mathbb C})$
.
$G_2({\mathbb C})$
.
8 Fibers of
 $\mathcal {L}$
$\mathcal {L}$
Let
![]() $\phi \in \Phi _{ds}^{\diamondsuit }(G_2)$
be a discrete series parameter so that
$\phi \in \Phi _{ds}^{\diamondsuit }(G_2)$
be a discrete series parameter so that
![]() $\iota \circ \phi $
is a discrete series parameter of
$\iota \circ \phi $
is a discrete series parameter of
![]() $\mathrm {PGSp_6}$
. Then we have shown in Proposition 6.1 that
$\mathrm {PGSp_6}$
. Then we have shown in Proposition 6.1 that
![]() $\mathcal {L}^{-1}(\phi )$
contains a generic discrete series representation and is thus nonempty. In this section, we shall enumerate the fiber
$\mathcal {L}^{-1}(\phi )$
contains a generic discrete series representation and is thus nonempty. In this section, we shall enumerate the fiber
![]() $\mathcal {L}^{-1}(\phi )$
.
$\mathcal {L}^{-1}(\phi )$
.
For ease of notation, let us set
It is clear from the construction of
![]() $\mathcal {L}$
that
$\mathcal {L}$
that
and as we discussed in the previous section, the latter set is the disjoint union of Xu’s packets.
8.1 Uniqueness of generic member
We first show:
Proposition 8.1. For
![]() $\phi \in \Phi _{ds}^{\diamondsuit }(G_2)$
, there is a unique generic representation in
$\phi \in \Phi _{ds}^{\diamondsuit }(G_2)$
, there is a unique generic representation in
![]() $\mathcal {L}^{-1}(\phi )$
.
$\mathcal {L}^{-1}(\phi )$
.
Proof. Since the existence part has been shown in Proposition 6.1, the main issue here is the uniqueness. Suppose, for the sake of contradiction, that
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
are two distinct generic representations of
$\pi '$
are two distinct generic representations of
![]() $G_2$
such that
$G_2$
such that
![]() $\mathcal {L}(\pi ) = \mathcal {L}(\pi ') = \phi $
. Then
$\mathcal {L}(\pi ) = \mathcal {L}(\pi ') = \phi $
. Then
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
belongs to
$\pi '$
belongs to
![]() $\mathrm {Irr}_{ds}^{\diamondsuit }(G_2)$
and we set
$\mathrm {Irr}_{ds}^{\diamondsuit }(G_2)$
and we set
Both
![]() $\sigma $
and
$\sigma $
and
![]() $\sigma '$
are distinct generic discrete series representations of
$\sigma '$
are distinct generic discrete series representations of
![]() $\mathrm {PGSp_6}$
(by Howe duality) belonging to
$\mathrm {PGSp_6}$
(by Howe duality) belonging to
![]() $\tilde {\Pi }_{\phi ^{\flat }}$
(see (7.1)). Hence, there is a quadratic character
$\tilde {\Pi }_{\phi ^{\flat }}$
(see (7.1)). Hence, there is a quadratic character
![]() $\chi $
such that
$\chi $
such that
![]() $\sigma ' \cong \sigma \otimes \chi \ncong \sigma $
.
$\sigma ' \cong \sigma \otimes \chi \ncong \sigma $
.
Now by Proposition 5.2,
![]() $\sigma $
has (unique) Kret-Shin parameter
$\sigma $
has (unique) Kret-Shin parameter
![]() $\iota \circ \phi $
which is an element of
$\iota \circ \phi $
which is an element of
![]() $\tilde {\Phi }_{\phi ^{\flat }}$
(see (7.2). On the other hand,
$\tilde {\Phi }_{\phi ^{\flat }}$
(see (7.2). On the other hand,
-
• by Proposition 4.1(ii), since
 $\sigma ' \cong \sigma \otimes \chi $
,
$\sigma ' \cong \sigma \otimes \chi $
,
 $\sigma '$
has Kret-Shin parameter
$\sigma '$
has Kret-Shin parameter
 $(\iota \circ \phi ) \otimes \chi $
;
$(\iota \circ \phi ) \otimes \chi $
; -
• by Proposition 5.2,
 $\sigma ' = \theta (\pi ')$
has Kret-Shin parameter
$\sigma ' = \theta (\pi ')$
has Kret-Shin parameter
 $\iota \circ \phi $
.
$\iota \circ \phi $
.
By the uniqueness part of Proposition 5.2, we have
Hence the quadratic character
![]() $\chi $
stabilizes
$\chi $
stabilizes
![]() $\iota \circ \phi \in \tilde {\Phi }_{\phi ^{\flat }}$
but does not stabilize
$\iota \circ \phi \in \tilde {\Phi }_{\phi ^{\flat }}$
but does not stabilize
![]() $\sigma \in \tilde {\Pi }_{\phi ^{\flat }}$
. This contradicts statement (e) of §7.
$\sigma \in \tilde {\Pi }_{\phi ^{\flat }}$
. This contradicts statement (e) of §7.
8.2 A distinguished Xu’s packet
In view of Proposition 8.1, we can now pick out a distinguished Xu’s packet contained in
![]() $\tilde {\Pi }_{\phi ^{\flat }}$
. Namely, we set
$\tilde {\Pi }_{\phi ^{\flat }}$
. Namely, we set
Another way to say this is:
We shall show:
Proposition 8.2. Let
![]() $\phi \in \Phi _{ds}^{\diamondsuit }(G_2)$
. The local theta correspondence defines a bijection
$\phi \in \Phi _{ds}^{\diamondsuit }(G_2)$
. The local theta correspondence defines a bijection
8.3 Parametrization of fiber of
 $\mathcal {L}$
$\mathcal {L}$
Let us assume this proposition for a moment and explain how it leads to a proof of (vii) of the Main Theorem. It was shown in [Reference Gross and SavinGrS2, Section 4, Prop. 1.10] that the inclusion
![]() $\iota $
gives rise to an isomorphism
$\iota $
gives rise to an isomorphism
and thus a bijection
On the other hand, statement (c) of §7 gives a bijection
Combining this with Proposition 8.2, we obtain a bijection
This finishes the proof of (vii) of the Main Theorem.
8.4 One in, all in
It remains to prove Proposition 8.2. The following is the key lemma:
Lemma 8.3. Let
![]() $\tilde {\Pi }^X_{\phi ^{\flat }} \subset \tilde {\Pi }_{\phi ^{\flat }}$
be any Xu’s packet. Then either all elements of
$\tilde {\Pi }^X_{\phi ^{\flat }} \subset \tilde {\Pi }_{\phi ^{\flat }}$
be any Xu’s packet. Then either all elements of
![]() $\tilde {\Pi }^X_{\phi ^{\flat }}$
have nonzero theta lift to
$\tilde {\Pi }^X_{\phi ^{\flat }}$
have nonzero theta lift to
![]() $G_2$
or none of them has.
$G_2$
or none of them has.
Proof. It suffices to show that if
![]() $\sigma \in \tilde {\Pi }^X_{\phi ^{\flat }}$
has nonzero theta lift to
$\sigma \in \tilde {\Pi }^X_{\phi ^{\flat }}$
has nonzero theta lift to
![]() $G_2$
, then so does any other
$G_2$
, then so does any other
![]() $\sigma ' \in \tilde {\Pi }^X_{\phi ^{\flat }}$
. This will proceed by a global argument.
$\sigma ' \in \tilde {\Pi }^X_{\phi ^{\flat }}$
. This will proceed by a global argument.
Suppose that
![]() $\sigma = \theta (\pi )$
for
$\sigma = \theta (\pi )$
for
![]() $\pi \in \mathrm {Irr}^{\diamondsuit }_{ds}(G_2)$
. Note that all non-supercuspidal representations in
$\pi \in \mathrm {Irr}^{\diamondsuit }_{ds}(G_2)$
. Note that all non-supercuspidal representations in
![]() $\mathrm {Irr}^{\diamondsuit }_{ds}(G_2)$
are generic (see [Reference Gan and SavinGS23, Thm. 15.3]). We shall globalize
$\mathrm {Irr}^{\diamondsuit }_{ds}(G_2)$
are generic (see [Reference Gan and SavinGS23, Thm. 15.3]). We shall globalize
![]() $\pi $
to a cuspidal representation
$\pi $
to a cuspidal representation
![]() $\Pi $
in one of the following two ways, depending on the type of
$\Pi $
in one of the following two ways, depending on the type of
![]() $\pi $
.
$\pi $
.
-
(i) Suppose that
 $\pi $
is generic (this includes all non-supercuspidal
$\pi $
is generic (this includes all non-supercuspidal
 $\pi $
). Let k be a totally real number field with two places
$\pi $
). Let k be a totally real number field with two places
 $w_1$
and
$w_1$
and
 $w_2$
such that
$w_2$
such that
 $k_{w_1}\cong k_{w_2}\cong F$
. Let
$k_{w_1}\cong k_{w_2}\cong F$
. Let
 $\mathbb O$
be the split octonion algebra over k, and let
$\mathbb O$
be the split octonion algebra over k, and let
 $G=\mathrm {Aut}(\mathbb O)$
. Fix an additional place w and a generic supercuspidal representation
$G=\mathrm {Aut}(\mathbb O)$
. Fix an additional place w and a generic supercuspidal representation
 $\delta $
of
$\delta $
of
 $G(k_w)$
such that
$G(k_w)$
such that
 $\theta (\delta )$
is a generic supercuspidal representation of
$\theta (\delta )$
is a generic supercuspidal representation of
 $H(k_w)$
. (Using [Reference GanG] there are such representations
$H(k_w)$
. (Using [Reference GanG] there are such representations
 $\delta $
of depth 0.) By Proposition 10.7 and Lemma 10.8, one can find a globally generic cuspidal automorphic representation
$\delta $
of depth 0.) By Proposition 10.7 and Lemma 10.8, one can find a globally generic cuspidal automorphic representation
 $\Pi =\otimes _v \Pi _v$
of G such that
$\Pi =\otimes _v \Pi _v$
of G such that-
–
 $\Pi _{\infty }$
is a discrete series representation, with the infinitesimal character sufficiently away from walls, for every archimedean place
$\Pi _{\infty }$
is a discrete series representation, with the infinitesimal character sufficiently away from walls, for every archimedean place
 $\infty $
;
$\infty $
; -
–
 $\Pi _{w_1}\cong \Pi _{w_2}\cong \pi $
;
$\Pi _{w_1}\cong \Pi _{w_2}\cong \pi $
; -
–
 $\Pi _w = \delta $
.
$\Pi _w = \delta $
.
Then the global theta lift of
 $\Pi $
to
$\Pi $
to
 $\mathrm {PGSp_6}$
is a globally generic cuspidal representation
$\mathrm {PGSp_6}$
is a globally generic cuspidal representation
 $\Sigma $
satisfying
$\Sigma $
satisfying-
–
 $\Sigma _{\infty }$
is a discrete series representation for every archimedean place
$\Sigma _{\infty }$
is a discrete series representation for every archimedean place
 $\infty $
;
$\infty $
; -
–
 $\Sigma _{w_1}\cong \Sigma _{w_2}\cong \sigma = \theta (\pi )$
;
$\Sigma _{w_1}\cong \Sigma _{w_2}\cong \sigma = \theta (\pi )$
; -
– the restriction of
 $\Sigma $
to
$\Sigma $
to
 $\mathrm {Sp_6}$
is attached to a generic A-parameter.
$\mathrm {Sp_6}$
is attached to a generic A-parameter.
Here, the first item holds by the matching of infinitesimal characters [Reference Huang, Pandžić and SavinHPS] and the fact that, at infinitesimal characters of discrete series sufficiently away from walls, only discrete series representations are unitary. The third item is assured by the first.
-
-
(ii) Suppose that
 $\pi $
is supercuspidal. Let k be a totally real number field as in (i). Let
$\pi $
is supercuspidal. Let k be a totally real number field as in (i). Let
 $\mathbb O$
be the totally definite octonion algebra over k, and let
$\mathbb O$
be the totally definite octonion algebra over k, and let
 $G=\mathrm {Aut}(\mathbb O)$
. By Proposition 10.5 and Corollary 10.6, one can find a cuspidal automorphic representation
$G=\mathrm {Aut}(\mathbb O)$
. By Proposition 10.5 and Corollary 10.6, one can find a cuspidal automorphic representation
 $\Pi $
such that:
$\Pi $
such that:-
–
 $\Pi _{w_1} \cong \Pi _{w_2} \cong \pi $
;
$\Pi _{w_1} \cong \Pi _{w_2} \cong \pi $
; -
–
 $\Pi _u$
is the Steinberg representation for some other finite place u;
$\Pi _u$
is the Steinberg representation for some other finite place u; -
–
 $\Pi $
has nonzero cuspidal global theta lift
$\Pi $
has nonzero cuspidal global theta lift
 $\Sigma $
on
$\Sigma $
on
 $\mathrm {PGSp_6}$
.
$\mathrm {PGSp_6}$
.
Thus,
 $\Sigma $
is a nonzero cuspidal automorphic representation of
$\Sigma $
is a nonzero cuspidal automorphic representation of
 $\mathrm {PGSp_6}$
satisfying:
$\mathrm {PGSp_6}$
satisfying:-
–
 $\Sigma _{w_1}\cong \Sigma _{w_2}\cong \sigma = \theta (\pi )$
;
$\Sigma _{w_1}\cong \Sigma _{w_2}\cong \sigma = \theta (\pi )$
; -
–
 $\Sigma _u$
is the Steinberg representation;
$\Sigma _u$
is the Steinberg representation; -
– the restriction of
 $\Sigma $
to
$\Sigma $
to
 $\mathrm {Sp_6}$
is attached to a generic A-parameter.
$\mathrm {Sp_6}$
is attached to a generic A-parameter.
-
Here the last item is a consequence of the second.
Now let
![]() $\sigma '$
be a representation in
$\sigma '$
be a representation in
![]() $\tilde {\Pi }^X_{\phi ^{\flat }}$
. Then by the Arthur multiplicity formula for
$\tilde {\Pi }^X_{\phi ^{\flat }}$
. Then by the Arthur multiplicity formula for
![]() $\mathrm {PGSp_6}$
established by Xu, there exists a cuspidal automorphic representation
$\mathrm {PGSp_6}$
established by Xu, there exists a cuspidal automorphic representation
![]() $\Sigma '$
satisfying:
$\Sigma '$
satisfying:
-
•
 $\Sigma ^{\prime }_v \cong \Sigma _v$
for all
$\Sigma ^{\prime }_v \cong \Sigma _v$
for all
 $v \ne w_1$
or
$v \ne w_1$
or
 $w_2$
;
$w_2$
; -
•
 $\Sigma ^{\prime }_{w_1} \cong \Sigma ^{\prime }_{w_2} \cong \sigma '$
.
$\Sigma ^{\prime }_{w_1} \cong \Sigma ^{\prime }_{w_2} \cong \sigma '$
.
In addition, one has an equality of partial Spin L-functions:
In particular, since
![]() $L^S(s, \Sigma , \mathrm {std})$
is nonzero at
$L^S(s, \Sigma , \mathrm {std})$
is nonzero at
![]() $s=1$
(as
$s=1$
(as
![]() $\mathrm {rest}(\Sigma )$
is associated with a generic A-parameter), we see that
$\mathrm {rest}(\Sigma )$
is associated with a generic A-parameter), we see that
![]() $L^S(s, \Sigma ', {\mathrm {spin}})$
has a pole at
$L^S(s, \Sigma ', {\mathrm {spin}})$
has a pole at
![]() $s=1$
. By [Reference Gan and SavinGS20, Thm. 1.1],
$s=1$
. By [Reference Gan and SavinGS20, Thm. 1.1],
![]() $\Sigma '$
has nonzero global theta lift to a form of
$\Sigma '$
has nonzero global theta lift to a form of
![]() $G_2$
over k. Specializing to the place
$G_2$
over k. Specializing to the place
![]() $w_1$
, we see that
$w_1$
, we see that
![]() $\sigma '$
has nonzero local theta lift to the split
$\sigma '$
has nonzero local theta lift to the split
![]() $G_2$
, as desired. This concludes the proof.
$G_2$
, as desired. This concludes the proof.
8.5 Proof of Proposition 8.2
Using Lemma 8.3, we can now give the proof of Proposition 8.2. Lemma 8.3 implies that all members of the distinguished Xu’s packet
![]() $\tilde {\Pi }^{X \ast }_{\phi ^{\flat }}$
has nonzero theta lift to
$\tilde {\Pi }^{X \ast }_{\phi ^{\flat }}$
has nonzero theta lift to
![]() $G_2$
(since the generic member does). On the other hand, for any other Xu’s packet contained in
$G_2$
(since the generic member does). On the other hand, for any other Xu’s packet contained in
![]() $\tilde {\Pi }_{\phi ^{\flat }}$
, the generic member does not participate in theta correspondence with
$\tilde {\Pi }_{\phi ^{\flat }}$
, the generic member does not participate in theta correspondence with
![]() $G_2$
by Proposition 8.1. Hence, Lemma 8.3 implies that none of the members does. This proves Proposition 8.2.
$G_2$
by Proposition 8.1. Hence, Lemma 8.3 implies that none of the members does. This proves Proposition 8.2.
9 Applications to Theta Correspondence
The starting point of this paper is the Howe duality and theta dichotomy result of [Reference Gan and SavinGS23] for the dual pairs

The investigation of these dual pair correspondences was begun by Gross and the second author [Reference Gross and SavinGrS1, Reference Gross and SavinGrS2] in the 1990’s, and precise conjectures for the behaviour of these theta correspondences were formulated in [Reference Gross and SavinGrS1, Reference Gross and SavinGrS2] in terms of the conjectural LLC for the groups involved. Our construction of the (refined) LLC for
![]() $G_2$
in this paper is to a large extent guided by these conjectures. With the results established in this paper, we can turn the table around and establish these conjectures from [Reference Gross and SavinGrS1, Reference Gross and SavinGrS2].
$G_2$
in this paper is to a large extent guided by these conjectures. With the results established in this paper, we can turn the table around and establish these conjectures from [Reference Gross and SavinGrS1, Reference Gross and SavinGrS2].
For this, we first need to establish a partial LLC for
![]() $\mathrm {PGSp_6}$
. Namely, suppose that
$\mathrm {PGSp_6}$
. Namely, suppose that
![]() $\phi \in \Phi ^{\diamondsuit }_{ds}(G_2)$
and we set
$\phi \in \Phi ^{\diamondsuit }_{ds}(G_2)$
and we set
We have noted in §7 that the two sets
are noncanonically isomorphic as
![]() $\mathrm {Hom}(F^{\times }, \mu _2)$
-sets. However, we have seen in §8.2 that one has a distinguished Xu’s packet
$\mathrm {Hom}(F^{\times }, \mu _2)$
-sets. However, we have seen in §8.2 that one has a distinguished Xu’s packet
![]() $\tilde {\Pi }^{X\ast }_{\phi ^{\flat }}$
in the first set. Moreover, the second set contains the distinguished L-parameter
$\tilde {\Pi }^{X\ast }_{\phi ^{\flat }}$
in the first set. Moreover, the second set contains the distinguished L-parameter
![]() $\iota \circ \phi $
. The existence of these distinguished base points gives rise to a canonical isomorphism of
$\iota \circ \phi $
. The existence of these distinguished base points gives rise to a canonical isomorphism of
![]() $\mathrm {Hom}(F^{\times } ,\mu _2)$
-sets.
$\mathrm {Hom}(F^{\times } ,\mu _2)$
-sets.
In other words, for
![]() $\phi \in \Phi ^{\diamondsuit }_{ds}(G_2)$
, we define the L-parameter of the distinguished Xu’s packet
$\phi \in \Phi ^{\diamondsuit }_{ds}(G_2)$
, we define the L-parameter of the distinguished Xu’s packet
![]() $\tilde {\Pi }^{X\ast }_{\phi ^{\flat }}$
to be
$\tilde {\Pi }^{X\ast }_{\phi ^{\flat }}$
to be
![]() $\iota \circ \phi $
. This definition is not really ad hoc. Indeed, the distinguished Xu’s packet
$\iota \circ \phi $
. This definition is not really ad hoc. Indeed, the distinguished Xu’s packet
![]() $\tilde {\Pi }^{X\ast }_{\phi ^{\flat }}$
is the unique one in
$\tilde {\Pi }^{X\ast }_{\phi ^{\flat }}$
is the unique one in
![]() $ \tilde {\Phi }_{\phi ^{\flat }}$
for which the Langlands-Shahidi Spin L-function of its unique generic member is equal to the local L-factor of
$ \tilde {\Phi }_{\phi ^{\flat }}$
for which the Langlands-Shahidi Spin L-function of its unique generic member is equal to the local L-factor of
![]() ${\mathrm {spin}} \circ \iota \circ \phi $
(and hence has a pole at
${\mathrm {spin}} \circ \iota \circ \phi $
(and hence has a pole at
![]() $s = 0$
). Further, by extending the spin lifting constructed in §4 and using the results of Kret-Shin recalled in §5.1, we construct in Appendix C below a weak LLC for
$s = 0$
). Further, by extending the spin lifting constructed in §4 and using the results of Kret-Shin recalled in §5.1, we construct in Appendix C below a weak LLC for
![]() $\mathrm {PGSp_6}$
, of which this particular L-packet is an instance.
$\mathrm {PGSp_6}$
, of which this particular L-packet is an instance.
In any case, with this definition of the L-packet of
![]() $\mathrm {PGSp_6}$
associated to
$\mathrm {PGSp_6}$
associated to
![]() $\iota \circ \phi $
, and the results of [Reference Gan and SavinGS23] as well as the LLC of
$\iota \circ \phi $
, and the results of [Reference Gan and SavinGS23] as well as the LLC of
![]() $G_2$
established in this paper, we have:
$G_2$
established in this paper, we have:
Theorem 9.1.
(i) Conjecture 3.1 in [Reference Gross and SavinGrS1] holds when
![]() $p \ne 3$
. More precisely,
$p \ne 3$
. More precisely,
-
(a) For
 $\tau \in \mathrm {Irr}(\mathrm {PGL}_3)$
with L-parameter
$\tau \in \mathrm {Irr}(\mathrm {PGL}_3)$
with L-parameter
 $\phi _{\tau }$
, the local theta lifts of
$\phi _{\tau }$
, the local theta lifts of
 $\tau $
to
$\tau $
to
 $G_2$
is the set of
$G_2$
is the set of
 $\pi \in \mathrm {Irr}(G_2)$
whose (enhanced) L-parameter
$\pi \in \mathrm {Irr}(G_2)$
whose (enhanced) L-parameter
 $(\phi ,\eta )$
satisfies where we recall that
$(\phi ,\eta )$
satisfies where we recall that $$\begin{align*}\phi = \iota' \circ \phi_{\tau} \quad \text{and} \quad \eta \circ \iota^{\prime}_* = 1, \end{align*}$$
is the natural embedding which induces a map of component groups
$$\begin{align*}\phi = \iota' \circ \phi_{\tau} \quad \text{and} \quad \eta \circ \iota^{\prime}_* = 1, \end{align*}$$
is the natural embedding which induces a map of component groups $$\begin{align*}\iota': \mathrm{SL}_3({\mathbb C}) \longrightarrow G_2({\mathbb C}) \end{align*}$$
$$\begin{align*}\iota': \mathrm{SL}_3({\mathbb C}) \longrightarrow G_2({\mathbb C}) \end{align*}$$
 $$\begin{align*}\iota^{\prime}_* : \pi_0(Z_{\mathrm{SL}_3}(\phi_{\tau})) \longrightarrow S_{\iota' \circ \phi_{\tau}} = \pi_0(Z_{G_2}(\iota' \circ \phi_{\tau})). \end{align*}$$
$$\begin{align*}\iota^{\prime}_* : \pi_0(Z_{\mathrm{SL}_3}(\phi_{\tau})) \longrightarrow S_{\iota' \circ \phi_{\tau}} = \pi_0(Z_{G_2}(\iota' \circ \phi_{\tau})). \end{align*}$$
-
(b) If
 $\tau _D$
denotes the Jacquet-Langlands lift of
$\tau _D$
denotes the Jacquet-Langlands lift of
 $\tau $
to
$\tau $
to
 $D^{\times }$
, then the set of local theta lifts of
$D^{\times }$
, then the set of local theta lifts of
 $\tau _D$
and
$\tau _D$
and
 $\tau _D^{\vee }$
to
$\tau _D^{\vee }$
to
 $G_2$
consists of those
$G_2$
consists of those
 $\pi \in \mathrm {Irr}(G_2)$
whose (enhanced) L-parameter
$\pi \in \mathrm {Irr}(G_2)$
whose (enhanced) L-parameter
 $(\phi , \eta )$
satisfies
$(\phi , \eta )$
satisfies  $$\begin{align*}\phi = \iota' \circ \phi_{\tau} \quad \text{and} \quad \eta \circ \iota^{\prime}_* \ne 1, \end{align*}$$
$$\begin{align*}\phi = \iota' \circ \phi_{\tau} \quad \text{and} \quad \eta \circ \iota^{\prime}_* \ne 1, \end{align*}$$
(ii) Conjecture 1.13 (as well as Conjectures 2.3 and 2.5) in [Reference Gross and SavinGrS2, Section 4, Pg. 188] hold. More precisely, suppose that
![]() $\pi \in \mathrm {Irr}(G_2)$
has (enhanced) L-parameter
$\pi \in \mathrm {Irr}(G_2)$
has (enhanced) L-parameter
![]() $(\phi , \eta )$
, then its local theta lift
$(\phi , \eta )$
, then its local theta lift
![]() $\theta (\pi ) \in \mathrm {Irr}(\mathrm {PGSp_6})$
has (enhanced) L-parameter
$\theta (\pi ) \in \mathrm {Irr}(\mathrm {PGSp_6})$
has (enhanced) L-parameter
![]() $(\phi ', \eta ')$
satisfying
$(\phi ', \eta ')$
satisfying
where we recall that
is the natural embedding which induces a map of component groups
Thus, in a sense, we have come full circle.
10 Appendix A: Some Globalization Results
In this appendix, we record some globalization results that were used in the main body of the paper.
10.1 A local non-vanishing result
Let F be a p-adic field and
![]() ${\mathbb O}$
be an octonion algebra over F, and let
${\mathbb O}$
be an octonion algebra over F, and let
![]() $G=\mathrm {Aut}({\mathbb O})$
. Let D be a quaternion algebra over F and fix an embedding
$G=\mathrm {Aut}({\mathbb O})$
. Let D be a quaternion algebra over F and fix an embedding
![]() $D \hookrightarrow \mathbb {O}$
, unique up to conjugation by G. Let
$D \hookrightarrow \mathbb {O}$
, unique up to conjugation by G. Let
![]() $G_D\subset G$
be the pointwise stabilizer of
$G_D\subset G$
be the pointwise stabilizer of
![]() $D\subset {\mathbb O}$
. Then
$D\subset {\mathbb O}$
. Then
![]() $G_D$
is isomorphic to the group of norm one elements in D.
$G_D$
is isomorphic to the group of norm one elements in D.
Let
![]() $H= \mathrm {PGSp_6}(F)$
, and
$H= \mathrm {PGSp_6}(F)$
, and
![]() $P=MN$
the Siegel maximal parabolic subgroup. Let
$P=MN$
the Siegel maximal parabolic subgroup. Let
![]() $\hat N$
be the unitary dual of the unipotent radical N. The group M acts on
$\hat N$
be the unitary dual of the unipotent radical N. The group M acts on
![]() $\hat N$
with open orbits parameterized by quaternion algebras D: the stabilizer in M of an element in the orbit parameterized by is isomorphic to
$\hat N$
with open orbits parameterized by quaternion algebras D: the stabilizer in M of an element in the orbit parameterized by is isomorphic to
![]() $\mathrm {Aut}(D)$
.
$\mathrm {Aut}(D)$
.
Recall that we have the dual pair
![]() $G \times H \subset E_7$
and the minimal representation
$G \times H \subset E_7$
and the minimal representation
![]() $\Pi $
of
$\Pi $
of
![]() $E_7$
induces a local theta correspondence
$E_7$
induces a local theta correspondence
![]() $\theta : \mathrm {Irr}^{\heartsuit }(G) \longrightarrow \mathrm {Irr}(H)$
. Now we note:
$\theta : \mathrm {Irr}^{\heartsuit }(G) \longrightarrow \mathrm {Irr}(H)$
. Now we note:
Lemma 10.1. Let
![]() $\pi $
be an irreducible representation of G such that
$\pi $
be an irreducible representation of G such that
![]() $\theta (\pi )$
is a tempered representation of H. Then there exists a quaternion algebra
$\theta (\pi )$
is a tempered representation of H. Then there exists a quaternion algebra
![]() $D \subset {\mathbb O}$
such that
$D \subset {\mathbb O}$
such that
![]() $\pi $
is a quotient of
$\pi $
is a quotient of
![]() $\mathrm {ind}^G_{G_D}(1)$
.
$\mathrm {ind}^G_{G_D}(1)$
.
Proof. We claim that there exists
![]() $\psi _N$
, in one of the open orbits, such that
$\psi _N$
, in one of the open orbits, such that
![]() $\theta (\pi )_{N,\psi _N} \neq 0$
. If not then any summand of
$\theta (\pi )_{N,\psi _N} \neq 0$
. If not then any summand of
![]() $\theta (\pi )$
restricted to
$\theta (\pi )$
restricted to
![]() $\mathrm {Sp_6}(F)$
is of Howe’s N-rank 2, and thus a classical theta lift of a unitary representation of an orthogonal group
$\mathrm {Sp_6}(F)$
is of Howe’s N-rank 2, and thus a classical theta lift of a unitary representation of an orthogonal group
![]() $\mathrm {O}(2)$
[Reference LiLi]. But these theta lifts are not tempered, hence the claim
$\mathrm {O}(2)$
[Reference LiLi]. But these theta lifts are not tempered, hence the claim
Let
![]() $\Pi $
be the minimal representation of the group
$\Pi $
be the minimal representation of the group
![]() $E_7$
, so that
$E_7$
, so that
![]() $\pi \otimes \theta (\pi )$
is its quotient. From [Reference Gross and SavinGrS2, Section 5, Lemma 3.4] (case (4) in the proof) we have
$\pi \otimes \theta (\pi )$
is its quotient. From [Reference Gross and SavinGrS2, Section 5, Lemma 3.4] (case (4) in the proof) we have
where D is such that
![]() $\psi _N$
belongs to the open orbit parameterized by D. The lemma follows.
$\psi _N$
belongs to the open orbit parameterized by D. The lemma follows.
Corollary 10.2. Let
![]() $\pi $
be a supercuspidal representation of G such that
$\pi $
be a supercuspidal representation of G such that
![]() $\theta (\pi )\neq 0$
. Then there exists a quaternion algebra D such that
$\theta (\pi )\neq 0$
. Then there exists a quaternion algebra D such that
![]() $\pi $
is a submodule of
$\pi $
is a submodule of
![]() $\mathrm {ind}^G_{G_D}(1)$
.
$\mathrm {ind}^G_{G_D}(1)$
.
Proof. Since
![]() $\theta $
preserves tempered representations, it follows from Lemma 10.1 that
$\theta $
preserves tempered representations, it follows from Lemma 10.1 that
![]() $\pi $
is a quotient of
$\pi $
is a quotient of
![]() $\mathrm {ind}^G_{G_D}(1)$
for some D. The corollary follows from projectivity of
$\mathrm {ind}^G_{G_D}(1)$
for some D. The corollary follows from projectivity of
![]() $\pi $
.
$\pi $
.
Lemma 10.3. Let
![]() $\mathrm {St}$
be the Steinberg representation of G. Let D be a division quaternion algebra. Then
$\mathrm {St}$
be the Steinberg representation of G. Let D be a division quaternion algebra. Then
![]() $\mathrm {St}$
is a direct summand of
$\mathrm {St}$
is a direct summand of
![]() $L^2(G_D \backslash G)$
.
$L^2(G_D \backslash G)$
.
Proof. Recall that
![]() $\theta (\mathrm {St})$
is the Steinberg representation of H. Let U be a maximal unipotent subgroup of H containing N. By [Reference Chan and SavinCS, Prop. 5], the restriction of the Steinberg representation of H to U is the regular representation of U. It follows at once that
$\theta (\mathrm {St})$
is the Steinberg representation of H. Let U be a maximal unipotent subgroup of H containing N. By [Reference Chan and SavinCS, Prop. 5], the restriction of the Steinberg representation of H to U is the regular representation of U. It follows at once that
![]() $\theta (\mathrm {St})_{N,\psi _N} \neq 0$
for any character
$\theta (\mathrm {St})_{N,\psi _N} \neq 0$
for any character
![]() $\psi _N$
of N. Hence, arguing as in Lemma 10.1,
$\psi _N$
of N. Hence, arguing as in Lemma 10.1,
![]() $\mathrm {St}$
is a quotient of
$\mathrm {St}$
is a quotient of
![]() $\mathrm {ind}^G_{G_D}(1)$
with D non-split. Since
$\mathrm {ind}^G_{G_D}(1)$
with D non-split. Since
and
![]() $G_D$
is anisotropic, there exists a non-zero vector in
$G_D$
is anisotropic, there exists a non-zero vector in
![]() $\mathrm {St}$
fixed by
$\mathrm {St}$
fixed by
![]() $G_D$
. The corresponding matrix coefficient gives us
$G_D$
. The corresponding matrix coefficient gives us
We have a complementary result for the compact Lie group
![]() $G^c_2(\mathbb {R})$
which is the automorphism group of the octonion division
$G^c_2(\mathbb {R})$
which is the automorphism group of the octonion division
![]() $\mathbb {R}$
-algebra.
$\mathbb {R}$
-algebra.
Lemma 10.4. Let
![]() $\mathbb H$
be the quaternion division
$\mathbb H$
be the quaternion division
![]() $\mathbb {R}$
-algebra. For any irreducible (finite-dimensional) representation
$\mathbb {R}$
-algebra. For any irreducible (finite-dimensional) representation
![]() $\pi $
of
$\pi $
of
![]() $G^c_2(\mathbb {R})$
, one has
$G^c_2(\mathbb {R})$
, one has
![]() $\pi ^{G_{\mathbb H}(\mathbb {R})} \ne 0$
, so that
$\pi ^{G_{\mathbb H}(\mathbb {R})} \ne 0$
, so that
Proof. One has
![]() $G_{\mathbb H}(\mathbb {R}) \subset \mathrm {SU}_3 \subset G^c_2(\mathbb {R})$
. By the Gelfand-Zetlin branching rule, any irreducible representation of
$G_{\mathbb H}(\mathbb {R}) \subset \mathrm {SU}_3 \subset G^c_2(\mathbb {R})$
. By the Gelfand-Zetlin branching rule, any irreducible representation of
![]() ${\mathrm {SU}}_3$
has nonzero vectors fixed by
${\mathrm {SU}}_3$
has nonzero vectors fixed by
![]() $G_{\mathbb H}(\mathbb {R}) \cong \mathrm {SU}_2$
. The proposition follows.
$G_{\mathbb H}(\mathbb {R}) \cong \mathrm {SU}_2$
. The proposition follows.
10.2 First globalization result
Let k be a totally real number field and
![]() $\mathbb O$
be a totally definite octonion algebra over k, so that
$\mathbb O$
be a totally definite octonion algebra over k, so that
![]() $\mathbb O_{\infty }$
is non-split for all archimedean places
$\mathbb O_{\infty }$
is non-split for all archimedean places
![]() $\infty $
of k, and set
$\infty $
of k, and set
![]() $G=\mathrm {Aut}({\mathbb O})$
. For any place v of k, write
$G=\mathrm {Aut}({\mathbb O})$
. For any place v of k, write
![]() $G_v=G(k_v)$
for simplicity. Then
$G_v=G(k_v)$
for simplicity. Then
![]() $G_v$
is anisotropic for archimedean places v and split otherwise.
$G_v$
is anisotropic for archimedean places v and split otherwise.
Let
![]() $D\subseteq \mathbb O$
be a quaternion subalgebra. Define
$D\subseteq \mathbb O$
be a quaternion subalgebra. Define
be the Hilbert subspace which is orthogonal to the span of all automorphic representations
![]() $\Pi =\otimes _v \Pi _v$
such that
$\Pi =\otimes _v \Pi _v$
such that
for all
![]() $f\in \Pi $
. Hence, for any
$f\in \Pi $
. Hence, for any
![]() $\Pi \subset L^2_{D}(G(k)\backslash G(\mathbb A))$
, the global period integral over
$\Pi \subset L^2_{D}(G(k)\backslash G(\mathbb A))$
, the global period integral over
![]() $G_D$
is nonzero on
$G_D$
is nonzero on
![]() $\Pi $
.
$\Pi $
.
Proposition 10.5. Let
![]() $v_1, \ldots , v_n$
be a (nonempty) set of places of k. For nonarchimedean
$v_1, \ldots , v_n$
be a (nonempty) set of places of k. For nonarchimedean
![]() $v_i$
, let
$v_i$
, let
![]() $\pi _i$
be either the Steinberg representation
$\pi _i$
be either the Steinberg representation
![]() $\mathrm {St}$
or a supercuspidal representation of
$\mathrm {St}$
or a supercuspidal representation of
![]() $G_{v_i}$
such that
$G_{v_i}$
such that
![]() $\theta (\pi _i) \neq 0$
. For a real
$\theta (\pi _i) \neq 0$
. For a real
![]() $v_i$
, let
$v_i$
, let
![]() $\pi _i$
be any irreducible (finite dimensional) representation. Then there exist a quaternion algebra
$\pi _i$
be any irreducible (finite dimensional) representation. Then there exist a quaternion algebra
![]() $D \subseteq \mathbb {O}$
and an automorphic representation
$D \subseteq \mathbb {O}$
and an automorphic representation
![]() $\Pi =\otimes _v \Pi _v$
in
$\Pi =\otimes _v \Pi _v$
in
![]() $L^2_{D}(G(k)\backslash G(\mathbb A))$
such that
$L^2_{D}(G(k)\backslash G(\mathbb A))$
such that
![]() $\Pi _{v_i}\cong \pi _i$
for
$\Pi _{v_i}\cong \pi _i$
for
![]() $i=1, \ldots , n$
.
$i=1, \ldots , n$
.
Proof. Pick D such that for all
![]() $i=1, \ldots , n$
,
$i=1, \ldots , n$
,
This is possible by Corollary 10.2, Lemma 10.3 and Lemma 10.4. We can now proceed following [Reference Sakellaridis and VenkateshSV, Theorem 16.3.2 and Remark 16.4.1]. Using Poincaré series arising from compactly supported functions on
![]() $G_D\backslash G$
, one shows that
$G_D\backslash G$
, one shows that
 $$\begin{align*}\bigotimes_{i=1}^n L^2(G_{D, v_i} \backslash G_{v_i}) \quad \text{is weakly contained in} \quad L^2_{D} (G(k)\backslash G(\mathbb A)) \end{align*}$$
$$\begin{align*}\bigotimes_{i=1}^n L^2(G_{D, v_i} \backslash G_{v_i}) \quad \text{is weakly contained in} \quad L^2_{D} (G(k)\backslash G(\mathbb A)) \end{align*}$$
in the sense of Definition 11.5. Hence,
![]() $\otimes _i \pi _i$
is weakly contained there as well. The proposition now follows from Corollary 11.7, since supercuspidal representations and
$\otimes _i \pi _i$
is weakly contained there as well. The proposition now follows from Corollary 11.7, since supercuspidal representations and
![]() $\mathrm {St}$
are isolated in the unitary dual of
$\mathrm {St}$
are isolated in the unitary dual of
![]() $G_{v_i}$
by Proposition 11.3 (for the Steinberg representation).
$G_{v_i}$
by Proposition 11.3 (for the Steinberg representation).
We consider the global theta correspondence for the dual pair
![]() $G \times H$
in the adjoint group of absolute type
$G \times H$
in the adjoint group of absolute type
![]() $E_7$
(and k-rank
$E_7$
(and k-rank
![]() $3$
), that corresponds to the Albert algebra
$3$
), that corresponds to the Albert algebra
![]() $J_3(\mathbb O)$
via the Koecher-Tits construction, with respect to the minimal representation constructed in [Reference Hanzer and SavinHS, Theorem 6.4].
$J_3(\mathbb O)$
via the Koecher-Tits construction, with respect to the minimal representation constructed in [Reference Hanzer and SavinHS, Theorem 6.4].
Corollary 10.6. In the context of Proposition 10.5, the representation
![]() $\Pi $
has nonzero global theta lift to
$\Pi $
has nonzero global theta lift to
![]() $H = \mathrm {PGSp_6}$
. Moreover, this global theta lift is cuspidal if one of the following conditions hold:
$H = \mathrm {PGSp_6}$
. Moreover, this global theta lift is cuspidal if one of the following conditions hold:
-
• at some nonarchimedean
 $v_i$
,
$v_i$
,
 $\pi _i$
is the Steinberg representation;
$\pi _i$
is the Steinberg representation; -
• at a real
 $v_i$
,
$v_i$
,
 $\pi _i$
has regular highest weight.
$\pi _i$
has regular highest weight.
Proof. The nonvanishing of the global theta lift follows by [Reference Gross and SavinGrS2, Chapter 5, Prop. 4.5]: it is for this global nonvanishing result that we insist on globalizing with a nonzero
![]() $G_D$
-period in Proposition 10.5. The cuspidality of the global theta lift follows by [Reference Gross and SavinGrS2, Chapter 5, Cor. 4.9]. We note that though [Reference Gross and SavinGrS2] works over the base field
$G_D$
-period in Proposition 10.5. The cuspidality of the global theta lift follows by [Reference Gross and SavinGrS2, Chapter 5, Cor. 4.9]. We note that though [Reference Gross and SavinGrS2] works over the base field
![]() ${\mathbb Q}$
, the results from [Reference Gross and SavinGrS2] that we use in this proof hold over a general number field k with the same proofs given there.
${\mathbb Q}$
, the results from [Reference Gross and SavinGrS2] that we use in this proof hold over a general number field k with the same proofs given there.
10.3 Second globalization result
Assume now that k is an arbitrary number field and G is a simple split group over k. Let U be the unipotent radical of a Borel subgroup of G, and fix a Whittaker character
![]() $\psi = \prod _v \psi _v: U(\mathbb A)/U(k) \rightarrow \mathbb C^{\times }$
. In particular, we have a notion of local and automorphic Whittaker functional (relative to
$\psi = \prod _v \psi _v: U(\mathbb A)/U(k) \rightarrow \mathbb C^{\times }$
. In particular, we have a notion of local and automorphic Whittaker functional (relative to
![]() $\psi $
) and the notion of (Whittaker) generic representations, both locally and globally.
$\psi $
) and the notion of (Whittaker) generic representations, both locally and globally.
Fix a place w of k and a
![]() $\psi _w$
-generic supercuspidal representation
$\psi _w$
-generic supercuspidal representation
![]() $\sigma $
of
$\sigma $
of
![]() $G(k_w)$
. Let
$G(k_w)$
. Let
be the Hilbert subspace of the automorphic discrete spectrum of G which is orthogonal to the span of all square-integrable automorphic representations
![]() $\Pi =\otimes _v \Pi _v$
such that either the automorphic
$\Pi =\otimes _v \Pi _v$
such that either the automorphic
![]() $\psi $
-Whittaker functional vanishes on
$\psi $
-Whittaker functional vanishes on
![]() $\Pi $
or
$\Pi $
or
![]() $\Pi _w\ncong \sigma $
. Then any
$\Pi _w\ncong \sigma $
. Then any
![]() $\Pi \subset L^2_{\psi -\mathrm {gen}, \sigma } (G(k)\backslash G(\mathbb A))$
is globally (Whittaker) generic and
$\Pi \subset L^2_{\psi -\mathrm {gen}, \sigma } (G(k)\backslash G(\mathbb A))$
is globally (Whittaker) generic and
![]() $\Pi _w \cong \sigma $
.
$\Pi _w \cong \sigma $
.
For any place v, let
![]() $L^2_{\psi _v}(U(k_v)\backslash G(k_v))$
be the space of square integrable Whittaker functions. Recall that all generic square integrable representations of
$L^2_{\psi _v}(U(k_v)\backslash G(k_v))$
be the space of square integrable Whittaker functions. Recall that all generic square integrable representations of
![]() $G(k_v)$
are direct summands of
$G(k_v)$
are direct summands of
![]() $L^2_{\psi _v}(U(k_v)\backslash G(k_v))$
[Reference Sakellaridis and VenkateshSV].
$L^2_{\psi _v}(U(k_v)\backslash G(k_v))$
[Reference Sakellaridis and VenkateshSV].
Proposition 10.7. Let
![]() $v_1, \ldots , v_n$
be a set of (possibly archimedean) places of k, different from w. For
$v_1, \ldots , v_n$
be a set of (possibly archimedean) places of k, different from w. For
![]() $i=1, \ldots , n$
, let
$i=1, \ldots , n$
, let
![]() $\delta _i$
be a
$\delta _i$
be a
![]() $\psi _{v_i}$
-generic square integrable representation of
$\psi _{v_i}$
-generic square integrable representation of
![]() $G(k_{v_i})$
. Assume that these representations are isolated in
$G(k_{v_i})$
. Assume that these representations are isolated in
![]() $ L^2_{\psi -\mathrm {gen}, \sigma } (G(k)\backslash G(\mathbb A))$
. Then there exists an irreducible cuspidal automorphic representation
$ L^2_{\psi -\mathrm {gen}, \sigma } (G(k)\backslash G(\mathbb A))$
. Then there exists an irreducible cuspidal automorphic representation
![]() $\Pi $
in
$\Pi $
in
![]() $ L^2_{\psi -\mathrm {gen}, \sigma } (G(k)\backslash G(\mathbb A))$
such that
$ L^2_{\psi -\mathrm {gen}, \sigma } (G(k)\backslash G(\mathbb A))$
such that
![]() $\Pi _{v_i} \cong \delta _i$
for
$\Pi _{v_i} \cong \delta _i$
for
![]() $i=1, \ldots , n$
. Moreover, for all but one place different from w or
$i=1, \ldots , n$
. Moreover, for all but one place different from w or
![]() $v_i$
, we may assume that
$v_i$
, we may assume that
![]() $\Pi _v$
is a spherical representation.
$\Pi _v$
is a spherical representation.
Proof. Again, using Poincaré series [Reference Sakellaridis and VenkateshSV, Theorem 16.3.2 and Remark 16.4.1], one proves that
is weakly contained in
![]() $L^2_{\psi -\mathrm {gen}, \sigma } (G(k)\backslash G(\mathbb A))$
. In particular,
$L^2_{\psi -\mathrm {gen}, \sigma } (G(k)\backslash G(\mathbb A))$
. In particular,
![]() $\delta _1\otimes \cdots \otimes \delta _n$
is weakly contained there as well. The existence of the globalization
$\delta _1\otimes \cdots \otimes \delta _n$
is weakly contained there as well. The existence of the globalization
![]() $\Pi $
now follows from Proposition 11.6 and the hypothesis of isolation of the
$\Pi $
now follows from Proposition 11.6 and the hypothesis of isolation of the
![]() $\delta _i$
’s. The extra control at the places different from w and
$\delta _i$
’s. The extra control at the places different from w and
![]() $v_i$
is achieved by using appropriate test functions at these other places as the input for the Poincaré series, see [Reference Gan and IchinoGI, proof of Prop. Reference ArthurA.2].
$v_i$
is achieved by using appropriate test functions at these other places as the input for the Poincaré series, see [Reference Gan and IchinoGI, proof of Prop. Reference ArthurA.2].
In applications of Proposition 10.7, one would need to verify the hypothesis of isolation in the proposition. For classical groups and their associated similitude groups, the isolation for all generic discrete series representations is a consequence of estimates towards the Ramanujan conjecture for globally generic cuspidal representations; see [Reference Ichino, Lapid and MaoILM, Prop. A.5 and Lemma A.2]. The following verifies it for the group
![]() $G_2$
to the extent we shall need it in this paper.
$G_2$
to the extent we shall need it in this paper.
Lemma 10.8. Let
![]() $G=G_2$
and
$G=G_2$
and
![]() $H=\mathrm {PGSp_6}$
. Let
$H=\mathrm {PGSp_6}$
. Let
![]() $u\neq w$
be two finite places. Assume that
$u\neq w$
be two finite places. Assume that
![]() $\sigma $
is a generic supercuspidal representation of
$\sigma $
is a generic supercuspidal representation of
![]() $G(k_w)$
whose local theta lift to
$G(k_w)$
whose local theta lift to
![]() $H(k_w)$
is a generic supercuspidal representation (using [Reference GanG], there are such representations of depth 0). Assume that
$H(k_w)$
is a generic supercuspidal representation (using [Reference GanG], there are such representations of depth 0). Assume that
![]() $\delta $
is a generic discrete series representation of
$\delta $
is a generic discrete series representation of
![]() $G(k_u)$
such that
$G(k_u)$
such that
![]() $\theta (\delta )$
is a generic discrete series representation of
$\theta (\delta )$
is a generic discrete series representation of
![]() $H(k_u)$
. Then
$H(k_u)$
. Then
![]() $\delta $
is isolated in
$\delta $
is isolated in
![]() $ L^2_{\psi -\mathrm {gen}, \sigma } (G(k)\backslash G(\mathbb A))$
with respect to the Fell topology.
$ L^2_{\psi -\mathrm {gen}, \sigma } (G(k)\backslash G(\mathbb A))$
with respect to the Fell topology.
Proof. We argue by way of contradiction. Assume that there exists a sequence
![]() $\pi _n$
of local components of automorphic representations in
$\pi _n$
of local components of automorphic representations in
![]() $L^2_{\mathrm {gen}, \sigma } (G(k)\backslash G(\mathbb A))$
such that
$L^2_{\mathrm {gen}, \sigma } (G(k)\backslash G(\mathbb A))$
such that
![]() $\delta $
is a limit point of the sequence in Fell topology. Since discrete series representations are isolated in the tempered dual, the
$\delta $
is a limit point of the sequence in Fell topology. Since discrete series representations are isolated in the tempered dual, the
![]() $\pi _n$
’s may be assumed to be nontempered for any n. Further, since any irreducible
$\pi _n$
’s may be assumed to be nontempered for any n. Further, since any irreducible
![]() $\Pi \subset L^2_{\mathrm {gen}, \sigma } (G(k)\backslash G(\mathbb A))$
has a nonzero globally generic global theta lift
$\Pi \subset L^2_{\mathrm {gen}, \sigma } (G(k)\backslash G(\mathbb A))$
has a nonzero globally generic global theta lift
![]() $\Sigma \subset L^2_{\mathrm {gen}, \theta (\sigma )} (H(k)\backslash H(\mathbb A))$
(see [Reference Harris, Khare and ThorneHKT, appendix]), the local theta lifts
$\Sigma \subset L^2_{\mathrm {gen}, \theta (\sigma )} (H(k)\backslash H(\mathbb A))$
(see [Reference Harris, Khare and ThorneHKT, appendix]), the local theta lifts
![]() $\theta (\pi _n)$
are generic and unitarizable. We shall show that
$\theta (\pi _n)$
are generic and unitarizable. We shall show that
![]() $\theta (\pi _i)$
converges to
$\theta (\pi _i)$
converges to
![]() $\theta (\delta )$
and this will give the desired contradiction, since as we remarked before the lemma,
$\theta (\delta )$
and this will give the desired contradiction, since as we remarked before the lemma,
![]() $\theta (\delta )$
is known to be isolated in
$\theta (\delta )$
is known to be isolated in
![]() $L^2_{\mathrm {gen}, \theta (\sigma )} (H(k)\backslash H(\mathbb A))$
.
$L^2_{\mathrm {gen}, \theta (\sigma )} (H(k)\backslash H(\mathbb A))$
.
By [Reference TadićTa1], the supercuspidal support of
![]() $\delta $
is the limit of the sequence of supercuspidal supports of
$\delta $
is the limit of the sequence of supercuspidal supports of
![]() $\pi _n$
. For generic representations, the theta correspondence is continuous for supercupidal supports. Thus the supercuspidal support of
$\pi _n$
. For generic representations, the theta correspondence is continuous for supercupidal supports. Thus the supercuspidal support of
![]() $\theta (\delta )$
is the limit of the sequence of supercuspidal supports of
$\theta (\delta )$
is the limit of the sequence of supercuspidal supports of
![]() $\theta (\pi _n)$
. Now this should imply that
$\theta (\pi _n)$
. Now this should imply that
![]() $\theta (\delta )$
is a limit point of a subsequence of
$\theta (\delta )$
is a limit point of a subsequence of
![]() $\theta (\pi _n)$
, since any sequence of generic unitary representations should have a generic representation as a cluster point. For example, this will be true if genericity can be detected by a certain K-type. Since we could not find a reference for this result, we proceed as follows, using Proposition 11.2 shown below.
$\theta (\pi _n)$
, since any sequence of generic unitary representations should have a generic representation as a cluster point. For example, this will be true if genericity can be detected by a certain K-type. Since we could not find a reference for this result, we proceed as follows, using Proposition 11.2 shown below.
By Proposition 11.2, on passing to a subsequence of the given
![]() $\pi _n$
’s, we may realize
$\pi _n$
’s, we may realize
![]() $\delta $
as a limit point of a sequence of non-tempered representations
$\delta $
as a limit point of a sequence of non-tempered representations
![]() $\pi _n=\mathrm {Ind}_P^G(\tau _n)$
such that
$\pi _n=\mathrm {Ind}_P^G(\tau _n)$
such that
![]() $\delta $
is a subquotient of
$\delta $
is a subquotient of
![]() $\mathrm {Ind}_P^G(\tau )$
, where
$\mathrm {Ind}_P^G(\tau )$
, where
![]() $\tau $
is an irreducible generic representation which is a limit point of the sequence
$\tau $
is an irreducible generic representation which is a limit point of the sequence
![]() $\tau _n$
. Now the local theta correspondence for non-tempered representation is known by [Reference Gan and SavinGS23]. In particular, there exists a parabolic subgroup
$\tau _n$
. Now the local theta correspondence for non-tempered representation is known by [Reference Gan and SavinGS23]. In particular, there exists a parabolic subgroup
![]() $Q=LU \subset H$
, depending on P, such that
$Q=LU \subset H$
, depending on P, such that
where
![]() $\nu _n$
is irreducible and explicitly constructed from
$\nu _n$
is irreducible and explicitly constructed from
![]() $\tau _n$
.
$\tau _n$
.
Let
![]() $\nu $
be the irreducible representation of L explicitly constructed from
$\nu $
be the irreducible representation of L explicitly constructed from
![]() $\tau $
in the same way as
$\tau $
in the same way as
![]() $\nu _n$
is constructed from
$\nu _n$
is constructed from
![]() $\tau _n$
. Then it follows (by the continuity of induction) that the irreducible subquotients of
$\tau _n$
. Then it follows (by the continuity of induction) that the irreducible subquotients of
![]() $\mathrm {Ind}_Q^H(\nu )$
are limit points of the sequence
$\mathrm {Ind}_Q^H(\nu )$
are limit points of the sequence
![]() $\mathrm {Ind}_Q^H(\nu _n) = \theta (\pi _n)$
. Now the irreducible representation
$\mathrm {Ind}_Q^H(\nu _n) = \theta (\pi _n)$
. Now the irreducible representation
![]() $\nu $
is generic (since
$\nu $
is generic (since
![]() $\tau $
is generic), so that
$\tau $
is generic), so that
![]() $\mathrm {Ind}_Q^H(\nu )$
has a unique irreducible generic subquotient. Since the supercuspidal support of
$\mathrm {Ind}_Q^H(\nu )$
has a unique irreducible generic subquotient. Since the supercuspidal support of
![]() $\mathrm {Ind}_Q^H(\nu )$
is the same as the superccuspidal support of
$\mathrm {Ind}_Q^H(\nu )$
is the same as the superccuspidal support of
![]() $\theta (\delta )$
, we see that
$\theta (\delta )$
, we see that
![]() $\theta (\delta )$
is the unique irreducible generic subquotient of
$\theta (\delta )$
is the unique irreducible generic subquotient of
![]() $\mathrm {Ind}_Q^H(\nu )$
. In particular,
$\mathrm {Ind}_Q^H(\nu )$
. In particular,
![]() $\theta (\delta )$
is a limit point of
$\theta (\delta )$
is a limit point of
![]() $\theta (\pi _n)$
. Thus we have proved that
$\theta (\pi _n)$
. Thus we have proved that
![]() $\theta (\delta )$
is not isolated in
$\theta (\delta )$
is not isolated in
![]() $L^2_{\mathrm {gen}, \theta (\sigma )} (H(k)\backslash H(\mathbb A))$
, giving the desired contradiction.
$L^2_{\mathrm {gen}, \theta (\sigma )} (H(k)\backslash H(\mathbb A))$
, giving the desired contradiction.
11 Appendix B: Topology of Unitary dual
Let G be a (simple) Chevalley group over a p-adic field F. Recall that a unitary representation
![]() $\pi $
of G on a Hilbert space
$\pi $
of G on a Hilbert space
![]() $H_{\pi }$
is continuous if, for every
$H_{\pi }$
is continuous if, for every
![]() $v\in H_{\pi }$
, the map
$v\in H_{\pi }$
, the map
![]() $g\mapsto \pi (g) v$
, where
$g\mapsto \pi (g) v$
, where
![]() $g\in G$
, is continuous. In that case, the subspace
$g\in G$
, is continuous. In that case, the subspace
![]() $V_{\pi } \subseteq H_{\pi }$
of smooth vectors is dense. All unitary representations are assumed to be continuous. We say that a smooth irreducible representation of G is unitarizable if it has a G-invariant positive-definite hermitian form, or equivalently if it is the space of smooth vectors in an irreducible unitary representation.
$V_{\pi } \subseteq H_{\pi }$
of smooth vectors is dense. All unitary representations are assumed to be continuous. We say that a smooth irreducible representation of G is unitarizable if it has a G-invariant positive-definite hermitian form, or equivalently if it is the space of smooth vectors in an irreducible unitary representation.
11.1 Steinberg is isolated
Using an argument due to Miličić, we prove that the Steinberg representation of G is isolated, with respect of the Fell topology, in the unitary dual of G. (We refer the reader to [Reference Bekka, de la Harpe and ValetteBHV, Appendix F], for a nice summary of Fell topology, definitions and basic properties). Here we work with smooth representations.
We first recall some basic notions:
-
• An irreducible unitarizable representation
 $\pi $
of G is a limit point of a sequence
$\pi $
of G is a limit point of a sequence
 $\pi _n$
of irreducible unitarizable representations
$\pi _n$
of irreducible unitarizable representations
 $\pi _n$
of G if for some (or equivalently for any) matrix coefficient
$\pi _n$
of G if for some (or equivalently for any) matrix coefficient
 $\langle \pi (g) v, v\rangle $
of
$\langle \pi (g) v, v\rangle $
of
 $\pi $
, there is a sequence of matrix coefficients
$\pi $
, there is a sequence of matrix coefficients
 $\langle \pi _n(g) v_n, v_n\rangle $
of
$\langle \pi _n(g) v_n, v_n\rangle $
of
 $\pi _n$
converging uniformly on all compact sets in G to
$\pi _n$
converging uniformly on all compact sets in G to
 $\langle \pi (g) v, v\rangle $
.
$\langle \pi (g) v, v\rangle $
. -
• An irreducible unitarizable representation
 $\pi $
of G is a cluster point of the sequence
$\pi $
of G is a cluster point of the sequence
 $\pi _n$
if it is a limit point of a subsequence of
$\pi _n$
if it is a limit point of a subsequence of
 $\pi _n$
.
$\pi _n$
.
Let
![]() $L[\pi _n]$
and
$L[\pi _n]$
and
![]() $C[\pi _n]$
denote the sets of limit and cluster points of
$C[\pi _n]$
denote the sets of limit and cluster points of
![]() $\pi _n$
respectively, so that clearly,
$\pi _n$
respectively, so that clearly,
However, since the unitary dual is not a Hausdorff space, a nonempty
![]() $L[\pi _n]$
does not have to be a singleton and the inclusion
$L[\pi _n]$
does not have to be a singleton and the inclusion
![]() $L[\pi _n] \subseteq C[\pi _n]$
can be strict. However, as explained by Miličić, one can have the equality
$L[\pi _n] \subseteq C[\pi _n]$
can be strict. However, as explained by Miličić, one can have the equality
![]() $L[\pi _n] = C[\pi _n]$
under some conditions.
$L[\pi _n] = C[\pi _n]$
under some conditions.
More precisely, let
![]() $\chi _{\pi _n}$
be the character distribution of
$\chi _{\pi _n}$
be the character distribution of
![]() $\pi _n$
. We say that a sequence
$\pi _n$
. We say that a sequence
![]() $\chi _{\pi _n}$
is weakly converging if, for every
$\chi _{\pi _n}$
is weakly converging if, for every
![]() $f\in C_c(G)$
, the sequence of complex numbers
$f\in C_c(G)$
, the sequence of complex numbers
![]() $\chi _{\pi _n}(f)$
is convergent. We have the following result [Reference MiličićMi, Thm. 5]; see also [Reference TadićTa1].
$\chi _{\pi _n}(f)$
is convergent. We have the following result [Reference MiličićMi, Thm. 5]; see also [Reference TadićTa1].
Theorem 11.1. Let
![]() $\pi _n$
be a sequence of irreducible unitarizable representations of G. Assume that the corresponding sequence of characters is weakly converging. Then there exists a finite set S of unitary representations such that
$\pi _n$
be a sequence of irreducible unitarizable representations of G. Assume that the corresponding sequence of characters is weakly converging. Then there exists a finite set S of unitary representations such that
for all
![]() $f\in C_c(G)$
, where
$f\in C_c(G)$
, where
![]() $n_{\sigma }>0$
are natural numbers. Moreover, one has
$n_{\sigma }>0$
are natural numbers. Moreover, one has
We shall need the following proposition which, for real groups, was established by Vogan [Reference VoganVo] in a greater generality.
Proposition 11.2. Let G be a simple split group over F. Let
![]() $\delta $
be a generic unitarizable representation of G. Let
$\delta $
be a generic unitarizable representation of G. Let
![]() $\pi _n$
be a sequence of generic unitarizable representations of G such that
$\pi _n$
be a sequence of generic unitarizable representations of G such that
![]() $\delta $
is a limit point of the sequence
$\delta $
is a limit point of the sequence
![]() $\pi _n$
. Then, after passing to a subsequence of
$\pi _n$
. Then, after passing to a subsequence of
![]() $\pi _n$
if necessary, there exists a parabolic
$\pi _n$
if necessary, there exists a parabolic
![]() $P\subseteq G$
and a sequence of standard modules
$P\subseteq G$
and a sequence of standard modules
![]() $\mathrm {Ind}_P^G(\tau _n)$
such that
$\mathrm {Ind}_P^G(\tau _n)$
such that
-
•
 $\pi _n \cong \mathrm {Ind}_P^G(\tau _n)$
for all n;
$\pi _n \cong \mathrm {Ind}_P^G(\tau _n)$
for all n; -
• the character distributions of
 ${\tau _n}$
weakly converge to the character distribution of
${\tau _n}$
weakly converge to the character distribution of
 ${\tau }$
, where
${\tau }$
, where
 $\tau $
is a not necessarily irreducible representation;
$\tau $
is a not necessarily irreducible representation; -
•
 $\delta $
is a subquotient of
$\delta $
is a subquotient of
 $\mathrm {Ind}_P^G(\tau )$
.
$\mathrm {Ind}_P^G(\tau )$
.
In particular, the representation
![]() $\tau $
is generic.
$\tau $
is generic.
Proof. Fix a Borel subgroup
![]() $B=TU$
. Let
$B=TU$
. Let
![]() $\Delta $
be the set of simple roots given by the choice of B. Let
$\Delta $
be the set of simple roots given by the choice of B. Let
![]() $P=MN$
be a parabolic subgroup of G corresponding to a subset
$P=MN$
be a parabolic subgroup of G corresponding to a subset
![]() $S\subset \Delta $
. Let
$S\subset \Delta $
. Let
![]() $\tau $
be an irreducible representation of M with a polar decomposition
$\tau $
be an irreducible representation of M with a polar decomposition
![]() $\tau = \tau ^{\circ } \cdot \chi $
where
$\tau = \tau ^{\circ } \cdot \chi $
where
-
•
 $\tau ^{\circ }$
is a tempered representation of M.
$\tau ^{\circ }$
is a tempered representation of M. -
•
 $\chi : M \rightarrow \mathbb R^{\times }_+$
is an unramified multiplicative character, with associated “differential” where
$\chi : M \rightarrow \mathbb R^{\times }_+$
is an unramified multiplicative character, with associated “differential” where $$\begin{align*}d \chi = \sum_{\alpha \in \Delta\setminus S} s_{\alpha} \varpi_{\alpha} \end{align*}$$
$$\begin{align*}d \chi = \sum_{\alpha \in \Delta\setminus S} s_{\alpha} \varpi_{\alpha} \end{align*}$$
 $s_{\alpha }>0$
and
$s_{\alpha }>0$
and
 $ \varpi _{\alpha }$
is the fundamental weight corresponding to
$ \varpi _{\alpha }$
is the fundamental weight corresponding to
 $\alpha $
.
$\alpha $
.
A standard module corresponding to the pair
![]() $(M,\tau )$
is the induced representation
$(M,\tau )$
is the induced representation
![]() $\mathrm {Ind}_P^G(\tau )$
. Recall from [Reference Heiermann and OpdamHO] that any generic representation is isomorphic to a standard module
$\mathrm {Ind}_P^G(\tau )$
. Recall from [Reference Heiermann and OpdamHO] that any generic representation is isomorphic to a standard module
![]() $\mathrm {Ind}_P^G(\tau )$
for some pair
$\mathrm {Ind}_P^G(\tau )$
for some pair
![]() $(M,\tau )$
.
$(M,\tau )$
.
Thus any
![]() $\pi _n$
is isomorphic to a standard module
$\pi _n$
is isomorphic to a standard module
![]() $\mathrm {Ind}_P^G(\tau _n)$
where the parabolic P depends on n. However, since there are finitely many parabolic subgroups in the standard position, after passing to a subsequence of
$\mathrm {Ind}_P^G(\tau _n)$
where the parabolic P depends on n. However, since there are finitely many parabolic subgroups in the standard position, after passing to a subsequence of
![]() $\pi $
if necessary, we can assume that P is independent of n. This takes care of the first bullet.
$\pi $
if necessary, we can assume that P is independent of n. This takes care of the first bullet.
Write
![]() $\tau _n=\tau _n^{\circ } \cdot \chi _n$
, the polar decompostion. Then by [Reference TadićTa1], there exists a subsequence of
$\tau _n=\tau _n^{\circ } \cdot \chi _n$
, the polar decompostion. Then by [Reference TadićTa1], there exists a subsequence of
![]() $\tau _n^{\circ }$
such that the corresponding character distributions weakly converge. Replace the sequence
$\tau _n^{\circ }$
such that the corresponding character distributions weakly converge. Replace the sequence
![]() $\tau _n^{\circ }$
by that subsequence. Hence there exists a representation
$\tau _n^{\circ }$
by that subsequence. Hence there exists a representation
![]() $\tau ^{\circ }$
, not necessarily irreducible, such that its character distribution is the weak limit of the character distributions of
$\tau ^{\circ }$
, not necessarily irreducible, such that its character distribution is the weak limit of the character distributions of
![]() $\tau _n^{\circ }$
. Since
$\tau _n^{\circ }$
. Since
![]() $\pi _n$
are unitary, the differentials
$\pi _n$
are unitary, the differentials
![]() $d\chi _n$
must be bounded. Hence, after passing to a subsequence again, we can assume that
$d\chi _n$
must be bounded. Hence, after passing to a subsequence again, we can assume that
![]() $\chi _n$
converge to a character
$\chi _n$
converge to a character
![]() $\chi $
. Let
$\chi $
. Let
![]() $\tau =\tau ^{\circ } \cdot \chi $
. This takes care of the second bullet.
$\tau =\tau ^{\circ } \cdot \chi $
. This takes care of the second bullet.
Finally, since the character distributions of
![]() $\tau _n$
weakly converge to the character distribution of
$\tau _n$
weakly converge to the character distribution of
![]() $\tau $
, the character distributions of
$\tau $
, the character distributions of
![]() $\mathrm {Ind}_P^G(\tau _n)$
weakly converge to the character distribution of
$\mathrm {Ind}_P^G(\tau _n)$
weakly converge to the character distribution of
![]() $\mathrm {Ind}_P^G(\tau )$
. Hence, by Theorem 11.1, the limit points of the sequence
$\mathrm {Ind}_P^G(\tau )$
. Hence, by Theorem 11.1, the limit points of the sequence
![]() $\pi _n$
are precisely the subquotients of
$\pi _n$
are precisely the subquotients of
![]() $\mathrm {Ind}_P^G(\tau )$
. This completes the third bullet.
$\mathrm {Ind}_P^G(\tau )$
. This completes the third bullet.
Now we are ready to prove the main result in this section:
Proposition 11.3. Let
![]() $\sigma $
be the Steinberg representation of G. If the rank of G is at least 2, then
$\sigma $
be the Steinberg representation of G. If the rank of G is at least 2, then
![]() $\sigma $
is isolated in the unitary dual of G.
$\sigma $
is isolated in the unitary dual of G.
Proof. We shall prove this by contradiction, so let’s assume that
![]() $\sigma $
is a limit point of a sequence
$\sigma $
is a limit point of a sequence
![]() $\pi _n$
.
$\pi _n$
.
Let K be an open compact subgroup of G. Let
![]() $\tau $
be any smooth irreducible representation of K. Let
$\tau $
be any smooth irreducible representation of K. Let
![]() $f_{\tau }$
be a smooth function on G, supported on K, and equal to the complex conjugate of the character of
$f_{\tau }$
be a smooth function on G, supported on K, and equal to the complex conjugate of the character of
![]() $\tau $
, divided by the volume of K, on K. Thus, for any unitary representation
$\tau $
, divided by the volume of K, on K. Thus, for any unitary representation
![]() $(\pi ,V)$
of G, the operator
$(\pi ,V)$
of G, the operator
![]() $\pi (f_{\tau })$
is the projector on the
$\pi (f_{\tau })$
is the projector on the
![]() $\tau $
-isotypic subspace of V.
$\tau $
-isotypic subspace of V.
Lemma 11.4. Let
![]() $\pi $
be an irreducible unitarizable representation such that the K-type
$\pi $
be an irreducible unitarizable representation such that the K-type
![]() $\tau $
occurs in
$\tau $
occurs in
![]() $\pi $
. Assume that
$\pi $
. Assume that
![]() $\pi $
is a limit point of a sequence of irreducible representations
$\pi $
is a limit point of a sequence of irreducible representations
![]() $\pi _n$
. Then, for almost all n, the K-type
$\pi _n$
. Then, for almost all n, the K-type
![]() $\tau $
occurs in
$\tau $
occurs in
![]() $\pi _n$
.
$\pi _n$
.
Proof. By the assumption there exists a non-zero
![]() $v\in V$
, such that
$v\in V$
, such that
![]() $\langle \pi (f_{\tau }) v, v\rangle = \langle v, v\rangle \neq 0$
. Let
$\langle \pi (f_{\tau }) v, v\rangle = \langle v, v\rangle \neq 0$
. Let
![]() $\langle \pi _n(g) v_n, v_n\rangle $
be a sequence of matrix coefficients of
$\langle \pi _n(g) v_n, v_n\rangle $
be a sequence of matrix coefficients of
![]() $\pi _n$
converging uniformly on all compact sets in G, in particular on K, to
$\pi _n$
converging uniformly on all compact sets in G, in particular on K, to
![]() $\langle \pi (g) v, v\rangle $
. Thus the limit of
$\langle \pi (g) v, v\rangle $
. Thus the limit of
![]() $\langle \pi _n(f_{\tau }) v_n, v_n\rangle $
is
$\langle \pi _n(f_{\tau }) v_n, v_n\rangle $
is
![]() $\langle \pi (f_{\tau }) v, v\rangle $
, and the lemma follows.
$\langle \pi (f_{\tau }) v, v\rangle $
, and the lemma follows.
Now assume that K is a special maximal compact subgroup. Then K has a quotient
![]() $G(\mathbb F_q)$
where
$G(\mathbb F_q)$
where
![]() $\mathbb F_q$
is the residual field of F. Let
$\mathbb F_q$
is the residual field of F. Let
![]() $\mathrm {st}_G$
be the inflation to K of the Steinberg representation of the finite group
$\mathrm {st}_G$
be the inflation to K of the Steinberg representation of the finite group
![]() $G(\mathbb F_q)$
. The restriction of
$G(\mathbb F_q)$
. The restriction of
![]() $\sigma $
to K contains
$\sigma $
to K contains
![]() $\mathrm {st}_G$
. By Lemma 11.4, after passing to a subsequence, we may assume that all
$\mathrm {st}_G$
. By Lemma 11.4, after passing to a subsequence, we may assume that all
![]() $\pi _n$
contain
$\pi _n$
contain
![]() $\mathrm {st}_G$
. But this implies that
$\mathrm {st}_G$
. But this implies that
![]() $\pi _n$
are generic [Reference Barbasch and MoyBM], hence we can apply Proposition 11.2. In particular,
$\pi _n$
are generic [Reference Barbasch and MoyBM], hence we can apply Proposition 11.2. In particular,
![]() $\sigma $
is a subquotient of some induced representation
$\sigma $
is a subquotient of some induced representation
![]() $\mathrm {Ind}_P^G(\tau )$
where all subquotients are unitarzable. Observe that P is a proper parabolic subgroup. Indeed, since square integrable representations are isolated in the tempered dual of G, we see that the
$\mathrm {Ind}_P^G(\tau )$
where all subquotients are unitarzable. Observe that P is a proper parabolic subgroup. Indeed, since square integrable representations are isolated in the tempered dual of G, we see that the
![]() $\pi _n$
may be assumed to be nontempered; in particular,
$\pi _n$
may be assumed to be nontempered; in particular,
![]() $P \neq G$
. Furthermore, since convergence in Fell topology implies convergence in Bernstein center [Reference TadićTa2], all irreducible subquotients of
$P \neq G$
. Furthermore, since convergence in Fell topology implies convergence in Bernstein center [Reference TadićTa2], all irreducible subquotients of
![]() $\mathrm {Ind}_P^G(\tau )$
are contained in any principal series
$\mathrm {Ind}_P^G(\tau )$
are contained in any principal series
![]() $\mathrm {Ind}_B^G(\chi )$
containing
$\mathrm {Ind}_B^G(\chi )$
containing
![]() $\sigma $
.
$\sigma $
.
Next, recall that
![]() $\mathrm {st}_G$
is the unique K-type of
$\mathrm {st}_G$
is the unique K-type of
![]() $\sigma $
with Iwahori-fixed vectors. Observe that K-types of
$\sigma $
with Iwahori-fixed vectors. Observe that K-types of
![]() $\mathrm {Ind}_P^G(\tau )$
are easily determined from
$\mathrm {Ind}_P^G(\tau )$
are easily determined from
![]() $K\cap M$
-types of
$K\cap M$
-types of
![]() $\tau $
. Observe that
$\tau $
. Observe that
![]() $\tau $
is generic, and hence
$\tau $
is generic, and hence
![]() $\mathrm {st}_M$
is a type of
$\mathrm {st}_M$
is a type of
![]() $\tau $
. If the rank of G is greater than one, it is easy to see that there is an Iwahori type in
$\tau $
. If the rank of G is greater than one, it is easy to see that there is an Iwahori type in
![]() $\mathrm {Ind}_P^G(\tau )$
, different from
$\mathrm {Ind}_P^G(\tau )$
, different from
![]() $\mathrm {st}_G$
, that contains
$\mathrm {st}_G$
, that contains
![]() $\mathrm {st}_M$
. Hence
$\mathrm {st}_M$
. Hence
![]() $\mathrm {Ind}_P^G(\tau )$
and therefore
$\mathrm {Ind}_P^G(\tau )$
and therefore
![]() $\mathrm {Ind}_B^G(\chi )$
contains a unitarizable representation different from
$\mathrm {Ind}_B^G(\chi )$
contains a unitarizable representation different from
![]() $\sigma $
and the trivial representation of G. We claim that there is no such representation. Indeed, by Rodier [Reference RodierRo],
$\sigma $
and the trivial representation of G. We claim that there is no such representation. Indeed, by Rodier [Reference RodierRo],
![]() $\mathrm {Ind}_B^G(\chi )$
has
$\mathrm {Ind}_B^G(\chi )$
has
![]() $2^r$
irreducible suqbquotients. Their exponents are known, and thus the asymptotics of their matrix coefficients. It follows that the matrix coefficients of subquotients, different from the Steinberg representation, are not decaying at infinity. Thus, by a theorem of Howe and Moore the only unitarizable subquotients of
$2^r$
irreducible suqbquotients. Their exponents are known, and thus the asymptotics of their matrix coefficients. It follows that the matrix coefficients of subquotients, different from the Steinberg representation, are not decaying at infinity. Thus, by a theorem of Howe and Moore the only unitarizable subquotients of
![]() $\mathrm {Ind}_B^G(\chi _)$
are the trivial representation and
$\mathrm {Ind}_B^G(\chi _)$
are the trivial representation and
![]() $\sigma $
.
$\sigma $
.
11.2 Weak containment
Definition 11.5. Let
![]() $\pi $
and
$\pi $
and
![]() $\sigma $
be two unitary representations of G. We say that
$\sigma $
be two unitary representations of G. We say that
![]() $\sigma $
is weakly contained in
$\sigma $
is weakly contained in
![]() $\pi $
if every normalized matrix coefficient
$\pi $
if every normalized matrix coefficient
![]() $\langle \sigma (g) v,v\rangle $
of
$\langle \sigma (g) v,v\rangle $
of
![]() $\sigma $
, that is
$\sigma $
, that is
![]() $||v||=1$
, can be approximated uniformly, on compact subsets of G, by convex combinations of normalized matrix coefficients of
$||v||=1$
, can be approximated uniformly, on compact subsets of G, by convex combinations of normalized matrix coefficients of
![]() $\pi $
.
$\pi $
.
Proposition 11.6. Let
![]() $\pi _1, \pi _2, \ldots $
be a sequence of irreducible unitary representations of G. Let
$\pi _1, \pi _2, \ldots $
be a sequence of irreducible unitary representations of G. Let
![]() $\pi = \hat \oplus _{i=1}^{\infty } \pi _i$
. Let
$\pi = \hat \oplus _{i=1}^{\infty } \pi _i$
. Let
![]() $\sigma $
be an irreducible unitary representation of G. If
$\sigma $
be an irreducible unitary representation of G. If
![]() $\sigma $
is weakly contained in
$\sigma $
is weakly contained in
![]() $\pi $
then
$\pi $
then
![]() $\sigma $
is a limit of a subsequence of
$\sigma $
is a limit of a subsequence of
![]() $\pi _n$
.
$\pi _n$
.
Proof. Recall that
![]() $L^{\infty }(G)$
is the dual space of
$L^{\infty }(G)$
is the dual space of
![]() $L^1(G)$
, and the unit ball in
$L^1(G)$
, and the unit ball in
![]() $L^{\infty }(G)$
is compact in the weak-
$L^{\infty }(G)$
is compact in the weak-
![]() $\ast $
topology. Let
$\ast $
topology. Let
![]() $\mathcal C$
be the weak-
$\mathcal C$
be the weak-
![]() $\ast $
closure, in
$\ast $
closure, in
![]() $L^{\infty }(G)$
, of the convex hull of
$L^{\infty }(G)$
, of the convex hull of
Then
![]() $\mathcal C$
is closed and convex subset of the unit ball, in particular, it is compact by Alaoglu’s Theorem [Reference ConwayCo, page 130]. Recall that an element of a convex set is extremal if it is not a proper convex combination of two other elements of the set. By [Reference Bekka, de la Harpe and ValetteBHV, Thm. Reference ChenevierC.5.2], elements of
$\mathcal C$
is closed and convex subset of the unit ball, in particular, it is compact by Alaoglu’s Theorem [Reference ConwayCo, page 130]. Recall that an element of a convex set is extremal if it is not a proper convex combination of two other elements of the set. By [Reference Bekka, de la Harpe and ValetteBHV, Thm. Reference ChenevierC.5.2], elements of
![]() $\mathcal F$
are extremal in
$\mathcal F$
are extremal in
![]() $\mathcal C$
. (That theorem states that normalized matrix coefficients associated to an irreducible representation are extremal in a larger convex set.) By our assumption,
$\mathcal C$
. (That theorem states that normalized matrix coefficients associated to an irreducible representation are extremal in a larger convex set.) By our assumption,
![]() $f(g)= \langle \sigma (g) v, v \rangle $
, for
$f(g)= \langle \sigma (g) v, v \rangle $
, for
![]() $v\in \sigma $
of norm 1, is contained in
$v\in \sigma $
of norm 1, is contained in
![]() $\mathcal C$
. Thus it is also an extremal point of
$\mathcal C$
. Thus it is also an extremal point of
![]() $\mathcal C$
since
$\mathcal C$
since
![]() $\sigma $
is irreducible. By the Krein-Milman Theorem [Reference ConwayCo, page 141], any extremal point in
$\sigma $
is irreducible. By the Krein-Milman Theorem [Reference ConwayCo, page 141], any extremal point in
![]() $\mathcal C$
is in the closure of
$\mathcal C$
is in the closure of
![]() $\mathcal F$
. In particular, f is a limit of a sequence
$\mathcal F$
. In particular, f is a limit of a sequence
![]() $f_n(g)=\langle \pi _n(g) v_n, v_n \rangle $
in
$f_n(g)=\langle \pi _n(g) v_n, v_n \rangle $
in
![]() $\mathcal F$
. Of course, the limit is in the weak-
$\mathcal F$
. Of course, the limit is in the weak-
![]() $\ast $
topology, however, by a theorem of Raikov [Reference Bekka, de la Harpe and ValetteBHV, Thm. C.5.6], the sequence
$\ast $
topology, however, by a theorem of Raikov [Reference Bekka, de la Harpe and ValetteBHV, Thm. C.5.6], the sequence
![]() $f_n$
converges uniformly on compact sets to f. This is banal for p-adic groups. Indeed, we can assume that v and all
$f_n$
converges uniformly on compact sets to f. This is banal for p-adic groups. Indeed, we can assume that v and all
![]() $v_n$
are K-fixed for a small open compact subgroup of G. Thus these functions are constant on K-double cosets, and uniform convergence on compact sets is equivalent to point-wise convergence. Thus, if
$v_n$
are K-fixed for a small open compact subgroup of G. Thus these functions are constant on K-double cosets, and uniform convergence on compact sets is equivalent to point-wise convergence. Thus, if
![]() $g\in G$
and
$g\in G$
and
![]() $\chi _g$
is the characteristic function of
$\chi _g$
is the characteristic function of
![]() $KgK$
divided by the volume of
$KgK$
divided by the volume of
![]() $KgK$
volume, then we have
$KgK$
volume, then we have
since
![]() $f_n \rightarrow f$
in the weak-
$f_n \rightarrow f$
in the weak-
![]() $\ast $
topology.
$\ast $
topology.
Corollary 11.7. Let
![]() $\pi _1, \pi _2, \ldots $
be a sequence of irreducible unitary representations of G. Let
$\pi _1, \pi _2, \ldots $
be a sequence of irreducible unitary representations of G. Let
![]() $\pi = \hat \oplus _{i=1}^{\infty } \pi _i$
. Let
$\pi = \hat \oplus _{i=1}^{\infty } \pi _i$
. Let
![]() $\sigma $
be an irreducible unitary representation of G isolated in the unitary dual. If
$\sigma $
be an irreducible unitary representation of G isolated in the unitary dual. If
![]() $\sigma $
is weakly contained in
$\sigma $
is weakly contained in
![]() $\pi $
then
$\pi $
then
![]() $\sigma \cong \pi _i$
for some i.
$\sigma \cong \pi _i$
for some i.
12 Appendix C: A Weak LLC for
 $\mathrm {PGSp_6}$
$\mathrm {PGSp_6}$
We have mentioned that the ideas involved in the construction of the Spin lifting in §4 via an application of triality and the results of Kret-Shin allow one to construct a weak LLC for
![]() $\mathrm {PGSp_6}$
refining the results of B. Xu in this specific case. In this appendix, let us give an outline of this, explaining in particular what “weak” means. The reader will notice that the general structure is very similar to our treatment of the LLC for
$\mathrm {PGSp_6}$
refining the results of B. Xu in this specific case. In this appendix, let us give an outline of this, explaining in particular what “weak” means. The reader will notice that the general structure is very similar to our treatment of the LLC for
![]() $G_2$
.
$G_2$
.
12.1 Weak equivalence of L-parameters
In §5.2, we have encountered the natural map
As mentioned there, this map is not injective, because
![]() $\mathrm {Spin}_7({\mathbb C})$
is not acceptable in the sense of Larsen [Reference Chenevier and GanCG1]. On the other hand, the standard and Spin L-functions of
$\mathrm {Spin}_7({\mathbb C})$
is not acceptable in the sense of Larsen [Reference Chenevier and GanCG1]. On the other hand, the standard and Spin L-functions of
![]() $\phi \in \Phi (\mathrm {PGSp_6})$
is completely determined by its image in
$\phi \in \Phi (\mathrm {PGSp_6})$
is completely determined by its image in
![]() $\Phi (\mathrm {Sp_6}) \times \Phi (\mathrm {GL}_8)$
. This motivates us to define the coarser equivalence relation on L-parameters:
$\Phi (\mathrm {Sp_6}) \times \Phi (\mathrm {GL}_8)$
. This motivates us to define the coarser equivalence relation on L-parameters:
Definition 12.1. Two elements
![]() $\phi _1, \phi _2 \in \Phi (\mathrm {PGSp_6})$
are said to be weakly equivalent if
$\phi _1, \phi _2 \in \Phi (\mathrm {PGSp_6})$
are said to be weakly equivalent if
We denote the set of weak equivalence classes by
![]() $\Phi _w(\mathrm {PGSp_6})$
.
$\Phi _w(\mathrm {PGSp_6})$
.
One has [Reference Chenevier and GanCG1, §1]:
Lemma 12.2. The following are equivalent for two elements
![]() $\phi _1$
and
$\phi _1$
and
![]() $\phi _2$
of
$\phi _2$
of
![]() $\Phi (\mathrm {PGSp_6})$
:
$\Phi (\mathrm {PGSp_6})$
:
-
•
 $\phi _1$
and
$\phi _1$
and
 $\phi _2$
are weakly equivalent;
$\phi _2$
are weakly equivalent; -
•
 $\phi _1$
and
$\phi _1$
and
 $\phi _2$
are elementwise conjugate.
$\phi _2$
are elementwise conjugate.
Our goal in this appendix is to construct a canonical map
satisfying some desirable properties.
12.2 Theta dichotomy
We shall make use of the similitude theta correspondence associated to the following dual pairs:

Here, the orthogonal similitude groups in the right tower are split, whereas the one on the left has F-rank
![]() $1$
and is isomorphic to
$1$
and is isomorphic to
![]() $\mathrm {PGL}_2(D) \rtimes {\mathbb Z}/2{\mathbb Z}$
where D is the quaternion division F-algebra.
$\mathrm {PGL}_2(D) \rtimes {\mathbb Z}/2{\mathbb Z}$
where D is the quaternion division F-algebra.
As a consequence of the conservation relation [Reference Sun and ZhuSZ], any
![]() $\sigma \in \mathrm {Irr}(\mathrm {PGSp_6})$
has a nonzero theta lift to exactly one of
$\sigma \in \mathrm {Irr}(\mathrm {PGSp_6})$
has a nonzero theta lift to exactly one of
![]() $\mathrm {PGO}_8$
or
$\mathrm {PGO}_8$
or
![]() $\mathrm {PGO}_{5,1}$
. This gives a partition
$\mathrm {PGO}_{5,1}$
. This gives a partition
where the elements in
![]() $\mathrm {Irr}^{\heartsuit }(\mathrm {PGSp_6})$
are those with nonzero theta lifts to
$\mathrm {Irr}^{\heartsuit }(\mathrm {PGSp_6})$
are those with nonzero theta lifts to
![]() $\mathrm {PGO}_8$
. Among the representations in
$\mathrm {PGO}_8$
. Among the representations in
![]() $\mathrm {Irr}^{\heartsuit }(\mathrm {PGSp_6})$
, some will participate in the theta correspondence with the lower step of the tower, i.e. with
$\mathrm {Irr}^{\heartsuit }(\mathrm {PGSp_6})$
, some will participate in the theta correspondence with the lower step of the tower, i.e. with
![]() $\mathrm {PGO}_6 = \mathrm {PGL}_4(F) \rtimes {\mathbb Z}/2{\mathbb Z}$
. Thus, we have a further decomposition
$\mathrm {PGO}_6 = \mathrm {PGL}_4(F) \rtimes {\mathbb Z}/2{\mathbb Z}$
. Thus, we have a further decomposition
where
![]() $\mathrm {Irr}^{\clubsuit }(\mathrm {PGSp_6})$
denotes the subset of those representations which has nonzero theta lifting to
$\mathrm {Irr}^{\clubsuit }(\mathrm {PGSp_6})$
denotes the subset of those representations which has nonzero theta lifting to
![]() $\mathrm {PGO}_6$
. It will be better to group
$\mathrm {PGO}_6$
. It will be better to group
![]() $\mathrm {Irr}^{\spadesuit }(\mathrm {PGSp_6})$
and
$\mathrm {Irr}^{\spadesuit }(\mathrm {PGSp_6})$
and
![]() $\mathrm {Irr}^{\clubsuit }(\mathrm {PGSp_6})$
together, denoting their union by
$\mathrm {Irr}^{\clubsuit }(\mathrm {PGSp_6})$
together, denoting their union by
![]() $\mathrm {Irr}^{\spadesuit \clubsuit }(\mathrm {PGSp_6})$
.
$\mathrm {Irr}^{\spadesuit \clubsuit }(\mathrm {PGSp_6})$
.
In short, the similitude theta correspondence gives maps:
and
The latter map is in fact injective and takes value in the
![]() ${\mathbb Z}/2{\mathbb Z}$
-fixed points in
${\mathbb Z}/2{\mathbb Z}$
-fixed points in
![]() $\mathrm {Irr}(\mathrm {PGSO}_8)$
.
$\mathrm {Irr}(\mathrm {PGSO}_8)$
.
12.3 Spin lifting
We have defined the Spin lifting of generic representations of
![]() $\mathrm {PGSp_6}$
in §4.3. In fact, this definition can be extended to the whole of
$\mathrm {PGSp_6}$
in §4.3. In fact, this definition can be extended to the whole of
![]() $\mathrm {Irr}(\mathrm {PGSp_6})$
to give:
$\mathrm {Irr}(\mathrm {PGSp_6})$
to give:
We consider two cases, according to the decomposition of
![]() $\mathrm {Irr}(G)$
.
$\mathrm {Irr}(G)$
.
(a) if
![]() $\sigma \in \mathrm {Irr}^{\heartsuit }(\mathrm {PGSp_6})$
, we set:
$\sigma \in \mathrm {Irr}^{\heartsuit }(\mathrm {PGSp_6})$
, we set:
and
Here, we refer to §4.1 for the definition of
![]() $f_2$
. This definition of
$f_2$
. This definition of
![]() ${\mathrm {spin}}_*$
is the same as that given in §4.3 for generic representations.
${\mathrm {spin}}_*$
is the same as that given in §4.3 for generic representations.
(b) if
![]() $\sigma \in \mathrm {Irr}^{\spadesuit \clubsuit }(\mathrm {PGSp_6})$
, then recall that we have the theta lifting map
$\sigma \in \mathrm {Irr}^{\spadesuit \clubsuit }(\mathrm {PGSp_6})$
, then recall that we have the theta lifting map
Moreover, one has a commutative diagram

where the horizontal arrows are LLC maps, the first vertical arrow is the isobaric sum and the second vertical arrow is the map sending
![]() $(\phi , \phi ^{\vee })$
to
$(\phi , \phi ^{\vee })$
to
![]() $\phi \oplus \phi ^{\vee }$
. More precisely,
$\phi \oplus \phi ^{\vee }$
. More precisely,
![]() $\boxplus $
is given concretely as:
$\boxplus $
is given concretely as:
where P is the maximal parabolic subgroup of
![]() $\mathrm {GL}_8$
with Levi factor
$\mathrm {GL}_8$
with Levi factor
![]() $\mathrm {GL}_4 \times \mathrm {GL}_4$
.
$\mathrm {GL}_4 \times \mathrm {GL}_4$
.
We may now set:
The representations in
![]() $\mathrm {Irr}^{\clubsuit }(\mathrm {PGSp_6})$
have been treated in both (a) and (b) above. One can check that the two definitions of
$\mathrm {Irr}^{\clubsuit }(\mathrm {PGSp_6})$
have been treated in both (a) and (b) above. One can check that the two definitions of
![]() ${\mathrm {spin}}_*$
agree on
${\mathrm {spin}}_*$
agree on
![]() $\mathrm {Irr}^{\clubsuit }(\mathrm {PGSp_6})$
. Thus, we have now a well-defined map
$\mathrm {Irr}^{\clubsuit }(\mathrm {PGSp_6})$
. Thus, we have now a well-defined map
12.4 Kret-Shin parameters
Now a key result in the construction of our map
![]() $\mathcal {L}_w$
is the following:
$\mathcal {L}_w$
is the following:
Theorem 12.3. Given
![]() $\sigma \in \mathrm {Irr}(\mathrm {PGSp_6})$
, there exists a unique
$\sigma \in \mathrm {Irr}(\mathrm {PGSp_6})$
, there exists a unique
![]() $\phi \in \Phi _w(\mathrm {PGSp_6})$
such that
$\phi \in \Phi _w(\mathrm {PGSp_6})$
such that
and
Here we recall that
![]() $\mathrm {rest}: \mathrm {Irr}(\mathrm {PGSp_6}) \longrightarrow \mathrm {Irr}(\mathrm {Sp_6})_{/\mathrm {PGSp_6}}$
is the restriction of representations from
$\mathrm {rest}: \mathrm {Irr}(\mathrm {PGSp_6}) \longrightarrow \mathrm {Irr}(\mathrm {Sp_6})_{/\mathrm {PGSp_6}}$
is the restriction of representations from
![]() $\mathrm {PGSp_6}$
to
$\mathrm {PGSp_6}$
to
![]() $\mathrm {Sp_6}$
.
$\mathrm {Sp_6}$
.
Proposition 5.1 is a special case of this for
![]() $\sigma \in \mathrm {Irr}_{gen, ds}(\mathrm {PGSp_6})$
. Recall that we have called a
$\sigma \in \mathrm {Irr}_{gen, ds}(\mathrm {PGSp_6})$
. Recall that we have called a
![]() $\phi $
as in the Theorem a Kret-Shin parameter of
$\phi $
as in the Theorem a Kret-Shin parameter of
![]() $\sigma $
.
$\sigma $
.
Proof. To prove the Theorem, we consider two cases:
-
• If
 $\sigma \in \mathrm {Irr}^{\spadesuit \clubsuit }(\mathrm {PGSp_6})$
, then our discussion in Case (b) in the previous subsection already gives the desired
$\sigma \in \mathrm {Irr}^{\spadesuit \clubsuit }(\mathrm {PGSp_6})$
, then our discussion in Case (b) in the previous subsection already gives the desired
 $\phi $
. In the notation there, we set where
$\phi $
. In the notation there, we set where $$\begin{align*}\phi = j \circ \phi_{\theta^{\spadesuit\clubsuit}(\sigma)}, \end{align*}$$
This satisfies
$$\begin{align*}\phi = j \circ \phi_{\theta^{\spadesuit\clubsuit}(\sigma)}, \end{align*}$$
This satisfies $$\begin{align*}j: \mathrm{PGL}_4^{\vee} = \mathrm{Spin}_6({\mathbb C}) \longrightarrow \mathrm{Spin}_7({\mathbb C}). \end{align*}$$
$$\begin{align*}j: \mathrm{PGL}_4^{\vee} = \mathrm{Spin}_6({\mathbb C}) \longrightarrow \mathrm{Spin}_7({\mathbb C}). \end{align*}$$
 ${\mathrm {spin}} \circ \phi = \mathcal {L}_{\mathrm {GL}_8}( {\mathrm {spin}}_*(\sigma ))$
. Moreover, by the theory of theta correspondence, it is easy to see that
${\mathrm {spin}} \circ \phi = \mathcal {L}_{\mathrm {GL}_8}( {\mathrm {spin}}_*(\sigma ))$
. Moreover, by the theory of theta correspondence, it is easy to see that  $$\begin{align*}\mathrm{std} \circ \phi = \mathcal{L}_{\mathrm{SO}_6}(\theta^{\spadesuit\clubsuit}(\sigma)) \oplus 1 = \mathcal{L}_{\mathrm{Sp_6}_6}(\mathrm{rest}(\sigma)). \end{align*}$$
$$\begin{align*}\mathrm{std} \circ \phi = \mathcal{L}_{\mathrm{SO}_6}(\theta^{\spadesuit\clubsuit}(\sigma)) \oplus 1 = \mathcal{L}_{\mathrm{Sp_6}_6}(\mathrm{rest}(\sigma)). \end{align*}$$
-
• Suppose now that
 $\sigma \in \mathrm {Irr}^{\heartsuit }(\mathrm {PGSp_6})$
. If
$\sigma \in \mathrm {Irr}^{\heartsuit }(\mathrm {PGSp_6})$
. If
 $\sigma $
is not a discrete series representation, then one can determine its local theta lift to
$\sigma $
is not a discrete series representation, then one can determine its local theta lift to
 $\mathrm {PGSO}_8$
completely (using the fact that the LLC for Levi subgroups of
$\mathrm {PGSO}_8$
completely (using the fact that the LLC for Levi subgroups of
 $\mathrm {PGSp_6}$
and
$\mathrm {PGSp_6}$
and
 $\mathrm {PGSO}_8$
are known). From this knowledge, one can write down the desired
$\mathrm {PGSO}_8$
are known). From this knowledge, one can write down the desired
 $\phi \in \Phi (\mathrm {PGSp_6})$
: it will factor through a Levi subgroup of
$\phi \in \Phi (\mathrm {PGSp_6})$
: it will factor through a Levi subgroup of
 $\mathrm {Spin}_7({\mathbb C})$
. We omit the details here.
$\mathrm {Spin}_7({\mathbb C})$
. We omit the details here.The key case is that of discrete series representations. Here the proof is along the same lines as that of Proposition 5.1, where we demonstrated this for generic discrete series representations. To carry out the same proof, for
 $\sigma \in \mathrm {Irr}_{ds}(\mathrm {PGSp_6})$
, one needs to globalize
$\sigma \in \mathrm {Irr}_{ds}(\mathrm {PGSp_6})$
, one needs to globalize
 $\sigma $
appropriately. We discuss this globalization below.
$\sigma $
appropriately. We discuss this globalization below.
12.5 Globalization
Let k be a totally real number field with adele ring
![]() $\mathbb {A}$
and a place
$\mathbb {A}$
and a place
![]() $v_0$
such that
$v_0$
such that
![]() $k_{v_0} = F$
, and let
$k_{v_0} = F$
, and let
![]() $v_1\ne v_0$
be another finite place. Consider the split group
$v_1\ne v_0$
be another finite place. Consider the split group
![]() $\mathrm {PGSp_6}$
over k. We have:
$\mathrm {PGSp_6}$
over k. We have:
Lemma 12.4. There is a cuspidal automorphic representation
![]() $\Sigma $
of
$\Sigma $
of
![]() $\mathrm {PGSp_6}$
satisfying:
$\mathrm {PGSp_6}$
satisfying:
-
•
 $\Sigma _{v_0} = \sigma $
;
$\Sigma _{v_0} = \sigma $
; -
•
 $\Sigma _{v_1} = \mathrm {St}_{v_1}$
is the Steinberg representation;
$\Sigma _{v_1} = \mathrm {St}_{v_1}$
is the Steinberg representation; -
• for each real place
 $v_{\infty }$
of k,
$v_{\infty }$
of k,
 $\Sigma _{v_{\infty }}$
is a generic discrete series representation with very regular infinitesimal character so that it is spin-regular in the sense of [Reference Kret and ShinKS];
$\Sigma _{v_{\infty }}$
is a generic discrete series representation with very regular infinitesimal character so that it is spin-regular in the sense of [Reference Kret and ShinKS]; -
•
 $\Sigma _v$
is a quadratic twist of an unramified representation for all other v.
$\Sigma _v$
is a quadratic twist of an unramified representation for all other v.
Proof. Using [Reference ShinS, Theorem 5.8], we can find a cuspidal automorphic representation
![]() $\Sigma '$
of
$\Sigma '$
of
![]() $\mathrm {PGSp_6}$
satisfying:
$\mathrm {PGSp_6}$
satisfying:
-
•
 $\Sigma ^{\prime }_{v_0} = \pi $
;
$\Sigma ^{\prime }_{v_0} = \pi $
; -
•
 $\Sigma ^{\prime }_{v_1} = \mathrm {St}_{v_1}$
;
$\Sigma ^{\prime }_{v_1} = \mathrm {St}_{v_1}$
; -
• for each real place
 $v_{\infty }$
,
$v_{\infty }$
,
 $\Sigma ^{\prime }_{v_{\infty }}$
is a discrete series representation with very regular infinitesimal character and is spin-regular;
$\Sigma ^{\prime }_{v_{\infty }}$
is a discrete series representation with very regular infinitesimal character and is spin-regular; -
• for all other places v,
 $\Sigma ^{\prime }_v$
is unramified.
$\Sigma ^{\prime }_v$
is unramified.
The only condition potentially missing from
![]() $\Sigma '$
is the genericity of its archimedean components.
$\Sigma '$
is the genericity of its archimedean components.
Now the restriction of
![]() $\Sigma '$
to
$\Sigma '$
to
![]() $\mathrm {Sp_6}$
determines a near equivalence class of square-integrable automorphic representations with a generic A-parameter
$\mathrm {Sp_6}$
determines a near equivalence class of square-integrable automorphic representations with a generic A-parameter
![]() $\Psi $
of
$\Psi $
of
![]() $\mathrm {Sp_6}$
, because of the Steinberg local component. Moreover, again because of the Steinberg local component, the global component group of the A-parameter
$\mathrm {Sp_6}$
, because of the Steinberg local component. Moreover, again because of the Steinberg local component, the global component group of the A-parameter
![]() $\Psi $
is trivial. As a consequence, every representation of
$\Psi $
is trivial. As a consequence, every representation of
![]() $\mathrm {Sp_6}(\mathbb {A})$
in the global A-packet attached to
$\mathrm {Sp_6}(\mathbb {A})$
in the global A-packet attached to
![]() $\Psi $
occurs in the space of cusp forms by Arthur’s multiplicity formula [Reference ArthurA]. In particular, if we take an irreducible automorphic summand
$\Psi $
occurs in the space of cusp forms by Arthur’s multiplicity formula [Reference ArthurA]. In particular, if we take an irreducible automorphic summand
![]() $\Sigma ^{\prime }{\flat }$
of
$\Sigma ^{\prime }{\flat }$
of
![]() $\Sigma '|_{\mathrm {Sp_6}}$
, we may replace the archimedean components of
$\Sigma '|_{\mathrm {Sp_6}}$
, we may replace the archimedean components of
![]() $\Sigma ^{\prime }{\prime \flat }$
by the generic discrete series representations in the local A-packets (which are just L-packets) and obtain a cuspidal automorphic representation
$\Sigma ^{\prime }{\prime \flat }$
by the generic discrete series representations in the local A-packets (which are just L-packets) and obtain a cuspidal automorphic representation
![]() $\Sigma ^{\flat }$
in the same A-packet such that
$\Sigma ^{\flat }$
in the same A-packet such that
![]() $\Sigma ^{\flat }_f = \Sigma ^{\prime \flat }_f$
. Note also that the central character of
$\Sigma ^{\flat }_f = \Sigma ^{\prime \flat }_f$
. Note also that the central character of
![]() $\Sigma ^{\flat }$
is the same as that of
$\Sigma ^{\flat }$
is the same as that of
![]() $\Sigma ^{\prime \flat }$
, which is trivial.
$\Sigma ^{\prime \flat }$
, which is trivial.
Now let
![]() $\Sigma $
be a cuspidal automorphic representation of
$\Sigma $
be a cuspidal automorphic representation of
![]() $\mathrm {PGSp_6}$
whose restriction to
$\mathrm {PGSp_6}$
whose restriction to
![]() $\mathrm {Sp_6}$
contains
$\mathrm {Sp_6}$
contains
![]() $\Sigma ^{\flat }$
. Then the archimedean components of
$\Sigma ^{\flat }$
. Then the archimedean components of
![]() $\Sigma $
are generic discrete series which are spin-regular. Moreover,
$\Sigma $
are generic discrete series which are spin-regular. Moreover,
![]() $\Sigma _{v_0} = \pi \otimes \chi _0$
and
$\Sigma _{v_0} = \pi \otimes \chi _0$
and
![]() $\Sigma _{v_1} = \mathrm {St}_{v_1} \otimes \chi _1$
for some quadratic characters
$\Sigma _{v_1} = \mathrm {St}_{v_1} \otimes \chi _1$
for some quadratic characters
![]() $\chi _0$
and
$\chi _0$
and
![]() $\chi _1$
. Thus, after replacing
$\chi _1$
. Thus, after replacing
![]() $\Sigma $
by its twist by an automorphic quadratic character
$\Sigma $
by its twist by an automorphic quadratic character
![]() $\chi $
such that
$\chi $
such that
![]() $\chi _{v_0} = \chi _0$
and
$\chi _{v_0} = \chi _0$
and
![]() $\chi _{v_1} = \chi _1$
, we obtain the desired
$\chi _{v_1} = \chi _1$
, we obtain the desired
![]() $\Sigma $
as in the Lemma.
$\Sigma $
as in the Lemma.
12.6 Global Theta lift
With the cuspidal automorphic representation
![]() $\Sigma $
given by the lemma, we may now consider the global theta lift of
$\Sigma $
given by the lemma, we may now consider the global theta lift of
![]() $\Sigma $
to the split group
$\Sigma $
to the split group
![]() $\mathrm {PGSO}_8$
over k. We have:
$\mathrm {PGSO}_8$
over k. We have:
Lemma 12.5. The global theta lift
![]() $\Theta (\Sigma )$
of
$\Theta (\Sigma )$
of
![]() $\Sigma $
to
$\Sigma $
to
![]() $\mathrm {PGSO}_8$
is a nonzero cuspidal automorphic representation.
$\mathrm {PGSO}_8$
is a nonzero cuspidal automorphic representation.
Proof. We first note that
![]() $\Theta (\Sigma )$
must be cuspidal because of the tower property of theta correspondence. Indeed, the Steinberg representation
$\Theta (\Sigma )$
must be cuspidal because of the tower property of theta correspondence. Indeed, the Steinberg representation
![]() $St_{v_1}$
of
$St_{v_1}$
of
![]() $\mathrm {PGSp_6}(k_{v_1})$
does not participate in the local theta correspondence with
$\mathrm {PGSp_6}(k_{v_1})$
does not participate in the local theta correspondence with
![]() $\mathrm {PGO}_6(k_{v_1})$
, so that the global theta lift of
$\mathrm {PGO}_6(k_{v_1})$
, so that the global theta lift of
![]() $\Sigma $
to the split
$\Sigma $
to the split
![]() $\mathrm {PGO}_6$
is zero.
$\mathrm {PGO}_6$
is zero.
By [Reference Gan, Qiu and TakedaGQT, Thm. 1.4(ii)], to show the nonvanishing of the global theta lift
![]() $\Theta (\Sigma )$
, it suffices to show:
$\Theta (\Sigma )$
, it suffices to show:
-
• For any place v of k, the local component
 $\Sigma _v$
has nonzero theta lift to
$\Sigma _v$
has nonzero theta lift to
 $\mathrm {PGSO}_8(k_v)$
. This follows because unramified representations or generic representations have nonzero theta lifting to
$\mathrm {PGSO}_8(k_v)$
. This follows because unramified representations or generic representations have nonzero theta lifting to
 $\mathrm {PGSO}_8(k_v)$
; this takes care of all places
$\mathrm {PGSO}_8(k_v)$
; this takes care of all places
 $v \ne v_0$
, and for the place
$v \ne v_0$
, and for the place
 $v_0$
, it follows by our assumption that
$v_0$
, it follows by our assumption that
 $\Sigma _{v_0} = \sigma \in \mathrm {Irr}^{\heartsuit }(\mathrm {PGSp_6})$
.
$\Sigma _{v_0} = \sigma \in \mathrm {Irr}^{\heartsuit }(\mathrm {PGSp_6})$
. -
• The degree 7 standard L-function
 $L(s, \Sigma , std)$
is nonzero at
$L(s, \Sigma , std)$
is nonzero at
 $s=1$
. This follows because
$s=1$
. This follows because
 $\Sigma |_{\mathrm {Sp_6}}$
has a generic A-parameter.
$\Sigma |_{\mathrm {Sp_6}}$
has a generic A-parameter.
By the Rallis inner product formula [Reference Gan, Qiu and TakedaGQT, Thm. 1.4(ii)], we deduce that the global theta lift
![]() $\Theta (\Sigma )$
to
$\Theta (\Sigma )$
to
![]() $\mathrm {PGSO}_8$
is nonzero and the lemma is proved.
$\mathrm {PGSO}_8$
is nonzero and the lemma is proved.
We may thus consider the global Spin lifting of
![]() $\Sigma $
:
$\Sigma $
:
Then
![]() ${\mathrm {spin}}_*(\Sigma )$
is in fact a cuspidal representation of
${\mathrm {spin}}_*(\Sigma )$
is in fact a cuspidal representation of
![]() $\mathrm {GL}_8$
(because of the spin-regularity of the infinitesimal character at infinite places). Applying the results of Kret-Shin, as recounted in §5.1, and arguing as in the proof of Proposition 5.1, we conclude the proof of Theorem 12.3.
$\mathrm {GL}_8$
(because of the spin-regularity of the infinitesimal character at infinite places). Applying the results of Kret-Shin, as recounted in §5.1, and arguing as in the proof of Proposition 5.1, we conclude the proof of Theorem 12.3.
12.7 Construction of
 $\mathcal {L}_w$
$\mathcal {L}_w$
By Theorem 12.3, we have shown:
Theorem 12.6. Let
be defined by
for each
![]() $\sigma \in \mathrm {Irr}(\mathrm {PGSp_6})$
. Then
$\sigma \in \mathrm {Irr}(\mathrm {PGSp_6})$
. Then
![]() $\mathcal {L}_w$
features in and is characterized by the following commutative diagram:
$\mathcal {L}_w$
features in and is characterized by the following commutative diagram:

Moreover, the map
![]() $\mathcal {L}_w$
sends tempered (respectively discrete series) representations to (weak equivalence classes of) tempered (respectively discrete series) L-parameters and satisfies
$\mathcal {L}_w$
sends tempered (respectively discrete series) representations to (weak equivalence classes of) tempered (respectively discrete series) L-parameters and satisfies
for any quadratic character
![]() $\chi $
of
$\chi $
of
![]() $F^{\times }$
.
$F^{\times }$
.
Proof. It remains to verify the last statement: the compatibility of
![]() $\mathcal {L}_w$
with twisting by quadratic characters, It comes down to the fact that the similitude theta correspondence is compatible with such twisting. More precisely, if
$\mathcal {L}_w$
with twisting by quadratic characters, It comes down to the fact that the similitude theta correspondence is compatible with such twisting. More precisely, if
![]() $\sigma \in \mathrm {Irr}^{\heartsuit }(\mathrm {PGSp_6})$
, then
$\sigma \in \mathrm {Irr}^{\heartsuit }(\mathrm {PGSp_6})$
, then
Here, it is important to note that the similitude character of
![]() $\mathrm {PGSO}_8$
implicit on the right hand side of the equation is the one which is trivial on
$\mathrm {PGSO}_8$
implicit on the right hand side of the equation is the one which is trivial on
![]() $f_1(\mathrm {SO}_8(F))$
. In particular, it is not trivial on
$f_1(\mathrm {SO}_8(F))$
. In particular, it is not trivial on
![]() $f_2(\mathrm {SO}_8(F))$
(see §4.1 for
$f_2(\mathrm {SO}_8(F))$
(see §4.1 for
![]() $f_1$
and
$f_1$
and
![]() $f_2$
). Thus, for any representation
$f_2$
). Thus, for any representation
![]() $\pi $
of
$\pi $
of
![]() $\mathrm {PGSO}_8(F)$
,
$\mathrm {PGSO}_8(F)$
,
where we regard
![]() $\chi $
as a character of
$\chi $
as a character of
![]() $\mathrm {SO}_8(F)$
via composition with the spinor norm. Since the LLC for
$\mathrm {SO}_8(F)$
via composition with the spinor norm. Since the LLC for
![]() $\mathrm {SO}_8$
is compatible with twisting by quadratic characters, we deduce that
$\mathrm {SO}_8$
is compatible with twisting by quadratic characters, we deduce that
For
![]() $\sigma \in \mathrm {Irr}^{\spadesuit \clubsuit }(G)$
, one verifies this identity along similar lines; we omit the details.
$\sigma \in \mathrm {Irr}^{\spadesuit \clubsuit }(G)$
, one verifies this identity along similar lines; we omit the details.
12.8 Fibers of
 $\mathcal {L}_w$
$\mathcal {L}_w$
Finally, we would like to understand the fibers of
![]() $\mathcal {L}_w$
. We shall show:
$\mathcal {L}_w$
. We shall show:
Theorem 12.7.
(i) The map
![]() $\mathcal {L}_w$
is surjective. Moreover, the natural restriction map
$\mathcal {L}_w$
is surjective. Moreover, the natural restriction map
is surjective.
(ii) The fibers of
![]() $\mathcal {L}_w$
are unions of Xu’s packets (introduced in §7).
$\mathcal {L}_w$
are unions of Xu’s packets (introduced in §7).
Proof. (i) For given
![]() $\phi \in \Phi _w(\mathrm {PGSp_6})$
, with
$\phi \in \Phi _w(\mathrm {PGSp_6})$
, with
![]() $\phi ^{\flat } := \mathrm {std} \circ \phi \in \Phi (\mathrm {Sp_6})$
, write
$\phi ^{\flat } := \mathrm {std} \circ \phi \in \Phi (\mathrm {Sp_6})$
, write
be the corresponding L-packet for
![]() $\mathrm {Sp_6}$
, which is non-empty. Pick
$\mathrm {Sp_6}$
, which is non-empty. Pick
![]() $\sigma ^{\flat } \in \Pi _{\phi ^{\flat }}$
. Because
$\sigma ^{\flat } \in \Pi _{\phi ^{\flat }}$
. Because
![]() $\phi ^{\flat }$
can be lifted to
$\phi ^{\flat }$
can be lifted to
![]() $\mathrm {Spin}_7({\mathbb C})$
, the representations in
$\mathrm {Spin}_7({\mathbb C})$
, the representations in
![]() $\Pi _{\phi ^{\flat }}$
have trivial central character. Hence we can pick
$\Pi _{\phi ^{\flat }}$
have trivial central character. Hence we can pick
![]() $\sigma \in \mathrm {Irr}(\mathrm {PGSp_6})$
such that
$\sigma \in \mathrm {Irr}(\mathrm {PGSp_6})$
such that
![]() $\sigma ^{\flat } \subset \mathrm {rest}(\sigma ) $
. Then
$\sigma ^{\flat } \subset \mathrm {rest}(\sigma ) $
. Then
![]() $\mathcal {L}_w(\sigma )$
is a lift of
$\mathcal {L}_w(\sigma )$
is a lift of
![]() $\phi ^{\flat }$
, so that
$\phi ^{\flat }$
, so that
for some quadratic character
![]() $\chi $
. Hence
$\chi $
. Hence
![]() $\mathcal {L}(\sigma \otimes \chi ) = \phi $
. This proves the first assertion. Indeed, the proof shows that for any
$\mathcal {L}(\sigma \otimes \chi ) = \phi $
. This proves the first assertion. Indeed, the proof shows that for any
![]() $\sigma ^{\flat } \in \Pi _{\phi ^{\flat }}$
, there exists
$\sigma ^{\flat } \in \Pi _{\phi ^{\flat }}$
, there exists
![]() $\sigma \in \mathrm {Irr}(\mathrm {PGSp_6})$
such that
$\sigma \in \mathrm {Irr}(\mathrm {PGSp_6})$
such that
![]() $\sigma ^{\flat } \subset \mathrm {rest}(\sigma )$
and
$\sigma ^{\flat } \subset \mathrm {rest}(\sigma )$
and
![]() $\mathcal {L}_w(\sigma ) = \phi $
. This gives the second assertion.
$\mathcal {L}_w(\sigma ) = \phi $
. This gives the second assertion.
(ii) It is not hard to reduce this issue to the case of a discrete series L-parameter
![]() $\phi $
. Moreover, we shall assume that
$\phi $
. Moreover, we shall assume that
![]() $\phi $
does not factor through
$\phi $
does not factor through
![]() $\mathrm {Spin}_6({\mathbb C})$
so that
$\mathrm {Spin}_6({\mathbb C})$
so that
The case when
![]() $\mathcal {L}_w^{-1}(\phi ) \subset \mathrm {Irr}^{\spadesuit \clubsuit }(\mathrm {PGSp_6})$
is checked along similar lines and we leave it to the reader.
$\mathcal {L}_w^{-1}(\phi ) \subset \mathrm {Irr}^{\spadesuit \clubsuit }(\mathrm {PGSp_6})$
is checked along similar lines and we leave it to the reader.
Suppose then that
![]() $\sigma \in \mathcal {L}_w^{-1}(\phi )$
. Writing
$\sigma \in \mathcal {L}_w^{-1}(\phi )$
. Writing
![]() $\phi ^{\flat } = \mathrm {std} \circ \phi $
, we know that
$\phi ^{\flat } = \mathrm {std} \circ \phi $
, we know that
![]() $\sigma $
lies in a unique Xu’s packet
$\sigma $
lies in a unique Xu’s packet
![]() $\tilde {\Pi }^X_{\phi ^{\flat }}$
, where we are using the notations from §7. Thus, we need to show that
$\tilde {\Pi }^X_{\phi ^{\flat }}$
, where we are using the notations from §7. Thus, we need to show that
By Lemma 12.4, we globalize
![]() $\sigma $
to a cuspidal automorphic representation
$\sigma $
to a cuspidal automorphic representation
![]() $\Sigma $
over a number field k such that
$\Sigma $
over a number field k such that
![]() $\Sigma _{v_0} = \sigma $
and
$\Sigma _{v_0} = \sigma $
and
![]() $\Sigma _{v_1} = \mathrm {St}_{v_1}$
is the Steinberg representation; moreover, the global theta lift
$\Sigma _{v_1} = \mathrm {St}_{v_1}$
is the Steinberg representation; moreover, the global theta lift
![]() $\Theta (\Sigma )$
of
$\Theta (\Sigma )$
of
![]() $\Pi $
to
$\Pi $
to
![]() $\mathrm {PGSO}_8$
is a nonzero cuspidal representation by Lemma 12.5.
$\mathrm {PGSO}_8$
is a nonzero cuspidal representation by Lemma 12.5.
As we saw in the proof of Lemma 12.4,
![]() $\mathrm {rest}(\Sigma )$
gives rise to a generic A-parameter
$\mathrm {rest}(\Sigma )$
gives rise to a generic A-parameter
![]() $\Psi ^{\flat }$
with trivial global component group
$\Psi ^{\flat }$
with trivial global component group
![]() $S_{\Psi ^{\flat }}$
. Now we appeal to the global results of Xu [Reference XuXu3, Thm. 4.1]. Under these circumstances, Xu showed that
$S_{\Psi ^{\flat }}$
. Now we appeal to the global results of Xu [Reference XuXu3, Thm. 4.1]. Under these circumstances, Xu showed that
![]() $\Sigma $
belongs to a global generic A-packet for
$\Sigma $
belongs to a global generic A-packet for
![]() $\mathrm {PGSp_6}$
of the form
$\mathrm {PGSp_6}$
of the form
where the local packets
![]() $\tilde {\Pi }_{\Psi ^{\flat }_{v}}^X$
were introduced in §7. The contribution of
$\tilde {\Pi }_{\Psi ^{\flat }_{v}}^X$
were introduced in §7. The contribution of
![]() $ \tilde {\Pi }^X_{\Psi ^{\flat }} $
to the automorphic discrete spectrum is governed by the Arthur multiplicity formula. In particular, since the global component group
$ \tilde {\Pi }^X_{\Psi ^{\flat }} $
to the automorphic discrete spectrum is governed by the Arthur multiplicity formula. In particular, since the global component group
![]() $S_{\Psi ^{\flat }}$
is trivial, [Reference XuXu3, Thm. 4.1] says that every element of
$S_{\Psi ^{\flat }}$
is trivial, [Reference XuXu3, Thm. 4.1] says that every element of
![]() $\tilde {\Pi }^X_{\Psi ^{\flat }}$
is automorphic.
$\tilde {\Pi }^X_{\Psi ^{\flat }}$
is automorphic.
Now we know that
![]() $\sigma = \Sigma _{v_0} \in \Pi _{\Psi ^{\flat }_{v_0}}^X$
and we would like to show that
$\sigma = \Sigma _{v_0} \in \Pi _{\Psi ^{\flat }_{v_0}}^X$
and we would like to show that
For any
![]() $\sigma ' \in \tilde {\Pi }_{\Psi ^{\flat }_{v_0}}^X$
, we thus need to show that
$\sigma ' \in \tilde {\Pi }_{\Psi ^{\flat }_{v_0}}^X$
, we thus need to show that
For this, let
![]() $\Sigma '$
be the representation of
$\Sigma '$
be the representation of
![]() $PGSp_6(\mathbb {A})$
such that
$PGSp_6(\mathbb {A})$
such that
As we noted above,
![]() $\Sigma '$
is cuspidal automorphic as well. Moreover, as we showed in the proof of Lemma 12.5, the global theta lift
$\Sigma '$
is cuspidal automorphic as well. Moreover, as we showed in the proof of Lemma 12.5, the global theta lift
![]() $\Theta (\Sigma ')$
to
$\Theta (\Sigma ')$
to
![]() $\mathrm {PGSO}_8$
is nonzero.
$\mathrm {PGSO}_8$
is nonzero.
Now we have two cuspidal representations
![]() $\Theta (\Sigma )$
and
$\Theta (\Sigma )$
and
![]() $\Theta (\Sigma ')$
on
$\Theta (\Sigma ')$
on
![]() $\mathrm {PGSO}_8$
which are nearly equivalent. Hence
$\mathrm {PGSO}_8$
which are nearly equivalent. Hence
give the same generic A-parameter on
![]() $\mathrm {GL}_8$
. In particular, their local component at
$\mathrm {GL}_8$
. In particular, their local component at
![]() $v_0$
are the same. Likewise, both
$v_0$
are the same. Likewise, both
![]() $f_1^*(\Theta (\Sigma ))$
and
$f_1^*(\Theta (\Sigma ))$
and
![]() $f_1^*(\Theta (\Sigma '))$
have A-parameter
$f_1^*(\Theta (\Sigma '))$
have A-parameter
![]() $1 \oplus \Psi ^{\flat }$
. Hence, on extracting the
$1 \oplus \Psi ^{\flat }$
. Hence, on extracting the
![]() $v_0$
-component, it follows that
$v_0$
-component, it follows that
![]() $\mathcal {L}_w(\sigma ') = \mathcal {L}_w(\sigma ) = \phi $
, as desired.
$\mathcal {L}_w(\sigma ') = \mathcal {L}_w(\sigma ) = \phi $
, as desired.
As one believes that Xu’s packets are precisely the L-packets of
![]() $\mathrm {PGSp_6}$
, the map
$\mathrm {PGSp_6}$
, the map
![]() $\mathcal {L}_w$
is not the ultimate LLC map. However, it is a strict refinement of the results of Xu in the setting of
$\mathcal {L}_w$
is not the ultimate LLC map. However, it is a strict refinement of the results of Xu in the setting of
![]() $\mathrm {PGSp_6}$
. Indeed, as we showed in the main body of the paper (see Proposition 5.2), if
$\mathrm {PGSp_6}$
. Indeed, as we showed in the main body of the paper (see Proposition 5.2), if
![]() $\phi \in \Phi (\mathrm {PGSp_6})$
is valued in
$\phi \in \Phi (\mathrm {PGSp_6})$
is valued in
![]() $G_2({\mathbb C})$
, then
$G_2({\mathbb C})$
, then
![]() $\mathcal {L}_w^{-1}(\phi )$
is a single Xu’s packet and hence is an honest L-packet of
$\mathcal {L}_w^{-1}(\phi )$
is a single Xu’s packet and hence is an honest L-packet of
![]() $\mathrm {PGSp_6}$
. This fact plays a crucial role in our proof of the LLC for
$\mathrm {PGSp_6}$
. This fact plays a crucial role in our proof of the LLC for
![]() $G_2$
.
$G_2$
.
Acknowledgments
The final part of this work was completed when the authors participated in a Research in Teams (RIT) project “Modular Forms and Theta Correspondence for Exceptional Groups” hosted by the Erwin Schrodinger Institute, University of Vienna. We thank the Erwin Schrodinger Institute for its generous support and wonderful working environment, as well as our other RIT members Nadya Gurevich and Aaron Pollack for helpful discussions. We would like to thank B. Bekka and M. Tadić for their help with the Fell topology and G. Chenevier for his help with the unacceptability of
![]() $\mathrm {Spin}_7$
. Finally, we are grateful to Benedict Gross, whose inspirational ideas on the exceptional theta correspondence have been sustaining our work for the past 25 years.
$\mathrm {Spin}_7$
. Finally, we are grateful to Benedict Gross, whose inspirational ideas on the exceptional theta correspondence have been sustaining our work for the past 25 years.
Competing interest
The authors have no competing interest to declare.
Financial support
W.T. Gan is partially supported by a Singapore government MOE Tier 1 grant R-146-000-320-114 and a Tan Chin Tuan Centennial Professorship. G. Savin is partially supported by a National Science Foundation grant DMS-1901745.