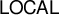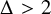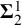Descriptive combinatorics is an area concerned with the investigation of combinatorial problems on infinite graphs that satisfy additional regularity properties (see, e.g. [Reference PikhurkoPik21, Reference Kechris and MarksKM20] for surveys of the most important results). In recent years, the study of such problems revealed deep connections to other areas of mathematics and computer science. The most relevant to our study are the connections with the so-called
![]() $\mathsf {LOCAL}$
model from the area of distributed computing. There are several recent results that use distributed computing techniques in order to get results either in descriptive combinatorics [Reference BernshteynBer23, Reference BernshteynBer21, Reference Brandt, Chang, Grebík, Grunau, Rozhoň and VidnyánszkyBCG+21, Reference ElekEle18, Reference Grebík and RozhoňGR21a], or in the theory of random processes [Reference Holroyd, Schramm and WilsonHSW17, Reference Grebík and RozhoňGR21b]. The starting point of our work was the investigation of the opposite direction. Namely, our aim was to adapt the celebrated determinacy technique of Marks [Reference MarksMar16] to the
$\mathsf {LOCAL}$
model from the area of distributed computing. There are several recent results that use distributed computing techniques in order to get results either in descriptive combinatorics [Reference BernshteynBer23, Reference BernshteynBer21, Reference Brandt, Chang, Grebík, Grunau, Rozhoň and VidnyánszkyBCG+21, Reference ElekEle18, Reference Grebík and RozhoňGR21a], or in the theory of random processes [Reference Holroyd, Schramm and WilsonHSW17, Reference Grebík and RozhoňGR21b]. The starting point of our work was the investigation of the opposite direction. Namely, our aim was to adapt the celebrated determinacy technique of Marks [Reference MarksMar16] to the
![]() $\mathsf {LOCAL}$
model of distributed computing. In order to perform the adaptation (which is indeed possible, see our conference paper [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and VidnyánszkyBCG+21]Footnote
1
), we had to circumvent several technical hurdles that, rather surprisingly, lead to the main objects that we study in this paper, homomorphism graphs (defined in Section 2). We refer the reader to [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and VidnyánszkyBCG+21] for a detailed discussion of the concepts and their connections to the
$\mathsf {LOCAL}$
model of distributed computing. In order to perform the adaptation (which is indeed possible, see our conference paper [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and VidnyánszkyBCG+21]Footnote
1
), we had to circumvent several technical hurdles that, rather surprisingly, lead to the main objects that we study in this paper, homomorphism graphs (defined in Section 2). We refer the reader to [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and VidnyánszkyBCG+21] for a detailed discussion of the concepts and their connections to the
![]() $\mathsf {LOCAL}$
model.
$\mathsf {LOCAL}$
model.
Before we state our results, we recall several basic notions and facts. A graph G on a set X is a symmetric subset of
![]() $X^2 \setminus \{(x,x):x \in X\}$
. We will refer to X as the vertex set of G, in symbols
$X^2 \setminus \{(x,x):x \in X\}$
. We will refer to X as the vertex set of G, in symbols
![]() $V(G)$
, and to G as the edge set. If
$V(G)$
, and to G as the edge set. If
![]() $n \in \{1,2,\dots ,\aleph _0\}$
, a (proper) n-coloring of G is a mapping
$n \in \{1,2,\dots ,\aleph _0\}$
, a (proper) n-coloring of G is a mapping
![]() $c:V(G) \to n$
, such that
$c:V(G) \to n$
, such that
![]() $(x,y) \in G \implies c(x) \neq c(y)$
. The chromatic number of G,
$(x,y) \in G \implies c(x) \neq c(y)$
. The chromatic number of G,
![]() $\chi (G)$
is the minimal n for which an n-coloring exists. If G and H are graphs, a homomorphism from G to H is a mapping
$\chi (G)$
is the minimal n for which an n-coloring exists. If G and H are graphs, a homomorphism from G to H is a mapping
![]() $c:V(G) \to V(H)$
that preserves edges. Note that
$c:V(G) \to V(H)$
that preserves edges. Note that
![]() $\chi (G) \leq n$
if and only if G admits a homomorphism to the complete graph on n vertices,
$\chi (G) \leq n$
if and only if G admits a homomorphism to the complete graph on n vertices,
![]() $K_n$
. We denote by
$K_n$
. We denote by
![]() $\Delta (G)$
the supremum of the vertex degrees of G. In what follows, we will only consider graphs with degrees bounded by a finite number, unless explicitly stated otherwise. A graph is called
$\Delta (G)$
the supremum of the vertex degrees of G. In what follows, we will only consider graphs with degrees bounded by a finite number, unless explicitly stated otherwise. A graph is called
![]() $\Delta $
-regular if every vertex has degree
$\Delta $
-regular if every vertex has degree
![]() $\Delta $
. It is easy to see that
$\Delta $
. It is easy to see that
![]() $\chi (G) \leq \Delta (G)+1$
. Moreover, Brooks’s theorem states that this inequality is sharp only in trivial situations: if
$\chi (G) \leq \Delta (G)+1$
. Moreover, Brooks’s theorem states that this inequality is sharp only in trivial situations: if
![]() $\Delta (G)>2$
, it happens if and only if G contains a complete graph on
$\Delta (G)>2$
, it happens if and only if G contains a complete graph on
![]() $\Delta (G)+1$
vertices, and if
$\Delta (G)+1$
vertices, and if
![]() $\Delta (G)=2$
, it happens if and only if G contains an odd cycle.
$\Delta (G)=2$
, it happens if and only if G contains an odd cycle.
We say that G is a Borel graph if
![]() $V(G)$
is a standard Borel space, see [Reference KechrisKec95], and the set of edges of G is a Borel subset of
$V(G)$
is a standard Borel space, see [Reference KechrisKec95], and the set of edges of G is a Borel subset of
![]() $V(G)\times V(G)$
endowed with the product Borel structure. The Borel chromatic number,
$V(G)\times V(G)$
endowed with the product Borel structure. The Borel chromatic number,
![]() $\chi _B(G)$
, of G is defined as the minimal n for which a Borel n-coloring exists, here, we endow n with the trivial Borel structure. Similar concepts are studied when we relax the notion of Borel measurable to merely measurable with respect to some probability measure, or Baire measurable with respect to some compatible Polish topology. It has been shown by Kechris-Solecki-Todorčević [Reference Kechris, Solecki and TodorčevićKST99] that
$\chi _B(G)$
, of G is defined as the minimal n for which a Borel n-coloring exists, here, we endow n with the trivial Borel structure. Similar concepts are studied when we relax the notion of Borel measurable to merely measurable with respect to some probability measure, or Baire measurable with respect to some compatible Polish topology. It has been shown by Kechris-Solecki-Todorčević [Reference Kechris, Solecki and TodorčevićKST99] that
![]() $\chi _B(G) \leq \Delta (G)+1$
, and it was a long-standing open problem, whether Brooks’s theorem has a literal extension to the Borel context, at least in the case
$\chi _B(G) \leq \Delta (G)+1$
, and it was a long-standing open problem, whether Brooks’s theorem has a literal extension to the Borel context, at least in the case
![]() $\Delta (G)>2$
. For example, it has been proved by Conley-Marks-Tucker-Drob [Reference Conley, Marks and Tucker-DrobCMTD16] that in the measurable or Baire measurable setting, the answer is affirmative. Eventually, this problem has been solved by Marks [Reference MarksMar16], who showed the existence of
$\Delta (G)>2$
. For example, it has been proved by Conley-Marks-Tucker-Drob [Reference Conley, Marks and Tucker-DrobCMTD16] that in the measurable or Baire measurable setting, the answer is affirmative. Eventually, this problem has been solved by Marks [Reference MarksMar16], who showed the existence of
![]() $\Delta $
-regular acyclic Borel graphs with Borel chromatic number
$\Delta $
-regular acyclic Borel graphs with Borel chromatic number
![]() $\Delta +1$
. Remarkably, this result relies on Martin’s Borel determinacy theorem, one of the cornerstones of modern descriptive set theory.
$\Delta +1$
. Remarkably, this result relies on Martin’s Borel determinacy theorem, one of the cornerstones of modern descriptive set theory.
Results
First, let us give a high-level overview of our new method for constructing Borel graphs (for the precise definition of the notions discussed below, see Section 2). Fix a
![]() $\Delta>2$
. To a given Borel graph
$\Delta>2$
. To a given Borel graph
![]() $\mathcal {H}$
we will associate a
$\mathcal {H}$
we will associate a
![]() $\Delta $
-regular acyclic Borel graph
$\Delta $
-regular acyclic Borel graph
![]() $\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H})$
. Roughly speaking, the vertex set of the graph will be a collection of pairs
$\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H})$
. Roughly speaking, the vertex set of the graph will be a collection of pairs
![]() $(x,h)$
, where
$(x,h)$
, where
![]() $x \in V(\mathcal {H})$
and h is a homomorphism from the
$x \in V(\mathcal {H})$
and h is a homomorphism from the
![]() $\Delta $
-regular infinite rooted tree
$\Delta $
-regular infinite rooted tree
![]() $T_\Delta $
to
$T_\Delta $
to
![]() $\mathcal {H}$
that maps the root to x, and
$\mathcal {H}$
that maps the root to x, and
![]() $(x,h)$
is adjacent to
$(x,h)$
is adjacent to
![]() $(x',h')$
if
$(x',h')$
if
![]() $h'$
is obtained from h by moving the root to a neighboring vertex.
$h'$
is obtained from h by moving the root to a neighboring vertex.
The main idea is that the we can use the combinatorial properties of
![]() $\mathcal {H}$
to control the properties of
$\mathcal {H}$
to control the properties of
![]() $\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H})$
. Most importantly, we will argue that from a Borel
$\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H})$
. Most importantly, we will argue that from a Borel
![]() $\Delta $
-coloring c of
$\Delta $
-coloring c of
![]() $\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H})$
we can construct a
$\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H})$
we can construct a
![]() $\Delta $
-coloring of
$\Delta $
-coloring of
![]() $\mathcal {H}$
: to each x we associate games analogous to the ones developed by Marks, in order to select one of the sets
$\mathcal {H}$
: to each x we associate games analogous to the ones developed by Marks, in order to select one of the sets
![]() $\{h:c(x,h)=i\}$
for
$\{h:c(x,h)=i\}$
for
![]() $i \leq \Delta $
(in some sense, we select the largest), and color x with the appropriate i. As this selection will be based on the existence of winning strategies, the coloring of
$i \leq \Delta $
(in some sense, we select the largest), and color x with the appropriate i. As this selection will be based on the existence of winning strategies, the coloring of
![]() $\mathcal {H}$
will not be Borel. However, it will still be in a class that has all the usual regularity properties (see Section 1 for the definition of this class and the corresponding chromatic number,
$\mathcal {H}$
will not be Borel. However, it will still be in a class that has all the usual regularity properties (see Section 1 for the definition of this class and the corresponding chromatic number,
![]() $\chi _{\Game \mathbf {\Delta }^1_1}$
). Thus, we will be able to prove the following.
$\chi _{\Game \mathbf {\Delta }^1_1}$
). Thus, we will be able to prove the following.
Theorem 0.1. Let
![]() $\mathcal {H}$
be a locally countable Borel graph. Then we have
$\mathcal {H}$
be a locally countable Borel graph. Then we have
In particular,
![]() $\chi _{\Game \mathbf {\Delta }^1_1}(\mathcal {H})>\Delta $
holds if the Ramsey measurable (if
$\chi _{\Game \mathbf {\Delta }^1_1}(\mathcal {H})>\Delta $
holds if the Ramsey measurable (if
![]() $V(\mathcal {H})=[\mathbb {N}]^{\mathbb {N}}$
), Baire measurable, or
$V(\mathcal {H})=[\mathbb {N}]^{\mathbb {N}}$
), Baire measurable, or
![]() $\mu $
measurable chromatic number of
$\mu $
measurable chromatic number of
![]() $\mathcal {H}$
is
$\mathcal {H}$
is
![]() $>\Delta $
.
$>\Delta $
.
Next, we list the applications. In each instance, we use a version of Theorem 0.1 for a carefully chosen target graph
![]() $\mathcal {H}$
. These graphs come from well-studied contexts of descriptive combinatorics, namely, Ramsey property and Baire category.
$\mathcal {H}$
. These graphs come from well-studied contexts of descriptive combinatorics, namely, Ramsey property and Baire category.
a) Complexity result
We apply homomorphism graphs in connection to projective complexity and Brooks’s theorem. One might conjecture that the right generalization of Brooks’s theorem to the Borel context is that Marks’s examples serve as the analogues of the complete graph, that is, whenever G is a Borel graph with
![]() $\chi _B(G)=\Delta (G)+1$
, then G must contain a Borel homomorphic copy of the corresponding example of Marks. Note that in the case
$\chi _B(G)=\Delta (G)+1$
, then G must contain a Borel homomorphic copy of the corresponding example of Marks. Note that in the case
![]() $\Delta (G)=2$
, this is the situation, as there is a Borel analogue of odd cycles that admits a homomorphism into each Borel graph G with
$\Delta (G)=2$
, this is the situation, as there is a Borel analogue of odd cycles that admits a homomorphism into each Borel graph G with
![]() $\chi _B(G)>2$
(see [Reference Carroy, Miller, Schrittesser and VidnyánszkyCMSV21]).
$\chi _B(G)>2$
(see [Reference Carroy, Miller, Schrittesser and VidnyánszkyCMSV21]).
In [Reference Todorčević and VidnyánszkyTV21], it has been shown that it is impossible to give a simple characterization of acyclic Borel graphs with Borel chromatic number
![]() $\leq 3$
. The construction there was based on a Ramsey theoretic statement, the Galvin-Prikry theorem [Reference Galvin and PrikryGP73]. An important weakness of that proof is that it uses graphs of finite but unbounded degrees. Using the homomorphism graph combined with the method developed in [Reference Todorčević and VidnyánszkyTV21] and Marks’s technique, we obtain the analogous result for bounded degree graphs.
$\leq 3$
. The construction there was based on a Ramsey theoretic statement, the Galvin-Prikry theorem [Reference Galvin and PrikryGP73]. An important weakness of that proof is that it uses graphs of finite but unbounded degrees. Using the homomorphism graph combined with the method developed in [Reference Todorčević and VidnyánszkyTV21] and Marks’s technique, we obtain the analogous result for bounded degree graphs.
Theorem 0.2. For each
![]() $\Delta>2$
, the family of
$\Delta>2$
, the family of
![]() $\Delta $
-regular acyclic Borel graphs with Borel chromatic number
$\Delta $
-regular acyclic Borel graphs with Borel chromatic number
![]() $\leq \Delta $
has no simple characterization, namely, it is
$\leq \Delta $
has no simple characterization, namely, it is
![]() $\mathbf {\Sigma }^1_2$
-complete.
$\mathbf {\Sigma }^1_2$
-complete.
From this, we deduce a strong negative answer to the conjecture described above.
Corollary 0.3. Brooks’s theorem has no analogue for Borel graphs in the following sense. Let
![]() $\Delta>2$
. There is no countable family
$\Delta>2$
. There is no countable family
![]() $\{\mathcal {H}_i\}_{i \in I}$
of Borel graphs, such that for any Borel graph
$\{\mathcal {H}_i\}_{i \in I}$
of Borel graphs, such that for any Borel graph
![]() $\mathcal {G}$
with
$\mathcal {G}$
with
![]() $\Delta (\mathcal {G})\leq \Delta $
, we have
$\Delta (\mathcal {G})\leq \Delta $
, we have
![]() $\chi _B(\mathcal {G})>\Delta $
if and only if for some
$\chi _B(\mathcal {G})>\Delta $
if and only if for some
![]() $i \in I$
, the graph
$i \in I$
, the graph
![]() $\mathcal {G}$
contains a Borel homomorphic copy of
$\mathcal {G}$
contains a Borel homomorphic copy of
![]() $\mathcal {H}_i$
.
$\mathcal {H}_i$
.
b) Chromatic number and hyperfiniteness
Recall that a Borel graph
![]() $\mathcal {G}$
is called hyperfinite if it is the increasing union of Borel graphs with finite connected components. In [Reference Conley, Jackson, Marks, Seward and Tucker-DrobCJM+20], the authors examine the connection between hyperfiniteness and notions of Borel combinatorics, such as Borel chromatic number and the Lovász Local Lemma [Reference Erdős and LovászEL75]. Roughly speaking, they show that hyperfiniteness has no effect on Borel combinatorics, for example, they establish the following.
$\mathcal {G}$
is called hyperfinite if it is the increasing union of Borel graphs with finite connected components. In [Reference Conley, Jackson, Marks, Seward and Tucker-DrobCJM+20], the authors examine the connection between hyperfiniteness and notions of Borel combinatorics, such as Borel chromatic number and the Lovász Local Lemma [Reference Erdős and LovászEL75]. Roughly speaking, they show that hyperfiniteness has no effect on Borel combinatorics, for example, they establish the following.
Theorem 0.4 [Reference Conley, Jackson, Marks, Seward and Tucker-DrobCJM+20].
There exists a hyperfinite
![]() $\Delta $
-regular acyclic Borel graph with Borel chromatic number
$\Delta $
-regular acyclic Borel graph with Borel chromatic number
![]() $\Delta +1$
.
$\Delta +1$
.
Using homomorphism graphs, we provide a new, short, and more streamlined proof of this result. In particular, the conclusion about the chromatic number follows from our general result about
![]() $\operatorname {\mathbf { Hom}}^{e}$
(a version of
$\operatorname {\mathbf { Hom}}^{e}$
(a version of
![]() $\operatorname {\mathbf { Hom}}^{ac}$
), while to get hyperfiniteness, we can basically choose any acyclic hyperfinite graph as a target graph. To get both properties at once, we simply pick a variant of the graph
$\operatorname {\mathbf { Hom}}^{ac}$
), while to get hyperfiniteness, we can basically choose any acyclic hyperfinite graph as a target graph. To get both properties at once, we simply pick a variant of the graph
![]() $\mathbb {G}_0$
(see [Reference Kechris, Solecki and TodorčevićKST99, Section 6]) as our target graph.
$\mathbb {G}_0$
(see [Reference Kechris, Solecki and TodorčevićKST99, Section 6]) as our target graph.
c) Graph homomorphism
We also consider a slightly more general context: homomorphisms to finite graphs. Clearly, the
![]() $\Delta $
-regular examples constructed by Marks do not admit a Borel homomorphism to finite graphs of chromatic number at most
$\Delta $
-regular examples constructed by Marks do not admit a Borel homomorphism to finite graphs of chromatic number at most
![]() $\Delta $
, as this would imply that their Borel chromatic number is
$\Delta $
, as this would imply that their Borel chromatic number is
![]() $\leq \Delta $
. No other examples of such graphs were known. We show the following.
$\leq \Delta $
. No other examples of such graphs were known. We show the following.
Theorem 0.5. For every
![]() $\Delta>2$
and every
$\Delta>2$
and every
![]() $\ell \leq 2\Delta -2$
, there are a finite graph H and a
$\ell \leq 2\Delta -2$
, there are a finite graph H and a
![]() $\Delta $
-regular acyclic Borel graph
$\Delta $
-regular acyclic Borel graph
![]() $\mathcal {G}$
, such that
$\mathcal {G}$
, such that
![]() $\chi (H)=\ell $
and
$\chi (H)=\ell $
and
![]() $\mathcal {G}$
does not admit Borel homomorphism to H. The graph
$\mathcal {G}$
does not admit Borel homomorphism to H. The graph
![]() $\mathcal {G}$
can be chosen to be hyperfinite.
$\mathcal {G}$
can be chosen to be hyperfinite.
This theorem is a step toward the better understanding of Problem 8.12 from [Reference Kechris and MarksKM20].
Remark 0.6. The upper bound
![]() $2\Delta -2$
on the chromatic number is implied by the combinatorial condition almost
$2\Delta -2$
on the chromatic number is implied by the combinatorial condition almost
![]() $\Delta $
-colorable, see Definition 3.6, that is utilized in the generalization of Marks’s determinacy technique. It is an interesting open problem to determine exactly to what graphs the determinacy argument may be applied. Recently, Csóka and the last author showed that there is no factor of iid homomorphism from the
$\Delta $
-colorable, see Definition 3.6, that is utilized in the generalization of Marks’s determinacy technique. It is an interesting open problem to determine exactly to what graphs the determinacy argument may be applied. Recently, Csóka and the last author showed that there is no factor of iid homomorphism from the
![]() $\Delta $
-regular tree to finite graphs of arbitrarily large chromatic number using the theory of entropy inequalities. This, of course, implies the same result in the Borel setting. Observe, however, that there is a factor of iid homomorphism from the
$\Delta $
-regular tree to finite graphs of arbitrarily large chromatic number using the theory of entropy inequalities. This, of course, implies the same result in the Borel setting. Observe, however, that there is a factor of iid homomorphism from the
![]() $\Delta $
-regular tree to examples constructed in this paper as the universal graph
$\Delta $
-regular tree to examples constructed in this paper as the universal graph
![]() $H_\Delta $
that is almost
$H_\Delta $
that is almost
![]() $\Delta $
-colorable, see Section 4.3, and Figure 2 contains the complete graph on
$\Delta $
-colorable, see Section 4.3, and Figure 2 contains the complete graph on
![]() $\Delta $
vertices. This shows that the difference between a factor of iid and Borel chromatic numbers extends nontrivially to the question about graph homomorphism. The exact relationship between the existence of a factor of iid and Borel homomorphisms is wide open.
$\Delta $
vertices. This shows that the difference between a factor of iid and Borel chromatic numbers extends nontrivially to the question about graph homomorphism. The exact relationship between the existence of a factor of iid and Borel homomorphisms is wide open.
Roadmap
The paper is structured as follows. In Section 1, we collect the most important definitions and theorems that are going to be used. Then, in Section 2, we establish the basic properties of homomorphism graphs and their various modifications. Section 3 contains Marks’s technique’s adaptation to our context, while in Section 4, we prove our main results. We conclude the paper with a couple of remarks in Section 5.
1 Preliminaries
For standard facts and notations of descriptive set theory not explained here, we refer the reader to [Reference KechrisKec95] (see also [Reference MoschovakisMos09]).
Given a graph G, we refer to maps
![]() $V(G) \to S$
and
$V(G) \to S$
and
![]() $G \to S$
as vertex (S)-labelings and edge (S)-labelings, respectively. An edge labeling is called an edge coloring, if incident edges have different labels. Let
$G \to S$
as vertex (S)-labelings and edge (S)-labelings, respectively. An edge labeling is called an edge coloring, if incident edges have different labels. Let
![]() $\mathcal {F}$
be a family of subsets of
$\mathcal {F}$
be a family of subsets of
![]() $V(G)$
, and
$V(G)$
, and
![]() $n \in \{1,2,\dots , \aleph _0\}$
. An
$n \in \{1,2,\dots , \aleph _0\}$
. An
![]() $\mathcal {F}$
measurable n-coloring is an n-coloring c of G, such that
$\mathcal {F}$
measurable n-coloring is an n-coloring c of G, such that
![]() $c^{-1}(i) \in \mathcal {F}$
for each
$c^{-1}(i) \in \mathcal {F}$
for each
![]() $i<n$
. Using this notion, we define the
$i<n$
. Using this notion, we define the
![]() $\mathcal {F}$
measurable chromatic number of G,
$\mathcal {F}$
measurable chromatic number of G,
![]() $\chi _{\mathcal {F}}(G)$
to be the minimal n for which such a coloring exists.
$\chi _{\mathcal {F}}(G)$
to be the minimal n for which such a coloring exists.
We denote by
![]() $[S]^{\mathbb {N}}$
the collection of infinite subsets of the set S, and by
$[S]^{\mathbb {N}}$
the collection of infinite subsets of the set S, and by
![]() $S^{<\mathbb {N}}$
the family of finite sequences of elements of S. Points of the space
$S^{<\mathbb {N}}$
the family of finite sequences of elements of S. Points of the space
![]() $[\mathbb {N}]^{\mathbb {N}}$
will be identified with their increasing enumeration, making
$[\mathbb {N}]^{\mathbb {N}}$
will be identified with their increasing enumeration, making
![]() $[\mathbb {N}]^{\mathbb {N}}$
a
$[\mathbb {N}]^{\mathbb {N}}$
a
![]() $G_\delta $
subset of
$G_\delta $
subset of
![]() $ \mathbb {N}^{\mathbb {N}}$
, and hence, the product topology of
$ \mathbb {N}^{\mathbb {N}}$
, and hence, the product topology of
![]() $\mathbb {N}^{\mathbb {N}}$
gives rise to a Polish topology on
$\mathbb {N}^{\mathbb {N}}$
gives rise to a Polish topology on
![]() $[\mathbb {N}]^{\mathbb {N}}$
.
$[\mathbb {N}]^{\mathbb {N}}$
.
Define the shift-graph (on
![]() $[\mathbb {N}]^{\mathbb {N}}$
),
$[\mathbb {N}]^{\mathbb {N}}$
),
![]() $\mathcal {G}_S$
, by letting x and y be adjacent if
$\mathcal {G}_S$
, by letting x and y be adjacent if
![]() $y=x \setminus \min x$
or
$y=x \setminus \min x$
or
![]() $x=y \setminus \min y$
. The shift-graph has a close connection to the notion of so-called Ramsey property: for
$x=y \setminus \min y$
. The shift-graph has a close connection to the notion of so-called Ramsey property: for
![]() $s \subset \mathbb {N}$
finite and
$s \subset \mathbb {N}$
finite and
![]() $A \in [\mathbb {N}]^{\mathbb {N}}$
with
$A \in [\mathbb {N}]^{\mathbb {N}}$
with
![]() $\max s < \min A$
, let
$\max s < \min A$
, let
![]() $[s,A]=\{B \in [\mathbb {N}]^{\mathbb {N}}: s \subset B, A \supseteq B \setminus s\}$
. A set
$[s,A]=\{B \in [\mathbb {N}]^{\mathbb {N}}: s \subset B, A \supseteq B \setminus s\}$
. A set
![]() $S \subseteq [\mathbb {N}]^{\mathbb {N}}$
is called Ramsey if for each set of the form
$S \subseteq [\mathbb {N}]^{\mathbb {N}}$
is called Ramsey if for each set of the form
![]() $[s,A]$
, there exists
$[s,A]$
, there exists
![]() $B\in [A]^{\mathbb {N}}$
, such that
$B\in [A]^{\mathbb {N}}$
, such that
![]() $[s,B] \cap S= \emptyset $
or
$[s,B] \cap S= \emptyset $
or
![]() $[s,B] \subseteq S$
(see, e.g. [Reference Kechris, Solecki and TodorčevićKST99, Reference KhomskiiKho12, Reference TodorcevicTod10] for results on the shift-graph and Ramsey measurability). The following follows from the definition.
$[s,B] \subseteq S$
(see, e.g. [Reference Kechris, Solecki and TodorčevićKST99, Reference KhomskiiKho12, Reference TodorcevicTod10] for results on the shift-graph and Ramsey measurability). The following follows from the definition.
Theorem 1.1. The graph
![]() $\mathcal {G}_S$
has no Ramsey measurable finite coloring.
$\mathcal {G}_S$
has no Ramsey measurable finite coloring.
Note that the Galvin-Prikry theorem asserts that Borel sets are Ramsey measurable. However, adapting Marks’s technique to our setting will require the usage of families of sets that are much larger than the collection of Borel sets.
If
![]() $T \subseteq \mathbb {N}^{<\mathbb {N}}$
is a nonempty pruned tree, and
$T \subseteq \mathbb {N}^{<\mathbb {N}}$
is a nonempty pruned tree, and
![]() $A \subseteq \mathbb {N}^{\mathbb {N}}$
,
$A \subseteq \mathbb {N}^{\mathbb {N}}$
,
![]() $G(T,A)$
will denote the two-player infinite game on
$G(T,A)$
will denote the two-player infinite game on
![]() $\mathbb {N}$
with legal positions in T and payoff set A. We will call the first player
$\mathbb {N}$
with legal positions in T and payoff set A. We will call the first player
![]() $\operatorname {Alice}$
and the second
$\operatorname {Alice}$
and the second
![]() $\operatorname {Bob}$
,
$\operatorname {Bob}$
,
![]() $\operatorname {Alice}$
wins the game if the resulting element is in A. Note that the Borel determinacy theorem [Reference MartinMar75] states that one of the players has a winning strategy in
$\operatorname {Alice}$
wins the game if the resulting element is in A. Note that the Borel determinacy theorem [Reference MartinMar75] states that one of the players has a winning strategy in
![]() $G(T,A),$
whenever A is Borel.
$G(T,A),$
whenever A is Borel.
Recall that a subset of A, a Polish space X, is in the class
![]() $\Game \mathbf {\Delta }^1_1$
if there is some Borel set
$\Game \mathbf {\Delta }^1_1$
if there is some Borel set
![]() $B \subset X \times \mathbb {N}^{\mathbb {N}}$
, such that
$B \subset X \times \mathbb {N}^{\mathbb {N}}$
, such that
see [Reference MoschovakisMos09].
By modifying the payoff sets, it is easy to see the following (see, [Reference KechrisKec95, p138]).
Lemma 1.2. Let X be a Polish space,
![]() $B \subseteq X \times \mathbb {N}^{\mathbb {N}}$
be Borel, and
$B \subseteq X \times \mathbb {N}^{\mathbb {N}}$
be Borel, and
![]() $x \mapsto T_x$
be a Borel map, such that
$x \mapsto T_x$
be a Borel map, such that
![]() $T_x$
is a pruned subtree of
$T_x$
is a pruned subtree of
![]() $\mathbb {N}^{<\mathbb {N}}$
. Then the set
$\mathbb {N}^{<\mathbb {N}}$
. Then the set
is
![]() $\Game \mathbf {\Delta }^1_1$
.
$\Game \mathbf {\Delta }^1_1$
.
The class
![]() $\Game \mathbf {\Delta }^1_1$
enjoys a number of regularity properties.
$\Game \mathbf {\Delta }^1_1$
enjoys a number of regularity properties.
Proposition 1.3. Let X be a Polish space.
![]() $\Game \mathbf {\Delta }^1_1$
sets
$\Game \mathbf {\Delta }^1_1$
sets
-
1. form a
 $\sigma $
-algebra,
$\sigma $
-algebra, -
2. have the Baire property w.r.t. any compatible Polish topology,
-
3. are measurable with respect to any Borel probability measure,
-
4. in the case
 $X=[\mathbb {N}]^{\mathbb {N}}$
, have the Ramsey property.
$X=[\mathbb {N}]^{\mathbb {N}}$
, have the Ramsey property.
Before proving this statement, we need to fix an encoding of Borel sets. Let
![]() $\mathbf {BC}(X)$
be a set of Borel codes and sets
$\mathbf {BC}(X)$
be a set of Borel codes and sets
![]() $\mathbf {A}(X)$
and
$\mathbf {A}(X)$
and
![]() $\mathbf {C}(X)$
with the properties summarized below:
$\mathbf {C}(X)$
with the properties summarized below:
Proposition 1.4. (see [Reference MoschovakisMos09, 3.H])
-
•
 $\mathbf {BC}(X) \in \mathbf {\Pi }^1_1(\mathbb {N}^{\mathbb {N}})$
,
$\mathbf {BC}(X) \in \mathbf {\Pi }^1_1(\mathbb {N}^{\mathbb {N}})$
,
 $\mathbf {A}(X) \in \mathbf {\Sigma }^1_1(\mathbb {N}^{\mathbb {N}} \times X)$
,
$\mathbf {A}(X) \in \mathbf {\Sigma }^1_1(\mathbb {N}^{\mathbb {N}} \times X)$
,
 $\mathbf {C}(X) \in \mathbf {\Pi }^1_1(\mathbb {N}^{\mathbb {N}} \times X)$
,
$\mathbf {C}(X) \in \mathbf {\Pi }^1_1(\mathbb {N}^{\mathbb {N}} \times X)$
, -
• for
 $c\in \mathbf {BC}(X)$
and
$c\in \mathbf {BC}(X)$
and
 $x \in X$
, we have
$x \in X$
, we have
 $(c,x) \in \mathbf {A}(X) \iff (c,x) \in \mathbf {C}(X)$
,
$(c,x) \in \mathbf {A}(X) \iff (c,x) \in \mathbf {C}(X)$
, -
• if P is a Polish space and
 $B \in \mathbf {\Delta }^1_1(P \times X)$
, then there exists a Borel map
$B \in \mathbf {\Delta }^1_1(P \times X)$
, then there exists a Borel map
 $f:P \to \mathbb {N}^{\mathbb {N}}$
so that
$f:P \to \mathbb {N}^{\mathbb {N}}$
so that
 $ran(f) \subset \mathbf {BC}(X)$
and for every
$ran(f) \subset \mathbf {BC}(X)$
and for every
 $p \in P$
, we have
$p \in P$
, we have
 $\mathbf {A}(X)_{f(p)}=B_p$
.
$\mathbf {A}(X)_{f(p)}=B_p$
.
Moreover, in the case
![]() $X=(\mathbb {N}^{\mathbb {N}})^k$
, the sets
$X=(\mathbb {N}^{\mathbb {N}})^k$
, the sets
![]() $\mathbf {BC}(X)$
,
$\mathbf {BC}(X)$
,
![]() $\mathbf {A}(X)$
, and
$\mathbf {A}(X)$
, and
![]() $\mathbf {C}(X)$
can be described by
$\mathbf {C}(X)$
can be described by
![]() $\Pi ^1_1$
,
$\Pi ^1_1$
,
![]() $\Sigma ^1_1$
, and
$\Sigma ^1_1$
, and
![]() $\Pi ^1_1$
formulas, respectively.
$\Pi ^1_1$
formulas, respectively.
Now we can prove Proposition 1.3.
Proof of Proposition 1.3.
The first statement is a consequence of [Reference MoschovakisMos09, Lemma 6D.1] and not very hard to verify.
In order to see the rest, we rely on results of Feng-Magidor-Woodin [Reference Feng, Magidor and WoodinFMW92]. Recall that a subset S of
![]() $\mathbb {N}^{\mathbb {N}}$
is universally Baire if for every topological space Y that has a basis consisting of regular open sets and every continuous
$\mathbb {N}^{\mathbb {N}}$
is universally Baire if for every topological space Y that has a basis consisting of regular open sets and every continuous
![]() $f:Y \to \mathbb {N}^{\mathbb {N}}$
, the set
$f:Y \to \mathbb {N}^{\mathbb {N}}$
, the set
![]() $f^{-1}(S)$
has the Baire property.
$f^{-1}(S)$
has the Baire property.
It is not hard to check the following properties of universally Baire sets (see [Reference Feng, Magidor and WoodinFMW92, Theorem 2.2] and the discussion on p212).
Claim 1.5. Assume that
![]() $S \subseteq \mathbb {N}^{\mathbb {N}}$
is universally Baire, X is a Polish space, and
$S \subseteq \mathbb {N}^{\mathbb {N}}$
is universally Baire, X is a Polish space, and
![]() $\varphi :X \to \mathbb {N}^{\mathbb {N}}$
is an injection.
$\varphi :X \to \mathbb {N}^{\mathbb {N}}$
is an injection.
-
1. S has the Baire property w.r.t. any compatible Polish topology, is measurable w.r.t. any Borel probability measure, and, in case
 $S \subseteq [\mathbb {N}]^{\mathbb {N}}$
, S has the Ramsey property.
$S \subseteq [\mathbb {N}]^{\mathbb {N}}$
, S has the Ramsey property. -
2. If
 $X \subseteq \mathbb {N}^{\mathbb {N}}$
and
$X \subseteq \mathbb {N}^{\mathbb {N}}$
and
 $\varphi $
is continuous, then
$\varphi $
is continuous, then
 $\varphi ^{-1}(S)$
is universally Baire.
$\varphi ^{-1}(S)$
is universally Baire. -
3. If
 $\varphi $
is Borel, then
$\varphi $
is Borel, then
 $\varphi ^{-1}(S)$
has the Baire property w.r.t. any compatible Polish topology and is measurable w.r.t. any Borel probability measure.
$\varphi ^{-1}(S)$
has the Baire property w.r.t. any compatible Polish topology and is measurable w.r.t. any Borel probability measure.
Now, we consider a set which encompasses all the
![]() $\Game \mathbf {\Delta }^1_1$
sets and show that it is universally Baire. To ease the notation, set
$\Game \mathbf {\Delta }^1_1$
sets and show that it is universally Baire. To ease the notation, set
![]() $\mathbf {BC}:=\mathbf {BC}(\mathbb {N}^{\mathbb {N}} \times \mathbb {N}^{\mathbb {N}})$
,
$\mathbf {BC}:=\mathbf {BC}(\mathbb {N}^{\mathbb {N}} \times \mathbb {N}^{\mathbb {N}})$
,
![]() $\mathbf {C}:=\mathbf {C}(\mathbb {N}^{\mathbb {N}} \times \mathbb {N}^{\mathbb {N}})$
, and
$\mathbf {C}:=\mathbf {C}(\mathbb {N}^{\mathbb {N}} \times \mathbb {N}^{\mathbb {N}})$
, and
![]() $\mathbf {A}:=\mathbf {A}(\mathbb {N}^{\mathbb {N}} \times \mathbb {N}^{\mathbb {N}})$
. Note that we have
$\mathbf {A}:=\mathbf {A}(\mathbb {N}^{\mathbb {N}} \times \mathbb {N}^{\mathbb {N}})$
. Note that we have
![]() $\mathbf {BC} \in \mathbf {\Pi }^1_1(\mathbb {N}^{\mathbb {N}})$
,
$\mathbf {BC} \in \mathbf {\Pi }^1_1(\mathbb {N}^{\mathbb {N}})$
,
![]() $\mathbf {A} \in \mathbf {\Sigma }^1_1(\mathbb {N}^{\mathbb {N}} \times (\mathbb {N}^{\mathbb {N}}\times \mathbb {N}^{\mathbb {N}}))$
,
$\mathbf {A} \in \mathbf {\Sigma }^1_1(\mathbb {N}^{\mathbb {N}} \times (\mathbb {N}^{\mathbb {N}}\times \mathbb {N}^{\mathbb {N}}))$
,
![]() $\mathbf {C} \in \mathbf {\Pi }^1_1(\mathbb {N}^{\mathbb {N}} \times (\mathbb {N}^{\mathbb {N}}\times \mathbb {N}^{\mathbb {N}}))$
. Consider first the set
$\mathbf {C} \in \mathbf {\Pi }^1_1(\mathbb {N}^{\mathbb {N}} \times (\mathbb {N}^{\mathbb {N}}\times \mathbb {N}^{\mathbb {N}}))$
. Consider first the set
Claim 1.6.
![]() $WS$
is universally Baire.
$WS$
is universally Baire.
Proof. By the characterization result of Feng-Magidor-Woodin [Reference Feng, Magidor and WoodinFMW92], a set
![]() $Z \subseteq \mathbb {N}^{\mathbb {N}}$
is universally Baire if and only if there exist a cardinal
$Z \subseteq \mathbb {N}^{\mathbb {N}}$
is universally Baire if and only if there exist a cardinal
![]() $\lambda $
and trees
$\lambda $
and trees
![]() $T,T^* \subseteq \mathbb {N}^{<\mathbb {N}} \times \lambda ^{<\mathbb {N}}$
, such that
$T,T^* \subseteq \mathbb {N}^{<\mathbb {N}} \times \lambda ^{<\mathbb {N}}$
, such that
![]() $Z=proj_{\mathbb {N}^{\mathbb {N}}}([T])$
and
$Z=proj_{\mathbb {N}^{\mathbb {N}}}([T])$
and
![]() $\mathbb {N}^{\mathbb {N}} \setminus Z = proj_{\mathbb {N}^{\mathbb {N}}}([T^*])$
, and for every forcing notion
$\mathbb {N}^{\mathbb {N}} \setminus Z = proj_{\mathbb {N}^{\mathbb {N}}}([T^*])$
, and for every forcing notion
![]() $\mathbb {P}$
, we have that
$\mathbb {P}$
, we have that
We show this condition for
![]() $WS$
. Note that S is a winning strategy for
$WS$
. Note that S is a winning strategy for
![]() $\operatorname {Alice}$
in
$\operatorname {Alice}$
in
![]() $G(\mathbb {N}^{<\mathbb {N}},(\mathbf {C}_c)_x)$
if and only if S is a strategy for
$G(\mathbb {N}^{<\mathbb {N}},(\mathbf {C}_c)_x)$
if and only if S is a strategy for
![]() $\operatorname {Alice}$
, such that
$\operatorname {Alice}$
, such that
![]() $\forall y \ (y \not \in [S] \lor y \in (\mathbf {C}_c)_x)$
. Using the last sentence of Proposition 1.4, this yields that
$\forall y \ (y \not \in [S] \lor y \in (\mathbf {C}_c)_x)$
. Using the last sentence of Proposition 1.4, this yields that
![]() $WS$
can be described by a
$WS$
can be described by a
![]() $\Sigma ^1_2$
formula. Moreover, as
$\Sigma ^1_2$
formula. Moreover, as
![]() $\mathbf {A}_c=\mathbf {C}_c$
whenever
$\mathbf {A}_c=\mathbf {C}_c$
whenever
![]() $c \in \mathbf {BC}$
, and
$c \in \mathbf {BC}$
, and
![]() $\mathbf {C}_c$
is Borel, by the Borel determinacy theorem,
$\mathbf {C}_c$
is Borel, by the Borel determinacy theorem,
![]() $\operatorname {Alice}$
has a winning strategy in
$\operatorname {Alice}$
has a winning strategy in
![]() $G(\mathbb {N}^{<\mathbb {N}},(\mathbf {C}_c)_x)$
if and only if
$G(\mathbb {N}^{<\mathbb {N}},(\mathbf {C}_c)_x)$
if and only if
![]() $\operatorname {Bob}$
has no winning strategy. That is, for every S strategy for
$\operatorname {Bob}$
has no winning strategy. That is, for every S strategy for
![]() $\operatorname {Bob}$
, we have
$\operatorname {Bob}$
, we have
![]() $\exists y \ (y \in [S] \land y \in (\mathbf {A}_c)_x)$
. This yields a description of
$\exists y \ (y \in [S] \land y \in (\mathbf {A}_c)_x)$
. This yields a description of
![]() $\mathbb {N}^{\mathbb {N}} \setminus WS$
using a
$\mathbb {N}^{\mathbb {N}} \setminus WS$
using a
![]() $\Sigma ^1_2$
formula. By [Reference MoschovakisMos09, 2D.3], there are trees
$\Sigma ^1_2$
formula. By [Reference MoschovakisMos09, 2D.3], there are trees
![]() $T,T^* \subseteq \mathbb {N}^{<\mathbb {N}} \times \omega _1^{<\mathbb {N}}$
(together with formulas defining them), such that
$T,T^* \subseteq \mathbb {N}^{<\mathbb {N}} \times \omega _1^{<\mathbb {N}}$
(together with formulas defining them), such that
![]() $WS=proj_{\mathbb {N}^{\mathbb {N}}}([T])$
and
$WS=proj_{\mathbb {N}^{\mathbb {N}}}([T])$
and
![]() $\mathbb {N}^{\mathbb {N}} \setminus WS = proj_{\mathbb {N}^{\mathbb {N}}}([T^*])$
holds in every model of ZFC, showing that the desired property holds.
$\mathbb {N}^{\mathbb {N}} \setminus WS = proj_{\mathbb {N}^{\mathbb {N}}}([T^*])$
holds in every model of ZFC, showing that the desired property holds.
Claim 1.7. Let S be a
![]() $\Game \mathbf {\Delta }^1_1$
subset of a Polish space X. Then there is a Borel injection
$\Game \mathbf {\Delta }^1_1$
subset of a Polish space X. Then there is a Borel injection
![]() $\varphi $
and some
$\varphi $
and some
![]() $c \in \mathbb {N}^{\mathbb {N}}$
, such that
$c \in \mathbb {N}^{\mathbb {N}}$
, such that
![]() $S=\varphi ^{-1}(WS^{c})$
, where
$S=\varphi ^{-1}(WS^{c})$
, where
![]() $WS^c=\{x\in \mathbb {N}^{\mathbb {N}}:(x,c)\in WS\}$
. If X is zero dimensional, then there is even a homeomorphism with such a property.
$WS^c=\{x\in \mathbb {N}^{\mathbb {N}}:(x,c)\in WS\}$
. If X is zero dimensional, then there is even a homeomorphism with such a property.
Proof. Let B be a Borel set in
![]() $X \times \mathbb {N}^{\mathbb {N}}$
, such that
$X \times \mathbb {N}^{\mathbb {N}}$
, such that
Since X is Polish, there exists a Borel injection
![]() $\varphi :X \to \mathbb {N}^{\mathbb {N}}$
. Moreover, if X is zero dimensional, then
$\varphi :X \to \mathbb {N}^{\mathbb {N}}$
. Moreover, if X is zero dimensional, then
![]() $\varphi $
can be chosen to be a homeomorphism. Now let
$\varphi $
can be chosen to be a homeomorphism. Now let
![]() $(s,r) \in B' \iff (\varphi ^{-1}(s),r) \in B$
. Then
$(s,r) \in B' \iff (\varphi ^{-1}(s),r) \in B$
. Then
![]() $B'$
is Borel, and there is some
$B'$
is Borel, and there is some
![]() $c \in \mathbf {BC}$
with
$c \in \mathbf {BC}$
with
![]() $\mathbf {C}_c=B'$
. Then, by definition, we have
$\mathbf {C}_c=B'$
. Then, by definition, we have
![]() $S=\varphi ^{-1}(WS^{c})$
.
$S=\varphi ^{-1}(WS^{c})$
.
Now, let first S be a
![]() $\Game \mathbf {\Delta }^1_1$
subset of an arbitrary Polish space X. By the claim above, there exist a Borel injection
$\Game \mathbf {\Delta }^1_1$
subset of an arbitrary Polish space X. By the claim above, there exist a Borel injection
![]() $\varphi $
and a c with
$\varphi $
and a c with
![]() $\varphi ^{-1}(WS^{c})$
. Using Claim 1.5, S has Properties (2) and (3).
$\varphi ^{-1}(WS^{c})$
. Using Claim 1.5, S has Properties (2) and (3).
Finally, if
![]() $X=[\mathbb {N}]^{\mathbb {N}}$
, then
$X=[\mathbb {N}]^{\mathbb {N}}$
, then
![]() $\varphi $
can be taken to be a homeomorphism. Then S is universally Baire, and hence, Ramsey measurable by Claim 1.5.
$\varphi $
can be taken to be a homeomorphism. Then S is universally Baire, and hence, Ramsey measurable by Claim 1.5.
Remark 1.8. In the original version of this paper, we introduced the family of weakly provably
![]() $\mathbf {\Delta }^1_2$
sets, which contains
$\mathbf {\Delta }^1_2$
sets, which contains
![]() $\Game \mathbf {\Delta }^1_1$
sets, in order to be able to handle definability issues. Subsequently, Kastner and Lyons pointed out that these results also follow from the theorems of Feng-Magidor-Woodin.
$\Game \mathbf {\Delta }^1_1$
sets, in order to be able to handle definability issues. Subsequently, Kastner and Lyons pointed out that these results also follow from the theorems of Feng-Magidor-Woodin.
In an upcoming work, Kastner and Lyons will prove the required regularity properties of the class
![]() $\Game \mathbf {\Delta }^1_1$
with a more streamlined, purely game theoretic argument, based on the one given in Kechris [Reference KechrisKec78].
$\Game \mathbf {\Delta }^1_1$
with a more streamlined, purely game theoretic argument, based on the one given in Kechris [Reference KechrisKec78].
Finally, all the regularity properties of
![]() $\Game \mathbf {\Delta }^1_1$
sets follow from projective determinacy.
$\Game \mathbf {\Delta }^1_1$
sets follow from projective determinacy.
2 The homomorphism graph
In this section, we define the main objects of our study, homomorphism graphs, and establish a couple of their properties.
Let
![]() $\Gamma $
be a countable group and
$\Gamma $
be a countable group and
![]() $S \subseteq \Gamma $
be a generating set. Assume that
$S \subseteq \Gamma $
be a generating set. Assume that
![]() $\Gamma \curvearrowright X$
is an action of
$\Gamma \curvearrowright X$
is an action of
![]() $\Gamma $
on the set X. As there is no danger of confusion, we always denote the action with the symbol
$\Gamma $
on the set X. As there is no danger of confusion, we always denote the action with the symbol
![]() $\cdot $
. The Schreier graph
$\cdot $
. The Schreier graph ![]() of such an action is a graph on the set X, such that
of such an action is a graph on the set X, such that
![]() $x \neq x'$
are adjacent iff for some
$x \neq x'$
are adjacent iff for some
![]() $\gamma \in S \cup S^{-1}$
, we have that
$\gamma \in S \cup S^{-1}$
, we have that
![]() $\gamma \cdot x=x'$
.
$\gamma \cdot x=x'$
.
Probably the most important example of a Schreier graph is the (right) Cayley graph,
![]() $\operatorname {Cay}(\Gamma ,S)$
that comes from the right multiplication action of
$\operatorname {Cay}(\Gamma ,S)$
that comes from the right multiplication action of
![]() $\Gamma $
on itself. That is,
$\Gamma $
on itself. That is,
![]() $g,h\in \Gamma $
form an edge in
$g,h\in \Gamma $
form an edge in
![]() $\operatorname {Cay}(\Gamma ,S)$
if there is
$\operatorname {Cay}(\Gamma ,S)$
if there is
![]() $\sigma \in S$
, such that
$\sigma \in S$
, such that
![]() $g\cdot \sigma =h$
. Another example is the graph of the left-shift action of
$g\cdot \sigma =h$
. Another example is the graph of the left-shift action of
![]() $\Gamma $
on the space
$\Gamma $
on the space
![]() $2^\Gamma $
: recall that the left-shift action is defined by
$2^\Gamma $
: recall that the left-shift action is defined by
for
![]() $\gamma \in \Gamma $
and
$\gamma \in \Gamma $
and
![]() $x \in 2^\Gamma $
. Observe that the Schreier graph of these actions is a Borel graph, when we endow the space
$x \in 2^\Gamma $
. Observe that the Schreier graph of these actions is a Borel graph, when we endow the space
![]() $2^\Gamma $
with the product topology.
$2^\Gamma $
with the product topology.
Our examples will come from a generalization of this graph. First, note that if we replace
![]() $2$
by any other standard Borel space X, the space
$2$
by any other standard Borel space X, the space
![]() $X^\Gamma $
still admits a Borel product structure with respect to which the Schreier graph of the left-shift action defined as above is a Borel graph. The main idea is to start with a Borel graph
$X^\Gamma $
still admits a Borel product structure with respect to which the Schreier graph of the left-shift action defined as above is a Borel graph. The main idea is to start with a Borel graph
![]() $\mathcal {H}$
and restrict the corresponding Schreier graph on
$\mathcal {H}$
and restrict the corresponding Schreier graph on
![]() $V(\mathcal {H})^\Gamma $
to an appropriate subset on which the elements
$V(\mathcal {H})^\Gamma $
to an appropriate subset on which the elements
![]() $h \in V(\mathcal {H})^\Gamma $
are graph homomorphisms from
$h \in V(\mathcal {H})^\Gamma $
are graph homomorphisms from
![]() $\operatorname {Cay}(\Gamma ,S)$
to
$\operatorname {Cay}(\Gamma ,S)$
to
![]() $\mathcal {H}$
. This allows us to control certain properties (such as chromatic number or hyperfiniteness) of the resulting graph by the properties of
$\mathcal {H}$
. This allows us to control certain properties (such as chromatic number or hyperfiniteness) of the resulting graph by the properties of
![]() $\mathcal {H}$
. More precisely:
$\mathcal {H}$
. More precisely:
Definition 2.1. Let
![]() $\mathcal {H}$
be a Borel graph and
$\mathcal {H}$
be a Borel graph and
![]() $\Gamma $
be a countable group with a generating set S. Let
$\Gamma $
be a countable group with a generating set S. Let
![]() $\operatorname {\mathbf { Hom}}(\Gamma ,S,\mathcal {H})$
be the restriction of
$\operatorname {\mathbf { Hom}}(\Gamma ,S,\mathcal {H})$
be the restriction of ![]() to the set
to the set
We will refer to
![]() $\mathcal {H}$
as the target graph, and we will denote the map
$\mathcal {H}$
as the target graph, and we will denote the map
![]() $h \mapsto h(1)$
by
$h \mapsto h(1)$
by
![]() $Root$
(note that the vertices of
$Root$
(note that the vertices of
![]() $\operatorname {Cay}(\Gamma ,S)$
are labeled by the elements of
$\operatorname {Cay}(\Gamma ,S)$
are labeled by the elements of
![]() $\Gamma $
). It is clear from the definition that
$\Gamma $
). It is clear from the definition that
![]() $\operatorname {\mathbf { Hom}}(\Gamma ,S,\mathcal {H})$
is a Borel graph with degrees at most
$\operatorname {\mathbf { Hom}}(\Gamma ,S,\mathcal {H})$
is a Borel graph with degrees at most
![]() $|S \cup S^{-1}|$
and that
$|S \cup S^{-1}|$
and that
![]() $Root$
is a Borel map. We can immediately make the following observation.
$Root$
is a Borel map. We can immediately make the following observation.
Proposition 2.2. The map
![]() $Root$
is a Borel homomorphism from
$Root$
is a Borel homomorphism from
![]() $\operatorname {\mathbf { Hom}}(\Gamma ,S,\mathcal {H})$
to
$\operatorname {\mathbf { Hom}}(\Gamma ,S,\mathcal {H})$
to
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
In particular,
![]() $\chi _B(\operatorname {\mathbf { Hom}}(\Gamma ,S,\mathcal {H})) \leq \chi _B(\mathcal {H})$
and the action of
$\chi _B(\operatorname {\mathbf { Hom}}(\Gamma ,S,\mathcal {H})) \leq \chi _B(\mathcal {H})$
and the action of
![]() $1 \neq \gamma \in S$
on
$1 \neq \gamma \in S$
on
![]() $\operatorname {\mathbf { Hom}}(\Gamma ,S,\mathcal {H})$
has no fixed-points.
$\operatorname {\mathbf { Hom}}(\Gamma ,S,\mathcal {H})$
has no fixed-points.
Proof. Let
![]() $h\in \operatorname {\mathbf { Hom}}(\Gamma ,S,\mathcal {H})$
and
$h\in \operatorname {\mathbf { Hom}}(\Gamma ,S,\mathcal {H})$
and
![]() $1\not = \gamma \in S\cup S^{-1}$
. Note that as
$1\not = \gamma \in S\cup S^{-1}$
. Note that as
![]() $\gamma ^{-1}$
and
$\gamma ^{-1}$
and
![]() $1$
are adjacent in
$1$
are adjacent in
![]() $\operatorname {Cay}(\Gamma ,S)$
, it follows that
$\operatorname {Cay}(\Gamma ,S)$
, it follows that
![]() $Root(\gamma \cdot h)=h(\gamma ^{-1})$
and
$Root(\gamma \cdot h)=h(\gamma ^{-1})$
and
![]() $Root(h)=h(1)$
are adjacent in
$Root(h)=h(1)$
are adjacent in
![]() $\mathcal {H}$
as h is a homomorphism. Consequently, the map
$\mathcal {H}$
as h is a homomorphism. Consequently, the map
![]() $Root$
is a Borel homomorphism from
$Root$
is a Borel homomorphism from
![]() $\operatorname {\mathbf { Hom}}(\Gamma ,S,\mathcal {H})$
to
$\operatorname {\mathbf { Hom}}(\Gamma ,S,\mathcal {H})$
to
![]() $\mathcal {H}$
and
$\mathcal {H}$
and
![]() $h\not =\gamma \cdot h$
as there are no loops in
$h\not =\gamma \cdot h$
as there are no loops in
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
The
 $\Delta $
-regular tree
$\Delta $
-regular tree
 $T_\Delta $
.
$T_\Delta $
.
In this paper, we only consider the case of the group
together with the generating set
![]() $S_\Delta =\{\alpha _1,\dots ,\alpha _\Delta \}$
. Since
$S_\Delta =\{\alpha _1,\dots ,\alpha _\Delta \}$
. Since
![]() $\operatorname {Cay}(\mathbb {Z}^{*\Delta }_2,S_\Delta )$
is isomorphic to the
$\operatorname {Cay}(\mathbb {Z}^{*\Delta }_2,S_\Delta )$
is isomorphic to the
![]() $\Delta $
-regular infinite tree,
$\Delta $
-regular infinite tree,
![]() $T_\Delta $
, we use
$T_\Delta $
, we use
![]() $\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})$
to denote the graph
$\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})$
to denote the graph
![]() $\operatorname {\mathbf { Hom}}(\mathbb {Z}^{*\Delta }_2,S_\Delta ,\mathcal {H})$
. Note also that we consider
$\operatorname {\mathbf { Hom}}(\mathbb {Z}^{*\Delta }_2,S_\Delta ,\mathcal {H})$
. Note also that we consider
![]() $\operatorname {Cay}(\mathbb {Z}^{*\Delta }_2,S_\Delta )$
and
$\operatorname {Cay}(\mathbb {Z}^{*\Delta }_2,S_\Delta )$
and
![]() $T_\Delta $
equipped with a
$T_\Delta $
equipped with a
![]() $\Delta $
-edge coloring. As suggested above, an equivalent description of the vertex set of
$\Delta $
-edge coloring. As suggested above, an equivalent description of the vertex set of
![]() $\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})$
is that it is the set of pairs
$\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})$
is that it is the set of pairs
![]() $(x,h)$
, where h is a homomorphism from the tree
$(x,h)$
, where h is a homomorphism from the tree
![]() $T_\Delta $
to
$T_\Delta $
to
![]() $\mathcal {H}$
and x is a distinguished vertex of
$\mathcal {H}$
and x is a distinguished vertex of
![]() $T_\Delta $
, a root. Then we have that
$T_\Delta $
, a root. Then we have that
![]() $(x,h)$
and
$(x,h)$
and
![]() $(y,g)$
form an (
$(y,g)$
form an (
![]() $\alpha $
-)edge if and only if
$\alpha $
-)edge if and only if
![]() $h=g$
and
$h=g$
and
![]() $(x, y)$
is an (
$(x, y)$
is an (
![]() $\alpha $
-)edge in
$\alpha $
-)edge in
![]() $T_\Delta $
. This is because (a) there is a one-to-one correspondence between a homomorphism from
$T_\Delta $
. This is because (a) there is a one-to-one correspondence between a homomorphism from
![]() $\operatorname {Cay}(\mathbb {Z}^{*\Delta }_2,S_\Delta )$
to
$\operatorname {Cay}(\mathbb {Z}^{*\Delta }_2,S_\Delta )$
to
![]() $\mathcal {H}$
and the pairs
$\mathcal {H}$
and the pairs
![]() $(x,h)$
, and (b) the shift action
$(x,h)$
, and (b) the shift action
![]() $\mathbb {Z}^{*\Delta }_2 \curvearrowright \operatorname {\mathbf { Hom}}(\mathbb {Z}^{*\Delta }_2,S_\Delta ,\mathcal {H})$
corresponds to changing the root for a fixed homomorphism h from
$\mathbb {Z}^{*\Delta }_2 \curvearrowright \operatorname {\mathbf { Hom}}(\mathbb {Z}^{*\Delta }_2,S_\Delta ,\mathcal {H})$
corresponds to changing the root for a fixed homomorphism h from
![]() $T_\Delta $
to
$T_\Delta $
to
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
Recall that an action
![]() $\Gamma \curvearrowright X$
is free if for each
$\Gamma \curvearrowright X$
is free if for each
![]() $1 \neq \gamma \in \Gamma $
and
$1 \neq \gamma \in \Gamma $
and
![]() $x \in X$
, we have
$x \in X$
, we have
![]() $\gamma \cdot x \neq x$
. The free part, denoted by
$\gamma \cdot x \neq x$
. The free part, denoted by
![]() $Free(X)$
, is the set
$Free(X)$
, is the set
![]() $\{x:\forall 1 \neq \gamma \in \Gamma \ \gamma \cdot x \neq x\}$
. Note that the left-shift action of
$\{x:\forall 1 \neq \gamma \in \Gamma \ \gamma \cdot x \neq x\}$
. Note that the left-shift action of
![]() $\mathbb {Z}^{*\Delta }_2$
on, say,
$\mathbb {Z}^{*\Delta }_2$
on, say,
![]() $\mathbb {N}^{\mathbb {Z}^{*\Delta }_2}$
is not free, in particular, the corresponding Schreier-graph has cycles. To remedy this, Marks used a restriction of the graph to the free part, showing that for each
$\mathbb {N}^{\mathbb {Z}^{*\Delta }_2}$
is not free, in particular, the corresponding Schreier-graph has cycles. To remedy this, Marks used a restriction of the graph to the free part, showing that for each
![]() $\Delta> 2$
, this graph has Borel chromatic number
$\Delta> 2$
, this graph has Borel chromatic number
![]() $\Delta +1$
. Analogously, we have the following.
$\Delta +1$
. Analogously, we have the following.
Definition 2.3. Let
![]() $\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H})=\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H}) \restriction Free(V(\mathcal {H})^{\mathbb {Z}^{*\Delta }_2}),$
that is, the restriction of the graph
$\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H})=\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H}) \restriction Free(V(\mathcal {H})^{\mathbb {Z}^{*\Delta }_2}),$
that is, the restriction of the graph
![]() $\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})$
to the free part of the
$\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})$
to the free part of the
![]() $\mathbb {Z}^{*\Delta }_2$
action.
$\mathbb {Z}^{*\Delta }_2$
action.
In our first application, we will use this remedy to get acyclic graphs. Note that for each edge in
![]() $\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H})$
, there is a unique generator
$\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H})$
, there is a unique generator
![]() $\alpha \in S_\Delta $
that induces it. In particular, the graph
$\alpha \in S_\Delta $
that induces it. In particular, the graph
![]() $\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H})$
admits a canonical Borel edge
$\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H})$
admits a canonical Borel edge
![]() $\Delta $
-coloring. The following is straightforward.
$\Delta $
-coloring. The following is straightforward.
Proposition 2.4. Let
![]() $\mathcal {H}$
be a locally countable Borel graph. If
$\mathcal {H}$
be a locally countable Borel graph. If
![]() $\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H})$
is nonempty, then it is
$\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H})$
is nonempty, then it is
![]() $\Delta $
-regular and acylic.
$\Delta $
-regular and acylic.
However, utilizing the homomorphism graph together with an appropriate target graph, we will be able to completely avoid the nonfree part, in an automatic manner. This way, we will be able to guarantee the hyperfiniteness of the homomorphism graph as well. Recall that
![]() $T_\Delta =\operatorname {Cay}(\mathbb {Z}^{*\Delta }_2,S_\Delta )$
comes with a
$T_\Delta =\operatorname {Cay}(\mathbb {Z}^{*\Delta }_2,S_\Delta )$
comes with a
![]() $\Delta $
-edge coloring by the elements of
$\Delta $
-edge coloring by the elements of
![]() $S_\Delta $
. Let us consider the a subgraph of the homomorphism graph that arises by requiring h to preserve this information.
$S_\Delta $
. Let us consider the a subgraph of the homomorphism graph that arises by requiring h to preserve this information.
Definition 2.5. Assume that the graph
![]() $\mathcal {H}$
is equipped with a Borel edge
$\mathcal {H}$
is equipped with a Borel edge
![]() $S_\Delta $
-labeling. Let
$S_\Delta $
-labeling. Let
![]() $\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
be the restriction of
$\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
be the restriction of
![]() $\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})$
to the set
$\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})$
to the set
Clearly,
![]() $\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
is also a Borel graph. Note that in the following statement, the labeling of the edges of the target graph
$\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
is also a Borel graph. Note that in the following statement, the labeling of the edges of the target graph
![]() $\mathcal {H}$
is typically not a coloring.
$\mathcal {H}$
is typically not a coloring.
Proposition 2.6. Assume that
![]() $\mathcal {H}$
is an acyclic graph equipped with a Borel edge
$\mathcal {H}$
is an acyclic graph equipped with a Borel edge
![]() $S_{\Delta }$
-labeling and
$S_{\Delta }$
-labeling and
![]() $\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
is nonempty. Then
$\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
is nonempty. Then
-
1.
 $\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
is acyclic,
$\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
is acyclic, -
2. If
 $\mathcal {H}$
is hyperfinite, then so is
$\mathcal {H}$
is hyperfinite, then so is
 $\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
,
$\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
, -
3.
 $\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
is
$\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
is
 $\Delta $
-regular.
$\Delta $
-regular.
Proof. Observe that if h is a homomorphism from a tree to an acyclic graph that is not injective, then there must be adjacent pairs of vertices
![]() $(x,y)$
and
$(x,y)$
and
![]() $(y,z)$
with
$(y,z)$
with
![]() $x \neq z$
and
$x \neq z$
and
![]() $h(z)=h(x)$
. Thus, if
$h(z)=h(x)$
. Thus, if
![]() $h \in \operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
is edge label preserving, then it must be injective, as incident edges have different labels in
$h \in \operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
is edge label preserving, then it must be injective, as incident edges have different labels in
![]() $T_\Delta $
. Therefore, the map
$T_\Delta $
. Therefore, the map
![]() $Root$
is injective on each connected component of
$Root$
is injective on each connected component of
![]() $\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
, yielding (1).
$\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
, yielding (1).
To see (2), let
![]() $(\mathcal {H}_n)_{n \in \mathbb {N}}$
be a witness to the hyperfiniteness of
$(\mathcal {H}_n)_{n \in \mathbb {N}}$
be a witness to the hyperfiniteness of
![]() $\mathcal {H}$
. Let
$\mathcal {H}$
. Let
![]() $\mathcal {H}^{\prime }_n$
be the pullback of
$\mathcal {H}^{\prime }_n$
be the pullback of
![]() $\mathcal {H}_n$
by the map
$\mathcal {H}_n$
by the map
![]() $Root$
. Since
$Root$
. Since
![]() $Root$
is injective on every connected component, the graphs
$Root$
is injective on every connected component, the graphs
![]() $\mathcal {H}^{\prime }_n$
also have finite components and their union is
$\mathcal {H}^{\prime }_n$
also have finite components and their union is
![]() $\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
.
$\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
.
For (3), just notice that using the injectivity of
![]() $Root$
again, it follows that
$Root$
again, it follows that
![]() $\{\gamma \cdot h\}_{\gamma \in \{1\}\cup S_\Delta }$
has cardinality
$\{\gamma \cdot h\}_{\gamma \in \{1\}\cup S_\Delta }$
has cardinality
![]() $\Delta +1$
.
$\Delta +1$
.
3 Variations on Marks’s technique
Now we are ready to adapt Marks’s technique [Reference MarksMar16] to homomorphism graphs. Let us denote by
![]() $\chi _{\Game \mathbf {\Delta }^1_1}(\mathcal {H})$
the
$\chi _{\Game \mathbf {\Delta }^1_1}(\mathcal {H})$
the
![]() $\Game \mathbf {\Delta }^1_1$
-chromatic number of
$\Game \mathbf {\Delta }^1_1$
-chromatic number of
![]() $\mathcal {H}$
(see Section 1).
$\mathcal {H}$
(see Section 1).
Theorem 0.1. Let
![]() $\mathcal {H}$
be a locally countable Borel graph. Then
$\mathcal {H}$
be a locally countable Borel graph. Then
The games we will define naturally yield elements
![]() $h \in \operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})$
rather than
$h \in \operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})$
rather than
![]() $\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H})$
. In order to deal with the cyclic part of the graph, we will show slightly more, using the same strategy as Marks. Let
$\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H})$
. In order to deal with the cyclic part of the graph, we will show slightly more, using the same strategy as Marks. Let
![]() $V \subseteq V(\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H}))$
, an antigame labeling of V is a map
$V \subseteq V(\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H}))$
, an antigame labeling of V is a map
![]() $c:V \to \Delta $
, such that there are no
$c:V \to \Delta $
, such that there are no
![]() $i \in \Delta $
and distinct vertices
$i \in \Delta $
and distinct vertices
![]() $h,h'\in V$
with
$h,h'\in V$
with
![]() $c(h)=c(h')=i$
and
$c(h)=c(h')=i$
and
![]() $\alpha _i \cdot h=h'$
. Observe that every
$\alpha _i \cdot h=h'$
. Observe that every
![]() $\Delta $
-coloring is automatically antigame labeling.
$\Delta $
-coloring is automatically antigame labeling.
Remark 3.1. One can define analogously antigame labelings for graphs with edges labeled by
![]() $\Delta $
. Note that in the case when the graph is
$\Delta $
. Note that in the case when the graph is
![]() $\Delta $
-regular and the labeling is an edge
$\Delta $
-regular and the labeling is an edge
![]() $\Delta $
-coloring, the existence of an antigame labeling is equivalent with solving the well known edge grabbing problem (that is, every vertex picks one adjacent edge, but no edge can be picked from both sides (see [Reference Balliu, Brandt, Efron, Hirvonen, Maus, Olivetti and SuomelaBBE+20] or the sinkless orientation problem). Observe that the sinkless orientation problem, and hence, the existence of antigame labeling, can be easily solved on graphs with cycles. This observation is crucially utilized in both Marks’s and this paper (see Lemma 3.2).
$\Delta $
-coloring, the existence of an antigame labeling is equivalent with solving the well known edge grabbing problem (that is, every vertex picks one adjacent edge, but no edge can be picked from both sides (see [Reference Balliu, Brandt, Efron, Hirvonen, Maus, Olivetti and SuomelaBBE+20] or the sinkless orientation problem). Observe that the sinkless orientation problem, and hence, the existence of antigame labeling, can be easily solved on graphs with cycles. This observation is crucially utilized in both Marks’s and this paper (see Lemma 3.2).
Lemma 3.2. There exists a Borel antigame labeling
![]() $c:V(\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})) \setminus V(\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H})) \to \Delta $
.
$c:V(\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})) \setminus V(\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H})) \to \Delta $
.
Proof. Let us use the notation
![]() $C=V(\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})) \setminus V(\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H}))$
. By definition, the
$C=V(\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})) \setminus V(\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H}))$
. By definition, the
![]() $\mathbb {Z}^{*\Delta }_2$
action on every connected component
$\mathbb {Z}^{*\Delta }_2$
action on every connected component
![]() $\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H}) \restriction C$
is not free. Using [Reference Kechris and MillerKM04, Lemma 7.3], we can find a Borel maximal family
$\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H}) \restriction C$
is not free. Using [Reference Kechris and MillerKM04, Lemma 7.3], we can find a Borel maximal family
![]() $\mathcal {F} \subseteq C^{<\mathbb {N}}$
of pairwise disjoint finite sequences each of length at least
$\mathcal {F} \subseteq C^{<\mathbb {N}}$
of pairwise disjoint finite sequences each of length at least
![]() $2$
, such that for each
$2$
, such that for each
![]() $(h_i)_{i<k} \in \mathcal {F}$
, there is a sequence
$(h_i)_{i<k} \in \mathcal {F}$
, there is a sequence
![]() $(\alpha _{n_i})_{i<k} \in S^k_{\Delta }$
, such that
$(\alpha _{n_i})_{i<k} \in S^k_{\Delta }$
, such that
![]() $\alpha _{n_i}\not =\alpha _{n_{i+1}}$
,
$\alpha _{n_i}\not =\alpha _{n_{i+1}}$
,
![]() $\alpha _{n_i} \cdot h_i=h_{i+1}$
for
$\alpha _{n_i} \cdot h_i=h_{i+1}$
for
![]() $i<k-1$
, and
$i<k-1$
, and
![]() $\alpha _{n_0}\not =\alpha _{n_{k-1}}$
,
$\alpha _{n_0}\not =\alpha _{n_{k-1}}$
,
![]() $\alpha _{n_{k-1}} \cdot h_{k-1}=h_0$
(note that it is possible that
$\alpha _{n_{k-1}} \cdot h_{k-1}=h_0$
(note that it is possible that
![]() $k=2$
, in which case, there are two distinct generators
$k=2$
, in which case, there are two distinct generators
![]() $\alpha _{n_0}\not = \alpha _{n_1}$
, such that
$\alpha _{n_0}\not = \alpha _{n_1}$
, such that
![]() $\alpha _{n_0}\cdot h_0=\alpha _{n_1}\cdot h_0=h_1$
).
$\alpha _{n_0}\cdot h_0=\alpha _{n_1}\cdot h_0=h_1$
).
Now label an element
![]() $h \in C$
by
$h \in C$
by
![]() $n_i$
if
$n_i$
if
![]() $h=h_i$
for some
$h=h_i$
for some
![]() $(h_i)_{i<k} \in \mathcal {F}$
. Otherwise, let
$(h_i)_{i<k} \in \mathcal {F}$
. Otherwise, let
![]() $c(h)$
be the minimal i, such that
$c(h)$
be the minimal i, such that
![]() $\alpha _i \cdot h$
has strictly smaller distance to
$\alpha _i \cdot h$
has strictly smaller distance to
![]() $\mathcal {F}$
than h with respect to the graph distance in
$\mathcal {F}$
than h with respect to the graph distance in
![]() $\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})$
. It is easy to check that c is an antigame labeling.
$\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})$
. It is easy to check that c is an antigame labeling.
Proof of Theorem 0.1.
We show that there is no Borel antigame labeling
![]() $c:V(\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})) \to \Delta $
. Once we have that, the proof of Theorem 0.1 is finished as follows. Suppose that d is a Borel
$c:V(\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})) \to \Delta $
. Once we have that, the proof of Theorem 0.1 is finished as follows. Suppose that d is a Borel
![]() $\Delta $
-coloring of
$\Delta $
-coloring of
![]() $\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H})$
. As observed above, every
$\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {H})$
. As observed above, every
![]() $\Delta $
-coloring is also antigame labeling. Consequently, the union of d and the antigame labeling produced in Lemma 3.2 is a Borel antigame labeling of
$\Delta $
-coloring is also antigame labeling. Consequently, the union of d and the antigame labeling produced in Lemma 3.2 is a Borel antigame labeling of
![]() $V(\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H}))$
, contradiction.
$V(\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H}))$
, contradiction.
Assume toward contradiction that
![]() $c:V(\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})) \to \Delta $
is a Borel antigame labeling. Without loss of generality, we may assume that
$c:V(\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})) \to \Delta $
is a Borel antigame labeling. Without loss of generality, we may assume that
![]() $\mathcal {H}$
has no isolated points. This ensures that the games below can be always continued.
$\mathcal {H}$
has no isolated points. This ensures that the games below can be always continued.
We define a family of two-player games
![]() $\mathbb {G}(x,i)$
parametrized by elements
$\mathbb {G}(x,i)$
parametrized by elements
![]() $x \in V(\mathcal {H})$
and
$x \in V(\mathcal {H})$
and
![]() $i \in \Delta $
. In a run of the game,
$i \in \Delta $
. In a run of the game,
![]() $\mathbb {G}(x,i)$
players
$\mathbb {G}(x,i)$
players
![]() $\operatorname {Alice}$
and
$\operatorname {Alice}$
and
![]() $\operatorname {Bob}$
alternate and build a homomorphism h from
$\operatorname {Bob}$
alternate and build a homomorphism h from
![]() $T_\Delta $
to
$T_\Delta $
to
![]() $\mathcal {H}$
, that is, an element of
$\mathcal {H}$
, that is, an element of
![]() $\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H}) \subset V(\mathcal {H})^{\mathbb {Z}^{*\Delta }_2}$
, with the property that
$\operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H}) \subset V(\mathcal {H})^{\mathbb {Z}^{*\Delta }_2}$
, with the property that
![]() $Root(h)=x$
.
$Root(h)=x$
.
In the k-th round, first
![]() $\operatorname {Alice}$
labels vertices of distance k from the
$\operatorname {Alice}$
labels vertices of distance k from the
![]() $1$
on the side of the
$1$
on the side of the
![]() $\alpha _i$
edge. After that,
$\alpha _i$
edge. After that,
![]() $\operatorname {Bob}$
labels all remaining vertices of distance k, etc. (see Figure 1). In other words,
$\operatorname {Bob}$
labels all remaining vertices of distance k, etc. (see Figure 1). In other words,
![]() $\operatorname {Alice}$
labels the elements of
$\operatorname {Alice}$
labels the elements of
![]() $\mathbb {Z}^{*\Delta }_2$
corresponding to reduced words of length k starting with
$\mathbb {Z}^{*\Delta }_2$
corresponding to reduced words of length k starting with
![]() $\alpha _i$
, then
$\alpha _i$
, then
![]() $\operatorname {Bob}$
labels the rest of the reduced words of length k.
$\operatorname {Bob}$
labels the rest of the reduced words of length k.

Figure 1 The game
![]() $\mathbb {G}(x,i)$
.
$\mathbb {G}(x,i)$
.
Note that once the parameters of the game are fixed, the definition of the game is analoguous to the one defined by Marks [Reference MarksMar16]. There is, however, one important difference. The allowed moves are vertices of the target graph
![]() $\mathcal {H}$
restricted by its edge relation. Observe that the original construction of Marks can be interpreted in our setting by taking
$\mathcal {H}$
restricted by its edge relation. Observe that the original construction of Marks can be interpreted in our setting by taking
![]() $\mathcal {H}$
to be the the complete graph on
$\mathcal {H}$
to be the the complete graph on
![]() $\mathbb {N}$
.
$\mathbb {N}$
.
The winning condition is defined as follows:
Lemma 3.3.
-
1. For any
 $x \in V(\mathcal {H})$
and
$x \in V(\mathcal {H})$
and
 $i \in \Delta $
, one of the players has a winning strategy in the game
$i \in \Delta $
, one of the players has a winning strategy in the game
 $\mathbb {G}(x,i)$
.
$\mathbb {G}(x,i)$
. -
2. The set
 $\{(x,i): \operatorname {Alice} \text { has a winning strategy in } \mathbb {G}(x,i)\}$
is
$\{(x,i): \operatorname {Alice} \text { has a winning strategy in } \mathbb {G}(x,i)\}$
is
 $\Game \mathbf {\Delta }^1_1$
.
$\Game \mathbf {\Delta }^1_1$
.
Proof. We encode the games
![]() $\mathbb {G}(x,i)$
in a way that allows the use of Borel determinacy theorem and Lemma 1.2. Let us denote by
$\mathbb {G}(x,i)$
in a way that allows the use of Borel determinacy theorem and Lemma 1.2. Let us denote by
![]() $E_{\mathcal {H}}$
the connected component equivalence relation of
$E_{\mathcal {H}}$
the connected component equivalence relation of
![]() $\mathcal {H}$
. Observe that as
$\mathcal {H}$
. Observe that as
![]() $T_\Delta $
is connected, the range of any element
$T_\Delta $
is connected, the range of any element
![]() $h \in \operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})$
is contained in a single
$h \in \operatorname {\mathbf { Hom}}(T_\Delta ,\mathcal {H})$
is contained in a single
![]() $E_{\mathcal {H}}$
class. By the Feldman-Moore theorem, there is a countable collection of Borel functions
$E_{\mathcal {H}}$
class. By the Feldman-Moore theorem, there is a countable collection of Borel functions
![]() $f_i:V(\mathcal {H}) \to V(\mathcal {H})$
, such that
$f_i:V(\mathcal {H}) \to V(\mathcal {H})$
, such that
![]() $E_{\mathcal {H}}=\bigcup _{j \in \mathbb {N}} graph(f^{\pm 1}_j)$
. Therefore, the games
$E_{\mathcal {H}}=\bigcup _{j \in \mathbb {N}} graph(f^{\pm 1}_j)$
. Therefore, the games
![]() $\mathbb {G}(x,i)$
above can be identified by games played on
$\mathbb {G}(x,i)$
above can be identified by games played on
![]() $\mathbb {N}$
, namely, labeling a vertex in
$\mathbb {N}$
, namely, labeling a vertex in
![]() $T_\Delta $
by a vertex
$T_\Delta $
by a vertex
![]() $y\in V(\mathcal {H})$
corresponds to playing the minimal natural number j with
$y\in V(\mathcal {H})$
corresponds to playing the minimal natural number j with
![]() $f_j(x)=y$
. Since the functions
$f_j(x)=y$
. Since the functions
![]() $(f_j)_{j \in \mathbb {N}}$
are Borel, this correspondence is Borel as well. Moreover, the rule that h must be homomorphism determines a pruned subtree of legal positions
$(f_j)_{j \in \mathbb {N}}$
are Borel, this correspondence is Borel as well. Moreover, the rule that h must be homomorphism determines a pruned subtree of legal positions
![]() $T_{x,i} \subset \mathbb {N}^{<\mathbb {N}}$
and the map
$T_{x,i} \subset \mathbb {N}^{<\mathbb {N}}$
and the map
![]() $(x,i) \mapsto T_{x,i}$
is Borel. This yields that there exists a Borel set
$(x,i) \mapsto T_{x,i}$
is Borel. This yields that there exists a Borel set
![]() $B \subseteq V(\mathcal {H}) \times \Delta \times \mathbb {N}^{\mathbb {N}}$
, such that
$B \subseteq V(\mathcal {H}) \times \Delta \times \mathbb {N}^{\mathbb {N}}$
, such that
Now, the first claim follows from the Borel determinacy theorem, while the second follows from Lemma 1.2.
Claim 3.4. For every
![]() $x\in X$
, there is an
$x\in X$
, there is an
![]() $i\in \Delta $
, such that
$i\in \Delta $
, such that
![]() $\operatorname {Bob}$
wins
$\operatorname {Bob}$
wins
![]() $\mathbb {G}(x,i)$
.
$\mathbb {G}(x,i)$
.
Proof. Suppose not. Then we can combine strategies of
![]() $\operatorname {Alice}$
for each i in the natural way to build a homomorphism that is not in the domain of c (see, e.g. [Reference MarksMar] or [Reference MarksMar16]).
$\operatorname {Alice}$
for each i in the natural way to build a homomorphism that is not in the domain of c (see, e.g. [Reference MarksMar] or [Reference MarksMar16]).
Now, we can finish the proof of Theorem 0.1. Define
![]() $d:V(\mathcal {H}) \to \Delta $
by
$d:V(\mathcal {H}) \to \Delta $
by
Since
![]() $\Game \mathbf {\Delta }^1_1$
sets form an algebra, d is
$\Game \mathbf {\Delta }^1_1$
sets form an algebra, d is
![]() $\Game \mathbf {\Delta }^1_1$
measurable, and by Claim 3.4, it is everywhere defined. By our assumptions on
$\Game \mathbf {\Delta }^1_1$
measurable, and by Claim 3.4, it is everywhere defined. By our assumptions on
![]() $\mathcal {H}$
, there are
$\mathcal {H}$
, there are
![]() $x \neq x'$
adjacent with
$x \neq x'$
adjacent with
![]() $d(x)=d(x')=i$
. Now, we can play the two winning strategies corresponding to games
$d(x)=d(x')=i$
. Now, we can play the two winning strategies corresponding to games
![]() $\mathbb {G}(x,i)$
and
$\mathbb {G}(x,i)$
and
![]() $\mathbb {G}(x',i)$
of
$\mathbb {G}(x',i)$
of
![]() $\operatorname {Bob}$
against each other, as if the first move of
$\operatorname {Bob}$
against each other, as if the first move of
![]() $\operatorname {Alice}$
was
$\operatorname {Alice}$
was
![]() $x'$
(respectively, x). This yields distinct homomorphisms
$x'$
(respectively, x). This yields distinct homomorphisms
![]() $h,h'$
with
$h,h'$
with
![]() $\alpha _i \cdot h=h'$
and
$\alpha _i \cdot h=h'$
and
![]() $c(h)=c(h')=i$
, contradicting that c is an antigame labeling.
$c(h)=c(h')=i$
, contradicting that c is an antigame labeling.
3.1 Generalizations
Edge labeled graphs
As mentioned above, a novel feature of our approach is that requiring the homomorphisms to be edge label preserving and ensuring that
![]() $\mathcal {H}$
is acyclic, we can get rid of the investigation of the cyclic part (see Proposition 2.6). In order to achieve this, we have to assume slightly more about the chromatic properties of the target graph.
$\mathcal {H}$
is acyclic, we can get rid of the investigation of the cyclic part (see Proposition 2.6). In order to achieve this, we have to assume slightly more about the chromatic properties of the target graph.
Assume that
![]() $\mathcal {H}$
is equipped with an edge S-labeling. The edge-labeled chromatic number
$\mathcal {H}$
is equipped with an edge S-labeling. The edge-labeled chromatic number
![]() $el\chi (\mathcal {H})$
of
$el\chi (\mathcal {H})$
of
![]() $\mathcal {H}$
is the minimal n, for which there exists a map
$\mathcal {H}$
is the minimal n, for which there exists a map
![]() $c:V(\mathcal {H}) \to n$
, so that for each
$c:V(\mathcal {H}) \to n$
, so that for each
![]() $i \in n$
, the set
$i \in n$
, the set
![]() $c^{-1}(i)$
doesn’t span edges with every possible label. In other words,
$c^{-1}(i)$
doesn’t span edges with every possible label. In other words,
![]() $el\chi (\mathcal {H})>n$
if and only if no matter how we assign n many colors to the vertices of
$el\chi (\mathcal {H})>n$
if and only if no matter how we assign n many colors to the vertices of
![]() $\mathcal {H}$
, there will be a color class containing edges with every label. We define
$\mathcal {H}$
, there will be a color class containing edges with every label. We define
![]() $\mu $
measurable, Baire measurable, etc. versions of the edge-labeled chromatic number in the natural way.
$\mu $
measurable, Baire measurable, etc. versions of the edge-labeled chromatic number in the natural way.
Theorem 3.5. Let
![]() $\mathcal {H}$
be a locally countable Borel graph with a Borel
$\mathcal {H}$
be a locally countable Borel graph with a Borel
![]() $S_\Delta $
-edge labeling, such that for every vertex x and every label
$S_\Delta $
-edge labeling, such that for every vertex x and every label
![]() $\alpha $
, there is an
$\alpha $
, there is an
![]() $\alpha $
-labeled edge incident to x. Then
$\alpha $
-labeled edge incident to x. Then
Proof. The proof is similar to the proof of Theorem 0.1 but with taking the edge colors into consideration. Let us indicate the required modifications. We define
![]() $\mathbb {G}(x,i)$
as above, with the extra assumption that players must build a homomorphism that respects edge labels, that is, an element
$\mathbb {G}(x,i)$
as above, with the extra assumption that players must build a homomorphism that respects edge labels, that is, an element
![]() $h \in \operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
. The condition on the edge-labeling ensures that the players can continue the game respecting the rules at every given finite step.
$h \in \operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
. The condition on the edge-labeling ensures that the players can continue the game respecting the rules at every given finite step.
The analogue of Claim 3.4 clearly holds in this case, and we can define d as in (3.1). Finally,
![]() ${el\chi }_{\Game \mathbf {\Delta }^1_1}(\mathcal {H})>\Delta $
guarantees the existence of
${el\chi }_{\Game \mathbf {\Delta }^1_1}(\mathcal {H})>\Delta $
guarantees the existence of
![]() $i \in \Delta $
and
$i \in \Delta $
and
![]() $x,x' \in V(\mathcal {H})$
, such that
$x,x' \in V(\mathcal {H})$
, such that
![]() $d(x)=d(x')=i$
and that the edge between x and
$d(x)=d(x')=i$
and that the edge between x and
![]() $x'$
has label
$x'$
has label
![]() $\alpha _i$
, which, in turn, allows us to use the winning strategies of
$\alpha _i$
, which, in turn, allows us to use the winning strategies of
![]() $\operatorname {Bob}$
in
$\operatorname {Bob}$
in
![]() $\mathbb {G}(x,i)$
and
$\mathbb {G}(x,i)$
and
![]() $\mathbb {G}(x',i)$
against each other, as above.
$\mathbb {G}(x',i)$
against each other, as above.
Graph homomorphism
In what follows, we will consider a slightly more general context, namely, instead of the question of the existence of Borel colorings, we will investigate the existence of Borel homomorphisms to a given finite graph H. The following notion is going to be our key technical tool.
Definition 3.6 (Almost
 $\Delta $
-colorable).
$\Delta $
-colorable).
Let
![]() $\Delta>2$
and H be a finite graph. We say that H is almost
$\Delta>2$
and H be a finite graph. We say that H is almost
![]() $\Delta $
-colorable if there are sets
$\Delta $
-colorable if there are sets
![]() $R_0,R_1\subseteq V(H)$
, such that H restricted to
$R_0,R_1\subseteq V(H)$
, such that H restricted to
![]() $V(H) \setminus R_i$
has chromatic number at most
$V(H) \setminus R_i$
has chromatic number at most
![]() $(\Delta -1)$
for
$(\Delta -1)$
for
![]() $i\in \{0,1\}$
, and there is no edge between vertices of
$i\in \{0,1\}$
, and there is no edge between vertices of
![]() $R_0$
and
$R_0$
and
![]() $R_1$
.
$R_1$
.
Note that if
![]() $\chi (H) \leq \Delta $
, then H is almost
$\chi (H) \leq \Delta $
, then H is almost
![]() $\Delta $
-colorable. Indeed, if
$\Delta $
-colorable. Indeed, if
![]() $A_1,\dots ,A_\Delta $
are independent sets that cover
$A_1,\dots ,A_\Delta $
are independent sets that cover
![]() $V(H)$
, we can set
$V(H)$
, we can set
![]() $R_0=R_1=A_1$
. The basic properties of almost
$R_0=R_1=A_1$
. The basic properties of almost
![]() $\Delta $
-colorable graphs are summarized in Section 4.3. In particular, we show that every almost
$\Delta $
-colorable graphs are summarized in Section 4.3. In particular, we show that every almost
![]() $\Delta $
-colorable graph has chromatic number at most
$\Delta $
-colorable graph has chromatic number at most
![]() $2\Delta -2$
, a bound that appears in Theorem 0.5.
$2\Delta -2$
, a bound that appears in Theorem 0.5.
Theorem 3.7. Let
![]() $\mathcal {H}$
be a locally countable Borel graph, and assume that H is a finite graph that is almost
$\mathcal {H}$
be a locally countable Borel graph, and assume that H is a finite graph that is almost
![]() $\Delta $
-colorable. Assume that
$\Delta $
-colorable. Assume that
![]() $\mathcal {H}$
is equipped with a Borel
$\mathcal {H}$
is equipped with a Borel
![]() $S_\Delta $
-edge labeling, with the property that for every vertex v and every edge label
$S_\Delta $
-edge labeling, with the property that for every vertex v and every edge label
![]() $\alpha _i \in S_\Delta $
, there exists an edge from v with label
$\alpha _i \in S_\Delta $
, there exists an edge from v with label
![]() $\alpha _i$
. Then
$\alpha _i$
. Then
Proof. Assume for contradiction that such a Borel homomorphism c exists. We will need a further modification of Marks’s games. Let
![]() $R \subseteq V(H)$
. For
$R \subseteq V(H)$
. For
![]() $x \in V(\mathcal {H})$
, define the game
$x \in V(\mathcal {H})$
, define the game
![]() $\mathbb {G}(x,i,R)$
as in the proof of Theorem 3.5, with the winning condition modified to
$\mathbb {G}(x,i,R)$
as in the proof of Theorem 3.5, with the winning condition modified to
Observe that by playing the strategies of
![]() $\operatorname {Alice}$
against each other, as in Claim 3.4, we can establish the following.
$\operatorname {Alice}$
against each other, as in Claim 3.4, we can establish the following.
Claim 3.8. For every
![]() $x \in V(\mathcal {H})$
and every sequence
$x \in V(\mathcal {H})$
and every sequence
![]() $(R_{i})_{i\in \Delta }$
with
$(R_{i})_{i\in \Delta }$
with
![]() $\bigcup _{i} R_{i}=V(H)$
, there is some i, such that
$\bigcup _{i} R_{i}=V(H)$
, there is some i, such that
![]() $\operatorname {Alice}$
has no winning strategy in
$\operatorname {Alice}$
has no winning strategy in
![]() $\mathbb {G}(x,i,R_{i})$
.
$\mathbb {G}(x,i,R_{i})$
.
Now, let N be the powerset of the set
![]() $\{(i,R):i \in \Delta ,R \subseteq V(H)\}$
. Of course,
$\{(i,R):i \in \Delta ,R \subseteq V(H)\}$
. Of course,
![]() $|N|=2^{\Delta \cdot 2^{|V(H)|}}$
. Define a mapping
$|N|=2^{\Delta \cdot 2^{|V(H)|}}$
. Define a mapping
![]() $d:V(\mathcal {H}) \to N$
by
$d:V(\mathcal {H}) \to N$
by
Using Lemma 1.2 as in the proof of Lemma 3.3, the map d is
![]() $\Game \mathbf {\Delta }^1_1$
-measurable. By our assumption on
$\Game \mathbf {\Delta }^1_1$
-measurable. By our assumption on
![]() $\mathcal {H}$
, there is a subset C on which d is constant and C spans an edge with each label.
$\mathcal {H}$
, there is a subset C on which d is constant and C spans an edge with each label.
Lemma 3.9. Let
![]() $i\in \Delta $
and
$i\in \Delta $
and
![]() $R_0,R_1\subseteq V(H)$
be sets, such that there is no edge between points of
$R_0,R_1\subseteq V(H)$
be sets, such that there is no edge between points of
![]() $R_0$
and
$R_0$
and
![]() $R_1$
in G. Then for every
$R_1$
in G. Then for every
![]() $x \in C$
,
$x \in C$
,
![]() $\operatorname {Bob}$
has no winning strategy in at least one of
$\operatorname {Bob}$
has no winning strategy in at least one of
![]() $\mathbb {G}(x,i,R_0)$
and
$\mathbb {G}(x,i,R_0)$
and
![]() $\mathbb {G}(x,i,R_1)$
. In particular, if R is independent in G, then
$\mathbb {G}(x,i,R_1)$
. In particular, if R is independent in G, then
![]() $\operatorname {Bob}$
cannot have a winning strategy in
$\operatorname {Bob}$
cannot have a winning strategy in
![]() $\mathbb {G}(x,i,R)$
.
$\mathbb {G}(x,i,R)$
.
Proof. If there exists an
![]() $x\in C$
for which
$x\in C$
for which
![]() $\mathbb {G}(x,i,R_0)$
and
$\mathbb {G}(x,i,R_0)$
and
![]() $\mathbb {G}(x,i,R_1)$
can be won by
$\mathbb {G}(x,i,R_1)$
can be won by
![]() $\operatorname {Bob}$
, then, as d is constant on C, this is the case for every
$\operatorname {Bob}$
, then, as d is constant on C, this is the case for every
![]() $x\in C$
. So we could find
$x\in C$
. So we could find
![]() $x_0,x_1 \in C$
connected with an
$x_0,x_1 \in C$
connected with an
![]() $\alpha _i$
labeled edge so that
$\alpha _i$
labeled edge so that
![]() $\operatorname {Bob}$
has winning strategies in
$\operatorname {Bob}$
has winning strategies in
![]() $\mathbb {G}(x_0,i,R_0)$
and
$\mathbb {G}(x_0,i,R_0)$
and
![]() $\mathbb {G}(x_1,i,R_1)$
. Then we can play the two winning strategies of
$\mathbb {G}(x_1,i,R_1)$
. Then we can play the two winning strategies of
![]() $\operatorname {Bob}$
against each other as in the proof of Theorem 0.1. This would yield elements
$\operatorname {Bob}$
against each other as in the proof of Theorem 0.1. This would yield elements
![]() $h_0,h_1$
in
$h_0,h_1$
in
![]() $\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
that form an
$\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
that form an
![]() $\alpha _i$
-edge with
$\alpha _i$
-edge with
![]() $c(h_i)\in R_i$
, contradicting our assumption on c and
$c(h_i)\in R_i$
, contradicting our assumption on c and
![]() $R_i$
.
$R_i$
.
To finish the proof of the theorem, fix the sets
![]() $R_0,R_1$
from Definition 3.6, and take an arbitrary
$R_0,R_1$
from Definition 3.6, and take an arbitrary
![]() $x \in C$
. By Lemma 3.9, we get that for one of them, say
$x \in C$
. By Lemma 3.9, we get that for one of them, say
![]() $R_0$
,
$R_0$
,
![]() $\operatorname {Alice}$
has a winning strategy
$\operatorname {Alice}$
has a winning strategy
![]() $\mathbb {G}(x,\alpha _0,R_0)$
. Let
$\mathbb {G}(x,\alpha _0,R_0)$
. Let
![]() $A_1,\dots ,A_{\Delta -1}$
be independent sets as in Definition 3.6, that is, with the property that
$A_1,\dots ,A_{\Delta -1}$
be independent sets as in Definition 3.6, that is, with the property that
![]() $R_0 \cup \bigcup _i A_i=V(G)$
. Using Lemma 3.9 again, we obtain that
$R_0 \cup \bigcup _i A_i=V(G)$
. Using Lemma 3.9 again, we obtain that
![]() $\operatorname {Alice}$
has a winning strategy in
$\operatorname {Alice}$
has a winning strategy in
![]() $\mathbb {G}(x,\alpha _i,A_i)$
for each
$\mathbb {G}(x,\alpha _i,A_i)$
for each
![]() $i \in \Delta $
. This contradicts Claim 3.8.
$i \in \Delta $
. This contradicts Claim 3.8.
4 Applications
In this section, we apply the theorems proven before to establish our main results. We will choose a target graph using two prominent notions from descriptive set theory: category and Ramsey property.
4.1 Complexity of the coloring problem
First, we will utilize the shift-graph
![]() $\mathcal {G}_S$
on
$\mathcal {G}_S$
on
![]() $[\mathbb {N}]^{\mathbb {N}}$
to establish the complexity results. Let us mention that it would be ideal to use the main result of [Reference Todorčević and VidnyánszkyTV21] (i.e. that deciding the Borel chromatic number of graphs is complicated) directly and apply the
$[\mathbb {N}]^{\mathbb {N}}$
to establish the complexity results. Let us mention that it would be ideal to use the main result of [Reference Todorčević and VidnyánszkyTV21] (i.e. that deciding the Borel chromatic number of graphs is complicated) directly and apply the
![]() $\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\cdot )$
map together with Theorem 0.1 to show that this already holds for acyclic bounded degree graphs. Unfortunately, since the mentioned theorem requires large
$\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\cdot )$
map together with Theorem 0.1 to show that this already holds for acyclic bounded degree graphs. Unfortunately, since the mentioned theorem requires large
![]() $\Game \mathbf {\Delta }^1_1$
-measurable chromatic number, this does not seem to be possible (the graphs constructed in [Reference Todorčević and VidnyánszkyTV21] only have large Borel chromatic numbers, at least a priori). Instead, we will rely on the uniformization technique from [Reference Todorčević and VidnyánszkyTV21]. Roughly speaking, the technique enables us to prove that in certain situations deciding the existence of, say, Borel colorings is
$\Game \mathbf {\Delta }^1_1$
-measurable chromatic number, this does not seem to be possible (the graphs constructed in [Reference Todorčević and VidnyánszkyTV21] only have large Borel chromatic numbers, at least a priori). Instead, we will rely on the uniformization technique from [Reference Todorčević and VidnyánszkyTV21]. Roughly speaking, the technique enables us to prove that in certain situations deciding the existence of, say, Borel colorings is
![]() $\mathbf {\Sigma }^1_2$
-hard, whenever we are allowed to put graphs “next to each other.”
$\mathbf {\Sigma }^1_2$
-hard, whenever we are allowed to put graphs “next to each other.”
Let
![]() $X,Y$
be uncountable Polish spaces,
$X,Y$
be uncountable Polish spaces,
![]() $\mathbf {\Gamma }$
be a class of Borel sets, and
$\mathbf {\Gamma }$
be a class of Borel sets, and
![]() $\Phi :\mathbf {\Gamma }(X) \to \mathbf {\Pi }^1_1(Y)$
be a map. Define
$\Phi :\mathbf {\Gamma }(X) \to \mathbf {\Pi }^1_1(Y)$
be a map. Define
![]() $\mathcal {F}^{\Phi }\subset \mathbf {\Gamma }(X)$
by
$\mathcal {F}^{\Phi }\subset \mathbf {\Gamma }(X)$
by
![]() $A \in \mathcal {F}^{\Phi } \iff \Phi (A) \not = \emptyset $
, and let the uniform family,
$A \in \mathcal {F}^{\Phi } \iff \Phi (A) \not = \emptyset $
, and let the uniform family,
![]() $\mathcal {U}^{\Phi }$
, be defined as follows: for
$\mathcal {U}^{\Phi }$
, be defined as follows: for
![]() $B \in \mathbf {\Gamma }(\mathbb {N}^{\mathbb {N}} \times X)$
, let
$B \in \mathbf {\Gamma }(\mathbb {N}^{\mathbb {N}} \times X)$
, let
and
(that is, it contains the graph of a Borel function
![]() $\mathbb {N}^{\mathbb {N}} \to Y$
).
$\mathbb {N}^{\mathbb {N}} \to Y$
).
Let
![]() $\mathbf {\Delta }$
be a family of subsets of Polish spaces. Recall that a subset A of a Polish space X is
$\mathbf {\Delta }$
be a family of subsets of Polish spaces. Recall that a subset A of a Polish space X is
![]() $\mathbf {\Delta }$
-hard, if for every Y Polish and
$\mathbf {\Delta }$
-hard, if for every Y Polish and
![]() $B \in \mathbf {\Delta }(Y)$
, there exists a continuous map
$B \in \mathbf {\Delta }(Y)$
, there exists a continuous map
![]() $f:Y \to X$
with
$f:Y \to X$
with
![]() $f^{-1}(A)=B$
. A set is
$f^{-1}(A)=B$
. A set is
![]() $\mathbf {\Delta }$
-complete if it is
$\mathbf {\Delta }$
-complete if it is
![]() $\mathbf {\Delta }$
-hard and in
$\mathbf {\Delta }$
-hard and in
![]() $\mathbf {\Delta }$
. A family
$\mathbf {\Delta }$
. A family
![]() $\mathcal {F}$
of subsets of a Polish space X is said to be
$\mathcal {F}$
of subsets of a Polish space X is said to be
![]() $\mathbf {\Delta }$
-hard on
$\mathbf {\Delta }$
-hard on
![]() $\mathbf {\Gamma }$
, if there exists a set
$\mathbf {\Gamma }$
, if there exists a set
![]() $B \in \mathbf {\Gamma }(\mathbb {N}^{\mathbb {N}} \times X)$
, so that the set
$B \in \mathbf {\Gamma }(\mathbb {N}^{\mathbb {N}} \times X)$
, so that the set
![]() $\{s \in \mathbb {N}^{\mathbb {N}}:B_s \in \mathcal {F}\}$
is
$\{s \in \mathbb {N}^{\mathbb {N}}:B_s \in \mathcal {F}\}$
is
![]() $\mathbf {\Delta }$
-hard. The next definition captures the central technical condition.
$\mathbf {\Delta }$
-hard. The next definition captures the central technical condition.
Definition 4.1. The family
![]() $\mathcal {F}^{\Phi }$
is said to be nicely
$\mathcal {F}^{\Phi }$
is said to be nicely
![]() $\mathbf {\Sigma }^1_1$
-hard on
$\mathbf {\Sigma }^1_1$
-hard on
![]() $\mathbf {\Gamma }$
if for every
$\mathbf {\Gamma }$
if for every
![]() $A \in \mathbf {\Sigma }^1_1(\mathbb {N}^{\mathbb {N}})$
, there exist sets
$A \in \mathbf {\Sigma }^1_1(\mathbb {N}^{\mathbb {N}})$
, there exist sets
![]() $B \in \mathbf {\Gamma }(\mathbb {N}^{\mathbb {N}} \times X)$
and
$B \in \mathbf {\Gamma }(\mathbb {N}^{\mathbb {N}} \times X)$
and
![]() $D \in \mathbf {\Sigma }^1_1(\mathbb {N}^{\mathbb {N}} \times Y)$
, so that
$D \in \mathbf {\Sigma }^1_1(\mathbb {N}^{\mathbb {N}} \times Y)$
, so that
![]() $D \subset \bar {\Phi }(B)$
and for all
$D \subset \bar {\Phi }(B)$
and for all
![]() $s \in \mathbb {N}^{\mathbb {N}}$
, we have
$s \in \mathbb {N}^{\mathbb {N}}$
, we have
A map
![]() $\Phi : \mathbf {\Gamma }(X)\to \mathbf {\Pi }^1_1(Y)$
is called
$\Phi : \mathbf {\Gamma }(X)\to \mathbf {\Pi }^1_1(Y)$
is called
![]() $\mathbf {\Pi }^1_1$
on
$\mathbf {\Pi }^1_1$
on
![]() $\mathbf {\Gamma }$
if for every Polish space P and
$\mathbf {\Gamma }$
if for every Polish space P and
![]() $A\in \mathbf {\Gamma }(P \times X)$
, we have
$A\in \mathbf {\Gamma }(P \times X)$
, we have
![]() $\{(s,y) \in P \times Y:y \in \Phi (A_s)\}\in \mathbf {\Pi }^1_1$
. Now we have the following theorem.
$\{(s,y) \in P \times Y:y \in \Phi (A_s)\}\in \mathbf {\Pi }^1_1$
. Now we have the following theorem.
Theorem 4.2 ([Reference Todorčević and VidnyánszkyTV21], Theorem 1.6).
Let
![]() $X,Y$
be uncountable Polish spaces,
$X,Y$
be uncountable Polish spaces,
![]() $\mathbf {\Gamma }$
be a class of subsets of Polish spaces which is closed under continuous preimages, finite unions, and intersections, and
$\mathbf {\Gamma }$
be a class of subsets of Polish spaces which is closed under continuous preimages, finite unions, and intersections, and
![]() $\mathbf {\Pi }^0_1 \cup \mathbf {\Sigma }^0_1 \subset \mathbf {\Gamma }$
. Suppose that
$\mathbf {\Pi }^0_1 \cup \mathbf {\Sigma }^0_1 \subset \mathbf {\Gamma }$
. Suppose that
![]() $\Phi :\mathbf {\Gamma }(X) \to \mathbf {\Pi }^1_1(Y)$
is
$\Phi :\mathbf {\Gamma }(X) \to \mathbf {\Pi }^1_1(Y)$
is
![]() $\mathbf {\Pi }^1_1$
on
$\mathbf {\Pi }^1_1$
on
![]() $\mathbf {\Gamma }$
and that
$\mathbf {\Gamma }$
and that
![]() $\mathcal {F}^\Phi $
is nicely
$\mathcal {F}^\Phi $
is nicely
![]() $\mathbf {\Sigma }^1_1$
-hard on
$\mathbf {\Sigma }^1_1$
-hard on
![]() $\mathbf {\Gamma }$
. Then the family
$\mathbf {\Gamma }$
. Then the family
![]() $\mathcal {U}^\Phi $
is
$\mathcal {U}^\Phi $
is
![]() $\mathbf {\Sigma }^1_2$
-hard on
$\mathbf {\Sigma }^1_2$
-hard on
![]() $\mathbf {\Gamma }$
.
$\mathbf {\Gamma }$
.
Let us identify infinite subsets of
![]() $\mathbb {N}$
with their increasing enumeration. If
$\mathbb {N}$
with their increasing enumeration. If
![]() $x,y \in [\mathbb {N}]^{\mathbb {N}}$
, let us use the notation
$x,y \in [\mathbb {N}]^{\mathbb {N}}$
, let us use the notation
![]() $y \leq ^\infty x$
in the case the set
$y \leq ^\infty x$
in the case the set
![]() $\{n:y(n) \leq x(n)\}$
is infinite and
$\{n:y(n) \leq x(n)\}$
is infinite and
![]() $y \leq ^* x$
if it is cofinite. Set
$y \leq ^* x$
if it is cofinite. Set
![]() $\mathcal {D}=\{(x,y):y \leq ^\infty x\}.$
It follows from the fact that
$\mathcal {D}=\{(x,y):y \leq ^\infty x\}.$
It follows from the fact that
![]() $\mathcal {G}_S$
restricted to sets of the form
$\mathcal {G}_S$
restricted to sets of the form
![]() $\mathcal {D}_x$
has a Borel
$\mathcal {D}_x$
has a Borel
![]() $3$
-coloring that the graphs
$3$
-coloring that the graphs
![]() $\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S\restriction \mathcal {D}_x)$
admit a Borel
$\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S\restriction \mathcal {D}_x)$
admit a Borel
![]() $3$
-coloring, uniformly in x:
$3$
-coloring, uniformly in x:
Lemma 4.3. There exists a Borel function
![]() $f_{dom}: [\mathbb {N}]^{\mathbb {N}} \to \mathbb {N}^{\mathbb {N}}$
, so that for each
$f_{dom}: [\mathbb {N}]^{\mathbb {N}} \to \mathbb {N}^{\mathbb {N}}$
, so that for each
![]() $x\in [\mathbb {N}]^{\mathbb {N}}$
, we have
$x\in [\mathbb {N}]^{\mathbb {N}}$
, we have
![]() $f_{dom}(x)=\langle c_0,\dots ,c_{\Delta -1}\rangle $
with
$f_{dom}(x)=\langle c_0,\dots ,c_{\Delta -1}\rangle $
with
![]() $c_i \in \mathbf {BC}([\mathbb {N}]^{\mathbb {N}})$
,
$c_i \in \mathbf {BC}([\mathbb {N}]^{\mathbb {N}})$
,
![]() $\mathbf {A}([\mathbb {N}]^{\mathbb {N}})_{c_i}$
are
$\mathbf {A}([\mathbb {N}]^{\mathbb {N}})_{c_i}$
are
![]() $\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S)$
-independent subsets of
$\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S)$
-independent subsets of
![]() $V(\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S))$
for every
$V(\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S))$
for every
![]() $i<\Delta $
, and
$i<\Delta $
, and
 $$\begin{align*}V(\operatorname{\mathbf{ Hom}}^{ac}(T_\Delta,\mathcal{G}_S\restriction \mathcal{D}_x)) = \bigcup^{\Delta-1}_{i=0} \mathbf{A}([\mathbb{N}]^{\mathbb{N}})_{c_i}.\end{align*}$$
$$\begin{align*}V(\operatorname{\mathbf{ Hom}}^{ac}(T_\Delta,\mathcal{G}_S\restriction \mathcal{D}_x)) = \bigcup^{\Delta-1}_{i=0} \mathbf{A}([\mathbb{N}]^{\mathbb{N}})_{c_i}.\end{align*}$$
Proof. Note that it suffices to construct a Borel map
![]() $c:[\mathbb {N}]^{\mathbb {N}} \times \operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S) \to \Delta $
that is a coloring of the graph
$c:[\mathbb {N}]^{\mathbb {N}} \times \operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S) \to \Delta $
that is a coloring of the graph
![]() $\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S \restriction \mathcal {D}_x)$
for each x: indeed, we can use Proposition 1.4 for
$\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S \restriction \mathcal {D}_x)$
for each x: indeed, we can use Proposition 1.4 for
![]() $(B_i)_x=\{(x,h):c(x,h)=i\}$
to obtain Borel maps
$(B_i)_x=\{(x,h):c(x,h)=i\}$
to obtain Borel maps
![]() $f_i:[\mathbb {N}]^{\mathbb {N}} \to \mathbb {N}^{\mathbb {N}}$
, so that for every
$f_i:[\mathbb {N}]^{\mathbb {N}} \to \mathbb {N}^{\mathbb {N}}$
, so that for every
![]() $x \in [\mathbb {N}]^{\mathbb {N}}$
, we have
$x \in [\mathbb {N}]^{\mathbb {N}}$
, we have
![]() $\mathbf {A}([\mathbb {N}]^{\mathbb {N}})_{f_i(x)}=B_i$
, and let
$\mathbf {A}([\mathbb {N}]^{\mathbb {N}})_{f_i(x)}=B_i$
, and let
![]() $f_{dom}(x)=\langle f_0(x),\dots ,f_{\Delta -1}(x)\rangle $
.
$f_{dom}(x)=\langle f_0(x),\dots ,f_{\Delta -1}(x)\rangle $
.
It has been established in [Reference Todorčević and VidnyánszkyTV21, Lemma 4.5] (see also [Reference Di Prisco and TodorčevićDPT15]) that there exists a Borel map
![]() $c':\mathcal {D} \to 3$
, such that for each x, it is a
$c':\mathcal {D} \to 3$
, such that for each x, it is a
![]() $3$
-coloring of the graph
$3$
-coloring of the graph
![]() $\mathcal {G}_S \restriction \mathcal {D}_x$
. As the map
$\mathcal {G}_S \restriction \mathcal {D}_x$
. As the map
![]() $Root:\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S) \to \mathcal {G}_S$
is a Borel homomorphism by Proposition 2.2, it follows that the map
$Root:\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S) \to \mathcal {G}_S$
is a Borel homomorphism by Proposition 2.2, it follows that the map
![]() $c(x,h):=c'(x, Root(h))$
is the desired
$c(x,h):=c'(x, Root(h))$
is the desired
![]() $\Delta $
-coloring (in fact,
$\Delta $
-coloring (in fact,
![]() $3$
-coloring).
$3$
-coloring).
Let
![]() $\mathcal {H}$
be the graph on
$\mathcal {H}$
be the graph on
![]() $\mathbb {N}^{\mathbb {N}} \times V(\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S))$
defined by making
$\mathbb {N}^{\mathbb {N}} \times V(\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S))$
defined by making
![]() $(x,h), (x',h')$
adjacent if
$(x,h), (x',h')$
adjacent if
![]() $x=x'$
and h is adjacent to
$x=x'$
and h is adjacent to
![]() $h'$
in
$h'$
in
![]() $\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S)$
. Fixing a Polish topology on
$\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S)$
. Fixing a Polish topology on
![]() $V(\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S))$
that is compatible with the Borel structure, we might assume that
$V(\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S))$
that is compatible with the Borel structure, we might assume that
![]() $V(\mathcal {H})$
is a Polish space.
$V(\mathcal {H})$
is a Polish space.
Putting together results proved in the previous sections, we get the following corollary.
Corollary 4.4. The Borel chromatic number of
![]() $\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S)$
is
$\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S)$
is
![]() $\Delta +1$
.
$\Delta +1$
.
Now, we are ready to prove the following.
Proposition 4.5. There exists a Borel set
![]() $C \subseteq \mathbb {N}^{\mathbb {N}} \times \mathbb {N}^{\mathbb {N}} \times V(\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S))$
so that the set
$C \subseteq \mathbb {N}^{\mathbb {N}} \times \mathbb {N}^{\mathbb {N}} \times V(\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S))$
so that the set
![]() $\{s: \chi _B (\mathcal {H} \restriction C_s)\leq \Delta \}$
is
$\{s: \chi _B (\mathcal {H} \restriction C_s)\leq \Delta \}$
is
![]() $\mathbf {\Sigma }^1_2$
-hard.
$\mathbf {\Sigma }^1_2$
-hard.
Proof. We check the applicability of Theorem 4.2, with
![]() $X=V(\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S))$
,
$X=V(\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S))$
,
![]() $Y=\mathbb {N}^{\mathbb {N}}$
,
$Y=\mathbb {N}^{\mathbb {N}}$
,
![]() $\mathbf {\Gamma }=\mathbf {\Delta }^1_1$
and
$\mathbf {\Gamma }=\mathbf {\Delta }^1_1$
and
in other words,
![]() $\Phi (A)$
contains the Borel codes of the Borel
$\Phi (A)$
contains the Borel codes of the Borel
![]() $\Delta $
-colorings of
$\Delta $
-colorings of
![]() $\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S) \restriction A$
. Let
$\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S) \restriction A$
. Let
![]() $A \subseteq \mathbb {N}^{\mathbb {N}}$
be analytic, and take a closed set
$A \subseteq \mathbb {N}^{\mathbb {N}}$
be analytic, and take a closed set
![]() $F \subset \mathbb {N}^{\mathbb {N}} \times [\mathbb {N}]^{\mathbb {N}}$
so that
$F \subset \mathbb {N}^{\mathbb {N}} \times [\mathbb {N}]^{\mathbb {N}}$
so that
![]() $proj_0(F)=A$
. Let
$proj_0(F)=A$
. Let
Lemma 4.6.
-
1.
 $B' \in \mathbf {\Pi }^0_2$
.
$B' \in \mathbf {\Pi }^0_2$
. -
2.
 $\Phi $
is
$\Phi $
is
 $\mathbf {\Pi }^1_1$
on
$\mathbf {\Pi }^1_1$
on
 $\mathbf {\Delta }^1_1$
.
$\mathbf {\Delta }^1_1$
. -
3. For any Borel set C, we have
 $C \in \mathcal {U}^\Phi $
if and only if
$C \in \mathcal {U}^\Phi $
if and only if
 $\chi _B(\mathcal {H} \restriction C)\leq \Delta $
.
$\chi _B(\mathcal {H} \restriction C)\leq \Delta $
.
Proof. The first statement has been proved in the stated form in [Reference Todorčević and VidnyánszkyTV21, Lemma 4.6]. The second statement also follows from the straightforward modification of the argument presented in [Reference Todorčević and VidnyánszkyTV21, Lemma 4.6]: in fact,
![]() $\Phi $
is
$\Phi $
is
![]() $\mathbf { \Pi }^1_1$
on
$\mathbf { \Pi }^1_1$
on
![]() $\mathbf {\Delta }^1_1$
if
$\mathbf {\Delta }^1_1$
if
![]() $\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S)$
is replaced with any Borel graph, and the last statement works for every Borel graph on a product space, where edges only go between points in the same vertical section, in particular, for
$\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S)$
is replaced with any Borel graph, and the last statement works for every Borel graph on a product space, where edges only go between points in the same vertical section, in particular, for
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
Now define
and
where
![]() $f_{dom}$
is the function from Lemma 4.3.
$f_{dom}$
is the function from Lemma 4.3.
We will show that B and D witness that
![]() $\mathcal {F}^\Phi $
is nicely
$\mathcal {F}^\Phi $
is nicely
![]() $\mathbf {\Sigma }^1_1$
-hard. The set B is Borel by (1) of the lemma above, while by its definition, D is analytic.
$\mathbf {\Sigma }^1_1$
-hard. The set B is Borel by (1) of the lemma above, while by its definition, D is analytic.
Suppose that
![]() $s \in A$
. Then for each
$s \in A$
. Then for each
![]() $x' \in F_s$
, we have
$x' \in F_s$
, we have
Thus, by Lemma 4.3,
![]() $B_s \in \mathcal {F}^\Phi $
and
$B_s \in \mathcal {F}^\Phi $
and
![]() $D_s \not = \emptyset $
. Moreover, if
$D_s \not = \emptyset $
. Moreover, if
![]() $c \in D_s$
, then for some
$c \in D_s$
, then for some
![]() $x \in F_s$
, we have
$x \in F_s$
, we have
![]() $f_{dom}(x)=c$
with
$f_{dom}(x)=c$
with
![]() $c=\langle c_0,\dots ,c_{\Delta -1}\rangle $
, again, by Lemma 4.3, we have
$c=\langle c_0,\dots ,c_{\Delta -1}\rangle $
, again, by Lemma 4.3, we have
![]() $B_s \subseteq \bigcup ^{\Delta -1}_{i=0} \mathbf {A}([\mathbb {N}]^{\mathbb {N}})_{c_i}$
and the sets
$B_s \subseteq \bigcup ^{\Delta -1}_{i=0} \mathbf {A}([\mathbb {N}]^{\mathbb {N}})_{c_i}$
and the sets
![]() $\mathbf {A}([\mathbb {N}]^{\mathbb {N}})_{c_i}$
are
$\mathbf {A}([\mathbb {N}]^{\mathbb {N}})_{c_i}$
are
![]() $\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S)$
-independent, thus,
$\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S)$
-independent, thus,
![]() $D_{s} \subseteq \Phi (B_s)$
. Conversely, if
$D_{s} \subseteq \Phi (B_s)$
. Conversely, if
![]() $s \not \in A$
, then
$s \not \in A$
, then
![]() $F_s=D_s=\emptyset $
and
$F_s=D_s=\emptyset $
and
![]() $B^{\prime }_s=[\mathbb {N}]^{\mathbb {N}}$
. Then
$B^{\prime }_s=[\mathbb {N}]^{\mathbb {N}}$
. Then
![]() $B_s=\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S)$
, which set does not admit a Borel
$B_s=\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S)$
, which set does not admit a Borel
![]() $\Delta $
-coloring by Corollary 4.4. Consequently,
$\Delta $
-coloring by Corollary 4.4. Consequently,
![]() $\Phi (B_s)=\emptyset $
.
$\Phi (B_s)=\emptyset $
.
So, Theorem 4.2 is applicable, and it yields a Borel set
![]() $C \subseteq \mathbb {N}^{\mathbb {N}} \times \mathbb {N}^{\mathbb {N}} \times [\mathbb {N}]^{\mathbb {N}}$
so that
$C \subseteq \mathbb {N}^{\mathbb {N}} \times \mathbb {N}^{\mathbb {N}} \times [\mathbb {N}]^{\mathbb {N}}$
so that
![]() $\{s:C_s \in \mathcal {U}^\Phi \}$
is
$\{s:C_s \in \mathcal {U}^\Phi \}$
is
![]() $\mathbf {\Sigma }^1_2$
-hard. This implies the desired conclusion by (3) of the lemma above.
$\mathbf {\Sigma }^1_2$
-hard. This implies the desired conclusion by (3) of the lemma above.
We can prove Theorem 0.2. Let us restate the theorem, describing precisely what we mean by “form a
![]() $\mathbf {\Sigma }^1_2$
-complete set.”
$\mathbf {\Sigma }^1_2$
-complete set.”
Theorem 0.2. Let X be an uncountable Polish space and
![]() $\Delta>2$
. The set
$\Delta>2$
. The set
is
![]() $\mathbf {\Sigma }^1_2$
-complete.
$\mathbf {\Sigma }^1_2$
-complete.
In particular, Brooks’s theorem has no analogue for Borel graphs in the following sense: there is no countable family
![]() $\{\mathcal {H}_i\}_{i \in I}$
of Borel graphs, such that for any Borel graph
$\{\mathcal {H}_i\}_{i \in I}$
of Borel graphs, such that for any Borel graph
![]() $\mathcal {G}$
with
$\mathcal {G}$
with
![]() $\Delta (\mathcal {G})\leq \Delta $
, we have
$\Delta (\mathcal {G})\leq \Delta $
, we have
![]() $\chi _B(\mathcal {G})>\Delta $
if and only if for some
$\chi _B(\mathcal {G})>\Delta $
if and only if for some
![]() $i \in I$
, the graph
$i \in I$
, the graph
![]() $\mathcal {G}$
contains a Borel homomorphic copy of
$\mathcal {G}$
contains a Borel homomorphic copy of
![]() $\mathcal {H}_i$
.
$\mathcal {H}_i$
.
Proof of Theorem 0.2.
First, note that using the fact that the codes of Borel functions between Polish spaces form a
![]() $\mathbf {\Pi }^1_1$
set, it is straightforward to show that S is a
$\mathbf {\Pi }^1_1$
set, it is straightforward to show that S is a
![]() $\mathbf {\Sigma }^1_2$
set (see e.g. [Reference Todorčević and VidnyánszkyTV21, Proof of Theorem 1.3]). Similarly, one can check that if there was a collection
$\mathbf {\Sigma }^1_2$
set (see e.g. [Reference Todorčević and VidnyánszkyTV21, Proof of Theorem 1.3]). Similarly, one can check that if there was a collection
![]() $\{\mathcal {H}_i:i \in I\}$
as above, then this would yield that the set S is
$\{\mathcal {H}_i:i \in I\}$
as above, then this would yield that the set S is
![]() $\mathbf {\Pi }^1_2$
. Thus, in order to show both parts of the theorem, it suffices to prove that S is
$\mathbf {\Pi }^1_2$
. Thus, in order to show both parts of the theorem, it suffices to prove that S is
![]() $\mathbf {\Sigma }^1_2$
-hard.
$\mathbf {\Sigma }^1_2$
-hard.
Second, by [Reference SabokSab12], it follows that if we replace continuous functions with Borel ones in the definition of
![]() $\mathbf {\Sigma }^1_2$
-hard sets, we get the same class. As uncountable Polish spaces are Borel isomorphic, it is enough to show that S is
$\mathbf {\Sigma }^1_2$
-hard sets, we get the same class. As uncountable Polish spaces are Borel isomorphic, it is enough to show that S is
![]() $\mathbf {\Sigma }^1_2$
-hard for some X.
$\mathbf {\Sigma }^1_2$
-hard for some X.
Take the graph
![]() $\mathcal {H}$
and the set C from Proposition 4.5. Note that the graph
$\mathcal {H}$
and the set C from Proposition 4.5. Note that the graph
![]() $\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S)$
is acyclic and has degrees
$\operatorname {\mathbf { Hom}}^{ac}(T_\Delta ,\mathcal {G}_S)$
is acyclic and has degrees
![]() $\leq \Delta $
by its construction. Therefore, the same holds for
$\leq \Delta $
by its construction. Therefore, the same holds for
![]() $\mathcal {H} \restriction C_s$
for each s. Using that the sets
$\mathcal {H} \restriction C_s$
for each s. Using that the sets
![]() $D_i=\{(s,x,h):\text {the degree of }(x,h)\text { in }\mathcal {H} \restriction C_s\text { is }i\}$
are Borel, it is straightforward to modify
$D_i=\{(s,x,h):\text {the degree of }(x,h)\text { in }\mathcal {H} \restriction C_s\text { is }i\}$
are Borel, it is straightforward to modify
![]() $\mathcal {H}$
so that we obtain a Borel graph
$\mathcal {H}$
so that we obtain a Borel graph
![]() $\mathcal {H}_\Delta $
on a Polish space of the form
$\mathcal {H}_\Delta $
on a Polish space of the form
![]() $X=\mathbb {N}^{\mathbb {N}} \times Y$
, such that for each s, the graph
$X=\mathbb {N}^{\mathbb {N}} \times Y$
, such that for each s, the graph
![]() $\mathcal {H}_\Delta \restriction \{s\} \times Y$
is
$\mathcal {H}_\Delta \restriction \{s\} \times Y$
is
![]() $\Delta $
-regular, acyclic, and that the set
$\Delta $
-regular, acyclic, and that the set
![]() $\{s:\chi _B(\mathcal {H}_\Delta \restriction \{s\} \times Y)) \leq \Delta \}= \{s:\chi _B(\mathcal {H}\restriction C_s)\leq \Delta \}$
(indeed, to vertices in
$\{s:\chi _B(\mathcal {H}_\Delta \restriction \{s\} \times Y)) \leq \Delta \}= \{s:\chi _B(\mathcal {H}\restriction C_s)\leq \Delta \}$
(indeed, to vertices in
![]() $D_i$
, we can attach
$D_i$
, we can attach
![]() $\Delta -i$
-many disjoint infinite rooted trees that are
$\Delta -i$
-many disjoint infinite rooted trees that are
![]() $\Delta $
-regular except for the root, which has degree
$\Delta $
-regular except for the root, which has degree
![]() $\Delta -1$
, in a Borel way). The third part of Proposition 1.4 gives a Borel reduction from the former set to S. Since the latter set is
$\Delta -1$
, in a Borel way). The third part of Proposition 1.4 gives a Borel reduction from the former set to S. Since the latter set is
![]() $\mathbf {\Sigma }^1_2$
-hard, this yields the desired result by using [Reference SabokSab12] as above.
$\mathbf {\Sigma }^1_2$
-hard, this yields the desired result by using [Reference SabokSab12] as above.
4.2 Hyperfiniteness
In this section, we use Baire category arguments to obtain a new proof of Theorem 0.4.
Theorem 0.4. There exists a hyperfinite
![]() $\Delta $
-regular acyclic Borel graph with Borel chromatic number
$\Delta $
-regular acyclic Borel graph with Borel chromatic number
![]() $\Delta +1$
.
$\Delta +1$
.
We will utilize a version of the graph
![]() $\mathbb {G}_0$
constructed in [Reference Kechris, Solecki and TodorčevićKST99]. For
$\mathbb {G}_0$
constructed in [Reference Kechris, Solecki and TodorčevićKST99]. For
![]() $s\in 2^{<\mathbb N}$
, define
$s\in 2^{<\mathbb N}$
, define
on
![]() $2^{\mathbb N}$
. Fix some collection
$2^{\mathbb N}$
. Fix some collection
![]() $(s_n)_{n\in \mathbb N}\subseteq 2^{<\mathbb N}$
, such that
$(s_n)_{n\in \mathbb N}\subseteq 2^{<\mathbb N}$
, such that
![]() $|s_n|=n$
, that is,
$|s_n|=n$
, that is,
![]() $s_n\in 2^n$
, for every
$s_n\in 2^n$
, for every
![]() $n\in \mathbb N$
, together with a function
$n\in \mathbb N$
, together with a function
![]() $e:\mathbb {N}\to \Delta $
, such that
$e:\mathbb {N}\to \Delta $
, such that
![]() $(s_n)_{e(n)=i}\subseteq 2^{<\mathbb N}$
is dense in
$(s_n)_{e(n)=i}\subseteq 2^{<\mathbb N}$
is dense in
![]() $2^{<\mathbb {N}}$
for every
$2^{<\mathbb {N}}$
for every
![]() $i\in \Delta $
. Set
$i\in \Delta $
. Set
![]() $\mathbb {G}_0=\bigcup _{n \in \mathbb {N}}\mathbb {G}_{s_n}$
. Label an edge
$\mathbb {G}_0=\bigcup _{n \in \mathbb {N}}\mathbb {G}_{s_n}$
. Label an edge
![]() $\alpha _i$
if it is in the graph
$\alpha _i$
if it is in the graph
![]() $\bigcup _{e(n)=i} \mathbb {G}_{s_n}$
. Finally, write
$\bigcup _{e(n)=i} \mathbb {G}_{s_n}$
. Finally, write
![]() $\mathcal {H}$
for the restriction of
$\mathcal {H}$
for the restriction of
![]() $\mathbb {G}_0$
to those vertices x such that every vertex in the connected component of x is adjacent to at least one edge of each label. Standard arguments yield the following claim.
$\mathbb {G}_0$
to those vertices x such that every vertex in the connected component of x is adjacent to at least one edge of each label. Standard arguments yield the following claim.
Claim 4.7.
-
1.
 $\mathcal {H}$
is acyclic and locally countable.
$\mathcal {H}$
is acyclic and locally countable. -
2.
 $\mathcal {H}$
is defined on a comeager subset of
$\mathcal {H}$
is defined on a comeager subset of
 $2^{\mathbb {N}}$
.
$2^{\mathbb {N}}$
. -
3. The Baire measurable edge-labeled chromatic number of
 $\mathcal {H}$
is infinite (in fact, uncountable).
$\mathcal {H}$
is infinite (in fact, uncountable). -
4.
 $\mathcal {H}$
is hyperfinite.
$\mathcal {H}$
is hyperfinite.
Proof. The fact the
![]() $\mathcal {H}$
is locally countable is clear from its definition, while acyclicity follows from the assumption that
$\mathcal {H}$
is locally countable is clear from its definition, while acyclicity follows from the assumption that
![]() $|s_n|=n$
. To see the second part, note that the set
$|s_n|=n$
. To see the second part, note that the set
![]() $\{x \in 2^{\mathbb {N}}: \forall i \in \Delta \ \exists n \ (e(n)=i \land s_n \sqsubset x) \}$
is open and dense in
$\{x \in 2^{\mathbb {N}}: \forall i \in \Delta \ \exists n \ (e(n)=i \land s_n \sqsubset x) \}$
is open and dense in
![]() $2^{\mathbb {N}}$
. Now,
$2^{\mathbb {N}}$
. Now,
![]() $\mathcal {H}$
is the restriction of
$\mathcal {H}$
is the restriction of
![]() $\mathbb {G}_0$
to a set that is an intersection of the image of this set under countably many homeomorphisms of the form
$\mathbb {G}_0$
to a set that is an intersection of the image of this set under countably many homeomorphisms of the form
![]() $s_n^\frown (i)^\frown c \mapsto s_n^\frown (1-i)^\frown c$
, hence, its vertex set is comeager.
$s_n^\frown (i)^\frown c \mapsto s_n^\frown (1-i)^\frown c$
, hence, its vertex set is comeager.
The proof of the third part is identical to the proof of [Reference Kechris, Solecki and TodorčevićKST99, Proposition 6.2]. We include the argument for completeness. Assume that
![]() $c:2^{\mathbb {N}} \to \aleph _0$
is a Baire measurable coloring and
$c:2^{\mathbb {N}} \to \aleph _0$
is a Baire measurable coloring and
![]() $j \in \Delta $
is arbitrary. Then, for some i, the set
$j \in \Delta $
is arbitrary. Then, for some i, the set
![]() $c^{-1}(i)$
is nonmeager. Since
$c^{-1}(i)$
is nonmeager. Since
![]() $c^{-1}(i)$
is Baire-measurable, there is some neighborhood
$c^{-1}(i)$
is Baire-measurable, there is some neighborhood
![]() $N_t$
, such that
$N_t$
, such that
![]() $N_t \setminus c^{-1}(i)$
is comeager. In turn, there is some n with
$N_t \setminus c^{-1}(i)$
is comeager. In turn, there is some n with
![]() $e(n)=j$
and
$e(n)=j$
and
![]() $N_{s_n} \setminus c^{-1}(i)$
comeager. Since the map
$N_{s_n} \setminus c^{-1}(i)$
comeager. Since the map ![]() is category preserving from
is category preserving from
![]() $N_{s_n}$
to
$N_{s_n}$
to
![]() $N_{s_n}$
, there will be some
$N_{s_n}$
, there will be some
![]() $x,y \in c^{-1}(i) \cap N_{s_n}$
, with
$x,y \in c^{-1}(i) \cap N_{s_n}$
, with
![]() $(x,y) \in \mathbb {G}_{s_n}$
, in other words, the edge
$(x,y) \in \mathbb {G}_{s_n}$
, in other words, the edge
![]() $(x,y)$
is labeled j.
$(x,y)$
is labeled j.
Finally, the hyperfiniteness of
![]() $\mathcal {H}$
follows from the fact that
$\mathcal {H}$
follows from the fact that
![]() $E_{\mathcal {H}} \subset \mathbb {E}_0$
(see, e.g. [Reference Jackson, Kechris and LouveauJKL02, Proposition 1.3]).
$E_{\mathcal {H}} \subset \mathbb {E}_0$
(see, e.g. [Reference Jackson, Kechris and LouveauJKL02, Proposition 1.3]).
Proof of Theorem 0.4.
By Claim 4.7 and Proposition 2.6, the graph
![]() $\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
is hyperfinite,
$\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
is hyperfinite,
![]() $\Delta $
-regular, and acyclic. By Theorem 3.5 and Proposition 1.3, its Borel chromatic number is
$\Delta $
-regular, and acyclic. By Theorem 3.5 and Proposition 1.3, its Borel chromatic number is
![]() $\Delta +1$
.
$\Delta +1$
.
Note that the above theorem also implies Theorem 1.6 in [Reference Conley, Jackson, Marks, Seward and Tucker-DrobCJM+20], namely, that there is no Borel version of the Lovász Local Lemma (LLL) even on hyperfinite graphs and if the probability of a bad event is polynomial in the degree of the dependency graph (for related results and precise definitions see [Reference Csóka, Grabowski, András, Pikhurko and TyrosCGA+16] and [Reference BernshteynBer23]). In order to see this, observe that the sinkless orientation problem from [Reference Brandt, Fischer, Hirvonen, Keller, Lempiäinen, Rybicki, Suomela and UittoBFH+16] can be thought of as an instance of the LLL as follows: Each edge corresponds to a random binary variable representing its orientation. At each node, the bad event has probability
![]() $2^{-\Delta }$
: all incident edges are oriented toward it. It remains to observe that a Borel solution to the sinkless orientation problem implies easily a Borel solution to the edge grabbing problem which, in turn, by Remark 3.1, implies the existence of a Borel antigame labeling. However, it follows from the proof of Theorem 3.5 that
$2^{-\Delta }$
: all incident edges are oriented toward it. It remains to observe that a Borel solution to the sinkless orientation problem implies easily a Borel solution to the edge grabbing problem which, in turn, by Remark 3.1, implies the existence of a Borel antigame labeling. However, it follows from the proof of Theorem 3.5 that
![]() $\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
does not admit a Borel antigame labeling.
$\operatorname {\mathbf { Hom}}^{e}(T_\Delta ,\mathcal {H})$
does not admit a Borel antigame labeling.
4.3 Graph homomorphisms
In this section, we prove Theorem 0.5 that we restate here for the convenience of the reader.
Theorem 0.5. For every
![]() $\Delta>2$
and every
$\Delta>2$
and every
![]() $\ell \leq 2\Delta -2$
, there are a finite graph H and a
$\ell \leq 2\Delta -2$
, there are a finite graph H and a
![]() $\Delta $
-regular acyclic Borel graph
$\Delta $
-regular acyclic Borel graph
![]() $\mathcal {G}$
, such that
$\mathcal {G}$
, such that
![]() $\chi (H)=\ell $
and
$\chi (H)=\ell $
and
![]() $\mathcal {G}$
does not admit Borel homomorphism to H. The graph
$\mathcal {G}$
does not admit Borel homomorphism to H. The graph
![]() $\mathcal {G}$
can be chosen to be hyperfinite.
$\mathcal {G}$
can be chosen to be hyperfinite.
We remark that the first proof of the theorem (without the conclusion about hyperfiniteness) relied on a construction from the random graph theory (see [Reference Brandt, Chang, Grebík, Grunau, Rozhoň and VidnyánszkyBCG+21] for motivation and connection to the
![]() $\mathsf {LOCAL}$
model). We sketch the construction here for completeness. Fix
$\mathsf {LOCAL}$
model). We sketch the construction here for completeness. Fix
![]() $k\in \mathbb {N}$
, large enough depending on
$k\in \mathbb {N}$
, large enough depending on
![]() $\Delta $
, and consider
$\Delta $
, and consider
![]() $k\Delta $
pairings on a set n sampled independently uniformly at random. In other words, we have a
$k\Delta $
pairings on a set n sampled independently uniformly at random. In other words, we have a
![]() $k\Delta $
-regular graph and there is a canonical edge
$k\Delta $
-regular graph and there is a canonical edge
![]() $\Delta $
-labeling, such that each vertex is adjacent to exactly k edges of each color. Now taking a local-global limit of such graphs as
$\Delta $
-labeling, such that each vertex is adjacent to exactly k edges of each color. Now taking a local-global limit of such graphs as
![]() $n\to \infty $
produces with probability
$n\to \infty $
produces with probability
![]() $1$
an acyclic graphing with large edge-labeled chromatic number as needed (see [Reference BollobásBol81, Reference Hatami, Lovász and SzegedyHLS14]).
$1$
an acyclic graphing with large edge-labeled chromatic number as needed (see [Reference BollobásBol81, Reference Hatami, Lovász and SzegedyHLS14]).
Before we prove Theorem 0.5, we discuss graphs that are almost
![]() $\Delta $
-colorable.
$\Delta $
-colorable.
Almost
 $\Delta $
-colorable graphs
$\Delta $
-colorable graphs
As we have seen, in Section 3.1, being almost
![]() $\Delta $
-colorable is (formally) a weaker condition than having chromatic number at most
$\Delta $
-colorable is (formally) a weaker condition than having chromatic number at most
![]() $\Delta $
but still allows us to use a version of Marks’s technique. Similarly to the way the complete graph on
$\Delta $
but still allows us to use a version of Marks’s technique. Similarly to the way the complete graph on
![]() $\Delta $
-many vertices,
$\Delta $
-many vertices,
![]() $K_\Delta $
, is maximal among graphs of chromatic number
$K_\Delta $
, is maximal among graphs of chromatic number
![]() $\leq \Delta $
, we show that there exists a maximal graph (under homomorphisms) that is almost
$\leq \Delta $
, we show that there exists a maximal graph (under homomorphisms) that is almost
![]() $\Delta $
-colorable. It turns out that the chromatic number of the maximal graph is
$\Delta $
-colorable. It turns out that the chromatic number of the maximal graph is
![]() $2\Delta -2$
.
$2\Delta -2$
.
Let us describe the maximal examples of graphs that are almost
![]() $\Delta $
-colorable for
$\Delta $
-colorable for
![]() $\Delta>2$
. Recall that the (categorical) product
$\Delta>2$
. Recall that the (categorical) product
![]() $G \times H$
of graphs
$G \times H$
of graphs
![]() $G,H$
is the graph on
$G,H$
is the graph on
![]() $V(G) \times V(H)$
, such that
$V(G) \times V(H)$
, such that
![]() $((g,h),(g',h')) \in E(G \times H)$
if and only if
$((g,h),(g',h')) \in E(G \times H)$
if and only if
![]() $(g,g') \in E(G)$
and
$(g,g') \in E(G)$
and
![]() $(h,h') \in E(H)$
.
$(h,h') \in E(H)$
.

Figure 2 The maximal graph that is almost
![]() $\Delta $
-colorable for
$\Delta $
-colorable for
![]() $\Delta =3$
.
$\Delta =3$
.
Write P for the product
![]() $K_{\Delta -1}\times K_{\Delta -1}$
. Let
$K_{\Delta -1}\times K_{\Delta -1}$
. Let
![]() $V_0$
and
$V_0$
and
![]() $V_1$
be vertex disjoint copies of
$V_1$
be vertex disjoint copies of
![]() $K_{\Delta -1}$
. We think of vertices in
$K_{\Delta -1}$
. We think of vertices in
![]() $V_i$
and P as having labels from
$V_i$
and P as having labels from
![]() $[\Delta -1]$
and
$[\Delta -1]$
and
![]() $[\Delta -1] \times [\Delta -1]$
, respectively. The graph
$[\Delta -1] \times [\Delta -1]$
, respectively. The graph
![]() $H_\Delta $
is the disjoint union of
$H_\Delta $
is the disjoint union of
![]() $V_0$
,
$V_0$
,
![]() $V_1$
, P, and an extra vertex
$V_1$
, P, and an extra vertex
![]() $\dagger $
that is connected by an edge to every vertex in P, and additionally, if v is a vertex in
$\dagger $
that is connected by an edge to every vertex in P, and additionally, if v is a vertex in
![]() $V_0$
with label
$V_0$
with label
![]() $i\in [\Delta -1]$
, then we connect it by an edge with
$i\in [\Delta -1]$
, then we connect it by an edge with
![]() $(i',j)\in P$
for every
$(i',j)\in P$
for every
![]() $i'\not =i$
and
$i'\not =i$
and
![]() $j\in [\Delta -1]$
, and if v is a vertex in
$j\in [\Delta -1]$
, and if v is a vertex in
![]() $V_1$
with label
$V_1$
with label
![]() $j\in \Delta -1$
, then we connect it by an edge with
$j\in \Delta -1$
, then we connect it by an edge with
![]() $(i,j')\in P$
for every
$(i,j')\in P$
for every
![]() $j'\not =j$
and
$j'\not =j$
and
![]() $i \in [\Delta -1]$
. The graph
$i \in [\Delta -1]$
. The graph
![]() $H_{3}$
is depicted in Figure 2.
$H_{3}$
is depicted in Figure 2.
Proposition 4.8.
-
1.
 $H_\Delta $
is almost
$H_\Delta $
is almost
 $\Delta $
-colorable.
$\Delta $
-colorable. -
2.
 $\chi (H_\Delta )=2\Delta -2$
.
$\chi (H_\Delta )=2\Delta -2$
. -
3. A graph G is almost
 $\Delta $
colorable if and only if it admits a homomorphism to
$\Delta $
colorable if and only if it admits a homomorphism to
 $H_\Delta $
.
$H_\Delta $
.
Proof. (1) Set
![]() $R_0=V(V_0)\cup \{\dagger \}$
and
$R_0=V(V_0)\cup \{\dagger \}$
and
![]() $R_1=V(V_1)\cup \{\dagger \}$
. By the definition, there are no edges between
$R_1=V(V_1)\cup \{\dagger \}$
. By the definition, there are no edges between
![]() $R_0$
and
$R_0$
and
![]() $R_1$
. Consider now, for example,
$R_1$
. Consider now, for example,
![]() $V(H_\Delta )\setminus R_0$
. Let
$V(H_\Delta )\setminus R_0$
. Let
![]() $A_j$
consist of all elements in P that have second coordinate equal to j together with the vertex in
$A_j$
consist of all elements in P that have second coordinate equal to j together with the vertex in
![]() $V_1$
that has the label j. By the definition, the set
$V_1$
that has the label j. By the definition, the set
![]() $A_i$
is independent and
$A_i$
is independent and
![]() $\bigcup _{i\in [\Delta -1]}A_i$
covers
$\bigcup _{i\in [\Delta -1]}A_i$
covers
![]() $H_\Delta \setminus R_0$
, and similarly for
$H_\Delta \setminus R_0$
, and similarly for
![]() $R_1$
.
$R_1$
.
(2) First, we show that
![]() $\chi (H_\Delta )\le 2\Delta -2$
. Observe that there is no edge between
$\chi (H_\Delta )\le 2\Delta -2$
. Observe that there is no edge between
![]() $R_0 \setminus R_1$
and
$R_0 \setminus R_1$
and
![]() $R_0 \cap R_1$
, as there is no edge between
$R_0 \cap R_1$
, as there is no edge between
![]() $R_0$
and
$R_0$
and
![]() $R_1$
. It follows that the chromatic number of the induced subgraph of
$R_1$
. It follows that the chromatic number of the induced subgraph of
![]() $H_\Delta $
to
$H_\Delta $
to
![]() $R_0$
is
$R_0$
is
![]() $\Delta -1$
. The desired
$\Delta -1$
. The desired
![]() $2\Delta -2$
coloring of
$2\Delta -2$
coloring of
![]() $H_\Delta $
is then defined as the disjoint union of the
$H_\Delta $
is then defined as the disjoint union of the
![]() $\Delta -1$
-colorings of
$\Delta -1$
-colorings of
![]() $R_0$
and
$R_0$
and
![]() $V(H) \setminus R_0$
.
$V(H) \setminus R_0$
.
Next, we show that
![]() $\chi (H_\Delta )\geq 2\Delta -2$
. Toward a contradiction, assume that c is a coloring of
$\chi (H_\Delta )\geq 2\Delta -2$
. Toward a contradiction, assume that c is a coloring of
![]() $H_\Delta $
with
$H_\Delta $
with
![]() $<2\Delta -2$
-many colors. It follows that
$<2\Delta -2$
-many colors. It follows that
![]() $|c(V(P))|\leq 2\Delta -4$
, and also
$|c(V(P))|\leq 2\Delta -4$
, and also
![]() $\Delta -1 \leq |c(V(P))|$
. First, we claim that there are no indices
$\Delta -1 \leq |c(V(P))|$
. First, we claim that there are no indices
![]() $i,j\in [\Delta -1]$
(even with
$i,j\in [\Delta -1]$
(even with
![]() $i=j$
), such that
$i=j$
), such that
![]() $c(i,r)\not =c(i,s)$
and
$c(i,r)\not =c(i,s)$
and
![]() $c(r,j)\not =c(s,j)$
for every
$c(r,j)\not =c(s,j)$
for every
![]() $s\not =r$
: indeed, otherwise, by the definition of P, we had
$s\not =r$
: indeed, otherwise, by the definition of P, we had
![]() $c(i,r)\not =c(s,j)$
for every
$c(i,r)\not =c(s,j)$
for every
![]() $r,s$
unless
$r,s$
unless
![]() $(i,r)=(s,j)$
, which would be the upper bound on the size of
$(i,r)=(s,j)$
, which would be the upper bound on the size of
![]() $c(V(P))$
.
$c(V(P))$
.
Therefore, without loss of generality, we may assume that for every
![]() $i\in [\Delta -1]$
, there is a color
$i\in [\Delta -1]$
, there is a color
![]() $\alpha _i$
and two indices
$\alpha _i$
and two indices
![]() $j_i \neq j^{\prime }_i$
, such that
$j_i \neq j^{\prime }_i$
, such that
![]() $c(i,j_i)=c(i,j^{\prime }_i)=\alpha _i$
. It follows from the definition of P and
$c(i,j_i)=c(i,j^{\prime }_i)=\alpha _i$
. It follows from the definition of P and
![]() $j_i \neq j^{\prime }_i$
that
$j_i \neq j^{\prime }_i$
that
![]() $\alpha _i\not =\alpha _{i'}$
whenever
$\alpha _i\not =\alpha _{i'}$
whenever
![]() $i\not = i'$
.
$i\not = i'$
.
Moreover, note that any vertex in
![]() $V_1$
is connected to at least one of the vertices
$V_1$
is connected to at least one of the vertices
![]() $(i,j_i)$
and
$(i,j_i)$
and
![]() $(i,j^{\prime }_i)$
, hence, none of the colors
$(i,j^{\prime }_i)$
, hence, none of the colors
![]() $\{\alpha _i\}_{i \in [\Delta -1]}$
can appear on
$\{\alpha _i\}_{i \in [\Delta -1]}$
can appear on
![]() $V_1$
. Consequently, since
$V_1$
. Consequently, since
![]() $V_1$
is isomorphic to
$V_1$
is isomorphic to
![]() $K_{\Delta -1}$
, we need to use at least
$K_{\Delta -1}$
, we need to use at least
![]() $\Delta -1$
additional colors, a contradiction.
$\Delta -1$
additional colors, a contradiction.
(3) First, note that if G admits a homomorphism into
![]() $H_\Delta $
, then the pullback of the sets
$H_\Delta $
, then the pullback of the sets
![]() $R_0$
,
$R_0$
,
![]() $R_1$
, and
$R_1$
, and
![]() $A_i$
for
$A_i$
for
![]() $i\in [\Delta -1]$
witnesses that G is almost
$i\in [\Delta -1]$
witnesses that G is almost
![]() $\Delta $
-colorable.
$\Delta $
-colorable.
Conversely, let G be almost
![]() $\Delta $
-colorable. Fix the corresponding sets
$\Delta $
-colorable. Fix the corresponding sets
![]() $R_0,R_1$
together with
$R_0,R_1$
together with
![]() $(\Delta -1)$
-colorings
$(\Delta -1)$
-colorings
![]() $c_0,c_1$
of their complements. We construct a homomorphism
$c_0,c_1$
of their complements. We construct a homomorphism
![]() $\Theta $
from G to
$\Theta $
from G to
![]() $H_\Delta $
. Let
$H_\Delta $
. Let
 $$\begin{align*}\Theta(v)= \begin{cases} \dagger &\mbox{if } v \in R_0 \cap R_1, \\ c_0(v) & \mbox{if } v \in R_1 \setminus R_0, \\ c_1(v) & \mbox{if } v \in R_0 \setminus R_1, \\ (c_0(v),c_1(v)) & \mbox{if } v \not \in R_0 \cup R_1. \end{cases} \end{align*}$$
$$\begin{align*}\Theta(v)= \begin{cases} \dagger &\mbox{if } v \in R_0 \cap R_1, \\ c_0(v) & \mbox{if } v \in R_1 \setminus R_0, \\ c_1(v) & \mbox{if } v \in R_0 \setminus R_1, \\ (c_0(v),c_1(v)) & \mbox{if } v \not \in R_0 \cup R_1. \end{cases} \end{align*}$$
Observe that
![]() $R=R_0\cap R_1$
is an independent set, such that there is no edge between R and
$R=R_0\cap R_1$
is an independent set, such that there is no edge between R and
![]() $R_0 \cup R_1$
. Using this observation, one easily checks case-by-case that
$R_0 \cup R_1$
. Using this observation, one easily checks case-by-case that
![]() $\Theta $
is indeed a homomorphism.
$\Theta $
is indeed a homomorphism.
Remark 4.9. It can be shown that for
![]() $\Delta =3$
, both the Chvátal and Grötsch graphs are almost
$\Delta =3$
, both the Chvátal and Grötsch graphs are almost
![]() $\Delta $
-colorable.
$\Delta $
-colorable.
Proof of Theorem 0.5.
Note that it is enough to show the existence of such H and
![]() $\mathcal {G}$
with
$\mathcal {G}$
with
![]() $\chi (H)=2\Delta -2$
. Indeed, since erasing a vertex decreases the chromatic number by at most
$\chi (H)=2\Delta -2$
. Indeed, since erasing a vertex decreases the chromatic number by at most
![]() $1$
, we can produce subgraphs of H with chromatic number exactly
$1$
, we can produce subgraphs of H with chromatic number exactly
![]() $\ell $
for each
$\ell $
for each
![]() $\ell \leq 2\Delta -2$
.
$\ell \leq 2\Delta -2$
.
By Proposition 4.8, the graph
![]() $H_\Delta $
is almost
$H_\Delta $
is almost
![]() $\Delta $
-colorable and has chromatic number
$\Delta $
-colorable and has chromatic number
![]() $2\Delta -2$
. Then it is easy to see that taking the target graph
$2\Delta -2$
. Then it is easy to see that taking the target graph
![]() $\mathcal {H}$
as in Claim 4.7 gives the conclusion by Proposition 2.6 and Theorem 3.7.
$\mathcal {H}$
as in Claim 4.7 gives the conclusion by Proposition 2.6 and Theorem 3.7.
Remark 4.10. Interestingly, recent results connected to counterexamples to Hedetniemi’s conjecture yield Theorem 0.5 asymptotically, as
![]() $\Delta \to \infty $
. Recall that Hedetniemi’s conjecture is the statement that if
$\Delta \to \infty $
. Recall that Hedetniemi’s conjecture is the statement that if
![]() $G,H$
are finite graphs, then
$G,H$
are finite graphs, then
![]() $\chi (G \times H)=\min \{\chi (G),\chi (H)\}$
. This conjecture has been recently disproven by Shitov [Reference ShitovShi19], and strong counterexamples have been constructed later (see, [Reference Tardif and ZhuTZ19, Reference ZhuZhu21]). We claim that these imply for
$\chi (G \times H)=\min \{\chi (G),\chi (H)\}$
. This conjecture has been recently disproven by Shitov [Reference ShitovShi19], and strong counterexamples have been constructed later (see, [Reference Tardif and ZhuTZ19, Reference ZhuZhu21]). We claim that these imply for
![]() $\varepsilon>0$
the existence of finite graphs H with
$\varepsilon>0$
the existence of finite graphs H with
![]() $\chi (H) \geq (2-\varepsilon )\Delta $
to which
$\chi (H) \geq (2-\varepsilon )\Delta $
to which
![]() $\Delta $
-regular Borel forests cannot have, in general, a Borel homomorphism, for every large enough
$\Delta $
-regular Borel forests cannot have, in general, a Borel homomorphism, for every large enough
![]() $\Delta $
. Indeed, if a
$\Delta $
. Indeed, if a
![]() $\Delta $
-regular Borel forest admitted a Borel homomorphism to each finite graph of chromatic number at least
$\Delta $
-regular Borel forest admitted a Borel homomorphism to each finite graph of chromatic number at least
![]() $(2-\varepsilon )\Delta $
, it would have such a homomorphism to their product as well. Thus, we would obtain that the chromatic number of the product of any graphs of chromatic number
$(2-\varepsilon )\Delta $
, it would have such a homomorphism to their product as well. Thus, we would obtain that the chromatic number of the product of any graphs of chromatic number
![]() $(2-\varepsilon )\Delta $
is at least
$(2-\varepsilon )\Delta $
is at least
![]() $\Delta +1$
. This contradicts Zhu’s result [Reference ZhuZhu21], which states that the chromatic number of the product of graphs with chromatic number n can drop to
$\Delta +1$
. This contradicts Zhu’s result [Reference ZhuZhu21], which states that the chromatic number of the product of graphs with chromatic number n can drop to
![]() $\approx \frac {n}{2}$
.
$\approx \frac {n}{2}$
.
5 Remarks and further directions
Since the construction of homomorphism graphs is rather flexible, we expect that this method will find further applications. A direction that we do not take in this paper is to investigate homomorphism graphs corresponding to countable groups other than
![]() $\mathbb {Z}^{*\Delta }_2$
. Another possible direction could be to understand the connection of our method with hyperfiniteness.
$\mathbb {Z}^{*\Delta }_2$
. Another possible direction could be to understand the connection of our method with hyperfiniteness.
While Theorem 0.2 is optimal in the Borel context, one might hope that there is a positive answer in the case of graphs arising as compact, free subshifts of
![]() $2^{\mathbb {Z}^{*\Delta }_2}$
.
$2^{\mathbb {Z}^{*\Delta }_2}$
.
Question 5.1. Is there a characterization of Borel graphs with Borel chromatic number
![]() $\leq \Delta $
that are compact, free subshifts of the left-shift action of
$\leq \Delta $
that are compact, free subshifts of the left-shift action of
![]() $\mathbb {Z}^{*\Delta }_2$
on
$\mathbb {Z}^{*\Delta }_2$
on
![]() $2^{\mathbb {Z}^{*\Delta }_2}$
?
$2^{\mathbb {Z}^{*\Delta }_2}$
?
A way to answer this question on the negative would be to extend the machinery developed in [Reference Seward and Tucker-DrobSTD16] or [Reference BernshteynBer21], so that the produced equivariant maps preserve the Borel chromatic number, their range is compact, and then apply Theorem 0.2; however, this seems to require a significant amount of new ideas.
Let us point out that Theorem 0.1 has a particularly nice form, if we assume Projective Determinacy or replace the Axiom of Choice with the Axiom of Determinacy (see, e.g. [Reference Caicedo and KetchersidCK11] for related results).
Theorem 5.2. Let
![]() $\Delta>2$
.
$\Delta>2$
.
-
• (
 $\mathtt {PD}$
) Let
$\mathtt {PD}$
) Let
 $\mathcal {H}$
be a locally countable Borel graph. Then where
$\mathcal {H}$
be a locally countable Borel graph. Then where $$\begin{align*}\chi_{pr}(\mathcal{H})>\Delta \iff \chi_{pr}(\operatorname{\mathbf{ Hom}}^{ac}(T_\Delta,\mathcal{H}))>\Delta,\end{align*}$$
$$\begin{align*}\chi_{pr}(\mathcal{H})>\Delta \iff \chi_{pr}(\operatorname{\mathbf{ Hom}}^{ac}(T_\Delta,\mathcal{H}))>\Delta,\end{align*}$$
 $\chi _{pr}$
stands for the projective chromatic number of
$\chi _{pr}$
stands for the projective chromatic number of
 $\mathcal {H}$
.
$\mathcal {H}$
.
-
• (
 $\mathtt {AD}+\mathtt {DC}_{\aleph _0}$
) Let
$\mathtt {AD}+\mathtt {DC}_{\aleph _0}$
) Let
 $\mathcal {H}$
be a locally countable graph on a Polish space. Then
$\mathcal {H}$
be a locally countable graph on a Polish space. Then  $$\begin{align*}\chi(\mathcal{H})>\Delta \iff \chi(\operatorname{\mathbf{ Hom}}^{ac}(T_\Delta,\mathcal{H}))>\Delta.\end{align*}$$
$$\begin{align*}\chi(\mathcal{H})>\Delta \iff \chi(\operatorname{\mathbf{ Hom}}^{ac}(T_\Delta,\mathcal{H}))>\Delta.\end{align*}$$
Acknowledgements
We would like to thank Anton Bernshteyn, Mohsen Ghaffari, Steve Jackson, Alex Kastner, Alexander Kechris, Yurii Khomskii, Clark Lyons, Andrew Marks, Oleg Pikhurko, Brandon Seward, Jukka Suomela, and Yufan Zheng for insightful discussions. The second author was partially supported by Dr. Max Rössler, by the Walter Haefner Foundation, and by the Eidgenössische Technische Hochschule (ETH) Zürich Foundation. The third author was supported by Leverhulme Research Project Grant RPG-2018-424. The main part of this work was carried out while he was affiliated with University of Warwick. The fourth author was supported by the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation programme (grant agreement No. 853109). The sixth author was partially supported by the National Research, Development and Innovation Office – Nemzeti Kutatási, Fejlesztési és Innovációs Hivatal (NKFIH), grants no. 113047, no. 129211 and Fonds zur Förderung der wissenschaftlichen Forschung (FWF) Grant M2779. The main part of this work was carried out while affiliated with California Institute of Technology (Caltech).
Competing interests
The authors have no competing interest to declare.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.