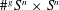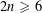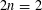Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Krannich, Manuel
2020.
A NOTE ON RATIONAL HOMOLOGICAL STABILITY OF AUTOMORPHISMS OF MANIFOLDS.
The Quarterly Journal of Mathematics,
Vol. 71,
Issue. 3,
p.
1069.
Botvinnik, Boris
Ebert, Johannes
and
Wraith, David
2020.
On the topology of the space of Ricci-positive metrics.
Proceedings of the American Mathematical Society,
Vol. 148,
Issue. 9,
p.
3997.
Kupers, Alexander
and
Randal-Williams, Oscar
2020.
The cohomology of Torelli groups is algebraic.
Forum of Mathematics, Sigma,
Vol. 8,
Issue. ,
Gaifullin, A. A.
2021.
On a spectral sequence for the action of the Torelli group of genus
on the complex of cycles.
Izvestiya: Mathematics,
Vol. 85,
Issue. 6,
p.
1060.
Gaifullin, Alexander Aleksandrovich
2021.
О спектральной последовательности для действия группы Торелли рода $3$ на комплексе циклов.
Известия Российской академии наук. Серия математическая,
Vol. 85,
Issue. 6,
p.
27.
Lindell, Erik
2023.
ABELIAN CYCLES IN THE HOMOLOGY OF THE TORELLI GROUP.
Journal of the Institute of Mathematics of Jussieu,
Vol. 22,
Issue. 4,
p.
1703.
Kupers, Alexander
and
Randal-Williams, Oscar
2023.
On the Torelli Lie algebra.
Forum of Mathematics, Pi,
Vol. 11,
Issue. ,
Felder, Matteo
Naef, Florian
and
Willwacher, Thomas
2023.
Stable cohomology of graph complexes.
Selecta Mathematica,
Vol. 29,
Issue. 2,
Kupers, Alexander
and
Randal-Williams, Oscar
2024.
On diffeomorphisms of even-dimensional discs.
Journal of the American Mathematical Society,
Vol. 38,
Issue. 1,
p.
63.
Kawazumi, Nariya
and
Soulié, Arthur
2024.
Stable twisted cohomology of the mapping class groups in the unit tangent bundle homology.
Bulletin of the London Mathematical Society,
Vol. 56,
Issue. 11,
p.
3358.
Randal-Williams, Oscar
2024.
On the Cohomology of Torelli Groups. II.
International Mathematics Research Notices,
Vol. 2024,
Issue. 3,
p.
2339.
HABIRO, Kazuo
and
KATADA, Mai
2025.
On the stable cohomology of the $\operatorname{IA}$-automorphism groups of free groups.
Journal of the Mathematical Society of Japan,
Vol. 77,
Issue. 2,