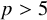1 Introduction
In recent years, there has been much progress in understanding the birational geometry of threefolds over algebraically closed fields of characteristic
![]() $p>0$
by using methods inspired by the theory of F-singularities. One of the main achievements in this area is the proof of the minimal model program (MMP) in dimension three in wide generality (see, e.g., [Reference Hacon and XuHX15], [Reference Cascini, Tanaka and XuCTX15], [Reference BirkarBir16], [Reference Birkar and WaldronBW17], [Reference Hacon and WitaszekHW21], [Reference Hacon and WitaszekHW22]).
$p>0$
by using methods inspired by the theory of F-singularities. One of the main achievements in this area is the proof of the minimal model program (MMP) in dimension three in wide generality (see, e.g., [Reference Hacon and XuHX15], [Reference Cascini, Tanaka and XuCTX15], [Reference BirkarBir16], [Reference Birkar and WaldronBW17], [Reference Hacon and WitaszekHW21], [Reference Hacon and WitaszekHW22]).
Long before these developments, Kawamata has established the validity of the semistable MMP in dimension three based on classification results ([Reference KawamataKaw94]). Although weaker than the general form of the MMP, this has nevertheless led to plenty of applications, especially concerning Tate’s conjecture and criteria for the existence of good reductions for K3 surfaces and other classes of varieties, generalising Serre–Tate’s and Néron-Ogg–Shafarevich results for abelian varieties (see, e.g., [Reference MaulikMau14, Reference Liedtke and YuyaLM18, Reference Chiarellotto, Lazda and LiedtkeCLL22, Reference Chiarellotto and LazdaCL16]). The purpose of our paper is to extend the semistable MMP (and also the MMP for resolutions of singularities) to dimension four and derive applications thereof. This is the first step towards establishing the MMP in full generality for fourfolds in high characteristic. In view of the recent developments in mixed characteristic ([Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20]), we are also able to provide results on the MMP for arithmetic fourfolds. In particular, we can address questions about the MMP of lifts of positive characteristic three-dimensional varieties which arose after the work of Kawamata.
For the convenience of the reader, we state the simplified versions of our main theorems and refer to Theorems 4.1, 5.1, 6.1, 6.2 for the precise statements. In particular, in all the results below we assume that log resolution of four-dimensional varieties exists.
Theorem 1.1 (Theorem 4.1)
Every log resolution of a four-dimensional
![]() ${\mathbb {Q}}$
-factorial klt singularity with perfect residue field of characteristic
${\mathbb {Q}}$
-factorial klt singularity with perfect residue field of characteristic
![]() $p>5$
decomposes into a sequence of steps of the MMP.
$p>5$
decomposes into a sequence of steps of the MMP.
More generally, we show that we can run a dlt MMP on a log resolution of every
![]() ${\mathbb {Q}}$
-factorial singularity.
${\mathbb {Q}}$
-factorial singularity.
Theorem 1.2 (Theorem 5.1)
The MMP may be run on every four-dimensional semistable variety of nonnegative Kodaira dimension which is projective over a discrete valuation ring with perfect residue field of characteristic
![]() $p>5$
.
$p>5$
.
The assumption on the residue field being perfect is necessary as the three-dimensional base point free theorem is not known in full generality in a more general setting (for example, when the residue field is F-finite). Note that the assumptions on the Kodaira dimension and the base of the MMP have been weakened after our article was made available by improving on our termination results (see [Reference Xie and XueXX21a]).
In order to show the above theorems, we find a new way of constructing flips when the boundary contains an ample divisor (see Theorem 1.6). This key technical result is explained in the next subsection of the introduction.
As in [Reference Hacon and WitaszekHW21], Theorem 1.1 allows us to derive a series of results for
![]() ${\mathbb {Q}}$
-factorial four-dimensional singularities, which in characteristic 0 are proven using vanishing theorems. In particular, we show that positive characteristic klt singularities are
${\mathbb {Q}}$
-factorial four-dimensional singularities, which in characteristic 0 are proven using vanishing theorems. In particular, we show that positive characteristic klt singularities are
![]() $W{\mathcal {O}}_X$
-rational, dlt modifications exist and the inversion of adjunction holds (Corollaries 4.7, 4.8, 4.9). The first result implies the following generalisation of the Chevalley–Warning criterion (see [Reference EsnaultEsn03, Corollary 1.3] for the smooth rationally chain connected case in any dimension and its generalisation to the klt case in dimension three by [Reference Gongyo, Nakamura and HiromuGNH19]).
$W{\mathcal {O}}_X$
-rational, dlt modifications exist and the inversion of adjunction holds (Corollaries 4.7, 4.8, 4.9). The first result implies the following generalisation of the Chevalley–Warning criterion (see [Reference EsnaultEsn03, Corollary 1.3] for the smooth rationally chain connected case in any dimension and its generalisation to the klt case in dimension three by [Reference Gongyo, Nakamura and HiromuGNH19]).
Corollary 1.3. Every four-dimensional geometrically connected
![]() ${\mathbb {Q}}$
-factorial klt variety X which is projective over a finite field
${\mathbb {Q}}$
-factorial klt variety X which is projective over a finite field
![]() $\mathbb {F}_{q}$
of characteristic
$\mathbb {F}_{q}$
of characteristic
![]() $p>5$
and which admits a rationally chain connected log resolution satisfies
$p>5$
and which admits a rationally chain connected log resolution satisfies
![]() $|X(\mathbb {F}_q)| \equiv 1 \pmod q$
.
$|X(\mathbb {F}_q)| \equiv 1 \pmod q$
.
In particular, X admits a rational point. For the definition of rational chain connectedness, we refer to [Reference Gongyo, Nakamura and HiromuGNH19, Definition 4.5].
Similarly, one should be able to extend other statements from dimension three in positive characteristic to dimension four, such as finite generatedness of the local Picard group (cf. [Reference Carvajal-Rojas, Stäbler and KollárCSK20]) or, assuming the Borisov-Alexeev-Borisov (BAB) conjecture in dimension three, finiteness of the tame étale fundamental group. To avoid making our article too long, we do not write down proofs of these results here.
Theorem 1.2 can be used, for example, to construct canonical skeleta of degenerations of varieties with nonnegative Kodaira dimension ([Reference Nicaise and XuNX16]) and allows for descending deformations of threefolds under operations of the MMP. In particular, we are able to provide a positive answer to [Reference Hacon and WitaszekHW19, Question 5.2] for lifts to characteristic 0 contingent upon the resolutions of singularities. This gives a new insight into the results of [Reference Liedtke and MatthewLS14] on the behaviour of liftability under birational maps.
Corollary 1.4 (Theorem 6.1)
Let X be a
![]() ${\mathbb {Q}}$
-factorial terminal projective three-dimensional variety over a perfect field of characteristic
${\mathbb {Q}}$
-factorial terminal projective three-dimensional variety over a perfect field of characteristic
![]() $p>5$
. Suppose that
$p>5$
. Suppose that
![]() $K_X$
is pseudo-effective and that X lifts to characteristic 0. Then a (possibly non-
$K_X$
is pseudo-effective and that X lifts to characteristic 0. Then a (possibly non-
![]() ${\mathbb {Q}}$
-factorial) minimal model of X lifts to characteristic 0 as well.
${\mathbb {Q}}$
-factorial) minimal model of X lifts to characteristic 0 as well.
As a corollary to the full statement of the above result (Theorem 6.1), we get that liftability of three-dimensional terminal Calabi–Yau varieties is a birational invariant. Here, we say that a projective variety X is Calabi–Yau if
![]() $\omega _X$
is trivial and
$\omega _X$
is trivial and
![]() $H^i(X,{\mathcal {O}}_X)=0$
for
$H^i(X,{\mathcal {O}}_X)=0$
for
![]() $0 < i < \mathrm {dim}\, X$
.
$0 < i < \mathrm {dim}\, X$
.
Corollary 1.5 (Theorem 6.2)
Let X and Y be three-dimensional terminal
![]() ${\mathbb {Q}}$
-factorial projective Calabi–Yau varieties defined over a perfect field of characteristic
${\mathbb {Q}}$
-factorial projective Calabi–Yau varieties defined over a perfect field of characteristic
![]() $p>5$
. Suppose that X and Y are birational and that X lifts to characteristic 0. Then Y lifts to characteristic 0 as well.
$p>5$
. Suppose that X and Y are birational and that X lifts to characteristic 0. Then Y lifts to characteristic 0 as well.
We hope that Theorem 1.2 will also find applications in the study of Néron–Ogg–Shafarevich-type criteria for good reductions of three-dimensional varieties.
The idea of the proof of Theorem 1.1
Here, we explain the proof in positive characteristic. The mixed characteristic case is analogous with
![]() $S^0$
and F-regularity replaced by
$S^0$
and F-regularity replaced by
![]() $B^0$
and
$B^0$
and
![]() $+$
-regularity, respectively, as developed in [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20].
$+$
-regularity, respectively, as developed in [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20].
By the same arguments as in [Reference BirkarBir16], we can assume that
![]() $\Delta $
has standard coefficients. Our strategy follows the ideas developed in [Reference Hacon and WitaszekHW21]. The main new difficulty is to show the existence of pl-flips occurring in the above MMP. As observed in [Reference Hacon and WitaszekHW21], the corresponding pl-flipping contractions contain a relatively ample divisor in the boundary. In particular, by applying inversion of F-adjunction twice and using the F-regularity of relative log Fano surfaces in the birational case (see [Reference Hacon and XuHX15, Theorem 3.1]) we can deduce that these pl-flipping contractions are relatively purely F-regular (up to a small perturbation); see Theorem 4.3.
$\Delta $
has standard coefficients. Our strategy follows the ideas developed in [Reference Hacon and WitaszekHW21]. The main new difficulty is to show the existence of pl-flips occurring in the above MMP. As observed in [Reference Hacon and WitaszekHW21], the corresponding pl-flipping contractions contain a relatively ample divisor in the boundary. In particular, by applying inversion of F-adjunction twice and using the F-regularity of relative log Fano surfaces in the birational case (see [Reference Hacon and XuHX15, Theorem 3.1]) we can deduce that these pl-flipping contractions are relatively purely F-regular (up to a small perturbation); see Theorem 4.3.
Unluckily, in contrast to the three-dimensional case ([Reference Hacon and XuHX15]), this is not enough to conclude the existence of flips. Indeed, [Reference Hacon and XuHX15] employs a strategy of Shokurov for constructing flips which is not valid in higher dimensions. On the other hand, it is not clear how to generalise the higher-dimensional proof of the existence of flips ([Reference Hacon and McKernanHMK10]) from characteristic 0 to positive characteristic in this setting, as the proof calls for applying vanishing theorems on a log resolution, in which case the relative pure F-regularity is lost.
As mentioned earlier, we address this problem by finding a new way of constructing flips when the boundary contains a relatively ample divisor.
Theorem 1.6 (cf. Theorem 4.3)
Let
![]() $(X,S+A+B)$
be an n-dimensional
$(X,S+A+B)$
be an n-dimensional
![]() ${\mathbb {Q}}$
-factorial dlt pair defined over an F-finite field of characteristic
${\mathbb {Q}}$
-factorial dlt pair defined over an F-finite field of characteristic
![]() $p>0$
and let
$p>0$
and let
![]() $f \colon X \to Z$
be a
$f \colon X \to Z$
be a
![]() $(K_X+S+A+B)$
-flipping contraction with
$(K_X+S+A+B)$
-flipping contraction with
![]() $\rho (X/Z)=1$
, where S is an f-anti-ample divisor, A is an f-ample divisor and
$\rho (X/Z)=1$
, where S is an f-anti-ample divisor, A is an f-ample divisor and
![]() $\lfloor B \rfloor = 0$
. Suppose that the MMP is valid in dimension
$\lfloor B \rfloor = 0$
. Suppose that the MMP is valid in dimension
![]() $n-1$
. If
$n-1$
. If
![]() $(X,S+(1-\epsilon )A+B)$
is relatively purely F-regular for all
$(X,S+(1-\epsilon )A+B)$
is relatively purely F-regular for all
![]() $0 < \epsilon < 1$
, then the flip of f exists.
$0 < \epsilon < 1$
, then the flip of f exists.
In fact, we show that
![]() $H^0(X, m(K_X+S+A+B))\to H^0(S, m(K_{S}+A_{S}+B_{S}))$
is surjective for all
$H^0(X, m(K_X+S+A+B))\to H^0(S, m(K_{S}+A_{S}+B_{S}))$
is surjective for all
![]() $m>0$
sufficiently divisible, where
$m>0$
sufficiently divisible, where
![]() $K_S+A_S+B_S = (K_X+S+A+B)|_S$
(Proposition 3.1). In particular, the finite generatedness of canonical rings in dimension
$K_S+A_S+B_S = (K_X+S+A+B)|_S$
(Proposition 3.1). In particular, the finite generatedness of canonical rings in dimension
![]() $n-1$
implies that the canonical ring of
$n-1$
implies that the canonical ring of
![]() $(X,S+A+B)$
is finitely generated as well, and so its projectivisation is the sought-for flip. Note that this surjectivity is false without the ample divisor in the boundary (see [Reference de Fernex and HacondFH11, Remark 4.9]).
$(X,S+A+B)$
is finitely generated as well, and so its projectivisation is the sought-for flip. Note that this surjectivity is false without the ample divisor in the boundary (see [Reference de Fernex and HacondFH11, Remark 4.9]).
Resolutions of singularities
It is natural to wonder if the assumption on the existence of log resolutions can be dropped. In general, this seems to be a very difficult problem in view of the fact that alterations or quasi-resolutions do not behave nicely with respect to the canonical divisor. However, one may hope to remove this assumption if we start to run the MMP on a regular variety, and this is, to some extent, the case (see Proposition 5.8) provided a much weaker assertion: that embedded log resolutions of subschemes of smooth fourfolds exist. Note, however, that the current proofs of Theorem 1.1 and of Theorem 1.2 (and so that of Corollary 1.3, Corollary 1.4 and Corollary 1.5 as well) require additionally that the log resolutions are constructed by a sequence of blowups along the non-simple normal crossing locus (non-snc locus) (see the second paragraph of the proof of Theorem 4.1 and of the proof of Claim 5.5).
Mixed charactieristic
The original version of this article covered the positive characteristic case only. A few months after its submission to the arxiv, [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20] developed the mixed characteristic analogues of
![]() $S^0$
and F-regularity and proved the validity of the three-dimensional MMP for arithmetic threefolds. In view of this and recent results on relative semiampleness ([Reference WitaszekWit21b]), the original results of our article generalise to mixed characteristic with small modifications. The current updated version of our paper incorporates these generalisations and several applications thereof.
$S^0$
and F-regularity and proved the validity of the three-dimensional MMP for arithmetic threefolds. In view of this and recent results on relative semiampleness ([Reference WitaszekWit21b]), the original results of our article generalise to mixed characteristic with small modifications. The current updated version of our paper incorporates these generalisations and several applications thereof.
We also note that results on the three-dimensional MMP in mixed characteristic in the semistable case (in a wider generality than that of Kawamata) were obtained in [Reference Takamatsu and YoshikawaTY20] independently of [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20]. The geometric part of their proof is based on the ideas of the original version of our article and on [Reference Hacon and WitaszekHW21]. In particular, [Reference Takamatsu and YoshikawaTY20] generalised our Theorem 1.6 to mixed characteristic before this updated version of our article was submitted.
The notions of
![]() $+$
-regularity and
$+$
-regularity and
![]() $+$
-stable sections (
$+$
-stable sections (
![]() $B^0$
) work in both positive and mixed characteristic, and so we could restate the whole article to avoid the use of F-regularity and Frobenius stable sections (
$B^0$
) work in both positive and mixed characteristic, and so we could restate the whole article to avoid the use of F-regularity and Frobenius stable sections (
![]() $S^0$
). We decided against doing so, instead treating positive and mixed characteristic cases separately, to prevent our article from being unnecessarily technical for the readers interested in the positive characteristic case only. The notion of F-regularity has been in use for a long time, in contrast to
$S^0$
). We decided against doing so, instead treating positive and mixed characteristic cases separately, to prevent our article from being unnecessarily technical for the readers interested in the positive characteristic case only. The notion of F-regularity has been in use for a long time, in contrast to
![]() $+$
-regularity which was introduced recently and is more technically involved.
$+$
-regularity which was introduced recently and is more technically involved.
In the mixed characteristic case, some of our results are valid beyond the case of schemes defined over discrete valuation rings (DVRs) (see, e.g., the setting of [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20]). For the sake of readability and in order to avoid dealing with unnecessary technicalities, we do not strive to provide the most general version. Note, however, that there is a fundamental obstacle to generalising Theorem 5.1 to the case of Dedekind domains such as
![]() $\operatorname {\mathrm {Spec}} \mathbb {Z}$
(or
$\operatorname {\mathrm {Spec}} \mathbb {Z}$
(or
![]() $\operatorname {\mathrm {Spec}} k[t])$
) due to the issues with termination of flips; indeed, over such a base it could a priori happen that there is an infinite sequence of flipping curves contained in fibres over different prime numbers (fortunately, this has been now resolved in [Reference Xie and XueXX21a]). Furthermore, Theorem 5.1 needs the residue field to be perfect so that we can invoke the three-dimensional base point free theorem as well as [Reference Nakamura and TanakaNT20], and the positive characteristic case thereof requires essentially that the base spreads out over an algebraically closed field so that we can apply positive characteristic Bertini theorems from [Reference Schwede and ZhangSZ13].
$\operatorname {\mathrm {Spec}} k[t])$
) due to the issues with termination of flips; indeed, over such a base it could a priori happen that there is an infinite sequence of flipping curves contained in fibres over different prime numbers (fortunately, this has been now resolved in [Reference Xie and XueXX21a]). Furthermore, Theorem 5.1 needs the residue field to be perfect so that we can invoke the three-dimensional base point free theorem as well as [Reference Nakamura and TanakaNT20], and the positive characteristic case thereof requires essentially that the base spreads out over an algebraically closed field so that we can apply positive characteristic Bertini theorems from [Reference Schwede and ZhangSZ13].
To align with the notation in the positive characteristic case, we use the word variety (as defined in the preliminaries below) even for schemes over DVRs. We hope that this will not cause any confusion for the reader.
2 Preliminaries
A scheme X will be called a variety if it is integral, separated and of finite type over a field k or a divisorial valuation ring R. Throughout this paper, unless otherwise stated, we work over F-finite fields k of characteristic
![]() $p>0$
or DVRs R of characteristic
$p>0$
or DVRs R of characteristic
![]() $(0,p)$
for
$(0,p)$
for
![]() $p\geq 0$
.
$p\geq 0$
.
We refer the reader to [Reference Kollár and MoriKM98] for the standard definitions and results of the MMP, to [Reference Hacon and WitaszekHW21] for a brief introduction to F-singularities and to [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20] for the results on
![]() $+$
-regularity. Further, we refer to [Reference Gongyo, Nakamura and HiromuGNH19, Remark 2.7] for a discussion on properties of varieties which are independent of a base change from a perfect field. We warn the reader that
$+$
-regularity. Further, we refer to [Reference Gongyo, Nakamura and HiromuGNH19, Remark 2.7] for a discussion on properties of varieties which are independent of a base change from a perfect field. We warn the reader that
![]() ${\mathbb {Q}}$
-factoriality is not such a property.
${\mathbb {Q}}$
-factoriality is not such a property.
In this paper, a pair
![]() $(X,B)$
consists of a normal variety X and an effective
$(X,B)$
consists of a normal variety X and an effective
![]() ${\mathbb {Q}}$
-divisor B such that
${\mathbb {Q}}$
-divisor B such that
![]() $K_X+B$
is
$K_X+B$
is
![]() ${\mathbb {Q}}$
-Cartier. The pair
${\mathbb {Q}}$
-Cartier. The pair
![]() $(X,B)$
is kawamata log terminal (klt) (resp. log canonical (lc)) if for any proper birational morphism
$(X,B)$
is kawamata log terminal (klt) (resp. log canonical (lc)) if for any proper birational morphism
![]() $f \colon Y\to X$
and any prime divisor E on Y we have
$f \colon Y\to X$
and any prime divisor E on Y we have
![]() $\textrm {mult}_E(B_Y)<1$
(resp.
$\textrm {mult}_E(B_Y)<1$
(resp.
![]() $\textrm {mult}_E(B_Y)\leq 1$
), where
$\textrm {mult}_E(B_Y)\leq 1$
), where
![]() $K_Y+B_Y=f^*(K_X+B)$
. If
$K_Y+B_Y=f^*(K_X+B)$
. If
![]() $(X,B)$
admits a log resolution
$(X,B)$
admits a log resolution
![]() $f \colon Y\to X$
, then it suffices to check the above condition for all prime divisors E on Y.
$f \colon Y\to X$
, then it suffices to check the above condition for all prime divisors E on Y.
In the article, we often consider log resolutions of singularities
![]() $f \colon Y \to X$
of dlt pairs
$f \colon Y \to X$
of dlt pairs
![]() $(X,\Delta )$
which are isomorphisms over the generic points of the strata of
$(X,\Delta )$
which are isomorphisms over the generic points of the strata of
![]() $(X,\Delta )$
. Every log resolution f constructed by a sequence of blowups along the non-snc locus satisfies this property. Note that using the notation from [Reference KollárKol13, Definition 2.79 and Theorem 2.87], such f is a morphism which is both a log resolution and a thrifty resolution.
$(X,\Delta )$
. Every log resolution f constructed by a sequence of blowups along the non-snc locus satisfies this property. Note that using the notation from [Reference KollárKol13, Definition 2.79 and Theorem 2.87], such f is a morphism which is both a log resolution and a thrifty resolution.
The definitions of singularities in birational geometry may be found in [Reference KollárKol13] and [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Section 2.5]. We say that a pair
![]() $(X,B)$
such that
$(X,B)$
such that
![]() $B=\sum b_iB_i$
with
$B=\sum b_iB_i$
with
![]() $0\leq b_i\leq 1$
is divisorially log terminal (dlt) if there exists an open subset
$0\leq b_i\leq 1$
is divisorially log terminal (dlt) if there exists an open subset
![]() $U\subset X$
such that U is regular and
$U\subset X$
such that U is regular and
![]() $B|_U$
has simple normal crossings support and for every proper birational morphism
$B|_U$
has simple normal crossings support and for every proper birational morphism
![]() $f \colon Y\to X$
and any prime divisor E on Y with centre Z contained in
$f \colon Y\to X$
and any prime divisor E on Y with centre Z contained in
![]() $X\setminus U$
, we have
$X\setminus U$
, we have
![]() $\textrm {mult}_E(B_Y)<1$
. We say that
$\textrm {mult}_E(B_Y)<1$
. We say that
![]() $a_E(X,B):=1-\textrm {mult}_E(B_Y)$
is the log discrepancy of
$a_E(X,B):=1-\textrm {mult}_E(B_Y)$
is the log discrepancy of
![]() $(X,B)$
along E. A pair
$(X,B)$
along E. A pair
![]() $(X,S+B)$
with
$(X,S+B)$
with
![]() $\lfloor S+B\rfloor =S$
irreducible is purely log terminal (plt) if
$\lfloor S+B\rfloor =S$
irreducible is purely log terminal (plt) if
![]() $a_E(X,S+B)>0$
for any
$a_E(X,S+B)>0$
for any
![]() $E\ne S$
.
$E\ne S$
.
A morphism of schemes
![]() $f\colon X\to Y$
is a universal homeomorphism if for any morphism
$f\colon X\to Y$
is a universal homeomorphism if for any morphism
![]() $Y'\to Y$
, the induced morphism
$Y'\to Y$
, the induced morphism
![]() $X'=X\times _Y Y'\to Y'$
is a homeomorphism. In positive characteristic, it is known that a finite morphism is a universal homeomorphism if and only if it factors a sufficiently high power of the Frobenius morphism [Reference KollárKol97, Proposition 6.6]. We say that a variety X is normal up to universal homeomorphism if its normalisation
$X'=X\times _Y Y'\to Y'$
is a homeomorphism. In positive characteristic, it is known that a finite morphism is a universal homeomorphism if and only if it factors a sufficiently high power of the Frobenius morphism [Reference KollárKol97, Proposition 6.6]. We say that a variety X is normal up to universal homeomorphism if its normalisation
![]() $X^{\nu } \to X$
is a universal homeomorphism. We learned the following result from János Kollár.
$X^{\nu } \to X$
is a universal homeomorphism. We learned the following result from János Kollár.
Lemma 2.1. Let
![]() $(X,D+\Delta )$
be a dlt pair with D prime and
$(X,D+\Delta )$
be a dlt pair with D prime and
![]() ${\mathbb {Q}}$
-Cartier. Then D is normal up to universal homeomorphism.
${\mathbb {Q}}$
-Cartier. Then D is normal up to universal homeomorphism.
Proof. By [Reference KollárKol16, Theorem 41], it is enough to show that
![]() $D^{\mathrm sh} \,\backslash \, \{x^{\mathrm sh}\}$
is connected for the Henselisation
$D^{\mathrm sh} \,\backslash \, \{x^{\mathrm sh}\}$
is connected for the Henselisation
![]() $D^{\mathrm sh}$
of D at every point
$D^{\mathrm sh}$
of D at every point
![]() $x \in D$
. If x is a point of codimension at most two in X, then this follows by surface theory (cf. [Reference KollárKol13]) as
$x \in D$
. If x is a point of codimension at most two in X, then this follows by surface theory (cf. [Reference KollárKol13]) as
![]() $(X,D+\Delta )$
is dlt. Thus, we may assume that x is of codimension at least three in X. Let
$(X,D+\Delta )$
is dlt. Thus, we may assume that x is of codimension at least three in X. Let
![]() $X^{\wedge }$
and
$X^{\wedge }$
and
![]() $D^{\wedge }$
be the completions of X and D at x, respectively. It is enough to show that
$D^{\wedge }$
be the completions of X and D at x, respectively. It is enough to show that
![]() $D^{\wedge } \,\backslash \, \{x\}$
is connected. Note that
$D^{\wedge } \,\backslash \, \{x\}$
is connected. Note that
![]() $X^{\wedge }$
is normal ([Sta14, Tag 033C, 07GC, 037D] and [Reference PopescuPop00, Lemma 2.7]), hence
$X^{\wedge }$
is normal ([Sta14, Tag 033C, 07GC, 037D] and [Reference PopescuPop00, Lemma 2.7]), hence
![]() $S_2$
, and so
$S_2$
, and so
![]() $X^{\wedge } \,\backslash \, \{x\}$
is connected. Moreover,
$X^{\wedge } \,\backslash \, \{x\}$
is connected. Moreover,
![]() $X^{\wedge } \,\backslash \, \{x\}$
is S2 at every closed point
$X^{\wedge } \,\backslash \, \{x\}$
is S2 at every closed point
![]() $x' \in X^{\wedge } \,\backslash \, \{x\}$
(as the scheme is Catenary, the codimension of
$x' \in X^{\wedge } \,\backslash \, \{x\}$
(as the scheme is Catenary, the codimension of
![]() $x'$
in
$x'$
in
![]() $X^{\wedge }$
is at least two). Since
$X^{\wedge }$
is at least two). Since
![]() $D^{\wedge }$
is of codimension one ([Sta14, Tag 07NV]) and
$D^{\wedge }$
is of codimension one ([Sta14, Tag 07NV]) and
![]() ${\mathbb {Q}}$
-Cartier, we can apply the local Lefschetz property of [Reference GrothendieckGro62, XIII.2, Theorem 2.1, p. 139] to a Cartier multiple of
${\mathbb {Q}}$
-Cartier, we can apply the local Lefschetz property of [Reference GrothendieckGro62, XIII.2, Theorem 2.1, p. 139] to a Cartier multiple of
![]() $D^{\wedge }$
to conclude the proof.
$D^{\wedge }$
to conclude the proof.
We refer to [Reference Gongyo, Nakamura and HiromuGNH19] and [Reference Hacon and WitaszekHW21, Subsection 2.3] for the notion of
![]() $W{\mathcal {O}}$
-rational singularities in positive characteristic. Since log resolutions of singularities are not known to exist beyond dimension three, a positive characteristic singularity X is called
$W{\mathcal {O}}$
-rational singularities in positive characteristic. Since log resolutions of singularities are not known to exist beyond dimension three, a positive characteristic singularity X is called
![]() $W{\mathcal {O}}$
-rational if
$W{\mathcal {O}}$
-rational if
![]() $R^if_*W{\mathcal {O}}_{V,{\mathbb {Q}}}= 0$
for
$R^if_*W{\mathcal {O}}_{V,{\mathbb {Q}}}= 0$
for
![]() $i>0$
and every quasi-resolution
$i>0$
and every quasi-resolution
![]() $f \colon V \to X$
(see [Reference Gongyo, Nakamura and HiromuGNH19, Section 3]). Note that it is enough to verify this condition on a single quasi-resolution ([Reference Chatzistamatiou and RüllingCR12, Corollary 4.5.1]). In particular, if X admits a usual resolution of singularities, we can verify this condition on it.
$f \colon V \to X$
(see [Reference Gongyo, Nakamura and HiromuGNH19, Section 3]). Note that it is enough to verify this condition on a single quasi-resolution ([Reference Chatzistamatiou and RüllingCR12, Corollary 4.5.1]). In particular, if X admits a usual resolution of singularities, we can verify this condition on it.
Lemma 2.2. Let
![]() $(X,\Delta )$
be a
$(X,\Delta )$
be a
![]() ${\mathbb {Q}}$
-factorial dlt pair and S an irreducible component of
${\mathbb {Q}}$
-factorial dlt pair and S an irreducible component of
![]() $\lfloor \Delta \rfloor $
. If
$\lfloor \Delta \rfloor $
. If
![]() $S^{\nu } \to S$
is the normalisation and
$S^{\nu } \to S$
is the normalisation and
![]() $K_{S^{\nu }}+\Delta _{S^{\nu }}=(K_X+\Delta )|_{S^{\nu }}$
, then
$K_{S^{\nu }}+\Delta _{S^{\nu }}=(K_X+\Delta )|_{S^{\nu }}$
, then
![]() $(S^{\nu },\Delta _{S^{\nu }})$
is dlt and there is a bijection between the strata of
$(S^{\nu },\Delta _{S^{\nu }})$
is dlt and there is a bijection between the strata of
![]() $\lfloor \Delta _{S^{\nu }}\rfloor $
and the strata of
$\lfloor \Delta _{S^{\nu }}\rfloor $
and the strata of
![]() $\lfloor \Delta \rfloor $
that are contained in S.
$\lfloor \Delta \rfloor $
that are contained in S.
Let
![]() $P\in S$
be any codimension 1 point on S and m the Cartier index of
$P\in S$
be any codimension 1 point on S and m the Cartier index of
![]() $K_X$
at P. Then on a neighbourhood of
$K_X$
at P. Then on a neighbourhood of
![]() $P\in X$
,
$P\in X$
,
![]() $mD$
is Cartier for any divisor D, and S is normal, and
$mD$
is Cartier for any divisor D, and S is normal, and
![]() $(K_X+S)|_S=K_S+(1-\frac 1 m )P$
.
$(K_X+S)|_S=K_S+(1-\frac 1 m )P$
.
Proof. By assumption, there is an open subset
![]() $U\subset X$
containing the generic points of every strata of
$U\subset X$
containing the generic points of every strata of
![]() $\lfloor \Delta \rfloor $
such that
$\lfloor \Delta \rfloor $
such that
![]() $(U,\lfloor \Delta \rfloor |_U)$
has simple normal crossings and the complement
$(U,\lfloor \Delta \rfloor |_U)$
has simple normal crossings and the complement
![]() $Z=X\setminus U$
contains no non-klt centres. Then, it is easy to see that
$Z=X\setminus U$
contains no non-klt centres. Then, it is easy to see that
![]() $(S\cap U, \lfloor \Delta \rfloor |_{S\cap U})=(S^{\nu }\cap U,\lfloor \Delta _{S^{\nu }}\rfloor |_{S^{\nu }\cap U})$
has simple normal crossings. Let E be an exceptional divisor over S with centre
$(S\cap U, \lfloor \Delta \rfloor |_{S\cap U})=(S^{\nu }\cap U,\lfloor \Delta _{S^{\nu }}\rfloor |_{S^{\nu }\cap U})$
has simple normal crossings. Let E be an exceptional divisor over S with centre
![]() $c_E$
whose generic point is not contained in
$c_E$
whose generic point is not contained in
![]() $\lfloor \Delta \rfloor |_{S\cap U}$
, and let I be an ideal sheaf on S, the blowup of which contains E. By blowing up the pushforward of I on X and taking the normalisation, we may construct a morphism
$\lfloor \Delta \rfloor |_{S\cap U}$
, and let I be an ideal sheaf on S, the blowup of which contains E. By blowing up the pushforward of I on X and taking the normalisation, we may construct a morphism
![]() $X'\to X$
such that if
$X'\to X$
such that if
![]() $S'\subset X'$
is the strict transform of S, then E is a divisor on
$S'\subset X'$
is the strict transform of S, then E is a divisor on
![]() $S'$
. After possibly further blowups of X, we may assume that there is an exceptional divisor
$S'$
. After possibly further blowups of X, we may assume that there is an exceptional divisor
![]() $F\subset X'$
such that
$F\subset X'$
such that
![]() $S'\cap F= E$
and
$S'\cap F= E$
and
![]() $S',F$
intersect transversely at the generic point of E. But then the log discrepancies satisfy
$S',F$
intersect transversely at the generic point of E. But then the log discrepancies satisfy
![]() $a_E(S^{\nu } , \Delta _{S^{\nu }})=a_F(X,\Delta )>0$
. The first part of the lemma now follows easily.
$a_E(S^{\nu } , \Delta _{S^{\nu }})=a_F(X,\Delta )>0$
. The first part of the lemma now follows easily.
The second part of the lemma follows by standard results for surfaces once we localise at
![]() $P\in X$
.
$P\in X$
.
We state an application of [Reference WitaszekWit22].
Theorem 2.3 [Reference WitaszekWit21b, Theorem 2.22]
Let
![]() $f \colon Y \to X$
be a finite universal homeomorphism of schemes which are proper over a Noetherian base scheme S. Let
$f \colon Y \to X$
be a finite universal homeomorphism of schemes which are proper over a Noetherian base scheme S. Let
![]() $\mathcal {L}$
be a nef line bundle on X such that
$\mathcal {L}$
be a nef line bundle on X such that
![]() $\mathcal {L}|_{X_{{\mathbb {Q}}}}$
and
$\mathcal {L}|_{X_{{\mathbb {Q}}}}$
and
![]() $f^*\mathcal {L}$
are semiample, where
$f^*\mathcal {L}$
are semiample, where
![]() $X_{{\mathbb {Q}}}$
is the characteristic 0 fibre of
$X_{{\mathbb {Q}}}$
is the characteristic 0 fibre of
![]() $X \to \operatorname {\mathrm {Spec}} \mathbb {Z}$
. Then
$X \to \operatorname {\mathrm {Spec}} \mathbb {Z}$
. Then
![]() $\mathcal {L}$
is semiample.
$\mathcal {L}$
is semiample.
2.1 F-regularity and
 $+$
-regularity
$+$
-regularity
Since the work of Hacon and Xu [Reference Hacon and XuHX15], (global) F-regularity has been one of the main tools in the MMP in positive characteristics. In the local setting, it gives a good analog of (and often coincides with) klt singularities and in the global setting it provides us with a log Fano structure and implies vanishing theorems. For the convenience of the reader, we recall several definitions and key results.
Definition 2.4. Let X be an F-finite
![]() $\mathbb F _p$
-scheme. Given an effective
$\mathbb F _p$
-scheme. Given an effective
![]() ${\mathbb {Q}}$
-divisor B, we say that
${\mathbb {Q}}$
-divisor B, we say that
![]() $(X,B) $
is globally F-split if for every integer
$(X,B) $
is globally F-split if for every integer
![]() $e>0$
, the natural homomorphism of
$e>0$
, the natural homomorphism of
![]() ${\mathcal {O}} _X$
-modules
${\mathcal {O}} _X$
-modules
has an
![]() ${\mathcal {O}}_X$
-module splitting. We say that
${\mathcal {O}}_X$
-module splitting. We say that
![]() $(X,B) $
is globally F-regular (resp. purely globally F-regular) if for every effective divisor D on X (resp. every
$(X,B) $
is globally F-regular (resp. purely globally F-regular) if for every effective divisor D on X (resp. every
![]() $D\geq 0$
intersecting
$D\geq 0$
intersecting
![]() $\lfloor B \rfloor $
properly) and every integer
$\lfloor B \rfloor $
properly) and every integer
![]() $e\gg 0$
, the natural homomorphism of
$e\gg 0$
, the natural homomorphism of
![]() ${\mathcal {O}} _X$
-modules
${\mathcal {O}} _X$
-modules
splits.
If the above splittings hold locally on X, then we refer to these notions as F-purity, strong F-regularity, and pure F-regularity, respectively. Given a morphism
![]() $f\colon X\to Y$
, we say that
$f\colon X\to Y$
, we say that
![]() $(X,B)$
is relatively (over Y) F-split, F-regular, or purely F-regular, if the above splittings hold locally over Y.
$(X,B)$
is relatively (over Y) F-split, F-regular, or purely F-regular, if the above splittings hold locally over Y.
Let L be a divisor and
![]() $(X,B)$
be a log pair where p does not divide the index of B. We let
$(X,B)$
be a log pair where p does not divide the index of B. We let
where the intersection is taken over
![]() $e>0$
sufficiently divisible so that
$e>0$
sufficiently divisible so that
![]() $(p^e-1)B$
is integral. Note that if
$(p^e-1)B$
is integral. Note that if
![]() $f\colon X\to U$
is a projective morphism to an affine variety such that L is
$f\colon X\to U$
is a projective morphism to an affine variety such that L is
![]() ${\mathbb {Q}}$
-Cartier and
${\mathbb {Q}}$
-Cartier and
![]() $L-(K_X+B)$
is f-ample, then (identifying
$L-(K_X+B)$
is f-ample, then (identifying
![]() $f_*{\mathcal {O}}_X(L)$
with
$f_*{\mathcal {O}}_X(L)$
with
![]() $H^0(X,{\mathcal {O}} _X(L))$
) the subsheaf
$H^0(X,{\mathcal {O}} _X(L))$
) the subsheaf
![]() $S^0(X,B;L)\subset f_*{\mathcal {O}}_X(L)$
is coherent and equal to the single image for a sufficiently big and divisible
$S^0(X,B;L)\subset f_*{\mathcal {O}}_X(L)$
is coherent and equal to the single image for a sufficiently big and divisible
![]() $e>0$
(see the proof of [Reference Hacon and XuHX15, Proposition 2.15]).
$e>0$
(see the proof of [Reference Hacon and XuHX15, Proposition 2.15]).
We quickly review the theory of
![]() $+$
-regularity ([Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20]). Let X be a normal integral scheme which is proper over a complete Noetherian local domain
$+$
-regularity ([Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20]). Let X be a normal integral scheme which is proper over a complete Noetherian local domain
![]() $(R,\mathfrak {m})$
with characteristic
$(R,\mathfrak {m})$
with characteristic
![]() $p>0$
residue field. Let
$p>0$
residue field. Let
![]() $B \geq 0$
be a
$B \geq 0$
be a
![]() ${\mathbb {Q}}$
-divisor on X. For a Weil divisor L on X, we define the subspace of
${\mathbb {Q}}$
-divisor on X. For a Weil divisor L on X, we define the subspace of
![]() $+$
-stable sections
$+$
-stable sections
![]() $B^0(X, B; {\mathcal {O}}_X(L))$
to be
$B^0(X, B; {\mathcal {O}}_X(L))$
to be
 $$\begin{align*}\bigcap_{\substack{f \colon Y \to X\\ \mathrm{finite}}}\textrm{Im}\,\big(H^0(Y, {\mathcal{O}}_Y( K_Y + \lceil{f^* (L - K_X - B)}\rceil)) \to H^0(X, {\mathcal{O}}_X(L))\big),\\[-17pt] \end{align*}$$
$$\begin{align*}\bigcap_{\substack{f \colon Y \to X\\ \mathrm{finite}}}\textrm{Im}\,\big(H^0(Y, {\mathcal{O}}_Y( K_Y + \lceil{f^* (L - K_X - B)}\rceil)) \to H^0(X, {\mathcal{O}}_X(L))\big),\\[-17pt] \end{align*}$$
where the intersection taken over all finite covers
![]() $f \colon Y \to X$
by a normal integral scheme Y (more precisely, here and throughout the article, this means that we take the intersection over the category of all finite covers equipped with an embedding of
$f \colon Y \to X$
by a normal integral scheme Y (more precisely, here and throughout the article, this means that we take the intersection over the category of all finite covers equipped with an embedding of
![]() $K(Y)$
into a fixed algebraic closure
$K(Y)$
into a fixed algebraic closure
![]() $\overline {K(X)}$
of
$\overline {K(X)}$
of
![]() $K(X)$
; see [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Convention 4.1]). When X is not irreducible, but still normal, we define
$K(X)$
; see [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Convention 4.1]). When X is not irreducible, but still normal, we define
![]() $B^0(X, B; {\mathcal {O}}_X(L))$
to be the direct sum of
$B^0(X, B; {\mathcal {O}}_X(L))$
to be the direct sum of
![]() $B^0$
for each connected (thus irreducible) component of X.
$B^0$
for each connected (thus irreducible) component of X.
Similarly, for a reduced divisor S having no common components with an effective
![]() ${\mathbb {Q}}$
-divisor B, we define the adjoint variant
${\mathbb {Q}}$
-divisor B, we define the adjoint variant
![]() $B^0_{S}(X, S+B; {\mathcal {O}}_X(L))$
to be equal to
$B^0_{S}(X, S+B; {\mathcal {O}}_X(L))$
to be equal to
 $$\begin{align*}\bigcap_{\substack{f \colon Y \to X\\ \mathrm{finite}}}\textrm{Im}\,\Big(H^0(Y, \bigoplus_{i=1}^t{\mathcal{O}}_Y( K_Y +S_{i,Y} + \lceil{f^* (L - K_X-S-B)}\rceil)) \to H^0(X, {\mathcal{O}}_X(L))\Big),\\[-17pt] \end{align*}$$
$$\begin{align*}\bigcap_{\substack{f \colon Y \to X\\ \mathrm{finite}}}\textrm{Im}\,\Big(H^0(Y, \bigoplus_{i=1}^t{\mathcal{O}}_Y( K_Y +S_{i,Y} + \lceil{f^* (L - K_X-S-B)}\rceil)) \to H^0(X, {\mathcal{O}}_X(L))\Big),\\[-17pt] \end{align*}$$
where
![]() $S_{i,Y}$
are compatibly chosen prime divisors lying over
$S_{i,Y}$
are compatibly chosen prime divisors lying over
![]() $S_{i}$
for
$S_{i}$
for
![]() $S = \sum _{i=1}^t S_i$
and
$S = \sum _{i=1}^t S_i$
and
![]() $S_i$
prime. The choice of such divisors
$S_i$
prime. The choice of such divisors
![]() $S_{i,Y}$
is equivalent to choosing prime divisors
$S_{i,Y}$
is equivalent to choosing prime divisors
![]() $S_i^+$
in
$S_i^+$
in
![]() $X^+$
lying over
$X^+$
lying over
![]() $S_i$
. Note that the definition of
$S_i$
. Note that the definition of
![]() $B^0_S$
is independent of the choice of these
$B^0_S$
is independent of the choice of these
![]() $S_i^+$
(see [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Lemma 4.23]).
$S_i^+$
(see [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Lemma 4.23]).
Definition 2.5. Let X be a normal, integral, excellent scheme with a dualising complex and with every closed point having positive characteristic residue field. Further, let
![]() $B \geq 0$
be a
$B \geq 0$
be a
![]() ${\mathbb {Q}}$
-divisor on X.
${\mathbb {Q}}$
-divisor on X.
We say that
![]() $(X,B)$
is globally
$(X,B)$
is globally
![]() $+$
-regular if for every finite dominant map
$+$
-regular if for every finite dominant map
![]() $f \colon Y \to X$
with Y normal, the morphism
$f \colon Y \to X$
with Y normal, the morphism
splits. When X is not integral, but still normal with all connected components of the same dimension, we say that X is globally
![]() $+$
-regular if also all of its connected components are.
$+$
-regular if also all of its connected components are.
Let
![]() $(X,S+B)$
be a log pair such that S is a reduced divisor having no common components with an effective
$(X,S+B)$
be a log pair such that S is a reduced divisor having no common components with an effective
![]() ${\mathbb {Q}}$
-divisor B. We say that
${\mathbb {Q}}$
-divisor B. We say that
![]() $(X,S+B)$
such that
$(X,S+B)$
such that
![]() $\lfloor B \rfloor =0$
, is purely globally
$\lfloor B \rfloor =0$
, is purely globally
![]() $+$
-regular (along S), if for every finite dominant map
$+$
-regular (along S), if for every finite dominant map
![]() $f \colon Y \to X$
with Y normal, the morphism
$f \colon Y \to X$
with Y normal, the morphism
 $$\begin{align*}{\mathcal{O}}_X \to f_* \bigoplus_{i=1}^t{\mathcal{O}}_Y(\lfloor f^*(S+B)\rfloor - S_{i,Y}) \end{align*}$$
$$\begin{align*}{\mathcal{O}}_X \to f_* \bigoplus_{i=1}^t{\mathcal{O}}_Y(\lfloor f^*(S+B)\rfloor - S_{i,Y}) \end{align*}$$
splits, where
![]() $S_{i,Y}$
are chosen as in the definition of
$S_{i,Y}$
are chosen as in the definition of
![]() $B^0_S$
above.
$B^0_S$
above.
In what follows, we recall the relative analogs of the above notions. Note that the completion
![]() $\hat {R}$
of an excellent normal local ring R is automatically normal (see [Sta14, Tag 0C23]). Similarly, if X is a normal excellent scheme over R, then the base change
$\hat {R}$
of an excellent normal local ring R is automatically normal (see [Sta14, Tag 0C23]). Similarly, if X is a normal excellent scheme over R, then the base change
![]() $X_{\hat R}$
is also normal (see [Sta14, Tag 0C22]).
$X_{\hat R}$
is also normal (see [Sta14, Tag 0C22]).
Definition 2.6. Let Z be a normal integral excellent scheme with a dualising complex. Let
![]() $f \colon X \to Z$
be a proper morphism for a normal integral scheme X.
$f \colon X \to Z$
be a proper morphism for a normal integral scheme X.
We say that
![]() $(X,B)$
for a
$(X,B)$
for a
![]() ${\mathbb {Q}}$
-divisor
${\mathbb {Q}}$
-divisor
![]() $B\geq 0$
is completely relatively
$B\geq 0$
is completely relatively
![]() $+$
-regular over Z if for every closed point
$+$
-regular over Z if for every closed point
![]() $z \in Z$
with positive residue characteristic its base change
$z \in Z$
with positive residue characteristic its base change
![]() $(X_{\widehat {Z}_z}, B_{\widehat {Z}_z})$
to the completion of
$(X_{\widehat {Z}_z}, B_{\widehat {Z}_z})$
to the completion of
![]() ${\mathcal {O}}_{Z,z}$
at z is globally
${\mathcal {O}}_{Z,z}$
at z is globally
![]() $+$
-regular.
$+$
-regular.
We say that
![]() $(X,S+B)$
for a reduced divisor S having no common components with a
$(X,S+B)$
for a reduced divisor S having no common components with a
![]() ${\mathbb {Q}}$
-divisor
${\mathbb {Q}}$
-divisor
![]() $B\geq 0$
is completely relatively purely
$B\geq 0$
is completely relatively purely
![]() $+$
-regular over Z if for every closed point
$+$
-regular over Z if for every closed point
![]() $z \in Z$
with positive residue characteristic its base change
$z \in Z$
with positive residue characteristic its base change
![]() $(X_{\widehat {Z}_z}, S_{\widehat {Z}_z} + B_{\widehat {Z}_z})$
to the completion of
$(X_{\widehat {Z}_z}, S_{\widehat {Z}_z} + B_{\widehat {Z}_z})$
to the completion of
![]() ${\mathcal {O}}_{Z,z}$
at z is purely globally
${\mathcal {O}}_{Z,z}$
at z is purely globally
![]() $+$
-regular.
$+$
-regular.
Note that in contrast to [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20], we do not assume that Z has all closed points of positive residue characteristics. In particular, our definition is meaningless in a neighbourhood of closed points of characteristic 0. However, such a formulation of the definition allows us to simplify some of the statements later on.
The scheme X proper over
![]() $Z=\operatorname {\mathrm {Spec}} R$
having all closed points of positive residue characteristics is globally
$Z=\operatorname {\mathrm {Spec}} R$
having all closed points of positive residue characteristics is globally
![]() $+$
-regular if and only if it is completely relatively
$+$
-regular if and only if it is completely relatively
![]() $+$
-regular over R ([Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Corollary 6.9]). However, this is not known for pure global
$+$
-regular over R ([Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Corollary 6.9]). However, this is not known for pure global
![]() $+$
-regularity (unless
$+$
-regularity (unless
![]() $H^0(X,{\mathcal {O}}_X)=R$
and
$H^0(X,{\mathcal {O}}_X)=R$
and
![]() $-(K_X+S+B)$
is big and semiample; see [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Corollary 7.6]), and so for coherence of notation, we shall always add the prefix completely when talking about any of these notions in the relative setting.
$-(K_X+S+B)$
is big and semiample; see [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Corollary 7.6]), and so for coherence of notation, we shall always add the prefix completely when talking about any of these notions in the relative setting.
We also point out to the reader that, with notation as above, if X is proper over a complete Noetherian local domain R of positive residue characteristic, then global
![]() $+$
-regularity and pure global
$+$
-regularity and pure global
![]() $+$
-regularity of
$+$
-regularity of
![]() $(X,B)$
and
$(X,B)$
and
![]() $(X,S+B)$
, respectively, are equivalent to
$(X,S+B)$
, respectively, are equivalent to
![]() $B^0(X,B; {\mathcal {O}}_X) = H^0(X,{\mathcal {O}}_X)$
and
$B^0(X,B; {\mathcal {O}}_X) = H^0(X,{\mathcal {O}}_X)$
and
![]() $B^0_{S}(X,S+B; {\mathcal {O}}_X) = H^0(X,{\mathcal {O}}_X)$
by [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Proposition 6.8 and Proposition 6.26].
$B^0_{S}(X,S+B; {\mathcal {O}}_X) = H^0(X,{\mathcal {O}}_X)$
by [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Proposition 6.8 and Proposition 6.26].
Lemma 2.7. Let X and
![]() $X'$
be two normal varieties defined over an F-finite field of characteristic
$X'$
be two normal varieties defined over an F-finite field of characteristic
![]() $p>0$
, and let
$p>0$
, and let
![]() be a birational map which is an isomorphism at any codimension one point. Let
be a birational map which is an isomorphism at any codimension one point. Let
![]() $B\geq 0$
be a
$B\geq 0$
be a
![]() ${\mathbb {Q}}$
-divisor on X and
${\mathbb {Q}}$
-divisor on X and
![]() $B'=\phi _* B$
the corresponding
$B'=\phi _* B$
the corresponding
![]() ${\mathbb {Q}}$
-divisor on
${\mathbb {Q}}$
-divisor on
![]() $X'$
. Then
$X'$
. Then
![]() $(X,B)$
is globally F-split (resp. globally F-regular or purely globally F-regular) if and only if
$(X,B)$
is globally F-split (resp. globally F-regular or purely globally F-regular) if and only if
![]() $(X',B')$
is globally F-split (resp. globally F-regular or purely globally F-regular).
$(X',B')$
is globally F-split (resp. globally F-regular or purely globally F-regular).
The same result holds for global
![]() $+$
-regularity and global pure
$+$
-regularity and global pure
![]() $+$
-regularity when X and
$+$
-regularity when X and
![]() $X'$
are as in Definition 2.5.
$X'$
are as in Definition 2.5.
Proof. This follows from the fact that a splitting of structure sheaves for a finite map of normal varieties may be checked on an open subset with complement of codimension at least two. In positive characteristic, this lemma has been observed in [Reference Schwede and SmithSS10, Proof of Proposition 6.3]. In mixed characteristic, the proof is analogous to [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Proposition 6.18].
Proposition 2.8. Suppose that
![]() $(X,S+B)$
is a purely F-regular pair over an F-finite field of characteristic
$(X,S+B)$
is a purely F-regular pair over an F-finite field of characteristic
![]() $p>0$
(or a purely
$p>0$
(or a purely
![]() $+$
-regular pair as in Definition 2.5), where
$+$
-regular pair as in Definition 2.5), where
![]() $\lfloor S+B\rfloor =S$
is a prime divisor. Then S is normal.
$\lfloor S+B\rfloor =S$
is a prime divisor. Then S is normal.
Proof. In positive characteristic, see [Reference Ma, Schwede, Tucker, Waldron and WitaszekMSTWW22, Theorem A] or the proof of [Reference DasDas15, Theorem A]. In mixed characteristic, this is [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Corollary 7.9].
Further, recall the following result known as inversion of F-adjunction (
![]() $+$
-adjunction, resp.).
$+$
-adjunction, resp.).
Lemma 2.9. Let
![]() $(X,S+B)$
be a plt pair, where
$(X,S+B)$
be a plt pair, where
![]() $S=\lfloor S+B\rfloor $
is a prime divisor and
$S=\lfloor S+B\rfloor $
is a prime divisor and
![]() $B\geq 0$
has no common components with S, and let
$B\geq 0$
has no common components with S, and let
![]() $f \colon X\to Z$
be a projective birational morphism of normal varieties over an F-finite field of characteristic
$f \colon X\to Z$
be a projective birational morphism of normal varieties over an F-finite field of characteristic
![]() $p>0$
(resp. over a DVR of characteristic
$p>0$
(resp. over a DVR of characteristic
![]() $(0,p)$
for
$(0,p)$
for
![]() $p>0$
). Assume that
$p>0$
). Assume that
![]() $-(K_X+S+B)$
is f-ample and write
$-(K_X+S+B)$
is f-ample and write
![]() $K_{S^{\nu }}+B_{S^{\nu }}=(K_X+S+B)|_{S^{\nu }}$
for the normalisation
$K_{S^{\nu }}+B_{S^{\nu }}=(K_X+S+B)|_{S^{\nu }}$
for the normalisation
![]() $S^{\nu }\to S$
.
$S^{\nu }\to S$
.
Then
![]() $(X,S+B)$
is relatively purely F-regular (resp. completely relatively purely
$(X,S+B)$
is relatively purely F-regular (resp. completely relatively purely
![]() $+$
-regular) over a neighbourhood of
$+$
-regular) over a neighbourhood of
![]() $f(S)\subset Z$
if and only if
$f(S)\subset Z$
if and only if
![]() $(S^{\nu },B_{S^{\nu }})$
is relatively F-regular (resp. completely relatively
$(S^{\nu },B_{S^{\nu }})$
is relatively F-regular (resp. completely relatively
![]() $+$
-regular) over
$+$
-regular) over
![]() $f(S)$
. Under these equivalent assumptions, S is normal.
$f(S)$
. Under these equivalent assumptions, S is normal.
Proof. In positive characteristic, this follows by the same proof as [Reference Hacon and WitaszekHW19, Lemma 2.10]. It uses the equality between the different and the F-different. For this, note that [Reference DasDas15, Theorem B] assumes that the base field is algebraically closed, but the proof goes through for every F-finite base field.
In mixed characteristic, this is [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Corollary 7.5] (after completing or invoking [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Corollary 7.6]).
Finally, the normality of S around positive characteristic closed points follows from Proposition 2.8, and around characteristic 0 closed points by standard results ([Reference Kollár and MoriKM98, Theorem 5.50]).
We also have the following immediate consequence of [Reference SchwedeSch14, 5.3].
Proposition 2.10. Let
![]() $f\colon X\to U$
be a projective morphism of normal varieties over an F-finite field of positive characteristic, where U is affine, L a
$f\colon X\to U$
be a projective morphism of normal varieties over an F-finite field of positive characteristic, where U is affine, L a
![]() ${\mathbb {Q}}$
-Cartier Weil divisor and
${\mathbb {Q}}$
-Cartier Weil divisor and
![]() $(X,S+B)$
a log pair such that
$(X,S+B)$
a log pair such that
-
(1)
 $\lfloor S+B\rfloor =S$
is normal and integral;
$\lfloor S+B\rfloor =S$
is normal and integral; -
(2) p does not divide the index of B;
-
(3)
 $L-(K_X+S+B)$
is f-ample;
$L-(K_X+S+B)$
is f-ample; -
(4) L is Cartier on an open neighbourhood of
 $S\,\backslash \, Z$
, where
$S\,\backslash \, Z$
, where
 $Z \subseteq S$
is a closed subset of codimension at least two;
$Z \subseteq S$
is a closed subset of codimension at least two; -
(5) X is
 $\mathbb {Q}$
-factorial, strongly F-regular and of dimension at least three.
$\mathbb {Q}$
-factorial, strongly F-regular and of dimension at least three.
Then
![]() $S^0(X,S+B;L)\to S^0(S,B_S; L|_S)$
is surjective, where
$S^0(X,S+B;L)\to S^0(S,B_S; L|_S)$
is surjective, where
![]() $(K_X+S+B)|_S=K_S+B_S$
.
$(K_X+S+B)|_S=K_S+B_S$
.
Since
![]() $Z \subseteq S$
is a closed subset of codimension at least two,
$Z \subseteq S$
is a closed subset of codimension at least two,
![]() $L|_S$
is well defined as a Weil divisor. If L is Cartier, then the assumption that X is
$L|_S$
is well defined as a Weil divisor. If L is Cartier, then the assumption that X is
![]() $\mathbb {Q}$
-factorial, strongly F-regular and of dimension at least three is not needed (cf. [Reference SchwedeSch14, 5.3]).
$\mathbb {Q}$
-factorial, strongly F-regular and of dimension at least three is not needed (cf. [Reference SchwedeSch14, 5.3]).
Proof. This follows easily from the following commutative diagram, which exists as the different is equal to the F-different

Here, we use that
![]() $(X,S+B)$
is
$(X,S+B)$
is
![]() $\mathbb {Q}$
-factorial, strongly F-regular and of dimension at least three to guarantee that divisorial sheaves on X are
$\mathbb {Q}$
-factorial, strongly F-regular and of dimension at least three to guarantee that divisorial sheaves on X are
![]() $S_3$
(cf. [Reference Hacon and WitaszekHW19, Proposition 2.7]), which implies that the upper horizontal arrow is a surjection of sheaves (cf. [Reference Hacon and WitaszekHW19, Lemma 2.4]). This is turn gives the surjection on global sections for
$S_3$
(cf. [Reference Hacon and WitaszekHW19, Proposition 2.7]), which implies that the upper horizontal arrow is a surjection of sheaves (cf. [Reference Hacon and WitaszekHW19, Lemma 2.4]). This is turn gives the surjection on global sections for
![]() $e \gg 0$
by Serre’s vanishing.
$e \gg 0$
by Serre’s vanishing.
In the case of
![]() $B^0$
, the assumption on
$B^0$
, the assumption on
![]() $+$
-regularity of singularities when L is not Cartier is not needed. This discrepancy stems from
$+$
-regularity of singularities when L is not Cartier is not needed. This discrepancy stems from
![]() $X^+$
being cohomologically Cohen–Macaulay in positive and mixed characteristic (informally speaking, the ‘non-Cohen–Macauliness’ is not necessarily killed by Frobenii but is always killed by finite covers).
$X^+$
being cohomologically Cohen–Macaulay in positive and mixed characteristic (informally speaking, the ‘non-Cohen–Macauliness’ is not necessarily killed by Frobenii but is always killed by finite covers).
Proposition 2.11. Let X be a projective normal integral scheme over a complete local Noetherian domain
![]() $(R, \mathfrak {m})$
of characteristic
$(R, \mathfrak {m})$
of characteristic
![]() $(0,p)$
for
$(0,p)$
for
![]() $p> 0$
. Let L be a
$p> 0$
. Let L be a
![]() ${\mathbb {Q}}$
-Cartier Weil divisor, and let
${\mathbb {Q}}$
-Cartier Weil divisor, and let
![]() $(X,S+B)$
a log pair such that
$(X,S+B)$
a log pair such that
-
(1)
 $\lfloor S+B\rfloor =S$
is normal and integral,
$\lfloor S+B\rfloor =S$
is normal and integral, -
(2)
 $L-(K_X+S+B)$
is f-ample,
$L-(K_X+S+B)$
is f-ample, -
(3) L is Cartier on an open neighbourhood of
 $S\,\backslash \, Z$
, where
$S\,\backslash \, Z$
, where
 $Z \subseteq S$
is a closed subset of codimension at least two.
$Z \subseteq S$
is a closed subset of codimension at least two.
Then
![]() $B^0_S(X,S+B;L)\to B^0(S,B_S; L|_S)$
is surjective, where
$B^0_S(X,S+B;L)\to B^0(S,B_S; L|_S)$
is surjective, where
![]() $(K_X+S+B)|_S=K_S+B_S$
.
$(K_X+S+B)|_S=K_S+B_S$
.
The assumption that S is connected is unnecessary, but we kept it for simplicity as in our applications the connectedness will be preserved under completion. In general, however, this is not always the case.
Proof. The proof is the same as in [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Theorem 7.2]. We recall it for the convenience of the reader. We refer to [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Subsection 2.1] for a primer on Matlis duality.
Set
![]() $\mathcal {N} = {\mathcal {O}}_{X^+}(N)$
for
$\mathcal {N} = {\mathcal {O}}_{X^+}(N)$
for
![]() $N = \pi ^*(K_X+S+B-L)$
, where
$N = \pi ^*(K_X+S+B-L)$
, where
![]() $\pi \colon X^+ \to X$
is the natural map. Note that
$\pi \colon X^+ \to X$
is the natural map. Note that
![]() $\mathcal {N}$
is a line bundle as every
$\mathcal {N}$
is a line bundle as every
![]() ${\mathbb {Q}}$
-Cartier
${\mathbb {Q}}$
-Cartier
![]() ${\mathbb {Q}}$
-divisor is rendered Cartier by some finite cover. Let
${\mathbb {Q}}$
-divisor is rendered Cartier by some finite cover. Let
![]() $S^+$
be the chosen prime divisor on
$S^+$
be the chosen prime divisor on
![]() $X^+$
such that
$X^+$
such that
![]() $\pi (S^+)=S$
, and consider the following diagram wherein the left square exists as B is effective:
$\pi (S^+)=S$
, and consider the following diagram wherein the left square exists as B is effective:

Here, the right vertical dashed arrow exists by an easy diagram chase. Moreover, this arrow factorises through the
![]() $S_2$
-fification
$S_2$
-fification
![]() ${\mathcal {O}}_{S}(K_{S}-L|_S)$
of the upper term as
${\mathcal {O}}_{S}(K_{S}-L|_S)$
of the upper term as
![]() $S^+$
is normal, and so
$S^+$
is normal, and so
![]() ${\mathcal {O}}_{S^+} \otimes \mathcal {N}$
is
${\mathcal {O}}_{S^+} \otimes \mathcal {N}$
is
![]() $S_2$
. Now, apply local cohomology with
$S_2$
. Now, apply local cohomology with
![]() $d = \dim X$
to get:
$d = \dim X$
to get:

Here, the upper left vertical arrow is surjective as the cokernel of
has codimension at least
![]() $1$
in S, and so the top local cohomology (
$1$
in S, and so the top local cohomology (
![]() $H^{d-1} R\Gamma _{\mathfrak {m}} R\Gamma $
) thereof vanishes. The bottom horizontal arrow is injective as
$H^{d-1} R\Gamma _{\mathfrak {m}} R\Gamma $
) thereof vanishes. The bottom horizontal arrow is injective as
by [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Corollary 3.7].
The upshot is that the image of
![]() $(*)$
injects into the image of
$(*)$
injects into the image of
![]() $(**)$
. Note that
$(**)$
. Note that
by definition of the different (cf. the second part of [Reference Ma, Schwede, Tucker, Waldron and WitaszekMSTWW22, Subsection 2.1]), and so by taking Matlis duality we get that
is surjective. Here, the left-hand side is Matlis dual to the image of
![]() $(**)$
by [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Definition 4.21 and Lemma 4.24], while the right-hand side is Matlis dual to the image of
$(**)$
by [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Definition 4.21 and Lemma 4.24], while the right-hand side is Matlis dual to the image of
![]() $(*)$
by [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Lemma 4.8].
$(*)$
by [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Lemma 4.8].
2.2 Special termination
In this section, X is a normal variety defined over a field k of characteristic
![]() $p>0$
or a DVR R of characteristic
$p>0$
or a DVR R of characteristic
![]() $(0,p)$
for
$(0,p)$
for
![]() $p>0$
. Recall the following result known as special termination [Reference FujinoFuj07, Theorem 4.2.1].
$p>0$
. Recall the following result known as special termination [Reference FujinoFuj07, Theorem 4.2.1].
Theorem 2.12. Assume that the log MMP for
![]() ${\mathbb {Q}}$
-factorial dlt pairs holds in dimension
${\mathbb {Q}}$
-factorial dlt pairs holds in dimension
![]() $\leq n-1$
(including the termination of all flips). Let X be a normal
$\leq n-1$
(including the termination of all flips). Let X be a normal
![]() ${\mathbb {Q}}$
-factorial n-dimensional variety, let B be an effective
${\mathbb {Q}}$
-factorial n-dimensional variety, let B be an effective
![]() $\mathbb R$
-divisor such that
$\mathbb R$
-divisor such that
![]() $(X,B)$
is dlt and let
$(X,B)$
is dlt and let
be a sequence of
![]() $(K_X+B)$
-flips. Then after finitely many steps, the flipping loci are disjoint from
$(K_X+B)$
-flips. Then after finitely many steps, the flipping loci are disjoint from
![]() $\lfloor B_i \rfloor $
.
$\lfloor B_i \rfloor $
.
Since the MMP for surfaces is known in full generality, the above result implies special termination for threefolds and in some special cases for fourfolds over perfect F-finite fields of characteristic
![]() $p>0$
. Note that it is not true that in positive characteristic log canonical centres are normal. However, by Lemma 2.2, we know that if
$p>0$
. Note that it is not true that in positive characteristic log canonical centres are normal. However, by Lemma 2.2, we know that if
![]() $W^{\nu }\to W$
is the normalisation of a log canonical centre of a dlt pair
$W^{\nu }\to W$
is the normalisation of a log canonical centre of a dlt pair
![]() $(X,B)$
, then the induced pair
$(X,B)$
, then the induced pair
![]() $K_{W^{\nu }}+B_{W^{\nu }}=(K_X+B)|_{W^{\nu }}$
is also dlt, its log canonical centres are in bijection with the log canonical centres of
$K_{W^{\nu }}+B_{W^{\nu }}=(K_X+B)|_{W^{\nu }}$
is also dlt, its log canonical centres are in bijection with the log canonical centres of
![]() $(X,B)$
contained in W and the coefficients of
$(X,B)$
contained in W and the coefficients of
![]() $B_{W^{\nu }}$
are the same as those given by the usual adjunction in characteristic 0.
$B_{W^{\nu }}$
are the same as those given by the usual adjunction in characteristic 0.
Theorem 2.13. The statement of Theorem 2.12 holds in dimension three over all F-finite fields k of characteristic
![]() $p>5$
or DVRs R of characteristic
$p>5$
or DVRs R of characteristic
![]() $(0,p)$
for
$(0,p)$
for
![]() $p>5$
.
$p>5$
.
Proof. The three-dimensional case of Theorem 2.12 is an immediate consequence of the proof of [Reference FujinoFuj07, Theorem 4.2.1] and the two-dimensional MMP [Reference TanakaTan18].
Theorem 2.14. Let
![]() $(X,B)$
be a
$(X,B)$
be a
![]() ${\mathbb {Q}}$
-factorial four-dimensional dlt pair defined over a field of characteristic
${\mathbb {Q}}$
-factorial four-dimensional dlt pair defined over a field of characteristic
![]() $p \geq 0$
or a DVR of characteristic
$p \geq 0$
or a DVR of characteristic
![]() $(0,p)$
for
$(0,p)$
for
![]() $p>0$
, where B is an effective
$p>0$
, where B is an effective
![]() $\mathbb R$
-divisor. Let
$\mathbb R$
-divisor. Let
![]() $\pi \colon X\to U$
be a projective morphism, and suppose that
$\pi \colon X\to U$
be a projective morphism, and suppose that
is a sequence of
![]() $(K_X+B)$
-flips and divisorial contractions over U. Then after finitely many steps, the intersections of the flipping and flipped loci with the non-klt locus are at most one dimensional. In particular, the flipping and flipped loci for
$(K_X+B)$
-flips and divisorial contractions over U. Then after finitely many steps, the intersections of the flipping and flipped loci with the non-klt locus are at most one dimensional. In particular, the flipping and flipped loci for
cannot be both contained in
![]() $\lfloor B_i \rfloor $
and
$\lfloor B_i \rfloor $
and
![]() $\lfloor B_{i+1} \rfloor $
.
$\lfloor B_{i+1} \rfloor $
.
Moreover, if
![]() $\dim U=1$
,
$\dim U=1$
,
![]() $\kappa (K_X+B/U)\geq 0$
and
$\kappa (K_X+B/U)\geq 0$
and
![]() $\lfloor B \rfloor $
contains the fibre
$\lfloor B \rfloor $
contains the fibre
![]() $X_u$
for some point
$X_u$
for some point
![]() $u\in U$
, then after finitely many steps, the flipping loci are disjoint from
$u\in U$
, then after finitely many steps, the flipping loci are disjoint from
![]() $X_u$
.
$X_u$
.
Proof. Since divisorial contractions decrease the Picard rank, we may assume that the above sequence consists only of flips. Denote the flips by
![]() $\phi _i \colon X_i \dashrightarrow X_{i+1}$
, and denote the flipping and the flipped contractions by
$\phi _i \colon X_i \dashrightarrow X_{i+1}$
, and denote the flipping and the flipped contractions by
![]() $f_i \colon X_i \to Z_i$
and
$f_i \colon X_i \to Z_i$
and
![]() $f_i^+ \colon X_{i+1} \to Z_i$
, respectively. Let S be an irreducible component of
$f_i^+ \colon X_{i+1} \to Z_i$
, respectively. Let S be an irreducible component of
![]() $\lfloor B \rfloor $
, let
$\lfloor B \rfloor $
, let
![]() $S_i$
be its strict transform on
$S_i$
be its strict transform on
![]() $X_i$
and let
$X_i$
and let
![]() $T_i := f_i(S_i)$
. Note that the normalisation of
$T_i := f_i(S_i)$
. Note that the normalisation of
![]() $S_i$
need not be
$S_i$
need not be
![]() ${\mathbb {Q}}$
-factorial.
${\mathbb {Q}}$
-factorial.
By [Reference FujinoFuj07, Proposition 4.2.14], we may assume that
![]() $f^+_i|_{S_{i+1}} \colon S_{i+1} \to T_i$
is small. Moreover, if
$f^+_i|_{S_{i+1}} \colon S_{i+1} \to T_i$
is small. Moreover, if
![]() $f_i|_{S_i} \colon S_i \to T_i$
is divisorial, then the Picard rank as defined in [Reference Alexeev, Hacon and KawamataAHK07, Lemma 1.6] satisfies
$f_i|_{S_i} \colon S_i \to T_i$
is divisorial, then the Picard rank as defined in [Reference Alexeev, Hacon and KawamataAHK07, Lemma 1.6] satisfies
![]() $\rho (S^{\nu }_i/U)>\rho (S^{\nu }_{i+1}/U)$
, where
$\rho (S^{\nu }_i/U)>\rho (S^{\nu }_{i+1}/U)$
, where
![]() $S^{\nu }_i$
and
$S^{\nu }_i$
and
![]() $S^{\nu }_{i+1}$
are appropriate normalisations. Thus, again we may assume
$S^{\nu }_{i+1}$
are appropriate normalisations. Thus, again we may assume
![]() $f_i|_{S_i}$
is small, that is,
$f_i|_{S_i}$
is small, that is,
![]() $\phi _i|_{S_i} \colon S_i \dashrightarrow S_{i+1}$
is of type (SS). The sum of the dimensions of the flipping and the flipped locus of
$\phi _i|_{S_i} \colon S_i \dashrightarrow S_{i+1}$
is of type (SS). The sum of the dimensions of the flipping and the flipped locus of
![]() is at least three, so one of them must be two-dimensional (in fact, they must be of type
is at least three, so one of them must be two-dimensional (in fact, they must be of type
![]() $(2,1)$
,
$(2,1)$
,
![]() $(2,2)$
or
$(2,2)$
or
![]() $(1,2)$
[Reference Kawamata, Matsuda and MatsukiKMM87, Lemma 5.1.17] and [Reference Alexeev, Hacon and KawamataAHK07, Lemma 1.2]), and so they cannot be both contained in the non-klt locus.
$(1,2)$
[Reference Kawamata, Matsuda and MatsukiKMM87, Lemma 5.1.17] and [Reference Alexeev, Hacon and KawamataAHK07, Lemma 1.2]), and so they cannot be both contained in the non-klt locus.
Now, assume that
![]() $\dim U=1$
,
$\dim U=1$
,
![]() $\kappa (K_X+B/U)\geq 0$
, and
$\kappa (K_X+B/U)\geq 0$
, and
![]() $\lfloor B \rfloor $
contains the support of the fibre
$\lfloor B \rfloor $
contains the support of the fibre
![]() $X_u$
for some point
$X_u$
for some point
![]() $u\in U$
. As observed above, after finitely many steps,
$u\in U$
. As observed above, after finitely many steps,
![]() $\lfloor B_i\rfloor $
contains no two-dimensional component of the flipping or flipped loci. Suppose that the flipping locus (and thus also the flipped locus) is contained in the fibre over u and hence in the non-klt locus. Since either the flipping or flipped locus is two dimensional, this can not happen infinitely often. Therefore, we may assume that for
$\lfloor B_i\rfloor $
contains no two-dimensional component of the flipping or flipped loci. Suppose that the flipping locus (and thus also the flipped locus) is contained in the fibre over u and hence in the non-klt locus. Since either the flipping or flipped locus is two dimensional, this can not happen infinitely often. Therefore, we may assume that for
![]() $i\gg 0$
the flipping and flipped loci dominate U.
$i\gg 0$
the flipping and flipped loci dominate U.
Therefore, we can replace
![]() $(X,B)$
and
$(X,B)$
and
![]() $(X_i,B_i)$
by
$(X_i,B_i)$
by
![]() $(X_{\eta }, B_{\eta })$
and
$(X_{\eta }, B_{\eta })$
and
![]() $((X_i)_{\eta }, (B_i)_{\eta })$
, respectively, so that these are three-dimensional
$((X_i)_{\eta }, (B_i)_{\eta })$
, respectively, so that these are three-dimensional
![]() ${\mathbb {Q}}$
-factorial pairs defined over a field of characteristic 0 or an F-finite field
${\mathbb {Q}}$
-factorial pairs defined over a field of characteristic 0 or an F-finite field
![]() $k(\eta )$
for the generic point
$k(\eta )$
for the generic point
![]() $\eta \in U$
. In particular, we can assume that log resolutions and terminalisations exist (see [Reference Das and WaldronDW19b] when
$\eta \in U$
. In particular, we can assume that log resolutions and terminalisations exist (see [Reference Das and WaldronDW19b] when
![]() $\eta $
is of positive characteristic and [Reference Birkar, Cascini, Hacon and McKernanBCHM10] when it is of characteristic 0).
$\eta $
is of positive characteristic and [Reference Birkar, Cascini, Hacon and McKernanBCHM10] when it is of characteristic 0).
First, we will show that
![]() $\lfloor B_i \rfloor $
is disjoint from the flipping, and so the flipped, locus. By what we have proven above, we may also assume that the intersection of the non-klt locus with the flipping and the flipped locus is at most zero dimensional. Now, suppose that a flipping curve C intersects
$\lfloor B_i \rfloor $
is disjoint from the flipping, and so the flipped, locus. By what we have proven above, we may also assume that the intersection of the non-klt locus with the flipping and the flipped locus is at most zero dimensional. Now, suppose that a flipping curve C intersects
![]() $\lfloor B_i\rfloor $
. Then
$\lfloor B_i\rfloor $
. Then
![]() $C \cdot \lfloor B_i \rfloor> 0$
, and so the flipped locus is contained in
$C \cdot \lfloor B_i \rfloor> 0$
, and so the flipped locus is contained in
![]() $\lfloor B_{i+1} \rfloor $
which is impossible. Now, replacing
$\lfloor B_{i+1} \rfloor $
which is impossible. Now, replacing
![]() $B_i$
by
$B_i$
by
![]() $\{B_i\}$
, we may assume that
$\{B_i\}$
, we may assume that
![]() $(X_i,B_i)$
are klt, and so the MMP should terminate by Proposition 2.15 for
$(X_i,B_i)$
are klt, and so the MMP should terminate by Proposition 2.15 for
![]() $U = \operatorname {\mathrm {Spec}} k(\eta )$
.
$U = \operatorname {\mathrm {Spec}} k(\eta )$
.
However, the above replacement may render the assumption
![]() $\kappa (K_X+B) \geq 0$
invalid, so we need to be more careful. Precisely, write
$\kappa (K_X+B) \geq 0$
invalid, so we need to be more careful. Precisely, write
![]() $K_X+B\sim _{{\mathbb {Q}}}M\geq 0$
, where the supports of the strict transforms
$K_X+B\sim _{{\mathbb {Q}}}M\geq 0$
, where the supports of the strict transforms
![]() $M_i$
on
$M_i$
on
![]() $X_i$
contain the flipping loci for all i. Since the flipping loci are disjoint from
$X_i$
contain the flipping loci for all i. Since the flipping loci are disjoint from
![]() $\lfloor B_i \rfloor $
, the above
$\lfloor B_i \rfloor $
, the above
![]() $(K_X+B)$
-MMP (equivalently, a
$(K_X+B)$
-MMP (equivalently, a
![]() $(K_X+B+\epsilon M)$
-MMP), is also a
$(K_X+B+\epsilon M)$
-MMP), is also a
![]() $(K_X+\{B\} + \epsilon M)$
-MMP for
$(K_X+\{B\} + \epsilon M)$
-MMP for
![]() $0 < \epsilon \ll 1$
. Since the flipping loci are contained in
$0 < \epsilon \ll 1$
. Since the flipping loci are contained in
![]() ${\mathrm {Supp}}(\{B\}+ \epsilon M)$
, this MMP terminates by Proposition 2.15.
${\mathrm {Supp}}(\{B\}+ \epsilon M)$
, this MMP terminates by Proposition 2.15.
Proposition 2.15. Let
![]() $(X,B)$
be a
$(X,B)$
be a
![]() ${\mathbb {Q}}$
-factorial klt log pair of dimension n defined over a field of characteristic
${\mathbb {Q}}$
-factorial klt log pair of dimension n defined over a field of characteristic
![]() $p\geq 0$
, where B is an effective
$p\geq 0$
, where B is an effective
![]() $\mathbb R$
-divisor. Let
$\mathbb R$
-divisor. Let
![]() $\pi \colon X\to U$
be a projective morphism and suppose that
$\pi \colon X\to U$
be a projective morphism and suppose that
is a sequence of
![]() $(K_X+B)$
-flips over U.
$(K_X+B)$
-flips over U.
Assume that log resolutions of all n-dimensional log pairs with the underlying variety being birational to X exist and so do terminalisations for n-dimensional
![]() ${\mathbb {Q}}$
-factorial klt pairs. Then it can happen only finitely many times that the flipping or the flipped locus has a component of codimension two in
${\mathbb {Q}}$
-factorial klt pairs. Then it can happen only finitely many times that the flipping or the flipped locus has a component of codimension two in
![]() $X_n$
and which is contained in
$X_n$
and which is contained in
![]() ${\mathrm {Supp}}\, B_n$
. In particular, if
${\mathrm {Supp}}\, B_n$
. In particular, if
![]() $\kappa (K_X+B/U) \geq 0$
, then the flipping locus is of codimension at least three for
$\kappa (K_X+B/U) \geq 0$
, then the flipping locus is of codimension at least three for
![]() $n \gg 0$
.
$n \gg 0$
.
This result holds in a more general setting (that is, as in [Reference KollárKol13] or [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20]).
Proof. This follows by the same argument as [Reference Alexeev, Hacon and KawamataAHK07, Theorem 2.15]. For the convenience of the reader, we recall the argument briefly. Define the following functions
![]() $w^{-}_{\alpha }, w^{+}_{\alpha }, W^{-}_{\alpha }, W^+_{\alpha } \colon (-\infty , 1) \to \mathbb {R}_{\geq 0}$
for
$w^{-}_{\alpha }, w^{+}_{\alpha }, W^{-}_{\alpha }, W^+_{\alpha } \colon (-\infty , 1) \to \mathbb {R}_{\geq 0}$
for
![]() $\alpha \in (0,1)$
by
$\alpha \in (0,1)$
by
 $$ \begin{align*} w_{\alpha}^-(x) &= 1-x \text{ for } x \leq \alpha, \text{ and } w_{\alpha}^-(x) =0 \text{ otherwise, }\\ w_{\alpha}^+(x) &= 1-x \text{ for } x < \alpha, \text{ and } w_{\alpha}^+(x) =0 \text{ otherwise, }\\ W_{\alpha}^-(b) &= {\textstyle \sum_{k=1}^{\infty}} w_{\alpha}^-(k(1-b)), \\ W_{\alpha}^+(b) &= {\textstyle \sum_{k=1}^{\infty}} w_{\alpha}^+(k(1-b)). \end{align*} $$
$$ \begin{align*} w_{\alpha}^-(x) &= 1-x \text{ for } x \leq \alpha, \text{ and } w_{\alpha}^-(x) =0 \text{ otherwise, }\\ w_{\alpha}^+(x) &= 1-x \text{ for } x < \alpha, \text{ and } w_{\alpha}^+(x) =0 \text{ otherwise, }\\ W_{\alpha}^-(b) &= {\textstyle \sum_{k=1}^{\infty}} w_{\alpha}^-(k(1-b)), \\ W_{\alpha}^+(b) &= {\textstyle \sum_{k=1}^{\infty}} w_{\alpha}^+(k(1-b)). \end{align*} $$
For any subterminal log pair
![]() $(Y,B_Y)$
and
$(Y,B_Y)$
and
![]() $B_Y = \sum b_i B_i$
with
$B_Y = \sum b_i B_i$
with
![]() $B_i$
irreducible, we define the difficulty ([Reference Alexeev, Hacon and KawamataAHK07, Definition 2.3])
$B_i$
irreducible, we define the difficulty ([Reference Alexeev, Hacon and KawamataAHK07, Definition 2.3])
 $$\begin{align*}d^+_{\alpha}(Y,B_Y) = \sum_{b_i \leq 0} W^{+}_{\alpha}(b_i) \rho(\tilde B_i) + \sum_{v} w_{\alpha}^+(a_v) - \sum_{\tilde C_{i,j}} W^{+}_{\alpha}(b_i), \text{ where}\end{align*}$$
$$\begin{align*}d^+_{\alpha}(Y,B_Y) = \sum_{b_i \leq 0} W^{+}_{\alpha}(b_i) \rho(\tilde B_i) + \sum_{v} w_{\alpha}^+(a_v) - \sum_{\tilde C_{i,j}} W^{+}_{\alpha}(b_i), \text{ where}\end{align*}$$
-
•
 $\rho $
is as in [Reference Alexeev, Hacon and KawamataAHK07, Lemma 1.6] (in particular, stable under small birational maps),
$\rho $
is as in [Reference Alexeev, Hacon and KawamataAHK07, Lemma 1.6] (in particular, stable under small birational maps), -
• v is taken over all valuations which are not echoes on Y (here,
 $a_v$
denotes the discrepancy of
$a_v$
denotes the discrepancy of
 $(Y,B_Y\hspace{-1pt})$
at v) and
$(Y,B_Y\hspace{-1pt})$
at v) and -
•
 $\tilde C_{i,j}$
are codimension one irreducible components in
$\tilde C_{i,j}$
are codimension one irreducible components in
 $\tilde B_i$
of the inverse image of a codimension two integral subscheme
$\tilde B_i$
of the inverse image of a codimension two integral subscheme
 $C \subseteq Y$
under the normalisation
$C \subseteq Y$
under the normalisation
 $\bigsqcup \tilde B_i \to \bigcup B_i$
. Here, we exclude those C which are centres of echoes.
$\bigsqcup \tilde B_i \to \bigcup B_i$
. Here, we exclude those C which are centres of echoes.
We say that an irreducible
![]() $C \subseteq Y$
is a centre of an echo if it is of codimension two, contained in exactly one
$C \subseteq Y$
is a centre of an echo if it is of codimension two, contained in exactly one
![]() $B_i$
, but not in
$B_i$
, but not in
![]() $\mathrm {Sing}\, B_i$
. Here, a valuation is called a (k-th) echo for such C if it corresponds to the last exceptional divisor of a sequence of k blowups at strict transforms of C (see [Reference Alexeev, Hacon and KawamataAHK07, Example 1.4]). The discrepancy of the k-th echo is
$\mathrm {Sing}\, B_i$
. Here, a valuation is called a (k-th) echo for such C if it corresponds to the last exceptional divisor of a sequence of k blowups at strict transforms of C (see [Reference Alexeev, Hacon and KawamataAHK07, Example 1.4]). The discrepancy of the k-th echo is
![]() $k(1-b_i)$
. The difficulty is well defined and finite because there are only finitely many valuations with discrepancy in
$k(1-b_i)$
. The difficulty is well defined and finite because there are only finitely many valuations with discrepancy in
![]() $(-1,0]$
and also finitely many in
$(-1,0]$
and also finitely many in
![]() $(0,1)$
if we exclude echoes ([Reference Alexeev, Hacon and KawamataAHK07, Lemma 1.5]; here, we use log resolutions).
$(0,1)$
if we exclude echoes ([Reference Alexeev, Hacon and KawamataAHK07, Lemma 1.5]; here, we use log resolutions).
We can similarly define
![]() $d^-_{\alpha }$
. The difficulties are stable under log pullbacks ([Reference Alexeev, Hacon and KawamataAHK07, Lemma 2.7]), and so we extend these definitions to arbitrary
$d^-_{\alpha }$
. The difficulties are stable under log pullbacks ([Reference Alexeev, Hacon and KawamataAHK07, Lemma 2.7]), and so we extend these definitions to arbitrary
![]() ${\mathbb {Q}}$
-factorial klt pairs by taking the difficulty of a terminalisation ([Reference Alexeev, Hacon and KawamataAHK07, Definition 2.8]). The difficulties are nonnegative for klt pairs ([Reference Alexeev, Hacon and KawamataAHK07, Lemma 2.9]) and decreasing for a sequence of flips
${\mathbb {Q}}$
-factorial klt pairs by taking the difficulty of a terminalisation ([Reference Alexeev, Hacon and KawamataAHK07, Definition 2.8]). The difficulties are nonnegative for klt pairs ([Reference Alexeev, Hacon and KawamataAHK07, Lemma 2.9]) and decreasing for a sequence of flips
![]() $(X_n,B_n) \dashrightarrow (X_{n+1},B_{n+1})$
if we start with
$(X_n,B_n) \dashrightarrow (X_{n+1},B_{n+1})$
if we start with
![]() $n \gg 0$
([Reference Alexeev, Hacon and KawamataAHK07, Theorem 2.12]).
$n \gg 0$
([Reference Alexeev, Hacon and KawamataAHK07, Theorem 2.12]).
We are ready to give the proof of the proposition. First, we show that there are only finitely many flips with flipping or flipped loci admitting a component C of codimension two and contained in
![]() $\mathrm {Sing}\, X_n$
(this is [Reference Alexeev, Hacon and KawamataAHK07, Lemma 2.14] with the use of Bertini replaced by localisation at C). By taking
$\mathrm {Sing}\, X_n$
(this is [Reference Alexeev, Hacon and KawamataAHK07, Lemma 2.14] with the use of Bertini replaced by localisation at C). By taking
![]() $n\gg 0$
, we can assume that the places with discrepancies smaller or equal to 0 are stable under flips: Let
$n\gg 0$
, we can assume that the places with discrepancies smaller or equal to 0 are stable under flips: Let
![]() $E_1, \ldots , E_m$
be such places over
$E_1, \ldots , E_m$
be such places over
![]() $X_n$
with discrepancies
$X_n$
with discrepancies
![]() $a_1, \ldots , a_m \leq 0$
. In particular, the minimal discrepancy of the two-dimensional singularity obtained by localisation at C must be equal to
$a_1, \ldots , a_m \leq 0$
. In particular, the minimal discrepancy of the two-dimensional singularity obtained by localisation at C must be equal to
![]() $a_i$
for some i. It is known by experts that minimal log discrepancies (mlds) for klt surface singularities satisfy the ascending chain condition, and since flips increase discrepancies, the statement follows. As this result is unpublished, we refer to Lemma 2.16 instead.
$a_i$
for some i. It is known by experts that minimal log discrepancies (mlds) for klt surface singularities satisfy the ascending chain condition, and since flips increase discrepancies, the statement follows. As this result is unpublished, we refer to Lemma 2.16 instead.
We are left to show that there are only finitely many flips with flipping or flipped loci admitting a component C of codimension two and contained in
![]() ${\mathrm {Supp}}\, B_n$
but not
${\mathrm {Supp}}\, B_n$
but not
![]() $\mathrm {Sing}\, X_n$
. The blowup along C produces a divisor with discrepancy
$\mathrm {Sing}\, X_n$
. The blowup along C produces a divisor with discrepancy
![]() $1 - \sum m_i b_i$
for
$1 - \sum m_i b_i$
for
![]() $m_i \in \mathbb {Z}_{\geq 0}$
. There are only finitely many such discrepancies, and, thus, it is enough to prove the following claim: Given
$m_i \in \mathbb {Z}_{\geq 0}$
. There are only finitely many such discrepancies, and, thus, it is enough to prove the following claim: Given
![]() $\alpha \in (-1,1)$
, there cannot be infinitely many flips for which there exists a valuation v with
$\alpha \in (-1,1)$
, there cannot be infinitely many flips for which there exists a valuation v with
![]() $a_v = \alpha $
and centre contained in the flipping or the flipped locus ([Reference Alexeev, Hacon and KawamataAHK07, Theorem 2.13]). The case
$a_v = \alpha $
and centre contained in the flipping or the flipped locus ([Reference Alexeev, Hacon and KawamataAHK07, Theorem 2.13]). The case
![]() $\alpha \in (-1,0]$
follows by finiteness, while for
$\alpha \in (-1,0]$
follows by finiteness, while for
![]() $\alpha \in (0,1)$
we notice that
$\alpha \in (0,1)$
we notice that
![]() $d^-_{\alpha }$
drops by at least
$d^-_{\alpha }$
drops by at least
![]() $1-\alpha $
if the flipping locus admits such a valuation and so does
$1-\alpha $
if the flipping locus admits such a valuation and so does
![]() $d^+_{\alpha }$
for the flipped locus. Since the difficulties are positive and finite, this can only happen finitely many times.
$d^+_{\alpha }$
for the flipped locus. Since the difficulties are positive and finite, this can only happen finitely many times.
The last assertions follows by replacing B by
![]() $B + \epsilon M$
for
$B + \epsilon M$
for
![]() $0 \leq M \sim _{{\mathbb {Q}}, U} K_X + B$
and
$0 \leq M \sim _{{\mathbb {Q}}, U} K_X + B$
and
![]() $0 < \epsilon \ll 1$
since then every flipping curve
$0 < \epsilon \ll 1$
since then every flipping curve
![]() $\Sigma $
satisfies
$\Sigma $
satisfies
![]() $\Sigma \cdot M < 0$
, and so is contained in M.
$\Sigma \cdot M < 0$
, and so is contained in M.
Lemma 2.16. Fix
![]() $m \in \mathbb {N}$
and
$m \in \mathbb {N}$
and
![]() $\epsilon>0$
. Consider all
$\epsilon>0$
. Consider all
![]() $\epsilon $
-lc excellent two-dimensional pairs
$\epsilon $
-lc excellent two-dimensional pairs
![]() $(S,B)$
with the minimal log resolution having at most m distinct discrepancies. Then the set of all these discrepancies for such surfaces is finite.
$(S,B)$
with the minimal log resolution having at most m distinct discrepancies. Then the set of all these discrepancies for such surfaces is finite.
This result holds in a more general setting (that is, as in [Reference KollárKol13] or [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20]).
Proof. Let
![]() $f \colon S'\to S$
be the minimal resolution at a point
$f \colon S'\to S$
be the minimal resolution at a point
![]() $s \in S$
with k exceptional curves
$s \in S$
with k exceptional curves
![]() $C_i$
(which are
$C_i$
(which are
![]() $k(s)$
-schemes), and let
$k(s)$
-schemes), and let
![]() $\Gamma $
be the corresponding graph. Write
$\Gamma $
be the corresponding graph. Write
![]() $K_{S'} + B_{S'} = f^*(K_S+B_S)$
, and let
$K_{S'} + B_{S'} = f^*(K_S+B_S)$
, and let
![]() $a_i$
be the log discrepancy of
$a_i$
be the log discrepancy of
![]() $C_i$
in
$C_i$
in
![]() $(S',B_{S'})$
. We will use the results of [Reference KollárKol13]. Set
$(S',B_{S'})$
. We will use the results of [Reference KollárKol13]. Set
![]() $r_i:=\dim _{k(s)}H^0(C_i, \mathcal O _{C_i})$
. Then
$r_i:=\dim _{k(s)}H^0(C_i, \mathcal O _{C_i})$
. Then
![]() $C_i^2=-r_ic_i$
for
$C_i^2=-r_ic_i$
for
![]() $c_i \in \mathbb {Z}$
. Note that
$c_i \in \mathbb {Z}$
. Note that
![]() $C_i$
are conics over the field
$C_i$
are conics over the field
![]() $H^0(C_i, \mathcal {O}_{C_i})$
and in particular
$H^0(C_i, \mathcal {O}_{C_i})$
and in particular
![]() $\deg \omega _{C_i}=-2r_i$
([Reference KollárKol13, Reduction 3.30.2]). By adjunction,
$\deg \omega _{C_i}=-2r_i$
([Reference KollárKol13, Reduction 3.30.2]). By adjunction,
and so
![]() $-c_i \leq \frac {2}{a_i}$
is bounded. By classification ([Reference KollárKol13, 3.31 and 3.41]),
$-c_i \leq \frac {2}{a_i}$
is bounded. By classification ([Reference KollárKol13, 3.31 and 3.41]),
![]() $r_i \leq 4$
, and so
$r_i \leq 4$
, and so
![]() $-C_i^2$
is bounded. Further,
$-C_i^2$
is bounded. Further,
![]() $C_i \cdot C_j$
is bounded as well for every
$C_i \cdot C_j$
is bounded as well for every
![]() $i\neq j$
(see [Reference KollárKol13, 3.41]).
$i\neq j$
(see [Reference KollárKol13, 3.41]).
Recall that
![]() $\Gamma $
is a tree with at most one fork and three legs ([Reference KollárKol13, 3.31]), there are no
$\Gamma $
is a tree with at most one fork and three legs ([Reference KollárKol13, 3.31]), there are no
![]() $K_X$
-negative curves and the convexity of discrepancies holds ([Reference KollárKol13, Proposition 2.37]), that is, given three consecutive curves
$K_X$
-negative curves and the convexity of discrepancies holds ([Reference KollárKol13, Proposition 2.37]), that is, given three consecutive curves
![]() $C_1$
,
$C_1$
,
![]() $C_2$
and
$C_2$
and
![]() $C_3$
on a leg, we have
$C_3$
on a leg, we have
![]() $2a_2\leq a_1+a_3$
. In fact, it follows easily from the same proof that if
$2a_2\leq a_1+a_3$
. In fact, it follows easily from the same proof that if
![]() $2a_2= a_1+a_3$
, then
$2a_2= a_1+a_3$
, then
![]() $c_2=-2$
,
$c_2=-2$
,
![]() $f^{-1}_*B\cdot C_2=0$
and
$f^{-1}_*B\cdot C_2=0$
and
![]() $C_2 \cdot C_1 = C_2 \cdot C_3 = r_2$
.
$C_2 \cdot C_1 = C_2 \cdot C_3 = r_2$
.
By the negativity lemma, the k equations
are linearly independent and uniquely determine the discrepancies. Given a maximal sequence of successive curves
![]() $C_1,\ldots , C_r$
on one leg with the same discrepancies
$C_1,\ldots , C_r$
on one leg with the same discrepancies
![]() $a_i$
and parameters
$a_i$
and parameters
![]() $r_i$
, we remove the equations corresponding to
$r_i$
, we remove the equations corresponding to
![]() $C_2, \ldots , C_{r-1}$
and replace all occurrences of
$C_2, \ldots , C_{r-1}$
and replace all occurrences of
![]() $a_2,\ldots , a_r$
by
$a_2,\ldots , a_r$
by
![]() $a_1$
. This operation does not change the set of solutions (indeed, this is equivalent to adding equations
$a_1$
. This operation does not change the set of solutions (indeed, this is equivalent to adding equations
![]() $a_1=a_2=\ldots =a_r$
which does not change the set of solutions but renders the equations corresponding to
$a_1=a_2=\ldots =a_r$
which does not change the set of solutions but renders the equations corresponding to
![]() $C_2, \ldots , C_{r-1}$
trivial), and so, eventually, given the shape of
$C_2, \ldots , C_{r-1}$
trivial), and so, eventually, given the shape of
![]() $\Gamma $
([Reference KollárKol13, 3.31]), we are left with bounded-in-m number of equations with bounded coefficients and in the same or lower number of variables. Therefore, the set of discrepancies is bounded in terms of m as well.
$\Gamma $
([Reference KollárKol13, 3.31]), we are left with bounded-in-m number of equations with bounded coefficients and in the same or lower number of variables. Therefore, the set of discrepancies is bounded in terms of m as well.
Remark 2.17. Special termination of sequences of the fourfold MMP with scaling now holds by [Reference Xie and XueXX21a, Remark 2.17].
3 Extending sections
In this section, we prove an extension result for purely F-regular (and purely
![]() $+$
-regular) pairs. In particular, the following proposition implies Theorem 1.6. Our original arXiv submission covered the positive characteristic case only. Its generalisation to mixed characteristic was then obtained in [Reference Takamatsu and YoshikawaTY20, Proposition 3.28]. For the convenience of the reader, we append the proof of the mixed characteristic case at the end of the argument using the techniques of [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20].
$+$
-regular) pairs. In particular, the following proposition implies Theorem 1.6. Our original arXiv submission covered the positive characteristic case only. Its generalisation to mixed characteristic was then obtained in [Reference Takamatsu and YoshikawaTY20, Proposition 3.28]. For the convenience of the reader, we append the proof of the mixed characteristic case at the end of the argument using the techniques of [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20].
Proposition 3.1. Let
![]() $(X,S+A+B)$
be a
$(X,S+A+B)$
be a
![]() ${\mathbb {Q}}$
-factorial dlt pair of dimension at least three defined over an F-finite field of characteristic
${\mathbb {Q}}$
-factorial dlt pair of dimension at least three defined over an F-finite field of characteristic
![]() $p>0$
(resp. over a DVR of characteristic
$p>0$
(resp. over a DVR of characteristic
![]() $(0,p)$
for
$(0,p)$
for
![]() $p>0$
), where
$p>0$
), where
![]() $\lfloor S+A+B\rfloor =S+A$
, the
$\lfloor S+A+B\rfloor =S+A$
, the
![]() ${\mathbb {Q}}$
-Cartier Weil divisor A is ample, and the Weil divisor S is irreducible. Further, let
${\mathbb {Q}}$
-Cartier Weil divisor A is ample, and the Weil divisor S is irreducible. Further, let
![]() $f\colon X\to Z$
be a contraction with Z an affine variety such that
$f\colon X\to Z$
be a contraction with Z an affine variety such that
![]() $(X,S+(1-\epsilon )A+B)$
is relatively purely F-regular (resp. completely relatively purely
$(X,S+(1-\epsilon )A+B)$
is relatively purely F-regular (resp. completely relatively purely
![]() $+$
-regular) over Z for any
$+$
-regular) over Z for any
![]() $\epsilon>0$
. Write
$\epsilon>0$
. Write
![]() $K_S+B_S = (K_X+S+B)|_S$
and
$K_S+B_S = (K_X+S+B)|_S$
and
![]() $A_S = A|_S$
.
$A_S = A|_S$
.
In the mixed characteristic case, we also assume that
![]() $-(K_X+S+B+A)$
is relatively ample and that closed points of Z are of positive residue characteristic. Then
$-(K_X+S+B+A)$
is relatively ample and that closed points of Z are of positive residue characteristic. Then
is surjective for every
![]() $k\geq 1$
such that
$k\geq 1$
such that
![]() $k(K_X+S+B+A)$
is Cartier.
$k(K_X+S+B+A)$
is Cartier.
Note that S is normal by Lemma 2.9. Also, observe that the assumption on
![]() ${\mathbb {Q}}$
-factoriality and the dimension being at least three is unnecessary in mixed characteristic. Further, the statement is in fact true over characteristic 0 closed points by Remark 3.3 or by an analogous argument with
${\mathbb {Q}}$
-factoriality and the dimension being at least three is unnecessary in mixed characteristic. Further, the statement is in fact true over characteristic 0 closed points by Remark 3.3 or by an analogous argument with
![]() $S^0$
replaced by
$S^0$
replaced by
![]() $H^0$
using Nadel vanishing.
$H^0$
using Nadel vanishing.
Proof. We tackle the positive characteristic case first. Let
![]() $F \in |k(K_S+B_S+A_S)|$
. We will construct divisors
$F \in |k(K_S+B_S+A_S)|$
. We will construct divisors
![]() $G_m \in |k(K_X+S+B+A) + mA|$
such that
$G_m \in |k(K_X+S+B+A) + mA|$
such that
![]() $G_m|_S = F + mA_S$
by descending induction. First, we take
$G_m|_S = F + mA_S$
by descending induction. First, we take
![]() $M \gg 0$
for which we can construct
$M \gg 0$
for which we can construct
![]() $G_M$
by Serre vanishing. Now, assume that we constructed
$G_M$
by Serre vanishing. Now, assume that we constructed
![]() $G_{m+1}$
as above. To construct
$G_{m+1}$
as above. To construct
![]() $G_m$
we proceed as follows. Write
$G_m$
we proceed as follows. Write
 $$ \begin{align*} L &= k(K_X+S+B+A) + mA \\ &= K_X+S+B + (k-1)(K_X+S+B+A) + (m+1)A \\ &\sim_{{\mathbb{Q}}} K_X+S+B + {\textstyle \frac{k-1}{k}}G_{m+1} + {\textstyle \frac{m+1}{k}}A. \end{align*} $$
$$ \begin{align*} L &= k(K_X+S+B+A) + mA \\ &= K_X+S+B + (k-1)(K_X+S+B+A) + (m+1)A \\ &\sim_{{\mathbb{Q}}} K_X+S+B + {\textstyle \frac{k-1}{k}}G_{m+1} + {\textstyle \frac{m+1}{k}}A. \end{align*} $$
Since
![]() $L-(K_X+S+B + \frac {k-1}{k}G_{m+1})$
is ample, up to a small perturbation of the coefficients, by Proposition 2.10 we have a surjection (the assumption on the non-Cartier locus of A, and hence of L, is satisfied as
$L-(K_X+S+B + \frac {k-1}{k}G_{m+1})$
is ample, up to a small perturbation of the coefficients, by Proposition 2.10 we have a surjection (the assumption on the non-Cartier locus of A, and hence of L, is satisfied as
![]() $(X,S+A+B)$
is dlt)
$(X,S+A+B)$
is dlt)
Since
![]() $(S,B_S + \frac {k-1}{k}A_S)$
is relatively F-regular and
$(S,B_S + \frac {k-1}{k}A_S)$
is relatively F-regular and
Lemma 3.2 implies that the section corresponding to
![]() $F + mA_S$
lies in the image of the above map. This concludes the construction of
$F + mA_S$
lies in the image of the above map. This concludes the construction of
![]() $G_m$
, and so we obtain a lift
$G_m$
, and so we obtain a lift
![]() $G_0 \in |k(K_X+S+B+A)|$
of F.
$G_0 \in |k(K_X+S+B+A)|$
of F.
In mixed characteristic, since surjectivity of maps of coherent sheaves may be checked on completions of closed points (see [Sta14, Tag 00MC and Tag 00MA(3)]), we can complete at a closed point
![]() $z \in Z$
of positive residue characteristic and assume that
$z \in Z$
of positive residue characteristic and assume that
![]() $Z = \operatorname {\mathrm {Spec}} R$
for a complete Noetherian local domain R (note that this need not preserve
$Z = \operatorname {\mathrm {Spec}} R$
for a complete Noetherian local domain R (note that this need not preserve
![]() ${\mathbb {Q}}$
-factoriality). By [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Corollary 7.8] (and [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Corollary 7.5]), S stays prime after the base change to the completion (here, we use that
${\mathbb {Q}}$
-factoriality). By [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Corollary 7.8] (and [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Corollary 7.5]), S stays prime after the base change to the completion (here, we use that
![]() $-(K_X+S+B+A)$
is relatively ample). Now the proof follows the positive characteristic case word for word with F-regular replaced by
$-(K_X+S+B+A)$
is relatively ample). Now the proof follows the positive characteristic case word for word with F-regular replaced by
![]() $+$
-regular, Proposition 2.10 replaced by Proposition 2.11 and the surjectivity of
$+$
-regular, Proposition 2.10 replaced by Proposition 2.11 and the surjectivity of
![]() $S^0$
replaced by the surjectivity of
$S^0$
replaced by the surjectivity of
Lemma 3.2. Let
![]() $(X,B)$
be a projective globally F-regular pair defined over an affine variety over an F-finite field of characteristic
$(X,B)$
be a projective globally F-regular pair defined over an affine variety over an F-finite field of characteristic
![]() $p>0$
(resp. a globally
$p>0$
(resp. a globally
![]() $+$
-regular pair defined over a complete local Noetherian domain of characteristic
$+$
-regular pair defined over a complete local Noetherian domain of characteristic
![]() $(0,p)$
for
$(0,p)$
for
![]() $p>0$
), let L be a Weil divisor and let
$p>0$
), let L be a Weil divisor and let
![]() $ \Gamma $
be an effective
$ \Gamma $
be an effective
![]() ${\mathbb {Q}}$
-divisor. If
${\mathbb {Q}}$
-divisor. If
![]() $g\in H^0(X, {\mathcal {O}}_X(L))$
corresponds to a divisor
$g\in H^0(X, {\mathcal {O}}_X(L))$
corresponds to a divisor
![]() $G\in |L|$
such that
$G\in |L|$
such that
![]() $G\geq \Gamma $
, then
$G\geq \Gamma $
, then
![]() $g\in S^0(X, B+\Gamma; L)$
(resp.
$g\in S^0(X, B+\Gamma; L)$
(resp.
![]() $g\in B^0(X, B+\Gamma; L)$
).
$g\in B^0(X, B+\Gamma; L)$
).
Proof. First, we deal with the positive characteristic case. By replacing X by its regular locus, we can assume that it is regular and hence factorial. Further, we perturb B so that its index is not divisible by p. Since
![]() $(X,B)$
is globally F-regular, we have a splitting of
$(X,B)$
is globally F-regular, we have a splitting of
and so
![]() $H^0(X, {\mathcal {O}}_X) = S^0(X,B;{\mathcal {O}}_X)$
.
$H^0(X, {\mathcal {O}}_X) = S^0(X,B;{\mathcal {O}}_X)$
.
Thus, we have the following diagram

Therefore, g is in the image of the map on global sections induced by
Since
![]() $G\geq \Gamma $
, we have the following sequence of homomorphisms
$G\geq \Gamma $
, we have the following sequence of homomorphisms
Applying Grothendieck duality to these maps shows that (
![]() $\dagger $
) factors through
$\dagger $
) factors through
concluding the proof.
In mixed characteristic, take a finite cover
![]() $f \colon Y \to X$
with Y normal. By global
$f \colon Y \to X$
with Y normal. By global
![]() $+$
-regularity of
$+$
-regularity of
![]() $(X,B)$
, the trace map
$(X,B)$
, the trace map
is split surjective (see the proof of [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Proposition 6.8]). Hence, by
![]() $B^0(X,B; {\mathcal {O}}_X) = H^0(X, {\mathcal {O}}_X)$
(see also [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Lemma 6.11]). By the same argument as above, g is in the image of the map on global sections induced by
$B^0(X,B; {\mathcal {O}}_X) = H^0(X, {\mathcal {O}}_X)$
(see also [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Lemma 6.11]). By the same argument as above, g is in the image of the map on global sections induced by
and as
![]() $G \geq \Gamma $
, this homomorphism factors through
$G \geq \Gamma $
, this homomorphism factors through
concluding the proof.
Remark 3.3. (C. Xu) Let k be a field of characteristic 0 or any field of positive characteristic, respectively. Suppose that
![]() $f\colon X\to Z$
is a flipping contraction and
$f\colon X\to Z$
is a flipping contraction and
![]() is the flip of a dlt pair
is the flip of a dlt pair
![]() $(X,S+A+B)$
, where A is an f-ample Weil divisors, S is irreducible and
$(X,S+A+B)$
, where A is an f-ample Weil divisors, S is irreducible and
![]() $\lfloor S+A+B\rfloor = S+A$
. Write
$\lfloor S+A+B\rfloor = S+A$
. Write
![]() $K_S+B_S = (K_X+S+B)|_S$
and
$K_S+B_S = (K_X+S+B)|_S$
and
![]() $A_S=A|_S$
. Assume for simplicity that S is normal.
$A_S=A|_S$
. Assume for simplicity that S is normal.
We claim that
![]() $|k(K_X+S+A+B)|_S=|k(K_S+A_S+B_S)|$
for every integer
$|k(K_X+S+A+B)|_S=|k(K_S+A_S+B_S)|$
for every integer
![]() $k>1$
such that
$k>1$
such that
![]() $k(K_X+S+A+B)$
is integral (resp. any sufficiently divisible integer). This explains why we can obtain such strong liftability results, which are normally false when there is no ample divisor in the boundary (cf. [Reference Hacon and McKernanHMK10]).
$k(K_X+S+A+B)$
is integral (resp. any sufficiently divisible integer). This explains why we can obtain such strong liftability results, which are normally false when there is no ample divisor in the boundary (cf. [Reference Hacon and McKernanHMK10]).
To see the claim, notice that if
![]() $S^+=\phi _*S$
, then
$S^+=\phi _*S$
, then
![]() extracts no divisors. In fact, if
extracts no divisors. In fact, if
![]() $P\subset S^+$
is an extracted divisor, then since
$P\subset S^+$
is an extracted divisor, then since
![]() $A^+=\phi _* A$
is
$A^+=\phi _* A$
is
![]() $f^+\colon X^+\to Z$
antiample (as A is f-ample), it contains P and hence there is a divisor F over
$f^+\colon X^+\to Z$
antiample (as A is f-ample), it contains P and hence there is a divisor F over
![]() $X^+$
with centre P such that the log-discrepancy
$X^+$
with centre P such that the log-discrepancy
![]() $a_F(X^+,S^++A^++B^+)=0$
which is impossible, as
$a_F(X^+,S^++A^++B^+)=0$
which is impossible, as
![]() $(X,S+A+B)$
is dlt and discrepancies improve after flips.
$(X,S+A+B)$
is dlt and discrepancies improve after flips.
Now, since
![]() $K_{X^+}+S^++A^++B^+$
is
$K_{X^+}+S^++A^++B^+$
is
![]() $f^+$
-ample, by Kawamata–Viehweg vanishing (resp. Serre vanishing)
$f^+$
-ample, by Kawamata–Viehweg vanishing (resp. Serre vanishing)
is surjective. Since
![]() $\phi $
is a small birational morphism,
$\phi $
is a small birational morphism,
![]() $ H^0(X^+, k(K_{X^+}+S^++A^++B^+))\cong H^0(X, k(K_{X}+S+A+B)) $
and since
$ H^0(X^+, k(K_{X^+}+S^++A^++B^+))\cong H^0(X, k(K_{X}+S+A+B)) $
and since
![]() is a
is a
![]() $(K_S+A_S+B_S)$
-nonpositive birational contraction,
$(K_S+A_S+B_S)$
-nonpositive birational contraction,
4 Relative MMP over
 ${\mathbb {Q}}$
-factorial fourfolds
${\mathbb {Q}}$
-factorial fourfolds
In this section, we prove Theorem 1.1 whose statement in full generality is as follows.
Theorem 4.1. Let
![]() $(Y,\Delta )$
be a four-dimensional
$(Y,\Delta )$
be a four-dimensional
![]() ${\mathbb {Q}}$
-factorial dlt pair defined over a perfect field of characteristic
${\mathbb {Q}}$
-factorial dlt pair defined over a perfect field of characteristic
![]() $p>5$
or a DVR of characteristic
$p>5$
or a DVR of characteristic
![]() $(0,p)$
for
$(0,p)$
for
![]() $p>5$
with a perfect residue field. Suppose that
$p>5$
with a perfect residue field. Suppose that
![]() $\Delta $
has standard coefficients or that log resolutions of all log pairs with the underlying variety being birational to Y exist (and are given by a sequence of blowups along the non-snc locus). Let
$\Delta $
has standard coefficients or that log resolutions of all log pairs with the underlying variety being birational to Y exist (and are given by a sequence of blowups along the non-snc locus). Let
![]() $\pi \colon Y\to X$
be a projective birational morphism to a normal
$\pi \colon Y\to X$
be a projective birational morphism to a normal
![]() ${\mathbb {Q}}$
-factorial variety X such that
${\mathbb {Q}}$
-factorial variety X such that
![]() $\textrm {Ex}(\pi )\subset \lfloor \Delta \rfloor $
. Then we may run a
$\textrm {Ex}(\pi )\subset \lfloor \Delta \rfloor $
. Then we may run a
![]() $(K_Y+\Delta )$
-MMP over X, which terminates with a minimal model.
$(K_Y+\Delta )$
-MMP over X, which terminates with a minimal model.
4.1 Existence of pl-flips with ample divisor in the boundary
In order to show Theorem 4.3, we need the following lemma.
Lemma 4.2. Let
![]() $(S,C+B)$
be a three-dimensional plt pair with standard coefficients defined over an F-finite field of characteristic
$(S,C+B)$
be a three-dimensional plt pair with standard coefficients defined over an F-finite field of characteristic
![]() $p>5$
(resp. a DVR of characteristic
$p>5$
(resp. a DVR of characteristic
![]() $(0,p)$
for
$(0,p)$
for
![]() $p>5$
), where
$p>5$
), where
![]() $f\colon S\to T$
is a projective birational morphism, C is a prime divisor with
$f\colon S\to T$
is a projective birational morphism, C is a prime divisor with
![]() $f|_{C} \colon C \to f(C)$
birational, and
$f|_{C} \colon C \to f(C)$
birational, and
![]() $-(K_S+C+B)$
is an f-ample
$-(K_S+C+B)$
is an f-ample
![]() ${\mathbb {Q}}$
-divisor.
${\mathbb {Q}}$
-divisor.
Then
![]() $(S,C+B)$
is relatively purely F-regular (resp. completely relatively purely
$(S,C+B)$
is relatively purely F-regular (resp. completely relatively purely
![]() $+$
-regular) over a neighbourhood of
$+$
-regular) over a neighbourhood of
![]() $f(C)\subset T$
.
$f(C)\subset T$
.
Proof. Let
![]() $\tilde {C}$
be the normalisation of C, and write
$\tilde {C}$
be the normalisation of C, and write
![]() $K_{\tilde C} + B_{\tilde C} = (K_S+C+B)|_{\tilde C}$
. Then
$K_{\tilde C} + B_{\tilde C} = (K_S+C+B)|_{\tilde C}$
. Then
![]() $(\tilde C, B_{\tilde C})$
is klt with standard coefficients (see Lemma 2.2). Since
$(\tilde C, B_{\tilde C})$
is klt with standard coefficients (see Lemma 2.2). Since
![]() $\tilde C \to f(C)$
is birational,
$\tilde C \to f(C)$
is birational,
![]() $(\tilde C, B_{\tilde C})$
is relatively globally F-regular ([Reference Das and WaldronDW19a, Theorem 5.1], cf. [Reference Hacon and XuHX15, Theorem 3.1], [Reference Hacon and WitaszekHW22, Proposition 2.9]) or completely relatively globally
$(\tilde C, B_{\tilde C})$
is relatively globally F-regular ([Reference Das and WaldronDW19a, Theorem 5.1], cf. [Reference Hacon and XuHX15, Theorem 3.1], [Reference Hacon and WitaszekHW22, Proposition 2.9]) or completely relatively globally
![]() $+$
-regular ([Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Theorem 7.14]), respectively. Lemma 2.9 implies that
$+$
-regular ([Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Theorem 7.14]), respectively. Lemma 2.9 implies that
![]() $(S,C+B)$
is relatively purely F-regular (resp. completely relatively purely
$(S,C+B)$
is relatively purely F-regular (resp. completely relatively purely
![]() $+$
-regular) over a neighbourhood of
$+$
-regular) over a neighbourhood of
![]() $f(C)$
.
$f(C)$
.
Theorem 4.3. Let
![]() $(X,\Delta )$
be a four-dimensional
$(X,\Delta )$
be a four-dimensional
![]() ${\mathbb {Q}}$
-factorial dlt pair with standard coefficients defined over an F-finite field k of characteristic
${\mathbb {Q}}$
-factorial dlt pair with standard coefficients defined over an F-finite field k of characteristic
![]() $p>5$
(resp. a DVR of characteristic
$p>5$
(resp. a DVR of characteristic
![]() $(0,p)$
for
$(0,p)$
for
![]() $p>5$
) and
$p>5$
) and
![]() $\phi \colon X\to Z$
a flipping contraction of a
$\phi \colon X\to Z$
a flipping contraction of a
![]() $(K_X+\Delta )$
-negative extremal ray R with
$(K_X+\Delta )$
-negative extremal ray R with
![]() $\rho (X/Z)=1$
. Suppose that there exist irreducible divisors
$\rho (X/Z)=1$
. Suppose that there exist irreducible divisors
![]() $S,A\subset \lfloor \Delta \rfloor $
such that
$S,A\subset \lfloor \Delta \rfloor $
such that
![]() $R\cdot S<0$
and
$R\cdot S<0$
and
![]() $R\cdot A>0$
.
$R\cdot A>0$
.
Then the flip
![]() $(X^+,\Delta ^+)$
exists. Moreover, both X and
$(X^+,\Delta ^+)$
exists. Moreover, both X and
![]() $X^+$
are relatively F-regular (resp. completely relatively
$X^+$
are relatively F-regular (resp. completely relatively
![]() $+$
-regular) over a neighbourhood of the image of the flipping locus in Z.
$+$
-regular) over a neighbourhood of the image of the flipping locus in Z.
Proof. The statement is local, and hence we may assume that Z is affine and we work in a neighbourhood of some closed point
![]() $z\in Z$
of positive residue characteristic in the image of the flipping locus. Replacing
$z\in Z$
of positive residue characteristic in the image of the flipping locus. Replacing
![]() $\lfloor \Delta \rfloor -S-A$
by
$\lfloor \Delta \rfloor -S-A$
by
![]() $(1-\frac 1m)(\lfloor \Delta \rfloor -S-A)$
for some
$(1-\frac 1m)(\lfloor \Delta \rfloor -S-A)$
for some
![]() $m\gg 0$
, we may assume that
$m\gg 0$
, we may assume that
![]() $\lfloor \Delta \rfloor =S+A$
. Let
$\lfloor \Delta \rfloor =S+A$
. Let
![]() $K_{S^{\nu }}+A_{S^{\nu }}+B_{S^{\nu }}=(K_X+S+A+B)|_{S^{\nu }}$
with
$K_{S^{\nu }}+A_{S^{\nu }}+B_{S^{\nu }}=(K_X+S+A+B)|_{S^{\nu }}$
with
![]() $A_{S^{\nu }} = A|_{S^{\nu }}$
and
$A_{S^{\nu }} = A|_{S^{\nu }}$
and
![]() $S^{\nu }$
being the normalisation of S. Then
$S^{\nu }$
being the normalisation of S. Then
![]() $(S^{\nu },A_{S^{\nu }}+B_{S^{\nu }})$
is a plt threefold with standard coefficients. Since
$(S^{\nu },A_{S^{\nu }}+B_{S^{\nu }})$
is a plt threefold with standard coefficients. Since
![]() $A_{S^{\nu }}$
is relatively ample, it is not exceptional, and so it is birational over its image in Z. As
$A_{S^{\nu }}$
is relatively ample, it is not exceptional, and so it is birational over its image in Z. As
![]() $-(K_{S^{\nu }}+A_{S^{\nu }}+B_{S^{\nu }})$
is relatively ample, Lemma 4.2 implies that
$-(K_{S^{\nu }}+A_{S^{\nu }}+B_{S^{\nu }})$
is relatively ample, Lemma 4.2 implies that
![]() $(S^{\nu },A_{S^{\nu }}+B_{S^{\nu }})$
is purely F-regular (resp. completely purely
$(S^{\nu },A_{S^{\nu }}+B_{S^{\nu }})$
is purely F-regular (resp. completely purely
![]() $+$
-regular) over a neighbourhood of
$+$
-regular) over a neighbourhood of
![]() $f(A_{S^{\nu }})$
. By Lemma 2.9,
$f(A_{S^{\nu }})$
. By Lemma 2.9,
![]() $(X,S+(1-\epsilon )A+B)$
is purely F-regular (resp. completely purely
$(X,S+(1-\epsilon )A+B)$
is purely F-regular (resp. completely purely
![]() $+$
-regular) over a neighbourhood of
$+$
-regular) over a neighbourhood of
![]() $f(A_S)$
for any
$f(A_S)$
for any
![]() $\epsilon>0$
. Since every flipping curve is contained in S and intersects A,
$\epsilon>0$
. Since every flipping curve is contained in S and intersects A,
![]() $(X,S+(1-\epsilon )A+B)$
is purely F-regular (resp. completely purely
$(X,S+(1-\epsilon )A+B)$
is purely F-regular (resp. completely purely
![]() $+$
-regular) over a neighbourhood of the image of the flipping locus. In particular, S is normal (Lemma 2.9).
$+$
-regular) over a neighbourhood of the image of the flipping locus. In particular, S is normal (Lemma 2.9).
By Shokurov’s reduction to pl-flips (see, e.g., [Reference CortiCor07, Lemma 2.3.6]), it suffices to show that the restricted algebra
is finitely generated. By Proposition 3.1 in fact
![]() $R_S(K_X+S+A+B)=R(K_S+A_S+B_S)$
(in divisible enough degrees). Since
$R_S(K_X+S+A+B)=R(K_S+A_S+B_S)$
(in divisible enough degrees). Since
![]() $(S,(1-\epsilon )A_S+B_S)$
is a klt threefold for
$(S,(1-\epsilon )A_S+B_S)$
is a klt threefold for
![]() $0 < \epsilon \leq 1$
, the ring
$0 < \epsilon \leq 1$
, the ring
![]() $R(K_S+A_S+B_S)$
is finitely generated (see [Reference Das and WaldronDW19b, Theorem 1.4 and 1.6] when S is purely positive characteristic and [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Theorem F and G] when S is of mixed characteristic).
$R(K_S+A_S+B_S)$
is finitely generated (see [Reference Das and WaldronDW19b, Theorem 1.4 and 1.6] when S is purely positive characteristic and [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Theorem F and G] when S is of mixed characteristic).
If
![]() $\phi \colon X \dashrightarrow X^+$
is the corresponding flip, then since the flipping contraction
$\phi \colon X \dashrightarrow X^+$
is the corresponding flip, then since the flipping contraction
![]() $f \colon X \to Z$
is relatively F-regular (resp. completely relatively
$f \colon X \to Z$
is relatively F-regular (resp. completely relatively
![]() $+$
-regular) over a neighbourhood of the image of the flipping locus and
$+$
-regular) over a neighbourhood of the image of the flipping locus and
![]() $\phi $
is an isomorphism in codimension two, the flipped contraction
$\phi $
is an isomorphism in codimension two, the flipped contraction
![]() $f^+ \colon X^+ \to Z$
is also relatively F-regular (resp. completely relatively
$f^+ \colon X^+ \to Z$
is also relatively F-regular (resp. completely relatively
![]() $+$
-regular); see Lemma 2.7.
$+$
-regular); see Lemma 2.7.
Remark 4.4. The same argument shows that Lemma 4.2 holds in dimension two for every F-finite field of characteristic
![]() $p>0$
without the assumption that B has standard coefficients, and so Theorem 4.3 holds in dimension three for
$p>0$
without the assumption that B has standard coefficients, and so Theorem 4.3 holds in dimension three for
![]() $p>0$
without the assumption that
$p>0$
without the assumption that
![]() $\Delta $
has standard coefficients (the required result on the canonical ring being finitely generated in dimension two follows from [Reference TanakaTan18, Theorem 1.1 and 4.2]). This gives a direct proof of the existence of flips needed in [Reference Hacon and WitaszekHW21] without referring to [Reference Hacon and XuHX15].
$\Delta $
has standard coefficients (the required result on the canonical ring being finitely generated in dimension two follows from [Reference TanakaTan18, Theorem 1.1 and 4.2]). This gives a direct proof of the existence of flips needed in [Reference Hacon and WitaszekHW21] without referring to [Reference Hacon and XuHX15].
4.2 Proof of Theorem 4.1
We start by constructing contractions.
Proposition 4.5. Let
![]() $(X,S+B)$
be a
$(X,S+B)$
be a
![]() ${\mathbb {Q}}$
-factorial dlt fourfold defined over perfect field of characteristic
${\mathbb {Q}}$
-factorial dlt fourfold defined over perfect field of characteristic
![]() $p>5$
(or a DVR of characteristic
$p>5$
(or a DVR of characteristic
![]() $(0,p)$
for
$(0,p)$
for
![]() $p>5$
with perfect residue field) and equipped with a projective morphism
$p>5$
with perfect residue field) and equipped with a projective morphism
![]() $\pi \colon X\to U$
to a quasi-projective variety. Let
$\pi \colon X\to U$
to a quasi-projective variety. Let
![]() $\Sigma $
be a
$\Sigma $
be a
![]() $(K_X+S+B)$
-negative extremal ray over U such that
$(K_X+S+B)$
-negative extremal ray over U such that
![]() $S\cdot \Sigma <0$
. Further, suppose the Mori cone
$S\cdot \Sigma <0$
. Further, suppose the Mori cone
![]() $\overline {\mathrm {NE}}(X/U)$
is generated by
$\overline {\mathrm {NE}}(X/U)$
is generated by
![]() $\overline {\mathrm {NE}}(X/U)_{K_X+S+B{\geq }0}$
and countably many extremal rays which do not accumulate in
$\overline {\mathrm {NE}}(X/U)_{K_X+S+B{\geq }0}$
and countably many extremal rays which do not accumulate in
![]() $\overline {\mathrm {NE}}(X/U)_{K_X+S+B<0}$
. Then the contraction
$\overline {\mathrm {NE}}(X/U)_{K_X+S+B<0}$
. Then the contraction
![]() $f\colon X\to Z$
of
$f\colon X\to Z$
of
![]() $\Sigma $
exists so that f is a projective morphism with
$\Sigma $
exists so that f is a projective morphism with
![]() $\rho (X/Z)=1$
.
$\rho (X/Z)=1$
.
Proof. Perturbing the coefficients, we may assume that
![]() $(X,S+B)$
is plt. We may pick an ample over
$(X,S+B)$
is plt. We may pick an ample over
![]() $U \ {\mathbb {Q}}$
-divisor H such that
$U \ {\mathbb {Q}}$
-divisor H such that
![]() $L=K_X+S+B+H$
is nef over U, and
$L=K_X+S+B+H$
is nef over U, and
![]() $L^{\perp }$
is spanned by
$L^{\perp }$
is spanned by
![]() $\Sigma $
. Let A be an ample
$\Sigma $
. Let A be an ample
![]() ${\mathbb {Q}}$
-divisor such that
${\mathbb {Q}}$
-divisor such that
![]() $(S+A)\cdot \Sigma =0$
, then for any
$(S+A)\cdot \Sigma =0$
, then for any
![]() $0<\epsilon \ll 1$
we may pick an ample
$0<\epsilon \ll 1$
we may pick an ample
![]() ${\mathbb {Q}}$
-divisor
${\mathbb {Q}}$
-divisor
![]() $H_{\epsilon } \sim _{\mathbb {Q}} H+ \epsilon (S+A)$
such that
$H_{\epsilon } \sim _{\mathbb {Q}} H+ \epsilon (S+A)$
such that
![]() $L_{\epsilon } =K_X+S+B+H_{\epsilon }$
is nef over U,
$L_{\epsilon } =K_X+S+B+H_{\epsilon }$
is nef over U,
![]() $(L_{\epsilon })^{\perp }=\mathbb R [\Sigma ]$
. Let
$(L_{\epsilon })^{\perp }=\mathbb R [\Sigma ]$
. Let
![]() $\mathbb E(L_{\epsilon })$
be the exceptional locus of the nef line bundle
$\mathbb E(L_{\epsilon })$
be the exceptional locus of the nef line bundle
![]() $L_{\epsilon }$
given by the union of the integral subvarieties
$L_{\epsilon }$
given by the union of the integral subvarieties
![]() $V\subset X$
such that
$V\subset X$
such that
![]() $(L_{\epsilon }|_V)$
is not relatively big (cf. [Reference Keelkee99, Definition 0.1] and [Reference WitaszekWit22, Lemma 2.2]). Then
$(L_{\epsilon }|_V)$
is not relatively big (cf. [Reference Keelkee99, Definition 0.1] and [Reference WitaszekWit22, Lemma 2.2]). Then
![]() $\mathbb E(L_{\epsilon })\subset S$
. To verify the last inclusion, notice that if
$\mathbb E(L_{\epsilon })\subset S$
. To verify the last inclusion, notice that if
![]() $V\subset X$
is a subvariety not contained in S, then
$V\subset X$
is a subvariety not contained in S, then
![]() $L_{\epsilon } |_V=(L+\epsilon (S+A))|_V$
is nef and big over U, and so
$L_{\epsilon } |_V=(L+\epsilon (S+A))|_V$
is nef and big over U, and so
![]() $ L_{\epsilon }^{\dim V}\cdot V>0$
. Replacing L by
$ L_{\epsilon }^{\dim V}\cdot V>0$
. Replacing L by
![]() $L_{\epsilon }$
, we may assume that
$L_{\epsilon }$
, we may assume that
![]() $\mathbb E(L)\subset S$
.
$\mathbb E(L)\subset S$
.
By adjunction,
![]() $(S^{\nu },B_{S^{\nu }})$
is klt, where
$(S^{\nu },B_{S^{\nu }})$
is klt, where
![]() $K_{S^{\nu }}+B_{S^{\nu }} = (K_X+S+B)|_{S^{\nu }}$
, the map
$K_{S^{\nu }}+B_{S^{\nu }} = (K_X+S+B)|_{S^{\nu }}$
, the map
![]() $S^{\nu } \to S$
is the normalisation, and
$S^{\nu } \to S$
is the normalisation, and
![]() $H_{S^{\nu }} = H|_{S^{\nu }}$
. By [Reference Hashizume, Nakamura and TanakaHNT20, Theorem 1.4(1)] and [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Theorem G],
$H_{S^{\nu }} = H|_{S^{\nu }}$
. By [Reference Hashizume, Nakamura and TanakaHNT20, Theorem 1.4(1)] and [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Theorem G],
![]() $L|_{S^{\nu }}$
is semiample over U (note that in the mixed characteristic case, by [Reference Hashizume, Nakamura and TanakaHNT20, Theorem 1.4(1)], we may assume that
$L|_{S^{\nu }}$
is semiample over U (note that in the mixed characteristic case, by [Reference Hashizume, Nakamura and TanakaHNT20, Theorem 1.4(1)], we may assume that
![]() $\dim \pi (S) \geq 1$
, and so [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Theorem G] applies). Since S is normal up to universal morphism,
$\dim \pi (S) \geq 1$
, and so [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Theorem G] applies). Since S is normal up to universal morphism,
![]() $L|_S$
is semiample by [Reference Keelkee99, Lemma 1.4] and Theorem 2.3. Since
$L|_S$
is semiample by [Reference Keelkee99, Lemma 1.4] and Theorem 2.3. Since
![]() $\mathbb {E}(L) \subseteq S$
, [Reference Keelkee99, Theorem 0.2] and [Reference WitaszekWit22, Theorem 1.2] imply that L is semiample over U, and thus it induces a projective morphism
$\mathbb {E}(L) \subseteq S$
, [Reference Keelkee99, Theorem 0.2] and [Reference WitaszekWit22, Theorem 1.2] imply that L is semiample over U, and thus it induces a projective morphism
![]() $f\colon X\to Z$
contracting
$f\colon X\to Z$
contracting
![]() $\Sigma $
and such that
$\Sigma $
and such that
![]() $f_*{\mathcal {O}} _X={\mathcal {O}} _Z$
and
$f_*{\mathcal {O}} _X={\mathcal {O}} _Z$
and
![]() $\rho (X/Z)=1$
.
$\rho (X/Z)=1$
.
Theorem 4.6. Let
![]() $(Y,\Delta )$
be a four-dimensional
$(Y,\Delta )$
be a four-dimensional
![]() ${\mathbb {Q}}$
-factorial dlt pair with standard coefficients defined over a perfect field of characteristic
${\mathbb {Q}}$
-factorial dlt pair with standard coefficients defined over a perfect field of characteristic
![]() $p> 5$
(or a DVR of characteristic
$p> 5$
(or a DVR of characteristic
![]() $(0,p)$
for
$(0,p)$
for
![]() $p>5$
with perfect residue field). Assume that there exists a projective birational morphism
$p>5$
with perfect residue field). Assume that there exists a projective birational morphism
![]() $\pi \colon Y \to X$
over a normal
$\pi \colon Y \to X$
over a normal
![]() ${\mathbb {Q}}$
-factorial variety X such that
${\mathbb {Q}}$
-factorial variety X such that
![]() $\textrm {Ex}(\pi ) \subset \lfloor \Delta \rfloor $
. Then
$\textrm {Ex}(\pi ) \subset \lfloor \Delta \rfloor $
. Then
![]() $\pi $
-relative divisorial and flipping contractions and flips exist for
$\pi $
-relative divisorial and flipping contractions and flips exist for
![]() $K_Y + \Delta $
, and we can run a
$K_Y + \Delta $
, and we can run a
![]() $(K_Y + \Delta )$
-MMP over X which terminates with a minimal model
$(K_Y + \Delta )$
-MMP over X which terminates with a minimal model
![]() .
.
Proof. If
![]() $K_Y+\Delta $
is
$K_Y+\Delta $
is
![]() $\pi $
-nef, then we are done. Otherwise, we run a
$\pi $
-nef, then we are done. Otherwise, we run a
![]() $(K_Y+\Delta )$
-MMP over X. Let
$(K_Y+\Delta )$
-MMP over X. Let
![]() be a sequence of flips and contractions, and let
be a sequence of flips and contractions, and let
![]() $\Delta _l$
be the strict transforms of
$\Delta _l$
be the strict transforms of
![]() $\Delta $
on
$\Delta $
on
![]() $Y_l$
. Since X is
$Y_l$
. Since X is
![]() ${\mathbb {Q}}$
-factorial, there exists an effective exceptional divisor E on
${\mathbb {Q}}$
-factorial, there exists an effective exceptional divisor E on
![]() $Y_l$
such that
$Y_l$
such that
![]() $-E$
is ample over X. In particular,
$-E$
is ample over X. In particular,
![]() $\lfloor \Delta _l\rfloor $
contains all
$\lfloor \Delta _l\rfloor $
contains all
![]() $\pi _l\colon Y_l\to X$
exceptional curves. We must show that we can continue the MMP. The termination will then follow by Theorem 2.14 as both the flipping and flipped locus must be contained in
$\pi _l\colon Y_l\to X$
exceptional curves. We must show that we can continue the MMP. The termination will then follow by Theorem 2.14 as both the flipping and flipped locus must be contained in
![]() $\mathrm {Ex}(\pi )\subseteq \lfloor \Delta \rfloor $
. Note that if
$\mathrm {Ex}(\pi )\subseteq \lfloor \Delta \rfloor $
. Note that if
![]() $K_{Y_l}+\Delta _l $
is nef over X, then
$K_{Y_l}+\Delta _l $
is nef over X, then
![]() $Y_l$
is the required minimal model. Therefore, we may assume that
$Y_l$
is the required minimal model. Therefore, we may assume that
![]() $K_{Y_l}+\Delta _l $
is not nef over X.
$K_{Y_l}+\Delta _l $
is not nef over X.
We start by establishing the cone theorem. Let
![]() $S_i$
be all the
$S_i$
be all the
![]() $\pi _l$
-exceptional divisors for
$\pi _l$
-exceptional divisors for
![]() $1 \leq i \leq r$
. Restricting to the normalisation
$1 \leq i \leq r$
. Restricting to the normalisation
![]() $S_i^{\nu }$
of
$S_i^{\nu }$
of
![]() $S_i$
, we get that
$S_i$
, we get that
![]() $(S_i^{\nu }, \Delta _{S_i^{\nu }})$
is dlt, where
$(S_i^{\nu }, \Delta _{S_i^{\nu }})$
is dlt, where
![]() $K_{S_i^{\nu }}+\Delta _{S_i^{\nu }}=(K_{Y_l}+\Delta _l)| _{S_i^{\nu }}$
. The three-dimensional cone theorem ([Reference Das and WaldronDW19b, Theorem 1.1] and [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Theorem H]) states that
$K_{S_i^{\nu }}+\Delta _{S_i^{\nu }}=(K_{Y_l}+\Delta _l)| _{S_i^{\nu }}$
. The three-dimensional cone theorem ([Reference Das and WaldronDW19b, Theorem 1.1] and [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Theorem H]) states that
 $$\begin{align*}\mathrm{NE}(S_i^{\nu}/X)=\mathrm{NE}(S_i^{\nu}/X)_{K_{S_i^{\nu}}+\Delta_{S_i^{\nu}} \geq 0}+\sum _{j\geq 1}\mathbb R _{\geq 0}[\overline{\Gamma}_{i,j}],\end{align*}$$
$$\begin{align*}\mathrm{NE}(S_i^{\nu}/X)=\mathrm{NE}(S_i^{\nu}/X)_{K_{S_i^{\nu}}+\Delta_{S_i^{\nu}} \geq 0}+\sum _{j\geq 1}\mathbb R _{\geq 0}[\overline{\Gamma}_{i,j}],\end{align*}$$
where
![]() $0> (K_{S_i^{\nu }}+\Delta _{S_i^{\nu }})\cdot \overline {\Gamma }_{i,j}= (K_{Y_l}+\Delta _l)\cdot \Gamma _{i,j}.$
Here
$0> (K_{S_i^{\nu }}+\Delta _{S_i^{\nu }})\cdot \overline {\Gamma }_{i,j}= (K_{Y_l}+\Delta _l)\cdot \Gamma _{i,j}.$
Here
![]() $\{\overline {\Gamma }_{i,j}\}_{j\geq 1}$
is a countable collection of curves on
$\{\overline {\Gamma }_{i,j}\}_{j\geq 1}$
is a countable collection of curves on
![]() $S_i^{\nu }$
and
$S_i^{\nu }$
and
![]() $\Gamma _{i,j}$
denote their images on
$\Gamma _{i,j}$
denote their images on
![]() $S_i \subseteq Y_l$
. Since
$S_i \subseteq Y_l$
. Since
![]() $\textrm {Ex }(\pi _l ) \subset \textrm {Supp }(E)$
, there is a surjection
$\textrm {Ex }(\pi _l ) \subset \textrm {Supp }(E)$
, there is a surjection
![]() $\sum _{i=1}^r \mathrm {NE}(S_i^{\nu }/X)\to \mathrm {NE}(Y_l/X)$
and hence
$\sum _{i=1}^r \mathrm {NE}(S_i^{\nu }/X)\to \mathrm {NE}(Y_l/X)$
and hence
 $$\begin{align*}\mathrm{NE}(Y_l/X)=\mathrm{NE}(Y_l/X)_{K_{Y_l}+\Delta_l \geq 0}+\sum _{1 \leq i \leq r, 1 \leq j}\mathbb R _{\geq 0}[\Gamma_{i,j}]. \end{align*}$$
$$\begin{align*}\mathrm{NE}(Y_l/X)=\mathrm{NE}(Y_l/X)_{K_{Y_l}+\Delta_l \geq 0}+\sum _{1 \leq i \leq r, 1 \leq j}\mathbb R _{\geq 0}[\Gamma_{i,j}]. \end{align*}$$
Note that for any ample
![]() ${\mathbb {Q}}$
-divisor
${\mathbb {Q}}$
-divisor
![]() $H_l$
on
$H_l$
on
![]() $Y_l$
, the set
$Y_l$
, the set
![]() $\{ \Gamma _{i,j} \mid (K_{Y_l}+\Delta _l+H_l)\cdot \Gamma _{i,j}\leq 0\}$
is finite, and so extremal rays do not accumulate in
$\{ \Gamma _{i,j} \mid (K_{Y_l}+\Delta _l+H_l)\cdot \Gamma _{i,j}\leq 0\}$
is finite, and so extremal rays do not accumulate in
![]() $\mathrm {NE}(Y_l/X)_{K_{Y_l}+\Delta _l < 0}$
.
$\mathrm {NE}(Y_l/X)_{K_{Y_l}+\Delta _l < 0}$
.
Now, pick an extremal curve
![]() $C = \Gamma _{i,j}$
for some
$C = \Gamma _{i,j}$
for some
![]() $i,j$
. Then, there is an effective
$i,j$
. Then, there is an effective
![]() $\pi _l$
-exceptional divisor S such that
$\pi _l$
-exceptional divisor S such that
![]() $S \cdot C < 0$
, and hence a contraction
$S \cdot C < 0$
, and hence a contraction
![]() $f \colon Y_l \to Z$
of C exists by Proposition 4.5 applied to
$f \colon Y_l \to Z$
of C exists by Proposition 4.5 applied to
![]() $(Y_l,\Delta _l)$
. If f is a divisorial contraction, we let
$(Y_l,\Delta _l)$
. If f is a divisorial contraction, we let
![]() $Y_{l+1}=Z$
. If f is a flipping contraction, then by [Reference Hacon and WitaszekHW21, Lemma 3.1] (this lemma is stated over a field but it holds in much wider generality such as over DVRs), there exists an f-ample irreducible divisor A which is
$Y_{l+1}=Z$
. If f is a flipping contraction, then by [Reference Hacon and WitaszekHW21, Lemma 3.1] (this lemma is stated over a field but it holds in much wider generality such as over DVRs), there exists an f-ample irreducible divisor A which is
![]() $\pi $
-exceptional and hence contained in
$\pi $
-exceptional and hence contained in
![]() $\lfloor \Delta _l \rfloor $
. By Theorem 4.3, the flip
$\lfloor \Delta _l \rfloor $
. By Theorem 4.3, the flip
![]() $f^+\colon Y^+\to Z$
exists. We let
$f^+\colon Y^+\to Z$
exists. We let
![]() $Y_{l+1}=Y^+$
,
$Y_{l+1}=Y^+$
,
![]() , and
, and
![]() $K_{Y_{l+1}}+\Delta _{l+1}=\psi _*(K_{Y_{l}}+\Delta _{l})$
.
$K_{Y_{l+1}}+\Delta _{l+1}=\psi _*(K_{Y_{l}}+\Delta _{l})$
.
Proof of Theorem 4.1
Note that the proof of Theorem 4.6 implies the existence of all relevant divisorial and flipping contractions and the termination of the relevant flips. It suffices therefore to show the existence of flips. Suppose that
![]() $f\colon Y\to Z$
is a flipping contraction over X. We must show that the corresponding flip
$f\colon Y\to Z$
is a flipping contraction over X. We must show that the corresponding flip
![]() $Y^+\to Z$
exists. Let
$Y^+\to Z$
exists. Let
![]() $\zeta (\Delta )$
be the number of components of
$\zeta (\Delta )$
be the number of components of
![]() $\Delta $
whose coefficient is not contained in the standard set
$\Delta $
whose coefficient is not contained in the standard set
![]() $\{ 1-\frac 1 m \mid m\in \mathbb N \}\cup \{ 1\}$
. We will prove the result by induction on
$\{ 1-\frac 1 m \mid m\in \mathbb N \}\cup \{ 1\}$
. We will prove the result by induction on
![]() $\zeta (\Delta )$
.
$\zeta (\Delta )$
.
Note that if
![]() $\zeta (\Delta )=0$
, then by Theorem 4.6 the required flip exists. Therefore, we assume that
$\zeta (\Delta )=0$
, then by Theorem 4.6 the required flip exists. Therefore, we assume that
![]() $\zeta (\Delta )>0$
, and so we may write
$\zeta (\Delta )>0$
, and so we may write
![]() $\Delta =aS+B$
, where
$\Delta =aS+B$
, where
![]() $a\not \in \{ 1-\frac 1 m \mid m\in \mathbb N \}\cup \{ 1\}$
. Note that S is not exceptional over X (as the exceptional divisors occur with coefficient one). Let
$a\not \in \{ 1-\frac 1 m \mid m\in \mathbb N \}\cup \{ 1\}$
. Note that S is not exceptional over X (as the exceptional divisors occur with coefficient one). Let
![]() $\nu \colon Y'\to Y$
be a log resolution which is an isomorphism at the generic points of strata of
$\nu \colon Y'\to Y$
be a log resolution which is an isomorphism at the generic points of strata of
![]() $\lfloor \Delta \rfloor $
, and let
$\lfloor \Delta \rfloor $
, and let
![]() $B'=\nu ^{-1}_*B+\textrm {Ex}(\nu )$
,
$B'=\nu ^{-1}_*B+\textrm {Ex}(\nu )$
,
![]() $S'=\nu ^{-1}_* S$
. Since
$S'=\nu ^{-1}_* S$
. Since
![]() $\zeta (S'+B')<\zeta (\Delta )$
, we may run the
$\zeta (S'+B')<\zeta (\Delta )$
, we may run the
![]() $(K_{Y'}+S'+B')$
-MMP over Z. We obtain a birational contraction
$(K_{Y'}+S'+B')$
-MMP over Z. We obtain a birational contraction
![]() such that
such that
![]() $K_{Y''}+S''+B''=\phi _*(K_{Y'}+S'+B')$
is nef over Z and all components of
$K_{Y''}+S''+B''=\phi _*(K_{Y'}+S'+B')$
is nef over Z and all components of
![]() $\lfloor S''+B''\rfloor $
are normal up to universal homeomorphism. We now run a
$\lfloor S''+B''\rfloor $
are normal up to universal homeomorphism. We now run a
![]() $(K_{Y''}+aS''+B'')$
-MMP over Z with scaling of
$(K_{Y''}+aS''+B'')$
-MMP over Z with scaling of
![]() $(1-a)S''$
. Note that this is also a
$(1-a)S''$
. Note that this is also a
![]() $(K_{Y''}+B'')$
-MMP and
$(K_{Y''}+B'')$
-MMP and
![]() $\zeta (B'')<\zeta (\Delta )$
. Therefore, the required minimal model
$\zeta (B'')<\zeta (\Delta )$
. Therefore, the required minimal model
![]() exists. Since the log resolution was an isomorphism at the generic points of strata of
exists. Since the log resolution was an isomorphism at the generic points of strata of
![]() $\lfloor \Delta \rfloor $
, it is easy to see that this is the required flip (cf. [Reference Hacon and WitaszekHW22, Section 7.1]).
$\lfloor \Delta \rfloor $
, it is easy to see that this is the required flip (cf. [Reference Hacon and WitaszekHW22, Section 7.1]).
4.3 Applications
We begin by proving that fourfold
![]() ${\mathbb {Q}}$
-factorial klt singularities in positive characteristic are
${\mathbb {Q}}$
-factorial klt singularities in positive characteristic are
![]() $W{\mathcal {O}}$
-rational.
$W{\mathcal {O}}$
-rational.
Corollary 4.7. Let X be a
![]() ${\mathbb {Q}}$
-factorial klt four-dimensional variety over a perfect field k of characteristic
${\mathbb {Q}}$
-factorial klt four-dimensional variety over a perfect field k of characteristic
![]() $p>5$
admitting a log resolution of singularities. Then X has
$p>5$
admitting a log resolution of singularities. Then X has
![]() $W\mathcal O$
-rational singularities.
$W\mathcal O$
-rational singularities.
Proof. Let
![]() $\pi \colon Y \to X$
be a log resolution, and run the
$\pi \colon Y \to X$
be a log resolution, and run the
![]() $(K_Y+\textrm {Ex}(\pi ))$
-MMP over X. By standard arguments, this MMP contracts
$(K_Y+\textrm {Ex}(\pi ))$
-MMP over X. By standard arguments, this MMP contracts
![]() $\textrm {Ex}(\pi )$
, and so its output
$\textrm {Ex}(\pi )$
, and so its output
![]() $Y'\to X$
is a small birational morphism and hence an isomorphism as X is
$Y'\to X$
is a small birational morphism and hence an isomorphism as X is
![]() ${\mathbb {Q}}$
-factorial. We shall show that if
${\mathbb {Q}}$
-factorial. We shall show that if
![]() $g \colon Y \dashrightarrow Y_n$
is a sequence of steps of the MMP, with the induced map
$g \colon Y \dashrightarrow Y_n$
is a sequence of steps of the MMP, with the induced map
![]() $\pi _n \colon Y_n \to X$
, then
$\pi _n \colon Y_n \to X$
, then
![]() $R^i\pi _*W{\mathcal {O}}_{Y,{\mathbb {Q}}} = R^i(\pi _n)_*W{\mathcal {O}}_{Y_n,{\mathbb {Q}}}$
. As a consequence,
$R^i\pi _*W{\mathcal {O}}_{Y,{\mathbb {Q}}} = R^i(\pi _n)_*W{\mathcal {O}}_{Y_n,{\mathbb {Q}}}$
. As a consequence,
![]() $R^i\pi _*W{\mathcal {O}}_{Y,{\mathbb {Q}}} = 0$
for
$R^i\pi _*W{\mathcal {O}}_{Y,{\mathbb {Q}}} = 0$
for
![]() $i>0$
, and so X has
$i>0$
, and so X has
![]() $W{\mathcal {O}}$
-rational singularities. Thus, inductively, after replacing Y by some steps of the MMP, we may assume that
$W{\mathcal {O}}$
-rational singularities. Thus, inductively, after replacing Y by some steps of the MMP, we may assume that
![]() $(Y, \textrm {Ex}(f))$
is dlt. Let
$(Y, \textrm {Ex}(f))$
is dlt. Let
![]() $f \colon Y \to Z$
be a Mori contraction over X with
$f \colon Y \to Z$
be a Mori contraction over X with
![]() $\rho (Y/Z)=1$
.
$\rho (Y/Z)=1$
.
Assume that f is divisorial. There exists an f-antiample irreducible divisor
![]() $S \subseteq \textrm {Ex}(f)$
with the induced map
$S \subseteq \textrm {Ex}(f)$
with the induced map
![]() $f_S \colon S \to X$
. Set
$f_S \colon S \to X$
. Set
![]() $K_{S^{\nu }}+\Delta _{S^{\nu }} = (K_Y + \textrm {Ex}(f))|_{S^{\nu }}$
, where
$K_{S^{\nu }}+\Delta _{S^{\nu }} = (K_Y + \textrm {Ex}(f))|_{S^{\nu }}$
, where
![]() $S^{\nu }$
is the normalisation of S with the induced map
$S^{\nu }$
is the normalisation of S with the induced map
![]() $f_{S^{\nu }} \colon S^{\nu } \to X$
. Then
$f_{S^{\nu }} \colon S^{\nu } \to X$
. Then
![]() $(S^{\nu },\Delta _{S^{\nu }})$
is dlt by Lemma 2.2 and
$(S^{\nu },\Delta _{S^{\nu }})$
is dlt by Lemma 2.2 and
![]() $-(K_{S^{\nu }}+\Delta _{S^{\nu }})$
is
$-(K_{S^{\nu }}+\Delta _{S^{\nu }})$
is
![]() $f_{S^{\nu }}$
-ample. Up to perturbation, we can assume that
$f_{S^{\nu }}$
-ample. Up to perturbation, we can assume that
![]() $(S^{\nu }, \Delta _{S^{\nu }})$
is klt, and so, by [Reference Nakamura and TanakaNT20, Theorem 3.11],
$(S^{\nu }, \Delta _{S^{\nu }})$
is klt, and so, by [Reference Nakamura and TanakaNT20, Theorem 3.11],
for
![]() $i>0$
. Since S is normal up to universal homeomorphism (Lemma 2.1), [Reference Nakamura and TanakaNT20, Lemma 2.17] and [Reference Gongyo, Nakamura and HiromuGNH19, Lemma 2.20 and 2.21] together with the Leray spectral sequence imply that
$i>0$
. Since S is normal up to universal homeomorphism (Lemma 2.1), [Reference Nakamura and TanakaNT20, Lemma 2.17] and [Reference Gongyo, Nakamura and HiromuGNH19, Lemma 2.20 and 2.21] together with the Leray spectral sequence imply that
![]() $R^i(f_{S})_*W{\mathcal {O}}_{S,{\mathbb {Q}}}=0$
for
$R^i(f_{S})_*W{\mathcal {O}}_{S,{\mathbb {Q}}}=0$
for
![]() $i>0$
. Let
$i>0$
. Let
![]() $u \colon S \to Y$
be the inclusion, and let
$u \colon S \to Y$
be the inclusion, and let
![]() $I_S$
be the ideal sheaf defining S. Then, we get the following short exact sequence (cf. [Reference Gongyo, Nakamura and HiromuGNH19, Proof of Proposition 3.4])
$I_S$
be the ideal sheaf defining S. Then, we get the following short exact sequence (cf. [Reference Gongyo, Nakamura and HiromuGNH19, Proof of Proposition 3.4])
By [Reference Gongyo, Nakamura and HiromuGNH19, Proposition 2.23],
![]() $R^if_* WI_{S,{\mathbb {Q}}}=0$
for
$R^if_* WI_{S,{\mathbb {Q}}}=0$
for
![]() $i>0$
, and so
$i>0$
, and so
where the second equality follows from [Reference Gongyo, Nakamura and HiromuGNH19, Lemma 2.20 and Lemma 2.21]. Moreover,
![]() $f_*W{\mathcal {O}}_{Y,{\mathbb {Q}}} = W{\mathcal {O}}_{Z,{\mathbb {Q}}}$
by [Reference Nakamura and TanakaNT20, Lemma 2.17], and so we can conclude the proof when f is divisorial by the Leray spectral sequence.
$f_*W{\mathcal {O}}_{Y,{\mathbb {Q}}} = W{\mathcal {O}}_{Z,{\mathbb {Q}}}$
by [Reference Nakamura and TanakaNT20, Lemma 2.17], and so we can conclude the proof when f is divisorial by the Leray spectral sequence.
Suppose that f is a flipping contraction, and let
![]() $\pi _Z \colon Z \to X$
be the induced map. Let
$\pi _Z \colon Z \to X$
be the induced map. Let
![]() $\phi \colon Y \dashrightarrow Y^+$
be the flip, let
$\phi \colon Y \dashrightarrow Y^+$
be the flip, let
![]() $f^+ \colon Y^+ \to Z$
be the flipped contraction and let
$f^+ \colon Y^+ \to Z$
be the flipped contraction and let
![]() $\pi ^+ \colon Y^+ \to X$
be the induced map. As before, by [Reference Hacon and WitaszekHW21, Lemma 3.1] and Theorem 4.3, both Y and
$\pi ^+ \colon Y^+ \to X$
be the induced map. As before, by [Reference Hacon and WitaszekHW21, Lemma 3.1] and Theorem 4.3, both Y and
![]() $Y^+$
are relatively F-regular over Z. In particular,
$Y^+$
are relatively F-regular over Z. In particular,
![]() $Rf_* {\mathcal {O}}_Y = {\mathcal {O}}_Z$
and
$Rf_* {\mathcal {O}}_Y = {\mathcal {O}}_Z$
and
![]() $Rf^+_* {\mathcal {O}}_{Y^+} = {\mathcal {O}}_Z$
(see [Reference Schwede and SmithSS10, Theorem 6.8] and the proof of [Reference Hacon and WitaszekHW22, Proposition 3.4]). By [Reference Nakamura and TanakaNT20, Lemma 2.17] and [Reference Gongyo, Nakamura and HiromuGNH19, Lemma 2.19 and Lemma 2.21],
$Rf^+_* {\mathcal {O}}_{Y^+} = {\mathcal {O}}_Z$
(see [Reference Schwede and SmithSS10, Theorem 6.8] and the proof of [Reference Hacon and WitaszekHW22, Proposition 3.4]). By [Reference Nakamura and TanakaNT20, Lemma 2.17] and [Reference Gongyo, Nakamura and HiromuGNH19, Lemma 2.19 and Lemma 2.21],
![]() $f_* W{\mathcal {O}}_{Y,{\mathbb {Q}}} = f^+_* W{\mathcal {O}}_{Y^+,{\mathbb {Q}}} = W{\mathcal {O}}_{Z,{\mathbb {Q}}}$
and
$f_* W{\mathcal {O}}_{Y,{\mathbb {Q}}} = f^+_* W{\mathcal {O}}_{Y^+,{\mathbb {Q}}} = W{\mathcal {O}}_{Z,{\mathbb {Q}}}$
and
![]() $R^if_* W{\mathcal {O}}_{Y,{\mathbb {Q}}} = R^if^+_* W{\mathcal {O}}_{Y^+,{\mathbb {Q}}} = 0$
for
$R^if_* W{\mathcal {O}}_{Y,{\mathbb {Q}}} = R^if^+_* W{\mathcal {O}}_{Y^+,{\mathbb {Q}}} = 0$
for
![]() $i>0$
. By the Leray spectral sequence:
$i>0$
. By the Leray spectral sequence:
We can now prove Corollary 1.3.
Proof of Corollary 1.3
Let
![]() $\pi \colon Y \to X$
be a resolution of singularities such that Y is rationally chain connected. Since X has
$\pi \colon Y \to X$
be a resolution of singularities such that Y is rationally chain connected. Since X has
![]() $W\mathcal {O}_X$
-rational singularities by the above corollary, [Reference Gongyo, Nakamura and HiromuGNH19, Remark 3.1] and [Reference Berthelot, Bloch and EsnaultBBE07, Proposition 6.9] imply that
$W\mathcal {O}_X$
-rational singularities by the above corollary, [Reference Gongyo, Nakamura and HiromuGNH19, Remark 3.1] and [Reference Berthelot, Bloch and EsnaultBBE07, Proposition 6.9] imply that
![]() $|X(\mathbb {F}_q)| \equiv |Y(\mathbb {F}_q)| \pmod q$
.
$|X(\mathbb {F}_q)| \equiv |Y(\mathbb {F}_q)| \pmod q$
.
We can conclude the proof as
![]() $|Y(\mathbb {F}_q)| \equiv 1\ \pmod q$
by [Reference EsnaultEsn03, Theorem 1.1] and the argument explained between this theorem and [Reference EsnaultEsn03, Corollary 1.3]. Specifically, this follows from the Lefschetz trace formula for crystalline cohomology
$|Y(\mathbb {F}_q)| \equiv 1\ \pmod q$
by [Reference EsnaultEsn03, Theorem 1.1] and the argument explained between this theorem and [Reference EsnaultEsn03, Corollary 1.3]. Specifically, this follows from the Lefschetz trace formula for crystalline cohomology
given that Y is rationally chain connected, and so all the slopes of Frobenius are
![]() $\geq 1$
by [Reference EsnaultEsn03, Theorem 1.1].
$\geq 1$
by [Reference EsnaultEsn03, Theorem 1.1].
Next, we show the existence of dlt modifications.
Corollary 4.8. Let
![]() $(X,\Delta )$
be a four-dimensional
$(X,\Delta )$
be a four-dimensional
![]() ${\mathbb {Q}}$
-factorial log pair with standard coefficients admitting a log resolution and defined over a perfect field of characteristic
${\mathbb {Q}}$
-factorial log pair with standard coefficients admitting a log resolution and defined over a perfect field of characteristic
![]() $p>5$
or a DVR of characteristic
$p>5$
or a DVR of characteristic
![]() $(0,p)$
for
$(0,p)$
for
![]() $p>5$
with perfect residue field. Then a dlt modification of
$p>5$
with perfect residue field. Then a dlt modification of
![]() $(X,\Delta )$
exists, that is, a birational morphism
$(X,\Delta )$
exists, that is, a birational morphism
![]() $\pi \colon Y \to X$
such that
$\pi \colon Y \to X$
such that
![]() $(Y, \pi ^{-1}_*\Delta + \textrm {Ex}(\pi ))$
is dlt,
$(Y, \pi ^{-1}_*\Delta + \textrm {Ex}(\pi ))$
is dlt,
![]() ${\mathbb {Q}}$
-factorial and minimal over X.
${\mathbb {Q}}$
-factorial and minimal over X.
Proof. Let
![]() $\pi \colon Y \to X$
be a log resolution of
$\pi \colon Y \to X$
be a log resolution of
![]() $(X, \Delta )$
. Then, a dlt modification is a minimal model of
$(X, \Delta )$
. Then, a dlt modification is a minimal model of
![]() $(Y,\pi ^{-1}_*\Delta + \textrm {Ex}(\pi ))$
over X (see Theorem 4.1).
$(Y,\pi ^{-1}_*\Delta + \textrm {Ex}(\pi ))$
over X (see Theorem 4.1).
Finally, we prove that inversion of adjunction holds.
Corollary 4.9. Consider a
![]() ${\mathbb {Q}}$
-factorial four-dimensional log pair
${\mathbb {Q}}$
-factorial four-dimensional log pair
![]() $(X,S+B)$
with standard coefficients defined over a perfect field of characteristic
$(X,S+B)$
with standard coefficients defined over a perfect field of characteristic
![]() $p>5$
or a DVR of characteristic
$p>5$
or a DVR of characteristic
![]() $(0,p)$
for
$(0,p)$
for
![]() $p>5$
with perfect residue field, where S is a prime divisor with no common component with
$p>5$
with perfect residue field, where S is a prime divisor with no common component with
![]() $B\geq 0$
. Assume that
$B\geq 0$
. Assume that
![]() $(X,S+B)$
admits a log resolution.
$(X,S+B)$
admits a log resolution.
Then
![]() $(X,S+B)$
is plt on a neighbourhood of S if and only if
$(X,S+B)$
is plt on a neighbourhood of S if and only if
![]() $(\tilde S,B_{\tilde S})$
is klt, where
$(\tilde S,B_{\tilde S})$
is klt, where
![]() $\tilde S$
is the normalisation of S and
$\tilde S$
is the normalisation of S and
![]() $B_{\tilde S}$
is the different.
$B_{\tilde S}$
is the different.
Proof. By considering a log resolution of
![]() $(X,S+B)$
, it is easy to see that if
$(X,S+B)$
, it is easy to see that if
![]() $(X,S+B)$
is plt, then
$(X,S+B)$
is plt, then
![]() $(\tilde S,B_{\tilde S})$
is klt. Thus, we can assume that
$(\tilde S,B_{\tilde S})$
is klt. Thus, we can assume that
![]() $(\tilde S,B_{\tilde S})$
is klt and aim to show that
$(\tilde S,B_{\tilde S})$
is klt and aim to show that
![]() $(X,S+B)$
is plt near S.
$(X,S+B)$
is plt near S.
Let
![]() $\pi \colon Y \to X$
be a dlt modification of
$\pi \colon Y \to X$
be a dlt modification of
![]() $(X,S+B)$
(see Corollary 4.8), and write
$(X,S+B)$
(see Corollary 4.8), and write
![]() $K_Y + S_Y + B_Y = \pi ^*(K_X+S+B)$
. By definition (of a dlt modification) for any
$K_Y + S_Y + B_Y = \pi ^*(K_X+S+B)$
. By definition (of a dlt modification) for any
![]() $\pi $
-exceptional irreducible divisor E, we have that
$\pi $
-exceptional irreducible divisor E, we have that
![]() $E \subseteq \lfloor B_Y \rfloor $
. Write
$E \subseteq \lfloor B_Y \rfloor $
. Write
where
![]() $\tilde S_Y \to S_Y$
is the normalisation of
$\tilde S_Y \to S_Y$
is the normalisation of
![]() $S_Y$
, and
$S_Y$
, and
![]() $B_{\tilde S_Y}$
is the different. Let E be a
$B_{\tilde S_Y}$
is the different. Let E be a
![]() $\pi $
-exceptional divisor intersecting
$\pi $
-exceptional divisor intersecting
![]() $S_Y$
. Since
$S_Y$
. Since
![]() $E \subseteq \lfloor B_Y \rfloor $
and
$E \subseteq \lfloor B_Y \rfloor $
and
![]() $(Y,S_Y+\textrm {Ex}(\pi ))$
is dlt, we must have that
$(Y,S_Y+\textrm {Ex}(\pi ))$
is dlt, we must have that
![]() $E \cap S_Y \subseteq \lfloor B_{\tilde S_Y} \rfloor $
. Since
$E \cap S_Y \subseteq \lfloor B_{\tilde S_Y} \rfloor $
. Since
![]() $E \cap S_Y \neq \emptyset $
, this contradicts
$E \cap S_Y \neq \emptyset $
, this contradicts
![]() $(\tilde S, B_{\tilde S})$
being klt.
$(\tilde S, B_{\tilde S})$
being klt.
Therefore, we may assume that
![]() $E\cap S_Y=\emptyset $
so that
$E\cap S_Y=\emptyset $
so that
![]() $Y=X$
near S, and hence
$Y=X$
near S, and hence
![]() $(X,S+B)$
is dlt on a neighbourhood of S. Since S is irreducible,
$(X,S+B)$
is dlt on a neighbourhood of S. Since S is irreducible,
![]() $(X,S+B)$
is in fact plt.
$(X,S+B)$
is in fact plt.
5 Relative MMP over a DVR
Throughout this section, we assume that log resolutions of all log pairs with the underlying variety being birational to X as below exist (and are given by a sequence of blowups along the non-snc locus). The assumption on the field (in the positive characteristic case) being algebraically closed is necessary to invoke Bertini’s theorem for strongly F-regular singularities.
In what follows, given a scheme X over an integral scheme S and a
![]() $\mathbb {Q}$
-Cartier
$\mathbb {Q}$
-Cartier
![]() ${\mathbb {Q}}$
-divisor L on X, we define
${\mathbb {Q}}$
-divisor L on X, we define
![]() $\kappa (L/S) := \kappa (L|_{X_{\eta }})$
, where
$\kappa (L/S) := \kappa (L|_{X_{\eta }})$
, where
![]() $X_{\eta }$
is the fibre over the generic point
$X_{\eta }$
is the fibre over the generic point
![]() $\eta \in S$
.
$\eta \in S$
.
Our goal is to show Theorem 1.2, whose statement in full generality is as follows. Note that when
![]() $\phi $
is smooth or X is semistable, the
$\phi $
is smooth or X is semistable, the
![]() $K_X$
-MMP and the
$K_X$
-MMP and the
![]() $(K_X+{\mathrm {Supp}}\,\phi ^{-1}(s))$
-MMP coincide.
$(K_X+{\mathrm {Supp}}\,\phi ^{-1}(s))$
-MMP coincide.
Theorem 5.1. Let
![]() $(X,\Delta )$
be a four-dimensional
$(X,\Delta )$
be a four-dimensional
![]() ${\mathbb {Q}}$
-factorial dlt pair with standard coefficients projective over a DVR R with perfect residue field of characteristic
${\mathbb {Q}}$
-factorial dlt pair with standard coefficients projective over a DVR R with perfect residue field of characteristic
![]() $p>5$
. Let
$p>5$
. Let
![]() $s \in \operatorname {\mathrm {Spec}} R$
be its special point, and let
$s \in \operatorname {\mathrm {Spec}} R$
be its special point, and let
![]() $\phi \colon X \to \operatorname {\mathrm {Spec}} R$
be the natural projection. When R is purely positive characteristic, we also assume that it is a local ring of a curve C defined over an algebraically closed field and that
$\phi \colon X \to \operatorname {\mathrm {Spec}} R$
be the natural projection. When R is purely positive characteristic, we also assume that it is a local ring of a curve C defined over an algebraically closed field and that
![]() $(X,\Delta ) := ({\mathcal {X}}, \Phi ) \times _C \operatorname {\mathrm {Spec}}(R)$
for a
$(X,\Delta ) := ({\mathcal {X}}, \Phi ) \times _C \operatorname {\mathrm {Spec}}(R)$
for a
![]() ${\mathbb {Q}}$
-factorial four-dimensional dlt pair
${\mathbb {Q}}$
-factorial four-dimensional dlt pair
![]() $({\mathcal {X}}, \Phi )$
which is projective over C.
$({\mathcal {X}}, \Phi )$
which is projective over C.
Further, suppose that log resolutions of all log pairs with the underlying variety being birational to X exist (and are constructed by a sequence of blowups along the non-snc locus).
If
![]() $\kappa (K_X +\Delta \,/\,\textrm {Spec}(R))\geq 0$
and
$\kappa (K_X +\Delta \,/\,\textrm {Spec}(R))\geq 0$
and
![]() $\textrm {Supp}(\phi ^{-1}(s))\subset \lfloor \Delta \rfloor $
, then we can run an arbitrary
$\textrm {Supp}(\phi ^{-1}(s))\subset \lfloor \Delta \rfloor $
, then we can run an arbitrary
![]() $(K_X+\Delta )$
-MMP over
$(K_X+\Delta )$
-MMP over
![]() $\operatorname {\mathrm {Spec}} R$
which terminates with a minimal model. In particular, every sequence of steps of the MMP terminates.
$\operatorname {\mathrm {Spec}} R$
which terminates with a minimal model. In particular, every sequence of steps of the MMP terminates.
In mixed characteristic, it is enough to assume that
![]() $K_X+\Delta $
is pseudo-effective, as then
$K_X+\Delta $
is pseudo-effective, as then
![]() $\kappa (K_X+\Delta )\geq 0$
holds by the nonvanishing theorem for characteristic 0 threefolds. Similarly, in the equicharacteristic case
$\kappa (K_X+\Delta )\geq 0$
holds by the nonvanishing theorem for characteristic 0 threefolds. Similarly, in the equicharacteristic case
![]() $p>5$
, if the generic fibre is geometrically klt, then nonvanishing follows from [Reference Xu and ZhangXZ19, Theorem 1.1] and [Reference WitaszekWit21a].
$p>5$
, if the generic fibre is geometrically klt, then nonvanishing follows from [Reference Xu and ZhangXZ19, Theorem 1.1] and [Reference WitaszekWit21a].
We start by proving the following base point free theorem. This result would follow easily from [Reference Cascini and TanakaCT20] and [Reference WitaszekWit21b] if we knew the abundance for slc threefolds.
Proposition 5.2. Let
![]() $(X,\Delta )$
be a four-dimensional
$(X,\Delta )$
be a four-dimensional
![]() ${\mathbb {Q}}$
-factorial dlt pair with standard coefficients projective over a DVR R with perfect residue field of characteristic
${\mathbb {Q}}$
-factorial dlt pair with standard coefficients projective over a DVR R with perfect residue field of characteristic
![]() $p>5$
. Let
$p>5$
. Let
![]() $s, \eta \in \operatorname {\mathrm {Spec}} R$
be the special and the generic point, respectively, and let
$s, \eta \in \operatorname {\mathrm {Spec}} R$
be the special and the generic point, respectively, and let
![]() $\phi \colon X \to \operatorname {\mathrm {Spec}} R$
be the natural projection. When R is purely positive characteristic, we also assume that it is a local ring of a curve C defined over an algebraically closed field and that
$\phi \colon X \to \operatorname {\mathrm {Spec}} R$
be the natural projection. When R is purely positive characteristic, we also assume that it is a local ring of a curve C defined over an algebraically closed field and that
![]() $(X,\Delta ) := ({\mathcal {X}}, \Phi ) \times _C \operatorname {\mathrm {Spec}}(R)$
for a
$(X,\Delta ) := ({\mathcal {X}}, \Phi ) \times _C \operatorname {\mathrm {Spec}}(R)$
for a
![]() ${\mathbb {Q}}$
-factorial four dimensional dlt pair
${\mathbb {Q}}$
-factorial four dimensional dlt pair
![]() $({\mathcal {X}}, \Phi )$
which is projective over C.
$({\mathcal {X}}, \Phi )$
which is projective over C.
Suppose that
![]() $K_X+\Delta $
is nef and big, and
$K_X+\Delta $
is nef and big, and
![]() $\lfloor \Delta \rfloor = \textrm {Supp}(\phi ^{-1}(s))$
. Then
$\lfloor \Delta \rfloor = \textrm {Supp}(\phi ^{-1}(s))$
. Then
![]() $K_X+\Delta $
is semiample.
$K_X+\Delta $
is semiample.
Proof. Write
![]() ${\mathrm {Supp}}\, X_{s}=\sum _{i=1}^r E_i$
for irreducible divisors
${\mathrm {Supp}}\, X_{s}=\sum _{i=1}^r E_i$
for irreducible divisors
![]() $E_i$
, and
$E_i$
, and
![]() $L := K_X+\Delta $
. Since
$L := K_X+\Delta $
. Since
![]() $(X, \Delta )$
is klt over
$(X, \Delta )$
is klt over
![]() $\eta $
, we get that
$\eta $
, we get that
![]() $L|_{X_{\eta }}$
is semiample by [Reference Das and WaldronDW19b, Theorem 1.4] or the base point free theorem in characteristic 0 [Reference Kollár and MoriKM98]. By [Reference Cascini and TanakaCT20, Theorem 1.1] and [Reference WitaszekWit21b, Theorem 1.2], it thus suffices to show that
$L|_{X_{\eta }}$
is semiample by [Reference Das and WaldronDW19b, Theorem 1.4] or the base point free theorem in characteristic 0 [Reference Kollár and MoriKM98]. By [Reference Cascini and TanakaCT20, Theorem 1.1] and [Reference WitaszekWit21b, Theorem 1.2], it thus suffices to show that
![]() $L|_{X_s}$
is semiample.
$L|_{X_s}$
is semiample.
Since L is big, we may assume that
![]() $\Delta + L \sim _{{\mathbb {Q}}}H+F+G$
, where H is ample,
$\Delta + L \sim _{{\mathbb {Q}}}H+F+G$
, where H is ample,
![]() $F\geq 0$
is supported on
$F\geq 0$
is supported on
![]() $X_s$
and the support of
$X_s$
and the support of
![]() $G \geq 0$
contains no divisors of
$G \geq 0$
contains no divisors of
![]() $X_s$
. In this paragraph, we reduce the proposition to the case when G does not contain any log canonical centres of
$X_s$
. In this paragraph, we reduce the proposition to the case when G does not contain any log canonical centres of
![]() $(X,\Delta )$
. To this end, let
$(X,\Delta )$
. To this end, let
![]() $\pi \colon Y\to X$
be a dlt modification of
$\pi \colon Y\to X$
be a dlt modification of
![]() $(X, \Delta +\delta G)$
for some
$(X, \Delta +\delta G)$
for some
![]() $0<\delta \ll 1$
(see Corollary 4.8). Then we may assume that
$0<\delta \ll 1$
(see Corollary 4.8). Then we may assume that
![]() $K_Y+\Delta _Y=\pi ^*(K_X+\Delta )$
, where
$K_Y+\Delta _Y=\pi ^*(K_X+\Delta )$
, where
![]() $\Delta _Y=\pi ^{-1}_*\Delta +\textrm {Ex}(\pi )$
and
$\Delta _Y=\pi ^{-1}_*\Delta +\textrm {Ex}(\pi )$
and
![]() $\pi ^{-1}_* G$
contains no strata of
$\pi ^{-1}_* G$
contains no strata of
![]() $\lfloor \Delta _Y \rfloor $
; indeed as
$\lfloor \Delta _Y \rfloor $
; indeed as
![]() $(X,\Delta )$
is dlt, the divisorial non-klt places of
$(X,\Delta )$
is dlt, the divisorial non-klt places of
![]() $(X,\Delta +\delta G)$
and
$(X,\Delta +\delta G)$
and
![]() $(X,\Delta )$
coincide on a given resolution (on which we run the MMP to construct the dlt modification) for
$(X,\Delta )$
coincide on a given resolution (on which we run the MMP to construct the dlt modification) for
![]() $0 < \delta \ll 1$
. Let P be an effective
$0 < \delta \ll 1$
. Let P be an effective
![]() $\pi $
-exceptional divisor such that
$\pi $
-exceptional divisor such that
![]() $-P$
is
$-P$
is
![]() $\pi $
-ample. Then the support of P is contained in
$\pi $
-ample. Then the support of P is contained in
![]() $Y_s$
and we may assume that
$Y_s$
and we may assume that
![]() $\pi ^*H-P$
is ample over
$\pi ^*H-P$
is ample over
![]() $\operatorname {\mathrm {Spec}} R$
. Note that
$\operatorname {\mathrm {Spec}} R$
. Note that
![]() $\Delta _Y-\pi ^* \Delta $
is supported on
$\Delta _Y-\pi ^* \Delta $
is supported on
![]() $\textrm {Ex}(\pi ) \subseteq Y_s$
. We have
$\textrm {Ex}(\pi ) \subseteq Y_s$
. We have
 $$ \begin{align*} \Delta _Y+\pi ^*L &= \Delta_Y-\pi^*\Delta + \pi^*(H+F+G)\\ &= (\pi^*H-P)+(P+\Delta _Y-\pi ^* \Delta +\pi ^*F+\pi ^*G-\pi^{-1}_*G) + \pi^{-1}_*G\\ &= H_Y+F_Y+G_Y, \end{align*} $$
$$ \begin{align*} \Delta _Y+\pi ^*L &= \Delta_Y-\pi^*\Delta + \pi^*(H+F+G)\\ &= (\pi^*H-P)+(P+\Delta _Y-\pi ^* \Delta +\pi ^*F+\pi ^*G-\pi^{-1}_*G) + \pi^{-1}_*G\\ &= H_Y+F_Y+G_Y, \end{align*} $$
where
![]() $G_Y=\pi ^{-1}_*G$
,
$G_Y=\pi ^{-1}_*G$
,
![]() $H_Y=\pi ^*H-P - aY_s$
is ample over
$H_Y=\pi ^*H-P - aY_s$
is ample over
![]() $\operatorname {\mathrm {Spec}} R$
, and
$\operatorname {\mathrm {Spec}} R$
, and
![]() $F_Y=P+(\Delta _Y-\pi ^* \Delta ) +\pi ^*F+(\pi ^*G-\pi ^{-1}_*G) + aY_s$
is supported on
$F_Y=P+(\Delta _Y-\pi ^* \Delta ) +\pi ^*F+(\pi ^*G-\pi ^{-1}_*G) + aY_s$
is supported on
![]() $Y_s$
(we choose
$Y_s$
(we choose
![]() $a \gg 0$
so that
$a \gg 0$
so that
![]() $F_Y \geq 0$
). Replacing
$F_Y \geq 0$
). Replacing
![]() $X, \Delta ,L, H,F,G$
by
$X, \Delta ,L, H,F,G$
by
![]() $Y,\Delta _Y,\pi ^*L, H_Y, F_Y, G_Y$
, we may assume that
$Y,\Delta _Y,\pi ^*L, H_Y, F_Y, G_Y$
, we may assume that
![]() $(X,\Delta +\delta G)$
is dlt,
$(X,\Delta +\delta G)$
is dlt,
![]() $\lfloor \Delta \rfloor = {\mathrm {Supp}}\, X_s$
, F is supported on
$\lfloor \Delta \rfloor = {\mathrm {Supp}}\, X_s$
, F is supported on
![]() $X_s$
, and H is ample.
$X_s$
, and H is ample.
Since H is ample, we may further assume that the support of
![]() $F=\sum f_iF_i$
equals
$F=\sum f_iF_i$
equals
![]() $X_s$
, where the
$X_s$
, where the
![]() $f_i$
are chosen generically (here,
$f_i$
are chosen generically (here,
![]() $F_i$
are distinct prime divisor). Moreover, we have that
$F_i$
are distinct prime divisor). Moreover, we have that
is klt for
![]() $0 < \delta \ll 1$
and some possibly negative
$0 < \delta \ll 1$
and some possibly negative
![]() $\epsilon $
such that
$\epsilon $
such that
![]() $|\epsilon |\ll 1$
. Note that
$|\epsilon |\ll 1$
. Note that
![]() $K_X + \Delta _{\epsilon ,\delta } \sim _{{\mathbb {Q}}} (1+\delta )L$
.
$K_X + \Delta _{\epsilon ,\delta } \sim _{{\mathbb {Q}}} (1+\delta )L$
.
Fixing
![]() $\delta $
and increasing
$\delta $
and increasing
![]() $\epsilon $
, since the
$\epsilon $
, since the
![]() $f_i$
are chosen generically, we obtain a sequence of rational numbers
$f_i$
are chosen generically, we obtain a sequence of rational numbers
![]() $\epsilon <\epsilon _1<\epsilon _2<\ldots <\epsilon _r$
such that
$\epsilon <\epsilon _1<\epsilon _2<\ldots <\epsilon _r$
such that
![]() $\lfloor \Delta _{\epsilon _i,\delta }\rfloor =U_i:=\sum _{j=1}^iE_j$
and
$\lfloor \Delta _{\epsilon _i,\delta }\rfloor =U_i:=\sum _{j=1}^iE_j$
and
![]() $E_i$
occurs with coefficient one in
$E_i$
occurs with coefficient one in
![]() $\Delta _{\epsilon _i,\delta }$
. Here, of course, we have reindexed the
$\Delta _{\epsilon _i,\delta }$
. Here, of course, we have reindexed the
![]() $E_i$
accordingly. Note that all
$E_i$
accordingly. Note that all
![]() $E_i$
are defined over a perfect field of positive characteristic. We claim that
$E_i$
are defined over a perfect field of positive characteristic. We claim that
Claim 5.3.
![]() $(K_X + \Delta )|_{E_i^{\nu }}$
is semiample, where
$(K_X + \Delta )|_{E_i^{\nu }}$
is semiample, where
![]() $E_i^{\nu }\to E_i$
is the normalisation, and hence also
$E_i^{\nu }\to E_i$
is the normalisation, and hence also
![]() $(K_X + \Delta )|_{E_i}$
is semiample as the
$(K_X + \Delta )|_{E_i}$
is semiample as the
![]() $E_i$
are normal up to universal homeomorphism (see Theorem 2.3).
$E_i$
are normal up to universal homeomorphism (see Theorem 2.3).
Granting the claim and proceeding by induction, we may assume that
![]() $(K_X+\Delta )|_{U_{i-1}}$
is semiample and we must show that
$(K_X+\Delta )|_{U_{i-1}}$
is semiample and we must show that
![]() $(K_X+\Delta )|_{U_i}$
is semiample. By [Reference Keelkee99, Corollary 2.9], it suffices to show that
$(K_X+\Delta )|_{U_i}$
is semiample. By [Reference Keelkee99, Corollary 2.9], it suffices to show that
![]() $g_2|_{U_{i-1}\cap E^{\nu } _i}$
has connected geometric fibres, where
$g_2|_{U_{i-1}\cap E^{\nu } _i}$
has connected geometric fibres, where
![]() $g_2 \colon E_i^{\nu } \to V$
is the morphism associated to the semiample
$g_2 \colon E_i^{\nu } \to V$
is the morphism associated to the semiample
![]() ${\mathbb {Q}}$
-divisor
${\mathbb {Q}}$
-divisor
![]() $(K_X+\Delta )|_{E_i^{\nu }}$
. Note that
$(K_X+\Delta )|_{E_i^{\nu }}$
. Note that
![]() $(K_X+\Delta )|_{E_i^{\nu }}\equiv _{V}0$
, hence
$(K_X+\Delta )|_{E_i^{\nu }}\equiv _{V}0$
, hence
![]() $-(K_{E_i^{\nu }}+\Delta ^{\prime }_{E_i^{\nu }}):=-(K_X+\Delta _{\epsilon _i,\delta }-\delta H)|_{E_i^{\nu } }$
is ample over V. By [Reference Nakamura and TanakaNT20, Theorem 1.2] (this requires the base field to be perfect), the fibres of the non-klt locus of
$-(K_{E_i^{\nu }}+\Delta ^{\prime }_{E_i^{\nu }}):=-(K_X+\Delta _{\epsilon _i,\delta }-\delta H)|_{E_i^{\nu } }$
is ample over V. By [Reference Nakamura and TanakaNT20, Theorem 1.2] (this requires the base field to be perfect), the fibres of the non-klt locus of
![]() $({E_i^{\nu }},\Delta ^{\prime }_{E_i^{\nu }})$
are geometrically connected. Since this non-klt locus coincides with
$({E_i^{\nu }},\Delta ^{\prime }_{E_i^{\nu }})$
are geometrically connected. Since this non-klt locus coincides with
![]() $U_{i-1}\cap {E_i}$
(as
$U_{i-1}\cap {E_i}$
(as
![]() $K_X+\Delta +\delta (H+G)$
is dlt), the statement of the proposition follows.
$K_X+\Delta +\delta (H+G)$
is dlt), the statement of the proposition follows.
Proof of Claim 5.3
We proceed by induction. We warn the reader that
![]() $E^{\nu }_i$
need not be
$E^{\nu }_i$
need not be
![]() ${\mathbb {Q}}$
-factorial. Set
${\mathbb {Q}}$
-factorial. Set
![]() $K_{E_i^{\nu }}+\Delta _{E_i^{\nu }}=(K_X+\Delta )|_{E_i^{\nu }}$
.
$K_{E_i^{\nu }}+\Delta _{E_i^{\nu }}=(K_X+\Delta )|_{E_i^{\nu }}$
.
First, if
![]() $L|_{E^{\nu }_i}$
is big, then it is semiample by [Reference WaldronWal18, Theorem 1.1] and base change to an algebraically closed field. Hence, we can assume that it is not big. In particular,
$L|_{E^{\nu }_i}$
is big, then it is semiample by [Reference WaldronWal18, Theorem 1.1] and base change to an algebraically closed field. Hence, we can assume that it is not big. In particular,
![]() $L|_{E^{\nu }_i}-\gamma \lfloor \Delta _{E_i^{\nu }}\rfloor $
is not pseudo-effective for any
$L|_{E^{\nu }_i}-\gamma \lfloor \Delta _{E_i^{\nu }}\rfloor $
is not pseudo-effective for any
![]() $\gamma> 0$
(note that
$\gamma> 0$
(note that
![]() $\lfloor \Delta _{E_i^{\nu }}\rfloor = \lfloor \Delta - E_i \rfloor |_{E_i^{\nu }}$
is
$\lfloor \Delta _{E_i^{\nu }}\rfloor = \lfloor \Delta - E_i \rfloor |_{E_i^{\nu }}$
is
![]() ${\mathbb {Q}}$
-Cartier). Indeed, assume otherwise and write
${\mathbb {Q}}$
-Cartier). Indeed, assume otherwise and write
![]() $L \sim _{{\mathbb {Q}}} H'+F'+G'$
, where
$L \sim _{{\mathbb {Q}}} H'+F'+G'$
, where
![]() $H'$
is ample,
$H'$
is ample,
![]() $F'\geq 0$
is supported on
$F'\geq 0$
is supported on
![]() $X_s$
and the support of
$X_s$
and the support of
![]() $G'\geq 0$
contains no divisors of
$G'\geq 0$
contains no divisors of
![]() $X_s$
. By shifting
$X_s$
. By shifting
![]() $F'$
by a multiple of
$F'$
by a multiple of
![]() $\phi ^{-1}(s)$
, we may assume that
$\phi ^{-1}(s)$
, we may assume that
![]() $F'$
does not contain
$F'$
does not contain
![]() $E_i$
in its support (but it is not necessarily effective any more). Thus, we can write
$E_i$
in its support (but it is not necessarily effective any more). Thus, we can write
 $$ \begin{align*} (m+1)L|_{E^{\nu}_i} &\sim_{{\mathbb{Q}}} H'|_{E^{\nu}_i} + mL|_{E^{\nu}_i} + F'|_{E^{\nu}_i} + G'|_{E^{\nu}_i} \\ &\sim_{{\mathbb{Q}}} H'|_{E^{\nu}_i} + (mL|_{E^{\nu}_i}-t\lfloor \Delta_{E_i^{\nu}}\rfloor) + (F'|_{E^{\nu}_i}+t\lfloor \Delta_{E_i^{\nu}}\rfloor) + G'|_{E^{\nu}_i} \end{align*} $$
$$ \begin{align*} (m+1)L|_{E^{\nu}_i} &\sim_{{\mathbb{Q}}} H'|_{E^{\nu}_i} + mL|_{E^{\nu}_i} + F'|_{E^{\nu}_i} + G'|_{E^{\nu}_i} \\ &\sim_{{\mathbb{Q}}} H'|_{E^{\nu}_i} + (mL|_{E^{\nu}_i}-t\lfloor \Delta_{E_i^{\nu}}\rfloor) + (F'|_{E^{\nu}_i}+t\lfloor \Delta_{E_i^{\nu}}\rfloor) + G'|_{E^{\nu}_i} \end{align*} $$
for
![]() $m,t \in \mathbb {N}$
such that
$m,t \in \mathbb {N}$
such that
![]() $mL|_{E^{\nu }_i}-t\lfloor \Delta _{E_i^{\nu }}\rfloor $
and
$mL|_{E^{\nu }_i}-t\lfloor \Delta _{E_i^{\nu }}\rfloor $
and
![]() $F'|_{E^{\nu }_i}+t\lfloor \Delta _{E_i^{\nu }}\rfloor $
are pseudo-effective. This shows that
$F'|_{E^{\nu }_i}+t\lfloor \Delta _{E_i^{\nu }}\rfloor $
are pseudo-effective. This shows that
![]() $L|_{E^{\nu }_i}$
is big, which is the required contradiction.
$L|_{E^{\nu }_i}$
is big, which is the required contradiction.
Let
![]() $(\overline {E}_i, \Delta _{\overline {E}_i})$
be a dlt modification of
$(\overline {E}_i, \Delta _{\overline {E}_i})$
be a dlt modification of
![]() $(E^{\nu }_i, \Delta _{E^{\nu }_i})$
so that
$(E^{\nu }_i, \Delta _{E^{\nu }_i})$
so that
![]() $\overline {E}_i$
is
$\overline {E}_i$
is
![]() ${\mathbb {Q}}$
-factorial (see [Reference Hashizume, Nakamura and TanakaHNT20, Corollary 3.6]). Let r be the Cartier index of
${\mathbb {Q}}$
-factorial (see [Reference Hashizume, Nakamura and TanakaHNT20, Corollary 3.6]). Let r be the Cartier index of
![]() $K_{\overline {E}_i} + \Delta _{\overline {E}_i}$
, and let
$K_{\overline {E}_i} + \Delta _{\overline {E}_i}$
, and let
![]() $L_i$
be the pullback of
$L_i$
be the pullback of
![]() $L|_{E_i^{\nu }}$
. Note that
$L|_{E_i^{\nu }}$
. Note that
![]() $L_i = K_{\overline {E}_i} + \Delta _{\overline {E}_i}$
. We will run the
$L_i = K_{\overline {E}_i} + \Delta _{\overline {E}_i}$
. We will run the
![]() $(K_{\overline {E}_i}+\Delta _{\overline {E}_i}-\gamma \lfloor \Delta _{\overline {E}_i}\rfloor )$
-MMP for
$(K_{\overline {E}_i}+\Delta _{\overline {E}_i}-\gamma \lfloor \Delta _{\overline {E}_i}\rfloor )$
-MMP for
![]() $\gamma = \frac {1}{6r+1}$
, which by the above must terminate with a Mori fibre space (cf. [Reference Gongyo, Nakamura and HiromuGNH19, Theorem 2.13]).
$\gamma = \frac {1}{6r+1}$
, which by the above must terminate with a Mori fibre space (cf. [Reference Gongyo, Nakamura and HiromuGNH19, Theorem 2.13]).
We claim that each step of the MMP is
![]() $(K_{\overline {E}_i}+\Delta _{\overline {E}_i})$
-trivial. We start by showing this for the first step. Note that
$(K_{\overline {E}_i}+\Delta _{\overline {E}_i})$
-trivial. We start by showing this for the first step. Note that
![]() $(K_{\overline {E}_i}+\Delta _{\overline {E}_i}-\lfloor \Delta _{\overline {E}_i}\rfloor )\cdot \Gamma \geq -6d_{\Gamma }$
for any
$(K_{\overline {E}_i}+\Delta _{\overline {E}_i}-\lfloor \Delta _{\overline {E}_i}\rfloor )\cdot \Gamma \geq -6d_{\Gamma }$
for any
![]() $(K_{\overline {E}_i}+\Delta _{\overline {E}_i}-\gamma \lfloor \Delta _{\overline {E}_i}\rfloor )$
-negative extremal ray
$(K_{\overline {E}_i}+\Delta _{\overline {E}_i}-\gamma \lfloor \Delta _{\overline {E}_i}\rfloor )$
-negative extremal ray
![]() $\Gamma $
(see [Reference Das and WaldronDW19b, Theorem 1.1]; here,
$\Gamma $
(see [Reference Das and WaldronDW19b, Theorem 1.1]; here,
![]() $d_{\Gamma }$
satisfies
$d_{\Gamma }$
satisfies
![]() $d_{\Gamma } \mid \Gamma \cdot M$
for every Cartier divisor M). But if
$d_{\Gamma } \mid \Gamma \cdot M$
for every Cartier divisor M). But if
![]() $(K_{\overline {E}_i}+\Delta _{\overline {E}_i})\cdot \Gamma>0$
, then
$(K_{\overline {E}_i}+\Delta _{\overline {E}_i})\cdot \Gamma>0$
, then
![]() $(K_{\overline {E}_i}+\Delta _{\overline {E}_i})\cdot \Gamma \geq d_{\Gamma }/r$
by the definition of r, and hence
$(K_{\overline {E}_i}+\Delta _{\overline {E}_i})\cdot \Gamma \geq d_{\Gamma }/r$
by the definition of r, and hence
which is a contradiction. In particular,
![]() $(K_{\overline {E}_i}+\Delta _{\overline {E}_i})\cdot \Gamma =0$
. Hence, the nefness of
$(K_{\overline {E}_i}+\Delta _{\overline {E}_i})\cdot \Gamma =0$
. Hence, the nefness of
![]() $K_{\overline {E}_i}+\Delta _{\overline {E}_i}$
is preserved by the first step of the MMP and so is its Cartier index r by [Reference BernasconiBer21, Theorem 1.1], [Reference Arvidsson, Bernasconi and JustinABL22, Corollary 1.5] (precisely, if
$K_{\overline {E}_i}+\Delta _{\overline {E}_i}$
is preserved by the first step of the MMP and so is its Cartier index r by [Reference BernasconiBer21, Theorem 1.1], [Reference Arvidsson, Bernasconi and JustinABL22, Corollary 1.5] (precisely, if
![]() $\overline {E}_i \to Z$
is the contraction of
$\overline {E}_i \to Z$
is the contraction of
![]() $\Gamma $
given by
$\Gamma $
given by
![]() $L' = K_{\overline {E}_i}+\Delta _{\overline {E}_i}-\gamma \lfloor \Delta _{\overline {E}_i}\rfloor +A$
for some ample
$L' = K_{\overline {E}_i}+\Delta _{\overline {E}_i}-\gamma \lfloor \Delta _{\overline {E}_i}\rfloor +A$
for some ample
![]() ${\mathbb {Q}}$
-divisor A, then we apply this result to
${\mathbb {Q}}$
-divisor A, then we apply this result to
![]() $rL_i \sim _{{\mathbb {Q}},Z} K_{\overline {E}_i}+\Delta _{\overline {E}_i}-\gamma \lfloor \Delta _{\overline {E}_i}\rfloor +A + (rL_i - L')$
over Z). Hence, we may repeat this procedure for all steps of the
$rL_i \sim _{{\mathbb {Q}},Z} K_{\overline {E}_i}+\Delta _{\overline {E}_i}-\gamma \lfloor \Delta _{\overline {E}_i}\rfloor +A + (rL_i - L')$
over Z). Hence, we may repeat this procedure for all steps of the
![]() $(K_{\overline {E}_i}+\Delta _{\overline {E}_i}-\gamma \lfloor \Delta _{\overline {E}_i}\rfloor )$
-MMP.
$(K_{\overline {E}_i}+\Delta _{\overline {E}_i}-\gamma \lfloor \Delta _{\overline {E}_i}\rfloor )$
-MMP.
By replacing
![]() $\overline {E}_i$
by the output of this MMP and
$\overline {E}_i$
by the output of this MMP and
![]() $\Delta _{\overline {E}_i}$
together with
$\Delta _{\overline {E}_i}$
together with
![]() $L_i$
by their pushforwards, we can assume that we have a
$L_i$
by their pushforwards, we can assume that we have a
![]() $(K_{\overline {E}_i}+\Delta _{\overline {E}_i}-\gamma \lfloor \Delta _{\overline {E}_i}\rfloor )$
-Mori fibre space
$(K_{\overline {E}_i}+\Delta _{\overline {E}_i}-\gamma \lfloor \Delta _{\overline {E}_i}\rfloor )$
-Mori fibre space
![]() $\psi \colon \overline {E}_i\to Z$
(in particular Z is normal). Since
$\psi \colon \overline {E}_i\to Z$
(in particular Z is normal). Since
![]() $\psi $
is
$\psi $
is
![]() $L_i$
-trivial,
$L_i$
-trivial,
![]() $\lfloor \Delta _{\overline {E}_i}\rfloor $
is relatively ample so that one of its components, say W, dominates Z. We claim that
$\lfloor \Delta _{\overline {E}_i}\rfloor $
is relatively ample so that one of its components, say W, dominates Z. We claim that
![]() $L_i|_{\lfloor \Delta _{\overline {E}_i}\rfloor }$
(and so
$L_i|_{\lfloor \Delta _{\overline {E}_i}\rfloor }$
(and so
![]() $L_i|_W$
) is semiample. This can be checked after a base change to an algebraically closed field and on a dlt modification of
$L_i|_W$
) is semiample. This can be checked after a base change to an algebraically closed field and on a dlt modification of
![]() $(\overline {E}_i, \Delta _{\overline {E}_i})$
(cf. [Reference Cascini and TanakaCT20, Lemma 2.11(3)]) in which case it follows from [Reference WaldronWal18, Theorem 1.3]. Now,
$(\overline {E}_i, \Delta _{\overline {E}_i})$
(cf. [Reference Cascini and TanakaCT20, Lemma 2.11(3)]) in which case it follows from [Reference WaldronWal18, Theorem 1.3]. Now,
![]() $L_i \sim _{{\mathbb {Q}}} \psi ^* D$
for some
$L_i \sim _{{\mathbb {Q}}} \psi ^* D$
for some
![]() ${\mathbb {Q}}$
-divisor D on Z. But then
${\mathbb {Q}}$
-divisor D on Z. But then
![]() $(\psi |_W)^*D \sim _{{\mathbb {Q}}} L_i|_W$
, which is semiample, and hence both D and
$(\psi |_W)^*D \sim _{{\mathbb {Q}}} L_i|_W$
, which is semiample, and hence both D and
![]() $L_i$
are semiample as Z is normal (cf. [Reference Cascini and TanakaCT20, Lemma 2.11(4)]).
$L_i$
are semiample as Z is normal (cf. [Reference Cascini and TanakaCT20, Lemma 2.11(4)]).
Proposition 5.4. With notation as in the first paragraph of Proposition 5.2, suppose that
![]() $\textrm {Supp}(\phi ^{-1}(s))\subset \lfloor \Delta \rfloor $
. Let L be a nef and big
$\textrm {Supp}(\phi ^{-1}(s))\subset \lfloor \Delta \rfloor $
. Let L be a nef and big
![]() ${\mathbb {Q}}$
-Cartier
${\mathbb {Q}}$
-Cartier
![]() ${\mathbb {Q}}$
-divisor on X such that
${\mathbb {Q}}$
-divisor on X such that
![]() $L-(K_X+\Delta )$
is ample. Then L is semiample and induces a morphism
$L-(K_X+\Delta )$
is ample. Then L is semiample and induces a morphism
![]() $f\colon X \to Z$
over
$f\colon X \to Z$
over
![]() $\operatorname {\mathrm {Spec}} R$
. In particular, every f-numerically trivial
$\operatorname {\mathrm {Spec}} R$
. In particular, every f-numerically trivial
![]() ${\mathbb {Q}}$
-Cartier divisor descends to a
${\mathbb {Q}}$
-Cartier divisor descends to a
![]() ${\mathbb {Q}}$
-Cartier divisor on Z.
${\mathbb {Q}}$
-Cartier divisor on Z.
Proof. This follows from Proposition 5.2 by perturbation.
Proof of Theorem 5.1
The proof is similar to that of [Reference Hacon and WitaszekHW21, Proposition 4.1]. We will run an arbitrary
![]() $(K_{X}+\Delta )$
-MMP.
$(K_{X}+\Delta )$
-MMP.
In the positive characteristic case, we will implicitly work with the spread-out
![]() $\mathcal {X}$
of X and repeatedly replace C by an appropriate neighbourhood of the special point
$\mathcal {X}$
of X and repeatedly replace C by an appropriate neighbourhood of the special point
![]() $s\in U\subset C$
and
$s\in U\subset C$
and
![]() $\mathcal X$
by
$\mathcal X$
by
![]() $\mathcal X\times _C U$
so that we can apply results on the MMP for finite type schemes over a field. Let
$\mathcal X\times _C U$
so that we can apply results on the MMP for finite type schemes over a field. Let
![]() $\eta $
be the generic point of
$\eta $
be the generic point of
![]() $\operatorname {\mathrm {Spec}} R$
.
$\operatorname {\mathrm {Spec}} R$
.
Following the proof of Theorem 4.6, we will run a
![]() $(K_X+\Delta )$
-MMP
$(K_X+\Delta )$
-MMP
![]() . We will denote the central fibre by
. We will denote the central fibre by
![]() $ X_{l,s}$
and the pushforward of
$ X_{l,s}$
and the pushforward of
![]() $\Delta $
on
$\Delta $
on
![]() $X_l$
by
$X_l$
by
![]() $\Delta _l$
. Note that
$\Delta _l$
. Note that
![]() $X_{l,s}\sim _{\operatorname {\mathrm {Spec}} R} 0$
. By the same argument as that in Theorem 4.6, the cone theorem is valid for
$X_{l,s}\sim _{\operatorname {\mathrm {Spec}} R} 0$
. By the same argument as that in Theorem 4.6, the cone theorem is valid for
![]() $K_{ X_l}+\Delta _l$
. Hence, if
$K_{ X_l}+\Delta _l$
. Hence, if
![]() $K_{ X_l}+\Delta _l$
is not nef over
$K_{ X_l}+\Delta _l$
is not nef over
![]() $\operatorname {\mathrm {Spec}} R$
, then there exists a
$\operatorname {\mathrm {Spec}} R$
, then there exists a
![]() $(K_{ X_l}+\Delta _l)$
-negative extremal ray over
$(K_{ X_l}+\Delta _l)$
-negative extremal ray over
![]() $\operatorname {\mathrm {Spec}} R$
spanned by a curve
$\operatorname {\mathrm {Spec}} R$
spanned by a curve
![]() $\Sigma \subset X _{l,s}$
.
$\Sigma \subset X _{l,s}$
.
Let G be an ample
![]() ${\mathbb {Q}}$
-divisor such that
${\mathbb {Q}}$
-divisor such that
![]() $L = K_{ X_l} + \Delta _l + G$
is nef and
$L = K_{ X_l} + \Delta _l + G$
is nef and
![]() $L^{\perp } = \mathbb R[\Sigma ]$
. Then L is semiample by Proposition 5.4. Let
$L^{\perp } = \mathbb R[\Sigma ]$
. Then L is semiample by Proposition 5.4. Let
![]() $f\colon X _l\to Z$
be the corresponding contraction, which is birational as
$f\colon X _l\to Z$
be the corresponding contraction, which is birational as
![]() $\kappa (K_X+\Delta \,/\,\textrm { Spec}(R))\geq 0$
. There are two cases. If
$\kappa (K_X+\Delta \,/\,\textrm { Spec}(R))\geq 0$
. There are two cases. If
![]() $f\colon X _l\to Z$
is a divisorial contraction (over
$f\colon X _l\to Z$
is a divisorial contraction (over
![]() $\operatorname {\mathrm {Spec}} R$
), then we may set
$\operatorname {\mathrm {Spec}} R$
), then we may set
![]() $X _{l+1}:= Z$
and continue our MMP over
$X _{l+1}:= Z$
and continue our MMP over
![]() $\operatorname {\mathrm {Spec}} R$
. Thus, we must show that if the induced morphism
$\operatorname {\mathrm {Spec}} R$
. Thus, we must show that if the induced morphism
![]() $f\colon X _l\to Z$
(over
$f\colon X _l\to Z$
(over
![]() $\operatorname {\mathrm {Spec}} R$
) is a flipping contraction, then the flip
$\operatorname {\mathrm {Spec}} R$
) is a flipping contraction, then the flip
![]() $f^+ \colon X_{l+1}\to Z$
exists. Further, we must show that there is no infinite sequence of flips. The latter follows from Theorem 2.14. As for the former, by means of perturbation, we may assume that
$f^+ \colon X_{l+1}\to Z$
exists. Further, we must show that there is no infinite sequence of flips. The latter follows from Theorem 2.14. As for the former, by means of perturbation, we may assume that
![]() $\lfloor \Delta _l \rfloor = {\mathrm {Supp}}\, X_{l,s}$
, and consider two cases.
$\lfloor \Delta _l \rfloor = {\mathrm {Supp}}\, X_{l,s}$
, and consider two cases.
Claim 5.5. If the flipping locus is contained in the special fibre
![]() $ X_{l,s}$
, then the flip
$ X_{l,s}$
, then the flip
![]() exists.
exists.
Proof. Let
![]() $\Sigma $
be a flipping curve. If
$\Sigma $
be a flipping curve. If
![]() $\Sigma \cdot S\ne 0$
for some component S of
$\Sigma \cdot S\ne 0$
for some component S of
![]() $ X _{l,s}$
, then since
$ X _{l,s}$
, then since
![]() $\Sigma \cdot X _{l,s}=0$
, we may assume that there is another component E of
$\Sigma \cdot X _{l,s}=0$
, we may assume that there is another component E of
![]() $X _{l,s}$
such that
$X _{l,s}$
such that
![]() $\Sigma \cdot S<0$
and
$\Sigma \cdot S<0$
and
![]() $\Sigma \cdot E>0$
(up to swapping S and E). Thus, the flip exists by Theorem 4.3. We may therefore assume that
$\Sigma \cdot E>0$
(up to swapping S and E). Thus, the flip exists by Theorem 4.3. We may therefore assume that
![]() $\Sigma \cdot S=0$
for every component of
$\Sigma \cdot S=0$
for every component of
![]() $\mathcal X _{l,s}$
. We follow the proof of [Reference Hacon and WitaszekHW21, Proposition 4.1]. Now, let S be a component of
$\mathcal X _{l,s}$
. We follow the proof of [Reference Hacon and WitaszekHW21, Proposition 4.1]. Now, let S be a component of
![]() $X_{l,s}$
such that
$X_{l,s}$
such that
![]() $\Sigma \subseteq S$
. Since
$\Sigma \subseteq S$
. Since
![]() $S\cdot \Sigma =0$
, we may assume that
$S\cdot \Sigma =0$
, we may assume that
![]() $S':=f_*S$
is also
$S':=f_*S$
is also
![]() ${\mathbb {Q}}$
-Cartier (as f is a flip, then
${\mathbb {Q}}$
-Cartier (as f is a flip, then
![]() $\rho (X/Z)=1$
and so every divisor that intersects
$\rho (X/Z)=1$
and so every divisor that intersects
![]() $\Sigma $
trivially is pulled back from Z, equivalently apply Proposition 5.4). Let
$\Sigma $
trivially is pulled back from Z, equivalently apply Proposition 5.4). Let
![]() $H'$
be a reduced
$H'$
be a reduced
![]() ${\mathbb {Q}}$
-Cartier divisor on Z such that
${\mathbb {Q}}$
-Cartier divisor on Z such that
-
(1)
 $H=f^{-1}_*H'$
contains
$H=f^{-1}_*H'$
contains
 $\textrm {Ex}(f)$
,
$\textrm {Ex}(f)$
, -
(2)
 $(X_l, \Delta _l + H)$
is dlt over the generic point
$(X_l, \Delta _l + H)$
is dlt over the generic point
 $\eta \in \operatorname {\mathrm {Spec}} R$
,
$\eta \in \operatorname {\mathrm {Spec}} R$
, -
(3) For any proper birational morphism
 $h\colon Y\to Z$
such that Y is
$h\colon Y\to Z$
such that Y is
 ${\mathbb {Q}}$
-factorial, we have that
${\mathbb {Q}}$
-factorial, we have that
 $N^1(Y/Z)$
is generated by the irreducible components of the strict transform of
$N^1(Y/Z)$
is generated by the irreducible components of the strict transform of
 $H'$
and the h-exceptional divisors, and
$H'$
and the h-exceptional divisors, and -
(4) H and
 $\Delta _l$
have no common components.
$\Delta _l$
have no common components.
Explicitly, we take
![]() $H_1$
and
$H_1$
and
![]() $H_2$
as in Lemma 5.6. Then
$H_2$
as in Lemma 5.6. Then
![]() $H=H_1+H_2$
descends to a
$H=H_1+H_2$
descends to a
![]() ${\mathbb {Q}}$
-Cartier divisor
${\mathbb {Q}}$
-Cartier divisor
![]() $H'$
on Z by Proposition 5.4. We leave the verification of (3) to the reader (here, we use that
$H'$
on Z by Proposition 5.4. We leave the verification of (3) to the reader (here, we use that
![]() $\rho (X_l/Z)=1$
, otherwise we would need to enlarge
$\rho (X_l/Z)=1$
, otherwise we would need to enlarge
![]() $H'$
).
$H'$
).
Let
![]() $p\colon Y\to X_l$
be a dlt modification of
$p\colon Y\to X_l$
be a dlt modification of
![]() $(X_l,\Delta _l + H)$
(see Corollary 4.8). Since the generic points of
$(X_l,\Delta _l + H)$
(see Corollary 4.8). Since the generic points of
![]() $H_1\cap H_2$
are simple normal crossing in
$H_1\cap H_2$
are simple normal crossing in
![]() $X_{l,\eta }$
, we may assume that the dlt modification is constructed from a log resolution which is an isomorphism over the generic points of
$X_{l,\eta }$
, we may assume that the dlt modification is constructed from a log resolution which is an isomorphism over the generic points of
![]() $(H_1 \cap H_2)|_{X_{l,\eta }}$
. In particular, p must be an isomorphism over the generic point
$(H_1 \cap H_2)|_{X_{l,\eta }}$
. In particular, p must be an isomorphism over the generic point
![]() $\eta \in R$
. Set
$\eta \in R$
. Set
![]() $h = f \circ p \colon Y \to Z$
.
$h = f \circ p \colon Y \to Z$
.
First, we will run a
![]() $(K_Y+\Delta _Y+H_Y)$
-MMP over Z, where
$(K_Y+\Delta _Y+H_Y)$
-MMP over Z, where
![]() $H_Y=p^{-1}_* H$
and
$H_Y=p^{-1}_* H$
and
![]() $\Delta _Y=p_*^{-1}\Delta _l +\textrm {Ex}(p)$
. All extremal rays R are contained in the support of
$\Delta _Y=p_*^{-1}\Delta _l +\textrm {Ex}(p)$
. All extremal rays R are contained in the support of
![]() $h^*H'$
and some component of
$h^*H'$
and some component of
![]() $h^*H'$
has a nonzero intersection number with R (by condition (3) above). Since
$h^*H'$
has a nonzero intersection number with R (by condition (3) above). Since
![]() $h^*H'\cdot R=0$
, there are components
$h^*H'\cdot R=0$
, there are components
![]() $E,E'$
of
$E,E'$
of
![]() ${{\mathrm {Supp}}}\, h^*H'$
such that
${{\mathrm {Supp}}}\, h^*H'$
such that
![]() $E\cdot R<0$
and
$E\cdot R<0$
and
![]() $E'\cdot R>0$
. Since the support of
$E'\cdot R>0$
. Since the support of
![]() $h^*H'$
is contained in the support of
$h^*H'$
is contained in the support of
![]() $\lfloor \Delta _Y+H_Y\rfloor $
, the necessary flips exist by Theorem 4.3 and we may run the required MMP. Note that by Theorem 2.14, there is no infinite sequence of such flips and hence we may assume that, up to replacing Y by the output of the MMP,
$\lfloor \Delta _Y+H_Y\rfloor $
, the necessary flips exist by Theorem 4.3 and we may run the required MMP. Note that by Theorem 2.14, there is no infinite sequence of such flips and hence we may assume that, up to replacing Y by the output of the MMP,
![]() $K_Y+\Delta _Y+H_Y$
is nef over Z. We now run a
$K_Y+\Delta _Y+H_Y$
is nef over Z. We now run a
![]() $(K_Y+\Delta _Y)$
-MMP with scaling of
$(K_Y+\Delta _Y)$
-MMP with scaling of
![]() $H_Y$
over Z. If R is a corresponding
$H_Y$
over Z. If R is a corresponding
![]() $(K_Y+\Delta _Y)$
-negative extremal ray, then
$(K_Y+\Delta _Y)$
-negative extremal ray, then
![]() $H_Y\cdot R>0$
. Since
$H_Y\cdot R>0$
. Since
for some h-exceptional divisors
![]() $E_j$
, it follows that
$E_j$
, it follows that
![]() $R\cdot E_j<0$
for some j. Since
$R\cdot E_j<0$
for some j. Since
![]() $E_j$
is contained in
$E_j$
is contained in
![]() $Y_s$
, it is contained in the support of
$Y_s$
, it is contained in the support of
![]() $h^*Z_s$
. Since
$h^*Z_s$
. Since
![]() $R\cdot h^*Z_s=0$
, there is a component
$R\cdot h^*Z_s=0$
, there is a component
![]() $E'$
of
$E'$
of
![]() $\lfloor \Delta _Y\rfloor $
such that
$\lfloor \Delta _Y\rfloor $
such that
![]() $R\cdot E'>0$
and the necessary flip exists by Theorem 4.3.
$R\cdot E'>0$
and the necessary flip exists by Theorem 4.3.
By Theorem 2.14, there is no infinite sequence of such flips and hence we may assume that
![]() $K_Y+\Delta _Y$
is nef over Z. By Proposition 5.2 applied to
$K_Y+\Delta _Y$
is nef over Z. By Proposition 5.2 applied to
![]() $K_Y+ \Delta _Y+h^*A$
for a sufficiently ample divisor A on Z, we get that
$K_Y+ \Delta _Y+h^*A$
for a sufficiently ample divisor A on Z, we get that
![]() $K_Y+\Delta _Y$
is semiample over Z, and thus by replacing Y by the image of the associated semiample fibration, we can assume that
$K_Y+\Delta _Y$
is semiample over Z, and thus by replacing Y by the image of the associated semiample fibration, we can assume that
![]() $K_Y + \Delta _Y$
is relatively ample over Z. We claim that
$K_Y + \Delta _Y$
is relatively ample over Z. We claim that
![]() $Y\to Z$
is small, and hence
$Y\to Z$
is small, and hence
![]() $X _{l+1}:=Y$
is the required flip (the canonical ring
$X _{l+1}:=Y$
is the required flip (the canonical ring
![]() $R(K_{X_{l}} + \Delta _l) = R(K_Z + f_* \Delta _l) = R(K_Y + \Delta _Y)$
is finitely generated). To this end, note that if
$R(K_{X_{l}} + \Delta _l) = R(K_Z + f_* \Delta _l) = R(K_Y + \Delta _Y)$
is finitely generated). To this end, note that if
![]() $p \colon W\to X _{l}$
and
$p \colon W\to X _{l}$
and
![]() $q \colon W\to Y$
is the normalisation of the graph of the rational map
$q \colon W\to Y$
is the normalisation of the graph of the rational map
![]() , then we may write
, then we may write
where
![]() $p_*E=0$
(as
$p_*E=0$
(as
![]() $X _{l}\to Z$
is small) and
$X _{l}\to Z$
is small) and
![]() $-E$
is relatively ample over Z. By the negativity lemma,
$-E$
is relatively ample over Z. By the negativity lemma,
![]() $E\geq 0$
. On the other hand, by construction, if F is a p-exceptional but not q-exceptional divisor on W, then by definition of
$E\geq 0$
. On the other hand, by construction, if F is a p-exceptional but not q-exceptional divisor on W, then by definition of
![]() $\Delta _Y$
we have
$\Delta _Y$
we have
and so, in fact,
![]() $\textrm {mult}_F(E) = 0$
. This contradicts
$\textrm {mult}_F(E) = 0$
. This contradicts
![]() $-E$
being relatively ample over Z.
$-E$
being relatively ample over Z.
Let
![]() $f_{\eta }\colon (X_{l,\eta }, \Delta _{l,\eta })\to Z_{\eta } $
be the restriction of f to
$f_{\eta }\colon (X_{l,\eta }, \Delta _{l,\eta })\to Z_{\eta } $
be the restriction of f to
![]() $X_{\eta }$
. By the above claim, we may assume that
$X_{\eta }$
. By the above claim, we may assume that
![]() $f_{\eta }$
is not the identity. Since f is a flipping contraction, it is easy to see that
$f_{\eta }$
is not the identity. Since f is a flipping contraction, it is easy to see that
![]() $f_{\eta }$
is a flipping contraction and in particular
$f_{\eta }$
is a flipping contraction and in particular
![]() $X_{l,\eta }$
is
$X_{l,\eta }$
is
![]() ${\mathbb {Q}}$
-factorial,
${\mathbb {Q}}$
-factorial,
![]() $\rho (X_{l,\eta }/Z_{\eta } )=1$
,
$\rho (X_{l,\eta }/Z_{\eta } )=1$
,
![]() $X_{l,\eta }\to Z_{\eta } $
is small and
$X_{l,\eta }\to Z_{\eta } $
is small and
![]() $-(K_{X_{l,\eta } }+ \Delta _{l,\eta })$
is ample over
$-(K_{X_{l,\eta } }+ \Delta _{l,\eta })$
is ample over
![]() $Z_{\eta } $
. By [Reference Das and WaldronDW19b, Theorem 1.3] in positive characteristic (and [Reference Birkar, Cascini, Hacon and McKernanBCHM10] in characteristic 0), the corresponding flip
$Z_{\eta } $
. By [Reference Das and WaldronDW19b, Theorem 1.3] in positive characteristic (and [Reference Birkar, Cascini, Hacon and McKernanBCHM10] in characteristic 0), the corresponding flip
![]() $f_{\eta } ^+\colon X_{l,\eta }^+\to Z_{\eta } $
exists. Let
$f_{\eta } ^+\colon X_{l,\eta }^+\to Z_{\eta } $
exists. Let
![]() $f' \colon X^{\prime }_l \to Z$
be the closure of the projective morphism
$f' \colon X^{\prime }_l \to Z$
be the closure of the projective morphism
![]() $f^+_{\eta }$
. Note that the fibre of
$f^+_{\eta }$
. Note that the fibre of
![]() $X^{\prime }_l$
over s may be highly singular and in particular nonnormal and not even
$X^{\prime }_l$
over s may be highly singular and in particular nonnormal and not even
![]() $R_1$
; therefore, to construct the flip we will consider an appropriate log resolution and then run an MMP over Z.
$R_1$
; therefore, to construct the flip we will consider an appropriate log resolution and then run an MMP over Z.
Let
![]() $\Delta ^{\prime }_l$
be a divisor on
$\Delta ^{\prime }_l$
be a divisor on
![]() $X^{\prime }_l$
given as the sum of the closure of
$X^{\prime }_l$
given as the sum of the closure of
![]() $\Delta ^+_{l,\eta }$
and the support of
$\Delta ^+_{l,\eta }$
and the support of
![]() $X^{\prime }_{l,s}$
. Let
$X^{\prime }_{l,s}$
. Let
![]() $p \colon Y \to X^{\prime }_l$
be a log resolution of
$p \colon Y \to X^{\prime }_l$
be a log resolution of
![]() $(X^{\prime }_l, \Delta ^{\prime }_l)$
, and set
$(X^{\prime }_l, \Delta ^{\prime }_l)$
, and set
![]() $\Delta ' _Y=p_*^{-1}\Delta ^{\prime }_l +\textrm {Ex}(p)$
. We now run a
$\Delta ' _Y=p_*^{-1}\Delta ^{\prime }_l +\textrm {Ex}(p)$
. We now run a
![]() $(K_Y+\Delta ^{\prime }_Y)$
-MMP over
$(K_Y+\Delta ^{\prime }_Y)$
-MMP over
![]() $X^{\prime }_{l}$
. We must show that the necessary flips exist and that the corresponding MMP terminates. Let
$X^{\prime }_{l}$
. We must show that the necessary flips exist and that the corresponding MMP terminates. Let
![]() $v \colon Y\to V$
be a flipping contraction. Note that if the flipping locus is contained in the central fibre
$v \colon Y\to V$
be a flipping contraction. Note that if the flipping locus is contained in the central fibre
![]() $Y_s$
, then the flip exists by Claim 5.5. If the flipping locus dominates
$Y_s$
, then the flip exists by Claim 5.5. If the flipping locus dominates
![]() $\operatorname {\mathrm {Spec}} R$
, then as
$\operatorname {\mathrm {Spec}} R$
, then as
![]() $X^{\prime }_{l,\eta }$
is
$X^{\prime }_{l,\eta }$
is
![]() ${\mathbb {Q}}$
-factorial, by [Reference Hacon and WitaszekHW21, Lemma 3.1] (the same argument works in mixed characteristic), there is a v-ample p-exceptional divisor
${\mathbb {Q}}$
-factorial, by [Reference Hacon and WitaszekHW21, Lemma 3.1] (the same argument works in mixed characteristic), there is a v-ample p-exceptional divisor
![]() $A_{\eta }\subset Y_{\eta }$
. As
$A_{\eta }\subset Y_{\eta }$
. As
![]() $\rho (Y/V)=1$
, its closure
$\rho (Y/V)=1$
, its closure
![]() $A\subset Y$
is also relatively ample and is contained in the support of
$A\subset Y$
is also relatively ample and is contained in the support of
![]() $\lfloor \Delta ' _Y\rfloor $
. Similarly, we also have an effective p-exceptional divisor
$\lfloor \Delta ' _Y\rfloor $
. Similarly, we also have an effective p-exceptional divisor
![]() $F_{\eta }\subset Y_{\eta }$
which is p-antiample. Therefore, there is a component
$F_{\eta }\subset Y_{\eta }$
which is p-antiample. Therefore, there is a component
![]() $S_{\eta }$
of
$S_{\eta }$
of
![]() $F_{\eta }$
such that its closure
$F_{\eta }$
such that its closure
![]() $S\subset Y$
is v-antiample. Thus, the flip exists by Theorem 4.3. By Theorem 2.14 the above sequence terminates with the required dlt model which we again denote by
$S\subset Y$
is v-antiample. Thus, the flip exists by Theorem 4.3. By Theorem 2.14 the above sequence terminates with the required dlt model which we again denote by
![]() $(Y,\Delta ^{\prime }_Y)$
. Since
$(Y,\Delta ^{\prime }_Y)$
. Since
![]() $(X^{\prime }_l, \Delta ^{\prime }_l)$
is klt and
$(X^{\prime }_l, \Delta ^{\prime }_l)$
is klt and
![]() ${\mathbb {Q}}$
-factorial over
${\mathbb {Q}}$
-factorial over
![]() $\eta $
, we can assume that p is an isomorphism over
$\eta $
, we can assume that p is an isomorphism over
![]() $\eta $
. Set
$\eta $
. Set
![]() $h = f' \circ p \colon Y \to Z$
.
$h = f' \circ p \colon Y \to Z$
.
We will run a
![]() $(K_Y+\Delta ^{\prime }_Y)$
-MMP over Z, where
$(K_Y+\Delta ^{\prime }_Y)$
-MMP over Z, where
![]() $(Y,\Delta ' _Y=p_*^{-1}\Delta ^{\prime }_l +\textrm {Ex}(p))$
is dlt. Contractions exist for the same reason as before (see Proposition 5.4). Since
$(Y,\Delta ' _Y=p_*^{-1}\Delta ^{\prime }_l +\textrm {Ex}(p))$
is dlt. Contractions exist for the same reason as before (see Proposition 5.4). Since
![]() $K_{Y_{\eta }} + \Delta ^{\prime }_{Y_{\eta }}$
is ample over
$K_{Y_{\eta }} + \Delta ^{\prime }_{Y_{\eta }}$
is ample over
![]() $Z_{\eta }$
, the contracted locus is contained in the fibre over
$Z_{\eta }$
, the contracted locus is contained in the fibre over
![]() $s \in \operatorname {\mathrm {Spec}} R$
. In particular, the necessary flips exist by Claim 5.5. The MMP terminates by Theorem 2.14.
$s \in \operatorname {\mathrm {Spec}} R$
. In particular, the necessary flips exist by Claim 5.5. The MMP terminates by Theorem 2.14.
Hence, we can assume that
![]() $K_Y+\Delta ^{\prime }_Y$
is nef over Z. By Proposition 5.2,
$K_Y+\Delta ^{\prime }_Y$
is nef over Z. By Proposition 5.2,
![]() $K_Y+\Delta ^{\prime }_Y$
is semiample over
$K_Y+\Delta ^{\prime }_Y$
is semiample over
![]() $\operatorname {\mathrm {Spec}} R$
. Replacing Y by the image of the associated semiample fibration, we can assume that
$\operatorname {\mathrm {Spec}} R$
. Replacing Y by the image of the associated semiample fibration, we can assume that
![]() $K_Y + \Delta ^{\prime }_Y$
is relatively ample. We claim that
$K_Y + \Delta ^{\prime }_Y$
is relatively ample. We claim that
![]() $Y\to Z$
is small, and hence,
$Y\to Z$
is small, and hence,
![]() $X _{l+1}:=Y$
is the required flip. To this end, note that if
$X _{l+1}:=Y$
is the required flip. To this end, note that if
![]() $p \colon W\to X _{l}$
and
$p \colon W\to X _{l}$
and
![]() $q \colon W\to Y$
is the normalisation of the graph of the rational map
$q \colon W\to Y$
is the normalisation of the graph of the rational map
![]() , then we may write
, then we may write
where
![]() $p_*E=0$
(as
$p_*E=0$
(as
![]() $X _{l}\to Z$
is small) and
$X _{l}\to Z$
is small) and
![]() $-E$
is relatively ample over Z. By the negativity lemma,
$-E$
is relatively ample over Z. By the negativity lemma,
![]() $E\geq 0$
. On the other hand, by construction, if F is p-exceptional but not q-exceptional, then by definition of
$E\geq 0$
. On the other hand, by construction, if F is p-exceptional but not q-exceptional, then by definition of
![]() $\Delta ^{\prime }_Y$
we have
$\Delta ^{\prime }_Y$
we have
and so, in fact,
![]() $\textrm {mult}_F(E) = 0$
. This contradicts
$\textrm {mult}_F(E) = 0$
. This contradicts
![]() $-E$
being relatively ample over Z.
$-E$
being relatively ample over Z.
In the proof we used the following technical lemma.
Lemma 5.6. Let C be a regular affine curve defined over an algebraically closed field k of positive characteristic
![]() $p>0$
. Let
$p>0$
. Let
![]() $s \in C$
be a closed point, and let
$s \in C$
be a closed point, and let
![]() $\eta \in C$
be the generic point. Let
$\eta \in C$
be the generic point. Let
![]() $(X,S+B)$
be a
$(X,S+B)$
be a
![]() ${\mathbb {Q}}$
-factorial dlt pair of absolute dimension four, projective and dominant over the curve C such that
${\mathbb {Q}}$
-factorial dlt pair of absolute dimension four, projective and dominant over the curve C such that
![]() $S = \lfloor S + B \rfloor = {\mathrm {Supp}}\, X_s \neq 0$
and B has standard coefficients. Let
$S = \lfloor S + B \rfloor = {\mathrm {Supp}}\, X_s \neq 0$
and B has standard coefficients. Let
![]() $f \colon X \to Z$
be a small contraction with
$f \colon X \to Z$
be a small contraction with
![]() $\rho (X/Z)=1$
and exceptional locus
$\rho (X/Z)=1$
and exceptional locus
![]() $\textrm {Ex}(f)$
contained in
$\textrm {Ex}(f)$
contained in
![]() $X_s$
. Suppose that every irreducible component
$X_s$
. Suppose that every irreducible component
![]() $S_i$
of S is f-numerically trivial.
$S_i$
of S is f-numerically trivial.
Then there exist
![]() ${\mathbb {Q}}$
-Cartier Weil divisors
${\mathbb {Q}}$
-Cartier Weil divisors
![]() $H_i$
for
$H_i$
for
![]() $i \in \{1,2\}$
such that
$i \in \{1,2\}$
such that
![]() $H_1$
and
$H_1$
and
![]() $H_2$
are f-ample and f-antiample, respectively,
$H_2$
are f-ample and f-antiample, respectively,
![]() $H_1+H_2$
is f-numerically trivial, and
$H_1+H_2$
is f-numerically trivial, and
![]() $(X,S+B+H_1+H_2)$
is dlt over
$(X,S+B+H_1+H_2)$
is dlt over
![]() $\eta $
.
$\eta $
.
The same statement holds if X is defined over
![]() $C=\operatorname {\mathrm {Spec}} R$
for a DVR R of mixed characteristic
$C=\operatorname {\mathrm {Spec}} R$
for a DVR R of mixed characteristic
![]() $(0,p>0)$
.
$(0,p>0)$
.
Proof. Pick an f-ample Cartier divisor D on X and an ample Cartier divisor A on Z. Set
![]() $D_i = (-1)^{i+1}D$
and
$D_i = (-1)^{i+1}D$
and
![]() $L_i := D_i + m_if^*A$
for
$L_i := D_i + m_if^*A$
for
![]() $m_2 \gg m_1 \gg 0$
and
$m_2 \gg m_1 \gg 0$
and
![]() $i \in \{1,2\}$
. We claim that there exist effective divisors
$i \in \{1,2\}$
. We claim that there exist effective divisors
![]() $H_{i,\eta } \in |L_i|_{X_{\eta }}|$
such that
$H_{i,\eta } \in |L_i|_{X_{\eta }}|$
such that
![]() $(X_{\eta }, B|_{X_{\eta }} + H_{1,\eta }+H_{2,\eta })$
is dlt. Assuming this claim, we pick
$(X_{\eta }, B|_{X_{\eta }} + H_{1,\eta }+H_{2,\eta })$
is dlt. Assuming this claim, we pick
![]() $H_i$
to be the closures of
$H_i$
to be the closures of
![]() $H_{i,\eta }$
in X. Then
$H_{i,\eta }$
in X. Then
![]() $H_{i} \sim _{{\mathbb {Q}}} L_i + \sum a_i S_i$
for irreducible divisors
$H_{i} \sim _{{\mathbb {Q}}} L_i + \sum a_i S_i$
for irreducible divisors
![]() $S_i$
of S and some
$S_i$
of S and some
![]() $a_i \in {\mathbb {Q}}$
. Since
$a_i \in {\mathbb {Q}}$
. Since
![]() $S_i$
are f-numerically trivial, we get that
$S_i$
are f-numerically trivial, we get that
![]() $H_1$
is f-ample,
$H_1$
is f-ample,
![]() $H_2$
is f-antiample and
$H_2$
is f-antiample and
![]() $H_1 + H_2$
is f-numerically trivial.
$H_1 + H_2$
is f-numerically trivial.
Thus, we are left to show the claim. In the mixed characteristic case, it follows automatically from the standard Bertini results in characteristic 0. Hence, we can assume that we are in the purely positive characteristic case. First, we replace C by
![]() $C \,\backslash \, \{s\}$
, and so we can assume that
$C \,\backslash \, \{s\}$
, and so we can assume that
![]() $S=0$
and
$S=0$
and
![]() $L_i$
are very ample. Let
$L_i$
are very ample. Let
![]() $V \subseteq X$
be the subset of points on which
$V \subseteq X$
be the subset of points on which
![]() $(X,B)$
is strongly F-regular. By standard argument, V is open. Now, by localising at codimension two points and applying [Reference Sato and TakagiST18, Theorem 5.7], we get that
$(X,B)$
is strongly F-regular. By standard argument, V is open. Now, by localising at codimension two points and applying [Reference Sato and TakagiST18, Theorem 5.7], we get that
![]() $Z := X \, \backslash \, V$
is at most one dimensional.
$Z := X \, \backslash \, V$
is at most one dimensional.
Let
![]() $H_{1}$
be a general member of
$H_{1}$
be a general member of
![]() $|L_1|$
. By [Reference Schwede and ZhangSZ13, Corollary 6.10],
$|L_1|$
. By [Reference Schwede and ZhangSZ13, Corollary 6.10],
![]() $(V,B|_V+H_1|_V)$
is purely F-regular (note that [Reference Schwede and ZhangSZ13] uses a different name: divisorially F-regular), and hence plt with
$(V,B|_V+H_1|_V)$
is purely F-regular (note that [Reference Schwede and ZhangSZ13] uses a different name: divisorially F-regular), and hence plt with
![]() $H_1|_V$
normal. Since
$H_1|_V$
normal. Since
![]() $H_1 \cap Z$
is 0-dimensional, we can replace C by an open subset so that
$H_1 \cap Z$
is 0-dimensional, we can replace C by an open subset so that
![]() $(X,B+H_1)$
is plt and
$(X,B+H_1)$
is plt and
![]() $H_1$
is normal.
$H_1$
is normal.
Let
![]() $H_2$
be a general member of
$H_2$
be a general member of
![]() $|L_2|$
. Since
$|L_2|$
. Since
![]() $m_2 \gg m_1$
, Serre’s vanishing implies that
$m_2 \gg m_1$
, Serre’s vanishing implies that
![]() $H^0(X, L_2) \to H^0(H_1, L_2|_{H_1})$
is surjective, and so
$H^0(X, L_2) \to H^0(H_1, L_2|_{H_1})$
is surjective, and so
![]() $H_2|_{H_1}$
is a general member of
$H_2|_{H_1}$
is a general member of
![]() $L_2|_{H_1}$
. By the same argument as above, we have that
$L_2|_{H_1}$
. By the same argument as above, we have that
![]() $(X,B+H_1+H_2)$
is plt outside
$(X,B+H_1+H_2)$
is plt outside
![]() $H_1 \cap H_2$
up to replacing C by an open subset. Write
$H_1 \cap H_2$
up to replacing C by an open subset. Write
![]() $K_{H_1} + B_{H_1} = (K_X+B+H_1)|_{H_1}$
. By [Reference Sato and TakagiST18, Theorem 5.9] and inversion of adjunction for threefolds, we get that
$K_{H_1} + B_{H_1} = (K_X+B+H_1)|_{H_1}$
. By [Reference Sato and TakagiST18, Theorem 5.9] and inversion of adjunction for threefolds, we get that
![]() $(H_1, B_{H_1}+H_2|_{H_1})$
is plt. In particular, the inversion of adjunction for fourfolds (Corollary 4.9) and the standard argument implies that the only log canonical centres of
$(H_1, B_{H_1}+H_2|_{H_1})$
is plt. In particular, the inversion of adjunction for fourfolds (Corollary 4.9) and the standard argument implies that the only log canonical centres of
![]() $(X,B+H_1+H_2)$
are the generic points of
$(X,B+H_1+H_2)$
are the generic points of
![]() $H_1\cap H_2$
. The generic points of
$H_1\cap H_2$
. The generic points of
![]() $H_1\cap H_2$
are contained in the smooth locus
$H_1\cap H_2$
are contained in the smooth locus
![]() $X^{\textrm {sm}} \subseteq X$
, and hence
$X^{\textrm {sm}} \subseteq X$
, and hence
![]() $(X,B+H_1+H_2)$
is simple normal crossing at them by the standard Bertini theorem applied to the smooth locus of
$(X,B+H_1+H_2)$
is simple normal crossing at them by the standard Bertini theorem applied to the smooth locus of
![]() $H_2$
(cf. [Reference Jannsen and SaitoJS12, Theorem 3]).
$H_2$
(cf. [Reference Jannsen and SaitoJS12, Theorem 3]).
Let us point out that some of the assumptions on the existence of log resolutions of singularities may be weakened.
Conjecture 5.7 (Embedded resolution of singularities)
Let X be a regular quasi-projective variety and Z a closed subscheme, then there exists a projective birational morphism
![]() $\nu \colon X'\to X$
such that the schemes associated to
$\nu \colon X'\to X$
such that the schemes associated to
![]() $\textrm {Ex}(\nu )$
and
$\textrm {Ex}(\nu )$
and
![]() $\nu ^{-1}(Z)$
are divisors (in particular,
$\nu ^{-1}(Z)$
are divisors (in particular,
![]() $\nu ^{-1}I_Z$
is locally free) and
$\nu ^{-1}I_Z$
is locally free) and
![]() $\nu ^{-1}Z\cup \textrm {Ex}(\nu )$
has simple normal crossing support.
$\nu ^{-1}Z\cup \textrm {Ex}(\nu )$
has simple normal crossing support.
From this conjecture, we can deduce the existence of log resolutions for varieties birational to a regular variety.
Proposition 5.8. Assume that Conjecture 5.7 holds for a regular projective variety X and all of its subschemes. Let Y be a quasi-projective variety birational to X. Then for any scheme
![]() $W\subset Y$
, there exists a proper birational morphism from a regular variety
$W\subset Y$
, there exists a proper birational morphism from a regular variety
![]() $\mu \colon Y'\to Y$
such that schemes associated to
$\mu \colon Y'\to Y$
such that schemes associated to
![]() $\textrm {Ex }(\mu )$
and
$\textrm {Ex }(\mu )$
and
![]() $\mu ^{-1}(W)$
are divisors and
$\mu ^{-1}(W)$
are divisors and
![]() $\textrm {Ex}(\mu ) \cup \mu ^{-1}(W)$
has simple normal crossing support.
$\textrm {Ex}(\mu ) \cup \mu ^{-1}(W)$
has simple normal crossing support.
Proof. Let
![]() be a birational map, and let Z be the indeterminacy locus of f. More precisely, let V be the normalisation of the graph of f with projections
be a birational map, and let Z be the indeterminacy locus of f. More precisely, let V be the normalisation of the graph of f with projections
![]() $p\colon V\to X$
and
$p\colon V\to X$
and
![]() $q\colon V\to Y$
. If H is a very ample divisor on Y and
$q\colon V\to Y$
. If H is a very ample divisor on Y and
![]() $H_1,\ldots , H_{d+1}\in |H|$
are general elements, where
$H_1,\ldots , H_{d+1}\in |H|$
are general elements, where
![]() $d=\dim Y$
, then Z is cut out by
$d=\dim Y$
, then Z is cut out by
![]() $H^{\prime }_i=p_*q^*H_i\in |H'|$
, where
$H^{\prime }_i=p_*q^*H_i\in |H'|$
, where
![]() $H'$
is the strict transform of H.
$H'$
is the strict transform of H.
Let
![]() $\nu \colon X'\to X$
be the resolution of Z given by Conjecture 5.7. Then
$\nu \colon X'\to X$
be the resolution of Z given by Conjecture 5.7. Then
![]() $\nu ^*H'=F+M$
and
$\nu ^*H'=F+M$
and
![]() $\nu ^* H^{\prime }_i=F+M_i$
, where F is a simple normal crossings divisor and the divisors
$\nu ^* H^{\prime }_i=F+M_i$
, where F is a simple normal crossings divisor and the divisors
![]() $M_1,\ldots ,M_{d+1}$
give rise to a base point free linear series. Consider the corresponding morphism
$M_1,\ldots ,M_{d+1}$
give rise to a base point free linear series. Consider the corresponding morphism
![]() $f'\colon X'\to Y$
.
$f'\colon X'\to Y$
.
We will now apply Conjecture 5.7 to
![]() $\textrm {Ex}(f')$
and
$\textrm {Ex}(f')$
and
![]() $(f')^{-1}(W)$
. Let
$(f')^{-1}(W)$
. Let
![]() $g\colon Y'\to X'$
and
$g\colon Y'\to X'$
and
![]() $\mu \colon Y'\to Y$
be the induced morphisms. Since
$\mu \colon Y'\to Y$
be the induced morphisms. Since
![]() $\textrm {Ex}(\mu )=\textrm {Ex }(g)\cup g^{-1}(\textrm {Ex}(f'))$
, then
$\textrm {Ex}(\mu )=\textrm {Ex }(g)\cup g^{-1}(\textrm {Ex}(f'))$
, then
![]() $\textrm {Ex}(\mu )$
is a divisor and so is
$\textrm {Ex}(\mu )$
is a divisor and so is
![]() $\mu ^{-1}(W)=g^{-1}((f')^{-1}(W))$
. It is clear that their union has simple normal crossings.
$\mu ^{-1}(W)=g^{-1}((f')^{-1}(W))$
. It is clear that their union has simple normal crossings.
6 Liftability to characteristic 0
Throughout this section, k is a perfect field of characteristic
![]() $p>0$
. Our goal is to show Corollary 1.4 and Corollary 1.5, whose statements in full generality are as follows.
$p>0$
. Our goal is to show Corollary 1.4 and Corollary 1.5, whose statements in full generality are as follows.
Theorem 6.1. Let
![]() $(R,\mathfrak {m})$
be a DVR of mixed characteristic
$(R,\mathfrak {m})$
be a DVR of mixed characteristic
![]() $(0,p)$
for
$(0,p)$
for
![]() $p>5$
, with a perfect residue field k.
$p>5$
, with a perfect residue field k.
Let X be a three-dimensional
![]() ${\mathbb {Q}}$
-factorial terminal variety projective over k. Suppose that
${\mathbb {Q}}$
-factorial terminal variety projective over k. Suppose that
![]() $K_X$
is pseudo-effective and that X lifts to a scheme
$K_X$
is pseudo-effective and that X lifts to a scheme
![]() ${\mathcal {X}}$
over R. Further, assume that log resolutions of all log pairs with the underlying variety being birational to
${\mathcal {X}}$
over R. Further, assume that log resolutions of all log pairs with the underlying variety being birational to
![]() ${\mathcal {X}}$
exist (and are given by a sequence of blowups along the non-snc locus). Then the following hold.
${\mathcal {X}}$
exist (and are given by a sequence of blowups along the non-snc locus). Then the following hold.
-
(1) A (possibly non-
 ${\mathbb {Q}}$
-factorial) minimal model of X lifts over R.
${\mathbb {Q}}$
-factorial) minimal model of X lifts over R. -
(2) If
 $N^1({\mathcal {X}}/\operatorname {\mathrm {Spec}} R)\to N^1(X)$
is surjective, then
$N^1({\mathcal {X}}/\operatorname {\mathrm {Spec}} R)\to N^1(X)$
is surjective, then-
(a) every sequence of steps of a
 $K_X$
-MMP lifts over R, and
$K_X$
-MMP lifts over R, and -
(b) all
 ${\mathbb {Q}}$
-factorial minimal models of X lift over R.
${\mathbb {Q}}$
-factorial minimal models of X lift over R.
-
-
(3) If
 $K_X$
is big, then the canonical model of X lifts over R.
$K_X$
is big, then the canonical model of X lifts over R.
Here,
![]() $N^1(X) = \operatorname {Pic}(X) \otimes {\mathbb {Q}} /{\equiv }$
; this is the set of
$N^1(X) = \operatorname {Pic}(X) \otimes {\mathbb {Q}} /{\equiv }$
; this is the set of
![]() ${\mathbb {Q}}$
-line bundles up to numerical equivalence. Further, we say that a scheme X lifts over R if there exists a flat projective morphism
${\mathbb {Q}}$
-line bundles up to numerical equivalence. Further, we say that a scheme X lifts over R if there exists a flat projective morphism
![]() ${\mathcal {X}} \to \operatorname {\mathrm {Spec}} R$
such that the central fibre
${\mathcal {X}} \to \operatorname {\mathrm {Spec}} R$
such that the central fibre
![]() ${\mathcal {X}}_{{\mathfrak {m}}}$
is isomorphic to X. Finally, recall that a birational map of terminal varieties
${\mathcal {X}}_{{\mathfrak {m}}}$
is isomorphic to X. Finally, recall that a birational map of terminal varieties
![]() is a minimal model if
is a minimal model if
![]() $K_{X_{\textrm {min}}}$
is nef [Reference Kollár and MoriKM98, Definition 2.13]. It is easy to see that
$K_{X_{\textrm {min}}}$
is nef [Reference Kollár and MoriKM98, Definition 2.13]. It is easy to see that
![]() $a(X,0,E)<a(X_{\textrm {min}},0;E)$
for every
$a(X,0,E)<a(X_{\textrm {min}},0;E)$
for every
![]() $\phi $
-exceptional divisor E. A well-known consequence of the negativity lemma then implies that
$\phi $
-exceptional divisor E. A well-known consequence of the negativity lemma then implies that
![]() $a(X,0,E)\leq a(X_{\textrm {min}},0;E)$
for every divisor E over
$a(X,0,E)\leq a(X_{\textrm {min}},0;E)$
for every divisor E over
![]() $X_{\textrm {min}}$
. However, since
$X_{\textrm {min}}$
. However, since
![]() $X_{\textrm {min}}$
is possibly not
$X_{\textrm {min}}$
is possibly not
![]() ${\mathbb {Q}}$
-factorial, it is not necessarily the case that
${\mathbb {Q}}$
-factorial, it is not necessarily the case that
![]() $\phi $
is given by an MMP.
$\phi $
is given by an MMP.
As a corollary to (2b), we get that liftability of three-dimensional terminal Calabi–Yau varieties is a birational invariant. Recall that a projective variety X is Calabi–Yau if
![]() $\omega _X$
is trivial and
$\omega _X$
is trivial and
![]() $H^i(X,{\mathcal {O}}_X)=0$
for
$H^i(X,{\mathcal {O}}_X)=0$
for
![]() $0 < i < \mathrm {dim} X$
.
$0 < i < \mathrm {dim} X$
.
Theorem 6.2. Let
![]() $(R,\mathfrak {m})$
be a complete DVR of mixed characteristic
$(R,\mathfrak {m})$
be a complete DVR of mixed characteristic
![]() $(0,p)$
for
$(0,p)$
for
![]() $p>5$
, with a perfect residue field k.
$p>5$
, with a perfect residue field k.
Let X and Y be three-dimensional terminal
![]() ${\mathbb {Q}}$
-factorial projective Calabi–Yau varieties defined over k. Suppose that X and Y are birational and that X lifts to a scheme
${\mathbb {Q}}$
-factorial projective Calabi–Yau varieties defined over k. Suppose that X and Y are birational and that X lifts to a scheme
![]() $\mathcal {X}$
over R. Further, assume that log resolutions of all log pairs with the underlying variety being birational to
$\mathcal {X}$
over R. Further, assume that log resolutions of all log pairs with the underlying variety being birational to
![]() $\mathcal {X}$
exist (and are given by a sequence of blowups along the non-snc locus).
$\mathcal {X}$
exist (and are given by a sequence of blowups along the non-snc locus).
Then Y lifts over R as well.
It is necessary to assume that R is complete to guarantee that
![]() $N^1({\mathcal {X}}/\operatorname {\mathrm {Spec}} R) \to N^1(X)$
is surjective (see Lemma 6.5).
$N^1({\mathcal {X}}/\operatorname {\mathrm {Spec}} R) \to N^1(X)$
is surjective (see Lemma 6.5).
6.1 Normality of plt centres
Although we do not know that plt centres of four-dimensional pairs are normal in general, we can show this in the setting of lifting using deformation theory. This will be important in the later parts of this section.
Lemma 6.3. Let
![]() ${\mathcal {X}}\to \operatorname {\mathrm {Spec}} R$
be a projective morphism from a normal scheme to a complete DVR
${\mathcal {X}}\to \operatorname {\mathrm {Spec}} R$
be a projective morphism from a normal scheme to a complete DVR
![]() $(R,{\mathfrak {m}})$
of mixed characteristic
$(R,{\mathfrak {m}})$
of mixed characteristic
![]() $(0,p>5)$
with perfect residue field. Suppose that the special fibre X is three-dimensional, reduced, and
$(0,p>5)$
with perfect residue field. Suppose that the special fibre X is three-dimensional, reduced, and
![]() $({\mathcal {X}}, X)$
is plt. Then X is normal.
$({\mathcal {X}}, X)$
is plt. Then X is normal.
Moreover, if
![]() $({\mathcal {X}}, X)$
admits a log resolution of singularities, then the assumption that
$({\mathcal {X}}, X)$
admits a log resolution of singularities, then the assumption that
![]() $(R,{\mathfrak {m}})$
is complete may be dropped.
$(R,{\mathfrak {m}})$
is complete may be dropped.
Proof. As for the last part: The completion
![]() $\hat {R} \to R$
is faithfully flat (see [Sta14, Tag 00MC]), so we can replace R by
$\hat {R} \to R$
is faithfully flat (see [Sta14, Tag 00MC]), so we can replace R by
![]() $\hat {R}$
and assume that
$\hat {R}$
and assume that
![]() $(R,{\mathfrak {m}})$
is complete (see [Sta14, Tag 033G]). The plt-ness of
$(R,{\mathfrak {m}})$
is complete (see [Sta14, Tag 033G]). The plt-ness of
![]() $({\mathcal {X}},X)$
is preserved by the same argument as in [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Lemma 2.7] (here, we use the existence of a resolution).
$({\mathcal {X}},X)$
is preserved by the same argument as in [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Lemma 2.7] (here, we use the existence of a resolution).
Let
![]() $\nu :X^{\nu }\to X$
be the normalisation. Since
$\nu :X^{\nu }\to X$
be the normalisation. Since
![]() $({\mathcal {X}}, X)$
is plt, Lemma 2.1 shows that the special fibre
$({\mathcal {X}}, X)$
is plt, Lemma 2.1 shows that the special fibre
![]() $X={\mathcal {X}}_{\mathfrak m}$
is normal up to universal homeomorphism. By localising at points of X of dimension one and applying [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Corollary 7.17], we get that that X is normal except at possibly finitely many points; explicitly let
$X={\mathcal {X}}_{\mathfrak m}$
is normal up to universal homeomorphism. By localising at points of X of dimension one and applying [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Corollary 7.17], we get that that X is normal except at possibly finitely many points; explicitly let
![]() $Z\subset X^{\nu }$
be a finite set of points such that
$Z\subset X^{\nu }$
be a finite set of points such that
![]() $\nu |_{X^{\nu }\setminus Z}$
is an isomorphism onto its image. We then have that
$\nu |_{X^{\nu }\setminus Z}$
is an isomorphism onto its image. We then have that
is
![]() ${\mathbb {Q}}$
-Cartier. Moreover, as
${\mathbb {Q}}$
-Cartier. Moreover, as
![]() $({\mathcal {X}}, X)$
is plt, we get that
$({\mathcal {X}}, X)$
is plt, we get that
![]() $X^{\nu }$
is klt and so Cohen–Macaulay ([Reference Arvidsson, Bernasconi and JustinABL22, Corollary 1.3], cf. [Reference Hacon and WitaszekHW19, Theorem 1.1]).
$X^{\nu }$
is klt and so Cohen–Macaulay ([Reference Arvidsson, Bernasconi and JustinABL22, Corollary 1.3], cf. [Reference Hacon and WitaszekHW19, Theorem 1.1]).
Let
![]() $U=X^{\nu }\setminus Z$
. Since X lifts to any order (to
$U=X^{\nu }\setminus Z$
. Since X lifts to any order (to
![]() $X_i = \mathcal {X} \times _R R/{\mathfrak {m}}^{i+1}$
) and
$X_i = \mathcal {X} \times _R R/{\mathfrak {m}}^{i+1}$
) and
![]() $U \simeq \nu (U) \subseteq X$
, we have that U also lifts to any order. Explicitly, let
$U \simeq \nu (U) \subseteq X$
, we have that U also lifts to any order. Explicitly, let
![]() $U_i$
be the induced compatible lifts of U to
$U_i$
be the induced compatible lifts of U to
![]() $R/{\mathfrak {m}}^{i+1}$
.
$R/{\mathfrak {m}}^{i+1}$
.
By [Reference ZdanowiczZda17, Lemma A.23],
![]() $X^{\nu }$
also lifts to any order. For the convenience of the reader, we explicate this result. Consider short exact sequences
$X^{\nu }$
also lifts to any order. For the convenience of the reader, we explicate this result. Consider short exact sequences
of sheaves of rings on
![]() $|U|$
. Define a sheaf
$|U|$
. Define a sheaf
![]() ${\mathcal {O}}_{X^{\nu }_i}$
of abelian groups on
${\mathcal {O}}_{X^{\nu }_i}$
of abelian groups on
![]() $|X^{\nu }|$
by the formula:
$|X^{\nu }|$
by the formula:
where
![]() $i \colon U \to X^{\nu }$
is the inclusion of topological spaces. Pushing forward the above short exact sequence of abelian groups by i and using normality of
$i \colon U \to X^{\nu }$
is the inclusion of topological spaces. Pushing forward the above short exact sequence of abelian groups by i and using normality of
![]() $X^{\nu }$
, we get
$X^{\nu }$
, we get
Here,
![]() $R^1i_*{\mathcal {O}}_U$
is calculated in the category of abelian groups, but the answer is the same when it is calculated in the category of coherent sheaves (for example, thanks to Čech resolution, cf. [Sta14, Tag 09V2]), and so it is 0 as
$R^1i_*{\mathcal {O}}_U$
is calculated in the category of abelian groups, but the answer is the same when it is calculated in the category of coherent sheaves (for example, thanks to Čech resolution, cf. [Sta14, Tag 09V2]), and so it is 0 as
![]() $X^{\nu }$
is
$X^{\nu }$
is
![]() $S_3$
and Z has codimension
$S_3$
and Z has codimension
![]() $\geq 3$
. Finally,
$\geq 3$
. Finally,
![]() $\mathcal O _{X^{\nu }_i}$
inherits a structure of a ring from
$\mathcal O _{X^{\nu }_i}$
inherits a structure of a ring from
![]() $U_i$
and so defines a scheme
$U_i$
and so defines a scheme
![]() $X^{\nu }_i$
lifting
$X^{\nu }_i$
lifting
![]() $X^{\nu }$
over
$X^{\nu }$
over
![]() $R/{\mathfrak {m}}^{i+1}$
(here, the flatness follows from the exactness of (1)).
$R/{\mathfrak {m}}^{i+1}$
(here, the flatness follows from the exactness of (1)).
Let
![]() $j=\nu \circ i: U\to X$
. Then we have compatible homomorphisms
$j=\nu \circ i: U\to X$
. Then we have compatible homomorphisms
and so compatible maps of schemes
![]() $X^{\nu }_i \to X_i$
. Hence, we can apply [Sta14, Tag 09ZT and Tag 09ZW(8)], to get a finite map of schemes
$X^{\nu }_i \to X_i$
. Hence, we can apply [Sta14, Tag 09ZT and Tag 09ZW(8)], to get a finite map of schemes
![]() $\psi \colon \overline {{\mathcal {X}}} \to {\mathcal {X}}$
which reduces to
$\psi \colon \overline {{\mathcal {X}}} \to {\mathcal {X}}$
which reduces to
![]() $X^{\nu }_i \to X_i$
modulo
$X^{\nu }_i \to X_i$
modulo
![]() ${\mathfrak {m}}^{i+1}$
.
${\mathfrak {m}}^{i+1}$
.
Moreover,
![]() $\psi \colon \overline {{\mathcal {X}}} \to {\mathcal {X}}$
is birational. Indeed, this is equivalent to showing that the coherent sheaf
$\psi \colon \overline {{\mathcal {X}}} \to {\mathcal {X}}$
is birational. Indeed, this is equivalent to showing that the coherent sheaf
![]() $ \psi _*{\mathcal {O}}_{\overline {{\mathcal {X}}}}/{\mathcal {O}}_{{\mathcal {X}}}$
is not supported on all of
$ \psi _*{\mathcal {O}}_{\overline {{\mathcal {X}}}}/{\mathcal {O}}_{{\mathcal {X}}}$
is not supported on all of
![]() ${\mathcal {X}}$
, which can be checked after localising at a generic point
${\mathcal {X}}$
, which can be checked after localising at a generic point
![]() $\eta _X$
of
$\eta _X$
of
![]() $X \subseteq {\mathcal {X}}$
. As
$X \subseteq {\mathcal {X}}$
. As
![]() $ \psi _*{\mathcal {O}}_{\overline {{\mathcal {X}}}}/{\mathcal {O}}_{{\mathcal {X}}}$
is 0 on
$ \psi _*{\mathcal {O}}_{\overline {{\mathcal {X}}}}/{\mathcal {O}}_{{\mathcal {X}}}$
is 0 on
![]() $\eta _X$
, this yields a finite module M over a Noetherian R-algebra
$\eta _X$
, this yields a finite module M over a Noetherian R-algebra
![]() $A = {\mathcal {O}}_{{\mathcal {X}},\eta _X}$
such that
$A = {\mathcal {O}}_{{\mathcal {X}},\eta _X}$
such that
![]() $M/{\mathfrak {m}} M=0$
(equivalently,
$M/{\mathfrak {m}} M=0$
(equivalently,
![]() ${\mathfrak {m}} M = M$
), and so there exists
${\mathfrak {m}} M = M$
), and so there exists
![]() $f \in 1+{\mathfrak {m}}$
satisfying
$f \in 1+{\mathfrak {m}}$
satisfying
![]() $fM=0$
by Nakayama’s lemma (see [Sta14, Tag 00DV(1)]). In particular,
$fM=0$
by Nakayama’s lemma (see [Sta14, Tag 00DV(1)]). In particular,
![]() $\operatorname {\mathrm {Ann}}(M) \neq 0$
, and so
$\operatorname {\mathrm {Ann}}(M) \neq 0$
, and so
![]() ${\mathrm {Supp}}\, M \neq \operatorname {\mathrm {Spec}} A$
as A is integral.
${\mathrm {Supp}}\, M \neq \operatorname {\mathrm {Spec}} A$
as A is integral.
Since
![]() ${\mathcal {X}}$
is normal,
${\mathcal {X}}$
is normal,
![]() $\psi \colon \overline {{\mathcal {X}}} \to {\mathcal {X}}$
must thus be an isomorphism, and so
$\psi \colon \overline {{\mathcal {X}}} \to {\mathcal {X}}$
must thus be an isomorphism, and so
![]() $X\simeq X^{\nu }$
is normal concluding the proof of the lemma.
$X\simeq X^{\nu }$
is normal concluding the proof of the lemma.
6.2 Liftability of minimal models to characteristic 0
Definition 6.4. Let
![]() $(R, {\mathfrak {m}})$
be a DVR of mixed characteristic and with residue field k. We say that a projective scheme X over k lifts over R if there exists a flat projective morphism
$(R, {\mathfrak {m}})$
be a DVR of mixed characteristic and with residue field k. We say that a projective scheme X over k lifts over R if there exists a flat projective morphism
![]() ${\mathcal {X}} \to \operatorname {\mathrm {Spec}} R$
with the central fibre
${\mathcal {X}} \to \operatorname {\mathrm {Spec}} R$
with the central fibre
![]() ${\mathcal {X}}_{{\mathfrak {m}}}$
isomorphic to X.
${\mathcal {X}}_{{\mathfrak {m}}}$
isomorphic to X.
We say that a projective scheme X defined over k lifts to characteristic 0 if there exists a DVR
![]() $(R, {\mathfrak {m}})$
of mixed characteristic and with residue field k such that X lifts over R.
$(R, {\mathfrak {m}})$
of mixed characteristic and with residue field k such that X lifts over R.
Note that if X is normal, then so is
![]() ${\mathcal {X}}$
. Indeed,
${\mathcal {X}}$
. Indeed,
![]() ${\mathcal {X}}$
is regular in neighbourhoods of regular points of X (cf. [Sta14, Tag 00NU]), and so it is
${\mathcal {X}}$
is regular in neighbourhoods of regular points of X (cf. [Sta14, Tag 00NU]), and so it is
![]() $G_1$
, and since X is
$G_1$
, and since X is
![]() $S_2$
and Cartier,
$S_2$
and Cartier,
![]() ${\mathcal {X}}$
is
${\mathcal {X}}$
is
![]() $S_3$
.
$S_3$
.
In what follows, we shall often write
![]() $S = \operatorname {\mathrm {Spec}} R$
.
$S = \operatorname {\mathrm {Spec}} R$
.
Lemma 6.5. Let
![]() $(R, {\mathfrak {m}})$
be a complete DVR of mixed characteristic
$(R, {\mathfrak {m}})$
be a complete DVR of mixed characteristic
![]() $(0,p)$
with residue field k. Let X be a projective scheme over k and which lifts to
$(0,p)$
with residue field k. Let X be a projective scheme over k and which lifts to
![]() ${\mathcal {X}}$
over R. Further, suppose that
${\mathcal {X}}$
over R. Further, suppose that
![]() $H^2(X, \mathcal O _X)=0$
.
$H^2(X, \mathcal O _X)=0$
.
Then any line bundle L on X lifts to a line bundle
![]() $\mathcal L$
on
$\mathcal L$
on
![]() ${\mathcal {X}}$
such that
${\mathcal {X}}$
such that
![]() $\mathcal L|_X=L$
(in particular,
$\mathcal L|_X=L$
(in particular,
![]() $N^1({\mathcal {X}}/\operatorname {\mathrm {Spec}} R) \to N^1(X)$
is surjective). If moreover L is ample, then so is
$N^1({\mathcal {X}}/\operatorname {\mathrm {Spec}} R) \to N^1(X)$
is surjective). If moreover L is ample, then so is
![]() $\mathcal L$
.
$\mathcal L$
.
Proof. Let
![]() $X_n={\mathcal {X}} \times _S \textrm {Spec }(R/\mathfrak m ^{n+1})$
, and suppose that L on X lifts to a line bundle
$X_n={\mathcal {X}} \times _S \textrm {Spec }(R/\mathfrak m ^{n+1})$
, and suppose that L on X lifts to a line bundle
![]() $L_n$
on
$L_n$
on
![]() $X_n$
. By [Reference HartshorneHar10, Theorem 6.4], the obstruction to lifting
$X_n$
. By [Reference HartshorneHar10, Theorem 6.4], the obstruction to lifting
![]() $L_n$
on
$L_n$
on
![]() $X_n$
to
$X_n$
to
![]() $L_{n+1}$
on
$L_{n+1}$
on
![]() $X_{n+1}$
lies in
$X_{n+1}$
lies in
![]() $H^2(X, \mathcal O _X)$
and hence vanishes by assumption. By [Sta14, Tag 08BE], there is a line bundle
$H^2(X, \mathcal O _X)$
and hence vanishes by assumption. By [Sta14, Tag 08BE], there is a line bundle
![]() $\mathcal L$
on
$\mathcal L$
on
![]() ${\mathcal {X}}$
such that
${\mathcal {X}}$
such that
![]() $\mathcal L|_{X_n}\cong L_n$
for every
$\mathcal L|_{X_n}\cong L_n$
for every
![]() $n>0$
.
$n>0$
.
The last assertion follows from the fact that ampleness may be checked over closed points (see [Sta14, Tag 0D3A]).
Lemma 6.6. Let
![]() ${\mathcal {X}}$
be a normal scheme over a DVR
${\mathcal {X}}$
be a normal scheme over a DVR
![]() $(R, {\mathfrak {m}})$
of characteristic
$(R, {\mathfrak {m}})$
of characteristic
![]() $(0,p)$
for
$(0,p)$
for
![]() $p\geq 0$
. Suppose that the central fibre X of
$p\geq 0$
. Suppose that the central fibre X of
![]() ${\mathcal {X}}$
is a normal
${\mathcal {X}}$
is a normal
![]() $S_3$
scheme.
$S_3$
scheme.
Let
![]() $\mathcal D$
be a Weil divisor on
$\mathcal D$
be a Weil divisor on
![]() ${\mathcal {X}}$
whose support does not contain X and such that
${\mathcal {X}}$
whose support does not contain X and such that
![]() $D=\mathcal D|_X$
is
$D=\mathcal D|_X$
is
![]() ${\mathbb {Q}}$
-Cartier. Further, assume that there is a closed subset
${\mathbb {Q}}$
-Cartier. Further, assume that there is a closed subset
![]() $Z\subset {\mathcal {X}}$
satisfying
$Z\subset {\mathcal {X}}$
satisfying
![]() $\textrm {codim}(Z\cap X,X)\geq 3$
and for which
$\textrm {codim}(Z\cap X,X)\geq 3$
and for which
![]() $D|_{{\mathcal {X}} \setminus Z}$
is
$D|_{{\mathcal {X}} \setminus Z}$
is
![]() ${\mathbb {Q}}$
-Cartier. Then
${\mathbb {Q}}$
-Cartier. Then
![]() $\mathcal D$
is also
$\mathcal D$
is also
![]() ${\mathbb {Q}}$
-Cartier.
${\mathbb {Q}}$
-Cartier.
Note that since X is normal, it is regular in codimension 1 and as observed above, so is
![]() ${\mathcal {X}}$
(cf. [Sta14, Tag 00NU]). Therefore,
${\mathcal {X}}$
(cf. [Sta14, Tag 00NU]). Therefore,
![]() $\mathcal {D}|_X$
is defined by taking the closure of the restriction to the regular locus.
$\mathcal {D}|_X$
is defined by taking the closure of the restriction to the regular locus.
Proof. See [Reference Kollár and MoriKM92, 12.1.8] and [Reference de Fernex and HacondFH11, Proposition 3.1].
Corollary 6.7. Let
![]() ${\mathcal {X}}$
be a normal scheme over a DVR
${\mathcal {X}}$
be a normal scheme over a DVR
![]() $(R, {\mathfrak {m}})$
of characteristic
$(R, {\mathfrak {m}})$
of characteristic
![]() $(0,p)$
for
$(0,p)$
for
![]() $p> 5$
. Suppose that the central fibre X is a three-dimensional terminal variety. Then
$p> 5$
. Suppose that the central fibre X is a three-dimensional terminal variety. Then
-
(1)
 $\mathcal X$
is Cohen–Macaulay,
$\mathcal X$
is Cohen–Macaulay,
 $K_{\mathcal {X}}$
is
$K_{\mathcal {X}}$
is
 ${\mathbb {Q}}$
-Cartier and if X is
${\mathbb {Q}}$
-Cartier and if X is
 ${\mathbb {Q}}$
-factorial, then so is
${\mathbb {Q}}$
-factorial, then so is
 $\mathcal X$
,
$\mathcal X$
, -
(2) If X is
 ${\mathbb {Q}}$
-factorial and log resolutions of all log pairs with the underlying variety being birational to
${\mathbb {Q}}$
-factorial and log resolutions of all log pairs with the underlying variety being birational to
 ${\mathcal {X}}$
exist (and are constructed by a sequence of blowups along the non-snc locus), then
${\mathcal {X}}$
exist (and are constructed by a sequence of blowups along the non-snc locus), then
 $({\mathcal {X}}, X)$
is plt and
$({\mathcal {X}}, X)$
is plt and
 $\mathcal X$
is terminal.
$\mathcal X$
is terminal.
Note that the terminality of
![]() ${\mathcal {X}}$
in (2) is not used later on, but we believe that it is of independent interest.
${\mathcal {X}}$
in (2) is not used later on, but we believe that it is of independent interest.
Proof. By [Reference Arvidsson, Bernasconi and JustinABL22, Corollary 1.3], X is Cohen–Macaulay and as X is a Cartier divisor,
![]() ${\mathcal {X}}$
is also Cohen–Macaulay. Since X is terminal, it is normal and regular in codimension 2, thus so is
${\mathcal {X}}$
is also Cohen–Macaulay. Since X is terminal, it is normal and regular in codimension 2, thus so is
![]() ${\mathcal {X}}$
(cf. [Sta14, Tag 00NU]).
${\mathcal {X}}$
(cf. [Sta14, Tag 00NU]).
For the rest of (1), pick a divisor
![]() $\mathcal D$
whose support does not contain X and such that
$\mathcal D$
whose support does not contain X and such that
![]() $\mathcal D|_X$
is
$\mathcal D|_X$
is
![]() ${\mathbb {Q}}$
-Cartier. We claim that then
${\mathbb {Q}}$
-Cartier. We claim that then
![]() $\mathcal D$
is also
$\mathcal D$
is also
![]() ${\mathbb {Q}}$
-Cartier. Replacing
${\mathbb {Q}}$
-Cartier. Replacing
![]() $\mathcal D$
by a multiple, we may assume that
$\mathcal D$
by a multiple, we may assume that
![]() $\mathcal D|_X$
is Cartier. Notice that if
$\mathcal D|_X$
is Cartier. Notice that if
![]() $U={\mathcal {X}} \setminus \mathcal Z$
is the regular locus, then
$U={\mathcal {X}} \setminus \mathcal Z$
is the regular locus, then
![]() $\mathcal D$
is Cartier on
$\mathcal D$
is Cartier on
![]() ${\mathcal {X}} \setminus \mathcal Z$
and
${\mathcal {X}} \setminus \mathcal Z$
and
![]() $\textrm {codim}( Z, X)\geq 3$
where
$\textrm {codim}( Z, X)\geq 3$
where
![]() $Z=\mathcal Z\cap X$
. Hence, the hypotheses of Lemma 6.6 are satisfied, and so
$Z=\mathcal Z\cap X$
. Hence, the hypotheses of Lemma 6.6 are satisfied, and so
![]() $\mathcal D$
is Cartier.
$\mathcal D$
is Cartier.
In particular, the above paragraph shows that
![]() $K_{{\mathcal {X}}}$
is
$K_{{\mathcal {X}}}$
is
![]() ${\mathbb {Q}}$
-Cartier, as
${\mathbb {Q}}$
-Cartier, as
![]() $K_X$
is
$K_X$
is
![]() ${\mathbb {Q}}$
-Cartier and
${\mathbb {Q}}$
-Cartier and
![]() $K_{\mathcal {X}}|_X=K_X$
. Suppose now that X is
$K_{\mathcal {X}}|_X=K_X$
. Suppose now that X is
![]() ${\mathbb {Q}}$
-factorial, and let
${\mathbb {Q}}$
-factorial, and let
![]() $\mathcal D$
be a
$\mathcal D$
be a
![]() ${\mathbb {Q}}$
-divisor on
${\mathbb {Q}}$
-divisor on
![]() ${\mathcal {X}}$
. We need to show that
${\mathcal {X}}$
. We need to show that
![]() $\mathcal D$
is
$\mathcal D$
is
![]() ${\mathbb {Q}}$
-Cartier. Since
${\mathbb {Q}}$
-Cartier. Since
![]() $X \subseteq {\mathcal {X}}$
is Cartier and irreducible, we may assume that the support of
$X \subseteq {\mathcal {X}}$
is Cartier and irreducible, we may assume that the support of
![]() $\mathcal D$
does not contain X. Since X is
$\mathcal D$
does not contain X. Since X is
![]() ${\mathbb {Q}}$
-factorial, we have that
${\mathbb {Q}}$
-factorial, we have that
![]() $\mathcal D|_X$
is
$\mathcal D|_X$
is
![]() ${\mathbb {Q}}$
-Cartier, and so by the above paragraph,
${\mathbb {Q}}$
-Cartier, and so by the above paragraph,
![]() $\mathcal D$
is
$\mathcal D$
is
![]() ${\mathbb {Q}}$
-Cartier as well, concluding the proof of the
${\mathbb {Q}}$
-Cartier as well, concluding the proof of the
![]() ${\mathbb {Q}}$
-factoriality of
${\mathbb {Q}}$
-factoriality of
![]() ${\mathcal {X}}$
.
${\mathcal {X}}$
.
Now, we move to (2) assuming the existence of appropriate resolutions. Note that as X is terminal, it is klt, and so
![]() $({\mathcal {X}},X)$
is plt by Corollary 4.9.
$({\mathcal {X}},X)$
is plt by Corollary 4.9.
Next, we woud like to construct a terminalisation of
![]() $\mathcal {X}$
. Alas, due to the limitations of our MMP results (Theorem 4.1 and Theorem 5.1), we can only construct a partial terminalisation, but fortunately that will be enough for our application.
$\mathcal {X}$
. Alas, due to the limitations of our MMP results (Theorem 4.1 and Theorem 5.1), we can only construct a partial terminalisation, but fortunately that will be enough for our application.
Claim 6.8. There exists a projective birational morphism
![]() $\phi \colon {\mathcal {Y}} \to {\mathcal {X}}$
such that
$\phi \colon {\mathcal {Y}} \to {\mathcal {X}}$
such that
-
(1)
 ${\mathcal {Y}}$
is terminal,
${\mathcal {Y}}$
is terminal, -
(2) The central fibre Y of
 ${\mathcal {Y}}$
over
${\mathcal {Y}}$
over
 $\operatorname {\mathrm {Spec}} R$
is integral,
$\operatorname {\mathrm {Spec}} R$
is integral, -
(3)
 $({\mathcal {Y}}, Y)$
is plt and
$({\mathcal {Y}}, Y)$
is plt and -
(4)
 $\Delta _{{\mathcal {Y}}} \geq 0$
, where
$\Delta _{{\mathcal {Y}}} \geq 0$
, where
 $K_{{\mathcal {Y}}} + \Delta _{{\mathcal {Y}}} = \phi ^*K_{{\mathcal {X}}}$
.
$K_{{\mathcal {Y}}} + \Delta _{{\mathcal {Y}}} = \phi ^*K_{{\mathcal {X}}}$
.
Proof. Let
![]() $\pi \colon {\mathcal {Z}} \to {\mathcal {X}}$
be a log resolution of
$\pi \colon {\mathcal {Z}} \to {\mathcal {X}}$
be a log resolution of
![]() $({\mathcal {X}},X)$
, and set Z to be the reduced central fibre of
$({\mathcal {X}},X)$
, and set Z to be the reduced central fibre of
![]() ${\mathcal {Z}}$
over
${\mathcal {Z}}$
over
![]() $\operatorname {\mathrm {Spec}} R$
. Let
$\operatorname {\mathrm {Spec}} R$
. Let
![]() $h\colon {\mathcal {Z}} \dashrightarrow {\mathcal {Y}}$
be the output of a
$h\colon {\mathcal {Z}} \dashrightarrow {\mathcal {Y}}$
be the output of a
![]() $(K_{{\mathcal {Z}}} + Z)$
-MMP over
$(K_{{\mathcal {Z}}} + Z)$
-MMP over
![]() ${\mathcal {X}}$
. We can run this MMP by Theorem 5.1 (note that we can run it over
${\mathcal {X}}$
. We can run this MMP by Theorem 5.1 (note that we can run it over
![]() ${\mathcal {X}}$
as we can always add to the boundary a pullback of a sufficiently ample divisor from
${\mathcal {X}}$
as we can always add to the boundary a pullback of a sufficiently ample divisor from
![]() ${\mathcal {X}}$
and by boundedness of extremal rays, such an MMP would only contract rays over
${\mathcal {X}}$
and by boundedness of extremal rays, such an MMP would only contract rays over
![]() ${\mathcal {X}}$
). Then
${\mathcal {X}}$
). Then
![]() $K_{{\mathcal {Y}}} + h_*Z$
is nef over
$K_{{\mathcal {Y}}} + h_*Z$
is nef over
![]() ${\mathcal {X}}$
.
${\mathcal {X}}$
.
Denote by
![]() $\phi $
the induced map
$\phi $
the induced map
![]() ${\mathcal {Y}} \to {\mathcal {X}}$
, and write
${\mathcal {Y}} \to {\mathcal {X}}$
, and write
In particular,
![]() $K_{{\mathcal {Y}}} + \phi ^*X+ \Delta _{{\mathcal {Y}}} = \phi ^*(K_{{\mathcal {X}}}+X)$
, and since
$K_{{\mathcal {Y}}} + \phi ^*X+ \Delta _{{\mathcal {Y}}} = \phi ^*(K_{{\mathcal {X}}}+X)$
, and since
![]() $({\mathcal {X}},X)$
is plt, we get that all the coefficients of
$({\mathcal {X}},X)$
is plt, we get that all the coefficients of
![]() $\phi ^*X+ \Delta _{{\mathcal {Y}}}$
, except for
$\phi ^*X+ \Delta _{{\mathcal {Y}}}$
, except for
![]() $\phi ^{-1}_*X$
are smaller than
$\phi ^{-1}_*X$
are smaller than
![]() $1$
. Then
$1$
. Then
is nef and exceptional and so antieffective. As the coefficients of
![]() $\phi ^*X+ \Delta _{{\mathcal {Y}}}$
, except for
$\phi ^*X+ \Delta _{{\mathcal {Y}}}$
, except for
![]() $\phi ^{-1}_*X$
, are smaller than
$\phi ^{-1}_*X$
, are smaller than
![]() $1$
, we get that
$1$
, we get that
![]() $h_*Z = \phi ^{-1}_*X$
. Thus, the central fibre Y of
$h_*Z = \phi ^{-1}_*X$
. Thus, the central fibre Y of
![]() ${\mathcal {Y}}$
is irreducible. Since the central fibres of
${\mathcal {Y}}$
is irreducible. Since the central fibres of
![]() ${\mathcal {Y}}$
and
${\mathcal {Y}}$
and
![]() ${\mathcal {X}}$
agree generically, Y must also be reduced, and so
${\mathcal {X}}$
agree generically, Y must also be reduced, and so
![]() $h_*Z = Y$
. This proves (2). Since Y is irreducible and
$h_*Z = Y$
. This proves (2). Since Y is irreducible and
![]() $({\mathcal {Y}},Y)$
is dlt as an output of a dlt MMP,
$({\mathcal {Y}},Y)$
is dlt as an output of a dlt MMP,
![]() $({\mathcal {Y}},Y)$
is plt proving (3).
$({\mathcal {Y}},Y)$
is plt proving (3).
Since Y is the central fibre,
![]() $K_{{\mathcal {Y}}} \sim K_{{\mathcal {Y}}} + Y$
is nef, and so by negativity lemma and (2), we have that
$K_{{\mathcal {Y}}} \sim K_{{\mathcal {Y}}} + Y$
is nef, and so by negativity lemma and (2), we have that
![]() $\Delta _{{\mathcal {Y}}} \geq 0$
concluding the proof of (4).
$\Delta _{{\mathcal {Y}}} \geq 0$
concluding the proof of (4).
Finally, to show (1) we observe that
![]() ${\mathcal {Y}}_{{\mathbb {Q}}}$
is terminal, as
${\mathcal {Y}}_{{\mathbb {Q}}}$
is terminal, as
![]() ${\mathcal {Z}}_{{\mathbb {Q}}}$
is smooth and we were running a
${\mathcal {Z}}_{{\mathbb {Q}}}$
is smooth and we were running a
![]() $(K_{{\mathcal {Z}}} + Z)$
-MMP which, over
$(K_{{\mathcal {Z}}} + Z)$
-MMP which, over
![]() ${\mathbb {Q}}$
, is a
${\mathbb {Q}}$
, is a
![]() $K_{{\mathcal {Z}}_{{\mathbb {Q}}}}$
-MMP. Thus, to show that
$K_{{\mathcal {Z}}_{{\mathbb {Q}}}}$
-MMP. Thus, to show that
![]() ${\mathcal {Y}}$
is terminal, we need to show that the log discrepancy with respect to
${\mathcal {Y}}$
is terminal, we need to show that the log discrepancy with respect to
![]() $({\mathcal {X}}, 0)$
of every divisor E lying over
$({\mathcal {X}}, 0)$
of every divisor E lying over
![]() ${\mathfrak {m}}$
, is greater than
${\mathfrak {m}}$
, is greater than
![]() $one$
. This is clear, because such divisors have positive log discrepancy with respect to the plt pair
$one$
. This is clear, because such divisors have positive log discrepancy with respect to the plt pair
![]() $({\mathcal {X}}, X)$
and X is Cartier.
$({\mathcal {X}}, X)$
and X is Cartier.
Now, assume that X is terminal, but suppose by contradiction that
![]() ${\mathcal {X}}$
is not terminal, or equivalently (by property (4) in the above claim) that
${\mathcal {X}}$
is not terminal, or equivalently (by property (4) in the above claim) that
![]() $\phi \colon {\mathcal {Y}} \to {\mathcal {X}}$
is not an isomorphism. Let
$\phi \colon {\mathcal {Y}} \to {\mathcal {X}}$
is not an isomorphism. Let
![]() $\mathcal {E}$
be a
$\mathcal {E}$
be a
![]() $\phi $
-exceptional prime divisor on
$\phi $
-exceptional prime divisor on
![]() ${\mathcal {Y}}$
(which exists as
${\mathcal {Y}}$
(which exists as
![]() ${\mathcal {X}}$
is
${\mathcal {X}}$
is
![]() ${\mathbb {Q}}$
-factorial). Since Y is the reduced special fibre and
${\mathbb {Q}}$
-factorial). Since Y is the reduced special fibre and
![]() $\operatorname {\mathrm {Spec}} R$
admits only one closed point, we have that
$\operatorname {\mathrm {Spec}} R$
admits only one closed point, we have that
![]() $E = \mathcal {E} \cap Y$
is nonempty.
$E = \mathcal {E} \cap Y$
is nonempty.
Since the central fibre Y is integral (and so must be equal to
![]() $\phi ^{-1}_*X$
), our divisor
$\phi ^{-1}_*X$
), our divisor
![]() $\mathcal {E}$
must be dominant over
$\mathcal {E}$
must be dominant over
![]() $\operatorname {\mathrm {Spec}} R$
. In particular, the irreducible subscheme
$\operatorname {\mathrm {Spec}} R$
. In particular, the irreducible subscheme
![]() $\phi (\mathcal {E})$
is also dominant over
$\phi (\mathcal {E})$
is also dominant over
![]() $\operatorname {\mathrm {Spec}} R$
and of codimension at least two in
$\operatorname {\mathrm {Spec}} R$
and of codimension at least two in
![]() ${\mathcal {X}}$
. Hence,
${\mathcal {X}}$
. Hence,
![]() $\phi |_Y(E) \subseteq X$
is of codimension at least two in X, and so
$\phi |_Y(E) \subseteq X$
is of codimension at least two in X, and so
![]() $E \subseteq Y$
is exceptional over X. This contradicts the fact that X is terminal as
$E \subseteq Y$
is exceptional over X. This contradicts the fact that X is terminal as
 $$ \begin{align*} K_Y &= K_{{\mathcal{Y}}}|_Y = (\phi^*K_{{\mathcal{X}}} + G)|_Y = (\phi|_Y)^{-1}K_X + G|_Y \\ K_Y &= (\phi|_Y)^*K_X + F, \end{align*} $$
$$ \begin{align*} K_Y &= K_{{\mathcal{Y}}}|_Y = (\phi^*K_{{\mathcal{X}}} + G)|_Y = (\phi|_Y)^{-1}K_X + G|_Y \\ K_Y &= (\phi|_Y)^*K_X + F, \end{align*} $$
where
![]() $G := -\Delta _{{\mathcal {Y}}} \leq 0$
by (4) in the above claim, and
$G := -\Delta _{{\mathcal {Y}}} \leq 0$
by (4) in the above claim, and
![]() $F \geq 0$
with
$F \geq 0$
with
![]() ${\mathrm {Supp}}\, F = \mathrm {Exc}(\phi |_Y)$
(in particular, it contains the exceptional divisor E with positive coefficient) as X is terminal.
${\mathrm {Supp}}\, F = \mathrm {Exc}(\phi |_Y)$
(in particular, it contains the exceptional divisor E with positive coefficient) as X is terminal.
Proof of Theorem 6.1
By Theorem 6.7,
![]() $\mathcal X$
is Cohen Macaulay,
$\mathcal X$
is Cohen Macaulay,
![]() ${\mathbb {Q}}$
-factorial, terminal and
${\mathbb {Q}}$
-factorial, terminal and
![]() $({\mathcal {X}},X)$
is plt. Let
$({\mathcal {X}},X)$
is plt. Let
![]() $\eta $
be the generic point of
$\eta $
be the generic point of
![]() $S=\operatorname {\mathrm {Spec}} R$
, then we claim that
$S=\operatorname {\mathrm {Spec}} R$
, then we claim that
![]() $K_{X_{\eta }}$
is pseudo-effective.
$K_{X_{\eta }}$
is pseudo-effective.
To see this, let
![]() $\mathcal {A}$
be an ample Cartier divisor on
$\mathcal {A}$
be an ample Cartier divisor on
![]() $\mathcal {X}$
, and let
$\mathcal {X}$
, and let
![]() $t\in \mathbb Q$
be the pseudo-effective threshold (or
$t\in \mathbb Q$
be the pseudo-effective threshold (or
![]() $0$
, if
$0$
, if
![]() $K_{{\mathcal {X}}}$
is already pseudo-effective) so that
$K_{{\mathcal {X}}}$
is already pseudo-effective) so that
![]() $0\leq \kappa (K_{{\mathcal {X}}_{\eta }}+t\mathcal {A}_{\eta })$
(the fact that t is rational follows by running a characteristic 0
$0\leq \kappa (K_{{\mathcal {X}}_{\eta }}+t\mathcal {A}_{\eta })$
(the fact that t is rational follows by running a characteristic 0
![]() $K_{X_{\eta }}$
-MMP with scaling of
$K_{X_{\eta }}$
-MMP with scaling of
![]() $\mathcal {A}_{\eta }$
and the cone theorem applied to a resulting Mori fibre space if
$\mathcal {A}_{\eta }$
and the cone theorem applied to a resulting Mori fibre space if
![]() $t>0$
). We wish to show that
$t>0$
). We wish to show that
![]() $t=0$
. We may assume that
$t=0$
. We may assume that
![]() $({\mathcal {X}},X+t\mathcal A)$
is plt and
$({\mathcal {X}},X+t\mathcal A)$
is plt and
![]() $(X,tA)$
is terminal, where
$(X,tA)$
is terminal, where
![]() $A=\mathcal A |_X$
. By Theorem 5.1, we may run the
$A=\mathcal A |_X$
. By Theorem 5.1, we may run the
![]() $K_{{\mathcal {X}}}+X+t\mathcal {A}$
MMP with scaling over S which terminates with a minimal model
$K_{{\mathcal {X}}}+X+t\mathcal {A}$
MMP with scaling over S which terminates with a minimal model
. Let
![]() $X'$
be the special fibre of
$X'$
be the special fibre of
![]() ${\mathcal {X}}'$
over
${\mathcal {X}}'$
over
![]() $\operatorname {\mathrm {Spec}} R$
; equivalently
$\operatorname {\mathrm {Spec}} R$
; equivalently
![]() $X' = \phi _*X$
. By definition,
$X' = \phi _*X$
. By definition,
![]() $X'$
is Cartier and
$X'$
is Cartier and
![]() $K_{{\mathcal {X}}'}+X'+t\mathcal A'$
is nef over S. As
$K_{{\mathcal {X}}'}+X'+t\mathcal A'$
is nef over S. As
![]() $({\mathcal {X}} ',X'+t\mathcal A')$
is plt (and so is
$({\mathcal {X}} ',X'+t\mathcal A')$
is plt (and so is
![]() $({\mathcal {X}}',X')$
in view of
$({\mathcal {X}}',X')$
in view of
![]() ${\mathcal {X}}'$
being
${\mathcal {X}}'$
being
![]() ${\mathbb {Q}}$
-factorial), Lemma 6.3 shows that
${\mathbb {Q}}$
-factorial), Lemma 6.3 shows that
![]() $X'$
is normal. Note that as X is terminal,
$X'$
is normal. Note that as X is terminal,
does not extract any divisors. Indeed, let
![]() $\mathcal A'=\phi _* \mathcal A$
and
$\mathcal A'=\phi _* \mathcal A$
and
![]() $A'=\mathcal A'|_{X'}$
, then every divisor on
$A'=\mathcal A'|_{X'}$
, then every divisor on
![]() $X'$
, say
$X'$
, say
![]() $E \subseteq X'$
, has log discrepancy
$E \subseteq X'$
, has log discrepancy
![]() $\leq 1$
with respect to
$\leq 1$
with respect to
![]() $(X',tA')$
, and so log discrepancy
$(X',tA')$
, and so log discrepancy
![]() $\leq 1$
with respect to
$\leq 1$
with respect to
![]() $(X,tA)$
(running a
$(X,tA)$
(running a
![]() $(K_{{\mathcal {X}}}+X+t\mathcal A)$
-MMP can only increase the discrepancies of
$(K_{{\mathcal {X}}}+X+t\mathcal A)$
-MMP can only increase the discrepancies of
![]() $({\mathcal {X}},X+t\mathcal A)$
, and hence cannot decrease those of
$({\mathcal {X}},X+t\mathcal A)$
, and hence cannot decrease those of
![]() $(X,tA)$
by adjunction). Thus, it is impossible for E to be extracted because then E is not a divisor on X, and so by definition of terminality has log discrepancy
$(X,tA)$
by adjunction). Thus, it is impossible for E to be extracted because then E is not a divisor on X, and so by definition of terminality has log discrepancy
![]() $>1$
.
$>1$
.
Note that
![]() $K_{X'}+tA'$
and
$K_{X'}+tA'$
and
![]() $K_{{\mathcal {X}}^{\prime }_{\eta } }+t\mathcal A^{\prime }_{\eta }$
are nef and if
$K_{{\mathcal {X}}^{\prime }_{\eta } }+t\mathcal A^{\prime }_{\eta }$
are nef and if
![]() $t>0$
, then
$t>0$
, then
![]() $K_{X' }+t A'$
is big. It then follows that
$K_{X' }+t A'$
is big. It then follows that
so that
![]() $K_{{\mathcal {X}}^{\prime }_{\eta } }+t\mathcal A^{\prime }_{\eta }$
is also big, a contradiction to t being positive. Therefore, we may assume that
$K_{{\mathcal {X}}^{\prime }_{\eta } }+t\mathcal A^{\prime }_{\eta }$
is also big, a contradiction to t being positive. Therefore, we may assume that
![]() $t= 0$
and hence
$t= 0$
and hence
![]() $K_{{\mathcal {X}}'}+X'$
is nef over S. Since
$K_{{\mathcal {X}}'}+X'$
is nef over S. Since
![]() $ K_{X'}=(K_{{\mathcal {X}}'}+X')|_{X'}$
is
$ K_{X'}=(K_{{\mathcal {X}}'}+X')|_{X'}$
is
![]() ${\mathbb {Q}}$
-Cartier and
${\mathbb {Q}}$
-Cartier and
![]() $({\mathcal {X}} ',X')$
is plt, we get that
$({\mathcal {X}} ',X')$
is plt, we get that
![]() $X'$
is klt and
$X'$
is klt and
![]() $K_{X'}$
is nef. It follows that
$K_{X'}$
is nef. It follows that
![]() is a (possibly non-
is a (possibly non-
![]() ${\mathbb {Q}}$
-factorial) minimal model concluding the proof of (1).
${\mathbb {Q}}$
-factorial) minimal model concluding the proof of (1).
We move on to the proof of (2a). Suppose now that
![]() $N^1({\mathcal {X}}/S)\to N^1(X)$
is surjective. In particular,
$N^1({\mathcal {X}}/S)\to N^1(X)$
is surjective. In particular,
![]() $\overline {\mathrm {NE}}(\mathcal {X}/S)=\overline {\mathrm {NE}}(X)$
; indeed this is true because only curves which are projective over S (and hence lie on the special fibre X) are used in the definition of
$\overline {\mathrm {NE}}(\mathcal {X}/S)=\overline {\mathrm {NE}}(X)$
; indeed this is true because only curves which are projective over S (and hence lie on the special fibre X) are used in the definition of
![]() $\overline {\mathrm {NE}}$
(cf. [Reference TanakaTan18] or [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20]) and numerical equivalence relations on X and
$\overline {\mathrm {NE}}$
(cf. [Reference TanakaTan18] or [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20]) and numerical equivalence relations on X and
![]() ${\mathcal {X}}$
are the same in view of
${\mathcal {X}}$
are the same in view of
![]() $N^1({\mathcal {X}}/ S)\to N^1(X)$
being surjective.
$N^1({\mathcal {X}}/ S)\to N^1(X)$
being surjective.
Our goal is to show that any sequence of
![]() $K_X$
-MMP steps
$K_X$
-MMP steps
(where
![]() $X_l$
is a minimal model of X) lifts to a sequence of
$X_l$
is a minimal model of X) lifts to a sequence of
![]() $K_{{\mathcal {X}}}$
-MMP steps
$K_{{\mathcal {X}}}$
-MMP steps
Consider the first step
![]() $h \colon X \dashrightarrow X_1$
. Let A be an ample
$h \colon X \dashrightarrow X_1$
. Let A be an ample
![]() ${\mathbb {Q}}$
-divisor on X such that
${\mathbb {Q}}$
-divisor on X such that
![]() $(K_X+A)^{\perp } \subseteq \overline {\mathrm {NE}}(X)$
is equal to the extremal ray
$(K_X+A)^{\perp } \subseteq \overline {\mathrm {NE}}(X)$
is equal to the extremal ray
![]() $\Sigma $
defining h. Since
$\Sigma $
defining h. Since
![]() $N^1({\mathcal {X}}/S)\to N^1(X)$
is surjective, there exists an ample
$N^1({\mathcal {X}}/S)\to N^1(X)$
is surjective, there exists an ample
![]() ${\mathbb {Q}}$
-divisor
${\mathbb {Q}}$
-divisor
![]() $\mathcal {A}$
on
$\mathcal {A}$
on
![]() ${\mathcal {X}}$
such that
${\mathcal {X}}$
such that
![]() $\mathcal {A}|_X \equiv A$
. Then
$\mathcal {A}|_X \equiv A$
. Then
![]() $(K_{{\mathcal {X}}}+X+\mathcal {A})^{\perp } = \Sigma \subseteq \overline {\mathrm {NE}}(\mathcal {X}/S)$
.
$(K_{{\mathcal {X}}}+X+\mathcal {A})^{\perp } = \Sigma \subseteq \overline {\mathrm {NE}}(\mathcal {X}/S)$
.
We set
![]() $\phi \colon \mathcal X \dashrightarrow \mathcal X_1$
to be the step of a
$\phi \colon \mathcal X \dashrightarrow \mathcal X_1$
to be the step of a
![]() $(K_{{\mathcal {X}}}+X)$
-MMP (equivalently,
$(K_{{\mathcal {X}}}+X)$
-MMP (equivalently,
![]() $K_{{\mathcal {X}}}$
-MMP) corresponding to
$K_{{\mathcal {X}}}$
-MMP) corresponding to
![]() $\Sigma $
. In particular,
$\Sigma $
. In particular,
![]() $({\mathcal {X}}_1, ({\mathcal {X}}_1)_{{\mathfrak {m}}})$
is plt, where
$({\mathcal {X}}_1, ({\mathcal {X}}_1)_{{\mathfrak {m}}})$
is plt, where
![]() $({\mathcal {X}}_1)_{{\mathfrak {m}}}$
is the special fibre, hence
$({\mathcal {X}}_1)_{{\mathfrak {m}}}$
is the special fibre, hence
![]() $({\mathcal {X}}_1)_{{\mathfrak {m}}}$
is normal by Lemma 6.3. As explained before, the terminality of X ensures that
$({\mathcal {X}}_1)_{{\mathfrak {m}}}$
is normal by Lemma 6.3. As explained before, the terminality of X ensures that
![]() $\phi |_X \colon X \dashrightarrow ({\mathcal {X}}_1)_{{\mathfrak {m}}}$
does not extract any divisors.
$\phi |_X \colon X \dashrightarrow ({\mathcal {X}}_1)_{{\mathfrak {m}}}$
does not extract any divisors.
We claim that
![]() $\phi |_X \colon X \dashrightarrow ({\mathcal {X}}_1)_{{\mathfrak {m}}}$
and
$\phi |_X \colon X \dashrightarrow ({\mathcal {X}}_1)_{{\mathfrak {m}}}$
and
![]() $h \colon X \dashrightarrow X_1$
coincide. To this end, let
$h \colon X \dashrightarrow X_1$
coincide. To this end, let
![]() $f \colon X \to Z$
be the contraction of
$f \colon X \to Z$
be the contraction of
![]() $\Sigma \subseteq \overline {\mathrm {NE}}(X)$
induced by
$\Sigma \subseteq \overline {\mathrm {NE}}(X)$
induced by
![]() $K_{X}+A$
, and let
$K_{X}+A$
, and let
![]() $\psi \colon {\mathcal {X}} \to {\mathcal {Z}}$
be the contraction of
$\psi \colon {\mathcal {X}} \to {\mathcal {Z}}$
be the contraction of
![]() $\Sigma \subseteq \overline {\mathrm {NE}}(\mathcal {X}/S)$
induced by
$\Sigma \subseteq \overline {\mathrm {NE}}(\mathcal {X}/S)$
induced by
![]() $K_{{\mathcal {X}}}+X+\mathcal {A}$
. Note that
$K_{{\mathcal {X}}}+X+\mathcal {A}$
. Note that
![]() $\psi |_X \colon X \to {\mathcal {Z}}_{{\mathfrak {m}}}$
contracts exactly
$\psi |_X \colon X \to {\mathcal {Z}}_{{\mathfrak {m}}}$
contracts exactly
![]() $\Sigma $
and no other numerical class of a curve; hence, we have a factorisation
$\Sigma $
and no other numerical class of a curve; hence, we have a factorisation
and Z is the normalisation of
![]() ${\mathcal {Z}}_{{\mathfrak {m}}}$
.
${\mathcal {Z}}_{{\mathfrak {m}}}$
.
Before proceeding with the proof of the claim, we will show that
![]() ${\mathcal {Z}}_{{\mathfrak {m}}} \simeq Z$
and
${\mathcal {Z}}_{{\mathfrak {m}}} \simeq Z$
and
![]() $\psi |_X = f$
. To this end, we may assume that
$\psi |_X = f$
. To this end, we may assume that
![]() $(X,A)$
is klt (cf. [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Lemma 2.29] or [Reference BirkarBir16, Lemma 9.2]; this uses the existence of a resolution with an ample exceptional divisor). Hence,
$(X,A)$
is klt (cf. [Reference Bhatt, Ma, Patakfalvi, Schwede, Tucker, Waldron and WitaszekBMPSTWW20, Lemma 2.29] or [Reference BirkarBir16, Lemma 9.2]; this uses the existence of a resolution with an ample exceptional divisor). Hence,
![]() $(Z, f_*A)$
is also klt, and so both X and Z have rational singularities by [Reference Arvidsson, Bernasconi and JustinABL22, Corollary 1.3]. Therefore,
$(Z, f_*A)$
is also klt, and so both X and Z have rational singularities by [Reference Arvidsson, Bernasconi and JustinABL22, Corollary 1.3]. Therefore,
![]() $R^1f_*{\mathcal {O}}_X=0$
(equivalently,
$R^1f_*{\mathcal {O}}_X=0$
(equivalently,
![]() $R^1(\psi |_X)_*{\mathcal {O}}_{X}=0$
), which in turn implies that
$R^1(\psi |_X)_*{\mathcal {O}}_{X}=0$
), which in turn implies that
![]() $R^1\psi _*{\mathcal {O}}_{{\mathcal {X}}}=0$
(specifically, we apply the semicontinuity theorem, [Reference HartshorneHar77, Theorem III.2.18], to the flat morphism
$R^1\psi _*{\mathcal {O}}_{{\mathcal {X}}}=0$
(specifically, we apply the semicontinuity theorem, [Reference HartshorneHar77, Theorem III.2.18], to the flat morphism
![]() $X \to \operatorname {\mathrm {Spec}} R$
and the sheaf
$X \to \operatorname {\mathrm {Spec}} R$
and the sheaf
![]() $\psi ^*\mathcal {L}^m$
for an ample line bundle
$\psi ^*\mathcal {L}^m$
for an ample line bundle
![]() $\mathcal {L}$
on
$\mathcal {L}$
on
![]() ${\mathcal {Z}}$
and
${\mathcal {Z}}$
and
![]() $m\gg 0$
). Hence, by the projection formula
$m\gg 0$
). Hence, by the projection formula
for m divisible enough, and so
is surjective. In particular,
![]() ${\mathcal {Z}}_{{\mathfrak {m}}} \simeq Z$
and
${\mathcal {Z}}_{{\mathfrak {m}}} \simeq Z$
and
![]() $\psi |_X = f$
.
$\psi |_X = f$
.
Now, we consider the following cases:
-
(1)
 is a divisorial contraction (that is,
is a divisorial contraction (that is,
 $\psi =\phi $
): Then
$\psi =\phi $
): Then
 $\psi |_X=f$
is also divisorial by semicontinuity of fibre dimension [Reference GrothendieckGro67, Corollaire (13.1.5)]; in particular, the first step
$\psi |_X=f$
is also divisorial by semicontinuity of fibre dimension [Reference GrothendieckGro67, Corollaire (13.1.5)]; in particular, the first step
 $h \colon X \dashrightarrow X_1$
of the
$h \colon X \dashrightarrow X_1$
of the
 $K_X$
-MMP is the contraction
$K_X$
-MMP is the contraction
 $f \colon X \to Z$
; and hence, it lifts to
$f \colon X \to Z$
; and hence, it lifts to
 $\phi =\psi \colon {\mathcal {X}} \to {\mathcal {Z}}$
.
$\phi =\psi \colon {\mathcal {X}} \to {\mathcal {Z}}$
. -
(2)
 is a flip over the flipping contraction
is a flip over the flipping contraction
 $\psi \colon {\mathcal {X}} \to {\mathcal {Z}}$
(in particular,
$\psi \colon {\mathcal {X}} \to {\mathcal {Z}}$
(in particular,
 ${\mathcal {Z}}$
is not
${\mathcal {Z}}$
is not
 ${\mathbb {Q}}$
-Gorenstein) and
${\mathbb {Q}}$
-Gorenstein) and-
(a)
 $f \colon X \to Z$
is divisorial: Then Z is
$f \colon X \to Z$
is divisorial: Then Z is
 ${\mathbb {Q}}$
-Gorenstein, Cohen–Macaulay (as it has rational singularities), and
${\mathbb {Q}}$
-Gorenstein, Cohen–Macaulay (as it has rational singularities), and
 $\mathrm {codim}\, \mathrm {Sing}(Z) \geq 3$
(as X is terminal). Since
$\mathrm {codim}\, \mathrm {Sing}(Z) \geq 3$
(as X is terminal). Since
 $Z \simeq {\mathcal {Z}}_{{\mathfrak {m}}}$
, we get that
$Z \simeq {\mathcal {Z}}_{{\mathfrak {m}}}$
, we get that
 ${\mathcal {Z}}$
is
${\mathcal {Z}}$
is
 ${\mathbb {Q}}$
-Gorenstein by Lemma 6.6 (cf. the proof of Corollary 6.7) which is impossible. This shows that f can never be divisorial when
${\mathbb {Q}}$
-Gorenstein by Lemma 6.6 (cf. the proof of Corollary 6.7) which is impossible. This shows that f can never be divisorial when
 $\phi $
is a flip.
$\phi $
is a flip. -
(b)
 $f \colon X \to Z$
is small: Then,
$f \colon X \to Z$
is small: Then,
 $({\mathcal {X}}_1)_{{\mathfrak {m}}}$
is normal (cf. Lemma 6.3), and since
$({\mathcal {X}}_1)_{{\mathfrak {m}}}$
is normal (cf. Lemma 6.3), and since
 $\phi |_X \colon X \dashrightarrow ({\mathcal {X}}_1)_{{\mathfrak {m}}}$
does not extract any divisors, the induced map
$\phi |_X \colon X \dashrightarrow ({\mathcal {X}}_1)_{{\mathfrak {m}}}$
does not extract any divisors, the induced map
 $({\mathcal {X}}_1)_{{\mathfrak {m}}} \to Z$
is also small. As
$({\mathcal {X}}_1)_{{\mathfrak {m}}} \to Z$
is also small. As
 $({\mathcal {X}}_1)_{{\mathfrak {m}}}$
is
$({\mathcal {X}}_1)_{{\mathfrak {m}}}$
is
 ${\mathbb {Q}}$
-Gorenstein and
${\mathbb {Q}}$
-Gorenstein and
 $K_{({\mathcal {X}}_1)_{{\mathfrak {m}}}} = K_{{\mathcal {X}}_1}|_{({\mathcal {X}}_1)_{{\mathfrak {m}}}}$
is ample over Z, we have that
$K_{({\mathcal {X}}_1)_{{\mathfrak {m}}}} = K_{{\mathcal {X}}_1}|_{({\mathcal {X}}_1)_{{\mathfrak {m}}}}$
is ample over Z, we have that
 $({\mathcal {X}}_1)_{{\mathfrak {m}}}$
is the canonical model of X over Z. Hence it is a flip,
$({\mathcal {X}}_1)_{{\mathfrak {m}}}$
is the canonical model of X over Z. Hence it is a flip,
 $({\mathcal {X}}_1)_{{\mathfrak {m}}} \simeq X_1$
and
$({\mathcal {X}}_1)_{{\mathfrak {m}}} \simeq X_1$
and
 $\phi |_X=h$
.
$\phi |_X=h$
.
-
Having lifted
![]() $h \colon X \dashrightarrow X_1$
, we would like to replace X and
$h \colon X \dashrightarrow X_1$
, we would like to replace X and
![]() ${\mathcal {X}}$
by
${\mathcal {X}}$
by
![]() $X_1$
and
$X_1$
and
![]() ${\mathcal {X}}_1$
, respectively, and repeat the above procedure. To be able to do this, we deduce the surjectivity of
${\mathcal {X}}_1$
, respectively, and repeat the above procedure. To be able to do this, we deduce the surjectivity of
![]() $N^1(\mathcal {X}_1/S) \to N^1(X_1)$
from that of
$N^1(\mathcal {X}_1/S) \to N^1(X_1)$
from that of
![]() $N^1(\mathcal {X}/S) \to N^1(X)$
. Pick a line bundle L on
$N^1(\mathcal {X}/S) \to N^1(X)$
. Pick a line bundle L on
![]() $X_1$
. We need to show that
$X_1$
. We need to show that
![]() $L^m \equiv \mathcal {L}|_{X_1}$
for some line bundle
$L^m \equiv \mathcal {L}|_{X_1}$
for some line bundle
![]() $\mathcal L$
on
$\mathcal L$
on
![]() ${\mathcal {X}}_1$
and
${\mathcal {X}}_1$
and
![]() $m \in \mathbb {N}$
. This is a standard consequence of the base point free theorem as explained by the following case by case analysis:
$m \in \mathbb {N}$
. This is a standard consequence of the base point free theorem as explained by the following case by case analysis:
-
(1)
 $\phi =\psi \colon \mathcal {X} \to \mathcal {Z}$
is a divisorial contraction (in particular,
$\phi =\psi \colon \mathcal {X} \to \mathcal {Z}$
is a divisorial contraction (in particular,
 $Z=X_1$
): Then up to replacing L by a multiple, we may pick
$Z=X_1$
): Then up to replacing L by a multiple, we may pick
 $\mathcal {L}'$
on
$\mathcal {L}'$
on
 ${\mathcal {X}}$
such that
${\mathcal {X}}$
such that
 $f^*L \equiv \mathcal {L}'|_X $
. Since
$f^*L \equiv \mathcal {L}'|_X $
. Since
 $\mathcal {L}'$
is numerically trivial over
$\mathcal {L}'$
is numerically trivial over
 ${\mathcal {Z}}$
, it descends, up to some multiple, to a line bundle
${\mathcal {Z}}$
, it descends, up to some multiple, to a line bundle
 $\mathcal {L}$
on
$\mathcal {L}$
on
 ${\mathcal {Z}}$
by the base point free theorem (cf. Proposition 5.4), and
${\mathcal {Z}}$
by the base point free theorem (cf. Proposition 5.4), and
 $\mathcal {L}|_Z \equiv L$
by construction.
$\mathcal {L}|_Z \equiv L$
by construction. -
(2)
 $\phi \colon {\mathcal {X}} \dashrightarrow {\mathcal {X}}_1$
is small: Then since
$\phi \colon {\mathcal {X}} \dashrightarrow {\mathcal {X}}_1$
is small: Then since
 $K_{{\mathcal {X}}_1}|_{X_1} = K_{X_1}$
is ample over Z and
$K_{{\mathcal {X}}_1}|_{X_1} = K_{X_1}$
is ample over Z and
 $\rho (X_1/Z)=1$
, we can replace L by
$\rho (X_1/Z)=1$
, we can replace L by
 $L+aK_{X_1}$
for some
$L+aK_{X_1}$
for some
 $a \in {\mathbb {Q}}$
and assume that
$a \in {\mathbb {Q}}$
and assume that
 $L\equiv _Z 0$
. Then by the base point free theorem (cf. Proposition 5.4), up to some multiple, L descends to a line bundle
$L\equiv _Z 0$
. Then by the base point free theorem (cf. Proposition 5.4), up to some multiple, L descends to a line bundle
 $L_Z$
on
$L_Z$
on
 $Z = {\mathcal {Z}}_{{\mathfrak {m}}}$
. By the same argument as in (1), up to some multiple, there exists
$Z = {\mathcal {Z}}_{{\mathfrak {m}}}$
. By the same argument as in (1), up to some multiple, there exists
 $\mathcal {L}_{\mathcal Z}$
on
$\mathcal {L}_{\mathcal Z}$
on
 ${\mathcal {Z}}$
such that
${\mathcal {Z}}$
such that
 $\mathcal {L}_{\mathcal Z}|_Z \equiv L_Z$
. Then
$\mathcal {L}_{\mathcal Z}|_Z \equiv L_Z$
. Then
 $(\psi ^+)^*\mathcal {L}_{\mathcal Z}|_{X_1} \equiv L$
, where
$(\psi ^+)^*\mathcal {L}_{\mathcal Z}|_{X_1} \equiv L$
, where
 $\psi ^+\colon {\mathcal {X}}_1 \to {\mathcal {Z}}$
is the flipped contraction.
$\psi ^+\colon {\mathcal {X}}_1 \to {\mathcal {Z}}$
is the flipped contraction.
Thus, we can repeat the above procedure until we get a lift
![]() $\mathcal {X}_l$
of
$\mathcal {X}_l$
of
![]() $X_l$
. Since
$X_l$
. Since
![]() $K_{X_l}$
is nef, so is
$K_{X_l}$
is nef, so is
![]() $K_{\mathcal {X}_l}$
. Hence,
$K_{\mathcal {X}_l}$
. Hence,
![]() $\mathcal {X}_l$
is a minimal model of
$\mathcal {X}_l$
is a minimal model of
![]() ${\mathcal {X}}$
.
${\mathcal {X}}$
.
Next, we tackle (2b). By (2a), we can replace X by the output of a
![]() $K_X$
-MMP, and so assume that X is minimal. Let
$K_X$
-MMP, and so assume that X is minimal. Let
![]() $h \colon X \dashrightarrow Y$
be a small birational map to another
$h \colon X \dashrightarrow Y$
be a small birational map to another
![]() ${\mathbb {Q}}$
-factorial minimal model Y. It is well known (cf. [Reference KawamataKaw08]) that
${\mathbb {Q}}$
-factorial minimal model Y. It is well known (cf. [Reference KawamataKaw08]) that
![]() is a small birational map given by a finite sequence of flops. To see this, pick
is a small birational map given by a finite sequence of flops. To see this, pick
![]() $A_Y$
an ample Cartier divisor on Y and let A be its strict transform on X. Since
$A_Y$
an ample Cartier divisor on Y and let A be its strict transform on X. Since
![]() is small, A is
is small, A is
![]() ${\mathbb {Q}}$
-movable and big. Pick
${\mathbb {Q}}$
-movable and big. Pick
![]() $0\leq D\sim _{\mathbb {Q}} A$
. We may assume that
$0\leq D\sim _{\mathbb {Q}} A$
. We may assume that
![]() $(X,\epsilon D)$
is terminal. We claim that for
$(X,\epsilon D)$
is terminal. We claim that for
![]() $0<\epsilon \ll 1$
there is a finite sequence of
$0<\epsilon \ll 1$
there is a finite sequence of
![]() $(K_X+\epsilon D)$
-flips which are
$(K_X+\epsilon D)$
-flips which are
![]() $K_X$
-flops inducing a
$K_X$
-flops inducing a
![]() $(K_X+\epsilon D)$
-minimal model
$(K_X+\epsilon D)$
-minimal model
![]() . We proceed as follows. If
. We proceed as follows. If
![]() $K_X+tD$
is nef for some
$K_X+tD$
is nef for some
![]() $0<t< \epsilon /(6r+1)$
, we may replace
$0<t< \epsilon /(6r+1)$
, we may replace
![]() $\epsilon $
by t and we are done. If on the other hand
$\epsilon $
by t and we are done. If on the other hand
![]() $K_X+tD$
is not nef for any
$K_X+tD$
is not nef for any
![]() $0<t<\epsilon /(6r+1)$
, then let
$0<t<\epsilon /(6r+1)$
, then let
![]() $\Sigma $
be a negative extremal ray generated by a curve C. Note that
$\Sigma $
be a negative extremal ray generated by a curve C. Note that
![]() $\Sigma $
is also a
$\Sigma $
is also a
![]() $(K_X+\epsilon D)$
-negative extremal ray, and so by cf. [Reference Das and WaldronDW19b, Theorem 1.1], we may assume that there is an integer
$(K_X+\epsilon D)$
-negative extremal ray, and so by cf. [Reference Das and WaldronDW19b, Theorem 1.1], we may assume that there is an integer
![]() $d=d_{\Sigma }$
(depending only on
$d=d_{\Sigma }$
(depending only on
![]() $\Sigma $
) such that
$\Sigma $
) such that
![]() $(K_X+\epsilon D)\cdot C\geq -6d$
and if
$(K_X+\epsilon D)\cdot C\geq -6d$
and if
![]() $rK_X$
is Cartier and
$rK_X$
is Cartier and
![]() $K_X\cdot C\ne 0$
, then we have
$K_X\cdot C\ne 0$
, then we have
![]() $K_X\cdot C\geq d/r$
. But then
$K_X\cdot C\geq d/r$
. But then
This is impossible and so
![]() $K_X\cdot C=0$
. It follows that
$K_X\cdot C=0$
. It follows that
![]() $\Sigma $
is a
$\Sigma $
is a
![]() $(K_X+\epsilon D)$
-negative extremal ray which is
$(K_X+\epsilon D)$
-negative extremal ray which is
![]() $K_X$
trivial. Let
$K_X$
trivial. Let
![]() be the corresponding flop, then
be the corresponding flop, then
![]() $K_{X^+}$
is nef and
$K_{X^+}$
is nef and
![]() $rK_{X^+}$
is Cartier (cf. [Reference Arvidsson, Bernasconi and JustinABL22, Corollary 1.5]). We may replace X by
$rK_{X^+}$
is Cartier (cf. [Reference Arvidsson, Bernasconi and JustinABL22, Corollary 1.5]). We may replace X by
![]() $X^+$
and repeat the procedure which terminates after finitely many steps by Proposition 2.15 (note in fact that each flip is D-negative, and hence the flipping locus is always contained in the support of D).
$X^+$
and repeat the procedure which terminates after finitely many steps by Proposition 2.15 (note in fact that each flip is D-negative, and hence the flipping locus is always contained in the support of D).
Let
![]() be the corresponding minimal model. Since D is movable,
be the corresponding minimal model. Since D is movable,
![]() $\phi $
is an isomorphism in codimension 1. Since
$\phi $
is an isomorphism in codimension 1. Since
![]() $K_Y+\epsilon A_Y$
is ample, the (unique) canonical model of
$K_Y+\epsilon A_Y$
is ample, the (unique) canonical model of
![]() $K_X+\epsilon D$
is isomorphic to Y and the induced morphism
$K_X+\epsilon D$
is isomorphic to Y and the induced morphism
![]() $X'\to Y$
is a small birational morphism of
$X'\to Y$
is a small birational morphism of
![]() ${\mathbb {Q}}$
-factorial varieties and hence an isomorphism. Therefore we may assume that
${\mathbb {Q}}$
-factorial varieties and hence an isomorphism. Therefore we may assume that
![]() is a
is a
![]() $K_X$
-flop and we must show that Y lifts to
$K_X$
-flop and we must show that Y lifts to
![]() $\mathcal Y$
over R and
$\mathcal Y$
over R and
![]() $N^1(\mathcal Y/\textrm {Spec}(R))\to N^1(Y)$
is surjective.
$N^1(\mathcal Y/\textrm {Spec}(R))\to N^1(Y)$
is surjective.
Let
![]() $f\colon X\to Z$
be the flopping contraction and
$f\colon X\to Z$
be the flopping contraction and
![]() $H=f^*H_Z$
the pullback of an ample divisor
$H=f^*H_Z$
the pullback of an ample divisor
![]() $H_Z$
on Z. We also set
$H_Z$
on Z. We also set
![]() $\Sigma \in \overline {\textrm {NE}}(X)$
to be the corresponding
$\Sigma \in \overline {\textrm {NE}}(X)$
to be the corresponding
![]() $(K_X+A)$
-negative extremal ray.
$(K_X+A)$
-negative extremal ray.
Since
![]() $N^1({\mathcal {X}}/S) \to N^1(X)$
is surjective, there exist Cartier divisors
$N^1({\mathcal {X}}/S) \to N^1(X)$
is surjective, there exist Cartier divisors
![]() $\mathcal A$
and
$\mathcal A$
and
![]() $\mathcal H$
on
$\mathcal H$
on
![]() ${\mathcal {X}}$
such that
${\mathcal {X}}$
such that
![]() $\mathcal A |_X = A$
and
$\mathcal A |_X = A$
and
![]() $\mathcal H |_X = H$
. Since H is nef and big, it is easy to see that
$\mathcal H |_X = H$
. Since H is nef and big, it is easy to see that
![]() $\mathcal H _{\eta } $
is nef and big as well, and hence
$\mathcal H _{\eta } $
is nef and big as well, and hence
![]() $\mathcal H$
is big over S. Replacing
$\mathcal H$
is big over S. Replacing
![]() $\mathcal H$
by a multiple, we may assume that
$\mathcal H$
by a multiple, we may assume that
![]() $\mathcal H+ \mathcal A$
is big. Pick
$\mathcal H+ \mathcal A$
is big. Pick
![]() $0\leq \mathcal D\sim _{\mathbb {Q}} \mathcal H+ \mathcal A$
an effective
$0\leq \mathcal D\sim _{\mathbb {Q}} \mathcal H+ \mathcal A$
an effective
![]() ${\mathbb {Q}}$
-divisor whose support does not contain X. For
${\mathbb {Q}}$
-divisor whose support does not contain X. For
![]() $0<\epsilon \ll 1$
, we may assume that
$0<\epsilon \ll 1$
, we may assume that
![]() $({\mathcal {X}},X+\epsilon \mathcal D)$
is plt and
$({\mathcal {X}},X+\epsilon \mathcal D)$
is plt and
![]() $(X,\epsilon D)$
is terminal, where
$(X,\epsilon D)$
is terminal, where
![]() $D=\mathcal D |_X$
. Arguing as in the proof of (2a), we have a
$D=\mathcal D |_X$
. Arguing as in the proof of (2a), we have a
![]() $(K_{\mathcal {X}}+\epsilon \mathcal D)$
-flip
$(K_{\mathcal {X}}+\epsilon \mathcal D)$
-flip
![]() corresponding to the extremal ray
corresponding to the extremal ray
![]() $\Sigma \in \overline {\textrm {NE}}({\mathcal {X}} /S)$
and
$\Sigma \in \overline {\textrm {NE}}({\mathcal {X}} /S)$
and
![]() ${\mathcal {X}} ^+_{\mathfrak m}=Y$
. The surjectivity of
${\mathcal {X}} ^+_{\mathfrak m}=Y$
. The surjectivity of
![]() $N^1(\mathcal Y/\textrm {Spec}(R))\to N^1(Y)$
also follows as in the proof of (2a). This concludes the proof of (2b).
$N^1(\mathcal Y/\textrm {Spec}(R))\to N^1(Y)$
also follows as in the proof of (2a). This concludes the proof of (2b).
Finally, we tackle (3). By (1), we can replace X by a (possibly non-
![]() ${\mathbb {Q}}$
-factorial) minimal model and assume that
${\mathbb {Q}}$
-factorial) minimal model and assume that
![]() $K_X$
is nef and big. Note, however, that the lift
$K_X$
is nef and big. Note, however, that the lift
![]() ${\mathcal {X}}$
of X constructed in (1) is
${\mathcal {X}}$
of X constructed in (1) is
![]() ${\mathbb {Q}}$
-factorial. Now,
${\mathbb {Q}}$
-factorial. Now,
![]() $K_{{\mathcal {X}}} +X \sim _{{\mathbb {Q}}} K_{{\mathcal {X}}}$
is also nef and big, and so it is semiample by Proposition 5.2. Let
$K_{{\mathcal {X}}} +X \sim _{{\mathbb {Q}}} K_{{\mathcal {X}}}$
is also nef and big, and so it is semiample by Proposition 5.2. Let
![]() $\psi \colon \mathcal {X} \to \mathcal {X}^c$
be the induced birational morphism. Since
$\psi \colon \mathcal {X} \to \mathcal {X}^c$
be the induced birational morphism. Since
![]() $(\mathcal {X}^c, (\mathcal {X}^c)_{{\mathfrak {m}}})$
is plt, Lemma 6.3 shows that
$(\mathcal {X}^c, (\mathcal {X}^c)_{{\mathfrak {m}}})$
is plt, Lemma 6.3 shows that
![]() $(\mathcal {X}^c)_{{\mathfrak {m}}}$
is normal. In particular,
$(\mathcal {X}^c)_{{\mathfrak {m}}}$
is normal. In particular,
![]() $\psi |_X = f$
, where
$\psi |_X = f$
, where
![]() $f \colon X \to X^c$
is the map induced by
$f \colon X \to X^c$
is the map induced by
![]() $K_{X}$
. Therefore,
$K_{X}$
. Therefore,
![]() $\mathcal {X}^c$
is the lift of
$\mathcal {X}^c$
is the lift of
![]() $X^c$
, which concludes the proof of (3).
$X^c$
, which concludes the proof of (3).
Acknowledgements
We would like to thank Bhargav Bhatt, János Kollár, Karl Schwede, Zsolt Patakfalvi, Joe Waldron and Chenyang Xu for comments and helpful suggestions. We are very grateful to the reviewer for carefully reading our article and for suggesting multiple improvements.
The first author was partially supported by NSF research grants no: DMS-1300750, DMS-1952522, DMS-1801851 and by a grant from the Simons Foundation; Award Number: 256202. He would also like to thank the Mathematics Department and the Research Institute for Mathematical Sciences, located Kyoto University and the Mathematical Sciences Research Institute in Berkeley were some of this research was conducted. The second author was supported by the National Science Foundation under Grant No. DMS-1638352 at the Institute for Advanced Study in Princeton and by the National Science Foundation under Grant No. DMS-1440140 while the author was in residence at the Mathematical Sciences Research Institute in Berkeley, California, during the Spring 2019 semester. He is currently supported by the NSF research grant no: DMS-2101897.
Conflict of Interest
The authors have no conflict of interest to declare.