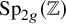1 Introduction
Let
![]() $\Sigma _{g,1}$
denote a compact oriented surface of genus g with one boundary component. Its Torelli group is the group
$\Sigma _{g,1}$
denote a compact oriented surface of genus g with one boundary component. Its Torelli group is the group
![]() $T_{g,1}$
of isotopy classes of orientation-preserving diffeomorphisms of
$T_{g,1}$
of isotopy classes of orientation-preserving diffeomorphisms of
![]() $\Sigma _{g,1}$
which act as the identity on
$\Sigma _{g,1}$
which act as the identity on
![]() $H_1(\Sigma _{g,1};\mathbb {Z})$
. There is an initial pro-unipotent
$H_1(\Sigma _{g,1};\mathbb {Z})$
. There is an initial pro-unipotent
![]() $\mathbb {Q}$
-algebraic group under
$\mathbb {Q}$
-algebraic group under
![]() $T_{g,1}$
, whose pro-nilpotent Lie algebra is the unipotent completion, or Malcev completion,
$T_{g,1}$
, whose pro-nilpotent Lie algebra is the unipotent completion, or Malcev completion,
![]() $\mathfrak {t}_{g,1}$
of
$\mathfrak {t}_{g,1}$
of
![]() $T_{g,1}$
. Hain has proved that, as long as
$T_{g,1}$
. Hain has proved that, as long as
![]() $g \geq 4$
,
$g \geq 4$
,
![]() $\mathfrak {t}_{g,1}$
is isomorphic to the completion of the associated graded
$\mathfrak {t}_{g,1}$
is isomorphic to the completion of the associated graded
![]() $\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\, \mathfrak {t}_{g,1}$
of its lower central series and that this Lie algebra is quadratically presented. In this paper, we will prove that it is Koszul in a stable range. Throughout this paper, we shall take ‘Koszul’ to mean the diagonal criterion: the additional ‘weight’ grading of
$\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\, \mathfrak {t}_{g,1}$
of its lower central series and that this Lie algebra is quadratically presented. In this paper, we will prove that it is Koszul in a stable range. Throughout this paper, we shall take ‘Koszul’ to mean the diagonal criterion: the additional ‘weight’ grading of
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
induces a weight grading on its Lie algebra homology (see Section 2 for our grading conventions), and Koszulness means vanishing of this bigraded Lie algebra homology away from the diagonal.
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
induces a weight grading on its Lie algebra homology (see Section 2 for our grading conventions), and Koszulness means vanishing of this bigraded Lie algebra homology away from the diagonal.
Theorem A. The Lie algebra
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
is Koszul in weight
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
is Koszul in weight
![]() $ \leq \tfrac {g}{3}$
.
$ \leq \tfrac {g}{3}$
.
More generally, for
![]() $\Sigma _{g,n}^r$
a surface of genus g with n boundary components and r marked points, let
$\Sigma _{g,n}^r$
a surface of genus g with n boundary components and r marked points, let
![]() $\smash {\mathfrak {t}^r_{g,n}}$
be the unipotent completion of its Torelli group. We also prove that
$\smash {\mathfrak {t}^r_{g,n}}$
be the unipotent completion of its Torelli group. We also prove that
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm { LCS}}\,}\mathfrak {t}_g$
and
${\mathrm {Gr}^{\bullet }_{\mathrm { LCS}}\,}\mathfrak {t}_g$
and
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g}^1$
are Koszul in the same range, as well as the relative unipotent completions
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g}^1$
are Koszul in the same range, as well as the relative unipotent completions
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g}$
,
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g}$
,
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_g^1$
and
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_g^1$
and
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g,1}$
(see Section 3.1.1 for detailed definitions). This result for
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g,1}$
(see Section 3.1.1 for detailed definitions). This result for
![]() ${\mathrm { Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g}$
has simultaneously been obtained by Felder–Naef–Willwacher [Reference Garoufalidis and GetzlerFNW23]; we discuss the relation between the arguments in Remark 7.4.
${\mathrm { Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g}$
has simultaneously been obtained by Felder–Naef–Willwacher [Reference Garoufalidis and GetzlerFNW23]; we discuss the relation between the arguments in Remark 7.4.
Remark.
-
(i) Theorem A and its variants imply Conjecture 16.2 of [Reference HirschhornHai20] and answer Questions 9.13 and 9.14 of [Reference Habiro and MassuyeauHL97] affirmatively. By Corollary 16.5 of [Reference HirschhornHai20], Conjecture 16.1 of loc. cit. is also true. This is part (iii) of ‘the most optimistic landscape’ in Section 19 of [Reference HirschhornHai20].
-
(ii) Remark 3.5 shows that the Lie algebra
 ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,}\mathfrak {t}_{g,1}$
cannot actually be Koszul.
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,}\mathfrak {t}_{g,1}$
cannot actually be Koszul.
Garoufalidis–Getzler [Reference Ginzburg and KapranovGG17] have used work of Looijenga and Madsen–Weiss to compute the stable character of the quadratic dual of
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_g$
as graded algebraic
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_g$
as graded algebraic
![]() $\mathrm {Sp}_{2g}(\mathbb {Z})$
-representation and then in Theorem 1.3 of loc. cit. have computed from this—under the assumption of stable Koszulness—the stable character of
$\mathrm {Sp}_{2g}(\mathbb {Z})$
-representation and then in Theorem 1.3 of loc. cit. have computed from this—under the assumption of stable Koszulness—the stable character of
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm { LCS}}\,} \mathfrak {t}_g$
as a graded algebraic
${\mathrm {Gr}^{\bullet }_{\mathrm { LCS}}\,} \mathfrak {t}_g$
as a graded algebraic
![]() $\mathrm {Sp}_{2g}(\mathbb {Z})$
-representation. In [Reference Koike and TeradaKRW20c, Sections 6, 8.1], we gave a different approach to the first of these computations and explained how it applies to surfaces with a boundary component or a marked point too. This method, along with Theorem A and its generalisation, renders the characters of the graded algebraic
$\mathrm {Sp}_{2g}(\mathbb {Z})$
-representation. In [Reference Koike and TeradaKRW20c, Sections 6, 8.1], we gave a different approach to the first of these computations and explained how it applies to surfaces with a boundary component or a marked point too. This method, along with Theorem A and its generalisation, renders the characters of the graded algebraic
![]() $\mathrm {Sp}_{2g}(\mathbb {Z})$
-representations
$\mathrm {Sp}_{2g}(\mathbb {Z})$
-representations
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g$
,
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g$
,
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,}\mathfrak {t}^1_g$
,
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,}\mathfrak {t}^1_g$
,
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
,
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
,
![]() ${\mathrm { Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g}$
,
${\mathrm { Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g}$
,
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_g^1$
and
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_g^1$
and
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g,1}$
, amenable to computer calculation in weight
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g,1}$
, amenable to computer calculation in weight
![]() $\leq \tfrac {g}{3}$
.
$\leq \tfrac {g}{3}$
.
We further use Theorem A to analyse the map
obtained from the action of the mapping class group of
![]() $\Sigma _{g,1}$
on its fundamental group, whose image lies in the Lie subalgebra
$\Sigma _{g,1}$
on its fundamental group, whose image lies in the Lie subalgebra
![]() $\mathfrak {h}_{g,1} \subset \mathrm {Der}(\mathrm {Lie}(H))$
of symplectic derivations. Following Hain, we call this the geometric Johnson homomorphism, and Morita has asked whether it is injective in weight
$\mathfrak {h}_{g,1} \subset \mathrm {Der}(\mathrm {Lie}(H))$
of symplectic derivations. Following Hain, we call this the geometric Johnson homomorphism, and Morita has asked whether it is injective in weight
![]() $\neq 2$
. The map
$\neq 2$
. The map
![]() $\tau _{g,1}$
is one of Lie algebras with additional weight grading in the category of algebraic
$\tau _{g,1}$
is one of Lie algebras with additional weight grading in the category of algebraic
![]() $\mathrm {Sp}_{2g}(\mathbb {Z})$
-representations and here we give strong evidence for this injectivity by tightly constraining its kernel in a range.
$\mathrm {Sp}_{2g}(\mathbb {Z})$
-representations and here we give strong evidence for this injectivity by tightly constraining its kernel in a range.
Theorem B. In weight
![]() $\leq \frac {g}{3}$
, the kernel of
$\leq \frac {g}{3}$
, the kernel of
![]() $\tau _{g,1}$
lies in the centre of the Lie algebra
$\tau _{g,1}$
lies in the centre of the Lie algebra
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
and consists of trivial
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
and consists of trivial
![]() $\mathrm {Sp}_{2g}(\mathbb {Z})$
-representations.
$\mathrm {Sp}_{2g}(\mathbb {Z})$
-representations.
We also prove the analogous statement for
![]() $\mathfrak {t}_g^1$
,
$\mathfrak {t}_g^1$
,
![]() $\mathfrak {t}_g$
,
$\mathfrak {t}_g$
,
![]() $\mathfrak {u}_{g,1}$
,
$\mathfrak {u}_{g,1}$
,
![]() $\mathfrak {u}_g^1$
and
$\mathfrak {u}_g^1$
and
![]() $\mathfrak {u}_g$
.
$\mathfrak {u}_g$
.
Remark.
-
(i) The map
 $\tau _{g,1}$
factors over a map
$\tau _{g,1}$
factors over a map
 ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1} \to {\mathrm {Gr}^{\bullet }_{\mathrm { LCS}}\,} \mathfrak {u}_{g,1}$
whose kernel is a central
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1} \to {\mathrm {Gr}^{\bullet }_{\mathrm { LCS}}\,} \mathfrak {u}_{g,1}$
whose kernel is a central
 $\mathbb {Q}$
in weight 2 on which
$\mathbb {Q}$
in weight 2 on which
 $\mathrm { Sp}_{2g}(\mathbb {Z})$
acts trivially [Reference HainHai97, Theoren 3.4], so Theorem B is sharp in this sense. However, comparing [Reference Ginzburg and KapranovGG17, Section 7] with [Reference Morita, Sakasai and SuzukiMSS15, Table 1] one sees that
$\mathrm { Sp}_{2g}(\mathbb {Z})$
acts trivially [Reference HainHai97, Theoren 3.4], so Theorem B is sharp in this sense. However, comparing [Reference Ginzburg and KapranovGG17, Section 7] with [Reference Morita, Sakasai and SuzukiMSS15, Table 1] one sees that
 ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g,1} \to \mathfrak {h}_{g,1}$
is injective in weight
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g,1} \to \mathfrak {h}_{g,1}$
is injective in weight
 $\leq 6$
in a stable range, and it might well be the case that this map is injective.
$\leq 6$
in a stable range, and it might well be the case that this map is injective. -
(ii) Stably and neglecting trivial
 $\mathrm {Sp}_{2g}(\mathbb {Z})$
-representations in the centre, this answers several questions in the literature: part (i) of ‘the most optimistic landscape’ in Section 1.9 of [Reference HirschhornHai20], [Reference Habiro and MassuyeauHL97, Question 9.7], [Reference MoritaMor99, Problem 6.2], [Reference Morita, Sakasai and SuzukiMor06, Problem 3.3, Problem 8.1], [Reference Habegger and SorgerHM09, Question 8.2], [Reference Sam and SnowdenMSS20, Conjecture 1.8]. It also has consequences for finite type invariants of 3-manifolds (see Remark 8.6), c.f. p. 381 of [Reference MoritaMor99].
$\mathrm {Sp}_{2g}(\mathbb {Z})$
-representations in the centre, this answers several questions in the literature: part (i) of ‘the most optimistic landscape’ in Section 1.9 of [Reference HirschhornHai20], [Reference Habiro and MassuyeauHL97, Question 9.7], [Reference MoritaMor99, Problem 6.2], [Reference Morita, Sakasai and SuzukiMor06, Problem 3.3, Problem 8.1], [Reference Habegger and SorgerHM09, Question 8.2], [Reference Sam and SnowdenMSS20, Conjecture 1.8]. It also has consequences for finite type invariants of 3-manifolds (see Remark 8.6), c.f. p. 381 of [Reference MoritaMor99].
Our arguments use in an essential manner the classifying spaces
![]() $B\mathrm {Tor}_{\partial }(W_{g,1})$
of the Torelli groups of the high-dimensional analogue of a surface of genus g with one boundary component. As a consequence, we also obtain results about the rational homotopy Lie algebra of
$B\mathrm {Tor}_{\partial }(W_{g,1})$
of the Torelli groups of the high-dimensional analogue of a surface of genus g with one boundary component. As a consequence, we also obtain results about the rational homotopy Lie algebra of
![]() $B\mathrm {Tor}_{\partial }(W_{g,1})$
(see Section 7.1).
$B\mathrm {Tor}_{\partial }(W_{g,1})$
(see Section 7.1).
Outline of proofs. We now outline the proof of Theorem A. We will suppress explicit ranges for the sake of readability, writing ‘in a stable range’ when a statement holds in a range of degrees or weights tending to
![]() $\infty $
with g.
$\infty $
with g.
-
(1) Use Koszul duality, and relate different genera g and dimensions n. By a result of Hain, the Lie algebra
 $\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,\mathfrak {t}_{g,1}$
is quadratically presented when
$\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,\mathfrak {t}_{g,1}$
is quadratically presented when
 $g \geq 4$
. Hence, to prove Theorem A, it suffices to prove the quadratic dual commutative algebra of
$g \geq 4$
. Hence, to prove Theorem A, it suffices to prove the quadratic dual commutative algebra of
 $\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,\mathfrak {t}_{g,1}$
is Koszul in a stable range, in the sense that its bigraded commutative algebra homology groups vanish away from the diagonal.
$\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,\mathfrak {t}_{g,1}$
is Koszul in a stable range, in the sense that its bigraded commutative algebra homology groups vanish away from the diagonal.The quadratic dual of
 $\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,\mathfrak {t}_{g,1}$
can be identified as an algebra of twisted Miller–Morita–Mumford classes as in [Reference Koike and TeradaKRW20c, Section 5]. Taking into account the
$\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,\mathfrak {t}_{g,1}$
can be identified as an algebra of twisted Miller–Morita–Mumford classes as in [Reference Koike and TeradaKRW20c, Section 5]. Taking into account the
 $\mathrm { Sp}_{2g}(\mathbb {Z})$
-action this description is uniform in g: There is a commutative algebra object
$\mathrm { Sp}_{2g}(\mathbb {Z})$
-action this description is uniform in g: There is a commutative algebra object
 $E_1/(\kappa _{e^2}) \colon \mathsf {dsBr} \to \mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
in the category of representations of the downward signed Brauer category whose realisation
$E_1/(\kappa _{e^2}) \colon \mathsf {dsBr} \to \mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
in the category of representations of the downward signed Brauer category whose realisation
 $K^{\vee } \otimes ^{\mathsf {dsBr}} E_1/(\kappa _{e^2}) \in \mathsf {Gr}(\mathsf {Rep}(\mathrm {Sp}_{2g}(\mathbb {Z})))$
is the quadratic dual of
$K^{\vee } \otimes ^{\mathsf {dsBr}} E_1/(\kappa _{e^2}) \in \mathsf {Gr}(\mathsf {Rep}(\mathrm {Sp}_{2g}(\mathbb {Z})))$
is the quadratic dual of
 $\mathrm { Gr}^{\bullet }_{\mathrm {LCS}}\,\mathfrak {t}_{g,1}$
in a stable range (implicitly
$\mathrm { Gr}^{\bullet }_{\mathrm {LCS}}\,\mathfrak {t}_{g,1}$
in a stable range (implicitly
 $K^{\vee }$
depends on g but
$K^{\vee }$
depends on g but
 $E_1/(\kappa _{e^2})$
does not). This realisation is Koszul in a stable range if and only if
$E_1/(\kappa _{e^2})$
does not). This realisation is Koszul in a stable range if and only if
 $E_1/(\kappa _{e^2})$
is if and only if
$E_1/(\kappa _{e^2})$
is if and only if
 $E_1$
is. The algebra object
$E_1$
is. The algebra object
 $E_1$
is one of a family
$E_1$
is one of a family
 $E_n$
which up to rescaling only depends on the parity of n, and this has a closely related variant
$E_n$
which up to rescaling only depends on the parity of n, and this has a closely related variant
 $Z_n$
. The commutative algebra object
$Z_n$
. The commutative algebra object
 $E_1$
is Koszul in a stable range if and only if
$E_1$
is Koszul in a stable range if and only if
 $E_n$
is if and only if
$E_n$
is if and only if
 $Z_n$
is.
$Z_n$
is. -
(2) Use high-dimensional manifold theory to get vanishing of the nontrivial
 $\mathrm { Sp}_{2g}(\mathbb {Z})$
-representations. The reason for the reductions performed in Step (1) is that the algebra object
$\mathrm { Sp}_{2g}(\mathbb {Z})$
-representations. The reason for the reductions performed in Step (1) is that the algebra object
 $Z_n$
has appeared in [Reference Kupers and Randal-WilliamsKRW20b]: Its realisation
$Z_n$
has appeared in [Reference Kupers and Randal-WilliamsKRW20b]: Its realisation
 $K^{\vee } \otimes ^{\mathsf {d(s)Br}} Z_n$
is an algebra of twisted Miller–Morita–Mumford classes for the framed Torelli group
$K^{\vee } \otimes ^{\mathsf {d(s)Br}} Z_n$
is an algebra of twisted Miller–Morita–Mumford classes for the framed Torelli group
 $\mathrm {Tor}^{\mathrm {fr}}_{\partial }(W_{g,1})$
of the
$\mathrm {Tor}^{\mathrm {fr}}_{\partial }(W_{g,1})$
of the
 $2n$
-dimensional analogue
$2n$
-dimensional analogue
 $W_{g,1} = D^{2n} \# (S^n \times S^n)^{\# g}$
of the surface
$W_{g,1} = D^{2n} \# (S^n \times S^n)^{\# g}$
of the surface
 $\Sigma _{g,1}$
. These classes account for nearly all of the cohomology of this group: When
$\Sigma _{g,1}$
. These classes account for nearly all of the cohomology of this group: When
 $2n \geq 6$
, a finite cover of the classifying space of this group fits in a fibration sequence of nilpotent spaces with
$2n \geq 6$
, a finite cover of the classifying space of this group fits in a fibration sequence of nilpotent spaces with $$\begin{align*}X_1(g) \longrightarrow \overline{B\mathrm{Tor}}^{\mathrm{fr}}_{\partial}(W_{g,1}) \longrightarrow X_0\end{align*}$$
$$\begin{align*}X_1(g) \longrightarrow \overline{B\mathrm{Tor}}^{\mathrm{fr}}_{\partial}(W_{g,1}) \longrightarrow X_0\end{align*}$$
 $\mathrm {Sp}_{2g}(\mathbb {Z})$
-action (the action is trivial on
$\mathrm {Sp}_{2g}(\mathbb {Z})$
-action (the action is trivial on
 $X_0$
) and
$X_0$
) and
 $K^{\vee } \otimes ^{\mathsf {d(s)Br}} Z_n = H^*(X_1(g);\mathbb {Q})$
in a stable range. It thus suffices to verify the diagonal criterion for the commutative algebra homology of
$K^{\vee } \otimes ^{\mathsf {d(s)Br}} Z_n = H^*(X_1(g);\mathbb {Q})$
in a stable range. It thus suffices to verify the diagonal criterion for the commutative algebra homology of
 $H^*(X_1(g);\mathbb {Q})$
.
$H^*(X_1(g);\mathbb {Q})$
.
There is an unstable rational Adams spectral sequence of
 $\mathrm {Sp}_{2g}(\mathbb {Z})$
-representations
$\mathrm {Sp}_{2g}(\mathbb {Z})$
-representations  $$\begin{align*}H^{\mathrm{Com}}_s(H^*(X_1(g);\mathbb{Q}))_{rn} \Longrightarrow \mathrm{Hom}(\pi_{rn-s+1}(X_1(g)),\mathbb{Q}).\end{align*}$$
$$\begin{align*}H^{\mathrm{Com}}_s(H^*(X_1(g);\mathbb{Q}))_{rn} \Longrightarrow \mathrm{Hom}(\pi_{rn-s+1}(X_1(g)),\mathbb{Q}).\end{align*}$$
As
 $H^*(X_1(g);\mathbb {Q})$
is sparse, so are the entries in this spectral sequence. Not only does this imply a sparsity result for
$H^*(X_1(g);\mathbb {Q})$
is sparse, so are the entries in this spectral sequence. Not only does this imply a sparsity result for
 $\pi _*(X_1(g)) \otimes \mathbb {Q}$
, but we can exclude differentials in any desired range by increasing the dimension
$\pi _*(X_1(g)) \otimes \mathbb {Q}$
, but we can exclude differentials in any desired range by increasing the dimension
 $2n$
. In [Reference Kupers and Randal-WilliamsKRW20b], we also accessed the rational homotopy groups of
$2n$
. In [Reference Kupers and Randal-WilliamsKRW20b], we also accessed the rational homotopy groups of
 $\smash {\overline {B\mathrm {Tor}}^{\mathrm {fr}}_{\partial }}(W_{g,1})$
using embedding calculus. Up to contributions from
$\smash {\overline {B\mathrm {Tor}}^{\mathrm {fr}}_{\partial }}(W_{g,1})$
using embedding calculus. Up to contributions from
 $\pi _*(X_0)\otimes \mathbb {Q}$
, this gives a different sparsity result for
$\pi _*(X_0)\otimes \mathbb {Q}$
, this gives a different sparsity result for
 $\pi _*(X_1(g))$
. Verification of the diagonal criterion up to trivial representations then follows in a stable range by combining the two sparsity results.
$\pi _*(X_1(g))$
. Verification of the diagonal criterion up to trivial representations then follows in a stable range by combining the two sparsity results. -
(3) Apply a transfer argument in graph complexes to get vanishing of the trivial
 $\mathrm { Sp}_{2g}(\mathbb {Z})$
-representations. In terms of the commutative algebra object
$\mathrm { Sp}_{2g}(\mathbb {Z})$
-representations. In terms of the commutative algebra object
 $Z_n$
, we have proven that its commutative algebra homology vanishes away from the diagonal when evaluated on those objects of
$Z_n$
, we have proven that its commutative algebra homology vanishes away from the diagonal when evaluated on those objects of
 $\mathsf {d(s)Br}$
given by nonempty sets, and it remains to prove the same holds for the empty set. To do so, we resolve
$\mathsf {d(s)Br}$
given by nonempty sets, and it remains to prove the same holds for the empty set. To do so, we resolve
 $Z_n$
by a complex
$Z_n$
by a complex
 $RB^{Z_n}$
of red-and-black graphs: The commutative algebra homology groups of
$RB^{Z_n}$
of red-and-black graphs: The commutative algebra homology groups of
 $RB^{Z_n}$
equal those of
$RB^{Z_n}$
equal those of
 $Z_n$
, but
$Z_n$
, but
 $RB^{Z_n}$
is chosen so that these can be computed by taking strict commutative algebra indecomposables; this is a graph complex
$RB^{Z_n}$
is chosen so that these can be computed by taking strict commutative algebra indecomposables; this is a graph complex
 $RB^{Z_n}_{\mathrm {conn}}$
of connected red-and-black graphs. We show that this is closely related to a complex
$RB^{Z_n}_{\mathrm {conn}}$
of connected red-and-black graphs. We show that this is closely related to a complex
 $G^{Z_n}$
of connected black graphs, and in particular certain vanishing ranges can be passed back and forth between these complexes.
$G^{Z_n}$
of connected black graphs, and in particular certain vanishing ranges can be passed back and forth between these complexes.Step (2) gives the required vanishing of the homology of
 $RB^{Z_n}_{\mathrm {conn}}(S)$
for all nonempty sets S, and in turn this implies a certain vanishing of the homology of
$RB^{Z_n}_{\mathrm {conn}}(S)$
for all nonempty sets S, and in turn this implies a certain vanishing of the homology of
 $G^{Z_n}(S)$
for all nonempty sets S. A transfer argument shows that the homology of
$G^{Z_n}(S)$
for all nonempty sets S. A transfer argument shows that the homology of
 $G^{Z_n}(\varnothing )$
injects into that of
$G^{Z_n}(\varnothing )$
injects into that of
 $G^{Z_n}(\underline {1})$
, giving a certain vanishing of the homology of
$G^{Z_n}(\underline {1})$
, giving a certain vanishing of the homology of
 $G^{Z_n}(\varnothing )$
; this then implies the required vanishing of the homology of
$G^{Z_n}(\varnothing )$
; this then implies the required vanishing of the homology of
 $RB^{Z_n}_{\mathrm {conn}}(\varnothing )$
.
$RB^{Z_n}_{\mathrm {conn}}(\varnothing )$
.
We next outline the proof of Theorem B. Using Theorem A, we can identify the geometric Johnson homomorphism in terms of high-dimensional manifold theory: Up to trivial representations, it amounts to the map induced on rational homotopy groups by the composition
Its injectivity can then be deduced from the unstable rational Adams spectral sequence and sparsity results of Step (2).
2 Preliminaries
Notation 2.1. Let
![]() $\mathbb {Q}\text {-}\mathsf {mod}$
denote the category of
$\mathbb {Q}\text {-}\mathsf {mod}$
denote the category of
![]() $\mathbb {Q}$
-vector spaces,
$\mathbb {Q}$
-vector spaces,
![]() $\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
the category of nonnegatively graded
$\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
the category of nonnegatively graded
![]() $\mathbb {Q}$
-vector spaces, and
$\mathbb {Q}$
-vector spaces, and
![]() $\mathsf {Ch}$
the category of nonnegatively graded chain complexes over
$\mathsf {Ch}$
the category of nonnegatively graded chain complexes over
![]() $\mathbb {Q}$
. We consider
$\mathbb {Q}$
. We consider
![]() $\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
as the subcategory of
$\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
as the subcategory of
![]() $\mathsf {Ch}$
of chain complexes without differential, and
$\mathsf {Ch}$
of chain complexes without differential, and
![]() $\mathbb {Q}\text {-}\mathsf {mod}$
as the subcategory of
$\mathbb {Q}\text {-}\mathsf {mod}$
as the subcategory of
![]() $\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
of graded vector spaces supported in degree 0. We endow
$\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
of graded vector spaces supported in degree 0. We endow
![]() $\mathsf {Ch}$
with the usual symmetric monoidality, incorporating the Koszul sign rule and give the other categories the induced symmetric monoidalities.
$\mathsf {Ch}$
with the usual symmetric monoidality, incorporating the Koszul sign rule and give the other categories the induced symmetric monoidalities.
We will want to consider objects (chain complexes, etc.) equipped with an additional
![]() $\mathbb {N}$
-grading, called the ‘weight grading’, and we write
$\mathbb {N}$
-grading, called the ‘weight grading’, and we write
![]() $\mathsf {Ch}^{\mathbb {N}} := \mathsf {Fun}(\mathbb {N}, \mathsf {Ch})$
and so on for the categories of these. Treating
$\mathsf {Ch}^{\mathbb {N}} := \mathsf {Fun}(\mathbb {N}, \mathsf {Ch})$
and so on for the categories of these. Treating
![]() $\mathbb {N}$
as a symmetric monoidal category having only identity maps and symmetric monoidal structure given by addition, Day convolution endows these categories with their own symmetric monoidalities. We emphasise that when interchanging elements the sign incurred depends only on the homological degree and not on the weight. In particular,
$\mathbb {N}$
as a symmetric monoidal category having only identity maps and symmetric monoidal structure given by addition, Day convolution endows these categories with their own symmetric monoidalities. We emphasise that when interchanging elements the sign incurred depends only on the homological degree and not on the weight. In particular,
![]() $X \mapsto \bigoplus _{n \in \mathbb {N}} X(n): \mathsf {Ch}^{\mathbb {N}} \to \mathsf {Ch}$
is symmetric monoidal.
$X \mapsto \bigoplus _{n \in \mathbb {N}} X(n): \mathsf {Ch}^{\mathbb {N}} \to \mathsf {Ch}$
is symmetric monoidal.
2.1 Commutative algebras
Let
![]() $\mathsf {Com}$
denote the nonunital commutative operad in
$\mathsf {Com}$
denote the nonunital commutative operad in
![]() $\mathbb {Q}\text {-}\mathsf {mod}$
, having
$\mathbb {Q}\text {-}\mathsf {mod}$
, having
![]() $\mathsf {Com}(r) = 0$
for
$\mathsf {Com}(r) = 0$
for
![]() $r=0$
and
$r=0$
and
![]() $\mathsf {Com}(r) = \mathbb {Q}$
as a trivial
$\mathsf {Com}(r) = \mathbb {Q}$
as a trivial
![]() $\mathfrak {S}_r$
-representations otherwise. A commutative algebra in
$\mathfrak {S}_r$
-representations otherwise. A commutative algebra in
![]() $\mathsf {Ch}$
is an algebra for the operad
$\mathsf {Ch}$
is an algebra for the operad
![]() $\mathsf {Com}$
or, equivalently, the associated monad.
$\mathsf {Com}$
or, equivalently, the associated monad.
The (desuspended) Harrison complex of commutative algebra A is
where
![]() $[1]$
denotes suspension and
$[1]$
denotes suspension and
![]() $[-1]$
denotes desuspension of chain complexes, and the differential
$[-1]$
denotes desuspension of chain complexes, and the differential
![]() $d=d_A + d_{\mathrm {Harr}}$
is the sum of the differential
$d=d_A + d_{\mathrm {Harr}}$
is the sum of the differential
![]() $d_A$
induced by that on A and the differential
$d_A$
induced by that on A and the differential
![]() $d_{\mathrm {Harr}}$
induced by the unique map of Lie coalgebras given on cogenerators by the commutative multiplication map
$d_{\mathrm {Harr}}$
induced by the unique map of Lie coalgebras given on cogenerators by the commutative multiplication map
![]() $\mathrm {coLie}^2(A[1]) = \Lambda ^2(A[1])= \mathrm {Sym}^2(A)[2] \to A[1]$
. These satisfy
$\mathrm {coLie}^2(A[1]) = \Lambda ^2(A[1])= \mathrm {Sym}^2(A)[2] \to A[1]$
. These satisfy
![]() $d_Ad_{\mathrm {Harr}}+d_{\mathrm {Harr}}d_A = 0$
, so
$d_Ad_{\mathrm {Harr}}+d_{\mathrm {Harr}}d_A = 0$
, so
![]() $d^2 = 0$
.
$d^2 = 0$
.
If A is a nonunital commutative algebra object in the subcategory
![]() $\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod}) \subset \mathsf {Ch}$
, then the objects
$\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod}) \subset \mathsf {Ch}$
, then the objects
![]() $\mathrm {Harr}(A)$
inherit a further grading, as usual in homological algebra. We may think of this as follows: The grading of A determines a
$\mathrm {Harr}(A)$
inherit a further grading, as usual in homological algebra. We may think of this as follows: The grading of A determines a
![]() $\mathbb {Q}^{\times }$
-action on A, where
$\mathbb {Q}^{\times }$
-action on A, where
![]() $u \in \mathbb {Q}^{\times }$
acts as
$u \in \mathbb {Q}^{\times }$
acts as
![]() $u^q$
in degree q. Functoriality gives a
$u^q$
in degree q. Functoriality gives a
![]() $\mathbb {Q}^{\times }$
-action on
$\mathbb {Q}^{\times }$
-action on
![]() $\mathrm {Harr}(A)$
, and we write
$\mathrm {Harr}(A)$
, and we write
![]() $\mathrm {Harr}_{*}(A)_q$
for the subspace on which
$\mathrm {Harr}_{*}(A)_q$
for the subspace on which
![]() $u \in \mathbb {Q}^{\times }$
acts as
$u \in \mathbb {Q}^{\times }$
acts as
![]() $u^q$
. It is clear that such eigenspaces exhaust
$u^q$
. It is clear that such eigenspaces exhaust
![]() $\mathrm {Harr}(A)$
, and we set
$\mathrm {Harr}(A)$
, and we set
and call p the Harrison degree, q the internal degree and
![]() $p+q-1$
the total degree.
$p+q-1$
the total degree.
If A also has a weight grading, that is, is a nonunital commutative algebra object in
![]() $\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})^{\mathbb {N}}$
, then the Harrison complex and its homology obtains a further weight grading, and we write
$\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})^{\mathbb {N}}$
, then the Harrison complex and its homology obtains a further weight grading, and we write
for the piece of weight w.
Definition 2.2. For
![]() $A \in \mathsf {Alg}_{\mathrm {Com}}(\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})^{\mathbb {N}})$
, we say that A is Koszul in weight
$A \in \mathsf {Alg}_{\mathrm {Com}}(\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})^{\mathbb {N}})$
, we say that A is Koszul in weight
![]() $ \leq W$
if
$ \leq W$
if
![]() $H^{\mathrm {Com}}_p(A)_{q,w}=0$
when
$H^{\mathrm {Com}}_p(A)_{q,w}=0$
when
![]() $p \neq w$
and
$p \neq w$
and
![]() $w \leq W$
. If
$w \leq W$
. If
![]() $W=\infty $
, then we simply say that A is Koszul.
$W=\infty $
, then we simply say that A is Koszul.
2.2 Lie algebras
Let
![]() $\mathsf {Lie}$
denote the Lie operad, whose definition can be found in [Reference MillèsLV12, Section 13.2.3]. A Lie algebra in
$\mathsf {Lie}$
denote the Lie operad, whose definition can be found in [Reference MillèsLV12, Section 13.2.3]. A Lie algebra in
![]() $\mathsf {Ch}$
is an algebra for the operad
$\mathsf {Ch}$
is an algebra for the operad
![]() $\mathsf {Lie}$
, or equivalently the associated monad. The (desuspended) Chevalley–Eilenberg complex of a Lie algebra L is
$\mathsf {Lie}$
, or equivalently the associated monad. The (desuspended) Chevalley–Eilenberg complex of a Lie algebra L is
where the differential
![]() $d=d_L + d_{\mathrm {CE}}$
is again the sum of the differential
$d=d_L + d_{\mathrm {CE}}$
is again the sum of the differential
![]() $d_L$
induced by that on L and the differential
$d_L$
induced by that on L and the differential
![]() $d_{\mathrm { CE}}$
induced by the unique map of cocommutative coalgebras given on cogenerators by the Lie bracket map
$d_{\mathrm { CE}}$
induced by the unique map of cocommutative coalgebras given on cogenerators by the Lie bracket map
![]() $\mathrm {coCom}^2(L[1]) = \mathrm { Sym}^2(L[1]) = \mathrm {Lie}^2(L)[2] \to L[1]$
. These satisfy
$\mathrm {coCom}^2(L[1]) = \mathrm { Sym}^2(L[1]) = \mathrm {Lie}^2(L)[2] \to L[1]$
. These satisfy
![]() $d_Ld_{\mathrm {CE}}+d_{\mathrm {CE}}d_L = 0$
, so
$d_Ld_{\mathrm {CE}}+d_{\mathrm {CE}}d_L = 0$
, so
![]() $d^2 = 0$
.
$d^2 = 0$
.
If L is a Lie algebra object in
![]() $\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
, then as above we can endow the Chevalley–Eilenberg complex with a further grading, and we set
$\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
, then as above we can endow the Chevalley–Eilenberg complex with a further grading, and we set
If L also has a weight grading, then we write
for the piece of weight w.
Definition 2.3. For
![]() $L \in \mathsf {Alg}_{\mathsf {Lie}}(\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})^{\mathbb {N}})$
, we say that L is Koszul in weight
$L \in \mathsf {Alg}_{\mathsf {Lie}}(\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})^{\mathbb {N}})$
, we say that L is Koszul in weight
![]() $\leq W$
if
$\leq W$
if
![]() $H^{\mathrm {Lie}}_p(L)_{q,w} = 0$
when
$H^{\mathrm {Lie}}_p(L)_{q,w} = 0$
when
![]() $p \neq w$
and
$p \neq w$
and
![]() $w \leq W$
. If
$w \leq W$
. If
![]() $W=\infty $
, then we simply say that L is Koszul.
$W=\infty $
, then we simply say that L is Koszul.
2.3 Koszul duality
The operads
![]() $\mathsf {Com}$
and
$\mathsf {Com}$
and
![]() $\mathsf {Lie}$
are Koszul dual [Reference Garoufalidis and NakamuraGK94, Corollary 4.2.7], [Reference MillèsLV12, Proposition 13.1.5], and thus there is a Koszul duality between nonunital commutative algebras and Lie algebras.
$\mathsf {Lie}$
are Koszul dual [Reference Garoufalidis and NakamuraGK94, Corollary 4.2.7], [Reference MillèsLV12, Proposition 13.1.5], and thus there is a Koszul duality between nonunital commutative algebras and Lie algebras.
A quadratic datum for a nonunital commutative algebra is a pair
![]() $(V,S)$
of a finite-dimensional graded vector space V and a subspace
$(V,S)$
of a finite-dimensional graded vector space V and a subspace
![]() $S \subset \mathrm {Com}(2) \otimes _{\mathfrak {S}_2} V^{\otimes 2}$
. From this, we may form the quadratic nonunital commutative algebra
$S \subset \mathrm {Com}(2) \otimes _{\mathfrak {S}_2} V^{\otimes 2}$
. From this, we may form the quadratic nonunital commutative algebra
![]() $A(V,S)$
as the quotient of the free graded nonunital commutative algebra
$A(V,S)$
as the quotient of the free graded nonunital commutative algebra
![]() $\mathrm {Com}(V)$
by the ideal generated by S. As the relations are homogeneous in V (namely purely quadratic), we can endow this with a weight grading by declaring V to have weight 1. Similarly, a quadratic datum for a Lie algebra, given by a pair
$\mathrm {Com}(V)$
by the ideal generated by S. As the relations are homogeneous in V (namely purely quadratic), we can endow this with a weight grading by declaring V to have weight 1. Similarly, a quadratic datum for a Lie algebra, given by a pair
![]() $(W,R)$
of a finite-dimensional graded vector space W and a subspace
$(W,R)$
of a finite-dimensional graded vector space W and a subspace
![]() $R \subset \mathrm { Lie}(2) \otimes _{\mathfrak {S}_2} W^{\otimes 2}$
, yields a quadratic Lie algebra
$R \subset \mathrm { Lie}(2) \otimes _{\mathfrak {S}_2} W^{\otimes 2}$
, yields a quadratic Lie algebra
![]() $L(W,R)$
; it has a weight grading by declaring W to have weight 1.
$L(W,R)$
; it has a weight grading by declaring W to have weight 1.
Given a quadratically presented nonunital commutative algebra
![]() $A=A(V,S)$
, its quadratic dual Lie algebra is
$A=A(V,S)$
, its quadratic dual Lie algebra is
![]() .Footnote 1 Similarly, given a quadratically presented Lie algebra
.Footnote 1 Similarly, given a quadratically presented Lie algebra
![]() $L = L(W,R)$
, its quadratic dual nonunital commutative algebra is
$L = L(W,R)$
, its quadratic dual nonunital commutative algebra is
![]() . These constructions are natural in the quadratic data, and are dualities in the sense that there are natural isomorphisms
. These constructions are natural in the quadratic data, and are dualities in the sense that there are natural isomorphisms
![]() $A \cong (A^!)^!$
and
$A \cong (A^!)^!$
and
![]() $L \cong (L^!)^!$
. In particular, the quadratic dual preserves any group actions on the objects in question.
$L \cong (L^!)^!$
. In particular, the quadratic dual preserves any group actions on the objects in question.
The definitions of Koszulness given in Definition 2.2 and Definition 2.3 are the diagonal criteria; a reference is [Reference MoritaMil12, Theorem 4.9 (ii)]. By [Reference MoritaMil12, Theorem 4.11], A is Koszul if and only if
![]() $A^!$
is Koszul. The same is true for the notions of Koszulness in a range by the same argument:
$A^!$
is Koszul. The same is true for the notions of Koszulness in a range by the same argument:
Lemma 2.4. A quadratic nonunital commutative algebra A is Koszul in weight
![]() $\leq W$
if and only if its quadratic dual Lie algebra
$\leq W$
if and only if its quadratic dual Lie algebra
![]() $A^!$
is Koszul in weight
$A^!$
is Koszul in weight
![]() $\leq W$
.
$\leq W$
.
![]() $ \Box $
$ \Box $
2.4 Orthogonal and symplectic representation theory
We recall some facts from [Reference Koike and TeradaKRW20c, Section 2.1]. Let
![]() $H(g)$
be a
$H(g)$
be a
![]() $2g$
-dimensional rational vector space with nonsingular
$2g$
-dimensional rational vector space with nonsingular
![]() $\epsilon $
-symmetric pairing
$\epsilon $
-symmetric pairing
![]() $\lambda \colon H(g) \otimes H(g) \to \mathbb {Q}$
given by the hyperbolic form. Its dual
$\lambda \colon H(g) \otimes H(g) \to \mathbb {Q}$
given by the hyperbolic form. Its dual
![]() $\epsilon $
-symmetric form
$\epsilon $
-symmetric form
![]() $\omega \colon \mathbb {Q} \to H(g) \otimes H(g)$
characteristic by
$\omega \colon \mathbb {Q} \to H(g) \otimes H(g)$
characteristic by
![]() $(\lambda \otimes \mathrm {id})(- \otimes \omega ) = \mathrm {id}(-)$
. The automorphisms of
$(\lambda \otimes \mathrm {id})(- \otimes \omega ) = \mathrm {id}(-)$
. The automorphisms of
![]() $H(g)$
preserving
$H(g)$
preserving
![]() $\lambda $
are denoted
$\lambda $
are denoted
![]() $\mathrm {O}_{\epsilon }(H(g))$
; these are the
$\mathrm {O}_{\epsilon }(H(g))$
; these are the
![]() $\mathbb {Q}$
-points of an algebraic group
$\mathbb {Q}$
-points of an algebraic group
![]() $\mathbf {O}_{g,g}$
for
$\mathbf {O}_{g,g}$
for
![]() $\epsilon =1$
and
$\epsilon =1$
and
![]() $\mathbf {Sp}_{2g}$
for
$\mathbf {Sp}_{2g}$
for
![]() $\epsilon =-1$
. Observe that
$\epsilon =-1$
. Observe that
![]() $\mathrm {O}_{\epsilon }(H(g))$
is a subgroup of
$\mathrm {O}_{\epsilon }(H(g))$
is a subgroup of
![]() $\mathrm {GL}_{2g}(\mathbb {Q})$
and the intersection
$\mathrm {GL}_{2g}(\mathbb {Q})$
and the intersection
![]() $\mathrm {O}_{\epsilon }(H(g)) \cap \mathrm {GL}_{2g}(\mathbb {Z})$
is
$\mathrm {O}_{\epsilon }(H(g)) \cap \mathrm {GL}_{2g}(\mathbb {Z})$
is
![]() $\mathrm {O}_{g,g}(\mathbb {Z})$
if
$\mathrm {O}_{g,g}(\mathbb {Z})$
if
![]() $\epsilon =1$
and
$\epsilon =1$
and
![]() $\mathrm {Sp}_{2g}(\mathbb {Z})$
if
$\mathrm {Sp}_{2g}(\mathbb {Z})$
if
![]() $\epsilon =-1$
.
$\epsilon =-1$
.
For distinct i and j in
![]() $\{1,2,\ldots ,q\}$
, applying the pairing
$\{1,2,\ldots ,q\}$
, applying the pairing
![]() $\lambda $
to the ith and jth factors yields a map
$\lambda $
to the ith and jth factors yields a map
and inserting the form
![]() $\omega $
in the ith and jth factors yields a map
$\omega $
in the ith and jth factors yields a map
We obtain representations of
![]() $\mathrm {O}_{\epsilon }(H(g))$
by
$\mathrm {O}_{\epsilon }(H(g))$
by

and the composition
![]() $H(g)^{[q]} \to H(g)^{\otimes q} \to H(g)_{[q]}$
is an isomorphism. The action of the symmetric group
$H(g)^{[q]} \to H(g)^{\otimes q} \to H(g)_{[q]}$
is an isomorphism. The action of the symmetric group
![]() $\Sigma _q$
permuting the terms in the tensor product
$\Sigma _q$
permuting the terms in the tensor product
![]() $H(g)^{\otimes q}$
descends to an action on
$H(g)^{\otimes q}$
descends to an action on
![]() $H(g)^{[q]}$
and
$H(g)^{[q]}$
and
![]() $H(g)_{[q]}$
.
$H(g)_{[q]}$
.
Recall that the irreducible rational representations of
![]() $\mathfrak {S}_q$
are in bijection with partitions
$\mathfrak {S}_q$
are in bijection with partitions
![]() $\lambda $
of q into positive integers; these are denoted
$\lambda $
of q into positive integers; these are denoted
![]() $S^{\lambda }$
. Then we define
$S^{\lambda }$
. Then we define
By construction, these are algebraic
![]() $\mathrm {O}_{\epsilon }(H(g))$
-representations. They are either zero or irreducible, and the irreducible ones are distinct and exhaust all isomorphism classes.
$\mathrm {O}_{\epsilon }(H(g))$
-representations. They are either zero or irreducible, and the irreducible ones are distinct and exhaust all isomorphism classes.
We will have a use for representations of arithmetic subgroups
![]() $G \subset \mathrm {O}_{\epsilon }(H(g))$
, that is, groups
$G \subset \mathrm {O}_{\epsilon }(H(g))$
, that is, groups
![]() $G \subset \mathrm { O}_{\epsilon }(H(g))$
which are commensurable with
$G \subset \mathrm { O}_{\epsilon }(H(g))$
which are commensurable with
![]() $\mathrm {O}_{g,g}(\mathbb {Z})$
or
$\mathrm {O}_{g,g}(\mathbb {Z})$
or
![]() $\mathrm {Sp}_{2g}(\mathbb {Z})$
. As long as
$\mathrm {Sp}_{2g}(\mathbb {Z})$
. As long as
![]() $g \geq 2$
, the
$g \geq 2$
, the
![]() $V_{\lambda }$
restrict to irreducible algebraic representations of G and any algebraic representation of G is a direct sum of these [Reference Koike and TeradaKRW20c, Section 2.1].
$V_{\lambda }$
restrict to irreducible algebraic representations of G and any algebraic representation of G is a direct sum of these [Reference Koike and TeradaKRW20c, Section 2.1].
3 The Torelli Lie algebra
3.1 Basic results
3.1.1 Definitions
Let
![]() $\Sigma ^r_{g,n}$
be a surface of genus g with n boundary components and r marked points, and
$\Sigma ^r_{g,n}$
be a surface of genus g with n boundary components and r marked points, and
![]() $\Gamma ^r_{g,n}$
its mapping class group, consisting of isotopy classes of orientation-preserving diffeomorphism fixing pointwise the boundary components and the marked points. Its Torelli group is the subgroup
$\Gamma ^r_{g,n}$
its mapping class group, consisting of isotopy classes of orientation-preserving diffeomorphism fixing pointwise the boundary components and the marked points. Its Torelli group is the subgroup
![]() $T_{g,n}^r \subset \Gamma _{g,n}^r$
of those isotopy classes which act as the identity on
$T_{g,n}^r \subset \Gamma _{g,n}^r$
of those isotopy classes which act as the identity on
![]() $H_1(\Sigma _g;\mathbb {Z})$
through the inclusion
$H_1(\Sigma _g;\mathbb {Z})$
through the inclusion
![]() $\Sigma _{g,n}^r \hookrightarrow \Sigma _g$
. Its pro-unipotent, or Malcev, completion
$\Sigma _{g,n}^r \hookrightarrow \Sigma _g$
. Its pro-unipotent, or Malcev, completion
![]() $\mathfrak {t}^r_{g,n}$
is the Lie algebra of the initial pro-unipotent algebraic group over
$\mathfrak {t}^r_{g,n}$
is the Lie algebra of the initial pro-unipotent algebraic group over
![]() $\mathbb {Q}$
under
$\mathbb {Q}$
under
![]() $T^r_{g,n}$
.
$T^r_{g,n}$
.
There is a tautological extension of groups
![]() $T_{g,n}^r \to \Gamma _{g,n}^r \to \mathrm {Sp}_{2g}(\mathbb {Z})$
, and the induced representation
$T_{g,n}^r \to \Gamma _{g,n}^r \to \mathrm {Sp}_{2g}(\mathbb {Z})$
, and the induced representation
![]() $\Gamma _{g,n}^r \to \mathrm {Sp}_{2g}(\mathbb {Q})$
into the
$\Gamma _{g,n}^r \to \mathrm {Sp}_{2g}(\mathbb {Q})$
into the
![]() $\mathbb {Q}$
-points of the algebraic group
$\mathbb {Q}$
-points of the algebraic group
![]() $\mathbf {Sp}_{2g}$
is Zariski dense. There is an initial pro-algebraic group
$\mathbf {Sp}_{2g}$
is Zariski dense. There is an initial pro-algebraic group
![]() $\mathcal {G}_{g,n}^r$
over
$\mathcal {G}_{g,n}^r$
over
![]() $\mathbb {Q}$
with Zariski dense homomorphism to
$\mathbb {Q}$
with Zariski dense homomorphism to
![]() $\mathbf {Sp}_{2g}$
and pro-unipotent kernel [Reference HainHai93, §2]. The Lie algebra of
$\mathbf {Sp}_{2g}$
and pro-unipotent kernel [Reference HainHai93, §2]. The Lie algebra of
![]() $\mathcal {G}_{g,n}^r$
is
$\mathcal {G}_{g,n}^r$
is
![]() $\mathfrak {g}_{g,n}^r$
and the pro-nilpotent Lie algebra of this kernel is the relative unipotent completion
$\mathfrak {g}_{g,n}^r$
and the pro-nilpotent Lie algebra of this kernel is the relative unipotent completion
![]() $\mathfrak {u}_{g,n}^r$
of
$\mathfrak {u}_{g,n}^r$
of
![]() $T_{g,n}^r$
.
$T_{g,n}^r$
.
Let
![]() $\mathfrak {p}^r_{g,n}$
denote the Lie algebra of the pro-unipotent completion of the fundamental group
$\mathfrak {p}^r_{g,n}$
denote the Lie algebra of the pro-unipotent completion of the fundamental group
![]() $\pi ^r_{g,n}$
of the ordered configuration space in
$\pi ^r_{g,n}$
of the ordered configuration space in
![]() $\Sigma _g$
of r points and n points with nonzero tangent vector (in the notation of [Reference HainHai97] we have
$\Sigma _g$
of r points and n points with nonzero tangent vector (in the notation of [Reference HainHai97] we have
![]() $\mathfrak {p}_g = \mathfrak {p}^1_g$
). The usual extensions of groups relating mapping class groups yield extensions of Lie algebras (Theorem 3.4 and Proposition 3.6 of [Reference HainHai97]).
$\mathfrak {p}_g = \mathfrak {p}^1_g$
). The usual extensions of groups relating mapping class groups yield extensions of Lie algebras (Theorem 3.4 and Proposition 3.6 of [Reference HainHai97]).
Lemma 3.1. For
![]() $g \geq 3$
, there are extensions of Lie algebras
$g \geq 3$
, there are extensions of Lie algebras
3.1.2 Mixed Hodge structures and lower central series
The associated graded of the lower central series of a Lie algebra
![]() $\mathfrak {g}$
is a Lie algebra
$\mathfrak {g}$
is a Lie algebra
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {g}$
. We consider this as a Lie algebra in
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {g}$
. We consider this as a Lie algebra in
![]() $\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})^{\mathbb {N}}$
by giving it homological degree 0 and giving
$\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})^{\mathbb {N}}$
by giving it homological degree 0 and giving
![]() $\mathrm {Gr}^w_{\mathrm {LCS}}\, \mathfrak {g}$
weight w. In the following, there are unfortunately two things called weight: our additional grading and the Hodge theoretic weight filtration. We do not think any confusion is likely, but we shall refer to our weight grading as ‘the additional grading’ in places where confusion is possible.
$\mathrm {Gr}^w_{\mathrm {LCS}}\, \mathfrak {g}$
weight w. In the following, there are unfortunately two things called weight: our additional grading and the Hodge theoretic weight filtration. We do not think any confusion is likely, but we shall refer to our weight grading as ‘the additional grading’ in places where confusion is possible.
As long as
![]() $g \geq 3$
, Theorem 4.10 of [Reference HainHai97] says that
$g \geq 3$
, Theorem 4.10 of [Reference HainHai97] says that
![]() $\mathfrak {t}_{g,n}^r$
is equipped with a mixed Hodge structure whose weight filtration agrees, up to negation of the indexing, with the lower central filtration. By Corollary 4.8 and 4.9 of loc. cit., the same is true for
$\mathfrak {t}_{g,n}^r$
is equipped with a mixed Hodge structure whose weight filtration agrees, up to negation of the indexing, with the lower central filtration. By Corollary 4.8 and 4.9 of loc. cit., the same is true for
![]() $\mathfrak {u}_{g,n}^r$
. Corollary 5.3 of loc. cit. (stated over
$\mathfrak {u}_{g,n}^r$
. Corollary 5.3 of loc. cit. (stated over
![]() $\mathbb {C}$
, see [Reference HirschhornHai20, Section 7.4] for why it is also true over
$\mathbb {C}$
, see [Reference HirschhornHai20, Section 7.4] for why it is also true over
![]() $\mathbb {Q}$
) implies that for
$\mathbb {Q}$
) implies that for
![]() $g \geq 3$
there are isomorphisms of pro-nilpotent Lie algebras
$g \geq 3$
there are isomorphisms of pro-nilpotent Lie algebras
Similarly,
![]() $\mathfrak {p}^r_{g,n}$
comes with a mixed Hodge structure [Reference HainHai87, Theorem 1], and by Section 2 and Lemma 4.7 of [Reference HainHai97] its weight filtration agrees, up to negation of the indexing, with the lower central series filtration.
$\mathfrak {p}^r_{g,n}$
comes with a mixed Hodge structure [Reference HainHai87, Theorem 1], and by Section 2 and Lemma 4.7 of [Reference HainHai97] its weight filtration agrees, up to negation of the indexing, with the lower central series filtration.
The existence of compatible mixed Hodge structures implies that taking the associated graded of the weight filtration is exact and hence so is taking the associated graded of the lower central series filtration. In Lemma 3.1, the two copies of
![]() $\mathbb {Q}$
are the Hodge structures
$\mathbb {Q}$
are the Hodge structures
![]() $\mathbb {Q}(1)$
, so we obtain the following (using Section 13 and Theorem 4.10 of [Reference HainHai97]), where we clarify that the
$\mathbb {Q}(1)$
, so we obtain the following (using Section 13 and Theorem 4.10 of [Reference HainHai97]), where we clarify that the
![]() $\mathbb {Q}[2]$
are in weight
$\mathbb {Q}[2]$
are in weight
![]() $2$
and homological degree
$2$
and homological degree
![]() $0$
.
$0$
.
Lemma 3.2. For
![]() $g \geq 3$
, there are extensions of Lie algebras with additional grading
$g \geq 3$
, there are extensions of Lie algebras with additional grading
3.1.3 Koszulness
The general version of Theorem A is as follows.
Theorem 3.3. The Lie algebras with additional grading
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
,
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
,
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g}^1$
,
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g}^1$
,
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g$
,
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g$
,
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g,1}$
,
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g,1}$
,
![]() ${\mathrm { Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}^1_g$
and
${\mathrm { Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}^1_g$
and
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_g$
are Koszul in weight
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_g$
are Koszul in weight
![]() $\leq \tfrac {g}{3}$
.
$\leq \tfrac {g}{3}$
.
The following proposition shows that Theorem A implies Theorem 3.3, so we may focus on Theorem A for the remainder of this paper.
Proposition 3.4. Suppose
![]() $g \geq 3$
and that
$g \geq 3$
and that
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
is Koszul in weight
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
is Koszul in weight
![]() $\leq W$
. Then the same is true for
$\leq W$
. Then the same is true for
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g}^1$
,
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g}^1$
,
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g$
,
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g$
,
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g,1}$
,
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g,1}$
,
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}^1_g$
and
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}^1_g$
and
![]() ${\mathrm { Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_g$
.
${\mathrm { Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_g$
.
Proof. Though we defined Koszulness in terms of Chevalley–Eilenberg homology, to verify its vanishing we may as well use Chevalley–Eilenberg cohomology, and take advantage of its multiplicative structure. We first prove that
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}^1_g$
is Koszul in additional gradings
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}^1_g$
is Koszul in additional gradings
![]() $ \leq W$
, by considering the spectral sequence in Lie algebra cohomology for the extension
$ \leq W$
, by considering the spectral sequence in Lie algebra cohomology for the extension
of Lemma 3.2. This yields a Gysin sequence
If
![]() $w \leq W$
, then the right-hand term is zero whenever
$w \leq W$
, then the right-hand term is zero whenever
![]() $p \neq w$
, in which case
$p \neq w$
, in which case
![]() $H_{\mathrm {Lie}}^{p}({\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g}^1)_{0,w}$
is infinitely divisible by e and hence vanishes. Thus,
$H_{\mathrm {Lie}}^{p}({\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g}^1)_{0,w}$
is infinitely divisible by e and hence vanishes. Thus,
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g}^1$
is also Koszul in additional gradings
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g}^1$
is also Koszul in additional gradings
![]() $ \leq W$
.
$ \leq W$
.
We next prove that
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,}\mathfrak {t}_g$
is Koszul in additional gradings
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,}\mathfrak {t}_g$
is Koszul in additional gradings
![]() $ \leq W$
, using the extension
$ \leq W$
, using the extension
of Lemma 3.2. We will make use of continuous Lie algebra cohomology; see [Reference HainHai97, Section 5] for background. By Proposition 5.5 of [Reference HainHai97], we have an isomorphism
and as surface groups are pseudo-nilpotent [Reference Kupers and Randal-WilliamsKO87] we have
![]() $H^*_{\mathrm {Lie}, \text {cts}}(\mathfrak {p}_g) = H^*(\Sigma _g; \mathbb {Q})$
. In particular, we have
$H^*_{\mathrm {Lie}, \text {cts}}(\mathfrak {p}_g) = H^*(\Sigma _g; \mathbb {Q})$
. In particular, we have
![]() $H_{\mathrm {Lie}}^2({\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {p}_g) = \mathbb {Q}$
and the cohomology in higher degrees vanishes. Thus, in the spectral sequence for this extension projection to the top row provides a fibre-integration map
$H_{\mathrm {Lie}}^2({\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {p}_g) = \mathbb {Q}$
and the cohomology in higher degrees vanishes. Thus, in the spectral sequence for this extension projection to the top row provides a fibre-integration map
which as usual is a map of
![]() $H^{*}_{\mathrm {Lie}}({\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g)$
-modules and satisfies
$H^{*}_{\mathrm {Lie}}({\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g)$
-modules and satisfies
![]() $\pi _!(e) = 2-2g \neq 0 \in H_{\mathrm {Lie}}^{0}({\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g)$
by comparison to the corresponding extension of groups
$\pi _!(e) = 2-2g \neq 0 \in H_{\mathrm {Lie}}^{0}({\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g)$
by comparison to the corresponding extension of groups
![]() $\pi _1(\Sigma _g) \to T_g^1 \to T_g$
. In particular, this implies that
$\pi _1(\Sigma _g) \to T_g^1 \to T_g$
. In particular, this implies that
![]() $\pi ^*\colon H_{\mathrm {Lie}}^{p}({\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g)_{0,w} \to H_{\mathrm {Lie}}^{p}({\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g^1)_{0,w}$
is injective. Assuming
$\pi ^*\colon H_{\mathrm {Lie}}^{p}({\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g)_{0,w} \to H_{\mathrm {Lie}}^{p}({\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g^1)_{0,w}$
is injective. Assuming
![]() ${\mathrm { Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g^1$
is Koszul the target of this map vanishes for
${\mathrm { Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g^1$
is Koszul the target of this map vanishes for
![]() $p \neq w$
and
$p \neq w$
and
![]() $w \leq W$
: Thus, the source does too.
$w \leq W$
: Thus, the source does too.
For
![]() $\mathfrak {u}_{g,1}$
, we use the extension
$\mathfrak {u}_{g,1}$
, we use the extension
![]() $\mathbb {Q}(1) \to \mathfrak {t}_{g,1} \to \mathfrak {u}_{g,1}$
of Lie algebras with mixed Hodge structure and proceed as we did above for
$\mathbb {Q}(1) \to \mathfrak {t}_{g,1} \to \mathfrak {u}_{g,1}$
of Lie algebras with mixed Hodge structure and proceed as we did above for
![]() $\mathfrak {t}^1_g$
, taking associated graded and using the Gysin sequence;
$\mathfrak {t}^1_g$
, taking associated graded and using the Gysin sequence;
![]() $\mathfrak {u}_g^1$
and
$\mathfrak {u}_g^1$
and
![]() $\mathfrak {u}_g$
may be treated similarly.
$\mathfrak {u}_g$
may be treated similarly.
Remark 3.5. The Lie algebra
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g}$
for
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g}$
for
![]() $g \geq 4$
can never actually be Koszul, and hence neither can
$g \geq 4$
can never actually be Koszul, and hence neither can
![]() ${\mathrm { Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g}^1$
or
${\mathrm { Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g}^1$
or
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
be by the proof of Proposition 3.4. If
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
be by the proof of Proposition 3.4. If
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g}$
were Koszul, then
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g}$
were Koszul, then
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g}$
would be too by the Gysin sequence argument of Proposition 3.4 applied to
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g}$
would be too by the Gysin sequence argument of Proposition 3.4 applied to
This would imply that the cohomology algebras
![]() $H^*_{\mathrm {Lie}}({\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g})$
and
$H^*_{\mathrm {Lie}}({\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g})$
and
![]() $H^*_{\mathrm {Lie}}({\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g})$
are both generated in tridegree
$H^*_{\mathrm {Lie}}({\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g})$
are both generated in tridegree
![]() $(1,0,1)$
by the same vector space
$(1,0,1)$
by the same vector space
![]() $(\mathrm {Gr}_{\text {LCS}}^1\, \mathfrak {u}_{g})^{\vee } \overset {\sim } \to (\mathrm {Gr}_{\text {LCS}}^1\, \mathfrak {t}_{g})^{\vee }$
. This is finite-dimensional for
$(\mathrm {Gr}_{\text {LCS}}^1\, \mathfrak {u}_{g})^{\vee } \overset {\sim } \to (\mathrm {Gr}_{\text {LCS}}^1\, \mathfrak {t}_{g})^{\vee }$
. This is finite-dimensional for
![]() $g \geq 3$
by a theorem of Johnson [Reference Kawazumi and MoritaJoh85], so the map
$g \geq 3$
by a theorem of Johnson [Reference Kawazumi and MoritaJoh85], so the map
is surjective and both cohomology groups vanish above some cohomological degree. Let the top degrees in which the cohomologies are nontrivial be called U and T, so this surjection shows that
![]() $U \geq T$
. On the other hand the Gysin sequence for the extension shows that
$U \geq T$
. On the other hand the Gysin sequence for the extension shows that
![]() $T = U+1$
, a contradiction.
$T = U+1$
, a contradiction.
As far as we can tell Koszulness of
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,}\mathfrak {u}_g$
cannot be ruled out in this way:
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,}\mathfrak {u}_g$
cannot be ruled out in this way:
Question 3.6. Is it possible that
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,}\mathfrak {u}_g$
is Koszul?
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,}\mathfrak {u}_g$
is Koszul?
3.1.4 Quadratic presentations
We will take from the work of Hain only the fact that the Lie algebra
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
is quadratically presented and not a particular presentation: In the following section, we will deduce from this fact a presentation that is convenient for us.
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
is quadratically presented and not a particular presentation: In the following section, we will deduce from this fact a presentation that is convenient for us.
For
![]() $g \geq 6$
, the following is [Reference HainHai97, Corollary 7.8] (beware that what is denoted
$g \geq 6$
, the following is [Reference HainHai97, Corollary 7.8] (beware that what is denoted
![]() $\mathfrak {t}_{g,n}$
in [Reference HainHai15, Theorem 7.8] is denoted
$\mathfrak {t}_{g,n}$
in [Reference HainHai15, Theorem 7.8] is denoted
![]() $\mathfrak {t}_{g}^n$
in [Reference HainHai97] and here). It can be generalised to
$\mathfrak {t}_{g}^n$
in [Reference HainHai97] and here). It can be generalised to
![]() $g \geq 4$
using the results in [Reference HainHai15, Section 7].
$g \geq 4$
using the results in [Reference HainHai15, Section 7].
Theorem 3.7 (Hain)
For
![]() $g \geq 4$
and
$g \geq 4$
and
![]() $r,n \geq 0$
, the Lie algebras with additional grading
$r,n \geq 0$
, the Lie algebras with additional grading
![]() ${\mathrm { Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,r}^n$
and
${\mathrm { Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,r}^n$
and
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g,r}^n$
are quadratically presented.
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {u}_{g,r}^n$
are quadratically presented.
![]() $ \Box $
$ \Box $
3.2 Cohomology of
 $\mathfrak {t}_{g,1}$
in low degrees
$\mathfrak {t}_{g,1}$
in low degrees
Following Morita and Kawazumi [Reference Kohno and OdaKM96], in [Reference Koike and TeradaKRW20c, Section 5.1] we have constructed, for each
![]() $a,r \geq 0$
with
$a,r \geq 0$
with
![]() $r+2a -2 \geq 0$
and tuple
$r+2a -2 \geq 0$
and tuple
![]() $v_1, v_2, \ldots , v_r \in H^1(\Sigma _g;\mathbb {Q})$
, a cohomology class
$v_1, v_2, \ldots , v_r \in H^1(\Sigma _g;\mathbb {Q})$
, a cohomology class
generalising the Miller–Morita–Mumford class
![]() $\kappa _{e^a}$
; we refer to it as a twisted MMM-class. (We often write
$\kappa _{e^a}$
; we refer to it as a twisted MMM-class. (We often write
![]() $1$
for
$1$
for
![]() $e^0$
.) This construction is linear in the
$e^0$
.) This construction is linear in the
![]() $v_i$
, is alternating under permuting the
$v_i$
, is alternating under permuting the
![]() $v_i$
and is
$v_i$
and is
![]() $\mathrm {Sp}_{2g}(\mathbb {Z})$
-equivariant.
$\mathrm {Sp}_{2g}(\mathbb {Z})$
-equivariant.
Lemma 3.8. If
![]() $\{a_i\}$
is a basis of
$\{a_i\}$
is a basis of
![]() $H^1(\Sigma _g;\mathbb {Q})$
and
$H^1(\Sigma _g;\mathbb {Q})$
and
![]() $\{a_i^{\#}\}$
is the dual basis characterised by
$\{a_i^{\#}\}$
is the dual basis characterised by
![]() $\langle a_i^{\#} \cdot a_j, [\Sigma _g] \rangle = \delta _{ij}$
, then there are relations
$\langle a_i^{\#} \cdot a_j, [\Sigma _g] \rangle = \delta _{ij}$
, then there are relations
 $$ \begin{align*} \sum_i \kappa_{e^a}(v_1 \otimes \cdots \otimes v_j \otimes a_i) \cdot \kappa_{e^b}(a_i^{\#} \otimes v_{j+1} \otimes \cdots \otimes v_r) &= \kappa_{e^{a+b}}(v_1 \otimes \cdots \otimes v_r)\\ \sum_i \kappa_{e^a}(v_1 \otimes \cdots \otimes v_r \otimes a_i \otimes a_i^{\#}) &=\kappa_{e^{a+1}}(v_1 \otimes \cdots \otimes v_r)\\ \sum_{i,j,k} \kappa_1(a_i \otimes a_j \otimes a_k) \cdot \kappa_1(a_i^{\#} \otimes a_j^{\#} \otimes a_k^{\#}) &=0. \end{align*} $$
$$ \begin{align*} \sum_i \kappa_{e^a}(v_1 \otimes \cdots \otimes v_j \otimes a_i) \cdot \kappa_{e^b}(a_i^{\#} \otimes v_{j+1} \otimes \cdots \otimes v_r) &= \kappa_{e^{a+b}}(v_1 \otimes \cdots \otimes v_r)\\ \sum_i \kappa_{e^a}(v_1 \otimes \cdots \otimes v_r \otimes a_i \otimes a_i^{\#}) &=\kappa_{e^{a+1}}(v_1 \otimes \cdots \otimes v_r)\\ \sum_{i,j,k} \kappa_1(a_i \otimes a_j \otimes a_k) \cdot \kappa_1(a_i^{\#} \otimes a_j^{\#} \otimes a_k^{\#}) &=0. \end{align*} $$
Proof. The first two are given in [Reference Koike and TeradaKRW20c, Section 5.2]. Repeatedly applying the first two relations shows that
![]() $\sum _{i,j,k} \kappa _1(a_i \otimes a_j \otimes a_k) \cdot \kappa _1(a_i^{\#} \otimes a_j^{\#} \otimes a_k^{\#}) = - \kappa _{e^2}$
. Now,
$\sum _{i,j,k} \kappa _1(a_i \otimes a_j \otimes a_k) \cdot \kappa _1(a_i^{\#} \otimes a_j^{\#} \otimes a_k^{\#}) = - \kappa _{e^2}$
. Now,
![]() $e^2 = p_1 = 3 \mathcal {L}_1$
and we have
$e^2 = p_1 = 3 \mathcal {L}_1$
and we have
![]() $\kappa _{\mathcal {L}_1}=0 \in H^2(T_{g,1};\mathbb {Q})$
as a consequence of the family signature theorem (see, e.g., [Reference Andersson, Willwacher and ZivkovicAti69]).
$\kappa _{\mathcal {L}_1}=0 \in H^2(T_{g,1};\mathbb {Q})$
as a consequence of the family signature theorem (see, e.g., [Reference Andersson, Willwacher and ZivkovicAti69]).
This construction for
![]() $a=0$
and
$a=0$
and
![]() $r=3$
gives a map of
$r=3$
gives a map of
![]() $\mathrm {Sp}_{2g}(\mathbb {Z})$
-representations
$\mathrm {Sp}_{2g}(\mathbb {Z})$
-representations
Remark 3.9. The linear dual
![]() $H_{1}(T_{g,1};\mathbb {Q}) \to \Lambda ^3 V_1$
of
$H_{1}(T_{g,1};\mathbb {Q}) \to \Lambda ^3 V_1$
of
![]() $\kappa _1$
may be identified with the Johnson homomorphism [Reference Kawazumi and MoritaJoh85].
$\kappa _1$
may be identified with the Johnson homomorphism [Reference Kawazumi and MoritaJoh85].
Taking cup products of such classes determines an algebra homomorphism
It follows from the discussion in [Reference Koike and TeradaKRW20c, Section 8.2] and the estimate in [Reference Koike and TeradaKRW20c, Section 9.3] that as long as
![]() $g \geq 4$
this map is an isomorphism in degree 1 and its kernel in degree 2 is spanned by the terms
$g \geq 4$
this map is an isomorphism in degree 1 and its kernel in degree 2 is spanned by the terms
 $$ \begin{align} \sum_i \kappa_1(v_1 \otimes v_2 \otimes a_i) \cdot \kappa_1(a_i^{\#} \otimes v_5 \otimes v_6) - \sum_i \kappa_1(v_1 \otimes v_5 \otimes a_i) \cdot \kappa_1(a_i^{\#} \otimes v_6 \otimes v_2) \end{align} $$
$$ \begin{align} \sum_i \kappa_1(v_1 \otimes v_2 \otimes a_i) \cdot \kappa_1(a_i^{\#} \otimes v_5 \otimes v_6) - \sum_i \kappa_1(v_1 \otimes v_5 \otimes a_i) \cdot \kappa_1(a_i^{\#} \otimes v_6 \otimes v_2) \end{align} $$
for
![]() $v_1, v_2, v_5, v_6 \in H^1(\Sigma _{g,1};\mathbb {Q})$
, as well as the invariant vector
$v_1, v_2, v_5, v_6 \in H^1(\Sigma _{g,1};\mathbb {Q})$
, as well as the invariant vector
(which, as we showed in the proof of Lemma 3.8 above, represents
![]() $-3 \kappa _{\mathcal {L}_1}$
). Furthermore, in degrees
$-3 \kappa _{\mathcal {L}_1}$
). Furthermore, in degrees
![]() $\leq 2$
the image of
$\leq 2$
the image of
![]() $\phi $
is the maximal algebraic subrepresentation
$\phi $
is the maximal algebraic subrepresentation
![]() $H^{*}(T_{g,1};\mathbb {Q})^{\text {alg}}$
.
$H^{*}(T_{g,1};\mathbb {Q})^{\text {alg}}$
.
Theorem 3.10. There is a homomorphism of trigraded algebras
 $$\begin{align*}\psi \colon \frac{\Lambda^*[\Lambda^3 V_1[1,0,1]]}{((\text{IH}), (\Theta))} \longrightarrow H_{\mathrm{Lie}}^{*}({\mathrm{Gr}^{\bullet}_{\mathrm{LCS}}\,} \mathfrak{t}_{g,1})_{*,*},\end{align*}$$
$$\begin{align*}\psi \colon \frac{\Lambda^*[\Lambda^3 V_1[1,0,1]]}{((\text{IH}), (\Theta))} \longrightarrow H_{\mathrm{Lie}}^{*}({\mathrm{Gr}^{\bullet}_{\mathrm{LCS}}\,} \mathfrak{t}_{g,1})_{*,*},\end{align*}$$
which as long as
![]() $g \geq 4$
is an isomorphism in cohomological degrees
$g \geq 4$
is an isomorphism in cohomological degrees
![]() $* \leq 2$
.
$* \leq 2$
.
Proof. We will work with the continuous Lie algebra cohomology
![]() $H_{\mathrm {Lie}, \text {cts}}^*(\mathfrak {t}_{g,1})$
, cf. [Reference HainHai97, Section 5]. By [Reference HainHai97, Proposition 5.5], there is an isomorphism
$H_{\mathrm {Lie}, \text {cts}}^*(\mathfrak {t}_{g,1})$
, cf. [Reference HainHai97, Section 5]. By [Reference HainHai97, Proposition 5.5], there is an isomorphism
and by [Reference HainHai97, Theorem 4.10] there is an identification
By definition of the lower central series, this Lie algebra with additional grading is generated by its piece of grading 1. Its grading 1 piece is by definition the abelianisation of the Lie algebra
![]() $\mathfrak {t}_{g,1}$
, which is tautologically identified with
$\mathfrak {t}_{g,1}$
, which is tautologically identified with
![]() $H_1(T_{g,1};\mathbb {Q})$
and so for
$H_1(T_{g,1};\mathbb {Q})$
and so for
![]() $g \geq 3$
is the algebraic
$g \geq 3$
is the algebraic
![]() $\mathrm {Sp}_{2g}(\mathbb {Z})$
-representation
$\mathrm {Sp}_{2g}(\mathbb {Z})$
-representation
![]() $\Lambda ^3 V_1$
by a theorem of Johnson [Reference Kawazumi and MoritaJoh85]. It follows that the Lie algebra with additional grading
$\Lambda ^3 V_1$
by a theorem of Johnson [Reference Kawazumi and MoritaJoh85]. It follows that the Lie algebra with additional grading
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
is a finite-dimensional algebraic
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
is a finite-dimensional algebraic
![]() $\mathrm {Sp}_{2g}(\mathbb {Z})$
-representation in each additional grading, so
$\mathrm {Sp}_{2g}(\mathbb {Z})$
-representation in each additional grading, so
![]() $\smash {\mathrm { Gr}^W_{\bullet }} H_{\mathrm {Lie}, \text {cts}}^*(\mathfrak {t}_{g,1})$
is a finite-dimensional algebraic
$\smash {\mathrm { Gr}^W_{\bullet }} H_{\mathrm {Lie}, \text {cts}}^*(\mathfrak {t}_{g,1})$
is a finite-dimensional algebraic
![]() $\mathrm { Sp}_{2g}(\mathbb {Z})$
-representation in each bigrading. As the weight filtration is finite in each cohomological degree, it follows that
$\mathrm { Sp}_{2g}(\mathbb {Z})$
-representation in each bigrading. As the weight filtration is finite in each cohomological degree, it follows that
![]() $H_{\mathrm {Lie}, \text {cts}}^*(\mathfrak {t}_{g,1})$
is a finite-dimensional algebraic
$H_{\mathrm {Lie}, \text {cts}}^*(\mathfrak {t}_{g,1})$
is a finite-dimensional algebraic
![]() $\mathrm {Sp}_{2g}(\mathbb {Z})$
-representation in each degree.
$\mathrm {Sp}_{2g}(\mathbb {Z})$
-representation in each degree.
Consider the natural map
By the discussion above, it has image in the maximal algebraic subrepresentation
![]() $ H^{*}(T_{g,1};\mathbb {Q})^{\text {alg}}$
. As
$ H^{*}(T_{g,1};\mathbb {Q})^{\text {alg}}$
. As
![]() $H^1(T_{g,1};\mathbb {Q}) \cong \Lambda ^3 V_1$
is finite-dimensional, [Reference HainHai97, Proposition 5.1] implies that (3) is an isomorphism in degree 1 and a monomorphism in degree 2. Thus,
$H^1(T_{g,1};\mathbb {Q}) \cong \Lambda ^3 V_1$
is finite-dimensional, [Reference HainHai97, Proposition 5.1] implies that (3) is an isomorphism in degree 1 and a monomorphism in degree 2. Thus,
![]() $\phi $
factors as
$\phi $
factors as
and the relations (IH) and (Θ) hold in
![]() $H_{\mathrm {Lie}, \text {cts}}^2(\mathfrak {t}_{g,1})$
, so
$H_{\mathrm {Lie}, \text {cts}}^2(\mathfrak {t}_{g,1})$
, so
![]() $\psi "$
descends to give
$\psi "$
descends to give
 $$\begin{align*}\frac{\Lambda^*[\Lambda^3 V_1[1]]}{(({IH}), (\Theta))} \overset{\psi'}\longrightarrow H_{\mathrm{Lie}, \text{cts}}^{*}(\mathfrak{t}_{g,1}) \longrightarrow H^{*}(T_{g,1};\mathbb{Q})^{\text{alg}}\end{align*}$$
$$\begin{align*}\frac{\Lambda^*[\Lambda^3 V_1[1]]}{(({IH}), (\Theta))} \overset{\psi'}\longrightarrow H_{\mathrm{Lie}, \text{cts}}^{*}(\mathfrak{t}_{g,1}) \longrightarrow H^{*}(T_{g,1};\mathbb{Q})^{\text{alg}}\end{align*}$$
with
![]() $\psi '$
an isomorphism in degree 1 and a monomorphism in degree 2. By the discussion above the composition is an isomorphism in degrees
$\psi '$
an isomorphism in degree 1 and a monomorphism in degree 2. By the discussion above the composition is an isomorphism in degrees
![]() $\leq 2$
, so it follows that
$\leq 2$
, so it follows that
![]() $\psi '$
is too.
$\psi '$
is too.
It follows from (1) and (2) that
![]() $H_{\mathrm {Lie}, \text {cts}}^{1}(\mathfrak {t}_{g,1})$
is a pure Hodge structure of weight
$H_{\mathrm {Lie}, \text {cts}}^{1}(\mathfrak {t}_{g,1})$
is a pure Hodge structure of weight
![]() $-1$
, so if we give the domain of
$-1$
, so if we give the domain of
![]() $\psi '$
the weight filtration given by minus its degree, then
$\psi '$
the weight filtration given by minus its degree, then
![]() $\psi '$
is an isomorphism of weight-filtered graded vector spaces in degrees
$\psi '$
is an isomorphism of weight-filtered graded vector spaces in degrees
![]() $* \leq 2$
: passing to associated graded for the weight filtration, applying (1) and (2) again, and recalling that
$* \leq 2$
: passing to associated graded for the weight filtration, applying (1) and (2) again, and recalling that
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
is supported in homological degree 0, gives the map
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
is supported in homological degree 0, gives the map
![]() $\psi $
in the statement of the lemma and shows it is an isomorphism in cohomological degrees
$\psi $
in the statement of the lemma and shows it is an isomorphism in cohomological degrees
![]() $* \leq 2$
.
$* \leq 2$
.
Remark 3.11. It will be a consequence of Theorem A that
![]() $\psi $
is in fact an isomorphism in a stable range of degrees.
$\psi $
is in fact an isomorphism in a stable range of degrees.
Our next goal is to describe the quadratic presentation of
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
. This uses the following lemma.
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
. This uses the following lemma.
Lemma 3.12. Let W be a vector space and
![]() $Q \leq \Lambda ^2 W$
be a subspace, and form the quadratic Lie algebra
$Q \leq \Lambda ^2 W$
be a subspace, and form the quadratic Lie algebra
![]() $\mathfrak {g} = \mathrm {Lie}(W)/(Q)$
. Then
$\mathfrak {g} = \mathrm {Lie}(W)/(Q)$
. Then
-
(i) The abelianisation map
 $\mathfrak {g} \to W$
induces an isomorphism
$\mathfrak {g} \to W$
induces an isomorphism
 $W^{\vee } \overset {\sim }\to H_{\mathrm {Lie}}^1(\mathfrak {g})$
.
$W^{\vee } \overset {\sim }\to H_{\mathrm {Lie}}^1(\mathfrak {g})$
. -
(ii) The kernel of
 $\Lambda ^2 H_{\mathrm {Lie}}^1(\mathfrak {g}) \to H_{\mathrm {Lie}}^2(\mathfrak {g})$
is the annihilator of Q.
$\Lambda ^2 H_{\mathrm {Lie}}^1(\mathfrak {g}) \to H_{\mathrm {Lie}}^2(\mathfrak {g})$
is the annihilator of Q.
Proof. As
![]() $\mathfrak {g}$
is quadratically presented it admits an additional grading by weight, where W is put in weight 1. This endows the Chevalley–Eilenberg chains
$\mathfrak {g}$
is quadratically presented it admits an additional grading by weight, where W is put in weight 1. This endows the Chevalley–Eilenberg chains
![]() $(\mathrm {coCom}(\mathfrak {g}[1])[-1], d_{CE})$
with an additional weight grading, with respect to which it takes the form (homological degree is displayed horizontally, weight vertically)
$(\mathrm {coCom}(\mathfrak {g}[1])[-1], d_{CE})$
with an additional weight grading, with respect to which it takes the form (homological degree is displayed horizontally, weight vertically)

The maps from the second to the first column are given by
![]() $[-,-] \colon \Lambda ^2 \mathfrak {g} \to \mathfrak {g}$
so are surjective in weights
$[-,-] \colon \Lambda ^2 \mathfrak {g} \to \mathfrak {g}$
so are surjective in weights
![]() $>1$
, as
$>1$
, as
![]() $\mathfrak {g}$
is generated in weight 1. Dualising this complex, it follows that
$\mathfrak {g}$
is generated in weight 1. Dualising this complex, it follows that
![]() $H^1_{\mathrm {Lie}}(\mathfrak {g})=W^{\vee }$
and that there is an exact sequence as claimed
$H^1_{\mathrm {Lie}}(\mathfrak {g})=W^{\vee }$
and that there is an exact sequence as claimed
Let us write
![]() and
and
![]() $R^{\perp } \leq (\Lambda ^2 \Lambda ^3 V_1)^{\vee } \cong \Lambda ^2 \Lambda ^3 V_1$
for its annihilator.
$R^{\perp } \leq (\Lambda ^2 \Lambda ^3 V_1)^{\vee } \cong \Lambda ^2 \Lambda ^3 V_1$
for its annihilator.
Remark 3.13. As long as
![]() $g \geq 6$
we have the decomposition
$g \geq 6$
we have the decomposition
into irreducible
![]() $\mathrm {Sp}_{2g}(\mathbb {Z})$
-representations. The vectors (IH) generate the representation
$\mathrm {Sp}_{2g}(\mathbb {Z})$
-representations. The vectors (IH) generate the representation
![]() $V_0 + V_{1^2} + V_{2^2}$
(see [Reference Galatius and Randal-WilliamsGN98, Proof of Corollary 2.2 (ii)]Footnote 2), and the invariant vector (
$V_0 + V_{1^2} + V_{2^2}$
(see [Reference Galatius and Randal-WilliamsGN98, Proof of Corollary 2.2 (ii)]Footnote 2), and the invariant vector (
![]() $\Theta $
) can be checked not to lie in (IH). Therefore,
$\Theta $
) can be checked not to lie in (IH). Therefore,
![]() $R^{\perp } \cong 2 V_{1^2} + 2V_{1^4} + V_{1^6} + V_{2,1^2} + V_{2^2,1^2}$
. For
$R^{\perp } \cong 2 V_{1^2} + 2V_{1^4} + V_{1^6} + V_{2,1^2} + V_{2^2,1^2}$
. For
![]() $g < 6$
, the representation theory is degenerate but in principle a similar analysis can be made.
$g < 6$
, the representation theory is degenerate but in principle a similar analysis can be made.
The following is essentially in [Reference HainHai97], though Hain does not give the final answer in the case of
![]() $\mathfrak {t}_{g,1}$
. The explicit presentation produced by Hain’s method in this case was given in [Reference IsaacsonHS00] (and agrees with the following).
$\mathfrak {t}_{g,1}$
. The explicit presentation produced by Hain’s method in this case was given in [Reference IsaacsonHS00] (and agrees with the following).
Corollary 3.14 (Hain)
For
![]() $g \geq 4$
, there is an isomorphism
$g \geq 4$
, there is an isomorphism
Proof. As
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
admits a quadratic presentation by Theorem 3.7, it is isomorphic to
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
admits a quadratic presentation by Theorem 3.7, it is isomorphic to
![]() $\mathrm {Lie}(W)/ ( Q )$
for some vector space W of homological degree 0 and weight 1 and some
$\mathrm {Lie}(W)/ ( Q )$
for some vector space W of homological degree 0 and weight 1 and some
![]() $Q \leq \Lambda ^2 W$
, and we may apply Lemma 3.12 to determine W and Q in terms of
$Q \leq \Lambda ^2 W$
, and we may apply Lemma 3.12 to determine W and Q in terms of
![]() $H_{\mathrm {Lie}}^*({\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1})$
for
$H_{\mathrm {Lie}}^*({\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1})$
for
![]() $* \leq 2$
, which is given by Theorem 3.10. This gives
$* \leq 2$
, which is given by Theorem 3.10. This gives
![]() $W = (\Lambda ^3 V_1)^{\vee } \cong \Lambda ^3 V_1$
and
$W = (\Lambda ^3 V_1)^{\vee } \cong \Lambda ^3 V_1$
and
![]() $Q = R^{\perp }$
.
$Q = R^{\perp }$
.
Using Lemma 2.4, it follows that for
![]() $g \geq 4$
the Lie algebra
$g \geq 4$
the Lie algebra
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
is Koszul in weight
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
is Koszul in weight
![]() $\leq W$
if and only if the commutative algebra object
$\leq W$
if and only if the commutative algebra object
![]() $\frac {\Lambda ^*[\Lambda ^3 V_1[1,1]]}{(({IH}), (\Theta ))}$
in
$\frac {\Lambda ^*[\Lambda ^3 V_1[1,1]]}{(({IH}), (\Theta ))}$
in
![]() $\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})^{\mathbb {N}}$
is Koszul in weight
$\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})^{\mathbb {N}}$
is Koszul in weight
![]() $\leq W$
, allowing us to work with the latter.
$\leq W$
, allowing us to work with the latter.
4 Representations of the downward Brauer category
In this section, we define the objects
![]() $E_n$
and
$E_n$
and
![]() $Z_n$
, which are augmented unital commutative algebra objects in the category of representations of the downward (signed) Brauer category and explain how they relate to
$Z_n$
, which are augmented unital commutative algebra objects in the category of representations of the downward (signed) Brauer category and explain how they relate to
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
as well as each other.
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
as well as each other.
4.1 The downward Brauer category
The following is identical to [Reference Koike and TeradaKRW20c, Definition 2.15]. One thinks of the morphisms of this category as in Figure 1.

Figure 1 A graphical representation of a morphism
![]() $(f,m_S)$
in
$(f,m_S)$
in
![]() $\mathsf {dBr}(S,T)$
from a 7-element set S to a 5-element set T. The order of crossings is irrelevant.
$\mathsf {dBr}(S,T)$
from a 7-element set S to a 5-element set T. The order of crossings is irrelevant.
Definition 4.1. The downward Brauer category
![]() $\mathsf {dBr}$
is the
$\mathsf {dBr}$
is the
![]() $\mathbb {Q}\text {-}\mathsf {mod}$
-enriched category with objects finite sets, and with vector space of morphisms
$\mathbb {Q}\text {-}\mathsf {mod}$
-enriched category with objects finite sets, and with vector space of morphisms
![]() $\mathsf {dBr}(S,T)$
having basis the pairs
$\mathsf {dBr}(S,T)$
having basis the pairs
![]() $(f, m_S)$
of an injection
$(f, m_S)$
of an injection
![]() $f\colon T \hookrightarrow S$
and an unordered matching
$f\colon T \hookrightarrow S$
and an unordered matching
![]() $m_S$
on the set
$m_S$
on the set
![]() $S \setminus f(T)$
. It has a symmetric monoidality given by disjoint union.
$S \setminus f(T)$
. It has a symmetric monoidality given by disjoint union.
There is also the following signed version, identical to [Reference Koike and TeradaKRW20c, Definition 2.20].
Definition 4.2. The downward signed Brauer category
![]() $\mathsf {dsBr}$
is the
$\mathsf {dsBr}$
is the
![]() $\mathbb {Q}\text {-}\mathsf {mod}$
-enriched category with objects finite sets, and with vector space of morphisms
$\mathbb {Q}\text {-}\mathsf {mod}$
-enriched category with objects finite sets, and with vector space of morphisms
![]() $\mathsf {dsBr}(S,T)$
given as follows. First, let
$\mathsf {dsBr}(S,T)$
given as follows. First, let
![]() $\mathsf {dsBr}(S,T)'$
denote the vector space with basis the pairs
$\mathsf {dsBr}(S,T)'$
denote the vector space with basis the pairs
![]() $(f, m_S)$
of an injection
$(f, m_S)$
of an injection
![]() $f \colon T \hookrightarrow S$
and an ordered matching
$f \colon T \hookrightarrow S$
and an ordered matching
![]() $m_S$
of
$m_S$
of
![]() $S \setminus f(T)$
. Then let
$S \setminus f(T)$
. Then let
![]() $\mathsf {dsBr}(S,T)$
be the quotient space of
$\mathsf {dsBr}(S,T)$
be the quotient space of
![]() $\mathsf {dsBr}(S,T)'$
by the subspace spanned by elements
$\mathsf {dsBr}(S,T)'$
by the subspace spanned by elements
![]() $(f, m_S) - (-1)^r (f, m^{\prime }_S)$
whenever
$(f, m_S) - (-1)^r (f, m^{\prime }_S)$
whenever
![]() $m^{\prime }_S$
differ from
$m^{\prime }_S$
differ from
![]() $m_S$
by reversing precisely r pairs. It has a symmetric monoidality given by disjoint union.
$m_S$
by reversing precisely r pairs. It has a symmetric monoidality given by disjoint union.
We will also write
![]() $\mathsf {FB}$
for the category of finite sets and bijections and consider it (after
$\mathsf {FB}$
for the category of finite sets and bijections and consider it (after
![]() $\mathbb {Q}$
-linearising) as a subcategory of both
$\mathbb {Q}$
-linearising) as a subcategory of both
![]() $\mathsf {dBr}$
and
$\mathsf {dBr}$
and
![]() $\mathsf {dsBr}$
, consisting of all objects and morphisms spanned by those
$\mathsf {dsBr}$
, consisting of all objects and morphisms spanned by those
![]() $(f,m_S)$
with f a bijection and
$(f,m_S)$
with f a bijection and
![]() $m_S=\varnothing $
. To treat the symmetric and skew-symmetric cases simultaneously, we will write
$m_S=\varnothing $
. To treat the symmetric and skew-symmetric cases simultaneously, we will write
![]() $\mathsf {d(s)Br}$
for
$\mathsf {d(s)Br}$
for
![]() $\mathsf {dBr}$
if n is even and
$\mathsf {dBr}$
if n is even and
![]() $\mathsf {dsBr}$
if n is odd.
$\mathsf {dsBr}$
if n is odd.
Recall that
![]() $\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
is the category of nonnegatively graded
$\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
is the category of nonnegatively graded
![]() $\mathbb {Q}$
-vector spaces, considered as a
$\mathbb {Q}$
-vector spaces, considered as a
![]() $\mathbb {Q}\text {-}\mathsf {mod}$
-enriched category. We shall be interested in (graded) representations of the downward (signed) Brauer category, that is, enriched functors
$\mathbb {Q}\text {-}\mathsf {mod}$
-enriched category. We shall be interested in (graded) representations of the downward (signed) Brauer category, that is, enriched functors
![]() $F\colon \mathsf {d(s)Br} \to \mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
. The category of such functors
$F\colon \mathsf {d(s)Br} \to \mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
. The category of such functors
![]() $\mathsf {Fun}({\mathsf {d(s)Br}}, \mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod}))$
is again symmetric monoidal under Day convolution, using the symmetric monoidality on
$\mathsf {Fun}({\mathsf {d(s)Br}}, \mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod}))$
is again symmetric monoidal under Day convolution, using the symmetric monoidality on
![]() $\mathsf {d(s)Br}$
given by disjoint union and that on
$\mathsf {d(s)Br}$
given by disjoint union and that on
![]() $\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
given by tensor product of graded vector spaces and the Koszul sign rule. Using the tensoring of
$\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
given by tensor product of graded vector spaces and the Koszul sign rule. Using the tensoring of
![]() $\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
over
$\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
over
![]() $\mathbb {Q}\text {-}\mathsf {mod}$
, it is given by the enriched coend
$\mathbb {Q}\text {-}\mathsf {mod}$
, it is given by the enriched coend
 $$\begin{align*}(F \otimes G)(S) = \int^{S',S" \in \mathsf{d(s)Br}} \mathsf{d(s)Br}(S' \sqcup S",S) \otimes F(S') \otimes G(S"),\end{align*}$$
$$\begin{align*}(F \otimes G)(S) = \int^{S',S" \in \mathsf{d(s)Br}} \mathsf{d(s)Br}(S' \sqcup S",S) \otimes F(S') \otimes G(S"),\end{align*}$$
and the monoidal unit is the functor
![]() given by
given by
![]() $\mathbb {Q}$
on the empty set and 0 on all other finite sets. One can compute the values of the Day convolution explicitly as
$\mathbb {Q}$
on the empty set and 0 on all other finite sets. One can compute the values of the Day convolution explicitly as
where the indexing set runs over all isomorphism classes of pairs of finite sets and
![]() $\mathsf {Pair}(S' \sqcup S",S) \subset \mathsf {d(s)Br}(S' \sqcup S",S)$
is the span of those
$\mathsf {Pair}(S' \sqcup S",S) \subset \mathsf {d(s)Br}(S' \sqcup S",S)$
is the span of those
![]() $(f,m_{S' \sqcup S"})$
, where each pair in
$(f,m_{S' \sqcup S"})$
, where each pair in
![]() $m_{S' \sqcup S"}$
contains elements of both
$m_{S' \sqcup S"}$
contains elements of both
![]() $S'$
and
$S'$
and
![]() $S"$
. To see this, use that Day convolution preserves colimits in each variable to reduce to the case that F and G are representable and verify it by hand there.
$S"$
. To see this, use that Day convolution preserves colimits in each variable to reduce to the case that F and G are representable and verify it by hand there.
4.1.1 Homotopy theory of representations of the downward Brauer category
We can do homotopy theory with these objects if we enlarge their target to
![]() $\mathsf {Ch}$
. One can use
$\mathsf {Ch}$
. One can use
![]() $\infty $
-categories or model structures; we opt for the latter because we need to do some explicit computations.
$\infty $
-categories or model structures; we opt for the latter because we need to do some explicit computations.
We endow
![]() $\mathsf {Ch}$
with the projective model structure [Reference HainGS07, Theorem 1.5]: the weak equivalences are quasi-isomorphisms, the cofibrations are degreewise monomorphisms and the fibrations are epimorphisms in positive degrees. Let us define chain complexes
$\mathsf {Ch}$
with the projective model structure [Reference HainGS07, Theorem 1.5]: the weak equivalences are quasi-isomorphisms, the cofibrations are degreewise monomorphisms and the fibrations are epimorphisms in positive degrees. Let us define chain complexes

Then this model structure is cofibrantly generated by the set I of generating cofibrations given by
![]() $0 \to S(0)$
and the inclusions
$0 \to S(0)$
and the inclusions
![]() $S(n-1) \hookrightarrow D(n)$
for
$S(n-1) \hookrightarrow D(n)$
for
![]() $n \geq 1$
, and the set J of generating trivial cofibrations given by the inclusions
$n \geq 1$
, and the set J of generating trivial cofibrations given by the inclusions
![]() $0 \hookrightarrow D(n)$
for
$0 \hookrightarrow D(n)$
for
![]() $n \geq 1$
[Reference HainGS07, Examples 3.4(1)].
$n \geq 1$
[Reference HainGS07, Examples 3.4(1)].
Lemma 4.3. The category
![]() $\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Ch})$
has a model structure whose weak equivalences and fibrations are objectwise. This is cofibrantly generated and monoidal with respect to Day convolution.
$\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Ch})$
has a model structure whose weak equivalences and fibrations are objectwise. This is cofibrantly generated and monoidal with respect to Day convolution.
The proof proceeds as in the unenriched case [Reference Hain and LooijengaHir03, Theorem 11.6.1] by right transfer as in [Reference Hain and LooijengaHir03, Theorem 11.3.2]. The set of generating cofibrations
![]() $I'$
is given by the union over all
$I'$
is given by the union over all
![]() $S \in \mathrm { ob}(\mathsf {d(s)Br})$
of the image of I under the left adjoint
$S \in \mathrm { ob}(\mathsf {d(s)Br})$
of the image of I under the left adjoint
![]() $S_*$
to the evaluation
$S_*$
to the evaluation
![]() $ \mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Ch}) \to \mathsf {Ch}$
given by
$ \mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Ch}) \to \mathsf {Ch}$
given by
![]() $F \mapsto F(S)$
, and the set of generating trivial cofibrations
$F \mapsto F(S)$
, and the set of generating trivial cofibrations
![]() $J'$
is in the same manner with J in place of I. That this model structure is monoidal is [Reference JohnsonIsa09, Proposition 2.2.15].
$J'$
is in the same manner with J in place of I. That this model structure is monoidal is [Reference JohnsonIsa09, Proposition 2.2.15].
By Lemma 4.3, the Day convolution tensor product preserves weak equivalences in each entry when all objects involved are cofibrant. The latter hypothesis is in fact unnecessary.
Lemma 4.4. The Day convolution tensor product on
![]() $\mathsf {d(s)Br}$
preserves weak equivalences in each entry.
$\mathsf {d(s)Br}$
preserves weak equivalences in each entry.
Proof. Using (4), the result follows from the facts that for rational chain complexes tensor products and quotients by finite group actions preserve weak equivalences.
4.2 Commutative algebras on the downward Brauer category
Recall that
![]() $\mathsf {Com}$
denotes the nonunital commutative algebra operad. We write
$\mathsf {Com}$
denotes the nonunital commutative algebra operad. We write
![]() $\mathsf {Alg}_{\mathsf {Com}}(\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Ch}))$
for the category of
$\mathsf {Alg}_{\mathsf {Com}}(\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Ch}))$
for the category of
![]() $\mathsf {Com}$
-algebra objects in the symmetric monoidal category
$\mathsf {Com}$
-algebra objects in the symmetric monoidal category
![]() $\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Ch})$
; these are nonunital commutative algebra objects.
$\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Ch})$
; these are nonunital commutative algebra objects.
4.2.1 Unital commutative algebras
Let
![]() $\mathsf {Com}^+$
denote the unital commutative algebra operad, having
$\mathsf {Com}^+$
denote the unital commutative algebra operad, having
![]() $\mathsf {Com}^+(r) = \mathbb {Q}$
with trivial
$\mathsf {Com}^+(r) = \mathbb {Q}$
with trivial
![]() $\mathfrak {S}_r$
-action for all
$\mathfrak {S}_r$
-action for all
![]() $r \geq 0$
. We will write
$r \geq 0$
. We will write
![]() $\mathsf {Alg}_{\mathsf {Com}^+}(\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Ch}))$
for the category of
$\mathsf {Alg}_{\mathsf {Com}^+}(\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Ch}))$
for the category of
![]() $\mathsf {Com}^+$
-algebra objects in
$\mathsf {Com}^+$
-algebra objects in
![]() $\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Ch})$
; these are unital commutative algebra objects.
$\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Ch})$
; these are unital commutative algebra objects.
The object
is canonically a unital commutative algebra object; an augmentation for a unital commutative algebra object R is a morphism
. Since the unit provides a section, there is a splitting
with
![]() $\overline {R} = \ker (\epsilon )$
the augmentation ideal. This is canonically a nonunital commutative algebra object and taking the augmentation ideal yields an equivalence of categories
$\overline {R} = \ker (\epsilon )$
the augmentation ideal. This is canonically a nonunital commutative algebra object and taking the augmentation ideal yields an equivalence of categories
which has an inverse given by unitalisation.
4.2.2 Homotopy theory of commutative algebras and André–Quillen homology
To do homotopy theory with the nonunital commutative algebras in
![]() $\mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Ch})$
, we transfer the model structure to these objects.
$\mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Ch})$
, we transfer the model structure to these objects.
Lemma 4.5. The category
![]() $\mathsf {Alg}_{\mathsf {Com}}(\mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Ch}))$
has a model structure whose weak equivalences and fibrations are objectwise. This is cofibrantly generated.
$\mathsf {Alg}_{\mathsf {Com}}(\mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Ch}))$
has a model structure whose weak equivalences and fibrations are objectwise. This is cofibrantly generated.
![]() $ \Box $
$ \Box $
The proof proceeds as in the unenriched case by right transfer [Reference HainGS07, Example 3.7]. The set of generating cofibrations is
![]() $F^{\mathrm {Com}}I'$
and the set of generating trivial cofibrations is
$F^{\mathrm {Com}}I'$
and the set of generating trivial cofibrations is
![]() $F^{\mathrm {Com}} J'$
with
$F^{\mathrm {Com}} J'$
with
![]() $F^{\mathrm {Com}}$
the left adjoint in the free-forgetful adjunction
$F^{\mathrm {Com}}$
the left adjoint in the free-forgetful adjunction
Remark 4.6. The same construction endows
![]() $\mathsf {Alg}_{\mathsf {Com}^+}(\mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Ch}))$
with a model structure whose weak equivalences and fibrations are objectwise. Moreover, [Reference Hain and LooijengaHir03, Theorem 7.6.5] endows
$\mathsf {Alg}_{\mathsf {Com}^+}(\mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Ch}))$
with a model structure whose weak equivalences and fibrations are objectwise. Moreover, [Reference Hain and LooijengaHir03, Theorem 7.6.5] endows
![]() $\mathsf {Alg}^{\mathrm { augm}}_{\mathsf {Com}^+}(\mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Ch}))$
with a model structure whose weak equivalences, cofibrations and fibrations are such when forgetting the augmentation. Then (6) is a Quillen equivalence.
$\mathsf {Alg}^{\mathrm { augm}}_{\mathsf {Com}^+}(\mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Ch}))$
with a model structure whose weak equivalences, cofibrations and fibrations are such when forgetting the augmentation. Then (6) is a Quillen equivalence.
The monad
![]() $\mathrm {Com}$
has an augmentation
$\mathrm {Com}$
has an augmentation
![]() $\epsilon \colon \mathrm {Com} \to \mathrm {Id}$
by projection to the
$\epsilon \colon \mathrm {Com} \to \mathrm {Id}$
by projection to the
![]() $n=1$
summand, and we define indecomposables
$n=1$
summand, and we define indecomposables
![]() $Q^{\mathrm {Com}}(\overline {R})$
of a nonunital commutative algebra object
$Q^{\mathrm {Com}}(\overline {R})$
of a nonunital commutative algebra object
![]() $\overline {R}$
as the following reflexive coequaliser in
$\overline {R}$
as the following reflexive coequaliser in
![]() $\mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Ch})$
$\mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Ch})$
This is the left adjoint in an adjunction

with right adjoint the trivial algebra functor
![]() $Z^{\mathrm {Com}}$
endowing F with the zero multiplication. With the model structures of Lemma 4.3 and Lemma 4.5 this is a Quillen adjunction, because the right adjoint preserves the underlying objects and hence (trivial) fibrations. We write
$Z^{\mathrm {Com}}$
endowing F with the zero multiplication. With the model structures of Lemma 4.3 and Lemma 4.5 this is a Quillen adjunction, because the right adjoint preserves the underlying objects and hence (trivial) fibrations. We write
![]() $\mathbb {L} Q^{\mathrm {Com}}$
for the total left derived functor of
$\mathbb {L} Q^{\mathrm {Com}}$
for the total left derived functor of
![]() $Q^{\mathrm {Com}}$
.
$Q^{\mathrm {Com}}$
.
Definition 4.7. For a nonunital commutative algebra object
![]() $\overline {R} \colon \mathsf {d(s)Br} \to \mathsf {Ch}$
we define its André–Quillen homology
$\overline {R} \colon \mathsf {d(s)Br} \to \mathsf {Ch}$
we define its André–Quillen homology
Notation 4.8. By a slight abuse of notation, for an augmented commutative algebra R with augmentation ideal
![]() $\overline {R}$
, we write
$\overline {R}$
, we write
![]() $\mathbb {L} Q^{\mathrm {Com}^+}(R)$
for
$\mathbb {L} Q^{\mathrm {Com}^+}(R)$
for
![]() $\mathbb {L} Q^{\mathrm {Com}}(\overline {R})$
, and
$\mathbb {L} Q^{\mathrm {Com}}(\overline {R})$
, and
![]() $\mathrm {AQ}_*(R)$
for
$\mathrm {AQ}_*(R)$
for
![]() $\mathrm { AQ}_*(\overline {R})$
.
$\mathrm { AQ}_*(\overline {R})$
.
4.2.3 Regular sequences
If
![]() $R \in \mathsf {Alg}^{\mathrm {augm}}_{\mathsf {Com}^+}(\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Ch}))$
and
$R \in \mathsf {Alg}^{\mathrm {augm}}_{\mathsf {Com}^+}(\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Ch}))$
and
![]() $z \in \overline {R}(\varnothing )$
is a cycle of degree
$z \in \overline {R}(\varnothing )$
is a cycle of degree
![]() $k \geq 0$
, then by adjunction there is a map
$k \geq 0$
, then by adjunction there is a map
![]() $(\varnothing )_* S(k) \to R$
, where
$(\varnothing )_* S(k) \to R$
, where
![]() $(\varnothing )_*$
denotes the left Kan extension along the inclusion
$(\varnothing )_*$
denotes the left Kan extension along the inclusion
![]() $\{\varnothing \} \to \mathsf {d(s)Br}$
and
$\{\varnothing \} \to \mathsf {d(s)Br}$
and
![]() $S(k)$
is the chain complex of (5). Using that R is a unital commutative algebra object, this further extends to a morphism
$S(k)$
is the chain complex of (5). Using that R is a unital commutative algebra object, this further extends to a morphism
![]() $F^{\mathrm { Com}^+}((\varnothing )_* S(k)) \to R$
, using which we may form the pushout
$F^{\mathrm { Com}^+}((\varnothing )_* S(k)) \to R$
, using which we may form the pushout

in the category
![]() $\mathsf {Alg}^{\mathrm {augm}}_{\mathsf {Com}^+}(\mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Ch}))$
.
$\mathsf {Alg}^{\mathrm {augm}}_{\mathsf {Com}^+}(\mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Ch}))$
.
Definition 4.9. Let R and z be as above, then we say that z is not a zero divisor if the morphisms
![]() $z \cdot -\colon \mathbb {Q}[k] \otimes R(S) \to R(S)$
are injective for all finite sets S.
$z \cdot -\colon \mathbb {Q}[k] \otimes R(S) \to R(S)$
are injective for all finite sets S.
In particular, as
![]() $z^2 = (-1)^k z^2$
by graded-commutativity, k must be even.
$z^2 = (-1)^k z^2$
by graded-commutativity, k must be even.
Lemma 4.10. If
![]() $z \in \overline {R}(\varnothing )$
is not a zero divisor, then (7) is a homotopy pushout.
$z \in \overline {R}(\varnothing )$
is not a zero divisor, then (7) is a homotopy pushout.
Proof. Consider the generating cofibration
![]() $S(k) \hookrightarrow D(k+1)$
of (5). Then
$S(k) \hookrightarrow D(k+1)$
of (5). Then
is a cofibration modelling the left vertical map of (7) (it is a generating cofibration). If
![]() $cR \overset {\sim }\to R$
is a cofibrant replacement (we may assume it is surjective) and
$cR \overset {\sim }\to R$
is a cofibrant replacement (we may assume it is surjective) and
![]() $z' \in \overline {cR}(\varnothing )$
is a lift of z, the homotopy pushout is by definition given by
$z' \in \overline {cR}(\varnothing )$
is a lift of z, the homotopy pushout is by definition given by
which is
![]() $cR \otimes F^{\mathrm {Com}^+}((\varnothing )_*S(k+1))$
with differential determined by
$cR \otimes F^{\mathrm {Com}^+}((\varnothing )_*S(k+1))$
with differential determined by
![]() $d (x \otimes 1) = d_{cR}(x) \otimes 1$
,
$d (x \otimes 1) = d_{cR}(x) \otimes 1$
,
![]() $d (1 \otimes z_{k+1}) = z' \otimes 1$
and the Leibniz rule.
$d (1 \otimes z_{k+1}) = z' \otimes 1$
and the Leibniz rule.
We thus first prove that the map
induced by
![]() $cR \overset {\sim }\to R$
is a weak equivalence. To do so, we use that there is an isomorphism
$cR \overset {\sim }\to R$
is a weak equivalence. To do so, we use that there is an isomorphism
and filter both sides by powers of
![]() $z_{k+1}$
(there will be only two nonzero powers,
$z_{k+1}$
(there will be only two nonzero powers,
![]() $1$
and
$1$
and
![]() $z_{k+1}$
, since
$z_{k+1}$
, since
![]() $k+1$
is odd). On the associated gradeds, we get either a shift of the map
$k+1$
is odd). On the associated gradeds, we get either a shift of the map
![]() $cR \to R$
or the map
$cR \to R$
or the map
![]() $0 \to 0$
, so the result follows.
$0 \to 0$
, so the result follows.
Next, we observe that the isomorphism (8) together with the fact that
![]() $k+1$
is odd, identifies
$k+1$
is odd, identifies
![]() $R \otimes F^{\mathrm { Com}^+}((\varnothing )_*S(k+1))$
with the mapping cone of
$R \otimes F^{\mathrm { Com}^+}((\varnothing )_*S(k+1))$
with the mapping cone of
As we have assumed that z is not a zero divisor, this map is injective when evaluated on any finite set, so its cokernel and mapping cone are quasi-isomorphic: It follows that
![]() $R \otimes F^{\mathrm {Com}^+}((\varnothing )_*S(k+1)) \simeq R/(z)$
.
$R \otimes F^{\mathrm {Com}^+}((\varnothing )_*S(k+1)) \simeq R/(z)$
.
Corollary 4.11. If
![]() $z \in \overline {R}(\varnothing )$
is not a zero divisor, then there is a homotopy cofibre sequence
$z \in \overline {R}(\varnothing )$
is not a zero divisor, then there is a homotopy cofibre sequence
4.2.4 The Harrison complex
Koszul duality between the nonunital commutative and Lie operads [Reference MillèsLV12, Section 13.1.5] gives for
![]() $\overline {R} \in \mathsf {Alg}_{\mathsf {Com}}(\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Ch}))$
a weak equivalence of the form
$\overline {R} \in \mathsf {Alg}_{\mathsf {Com}}(\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Ch}))$
a weak equivalence of the form
where the differential of the domain is a certain functorial deformation of the differential induced by that on
![]() $\overline {R}$
[Reference MillèsLV12, Corollary 11.3.5], and the domain is in addition cofibrant [Reference MillèsLV12, Proof of Theorem 12.1.6]; the proofs in [Reference MillèsLV12] are given in
$\overline {R}$
[Reference MillèsLV12, Corollary 11.3.5], and the domain is in addition cofibrant [Reference MillèsLV12, Proof of Theorem 12.1.6]; the proofs in [Reference MillèsLV12] are given in
![]() $\mathsf {Ch}$
but go through for
$\mathsf {Ch}$
but go through for
![]() $\mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Ch})$
. Taking indecomposables shows that the (shifted) Harrison complex (c.f. Section 2.1),
$\mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Ch})$
. Taking indecomposables shows that the (shifted) Harrison complex (c.f. Section 2.1),
is a model for the derived indecomposables (cf. [Reference MillèsLV12, Proposition 13.1.4]).
Lemma 4.12.
![]() $\mathbb {L} Q^{\mathrm {Com}}(\overline {R}) \simeq \mathrm {Harr}(\overline {R})[-1]$
.
$\mathbb {L} Q^{\mathrm {Com}}(\overline {R}) \simeq \mathrm {Harr}(\overline {R})[-1]$
.
Proof. For
![]() $c\overline {R} \overset {\sim }\longrightarrow \overline {R}$
a cofibrant replacement, there is a commutative diagram
$c\overline {R} \overset {\sim }\longrightarrow \overline {R}$
a cofibrant replacement, there is a commutative diagram

By definition
![]() $c\overline {R}$
is a cofibrant, and
$c\overline {R}$
is a cofibrant, and
![]() $F^{\mathrm {Com}}(\mathrm {coLie}(c\overline {R}[1])[-1])$
is too by the discussion above. The left horizontal map is thus a weak equivalence; it is a left Quillen functor applied to a weak equivalence between cofibrant objects. The right vertical map is a weak equivalence as
$F^{\mathrm {Com}}(\mathrm {coLie}(c\overline {R}[1])[-1])$
is too by the discussion above. The left horizontal map is thus a weak equivalence; it is a left Quillen functor applied to a weak equivalence between cofibrant objects. The right vertical map is a weak equivalence as
![]() $\mathrm {coLie}(-)$
preserves weak equivalences (as the tensor product does by Lemma 4.4 and coinvariants for a finite group action do).
$\mathrm {coLie}(-)$
preserves weak equivalences (as the tensor product does by Lemma 4.4 and coinvariants for a finite group action do).
4.2.5 Additional gradings and Koszulness
If a nonunital commutative algebra object
![]() $\overline {R}$
takes values in the subcategory
$\overline {R}$
takes values in the subcategory
![]() $\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod}) \subset \mathsf {Ch}$
, then the objects
$\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod}) \subset \mathsf {Ch}$
, then the objects
![]() $\mathrm {AQ}_p(\overline {R})$
inherit a further grading, as in Section 2.1. We set
$\mathrm {AQ}_p(\overline {R})$
inherit a further grading, as in Section 2.1. We set
and call p the Harrison degree, q the internal degree and
![]() $p+q-1$
the total degree. If
$p+q-1$
the total degree. If
![]() $\overline {R}$
also has a weight grading, that is,
$\overline {R}$
also has a weight grading, that is,
![]() $\overline {R} \in \mathsf {Alg}_{\mathsf {Com}}(\mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})^{\mathbb {N}}))$
, then its derived indecomposables can be formed in
$\overline {R} \in \mathsf {Alg}_{\mathsf {Com}}(\mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})^{\mathbb {N}}))$
, then its derived indecomposables can be formed in
![]() $\mathsf {Ch}^{\mathbb {N}}$
, giving them an additional weight grading (and similarly for the Harrison complex) and we write
$\mathsf {Ch}^{\mathbb {N}}$
, giving them an additional weight grading (and similarly for the Harrison complex) and we write
for the piece of weight w.
Definition 4.13. For
![]() $\overline {R} \in \mathsf {Alg}_{\mathrm { Com}}(\mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})^{\mathbb {N}}))$
, we say that
$\overline {R} \in \mathsf {Alg}_{\mathrm { Com}}(\mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})^{\mathbb {N}}))$
, we say that
![]() $\overline {R}$
is Koszul in weight
$\overline {R}$
is Koszul in weight
![]() $ \leq W$
if
$ \leq W$
if
![]() $H^{\mathrm {Com}}_p(\overline {R})_{q,w}=0$
when
$H^{\mathrm {Com}}_p(\overline {R})_{q,w}=0$
when
![]() $p \neq w$
and
$p \neq w$
and
![]() $w \leq W$
. If
$w \leq W$
. If
![]() $W=\infty $
, then we simply say that R is Koszul.
$W=\infty $
, then we simply say that R is Koszul.
The following lemma gives an easy criterion for half of this inequation:
Lemma 4.14. If each
![]() $\overline {R}(S)$
is supported in weight
$\overline {R}(S)$
is supported in weight
![]() $\geq 1$
, then
$\geq 1$
, then
![]() $H^{\mathrm {Com}}_p(\overline {R})_{q,w} = 0 \text { if } p> w$
.
$H^{\mathrm {Com}}_p(\overline {R})_{q,w} = 0 \text { if } p> w$
.
Proof. Neglecting the differential, the Harrison complex splits as
The weight of
![]() $\overline {R}[1]$
is
$\overline {R}[1]$
is
![]() $\geq 1$
, so the weight of
$\geq 1$
, so the weight of
![]() $(\overline {R}[1])^{\otimes p}$
is
$(\overline {R}[1])^{\otimes p}$
is
![]() $\geq p$
. As
$\geq p$
. As
![]() $H^{\mathrm {Com}}_p(\overline {R})$
is a subquotient of
$H^{\mathrm {Com}}_p(\overline {R})$
is a subquotient of
![]() $\mathrm {coLie}(p) \otimes _{\mathfrak {S}_p} (\overline {R}[1])^{\otimes p}$
, it is supported in weight
$\mathrm {coLie}(p) \otimes _{\mathfrak {S}_p} (\overline {R}[1])^{\otimes p}$
, it is supported in weight
![]() $\geq p$
.
$\geq p$
.
4.3 Realisation
If H is a vector space with a (skew) symmetric form
![]() $\lambda $
, then we will now explain how a representation of the downward (signed) Brauer category yields a representation of
$\lambda $
, then we will now explain how a representation of the downward (signed) Brauer category yields a representation of
![]() $\mathrm {Aut}(H,\lambda )$
.
$\mathrm {Aut}(H,\lambda )$
.
Definition 4.15. If
![]() $\lambda $
is a symmetric form on H, there is associated a functor
$\lambda $
is a symmetric form on H, there is associated a functor
given as follows: To the object S, we assign
![]() $K(S) = {H}^{\otimes S}$
, considered as a graded vector space in grading zero, and to the morphism
$K(S) = {H}^{\otimes S}$
, considered as a graded vector space in grading zero, and to the morphism
![]() $(f, m_S)\colon S \to T$
we assign the map
$(f, m_S)\colon S \to T$
we assign the map
![]() ${H}^{\otimes S} \to {H}^{\otimes T}$
given by applying
${H}^{\otimes S} \to {H}^{\otimes T}$
given by applying
![]() ${\lambda }$
to each of the pairs in
${\lambda }$
to each of the pairs in
![]() $m_S$
and using the bijection
$m_S$
and using the bijection
![]() $f(T) \overset {\sim }\to T$
to induce an isomorphism
$f(T) \overset {\sim }\to T$
to induce an isomorphism
![]() ${H}^{\otimes f(T)} \overset {\sim }\to {H}^{\otimes T}$
on the remaining factors.
${H}^{\otimes f(T)} \overset {\sim }\to {H}^{\otimes T}$
on the remaining factors.
Similarly, if
![]() $\lambda $
is a skew-symmetric form on H there is associated a functor
$\lambda $
is a skew-symmetric form on H there is associated a functor
given in the same way on objects and given on a morphism
![]() $[(f,m_S)]\colon S \to T$
by applying
$[(f,m_S)]\colon S \to T$
by applying
![]() $\lambda $
to each of the ordered pairs in
$\lambda $
to each of the ordered pairs in
![]() $m_S$
; as
$m_S$
; as
![]() $\lambda $
is skew-symmetric this is well defined.
$\lambda $
is skew-symmetric this is well defined.
Remark 4.16. In [Reference Koike and TeradaKRW20c] K was defined on the full Brauer category
![]() $\mathsf {(s)Br}$
, and its restriction to
$\mathsf {(s)Br}$
, and its restriction to
![]() $\mathsf {d(s)Br}$
was denoted
$\mathsf {d(s)Br}$
was denoted
![]() $i^*K$
. We have no need for the full Brauer category here and hence opt to simplify the notation.
$i^*K$
. We have no need for the full Brauer category here and hence opt to simplify the notation.
In either case, dualising K gives a functor
![]() $K^{\vee }\colon \mathsf {d(s)Br}^{\mathrm {op}} \to \mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
, and taking the coend with this defines a functor
$K^{\vee }\colon \mathsf {d(s)Br}^{\mathrm {op}} \to \mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
, and taking the coend with this defines a functor
As explained in [Reference Koike and TeradaKRW20c, Section 2.2.1] (following [Reference Turchin and WillwacherSS15]), this has a strong symmetric monoidality.
The data
![]() $({H},{\lambda })$
is – tautologically – equipped with an action of the group
$({H},{\lambda })$
is – tautologically – equipped with an action of the group
![]() $\mathrm {Aut}({H},{\lambda })$
, and hence the functor K is too. Thus, the above construction may be promoted to a functor
$\mathrm {Aut}({H},{\lambda })$
, and hence the functor K is too. Thus, the above construction may be promoted to a functor
that is, to take values in graded
![]() $\mathrm {Aut}({H},{\lambda })$
-representations.
$\mathrm {Aut}({H},{\lambda })$
-representations.
From now on, we take
![]() $(H,\lambda )$
to be
$(H,\lambda )$
to be
![]() $(H(g),\lambda )$
as in Section 2.4 so that
$(H(g),\lambda )$
as in Section 2.4 so that
![]() $\mathrm {Aut}(H,\lambda ) = \mathrm { O}_{\epsilon }(H(g))$
. This functor is a left adjoint so is right exact but is not left exact in general. However, it has the following stable left exactness property. Let us say that a functor
$\mathrm {Aut}(H,\lambda ) = \mathrm { O}_{\epsilon }(H(g))$
. This functor is a left adjoint so is right exact but is not left exact in general. However, it has the following stable left exactness property. Let us say that a functor
![]() $A\colon \mathsf {d(s)Br} \to \mathbb {Q}\text {-}\mathsf {mod}$
is supported on sets of size
$A\colon \mathsf {d(s)Br} \to \mathbb {Q}\text {-}\mathsf {mod}$
is supported on sets of size
![]() $\leq N$
if
$\leq N$
if
![]() $A(S)=0$
whenever
$A(S)=0$
whenever
![]() $|S|> N$
. (We take the target to be
$|S|> N$
. (We take the target to be
![]() $\mathbb {Q}$
-modules rather than graded
$\mathbb {Q}$
-modules rather than graded
![]() $\mathbb {Q}$
-modules as we will later wish to consider functors to graded
$\mathbb {Q}$
-modules as we will later wish to consider functors to graded
![]() $\mathbb {Q}$
-modules whose support depends on the grading.)
$\mathbb {Q}$
-modules whose support depends on the grading.)
Lemma 4.17. For each
![]() $A \in \mathsf {Fun}(\mathsf {d(s)Br},\mathbb {Q}\text {-}\mathsf {mod})$
and finite set S there is a surjective map
$A \in \mathsf {Fun}(\mathsf {d(s)Br},\mathbb {Q}\text {-}\mathsf {mod})$
and finite set S there is a surjective map
which is injective when
![]() $|S| \leq g$
.
$|S| \leq g$
.
Proof. Recall from Section 2.4 that
![]() $H(g)_{[S]}$
is a certain quotient of
$H(g)_{[S]}$
is a certain quotient of
![]() $H(g)^{\otimes S}$
, and consider
$H(g)^{\otimes S}$
, and consider
 $$\begin{align*}[H(g)_{[S]} \otimes (K^{\vee} \otimes^{\mathsf{d(s)Br}} A)]^{\mathrm{O}_{\epsilon}(H(g))} = \int^{T \in \mathsf{d(s)Br}} [H(g)_{[S]} \otimes K(T)^{\vee}]^{\mathrm{O}_{\epsilon}(H(g))} \otimes A(T).\end{align*}$$
$$\begin{align*}[H(g)_{[S]} \otimes (K^{\vee} \otimes^{\mathsf{d(s)Br}} A)]^{\mathrm{O}_{\epsilon}(H(g))} = \int^{T \in \mathsf{d(s)Br}} [H(g)_{[S]} \otimes K(T)^{\vee}]^{\mathrm{O}_{\epsilon}(H(g))} \otimes A(T).\end{align*}$$
There is a natural transformation of two variables
given by the functoriality of K, which is surjective, and is injective if
![]() $|S|+|T| \leq 2g$
, by [Reference Koike and TeradaKRW20c, Theorem 2.6]. By the co-Yoneda lemma it gives a map
$|S|+|T| \leq 2g$
, by [Reference Koike and TeradaKRW20c, Theorem 2.6]. By the co-Yoneda lemma it gives a map
which is surjective, and injective for
![]() $|S| \leq g$
.
$|S| \leq g$
.
Lemma 4.18. If
![]() $0 \to A \to B \to C \to 0$
is a short exact sequence in the category
$0 \to A \to B \to C \to 0$
is a short exact sequence in the category
![]() $\mathsf {Fun}(\mathsf {d(s)Br},\mathbb {Q}\text {-}\mathsf {mod})$
such that B is supported on sets of size
$\mathsf {Fun}(\mathsf {d(s)Br},\mathbb {Q}\text {-}\mathsf {mod})$
such that B is supported on sets of size
![]() $\leq g$
, then
$\leq g$
, then
is again exact.
(The following argument provides the missing second half of the proof of [Reference Koike and TeradaKRW20c, Corollary 2.18], which is not as immediate as we had suggested.)
Proof. It is right exact as
![]() $K^{\vee } \otimes ^{\mathsf {d(s)Br}} -$
is a left adjoint, so we only need to show that the left-hand map is injective. As B is supported on sets of size
$K^{\vee } \otimes ^{\mathsf {d(s)Br}} -$
is a left adjoint, so we only need to show that the left-hand map is injective. As B is supported on sets of size
![]() $\leq g$
and A is a subobject of B, A also is supported on sets of size
$\leq g$
and A is a subobject of B, A also is supported on sets of size
![]() $\leq g$
.
$\leq g$
.
The map
of Lemma 4.17 is an isomorphism for
![]() $|S| \leq g$
. As the domain vanishes if
$|S| \leq g$
. As the domain vanishes if
![]() $|S|> g$
, this map is an isomorphism. The same argument holds with A replaced by B, and so we deduce that the map
$|S|> g$
, this map is an isomorphism. The same argument holds with A replaced by B, and so we deduce that the map
is injective for all finite sets S.
If
![]() $K^{\vee } \otimes ^{\mathsf {d(s)Br}} A \to K^{\vee } \otimes ^{\mathsf {d(s)Br}} B$
were not injective, then its kernel would contain an irreducible algebraic
$K^{\vee } \otimes ^{\mathsf {d(s)Br}} A \to K^{\vee } \otimes ^{\mathsf {d(s)Br}} B$
were not injective, then its kernel would contain an irreducible algebraic
![]() $\mathrm {O}_{\epsilon }(H(g))$
-representation, which would be detected by applying
$\mathrm {O}_{\epsilon }(H(g))$
-representation, which would be detected by applying
![]() $[H_{[S]} \otimes -]^{\mathrm {O}_{\epsilon }(H(g))}$
for some finite set S. Thus, the map is injective as claimed.
$[H_{[S]} \otimes -]^{\mathrm {O}_{\epsilon }(H(g))}$
for some finite set S. Thus, the map is injective as claimed.
4.3.1 Realisation and Koszulness
The above results imply that realisation preserves Koszulness in a range increasing with g.
Lemma 4.19. Suppose that the weight w piece of a nonunital commutative algebra
![]() $\overline {R} \in \mathsf {Alg}_{\mathrm { Com}}(\mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})^{\mathbb {N}}))$
is supported on sets of size
$\overline {R} \in \mathsf {Alg}_{\mathrm { Com}}(\mathsf {Fun}(\mathsf {d(s)Br},\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})^{\mathbb {N}}))$
is supported on sets of size
![]() $\leq \lambda w$
for some
$\leq \lambda w$
for some
![]() $\lambda \in \mathbb {N}_{>0}$
. Then as long as
$\lambda \in \mathbb {N}_{>0}$
. Then as long as
![]() $w \leq \tfrac {1}{\lambda }g$
we have
$w \leq \tfrac {1}{\lambda }g$
we have
Proof. As an explicit model for the derived indecomposables of
![]() $\overline {R}$
we can take the Harrison complex (Lemma 4.12):
$\overline {R}$
we can take the Harrison complex (Lemma 4.12):
The weight w piece of
![]() $\overline {R}$
is supported on sets of size
$\overline {R}$
is supported on sets of size
![]() $\leq \lambda w$
, that is,
$\leq \lambda w$
, that is,
![]() $\overline {R}(S)_{q,w}=0$
if
$\overline {R}(S)_{q,w}=0$
if
![]() $w < \tfrac {1}{\lambda }|S|$
. It follows that tensor powers of
$w < \tfrac {1}{\lambda }|S|$
. It follows that tensor powers of
![]() $\overline {R}$
have the same property, and so Schur functors of
$\overline {R}$
have the same property, and so Schur functors of
![]() $\overline {R}$
have the same property, and hence the chain complex with additional grading
$\overline {R}$
have the same property, and hence the chain complex with additional grading
![]() $\mathrm {Harr}(\overline {R})$
has this vanishing property too. In particular, for each
$\mathrm {Harr}(\overline {R})$
has this vanishing property too. In particular, for each
![]() $w \leq \tfrac {1}{\lambda } g$
,
$w \leq \tfrac {1}{\lambda } g$
,
![]() $\mathrm {Harr}(\overline {R})_{q,w}$
is a chain complex supported on sets of size
$\mathrm {Harr}(\overline {R})_{q,w}$
is a chain complex supported on sets of size
![]() $\leq g$
, so by Lemma 4.18 the operation
$\leq g$
, so by Lemma 4.18 the operation
![]() $K^{\vee } \otimes ^{\mathsf {dsBr}} -$
is exact on it. Thus, as long as
$K^{\vee } \otimes ^{\mathsf {dsBr}} -$
is exact on it. Thus, as long as
![]() $w \leq \tfrac {1}{\lambda } g$
, we have
$w \leq \tfrac {1}{\lambda } g$
, we have
 $$ \begin{align*} K^{\vee} \otimes^{\mathsf{d(s)Br}} H^{\mathrm{Com}}_{p}(\overline{R})_{q,w} &\cong H_{p+q}(K^{\vee} \otimes^{\mathsf{d(s)Br}} \mathrm{ Harr}(\overline{R}))_{q,w} \\ &\cong H_{p+q}( \mathrm{Harr}(K^{\vee} \otimes^{\mathsf{d(s)Br}} \overline{R}))_{q,w} \\ &\cong H^{\mathrm{Com}}_{p}(K^{\vee} \otimes^{\mathsf{d(s)Br}} \overline{R})_{q,w}, \end{align*} $$
$$ \begin{align*} K^{\vee} \otimes^{\mathsf{d(s)Br}} H^{\mathrm{Com}}_{p}(\overline{R})_{q,w} &\cong H_{p+q}(K^{\vee} \otimes^{\mathsf{d(s)Br}} \mathrm{ Harr}(\overline{R}))_{q,w} \\ &\cong H_{p+q}( \mathrm{Harr}(K^{\vee} \otimes^{\mathsf{d(s)Br}} \overline{R}))_{q,w} \\ &\cong H^{\mathrm{Com}}_{p}(K^{\vee} \otimes^{\mathsf{d(s)Br}} \overline{R})_{q,w}, \end{align*} $$
where for the second step we have used that
![]() $K^{\vee } \otimes ^{\mathsf {d(s)Br}}-$
is an additive strong symmetric monoidal left adjoint and so commutes with the formation of the Harrison complex.
$K^{\vee } \otimes ^{\mathsf {d(s)Br}}-$
is an additive strong symmetric monoidal left adjoint and so commutes with the formation of the Harrison complex.
4.4 The main examples
There are two families of examples we shall work with, which are both special cases of the functors
![]() $\mathcal {P}(-; \mathcal {B})^{\prime }_{\geq 0} \otimes \det ^{\otimes n}$
from [Reference Koike and TeradaKRW20c, Definition 1.3], and we follow that definition.
$\mathcal {P}(-; \mathcal {B})^{\prime }_{\geq 0} \otimes \det ^{\otimes n}$
from [Reference Koike and TeradaKRW20c, Definition 1.3], and we follow that definition.
Definition 4.20. A partition of a finite set S is a finite collection of possibly empty subsets
![]() $\{S_{\alpha }\}_{\alpha \in I}$
of S which are pairwise disjoint and whose union is S. A partition is admissible if each part has size
$\{S_{\alpha }\}_{\alpha \in I}$
of S which are pairwise disjoint and whose union is S. A partition is admissible if each part has size
![]() $\geq 3$
.
$\geq 3$
.
For
![]() $n \in \mathbb {N}_{>0}$
, let
$n \in \mathbb {N}_{>0}$
, let
![]() $Z_n\colon \mathsf {d(s)Br} \to \mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
be the functor which to a finite set S assigns the vector space
$Z_n\colon \mathsf {d(s)Br} \to \mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
be the functor which to a finite set S assigns the vector space
made into a graded vector space by declaring a part
![]() $S_{\alpha }$
to have degree
$S_{\alpha }$
to have degree
![]() $n(|S_{\alpha }|-2)$
, and a partition to have degree the sum of the degrees of its parts.
$n(|S_{\alpha }|-2)$
, and a partition to have degree the sum of the degrees of its parts.
The linear map
![]() $Z_n(S) \to Z_n(T)$
induced by a bijection
$Z_n(S) \to Z_n(T)$
induced by a bijection
![]() $(f, \varnothing )\colon S \to T$
is simply given by relabelling elements in a partition and by the induced map on determinants. The linear map induced by
$(f, \varnothing )\colon S \to T$
is simply given by relabelling elements in a partition and by the induced map on determinants. The linear map induced by
![]() $(inc, (x,y))\colon S \to S \setminus \{x,y\}$
assigns to the element
$(inc, (x,y))\colon S \to S \setminus \{x,y\}$
assigns to the element
![]() $[\{S_{\alpha }\}_{\alpha \in I}] \otimes (x \wedge y \wedge s_3 \wedge \cdots \wedge s_{|S|})^{\otimes n}$
the following:
$[\{S_{\alpha }\}_{\alpha \in I}] \otimes (x \wedge y \wedge s_3 \wedge \cdots \wedge s_{|S|})^{\otimes n}$
the following:
-
(i) If some
 $S_{\beta }$
contains
$S_{\beta }$
contains
 $\{x,y\}$
, then it assigns 0.
$\{x,y\}$
, then it assigns 0. -
(ii) If x and y lie in different parts
 $S_{\beta }$
and
$S_{\beta }$
and
 $S_{\gamma }$
, then these are merged into a single new part
$S_{\gamma }$
, then these are merged into a single new part
 $S_{\beta } \setminus \{x\} \cup S_{\gamma } \setminus \{y\}$
and it assigns
$S_{\beta } \setminus \{x\} \cup S_{\gamma } \setminus \{y\}$
and it assigns  $$\begin{align*}[\{S_{\alpha}\}_{\alpha \neq \beta, \gamma} \cup \{S_{\beta} \setminus\{x\} \cup S_{\gamma} \setminus\{y\}\}] \otimes (s_3 \wedge \cdots \wedge s_{|S|})^{\otimes n}.\end{align*}$$
$$\begin{align*}[\{S_{\alpha}\}_{\alpha \neq \beta, \gamma} \cup \{S_{\beta} \setminus\{x\} \cup S_{\gamma} \setminus\{y\}\}] \otimes (s_3 \wedge \cdots \wedge s_{|S|})^{\otimes n}.\end{align*}$$
On a more general morphism in
![]() $\mathsf {d(s)Br}$
, the effect of
$\mathsf {d(s)Br}$
, the effect of
![]() $Z_n$
is determined by the above and functoriality.
$Z_n$
is determined by the above and functoriality.

Figure 2 The effect of the morphism
![]() $(inc,\{1,2\}) \colon S = \underline {8} \to S' = \underline {8} \setminus \{1,2\}$
on two elements of
$(inc,\{1,2\}) \colon S = \underline {8} \to S' = \underline {8} \setminus \{1,2\}$
on two elements of
![]() $Z_n(S)$
: The first is the partition of S into parts
$Z_n(S)$
: The first is the partition of S into parts
![]() $S_{ \alpha } = \{1,\ldots ,5\}$
and
$S_{ \alpha } = \{1,\ldots ,5\}$
and
![]() $S_{ \beta } = \{6,7,8\}$
and the second is the partition into parts
$S_{ \beta } = \{6,7,8\}$
and the second is the partition into parts
![]() $S^{\prime }_{ \alpha '} = \{2,\ldots ,6\}$
and
$S^{\prime }_{ \alpha '} = \{2,\ldots ,6\}$
and
![]() $S^{\prime }_{ \beta '} = \{1,7,8\}$
. Similarly to [Reference Koike and TeradaKRW20c, Section 5.3], we represent each part in a partition by a corolla whose legs are labelled by the elements in that part; we have suppressed the orientations. In this graphical notation, morphisms in
$S^{\prime }_{ \beta '} = \{1,7,8\}$
. Similarly to [Reference Koike and TeradaKRW20c, Section 5.3], we represent each part in a partition by a corolla whose legs are labelled by the elements in that part; we have suppressed the orientations. In this graphical notation, morphisms in
![]() $\mathsf {d(s)Br}$
act by reordering labels and connecting legs, collapsing internal edges and mapping to zero whenever a loop appears.
$\mathsf {d(s)Br}$
act by reordering labels and connecting legs, collapsing internal edges and mapping to zero whenever a loop appears.
Definition 4.21. A weighted partition of a set S is a partition
![]() $\{S_{\alpha }\}_{\alpha \in I}$
of S along with a weight
$\{S_{\alpha }\}_{\alpha \in I}$
of S along with a weight
![]() $g_{\alpha } \in \{0,1,2,3,\ldots \}$
for each part. A weighted partition is admissible if
$g_{\alpha } \in \{0,1,2,3,\ldots \}$
for each part. A weighted partition is admissible if
-
(i) Each part of size 0 has weight
 $\geq 2$
.
$\geq 2$
. -
(ii) Each part of size 1 or 2 has weight
 $\geq 1$
.
$\geq 1$
.
For
![]() $n \in \mathbb {N}_{>0}$
, let
$n \in \mathbb {N}_{>0}$
, let
![]() $E_n\colon \mathsf {d(s)Br} \to \mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
be the functor which to a finite set S assigns the vector space
$E_n\colon \mathsf {d(s)Br} \to \mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod})$
be the functor which to a finite set S assigns the vector space
made into a graded vector space by declaring a weighted part
![]() $(S_{\alpha }, g_{\alpha })$
to have degree
$(S_{\alpha }, g_{\alpha })$
to have degree
![]() $n(2 g_{\alpha } + |S_{\alpha }|-2)$
, and a weighted partition to have degree the sum of the degrees of its weighted parts.
$n(2 g_{\alpha } + |S_{\alpha }|-2)$
, and a weighted partition to have degree the sum of the degrees of its weighted parts.
The linear map
![]() $E_n(S) \to E_n(T)$
induced by a bijection
$E_n(S) \to E_n(T)$
induced by a bijection
![]() $(f, \varnothing )\colon S \to T$
is simply given by relabelling elements in a partition and by the induced map on determinants. The linear map induced by
$(f, \varnothing )\colon S \to T$
is simply given by relabelling elements in a partition and by the induced map on determinants. The linear map induced by
![]() $(inc, (x,y))\colon S \to S \setminus \{x,y\}$
assigns to the element
$(inc, (x,y))\colon S \to S \setminus \{x,y\}$
assigns to the element
![]() $[\{(S_{\alpha }, g_{\alpha })\}_{\alpha \in I}] \otimes (x \wedge y \wedge s_3 \wedge \cdots \wedge s_{|S|})^{\otimes n}$
the following:
$[\{(S_{\alpha }, g_{\alpha })\}_{\alpha \in I}] \otimes (x \wedge y \wedge s_3 \wedge \cdots \wedge s_{|S|})^{\otimes n}$
the following:
-
(i) If some
 $S_{\beta }$
contains
$S_{\beta }$
contains
 $\{x,y\}$
, then it assigns
$\{x,y\}$
, then it assigns  $$\begin{align*}[\{(S_{\alpha}, g_{\alpha})\}_{\alpha \neq \beta} \cup \{(S_{\beta} \setminus \{x,y\}, g_{\beta}+1)\}] \otimes ( s_3 \wedge \cdots \wedge s_{|S|})^{\otimes n},\end{align*}$$
$$\begin{align*}[\{(S_{\alpha}, g_{\alpha})\}_{\alpha \neq \beta} \cup \{(S_{\beta} \setminus \{x,y\}, g_{\beta}+1)\}] \otimes ( s_3 \wedge \cdots \wedge s_{|S|})^{\otimes n},\end{align*}$$
-
(ii) If x and y lie in different parts
 $S_{\beta }$
and
$S_{\beta }$
and
 $S_{\gamma }$
, then it assigns
$S_{\gamma }$
, then it assigns  $$\begin{align*}[\{(S_{\alpha}, g_{\alpha})\}_{\alpha \neq \beta, \gamma} \cup \{(S_{\beta} \setminus\{x\} \cup S_{\gamma} \setminus\{y\}, g_{\beta}+g_{\gamma})\}] \otimes ( s_3 \wedge \cdots \wedge s_{|S|})^{\otimes n}.\end{align*}$$
$$\begin{align*}[\{(S_{\alpha}, g_{\alpha})\}_{\alpha \neq \beta, \gamma} \cup \{(S_{\beta} \setminus\{x\} \cup S_{\gamma} \setminus\{y\}, g_{\beta}+g_{\gamma})\}] \otimes ( s_3 \wedge \cdots \wedge s_{|S|})^{\otimes n}.\end{align*}$$
On a more general morphism in
![]() $\mathsf {d(s)Br}$
, the effect of
$\mathsf {d(s)Br}$
, the effect of
![]() $E_n$
is determined by the above and functoriality.
$E_n$
is determined by the above and functoriality.

Figure 3 The effect of the morphism
![]() $(inc,\{1,2\}) \colon S = \underline {8} \to S' = \underline {8} \setminus \{1,2\}$
on two elements of
$(inc,\{1,2\}) \colon S = \underline {8} \to S' = \underline {8} \setminus \{1,2\}$
on two elements of
![]() $E_n(S)$
, once more representing each part in a partition by a corolla and suppressing the orientations. Each part
$E_n(S)$
, once more representing each part in a partition by a corolla and suppressing the orientations. Each part
![]() $S_{ \alpha }$
in a partition – that is, each corolla – has a weight
$S_{ \alpha }$
in a partition – that is, each corolla – has a weight
![]() $g_{ \alpha } \geq 0$
indicated with a label at the vertex. Morphisms in
$g_{ \alpha } \geq 0$
indicated with a label at the vertex. Morphisms in
![]() $\mathsf {d(s)Br}$
act by reordering labels and connecting labels, collapsing internal edges (adding their weights) and removing loops (adding
$\mathsf {d(s)Br}$
act by reordering labels and connecting labels, collapsing internal edges (adding their weights) and removing loops (adding
![]() $1$
to the weight of the vertex it is attached to).
$1$
to the weight of the vertex it is attached to).
The functors
![]() $Z_n$
and
$Z_n$
and
![]() $E_n$
have lax symmetric monoidalities given by disjoint union, making them into unital commutative algebra objects in
$E_n$
have lax symmetric monoidalities given by disjoint union, making them into unital commutative algebra objects in
![]() $\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod}))$
. As they are concentrated in homological degrees which are multiples of n, we can give them an additional weight grading by declaring it to be the homological degree divided by n. Furthermore, both
$\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod}))$
. As they are concentrated in homological degrees which are multiples of n, we can give them an additional weight grading by declaring it to be the homological degree divided by n. Furthermore, both
![]() $Z_n$
and
$Z_n$
and
![]() $E_n$
have unique augmentations, by sending all (weighted) partitions of nonempty sets to zero and the empty partition of the empty set to
$E_n$
have unique augmentations, by sending all (weighted) partitions of nonempty sets to zero and the empty partition of the empty set to
![]() $1$
. Up to scaling the homological grading each of these augmented unital commutative algebra objects only depends on the parity of n.
$1$
. Up to scaling the homological grading each of these augmented unital commutative algebra objects only depends on the parity of n.
For each n, there is a (lax symmetric monoidal) epimorphism
![]() $E_n \to Z_n$
given by sending a part
$E_n \to Z_n$
given by sending a part
![]() $(S_{\alpha }, 0)$
to
$(S_{\alpha }, 0)$
to
![]() $S_{\alpha }$
, and parts with strictly positive weight to zero. It is compatible with the augmentations.
$S_{\alpha }$
, and parts with strictly positive weight to zero. It is compatible with the augmentations.
After having introduced
![]() $E_n$
and
$E_n$
and
![]() $Z_n$
we will now explain that, as commutative algebra objects, they differ only by the attachment of a single commutative algebra cell. As we mentioned above, there is a map of commutative algebra objects
$Z_n$
we will now explain that, as commutative algebra objects, they differ only by the attachment of a single commutative algebra cell. As we mentioned above, there is a map of commutative algebra objects
![]() $E_n \to Z_n$
and hence maps
$E_n \to Z_n$
and hence maps
![]() $\mathbb {L} Q^{\mathrm { Com}^+}(E_n) \to \mathbb {L} Q^{\mathrm {Com}^+}(Z_n)$
. Taking the homotopy cofibre of this, we may define the relative homology groups
$\mathbb {L} Q^{\mathrm { Com}^+}(E_n) \to \mathbb {L} Q^{\mathrm {Com}^+}(Z_n)$
. Taking the homotopy cofibre of this, we may define the relative homology groups
![]() $H_p^{\mathrm {Com}}(Z_n, E_n)_{q,w}$
which participate in the usual long exact sequence. We have the following description of this relative homology.
$H_p^{\mathrm {Com}}(Z_n, E_n)_{q,w}$
which participate in the usual long exact sequence. We have the following description of this relative homology.
Theorem 4.22. We have
 $$\begin{align*}H_p^{\mathrm{Com}}(Z_n, E_n)_{q,w}(S) \cong \begin{cases} \mathbb{Q} & \text{ if } |S|=1 \text{ and } (p,q,w)=(2,n,1),\\ 0 & \text{ otherwise.} \end{cases}\end{align*}$$
$$\begin{align*}H_p^{\mathrm{Com}}(Z_n, E_n)_{q,w}(S) \cong \begin{cases} \mathbb{Q} & \text{ if } |S|=1 \text{ and } (p,q,w)=(2,n,1),\\ 0 & \text{ otherwise.} \end{cases}\end{align*}$$
Proof. As the weight is given by the homological grading divided by n, we may neglect it. Let us write
and in particular
![]() $\underline {1} = \{1\}$
. There is a map
$\underline {1} = \{1\}$
. There is a map
![]() $S(n) \to E_n(\underline {1})$
corresponding to the weighted partition
$S(n) \to E_n(\underline {1})$
corresponding to the weighted partition
![]() $(\underline {1}, 1)$
of the set
$(\underline {1}, 1)$
of the set
![]() $\underline {1}$
, with
$\underline {1}$
, with
![]() $S(n)$
as in (5). This is adjoint to a map
$S(n)$
as in (5). This is adjoint to a map
![]() $\underline {1}_*S(n) \to E_n$
and hence, as the target is a unital commutative algebra object, to a map
$\underline {1}_*S(n) \to E_n$
and hence, as the target is a unital commutative algebra object, to a map
![]() $\phi \colon F^{\mathrm {Com}^+}(\underline {1}_*S(n)) \longrightarrow E_n$
. Using this we may form the pushout
$\phi \colon F^{\mathrm {Com}^+}(\underline {1}_*S(n)) \longrightarrow E_n$
. Using this we may form the pushout

of unital commutative algebra objects. As
![]() $(\underline {1}, 1)$
maps to zero in
$(\underline {1}, 1)$
maps to zero in
![]() $Z_n(\underline {1})$
, there is a factorisation
$Z_n(\underline {1})$
, there is a factorisation
Although
![]() $E^{\prime }_n : \mathsf {d(s)Br} \to \mathsf {Ch}$
does not take values in the subcategory
$E^{\prime }_n : \mathsf {d(s)Br} \to \mathsf {Ch}$
does not take values in the subcategory
![]() $\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod}) \subset \mathsf {Ch}$
, we can nonetheless give it an ‘internal grading’ and ‘weight’ by declaring both
$\mathsf {Gr}(\mathbb {Q}\text {-}\mathsf {mod}) \subset \mathsf {Ch}$
, we can nonetheless give it an ‘internal grading’ and ‘weight’ by declaring both
![]() $\underline {1}_* S(n)$
and
$\underline {1}_* S(n)$
and
![]() $\underline {1}_* D(n+1)$
to have internal degree n and weight 1. Then the maps (9) both preserve these two additional gradings. We will show that the map
$\underline {1}_* D(n+1)$
to have internal degree n and weight 1. Then the maps (9) both preserve these two additional gradings. We will show that the map
![]() $E^{\prime }_n \to Z_n$
is a weak equivalence: As the cofibre of the map
$E^{\prime }_n \to Z_n$
is a weak equivalence: As the cofibre of the map
![]() $\mathbb {L} Q^{\mathrm {Com}^+}(E_n) \to \mathbb {L} Q^{\mathrm { Com}^+}(E^{\prime }_n)$
is
$\mathbb {L} Q^{\mathrm {Com}^+}(E_n) \to \mathbb {L} Q^{\mathrm { Com}^+}(E^{\prime }_n)$
is
![]() $\underline {1}_* (D(n+1)/S(n)) = \underline {1}_* S(n+1)$
by construction (supported in total degree
$\underline {1}_* (D(n+1)/S(n)) = \underline {1}_* S(n+1)$
by construction (supported in total degree
![]() $n+1$
, internal degree n, and weight
$n+1$
, internal degree n, and weight
![]() $1$
) the formula in the statement of the theorem follows.
$1$
) the formula in the statement of the theorem follows.
Pushouts of commutative algebra objects are given by the relative tensor product, and – neglecting the differential – we have
 $$ \begin{align*} F^{\mathrm{Com}^+}(\underline{1}_*D(n+1)) &= F^{\mathrm{Com}^+}(\underline{1}_*S(n) \oplus \underline{1}_*S(n+1))\\ &= F^{\mathrm{Com}^+}(\underline{1}_*S(n)) \otimes F^{\mathrm{Com}^+}(\underline{1}_*S(n+1)) \end{align*} $$
$$ \begin{align*} F^{\mathrm{Com}^+}(\underline{1}_*D(n+1)) &= F^{\mathrm{Com}^+}(\underline{1}_*S(n) \oplus \underline{1}_*S(n+1))\\ &= F^{\mathrm{Com}^+}(\underline{1}_*S(n)) \otimes F^{\mathrm{Com}^+}(\underline{1}_*S(n+1)) \end{align*} $$
so that – neglecting the differential – we have
Claim. We have
![]() $F^{\mathrm {Com}^+}(\underline {1}_*S(n+1))(T) \cong \det (\mathbb {Q}^T)^{\otimes n+1}[(n+1)|T|]$
, and the functoriality is such that a morphism
$F^{\mathrm {Com}^+}(\underline {1}_*S(n+1))(T) \cong \det (\mathbb {Q}^T)^{\otimes n+1}[(n+1)|T|]$
, and the functoriality is such that a morphism
![]() $(f,m)$
in
$(f,m)$
in
![]() $\mathsf {d(s)Br}$
with
$\mathsf {d(s)Br}$
with
![]() $m \neq \varnothing $
acts as zero.
$m \neq \varnothing $
acts as zero.
Proof of claim
By definition of Day convolution, we have
where
![]() $\mathfrak {S}_p$
acts diagonally, and so
$\mathfrak {S}_p$
acts diagonally, and so
Write
![]() $e_{n+1} \in S(n+1)$
for the basis element. If
$e_{n+1} \in S(n+1)$
for the basis element. If
![]() $(f, m) \in \mathsf {d(s)Br}(\{1,2,\ldots , p\}, T)$
has
$(f, m) \in \mathsf {d(s)Br}(\{1,2,\ldots , p\}, T)$
has
![]() $m \neq \varnothing $
, say with
$m \neq \varnothing $
, say with
![]() $(x,y) \in m$
, then
$(x,y) \in m$
, then
 $$ \begin{align*} (e_{n+1} \otimes \cdots \otimes e_{n+1}) \otimes_{\mathfrak{S}_p} (f, m) &= (x \, y) \cdot(e_{n+1} \otimes \cdots \otimes e_{n+1}) \otimes_{\mathfrak{S}_p} (x \, y) \cdot(f, m)\\ &= (-1)^{n+1} (e_{n+1} \otimes \cdots \otimes e_{n+1}) \otimes_{\mathfrak{S}_p} (-1)^n (f, m)\\ &= - (e_{n+1} \otimes \cdots \otimes e_{n+1}) \otimes_{\mathfrak{S}_p} (f, m) \end{align*} $$
$$ \begin{align*} (e_{n+1} \otimes \cdots \otimes e_{n+1}) \otimes_{\mathfrak{S}_p} (f, m) &= (x \, y) \cdot(e_{n+1} \otimes \cdots \otimes e_{n+1}) \otimes_{\mathfrak{S}_p} (x \, y) \cdot(f, m)\\ &= (-1)^{n+1} (e_{n+1} \otimes \cdots \otimes e_{n+1}) \otimes_{\mathfrak{S}_p} (-1)^n (f, m)\\ &= - (e_{n+1} \otimes \cdots \otimes e_{n+1}) \otimes_{\mathfrak{S}_p} (f, m) \end{align*} $$
and so this term vanishes. Hence, only the term with
![]() $p=|T|$
contributes, giving
$p=|T|$
contributes, giving
![]() $F^{\mathrm {Com}^+}(\underline {1}_*S(n+1))(T) = S(n+1)^{\otimes |T|} \otimes _{\mathfrak {S}_{|T|}} \mathsf {d(s)Br}(\{1,2,\ldots , |T|\}, T)$
. The claim is simply an interpretation of this formula.
$F^{\mathrm {Com}^+}(\underline {1}_*S(n+1))(T) = S(n+1)^{\otimes |T|} \otimes _{\mathfrak {S}_{|T|}} \mathsf {d(s)Br}(\{1,2,\ldots , |T|\}, T)$
. The claim is simply an interpretation of this formula.
Using the expression (4) for Day convolution, neglecting the differential we have
We will give an interpretation of this in terms of decorated partitions. Define a biweighted partition of a set S to be a partition
![]() $\{S_{\alpha }\}_{\alpha \in I}$
of a subset of S along with a weight
$\{S_{\alpha }\}_{\alpha \in I}$
of a subset of S along with a weight
![]() $g_{\alpha } \in \{0,1,2,3,\ldots \}$
and a further weight
$g_{\alpha } \in \{0,1,2,3,\ldots \}$
and a further weight
![]() $h_{\alpha } \in \{0,1\}$
for each part. A biweighted partition is admissible if
$h_{\alpha } \in \{0,1\}$
for each part. A biweighted partition is admissible if
-
(i) when
 $|S_{\alpha }|=0$
then
$|S_{\alpha }|=0$
then
 $g_{\alpha }+h_{\alpha }\geq 2$
,
$g_{\alpha }+h_{\alpha }\geq 2$
, -
(ii) when
 $|S_{\alpha }|=1,2$
then
$|S_{\alpha }|=1,2$
then
 $g_{\alpha }+h_{\alpha }\geq 1$
.
$g_{\alpha }+h_{\alpha }\geq 1$
.
For such a biweighted partition, we let
![]() ,
,
![]() and
and
![]() . Define
. Define
 $$\begin{align*}E^{\prime\prime}_n(S) = \bigoplus_{\substack{\text{admissible biweighted partitions} \\ \{(S_{\alpha}, g_{\alpha}, h_{\alpha})\}_{\alpha \in I} \text{ of } S}} \det(\mathbb{Q}^{J}) \otimes \det(\mathbb{Q}^{B}) \otimes \det(\mathbb{Q}^{S})^{\otimes n}\end{align*}$$
$$\begin{align*}E^{\prime\prime}_n(S) = \bigoplus_{\substack{\text{admissible biweighted partitions} \\ \{(S_{\alpha}, g_{\alpha}, h_{\alpha})\}_{\alpha \in I} \text{ of } S}} \det(\mathbb{Q}^{J}) \otimes \det(\mathbb{Q}^{B}) \otimes \det(\mathbb{Q}^{S})^{\otimes n}\end{align*}$$
made into a graded vector space by declaring a biweighted partition to have degree
![]() $(n+1)|B| + \sum _{\alpha \in I} n(2 g_{\alpha } + |S_{\alpha }|-2) + (2n+1)h_{\alpha }$
.
$(n+1)|B| + \sum _{\alpha \in I} n(2 g_{\alpha } + |S_{\alpha }|-2) + (2n+1)h_{\alpha }$
.

Figure 4 Intuitive indication of the map
![]() $\chi $
. Weights
$\chi $
. Weights
![]() $g_{\alpha }$
are not indicated, and weights
$g_{\alpha }$
are not indicated, and weights
![]() $h_{\alpha }=1$
are indicated by a half-edge with a red end.
$h_{\alpha }=1$
are indicated by a half-edge with a red end.
Define a morphism of graded vector spaces
on
![]() $(\{S_{\alpha }\}_{\alpha \in I}, g_{\alpha }, h_{\alpha }) \otimes (j_1 \wedge \cdots \wedge j_{|J|}) \otimes (b_1 \wedge \cdots \wedge b_{|B|}) \otimes (a_1 \wedge \cdots \wedge a_{|A|} \wedge b_1 \wedge \cdots \wedge b_{|B|})^{\otimes n}$
as follows. Let
$(\{S_{\alpha }\}_{\alpha \in I}, g_{\alpha }, h_{\alpha }) \otimes (j_1 \wedge \cdots \wedge j_{|J|}) \otimes (b_1 \wedge \cdots \wedge b_{|B|}) \otimes (a_1 \wedge \cdots \wedge a_{|A|} \wedge b_1 \wedge \cdots \wedge b_{|B|})^{\otimes n}$
as follows. Let
and
, and let
![]() $\phi = (f, m) \colon S' \sqcup S" \to S$
be the morphism in
$\phi = (f, m) \colon S' \sqcup S" \to S$
be the morphism in
![]() $\mathsf {d(s)Br}$
with injection
$\mathsf {d(s)Br}$
with injection
![]() $f \colon S \to S' \sqcup S"$
given by sending
$f \colon S \to S' \sqcup S"$
given by sending
![]() $s \in S$
to
$s \in S$
to
![]() $s \in S'$
if
$s \in S'$
if
![]() $s \in A$
, and to
$s \in A$
, and to
![]() $s \in S"$
if
$s \in S"$
if
![]() $s \in B$
, and matching m given by pairing each element of
$s \in B$
, and matching m given by pairing each element of
![]() $J \subset S'$
with the same element of
$J \subset S'$
with the same element of
![]() $J \subset S"$
, putting that of
$J \subset S"$
, putting that of
![]() $S'$
first. For
$S'$
first. For
![]() $\alpha \in I$
, let
$\alpha \in I$
, let

Then
![]() $\phi $
,
$\phi $
,
![]() $(\{S^{\prime }_{\alpha }\}_{\alpha \in I}, g_{\alpha }) \otimes (a_1 \wedge \cdots \wedge a_{|A|} \wedge j_1 \wedge \cdots \wedge j_{|J|})^{\otimes n}$
,
$(\{S^{\prime }_{\alpha }\}_{\alpha \in I}, g_{\alpha }) \otimes (a_1 \wedge \cdots \wedge a_{|A|} \wedge j_1 \wedge \cdots \wedge j_{|J|})^{\otimes n}$
,
![]() $(b_1 \wedge \cdots \wedge b_{|B|} \wedge j_1 \wedge \cdots \wedge j_{|J|})^{\otimes n+1}$
represents an element of (10). Note that permuting the
$(b_1 \wedge \cdots \wedge b_{|B|} \wedge j_1 \wedge \cdots \wedge j_{|J|})^{\otimes n+1}$
represents an element of (10). Note that permuting the
![]() $j_i$
acts by the sign, permuting the
$j_i$
acts by the sign, permuting the
![]() $a_i$
acts by the nth power of the sign and permuting the
$a_i$
acts by the nth power of the sign and permuting the
![]() $b_i$
acts via the
$b_i$
acts via the
![]() $(n+1)$
st power of the sign, making this map well defined.
$(n+1)$
st power of the sign, making this map well defined.
Claim. The map
![]() $\chi $
is an isomorphism.
$\chi $
is an isomorphism.
Proof of claim
Suppose we are given a morphism
![]() $\phi = (f, m) \colon S' \sqcup S" \to S$
,
$\phi = (f, m) \colon S' \sqcup S" \to S$
,
![]() $(\{S^{\prime }_{\alpha }\}_{\alpha \in I}, g_{\alpha }) \otimes (s^{\prime }_1 \wedge \cdots \wedge s^{\prime }_{|S'|})^{\otimes n} \in E_n(S')$
, and
$(\{S^{\prime }_{\alpha }\}_{\alpha \in I}, g_{\alpha }) \otimes (s^{\prime }_1 \wedge \cdots \wedge s^{\prime }_{|S'|})^{\otimes n} \in E_n(S')$
, and
![]() $(s^{\prime \prime }_1 \wedge \cdots \wedge s^{\prime \prime }_{|S"|})^{\otimes n+1} \in \det (\mathbb {Q}^{S"})^{\otimes n+1}[(n+1)|S"|]$
, representing an element of
$(s^{\prime \prime }_1 \wedge \cdots \wedge s^{\prime \prime }_{|S"|})^{\otimes n+1} \in \det (\mathbb {Q}^{S"})^{\otimes n+1}[(n+1)|S"|]$
, representing an element of
![]() $E^{\prime }_n(S)$
in the description (10).
$E^{\prime }_n(S)$
in the description (10).
Suppose that this data is such that there are ordered pairs
![]() $(s^{\prime }_i, s^{\prime \prime }_i), (s^{\prime }_j, s^{\prime \prime }_j)$
with
$(s^{\prime }_i, s^{\prime \prime }_i), (s^{\prime }_j, s^{\prime \prime }_j)$
with
![]() $i \neq j$
, but
$i \neq j$
, but
![]() $s^{\prime }_i, s^{\prime }_j \in S^{\prime }_{\alpha }$
. The permutation
$s^{\prime }_i, s^{\prime }_j \in S^{\prime }_{\alpha }$
. The permutation
![]() $(s^{\prime }_i \, s^{\prime }_j)(s^{\prime \prime }_i \, s^{\prime \prime }_j)$
gives a morphism
$(s^{\prime }_i \, s^{\prime }_j)(s^{\prime \prime }_i \, s^{\prime \prime }_j)$
gives a morphism
![]() $\psi \colon S' \sqcup S" \to S' \sqcup S"$
such that
$\psi \colon S' \sqcup S" \to S' \sqcup S"$
such that
![]() $\phi \circ \psi = \psi $
. Thus, the data above is equivalent to the data
$\phi \circ \psi = \psi $
. Thus, the data above is equivalent to the data
![]() $\phi $
,
$\phi $
,
![]() $(s^{\prime }_i \, s^{\prime }_j) \cdot ((\{S^{\prime }_{\alpha }\}_{\alpha \in I}, g_{\alpha }) \otimes (s^{\prime }_1 \wedge \cdots \wedge s^{\prime }_{|S'|})^{\otimes n})$
,
$(s^{\prime }_i \, s^{\prime }_j) \cdot ((\{S^{\prime }_{\alpha }\}_{\alpha \in I}, g_{\alpha }) \otimes (s^{\prime }_1 \wedge \cdots \wedge s^{\prime }_{|S'|})^{\otimes n})$
,
![]() $(s^{\prime \prime }_i \, s^{\prime \prime }_j) \cdot (s^{\prime \prime }_1 \wedge \cdots \wedge s^{\prime \prime }_{|S"|})^{\otimes n+1}$
. That is: The data
$(s^{\prime \prime }_i \, s^{\prime \prime }_j) \cdot (s^{\prime \prime }_1 \wedge \cdots \wedge s^{\prime \prime }_{|S"|})^{\otimes n+1}$
. That is: The data
![]() $\phi $
,
$\phi $
,
![]() $(-1)^n (\{S^{\prime }_{\alpha }\}_{\alpha \in I}, g_{\alpha }) \otimes (s^{\prime }_1 \wedge \cdots \wedge s^{\prime }_{|S'|})$
, and
$(-1)^n (\{S^{\prime }_{\alpha }\}_{\alpha \in I}, g_{\alpha }) \otimes (s^{\prime }_1 \wedge \cdots \wedge s^{\prime }_{|S'|})$
, and
![]() $(-1)^{n+1}(s^{\prime \prime }_1 \wedge \cdots \wedge s^{\prime \prime }_{|S"|})^{\otimes n+1}$
and so minus the original element. Thus, such elements vanish, and we may suppose that for each
$(-1)^{n+1}(s^{\prime \prime }_1 \wedge \cdots \wedge s^{\prime \prime }_{|S"|})^{\otimes n+1}$
and so minus the original element. Thus, such elements vanish, and we may suppose that for each
![]() $\alpha $
there is at most one pair
$\alpha $
there is at most one pair
![]() $(s',s") \in m$
with
$(s',s") \in m$
with
![]() $s' \in S^{\prime }_{\alpha }$
. Using this, it is easy to produce an inverse to the map
$s' \in S^{\prime }_{\alpha }$
. Using this, it is easy to produce an inverse to the map
![]() $\chi $
: we set
$\chi $
: we set
![]() and
and
![]() $h_{\alpha }=1$
if
$h_{\alpha }=1$
if
![]() $(s',s") \in m$
with
$(s',s") \in m$
with
![]() $s' \in S^{\prime }_{\alpha }$
, and otherwise set
$s' \in S^{\prime }_{\alpha }$
, and otherwise set
![]() and
and
![]() $h_{\alpha }=0$
.
$h_{\alpha }=0$
.
The differential of
![]() $E^{\prime }_n(S)$
is given under the isomorphism
$E^{\prime }_n(S)$
is given under the isomorphism
![]() $\chi $
by sending the element
$\chi $
by sending the element
![]() $(\{S_{\alpha }\}_{\alpha \in I}, g_{\alpha }, h_{\alpha }) \otimes (j_1 \wedge \cdots \wedge j_{|J|}) \otimes (b_1 \wedge \cdots \wedge b_{|B|}) \otimes (a_1 \wedge \cdots \wedge a_{|A|} \wedge b_1 \wedge \cdots \wedge b_{|B|})^{\otimes n}$
of
$(\{S_{\alpha }\}_{\alpha \in I}, g_{\alpha }, h_{\alpha }) \otimes (j_1 \wedge \cdots \wedge j_{|J|}) \otimes (b_1 \wedge \cdots \wedge b_{|B|}) \otimes (a_1 \wedge \cdots \wedge a_{|A|} \wedge b_1 \wedge \cdots \wedge b_{|B|})^{\otimes n}$
of
![]() $E^{\prime \prime }_n(S)$
to
$E^{\prime \prime }_n(S)$
to
 $$ \begin{align*} &\sum_{\beta \in J \subset I} (\{S_{\alpha}\}_{\alpha \in I}, g_{\alpha} + \delta_{\alpha \beta}, h_{\alpha} - \delta_{\alpha \beta}) \otimes (j_1 \wedge \cdots \wedge j_{|J|})/\beta \\ &\quad\quad\quad\quad\quad \otimes (b_1 \wedge \cdots \wedge b_{|B|}) \otimes (a_1 \wedge \cdots \wedge a_{|A|} \wedge b_1 \wedge \cdots \wedge b_{|B|})^{\otimes n}\\ &+ \sum_{b \in B} (\{S_{\alpha}\}_{\alpha \in I \cup \{b\}}, g_{\alpha}, h_{\alpha}) \otimes (j_1 \wedge \cdots \wedge j_{|J|})\\ &\quad\quad\quad\quad\quad \otimes (b_1 \wedge \cdots \wedge b_{|B|})/b \otimes (a_1 \wedge \cdots \wedge a_{|A|} \wedge b_1 \wedge \cdots \wedge b_{|B|})^{\otimes n,} \end{align*} $$
$$ \begin{align*} &\sum_{\beta \in J \subset I} (\{S_{\alpha}\}_{\alpha \in I}, g_{\alpha} + \delta_{\alpha \beta}, h_{\alpha} - \delta_{\alpha \beta}) \otimes (j_1 \wedge \cdots \wedge j_{|J|})/\beta \\ &\quad\quad\quad\quad\quad \otimes (b_1 \wedge \cdots \wedge b_{|B|}) \otimes (a_1 \wedge \cdots \wedge a_{|A|} \wedge b_1 \wedge \cdots \wedge b_{|B|})^{\otimes n}\\ &+ \sum_{b \in B} (\{S_{\alpha}\}_{\alpha \in I \cup \{b\}}, g_{\alpha}, h_{\alpha}) \otimes (j_1 \wedge \cdots \wedge j_{|J|})\\ &\quad\quad\quad\quad\quad \otimes (b_1 \wedge \cdots \wedge b_{|B|})/b \otimes (a_1 \wedge \cdots \wedge a_{|A|} \wedge b_1 \wedge \cdots \wedge b_{|B|})^{\otimes n,} \end{align*} $$
where
![]() $S_b = \{b\}$
,
$S_b = \{b\}$
,
![]() $g_b = 1$
,
$g_b = 1$
,
![]() $h_b=0$
. In particular, the partition
$h_b=0$
. In particular, the partition
![]() $S = \bigcup _{\alpha } S_{\alpha } \cup \bigcup _{b \in B} \{b\}$
of S is preserved by the differential, so we recognise the chain complex
$S = \bigcup _{\alpha } S_{\alpha } \cup \bigcup _{b \in B} \{b\}$
of S is preserved by the differential, so we recognise the chain complex
![]() $E^{\prime \prime }_n(S)$
as a direct sum of complexes, one for each partition of S. Furthermore, we recognise the chain complex for the partition
$E^{\prime \prime }_n(S)$
as a direct sum of complexes, one for each partition of S. Furthermore, we recognise the chain complex for the partition
![]() $S = \bigcup _{\alpha } S_{\alpha } \cup \bigcup _{b \in B} \{b\}$
as the tensor product of chain complexes, one for each part of this partition.
$S = \bigcup _{\alpha } S_{\alpha } \cup \bigcup _{b \in B} \{b\}$
as the tensor product of chain complexes, one for each part of this partition.
-
(i) That corresponding to the part
 $S_{\alpha }$
is given by (tensored with
$S_{\alpha }$
is given by (tensored with $$\begin{align*}\bigoplus_{g_{\alpha} + 1 \geq r_{\alpha}} (S_{\alpha}, g_{\alpha}, 1) \otimes \alpha \otimes 1 \overset{d}\longrightarrow \bigoplus_{g_{\alpha} \geq r_{\alpha}} (S_{\alpha}, g_{\alpha}, 0) \otimes 1 \otimes 1 \end{align*}$$
$$\begin{align*}\bigoplus_{g_{\alpha} + 1 \geq r_{\alpha}} (S_{\alpha}, g_{\alpha}, 1) \otimes \alpha \otimes 1 \overset{d}\longrightarrow \bigoplus_{g_{\alpha} \geq r_{\alpha}} (S_{\alpha}, g_{\alpha}, 0) \otimes 1 \otimes 1 \end{align*}$$
 $\det (\mathbb {Q}^{S_{\alpha }})^{\otimes n}$
) with
$\det (\mathbb {Q}^{S_{\alpha }})^{\otimes n}$
) with
 $d((S_{\alpha }, g_{\alpha }, 1) \otimes \alpha \otimes 1) = (S_{\alpha }, g_{\alpha }+1, 0) \otimes 1 \otimes 1$
, where
$d((S_{\alpha }, g_{\alpha }, 1) \otimes \alpha \otimes 1) = (S_{\alpha }, g_{\alpha }+1, 0) \otimes 1 \otimes 1$
, where
 $r_{\alpha }$
is 2 if
$r_{\alpha }$
is 2 if
 $|S_{\alpha }|$
is 0, is 1 if
$|S_{\alpha }|$
is 0, is 1 if
 $|S_{\alpha }|$
is 1 or 2, and is 0 otherwise. The homology of this complex is given by
$|S_{\alpha }|$
is 1 or 2, and is 0 otherwise. The homology of this complex is given by
 $\bigoplus _{0 \geq r_{\alpha }} (S_{\alpha }, 0, 0) \otimes 1 \otimes 1$
, that is, is 1-dimensional as long as
$\bigoplus _{0 \geq r_{\alpha }} (S_{\alpha }, 0, 0) \otimes 1 \otimes 1$
, that is, is 1-dimensional as long as
 $|S_{\alpha }|> 2$
and zero otherwise, recalling the requirement
$|S_{\alpha }|> 2$
and zero otherwise, recalling the requirement
 $g_{\alpha } \geq 0$
.
$g_{\alpha } \geq 0$
.
-
(ii) That corresponding to the part
 $\{b\}$
with
$\{b\}$
with
 $b \in B$
is given by (tensored with
$b \in B$
is given by (tensored with $$\begin{align*}(\varnothing, -, -) \otimes 1 \otimes s \underset{\sim}{\overset{d}\longrightarrow} (\{b\}, 1, 0) \otimes 1 \otimes 1\end{align*}$$
$$\begin{align*}(\varnothing, -, -) \otimes 1 \otimes s \underset{\sim}{\overset{d}\longrightarrow} (\{b\}, 1, 0) \otimes 1 \otimes 1\end{align*}$$
 $\det (\mathbb {Q}^{b})^{\otimes n}$
) so is acyclic.
$\det (\mathbb {Q}^{b})^{\otimes n}$
) so is acyclic.
Thus, the homology of
![]() $E_n"(S)$
is supported on those partitions with
$E_n"(S)$
is supported on those partitions with
![]() $B=\varnothing $
,
$B=\varnothing $
,
![]() $|S_{\alpha }|> 2$
and
$|S_{\alpha }|> 2$
and
![]() $g_{\alpha }=h_{\alpha }=0$
, and we recognise it as being isomorphic to
$g_{\alpha }=h_{\alpha }=0$
, and we recognise it as being isomorphic to
![]() $Z_n(S)$
. By considering the maps involved (or by counting dimensions) it follows that the map
$Z_n(S)$
. By considering the maps involved (or by counting dimensions) it follows that the map
![]() $E^{\prime }_n(S) \to Z_n(S)$
is an isomorphism on homology, so
$E^{\prime }_n(S) \to Z_n(S)$
is an isomorphism on homology, so
![]() $E^{\prime }_n \to Z_n$
is a weak equivalence.
$E^{\prime }_n \to Z_n$
is a weak equivalence.
Corollary 4.23.
![]() $E_n$
is Koszul if and only if
$E_n$
is Koszul if and only if
![]() $Z_n$
is.
$Z_n$
is.
Proof. In the portion of the long exact sequence

we must show that the connecting map is injective. By the proof of the previous theorem, this connecting map sends the generator to the map
a class in
![]() $\mathrm {AQ}_n(E_n)_{n,1}(\underline {1}) = H_1^{\mathrm {Com}}(E_n)_{n,1}(\underline {1})$
. As
$\mathrm {AQ}_n(E_n)_{n,1}(\underline {1}) = H_1^{\mathrm {Com}}(E_n)_{n,1}(\underline {1})$
. As
![]() $1$
is the lowest weight in which
$1$
is the lowest weight in which
![]() $\overline {E_n}$
has nontrivial elements, elements of this weight cannot be decomposable: Thus, as
$\overline {E_n}$
has nontrivial elements, elements of this weight cannot be decomposable: Thus, as
![]() $\phi $
is nontrivial the connecting map is too.
$\phi $
is nontrivial the connecting map is too.
4.5 Relation to Torelli Lie algebras
The relation between
![]() $E_1$
and the Torelli Lie algebra was already indicated in [Reference Koike and TeradaKRW20c, Remark 8.4], but we explain it again here.
$E_1$
and the Torelli Lie algebra was already indicated in [Reference Koike and TeradaKRW20c, Remark 8.4], but we explain it again here.
Notation 4.24. We write
![]() .
.
Theorem 4.25. The realisation
is a commutative algebra object, and as long as
![]() $g \geq 4$
it agrees in degrees
$g \geq 4$
it agrees in degrees
![]() $* \leq g$
with the quadratic dual of the Lie algebra object
$* \leq g$
with the quadratic dual of the Lie algebra object
Proof. In the language of [Reference Koike and TeradaKRW20c, Section 5], we have
![]() $E_1 = \mathcal {P}(-;\mathcal {V})^{\prime }_{\geq 0} \otimes \det $
with
$E_1 = \mathcal {P}(-;\mathcal {V})^{\prime }_{\geq 0} \otimes \det $
with
![]() $\mathcal {V}=\mathbb {Q}[e]$
having
$\mathcal {V}=\mathbb {Q}[e]$
having
![]() $|e|=2$
, and so
$|e|=2$
, and so
![]() $K^{\vee } \otimes ^{\mathsf {dsBr}} E_1$
is the object denoted
$K^{\vee } \otimes ^{\mathsf {dsBr}} E_1$
is the object denoted
![]() $R^{\mathcal {V}}$
there. By the discussion of [Reference Koike and TeradaKRW20c, Section 8.2] (especially Remark 8.4), and using the notation of Section 3.2, there is a map of graded commutative algebras
$R^{\mathcal {V}}$
there. By the discussion of [Reference Koike and TeradaKRW20c, Section 8.2] (especially Remark 8.4), and using the notation of Section 3.2, there is a map of graded commutative algebras
 $$\begin{align*}\frac{\Lambda^*[\Lambda^3 V_1[1]]}{(({IH}))} \longrightarrow R^{\mathcal{V}}\end{align*}$$
$$\begin{align*}\frac{\Lambda^*[\Lambda^3 V_1[1]]}{(({IH}))} \longrightarrow R^{\mathcal{V}}\end{align*}$$
which is an isomorphism in a stable range of degrees. As in the proof of Lemma 3.8, the element
![]() $\Theta = \sum _{i,j,k} \kappa _1(a_i \otimes a_j \otimes a_k) \cdot \kappa _1(a_i^{\#} \otimes a_j^{\#} \otimes a_k^{\#})$
corresponds to
$\Theta = \sum _{i,j,k} \kappa _1(a_i \otimes a_j \otimes a_k) \cdot \kappa _1(a_i^{\#} \otimes a_j^{\#} \otimes a_k^{\#})$
corresponds to
![]() $-\kappa _{e^2}$
. As the weight grading on
$-\kappa _{e^2}$
. As the weight grading on
![]() $E_1$
coincides with its homological grading, there is a map
$E_1$
coincides with its homological grading, there is a map
 $$\begin{align*}\frac{\Lambda^*[\Lambda^3 V_1[1,1]]}{(({IH}), (\Theta))} \longrightarrow K^{\vee} \otimes^{\mathsf{dsBr}} E_1/(\kappa_{e^2})\end{align*}$$
$$\begin{align*}\frac{\Lambda^*[\Lambda^3 V_1[1,1]]}{(({IH}), (\Theta))} \longrightarrow K^{\vee} \otimes^{\mathsf{dsBr}} E_1/(\kappa_{e^2})\end{align*}$$
which is an isomorphism in a stable range of degrees, and the domain is the quadratic dual of
![]() $\mathrm {Gr}^{\bullet }_{\mathrm {LCS}} \mathfrak {t}_{g,1}$
as long as
$\mathrm {Gr}^{\bullet }_{\mathrm {LCS}} \mathfrak {t}_{g,1}$
as long as
![]() $g \geq 4$
by the discussion in Section 3.2. Finally, the stability range is determined in [Reference Koike and TeradaKRW20c, Section 9.5]: This map is an isomorphism in degrees
$g \geq 4$
by the discussion in Section 3.2. Finally, the stability range is determined in [Reference Koike and TeradaKRW20c, Section 9.5]: This map is an isomorphism in degrees
![]() $* \leq g$
.
$* \leq g$
.
This yields a relation between Koszulness of
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
and of
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
and of
![]() $E_1$
.
$E_1$
.
Proposition 4.26. If
![]() $E_1$
is Koszul, then
$E_1$
is Koszul, then
![]() $K^{\vee } \otimes ^{\mathsf {dsBr}} E_1/(\kappa _{e^2})$
is Koszul in weight
$K^{\vee } \otimes ^{\mathsf {dsBr}} E_1/(\kappa _{e^2})$
is Koszul in weight
![]() $ \leq \tfrac {1}{3} g$
.
$ \leq \tfrac {1}{3} g$
.
Proof. Note that
![]() $E_1(\varnothing )$
is the polynomial algebra on the elements
$E_1(\varnothing )$
is the polynomial algebra on the elements
![]() $\kappa _{e^j} = (\varnothing , j)$
for
$\kappa _{e^j} = (\varnothing , j)$
for
![]() $j> 1$
, and each
$j> 1$
, and each
![]() $E_1(S)$
is a free
$E_1(S)$
is a free
![]() $E_1(\varnothing )$
-module, so the element
$E_1(\varnothing )$
-module, so the element
![]() $\kappa _{e^2} = (\varnothing ,2) \in E_1(\varnothing )_{2,2}$
is not a zero divisor in the sense of Section 4.2.3, and hence we may apply Corollary 4.11. Recalling the definition
$\kappa _{e^2} = (\varnothing ,2) \in E_1(\varnothing )_{2,2}$
is not a zero divisor in the sense of Section 4.2.3, and hence we may apply Corollary 4.11. Recalling the definition
![]() $\mathrm {AQ}_*({R}) = H_*(\mathbb {L} Q^{\mathrm {Com}}(\overline {R}))$
, there is a long exact sequence
$\mathrm {AQ}_*({R}) = H_*(\mathbb {L} Q^{\mathrm {Com}}(\overline {R}))$
, there is a long exact sequence
As
![]() $\kappa _{e^2}$
is decomposable in
$\kappa _{e^2}$
is decomposable in
![]() $E_1$
by the formula for (Θ), taking internal gradings and weight into account this gives short exact sequences
$E_1$
by the formula for (Θ), taking internal gradings and weight into account this gives short exact sequences
 $$\begin{align*}0 \to H_p^{\mathrm{Com}}(E_1)_{q,w}(S) \to H_p^{\mathrm{Com}}(E_1/(\kappa_{e^2}))_{q,w}(S) \to \begin{cases} \mathbb{Q} & (p,q,w)=(2,2,2),\ S=\varnothing\\ 0 & \text{ otherwise} \end{cases} \to 0,\end{align*}$$
$$\begin{align*}0 \to H_p^{\mathrm{Com}}(E_1)_{q,w}(S) \to H_p^{\mathrm{Com}}(E_1/(\kappa_{e^2}))_{q,w}(S) \to \begin{cases} \mathbb{Q} & (p,q,w)=(2,2,2),\ S=\varnothing\\ 0 & \text{ otherwise} \end{cases} \to 0,\end{align*}$$
so
![]() $E_1$
is Koszul if and only if
$E_1$
is Koszul if and only if
![]() $E_1/(\kappa _{e^2})$
is.
$E_1/(\kappa _{e^2})$
is.
Observe that the weight w part of
![]() $E_1/(\kappa _{e^2})$
is supported on sets of size
$E_1/(\kappa _{e^2})$
is supported on sets of size
![]() $\leq 3w$
, so by Lemma 4.19 we have
$\leq 3w$
, so by Lemma 4.19 we have
as long as
![]() $w \leq \tfrac {1}{3}g$
. Now, if
$w \leq \tfrac {1}{3}g$
. Now, if
![]() $E_1/(\kappa _{e^2})$
is Koszul, then
$E_1/(\kappa _{e^2})$
is Koszul, then
![]() $H^{\mathrm {Com}}_{p}(E_1/(\kappa _{e^2}))_{q,w}=0$
for
$H^{\mathrm {Com}}_{p}(E_1/(\kappa _{e^2}))_{q,w}=0$
for
![]() $p \neq w$
, and it follows that
$p \neq w$
, and it follows that
![]() $H^{\mathrm {Com}}_{p}(K^{\vee } \otimes ^{\mathsf {dsBr}} E_1/(\kappa _{e^2}))_{q,w}=0$
for
$H^{\mathrm {Com}}_{p}(K^{\vee } \otimes ^{\mathsf {dsBr}} E_1/(\kappa _{e^2}))_{q,w}=0$
for
![]() $p \neq w$
and
$p \neq w$
and
![]() $w \leq \tfrac {1}{3} g$
.
$w \leq \tfrac {1}{3} g$
.
Corollary 4.27. If
![]() $E_1$
is Koszul, then
$E_1$
is Koszul, then
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
is Koszul in weight
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
is Koszul in weight
![]() $\leq \tfrac {1}{3}g$
.
$\leq \tfrac {1}{3}g$
.
Proof. If
![]() $E_1$
is Koszul, then, by Proposition 4.26,
$E_1$
is Koszul, then, by Proposition 4.26,
![]() $K^{\vee } \otimes ^{\mathsf {dsBr}} E_1/(\kappa _{e^2})$
is Koszul in weight
$K^{\vee } \otimes ^{\mathsf {dsBr}} E_1/(\kappa _{e^2})$
is Koszul in weight
![]() $ \leq \tfrac {1}{3} g$
. By Theorem 4.25,
$ \leq \tfrac {1}{3} g$
. By Theorem 4.25,
![]() $K^{\vee } \otimes ^{\mathsf {dsBr}} E_1/(\kappa _{e^2})$
agrees with the quadratic dual of the Lie algebra
$K^{\vee } \otimes ^{\mathsf {dsBr}} E_1/(\kappa _{e^2})$
agrees with the quadratic dual of the Lie algebra
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
in weight
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
in weight
![]() $ \leq g$
, so by Lemma 2.4 this Lie algebra is Koszul in weight
$ \leq g$
, so by Lemma 2.4 this Lie algebra is Koszul in weight
![]() $ \leq \tfrac {1}{3}g$
.
$ \leq \tfrac {1}{3}g$
.
For any odd
![]() $n \geq 1$
, the commutative algebra object
$n \geq 1$
, the commutative algebra object
![]() $E_n$
is isomorphic to
$E_n$
is isomorphic to
![]() $E_1$
with its homological grading scaled by n. Thus,
$E_1$
with its homological grading scaled by n. Thus,
![]() $E_1$
is Koszul if and only if
$E_1$
is Koszul if and only if
![]() $E_n$
is Koszul, and using Corollary 4.27 and Proposition 3.4 this is what we shall show to prove Theorem A and hence Theorem 3.3. We will do so by showing that the
$E_n$
is Koszul, and using Corollary 4.27 and Proposition 3.4 this is what we shall show to prove Theorem A and hence Theorem 3.3. We will do so by showing that the
![]() $Z_n$
are Koszul and appealing to Corollary 4.23. Koszulness of the
$Z_n$
are Koszul and appealing to Corollary 4.23. Koszulness of the
![]() $Z_n$
has its own applications, to the rational homotopy Lie algebra of diffeomorphism groups of high-dimensional manifolds: We will explain these applications in Section 7.1.
$Z_n$
has its own applications, to the rational homotopy Lie algebra of diffeomorphism groups of high-dimensional manifolds: We will explain these applications in Section 7.1.
5 High-dimensional manifolds: starting the proof of Theorem A
The goal of this section is to prove the following theorem, which almost proves that the objects
![]() $Z_n, E_n \in \mathsf {Alg}_{\mathsf {Com}^+}^{\mathrm {augm}}(\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Ch}^{\mathbb {N}}))$
are Koszul.
$Z_n, E_n \in \mathsf {Alg}_{\mathsf {Com}^+}^{\mathrm {augm}}(\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Ch}^{\mathbb {N}}))$
are Koszul.
Theorem 5.1. If
![]() $q \neq n \cdot p$
, then the functors
$q \neq n \cdot p$
, then the functors
vanish when evaluated on nonempty sets.
As
![]() $Z_n$
and
$Z_n$
and
![]() $E_n$
have a weight grading which is equal to the homological grading divided by n, the above is equivalent to the vanishing on nonempty sets of
$E_n$
have a weight grading which is equal to the homological grading divided by n, the above is equivalent to the vanishing on nonempty sets of
![]() $H^{\mathrm {Com}}_{p}(Z_n)_{q,w}$
and
$H^{\mathrm {Com}}_{p}(Z_n)_{q,w}$
and
![]() $H^{\mathrm {Com}}_{p}(E_n)_{q,w}$
for
$H^{\mathrm {Com}}_{p}(E_n)_{q,w}$
for
![]() $p \neq w$
, that is, to Koszulness, but only on nonempty sets. Because of this, we can and will refrain from mentioning the weight grading from now on.
$p \neq w$
, that is, to Koszulness, but only on nonempty sets. Because of this, we can and will refrain from mentioning the weight grading from now on.
By Corollary 4.23, it is enough to prove Theorem 5.1 for
![]() $Z_n$
, which we will do by relating
$Z_n$
, which we will do by relating
![]() $Z_n$
to the cohomology of moduli spaces of certain high-dimensional manifolds with framings. We have already developed these results in [Reference Kupers and Randal-WilliamsKRW20b], relying on results from [Reference Koike and TeradaKRW20c, Reference Kupers and Randal-WilliamsKRW20a], and it will suffice to merely recall them here.
$Z_n$
to the cohomology of moduli spaces of certain high-dimensional manifolds with framings. We have already developed these results in [Reference Kupers and Randal-WilliamsKRW20b], relying on results from [Reference Koike and TeradaKRW20c, Reference Kupers and Randal-WilliamsKRW20a], and it will suffice to merely recall them here.
5.1 Torelli groups of high-dimensional manifolds
For the remainder of this section, we suppose that
![]() $2n \geq 6$
. We will use the
$2n \geq 6$
. We will use the
![]() $2n$
-manifolds
$2n$
-manifolds
A tangential structure for
![]() $2n$
-manifolds can equivalently be described by a map
$2n$
-manifolds can equivalently be described by a map
![]() $\theta \colon B \to B\mathrm {O}(2n)$
, or by a
$\theta \colon B \to B\mathrm {O}(2n)$
, or by a
![]() $\mathrm { GL}_{2n}(\mathbb {R})$
-space
$\mathrm { GL}_{2n}(\mathbb {R})$
-space
![]() $\Theta $
(see [Reference Goerss and SchemmerhornGRW19, Section 4.5]). Here, we use the former, as in [Reference Koike and TeradaKRW20c, Reference Kupers and Randal-WilliamsKRW20a], though we cite extensively from [Reference Kupers and Randal-WilliamsKRW20b], which uses the latter.
$\Theta $
(see [Reference Goerss and SchemmerhornGRW19, Section 4.5]). Here, we use the former, as in [Reference Koike and TeradaKRW20c, Reference Kupers and Randal-WilliamsKRW20a], though we cite extensively from [Reference Kupers and Randal-WilliamsKRW20b], which uses the latter.
Fix a tangential structure
![]() $\theta \colon B \to B\mathrm {O}(2n)$
. A
$\theta \colon B \to B\mathrm {O}(2n)$
. A
![]() $\theta $
-structure on
$\theta $
-structure on
![]() $W_{g,1}$
is a map of vector bundles
$W_{g,1}$
is a map of vector bundles
![]() $\ell \colon TW_{g,1} \to \theta ^* \gamma _{2n}$
, where
$\ell \colon TW_{g,1} \to \theta ^* \gamma _{2n}$
, where
![]() $\gamma _{2n}$
is the universal bundle over
$\gamma _{2n}$
is the universal bundle over
![]() $B\mathrm {O}(2n)$
. We will fix a boundary condition
$B\mathrm {O}(2n)$
. We will fix a boundary condition
![]() $\ell _{\partial } \colon TW_{g,1}|_{\partial W_{g,1}} \to \theta ^*\gamma _{2n}$
and consider only those
$\ell _{\partial } \colon TW_{g,1}|_{\partial W_{g,1}} \to \theta ^*\gamma _{2n}$
and consider only those
![]() $\theta $
-structures which extend it; we let
$\theta $
-structures which extend it; we let
![]() $\mathrm {Bun}_{\partial }(TW_{g,1},\theta ^*\gamma _{2n})$
denote the space of such bundle maps. The topological group
$\mathrm {Bun}_{\partial }(TW_{g,1},\theta ^*\gamma _{2n})$
denote the space of such bundle maps. The topological group
![]() $\mathrm {Diff}_{\partial }(W_{g,1})$
of diffeomorphisms of
$\mathrm {Diff}_{\partial }(W_{g,1})$
of diffeomorphisms of
![]() $W_{g,1}$
which fix its boundary pointwise (in the
$W_{g,1}$
which fix its boundary pointwise (in the
![]() $C^{\infty }$
-topology) acts on it through the derivative. We define
$C^{\infty }$
-topology) acts on it through the derivative. We define
We will only use tangential structures which satisfy the assumptions of Section 8 of [Reference Kupers and Randal-WilliamsKRW20a]. By Lemma 8.5 (i) of [Reference Kupers and Randal-WilliamsKRW20a], there then exists up to homotopy a unique orientation-preserving boundary condition
![]() $\ell _{\partial } \colon TW_{g,1}|_{\partial W_{g,1}} \to \theta ^* \gamma _{2n}$
which extends to
$\ell _{\partial } \colon TW_{g,1}|_{\partial W_{g,1}} \to \theta ^* \gamma _{2n}$
which extends to
![]() $W_{g,1}$
. For a
$W_{g,1}$
. For a
![]() $\theta $
-structure
$\theta $
-structure
![]() $\ell $
on
$\ell $
on
![]() $W_{g,1}$
, we denote by
$W_{g,1}$
, we denote by
![]() $B\mathrm {Diff}^{\theta }_{\partial }(W_{g,1})_{\ell }$
the path-component of
$B\mathrm {Diff}^{\theta }_{\partial }(W_{g,1})_{\ell }$
the path-component of
![]() $B\mathrm {Diff}^{\theta }_{\partial }(W_{g,1})$
which contains it.
$B\mathrm {Diff}^{\theta }_{\partial }(W_{g,1})$
which contains it.
The intersection product endows
![]() $H_n(W_{g,1};\mathbb {Z})$
with a nondegenerate
$H_n(W_{g,1};\mathbb {Z})$
with a nondegenerate
![]() $(-1)^n$
-symmetric form. Every diffeomorphism of
$(-1)^n$
-symmetric form. Every diffeomorphism of
![]() $W_{g,1}$
induces an automorphism of this form, so we get a homomorphism
$W_{g,1}$
induces an automorphism of this form, so we get a homomorphism
 $$\begin{align*}\pi_1(B\mathrm{Diff}_{\partial}(W_{g,1})) \longrightarrow G_g = \begin{cases} \mathrm{Sp}_{2g}(\mathbb{Z}) & \text{if }n\text{ is odd,} \\ \mathrm{O}_{g,g}(\mathbb{Z}) & \text{if }n\text{ is even.}\end{cases}\end{align*}$$
$$\begin{align*}\pi_1(B\mathrm{Diff}_{\partial}(W_{g,1})) \longrightarrow G_g = \begin{cases} \mathrm{Sp}_{2g}(\mathbb{Z}) & \text{if }n\text{ is odd,} \\ \mathrm{O}_{g,g}(\mathbb{Z}) & \text{if }n\text{ is even.}\end{cases}\end{align*}$$
We will let
![]() $\smash {G^{\theta ,[\ell ]}_g} \subset G_g$
denote the image of the composition
$\smash {G^{\theta ,[\ell ]}_g} \subset G_g$
denote the image of the composition
It is a finite index subgroup by [Reference Kupers and Randal-WilliamsKRW20a, Lemma 8.9]. There is an induced map
![]() $B\mathrm { Diff}^{\theta }_{\partial }(W_{g,1})_{\ell } \to BG^{\theta ,[\ell ]}_g$
, and we define
$B\mathrm { Diff}^{\theta }_{\partial }(W_{g,1})_{\ell } \to BG^{\theta ,[\ell ]}_g$
, and we define
5.2
 $Z_n$
and high-dimensional manifolds with framings
$Z_n$
and high-dimensional manifolds with framings
For
![]() $Z_n$
, we will use the above constructions with tangential structure
$Z_n$
, we will use the above constructions with tangential structure
![]() $\theta _{\mathrm {fr}} \colon E\mathrm {O}(2n) \to B\mathrm {O}(2n)$
to obtain Torelli groups
$\theta _{\mathrm {fr}} \colon E\mathrm {O}(2n) \to B\mathrm {O}(2n)$
to obtain Torelli groups
![]() $B\mathrm {Tor}^{\mathrm {fr}}_{\partial }(W_{g,1})_{\ell }$
with framings. From this, we developed the commutative diagram [Reference Kupers and Randal-WilliamsKRW20b, (15)] with rows and columns fibration sequences
$B\mathrm {Tor}^{\mathrm {fr}}_{\partial }(W_{g,1})_{\ell }$
with framings. From this, we developed the commutative diagram [Reference Kupers and Randal-WilliamsKRW20b, (15)] with rows and columns fibration sequences

with overlines denoting a passage to a finite cover or finite index subgroup which has no effect on rational cohomology (we refer to loc. cit. for definitions and details). The proof of Theorem 5.1 uses the following facts about
![]() $X_1(g)$
, which combines Lemma 4.9, Theorem 4.11, Corollary 4.20 and Remark 6.5 of [Reference Kupers and Randal-WilliamsKRW20b].
$X_1(g)$
, which combines Lemma 4.9, Theorem 4.11, Corollary 4.20 and Remark 6.5 of [Reference Kupers and Randal-WilliamsKRW20b].
Theorem 5.2. Fix
![]() $2n \geq 6$
.
$2n \geq 6$
.
-
(i) The space
 $X_1(g)$
is nilpotent and of finite type.
$X_1(g)$
is nilpotent and of finite type. -
(ii) The action of
 $\pi _1(A_2(g))$
on
$\pi _1(A_2(g))$
on
 $H^*(X_1(g);\mathbb {Q})$
and
$H^*(X_1(g);\mathbb {Q})$
and
 $\pi _*(X_1(g)) \otimes \mathbb {Q}$
factors over
$\pi _*(X_1(g)) \otimes \mathbb {Q}$
factors over
 $\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
.
$\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
. -
(iii) There is a map
 $K^{\vee } \otimes ^{\mathsf {d(s)Br}} Z_n \to H^*(X_1(g);\mathbb {Q})$
of
$K^{\vee } \otimes ^{\mathsf {d(s)Br}} Z_n \to H^*(X_1(g);\mathbb {Q})$
of
 $\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
-representations which is an isomorphism in a range of homological degrees tending to
$\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
-representations which is an isomorphism in a range of homological degrees tending to
 $\infty $
as
$\infty $
as
 $g \to \infty $
.
$g \to \infty $
. -
(iv) In a range tending to
 $\infty $
as
$\infty $
as
 $g \to \infty $
, in degrees
$g \to \infty $
, in degrees
 $* \leq \tfrac {n(n-3)}{2}$
the nontrivial
$* \leq \tfrac {n(n-3)}{2}$
the nontrivial
 $\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
-representations in
$\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
-representations in
 $\pi _{*+1}(X_1(g)) \otimes \mathbb {Q}$
vanish except with
$\pi _{*+1}(X_1(g)) \otimes \mathbb {Q}$
vanish except with
 $* = r(n-1)$
for some
$* = r(n-1)$
for some
 $r \geq 1$
.
$r \geq 1$
.
 $ \Box $
$ \Box $
5.3 Proof of Theorem 5.1
We first prove Theorem 5.1 for
![]() $Z_n$
, using the above theorem as input. As a consequence of Theorem 5.2 (i), there is a strongly convergent unstable rational Adams spectral sequence
$Z_n$
, using the above theorem as input. As a consequence of Theorem 5.2 (i), there is a strongly convergent unstable rational Adams spectral sequence
with
![]() $d^r$
-differential of bidegree
$d^r$
-differential of bidegree
![]() $(-r,-r+1)$
which, by naturality and Theorem 5.2 (ii), is a spectral sequence of
$(-r,-r+1)$
which, by naturality and Theorem 5.2 (ii), is a spectral sequence of
![]() $\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
-representations.
$\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
-representations.
By Theorem 5.2 (iii), in a stable range the rational cohomology of
![]() $X_1(g)$
is concentrated in degrees which are multiples of n. Thus, in a stable range the groups
$X_1(g)$
is concentrated in degrees which are multiples of n. Thus, in a stable range the groups
![]() $E^2_{s,t}$
are supported along the lines
$E^2_{s,t}$
are supported along the lines
![]() $t = r \cdot n$
with
$t = r \cdot n$
with
![]() $r \in \mathbb {N}$
and by the argument of Lemma 4.14 we have
$r \in \mathbb {N}$
and by the argument of Lemma 4.14 we have
![]() $E^2_{s,rn}=0$
for
$E^2_{s,rn}=0$
for
![]() $r < s$
. Thus,
$r < s$
. Thus,
![]() $E^2_{s,t}$
with
$E^2_{s,t}$
with
![]() $t=r\cdot n$
is nontrivial only for
$t=r\cdot n$
is nontrivial only for
![]() $1 \leq s \leq r$
, contributing to degrees
$1 \leq s \leq r$
, contributing to degrees
Furthermore, as long as these ranges of total degrees are separated from each other there can be no differentials between the corresponding lines: In particular, as long as
![]() $n \geq r-2$
the spectral sequence must collapse in degrees
$n \geq r-2$
the spectral sequence must collapse in degrees
![]() $t-s+1 \leq r \cdot n$
. Thus, as long as
$t-s+1 \leq r \cdot n$
. Thus, as long as
![]() $r \leq n+2$
, there is an isomorphism of
$r \leq n+2$
, there is an isomorphism of
![]() $\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
-representations in a stable range
$\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
-representations in a stable range
By Theorem 5.2 (iv), in degrees
![]() $* \leq \tfrac {n(n-3)}{2}$
the nontrivial representations on the right side vanish except when
$* \leq \tfrac {n(n-3)}{2}$
the nontrivial representations on the right side vanish except when
![]() $r=s$
. Hence the same is true for the left side.
$r=s$
. Hence the same is true for the left side.
By Theorem 5.2 (iii) there is a map
of
![]() $\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
-representations which is an isomorphism in a stable range. By Lemma 4.19
$\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
-representations which is an isomorphism in a stable range. By Lemma 4.19
as long as
![]() $\tfrac {q}{n} \leq \tfrac {1}{3} g$
, which is satisfied by taking g large enough. By the vanishing result established above, for all large enough g and for
$\tfrac {q}{n} \leq \tfrac {1}{3} g$
, which is satisfied by taking g large enough. By the vanishing result established above, for all large enough g and for
![]() $q \leq \smash {\tfrac {n(n-3)}{2}}$
, this is a trivial representation whenever
$q \leq \smash {\tfrac {n(n-3)}{2}}$
, this is a trivial representation whenever
![]() $q \neq n\cdot p$
. By the discussion in Section 2.4, the same is true as
$q \neq n\cdot p$
. By the discussion in Section 2.4, the same is true as
![]() $\mathrm {O}_{\epsilon }(H(g))$
-representations.
$\mathrm {O}_{\epsilon }(H(g))$
-representations.
By Lemma 4.17, if
![]() $H^{\mathrm {Com}}_p(Z_n)_q(S)$
were not zero for a nonempty finite set S, then for
$H^{\mathrm {Com}}_p(Z_n)_q(S)$
were not zero for a nonempty finite set S, then for
![]() $g \geq |S|$
so would be
$g \geq |S|$
so would be
![]() $[H_{[S]} \otimes (K^{\vee } \otimes ^{\mathsf {d(s)Br}} H^{\mathrm {Com}}_p(Z_n)_q]^{\mathrm {O}_{\epsilon }(H(g))}$
. As
$[H_{[S]} \otimes (K^{\vee } \otimes ^{\mathsf {d(s)Br}} H^{\mathrm {Com}}_p(Z_n)_q]^{\mathrm {O}_{\epsilon }(H(g))}$
. As
![]() $H_{[S]}$
for a nonempty set S is a direct sum of irreducibles that are not equal to the trivial representation, this implies that
$H_{[S]}$
for a nonempty set S is a direct sum of irreducibles that are not equal to the trivial representation, this implies that
![]() $K^{\vee } \otimes ^{\mathsf {d(s)Br}} H^{\mathrm {Com}}_p(Z_n)_q$
would contain a nontrivial subrepresentation. Using the above, we conclude that
$K^{\vee } \otimes ^{\mathsf {d(s)Br}} H^{\mathrm {Com}}_p(Z_n)_q$
would contain a nontrivial subrepresentation. Using the above, we conclude that
We now use that for all n’s of the same parity the commutative algebra objects
![]() $Z_n$
are isomorphic up to a linear scaling of degrees. As the bound ‘
$Z_n$
are isomorphic up to a linear scaling of degrees. As the bound ‘
![]() $q \leq \tfrac {n(n-3)}{2}$
’ scales quadratically with n it can therefore be ignored, yielding Theorem 5.1 for
$q \leq \tfrac {n(n-3)}{2}$
’ scales quadratically with n it can therefore be ignored, yielding Theorem 5.1 for
![]() $Z_n$
.
$Z_n$
.
5.4
 $E_n$
and high-dimensional manifolds with Euler structure
$E_n$
and high-dimensional manifolds with Euler structure
Instead of using Corollary 4.23 to deduce Theorem 5.1 for
![]() $E_n$
from
$E_n$
from
![]() $Z_n$
, one may prove it directly using a custom tangential structure which mimics in high dimensions the moduli spaces of surfaces. We explain this in this extended remark, as it may be of independent interest. It was in fact our original approach to Theorem A.
$Z_n$
, one may prove it directly using a custom tangential structure which mimics in high dimensions the moduli spaces of surfaces. We explain this in this extended remark, as it may be of independent interest. It was in fact our original approach to Theorem A.
The Pontrjagin classes
![]() $p_j \in H^{4j}(B\mathrm {SO}(2n);\mathbb {Z})$
for
$p_j \in H^{4j}(B\mathrm {SO}(2n);\mathbb {Z})$
for
![]() $1 \leq j < n$
induce a map
$1 \leq j < n$
induce a map
 $$\begin{align*}B\mathrm{SO}(2n) \longrightarrow \prod_{1 \leq j<n} K(\mathbb{Z},4j).\end{align*}$$
$$\begin{align*}B\mathrm{SO}(2n) \longrightarrow \prod_{1 \leq j<n} K(\mathbb{Z},4j).\end{align*}$$
We denote its homotopy fibre by
![]() $\widetilde {B}^e$
, which has n-connected cover
$\widetilde {B}^e$
, which has n-connected cover
![]() .
.
Definition 5.3. The Euler tangential structure is the map
![]() $\theta _e \colon B^e \to B\mathrm {O}(2n)$
.
$\theta _e \colon B^e \to B\mathrm {O}(2n)$
.
The name is justified by the calculation
![]() $H^*(B^e;\mathbb {Q}) = \mathbb {Q}[e]$
where e denotes the Euler class, of degree
$H^*(B^e;\mathbb {Q}) = \mathbb {Q}[e]$
where e denotes the Euler class, of degree
![]() $2n$
. By construction
$2n$
. By construction
![]() $B^e$
is n-connected, and since
$B^e$
is n-connected, and since
![]() $B\mathrm {SO}(2n)$
has finitely generated homotopy groups, so does
$B\mathrm {SO}(2n)$
has finitely generated homotopy groups, so does
![]() $B^e$
. Thus, this tangential structure satisfies the hypotheses for Section 8 of [Reference Kupers and Randal-WilliamsKRW20a]. From Section 5.1, we obtain
$B^e$
. Thus, this tangential structure satisfies the hypotheses for Section 8 of [Reference Kupers and Randal-WilliamsKRW20a]. From Section 5.1, we obtain
![]() $B\mathrm { Tor}^{\theta _e}_{\partial }(W_{g,1})$
which we shorten to
$B\mathrm { Tor}^{\theta _e}_{\partial }(W_{g,1})$
which we shorten to
![]() $B\mathrm {Tor}^e_{\partial }(W_{g,1})$
. A straightforward adaptation of the techniques of [Reference Koike and TeradaKRW20c, Reference Kupers and Randal-WilliamsKRW20b] yields a homotopy-commutative diagram
$B\mathrm {Tor}^e_{\partial }(W_{g,1})$
. A straightforward adaptation of the techniques of [Reference Koike and TeradaKRW20c, Reference Kupers and Randal-WilliamsKRW20b] yields a homotopy-commutative diagram

with rows and columns fibration sequences, and an analogue of Theorem 5.2 sufficient to directly prove Theorem 5.1 for
![]() $E_n$
.
$E_n$
.
Theorem 5.4.
-
(i) The space
 $X_1^e(g)$
is nilpotent and of finite type.
$X_1^e(g)$
is nilpotent and of finite type. -
(ii) The action of
 $\pi _1(A^e_2(g))$
on
$\pi _1(A^e_2(g))$
on
 $H^*(X^e_1(g);\mathbb {Q})$
and
$H^*(X^e_1(g);\mathbb {Q})$
and
 $\pi _*(X^e_1(g)) \otimes \mathbb {Q}$
factors over
$\pi _*(X^e_1(g)) \otimes \mathbb {Q}$
factors over
 $\overline {G}{}^{e,[\ell ]}_g$
.
$\overline {G}{}^{e,[\ell ]}_g$
. -
(iii) There is a map
of $$\begin{align*}\frac{K^{\vee} \otimes^{\mathsf{d(s)Br}} E_n}{(\kappa_{e^{j}} \mid j> 1)} \longrightarrow H^*(X^e_1(g);\mathbb{Q})\end{align*}$$
$$\begin{align*}\frac{K^{\vee} \otimes^{\mathsf{d(s)Br}} E_n}{(\kappa_{e^{j}} \mid j> 1)} \longrightarrow H^*(X^e_1(g);\mathbb{Q})\end{align*}$$
 $\overline {G}{}^{e,[\ell ]}_g$
-representations which is an isomorphism in a range of homological degrees tending to
$\overline {G}{}^{e,[\ell ]}_g$
-representations which is an isomorphism in a range of homological degrees tending to
 $\infty $
as
$\infty $
as
 $g \to \infty $
.
$g \to \infty $
.
-
(iv) In a stable range, in degrees
 $* \leq \tfrac {n(n-3)}{2}$
the nontrivial
$* \leq \tfrac {n(n-3)}{2}$
the nontrivial
 $\overline {G}{}^{e,[\ell ]}_g$
-representations in
$\overline {G}{}^{e,[\ell ]}_g$
-representations in
 $\pi _{*+1}(X^e_1(g)) \otimes \mathbb {Q}$
vanish except with
$\pi _{*+1}(X^e_1(g)) \otimes \mathbb {Q}$
vanish except with
 $* = r(n-1)$
for some
$* = r(n-1)$
for some
 $r \geq 1$
.
$r \geq 1$
.
 $ \Box $
$ \Box $
6 Graph complexes: finishing the proof of Theorem A
Our strategy to complete the proof of Theorem 3.3 is as follows. Firstly, we will establish graph complex models
![]() $RB^{Z_n}_{\mathrm {conn}}$
and
$RB^{Z_n}_{\mathrm {conn}}$
and
![]() $RB^{E_n}_{\mathrm {conn}}$
for
$RB^{E_n}_{\mathrm {conn}}$
for
![]() $\mathbb {L} Q^{\mathrm {Com}}(Z_n)$
and
$\mathbb {L} Q^{\mathrm {Com}}(Z_n)$
and
![]() $\mathbb {L} Q^{\mathrm {Com}}(E_n)$
, in terms of graphs with red and black edges whose black subgraph is connected, equipped with a certain differential. Once these models have been established, there are several ways in which one can proceed: We have chosen to proceed in the most self-contained way, but see Section 7.2.2 for alternatives using vanishing results for graph complexes from the literature. In this section, we will disregard the weight grading on
$\mathbb {L} Q^{\mathrm {Com}}(E_n)$
, in terms of graphs with red and black edges whose black subgraph is connected, equipped with a certain differential. Once these models have been established, there are several ways in which one can proceed: We have chosen to proceed in the most self-contained way, but see Section 7.2.2 for alternatives using vanishing results for graph complexes from the literature. In this section, we will disregard the weight grading on
![]() $E_n$
and
$E_n$
and
![]() $Z_n$
.
$Z_n$
.
6.1 Red and black graphs
We will first describe explicit cofibrant replacements for the augmented unital commutative algebra objects
![]() $Z_n, E_n \in \mathsf {Alg}_{\mathsf {Com}^+}^{\mathrm {augm}}(\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Ch}))$
.
$Z_n, E_n \in \mathsf {Alg}_{\mathsf {Com}^+}^{\mathrm {augm}}(\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Ch}))$
.
Definition 6.1.
-
(i) A graph
 $\Gamma $
is a tuple
$\Gamma $
is a tuple
 $(V, H, \iota , \partial )$
of a set V of vertices, a set H of half-edges, a function
$(V, H, \iota , \partial )$
of a set V of vertices, a set H of half-edges, a function
 $\partial \colon H \to V$
and an involution
$\partial \colon H \to V$
and an involution
 $\iota $
on H. The edges E of
$\iota $
on H. The edges E of
 $\Gamma $
is the set of free orbits of
$\Gamma $
is the set of free orbits of
 $\iota $
, and the legs L is the set of trivial orbits. For a graph
$\iota $
, and the legs L is the set of trivial orbits. For a graph
 $\Gamma $
, we will write
$\Gamma $
, we will write
 $V(\Gamma ), H(\Gamma ), E(\Gamma ), L(\Gamma ), \iota _{\Gamma }$
and
$V(\Gamma ), H(\Gamma ), E(\Gamma ), L(\Gamma ), \iota _{\Gamma }$
and
 $\partial _{\Gamma }$
for its associated data.
$\partial _{\Gamma }$
for its associated data. -
(ii) An isomorphism of graphs
 $\Gamma \leadsto \Gamma '$
is a pair of bijections between their sets of vertices and half-edges which intertwine the
$\Gamma \leadsto \Gamma '$
is a pair of bijections between their sets of vertices and half-edges which intertwine the
 $\iota $
’s and
$\iota $
’s and
 $\partial $
’s.
$\partial $
’s.
Definition 6.2. If
![]() $e = \{h_1, h_2\} \in E(\Gamma )$
is an edge, the graph
$e = \{h_1, h_2\} \in E(\Gamma )$
is an edge, the graph
![]() $\Gamma ' = \Gamma /e$
obtained by contracting the edge e has vertices
$\Gamma ' = \Gamma /e$
obtained by contracting the edge e has vertices
![]() , half-edges
, half-edges
![]() , boundary map
, boundary map
and involution
![]() $\iota _{\Gamma '} = \iota _{\Gamma }\vert _{H(\Gamma ')}$
.
$\iota _{\Gamma '} = \iota _{\Gamma }\vert _{H(\Gamma ')}$
.
Definition 6.3.
-
(i) A weighted red and black graph
 $\Gamma $
is a graph
$\Gamma $
is a graph
 $(V, H, \iota , \partial )$
along with a function
$(V, H, \iota , \partial )$
along with a function
 $c = c_{\Gamma }\colon E(\Gamma ) \to \{R,B\}$
colouring each edge either red or black, and a function
$c = c_{\Gamma }\colon E(\Gamma ) \to \{R,B\}$
colouring each edge either red or black, and a function
 $w\colon V(\Gamma ) \to \mathbb {N}$
assigning to each vertex a weight
Footnote 3 .
$w\colon V(\Gamma ) \to \mathbb {N}$
assigning to each vertex a weight
Footnote 3 . -
(ii) We write
 and
and
 for the sets of red edges and black edges, respectively. The black subgraph of
for the sets of red edges and black edges, respectively. The black subgraph of
 $\Gamma $
is the subgraph consisting of all vertices and the black edges.
$\Gamma $
is the subgraph consisting of all vertices and the black edges. -
(iii) An isomorphism of weighted red and black graphs
 $\Gamma \leadsto \Gamma '$
is an isomorphism of graphs which commutes with the colour and weight functions.
$\Gamma \leadsto \Gamma '$
is an isomorphism of graphs which commutes with the colour and weight functions. -
(iv) A weighted red and black graph is admissible if for each
 $v \in V(\Gamma )$
we have
$v \in V(\Gamma )$
we have
 $2 w(v) + \# \partial ^{-1}(v) \geq 3$
.
$2 w(v) + \# \partial ^{-1}(v) \geq 3$
.
Definition 6.4. If
![]() $e \in E_B(\Gamma )$
, we let
$e \in E_B(\Gamma )$
, we let
![]() $\Gamma /e$
be the weighted red and black graph obtained by contracting the edge
$\Gamma /e$
be the weighted red and black graph obtained by contracting the edge
![]() $e = \{h_1, h_2\}$
, taking the induced colouring, and
$e = \{h_1, h_2\}$
, taking the induced colouring, and
-
(i) If
 $\partial (h_1) \neq \partial (h_2)$
, then giving the new vertex weight
$\partial (h_1) \neq \partial (h_2)$
, then giving the new vertex weight
 $w(\partial (h_1)) + w(\partial (h_2))$
;
$w(\partial (h_1)) + w(\partial (h_2))$
; -
(ii) If
 $\partial (h_1) = \partial (h_2)$
, then giving the new vertex weight
$\partial (h_1) = \partial (h_2)$
, then giving the new vertex weight
 $w(\partial (h_1))+1$
.
$w(\partial (h_1))+1$
.
Similarly let
![]() $\Gamma {\setminus }e$
be the red and black graph obtained by turning the black edge e red.
$\Gamma {\setminus }e$
be the red and black graph obtained by turning the black edge e red.
Note that if
![]() $\Gamma $
is admissible, so are
$\Gamma $
is admissible, so are
![]() $\Gamma /e$
and
$\Gamma /e$
and
![]() $\Gamma \backslash e$
. Recall that
$\Gamma \backslash e$
. Recall that
![]() . Define 1-dimensional vector spaces
. Define 1-dimensional vector spaces
Isomorphisms of weighted red and black graphs induce isomorphisms of these vector spaces.
If
![]() $e \in E_B(\Gamma )$
, there are maps
$e \in E_B(\Gamma )$
, there are maps
![]() $-/e\colon \mathfrak {K}_B(\Gamma ) \to \mathfrak {K}_B(\Gamma /e)$
and
$-/e\colon \mathfrak {K}_B(\Gamma ) \to \mathfrak {K}_B(\Gamma /e)$
and
![]() $- {\setminus } e\colon \mathfrak {K}_B(\Gamma ) \to \mathfrak {K}_B(\Gamma {\setminus } e)$
given by contracting with e. As contracting or colouring an edge does not change the set of legs, there are also canonical identifications
$- {\setminus } e\colon \mathfrak {K}_B(\Gamma ) \to \mathfrak {K}_B(\Gamma {\setminus } e)$
given by contracting with e. As contracting or colouring an edge does not change the set of legs, there are also canonical identifications
![]() $\mathfrak {L}(\Gamma ) \overset {\sim }\to \mathfrak {L}(\Gamma /e)$
and
$\mathfrak {L}(\Gamma ) \overset {\sim }\to \mathfrak {L}(\Gamma /e)$
and
![]() $\mathfrak {L}(\Gamma ) \overset {\sim }\to \mathfrak {L}(\Gamma {\setminus } e)$
.
$\mathfrak {L}(\Gamma ) \overset {\sim }\to \mathfrak {L}(\Gamma {\setminus } e)$
.
Definition 6.5. For an admissible weighted red and black graph
![]() $\Gamma $
, we set
$\Gamma $
, we set

and define a graded vector space

where the sum is over all admissible weighted red and black graphs with legs identified with S, and
![]() $\sim $
is the equivalence relation induced by isomorphism of such graphs.
$\sim $
is the equivalence relation induced by isomorphism of such graphs.
We define a differential by summing over all ways of contracting a black edge or turning a black edge red, with certain signs. More formally, we define
![]() $d=d_{\text {con}}+d_{\text {col}}$
on this graded vector space by
$d=d_{\text {con}}+d_{\text {col}}$
on this graded vector space by
 $$ \begin{align*} d_{\text{con}}(\Gamma, \ell, \nu, \omega^{\otimes n}) &= \sum_{e \in E_B(\Gamma)} (\Gamma/e, \ell, \nu/e, \omega^{\otimes n})\\ d_{\text{col}}(\Gamma, \ell, \nu, \omega^{\otimes n}) &= -\sum_{e \in E_B(\Gamma)} (\Gamma {\setminus} e, \ell, \nu {\setminus} e, \omega^{\otimes n}). \end{align*} $$
$$ \begin{align*} d_{\text{con}}(\Gamma, \ell, \nu, \omega^{\otimes n}) &= \sum_{e \in E_B(\Gamma)} (\Gamma/e, \ell, \nu/e, \omega^{\otimes n})\\ d_{\text{col}}(\Gamma, \ell, \nu, \omega^{\otimes n}) &= -\sum_{e \in E_B(\Gamma)} (\Gamma {\setminus} e, \ell, \nu {\setminus} e, \omega^{\otimes n}). \end{align*} $$
We consider these complexes as defining a functor
![]() $RB^{E_n}\colon \mathsf {d(s)Br} \to \mathsf {Ch}$
, by letting the morphism
$RB^{E_n}\colon \mathsf {d(s)Br} \to \mathsf {Ch}$
, by letting the morphism
![]() $[(f, m_S)] \in \mathsf {d(s)Br}(S, T)$
induce the map
$[(f, m_S)] \in \mathsf {d(s)Br}(S, T)$
induce the map
![]() $RB^{E_n}(S) \to RB^{E_n}(T)$
given by creating (oriented) red edges according to the (ordered) matching
$RB^{E_n}(S) \to RB^{E_n}(T)$
given by creating (oriented) red edges according to the (ordered) matching
![]() $m_S$
and then relabelling the remaining legs according to f. (This is well defined as a functor on
$m_S$
and then relabelling the remaining legs according to f. (This is well defined as a functor on
![]() $\mathsf {d(s)Br}$
because of the twisting by
$\mathsf {d(s)Br}$
because of the twisting by
![]() $\mathfrak {L}(\Gamma )^{\otimes n}$
.) Disjoint union makes
$\mathfrak {L}(\Gamma )^{\otimes n}$
.) Disjoint union makes
![]() $RB^{E_n}$
into a commutative algebra object.
$RB^{E_n}$
into a commutative algebra object.

Figure 5 A weighted red and black graph with two vertices, of weight
![]() $g_{ \alpha }$
and
$g_{ \alpha }$
and
![]() $g_{ \beta }$
respectively, and two legs, labelled by
$g_{ \beta }$
respectively, and two legs, labelled by
![]() $ \underline {2}$
. We have also indicated the terms
$ \underline {2}$
. We have also indicated the terms
![]() $d_{\mathrm {col}}$
and
$d_{\mathrm {col}}$
and
![]() $d_{\mathrm {con}}$
of the differential, assuming n is even (if n were odd, then the graph would be zero by symmetry of the legs). In
$d_{\mathrm {con}}$
of the differential, assuming n is even (if n were odd, then the graph would be zero by symmetry of the legs). In
![]() $d_{\mathrm {col}}$
, the reader maybe expected two terms obtained by turning red one of the two black edges connecting the two vertices, by these yield the same graph with opposite sign and hence cancel. The same happens in
$d_{\mathrm {col}}$
, the reader maybe expected two terms obtained by turning red one of the two black edges connecting the two vertices, by these yield the same graph with opposite sign and hence cancel. The same happens in
![]() $d_{\mathrm {con}}$
, where two terms obtained by collapsing one of the two black edges connecting the two vertices cancel.
$d_{\mathrm {con}}$
, where two terms obtained by collapsing one of the two black edges connecting the two vertices cancel.
We let
![]() $RB^{Z_n}(S)$
be the quotient of
$RB^{Z_n}(S)$
be the quotient of
![]() $RB^{E_n}(S)$
by those weighted red and black graphs having some vertex of weight
$RB^{E_n}(S)$
by those weighted red and black graphs having some vertex of weight
![]() $>0$
. These assemble into a functor
$>0$
. These assemble into a functor
![]() $RB^{Z_n}\colon \mathsf {d(s)Br} \to \mathsf {Ch}$
which is a quotient of
$RB^{Z_n}\colon \mathsf {d(s)Br} \to \mathsf {Ch}$
which is a quotient of
![]() $RB^{E_n}$
, having an induced augmented unital commutative algebra structure. Concretely
$RB^{E_n}$
, having an induced augmented unital commutative algebra structure. Concretely
![]() $RB^{Z_n}(S)$
is given by weighted red and black graphs having all weights zero (equivalently, no weights), and the differential is given by the same formula with the understanding that
$RB^{Z_n}(S)$
is given by weighted red and black graphs having all weights zero (equivalently, no weights), and the differential is given by the same formula with the understanding that
![]() $\Gamma /e$
is zero when e is a loop (as then
$\Gamma /e$
is zero when e is a loop (as then
![]() $\Gamma /e$
has a vertex of weight
$\Gamma /e$
has a vertex of weight
![]() $>0$
).
$>0$
).
Proposition 6.6. There are weak equivalences of unital commutative algebras
and
![]() $RB^{Z_n}$
and
$RB^{Z_n}$
and
![]() $RB^{E_n}$
are cofibrant in
$RB^{E_n}$
are cofibrant in
![]() $\mathsf {Alg}_{\mathsf {Com}^+}^{\mathrm {augm}}(\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Ch}))$
.
$\mathsf {Alg}_{\mathsf {Com}^+}^{\mathrm {augm}}(\mathsf {Fun}(\mathsf {d(s)Br}, \mathsf {Ch}))$
.
Proof. Let
![]() $\phi \colon RB^{E_n} \to E_n$
be the map which
$\phi \colon RB^{E_n} \to E_n$
be the map which
-
(i) kills weighted red and black graphs having any black edges, and
-
(ii) assigns to a graph having only red edges the induced partition of its set of legs given by the connected components of the graph, with the part corresponding to the connected subgraph
 $\Gamma _{\alpha }$
assigned weight
$\Gamma _{\alpha }$
assigned weight
 $\left (\sum _{v \in V(\Gamma _{\alpha })} w(v)\right ) + 1 - \chi (\Gamma _{\alpha })$
, that is, the sum of the weights of its vertices and its genus.
$\left (\sum _{v \in V(\Gamma _{\alpha })} w(v)\right ) + 1 - \chi (\Gamma _{\alpha })$
, that is, the sum of the weights of its vertices and its genus.
This is a map of commutative algebra objects. It is also – when evaluated on any S – a map of chain complexes, as follows. If
![]() $(\Gamma , \ell , \omega ^{\otimes n}, \nu )$
is such that
$(\Gamma , \ell , \omega ^{\otimes n}, \nu )$
is such that
![]() $\Gamma $
has at least two black edges, then every term of
$\Gamma $
has at least two black edges, then every term of
![]() $d(\Gamma , \ell , \omega ^{\otimes n}, \nu )$
has a black edge and so vanishes under
$d(\Gamma , \ell , \omega ^{\otimes n}, \nu )$
has a black edge and so vanishes under
![]() $\phi $
;
$\phi $
;
![]() $(\Gamma , \ell , \omega ^{\otimes n}, \nu )$
does too. If
$(\Gamma , \ell , \omega ^{\otimes n}, \nu )$
does too. If
![]() $(\Gamma , \ell , \omega ^{\otimes n}, \nu )$
is such that
$(\Gamma , \ell , \omega ^{\otimes n}, \nu )$
is such that
![]() $\Gamma $
has a single black edge e, then
$\Gamma $
has a single black edge e, then
and
![]() $\Gamma /e$
and
$\Gamma /e$
and
![]() $\Gamma {\setminus } e$
induce the same partition on S with the same weights so this vanishes on applying
$\Gamma {\setminus } e$
induce the same partition on S with the same weights so this vanishes on applying
![]() $\phi $
;
$\phi $
;
![]() $(\Gamma , \ell , \omega ^{\otimes n}, \nu )$
does too.
$(\Gamma , \ell , \omega ^{\otimes n}, \nu )$
does too.
To check that
![]() $\phi $
is a weak equivalence, we consider the filtration given by letting
$\phi $
is a weak equivalence, we consider the filtration given by letting
![]() $F^p RB^{E_n}(S)$
be spanned by those graphs with
$F^p RB^{E_n}(S)$
be spanned by those graphs with
![]() $\leq p$
edges. As
$\leq p$
edges. As
![]() $d_{\text {con}}$
reduces the number of edges and
$d_{\text {con}}$
reduces the number of edges and
![]() $d_{\text {col}}$
preserves the number of edges, we have
$d_{\text {col}}$
preserves the number of edges, we have
This complex splits over isomorphism classes of weighted graphs
![]() $\Gamma $
as a sum of chain complexes
$\Gamma $
as a sum of chain complexes
![]() $\mathrm {Colour}_*(\Gamma )_{\mathrm { Aut}(\Gamma )}$
, where
$\mathrm {Colour}_*(\Gamma )_{\mathrm { Aut}(\Gamma )}$
, where
![]() $\mathrm {Colour}_*(\Gamma )$
has basis the set of subgraphs of
$\mathrm {Colour}_*(\Gamma )$
has basis the set of subgraphs of
![]() $\Gamma $
, considered as those edges to be coloured red: Such a subgraph has degree given by
$\Gamma $
, considered as those edges to be coloured red: Such a subgraph has degree given by
![]() $n\left (\sum _{v \in V(\Gamma )}(2w(v)+\mathrm {val}(v)-2)\right ) + \# E_B(\Gamma )$
, and the differential sums over all ways of adding a single edge to the red subgraph. In other words, up to a shift of degrees
$n\left (\sum _{v \in V(\Gamma )}(2w(v)+\mathrm {val}(v)-2)\right ) + \# E_B(\Gamma )$
, and the differential sums over all ways of adding a single edge to the red subgraph. In other words, up to a shift of degrees
![]() $\mathrm {Colour}_*(\Gamma )$
is the reduced simplicial chain complex of the simplex
$\mathrm {Colour}_*(\Gamma )$
is the reduced simplicial chain complex of the simplex
![]() $\Delta ^{E(\Gamma )}$
on the set of edges of
$\Delta ^{E(\Gamma )}$
on the set of edges of
![]() $\Gamma $
. It is therefore acyclic if
$\Gamma $
. It is therefore acyclic if
![]() $\Gamma $
contains any edges and has homology
$\Gamma $
contains any edges and has homology
![]() $\mathbb {Q}[n\sum _{v \in V(\Gamma )}(2w(v)+\mathrm {val}(v)-2)]$
otherwise. As it is supported on graphs with no edges, the differential
$\mathbb {Q}[n\sum _{v \in V(\Gamma )}(2w(v)+\mathrm {val}(v)-2)]$
otherwise. As it is supported on graphs with no edges, the differential
![]() $d_{\text {con}}$
has no effect and so the spectral sequence for this filtration collapses, to give
$d_{\text {con}}$
has no effect and so the spectral sequence for this filtration collapses, to give
 $$\begin{align*}H_*(RB^{E_n}(S), d) \cong \bigoplus_{\substack{\text{weighted graphs } \Gamma \\ \text{ with no edges}}} \mathbb{Q}[n\sum_{v \in V(\Gamma)}(2w(v)+\mathrm{val}(v)-2)],\end{align*}$$
$$\begin{align*}H_*(RB^{E_n}(S), d) \cong \bigoplus_{\substack{\text{weighted graphs } \Gamma \\ \text{ with no edges}}} \mathbb{Q}[n\sum_{v \in V(\Gamma)}(2w(v)+\mathrm{val}(v)-2)],\end{align*}$$
and with this description we observe that
![]() $\phi _*\colon H_*(RB^{E_n}(S), d) \to E_n$
is an isomorphism as required. The argument for
$\phi _*\colon H_*(RB^{E_n}(S), d) \to E_n$
is an isomorphism as required. The argument for
![]() $Z_n$
is completely parallel.
$Z_n$
is completely parallel.
Neglecting for a moment the differential, let
![]() $X \subset RB^{E_n}$
be the subobject spanned by those weighted red and black graphs whose black subgraphs are connected (we take this to also mean nonempty). The commutative unital algebra structure on
$X \subset RB^{E_n}$
be the subobject spanned by those weighted red and black graphs whose black subgraphs are connected (we take this to also mean nonempty). The commutative unital algebra structure on
![]() $RB^{E_n}$
induces a map
$RB^{E_n}$
induces a map
which we claim is an isomorphism. By definition of Day convolution, we have
 $$\begin{align*}(X^{\otimes k})(S) = \operatorname*{\mathrm{colim}}_{\substack{f: S_1 \sqcup \cdots \sqcup S_k \to S \\ \in \mathsf{d(s)Br}}} X(S_1) \otimes \cdots \otimes X(S_k).\end{align*}$$
$$\begin{align*}(X^{\otimes k})(S) = \operatorname*{\mathrm{colim}}_{\substack{f: S_1 \sqcup \cdots \sqcup S_k \to S \\ \in \mathsf{d(s)Br}}} X(S_1) \otimes \cdots \otimes X(S_k).\end{align*}$$
Spelling this out, it is the space of weighted red and black graphs with legs S whose black subgraph has precisely k components, and the components are ordered;
![]() $(X^{\otimes k})_{\mathfrak {S}_k}(S)$
is then the same without the ordering of components. We therefore see that (12) is indeed an isomorphism.
$(X^{\otimes k})_{\mathfrak {S}_k}(S)$
is then the same without the ordering of components. We therefore see that (12) is indeed an isomorphism.
Reincorporating the differential, we have just shown that
![]() $RB^{E_n}$
is quasi-free, and it is also nonnegatively graded, so a standard induction over skeleta of X shows that it is cofibrant, cf. [Reference MillèsLV12, Proposition B.6.6]. The same goes for
$RB^{E_n}$
is quasi-free, and it is also nonnegatively graded, so a standard induction over skeleta of X shows that it is cofibrant, cf. [Reference MillèsLV12, Proposition B.6.6]. The same goes for
![]() $RB^{Z_n}$
.
$RB^{Z_n}$
.
Let
![]() $RB^{E_n}_{\mathrm {conn}}$
be the quotient of
$RB^{E_n}_{\mathrm {conn}}$
be the quotient of
![]() $RB^{E_n}$
by the unit and those weighted red and black graphs whose black subgraph is not connected, and
$RB^{E_n}$
by the unit and those weighted red and black graphs whose black subgraph is not connected, and
![]() $RB^{Z_n}_{\mathrm {conn}}$
be the analogous quotient of
$RB^{Z_n}_{\mathrm {conn}}$
be the analogous quotient of
![]() $RB^{Z_n}$
. As the red and black graphs whose black subgraph is not connected are precisely the decomposables, we find the following.
$RB^{Z_n}$
. As the red and black graphs whose black subgraph is not connected are precisely the decomposables, we find the following.
Corollary 6.7. We have
![]() $\mathbb {L} Q^{\mathrm {Com}}(Z_n) \simeq RB^{Z_n}_{\mathrm {conn}}$
and
$\mathbb {L} Q^{\mathrm {Com}}(Z_n) \simeq RB^{Z_n}_{\mathrm {conn}}$
and
![]() $\mathbb {L} Q^{\mathrm {Com}}(E_n) \simeq RB^{E_n}_{\mathrm {conn}}$
.
$\mathbb {L} Q^{\mathrm {Com}}(E_n) \simeq RB^{E_n}_{\mathrm {conn}}$
.
Following Section 4.2.5, as
![]() $Z_n$
and
$Z_n$
and
![]() $E_n$
have trivial differential the homology groups
$E_n$
have trivial differential the homology groups
![]() $\mathrm {AQ}_*(Z_n)$
and
$\mathrm {AQ}_*(Z_n)$
and
![]() $\mathrm {AQ}_*(E_n)$
are equipped with an additional internal grading. This may be implemented in terms of the resolutions
$\mathrm {AQ}_*(E_n)$
are equipped with an additional internal grading. This may be implemented in terms of the resolutions
![]() $RB^{Z_n}$
and
$RB^{Z_n}$
and
![]() $RB^{E_n}$
, and so in the models
$RB^{E_n}$
, and so in the models
![]() $RB^{Z_n}_{\mathrm {conn}}$
and
$RB^{Z_n}_{\mathrm {conn}}$
and
![]() $RB^{E_n}_{\mathrm {conn}}$
, by giving a (weighted) red and black graph
$RB^{E_n}_{\mathrm {conn}}$
, by giving a (weighted) red and black graph
![]() $\Gamma $
internal degree
$\Gamma $
internal degree

It is indeed preserved by the differential, and by the quasi-isomorphisms to
![]() $Z_n$
and
$Z_n$
and
![]() $E_n$
. As the total degree of
$E_n$
. As the total degree of
![]() $\Gamma $
is
$\Gamma $
is
![]() $ n\left (\sum _{v \in V(\Gamma )}(2 w(v)+\mathrm {val}(v)-2)\right ) + \#E_B(\Gamma )$
, its Harrison degree is then
$ n\left (\sum _{v \in V(\Gamma )}(2 w(v)+\mathrm {val}(v)-2)\right ) + \#E_B(\Gamma )$
, its Harrison degree is then
![]() $\# E_B(\Gamma ) + 1$
.
$\# E_B(\Gamma ) + 1$
.
6.2 Black graphs
Definition 6.8. Let
![]() $G^{E_n}(S)$
be the quotient of
$G^{E_n}(S)$
be the quotient of
![]() $RB^{E_n}_{\mathrm {conn}}(S)$
by the subcomplex spanned by those red and black graphs having a nonzero number of red edges, and
$RB^{E_n}_{\mathrm {conn}}(S)$
by the subcomplex spanned by those red and black graphs having a nonzero number of red edges, and
![]() $G^{Z_n}(S)$
be the analogous quotient of
$G^{Z_n}(S)$
be the analogous quotient of
![]() $RB^{Z_n}_{\mathrm {conn}}(S)$
.
$RB^{Z_n}_{\mathrm {conn}}(S)$
.
By the discussion above, these complexes inherit an internal grading, giving homology groups
![]() $H_{p+q}(G^{E_n}(S))_q$
and
$H_{p+q}(G^{E_n}(S))_q$
and
![]() $H_{p+q}(G^{Z_n}(S))_q$
in total degree
$H_{p+q}(G^{Z_n}(S))_q$
in total degree
![]() $p+q$
and internal degree q. Moreover,
$p+q$
and internal degree q. Moreover,
![]() $G^{E_n}(S)$
and
$G^{E_n}(S)$
and
![]() $G^{Z_n}(S)$
are functorial with respect to bijections of S, and may be organised into objects
$G^{Z_n}(S)$
are functorial with respect to bijections of S, and may be organised into objects
![]() $G^{E_n}$
and
$G^{E_n}$
and
![]() $G^{Z_n}$
of
$G^{Z_n}$
of
![]() $\mathsf {Fun}(\mathsf {FB},\mathsf {Ch})$
. In Section 7.2.1, we explain how these are related to other graph complexes in the literature.
$\mathsf {Fun}(\mathsf {FB},\mathsf {Ch})$
. In Section 7.2.1, we explain how these are related to other graph complexes in the literature.
Neglecting the differential, every red and black graph whose black subgraph is connected can, tautologically, be obtained from a connected black graph by attaching some red edges. This gives the decompositions
 $$ \begin{align} \begin{aligned} RB^{Z_n}_{\mathrm{conn}}(-) &\cong \bigoplus_{n \geq 0} G^{Z_n}(\underline{n}) \otimes_{\mathfrak{S}_n} \mathsf{d(s)Br}(\underline{n}, -)\\ RB^{E_n}_{\mathrm{conn}}(-) &\cong \bigoplus_{n \geq 0} G^{E_n}(\underline{n}) \otimes_{\mathfrak{S}_n} \mathsf{d(s)Br}(\underline{n}, -) \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} RB^{Z_n}_{\mathrm{conn}}(-) &\cong \bigoplus_{n \geq 0} G^{Z_n}(\underline{n}) \otimes_{\mathfrak{S}_n} \mathsf{d(s)Br}(\underline{n}, -)\\ RB^{E_n}_{\mathrm{conn}}(-) &\cong \bigoplus_{n \geq 0} G^{E_n}(\underline{n}) \otimes_{\mathfrak{S}_n} \mathsf{d(s)Br}(\underline{n}, -) \end{aligned} \end{align} $$
as functors to graded vector spaces, where we recall
![]() .
.
The inclusion
![]() $i \colon \mathsf {FB} \to \mathsf {d(s)Br}$
of the (
$i \colon \mathsf {FB} \to \mathsf {d(s)Br}$
of the (
![]() $\mathbb {Q}$
-linearised) category of finite sets and bijections has a retraction
$\mathbb {Q}$
-linearised) category of finite sets and bijections has a retraction
![]() $r \colon \mathsf {d(s)Br} \to \mathsf {FB}$
, which is the identity on objects, and on morphisms
$r \colon \mathsf {d(s)Br} \to \mathsf {FB}$
, which is the identity on objects, and on morphisms
![]() $r \colon \mathsf {d(s)Br}(A,B) \to \mathsf {FB}(A,B)$
is the identity if
$r \colon \mathsf {d(s)Br}(A,B) \to \mathsf {FB}(A,B)$
is the identity if
![]() $|A|=|B|$
, and is the zero map otherwise. Left Kan extension gives a functor
$|A|=|B|$
, and is the zero map otherwise. Left Kan extension gives a functor
In Lemma 4.3, we discussed the model structure on the domain, and the codomain has a similar model structure, such that
![]() $r_* \dashv r^*$
is a Quillen adjunction, and in particular
$r_* \dashv r^*$
is a Quillen adjunction, and in particular
![]() $r_*$
admits a total left derived functor
$r_*$
admits a total left derived functor
![]() $\mathbb {L} r_*$
. Unwinding definitions shows that
$\mathbb {L} r_*$
. Unwinding definitions shows that
![]() $G^{E_n} = r_*(RB_{conn}^{E_n})$
and
$G^{E_n} = r_*(RB_{conn}^{E_n})$
and
![]() $G^{Z_n} = r_*(RB_{conn}^{Z_n})$
, and we first argue that these are in fact also derived left Kan extensions.
$G^{Z_n} = r_*(RB_{conn}^{Z_n})$
, and we first argue that these are in fact also derived left Kan extensions.
Lemma 6.9. The natural maps
 $$ \begin{align*} \mathbb{L} r_* (RB_{conn}^{E_n}) &\longrightarrow r_* (RB_{conn}^{E_n}) = G^{E_n},\\ \mathbb{L} r_* (RB_{conn}^{Z_n}) &\longrightarrow r_* (RB_{conn}^{Z_n}) = G^{Z_n} \end{align*} $$
$$ \begin{align*} \mathbb{L} r_* (RB_{conn}^{E_n}) &\longrightarrow r_* (RB_{conn}^{E_n}) = G^{E_n},\\ \mathbb{L} r_* (RB_{conn}^{Z_n}) &\longrightarrow r_* (RB_{conn}^{Z_n}) = G^{Z_n} \end{align*} $$
are equivalences.
Proof. We consider the case of
![]() $E_n$
; that of
$E_n$
; that of
![]() $Z_n$
is identical. Filtering
$Z_n$
is identical. Filtering
![]() $RB^{E_n}_{conn}(-)$
by its grading, we obtain compatible filtrations of the two sides. This gives a map of spectral sequences, which are strongly convergent as the values of
$RB^{E_n}_{conn}(-)$
by its grading, we obtain compatible filtrations of the two sides. This gives a map of spectral sequences, which are strongly convergent as the values of
![]() ${RB}_{conn}^{E_n}$
are nonnegatively graded. As
${RB}_{conn}^{E_n}$
are nonnegatively graded. As
![]() $r_*$
preserves exact sequences the map of
$r_*$
preserves exact sequences the map of
![]() $E^1$
-pages is
$E^1$
-pages is
Thus, it suffices to show that this is an equivalence. By (13), we have
![]() $\mathrm {Gr}(RB_{conn}^{E_n})(-) = i_*(G^{E_n})(-)$
, where the latter has trivial differential. As we are working over a field of characteristic zero all objects of
$\mathrm {Gr}(RB_{conn}^{E_n})(-) = i_*(G^{E_n})(-)$
, where the latter has trivial differential. As we are working over a field of characteristic zero all objects of
![]() $\mathsf {Fun}(\mathsf {FB}, \mathsf {Ch})$
are cofibrant, so
$\mathsf {Fun}(\mathsf {FB}, \mathsf {Ch})$
are cofibrant, so
![]() $\mathbb {L} i_*(G^{E_n})(-) \overset {\sim }\to i_*(G^{E_n})(-)$
. Using that
$\mathbb {L} i_*(G^{E_n})(-) \overset {\sim }\to i_*(G^{E_n})(-)$
. Using that
![]() $r_* \circ i_* = (r \circ i)_* = \mathrm {id}$
and similarly
$r_* \circ i_* = (r \circ i)_* = \mathrm {id}$
and similarly
![]() $\mathbb {L} r_* \circ \mathbb {L} i_* \simeq \mathrm {id}$
, the claim follows.
$\mathbb {L} r_* \circ \mathbb {L} i_* \simeq \mathrm {id}$
, the claim follows.
Let us analyse
![]() $\mathbb {L} r_*(A)$
for
$\mathbb {L} r_*(A)$
for
![]() $A \colon \mathsf {d(s)Br} \to \mathsf {Ch}$
using the colimit description of Kan extension and the bar construction model for homotopy colimits. This is the simplicial object with s-simplices
$A \colon \mathsf {d(s)Br} \to \mathsf {Ch}$
using the colimit description of Kan extension and the bar construction model for homotopy colimits. This is the simplicial object with s-simplices
 $$\begin{align*}[s] \longmapsto \bigoplus_{S_0, \ldots, S_s \in \mathsf{d(s)Br}} A(S_0) \otimes \mathsf{d(s)Br}(S_0, S_1) \otimes \cdots \otimes \mathsf{d(s)Br}(S_{s-1}, S_s) \otimes \mathsf{FB}(r(S_s), -)\end{align*}$$
$$\begin{align*}[s] \longmapsto \bigoplus_{S_0, \ldots, S_s \in \mathsf{d(s)Br}} A(S_0) \otimes \mathsf{d(s)Br}(S_0, S_1) \otimes \cdots \otimes \mathsf{d(s)Br}(S_{s-1}, S_s) \otimes \mathsf{FB}(r(S_s), -)\end{align*}$$
(implicitly replacing
![]() $\mathsf {d(s)Br}$
by a skeletal subcategory), and face maps given by composing morphisms in
$\mathsf {d(s)Br}$
by a skeletal subcategory), and face maps given by composing morphisms in
![]() $\mathsf {d(s)Br}$
, acting with them on
$\mathsf {d(s)Br}$
, acting with them on
![]() $A(-)$
, or applying
$A(-)$
, or applying
![]() $r \colon \mathsf {d(s)Br} \to \mathsf {FB}$
to them and composing in
$r \colon \mathsf {d(s)Br} \to \mathsf {FB}$
to them and composing in
![]() $\mathsf {FB}$
; its geometric realisation models
$\mathsf {FB}$
; its geometric realisation models
![]() $\mathbb {L} r_*(A)$
. Filtering this geometric realisation by skeleta gives a spectral sequence with
$\mathbb {L} r_*(A)$
. Filtering this geometric realisation by skeleta gives a spectral sequence with
 $$\begin{align*}E^1_{s,t} = \bigoplus_{S_0, \ldots, S_s \in \mathsf{d(s)Br}} H_{t}(A)(S_0) \otimes \mathsf{d(s)Br}(S_0, S_1) \otimes \cdots \otimes \mathsf{d(s)Br}(S_{s-1}, S_s) \otimes \mathsf{FB}(r(S_s), -),\end{align*}$$
$$\begin{align*}E^1_{s,t} = \bigoplus_{S_0, \ldots, S_s \in \mathsf{d(s)Br}} H_{t}(A)(S_0) \otimes \mathsf{d(s)Br}(S_0, S_1) \otimes \cdots \otimes \mathsf{d(s)Br}(S_{s-1}, S_s) \otimes \mathsf{FB}(r(S_s), -),\end{align*}$$
converging strongly to
![]() $H_{s+t}(\mathbb {L} r_*(A))$
as the values of A are by definition nonnegatively graded. The
$H_{s+t}(\mathbb {L} r_*(A))$
as the values of A are by definition nonnegatively graded. The
![]() $d^1$
-differential is given by the alternating sum of the face maps.
$d^1$
-differential is given by the alternating sum of the face maps.
If A also has an additional grading, then this gets carried along too. Applied to
![]() with its additional internal grading this gives a spectral sequence
with its additional internal grading this gives a spectral sequence

where the top expression is
![]() $E^1_{s,t,q}$
, and similarly for
$E^1_{s,t,q}$
, and similarly for
![]() $RB_{conn}^{Z_n}$
.
$RB_{conn}^{Z_n}$
.
6.3 Finishing the proof of Theorem A
Lemma 6.10.
![]() $H_{p+q}(G^{Z_n}(T))_q$
and
$H_{p+q}(G^{Z_n}(T))_q$
and
![]() $H_{p+q}(G^{E_n}(T))_q$
vanish if
$H_{p+q}(G^{E_n}(T))_q$
vanish if
![]() $n \cdot (p+1) < q$
and
$n \cdot (p+1) < q$
and
![]() $T \neq \varnothing $
.
$T \neq \varnothing $
.
Proof. We consider the case of
![]() $E_n$
; that of
$E_n$
; that of
![]() $Z_n$
is identical. We apply the spectral sequence (14) for a fixed q and evaluated at
$Z_n$
is identical. We apply the spectral sequence (14) for a fixed q and evaluated at
![]() $T \neq \varnothing $
, which starts from
$T \neq \varnothing $
, which starts from

and converges to
![]() $H_{s+t}(G^{E_n}(T))$
. For the latter tensor factors to be nonzero, we must have
$H_{s+t}(G^{E_n}(T))$
. For the latter tensor factors to be nonzero, we must have
![]() $|S_0| \geq |S_1| \geq \cdots \geq |S_s|=|T|$
, and so if
$|S_0| \geq |S_1| \geq \cdots \geq |S_s|=|T|$
, and so if
![]() $T \neq \varnothing $
then
$T \neq \varnothing $
then
![]() $S_0 \neq \varnothing $
. In this case, for the first tensor factor to be nonzero we must have
$S_0 \neq \varnothing $
. In this case, for the first tensor factor to be nonzero we must have
![]() $q = n \cdot (t-q+1)$
by Theorem 5.1. Thus, if
$q = n \cdot (t-q+1)$
by Theorem 5.1. Thus, if
![]() $q \neq n \cdot (t-q+1)$
then
$q \neq n \cdot (t-q+1)$
then
![]() $E^1_{s,t,q}=0$
.
$E^1_{s,t,q}=0$
.
In particular, if
![]() $t < \tfrac {n+1}{n}q-1$
then
$t < \tfrac {n+1}{n}q-1$
then
![]() $E^1_{s,t,q}=0$
, so
$E^1_{s,t,q}=0$
, so
![]() $H_{s+t}(G^{E_n}(T))_q=0$
if
$H_{s+t}(G^{E_n}(T))_q=0$
if
![]() $s+t < \tfrac {n+1}{n}q-1$
. Writing
$s+t < \tfrac {n+1}{n}q-1$
. Writing
![]() $s+t = p+q$
and rearranging, we see that
$s+t = p+q$
and rearranging, we see that
![]() $H_{p+q}(G^{E_n}(T))_q=0$
for
$H_{p+q}(G^{E_n}(T))_q=0$
for
![]() $n \cdot (p+1)< q$
as claimed.
$n \cdot (p+1)< q$
as claimed.
The following lemma is due to Turchin–Willwacher [Reference Turchin and WillwacherTW17, Section 6.1] for
![]() $Z_n$
and Chan–Galatius–Payne [Reference Felder, Naef and WillwacherCGP22, Theorem 1.7] for
$Z_n$
and Chan–Galatius–Payne [Reference Felder, Naef and WillwacherCGP22, Theorem 1.7] for
![]() $E_n$
. As its proof is quite elementary, we give it, following [Reference Felder, Naef and WillwacherCGP22, Section 5.3].
$E_n$
. As its proof is quite elementary, we give it, following [Reference Felder, Naef and WillwacherCGP22, Section 5.3].
Lemma 6.11 (Turchin–Willwacher, Chan–Galatius–Payne)
There are injections
 $$ \begin{align*} H_{p+q}(G^{Z_n}(\varnothing))_q &\longrightarrow H_{p+q+n}(G^{Z_n}(\underline{1}))_{q+n},\\ H_{p+q}(G^{E_n}(\varnothing))_q &\longrightarrow H_{p+q+n}(G^{E_n}(\underline{1}))_{q+n}. \end{align*} $$
$$ \begin{align*} H_{p+q}(G^{Z_n}(\varnothing))_q &\longrightarrow H_{p+q+n}(G^{Z_n}(\underline{1}))_{q+n},\\ H_{p+q}(G^{E_n}(\varnothing))_q &\longrightarrow H_{p+q+n}(G^{E_n}(\underline{1}))_{q+n}. \end{align*} $$
Proof. We explain the proof for
![]() $G^{E_n}$
; the proof for
$G^{E_n}$
; the proof for
![]() $G^{Z_n}$
is identical without weights.
$G^{Z_n}$
is identical without weights.
For
![]() $q \leq 0$
, there is nothing to prove: the admissibility condition for graphs in
$q \leq 0$
, there is nothing to prove: the admissibility condition for graphs in
![]() $G^{E_n}(\varnothing )$
implies that
$G^{E_n}(\varnothing )$
implies that
![]() $2 w(v)+\mathrm {val}(v) -2 \geq 1$
for all vertices v, so the internal grading satisfies
$2 w(v)+\mathrm {val}(v) -2 \geq 1$
for all vertices v, so the internal grading satisfies
![]() $q = n\sum _{v \in V(\Gamma )} (2w(v)+\mathrm {val}(v)-2)> 0$
.
$q = n\sum _{v \in V(\Gamma )} (2w(v)+\mathrm {val}(v)-2)> 0$
.
We will define maps of chain complexes
whose composition preserves the internal grading and on the summand with internal grading q is given by multiplication by q. In particular, it is an isomorphism for
![]() $q>0$
. Informally, t sums over all ways to add a single leg and
$q>0$
. Informally, t sums over all ways to add a single leg and
![]() $\pi $
deletes the leg.
$\pi $
deletes the leg.
Suppose we are given a weighted black graph
![]() $(\Gamma ,\ell ,\nu ,\omega ^{\otimes n}) \in G^{E_n}(\varnothing )$
;
$(\Gamma ,\ell ,\nu ,\omega ^{\otimes n}) \in G^{E_n}(\varnothing )$
;
![]() $\Gamma $
is the graph with w the weights of its vertices,
$\Gamma $
is the graph with w the weights of its vertices,
![]() $\ell $
the labelling of its legs, and
$\ell $
the labelling of its legs, and
![]() $\nu $
and
$\nu $
and
![]() $\omega ^{\otimes n}$
are orientations in
$\omega ^{\otimes n}$
are orientations in
![]() $\mathfrak {K}_B(\Gamma )$
and
$\mathfrak {K}_B(\Gamma )$
and
![]() $\mathfrak {L}(\Gamma )^{\otimes n}$
respectively, as in (11). For each vertex
$\mathfrak {L}(\Gamma )^{\otimes n}$
respectively, as in (11). For each vertex
![]() $v \in V(\Gamma )$
adding a leg at v yields a graph
$v \in V(\Gamma )$
adding a leg at v yields a graph
![]() $\Gamma _v$
with
$\Gamma _v$
with
![]() $V(\Gamma _v) = V(\Gamma )$
,
$V(\Gamma _v) = V(\Gamma )$
,
![]() $E_B(\Gamma _v) = E_B(\Gamma )$
, and
$E_B(\Gamma _v) = E_B(\Gamma )$
, and
![]() $L(\Gamma _v) = \{l\}$
. Using the same w and
$L(\Gamma _v) = \{l\}$
. Using the same w and
![]() $\nu $
,
$\nu $
,
![]() $\ell _v \colon \{l\} \to \{1\}$
the unique bijection and
$\ell _v \colon \{l\} \to \{1\}$
the unique bijection and
![]() $\omega _v$
induced from
$\omega _v$
induced from
![]() $\omega $
by
$\omega $
by
![]() $- \wedge l \colon \det (\mathbb {Q}^{L(\Gamma )}) \overset {\sim }\to \det (\mathbb {Q}^{L(\Gamma _v)})$
, we obtain
$- \wedge l \colon \det (\mathbb {Q}^{L(\Gamma )}) \overset {\sim }\to \det (\mathbb {Q}^{L(\Gamma _v)})$
, we obtain
![]() $(\Gamma _v,\ell _v,\nu ,\omega _v^{\otimes n}) \in G^{E_n}(\underline {1})$
. Since the valence of v has increased by
$(\Gamma _v,\ell _v,\nu ,\omega _v^{\otimes n}) \in G^{E_n}(\underline {1})$
. Since the valence of v has increased by
![]() $1$
,
$1$
,
![]() $\mathrm {deg}_{\mathrm {int}}(\Gamma _v) = \mathrm {deg}_{\mathrm {int}}(\Gamma )+n$
and the same is true for the total degree since the number of black edges did not change. Introducing the notation
$\mathrm {deg}_{\mathrm {int}}(\Gamma _v) = \mathrm {deg}_{\mathrm {int}}(\Gamma )+n$
and the same is true for the total degree since the number of black edges did not change. Introducing the notation
![]() , then t is defined by
, then t is defined by
 $$ \begin{align*} t \colon G^{E_n}_{p+q}(\varnothing) & \longrightarrow G^{E_n}_{p+q+n}(\underline{1}) \\ (\Gamma,\ell,\nu,\omega^{\otimes n}) &\longmapsto \sum_{v \in V(\Gamma)} \chi(v) \cdot (\Gamma_v,,\ell_v,\nu,\omega_v^{\otimes n}).\end{align*} $$
$$ \begin{align*} t \colon G^{E_n}_{p+q}(\varnothing) & \longrightarrow G^{E_n}_{p+q+n}(\underline{1}) \\ (\Gamma,\ell,\nu,\omega^{\otimes n}) &\longmapsto \sum_{v \in V(\Gamma)} \chi(v) \cdot (\Gamma_v,,\ell_v,\nu,\omega_v^{\otimes n}).\end{align*} $$
To verify t is a chain map, we need to show it commutes with
![]() $d_{\mathrm {con}}$
(since
$d_{\mathrm {con}}$
(since
![]() $d_{\mathrm {col}}$
vanishes upon taking the quotient by graphs with at least one red edge). This follows by observing that if an edge e connecting vertices
$d_{\mathrm {col}}$
vanishes upon taking the quotient by graphs with at least one red edge). This follows by observing that if an edge e connecting vertices
![]() $v'$
and
$v'$
and
![]() $v"$
(these can be equal, when e is a loop) is collapsed to a vertex v, then
$v"$
(these can be equal, when e is a loop) is collapsed to a vertex v, then
![]() $(\Gamma /e)_v = \Gamma _{v'}/e = \Gamma _{v"}/e$
and
$(\Gamma /e)_v = \Gamma _{v'}/e = \Gamma _{v"}/e$
and
![]() $\chi (v) = \chi (v')+\chi (v")$
.
$\chi (v) = \chi (v')+\chi (v")$
.
Suppose we are given a weighted black graph
![]() $(\Gamma ,\ell ,\nu ,\omega ^{\otimes n}) \in G^{E_n}(\underline {1})$
. Removing the unique leg l from
$(\Gamma ,\ell ,\nu ,\omega ^{\otimes n}) \in G^{E_n}(\underline {1})$
. Removing the unique leg l from
![]() $\Gamma $
yields a graph
$\Gamma $
yields a graph
![]() $\Gamma ^l$
with
$\Gamma ^l$
with
![]() $V(\Gamma ^l) = V(\Gamma )$
,
$V(\Gamma ^l) = V(\Gamma )$
,
![]() $E_B(\Gamma ^l) = E_B(\Gamma )$
, and
$E_B(\Gamma ^l) = E_B(\Gamma )$
, and
![]() $L(\Gamma ^l) = \varnothing $
. Using the same w and
$L(\Gamma ^l) = \varnothing $
. Using the same w and
![]() $\nu $
,
$\nu $
,
![]() $\ell ^l$
the unique map between empty sets, and
$\ell ^l$
the unique map between empty sets, and
![]() $\omega ^l$
induced from
$\omega ^l$
induced from
![]() $\omega $
by the map
$\omega $
by the map
![]() $\det (\mathbb {Q}^{L(\Gamma )}) \smash {\overset {\sim }\to } \det (\mathbb {Q}^{L(\Gamma ^l)})$
that contracts with l, we obtain
$\det (\mathbb {Q}^{L(\Gamma )}) \smash {\overset {\sim }\to } \det (\mathbb {Q}^{L(\Gamma ^l)})$
that contracts with l, we obtain
![]() $(\Gamma ^l,\ell ^l,\nu ,(\omega ^l)^{\otimes n}) \in G^{E_n}(\varnothing )$
. Since the valence of
$(\Gamma ^l,\ell ^l,\nu ,(\omega ^l)^{\otimes n}) \in G^{E_n}(\varnothing )$
. Since the valence of
![]() has decreased by
has decreased by
![]() $1$
,
$1$
,
![]() $\mathrm {deg}_{\mathrm {int}}(\Gamma ^l) = \mathrm { deg}_{\mathrm {int}}(\Gamma )-n$
and the same is true for the total degree since the number of black edges did not change. This weighted graph is admissible if and only if
$\mathrm {deg}_{\mathrm {int}}(\Gamma ^l) = \mathrm { deg}_{\mathrm {int}}(\Gamma )-n$
and the same is true for the total degree since the number of black edges did not change. This weighted graph is admissible if and only if
![]() $2 w(v_l) + \mathrm {val}(v_l) \geq 3$
. Then define
$2 w(v_l) + \mathrm {val}(v_l) \geq 3$
. Then define
 $$ \begin{align*} \pi \colon G^{E_n}_{p+q+n}(\underline{1}) & \longrightarrow G^{E_n}_{p+q}(\varnothing) \\ (\Gamma,\ell,\nu,\omega^{\otimes n}) &\longmapsto \begin{cases} (\Gamma^l,\ell^l,\nu,(\omega^l)^{\otimes n}) & \text{if }2 w(v_l) + \mathrm{ val}(v_l) \geq 3, \\ 0 & \text{otherwise.}\end{cases}\end{align*} $$
$$ \begin{align*} \pi \colon G^{E_n}_{p+q+n}(\underline{1}) & \longrightarrow G^{E_n}_{p+q}(\varnothing) \\ (\Gamma,\ell,\nu,\omega^{\otimes n}) &\longmapsto \begin{cases} (\Gamma^l,\ell^l,\nu,(\omega^l)^{\otimes n}) & \text{if }2 w(v_l) + \mathrm{ val}(v_l) \geq 3, \\ 0 & \text{otherwise.}\end{cases}\end{align*} $$
To verify that
![]() $\pi $
is a chain map, we observe that
$\pi $
is a chain map, we observe that
![]() $(\Gamma /e)^l = \Gamma ^l/e$
. A subtlety is that deleting a leg may make a graph inadmissible; this occurs either when (a) the leg l is at a trivalent vertex of weight
$(\Gamma /e)^l = \Gamma ^l/e$
. A subtlety is that deleting a leg may make a graph inadmissible; this occurs either when (a) the leg l is at a trivalent vertex of weight
![]() $0$
, or (b) the leg l is at a univalent vertex with weight 1. The case (a) is verified in Figure 6, and case (b) is left to the reader.
$0$
, or (b) the leg l is at a univalent vertex with weight 1. The case (a) is verified in Figure 6, and case (b) is left to the reader.

Figure 6 This figure illustrates that
![]() $ \pi $
is a chain map when deleting the unique leg creates inadmissible graphs, in case (a). Weights are not displayed.
$ \pi $
is a chain map when deleting the unique leg creates inadmissible graphs, in case (a). Weights are not displayed.
The composition
![]() $\pi \circ t$
is given on the element
$\pi \circ t$
is given on the element
![]() $(\Gamma ,\ell ,\nu ,\omega ^{\otimes n})$
by multiplication by
$(\Gamma ,\ell ,\nu ,\omega ^{\otimes n})$
by multiplication by
![]() $ \sum _{v \in V(\Gamma )} \chi (v) = \mathrm {deg}_{\mathrm {int}}(\Gamma )$
; the result follows.
$ \sum _{v \in V(\Gamma )} \chi (v) = \mathrm {deg}_{\mathrm {int}}(\Gamma )$
; the result follows.
Combining this with Lemma 6.10 shows that the conclusion of that lemma holds for
![]() $T=\varnothing $
too, with a slightly better range.
$T=\varnothing $
too, with a slightly better range.
Corollary 6.12.
![]() $H_{p+q}(G^{Z_n}(\varnothing ))_q$
and
$H_{p+q}(G^{Z_n}(\varnothing ))_q$
and
![]() $H_{p+q}(G^{E_n}(\varnothing ))_q$
vanish if
$H_{p+q}(G^{E_n}(\varnothing ))_q$
vanish if
![]() $n \cdot p < q$
.
$n \cdot p < q$
.
Proof. By Lemma 6.11,
![]() $H_{p+q}(G^{Z_n}(\varnothing ))_q$
injects into
$H_{p+q}(G^{Z_n}(\varnothing ))_q$
injects into
![]() $H_{p+q+n}(G^{Z_n}(\underline {1}))_{q+n}$
for
$H_{p+q+n}(G^{Z_n}(\underline {1}))_{q+n}$
for
![]() $q \neq 0$
. By Lemma 6.10 for
$q \neq 0$
. By Lemma 6.10 for
![]() $T = \underline {1}$
, this vanishes as long as
$T = \underline {1}$
, this vanishes as long as
![]() $n(p+1)<q+n$
. Rearranging gives the result.
$n(p+1)<q+n$
. Rearranging gives the result.
Using this we can reverse the logic of the proof of Lemma 6.10 to access
![]() $H_{p}^{\mathrm {Com}}(Z_n)_q(\varnothing )$
and
$H_{p}^{\mathrm {Com}}(Z_n)_q(\varnothing )$
and
![]() $H_{p}^{\mathrm {Com}}(E_n)_q(\varnothing )$
.
$H_{p}^{\mathrm {Com}}(E_n)_q(\varnothing )$
.
Theorem 6.13.
![]() $H^{\mathrm {Com}}_{p}(Z_n)_q(\varnothing )$
and
$H^{\mathrm {Com}}_{p}(Z_n)_q(\varnothing )$
and
![]() $H^{\mathrm {Com}}_{p}(E_n)_q(\varnothing )$
vanish if
$H^{\mathrm {Com}}_{p}(E_n)_q(\varnothing )$
vanish if
![]() $q \neq n \cdot p$
.
$q \neq n \cdot p$
.
Proof. We consider the case of
![]() $E_n$
; that of
$E_n$
; that of
![]() $Z_n$
is identical. Consider the spectral sequence of (14) for
$Z_n$
is identical. Consider the spectral sequence of (14) for
![]() $T=\varnothing $
. This has
$T=\varnothing $
. This has

and converges strongly to
![]() $H_{s+t}(G^{E_n}(\varnothing ))_q$
. The terms with
$H_{s+t}(G^{E_n}(\varnothing ))_q$
. The terms with
![]() $S_0 = \varnothing $
form a subcomplex
$S_0 = \varnothing $
form a subcomplex
![]() $D_{*,t,q}$
of
$D_{*,t,q}$
of
![]() $(E^1_{*,t,q}, d^1)$
, as in this case for the latter tensor factors to be nonzero we must have
$(E^1_{*,t,q}, d^1)$
, as in this case for the latter tensor factors to be nonzero we must have
![]() $\varnothing = S_0 = S_1 = \cdots = S_s$
, and
$\varnothing = S_0 = S_1 = \cdots = S_s$
, and
![]() $d^1$
preserves this property. Furthermore, this subcomplex is
$d^1$
preserves this property. Furthermore, this subcomplex is
so is acyclic in degrees
![]() $s>0$
. The quotient complex
$s>0$
. The quotient complex
![]() $E^1_{*,t,q}/D_{*,t,q}$
is given by the analogous formula to the above but only summing over
$E^1_{*,t,q}/D_{*,t,q}$
is given by the analogous formula to the above but only summing over
![]() $S_0 \neq \varnothing $
. In this case, for
$S_0 \neq \varnothing $
. In this case, for
![]() $H_{t-q+1}^{\mathrm {Com}}(E_n)_q(S_0)$
to be nonzero we must have
$H_{t-q+1}^{\mathrm {Com}}(E_n)_q(S_0)$
to be nonzero we must have
![]() $q = n \cdot (t-q+1)$
. In total we find that
$q = n \cdot (t-q+1)$
. In total we find that
![]() $E^2_{0,t,q} = H_{t-q+1}^{\mathrm {Com}}(E_n)_q(\varnothing )$
and if
$E^2_{0,t,q} = H_{t-q+1}^{\mathrm {Com}}(E_n)_q(\varnothing )$
and if
![]() $q \neq n \cdot (t-q+1)$
and
$q \neq n \cdot (t-q+1)$
and
![]() $s> 0$
, then
$s> 0$
, then
![]() $E^2_{s,t,q}=0$
.
$E^2_{s,t,q}=0$
.
We combine these properties as follows. By Lemma 4.14, we already know that the claimed vanishing occurs for
![]() $q < n \cdot p$
, so suppose that
$q < n \cdot p$
, so suppose that
![]() $q> n \cdot p$
and consider
$q> n \cdot p$
and consider
![]() $H_{p}^{\mathrm {Com}}(E_n)_q(\varnothing ) = E^2_{0,p+q-1,q}$
. There are no differentials leaving this position in the spectral sequence. Differentials arriving at it come from
$H_{p}^{\mathrm {Com}}(E_n)_q(\varnothing ) = E^2_{0,p+q-1,q}$
. There are no differentials leaving this position in the spectral sequence. Differentials arriving at it come from
![]() $E^r_{r,p+q-r,q}$
with
$E^r_{r,p+q-r,q}$
with
![]() $r \geq 2$
, but for this to be nontrivial we must have
$r \geq 2$
, but for this to be nontrivial we must have
![]() $q=n \cdot (p-r+1) \leq n \cdot p$
, which is not possible by our assumption that
$q=n \cdot (p-r+1) \leq n \cdot p$
, which is not possible by our assumption that
![]() $q> n \cdot p$
. Thus, no differentials can enter this position either, and so
$q> n \cdot p$
. Thus, no differentials can enter this position either, and so
But
![]() $E^{\infty }_{0,p+q-1,q}$
is a filtration quotient of
$E^{\infty }_{0,p+q-1,q}$
is a filtration quotient of
![]() $H_{p+q-1}(G^{E_n}(\varnothing ))_q$
, which by Corollary 6.12 vanishes for
$H_{p+q-1}(G^{E_n}(\varnothing ))_q$
, which by Corollary 6.12 vanishes for
![]() $n\cdot (p-1) < q$
so in particular for
$n\cdot (p-1) < q$
so in particular for
![]() $q> n \cdot p$
which is what we assumed.
$q> n \cdot p$
which is what we assumed.
Remark 6.14. The reader may wonder why we did not apply a transfer argument as in Lemma 6.11 directly to
![]() $RB^{Z_n}_{conn}$
and
$RB^{Z_n}_{conn}$
and
![]() $RB^{E_n}_{conn}$
to deduce Theorem 6.13 from the corresponding result with
$RB^{E_n}_{conn}$
to deduce Theorem 6.13 from the corresponding result with
![]() $\underline {1}$
in place of
$\underline {1}$
in place of
![]() $\varnothing $
. The reason is that the analogue of the map
$\varnothing $
. The reason is that the analogue of the map
![]() $\pi $
, which removes the unique leg from a red-and-black graph whose legs are labelled by
$\pi $
, which removes the unique leg from a red-and-black graph whose legs are labelled by
![]() $\underline {1}$
, is not a chain map in this case. We invite the reader to verify this for the following red-and-black graph:
$\underline {1}$
, is not a chain map in this case. We invite the reader to verify this for the following red-and-black graph:

Recalling that the internal degree is n times the weight, Theorem 5.1 and Theorem 6.13 together show that the
![]() $Z_n$
and
$Z_n$
and
![]() $E_n$
are all Koszul, and hence by Corollary 4.27 imply that
$E_n$
are all Koszul, and hence by Corollary 4.27 imply that
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
is Koszul in gradings
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
is Koszul in gradings
![]() $\leq \tfrac {g}{3}$
, and hence by Proposition 3.4 imply Theorem 3.3.
$\leq \tfrac {g}{3}$
, and hence by Proposition 3.4 imply Theorem 3.3.
7 Applications of Koszulness
In this section, we give two applications of Theorem A, to high-dimensional manifolds and graph complexes respectively.
7.1 Applications to high-dimensional manifolds
In this subsection, we follow Section 5 in refraining from mentioning the weight grading (as it coincides with the homological grading divided by n). Given the Koszulness of
![]() $Z_n$
, we can now revisit Section 5.2 and determine the rational homotopy groups of
$Z_n$
, we can now revisit Section 5.2 and determine the rational homotopy groups of
![]() $X_1(g)$
in a stable range of degrees. Let
$X_1(g)$
in a stable range of degrees. Let
![]() $2n \geq 6$
and recall that by Theorem 5.2 (iii) the construction of twisted MMM-classes yields an algebra homomorphism
$2n \geq 6$
and recall that by Theorem 5.2 (iii) the construction of twisted MMM-classes yields an algebra homomorphism
which is an isomorphism of
![]() $\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
-representations in a stable range; in fact,
$\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
-representations in a stable range; in fact,
![]() $* \leq \frac {g-3}{2}$
suffices by [Reference Koike and TeradaKRW20c, Section 9.2]. The discussion in [Reference Koike and TeradaKRW20c, Section 5] gives in degrees
$* \leq \frac {g-3}{2}$
suffices by [Reference Koike and TeradaKRW20c, Section 9.2]. The discussion in [Reference Koike and TeradaKRW20c, Section 5] gives in degrees
![]() $* \leq n \cdot g$
(cf. Theorem 4.25) an expression for the left side as a quadratic commutative algebra:
$* \leq n \cdot g$
(cf. Theorem 4.25) an expression for the left side as a quadratic commutative algebra:

and
. We write
![]() $R^{\prime \perp } \subset \Lambda ^2[W[n]]^{\vee } \cong \Lambda ^2[W[n]]$
for its annihilator.
$R^{\prime \perp } \subset \Lambda ^2[W[n]]^{\vee } \cong \Lambda ^2[W[n]]$
for its annihilator.
Remark 7.1. When n is odd, as long as
![]() $g \geq 6$
we have the decomposition
$g \geq 6$
we have the decomposition
into irreducible
![]() $\mathrm {Sp}_{2g}(\mathbb {Z})$
-representations. The vectors (IH) generate the representation
$\mathrm {Sp}_{2g}(\mathbb {Z})$
-representations. The vectors (IH) generate the representation
![]() $V_0 + V_{1^2} + V_{2^2}$
(c.f. Remark 3.13), so
$V_0 + V_{1^2} + V_{2^2}$
(c.f. Remark 3.13), so
![]() $R^{\prime \perp } \cong V_{1^4}+V_{1^6} + V_{2^2,1^2}$
. For n even, one takes the transpose [Reference Kupers and Randal-WilliamsKRW20b, Remark 4.23].
$R^{\prime \perp } \cong V_{1^4}+V_{1^6} + V_{2^2,1^2}$
. For n even, one takes the transpose [Reference Kupers and Randal-WilliamsKRW20b, Remark 4.23].
Theorem 7.2. In degrees
![]() $* \leq \frac {g-3}{2}$
, there is a Lie algebra isomorphism
$* \leq \frac {g-3}{2}$
, there is a Lie algebra isomorphism
Proof. The map
![]() $\psi \colon K^{\vee } \otimes ^{\mathsf {d(s)Br}} Z_n \to H^*(X_1(g);\mathbb {Q})$
of
$\psi \colon K^{\vee } \otimes ^{\mathsf {d(s)Br}} Z_n \to H^*(X_1(g);\mathbb {Q})$
of
![]() $\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
-representations is an isomorphism in degrees
$\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
-representations is an isomorphism in degrees
![]() $* \leq \frac {g-3}{2}$
. The left side is Koszul in degrees
$* \leq \frac {g-3}{2}$
. The left side is Koszul in degrees
![]() $* \leq n\cdot \frac {g}{3}$
by Theorem 6.13 and Lemma 4.19. Thus, the unstable rational Adams spectral sequence of the proof of Theorem 5.1 (see Section 5.3)
$* \leq n\cdot \frac {g}{3}$
by Theorem 6.13 and Lemma 4.19. Thus, the unstable rational Adams spectral sequence of the proof of Theorem 5.1 (see Section 5.3)
vanishes except when
![]() $t = s \cdot n$
as long as
$t = s \cdot n$
as long as
![]() $t \leq \min (\frac {g-3}{2},n\cdot \frac {g}{3})$
but since
$t \leq \min (\frac {g-3}{2},n\cdot \frac {g}{3})$
but since
![]() $2n \geq 6$
the first term is always smaller. Moreover, in this range the
$2n \geq 6$
the first term is always smaller. Moreover, in this range the
![]() $E^2$
-page is dual to the quadratic dual of
$E^2$
-page is dual to the quadratic dual of
![]() $\Lambda ^*[W[n]]/(R')$
and the spectral sequence collapses for degree reasons because the differentials have bidegree
$\Lambda ^*[W[n]]/(R')$
and the spectral sequence collapses for degree reasons because the differentials have bidegree
![]() $(-r,-r+1)$
.
$(-r,-r+1)$
.
This in turn has consequences for diffeomorphisms of the disc
![]() $D^{2n}$
and homeomorphisms of the Euclidean space
$D^{2n}$
and homeomorphisms of the Euclidean space
![]() $\mathbb {R}^{2n}$
. The fundamental diagram of [Reference Kupers and Randal-WilliamsKRW20b] is (30) in Section 6.1 of loc. cit.:
$\mathbb {R}^{2n}$
. The fundamental diagram of [Reference Kupers and Randal-WilliamsKRW20b] is (30) in Section 6.1 of loc. cit.:

The row and column are fibration sequences, and all spaces are nilpotent, connected and of finite type. The common homotopy fibre
![]() $F_n$
of the rationalisations of the dashed maps [Reference Kupers and Randal-WilliamsKRW20b, Definition 6.1] fits into a map of fibration sequences (cf. [Reference Kupers and Randal-WilliamsKRW20b, (3)])
$F_n$
of the rationalisations of the dashed maps [Reference Kupers and Randal-WilliamsKRW20b, Definition 6.1] fits into a map of fibration sequences (cf. [Reference Kupers and Randal-WilliamsKRW20b, (3)])

In particular,
![]() $(X_0)_{\mathbb {Q}} \simeq \prod K(\mathbb {Q},d)$
with product indexed by integers
$(X_0)_{\mathbb {Q}} \simeq \prod K(\mathbb {Q},d)$
with product indexed by integers
![]() $d>0$
such that
$d>0$
such that
![]() $d \equiv 2n-1 \pmod 4$
. This directly yields the following improvement of Theorem C of [Reference Kupers and Randal-WilliamsKRW20b], also improving Theorem B of loc. cit.
$d \equiv 2n-1 \pmod 4$
. This directly yields the following improvement of Theorem C of [Reference Kupers and Randal-WilliamsKRW20b], also improving Theorem B of loc. cit.
Corollary 7.3. The rational homotopy groups of
![]() $\Omega ^{2n+1}_0 \tfrac {\mathrm {Top}}{\mathrm {Top}(2n)}$
are supported in degrees
$\Omega ^{2n+1}_0 \tfrac {\mathrm {Top}}{\mathrm {Top}(2n)}$
are supported in degrees
![]() $* \in \bigcup _{r \geq 2} [2r(n-2)-1,2r(n-1)+1]$
.
$* \in \bigcup _{r \geq 2} [2r(n-2)-1,2r(n-1)+1]$
.
7.2 Applications to graph complexes
7.2.1 Relation to classical graph complexes
Up to a change of degrees the chain complex
![]() $G^{Z_n}(S)$
may be identified with the sum
$G^{Z_n}(S)$
may be identified with the sum
![]() $\bigoplus _{g} G^{(g,|S|)}$
of the graph complexes studied by Chan–Galatius–Payne [Reference Chan, Galatius and PayneCGP21, Reference Felder, Naef and WillwacherCGP22]. When
$\bigoplus _{g} G^{(g,|S|)}$
of the graph complexes studied by Chan–Galatius–Payne [Reference Chan, Galatius and PayneCGP21, Reference Felder, Naef and WillwacherCGP22]. When
![]() $S=\varnothing $
, this is predual to Kontsevich’s graph complex
$S=\varnothing $
, this is predual to Kontsevich’s graph complex
![]() $\mathsf {GC}_2$
as studied by Willwacher [Reference WillwacherWil15], and for general S it is predual to the ‘hairy graph complex’
$\mathsf {GC}_2$
as studied by Willwacher [Reference WillwacherWil15], and for general S it is predual to the ‘hairy graph complex’
![]() $\mathsf {HGC}_2^{S}$
of Andersson–Willwacher–Zivkovic [Reference Bousfield and KanAWZ20]. Similarly, the chain complex
$\mathsf {HGC}_2^{S}$
of Andersson–Willwacher–Zivkovic [Reference Bousfield and KanAWZ20]. Similarly, the chain complex
![]() $G^{E_n}(S)$
may be identified with the sum
$G^{E_n}(S)$
may be identified with the sum
![]() $\bigoplus _{g} \widetilde {C}_*(\Delta _{g,|S|};\mathbb {Q})$
of the reduced chains on the moduli spaces of tropical curves of genus g with
$\bigoplus _{g} \widetilde {C}_*(\Delta _{g,|S|};\mathbb {Q})$
of the reduced chains on the moduli spaces of tropical curves of genus g with
![]() $|S|$
marked points from [Reference Felder, Naef and WillwacherCGP22], or the predual of
$|S|$
marked points from [Reference Felder, Naef and WillwacherCGP22], or the predual of
![]() $\mathsf {HGC}_2^{S, \text {mod}}$
from [Reference Bousfield and KanAWZ20].
$\mathsf {HGC}_2^{S, \text {mod}}$
from [Reference Bousfield and KanAWZ20].
In the degree convention of [Reference Felder, Naef and WillwacherCGP22], a connected (weighted) graph
![]() $\Gamma $
is given degree
$\Gamma $
is given degree
![]() $\mathrm {deg}_{CGP}(\Gamma ) := \# E(\Gamma )-2g(\Gamma )$
, where
$\mathrm {deg}_{CGP}(\Gamma ) := \# E(\Gamma )-2g(\Gamma )$
, where
![]() $g(\Gamma )$
is the sum of the first Betti number of
$g(\Gamma )$
is the sum of the first Betti number of
![]() $\Gamma $
and the weights at all its vertices. Our internal degree can be compared to
$\Gamma $
and the weights at all its vertices. Our internal degree can be compared to
![]() $g(\Gamma )$
via
$g(\Gamma )$
via
and our total degree is
![]() $\mathrm {deg}(\Gamma ) = \#E(\Gamma ) + \deg _{\text {int}}(\Gamma )$
, so
$\mathrm {deg}(\Gamma ) = \#E(\Gamma ) + \deg _{\text {int}}(\Gamma )$
, so
7.2.2 An alternative approach
Complementary to the filtration used in the proof of Proposition 6.6 by number of edges, we may filter
![]() $RB^{E_n}_{\text {conn}}$
by the number of red edges: This kills the
$RB^{E_n}_{\text {conn}}$
by the number of red edges: This kills the
![]() $d_{\text {col}}$
part of the differential, leaving
$d_{\text {col}}$
part of the differential, leaving
In particular, it gives a spectral sequence

Using this and the spectral sequence (14), it follows that Koszulness of
![]() $E_n$
is equivalent to the vanishing range
$E_n$
is equivalent to the vanishing range
The same goes with
![]() $E_n$
replaced by
$E_n$
replaced by
![]() $Z_n$
.
$Z_n$
.
Remark 7.4. Willwacher has pointed out the following line of reasoning to us, which is essentially the argument of [Reference Garoufalidis and GetzlerFNW23]: Combining the above with the discussion of Chan–Galatius–Payne’s complexes in the last section, it follows that Koszulness of
![]() $Z_n$
is equivalent to
$Z_n$
is equivalent to
![]() $H_*(G^{(g, n)})=0$
for
$H_*(G^{(g, n)})=0$
for
![]() $* < n-3$
, and Koszulness of
$* < n-3$
, and Koszulness of
![]() $E_n$
is equivalent to
$E_n$
is equivalent to
![]() $\widetilde {H}_*(\Delta _{g,n};\mathbb {Q})=0$
for
$\widetilde {H}_*(\Delta _{g,n};\mathbb {Q})=0$
for
![]() $* < n-3+2g-1$
, but both follow from [Reference Felder, Naef and WillwacherCGP22, Theorem 1.6].
$* < n-3+2g-1$
, but both follow from [Reference Felder, Naef and WillwacherCGP22, Theorem 1.6].
7.2.3 Comparing
 $E_n$
and
$E_n$
and
 $Z_n$
$Z_n$
We can use our results to give a new proof of [Reference Chan, Galatius and PayneCGP21, Theorem 1.3] and [Reference Felder, Naef and WillwacherCGP22, Theorem 1.4] (another has been sketched in [Reference Bousfield and KanAWZ20, Lemma 5]). As explained in Section 4.4, there is a map of commutative algebra objects
![]() $E_n \to Z_n$
, and by Theorem 4.22 we have
$E_n \to Z_n$
, and by Theorem 4.22 we have
 $$ \begin{align} H_p^{\mathrm{Com}}(Z_n, E_n)_q(S) = \begin{cases} \mathbb{Q} & \text{ if } |S|=1 \text{ and } (p,q)=(2,n),\\ 0 & \text{ otherwise}. \end{cases} \end{align} $$
$$ \begin{align} H_p^{\mathrm{Com}}(Z_n, E_n)_q(S) = \begin{cases} \mathbb{Q} & \text{ if } |S|=1 \text{ and } (p,q)=(2,n),\\ 0 & \text{ otherwise}. \end{cases} \end{align} $$
Corollary 7.5. We have
 $$\begin{align*}H_{p+q}(G^{Z_n}(S), G^{E_n}(S))_q = \begin{cases} \mathbb{Q} & \text{ if } |S|=1 \text{ and } (p,q)=(1,n),\\ 0 & \text{ otherwise} .\end{cases}\end{align*}$$
$$\begin{align*}H_{p+q}(G^{Z_n}(S), G^{E_n}(S))_q = \begin{cases} \mathbb{Q} & \text{ if } |S|=1 \text{ and } (p,q)=(1,n),\\ 0 & \text{ otherwise} .\end{cases}\end{align*}$$
Proof. There is a relative form of the spectral sequence (14), obtained by taking mapping cones of filtered chain complexes, starting with
![]() $E^1_{s,t,q}$
given by
$E^1_{s,t,q}$
given by

and converging to
![]() $H_{s+t}(G^{Z_n}(T), G^{E_n}(T))_q$
. If
$H_{s+t}(G^{Z_n}(T), G^{E_n}(T))_q$
. If
![]() $|T| \geq 2$
, then only terms with
$|T| \geq 2$
, then only terms with
![]() $|S_0| \geq 2$
can contribute, but then
$|S_0| \geq 2$
can contribute, but then
![]() $H_{*}^{\mathrm {Com}}(Z_n, E_n)(A_0)=0$
by (16).
$H_{*}^{\mathrm {Com}}(Z_n, E_n)(A_0)=0$
by (16).
If
![]() $0 \leq |T|<2$
, then we may argue as in the proof of Theorem 6.13 that the subcomplex with
$0 \leq |T|<2$
, then we may argue as in the proof of Theorem 6.13 that the subcomplex with
![]() $|T| = |S_0| = \cdots = |S_s|$
is acyclic in degrees
$|T| = |S_0| = \cdots = |S_s|$
is acyclic in degrees
![]() $s>0$
. Once we quotient by this complex, the remaining terms must have
$s>0$
. Once we quotient by this complex, the remaining terms must have
![]() $|S_0| \geq |T|+2$
and the above argument still applies. Thus, the
$|S_0| \geq |T|+2$
and the above argument still applies. Thus, the
![]() $E^2$
-page of the spectral sequence is supported along
$E^2$
-page of the spectral sequence is supported along
![]() $s=0$
so collapses to give an isomorphism
$s=0$
so collapses to give an isomorphism
The result then follows from (16).
8 Injectivity of the geometric Johnson homomorphism
8.1 The geometric Johnson homomorphism
8.1.1 Construction
Recall from Lemma 3.2 that there is an extension of Lie algebras with additional grading
This exhibits
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {p}^r_{g,n}$
as a Lie ideal in
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {p}^r_{g,n}$
as a Lie ideal in
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}^r_{g,n}$
and hence the adjoint representation induces a map
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}^r_{g,n}$
and hence the adjoint representation induces a map
Specializing to
![]() $\Sigma _{g,1}$
, we have
$\Sigma _{g,1}$
, we have
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {p}_{g,1} = \mathrm {Lie}(H)$
, the free Lie algebra on
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {p}_{g,1} = \mathrm {Lie}(H)$
, the free Lie algebra on
![]() in weight 1. The map
in weight 1. The map
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1} \to \mathrm {Der}(\mathrm { Lie}(H))$
has image in the derivations which increase the weight and annihilate the element
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1} \to \mathrm {Der}(\mathrm { Lie}(H))$
has image in the derivations which increase the weight and annihilate the element
![]() $\omega = \sum _{i=1}^g [e_i,f_i]$
with
$\omega = \sum _{i=1}^g [e_i,f_i]$
with
![]() $e_1,\ldots ,e_g,f_1,\ldots ,f_g$
a symplectic basis of
$e_1,\ldots ,e_g,f_1,\ldots ,f_g$
a symplectic basis of
![]() $H_1(\Sigma _{g,1};\mathbb {Q}) = H_1(\Sigma _g;\mathbb {Q})$
[Reference MoritaMor93, Corollary 3.2]. This is denoted by
$H_1(\Sigma _{g,1};\mathbb {Q}) = H_1(\Sigma _g;\mathbb {Q})$
[Reference MoritaMor93, Corollary 3.2]. This is denoted by
![]() $\mathfrak {h}_{g,1} \subset \mathrm {Der}(\mathrm {Lie}(H))$
and called the Lie algebra of positive degree symplectic derivations.
$\mathfrak {h}_{g,1} \subset \mathrm {Der}(\mathrm {Lie}(H))$
and called the Lie algebra of positive degree symplectic derivations.
Following Hain, we refer to the resulting map
as the geometric Johnson homomorphism. Since this is a map of Lie algebras and its domain is generated in weight 1 as long as
![]() $g \geq 4$
(see Corollary 3.14), it is determined by its restriction to
$g \geq 4$
(see Corollary 3.14), it is determined by its restriction to
![]() $\mathrm {Gr}^1_{\mathrm {LCS}}\,\mathfrak {t}_{g,1}$
. Furthermore, it is a map of algebraic
$\mathrm {Gr}^1_{\mathrm {LCS}}\,\mathfrak {t}_{g,1}$
. Furthermore, it is a map of algebraic
![]() $\mathrm {Sp}_{2g}(\mathbb {Z})$
-representations, and
$\mathrm {Sp}_{2g}(\mathbb {Z})$
-representations, and
![]() $\mathrm {Gr}^1_{\mathrm {LCS}}\,\mathfrak {t}_{g,1}$
and
$\mathrm {Gr}^1_{\mathrm {LCS}}\,\mathfrak {t}_{g,1}$
and
![]() $(\mathfrak {h}_{g,1})_1$
are both given by
$(\mathfrak {h}_{g,1})_1$
are both given by
![]() $V_1 \oplus V_{1^3}$
by Corollary 3.14 and [Reference Kupers and Randal-WilliamsKRW20b, Computation 5.8]. This map
$V_1 \oplus V_{1^3}$
by Corollary 3.14 and [Reference Kupers and Randal-WilliamsKRW20b, Computation 5.8]. This map
![]() $\mathrm {Gr}^1_{\mathrm {LCS}}\,\mathfrak {t}_{g,1} \to (\mathfrak {h}_{g,1})_1$
is an isomorphism, essentially by construction of
$\mathrm {Gr}^1_{\mathrm {LCS}}\,\mathfrak {t}_{g,1} \to (\mathfrak {h}_{g,1})_1$
is an isomorphism, essentially by construction of
![]() $\mathfrak {t}_{g,1}$
, and thus up to isomorphism
$\mathfrak {t}_{g,1}$
, and thus up to isomorphism
![]() $\tau _{g,1}$
is the unique map of Lie algebras that is injective in weight 1. Theorem B asserts that in weight
$\tau _{g,1}$
is the unique map of Lie algebras that is injective in weight 1. Theorem B asserts that in weight
![]() $\leq \frac {1}{3}g$
the kernel of
$\leq \frac {1}{3}g$
the kernel of
![]() $\tau _{g,1}$
lies in the centre of
$\tau _{g,1}$
lies in the centre of
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
and consists of trivial representations of
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
and consists of trivial representations of
![]() $\mathrm {Sp}_{2g}(\mathbb {Z})$
.
$\mathrm {Sp}_{2g}(\mathbb {Z})$
.
Remark 8.1. Theorem B may be rephrased as saying that in weight
![]() $\leq \frac {1}{3}g$
the kernel of
$\leq \frac {1}{3}g$
the kernel of
![]() $\tau _{g,1}$
lies in the centre of
$\tau _{g,1}$
lies in the centre of
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {g}_{g,1}$
, the lower central series Lie algebra of the pro-algebraic group
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {g}_{g,1}$
, the lower central series Lie algebra of the pro-algebraic group
![]() $\mathcal {G}_{g,1}$
of Section 3.1.1. See [Reference HirschhornHai20, Question 5.11] for a question about this centre.
$\mathcal {G}_{g,1}$
of Section 3.1.1. See [Reference HirschhornHai20, Question 5.11] for a question about this centre.
We know that
![]() $K^{\vee } \otimes ^{\mathsf {dsBr}} E_1$
and
$K^{\vee } \otimes ^{\mathsf {dsBr}} E_1$
and
![]() $K^{\vee } \otimes ^{\mathsf {dsBr}} Z_1$
are Koszul in weight
$K^{\vee } \otimes ^{\mathsf {dsBr}} Z_1$
are Koszul in weight
![]() $\leq \frac {1}{3}g$
by Theorem 6.13 and the argument of Corollary 4.27. In particular, they are quadratic in this range and as long as
$\leq \frac {1}{3}g$
by Theorem 6.13 and the argument of Corollary 4.27. In particular, they are quadratic in this range and as long as
![]() $g \geq 6$
we let
$g \geq 6$
we let
![]() $(K^{\vee } \otimes ^{\mathsf {dsBr}} E_1)^{\mathrm {quad}}$
and
$(K^{\vee } \otimes ^{\mathsf {dsBr}} E_1)^{\mathrm {quad}}$
and
![]() $(K^{\vee } \otimes ^{\mathsf {dsBr}} Z_1)^{\mathrm {quad}}$
denote the quadratic algebras given by the quadratic duals of the presentations of
$(K^{\vee } \otimes ^{\mathsf {dsBr}} Z_1)^{\mathrm {quad}}$
denote the quadratic algebras given by the quadratic duals of the presentations of
![]() $K^{\vee } \otimes ^{\mathsf {dsBr}} E_1$
and
$K^{\vee } \otimes ^{\mathsf {dsBr}} E_1$
and
![]() $K^{\vee } \otimes ^{\mathsf {dsBr}} Z_1$
in weights
$K^{\vee } \otimes ^{\mathsf {dsBr}} Z_1$
in weights
![]() $\leq 2$
. These are explicitly described by (see the proofs of Theorem 4.25 and Theorem 7.2)
$\leq 2$
. These are explicitly described by (see the proofs of Theorem 4.25 and Theorem 7.2)
 $$\begin{align*}(K^{\vee} \otimes^{\mathsf{dsBr}} E_1)^{\mathrm{quad}} \cong \frac{\mathrm{Lie}(\Lambda^3(V_1)[0,1])}{(({IH})^{\perp})} \qquad \text{and} \qquad (K^{\vee} \otimes^{\mathsf{dsBr}} Z_1)^{\mathrm{quad}} \cong \frac{\mathrm{Lie}(V_{1^3}[0,1])}{(({IH})^{\perp})};\end{align*}$$
$$\begin{align*}(K^{\vee} \otimes^{\mathsf{dsBr}} E_1)^{\mathrm{quad}} \cong \frac{\mathrm{Lie}(\Lambda^3(V_1)[0,1])}{(({IH})^{\perp})} \qquad \text{and} \qquad (K^{\vee} \otimes^{\mathsf{dsBr}} Z_1)^{\mathrm{quad}} \cong \frac{\mathrm{Lie}(V_{1^3}[0,1])}{(({IH})^{\perp})};\end{align*}$$
in both cases the generators are in homological degree 0 and weight 1, so in particular these Lie algebras are supported in homological degree 0. For
![]() $g \geq 6$
, there is therefore a commutative diagram
$g \geq 6$
, there is therefore a commutative diagram

with horizontal maps isomorphisms for
![]() $w \leq \frac {1}{3}g$
.
$w \leq \frac {1}{3}g$
.
Lemma 8.2. Suppose
![]() $g \geq 6$
, then the map
$g \geq 6$
, then the map
is injective for
![]() $w=1$
and an isomorphism for
$w=1$
and an isomorphism for
![]() $2 \leq w \leq \frac {1}{3}g$
$2 \leq w \leq \frac {1}{3}g$
Proof. Since the weight w parts of
![]() $Z_1$
and
$Z_1$
and
![]() $E_1$
are supported on sets of size
$E_1$
are supported on sets of size
![]() $\leq 3w$
, by Lemma 4.19 the right vertical map is dual to
$\leq 3w$
, by Lemma 4.19 the right vertical map is dual to
as long as
![]() $w \leq \tfrac {1}{3}g$
. By Theorem 4.22, the map
$w \leq \tfrac {1}{3}g$
. By Theorem 4.22, the map
![]() $H^{\mathrm {Com}}_p(E_1)_{q,w} \to H^{\mathrm {Com}}_p(Z_1)_{q,w}$
is an isomorphism except when
$H^{\mathrm {Com}}_p(E_1)_{q,w} \to H^{\mathrm {Com}}_p(Z_1)_{q,w}$
is an isomorphism except when
![]() $(p,q,w) = (1,1,1)$
and evaluated on sets of size
$(p,q,w) = (1,1,1)$
and evaluated on sets of size
![]() $1$
, in which case it is surjective by the proof of Corollary 4.23. The lemma is then obtained by dualising.
$1$
, in which case it is surjective by the proof of Corollary 4.23. The lemma is then obtained by dualising.
By the proof of Proposition 4.26, the map
is injective with cokernel a single trivial representation in weight 2. Since the geometric Johnson homomorphism is injective in weight
![]() $1$
and we work up to trivial representations, we thus may as well study the composition
$1$
and we work up to trivial representations, we thus may as well study the composition
Up to isomorphism, this is the unique map of Lie algebras with additional weight grading which is injective in weight 1.
8.1.2 A high-dimensional geometric Johnson homomorphism
We next describe a higher-dimensional incarnation of (17), and first give its domain and codomain. By Theorem 7.2, for n odd and degrees
![]() $w(n-1) \leq \frac {g-3}{2}$
[Reference Koike and TeradaKRW20c, Section 9.2], there is an isomorphism
$w(n-1) \leq \frac {g-3}{2}$
[Reference Koike and TeradaKRW20c, Section 9.2], there is an isomorphism
of algebraic
![]() $\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
-representations, with
$\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
-representations, with
![]() $\overline {G}{}^{\mathrm {fr},[\ell ]}_g \subset \mathrm { Sp}_{2g}(\mathbb {Z})$
a finite index subgroup. The left-hand side is identified with
$\overline {G}{}^{\mathrm {fr},[\ell ]}_g \subset \mathrm { Sp}_{2g}(\mathbb {Z})$
a finite index subgroup. The left-hand side is identified with
![]() $((K^{\vee } \otimes ^{\mathsf {dsBr}} Z_1)^{\mathrm {quad}})_{0,w}$
, so the domain of our higher-dimensional geometric Johnson homomorphism is the rational homotopy Lie algebra of
$((K^{\vee } \otimes ^{\mathsf {dsBr}} Z_1)^{\mathrm {quad}})_{0,w}$
, so the domain of our higher-dimensional geometric Johnson homomorphism is the rational homotopy Lie algebra of
![]() $X_1(g)$
with a certain regrading.
$X_1(g)$
with a certain regrading.
For the codomain, we let
![]() $\mathrm {Der}^+(\mathrm {Lie}(H[n-1]))$
denote the graded Lie algebra of positive degree derivations of the free graded Lie algebra on
$\mathrm {Der}^+(\mathrm {Lie}(H[n-1]))$
denote the graded Lie algebra of positive degree derivations of the free graded Lie algebra on
![]() $H = H_n(W_{g,1};\mathbb {Q})$
placed in degree
$H = H_n(W_{g,1};\mathbb {Q})$
placed in degree
![]() $n-1$
and weight 1. Writing
$n-1$
and weight 1. Writing
![]() $\mathrm {Der}^+_{\omega }(\mathrm {Lie}(H[n-1]) \subset \mathrm {Der}^+(\mathrm {Lie}(H[n-1])$
for those derivations which annihilate
$\mathrm {Der}^+_{\omega }(\mathrm {Lie}(H[n-1]) \subset \mathrm {Der}^+(\mathrm {Lie}(H[n-1])$
for those derivations which annihilate
![]() $\omega $
, we get a graded Lie algebra which agrees with
$\omega $
, we get a graded Lie algebra which agrees with
![]() $\mathfrak {h}_{g,1}$
up to regrading; that is,
$\mathfrak {h}_{g,1}$
up to regrading; that is,
![]() $(\mathfrak {h}_{g,1})_{0,w}$
is identified with
$(\mathfrak {h}_{g,1})_{0,w}$
is identified with
![]() $\mathrm {Der}^+_{\omega }(\mathrm {Lie}(H[n-1])_{w(n-1),w}$
. It is well known that there is an isomorphism of graded Lie algebras
$\mathrm {Der}^+_{\omega }(\mathrm {Lie}(H[n-1])_{w(n-1),w}$
. It is well known that there is an isomorphism of graded Lie algebras
in algebraic
![]() $\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
-representations (see [Reference Chan, Galatius and PayneBM20, Corollary 3.3]), with the superscript
$\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
-representations (see [Reference Chan, Galatius and PayneBM20, Corollary 3.3]), with the superscript
![]() $\mathrm {id}$
indicating the identity component. So the codomain of our higher-dimensional geometric Johnson homomorphism is the rational homotopy Lie algebra of
$\mathrm {id}$
indicating the identity component. So the codomain of our higher-dimensional geometric Johnson homomorphism is the rational homotopy Lie algebra of
![]() $B\mathrm {hAut}^{\mathrm {id}}_{\partial }(W_{g,1})$
.
$B\mathrm {hAut}^{\mathrm {id}}_{\partial }(W_{g,1})$
.
There are maps
which induce a map
![]() $\pi _{*+1}(X_1(g)) \otimes \mathbb {Q} \to \pi _{*+1}(B\mathrm {hAut}^{\mathrm {id}}_{\partial }(W_{g,1})) \otimes \mathbb {Q}$
of graded Lie algebras in algebraic
$\pi _{*+1}(X_1(g)) \otimes \mathbb {Q} \to \pi _{*+1}(B\mathrm {hAut}^{\mathrm {id}}_{\partial }(W_{g,1})) \otimes \mathbb {Q}$
of graded Lie algebras in algebraic
![]() $\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
-representations. This is the higher-dimensional geometric Johnson homomorphism. To see that it coincides with
$\overline {G}{}^{\mathrm {fr},[\ell ]}_g$
-representations. This is the higher-dimensional geometric Johnson homomorphism. To see that it coincides with
![]() $\tau _{g,1}$
, in a stable range and up to isomorphism and regrading, it suffices to verify that it is injective in degree
$\tau _{g,1}$
, in a stable range and up to isomorphism and regrading, it suffices to verify that it is injective in degree
![]() $*=n-1$
in a stable range. This is the content of [Reference Kupers and Randal-WilliamsKRW20b, Proposition 5.10]. To prove Theorem B, we may thus use this higher-dimensional incarnation instead.
$*=n-1$
in a stable range. This is the content of [Reference Kupers and Randal-WilliamsKRW20b, Proposition 5.10]. To prove Theorem B, we may thus use this higher-dimensional incarnation instead.
8.2 Proof of Theorem B
Translated to high dimensions, Theorem B says that in a stable range the kernel of the map induced by (18) on rational homotopy groups consists solely of trivial
![]() $\smash {\overline {G}{}^{\mathrm { fr},[\ell ]}_g}$
-representations in the centre of
$\smash {\overline {G}{}^{\mathrm { fr},[\ell ]}_g}$
-representations in the centre of
![]() $\pi _{*+1}(X_1(g)) \otimes \mathbb {Q}$
.
$\pi _{*+1}(X_1(g)) \otimes \mathbb {Q}$
.
We need to recall some of the setup from [Reference Kupers and Randal-WilliamsKRW20b, Section 3]. Let us write
for a fixed subset
![]() $D^{2n-1} \subset S^{2n-1} = \partial W_{g,1}$
. Then we let
$D^{2n-1} \subset S^{2n-1} = \partial W_{g,1}$
. Then we let
denote the path component of the homotopy quotient
containing
![]() $\ell $
. Let us consider the commutative diagram
$\ell $
. Let us consider the commutative diagram

The map
is injective on rational homotopy groups in all degrees, as the following commutes

We claim that
is also injective. To see this is the case, we use the Bousfield–Kan spectral sequence for the embedding calculus Taylor tower [Reference Kupers and Randal-WilliamsKRW20b, Section 5.2.3]. This is an extended spectral sequence in the sense of [Reference Berglund and MadsenBK72], given by

and converging completely to
. In [Reference Kupers and Randal-WilliamsKRW20b, Proposition 5.32], we described which entries on the
![]() $E^1$
-page can be nonzero. In particular, there is a pattern of ‘bands’: for
$E^1$
-page can be nonzero. In particular, there is a pattern of ‘bands’: for
![]() $r \geq 1$
there are nonzero entries only in bidegrees
$r \geq 1$
there are nonzero entries only in bidegrees
![]() $(p,q)$
lying in the intervals
$(p,q)$
lying in the intervals
![]() $[0,r+1] \times \{r(n-1)+1\}$
with
$[0,r+1] \times \{r(n-1)+1\}$
with
![]() $r \geq 1$
. Since the differentials have bidegree
$r \geq 1$
. Since the differentials have bidegree
![]() $(r,r-1)$
, the spectral sequence collapses rationally at the
$(r,r-1)$
, the spectral sequence collapses rationally at the
![]() $E^2$
-page in a range. As we increase n, the number of intervals in which this collapse occurs increases. Thus, by making n large enough, we see that the map
$E^2$
-page in a range. As we increase n, the number of intervals in which this collapse occurs increases. Thus, by making n large enough, we see that the map
induces an identification

so in particular is injective.
Thus, the kernel of (18) coincides with that of the map induced on rational homotopy by the composition
The kernel of the left map coincides with the image of the rational homotopy of
![]() $X_0$
under the connecting homomorphism and hence consists of trivial representations in the centre of
$X_0$
under the connecting homomorphism and hence consists of trivial representations in the centre of
![]() $\pi _{*+1}(X_1(g)) \otimes \mathbb {Q}$
. Using the framed Weiss fibre sequence [Reference Kupers and Randal-WilliamsKRW20b, Theorem 3.12]
$\pi _{*+1}(X_1(g)) \otimes \mathbb {Q}$
. Using the framed Weiss fibre sequence [Reference Kupers and Randal-WilliamsKRW20b, Theorem 3.12]
the kernel of the right map coincides with the image of the rational homotopy of
![]() $B^2\mathrm {Diff}^{\mathrm {fr}}_{\partial }(D^{2n})_{\ell _0}$
under the connecting homomorphism and hence consists of trivial representations in the centre of
$B^2\mathrm {Diff}^{\mathrm {fr}}_{\partial }(D^{2n})_{\ell _0}$
under the connecting homomorphism and hence consists of trivial representations in the centre of
![]() $\pi _{*+1}(B\mathrm {Diff}_{\partial }^{\mathrm {fr}}(W_{g,1})_{\ell }) \otimes \mathbb {Q}$
.
$\pi _{*+1}(B\mathrm {Diff}_{\partial }^{\mathrm {fr}}(W_{g,1})_{\ell }) \otimes \mathbb {Q}$
.
To complete the proof of Theorem B, it remains to establish the explicit ranges. To do so, we use a version of representation stability (cf. [Reference HirschhornHai20, Proposition 15.1]) for the domain and codomain of
![]() $\tau _{g,1}$
. By Corollary 3.14, the Lie algebra
$\tau _{g,1}$
. By Corollary 3.14, the Lie algebra
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
is quadratically generated by
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
is quadratically generated by
![]() $\Lambda ^3 V_1$
in weight 1, so by stability for symplectic Schur functors and the branching rule (e.g., [Reference Loday and ValletteKT87]), its decomposition into nonzero irreducibles stabilises in weight
$\Lambda ^3 V_1$
in weight 1, so by stability for symplectic Schur functors and the branching rule (e.g., [Reference Loday and ValletteKT87]), its decomposition into nonzero irreducibles stabilises in weight
![]() $\leq \frac {1}{3}g$
. The Lie algebra
$\leq \frac {1}{3}g$
. The Lie algebra
![]() $\mathfrak {h}_{g,1}$
fits into the short exact sequence
$\mathfrak {h}_{g,1}$
fits into the short exact sequence
where
![]() $\mathrm {Lie}^{\geq 2}$
means we discard bracketings of
$\mathrm {Lie}^{\geq 2}$
means we discard bracketings of
![]() $<2$
elements. Once more invoking stability for symplectic Schur functors and the branching rule, its decomposition into nonzero irreducibles stabilises in weight
$<2$
elements. Once more invoking stability for symplectic Schur functors and the branching rule, its decomposition into nonzero irreducibles stabilises in weight
![]() $\leq g-2$
. These observations imply that for
$\leq g-2$
. These observations imply that for
![]() $g'>g$
, in the commutative diagram
$g'>g$
, in the commutative diagram

induced by the inclusion
![]() $\Sigma _{g,1} \subset \Sigma _{g',1}$
, the left vertical map is an isomorphism in weight
$\Sigma _{g,1} \subset \Sigma _{g',1}$
, the left vertical map is an isomorphism in weight
![]() $\leq \frac {1}{3}g$
and the right vertical map is in weight
$\leq \frac {1}{3}g$
and the right vertical map is in weight
![]() $ \leq g-2$
. Since we can make the bottom horizontal map have kernel consisting of trivial representations that are contained in the centre for arbitrary large weight by increasing
$ \leq g-2$
. Since we can make the bottom horizontal map have kernel consisting of trivial representations that are contained in the centre for arbitrary large weight by increasing
![]() $g'$
, we conclude that the same is true for the top horizontal map in weight
$g'$
, we conclude that the same is true for the top horizontal map in weight
![]() $\leq \min (\frac {1}{3}g,g-2)$
. Since
$\leq \min (\frac {1}{3}g,g-2)$
. Since
![]() $g-2 \geq \frac {1}{3}g$
unless
$g-2 \geq \frac {1}{3}g$
unless
![]() $g \leq 2$
—in which case the injectivity of the geometric Johnson homomorphism in weight
$g \leq 2$
—in which case the injectivity of the geometric Johnson homomorphism in weight
![]() $\leq \tfrac {g}{3}$
is clear — we conclude that the top map has a kernel consisting of trivial representations that are contained in the centre for weight
$\leq \tfrac {g}{3}$
is clear — we conclude that the top map has a kernel consisting of trivial representations that are contained in the centre for weight
![]() $\leq \frac {1}{3}g$
.
$\leq \frac {1}{3}g$
.
Remark 8.3. The proof of Theorem B also gives a version of this theorem for n even.
8.3 Further remarks
8.3.1 The Euler tangential structure
To prove Theorem B, we could have used the Euler tangential structure of Section 5.4 instead of framings. Doing so, the space
![]() $X_1(g)$
gets replaced by
$X_1(g)$
gets replaced by
![]() $X_1^e(g)$
and
$X_1^e(g)$
and
![]() $K^{\vee } \otimes ^{\mathsf {d(s)Br}} Z_n$
by
$K^{\vee } \otimes ^{\mathsf {d(s)Br}} Z_n$
by
![]() $(K^{\vee } \otimes ^{\mathsf {d(s)Br}} E_n)/(\kappa _{e^j} \mid j>1)$
, but otherwise the proof proceeds in a similar manner. From this point of view, Lemma 8.2 amounts to the statement that map induced on rational homotopy groups by
$(K^{\vee } \otimes ^{\mathsf {d(s)Br}} E_n)/(\kappa _{e^j} \mid j>1)$
, but otherwise the proof proceeds in a similar manner. From this point of view, Lemma 8.2 amounts to the statement that map induced on rational homotopy groups by
is an isomorphism in degrees
![]() $*>n$
.
$*>n$
.
8.3.2 Computing the Johnson cokernel
Both
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
and
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
and
![]() $\mathfrak {h}_{g,1}$
are accessible to computer calculations: More precisely, one can compute the multiplicities of the irreducibles in each degree. As pointed out in the introduction, for
$\mathfrak {h}_{g,1}$
are accessible to computer calculations: More precisely, one can compute the multiplicities of the irreducibles in each degree. As pointed out in the introduction, for
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
one uses the computation of the stable character of
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1}$
one uses the computation of the stable character of
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g$
of Garoufalidis–Getzler [Reference Ginzburg and KapranovGG17], which was conditional on Theorem A (or rather Theorem 3.3), while
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g$
of Garoufalidis–Getzler [Reference Ginzburg and KapranovGG17], which was conditional on Theorem A (or rather Theorem 3.3), while
![]() $\mathfrak {h}_{g,1}$
admits a description in terms of Schur functors (see [Reference Kupers and Randal-WilliamsKRW20b, Section 5.4.1]). Then Theorem B implies that, up to trivial representations, the Johnson cokernel
$\mathfrak {h}_{g,1}$
admits a description in terms of Schur functors (see [Reference Kupers and Randal-WilliamsKRW20b, Section 5.4.1]). Then Theorem B implies that, up to trivial representations, the Johnson cokernel
![]() $\mathrm {coker}(\tau _{g,1} \colon {\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1} \to \mathfrak {h}_{g,1})$
is also accessible to computer calculations in a stable range.
$\mathrm {coker}(\tau _{g,1} \colon {\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1} \to \mathfrak {h}_{g,1})$
is also accessible to computer calculations in a stable range.
In fact, up to trivial representations the Johnson image is the kernel of the restriction to
![]() $\mathfrak {h}_{g,1}$
of the connecting homomorphism
$\mathfrak {h}_{g,1}$
of the connecting homomorphism
in the fibration sequence
arising from the framed embedding calculus Taylor tower. It would be interesting to relate
![]() $\partial $
to Morita’s trace maps and its variants, and to approach Question 12.8 of [Reference HirschhornHai20] from this perspective (cf. part (ii) of ‘the most optimistic landscape’ in Section 1.9 of loc. cit.).
$\partial $
to Morita’s trace maps and its variants, and to approach Question 12.8 of [Reference HirschhornHai20] from this perspective (cf. part (ii) of ‘the most optimistic landscape’ in Section 1.9 of loc. cit.).
8.3.3 Variants
Let us next consider the analogous geometric Johnson homomorphisms
where
![]() $\smash {\mathfrak {h}_{g}^1}$
(also denoted
$\smash {\mathfrak {h}_{g}^1}$
(also denoted
![]() $\mathfrak {h}_{g,\ast }$
in the literature) is the Lie algebra of the positive degree symplectic derivations of
$\mathfrak {h}_{g,\ast }$
in the literature) is the Lie algebra of the positive degree symplectic derivations of
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {p}_g^1$
and
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {p}_g^1$
and
![]() $\mathfrak {h}_g$
is the quotient of
$\mathfrak {h}_g$
is the quotient of
![]() $\mathfrak {g}_{g}^1$
by the inner derivations [Reference MoritaMor99, p. 370].
$\mathfrak {g}_{g}^1$
by the inner derivations [Reference MoritaMor99, p. 370].
Corollary 8.4. In weight
![]() $\leq \frac {1}{3}g$
, the kernels of
$\leq \frac {1}{3}g$
, the kernels of
![]() $\tau _g^1 \colon {\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g^1 \to \mathfrak {h}_{g}^1$
and
$\tau _g^1 \colon {\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g^1 \to \mathfrak {h}_{g}^1$
and
![]() $\tau _g \colon {\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g \to \mathfrak {h}_g$
lie in the centre and consists of trivial
$\tau _g \colon {\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g \to \mathfrak {h}_g$
lie in the centre and consists of trivial
![]() $\mathrm {Sp}_{2g}(\mathbb {Z})$
-representations.
$\mathrm {Sp}_{2g}(\mathbb {Z})$
-representations.
Proof. For
![]() $\tau _g^1$
, we use the extension
$\tau _g^1$
, we use the extension
![]() $\mathbb {Q}[2\to {\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1} \to {\mathrm { Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g^1$
of Lemma 3.2. The statement in weight
$\mathbb {Q}[2\to {\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_{g,1} \to {\mathrm { Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {t}_g^1$
of Lemma 3.2. The statement in weight
![]() $\neq 2$
follows because the images of
$\neq 2$
follows because the images of
![]() $\tau _{g,1}$
and
$\tau _{g,1}$
and
![]() $\tau ^1_g$
coincide by [Reference Morita, Sakasai and SuzukiMSS15, Proposition 3.5 (ii)]. In weight 2,
$\tau ^1_g$
coincide by [Reference Morita, Sakasai and SuzukiMSS15, Proposition 3.5 (ii)]. In weight 2,
![]() $\mathfrak {h}_{g,1}$
and
$\mathfrak {h}_{g,1}$
and
![]() $\mathfrak {h}_{g}^1$
differ only in a trivial representation, by [Reference Morita, Sakasai and SuzukiMSS15, Table 1] (
$\mathfrak {h}_{g}^1$
differ only in a trivial representation, by [Reference Morita, Sakasai and SuzukiMSS15, Table 1] (
![]() $\mathfrak {j}_{g,1}$
is the kernel of the surjection
$\mathfrak {j}_{g,1}$
is the kernel of the surjection
![]() $\mathfrak {h}_{g,1} \to \mathfrak {h}_g^1$
[Reference Morita, Sakasai and SuzukiMSS15, p. 307]).
$\mathfrak {h}_{g,1} \to \mathfrak {h}_g^1$
[Reference Morita, Sakasai and SuzukiMSS15, p. 307]).
For
![]() $\tau _g$
, we use the diagram of extensions
$\tau _g$
, we use the diagram of extensions

The top row appears in Lemma 3.2, the bottom row appears on p. 370 of [Reference MoritaMor99] (Morita uses
![]() $\mathcal {L}_g$
and
$\mathcal {L}_g$
and
![]() $\mathfrak {h}_{g,*}$
in place of
$\mathfrak {h}_{g,*}$
in place of
![]() ${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {p}^1_g$
and
${\mathrm {Gr}^{\bullet }_{\mathrm {LCS}}\,} \mathfrak {p}^1_g$
and
![]() $\mathfrak {h}_g^1$
). See also p. 643 of [Reference HainHai97].
$\mathfrak {h}_g^1$
). See also p. 643 of [Reference HainHai97].
Remark 8.5. Theorem B and Corollary 8.4 remain true when we replace the unipotent completions
![]() $\mathfrak {t}_{g,1}$
,
$\mathfrak {t}_{g,1}$
,
![]() $\mathfrak {t}_g^1$
and
$\mathfrak {t}_g^1$
and
![]() $\mathfrak {t}_g$
with the relative unipotent completions
$\mathfrak {t}_g$
with the relative unipotent completions
![]() $\mathfrak {u}_{g,1}$
,
$\mathfrak {u}_{g,1}$
,
![]() $\mathfrak {u}_g^1$
and
$\mathfrak {u}_g^1$
and
![]() $\mathfrak {u}_g$
respectively since these only differ by trivial representations in the centre by Lemma 3.1.
$\mathfrak {u}_g$
respectively since these only differ by trivial representations in the centre by Lemma 3.1.
Remark 8.6. Let
![]() $\mathcal {C}_{g,1}$
be the monoid of 3-dimensional homology cylinders under concatenation, which has a filtration by Y-equivalence. There is a map of filtered monoids
$\mathcal {C}_{g,1}$
be the monoid of 3-dimensional homology cylinders under concatenation, which has a filtration by Y-equivalence. There is a map of filtered monoids
![]() $T_{g,1} \to C_{g,1}$
, if the left side is given the lower central series filtration. Taking associated gradeds and rationalising, we get a map of Lie algebras with additional weight grading
$T_{g,1} \to C_{g,1}$
, if the left side is given the lower central series filtration. Taking associated gradeds and rationalising, we get a map of Lie algebras with additional weight grading
In [Reference Habegger and SorgerHM09, Question 1.3], Habiro and Massuyeau ask whether this map is injective. Rationally, in a stable range, and up to trivial representations in the centre, it follows from Theorem B that it is. To see this, consider Figure 8.1 of [Reference Habegger and SorgerHM09] and observe that the map denoted by
![]() $\mathrm {Gr}^{\Gamma } \mathcal {I}_{g,1} \otimes \mathbb {Q} \to \mathrm { Gr}^{[-]} \mathcal {I}_{g,1} \otimes \mathbb {Q}$
is
$\mathrm {Gr}^{\Gamma } \mathcal {I}_{g,1} \otimes \mathbb {Q} \to \mathrm { Gr}^{[-]} \mathcal {I}_{g,1} \otimes \mathbb {Q}$
is
![]() $\tau _{g,1}$
.
$\tau _{g,1}$
.
Acknowledgements
The authors thank M. Kassabov and T. Willwacher for useful discussions, and both anonymous referees for helpful comments.
Conflicts of Interest
The authors have no conflict of interest to declare.
Financial Support
AK acknowledges the support of the Natural Sciences and Engineering Research Council of Canada (NSERC) [funding reference number 512156 and 512250], as well as the Research Competitiveness Fund of the University of Toronto at Scarborough. AK was supported by an Alfred J. Sloan Research Fellowship. ORW was partially supported by the ERC under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 756444) and by a Philip Leverhulme Prize from the Leverhulme Trust.