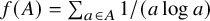1 Introduction
A set of integers
![]() $A\subset \mathbb {Z}_{>1}$
is primitive if no member in A divides another. For example, the integers in a dyadic interval
$A\subset \mathbb {Z}_{>1}$
is primitive if no member in A divides another. For example, the integers in a dyadic interval
![]() $(x,2x]$
form a primitive set. Similarly, the set of primes is primitive, along with the set
$(x,2x]$
form a primitive set. Similarly, the set of primes is primitive, along with the set
![]() $\mathbb {N}_k$
of numbers with exactly k prime factors (with multiplicity), for each
$\mathbb {N}_k$
of numbers with exactly k prime factors (with multiplicity), for each
![]() $k\ge 1$
. Another well-known example is the set of perfect numbers.Footnote
1
$k\ge 1$
. Another well-known example is the set of perfect numbers.Footnote
1
The study of primitive sets emerged in the 1930s as a generalization of one special problem. A classical theorem of Davenport asserts that the set of abundant numbers has a positive asymptotic density. This was originally proved by sophisticated analytic methods, but Erdős soon found an elementary proof by using primitive abundant numbers.Footnote 2 The proof ideas led people to introduce the abstract definition of primitive sets and study them for their own sake. See Hall [Reference Hall21] or Halberstam–Roth [Reference Halberstam and Roth20, §5] for detailed introductions to the subject.
There are a number of interesting and sometimes unexpected theorems about primitive sets. For instance, in 1934 Besicovitch [Reference Besicovitch5] showed that the upper asymptotic density of a primitive set can be arbitrarily close to
![]() $1/2$
, whereas in 1935 Behrend [Reference Behrend4] and Erdős [Reference Erdős13] proved the lower asymptotic density is always
$1/2$
, whereas in 1935 Behrend [Reference Behrend4] and Erdős [Reference Erdős13] proved the lower asymptotic density is always
![]() $0$
. In fact, Erdős proved the stronger result that
$0$
. In fact, Erdős proved the stronger result that
 $$ \begin{align*} f(A) := \sum_{a\in A}\frac{1}{a\log a} \ < \ \infty, \end{align*} $$
$$ \begin{align*} f(A) := \sum_{a\in A}\frac{1}{a\log a} \ < \ \infty, \end{align*} $$
uniformly over all primitive sets A. Later in 1986, Erdős [Reference Erdős15, Conjecture 2.1] famously asked if the maximum is attained by the primes
![]() $\mathcal {P}$
.
$\mathcal {P}$
.
Conjecture 1.1 (Erdős primitive set conjecture).
For any primitive set A,
![]() $f(A) \le f(\mathcal P)$
.
$f(A) \le f(\mathcal P)$
.
The prime sum is
![]() $f(\mathcal {P}) = \sum _p 1/(p\log p)=1.6366\cdots $
after computations of Cohen [Reference Cohen10]. In 1993, Erdős and Zhang [Reference Erdős and Zhang19] proved the bound
$f(\mathcal {P}) = \sum _p 1/(p\log p)=1.6366\cdots $
after computations of Cohen [Reference Cohen10]. In 1993, Erdős and Zhang [Reference Erdős and Zhang19] proved the bound
![]() $f(A) < 1.84$
for all primitive A. Recently in 2019, Lichtman and Pomerance [Reference Lichtman and Pomerance27] improved the bound to
$f(A) < 1.84$
for all primitive A. Recently in 2019, Lichtman and Pomerance [Reference Lichtman and Pomerance27] improved the bound to
![]() $f(A) < e^{\gamma }=1.781\cdots $
, where
$f(A) < e^{\gamma }=1.781\cdots $
, where
![]() $\gamma $
is the Euler–Mascheroni constant. Note the tail of the series for
$\gamma $
is the Euler–Mascheroni constant. Note the tail of the series for
![]() $f(\mathcal {P})$
converges quite slowly
$f(\mathcal {P})$
converges quite slowly
![]() $O(1/\log x)$
, and moreover there are sets
$O(1/\log x)$
, and moreover there are sets
![]() $A\subset [x,\infty )$
for which
$A\subset [x,\infty )$
for which
![]() $f(A)\sim 1$
as
$f(A)\sim 1$
as
![]() $x\to \infty $
(in this connection, see Conjecture 1.4 below). As such, Conjecture 1.1 is not susceptible to direct attack by computing partial sums up to x.
$x\to \infty $
(in this connection, see Conjecture 1.4 below). As such, Conjecture 1.1 is not susceptible to direct attack by computing partial sums up to x.
One potential strategy to approach Conjecture 1.1 is via integration. Namely,
 $$ \begin{align*} f(A) = \sum_{a\in A}\frac{1}{a\log a} = \sum_{a\in A}\int_1^{\infty} a^{-t}\mathrm{d}{t} = \int_1^{\infty} f_t(A)\,\mathrm{d}{t}, \end{align*} $$
$$ \begin{align*} f(A) = \sum_{a\in A}\frac{1}{a\log a} = \sum_{a\in A}\int_1^{\infty} a^{-t}\mathrm{d}{t} = \int_1^{\infty} f_t(A)\,\mathrm{d}{t}, \end{align*} $$
letting
![]() $f_t(A) = \sum _{a\in A} a^{-t}$
. So Conjecture 1 would follow if for any
$f_t(A) = \sum _{a\in A} a^{-t}$
. So Conjecture 1 would follow if for any
![]() $t>1$
, primitive set A,
$t>1$
, primitive set A,
However, it was shown in [Reference Banks and Martin2] that equation (1) holds if and only if
where
![]() $t=\tau $
is the unique real solution to the equation
$t=\tau $
is the unique real solution to the equation
 $$ \begin{align*} \sum_p p^{-t} = 1+\Big(1-\sum_p p^{-2t}\Big)^{1/2}. \end{align*} $$
$$ \begin{align*} \sum_p p^{-t} = 1+\Big(1-\sum_p p^{-2t}\Big)^{1/2}. \end{align*} $$
The fact that
![]() $\tau $
is markedly larger than 1 gives some indication as to why the Erdős primitive set conjecture has remained open.
$\tau $
is markedly larger than 1 gives some indication as to why the Erdős primitive set conjecture has remained open.
Similar analysis actually enables a disproof of a natural analogue of Conjecture 1.1 for the translated sum
![]() $f(A,h)=\sum _{a\in A}1/a(\log a+h)$
, in that there are primitive A for which
$f(A,h)=\sum _{a\in A}1/a(\log a+h)$
, in that there are primitive A for which
![]() $f(A,h)>f(\mathcal P,h)$
once
$f(A,h)>f(\mathcal P,h)$
once
![]() $h\ge 81$
[Reference Laib, Derbal and Mechik24], [Reference Laib23]. This was refined down to just
$h\ge 81$
[Reference Laib, Derbal and Mechik24], [Reference Laib23]. This was refined down to just
![]() $h\ge 1.04$
in [Reference Lichtman26] and suggests that the original conjecture (when
$h\ge 1.04$
in [Reference Lichtman26] and suggests that the original conjecture (when
![]() $h=0$
), if true, is only ‘barely’ so.
$h=0$
), if true, is only ‘barely’ so.
Concerning equation (1), we also note Chan et al. [Reference Chan, Lichtman and Pomerance8] proved
![]() $f_t(A) \ \le \ f_t(\mathcal P)$
for all
$f_t(A) \ \le \ f_t(\mathcal P)$
for all
![]() $t\ge .7983$
for all 2-primitive sets A, thereby resolving Conjecture 1 in this special case (also see [Reference Chan, Lichtman and Pomerance9]). Here, a set A is 2-primitive if no member of A divides the product of two others.
$t\ge .7983$
for all 2-primitive sets A, thereby resolving Conjecture 1 in this special case (also see [Reference Chan, Lichtman and Pomerance9]). Here, a set A is 2-primitive if no member of A divides the product of two others.
A separate strategy for the problem is to split up A according to the smallest prime factor. That is, for each prime p let
As in [Reference Lichtman and Pomerance27], we say p is Erdős strong if the singleton set
![]() $\{p\}$
maximizes
$\{p\}$
maximizes
![]() $f(A)$
among all primitive sets A all of whose elements have least prime factor p. That is,
$f(A)$
among all primitive sets A all of whose elements have least prime factor p. That is,
![]() $f(A_p)\le f(\{p\})=:f(p)$
for all primitive A. Conjecture 1.1 would follow if every prime is Erdős strong since then
$f(A_p)\le f(\{p\})=:f(p)$
for all primitive A. Conjecture 1.1 would follow if every prime is Erdős strong since then
![]() $f(A) = \sum _p f(A_p) \le f(\mathcal {P})$
.
$f(A) = \sum _p f(A_p) \le f(\mathcal {P})$
.
By a short argument in [Reference Lichtman and Pomerance27] (also see Lemma 2.3), a sufficient condition for a prime p to be Erdős strong is that
 $$ \begin{align} e^{\gamma}\prod_{q<p}\Big(1-\frac{1}{q}\Big) \ \le \ \frac{1}{\log p}. \end{align} $$
$$ \begin{align} e^{\gamma}\prod_{q<p}\Big(1-\frac{1}{q}\Big) \ \le \ \frac{1}{\log p}. \end{align} $$
Here, q runs over primes. Note the two sides of this inequality are asymptotically equal by Mertens’ prime product theorem. By direct computation, equation (2) is satisfied by the first
![]() $10^8$
odd primes but fails for
$10^8$
odd primes but fails for
![]() $p=2$
since
$p=2$
since
![]() $\log 2> e^{-\gamma }$
.
$\log 2> e^{-\gamma }$
.
Moreover,
![]() $99.999973\%$
of primesFootnote
3
satisfy equation (2), assuming the Riemann hypothesis and the linear independence hypothesisFootnote
4
[Reference Lichtman, Martin and Pomerance28]. This result is intimately related to the celebrated work of Rubinstein and Sarnak [Reference Rubinstein and Sarnak30] on the prime number race between
$99.999973\%$
of primesFootnote
3
satisfy equation (2), assuming the Riemann hypothesis and the linear independence hypothesisFootnote
4
[Reference Lichtman, Martin and Pomerance28]. This result is intimately related to the celebrated work of Rubinstein and Sarnak [Reference Rubinstein and Sarnak30] on the prime number race between
![]() $\pi (x)$
and
$\pi (x)$
and
![]() $\text {li}(x)$
. On the Riemann hypothesis alone, equation (2) fails for a positive proportion of primes p (in log density), and even unconditionally equation (2) is known to fail for infinitely many primes p. This perhaps suggests Conjecture 1.1 might be false, or at least beyond the reach of unconditional tools.
$\text {li}(x)$
. On the Riemann hypothesis alone, equation (2) fails for a positive proportion of primes p (in log density), and even unconditionally equation (2) is known to fail for infinitely many primes p. This perhaps suggests Conjecture 1.1 might be false, or at least beyond the reach of unconditional tools.
In this article, we establish Conjecture 1.1.
Theorem 1.2. For any primitive set A, we have
![]() $f(A) \le f(\mathcal P)$
.
$f(A) \le f(\mathcal P)$
.
Moreover, we show that every odd prime is Erdős strong.
Theorem 1.3. For any primitive set A and any prime
![]() $p>2$
, we have
$p>2$
, we have
![]() $f(A_p) \le f(p)$
.
$f(A_p) \le f(p)$
.
It remains an open question whether
![]() $p=2$
is Erdős strong.
$p=2$
is Erdős strong.
Another question related to Conjecture 1.1, in 1968 Erdős, Sárközy and Szemerédi posed the following [Reference Erdős, Sárközy and Szemerédi18, eq. (11)].
Conjecture 1.4 (Erdős–Sárközy–Szemerédi).
We have
 $$ \begin{align*} \lim_{x\to\infty}\sup_{\substack{A\subset[x,\infty)\\A\ \mathrm{primitive}}}f(A) \ \le \ 1. \end{align*} $$
$$ \begin{align*} \lim_{x\to\infty}\sup_{\substack{A\subset[x,\infty)\\A\ \mathrm{primitive}}}f(A) \ \le \ 1. \end{align*} $$
This also appears in [Reference Sárközy, Graham and Nesetril31, p. 244] as Problem 2.2, and in [Reference Sárközy, Graham and Nesetril32, p. 224] as Problem 2.
Not much has been proven in this direction until very recently. Recall the set
![]() $\mathbb {N}_k$
of numbers with exactly k prime factors (with multiplicity) lies in
$\mathbb {N}_k$
of numbers with exactly k prime factors (with multiplicity) lies in
![]() $[2^k,\infty )$
. Lichtman and Pomerance [Reference Lichtman and Pomerance27] proved
$[2^k,\infty )$
. Lichtman and Pomerance [Reference Lichtman and Pomerance27] proved
![]() $f({\mathbb N}_k)\gg 1$
, and in [Reference Lichtman25] it was shown
$f({\mathbb N}_k)\gg 1$
, and in [Reference Lichtman25] it was shown
![]() $f({\mathbb N}_k)\sim 1$
as
$f({\mathbb N}_k)\sim 1$
as
![]() $k\to \infty $
. This means that if Conjecture 1.4 holds, then the limit must attain an equality of 1. We note [Reference Lichtman25, Theorem 4.1] gives for all
$k\to \infty $
. This means that if Conjecture 1.4 holds, then the limit must attain an equality of 1. We note [Reference Lichtman25, Theorem 4.1] gives for all
![]() ${\epsilon }>0$
,
${\epsilon }>0$
,
Moreover, computations up to
![]() $k=20$
suggest the true rate of decay may be exponential
$k=20$
suggest the true rate of decay may be exponential
![]() $O(2^{-k})$
; see [Reference Lichtman25].
$O(2^{-k})$
; see [Reference Lichtman25].
The methods in this paper enable the following progress towards Conjecture 1.4.
Theorem 1.5. We have
 $$ \begin{align*} \lim_{x\to\infty}\sup_{\substack{A\subset[x,\infty)\\ A\ \mathrm{primitive}}}f(A) \ \le \ e^{\gamma}\frac{\pi}{4} \approx 1.399. \end{align*} $$
$$ \begin{align*} \lim_{x\to\infty}\sup_{\substack{A\subset[x,\infty)\\ A\ \mathrm{primitive}}}f(A) \ \le \ e^{\gamma}\frac{\pi}{4} \approx 1.399. \end{align*} $$
Notation
Let
![]() $p(a),P(a)$
denote the smallest and largest prime factors of
$p(a),P(a)$
denote the smallest and largest prime factors of
![]() $a\in {\mathbb Z}_{>1}$
, respectively, and denote
$a\in {\mathbb Z}_{>1}$
, respectively, and denote
![]() $a^*=a/P(a)$
. Let
$a^*=a/P(a)$
. Let
![]() $\Omega (n)$
denote the number of prime factors of n (with multiplicity), and let
$\Omega (n)$
denote the number of prime factors of n (with multiplicity), and let
![]() ${\mathbb N}_k = \{n: \Omega (n)=k\}$
. Define
${\mathbb N}_k = \{n: \Omega (n)=k\}$
. Define
![]() $f(a) = 1/(a\log a)$
and
$f(a) = 1/(a\log a)$
and
![]() $f(A) = \sum _{a\in A}f(a)$
for
$f(A) = \sum _{a\in A}f(a)$
for
![]() $A\subset {\mathbb Z}_{>1}$
. Let
$A\subset {\mathbb Z}_{>1}$
. Let
![]() $\mathcal P$
be the set of prime numbers, whose elements we denote by p and q, unless otherwise stated. Also,
$\mathcal P$
be the set of prime numbers, whose elements we denote by p and q, unless otherwise stated. Also,
![]() $p^k\| n$
means
$p^k\| n$
means
![]() $p^k\mid n$
and
$p^k\mid n$
and
![]() $p^{k+1}\nmid n$
.
$p^{k+1}\nmid n$
.
1.1 Proof outline of Theorem 1.2
The proof is a refinement of the argument of [Reference Lichtman and Pomerance27]. The key new idea is to exploit the fact that A cannot contain too many elements a with
![]() $P(a)$
just slightly less than a. This improves the critical case in the argument of [Reference Lichtman and Pomerance27] and ultimately leads to an improvement by a factor of
$P(a)$
just slightly less than a. This improves the critical case in the argument of [Reference Lichtman and Pomerance27] and ultimately leads to an improvement by a factor of
![]() $\pi /4$
from a contribution from each
$\pi /4$
from a contribution from each
![]() $a\in A$
which is not prime. Since
$a\in A$
which is not prime. Since
![]() $e^{\gamma }\pi /4<f(\mathcal P)$
, this ultimately means that
$e^{\gamma }\pi /4<f(\mathcal P)$
, this ultimately means that
![]() $f(A)$
is maximized when all elements are prime. (Additional care is needed for small numbers, using explicit bounds.)
$f(A)$
is maximized when all elements are prime. (Additional care is needed for small numbers, using explicit bounds.)
Let us recall the rough argument of [Reference Lichtman and Pomerance27] (suppressing details for primes and small numbers). By Mertens’ product theorem,
 $$ \begin{align} f(A)=\sum_{a\in A}\frac{1}{a\log{a}} < \sum_{a\in A}\frac{1}{a\log P(a)}\approx e^{\gamma}\sum_{a\in A}\frac{1}{a}\prod_{p<P(a)}\Big(1-\frac{1}{p}\Big). \end{align} $$
$$ \begin{align} f(A)=\sum_{a\in A}\frac{1}{a\log{a}} < \sum_{a\in A}\frac{1}{a\log P(a)}\approx e^{\gamma}\sum_{a\in A}\frac{1}{a}\prod_{p<P(a)}\Big(1-\frac{1}{p}\Big). \end{align} $$
But
![]() $a^{-1}\prod _{p<P(a)}(1-p^{-1})$
is the natural density of
$a^{-1}\prod _{p<P(a)}(1-p^{-1})$
is the natural density of
![]() $\mathrm {L}_a=\{ba\;:\;p\mid b \Rightarrow p\ge P(a)\}$
, and these sets turn out to be disjoint by primitivity of A (Lemma 2.1). So the sum of densities in equation (4) is trivially at most 1, leading to the bound
$\mathrm {L}_a=\{ba\;:\;p\mid b \Rightarrow p\ge P(a)\}$
, and these sets turn out to be disjoint by primitivity of A (Lemma 2.1). So the sum of densities in equation (4) is trivially at most 1, leading to the bound
![]() $f(A)<e^{\gamma }$
for primitive A. This is inspired by the original 1935 argument of Erdős [Reference Erdős13].
$f(A)<e^{\gamma }$
for primitive A. This is inspired by the original 1935 argument of Erdős [Reference Erdős13].
There is a loss in the above argument when bounding a by
![]() $P(a)$
, and this loss is largest when a is far from prime. We can save an additional factor of
$P(a)$
, and this loss is largest when a is far from prime. We can save an additional factor of
![]() $\log {P(a)}/\log a$
for any individual
$\log {P(a)}/\log a$
for any individual
![]() $a\in A$
, and this would be a significant improvement in the case
$a\in A$
, and this would be a significant improvement in the case
![]() $P(a)^2<a$
, say. Therefore, the critical case to handle is when
$P(a)^2<a$
, say. Therefore, the critical case to handle is when
![]() $a\in A$
is composite with
$a\in A$
is composite with
![]() $P(a)$
close to a in size. The key new ingredient (Proposition 3.3) shows that if
$P(a)$
close to a in size. The key new ingredient (Proposition 3.3) shows that if
![]() $P(a)^{1+v}>a$
uniformly for all
$P(a)^{1+v}>a$
uniformly for all
![]() $a\in A$
(so the savings factor is
$a\in A$
(so the savings factor is
![]() $\log P(a)/\log a> 1/(1+v)$
), then we can bound the sum of densities in equation (4) by
$\log P(a)/\log a> 1/(1+v)$
), then we can bound the sum of densities in equation (4) by
![]() $\sqrt {v}$
. This refines the trivial bound of 1 in the range
$\sqrt {v}$
. This refines the trivial bound of 1 in the range
![]() $0<v<1$
, and quantifies the earlier statement that A contains few elements a with
$0<v<1$
, and quantifies the earlier statement that A contains few elements a with
![]() $P(a)$
slightly less than a. As the savings
$P(a)$
slightly less than a. As the savings
![]() $1/(1+v)$
improves with v, the worst-case scenario is when the subset of
$1/(1+v)$
improves with v, the worst-case scenario is when the subset of
![]() $a\in A$
with
$a\in A$
with
![]() $P(a)^{1+v}\approx a$
contributes about
$P(a)^{1+v}\approx a$
contributes about
![]() $\frac {\mathrm{d} }{\mathrm{d} v}[\sqrt {v}]=1/2\sqrt {v}$
to the sum of densities in equation (4). Combining these ingredients ultimately leads to a savings of
$\frac {\mathrm{d} }{\mathrm{d} v}[\sqrt {v}]=1/2\sqrt {v}$
to the sum of densities in equation (4). Combining these ingredients ultimately leads to a savings of
![]() $\int _0^1\mathrm{d} v/2\sqrt {v}(1+v)=\pi /4$
, as desired.
$\int _0^1\mathrm{d} v/2\sqrt {v}(1+v)=\pi /4$
, as desired.
Lastly, the key Proposition 3.3 relies on the following observation (Lemma 3.1): Not only are the sets
![]() $\mathrm {L}_a$
disjoint but so too are
$\mathrm {L}_a$
disjoint but so too are
![]() $\mathrm {L}_{ac}$
for many choices of integers c (in fact, all choices of c with prime factors between
$\mathrm {L}_{ac}$
for many choices of integers c (in fact, all choices of c with prime factors between
![]() $P_2(a)$
and
$P_2(a)$
and
![]() $P_2(a)^{1/\sqrt {v}})$
. Thus, the sum of densities of these
$P_2(a)^{1/\sqrt {v}})$
. Thus, the sum of densities of these
![]() $\mathrm {L}_{ac}$
must be at most 1. But these sets
$\mathrm {L}_{ac}$
must be at most 1. But these sets
![]() $\mathrm {L}_{ac}$
are self-similar to the
$\mathrm {L}_{ac}$
are self-similar to the
![]() $\mathrm {L}_a$
, and so the sum of their densities is roughly
$\mathrm {L}_a$
, and so the sum of their densities is roughly
![]() $1/\sqrt {v}$
times that of the
$1/\sqrt {v}$
times that of the
![]() $\mathrm {L}_a$
, giving the desired bound
$\mathrm {L}_a$
, giving the desired bound
![]() $\sqrt {v}$
.
$\sqrt {v}$
.
1.2 L-primitive sets
As outlined above, the subset of multiples of each
![]() $a\in A$
,
$a\in A$
,
arises naturally in our proof. As such, we shall introduce ‘L’ refinements of our common notions (here, L alludes to ‘lexicographic’). Specifically, if
![]() $n\in \mathrm {L}_a$
, we say n is an L-multiple of a, and a is an L-divisor of n. Most importantly, we introduce the following key definition.
$n\in \mathrm {L}_a$
, we say n is an L-multiple of a, and a is an L-divisor of n. Most importantly, we introduce the following key definition.
Definition 1.6. A set
![]() $A\subset {\mathbb Z}_{>1}$
is
$A\subset {\mathbb Z}_{>1}$
is
![]() $\mathrm {L}$
-primitive if
$\mathrm {L}$
-primitive if
![]() $a'\notin {\mathrm L}_a$
for all distinct
$a'\notin {\mathrm L}_a$
for all distinct
![]() $a,a'\in A$
.
$a,a'\in A$
.
That is, A is L-primitive if no member of A is an L-multiple of another. In particular, this definition is weaker than primitive.
One may apply the basic argument as in equation (4) more generally for L-primitive sets A, leading to the same bound
![]() $f(A) < e^{\gamma }$
(again ignoring small numbers). Moreover, L-primitive sets play a central role in the proof of Theorem 1.2. However, it turns out the bound
$f(A) < e^{\gamma }$
(again ignoring small numbers). Moreover, L-primitive sets play a central role in the proof of Theorem 1.2. However, it turns out the bound
![]() $e^{\gamma }$
is essentially best possible for L-primitive sets (see Proposition 5.3), which is markedly larger than
$e^{\gamma }$
is essentially best possible for L-primitive sets (see Proposition 5.3), which is markedly larger than
![]() $f(\mathcal P)$
. This further highlights the subtlety of Conjecture 1.1.
$f(\mathcal P)$
. This further highlights the subtlety of Conjecture 1.1.
1.3 Density and divisibility chains
Recall the natural (asymptotic) density
![]() ${\mathrm d}(S)=\lim _{x\to \infty } |S\cap [1,x]|/x$
of a set
${\mathrm d}(S)=\lim _{x\to \infty } |S\cap [1,x]|/x$
of a set
![]() $S\subset {\mathbb N}$
. We also consider
$S\subset {\mathbb N}$
. We also consider
![]() $\log $
density
$\log $
density
![]() $\delta (S)$
and
$\delta (S)$
and
![]() $\log \log $
density
$\log \log $
density
![]() $\Delta (S)$
, given by
$\Delta (S)$
, given by
 $$ \begin{align} \delta(S) & = \lim_{x\to\infty} \frac{1}{\log x}\sum_{n\in S, n\le x}\frac{1}{n},\qquad\text{and}\quad &\Delta(S) = \lim_{x\to\infty} \frac{1}{\log\log x}\sum_{n\in S, 1<n\le x}\frac{1}{n\log n}, \end{align} $$
$$ \begin{align} \delta(S) & = \lim_{x\to\infty} \frac{1}{\log x}\sum_{n\in S, n\le x}\frac{1}{n},\qquad\text{and}\quad &\Delta(S) = \lim_{x\to\infty} \frac{1}{\log\log x}\sum_{n\in S, 1<n\le x}\frac{1}{n\log n}, \end{align} $$
provided these limits exist. Recall the corresponding upper densities
![]() $\overline {\mathrm d}(S)$
,
$\overline {\mathrm d}(S)$
,
![]() $\overline {\delta }(S)$
,
$\overline {\delta }(S)$
,
![]() $\overline {\Delta }(S)$
always exist, by replacing
$\overline {\Delta }(S)$
always exist, by replacing
![]() $\lim _{x\to \infty }$
with
$\lim _{x\to \infty }$
with
![]() $\limsup _{x\to \infty }$
(and similarly
$\limsup _{x\to \infty }$
(and similarly
![]() $\liminf _{x\to \infty }$
for lower densities).
$\liminf _{x\to \infty }$
for lower densities).
Taking an abstract view, a primitive set is an antichain for the partial ordering of integers by divisibility. As such, this naturally leads to the dual notion of a chain in this context. Namely, an infinite sequence of integers
![]() $1<d_1<d_2<\cdots $
is a divisibility chain if
$1<d_1<d_2<\cdots $
is a divisibility chain if
![]() $d_j\mid d_{j+1}$
for all
$d_j\mid d_{j+1}$
for all
![]() $j\ge 1$
. A classical 1937 theorem of Davenport and Erdos [Reference Davenport and Erdős11] asserts that if set
$j\ge 1$
. A classical 1937 theorem of Davenport and Erdos [Reference Davenport and Erdős11] asserts that if set
![]() $A\subset {\mathbb N}$
has upper
$A\subset {\mathbb N}$
has upper
![]() $\log $
density
$\log $
density
![]() $\overline {\delta }(A)>0$
, then it contains an infinite divisibility chain
$\overline {\delta }(A)>0$
, then it contains an infinite divisibility chain
![]() $D\subset A$
.
$D\subset A$
.
Analogously, we introduce the following refinement.
Definition 1.7. An infinite sequence of integers
![]() $1<d_1<d_2<\cdots $
is an
$1<d_1<d_2<\cdots $
is an
![]() ${\mathrm L}$
-divisibility chain if
${\mathrm L}$
-divisibility chain if
![]() $d_{j+1}\in {\mathrm L}_{d_j}$
for all
$d_{j+1}\in {\mathrm L}_{d_j}$
for all
![]() $j\ge 1$
.
$j\ge 1$
.
That is,
![]() $d_{j+1}$
is an L-multiple of
$d_{j+1}$
is an L-multiple of
![]() $d_j$
for all
$d_j$
for all
![]() $j\ge 1$
. In particular, this definition is stronger than a (mere) divisibility chain.
$j\ge 1$
. In particular, this definition is stronger than a (mere) divisibility chain.
We refine the Davenport–Erdos theorem to L-divisibility chains.
Theorem 1.8. If a set
![]() $A\subset {\mathbb N}$
has upper
$A\subset {\mathbb N}$
has upper
![]() $\log $
density
$\log $
density
![]() $\overline {\delta }(A)>0$
, then A contains an infinite L-divisibility chain.
$\overline {\delta }(A)>0$
, then A contains an infinite L-divisibility chain.
In 1966, Erdős, Sárközy and Szemerédi [Reference Erdős, Sárközy and Szemerédi16, Theorem 1] quantified the Davenport–Erdős theorem by showing such a divisibility chain D satisfies
![]() $\limsup _{y\to \infty }\sum _{d\in D,d\le y}1/\sqrt {\log \log y}> 0$
and proved such growth rate is best possible.
$\limsup _{y\to \infty }\sum _{d\in D,d\le y}1/\sqrt {\log \log y}> 0$
and proved such growth rate is best possible.
They also studied the analogous question for upper
![]() $\log \log $
density, which they write ‘seems more interesting to us’. Namely, in [Reference Erdős, Sárközy and Szemerédi16, Theorem 2] they established the following quantitative result.
$\log \log $
density, which they write ‘seems more interesting to us’. Namely, in [Reference Erdős, Sárközy and Szemerédi16, Theorem 2] they established the following quantitative result.
Theorem 1.9 (Erdős–Sárközy–Szemerédi).
If
![]() $A\subset {\mathbb N}$
has upper
$A\subset {\mathbb N}$
has upper
![]() $\log \log $
density
$\log \log $
density
![]() $\overline {\Delta }(A)>0$
, then there is an infinite divisibility chain
$\overline {\Delta }(A)>0$
, then there is an infinite divisibility chain
![]() $D\subset A$
of growth
$D\subset A$
of growth
 $$ \begin{align} \limsup_{y\to\infty}\sum_{\substack{d\in D\\d\le y}}\frac{1}{\log\log y} \ \ge \ \frac{\overline{\Delta}(A)}{e^{\gamma}}. \end{align} $$
$$ \begin{align} \limsup_{y\to\infty}\sum_{\substack{d\in D\\d\le y}}\frac{1}{\log\log y} \ \ge \ \frac{\overline{\Delta}(A)}{e^{\gamma}}. \end{align} $$
Analogously, we quantify Theorem 1.8 in the case of
![]() $\log \log $
density, thereby refining Theorem 1.9 of Erdős–Sárközy–Szemerédi to L-divisibility chains.
$\log \log $
density, thereby refining Theorem 1.9 of Erdős–Sárközy–Szemerédi to L-divisibility chains.
Theorem 1.10. If
![]() $A\subset {\mathbb N}$
has upper
$A\subset {\mathbb N}$
has upper
![]() $\log \log $
density
$\log \log $
density
![]() $\overline {\Delta }(A)>0$
, then there is an infinite L-divisibility chain
$\overline {\Delta }(A)>0$
, then there is an infinite L-divisibility chain
![]() $D\subset A$
of growth
$D\subset A$
of growth
 $$ \begin{align*} \limsup_{y\to\infty}\sum_{\substack{d\in D\\d\le y}}\frac{1}{\log\log y} \ \ge \ \frac{\overline{\Delta}(A)}{e^{\gamma}}. \end{align*} $$
$$ \begin{align*} \limsup_{y\to\infty}\sum_{\substack{d\in D\\d\le y}}\frac{1}{\log\log y} \ \ge \ \frac{\overline{\Delta}(A)}{e^{\gamma}}. \end{align*} $$
In view of Proposition 5.3, we believe that the lower bound
![]() $\overline {\Delta }(A)/e^{\gamma }$
above is best possible for L-divisibility chains, though we are unable to settle this. Notably, this contrasts the situation in Theorem 1.9, as Erdős–Sárközy–Szemerédi conjectured
$\overline {\Delta }(A)/e^{\gamma }$
above is best possible for L-divisibility chains, though we are unable to settle this. Notably, this contrasts the situation in Theorem 1.9, as Erdős–Sárközy–Szemerédi conjectured
![]() $\overline {\Delta }(A)/e^{\gamma }$
in equation (7) might be improved to
$\overline {\Delta }(A)/e^{\gamma }$
in equation (7) might be improved to
![]() $\overline {\Delta }(A)$
, which would be best possible for divisibility chains, if true [Reference Erdős, Sárközy and Szemerédi16, eq. (5)].
$\overline {\Delta }(A)$
, which would be best possible for divisibility chains, if true [Reference Erdős, Sárközy and Szemerédi16, eq. (5)].
2 Preliminaries on L-primitive sets
Recall the set of L-multiples
![]() $\mathrm {L}_a:=\{ba\in {\mathbb N} \,:\,p\mid b \Rightarrow p\ge P(a)\}$
from equation (5). In particular,
$\mathrm {L}_a:=\{ba\in {\mathbb N} \,:\,p\mid b \Rightarrow p\ge P(a)\}$
from equation (5). In particular,
![]() $a\in {\mathrm L}_a$
for
$a\in {\mathrm L}_a$
for
![]() $b=1$
, and
$b=1$
, and
![]() $p(b) \ge P(a)$
for
$p(b) \ge P(a)$
for
![]() $b>1$
. For
$b>1$
. For
![]() $A\subset {\mathbb N}$
, define
$A\subset {\mathbb N}$
, define
![]() $\mathrm {L}_A :=\bigcup _{a\in A}{\mathrm L}_a$
. Also, let
$\mathrm {L}_A :=\bigcup _{a\in A}{\mathrm L}_a$
. Also, let
![]() $A_a =A\cap {\mathrm L}_a$
so that
$A_a =A\cap {\mathrm L}_a$
so that
![]() ${\mathbb N}_a={\mathrm L}_a$
and
${\mathbb N}_a={\mathrm L}_a$
and
![]() $A_q = \{a\in A : p(a)=q\}$
for prime q.Footnote
5
$A_q = \{a\in A : p(a)=q\}$
for prime q.Footnote
5
Observe that
![]() $a\in {\mathrm L}_{a'}$
if and only if
$a\in {\mathrm L}_{a'}$
if and only if
![]() $\mathrm {L}_a\subset {\mathrm L}_{a'}$
, as well as the following trichotomy.
$\mathrm {L}_a\subset {\mathrm L}_{a'}$
, as well as the following trichotomy.
Lemma 2.1. For any integers
![]() $a,a'>1$
, if
$a,a'>1$
, if
![]() $\mathrm {L}_a\cap {\mathrm L}_{a'}\neq \emptyset $
then
$\mathrm {L}_a\cap {\mathrm L}_{a'}\neq \emptyset $
then
![]() $a\in {\mathrm L}_{a'}$
or
$a\in {\mathrm L}_{a'}$
or
![]() $a'\in {\mathrm L}_a$
. Thus
$a'\in {\mathrm L}_a$
. Thus
![]() $\mathrm {L}_a\cap {\mathrm L}_{a'}=\emptyset $
or
$\mathrm {L}_a\cap {\mathrm L}_{a'}=\emptyset $
or
![]() $\mathrm {L}_a\subset {\mathrm L}_{a'}$
or
$\mathrm {L}_a\subset {\mathrm L}_{a'}$
or
![]() $\mathrm {L}_a\supset {\mathrm L}_{a'}$
.
$\mathrm {L}_a\supset {\mathrm L}_{a'}$
.
Proof. Suppose
![]() $ba=b'a' \in {\mathrm L}_a\cap {\mathrm L}_{a'}$
. If
$ba=b'a' \in {\mathrm L}_a\cap {\mathrm L}_{a'}$
. If
![]() $b=1$
or
$b=1$
or
![]() $b'=1$
, then
$b'=1$
, then
![]() $a\in {\mathrm L}_{a'}$
or
$a\in {\mathrm L}_{a'}$
or
![]() $a'\in {\mathrm L}_a$
. Otherwise,
$a'\in {\mathrm L}_a$
. Otherwise,
![]() $b,b'>1$
, so
$b,b'>1$
, so
![]() $P(a) \le p(b)$
and
$P(a) \le p(b)$
and
![]() $P(a')\le p(b')$
imply
$P(a')\le p(b')$
imply
![]() $b\mid b'$
or
$b\mid b'$
or
![]() $b'\mid b$
. Thus,
$b'\mid b$
. Thus,
![]() $a' = a(b/b')\in {\mathrm L}_a$
or
$a' = a(b/b')\in {\mathrm L}_a$
or
![]() $a = a'(b'/b)\in {\mathrm L}_{a'}$
as well.
$a = a'(b'/b)\in {\mathrm L}_{a'}$
as well.
As such, we see A is L-primitive if and only if the sets
![]() $\{{\mathrm L}_a\}_{a\in A}$
are pairwise disjoint.
$\{{\mathrm L}_a\}_{a\in A}$
are pairwise disjoint.
Corollary 2.2. If A is an L-primitive set, then
![]() $\mathrm {L}_a$
and
$\mathrm {L}_a$
and
![]() $\mathrm {L}_{a'}$
are disjoint for distinct
$\mathrm {L}_{a'}$
are disjoint for distinct
![]() $a,a'\in A$
.
$a,a'\in A$
.
Recall
![]() $\mathrm {L}_a$
has natural density
$\mathrm {L}_a$
has natural density
![]() ${\mathrm d}({\mathrm L}_a) = \frac {1}{a}\prod _{p<P(a)}(1-\frac {1}{p})$
. And by Mertens’ product theorem
${\mathrm d}({\mathrm L}_a) = \frac {1}{a}\prod _{p<P(a)}(1-\frac {1}{p})$
. And by Mertens’ product theorem
![]() $\prod _{p<x}(1-\frac {1}{p})\sim 1/e^{\gamma } \log x$
, where
$\prod _{p<x}(1-\frac {1}{p})\sim 1/e^{\gamma } \log x$
, where
![]() $\gamma =.57721\cdots $
is the Euler–Mascheroni constant. By a show argument below, we relate
$\gamma =.57721\cdots $
is the Euler–Mascheroni constant. By a show argument below, we relate
![]() $f(A)$
to density of L-multiples. This is essentially based on Erdős [Reference Erdős13] (also see [Reference Erdős, Sárközy and Szemerédi17, Lemma 1], [Reference Lichtman and Pomerance27, Proposition 2.1]).
$f(A)$
to density of L-multiples. This is essentially based on Erdős [Reference Erdős13] (also see [Reference Erdős, Sárközy and Szemerédi17, Lemma 1], [Reference Lichtman and Pomerance27, Proposition 2.1]).
Lemma 2.3. For an L-primitive set A and an integer
![]() $1<n\notin A$
, we have
$1<n\notin A$
, we have
![]() $f(A_n) < e^{\gamma }\,{\mathrm d}({\mathrm L}_n)$
.
$f(A_n) < e^{\gamma }\,{\mathrm d}({\mathrm L}_n)$
.
Proof. We may assume
![]() $A=A_n$
is finite since
$A=A_n$
is finite since
![]() $f(A) = \lim _{x\to \infty } f(A\cap [1,x])$
. As
$f(A) = \lim _{x\to \infty } f(A\cap [1,x])$
. As
![]() $n\notin A$
, all elements of A are composite. Also, A is L-primitive so
$n\notin A$
, all elements of A are composite. Also, A is L-primitive so
![]() ${\mathrm d}({\mathrm L}_A)=\sum _{a\in A}{\mathrm d}({\mathrm L}_a)$
by Corollary 2.2. Next, Theorem 7 in [Reference Rosser and Schoenfeld29] implies
${\mathrm d}({\mathrm L}_A)=\sum _{a\in A}{\mathrm d}({\mathrm L}_a)$
by Corollary 2.2. Next, Theorem 7 in [Reference Rosser and Schoenfeld29] implies
![]() $\prod _{p < x} \frac {p}{p-1} < e^{\gamma } \log (2x)$
for all
$\prod _{p < x} \frac {p}{p-1} < e^{\gamma } \log (2x)$
for all
![]() $x> 1$
. Thus, for any composite integer
$x> 1$
. Thus, for any composite integer
![]() $a>1$
, we have
$a>1$
, we have
![]() $a>2P(a)$
so that
$a>2P(a)$
so that
 $$ \begin{align*} f(a) = \frac{1}{a\log a} \ \le \ \frac{1}{a\log 2P(a)} \ < \ \frac{e^{\gamma}}{a}\prod_{p<P(a)}\Big(1-\frac{1}{p}\Big) \ = \ e^{\gamma}\,{\mathrm d}({\mathrm L}_a). \end{align*} $$
$$ \begin{align*} f(a) = \frac{1}{a\log a} \ \le \ \frac{1}{a\log 2P(a)} \ < \ \frac{e^{\gamma}}{a}\prod_{p<P(a)}\Big(1-\frac{1}{p}\Big) \ = \ e^{\gamma}\,{\mathrm d}({\mathrm L}_a). \end{align*} $$
Hence,
![]() $f(A) = \sum _{a\in A}f(a) < e^{\gamma }\,{\mathrm d}({\mathrm L}_A) \le e^{\gamma }\,{\mathrm d}({\mathrm L}_n)$
since
$f(A) = \sum _{a\in A}f(a) < e^{\gamma }\,{\mathrm d}({\mathrm L}_A) \le e^{\gamma }\,{\mathrm d}({\mathrm L}_n)$
since
![]() $A\subset {\mathrm L}_n$
.
$A\subset {\mathrm L}_n$
.
We shall also need a technical refinement of Lemma 2.3. For this, we rewrite Mertens’ product theorem as
![]() $\mu _x\sim 1$
, where we denote
$\mu _x\sim 1$
, where we denote
 $$ \begin{align} \mu_x := e^{\gamma} \log x\prod_{p<x}\Big(1-\frac{1}{p}\Big). \end{align} $$
$$ \begin{align} \mu_x := e^{\gamma} \log x\prod_{p<x}\Big(1-\frac{1}{p}\Big). \end{align} $$
In particular, for a prime q we have
 $$ \begin{align} f(q) = \frac{1}{q\log q} = \frac{1}{q}\frac{e^{\gamma}}{\mu_q}\prod_{p<q}\Big(1-\frac{1}{p}\Big) =\frac{e^{\gamma}}{\mu_q}{\mathrm d}({\mathrm L}_q). \end{align} $$
$$ \begin{align} f(q) = \frac{1}{q\log q} = \frac{1}{q}\frac{e^{\gamma}}{\mu_q}\prod_{p<q}\Big(1-\frac{1}{p}\Big) =\frac{e^{\gamma}}{\mu_q}{\mathrm d}({\mathrm L}_q). \end{align} $$
We have the following explicit bounds for
![]() $\mu _x$
, which critically are monotonic. We give upper bounds which hold on real
$\mu _x$
, which critically are monotonic. We give upper bounds which hold on real
![]() $x\in {\mathbb R}$
, but for lower bounds it turns out it suffices to restrict to the subsequence of primes
$x\in {\mathbb R}$
, but for lower bounds it turns out it suffices to restrict to the subsequence of primes
![]() $q\in \mathcal P$
.
$q\in \mathcal P$
.
Lemma 2.4 (Monotonic bounds).
For
![]() $q\in \mathcal P$
and
$q\in \mathcal P$
and
![]() $x\in {\mathbb R}$
, define
$x\in {\mathbb R}$
, define
 $$ \begin{align*} m_q := \inf_{\substack{p\ge q\\ p\in \mathcal P}}\mu_p, \quad\text{and}\quad M_x := \sup_{\substack{y\ge x\\ y\in {\mathbb R}}}\mu_y. \end{align*} $$
$$ \begin{align*} m_q := \inf_{\substack{p\ge q\\ p\in \mathcal P}}\mu_p, \quad\text{and}\quad M_x := \sup_{\substack{y\ge x\\ y\in {\mathbb R}}}\mu_y. \end{align*} $$
Then we have
 $$\begin{align*}m_q \ge \begin{cases} \mu_7 = 0.9242\cdots & q \le 7\\ \mu_{19} = 0.9467\cdots & 7< q \le 300\\ 1- \frac{1}{2(\log q)^2} & q> 300. \end{cases} \quad\text{and}\quad M_x \le \begin{cases} \mu_2 = 1.235\cdots & x \le 2\\ 1 + \frac{1}{2\log(2\cdot10^9)^2} & 2< x \le 2\cdot10^9\\ 1 + \frac{1}{2(\log x)^2} & x> 2\cdot10^9. \end{cases} \end{align*}$$
$$\begin{align*}m_q \ge \begin{cases} \mu_7 = 0.9242\cdots & q \le 7\\ \mu_{19} = 0.9467\cdots & 7< q \le 300\\ 1- \frac{1}{2(\log q)^2} & q> 300. \end{cases} \quad\text{and}\quad M_x \le \begin{cases} \mu_2 = 1.235\cdots & x \le 2\\ 1 + \frac{1}{2\log(2\cdot10^9)^2} & 2< x \le 2\cdot10^9\\ 1 + \frac{1}{2(\log x)^2} & x> 2\cdot10^9. \end{cases} \end{align*}$$
Proof. First, Rosser–Schoenfeld [Reference Rosser and Schoenfeld29, Theorem 7] implies the product over primes
![]() $p< x$
is bounded in between
$p< x$
is bounded in between
 $$ \begin{align*} 1-\frac{1}{2(\log x)^2} \ \overset{(x>285)}{\le} \ e^{\gamma} \log x\prod_{p< x}\Big(1-\frac{1}{p}\Big) \ \overset{(x>1)}{\le} \ 1+\frac{1}{2(\log x)^2}. \end{align*} $$
$$ \begin{align*} 1-\frac{1}{2(\log x)^2} \ \overset{(x>285)}{\le} \ e^{\gamma} \log x\prod_{p< x}\Big(1-\frac{1}{p}\Big) \ \overset{(x>1)}{\le} \ 1+\frac{1}{2(\log x)^2}. \end{align*} $$
Note
![]() $\mu _x$
is increasing on
$\mu _x$
is increasing on
![]() $x\in (p,p']$
for consecutive primes
$x\in (p,p']$
for consecutive primes
![]() $p,p'$
. So the upper bound follows by computing
$p,p'$
. So the upper bound follows by computing
![]() $\mu _p<1$
for the first
$\mu _p<1$
for the first
![]() $10^8$
odd primes p (note
$10^8$
odd primes p (note
![]() $p_{10^8} \ge 2\cdot 10^9$
). Hence,
$p_{10^8} \ge 2\cdot 10^9$
). Hence,
![]() $\mu _x<1$
for real
$\mu _x<1$
for real
![]() $2< x\le 2\cdot 10^9$
. Below we display
$2< x\le 2\cdot 10^9$
. Below we display
![]() $\mu _q$
for the first few primes q, rounded to four significant digits.
$\mu _q$
for the first few primes q, rounded to four significant digits.

The lower bound follows by identifying the primes q for which
![]() $\mu _q = \inf _{p\ge q} \mu _p$
(in bold above), and then computing
$\mu _q = \inf _{p\ge q} \mu _p$
(in bold above), and then computing
![]() $\mu _{199} < \mu _p$
for
$\mu _{199} < \mu _p$
for
![]() $199<p\le 300$
, as well as checking
$199<p\le 300$
, as well as checking
![]() $\mu _{199} < 0.9846 < 1-\frac {1}{2(\log x)^2}$
for
$\mu _{199} < 0.9846 < 1-\frac {1}{2(\log x)^2}$
for
![]() $x>300$
. (In practice, we shall only need
$x>300$
. (In practice, we shall only need
![]() $\mu _q$
for
$\mu _q$
for
![]() $q=7,19$
.)
$q=7,19$
.)
We may now prove a technical refinement of Lemma 2.3 using
![]() $\mu _q$
.
$\mu _q$
.
Lemma 2.5. Let A be an L-primitive set. Take
![]() $v\ge 0$
, an integer
$v\ge 0$
, an integer
![]() $n\notin A$
and denote
$n\notin A$
and denote
![]() $q=P(n)$
. If
$q=P(n)$
. If
![]() $P(a)^{1+v}\le a$
for all
$P(a)^{1+v}\le a$
for all
![]() $a\in A_n$
, then
$a\in A_n$
, then
 $$ \begin{align*} f(A_n) = \sum_{a\in A_n}\frac{1}{a\log a} \ &\le \ \frac{e^{\gamma}}{m_q}\,\frac{{\mathrm d}({\mathrm L}_{A_n})}{1+v}. \end{align*} $$
$$ \begin{align*} f(A_n) = \sum_{a\in A_n}\frac{1}{a\log a} \ &\le \ \frac{e^{\gamma}}{m_q}\,\frac{{\mathrm d}({\mathrm L}_{A_n})}{1+v}. \end{align*} $$
Proof. We may assume
![]() $A = A_n$
is finite, since
$A = A_n$
is finite, since
![]() $f(A) = \lim _{x\to \infty } f(A\cap [1,x])$
. As
$f(A) = \lim _{x\to \infty } f(A\cap [1,x])$
. As
![]() $n\notin A$
, all elements of A are composite. Also, A is L-primitive so
$n\notin A$
, all elements of A are composite. Also, A is L-primitive so
![]() ${\mathrm d}({\mathrm L}_A)=\sum _{a\in A}{\mathrm d}({\mathrm L}_a)$
by Corollary 2.2. Moreover,
${\mathrm d}({\mathrm L}_A)=\sum _{a\in A}{\mathrm d}({\mathrm L}_a)$
by Corollary 2.2. Moreover,
![]() $(1+v)\log P(a) \le \log a$
for all
$(1+v)\log P(a) \le \log a$
for all
![]() $a\in A$
. Thus, by definition of
$a\in A$
. Thus, by definition of
![]() $\mu _{P(a)}$
in (8),
$\mu _{P(a)}$
in (8),
 $$ \begin{align*} \frac{1}{a\log a} \ \le \ \frac{1}{1+v}\frac{1}{a\log P(a)} = \frac{e^{\gamma}}{\mu_{P(a)}}\frac{1}{(1+v)a}\prod_{p<P(a)}\Big(1-\frac{1}{p}\Big) = \frac{e^{\gamma}}{\mu_{P(a)}}\frac{{\mathrm d}({\mathrm L}_a)}{1+v}. \end{align*} $$
$$ \begin{align*} \frac{1}{a\log a} \ \le \ \frac{1}{1+v}\frac{1}{a\log P(a)} = \frac{e^{\gamma}}{\mu_{P(a)}}\frac{1}{(1+v)a}\prod_{p<P(a)}\Big(1-\frac{1}{p}\Big) = \frac{e^{\gamma}}{\mu_{P(a)}}\frac{{\mathrm d}({\mathrm L}_a)}{1+v}. \end{align*} $$
By monotonicity
![]() $\mu _{P(a)}\ge m_{P(a)}\ge m_q$
for
$\mu _{P(a)}\ge m_{P(a)}\ge m_q$
for
![]() $a\in A\subset {\mathrm L}_n$
. Hence, we conclude
$a\in A\subset {\mathrm L}_n$
. Hence, we conclude
 $$ \begin{align*} f(A) = \sum_{a\in A}\frac{1}{a\log a} \ \le \ \frac{e^{\gamma}}{m_q}\frac{1}{1+v}\sum_{a\in A}{\mathrm d}({\mathrm L}_a) = \frac{e^{\gamma}}{m_q}\frac{{\mathrm d}({\mathrm L}_A)}{1+v}.\\[-38pt] \end{align*} $$
$$ \begin{align*} f(A) = \sum_{a\in A}\frac{1}{a\log a} \ \le \ \frac{e^{\gamma}}{m_q}\frac{1}{1+v}\sum_{a\in A}{\mathrm d}({\mathrm L}_a) = \frac{e^{\gamma}}{m_q}\frac{{\mathrm d}({\mathrm L}_A)}{1+v}.\\[-38pt] \end{align*} $$
3 Primitive sets
Given
![]() $v\in (0,1)$
, we shall be interested in elements
$v\in (0,1)$
, we shall be interested in elements
![]() $a\in A$
for which
$a\in A$
for which
![]() $P(a)^{1+v}>a$
, and their multiples
$P(a)^{1+v}>a$
, and their multiples
![]() $ac$
, where
$ac$
, where
![]() $c\in C_a^v$
for
$c\in C_a^v$
for
Note
![]() $c=1\in C_a^v$
. Recall
$c=1\in C_a^v$
. Recall
![]() $a^*=a/P(a)$
, so
$a^*=a/P(a)$
, so
![]() $P(a^*)$
is the second largest prime of a. Also if
$P(a^*)$
is the second largest prime of a. Also if
![]() $1<c\in C_a^v$
then
$1<c\in C_a^v$
then
![]() $P(c)\le P(a^*)^{1/\sqrt {v}}$
is markedly smaller than
$P(c)\le P(a^*)^{1/\sqrt {v}}$
is markedly smaller than
![]() $P(a) \ge P(a^*)^{1/v}$
.
$P(a) \ge P(a^*)^{1/v}$
.
The following key lemma provides an upgrade to Corollary 2.2 in the case when A is primitive, not just
![]() $\mathrm {L}$
-primitive. Namely, the
$\mathrm {L}$
-primitive. Namely, the
![]() $\mathrm {L}_{ac}$
are disjoint, and so the larger set
$\mathrm {L}_{ac}$
are disjoint, and so the larger set
![]() $\{ac : a\in A, c\in C_a^v\}$
is
$\{ac : a\in A, c\in C_a^v\}$
is
![]() $\mathrm {L}$
-primitive.
$\mathrm {L}$
-primitive.
Lemma 3.1. Let A be a primitive set of composite numbers, and take
![]() $v\in (0,1)$
. If
$v\in (0,1)$
. If
![]() $P(a)^{1+v}>a$
for all
$P(a)^{1+v}>a$
for all
![]() $a\in A$
, then the collection of sets
$a\in A$
, then the collection of sets
![]() $\mathrm {L}_{ac}$
, ranging over
$\mathrm {L}_{ac}$
, ranging over
![]() $a\in A, c\in C_a^v$
, are pairwise disjoint.
$a\in A, c\in C_a^v$
, are pairwise disjoint.
Proof. Suppose
![]() $\mathrm {L}_{ac}\cap {\mathrm L}_{a'c'}\neq \emptyset $
for some
$\mathrm {L}_{ac}\cap {\mathrm L}_{a'c'}\neq \emptyset $
for some
![]() $a, a'\in A$
and
$a, a'\in A$
and
![]() $c\in C_a^v$
,
$c\in C_a^v$
,
![]() $c'\in C_{a'}^v$
. Without loss, by Lemma 2.1 we may assume
$c'\in C_{a'}^v$
. Without loss, by Lemma 2.1 we may assume
![]() $ac\in {\mathrm L}_{a'c'}$
. Note if
$ac\in {\mathrm L}_{a'c'}$
. Note if
![]() $c=1$
, then
$c=1$
, then
![]() $a\in {\mathrm L}_{a'c'}$
implies
$a\in {\mathrm L}_{a'c'}$
implies
![]() $a'\mid a'c'\mid a$
, which forces
$a'\mid a'c'\mid a$
, which forces
![]() $a=a'$
and
$a=a'$
and
![]() $c'=1$
by primitivity of A. So assuming
$c'=1$
by primitivity of A. So assuming
![]() $(a,c)\neq (a',c')$
, we deduce
$(a,c)\neq (a',c')$
, we deduce
![]() $c>1$
.
$c>1$
.
We factor
![]() $ac=p_1\cdots p_k$
into primes
$ac=p_1\cdots p_k$
into primes
![]() $p_1\ge \cdots \ge p_k$
, so
$p_1\ge \cdots \ge p_k$
, so
![]() $ac\in {\mathrm L}_{a'c'}$
implies
$ac\in {\mathrm L}_{a'c'}$
implies
![]() $a'c'=p_j\cdots p_k$
for some index
$a'c'=p_j\cdots p_k$
for some index
![]() $1<j<k$
. Since
$1<j<k$
. Since
![]() $P(a)>P(c),p(c)\ge P(a^*)$
, we also have
$P(a)>P(c),p(c)\ge P(a^*)$
, we also have
![]() $a^* = p_i\cdots p_k$
for some
$a^* = p_i\cdots p_k$
for some
![]() $2<i\le k$
. If
$2<i\le k$
. If
![]() $i\le j$
, then
$i\le j$
, then
![]() $a'c'\mid a^*$
so
$a'c'\mid a^*$
so
![]() $a'\mid a$
, contradicting A as primitive. Hence,
$a'\mid a$
, contradicting A as primitive. Hence,
![]() $i>j$
so
$i>j$
so
![]() $a^*\mid a'c'$
. Write
$a^*\mid a'c'$
. Write
![]() $da^*=a'c'$
, where
$da^*=a'c'$
, where
![]() $d=p_j\cdots p_{i-1}$
, and note
$d=p_j\cdots p_{i-1}$
, and note
![]() $P(d)=p_j=P(a')$
. By definition of
$P(d)=p_j=P(a')$
. By definition of
![]() $1<c\in C_a^v$
, we have
$1<c\in C_a^v$
, we have
Recall
![]() $P(a')^{v}> (a')^* \ge P((a')^*)$
for
$P(a')^{v}> (a')^* \ge P((a')^*)$
for
![]() $a'\in A$
. Now consider cases
$a'\in A$
. Now consider cases
![]() $c'>1$
and
$c'>1$
and
![]() $c'=1$
. When
$c'=1$
. When
![]() $1<c'\in C_{a'}^v$
, we have
$1<c'\in C_{a'}^v$
, we have
![]() $P(c')=p_{j+1}\ge p_i= P(a^*)$
. Thus,
$P(c')=p_{j+1}\ge p_i= P(a^*)$
. Thus,
But equation (12) contradicts equation (11), so
![]() $\mathrm {L}_{ac}$
and
$\mathrm {L}_{ac}$
and
![]() $\mathrm {L}_{a'c'}$
are disjoint.
$\mathrm {L}_{a'c'}$
are disjoint.
Similarly, when
![]() $c'=1$
, we have
$c'=1$
, we have
![]() $P((a')^*) = p_{j+1} \ge p_i = P(a^*)$
and so
$P((a')^*) = p_{j+1} \ge p_i = P(a^*)$
and so
This also contradicts equation (11) (indeed
![]() $v<\sqrt {v}$
). Hence,
$v<\sqrt {v}$
). Hence,
![]() $\mathrm {L}_{ac}$
and
$\mathrm {L}_{ac}$
and
![]() $\mathrm {L}_{a'}$
are disjoint in both cases.
$\mathrm {L}_{a'}$
are disjoint in both cases.
Remark 3.2. The exponent
![]() $1/\sqrt {v}$
in the definition of
$1/\sqrt {v}$
in the definition of
![]() $C_a^v$
in equation (10) is chosen as large as possible, constrained by the final steps (11), (12) above. If one established a larger exponent in Lemma 3.1, this would improve the final savings factor
$C_a^v$
in equation (10) is chosen as large as possible, constrained by the final steps (11), (12) above. If one established a larger exponent in Lemma 3.1, this would improve the final savings factor
![]() $\int _0^1\frac {\mathrm{d} }{\mathrm{d} v}[v^{1/2}]\frac {\mathrm{d} {v}}{1+v} = \pi /4$
.
$\int _0^1\frac {\mathrm{d} }{\mathrm{d} v}[v^{1/2}]\frac {\mathrm{d} {v}}{1+v} = \pi /4$
.
In the following proposition, we use Lemma 3.1 in order to bound the density of
![]() $\mathrm {L}_{A_n}$
by essentially a savings factor
$\mathrm {L}_{A_n}$
by essentially a savings factor
![]() $\sqrt {v}$
from the trivial bound
$\sqrt {v}$
from the trivial bound
![]() ${\mathrm d}({\mathrm L}_{n})$
, when
${\mathrm d}({\mathrm L}_{n})$
, when
![]() $P(a)^{1+v}>a$
for all
$P(a)^{1+v}>a$
for all
![]() $a\in A_n$
.
$a\in A_n$
.
Proposition 3.3. Let A be a finite primitive set. Take
![]() $v\in (0,1)$
, an integer
$v\in (0,1)$
, an integer
![]() $n>1$
with
$n>1$
with
![]() $n\notin A$
, and denote
$n\notin A$
, and denote
![]() $q=P(n)$
. If
$q=P(n)$
. If
![]() $P(a)^{1+v}>a$
for all
$P(a)^{1+v}>a$
for all
![]() $a\in A_n$
, then
$a\in A_n$
, then
for the ratio
![]() $r_q := M_q/m_q$
when
$r_q := M_q/m_q$
when
![]() $q\ge 3$
, and
$q\ge 3$
, and
![]() $r_2:=r_3$
.
$r_2:=r_3$
.
Proof. Without loss assume
![]() $A = A_n$
. Then
$A = A_n$
. Then
![]() $ac\in {\mathrm L}_n$
for all
$ac\in {\mathrm L}_n$
for all
![]() $a\in A$
,
$a\in A$
,
![]() $c\in C_a^v$
(recall
$c\in C_a^v$
(recall
![]() $p(ac)=p(a)$
), and so
$p(ac)=p(a)$
), and so
![]() $\mathrm {L}_{ac} \subset {\mathrm L}_n$
. Note the condition
$\mathrm {L}_{ac} \subset {\mathrm L}_n$
. Note the condition
![]() $P(a)^{1+v}> a$
is equivalent to
$P(a)^{1+v}> a$
is equivalent to
![]() $P(a)^v> a^*$
, and
$P(a)^v> a^*$
, and
![]() $v<1$
implies
$v<1$
implies
![]() $P(a)\nmid a^*$
. By Lemma 3.1, we have the following (finite) disjoint union,
$P(a)\nmid a^*$
. By Lemma 3.1, we have the following (finite) disjoint union,
Thus, taking the density of equation (14), we obtain
 $$ \begin{align} {\mathrm d}({\mathrm L}_n) & \ge {\mathrm d}\bigg(\bigcup_{a\in A} \bigcup_{c\in C_a^v}{\mathrm L}_{ac}\bigg) = \sum_{a\in A}\sum_{c\in C_a^v}{\mathrm d}({\mathrm L}_{ac}) = \sum_{a\in A}{\mathrm d}({\mathrm L}_a)\,\sum_{c\in C_a}\frac{1}{c}, \end{align} $$
$$ \begin{align} {\mathrm d}({\mathrm L}_n) & \ge {\mathrm d}\bigg(\bigcup_{a\in A} \bigcup_{c\in C_a^v}{\mathrm L}_{ac}\bigg) = \sum_{a\in A}\sum_{c\in C_a^v}{\mathrm d}({\mathrm L}_{ac}) = \sum_{a\in A}{\mathrm d}({\mathrm L}_a)\,\sum_{c\in C_a}\frac{1}{c}, \end{align} $$
noting
![]() $P(a)>P(c)$
for
$P(a)>P(c)$
for
![]() $1<c\in C_a^v$
, so
$1<c\in C_a^v$
, so
![]() $\mathrm {L}_{ac} = \{bac: p(b) \ge P(a)\} = c\cdot {\mathrm L}_{a}$
. Then by definitions of
$\mathrm {L}_{ac} = \{bac: p(b) \ge P(a)\} = c\cdot {\mathrm L}_{a}$
. Then by definitions of
![]() $C_a^v$
and
$C_a^v$
and
![]() $\mu _q$
in equations (10) and (8),
$\mu _q$
in equations (10) and (8),
 $$ \begin{align} \sum_{c\in C_a^v}\frac{1}{c}\ & = \prod_{p\in [P(a^*), P(a^*)^{1/\sqrt{v}})}\Big(1-\frac{1}{p}\Big)^{-1} = \prod_{p<P(a^*)^{1/\sqrt{v}}}\Big(1-\frac{1}{p}\Big)^{-1}\prod_{p<P(a^*)}\Big(1-\frac{1}{p}\Big) \nonumber\\ &= \frac{\log P(a^*)^{1/\sqrt{v}}}{\mu_{P(a^*)^{1/\sqrt{v}}}} \frac{\mu_{P(a^*)}}{\log P(a^*)} = \frac{\mu_{P(a^*)}}{\mu_{P(a^*)^{1/\sqrt{v}}}}\frac{1}{\sqrt{v}}. \end{align} $$
$$ \begin{align} \sum_{c\in C_a^v}\frac{1}{c}\ & = \prod_{p\in [P(a^*), P(a^*)^{1/\sqrt{v}})}\Big(1-\frac{1}{p}\Big)^{-1} = \prod_{p<P(a^*)^{1/\sqrt{v}}}\Big(1-\frac{1}{p}\Big)^{-1}\prod_{p<P(a^*)}\Big(1-\frac{1}{p}\Big) \nonumber\\ &= \frac{\log P(a^*)^{1/\sqrt{v}}}{\mu_{P(a^*)^{1/\sqrt{v}}}} \frac{\mu_{P(a^*)}}{\log P(a^*)} = \frac{\mu_{P(a^*)}}{\mu_{P(a^*)^{1/\sqrt{v}}}}\frac{1}{\sqrt{v}}. \end{align} $$
When
![]() $q\ge 3$
, we use
$q\ge 3$
, we use
![]() $\mu _{P(a^*)}/\mu _{P(a^*)^{1/\sqrt {v}}} \ge m_q/M_q=1/r_q$
, which follows by monotonicity of
$\mu _{P(a^*)}/\mu _{P(a^*)^{1/\sqrt {v}}} \ge m_q/M_q=1/r_q$
, which follows by monotonicity of
![]() $m_q,M_q$
in Lemma 2.4, and that
$m_q,M_q$
in Lemma 2.4, and that
![]() $P(a^*),q\in \mathcal P$
. Hence, plugging equation (16) back into equation (15),
$P(a^*),q\in \mathcal P$
. Hence, plugging equation (16) back into equation (15),
 $$ \begin{align*} {\mathrm d}({\mathrm L}_n) & \ge \frac{1}{\sqrt{v}\,r_q}\sum_{a\in A}{\mathrm d}({\mathrm L}_a) = \frac{1}{\sqrt{v}\,r_q}\,{\mathrm d}({\mathrm L}_A) \end{align*} $$
$$ \begin{align*} {\mathrm d}({\mathrm L}_n) & \ge \frac{1}{\sqrt{v}\,r_q}\sum_{a\in A}{\mathrm d}({\mathrm L}_a) = \frac{1}{\sqrt{v}\,r_q}\,{\mathrm d}({\mathrm L}_A) \end{align*} $$
as desired.
The result similarly holds when
![]() $q=2$
: If
$q=2$
: If
![]() $P(a^*)\ge 3$
, then
$P(a^*)\ge 3$
, then
![]() $\mu _{P(a^*)}/\mu _{P(a^*)^{1/\sqrt {v}}} \ge m_3/M_3=1/r_3$
as before. And if
$\mu _{P(a^*)}/\mu _{P(a^*)^{1/\sqrt {v}}} \ge m_3/M_3=1/r_3$
as before. And if
![]() $P(a^*)= 2$
, then
$P(a^*)= 2$
, then
![]() $\mu _{2}/\mu _{2^{1/\sqrt {v}}} \ge 1$
also suffices.
$\mu _{2}/\mu _{2^{1/\sqrt {v}}} \ge 1$
also suffices.
4 Deduction of Theorems 1.2, 1.3, 1.5
We now apply our analysis of the density of L-multiples to our original sum of interest
![]() $f(A) = \sum _{a\in A}\frac {1}{a\log a}$
. First, we need a simple lemma on bounding certain monotonic sequences.
$f(A) = \sum _{a\in A}\frac {1}{a\log a}$
. First, we need a simple lemma on bounding certain monotonic sequences.
Lemma 4.1. For
![]() $k\ge 1$
, let
$k\ge 1$
, let
![]() $c_0\ge c_1\ge \cdots \ge c_k\ge 0$
and
$c_0\ge c_1\ge \cdots \ge c_k\ge 0$
and
![]() $0=D_0\le D_1\le \cdots \le D_k$
. If
$0=D_0\le D_1\le \cdots \le D_k$
. If
![]() $d_1,\ldots ,d_k\ge 0$
satisfy
$d_1,\ldots ,d_k\ge 0$
satisfy
![]() $\sum _{j\le i}d_j \le D_i$
for all
$\sum _{j\le i}d_j \le D_i$
for all
![]() $i\le k$
, then we have
$i\le k$
, then we have
Proof. By rearranging sums,
 $$ \begin{align*} \sum_{i\le k}c_id_i=\sum_{i\le k}c_i\Big(\sum_{j\le i}d_j-\sum_{j\le i-1}d_j\Big) =\sum_{i\le k-1}(c_i-c_{i+1})\sum_{j\le i}d_j \ + \ c_k\sum_{i\le k}d_i. \end{align*} $$
$$ \begin{align*} \sum_{i\le k}c_id_i=\sum_{i\le k}c_i\Big(\sum_{j\le i}d_j-\sum_{j\le i-1}d_j\Big) =\sum_{i\le k-1}(c_i-c_{i+1})\sum_{j\le i}d_j \ + \ c_k\sum_{i\le k}d_i. \end{align*} $$
Since
![]() $c_i \ge c_{i+1}$
and
$c_i \ge c_{i+1}$
and
![]() $\sum _{j\le i} d_j \le D_i$
, we conclude
$\sum _{j\le i} d_j \le D_i$
, we conclude
To motivate the remainder of the proof, we offer a probabilistic interpretation of Proposition 3.3: For
![]() $v\ge 0$
, consider
$v\ge 0$
, consider
![]() $D(v):=\sup _A{\mathrm d}({\mathrm L}_{A_n})/{\mathrm d}({\mathrm L}_n)$
, ranging over primitive sets A such that
$D(v):=\sup _A{\mathrm d}({\mathrm L}_{A_n})/{\mathrm d}({\mathrm L}_n)$
, ranging over primitive sets A such that
![]() $P(a)^{1+v}> a$
for all
$P(a)^{1+v}> a$
for all
![]() $a\in A$
. Note
$a\in A$
. Note
![]() $D(v)$
may be viewed as a ‘cumulative distribution function’, since
$D(v)$
may be viewed as a ‘cumulative distribution function’, since
![]() $D(0)=0$
and
$D(0)=0$
and
![]() $D(v)\to 1$
as
$D(v)\to 1$
as
![]() $v\to \infty $
. Now, Proposition 3.3 essentially bounds
$v\to \infty $
. Now, Proposition 3.3 essentially bounds
![]() $D(v)$
by
$D(v)$
by
![]() $\sqrt {v}$
. Using the corresponding bound
$\sqrt {v}$
. Using the corresponding bound
![]() $1/2\sqrt {v}$
for the ‘probability density function’, we establish quantitative bounds below.
$1/2\sqrt {v}$
for the ‘probability density function’, we establish quantitative bounds below.
Proposition 4.2. For any primitive set A, and any integer
![]() $n\notin A$
with
$n\notin A$
with
![]() $q=P(n)\ge 3$
,
$q=P(n)\ge 3$
,
 $$ \begin{align*} f(A_n) \ \le \ \frac{\pi}{4}\frac{M_q}{m_q^2}\;e^{\gamma} {\mathrm d}({\mathrm L}_n). \end{align*} $$
$$ \begin{align*} f(A_n) \ \le \ \frac{\pi}{4}\frac{M_q}{m_q^2}\;e^{\gamma} {\mathrm d}({\mathrm L}_n). \end{align*} $$
Proof. Without loss, we may assume
![]() $A=A_n$
is finite since
$A=A_n$
is finite since
![]() $f(A) = \lim _{x\to \infty } f(A\cap [1,x])$
. Also,
$f(A) = \lim _{x\to \infty } f(A\cap [1,x])$
. Also,
![]() $n\notin A$
implies all elements of A are composite.
$n\notin A$
implies all elements of A are composite.
Take
![]() $k\ge 1$
and any sequence
$k\ge 1$
and any sequence
![]() $0=v_0<v_1<\cdots <v_k=1$
, and partition the set
$0=v_0<v_1<\cdots <v_k=1$
, and partition the set
![]() $A = \bigcup _{0\le i\le k} A_{(i)}$
, where
$A = \bigcup _{0\le i\le k} A_{(i)}$
, where
![]() $A_{(k)}=\{a\in A: P(a)^2 \le a\}$
and for
$A_{(k)}=\{a\in A: P(a)^2 \le a\}$
and for
![]() $0\le i\le k$
,
$0\le i\le k$
,
Then applying Lemma 2.5 to each
![]() $A_{(i)}$
,
$A_{(i)}$
,
 $$ \begin{align} f(A) & = \sum_{0\le i\le k} f(A_{(i)}) \ \le \ \frac{e^{\gamma}}{m_q} \sum_{0\le i\le k} \frac{{\mathrm d}({\mathrm L}_{A_{(i)}})}{1+v_i}. \end{align} $$
$$ \begin{align} f(A) & = \sum_{0\le i\le k} f(A_{(i)}) \ \le \ \frac{e^{\gamma}}{m_q} \sum_{0\le i\le k} \frac{{\mathrm d}({\mathrm L}_{A_{(i)}})}{1+v_i}. \end{align} $$
Note since A is primitive,
![]() $\{{\mathrm L}_{A_{(i)}}\}_{i\le k}$
are pairwise disjoint. Also, for each
$\{{\mathrm L}_{A_{(i)}}\}_{i\le k}$
are pairwise disjoint. Also, for each
![]() $j< k$
, the first j components are
$j< k$
, the first j components are
![]() $\bigcup _{0\le i\le j}A_{(i)}=\{a\in A:a<P(a)^{1+v_{j+1}}\}=:A^{(j)}$
, so by Proposition 3.3 they have density
$\bigcup _{0\le i\le j}A_{(i)}=\{a\in A:a<P(a)^{1+v_{j+1}}\}=:A^{(j)}$
, so by Proposition 3.3 they have density
 $$ \begin{align*} \sum_{0\le i\le j}{\mathrm d}({\mathrm L}_{A_{(i)}}) = {\mathrm d}({\mathrm L}_{A^{(j)}})\le \sqrt{v_{j+1}} \,r_q\,{\mathrm d}({\mathrm L}_n). \end{align*} $$
$$ \begin{align*} \sum_{0\le i\le j}{\mathrm d}({\mathrm L}_{A_{(i)}}) = {\mathrm d}({\mathrm L}_{A^{(j)}})\le \sqrt{v_{j+1}} \,r_q\,{\mathrm d}({\mathrm L}_n). \end{align*} $$
Also, for
![]() $j=k$
we have
$j=k$
we have
![]() $\sum _{0\le i\le k}{\mathrm d}({\mathrm L}_{A_{(i)}}) = {\mathrm d}({\mathrm L}_{A}) \le {\mathrm d}({\mathrm L}_n)$
, which is trivially less than
$\sum _{0\le i\le k}{\mathrm d}({\mathrm L}_{A_{(i)}}) = {\mathrm d}({\mathrm L}_{A}) \le {\mathrm d}({\mathrm L}_n)$
, which is trivially less than
![]() $r_q{\mathrm d}({\mathrm L}_n)$
. Let
$r_q{\mathrm d}({\mathrm L}_n)$
. Let
![]() $c_i = \frac {1}{1+v_{i}}$
,
$c_i = \frac {1}{1+v_{i}}$
,
![]() $d_i = {\mathrm d}({\mathrm L}_{A_{(i)}})$
,
$d_i = {\mathrm d}({\mathrm L}_{A_{(i)}})$
,
![]() $D_i = \sqrt {v_{i+1}} \,r_q\,{\mathrm d}({\mathrm L}_n)$
(here, we let
$D_i = \sqrt {v_{i+1}} \,r_q\,{\mathrm d}({\mathrm L}_n)$
(here, we let
![]() $v_{k+1}=v_k$
so that
$v_{k+1}=v_k$
so that
![]() $D_k - D_{k-1}=0$
). Thus, by Lemma 4.1 we have
$D_k - D_{k-1}=0$
). Thus, by Lemma 4.1 we have
 $$ \begin{align*} \sum_{0\le i\le k} \frac{{\mathrm d}({\mathrm L}_{A_{(i)}})}{1+v_{i}} = \sum_{0\le i\le k}c_id_i \ \le \ \sum_{0\le i\le k}c_i(D_i - D_{i-1}) =r_q\,{\mathrm d}({\mathrm L}_n)\sum_{0\le i\le k} \frac{\sqrt{v_{i+1}}-\sqrt{v_{i}}}{1+v_{i}}. \end{align*} $$
$$ \begin{align*} \sum_{0\le i\le k} \frac{{\mathrm d}({\mathrm L}_{A_{(i)}})}{1+v_{i}} = \sum_{0\le i\le k}c_id_i \ \le \ \sum_{0\le i\le k}c_i(D_i - D_{i-1}) =r_q\,{\mathrm d}({\mathrm L}_n)\sum_{0\le i\le k} \frac{\sqrt{v_{i+1}}-\sqrt{v_{i}}}{1+v_{i}}. \end{align*} $$
Hence, the weighted sum in equation (17) is bounded by
 $$ \begin{align} f(A) & \le \frac{r_q}{m_q}\,e^{\gamma}\,{\mathrm d}({\mathrm L}_n)\sum_{1\le i\le k} \frac{\sqrt{v_{i}}-\sqrt{v_{i-1}}}{1+v_{i-1}}. \end{align} $$
$$ \begin{align} f(A) & \le \frac{r_q}{m_q}\,e^{\gamma}\,{\mathrm d}({\mathrm L}_n)\sum_{1\le i\le k} \frac{\sqrt{v_{i}}-\sqrt{v_{i-1}}}{1+v_{i-1}}. \end{align} $$
As equation (18) holds for any partition
![]() $0=v_0<v_1<\cdots <v_k=1$
, we may set
$0=v_0<v_1<\cdots <v_k=1$
, we may set
![]() $v_i=\frac {i}{k}$
and obtain the corresponding integral,
$v_i=\frac {i}{k}$
and obtain the corresponding integral,
 $$ \begin{align*} \lim_{k\to\infty}\sum_{1\le i\le k} \frac{\sqrt{v_i}-\sqrt{v_{i-1}}}{1+v_{i-1}} = \lim_{k\to\infty}\sum_{1\le i\le k}\int_{v_{i-1}}^{v_i} \frac{\mathrm{d}}{\mathrm{d} v}\Big[\sqrt{v}\Big]\frac{\mathrm{d}{v}}{1+v_{i-1}} = \int_0^1 \frac{\mathrm{d}{v}}{2\sqrt{v}(1+v)} = \frac{\pi}{4}. \end{align*} $$
$$ \begin{align*} \lim_{k\to\infty}\sum_{1\le i\le k} \frac{\sqrt{v_i}-\sqrt{v_{i-1}}}{1+v_{i-1}} = \lim_{k\to\infty}\sum_{1\le i\le k}\int_{v_{i-1}}^{v_i} \frac{\mathrm{d}}{\mathrm{d} v}\Big[\sqrt{v}\Big]\frac{\mathrm{d}{v}}{1+v_{i-1}} = \int_0^1 \frac{\mathrm{d}{v}}{2\sqrt{v}(1+v)} = \frac{\pi}{4}. \end{align*} $$
Hence, we conclude
![]() $f(A) \le \frac {\pi }{4}\,\frac {r_q}{m_q}\,e^{\gamma }\,{\mathrm d}({\mathrm L}_n)$
as desired.
$f(A) \le \frac {\pi }{4}\,\frac {r_q}{m_q}\,e^{\gamma }\,{\mathrm d}({\mathrm L}_n)$
as desired.
We illustrate the value of these bounds by deducing Theorem 1.3 in quantitative form.
Corollary 4.3. Let A be a primitive set, and take an odd prime p. If
![]() $p\notin A$
, then we have
$p\notin A$
, then we have
![]() $f(A_p) <.901\,f(p)$
, and moreover
$f(A_p) <.901\,f(p)$
, and moreover
![]() $f(A_p) \le (\frac {\pi }{4}+o(1))f(p)$
as
$f(A_p) \le (\frac {\pi }{4}+o(1))f(p)$
as
![]() $p\to \infty $
. In addition, if
$p\to \infty $
. In addition, if
![]() $p>23$
and
$p>23$
and
![]() $2p\notin A$
, then
$2p\notin A$
, then
![]() $f(A_{2p}) < f(2p)$
.
$f(A_{2p}) < f(2p)$
.
Proof. For an odd prime q, define
![]() $b_q:=\frac {\pi }{4}\frac {M_q}{m_q^2}\mu _q$
. Then Proposition 4.2 shows that if
$b_q:=\frac {\pi }{4}\frac {M_q}{m_q^2}\mu _q$
. Then Proposition 4.2 shows that if
![]() $n\notin A$
we have
$n\notin A$
we have
 $$ \begin{align*} f(A_n) \le \frac{\pi}{4}\frac{M_q}{m_q^2}e^{\gamma} {\mathrm d}({\mathrm L}_n) = \frac{q}{n}\,b_q f(q) \end{align*} $$
$$ \begin{align*} f(A_n) \le \frac{\pi}{4}\frac{M_q}{m_q^2}e^{\gamma} {\mathrm d}({\mathrm L}_n) = \frac{q}{n}\,b_q f(q) \end{align*} $$
with
![]() $q=P(n)\ge 3$
, recalling
$q=P(n)\ge 3$
, recalling
![]() ${\mathrm d}({\mathrm L}_n) = \frac {q}{n}{\mathrm d}({\mathrm L}_q)$
and equation (9). In particular for
${\mathrm d}({\mathrm L}_n) = \frac {q}{n}{\mathrm d}({\mathrm L}_q)$
and equation (9). In particular for
![]() $n=q,2q$
, we have
$n=q,2q$
, we have
![]() $f(A_q)\le b_qf(q)$
and
$f(A_q)\le b_qf(q)$
and
![]() $f(A_{2q})\le \frac {1}{2}b_qf(q)$
. Note
$f(A_{2q})\le \frac {1}{2}b_qf(q)$
. Note
![]() $\mu _q,m_q,M_q\sim 1$
implies
$\mu _q,m_q,M_q\sim 1$
implies
![]() $b_q \sim \frac {\pi }{4}$
as claimed. Also, the first few values of
$b_q \sim \frac {\pi }{4}$
as claimed. Also, the first few values of
![]() $b_q$
are displayed below.
$b_q$
are displayed below.

Observe for
![]() $q>7$
, we have
$q>7$
, we have
 $$ \begin{align*} f(A_q) \le \frac{\pi}{4} \Big(\frac{M_q}{m_{11}}\Big)^2 f(q) \le \frac{\pi}{4} \Big(\frac{1+1/2\log(2\cdot 10^9)^2}{\mu_{19}}\Big)^2 f(q) < .879 f(q). \end{align*} $$
$$ \begin{align*} f(A_q) \le \frac{\pi}{4} \Big(\frac{M_q}{m_{11}}\Big)^2 f(q) \le \frac{\pi}{4} \Big(\frac{1+1/2\log(2\cdot 10^9)^2}{\mu_{19}}\Big)^2 f(q) < .879 f(q). \end{align*} $$
In particular, with the table, we see
![]() $f(A_q) < .901 f(q)$
for all
$f(A_q) < .901 f(q)$
for all
![]() $q>2$
as claimed.
$q>2$
as claimed.
Finally, we note
![]() $f(A_{2q}) < f(2q)$
whenever
$f(A_{2q}) < f(2q)$
whenever
![]() $b_q < \frac {\log q}{\log (2q)}$
. The result then follows since
$b_q < \frac {\log q}{\log (2q)}$
. The result then follows since
 $$ \begin{align} b_q = \frac{\pi}{4}\frac{M_q}{m_q^2} \mu_q \> \ \frac{\log q}{\log(2q)} \quad\qquad\text{iff} \quad q\le 23. \end{align} $$
$$ \begin{align} b_q = \frac{\pi}{4}\frac{M_q}{m_q^2} \mu_q \> \ \frac{\log q}{\log(2q)} \quad\qquad\text{iff} \quad q\le 23. \end{align} $$
Indeed, this may be checked directly for
![]() $q< 47$
. And for
$q< 47$
. And for
![]() $q\ge 47$
we observe that
$q\ge 47$
we observe that
![]() $\log q/\log (2q)\ge \log 47/\log 94\ge .847$
exceeds
$\log q/\log (2q)\ge \log 47/\log 94\ge .847$
exceeds
![]() $b_q \le \frac {\pi }{4}(M_{2\cdot 10^9}/m_{47})^2 \le .834$
.
$b_q \le \frac {\pi }{4}(M_{2\cdot 10^9}/m_{47})^2 \le .834$
.
Importantly,
![]() $b_q<1$
for all odd q, which means every odd prime is Erdős strong. However, it remains an open question whether
$b_q<1$
for all odd q, which means every odd prime is Erdős strong. However, it remains an open question whether
![]() $q=2$
is Erdős strong. Now, if
$q=2$
is Erdős strong. Now, if
![]() $2\in A$
we immediately deduce
$2\in A$
we immediately deduce
![]() $f(A) \le f(\mathcal P)=1.6366\cdots $
. Thus, to complete the proof of Theorem 1.2, it suffices to assume
$f(A) \le f(\mathcal P)=1.6366\cdots $
. Thus, to complete the proof of Theorem 1.2, it suffices to assume
![]() $2\notin A$
.
$2\notin A$
.
We achieve this in the result below. The argument is somewhat similar in spirit to that of Theorem 1.1 and Lemma 2.4 in [Reference Lichtman and Pomerance27].
Theorem 4.4. For any primitive set A with
![]() $2\notin A$
, we have
$2\notin A$
, we have
![]() $f(A) < 1.60$
.
$f(A) < 1.60$
.
Proof. As
![]() $2\notin A$
, denote by
$2\notin A$
, denote by
![]() $K\ge 2$
the exponent for which
$K\ge 2$
the exponent for which
![]() $2^K \in A$
. Note K is unique by primitivity (Also, if
$2^K \in A$
. Note K is unique by primitivity (Also, if
![]() $2^k\notin A$
for all k let
$2^k\notin A$
for all k let
![]() $K=\infty $
, in which case let
$K=\infty $
, in which case let
![]() $f(2^K)=0$
). Partition A into sets
$f(2^K)=0$
). Partition A into sets
![]() $A^0=\{a\in A : 2\nmid a\}$
and
$A^0=\{a\in A : 2\nmid a\}$
and
![]() $A^k = \{a\in A: 2^k\| a\}$
for
$A^k = \{a\in A: 2^k\| a\}$
for
![]() $k\ge 1$
, and let
$k\ge 1$
, and let
![]() $B^k = \{a/2^{k}: a\in A^k\}$
. We have
$B^k = \{a/2^{k}: a\in A^k\}$
. We have
 $$ \begin{align} f(A) & = f(2^K)+\sum_{p\in A}f(p) +\sum_{p\notin A}f(A_{p}) \nonumber\\ &\le f(2^K) + \sum_{\substack{p>2\\p\in A}} f(p) + \sum_{\substack{p>2\\p\notin A}} b_pf(p) + \sum_{\substack{p>2\\p\notin A}}\sum_{k=1}^{K-1} f((A^k)_{2^k p}), \end{align} $$
$$ \begin{align} f(A) & = f(2^K)+\sum_{p\in A}f(p) +\sum_{p\notin A}f(A_{p}) \nonumber\\ &\le f(2^K) + \sum_{\substack{p>2\\p\in A}} f(p) + \sum_{\substack{p>2\\p\notin A}} b_pf(p) + \sum_{\substack{p>2\\p\notin A}}\sum_{k=1}^{K-1} f((A^k)_{2^k p}), \end{align} $$
since
![]() $f((A^0)_p) \le b_pf(p)$
if
$f((A^0)_p) \le b_pf(p)$
if
![]() $p\notin A$
by Proposition 4.2. More generally, if
$p\notin A$
by Proposition 4.2. More generally, if
![]() $2^kp\notin A$
, then
$2^kp\notin A$
, then
By comparison, if
![]() $2^kp\in A$
, then
$2^kp\in A$
, then
![]() $f((A^k)_{2^k p}) = f(2^kp) \le 2^{-k}f(p)\frac {\log p}{\log (2p)}$
.
$f((A^k)_{2^k p}) = f(2^kp) \le 2^{-k}f(p)\frac {\log p}{\log (2p)}$
.
Observe that either
![]() $2^kp\notin A$
for all
$2^kp\notin A$
for all
![]() $k\ge 1$
, or
$k\ge 1$
, or
![]() $2^Jp\in A$
for a (unique)
$2^Jp\in A$
for a (unique)
![]() $J=J_p\in [1,K)$
, in which case
$J=J_p\in [1,K)$
, in which case
![]() $(A^k)_{2^k p}=\emptyset $
for all
$(A^k)_{2^k p}=\emptyset $
for all
![]() $k>J$
by primitivity. Thus, by equation (19), it suffices to assume
$k>J$
by primitivity. Thus, by equation (19), it suffices to assume
![]() $2^kp\notin A$
for all
$2^kp\notin A$
for all
![]() $k\ge 1$
when
$k\ge 1$
when
![]() $p\le 23$
, and
$p\le 23$
, and
![]() $2^Jp\in A$
for some
$2^Jp\in A$
for some
![]() $J\in [1,K)$
when
$J\in [1,K)$
when
![]() $p> 23$
, so
$p> 23$
, so
 $$ \begin{align*} \sum_{\substack{p>2\\ p\notin A}}\sum_{k=1}^{K-1} f((A^k)_{2^k p}) & \le (1-2^{1-K})\sum_{\substack{2<p\le 23\\ p\notin A}} b_pf(p) + \sum_{\substack{p>23\\ p\notin A}}f(p)\Big((1-2^{1-J})b_p + 2^{-J}\frac{\log p}{\log(2p)} \Big)\\ & \le (1-2^{1-K})\sum_{\substack{2<p\le 23\\ p\notin A}} b_pf(p) + \sum_{\substack{p>23\\ p\notin A}}b_p f(p), \end{align*} $$
$$ \begin{align*} \sum_{\substack{p>2\\ p\notin A}}\sum_{k=1}^{K-1} f((A^k)_{2^k p}) & \le (1-2^{1-K})\sum_{\substack{2<p\le 23\\ p\notin A}} b_pf(p) + \sum_{\substack{p>23\\ p\notin A}}f(p)\Big((1-2^{1-J})b_p + 2^{-J}\frac{\log p}{\log(2p)} \Big)\\ & \le (1-2^{1-K})\sum_{\substack{2<p\le 23\\ p\notin A}} b_pf(p) + \sum_{\substack{p>23\\ p\notin A}}b_p f(p), \end{align*} $$
since
![]() $2b_p> 1 > \frac {\log p}{\log (2p)}$
for all
$2b_p> 1 > \frac {\log p}{\log (2p)}$
for all
![]() $p>2$
. Moreover,
$p>2$
. Moreover,
![]() $(2-2^{1-K})b_p \ge (2-1/2)\frac {\pi }{4}> 1.1$
, so equation (20) becomes
$(2-2^{1-K})b_p \ge (2-1/2)\frac {\pi }{4}> 1.1$
, so equation (20) becomes
 $$ \begin{align} f(A) & \le f(2^K) + \sum_{\substack{p>2\\p\in A}} f(p) + (2-2^{1-K})\sum_{\substack{2<p\le 23\\p\notin A}} b_pf(p) + 2\sum_{\substack{p>23\\p\notin A}}b_p f(p) \nonumber\\ & \le f(2^K) + (2-2^{1-K})\sum_{2<p\le 23} b_pf(p) + 2\sum_{p>23}b_p f(p)\nonumber\\ & =: \ f(2^K) + (2-2^{1-K})C_1 + 2C_2. \end{align} $$
$$ \begin{align} f(A) & \le f(2^K) + \sum_{\substack{p>2\\p\in A}} f(p) + (2-2^{1-K})\sum_{\substack{2<p\le 23\\p\notin A}} b_pf(p) + 2\sum_{\substack{p>23\\p\notin A}}b_p f(p) \nonumber\\ & \le f(2^K) + (2-2^{1-K})\sum_{2<p\le 23} b_pf(p) + 2\sum_{p>23}b_p f(p)\nonumber\\ & =: \ f(2^K) + (2-2^{1-K})C_1 + 2C_2. \end{align} $$
Now, we compute the constants
![]() $C_1,C_2$
. First, let
$C_1,C_2$
. First, let
![]() $M=M_{2\cdot 10^9}=1.001\cdots $
. Recalling
$M=M_{2\cdot 10^9}=1.001\cdots $
. Recalling
![]() $\mu _p f(p) = e^{\gamma } {\mathrm d}({\mathrm L}_p)$
,
$\mu _p f(p) = e^{\gamma } {\mathrm d}({\mathrm L}_p)$
,
 $$ \begin{align} C_2 :=\sum_{p>23}b_p f(p) = \frac{\pi}{4} e^{\gamma} \sum_{p> 23}\frac{M_p}{m_p^2}{\mathrm d}({\mathrm L}_p) \le \frac{\pi}{4}\frac{Me^{\gamma}}{\mu_{23}^2} \prod_{p\le 23}\big(1-\tfrac{1}{p}\big) = 0.251135\cdots, \end{align} $$
$$ \begin{align} C_2 :=\sum_{p>23}b_p f(p) = \frac{\pi}{4} e^{\gamma} \sum_{p> 23}\frac{M_p}{m_p^2}{\mathrm d}({\mathrm L}_p) \le \frac{\pi}{4}\frac{Me^{\gamma}}{\mu_{23}^2} \prod_{p\le 23}\big(1-\tfrac{1}{p}\big) = 0.251135\cdots, \end{align} $$
since
![]() $\sum _{p> q}{\mathrm d}({\mathrm L}_{p}) = \prod _{p\le q}(1-\frac {1}{p})$
. Similarly, we have
$\sum _{p> q}{\mathrm d}({\mathrm L}_{p}) = \prod _{p\le q}(1-\frac {1}{p})$
. Similarly, we have
 $$ \begin{align} C_1 :=\sum_{2<p\le 23}b_p f(p)= \sum_{2< p\le 23} \frac{\pi}{4}\frac{M}{m_p^2} e^{\gamma}{\mathrm d}({\mathrm L}_p) = \frac{\pi}{4}\,M e^{\gamma}\cdot 0.39012\cdots = 0.5463\cdots \end{align} $$
$$ \begin{align} C_1 :=\sum_{2<p\le 23}b_p f(p)= \sum_{2< p\le 23} \frac{\pi}{4}\frac{M}{m_p^2} e^{\gamma}{\mathrm d}({\mathrm L}_p) = \frac{\pi}{4}\,M e^{\gamma}\cdot 0.39012\cdots = 0.5463\cdots \end{align} $$
Here, we computed
 $$ \begin{align*} \sum_{2< p\le 23} \frac{1}{m_p^2} {\mathrm d}({\mathrm L}_{p}) & = \frac{1}{\mu_7^2}\sum_{2< p\le 7}{\mathrm d}({\mathrm L}_{p}) + \frac{1}{\mu_{19}^2}\sum_{7< p\le 19}{\mathrm d}({\mathrm L}_{p}) + \frac{1}{\mu_{23}^2} {\mathrm d}({\mathrm L}_{23}) = 0.390126\cdots, \end{align*} $$
$$ \begin{align*} \sum_{2< p\le 23} \frac{1}{m_p^2} {\mathrm d}({\mathrm L}_{p}) & = \frac{1}{\mu_7^2}\sum_{2< p\le 7}{\mathrm d}({\mathrm L}_{p}) + \frac{1}{\mu_{19}^2}\sum_{7< p\le 19}{\mathrm d}({\mathrm L}_{p}) + \frac{1}{\mu_{23}^2} {\mathrm d}({\mathrm L}_{23}) = 0.390126\cdots, \end{align*} $$
using
![]() $\sum _{q< p\le q'}{\mathrm d}({\mathrm L}_{p}) = \prod _{p\le q}(1-\frac {1}{p})-\prod _{p\le q'}(1-\frac {1}{p})$
.
$\sum _{q< p\le q'}{\mathrm d}({\mathrm L}_{p}) = \prod _{p\le q}(1-\frac {1}{p})-\prod _{p\le q'}(1-\frac {1}{p})$
.
Hence, plugging equations (22) and (23) back into equation (21),
 $$ \begin{align} f(A) & \le f(2^K) + (2-2^{1-K})C_1 + 2C_2 \nonumber\\ & \le 2^{-K}\Big(\frac{1}{\log 4} - 2C_1\Big) + 2(C_1 + C_2) \le 2(C_1 + C_2) \le 1.595. \end{align} $$
$$ \begin{align} f(A) & \le f(2^K) + (2-2^{1-K})C_1 + 2C_2 \nonumber\\ & \le 2^{-K}\Big(\frac{1}{\log 4} - 2C_1\Big) + 2(C_1 + C_2) \le 2(C_1 + C_2) \le 1.595. \end{align} $$
Here, we used
![]() $2C_1> .722 > 1/\log 4$
. This completes the proof.
$2C_1> .722 > 1/\log 4$
. This completes the proof.
Remark 4.5. A similar argument as in Theorem 4.4 shows
![]() $f(A_2) < C_1+C_2 < 0.80$
when
$f(A_2) < C_1+C_2 < 0.80$
when
![]() $2\notin A$
. We leave this to the interested reader. Note this bound improves on
$2\notin A$
. We leave this to the interested reader. Note this bound improves on
![]() $f(A_2) < e^{\gamma }/2\approx 0.89$
from [Reference Lichtman and Pomerance27, Proposition 2.1] but unfortunately still exceeds
$f(A_2) < e^{\gamma }/2\approx 0.89$
from [Reference Lichtman and Pomerance27, Proposition 2.1] but unfortunately still exceeds
![]() $f(2) \approx 0.72$
.
$f(2) \approx 0.72$
.
4.1 Proof of Theorem 1.5
Take
![]() ${\epsilon }>0$
. We shall introduce large parameters
${\epsilon }>0$
. We shall introduce large parameters
![]() $y=y_{\epsilon }$
,
$y=y_{\epsilon }$
,
![]() $k=k_{{\epsilon },y}$
and
$k=k_{{\epsilon },y}$
and
![]() $x=x_{{\epsilon },k}$
.
$x=x_{{\epsilon },k}$
.
By Lemma 2.3, we have
![]() $f(A_n) \le e^{\gamma }{\mathrm d}({\mathrm L}_n)$
for any integer
$f(A_n) \le e^{\gamma }{\mathrm d}({\mathrm L}_n)$
for any integer
![]() $n\notin A$
,
$n\notin A$
,
![]() $n>1$
and when
$n>1$
and when
![]() $y=y_{\epsilon }\in {\mathbb R}$
is sufficiently large by Proposition 4.2 we have the sharper bound
$y=y_{\epsilon }\in {\mathbb R}$
is sufficiently large by Proposition 4.2 we have the sharper bound
Next, by [?, Lemma 2], for
![]() $k=k_{{\epsilon }}=k_{{\epsilon },y}\in {\mathbb N}$
sufficiently large,
$k=k_{{\epsilon }}=k_{{\epsilon },y}\in {\mathbb N}$
sufficiently large,
 $$ \begin{align} \sum_{\substack{n\in {\mathbb N}_{k}\\P(n)\le y}}{\mathrm d}({\mathrm L}_n) \ll \frac{1}{k}\sum_{\substack{\Omega(n)=k\\P(n)\le y}}\frac{1}{n} \ll (\log y)^2\,2^{-k} < {\epsilon}. \end{align} $$
$$ \begin{align} \sum_{\substack{n\in {\mathbb N}_{k}\\P(n)\le y}}{\mathrm d}({\mathrm L}_n) \ll \frac{1}{k}\sum_{\substack{\Omega(n)=k\\P(n)\le y}}\frac{1}{n} \ll (\log y)^2\,2^{-k} < {\epsilon}. \end{align} $$
Finally, since
![]() $f({\mathbb N}_j)<2$
crudely for all j there exists
$f({\mathbb N}_j)<2$
crudely for all j there exists
![]() $x=x_{{\epsilon },k}\in {\mathbb R}$
sufficiently large so that
$x=x_{{\epsilon },k}\in {\mathbb R}$
sufficiently large so that
![]() $f\big (\bigcup _{j \le k}{\mathbb N}_j\cap [x,\infty )\big )<{\epsilon }$
.
$f\big (\bigcup _{j \le k}{\mathbb N}_j\cap [x,\infty )\big )<{\epsilon }$
.
Now, take a primitive set
![]() $A\subset [x,\infty )$
, and consider the partition
$A\subset [x,\infty )$
, and consider the partition
![]() $A = A'\cup \bigcup _{n\in {\mathbb N}_k \setminus A}A_n$
, where
$A = A'\cup \bigcup _{n\in {\mathbb N}_k \setminus A}A_n$
, where
![]() $A'$
consists of elements
$A'$
consists of elements
![]() $a\in A$
with at most k prime factors, and each other element
$a\in A$
with at most k prime factors, and each other element
![]() $a\in A$
(with at least
$a\in A$
(with at least
![]() $k+1$
prime factors) then lies in
$k+1$
prime factors) then lies in
![]() $A_n=A\cap {\mathrm L}_n$
, where
$A_n=A\cap {\mathrm L}_n$
, where
![]() $n\notin A$
is the product of the smallest k primes of a. Hence, we conclude
$n\notin A$
is the product of the smallest k primes of a. Hence, we conclude
 $$ \begin{align*} f(A) & = f(A') + \sum_{\substack{n\in {\mathbb N}_{k}\setminus A}}f(A_n)\\ & \le f\big(\bigcup_{j \le k}{\mathbb N}_j\cap [x,\infty)\big) + \sum_{\substack{n\in {\mathbb N}_{k}\setminus A\\P(n)\le y}}f(A_n)+ \sum_{\substack{n\in {\mathbb N}_{k}\setminus A\\P(n)> y}}f(A_n)\\ & \le {\epsilon} + e^{\gamma}\sum_{\substack{n\in {\mathbb N}_{k}\\P(n)\le y}}{\mathrm d}({\mathrm L}_n)+ (\frac{\pi}{4}e^{\gamma} + {\epsilon})\sum_{\substack{n\in {\mathbb N}_{k}\\P(n)>y}}{\mathrm d}({\mathrm L}_n) \ \le \ {\epsilon} + e^{\gamma}\,{\epsilon}+ (\frac{\pi}{4}e^{\gamma} + {\epsilon}), \end{align*} $$
$$ \begin{align*} f(A) & = f(A') + \sum_{\substack{n\in {\mathbb N}_{k}\setminus A}}f(A_n)\\ & \le f\big(\bigcup_{j \le k}{\mathbb N}_j\cap [x,\infty)\big) + \sum_{\substack{n\in {\mathbb N}_{k}\setminus A\\P(n)\le y}}f(A_n)+ \sum_{\substack{n\in {\mathbb N}_{k}\setminus A\\P(n)> y}}f(A_n)\\ & \le {\epsilon} + e^{\gamma}\sum_{\substack{n\in {\mathbb N}_{k}\\P(n)\le y}}{\mathrm d}({\mathrm L}_n)+ (\frac{\pi}{4}e^{\gamma} + {\epsilon})\sum_{\substack{n\in {\mathbb N}_{k}\\P(n)>y}}{\mathrm d}({\mathrm L}_n) \ \le \ {\epsilon} + e^{\gamma}\,{\epsilon}+ (\frac{\pi}{4}e^{\gamma} + {\epsilon}), \end{align*} $$
by equations (25) and (26) and noting
![]() $\sum _{n\in {\mathbb N}_{k}, P(n)>y}{\mathrm d}({\mathrm L}_n) \le 1$
. Hence, letting
$\sum _{n\in {\mathbb N}_{k}, P(n)>y}{\mathrm d}({\mathrm L}_n) \le 1$
. Hence, letting
![]() ${\epsilon }\to 0$
completes the proof of Theorem 1.5.
${\epsilon }\to 0$
completes the proof of Theorem 1.5.
5 L-primitive sets revisited
5.1 Upper density
As mentioned in the introduction, one of the striking early results in the study of primitive sets was due to Besicovitch [Reference Besicovitch5], who showed
 $$ \begin{align*} \sup_{A\text{ primitive}}\overline{{\mathrm d}}(A) \;=\; \frac{1}{2}. \end{align*} $$
$$ \begin{align*} \sup_{A\text{ primitive}}\overline{{\mathrm d}}(A) \;=\; \frac{1}{2}. \end{align*} $$
This came as quite a surprise at the time, in particular disproving a conjecture of Davenport. We shall extend this phenomenon further to L-primitive sets, in Proposition 5.2.
To proceed, we recall a result of Erdős [Reference Erdős14], which bounds the density of the set of multiples of an interval. Also, see Hall–Tenenbaum [Reference Hall and Tenenbaum22, Theorem 21] for quantitatively stronger results. Denote the set of (all) multiples of
![]() $A\subset {\mathbb N}$
as
$A\subset {\mathbb N}$
as
![]() ${\mathrm M}_A = \{na : n\in {\mathbb N}, a\in A\}$
.
${\mathrm M}_A = \{na : n\in {\mathbb N}, a\in A\}$
.
Proposition 5.1 (Erdős, 1936).
Let
![]() $\varepsilon (x)$
be any function with
$\varepsilon (x)$
be any function with
![]() $\varepsilon (x)\to 0$
as
$\varepsilon (x)\to 0$
as
![]() $x\to \infty $
. Then the upper density of
$x\to \infty $
. Then the upper density of
![]() ${\mathrm M}_{(x^{1-\varepsilon (x)},x]}$
tends to zero as
${\mathrm M}_{(x^{1-\varepsilon (x)},x]}$
tends to zero as
![]() $x\to \infty $
.
$x\to \infty $
.
We prove a Besicovitch-type result for L-primitive sets, notably with full upper density.
Proposition 5.2. We have
![]() $\sup _A \overline {\mathrm d}(A) = 1$
over L-primitive sets A.
$\sup _A \overline {\mathrm d}(A) = 1$
over L-primitive sets A.
Proof. Take
![]() $h\in {\mathbb Z}_{>1}$
,
$h\in {\mathbb Z}_{>1}$
,
![]() ${\epsilon }>0$
, and let
${\epsilon }>0$
, and let
![]() $S = \{n\in {\mathbb N} : P(n)\le h\}$
be the set of h-smooth numbers. For a sequence of indices
$S = \{n\in {\mathbb N} : P(n)\le h\}$
be the set of h-smooth numbers. For a sequence of indices
![]() $k_1,k_2,\ldots $
to be determined, define intervals
$k_1,k_2,\ldots $
to be determined, define intervals
![]() $I_i = (h^{k_i-1}, h^{k_i}]$
. Let
$I_i = (h^{k_i-1}, h^{k_i}]$
. Let
![]() $S_i:=I_i\setminus S$
, and note for
$S_i:=I_i\setminus S$
, and note for
![]() $a\in S_i$
and
$a\in S_i$
and
![]() $n\in {\mathrm L}_a$
we have
$n\in {\mathrm L}_a$
we have
![]() $n\ge P(a)a>h^{k_i}$
, so
$n\ge P(a)a>h^{k_i}$
, so
![]() $n\notin I_i\supset S_i$
. In particular,
$n\notin I_i\supset S_i$
. In particular,
![]() $a'\notin {\mathrm L}_a$
for distinct
$a'\notin {\mathrm L}_a$
for distinct
![]() $a,a'\in S_i$
, so each set
$a,a'\in S_i$
, so each set
![]() $S_i$
is L-primitive. Now, define the L-primitive set
$S_i$
is L-primitive. Now, define the L-primitive set
 $$ \begin{align} A = \bigcup_{j\ge1}\bigg(S_j\setminus\bigcup_{1\le i<j}{\mathrm M}_{I_i}\bigg). \end{align} $$
$$ \begin{align} A = \bigcup_{j\ge1}\bigg(S_j\setminus\bigcup_{1\le i<j}{\mathrm M}_{I_i}\bigg). \end{align} $$
Note for each fixed
![]() $h>1$
the set S has zero density, so
$h>1$
the set S has zero density, so
![]() $|S\cap [1,x]| < \epsilon x$
for
$|S\cap [1,x]| < \epsilon x$
for
![]() $x\ge x_{h,\epsilon }$
sufficiently large. Also, by Proposition 5.1 we see
$x\ge x_{h,\epsilon }$
sufficiently large. Also, by Proposition 5.1 we see
![]() $\overline {\mathrm d}({\mathrm M}_{(x/h,x]})\to 0$
as
$\overline {\mathrm d}({\mathrm M}_{(x/h,x]})\to 0$
as
![]() $x\to \infty $
. So for
$x\to \infty $
. So for
![]() $k_i$
large enough, we may assume
$k_i$
large enough, we may assume
![]() $\overline {\mathrm d}({\mathrm M}_{I_i}) < {\epsilon }/2^i$
.
$\overline {\mathrm d}({\mathrm M}_{I_i}) < {\epsilon }/2^i$
.
For each i, the set of multiples
![]() ${\mathrm M}_{I_{i}}$
is a periodic set with period (dividing)
${\mathrm M}_{I_{i}}$
is a periodic set with period (dividing)
![]() $(h^{k_i})!$
. So assuming
$(h^{k_i})!$
. So assuming
![]() $k_{i+1} \ge (h^{k_{i}})!$
the relative density of
$k_{i+1} \ge (h^{k_{i}})!$
the relative density of
![]() ${\mathrm M}_{I_i}$
inside
${\mathrm M}_{I_i}$
inside
![]() $I_{i+1}$
is at most
$I_{i+1}$
is at most
![]() $2\overline {\mathrm d}({\mathrm M}_{I_i})$
. Hence,
$2\overline {\mathrm d}({\mathrm M}_{I_i})$
. Hence,
 $$ \begin{align*} |A\cap [1,h^{k_j}]| &\ge |I_j| - \big|S\cap [1,h^{k_j}]\big| - 2h^{k_j}\sum_{1\le i<j}\overline{\mathrm d}({\mathrm M}_{I_i})\\ &\ge (h^{k_j}-h^{k_j-1}) - \epsilon h^{k_j} - 2{\epsilon} h^{k_j}\sum_{i\ge1}2^{-i}. \end{align*} $$
$$ \begin{align*} |A\cap [1,h^{k_j}]| &\ge |I_j| - \big|S\cap [1,h^{k_j}]\big| - 2h^{k_j}\sum_{1\le i<j}\overline{\mathrm d}({\mathrm M}_{I_i})\\ &\ge (h^{k_j}-h^{k_j-1}) - \epsilon h^{k_j} - 2{\epsilon} h^{k_j}\sum_{i\ge1}2^{-i}. \end{align*} $$
Thus, dividing by
![]() $x=h^{k_j}$
we see
$x=h^{k_j}$
we see
![]() $\overline {\mathrm d}(A)=\limsup _{x\to \infty }|A\cap [1,x]|/x \ge 1 - 1/h - 3{\epsilon }$
. Taking
$\overline {\mathrm d}(A)=\limsup _{x\to \infty }|A\cap [1,x]|/x \ge 1 - 1/h - 3{\epsilon }$
. Taking
![]() $h\to \infty $
and
$h\to \infty $
and
![]() ${\epsilon }\to 0$
completes the proof.
${\epsilon }\to 0$
completes the proof.
5.2 The Erdős L-primitive set conjecture
Sets of L-multiples play a central role in our proof of Theorem 1.2, as the mathematical structures arising from a probabilistic interpretation of equation (4),Footnote
6
and implicit in the original 1935 argument of Erdős [Reference Erdős13].Footnote
7
As such, it is natural to pose the L-primitive analogue of Conjecture 1.1, namely that
![]() $f(A) \le f(\mathcal P)$
for all L-primitive sets A.
$f(A) \le f(\mathcal P)$
for all L-primitive sets A.
However, this conjecture turns out to be false.
Proposition 5.3. We have
 $$ \begin{align} \sup_{A\mathrm{ L-primitive}} f(A) \ &= \ \sum_p\max\{f(p),e^{\gamma}{\mathrm d}({\mathrm L}_p)\}, \quad \text{and} \qquad \lim_{x\to\infty}\sup_{\substack{A\subset [x,\infty)\\ A\mathrm{ L-primitive}}} f(A) \ = \ e^{\gamma}. \end{align} $$
$$ \begin{align} \sup_{A\mathrm{ L-primitive}} f(A) \ &= \ \sum_p\max\{f(p),e^{\gamma}{\mathrm d}({\mathrm L}_p)\}, \quad \text{and} \qquad \lim_{x\to\infty}\sup_{\substack{A\subset [x,\infty)\\ A\mathrm{ L-primitive}}} f(A) \ = \ e^{\gamma}. \end{align} $$
Note the prime sum in equation (28) above is at least (and well approximated by)
![]() $f(\mathcal P)-f(2) + e^{\gamma }/2 \approx 1.805$
. In particular, it exceeds
$f(\mathcal P)-f(2) + e^{\gamma }/2 \approx 1.805$
. In particular, it exceeds
![]() $f(\mathcal P) \approx 1.636$
. As such, Proposition 5.3, along with Conjecture 7.1 and related work in the literature, highlights how the Erdős primitive set conjecture is quite fragile under certain seemingly natural directions of generalization.
$f(\mathcal P) \approx 1.636$
. As such, Proposition 5.3, along with Conjecture 7.1 and related work in the literature, highlights how the Erdős primitive set conjecture is quite fragile under certain seemingly natural directions of generalization.
We now proceed to set up the proof of Proposition 5.3. First, the trichotomy in Lemma 2.1 leads to the following.
Lemma 5.4. Every set
![]() $S\subset {\mathbb N}$
has a unique L-primitive subset
$S\subset {\mathbb N}$
has a unique L-primitive subset
![]() $\langle S\rangle $
with
$\langle S\rangle $
with
![]() $\mathrm {L}_{\langle S\rangle } = {\mathrm L}_S$
. In particular,
$\mathrm {L}_{\langle S\rangle } = {\mathrm L}_S$
. In particular,
![]() $\langle S\rangle =S$
if S is L-primitive.
$\langle S\rangle =S$
if S is L-primitive.
Proof. For any
![]() $s_1,s_2\in S$
, by Lemma 2.1 either
$s_1,s_2\in S$
, by Lemma 2.1 either
![]() $\mathrm {L}_{s_1}\cap {\mathrm L}_{s_2}=\emptyset $
or
$\mathrm {L}_{s_1}\cap {\mathrm L}_{s_2}=\emptyset $
or
![]() $\mathrm {L}_{s_1}\subset {\mathrm L}_{s_2}$
(or vice versa). Thus, each
$\mathrm {L}_{s_1}\subset {\mathrm L}_{s_2}$
(or vice versa). Thus, each
![]() $s\in S$
has a (unique) smallest L-divisor
$s\in S$
has a (unique) smallest L-divisor
![]() $s'\in S$
, inducing a map
$s'\in S$
, inducing a map
![]() $S\to S:s\mapsto s'$
. We define
$S\to S:s\mapsto s'$
. We define
![]() $\langle S\rangle $
as the image of this map. Explicitly, this is
$\langle S\rangle $
as the image of this map. Explicitly, this is
By minimality,
![]() $\mathrm {L}_{s_1}\cap {\mathrm L}_{s_2}=\emptyset $
for all
$\mathrm {L}_{s_1}\cap {\mathrm L}_{s_2}=\emptyset $
for all
![]() $s_1,s_2\in \langle S\rangle $
, so
$s_1,s_2\in \langle S\rangle $
, so
![]() $\langle S\rangle $
is L-primitive. Moreover,
$\langle S\rangle $
is L-primitive. Moreover,
![]() $\mathrm {L}_S = \bigcup _{s\in S}{\mathrm L}_s = \bigcup _{s'\in \langle S\rangle }{\mathrm L}_{s'} = {\mathrm L}_{\langle S\rangle }$
, where the latter union over
$\mathrm {L}_S = \bigcup _{s\in S}{\mathrm L}_s = \bigcup _{s'\in \langle S\rangle }{\mathrm L}_{s'} = {\mathrm L}_{\langle S\rangle }$
, where the latter union over
![]() $\langle S\rangle $
is disjoint by L-primitivity. This completes the proof.
$\langle S\rangle $
is disjoint by L-primitivity. This completes the proof.
Next, take
![]() $v>0$
,
$v>0$
,
![]() $n\in {\mathbb Z}_{>1}$
, and consider the set
$n\in {\mathbb Z}_{>1}$
, and consider the set
![]() $D_v(n)$
of prime divisors of n whose induced L-divisor is not smooth, that is,
$D_v(n)$
of prime divisors of n whose induced L-divisor is not smooth, that is,
 $$ \begin{align} D_v(n) = \Big\{ p\mid n \; :\, \prod_{q^e\| n, q< p} q^e \ \le \ p^v \Big\}. \end{align} $$
$$ \begin{align} D_v(n) = \Big\{ p\mid n \; :\, \prod_{q^e\| n, q< p} q^e \ \le \ p^v \Big\}. \end{align} $$
We cite the following result of Bovey, based on earlier work of Erdős [Reference Hall and Tenenbaum22, §1.2].
Proposition 5.5 (Bovey, 1977).
For each
![]() $v>0$
, there is a set
$v>0$
, there is a set
![]() $N_v\subset {\mathbb N}$
of full density with
$N_v\subset {\mathbb N}$
of full density with
as
![]() $n\to \infty $
on
$n\to \infty $
on
![]() $N_v$
. Here,
$N_v$
. Here,
![]() $\rho $
is the Dickman–de Bruijn function.
$\rho $
is the Dickman–de Bruijn function.
Remark 5.6. In probability, the right-hand side of equation (31) is called the Dickman distribution.
In particular,
![]() $|D_v(n)|\gg _v \log \log n$
for all
$|D_v(n)|\gg _v \log \log n$
for all
![]() $n\in N_v$
. Now, we may define a map
$n\in N_v$
. Now, we may define a map
![]() $\beta : N_u\to {\mathbb N}$
sending n to its L-divisor
$\beta : N_u\to {\mathbb N}$
sending n to its L-divisor
![]() $\beta (n)=p\prod _{q^e\| n, q< p} q^e$
, for the largest prime
$\beta (n)=p\prod _{q^e\| n, q< p} q^e$
, for the largest prime
![]() $p\in D_v(n)$
.
$p\in D_v(n)$
.
Define the L-primitive generating set
![]() $B(v) := \langle \beta (N_v)\rangle $
as in Lemma 5.4. By construction,
$B(v) := \langle \beta (N_v)\rangle $
as in Lemma 5.4. By construction,
![]() $\mathrm {L}_{B(v)} = {\mathrm L}_{\beta (N_v)} \supset N_u$
has full density. Also, by definition of
$\mathrm {L}_{B(v)} = {\mathrm L}_{\beta (N_v)} \supset N_u$
has full density. Also, by definition of
![]() $\beta , D_v$
,
$\beta , D_v$
,
We are now prepared to establish a local version of Proposition 5.3.
Proposition 5.7. For each prime q, we have
 $$ \begin{align*} \lim_{y\to\infty}\sup_{\substack{A\subset[y,\infty)\\ \mathrm{L-primitive }A\not\ni q}}f(A_q) \ = \ \sup_{\mathrm{L-primitive }A\not\ni q}f(A_q) \ = \ e^{\gamma} {\mathrm d}({\mathrm L}_q). \end{align*} $$
$$ \begin{align*} \lim_{y\to\infty}\sup_{\substack{A\subset[y,\infty)\\ \mathrm{L-primitive }A\not\ni q}}f(A_q) \ = \ \sup_{\mathrm{L-primitive }A\not\ni q}f(A_q) \ = \ e^{\gamma} {\mathrm d}({\mathrm L}_q). \end{align*} $$
Proof. By Lemma 2.3, we have
![]() $f(A_p) < e^{\gamma } {\mathrm d}({\mathrm L}_p)$
for all L-primitive A not containing p. It now suffices to provide L-primitive sets
$f(A_p) < e^{\gamma } {\mathrm d}({\mathrm L}_p)$
for all L-primitive A not containing p. It now suffices to provide L-primitive sets
![]() $B\subset [y,\infty )$
with
$B\subset [y,\infty )$
with
![]() $f(B_q) \to e^{\gamma } {\mathrm d}({\mathrm L}_q)$
as
$f(B_q) \to e^{\gamma } {\mathrm d}({\mathrm L}_q)$
as
![]() $y\to \infty $
.
$y\to \infty $
.
Fix
![]() $v>0$
. The L-primitive set
$v>0$
. The L-primitive set
![]() $B(v)$
in equation (32) satisfies
$B(v)$
in equation (32) satisfies
 $$ \begin{align} f(B(v)_q) = \sum_{b\in B(v)_q}\frac{1}{b\log b} \ & \ge \ \frac{1}{1+v}\sum_{b\in B(v)_q}\frac{1}{b\log P(b)}. \end{align} $$
$$ \begin{align} f(B(v)_q) = \sum_{b\in B(v)_q}\frac{1}{b\log b} \ & \ge \ \frac{1}{1+v}\sum_{b\in B(v)_q}\frac{1}{b\log P(b)}. \end{align} $$
Next, for
![]() $x>e^{e^{e^y}}$
we may assume
$x>e^{e^{e^y}}$
we may assume
![]() $N_v\subset [x,\infty )$
and retain full density. Observe then
$N_v\subset [x,\infty )$
and retain full density. Observe then
![]() $B(v)\subset [y,\infty )$
is our candidate L-primitive set. Indeed, for each
$B(v)\subset [y,\infty )$
is our candidate L-primitive set. Indeed, for each
![]() $n\in N_v$
by construction
$n\in N_v$
by construction
![]() $\beta (n)$
is divisible by all primes
$\beta (n)$
is divisible by all primes
![]() $q\in D_v(n)$
, so
$q\in D_v(n)$
, so
![]() $\beta (n)$
is composite with
$\beta (n)$
is composite with
![]() $\beta (n)\ge |D_v(n)| \gg _v \log \log n \ge \log \log \log x> y$
for each
$\beta (n)\ge |D_v(n)| \gg _v \log \log n \ge \log \log \log x> y$
for each
![]() $b\in B(v)$
, for y sufficiently large. And note Mertens’ product theorem gives
$b\in B(v)$
, for y sufficiently large. And note Mertens’ product theorem gives
 $$ \begin{align*} {\mathrm d}({\mathrm L}_b) = \frac{1}{b}\prod_{p< P(b)}\Big(1-\frac{1}{p}\Big) = \frac{e^{-\gamma}+o_y(1)}{b\log P(b)}. \end{align*} $$
$$ \begin{align*} {\mathrm d}({\mathrm L}_b) = \frac{1}{b}\prod_{p< P(b)}\Big(1-\frac{1}{p}\Big) = \frac{e^{-\gamma}+o_y(1)}{b\log P(b)}. \end{align*} $$
Plugging back into equation (33), we obtain
 $$ \begin{align*} f(B(v)_q) \ge \frac{e^{\gamma}+o_y(1)}{1+v}\sum_{b\in B(v)_q}{\mathrm d}({\mathrm L}_b). \end{align*} $$
$$ \begin{align*} f(B(v)_q) \ge \frac{e^{\gamma}+o_y(1)}{1+v}\sum_{b\in B(v)_q}{\mathrm d}({\mathrm L}_b). \end{align*} $$
Recall
![]() $\mathrm {L}_{B(v)} = {\mathrm L}_{\beta (N_v)} \supset N_v$
has full density, which implies
$\mathrm {L}_{B(v)} = {\mathrm L}_{\beta (N_v)} \supset N_v$
has full density, which implies
![]() $({\mathrm L}_{B(v)})_q={\mathrm L}_{B(v)_q}$
has full relative density
$({\mathrm L}_{B(v)})_q={\mathrm L}_{B(v)_q}$
has full relative density
![]() ${\mathrm d}({\mathrm L}_{B(v)_q}) = {\mathrm d}({\mathrm L}_q)$
. Hence, by Corollary 2.2 this latter sum is
${\mathrm d}({\mathrm L}_{B(v)_q}) = {\mathrm d}({\mathrm L}_q)$
. Hence, by Corollary 2.2 this latter sum is
 $$ \begin{align*} \sum_{b\in B(v)_q}{\mathrm d}({\mathrm L}_b) = {\mathrm d}({\mathrm L}_{B(v)_q}) = {\mathrm d}({\mathrm L}_q). \end{align*} $$
$$ \begin{align*} \sum_{b\in B(v)_q}{\mathrm d}({\mathrm L}_b) = {\mathrm d}({\mathrm L}_{B(v)_q}) = {\mathrm d}({\mathrm L}_q). \end{align*} $$
Thus, taking
![]() $y\to \infty $
and
$y\to \infty $
and
![]() $v\to 0$
gives
$v\to 0$
gives
![]() $f(B(v)_q)\to e^{\gamma }{\mathrm d}({\mathrm L}_q)$
as desired.
$f(B(v)_q)\to e^{\gamma }{\mathrm d}({\mathrm L}_q)$
as desired.
Proof of Proposition 5.3.
Take L-primitive
![]() $A\subset [x,\infty )$
, so
$A\subset [x,\infty )$
, so
![]() $p\ge x$
for all
$p\ge x$
for all
![]() $p\in A$
. Then by Lemma 2.3,
$p\in A$
. Then by Lemma 2.3,
 $$ \begin{align*} f(A) = \sum_p f(A_p) & = \sum_{\substack{p< x\\\text{or }p\notin A}} f(A_p) + \sum_{p\in A, p\ge x}f(p)\\ & \le e^{\gamma}\sum_{\substack{p< x\\\text{or }p\notin A}} {\mathrm d}({\mathrm L}_p) + \sum_{p\in A, p\ge x}f(p)\\ & \le e^{\gamma}\sum_{p} {\mathrm d}({\mathrm L}_p) + \big(e^{\gamma}+o_x(1)\big)\sum_{p\ge x}{\mathrm d}({\mathrm L}_p) \ \le \ e^{\gamma}+o_x(1) \end{align*} $$
$$ \begin{align*} f(A) = \sum_p f(A_p) & = \sum_{\substack{p< x\\\text{or }p\notin A}} f(A_p) + \sum_{p\in A, p\ge x}f(p)\\ & \le e^{\gamma}\sum_{\substack{p< x\\\text{or }p\notin A}} {\mathrm d}({\mathrm L}_p) + \sum_{p\in A, p\ge x}f(p)\\ & \le e^{\gamma}\sum_{p} {\mathrm d}({\mathrm L}_p) + \big(e^{\gamma}+o_x(1)\big)\sum_{p\ge x}{\mathrm d}({\mathrm L}_p) \ \le \ e^{\gamma}+o_x(1) \end{align*} $$
by Mertens’ theorem, and noting
![]() $\sum _p {\mathrm d}({\mathrm L}_p)=1$
. Thus,
$\sum _p {\mathrm d}({\mathrm L}_p)=1$
. Thus,
![]() $\lim _x\sup _{A\subset [x,\infty )}f(A) \le e^{\gamma }$
. Equality in the limsup holds for the choice of
$\lim _x\sup _{A\subset [x,\infty )}f(A) \le e^{\gamma }$
. Equality in the limsup holds for the choice of
![]() $B = \bigcup _{q} B(v)_q$
and taking
$B = \bigcup _{q} B(v)_q$
and taking
![]() $v\to 0$
as in Proposition 5.7. Observe such B inherits L-primitivity from the
$v\to 0$
as in Proposition 5.7. Observe such B inherits L-primitivity from the
![]() $B(v)_q$
. Note in general, a union
$B(v)_q$
. Note in general, a union
![]() $B=\bigcup _q B_q$
is L-primitive if each
$B=\bigcup _q B_q$
is L-primitive if each
![]() $B_q$
is L-primitive. (By contrast,
$B_q$
is L-primitive. (By contrast,
![]() $B=\bigcup _q B_q$
is not necessarily primitive even if each
$B=\bigcup _q B_q$
is not necessarily primitive even if each
![]() $B_q$
is primitive, e.g.,
$B_q$
is primitive, e.g.,
![]() $B=\{3,6\}$
.)
$B=\{3,6\}$
.)
Next, consider the primes
![]() $\mathcal Q = \{q : f(q)> e^{\gamma } {\mathrm d}({\mathrm L}_q)\} = \{q : 1/\log q > e^{\gamma }\prod _{p<q}(1-\frac {1}{p})\}$
. By Lemma 2.3
$\mathcal Q = \{q : f(q)> e^{\gamma } {\mathrm d}({\mathrm L}_q)\} = \{q : 1/\log q > e^{\gamma }\prod _{p<q}(1-\frac {1}{p})\}$
. By Lemma 2.3
![]() $f(A_q) < e^{\gamma } {\mathrm d}({\mathrm L}_q)$
when
$f(A_q) < e^{\gamma } {\mathrm d}({\mathrm L}_q)$
when
![]() $q\notin A$
, so in general
$q\notin A$
, so in general
![]() $f(A_q) < \max \{f(q),e^{\gamma } {\mathrm d}({\mathrm L}_q)\}$
for all L-primitive A and all primes q. Hence,
$f(A_q) < \max \{f(q),e^{\gamma } {\mathrm d}({\mathrm L}_q)\}$
for all L-primitive A and all primes q. Hence,
This bound is attained for the choice of
![]() $B' = \mathcal Q\cup \bigcup _{q\notin \mathcal Q} B(v)_q$
, and taking
$B' = \mathcal Q\cup \bigcup _{q\notin \mathcal Q} B(v)_q$
, and taking
![]() $v\to 0$
as in Proposition 5.7. Again,
$v\to 0$
as in Proposition 5.7. Again,
![]() $B'$
inherits L-primitivity from the
$B'$
inherits L-primitivity from the
![]() $B(v)_q$
, as desired.
$B(v)_q$
, as desired.
6 Deduction of Theorems 1.8, 1.10
Our study of sets of L-multiples leads to Theorem 1.8, refining Davenport–Erdős. This in turn enables the proof of Theorem 1.10, by a modification of the argument in [Reference Erdős, Sárközy and Szemerédi16, Theorem 2], with greater care given to the constants involved.
To proceed, we first establish some lemmas.
Lemma 6.1. For any L-primitive
![]() $A\subset {\mathbb N}$
, we have
$A\subset {\mathbb N}$
, we have
![]() $\underline {{\mathrm d}}({\mathrm L}_A)\ge \sum _{a\in A}{\mathrm d}({\mathrm L}_a)$
. Moreover, if
$\underline {{\mathrm d}}({\mathrm L}_A)\ge \sum _{a\in A}{\mathrm d}({\mathrm L}_a)$
. Moreover, if
![]() $\sum _{a\in A}1/a < \infty $
, then the natural density
$\sum _{a\in A}1/a < \infty $
, then the natural density
![]() ${\mathrm d}({\mathrm L}_A)$
exists and equals
${\mathrm d}({\mathrm L}_A)$
exists and equals
![]() $\sum _{a\in A}{\mathrm d}({\mathrm L}_a)$
.
$\sum _{a\in A}{\mathrm d}({\mathrm L}_a)$
.
Proof. For each
![]() $a\in A$
, we have
$a\in A$
, we have
![]() $\underline {{\mathrm d}}({\mathrm L}_a) = {\mathrm d}({\mathrm L}_a)$
. So taking the lower density of the finite (disjoint) union
$\underline {{\mathrm d}}({\mathrm L}_a) = {\mathrm d}({\mathrm L}_a)$
. So taking the lower density of the finite (disjoint) union
![]() $\bigcup _{a\in A, a\le x}{\mathrm L}_a \subset {\mathrm L}_A$
, we have
$\bigcup _{a\in A, a\le x}{\mathrm L}_a \subset {\mathrm L}_A$
, we have
![]() $\sum _{a\in A, a\le x}{\mathrm d}({\mathrm L}_a) \le \underline {{\mathrm d}}({\mathrm L}_A)$
for all
$\sum _{a\in A, a\le x}{\mathrm d}({\mathrm L}_a) \le \underline {{\mathrm d}}({\mathrm L}_A)$
for all
![]() $x>1$
. Thus,
$x>1$
. Thus,
![]() $\sum _{a\in A}{\mathrm d}({\mathrm L}_a) \le \underline {{\mathrm d}}({\mathrm L}_A)$
. Moreover, if
$\sum _{a\in A}{\mathrm d}({\mathrm L}_a) \le \underline {{\mathrm d}}({\mathrm L}_A)$
. Moreover, if
![]() $\sum _{a\in A}1/a < \infty $
, then for all
$\sum _{a\in A}1/a < \infty $
, then for all
![]() $y>1$
$y>1$
 $$ \begin{align*} \frac{1}{x}\sum_{\substack{n\le x\\ n\in {\mathrm L}_{A\cap (y,\infty)}}}1 \le \frac{1}{x}\sum_{a\in A,a> y}\left\lfloor \frac{x}{a}\right\rfloor \le \sum_{a\in A,a> y}\frac{1}{a} = o_y(1). \end{align*} $$
$$ \begin{align*} \frac{1}{x}\sum_{\substack{n\le x\\ n\in {\mathrm L}_{A\cap (y,\infty)}}}1 \le \frac{1}{x}\sum_{a\in A,a> y}\left\lfloor \frac{x}{a}\right\rfloor \le \sum_{a\in A,a> y}\frac{1}{a} = o_y(1). \end{align*} $$
Thus,
![]() $\overline {{\mathrm d}}({\mathrm L}_{A\cap (y,\infty )}) \to 0$
as
$\overline {{\mathrm d}}({\mathrm L}_{A\cap (y,\infty )}) \to 0$
as
![]() $y\to \infty $
, and so combining with
$y\to \infty $
, and so combining with
![]() ${\mathrm d}({\mathrm L}_{A\cap [1,y]})=\sum _{a\in A, a\le y}{\mathrm d}({\mathrm L}_a)$
completes the proof.
${\mathrm d}({\mathrm L}_{A\cap [1,y]})=\sum _{a\in A, a\le y}{\mathrm d}({\mathrm L}_a)$
completes the proof.
The following lemma shows that sets of L-multiples have a
![]() $\log $
density, refining Davenport–Erdős’ elementary proof for sets of (all) multiples [Reference Davenport and Erdős12].
$\log $
density, refining Davenport–Erdős’ elementary proof for sets of (all) multiples [Reference Davenport and Erdős12].
Lemma 6.2. For any L-primitive
![]() $A\subset {\mathbb N}$
, the
$A\subset {\mathbb N}$
, the
![]() $\log $
density
$\log $
density
![]() $\delta ({\mathrm L}_A)$
exists and equals
$\delta ({\mathrm L}_A)$
exists and equals
![]() $\sum _{a\in A}{\mathrm d}({\mathrm L}_a)$
.
$\sum _{a\in A}{\mathrm d}({\mathrm L}_a)$
.
Proof. In general,
![]() $\underline {{\mathrm d}}(S) \; \le \; \underline {\delta }(S) \;\le \; \overline {\delta }(S) \; \le \; \overline {{\mathrm d}}(S)$
for any
$\underline {{\mathrm d}}(S) \; \le \; \underline {\delta }(S) \;\le \; \overline {\delta }(S) \; \le \; \overline {{\mathrm d}}(S)$
for any
![]() $S\subset {\mathbb N}$
. So for
$S\subset {\mathbb N}$
. So for
![]() $S={\mathrm L}_A$
, by Lemma 6.1 it suffices to show
$S={\mathrm L}_A$
, by Lemma 6.1 it suffices to show
To this, for
![]() $y>1$
let
$y>1$
let
![]() $A^y = \{a\in A : P(a)\le y\}$
and
$A^y = \{a\in A : P(a)\le y\}$
and
![]() $L^y = \{n\in {\mathrm L}_A : P(n)\le y\}$
. Note
$L^y = \{n\in {\mathrm L}_A : P(n)\le y\}$
. Note
![]() $L^y \subset {\mathrm L}_{A^y}$
. Also
$L^y \subset {\mathrm L}_{A^y}$
. Also
![]() $\sum _{a\in A^y}\frac {1}{a} \le \prod _{p\le y}(1-\frac {1}{p})^{-1} = O_y(1)$
, so by Lemma 6.1
$\sum _{a\in A^y}\frac {1}{a} \le \prod _{p\le y}(1-\frac {1}{p})^{-1} = O_y(1)$
, so by Lemma 6.1
![]() ${\mathrm d}({\mathrm L}_{A^y})$
exists and equals
${\mathrm d}({\mathrm L}_{A^y})$
exists and equals
![]() $\sum _{a\in A^y}{\mathrm d}({\mathrm L}_a)$
for all
$\sum _{a\in A^y}{\mathrm d}({\mathrm L}_a)$
for all
![]() $y>1$
. In particular,
$y>1$
. In particular,
![]() ${\mathrm d}({\mathrm L}_{A^y})\to \sum _{a\in A}{\mathrm d}({\mathrm L}_a)$
as
${\mathrm d}({\mathrm L}_{A^y})\to \sum _{a\in A}{\mathrm d}({\mathrm L}_a)$
as
![]() $y\to \infty $
.
$y\to \infty $
.
Now, observe each
![]() $n\in {\mathrm L}_{A^y}$
is a L-multiple of a unique
$n\in {\mathrm L}_{A^y}$
is a L-multiple of a unique
![]() $a\in A^y$
, so for
$a\in A^y$
, so for
![]() $x\ge y>1$
we have
$x\ge y>1$
we have
 $$ \begin{align} \sum_{n\in L^x\cap {\mathrm L}_{A^y}}\frac{1}{n} &= \sum_{a\in A^y}\frac{1}{a}\prod_{P(a)\le p\le x}(1-\tfrac{1}{p})^{-1} = \sum_{a\in A^y}\frac{1}{a}\prod_{p<P(a)}(1-\tfrac{1}{p})\prod_{p\le x}(1-\tfrac{1}{p})^{-1} \nonumber\\ &= {\mathrm d}({\mathrm L}_{A^y})\prod_{p\le x}(1-\tfrac{1}{p})^{-1}. \end{align} $$
$$ \begin{align} \sum_{n\in L^x\cap {\mathrm L}_{A^y}}\frac{1}{n} &= \sum_{a\in A^y}\frac{1}{a}\prod_{P(a)\le p\le x}(1-\tfrac{1}{p})^{-1} = \sum_{a\in A^y}\frac{1}{a}\prod_{p<P(a)}(1-\tfrac{1}{p})\prod_{p\le x}(1-\tfrac{1}{p})^{-1} \nonumber\\ &= {\mathrm d}({\mathrm L}_{A^y})\prod_{p\le x}(1-\tfrac{1}{p})^{-1}. \end{align} $$
In particular, for
![]() $x=y$
we have
$x=y$
we have
![]() $\sum _{n\in L^x}\frac {1}{n}={\mathrm d}({\mathrm L}_{A^x})\prod _{p\le x}(1-\tfrac {1}{p})^{-1}$
.
$\sum _{n\in L^x}\frac {1}{n}={\mathrm d}({\mathrm L}_{A^x})\prod _{p\le x}(1-\tfrac {1}{p})^{-1}$
.
Then for all
![]() $x\ge y>1$
, by equation (35) and Mertens’ theorem
$x\ge y>1$
, by equation (35) and Mertens’ theorem
 $$ \begin{align} \sum_{n\in L^x \setminus {\mathrm L}_{A^y}}\frac{1}{n} &= \ \sum_{n\in L^x}\frac{1}{n} \ - \sum_{n\in L^x \cap {\mathrm L}_{A^y}}\frac{1}{n} \nonumber\\ &= \big({\mathrm d}({\mathrm L}_{A^x})-{\mathrm d}({\mathrm L}_{A^y})\big)\prod_{p\le x}(1-\tfrac{1}{p})^{-1} \ \ll \ (\log x)\big({\mathrm d}({\mathrm L}_{A^x})-{\mathrm d}({\mathrm L}_{A^y})\big). \end{align} $$
$$ \begin{align} \sum_{n\in L^x \setminus {\mathrm L}_{A^y}}\frac{1}{n} &= \ \sum_{n\in L^x}\frac{1}{n} \ - \sum_{n\in L^x \cap {\mathrm L}_{A^y}}\frac{1}{n} \nonumber\\ &= \big({\mathrm d}({\mathrm L}_{A^x})-{\mathrm d}({\mathrm L}_{A^y})\big)\prod_{p\le x}(1-\tfrac{1}{p})^{-1} \ \ll \ (\log x)\big({\mathrm d}({\mathrm L}_{A^x})-{\mathrm d}({\mathrm L}_{A^y})\big). \end{align} $$
Recall the natural density
![]() ${\mathrm d}({\mathrm L}_{A^y})$
exists, in which case equals the log density
${\mathrm d}({\mathrm L}_{A^y})$
exists, in which case equals the log density
![]() $\delta ({\mathrm L}_{A^y})$
. Hence, by equation (36), for each
$\delta ({\mathrm L}_{A^y})$
. Hence, by equation (36), for each
![]() $y>1$
the upper log density is
$y>1$
the upper log density is
 $$ \begin{align} \overline{\delta}({\mathrm L}_{A}) \ = \ \limsup_{x\to\infty}\frac{1}{\log x}\sum_{\substack{n\le x\\n\in {\mathrm L}_{A}}}\frac{1}{n} & \le \lim_{x\to\infty}\frac{1}{\log x}\sum_{\substack{n\le x\\n\in {\mathrm L}_{A^y}}}\frac{1}{n} \ + \ \limsup_{x\to\infty}\frac{1}{\log x}\sum_{n\in L^x \setminus {\mathrm L}_{A^y}}\frac{1}{n} \nonumber\\ & \ = \delta({\mathrm L}_{A^y}) \ + \ \lim_{x\to\infty}O\big({\mathrm d}({\mathrm L}_{A^x})-{\mathrm d}({\mathrm L}_{A^y})\big) \nonumber\\ & \ = {\mathrm d}({\mathrm L}_{A^y}) \ + \ O\Big(\sum_{a\in A}{\mathrm d}({\mathrm L}_a)-{\mathrm d}({\mathrm L}_{A^y})\Big). \end{align} $$
$$ \begin{align} \overline{\delta}({\mathrm L}_{A}) \ = \ \limsup_{x\to\infty}\frac{1}{\log x}\sum_{\substack{n\le x\\n\in {\mathrm L}_{A}}}\frac{1}{n} & \le \lim_{x\to\infty}\frac{1}{\log x}\sum_{\substack{n\le x\\n\in {\mathrm L}_{A^y}}}\frac{1}{n} \ + \ \limsup_{x\to\infty}\frac{1}{\log x}\sum_{n\in L^x \setminus {\mathrm L}_{A^y}}\frac{1}{n} \nonumber\\ & \ = \delta({\mathrm L}_{A^y}) \ + \ \lim_{x\to\infty}O\big({\mathrm d}({\mathrm L}_{A^x})-{\mathrm d}({\mathrm L}_{A^y})\big) \nonumber\\ & \ = {\mathrm d}({\mathrm L}_{A^y}) \ + \ O\Big(\sum_{a\in A}{\mathrm d}({\mathrm L}_a)-{\mathrm d}({\mathrm L}_{A^y})\Big). \end{align} $$
Hence,
![]() ${\mathrm d}({\mathrm L}_{A^y})\to \sum _{a\in A}{\mathrm d}({\mathrm L}_a)$
as
${\mathrm d}({\mathrm L}_{A^y})\to \sum _{a\in A}{\mathrm d}({\mathrm L}_a)$
as
![]() $y\to \infty $
implies
$y\to \infty $
implies
![]() $\overline {\delta }({\mathrm L}_{A})\le \sum _{a\in A}{\mathrm d}({\mathrm L}_a)$
, giving (34).
$\overline {\delta }({\mathrm L}_{A})\le \sum _{a\in A}{\mathrm d}({\mathrm L}_a)$
, giving (34).
Theorem 1.8. If
![]() $\overline {\delta }(A)>0$
, then A contains an infinite L-divisibility chain.
$\overline {\delta }(A)>0$
, then A contains an infinite L-divisibility chain.
Proof. We claim all such
![]() $A\subset {\mathbb N}$
contain an element
$A\subset {\mathbb N}$
contain an element
![]() $a\in A$
such that
$a\in A$
such that
![]() $A\cap {\mathrm L}_a$
has positive upper
$A\cap {\mathrm L}_a$
has positive upper
![]() $\log $
density. (In other words, if
$\log $
density. (In other words, if
![]() $\overline {\delta }(A)> 0$
, then there exists an element
$\overline {\delta }(A)> 0$
, then there exists an element
![]() $a\in A$
such that
$a\in A$
such that
![]() $\overline {\delta }(A\cap {\mathrm L}_a)>0$
.)
$\overline {\delta }(A\cap {\mathrm L}_a)>0$
.)
Assume this claim holds. Letting
![]() $A^1=A$
,
$A^1=A$
,
![]() $a_1=a$
, and for
$a_1=a$
, and for
![]() $i\ge 1$
suppose
$i\ge 1$
suppose
![]() $\overline {\delta }(A^i)>0$
. By the claim, there exists
$\overline {\delta }(A^i)>0$
. By the claim, there exists
![]() $a_i\in A^i$
such that
$a_i\in A^i$
such that
![]() $A^{i+1} := A^i\cap {\mathrm L}_{a_i}$
has positive upper
$A^{i+1} := A^i\cap {\mathrm L}_{a_i}$
has positive upper
![]() $\log $
density. Hence, by induction, we obtain an L-divisibility chain
$\log $
density. Hence, by induction, we obtain an L-divisibility chain
![]() $a_1,a_2,\cdots $
, as desired.
$a_1,a_2,\cdots $
, as desired.
Thus, it remains to establish the above claim. For sake of contradiction, suppose
![]() $A\cap {\mathrm L}_a$
has zero
$A\cap {\mathrm L}_a$
has zero
![]() $\log $
density for all
$\log $
density for all
![]() $a\in A$
. Next, for the L-primitive generating set
$a\in A$
. Next, for the L-primitive generating set
![]() $B = \langle A\rangle $
by Lemma 6.1
$B = \langle A\rangle $
by Lemma 6.1
![]() $\delta ({\mathrm L}_B)=\sum _{b\in B}{\mathrm d}({\mathrm L}_b)$
exists. Then for
$\delta ({\mathrm L}_B)=\sum _{b\in B}{\mathrm d}({\mathrm L}_b)$
exists. Then for
![]() $z>1$
large enough we have
$z>1$
large enough we have
![]() $\delta ({\mathrm L}_{B\cap (z,\infty )}) = \sum _{b\in B, b>z}{\mathrm d}({\mathrm L}_b)< \overline {\delta }(A)$
. Now, by assumption
$\delta ({\mathrm L}_{B\cap (z,\infty )}) = \sum _{b\in B, b>z}{\mathrm d}({\mathrm L}_b)< \overline {\delta }(A)$
. Now, by assumption
![]() $\overline {\delta }(A\cap {\mathrm L}_b)=0$
for all
$\overline {\delta }(A\cap {\mathrm L}_b)=0$
for all
![]() $b\le z$
,
$b\le z$
,
![]() $b\in B$
, and so
$b\in B$
, and so
a contradiction. Hence, there exists
![]() $a\in A$
such that
$a\in A$
such that
![]() $A\cap {\mathrm L}_a$
has positive upper
$A\cap {\mathrm L}_a$
has positive upper
![]() $\log $
density.
$\log $
density.
Theorem 1.10. If
![]() $\overline {\Delta }(A)>0$
, then there is an infinite L-divisibility chain
$\overline {\Delta }(A)>0$
, then there is an infinite L-divisibility chain
![]() $D\subset A$
of growth
$D\subset A$
of growth
 $$ \begin{align*} \limsup_{y\to\infty}\sum_{\substack{d\in D\\d\le y}}\frac{1}{\log\log y} \ \ge \ \frac{\overline{\Delta}(A)}{e^{\gamma}}. \end{align*} $$
$$ \begin{align*} \limsup_{y\to\infty}\sum_{\substack{d\in D\\d\le y}}\frac{1}{\log\log y} \ \ge \ \frac{\overline{\Delta}(A)}{e^{\gamma}}. \end{align*} $$
Proof. Take
![]() ${\epsilon }>0$
. Without loss, we may suppose
${\epsilon }>0$
. Without loss, we may suppose
![]() $A\subset [x_{\epsilon },\infty )$
for
$A\subset [x_{\epsilon },\infty )$
for
![]() $x_{\epsilon }$
sufficiently large so that by Proposition 5.3
$x_{\epsilon }$
sufficiently large so that by Proposition 5.3
![]() $f(A')\le e^{\gamma }+{\epsilon }$
for all L-primitive subsets
$f(A')\le e^{\gamma }+{\epsilon }$
for all L-primitive subsets
![]() $A'\subset A$
.
$A'\subset A$
.
By definition of upper
![]() $\log \log $
density
$\log \log $
density
![]() $\Delta :=\overline {\Delta }(A)>0$
, there exists an unbounded sequence
$\Delta :=\overline {\Delta }(A)>0$
, there exists an unbounded sequence
![]() $(x_j)_{j=0}^{\infty }\subset {\mathbb R}$
such that for all
$(x_j)_{j=0}^{\infty }\subset {\mathbb R}$
such that for all
![]() $j\ge 0$
,
$j\ge 0$
,
 $$ \begin{align} f(A\cap [1,x_j]) = \sum_{\substack{a\in A\\ a\le x_j}}\frac{1}{a\log a}> (\Delta-{\epsilon})\log\log x_j. \end{align} $$
$$ \begin{align} f(A\cap [1,x_j]) = \sum_{\substack{a\in A\\ a\le x_j}}\frac{1}{a\log a}> (\Delta-{\epsilon})\log\log x_j. \end{align} $$
Recall the L-primitive generating set
![]() $\langle S\rangle =\{s\in S: s\notin {\mathrm L}_t \; \forall t<s,t\in S\}$
of a set
$\langle S\rangle =\{s\in S: s\notin {\mathrm L}_t \; \forall t<s,t\in S\}$
of a set
![]() $S\subset {\mathbb N}$
from Lemma 5.4. We partition
$S\subset {\mathbb N}$
from Lemma 5.4. We partition
![]() $A = \bigcup _{i\ge 0} A^i$
into a disjoint collection of L-primitive subsets, where
$A = \bigcup _{i\ge 0} A^i$
into a disjoint collection of L-primitive subsets, where
![]() $A^0 = \langle A\rangle $
and inductively
$A^0 = \langle A\rangle $
and inductively
![]() $A^l = \langle A\setminus \bigcup _{i<l} A^i\rangle $
. By construction, each
$A^l = \langle A\setminus \bigcup _{i<l} A^i\rangle $
. By construction, each
![]() $a=a_l\in A^l$
has a (finite) chain of L-divisors
$a=a_l\in A^l$
has a (finite) chain of L-divisors
![]() $a_i\in A^i$
with
$a_i\in A^i$
with
![]() $\mathrm {L}_{a_0}\supset \cdots \supset {\mathrm L}_{a_l}={\mathrm L}_a$
. Also, note
$\mathrm {L}_{a_0}\supset \cdots \supset {\mathrm L}_{a_l}={\mathrm L}_a$
. Also, note
![]() $f(A^i)\le e^{\gamma }+{\epsilon }$
by assumption, so in particular
$f(A^i)\le e^{\gamma }+{\epsilon }$
by assumption, so in particular
![]() $A^i$
has zero
$A^i$
has zero
![]() $\log \log $
density. Hence, equation (38) implies each
$\log \log $
density. Hence, equation (38) implies each
![]() $A^i$
in
$A^i$
in
![]() $A=\bigcup _{i\ge 0} A^i$
is nonempty. Next, define the subset
$A=\bigcup _{i\ge 0} A^i$
is nonempty. Next, define the subset
![]() $B = \bigcup _{j\ge 0}B_j$
for
$B = \bigcup _{j\ge 0}B_j$
for
 $$ \begin{align*} B_j \ : = \ A\cap [1,x_j]\setminus \bigcup_{1\le i<r_j} A^i, \qquad\text{where}\quad r_j := \frac{\Delta-2{\epsilon}}{e^{\gamma}+{\epsilon}}\log\log x_j. \end{align*} $$
$$ \begin{align*} B_j \ : = \ A\cap [1,x_j]\setminus \bigcup_{1\le i<r_j} A^i, \qquad\text{where}\quad r_j := \frac{\Delta-2{\epsilon}}{e^{\gamma}+{\epsilon}}\log\log x_j. \end{align*} $$
Note the sets
![]() $B_j$
are pairwise disjoint: Indeed, since
$B_j$
are pairwise disjoint: Indeed, since
![]() $A = \bigcup _{i\ge 0} A^i$
, for each j we have
$A = \bigcup _{i\ge 0} A^i$
, for each j we have
![]() $A\cap [1,x_j]\subset \bigcup _{i<s_j} A^i$
for some finite
$A\cap [1,x_j]\subset \bigcup _{i<s_j} A^i$
for some finite
![]() $s_j$
, as determined by
$s_j$
, as determined by
![]() $x_j$
. Then since
$x_j$
. Then since
![]() $(x_j)_j$
is unbounded, (passing to a subsequence) we have
$(x_j)_j$
is unbounded, (passing to a subsequence) we have
![]() $r_{j+1}> s_j$
and so
$r_{j+1}> s_j$
and so
![]() $A\cap [1,x_j]\subset \bigcup _{i<r_{j+1}}A^i$
. Thus,
$A\cap [1,x_j]\subset \bigcup _{i<r_{j+1}}A^i$
. Thus,
![]() $B_j=A\cap [1,x_j]\setminus \bigcup _{i<r_j} A^i \; \subset \; \bigcup _{r_j\le i<r_{j+1}} A^i$
inherits disjointness from the
$B_j=A\cap [1,x_j]\setminus \bigcup _{i<r_j} A^i \; \subset \; \bigcup _{r_j\le i<r_{j+1}} A^i$
inherits disjointness from the
![]() $A^i$
, as claimed.
$A^i$
, as claimed.
Since
![]() $B = \bigcup _{j\ge 0}B_j$
forms a disjoint union, for each
$B = \bigcup _{j\ge 0}B_j$
forms a disjoint union, for each
![]() $b\in B$
there is a unique index
$b\in B$
there is a unique index
![]() $J(b)$
such that
$J(b)$
such that
![]() $b\in B_{J(b)}$
, that is,
$b\in B_{J(b)}$
, that is,
 $$ \begin{align} b \ \le \ x_{J(b)} \quad \text{and}\quad b\notin \bigcup_{i<r_{J(b)}} A^i. \end{align} $$
$$ \begin{align} b \ \le \ x_{J(b)} \quad \text{and}\quad b\notin \bigcup_{i<r_{J(b)}} A^i. \end{align} $$
In addition, B has positive upper
![]() $\log \log $
density, since by definitions of B,
$\log \log $
density, since by definitions of B,
![]() $r_j$
and equation (38),
$r_j$
and equation (38),
 $$ \begin{align*} f(B\cap [1,x_j]) \ \ge \ f(B_j) & \ \ge \ f(A\cap [1,x_j]) \ - \ \sum_{i < r_j}f(A^i)\\ & \ > \ (\Delta-{\epsilon})\log\log x_j - r_j(e^{\gamma}+{\epsilon}) \ = \ {\epsilon}\log\log x_j. \end{align*} $$
$$ \begin{align*} f(B\cap [1,x_j]) \ \ge \ f(B_j) & \ \ge \ f(A\cap [1,x_j]) \ - \ \sum_{i < r_j}f(A^i)\\ & \ > \ (\Delta-{\epsilon})\log\log x_j - r_j(e^{\gamma}+{\epsilon}) \ = \ {\epsilon}\log\log x_j. \end{align*} $$
In particular, B has positive upper
![]() $\log $
density, so by Theorem 1.8 there exists an infinite L–divisibility chain
$\log $
density, so by Theorem 1.8 there exists an infinite L–divisibility chain
![]() $D\subset B$
. Since
$D\subset B$
. Since
![]() $D:=(d_k)_{k=0}^{\infty }$
is unbounded, (by passing to a subchain) we may assume
$D:=(d_k)_{k=0}^{\infty }$
is unbounded, (by passing to a subchain) we may assume
![]() $J(d_k) < J(d_{k+1})$
for all
$J(d_k) < J(d_{k+1})$
for all
![]() $k\ge 0$
. Recall each
$k\ge 0$
. Recall each
![]() $a\in A^i$
is at the end of an
$a\in A^i$
is at the end of an
![]() $\mathrm {L}$
-divisibility chain of length i. As
$\mathrm {L}$
-divisibility chain of length i. As
![]() $b\in B_{J(b)}$
and
$b\in B_{J(b)}$
and
![]() $B_j$
is contained in
$B_j$
is contained in
![]() $\bigcup _{r_j\le i<r_{j+1}}A^i$
, we infer each
$\bigcup _{r_j\le i<r_{j+1}}A^i$
, we infer each
![]() $d\in D\subset B$
is at the end of an
$d\in D\subset B$
is at the end of an
![]() $\mathrm {L}$
-divisibility chain of length (at least)
$\mathrm {L}$
-divisibility chain of length (at least)
![]() $r_{J(d)}$
. Write it as
$r_{J(d)}$
. Write it as
![]() $c_0^{(k)}\mid c_1^{(k)}\mid \cdots \mid c_{r_{J(d_k)}}^{(k)}=d_k$
, with
$c_0^{(k)}\mid c_1^{(k)}\mid \cdots \mid c_{r_{J(d_k)}}^{(k)}=d_k$
, with
Now, let
![]() $i_k$
be the least index such that
$i_k$
be the least index such that
![]() $c_{i_k}^{(k)}>d_{k-1}$
and define
$c_{i_k}^{(k)}>d_{k-1}$
and define
We may assume
![]() $(r_j)_j$
grows fast enough so that
$(r_j)_j$
grows fast enough so that
![]() $\lfloor {\epsilon }\, r_{J(d_k)}\rfloor> d_{k-1}$
. Then the trivial bound
$\lfloor {\epsilon }\, r_{J(d_k)}\rfloor> d_{k-1}$
. Then the trivial bound
![]() $c_i^{(k)}> i$
implies
$c_i^{(k)}> i$
implies
![]() $c_{\lfloor {\epsilon } \,r_{J(d_k)\rfloor }}^{(k)}> d_{k-1}$
, and so
$c_{\lfloor {\epsilon } \,r_{J(d_k)\rfloor }}^{(k)}> d_{k-1}$
, and so
![]() $\lfloor {\epsilon } \,r_{J(d_k)}\rfloor \ge i_k$
. Thus,
$\lfloor {\epsilon } \,r_{J(d_k)}\rfloor \ge i_k$
. Thus,
Hence, taking
![]() ${\epsilon }\to 0$
in equation (40) above gives
${\epsilon }\to 0$
in equation (40) above gives
![]() $\limsup _{x\to \infty } \sum _{c\in C,c\le x}1/\log \log x \ge \Delta /e^{\gamma }$
as desired.
$\limsup _{x\to \infty } \sum _{c\in C,c\le x}1/\log \log x \ge \Delta /e^{\gamma }$
as desired.
Finally, note C forms an infinite L-divisibility chain: For each k we have
![]() $c_j^{(k)}\in {\mathrm L}_{c_i^{(k)}}$
for all
$c_j^{(k)}\in {\mathrm L}_{c_i^{(k)}}$
for all
![]() $i_k\le i<j$
, in particular
$i_k\le i<j$
, in particular
![]() $d_k\in {\mathrm L}_{c_i^{(k)}}$
. Also,
$d_k\in {\mathrm L}_{c_i^{(k)}}$
. Also,
![]() $d_k\in {\mathrm L}_{d_{k-1}}$
since D is an L-divisibility chain, so there exist factorizations
$d_k\in {\mathrm L}_{d_{k-1}}$
since D is an L-divisibility chain, so there exist factorizations
with
![]() $p(g)\ge P(c_i^{(k)})$
and
$p(g)\ge P(c_i^{(k)})$
and
![]() $p(h)\ge P(d_{k-1})$
. As
$p(h)\ge P(d_{k-1})$
. As
![]() $c_i^{(k)}> d_{k-1}$
, we deduce
$c_i^{(k)}> d_{k-1}$
, we deduce
![]() $c_i^{(k)}\in {\mathrm L}_{d_{k-1}}$
. Thus, the kth and
$c_i^{(k)}\in {\mathrm L}_{d_{k-1}}$
. Thus, the kth and
![]() $(k-1)$
th pieces of C are linked together. Hence, C is indeed an L-divisibility chain.
$(k-1)$
th pieces of C are linked together. Hence, C is indeed an L-divisibility chain.
7 Closing remarks
In this discussion, we attempt to sample just a few of the multitude of open questions that have quickly arisen in connection with the Erdős primitive set conjecture. We have already described a few in the introduction, including Conjecture 1.4, as well as whether
![]() $p=2$
is Erdős strong. We also note recent work has studied variants of the problem in function fields
$p=2$
is Erdős strong. We also note recent work has studied variants of the problem in function fields
![]() $\mathbb {F}_q[x]$
; see [Reference Gómez-Colunga, Kavaler, McNew and Zhu6], [Reference Gómez-Colunga, Kavaler, McNew and Zhu7]. In addition, it would be interesting to further extend the classical study of sets of (all) multiples and of primitive sets,for example, see Hall [Reference Hall21] or Halberstam–Roth [Reference Halberstam and Roth20, §5], to sets of L-multiples and L-primitive sets.
$\mathbb {F}_q[x]$
; see [Reference Gómez-Colunga, Kavaler, McNew and Zhu6], [Reference Gómez-Colunga, Kavaler, McNew and Zhu7]. In addition, it would be interesting to further extend the classical study of sets of (all) multiples and of primitive sets,for example, see Hall [Reference Hall21] or Halberstam–Roth [Reference Halberstam and Roth20, §5], to sets of L-multiples and L-primitive sets.
We conclude with a related question of Banks and Martin, which offers a potential unified framework to view the results described in this article. For
![]() $k\ge 1$
, recall
$k\ge 1$
, recall
![]() $\mathbb {N}_k=\{n : \Omega (n)=k\}$
, in particular
$\mathbb {N}_k=\{n : \Omega (n)=k\}$
, in particular
![]() $\mathbb {N}_1=\mathcal {P}$
. In 1993, Zhang [Reference Zhang33] proved
$\mathbb {N}_1=\mathcal {P}$
. In 1993, Zhang [Reference Zhang33] proved
![]() $f(\mathbb {N}_k)<f(\mathcal {P})$
for each
$f(\mathbb {N}_k)<f(\mathcal {P})$
for each
![]() $k>1$
. Later Bayless, Kinlaw and Klyve [Reference Bayless, Kinlaw and Klyve3] showed that
$k>1$
. Later Bayless, Kinlaw and Klyve [Reference Bayless, Kinlaw and Klyve3] showed that
![]() $f({\mathbb N}_2)> f({\mathbb N}_3)$
. Banks and Martin [Reference Banks and Martin2] predicted
$f({\mathbb N}_2)> f({\mathbb N}_3)$
. Banks and Martin [Reference Banks and Martin2] predicted
![]() $f(\mathbb {N}_k)<f(\mathbb {N}_{k-1})$
for each
$f(\mathbb {N}_k)<f(\mathbb {N}_{k-1})$
for each
![]() $k>1$
. In fact, they posed a vast generalization to Conjecture 1.1.
$k>1$
. In fact, they posed a vast generalization to Conjecture 1.1.
Conjecture 7.1 (odd Banks–Martin).
Let
![]() $k\ge 1$
and suppose A is a primitive set with
$k\ge 1$
and suppose A is a primitive set with
![]() $\Omega (n)\ge k$
for all
$\Omega (n)\ge k$
for all
![]() $n\in A$
. Then for any set of odd primes
$n\in A$
. Then for any set of odd primes
![]() $\mathcal Q$
, we have
$\mathcal Q$
, we have
Here,
![]() $A(\mathcal Q)$
denotes the set of members of A composed of primes in
$A(\mathcal Q)$
denotes the set of members of A composed of primes in
![]() $\mathcal Q$
.
$\mathcal Q$
.
Banks and Martin managed to show equation (41) in the special case when the set of primes
![]() $\mathcal Q$
is quite sparse, namely
$\mathcal Q$
is quite sparse, namely
![]() $\sum _{p\in \mathcal Q}1/p <1.74$
(even when
$\sum _{p\in \mathcal Q}1/p <1.74$
(even when
![]() $2\in \mathcal Q$
). We note the original formulation of Conjecture 7.1 included the cases
$2\in \mathcal Q$
). We note the original formulation of Conjecture 7.1 included the cases
![]() $2\in \mathcal Q$
, but this turns out to be false. Indeed, when
$2\in \mathcal Q$
, but this turns out to be false. Indeed, when
![]() $\mathcal Q=\mathcal P$
it was shown
$\mathcal Q=\mathcal P$
it was shown
![]() $f(\mathbb {N}_k)> f(\mathbb {N}_6)$
for each
$f(\mathbb {N}_k)> f(\mathbb {N}_6)$
for each
![]() $k\neq 6$
[Reference Lichtman25]. In fact, numerical evidence suggests that in fact the reverse holds
$k\neq 6$
[Reference Lichtman25]. In fact, numerical evidence suggests that in fact the reverse holds
![]() $f(\mathbb {N}_k)>f(\mathbb {N}_{k-1})$
for
$f(\mathbb {N}_k)>f(\mathbb {N}_{k-1})$
for
![]() $k>6$
. Nevertheless, for
$k>6$
. Nevertheless, for
![]() $\mathcal Q=\mathcal P\setminus \{2\}$
, the desired inequality
$\mathcal Q=\mathcal P\setminus \{2\}$
, the desired inequality
![]() $f(\mathbb {N}_k(\mathcal Q))<f(\mathbb {N}_{k-1}(\mathcal Q))$
holds up to at least
$f(\mathbb {N}_k(\mathcal Q))<f(\mathbb {N}_{k-1}(\mathcal Q))$
holds up to at least
![]() $k=20$
.
$k=20$
.
Observe that Theorem 1.3 implies Conjecture 7.1 in the special case
![]() $k=1$
. Indeed, if
$k=1$
. Indeed, if
![]() $p\notin \mathcal Q$
, then
$p\notin \mathcal Q$
, then
![]() $A(\mathcal Q)_p=\emptyset $
, so we deduce
$A(\mathcal Q)_p=\emptyset $
, so we deduce
![]() $f(A(\mathcal Q)) = \sum _{p\in \mathcal Q}f(A(\mathcal Q)_p) \le \sum _{p\in \mathcal Q}f(p) = f(\mathcal Q)$
. Moreover, if true, Conjecture 7.1 implies Conjecture 1.4 of Erdős–Sárközy–Szemerédi. This follows by an argument similar to Theorem 1.5, and using
$f(A(\mathcal Q)) = \sum _{p\in \mathcal Q}f(A(\mathcal Q)_p) \le \sum _{p\in \mathcal Q}f(p) = f(\mathcal Q)$
. Moreover, if true, Conjecture 7.1 implies Conjecture 1.4 of Erdős–Sárközy–Szemerédi. This follows by an argument similar to Theorem 1.5, and using
![]() $f({\mathbb N}_k(\mathcal Q))\to 1/2$
as
$f({\mathbb N}_k(\mathcal Q))\to 1/2$
as
![]() $k\to \infty $
when
$k\to \infty $
when
![]() $\mathcal Q=\mathcal P\setminus \{2\}$
; see [Reference Lichtman25, Corollary 4.2]. We leave this to the interested reader.
$\mathcal Q=\mathcal P\setminus \{2\}$
; see [Reference Lichtman25, Corollary 4.2]. We leave this to the interested reader.
Acknowledgements
The author expresses deep gratitude to Carl Pomerance for many discussions and to Paul Kinlaw and James Maynard for careful readings and feedback. The author more broadly thanks Tsz Ho Chan and Scott Neville for engaging conversations over the years. The author also thanks András Sárközy for bringing [Reference Sárközy, Graham and Nesetril32] and references therein to his attention, as well as Michel Balazard and François Morain for the reference [Reference Erdős15] on the Erdős primitive set conjecture.
Competing Interest
The authors have no competing interest to declare.
Financial Support
The author was supported by the Clarendon Scholarship and Balliol College at the University of Oxford, as well as the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 851318).