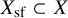1 Introduction
Two decades ago, in an attempt to understand mirror symmetry using the SYZ conjecture [Reference Strominger, Yau and Zaslow47], Fukaya [Reference Fukaya19] proposed two correspondences:
-
• Correspondence I: between the theory of pseudo-holomorphic curves (instanton corrections) on a Calabi–Yau manifold
 $\check {X}$
and the multivalued Morse theory on the base
$\check {X}$
and the multivalued Morse theory on the base
 $\check {B}$
of an SYZ fibration
$\check {B}$
of an SYZ fibration
 $\check {p}\colon \check {X}\to \check {B}$
, and
$\check {p}\colon \check {X}\to \check {B}$
, and -
• Correspondence II: between deformation theory of the mirror X and the same multivalued Morse theory on the base
 $\check {B}$
.
$\check {B}$
.
In this paper, we prove a reformulation of the main conjecture [Reference Fukaya19, Conj 5.3] in Fukaya’s Correspondence II, where multivalued Morse theory on the SYZ base
![]() $\check {B}$
is replaced by tropical geometry on the Legendre dual B. Such a reformulation of Fukaya’s conjecture was proposed and proved in [Reference Chan, Leung and Ma7] in a local setting; the main result of the current paper is a global version of the main result in loc. cit. A crucial ingredient in the proof is a precise link between tropical geometry on an integral affine manifold with singularities and smoothing of maximally degenerate Calabi–Yau varieties.
$\check {B}$
is replaced by tropical geometry on the Legendre dual B. Such a reformulation of Fukaya’s conjecture was proposed and proved in [Reference Chan, Leung and Ma7] in a local setting; the main result of the current paper is a global version of the main result in loc. cit. A crucial ingredient in the proof is a precise link between tropical geometry on an integral affine manifold with singularities and smoothing of maximally degenerate Calabi–Yau varieties.
The main conjecture [Reference Fukaya19, Conj. 5.3] in Fukaya’s Correspondence II asserts that there exists a Maurer–Cartan element of the Kodaira–Spencer differential graded Lie algebra (dgLa) associated to deformations of the semiflat part
![]() $X_{\mathrm {sf}}$
of X that is asymptotically close to a Fourier expansion ([Reference Fukaya19, Eq. (42)]), whose Fourier modes are given by smoothings of distribution-valued 1-forms defined by moduli spaces of gradient Morse flow trees which are expected to encode counting of nontrivial (Maslov index 0) holomorphic disks bounded by Lagrangian torus fibers (see [Reference Fukaya19, Rem. 5.4]). Also, the complex structure defined by this Maurer–Cartan element can be compactified to give a complex structure on X. At the same time, Fukaya’s Correspondence I suggests that these gradient Morse flow trees arise as adiabatic limits of loci of those Lagrangian torus fibers which bound nontrivial (Maslov index 0) holomorphic disks. This can be reformulated as a holomorphic/tropical correspondence, and much evidence has been found [Reference Bardwell-Evans, Cheung, Hong and Lin4, Reference Cheung and Lin10, Reference Cho, Hong and Lau11, Reference Cho, Hong and Lau12, Reference Floer18, Reference Fukaya and Oh20, Reference Lin38, Reference Mikhalkin39, Reference Nishinou and Siebert40].
$X_{\mathrm {sf}}$
of X that is asymptotically close to a Fourier expansion ([Reference Fukaya19, Eq. (42)]), whose Fourier modes are given by smoothings of distribution-valued 1-forms defined by moduli spaces of gradient Morse flow trees which are expected to encode counting of nontrivial (Maslov index 0) holomorphic disks bounded by Lagrangian torus fibers (see [Reference Fukaya19, Rem. 5.4]). Also, the complex structure defined by this Maurer–Cartan element can be compactified to give a complex structure on X. At the same time, Fukaya’s Correspondence I suggests that these gradient Morse flow trees arise as adiabatic limits of loci of those Lagrangian torus fibers which bound nontrivial (Maslov index 0) holomorphic disks. This can be reformulated as a holomorphic/tropical correspondence, and much evidence has been found [Reference Bardwell-Evans, Cheung, Hong and Lin4, Reference Cheung and Lin10, Reference Cho, Hong and Lau11, Reference Cho, Hong and Lau12, Reference Floer18, Reference Fukaya and Oh20, Reference Lin38, Reference Mikhalkin39, Reference Nishinou and Siebert40].
The tropical counterpart of such gradient Morse flow trees are given by consistent scattering diagrams, which were invented by Kontsevich–Soibelman [Reference Kontsevich and Soibelman36] and extensively used in the Gross–Siebert program [Reference Gross and Siebert29] to solve the reconstruction problem in mirror symmetry, namely, the construction of the mirror X from smoothing of a maximally degenerate Calabi–Yau variety ![]() . It is therefore natural to replace the distribution-valued 1-form in each Fourier mode in the Fourier expansion [Reference Fukaya19, Eq. (42)] by a distribution-valued 1-form associated to a wall-crossing factor of a consistent scattering diagram. This was exactly how Fukaya’s conjecture [Reference Fukaya19, Conj. 5.3] was reformulated and proved in the local case in [Reference Chan, Leung and Ma7].
. It is therefore natural to replace the distribution-valued 1-form in each Fourier mode in the Fourier expansion [Reference Fukaya19, Eq. (42)] by a distribution-valued 1-form associated to a wall-crossing factor of a consistent scattering diagram. This was exactly how Fukaya’s conjecture [Reference Fukaya19, Conj. 5.3] was reformulated and proved in the local case in [Reference Chan, Leung and Ma7].
In order to reformulate the global version of Fukaya’s conjecture, however, we must also relate deformations of the semiflat part
![]() $X_{\mathrm {sf}}$
with smoothings of the maximally degenerate Calabi–Yau variety
$X_{\mathrm {sf}}$
with smoothings of the maximally degenerate Calabi–Yau variety ![]() . This is because consistent scattering diagrams were used by Gross–Siebert [Reference Gross and Siebert28] to study the deformation theory of the compact log variety
. This is because consistent scattering diagrams were used by Gross–Siebert [Reference Gross and Siebert28] to study the deformation theory of the compact log variety ![]() (whose log structure is specified by slab functions), instead of
(whose log structure is specified by slab functions), instead of
![]() $X_{\mathrm {sf}}$
. For this purpose, we consider the open dense part
$X_{\mathrm {sf}}$
. For this purpose, we consider the open dense part
where ![]() is the generalized moment map in [Reference Ruddat and Siebert43] and
is the generalized moment map in [Reference Ruddat and Siebert43] and
![]() $W_0 \subseteq B$
is an open dense subset such that
$W_0 \subseteq B$
is an open dense subset such that
![]() $B\setminus W_0$
contains the tropical singular locus and all codimension
$B\setminus W_0$
contains the tropical singular locus and all codimension
![]() $2$
cells of B.
$2$
cells of B.
Equipping ![]() with the trivial log structure, there is a semiflat differential graded Batalin–Vilkovisky (dgBV) algebra
with the trivial log structure, there is a semiflat differential graded Batalin–Vilkovisky (dgBV) algebra ![]() governing its smoothings, and the general fiber of a smoothing is given by the semiflat Calabi–Yau
governing its smoothings, and the general fiber of a smoothing is given by the semiflat Calabi–Yau
![]() $X_{\mathrm {sf}}$
that appeared in Fukaya’s original conjecture [Reference Fukaya19, Conj. 5.3]. However, the Maurer–Cartan elements of
$X_{\mathrm {sf}}$
that appeared in Fukaya’s original conjecture [Reference Fukaya19, Conj. 5.3]. However, the Maurer–Cartan elements of ![]() cannot be compactified to give complex structures on X. On the other hand, in our previous work [Reference Chan, Leung and Ma8] we constructed a Kodaira–Spencer–type pre-dgBV algebra
cannot be compactified to give complex structures on X. On the other hand, in our previous work [Reference Chan, Leung and Ma8] we constructed a Kodaira–Spencer–type pre-dgBV algebra ![]() which controls the smoothing of
which controls the smoothing of ![]() . A key observation is that a twisting of
. A key observation is that a twisting of ![]() by slab functions is isomorphic to the restriction of
by slab functions is isomorphic to the restriction of ![]() to
to ![]() (Lemma 5.10).
(Lemma 5.10).
Our reformulation of the global Fukaya conjecture now claims the existence of a Maurer–Cartan element
![]() $\phi $
of this twisted semiflat dgBV algebra that is asymptotically close to a Fourier expansion whose Fourier modes give rise to the wall-crossing factors of a consistent scattering diagram. This conjecture follows from (the proof of) our main result, stated as Theorem 1.1 below, which is a combination of Theorem 4.18, the construction in §5.3.2 and Theorem 5.24:
$\phi $
of this twisted semiflat dgBV algebra that is asymptotically close to a Fourier expansion whose Fourier modes give rise to the wall-crossing factors of a consistent scattering diagram. This conjecture follows from (the proof of) our main result, stated as Theorem 1.1 below, which is a combination of Theorem 4.18, the construction in §5.3.2 and Theorem 5.24:
Theorem 1.1. There exists a solution
![]() $\phi $
to the classical Maurer–Cartan equation (4.11) giving rise to a smoothing of the maximally degenerate Calabi–Yau log variety
$\phi $
to the classical Maurer–Cartan equation (4.11) giving rise to a smoothing of the maximally degenerate Calabi–Yau log variety ![]() over
over
![]() $\mathbb {C}[[q]]$
, from which a consistent scattering diagram
$\mathbb {C}[[q]]$
, from which a consistent scattering diagram
![]() $\mathscr {D}(\phi )$
can be extracted by taking asymptotic expansions.
$\mathscr {D}(\phi )$
can be extracted by taking asymptotic expansions.
A brief outline of the proof of Theorem 1.1 is now in order. First, recall that the pre-dgBV algebra ![]() which governs smoothing of the maximally degenerate Calabi–Yau variety
which governs smoothing of the maximally degenerate Calabi–Yau variety ![]() was constructed in [Reference Chan, Leung and Ma8, Thm. 1.1 & §3.5], and we also proved a Bogomolov–Tian–Todorov–type theorem [Reference Chan, Leung and Ma8, Thm. 1.2 & §5] showing unobstructedness of the extended Maurer–Cartan equation (4.10), under the Hodge-to-de Rham degeneracy Condition 4.16 and a holomorphic Poincaré Lemma Condition 4.14 (both proven in [Reference Felten, Filip and Ruddat17, Reference Gross and Siebert28]). In Theorem 4.18, we will further show how one can extract from the extended Maurer–Cartan equation (4.10) a smoothing of
was constructed in [Reference Chan, Leung and Ma8, Thm. 1.1 & §3.5], and we also proved a Bogomolov–Tian–Todorov–type theorem [Reference Chan, Leung and Ma8, Thm. 1.2 & §5] showing unobstructedness of the extended Maurer–Cartan equation (4.10), under the Hodge-to-de Rham degeneracy Condition 4.16 and a holomorphic Poincaré Lemma Condition 4.14 (both proven in [Reference Felten, Filip and Ruddat17, Reference Gross and Siebert28]). In Theorem 4.18, we will further show how one can extract from the extended Maurer–Cartan equation (4.10) a smoothing of ![]() , described as a solution
, described as a solution ![]() to the classical Maurer–Cartan equation (4.11)
to the classical Maurer–Cartan equation (4.11)
together with a holomorphic volume form ![]() which satisfies the normalization condition
which satisfies the normalization condition
where T is a nearby vanishing torus in the smoothing.
Next, we need to tropicalize the pre-dgBV algebra ![]() . However, the original construction of
. However, the original construction of ![]() in [Reference Chan, Leung and Ma8] using the Thom–Whitney resolution [Reference Dupont14, Reference Whitney49] is too algebraic in nature. Here, we construct a geometric resolution exploiting the affine manifold structure on B. Using the generalized moment map
in [Reference Chan, Leung and Ma8] using the Thom–Whitney resolution [Reference Dupont14, Reference Whitney49] is too algebraic in nature. Here, we construct a geometric resolution exploiting the affine manifold structure on B. Using the generalized moment map ![]() [Reference Ruddat and Siebert43] and applying the techniques of asymptotic analysis (in particular the notion of asymptotic support) in [Reference Chan, Leung and Ma7], we define the sheaf
[Reference Ruddat and Siebert43] and applying the techniques of asymptotic analysis (in particular the notion of asymptotic support) in [Reference Chan, Leung and Ma7], we define the sheaf
![]() $\mathscr {T}^*$
of monodromy invariant tropical differential forms on B in §5.1. According to Definition 5.5, a tropical differential form can be regarded as a distribution-valued form supported on polyhedral subsets of B. Using the sheaf
$\mathscr {T}^*$
of monodromy invariant tropical differential forms on B in §5.1. According to Definition 5.5, a tropical differential form can be regarded as a distribution-valued form supported on polyhedral subsets of B. Using the sheaf
![]() $\mathscr {T}^*$
, we can take asymptotic expansions of elements in
$\mathscr {T}^*$
, we can take asymptotic expansions of elements in ![]() and hence connect differential geometric operations in dgBV/dgLa with tropical geometry. In this manner, we can extract local scattering diagrams from Maurer–Cartan solutions as we did in [Reference Chan, Leung and Ma7], but we need to glue them together to get a global object.
and hence connect differential geometric operations in dgBV/dgLa with tropical geometry. In this manner, we can extract local scattering diagrams from Maurer–Cartan solutions as we did in [Reference Chan, Leung and Ma7], but we need to glue them together to get a global object.
To achieve this, we need the aforementioned comparison between ![]() and the semiflat dgBV algebra
and the semiflat dgBV algebra ![]() which governs smoothing of the semiflat part
which governs smoothing of the semiflat part ![]() equipped with the trivial log structure. The key Lemma 5.10 says that the restriction of
equipped with the trivial log structure. The key Lemma 5.10 says that the restriction of ![]() to the semiflat part is isomorphic to
to the semiflat part is isomorphic to ![]() precisely after we twist the semiflat operator
precisely after we twist the semiflat operator
![]() $\bar {\partial }_{\circ }$
by elements corresponding to the slab functions associated to the initial walls of the form:
$\bar {\partial }_{\circ }$
by elements corresponding to the slab functions associated to the initial walls of the form:
here, the sum is over vertices in codimension one cells
![]() $\rho $
’s which intersect with the essential singular locus
$\rho $
’s which intersect with the essential singular locus
![]() $\mathscr {S}_e$
(defined in §3.3),
$\mathscr {S}_e$
(defined in §3.3),
![]() $\delta _{v,\rho }$
is a distribution-valued
$\delta _{v,\rho }$
is a distribution-valued
![]() $1$
-form supported on a component of
$1$
-form supported on a component of
![]() $\rho \setminus \mathscr {S}_e$
containing v,
$\rho \setminus \mathscr {S}_e$
containing v,
![]() $\partial _{\check {d}_{\rho }}$
is a holomorphic vector field and
$\partial _{\check {d}_{\rho }}$
is a holomorphic vector field and
![]() $f_{v,\rho }$
’s are the slab functions associated to the initial walls. We remark that slab functions were used to specify the log structure on
$f_{v,\rho }$
’s are the slab functions associated to the initial walls. We remark that slab functions were used to specify the log structure on ![]() as well as the local models for smoothing
as well as the local models for smoothing ![]() in the Gross–Siebert program; see §2 for a review.
in the Gross–Siebert program; see §2 for a review.
Now, the Maurer–Cartan solution ![]() obtained in Theorem 4.18 defines a new operator
obtained in Theorem 4.18 defines a new operator
![]() $\bar {\partial }_{\phi }$
on
$\bar {\partial }_{\phi }$
on ![]() which squares to zero. Applying the above comparison of dgBV algebras (Lemma 5.10) and the gauge transformation from Lemma 5.11, we show that, after restricting to
which squares to zero. Applying the above comparison of dgBV algebras (Lemma 5.10) and the gauge transformation from Lemma 5.11, we show that, after restricting to
![]() $W_0$
, there is an isomorphism
$W_0$
, there is an isomorphism
for some element
![]() $\phi _{\mathrm {s}}$
, where ‘s’ stands for scattering terms. From the description of
$\phi _{\mathrm {s}}$
, where ‘s’ stands for scattering terms. From the description of
![]() $\mathscr {T}^*$
, the element
$\mathscr {T}^*$
, the element
![]() $\phi _{\mathrm {s}}$
, to any fixed order k, is written locally as a finite sum of terms supported on codimension one walls/slabs (Definitions 5.13 and 5.14. For the purpose of a brief discussion in this introduction, we will restrict ourselves to a wall
$\phi _{\mathrm {s}}$
, to any fixed order k, is written locally as a finite sum of terms supported on codimension one walls/slabs (Definitions 5.13 and 5.14. For the purpose of a brief discussion in this introduction, we will restrict ourselves to a wall
![]() $\mathbf {w}$
below, though the same argument applies to a slab; see §5.3.2 for the details. In a neighborhood
$\mathbf {w}$
below, though the same argument applies to a slab; see §5.3.2 for the details. In a neighborhood
![]() $U_{\mathbf {w}}$
of each wall
$U_{\mathbf {w}}$
of each wall
![]() $\mathbf {w}$
, the operator
$\mathbf {w}$
, the operator
![]() $\bar {\partial }_{\circ }+[\phi _{\mathrm {in}}+\phi _{\mathrm {s}},\cdot ]$
is gauge equivalent to
$\bar {\partial }_{\circ }+[\phi _{\mathrm {in}}+\phi _{\mathrm {s}},\cdot ]$
is gauge equivalent to
![]() $\bar {\partial }_{\circ }$
via some vector field
$\bar {\partial }_{\circ }$
via some vector field ![]() , that is,
, that is,
Employing the techniques for analyzing the gauge which we developed in [Reference Chan, Leung and Ma7, Reference Chan and Ma9, Reference Leung, Ma and Young37], we see that the gauge will jump across the wall, resulting in a wall-crossing factor
![]() $\varTheta _{\mathbf {w}}$
satisfying
$\varTheta _{\mathbf {w}}$
satisfying
 $$ \begin{align*} e^{[\theta_{\mathbf{w}},\cdot]}|_{ \mathcal{C}_{\pm}} = \begin{cases} \varTheta_{\mathbf{w}}|_{ \mathcal{C}_+} & \text{on } U_{\mathbf{w}} \cap \mathcal{C}_+,\\ \mathrm{id} & \text{on } U_{\mathbf{w}} \cap \mathcal{C}_-, \end{cases} \end{align*} $$
$$ \begin{align*} e^{[\theta_{\mathbf{w}},\cdot]}|_{ \mathcal{C}_{\pm}} = \begin{cases} \varTheta_{\mathbf{w}}|_{ \mathcal{C}_+} & \text{on } U_{\mathbf{w}} \cap \mathcal{C}_+,\\ \mathrm{id} & \text{on } U_{\mathbf{w}} \cap \mathcal{C}_-, \end{cases} \end{align*} $$
where
![]() $\mathcal {C}_{\pm }$
are the two chambers separated by
$\mathcal {C}_{\pm }$
are the two chambers separated by
![]() $\mathbf {w}$
. Then from the fact that the volume form
$\mathbf {w}$
. Then from the fact that the volume form ![]() is normalized as in equation (1.1), it follows that
is normalized as in equation (1.1), it follows that
![]() $\phi _{\mathrm {s}}$
is closed under the semiflat BV operator
$\phi _{\mathrm {s}}$
is closed under the semiflat BV operator ![]() , and hence we deduce that the wall-crossing factor
, and hence we deduce that the wall-crossing factor
![]() $\varTheta _{\mathbf {w}}$
lies in the tropical vertex group. This defines a scattering diagram
$\varTheta _{\mathbf {w}}$
lies in the tropical vertex group. This defines a scattering diagram
![]() $\mathscr {D}(\phi )$
on the semiflat part
$\mathscr {D}(\phi )$
on the semiflat part
![]() $W_0$
associated to
$W_0$
associated to
![]() $\phi $
. Finally, we prove consistency of the scattering diagram
$\phi $
. Finally, we prove consistency of the scattering diagram
![]() $\mathscr {D}(\phi )$
in Theorem 5.24. We emphasize that the consistency is over the whole B even though the diagram is only defined on
$\mathscr {D}(\phi )$
in Theorem 5.24. We emphasize that the consistency is over the whole B even though the diagram is only defined on
![]() $W_0$
, because the Maurer–Cartan solution
$W_0$
, because the Maurer–Cartan solution
![]() $\phi $
is globally defined on B.
$\phi $
is globally defined on B.
Remark 1.2. Our notion of scattering diagrams (Definition 5.17) is a little bit more relaxed than the usual notion defined in [Reference Kontsevich and Soibelman36, Reference Gross and Siebert29] in two aspects: One is that we do not require the generator of the exponents of the wall-crossing factor to be orthogonal to the wall.Footnote 1 The other is that we allow possibly infinite number of walls/slabs approaching strata of the tropical singular locus. See the paragraph after Definition 5.17 for more details. In practice, this simply means that we are considering a larger gauge equivalence class (or equivalently, a weaker gauge equivalence), which is natural from the point of view of both the Bogomolov–Tian–Todorov Theorem and mirror symmetry (in the A-side, this amounts to flexibility in the choice of the almost complex structure). We also have a different, but more or less equivalent, formulation of the consistency of a scattering diagram; see Definition 5.21 and §5.3.1.
Along the way of proving Fukaya’s conjecture, besides figuring out the precise relation between the semiflat part
![]() $X_{\mathrm {sf}}$
and the maximally degenerate Calabi–Yau log variety
$X_{\mathrm {sf}}$
and the maximally degenerate Calabi–Yau log variety ![]() , we also find the correct description of the Maurer–Cartan solutions near the singular locus, namely, they should be extendable to the local models prescribed by the log structure (or slab functions), as was hinted by the Gross–Siebert program. This is related to a remark by Fukaya [Reference Fukaya19, Pt. (2) after Conj. 5.3].
, we also find the correct description of the Maurer–Cartan solutions near the singular locus, namely, they should be extendable to the local models prescribed by the log structure (or slab functions), as was hinted by the Gross–Siebert program. This is related to a remark by Fukaya [Reference Fukaya19, Pt. (2) after Conj. 5.3].
Another important point is that we have established in the global setting an interplay between the differential-geometric properties of the tropical dgBV algebra and the scattering (and other combinatorial) properties of tropical disks, which was speculated by Fukaya as well ([Reference Fukaya19, Pt. (1) after Conj. 5.3]) although he considered holomorphic disks instead of tropical ones.
Furthermore, by providing a direct linkage between Fukaya’s conjecture with the Gross–Siebert program [Reference Gross and Siebert27, Reference Gross and Siebert28, Reference Gross and Siebert29] and Katzarkov–Kontsevich–Pantev’s Hodge theoretic viewpoint [Reference Katzarkov, Kontsevich and Pantev33] through ![]() (recall from [Reference Chan, Leung and Ma8] that a semi-infinite variation of Hodge structures can be constructed from
(recall from [Reference Chan, Leung and Ma8] that a semi-infinite variation of Hodge structures can be constructed from ![]() , using the techniques of Barannikov–Kontsevich [Reference Barannikov and Kontsevich3, Reference Barannikov2] and Katzarkov–Kontsevich–Pantev [Reference Katzarkov, Kontsevich and Pantev33]), we obtain a more transparent understanding of mirror symmetry through the SYZ framework.
, using the techniques of Barannikov–Kontsevich [Reference Barannikov and Kontsevich3, Reference Barannikov2] and Katzarkov–Kontsevich–Pantev [Reference Katzarkov, Kontsevich and Pantev33]), we obtain a more transparent understanding of mirror symmetry through the SYZ framework.
Remark 1.3. A future direction is to apply the framework in this paper and the works [Reference Chan, Leung and Ma7, Reference Chan, Leung and Ma8] to develop a local-to-global approach to understand genus
![]() $0$
mirror symmetry. In view of the ideas of Seidel [Reference Seidel46] and Kontsevich [Reference Kontsevich35], and also recent breakthroughs by Ganatra–Pardon–Shende [Reference Ganatra, Pardon and Shende24, Reference Ganatra, Pardon and Shende25, Reference Ganatra, Pardon and Shende26] and Gammage–Shende [Reference Gammage and Shende22, Reference Gammage and Shende23], we expect that there is a sheaf of
$0$
mirror symmetry. In view of the ideas of Seidel [Reference Seidel46] and Kontsevich [Reference Kontsevich35], and also recent breakthroughs by Ganatra–Pardon–Shende [Reference Ganatra, Pardon and Shende24, Reference Ganatra, Pardon and Shende25, Reference Ganatra, Pardon and Shende26] and Gammage–Shende [Reference Gammage and Shende22, Reference Gammage and Shende23], we expect that there is a sheaf of
![]() $L_\infty $
algebras on the A-side mirror to (the
$L_\infty $
algebras on the A-side mirror to (the
![]() $L_\infty $
enhancement of)
$L_\infty $
enhancement of) ![]() that can be constructed by gluing local models. More precisely, a large volume limit of a Calabi–Yau manifold
that can be constructed by gluing local models. More precisely, a large volume limit of a Calabi–Yau manifold
![]() $\check {X}$
can be specified by removing from it a normal crossing divisor
$\check {X}$
can be specified by removing from it a normal crossing divisor
![]() $\check {D}$
which represents the Kähler class of
$\check {D}$
which represents the Kähler class of
![]() $\check {X}$
. This gives rise to a Weinstein manifold
$\check {X}$
. This gives rise to a Weinstein manifold
![]() $\check {X} \setminus \check {D}$
and produces a mirror pair
$\check {X} \setminus \check {D}$
and produces a mirror pair ![]() at the large volume/complex structure limits.
at the large volume/complex structure limits.
In [Reference Gammage and Shende23], Gammage–Shende constructed a Lagrangian skeleton
![]() $\Lambda (\Phi ) \subset \check {X} \setminus \check {D}$
from a combinatorial structure
$\Lambda (\Phi ) \subset \check {X} \setminus \check {D}$
from a combinatorial structure
![]() $\Phi $
called fanifold, which can be extracted from the integral tropical manifold B equipped with a polyhedral decomposition
$\Phi $
called fanifold, which can be extracted from the integral tropical manifold B equipped with a polyhedral decomposition
![]() $\mathscr {P}$
(here, we assume that the gluing data s is trivial). They also proved a Homological Mirror Symmetry statement at the large limits. We expect that an A-side analogue of
$\mathscr {P}$
(here, we assume that the gluing data s is trivial). They also proved a Homological Mirror Symmetry statement at the large limits. We expect that an A-side analogue of ![]() can be constructed from the Lagrangian skeleton
can be constructed from the Lagrangian skeleton
![]() $\Lambda (\Phi )$
in
$\Lambda (\Phi )$
in
![]() $\check {X} \setminus \check {D}$
, possibly together with a nice and compatible SYZ fibration on
$\check {X} \setminus \check {D}$
, possibly together with a nice and compatible SYZ fibration on
![]() $\check {X} \setminus \check {D}$
, via gluing of local models. A local-to-global comparsion on the A-side and isomorphisms between the local models on the two sides should then yield an isomorphism of Frobenius manifolds.
$\check {X} \setminus \check {D}$
, via gluing of local models. A local-to-global comparsion on the A-side and isomorphisms between the local models on the two sides should then yield an isomorphism of Frobenius manifolds.
Notation 1.4. We usually fix a rank s lattice
![]() $\mathbf {K}$
together with a strictly convex s-dimensional rational polyhedral cone
$\mathbf {K}$
together with a strictly convex s-dimensional rational polyhedral cone
![]() $Q_{\mathbb {R}} \subset \mathbf {K}_{\mathbb {R}} = \mathbf {K}\otimes _{\mathbb {Z}} \mathbb {R}$
. We call
$Q_{\mathbb {R}} \subset \mathbf {K}_{\mathbb {R}} = \mathbf {K}\otimes _{\mathbb {Z}} \mathbb {R}$
. We call
![]() $Q := Q_{\mathbb {R}} \cap \mathbf {K}$
the universal monoid. We consider the ring
$Q := Q_{\mathbb {R}} \cap \mathbf {K}$
the universal monoid. We consider the ring
![]() $R:=\mathbb {C}[Q]$
, a monomial element of which is written as
$R:=\mathbb {C}[Q]$
, a monomial element of which is written as
![]() $q^m \in R$
for
$q^m \in R$
for
![]() $m \in Q$
, and the maximal ideal
$m \in Q$
, and the maximal ideal
![]() $\mathbf {m}:= \mathbb {C}[Q\setminus \{0\}]$
. Then
$\mathbf {m}:= \mathbb {C}[Q\setminus \{0\}]$
. Then ![]() is an Artinian ring, and we denote by
is an Artinian ring, and we denote by ![]() the completion of R. We further equip R,
the completion of R. We further equip R, ![]() and
and
![]() $\hat {R}$
with the natural monoid homomorphism
$\hat {R}$
with the natural monoid homomorphism
![]() $Q \rightarrow R$
,
$Q \rightarrow R$
,
![]() $m \mapsto q^m$
, which gives them the structure of a log ring (see [Reference Gross and Siebert29, Definition 2.11]); the corresponding log analytic spaces are denoted as
$m \mapsto q^m$
, which gives them the structure of a log ring (see [Reference Gross and Siebert29, Definition 2.11]); the corresponding log analytic spaces are denoted as
![]() $S^{\dagger }$
,
$S^{\dagger }$
, ![]() and
and
![]() $\hat {S}^{\dagger }$
, respectively.
$\hat {S}^{\dagger }$
, respectively.
Furthermore, we let ![]() ,
, ![]() and
and
![]() $\hat {\Omega }^{*}_{S^{\dagger }} := \hat {R} \otimes _{\mathbb {C}} \bigwedge ^*\mathbf {K}_{\mathbb {C}}$
(here,
$\hat {\Omega }^{*}_{S^{\dagger }} := \hat {R} \otimes _{\mathbb {C}} \bigwedge ^*\mathbf {K}_{\mathbb {C}}$
(here,
![]() $\mathbf {K}_{\mathbb {C}} = \mathbf {K} \otimes _{\mathbb {Z}} \mathbb {C}$
) be the spaces of log de Rham differentials on
$\mathbf {K}_{\mathbb {C}} = \mathbf {K} \otimes _{\mathbb {Z}} \mathbb {C}$
) be the spaces of log de Rham differentials on
![]() $S^{\dagger }$
,
$S^{\dagger }$
, ![]() and
and
![]() $\hat {S}^{\dagger }$
respectively, where we write
$\hat {S}^{\dagger }$
respectively, where we write
![]() $1 \otimes m = d \log q^m$
for
$1 \otimes m = d \log q^m$
for
![]() $m \in \mathbf {K}$
; these are equipped with the de Rham differential
$m \in \mathbf {K}$
; these are equipped with the de Rham differential
![]() $\partial $
satisfying
$\partial $
satisfying
![]() $\partial (q^m) = q^m d\log q^m$
. We also denote by
$\partial (q^m) = q^m d\log q^m$
. We also denote by ![]() ,
, ![]() and
and
![]() $\hat {\Theta }_{S^{\dagger }}$
, respectively, the spaces of log derivations, which are equipped with a natural Lie bracket
$\hat {\Theta }_{S^{\dagger }}$
, respectively, the spaces of log derivations, which are equipped with a natural Lie bracket
![]() $[\cdot ,\cdot ]$
. We write
$[\cdot ,\cdot ]$
. We write
![]() $\partial _n$
for the element
$\partial _n$
for the element
![]() $1\otimes n$
with action
$1\otimes n$
with action
![]() $\partial _n (q^m) = (m,n) q^m$
, where
$\partial _n (q^m) = (m,n) q^m$
, where
![]() $(m,n)$
is the natural pairing between
$(m,n)$
is the natural pairing between
![]() $\mathbf {K}_{\mathbb {C}}$
and
$\mathbf {K}_{\mathbb {C}}$
and
![]() $\mathbf {K}^{\vee }_{\mathbb {C}}$
.
$\mathbf {K}^{\vee }_{\mathbb {C}}$
.
2 Gross–Siebert’s cone construction of maximally degenerate Calabi–Yau varieties
This section is a brief review of Gross–Siebert’s construction of the maximally degenerate Calabi–Yau variety ![]() from the affine manifold B and its log structures from slab functions [Reference Gross and Siebert27, Reference Gross and Siebert28, Reference Gross and Siebert29].
from the affine manifold B and its log structures from slab functions [Reference Gross and Siebert27, Reference Gross and Siebert28, Reference Gross and Siebert29].
2.1 Integral tropical manifolds
We first recall the notion of integral tropical manifolds from [Reference Gross and Siebert29, §1.1]. Given a lattice M of rank n, a rational convex polyhedron
![]() $\sigma $
is a convex subset in
$\sigma $
is a convex subset in
![]() $M_{\mathbb {R}}$
given by a finite intersection of rational (i.e., defined over
$M_{\mathbb {R}}$
given by a finite intersection of rational (i.e., defined over
![]() $M_{\mathbb {Q}}$
) affine half-spaces. We usually drop the attributes ‘rational’ and ‘convex’ for polyhedra. A polyhedron
$M_{\mathbb {Q}}$
) affine half-spaces. We usually drop the attributes ‘rational’ and ‘convex’ for polyhedra. A polyhedron
![]() $\sigma $
is said to be integral if all its vertices lie in M; a polytope is a compact polyhedron. The group
$\sigma $
is said to be integral if all its vertices lie in M; a polytope is a compact polyhedron. The group
![]() $\mathbf {Aff}(M):= M \rtimes \mathrm {GL}(M)$
of integral affine transformations acts on the set of polyhedra in
$\mathbf {Aff}(M):= M \rtimes \mathrm {GL}(M)$
of integral affine transformations acts on the set of polyhedra in
![]() $M_{\mathbb {R}}$
. Given a polyhedron
$M_{\mathbb {R}}$
. Given a polyhedron
![]() $\sigma \subset M_{\mathbb {R}}$
, let
$\sigma \subset M_{\mathbb {R}}$
, let
![]() $\Lambda _{\sigma ,\mathbb {R}} \subset M_{\mathbb {R}}$
be the smallest affine subspace containing
$\Lambda _{\sigma ,\mathbb {R}} \subset M_{\mathbb {R}}$
be the smallest affine subspace containing
![]() $\sigma $
, and denote by
$\sigma $
, and denote by
![]() $\Lambda _{\sigma } := \Lambda _{\sigma ,\mathbb {R}} \cap M$
the corresponding lattice. The relative interior
$\Lambda _{\sigma } := \Lambda _{\sigma ,\mathbb {R}} \cap M$
the corresponding lattice. The relative interior
![]() $\mathrm {int}_{\mathrm {re}}(\sigma )$
refers to taking the interior of
$\mathrm {int}_{\mathrm {re}}(\sigma )$
refers to taking the interior of
![]() $\sigma $
in
$\sigma $
in
![]() $\Lambda _{\sigma ,\mathbb {R}}$
. There is an identification
$\Lambda _{\sigma ,\mathbb {R}}$
. There is an identification
![]() $T_{\sigma ,x} \cong \Lambda _{\sigma ,\mathbb {R}}$
for the tangent space at
$T_{\sigma ,x} \cong \Lambda _{\sigma ,\mathbb {R}}$
for the tangent space at
![]() $x \in \mathrm {int}_{\mathrm {re}}(\sigma )$
. Write
$x \in \mathrm {int}_{\mathrm {re}}(\sigma )$
. Write
![]() $\partial \sigma = \sigma \setminus \mathrm {int}_{\mathrm {re}}(\sigma )$
. Then a face of
$\partial \sigma = \sigma \setminus \mathrm {int}_{\mathrm {re}}(\sigma )$
. Then a face of
![]() $\sigma $
is the intersection of
$\sigma $
is the intersection of
![]() $\partial \sigma $
with a supporting hyperplane. Codimension one faces are called facets.
$\partial \sigma $
with a supporting hyperplane. Codimension one faces are called facets.
Let
![]() $\underline {\mathrm {LPoly}}$
be the category whose objects are integral polyhedra and morphisms consist of the identity and integral affine isomorphisms onto faces (i.e., an integral affine morphism
$\underline {\mathrm {LPoly}}$
be the category whose objects are integral polyhedra and morphisms consist of the identity and integral affine isomorphisms onto faces (i.e., an integral affine morphism
![]() $\tau \rightarrow \sigma $
which is an isomorphism onto its image and identifies
$\tau \rightarrow \sigma $
which is an isomorphism onto its image and identifies
![]() $\tau $
with a face of
$\tau $
with a face of
![]() $\sigma $
). An integral polyhedral complex is a functor
$\sigma $
). An integral polyhedral complex is a functor
![]() $\mathtt {F}\colon \mathscr {P} \rightarrow \underline {\mathrm {LPoly}}$
from a finite category
$\mathtt {F}\colon \mathscr {P} \rightarrow \underline {\mathrm {LPoly}}$
from a finite category
![]() $\mathscr {P}$
to
$\mathscr {P}$
to
![]() $\underline {\mathrm {LPoly}}$
such that every face of
$\underline {\mathrm {LPoly}}$
such that every face of
![]() $\mathtt {F}(\sigma )$
still lies in the image of
$\mathtt {F}(\sigma )$
still lies in the image of
![]() $\mathtt {F}$
, and there is at most one arrow
$\mathtt {F}$
, and there is at most one arrow
![]() $\tau \rightarrow \sigma $
for every pair
$\tau \rightarrow \sigma $
for every pair
![]() $\tau ,\sigma \in \mathscr {P}$
. By abuse of notation, we usually drop the notation
$\tau ,\sigma \in \mathscr {P}$
. By abuse of notation, we usually drop the notation
![]() $\mathtt {F}$
and write
$\mathtt {F}$
and write
![]() $\sigma \in \mathscr {P}$
to represent an integral polyhedron in the image of the functor. From an integral polyhedral complex, we obtain a topological space
$\sigma \in \mathscr {P}$
to represent an integral polyhedron in the image of the functor. From an integral polyhedral complex, we obtain a topological space
![]() $B := \varinjlim _{\sigma \in \mathscr {P}} \sigma $
via gluing of the polyhedra along faces. We further assume that:
$B := \varinjlim _{\sigma \in \mathscr {P}} \sigma $
via gluing of the polyhedra along faces. We further assume that:
-
1. the natural map
 $\sigma \rightarrow B$
is injective for each
$\sigma \rightarrow B$
is injective for each
 $\sigma \in \mathscr {P}$
, so that
$\sigma \in \mathscr {P}$
, so that
 $\sigma $
can be identified with a closed subset of B called a cell, and a morphism
$\sigma $
can be identified with a closed subset of B called a cell, and a morphism
 $\tau \rightarrow \sigma $
can be identified with an inclusion of subsets;
$\tau \rightarrow \sigma $
can be identified with an inclusion of subsets; -
2. a finite intersection of cells is a cell; and
-
3. B is an orientable connected topological manifold of dimension n without boundary which in addition satisfies the condition that
 $H^1(B,\mathbb {Q}) = 0$
.
$H^1(B,\mathbb {Q}) = 0$
.
Remark 2.1. The condition
![]() $H^1(B,\mathbb {Q}) = 0$
will be used only in Theorem 4.18 to ensure that
$H^1(B,\mathbb {Q}) = 0$
will be used only in Theorem 4.18 to ensure that ![]() , where
, where ![]() is the degenerate Calabi–Yau variety that we are going to construct.Footnote
2
This corresponds to the condition that
is the degenerate Calabi–Yau variety that we are going to construct.Footnote
2
This corresponds to the condition that
![]() $b_1=0$
for smooth Calabi–Yau manifolds.
$b_1=0$
for smooth Calabi–Yau manifolds.
The set of k-dimensional cells is denoted by
![]() $\mathscr {P}^{[k]}$
and the k-skeleton by
$\mathscr {P}^{[k]}$
and the k-skeleton by
![]() $\mathscr {P}^{[\leq k]}$
. For every
$\mathscr {P}^{[\leq k]}$
. For every
![]() $\tau \in \mathscr {P}$
, we define its open star by
$\tau \in \mathscr {P}$
, we define its open star by
which is an open subset of B containing
![]() $\mathrm {int}_{\mathrm {re}}(\tau )$
. A fan structure along
$\mathrm {int}_{\mathrm {re}}(\tau )$
. A fan structure along
![]() $\tau \in \mathscr {P}^{[n-k]}$
is a continuous map
$\tau \in \mathscr {P}^{[n-k]}$
is a continuous map
![]() $S_{\tau } \colon U_{\tau } \rightarrow \mathbb {R}^{k}$
such that
$S_{\tau } \colon U_{\tau } \rightarrow \mathbb {R}^{k}$
such that
-
•
 $S^{-1}_{\tau }(0) = \mathrm {int}_{\mathrm {re}}(\tau )$
,
$S^{-1}_{\tau }(0) = \mathrm {int}_{\mathrm {re}}(\tau )$
, -
• for every
 $\sigma \supset \tau $
, the restriction
$\sigma \supset \tau $
, the restriction
 $S_{\tau }|_{\mathrm {int}_{\mathrm {re}}(\sigma )}$
is an integral affine submersion onto its image (meaning that it is induced by some epimorphism
$S_{\tau }|_{\mathrm {int}_{\mathrm {re}}(\sigma )}$
is an integral affine submersion onto its image (meaning that it is induced by some epimorphism
 $\Lambda _{\sigma } \rightarrow W \cap \mathbb {Z}^k$
for some vector subspace
$\Lambda _{\sigma } \rightarrow W \cap \mathbb {Z}^k$
for some vector subspace
 $W\subset \mathbb {R}^k$
), and
$W\subset \mathbb {R}^k$
), and -
• the collection of cones
 $\{ K_{\tau }\sigma := \mathbb {R}_{\geq 0} S_{\tau }(\sigma \cap U_{\tau }) \}_{\sigma \supset \tau }$
forms a complete finite fan
$\{ K_{\tau }\sigma := \mathbb {R}_{\geq 0} S_{\tau }(\sigma \cap U_{\tau }) \}_{\sigma \supset \tau }$
forms a complete finite fan
 $\Sigma _{\tau }$
.
$\Sigma _{\tau }$
.
Two fan structures along
![]() $\tau $
are equivalent if they differ by composition with an integral affine transformation of
$\tau $
are equivalent if they differ by composition with an integral affine transformation of
![]() $\mathbb {R}^{k}$
. If
$\mathbb {R}^{k}$
. If
![]() $S_\tau $
is a fan structure along
$S_\tau $
is a fan structure along
![]() $\tau $
and
$\tau $
and
![]() $\sigma \supset \tau $
, then
$\sigma \supset \tau $
, then
![]() $U_{\sigma } \subset U_{\tau }$
and there is a fan structure along
$U_{\sigma } \subset U_{\tau }$
and there is a fan structure along
![]() $\sigma $
induced from
$\sigma $
induced from
![]() $S_{\tau }$
via the composition:
$S_{\tau }$
via the composition:
where
![]() $\mathbb {R}^{k} \rightarrow \mathbb {R}^{k}/ \mathbb {R} S_{\tau }(\sigma \cap U_{\tau }) \cong \mathbb {R}^{l}$
is the quotient map.
$\mathbb {R}^{k} \rightarrow \mathbb {R}^{k}/ \mathbb {R} S_{\tau }(\sigma \cap U_{\tau }) \cong \mathbb {R}^{l}$
is the quotient map.
Definition 2.2 ([Reference Gross and Siebert29], Definition 1.2).
An integral tropical manifold is an integral polyhedral complex
![]() $(B,\mathscr {P})$
together with a fan structure
$(B,\mathscr {P})$
together with a fan structure
![]() $S_{\tau }$
along each
$S_{\tau }$
along each
![]() $\tau \in \mathscr {P}$
such that whenever
$\tau \in \mathscr {P}$
such that whenever
![]() $\tau \subset \sigma $
, the fan structure induced from
$\tau \subset \sigma $
, the fan structure induced from
![]() $S_{\tau }$
is equivalent to
$S_{\tau }$
is equivalent to
![]() $S_{\sigma }$
.
$S_{\sigma }$
.
Taking sufficiently small and mutually disjoint open subsets
![]() $W_{v} \subset U_{v}$
for
$W_{v} \subset U_{v}$
for
![]() $v \in \mathscr {P}^{[0]}$
and
$v \in \mathscr {P}^{[0]}$
and
![]() $\mathrm {int}_{\mathrm {re}}(\sigma )$
for
$\mathrm {int}_{\mathrm {re}}(\sigma )$
for
![]() $\sigma \in \mathscr {P}^{[n]}$
, there is an integral affine structure on
$\sigma \in \mathscr {P}^{[n]}$
, there is an integral affine structure on
![]() $\bigcup _{v \in \mathscr {P}^{[0]}} W_v \cup \bigcup _{\sigma \in \mathscr {P}^{[n]}} \mathrm {int}_{\mathrm {re}}(\sigma )$
. We will further choose the open subsets
$\bigcup _{v \in \mathscr {P}^{[0]}} W_v \cup \bigcup _{\sigma \in \mathscr {P}^{[n]}} \mathrm {int}_{\mathrm {re}}(\sigma )$
. We will further choose the open subsets
![]() $W_v$
’s and
$W_v$
’s and
![]() $\mathrm {int}_{\mathrm {re}}(\sigma )$
’s so that the affine structure is defined outside a closed subset
$\mathrm {int}_{\mathrm {re}}(\sigma )$
’s so that the affine structure is defined outside a closed subset
![]() $\Gamma $
of codimension two in B, as in [Reference Gross and Siebert27, §1.3]. This affine structure allows us to use parallel transport to identify the tangent spaces
$\Gamma $
of codimension two in B, as in [Reference Gross and Siebert27, §1.3]. This affine structure allows us to use parallel transport to identify the tangent spaces
![]() $T_x B$
for different points x outside the closed subset. For every
$T_x B$
for different points x outside the closed subset. For every
![]() $\tau $
, we choose a maximal cell
$\tau $
, we choose a maximal cell
![]() $\sigma \supset \tau $
and consider the lattice of normal vectors
$\sigma \supset \tau $
and consider the lattice of normal vectors
![]() $\mathscr {Q}_{\tau }=\Lambda _{\sigma }/\Lambda _{\tau }$
(we suppress the dependence on
$\mathscr {Q}_{\tau }=\Lambda _{\sigma }/\Lambda _{\tau }$
(we suppress the dependence on
![]() $\sigma $
because we will see that
$\sigma $
because we will see that
![]() $\Lambda _{\tau }$
is monodromy invariant under the monodromy transformation given by any two vertices of
$\Lambda _{\tau }$
is monodromy invariant under the monodromy transformation given by any two vertices of
![]() $\tau $
and any two maximal cells containing
$\tau $
and any two maximal cells containing
![]() $\tau $
). We can identify
$\tau $
). We can identify
![]() $\mathscr {Q}_{\tau }$
with
$\mathscr {Q}_{\tau }$
with
![]() $\mathbb {Z}^{k}$
via
$\mathbb {Z}^{k}$
via
![]() $S_{\tau }$
and write the fan structure as
$S_{\tau }$
and write the fan structure as
![]() $S_{\tau } \colon U_{\tau } \rightarrow \mathscr {Q}_{\tau ,\mathbb {R}}$
.
$S_{\tau } \colon U_{\tau } \rightarrow \mathscr {Q}_{\tau ,\mathbb {R}}$
.
Example 2.3. We take a two-dimensional example from [Reference Aspinwall, Bridgeland, Craw, Douglas, Gross, Kapustin, Moore, Segal, Szendrői and Wilson1, Ex. 6.74] to illustrate the above definitions. Let
![]() $\Xi $
be the convex hull of the points
$\Xi $
be the convex hull of the points
 $$ \begin{align*} p_0 = \begin{bmatrix} -1 \\ -1 \\ -1 \end{bmatrix}, \ p_1 = \begin{bmatrix} 3\\-1\\-1\end{bmatrix}, \ p_2 = \begin{bmatrix} -1 \\ 3 \\ -1 \end{bmatrix}, \ p_3 = \begin{bmatrix} -1 \\ -1 \\3 \end{bmatrix}, \end{align*} $$
$$ \begin{align*} p_0 = \begin{bmatrix} -1 \\ -1 \\ -1 \end{bmatrix}, \ p_1 = \begin{bmatrix} 3\\-1\\-1\end{bmatrix}, \ p_2 = \begin{bmatrix} -1 \\ 3 \\ -1 \end{bmatrix}, \ p_3 = \begin{bmatrix} -1 \\ -1 \\3 \end{bmatrix}, \end{align*} $$
so
![]() $\Xi $
is a
$\Xi $
is a
![]() $3$
-simplex. Take B (as a topological space) to be the boundary of
$3$
-simplex. Take B (as a topological space) to be the boundary of
![]() $\Xi $
. The polyhedral decomposition
$\Xi $
. The polyhedral decomposition
![]() $\mathscr {P}$
is defined so that the integral points are vertices as shown in Figure 1.
$\mathscr {P}$
is defined so that the integral points are vertices as shown in Figure 1.

Figure 1 The polyhedral decomposition.
Then we define affine coordinate charts on
![]() $\bigcup _{\sigma \in \mathscr {P}^{[n]}} \mathrm {int}_{\mathrm {re}}(\sigma ) \cup \bigcup _{v\in \mathscr {P}^{[0]}} W_v$
as follows. On
$\bigcup _{\sigma \in \mathscr {P}^{[n]}} \mathrm {int}_{\mathrm {re}}(\sigma ) \cup \bigcup _{v\in \mathscr {P}^{[0]}} W_v$
as follows. On
![]() $\mathrm {int}_{\mathrm {re}}(\sigma )$
, we take
$\mathrm {int}_{\mathrm {re}}(\sigma )$
, we take
![]() $\psi _{\sigma } \colon \mathrm {int}_{\mathrm {re}}(\sigma ) \rightarrow \Lambda _{\sigma ,\mathbb {R}}$
which maps homeomorphically onto its image. At a vertex v treated as a vector in
$\psi _{\sigma } \colon \mathrm {int}_{\mathrm {re}}(\sigma ) \rightarrow \Lambda _{\sigma ,\mathbb {R}}$
which maps homeomorphically onto its image. At a vertex v treated as a vector in
![]() $\mathbb {R}^3$
, we let
$\mathbb {R}^3$
, we let
![]() $\psi _v\colon W_v \subset \mathbb {R}^3 \rightarrow \mathbb {R}^3 / \mathbb {R} v$
, where
$\psi _v\colon W_v \subset \mathbb {R}^3 \rightarrow \mathbb {R}^3 / \mathbb {R} v$
, where
![]() $\mathbb {R}^3 \rightarrow \mathbb {R}^3/\mathbb {R} v$
is the natural projection onto the quotient. By [Reference Aspinwall, Bridgeland, Craw, Douglas, Gross, Kapustin, Moore, Segal, Szendrői and Wilson1, Prop. 6.81], this gives an integral affine manifold with singularities. The affine structure can be extended to the complement of a subset
$\mathbb {R}^3 \rightarrow \mathbb {R}^3/\mathbb {R} v$
is the natural projection onto the quotient. By [Reference Aspinwall, Bridgeland, Craw, Douglas, Gross, Kapustin, Moore, Segal, Szendrői and Wilson1, Prop. 6.81], this gives an integral affine manifold with singularities. The affine structure can be extended to the complement of a subset
![]() $\Gamma $
consisting of
$\Gamma $
consisting of
![]() $24$
points lying on the six edges of
$24$
points lying on the six edges of
![]() $\Xi $
, with each edge containing
$\Xi $
, with each edge containing
![]() $4$
points (colored in red in Figure 1). The fan structure
$4$
points (colored in red in Figure 1). The fan structure
![]() $S_\tau $
can be defined similarly.
$S_\tau $
can be defined similarly.
Locally near each singular point
![]() $p \in \Gamma $
contained in an edge
$p \in \Gamma $
contained in an edge
![]() $\rho $
, the affine structure is described as a gluing of two affine charts
$\rho $
, the affine structure is described as a gluing of two affine charts
![]() $U_{\mathrm {I}}\subset \mathbb {R}^2 \setminus \{0\} \times \mathbb {R}_{\geq 0}$
and
$U_{\mathrm {I}}\subset \mathbb {R}^2 \setminus \{0\} \times \mathbb {R}_{\geq 0}$
and
![]() $U_{\mathrm {II}}\subset \mathbb {R}^2 \setminus 0 \times \mathbb {R}_{\leq 0}$
as in [Reference Gross and Siebert30, §3.2]. The change of coordinates from
$U_{\mathrm {II}}\subset \mathbb {R}^2 \setminus 0 \times \mathbb {R}_{\leq 0}$
as in [Reference Gross and Siebert30, §3.2]. The change of coordinates from
![]() $U_{\mathrm {I}}$
to
$U_{\mathrm {I}}$
to
![]() $U_{\mathrm {II}}$
is given by the restriction of the map
$U_{\mathrm {II}}$
is given by the restriction of the map
![]() $\Upsilon $
from
$\Upsilon $
from
![]() $(\mathbb {R} \setminus \{0\}) \times \mathbb {R}$
to itself defined by
$(\mathbb {R} \setminus \{0\}) \times \mathbb {R}$
to itself defined by
 $$ \begin{align*} (x,y) \mapsto \begin{cases} (x,y), & x<0\\ (x,x+y), & x>0. \end{cases} \end{align*} $$
$$ \begin{align*} (x,y) \mapsto \begin{cases} (x,y), & x<0\\ (x,x+y), & x>0. \end{cases} \end{align*} $$
The fan structure
![]() $S_\rho \colon U_{\rho } \rightarrow \mathbb {R}$
is given as
$S_\rho \colon U_{\rho } \rightarrow \mathbb {R}$
is given as
![]() $S_{\rho }(x,y) = x$
and the fan
$S_{\rho }(x,y) = x$
and the fan
![]() $\Sigma _{\rho }$
is the toric fan for
$\Sigma _{\rho }$
is the toric fan for
![]() $\mathbb {P}^1$
. Figure 2 below illustrates the situation.
$\mathbb {P}^1$
. Figure 2 below illustrates the situation.

Figure 2 Affine coordinate charts.
With the structure of an integral tropical manifold, the corners and edges in Figure 1 are flattened via the affine coordinate charts, and we can view
![]() $(B,\mathscr {P})$
as the 2-sphere equipped with a polyhedral decomposition and with
$(B,\mathscr {P})$
as the 2-sphere equipped with a polyhedral decomposition and with
![]() $24$
affine singularities. Such an affine structure with singularities also appears in the base B of an SYZ fibration of a K3 surface.
$24$
affine singularities. Such an affine structure with singularities also appears in the base B of an SYZ fibration of a K3 surface.
Example 2.4. A three-dimensional example can be constructed as in [Reference Aspinwall, Bridgeland, Craw, Douglas, Gross, Kapustin, Moore, Segal, Szendrői and Wilson1, Ex. 6.74]. Take
![]() $\Xi $
to be the convex hull of the points
$\Xi $
to be the convex hull of the points
 $$ \begin{align*} p_0 = \begin{bmatrix} -1 \\ -1 \\ -1 \\-1 \end{bmatrix}, \ p_1 = \begin{bmatrix} 4 \\-1\\-1 \\ -1 \end{bmatrix}, \ p_2 = \begin{bmatrix} -1 \\ 4 \\ -1 \\ -1 \end{bmatrix}, \ p_3 = \begin{bmatrix} -1 \\ -1 \\4 \\ -1 \end{bmatrix}, \ p_4 = \begin{bmatrix} -1 \\ -1 \\-1 \\ 4 \end{bmatrix}, \end{align*} $$
$$ \begin{align*} p_0 = \begin{bmatrix} -1 \\ -1 \\ -1 \\-1 \end{bmatrix}, \ p_1 = \begin{bmatrix} 4 \\-1\\-1 \\ -1 \end{bmatrix}, \ p_2 = \begin{bmatrix} -1 \\ 4 \\ -1 \\ -1 \end{bmatrix}, \ p_3 = \begin{bmatrix} -1 \\ -1 \\4 \\ -1 \end{bmatrix}, \ p_4 = \begin{bmatrix} -1 \\ -1 \\-1 \\ 4 \end{bmatrix}, \end{align*} $$
which gives a
![]() $4$
-simplex. Take B (as a topological space) to be the boundary of
$4$
-simplex. Take B (as a topological space) to be the boundary of
![]() $\Xi $
. There are five three-dimensional maximal cells intersecting along 10 two-dimensional facets. The polyhedral decomposition
$\Xi $
. There are five three-dimensional maximal cells intersecting along 10 two-dimensional facets. The polyhedral decomposition
![]() $\mathscr {P}$
on each facet is as in Figure 3.
$\mathscr {P}$
on each facet is as in Figure 3.

Figure 3 The polyhedral decomposition on a facet.
The affine structure can be extended to the complement of codimension 2 closed subset
![]() $\Gamma $
whose intersection with a triangle in Figure 3 is a Y-shaped locus. Locally near each of these triangles, it looks like Figure 4a.
$\Gamma $
whose intersection with a triangle in Figure 3 is a Y-shaped locus. Locally near each of these triangles, it looks like Figure 4a.

Figure 4 Two types of Y-vertex.
![]() $\Xi $
has 10 one-dimensional faces, each of which is an edge with affine length
$\Xi $
has 10 one-dimensional faces, each of which is an edge with affine length
![]() $5$
. The polyhedral decomposition
$5$
. The polyhedral decomposition
![]() $\mathscr {P}$
divides each edge into
$\mathscr {P}$
divides each edge into
![]() $5$
intervals as we can see in Figure 3. Locally near each of these length
$5$
intervals as we can see in Figure 3. Locally near each of these length
![]() $1$
intervals, there are three
$1$
intervals, there are three
![]() $2$
-cells of
$2$
-cells of
![]() $\mathscr {P}$
intersecting along it. The locus
$\mathscr {P}$
intersecting along it. The locus
![]() $\Gamma $
on each
$\Gamma $
on each
![]() $2$
-cell intersects on the interval as shown in Figure 4b.
$2$
-cell intersects on the interval as shown in Figure 4b.
Definition 2.5 ([Reference Gross and Siebert27], Definition 1.43).
An integral affine function on an open subset
![]() $U \subset B$
is a continuous function
$U \subset B$
is a continuous function
![]() $\varphi $
on U which is integral affine on
$\varphi $
on U which is integral affine on
![]() $U \cap \mathrm {int}_{\mathrm {re}}(\sigma )$
for
$U \cap \mathrm {int}_{\mathrm {re}}(\sigma )$
for
![]() $\sigma \in \mathscr {P}^{[n]}$
and on
$\sigma \in \mathscr {P}^{[n]}$
and on
![]() $U \cap W_v$
for
$U \cap W_v$
for
![]() $v \in \mathscr {P}^{[0]}$
. We denote by
$v \in \mathscr {P}^{[0]}$
. We denote by
![]() $\mathcal {A}{ff}_{B}$
(or simply
$\mathcal {A}{ff}_{B}$
(or simply
![]() $\mathcal {A}{ff}$
) the sheaf of integral affine functions on B.
$\mathcal {A}{ff}$
) the sheaf of integral affine functions on B.
A piecewise integral affine function (abbreviated as PA-function) on U is a continuous function
![]() $\varphi $
on U which can be written as
$\varphi $
on U which can be written as
![]() $\varphi = \psi + S_{\tau }^*(\bar {\varphi })$
on
$\varphi = \psi + S_{\tau }^*(\bar {\varphi })$
on
![]() $U \cap U_{\tau }$
for every
$U \cap U_{\tau }$
for every
![]() $\tau \in \mathscr {P}$
, where
$\tau \in \mathscr {P}$
, where
![]() $\psi \in \mathcal {A}{ff}(U \cap U_\tau )$
and
$\psi \in \mathcal {A}{ff}(U \cap U_\tau )$
and
![]() $\bar {\varphi }$
is a piecewise linear function on
$\bar {\varphi }$
is a piecewise linear function on
![]() $\mathscr {Q}_{\tau ,\mathbb {R}}$
with respect to the fan
$\mathscr {Q}_{\tau ,\mathbb {R}}$
with respect to the fan
![]() $\Sigma _{\tau }$
. The sheaf of PA-functions on B is denoted by
$\Sigma _{\tau }$
. The sheaf of PA-functions on B is denoted by
![]() $\mathcal {PL}_{\mathscr {P}}$
.
$\mathcal {PL}_{\mathscr {P}}$
.
There is a natural inclusion
![]() $\mathcal {A}{ff}\hookrightarrow \mathcal {PL}_{\mathscr {P}}$
, and we let
$\mathcal {A}{ff}\hookrightarrow \mathcal {PL}_{\mathscr {P}}$
, and we let
![]() $\mathcal {MPL}_{\mathscr {P}}$
be the quotient:
$\mathcal {MPL}_{\mathscr {P}}$
be the quotient:
Locally, an element
![]() $\varphi \in \Gamma (B,\mathcal {MPL}_{\mathscr {P}})$
is a collection of piecewise affine functions
$\varphi \in \Gamma (B,\mathcal {MPL}_{\mathscr {P}})$
is a collection of piecewise affine functions
![]() $\{\varphi _U\}$
such that on each overlap
$\{\varphi _U\}$
such that on each overlap
![]() $U\cap V$
, the difference
$U\cap V$
, the difference
![]() $\varphi _U|_{V}-\varphi _V|_{U}$
is an integral affine function on
$\varphi _U|_{V}-\varphi _V|_{U}$
is an integral affine function on
![]() $U\cap V$
.
$U\cap V$
.
Definition 2.6 ([Reference Gross and Siebert27], Definitions 1.45 and 1.47).
The sheaf
![]() $\mathcal {MPL}_{\mathscr {P}}$
is called the sheaf of multivalued piecewise affine functions (abbreviated as MPA-funtions) of the pair
$\mathcal {MPL}_{\mathscr {P}}$
is called the sheaf of multivalued piecewise affine functions (abbreviated as MPA-funtions) of the pair
![]() $(B,\mathscr {P})$
. A section
$(B,\mathscr {P})$
. A section
![]() $\varphi \in H^0(B,\mathcal {MPL}_{\mathscr {P}})$
is said to be convex (resp. strictly convex) if for any vertex
$\varphi \in H^0(B,\mathcal {MPL}_{\mathscr {P}})$
is said to be convex (resp. strictly convex) if for any vertex
![]() $\{v\}\in \mathscr {P}$
, there is a convex (resp. strictly convex) representative
$\{v\}\in \mathscr {P}$
, there is a convex (resp. strictly convex) representative
![]() $\varphi _v$
on
$\varphi _v$
on
![]() $U_v$
. (Here, convexity (resp. strict convexity) means if we take any maximal cone
$U_v$
. (Here, convexity (resp. strict convexity) means if we take any maximal cone
![]() $\sigma \subset U_v$
with the affine function
$\sigma \subset U_v$
with the affine function
![]() $l_{\sigma }\colon U_v\rightarrow \mathbb {R}$
defined by requiring
$l_{\sigma }\colon U_v\rightarrow \mathbb {R}$
defined by requiring
![]() $\varphi _v|_{\sigma } = l_{\sigma }$
, we always have
$\varphi _v|_{\sigma } = l_{\sigma }$
, we always have
![]() $\varphi _v(y)\geq l_{\sigma }(y)$
(resp.
$\varphi _v(y)\geq l_{\sigma }(y)$
(resp.
![]() $\varphi _v(y)> l_{\sigma }(y)$
) for
$\varphi _v(y)> l_{\sigma }(y)$
) for
![]() $y\in U_v \setminus \sigma $
).
$y\in U_v \setminus \sigma $
).
The set of all convex multivalued piecewise affine functions gives a submonoid of
![]() $H^0(B,\mathcal {MPL}_{\mathscr {P}})$
under addition, denoted as
$H^0(B,\mathcal {MPL}_{\mathscr {P}})$
under addition, denoted as
![]() $H^0(B,\mathcal {MPL}_{\mathscr {P}},\mathbb {N})$
; we let Q be the dual monoid.
$H^0(B,\mathcal {MPL}_{\mathscr {P}},\mathbb {N})$
; we let Q be the dual monoid.
Definition 2.7 ([Reference Gross and Siebert27], Definition 1.48).
The polyhedral decomposition
![]() $\mathscr {P}$
is said to be regular if there exists a strictly convex multivalued piecewise linear function
$\mathscr {P}$
is said to be regular if there exists a strictly convex multivalued piecewise linear function
![]() $\varphi \in H^0(B,\mathcal {MPL}_{\mathscr {P}})$
.
$\varphi \in H^0(B,\mathcal {MPL}_{\mathscr {P}})$
.
We always assume that
![]() $\mathscr {P}$
is regular with a fixed strictly convex
$\mathscr {P}$
is regular with a fixed strictly convex
![]() $\varphi \in H^0(B,\mathcal {MPL}_{\mathscr {P}})$
.
$\varphi \in H^0(B,\mathcal {MPL}_{\mathscr {P}})$
.
2.2 Monodromy, positivity and simplicity
To describe monodromy, we consider two maximal cells
![]() $\sigma _{\pm }$
and two of their common vertices
$\sigma _{\pm }$
and two of their common vertices
![]() $v_{\pm }$
. Taking a path
$v_{\pm }$
. Taking a path
![]() $\gamma $
going from
$\gamma $
going from
![]() $v_+$
to
$v_+$
to
![]() $v_-$
through
$v_-$
through
![]() $\sigma _+$
, and then from
$\sigma _+$
, and then from
![]() $v_-$
back to
$v_-$
back to
![]() $v_+$
through
$v_+$
through
![]() $\sigma _-$
, we obtain a monodromy transformation
$\sigma _-$
, we obtain a monodromy transformation
![]() $T_{\gamma }$
. As in [Reference Gross and Siebert27, §1.5], we are interested in two cases. The first case is when
$T_{\gamma }$
. As in [Reference Gross and Siebert27, §1.5], we are interested in two cases. The first case is when
![]() $v_+$
is connected to
$v_+$
is connected to
![]() $v_-$
via a bounded edge
$v_-$
via a bounded edge
![]() $\omega \in \mathscr {P}^{[1]}$
. Let
$\omega \in \mathscr {P}^{[1]}$
. Let
![]() $d_{\omega } \in \Lambda _{\omega }$
be the unique primitive vector pointing to
$d_{\omega } \in \Lambda _{\omega }$
be the unique primitive vector pointing to
![]() $v_-$
along
$v_-$
along
![]() $\omega $
. For an integral tangent vector
$\omega $
. For an integral tangent vector
![]() $m \in T_{v_+} := T_{v_+,\mathbb {Z}}B$
, the monodromy transformation
$m \in T_{v_+} := T_{v_+,\mathbb {Z}}B$
, the monodromy transformation
![]() $T_{\gamma }$
is given by
$T_{\gamma }$
is given by
for some
![]() $n^{\sigma _+ \sigma _-}_{\omega } \in \mathscr {Q}_{\sigma _+ \cap \sigma _-}^*\subset T_{v_+}^* $
, where
$n^{\sigma _+ \sigma _-}_{\omega } \in \mathscr {Q}_{\sigma _+ \cap \sigma _-}^*\subset T_{v_+}^* $
, where
![]() $\langle \cdot , \cdot \rangle $
is the natural pairing between
$\langle \cdot , \cdot \rangle $
is the natural pairing between
![]() $T_{v_+}$
and
$T_{v_+}$
and
![]() $T_{v_+}^*$
. The second case is when
$T_{v_+}^*$
. The second case is when
![]() $\sigma _+$
and
$\sigma _+$
and
![]() $\sigma _-$
are separated by a codimension one cell
$\sigma _-$
are separated by a codimension one cell
![]() $\rho \in \mathscr {P}^{[n-1]}$
. Let
$\rho \in \mathscr {P}^{[n-1]}$
. Let
![]() $\check {d}_{\rho }\in \mathscr {Q}_{\rho }^*$
be the unique primitive covector which is positive on
$\check {d}_{\rho }\in \mathscr {Q}_{\rho }^*$
be the unique primitive covector which is positive on
![]() $\sigma _+$
. The monodromy transformation is given by
$\sigma _+$
. The monodromy transformation is given by
for some
![]() $m^{\rho }_{v_+v_-} \in \Lambda _{\tau }$
, where
$m^{\rho }_{v_+v_-} \in \Lambda _{\tau }$
, where
![]() $\tau \subset \rho $
is the smallest face of
$\tau \subset \rho $
is the smallest face of
![]() $\rho $
containing
$\rho $
containing
![]() $v_{\pm }$
. In particular, if we fix both
$v_{\pm }$
. In particular, if we fix both
![]() $v_{\pm } \in \omega \subset \rho \subset \sigma _{\pm }$
, one obtains the formula
$v_{\pm } \in \omega \subset \rho \subset \sigma _{\pm }$
, one obtains the formula
for some integer
![]() $\kappa _{\omega \rho }$
.
$\kappa _{\omega \rho }$
.
Definition 2.8 ([Reference Gross and Siebert27], Definition 1.54).
We say that
![]() $(B,\mathscr {P})$
is positive if
$(B,\mathscr {P})$
is positive if
![]() $\kappa _{\omega \rho } \geq 0$
for all
$\kappa _{\omega \rho } \geq 0$
for all
![]() $\omega \in \mathscr {P}^{[1]}$
and
$\omega \in \mathscr {P}^{[1]}$
and
![]() $\rho \in \mathscr {P}^{[n-1]}$
with
$\rho \in \mathscr {P}^{[n-1]}$
with
![]() $\omega \subset \rho $
.
$\omega \subset \rho $
.
Following [Reference Gross and Siebert27, Definition 1.58], we package the monodromy data into polytopes associated to
![]() $\tau \in \mathscr {P}^{[k]}$
for
$\tau \in \mathscr {P}^{[k]}$
for
![]() $1\leq k \leq n-1$
. The simplest case is when
$1\leq k \leq n-1$
. The simplest case is when
![]() $\rho \in \mathscr {P}^{[n-1]}$
, whose monodromy polytope is defined by fixing a vertex
$\rho \in \mathscr {P}^{[n-1]}$
, whose monodromy polytope is defined by fixing a vertex
![]() $v_0 \in \rho $
and setting
$v_0 \in \rho $
and setting
where
![]() $\mathrm {Conv}$
refers to taking the convex hull. It is well defined up to translation and independent of the choice of
$\mathrm {Conv}$
refers to taking the convex hull. It is well defined up to translation and independent of the choice of
![]() $v_0$
. The normal fan of
$v_0$
. The normal fan of
![]() $\rho $
in
$\rho $
in
![]() $\Lambda _{\rho ,\mathbb {R}}^*$
is a refinement of the normal fan of
$\Lambda _{\rho ,\mathbb {R}}^*$
is a refinement of the normal fan of
![]() $\Delta (\rho )$
. Similarly, when
$\Delta (\rho )$
. Similarly, when
![]() $\omega \in \mathscr {P}^{[1]}$
, one defines the dual monodromy polytope by fixing
$\omega \in \mathscr {P}^{[1]}$
, one defines the dual monodromy polytope by fixing
![]() $\sigma _0 \supset \omega $
and setting
$\sigma _0 \supset \omega $
and setting
Again, this is well defined up to translation and independent of the choice of
![]() $\sigma _0$
. The fan
$\sigma _0$
. The fan
![]() $\Sigma _{\omega }$
in
$\Sigma _{\omega }$
in
![]() $\mathscr {Q}_{\omega ,\mathbb {R}}$
is a refinement of the normal fan of
$\mathscr {Q}_{\omega ,\mathbb {R}}$
is a refinement of the normal fan of
![]() $\check {\Delta }(\omega )$
. For
$\check {\Delta }(\omega )$
. For
![]() $1< \dim _{\mathbb {R}}(\tau ) <n-1$
, a combination of monodromy and dual monodromy polytopes is needed. We let
$1< \dim _{\mathbb {R}}(\tau ) <n-1$
, a combination of monodromy and dual monodromy polytopes is needed. We let
![]() $\mathscr {P}_1(\tau ) = \{ \omega \ | \ \omega \in \mathscr {P}^{[1]}, \ \omega \subset \tau \}$
and
$\mathscr {P}_1(\tau ) = \{ \omega \ | \ \omega \in \mathscr {P}^{[1]}, \ \omega \subset \tau \}$
and
![]() $\mathscr {P}_{n-1}(\tau ) = \{ \rho \ | \ \rho \in \mathscr {P}^{[n-1]}, \ \rho \supset \tau \}$
. For each
$\mathscr {P}_{n-1}(\tau ) = \{ \rho \ | \ \rho \in \mathscr {P}^{[n-1]}, \ \rho \supset \tau \}$
. For each
![]() $\rho \in \mathscr {P}_{n-1}(\tau )$
, we choose a vertex
$\rho \in \mathscr {P}_{n-1}(\tau )$
, we choose a vertex
![]() $v_0 \in \rho $
and let
$v_0 \in \rho $
and let
Similarly, for each
![]() $\omega \in \mathscr {P}_1(\tau )$
, we choose
$\omega \in \mathscr {P}_1(\tau )$
, we choose
![]() $\sigma _0 \supset \tau $
and let
$\sigma _0 \supset \tau $
and let
These are well defined up to translation and independent of the choices of
![]() $v_0$
and
$v_0$
and
![]() $\sigma _0$
, respectively.
$\sigma _0$
, respectively.
Definition 2.9 ([Reference Gross and Siebert27], Definition 1.60).
We say
![]() $(B,\mathscr {P})$
is simple if, for every
$(B,\mathscr {P})$
is simple if, for every
![]() $\tau \in \mathscr {P}$
, there are disjoint nonempty subsets
$\tau \in \mathscr {P}$
, there are disjoint nonempty subsets
(where p depends on
![]() $\tau $
) such that
$\tau $
) such that
-
1. for
 $\omega \in \mathscr {P}_1(\tau )$
and
$\omega \in \mathscr {P}_1(\tau )$
and
 $\rho \in \mathscr {P}_{n-1}(\tau )$
,
$\rho \in \mathscr {P}_{n-1}(\tau )$
,
 $\kappa _{\omega \rho } \neq 0$
if and only if
$\kappa _{\omega \rho } \neq 0$
if and only if
 $\omega \in \Omega _i$
and
$\omega \in \Omega _i$
and
 $\rho \in R_i$
for some
$\rho \in R_i$
for some
 $1 \leq i \leq p$
;
$1 \leq i \leq p$
; -
2.
 $\Delta _{\rho }(\tau )$
is independent (up to translation) of
$\Delta _{\rho }(\tau )$
is independent (up to translation) of
 $\rho \in R_i$
and will be denoted by
$\rho \in R_i$
and will be denoted by
 $\Delta _i(\tau )$
; similarly,
$\Delta _i(\tau )$
; similarly,
 $\check {\Delta }_{\omega }(\tau )$
is independent (up to translation) of
$\check {\Delta }_{\omega }(\tau )$
is independent (up to translation) of
 $\omega \in \Omega _i$
and will be denoted by
$\omega \in \Omega _i$
and will be denoted by
 $\check {\Delta }_i(\tau )$
;
$\check {\Delta }_i(\tau )$
; -
3. if
 $\{e_1,\dots ,e_p\}$
is the standard basis in
$\{e_1,\dots ,e_p\}$
is the standard basis in
 $\mathbb {Z}^{p}$
, then are elementary simplices (i.e., a simplex whose only integral points are its vertices) in
$\mathbb {Z}^{p}$
, then are elementary simplices (i.e., a simplex whose only integral points are its vertices) in $$ \begin{align*} \Delta(\tau):= \mathrm{Conv} \left\{ \bigcup_{i=1}^{p} \Delta_i(\tau) \times \{e_i\} \right\}, \quad \check{\Delta}(\tau):= \mathrm{Conv} \left\{ \bigcup_{i=1}^{p} \check{\Delta}_i(\tau) \times \{e_i\} \right\} \end{align*} $$
$$ \begin{align*} \Delta(\tau):= \mathrm{Conv} \left\{ \bigcup_{i=1}^{p} \Delta_i(\tau) \times \{e_i\} \right\}, \quad \check{\Delta}(\tau):= \mathrm{Conv} \left\{ \bigcup_{i=1}^{p} \check{\Delta}_i(\tau) \times \{e_i\} \right\} \end{align*} $$
 $\left (\Lambda _{\tau } \oplus \mathbb {Z}^{p}\right )_{\mathbb {R}}$
and
$\left (\Lambda _{\tau } \oplus \mathbb {Z}^{p}\right )_{\mathbb {R}}$
and
 $\left ( \mathscr {Q}_{\tau }^*\oplus \mathbb {Z}^{p} \right )_{\mathbb {R}}$
, respectively.
$\left ( \mathscr {Q}_{\tau }^*\oplus \mathbb {Z}^{p} \right )_{\mathbb {R}}$
, respectively.
We need the following stronger condition in order to apply [Reference Gross and Siebert28, Thm. 3.21] in a later stage:
Definition 2.10. We say
![]() $(B,\mathscr {P})$
is strongly simple if it is simple, and for every
$(B,\mathscr {P})$
is strongly simple if it is simple, and for every
![]() $\tau \in \mathscr {P}$
, both
$\tau \in \mathscr {P}$
, both
![]() $\Delta (\tau )$
and
$\Delta (\tau )$
and
![]() $\check {\Delta }(\tau )$
are standard simplices.
$\check {\Delta }(\tau )$
are standard simplices.
Example 2.11. Consider the two-dimensional example in Example 2.3. Following [Reference Aspinwall, Bridgeland, Craw, Douglas, Gross, Kapustin, Moore, Segal, Szendrői and Wilson1, Ex. 6.82(1)], we may choose the two adjacent vertices in Figure 1 to be
![]() $v_1 = \begin {bmatrix} -1 & -1 & -1 \end {bmatrix}^T$
and
$v_1 = \begin {bmatrix} -1 & -1 & -1 \end {bmatrix}^T$
and
![]() $v_2 = \begin {bmatrix} 0 & -1 & -1 \end {bmatrix}^T$
which bound a
$v_2 = \begin {bmatrix} 0 & -1 & -1 \end {bmatrix}^T$
which bound a
![]() $1$
-cell
$1$
-cell
![]() $\rho $
. The two adjacent maximal cells are given by
$\rho $
. The two adjacent maximal cells are given by
![]() $\sigma _+ \subset \{ b \ | \ \langle w_+,b\rangle =1\}$
, where
$\sigma _+ \subset \{ b \ | \ \langle w_+,b\rangle =1\}$
, where
![]() $w_+ = \begin {bmatrix} 0 & 0 & -1 \end {bmatrix}^T$
and
$w_+ = \begin {bmatrix} 0 & 0 & -1 \end {bmatrix}^T$
and
![]() $\sigma _- \subset \{ b \ | \ \langle w_-,b\rangle =1\}$
, where
$\sigma _- \subset \{ b \ | \ \langle w_-,b\rangle =1\}$
, where
![]() $w_- = \begin {bmatrix} 0 & -1 & 0 \end {bmatrix}^T$
. The tangent lattice
$w_- = \begin {bmatrix} 0 & -1 & 0 \end {bmatrix}^T$
. The tangent lattice
![]() $T_{v_1}$
can be identified with
$T_{v_1}$
can be identified with
![]() $\mathbb {Z}^3/\mathbb {Z} \cdot v_1$
equipped with the basis
$\mathbb {Z}^3/\mathbb {Z} \cdot v_1$
equipped with the basis
![]() $e_1 = \begin {bmatrix} 1 & 0 &0 \end {bmatrix}^T$
,
$e_1 = \begin {bmatrix} 1 & 0 &0 \end {bmatrix}^T$
,
![]() $e_2 = \begin {bmatrix} 0 & 1& 0 \end {bmatrix}^T$
. If we let
$e_2 = \begin {bmatrix} 0 & 1& 0 \end {bmatrix}^T$
. If we let
![]() $\gamma $
be a loop going from
$\gamma $
be a loop going from
![]() $v_1$
to
$v_1$
to
![]() $v_2$
through
$v_2$
through
![]() $\sigma _+$
and going back to
$\sigma _+$
and going back to
![]() $v_1$
through
$v_1$
through
![]() $\sigma _-$
, we have
$\sigma _-$
, we have
for
![]() $m \in T_{v_1}$
. Therefore, we have
$m \in T_{v_1}$
. Therefore, we have
![]() $p=1$
,
$p=1$
,
![]() $\Delta _1(\rho ) = \mathrm {Conv} \{0,e_1\}$
and
$\Delta _1(\rho ) = \mathrm {Conv} \{0,e_1\}$
and
![]() $\check {\Delta }_{1}(\rho ) = \mathrm {Conv} \{ 0 , w_+ - w_-\}$
. This is an example of a positive and strongly simple
$\check {\Delta }_{1}(\rho ) = \mathrm {Conv} \{ 0 , w_+ - w_-\}$
. This is an example of a positive and strongly simple
![]() $(B,\mathscr {P})$
(Definitions 2.8 and 2.10).
$(B,\mathscr {P})$
(Definitions 2.8 and 2.10).
Example 2.12. Next, we consider the two types of Y-vertex in Example 2.4.
We begin with Y-vertex of type I in Figure 4a. Following [Reference Aspinwall, Bridgeland, Craw, Douglas, Gross, Kapustin, Moore, Segal, Szendrői and Wilson1, Ex. 6.82(2)], the three vertices
![]() $v_1,v_2,v_3$
can be chosen to be
$v_1,v_2,v_3$
can be chosen to be
and
![]() $\sigma _+ \subset \{ b \in \mathbb {R}^4 \ | \ \langle w_+ , b \rangle = 1 \}$
,
$\sigma _+ \subset \{ b \in \mathbb {R}^4 \ | \ \langle w_+ , b \rangle = 1 \}$
,
![]() $\sigma _- \subset \{ b \in \mathbb {R}^4 \ | \ \langle w_- , b \rangle = 1 \}$
are
$\sigma _- \subset \{ b \in \mathbb {R}^4 \ | \ \langle w_- , b \rangle = 1 \}$
are
![]() $3$
-cells of B lying in the affine hyperplanes with dual vector
$3$
-cells of B lying in the affine hyperplanes with dual vector
![]() $w_+ = \begin {bmatrix} 0 & 0 & -1 & 0 \end {bmatrix}^T$
and
$w_+ = \begin {bmatrix} 0 & 0 & -1 & 0 \end {bmatrix}^T$
and
![]() $w_- = \begin {bmatrix} 0 & 0 & 0 & -1 \end {bmatrix}^T$
, respectively. If we identify
$w_- = \begin {bmatrix} 0 & 0 & 0 & -1 \end {bmatrix}^T$
, respectively. If we identify
![]() $T_v$
with
$T_v$
with
![]() $\Lambda _{\sigma _+}$
via parallel transport and choose the basis of
$\Lambda _{\sigma _+}$
via parallel transport and choose the basis of
![]() $\Lambda _{\sigma _+}$
as
$\Lambda _{\sigma _+}$
as
then the monodromy transformations are given by
 $$ \begin{align*} T_{\gamma_1}= \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}, \ T_{\gamma_2} = \begin{bmatrix} 1 & 0 & -1 \\ 0 & 1 & -1 \\ 0 & 0 & 1 \end{bmatrix}, \ T_{\gamma_3} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{bmatrix}, \end{align*} $$
$$ \begin{align*} T_{\gamma_1}= \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}, \ T_{\gamma_2} = \begin{bmatrix} 1 & 0 & -1 \\ 0 & 1 & -1 \\ 0 & 0 & 1 \end{bmatrix}, \ T_{\gamma_3} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{bmatrix}, \end{align*} $$
where
![]() $\gamma _i$
is the loop going from
$\gamma _i$
is the loop going from
![]() $v_i$
to
$v_i$
to
![]() $v_{i+1}$
through
$v_{i+1}$
through
![]() $\sigma _+$
and going back to
$\sigma _+$
and going back to
![]() $v_i$
through
$v_i$
through
![]() $\sigma _-$
, with indices of
$\sigma _-$
, with indices of
![]() $v_i$
’s taken modulo
$v_i$
’s taken modulo
![]() $3$
. In this case, we have
$3$
. In this case, we have
![]() $p=1$
,
$p=1$
,
![]() $\Delta _1(\rho ) = \mathrm {Conv}\{0, e_1,-e_2\}$
is a
$\Delta _1(\rho ) = \mathrm {Conv}\{0, e_1,-e_2\}$
is a
![]() $2$
-simplex and
$2$
-simplex and
![]() $\check {\Delta }_{1}(\rho ) = \mathrm {Conv}\{0, w_+ - w_-\}$
is a
$\check {\Delta }_{1}(\rho ) = \mathrm {Conv}\{0, w_+ - w_-\}$
is a
![]() $1$
-simplex.
$1$
-simplex.
For the Y-vertex of type II in Figure 4b, we can choose
which are the end points of a
![]() $1$
-cell
$1$
-cell
![]() $\tau $
. We choose the three maximal cells
$\tau $
. We choose the three maximal cells
![]() $\sigma _1$
,
$\sigma _1$
,
![]() $\sigma _2$
and
$\sigma _2$
and
![]() $\sigma _3$
intersecting at
$\sigma _3$
intersecting at
![]() $\tau $
to be the
$\tau $
to be the
![]() $3$
-cells lying in affine hyperplanes defined by
$3$
-cells lying in affine hyperplanes defined by
![]() $\{b \ | \ \langle w_i, b \rangle = 1\}$
, where
$\{b \ | \ \langle w_i, b \rangle = 1\}$
, where
Let
![]() $\tilde {\gamma }_i$
be the loop going from
$\tilde {\gamma }_i$
be the loop going from
![]() $v_1$
to
$v_1$
to
![]() $v_2$
through
$v_2$
through
![]() $w_i$
and then going back to
$w_i$
and then going back to
![]() $v_1$
through
$v_1$
through
![]() $w_{i+1}$
, with indices taken to be modulo
$w_{i+1}$
, with indices taken to be modulo
![]() $3$
. Then the corresponding monodromy transformations are given by
$3$
. Then the corresponding monodromy transformations are given by
 $$ \begin{align*}T_{\gamma_1}= \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}, \ T_{\gamma_2} = \begin{bmatrix} 1 & 1& 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}, \ T_{\gamma_3} = \begin{bmatrix} 1 & -1& -1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}, \end{align*} $$
$$ \begin{align*}T_{\gamma_1}= \begin{bmatrix} 1 & 0 & 1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}, \ T_{\gamma_2} = \begin{bmatrix} 1 & 1& 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}, \ T_{\gamma_3} = \begin{bmatrix} 1 & -1& -1 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}, \end{align*} $$
with respect to the basis
In this case,
![]() $p=1$
,
$p=1$
,
![]() $\Delta _1(\tau ) = \mathrm {Conv}\{0, v_2 - v_1\}$
is a
$\Delta _1(\tau ) = \mathrm {Conv}\{0, v_2 - v_1\}$
is a
![]() $1$
-simplex and
$1$
-simplex and
![]() $\check {\Delta }_1(\tau )= \mathrm {Conv}\{0, w_1 - w_2, w_1-w_3\}$
is a
$\check {\Delta }_1(\tau )= \mathrm {Conv}\{0, w_1 - w_2, w_1-w_3\}$
is a
![]() $2$
-simplex.
$2$
-simplex.
Both examples are positive and strongly simple.
Throughout this paper, we always assume that
![]() $(B,\mathscr {P})$
is positive and strongly simple. In particular, both
$(B,\mathscr {P})$
is positive and strongly simple. In particular, both
![]() $\Delta _i(\tau )$
and
$\Delta _i(\tau )$
and
![]() $\check {\Delta }_i(\tau )$
are standard simplices of positive dimensions, and
$\check {\Delta }_i(\tau )$
are standard simplices of positive dimensions, and
![]() $\Lambda _{\Delta _1(\tau )}\oplus \cdots \oplus \Lambda _{\Delta _p(\tau )}$
(resp.
$\Lambda _{\Delta _1(\tau )}\oplus \cdots \oplus \Lambda _{\Delta _p(\tau )}$
(resp.
![]() $\Lambda _{\check {\Delta }_1(\tau )} \oplus \cdots \oplus \Lambda _{\check {\Delta }_p(\tau )}$
) is an internal direct summand of
$\Lambda _{\check {\Delta }_1(\tau )} \oplus \cdots \oplus \Lambda _{\check {\Delta }_p(\tau )}$
) is an internal direct summand of
![]() $\Lambda _{\tau }$
(resp.
$\Lambda _{\tau }$
(resp.
![]() $\mathscr {Q}_{\tau }^*$
).
$\mathscr {Q}_{\tau }^*$
).
2.3 Cone construction by gluing open affine charts
In this subsection, we recall the cone construction of the maximally degenerate Calabi–Yau ![]() , following [Reference Gross and Siebert27] and [Reference Gross and Siebert29, §1.2]. For this purpose, we take
, following [Reference Gross and Siebert27] and [Reference Gross and Siebert29, §1.2]. For this purpose, we take
![]() $\mathbf {K} = \mathbb {Z}$
and Q to be the positive real axis in Notation 1.4. Throughout this paper, we will work in the category of analytic schemes.
$\mathbf {K} = \mathbb {Z}$
and Q to be the positive real axis in Notation 1.4. Throughout this paper, we will work in the category of analytic schemes.
We will construct ![]() as a gluing of affine analytic schemes
as a gluing of affine analytic schemes
![]() $V(v)$
parametrized by the vertices of
$V(v)$
parametrized by the vertices of
![]() $\mathscr {P}$
. For each vertex v, we consider the fan
$\mathscr {P}$
. For each vertex v, we consider the fan
![]() $\Sigma _v$
and take the analytic affine toric variety
$\Sigma _v$
and take the analytic affine toric variety
where
![]() $\mathrm {Spec}_{\mathrm {an}}$
means analytification of the algebraic affine scheme given by
$\mathrm {Spec}_{\mathrm {an}}$
means analytification of the algebraic affine scheme given by
![]() $\mathrm {Spec}$
. Here, the monoid structure for a general fan
$\mathrm {Spec}$
. Here, the monoid structure for a general fan
![]() $\Sigma \subset M_{\mathbb {R}}$
is given by
$\Sigma \subset M_{\mathbb {R}}$
is given by
 $$ \begin{align*}p+q=\begin{cases} p+q &\text{ if }p,q \in M \text{ are in a common cone of } \Sigma, \\\infty & \text{ otherwise}, \end{cases}\end{align*} $$
$$ \begin{align*}p+q=\begin{cases} p+q &\text{ if }p,q \in M \text{ are in a common cone of } \Sigma, \\\infty & \text{ otherwise}, \end{cases}\end{align*} $$
and we set
![]() $z^{\infty } =0$
in taking
$z^{\infty } =0$
in taking
![]() $\mathrm {Spec}(\mathbb {C}[\Sigma ])$
(by abuse of notation, we use
$\mathrm {Spec}(\mathbb {C}[\Sigma ])$
(by abuse of notation, we use
![]() $\Sigma $
to stand for both the fan and the monoid associated to a fan if there is no confusion); in other words, the ring
$\Sigma $
to stand for both the fan and the monoid associated to a fan if there is no confusion); in other words, the ring
![]() $\mathbb {C}[\Sigma ]$
is defined explicitly as
$\mathbb {C}[\Sigma ]$
is defined explicitly as
 $$ \begin{align*}\mathbb{C}[\Sigma]:= \bigoplus_{p \in |\Sigma| \cap M} \mathbb{C} \cdot z^p, \quad z^p\cdot z^q=\begin{cases} z^{p+q} &\text{ if }p,q \in M \text{ are in a common cone of } \Sigma, \\0 & \text{ otherwise}, \end{cases}\end{align*} $$
$$ \begin{align*}\mathbb{C}[\Sigma]:= \bigoplus_{p \in |\Sigma| \cap M} \mathbb{C} \cdot z^p, \quad z^p\cdot z^q=\begin{cases} z^{p+q} &\text{ if }p,q \in M \text{ are in a common cone of } \Sigma, \\0 & \text{ otherwise}, \end{cases}\end{align*} $$
where
![]() $|\Sigma |$
denotes the support of the fan
$|\Sigma |$
denotes the support of the fan
![]() $\Sigma $
.
$\Sigma $
.
To glue these affine analytic schemes together, we need affine subschemes
![]() $\{V(\tau )\}$
associated to
$\{V(\tau )\}$
associated to
![]() $\tau \in \mathscr {P}$
with
$\tau \in \mathscr {P}$
with
![]() $v\in \tau $
and natural open embeddings
$v\in \tau $
and natural open embeddings
![]() $V(\tau )\hookrightarrow V(\omega )$
for
$V(\tau )\hookrightarrow V(\omega )$
for
![]() $v \in \omega \subset \tau $
. First, for
$v \in \omega \subset \tau $
. First, for
![]() $\tau \in \mathscr {P}$
such that
$\tau \in \mathscr {P}$
such that
![]() $v\in \tau $
, we consider the localization of
$v\in \tau $
, we consider the localization of
![]() $\Sigma _v$
at
$\Sigma _v$
at
![]() $\tau $
defined by
$\tau $
defined by
here recall that
![]() $K_v\sigma = \mathbb {R}_{\geq 0} S_{v}(\sigma \cap U_v)$
is the cone in
$K_v\sigma = \mathbb {R}_{\geq 0} S_{v}(\sigma \cap U_v)$
is the cone in
![]() $\Sigma _v$
(see the definition of a fan structure before Definition 2.2). This defines a new complete fan in
$\Sigma _v$
(see the definition of a fan structure before Definition 2.2). This defines a new complete fan in
![]() $T_{v,\mathbb {R}}$
consisting of convex, but not necessarily strictly convex, cones. If
$T_{v,\mathbb {R}}$
consisting of convex, but not necessarily strictly convex, cones. If
![]() $\tau $
contains another vertex
$\tau $
contains another vertex
![]() $v'$
, we can identify the fans
$v'$
, we can identify the fans
![]() $\tau ^{-1}\Sigma _v$
and
$\tau ^{-1}\Sigma _v$
and
![]() $\tau ^{-1}\Sigma _{v'}$
as follows: For each maximal
$\tau ^{-1}\Sigma _{v'}$
as follows: For each maximal
![]() $\sigma \supset \tau $
, we identify the maximal cones
$\sigma \supset \tau $
, we identify the maximal cones
![]() $K_{v}\sigma + \Lambda _{\tau ,\mathbb {R}}$
and
$K_{v}\sigma + \Lambda _{\tau ,\mathbb {R}}$
and
![]() $K_{v'}\sigma + \Lambda _{\tau ,\mathbb {R}}$
by identifying the tangent spaces
$K_{v'}\sigma + \Lambda _{\tau ,\mathbb {R}}$
by identifying the tangent spaces
![]() $T_v\cong T_{v'}$
using parallel transport through
$T_v\cong T_{v'}$
using parallel transport through
![]() $\sigma \supset \tau $
. Patching these identifications for all
$\sigma \supset \tau $
. Patching these identifications for all
![]() $\sigma \supset \tau $
together, we get a piecewise linear transformation from
$\sigma \supset \tau $
together, we get a piecewise linear transformation from
![]() $T_{v}$
to
$T_{v}$
to
![]() $T_{v'}$
, identifying the fans
$T_{v'}$
, identifying the fans
![]() $\tau ^{-1}\Sigma _v$
and
$\tau ^{-1}\Sigma _v$
and
![]() $\tau ^{-1}\Sigma _{v'}$
and hence the corresponding monoids. This defines the affine analytic scheme
$\tau ^{-1}\Sigma _{v'}$
and hence the corresponding monoids. This defines the affine analytic scheme
up to a unique isomorphism. Notice that
![]() $\tau ^{-1}\Sigma _v$
can be identified (noncanonically) with the fan
$\tau ^{-1}\Sigma _v$
can be identified (noncanonically) with the fan
![]() $\Sigma _{\tau } \times \Lambda _{\tau ,\mathbb {R}}$
in
$\Sigma _{\tau } \times \Lambda _{\tau ,\mathbb {R}}$
in
![]() $\mathscr {Q}_{\tau ,\mathbb {R}}\times \Lambda _{\tau ,\mathbb {R}}$
, so actually
$\mathscr {Q}_{\tau ,\mathbb {R}}\times \Lambda _{\tau ,\mathbb {R}}$
, so actually
where
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Lambda _{\tau }]) \cong \Lambda _{\tau }^* \otimes _{\mathbb {Z}} \mathbb {C}^* \cong (\mathbb {C}^{*})^l$
is a complex torus.
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Lambda _{\tau }]) \cong \Lambda _{\tau }^* \otimes _{\mathbb {Z}} \mathbb {C}^* \cong (\mathbb {C}^{*})^l$
is a complex torus.
For any
![]() $v\in \omega \subset \tau $
, there is a map of monoids
$v\in \omega \subset \tau $
, there is a map of monoids
![]() $ \omega ^{-1}\Sigma _v \to \tau ^{-1}\Sigma _v$
given by
$ \omega ^{-1}\Sigma _v \to \tau ^{-1}\Sigma _v$
given by
 $$ \begin{align*}p\mapsto\begin{cases} p & \text{ if }p\in K_{v}\sigma +\Lambda_{\omega,\mathbb{R}}\text{ for some }\sigma\supset\tau, \\\infty & \text{ otherwise} \end{cases}\end{align*} $$
$$ \begin{align*}p\mapsto\begin{cases} p & \text{ if }p\in K_{v}\sigma +\Lambda_{\omega,\mathbb{R}}\text{ for some }\sigma\supset\tau, \\\infty & \text{ otherwise} \end{cases}\end{align*} $$
(though there is no fan map from
![]() $\omega ^{-1}\Sigma _v$
to
$\omega ^{-1}\Sigma _v$
to
![]() $\tau ^{-1}\Sigma _v$
in general), and hence a ring map
$\tau ^{-1}\Sigma _v$
in general), and hence a ring map
This gives an open inclusion of affine schemes
and hence a functor
![]() $F\colon \mathscr {P}\to \mathbf {{Sch}}_{\mathrm {an}}$
defined by
$F\colon \mathscr {P}\to \mathbf {{Sch}}_{\mathrm {an}}$
defined by
for
![]() $\omega \subset \tau $
.
$\omega \subset \tau $
.
We can further introduce twistings of the gluing of the affine analytic schemes
![]() $\{V(\tau )\}_{\tau \in \mathscr {P}}$
. Toric automorphisms
$\{V(\tau )\}_{\tau \in \mathscr {P}}$
. Toric automorphisms
![]() $\mu $
of
$\mu $
of
![]() $V(\tau )$
are in bijection with the set of
$V(\tau )$
are in bijection with the set of
![]() $\mathbb {C}^{*}$
-valued piecewise multiplicative maps on
$\mathbb {C}^{*}$
-valued piecewise multiplicative maps on
![]() $T_v\cap |\tau ^{-1}\Sigma _v|$
with respect to the fan
$T_v\cap |\tau ^{-1}\Sigma _v|$
with respect to the fan
![]() $\tau ^{-1}\Sigma _v$
. Explicitly, for each maximal cone
$\tau ^{-1}\Sigma _v$
. Explicitly, for each maximal cone
![]() $\sigma \in \mathscr {P}^{[n]}$
with
$\sigma \in \mathscr {P}^{[n]}$
with
![]() $\tau \subset \sigma $
, there is a monoid homomorphism
$\tau \subset \sigma $
, there is a monoid homomorphism
![]() $\mu _{\sigma }\colon \Lambda _{\sigma }\to \mathbb {C}^{*}$
such that if
$\mu _{\sigma }\colon \Lambda _{\sigma }\to \mathbb {C}^{*}$
such that if
![]() $\sigma '\in \mathscr {P}^{[n]}$
also contains
$\sigma '\in \mathscr {P}^{[n]}$
also contains
![]() $\tau $
, then
$\tau $
, then
![]() $\mu _{\sigma }|_{\Lambda _{\sigma \cap \sigma '}}=\mu _{\sigma '}|_{\Lambda _{\sigma \cap \sigma '}}$
. Denote by
$\mu _{\sigma }|_{\Lambda _{\sigma \cap \sigma '}}=\mu _{\sigma '}|_{\Lambda _{\sigma \cap \sigma '}}$
. Denote by
![]() $\mathrm {PM}(\tau )$
the multiplicative group of
$\mathrm {PM}(\tau )$
the multiplicative group of
![]() $\mathbb {C}^{*}$
-valued piecewise multiplicative maps on
$\mathbb {C}^{*}$
-valued piecewise multiplicative maps on
![]() $T_v\cap |\tau ^{-1}\Sigma _v|$
. The group
$T_v\cap |\tau ^{-1}\Sigma _v|$
. The group
![]() $\mathrm {PM}(\tau )$
a priori depends on the choice of
$\mathrm {PM}(\tau )$
a priori depends on the choice of
![]() $v \in \tau $
; however, for different choices, say v and
$v \in \tau $
; however, for different choices, say v and
![]() $v'$
, the groups can be identified via the identification
$v'$
, the groups can be identified via the identification
![]() $\tau ^{-1}\Sigma _v \cong \tau ^{-1}\Sigma _{v'}$
. For
$\tau ^{-1}\Sigma _v \cong \tau ^{-1}\Sigma _{v'}$
. For
![]() $\omega \subset \tau $
, there is a natural restriction map
$\omega \subset \tau $
, there is a natural restriction map
![]() $|_{\tau } \colon \mathrm {PM}(\omega ) \rightarrow \mathrm {PM}(\tau )$
given by restricting to those maximal cells
$|_{\tau } \colon \mathrm {PM}(\omega ) \rightarrow \mathrm {PM}(\tau )$
given by restricting to those maximal cells
![]() $\sigma \supset \omega $
with
$\sigma \supset \omega $
with
![]() $\sigma \supset \tau $
.
$\sigma \supset \tau $
.
Definition 2.13 ([Reference Gross and Siebert29], Definition 1.18).
A choice of open gluing data (for the cone construction) for
![]() $(B,\mathscr {P})$
is a set
$(B,\mathscr {P})$
is a set
![]() $s=(s_{\omega \tau })_{\omega \subset \tau }$
of elements
$s=(s_{\omega \tau })_{\omega \subset \tau }$
of elements
![]() $s_{\omega \tau }\in \mathrm {PM}(\tau )$
such that
$s_{\omega \tau }\in \mathrm {PM}(\tau )$
such that
-
1.
 $s_{\tau \tau }=1$
for all
$s_{\tau \tau }=1$
for all
 $\tau \in \mathscr {P}$
, and
$\tau \in \mathscr {P}$
, and -
2. if
 $\omega \subset \tau \subset \rho $
, then
$\omega \subset \tau \subset \rho $
, then  $$ \begin{align*}s_{\omega\rho}=s_{\tau\rho}\cdot s_{\omega\tau}|_{\rho}.\end{align*} $$
$$ \begin{align*}s_{\omega\rho}=s_{\tau\rho}\cdot s_{\omega\tau}|_{\rho}.\end{align*} $$
Two choices of open gluing data
![]() $s,s'$
are said to be cohomologous if there exists a system
$s,s'$
are said to be cohomologous if there exists a system
![]() $\{t_{\tau }\}_{\tau \in \mathscr {P}}$
, with
$\{t_{\tau }\}_{\tau \in \mathscr {P}}$
, with
![]() $t_{\tau }\in \mathrm {PM}(\tau )$
for each
$t_{\tau }\in \mathrm {PM}(\tau )$
for each
![]() $\tau \in \mathscr {P}$
, such that
$\tau \in \mathscr {P}$
, such that
![]() $s_{\omega \tau }=t_{\tau }(t_{\omega }|_{\tau })^{-1}s_{\omega \tau }'$
whenever
$s_{\omega \tau }=t_{\tau }(t_{\omega }|_{\tau })^{-1}s_{\omega \tau }'$
whenever
![]() $\omega \subset \tau $
.
$\omega \subset \tau $
.
The set of cohomology classes of choices of open gluing data is a group under multiplication, denoted as
![]() $H^1(\mathscr {P},\mathscr {Q}_{\mathscr {P}}\otimes \mathbb {C}^{\times })$
. For
$H^1(\mathscr {P},\mathscr {Q}_{\mathscr {P}}\otimes \mathbb {C}^{\times })$
. For
![]() $s\in \mathrm {PM}(\tau )$
, we will denote also by s the corresponding toric automorphism on
$s\in \mathrm {PM}(\tau )$
, we will denote also by s the corresponding toric automorphism on
![]() $V(\tau )$
which is explicitly given by
$V(\tau )$
which is explicitly given by
![]() $s^*(z^m) = s_{\sigma }(m) z^m$
for
$s^*(z^m) = s_{\sigma }(m) z^m$
for
![]() $m \in \sigma \supset \tau $
. If s is a choice of open gluing data, then we can define an s-twisted functor
$m \in \sigma \supset \tau $
. If s is a choice of open gluing data, then we can define an s-twisted functor
![]() $F_s \colon \mathscr {P} \to \mathbf {{Sch}}_{\mathrm {an}}$
by setting
$F_s \colon \mathscr {P} \to \mathbf {{Sch}}_{\mathrm {an}}$
by setting
![]() $F_s(\tau ):=F(\tau )=V(\tau )$
on objects and
$F_s(\tau ):=F(\tau )=V(\tau )$
on objects and
![]() $F_s(\omega \subset \tau ):=F(\omega \subset \tau )\circ s_{\omega \tau }^{-1} \colon V(\tau ) \to V(\omega )$
on morphisms. This defines the analytic scheme
$F_s(\omega \subset \tau ):=F(\omega \subset \tau )\circ s_{\omega \tau }^{-1} \colon V(\tau ) \to V(\omega )$
on morphisms. This defines the analytic scheme
Gross–Siebert [Reference Gross and Siebert27] showed that ![]() as schemes when
as schemes when
![]() $s,s'$
are cohomologous.
$s,s'$
are cohomologous.
Remark 2.14. Given
![]() $\tau \in \mathscr {P}^{[k]}$
, one can define a closed stratum
$\tau \in \mathscr {P}^{[k]}$
, one can define a closed stratum ![]() of dimension k by gluing together the k-dimensional toric strata
of dimension k by gluing together the k-dimensional toric strata
![]() $V_\tau (\omega ) \subset V(\omega ) = \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\omega ^{-1}\Sigma _v])$
corresponding to the cones
$V_\tau (\omega ) \subset V(\omega ) = \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\omega ^{-1}\Sigma _v])$
corresponding to the cones
![]() $K_v\tau + \Lambda _{\omega ,\mathbb {R}}$
in
$K_v\tau + \Lambda _{\omega ,\mathbb {R}}$
in
![]() $\omega ^{-1}\Sigma _v$
, for all
$\omega ^{-1}\Sigma _v$
, for all
![]() $\omega \subset \tau $
. Abstractly, it is isomorphic to the toric variety associated to the polyhedron
$\omega \subset \tau $
. Abstractly, it is isomorphic to the toric variety associated to the polyhedron
![]() $\tau \subset \Lambda _{\tau ,\mathbb {R}}$
. Also, for every pair
$\tau \subset \Lambda _{\tau ,\mathbb {R}}$
. Also, for every pair
![]() $\omega \subset \tau $
, there is a natural inclusion
$\omega \subset \tau $
, there is a natural inclusion ![]() . One can alternatively construct
. One can alternatively construct ![]() by gluing along the closed strata
by gluing along the closed strata ![]() ’s according to the polyhedral decomposition; see [Reference Gross and Siebert27, §2.2].
’s according to the polyhedral decomposition; see [Reference Gross and Siebert27, §2.2].
We recall the following definition from [Reference Gross and Siebert27], which serves as an alternative set of combinatorial data for encoding
![]() $\mu \in \mathrm {PM}(\tau )$
.
$\mu \in \mathrm {PM}(\tau )$
.
Definition 2.15 ([Reference Gross and Siebert27], Definition 3.25 and [Reference Gross and Siebert29], Definition 1.20).
Let
![]() $\mu \in \mathrm {PM}(\tau )$
and
$\mu \in \mathrm {PM}(\tau )$
and
![]() $\rho \in \mathscr {P}^{[n-1]}$
with
$\rho \in \mathscr {P}^{[n-1]}$
with
![]() $\tau \subset \rho $
. For a vertex
$\tau \subset \rho $
. For a vertex
![]() $v\in \tau $
, we define
$v\in \tau $
, we define
where
![]() $\sigma ,\sigma '$
are the two unique maximal cells such that
$\sigma ,\sigma '$
are the two unique maximal cells such that
![]() $\sigma \cap \sigma '=\rho $
,
$\sigma \cap \sigma '=\rho $
,
![]() $m \in \Lambda _{\sigma }$
is an element projecting to the generator in
$m \in \Lambda _{\sigma }$
is an element projecting to the generator in
![]() $\mathscr {Q}_{\rho } \cong \Lambda _{\sigma }/\Lambda _{\rho }\cong \mathbb {Z}$
pointing to
$\mathscr {Q}_{\rho } \cong \Lambda _{\sigma }/\Lambda _{\rho }\cong \mathbb {Z}$
pointing to
![]() $\sigma '$
, and
$\sigma '$
, and
![]() $m'$
is the parallel transport of
$m'$
is the parallel transport of
![]() $m\in \Lambda _{\sigma }$
to
$m\in \Lambda _{\sigma }$
to
![]() $\Lambda _{\sigma '}$
through v.
$\Lambda _{\sigma '}$
through v.
![]() $D(\mu ,\rho ,v)$
is independent of the choice of m.
$D(\mu ,\rho ,v)$
is independent of the choice of m.
Let
![]() $\rho \in \mathscr {P}^{[d-1]}$
and
$\rho \in \mathscr {P}^{[d-1]}$
and
![]() $\sigma _+,\sigma _-$
be the two unique maximal cells such that
$\sigma _+,\sigma _-$
be the two unique maximal cells such that
![]() $\sigma _+\cap \sigma _-=\rho $
. Let
$\sigma _+\cap \sigma _-=\rho $
. Let
![]() $\check {d}_{\rho }\in \mathscr {Q}_{\rho }^*$
be the unique primitive generator pointing to
$\check {d}_{\rho }\in \mathscr {Q}_{\rho }^*$
be the unique primitive generator pointing to
![]() $\sigma _+$
. For any two vertices
$\sigma _+$
. For any two vertices
![]() $v,v'\in \tau $
, we have the formula
$v,v'\in \tau $
, we have the formula
relating monodromy data to the open gluing data, where
![]() $m_{vv'}^{\rho }\in \Lambda _{\rho }$
is as discussed in equation (2.2). The formula (2.6) describes the interaction between monodromy and a fixed
$m_{vv'}^{\rho }\in \Lambda _{\rho }$
is as discussed in equation (2.2). The formula (2.6) describes the interaction between monodromy and a fixed
![]() $\mu \in \mathrm {PM}(\tau )$
. We shall further impose the following lifting condition from [Reference Gross and Siebert27, Prop. 4.25] relating
$\mu \in \mathrm {PM}(\tau )$
. We shall further impose the following lifting condition from [Reference Gross and Siebert27, Prop. 4.25] relating
![]() $s_{v\tau }, s_{v'\tau } \in \mathrm {PM}(\tau )$
and monodromy data:
$s_{v\tau }, s_{v'\tau } \in \mathrm {PM}(\tau )$
and monodromy data:
Condition 2.16. We say a choice of open gluing data s satisfies the lifting condition if for any two vertices
![]() $v, v'\in \tau \subset \rho $
with
$v, v'\in \tau \subset \rho $
with
![]() $\rho \in \mathscr {P}^{[n-1]}$
, we have
$\rho \in \mathscr {P}^{[n-1]}$
, we have
![]() $D(s_{v\tau },\rho ,v) = D(s_{v'\tau },\rho ,v')$
whenever
$D(s_{v\tau },\rho ,v) = D(s_{v'\tau },\rho ,v')$
whenever
![]() $m^{\rho }_{vv'} = 0$
.
$m^{\rho }_{vv'} = 0$
.
2.4 Log structures
We need to equip the analytic scheme ![]() with log structures. The main reference is [Reference Gross and Siebert27, §3 - 5].
with log structures. The main reference is [Reference Gross and Siebert27, §3 - 5].
Definition 2.17. Let X be an analytic space, a log structure on X is a sheaf of monoids
![]() $\mathcal {M}_X$
together with a homomorphism
$\mathcal {M}_X$
together with a homomorphism
![]() $\alpha _X\colon \mathcal {M}_X \rightarrow \mathcal {O}_X$
of sheaves of (multiplicative) monoids such that
$\alpha _X\colon \mathcal {M}_X \rightarrow \mathcal {O}_X$
of sheaves of (multiplicative) monoids such that
![]() $\alpha _X \colon \alpha ^{-1}(\mathcal {O}_X^*) \rightarrow \mathcal {O}_X^*$
is an isomorphism. The ghost sheaf
$\alpha _X \colon \alpha ^{-1}(\mathcal {O}_X^*) \rightarrow \mathcal {O}_X^*$
is an isomorphism. The ghost sheaf
![]() $\overline {\mathcal {M}}_X$
of a log structure is defined as the quotient sheaf
$\overline {\mathcal {M}}_X$
of a log structure is defined as the quotient sheaf
![]() $\mathcal {M}_X/\alpha ^{-1}(\mathcal {O}_X^*)$
, whose monoid structure is written additively.
$\mathcal {M}_X/\alpha ^{-1}(\mathcal {O}_X^*)$
, whose monoid structure is written additively.
Example 2.18. Let X be an analytic space and
![]() $D\subset X$
be a closed analytic subspace of pure codimension one. We denote by
$D\subset X$
be a closed analytic subspace of pure codimension one. We denote by
![]() $j \colon X\setminus D \hookrightarrow X $
the inclusion. Then the sheaf of monoids
$j \colon X\setminus D \hookrightarrow X $
the inclusion. Then the sheaf of monoids
together with the natural inclusion
![]() $\alpha _X \colon \mathcal {M}_{X} \rightarrow \mathcal {O}_X$
defines a log structure on X.
$\alpha _X \colon \mathcal {M}_{X} \rightarrow \mathcal {O}_X$
defines a log structure on X.
We write
![]() $X^{\dagger }$
if we want to emphasize the log structure on X. A general way to define a log structure is to take an arbitrary homomorphism of sheaves of monoids
$X^{\dagger }$
if we want to emphasize the log structure on X. A general way to define a log structure is to take an arbitrary homomorphism of sheaves of monoids
and then define the associated log structure by
In particular, this allows us to define log structures on an analytic space Y by pulling back those on another analytic space X via a morphism
![]() $f \colon Y \rightarrow X$
. More precisely, given a log structure on X, the pullback log structure on Y is defined to be the log structure associated to the composition
$f \colon Y \rightarrow X$
. More precisely, given a log structure on X, the pullback log structure on Y is defined to be the log structure associated to the composition
![]() $\tilde {\alpha }_Y \colon f^{-1}(\mathcal {M}_X) \rightarrow f^{-1}(\mathcal {O}_X) \rightarrow \mathcal {O}_Y$
. For more details of the theory of log structures, readers are referred to, for example, [Reference Gross and Siebert27, §3].
$\tilde {\alpha }_Y \colon f^{-1}(\mathcal {M}_X) \rightarrow f^{-1}(\mathcal {O}_X) \rightarrow \mathcal {O}_Y$
. For more details of the theory of log structures, readers are referred to, for example, [Reference Gross and Siebert27, §3].
Example 2.19. Taking a toric monoid P (i.e.,
![]() $P= C \cap M$
for a cone
$P= C \cap M$
for a cone
![]() $C \subset M_{\mathbb {R}}$
), we can define
$C \subset M_{\mathbb {R}}$
), we can define
![]() $\tilde {\alpha } \colon \underline {P} \rightarrow \mathcal {O}_{\operatorname {\mathrm {Spec}}(\mathbb {C}[P])}$
by sending
$\tilde {\alpha } \colon \underline {P} \rightarrow \mathcal {O}_{\operatorname {\mathrm {Spec}}(\mathbb {C}[P])}$
by sending
![]() $m \mapsto z^{m}$
, where
$m \mapsto z^{m}$
, where
![]() $\underline {P}$
is the constant sheaf with stalk P. From this, we obtain a log structure on the analytic toric variety
$\underline {P}$
is the constant sheaf with stalk P. From this, we obtain a log structure on the analytic toric variety
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P])$
. Note that this is a special case of Example 2.18, where we take
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P])$
. Note that this is a special case of Example 2.18, where we take
![]() $X = \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P])$
and D to be the toric boundary divisor.
$X = \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P])$
and D to be the toric boundary divisor.
Before we describe the log structures on ![]() , let us first specify a ghost sheaf
, let us first specify a ghost sheaf
![]() $\overline {\mathcal {M}}$
over
$\overline {\mathcal {M}}$
over ![]() . Recall that the polyhedral decomposition
. Recall that the polyhedral decomposition
![]() $\mathscr {P}$
is assumed to be regular, namely, there exists a strictly convex multivalued piecewise linear function
$\mathscr {P}$
is assumed to be regular, namely, there exists a strictly convex multivalued piecewise linear function
![]() $\varphi \in H^0(B,\mathcal {MPL}_{\mathscr {P}})$
. For any
$\varphi \in H^0(B,\mathcal {MPL}_{\mathscr {P}})$
. For any
![]() $\tau \in \mathscr {P}$
, we take a strictly convex representative
$\tau \in \mathscr {P}$
, we take a strictly convex representative
![]() $\bar {\varphi }_{\tau }$
of
$\bar {\varphi }_{\tau }$
of
![]() $\varphi $
on
$\varphi $
on
![]() $\mathscr {Q}_{\tau ,\mathbb {R}}$
and define
$\mathscr {Q}_{\tau ,\mathbb {R}}$
and define
where
![]() $C_\tau :=\{(m,h)\in \mathscr {Q}_{\tau ,\mathbb {R}} \oplus \mathbb {R} \,|\, h\geq \bar {\varphi }_\tau (m)\}$
. For any
$C_\tau :=\{(m,h)\in \mathscr {Q}_{\tau ,\mathbb {R}} \oplus \mathbb {R} \,|\, h\geq \bar {\varphi }_\tau (m)\}$
. For any
![]() $\omega \subset \tau $
, we take an integral affine function
$\omega \subset \tau $
, we take an integral affine function
![]() $\psi _{\omega \tau }$
on
$\psi _{\omega \tau }$
on
![]() $U_{\omega }$
such that
$U_{\omega }$
such that
![]() $\psi _{\omega \tau }+ S_{\omega }^*( \bar {\varphi }_{\omega })$
vanishes on
$\psi _{\omega \tau }+ S_{\omega }^*( \bar {\varphi }_{\omega })$
vanishes on
![]() $K_{\omega }\tau $
and agrees with
$K_{\omega }\tau $
and agrees with
![]() $S_{\tau }^*(\bar {\varphi }_{\tau })$
on all of
$S_{\tau }^*(\bar {\varphi }_{\tau })$
on all of
![]() $\sigma \cap U_{\tau }$
for any
$\sigma \cap U_{\tau }$
for any
![]() $\sigma \supset \tau $
. This induces a map
$\sigma \supset \tau $
. This induces a map
![]() $C_{\omega } \rightarrow C_{\omega \tau } :=\{(m,h)\in \mathscr {Q}_{\omega ,\mathbb {R}} \oplus \mathbb {R} \,|\, h\geq \psi _{\omega \tau }(m)+\bar {\varphi }_\omega (m)\}$
by sending
$C_{\omega } \rightarrow C_{\omega \tau } :=\{(m,h)\in \mathscr {Q}_{\omega ,\mathbb {R}} \oplus \mathbb {R} \,|\, h\geq \psi _{\omega \tau }(m)+\bar {\varphi }_\omega (m)\}$
by sending
![]() $(m,h)\mapsto (m,h+\psi _{\omega \tau }(m))$
, whose composition with the quotient map
$(m,h)\mapsto (m,h+\psi _{\omega \tau }(m))$
, whose composition with the quotient map
![]() $\mathscr {Q}_{\omega ,\mathbb {R}}\oplus \mathbb {R} \rightarrow \mathscr {Q}_{\tau ,\mathbb {R}}\oplus \mathbb {R}$
gives a map
$\mathscr {Q}_{\omega ,\mathbb {R}}\oplus \mathbb {R} \rightarrow \mathscr {Q}_{\tau ,\mathbb {R}}\oplus \mathbb {R}$
gives a map
![]() $C_{\omega } \rightarrow C_{\tau }$
of cones that corresponds to the monoid homomorphism
$C_{\omega } \rightarrow C_{\tau }$
of cones that corresponds to the monoid homomorphism
![]() $\bar {P}_{\omega }\rightarrow \bar {P}_{\tau }$
. The
$\bar {P}_{\omega }\rightarrow \bar {P}_{\tau }$
. The
![]() $\bar {P}_{\tau }$
’s glue together to give the ghost sheaf
$\bar {P}_{\tau }$
’s glue together to give the ghost sheaf
![]() $\overline {\mathcal {M}}$
over
$\overline {\mathcal {M}}$
over ![]() . There is a well-defined section
. There is a well-defined section ![]() given by gluing
given by gluing
![]() $(0,1) \in C_{\tau }$
for each
$(0,1) \in C_{\tau }$
for each
![]() $\tau $
.
$\tau $
.
One may then hope to find a log structure on ![]() which is log smooth and with ghost sheaf given by
which is log smooth and with ghost sheaf given by
![]() $\overline {\mathcal {M}}$
. However, due to the presence of nontrivial monodromies of the affine structure, this can only be done away from a complex codimension
$\overline {\mathcal {M}}$
. However, due to the presence of nontrivial monodromies of the affine structure, this can only be done away from a complex codimension
![]() $2$
subset
$2$
subset ![]() not containing any toric strata. Such log structures can be described by sections of a coherent sheaf
not containing any toric strata. Such log structures can be described by sections of a coherent sheaf
![]() $\mathcal {LS}^+_{\mathrm {pre}}$
supported on the scheme-theoretic singular locus
$\mathcal {LS}^+_{\mathrm {pre}}$
supported on the scheme-theoretic singular locus ![]() . We now describe the sheaf
. We now describe the sheaf
![]() $\mathcal {LS}^+_{\mathrm {pre}}$
and some of its sections called slab functions; readers are referred to [Reference Gross and Siebert27, §3 and 4] for more details.
$\mathcal {LS}^+_{\mathrm {pre}}$
and some of its sections called slab functions; readers are referred to [Reference Gross and Siebert27, §3 and 4] for more details.
For every
![]() $\rho \in \mathscr {P}^{[n-1]}$
, we consider
$\rho \in \mathscr {P}^{[n-1]}$
, we consider ![]() , where
, where ![]() is the toric variety associated to the polytope
is the toric variety associated to the polytope
![]() $\rho \subset \Lambda _{\rho ,\mathbb {R}}$
. From the fact that the normal fan
$\rho \subset \Lambda _{\rho ,\mathbb {R}}$
. From the fact that the normal fan
![]() $\mathscr {N}_{\rho } \subset \Lambda _{\rho ,\mathbb {R}}^*$
of
$\mathscr {N}_{\rho } \subset \Lambda _{\rho ,\mathbb {R}}^*$
of
![]() $\rho $
is a refinement of the normal fan
$\rho $
is a refinement of the normal fan
![]() $\mathscr {N}_{\Delta (\rho )}\subset \Lambda _{\rho ,\mathbb {R}}^*$
of the
$\mathscr {N}_{\Delta (\rho )}\subset \Lambda _{\rho ,\mathbb {R}}^*$
of the
![]() $r_{\rho }$
-dimensional simplex
$r_{\rho }$
-dimensional simplex
![]() $\Delta (\rho )$
(as in §2.2), we have a toric morphism
$\Delta (\rho )$
(as in §2.2), we have a toric morphism
Now,
![]() $\Delta (\rho )$
corresponds to
$\Delta (\rho )$
corresponds to
![]() $\mathcal {O}(1)$
on
$\mathcal {O}(1)$
on
![]() $\mathbb {P}^{r_\rho }$
. We let
$\mathbb {P}^{r_\rho }$
. We let
![]() $\mathcal {N}_{\rho }:= \varkappa _{\rho }^*(\mathcal {O}(1))$
on
$\mathcal {N}_{\rho }:= \varkappa _{\rho }^*(\mathcal {O}(1))$
on ![]() and define
and define
 $$ \begin{align} \mathcal{LS}^+_{\mathrm{pre}} := \bigoplus_{\rho \in \mathscr{P}^{[n-1]}} \iota_{\rho,*} (\mathcal{N}_{\rho}). \end{align} $$
$$ \begin{align} \mathcal{LS}^+_{\mathrm{pre}} := \bigoplus_{\rho \in \mathscr{P}^{[n-1]}} \iota_{\rho,*} (\mathcal{N}_{\rho}). \end{align} $$
Sections of
![]() $\mathcal {LS}^+_{\mathrm {pre}}$
can be described explicitly. For each
$\mathcal {LS}^+_{\mathrm {pre}}$
can be described explicitly. For each
![]() $v \in \mathscr {P}^{[0]}$
, we consider the open subscheme
$v \in \mathscr {P}^{[0]}$
, we consider the open subscheme
![]() $V(v)$
of
$V(v)$
of ![]() and the local trivialization
and the local trivialization
whose sections over
![]() $V(v)$
are given by
$V(v)$
are given by
![]() $(f_{v\rho })_{v \in \rho }$
. Given
$(f_{v\rho })_{v \in \rho }$
. Given
![]() $v ,v' \in \tau $
where
$v ,v' \in \tau $
where
![]() $\tau $
corresponding to
$\tau $
corresponding to
![]() $V(\tau )$
, these local sections obey the change of coordinates given by
$V(\tau )$
, these local sections obey the change of coordinates given by
where
![]() $\rho \supset \tau $
and
$\rho \supset \tau $
and
![]() $s_{v\tau }, s_{v'\tau }$
are part of the open gluing data s. The section
$s_{v\tau }, s_{v'\tau }$
are part of the open gluing data s. The section
![]() $f := (f_{v\rho })_{v \in \rho }$
is said to be normalized if
$f := (f_{v\rho })_{v \in \rho }$
is said to be normalized if
![]() $f_{v\rho }$
takes the value
$f_{v\rho }$
takes the value
![]() $1$
at the zero-dimensional toric stratum corresponding to a vertex v, for all
$1$
at the zero-dimensional toric stratum corresponding to a vertex v, for all
![]() $\rho $
. We will restrict ourselves to normalized sections f of
$\rho $
. We will restrict ourselves to normalized sections f of
![]() $\mathcal {LS}^+_{\mathrm {pre}}$
. The complex codimension
$\mathcal {LS}^+_{\mathrm {pre}}$
. The complex codimension
![]() $2$
subset
$2$
subset ![]() is taken to be the zero locus of f on
is taken to be the zero locus of f on ![]() .
.
Only a subset of normalized sections of
![]() $\mathcal {LS}^+_{\mathrm {pre}}$
corresponds to log structures. For every vertex
$\mathcal {LS}^+_{\mathrm {pre}}$
corresponds to log structures. For every vertex
![]() $v \in \mathscr {P}^{[0]}$
and
$v \in \mathscr {P}^{[0]}$
and
![]() $\tau \in \mathscr {P}^{[n-2]}$
containing v, we choose a cyclic ordering
$\tau \in \mathscr {P}^{[n-2]}$
containing v, we choose a cyclic ordering
![]() $\rho _1,\dots ,\rho _l$
of codimension one cells containing
$\rho _1,\dots ,\rho _l$
of codimension one cells containing
![]() $\tau $
according to an orientation of
$\tau $
according to an orientation of
![]() $\mathscr {Q}_{\tau ,\mathbb {R}}$
. Let
$\mathscr {Q}_{\tau ,\mathbb {R}}$
. Let
![]() $\check {d}_{\rho _i} \in \mathscr {Q}_v^*$
be the positively oriented normal to
$\check {d}_{\rho _i} \in \mathscr {Q}_v^*$
be the positively oriented normal to
![]() $\rho _i$
. Then the condition for
$\rho _i$
. Then the condition for
![]() $f = (f_{v\rho })_{v\in \rho }\in \mathcal {LS}^+_{\mathrm {pre}}|_{V(v)}$
to define a log structure is given by
$f = (f_{v\rho })_{v\in \rho }\in \mathcal {LS}^+_{\mathrm {pre}}|_{V(v)}$
to define a log structure is given by
 $$ \begin{align} \prod_{i=1}^l \check{d}_{\rho_i} \otimes f_{v\rho_i}|_{V_{\tau}(v)} = 0 \otimes 1,\quad \text{in } \mathscr{Q}_v^* \otimes \Gamma(V_{\tau}(v)\setminus Z, \mathcal{O}_{V_{\tau}(v)}^*), \end{align} $$
$$ \begin{align} \prod_{i=1}^l \check{d}_{\rho_i} \otimes f_{v\rho_i}|_{V_{\tau}(v)} = 0 \otimes 1,\quad \text{in } \mathscr{Q}_v^* \otimes \Gamma(V_{\tau}(v)\setminus Z, \mathcal{O}_{V_{\tau}(v)}^*), \end{align} $$
where the group structure on
![]() $\mathscr {Q}_v^*$
is additive and that on
$\mathscr {Q}_v^*$
is additive and that on
![]() $\Gamma (V_{\tau }(v)\setminus Z, \mathcal {O}_{V_{\tau }(v)}^*)$
is multiplicative. If
$\Gamma (V_{\tau }(v)\setminus Z, \mathcal {O}_{V_{\tau }(v)}^*)$
is multiplicative. If
![]() $f = (f_{v\rho })_{v\in \rho }$
is a normalized section satisfying this condition, we call the
$f = (f_{v\rho })_{v\in \rho }$
is a normalized section satisfying this condition, we call the
![]() $f_{v\rho }$
’s slab functions.
$f_{v\rho }$
’s slab functions.
Theorem 2.20 ([Reference Gross and Siebert27], Theorem 5.2).
Suppose that B is compact and the pair
![]() $(B,\mathscr {P})$
is simple and positive. Let s be a choice of open gluing data satisfying the lifting condition (Condition 2.16). Then there exists a unique normalized section
$(B,\mathscr {P})$
is simple and positive. Let s be a choice of open gluing data satisfying the lifting condition (Condition 2.16). Then there exists a unique normalized section ![]() which defines a log structure on
which defines a log structure on ![]() (i.e., satisfying the condition (2.10)).
(i.e., satisfying the condition (2.10)).
From now on, we always assume that B is compact. To describe the log structure in Theorem 2.20, we first construct some local smoothing models: For each vertex
![]() $v \in \mathscr {P}^{[0]}$
, we represent the strictly convex piecewise linear function
$v \in \mathscr {P}^{[0]}$
, we represent the strictly convex piecewise linear function
![]() $\varphi $
in a small neighborhood U of v by a strictly convex piecewise linear
$\varphi $
in a small neighborhood U of v by a strictly convex piecewise linear
![]() $\varphi _v\colon \mathscr {Q}_{v,\mathbb {R}}\to \mathbb {R}$
(so that
$\varphi _v\colon \mathscr {Q}_{v,\mathbb {R}}\to \mathbb {R}$
(so that
![]() $\varphi = S_v^*(\varphi _v)$
) and set
$\varphi = S_v^*(\varphi _v)$
) and set
The element
![]() $\varrho = (0,1)\in \mathscr {Q}_v\oplus \mathbb {Z}$
gives rise to a regular function
$\varrho = (0,1)\in \mathscr {Q}_v\oplus \mathbb {Z}$
gives rise to a regular function
![]() $q:=z^{\varrho }$
on
$q:=z^{\varrho }$
on
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_v])$
. We have a natural identification
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_v])$
. We have a natural identification
through which we view
![]() $V(v)$
as the toric boundary divisor in
$V(v)$
as the toric boundary divisor in
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_v])$
that corresponds to the holomorphic function q, and
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_v])$
that corresponds to the holomorphic function q, and
![]() $\pi _v \colon \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_v]) \rightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[q])$
as a local model for smoothing
$\pi _v \colon \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_v]) \rightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[q])$
as a local model for smoothing
![]() $V(v)$
.
$V(v)$
.
Using these local models, we can now describe the log structure around a point ![]() . On a neighborhood
. On a neighborhood
![]() $V \subset V(v)\setminus Z$
of x, the local smoothing model is given by composing the two inclusions
$V \subset V(v)\setminus Z$
of x, the local smoothing model is given by composing the two inclusions ![]() and
and
![]() $V(v) \hookrightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_{v}])$
. The natural monoid homomorphism
$V(v) \hookrightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_{v}])$
. The natural monoid homomorphism
![]() $P_v \rightarrow \mathbb {C}[P_v]$
defined by sending
$P_v \rightarrow \mathbb {C}[P_v]$
defined by sending
![]() $m \mapsto z^m$
determines a log structure on
$m \mapsto z^m$
determines a log structure on
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_v])$
which restricts to one on the toric boundary divisor
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_v])$
which restricts to one on the toric boundary divisor
![]() $V(v) = \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _v])$
. We further twist the inclusion
$V(v) = \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _v])$
. We further twist the inclusion ![]() as
as
here, for each
![]() $m \in \Sigma _v$
,
$m \in \Sigma _v$
,
![]() $h_m$
is chosen as an invertible holomorphic function on
$h_m$
is chosen as an invertible holomorphic function on
![]() $V \cap \mathrm {Zero}(z^m;v)$
, where we denote
$V \cap \mathrm {Zero}(z^m;v)$
, where we denote
![]() $\mathrm {Zero}(z^m;v):=\overline { \{x \in V(v) \ | \ z^{m} \in \mathcal {O}_{x}^* \}}$
, and such that they satisfy the relations
$\mathrm {Zero}(z^m;v):=\overline { \{x \in V(v) \ | \ z^{m} \in \mathcal {O}_{x}^* \}}$
, and such that they satisfy the relations
Then pulling back the log structure on
![]() $V(v)$
via
$V(v)$
via ![]() produces a log structure on V which is log smooth.
produces a log structure on V which is log smooth.
These local choices of
![]() $h_m$
’s are also required to be determined by the slab functions
$h_m$
’s are also required to be determined by the slab functions
![]() $f_{v\rho }$
’s, up to equivalences. Here, we shall just give the formula relating them; see [Reference Gross and Siebert27, Thm. 3.22] for details. For any
$f_{v\rho }$
’s, up to equivalences. Here, we shall just give the formula relating them; see [Reference Gross and Siebert27, Thm. 3.22] for details. For any
![]() $\rho \in \mathscr {P}^{[n-1]}$
containing v and two maximal cells
$\rho \in \mathscr {P}^{[n-1]}$
containing v and two maximal cells
![]() $\sigma _{\pm }$
such that
$\sigma _{\pm }$
such that
![]() $\sigma _{+} \cap \sigma _- = \rho $
, we take
$\sigma _{+} \cap \sigma _- = \rho $
, we take
![]() $m_+ \in \mathscr {Q}_{v} \cap K_{v} \sigma _+$
generating
$m_+ \in \mathscr {Q}_{v} \cap K_{v} \sigma _+$
generating
![]() $\mathscr {Q}_{\rho }$
with some
$\mathscr {Q}_{\rho }$
with some
![]() $m_0 \in \mathscr {Q}_v\cap K_v \rho $
such that
$m_0 \in \mathscr {Q}_v\cap K_v \rho $
such that
![]() $m_0 - m_+ \in \mathscr {Q}_v \cap K_v \sigma _-$
. Then the required relation is given by
$m_0 - m_+ \in \mathscr {Q}_v \cap K_v \sigma _-$
. Then the required relation is given by
 $$ \begin{align} f_{v\rho} = \frac{h_{m_0}^2}{h_{m_0-m_+} \cdot h_{m_0 + m_+}}\Big|_{V_\rho(v)\cap V} \in \mathcal{O}^*_{V_\rho(v)}( V_\rho(v) \cap V), \end{align} $$
$$ \begin{align} f_{v\rho} = \frac{h_{m_0}^2}{h_{m_0-m_+} \cdot h_{m_0 + m_+}}\Big|_{V_\rho(v)\cap V} \in \mathcal{O}^*_{V_\rho(v)}( V_\rho(v) \cap V), \end{align} $$
which is independent of the choices of
![]() $m_0$
and
$m_0$
and
![]() $m_+$
.
$m_+$
.
By abuse of notation, we also let ![]() be the k-th order thickening of V over
be the k-th order thickening of V over
![]() $\mathbb {C}[q]/q^{k+1}$
in the model
$\mathbb {C}[q]/q^{k+1}$
in the model
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_v])$
under the above embedding. Then there is a natural divisorial log structure on
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_v])$
under the above embedding. Then there is a natural divisorial log structure on ![]() over
over ![]() coming from restriction of the log structure on
coming from restriction of the log structure on
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_{v}])^{\dagger }$
over
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_{v}])^{\dagger }$
over
![]() $S^{\dagger }$
(i.e., Example 2.18, which is the same as the one given by Example 2.19 in this case). Restricting to V reproduces the log structure we constructed above, which is the log structure of
$S^{\dagger }$
(i.e., Example 2.18, which is the same as the one given by Example 2.19 in this case). Restricting to V reproduces the log structure we constructed above, which is the log structure of ![]() over the log point
over the log point ![]() locally around x. We have a Cartesian diagram of log spaces
locally around x. We have a Cartesian diagram of log spaces

Next, we describe the log structure around a singular point ![]() for some
for some
![]() $\tau $
. Viewing
$\tau $
. Viewing
![]() $f = \sum _{\rho \in \mathscr {P}^{[n-1]}} f_{\rho }$
where
$f = \sum _{\rho \in \mathscr {P}^{[n-1]}} f_{\rho }$
where
![]() $f_{\rho }$
is a section of
$f_{\rho }$
is a section of
![]() $\mathcal {N}_{\rho }$
, we let
$\mathcal {N}_{\rho }$
, we let ![]() and write
and write
![]() $Z = \bigcup _{\rho } Z_{\rho }$
. For every
$Z = \bigcup _{\rho } Z_{\rho }$
. For every
![]() $\tau \in \mathscr {P}$
, we have the data
$\tau \in \mathscr {P}$
, we have the data
![]() $\Omega _i$
’s,
$\Omega _i$
’s,
![]() $R_i$
’s,
$R_i$
’s,
![]() $\Delta _i(\tau )$
and
$\Delta _i(\tau )$
and
![]() $\check {\Delta }_i(\tau )$
described in Definition 2.9 because
$\check {\Delta }_i(\tau )$
described in Definition 2.9 because
![]() $(B,\mathscr {P})$
is simple. Since the normal fan
$(B,\mathscr {P})$
is simple. Since the normal fan
![]() $\mathscr {N}_\tau \subset \Lambda _{\tau ,\mathbb {R}}^*$
of
$\mathscr {N}_\tau \subset \Lambda _{\tau ,\mathbb {R}}^*$
of
![]() $\tau $
is a refinement of
$\tau $
is a refinement of
![]() $\mathscr {N}_{\Delta _i(\tau )} \subset \Lambda _{\tau ,\mathbb {R}}^*$
, we have a natural toric morphism
$\mathscr {N}_{\Delta _i(\tau )} \subset \Lambda _{\tau ,\mathbb {R}}^*$
, we have a natural toric morphism
and the identification
![]() $\iota _{\tau \rho }^*(\mathcal {N}_{\rho }) \cong \varkappa _{\tau ,i}^*(\mathcal {O}(1))$
. By the proof of [Reference Gross and Siebert27, Thm. 5.2],
$\iota _{\tau \rho }^*(\mathcal {N}_{\rho }) \cong \varkappa _{\tau ,i}^*(\mathcal {O}(1))$
. By the proof of [Reference Gross and Siebert27, Thm. 5.2],
![]() $\iota _{\tau \rho }^*(f_{\rho })$
is completely determined by the gluing data s and the associated monodromy polytope
$\iota _{\tau \rho }^*(f_{\rho })$
is completely determined by the gluing data s and the associated monodromy polytope
![]() $\Delta _i(\tau )$
, where
$\Delta _i(\tau )$
, where
![]() $\rho \in R_i$
. In particular, we have
$\rho \in R_i$
. In particular, we have
![]() $\iota _{\tau \rho }^*(f_{\rho }) = \iota _{\tau \rho '}^*(f_{\rho '})$
and
$\iota _{\tau \rho }^*(f_{\rho }) = \iota _{\tau \rho '}^*(f_{\rho '})$
and ![]() for
for
![]() $\rho ,\rho ' \in R_i$
. Locally, if we write
$\rho ,\rho ' \in R_i$
. Locally, if we write
![]() $V(\tau ) = \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\tau ^{-1}\Sigma _v])$
by choosing some
$V(\tau ) = \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\tau ^{-1}\Sigma _v])$
by choosing some
![]() $v \in \tau $
, then, for each
$v \in \tau $
, then, for each
![]() $ 1 \leq i \leq p$
, there exists an analytic function
$ 1 \leq i \leq p$
, there exists an analytic function
![]() $f_{v,i}$
on
$f_{v,i}$
on
![]() $V(\tau )$
such that
$V(\tau )$
such that
![]() $f_{v,i}|_{V_{\rho }(\tau )} =s_{v\tau }^{-1}( f_{v\rho })$
for
$f_{v,i}|_{V_{\rho }(\tau )} =s_{v\tau }^{-1}( f_{v\rho })$
for
![]() $\rho \in R_i$
.
$\rho \in R_i$
.
According to [Reference Gross and Siebert28, §2.1], for each
![]() $ 1 \leq i \leq p$
, we have
$ 1 \leq i \leq p$
, we have
![]() $\check {\Delta }_i(\tau ) \subset \mathscr {Q}_{\tau ,\mathbb {R}}^*$
, which gives
$\check {\Delta }_i(\tau ) \subset \mathscr {Q}_{\tau ,\mathbb {R}}^*$
, which gives
By convention, we write
![]() $\psi _0:= \bar {\varphi }_{\tau }$
. By rearranging the indices i’s, we can assume that
$\psi _0:= \bar {\varphi }_{\tau }$
. By rearranging the indices i’s, we can assume that
![]() $x \in Z^\tau _{1} \cap \cdots \cap Z^\tau _{r}$
and
$x \in Z^\tau _{1} \cap \cdots \cap Z^\tau _{r}$
and
![]() $x \notin Z^{\tau }_{r+1} \cup \cdots \cup Z^{\tau }_{p} $
. We introduce the convention that
$x \notin Z^{\tau }_{r+1} \cup \cdots \cup Z^{\tau }_{p} $
. We introduce the convention that
![]() $\psi _{x,i} = \psi _{i}$
for
$\psi _{x,i} = \psi _{i}$
for
![]() $0\leq i \leq r$
and
$0\leq i \leq r$
and
![]() $\psi _{x,i} \equiv 0$
for
$\psi _{x,i} \equiv 0$
for
![]() $r<i\leq \dim _{\mathbb {R}}(\tau )$
. Then the local smoothing model near x is constructed as
$r<i\leq \dim _{\mathbb {R}}(\tau )$
. Then the local smoothing model near x is constructed as
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_{\tau ,x}])$
, where
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_{\tau ,x}])$
, where
![]() $l = \dim _{\mathbb {R}}(\tau )$
, and the distinguished element
$l = \dim _{\mathbb {R}}(\tau )$
, and the distinguished element
![]() $\varrho = (0,1,0,\dots ,0)$
defines a family
$\varrho = (0,1,0,\dots ,0)$
defines a family
by sending
![]() $q \mapsto z^{\varrho }$
. The central fiber is given by
$q \mapsto z^{\varrho }$
. The central fiber is given by
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[Q_{\tau ,x}])$
, where
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[Q_{\tau ,x}])$
, where
is equipped with the monoid structure
 $$ \begin{align*}m + m' = \begin{cases} m+m' & \text{if } m+m' \in Q_{\tau,x},\\ \infty & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*}m + m' = \begin{cases} m+m' & \text{if } m+m' \in Q_{\tau,x},\\ \infty & \text{otherwise.} \end{cases} \end{align*} $$
We have the ring isomorphism
![]() $\mathbb {C}[Q_{\tau ,x}] \cong \mathbb {C}[\Sigma _{\tau } \oplus \mathbb {N}^{l}]$
induced by the monoid isomorphism defined by sending
$\mathbb {C}[Q_{\tau ,x}] \cong \mathbb {C}[\Sigma _{\tau } \oplus \mathbb {N}^{l}]$
induced by the monoid isomorphism defined by sending
![]() $(m,a_0,a_1,\dots ,a_l) \mapsto (m,a_1 - \psi _1(m),\dots ,a_l - \psi _l(m))$
.
$(m,a_0,a_1,\dots ,a_l) \mapsto (m,a_1 - \psi _1(m),\dots ,a_l - \psi _l(m))$
.
We also fix some isomorphism
![]() $\mathbb {C}[\tau ^{-1}\Sigma _v] \cong \mathbb {C}[\Sigma _{\tau }\oplus \mathbb {Z}^{l}]$
coming from the identification of
$\mathbb {C}[\tau ^{-1}\Sigma _v] \cong \mathbb {C}[\Sigma _{\tau }\oplus \mathbb {Z}^{l}]$
coming from the identification of
![]() $\tau ^{-1}\Sigma _v $
with the fan
$\tau ^{-1}\Sigma _v $
with the fan
![]() $\Sigma _{\tau } \oplus \mathbb {R}^{l} = \{ \omega \oplus \mathbb {R}^{l} \ | \ \omega \text { is a cone of } \tau \} $
in
$\Sigma _{\tau } \oplus \mathbb {R}^{l} = \{ \omega \oplus \mathbb {R}^{l} \ | \ \omega \text { is a cone of } \tau \} $
in
![]() $\mathscr {Q}_{\tau ,\mathbb {R}} \oplus \mathbb {R}^{l}$
. Taking a sufficiently small neighborhood V of x such that
$\mathscr {Q}_{\tau ,\mathbb {R}} \oplus \mathbb {R}^{l}$
. Taking a sufficiently small neighborhood V of x such that
![]() $Z_\rho \cap V = \emptyset $
if
$Z_\rho \cap V = \emptyset $
if
![]() $x \notin Z_{\rho }$
, we define a map
$x \notin Z_{\rho }$
, we define a map
![]() $V \rightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[Q_{\tau ,x}])$
by composing the inclusion
$V \rightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[Q_{\tau ,x}])$
by composing the inclusion
![]() $V \hookrightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\tau ^{-1}\Sigma _v]) \cong \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }\oplus \mathbb {Z}^{l}])$
with the map
$V \hookrightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\tau ^{-1}\Sigma _v]) \cong \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }\oplus \mathbb {Z}^{l}])$
with the map
described on generators by
 $$ \begin{align} \begin{cases} z^m \mapsto h_m \cdot z^m & \text{if } m\in \Sigma_{\tau} ;\\ u_i \mapsto f_{v,i} & \text{if } 1\leq i \leq r;\\ u_i \mapsto z_i-z_i(x) & \text{if } r<i\leq l; \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} z^m \mapsto h_m \cdot z^m & \text{if } m\in \Sigma_{\tau} ;\\ u_i \mapsto f_{v,i} & \text{if } 1\leq i \leq r;\\ u_i \mapsto z_i-z_i(x) & \text{if } r<i\leq l; \end{cases} \end{align} $$
here,
![]() $u_i$
is the i-th coordinate function of
$u_i$
is the i-th coordinate function of
![]() $\mathbb {C}[\mathbb {N}^{l}]$
,
$\mathbb {C}[\mathbb {N}^{l}]$
,
![]() $z_i$
is the i-th coordinate function of
$z_i$
is the i-th coordinate function of
![]() $\mathbb {C}[\mathbb {Z}^{l}]$
chosen so that
$\mathbb {C}[\mathbb {Z}^{l}]$
chosen so that
![]() $\left (\frac {\partial f_{v,i}}{\partial {z_j}}\right )_{1\leq i \leq r, 1\leq j \leq r}$
is nondegenerate on V; also, each
$\left (\frac {\partial f_{v,i}}{\partial {z_j}}\right )_{1\leq i \leq r, 1\leq j \leq r}$
is nondegenerate on V; also, each
![]() $h_m$
is an invertible holomorphic functions on
$h_m$
is an invertible holomorphic functions on
![]() $V \cap \mathrm {Zero}(z^m;v)$
, and they satisfy the equations (2.12) and (2.13) where we replace
$V \cap \mathrm {Zero}(z^m;v)$
, and they satisfy the equations (2.12) and (2.13) where we replace
![]() $f_{v\rho }$
by
$f_{v\rho }$
by
 $$ \begin{align*}\tilde{f}_{v\rho} = \begin{cases} s_{v\tau}^{-1}( f_{v\rho}) & \text{if } x \notin Z_{\rho},\\ 1 & \text{if } x \in Z_{\rho}. \end{cases} \end{align*} $$
$$ \begin{align*}\tilde{f}_{v\rho} = \begin{cases} s_{v\tau}^{-1}( f_{v\rho}) & \text{if } x \notin Z_{\rho},\\ 1 & \text{if } x \in Z_{\rho}. \end{cases} \end{align*} $$
Letting ![]() be the k-th order thickening of V over
be the k-th order thickening of V over
![]() $\mathbb {C}[q]/q^{k+1}$
in the model
$\mathbb {C}[q]/q^{k+1}$
in the model
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_{\tau ,x}])$
under the above embedding, we have a natural divisorial log structure on
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_{\tau ,x}])$
under the above embedding, we have a natural divisorial log structure on ![]() over
over ![]() induced from the inclusion
induced from the inclusion
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[Q_{\tau ,x}]) \hookrightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_{\tau ,x}])$
(i.e., Example 2.18). Restricting it to V gives the log structure of
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[Q_{\tau ,x}]) \hookrightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_{\tau ,x}])$
(i.e., Example 2.18). Restricting it to V gives the log structure of ![]() over the log point
over the log point ![]() locally around x.
locally around x.
3 A generalized moment map and the tropical singular locus on B
In this section, we recall the construction of a generalized moment map ![]() from [Reference Ruddat and Siebert43, Prop. 2.1]. Then we construct some convenient charts on the base tropical manifold B and study its singular locus.
from [Reference Ruddat and Siebert43, Prop. 2.1]. Then we construct some convenient charts on the base tropical manifold B and study its singular locus.
3.1 A generalized moment map
From this point onward, we will assume the vanishing of an obstruction class associated to the open gluing data s, namely,
![]() $o(s) = 1$
, where the obstruction class
$o(s) = 1$
, where the obstruction class
![]() $o(s)$
is written multiplicatively (see [Reference Gross and Siebert27, Thm. 2.34]). Under this assumption, one can construct an ample line bundle
$o(s)$
is written multiplicatively (see [Reference Gross and Siebert27, Thm. 2.34]). Under this assumption, one can construct an ample line bundle
![]() $\mathcal {L}$
on
$\mathcal {L}$
on ![]() as follows: For each polytope
as follows: For each polytope
![]() $\tau \subset \Lambda _{\tau ,\mathbb {R}}$
, by identifying
$\tau \subset \Lambda _{\tau ,\mathbb {R}}$
, by identifying ![]() (a closed stratum of
(a closed stratum of ![]() described in Remark 2.14) with the projective toric variety associated to
described in Remark 2.14) with the projective toric variety associated to
![]() $\tau $
, we obtain an ample line bundle
$\tau $
, we obtain an ample line bundle
![]() $\mathcal {L}_\tau $
on
$\mathcal {L}_\tau $
on ![]() . When the assumption holds, then there exists an isomorphism
. When the assumption holds, then there exists an isomorphism
![]() $\mathbf {h}_{\omega \tau }\colon \iota _{\omega \tau }^*(\mathcal {L}_{\tau }) \cong \mathcal {L}_{\omega }$
, for every pair
$\mathbf {h}_{\omega \tau }\colon \iota _{\omega \tau }^*(\mathcal {L}_{\tau }) \cong \mathcal {L}_{\omega }$
, for every pair
![]() $\omega \subset \tau $
such that the isomorphisms
$\omega \subset \tau $
such that the isomorphisms
![]() $\mathbf {h}_{\omega \tau }$
’s satisfy the cocycle condition, that is,
$\mathbf {h}_{\omega \tau }$
’s satisfy the cocycle condition, that is,
![]() $\mathbf {h}_{\omega \tau }\circ \iota _{\omega \tau }^*(\mathbf {h}_{\tau \sigma }) = \mathbf {h}_{\omega \sigma }$
for every triple
$\mathbf {h}_{\omega \tau }\circ \iota _{\omega \tau }^*(\mathbf {h}_{\tau \sigma }) = \mathbf {h}_{\omega \sigma }$
for every triple
![]() $\omega \subset \tau \subset \sigma $
.Footnote
3
In particular, the degenerate Calabi–Yau
$\omega \subset \tau \subset \sigma $
.Footnote
3
In particular, the degenerate Calabi–Yau ![]() is projective.
is projective.
Sections of
![]() $\mathcal {L}$
correspond to the lattice points
$\mathcal {L}$
correspond to the lattice points
![]() $B_{\mathbb {Z}} \subset B$
. More precisely, given
$B_{\mathbb {Z}} \subset B$
. More precisely, given
![]() $m\in B_{\mathbb {Z}}$
, there is a unique
$m\in B_{\mathbb {Z}}$
, there is a unique
![]() $\tau \in \mathscr {P}$
such that
$\tau \in \mathscr {P}$
such that
![]() $m \in \mathrm {int}_{\mathrm {re}}(\tau )$
, and this determines a section
$m \in \mathrm {int}_{\mathrm {re}}(\tau )$
, and this determines a section
![]() $\vartheta _{m,\tau }$
of
$\vartheta _{m,\tau }$
of
![]() $\mathcal {L}_{\tau }$
by toric geometry. This section extends uniquely as
$\mathcal {L}_{\tau }$
by toric geometry. This section extends uniquely as
![]() $\vartheta _{m}$
to
$\vartheta _{m}$
to
![]() $\sigma \supset \tau $
such that
$\sigma \supset \tau $
such that
![]() $\mathbf {h}_{\tau \sigma }(\vartheta _m) = \vartheta _{m,\tau }$
. Further extending
$\mathbf {h}_{\tau \sigma }(\vartheta _m) = \vartheta _{m,\tau }$
. Further extending
![]() $\vartheta _m$
by
$\vartheta _m$
by
![]() $0$
to other cells gives a section of
$0$
to other cells gives a section of
![]() $\mathcal {L}$
corresponding to m, called a (
$\mathcal {L}$
corresponding to m, called a (
![]() $0^{\text {th}}$
-order) theta function. Now, for a vertex
$0^{\text {th}}$
-order) theta function. Now, for a vertex
![]() $v \in \mathscr {P}^{[0]}$
, we can trivialize
$v \in \mathscr {P}^{[0]}$
, we can trivialize
![]() $\mathcal {L}$
over
$\mathcal {L}$
over
![]() $V(v)$
using
$V(v)$
using
![]() $\vartheta _{v}$
as the holomorphic frame. Then, for m lying in a cell
$\vartheta _{v}$
as the holomorphic frame. Then, for m lying in a cell
![]() $\sigma $
that contains v,
$\sigma $
that contains v,
![]() $\vartheta _{m}$
is of the form
$\vartheta _{m}$
is of the form
![]() $g \vartheta _v$
, where g is a constant multiple of
$g \vartheta _v$
, where g is a constant multiple of
![]() $z^{m}$
.
$z^{m}$
.
Under the above projectivity assumption, one can define a generalized moment map
following [Reference Ruddat and Siebert43, Prop. 2.1]: First of all, the theta functions
![]() $\{\vartheta _m\}_{m \in B_{\mathbb {Z}}}$
defines an embedding of
$\{\vartheta _m\}_{m \in B_{\mathbb {Z}}}$
defines an embedding of ![]() , denoted by
, denoted by ![]() . Restricting to each closed toric stratum
. Restricting to each closed toric stratum ![]() , the only nonzero theta functions are those corresponding to
, the only nonzero theta functions are those corresponding to
![]() $m \in B_{\mathbb {Z}} \cap \tau $
. Also, there is an embedding
$m \in B_{\mathbb {Z}} \cap \tau $
. Also, there is an embedding
![]() $\mathfrak {j}_{\tau }\colon \mathtt {T}_{\tau } := \Lambda _{\tau ,\mathbb {R}}^*/\Lambda _{\tau ,\mathbb {Z}}^* \hookrightarrow \mathtt {U}(1)^{N}$
of real tori such that the composition
$\mathfrak {j}_{\tau }\colon \mathtt {T}_{\tau } := \Lambda _{\tau ,\mathbb {R}}^*/\Lambda _{\tau ,\mathbb {Z}}^* \hookrightarrow \mathtt {U}(1)^{N}$
of real tori such that the composition ![]() of
of
![]() $\Phi $
with the inclusion
$\Phi $
with the inclusion ![]() is equivariant. The map
is equivariant. The map
![]() $\mu $
is then defined by setting
$\mu $
is then defined by setting

which can be understood as a composition of maps
where
![]() $\mu _{\mathbb {P}}$
is the standard moment map for
$\mu _{\mathbb {P}}$
is the standard moment map for
![]() $\mathbb {P}^{N}$
and
$\mathbb {P}^{N}$
and
![]() $d\mathfrak {j}_{\tau }\colon \Lambda _{\tau ,\mathbb {R}}^* \rightarrow \mathbb {R}^{N}$
is the Lie algebra homomorphism induced by
$d\mathfrak {j}_{\tau }\colon \Lambda _{\tau ,\mathbb {R}}^* \rightarrow \mathbb {R}^{N}$
is the Lie algebra homomorphism induced by
![]() $\mathfrak {j}_{\tau }\colon \mathtt {T}_{\tau } \rightarrow \mathtt {U}(1)^N$
.
$\mathfrak {j}_{\tau }\colon \mathtt {T}_{\tau } \rightarrow \mathtt {U}(1)^N$
.
Fixing a vertex
![]() $v \in \mathscr {P}^{[0]}$
, we can naturally embed
$v \in \mathscr {P}^{[0]}$
, we can naturally embed
![]() $\Lambda _{\tau ,\mathbb {R}} \hookrightarrow T_{v,\mathbb {R}}$
for all
$\Lambda _{\tau ,\mathbb {R}} \hookrightarrow T_{v,\mathbb {R}}$
for all
![]() $\tau $
containing v. Furthermore, we can patch the
$\tau $
containing v. Furthermore, we can patch the
![]() $d\mathfrak {j}^*_{\tau }$
’s into a linear map
$d\mathfrak {j}^*_{\tau }$
’s into a linear map
![]() $d\mathfrak {j}^* \colon (\mathbb {R}^{N})^* \rightarrow T_{v,\mathbb {R}}$
so that
$d\mathfrak {j}^* \colon (\mathbb {R}^{N})^* \rightarrow T_{v,\mathbb {R}}$
so that
![]() $\mu _{\tau } = d\mathfrak {j}^* \circ \mu _{\mathbb {P}} \circ \Phi _{\tau }$
for each
$\mu _{\tau } = d\mathfrak {j}^* \circ \mu _{\mathbb {P}} \circ \Phi _{\tau }$
for each
![]() $\tau $
which contains v. In particular, on the local chart
$\tau $
which contains v. In particular, on the local chart
![]() $V(\tau )=\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\tau ^{-1}\Sigma _v])$
associated with
$V(\tau )=\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\tau ^{-1}\Sigma _v])$
associated with
![]() $v \in \tau $
, we have the local description
$v \in \tau $
, we have the local description
![]() $\mu |_{V(\tau )} = d \mathfrak {j}^*\circ \mu _{\mathbb {P}}\circ \Phi |_{V(\tau )}$
of the generalized moment map
$\mu |_{V(\tau )} = d \mathfrak {j}^*\circ \mu _{\mathbb {P}}\circ \Phi |_{V(\tau )}$
of the generalized moment map
![]() $\mu $
.
$\mu $
.
We consider the amoeba
![]() $\mathcal {A}:= \mu (Z)$
. As
$\mathcal {A}:= \mu (Z)$
. As ![]() , where
, where
![]() $Z^{\tau }_i$
is the zero set of a section of
$Z^{\tau }_i$
is the zero set of a section of
![]() $\varkappa _{\tau ,i}^*(\mathcal {O}(1))$
(see the discussion right after equation (2.15)), we can see that
$\varkappa _{\tau ,i}^*(\mathcal {O}(1))$
(see the discussion right after equation (2.15)), we can see that
![]() $\mathcal {A} \cap \tau = \bigcup _{i=1}^{p} \mu _{\tau }(Z^{\tau }_i)$
is a union of amoebas
$\mathcal {A} \cap \tau = \bigcup _{i=1}^{p} \mu _{\tau }(Z^{\tau }_i)$
is a union of amoebas
![]() $\mathcal {A}^{\tau }_i:= \mu _{\tau }(Z^{\tau }_i)$
. It was shown in [Reference Ruddat and Siebert43] that the affine structure defined right after Definition 2.2 extends to
$\mathcal {A}^{\tau }_i:= \mu _{\tau }(Z^{\tau }_i)$
. It was shown in [Reference Ruddat and Siebert43] that the affine structure defined right after Definition 2.2 extends to
![]() $B \setminus \mathcal {A}$
.
$B \setminus \mathcal {A}$
.
3.2 Construction of charts on B
For any
![]() $\tau \in \mathscr {P}$
, we have
$\tau \in \mathscr {P}$
, we have
For later purposes, we would like to relate sufficiently small open convex subsets
![]() $W \subset W(\tau )$
with Stein (or strongly
$W \subset W(\tau )$
with Stein (or strongly
![]() $1$
-completed, as defined in [Reference Demailly13]) open subsets
$1$
-completed, as defined in [Reference Demailly13]) open subsets
![]() $U \subset V(\tau )$
. To do so, we need to introduce a specific collection of (nonaffine) charts on B.
$U \subset V(\tau )$
. To do so, we need to introduce a specific collection of (nonaffine) charts on B.
Recall that there are natural maps
![]() $\Lambda _{\tau } \hookrightarrow \tau ^{-1} \Sigma _v $
and
$\Lambda _{\tau } \hookrightarrow \tau ^{-1} \Sigma _v $
and
![]() $\tau ^{-1} \Sigma _v \twoheadrightarrow \Sigma _{\tau }$
. By choosing a piecewise linear splitting
$\tau ^{-1} \Sigma _v \twoheadrightarrow \Sigma _{\tau }$
. By choosing a piecewise linear splitting
![]() $\mathsf {split}_\tau \colon \Sigma _{\tau } \rightarrow \tau ^{-1} \Sigma _v$
, we have an identification of monoids
$\mathsf {split}_\tau \colon \Sigma _{\tau } \rightarrow \tau ^{-1} \Sigma _v$
, we have an identification of monoids
![]() $\tau ^{-1} \Sigma _v \cong \Sigma _{\tau } \times \Lambda _{\tau }$
, which induces the biholomorphism
$\tau ^{-1} \Sigma _v \cong \Sigma _{\tau } \times \Lambda _{\tau }$
, which induces the biholomorphism
where
![]() $\Lambda _{\tau ,\mathbb {C}^*}^*:=\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Lambda _{\tau }]) \cong \Lambda _{\tau }^* \otimes _{\mathbb {Z}} \mathbb {C}^* \cong (\mathbb {C}^{*})^l$
is a complex torus. Fixing a set of generators
$\Lambda _{\tau ,\mathbb {C}^*}^*:=\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Lambda _{\tau }]) \cong \Lambda _{\tau }^* \otimes _{\mathbb {Z}} \mathbb {C}^* \cong (\mathbb {C}^{*})^l$
is a complex torus. Fixing a set of generators
![]() $\{m_i \}_{i \in \mathtt {B}_{\tau }}$
of the monoid
$\{m_i \}_{i \in \mathtt {B}_{\tau }}$
of the monoid
![]() $\Sigma _{\tau }$
, which is not necessarily a minimal set, we can define an embedding
$\Sigma _{\tau }$
, which is not necessarily a minimal set, we can define an embedding
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }])\hookrightarrow \mathbb {C}^{|\mathtt {B}_{\tau }|}$
as an analytic subset using the functions
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }])\hookrightarrow \mathbb {C}^{|\mathtt {B}_{\tau }|}$
as an analytic subset using the functions
![]() $z^{m_i}$
’s. We consider the real torus
$z^{m_i}$
’s. We consider the real torus
![]() $\mathtt {T}_{\tau ,\perp } := \mathscr {Q}_{\tau ,\mathbb {R}}^*/\mathscr {Q}_{\tau }^* \cong \mathtt {U}(1)^{n - l}$
and its action on
$\mathtt {T}_{\tau ,\perp } := \mathscr {Q}_{\tau ,\mathbb {R}}^*/\mathscr {Q}_{\tau }^* \cong \mathtt {U}(1)^{n - l}$
and its action on
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }])$
defined by
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }])$
defined by
![]() $t\cdot z^{m} = e^{2\pi i (t,m)} z^m$
, together with an embedding
$t\cdot z^{m} = e^{2\pi i (t,m)} z^m$
, together with an embedding
![]() $\mathtt {T}_{\tau ,\perp } \hookrightarrow \mathtt {U}(1)^{|\mathtt {B}_{\tau }|}$
of real tori via
$\mathtt {T}_{\tau ,\perp } \hookrightarrow \mathtt {U}(1)^{|\mathtt {B}_{\tau }|}$
of real tori via
![]() $t\mapsto (e^{2\pi i (t,m_i)})_{i \in \mathtt {B}_\tau }$
so that the inclusion
$t\mapsto (e^{2\pi i (t,m_i)})_{i \in \mathtt {B}_\tau }$
so that the inclusion
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }])\hookrightarrow \mathbb {C}^{|\mathtt {B}_{\tau }|}$
is
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }])\hookrightarrow \mathbb {C}^{|\mathtt {B}_{\tau }|}$
is
![]() $\mathtt {T}_{\tau ,\perp }$
-equivariant.
$\mathtt {T}_{\tau ,\perp }$
-equivariant.
We consider the moment map
![]() $\hat {\mu }_{\tau } \colon \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }]) \rightarrow \mathscr {Q}_{\tau ,\mathbb {R}}$
defined by
$\hat {\mu }_{\tau } \colon \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }]) \rightarrow \mathscr {Q}_{\tau ,\mathbb {R}}$
defined by
 $$ \begin{align} \hat{\mu}_{\tau} := \sum_{i \in \mathtt{B}_{\tau}} \frac{1}{2} |z^{m_i}|^2 \cdot m_i, \end{align} $$
$$ \begin{align} \hat{\mu}_{\tau} := \sum_{i \in \mathtt{B}_{\tau}} \frac{1}{2} |z^{m_i}|^2 \cdot m_i, \end{align} $$
which is obtained by composing the standard moment map
![]() $\mathbb {C}^{|\mathtt {B}_{\tau }|} \rightarrow \mathbb {R}^{|\mathtt {B}_{\tau }|}_{\geq 0}$
,
$\mathbb {C}^{|\mathtt {B}_{\tau }|} \rightarrow \mathbb {R}^{|\mathtt {B}_{\tau }|}_{\geq 0}$
,
![]() $(z_i)_{i\in \mathtt {B}_{\tau }} \mapsto (\frac {1}{2} |z_i|^2)_{i\in \mathtt {B}_{\tau }}$
with the projection
$(z_i)_{i\in \mathtt {B}_{\tau }} \mapsto (\frac {1}{2} |z_i|^2)_{i\in \mathtt {B}_{\tau }}$
with the projection
![]() $\mathbb {R}^{|\mathtt {B}_{\tau }|} \rightarrow \mathscr {Q}_{\tau ,\mathbb {R}}$
,
$\mathbb {R}^{|\mathtt {B}_{\tau }|} \rightarrow \mathscr {Q}_{\tau ,\mathbb {R}}$
,
![]() $e_i \mapsto m_i$
. By [Reference Fulton and William21, §4.2],
$e_i \mapsto m_i$
. By [Reference Fulton and William21, §4.2],
![]() $\hat {\mu }_{\tau }$
induces a homeomorphism between the quotient
$\hat {\mu }_{\tau }$
induces a homeomorphism between the quotient
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }])/\mathtt {T}_{\tau ,\perp }$
and
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }])/\mathtt {T}_{\tau ,\perp }$
and
![]() $\mathscr {Q}_{\tau ,\mathbb {R}}$
. Taking product with the log map
$\mathscr {Q}_{\tau ,\mathbb {R}}$
. Taking product with the log map
![]() $\log \colon \Lambda _{\tau ,\mathbb {C}^*}^* \rightarrow \Lambda _{\tau ,\mathbb {R}}^*$
(which is induced from the standard log map
$\log \colon \Lambda _{\tau ,\mathbb {C}^*}^* \rightarrow \Lambda _{\tau ,\mathbb {R}}^*$
(which is induced from the standard log map
![]() $\log \colon \mathbb {C}^* \rightarrow \mathbb {R}$
defined by
$\log \colon \mathbb {C}^* \rightarrow \mathbb {R}$
defined by
![]() $\log (e^{2\pi (x+i\theta )}) = x$
), we obtain a map
$\log (e^{2\pi (x+i\theta )}) = x$
), we obtain a map
![]() $\mu _{\tau } := (\log , \hat {\mu }_{\tau }) \colon V(\tau ) \rightarrow \Lambda _{\tau ,\mathbb {R}}^* \times \mathscr {Q}_{\tau ,\mathbb {R}}$
,Footnote
4
and the following diagram
$\mu _{\tau } := (\log , \hat {\mu }_{\tau }) \colon V(\tau ) \rightarrow \Lambda _{\tau ,\mathbb {R}}^* \times \mathscr {Q}_{\tau ,\mathbb {R}}$
,Footnote
4
and the following diagram

where
![]() $\Upsilon _{\tau }$
is a homeomorphism which serves as a chart.
$\Upsilon _{\tau }$
is a homeomorphism which serves as a chart.
The homeomorphism
![]() $\Upsilon _{\tau }$
exists because if we fix a vertex
$\Upsilon _{\tau }$
exists because if we fix a vertex
![]() $v \in \tau $
, then we can equip
$v \in \tau $
, then we can equip
![]() $V(\tau )$
with an action by the real torus
$V(\tau )$
with an action by the real torus
![]() $\mathtt {T}^{n} := T^*_{v, \mathbb {R}} / T^*_v$
such that both
$\mathtt {T}^{n} := T^*_{v, \mathbb {R}} / T^*_v$
such that both
![]() $\mu $
and
$\mu $
and
![]() $\mu _\tau $
induce homeomorphisms from the quotient
$\mu _\tau $
induce homeomorphisms from the quotient
![]() $V(\tau )/\mathtt {T}^{n}$
onto the images. The restriction of
$V(\tau )/\mathtt {T}^{n}$
onto the images. The restriction of
![]() $\Upsilon _{\tau }$
to
$\Upsilon _{\tau }$
to
![]() $\Lambda _{\tau ,\mathbb {R}}^* \times \{o\}$
, where
$\Lambda _{\tau ,\mathbb {R}}^* \times \{o\}$
, where
![]() $\{o\}$
is the zero cone, is a homeomorphism onto
$\{o\}$
is the zero cone, is a homeomorphism onto
![]() $\mathrm {int}_{\mathrm {re}}(\tau ) \subset W(\tau )$
, which is nothing but (a generalized version of) the Legendre transform (see [Reference Fulton and William21, §4.2] for the explicit formula); also, this homeomorphism is independent of the choices of the splitting
$\mathrm {int}_{\mathrm {re}}(\tau ) \subset W(\tau )$
, which is nothing but (a generalized version of) the Legendre transform (see [Reference Fulton and William21, §4.2] for the explicit formula); also, this homeomorphism is independent of the choices of the splitting
![]() $\mathsf {split}_{\tau }$
and the generators
$\mathsf {split}_{\tau }$
and the generators
![]() $\{m_i \}_{i \in \mathtt {B}_{\tau}}$
.
$\{m_i \}_{i \in \mathtt {B}_{\tau}}$
.
The dependencies of the chart
![]() $\Upsilon _{\tau }$
on the choices of the splitting
$\Upsilon _{\tau }$
on the choices of the splitting
![]() $\mathsf {split}_{\tau }\colon \Sigma _{\tau } \rightarrow \tau ^{-1} \Sigma _v$
and the generators
$\mathsf {split}_{\tau }\colon \Sigma _{\tau } \rightarrow \tau ^{-1} \Sigma _v$
and the generators
![]() $\{m_i \}_i$
can be described as follows. First, if we choose another piecewise linear splitting
$\{m_i \}_i$
can be described as follows. First, if we choose another piecewise linear splitting
![]() $\widetilde {\mathsf {split}}_{\tau }\colon \Sigma _{\tau } \rightarrow \tau ^{-1} \Sigma _v$
, then there is a piecewise linear map
$\widetilde {\mathsf {split}}_{\tau }\colon \Sigma _{\tau } \rightarrow \tau ^{-1} \Sigma _v$
, then there is a piecewise linear map
![]() $b \colon \Sigma _{\tau } \rightarrow \Lambda _{\tau ,\mathbb {R}}$
recording the difference between
$b \colon \Sigma _{\tau } \rightarrow \Lambda _{\tau ,\mathbb {R}}$
recording the difference between
![]() $\mathsf {split}_\tau $
and
$\mathsf {split}_\tau $
and
![]() $\widetilde {\mathsf {split}}_{\tau }$
. The two corresponding coordinate charts
$\widetilde {\mathsf {split}}_{\tau }$
. The two corresponding coordinate charts
![]() $\Upsilon _{\tau }$
and
$\Upsilon _{\tau }$
and
![]() $\tilde {\Upsilon }_{\tau }$
are then related by a homeomorphism
$\tilde {\Upsilon }_{\tau }$
are then related by a homeomorphism
![]() $\gimel $
such that
$\gimel $
such that
 $$ \begin{align*}\gimel\left(x,\sum_{i} y_i m_i\right) = \left(x , \sum_{i}y_i e^{4\pi \langle b(m_i),x\rangle } m_i \right), \end{align*} $$
$$ \begin{align*}\gimel\left(x,\sum_{i} y_i m_i\right) = \left(x , \sum_{i}y_i e^{4\pi \langle b(m_i),x\rangle } m_i \right), \end{align*} $$
where
![]() $y_i= \frac {1}{2} |z^{m_i}|^2$
for some point
$y_i= \frac {1}{2} |z^{m_i}|^2$
for some point
![]() $z\in \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }])$
and i runs through
$z\in \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }])$
and i runs through
![]() $m_i \in \sigma $
, via the formula
$m_i \in \sigma $
, via the formula
![]() $\tilde {\Upsilon }_{\tau } = \Upsilon _{\tau } \circ \gimel $
. Second, if we choose another set of generators
$\tilde {\Upsilon }_{\tau } = \Upsilon _{\tau } \circ \gimel $
. Second, if we choose another set of generators
![]() $\tilde {m}_j$
’s, then the corresponding maps
$\tilde {m}_j$
’s, then the corresponding maps
![]() $\hat {\mu }_{\tau }, \tilde {\mu }_{\tau } \colon \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }]) \rightarrow \mathscr {Q}_{\tau ,\mathbb {R}}$
are related by a continuous map
$\hat {\mu }_{\tau }, \tilde {\mu }_{\tau } \colon \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }]) \rightarrow \mathscr {Q}_{\tau ,\mathbb {R}}$
are related by a continuous map
![]() $\hat {\gimel } \colon \mathscr {Q}_{\tau ,\mathbb {R}} \rightarrow \mathscr {Q}_{\tau ,\mathbb {R}}$
which maps each cone
$\hat {\gimel } \colon \mathscr {Q}_{\tau ,\mathbb {R}} \rightarrow \mathscr {Q}_{\tau ,\mathbb {R}}$
which maps each cone
![]() $\sigma \in \Sigma _{\tau }$
back to itself. This is because both
$\sigma \in \Sigma _{\tau }$
back to itself. This is because both
![]() $\hat {\mu }_{\tau }, \tilde {\mu }_{\tau } $
induce a homeomorphism between
$\hat {\mu }_{\tau }, \tilde {\mu }_{\tau } $
induce a homeomorphism between
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }])/\mathtt {T}_{\tau ,\perp }$
and
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }])/\mathtt {T}_{\tau ,\perp }$
and
![]() $\mathscr {Q}_{\tau ,\mathbb {R}}$
.
$\mathscr {Q}_{\tau ,\mathbb {R}}$
.
Now, suppose that
![]() $\omega \subset \tau $
. We want to see how the charts
$\omega \subset \tau $
. We want to see how the charts
![]() $\Upsilon _{\omega }$
,
$\Upsilon _{\omega }$
,
![]() $\Upsilon _{\tau }$
can be glued together in a compatible manner. We first make a compatible choice of splittings. So we fix a vertex
$\Upsilon _{\tau }$
can be glued together in a compatible manner. We first make a compatible choice of splittings. So we fix a vertex
![]() $v \in \omega $
and a piecewise linear splitting
$v \in \omega $
and a piecewise linear splitting
![]() $\mathsf {split}_{\omega }\colon \Sigma _{\omega } \rightarrow \omega ^{-1} \Sigma _{v}$
. We then choose a piecewise linear splitting
$\mathsf {split}_{\omega }\colon \Sigma _{\omega } \rightarrow \omega ^{-1} \Sigma _{v}$
. We then choose a piecewise linear splitting
![]() $\mathsf {split}_{\omega \tau }\colon \Sigma _{\tau } \rightarrow \Sigma _{\omega }$
such that
$\mathsf {split}_{\omega \tau }\colon \Sigma _{\tau } \rightarrow \Sigma _{\omega }$
such that
![]() $K_\tau \sigma $
is mapped into
$K_\tau \sigma $
is mapped into
![]() $K_\omega \sigma $
for any
$K_\omega \sigma $
for any
![]() $\sigma \supset \tau $
. Together with the natural maps
$\sigma \supset \tau $
. Together with the natural maps
![]() $\Lambda _{\tau }/\Lambda _{\omega } \hookrightarrow \tau ^{-1}\Sigma _{\omega }$
and
$\Lambda _{\tau }/\Lambda _{\omega } \hookrightarrow \tau ^{-1}\Sigma _{\omega }$
and
![]() $\tau ^{-1}\Sigma _{\omega } \twoheadrightarrow \Sigma _{\tau }$
, we obtain an isomorphism
$\tau ^{-1}\Sigma _{\omega } \twoheadrightarrow \Sigma _{\tau }$
, we obtain an isomorphism
![]() $\tau ^{-1}\Sigma _{\omega } \cong (\Lambda _{\tau }/\Lambda _{\omega }) \times \Sigma _{\tau }$
. By composing together
$\tau ^{-1}\Sigma _{\omega } \cong (\Lambda _{\tau }/\Lambda _{\omega }) \times \Sigma _{\tau }$
. By composing together
![]() $\mathsf {split}_{\omega \tau }\colon \Sigma _{\tau } \rightarrow \Sigma _{\omega }$
,
$\mathsf {split}_{\omega \tau }\colon \Sigma _{\tau } \rightarrow \Sigma _{\omega }$
,
![]() $\mathsf {split}_{\omega }\colon \Sigma _{\omega } \rightarrow \omega ^{-1} \Sigma _{v}$
and the natural monoid homomorphism
$\mathsf {split}_{\omega }\colon \Sigma _{\omega } \rightarrow \omega ^{-1} \Sigma _{v}$
and the natural monoid homomorphism
![]() $ \omega ^{-1} \Sigma _{v} \rightarrow \tau ^{-1}\Sigma _{v}$
, we get a splitting
$ \omega ^{-1} \Sigma _{v} \rightarrow \tau ^{-1}\Sigma _{v}$
, we get a splitting
![]() $\mathsf {split}_{\tau }\colon \Sigma _{\tau } \rightarrow \tau ^{-1} \Sigma _{v}$
.
$\mathsf {split}_{\tau }\colon \Sigma _{\tau } \rightarrow \tau ^{-1} \Sigma _{v}$
.
Using these choices of splittings, we have a biholomorphism
which fits into the following diagram

Here, the bottom left horizontal map is induced from a splitting
![]() $(\Lambda _{\tau }/\Lambda _{\omega }) \rightarrow \Lambda _{\tau }$
obtained by composing
$(\Lambda _{\tau }/\Lambda _{\omega }) \rightarrow \Lambda _{\tau }$
obtained by composing
![]() $\Lambda _{\tau }/\Lambda _{\omega } \rightarrow \tau ^{-1}\Sigma _{\omega }$
with the splitting
$\Lambda _{\tau }/\Lambda _{\omega } \rightarrow \tau ^{-1}\Sigma _{\omega }$
with the splitting
![]() $\tau ^{-1}\Sigma _{\omega } \rightarrow \tau ^{-1}(\omega ^{-1} \Sigma _{v})$
and then identifying with the image lattice
$\tau ^{-1}\Sigma _{\omega } \rightarrow \tau ^{-1}(\omega ^{-1} \Sigma _{v})$
and then identifying with the image lattice
![]() $\Lambda _{\tau }$
. The appearance of
$\Lambda _{\tau }$
. The appearance of
![]() $s_{\omega \tau }$
in the diagram is due to the twisting of
$s_{\omega \tau }$
in the diagram is due to the twisting of
![]() $V(\tau )$
by the open gluing data
$V(\tau )$
by the open gluing data
![]() $(s_{\omega \tau })_{\omega \subset \tau }$
when it is glued to
$(s_{\omega \tau })_{\omega \subset \tau }$
when it is glued to
![]() $V(\omega )$
.
$V(\omega )$
.
We also have to make a compatible choice of the generators
![]() $\{m_i\}_{i \in \mathtt {B}_{\omega }}$
and
$\{m_i\}_{i \in \mathtt {B}_{\omega }}$
and
![]() $\{m_i\}_{i \in \mathtt {B}_{\tau }}$
. First, note that the restriction of
$\{m_i\}_{i \in \mathtt {B}_{\tau }}$
. First, note that the restriction of
![]() $\hat {\mu }_{\omega }$
to the open subset
$\hat {\mu }_{\omega }$
to the open subset
![]() $ \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\tau ^{-1}\Sigma _{\omega }]) \subset \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\omega }])$
depends only on the subcollection
$ \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\tau ^{-1}\Sigma _{\omega }]) \subset \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\omega }])$
depends only on the subcollection
![]() $\{m_i\}_{i \in \mathtt {B}_{\omega \subset \tau }}$
of
$\{m_i\}_{i \in \mathtt {B}_{\omega \subset \tau }}$
of
![]() $\{m_i\}_{i \in \mathtt {B}_{\omega }}$
which contains those
$\{m_i\}_{i \in \mathtt {B}_{\omega }}$
which contains those
![]() $m_i$
’s that belong to some cone
$m_i$
’s that belong to some cone
![]() $\sigma \supset \tau $
. We choose the set of generators
$\sigma \supset \tau $
. We choose the set of generators
![]() $\{\tilde {m}_i\}_{i \in \mathtt {B}_{\tau }}$
for
$\{\tilde {m}_i\}_{i \in \mathtt {B}_{\tau }}$
for
![]() $\Sigma _{\tau }$
, with
$\Sigma _{\tau }$
, with
![]() $\mathtt {B}_{\tau }=\mathtt {B}_{\omega \subset \tau }$
, to be the projection of
$\mathtt {B}_{\tau }=\mathtt {B}_{\omega \subset \tau }$
, to be the projection of
![]() $\{m_i\}_{i \in \mathtt {B}_{\omega \subset \tau }}$
through the natural map
$\{m_i\}_{i \in \mathtt {B}_{\omega \subset \tau }}$
through the natural map
![]() $\tau ^{-1} \Sigma _{\omega } \rightarrow \Sigma _{\tau }$
. Each
$\tau ^{-1} \Sigma _{\omega } \rightarrow \Sigma _{\tau }$
. Each
![]() $m_i$
can be expressed as
$m_i$
can be expressed as
![]() $m_i = \mathsf {split}_{\omega \tau }(\tilde {m}_i) + b_i$
for some
$m_i = \mathsf {split}_{\omega \tau }(\tilde {m}_i) + b_i$
for some
![]() $b_i \in \Lambda _{\tau }/\Lambda _{\omega }$
, through the splitting
$b_i \in \Lambda _{\tau }/\Lambda _{\omega }$
, through the splitting
![]() $\mathsf {split}_{\omega \tau }\colon \Sigma _{\tau } \rightarrow \Sigma _{\omega }$
. Notice that if
$\mathsf {split}_{\omega \tau }\colon \Sigma _{\tau } \rightarrow \Sigma _{\omega }$
. Notice that if
![]() $m_i \in K_{\omega } \tau $
, then we have
$m_i \in K_{\omega } \tau $
, then we have
![]() $\tilde {m}_i= o$
and hence
$\tilde {m}_i= o$
and hence
![]() $b_i \in K_{\omega }\tau $
. By tracing through the biholomorphism in equation (3.5) and taking either the modulus or the log map, we have a map
$b_i \in K_{\omega }\tau $
. By tracing through the biholomorphism in equation (3.5) and taking either the modulus or the log map, we have a map
satisfying
 $$ \begin{align} \gimel\left(x_1 - c_{\omega\tau,1},x_2-c_{\omega\tau,2},\sum_i y_i |s_{\omega\tau}(\mathsf{split}_{\omega\tau}(\tilde{m}_i))|^{-2} \tilde{m}_i\right) = \left(x_1,\sum_{i} y_i e^{4\pi \langle b_i,x_2 \rangle} m_i\right), \end{align} $$
$$ \begin{align} \gimel\left(x_1 - c_{\omega\tau,1},x_2-c_{\omega\tau,2},\sum_i y_i |s_{\omega\tau}(\mathsf{split}_{\omega\tau}(\tilde{m}_i))|^{-2} \tilde{m}_i\right) = \left(x_1,\sum_{i} y_i e^{4\pi \langle b_i,x_2 \rangle} m_i\right), \end{align} $$
where
![]() $y_i = \frac {1}{2} | z^{\tilde {m}_i}|^2$
. Here,
$y_i = \frac {1}{2} | z^{\tilde {m}_i}|^2$
. Here,
![]() $s_{\omega \tau } \in \mathrm {PM}(\tau )$
is the part of the open gluing data associated to
$s_{\omega \tau } \in \mathrm {PM}(\tau )$
is the part of the open gluing data associated to
![]() $\omega \subset \tau $
, and
$\omega \subset \tau $
, and
![]() $c_{\omega \tau }=c_{\omega \tau ,1}+c_{\omega \tau ,2} \in \Lambda _{\tau ,\mathbb {R}}^*$
is the unique element representing the linear map
$c_{\omega \tau }=c_{\omega \tau ,1}+c_{\omega \tau ,2} \in \Lambda _{\tau ,\mathbb {R}}^*$
is the unique element representing the linear map
![]() $\log |s_{\omega \tau }| \colon \Lambda _{\tau ,\mathbb {R}} \rightarrow \mathbb {R}$
defined by
$\log |s_{\omega \tau }| \colon \Lambda _{\tau ,\mathbb {R}} \rightarrow \mathbb {R}$
defined by
![]() $\log |s_{\omega \tau }|(b) = \log |s_{\omega \tau }(b)|$
. For instance, the holomorphic function
$\log |s_{\omega \tau }|(b) = \log |s_{\omega \tau }(b)|$
. For instance, the holomorphic function
![]() $z^{m_i} \in \mathbb {C}[\tau ^{-1}\Sigma _{\omega }]$
is identified with
$z^{m_i} \in \mathbb {C}[\tau ^{-1}\Sigma _{\omega }]$
is identified with
![]() $z^{b_i}\cdot z^{\tilde {m}_i}$
in
$z^{b_i}\cdot z^{\tilde {m}_i}$
in
![]() $(\Lambda _{\tau }/\Lambda _{\omega })^*\otimes _{\mathbb {Z}}\mathbb {C}^* \times \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }])$
, resulting in the expression
$(\Lambda _{\tau }/\Lambda _{\omega })^*\otimes _{\mathbb {Z}}\mathbb {C}^* \times \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }])$
, resulting in the expression
![]() $\sum _{i} y_i e^{4\pi \langle b_i,x_2 \rangle } m_i$
on the right-hand side. We have
$\sum _{i} y_i e^{4\pi \langle b_i,x_2 \rangle } m_i$
on the right-hand side. We have
![]() $\Upsilon _{\tau } = \Upsilon _{\omega } \circ \gimel $
, where we use the splitting
$\Upsilon _{\tau } = \Upsilon _{\omega } \circ \gimel $
, where we use the splitting
![]() $(\Lambda _{\tau }/\Lambda _{\omega }) \rightarrow \Lambda _{\tau }$
to obtain an isomorphism
$(\Lambda _{\tau }/\Lambda _{\omega }) \rightarrow \Lambda _{\tau }$
to obtain an isomorphism
![]() $\Lambda _{\omega ,\mathbb {R}}^* \times (\Lambda _{\tau ,\mathbb {R}}/\Lambda _{\omega ,\mathbb {R}})^* \cong \Lambda _{\tau ,\mathbb {R}}^*$
and an identification of the domains of the two maps
$\Lambda _{\omega ,\mathbb {R}}^* \times (\Lambda _{\tau ,\mathbb {R}}/\Lambda _{\omega ,\mathbb {R}})^* \cong \Lambda _{\tau ,\mathbb {R}}^*$
and an identification of the domains of the two maps
![]() $\Upsilon _{\tau }$
and
$\Upsilon _{\tau }$
and
![]() $\Upsilon _{\omega } \circ \gimel $
.
$\Upsilon _{\omega } \circ \gimel $
.
Lemma 3.1. There is a base
![]() $\mathscr {B}$
of open subsets of B such that the preimage
$\mathscr {B}$
of open subsets of B such that the preimage
![]() $\mu ^{-1}(W)$
is Stein for any
$\mu ^{-1}(W)$
is Stein for any
![]() $W \in \mathscr {B}$
.
$W \in \mathscr {B}$
.
Proof. First of all, it is well known that analytic spaces associated to affine varieties are Stein. So
![]() $V(\tau )$
is Stein for any
$V(\tau )$
is Stein for any
![]() $\tau $
. Now, we fix a point
$\tau $
. Now, we fix a point
![]() $x \in \mathrm {int}_{\mathrm {re}}(\tau ) \subset B$
. It suffices to show that there is a local base
$x \in \mathrm {int}_{\mathrm {re}}(\tau ) \subset B$
. It suffices to show that there is a local base
![]() $\mathscr {B}_x$
of x such that the preimage
$\mathscr {B}_x$
of x such that the preimage
![]() $\mu ^{-1}(W)$
is Stein for each
$\mu ^{-1}(W)$
is Stein for each
![]() $W \in \mathscr {B}_x$
. We work locally on
$W \in \mathscr {B}_x$
. We work locally on
![]() $\mu |_{V(\tau )} \colon V(\tau ) \rightarrow W(\tau )$
. Consider the diagram (3.4) and write
$\mu |_{V(\tau )} \colon V(\tau ) \rightarrow W(\tau )$
. Consider the diagram (3.4) and write
![]() $\Upsilon ^{-1}(x) = (\underline {x},o)$
, where
$\Upsilon ^{-1}(x) = (\underline {x},o)$
, where
![]() $o \in \mathscr {Q}_{\tau ,\mathbb {R}}$
is the origin. By [Reference Demailly13, Ch. 1, Ex. 7.4], the preimage
$o \in \mathscr {Q}_{\tau ,\mathbb {R}}$
is the origin. By [Reference Demailly13, Ch. 1, Ex. 7.4], the preimage
![]() $\log ^{-1}(W)$
under the log map
$\log ^{-1}(W)$
under the log map
![]() $\log \colon (\mathbb {C}^*)^l \rightarrow \Lambda _{\tau ,\mathbb {R}}^*$
is Stein for any convex
$\log \colon (\mathbb {C}^*)^l \rightarrow \Lambda _{\tau ,\mathbb {R}}^*$
is Stein for any convex
![]() $W \subset \Lambda _{\tau ,\mathbb {R}}^*$
which contains
$W \subset \Lambda _{\tau ,\mathbb {R}}^*$
which contains
![]() $\underline {x}$
. Again by [Reference Demailly13, Ch. 1, Ex. 7.4], any subset
$\underline {x}$
. Again by [Reference Demailly13, Ch. 1, Ex. 7.4], any subset
 $$ \begin{align*}\bigcap_{j=1}^N\{z \in \mathrm{Spec}_{\mathrm{an}}(\mathbb{C}[\Sigma_{\tau}]) \ | \ |f_j(z)|<\epsilon \},\end{align*} $$
$$ \begin{align*}\bigcap_{j=1}^N\{z \in \mathrm{Spec}_{\mathrm{an}}(\mathbb{C}[\Sigma_{\tau}]) \ | \ |f_j(z)|<\epsilon \},\end{align*} $$
where
![]() $f_j$
’s are holomorphic functions, is Stein. By taking
$f_j$
’s are holomorphic functions, is Stein. By taking
![]() $f_j$
’s to be the functions
$f_j$
’s to be the functions
![]() $z^{m_j}$
’s associated to the set of all nonzero generators in
$z^{m_j}$
’s associated to the set of all nonzero generators in
![]() $\{m_j\}_{j\in \mathtt {B}_{\tau }}$
and
$\{m_j\}_{j\in \mathtt {B}_{\tau }}$
and
![]() $\epsilon $
sufficiently small, we have a subset
$\epsilon $
sufficiently small, we have a subset
 $$ \begin{align*}W = \left\{ y \ \Big| \ y = \sum_{j} y_j m_j \text{ with } |y_j|<\frac{\epsilon^2}{2}, \ \text{where } y_j = \frac{1}{2} |z^{m_j}|^2 \text{ at some point } z \in \mathrm{Spec}_{\mathrm{an}}(\mathbb{C}[\Sigma_{\tau}])\right\}\end{align*} $$
$$ \begin{align*}W = \left\{ y \ \Big| \ y = \sum_{j} y_j m_j \text{ with } |y_j|<\frac{\epsilon^2}{2}, \ \text{where } y_j = \frac{1}{2} |z^{m_j}|^2 \text{ at some point } z \in \mathrm{Spec}_{\mathrm{an}}(\mathbb{C}[\Sigma_{\tau}])\right\}\end{align*} $$
of
![]() $\mathscr {Q}_{\tau ,\mathbb {R}}$
such that the preimage
$\mathscr {Q}_{\tau ,\mathbb {R}}$
such that the preimage
![]() $\hat {\mu }_{\tau }^{-1}(W)$
is Stein. Therefore, we can construct a local base
$\hat {\mu }_{\tau }^{-1}(W)$
is Stein. Therefore, we can construct a local base
![]() $\mathscr {B}_{o}$
of o such that the preimage
$\mathscr {B}_{o}$
of o such that the preimage
![]() $\hat {\mu }_{\tau }^{-1}(W)$
is Stein for any
$\hat {\mu }_{\tau }^{-1}(W)$
is Stein for any
![]() $W \in \mathscr {B}_o$
. Finally, since a product of Stein open subsets is Stein, we obtain our desired local base
$W \in \mathscr {B}_o$
. Finally, since a product of Stein open subsets is Stein, we obtain our desired local base
![]() $\mathscr {B}_x$
by taking the products of these subsets.
$\mathscr {B}_x$
by taking the products of these subsets.
3.3 The tropical singular locus
 $\mathscr {S}$
of B
$\mathscr {S}$
of B
We now specify a codimension
![]() $2$
singular locus
$2$
singular locus
![]() $\mathscr {S} \subset B$
of the affine structure using the charts
$\mathscr {S} \subset B$
of the affine structure using the charts
![]() $\Upsilon _{\tau }$
introduced in (3.4) for
$\Upsilon _{\tau }$
introduced in (3.4) for
![]() $\tau $
such that
$\tau $
such that
![]() $\dim _{\mathbb {R}}(\tau )<n$
. Given the chart
$\dim _{\mathbb {R}}(\tau )<n$
. Given the chart
![]() $\Upsilon _{\tau }$
that maps
$\Upsilon _{\tau }$
that maps
![]() $\Lambda _{\tau ,\mathbb {R}}^*$
to
$\Lambda _{\tau ,\mathbb {R}}^*$
to
![]() $\mathrm {int}_{\mathrm {re}}(\tau )$
, we define the tropical singular locus
$\mathrm {int}_{\mathrm {re}}(\tau )$
, we define the tropical singular locus
![]() $\mathscr {S}$
by requiring that
$\mathscr {S}$
by requiring that
 $$ \begin{align} \Upsilon_{\tau}^{-1}(\mathscr{S} \cap \mathrm{int}_{\mathrm{re}}(\tau)) = \bigcup_{\substack{\rho \in \mathscr{N}_{\tau};\\ \dim_{\mathbb{R}}(\rho) < \dim_{\mathbb{R}}(\tau)}} \big( (\mathrm{int}_{\mathrm{re}}(\rho) +c_{\tau}) \times \{o\} \big) , \end{align} $$
$$ \begin{align} \Upsilon_{\tau}^{-1}(\mathscr{S} \cap \mathrm{int}_{\mathrm{re}}(\tau)) = \bigcup_{\substack{\rho \in \mathscr{N}_{\tau};\\ \dim_{\mathbb{R}}(\rho) < \dim_{\mathbb{R}}(\tau)}} \big( (\mathrm{int}_{\mathrm{re}}(\rho) +c_{\tau}) \times \{o\} \big) , \end{align} $$
where
![]() $\mathscr {N}_{\tau } \subset \Lambda _{\tau ,\mathbb {R}}^*$
is the normal fan of the polytope
$\mathscr {N}_{\tau } \subset \Lambda _{\tau ,\mathbb {R}}^*$
is the normal fan of the polytope
![]() $\tau $
, and
$\tau $
, and
![]() $\{o\}$
is the zero cone in
$\{o\}$
is the zero cone in
![]() $\Sigma _{\tau } \subset \mathscr {Q}_{\tau ,\mathbb {R}}$
; here,
$\Sigma _{\tau } \subset \mathscr {Q}_{\tau ,\mathbb {R}}$
; here,
![]() $c_{\tau } = \log |s_{v\tau }|$
is the element in
$c_{\tau } = \log |s_{v\tau }|$
is the element in
![]() $\Lambda _{\tau ,\mathbb {R}}^*$
representing the linear map
$\Lambda _{\tau ,\mathbb {R}}^*$
representing the linear map
![]() $\log |s_{v\tau }|\colon \Lambda _{\tau ,\mathbb {R}} \rightarrow \mathbb {R}$
, which is independent of the vertex
$\log |s_{v\tau }|\colon \Lambda _{\tau ,\mathbb {R}} \rightarrow \mathbb {R}$
, which is independent of the vertex
![]() $v\in \tau $
. A subset of the form
$v\in \tau $
. A subset of the form
![]() $\mathscr {S}_{\tau ,\rho } := (\mathrm {int}_{\mathrm {re}}(\rho )+c_{\tau }) \times \{o\}$
in (3.7) is called a stratum of
$\mathscr {S}_{\tau ,\rho } := (\mathrm {int}_{\mathrm {re}}(\rho )+c_{\tau }) \times \{o\}$
in (3.7) is called a stratum of
![]() $\mathscr {S}$
in
$\mathscr {S}$
in
![]() $\mathrm {int}_{\mathrm {re}}(\tau )$
. The locus
$\mathrm {int}_{\mathrm {re}}(\tau )$
. The locus
![]() $\mathscr {S}$
is independent of the choices of the splittings
$\mathscr {S}$
is independent of the choices of the splittings
![]() $\mathsf {split}_{\tau }$
’s and generators
$\mathsf {split}_{\tau }$
’s and generators
![]() $\{m_i\}_{i \in \mathtt {B}_{\tau }}$
used to construct the charts
$\{m_i\}_{i \in \mathtt {B}_{\tau }}$
used to construct the charts
![]() $\Upsilon _{\tau }$
’s.
$\Upsilon _{\tau }$
’s.
Remark 3.2. Our definition of the singular locus is similar to those in [Reference Gross and Siebert27, Reference Gross and Siebert29]; the only difference is that our locus is a collection of polyhedra in
![]() $\Lambda _{\tau ,\mathbb {R}}^*$
, instead of
$\Lambda _{\tau ,\mathbb {R}}^*$
, instead of
![]() $\mathrm {int}_{\mathrm {re}}(\tau )$
. Note that
$\mathrm {int}_{\mathrm {re}}(\tau )$
. Note that
![]() $\Lambda _{\tau ,\mathbb {R}}^*$
is homeomorphic to
$\Lambda _{\tau ,\mathbb {R}}^*$
is homeomorphic to
![]() $\mathrm {int}_{\mathrm {re}}(\tau )$
by the Legendre transform. This modification is needed for our construction of the contraction map
$\mathrm {int}_{\mathrm {re}}(\tau )$
by the Legendre transform. This modification is needed for our construction of the contraction map
![]() $\mathscr {C}$
below, where we need to consider the convex open subsets in
$\mathscr {C}$
below, where we need to consider the convex open subsets in
![]() $\Lambda _{\tau ,\mathbb {R}}^*$
, instead of those in
$\Lambda _{\tau ,\mathbb {R}}^*$
, instead of those in
![]() $\mathrm {int}_{\mathrm {re}}(\tau )$
.
$\mathrm {int}_{\mathrm {re}}(\tau )$
.
Lemma 3.3. For
![]() $\omega \subset \tau $
and a stratum
$\omega \subset \tau $
and a stratum
![]() $\mathscr {S}_{\tau ,\rho }$
in
$\mathscr {S}_{\tau ,\rho }$
in
![]() $\mathrm {int}_{\mathrm {re}}(\tau )$
, the intersection of the closure
$\mathrm {int}_{\mathrm {re}}(\tau )$
, the intersection of the closure
![]() $\overline {\mathscr {S}_{\tau ,\rho }}$
in B with
$\overline {\mathscr {S}_{\tau ,\rho }}$
in B with
![]() $\mathrm {int}_{\mathrm {re}}(\omega )$
is a union of strata of
$\mathrm {int}_{\mathrm {re}}(\omega )$
is a union of strata of
![]() $\mathscr {S}$
in
$\mathscr {S}$
in
![]() $\mathrm {int}_{\mathrm {re}}(\omega )$
.
$\mathrm {int}_{\mathrm {re}}(\omega )$
.
Proof. We consider the map
![]() $\gimel $
described in equation (3.6) and take a neighborhood
$\gimel $
described in equation (3.6) and take a neighborhood
![]() $W = W_1 \times \mathscr {Q}_{\omega ,\mathbb {R}}$
of a point
$W = W_1 \times \mathscr {Q}_{\omega ,\mathbb {R}}$
of a point
![]() $(\underline {x},o)$
in
$(\underline {x},o)$
in
![]() $ \Lambda _{\omega ,\mathbb {R}}^* \times \mathscr {Q}_{\omega ,\mathbb {R}}$
, where
$ \Lambda _{\omega ,\mathbb {R}}^* \times \mathscr {Q}_{\omega ,\mathbb {R}}$
, where
![]() $W_1$
is some sufficiently small neighborhood of
$W_1$
is some sufficiently small neighborhood of
![]() $\underline {x}$
in
$\underline {x}$
in
![]() $\Lambda _{\omega ,\mathbb {R}}^*$
. By shrinking W if necessary, we may assume that
$\Lambda _{\omega ,\mathbb {R}}^*$
. By shrinking W if necessary, we may assume that
![]() $\gimel ^{-1}(W) = W_1 \times (a -\mathrm {int}_{\mathrm {re}}(K_{\omega }\tau ^{\vee })) \times \mathscr {Q}_{\tau ,\mathbb {R}}$
, where a is some element in
$\gimel ^{-1}(W) = W_1 \times (a -\mathrm {int}_{\mathrm {re}}(K_{\omega }\tau ^{\vee })) \times \mathscr {Q}_{\tau ,\mathbb {R}}$
, where a is some element in
![]() $-\mathrm {int}_{\mathrm {re}}(K_{\omega }\tau ^{\vee }) \subset (\Lambda _{\tau ,\mathbb {R}}/\Lambda _{\omega ,\mathbb {R}})^*$
. Writing
$-\mathrm {int}_{\mathrm {re}}(K_{\omega }\tau ^{\vee }) \subset (\Lambda _{\tau ,\mathbb {R}}/\Lambda _{\omega ,\mathbb {R}})^*$
. Writing
![]() $c_{\tau } = c_{\tau ,1}+c_{\tau ,2}$
, where
$c_{\tau } = c_{\tau ,1}+c_{\tau ,2}$
, where
![]() $c_{\tau ,1},c_{\tau ,2}$
are the components of
$c_{\tau ,1},c_{\tau ,2}$
are the components of
![]() $c_{\tau }$
according to the chosen decomposition
$c_{\tau }$
according to the chosen decomposition
![]() $\Lambda _{\tau ,\mathbb {R}}^* \cong \Lambda _{\omega ,\mathbb {R}}^* \times (\Lambda _{\tau ,\mathbb {R}}/\Lambda _{\omega ,\mathbb {R}})^*$
, the equality
$\Lambda _{\tau ,\mathbb {R}}^* \cong \Lambda _{\omega ,\mathbb {R}}^* \times (\Lambda _{\tau ,\mathbb {R}}/\Lambda _{\omega ,\mathbb {R}})^*$
, the equality
![]() $c_{\tau ,1} + c_{\omega \tau ,1} = c_{\omega }$
follows from the compatibility of the open gluing data in Definition 2.13. If
$c_{\tau ,1} + c_{\omega \tau ,1} = c_{\omega }$
follows from the compatibility of the open gluing data in Definition 2.13. If
![]() $\mathscr {S}_{\tau ,\rho }$
intersects the open subset
$\mathscr {S}_{\tau ,\rho }$
intersects the open subset
![]() $\gimel ^{-1}(W)$
, then
$\gimel ^{-1}(W)$
, then
![]() $\rho \subset \Lambda _{\tau ,\mathbb {R}}^*$
must be the dual cone of some face
$\rho \subset \Lambda _{\tau ,\mathbb {R}}^*$
must be the dual cone of some face
![]() $\rho ^{\vee } \subset \omega \subset \tau $
in
$\rho ^{\vee } \subset \omega \subset \tau $
in
![]() $\Lambda _{\tau ,\mathbb {R}}^*$
. The intersection is of the form
$\Lambda _{\tau ,\mathbb {R}}^*$
. The intersection is of the form
for some
![]() $\underline {\rho } \in \mathscr {N}_{\omega }$
(
$\underline {\rho } \in \mathscr {N}_{\omega }$
(
![]() $c_{\tau ,2}$
is absorbed by a), where
$c_{\tau ,2}$
is absorbed by a), where
![]() $\underline {\rho } \subset \Lambda _{\omega ,\mathbb {R}}^*$
is the dual cone of
$\underline {\rho } \subset \Lambda _{\omega ,\mathbb {R}}^*$
is the dual cone of
![]() $\rho ^{\vee }$
in
$\rho ^{\vee }$
in
![]() $\Lambda _{\omega ,\mathbb {R}}^*$
, and hence we have
$\Lambda _{\omega ,\mathbb {R}}^*$
, and hence we have
![]() $W \cap \mathscr {S}_{\tau ,\rho } =\gimel ((\mathrm {int}_{\mathrm {re}}(\underline {\rho })+c_{\tau ,1}) \times (a-\mathrm {int}_{\mathrm {re}}(K_{\omega }\tau ^{\vee })) \times \{o\})$
. Therefore, the intersection of
$W \cap \mathscr {S}_{\tau ,\rho } =\gimel ((\mathrm {int}_{\mathrm {re}}(\underline {\rho })+c_{\tau ,1}) \times (a-\mathrm {int}_{\mathrm {re}}(K_{\omega }\tau ^{\vee })) \times \{o\})$
. Therefore, the intersection of
![]() $\overline {\mathscr {S}_{\tau ,\rho }}$
with
$\overline {\mathscr {S}_{\tau ,\rho }}$
with
![]() $\Lambda _{\omega ,\mathbb {R}}^*$
in the open subset
$\Lambda _{\omega ,\mathbb {R}}^*$
in the open subset
![]() $W \subset \Lambda _{\omega ,\mathbb {R}}^* \times \mathscr {Q}_{\omega ,\mathbb {R}}$
is given by
$W \subset \Lambda _{\omega ,\mathbb {R}}^* \times \mathscr {Q}_{\omega ,\mathbb {R}}$
is given by
![]() $(\underline {\rho }+c_{\omega }) \times \{o\}$
, which is a union of strata.
$(\underline {\rho }+c_{\omega }) \times \{o\}$
, which is a union of strata.
The tropical singular locus
![]() $\mathscr {S}$
is naturally equipped with a stratification, where a stratum is given by
$\mathscr {S}$
is naturally equipped with a stratification, where a stratum is given by
![]() $\mathscr {S}_{\tau ,\rho }$
for some cone
$\mathscr {S}_{\tau ,\rho }$
for some cone
![]() $\rho \subset \mathscr {N}_{\tau }$
of
$\rho \subset \mathscr {N}_{\tau }$
of
![]() $\dim _{\mathbb {R}}(\rho ) < \dim _{\mathbb {R}}(\tau )$
for some
$\dim _{\mathbb {R}}(\rho ) < \dim _{\mathbb {R}}(\tau )$
for some
![]() $\tau \in \mathscr {P}^{[<n]}$
. We use the notation
$\tau \in \mathscr {P}^{[<n]}$
. We use the notation
![]() $\mathscr {S}^{[k]}$
to denote the set of k-dimensional strata of
$\mathscr {S}^{[k]}$
to denote the set of k-dimensional strata of
![]() $\mathscr {S}$
. The affine structure on
$\mathscr {S}$
. The affine structure on
![]() $\bigcup _{v \in \mathscr {P}^{[0]}} W_v \cup \bigcup _{\sigma \in \mathscr {P}^{[n]}} \mathrm {int}_{\mathrm {re}}(\sigma )$
introduced right after Definition 2.2 in §2.1 can be naturally extended to
$\bigcup _{v \in \mathscr {P}^{[0]}} W_v \cup \bigcup _{\sigma \in \mathscr {P}^{[n]}} \mathrm {int}_{\mathrm {re}}(\sigma )$
introduced right after Definition 2.2 in §2.1 can be naturally extended to
![]() $B \setminus \mathscr {S}$
as in [Reference Gross and Siebert29].
$B \setminus \mathscr {S}$
as in [Reference Gross and Siebert29].
If we consider
![]() $\omega \subset \tau \subset \rho $
for some
$\omega \subset \tau \subset \rho $
for some
![]() $\omega \in \mathscr {P}^{[1]}$
and
$\omega \in \mathscr {P}^{[1]}$
and
![]() $\rho \in \mathscr {P}^{[n-1]}$
, the corresponding monodromy transformation
$\rho \in \mathscr {P}^{[n-1]}$
, the corresponding monodromy transformation
![]() $T_{\gamma }$
is nontrivial if and only if
$T_{\gamma }$
is nontrivial if and only if
![]() $\omega \in \Omega _p$
and
$\omega \in \Omega _p$
and
![]() $\rho \in R_p$
, where p is as in Definition 2.9. Therefore, the part of the singular locus
$\rho \in R_p$
, where p is as in Definition 2.9. Therefore, the part of the singular locus
![]() $\mathscr {S}$
lying in
$\mathscr {S}$
lying in
![]() $\Upsilon _{\tau }^{-1}(\mathrm {int}_{\mathrm {re}}(\tau )) = \Lambda _{\tau ,\mathbb {R}}^* \times \{o\}$
is determined by the subsets
$\Upsilon _{\tau }^{-1}(\mathrm {int}_{\mathrm {re}}(\tau )) = \Lambda _{\tau ,\mathbb {R}}^* \times \{o\}$
is determined by the subsets
![]() $\Omega _p$
’s. We may further define the essential singular locus
$\Omega _p$
’s. We may further define the essential singular locus
![]() $\mathscr {S}_e$
to include only those strata contained in
$\mathscr {S}_e$
to include only those strata contained in
![]() $\mathscr {S}^{[n-2]}$
with nontrivial monodromy around them. We observe that the affine structure can be further extended to
$\mathscr {S}^{[n-2]}$
with nontrivial monodromy around them. We observe that the affine structure can be further extended to
![]() $B \setminus \mathscr {S}_e$
.
$B \setminus \mathscr {S}_e$
.
More explicitly, we have a projection
in which
![]() $\Lambda _{\Delta _1(\tau )}^* \oplus \cdots \oplus \Lambda _{\Delta _p(\tau )}^*$
can be treated as a direct summand as in §2.2. So we can consider the pullback of the fan
$\Lambda _{\Delta _1(\tau )}^* \oplus \cdots \oplus \Lambda _{\Delta _p(\tau )}^*$
can be treated as a direct summand as in §2.2. So we can consider the pullback of the fan
![]() $\mathscr {N}_{\Delta _1(\tau )} \times \cdots \times \mathscr {N}_{\Delta _p(\tau )}$
via the map
$\mathscr {N}_{\Delta _1(\tau )} \times \cdots \times \mathscr {N}_{\Delta _p(\tau )}$
via the map
![]() $\mathtt {i}_{\tau }$
and realize
$\mathtt {i}_{\tau }$
and realize
![]() $\mathscr {N}_{\tau } \subset \Lambda _{\tau ,\mathbb {R}}^*$
as a refinement of this fan. Similarly, we have
$\mathscr {N}_{\tau } \subset \Lambda _{\tau ,\mathbb {R}}^*$
as a refinement of this fan. Similarly, we have
![]() $\check {\mathtt {i}}_{\tau } =\check {\mathtt {i}}_{\tau ,1} \oplus \cdots \oplus \check {\mathtt {i}}_{\tau ,p} \colon \mathscr {Q}_{\tau }^* \rightarrow \Lambda ^*_{\check {\Delta }_1(\tau )} \oplus \cdots \oplus \Lambda ^*_{\check {\Delta }_p(\tau )}$
and the fan
$\check {\mathtt {i}}_{\tau } =\check {\mathtt {i}}_{\tau ,1} \oplus \cdots \oplus \check {\mathtt {i}}_{\tau ,p} \colon \mathscr {Q}_{\tau }^* \rightarrow \Lambda ^*_{\check {\Delta }_1(\tau )} \oplus \cdots \oplus \Lambda ^*_{\check {\Delta }_p(\tau )}$
and the fan
![]() $\mathscr {N}_{\check {\Delta }_1(\tau )} \times \cdots \times \mathscr {N}_{\check {\Delta }_p(\tau )}$
in
$\mathscr {N}_{\check {\Delta }_1(\tau )} \times \cdots \times \mathscr {N}_{\check {\Delta }_p(\tau )}$
in
![]() $\mathscr {Q}_{\tau ,\mathbb {R}}^*$
under pullback via
$\mathscr {Q}_{\tau ,\mathbb {R}}^*$
under pullback via
![]() $\check {\mathtt {i}}_{\tau }$
. The intersection
$\check {\mathtt {i}}_{\tau }$
. The intersection
![]() $\mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\tau ) $
can be described by replacing
$\mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\tau ) $
can be described by replacing
![]() $\rho \in \mathscr {N}_{\tau }$
with the condition
$\rho \in \mathscr {N}_{\tau }$
with the condition
![]() $\rho \in \mathtt {i}_{\tau }^{-1}(\mathscr {N}_{\Delta _1(\tau )} \times \cdots \times \mathscr {N}_{\Delta _p(\tau )})$
, with a stratum denoted by
$\rho \in \mathtt {i}_{\tau }^{-1}(\mathscr {N}_{\Delta _1(\tau )} \times \cdots \times \mathscr {N}_{\Delta _p(\tau )})$
, with a stratum denoted by
![]() $\mathscr {S}_{e,\tau ,\rho }$
. This gives a stratification on
$\mathscr {S}_{e,\tau ,\rho }$
. This gives a stratification on
![]() $\mathscr {S}_e$
.
$\mathscr {S}_e$
.
Lemma 3.4. For
![]() $\omega \subset \tau $
and a stratum
$\omega \subset \tau $
and a stratum
![]() $\mathscr {S}_{e,\tau ,\rho }$
in
$\mathscr {S}_{e,\tau ,\rho }$
in
![]() $\mathrm {int}_{\mathrm {re}}(\tau )$
, the intersection of the closure
$\mathrm {int}_{\mathrm {re}}(\tau )$
, the intersection of the closure
![]() $\overline {\mathscr {S}_{e,\tau ,\rho }}$
in B with
$\overline {\mathscr {S}_{e,\tau ,\rho }}$
in B with
![]() $\mathrm {int}_{\mathrm {re}}(\omega )$
is a union of strata of
$\mathrm {int}_{\mathrm {re}}(\omega )$
is a union of strata of
![]() $\mathscr {S}_e$
in
$\mathscr {S}_e$
in
![]() $\mathrm {int}_{\mathrm {re}}(\omega )$
.
$\mathrm {int}_{\mathrm {re}}(\omega )$
.
Proof. Given
![]() $\omega \subset \tau $
, we take a change of coordinate map
$\omega \subset \tau $
, we take a change of coordinate map
![]() $\gimel $
together with a neighborhood W as in the proof of Lemma 3.3. We need to show that
$\gimel $
together with a neighborhood W as in the proof of Lemma 3.3. We need to show that
![]() $W \cap \mathscr {S}_{\tau ,\rho } =\gimel ((\mathrm {int}_{\mathrm {re}}(\rho )+c_{\tau ,1}) \times (a-\mathrm {int}_{\mathrm {re}}(K_{\omega }\tau ^{\vee })) \times \{o\})$
for some cone
$W \cap \mathscr {S}_{\tau ,\rho } =\gimel ((\mathrm {int}_{\mathrm {re}}(\rho )+c_{\tau ,1}) \times (a-\mathrm {int}_{\mathrm {re}}(K_{\omega }\tau ^{\vee })) \times \{o\})$
for some cone
![]() $\rho \in \mathtt {i}_{\tau }^{-1}(\prod _{i=1}^p \mathscr {N}_{\Delta _i(\tau )})$
. Let
$\rho \in \mathtt {i}_{\tau }^{-1}(\prod _{i=1}^p \mathscr {N}_{\Delta _i(\tau )})$
. Let
![]() $\Delta _1(\tau ),\dots ,\Delta _r(\tau ),\dots ,\Delta _p(\tau )$
be the monodromy polytopes of
$\Delta _1(\tau ),\dots ,\Delta _r(\tau ),\dots ,\Delta _p(\tau )$
be the monodromy polytopes of
![]() $\tau $
, and
$\tau $
, and
![]() $\Delta _1(\omega ), \dots , \Delta _r(\omega ),\dots ,\Delta _{p'}(\omega )$
be those of
$\Delta _1(\omega ), \dots , \Delta _r(\omega ),\dots ,\Delta _{p'}(\omega )$
be those of
![]() $\omega $
such that
$\omega $
such that
![]() $\Delta _j(\omega )$
is the face of
$\Delta _j(\omega )$
is the face of
![]() $\Delta _j(\tau )$
parallel to
$\Delta _j(\tau )$
parallel to
![]() $\Lambda _{\omega }$
for
$\Lambda _{\omega }$
for
![]() $j=1,\dots ,r$
. Then we have direct sum decompositions
$j=1,\dots ,r$
. Then we have direct sum decompositions
![]() $\Lambda _{\Delta _{1}(\tau )}\oplus \cdots \oplus \Lambda _{\Delta _{p}(\tau )} \oplus A_{\tau } = \Lambda _{\tau }$
and
$\Lambda _{\Delta _{1}(\tau )}\oplus \cdots \oplus \Lambda _{\Delta _{p}(\tau )} \oplus A_{\tau } = \Lambda _{\tau }$
and
![]() $ \Lambda _{\Delta _{1}(\omega )}\oplus \cdots \oplus \Lambda _{\Delta _{p'}(\omega )} \oplus A_{\omega } = \Lambda _{\omega }$
. We can further choose an inclusion
$ \Lambda _{\Delta _{1}(\omega )}\oplus \cdots \oplus \Lambda _{\Delta _{p'}(\omega )} \oplus A_{\omega } = \Lambda _{\omega }$
. We can further choose an inclusion
in other words, for every
![]() $j=r+1,\dots ,p'$
, any
$j=r+1,\dots ,p'$
, any
![]() $f \in R_j \subset \mathscr {P}_{n-1}(\omega )$
in Definition 2.9 is not containing
$f \in R_j \subset \mathscr {P}_{n-1}(\omega )$
in Definition 2.9 is not containing
![]() $\tau $
. For every
$\tau $
. For every
![]() $j=r+1,\dots ,p$
and any
$j=r+1,\dots ,p$
and any
![]() $f \in R_j \subset \mathscr {P}_{n-1}(\tau )$
, the element
$f \in R_j \subset \mathscr {P}_{n-1}(\tau )$
, the element
![]() $m^{f}_{v_1v_2}$
is zero for any two vertices
$m^{f}_{v_1v_2}$
is zero for any two vertices
![]() $v_1,v_2$
of
$v_1,v_2$
of
![]() $\omega $
. We have the identification
$\omega $
. We have the identification
 $$ \begin{align*}\Lambda_{\tau}/\Lambda_{\omega} = \bigoplus_{j=1}^r (\Lambda_{\Delta_j(\tau)}/\Lambda_{\Delta_j(\omega)}) \oplus \bigoplus_{l=r+1}^{p} \Lambda_{\Delta_l(\tau)} \oplus \mathrm{coker}(\mathsf{a}_{\omega\tau}). \end{align*} $$
$$ \begin{align*}\Lambda_{\tau}/\Lambda_{\omega} = \bigoplus_{j=1}^r (\Lambda_{\Delta_j(\tau)}/\Lambda_{\Delta_j(\omega)}) \oplus \bigoplus_{l=r+1}^{p} \Lambda_{\Delta_l(\tau)} \oplus \mathrm{coker}(\mathsf{a}_{\omega\tau}). \end{align*} $$
As a result, any cone
![]() $\mathtt {i}^{-1}_{\tau }(\prod _{j=1}^{p} \rho _j) \in \mathtt {i}^{-1}_{\tau }\big (\prod _{i=1}^p \mathscr {N}_{\Delta _i(\tau )} \big )$
of codimension greater than
$\mathtt {i}^{-1}_{\tau }(\prod _{j=1}^{p} \rho _j) \in \mathtt {i}^{-1}_{\tau }\big (\prod _{i=1}^p \mathscr {N}_{\Delta _i(\tau )} \big )$
of codimension greater than
![]() $0$
intersecting
$0$
intersecting
![]() $\gimel ^{-1}(W)$
will be a pullback of a cone under the projection to
$\gimel ^{-1}(W)$
will be a pullback of a cone under the projection to
![]() $\Lambda _{\Delta _1(\tau ),\mathbb {R}}^* \oplus \cdots \oplus \Lambda _{\Delta _r(\tau ),\mathbb {R}}^*$
. Consider the commutative diagram of projection maps
$\Lambda _{\Delta _1(\tau ),\mathbb {R}}^* \oplus \cdots \oplus \Lambda _{\Delta _r(\tau ),\mathbb {R}}^*$
. Consider the commutative diagram of projection maps

We see that, in the open subset
![]() $\gimel ^{-1}(W)$
, every cone of codimension greater than
$\gimel ^{-1}(W)$
, every cone of codimension greater than
![]() $0$
coming from pullback via
$0$
coming from pullback via
![]() $\mathtt {p}_\tau $
is a further pullback via
$\mathtt {p}_\tau $
is a further pullback via
![]() $\Pi _{\omega \subset \tau } \circ \mathtt {p}_{\tau }$
. As a consequence, it must be of the form
$\Pi _{\omega \subset \tau } \circ \mathtt {p}_{\tau }$
. As a consequence, it must be of the form
![]() $\gimel ((\mathrm {int}_{\mathrm {re}}(\rho )+c_{\tau ,1}) \times (a-\mathrm {int}_{\mathrm {re}}(K_{\omega }\tau ^{\vee })) \times \{o\})$
in W.
$\gimel ((\mathrm {int}_{\mathrm {re}}(\rho )+c_{\tau ,1}) \times (a-\mathrm {int}_{\mathrm {re}}(K_{\omega }\tau ^{\vee })) \times \{o\})$
in W.
3.3.1 Contraction of
 $\mathcal {A}$
to
$\mathcal {A}$
to
 $\mathscr {S}$
$\mathscr {S}$
We would like to relate the amoeba
![]() $\mathcal {A} = \mu (Z)$
with the tropical singular locus
$\mathcal {A} = \mu (Z)$
with the tropical singular locus
![]() $\mathscr {S}$
introduced above.
$\mathscr {S}$
introduced above.
Assumption 3.5. We assume the existence of a surjective contraction map
![]() $\mathscr {C} \colon B \rightarrow B$
which is isotopic to the identity and satisfies the following conditions:
$\mathscr {C} \colon B \rightarrow B$
which is isotopic to the identity and satisfies the following conditions:
-
1.
 $\mathscr {C}^{-1}(B \setminus \mathscr {S}) \subset (B \setminus \mathscr {S})$
and the restriction
$\mathscr {C}^{-1}(B \setminus \mathscr {S}) \subset (B \setminus \mathscr {S})$
and the restriction
 $\mathscr {C}|_{\mathscr {C}^{-1}(B \setminus \mathscr {S})}\colon \mathscr {C}^{-1}(B \setminus \mathscr {S}) \to B \setminus \mathscr {S}$
is a homeomorphism.
$\mathscr {C}|_{\mathscr {C}^{-1}(B \setminus \mathscr {S})}\colon \mathscr {C}^{-1}(B \setminus \mathscr {S}) \to B \setminus \mathscr {S}$
is a homeomorphism. -
2.
 $\mathscr {C}$
maps
$\mathscr {C}$
maps
 $\mathcal {A}$
into the essential singular locus
$\mathcal {A}$
into the essential singular locus
 $\mathscr {S}_e$
.
$\mathscr {S}_e$
. -
3. For each
 $\tau \in \mathscr {P}$
, we have
$\tau \in \mathscr {P}$
, we have
 $\mathscr {C}^{-1}(\mathrm {int}_{\mathrm {re}}(\tau )) \subset \mathrm {int}_{\mathrm {re}}(\tau )$
.
$\mathscr {C}^{-1}(\mathrm {int}_{\mathrm {re}}(\tau )) \subset \mathrm {int}_{\mathrm {re}}(\tau )$
. -
4. For each
 $\tau \in \mathscr {P}$
with
$\tau \in \mathscr {P}$
with
 $0<\dim _{\mathbb {R}}(\tau )<n$
, we have a decomposition of the intersection
$0<\dim _{\mathbb {R}}(\tau )<n$
, we have a decomposition of the intersection $$ \begin{align*}\tau \cap \mathscr{C}^{-1}(B\setminus \mathscr{S}) = \bigcup_{v \in \tau^{[0]}} \tau_{v}\end{align*} $$
$$ \begin{align*}\tau \cap \mathscr{C}^{-1}(B\setminus \mathscr{S}) = \bigcup_{v \in \tau^{[0]}} \tau_{v}\end{align*} $$
 $\tau \cap \mathscr {C}^{-1}(B\setminus \mathscr {S})$
into connected components
$\tau \cap \mathscr {C}^{-1}(B\setminus \mathscr {S})$
into connected components
 $\tau _{v}$
’s, where each
$\tau _{v}$
’s, where each
 $\tau _{v}$
is contractible and is the unique component containing the vertex
$\tau _{v}$
is contractible and is the unique component containing the vertex
 $v \in \tau $
.
$v \in \tau $
.
-
5. For each
 $\tau \in \mathscr {P}$
and each point
$\tau \in \mathscr {P}$
and each point
 $x \in \mathrm {int}_{\mathrm {re}}(\tau ) \cap \mathscr {S}$
,
$x \in \mathrm {int}_{\mathrm {re}}(\tau ) \cap \mathscr {S}$
,
 $\mathscr {C}^{-1}(x) \subset \mathrm {int}_{\mathrm {re}}(\tau )$
is a connected compact subset.
$\mathscr {C}^{-1}(x) \subset \mathrm {int}_{\mathrm {re}}(\tau )$
is a connected compact subset. -
6. For each
 $\tau \in \mathscr {P}$
and each point
$\tau \in \mathscr {P}$
and each point
 $x \in \mathrm {int}_{\mathrm {re}}(\tau ) \cap \mathscr {S}$
, there exists a local base
$x \in \mathrm {int}_{\mathrm {re}}(\tau ) \cap \mathscr {S}$
, there exists a local base
 $\mathscr {B}_x$
around x such that
$\mathscr {B}_x$
around x such that
 $(\mathscr {C} \circ \mu )^{-1}(W) \subset V(\tau )$
is Stein for every
$(\mathscr {C} \circ \mu )^{-1}(W) \subset V(\tau )$
is Stein for every
 $W \in \mathscr {B}_x$
, and for any
$W \in \mathscr {B}_x$
, and for any
 $U \supset \mathscr {C}^{-1}(x)$
, we have
$U \supset \mathscr {C}^{-1}(x)$
, we have
 $\mathscr {C}^{-1}(W) \subset U$
for sufficiently small
$\mathscr {C}^{-1}(W) \subset U$
for sufficiently small
 $W \in \mathscr {B}_x$
.
$W \in \mathscr {B}_x$
.
Similar contraction maps appear in [Reference Ruddat and Siebert43, Rem. 2.4] (see also [Reference Ruddat and Zharkov45, 44]).
When
![]() $\dim _{\mathbb {R}}(B) = 2$
, we can take
$\dim _{\mathbb {R}}(B) = 2$
, we can take
![]() $\mathscr {C} = \mathrm {id}$
because from [Reference Gross and Siebert27, Ex. 1.62], we see that Z is a finite collection of points, with at most one point lying in each closed stratum
$\mathscr {C} = \mathrm {id}$
because from [Reference Gross and Siebert27, Ex. 1.62], we see that Z is a finite collection of points, with at most one point lying in each closed stratum ![]() , and the amoeba
, and the amoeba
![]() $\mathcal {A}$
is exactly the image of Z under the generalized moment map
$\mathcal {A}$
is exactly the image of Z under the generalized moment map
![]() $\mu $
.
$\mu $
.
When
![]() $\dim _{\mathbb {R}}(B) = 3$
, the amoeba
$\dim _{\mathbb {R}}(B) = 3$
, the amoeba
![]() $\mathcal {A}$
can possibly be of codimension one and we need to construct a contraction map as shown in Figure 5.
$\mathcal {A}$
can possibly be of codimension one and we need to construct a contraction map as shown in Figure 5.

Figure 5 Contraction map
![]() $\mathscr {C}$
when
$\mathscr {C}$
when
![]() $\dim _{\mathbb {R}}(B) = 3$
.
$\dim _{\mathbb {R}}(B) = 3$
.
For
![]() $\dim _{\mathbb {R}}(\tau ) = 1$
, again from [Reference Gross and Siebert27, Ex. 1.62], we see that if
$\dim _{\mathbb {R}}(\tau ) = 1$
, again from [Reference Gross and Siebert27, Ex. 1.62], we see that if
![]() $\mathcal {A} \cap \mathrm {int}_{\mathrm {re}}(\tau ) \neq \emptyset $
, then there is exactly one
$\mathcal {A} \cap \mathrm {int}_{\mathrm {re}}(\tau ) \neq \emptyset $
, then there is exactly one
![]() $\Omega _1$
and
$\Omega _1$
and
![]() $R_1$
, and
$R_1$
, and
![]() $\Delta _{1}(\tau )$
is a line segment of affine length
$\Delta _{1}(\tau )$
is a line segment of affine length
![]() $1$
. In this case,
$1$
. In this case, ![]() consists of only one point, given by the intersection of the zero locus
consists of only one point, given by the intersection of the zero locus
![]() $s_{v\tau }^{-1}(f_{v\rho })$
with
$s_{v\tau }^{-1}(f_{v\rho })$
with
![]() $\mathbb {C}^* \cong V_{\tau }(\tau ) \subset V(\tau )$
. Taking m to be the primitive vector in
$\mathbb {C}^* \cong V_{\tau }(\tau ) \subset V(\tau )$
. Taking m to be the primitive vector in
![]() $\Lambda _{\tau }$
starting at v that points into
$\Lambda _{\tau }$
starting at v that points into
![]() $\tau $
, we can write
$\tau $
, we can write
![]() $s_{v\tau }^{-1}(f_{v\rho }) = 1 + s_{v\tau }^{-1}(m) z^{m}$
. Applying the log map
$s_{v\tau }^{-1}(f_{v\rho }) = 1 + s_{v\tau }^{-1}(m) z^{m}$
. Applying the log map
![]() $\log \colon \mathbb {C}^* \rightarrow \mathbb {R}$
, we see that
$\log \colon \mathbb {C}^* \rightarrow \mathbb {R}$
, we see that
![]() $\mathcal {A} \cap \mathrm {int}_{\mathrm {re}}(\tau ) = c_{\tau }$
. Therefore, for an edge
$\mathcal {A} \cap \mathrm {int}_{\mathrm {re}}(\tau ) = c_{\tau }$
. Therefore, for an edge
![]() $\tau \in \mathscr {P}^{[1]}$
, we can define
$\tau \in \mathscr {P}^{[1]}$
, we can define
![]() $\mathscr {C}$
to be the identity on
$\mathscr {C}$
to be the identity on
![]() $\tau $
.
$\tau $
.
On a codimension one cell
![]() $\rho $
such that
$\rho $
such that
![]() $\mathrm {int}_{\mathrm {re}}(\rho ) \cap \mathcal {A} \neq \emptyset $
(see Figure 6), we consider the log map
$\mathrm {int}_{\mathrm {re}}(\rho ) \cap \mathcal {A} \neq \emptyset $
(see Figure 6), we consider the log map
![]() $\log \colon \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Lambda _{\rho }]) \cong (\mathbb {C}^*)^2 \rightarrow \Lambda _{\rho ,\mathbb {R}}^* \cong \mathbb {R}^2$
and take a sufficiently large polytope
$\log \colon \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Lambda _{\rho }]) \cong (\mathbb {C}^*)^2 \rightarrow \Lambda _{\rho ,\mathbb {R}}^* \cong \mathbb {R}^2$
and take a sufficiently large polytope
![]() $\mathtt {P}$
(colored purple in Figure 6) so that
$\mathtt {P}$
(colored purple in Figure 6) so that
![]() $\mathcal {A} \setminus \mathrm {int}_{\mathrm {re}}(\mathtt {P})$
is a disjoint union of legs. We first contract each leg to the tropical singular locus (colored blue in Figure 6) along the normal direction to the tropical singular locus. Next, we contract the polytope
$\mathcal {A} \setminus \mathrm {int}_{\mathrm {re}}(\mathtt {P})$
is a disjoint union of legs. We first contract each leg to the tropical singular locus (colored blue in Figure 6) along the normal direction to the tropical singular locus. Next, we contract the polytope
![]() $\mathtt {P}$
to the zero-dimensional stratum of
$\mathtt {P}$
to the zero-dimensional stratum of
![]() $\mathscr {S}_e$
. Notice that the restriction of
$\mathscr {S}_e$
. Notice that the restriction of
![]() $\mathscr {C}$
to the tropical singular locus
$\mathscr {C}$
to the tropical singular locus
![]() $\mathscr {S}$
is not the identity but rather a contraction onto itself. Once the contraction map is constructed for all codimension one cells
$\mathscr {S}$
is not the identity but rather a contraction onto itself. Once the contraction map is constructed for all codimension one cells
![]() $\rho $
, we can then extend it continuously to the whole of B so that it is a diffeomorphism on
$\rho $
, we can then extend it continuously to the whole of B so that it is a diffeomorphism on
![]() $\mathrm {int}_{\mathrm {re}}(\sigma )$
for every maximal cell
$\mathrm {int}_{\mathrm {re}}(\sigma )$
for every maximal cell
![]() $\sigma $
. The map is chosen such that the preimage
$\sigma $
. The map is chosen such that the preimage
![]() $\mathscr {C}^{-1}(x)$
for every point
$\mathscr {C}^{-1}(x)$
for every point
![]() $x \in \mathrm {int}_{\mathrm {re}}(\rho )$
is a convex polytope in
$x \in \mathrm {int}_{\mathrm {re}}(\rho )$
is a convex polytope in
![]() $\mathbb {R}^2$
. Therefore, given any open subset
$\mathbb {R}^2$
. Therefore, given any open subset
![]() $U\subset \mathbb {R}^2$
which contains
$U\subset \mathbb {R}^2$
which contains
![]() $\mathscr {C}^{-1}(x)$
, we can find some convex open neighborhood
$\mathscr {C}^{-1}(x)$
, we can find some convex open neighborhood
![]() $W_1 \subset U$
of
$W_1 \subset U$
of
![]() $\mathscr {C}^{-1}(x)$
giving the Stein open subset
$\mathscr {C}^{-1}(x)$
giving the Stein open subset
![]() $\log ^{-1}(W_1) \subset (\mathbb {C}^*)^2$
. By taking
$\log ^{-1}(W_1) \subset (\mathbb {C}^*)^2$
. By taking
![]() $W = W_1 \times W_2$
in the chart
$W = W_1 \times W_2$
in the chart
![]() $\Lambda _{\rho ,\mathbb {R}}^* \times \mathscr {Q}_{\rho ,\mathbb {R}}$
as in the proof of Lemma 3.1, we have the open subset W that satisfies condition (5) in Assumption 3.5.
$\Lambda _{\rho ,\mathbb {R}}^* \times \mathscr {Q}_{\rho ,\mathbb {R}}$
as in the proof of Lemma 3.1, we have the open subset W that satisfies condition (5) in Assumption 3.5.

Figure 6 Contraction at
![]() $\rho $
.
$\rho $
.
In general, we need to construct
![]() $\mathscr {C}|_{\mathrm {int}_{\mathrm {re}}(\tau )}$
inductively for each
$\mathscr {C}|_{\mathrm {int}_{\mathrm {re}}(\tau )}$
inductively for each
![]() $\tau \in \mathscr {P}$
such that
$\tau \in \mathscr {P}$
such that
![]() $\mathscr {C}^{-1}(x) \subset \mathrm {int}_{\mathrm {re}}(\tau )$
is convex in the chart
$\mathscr {C}^{-1}(x) \subset \mathrm {int}_{\mathrm {re}}(\tau )$
is convex in the chart
![]() $\Lambda _{\tau ,\mathbb {R}}^*\cong \mathrm {int}_{\mathrm {re}}(\tau )$
and the codimension one amoeba
$\Lambda _{\tau ,\mathbb {R}}^*\cong \mathrm {int}_{\mathrm {re}}(\tau )$
and the codimension one amoeba
![]() $\mathcal {A}$
is contracted to the codimension 2 tropical singular locus
$\mathcal {A}$
is contracted to the codimension 2 tropical singular locus
![]() $\mathscr {S}_e$
. The reason for introducing such a contraction map is that we can modify the generalized moment map
$\mathscr {S}_e$
. The reason for introducing such a contraction map is that we can modify the generalized moment map
![]() $\mu $
to one which is more closely related with tropical geometry:
$\mu $
to one which is more closely related with tropical geometry:
Definition 3.6. We call the composition ![]() the modified moment map.
the modified moment map.
One immediate consequence of property
![]() $(6)$
in Assumption 3.5 is that we have
$(6)$
in Assumption 3.5 is that we have
![]() $R\nu _* (\mathcal {F}) = \nu _*(\mathcal {F})$
for any coherent sheaf
$R\nu _* (\mathcal {F}) = \nu _*(\mathcal {F})$
for any coherent sheaf
![]() $\mathcal {F}$
on
$\mathcal {F}$
on ![]() , thanks to Lemma 3.1 and Cartan’s Theorem B:
, thanks to Lemma 3.1 and Cartan’s Theorem B:
Theorem 3.7 (Cartan’s Theorem B [Reference Cartan6]; see e.g. Ch. IX, Cor. 4.11 in [Reference Demailly13]).
For any coherent sheaf
![]() $\mathcal {F}$
over a Stein space U, we have
$\mathcal {F}$
over a Stein space U, we have
![]() $ H^{>0}(U,\mathcal {F}) = 0. $
$ H^{>0}(U,\mathcal {F}) = 0. $
3.3.2 Monodromy invariant differential forms on B
Outside of the essential singular locus
![]() $\mathscr {S}_e$
, we have a nice integral affine manifold
$\mathscr {S}_e$
, we have a nice integral affine manifold
![]() $B \setminus \mathscr {S}_e$
, on which we can talk about the sheaf
$B \setminus \mathscr {S}_e$
, on which we can talk about the sheaf
![]() $\Omega ^*$
of (
$\Omega ^*$
of (
![]() $\mathbb {R}$
-valued) de Rham differential forms. But in fact, we can extend its definition to
$\mathbb {R}$
-valued) de Rham differential forms. But in fact, we can extend its definition to
![]() $\mathscr {S}_e$
as well using monodromy invariant differential forms.
$\mathscr {S}_e$
as well using monodromy invariant differential forms.
We consider the inclusion
![]() $\iota \colon B_0 :=B \setminus \mathscr {S}_e \rightarrow B$
and the natural exact sequence
$\iota \colon B_0 :=B \setminus \mathscr {S}_e \rightarrow B$
and the natural exact sequence
where
![]() $\Lambda _{B_0}^*$
denotes the sheaf of integral cotangent vectors on
$\Lambda _{B_0}^*$
denotes the sheaf of integral cotangent vectors on
![]() $B_0$
. For any
$B_0$
. For any
![]() $\tau \in \mathscr {P}$
, the stalk
$\tau \in \mathscr {P}$
, the stalk
![]() $(\iota _*\Lambda _{B_0}^*)_x$
at a point
$(\iota _*\Lambda _{B_0}^*)_x$
at a point
![]() $x \in \mathrm {int}_{\mathrm {re}}(\tau ) \cap \mathscr {S}_e$
can be described using the chart
$x \in \mathrm {int}_{\mathrm {re}}(\tau ) \cap \mathscr {S}_e$
can be described using the chart
![]() $\Upsilon _{\tau }$
in equation (3.4). Using the description in §3.3, we have
$\Upsilon _{\tau }$
in equation (3.4). Using the description in §3.3, we have
![]() $x \in \mathscr {S}_{e,\tau ,\rho } = \mathrm {int}_{\mathrm {re}}(\rho ) \times \{o\}$
for some
$x \in \mathscr {S}_{e,\tau ,\rho } = \mathrm {int}_{\mathrm {re}}(\rho ) \times \{o\}$
for some
![]() $\rho \in \mathtt {i}_{\tau }^{-1}(\mathscr {N}_{\Delta _1(\tau )} \times \cdots \times \mathscr {N}_{\Delta _p(\tau )})$
. Taking a vertex
$\rho \in \mathtt {i}_{\tau }^{-1}(\mathscr {N}_{\Delta _1(\tau )} \times \cdots \times \mathscr {N}_{\Delta _p(\tau )})$
. Taking a vertex
![]() $v \in \tau $
, we can consider the monodromy transformations
$v \in \tau $
, we can consider the monodromy transformations
![]() $T_{\gamma }$
’s around the strata
$T_{\gamma }$
’s around the strata
![]() $\mathscr {S}_{e,\eta ,\rho }$
’s that contain x in their closures. We can identify the stalk
$\mathscr {S}_{e,\eta ,\rho }$
’s that contain x in their closures. We can identify the stalk
![]() $\iota _*(\Lambda _{B_0}^*)_{x}$
as the subset of invariant elements of
$\iota _*(\Lambda _{B_0}^*)_{x}$
as the subset of invariant elements of
![]() $T_{v}^*$
under all such monodromy transformations. Since
$T_{v}^*$
under all such monodromy transformations. Since
![]() $\rho \subset \Lambda _{\tau ,\mathbb {R}}^*$
is a cone, we have
$\rho \subset \Lambda _{\tau ,\mathbb {R}}^*$
is a cone, we have
![]() $\Lambda _{\rho } \subset \Lambda _{\tau }^*$
. Using the natural projection map
$\Lambda _{\rho } \subset \Lambda _{\tau }^*$
. Using the natural projection map
![]() $\pi _{v\tau }\colon T_{v}^* \rightarrow \Lambda _{\tau }^*$
, we have the identification
$\pi _{v\tau }\colon T_{v}^* \rightarrow \Lambda _{\tau }^*$
, we have the identification
![]() $\iota _*(\Lambda _{B_0}^*)_{x} \cong \pi _{v\tau }^{-1}(\Lambda _{\rho })$
. There is a direct sum decomposition
$\iota _*(\Lambda _{B_0}^*)_{x} \cong \pi _{v\tau }^{-1}(\Lambda _{\rho })$
. There is a direct sum decomposition
![]() $\iota _*(\Lambda _{B_0}^*)_{x} = \Lambda _{\rho } \oplus \mathscr {Q}_{\tau }^*$
, depending on a decomposition
$\iota _*(\Lambda _{B_0}^*)_{x} = \Lambda _{\rho } \oplus \mathscr {Q}_{\tau }^*$
, depending on a decomposition
![]() $T_{v} = \Lambda _{\tau } \oplus \mathscr {Q}_{\tau }$
. This gives the map
$T_{v} = \Lambda _{\tau } \oplus \mathscr {Q}_{\tau }$
. This gives the map
in a sufficiently small neighborhood
![]() $U_{x}$
, locally defined up to a translation in
$U_{x}$
, locally defined up to a translation in
![]() $\pi _{v\tau }^{-1}(\Lambda _{\rho })^*_{\mathbb {R}}$
. We need to describe the compatibility between the map associated to a point
$\pi _{v\tau }^{-1}(\Lambda _{\rho })^*_{\mathbb {R}}$
. We need to describe the compatibility between the map associated to a point
![]() $x \in \mathscr {S}_{e,\omega ,\rho }$
and that to a point
$x \in \mathscr {S}_{e,\omega ,\rho }$
and that to a point
![]() $\tilde {x} \in \mathscr {S}_{e,\tau ,\tilde {\rho }}$
such that
$\tilde {x} \in \mathscr {S}_{e,\tau ,\tilde {\rho }}$
such that
![]() $\mathscr {S}_{e,\omega ,\rho } \subset \overline {\mathscr {S}_{e,\tau ,\tilde {\rho }}}$
.
$\mathscr {S}_{e,\omega ,\rho } \subset \overline {\mathscr {S}_{e,\tau ,\tilde {\rho }}}$
.
The first case is when
![]() $\omega =\tau $
. We let
$\omega =\tau $
. We let
![]() $\tilde {x} \in \mathrm {int}_{\mathrm {re}}(\tilde {\rho }) \times \{o\} \cap U_{x}$
for some
$\tilde {x} \in \mathrm {int}_{\mathrm {re}}(\tilde {\rho }) \times \{o\} \cap U_{x}$
for some
![]() $\rho \subset \tilde {\rho }$
. Then, after choosing suitable translations in
$\rho \subset \tilde {\rho }$
. Then, after choosing suitable translations in
![]() $\pi _{v\tau }^{-1}(\Lambda _{\rho })^*_{\mathbb {R}}$
for the maps
$\pi _{v\tau }^{-1}(\Lambda _{\rho })^*_{\mathbb {R}}$
for the maps
![]() $\mathtt {x}$
and
$\mathtt {x}$
and
![]() $\tilde {\mathtt {x}}$
, we have the following commutative diagram:
$\tilde {\mathtt {x}}$
, we have the following commutative diagram:

The second case is when
![]() $\omega \subsetneq \tau $
. Making use of the change of charts
$\omega \subsetneq \tau $
. Making use of the change of charts
![]() $\gimel $
in equation (3.6), and the description in the proof of Lemma 3.4, we write
$\gimel $
in equation (3.6), and the description in the proof of Lemma 3.4, we write
for some cone
![]() $\tilde {\rho } = \mathtt {i}_{\tau }^{-1}(\prod _{j=1}^p \tilde {\rho }_j) \in \mathtt {i}_{\tau }^{-1}\big (\prod _{j=1}^p \Lambda _{\Delta _{j}(\tau )}^* \big )$
of positive codimension. In
$\tilde {\rho } = \mathtt {i}_{\tau }^{-1}(\prod _{j=1}^p \tilde {\rho }_j) \in \mathtt {i}_{\tau }^{-1}\big (\prod _{j=1}^p \Lambda _{\Delta _{j}(\tau )}^* \big )$
of positive codimension. In
![]() $\gimel ^{-1}(W)$
, we may assume
$\gimel ^{-1}(W)$
, we may assume
![]() $\tilde {\rho }$
is the pullback of a cone
$\tilde {\rho }$
is the pullback of a cone
![]() $\breve {\rho }$
via
$\breve {\rho }$
via
![]() $\Pi _{\omega \subset \tau } \circ \mathtt {p}_{\tau }$
as in equation (3.8). Since
$\Pi _{\omega \subset \tau } \circ \mathtt {p}_{\tau }$
as in equation (3.8). Since
![]() $\mathscr {S}_{e,\omega ,\rho } \subset \overline {\mathscr {S}_{e,\tau ,\tilde {\rho }}}$
, we have
$\mathscr {S}_{e,\omega ,\rho } \subset \overline {\mathscr {S}_{e,\tau ,\tilde {\rho }}}$
, we have
![]() $\rho \subset \mathtt {p}_{\omega }^{-1}(\breve {\rho })$
and hence
$\rho \subset \mathtt {p}_{\omega }^{-1}(\breve {\rho })$
and hence
![]() $\mathtt {p}_{\omega \subset \tau }^{-1}(\Lambda _{\rho }) \subset \Lambda _{\tilde {\rho }}$
. Therefore, from
$\mathtt {p}_{\omega \subset \tau }^{-1}(\Lambda _{\rho }) \subset \Lambda _{\tilde {\rho }}$
. Therefore, from
![]() $\mathtt {p}_{\omega \subset \tau } \circ \pi _{v\tau } = \pi _{v\omega }$
, we obtain
$\mathtt {p}_{\omega \subset \tau } \circ \pi _{v\tau } = \pi _{v\omega }$
, we obtain
![]() $\pi _{v\omega }^{-1}(\Lambda _{\rho }) \subset \pi _{v\tau }^{-1}(\Lambda _{\tilde {\rho }})$
, inducing the map
$\pi _{v\omega }^{-1}(\Lambda _{\rho }) \subset \pi _{v\tau }^{-1}(\Lambda _{\tilde {\rho }})$
, inducing the map
![]() $\mathtt {p}\colon \pi _{v\tau }^{-1}(\Lambda _{\tilde {\rho }})_{\mathbb {R}}^* \rightarrow \pi _{v\omega }^{-1}(\Lambda _{\rho })_{\mathbb {R}}^*$
. As a result, we still have the commutative diagram (3.11) for a point
$\mathtt {p}\colon \pi _{v\tau }^{-1}(\Lambda _{\tilde {\rho }})_{\mathbb {R}}^* \rightarrow \pi _{v\omega }^{-1}(\Lambda _{\rho })_{\mathbb {R}}^*$
. As a result, we still have the commutative diagram (3.11) for a point
![]() $\tilde {x}$
sufficiently close to x.
$\tilde {x}$
sufficiently close to x.
Definition 3.8. Given
![]() $x \in \mathscr {S}_e$
as above, the stalk of
$x \in \mathscr {S}_e$
as above, the stalk of
![]() $\Omega ^*$
at x is defined as the stalk
$\Omega ^*$
at x is defined as the stalk
![]() $\Omega ^*_{x}:= (\mathtt {x}^{-1}\Omega ^*)_{x}$
of the pullback of the sheaf of smooth de Rham forms on
$\Omega ^*_{x}:= (\mathtt {x}^{-1}\Omega ^*)_{x}$
of the pullback of the sheaf of smooth de Rham forms on
![]() $\pi _{v\tau }^{-1}(\Lambda _{\rho })^*_{\mathbb {R}}$
, which is equipped with the de Rham differential d. This defines the complex
$\pi _{v\tau }^{-1}(\Lambda _{\rho })^*_{\mathbb {R}}$
, which is equipped with the de Rham differential d. This defines the complex
![]() $(\Omega ^*, d)$
of monodromy invariant smooth differential forms on B. A section
$(\Omega ^*, d)$
of monodromy invariant smooth differential forms on B. A section
![]() $\alpha \in \Omega ^*(W)$
is a collection of elements
$\alpha \in \Omega ^*(W)$
is a collection of elements
![]() $\alpha _{x} \in \Omega ^*_{x}$
,
$\alpha _{x} \in \Omega ^*_{x}$
,
![]() $x \in W$
such that each
$x \in W$
such that each
![]() $\alpha _{x}$
can be represented by
$\alpha _{x}$
can be represented by
![]() $\mathtt {x}^{-1}\beta _{x}$
in a small neighborhood
$\mathtt {x}^{-1}\beta _{x}$
in a small neighborhood
![]() $U_{x} \subset \mathtt {p}^{-1}(\mathtt {U}_{x})$
for some smooth form
$U_{x} \subset \mathtt {p}^{-1}(\mathtt {U}_{x})$
for some smooth form
![]() $\beta _{x}$
on
$\beta _{x}$
on
![]() $\mathtt {U}_{x}$
, and satisfies the relation
$\mathtt {U}_{x}$
, and satisfies the relation
![]() $\alpha _{\tilde {x}} = \tilde {\mathtt {x}}^{-1}(\mathtt {p}^* \beta _{x})$
in
$\alpha _{\tilde {x}} = \tilde {\mathtt {x}}^{-1}(\mathtt {p}^* \beta _{x})$
in
![]() $\Omega ^*_{\tilde {x}}$
for every
$\Omega ^*_{\tilde {x}}$
for every
![]() $\tilde {x} \in U_{x}$
.
$\tilde {x} \in U_{x}$
.
Example 3.9. In the two-dimensional case in Example 2.11, we consider a singular point
for some
![]() $\tau \in \mathscr {P}^{[1]}$
. In this case, we can take
$\tau \in \mathscr {P}^{[1]}$
. In this case, we can take
![]() $\rho $
to be the zero-dimenisonal stratum in
$\rho $
to be the zero-dimenisonal stratum in
![]() $\mathscr {N}_{\tau }=\mathtt {i}_{\tau }^{-1}(\mathscr {N}_{\Delta _1(\tau )})$
and we have
$\mathscr {N}_{\tau }=\mathtt {i}_{\tau }^{-1}(\mathscr {N}_{\Delta _1(\tau )})$
and we have
![]() $\iota _*(\Lambda _{B_0}^*)_{x} = \mathscr {Q}_{\tau }^*$
. Taking a generator of
$\iota _*(\Lambda _{B_0}^*)_{x} = \mathscr {Q}_{\tau }^*$
. Taking a generator of
![]() $\mathscr {Q}_{\tau }^*$
, we get an invariant affine coordinate
$\mathscr {Q}_{\tau }^*$
, we get an invariant affine coordinate
![]() $\mathtt {x}\colon U_{x} \rightarrow \mathbb {R}$
which is the normal affine coordinate of
$\mathtt {x}\colon U_{x} \rightarrow \mathbb {R}$
which is the normal affine coordinate of
![]() $\tau $
. The stalk
$\tau $
. The stalk
![]() $\Omega ^*_{x}$
is then identified with the pullback of the space of germs of smooth differential forms from
$\Omega ^*_{x}$
is then identified with the pullback of the space of germs of smooth differential forms from
![]() $(\mathbb {R},0)$
via
$(\mathbb {R},0)$
via
![]() $\mathtt {x}$
. In particular,
$\mathtt {x}$
. In particular,
![]() $\Omega ^2_{x} =0$
.
$\Omega ^2_{x} =0$
.
For the Y-vertex of type II in Example 2.12, the situation is similar to the
![]() $2$
-dimensional case. For
$2$
-dimensional case. For
![]() $\{ x \} = \mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\tau )$
, we still have
$\{ x \} = \mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\tau )$
, we still have
![]() $\iota _*(\Lambda _{B_0}^*)_{x} = \mathscr {Q}_{\tau }^*$
, and in this case,
$\iota _*(\Lambda _{B_0}^*)_{x} = \mathscr {Q}_{\tau }^*$
, and in this case,
![]() $\mathtt {x} \colon U_{x} \rightarrow \mathbb {R}^2$
are the two invariant affine coordinates. We can identify
$\mathtt {x} \colon U_{x} \rightarrow \mathbb {R}^2$
are the two invariant affine coordinates. We can identify
![]() $\Omega ^*_{x}$
as the pullback of the space of germs of smooth differential forms from
$\Omega ^*_{x}$
as the pullback of the space of germs of smooth differential forms from
![]() $(\mathbb {R}^2,0)$
via
$(\mathbb {R}^2,0)$
via
![]() $\mathtt {x}$
.
$\mathtt {x}$
.
For the Y-vertex of type I in Example 2.12, we use the identification
![]() $ \Lambda _{\tau ,\mathbb {R}}^* \cong \mathrm {int}_{\mathrm {re}}(\tau )$
via
$ \Lambda _{\tau ,\mathbb {R}}^* \cong \mathrm {int}_{\mathrm {re}}(\tau )$
via
![]() $\Upsilon _{\tau }$
for the
$\Upsilon _{\tau }$
for the
![]() $2$
-dimensional cell
$2$
-dimensional cell
![]() $\tau $
separating two maximal cells
$\tau $
separating two maximal cells
![]() $\sigma _+$
and
$\sigma _+$
and
![]() $\sigma _-$
. In this case,
$\sigma _-$
. In this case,
![]() $\mathscr {S}_e$
is as shown (in blue color) in Figure 6 and
$\mathscr {S}_e$
is as shown (in blue color) in Figure 6 and
![]() $\mathscr {N}=\mathtt {i}_{\tau }^{-1}(\mathscr {N}_{\Delta _1(\tau )})$
is the fan of
$\mathscr {N}=\mathtt {i}_{\tau }^{-1}(\mathscr {N}_{\Delta _1(\tau )})$
is the fan of
![]() $\mathbb {P}^2$
. If x is the zero-dimensional stratum of
$\mathbb {P}^2$
. If x is the zero-dimensional stratum of
![]() $\mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\tau )$
, we have
$\mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\tau )$
, we have
![]() $\iota _*(\Lambda _{B_0}^*)_{x} = \mathscr {Q}_{\tau }^*$
and
$\iota _*(\Lambda _{B_0}^*)_{x} = \mathscr {Q}_{\tau }^*$
and
![]() $\mathtt {x}\colon U_{x} \rightarrow \mathbb {R}$
as an invariant affine coordinate. If x is a point on a leg of the Y-vertex, we have
$\mathtt {x}\colon U_{x} \rightarrow \mathbb {R}$
as an invariant affine coordinate. If x is a point on a leg of the Y-vertex, we have
![]() $\mathtt {x} =(\mathtt {x}_1,\mathtt {x}_2)\colon U_{x} \rightarrow \mathbb {R}^2$
with
$\mathtt {x} =(\mathtt {x}_1,\mathtt {x}_2)\colon U_{x} \rightarrow \mathbb {R}^2$
with
![]() $\mathtt {x}_1$
coming from a generator of
$\mathtt {x}_1$
coming from a generator of
![]() $\Lambda _{\rho }$
and
$\Lambda _{\rho }$
and
![]() $\mathtt {x}_2$
coming from a generator of
$\mathtt {x}_2$
coming from a generator of
![]() $\mathscr {Q}_{\tau }^*$
.
$\mathscr {Q}_{\tau }^*$
.
It follows from the definition that
![]() $\underline {\mathbb {R}} \rightarrow \Omega ^*$
is a resolution. We shall also prove the existence of a partition of unity.
$\underline {\mathbb {R}} \rightarrow \Omega ^*$
is a resolution. We shall also prove the existence of a partition of unity.
Lemma 3.10. Given any
![]() $x \in B$
and a sufficiently small neighborhood U, there exists
$x \in B$
and a sufficiently small neighborhood U, there exists
![]() $\varrho \in \Omega ^{0}(U)$
with compact support in U such that
$\varrho \in \Omega ^{0}(U)$
with compact support in U such that
![]() $0 \leq \varrho \leq 1$
and
$0 \leq \varrho \leq 1$
and
![]() $\varrho \equiv 1$
near x. (Since
$\varrho \equiv 1$
near x. (Since
![]() $\Omega ^0$
is a subsheaf of the sheaf
$\Omega ^0$
is a subsheaf of the sheaf
![]() $\mathcal {C}^{0}$
of continuous functions on B, we can talk about the value
$\mathcal {C}^{0}$
of continuous functions on B, we can talk about the value
![]() $f(x)$
for
$f(x)$
for
![]() $f \in \Omega ^{0}(W)$
and
$f \in \Omega ^{0}(W)$
and
![]() $x \in W$
.)
$x \in W$
.)
Proof. If
![]() $x \notin \mathscr {S}_e$
, the statement is a standard fact. So we assume that
$x \notin \mathscr {S}_e$
, the statement is a standard fact. So we assume that
![]() $x \in \mathrm {int}_{\mathrm {re}}(\tau ) \cap \mathscr {S}_e$
for some
$x \in \mathrm {int}_{\mathrm {re}}(\tau ) \cap \mathscr {S}_e$
for some
![]() $\tau \in \mathscr {P}$
. As above, we can write
$\tau \in \mathscr {P}$
. As above, we can write
![]() $x \in \mathrm {int}_{\mathrm {re}}(\rho ) \times \{o\}$
. Since
$x \in \mathrm {int}_{\mathrm {re}}(\rho ) \times \{o\}$
. Since
![]() $\rho $
is a cone in the fan
$\rho $
is a cone in the fan
![]() $\mathtt {i}_{\tau }^{-1}(\mathscr {N}_{\Delta _1(\tau )} \times \cdots \times \mathscr {N}_{\Delta _p(\tau )})$
,
$\mathtt {i}_{\tau }^{-1}(\mathscr {N}_{\Delta _1(\tau )} \times \cdots \times \mathscr {N}_{\Delta _p(\tau )})$
,
![]() $\Lambda _{\tau }^*$
has
$\Lambda _{\tau }^*$
has
![]() $\Lambda _{\Delta _1(\tau )}^* \oplus \cdots \oplus \Lambda _{\Delta _p(\tau )}^*$
as a direct summand, and the description of
$\Lambda _{\Delta _1(\tau )}^* \oplus \cdots \oplus \Lambda _{\Delta _p(\tau )}^*$
as a direct summand, and the description of
![]() $\iota _*(\Lambda _{B_0}^*)_x$
is compatible with the direct sum decomposition of
$\iota _*(\Lambda _{B_0}^*)_x$
is compatible with the direct sum decomposition of
![]() $\Lambda _{\tau }^*$
. We may further assume that
$\Lambda _{\tau }^*$
. We may further assume that
![]() $p=1$
and
$p=1$
and
![]() $\tau = \Delta _1(\tau )$
is a simplex.
$\tau = \Delta _1(\tau )$
is a simplex.
If
![]() $\rho $
is not the smallest cone (i.e., the one consisting of just the origin in
$\rho $
is not the smallest cone (i.e., the one consisting of just the origin in
![]() $\mathscr {N}_{\tau }$
), we have a decomposition
$\mathscr {N}_{\tau }$
), we have a decomposition
![]() $\Lambda _{\tau }^* = \Lambda _{\rho } \oplus \mathscr {Q}_{\rho }$
and the natural projection
$\Lambda _{\tau }^* = \Lambda _{\rho } \oplus \mathscr {Q}_{\rho }$
and the natural projection
![]() $\mathtt {p}\colon \Lambda _{\tau }^* \rightarrow \mathscr {Q}_{\rho }$
. Then, locally near
$\mathtt {p}\colon \Lambda _{\tau }^* \rightarrow \mathscr {Q}_{\rho }$
. Then, locally near
![]() $x_0$
, we can write the normal fan
$x_0$
, we can write the normal fan
![]() $\mathscr {N}_{\tau }$
as
$\mathscr {N}_{\tau }$
as
![]() $\mathtt {p}^{-1}(\Sigma _{\rho })$
for some normal fan
$\mathtt {p}^{-1}(\Sigma _{\rho })$
for some normal fan
![]() $\Sigma _{\rho } \subset \mathscr {Q}_{\rho }$
of a lower-dimensional simplex. For any vector v tangent to
$\Sigma _{\rho } \subset \mathscr {Q}_{\rho }$
of a lower-dimensional simplex. For any vector v tangent to
![]() $\rho $
at
$\rho $
at
![]() $x_0$
and the corresponding affine function
$x_0$
and the corresponding affine function
![]() $l_{v}$
locally near
$l_{v}$
locally near
![]() $x_0$
, we always have
$x_0$
, we always have
![]() $\frac {\partial l_{v}}{\partial {v}}>0$
. This allows us to construct a bump function
$\frac {\partial l_{v}}{\partial {v}}>0$
. This allows us to construct a bump function
![]() $\varrho = \sum _{v_i} (l_{v_i}(x) - l_{v_i}(x_0))^2$
along the
$\varrho = \sum _{v_i} (l_{v_i}(x) - l_{v_i}(x_0))^2$
along the
![]() $\Lambda _{\rho ,\mathbb {R}}$
-direction. So we are reduced to the case when
$\Lambda _{\rho ,\mathbb {R}}$
-direction. So we are reduced to the case when
![]() $\rho = \{o\}$
is the smallest cone in the fan
$\rho = \{o\}$
is the smallest cone in the fan
![]() $\mathscr {N}_{\tau }$
.
$\mathscr {N}_{\tau }$
.
Now, we construct the function
![]() $\varrho $
near the origin
$\varrho $
near the origin
![]() $o \in \mathscr {N}_{\tau }$
by induction on the dimension of the fan
$o \in \mathscr {N}_{\tau }$
by induction on the dimension of the fan
![]() $\mathscr {N}_{\tau }$
. When
$\mathscr {N}_{\tau }$
. When
![]() $\dim _{\mathbb {R}}(\mathscr {N}_{\tau }) = 1$
, it is the fan of
$\dim _{\mathbb {R}}(\mathscr {N}_{\tau }) = 1$
, it is the fan of
![]() $\mathbb {P}^1$
consisting of three cones
$\mathbb {P}^1$
consisting of three cones
![]() $\mathbb {R}_-$
,
$\mathbb {R}_-$
,
![]() $\{o\}$
and
$\{o\}$
and
![]() $\mathbb {R}_+$
. One can construct the bump function which is equal to
$\mathbb {R}_+$
. One can construct the bump function which is equal to
![]() $1$
near o and supported in a sufficiently small neighborhood of o. For the induction step, we consider an n-dimensional fan
$1$
near o and supported in a sufficiently small neighborhood of o. For the induction step, we consider an n-dimensional fan
![]() $\mathscr {N}_\tau $
. For any point x near but not equal to o, we have
$\mathscr {N}_\tau $
. For any point x near but not equal to o, we have
![]() $x \in \mathrm {int}_{\mathrm {re}}(\rho )$
for some
$x \in \mathrm {int}_{\mathrm {re}}(\rho )$
for some
![]() $\rho \neq \{o\}$
. Then we can decompose
$\rho \neq \{o\}$
. Then we can decompose
![]() $\mathscr {N}_\tau $
locally as
$\mathscr {N}_\tau $
locally as
![]() $\Lambda _{\rho } \oplus \mathscr {Q}_{\rho }$
. Applying the induction hypothesis to
$\Lambda _{\rho } \oplus \mathscr {Q}_{\rho }$
. Applying the induction hypothesis to
![]() $\mathscr {Q}_{\rho }$
gives a bump function
$\mathscr {Q}_{\rho }$
gives a bump function
![]() $\varrho _x$
compactly supported in any sufficiently small neighborhood of x (for the
$\varrho _x$
compactly supported in any sufficiently small neighborhood of x (for the
![]() $\Lambda _{\rho }$
directions, we do not need the induction hypothesis to get the bump function). This produces a partition of unity
$\Lambda _{\rho }$
directions, we do not need the induction hypothesis to get the bump function). This produces a partition of unity
![]() $\{\varrho _i\}$
outside o. Finally, letting
$\{\varrho _i\}$
outside o. Finally, letting
![]() $\varrho := 1 - \sum _i \varrho _i$
and extending it continuously to the origin o gives the desired function.
$\varrho := 1 - \sum _i \varrho _i$
and extending it continuously to the origin o gives the desired function.
Lemma 3.10 produces a partition of unity for the complex
![]() $(\Omega ^*, d)$
of monodromy invariant differential forms on B, which satisfies the requirement in Condition 4.7 below. In particular, the cohomology of
$(\Omega ^*, d)$
of monodromy invariant differential forms on B, which satisfies the requirement in Condition 4.7 below. In particular, the cohomology of
![]() $(\Omega ^*(B),d)$
computes
$(\Omega ^*(B),d)$
computes
![]() $R\Gamma (B,\underline {\mathbb {R}})$
. Given a point
$R\Gamma (B,\underline {\mathbb {R}})$
. Given a point
![]() $x \in B \setminus \mathscr {S}_e$
, we can take an element
$x \in B \setminus \mathscr {S}_e$
, we can take an element
![]() $\varrho _x \in \Omega ^n(B)$
, compactly supported in an arbitrarily small neighborhood
$\varrho _x \in \Omega ^n(B)$
, compactly supported in an arbitrarily small neighborhood
![]() $U_x \subset B \setminus \mathscr {S}_e$
, to represent a nonzero element in the cohomology
$U_x \subset B \setminus \mathscr {S}_e$
, to represent a nonzero element in the cohomology
![]() $H^n(\Omega ^*,d) = H^n(B,\mathbb {C}) \cong \mathbb {C}$
.
$H^n(\Omega ^*,d) = H^n(B,\mathbb {C}) \cong \mathbb {C}$
.
4 Smoothing of maximally degenerate Calabi–Yau varieties via dgBV algebras
In this section, we review and refine the results in [Reference Chan, Leung and Ma8] concerning smoothing of the maximally degenerate Calabi–Yau log variety ![]() over
over
![]() $\hat {S}^{\dagger } = \mathrm {Spec}_{\mathrm {an}}(\hat {R})^{\dagger } = \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[[q]])^{\dagger }$
using the local smoothing models
$\hat {S}^{\dagger } = \mathrm {Spec}_{\mathrm {an}}(\hat {R})^{\dagger } = \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[[q]])^{\dagger }$
using the local smoothing models ![]() ’s specified in §2.4. In order to relate with tropical geometry on B, we will choose V so that it is the preimage
’s specified in §2.4. In order to relate with tropical geometry on B, we will choose V so that it is the preimage
![]() $\nu ^{-1}(W)$
of an open subset W in B.
$\nu ^{-1}(W)$
of an open subset W in B.
4.1 Good covers and local smoothing data
Given
![]() $\tau \in \mathscr {P}$
and a point
$\tau \in \mathscr {P}$
and a point
![]() $x \in \mathrm {int}_{\mathrm {re}}(\tau ) \subset B$
, we take a sufficiently small open subset
$x \in \mathrm {int}_{\mathrm {re}}(\tau ) \subset B$
, we take a sufficiently small open subset
![]() $W \in \mathscr {B}_x$
. We need to construct a local smoothing model on the Stein open subset
$W \in \mathscr {B}_x$
. We need to construct a local smoothing model on the Stein open subset
![]() $V = \nu ^{-1}(W)$
.
$V = \nu ^{-1}(W)$
.
-
• If
 $x \notin \mathscr {S}_e$
, then we can simply take the local smoothing
$x \notin \mathscr {S}_e$
, then we can simply take the local smoothing  introduced in (2.14) in §2.4.
introduced in (2.14) in §2.4. -
• If
 $x \in \mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\tau )$
, we assume that
$x \in \mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\tau )$
, we assume that
 $\mathscr {C}^{-1}(W) \cap \mathcal {A}^{\tau }_i \neq \emptyset $
for
$\mathscr {C}^{-1}(W) \cap \mathcal {A}^{\tau }_i \neq \emptyset $
for
 $i = 1,\dots ,r$
and
$i = 1,\dots ,r$
and
 $\mathscr {C}^{-1}(W) \cap \mathcal {A}^{\tau }_i = \emptyset $
for other i’s. Note that
$\mathscr {C}^{-1}(W) \cap \mathcal {A}^{\tau }_i = \emptyset $
for other i’s. Note that
 $\mathscr {C}^{-1}(W) \cap \mathrm {int}_{\mathrm {re}}(\tau )$
may not be a small open subset in
$\mathscr {C}^{-1}(W) \cap \mathrm {int}_{\mathrm {re}}(\tau )$
may not be a small open subset in
 $\mathrm {int}_{\mathrm {re}}(\tau )$
as we may contract a polytope
$\mathrm {int}_{\mathrm {re}}(\tau )$
as we may contract a polytope
 $\mathtt {P}$
via
$\mathtt {P}$
via
 $\mathscr {C}$
(Figure 6). If we write
$\mathscr {C}$
(Figure 6). If we write
 $\Lambda _{\Delta _{1}(\tau )}\oplus \cdots \oplus \Lambda _{\Delta _{p}(\tau )} \oplus A_{\tau } = \Lambda _{\tau }$
as lattices, then for each direct summand
$\Lambda _{\Delta _{1}(\tau )}\oplus \cdots \oplus \Lambda _{\Delta _{p}(\tau )} \oplus A_{\tau } = \Lambda _{\tau }$
as lattices, then for each direct summand
 $\Lambda _{\Delta _{i}(\tau )}$
, we have a commutative diagram so that both
$\Lambda _{\Delta _{i}(\tau )}$
, we have a commutative diagram so that both
 $Z^{\tau }_i$
and
$Z^{\tau }_i$
and
 $\mathcal {A}^{\tau }_i$
are coming from pullbacks of some subsets under the projection maps
$\mathcal {A}^{\tau }_i$
are coming from pullbacks of some subsets under the projection maps
 $\mathtt {i}_{\tau ,i,\mathbb {C}^*}$
and
$\mathtt {i}_{\tau ,i,\mathbb {C}^*}$
and
 $\mathtt {i}_{\tau ,i,\mathbb {R}},$
respectively. From this, we see that
$\mathtt {i}_{\tau ,i,\mathbb {R}},$
respectively. From this, we see that
 $\mathscr {C}^{-1}(W) \cap \mathcal {A}^{\tau }_1 \cap \cdots \cap \mathcal {A}^{\tau }_r \neq \emptyset $
and
$\mathscr {C}^{-1}(W) \cap \mathcal {A}^{\tau }_1 \cap \cdots \cap \mathcal {A}^{\tau }_r \neq \emptyset $
and
 $\nu ^{-1}(W) \cap Z^{\tau }_1 \cap \cdots \cap Z^{\tau }_r \neq \emptyset $
while
$\nu ^{-1}(W) \cap Z^{\tau }_1 \cap \cdots \cap Z^{\tau }_r \neq \emptyset $
while
 $\nu ^{-1}(W) \cap Z^{\tau }_i = \emptyset $
for other i’s. Now, we take
$\nu ^{-1}(W) \cap Z^{\tau }_i = \emptyset $
for other i’s. Now, we take
 $\psi _{x,i} = \psi _i$
for
$\psi _{x,i} = \psi _i$
for
 $1\leq i\leq r$
and
$1\leq i\leq r$
and
 $\psi _{x,i} =0$
otherwise accordingly. Then we can take
$\psi _{x,i} =0$
otherwise accordingly. Then we can take
 $P_{\tau ,x}$
introduced in equation (2.17) and the map
$P_{\tau ,x}$
introduced in equation (2.17) and the map
 $V = \nu ^{-1}(W) \rightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }\oplus \mathbb {N}^{l}])$
defined by (4.1)Note that the third line of this formula is different from that of equation (2.19) because we do not specify a point
$V = \nu ^{-1}(W) \rightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }\oplus \mathbb {N}^{l}])$
defined by (4.1)Note that the third line of this formula is different from that of equation (2.19) because we do not specify a point $$ \begin{align} \begin{cases} z^m \mapsto h_m \cdot z^m & \text{if } m\in \Sigma_{\tau} ;\\ u_i \mapsto f_{v,i} & \text{if } 1\leq i \leq r;\\ u_i \mapsto z_i & \text{if } r<i\leq l. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} z^m \mapsto h_m \cdot z^m & \text{if } m\in \Sigma_{\tau} ;\\ u_i \mapsto f_{v,i} & \text{if } 1\leq i \leq r;\\ u_i \mapsto z_i & \text{if } r<i\leq l. \end{cases} \end{align} $$
 $x \in Z^{\tau }_1 \cap \cdots \cap Z^{\tau }_r$
. By shrinking W if necessary, one can show that it is an embedding using an argument similar to [Reference Gross and Siebert28, Thm. 2.6]. This is possible because we can check that the Jacobian appearing in the proof of [Reference Gross and Siebert28, Thm. 2.6] is invertible for all point in
$x \in Z^{\tau }_1 \cap \cdots \cap Z^{\tau }_r$
. By shrinking W if necessary, one can show that it is an embedding using an argument similar to [Reference Gross and Siebert28, Thm. 2.6]. This is possible because we can check that the Jacobian appearing in the proof of [Reference Gross and Siebert28, Thm. 2.6] is invertible for all point in
 $\nu ^{-1}(x) = \mu ^{-1}(\mathscr {C}^{-1}(x))$
, which is a connected compact subset by property
$\nu ^{-1}(x) = \mu ^{-1}(\mathscr {C}^{-1}(x))$
, which is a connected compact subset by property
 $(5)$
in Assumption 3.5.
$(5)$
in Assumption 3.5.
Condition 4.1. An open cover
![]() $\{ W_{\alpha } \}_{\alpha }$
of B is said to be good if
$\{ W_{\alpha } \}_{\alpha }$
of B is said to be good if
-
1. for each
 $W_{\alpha }$
, there exists a unique
$W_{\alpha }$
, there exists a unique
 $\tau _{\alpha } \in \mathscr {P}$
such that
$\tau _{\alpha } \in \mathscr {P}$
such that
 $W_{\alpha } \in \mathscr {B}_x$
for some
$W_{\alpha } \in \mathscr {B}_x$
for some
 $x \in \mathrm {int}_{\mathrm {re}}(\tau )$
;
$x \in \mathrm {int}_{\mathrm {re}}(\tau )$
; -
2.
 $W_{\alpha \beta }=W_{\alpha } \cap W_{\beta } \neq \emptyset $
only when
$W_{\alpha \beta }=W_{\alpha } \cap W_{\beta } \neq \emptyset $
only when
 $\tau _{\alpha } \subset \tau _{\beta }$
or
$\tau _{\alpha } \subset \tau _{\beta }$
or
 $\tau _{\beta } \subset \tau _{\alpha }$
, and if this is the case, we have either
$\tau _{\beta } \subset \tau _{\alpha }$
, and if this is the case, we have either
 $\mathrm {int}_{\mathrm {re}}(\alpha ) \cap W_{\alpha \beta } \neq \emptyset $
or
$\mathrm {int}_{\mathrm {re}}(\alpha ) \cap W_{\alpha \beta } \neq \emptyset $
or
 $\mathrm {int}_{\mathrm {re}}(\beta ) \cap W_{\alpha \beta } \neq \emptyset $
.
$\mathrm {int}_{\mathrm {re}}(\beta ) \cap W_{\alpha \beta } \neq \emptyset $
.
Given a good cover
![]() $\{ W_{\alpha } \}_{\alpha }$
of B, we have the corresponding Stein open cover
$\{ W_{\alpha } \}_{\alpha }$
of B, we have the corresponding Stein open cover
![]() $\mathcal {V} := \{V_\alpha \}_\alpha $
of
$\mathcal {V} := \{V_\alpha \}_\alpha $
of ![]() given by
given by
![]() $V_{\alpha } := \nu ^{-1}(W_{\alpha })$
for each
$V_{\alpha } := \nu ^{-1}(W_{\alpha })$
for each
![]() $\alpha $
. For each
$\alpha $
. For each
![]() $V_{\alpha }^{\dagger }$
, the infinitesimal local smoothing model is given as a log space
$V_{\alpha }^{\dagger }$
, the infinitesimal local smoothing model is given as a log space ![]() over
over
![]() $\hat {S}^{\dagger }$
(see equation (2.14)). Let
$\hat {S}^{\dagger }$
(see equation (2.14)). Let ![]() be the
be the
![]() $k^{\text {th}}$
-order thickening over
$k^{\text {th}}$
-order thickening over ![]() and
and
![]() $j \colon V_{\alpha } \setminus Z \hookrightarrow V_{\alpha }$
be the open inclusion. As in [Reference Chan, Leung and Ma8, §8], we obtain coherent sheaves of BV algebras (and modules) over
$j \colon V_{\alpha } \setminus Z \hookrightarrow V_{\alpha }$
be the open inclusion. As in [Reference Chan, Leung and Ma8, §8], we obtain coherent sheaves of BV algebras (and modules) over
![]() $V_\alpha $
from these local smoothing models. But for the purpose of this paper, we would like to push forward these coherent sheaves to B and work with the open subsets
$V_\alpha $
from these local smoothing models. But for the purpose of this paper, we would like to push forward these coherent sheaves to B and work with the open subsets
![]() $W_{\alpha }$
’s. This leads to the following modification of [Reference Chan, Leung and Ma8, Def. 7.6] (see also [Reference Chan, Leung and Ma8, Def. 2.14 and 2.20]):
$W_{\alpha }$
’s. This leads to the following modification of [Reference Chan, Leung and Ma8, Def. 7.6] (see also [Reference Chan, Leung and Ma8, Def. 2.14 and 2.20]):
Definition 4.2. For each
![]() $k \in \mathbb {Z}_{\geq 0}$
, we define
$k \in \mathbb {Z}_{\geq 0}$
, we define
-
• the sheaf of
 $k^{\text {th}}$
-order polyvector fields to be
$k^{\text {th}}$
-order polyvector fields to be  (i.e., push-forward of relative log polyvector fields on
(i.e., push-forward of relative log polyvector fields on  );
); -
• the
 $k^{\text {th}}$
-order log de Rham complex to be
$k^{\text {th}}$
-order log de Rham complex to be  (i.e., push-forward of log de Rham differentials) equipped with the de Rham differential
(i.e., push-forward of log de Rham differentials) equipped with the de Rham differential  which is naturally a dg module over
which is naturally a dg module over  ;
; -
•
 $k^{\text {th}}$
the local log volume form
$k^{\text {th}}$
the local log volume form  as a nowhere vanishing element in
as a nowhere vanishing element in  and the -order volume form to be
and the -order volume form to be  .
.
Given
![]() $k> l$
, there are natural maps
$k> l$
, there are natural maps ![]() which induce the maps
which induce the maps ![]() . Before taking the push-forward
. Before taking the push-forward
![]() $\mu _*$
, each
$\mu _*$
, each ![]() is a sheaf of flat
is a sheaf of flat ![]() -modules with the property that
-modules with the property that ![]() by [Reference Felten, Filip and Ruddat17, Cor. 7.4 and 7.9]. In other words, we have a short exact sequence of coherent sheaves
by [Reference Felten, Filip and Ruddat17, Cor. 7.4 and 7.9]. In other words, we have a short exact sequence of coherent sheaves
Applying
![]() $\mu _*$
, which is exact, we get
$\mu _*$
, which is exact, we get
As a result, we see that ![]() is a sheaf of flat
is a sheaf of flat ![]() -modules on
-modules on
![]() $W_{\alpha }$
, so we have
$W_{\alpha }$
, so we have ![]() for each r; a similar statement holds for
for each r; a similar statement holds for ![]() .
.
A natural filtration ![]() is given by
is given by ![]() and taking wedge product defines the natural sheaf isomorphism
and taking wedge product defines the natural sheaf isomorphism ![]() . We have the space
. We have the space ![]() of relative log de Rham differentials.
of relative log de Rham differentials.
There is a natural action
![]() $v \mathbin {\lrcorner } \varphi $
for
$v \mathbin {\lrcorner } \varphi $
for ![]() and
and ![]() given by contracting a logarithmic holomorphic vector field v with a logarithmic holomorphic form
given by contracting a logarithmic holomorphic vector field v with a logarithmic holomorphic form
![]() $\varphi $
. To simplify notations, for
$\varphi $
. To simplify notations, for ![]() , we often simply write
, we often simply write
![]() $v\varphi $
, suppressing the contraction
$v\varphi $
, suppressing the contraction
![]() $\mathbin {\lrcorner }$
. We define the Lie derivative via the formula
$\mathbin {\lrcorner }$
. We define the Lie derivative via the formula
![]() $\mathcal {L}_{v} := (-1)^{|v|} \partial \circ (v\mathbin {\lrcorner }) - (v\mathbin {\lrcorner }) \circ \partial $
(or equivalently,
$\mathcal {L}_{v} := (-1)^{|v|} \partial \circ (v\mathbin {\lrcorner }) - (v\mathbin {\lrcorner }) \circ \partial $
(or equivalently, ![]() ). By contracting with
). By contracting with ![]() , we get a sheaf isomorphism
, we get a sheaf isomorphism ![]() , which defines the BV operator
, which defines the BV operator ![]() by
by ![]() . We call it the BV operator because the BV identity:
. We call it the BV operator because the BV identity:
for ![]() , where we put
, where we put ![]() , defines a graded Lie bracket. This gives
, defines a graded Lie bracket. This gives ![]() the structure of a sheaf of BV algebras.
the structure of a sheaf of BV algebras.
4.2 An explicit description of the sheaf of log de Rham forms
Here, we apply the calculations in [Reference Felten, Filip and Ruddat17, Reference Gross and Siebert28] to give an explicit description of the stalk ![]() .
.
Let us consider
![]() $K=\nu ^{-1}(x)$
and the local model near K described in §4.1, with
$K=\nu ^{-1}(x)$
and the local model near K described in §4.1, with
![]() $P_{\tau ,x}$
and
$P_{\tau ,x}$
and
![]() $Q_{\tau ,x}$
as in equations (2.17), (2.18) and an embedding
$Q_{\tau ,x}$
as in equations (2.17), (2.18) and an embedding
![]() $V \rightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[Q_{\tau ,x}])$
. We may treat the subset
$V \rightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[Q_{\tau ,x}])$
. We may treat the subset
![]() $K \subset V$
as a compact subset of
$K \subset V$
as a compact subset of
![]() $\mathbb {C}^{l} = \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\mathbb {N}^l]) \hookrightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[Q_{\tau ,x}])$
via the identification of the analytic spaces
$\mathbb {C}^{l} = \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\mathbb {N}^l]) \hookrightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[Q_{\tau ,x}])$
via the identification of the analytic spaces
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }\oplus \mathbb {N}^l]) \cong \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[Q_{\tau ,x}])$
. For each
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }\oplus \mathbb {N}^l]) \cong \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[Q_{\tau ,x}])$
. For each
![]() $m \in \Sigma _{\tau }$
, we denote the corresponding element
$m \in \Sigma _{\tau }$
, we denote the corresponding element
![]() $(m,\psi _{x,0}(m),\dots ,\psi _{x,l}(m)) \in P_{\tau ,x}$
by
$(m,\psi _{x,0}(m),\dots ,\psi _{x,l}(m)) \in P_{\tau ,x}$
by
![]() $\hat {m}$
and the corresponding function by
$\hat {m}$
and the corresponding function by
![]() $z^{\hat {m}} \in \mathbb {C}[P_{\tau ,x}]$
. Similar to [Reference Felten, Filip and Ruddat17, Lem. 7.14], the germs of holomorphic functions
$z^{\hat {m}} \in \mathbb {C}[P_{\tau ,x}]$
. Similar to [Reference Felten, Filip and Ruddat17, Lem. 7.14], the germs of holomorphic functions ![]() near K in the analytic space
near K in the analytic space ![]() can be written as
can be written as

where
![]() $\mathtt {d}\colon \Sigma _{\tau } \rightarrow \mathbb {N}$
is a monoid morphism such that
$\mathtt {d}\colon \Sigma _{\tau } \rightarrow \mathbb {N}$
is a monoid morphism such that
![]() $\mathtt {d}^{-1}(0) = 0$
, and it is equipped with the product
$\mathtt {d}^{-1}(0) = 0$
, and it is equipped with the product
![]() $z^{\hat {m}_1} \cdot z^{\hat {m}_2} := z^{\hat {m}_1+\hat {m}_2}$
(but note that
$z^{\hat {m}_1} \cdot z^{\hat {m}_2} := z^{\hat {m}_1+\hat {m}_2}$
(but note that
![]() $\widehat {m_1+m_2}\neq \hat {m}_2 + \hat {m}_2$
in general). Thus, we have
$\widehat {m_1+m_2}\neq \hat {m}_2 + \hat {m}_2$
in general). Thus, we have ![]() .
.
To describe the differential forms, we consider the vector space
![]() $\mathscr {E} = P_{\tau ,x,\mathbb {C}}$
, regarded as the space of
$\mathscr {E} = P_{\tau ,x,\mathbb {C}}$
, regarded as the space of
![]() $1$
-forms on
$1$
-forms on
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_{\tau ,x}^{\mathrm {gp}}]) \cong (\mathbb {C}^*)^{n+1}$
. Write
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[P_{\tau ,x}^{\mathrm {gp}}]) \cong (\mathbb {C}^*)^{n+1}$
. Write
![]() $d\log z^{p}$
for
$d\log z^{p}$
for
![]() $p \in P_{\tau ,x,\mathbb {C}}$
and set
$p \in P_{\tau ,x,\mathbb {C}}$
and set
![]() $\mathscr {E}_1 := \mathbb {C} \langle d\log u_i \rangle _{i=1}^l$
, as a subset of
$\mathscr {E}_1 := \mathbb {C} \langle d\log u_i \rangle _{i=1}^l$
, as a subset of
![]() $\mathscr {E}$
. For an element
$\mathscr {E}$
. For an element
![]() $m\in \mathscr {Q}_{\tau ,\mathbb {C}}$
, we have the corresponding
$m\in \mathscr {Q}_{\tau ,\mathbb {C}}$
, we have the corresponding
![]() $1$
-form
$1$
-form
![]() $d\log z^{\hat {m}} \in P_{\tau ,x,\mathbb {C}}$
under the association between m and
$d\log z^{\hat {m}} \in P_{\tau ,x,\mathbb {C}}$
under the association between m and
![]() $z^{\hat {m}}$
. Let
$z^{\hat {m}}$
. Let
![]() $\mathtt {P}$
be the power set of
$\mathtt {P}$
be the power set of
![]() $\{1,\dots ,l\}$
, and write
$\{1,\dots ,l\}$
, and write
![]() $u^{I} = \prod _{i\in I} u_i$
for
$u^{I} = \prod _{i\in I} u_i$
for
![]() $I \in \mathtt {P}$
. A computation for sections of the sheaf
$I \in \mathtt {P}$
. A computation for sections of the sheaf ![]() from [Reference Gross and Siebert28, Prop. 1.12] and [Reference Felten, Filip and Ruddat17, Lem. 7.14] can then be rephrased as the following lemma.
from [Reference Gross and Siebert28, Prop. 1.12] and [Reference Felten, Filip and Ruddat17, Lem. 7.14] can then be rephrased as the following lemma.
Lemma 4.3 [Reference Felten, Filip and Ruddat17, Reference Gross and Siebert28].
The space of germs of sections of ![]() near K is a subspace of
near K is a subspace of ![]() given by elements of the form
given by elements of the form
 $$ \begin{align*}\displaystyle \alpha = \sum_{\substack{m \in \Sigma_{\tau}\\ 0\leq i \leq k }} \sum_{I} \alpha_{m,i,I} q^i z^{\hat{m}} u^I \otimes \beta_{m,I}, \quad \beta_{m,I} \in \bigwedge\nolimits^* \mathscr{E}_{m,I} = \bigwedge\nolimits^*(\mathscr{E}_{1,m,I}\oplus \mathscr{E}_{2,m,I} \oplus \langle d\log q\rangle), \end{align*} $$
$$ \begin{align*}\displaystyle \alpha = \sum_{\substack{m \in \Sigma_{\tau}\\ 0\leq i \leq k }} \sum_{I} \alpha_{m,i,I} q^i z^{\hat{m}} u^I \otimes \beta_{m,I}, \quad \beta_{m,I} \in \bigwedge\nolimits^* \mathscr{E}_{m,I} = \bigwedge\nolimits^*(\mathscr{E}_{1,m,I}\oplus \mathscr{E}_{2,m,I} \oplus \langle d\log q\rangle), \end{align*} $$
where
![]() $\mathscr {E}_{1,m,I} = \langle d\log u_i \rangle _{i\in I} \subset \mathscr {E}_1$
and the subspace
$\mathscr {E}_{1,m,I} = \langle d\log u_i \rangle _{i\in I} \subset \mathscr {E}_1$
and the subspace
![]() $\mathscr {E}_{2,m,I} \subset \mathscr {E}$
is given as follows: we consider the pullback of the product of normal fans
$\mathscr {E}_{2,m,I} \subset \mathscr {E}$
is given as follows: we consider the pullback of the product of normal fans
![]() $\prod _{i \notin I}\mathscr {N}_{\check {\Delta }_i(\tau )}$
to
$\prod _{i \notin I}\mathscr {N}_{\check {\Delta }_i(\tau )}$
to
![]() $ \mathscr {Q}_{\tau ,\mathbb {R}}$
and take
$ \mathscr {Q}_{\tau ,\mathbb {R}}$
and take
![]() $\mathscr {E}_{2,m,I} = \langle d\log z^{\hat {m}'} \rangle $
for
$\mathscr {E}_{2,m,I} = \langle d\log z^{\hat {m}'} \rangle $
for
![]() $m' \in \sigma _{m,I}$
, where
$m' \in \sigma _{m,I}$
, where
![]() $\sigma _{m,I}$
is the smallest cone in
$\sigma _{m,I}$
is the smallest cone in
![]() $\prod _{i \notin I}\mathscr {N}_{\check {\Delta }_i(\tau )} \subset \mathscr {Q}_{\tau ,\mathbb {R}}$
containing m.
$\prod _{i \notin I}\mathscr {N}_{\check {\Delta }_i(\tau )} \subset \mathscr {Q}_{\tau ,\mathbb {R}}$
containing m.
Here, we can treat
![]() $\prod _{i\notin I} \mathscr {N}_{\check {\Delta }_i(\tau )}\subset \mathscr {Q}_{\tau ,\mathbb {R}}$
since
$\prod _{i\notin I} \mathscr {N}_{\check {\Delta }_i(\tau )}\subset \mathscr {Q}_{\tau ,\mathbb {R}}$
since
![]() $\bigoplus _{i} \Lambda _{\check {\Delta }_i(\tau )}$
is a direct summand of
$\bigoplus _{i} \Lambda _{\check {\Delta }_i(\tau )}$
is a direct summand of
![]() $\mathscr {Q}_{\tau }^*$
. A similar description for
$\mathscr {Q}_{\tau }^*$
. A similar description for ![]() is simply given by quotienting out the direct summand
is simply given by quotienting out the direct summand
![]() $\langle d\log q\rangle $
in the above formula for
$\langle d\log q\rangle $
in the above formula for
![]() $\alpha $
. In particular, if we restrict ourselves to the case
$\alpha $
. In particular, if we restrict ourselves to the case
![]() $k=0$
, a general element
$k=0$
, a general element
![]() $\alpha $
can be written as
$\alpha $
can be written as
One can choose a nowhere vanishing element
for some nonzero element
![]() $\eta \in \wedge ^{n-\dim _{\mathbb {R}}(\tau )} \mathscr {E}_2$
, which is well defined up to rescaling. Any element in
$\eta \in \wedge ^{n-\dim _{\mathbb {R}}(\tau )} \mathscr {E}_2$
, which is well defined up to rescaling. Any element in ![]() can be written as
can be written as
![]() $f \Omega $
for some
$f \Omega $
for some ![]() .
.
Recall that the subset
![]() $K \subset \mathbb {C}^{l}$
is intersecting the singular locus
$K \subset \mathbb {C}^{l}$
is intersecting the singular locus
![]() $Z^{\tau }_1,\dots ,Z^{\tau }_{r}$
(as in §4.1), where
$Z^{\tau }_1,\dots ,Z^{\tau }_{r}$
(as in §4.1), where
![]() $u_i$
is the coordinate function of
$u_i$
is the coordinate function of
![]() $\mathbb {C}^{l}$
with simple zeros along
$\mathbb {C}^{l}$
with simple zeros along
![]() $Z_i^{\tau }$
for
$Z_i^{\tau }$
for
![]() $i=1,\dots ,r$
. There is a change of coordinates between a neighborhood of K in
$i=1,\dots ,r$
. There is a change of coordinates between a neighborhood of K in
![]() $\mathbb {C}^{l}$
and that of K in
$\mathbb {C}^{l}$
and that of K in
![]() $(\mathbb {C}^*)^l$
given by
$(\mathbb {C}^*)^l$
given by
 $$ \begin{align*} \begin{cases} u_i \mapsto f_{v,i}|_{(\mathbb{C}^{*})^l} & \text{if } 1\leq i \leq r;\\ u_i \mapsto z_i &\text{if } r<i\leq l. \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} u_i \mapsto f_{v,i}|_{(\mathbb{C}^{*})^l} & \text{if } 1\leq i \leq r;\\ u_i \mapsto z_i &\text{if } r<i\leq l. \end{cases} \end{align*} $$
Under the map
![]() $\log \colon (\mathbb {C}^*)^l \rightarrow \mathbb {R}^l$
, we have
$\log \colon (\mathbb {C}^*)^l \rightarrow \mathbb {R}^l$
, we have
![]() $K = \log ^{-1}(\mathscr {C})$
for some connected compact subset
$K = \log ^{-1}(\mathscr {C})$
for some connected compact subset
![]() $\mathscr {C}\subset \mathbb {R}^l$
. In the coordinates
$\mathscr {C}\subset \mathbb {R}^l$
. In the coordinates
![]() $z_1,\dots ,z_l$
, we find that
$z_1,\dots ,z_l$
, we find that
![]() $d\log z_1 \cdots d\log z_l\otimes \eta $
can be written as
$d\log z_1 \cdots d\log z_l\otimes \eta $
can be written as
![]() $f \Omega $
near K for some nowhere vanishing function
$f \Omega $
near K for some nowhere vanishing function ![]() .
.
Lemma 4.4. When
![]() $K \cap Z = \emptyset $
(i.e.,
$K \cap Z = \emptyset $
(i.e.,
![]() $r=0$
in the above discussion), the top cohomology group
$r=0$
in the above discussion), the top cohomology group ![]() is isomorphic to
is isomorphic to
![]() $\mathbb {C}$
, which is generated by the element
$\mathbb {C}$
, which is generated by the element
![]() $d\log z_1 \cdots d\log z_l\otimes \eta $
.
$d\log z_1 \cdots d\log z_l\otimes \eta $
.
Proof. Given a general element
![]() $f \Omega $
as above, first observe that we can write
$f \Omega $
as above, first observe that we can write
![]() $f = f_0 + f_{+}$
, where
$f = f_0 + f_{+}$
, where
![]() $f_+ = \sum _{m \in \Sigma _{\tau }\setminus \{0\}} f_m z^{\hat {m}}$
and
$f_+ = \sum _{m \in \Sigma _{\tau }\setminus \{0\}} f_m z^{\hat {m}}$
and
![]() $f_0 \in \mathcal {O}_{\mathbb {C}^l,K}$
. We take a basis
$f_0 \in \mathcal {O}_{\mathbb {C}^l,K}$
. We take a basis
![]() $e_1,\dots ,e_s$
of
$e_1,\dots ,e_s$
of
![]() $\mathscr {Q}_{\tau ,\mathbb {R}}^*$
, and also a partition
$\mathscr {Q}_{\tau ,\mathbb {R}}^*$
, and also a partition
![]() $I_1,\dots ,I_s$
of the lattice points in
$I_1,\dots ,I_s$
of the lattice points in
![]() $\Sigma _{\tau }\setminus \{0\}$
such that
$\Sigma _{\tau }\setminus \{0\}$
such that
![]() $\langle e_j,m\rangle \neq 0$
for
$\langle e_j,m\rangle \neq 0$
for
![]() $m \in I_j$
. Letting
$m \in I_j$
. Letting
 $$ \begin{align*} \alpha =(-1)^l \sum_{j} \sum_{m \in I_j} \frac{ f_m}{\langle e_j,m\rangle} z^{\hat{m}} du_1 \cdots du_l \otimes \iota_{e_j} \eta, \end{align*} $$
$$ \begin{align*} \alpha =(-1)^l \sum_{j} \sum_{m \in I_j} \frac{ f_m}{\langle e_j,m\rangle} z^{\hat{m}} du_1 \cdots du_l \otimes \iota_{e_j} \eta, \end{align*} $$
we have ![]() . So we only need to consider elements of the form
. So we only need to consider elements of the form
![]() $f_0 \Omega $
. If
$f_0 \Omega $
. If ![]() for some
for some
![]() $\alpha $
, we may take
$\alpha $
, we may take
![]() $\alpha = \sum _j \alpha _j du_1\cdots \widehat {du_j} \cdots du_l \otimes \eta $
for some
$\alpha = \sum _j \alpha _j du_1\cdots \widehat {du_j} \cdots du_l \otimes \eta $
for some
![]() $\alpha _j \in \mathcal {O}_{\mathbb {C}^{l},K}$
. Now, this is equivalent to
$\alpha _j \in \mathcal {O}_{\mathbb {C}^{l},K}$
. Now, this is equivalent to ![]() as forms in
as forms in
![]() $\Omega ^l_{\mathbb {C}^l,K}$
. This reduces the problem to
$\Omega ^l_{\mathbb {C}^l,K}$
. This reduces the problem to
![]() $\mathbb {C}^l$
.
$\mathbb {C}^l$
.
Working in
![]() $(\mathbb {C}^*)^l$
with coordinates
$(\mathbb {C}^*)^l$
with coordinates
![]() $z_i$
’s, we can write
$z_i$
’s, we can write
 $$ \begin{align*} \mathcal{O}_{(\mathbb{C}^*)^l,K} = \left\{ \sum_{m\in \mathbb{Z}^l} a_m z^{m} \ \Big| \ \sum_{m \in \mathbb{Z}^l} |a_m| e^{\langle v, m \rangle } < \infty, \ \text{for all } v \in W, \text{ for some open } W \supset \mathscr{C} \right\}, \end{align*} $$
$$ \begin{align*} \mathcal{O}_{(\mathbb{C}^*)^l,K} = \left\{ \sum_{m\in \mathbb{Z}^l} a_m z^{m} \ \Big| \ \sum_{m \in \mathbb{Z}^l} |a_m| e^{\langle v, m \rangle } < \infty, \ \text{for all } v \in W, \text{ for some open } W \supset \mathscr{C} \right\}, \end{align*} $$
using the fact that K is multicircular. By writing
![]() $\Omega ^*_{(\mathbb {C}^*)^l,K} = \mathcal {O}_{(\mathbb {C}^*)^l,K} \otimes \bigwedge ^* \mathscr {F}_1$
with
$\Omega ^*_{(\mathbb {C}^*)^l,K} = \mathcal {O}_{(\mathbb {C}^*)^l,K} \otimes \bigwedge ^* \mathscr {F}_1$
with
![]() $\mathscr {F}_1 = \langle d\log z_i \rangle _{i=1}^l$
, we can see that any element can be represented as
$\mathscr {F}_1 = \langle d\log z_i \rangle _{i=1}^l$
, we can see that any element can be represented as
![]() $c d\log z_1 \cdots d\log z_l$
in the quotient
$c d\log z_1 \cdots d\log z_l$
in the quotient ![]() , for some constant c.
, for some constant c.
From this lemma, we conclude that the top cohomology sheaf ![]() is isomorphic to the locally constant sheaf
is isomorphic to the locally constant sheaf
![]() $\underline {\mathbb {C}}$
over
$\underline {\mathbb {C}}$
over
![]() $B \setminus \mathscr {S}_e$
.
$B \setminus \mathscr {S}_e$
.
Lemma 4.5. The volume element ![]() is nonzero in
is nonzero in ![]() for every
for every
![]() $x \in B$
.
$x \in B$
.
Proof. We first consider the case when
![]() $x \in \mathrm {int}_{\mathrm {re}}(\sigma )$
for some maximal cell
$x \in \mathrm {int}_{\mathrm {re}}(\sigma )$
for some maximal cell
![]() $\sigma \in \mathscr {P}^{[n]}$
. The toric stratum
$\sigma \in \mathscr {P}^{[n]}$
. The toric stratum ![]() associated to
associated to
![]() $\sigma $
is equipped with the natural divisorial log structure induced from its boundary divisor. Then the sheaf
$\sigma $
is equipped with the natural divisorial log structure induced from its boundary divisor. Then the sheaf ![]() of log derivations for
of log derivations for ![]() is isomorphic to
is isomorphic to ![]() . By [Reference Gross and Siebert28, Lem. 3.12], we have
. By [Reference Gross and Siebert28, Lem. 3.12], we have ![]() in
in ![]() , where
, where
![]() $\mu _{\sigma } \in \bigwedge ^n \Lambda _{\sigma ,\mathbb {C}}$
is nowhere vanishing and c is a nonzero constant c. Thus
$\mu _{\sigma } \in \bigwedge ^n \Lambda _{\sigma ,\mathbb {C}}$
is nowhere vanishing and c is a nonzero constant c. Thus ![]() is nonzero in the cohomology as the same is true for
is nonzero in the cohomology as the same is true for ![]() . Next, we consider a general point
. Next, we consider a general point
![]() $x \in \mathrm {int}_{\mathrm {re}}(\tau )$
. If the statement is not true, we will have
$x \in \mathrm {int}_{\mathrm {re}}(\tau )$
. If the statement is not true, we will have ![]() for some
for some ![]() . Then there is an open neighborhood
. Then there is an open neighborhood
![]() $U \supset \mathscr {C}^{-1}(x)$
such that this relation continues to hold. As
$U \supset \mathscr {C}^{-1}(x)$
such that this relation continues to hold. As
![]() $U \cap \mathrm {int}_{\mathrm {re}}(\sigma ) \neq \emptyset $
, for those maximal cells
$U \cap \mathrm {int}_{\mathrm {re}}(\sigma ) \neq \emptyset $
, for those maximal cells
![]() $\sigma $
which contain the point x, we can take a nearby point
$\sigma $
which contain the point x, we can take a nearby point
![]() $y \in U \cap \mathrm {int}_{\mathrm {re}}(\sigma )$
and conclude that
$y \in U \cap \mathrm {int}_{\mathrm {re}}(\sigma )$
and conclude that ![]() in
in ![]() . This contradicts the previous case.
. This contradicts the previous case.
Lemma 4.6. Suppose that
![]() $x \in W_{\alpha } \setminus \mathscr {S}_e$
. For an element of the form
$x \in W_{\alpha } \setminus \mathscr {S}_e$
. For an element of the form
with ![]() satisfying
satisfying
![]() $f \equiv 0 (\text {mod } \mathbf {m})$
, there exist
$f \equiv 0 (\text {mod } \mathbf {m})$
, there exist ![]() and
and ![]() with
with
![]() $h,v \equiv 0 (\text {mod } \mathbf {m})$
such that
$h,v \equiv 0 (\text {mod } \mathbf {m})$
such that
in ![]() , where we recall that
, where we recall that
![]() $\mathcal {L}_{v} := (-1)^{|v|} \partial \circ (v\mathbin {\lrcorner }) - (v\mathbin {\lrcorner }) \circ \partial $
.
$\mathcal {L}_{v} := (-1)^{|v|} \partial \circ (v\mathbin {\lrcorner }) - (v\mathbin {\lrcorner }) \circ \partial $
.
Proof. To simplify notations in this proof, we will drop the subscript
![]() $\alpha $
. We prove the first statement by induction on k. The initial case is trivial. Assuming that this has been done for the
$\alpha $
. We prove the first statement by induction on k. The initial case is trivial. Assuming that this has been done for the
![]() $(k-1)^{\text {st}}$
-order, then, by taking an arbitrary lifting
$(k-1)^{\text {st}}$
-order, then, by taking an arbitrary lifting
![]() $\tilde {v}$
of v to the
$\tilde {v}$
of v to the
![]() $k^{\text {th}}$
-order, we have
$k^{\text {th}}$
-order, we have
for some ![]() . By Lemmas 4.4 and 4.5, we have
. By Lemmas 4.4 and 4.5, we have ![]() for some
for some
![]() $\gamma $
and some suitable constant c. Letting
$\gamma $
and some suitable constant c. Letting ![]() and
and
![]() $\breve {v} = \tilde {v} + q^{k} \theta $
, we have
$\breve {v} = \tilde {v} + q^{k} \theta $
, we have
By defining
![]() $\tilde {h}(q) := h(q) - cq^k$
in
$\tilde {h}(q) := h(q) - cq^k$
in
![]() $\mathbb {C}[q]/(q^{k+1})$
, we obtain the desired expression.
$\mathbb {C}[q]/(q^{k+1})$
, we obtain the desired expression.
4.3 A global pre-dgBV algebra from gluing
One approach for smoothing ![]() is to look for gluing morphisms
is to look for gluing morphisms ![]() between the local smoothing models which satisfy the cocycle condition, from which one obtain a
between the local smoothing models which satisfy the cocycle condition, from which one obtain a
![]() $k^{\text {th}}$
-order thickening
$k^{\text {th}}$
-order thickening ![]() over
over ![]() . This was done by Kontsevich–Soibelman [Reference Kontsevich and Soibelman36] (in two dimensions) and Gross–Siebert [Reference Gross and Siebert29] (in general dimensions) using consistent scattering diagrams. If such gluing morphisms
. This was done by Kontsevich–Soibelman [Reference Kontsevich and Soibelman36] (in two dimensions) and Gross–Siebert [Reference Gross and Siebert29] (in general dimensions) using consistent scattering diagrams. If such gluing morphisms ![]() ’s are available, one can certainly glue the global
’s are available, one can certainly glue the global
![]() $k^{\text {th}}$
-order sheaves
$k^{\text {th}}$
-order sheaves ![]() ,
, ![]() and the volume form
and the volume form ![]() .
.
In [Reference Chan, Leung and Ma8], we instead took suitable dg-resolutions ![]() ’s of the sheaves
’s of the sheaves ![]() ’s (more precisely, we used the Thom–Whitney resolution in [Reference Chan, Leung and Ma8, §3]) to construct gluings
’s (more precisely, we used the Thom–Whitney resolution in [Reference Chan, Leung and Ma8, §3]) to construct gluings
of sheaves which only preserve the Gerstenhaber algebra structure but not the differential. The key discovery in [Reference Chan, Leung and Ma8] was that, as the sheaves ![]() ’s are soft, such a gluing problem could be solved without any information from the complicated scattering diagrams. What we obtained is a pre-dgBV algebra
Footnote
5
’s are soft, such a gluing problem could be solved without any information from the complicated scattering diagrams. What we obtained is a pre-dgBV algebra
Footnote
5
![]() , in which the differential squares to zero only modulo
, in which the differential squares to zero only modulo
![]() $\mathbf {m} = (q)$
. Using well-known algebraic techniques [Reference Katzarkov, Kontsevich and Pantev33, Reference Terilla48], we can solve the Maurer–Cartan equation and construct the thickening
$\mathbf {m} = (q)$
. Using well-known algebraic techniques [Reference Katzarkov, Kontsevich and Pantev33, Reference Terilla48], we can solve the Maurer–Cartan equation and construct the thickening ![]() . In this subsection, we will summarize the whole procedure, incorporating the nice reformulation by Felten [Reference Felten16] in terms of deformations of Gerstenhaber algebras.
. In this subsection, we will summarize the whole procedure, incorporating the nice reformulation by Felten [Reference Felten16] in terms of deformations of Gerstenhaber algebras.
To begin with, we assume the following condition holds:
Condition 4.7. There is a sheaf
![]() $(\Omega ^*,d)$
of unital differential graded algebras (abbreviated as dga) (over
$(\Omega ^*,d)$
of unital differential graded algebras (abbreviated as dga) (over
![]() $\mathbb {R}$
or
$\mathbb {R}$
or
![]() $\mathbb {C}$
) over B, with degrees
$\mathbb {C}$
) over B, with degrees
![]() $0\leq * \leq L$
for some L such that
$0\leq * \leq L$
for some L such that
-
• the natural inclusion
 $\underline {\mathbb {R}} \rightarrow \Omega ^*$
(or
$\underline {\mathbb {R}} \rightarrow \Omega ^*$
(or
 $\underline {\mathbb {C}} \rightarrow \Omega ^*$
) of the locally constant sheaf (concentrated at degree
$\underline {\mathbb {C}} \rightarrow \Omega ^*$
) of the locally constant sheaf (concentrated at degree
 $0$
) gives a resolution, and
$0$
) gives a resolution, and -
• for any open cover
 $\mathcal {U} = \{ U_i \}_{i \in \mathcal {I}}$
, there is a partition of unity subordinate to
$\mathcal {U} = \{ U_i \}_{i \in \mathcal {I}}$
, there is a partition of unity subordinate to
 $\mathcal {U}$
, that is, we have
$\mathcal {U}$
, that is, we have
 $\{ \rho _i\}_{i\in \mathcal {I}}$
with
$\{ \rho _i\}_{i\in \mathcal {I}}$
with
 $\rho _i \in \Gamma (U_i,\Omega ^0)$
and
$\rho _i \in \Gamma (U_i,\Omega ^0)$
and
 $\overline {\mathrm {supp}(\rho _i)} \subset U_i$
such that
$\overline {\mathrm {supp}(\rho _i)} \subset U_i$
such that
 $\{\overline {\mathrm {supp}(\rho _i)} \}_i$
is locally finite and
$\{\overline {\mathrm {supp}(\rho _i)} \}_i$
is locally finite and
 $\sum _i \rho _i \equiv 1$
.
$\sum _i \rho _i \equiv 1$
.
It is easy to construct such an
![]() $\Omega ^*$
, and there are many natural choices. For instance, if B is a smooth manifold, then we can simply take the usual de Rham complex on B. In §3.3.2, the sheaf of monodromy invariant differential forms we constructed using the (singular) integral affine structure on B is another possible choice for
$\Omega ^*$
, and there are many natural choices. For instance, if B is a smooth manifold, then we can simply take the usual de Rham complex on B. In §3.3.2, the sheaf of monodromy invariant differential forms we constructed using the (singular) integral affine structure on B is another possible choice for
![]() $\Omega ^*$
(with degrees
$\Omega ^*$
(with degrees
![]() $0 \leq * \leq n$
). Yet another variant, namely the sheaf of monodromy invariant tropical differential forms, will be constructed in §5.1; this links tropical geometry on B with the smoothing of the maximally degenerate Calabi–Yau variety
$0 \leq * \leq n$
). Yet another variant, namely the sheaf of monodromy invariant tropical differential forms, will be constructed in §5.1; this links tropical geometry on B with the smoothing of the maximally degenerate Calabi–Yau variety ![]() .
.
Let us recall how to obtain a gluing of the dg resolutions of the sheaves ![]() and
and ![]() using any possible choice of such an
using any possible choice of such an
![]() $\Omega ^*$
. We fix a good cover
$\Omega ^*$
. We fix a good cover
![]() $\mathcal {W} := \{W_{\alpha }\}_{\alpha }$
of B and the corresponding Stein open cover
$\mathcal {W} := \{W_{\alpha }\}_{\alpha }$
of B and the corresponding Stein open cover
![]() $\mathcal {V} := \{V_\alpha \}_\alpha $
of
$\mathcal {V} := \{V_\alpha \}_\alpha $
of ![]() , where
, where
![]() $V_{\alpha } = \nu ^{-1}(W_{\alpha })$
for each
$V_{\alpha } = \nu ^{-1}(W_{\alpha })$
for each
![]() $\alpha $
.
$\alpha $
.
Definition 4.8. We define ![]() and
and ![]() , which gives a sheaf of dgBV algebras over
, which gives a sheaf of dgBV algebras over
![]() $W_{\alpha }$
. The dgBV structure
$W_{\alpha }$
. The dgBV structure ![]() is defined componentwise by
is defined componentwise by

for
![]() $\varphi , \psi \in \Omega ^*(U)$
and
$\varphi , \psi \in \Omega ^*(U)$
and ![]() for each open subset
for each open subset
![]() $U \subset W_{\alpha }$
.
$U \subset W_{\alpha }$
.
Definition 4.9. We define ![]() and
and ![]() , which gives a sheaf of dgas over
, which gives a sheaf of dgas over
![]() $W_{\alpha }$
equipped with the natural filtration
$W_{\alpha }$
equipped with the natural filtration ![]() inherited from
inherited from ![]() . The structures
. The structures ![]() are defined componentwise by
are defined componentwise by

for
![]() $\varphi , \psi \in \Omega ^*(U)$
and
$\varphi , \psi \in \Omega ^*(U)$
and ![]() for each open subset
for each open subset
![]() $U \subset W_{\alpha }$
.
$U \subset W_{\alpha }$
.
There is an action of ![]() on
on ![]() by contraction
by contraction
![]() $\mathbin {\lrcorner }$
defined by the formula
$\mathbin {\lrcorner }$
defined by the formula
for
![]() $\varphi , \psi \in \Omega ^*(U)$
,
$\varphi , \psi \in \Omega ^*(U)$
, ![]() and
and ![]() for each open subset
for each open subset
![]() $U \subset W_{\alpha }$
. Note that the local holomorphic volume form
$U \subset W_{\alpha }$
. Note that the local holomorphic volume form ![]() satisfies
satisfies ![]() , and we have the identity
, and we have the identity ![]() of operators.
of operators.
The next step is to consider gluing of the local sheaves ![]() ’s for higher orders k. Similar constructions have been done in [Reference Chan, Leung and Ma8, Reference Felten16] using the combinatorial Thom–Whitney resolution for the sheaves
’s for higher orders k. Similar constructions have been done in [Reference Chan, Leung and Ma8, Reference Felten16] using the combinatorial Thom–Whitney resolution for the sheaves ![]() ’s. We make suitable modifications of those arguments to fit into our current setting.
’s. We make suitable modifications of those arguments to fit into our current setting.
First, since ![]() and
and ![]() are divisorial deformations (in the sense of [Reference Gross and Siebert28, Def. 2.7]) of the intersection
are divisorial deformations (in the sense of [Reference Gross and Siebert28, Def. 2.7]) of the intersection
![]() $V^{\dagger }_{\alpha \beta }:= V^{\dagger }_{\alpha } \cap V^{\dagger }_{\beta }$
, we can use [Reference Gross and Siebert28, Thm. 2.11] and the fact that
$V^{\dagger }_{\alpha \beta }:= V^{\dagger }_{\alpha } \cap V^{\dagger }_{\beta }$
, we can use [Reference Gross and Siebert28, Thm. 2.11] and the fact that
![]() $V_{\alpha \beta }$
is Stein to obtain an isomorphism
$V_{\alpha \beta }$
is Stein to obtain an isomorphism ![]() of divisorial deformations which induces the gluing morphism
of divisorial deformations which induces the gluing morphism ![]() that in turn gives
that in turn gives ![]() .
.
Definition 4.10. A
![]() $k^{\text {th}}$
-order Gerstenhaber deformation of
$k^{\text {th}}$
-order Gerstenhaber deformation of ![]() is a collection of gluing morphisms
is a collection of gluing morphisms ![]() of the form
of the form
for some ![]() with
with
![]() $\theta _{\alpha \beta } \equiv 0 \ (\text {mod } \mathbf {m})$
, such that the cocycle condition
$\theta _{\alpha \beta } \equiv 0 \ (\text {mod } \mathbf {m})$
, such that the cocycle condition
is satisfied.
An isomorphism between two
![]() $k^{\text {th}}$
-order Gerstenhaber deformations
$k^{\text {th}}$
-order Gerstenhaber deformations ![]() and
and ![]() is a collection of automorphisms
is a collection of automorphisms ![]() of the form
of the form
for some ![]() with
with
![]() $\mathtt {b}_{\alpha } \equiv 0 (\text {mod } \mathbf {m})$
, such that
$\mathtt {b}_{\alpha } \equiv 0 (\text {mod } \mathbf {m})$
, such that
A slight modification of [Reference Felten16, Lem. 6.6], with essentially the same proof, gives the following:
Proposition 4.11. Given a
![]() $k^{\text {th}}$
-order Gerstenhaber deformation
$k^{\text {th}}$
-order Gerstenhaber deformation ![]() , the obstruction to the existence of a lifting to a
, the obstruction to the existence of a lifting to a
![]() $(k+1)^{\text {st}}$
-order deformation
$(k+1)^{\text {st}}$
-order deformation ![]() lies in the Čech cohomology (with respect to the cover
lies in the Čech cohomology (with respect to the cover
![]() $\mathcal {W} = \{W_{\alpha }\}_{\alpha }$
)
$\mathcal {W} = \{W_{\alpha }\}_{\alpha }$
)
The isomorphism classes of
![]() $(k+1)^{\text {st}}$
-order liftings are in
$(k+1)^{\text {st}}$
-order liftings are in
Fixing a
![]() $(k+1)^{\text {st}}$
-order lifting
$(k+1)^{\text {st}}$
-order lifting ![]() , the automorphisms fixing
, the automorphisms fixing ![]() are in
are in
Since
![]() $\Omega ^i$
satisfies Condition 4.7, we have
$\Omega ^i$
satisfies Condition 4.7, we have ![]() . In particular, we always have a set of compatible Gerstenhaber deformations
. In particular, we always have a set of compatible Gerstenhaber deformations ![]() , where
, where ![]() and any two of them are equivalent. Fixing such a set
and any two of them are equivalent. Fixing such a set ![]() , we obtain a set
, we obtain a set ![]() of Gerstenhaber algebras which is compatible, in the sense that there are natural identifications
of Gerstenhaber algebras which is compatible, in the sense that there are natural identifications ![]() .
.
We can also glue the local sheaves ![]() ’s of dgas using
’s of dgas using ![]() . First, we can define
. First, we can define ![]() using
using ![]() . For each fixed k, we can write
. For each fixed k, we can write ![]() as before. Then
as before. Then
where we recall that
![]() $\mathcal {L}_{v} := (-1)^{|v|} \partial \circ (v\mathbin {\lrcorner }) - (v\mathbin {\lrcorner }) \circ \partial $
, preserves the dga structure
$\mathcal {L}_{v} := (-1)^{|v|} \partial \circ (v\mathbin {\lrcorner }) - (v\mathbin {\lrcorner }) \circ \partial $
, preserves the dga structure ![]() and the filtration on
and the filtration on ![]() ’s. As a result, we obtain a set of compatible sheaves
’s. As a result, we obtain a set of compatible sheaves ![]() of dgas. The contraction action
of dgas. The contraction action
![]() $\mathbin {\lrcorner }$
is also compatible with the gluing construction, so we have a natural action
$\mathbin {\lrcorner }$
is also compatible with the gluing construction, so we have a natural action
![]() $\mathbin {\lrcorner }$
of
$\mathbin {\lrcorner }$
of ![]() on
on ![]() .
.
Next, we glue the operators
![]() $\bar {\partial }_{\alpha }$
’s and
$\bar {\partial }_{\alpha }$
’s and ![]() ’s.
’s.
Definition 4.12. A
![]() $k^{\text {th}}$
-order predifferential
$k^{\text {th}}$
-order predifferential
![]() $\bar {\partial }$
on
$\bar {\partial }$
on ![]() is a degree
is a degree
![]() $(0,1)$
operator obtained from gluing the operators
$(0,1)$
operator obtained from gluing the operators
![]() $\bar {\partial }_{\alpha }+[\eta _{\alpha },\cdot ]$
specified by a collection of elements
$\bar {\partial }_{\alpha }+[\eta _{\alpha },\cdot ]$
specified by a collection of elements ![]() such that
such that
![]() $\eta _{\alpha } \equiv 0 \ (\text {mod } \mathbf {m})$
and
$\eta _{\alpha } \equiv 0 \ (\text {mod } \mathbf {m})$
and
Two predifferentials
![]() $\bar {\partial }$
and
$\bar {\partial }$
and
![]() $\bar {\partial }'$
are equivalent if there is a Gerstenhaber automorphism (for the deformation
$\bar {\partial }'$
are equivalent if there is a Gerstenhaber automorphism (for the deformation ![]() )
) ![]() such that
such that
![]() $h^{-1}\circ \bar {\partial } \circ h = \bar {\partial }'$
.
$h^{-1}\circ \bar {\partial } \circ h = \bar {\partial }'$
.
Notice that we only have
![]() $\bar {\partial }^2 \equiv 0 (\text {mod} \mathbf {m})$
, which is why we call it a predifferential. Using the argument in [Reference Chan, Leung and Ma8, Thm. 3.34] or [Reference Felten16, Lem. 8.1], we can always lift any
$\bar {\partial }^2 \equiv 0 (\text {mod} \mathbf {m})$
, which is why we call it a predifferential. Using the argument in [Reference Chan, Leung and Ma8, Thm. 3.34] or [Reference Felten16, Lem. 8.1], we can always lift any
![]() $k^{\text {th}}$
-order predifferential
$k^{\text {th}}$
-order predifferential ![]() to a
to a
![]() $(k+1)^{\text {st}}$
-order predifferential. Furthermore, any two such liftings differ by a global element
$(k+1)^{\text {st}}$
-order predifferential. Furthermore, any two such liftings differ by a global element ![]() . We fix a set
. We fix a set ![]() of such compatible predifferentials. For each k, the action of
of such compatible predifferentials. For each k, the action of ![]() on
on ![]() is given by gluing of the action of
is given by gluing of the action of
![]() $\bar {\partial }_{\alpha } + \mathcal {L}_{\eta _{\alpha }}$
on
$\bar {\partial }_{\alpha } + \mathcal {L}_{\eta _{\alpha }}$
on ![]() . On the other hand, the elements
. On the other hand, the elements
glue to give a global element ![]() , and for different k’s, these elements are compatible. Computation shows that
, and for different k’s, these elements are compatible. Computation shows that
![]() $\bar {\partial }^{2} = [\mathfrak {l},\cdot ]$
on
$\bar {\partial }^{2} = [\mathfrak {l},\cdot ]$
on ![]() and
and
![]() $\bar {\partial }^{2} = \mathcal {L}_{\mathfrak {l}}$
on
$\bar {\partial }^{2} = \mathcal {L}_{\mathfrak {l}}$
on ![]() .
.
To glue the operators ![]() ’s, we need to glue the local volume elements
’s, we need to glue the local volume elements ![]() ’s to a global
’s to a global ![]() . We consider an element of the form
. We consider an element of the form ![]() , where
, where ![]() satisfies
satisfies
![]() $\mathfrak {f}_{\alpha } \equiv 0 \ (\text {mod } \mathbf {m})$
. Given a
$\mathfrak {f}_{\alpha } \equiv 0 \ (\text {mod } \mathbf {m})$
. Given a
![]() $k^{\text {th}}$
-order global volume element
$k^{\text {th}}$
-order global volume element ![]() , we take a lifting
, we take a lifting ![]() such that
such that
for some element ![]() . By construction,
. By construction,
![]() $\{\mathfrak {o}_{\alpha \beta }\}_{\alpha \beta }$
gives a Čech
$\{\mathfrak {o}_{\alpha \beta }\}_{\alpha \beta }$
gives a Čech
![]() $1$
-cycle in
$1$
-cycle in ![]() which is exact. So there exist
which is exact. So there exist
![]() $\mathfrak {u}_{\alpha }$
’s such that
$\mathfrak {u}_{\alpha }$
’s such that
![]() $\mathfrak {u}_{\beta }|_{W_{\alpha \beta }} - \mathfrak {u}_{\alpha }|_{W_{\alpha \beta }} = \mathfrak {o}_{\alpha \beta }$
, and we can modify
$\mathfrak {u}_{\beta }|_{W_{\alpha \beta }} - \mathfrak {u}_{\alpha }|_{W_{\alpha \beta }} = \mathfrak {o}_{\alpha \beta }$
, and we can modify
![]() $\tilde {\mathfrak {f}}_{\alpha }$
as
$\tilde {\mathfrak {f}}_{\alpha }$
as
![]() $\tilde {\mathfrak {f}}_{\alpha } + \mathfrak {u}_{\alpha }$
, which gives the desired
$\tilde {\mathfrak {f}}_{\alpha } + \mathfrak {u}_{\alpha }$
, which gives the desired
![]() $(k+1)^{\text {st}}$
-order volume element. Inductively, we can construct compatible volume elements
$(k+1)^{\text {st}}$
-order volume element. Inductively, we can construct compatible volume elements ![]() ,
,
![]() $k\in \mathbb {N}$
. Any two such volume elements
$k\in \mathbb {N}$
. Any two such volume elements ![]() and
and ![]() differ by
differ by ![]() , where
, where ![]() is some global element. Notice that
is some global element. Notice that ![]() unless
unless
![]() $\text {mod } \mathbf {m}$
.
$\text {mod } \mathbf {m}$
.
Using the volume element ![]() (we omit the dependence on k if there is no confusion), we may now define the global BV operator
(we omit the dependence on k if there is no confusion), we may now define the global BV operator ![]() by
by
which can locally be written as ![]() . We have
. We have ![]() . The local elements
. The local elements
glue to give a global element ![]() which satisfies
which satisfies ![]() . Also, the elements
. Also, the elements
![]() $\mathfrak {l}$
and
$\mathfrak {l}$
and
![]() $\mathfrak {n}$
satisfy the relation
$\mathfrak {n}$
satisfy the relation ![]() by a local calculation.
by a local calculation.
In summary, we obtain pre-dgBV algebras ![]() and pre-dgas
and pre-dgas ![]() with a natural contraction action
with a natural contraction action
![]() $\mathbin {\lrcorner }$
of
$\mathbin {\lrcorner }$
of ![]() on
on ![]() , and also volume elements
, and also volume elements ![]() . We set
. We set
and define a total de Rham operator ![]() by
by
which preserves the filtration ![]() . Using the contraction
. Using the contraction ![]() to pull back the operator, we obtain the operator
to pull back the operator, we obtain the operator ![]() acting on
acting on ![]() . Direct computation shows that
. Direct computation shows that
![]() $\mathbf {d}^2 = 0$
, and indeed it plays the role of the de Rham differential on a smooth manifold. Readers may consult [Reference Chan, Leung and Ma8, §4.2] for the computations and more details.
$\mathbf {d}^2 = 0$
, and indeed it plays the role of the de Rham differential on a smooth manifold. Readers may consult [Reference Chan, Leung and Ma8, §4.2] for the computations and more details.
Definition 4.13. We call ![]() (resp.
(resp. ![]() ) the sheaf of (resp.
) the sheaf of (resp.
![]() $k^{\text {th}}$
-order) smooth relative polyvector fields over
$k^{\text {th}}$
-order) smooth relative polyvector fields over
![]() $S^{\dagger }$
, and
$S^{\dagger }$
, and ![]() (resp.
(resp. ![]() ) the sheaf of (resp.
) the sheaf of (resp.
![]() $k^{\text {th}}$
-order) smooth forms over
$k^{\text {th}}$
-order) smooth forms over
![]() $S^{\dagger }$
. We denote the corresponding total complexes by
$S^{\dagger }$
. We denote the corresponding total complexes by ![]() (resp.
(resp. ![]() ) and
) and ![]() (resp.
(resp. ![]() ).
).
4.4 Smoothing by solving the Maurer–Cartan equation
With the sheaf ![]() of pre-dgBV algebras defined, we can now consider the extended Maurer–Cartan equation
of pre-dgBV algebras defined, we can now consider the extended Maurer–Cartan equation
for ![]() , where
, where ![]() . Setting
. Setting
![]() $t = 0$
gives the (classical) Maurer–Cartan equation
$t = 0$
gives the (classical) Maurer–Cartan equation
for ![]() . To inductively solve these equations, we need two conditions, namely the holomorphic Poincaré Lemma and the Hodge-to-de Rham degeneracy.
. To inductively solve these equations, we need two conditions, namely the holomorphic Poincaré Lemma and the Hodge-to-de Rham degeneracy.
We begin with the holomorphic Poincaré Lemma, which is a local condition on the sheaves ![]() ’s. We consider the complex
’s. We consider the complex ![]() , where
, where

There is a natural exact sequence

where ![]() as elements in
as elements in ![]() .
.
Condition 4.14. We say that the holomorphic Poincaré Lemma holds if at every point ![]() , the complex
, the complex ![]() is acyclic, where
is acyclic, where ![]() denotes the stalk of
denotes the stalk of ![]() at x.
at x.
The holomorphic Poincaré lemma for our setting was proved in [Reference Gross and Siebert28, proof of Thm. 4.1], but a gap was subsequently pointed out by Felten–Filip–Ruddat in [Reference Felten, Filip and Ruddat17], who used a different strategy to close the gap and give a correct proof in [Reference Felten, Filip and Ruddat17, Thm. 1.10]. From this condition, we can see that the cohomology sheaf ![]() is free over
is free over ![]() (cf. [Reference Kawamata and Namikawa34, Lem. 4.1]). We will need freeness of the cohomology
(cf. [Reference Kawamata and Namikawa34, Lem. 4.1]). We will need freeness of the cohomology ![]() over
over ![]() , which can be seen by the following lemma (see [Reference Kawamata and Namikawa34] and [Reference Chan, Leung and Ma8, §4.3.2] for similar arguments).
, which can be seen by the following lemma (see [Reference Kawamata and Namikawa34] and [Reference Chan, Leung and Ma8, §4.3.2] for similar arguments).
Lemma 4.15. Under Condition 4.14 (the holomorphic Poincaré Lemma), the natural map
is surjective for each
![]() $k \geq 0$
.
$k \geq 0$
.
Proof. First of all, applying the functor
![]() $\nu _*$
to the exact sequence
$\nu _*$
to the exact sequence

gives the following exact sequence of sheaves on B:
This is true because every sheaf in the first exact sequence is a direct limit of coherent analytic sheaves,
![]() $R\nu _{!}$
commutes with direct limits of sheaves, and
$R\nu _{!}$
commutes with direct limits of sheaves, and
![]() $R\nu _{!} = R\nu _* $
as the fiber
$R\nu _{!} = R\nu _* $
as the fiber
![]() $\nu ^{-1}(x)$
is a compact Hausdorff topological space; see, for example, [Reference Kashiwara and Schapira32]. By taking a Cartan–Eilenberg resolution, we have the implication:
$\nu ^{-1}(x)$
is a compact Hausdorff topological space; see, for example, [Reference Kashiwara and Schapira32]. By taking a Cartan–Eilenberg resolution, we have the implication:
for any open subset U, where
![]() $R\Gamma _U$
is the derived global section functor in the derived category of sheaves. In our case,
$R\Gamma _U$
is the derived global section functor in the derived category of sheaves. In our case,
![]() $U = \nu ^{-1}(W)$
and we have
$U = \nu ^{-1}(W)$
and we have
![]() $R\Gamma _{\nu ^{-1}(W)} = R\Gamma _{W} \circ R\nu _*$
. Furthermore, we see that
$R\Gamma _{\nu ^{-1}(W)} = R\Gamma _{W} \circ R\nu _*$
. Furthermore, we see that
This can be seen by taking a double complex
![]() $C^{*,*}$
resolving
$C^{*,*}$
resolving ![]() such that
such that
![]() $\nu _*(C^{*,*})$
computes
$\nu _*(C^{*,*})$
computes ![]() . The spectral sequence associated to the double complex has the
. The spectral sequence associated to the double complex has the
![]() $E_1$
-page given by
$E_1$
-page given by ![]() , which is
, which is
![]() $0$
if
$0$
if
![]() $q>0$
because
$q>0$
because ![]() is a direct limit of coherent analytic sheaves. Therefore,
is a direct limit of coherent analytic sheaves. Therefore, ![]() is a quasi-isomorphism. Combining these, we obtain that
is a quasi-isomorphism. Combining these, we obtain that ![]() for each i.
for each i.
Next, by Condition 4.7, ![]() is a resolution with a partition of unity, so the cohomology of the complex
is a resolution with a partition of unity, so the cohomology of the complex
computes ![]() . Through an isomorphism
. Through an isomorphism ![]() , we can identify the operator:
, we can identify the operator:
with ![]() , and hence deduce that
, and hence deduce that ![]() is acyclic for any open subset W.
is acyclic for any open subset W.
Now, we consider the global sheaf ![]() of complexes on B obtained by gluing the local sheaves
of complexes on B obtained by gluing the local sheaves ![]() . We also have
. We also have ![]() obtained by gluing
obtained by gluing ![]() , and
, and ![]() obtained by gluing
obtained by gluing ![]() . Then there is an exact sequence of complexes of sheaves
. Then there is an exact sequence of complexes of sheaves
To see that the complex ![]() is acyclic, we consider the total Čech complex associated to the cover
is acyclic, we consider the total Čech complex associated to the cover
![]() $\{W_{\alpha }\}_{\alpha }$
. The associated spectral sequence has zero
$\{W_{\alpha }\}_{\alpha }$
. The associated spectral sequence has zero
![]() $E_1$
page, thus
$E_1$
page, thus ![]() is indeed acyclic. As a result, the map
is indeed acyclic. As a result, the map ![]() is an isomorphism. Finally, surjectivity of the map
is an isomorphism. Finally, surjectivity of the map ![]() follows from the fact that the isomorphism
follows from the fact that the isomorphism ![]() factors through
factors through ![]() .
.
The Hodge-to-de Rham degeneracy is a global Hodge-theoretic condition on ![]() . We consider the Hodge filtration
. We consider the Hodge filtration ![]() ; the spectral sequence associated to it computes the hypercohomology of the complex of sheaves
; the spectral sequence associated to it computes the hypercohomology of the complex of sheaves ![]()
Condition 4.16. We say that the Hodge-to-de Rham degeneracy holds for ![]() if the spectral sequence associated to the above Hodge filtration degenerates at
if the spectral sequence associated to the above Hodge filtration degenerates at
![]() $E_1$
.
$E_1$
.
Under the assumption that
![]() $(B,\mathscr {P})$
is strongly simple (Definition 2.10), the Hodge-to-de Rham degeneracy for the maximally degenerate Calabi–Yau scheme
$(B,\mathscr {P})$
is strongly simple (Definition 2.10), the Hodge-to-de Rham degeneracy for the maximally degenerate Calabi–Yau scheme ![]() was proved in [Reference Gross and Siebert28, Thm. 3.26]. This was later generalized to the case when
was proved in [Reference Gross and Siebert28, Thm. 3.26]. This was later generalized to the case when
![]() $(B,\mathscr {P})$
is only simple (instead of strongly simple)Footnote
6
and further to log toroidal spaces in Felten–Filip–Ruddat [Reference Felten, Filip and Ruddat17] using different methods.
$(B,\mathscr {P})$
is only simple (instead of strongly simple)Footnote
6
and further to log toroidal spaces in Felten–Filip–Ruddat [Reference Felten, Filip and Ruddat17] using different methods.
We consider the dgBV algebra ![]() equipped with the operator
equipped with the operator ![]() .
.
Lemma 4.17. Under Condition 4.16 (the Hodge-to-de Rham degeneracy), ![]() is a free
is a free
![]() $\mathbb {C}[[t]]$
-module.
$\mathbb {C}[[t]]$
-module.
Proof. Recall that we are working with a good cover
![]() $\mathcal {W} = \{ W_\alpha \}_{\alpha }$
, so that the inverse image
$\mathcal {W} = \{ W_\alpha \}_{\alpha }$
, so that the inverse image
![]() $V_{\alpha } = \nu ^{-1}(W_{\alpha })$
is Stein for each
$V_{\alpha } = \nu ^{-1}(W_{\alpha })$
is Stein for each
![]() $\alpha $
. We have
$\alpha $
. We have
![]() $R\Gamma _{\nu ^{-1}(W)} = R\Gamma _{W} \circ R\nu _*$
and
$R\Gamma _{\nu ^{-1}(W)} = R\Gamma _{W} \circ R\nu _*$
and
If
![]() $\nu ^{-1}(W)$
is Stein, then
$\nu ^{-1}(W)$
is Stein, then ![]() and hence
and hence
The hypercohomology of ![]() is computed using the Čech double complex
is computed using the Čech double complex
with respect to the Stein open cover
![]() $\mathcal {V} = \{\nu ^{-1}(W_{\alpha })\}_{\alpha }$
. Similarly, the hypercohomology of the complex
$\mathcal {V} = \{\nu ^{-1}(W_{\alpha })\}_{\alpha }$
. Similarly, the hypercohomology of the complex ![]() is computed using the Čech double complex
is computed using the Čech double complex ![]() with respect to the open cover
with respect to the open cover
![]() $\mathcal {W} = \{ W_\alpha \}_{\alpha }$
; here, the Hodge filtration is induced from the filtration
$\mathcal {W} = \{ W_\alpha \}_{\alpha }$
; here, the Hodge filtration is induced from the filtration ![]() .
.
These two Čech complexes, as well as their corresponding Hodge filtrations, are identified as ![]() for each
for each
![]() $W = W_{\alpha _1} \cap \cdots \cap W_{\alpha _k}$
. Hence, under Condition 4.16, we have
$W = W_{\alpha _1} \cap \cdots \cap W_{\alpha _k}$
. Hence, under Condition 4.16, we have
![]() $E_1$
degeneracy also for
$E_1$
degeneracy also for ![]() , or equivalently, that
, or equivalently, that ![]() is a free
is a free
![]() $\mathbb {C}[[t]]$
-module. In view of the isomorphisms
$\mathbb {C}[[t]]$
-module. In view of the isomorphisms ![]() and
and
we conclude that ![]() is a free
is a free
![]() $\mathbb {C}[[t]]$
-module as well.
$\mathbb {C}[[t]]$
-module as well.
For the purpose of this paper, we restrict ourselves to the case that
where ![]() and
and ![]() . The extended Maurer-Cartan equation (4.10) can be decomposed, according to orders in t, into the (classical) Maurer–Cartan equation (4.11) for
. The extended Maurer-Cartan equation (4.10) can be decomposed, according to orders in t, into the (classical) Maurer–Cartan equation (4.11) for ![]() and the equation
and the equation
Theorem 4.18. Suppose that both Conditions 4.14 and 4.16 hold. Then for any
![]() $k^{\text {th}}$
-order solution
$k^{\text {th}}$
-order solution ![]() to the extended Maurer–Cartan equation (4.10), there exists a
to the extended Maurer–Cartan equation (4.10), there exists a
![]() $(k+1)^{\text {st}}$
-order solution
$(k+1)^{\text {st}}$
-order solution ![]() to equation (4.10) lifting
to equation (4.10) lifting ![]() . The same statement holds for the Maurer–Cartan equation (4.11) if we restrict to
. The same statement holds for the Maurer–Cartan equation (4.11) if we restrict to ![]() .
.
Proof. The first statement follows from [Reference Chan, Leung and Ma8, Thm. 5.6] and [Reference Chan, Leung and Ma8, Lem. 5.12]: Starting with a
![]() $k^{\text {th}}$
-order solution
$k^{\text {th}}$
-order solution ![]() for equation (4.10), one can always use [Reference Chan, Leung and Ma8, Thm. 5.6] to lift it to a general element
for equation (4.10), one can always use [Reference Chan, Leung and Ma8, Thm. 5.6] to lift it to a general element ![]() . The argument in [Reference Chan, Leung and Ma8, Lem. 5.12] shows that we can choose
. The argument in [Reference Chan, Leung and Ma8, Lem. 5.12] shows that we can choose ![]() such that the component of
such that the component of ![]() in
in ![]() is zero. As a result, the component of
is zero. As a result, the component of ![]() in
in ![]() is again a solution to (4.10).
is again a solution to (4.10).
For the second statement, we argue that, given ![]() , there always exists
, there always exists ![]() such that
such that ![]() is a solution to equation (4.10). We need to solve the equation (4.13) by induction on the order k. The initial case is trivial by taking
is a solution to equation (4.10). We need to solve the equation (4.13) by induction on the order k. The initial case is trivial by taking ![]() . Suppose the equation can be solved for
. Suppose the equation can be solved for ![]() . Then we take an arbitrary lifting
. Then we take an arbitrary lifting ![]() to the
to the
![]() $j^{\text {th}}$
-order. We can define an element
$j^{\text {th}}$
-order. We can define an element ![]() by
by
which satisfies
![]() $\bar {\partial }(\mathfrak {o}) = 0$
. Therefore, the class
$\bar {\partial }(\mathfrak {o}) = 0$
. Therefore, the class
![]() $[\mathfrak {o}]$
lies in the cohomology
$[\mathfrak {o}]$
lies in the cohomology
where the last equivalence is from [Reference Gross and Siebert27, Prop. 2.37]. By our assumption in §2, we have
![]() $H^1(B,\mathbb {C})=0$
, and hence we can find an element
$H^1(B,\mathbb {C})=0$
, and hence we can find an element
![]() $\breve {f}$
such that
$\breve {f}$
such that
![]() $\bar {\partial }(\breve {f}) = \mathfrak {o}$
. Letting
$\bar {\partial }(\breve {f}) = \mathfrak {o}$
. Letting ![]() proves the induction step from the
proves the induction step from the
![]() $(j-1)^{\text {st}}$
-order to the
$(j-1)^{\text {st}}$
-order to the
![]() $j^{\text {th}}$
-order. Now, applying the first statement, we can lift the solution
$j^{\text {th}}$
-order. Now, applying the first statement, we can lift the solution ![]() to
to ![]() which satisfies equation (4.10), and hence
which satisfies equation (4.10), and hence ![]() solves equation (4.11).
solves equation (4.11).
From Theorem 4.18, we obtain a solution ![]() to the Maurer–Cartan equation (4.11), from which we obtain the sheaves
to the Maurer–Cartan equation (4.11), from which we obtain the sheaves ![]() and
and ![]() over B. These sheaves are locally isomorphic to
over B. These sheaves are locally isomorphic to ![]() and
and ![]() , so we may treat them as obtained from gluing of the local sheaves
, so we may treat them as obtained from gluing of the local sheaves ![]() ’s and
’s and ![]() ’s. From these, we can extract consistent and compatible gluings
’s. From these, we can extract consistent and compatible gluings ![]() satisfying the cocycle condition, and hence obtain a k-th order thickening
satisfying the cocycle condition, and hence obtain a k-th order thickening ![]() of
of ![]() over
over ![]() ; see [Reference Chan, Leung and Ma8, §5.3]. Also,
; see [Reference Chan, Leung and Ma8, §5.3]. Also, ![]() , as a section of
, as a section of
![]() $\ker (\bar {\partial }+\mathcal {L}_{\phi })$
over B, defines a holomorphic volume form on the k-th order thickening
$\ker (\bar {\partial }+\mathcal {L}_{\phi })$
over B, defines a holomorphic volume form on the k-th order thickening ![]() .
.
4.4.1 Normalized volume form
For later purposes, we need to further normalize the holomorphic volume
by adding a suitable power series
![]() $h(q) \in (q) \subset \mathbb {C}[[q]]$
to f, so that the condition that
$h(q) \in (q) \subset \mathbb {C}[[q]]$
to f, so that the condition that ![]() , where T is a nearby n-torus in the smoothing, is satisfied.
, where T is a nearby n-torus in the smoothing, is satisfied.
The
![]() $k^{\text {th}}$
-order Hodge bundle over
$k^{\text {th}}$
-order Hodge bundle over
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[q]/q^{k+1})$
is defined as the cohomology
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[q]/q^{k+1})$
is defined as the cohomology
equipped with a Gauss–Manin connection ![]() , where
, where ![]() is the connecting homomorphism of the long exact sequence associated to
is the connecting homomorphism of the long exact sequence associated to
here
![]() $\mathbb {C} \langle d\log q \rangle $
is the one-dimensional graded vector space spanned by the degree
$\mathbb {C} \langle d\log q \rangle $
is the one-dimensional graded vector space spanned by the degree
![]() $1$
element
$1$
element
![]() $d\log q$
. We denote
$d\log q$
. We denote ![]() . Restricting to the
. Restricting to the
![]() $0^{\text {th}}$
-order, we have
$0^{\text {th}}$
-order, we have ![]() , which is a nilpotent operator acting on
, which is a nilpotent operator acting on ![]() , where
, where ![]() . If we consider the top cohomoloy
. If we consider the top cohomoloy ![]() , which is one-dimensional, we see that
, which is one-dimensional, we see that ![]() . So
. So ![]() is a flat connection without log poles at
is a flat connection without log poles at
![]() $q=0$
. Hence, we can find a basis (order by order in q) to identify
$q=0$
. Hence, we can find a basis (order by order in q) to identify ![]() , which also trivializes the flat connection
, which also trivializes the flat connection ![]() as
as
![]() $\frac {\partial }{\partial \log q}$
.
$\frac {\partial }{\partial \log q}$
.
Since
![]() $H^n(B,\mathbb {C})\cong \mathbb {C}$
, we can fix a nonzero generator and choose a representative
$H^n(B,\mathbb {C})\cong \mathbb {C}$
, we can fix a nonzero generator and choose a representative
![]() $\varrho \in \Omega ^n(B)$
. Then the element
$\varrho \in \Omega ^n(B)$
. Then the element ![]() (which may simply be written as
(which may simply be written as
![]() $\varrho $
) represents a section
$\varrho $
) represents a section
![]() $[\varrho ]$
in
$[\varrho ]$
in
![]() $\widehat {\mathcal {H}}$
. A direct computation shows that
$\widehat {\mathcal {H}}$
. A direct computation shows that ![]() , that is, it is a flat section to all orders. The pairing with the
, that is, it is a flat section to all orders. The pairing with the
![]() $0^{\text {th}}$
-order volume form
$0^{\text {th}}$
-order volume form ![]() gives a nonzero element
gives a nonzero element ![]() in
in ![]() .
.
Definition 4.19. The volume form ![]() is said to be normalized if
is said to be normalized if
![]() $[\varOmega \wedge \varrho ]$
is flat under
$[\varOmega \wedge \varrho ]$
is flat under ![]() .
.
In other words, we can write ![]() under the identification
under the identification
By modifying f to
![]() $f+h(q)$
, this can always be achieved. Further, after the modification,
$f+h(q)$
, this can always be achieved. Further, after the modification,
![]() $\varphi = \phi + t f$
still solves equation (4.10).
$\varphi = \phi + t f$
still solves equation (4.10).
5 From smoothing of Calabi–Yau varieties to tropical geometry
5.1 Tropical differential forms
To tropicalize the pre-dgBV algebra ![]() , we need to replace the Thom–Whitney resolution used in [Reference Chan, Leung and Ma8] by a geometric resolution. To do so, we first need to recall some background materials from our previous works [Reference Chan, Leung and Ma7, §4.2.3] and [Reference Chan and Ma9, §3.2]. Of crucial importance is the notion of differential forms with asymptotic support (which will be called tropical differential forms in this paper) that originated from multivalued Morse theory and Witten deformations. Such differential forms can be regarded as distribution-valued forms supported on tropical polyhedral subsets. This key notion allows us to develop tropical intersection theory via differential forms, and in particular, define the intersection pairing between possibly nontransversal tropical polyhedral subsets simply using the wedge product.
, we need to replace the Thom–Whitney resolution used in [Reference Chan, Leung and Ma8] by a geometric resolution. To do so, we first need to recall some background materials from our previous works [Reference Chan, Leung and Ma7, §4.2.3] and [Reference Chan and Ma9, §3.2]. Of crucial importance is the notion of differential forms with asymptotic support (which will be called tropical differential forms in this paper) that originated from multivalued Morse theory and Witten deformations. Such differential forms can be regarded as distribution-valued forms supported on tropical polyhedral subsets. This key notion allows us to develop tropical intersection theory via differential forms, and in particular, define the intersection pairing between possibly nontransversal tropical polyhedral subsets simply using the wedge product.
Let U be an open subset of
![]() $M_{\mathbb {R}}$
. We consider the space
$M_{\mathbb {R}}$
. We consider the space ![]() , where we take
, where we take
![]() $\mathcal {C}^{\infty }$
sections of
$\mathcal {C}^{\infty }$
sections of ![]() and
and
![]() $\hslash $
is a coordinate on
$\hslash $
is a coordinate on
![]() $\mathbb {R}_{>0}$
. Let
$\mathbb {R}_{>0}$
. Let
![]() $\mathcal {W}^{k}_{-\infty }(U) \subset \Omega ^k_\hslash (U)$
be the subset of k-forms
$\mathcal {W}^{k}_{-\infty }(U) \subset \Omega ^k_\hslash (U)$
be the subset of k-forms
![]() $\alpha $
such that, for each
$\alpha $
such that, for each
![]() $q \in U$
, there exist a neighborhood
$q \in U$
, there exist a neighborhood
![]() $q \in V \subset U$
, constants
$q \in V \subset U$
, constants
![]() $D_{j,V}$
,
$D_{j,V}$
,
![]() $c_V$
and a sufficiently small real number
$c_V$
and a sufficiently small real number
![]() $\hslash _0> 0$
such that
$\hslash _0> 0$
such that
![]() $\|\nabla ^j \alpha \|_{L^\infty (V)} \leq D_{j,V} e^{-c_V/\hslash }$
for all
$\|\nabla ^j \alpha \|_{L^\infty (V)} \leq D_{j,V} e^{-c_V/\hslash }$
for all
![]() $j \geq 0$
and for
$j \geq 0$
and for
![]() $0<\hslash < \hslash _0$
; here, the
$0<\hslash < \hslash _0$
; here, the
![]() $L^\infty $
-norm is defined by
$L^\infty $
-norm is defined by
![]() $\| \alpha \|_{L^{\infty }(V)} = \sup _{x\in V} \|\alpha (x)\|$
for any section
$\| \alpha \|_{L^{\infty }(V)} = \sup _{x\in V} \|\alpha (x)\|$
for any section
![]() $\alpha $
of the tensor bundle
$\alpha $
of the tensor bundle
![]() $TU^{\otimes k} \otimes T^{\vee }U^{\otimes l}$
, where we fix a constant metric on
$TU^{\otimes k} \otimes T^{\vee }U^{\otimes l}$
, where we fix a constant metric on
![]() $M_{\mathbb {R}}$
and use the induced metric on
$M_{\mathbb {R}}$
and use the induced metric on
![]() $TU^{\otimes k} \otimes T^{\vee }U^{\otimes l}$
;
$TU^{\otimes k} \otimes T^{\vee }U^{\otimes l}$
;
![]() $\nabla ^j$
denotes an operator of the form
$\nabla ^j$
denotes an operator of the form
![]() $\nabla _{\frac {\partial }{\partial x_{l_1}}}\cdots \nabla _{\frac {\partial }{\partial x_{l_j}}}$
, where
$\nabla _{\frac {\partial }{\partial x_{l_1}}}\cdots \nabla _{\frac {\partial }{\partial x_{l_j}}}$
, where
![]() $\nabla $
is a torsion-free, flat connection defining an affine structure on U and
$\nabla $
is a torsion-free, flat connection defining an affine structure on U and
![]() $x = (x_1,\dots , x_n)$
is an affine coordinate system (note that
$x = (x_1,\dots , x_n)$
is an affine coordinate system (note that
![]() $\nabla $
is not the Gauss–Manin connection in the previous section). Similarly, let
$\nabla $
is not the Gauss–Manin connection in the previous section). Similarly, let
![]() $\mathcal {W}^{k}_{\infty }(U) \subset \Omega ^k_\hslash (U)$
be the set of k-forms
$\mathcal {W}^{k}_{\infty }(U) \subset \Omega ^k_\hslash (U)$
be the set of k-forms
![]() $\alpha $
such that, for each
$\alpha $
such that, for each
![]() $q \in U$
, there exist a neighborhood
$q \in U$
, there exist a neighborhood
![]() $q \in V \subset U$
, a constant
$q \in V \subset U$
, a constant
![]() $D_{j,V}$
,
$D_{j,V}$
,
![]() $N_{j,V} \in \mathbb {Z}_{>0}$
and a sufficiently small real number
$N_{j,V} \in \mathbb {Z}_{>0}$
and a sufficiently small real number
![]() $\hslash _0> 0$
such that
$\hslash _0> 0$
such that
![]() $\|\nabla ^j \alpha \|_{L^\infty (V)} \leq D_{j,V} \hslash ^{-N_{j,V}}$
for all
$\|\nabla ^j \alpha \|_{L^\infty (V)} \leq D_{j,V} \hslash ^{-N_{j,V}}$
for all
![]() $j \geq 0$
and for
$j \geq 0$
and for
![]() $0<\hslash < \hslash _0$
.
$0<\hslash < \hslash _0$
.
The assignment
![]() $U \mapsto \mathcal {W}^{k}_{-\infty }(U)$
(resp.
$U \mapsto \mathcal {W}^{k}_{-\infty }(U)$
(resp.
![]() $U \mapsto \mathcal {W}^{k}_{\infty }(U)$
) defines a sheaf
$U \mapsto \mathcal {W}^{k}_{\infty }(U)$
) defines a sheaf
![]() $\mathcal {W}^{k}_{-\infty }$
(resp.
$\mathcal {W}^{k}_{-\infty }$
(resp.
![]() $\mathcal {W}^{k}_{\infty }$
) on
$\mathcal {W}^{k}_{\infty }$
) on
![]() $M_{\mathbb {R}}$
([Reference Chan, Leung and Ma7, Defs. 4.15 & 4.16]). Note that
$M_{\mathbb {R}}$
([Reference Chan, Leung and Ma7, Defs. 4.15 & 4.16]). Note that
![]() $\mathcal {W}^{k}_{-\infty }$
and
$\mathcal {W}^{k}_{-\infty }$
and
![]() $\mathcal {W}^{k}_{\infty }$
are closed under the wedge product,
$\mathcal {W}^{k}_{\infty }$
are closed under the wedge product,
![]() $\nabla _{\frac {\partial }{\partial x}}$
and the de Rham differential d. Since
$\nabla _{\frac {\partial }{\partial x}}$
and the de Rham differential d. Since
![]() $\mathcal {W}^{k}_{-\infty }$
is a dg ideal of
$\mathcal {W}^{k}_{-\infty }$
is a dg ideal of
![]() $\mathcal {W}^{k}_{\infty }$
, the quotient
$\mathcal {W}^{k}_{\infty }$
, the quotient
![]() $\mathcal {W}^{*}_{\infty }/\mathcal {W}^{*}_{-\infty }$
is a sheaf of dgas when equipped with the de Rham differential.
$\mathcal {W}^{*}_{\infty }/\mathcal {W}^{*}_{-\infty }$
is a sheaf of dgas when equipped with the de Rham differential.
Now, suppose U is a convex open set. By a tropical polyhedral subset of U, we mean a connected convex subset of U which is defined by finitely many affine equations or inequalities over
![]() $\mathbb {Q}$
of the form
$\mathbb {Q}$
of the form
![]() $a_1 x_1 + \cdots + a_n x_n \leq b$
.
$a_1 x_1 + \cdots + a_n x_n \leq b$
.
Definition 5.1 ([Reference Chan, Leung and Ma7], Definition 4.19).
A k-form
![]() $\alpha \in \mathcal {W}_{\infty }^k(U)$
is said to have asymptotic support on a closed codimension k tropical polyhedral subset
$\alpha \in \mathcal {W}_{\infty }^k(U)$
is said to have asymptotic support on a closed codimension k tropical polyhedral subset
![]() $P \subset U$
with weight
$P \subset U$
with weight
![]() $s \in \mathbb {Z}$
, denoted as
$s \in \mathbb {Z}$
, denoted as
![]() $\alpha \in \mathcal {W}_{P,s}(U)$
, if the following conditions are satisfied:
$\alpha \in \mathcal {W}_{P,s}(U)$
, if the following conditions are satisfied:
-
1. For any
 $p \in U \setminus P$
, there is a neighborhood
$p \in U \setminus P$
, there is a neighborhood
 $p \in V \subset U \setminus P$
such that
$p \in V \subset U \setminus P$
such that
 $\alpha |_V \in \mathcal {W}_{-\infty }^k(V)$
.
$\alpha |_V \in \mathcal {W}_{-\infty }^k(V)$
. -
2. There exists a neighborhood
 $W_P \subset U$
of P such that
$W_P \subset U$
of P such that
 $\alpha = h(x,\hslash ) \nu _P + \eta $
on
$\alpha = h(x,\hslash ) \nu _P + \eta $
on
 $W_P$
, where
$W_P$
, where
 $\nu _P \in \bigwedge ^k N_{\mathbb {R}}$
is a nonzero affine k-form (defined up to nonzero constant) which is normal to P,
$\nu _P \in \bigwedge ^k N_{\mathbb {R}}$
is a nonzero affine k-form (defined up to nonzero constant) which is normal to P,
 $h(x,\hslash ) \in C^\infty (W_P \times \mathbb {R}_{>0})$
and
$h(x,\hslash ) \in C^\infty (W_P \times \mathbb {R}_{>0})$
and
 $\eta \in \mathcal {W}_{-\infty }^k(W_P)$
.
$\eta \in \mathcal {W}_{-\infty }^k(W_P)$
. -
3. For any
 $p \in P$
, there exists a convex neighborhood
$p \in P$
, there exists a convex neighborhood
 $p \in V \subset U$
equipped with an affine coordinate system
$p \in V \subset U$
equipped with an affine coordinate system
 $x = (x_1,\dots , x_n)$
such that
$x = (x_1,\dots , x_n)$
such that
 $x' := (x_1, \dots , x_k)$
parametrizes codimension k affine linear subspaces of V parallel to P, with
$x' := (x_1, \dots , x_k)$
parametrizes codimension k affine linear subspaces of V parallel to P, with
 $x' = 0$
corresponding to the subspace containing P. With the foliation
$x' = 0$
corresponding to the subspace containing P. With the foliation
 $\{(P_{V, x'})\}_{x' \in N_V}$
, where
$\{(P_{V, x'})\}_{x' \in N_V}$
, where
 $P_{V,x'} = \{ (x_1,\dots ,x_n) \in V \ | \ (x_1,\dots ,x_k) = x' \}$
and
$P_{V,x'} = \{ (x_1,\dots ,x_n) \in V \ | \ (x_1,\dots ,x_k) = x' \}$
and
 $N_V$
is the normal bundle of V, we require that, for all
$N_V$
is the normal bundle of V, we require that, for all
 $j \in \mathbb {Z}_{\geq 0}$
and multi-indices
$j \in \mathbb {Z}_{\geq 0}$
and multi-indices
 $\beta = (\beta _1,\dots ,\beta _k) \in \mathbb {Z}_{\geq 0}^k$
, the estimate holds for some constant
$\beta = (\beta _1,\dots ,\beta _k) \in \mathbb {Z}_{\geq 0}^k$
, the estimate holds for some constant $$\begin{align*}\int_{x'} (x')^\beta \left(\sup_{P_{V,x'}}|\nabla^j (\iota_{\nu_P^\vee} \alpha)| \right) \nu_P \leq D_{j,V,\beta} \hslash^{-\frac{j+s-|\beta|-k}{2}} \end{align*}$$
$$\begin{align*}\int_{x'} (x')^\beta \left(\sup_{P_{V,x'}}|\nabla^j (\iota_{\nu_P^\vee} \alpha)| \right) \nu_P \leq D_{j,V,\beta} \hslash^{-\frac{j+s-|\beta|-k}{2}} \end{align*}$$
 $D_{j,V,\beta }$
and
$D_{j,V,\beta }$
and
 $s \in \mathbb {Z}$
, where
$s \in \mathbb {Z}$
, where
 $|\beta | = \sum _l \beta _l$
and
$|\beta | = \sum _l \beta _l$
and
 $\nu _P^\vee = \frac {\partial }{\partial x_1}\wedge \cdots \wedge \frac {\partial }{\partial x_k}$
.Footnote
7
$\nu _P^\vee = \frac {\partial }{\partial x_1}\wedge \cdots \wedge \frac {\partial }{\partial x_k}$
.Footnote
7
Observe that
![]() $\nabla _{\frac {\partial }{\partial x_l}} \mathcal {W}_{P,s}(U) \subset \mathcal {W}_{P,s+1}(U)$
and
$\nabla _{\frac {\partial }{\partial x_l}} \mathcal {W}_{P,s}(U) \subset \mathcal {W}_{P,s+1}(U)$
and
![]() $(x')^{\beta }\mathcal {W}_{P,s}(U) \subset \mathcal {W}_{P,s-|\beta |}(U)$
. It follows that
$(x')^{\beta }\mathcal {W}_{P,s}(U) \subset \mathcal {W}_{P,s-|\beta |}(U)$
. It follows that
The weight s defines a filtration of
![]() $\mathcal {W}^k_{\infty }$
(we drop the U dependence from the notation whenever it is clear from the context):Footnote
8
$\mathcal {W}^k_{\infty }$
(we drop the U dependence from the notation whenever it is clear from the context):Footnote
8
This filtration, which keeps track of the polynomial order of
![]() $\hslash $
for k-forms with asymptotic support on P, provides a convenient tool to express and prove results in asymptotic analysis.
$\hslash $
for k-forms with asymptotic support on P, provides a convenient tool to express and prove results in asymptotic analysis.
Definition 5.2 ([Reference Chan and Ma9], Definition 3.10).
A differential k-form
![]() $\alpha $
is in
$\alpha $
is in
![]() $\tilde {\mathcal {W}}_{s}^k(U)$
if there exist polyhedral subsets
$\tilde {\mathcal {W}}_{s}^k(U)$
if there exist polyhedral subsets
![]() $P_1, \dots , P_l \subset U$
of codimension k such that
$P_1, \dots , P_l \subset U$
of codimension k such that
![]() $\alpha \in \sum _{j=1}^l \mathcal {W}_{P_j,s}(U)$
. If, moreover,
$\alpha \in \sum _{j=1}^l \mathcal {W}_{P_j,s}(U)$
. If, moreover,
![]() $d \alpha \in \tilde {\mathcal {W}}_{s+1}^{k+1}(U)$
, then we write
$d \alpha \in \tilde {\mathcal {W}}_{s+1}^{k+1}(U)$
, then we write
![]() $\alpha \in \mathcal {W}_s^k(U)$
. For every
$\alpha \in \mathcal {W}_s^k(U)$
. For every
![]() $s \in \mathbb {Z}$
, let
$s \in \mathbb {Z}$
, let
![]() $\mathcal {W}_s^*(U) = \bigoplus _k \mathcal {W}_{s+k}^k(U)$
.
$\mathcal {W}_s^*(U) = \bigoplus _k \mathcal {W}_{s+k}^k(U)$
.
Example 5.3. Let
![]() $U = \mathbb {R}$
and x be an affine coordinate on U. Then we consider the
$U = \mathbb {R}$
and x be an affine coordinate on U. Then we consider the
![]() $\hslash $
-dependent
$\hslash $
-dependent
![]() $1$
-form
$1$
-form
 $$ \begin{align*} \delta:= \left( \frac{1}{\hslash \pi} \right)^{\frac{1}{2}} e^{-\frac{x^2}{\hslash}} dx. \end{align*} $$
$$ \begin{align*} \delta:= \left( \frac{1}{\hslash \pi} \right)^{\frac{1}{2}} e^{-\frac{x^2}{\hslash}} dx. \end{align*} $$
Direct calculations in [Reference Chan, Leung and Ma7, Lem 4.12] showed that
![]() $\delta \in \mathcal {W}_1^1(U)$
has asymptotic support on the hyperplane P defined by
$\delta \in \mathcal {W}_1^1(U)$
has asymptotic support on the hyperplane P defined by
![]() $x=0$
.
$x=0$
.
The hyperplane P separates U into two chambers
![]() $H_+$
and
$H_+$
and
![]() $H_-$
. If we fix a base point in
$H_-$
. If we fix a base point in
![]() $H_-$
and apply the integral operator I in [Reference Chan, Leung and Ma7, Lem. 4.23], we obtain
$H_-$
and apply the integral operator I in [Reference Chan, Leung and Ma7, Lem. 4.23], we obtain
![]() $I(\delta ) \in W^0_0(U)$
which has asymptotic support on
$I(\delta ) \in W^0_0(U)$
which has asymptotic support on
![]() $H_+ \cup P$
, playing the role of a step function.
$H_+ \cup P$
, playing the role of a step function.
Taking finite products of elements of the above form, we obtain
![]() $\alpha \in \mathcal {W}^k_k(U)$
with asymptotic support on arbitrary tropical polyhedral subsets of U. Any forms obtained from a finite number of steps of applying the differential d, applying the integral operator I and taking wedge product are in
$\alpha \in \mathcal {W}^k_k(U)$
with asymptotic support on arbitrary tropical polyhedral subsets of U. Any forms obtained from a finite number of steps of applying the differential d, applying the integral operator I and taking wedge product are in
![]() $W^*_0(U)$
.
$W^*_0(U)$
.
We say that two closed tropical polyhedral subsets
![]() $P_1, P_2 \subset U$
of codimension
$P_1, P_2 \subset U$
of codimension
![]() $k_1, k_2$
intersect transversally if the affine subspaces of codimension
$k_1, k_2$
intersect transversally if the affine subspaces of codimension
![]() $k_1$
and
$k_1$
and
![]() $k_2$
which contain
$k_2$
which contain
![]() $P_1$
and
$P_1$
and
![]() $P_2$
, respectively, intersect transversally. This definition applies also when
$P_2$
, respectively, intersect transversally. This definition applies also when
![]() $P_1 \cap P_2 = \emptyset $
or
$P_1 \cap P_2 = \emptyset $
or
![]() $\partial P_i \neq \emptyset $
.
$\partial P_i \neq \emptyset $
.
Lemma 5.4 [Reference Chan, Leung and Ma7, Lem. 4.22].
-
1. Let
 $P_1, P_2, P \subset U$
be closed tropical polyhedral subsets of codimension
$P_1, P_2, P \subset U$
be closed tropical polyhedral subsets of codimension
 $k_1$
,
$k_1$
,
 $k_2$
and
$k_2$
and
 $k_1+k_2$
, respectively, such that P contains
$k_1+k_2$
, respectively, such that P contains
 $P_1 \cap P_2$
and is normal to
$P_1 \cap P_2$
and is normal to
 $\nu _{P_1} \wedge \nu _{P_2}$
. Then
$\nu _{P_1} \wedge \nu _{P_2}$
. Then
 $\mathcal {W}_{P_1,s}(U) \wedge \mathcal {W}_{P_2,r}(U) \subset \mathcal {W}_{P,r+s}(U)$
if
$\mathcal {W}_{P_1,s}(U) \wedge \mathcal {W}_{P_2,r}(U) \subset \mathcal {W}_{P,r+s}(U)$
if
 $P_1$
and
$P_1$
and
 $P_2$
intersect transversally with
$P_2$
intersect transversally with
 $P_1 \cap P_2 \neq \emptyset $
, and
$P_1 \cap P_2 \neq \emptyset $
, and
 $\mathcal {W}_{P_1,s}(U) \wedge \mathcal {W}_{P_2,r}(U) \subset \mathcal {W}_{-\infty }^{k_1 + k_2}(U)$
otherwise.
$\mathcal {W}_{P_1,s}(U) \wedge \mathcal {W}_{P_2,r}(U) \subset \mathcal {W}_{-\infty }^{k_1 + k_2}(U)$
otherwise. -
2. We have
 $\mathcal {W}_{s_1}^{k_1}(U) \wedge \mathcal {W}_{s_2}^{k_2}(U) \subset \mathcal {W}_{s_1+s_2}^{k_1+k_2}(U)$
. In particular,
$\mathcal {W}_{s_1}^{k_1}(U) \wedge \mathcal {W}_{s_2}^{k_2}(U) \subset \mathcal {W}_{s_1+s_2}^{k_1+k_2}(U)$
. In particular,
 $\mathcal {W}_0^*(U) \subset \mathcal {W}_{\infty }^*(U)$
is a dg subalgebra and
$\mathcal {W}_0^*(U) \subset \mathcal {W}_{\infty }^*(U)$
is a dg subalgebra and
 $\mathcal {W}_{-1}^*(U) \subset \mathcal {W}_0^*(U)$
is a dg ideal.
$\mathcal {W}_{-1}^*(U) \subset \mathcal {W}_0^*(U)$
is a dg ideal.
Definition 5.5. Let
![]() $\mathcal {W}_s^*$
be the sheafification of the presheaf defined by
$\mathcal {W}_s^*$
be the sheafification of the presheaf defined by
![]() $U \mapsto \mathcal {W}_s^*(U)$
. We call the quotient sheaf
$U \mapsto \mathcal {W}_s^*(U)$
. We call the quotient sheaf
![]() $\mathscr {T}^*:=\mathcal {W}_0^*/\mathcal {W}_{-1}^*$
the sheaf of tropical differential forms, which is a sheaf of dgas on
$\mathscr {T}^*:=\mathcal {W}_0^*/\mathcal {W}_{-1}^*$
the sheaf of tropical differential forms, which is a sheaf of dgas on
![]() $M_{\mathbb {R}}$
with structures
$M_{\mathbb {R}}$
with structures
![]() $(\wedge ,d)$
.
$(\wedge ,d)$
.
From [Reference Chan and Ma9, Lem. 3.6], we learn that
![]() $\underline {\mathbb {R}} \rightarrow \mathscr {T}^*$
is a resolution. Furthermore, given any point
$\underline {\mathbb {R}} \rightarrow \mathscr {T}^*$
is a resolution. Furthermore, given any point
![]() $x \in U$
and a sufficiently small neighborhood
$x \in U$
and a sufficiently small neighborhood
![]() $x \in W \subset U$
, we can show that there exists
$x \in W \subset U$
, we can show that there exists
![]() $f \in \mathcal {W}_0^0(W)$
with compact support in W and satisfying
$f \in \mathcal {W}_0^0(W)$
with compact support in W and satisfying
![]() $f \equiv 1$
near x (using an argument similar to the proof of Lemma 3.10). Therefore,
$f \equiv 1$
near x (using an argument similar to the proof of Lemma 3.10). Therefore,
![]() $\mathscr {T}^*$
has a partition of unity subordinate to a given open cover. Replacing the sheaf of de Rham differential forms on
$\mathscr {T}^*$
has a partition of unity subordinate to a given open cover. Replacing the sheaf of de Rham differential forms on
![]() $\Lambda _{\rho _1,\mathbb {R}}^* \oplus \mathscr {Q}_{\tau ,\mathbb {R}}$
by the sheaf
$\Lambda _{\rho _1,\mathbb {R}}^* \oplus \mathscr {Q}_{\tau ,\mathbb {R}}$
by the sheaf
![]() $\mathscr {T}^*$
of tropical differential forms, we can construct a particular complex on the integral tropical manifold B satisfying Condition 4.7, which dictates the tropical geometry of B.
$\mathscr {T}^*$
of tropical differential forms, we can construct a particular complex on the integral tropical manifold B satisfying Condition 4.7, which dictates the tropical geometry of B.
Definition 5.6. Given a point x as in §3.3.2 (with a chart as in equation (3.10)), the stalk of
![]() $\mathscr {T}^*$
at x is defined as
$\mathscr {T}^*$
at x is defined as
![]() $\mathscr {T}^*_{x}:= (\mathtt {x}^{-1}\mathscr {T}^*)_{x}$
. This defines the complex
$\mathscr {T}^*_{x}:= (\mathtt {x}^{-1}\mathscr {T}^*)_{x}$
. This defines the complex
![]() $(\mathscr {T}^*,d)$
(or simply
$(\mathscr {T}^*,d)$
(or simply
![]() $\mathscr {T}^*$
) of monodromy invariant tropical differential forms on B. A section
$\mathscr {T}^*$
) of monodromy invariant tropical differential forms on B. A section
![]() $\alpha \in \mathscr {T}^*(W)$
is a collection of elements
$\alpha \in \mathscr {T}^*(W)$
is a collection of elements
![]() $\alpha _{x} \in \mathscr {T}^*_{x}$
,
$\alpha _{x} \in \mathscr {T}^*_{x}$
,
![]() $x \in W$
such that each
$x \in W$
such that each
![]() $\alpha _{x}$
can be represented by
$\alpha _{x}$
can be represented by
![]() $\mathtt {x}^{-1}\beta _{x}$
in a small neighborhood
$\mathtt {x}^{-1}\beta _{x}$
in a small neighborhood
![]() $U_{x} \subset \mathtt {p}^{-1}(\mathtt {U}_{x})$
for some tropical differential form
$U_{x} \subset \mathtt {p}^{-1}(\mathtt {U}_{x})$
for some tropical differential form
![]() $\beta _{x}$
on
$\beta _{x}$
on
![]() $\mathtt {U}_{x}$
, and satisfies the relation
$\mathtt {U}_{x}$
, and satisfies the relation
![]() $\alpha _{\tilde {x}} = \tilde {\mathtt {x}}^{-1}(\mathtt {p}^* \beta _{x})$
in
$\alpha _{\tilde {x}} = \tilde {\mathtt {x}}^{-1}(\mathtt {p}^* \beta _{x})$
in
![]() $\mathscr {T}^*_{\tilde {x}}$
for every
$\mathscr {T}^*_{\tilde {x}}$
for every
![]() $\tilde {x} \in U_{x}$
.
$\tilde {x} \in U_{x}$
.
Notice that the definition of
![]() $\mathscr {T}^*$
requires the projection map
$\mathscr {T}^*$
requires the projection map
![]() $\mathtt {p}$
in equation (3.11) to be affine, while that of
$\mathtt {p}$
in equation (3.11) to be affine, while that of
![]() $\Omega ^*$
in §3.3.2 does not. But like
$\Omega ^*$
in §3.3.2 does not. But like
![]() $\Omega ^*$
,
$\Omega ^*$
,
![]() $\mathscr {T}^*$
satisfies Condition 4.7 and can be used for the purpose of gluing the sheaf
$\mathscr {T}^*$
satisfies Condition 4.7 and can be used for the purpose of gluing the sheaf ![]() of dgBV algebras in §4.3. In the rest of this section, we shall use the notations
of dgBV algebras in §4.3. In the rest of this section, we shall use the notations ![]() and
and ![]() to denote the complexes of sheaves constructed using
to denote the complexes of sheaves constructed using
![]() $\mathscr {T}^*$
.
$\mathscr {T}^*$
.
5.2 The semiflat dgBV algebra and its comparison with the pre-dgBV algebra 
In this section, we define a twisting of the semiflat dgBV algebra by the slab functions (or initial wall-crossing factors) in §2.4 and compare it with the dgBV algebra we constructed in §4.3 using gluing of local smoothing models. The key result is Lemma 5.10, which is an important step in the proof of our main result.
We start by recalling some notations from §2.4. Recall that for each vertex v, we fix a representative
![]() $\varphi _v\colon U_v \rightarrow \mathbb {R}$
of the strictly convex multivalued piecewise linear function
$\varphi _v\colon U_v \rightarrow \mathbb {R}$
of the strictly convex multivalued piecewise linear function
![]() $\varphi \in H^0(B,\mathcal {MPL}_{\mathscr {P}})$
to define the cone
$\varphi \in H^0(B,\mathcal {MPL}_{\mathscr {P}})$
to define the cone
![]() $C_v$
and the monoid
$C_v$
and the monoid
![]() $P_v$
. The natural projection
$P_v$
. The natural projection
![]() $T_v \oplus \mathbb {Z} \rightarrow T_v$
induces a surjective ring homomorphism
$T_v \oplus \mathbb {Z} \rightarrow T_v$
induces a surjective ring homomorphism
![]() $\mathbb {C}[\rho ^{-1}P_v] \rightarrow \mathbb {C}[\rho ^{-1}\Sigma _v]$
; we denote by
$\mathbb {C}[\rho ^{-1}P_v] \rightarrow \mathbb {C}[\rho ^{-1}\Sigma _v]$
; we denote by
![]() $\bar {m} \in \rho ^{-1}\Sigma _v$
the image of
$\bar {m} \in \rho ^{-1}\Sigma _v$
the image of
![]() $m \in \rho ^{-1} P_v$
under the natural projection. We consider
$m \in \rho ^{-1} P_v$
under the natural projection. We consider
![]() $\mathbf {V}(\tau )_v := \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\tau ^{-1}P_v])$
for some
$\mathbf {V}(\tau )_v := \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\tau ^{-1}P_v])$
for some
![]() $\tau $
containing v and write
$\tau $
containing v and write
![]() $z^m$
for the function corresponding to
$z^m$
for the function corresponding to
![]() $m \in \tau ^{-1} P_v$
. The element
$m \in \tau ^{-1} P_v$
. The element
![]() $\varrho $
together with the corresponding function
$\varrho $
together with the corresponding function
![]() $z^{\varrho }$
determine a family
$z^{\varrho }$
determine a family
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\tau ^{-1}P_v]) \rightarrow \mathbb {C}$
, whose central fiber is given by
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\tau ^{-1}P_v]) \rightarrow \mathbb {C}$
, whose central fiber is given by
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\tau ^{-1}\Sigma _v])$
. The variety
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\tau ^{-1}\Sigma _v])$
. The variety
![]() $\mathbf {V}(\tau )_v = \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\tau ^{-1}P_v])$
is equipped with the divisorial log structure induced by
$\mathbf {V}(\tau )_v = \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\tau ^{-1}P_v])$
is equipped with the divisorial log structure induced by
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\tau ^{-1}\Sigma _v])$
, which is log smooth. We write
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\tau ^{-1}\Sigma _v])$
, which is log smooth. We write
![]() $\mathbf {V}(\tau )_v^{\dagger }$
if we need to emphasize the log structure.
$\mathbf {V}(\tau )_v^{\dagger }$
if we need to emphasize the log structure.
Since B is orientable, we can choose a nowhere vanishing integral element
![]() $\mu \in \Gamma (B\setminus \mathscr {S}_e,\bigwedge ^n T_{B,\mathbb {Z}})$
. We fix a local representative
$\mu \in \Gamma (B\setminus \mathscr {S}_e,\bigwedge ^n T_{B,\mathbb {Z}})$
. We fix a local representative
![]() $\mu _v \in \bigwedge ^n T_{v}$
for every vertex v and
$\mu _v \in \bigwedge ^n T_{v}$
for every vertex v and
![]() $\mu _{\sigma } \in \bigwedge ^n \Lambda _{\sigma }$
for every maximal cell
$\mu _{\sigma } \in \bigwedge ^n \Lambda _{\sigma }$
for every maximal cell
![]() $\sigma $
. Writing
$\sigma $
. Writing
![]() $\mu _v = m_1 \wedge \cdots \wedge m_n$
, we have the corresponding relative volume form
$\mu _v = m_1 \wedge \cdots \wedge m_n$
, we have the corresponding relative volume form
in
![]() $\Omega ^n_{\mathbf {V}(\tau )_v^{\dagger }/\mathbb {C}^{\dagger }}$
. Now, the relative log polyvector fields can be written as
$\Omega ^n_{\mathbf {V}(\tau )_v^{\dagger }/\mathbb {C}^{\dagger }}$
. Now, the relative log polyvector fields can be written as
 $$ \begin{align*}\bigwedge\nolimits^{-l} \Theta_{\mathbf{V}(\tau)_v^{\dagger}/\mathbb{C}^{\dagger}} = \bigoplus_{m \in \tau^{-1}P_v} z^m \partial_{n_1} \wedge \cdots \wedge \partial_{n_l}. \end{align*} $$
$$ \begin{align*}\bigwedge\nolimits^{-l} \Theta_{\mathbf{V}(\tau)_v^{\dagger}/\mathbb{C}^{\dagger}} = \bigoplus_{m \in \tau^{-1}P_v} z^m \partial_{n_1} \wedge \cdots \wedge \partial_{n_l}. \end{align*} $$
The volume form
![]() $\mu _v$
defines a BV operator via contraction
$\mu _v$
defines a BV operator via contraction ![]() , which is given explicitly by
, which is given explicitly by

A Schouten—Nijenhuis-type bracket is given by extending the following formulae skew-symmetrically:
 $$ \begin{align*} [z^{m_1} \partial_{n_1},z^{m_2}\partial_{n_2}] & = z^{m_1+m_2} \partial_{\langle \bar{m}_1, n_2 \rangle n_{1} - \langle \bar{m}_2, n_1 \rangle n_{2}},\\ [z^m , \partial_n] & = \langle \bar{m}, n \rangle z^m. \end{align*} $$
$$ \begin{align*} [z^{m_1} \partial_{n_1},z^{m_2}\partial_{n_2}] & = z^{m_1+m_2} \partial_{\langle \bar{m}_1, n_2 \rangle n_{1} - \langle \bar{m}_2, n_1 \rangle n_{2}},\\ [z^m , \partial_n] & = \langle \bar{m}, n \rangle z^m. \end{align*} $$
This gives
![]() $\bigwedge ^{-*} \Theta _{\mathbf {V}(\tau )_v^{\dagger }/\mathbb {C}^{\dagger }}$
the structure of a BV algebra.
$\bigwedge ^{-*} \Theta _{\mathbf {V}(\tau )_v^{\dagger }/\mathbb {C}^{\dagger }}$
the structure of a BV algebra.
5.2.1 Construction of the semiflat sheaves
For each
![]() $k \in \mathbb {N}$
, we shall define a sheaf
$k \in \mathbb {N}$
, we shall define a sheaf ![]() (resp.
(resp. ![]() ) of
) of
![]() $k^{\text {th}}$
-order semiflat log vector fields (resp. semiflat log de Rham forms) over the open dense subset
$k^{\text {th}}$
-order semiflat log vector fields (resp. semiflat log de Rham forms) over the open dense subset
![]() $W_0 \subset B$
defined by
$W_0 \subset B$
defined by
 $$ \begin{align*}W_0 := \bigcup_{\sigma \in \mathscr{P}^{[n]}} \mathrm{int}_{\mathrm{re}}(\sigma) \cup \bigcup_{\rho \in \mathscr{P}^{[n-1]}_0} \mathrm{int}_{\mathrm{re}}(\rho) \cup \bigcup_{\rho \in \mathscr{P}^{[n-1]}_1} \big( \mathrm{int}_{\mathrm{re}}(\rho) \setminus (\mathscr{S} \cap \mathrm{int}_{\mathrm{re}}(\rho)) \big), \end{align*} $$
$$ \begin{align*}W_0 := \bigcup_{\sigma \in \mathscr{P}^{[n]}} \mathrm{int}_{\mathrm{re}}(\sigma) \cup \bigcup_{\rho \in \mathscr{P}^{[n-1]}_0} \mathrm{int}_{\mathrm{re}}(\rho) \cup \bigcup_{\rho \in \mathscr{P}^{[n-1]}_1} \big( \mathrm{int}_{\mathrm{re}}(\rho) \setminus (\mathscr{S} \cap \mathrm{int}_{\mathrm{re}}(\rho)) \big), \end{align*} $$
where
![]() $\mathscr {P}^{[n-1]}_0$
consists of
$\mathscr {P}^{[n-1]}_0$
consists of
![]() $\rho $
’s such that
$\rho $
’s such that
![]() $\mathrm {int}_{\mathrm {re}}(\rho ) \cap \mathscr {S}_e = \emptyset $
and
$\mathrm {int}_{\mathrm {re}}(\rho ) \cap \mathscr {S}_e = \emptyset $
and
![]() $\mathscr {P}^{[n-1]}_1$
of
$\mathscr {P}^{[n-1]}_1$
of
![]() $\rho $
’s that intersect with
$\rho $
’s that intersect with
![]() $\mathscr {S}_e$
. These sheaves use the natural divisorial log structure on
$\mathscr {S}_e$
. These sheaves use the natural divisorial log structure on
![]() $\mathbf {V}(\rho )_v^{\dagger }$
and will not depend on the slab functions
$\mathbf {V}(\rho )_v^{\dagger }$
and will not depend on the slab functions
![]() $f_{v\rho }$
’s. This construction is possible because we are using the much more flexible Euclidean topology on
$f_{v\rho }$
’s. This construction is possible because we are using the much more flexible Euclidean topology on
![]() $W_0$
, instead of the Zariski topology on
$W_0$
, instead of the Zariski topology on ![]() .
.
For
![]() $\sigma \in \mathscr {P}^{[n]}$
, recall that we have
$\sigma \in \mathscr {P}^{[n]}$
, recall that we have
![]() $V(\sigma ) = \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\sigma ^{-1}\Sigma _{v}])$
for some
$V(\sigma ) = \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\sigma ^{-1}\Sigma _{v}])$
for some
![]() $v \in \sigma ^{[0]}$
. We also have
$v \in \sigma ^{[0]}$
. We also have
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\sigma ^{-1}\Sigma _{v}]) = \Lambda ^*_{\sigma ,\mathbb {C}}/\Lambda ^*_{\sigma } $
, which is isomorphic to
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\sigma ^{-1}\Sigma _{v}]) = \Lambda ^*_{\sigma ,\mathbb {C}}/\Lambda ^*_{\sigma } $
, which is isomorphic to
![]() $(\mathbb {C}^{*})^n$
, because
$(\mathbb {C}^{*})^n$
, because
![]() $\sigma ^{-1}\Sigma _v = \Lambda _{\sigma ,\mathbb {R}} = T_{v,\mathbb {R}}$
. The local
$\sigma ^{-1}\Sigma _v = \Lambda _{\sigma ,\mathbb {R}} = T_{v,\mathbb {R}}$
. The local
![]() $k^{\text {th}}$
-order thickening
$k^{\text {th}}$
-order thickening
is obtained by identifying
![]() $\sigma ^{-1}P_v$
as
$\sigma ^{-1}P_v$
as
![]() $\Lambda _{\sigma } \times \mathbb {N}$
. Choosing a different vertex
$\Lambda _{\sigma } \times \mathbb {N}$
. Choosing a different vertex
![]() $v'$
, we can use the parallel transport
$v'$
, we can use the parallel transport
![]() $T_{v} \cong T_{v'}$
from v to
$T_{v} \cong T_{v'}$
from v to
![]() $v'$
within
$v'$
within
![]() $\mathrm {int}_{\mathrm {re}}(\sigma )$
and the difference
$\mathrm {int}_{\mathrm {re}}(\sigma )$
and the difference
![]() $\varphi _v|_{\sigma } - \varphi _{v'}|_{\sigma }$
between two affine functions to identify the monoids
$\varphi _v|_{\sigma } - \varphi _{v'}|_{\sigma }$
between two affine functions to identify the monoids
![]() $\sigma ^{-1}P_{v}\cong \sigma ^{-1}P_{v'}$
. We take
$\sigma ^{-1}P_{v}\cong \sigma ^{-1}P_{v'}$
. We take
Next, we need to glue the sheaves ![]() ’s along neighborhoods of codimension one cells
’s along neighborhoods of codimension one cells
![]() $\rho $
’s. For each codimension, one cell
$\rho $
’s. For each codimension, one cell
![]() $\rho $
, we fix a primitive normal
$\rho $
, we fix a primitive normal
![]() $\check {d}_{\rho }$
to
$\check {d}_{\rho }$
to
![]() $\rho $
and label the two adjacent maximal cells
$\rho $
and label the two adjacent maximal cells
![]() $\sigma _+$
and
$\sigma _+$
and
![]() $\sigma _-$
so that
$\sigma _-$
so that
![]() $\check {d}_{\rho }$
is pointing into
$\check {d}_{\rho }$
is pointing into
![]() $\sigma _+$
. There are two situations to consider.
$\sigma _+$
. There are two situations to consider.
The simpler case is when
![]() $\mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\rho ) = \emptyset $
, where the monodromy is trivial. In this case, we have
$\mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\rho ) = \emptyset $
, where the monodromy is trivial. In this case, we have
![]() $V(\rho ) = \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\rho ^{-1}\Sigma _{v}])$
, with the gluing
$V(\rho ) = \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\rho ^{-1}\Sigma _{v}])$
, with the gluing
![]() $V(\sigma _{\pm }) \hookrightarrow V(\rho )$
as described below Definition 2.13 using the open gluing data
$V(\sigma _{\pm }) \hookrightarrow V(\rho )$
as described below Definition 2.13 using the open gluing data
![]() $s_{\rho \sigma _{\pm }}$
. We take the
$s_{\rho \sigma _{\pm }}$
. We take the
![]() $k^{\text {th}}$
-order thickening given by
$k^{\text {th}}$
-order thickening given by
equipped with the divisorial log structure induced by
![]() $V(\rho )$
. We extend the open gluing data
$V(\rho )$
. We extend the open gluing data
to
so that
![]() $s_{\rho \sigma _{\pm }}(0,1) = 1$
, which acts as an automorphism of
$s_{\rho \sigma _{\pm }}(0,1) = 1$
, which acts as an automorphism of
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\sigma ^{-1}\Sigma _{v}])$
. In this way, we can extend the gluing
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\sigma ^{-1}\Sigma _{v}])$
. In this way, we can extend the gluing
![]() $V(\sigma _{\pm }) \hookrightarrow V(\rho )$
to
$V(\sigma _{\pm }) \hookrightarrow V(\rho )$
to
by twisting with the ring homomorphism induced by
![]() $z^{m} \rightarrow s_{\rho \sigma _{\pm }}(m)^{-1}z^{m}$
. On a sufficiently small neighborhood
$z^{m} \rightarrow s_{\rho \sigma _{\pm }}(m)^{-1}z^{m}$
. On a sufficiently small neighborhood
![]() $\mathscr {W}_{\rho }$
of
$\mathscr {W}_{\rho }$
of
![]() $\mathrm {int}_{\mathrm {re}}(\rho )$
, we take
$\mathrm {int}_{\mathrm {re}}(\rho )$
, we take
Choosing a different vertex
![]() $v'$
, we may use parallel transport to identify the fans
$v'$
, we may use parallel transport to identify the fans
![]() $\rho ^{-1} \Sigma _{v} \cong \rho ^{-1} \Sigma _{v'}$
, and further use the difference
$\rho ^{-1} \Sigma _{v} \cong \rho ^{-1} \Sigma _{v'}$
, and further use the difference
![]() $\varphi _v|_{\mathscr {W}_{\rho }} - \varphi _{v'}|_{\mathscr {W}_{\rho }}$
to identify the monoids
$\varphi _v|_{\mathscr {W}_{\rho }} - \varphi _{v'}|_{\mathscr {W}_{\rho }}$
to identify the monoids
![]() $\rho ^{-1}P_v \cong \rho ^{-1}P_{v'}$
. One can check that the sheaf
$\rho ^{-1}P_v \cong \rho ^{-1}P_{v'}$
. One can check that the sheaf ![]() is well defined.
is well defined.
The more complicated case is when
![]() $\mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\rho ) \neq \emptyset $
, where the monodromy is nontrivial. We write
$\mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\rho ) \neq \emptyset $
, where the monodromy is nontrivial. We write
![]() $\mathrm {int}_{\mathrm {re}}(\rho ) \setminus \mathscr {S} = \bigcup _{v} \mathrm {int}_{\mathrm {re}}(\rho )_v$
, where
$\mathrm {int}_{\mathrm {re}}(\rho ) \setminus \mathscr {S} = \bigcup _{v} \mathrm {int}_{\mathrm {re}}(\rho )_v$
, where
![]() $\mathrm {int}_{\mathrm {re}}(\rho )_v$
is the unique component which contains the vertex v in its closure. We fix one v, the corresponding
$\mathrm {int}_{\mathrm {re}}(\rho )_v$
is the unique component which contains the vertex v in its closure. We fix one v, the corresponding
![]() $\mathrm {int}_{\mathrm {re}}(\rho )_v$
, and a sufficiently small open subset
$\mathrm {int}_{\mathrm {re}}(\rho )_v$
, and a sufficiently small open subset
![]() $\mathscr {W}_{\rho ,v}$
of
$\mathscr {W}_{\rho ,v}$
of
![]() $\mathrm {int}_{\mathrm {re}}(\rho )_v$
. We assume that the neighborhood
$\mathrm {int}_{\mathrm {re}}(\rho )_v$
. We assume that the neighborhood
![]() $\mathscr {W}_{\rho ,v}$
of
$\mathscr {W}_{\rho ,v}$
of
![]() $\mathrm {int}_{\mathrm {re}}(\rho )_v$
intersects neither
$\mathrm {int}_{\mathrm {re}}(\rho )_v$
intersects neither
![]() $\mathscr {W}_{v',\rho '}$
nor
$\mathscr {W}_{v',\rho '}$
nor
![]() $\mathscr {W}_{\rho '}$
for any possible
$\mathscr {W}_{\rho '}$
for any possible
![]() $v'$
and
$v'$
and
![]() $\rho '$
. Then we consider the scheme-theoretic embedding
$\rho '$
. Then we consider the scheme-theoretic embedding
given by
 $$ \begin{align*}z^{m} \mapsto \begin{cases} z^{\bar{m}} & \text{if } m \text{ lies on the boundary of the cone } \rho^{-1}P_{v},\\ 0 & \text{if } m \text{ lies in the interior of the cone } \rho^{-1}P_{v}. \end{cases} \end{align*} $$
$$ \begin{align*}z^{m} \mapsto \begin{cases} z^{\bar{m}} & \text{if } m \text{ lies on the boundary of the cone } \rho^{-1}P_{v},\\ 0 & \text{if } m \text{ lies in the interior of the cone } \rho^{-1}P_{v}. \end{cases} \end{align*} $$
We denote by ![]() the
the
![]() $k^{\text {th}}$
-order thickening of
$k^{\text {th}}$
-order thickening of
![]() $V(\rho )|_{\nu ^{-1}(\mathscr {W}_{\rho ,v})}$
in
$V(\rho )|_{\nu ^{-1}(\mathscr {W}_{\rho ,v})}$
in
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\rho ^{-1}P_{v}])$
and equip it with the divisorial log structure which is log smooth over
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\rho ^{-1}P_{v}])$
and equip it with the divisorial log structure which is log smooth over ![]() (note that it is different from the local model
(note that it is different from the local model ![]() introduced earlier in §4 because the latter depends on the slab functions
introduced earlier in §4 because the latter depends on the slab functions
![]() $f_{v,\rho }$
, as we can see explicitly in §5.2.2, while the former doesn’t). We take
$f_{v,\rho }$
, as we can see explicitly in §5.2.2, while the former doesn’t). We take
The gluing with nearby maximal cells
![]() $\sigma _{\pm }$
on the overlap
$\sigma _{\pm }$
on the overlap
![]() $\mathrm {int}_{\mathrm {re}}(\sigma _{\pm }) \cap \mathscr {W}_{\rho ,v}$
is given by parallel transporting through the vertex v to relate the monoids
$\mathrm {int}_{\mathrm {re}}(\sigma _{\pm }) \cap \mathscr {W}_{\rho ,v}$
is given by parallel transporting through the vertex v to relate the monoids
![]() $\sigma _{\pm }^{-1}P_v$
and
$\sigma _{\pm }^{-1}P_v$
and
![]() $\rho ^{-1}P_v$
constructed from
$\rho ^{-1}P_v$
constructed from
![]() $P_v$
, and twisting the map
$P_v$
, and twisting the map
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\sigma ^{-1}_{\pm }P_v]) \rightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\rho ^{-1}P_v])$
with the open gluing data
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\sigma ^{-1}_{\pm }P_v]) \rightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\rho ^{-1}P_v])$
with the open gluing data
using previous liftings of
![]() $s_{\rho \sigma _{\pm }}$
to
$s_{\rho \sigma _{\pm }}$
to
![]() $\Lambda _{\sigma _{\pm }}\oplus \mathbb {Z}$
. We obtain a commutative diagram of holomorphic maps
$\Lambda _{\sigma _{\pm }}\oplus \mathbb {Z}$
. We obtain a commutative diagram of holomorphic maps

where
![]() $\mathscr {D} =\nu ^{-1}( \mathscr {W}_{\rho ,v} \cap \mathrm {int}_{\mathrm {re}}(\sigma _{\pm }))$
and the vertical arrow on the right-hand side respects the log structures. The induced isomorphism
$\mathscr {D} =\nu ^{-1}( \mathscr {W}_{\rho ,v} \cap \mathrm {int}_{\mathrm {re}}(\sigma _{\pm }))$
and the vertical arrow on the right-hand side respects the log structures. The induced isomorphism
of sheaves on the overlap
![]() $\mathscr {W}_{\rho ,v} \cap \mathrm {int}_{\mathrm {re}}(\sigma _{\pm })$
then gives the desired gluing for defining the sheaf
$\mathscr {W}_{\rho ,v} \cap \mathrm {int}_{\mathrm {re}}(\sigma _{\pm })$
then gives the desired gluing for defining the sheaf ![]() on
on
![]() $W_0$
. Note that the cocycle condition is trivial here as there is no triple intersection of any three open subsets from
$W_0$
. Note that the cocycle condition is trivial here as there is no triple intersection of any three open subsets from
![]() $\mathrm {int}_{\mathrm {re}}(\sigma )$
,
$\mathrm {int}_{\mathrm {re}}(\sigma )$
,
![]() $\mathscr {W}_\rho $
and
$\mathscr {W}_\rho $
and
![]() $\mathscr {W}_{\rho ,v}$
.
$\mathscr {W}_{\rho ,v}$
.
Similarly, we can define the sheaf ![]() of semiflat log de Rham forms, together with a relative volume form
of semiflat log de Rham forms, together with a relative volume form ![]() obtained from gluing the local
obtained from gluing the local
![]() $\mu _v$
’s specified by the element
$\mu _v$
’s specified by the element
![]() $\mu $
as described in the beginning of §5.2.
$\mu $
as described in the beginning of §5.2.
It would be useful to write down elements of the sheaf ![]() more explicitly. For instance, fixing a point
more explicitly. For instance, fixing a point
![]() $x \in \mathrm {int}_{\mathrm {re}}(\rho )_v$
, we may write
$x \in \mathrm {int}_{\mathrm {re}}(\rho )_v$
, we may write
and use
![]() $\partial _n$
to stand for the semiflat holomorphic vector field associated to an element
$\partial _n$
to stand for the semiflat holomorphic vector field associated to an element
![]() $n \in T^*_{v,\mathbb {R}}$
.
$n \in T^*_{v,\mathbb {R}}$
.
Note that analytic continuation around the singular locus
![]() $\mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\rho )$
acts nontrivially on the semiflat sheaf
$\mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\rho )$
acts nontrivially on the semiflat sheaf ![]() due to the presence of nontrivial monodromy of the affine structure. Below is a simple example.
due to the presence of nontrivial monodromy of the affine structure. Below is a simple example.
Example 5.7. We consider the local affine charts which appeared in Example 2.3, equipped with a strictly convex piecewise linear affine function
![]() $\varphi $
on
$\varphi $
on
![]() $\Sigma _{\rho }$
whose change of slopes is
$\Sigma _{\rho }$
whose change of slopes is
![]() $1$
. Let us study the analytic continuation of a local section along the loop
$1$
. Let us study the analytic continuation of a local section along the loop
![]() $\gamma $
which starts at a point
$\gamma $
which starts at a point
![]() $b_+$
, as shown in Figure 7. First, we can identify both
$b_+$
, as shown in Figure 7. First, we can identify both
![]() $\rho ^{-1}P_{v_+}$
and
$\rho ^{-1}P_{v_+}$
and
![]() $\rho ^{-1}P_{v_-}$
with the monoid in the cone
$\rho ^{-1}P_{v_-}$
with the monoid in the cone
![]() $P = \{ (x,y,z) \ | \ z\geq \varphi (x) \}$
via parallel transport through
$P = \{ (x,y,z) \ | \ z\geq \varphi (x) \}$
via parallel transport through
![]() $\sigma _+$
. Writing
$\sigma _+$
. Writing
![]() $u = z^{(1,0,1)}$
,
$u = z^{(1,0,1)}$
,
![]() $v= z^{(-1,0,0)}$
,
$v= z^{(-1,0,0)}$
,
![]() $w = z^{(0,-1,0)}$
and
$w = z^{(0,-1,0)}$
and
![]() $q = z^{(0,0,1)}$
, we have
$q = z^{(0,0,1)}$
, we have
![]() $\mathbb {C}[P] \cong \mathbb {C}[u,v,w^{\pm }, q] / (uv-q)$
. Now, the analytic continuation of
$\mathbb {C}[P] \cong \mathbb {C}[u,v,w^{\pm }, q] / (uv-q)$
. Now, the analytic continuation of ![]() along
along
![]() $\gamma $
(going from the chart
$\gamma $
(going from the chart
![]() $U_{\mathrm {II}}$
to the chart
$U_{\mathrm {II}}$
to the chart
![]() $U_{\mathrm {I}}$
and then back to
$U_{\mathrm {I}}$
and then back to
![]() $U_{\mathrm {II}}$
) is given by as a sequence of elements:
$U_{\mathrm {II}}$
) is given by as a sequence of elements:
via the following sequence of maps between the stalks over
![]() $b_+, c_+ \in U_{\mathrm {II}}$
and
$b_+, c_+ \in U_{\mathrm {II}}$
and
![]() $b_-, c_- \in U_{\mathrm {I}}$
:
$b_-, c_- \in U_{\mathrm {I}}$
:
So we see that the analytic continuation along
![]() $\gamma $
maps u to
$\gamma $
maps u to
![]() $wu$
.
$wu$
.

Figure 7 Analytic continuation along
![]() $\gamma $
.
$\gamma $
.
![]() is equipped with the BV algebra structure inherited from
is equipped with the BV algebra structure inherited from
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\rho ^{-1}P_v])^{\dagger }$
(as described in the beginning of §5.2), which agrees with the one induced from the volume form
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\rho ^{-1}P_v])^{\dagger }$
(as described in the beginning of §5.2), which agrees with the one induced from the volume form ![]() . This allows us to define the sheaf of semiflat tropical vertex Lie algebras as
. This allows us to define the sheaf of semiflat tropical vertex Lie algebras as
Remark 5.8. The sheaf can actually be extended over the nonessential singular locus
![]() $\mathscr {S} \setminus \mathscr {S}_e$
because the monodromy around that locus acts trivially, but this is not necessary for our later discussion.
$\mathscr {S} \setminus \mathscr {S}_e$
because the monodromy around that locus acts trivially, but this is not necessary for our later discussion.
5.2.2 Explicit gluing away from codimension
 $2$
$2$
When we define the sheaves ![]() ’s in §4.1, the open subset
’s in §4.1, the open subset
![]() $W_{\alpha }$
is taken to be a sufficiently small neighborhood of
$W_{\alpha }$
is taken to be a sufficiently small neighborhood of
![]() $x \in \mathrm {int}_{\mathrm {re}}(\tau )$
for some
$x \in \mathrm {int}_{\mathrm {re}}(\tau )$
for some
![]() $\tau \in \mathscr {P}$
. In fact, we can choose one of these open subsets to be the large open dense subset
$\tau \in \mathscr {P}$
. In fact, we can choose one of these open subsets to be the large open dense subset
![]() $W_0$
. In this subsection, we construct the sheaves
$W_0$
. In this subsection, we construct the sheaves ![]() and
and ![]() on
on
![]() $W_0$
using an explicit gluing of the underlying complex analytic space.
$W_0$
using an explicit gluing of the underlying complex analytic space.
Over
![]() $\mathrm {int}_{\mathrm {re}}(\sigma )$
for
$\mathrm {int}_{\mathrm {re}}(\sigma )$
for
![]() $\sigma \in \mathscr {P}^{[n]}$
or over
$\sigma \in \mathscr {P}^{[n]}$
or over
![]() $\mathscr {W}_{\rho }$
for
$\mathscr {W}_{\rho }$
for
![]() $\rho \in \mathscr {P}^{[n-1]}$
with
$\rho \in \mathscr {P}^{[n-1]}$
with
![]() $\mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\rho ) = \emptyset $
, we have
$\mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\rho ) = \emptyset $
, we have ![]() , which was just constructed in §5.2.1. So it remains to consider
, which was just constructed in §5.2.1. So it remains to consider
![]() $\rho \in \mathscr {P}^{[n-1]}$
such that
$\rho \in \mathscr {P}^{[n-1]}$
such that
![]() $\mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\rho ) \neq \emptyset $
. The log structure of
$\mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\rho ) \neq \emptyset $
. The log structure of
![]() $V(\rho )^{\dagger }$
is prescribed by the slab functions
$V(\rho )^{\dagger }$
is prescribed by the slab functions
![]() $f_{v,\rho } \in \Gamma (\mathcal {O}_{V_{\rho }(v)})$
’s, which restrict to functions
$f_{v,\rho } \in \Gamma (\mathcal {O}_{V_{\rho }(v)})$
’s, which restrict to functions
![]() $s^{-1}_{v,\rho }(f_{v,\rho })$
’s on the torus
$s^{-1}_{v,\rho }(f_{v,\rho })$
’s on the torus
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Lambda _{\rho }]) \cong (\mathbb {C}^*)^{n-1}$
. Each of these can be pulled back via the natural projection
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Lambda _{\rho }]) \cong (\mathbb {C}^*)^{n-1}$
. Each of these can be pulled back via the natural projection
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\rho ^{-1}\Sigma _{v}]) \rightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Lambda _{\rho }])$
to give a function on
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\rho ^{-1}\Sigma _{v}]) \rightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Lambda _{\rho }])$
to give a function on
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\rho ^{-1}\Sigma _{v}])$
. In this case, we may fix the log chart
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\rho ^{-1}\Sigma _{v}])$
. In this case, we may fix the log chart
![]() $V(\rho )^{\dagger }|_{\nu ^{-1}(\mathscr {W}_{\rho ,v})} \rightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\rho ^{-1}P_{v}])^{\dagger }$
given by the equation
$V(\rho )^{\dagger }|_{\nu ^{-1}(\mathscr {W}_{\rho ,v})} \rightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\rho ^{-1}P_{v}])^{\dagger }$
given by the equation
 $$ \begin{align*} z^m \mapsto \left\{\begin{array}{lc} z^{\bar{m}} & \text{if } \langle \check{d}_{\rho}, \bar{m} \rangle \geq 0, \\ z^{\bar{m}} \big( s^{-1}_{v\rho}(f_{v,\rho})\big)^{\langle \check{d}_{\rho} , \bar{m} \rangle} & \text{if } \langle \check{d}_{\rho}, \bar{m} \rangle \leq 0.\end{array}\right. \end{align*} $$
$$ \begin{align*} z^m \mapsto \left\{\begin{array}{lc} z^{\bar{m}} & \text{if } \langle \check{d}_{\rho}, \bar{m} \rangle \geq 0, \\ z^{\bar{m}} \big( s^{-1}_{v\rho}(f_{v,\rho})\big)^{\langle \check{d}_{\rho} , \bar{m} \rangle} & \text{if } \langle \check{d}_{\rho}, \bar{m} \rangle \leq 0.\end{array}\right. \end{align*} $$
Write ![]() for the corresponding
for the corresponding
![]() $k^{\text {th}}$
-order thickening in
$k^{\text {th}}$
-order thickening in
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\rho ^{-1}P_{v}])$
, which gives a local model for smoothing
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\rho ^{-1}P_{v}])$
, which gives a local model for smoothing
![]() $V(\rho )|_{\nu ^{-1}(\mathscr {W}_{\rho ,v})}$
(as in §4). We take
$V(\rho )|_{\nu ^{-1}(\mathscr {W}_{\rho ,v})}$
(as in §4). We take
We have to specify the gluing on the overlap
![]() $\mathscr {W}_{\rho ,v} \cap \mathrm {int}_{\mathrm {re}}(\sigma _\pm )$
with the adjacent maximal cells
$\mathscr {W}_{\rho ,v} \cap \mathrm {int}_{\mathrm {re}}(\sigma _\pm )$
with the adjacent maximal cells
![]() $\sigma _{\pm }$
. This is given by first using parallel transport through v to relate the monoids
$\sigma _{\pm }$
. This is given by first using parallel transport through v to relate the monoids
![]() $\sigma _{\pm }^{-1}P_v$
and
$\sigma _{\pm }^{-1}P_v$
and
![]() $\rho ^{-1}P_v$
as in the semiflat case, and then an embedding
$\rho ^{-1}P_v$
as in the semiflat case, and then an embedding
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\sigma _{\pm }^{-1}P_{v}/q^{k+1}]) \rightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\rho ^{-1}P_{v}/q^{k+1}])$
via the formula
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\sigma _{\pm }^{-1}P_{v}/q^{k+1}]) \rightarrow \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\rho ^{-1}P_{v}/q^{k+1}])$
via the formula

where
![]() $s_{v\sigma _\pm }$
,
$s_{v\sigma _\pm }$
,
![]() $s_{\rho \sigma _\pm }$
are treated as maps
$s_{\rho \sigma _\pm }$
are treated as maps
![]() $\Lambda _{\sigma _{\pm }} \oplus \mathbb {Z} \rightarrow \mathbb {C}^*$
as before. We observe that there is a commutative diagram of log morphisms
$\Lambda _{\sigma _{\pm }} \oplus \mathbb {Z} \rightarrow \mathbb {C}^*$
as before. We observe that there is a commutative diagram of log morphisms

where
![]() $\mathscr {D} = \nu ^{-1}(\mathscr {W}_{\rho ,v} \cap \mathrm {int}_{\mathrm {re}}(\sigma _{\pm }))$
. The induced isomorphism
$\mathscr {D} = \nu ^{-1}(\mathscr {W}_{\rho ,v} \cap \mathrm {int}_{\mathrm {re}}(\sigma _{\pm }))$
. The induced isomorphism
of sheaves on the overlap
![]() $\mathscr {D}$
then provides the gluing for defining the sheaf
$\mathscr {D}$
then provides the gluing for defining the sheaf ![]() on
on
![]() $W_0$
. Hence, we obtain a sheaf
$W_0$
. Hence, we obtain a sheaf ![]() of BV algebras, where the BV structure is inherited from the local models
of BV algebras, where the BV structure is inherited from the local models
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\sigma ^{-1}P_v])$
and
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\sigma ^{-1}P_v])$
and
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\rho ^{-1}P_v])$
. Similarly, we can define the sheaf
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\rho ^{-1}P_v])$
. Similarly, we can define the sheaf ![]() of log de Rham forms over
of log de Rham forms over
![]() $W_0$
, together with a relative volume form
$W_0$
, together with a relative volume form ![]() by gluing the local
by gluing the local
![]() $\mu _v$
’s.
$\mu _v$
’s.
5.2.3 Relation between the semiflat dgBV algebra and the log structure
The difference between ![]() and
and ![]() is that analytic continuation along a path
is that analytic continuation along a path
![]() $\gamma $
in
$\gamma $
in
![]() $\mathrm {int}_{\mathrm {re}}(\sigma _{\pm }) \cup \mathrm {int}_{\mathrm {re}}(\rho )$
, where
$\mathrm {int}_{\mathrm {re}}(\sigma _{\pm }) \cup \mathrm {int}_{\mathrm {re}}(\rho )$
, where
![]() $\rho = \sigma _+ \cap \sigma _-$
, induces a nontrivial action on
$\rho = \sigma _+ \cap \sigma _-$
, induces a nontrivial action on ![]() (the semiflat sheaf) but not on
(the semiflat sheaf) but not on ![]() (the corrected sheaf). This is because, near a singular point
(the corrected sheaf). This is because, near a singular point
![]() $p \in \Gamma $
of the affine structure on B, there is another local model
$p \in \Gamma $
of the affine structure on B, there is another local model ![]() for
for
![]() $p \in W_{\alpha }$
constructed in 4.1, where restrictions of sections are invariant under analytic continuation (cf. Example 5.7). This is in line with the philosophy that monodromy is being cancelled by the slab functions
$p \in W_{\alpha }$
constructed in 4.1, where restrictions of sections are invariant under analytic continuation (cf. Example 5.7). This is in line with the philosophy that monodromy is being cancelled by the slab functions
![]() $f_{v,\rho }$
’s (which we also call initial wall-crossing factors). In view of this, we should be able to relate the sheaves
$f_{v,\rho }$
’s (which we also call initial wall-crossing factors). In view of this, we should be able to relate the sheaves ![]() and
and ![]() by adding back the initial wall-crossing factors
by adding back the initial wall-crossing factors
![]() $f_{v,\rho }$
’s.
$f_{v,\rho }$
’s.
Recall that the slab function
![]() $f_{v,\rho }$
is a function on
$f_{v,\rho }$
is a function on ![]() , whose zero locus is
, whose zero locus is
![]() $Z^{\rho }_1 \cap V_{\rho }(v)$
for
$Z^{\rho }_1 \cap V_{\rho }(v)$
for
![]() $\rho $
such that
$\rho $
such that
![]() $\mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\rho ) \neq \emptyset $
. Also, recall that, for
$\mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\rho ) \neq \emptyset $
. Also, recall that, for
![]() $\rho $
containing v,
$\rho $
containing v,
![]() $\rho _{v}$
is the unique contractible component in
$\rho _{v}$
is the unique contractible component in
![]() $\rho \cap \mathscr {C}^{-1}(B\setminus \mathscr {S})$
such that
$\rho \cap \mathscr {C}^{-1}(B\setminus \mathscr {S})$
such that
![]() $v \in \rho _{v}$
, as defined in Assumption 3.5. Note that the inverse image
$v \in \rho _{v}$
, as defined in Assumption 3.5. Note that the inverse image
![]() $\mu ^{-1}(\rho _v) \subset V_{\rho }(v)$
under the generalized moment map
$\mu ^{-1}(\rho _v) \subset V_{\rho }(v)$
under the generalized moment map
![]() $\mu $
is also a contractible open subset. It contains the zero-dimensional stratum
$\mu $
is also a contractible open subset. It contains the zero-dimensional stratum
![]() $x_v$
in
$x_v$
in
![]() $V_\rho (v)$
that corresponds to v. Since
$V_\rho (v)$
that corresponds to v. Since
![]() $f_{v,\rho } (x_v) =1$
, we can define
$f_{v,\rho } (x_v) =1$
, we can define
![]() $\log (f_{v,\rho })$
in a small neighborhood of
$\log (f_{v,\rho })$
in a small neighborhood of
![]() $x_v$
, and it can further be extended to the whole of
$x_v$
, and it can further be extended to the whole of
![]() $\mu ^{-1}(\rho _v) \subset V_{\rho }(v)$
because this subset is contractible. Restricting to the open dense torus orbit
$\mu ^{-1}(\rho _v) \subset V_{\rho }(v)$
because this subset is contractible. Restricting to the open dense torus orbit
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Lambda _{\rho }]) \cap \mu ^{-1}(\rho _v)$
, we obtain
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Lambda _{\rho }]) \cap \mu ^{-1}(\rho _v)$
, we obtain
![]() $\log (s_{v\rho }^{-1}(f_{v,\rho }))$
, which can in addition be lifted to a section in
$\log (s_{v\rho }^{-1}(f_{v,\rho }))$
, which can in addition be lifted to a section in ![]() for a sufficiently small
for a sufficiently small
![]() $\mathscr {W}_{\rho ,v}$
.
$\mathscr {W}_{\rho ,v}$
.
Now, we resolve the sheaves ![]() and
and ![]() by the complex
by the complex
![]() $\mathscr {T}^*$
introduced in §5.1. We let
$\mathscr {T}^*$
introduced in §5.1. We let
and equip it with
![]() $\bar {\partial }_{\circ }=d \otimes 1$
,
$\bar {\partial }_{\circ }=d \otimes 1$
, ![]() and
and
![]() $\wedge $
, making it a sheaf of dgBV algebras. Over the open subset
$\wedge $
, making it a sheaf of dgBV algebras. Over the open subset
![]() $\mathscr {W}_{\rho ,v}$
, using the explicit description of
$\mathscr {W}_{\rho ,v}$
, using the explicit description of ![]() , we consider the element
, we consider the element
where
![]() $\delta _{v,\rho }$
is any
$\delta _{v,\rho }$
is any
![]() $1$
-form with asymptotic support in
$1$
-form with asymptotic support in
![]() $\mathrm {int}_{\mathrm {re}}(\rho )_v$
and whose integral over any curve transversal to
$\mathrm {int}_{\mathrm {re}}(\rho )_v$
and whose integral over any curve transversal to
![]() $\mathrm {int}_{\mathrm {re}}(\rho )_v$
going from
$\mathrm {int}_{\mathrm {re}}(\rho )_v$
going from
![]() $\sigma _-$
to
$\sigma _-$
to
![]() $\sigma _+$
is asymptotically
$\sigma _+$
is asymptotically
![]() $1$
; such a 1-form can be constructed using a family of bump functions in the normal direction of
$1$
; such a 1-form can be constructed using a family of bump functions in the normal direction of
![]() $\mathrm {int}_{\mathrm {re}}(\rho )_v$
similar to Example 5.3 (see also [Reference Chan, Leung and Ma7, §4]). We can further extend the section
$\mathrm {int}_{\mathrm {re}}(\rho )_v$
similar to Example 5.3 (see also [Reference Chan, Leung and Ma7, §4]). We can further extend the section
![]() $\phi _{v,\rho }$
to the whole
$\phi _{v,\rho }$
to the whole
![]() $W_0$
by setting it to be
$W_0$
by setting it to be
![]() $0$
outside a small neighborhood of
$0$
outside a small neighborhood of
![]() $\mathrm {int}_{\mathrm {re}}(\rho )_v$
in
$\mathrm {int}_{\mathrm {re}}(\rho )_v$
in
![]() $\mathscr {W}_{\rho ,v}$
.
$\mathscr {W}_{\rho ,v}$
.
Definition 5.9. The sheaf of semiflat polyvector fields is defined as
which is equipped with a BV operator ![]() , a wedge product
, a wedge product
![]() $\wedge $
(and hence a Lie bracket
$\wedge $
(and hence a Lie bracket
![]() $[\cdot ,\cdot ]$
) and the operator
$[\cdot ,\cdot ]$
) and the operator
where
![]() $\bar {\partial }_{\circ } = d\otimes 1$
and
$\bar {\partial }_{\circ } = d\otimes 1$
and
![]() $\phi _{\mathrm {in}} := \sum _{v,\rho } \phi _{v,\rho }$
. We also define the sheaf of semiflat log de Rham forms as
$\phi _{\mathrm {in}} := \sum _{v,\rho } \phi _{v,\rho }$
. We also define the sheaf of semiflat log de Rham forms as
equipped with ![]() ,
,
![]() $\wedge $
,
$\wedge $
,
and a contraction action
![]() $\mathbin {\lrcorner }$
by elements in
$\mathbin {\lrcorner }$
by elements in ![]() .
.
It can be easily checked that ![]() , so we have a sheaf of dgBV algebras.
, so we have a sheaf of dgBV algebras.
On the other hand, we write
which is equipped with the operators
![]() $\bar {\partial }_0 = d\otimes 1$
,
$\bar {\partial }_0 = d\otimes 1$
, ![]() and
and
![]() $\wedge $
. The following important lemma is a comparison between the two sheaves of dgBV algebras.
$\wedge $
. The following important lemma is a comparison between the two sheaves of dgBV algebras.
Lemma 5.10. There exists a set of compatible isomorphisms
of sheaves of dgBV algebras such that
![]() $\varPhi \circ \bar {\partial }_0 = \bar {\partial }_{\mathrm {sf}} \circ \varPhi $
for each
$\varPhi \circ \bar {\partial }_0 = \bar {\partial }_{\mathrm {sf}} \circ \varPhi $
for each
![]() $k \in \mathbb {N}$
.
$k \in \mathbb {N}$
.
There also exists a set of compatible isomorphisms
of sheaves of dgas preserving the contraction action
![]() $\mathbin {\lrcorner }$
and such that
$\mathbin {\lrcorner }$
and such that
![]() $\varPhi \circ \bar {\partial }_0 = \bar {\partial }_{\mathrm {sf}} \circ \varPhi $
for each
$\varPhi \circ \bar {\partial }_0 = \bar {\partial }_{\mathrm {sf}} \circ \varPhi $
for each
![]() $k \in \mathbb {N}$
. Furthermore, the relative volume form
$k \in \mathbb {N}$
. Furthermore, the relative volume form ![]() is identified via
is identified via
![]() $\varPhi $
.
$\varPhi $
.
Proof. Outside those
![]() $\mathrm {int}_{\mathrm {re}}(\rho )$
’s such that
$\mathrm {int}_{\mathrm {re}}(\rho )$
’s such that
![]() $\mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\rho ) \neq \emptyset $
, the two sheaves are identical. So we will take a component
$\mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\rho ) \neq \emptyset $
, the two sheaves are identical. So we will take a component
![]() $\mathrm {int}_{\mathrm {re}}(\rho )_v$
of
$\mathrm {int}_{\mathrm {re}}(\rho )_v$
of
![]() $\mathrm {int}_{\mathrm {re}}(\rho ) \setminus \mathscr {S}$
and compare the sheaves on a neighborhood
$\mathrm {int}_{\mathrm {re}}(\rho ) \setminus \mathscr {S}$
and compare the sheaves on a neighborhood
![]() $\mathscr {W}_{\rho ,v}$
.
$\mathscr {W}_{\rho ,v}$
.
We fix a point
![]() $x \in \mathrm {int}_{\mathrm {re}}(\rho )_v$
and describe the map
$x \in \mathrm {int}_{\mathrm {re}}(\rho )_v$
and describe the map
![]() $\Phi $
at the stalks of the two sheaves. First, the preimage
$\Phi $
at the stalks of the two sheaves. First, the preimage
![]() $K:=\nu ^{-1}(x) \cong \Lambda _{\rho ,\mathbb {R}}^*/\Lambda _{\rho }^*$
can be identified as a real
$K:=\nu ^{-1}(x) \cong \Lambda _{\rho ,\mathbb {R}}^*/\Lambda _{\rho }^*$
can be identified as a real
![]() $(n-1)$
-dimensional torus in the analytic space
$(n-1)$
-dimensional torus in the analytic space
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Lambda _{\rho }]) \cong (\mathbb {C}^*)^{n-1}$
. We have an identification
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Lambda _{\rho }]) \cong (\mathbb {C}^*)^{n-1}$
. We have an identification
![]() $\rho ^{-1}\Sigma _v \cong \Sigma _{\rho } \times \Lambda _{\rho }$
, and we choose the unique primitive element
$\rho ^{-1}\Sigma _v \cong \Sigma _{\rho } \times \Lambda _{\rho }$
, and we choose the unique primitive element
![]() $m_{\rho } \in \Sigma _{\rho }$
in the ray pointing into
$m_{\rho } \in \Sigma _{\rho }$
in the ray pointing into
![]() $\sigma _+$
. As analytic spaces, we write
$\sigma _+$
. As analytic spaces, we write
where
![]() $u = z^{m_\rho }$
and
$u = z^{m_\rho }$
and
![]() $v = z^{-m_{\rho }}$
, and
$v = z^{-m_{\rho }}$
, and
The germ
![]() $\mathcal {O}_{V(\rho ),K}$
of analytic functions can be written as
$\mathcal {O}_{V(\rho ),K}$
of analytic functions can be written as
 $$ \begin{align*} \mathcal{O}_{V(\rho),K} = \left\{a_0 + \sum_{i=1}^{\infty} a_i u^i + \sum_{i=-1}^{-\infty}a_i v^{-i} \ \Big| \ a_i \in \mathcal{O}_{(\mathbb{C}^*)^{n-1}}(U) \ \text{for neigh. } U\supset K, \ \sup_{i\neq 0} \frac{\log|a_i|}{|i|} < \infty \right\}. \end{align*} $$
$$ \begin{align*} \mathcal{O}_{V(\rho),K} = \left\{a_0 + \sum_{i=1}^{\infty} a_i u^i + \sum_{i=-1}^{-\infty}a_i v^{-i} \ \Big| \ a_i \in \mathcal{O}_{(\mathbb{C}^*)^{n-1}}(U) \ \text{for neigh. } U\supset K, \ \sup_{i\neq 0} \frac{\log|a_i|}{|i|} < \infty \right\}. \end{align*} $$
Using the embedding ![]() in §5.2.2, we can write
in §5.2.2, we can write

with the relation
![]() $uv = q^l s_{v\rho }^{-1}(f_{v,\rho })$
(here, l is the change of slopes for
$uv = q^l s_{v\rho }^{-1}(f_{v,\rho })$
(here, l is the change of slopes for
![]() $\varphi _v$
across
$\varphi _v$
across
![]() $\rho $
). For the elements
$\rho $
). For the elements
![]() $(m_{\rho },\varphi _v(m_{\rho }))$
and
$(m_{\rho },\varphi _v(m_{\rho }))$
and
![]() $(-m_{\rho },\varphi _v(-m_{\rho }))$
in
$(-m_{\rho },\varphi _v(-m_{\rho }))$
in
![]() $\rho ^{-1}P_v$
, we have the identities (we omit the dependence on k when we write elements in the stalks of sheaves):
$\rho ^{-1}P_v$
, we have the identities (we omit the dependence on k when we write elements in the stalks of sheaves):
 $$ \begin{align*} z^{(m_{\rho},\varphi_v(m_{\rho}))} & = u, \\ z^{-(-m_{\rho},\varphi_v(-m_{\rho}))} & = s_{v\rho}^{-1}(f_{v,\rho})^{-1} v, \end{align*} $$
$$ \begin{align*} z^{(m_{\rho},\varphi_v(m_{\rho}))} & = u, \\ z^{-(-m_{\rho},\varphi_v(-m_{\rho}))} & = s_{v\rho}^{-1}(f_{v,\rho})^{-1} v, \end{align*} $$
describing the embedding ![]() . For polyvector fields, we can write
. For polyvector fields, we can write
The BV operator is described by the relations ![]() ,
,
![]() $[\partial _{n_1},\partial _{n_2}] =0$
, and
$[\partial _{n_1},\partial _{n_2}] =0$
, and

Similarly, we can write down the stalk for ![]() . As a module over ring
. As a module over ring
![]() $\mathcal {O}_{(\mathbb {C}^*)^{n-1},K}\otimes _{\mathbb {C}} \mathbb {C}[q]/(q^{k+1})$
, we have
$\mathcal {O}_{(\mathbb {C}^*)^{n-1},K}\otimes _{\mathbb {C}} \mathbb {C}[q]/(q^{k+1})$
, we have ![]() ; the ring structure on
; the ring structure on ![]() differs from that on
differs from that on ![]() and is determined by the relation
and is determined by the relation
![]() $uv = q^l$
. The embedding
$uv = q^l$
. The embedding ![]() is given by
is given by
 $$ \begin{align*} z^{(m_{\rho},\varphi_v(m_{\rho}))} & = u, \\ z^{-(-m_{\rho},\varphi_v(-m_{\rho}))} & = v. \end{align*} $$
$$ \begin{align*} z^{(m_{\rho},\varphi_v(m_{\rho}))} & = u, \\ z^{-(-m_{\rho},\varphi_v(-m_{\rho}))} & = v. \end{align*} $$
The formulae for the BV operator are the same as that for ![]() , except that for the last equation in (5.5), we have
, except that for the last equation in (5.5), we have ![]() instead.
instead.
We apply the argument in [Reference Chan, Leung and Ma7, §4], where we considered a scattering diagram consisting of only one wall, to relate these two sheaves. We can find a set of compatible elements ![]() , where
, where ![]() for
for
![]() $k\in \mathbb {N}$
, such that
$k\in \mathbb {N}$
, such that
![]() $e^{\theta }*\bar {\partial }_{\circ } = \bar {\partial }_{\mathrm {sf}}$
and
$e^{\theta }*\bar {\partial }_{\circ } = \bar {\partial }_{\mathrm {sf}}$
and ![]() . Explicitly,
. Explicitly,
![]() $\theta $
is a step-function-like section of the form
$\theta $
is a step-function-like section of the form
 $$ \begin{align*}\theta = \begin{cases} \log(s_{v\rho}^{-1}(f_{v,\rho})) \partial_{\check{d}_{\rho}} & \text{on } \mathrm{int}_{\mathrm{re}}(\sigma_+) \cap \mathscr{W}_{\rho,v},\\ 0 & \text{on } \mathrm{int}_{\mathrm{re}}(\sigma_-) \cap \mathscr{W}_{\rho,v}. \end{cases} \end{align*} $$
$$ \begin{align*}\theta = \begin{cases} \log(s_{v\rho}^{-1}(f_{v,\rho})) \partial_{\check{d}_{\rho}} & \text{on } \mathrm{int}_{\mathrm{re}}(\sigma_+) \cap \mathscr{W}_{\rho,v},\\ 0 & \text{on } \mathrm{int}_{\mathrm{re}}(\sigma_-) \cap \mathscr{W}_{\rho,v}. \end{cases} \end{align*} $$
For each
![]() $k\in \mathbb {N}$
, we also define
$k\in \mathbb {N}$
, we also define
![]() $\theta _0:= \log (s_{v\rho }^{-1}(f_{v,\rho })) \partial _{\check {d}_{\rho }}$
, as an element in
$\theta _0:= \log (s_{v\rho }^{-1}(f_{v,\rho })) \partial _{\check {d}_{\rho }}$
, as an element in ![]() . Now, we define the map
. Now, we define the map ![]() at the stalks by writing
at the stalks by writing
(and similarly for ![]() ) and extending the formulae
) and extending the formulae
 $$ \begin{align*} \begin{cases} \varPhi_x(\alpha) = \alpha & \text{for } \alpha \in \mathscr{T}_x,\\ \varPhi_x(f) = e^{[\theta,\cdot]}f = f & \text{for } f \in \mathcal{O}_{(\mathbb{C}^*)^{n-1},K}, \\ \varPhi_x(u) = e^{[\theta-\theta_0,\cdot]} u, & \\ \varPhi_x(v) = e^{[\theta,\cdot]} v ,& \\ \varPhi_x(\partial_n) = e^{[\theta-\theta_0,\cdot]} \partial_n & \text{for } n \in T_{v,\mathbb{R}}^* \end{cases} \end{align*} $$
$$ \begin{align*} \begin{cases} \varPhi_x(\alpha) = \alpha & \text{for } \alpha \in \mathscr{T}_x,\\ \varPhi_x(f) = e^{[\theta,\cdot]}f = f & \text{for } f \in \mathcal{O}_{(\mathbb{C}^*)^{n-1},K}, \\ \varPhi_x(u) = e^{[\theta-\theta_0,\cdot]} u, & \\ \varPhi_x(v) = e^{[\theta,\cdot]} v ,& \\ \varPhi_x(\partial_n) = e^{[\theta-\theta_0,\cdot]} \partial_n & \text{for } n \in T_{v,\mathbb{R}}^* \end{cases} \end{align*} $$
through the tensor product
![]() $\otimes _{\mathbb {R}}$
and skew-symmetrically in
$\otimes _{\mathbb {R}}$
and skew-symmetrically in
![]() $\partial _n$
’s.
$\partial _n$
’s.
To see that
![]() $\varPhi $
is the desired isomorphism, we check all the relations by computations:
$\varPhi $
is the desired isomorphism, we check all the relations by computations:
-
• Since
 $e^{[\theta ,\cdot ]} \circ \bar {\partial }_{\circ } \circ e^{-[\theta ,\cdot ]} = \bar {\partial }_{\mathrm {sf}}$
, we have similarly, we have
$e^{[\theta ,\cdot ]} \circ \bar {\partial }_{\circ } \circ e^{-[\theta ,\cdot ]} = \bar {\partial }_{\mathrm {sf}}$
, we have similarly, we have $$ \begin{align*} \bar{\partial}_{\mathrm{sf}} \varPhi_x(u) = e^{[\theta,\cdot]} \bar{\partial}_{\circ} ( e^{-[\theta_0,\cdot]} u) = 0; \end{align*} $$
$$ \begin{align*} \bar{\partial}_{\mathrm{sf}} \varPhi_x(u) = e^{[\theta,\cdot]} \bar{\partial}_{\circ} ( e^{-[\theta_0,\cdot]} u) = 0; \end{align*} $$
 $\bar {\partial }_{\mathrm {sf}}( \varPhi _x(v) ) = 0 = \bar {\partial }_{\mathrm {sf}}(\varPhi _x (\partial _n))$
. Hence, we have
$\bar {\partial }_{\mathrm {sf}}( \varPhi _x(v) ) = 0 = \bar {\partial }_{\mathrm {sf}}(\varPhi _x (\partial _n))$
. Hence, we have
 $\varPhi _x \circ \bar {\partial }_0 = \bar {\partial }_{\mathrm {sf}} \circ \varPhi _x$
.
$\varPhi _x \circ \bar {\partial }_0 = \bar {\partial }_{\mathrm {sf}} \circ \varPhi _x$
.
-
• We have
 $e^{-[\theta _0,\cdot ]} u = s^{-1}_{v\rho }(f_{v,\rho }) u$
and that is, the map
$e^{-[\theta _0,\cdot ]} u = s^{-1}_{v\rho }(f_{v,\rho }) u$
and that is, the map $$ \begin{align*}\varPhi_x(u) \varPhi_x(v) = e^{[\theta,\cdot]} (s^{-1}_{v\rho}(f_{v,\rho}) u) e^{[\theta,\cdot]}v =s^{-1}_{v\rho}(f_{v,\rho}) e^{[\theta,\cdot]} (uv) = q^l s^{-1}_{v\rho}(f_{v,\rho}) = \varPhi_x(uv ), \end{align*} $$
$$ \begin{align*}\varPhi_x(u) \varPhi_x(v) = e^{[\theta,\cdot]} (s^{-1}_{v\rho}(f_{v,\rho}) u) e^{[\theta,\cdot]}v =s^{-1}_{v\rho}(f_{v,\rho}) e^{[\theta,\cdot]} (uv) = q^l s^{-1}_{v\rho}(f_{v,\rho}) = \varPhi_x(uv ), \end{align*} $$
 $\varPhi _x$
preserves the product structure.
$\varPhi _x$
preserves the product structure.
-
• From the fact that
 , we see that
, we see that
 $e^{[\theta -\theta _0,\cdot ]}$
commutes with
$e^{[\theta -\theta _0,\cdot ]}$
commutes with  , and hence
, and hence  . We also have
. We also have
 $[\varPhi _x(\partial _{n_1}),\varPhi _x(\partial _{n_2})] = e^{[\theta -\theta _0,\cdot ]} [\partial _{n_1},\partial _{n_2}] = 0$
.
$[\varPhi _x(\partial _{n_1}),\varPhi _x(\partial _{n_2})] = e^{[\theta -\theta _0,\cdot ]} [\partial _{n_1},\partial _{n_2}] = 0$
. -
• Again from
 , we have
, we have 
-
• Finally, we have

We conclude that ![]() is an isomorphism of dgBV algebras. We need to check that the map
is an isomorphism of dgBV algebras. We need to check that the map
![]() $\varPhi _x$
agrees with the isomorphism
$\varPhi _x$
agrees with the isomorphism ![]() induced simply by the identity
induced simply by the identity ![]() , where
, where
![]() $\mathscr {C} = W_0 \setminus \bigcup _{\mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\rho ) \neq \emptyset } \mathrm {int}_{\mathrm {re}}(\rho )$
. For this purpose, we consider two nearby maximal cells
$\mathscr {C} = W_0 \setminus \bigcup _{\mathscr {S}_e \cap \mathrm {int}_{\mathrm {re}}(\rho ) \neq \emptyset } \mathrm {int}_{\mathrm {re}}(\rho )$
. For this purpose, we consider two nearby maximal cells
![]() $\sigma _{\pm }$
such that
$\sigma _{\pm }$
such that
![]() $\sigma _+ \cap \sigma _- = \rho $
. We have
$\sigma _+ \cap \sigma _- = \rho $
. We have ![]() , and the gluing of
, and the gluing of ![]() over
over
![]() $\mathscr {W}_{\rho ,v} \cap \sigma _+$
is given by parallel transporting through v, and then by the formulae
$\mathscr {W}_{\rho ,v} \cap \sigma _+$
is given by parallel transporting through v, and then by the formulae
 $$ \begin{align} \begin{cases} z^{m} \mapsto s^{-1}_{\rho\sigma_{+}}(m) z^m & \text{for } m \in \Lambda_{\rho},\\ u \mapsto s^{-1}_{\rho\sigma_+}(m_{\rho}) z^{m_{\rho}}, & \\ v \mapsto q^{l} s^{-1}_{v\sigma_+}(f_{v,\rho}) s^{-1}_{\rho\sigma_+}(-m_{\rho}) z^{-m_{\rho}}. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} z^{m} \mapsto s^{-1}_{\rho\sigma_{+}}(m) z^m & \text{for } m \in \Lambda_{\rho},\\ u \mapsto s^{-1}_{\rho\sigma_+}(m_{\rho}) z^{m_{\rho}}, & \\ v \mapsto q^{l} s^{-1}_{v\sigma_+}(f_{v,\rho}) s^{-1}_{\rho\sigma_+}(-m_{\rho}) z^{-m_{\rho}}. \end{cases} \end{align} $$
The only difference for gluing of ![]() is the last equation in (5.6), which is now replaced by the formula
is the last equation in (5.6), which is now replaced by the formula
![]() $v \mapsto q^{l} s^{-1}_{\rho \sigma _+}(-m_{\rho }) z^{-m_{\rho }}$
. Since we have
$v \mapsto q^{l} s^{-1}_{\rho \sigma _+}(-m_{\rho }) z^{-m_{\rho }}$
. Since we have
 $$ \begin{align*}\varPhi_x(v) = \begin{cases} s_{v\rho}^{-1}(f_{v,\rho}) v & \text{on } U_x \cap \mathrm{int}_{\mathrm{re}}(\sigma_+), \\ v & \text{on } U_x \cap \mathrm{int}_{\mathrm{re}}(\sigma_-) \end{cases} \end{align*} $$
$$ \begin{align*}\varPhi_x(v) = \begin{cases} s_{v\rho}^{-1}(f_{v,\rho}) v & \text{on } U_x \cap \mathrm{int}_{\mathrm{re}}(\sigma_+), \\ v & \text{on } U_x \cap \mathrm{int}_{\mathrm{re}}(\sigma_-) \end{cases} \end{align*} $$
on a sufficiently small neighborhood
![]() $U_x$
of x, we see that
$U_x$
of x, we see that
![]() $\varPhi _x(v) \mapsto q^{l} s^{-1}_{v\sigma _+}(f_{v,\rho }) s^{-1}_{\rho \sigma _+}(-m_{\rho }) z^{-m_{\rho }}$
under the gluing map of
$\varPhi _x(v) \mapsto q^{l} s^{-1}_{v\sigma _+}(f_{v,\rho }) s^{-1}_{\rho \sigma _+}(-m_{\rho }) z^{-m_{\rho }}$
under the gluing map of ![]() on
on
![]() $U_x \cap \mathrm {int}_{\mathrm {re}}(\sigma _+)$
. This shows the compatibility of
$U_x \cap \mathrm {int}_{\mathrm {re}}(\sigma _+)$
. This shows the compatibility of
![]() $\varPhi _x$
with the gluing of
$\varPhi _x$
with the gluing of ![]() and
and ![]() over
over
![]() $U_x \cap \mathrm {int}_{\mathrm {re}}(\sigma _+)$
. A similar argument applies for
$U_x \cap \mathrm {int}_{\mathrm {re}}(\sigma _+)$
. A similar argument applies for
![]() $U_x \cap \mathrm {int}_{\mathrm {re}}(\sigma _-)$
.
$U_x \cap \mathrm {int}_{\mathrm {re}}(\sigma _-)$
.
The proof for ![]() is similar and will be omitted. The volume form is preserved under
is similar and will be omitted. The volume form is preserved under
![]() $\varPhi $
because we have
$\varPhi $
because we have ![]() . This completes the proof of the lemma.
. This completes the proof of the lemma.
5.2.4 A global sheaf of dgLas from gluing of the semiflat sheaves
We shall apply the procedure described in §4.3 to the semiflat sheaves to glue a global sheaf of dgLas. First of all, we choose an open cover
![]() $\{W_{\alpha }\}_{\alpha \in \mathscr {I}}$
satisfying the Condition 4.1, together with a decomposition
$\{W_{\alpha }\}_{\alpha \in \mathscr {I}}$
satisfying the Condition 4.1, together with a decomposition
![]() $\mathscr {I} = \mathscr {I}_1 \sqcup \mathscr {I}_2$
such that
$\mathscr {I} = \mathscr {I}_1 \sqcup \mathscr {I}_2$
such that
![]() $\mathcal {W}_1 = \{W_{\alpha }\}_{\alpha \in \mathscr {I}_1}$
is a cover of the semiflat part
$\mathcal {W}_1 = \{W_{\alpha }\}_{\alpha \in \mathscr {I}_1}$
is a cover of the semiflat part
![]() $W_0$
, and
$W_0$
, and
![]() $\mathcal {W}_2 = \{W_{\alpha }\}_{\alpha \in \mathscr {I}_2}$
is a cover of a neighborhood of
$\mathcal {W}_2 = \{W_{\alpha }\}_{\alpha \in \mathscr {I}_2}$
is a cover of a neighborhood of
![]() $\big ( \bigcup _{\tau \in \mathscr {P}^{[n-2]}}\tau \big ) \cup \big ( \bigcup _{\rho \cap \mathscr {S}_e \neq \emptyset } \mathscr {S} \cap \mathrm {int}_{\mathrm {re}}(\rho ) \big )$
.
$\big ( \bigcup _{\tau \in \mathscr {P}^{[n-2]}}\tau \big ) \cup \big ( \bigcup _{\rho \cap \mathscr {S}_e \neq \emptyset } \mathscr {S} \cap \mathrm {int}_{\mathrm {re}}(\rho ) \big )$
.
For each
![]() $W_{\alpha }$
, we have a compatible set of local sheaves
$W_{\alpha }$
, we have a compatible set of local sheaves ![]() of BV algebras, local sheaves
of BV algebras, local sheaves ![]() of dgas, and relative volume elements
of dgas, and relative volume elements ![]() ,
,
![]() $k \in \mathbb {N}$
(as in §4.1). We can further demand that, over the semiflat part
$k \in \mathbb {N}$
(as in §4.1). We can further demand that, over the semiflat part
![]() $W_0$
, we have
$W_0$
, we have ![]() ,
, ![]() and
and ![]() , and hence
, and hence ![]() and
and ![]() for
for
![]() $\alpha \in \mathscr {I}_1$
.
$\alpha \in \mathscr {I}_1$
.
Using the construction in §4.3, we obtain a Gerstenhaber deformation ![]() specified by
specified by ![]() , which give rise to sets of compatible global sheaves
, which give rise to sets of compatible global sheaves ![]() and
and ![]() ,
,
![]() $k \in \mathbb {N}$
. Restricting to the semiflat part, we get two Gerstenhaber deformations
$k \in \mathbb {N}$
. Restricting to the semiflat part, we get two Gerstenhaber deformations ![]() and
and ![]() , which must be equivalent as
, which must be equivalent as ![]() . So we have a set of compatible isomorphisms locally given by
. So we have a set of compatible isomorphisms locally given by ![]() for some element
for some element ![]() , for each
, for each
![]() $k \in \mathbb {N}$
, and they fit into the following commutative diagram
$k \in \mathbb {N}$
, and they fit into the following commutative diagram

Since the predifferential on ![]() obtained from the construction in §4.3 is of the form
obtained from the construction in §4.3 is of the form
![]() $\bar {\partial }_\alpha + [\eta _{\alpha },\cdot ]$
for some
$\bar {\partial }_\alpha + [\eta _{\alpha },\cdot ]$
for some ![]() , pulling back via
, pulling back via
![]() $h_{\alpha }$
gives a global element
$h_{\alpha }$
gives a global element ![]() such that
such that
Theorem 4.18 gives a Maurer–Cartan solution ![]() such that
such that
![]() $(\bar {\partial }+[\phi ,\cdot ])^2=0$
, together with a holomorphic volume form
$(\bar {\partial }+[\phi ,\cdot ])^2=0$
, together with a holomorphic volume form ![]() , compatible for each k. We denote the pullback of
, compatible for each k. We denote the pullback of
![]() $\phi $
under
$\phi $
under
![]() $h_{\alpha }$
’s to
$h_{\alpha }$
’s to ![]() as
as
![]() $\phi _0$
and that of volume form to
$\phi _0$
and that of volume form to ![]() as
as ![]() . We see that the equation
. We see that the equation
is satisfied, or equivalently, that
![]() $\eta +\phi _0 + tg$
is a solution to the extended Maurer–Cartan equation 4.10.
$\eta +\phi _0 + tg$
is a solution to the extended Maurer–Cartan equation 4.10.
Lemma 5.11. If the holomorphic volume form ![]() is normalized in the sense of Definition 4.19, then we can find a set of compatible
is normalized in the sense of Definition 4.19, then we can find a set of compatible ![]() ,
,
![]() $k \in \mathbb {N}$
such that
$k \in \mathbb {N}$
such that
As a consequence, the Maurer–Cartan solution
![]() $\eta +\phi _0 + tg$
is gauge equivalent to a solution of the form
$\eta +\phi _0 + tg$
is gauge equivalent to a solution of the form
![]() $\zeta _0 + t\cdot 0$
for some
$\zeta _0 + t\cdot 0$
for some ![]() , via the gauge transformation
, via the gauge transformation ![]() .
.
Proof. We should construct
![]() $\mathcal {V}$
by induction on k as in the proof of Lemma 4.6. Namely, suppose
$\mathcal {V}$
by induction on k as in the proof of Lemma 4.6. Namely, suppose
![]() $\mathcal {V}$
is constructed for the
$\mathcal {V}$
is constructed for the
![]() $(k-1)^{\text {st}}$
-order, then we shall lift it to the
$(k-1)^{\text {st}}$
-order, then we shall lift it to the
![]() $k^{\text {th}}$
-order. We prove the existence of a lifting
$k^{\text {th}}$
-order. We prove the existence of a lifting ![]() at every stalk
at every stalk
![]() $x \in W_0$
and use partition of unity to glue a global lifting
$x \in W_0$
and use partition of unity to glue a global lifting
![]() $\mathcal {V}$
.
$\mathcal {V}$
.
First of all, we can always find a gauge transformation ![]() such that
such that
So we have ![]() , which implies that
, which implies that ![]() . We can write
. We can write ![]() in the stalk at x for some germ
in the stalk at x for some germ ![]() of holomorphic functions. Applying Lemma 4.6, we can further choose
of holomorphic functions. Applying Lemma 4.6, we can further choose
![]() $\theta $
so that
$\theta $
so that
![]() $h=h(q) \in (q)\subset \mathbb {C}[q]/q^{k+1}$
. In a sufficiently small neighborhood
$h=h(q) \in (q)\subset \mathbb {C}[q]/q^{k+1}$
. In a sufficiently small neighborhood
![]() $U_x$
, we find an element
$U_x$
, we find an element
![]() $\varrho _x \in \mathscr {T}^n(U_x)$
as in Definition 4.19. The fact that the volume form is normalized forces
$\varrho _x \in \mathscr {T}^n(U_x)$
as in Definition 4.19. The fact that the volume form is normalized forces ![]() to be constant with respect to the Gauss–Manin connection
to be constant with respect to the Gauss–Manin connection ![]() . Tracing through the exact sequence (4.14) on
. Tracing through the exact sequence (4.14) on
![]() $U_x$
, we can lift
$U_x$
, we can lift ![]() to
to ![]() which is closed under
which is closed under ![]() . As a consequence, we have
. As a consequence, we have ![]() , and hence we conclude that
, and hence we conclude that
![]() $h(q) =0$
.
$h(q) =0$
.
Now, we have to solve for a lifting
![]() $\mathcal {V}_x$
such that
$\mathcal {V}_x$
such that ![]() up to the
up to the
![]() $k^{\text {th}}$
-order. This is equivalent to solving for a lifting u satisfying
$k^{\text {th}}$
-order. This is equivalent to solving for a lifting u satisfying ![]() for the
for the
![]() $k^{\text {th}}$
-order once the
$k^{\text {th}}$
-order once the
![]() $(k-1)^{\text {st}}$
-order is given. Take an arbitrary lifting
$(k-1)^{\text {st}}$
-order is given. Take an arbitrary lifting
![]() $\tilde {u}$
to the
$\tilde {u}$
to the
![]() $k^{\text {th}}$
-order, and making use of the formula in [Reference Chan, Leung and Ma8, Lem. 2.8], we have
$k^{\text {th}}$
-order, and making use of the formula in [Reference Chan, Leung and Ma8, Lem. 2.8], we have

where
![]() $\delta _{\tilde {u}} = -[\tilde {u},\cdot ]$
. From
$\delta _{\tilde {u}} = -[\tilde {u},\cdot ]$
. From ![]() , we use induction on the order j to prove that
, we use induction on the order j to prove that ![]() up to order
up to order
![]() $(k-1)$
. Therefore, we can write
$(k-1)$
. Therefore, we can write
for some ![]() by the fact that the cohomology sheaf under
by the fact that the cohomology sheaf under ![]() is free over
is free over ![]() (see the discussion right after Condition 4.14). Setting
(see the discussion right after Condition 4.14). Setting
![]() $u = \tilde {u} - q^{k} \breve {u}$
will then solve the equation.
$u = \tilde {u} - q^{k} \breve {u}$
will then solve the equation.
The element
![]() $\mathcal {V}$
obtained in Lemma 5.11 can be used to conjugate the operator
$\mathcal {V}$
obtained in Lemma 5.11 can be used to conjugate the operator
![]() $\bar {\partial }_0+[\eta +\phi _0,\cdot ]$
to get
$\bar {\partial }_0+[\eta +\phi _0,\cdot ]$
to get
![]() $\bar {\partial }_0 + [\zeta _0,\cdot ]$
, that is,
$\bar {\partial }_0 + [\zeta _0,\cdot ]$
, that is,
The volume form ![]() will be holomorphic under the operator
will be holomorphic under the operator
![]() $\bar {\partial }_0 + [\zeta _0,\cdot ]$
. From the equation (4.13), we observe that
$\bar {\partial }_0 + [\zeta _0,\cdot ]$
. From the equation (4.13), we observe that ![]() . Furthermore, the image of
. Furthermore, the image of
![]() $\zeta _0$
under the isomorphism
$\zeta _0$
under the isomorphism ![]() in Lemma 5.10 gives
in Lemma 5.10 gives ![]() , and an operator of the form
, and an operator of the form
where
![]() $\phi _{\mathrm {in}} = \sum _{v,\rho } \phi _{v,\rho }$
, that acts on
$\phi _{\mathrm {in}} = \sum _{v,\rho } \phi _{v,\rho }$
, that acts on ![]() .
.
Equipping with this operator, the semiflat sheaf ![]() can be glued to the sheaves
can be glued to the sheaves ![]() ’s for
’s for
![]() $\alpha \in \mathscr {I}_2$
, preserving all the operators. More explicitly, on each overlap
$\alpha \in \mathscr {I}_2$
, preserving all the operators. More explicitly, on each overlap
![]() $W_{0\alpha }:=W_0 \cap W_{\alpha }$
, we have
$W_{0\alpha }:=W_0 \cap W_{\alpha }$
, we have
defined by
for
![]() $\beta \in \mathscr {I}_1$
, which sends the operator
$\beta \in \mathscr {I}_1$
, which sends the operator
![]() $\bar {\partial }_{\circ } + [\phi _{\mathrm {in}} + \phi _{\mathrm {s}},\cdot ]$
to
$\bar {\partial }_{\circ } + [\phi _{\mathrm {in}} + \phi _{\mathrm {s}},\cdot ]$
to
![]() $\bar {\partial }_\alpha + [\eta _{\alpha }+\phi ,\cdot ]$
.
$\bar {\partial }_\alpha + [\eta _{\alpha }+\phi ,\cdot ]$
.
Definition 5.12. We call ![]() , equipped with the structure of a dgLa using
, equipped with the structure of a dgLa using
![]() $\bar {\partial }_{\circ }$
and
$\bar {\partial }_{\circ }$
and
![]() $[\cdot ,\cdot ]$
inherited from
$[\cdot ,\cdot ]$
inherited from ![]() , the sheaf of semiflat tropical vertex differential graded Lie algebras (abbreviated as sf-TVdgLa).
, the sheaf of semiflat tropical vertex differential graded Lie algebras (abbreviated as sf-TVdgLa).
Note that ![]() . Also, we have
. Also, we have ![]() since
since ![]() , and a direct computation shows that
, and a direct computation shows that ![]() . Thus,
. Thus, ![]() , and the operator
, and the operator
![]() $\bar {\partial }_{\circ } + [\phi _{\mathrm {in}}+\phi _{\mathrm {s}},\cdot ]$
preserves the sub-dgLa
$\bar {\partial }_{\circ } + [\phi _{\mathrm {in}}+\phi _{\mathrm {s}},\cdot ]$
preserves the sub-dgLa ![]() .
.
From the description of the sheaf
![]() $\mathscr {T}^*$
, we can see that locally on
$\mathscr {T}^*$
, we can see that locally on
![]() $U \subset W_0$
,
$U \subset W_0$
,
![]() $\phi _{\mathrm {s}}$
is supported on finitely many codimension one polyhedral subsets, called walls or slabs, which are constituents of a scattering diagram. This is why we use the subscript ‘s’ in
$\phi _{\mathrm {s}}$
is supported on finitely many codimension one polyhedral subsets, called walls or slabs, which are constituents of a scattering diagram. This is why we use the subscript ‘s’ in
![]() $\phi _{\mathrm {s}}$
, which stands for ‘scattering’.
$\phi _{\mathrm {s}}$
, which stands for ‘scattering’.
5.3 Consistent scattering diagrams and Maurer–Cartan solutions
5.3.1 Scattering diagrams
In this subsection, we recall the notion of scattering diagrams introduced by Kontsevich–Soibelman [Reference Kontsevich and Soibelman36] and Gross–Siebert [Reference Gross and Siebert29], and make modifications to suit our needs. We begin with the notion of walls from [Reference Gross and Siebert29, §2]. Let
 $$ \begin{align*}\hat{\mathscr{S}} = \left( \bigcup_{\tau \in \mathscr{P}^{[n-2]}}\tau \right) \cup \left( \bigcup_{\substack{\rho \in \mathscr{P}^{[n-1]}\\ \rho \cap \mathscr{S}_e \neq \emptyset}} \mathscr{S} \cap \mathrm{int}_{\mathrm{re}}(\rho) \right)\end{align*} $$
$$ \begin{align*}\hat{\mathscr{S}} = \left( \bigcup_{\tau \in \mathscr{P}^{[n-2]}}\tau \right) \cup \left( \bigcup_{\substack{\rho \in \mathscr{P}^{[n-1]}\\ \rho \cap \mathscr{S}_e \neq \emptyset}} \mathscr{S} \cap \mathrm{int}_{\mathrm{re}}(\rho) \right)\end{align*} $$
be equipped with a polyhedral decomposition induced from
![]() $\mathscr {P}$
and
$\mathscr {P}$
and
![]() $\mathscr {S}$
. For the exposition below, we will always fix
$\mathscr {S}$
. For the exposition below, we will always fix
![]() $k>0$
and consider all these structures modulo
$k>0$
and consider all these structures modulo
![]() $\mathbf {m}^{k+1} = (q^{k+1})$
.
$\mathbf {m}^{k+1} = (q^{k+1})$
.
Definition 5.13. A wall
![]() $(\mathbf {w},\sigma _{\mathbf {w}}, \check {d}_{\mathbf {w}}, \Theta _{\mathbf {w}})$
consists of
$(\mathbf {w},\sigma _{\mathbf {w}}, \check {d}_{\mathbf {w}}, \Theta _{\mathbf {w}})$
consists of
-
• a maximal cell
 $\sigma _{\mathbf {w}}\in \mathscr {P}^{[n]}$
,
$\sigma _{\mathbf {w}}\in \mathscr {P}^{[n]}$
, -
• a closed
 $(n-1)$
-dimensional tropical polyhedral subset
$(n-1)$
-dimensional tropical polyhedral subset
 $\mathbf {w}$
of
$\mathbf {w}$
of
 $\sigma _{\mathbf {w}}$
such that
$\sigma _{\mathbf {w}}$
such that  $$ \begin{align*}\mathrm{int}_{\mathrm{re}}(\mathbf{w}) \cap \left( \bigcup_{\substack{\rho \in \mathscr{P}^{[n-1]}\\ \rho \cap \mathscr{S}_e \neq \emptyset}} \mathrm{int}_{\mathrm{re}}(\rho) \right) = \emptyset,\end{align*} $$
$$ \begin{align*}\mathrm{int}_{\mathrm{re}}(\mathbf{w}) \cap \left( \bigcup_{\substack{\rho \in \mathscr{P}^{[n-1]}\\ \rho \cap \mathscr{S}_e \neq \emptyset}} \mathrm{int}_{\mathrm{re}}(\rho) \right) = \emptyset,\end{align*} $$
-
• a choice of a primitive normal
 $\check {d}_{\mathbf {w}}$
, and
$\check {d}_{\mathbf {w}}$
, and -
• a section
 $\Theta _{\mathbf {w}}$
of the tropical vertex group
$\Theta _{\mathbf {w}}$
of the tropical vertex group  over a sufficiently small neighborhood of
over a sufficiently small neighborhood of
 $\mathbf {w}$
.
$\mathbf {w}$
.
We call
![]() $\Theta _{\mathbf {w}}$
the wall-crossing factor associated to the wall
$\Theta _{\mathbf {w}}$
the wall-crossing factor associated to the wall
![]() $\mathbf {w}$
. We may write a wall as
$\mathbf {w}$
. We may write a wall as
![]() $(\mathbf {w},\Theta _{\mathbf {w}})$
for simplicity.
$(\mathbf {w},\Theta _{\mathbf {w}})$
for simplicity.
A wall cannot be contained in
![]() $\rho $
with
$\rho $
with
![]() $\rho \cap \mathscr {S}_e \neq \emptyset $
. We define a notion of slabs for these subsets of codimension one strata
$\rho \cap \mathscr {S}_e \neq \emptyset $
. We define a notion of slabs for these subsets of codimension one strata
![]() $\rho $
intersecting
$\rho $
intersecting
![]() $\mathscr {S}_e$
. The difference is that we have an extra term
$\mathscr {S}_e$
. The difference is that we have an extra term
![]() $\varTheta _{v,\rho }$
coming from the slab function
$\varTheta _{v,\rho }$
coming from the slab function
![]() $f_{v,\rho }$
.
$f_{v,\rho }$
.
Definition 5.14. A slab
![]() $(\mathbf {b}, \rho _{\mathbf {b}}, \check {d}_{\rho }, \varXi _{\mathbf {b}})$
consists of
$(\mathbf {b}, \rho _{\mathbf {b}}, \check {d}_{\rho }, \varXi _{\mathbf {b}})$
consists of
-
• an
 $(n-1)$
-cell
$(n-1)$
-cell
 $\rho _{\mathbf {b}} \in \mathscr {P}^{[n-1]}$
such that
$\rho _{\mathbf {b}} \in \mathscr {P}^{[n-1]}$
such that
 $\rho _{\mathbf {b}} \cap \mathscr {S}_e \neq \emptyset $
,
$\rho _{\mathbf {b}} \cap \mathscr {S}_e \neq \emptyset $
, -
• a closed
 $(n-1)$
-dimensional tropical polyhedral subset
$(n-1)$
-dimensional tropical polyhedral subset
 $\mathbf {b}$
of
$\mathbf {b}$
of
 $\rho _{\mathbf {b}} \setminus (\rho _{\mathbf {b}} \cap \mathscr {S})$
,
$\rho _{\mathbf {b}} \setminus (\rho _{\mathbf {b}} \cap \mathscr {S})$
, -
• a choice of a primitive normal
 $\check {d}_{\rho }$
, and
$\check {d}_{\rho }$
, and -
• a section
 $\varXi _{\mathbf {b}}$
of
$\varXi _{\mathbf {b}}$
of  over a sufficiently small neighborhood of
over a sufficiently small neighborhood of
 $\mathbf {b}$
.
$\mathbf {b}$
.
The wall-crossing factor associated to the slab
![]() $\mathbf {b}$
is given by
$\mathbf {b}$
is given by
where v is the unique vertex such that
![]() $\mathrm {int}_{\mathrm {re}}(\rho )_v$
contains
$\mathrm {int}_{\mathrm {re}}(\rho )_v$
contains
![]() $\mathbf {b}$
and
$\mathbf {b}$
and
(cf. equation (5.4)). We may write a slab as
![]() $(\mathbf {b},\Theta _{\mathbf {b}})$
for simplicity.
$(\mathbf {b},\Theta _{\mathbf {b}})$
for simplicity.
Remark 5.15. In the above definition, a slab is not allowed to intersect the singular locus
![]() $\mathscr {S}$
. This is different from the situation in [Reference Gross and Siebert29, §2]. However, in our definition of consistent scattering diagrams, we will require consistency around each stratum of
$\mathscr {S}$
. This is different from the situation in [Reference Gross and Siebert29, §2]. However, in our definition of consistent scattering diagrams, we will require consistency around each stratum of
![]() $\mathscr {S}$
.
$\mathscr {S}$
.
Example 5.16. We consider the three-dimensional example shown in Figure 8, from which we can see possible supports of the walls and slabs. There are two adjacent maximal cells intersecting at
![]() $\rho \in \mathscr {P}^{[n-1]}$
with
$\rho \in \mathscr {P}^{[n-1]}$
with
![]() $\mathscr {S}_e \cap \rho = \mathscr {S} \cap \rho $
colored in red. The two-dimensional polyhedral subsets colored in blue can support walls and the polyhedral subset colored in green can support a slab because it is lying inside
$\mathscr {S}_e \cap \rho = \mathscr {S} \cap \rho $
colored in red. The two-dimensional polyhedral subsets colored in blue can support walls and the polyhedral subset colored in green can support a slab because it is lying inside
![]() $\rho $
with
$\rho $
with
![]() $\mathscr {S}_e \cap \rho \neq \emptyset $
.
$\mathscr {S}_e \cap \rho \neq \emptyset $
.

Figure 8 Supports of walls/slabs.
Definition 5.17. A (
![]() $k^{\text {th}}$
-order) scattering diagram is a countable collection
$k^{\text {th}}$
-order) scattering diagram is a countable collection
of walls or slabs such that the intersections of any two walls/slabs is at most an
![]() $(n-2)$
-dimensional tropical polyhedral subset, and
$(n-2)$
-dimensional tropical polyhedral subset, and
![]() $\{\mathbf {w}_i \cap W_0 \}_{i\in \mathbb {N}} \cup \{ \mathbf {b}_j\cap W_0\}_{j\in \mathbb {N}}$
is locally finite in
$\{\mathbf {w}_i \cap W_0 \}_{i\in \mathbb {N}} \cup \{ \mathbf {b}_j\cap W_0\}_{j\in \mathbb {N}}$
is locally finite in
![]() $W_0$
.
$W_0$
.
Our notion of scattering diagrams is more flexible than the one defined in [Reference Kontsevich and Soibelman36, Reference Gross and Siebert29] in two ways: First, there is no relation between the affine direction orthogonal to a wall
![]() $\mathbf {w}$
or a slab
$\mathbf {w}$
or a slab
![]() $\mathbf {b}$
and its wall crossing factor. As a result, we cannot allow overlapping of walls/slabs in their relative interior because in that case their associated wall crossing factors are not necessarily commuting. Second, we only require that the intersection of
$\mathbf {b}$
and its wall crossing factor. As a result, we cannot allow overlapping of walls/slabs in their relative interior because in that case their associated wall crossing factors are not necessarily commuting. Second, we only require that the intersection of
![]() $\mathscr {D}$
with
$\mathscr {D}$
with
![]() $W_0$
is a locally finite collection of
$W_0$
is a locally finite collection of
![]() $W_0$
, which implies that we allow a possibly infinite number of walls/slabs approaching strata of
$W_0$
, which implies that we allow a possibly infinite number of walls/slabs approaching strata of
![]() $\hat {\mathscr {S}}$
. In the construction of the scattering diagram
$\hat {\mathscr {S}}$
. In the construction of the scattering diagram
![]() $\mathscr {D}(\varphi )$
associated to a Maurer–Cartan solution
$\mathscr {D}(\varphi )$
associated to a Maurer–Cartan solution
![]() $\varphi $
below, all the walls/slabs will be compact subsets of
$\varphi $
below, all the walls/slabs will be compact subsets of
![]() $W_0$
. These walls will not intersect
$W_0$
. These walls will not intersect
![]() $\hat {\mathscr {S}}$
, as illustrated in Figure 8. However, there could be a union of infinitely many walls limiting to some strata of
$\hat {\mathscr {S}}$
, as illustrated in Figure 8. However, there could be a union of infinitely many walls limiting to some strata of
![]() $\hat {\mathscr {S}}$
. See also Remark 1.2.
$\hat {\mathscr {S}}$
. See also Remark 1.2.
Example 5.18. For the two-dimensional example shown in Figure 9, we see a vertex v and its adjacent cells, and the singular locus
![]() $\mathscr {S}_e$
consists of the red crosses. In our version of scattering diagrams, we allow infinitely many intervals limiting to
$\mathscr {S}_e$
consists of the red crosses. In our version of scattering diagrams, we allow infinitely many intervals limiting to
![]() $\{v\}$
or
$\{v\}$
or
![]() $\mathscr {S}_e$
.
$\mathscr {S}_e$
.

Figure 9 Walls/slabs around
![]() $\hat{\mathscr{S}}$
.
$\hat{\mathscr{S}}$
.
Given a scattering diagram
![]() $\hat{\mathscr {D}}$
, we can define its support as
$\hat{\mathscr {D}}$
, we can define its support as
![]() $|\mathscr {D}|:= \bigcup _{i \in \mathbb {N}} \mathbf {w}_i \cup \bigcup _{j \in \mathbb {N}} \mathbf {b}_j$
. There is an induced polyhedral decomposition on
$|\mathscr {D}|:= \bigcup _{i \in \mathbb {N}} \mathbf {w}_i \cup \bigcup _{j \in \mathbb {N}} \mathbf {b}_j$
. There is an induced polyhedral decomposition on
![]() $|\mathscr {D}|$
such that its
$|\mathscr {D}|$
such that its
![]() $(n-1)$
-cells are closed subsets of some walls or slabs, and all intersections of walls or slabs are lying in the union of the
$(n-1)$
-cells are closed subsets of some walls or slabs, and all intersections of walls or slabs are lying in the union of the
![]() $(n-2)$
-cells. We write
$(n-2)$
-cells. We write
![]() $|\mathscr {D}|^{[i]}$
for the collection of all the i-cells in this polyhedral decomposition. We may assume, after further subdividing the walls or slabs in
$|\mathscr {D}|^{[i]}$
for the collection of all the i-cells in this polyhedral decomposition. We may assume, after further subdividing the walls or slabs in
![]() $\mathscr {D}$
if necessary, that every wall or slab is an
$\mathscr {D}$
if necessary, that every wall or slab is an
![]() $(n-1)$
-cell in
$(n-1)$
-cell in
![]() $|\mathscr {D}|$
. We call an
$|\mathscr {D}|$
. We call an
![]() $(n-2)$
-cell
$(n-2)$
-cell
![]() $\mathfrak {j} \in |\mathscr {D}|^{[n-2]}$
a joint, and a connected component of
$\mathfrak {j} \in |\mathscr {D}|^{[n-2]}$
a joint, and a connected component of
![]() $W_0 \setminus |\mathscr {D}|$
a chamber.
$W_0 \setminus |\mathscr {D}|$
a chamber.
Given a wall or slab, we shall make sense of wall crossing in terms of jumping of holomorphic functions across it. Instead of formulating the definition in terms of path-ordered products of elements in the tropical vertex group as in [Reference Gross and Siebert29], we will express it in terms of the action by the tropical vertex group on the local sections of ![]() . There is no harm in doing so since we have the inclusion of sheaf of Lie algebra
. There is no harm in doing so since we have the inclusion of sheaf of Lie algebra ![]() , that is, a relative vector field is determined by its action on functions.
, that is, a relative vector field is determined by its action on functions.
In this regard, we would like to define the (
![]() $k^{\text {th}}$
-order) wall-crossing sheaf
$k^{\text {th}}$
-order) wall-crossing sheaf ![]() on the open set
on the open set
 $$ \begin{align*}W_{0}(\mathscr{D}):= W_0 \setminus \bigcup_{\mathfrak{j} \in |\mathscr{D}|^{[n-2]}} \mathfrak{j},\end{align*} $$
$$ \begin{align*}W_{0}(\mathscr{D}):= W_0 \setminus \bigcup_{\mathfrak{j} \in |\mathscr{D}|^{[n-2]}} \mathfrak{j},\end{align*} $$
which captures the jumping of holomorphic functions described by the wall-crossing factor when crossing a wall/slab. We first consider the sheaf ![]() of holomorphic functions over the subset
of holomorphic functions over the subset
![]() $W_0 \setminus |\mathscr {D}|$
, and let
$W_0 \setminus |\mathscr {D}|$
, and let
To extend it through the walls/slabs, we will specify the analytic continuation through
![]() $\mathrm {int}_{\mathrm {re}}(\mathbf {w})$
for each
$\mathrm {int}_{\mathrm {re}}(\mathbf {w})$
for each
![]() $\mathbf {w} \in |\mathscr {D}|^{[n-1]}$
. Given a wall/slab
$\mathbf {w} \in |\mathscr {D}|^{[n-1]}$
. Given a wall/slab
![]() $\mathbf {w}$
with two adjacent chambers
$\mathbf {w}$
with two adjacent chambers
![]() $\mathcal {C}_+$
,
$\mathcal {C}_+$
,
![]() $\mathcal {C}_-$
and
$\mathcal {C}_-$
and
![]() $\check {d}_{\mathbf {w}}$
pointing into
$\check {d}_{\mathbf {w}}$
pointing into
![]() $\mathcal {C}_+$
, and a point
$\mathcal {C}_+$
, and a point
![]() $x \in \mathrm {int}_{\mathrm {re}}(\mathbf {w})$
with the germ
$x \in \mathrm {int}_{\mathrm {re}}(\mathbf {w})$
with the germ
![]() $\Theta _{\mathbf {w},x}$
of wall-crossing factors near x, we let
$\Theta _{\mathbf {w},x}$
of wall-crossing factors near x, we let
but with a different gluing to nearby chambers
![]() $\mathcal {C}_{\pm }$
: In a sufficiently small neighborhood
$\mathcal {C}_{\pm }$
: In a sufficiently small neighborhood
![]() $U_x$
of x, the gluing of a local section
$U_x$
of x, the gluing of a local section ![]() is given by
is given by
 $$ \begin{align} f|_{U_x \cap \mathcal{C}_{\pm}} := \begin{cases} \Theta_{\mathbf{w},x}(f)|_{U_x \cap \mathcal{C}_+} & \text{on } U_x \cap \mathcal{C}_+,\\ f|_{U_x \cap \mathcal{C}_-} & \text{on } U_x \cap \mathcal{C}_-. \end{cases} \end{align} $$
$$ \begin{align} f|_{U_x \cap \mathcal{C}_{\pm}} := \begin{cases} \Theta_{\mathbf{w},x}(f)|_{U_x \cap \mathcal{C}_+} & \text{on } U_x \cap \mathcal{C}_+,\\ f|_{U_x \cap \mathcal{C}_-} & \text{on } U_x \cap \mathcal{C}_-. \end{cases} \end{align} $$
In this way, the sheaf ![]() extends to
extends to
![]() $W_0(\mathscr {D})$
.
$W_0(\mathscr {D})$
.
Now, we can formulate consistency of a scattering diagram
![]() $\mathscr {D}$
in terms of the behaviour of the sheaf
$\mathscr {D}$
in terms of the behaviour of the sheaf ![]() over the joints
over the joints
![]() $\mathfrak {j}$
’s and
$\mathfrak {j}$
’s and
![]() $(n-2)$
-dimensional strata of
$(n-2)$
-dimensional strata of
![]() $\hat {\mathscr {S}}$
. More precisely, we consider the push-forward
$\hat {\mathscr {S}}$
. More precisely, we consider the push-forward ![]() along the embedding
along the embedding
![]() $\mathfrak {i} \colon W_0(\mathscr {D}) \rightarrow B$
, and its stalk at
$\mathfrak {i} \colon W_0(\mathscr {D}) \rightarrow B$
, and its stalk at
![]() $x \in \mathrm {int}_{\mathrm {re}}(\mathfrak {j})$
and
$x \in \mathrm {int}_{\mathrm {re}}(\mathfrak {j})$
and
![]() $x \in \mathrm {int}_{\mathrm {re}}(\tau )$
for strata
$x \in \mathrm {int}_{\mathrm {re}}(\tau )$
for strata
![]() $\tau \subset \hat {\mathscr {S}}$
. Similar to above, we can define the (
$\tau \subset \hat {\mathscr {S}}$
. Similar to above, we can define the (
![]() $l^{\text {th}}$
-order) sheaf
$l^{\text {th}}$
-order) sheaf ![]() by using
by using ![]() and considering equation (5.9) modulo
and considering equation (5.9) modulo
![]() $(q)^{l+1}$
. There is a natural restriction map
$(q)^{l+1}$
. There is a natural restriction map ![]() . Taking tensor product, we have
. Taking tensor product, we have ![]() , where
, where ![]() .
.
The proof of the following lemma will be given in Appendix §A.
Lemma 5.19 (Hartogs extension property).
We have
where
![]() $\iota \colon W_0 \rightarrow B$
is the inclusion. Moreover, for any scattering diagram
$\iota \colon W_0 \rightarrow B$
is the inclusion. Moreover, for any scattering diagram
![]() $\mathscr {D}$
, we have
$\mathscr {D}$
, we have
where
![]() $\mathfrak {i} \colon W_0(\mathscr {D}) \rightarrow B$
is the inclusion.
$\mathfrak {i} \colon W_0(\mathscr {D}) \rightarrow B$
is the inclusion.
Lemma 5.20. The
![]() $0^{\text {th}}$
-order sheaf
$0^{\text {th}}$
-order sheaf ![]() is isomorphic to the sheaf
is isomorphic to the sheaf ![]() .
.
Proof. In view of Lemma 5.19, we only have to show that the two sheaves are isomorphic on the open subset
![]() $W_0(\mathscr {D})$
. Since we work modulo
$W_0(\mathscr {D})$
. Since we work modulo
![]() $(q)$
, only the wall-crossing factor
$(q)$
, only the wall-crossing factor
![]() $\varTheta _{v,\rho }$
associated to a slab matters. So we take a point
$\varTheta _{v,\rho }$
associated to a slab matters. So we take a point
![]() $x \in \mathrm {int}_{\mathrm {re}}(\mathbf {b}) \subset \mathrm {int}_{\mathrm {re}}(\rho )_v$
for some vertex v and compare
$x \in \mathrm {int}_{\mathrm {re}}(\mathbf {b}) \subset \mathrm {int}_{\mathrm {re}}(\rho )_v$
for some vertex v and compare ![]() with
with ![]() . From the proof of Lemma 5.10, we have
. From the proof of Lemma 5.10, we have

with the relation
![]() $uv= 0$
. The gluings with nearby maximal cells
$uv= 0$
. The gluings with nearby maximal cells
![]() $\sigma _{\pm }$
of both
$\sigma _{\pm }$
of both ![]() and
and ![]() are simply given by the parallel transport through v and the formulae
are simply given by the parallel transport through v and the formulae
 $$ \begin{align*} \sigma_+\colon\begin{cases} z^{m} \mapsto s^{-1}_{\rho\sigma_{+}}(m) z^m & \text{for } m \in \Lambda_{\rho},\\ u \mapsto s^{-1}_{\rho\sigma_+}(m_{\rho}) z^{m_{\rho}}, & \\ v \mapsto 0, & \end{cases} \qquad\quad \sigma_-\colon\begin{cases} z^{m} \mapsto s^{-1}_{\rho\sigma_{-}}(m) z^m & \text{for } m \in \Lambda_{\rho},\\ u \mapsto 0, & \\ v \mapsto s^{-1}_{\rho\sigma_-}(-m_{\rho})z^{-m_{\rho}} & \end{cases} \end{align*} $$
$$ \begin{align*} \sigma_+\colon\begin{cases} z^{m} \mapsto s^{-1}_{\rho\sigma_{+}}(m) z^m & \text{for } m \in \Lambda_{\rho},\\ u \mapsto s^{-1}_{\rho\sigma_+}(m_{\rho}) z^{m_{\rho}}, & \\ v \mapsto 0, & \end{cases} \qquad\quad \sigma_-\colon\begin{cases} z^{m} \mapsto s^{-1}_{\rho\sigma_{-}}(m) z^m & \text{for } m \in \Lambda_{\rho},\\ u \mapsto 0, & \\ v \mapsto s^{-1}_{\rho\sigma_-}(-m_{\rho})z^{-m_{\rho}} & \end{cases} \end{align*} $$
in the proof of Lemma 5.10.
Now, for the wall-crossing sheaf ![]() , the wall-crossing factor
, the wall-crossing factor
![]() $\varTheta _{v,\rho }$
acts trivially except on the two coordinate functions
$\varTheta _{v,\rho }$
acts trivially except on the two coordinate functions
![]() $u,v$
because
$u,v$
because
![]() $\langle m ,\check {d}_{\rho } \rangle = 0$
for
$\langle m ,\check {d}_{\rho } \rangle = 0$
for
![]() $m \in \Lambda _{\rho }$
. The gluing of u to the nearby maximal cells which obeys wall crossing is given by
$m \in \Lambda _{\rho }$
. The gluing of u to the nearby maximal cells which obeys wall crossing is given by
 $$ \begin{align*} u|_{U_x \cap \sigma_{\pm}} := \begin{cases} u|_{U_x \cap \sigma_+} & \text{on } U_x \cap \sigma_+,\\ \varTheta^{-1}_{v,\rho,x}(u)|_{U_x \cap \sigma_-} = 0 & \text{on } U_x \cap \sigma_-, \end{cases} \end{align*} $$
$$ \begin{align*} u|_{U_x \cap \sigma_{\pm}} := \begin{cases} u|_{U_x \cap \sigma_+} & \text{on } U_x \cap \sigma_+,\\ \varTheta^{-1}_{v,\rho,x}(u)|_{U_x \cap \sigma_-} = 0 & \text{on } U_x \cap \sigma_-, \end{cases} \end{align*} $$
in a sufficiently small neighborhood
![]() $U_x$
of x. Here, the reason that we have
$U_x$
of x. Here, the reason that we have
![]() $\varTheta ^{-1}_{v,\rho ,x}(u)|_{U_x \cap \sigma _-} = 0$
on
$\varTheta ^{-1}_{v,\rho ,x}(u)|_{U_x \cap \sigma _-} = 0$
on
![]() $U_x \cap \sigma _-$
is simply because we have
$U_x \cap \sigma _-$
is simply because we have
![]() $u \mapsto 0$
in the gluing of
$u \mapsto 0$
in the gluing of ![]() . For the same reason, we see that the gluing of v agrees with that of
. For the same reason, we see that the gluing of v agrees with that of ![]() and
and ![]() .
.
Definition 5.21. A (
![]() $k^{\text {th}}$
-order) scattering diagram
$k^{\text {th}}$
-order) scattering diagram
![]() $\mathscr {D}$
is said to be consistent if there is an isomorphism
$\mathscr {D}$
is said to be consistent if there is an isomorphism ![]() as sheaves of
as sheaves of
![]() $\mathbb {C}[q]/(q^{k+1})$
-algebras on each open subset
$\mathbb {C}[q]/(q^{k+1})$
-algebras on each open subset
![]() $W_{\alpha }$
.
$W_{\alpha }$
.
The above consistency condition would imply that ![]() is surjective for any
is surjective for any
![]() $l < k$
and hence
$l < k$
and hence ![]() is a sheaf of free
is a sheaf of free
![]() $\mathbb {C}[q]/(q^{k+1})$
-modules on B. We are going to see that
$\mathbb {C}[q]/(q^{k+1})$
-modules on B. We are going to see that ![]() agrees with the push-forward of the sheaf of holomorphic functions on a (
agrees with the push-forward of the sheaf of holomorphic functions on a (
![]() $k^{\text {th}}$
-order) thickening
$k^{\text {th}}$
-order) thickening ![]() of the central fiber
of the central fiber ![]() under the modified moment map
under the modified moment map
![]() $\nu $
.
$\nu $
.
Let us elaborate a bit on the relation between this definition of consistency and that in [Reference Gross and Siebert29]. Assuming we have a consistent scattering diagram in the sense of [Reference Gross and Siebert29], then we obtain a
![]() $k^{\text {th}}$
-order thickening
$k^{\text {th}}$
-order thickening ![]() of
of ![]() which is locally modeled on the thickenings
which is locally modeled on the thickenings ![]() ’s by [Reference Gross and Siebert28, Cor. 2.18]. Pushing forward via the modified moment map
’s by [Reference Gross and Siebert28, Cor. 2.18]. Pushing forward via the modified moment map
![]() $\nu $
, we obtain a sheaf of algebras over
$\nu $
, we obtain a sheaf of algebras over
![]() $\mathbb {C}[q]/(q^{k+1})$
lifting
$\mathbb {C}[q]/(q^{k+1})$
lifting ![]() , which is locally isomorphic to the
, which is locally isomorphic to the ![]() ’s. This consequence is exactly what we use to formulate our definition of consistency.
’s. This consequence is exactly what we use to formulate our definition of consistency.
Lemma 5.22. Suppose we have
![]() $W \subset W_{\alpha } \cap W_{\beta }$
such that
$W \subset W_{\alpha } \cap W_{\beta }$
such that
![]() $V = \nu ^{-1}(W)$
is Stein, and an isomorphism
$V = \nu ^{-1}(W)$
is Stein, and an isomorphism ![]() of sheaves of
of sheaves of
![]() $\mathbb {C}[q]/(q^{k+1})$
-algebras which is the identity modulo
$\mathbb {C}[q]/(q^{k+1})$
-algebras which is the identity modulo
![]() $(q)$
. Then there is a unique isomorphism
$(q)$
. Then there is a unique isomorphism ![]() of analytic spaces inducing h.
of analytic spaces inducing h.
Proof. From the description in §2.4, we can embed both families ![]() ,
, ![]() over
over
![]() $\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[q]/(q^{k+1}))$
as closed analytic subschemes of
$\mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[q]/(q^{k+1}))$
as closed analytic subschemes of
![]() $\mathbb {C}^{N+1} = \mathbb {C}^{N}\times \mathbb {C}_{q}$
and
$\mathbb {C}^{N+1} = \mathbb {C}^{N}\times \mathbb {C}_{q}$
and
![]() $\mathbb {C}^{L+1} = \mathbb {C}^{L} \times \mathbb {C}_q$
, respectively, where projection to the second factor defines the family over
$\mathbb {C}^{L+1} = \mathbb {C}^{L} \times \mathbb {C}_q$
, respectively, where projection to the second factor defines the family over
![]() $\mathbb {C}[q]/(q^{k+1})$
. Let
$\mathbb {C}[q]/(q^{k+1})$
. Let
![]() $\mathcal {J}_{\alpha }$
and
$\mathcal {J}_{\alpha }$
and
![]() $\mathcal {J}_{\beta }$
be the corresponding ideal sheaves, which can be generated by finitely many elements. We can take Stein open subsets
$\mathcal {J}_{\beta }$
be the corresponding ideal sheaves, which can be generated by finitely many elements. We can take Stein open subsets
![]() $U_{\alpha } \subseteq \mathbb {C}^{N+1}$
and
$U_{\alpha } \subseteq \mathbb {C}^{N+1}$
and
![]() $U_{\beta } \subseteq \mathbb {C}^{L+1}$
such that their intersections with the subschemes give
$U_{\beta } \subseteq \mathbb {C}^{L+1}$
such that their intersections with the subschemes give ![]() and
and ![]() , respectively. By taking global sections of the sheaves over W, we obtain the isomorphism
, respectively. By taking global sections of the sheaves over W, we obtain the isomorphism ![]() . Using the fact that
. Using the fact that
![]() $U_{\alpha }$
is Stein, we can lift
$U_{\alpha }$
is Stein, we can lift
![]() $h(z_i)$
’s, where
$h(z_i)$
’s, where
![]() $z_i$
’s are restrictions of coordinate functions to
$z_i$
’s are restrictions of coordinate functions to ![]() , to holomorphic functions on
, to holomorphic functions on
![]() $U_{\alpha }$
. In this way, h can be lifted as a holomorphic map
$U_{\alpha }$
. In this way, h can be lifted as a holomorphic map
![]() $\psi \colon U_{\alpha } \rightarrow U_{\beta }$
. Restricting to
$\psi \colon U_{\alpha } \rightarrow U_{\beta }$
. Restricting to ![]() , we see that the image lies in
, we see that the image lies in ![]() , and hence we obtain the isomorphism
, and hence we obtain the isomorphism
![]() $\psi $
. The uniqueness follows from the fact the
$\psi $
. The uniqueness follows from the fact the
![]() $\psi $
is determined by
$\psi $
is determined by
![]() $\psi ^*(z_i) = h(z_i)$
.
$\psi ^*(z_i) = h(z_i)$
.
Given a consistent scattering diagram
![]() $\mathscr {D}$
(in the sense of Definition 5.21), the sheaf
$\mathscr {D}$
(in the sense of Definition 5.21), the sheaf ![]() can be treated as a gluing of the local sheaves
can be treated as a gluing of the local sheaves ![]() ’s. Then from Lemma 5.22, we obtain a gluing of the local models
’s. Then from Lemma 5.22, we obtain a gluing of the local models ![]() ’s yielding a thickening
’s yielding a thickening ![]() of
of ![]() . This justifies Definition 5.21.
. This justifies Definition 5.21.
5.3.2 Constructing consistent scattering diagrams from Maurer–Cartan solutions
We are finally ready to demonstrate how to construct a consistent scattering diagram
![]() $\mathscr {D}(\varphi )$
in the sense of Definition 5.21 from a Maurer–Cartan solution
$\mathscr {D}(\varphi )$
in the sense of Definition 5.21 from a Maurer–Cartan solution
![]() $\varphi = \phi + t f$
obtained in Theorem 4.18. As in §5.2.4, we obtain a
$\varphi = \phi + t f$
obtained in Theorem 4.18. As in §5.2.4, we obtain a
![]() $k^{\text {th}}$
-order Maurer–Cartan solution
$k^{\text {th}}$
-order Maurer–Cartan solution
![]() $\zeta _0$
and define its scattered part as
$\zeta _0$
and define its scattered part as ![]() . From this, we want to construct a
. From this, we want to construct a
![]() $k^{\text {th}}$
-order scattering diagram
$k^{\text {th}}$
-order scattering diagram
![]() $\mathscr {D}(\varphi )$
.
$\mathscr {D}(\varphi )$
.
We take an open cover
![]() $\{U_i\}_{i}$
by precompact convex open subsets of
$\{U_i\}_{i}$
by precompact convex open subsets of
![]() $W_0$
such that, locally on
$W_0$
such that, locally on
![]() $U_i$
,
$U_i$
,
![]() $\phi _{\mathrm {in}}+\phi _{\mathrm {s}}$
can be written as a finite sum
$\phi _{\mathrm {in}}+\phi _{\mathrm {s}}$
can be written as a finite sum
where
![]() $\alpha _{ij} \in \mathscr {T}^1(U_i)$
has asymptotic support on a codimension one polyhedral subset
$\alpha _{ij} \in \mathscr {T}^1(U_i)$
has asymptotic support on a codimension one polyhedral subset
![]() $P_{ij} \subset U_i$
, and
$P_{ij} \subset U_i$
, and ![]() . We take a partition of unity
. We take a partition of unity
![]() $\{\varrho _i\}_{i}$
subordinate to the cover
$\{\varrho _i\}_{i}$
subordinate to the cover
![]() $\{U_i\}_{i}$
such that
$\{U_i\}_{i}$
such that
![]() $\mathrm {supp}(\varrho _i)$
has asymptotic support on a compact subset
$\mathrm {supp}(\varrho _i)$
has asymptotic support on a compact subset
![]() $C_i$
of
$C_i$
of
![]() $U_i$
. As a result, we can write
$U_i$
. As a result, we can write
where each
![]() $(\varrho _i \alpha _{ij})$
has asymptotic support on the compact codimension one subset
$(\varrho _i \alpha _{ij})$
has asymptotic support on the compact codimension one subset
![]() $C_i \cap P_{ij} \subset U_i$
. The subset
$C_i \cap P_{ij} \subset U_i$
. The subset
![]() $\bigcup _{ij}C_i \cap P_{ij}$
will be the support
$\bigcup _{ij}C_i \cap P_{ij}$
will be the support
![]() $|\mathscr {D}|$
of our scattering diagram
$|\mathscr {D}|$
of our scattering diagram
![]() $\mathscr {D} = \mathscr {D}(\varphi )$
.
$\mathscr {D} = \mathscr {D}(\varphi )$
.
We may equip
![]() $|\mathscr {D}| := \bigcup _{ij}C_i \cap P_{ij}$
with a polyhedral decomposition such that all the boundaries and mutual intersections of
$|\mathscr {D}| := \bigcup _{ij}C_i \cap P_{ij}$
with a polyhedral decomposition such that all the boundaries and mutual intersections of
![]() $C_i \cap P_{ij}$
’s are contained in
$C_i \cap P_{ij}$
’s are contained in
![]() $(n-2)$
-dimensional strata of
$(n-2)$
-dimensional strata of
![]() $|\mathscr {D}|$
. So, for each
$|\mathscr {D}|$
. So, for each
![]() $(n-1)$
-dimensional cell
$(n-1)$
-dimensional cell
![]() $\tau $
of
$\tau $
of
![]() $|\mathscr {D}|$
, if
$|\mathscr {D}|$
, if
![]() $\mathrm {int}_{\mathrm {re}}(\tau ) \cap (C_i \cap P_{ij} ) \neq \emptyset $
for some
$\mathrm {int}_{\mathrm {re}}(\tau ) \cap (C_i \cap P_{ij} ) \neq \emptyset $
for some
![]() $i,j$
, then we must have
$i,j$
, then we must have
![]() $\tau \subset C_i \cap P_{ij}$
. Let
$\tau \subset C_i \cap P_{ij}$
. Let
![]() $\mathtt {I}(\tau ):= \{ (i,j) \ | \ \tau \subset C_i \cap P_{ij} \}$
, which is a finite set of indices. We will equip the
$\mathtt {I}(\tau ):= \{ (i,j) \ | \ \tau \subset C_i \cap P_{ij} \}$
, which is a finite set of indices. We will equip the
![]() $(n-1)$
-cells
$(n-1)$
-cells
![]() $\tau $
’s of
$\tau $
’s of
![]() $|\mathscr {D}|$
with the structure of walls or slabs.
$|\mathscr {D}|$
with the structure of walls or slabs.
We first consider the case of a wall. Take
![]() $\tau \in |\mathscr {D}|^{[n-1]}$
such that
$\tau \in |\mathscr {D}|^{[n-1]}$
such that
![]() $\mathrm {int}_{\mathrm {re}}(\tau ) \cap \mathrm {int}_{\mathrm {re}}(\rho ) = \emptyset $
for all
$\mathrm {int}_{\mathrm {re}}(\tau ) \cap \mathrm {int}_{\mathrm {re}}(\rho ) = \emptyset $
for all
![]() $\rho $
with
$\rho $
with
![]() $\rho \cap \mathscr {S}_e \neq \emptyset $
. We let
$\rho \cap \mathscr {S}_e \neq \emptyset $
. We let
![]() $\mathbf {w} = \tau $
, choose a primitive normal
$\mathbf {w} = \tau $
, choose a primitive normal
![]() $\check {d}_{\mathbf {w}}$
of
$\check {d}_{\mathbf {w}}$
of
![]() $\tau $
, and give the labels
$\tau $
, and give the labels
![]() $\mathcal {C}_{\pm }$
to the two adjacent chambers
$\mathcal {C}_{\pm }$
to the two adjacent chambers
![]() $\mathcal {C}_{\pm }$
so that
$\mathcal {C}_{\pm }$
so that
![]() $\check {d}_{\mathbf {w}}$
is pointing into
$\check {d}_{\mathbf {w}}$
is pointing into
![]() $\mathcal {C}_{+}$
. In a sufficiently small neighborhood
$\mathcal {C}_{+}$
. In a sufficiently small neighborhood
![]() $U_\tau $
of
$U_\tau $
of
![]() $\mathrm {int}_{\mathrm {re}}(\tau )$
, we have
$\mathrm {int}_{\mathrm {re}}(\tau )$
, we have
![]() $\phi _{\mathrm {in}}|_{U_{\tau }} = 0$
and we may write
$\phi _{\mathrm {in}}|_{U_{\tau }} = 0$
and we may write
 $$ \begin{align*}\phi_{\mathrm{s}}|_{U_{\tau}} = \sum_{(i,j)\in \mathtt{I}(\tau)}(\varrho_i \alpha_{ij}) \otimes v_{ij}, \end{align*} $$
$$ \begin{align*}\phi_{\mathrm{s}}|_{U_{\tau}} = \sum_{(i,j)\in \mathtt{I}(\tau)}(\varrho_i \alpha_{ij}) \otimes v_{ij}, \end{align*} $$
where each
![]() $(\varrho _i \alpha _{ij})$
has asymptotic support on
$(\varrho _i \alpha _{ij})$
has asymptotic support on
![]() $\mathrm {int}_{\mathrm {re}}(\tau )$
. Since locally on
$\mathrm {int}_{\mathrm {re}}(\tau )$
. Since locally on
![]() $U_{\tau }$
any Maurer–Cartan solution is gauge equivalent to
$U_{\tau }$
any Maurer–Cartan solution is gauge equivalent to
![]() $0$
, there exists an element
$0$
, there exists an element ![]() such that
such that
Such an element can be constructed inductively using the procedure in [Reference Leung, Ma and Young37, §3.4.3] and can be chosen to be of the form
 $$ \begin{align} \theta_{\tau}|_{U_{\tau} \cap \mathcal{C}_{\pm}} = \begin{cases} \theta_{\tau,0}|_{U_{\tau} \cap \mathcal{C}_+} & \text{on } U_{\tau} \cap \mathcal{C}_+,\\ 0 & \text{on } U_{\tau} \cap \mathcal{C}_-, \end{cases} \end{align} $$
$$ \begin{align} \theta_{\tau}|_{U_{\tau} \cap \mathcal{C}_{\pm}} = \begin{cases} \theta_{\tau,0}|_{U_{\tau} \cap \mathcal{C}_+} & \text{on } U_{\tau} \cap \mathcal{C}_+,\\ 0 & \text{on } U_{\tau} \cap \mathcal{C}_-, \end{cases} \end{align} $$
for some ![]() . From this, we obtain the wall-crossing factor associated to the wall
. From this, we obtain the wall-crossing factor associated to the wall
![]() $\mathbf {w}$
$\mathbf {w}$
Remark 5.23. Here, we need to apply the procedure in [Reference Leung, Ma and Young37, §3.4.3], which is a generalization of that in [Reference Chan, Leung and Ma7], because of the potential noncommutativity:
![]() $[v_{ij},v_{ij'}]\neq 0$
for
$[v_{ij},v_{ij'}]\neq 0$
for
![]() $j \neq j'$
.
$j \neq j'$
.
For the case where
![]() $\tau \subset \mathrm {int}_{\mathrm {re}}(\rho )_v$
for some
$\tau \subset \mathrm {int}_{\mathrm {re}}(\rho )_v$
for some
![]() $\rho $
with
$\rho $
with
![]() $\rho \cap \mathscr {S}_e \neq \emptyset $
, we will define a slab. We take
$\rho \cap \mathscr {S}_e \neq \emptyset $
, we will define a slab. We take
![]() $U_{\tau }$
and
$U_{\tau }$
and
![]() $\mathtt {I}(\tau )$
as above, and let the slab
$\mathtt {I}(\tau )$
as above, and let the slab
![]() $\mathbf {b} = \tau $
. The primitive normal
$\mathbf {b} = \tau $
. The primitive normal
![]() $\check {d}_{\rho }$
is the one we chose earlier for each
$\check {d}_{\rho }$
is the one we chose earlier for each
![]() $\rho $
. Again, we work in a small neighborhood
$\rho $
. Again, we work in a small neighborhood
![]() $U_{\tau }$
of
$U_{\tau }$
of
![]() $\mathrm {int}_{\mathrm {re}}(\tau )$
with two adjacent chambers
$\mathrm {int}_{\mathrm {re}}(\tau )$
with two adjacent chambers
![]() $\mathcal {C}_{\pm }$
. As in the proof of Lemma 5.10, we can find a step-function-like element
$\mathcal {C}_{\pm }$
. As in the proof of Lemma 5.10, we can find a step-function-like element
![]() $\theta _{v,\rho }$
of the form
$\theta _{v,\rho }$
of the form
 $$ \begin{align*}\theta_{v,\rho} = \begin{cases} \log(s_{v\rho}^{-1}(f_{v,\rho})) \partial_{\check{d}_{\rho}} & \text{on } U_{\tau} \cap \mathcal{C}_+,\\ 0 & \text{on } U_{\tau} \cap \mathcal{C}_- \end{cases} \end{align*} $$
$$ \begin{align*}\theta_{v,\rho} = \begin{cases} \log(s_{v\rho}^{-1}(f_{v,\rho})) \partial_{\check{d}_{\rho}} & \text{on } U_{\tau} \cap \mathcal{C}_+,\\ 0 & \text{on } U_{\tau} \cap \mathcal{C}_- \end{cases} \end{align*} $$
to solve the equation
![]() $e^{[\theta _{v,\rho },\cdot ]}\circ \bar {\partial }_{\circ } \circ e^{-[\theta _{v,\rho },\cdot ]} = \bar {\partial }_{\circ } + [\phi _{\mathrm {in}},\cdot ]$
on
$e^{[\theta _{v,\rho },\cdot ]}\circ \bar {\partial }_{\circ } \circ e^{-[\theta _{v,\rho },\cdot ]} = \bar {\partial }_{\circ } + [\phi _{\mathrm {in}},\cdot ]$
on
![]() $U_\tau $
. In other words,
$U_\tau $
. In other words,
is an isomorphism of sheaves of dgLas. Computations using the formula in [Reference Chan, Leung and Ma8, Lem. 2.5] then gives the identity
Once again, we can find an element
![]() $\theta _{\tau }$
such that
$\theta _{\tau }$
such that
and hence a corresponding element ![]() of the form (5.11). From this, we get
of the form (5.11). From this, we get
and hence the wall-crossing factor
![]() $\Theta _{\mathbf {b}} :=\varTheta _{v,\rho } \circ \varXi _{\mathbf {b}} $
associated to the slab
$\Theta _{\mathbf {b}} :=\varTheta _{v,\rho } \circ \varXi _{\mathbf {b}} $
associated to the slab
![]() $\mathbf {b}$
.
$\mathbf {b}$
.
Next, we would like to argue that consistency of the scattering diagram
![]() $\mathscr {D}$
follows from the fact that
$\mathscr {D}$
follows from the fact that
![]() $\phi $
is a Maurer–Cartan solution. First of all, on the global sheaf
$\phi $
is a Maurer–Cartan solution. First of all, on the global sheaf ![]() over B, we have the operator
over B, we have the operator
![]() $\bar {\partial }_{\phi }:=\bar {\partial }+[\phi ,\cdot ]$
which satisfies
$\bar {\partial }_{\phi }:=\bar {\partial }+[\phi ,\cdot ]$
which satisfies ![]() and
and
![]() $\bar {\partial }_{\phi }^2 = 0$
. This allows us to define the sheaf of
$\bar {\partial }_{\phi }^2 = 0$
. This allows us to define the sheaf of
![]() $k^{\text {th}}$
-order holomorphic functions as
$k^{\text {th}}$
-order holomorphic functions as
for each
![]() $k\in \mathbb {N}$
. It is a sequence of sheaves of commutative
$k\in \mathbb {N}$
. It is a sequence of sheaves of commutative
![]() $\mathbb {C}[q]/(q^{k+1})$
-algebras over B, equipped with a natural map
$\mathbb {C}[q]/(q^{k+1})$
-algebras over B, equipped with a natural map ![]() for
for
![]() $l<k$
that is induced from the maps for
$l<k$
that is induced from the maps for ![]() . By construction, we see that
. By construction, we see that ![]() .
.
We claim that the maps ![]() ’s are surjective. To prove this, we fix a point
’s are surjective. To prove this, we fix a point
![]() $x\in B$
and take an open chart
$x\in B$
and take an open chart
![]() $W_{\alpha }$
containing x in the cover of B we chose at the beginning of §5.2.4. There is an isomorphism
$W_{\alpha }$
containing x in the cover of B we chose at the beginning of §5.2.4. There is an isomorphism ![]() identifying the differential
identifying the differential
![]() $\bar {\partial }$
with
$\bar {\partial }$
with
![]() $\bar {\partial }_{\alpha }+ [\eta _{\alpha },\cdot ]$
by our construction. Write
$\bar {\partial }_{\alpha }+ [\eta _{\alpha },\cdot ]$
by our construction. Write
![]() $\phi _{\alpha } = \varPhi _{\alpha }(\phi )$
and notice that
$\phi _{\alpha } = \varPhi _{\alpha }(\phi )$
and notice that
![]() $\bar {\partial }_{\alpha } + [\eta _{\alpha }+\phi _{\alpha },\cdot ]$
squares to zero, which means that
$\bar {\partial }_{\alpha } + [\eta _{\alpha }+\phi _{\alpha },\cdot ]$
squares to zero, which means that
![]() $\eta _{\alpha } + \phi _{\alpha }$
is a solution to the Maurer–Cartan equation for
$\eta _{\alpha } + \phi _{\alpha }$
is a solution to the Maurer–Cartan equation for ![]() . We apply the same trick as above to the local open subset
. We apply the same trick as above to the local open subset
![]() $W_{\alpha }$
, namely, any Maurer–Cartan solution lying in
$W_{\alpha }$
, namely, any Maurer–Cartan solution lying in ![]() is gauge equivalent to the trivial one, so there exists
is gauge equivalent to the trivial one, so there exists ![]() such that
such that
As a result, the map ![]() is an isomorphism of dgLas, sending
is an isomorphism of dgLas, sending ![]() isomorphically onto
isomorphically onto ![]() .
.
We shall now prove the consistency of the scattering diagram
![]() $\mathscr {D} = \mathscr {D}(\varphi )$
by identifying the associated wall-crossing sheaf
$\mathscr {D} = \mathscr {D}(\varphi )$
by identifying the associated wall-crossing sheaf ![]() with the sheaf
with the sheaf ![]() of
of
![]() $k^{\text {th}}$
-order holomorphic functions.
$k^{\text {th}}$
-order holomorphic functions.
Theorem 5.24. There is an isomorphism ![]() of sheaves of
of sheaves of
![]() $\mathbb {C}[q]/(q^{k+1})$
-algebras on
$\mathbb {C}[q]/(q^{k+1})$
-algebras on
![]() $W_0(\mathscr {D})$
. Furthermore, the scattering diagram
$W_0(\mathscr {D})$
. Furthermore, the scattering diagram
![]() $\mathscr {D} = \mathscr {D}(\varphi )$
associated to the Maurer–Cartan solution
$\mathscr {D} = \mathscr {D}(\varphi )$
associated to the Maurer–Cartan solution
![]() $\phi $
is consistent in the sense of Definition 5.21.
$\phi $
is consistent in the sense of Definition 5.21.
Proof. To prove the first statement, we first notice that there is a natural isomorphism
so we only need to consider those points
![]() $x \in \mathrm {int}_{\mathrm {re}}(\tau ),$
where
$x \in \mathrm {int}_{\mathrm {re}}(\tau ),$
where
![]() $\tau $
is either a wall or a slab. Since
$\tau $
is either a wall or a slab. Since
![]() $W_0(\mathscr {D}) \subset W_0$
, we will work on the semiflat locus
$W_0(\mathscr {D}) \subset W_0$
, we will work on the semiflat locus
![]() $W_0$
and use the model
$W_0$
and use the model ![]() , which is equipped with the operator
, which is equipped with the operator
![]() $ \bar {\partial }_{\circ }+ [\phi _{\mathrm {in}} + \phi _{\mathrm {s}},\cdot ]$
. Via the isomorphism
$ \bar {\partial }_{\circ }+ [\phi _{\mathrm {in}} + \phi _{\mathrm {s}},\cdot ]$
. Via the isomorphism
from Lemma 5.10, we may write
We fix a point
![]() $x \in W_0(\mathscr {D}) \cap |\mathscr {D}|$
and consider the stalk at x for both sheaves. In the above construction of walls and slabs from the Maurer–Cartan solution
$x \in W_0(\mathscr {D}) \cap |\mathscr {D}|$
and consider the stalk at x for both sheaves. In the above construction of walls and slabs from the Maurer–Cartan solution
![]() $\phi $
, we first take a sufficiently small open subset
$\phi $
, we first take a sufficiently small open subset
![]() $U_x$
and then find a gauge transformation of the form
$U_x$
and then find a gauge transformation of the form
![]() $\varPsi = e^{[\theta _{\tau },\cdot ]}$
in the case of a wall, and of the form
$\varPsi = e^{[\theta _{\tau },\cdot ]}$
in the case of a wall, and of the form
![]() $\varPsi =e^{[\theta _{v,\rho },\cdot ]} \circ e^{[\theta _{\tau },\cdot ]} $
in the case of a slab. We have
$\varPsi =e^{[\theta _{v,\rho },\cdot ]} \circ e^{[\theta _{\tau },\cdot ]} $
in the case of a slab. We have
by construction, so this further induces an isomorphism
of
![]() $\mathbb {C}[q]/(q^{k+1})$
-algebras.
$\mathbb {C}[q]/(q^{k+1})$
-algebras.
It remains to see how the stalk ![]() is glued to nearby chambers
is glued to nearby chambers
![]() $\mathcal {C}_{\pm }$
. For this purpose, we let
$\mathcal {C}_{\pm }$
. For this purpose, we let
as in equation (5.12) in the case of a wall, and
as in equation (5.13) in the case of a slab. Then, the restriction of an element ![]() to a nearby chamber is given by
to a nearby chamber is given by
 $$ \begin{align*} \varPsi (f) = \begin{cases} \Psi_0(f) & \text{on } U_{x} \cap \mathcal{C}_+,\\ f & \text{on } U_{x} \cap \mathcal{C}_- \end{cases} \end{align*} $$
$$ \begin{align*} \varPsi (f) = \begin{cases} \Psi_0(f) & \text{on } U_{x} \cap \mathcal{C}_+,\\ f & \text{on } U_{x} \cap \mathcal{C}_- \end{cases} \end{align*} $$
in a sufficiently small neighborhood
![]() $U_x$
. This agrees with the description of the wall-crossing sheaf
$U_x$
. This agrees with the description of the wall-crossing sheaf ![]() in equation (5.9). Hence, we obtain an isomorphism
in equation (5.9). Hence, we obtain an isomorphism ![]() .
.
To prove the second statement, we first apply pushing forward via
![]() $\mathfrak {i}\colon W_0(\mathscr {D}) \rightarrow B$
to the first statement to get the isomorphism
$\mathfrak {i}\colon W_0(\mathscr {D}) \rightarrow B$
to the first statement to get the isomorphism
Now, by the discussion right before this proof, we may identify ![]() with
with ![]() locally. But the sheaf
locally. But the sheaf ![]() , which is isomorphic to the restriction of
, which is isomorphic to the restriction of ![]() to
to
![]() $W_\alpha $
as sheaves of
$W_\alpha $
as sheaves of
![]() $\mathbb {C}[q]/(q^{k+1})$
-modules, satisfies the Hartogs extension property from
$\mathbb {C}[q]/(q^{k+1})$
-modules, satisfies the Hartogs extension property from
![]() $W_0(\mathscr {D})\cap W_{\alpha }$
to
$W_0(\mathscr {D})\cap W_{\alpha }$
to
![]() $W_{\alpha }$
by Lemma 5.19. So we have
$W_{\alpha }$
by Lemma 5.19. So we have ![]() . Hence, we obtain
. Hence, we obtain
from which follows the consistency of the diagram
![]() $\mathscr {D} = \mathscr {D}(\varphi )$
.
$\mathscr {D} = \mathscr {D}(\varphi )$
.
Remark 5.25. From the proof of Theorem 5.24, we actually have a correspondence between step-function-like elements in the gauge group and elements in the tropical vertex group as follows. We fix a generic point x in a joint
![]() $\mathfrak {j}$
, and consider a neighborhood of x of the form
$\mathfrak {j}$
, and consider a neighborhood of x of the form
![]() $U_x \times D_x$
, where
$U_x \times D_x$
, where
![]() $U_x$
is a neighborhood of x in
$U_x$
is a neighborhood of x in
![]() $\mathrm {int}_{\mathrm {re}}(\mathfrak {j})$
and
$\mathrm {int}_{\mathrm {re}}(\mathfrak {j})$
and
![]() $D_x$
is a disk in the normal direction of
$D_x$
is a disk in the normal direction of
![]() $\mathfrak {j}$
. We pick a compact annulus
$\mathfrak {j}$
. We pick a compact annulus
![]() $A_x \subset D_x$
surrounding x, intersecting finitely many walls/slabs. We let
$A_x \subset D_x$
surrounding x, intersecting finitely many walls/slabs. We let
![]() $\tau _1,\dots ,\tau _s$
be the walls/slabs in anticlockwise direction. For each
$\tau _1,\dots ,\tau _s$
be the walls/slabs in anticlockwise direction. For each
![]() $\tau _i$
, we take an open subset
$\tau _i$
, we take an open subset
![]() $\mathscr {W}_{i} $
just containing the wall
$\mathscr {W}_{i} $
just containing the wall
![]() $\tau _i$
such that
$\tau _i$
such that
![]() $\mathscr {W}_i \setminus \tau _i =\mathscr {W}_{i,+}\cup \mathscr {W}_{i,-}$
. The following Figure 10 below illustrates the situation.
$\mathscr {W}_i \setminus \tau _i =\mathscr {W}_{i,+}\cup \mathscr {W}_{i,-}$
. The following Figure 10 below illustrates the situation.

Figure 10 Wall crossing around a joint
![]() $\mathfrak {j}$
.
$\mathfrak {j}$
.
As in the proof of Theorem 5.24, there is a gauge transformation on each
![]() $\mathscr {W}_i$
of the form
$\mathscr {W}_i$
of the form
where
![]() $\varPsi _i = e^{[\theta _{v,\rho },\cdot ]} \circ e^{[\theta _{\tau },\cdot ]}$
for a slab and
$\varPsi _i = e^{[\theta _{v,\rho },\cdot ]} \circ e^{[\theta _{\tau },\cdot ]}$
for a slab and
![]() $\varPsi _i = e^{[\theta _{\tau },\cdot ]}$
for a wall. These are step-function-like elements in the gauge group satisfying
$\varPsi _i = e^{[\theta _{\tau },\cdot ]}$
for a wall. These are step-function-like elements in the gauge group satisfying
 $$ \begin{align*} \varPsi_i = \begin{cases} \Theta_{i} & \text{on } \mathscr{W}_{i,+},\\ \mathrm{id} & \text{on } \mathscr{W}_{i,-}, \end{cases} \end{align*} $$
$$ \begin{align*} \varPsi_i = \begin{cases} \Theta_{i} & \text{on } \mathscr{W}_{i,+},\\ \mathrm{id} & \text{on } \mathscr{W}_{i,-}, \end{cases} \end{align*} $$
where
![]() $\Theta _{i}$
is the wall crossing factor associated to
$\Theta _{i}$
is the wall crossing factor associated to
![]() $\tau _i$
.
$\tau _i$
.
On the overlap
![]() $\mathscr {W}_{i,+} = \mathscr {W}_i \cap \mathscr {W}_{i+1}$
(where we set
$\mathscr {W}_{i,+} = \mathscr {W}_i \cap \mathscr {W}_{i+1}$
(where we set
![]() $i+1=1$
if
$i+1=1$
if
![]() $i=s$
), there is a commutative diagram
$i=s$
), there is a commutative diagram

allowing us to interpret the wall crossing factor
![]() $\Theta _i$
as the gluing between the two sheaves
$\Theta _i$
as the gluing between the two sheaves ![]() and
and ![]() over
over
![]() $\mathscr {W}_{i,+}$
.
$\mathscr {W}_{i,+}$
.
Notice that the Maurer–Cartan element
![]() $\phi $
is global. On a small neighborhood
$\phi $
is global. On a small neighborhood
![]() $W_{\alpha }$
containing
$W_{\alpha }$
containing
![]() $U_x\times D_x$
, we have the sheaf
$U_x\times D_x$
, we have the sheaf ![]() on
on
![]() $W_{\alpha }$
, and there is an isomorphism
$W_{\alpha }$
, and there is an isomorphism
Composing with the isomorphism
we have a commutative diagram of isomorphisms

This is a Čech-type cocycle condition between the sheaves ![]() ’s and
’s and ![]() , which can be understood as the original consistency condition defined using path-ordered products in [Reference Kontsevich and Soibelman36, Reference Gross and Siebert29]. In particular, taking a local holomorphic function in
, which can be understood as the original consistency condition defined using path-ordered products in [Reference Kontsevich and Soibelman36, Reference Gross and Siebert29]. In particular, taking a local holomorphic function in ![]() and restricting it to
and restricting it to
![]() $U_x \times A_x$
, we obtain elements in
$U_x \times A_x$
, we obtain elements in ![]() that jump across the walls according to the wall crossing factors
that jump across the walls according to the wall crossing factors
![]() $\Theta _i$
’s.
$\Theta _i$
’s.
A The Hartogs extension property
The following lemma is an application of the Hartogs extension theorem [Reference Rossi41].
Lemma A.1. Consider the analytic space
![]() $(\mathbb {C}^*)^k \times \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }])$
for some
$(\mathbb {C}^*)^k \times \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }])$
for some
![]() $\tau $
and an open subset of the form
$\tau $
and an open subset of the form
![]() $U \times V$
, where
$U \times V$
, where
![]() $U \subset (\mathbb {C}^*)^k$
and V is a neighborhood of the origin
$U \subset (\mathbb {C}^*)^k$
and V is a neighborhood of the origin
![]() $o \in \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }])$
. Let
$o \in \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\tau }])$
. Let
![]() $W := V \setminus \big ( \bigcup _{\omega } V_{\omega } \big )$
, where
$W := V \setminus \big ( \bigcup _{\omega } V_{\omega } \big )$
, where
![]() $\dim _{\mathbb {R}}(\omega )+2 \leq \dim _{\mathbb {R}}(\Sigma _{\tau })$
(i.e., W is the complement of complex codimension
$\dim _{\mathbb {R}}(\omega )+2 \leq \dim _{\mathbb {R}}(\Sigma _{\tau })$
(i.e., W is the complement of complex codimension
![]() $2$
orbits in V). Then the restriction
$2$
orbits in V). Then the restriction
![]() $\mathcal {O}(U\times V) \rightarrow \mathcal {O}(U\times W)$
is a ring isomorphism.
$\mathcal {O}(U\times V) \rightarrow \mathcal {O}(U\times W)$
is a ring isomorphism.
Proof. We first consider the case where
![]() $\dim _{\mathbb {R}}(\Sigma _{\tau }) \geq 2$
and
$\dim _{\mathbb {R}}(\Sigma _{\tau }) \geq 2$
and
![]() $W = V \setminus \{0\}$
. We can further assume that
$W = V \setminus \{0\}$
. We can further assume that
![]() $\Sigma _{\tau }$
consists of just one cone
$\Sigma _{\tau }$
consists of just one cone
![]() $\sigma $
because the holomorphic functions on V are those on
$\sigma $
because the holomorphic functions on V are those on
![]() $V \cap \sigma $
that agree on the overlaps. So we can write
$V \cap \sigma $
that agree on the overlaps. So we can write
 $$ \begin{align*} \mathcal{O}(U \times W) = \left\{ \sum_{m \in \Lambda_{\sigma}} a_m z^m \ \Big| \ a_m \in \mathcal{O}_{(\mathbb{C}^*)^k}(U) \right\}, \end{align*} $$
$$ \begin{align*} \mathcal{O}(U \times W) = \left\{ \sum_{m \in \Lambda_{\sigma}} a_m z^m \ \Big| \ a_m \in \mathcal{O}_{(\mathbb{C}^*)^k}(U) \right\}, \end{align*} $$
that is, as Laurent series converging in W. We may further assume that W is a sufficiently small Stein open subset. Take
![]() $f = \sum _{m \in \Lambda _{\sigma }} a_m z^m \in \mathcal {O}(U\times W)$
. We have the corresponding holomorphic function
$f = \sum _{m \in \Lambda _{\sigma }} a_m z^m \in \mathcal {O}(U\times W)$
. We have the corresponding holomorphic function
![]() $\sum _{m \in \Lambda _{\sigma }} a_m(u) z^m$
on W for each point
$\sum _{m \in \Lambda _{\sigma }} a_m(u) z^m$
on W for each point
![]() $u \in U$
, which can be extended to V using the Hartogs extension theorem [Reference Rossi41] because
$u \in U$
, which can be extended to V using the Hartogs extension theorem [Reference Rossi41] because
![]() $\{0\}$
is a compact subset of V such that
$\{0\}$
is a compact subset of V such that
![]() $W = V \setminus \{0\}$
is connected. Therefore, we have
$W = V \setminus \{0\}$
is connected. Therefore, we have
![]() $a_m(u) = 0$
for
$a_m(u) = 0$
for
![]() $m \notin \sigma \cap \Lambda _{\sigma }$
for each u, and hence
$m \notin \sigma \cap \Lambda _{\sigma }$
for each u, and hence
![]() $f = \sum _{\sigma \cap \Lambda _{\sigma }} a_m z^m$
is an element in
$f = \sum _{\sigma \cap \Lambda _{\sigma }} a_m z^m$
is an element in
![]() $\mathcal {O}(U\times V)$
.
$\mathcal {O}(U\times V)$
.
For the general case, we use induction on the codimension of
![]() $\omega $
to show that any holomorphic function can be extended through
$\omega $
to show that any holomorphic function can be extended through
![]() $V_\omega \setminus \bigcup _{\tau } V_{\tau }$
with
$V_\omega \setminus \bigcup _{\tau } V_{\tau }$
with
![]() $\dim _{\mathbb {R}}(\tau ) < \dim _{\mathbb {R}}(\omega )$
. Taking a point
$\dim _{\mathbb {R}}(\tau ) < \dim _{\mathbb {R}}(\omega )$
. Taking a point
![]() $x \in V_{\omega } \setminus \bigcup _{\tau } V_\tau $
, a neighborhood of x can be written as
$x \in V_{\omega } \setminus \bigcup _{\tau } V_\tau $
, a neighborhood of x can be written as
![]() $(\mathbb {C}^*)^l \times \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\omega }])$
. By the induction hypothesis, we know that holomorphic functions can already be extended through
$(\mathbb {C}^*)^l \times \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\omega }])$
. By the induction hypothesis, we know that holomorphic functions can already be extended through
![]() $(\mathbb {C}^*)^l \times \{0\}$
. We conclude that any holomorphic function can be extended through
$(\mathbb {C}^*)^l \times \{0\}$
. We conclude that any holomorphic function can be extended through
![]() $V_\omega \setminus \bigcup _{\tau } V_{\tau }$
.
$V_\omega \setminus \bigcup _{\tau } V_{\tau }$
.
We will make use of the following version of the Hartogs extension theorem, which can be found in, for example, [Reference Jarnicki and Pflug31, p. 58], to handle extension within codimension one cells
![]() $\rho $
’s and maximal cells
$\rho $
’s and maximal cells
![]() $\sigma $
’s.
$\sigma $
’s.
Theorem A.2 (Hartogs extension theorem, see, for example, [Reference Jarnicki and Pflug31]).
Let
![]() $U \subset \mathbb {C}^n$
be a domain with
$U \subset \mathbb {C}^n$
be a domain with
![]() $n\geq 2$
, and
$n\geq 2$
, and
![]() $A \subset U$
such that
$A \subset U$
such that
![]() $U \setminus A$
is still a domain. Suppose
$U \setminus A$
is still a domain. Suppose
![]() $\pi (U) \setminus \pi (A)$
is a nonempty open subset, and
$\pi (U) \setminus \pi (A)$
is a nonempty open subset, and
![]() $\pi ^{-1}(\pi (x)) \cap A$
is compact for every
$\pi ^{-1}(\pi (x)) \cap A$
is compact for every
![]() $x\in A$
, where
$x\in A$
, where
![]() $\pi \colon \mathbb {C}^{n} \rightarrow \mathbb {C}^{n-1}$
is projection along one of the coordinate direction. Then the natural restriction
$\pi \colon \mathbb {C}^{n} \rightarrow \mathbb {C}^{n-1}$
is projection along one of the coordinate direction. Then the natural restriction
![]() $\mathcal {O}(U) \rightarrow \mathcal {O}(U\setminus A)$
is an isomorphism.
$\mathcal {O}(U) \rightarrow \mathcal {O}(U\setminus A)$
is an isomorphism.
Proof of Lemma 5.19.
To prove the first statement, we apply Lemma A.1. So we only need to show that, for
![]() $\rho \in \mathscr {P}^{[n-1]}$
, a holomorphic function f in
$\rho \in \mathscr {P}^{[n-1]}$
, a holomorphic function f in
![]() $U_x \setminus \mathscr {S} \subset V(\rho )$
can be extended uniquely to
$U_x \setminus \mathscr {S} \subset V(\rho )$
can be extended uniquely to
![]() $U_x$
, where
$U_x$
, where
![]() $U_x$
is some neighborhood of
$U_x$
is some neighborhood of
![]() $x \in \mathrm {int}_{\mathrm {re}}(\rho ) \cap \mathscr {S}$
. Writing
$x \in \mathrm {int}_{\mathrm {re}}(\rho ) \cap \mathscr {S}$
. Writing
![]() $V(\rho ) = (\mathbb {C}^*)^{n-1} \times \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\rho }])$
, we may simply prove that this is the case with
$V(\rho ) = (\mathbb {C}^*)^{n-1} \times \mathrm {Spec}_{\mathrm {an}}(\mathbb {C}[\Sigma _{\rho }])$
, we may simply prove that this is the case with
![]() $\Sigma _{\rho }$
consisting of a single ray
$\Sigma _{\rho }$
consisting of a single ray
![]() $\sigma $
as in the proof of Lemma A.1. Thus, we can assume that
$\sigma $
as in the proof of Lemma A.1. Thus, we can assume that
![]() $V(\rho ) = (\mathbb {C}^*)^{n-1} \times \mathbb {C}$
and the open subset
$V(\rho ) = (\mathbb {C}^*)^{n-1} \times \mathbb {C}$
and the open subset
![]() $U_x = U \times V$
for some connected U. We observe that extensions of holomorphic functions from
$U_x = U \times V$
for some connected U. We observe that extensions of holomorphic functions from
![]() $(U\setminus \mathscr {S}) \times V$
to
$(U\setminus \mathscr {S}) \times V$
to
![]() $U \times V$
can be done by covering the former open subset with Hartogs’ figures.
$U \times V$
can be done by covering the former open subset with Hartogs’ figures.
To prove the second statement, we need to further consider extensions through
![]() $\mathrm {int}_{\mathrm {re}}(\mathfrak {j})$
for a joint
$\mathrm {int}_{\mathrm {re}}(\mathfrak {j})$
for a joint
![]() $\mathfrak {j}$
. For those joints lying in some codimension one stratum
$\mathfrak {j}$
. For those joints lying in some codimension one stratum
![]() $\rho $
, the argument is similar to the above. So we assume that
$\rho $
, the argument is similar to the above. So we assume that
![]() $\sigma _{\mathfrak {j}} = \sigma $
is a maximal cell. We take a point
$\sigma _{\mathfrak {j}} = \sigma $
is a maximal cell. We take a point
![]() $x \in \mathrm {int}_{\mathrm {re}}(\mathfrak {j})$
and work in a sufficiently small neighborhood U of x. In this case, we may find a codimension one rational hyperplane
$x \in \mathrm {int}_{\mathrm {re}}(\mathfrak {j})$
and work in a sufficiently small neighborhood U of x. In this case, we may find a codimension one rational hyperplane
![]() $\omega $
containing
$\omega $
containing
![]() $\mathfrak {j}$
, together with a lattice embedding
$\mathfrak {j}$
, together with a lattice embedding
![]() $\Lambda _{\omega } \hookrightarrow \Lambda _{\sigma }$
which induces the projection
$\Lambda _{\omega } \hookrightarrow \Lambda _{\sigma }$
which induces the projection
![]() $\pi \colon (\mathbb {C}^*)^{n} \rightarrow (\mathbb {C}^*)^{n-1}$
along one of the coordinate directions. Letting
$\pi \colon (\mathbb {C}^*)^{n} \rightarrow (\mathbb {C}^*)^{n-1}$
along one of the coordinate directions. Letting
![]() $A = \nu ^{-1}(A \cap U)$
and applying Theorem A.2, we obtain extensions of holomorphic functions in U.
$A = \nu ^{-1}(A \cap U)$
and applying Theorem A.2, we obtain extensions of holomorphic functions in U.
List of notations

Acknowledgements
We thank Kenji Fukaya, Mark Gross and Richard Thomas for their interest and encouragement and also Helge Ruddat for useful comments on an earlier draft of this paper. We are very grateful to the anonymous referees for numerous constructive and extremely detailed comments/suggestions which have helped to greatly enhanced the exposition of the whole paper.
Competing interest
The authors have no competing interest to declare.
Funding statement
K. Chan was supported by grants of the Hong Kong Research Grants Council (Project No. CUHK14301420 and CUHK14301621) and direct grants from CUHK. N. C. Leung was supported by grants of the Hong Kong Research Grants Council (Project No. CUHK14301619 and CUHK14306720) and a direct grant (Project No. 4053400) from CUHK. Z. N. Ma was supported by National Science Fund for Excellent Young Scholars (Overseas).
Author contributions
These authors contributed equally to this work.

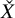
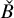
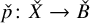
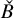
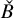
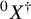 introduced in [8]. Then a comparison between this tropicalized algebra with the dgBV algebra associated to the deformation theory of the semiflat part
introduced in [8]. Then a comparison between this tropicalized algebra with the dgBV algebra associated to the deformation theory of the semiflat part