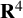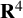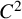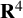1 Introduction
Consider
![]() $\Phi :\mathbf {R}^{n+1} \setminus \{0\} \to (0,\infty )$
a
$\Phi :\mathbf {R}^{n+1} \setminus \{0\} \to (0,\infty )$
a
![]() $1$
-homogeneous
$1$
-homogeneous
![]() $C^{3}_{\textrm {loc}}$
function (i.e.
$C^{3}_{\textrm {loc}}$
function (i.e.
![]() $\Phi (sv) = s\Phi (v)$
for
$\Phi (sv) = s\Phi (v)$
for
![]() $s>0$
). For
$s>0$
). For
![]() $M^{n}\to \mathbf {R}^{n+1}$
a two-sided immersion (with chosen unit normal field
$M^{n}\to \mathbf {R}^{n+1}$
a two-sided immersion (with chosen unit normal field
![]() $\nu (x)$
), we can define the anisotropic area functional
$\nu (x)$
), we can define the anisotropic area functional
Surfaces minimising the
![]() $\mathbf {\Phi }$
-functional arise as the equilibrium shape of crystallineFootnote
1
materials, as well as scaling limits of Ising and percolation models (see [Reference Cerf7, Chapter 5]). We say that M is
$\mathbf {\Phi }$
-functional arise as the equilibrium shape of crystallineFootnote
1
materials, as well as scaling limits of Ising and percolation models (see [Reference Cerf7, Chapter 5]). We say that M is
![]() $\mathbf {\Phi }$
-stationary if
$\mathbf {\Phi }$
-stationary if
![]() $\tfrac {d}{dt}\big |_{t=0} \mathbf {\Phi }(M_{t}) = 0$
for all compactly supported variations of M (fixing
$\tfrac {d}{dt}\big |_{t=0} \mathbf {\Phi }(M_{t}) = 0$
for all compactly supported variations of M (fixing
![]() $\partial M$
) and that M is
$\partial M$
) and that M is
![]() $\mathbf {\Phi }$
-stable if in addition
$\mathbf {\Phi }$
-stable if in addition
![]() $\tfrac {d^{2}}{dt^{2}}\big |_{t=0} \mathbf {\Phi }(M_{t}) \geq 0$
for such variations. Note that if
$\tfrac {d^{2}}{dt^{2}}\big |_{t=0} \mathbf {\Phi }(M_{t}) \geq 0$
for such variations. Note that if
![]() $\Phi (v) = |v|$
,
$\Phi (v) = |v|$
,
![]() $\mathbf {\Phi }$
reduces to the n-dimensional area functional and a
$\mathbf {\Phi }$
reduces to the n-dimensional area functional and a
![]() $\mathbf {\Phi }$
-stable hypersurface is known as a stable minimal hypersurface. We say that
$\mathbf {\Phi }$
-stable hypersurface is known as a stable minimal hypersurface. We say that
![]() $\mathbf {\Phi }$
is elliptic if the
$\mathbf {\Phi }$
is elliptic if the
![]() $\Phi $
-unit ball
$\Phi $
-unit ball
![]() $\Phi ^{-1}((0,1]) \cup \{0\}$
is uniformly convex.
$\Phi ^{-1}((0,1]) \cup \{0\}$
is uniformly convex.
This article is motivated by the following questions:
Question 1.1. For an anisotropic elliptic functional
![]() $\mathbf {\Phi }$
, is the flat hyperplane
$\mathbf {\Phi }$
, is the flat hyperplane
![]() $\mathbf {R}^{n}\subset \mathbf {R}^{n+1}$
the only complete, two-sided
$\mathbf {R}^{n}\subset \mathbf {R}^{n+1}$
the only complete, two-sided
![]() $\mathbf {\Phi }$
-stationary and stable immersion in
$\mathbf {\Phi }$
-stationary and stable immersion in
![]() $\mathbf {R}^{n+1}$
?
$\mathbf {R}^{n+1}$
?
Question 1.2. If
![]() $M^{n}\to \mathbf {R}^{n+1}$
is a complete, two-sided
$M^{n}\to \mathbf {R}^{n+1}$
is a complete, two-sided
![]() $\mathbf {\Phi }$
-stationary and stable immersion (for some anisotropic elliptic functional
$\mathbf {\Phi }$
-stationary and stable immersion (for some anisotropic elliptic functional
![]() $\mathbf {\Phi }$
), does M satisfy the intrinsic polynomial volume growth condition
$\mathbf {\Phi }$
), does M satisfy the intrinsic polynomial volume growth condition
![]() $\operatorname {\mathrm {Vol}}(B_{M}(p,\rho )) \leq C \rho ^{n}$
?
$\operatorname {\mathrm {Vol}}(B_{M}(p,\rho )) \leq C \rho ^{n}$
?
By a well-known blowup argument, an affirmative answer to Question 1.1 yields a priori interior curvature estimates for
![]() $\mathbf {\Phi }$
-stable immersions with boundary, and even for stable immersion with respect to a parametric elliptic integrand (where
$\mathbf {\Phi }$
-stable immersions with boundary, and even for stable immersion with respect to a parametric elliptic integrand (where
![]() $\Phi $
is allowed to also depend on x). We also note that for minimal surfaces, one can derive lower polynomial growth bounds (both intrinsic and extrinsic), but for general
$\Phi $
is allowed to also depend on x). We also note that for minimal surfaces, one can derive lower polynomial growth bounds (both intrinsic and extrinsic), but for general
![]() $\mathbf {\Phi }$
-stationary surfaces, no monotonicity type formula is known (cf. [Reference Allard3, Reference De Philippis, De Rosa and Ghiraldin16, Reference De Philippis, De Rosa and Hirsch17]) (on the other hand, stability can be used to derive a lower volume growth estimate; see Corollary 3.3 and [Reference De Philippis, De Rosa and Hirsch17]).
$\mathbf {\Phi }$
-stationary surfaces, no monotonicity type formula is known (cf. [Reference Allard3, Reference De Philippis, De Rosa and Ghiraldin16, Reference De Philippis, De Rosa and Hirsch17]) (on the other hand, stability can be used to derive a lower volume growth estimate; see Corollary 3.3 and [Reference De Philippis, De Rosa and Hirsch17]).
For the area functional, Question 1.1 (and thus, Question 1.2) has been completely resolved in the affirmative when
![]() $n=2$
(independently) by Fischer-Colbrie and Schoen, do Carmo and Peng and Pogorelov [Reference do Carmo and Peng19, Reference Fischer-Colbrie and Schoen23, Reference Pogorelov39] (see also [Reference Schoen42]) and recently, when
$n=2$
(independently) by Fischer-Colbrie and Schoen, do Carmo and Peng and Pogorelov [Reference do Carmo and Peng19, Reference Fischer-Colbrie and Schoen23, Reference Pogorelov39] (see also [Reference Schoen42]) and recently, when
![]() $n=3$
by the authors [Reference Chodosh and Li10]. In particular, we recall the result of Pogorelov (yielding a localised volume growth estimate).
$n=3$
by the authors [Reference Chodosh and Li10]. In particular, we recall the result of Pogorelov (yielding a localised volume growth estimate).
Theorem 1.3 [Reference Pogorelov39], cf. [Reference White51, Lemma 34], [Reference Munteanu, Sung and Wang36, Theorem 2].
Suppose that
![]() $M^{2}\to \mathbf {R}^{3}$
is a stable minimal immersion so that the intrinsic ball
$M^{2}\to \mathbf {R}^{3}$
is a stable minimal immersion so that the intrinsic ball
![]() $B_{M}(p,R) \subset M$
has compact closure in M and is topologically a disk. Then
$B_{M}(p,R) \subset M$
has compact closure in M and is topologically a disk. Then
On the other hand, Questions 1.1 and 1.2 remain open (even for the area functional) for
![]() $n=4,5,6$
. There exist nonflat stable minimal hypersurfaces (area minimisers) in
$n=4,5,6$
. There exist nonflat stable minimal hypersurfaces (area minimisers) in
![]() $\mathbf {R}^{8}$
and beyond [Reference Bombieri, De Giorgi and Giusti4, Reference Hardt and Simon28] (thus answering Question 1.1 in the negative), but all known examples satisfy the conclusion of Question 1.2. Note that Schoen, Simon and Yau [Reference Schoen, Simon and Yau41] (cf. [Reference Schoen and Simon43, Reference Simons47, Reference Wickramasekera52]) have shown that when
$\mathbf {R}^{8}$
and beyond [Reference Bombieri, De Giorgi and Giusti4, Reference Hardt and Simon28] (thus answering Question 1.1 in the negative), but all known examples satisfy the conclusion of Question 1.2. Note that Schoen, Simon and Yau [Reference Schoen, Simon and Yau41] (cf. [Reference Schoen and Simon43, Reference Simons47, Reference Wickramasekera52]) have shown that when
![]() $n\leq 5$
, a complete, two-sided stable minimal immersion satisfying the volume growth condition in Question 1.2 must be flat.
$n\leq 5$
, a complete, two-sided stable minimal immersion satisfying the volume growth condition in Question 1.2 must be flat.
For arbitrary elliptic functionals, there are nonflat minimisers for
![]() $n\geq 3$
[Reference Mooney and Yang34, Reference Morgan35], but as in the case of area, all known examples satisfy the intrinsic volume growth condition in Question 1.2. When
$n\geq 3$
[Reference Mooney and Yang34, Reference Morgan35], but as in the case of area, all known examples satisfy the intrinsic volume growth condition in Question 1.2. When
![]() $n=2$
, Question 1.1 is open for general elliptic functionals but is resolved in the affirmative assuming quadratic area growth (as shown by White [Reference White50]) or assuming the functional is sufficiently
$n=2$
, Question 1.1 is open for general elliptic functionals but is resolved in the affirmative assuming quadratic area growth (as shown by White [Reference White50]) or assuming the functional is sufficiently
![]() $C^{2}$
-closeFootnote
2
to area (as shown by Lin [Reference Lin30]; see also [Reference Jenkins29, Reference Simon46]). Still, for
$C^{2}$
-closeFootnote
2
to area (as shown by Lin [Reference Lin30]; see also [Reference Jenkins29, Reference Simon46]). Still, for
![]() $n=2$
, Colding and Minicozzi [Reference Colding and Minicozzi II14] have given a new proof of Theorem 1.3 that extends to show that Question 1.2 holds in the affimative for functionals sufficiently
$n=2$
, Colding and Minicozzi [Reference Colding and Minicozzi II14] have given a new proof of Theorem 1.3 that extends to show that Question 1.2 holds in the affimative for functionals sufficiently
![]() $C^{2}$
-close to area. When
$C^{2}$
-close to area. When
![]() $n\geq 3$
, Question 1.1 is answered in the negative by considering the nonflat area minimising solutions constructed by Mooney and Yang [Reference Mooney and Yang34] (see also [Reference Mooney33, Reference Morgan35]). On the other hand, Winklmann [Reference Winklmann53] has resolved Question 1.1 in the affirmative for
$n\geq 3$
, Question 1.1 is answered in the negative by considering the nonflat area minimising solutions constructed by Mooney and Yang [Reference Mooney and Yang34] (see also [Reference Mooney33, Reference Morgan35]). On the other hand, Winklmann [Reference Winklmann53] has resolved Question 1.1 in the affirmative for
![]() $n\leq 5$
under the assumptions that the functional is sufficiently
$n\leq 5$
under the assumptions that the functional is sufficiently
![]() $C^{4}$
-close to area and that the surface satisfies the growth condition from Question 1.2.
$C^{4}$
-close to area and that the surface satisfies the growth condition from Question 1.2.
1.1 Main results
In this article, we consider the volume growth problem (Question 1.2) for
![]() $\mathbf {\Phi }$
-stable hypersurfaces
$\mathbf {\Phi }$
-stable hypersurfaces
![]() $\mathbf {R}^{4}$
. In fact, the estimate we prove here is new even in the case of stable minimal hypersurfaces. As such, it yields an alternative approach to our recent result [Reference Chodosh and Li10] (this is discussed further in Section 2).
$\mathbf {R}^{4}$
. In fact, the estimate we prove here is new even in the case of stable minimal hypersurfaces. As such, it yields an alternative approach to our recent result [Reference Chodosh and Li10] (this is discussed further in Section 2).
We note that all constants in this paper can be given explicitly, see Remark 1.9.
Theorem 1.4. Assume that
![]() $\Phi $
satisfies
$\Phi $
satisfies
for all
![]() $v \in \nu ^{\perp }$
. Consider
$v \in \nu ^{\perp }$
. Consider
![]() $M^3\to \mathbf {R}^4$
a complete, two-sided,
$M^3\to \mathbf {R}^4$
a complete, two-sided,
![]() $\mathbf {\Phi }$
-stationary and stable immersion. Suppose
$\mathbf {\Phi }$
-stationary and stable immersion. Suppose
![]() $0\in M$
and M is simplyFootnote
3
connected. Then there exist explicit constants
$0\in M$
and M is simplyFootnote
3
connected. Then there exist explicit constants
![]() $V_0=V_0(\|\Phi \|_{C^1(S^{3})}), Q>0$
, such that
$V_0=V_0(\|\Phi \|_{C^1(S^{3})}), Q>0$
, such that
-
(i)
 $|B_{M}(0,\rho )|\le V_0 \rho ^3$
, for all
$|B_{M}(0,\rho )|\le V_0 \rho ^3$
, for all
 $\rho>0$
.
$\rho>0$
. -
(ii) For each connected component
 $\Sigma _0$
of
$\Sigma _0$
of
 $\partial B_{M}(0,\rho )$
, we have
$\partial B_{M}(0,\rho )$
, we have  $$\begin{align*}\max_{x\in \Sigma_0} r(x)\le Q \min_{x\in \Sigma_0} r(x),\end{align*}$$
$$\begin{align*}\max_{x\in \Sigma_0} r(x)\le Q \min_{x\in \Sigma_0} r(x),\end{align*}$$
where
 $r(x):=d_{\mathbf {R}^4}(0,x)$
.
$r(x):=d_{\mathbf {R}^4}(0,x)$
.
Note that (1.1) implies that
![]() $\nu \mapsto \Phi (\nu )$
is convex (since
$\nu \mapsto \Phi (\nu )$
is convex (since
![]() $D^{2}\Phi (\nu )(\nu ,\nu ) = 0$
by
$D^{2}\Phi (\nu )(\nu ,\nu ) = 0$
by
![]() $1$
-homogeneity). As such, all
$1$
-homogeneity). As such, all
![]() $\mathbf {\Phi }$
considered in Theorem 1.4 satisfy the ellipticity condition mentioned previously.
$\mathbf {\Phi }$
considered in Theorem 1.4 satisfy the ellipticity condition mentioned previously.
We note that by combining Theorem 1.4 with [Reference Winklmann53], we obtain:
Corollary 1.5. If
![]() $\Phi $
is
$\Phi $
is
![]() $C^{4}$
-sufficiently close to area, then any two-sided, complete
$C^{4}$
-sufficiently close to area, then any two-sided, complete
![]() $\mathbf {\Phi }$
-stationary and stable immersion is flat.
$\mathbf {\Phi }$
-stationary and stable immersion is flat.
Remark 1.6. Although it is not explicitly done in [Reference Winklmann53], the ‘sufficiently close’ requirement can be quantified. Alternatively, we note that by combining Theorem 1.4 with a contradiction argument in the spirit of [Reference Simon46], Corollary 1.5 actually holds under the weaker assumption of
![]() $C^{2,\alpha }$
-closeness (but with no numerical estimate of the required closeness).
$C^{2,\alpha }$
-closeness (but with no numerical estimate of the required closeness).
We can also prove a localised version of Theorem 1.4 more in the spirit of Pogorelov’s result (cf. Theorem 1.3). The estimate we prove here is slightly different, since it considers extrinsic balls, but is an interiorFootnote
4
estimate. Even for stable minimal surfaces, we are not aware of such an estimate in
![]() $\mathbf {R}^{3}$
with explicitFootnote
5
constants, cf. Remark 1.9.
$\mathbf {R}^{3}$
with explicitFootnote
5
constants, cf. Remark 1.9.
Theorem 1.7. Suppose that
![]() $\Phi $
satisfies (1.1). Assume
$\Phi $
satisfies (1.1). Assume
![]() $M^3\to B_1(0)\subset \mathbf {R}^4$
is a proper, two-sided
$M^3\to B_1(0)\subset \mathbf {R}^4$
is a proper, two-sided
![]() $\mathbf {\Phi }$
-stationary and stable immersion. Suppose
$\mathbf {\Phi }$
-stationary and stable immersion. Suppose
![]() $0\in M$
, M is simply connected and
$0\in M$
, M is simply connected and
![]() $\partial M$
is connected. Then there exist explicit constants
$\partial M$
is connected. Then there exist explicit constants
![]() $\rho _0 \in (0,1), V_1= V_1(\|\Phi \|_{C^1(S^{3})})$
, such that
$\rho _0 \in (0,1), V_1= V_1(\|\Phi \|_{C^1(S^{3})})$
, such that
where
![]() $M_{\rho _0}^*$
is the connected component of
$M_{\rho _0}^*$
is the connected component of
![]() $M\cap B_{\mathbf {R}^{4}}(0,\rho _{0})$
that contains
$M\cap B_{\mathbf {R}^{4}}(0,\rho _{0})$
that contains
![]() $0$
.
$0$
.
Remark 1.8. More generally, we can drop the requirement that M is simply connected and
![]() $\partial M$
is connected. In this case, we have:
$\partial M$
is connected. In this case, we have:
where E is the number of boundary connected components of M and
![]() $b_{1}(M)$
is the first Betti number.
$b_{1}(M)$
is the first Betti number.
Remark 1.9. One may explicitly compute the constants
![]() $V_0,V_{1}$
, Q,
$V_0,V_{1}$
, Q,
![]() $\rho _{0}$
as follows. Let
$\rho _{0}$
as follows. Let
 $$ \begin{align*} c_0 & = \frac{1}{\sqrt 2 - \frac 12},\\ \lambda & = \frac32 \left(\frac12 - \frac{3(c_0-1)}{8(\frac{1}{\sqrt 2} - \frac12)}\right) = \frac{3(5+3\sqrt 2)}{56} \approx 0.495. \end{align*} $$
$$ \begin{align*} c_0 & = \frac{1}{\sqrt 2 - \frac 12},\\ \lambda & = \frac32 \left(\frac12 - \frac{3(c_0-1)}{8(\frac{1}{\sqrt 2} - \frac12)}\right) = \frac{3(5+3\sqrt 2)}{56} \approx 0.495. \end{align*} $$
Then we have
 $$\begin{align*}V_0 = \frac{8\pi e^{\frac{15\pi}{\lambda}} \|\Phi\|_{C^1(S^3)} }{3\lambda \min_{\nu \in S^3} \Phi(\nu)}, \quad Q = e^{\frac{7\pi}{\sqrt \lambda}}\end{align*}$$
$$\begin{align*}V_0 = \frac{8\pi e^{\frac{15\pi}{\lambda}} \|\Phi\|_{C^1(S^3)} }{3\lambda \min_{\nu \in S^3} \Phi(\nu)}, \quad Q = e^{\frac{7\pi}{\sqrt \lambda}}\end{align*}$$
and
 $$\begin{align*}\rho_0 = e^{-\frac{5\pi}{\sqrt \lambda}},\quad V_1= \frac{8\pi \|\Phi\|_{C^1(S^3)}}{3\lambda\min_{\nu\in S^3}\Phi(\nu)}.\end{align*}$$
$$\begin{align*}\rho_0 = e^{-\frac{5\pi}{\sqrt \lambda}},\quad V_1= \frac{8\pi \|\Phi\|_{C^1(S^3)}}{3\lambda\min_{\nu\in S^3}\Phi(\nu)}.\end{align*}$$
1.2 Related work
We recall, here, some works (beyond those mentioned above) that are related to this paper. The regularity of hypersurfaces minimising parametric elliptic integrands has been studied in several places including [Reference Federer20, Reference Figalli21, Reference Schoen, Simon and Almgren40, Reference Schoen and Simon44]. See also [Reference Allard1, Reference White48] for estimates without the minimising hypothesis. Existence of critical points of parametric elliptic integrands has been considered in [Reference De Philippis and De Rosa15, Reference White49, Reference White50]. Finally, we note that stable solutions for the nonlocal area functional satisfy an a priori growth estimate (as in Question 1.2) in all dimensions [Reference Cinti, Serra and Valdinoci13] (see also [Reference Figalli and Serra22]).
1.3 Notation
We will use the following notation:
-
•
 $B_{\mathbf {R}^{n+1}}(0,\rho ) := \{x\in \mathbf {R}^{n+1}: |x| < \rho \}$
.
$B_{\mathbf {R}^{n+1}}(0,\rho ) := \{x\in \mathbf {R}^{n+1}: |x| < \rho \}$
. -
•
 $r(x) = \operatorname {\mathrm {dist}}_{\mathbf {R}^{n+1}} (0,x)$
.
$r(x) = \operatorname {\mathrm {dist}}_{\mathbf {R}^{n+1}} (0,x)$
. -
•
 $M^n\to \mathbf {R}^{n+1}$
is an immersion and g the induced Riemannian metric on M.
$M^n\to \mathbf {R}^{n+1}$
is an immersion and g the induced Riemannian metric on M. -
• D is the connection in
 $\mathbf {R}^{n+1}$
,
$\mathbf {R}^{n+1}$
,
 $\nabla $
is the induced connection on M.
$\nabla $
is the induced connection on M. -
•
 $\mu $
is the volume form of g.
$\mu $
is the volume form of g. -
•
 $B_{M}(0,\rho ) : = \{x\in M: \operatorname {\mathrm {dist}}_{M,g} (0,x)<\rho \}$
.
$B_{M}(0,\rho ) : = \{x\in M: \operatorname {\mathrm {dist}}_{M,g} (0,x)<\rho \}$
. -
•
 $\nu $
is a choice of unit normal vector field of M.
$\nu $
is a choice of unit normal vector field of M. -
• The shape operator will be written
 $S = \nabla \nu $
and the second fundamental form written
$S = \nabla \nu $
and the second fundamental form written
 $A(X,Y) = S(X)\cdot Y$
.
$A(X,Y) = S(X)\cdot Y$
. -
• The scalar curvature of g will be denoted by R.
-
• We will use the
 $\ell ^{2}$
-norm to define
$\ell ^{2}$
-norm to define
 $C^{k}$
-norms, that is
$C^{k}$
-norms, that is
 $\Vert f \Vert _{C^{k}} : = (\sum _{j=0}^{k} \Vert D^{(j)}f \Vert _{C^{0}}^{2})^{\frac 12}$
.
$\Vert f \Vert _{C^{k}} : = (\sum _{j=0}^{k} \Vert D^{(j)}f \Vert _{C^{0}}^{2})^{\frac 12}$
.
1.4 Organisation of the paper
In Section 2, we explain the techniques used in this paper in the special case of the area functional. The remaining part of the paper contains the details necessary for the generalisation to anisotropic integrands. We begin in Section 3 with some preliminary results. Section 4 contains a generalisation of the one-ended result for stable minimal hypersurfaces due to Cao, Shen and Zhu to the case of certain anisotropic integrands. We describe the conformally changed metric in Section 5 as introduced by Gulliver–Lawson and then combine these techniques with
![]() $\mu $
-bubbles to prove the main results in Section 5. Appendix A contains (well-known) computations of the first and second variation for elliptic integrands. Appendix B contains an auxiliary result comparing certain quadratic forms.
$\mu $
-bubbles to prove the main results in Section 5. Appendix A contains (well-known) computations of the first and second variation for elliptic integrands. Appendix B contains an auxiliary result comparing certain quadratic forms.
2 Volume growth for stable minimal hypersurfaces in
 $\mathbf {R}^{4}$
$\mathbf {R}^{4}$
In this section, we illustrate how one may use stability to deduce area estimates for stable minimal immersions
![]() $M^3\to \mathbf {R}^4$
. We will defer certain ancillary results and computation to later sections (where they were carried out for general
$M^3\to \mathbf {R}^4$
. We will defer certain ancillary results and computation to later sections (where they were carried out for general
![]() $\Phi $
-stationary and stable hypersurfaces) and instead focus on the geometric ideas and consequences.
$\Phi $
-stationary and stable hypersurfaces) and instead focus on the geometric ideas and consequences.
The main result we will prove here is as follows:
Theorem 2.1. Let
![]() $M^3\to \mathbf {R}^4$
be a complete, two-sided, simply connected, stable minimal immersion,
$M^3\to \mathbf {R}^4$
be a complete, two-sided, simply connected, stable minimal immersion,
![]() $0\in M$
. Then,
$0\in M$
. Then,
 $$\begin{align*}|B_{M}(0,\rho)| \leq \left(\frac{32\pi}{3}\right)^{\frac 32}\frac{e^{\frac{30\pi}{\sqrt 3}}}{6\sqrt \pi} \rho^{3}, \end{align*}$$
$$\begin{align*}|B_{M}(0,\rho)| \leq \left(\frac{32\pi}{3}\right)^{\frac 32}\frac{e^{\frac{30\pi}{\sqrt 3}}}{6\sqrt \pi} \rho^{3}, \end{align*}$$
for all
![]() $\rho \geq 0$
.
$\rho \geq 0$
.
Combined with the work of Schoen et al. [Reference Schoen, Simon and Yau41], this yields a new proof of our recent result [Reference Chodosh and Li10]:
Corollary 2.2. Any complete, two-sided, stable minimal immersion
![]() $M^{3}\to \mathbf {R}^{4}$
is flat.
$M^{3}\to \mathbf {R}^{4}$
is flat.
In fact, we have the following localised volume estimate in the spirit of Theorem 1.3.
Theorem 2.3. Let
![]() $M^3\to \mathbf {R}^4$
be a two-sided, simply connected stable minimal immersion, with
$M^3\to \mathbf {R}^4$
be a two-sided, simply connected stable minimal immersion, with
![]() $0\in M$
,
$0\in M$
,
![]() $\partial M$
connected and
$\partial M$
connected and
![]() $M\to B_{\mathbf {R}^{4}}(0,1) $
proper. Then,
$M\to B_{\mathbf {R}^{4}}(0,1) $
proper. Then,
 $$\begin{align*}|M_{\rho_{0}}^{*}| \leq \left(\frac{32\pi}{3}\right)^{\frac 32}\frac{1}{6\sqrt \pi}, \end{align*}$$
$$\begin{align*}|M_{\rho_{0}}^{*}| \leq \left(\frac{32\pi}{3}\right)^{\frac 32}\frac{1}{6\sqrt \pi}, \end{align*}$$
where
![]() $M_{\rho _0}^*$
is the connected component of
$M_{\rho _0}^*$
is the connected component of
![]() $M\cap B_{\mathbf {R}^{4}}(0,r_{0})$
that contains
$M\cap B_{\mathbf {R}^{4}}(0,r_{0})$
that contains
![]() $0$
and
$0$
and
![]() $\rho _{0} = e^{-\frac {10\pi }{\sqrt 3}}$
.
$\rho _{0} = e^{-\frac {10\pi }{\sqrt 3}}$
.
Proof of Theorem 2.1.
The first step is to consider a particular conformal deformation of
![]() $(M,g)$
. On
$(M,g)$
. On
![]() $M\setminus \{0\}$
, consider the conformally deformed metric
$M\setminus \{0\}$
, consider the conformally deformed metric
![]() $\tilde g = r^{-2}g$
(where we recall that r is the Euclidean distance to the origin and g is the induced metric on M). We use
$\tilde g = r^{-2}g$
(where we recall that r is the Euclidean distance to the origin and g is the induced metric on M). We use
![]() $\tilde \nabla , \tilde \mu , \tilde \Delta $
to denote the covariant derivative, the volume form and the Laplacian with respect to
$\tilde \nabla , \tilde \mu , \tilde \Delta $
to denote the covariant derivative, the volume form and the Laplacian with respect to
![]() $\tilde g$
, respectively. This conformal change was first used by Gulliver and Lawson [Reference Gulliver and Lawson27] to study isolated singularities for minimal hypersurfaces in
$\tilde g$
, respectively. This conformal change was first used by Gulliver and Lawson [Reference Gulliver and Lawson27] to study isolated singularities for minimal hypersurfaces in
![]() $\mathbf {R}^{n+1}$
.
$\mathbf {R}^{n+1}$
.
Remark 2.4. The relevance of the Gulliver and Lawson conformal deformation is a key insight in our work. Indeed, this allows us to apply tools from the study of strictly positive scalar curvature (cf. Remark 2.5). Our previous proof of Corollary 2.2 used tools from nonnegative scalar curvature (cf. [Reference Munteanu and Wang37, Reference Munteanu and Wang38]).Footnote 6
The computations in this part work for minimal immersions
![]() $M^n\to \mathbf {R}^{n+1}$
whenever
$M^n\to \mathbf {R}^{n+1}$
whenever
![]() $n\ge 3$
. For
$n\ge 3$
. For
![]() $\lambda \in \mathbf {R}$
,
$\lambda \in \mathbf {R}$
,
![]() $\varphi \in C_0^1(M\setminus \{0\})$
, consider the quadratic form
$\varphi \in C_0^1(M\setminus \{0\})$
, consider the quadratic form
where
![]() $\tilde R$
is the scalar curvature of
$\tilde R$
is the scalar curvature of
![]() $\tilde g$
. One computes (see Section 5 for details) that
$\tilde g$
. One computes (see Section 5 for details) that
 $$ \begin{align*} \mathcal Q(r^{\frac{n-2}{2}}\varphi) &= \int_M \left(r^2 |\nabla (r^{\frac{n-2}{2}}\varphi)|^2 + (\tfrac12 \tilde R - \lambda )r^{n-2}\varphi^2\right)r^{-n} d\mu\\ & = \int_M \left(|\nabla \varphi|^2 +\tfrac 12 R \varphi^2 + \left(\frac n2 \left(n - \frac{n+2}{2}|\nabla r|^2\right )-\lambda\right)r^{-2}\varphi^2\right)d\mu\\ & \ge \int_M \left(|\nabla \varphi|^2 + \tfrac 12 R \varphi^2 + \left(\frac{n(n-2)}{4} - \lambda\right)\right) d\mu. \end{align*} $$
$$ \begin{align*} \mathcal Q(r^{\frac{n-2}{2}}\varphi) &= \int_M \left(r^2 |\nabla (r^{\frac{n-2}{2}}\varphi)|^2 + (\tfrac12 \tilde R - \lambda )r^{n-2}\varphi^2\right)r^{-n} d\mu\\ & = \int_M \left(|\nabla \varphi|^2 +\tfrac 12 R \varphi^2 + \left(\frac n2 \left(n - \frac{n+2}{2}|\nabla r|^2\right )-\lambda\right)r^{-2}\varphi^2\right)d\mu\\ & \ge \int_M \left(|\nabla \varphi|^2 + \tfrac 12 R \varphi^2 + \left(\frac{n(n-2)}{4} - \lambda\right)\right) d\mu. \end{align*} $$
By the (traced) Gauss equations, minimality of M implies that
![]() $|A_{M}|^2 = -R_g$
. Thus, we can use stability of M to conclude
$|A_{M}|^2 = -R_g$
. Thus, we can use stability of M to conclude
 $$\begin{align*}\int_M \left( |\nabla \varphi|^2 - |A|^2 \varphi^2\right) d\mu \ge 0 \quad\Rightarrow \quad \int_M \left( |\nabla \varphi|^2 + \frac12 R \varphi^2\right) d\mu \ge 0,\end{align*}$$
$$\begin{align*}\int_M \left( |\nabla \varphi|^2 - |A|^2 \varphi^2\right) d\mu \ge 0 \quad\Rightarrow \quad \int_M \left( |\nabla \varphi|^2 + \frac12 R \varphi^2\right) d\mu \ge 0,\end{align*}$$
for all
![]() $\varphi \in C_0^1(M)$
. Note that we have used the fact that the scalar curvature of a minimal hypersurface in
$\varphi \in C_0^1(M)$
. Note that we have used the fact that the scalar curvature of a minimal hypersurface in
![]() $\mathbf {R}^{n+1}$
has
$\mathbf {R}^{n+1}$
has
![]() $R\le 0$
and that
$R\le 0$
and that
![]() $\tfrac 12 <1$
. In particular, choosing
$\tfrac 12 <1$
. In particular, choosing
![]() $\lambda = \frac {n(n-2)}{4}$
above, we find that
$\lambda = \frac {n(n-2)}{4}$
above, we find that
![]() $\mathcal Q(\varphi )\ge 0$
for any
$\mathcal Q(\varphi )\ge 0$
for any
![]() $\varphi \in C_0^1 (M\setminus \{0\})$
. Using [Reference Fischer-Colbrie and Schoen23, Theorem 1], there exists
$\varphi \in C_0^1 (M\setminus \{0\})$
. Using [Reference Fischer-Colbrie and Schoen23, Theorem 1], there exists
![]() $u\in C^\infty (M\setminus \{0\})$
,
$u\in C^\infty (M\setminus \{0\})$
,
![]() $u>0$
in the interior of
$u>0$
in the interior of
![]() $M\setminus \{0\}$
, such that
$M\setminus \{0\}$
, such that
 $$ \begin{align} \tilde \Delta u \le -\frac12 \left(\frac{n(n-2)}{2} - \tilde R\right)u. \end{align} $$
$$ \begin{align} \tilde \Delta u \le -\frac12 \left(\frac{n(n-2)}{2} - \tilde R\right)u. \end{align} $$
We note that (2.1) is an integral form of strictly positive scalar curvature.
In the second step, we restrict to the case of
![]() $n=3$
. We use warped
$n=3$
. We use warped
![]() $\mu $
-bubbles to derive geometric inequalities for
$\mu $
-bubbles to derive geometric inequalities for
![]() $3$
-manifolds
$3$
-manifolds
![]() $(N^3,g)$
admitting a positive function u with (2.1).
$(N^3,g)$
admitting a positive function u with (2.1).
Remark 2.5. The
![]() $\mu $
-bubble technique was first used by Gromov [Reference Catino, Mastrolia and Roncoroni8, Section 5
$\mu $
-bubble technique was first used by Gromov [Reference Catino, Mastrolia and Roncoroni8, Section 5
![]() $\frac{5}{6}$
] (see also [Reference Gromov25]). Warped
$\frac{5}{6}$
] (see also [Reference Gromov25]). Warped
![]() $\mu $
-bubbles have previously been combined with minimal hypersurface techniques to study problems in scalar curvature and in minimal surfaces (see, e.g. [Reference Chodosh and Li9, Reference Chodosh, Li and Liokumovich11, Reference Chodosh, Li and Stryker12, Reference Gromov26, Reference Zhu55, Reference Zhu56]). Precisely, suppose
$\mu $
-bubbles have previously been combined with minimal hypersurface techniques to study problems in scalar curvature and in minimal surfaces (see, e.g. [Reference Chodosh and Li9, Reference Chodosh, Li and Liokumovich11, Reference Chodosh, Li and Stryker12, Reference Gromov26, Reference Zhu55, Reference Zhu56]). Precisely, suppose
![]() $n=3$
and
$n=3$
and
![]() $\partial N\ne \emptyset $
. Then there exists an open set
$\partial N\ne \emptyset $
. Then there exists an open set
![]() $\Omega $
containing
$\Omega $
containing
![]() $\partial N$
,
$\partial N$
,
![]() $\Omega \subset B_{\frac {10\pi }{\sqrt 3}}(\partial N)$
, such that each connected component of
$\Omega \subset B_{\frac {10\pi }{\sqrt 3}}(\partial N)$
, such that each connected component of
![]() $\partial \Omega \setminus \partial N$
is a
$\partial \Omega \setminus \partial N$
is a
![]() $2$
-sphere with area at most
$2$
-sphere with area at most
![]() $\frac {32\pi }{3}$
and intrinsic diameter at most
$\frac {32\pi }{3}$
and intrinsic diameter at most
![]() $\frac {4\pi }{\sqrt 3}$
(see Lemma 6.1).
$\frac {4\pi }{\sqrt 3}$
(see Lemma 6.1).
Fix
![]() $\rho>0$
. By [Reference Cao, Shen and Zhu6],
$\rho>0$
. By [Reference Cao, Shen and Zhu6],
![]() $M\setminus B_M\left (0,e^{\frac {10\pi }{\sqrt 3}}\rho \right )$
has only one unbounded component E. Denote by
$M\setminus B_M\left (0,e^{\frac {10\pi }{\sqrt 3}}\rho \right )$
has only one unbounded component E. Denote by
![]() $M'=M\setminus E$
. We apply Remark 2.5 to
$M'=M\setminus E$
. We apply Remark 2.5 to
![]() $N=M'$
and find
$N=M'$
and find
![]() $M_0\subset M'$
with
$M_0\subset M'$
with
![]() $\operatorname {\mathrm {dist}}_{ \tilde g} (\partial M_0, \partial M')\le \frac {10\pi }{\sqrt 3}$
. The topological assumptions on M force
$\operatorname {\mathrm {dist}}_{ \tilde g} (\partial M_0, \partial M')\le \frac {10\pi }{\sqrt 3}$
. The topological assumptions on M force
![]() $\partial M_0$
to be connected, so
$\partial M_0$
to be connected, so
![]() $|\partial M_0|_{\tilde g}\le \tfrac {32\pi }{3}$
and
$|\partial M_0|_{\tilde g}\le \tfrac {32\pi }{3}$
and
![]() $\partial M_{0}$
has intrinsic diameter
$\partial M_{0}$
has intrinsic diameter
![]() $\leq \frac {4\pi }{\sqrt {3}}$
. By comparing g-distance with
$\leq \frac {4\pi }{\sqrt {3}}$
. By comparing g-distance with
![]() $\tilde g$
-distance (see (2) in Lemma 6.2), we find that
$\tilde g$
-distance (see (2) in Lemma 6.2), we find that
In particular, bounding intrinsic distance by extrinsic distance, we see that
![]() $\sup _{\partial M_{0}} r(x) \leq e^{\frac {10\pi }{\sqrt {3}}} \rho $
. Thus, we have
$\sup _{\partial M_{0}} r(x) \leq e^{\frac {10\pi }{\sqrt {3}}} \rho $
. Thus, we have
 $$\begin{align*}|B_{M}(0,\rho)| \le | M_0| \le \frac{1}{6\sqrt \pi} |\partial M_0|_g^{\frac 32} \le \frac{1}{6\sqrt \pi} (e^{\frac{10\pi}{\sqrt{3}}}\rho)^3 |\partial M_0|_{\tilde g}^{\frac 32} \le \left(\frac{32\pi}{3}\right)^{\frac 32}\frac{e^{\frac{30\pi}{\sqrt 3}}}{6\sqrt \pi}\rho^3, \end{align*}$$
$$\begin{align*}|B_{M}(0,\rho)| \le | M_0| \le \frac{1}{6\sqrt \pi} |\partial M_0|_g^{\frac 32} \le \frac{1}{6\sqrt \pi} (e^{\frac{10\pi}{\sqrt{3}}}\rho)^3 |\partial M_0|_{\tilde g}^{\frac 32} \le \left(\frac{32\pi}{3}\right)^{\frac 32}\frac{e^{\frac{30\pi}{\sqrt 3}}}{6\sqrt \pi}\rho^3, \end{align*}$$
where in the second step, we have used the isoperimetric inequality for minimal hypersurfaces in Euclidean spaces due to Brendle [Reference Brendle5] (cf. [Reference Michael and Simon32]). This completes the proof.
We now consider the requisite changes needed to prove the local result:
Proof of Theorem 2.3.
In the case where M is properly immersed in
![]() $B_1(0)\subset \mathbf {R}^4$
, we proceed similarly as before and obtain a region
$B_1(0)\subset \mathbf {R}^4$
, we proceed similarly as before and obtain a region
![]() $M'$
, such that
$M'$
, such that
![]() $\operatorname {\mathrm {dist}}_{ \tilde g} (\partial M',\partial B_1(0))\le \frac {10\pi }{\sqrt {3}}$
,
$\operatorname {\mathrm {dist}}_{ \tilde g} (\partial M',\partial B_1(0))\le \frac {10\pi }{\sqrt {3}}$
,
![]() $|\partial M'|_{\tilde g}\le \frac {32\pi }{3}$
and
$|\partial M'|_{\tilde g}\le \frac {32\pi }{3}$
and
![]() $\partial M'$
is connected. Again, using Lemma 6.2, we conclude that
$\partial M'$
is connected. Again, using Lemma 6.2, we conclude that
where
![]() $\rho _0 = e^{-\frac {10\pi }{\sqrt 3}}$
and
$\rho _0 = e^{-\frac {10\pi }{\sqrt 3}}$
and
![]() $M_{\rho _0}^*$
is the connected component of
$M_{\rho _0}^*$
is the connected component of
![]() $M\cap B_{\mathbf {R}^{4}}(0,\rho _{0})$
that contains
$M\cap B_{\mathbf {R}^{4}}(0,\rho _{0})$
that contains
![]() $0$
. Using [Reference Brendle5] as above,
$0$
. Using [Reference Brendle5] as above,
 $$\begin{align*}|M_{r_0}^*| \le |M'| \le \frac{1}{6\sqrt \pi} |\partial M'|_g^{\frac 32}\le \frac{1}{6\sqrt \pi} |\partial M'|_{\tilde g}^{\frac 32} \le \left(\frac{32\pi}{3}\right)^{\frac 32}\frac{1}{6\sqrt \pi}.\end{align*}$$
$$\begin{align*}|M_{r_0}^*| \le |M'| \le \frac{1}{6\sqrt \pi} |\partial M'|_g^{\frac 32}\le \frac{1}{6\sqrt \pi} |\partial M'|_{\tilde g}^{\frac 32} \le \left(\frac{32\pi}{3}\right)^{\frac 32}\frac{1}{6\sqrt \pi}.\end{align*}$$
This completes the proof.
3 Preliminaries on anisotropic integrands
We now consider a general anisotropic elliptic integrand. For
![]() $M^{n}\to \mathbf {R}^{n+1}$
two-sided immersion, we can set
$M^{n}\to \mathbf {R}^{n+1}$
two-sided immersion, we can set
In this section, we discuss the first and second variation formulae, as well as some important consequences to be used later.
3.1 First variation
Recall that M is
![]() $\mathbf {\Phi }$
-stationary means that
$\mathbf {\Phi }$
-stationary means that
![]() $\tfrac {d}{dt}\big |_{t=0} \mathbf {\Phi }(M_{t}) = 0$
for all compactly supported variations
$\tfrac {d}{dt}\big |_{t=0} \mathbf {\Phi }(M_{t}) = 0$
for all compactly supported variations
![]() $M_t$
fixing
$M_t$
fixing
![]() $\partial M$
. By (A.1), (A.2), (A.3) this is equivalent to
$\partial M$
. By (A.1), (A.2), (A.3) this is equivalent to
which we can interpret as vanishing of the
![]() $\mathbf {\Phi }$
-mean curvature. Here,
$\mathbf {\Phi }$
-mean curvature. Here,
![]() $\Psi (\nu ) : T\mathbf {R}^{n+1}\to T\mathbf {R}^{n+1}$
is defined by
$\Psi (\nu ) : T\mathbf {R}^{n+1}\to T\mathbf {R}^{n+1}$
is defined by
![]() $\Psi (\nu ): X \mapsto D^{2}\Phi (\nu )[X,\cdot ]$
and
$\Psi (\nu ): X \mapsto D^{2}\Phi (\nu )[X,\cdot ]$
and
![]() $S_{M}$
is the shape operator of M.
$S_{M}$
is the shape operator of M.
By the calculation in Section A.3, we find that if M is
![]() $\mathbf {\Phi }$
-stationary, then for any compactly supported (but not necessarily normal) vector field X along
$\mathbf {\Phi }$
-stationary, then for any compactly supported (but not necessarily normal) vector field X along
![]() $\Sigma $
, we have
$\Sigma $
, we have
By plugging the position vector field into (3.1), we obtain the following isoperimetric type inequality.
Corollary 3.1. Suppose
![]() $M^n\to \mathbf {R}^{n+1}$
is
$M^n\to \mathbf {R}^{n+1}$
is
![]() $\mathbf {\Phi }$
-stationary and the image of
$\mathbf {\Phi }$
-stationary and the image of
![]() $\partial M$
is contained in
$\partial M$
is contained in
![]() $B_{\mathbf {R}^{n+1}}(0,\rho )$
for some
$B_{\mathbf {R}^{n+1}}(0,\rho )$
for some
![]() $\rho>0$
. Then
$\rho>0$
. Then
 $$\begin{align*}|M| \le \frac{\rho\|\Phi\|_{C^1(S^{n})}}{n \cdot \min_{\nu\in S^n} \Phi(\nu)} |\partial M|.\end{align*}$$
$$\begin{align*}|M| \le \frac{\rho\|\Phi\|_{C^1(S^{n})}}{n \cdot \min_{\nu\in S^n} \Phi(\nu)} |\partial M|.\end{align*}$$
Proof. Recall that
![]() $r(x) = \operatorname {\mathrm {dist}}_{\mathbf {R}^{n+1}}(x,0)$
. Plug
$r(x) = \operatorname {\mathrm {dist}}_{\mathbf {R}^{n+1}}(x,0)$
. Plug
![]() $X = \sum _{i=1}^{n+1} x_i e_i$
, the position vector field in
$X = \sum _{i=1}^{n+1} x_i e_i$
, the position vector field in
![]() $\mathbf {R}^{n+1}$
, into (3.1). Then
$\mathbf {R}^{n+1}$
, into (3.1). Then
![]() $\operatorname {\mathrm {div}}_M X = n$
and
$\operatorname {\mathrm {div}}_M X = n$
and
On the other hand,
![]() $|X(x)|\le r(x)$
. Thus, we find (using
$|X(x)|\le r(x)$
. Thus, we find (using
![]() $\nu ,\eta $
orthonormal)
$\nu ,\eta $
orthonormal)
This completes the proof.
The next lemma generalises the traced Gauss equation
![]() $R = - |A|^{2}$
(valid for minimal hypersurfaces) to the case of
$R = - |A|^{2}$
(valid for minimal hypersurfaces) to the case of
![]() $\mathbf {\Phi }$
-stationary hypersurfaces in
$\mathbf {\Phi }$
-stationary hypersurfaces in
![]() $\mathbf {R}^{4}$
, under the assumption that
$\mathbf {R}^{4}$
, under the assumption that
![]() $D^{2}\Phi (\nu )$
is sufficiently pinched.
$D^{2}\Phi (\nu )$
is sufficiently pinched.
Lemma 3.2. Suppose
![]() $\Phi $
satisfies (1.1) and
$\Phi $
satisfies (1.1) and
![]() $M^{3}\to \mathbf {R}^{4}$
is
$M^{3}\to \mathbf {R}^{4}$
is
![]() $\mathbf {\Phi }$
-stationary. Then at each point on M, the induced scalar curvature satisfies
$\mathbf {\Phi }$
-stationary. Then at each point on M, the induced scalar curvature satisfies
![]() $R \le 0$
and
$R \le 0$
and
where
 $$\begin{align*}c_0 = \frac{1}{\sqrt 2 - \frac 12} \approx 1.09 .\end{align*}$$
$$\begin{align*}c_0 = \frac{1}{\sqrt 2 - \frac 12} \approx 1.09 .\end{align*}$$
Proof. Recall that
![]() $\mathbf {\Phi }$
-stationarity can be written as
$\mathbf {\Phi }$
-stationarity can be written as
![]() $\operatorname {\mathrm {tr}}_{M}(\Psi (\nu )S_{M}) = 0$
. Diagonalising
$\operatorname {\mathrm {tr}}_{M}(\Psi (\nu )S_{M}) = 0$
. Diagonalising
![]() $A_{M}$
at a given point, write
$A_{M}$
at a given point, write
![]() $k_{i}$
for the principal curvatures of M and
$k_{i}$
for the principal curvatures of M and
![]() $e_{i}$
for corresponding principal directions. Thus,
$e_{i}$
for corresponding principal directions. Thus,
![]() $\mathbf {\Phi }$
-stationarity can be written as
$\mathbf {\Phi }$
-stationarity can be written as
 $$\begin{align*}0 = \sum_{i=1}^{3} a_{i}k_{i}, \end{align*}$$
$$\begin{align*}0 = \sum_{i=1}^{3} a_{i}k_{i}, \end{align*}$$
where
![]() $a_{i} = D^{2}\Phi (\nu )[e_{i},e_{i}]$
. Without loss of generality, we can assume that
$a_{i} = D^{2}\Phi (\nu )[e_{i},e_{i}]$
. Without loss of generality, we can assume that
![]() $a_1\le a_2\le a_3$
. Note that the pinching assumption (1.1) yields
$a_1\le a_2\le a_3$
. Note that the pinching assumption (1.1) yields
We have
![]() $|A|^2 = \sum k_i^2$
,
$|A|^2 = \sum k_i^2$
,
![]() $R = 2\sum _{i< j} k_ik_j$
. Writing
$R = 2\sum _{i< j} k_ik_j$
. Writing
![]() $k_3= -\frac {a_1k_1 + a_2k_2}{a_3}$
, we have
$k_3= -\frac {a_1k_1 + a_2k_2}{a_3}$
, we have
 $$\begin{align*}|A|^2 = Q_1(k_1,k_2) :=\frac{a_1^2 +a_3^2}{a_3^2} k_1^2 + \frac{2a_1a_2}{a_3^2}k_1k_2 + \frac{a_2^2+a_3^2}{a_3^2} k_2^2,\end{align*}$$
$$\begin{align*}|A|^2 = Q_1(k_1,k_2) :=\frac{a_1^2 +a_3^2}{a_3^2} k_1^2 + \frac{2a_1a_2}{a_3^2}k_1k_2 + \frac{a_2^2+a_3^2}{a_3^2} k_2^2,\end{align*}$$
By the Gauss equation, we have
![]() $R + |A|^2 = H^2 \ge 0$
, and hence,
$R + |A|^2 = H^2 \ge 0$
, and hence,
![]() $|A|^2 \ge -R$
. Moreover, whenever
$|A|^2 \ge -R$
. Moreover, whenever
![]() $(a_1+a_2-a_3)^2<4a_1a_2$
(which is guaranteed by, for instance,
$(a_1+a_2-a_3)^2<4a_1a_2$
(which is guaranteed by, for instance,
![]() $a_3<4a_1$
),
$a_3<4a_1$
),
![]() $Q_2$
is a positive definite quadratic form, and hence,
$Q_2$
is a positive definite quadratic form, and hence,
![]() $-R$
is nonnegative. Given that
$-R$
is nonnegative. Given that
![]() $\frac {a_3}{a_1}, \frac {a_3}{a_2}\in [1,\sqrt {2}]$
, (3.2) follows from Appendix B.
$\frac {a_3}{a_1}, \frac {a_3}{a_2}\in [1,\sqrt {2}]$
, (3.2) follows from Appendix B.
3.2 Second variation
Suppose now that
![]() $M^{n}\to \mathbf {R}^{n+1}$
is
$M^{n}\to \mathbf {R}^{n+1}$
is
![]() $\mathbf {\Phi }$
-stationary and stable. In Section A.2, we derive the following second variation formula.
$\mathbf {\Phi }$
-stationary and stable. In Section A.2, we derive the following second variation formula.
 $$ \begin{align} \frac{d^2}{dt^2}\bigg\vert_{t=0}\mathbf{\Phi}(M_t) = \int_M {\left\langle {\nabla u, \Psi(\nu) \nabla u} \right\rangle} - \operatorname{\mathrm{tr}}_{M} \left(\Psi(\nu) S_M^2\right) u^2, \end{align} $$
$$ \begin{align} \frac{d^2}{dt^2}\bigg\vert_{t=0}\mathbf{\Phi}(M_t) = \int_M {\left\langle {\nabla u, \Psi(\nu) \nabla u} \right\rangle} - \operatorname{\mathrm{tr}}_{M} \left(\Psi(\nu) S_M^2\right) u^2, \end{align} $$
where
![]() $u\nu $
is the variation vector field. Note that stability and (3.3) imply that
$u\nu $
is the variation vector field. Note that stability and (3.3) imply that
for all
![]() $u\in C_c^1(M\setminus \partial M)$
. Here,
$u\in C_c^1(M\setminus \partial M)$
. Here,
![]() $\Lambda $
depends on the ellipticity of
$\Lambda $
depends on the ellipticity of
![]() $\mathbf {\Phi }$
. It is important to observe that if
$\mathbf {\Phi }$
. It is important to observe that if
![]() $\Phi $
satisfies (1.1), then
$\Phi $
satisfies (1.1), then
![]() $\Lambda \geq \tfrac {1}{\sqrt {2}}$
, and in particular,
$\Lambda \geq \tfrac {1}{\sqrt {2}}$
, and in particular,
for all
![]() $u\in C_c^1(M\setminus \partial M)$
.
$u\in C_c^1(M\setminus \partial M)$
.
3.3 Sobolev inequality and its consequences
In this section, we assume that
![]() $n\ge 3$
,
$n\ge 3$
,
![]() $M^n$
is a two-sided
$M^n$
is a two-sided
![]() $\mathbf {\Phi }$
-stationary and stable hypersurface immersed in
$\mathbf {\Phi }$
-stationary and stable hypersurface immersed in
![]() $\mathbf {R}^{n+1}$
, where
$\mathbf {R}^{n+1}$
, where
![]() $\mathbf {\Phi }$
is a general anisotropic elliptic integral. The Michael–Simon Sobolev inequality [Reference Michael and Simon32] implies that for any
$\mathbf {\Phi }$
is a general anisotropic elliptic integral. The Michael–Simon Sobolev inequality [Reference Michael and Simon32] implies that for any
![]() $f\in C_c^1(M)$
,
$f\in C_c^1(M)$
,
 $$\begin{align*}C_n \left(\int_M |f|^{\frac{n}{n-1}} \right)^{\frac{n-1}{n}}\le \int_{M } |\nabla f| + |fH|\end{align*}$$
$$\begin{align*}C_n \left(\int_M |f|^{\frac{n}{n-1}} \right)^{\frac{n-1}{n}}\le \int_{M } |\nabla f| + |fH|\end{align*}$$
(see also [Reference Brendle5]).
Replacing f by
![]() $f^{\frac {2(n-1)}{n-2}}$
, we find:
$f^{\frac {2(n-1)}{n-2}}$
, we find:
 $$ \begin{align} C_n \left(\int_ M |f|^{\frac{2n}{n-2}}\right)^{\frac{n-1}{n}}\le \int_ M \frac{2(n-1)}{n-2} |f|^{\frac{n}{n-2}} |\nabla f| + |f|^{\frac{2(n-1)}{n-2}} |H|. \end{align} $$
$$ \begin{align} C_n \left(\int_ M |f|^{\frac{2n}{n-2}}\right)^{\frac{n-1}{n}}\le \int_ M \frac{2(n-1)}{n-2} |f|^{\frac{n}{n-2}} |\nabla f| + |f|^{\frac{2(n-1)}{n-2}} |H|. \end{align} $$
By the Hölder inequality,
 $$\begin{align*}\int_ M |f|^{\frac{2(n-1)}{n-2}} |H| \le \left(\int_M f^2 H^2 \right)^{\frac 12} \left( \int_M |f|^{\frac{2n}{n-2}} \right)^{\frac 12}. \end{align*}$$
$$\begin{align*}\int_ M |f|^{\frac{2(n-1)}{n-2}} |H| \le \left(\int_M f^2 H^2 \right)^{\frac 12} \left( \int_M |f|^{\frac{2n}{n-2}} \right)^{\frac 12}. \end{align*}$$
The
![]() $\Phi $
-stability inequality implies
$\Phi $
-stability inequality implies
Now we use the Hölder inequality on the first term of the right hand of (3.6) and conclude the following Sobolev inequality:
 $$ \begin{align} \left(\int_{M } |f|^{\frac{2n}{n-2}}\right)^{\frac{n-2}{n}}\le C(n,\Phi) \int_{M } |\nabla f|^2. \end{align} $$
$$ \begin{align} \left(\int_{M } |f|^{\frac{2n}{n-2}}\right)^{\frac{n-2}{n}}\le C(n,\Phi) \int_{M } |\nabla f|^2. \end{align} $$
Corollary 3.3. Suppose
![]() $M^n\to \mathbf {R}^{n+1}$
is
$M^n\to \mathbf {R}^{n+1}$
is
![]() $\mathbf {\Phi }$
-stationary and stable. Assume that
$\mathbf {\Phi }$
-stationary and stable. Assume that
![]() $B_{M}(p,\rho )\subset M$
has compact closure. Then,
$B_{M}(p,\rho )\subset M$
has compact closure. Then,
Proof. For any
![]() $u\in C^1(M)$
, such that
$u\in C^1(M)$
, such that
![]() $u\ge 0$
and
$u\ge 0$
and
![]() $\Delta u\ge 0$
, the Sobolev inequality (3.7) and the standard Moser iteration implies that, for any
$\Delta u\ge 0$
, the Sobolev inequality (3.7) and the standard Moser iteration implies that, for any
![]() $\theta \in (0,1)$
,
$\theta \in (0,1)$
,
![]() $s>0$
,
$s>0$
,
 $$\begin{align*}\sup_{B_{M}(p,\theta\rho)} u \le C(n,\theta,\Phi, s)\left(\rho^{-n} \int_{B_{M}(p,\rho)} u^s\right)^{1/s}.\end{align*}$$
$$\begin{align*}\sup_{B_{M}(p,\theta\rho)} u \le C(n,\theta,\Phi, s)\left(\rho^{-n} \int_{B_{M}(p,\rho)} u^s\right)^{1/s}.\end{align*}$$
The result follows by taking
![]() $u=1$
,
$u=1$
,
![]() $s=1$
and
$s=1$
and
![]() $\theta = \tfrac 12$
.
$\theta = \tfrac 12$
.
Remark 3.4. The use of Sobolev inequality for volume lower bound was first used by Allard [Reference Allard2, Section 7.5].
Corollary 3.5. Suppose
![]() $M^n \to \mathbf {R}^{n+1}$
is two-sided complete,
$M^n \to \mathbf {R}^{n+1}$
is two-sided complete,
![]() $\mathbf {\Phi }$
-stationary and stable, and K is a compact subset of M. Then each unbounded component of
$\mathbf {\Phi }$
-stationary and stable, and K is a compact subset of M. Then each unbounded component of
![]() $M\setminus K$
has infinte volume.
$M\setminus K$
has infinte volume.
Proof. Let E be an unbounded component of
![]() $M\setminus K$
. Suppose the contrary, that
$M\setminus K$
. Suppose the contrary, that
![]() $|E|<V<\infty $
. Choose
$|E|<V<\infty $
. Choose
![]() $\rho $
, such that
$\rho $
, such that
![]() $C(n,\Phi ) \rho ^n>V$
. By completeness, there exists
$C(n,\Phi ) \rho ^n>V$
. By completeness, there exists
![]() $p\in E$
, such that
$p\in E$
, such that
![]() $d_M (p,\partial E)>\rho $
. Then we have
$d_M (p,\partial E)>\rho $
. Then we have
a contradiction. This completes the proof.
Combining (3.7) and Corollary 3.5, the same argument as used by Cao et al. [Reference Cao, Shen and Zhu6] implies the following result:
Corollary 3.6. If
![]() $M^{n}\to \mathbf {R}^{n+1}$
is a complete two-sided,
$M^{n}\to \mathbf {R}^{n+1}$
is a complete two-sided,
![]() $\mathbf {\Phi }$
-stationary and stable immersion with at least two ends, then there is a bounded nonconstant harmonic function on M with finite Dirichlet energy.
$\mathbf {\Phi }$
-stationary and stable immersion with at least two ends, then there is a bounded nonconstant harmonic function on M with finite Dirichlet energy.
4 One-endedness
Through this section, we assume that
![]() $n=3$
,
$n=3$
,
![]() $M^3\to \mathbf {R}^4$
is
$M^3\to \mathbf {R}^4$
is
![]() $\mathbf {\Phi }$
-stationary and stable. By analysing harmonic functions on M, we will show that M has only one end, if
$\mathbf {\Phi }$
-stationary and stable. By analysing harmonic functions on M, we will show that M has only one end, if
![]() $\mathbf {\Phi }$
satisfies (1.1) (following [Reference Cao, Shen and Zhu6, Reference Schoen and Yau45]).
$\mathbf {\Phi }$
satisfies (1.1) (following [Reference Cao, Shen and Zhu6, Reference Schoen and Yau45]).
Lemma 4.1. Suppose that
![]() $M^3$
is a complete two-sided,
$M^3$
is a complete two-sided,
![]() $\mathbf {\Phi }$
-stationary and stable immersion in
$\mathbf {\Phi }$
-stationary and stable immersion in
![]() $\mathbf {R}^4$
and u is a harmonic function on M. Then
$\mathbf {R}^4$
and u is a harmonic function on M. Then
for any
![]() $\varphi \in C_0^1(M)$
. Here,
$\varphi \in C_0^1(M)$
. Here,
![]() $\Lambda = \Lambda (\Phi )$
is the constant in (3.4).
$\Lambda = \Lambda (\Phi )$
is the constant in (3.4).
Proof. Fix
![]() $p\in M$
. Let
$p\in M$
. Let
![]() $k_i$
be the principal curvatures,
$k_i$
be the principal curvatures,
![]() $e_i$
be the corresponding orthonormal principal directions diagonalising
$e_i$
be the corresponding orthonormal principal directions diagonalising
![]() $A_{M}$
.
$A_{M}$
.
We first show that for any immersed hypersurface
![]() $M^3$
in
$M^3$
in
![]() $\mathbf {R}^4$
, equipped with the induced metric,
$\mathbf {R}^4$
, equipped with the induced metric,
![]() $p\in M$
, and any unit vector
$p\in M$
, and any unit vector
![]() $v\in T_p M$
, we have
$v\in T_p M$
, we have
Write
![]() $v=\sum y_i e_i$
. Then
$v=\sum y_i e_i$
. Then
![]() $\sum y_i^2=1$
. By the Gauss equation, we have
$\sum y_i^2=1$
. By the Gauss equation, we have
and thus,
![]() $\operatorname {\mathrm {Ric}}(e_i,e_j) = 0$
when
$\operatorname {\mathrm {Ric}}(e_i,e_j) = 0$
when
![]() $i\ne j$
and
$i\ne j$
and
![]() $\operatorname {\mathrm {Ric}}(e_i,e_i)= \sum _{j\ne i} A(e_i,e_i)A(e_j,e_j)$
. Therefore,
$\operatorname {\mathrm {Ric}}(e_i,e_i)= \sum _{j\ne i} A(e_i,e_i)A(e_j,e_j)$
. Therefore,
By Cauchy-Schwarz and the inequality of arithmetic and geometric means,
 $$ \begin{align*} k_1^2+k_2^2+k_3^2 \ge k_1^2 + \frac12 (k_2+k_3)^2 \ge -\sqrt 2 k_1(k_2+k_3) \\\Rightarrow k_1(k_2+k_3) \ge -\frac{1}{\sqrt 2} \sum_i k_i^2 = -\frac{1}{\sqrt 2} |A|^2. \end{align*} $$
$$ \begin{align*} k_1^2+k_2^2+k_3^2 \ge k_1^2 + \frac12 (k_2+k_3)^2 \ge -\sqrt 2 k_1(k_2+k_3) \\\Rightarrow k_1(k_2+k_3) \ge -\frac{1}{\sqrt 2} \sum_i k_i^2 = -\frac{1}{\sqrt 2} |A|^2. \end{align*} $$
Similarly,
Therefore,
 $$ \begin{align} \operatorname{\mathrm{Ric}}(v,v)\ge -\frac{1}{\sqrt 2}|A|^2 \sum_i y_i^2 = -\frac{1}{\sqrt 2}|A|^2. \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Ric}}(v,v)\ge -\frac{1}{\sqrt 2}|A|^2 \sum_i y_i^2 = -\frac{1}{\sqrt 2}|A|^2. \end{align} $$
Applying this to
![]() $\nabla u$
, we conclude that:
$\nabla u$
, we conclude that:
Since M is
![]() $\Phi $
-stable, (3.4) yields
$\Phi $
-stable, (3.4) yields
Replacing
![]() $\varphi $
by
$\varphi $
by
![]() $|\nabla u|\varphi $
, we have:
$|\nabla u|\varphi $
, we have:
 $$ \begin{align} \int_M \varphi^2 |\nabla u|^2 |A|^2 \le \int_M |\nabla \varphi|^2 |\nabla u|^2 + 2\int_M \left(\varphi |\nabla u| {\left\langle {\nabla \varphi, \nabla |\nabla u|} \right\rangle} + \varphi^2 |\nabla |\nabla u||^2\right)\nonumber\\ = \int_M |\nabla \varphi|^2 |\nabla u|^2 - \int_M \varphi^2 |\nabla u| \Delta|\nabla u|. \end{align} $$
$$ \begin{align} \int_M \varphi^2 |\nabla u|^2 |A|^2 \le \int_M |\nabla \varphi|^2 |\nabla u|^2 + 2\int_M \left(\varphi |\nabla u| {\left\langle {\nabla \varphi, \nabla |\nabla u|} \right\rangle} + \varphi^2 |\nabla |\nabla u||^2\right)\nonumber\\ = \int_M |\nabla \varphi|^2 |\nabla u|^2 - \int_M \varphi^2 |\nabla u| \Delta|\nabla u|. \end{align} $$
By the improved Kato inequality,
Combined with the Bochner formula and (4.2), we have:
 $$ \begin{align} \begin{split} \Delta |\nabla u|^2 &= 2\operatorname{\mathrm{Ric}}_M (\nabla u,\nabla u) + 2 |\nabla^{2} u|^2\\ &\ge -\sqrt 2 |A|^2 |\nabla u|^2 + \frac34 |\nabla u|^{-2} |\nabla |\nabla u|^2|^2. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \Delta |\nabla u|^2 &= 2\operatorname{\mathrm{Ric}}_M (\nabla u,\nabla u) + 2 |\nabla^{2} u|^2\\ &\ge -\sqrt 2 |A|^2 |\nabla u|^2 + \frac34 |\nabla u|^{-2} |\nabla |\nabla u|^2|^2. \end{split} \end{align} $$
Thus,
Proposition 4.2. Suppose
![]() $\Phi $
satisfies (1.1). Then any complete, two-sided
$\Phi $
satisfies (1.1). Then any complete, two-sided
![]() $\Phi $
-stable immersion
$\Phi $
-stable immersion
![]() $M^3$
in
$M^3$
in
![]() $\mathbf {R}^4$
has only one end.
$\mathbf {R}^4$
has only one end.
Proof. Suppose the contrary, that M has at least two ends. Then Corollary 3.6 implies that M admits a nontrivial harmonic function u with
![]() $\int _M |\nabla u|^2 \le C< \infty $
. For
$\int _M |\nabla u|^2 \le C< \infty $
. For
![]() $\rho>0$
, take
$\rho>0$
, take
![]() $\varphi \in C_c^1(M)$
, such that
$\varphi \in C_c^1(M)$
, such that
![]() $\varphi |_{B_M(0,\rho )}=1$
,
$\varphi |_{B_M(0,\rho )}=1$
,
![]() $\varphi |_{B_{M}(0,2\rho )}=0$
and
$\varphi |_{B_{M}(0,2\rho )}=0$
and
![]() $|\nabla \varphi |\le \tfrac 2\rho $
. Then (4.1) implies that
$|\nabla \varphi |\le \tfrac 2\rho $
. Then (4.1) implies that
 $$ \begin{align*} \int_{B_{M}(0,\rho)} (\Lambda - \tfrac{1}{\sqrt 2}) |A|^2 |\nabla u|^2 + \frac 12 |\nabla |\nabla u||^2 \le \frac{4}{\rho^2}\int_M |\nabla u|^2\le \frac{4C}{\rho^2}. \end{align*} $$
$$ \begin{align*} \int_{B_{M}(0,\rho)} (\Lambda - \tfrac{1}{\sqrt 2}) |A|^2 |\nabla u|^2 + \frac 12 |\nabla |\nabla u||^2 \le \frac{4}{\rho^2}\int_M |\nabla u|^2\le \frac{4C}{\rho^2}. \end{align*} $$
Here,
![]() $\Lambda \ge \tfrac {1}{\sqrt 2}$
by (1.1). Sending
$\Lambda \ge \tfrac {1}{\sqrt 2}$
by (1.1). Sending
![]() $\rho \to \infty $
, we conclude that
$\rho \to \infty $
, we conclude that
In particular, this implies that
![]() $|\nabla u|$
is a constant. Since u is nonconstant, we have that
$|\nabla u|$
is a constant. Since u is nonconstant, we have that
![]() $|\nabla u|>0$
. However, this implies that
$|\nabla u|>0$
. However, this implies that
contradicting Corollary 3.5.
5 A conformal deformation of metrics
Take
![]() $M^3\to \mathbf {R}^4$
to be
$M^3\to \mathbf {R}^4$
to be
![]() $\mathbf {\Phi }$
-stable, where
$\mathbf {\Phi }$
-stable, where
![]() $\Phi $
satisfies (1.1). In this section, we carry out the conformal deformation technique used by Gulliver and Lawson [Reference Gulliver and Lawson27] on M.
$\Phi $
satisfies (1.1). In this section, we carry out the conformal deformation technique used by Gulliver and Lawson [Reference Gulliver and Lawson27] on M.
Consider the function
![]() $r(x)=\operatorname {\mathrm {dist}}_{\mathbf {R}^{n+1}}(0,x)$
on M and the position vector field
$r(x)=\operatorname {\mathrm {dist}}_{\mathbf {R}^{n+1}}(0,x)$
on M and the position vector field
![]() $\vec X$
. Then
$\vec X$
. Then
![]() $\Delta \vec X = \vec H$
. Thus,
$\Delta \vec X = \vec H$
. Thus,
![]() $\Delta (r^2) = \Delta (\sum x_i^2 )= 2\vec X\cdot \Delta X + 2|\nabla \vec X|^2 = 2 \vec X\cdot \vec H + 2n$
. We find:
$\Delta (r^2) = \Delta (\sum x_i^2 )= 2\vec X\cdot \Delta X + 2|\nabla \vec X|^2 = 2 \vec X\cdot \vec H + 2n$
. We find:
here,
![]() $\hat x= \frac {\vec X}{|\vec X|}$
is the normalised position vector.
$\hat x= \frac {\vec X}{|\vec X|}$
is the normalised position vector.
Suppose that
![]() $w>0$
is a smooth function on
$w>0$
is a smooth function on
![]() $M^n\setminus \{0\}$
. On
$M^n\setminus \{0\}$
. On
![]() $M\setminus \{0\}$
, define
$M\setminus \{0\}$
, define
![]() $\tilde g = w^2 g$
. For
$\tilde g = w^2 g$
. For
![]() $\lambda \in \mathbf {R}$
,
$\lambda \in \mathbf {R}$
,
![]() $\varphi \in C_c^1(M\setminus \{0\})$
, consider the quadratic form
$\varphi \in C_c^1(M\setminus \{0\})$
, consider the quadratic form
where
![]() $\tilde \nabla $
,
$\tilde \nabla $
,
![]() $\tilde R$
,
$\tilde R$
,
![]() $\tilde \mu $
are the gradient, the scalar curvature and the volume form with respect to
$\tilde \mu $
are the gradient, the scalar curvature and the volume form with respect to
![]() $\tilde g$
, respectively. One relates the geometric quantities in g and
$\tilde g$
, respectively. One relates the geometric quantities in g and
![]() $\tilde g$
as follows:
$\tilde g$
as follows:
Moreover, we have
Denote by
![]() $\tilde {\mathcal Q}_w (\varphi ) := {\mathcal Q}_w(w^{\frac {2-n}{2}}\varphi )$
. We compute:
$\tilde {\mathcal Q}_w (\varphi ) := {\mathcal Q}_w(w^{\frac {2-n}{2}}\varphi )$
. We compute:
 $$ \begin{align*} &\tilde{\mathcal Q}_w(\varphi)\\ &=\int_M\left(w^{-2} |\nabla (w^{\frac{2-n}{2}}\varphi)|_{g}^2 + (\tfrac12 \tilde R - \lambda)w^{2-n} \varphi^2 \right)w^n d\mu\\ &=\int_M \left(w^{n-2} |w^{\frac{2-n}{2}} \nabla \varphi - \tfrac{n-2}{2} \varphi w^{-\frac n2} \nabla w|_{g}^2 + (\tfrac12w^2 \tilde R - w^2\lambda)\varphi^2 \right)d\mu\\ &=\int_M \left( |\nabla \varphi - \tfrac{n-2}{2} \varphi \nabla \log w|_{g}^2 + (\tfrac12 w^2 \tilde R - w^2 \lambda)\varphi^2 \right)d\mu\\ &=\int_M \left(|\nabla \varphi|_{g}^2 - \frac{n-2}{2} {\left\langle {\nabla (\varphi^2) , \nabla \log w } \right\rangle}_g +\frac{(n-2)^2}{4} |\nabla \log w|_{g}^2\varphi^2 + (\tfrac12 w^2 \tilde R - w^2 \lambda)\varphi^2 \right)d\mu\\ &= \int_M \left( |\nabla \varphi|_{g}^2 + \left(\frac{n-2}{2} \Delta \log w + \frac{(n-2)^2}{4}|\nabla \log w|_{g}^2 + \tfrac12 w^2 \tilde R - w^2\lambda\right)\varphi^2\right)d\mu\\ &= \int_M \left(|\nabla \varphi|_{g}^2 + \tfrac12 R\varphi^2 - \left(\frac n2 \left(\Delta \log w + \tfrac{(n-2)}{2} |\nabla \log w|_{g}^2\right) + w^2\lambda \right)\varphi^2 \right)d\mu. \end{align*} $$
$$ \begin{align*} &\tilde{\mathcal Q}_w(\varphi)\\ &=\int_M\left(w^{-2} |\nabla (w^{\frac{2-n}{2}}\varphi)|_{g}^2 + (\tfrac12 \tilde R - \lambda)w^{2-n} \varphi^2 \right)w^n d\mu\\ &=\int_M \left(w^{n-2} |w^{\frac{2-n}{2}} \nabla \varphi - \tfrac{n-2}{2} \varphi w^{-\frac n2} \nabla w|_{g}^2 + (\tfrac12w^2 \tilde R - w^2\lambda)\varphi^2 \right)d\mu\\ &=\int_M \left( |\nabla \varphi - \tfrac{n-2}{2} \varphi \nabla \log w|_{g}^2 + (\tfrac12 w^2 \tilde R - w^2 \lambda)\varphi^2 \right)d\mu\\ &=\int_M \left(|\nabla \varphi|_{g}^2 - \frac{n-2}{2} {\left\langle {\nabla (\varphi^2) , \nabla \log w } \right\rangle}_g +\frac{(n-2)^2}{4} |\nabla \log w|_{g}^2\varphi^2 + (\tfrac12 w^2 \tilde R - w^2 \lambda)\varphi^2 \right)d\mu\\ &= \int_M \left( |\nabla \varphi|_{g}^2 + \left(\frac{n-2}{2} \Delta \log w + \frac{(n-2)^2}{4}|\nabla \log w|_{g}^2 + \tfrac12 w^2 \tilde R - w^2\lambda\right)\varphi^2\right)d\mu\\ &= \int_M \left(|\nabla \varphi|_{g}^2 + \tfrac12 R\varphi^2 - \left(\frac n2 \left(\Delta \log w + \tfrac{(n-2)}{2} |\nabla \log w|_{g}^2\right) + w^2\lambda \right)\varphi^2 \right)d\mu. \end{align*} $$
We now choose
![]() $w= r^{-1}$
on
$w= r^{-1}$
on
![]() $M\setminus \{0\}$
. Note that (dropping the g subscript on the norm of the gradient)
$M\setminus \{0\}$
. Note that (dropping the g subscript on the norm of the gradient)
 $$ \begin{align*} \begin{split} \Delta \log w + \frac{n-2}{2} |\nabla \log w|^2 &= -\frac{\Delta r}{r} + \frac n2 \frac{|\nabla r|^2}{r^2}\\ &= -\frac {n}{r^2} - \frac{H(\hat x\cdot \nu)}{r} + \frac{n+2}{2} \frac{|\nabla r|^2}{r^2}. \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \Delta \log w + \frac{n-2}{2} |\nabla \log w|^2 &= -\frac{\Delta r}{r} + \frac n2 \frac{|\nabla r|^2}{r^2}\\ &= -\frac {n}{r^2} - \frac{H(\hat x\cdot \nu)}{r} + \frac{n+2}{2} \frac{|\nabla r|^2}{r^2}. \end{split} \end{align*} $$
Therefore,
 $$ \begin{align} \begin{split} &\tilde{\mathcal Q}_w(\varphi)= \int_M \left(|\nabla \varphi|^2 + \tfrac12 R\varphi^2 + \left(\frac n2 \left(n + rH(\hat x\cdot \nu) - \tfrac{n+2}{2} |\nabla r|^2 \right) - \lambda \right)r^{-2}\varphi^2 \right)d\mu\\ &\ge \int_M \left(|\nabla \varphi|^2 + \tfrac12 R\varphi^2 +\left(\frac n2 \left( n - \tfrac12 \beta r^2 H^2 - \tfrac{1}{2\beta} - \tfrac{n+2}{2} |\nabla r|^2\right) -\lambda \right)r^{-2}\varphi^2 \right)d\mu\\ &=\int_M \left(|\nabla \varphi|^2 + (\tfrac12 R - \tfrac n4 \beta H^2)\varphi^2 + \left(\frac n2 \left(n - \tfrac{1}{2\beta} - \tfrac{n+2}{2} |\nabla r|^2\right) -\lambda\right) r^{-2}\varphi^2\right)d\mu, \end{split} \end{align} $$
$$ \begin{align} \begin{split} &\tilde{\mathcal Q}_w(\varphi)= \int_M \left(|\nabla \varphi|^2 + \tfrac12 R\varphi^2 + \left(\frac n2 \left(n + rH(\hat x\cdot \nu) - \tfrac{n+2}{2} |\nabla r|^2 \right) - \lambda \right)r^{-2}\varphi^2 \right)d\mu\\ &\ge \int_M \left(|\nabla \varphi|^2 + \tfrac12 R\varphi^2 +\left(\frac n2 \left( n - \tfrac12 \beta r^2 H^2 - \tfrac{1}{2\beta} - \tfrac{n+2}{2} |\nabla r|^2\right) -\lambda \right)r^{-2}\varphi^2 \right)d\mu\\ &=\int_M \left(|\nabla \varphi|^2 + (\tfrac12 R - \tfrac n4 \beta H^2)\varphi^2 + \left(\frac n2 \left(n - \tfrac{1}{2\beta} - \tfrac{n+2}{2} |\nabla r|^2\right) -\lambda\right) r^{-2}\varphi^2\right)d\mu, \end{split} \end{align} $$
for
![]() $\beta>0$
to be chosen later.
$\beta>0$
to be chosen later.
By the Gauss equation and Lemma 3.2,
Combining with
![]() $|\nabla r|\le 1$
, we have
$|\nabla r|\le 1$
, we have
On the other hand, (3.5) and (3.2) imply that for every
![]() $\varphi \in C_c^1(M)$
,
$\varphi \in C_c^1(M)$
,
 $$\begin{align*}\int_M \left( |\nabla \varphi|^2 + \frac{1}{\sqrt 2} R\varphi^2\right)d\mu\ge 0. \end{align*}$$
$$\begin{align*}\int_M \left( |\nabla \varphi|^2 + \frac{1}{\sqrt 2} R\varphi^2\right)d\mu\ge 0. \end{align*}$$
Note that
![]() $R\le 0$
. Thus, by choosing
$R\le 0$
. Thus, by choosing
 $$\begin{align*}\beta = \frac{4(\frac{1}{\sqrt 2} - \frac12 )}{n(c_0 -1)}, \quad \lambda = \frac n2 \left(\frac{n-2}{2}- \frac{1}{2\beta}\right) = \frac n2 \left(\frac{n-2}{2} - \frac{n(c_0-1)}{8(\frac{1}{\sqrt 2} - \frac 12)}\right),\end{align*}$$
$$\begin{align*}\beta = \frac{4(\frac{1}{\sqrt 2} - \frac12 )}{n(c_0 -1)}, \quad \lambda = \frac n2 \left(\frac{n-2}{2}- \frac{1}{2\beta}\right) = \frac n2 \left(\frac{n-2}{2} - \frac{n(c_0-1)}{8(\frac{1}{\sqrt 2} - \frac 12)}\right),\end{align*}$$
we have that
![]() $\tilde {\mathcal Q}_w(\varphi )\ge 0 $
for all
$\tilde {\mathcal Q}_w(\varphi )\ge 0 $
for all
![]() $\varphi \in C_c^1(M\setminus \{0\})$
. We summarise these in the following proposition.
$\varphi \in C_c^1(M\setminus \{0\})$
. We summarise these in the following proposition.
Proposition 5.1. Suppose
![]() $n\ge 3$
,
$n\ge 3$
,
![]() $(M^n,g)$
is an immersed hypersurface in
$(M^n,g)$
is an immersed hypersurface in
![]() $\mathbf {R}^{n+1}$
,
$\mathbf {R}^{n+1}$
,
![]() $\Lambda , c_0 \in \mathbf {R}$
, such that:
$\Lambda , c_0 \in \mathbf {R}$
, such that:
Then the conformally deformed manifold
![]() $(M\setminus \{0\}, \tilde g = r^{-1} g)$
satisfies
$(M\setminus \{0\}, \tilde g = r^{-1} g)$
satisfies
where
![]() $\lambda = \frac n2 \left (\frac {n-2}{2} - \frac {n(c_0-1)}{8(\Lambda - \frac 12)}\right )$
.
$\lambda = \frac n2 \left (\frac {n-2}{2} - \frac {n(c_0-1)}{8(\Lambda - \frac 12)}\right )$
.
6 Volume estimates
We first recall a diameter bound for warped
![]() $\mu $
-bubbles in
$\mu $
-bubbles in
![]() $3$
-manifolds satisfying
$3$
-manifolds satisfying
![]() $\lambda _1(-\Delta + \tfrac 12 R)\ge \lambda>0$
.
$\lambda _1(-\Delta + \tfrac 12 R)\ge \lambda>0$
.
Lemma 6.1 (Warped
 $\mu $
-bubble area and diameter bound).
$\mu $
-bubble area and diameter bound).
Let
![]() $(N^3,g)$
be a
$(N^3,g)$
be a
![]() $3$
-manifold with compact connected boundary satisfying
$3$
-manifold with compact connected boundary satisfying
Suppose there exists
![]() $p\in N$
, such that
$p\in N$
, such that
![]() $d_N(p,\partial N)\ge \frac {5\pi }{\sqrt \lambda }$
. Then there exists a connected open set
$d_N(p,\partial N)\ge \frac {5\pi }{\sqrt \lambda }$
. Then there exists a connected open set
![]() $\Omega $
containing
$\Omega $
containing
![]() $\partial N$
,
$\partial N$
,
![]() $\Omega \subset B_{\frac {5\pi }{\sqrt \lambda }} (\partial N)$
, such that each connected component of
$\Omega \subset B_{\frac {5\pi }{\sqrt \lambda }} (\partial N)$
, such that each connected component of
![]() $\partial \Omega \setminus \partial N$
is a
$\partial \Omega \setminus \partial N$
is a
![]() $2$
-sphere with area at most
$2$
-sphere with area at most
![]() $\tfrac {8\pi }{\lambda }$
and intrinsic diameter at most
$\tfrac {8\pi }{\lambda }$
and intrinsic diameter at most
![]() $\frac {2\pi }{\sqrt \lambda }$
.
$\frac {2\pi }{\sqrt \lambda }$
.
Proof. This is an application of estimates for the warped
![]() $\mu $
-bubbles (see, e.g. [Reference Chodosh and Li9, Section 3]). Since N satisfies (6.1), there exists
$\mu $
-bubbles (see, e.g. [Reference Chodosh and Li9, Section 3]). Since N satisfies (6.1), there exists
![]() $u\in C^\infty (N)$
,
$u\in C^\infty (N)$
,
![]() $u>0$
in
$u>0$
in
![]() $\mathring {N}$
, such that
$\mathring {N}$
, such that
Take
![]() $\varphi _0\in C^\infty (M)$
to be a smoothing of
$\varphi _0\in C^\infty (M)$
to be a smoothing of
![]() $d_N(\cdot , \partial N)$
, such that
$d_N(\cdot , \partial N)$
, such that
![]() $|\operatorname {\mathrm {Lip}}(\varphi _0)|\le 2$
and
$|\operatorname {\mathrm {Lip}}(\varphi _0)|\le 2$
and
![]() $\varphi _0 = 0$
on
$\varphi _0 = 0$
on
![]() $\partial N$
. Choose
$\partial N$
. Choose
![]() $\varepsilon \in (0,\tfrac 12)$
, such that
$\varepsilon \in (0,\tfrac 12)$
, such that
![]() $\varepsilon , \frac {4}{\sqrt \lambda }\pi +2\varepsilon $
are regular values of
$\varepsilon , \frac {4}{\sqrt \lambda }\pi +2\varepsilon $
are regular values of
![]() $\varphi _0$
. Define
$\varphi _0$
. Define
 $$\begin{align*}\varphi = \frac{\varphi_0 - \varepsilon}{\frac{4}{\sqrt \lambda}+ \frac{\varepsilon}{\pi}} - \frac{\pi}{2},\end{align*}$$
$$\begin{align*}\varphi = \frac{\varphi_0 - \varepsilon}{\frac{4}{\sqrt \lambda}+ \frac{\varepsilon}{\pi}} - \frac{\pi}{2},\end{align*}$$
![]() $\Omega _1 = \{x\in N: -\tfrac {\pi }{2}<\varphi <\tfrac {\pi }{2}\}$
and
$\Omega _1 = \{x\in N: -\tfrac {\pi }{2}<\varphi <\tfrac {\pi }{2}\}$
and
![]() $\Omega _0 = \{x\in N: -\tfrac {\pi }{2}<\varphi \le 0 \}$
. We have that
$\Omega _0 = \{x\in N: -\tfrac {\pi }{2}<\varphi \le 0 \}$
. We have that
![]() $|\operatorname {\mathrm {Lip}}(\varphi )|<\tfrac {\sqrt {\lambda }}{2}$
. In
$|\operatorname {\mathrm {Lip}}(\varphi )|<\tfrac {\sqrt {\lambda }}{2}$
. In
![]() $\Omega _1$
, define
$\Omega _1$
, define
![]() $h(x)= -\tfrac 12 \tan (\varphi (x))$
. By a direct computation, we have
$h(x)= -\tfrac 12 \tan (\varphi (x))$
. By a direct computation, we have
Minimise
among Caccioppoli sets,
![]() $\Omega $
in
$\Omega $
in
![]() $\Omega _1$
with
$\Omega _1$
with
![]() $\Omega \Delta \Omega _0$
is compactly contained in
$\Omega \Delta \Omega _0$
is compactly contained in
![]() $\Omega _1$
. By [Reference Chodosh and Li9, Proposition 12], a minimiser
$\Omega _1$
. By [Reference Chodosh and Li9, Proposition 12], a minimiser
![]() $\tilde \Omega $
exists and has regular boundary. We take
$\tilde \Omega $
exists and has regular boundary. We take
![]() $\Omega $
to be the connected component of
$\Omega $
to be the connected component of
![]() $\{x\in N: 0\le \varphi _0(x)\le \varepsilon \}\cup \tilde {\Omega }$
that contains
$\{x\in N: 0\le \varphi _0(x)\le \varepsilon \}\cup \tilde {\Omega }$
that contains
![]() $\partial N$
(in other words, we disregard any component of
$\partial N$
(in other words, we disregard any component of
![]() $\tilde \Omega $
that is disjoint from
$\tilde \Omega $
that is disjoint from
![]() $\partial N$
). We verify that
$\partial N$
). We verify that
![]() $\Omega $
satisfies the conclusions of Lemma 6.1. Indeed, for any connected component
$\Omega $
satisfies the conclusions of Lemma 6.1. Indeed, for any connected component
![]() $\Sigma $
of
$\Sigma $
of
![]() $\partial \Omega \cap \Omega _1$
, the stability of
$\partial \Omega \cap \Omega _1$
, the stability of
![]() $\mathcal A$
implies [Reference Chodosh and Li9, Lemma 14]:
$\mathcal A$
implies [Reference Chodosh and Li9, Lemma 14]:
 $$ \begin{align} &\int_\Sigma |\nabla \psi|^2 u - \tfrac12 (R_N - \lambda - 2K_\Sigma) \psi^2 u + (\Delta_N u - \Delta_\Sigma u)\psi^2 \nonumber\\ &\quad-\tfrac 12 u^{-1} {\left\langle {\nabla_N u ,\nu} \right\rangle}^2 \psi^2 - \tfrac12 (\lambda +h^2 +2{\left\langle {\nabla_N h,\nu} \right\rangle})\psi^2 u \ge 0,\quad \forall \psi\in C^1(\Sigma). \end{align} $$
$$ \begin{align} &\int_\Sigma |\nabla \psi|^2 u - \tfrac12 (R_N - \lambda - 2K_\Sigma) \psi^2 u + (\Delta_N u - \Delta_\Sigma u)\psi^2 \nonumber\\ &\quad-\tfrac 12 u^{-1} {\left\langle {\nabla_N u ,\nu} \right\rangle}^2 \psi^2 - \tfrac12 (\lambda +h^2 +2{\left\langle {\nabla_N h,\nu} \right\rangle})\psi^2 u \ge 0,\quad \forall \psi\in C^1(\Sigma). \end{align} $$
Taking
![]() $\psi =u^{-\frac 12}$
and using (6.2), (6.3), we conclude that
$\psi =u^{-\frac 12}$
and using (6.2), (6.3), we conclude that
Note that we have used Gauss–Bonnet, which also implies that
![]() $\Sigma $
is a
$\Sigma $
is a
![]() $2$
-sphere. The diameter upper bound follows from [Reference Chodosh and Li9, Lemmas 16 and 18].
$2$
-sphere. The diameter upper bound follows from [Reference Chodosh and Li9, Lemmas 16 and 18].
For the next lemma, recall that
![]() $r(x)=\operatorname {\mathrm {dist}}_{\mathbf {R}^{m}}(0,x)$
.
$r(x)=\operatorname {\mathrm {dist}}_{\mathbf {R}^{m}}(0,x)$
.
Lemma 6.2. Below,
![]() $k\geq 2$
and
$k\geq 2$
and
![]() $N^{k}$
is a compact connected manifold, possibly with boundary.
$N^{k}$
is a compact connected manifold, possibly with boundary.
-
1. Consider an immersion
 $N^{k}\to \mathbf {R}^{m}\setminus \{0\}$
. Consider
$N^{k}\to \mathbf {R}^{m}\setminus \{0\}$
. Consider
 $p,q\in N$
with
$p,q\in N$
with
 $d_{\tilde g}(p,q)\le D$
, where
$d_{\tilde g}(p,q)\le D$
, where
 $\tilde g = r^{-2}g$
and g is the induced metric on N. Then
$\tilde g = r^{-2}g$
and g is the induced metric on N. Then
 $r(p)\le e^Dr(q)$
.
$r(p)\le e^Dr(q)$
. -
2. Consider an immersion
 $\varphi : N^{k} \to \mathbf {R}^{m}$
with
$\varphi : N^{k} \to \mathbf {R}^{m}$
with
 $0 \in \varphi (N)$
. Consider
$0 \in \varphi (N)$
. Consider
 $p,q\in N\setminus \varphi ^{-1}(0)$
with
$p,q\in N\setminus \varphi ^{-1}(0)$
with
 $d_{\tilde g}(p,q)\le D$
. Write g for the induced metric on N, and let
$d_{\tilde g}(p,q)\le D$
. Write g for the induced metric on N, and let
 $\bar r(x) = d_{g}(\varphi ^{-1}(0),x)$
denote the intrinsic distance on N. Then
$\bar r(x) = d_{g}(\varphi ^{-1}(0),x)$
denote the intrinsic distance on N. Then
 $\bar r(p) \leq e^{D} \bar r(q)$
.
$\bar r(p) \leq e^{D} \bar r(q)$
.
Proof. We first establish (1). Choose a curve
![]() $\gamma : [0,L]\to N$
, parametrised by
$\gamma : [0,L]\to N$
, parametrised by
![]() $\tilde g$
-unit speed, connecting p and q, such that
$\tilde g$
-unit speed, connecting p and q, such that
![]() $L\le D+\varepsilon $
. Using
$L\le D+\varepsilon $
. Using
![]() $|\nabla r|_g \le 1$
, we compute
$|\nabla r|_g \le 1$
, we compute
 $$ \begin{align*} \log r(q) - \log r(p) &= \int_0^L \frac{d}{dt} \log r(\gamma(t))dt\\ &= \int_0^L r(\gamma(t))^{-1} g(\nabla r, \gamma'(t)) dt \\ &\le \int_0^L r(\gamma(t))^{-1} |\nabla r|_g |\gamma'(t)|_g dt \\ &\le \int_0^L r(\gamma(t))^{-1} |\gamma'(t)|_g dt\\ &= \int_0^L |\gamma'(t)|_{\tilde g} dt =L\le D+\varepsilon. \end{align*} $$
$$ \begin{align*} \log r(q) - \log r(p) &= \int_0^L \frac{d}{dt} \log r(\gamma(t))dt\\ &= \int_0^L r(\gamma(t))^{-1} g(\nabla r, \gamma'(t)) dt \\ &\le \int_0^L r(\gamma(t))^{-1} |\nabla r|_g |\gamma'(t)|_g dt \\ &\le \int_0^L r(\gamma(t))^{-1} |\gamma'(t)|_g dt\\ &= \int_0^L |\gamma'(t)|_{\tilde g} dt =L\le D+\varepsilon. \end{align*} $$
Thus,
![]() $r(q)\le e^{D+\varepsilon } r(p)$
. The result follows by sending
$r(q)\le e^{D+\varepsilon } r(p)$
. The result follows by sending
![]() $\varepsilon \to 0$
.
$\varepsilon \to 0$
.
For (2), we begin by noting that
![]() $|\nabla \bar r|_g=1$
and
$|\nabla \bar r|_g=1$
and
![]() $r(x)\le \bar r(x)$
for any
$r(x)\le \bar r(x)$
for any
![]() $x\in N$
. Thus, arguing as above
$x\in N$
. Thus, arguing as above
 $$\begin{align*}\log \bar r(q) - \log \bar r(p) \le \int_0^L \bar r(\gamma(t))^{-1} |\gamma'(t)|_g dt \le \int_0^L r(\gamma(t))^{-1} |\gamma'(t)|_g dt = L.\end{align*}$$
$$\begin{align*}\log \bar r(q) - \log \bar r(p) \le \int_0^L \bar r(\gamma(t))^{-1} |\gamma'(t)|_g dt \le \int_0^L r(\gamma(t))^{-1} |\gamma'(t)|_g dt = L.\end{align*}$$
The proof is completed as above.
Proof of Theorem 1.4.
Let
![]() $r=\operatorname {\mathrm {dist}}_{\mathbf {R}^{4}}(\cdot , 0)$
and
$r=\operatorname {\mathrm {dist}}_{\mathbf {R}^{4}}(\cdot , 0)$
and
![]() $\bar r= \operatorname {\mathrm {dist}}_{M,g}(\cdot , 0)$
, and consider
$\bar r= \operatorname {\mathrm {dist}}_{M,g}(\cdot , 0)$
, and consider
![]() $\tilde g = r^{-2}g$
. Fix
$\tilde g = r^{-2}g$
. Fix
![]() $\rho>0$
, and consider the geodesic ball
$\rho>0$
, and consider the geodesic ball
![]() $B_{M}(0,e^{\frac {5\pi }{\sqrt {\lambda }}} \rho )$
. By Proposition 4.2,
$B_{M}(0,e^{\frac {5\pi }{\sqrt {\lambda }}} \rho )$
. By Proposition 4.2,
![]() $M\setminus B_{M}(0,e^{\frac {5\pi }{\sqrt \lambda }} \rho )$
has only one unbounded connected component E. Denote by
$M\setminus B_{M}(0,e^{\frac {5\pi }{\sqrt \lambda }} \rho )$
has only one unbounded connected component E. Denote by
![]() $M' = M\setminus E$
. We claim that
$M' = M\setminus E$
. We claim that
![]() $\partial M'=\partial E$
is connected. Indeed, since
$\partial M'=\partial E$
is connected. Indeed, since
![]() $M'$
and E are both connected, if
$M'$
and E are both connected, if
![]() $\partial M'$
has more than one connected component, then one can find a loop in M intersecting one component of
$\partial M'$
has more than one connected component, then one can find a loop in M intersecting one component of
![]() $\partial M'$
exactly once, contradicting that M is simply connected. Applying Lemma 6.1 to
$\partial M'$
exactly once, contradicting that M is simply connected. Applying Lemma 6.1 to
![]() $(M'\setminus \{0\},\tilde g)$
, we find a connected open set
$(M'\setminus \{0\},\tilde g)$
, we find a connected open set
![]() $\Omega $
in the
$\Omega $
in the
![]() $\frac {5\pi }{\sqrt \lambda }$
neighborhood of
$\frac {5\pi }{\sqrt \lambda }$
neighborhood of
![]() $\partial M'$
, such that each connected component of
$\partial M'$
, such that each connected component of
![]() $\partial \Omega \setminus \partial M'$
has area bounded by
$\partial \Omega \setminus \partial M'$
has area bounded by
![]() $\frac {8\pi }{\lambda }$
and diameter bounded by
$\frac {8\pi }{\lambda }$
and diameter bounded by
![]() $\frac {2\pi }{\sqrt \lambda }$
(we emphasise here that the distance, area and diameter are with respect to
$\frac {2\pi }{\sqrt \lambda }$
(we emphasise here that the distance, area and diameter are with respect to
![]() $\tilde g$
). Let
$\tilde g$
). Let
![]() $M_0$
be the connected component of
$M_0$
be the connected component of
![]() $ M'\setminus \Omega $
that contains
$ M'\setminus \Omega $
that contains
![]() $0$
.
$0$
.
We make a few observations about
![]() $M_0$
. First, we claim that
$M_0$
. First, we claim that
![]() $M\setminus M_0$
is connected. To see this, let
$M\setminus M_0$
is connected. To see this, let
![]() $M_1$
be the union of connected components of
$M_1$
be the union of connected components of
![]() $M'\setminus \Omega $
other than
$M'\setminus \Omega $
other than
![]() $M_0$
. Then
$M_0$
. Then
![]() $M\setminus M_0 = M_1\cup \Omega \cup E$
. Note that each connected component of
$M\setminus M_0 = M_1\cup \Omega \cup E$
. Note that each connected component of
![]() $M_1$
shares a common boundary with
$M_1$
shares a common boundary with
![]() $\Omega $
. Since
$\Omega $
. Since
![]() $\Omega $
is connected, so is
$\Omega $
is connected, so is
![]() $M_1\cup \Omega $
. Next, we claim that
$M_1\cup \Omega $
. Next, we claim that
![]() $M_0$
has only one boundary component: otherwise, since both
$M_0$
has only one boundary component: otherwise, since both
![]() $M_0$
and
$M_0$
and
![]() $M\setminus M_0$
are connected, as before, we can find a loop in M intersecting a connected component of
$M\setminus M_0$
are connected, as before, we can find a loop in M intersecting a connected component of
![]() $\partial M_0$
exactly once, contradicting that M is simply connected.
$\partial M_0$
exactly once, contradicting that M is simply connected.
Denote by
![]() $\Sigma = \partial M_0$
. By (2) in Lemma 6.2,
$\Sigma = \partial M_0$
. By (2) in Lemma 6.2,
![]() $\min _{x\in \Sigma } \bar r(x)\ge \rho $
. Since
$\min _{x\in \Sigma } \bar r(x)\ge \rho $
. Since
![]() $B_M(0,\rho )$
is connected, this implies that
$B_M(0,\rho )$
is connected, this implies that
![]() $B_{M}(0,\rho ) \subset M_0$
. On the other hand, by comparing intrinsic to extrinsic distance, we see that
$B_{M}(0,\rho ) \subset M_0$
. On the other hand, by comparing intrinsic to extrinsic distance, we see that
![]() $\max _{x \in \Sigma } r(x) \leq e^{\frac {5\pi }{\sqrt {\lambda }}} \rho $
, so
$\max _{x \in \Sigma } r(x) \leq e^{\frac {5\pi }{\sqrt {\lambda }}} \rho $
, so
Thus, Corollary 3.1 implies that
 $$ \begin{align*} |B_{M}(0,\rho)|_{g} \le |M_0|_{g} \le \frac{\|\Phi\|_{C^1}}{3\min_{\nu \in S^3} \Phi(\nu)} e^{\frac{5\pi}{\sqrt{\lambda}}} \rho |\partial M_0|_{g} \le \frac{8\pi e^{\frac{15\pi}{\lambda}} \|\Phi\|_{C^1}}{3\lambda \min_{\nu \in S^3} \Phi(\nu)} \rho^3. \end{align*} $$
$$ \begin{align*} |B_{M}(0,\rho)|_{g} \le |M_0|_{g} \le \frac{\|\Phi\|_{C^1}}{3\min_{\nu \in S^3} \Phi(\nu)} e^{\frac{5\pi}{\sqrt{\lambda}}} \rho |\partial M_0|_{g} \le \frac{8\pi e^{\frac{15\pi}{\lambda}} \|\Phi\|_{C^1}}{3\lambda \min_{\nu \in S^3} \Phi(\nu)} \rho^3. \end{align*} $$
This proves the first part of the assertion.
Now consider a connected component
![]() $\Sigma _0$
of
$\Sigma _0$
of
![]() $\partial B_{M}(0,\rho )$
, and let E be the connected component of
$\partial B_{M}(0,\rho )$
, and let E be the connected component of
![]() $M \setminus B_{M}(0,\rho )$
, such that
$M \setminus B_{M}(0,\rho )$
, such that
![]() $\partial E$
contains
$\partial E$
contains
![]() $\Sigma _0$
. Since M is simply connected, we must have that
$\Sigma _0$
. Since M is simply connected, we must have that
![]() $\partial E = \Sigma _0$
. Apply Lemma 6.1 to
$\partial E = \Sigma _0$
. Apply Lemma 6.1 to
![]() $M\setminus E$
, and obtain a connected surface
$M\setminus E$
, and obtain a connected surface
![]() $\Sigma $
, such that
$\Sigma $
, such that
![]() $\operatorname {\mathrm {dist}}_{ \tilde g} (\Sigma _0,\Sigma )\le \frac {5\pi }{\sqrt \lambda }$
and
$\operatorname {\mathrm {dist}}_{ \tilde g} (\Sigma _0,\Sigma )\le \frac {5\pi }{\sqrt \lambda }$
and
![]() $\operatorname {\mathrm {diam}}_{\tilde g}(\Sigma )\le \frac {2\pi }{\sqrt \lambda }$
(the proof that
$\operatorname {\mathrm {diam}}_{\tilde g}(\Sigma )\le \frac {2\pi }{\sqrt \lambda }$
(the proof that
![]() $\Sigma $
is connected follows a similar argument as used above). By the triangle inequality, we have that
$\Sigma $
is connected follows a similar argument as used above). By the triangle inequality, we have that
![]() $\operatorname {\mathrm {diam}}_{\tilde g} (\Sigma _0)\le \frac {7\pi }{\sqrt \lambda }$
. Thus, Lemma 6.2 implies that
$\operatorname {\mathrm {diam}}_{\tilde g} (\Sigma _0)\le \frac {7\pi }{\sqrt \lambda }$
. Thus, Lemma 6.2 implies that
This proves the assertion.
Proof of Theorem 1.7.
The proof is very similar to that of Theorem 1.4. We apply Lemma 6.1 to
![]() $(M\setminus \{0\}, \tilde g = r^{-2}g)$
and find a region
$(M\setminus \{0\}, \tilde g = r^{-2}g)$
and find a region
![]() $\Omega $
in the
$\Omega $
in the
![]() $\tfrac {5\pi }{\sqrt \lambda }$
neighborhood of
$\tfrac {5\pi }{\sqrt \lambda }$
neighborhood of
![]() $\partial M$
, such that each connected component of
$\partial M$
, such that each connected component of
![]() $\Omega \setminus \partial M$
has area bounded by
$\Omega \setminus \partial M$
has area bounded by
![]() $\frac {8\pi }{\lambda }$
(again, the distance and area are with respect to
$\frac {8\pi }{\lambda }$
(again, the distance and area are with respect to
![]() $\tilde g$
). Let
$\tilde g$
). Let
![]() $M'$
be the connected component of
$M'$
be the connected component of
![]() $M\setminus \Omega $
that contains
$M\setminus \Omega $
that contains
![]() $\{0\}$
. Then
$\{0\}$
. Then
![]() $\partial M'$
is connected.
$\partial M'$
is connected.
Denote by
![]() $\Sigma = \partial M'$
and
$\Sigma = \partial M'$
and
![]() $\rho _0 = e^{-\frac {5\pi }{\sqrt \lambda }}$
. By (1) in Lemma 6.2,
$\rho _0 = e^{-\frac {5\pi }{\sqrt \lambda }}$
. By (1) in Lemma 6.2,
![]() $\min _{x\in \Omega } r(x)\ge \rho _0$
. In particular, this implies that
$\min _{x\in \Omega } r(x)\ge \rho _0$
. In particular, this implies that
![]() $M_{r_0}^*\subset M'$
. We have
$M_{r_0}^*\subset M'$
. We have
Therefore, Corollary 3.1 implies that
This completes the proof.
Remark 6.3. In the more general case where we do not assume that M is simply connected or has one end (or boundary component), similar proofs work out. The only modification here is that
![]() $\partial M_0$
in the proof of Theorem 1.4 (or
$\partial M_0$
in the proof of Theorem 1.4 (or
![]() $\partial M'$
in the proof of Theorem 1.7) has connected components bounded by
$\partial M'$
in the proof of Theorem 1.7) has connected components bounded by
![]() $b_1(M) + E$
, where E is the number of ends if M is complete, and is the number of boundary components if
$b_1(M) + E$
, where E is the number of ends if M is complete, and is the number of boundary components if
![]() $M\subset B_1(0)$
. Thus, we have
$M\subset B_1(0)$
. Thus, we have
if M is complete and
if
![]() $M\subset B_1(0)$
.
$M\subset B_1(0)$
.
A First and second variation
We derive first and second variations of
![]() $\mathbf {\Phi }$
with emphasis on our geometric applications (see also [Reference De Philippis and Maggi18, Appendix A] and [Reference Winklmann54, Section 2]). For
$\mathbf {\Phi }$
with emphasis on our geometric applications (see also [Reference De Philippis and Maggi18, Appendix A] and [Reference Winklmann54, Section 2]). For
![]() $M^n\to \mathbf {R}^{n+1}$
a two-sided immersion, set
$M^n\to \mathbf {R}^{n+1}$
a two-sided immersion, set
for
![]() $\Phi : \mathbf {R}^{n+1}\to (0,\infty )$
an elliptic integrand.
$\Phi : \mathbf {R}^{n+1}\to (0,\infty )$
an elliptic integrand.
A.1 First variation
Consider a
![]() $1$
-parameter family of surfaces
$1$
-parameter family of surfaces
![]() $M_t$
with normal speed at
$M_t$
with normal speed at
![]() $t=0$
given by
$t=0$
given by
![]() $u \nu $
(with
$u \nu $
(with
![]() $u \in C^{1}_{c}(M\setminus \partial M)$
). Recall that
$u \in C^{1}_{c}(M\setminus \partial M)$
). Recall that
![]() $\dot \nu = - \nabla u$
. We find
$\dot \nu = - \nabla u$
. We find
 $$ \begin{align*} \frac{d}{dt}\bigg\vert_{t=0}\mathbf{\Phi}(M_t) & = \int_M \left( H u \Phi(\nu) - D_{\nabla u}\Phi(\nu) \right)\\ & = \int_M \left( H \Phi(\nu) + \operatorname{\mathrm{div}}_{M} ( D \Phi(\nu)^T) \right) u\\ & = \int_M \left( H \Phi(\nu) + \operatorname{\mathrm{div}}_M (D \Phi(\nu) - (D_{\nu} \Phi(\nu)) \nu) \right) u\\ & = \int_M \left( H \Phi(\nu) + \operatorname{\mathrm{div}}_M (D \Phi(\nu)) - (D_{\nu} \Phi(\nu))H \right) u. \end{align*} $$
$$ \begin{align*} \frac{d}{dt}\bigg\vert_{t=0}\mathbf{\Phi}(M_t) & = \int_M \left( H u \Phi(\nu) - D_{\nabla u}\Phi(\nu) \right)\\ & = \int_M \left( H \Phi(\nu) + \operatorname{\mathrm{div}}_{M} ( D \Phi(\nu)^T) \right) u\\ & = \int_M \left( H \Phi(\nu) + \operatorname{\mathrm{div}}_M (D \Phi(\nu) - (D_{\nu} \Phi(\nu)) \nu) \right) u\\ & = \int_M \left( H \Phi(\nu) + \operatorname{\mathrm{div}}_M (D \Phi(\nu)) - (D_{\nu} \Phi(\nu))H \right) u. \end{align*} $$
Now, we note that we have that
![]() $D \Phi (\nu )\cdot \nu = \Phi (\nu )$
by the Euler theorem for homogeneous functions. Thus, we find that
$D \Phi (\nu )\cdot \nu = \Phi (\nu )$
by the Euler theorem for homogeneous functions. Thus, we find that
 $$ \begin{align} \frac{d}{dt}\bigg\vert_{t=0}\mathbf{\Phi}(M_t) = \int_M \operatorname{\mathrm{div}}_M( D \Phi(\nu)) u. \end{align} $$
$$ \begin{align} \frac{d}{dt}\bigg\vert_{t=0}\mathbf{\Phi}(M_t) = \int_M \operatorname{\mathrm{div}}_M( D \Phi(\nu)) u. \end{align} $$
Thus,
vanishes if and only if M is a critical point of
![]() $\mathbf {\Phi }$
. Let us rewrite this as follows (with
$\mathbf {\Phi }$
. Let us rewrite this as follows (with
![]() $\{e_{i}\}_{i=1}^{n}$
a local orthonormal frame for M):
$\{e_{i}\}_{i=1}^{n}$
a local orthonormal frame for M):
 $$ \begin{align*} \operatorname{\mathrm{div}}_M( D \Phi(\nu)) & = \sum_{i=1}^n (D_{e_i} D \Phi(\nu)) \cdot e_i\\ & = \sum_{i=1}^n D^2\Phi(\nu)[D_{e_i}\nu,e_i]\\ & = \sum_{i=1}^n D^2\Phi(\nu)[S_\Sigma(e_i),e_i], \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{div}}_M( D \Phi(\nu)) & = \sum_{i=1}^n (D_{e_i} D \Phi(\nu)) \cdot e_i\\ & = \sum_{i=1}^n D^2\Phi(\nu)[D_{e_i}\nu,e_i]\\ & = \sum_{i=1}^n D^2\Phi(\nu)[S_\Sigma(e_i),e_i], \end{align*} $$
for
![]() $S_M$
the shape operator of M. Let us define
$S_M$
the shape operator of M. Let us define
![]() $\Psi (\nu ): T\mathbf {R}^{n+1}\to T\mathbf {R}^{n+1}$
by
$\Psi (\nu ): T\mathbf {R}^{n+1}\to T\mathbf {R}^{n+1}$
by
![]() $\Psi (\nu ): X \mapsto D^{2}\Phi (\nu )[X,\cdot ]$
(this is just the
$\Psi (\nu ): X \mapsto D^{2}\Phi (\nu )[X,\cdot ]$
(this is just the
![]() $(1,1)$
-tensor associated to
$(1,1)$
-tensor associated to
![]() $D^{2}\Phi (\nu )$
via the Euclidean metric).
$D^{2}\Phi (\nu )$
via the Euclidean metric).
Then, we find
Note that for
![]() $\Phi (\nu ) = |\nu |$
, we have
$\Phi (\nu ) = |\nu |$
, we have
so in particular, when
![]() $|\nu |=1$
, we find
$|\nu |=1$
, we find
![]() $\Psi (\nu )|_{T_{p}\Sigma } = \operatorname {\mathrm {Id}}_{T_{p}\Sigma }$
. Thus, this recovers the usual mean curvature.
$\Psi (\nu )|_{T_{p}\Sigma } = \operatorname {\mathrm {Id}}_{T_{p}\Sigma }$
. Thus, this recovers the usual mean curvature.
A.2 Second variation
Recall the tube formula:
(where we are regarding
![]() $\nabla ^{2}u$
as a
$\nabla ^{2}u$
as a
![]() $(1,1)$
-tensor via
$(1,1)$
-tensor via
![]() $g_{M}$
). Note also that the trace of a
$g_{M}$
). Note also that the trace of a
![]() $(1,1)$
-tensor is independent of the metric. Thus, we find
$(1,1)$
-tensor is independent of the metric. Thus, we find
Note that
Hence,
Integration on M gives
 $$ \begin{align} \frac{d^2}{dt^2}\bigg\vert_{t=0} \mathbf{\Phi}(M_t) = \int_M {\left\langle {\nabla u, \Psi(\nu) \nabla u} \right\rangle} - \operatorname{\mathrm{tr}}_{M} \left(\Psi(\nu) S_M^2\right) u^2. \end{align} $$
$$ \begin{align} \frac{d^2}{dt^2}\bigg\vert_{t=0} \mathbf{\Phi}(M_t) = \int_M {\left\langle {\nabla u, \Psi(\nu) \nabla u} \right\rangle} - \operatorname{\mathrm{tr}}_{M} \left(\Psi(\nu) S_M^2\right) u^2. \end{align} $$
Thus, stability implies that
Here,
![]() $\Lambda $
depends on the ellipticity of
$\Lambda $
depends on the ellipticity of
![]() $\Phi $
. In particular, if
$\Phi $
. In particular, if
![]() $\Phi $
satisfies (1.1), then (3.3) implies that for
$\Phi $
satisfies (1.1), then (3.3) implies that for
![]() $\Phi $
-stable surfaces M, we have
$\Phi $
-stable surfaces M, we have
Note that when
![]() $\Phi (X) = |X|$
, we have seen that
$\Phi (X) = |X|$
, we have seen that
![]() $\Psi (Y) = |Y|^{-1}\operatorname {\mathrm {Id}} - |Y|^{-3}Y \otimes Y^{\flat }$
. Hence,
$\Psi (Y) = |Y|^{-1}\operatorname {\mathrm {Id}} - |Y|^{-3}Y \otimes Y^{\flat }$
. Hence,
In particular,
![]() $D_{\nabla u} \Psi (\nu )|_{T_{p}M} = 0$
. Thus, we recover the standard second variation formula in this case.
$D_{\nabla u} \Psi (\nu )|_{T_{p}M} = 0$
. Thus, we recover the standard second variation formula in this case.
A.3 First variation through vector fields
We also deduce the first variation formula of
![]() $\mathbf {\Phi }$
through variations that are not necessarily normal to M. We compute as follows:
$\mathbf {\Phi }$
through variations that are not necessarily normal to M. We compute as follows:
 $$ \begin{align*} & \int_M \Phi(\nu) \operatorname{\mathrm{div}}_M X \\ & = \int_M \Phi(\nu) \operatorname{\mathrm{div}}_M X^T + \Phi(\nu) (X\cdot \nu) H\\ & = \int_M \operatorname{\mathrm{div}}_M(\Phi(\nu) X^T) - \nabla(\Phi(\nu))\cdot X^T + \Phi(\nu) (X\cdot \nu) H\\ & = \int_M \operatorname{\mathrm{div}}_M(\Phi(\nu) X^T) - D_{D\Phi(\nu)^T}\nu \cdot X^T + \Phi(\nu) (X\cdot \nu) H\\ & = \int_M \operatorname{\mathrm{div}}_M(\Phi(\nu) X^T) - D_{D\Phi(\nu)^T}X^T \cdot \nu + \Phi(\nu) (X\cdot \nu) H\\ & = \int_M \operatorname{\mathrm{div}}_M(\Phi(\nu) X^T) + D_{D\Phi(\nu)^T}(X\cdot \nu) - D_{D\Phi(\nu)^T}X \cdot \nu + \Phi(\nu) (X\cdot \nu) H\\ & = \int_M \operatorname{\mathrm{div}}_M(\Phi(\nu) X^T) + \operatorname{\mathrm{div}}((X\cdot\nu) D\Phi(\nu)^T) - (X\cdot \nu) \operatorname{\mathrm{div}}_\Sigma D\Phi(\nu)^T\\ &\qquad - D_{D\Phi(\nu)^T}X \cdot \nu + \Phi(\nu) (X\cdot \nu) H\\ & = \int_M - (X\cdot \nu) \operatorname{\mathrm{div}}_M D\Phi(\nu)^T - D_{D\Phi(\nu)^T}X \cdot \nu + \Phi(\nu) (X\cdot \nu) H \\ &\qquad + \int_{\partial M} \Phi(\nu) X\cdot \eta + (X\cdot\nu) D\Phi(\nu)\cdot \eta\\ & = \int_M - (X\cdot \nu) \operatorname{\mathrm{div}}_M D\Phi(\nu) - D_{D\Phi(\nu)^T}X \cdot \nu + \int_{\partial M} \Phi(\nu) X\cdot \eta + (X\cdot\nu) D\Phi(\nu)\cdot \eta. \end{align*} $$
$$ \begin{align*} & \int_M \Phi(\nu) \operatorname{\mathrm{div}}_M X \\ & = \int_M \Phi(\nu) \operatorname{\mathrm{div}}_M X^T + \Phi(\nu) (X\cdot \nu) H\\ & = \int_M \operatorname{\mathrm{div}}_M(\Phi(\nu) X^T) - \nabla(\Phi(\nu))\cdot X^T + \Phi(\nu) (X\cdot \nu) H\\ & = \int_M \operatorname{\mathrm{div}}_M(\Phi(\nu) X^T) - D_{D\Phi(\nu)^T}\nu \cdot X^T + \Phi(\nu) (X\cdot \nu) H\\ & = \int_M \operatorname{\mathrm{div}}_M(\Phi(\nu) X^T) - D_{D\Phi(\nu)^T}X^T \cdot \nu + \Phi(\nu) (X\cdot \nu) H\\ & = \int_M \operatorname{\mathrm{div}}_M(\Phi(\nu) X^T) + D_{D\Phi(\nu)^T}(X\cdot \nu) - D_{D\Phi(\nu)^T}X \cdot \nu + \Phi(\nu) (X\cdot \nu) H\\ & = \int_M \operatorname{\mathrm{div}}_M(\Phi(\nu) X^T) + \operatorname{\mathrm{div}}((X\cdot\nu) D\Phi(\nu)^T) - (X\cdot \nu) \operatorname{\mathrm{div}}_\Sigma D\Phi(\nu)^T\\ &\qquad - D_{D\Phi(\nu)^T}X \cdot \nu + \Phi(\nu) (X\cdot \nu) H\\ & = \int_M - (X\cdot \nu) \operatorname{\mathrm{div}}_M D\Phi(\nu)^T - D_{D\Phi(\nu)^T}X \cdot \nu + \Phi(\nu) (X\cdot \nu) H \\ &\qquad + \int_{\partial M} \Phi(\nu) X\cdot \eta + (X\cdot\nu) D\Phi(\nu)\cdot \eta\\ & = \int_M - (X\cdot \nu) \operatorname{\mathrm{div}}_M D\Phi(\nu) - D_{D\Phi(\nu)^T}X \cdot \nu + \int_{\partial M} \Phi(\nu) X\cdot \eta + (X\cdot\nu) D\Phi(\nu)\cdot \eta. \end{align*} $$
Thus, we find that if
![]() $H_\Phi = 0$
, then
$H_\Phi = 0$
, then
B Some computations for quadratic forms
In this section, we explicitly compute the constant
![]() $c_0$
that appeared in Lemma 3.2. The approach is elementary.
$c_0$
that appeared in Lemma 3.2. The approach is elementary.
Lemma B.1. Let
![]() $a_1\le a_2\le a_3$
be positive constants, such that
$a_1\le a_2\le a_3$
be positive constants, such that
![]() $\frac {a_3}{a_1}\le \sqrt 2$
. Consider quadratic forms
$\frac {a_3}{a_1}\le \sqrt 2$
. Consider quadratic forms
 $$\begin{align*}Q_1(k_1,k_2) = \frac{a_1^2 + a_3^2}{a_3^2} k_1^2 + \frac{2a_1a_2}{a_3^2} k_1k_2 + \frac{a_2^2+a_3^2}{a_3^2} k_2^2,\end{align*}$$
$$\begin{align*}Q_1(k_1,k_2) = \frac{a_1^2 + a_3^2}{a_3^2} k_1^2 + \frac{2a_1a_2}{a_3^2} k_1k_2 + \frac{a_2^2+a_3^2}{a_3^2} k_2^2,\end{align*}$$
Then we have
![]() $Q_1 \le c_0 Q_2$
, where
$Q_1 \le c_0 Q_2$
, where
 $$\begin{align*}c_0 = \frac{1}{\sqrt 2 - \frac12 } \approx 1.09.\end{align*}$$
$$\begin{align*}c_0 = \frac{1}{\sqrt 2 - \frac12 } \approx 1.09.\end{align*}$$
Proof. Write
![]() $\alpha = \frac {a_1}{a_3}$
,
$\alpha = \frac {a_1}{a_3}$
,
![]() $\beta = \frac {a_2}{a_3}$
, with
$\beta = \frac {a_2}{a_3}$
, with
![]() $2^{-\frac 12}\le \alpha \le \beta \le 1$
. Then
$2^{-\frac 12}\le \alpha \le \beta \le 1$
. Then
 $$ \begin{align} Q_1(k_1,k_2) &= (1+\alpha^2 )k_1^2 + 2\alpha \beta k_1k_2 + (1+\beta^2) k_2^2 \nonumber\\ &= (1+\alpha^2) \left(k_1 + \frac{\alpha\beta}{1+\alpha^2} k_2\right)^2 + \frac{1+\alpha^2+\beta^2}{1+\alpha^2} k_2^2. \end{align} $$
$$ \begin{align} Q_1(k_1,k_2) &= (1+\alpha^2 )k_1^2 + 2\alpha \beta k_1k_2 + (1+\beta^2) k_2^2 \nonumber\\ &= (1+\alpha^2) \left(k_1 + \frac{\alpha\beta}{1+\alpha^2} k_2\right)^2 + \frac{1+\alpha^2+\beta^2}{1+\alpha^2} k_2^2. \end{align} $$
Under the substitution
![]() $x= k_1 + \frac {\alpha \beta }{1+\alpha ^2} k_2$
,
$x= k_1 + \frac {\alpha \beta }{1+\alpha ^2} k_2$
,
![]() $y= k_2$
, we have
$y= k_2$
, we have
![]() $k_1 + k_2 + (-\alpha k_1 -\beta k_2)=(1-\alpha ) x + \frac {1- \beta -\alpha \beta +\alpha ^2}{1+\alpha ^2} y$
. Thus, by Cauchy-Schwartz,
$k_1 + k_2 + (-\alpha k_1 -\beta k_2)=(1-\alpha ) x + \frac {1- \beta -\alpha \beta +\alpha ^2}{1+\alpha ^2} y$
. Thus, by Cauchy-Schwartz,
 $$ \begin{align*} (Q_1-Q_2)(k_1,k_2) & = (k_1+k_2-\alpha k_1 -\beta k_2)^2 \\ & = \left((1-\alpha) x+ \frac{1 -\beta -\alpha \beta +\alpha^2}{1+\alpha^2}y\right)^2\\ & \le c_1\left((1+\alpha^2)x^2 +\frac{1+\alpha^2 +\beta^2}{1+\alpha^2}y^2\right) = c_1 Q_1(k_1,k_2), \end{align*} $$
$$ \begin{align*} (Q_1-Q_2)(k_1,k_2) & = (k_1+k_2-\alpha k_1 -\beta k_2)^2 \\ & = \left((1-\alpha) x+ \frac{1 -\beta -\alpha \beta +\alpha^2}{1+\alpha^2}y\right)^2\\ & \le c_1\left((1+\alpha^2)x^2 +\frac{1+\alpha^2 +\beta^2}{1+\alpha^2}y^2\right) = c_1 Q_1(k_1,k_2), \end{align*} $$
where
![]() $c_1= \frac {(1-\alpha )^2}{1+\alpha ^2} + \left (\frac {1-\beta -\alpha \beta +\alpha ^2}{1+\alpha ^2}\right )^2 \cdot \frac {1+\alpha ^2}{1+\alpha ^2+\beta ^2}$
. This gives
$c_1= \frac {(1-\alpha )^2}{1+\alpha ^2} + \left (\frac {1-\beta -\alpha \beta +\alpha ^2}{1+\alpha ^2}\right )^2 \cdot \frac {1+\alpha ^2}{1+\alpha ^2+\beta ^2}$
. This gives
![]() $Q_1 \le \frac {1}{1-c_1}Q_2$
. Using
$Q_1 \le \frac {1}{1-c_1}Q_2$
. Using
![]() $2^{-\frac 12}\le \alpha \le \beta \le 1$
, we have:
$2^{-\frac 12}\le \alpha \le \beta \le 1$
, we have:
 $$\begin{align*}c_1 \le \frac{(1-2^{-\frac 12})^2}{1+ \frac 12} + \left(\frac{1-2^{-\frac 12}}{1+\frac 12}\right)^2 \cdot \frac{1+ \frac 12}{2} = \frac32 - \sqrt 2.\end{align*}$$
$$\begin{align*}c_1 \le \frac{(1-2^{-\frac 12})^2}{1+ \frac 12} + \left(\frac{1-2^{-\frac 12}}{1+\frac 12}\right)^2 \cdot \frac{1+ \frac 12}{2} = \frac32 - \sqrt 2.\end{align*}$$
The result follows.
Acknowledgments
We are grateful to Fang-Hua Lin and Guido De Philippis for their interest and for several discussions, as well as Doug Stryker for pointing out a mistake in an earlier version of the paper and to the referees for some useful suggestions. O.C. was supported by an National Science Foundation grant (DMS-2016403), a Terman Fellowship and a Sloan Fellowship. C.L. was supported by an National Science Foundation grant (DMS-2202343).
Conflict of Interest
The authors have no conflict of interest to declare.