Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T17:33:29.425Z Has data issue: false hasContentIssue false
  • English
  • Français

STARK POINTS AND 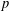$p$-ADIC ITERATED INTEGRALS ATTACHED TO MODULAR FORMS OF WEIGHT ONE

Part of: Discontinuous groups and automorphic forms Arithmetic algebraic geometry

Published online by Cambridge University Press:  13 October 2015

HENRI DARMON ,
ALAN LAUDER  and
VICTOR ROTGER
HENRI DARMON
Affiliation:
McGill University, Montreal, Canada; darmon@math.mcgill.ca
ALAN LAUDER
Affiliation:
University of Oxford, UK; lauder@maths.ox.ac.uk
VICTOR ROTGER
Affiliation:
Universitat Politècnica de Catalunya, Barcelona, Spain; victor.rotger@upc.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 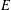$E$ be an elliptic curve over 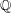$\mathbb{Q}$, and let 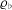${\it\varrho}_{\flat }$ and 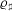${\it\varrho}_{\sharp }$ be odd two-dimensional Artin representations for which 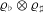${\it\varrho}_{\flat }\otimes {\it\varrho}_{\sharp }$ is self-dual. 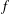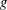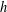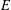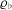The progress on modularity achieved in recent decades ensures the existence of normalized eigenforms $f$, $g$, and $h$ of respective weights two, one, and one, giving rise to $E$, ${\it\varrho}_{\flat }$, and 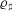${\it\varrho}_{\sharp }$ via the constructions of Eichler and Shimura, and of Deligne and Serre. This article examines certain 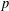$p$-adic iterated integrals attached to the triple 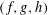$(f,g,h)$, which are 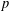$p$-adic avatars of the leading term of the Hasse–Weil–Artin 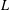$L$-series 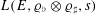$L(E,{\it\varrho}_{\flat }\otimes {\it\varrho}_{\sharp },s)$ when it has a double zero at the centre. A formula is proposed for these iterated integrals, involving the formal group logarithms of global points on 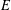$E$—referred to as Stark points—which are defined over the number field cut out by 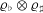${\it\varrho}_{\flat }\otimes {\it\varrho}_{\sharp }$. This formula can be viewed as an elliptic curve analogue of Stark’s conjecture on units attached to weight-one forms. It is proved when 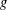$g$ and 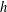$h$ are binary theta series attached to a common imaginary quadratic field in which 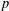$p$ splits, by relating the arithmetic quantities that arise in it to elliptic units and Heegner points. Fast algorithms for computing 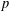$p$-adic iterated integrals based on Katz expansions of overconvergent modular forms are then exploited to gather numerical evidence in more exotic scenarios, encompassing Mordell–Weil groups over cyclotomic fields, ring class fields of real quadratic fields (a setting which may shed light on the theory of Stark–Heegner points attached to Shintani-type cycles on 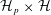${\mathcal{H}}_{p}\times {\mathcal{H}}$), and extensions of 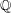$\mathbb{Q}$ with Galois group a central extension of the dihedral group 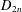$D_{2n}$ or of one of the exceptional subgroups 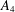$A_{4}$, 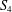$S_{4}$, and 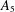$A_{5}$ of 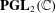$\mathbf{PGL}_{2}(\mathbb{C})$.

MSC classification

Primary: 11G05: Elliptic curves over global fields
Secondary: 11F11: Holomorphic modular forms of integral weight 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture
Type
Research Article
Information
Forum of Mathematics, Pi , Volume 3 , 2015 , e8
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2015

References

Atkin, A. O. L. and Li, W., ‘Twists of newforms and pseudo-eigenvalues of W-operators’, Invent. Math. 48(3) (1978), 221–243.Google Scholar
Bellaïche, J. and Dimitrov, M., ‘On the eigencurve at classical weight one points’, Duke Math. J. , to appear.Google Scholar
Bertolini, M., Castella, F., Darmon, H., Dasgupta, S., Prasanna, K. and Rotger, V., ‘p-adic L-functions and Euler systems: a tale in two trilogies’, inAutomorphic Forms and Galois Representations, Vol. 1, LMS Lecture Notes, 414 (Cambridge University Press, Cambridge, 2014), 52–102.Google Scholar
Bertolini, M. and Darmon, H., ‘Kolyvagin’s descent and Mordell–Weil groups over ring class fields’, J. reine angew. Math. 412 (1990), 63–74.Google Scholar
Bertolini, M. and Darmon, H., ‘Kato’s Euler system and rational points on elliptic curves I: A p-adic Beilinson formula’, Israel J. Math. 199 (2014), 163–188.Google Scholar
Bertolini, M., Darmon, H. and Prasanna, K., ‘p-adic Rankin L-series and rational points on CM elliptic curves’, Pacific J. Math. 260 (2012), 261–303.Google Scholar
Bertolini, M., Darmon, H. and Prasanna, K., ‘Generalised Heegner cycles and p-adic Rankin L-series’, Duke Math. J. 162(6) (2013), 1033–1148.Google Scholar
Bertolini, M., Darmon, H. and Rotger, V., ‘Beilinson–Flach elements and Euler Systems I: syntomic regulators and p-adic Rankin L-series’, J. Algebraic Geom. 24 (2015), 355–378.Google Scholar
Bertolini, M., Darmon, H. and Rotger, V., ‘Beilinson–Flach elements and Euler systems II: p-adic families and the Birch and Swinnerton-Dyer conjecture’, J. Algebraic Geom. 24 (2015), 569–604.Google Scholar
Brooks, E. H., ‘Generalized Heegner cycles, Shimura curves, and special values of $p$-adic $L$-functions’, PhD Dissertation, University of Michigan, 2013.Google Scholar
Buzzard, K., ‘Computing weight one modular forms over ℂ and F̄p ’, inComputations with Modular Forms: Proceedings of a Summer School and Conference, Heidelberg, August/September 2011 (eds. (ed. Böckle, G. and Wiese, G.) (Springer, 2014), 129–146.Google Scholar
Chinburg, T., ‘Stark’s conjecture for L-functions with first order zeroes at s = 0’, Adv. Math. 48 (1983), 82–113.Google Scholar
Cho, S. and Vatsal, V., ‘Deformations of induced Galois representations’, J. reine angew. Math. 556 (2003), 79–98.Google Scholar
Cowan, A., ‘Computational techniques for verifying the Birch and Swinnerton-Dyer conjecture for curves over cubic number fields’, NSERC USRA (Undergraduate Summer Research Award) project, available at http://www.math.mcgill.ca/darmon/theses/cowan.pdf.Google Scholar
Darmon, H., ‘Integration on Hp×H and arithmetic applications’, Ann. of Math. (2) 154(3) (2001), 589–639.Google Scholar
Darmon, H., Daub, M., Lichtenstein, S. and Rotger, V., ‘Algorithms for Chow–Heegner points via iterated integrals’, Math. Comp. 84 (2015), 2505–2547. With an appendix by W. Stein.Google Scholar
Darmon, H., Lauder, A. and Rotger, V., ‘Gross–Stark units and p-adic iterated integrals attached to modular forms of weight one’, Ann. Math. Québec , to appear. Volume dedicated to Prof. Glenn Stevens on his 60th birthday.Google Scholar
Darmon, H., Lauder, A. and Rotger, V., ‘Overconvergent generalised eigenforms of weight one and class fields of real quadratic fields’, Adv. Math. 283 (2015), 130–142.Google Scholar
Darmon, H., Lauder, A. and Rotger, V., ‘Elliptic Stark conjectures and irregular weight one forms’, in progress.Google Scholar
Darmon, H. and Pollack, R., ‘The efficient calculation of Stark–Heegner points via overconvergent modular symbols’, Israel J. Math. 153 (2006), 319–354.Google Scholar
Darmon, H. and Rotger, V., ‘Diagonal cycles and Euler systems I: a p-adic Gross–Zagier formula’, Ann. Sci. Éc. Norm. Supér. 47(4) , 47 p.Google Scholar
Darmon, H. and Rotger, V., ‘Diagonal cycles and Euler systems II: the Birch and Swinnerton-Dyer conjecture for Hasse–Weil–Artin $L$-series’, submitted.Google Scholar
Darmon, H. and Rotger, V., ‘Elliptic curves of rank two and generalised Kato classes’, submitted.Google Scholar
Darmon, H., Rotger, V. and Sols, I., ‘Iterated integrals, diagonal cycles, and rational points on elliptic curves’, Publ. Math. Besançon 2 (2012), 19–46.Google Scholar
David, C., Fearnley, J. and Kisilevsky, H., ‘Vanishing of L-functions of elliptic curves over number fields’, inRanks of Elliptic Curves and Random Matrix Theory, London Mathematical Society Lecture Note Series, 341 (Cambridge University Press, Cambridge, 2007), 247–259.Google Scholar
de Shalit, E., Iwasawa Theory of Elliptic Curves with Complex Multiplication. p-Adic L-Functions, Perspectives in Mathematics, 3 (Academic Press, Inc., Boston, MA, 1987).Google Scholar
Duke, W. and Li, Y., ‘Harmonic Maass forms of weight one’, Duke Math. J. 164 (2015), 39–113.Google Scholar
Ghate, E., ‘Ordinary forms and their local Galois representations’, available for download at http://www.math.tifr.res.in/ eghate/math.html.Google Scholar
Greenberg, M., ‘Stark–Heegner points and the cohomology of quaternionic Shimura varieties’, Duke Math. J. 147(3) (2009), 541–575.Google Scholar
Gross, B., ‘On the factorization of p-adic L-series’, Invent. Math. 57(1) (1980), 83–95.Google Scholar
Harris, M. and Kudla, S., ‘The central critical value of a triple product L-function’, Ann. Math. (2) 133 (1991), 605–672.Google Scholar
Hida, H., ‘Congruences of cusp forms and special values of their zeta functions’, Invent. Math. 63 (1981), 225–261.Google Scholar
Hida, H., ‘Elementary theory of L-functions and Eisenstein series’, Lond. Math. Soc. St. Texts 26 (1993).Google Scholar
Hida, H., ‘On the search of genuine p-adic modular L-functions for GL(n)’, inMémoires de la Société Mathématique de France, 2nd series, 67 (1996), 1–110.Google Scholar
Ichino, A., ‘Trilinear forms and the central values of triple product L-functions’, Duke Math. J. 145(2) (2008), 281–307.Google Scholar
Kato, K., ‘p-adic Hodge theory and values of zeta functions of modular forms’, inCohomologies p-Adiques et Applications Arithmétiques. III, Astérisque, No. 295 (2004), ix, 117–290.Google Scholar
Katz, N. M., ‘p-adic interpolation of real analytic Eisenstein series’, Ann. of Math. (2) 104(3) (1976), 459–571.Google Scholar
Katz, N. M., ‘p-adic L-functions for CM fields’, Invent. Math. 49 (1978), 199–297.Google Scholar
Khare, C. and Wintenberger, J.-P., ‘Serre’s modularity conjecture (I)’, Invent. Math. 178 (2009), 485–504.Google Scholar
Lauder, A., ‘Computations with classical and p-adic modular forms’, LMS J. Comput. Math. 14 (2011), 214–231.Google Scholar
Lauder, A., ‘Efficient computation of Rankin p-adic L-functions’, inComputations with Modular Forms: Proceedings of a Summer School and Conference, Heidelberg, August/September 2011 (eds. (ed. Böckle, G. and Wiese, G.) (Springer, 2014), 181–200.Google Scholar
Prasad, D., ‘Trilinear forms for representations of GL(2) and local epsilon factors’, Compos. Math. 75 (1990), 1–46.Google Scholar
Silverman, J. H., ‘Computing rational points on rank 1 elliptic curves via L-series and canonical heights’, Math. Comp. 68(226) (1999), 835–858.Google Scholar
Stark, H. M., ‘L-functions at s = 1. II. Artin L-functions with rational characters’, Adv. Math. 17 (1975), 60–92.Google Scholar
Stark, H. M., ‘Class fields and modular forms of weight one’, inModular Functions of One Variable, V (Proc. Second Internat. Conf., Univ. Bonn, Bonn, 1976), Lecture Notes in Mathematics, 601 (Springer, Berlin, 1977), 277–287.Google Scholar
Watson, T. C., ‘Rankin triple products and quantum chaos’. PhD Thesis, Princeton University, 2002, 81 pp.Google Scholar
Woodbury, M., ‘Trilinear forms and subconvexity of the triple product $L$-function’, submitted.Google Scholar
Woodbury, M., ‘On the triple product formula: real local calculations’, in preparation.Google Scholar
Yuan, X., Zhang, S. and Zhang, W., The Gross–Zagier Formula on Shimura Curves, Annals of Mathematics Studies, 184 (Princeton University Press, Princeton, NJ, 2013).Google Scholar
Zhang, S.-W., ‘Gross–Zagier formula for GL (2). II’, inHeegner Points and Rankin L-Series, Mathematical Sciences Research Institute Publications, 49 (Cambridge University Press, Cambridge, 2004), 191–214.Google Scholar