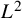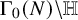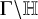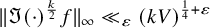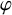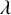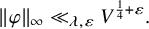1. Introduction
Let
![]() $\Gamma \backslash \mathbb {H}$
be a finite volume hyperbolic surface. A basic problem in quantum chaos is to understand the limiting behavior of
$\Gamma \backslash \mathbb {H}$
be a finite volume hyperbolic surface. A basic problem in quantum chaos is to understand the limiting behavior of
![]() $L^2$
-normalized Laplace eigenfunctions
$L^2$
-normalized Laplace eigenfunctions
![]() $\varphi $
on
$\varphi $
on
![]() $\Gamma \backslash \mathbb {H}$
. This behavior can be quantified through weak limits of
$\Gamma \backslash \mathbb {H}$
. This behavior can be quantified through weak limits of
![]() $L^2$
-masses (‘quantum ergodicity’), bounds for
$L^2$
-masses (‘quantum ergodicity’), bounds for
![]() $L^p$
-norms and so forth. We consider in this paper the sup-norm problem, which consists of bounding the supremum or
$L^p$
-norms and so forth. We consider in this paper the sup-norm problem, which consists of bounding the supremum or
![]() $L^\infty $
-norm of an
$L^\infty $
-norm of an
![]() $L^2$
-normalized eigenfunction
$L^2$
-normalized eigenfunction
![]() $\varphi $
with respect to the eigenvalue
$\varphi $
with respect to the eigenvalue
![]() $\lambda _\varphi $
and/or the geometry of the underlying manifold
$\lambda _\varphi $
and/or the geometry of the underlying manifold
![]() $\Gamma \backslash \mathbb {H}$
. A general bound in this direction, due to Bérard [Reference BérardBér77], asserts that
$\Gamma \backslash \mathbb {H}$
. A general bound in this direction, due to Bérard [Reference BérardBér77], asserts that
Here and henceforth,
![]() $A \ll B$
means that there is a constant C such that
$A \ll B$
means that there is a constant C such that
![]() $|A| \le CB$
; we allow C to depend on any subscripts of
$|A| \le CB$
; we allow C to depend on any subscripts of
![]() $\ll $
and write
$\ll $
and write
![]() $\varepsilon $
for an arbitrary, but sufficiently small, positive constant, which may change from line to line.
$\varepsilon $
for an arbitrary, but sufficiently small, positive constant, which may change from line to line.
Stronger bounds have been established in the arithmetic case that
-
∘
 $\Gamma \backslash \mathbb {H}$
is an arithmetic manifold, such as the modular surface
$\Gamma \backslash \mathbb {H}$
is an arithmetic manifold, such as the modular surface
 $\operatorname {\mathrm {SL}}_2(\mathbb {Z}) \backslash \mathbb {H}$
or a congruence cover, and
$\operatorname {\mathrm {SL}}_2(\mathbb {Z}) \backslash \mathbb {H}$
or a congruence cover, and -
∘
 $\varphi $
is a Hecke–Maaß form, that is, an eigenfunction not only of the Laplacian but also of the Hecke operators.
$\varphi $
is a Hecke–Maaß form, that is, an eigenfunction not only of the Laplacian but also of the Hecke operators.
The pioneering result in that case is due to Iwaniec–Sarnak [Reference Iwaniec and SarnakIS95], who showed for congruence lattices
![]() $\Gamma $
that
$\Gamma $
that
The above estimates depend in an unspecified manner upon the underlying manifold. Consider, for instance, the case that
![]() $\Gamma $
is the Hecke congruence subgroup
$\Gamma $
is the Hecke congruence subgroup
![]() $\Gamma _0(N) = \operatorname {\mathrm {SL}}_2(\mathbb {Z}) \cap \left ( \begin {smallmatrix} \mathbb {Z} &\mathbb {Z} \\ N \mathbb {Z} & \mathbb {Z} \end {smallmatrix} \right )$
so that
$\Gamma _0(N) = \operatorname {\mathrm {SL}}_2(\mathbb {Z}) \cap \left ( \begin {smallmatrix} \mathbb {Z} &\mathbb {Z} \\ N \mathbb {Z} & \mathbb {Z} \end {smallmatrix} \right )$
so that
![]() $\Gamma \backslash \mathbb {H}$
is an arithmetic manifold of volume
$\Gamma \backslash \mathbb {H}$
is an arithmetic manifold of volume
![]() $N^{1+o(1)}$
. We suppose that N is squarefree. A direct quantification of the Iwaniec–Sarnak argument (see [Reference Blomer and HolowinskyBH10, §10]) gives the estimate
$N^{1+o(1)}$
. We suppose that N is squarefree. A direct quantification of the Iwaniec–Sarnak argument (see [Reference Blomer and HolowinskyBH10, §10]) gives the estimate
where we normalize
![]() $\varphi $
to have
$\varphi $
to have
![]() $L^2$
-norm one with respect to the hyperbolic probability measure, that is, the multiple of the hyperbolic measure having total volume one. The level aspect case of the sup-norm problem is to improve the dependence of the bound (1.3) upon N. The first improvement in the exponent was a major breakthrough of Blomer–Holowinsky [Reference Blomer and HolowinskyBH10], achieved 13 years after the work of Iwaniec–Sarnak. For a Hecke–Maaß newform
$L^2$
-norm one with respect to the hyperbolic probability measure, that is, the multiple of the hyperbolic measure having total volume one. The level aspect case of the sup-norm problem is to improve the dependence of the bound (1.3) upon N. The first improvement in the exponent was a major breakthrough of Blomer–Holowinsky [Reference Blomer and HolowinskyBH10], achieved 13 years after the work of Iwaniec–Sarnak. For a Hecke–Maaß newform
![]() $\varphi $
of eigenvalue
$\varphi $
of eigenvalue
![]() $\lambda _{\varphi }$
, they managed to show
$\lambda _{\varphi }$
, they managed to show
(with explicit polynomial dependence upon
![]() $\lambda _\varphi $
). Subsequently, Templier [Reference TemplierTem10] and Harcos–Templier [Reference Harcos and TemplierHT12, Reference Harcos and TemplierHT13] established several improved bounds, culminating in
$\lambda _\varphi $
). Subsequently, Templier [Reference TemplierTem10] and Harcos–Templier [Reference Harcos and TemplierHT12, Reference Harcos and TemplierHT13] established several improved bounds, culminating in
The estimate (1.5) is comparable in strength to the Weyl bound for the Riemann zeta function and has long been regarded as a natural limit for the sup-norm problem in the squarefree level aspect [Reference Harcos and TemplierHT13, Remarks (i)]. It has been extended to number fields [Reference Blomer, Harcos and MilićevićBHM16, Reference Blomer, Harcos, Maga and MilićevićBHMM20, Reference AssingAss24] and to more general vectors than newforms [Reference Hu, Nelson and SahaHNS19, Reference AssingAss21]. For levels that are not squarefree (e.g., powers of a fixed prime), the flavor of the problem is quite different (see Remark 1.4), and stronger estimates have been achieved in [Reference SahaSah17, Reference MarshallMar16, Reference SahaSah20, Reference ComtatCom21, Reference Hu and SahaHS20].
In this work, we bring new methodology to bear on the sup-norm problem in the squarefree level aspect. By obtaining optimal solutions to the technical problems that arise in applying that methodology, we deduce the following improvement of Equation (1.5).
Theorem 1.1. Let N be a squarefree natural number. Let
![]() $\varphi $
be a cuspidal Hecke–Maaß newform for
$\varphi $
be a cuspidal Hecke–Maaß newform for
![]() $\Gamma _0(N)$
with trivial (central) character. Suppose that
$\Gamma _0(N)$
with trivial (central) character. Suppose that
![]() $\varphi $
is
$\varphi $
is
![]() $L^2$
-normalized with respect to the hyperbolic probability measure on
$L^2$
-normalized with respect to the hyperbolic probability measure on
![]() $\Gamma _0(N) \backslash \mathbb {H}$
. Then
$\Gamma _0(N) \backslash \mathbb {H}$
. Then
Our main results apply not only to
![]() $\Gamma _0(N) \backslash \mathbb {H}$
but also to compact arithmetic quotients. In general, such a manifold is of the shape
$\Gamma _0(N) \backslash \mathbb {H}$
but also to compact arithmetic quotients. In general, such a manifold is of the shape
![]() $\Gamma \backslash \mathbb {H}$
, where
$\Gamma \backslash \mathbb {H}$
, where
![]() $\Gamma $
is commensurable with a lattice attached to a maximal order in a quaternion algebra B over a totally real field F, with B split at exactly one Archimedean place. We are content here to consider the case
$\Gamma $
is commensurable with a lattice attached to a maximal order in a quaternion algebra B over a totally real field F, with B split at exactly one Archimedean place. We are content here to consider the case
![]() $F = \mathbb {Q}$
so that B is an indefinite quaternion algebra, characterized up to isomorphism by its reduced discriminant
$F = \mathbb {Q}$
so that B is an indefinite quaternion algebra, characterized up to isomorphism by its reduced discriminant
![]() $d_B$
. For each natural number N coprime to
$d_B$
. For each natural number N coprime to
![]() $d_B$
, we denote by
$d_B$
, we denote by
![]() $\Gamma _0^B(N)$
the group of proper (i.e., norm one) units arising from an Eichler order of level N in B (see Section 2.1 for details). For example, if
$\Gamma _0^B(N)$
the group of proper (i.e., norm one) units arising from an Eichler order of level N in B (see Section 2.1 for details). For example, if
![]() $B = \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {Q})$
, then we could take
$B = \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {Q})$
, then we could take
![]() $\Gamma _0^B(N) = \Gamma _0(N)$
. We prove the following theorem.
$\Gamma _0^B(N) = \Gamma _0(N)$
. We prove the following theorem.
Theorem 1.2. Let
![]() $\Gamma =\Gamma ^B_0(N)$
be as above with the level N being squarefree. Let
$\Gamma =\Gamma ^B_0(N)$
be as above with the level N being squarefree. Let
![]() $\varphi $
be a cuspidal Hecke–Maaß newform for
$\varphi $
be a cuspidal Hecke–Maaß newform for
![]() $\Gamma $
with trivial (central) character,
$\Gamma $
with trivial (central) character,
![]() $L^2$
-normalized with respect to the hyperbolic probability measure on
$L^2$
-normalized with respect to the hyperbolic probability measure on
![]() $\Gamma \backslash \mathbb {H}$
. Then, with
$\Gamma \backslash \mathbb {H}$
. Then, with
![]() $V = (d_BN)^{1+o(1)}$
the covolume of
$V = (d_BN)^{1+o(1)}$
the covolume of
![]() $\Gamma $
,
$\Gamma $
,
Theorem 1.2 specializes to Theorem 1.1 upon taking
![]() $B = \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {Q})$
. It improves upon (the
$B = \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {Q})$
. It improves upon (the
![]() $F = \mathbb {Q}$
case of) Templier’s result [Reference TemplierTem10], which gave the nontrivial bound
$F = \mathbb {Q}$
case of) Templier’s result [Reference TemplierTem10], which gave the nontrivial bound
![]() $V^{\frac {1}{2} - \frac {1}{24} + \varepsilon }$
. We emphasize that the estimate (1.6) is uniform in the quaternion algebra B, hence gives a strong saving in the ‘discriminant aspect’; the first nontrivial results in that aspect (for B indefinite, as we have assumed) were established only very recently by Toma [Reference TomaTom23], updating an earlier preprint, giving (among other things) the bound
$V^{\frac {1}{2} - \frac {1}{24} + \varepsilon }$
. We emphasize that the estimate (1.6) is uniform in the quaternion algebra B, hence gives a strong saving in the ‘discriminant aspect’; the first nontrivial results in that aspect (for B indefinite, as we have assumed) were established only very recently by Toma [Reference TomaTom23], updating an earlier preprint, giving (among other things) the bound
![]() $V^{\frac {1}{2}-\frac {1}{30}+\varepsilon }$
. Our method applies equally in the setting of definite quaternion algebras, where we improve the exponent
$V^{\frac {1}{2}-\frac {1}{30}+\varepsilon }$
. Our method applies equally in the setting of definite quaternion algebras, where we improve the exponent
![]() $\frac {1}{3}$
of Blomer–Michel [Reference Blomer and MichelBM11, Reference Blomer and MichelBM13] down to
$\frac {1}{3}$
of Blomer–Michel [Reference Blomer and MichelBM11, Reference Blomer and MichelBM13] down to
![]() $\frac {1}{4}$
in analogy with Theorem 1.2 (see Section §2.3 for details).
$\frac {1}{4}$
in analogy with Theorem 1.2 (see Section §2.3 for details).
Remark 1.3. The dependence on the eigenvalue in Equation (1.6) that follows from our proof is of exponential nature. With some finer Archimedean considerations, it seems likely that one could show
![]() $\|\varphi \|_{\infty } \ll _{\varepsilon } \lambda _\varphi ^{\frac {1}{4} +\varepsilon } V ^{\frac {1}{4} + \varepsilon }$
; indeed, by comparison, we obtain such an estimate for the definite analogue of Equation (1.6) (see Corollary 2.3). Such a refinement of Equation (1.6) seems to require lengthy Archimedean calculations that we feel would distract from the primary novelties of this paper concerning the level aspect.
$\|\varphi \|_{\infty } \ll _{\varepsilon } \lambda _\varphi ^{\frac {1}{4} +\varepsilon } V ^{\frac {1}{4} + \varepsilon }$
; indeed, by comparison, we obtain such an estimate for the definite analogue of Equation (1.6) (see Corollary 2.3). Such a refinement of Equation (1.6) seems to require lengthy Archimedean calculations that we feel would distract from the primary novelties of this paper concerning the level aspect.
Remark 1.4. We have noted already that we focus in this paper on the case of squarefree levels. The opposite case is the depth aspect, where the level is a power
![]() $N = p^n$
of a fixed prime p. In that case, local arguments give the bound
$N = p^n$
of a fixed prime p. In that case, local arguments give the bound
![]() $\|\varphi \|_\infty \ll _{p,d_B, \varepsilon } (\lambda _\varphi N)^{1/4+\varepsilon }$
[Reference MarshallMar16], which has been improved to
$\|\varphi \|_\infty \ll _{p,d_B, \varepsilon } (\lambda _\varphi N)^{1/4+\varepsilon }$
[Reference MarshallMar16], which has been improved to
![]() $\|\varphi \|_\infty \ll _{\lambda _\varphi ,p,d_B, \varepsilon } N^{5/24+\varepsilon }$
[Reference Hu and SahaHS20] via arithmetic amplification and refined local analysis.
$\|\varphi \|_\infty \ll _{\lambda _\varphi ,p,d_B, \varepsilon } N^{5/24+\varepsilon }$
[Reference Hu and SahaHS20] via arithmetic amplification and refined local analysis.
Remark 1.5. In a function field setting analogous to that of Theorem 1.1, Sawin [Reference SawinSaw21] has used geometric techniques to establish (among other things) the sup-norm bound
![]() $\ll N^{\frac {1}{4} + \alpha _q}$
, where
$\ll N^{\frac {1}{4} + \alpha _q}$
, where
![]() $\alpha _q> 0$
tends to zero as the cardinality q of the underlying finite field tends to
$\alpha _q> 0$
tends to zero as the cardinality q of the underlying finite field tends to
![]() $\infty $
. We do not see any obstruction to adapting the techniques of this paper to the function field setting, where we expect they would give the improved bound
$\infty $
. We do not see any obstruction to adapting the techniques of this paper to the function field setting, where we expect they would give the improved bound
![]() $\ll _{\varepsilon } N^{\frac {1}{4} + \varepsilon }$
.
$\ll _{\varepsilon } N^{\frac {1}{4} + \varepsilon }$
.
By combining the arguments of this paper with those of the prequel [Reference Khayutin and SteinerKS20] concerning the weight aspect for holomorphic forms, we obtain the following uniform hybrid bound in the weight and level aspects.
Theorem 1.6. Let
![]() $\Gamma = \Gamma ^B_0(N)$
be as in Theorem 1.2. Let f be a cuspidal holomorphic newform for
$\Gamma = \Gamma ^B_0(N)$
be as in Theorem 1.2. Let f be a cuspidal holomorphic newform for
![]() $\Gamma $
with trivial (central) character and weight
$\Gamma $
with trivial (central) character and weight
![]() $k\ge 2$
. Suppose f is
$k\ge 2$
. Suppose f is
![]() $L^2$
-normalized with respect to the hyperbolic probability measure on
$L^2$
-normalized with respect to the hyperbolic probability measure on
![]() $\Gamma \backslash \mathbb {H}$
. Then
$\Gamma \backslash \mathbb {H}$
. Then
where
![]() $V = (d_BN)^{1+o(1)}$
denotes the covolume of
$V = (d_BN)^{1+o(1)}$
denotes the covolume of
![]() $\Gamma $
.
$\Gamma $
.
1.1. Selected applications
A straightforward application of these improved sup-norms is to
![]() $L^p$
-norms for
$L^p$
-norms for
![]() $2\le p \le \infty $
by means of interpolation. We state here only the split holomorphic case, as in this case, strong
$2\le p \le \infty $
by means of interpolation. We state here only the split holomorphic case, as in this case, strong
![]() $L^4$
-bounds were given by Buttcane–Khan [Reference Buttcane and KhanBK15] with subconvexity input from [Reference YoungYou17].
$L^4$
-bounds were given by Buttcane–Khan [Reference Buttcane and KhanBK15] with subconvexity input from [Reference YoungYou17].
Corollary 1.7. Let q denote an odd prime and f a cuspidal holomorphic newform for
![]() $\Gamma _0(q)$
with trivial (central) character and weight k. Suppose f is
$\Gamma _0(q)$
with trivial (central) character and weight k. Suppose f is
![]() $L^2$
-normalized with respect to the hyperbolic probability measure on
$L^2$
-normalized with respect to the hyperbolic probability measure on
![]() $\Gamma _0(q) \backslash \mathbb {H}$
. Then, for
$\Gamma _0(q) \backslash \mathbb {H}$
. Then, for
![]() $2 \le p \le \infty $
and any
$2 \le p \le \infty $
and any
![]() $\eta>0$
, we have
$\eta>0$
, we have
 $$ \begin{align*} \| \Im(\cdot)^{\frac{k}{2}} f \|_p \ll_{k, \eta} \begin{cases} q^{\frac{1}{6}-\frac{1}{3p}+\eta} , & 2 \le p\le 4, \\ q^{\frac{1}{4}-\frac{2}{3p}+\eta} , & 4 \le p \le \infty, \end{cases} \end{align*} $$
$$ \begin{align*} \| \Im(\cdot)^{\frac{k}{2}} f \|_p \ll_{k, \eta} \begin{cases} q^{\frac{1}{6}-\frac{1}{3p}+\eta} , & 2 \le p\le 4, \\ q^{\frac{1}{4}-\frac{2}{3p}+\eta} , & 4 \le p \le \infty, \end{cases} \end{align*} $$
for k sufficiently large in terms of
![]() $\eta $
.
$\eta $
.
Further applications of sup-norm bounds include shifted convolution problems and subconvexity results for L-functions; see, for example, [Reference HarcosHar03, Reference Harcos and MichelHM06, Reference Hou and ChenHC19, Reference Hu and SahaHS20, Reference NordentoftNor21]. Often, such applications would be obtained from a uniform version of Wilton’s estimate. By applying the arguments of [Reference Harcos and MichelHM06, §2.7] with our improved sup-norm bound, we derive the following corollary.
Corollary 1.8. Let
![]() $\lambda (m)$
,
$\lambda (m)$
,
![]() $m \in \mathbb {N}$
, denote the Hecke eigenvalues, normalized so that the Ramanujan conjecture reads
$m \in \mathbb {N}$
, denote the Hecke eigenvalues, normalized so that the Ramanujan conjecture reads
![]() $|\lambda (m)| \ll _\varepsilon m^{\varepsilon }$
, of either a cuspidal Hecke–Maaß newform or a cuspidal holomorphic newform of weight k on
$|\lambda (m)| \ll _\varepsilon m^{\varepsilon }$
, of either a cuspidal Hecke–Maaß newform or a cuspidal holomorphic newform of weight k on
![]() $\Gamma _0(N)$
with trivial (central) character, where N is squarefree. Then, for any
$\Gamma _0(N)$
with trivial (central) character, where N is squarefree. Then, for any
![]() $\alpha \in \mathbb {R}$
, one has
$\alpha \in \mathbb {R}$
, one has

where the implied constant in the Maaß case further depends on the eigenvalue of the form.
As a consequence, we may, for example, improve the main theorem in [Reference Hou and ChenHC19].
Corollary 1.9. Let
![]() $\varphi $
either be a cuspidal Hecke–Maaß newform or a cuspidal holomorphic newform on
$\varphi $
either be a cuspidal Hecke–Maaß newform or a cuspidal holomorphic newform on
![]() $\Gamma _0(q)$
, with q prime. Let
$\Gamma _0(q)$
, with q prime. Let
![]() $\chi $
be a primitive Dirichlet character of modulus m with
$\chi $
be a primitive Dirichlet character of modulus m with
![]() $(m,q)=1$
. Suppose that
$(m,q)=1$
. Suppose that
![]() $q = m^{\eta }$
with
$q = m^{\eta }$
with
![]() $0 < \eta < 2$
. Then, we have
$0 < \eta < 2$
. Then, we have
where the implied constant depends on the eigenvalue respectively weight of
![]() $\varphi $
,
$\varphi $
,
![]() $\mathcal {C}=qm^2$
is the conductor of the L-function and
$\mathcal {C}=qm^2$
is the conductor of the L-function and
![]() $\vartheta $
is the current best bound towards the generalized Ramanujan conjecture if
$\vartheta $
is the current best bound towards the generalized Ramanujan conjecture if
![]() $\varphi $
is a Maaß form and
$\varphi $
is a Maaß form and
![]() $0$
if
$0$
if
![]() $\varphi $
is holomorphic.
$\varphi $
is holomorphic.
1.2. The fourth moment and further applications
The method underlying most previous works on this problem, including the work of Harcos–Templier giving the bound
![]() $\ll _{\epsilon } N^{1/3+\epsilon }$
, is based on the amplification method introduced in the original paper of Iwaniec–Sarnak. Recently, Steiner [Reference SteinerSte20] and Khayutin–Steiner [Reference Khayutin and SteinerKS20] introduced a new method based on analysis of fourth moments over families. The key observation of these papers was that such a fourth moment naturally arises as the
$\ll _{\epsilon } N^{1/3+\epsilon }$
, is based on the amplification method introduced in the original paper of Iwaniec–Sarnak. Recently, Steiner [Reference SteinerSte20] and Khayutin–Steiner [Reference Khayutin and SteinerKS20] introduced a new method based on analysis of fourth moments over families. The key observation of these papers was that such a fourth moment naturally arises as the
![]() $L^2$
-norm of a theta kernel. Alternatively, Blomer et al. [Reference Blomer, Harcos, Maga and MilićevićBHMM22] have demonstrated that one may use Voronoï summation for Rankin–Selberg convolutions in place of a theta kernel. Prior to the application to fourth moments, theta kernels have played similar roles in the study of quantum variance [Reference NelsonNel16, Reference NelsonNel17, Reference NelsonNel19, Reference NelsonNel20], numerical computations [Reference NelsonNel15] and in the proof of Waldspurger’s formula [Reference WaldspurgerWal85]. In each of these earlier works, theta kernels apparently served as a substitute for parabolic Fourier expansions, giving a tool for establishing analogues on compact quotients (where such expansions are not available) of results known already for noncompact quotients. The present work differs in that our main result is new even for the noncompact quotients
$L^2$
-norm of a theta kernel. Alternatively, Blomer et al. [Reference Blomer, Harcos, Maga and MilićevićBHMM22] have demonstrated that one may use Voronoï summation for Rankin–Selberg convolutions in place of a theta kernel. Prior to the application to fourth moments, theta kernels have played similar roles in the study of quantum variance [Reference NelsonNel16, Reference NelsonNel17, Reference NelsonNel19, Reference NelsonNel20], numerical computations [Reference NelsonNel15] and in the proof of Waldspurger’s formula [Reference WaldspurgerWal85]. In each of these earlier works, theta kernels apparently served as a substitute for parabolic Fourier expansions, giving a tool for establishing analogues on compact quotients (where such expansions are not available) of results known already for noncompact quotients. The present work differs in that our main result is new even for the noncompact quotients
![]() $\Gamma _0(N) \backslash \mathbb {H}$
.
$\Gamma _0(N) \backslash \mathbb {H}$
.
In this paper, we follow generally the theta kernel strategy of the prequel [Reference Khayutin and SteinerKS20] and prove a fourth moment bound from which one may deduce the Theorems 1.1, 1.2 and 1.6 after some additional analysis near any cusps. In what follows, we let
![]() $\Gamma = \Gamma ^B_0(N)$
be a lattice as in Theorem 1.2 and denote by
$\Gamma = \Gamma ^B_0(N)$
be a lattice as in Theorem 1.2 and denote by
![]() $V = (d_B N)^{1+o(1)}$
the volume of
$V = (d_B N)^{1+o(1)}$
the volume of
![]() $\Gamma \backslash \mathbb {H}$
.
$\Gamma \backslash \mathbb {H}$
.
The formulation of our results requires some quantification of the closeness of a point
![]() $z \in \Gamma \backslash \mathbb {H}$
to the cusps. If
$z \in \Gamma \backslash \mathbb {H}$
to the cusps. If
![]() $\Gamma \backslash \mathbb {H}$
is noncompact (i.e.,
$\Gamma \backslash \mathbb {H}$
is noncompact (i.e.,
![]() $d_B = 1$
), then we may assume that
$d_B = 1$
), then we may assume that
![]() $\Gamma = \Gamma _0(N)$
, and we set
$\Gamma = \Gamma _0(N)$
, and we set
where
![]() $A_0(N)$
denotes the lattice of Atkin–Lehner operators for
$A_0(N)$
denotes the lattice of Atkin–Lehner operators for
![]() $\Gamma _0(N)$
(see Section §2.2 for another formulation of the definition of H). If
$\Gamma _0(N)$
(see Section §2.2 for another formulation of the definition of H). If
![]() $\Gamma \backslash \mathbb {H}$
is compact, then we set
$\Gamma \backslash \mathbb {H}$
is compact, then we set
![]() $H(z) = 0$
.
$H(z) = 0$
.
Theorem 1.10. Let
![]() $\Gamma = \Gamma ^B_0(N)$
be as in Theorem 1.2. Fix
$\Gamma = \Gamma ^B_0(N)$
be as in Theorem 1.2. Fix
![]() $\Lambda> 0$
, and let
$\Lambda> 0$
, and let
![]() $(\varphi _i)_i$
be an orthonormal set of cuspidal Hecke–Maaß newforms with trivial (central) character and Laplace-eigenvalue bounded by
$(\varphi _i)_i$
be an orthonormal set of cuspidal Hecke–Maaß newforms with trivial (central) character and Laplace-eigenvalue bounded by
![]() $\Lambda $
on the hyperbolic surface
$\Lambda $
on the hyperbolic surface
![]() $\Gamma \backslash \mathbb {H}$
equipped with the hyperbolic probability measure. Then, for any two points
$\Gamma \backslash \mathbb {H}$
equipped with the hyperbolic probability measure. Then, for any two points
![]() $z,w \in \Gamma \backslash \mathbb {H}$
, we have
$z,w \in \Gamma \backslash \mathbb {H}$
, we have
 $$ \begin{align} \sum_i \left( |\varphi_i(z)|^2-|\varphi_i(w)|^2 \right)^2 \ll_{\epsilon, \Lambda} V^{1+\epsilon} \left(1+ V[H(z)^2+H(w)^2] \right). \end{align} $$
$$ \begin{align} \sum_i \left( |\varphi_i(z)|^2-|\varphi_i(w)|^2 \right)^2 \ll_{\epsilon, \Lambda} V^{1+\epsilon} \left(1+ V[H(z)^2+H(w)^2] \right). \end{align} $$
Similarly, for an orthonormal set
![]() $(f_i)_i$
of cuspidal holomorphic newforms for
$(f_i)_i$
of cuspidal holomorphic newforms for
![]() $\Gamma $
of weight k and trivial (central) character with respect to the hyperbolic probability measure on
$\Gamma $
of weight k and trivial (central) character with respect to the hyperbolic probability measure on
![]() $\Gamma \backslash \mathbb {H}$
, we have
$\Gamma \backslash \mathbb {H}$
, we have
 $$ \begin{align*} & \sum_i \left( |\Im(z)^{\frac{k}{2}}f_i(z)|^2-|\Im(w)^{\frac{k}{2}}f_i(w)|^2 \right)^2 \\ & \qquad\qquad\qquad\qquad\qquad\quad\qquad\ll_{\epsilon} (Vk)^{1+\epsilon} \left(1+V^{\frac{1}{2}}[H(z)+H(w)]+Vk^{-\frac{1}{2}}[H(z)^2+H(w)^2] \right) \end{align*} $$
$$ \begin{align*} & \sum_i \left( |\Im(z)^{\frac{k}{2}}f_i(z)|^2-|\Im(w)^{\frac{k}{2}}f_i(w)|^2 \right)^2 \\ & \qquad\qquad\qquad\qquad\qquad\quad\qquad\ll_{\epsilon} (Vk)^{1+\epsilon} \left(1+V^{\frac{1}{2}}[H(z)+H(w)]+Vk^{-\frac{1}{2}}[H(z)^2+H(w)^2] \right) \end{align*} $$
for any two points
![]() $z,w \in \Gamma \backslash \mathbb {H}$
.
$z,w \in \Gamma \backslash \mathbb {H}$
.
In the case that the hyperbolic surface
![]() $\Gamma \backslash \mathbb {H}$
is compact, we may integrate z and w over the whole surface and get an essentially sharp bound on the fourth moment of fourth norms in the level aspect, thereby extending a result of Blomer [Reference BlomerBlo13] to the case of cocompact lattices
$\Gamma \backslash \mathbb {H}$
is compact, we may integrate z and w over the whole surface and get an essentially sharp bound on the fourth moment of fourth norms in the level aspect, thereby extending a result of Blomer [Reference BlomerBlo13] to the case of cocompact lattices
![]() $\Gamma $
.
$\Gamma $
.
Corollary 1.11. With notation and assumptions as in Theorem 1.10 and assuming further that
![]() $\Gamma \backslash \mathbb {H}$
is compact, we have
$\Gamma \backslash \mathbb {H}$
is compact, we have
This result may also be recast as a double average of triple L-functions by means of Watson’s formula [Reference WatsonWat08, Theorem 3].
The final application of Theorem 1.10 we mention is to the diameter of compact arithmetic hyperbolic surfaces
![]() $\Gamma \backslash \mathbb {H}$
[Reference SteinerSte23]. Here, one may use the sharp bound on the ‘fourth moment’ of exceptional eigenforms, together with a strong density estimate for the exceptional eigenvalues, to get an optimal estimate on the almost diameter and an estimate on the diameter of the same strength as if one were to assume the Selberg eigenvalue conjecture.
$\Gamma \backslash \mathbb {H}$
[Reference SteinerSte23]. Here, one may use the sharp bound on the ‘fourth moment’ of exceptional eigenforms, together with a strong density estimate for the exceptional eigenvalues, to get an optimal estimate on the almost diameter and an estimate on the diameter of the same strength as if one were to assume the Selberg eigenvalue conjecture.
1.3. The added complexity of the level aspect
Compared to the weight aspect treated in the prequel, the level aspect requires many new ideas. Here, we tacitly restrict to the case of squarefree level; the general case would require a more nuanced discussion. In some sense, the level aspect may be understood as intermediate in difficulty between the holomorphic and eigenvalue aspects. Indeed, relative to known techniques, the difficulty in the sup-norm problem is reflected in the essential support of the matrix coefficient of the automorphic form being bounded. In the weight, (squarefree) level and eigenvalue aspects, the matrix coefficient concentrates on a space of dimension one, two and three, respectively.
We now briefly recall the main idea of the theta approach and discuss some of the new challenges that arise in the level aspect. We focus first on the case of Hecke–Maaß forms on
![]() $\Gamma _0(N) \backslash \mathbb {H}$
, as in Theorem 1.1. Take
$\Gamma _0(N) \backslash \mathbb {H}$
, as in Theorem 1.1. Take
![]() $R=\left (\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ N \mathbb {Z} & \mathbb {Z} \end {smallmatrix}\right )$
so that that the set of proper units of R is precisely
$R=\left (\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} \\ N \mathbb {Z} & \mathbb {Z} \end {smallmatrix}\right )$
so that that the set of proper units of R is precisely
![]() $\Gamma _0(N)$
. For
$\Gamma _0(N)$
. For
![]() $\ell \mid N$
, let
$\ell \mid N$
, let
![]() $R(\ell )= \left (\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} / \ell \\ N \mathbb {Z} / \ell & \mathbb {Z} \end {smallmatrix}\right )$
denote the partially dualized lattices of the order R. Let
$R(\ell )= \left (\begin {smallmatrix} \mathbb {Z} & \mathbb {Z} / \ell \\ N \mathbb {Z} / \ell & \mathbb {Z} \end {smallmatrix}\right )$
denote the partially dualized lattices of the order R. Let
![]() $\sigma _z \in \operatorname {\mathrm {SL}}_2(\mathbb {R})$
be any matrix taking i to
$\sigma _z \in \operatorname {\mathrm {SL}}_2(\mathbb {R})$
be any matrix taking i to
![]() $z \in \mathbb {H}$
. Let
$z \in \mathbb {H}$
. Let
![]() $\varphi $
be an arithmetically normalized cuspidal Hecke–Maaß newform. The theta identity at the heart of the argument then reads
$\varphi $
be an arithmetically normalized cuspidal Hecke–Maaß newform. The theta identity at the heart of the argument then reads
where V denotes the covolume of
![]() $\Gamma _0(N)$
and the theta function is given by
$\Gamma _0(N)$
and the theta function is given by
 $$ \begin{align} \theta(z,w;s) = \Im(s) \sum_{\left(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\right) \in \sigma_z^{-1} R \sigma_w} e^{- \pi (a^2+b^2+c^2+d^2) \Im(s)} e^{2 \pi i (ad-bc) \Re(s)}. \end{align} $$
$$ \begin{align} \theta(z,w;s) = \Im(s) \sum_{\left(\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}\right) \in \sigma_z^{-1} R \sigma_w} e^{- \pi (a^2+b^2+c^2+d^2) \Im(s)} e^{2 \pi i (ad-bc) \Re(s)}. \end{align} $$
By Bessel’s inequality, the left-hand side of Equation (1.7) is in essence captured by the
![]() $L^2$
-norm of the difference of the theta kernels
$L^2$
-norm of the difference of the theta kernels
![]() $\theta (z,z;\cdot )-\theta (w,w;\cdot )$
. From here, one may then proceed as in the prequel by covering a fundamental domain by Siegel sets and making use of the orthogonality relations in the unipotent direction. One ends up with a weighted sum over matrices
$\theta (z,z;\cdot )-\theta (w,w;\cdot )$
. From here, one may then proceed as in the prequel by covering a fundamental domain by Siegel sets and making use of the orthogonality relations in the unipotent direction. One ends up with a weighted sum over matrices
![]() $\gamma _1, \gamma _2 \in R(\ell )$
satisfying
$\gamma _1, \gamma _2 \in R(\ell )$
satisfying
![]() $\det (\gamma _1)=\det (\gamma _2)$
and for which the entries of
$\det (\gamma _1)=\det (\gamma _2)$
and for which the entries of
![]() $\sigma _z^{-1} \gamma _{i} \sigma _z$
,
$\sigma _z^{-1} \gamma _{i} \sigma _z$
,
![]() $i=1,2$
, satisfy certain bounds (and similarly for w). The bounds imposed on these entries depend crucially upon the precise choice of Siegel domains, so it is important that we make a good choice. Like in the prequel, we split the count according to whether
$i=1,2$
, satisfy certain bounds (and similarly for w). The bounds imposed on these entries depend crucially upon the precise choice of Siegel domains, so it is important that we make a good choice. Like in the prequel, we split the count according to whether
![]() $\operatorname {\mathrm {tr}}(\gamma _1) = \operatorname {\mathrm {tr}}(\gamma _2)$
or not.
$\operatorname {\mathrm {tr}}(\gamma _1) = \operatorname {\mathrm {tr}}(\gamma _2)$
or not.
In the case of nonequal trace, the naïve choice of Siegel domains consisting of
![]() $\Gamma _0(N) \backslash \operatorname {\mathrm {SL}}_2(\mathbb {Z})$
-translates of the standard Siegel domain for
$\Gamma _0(N) \backslash \operatorname {\mathrm {SL}}_2(\mathbb {Z})$
-translates of the standard Siegel domain for
![]() $\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
leads to a rather challenging counting problem. In order to get a sharp bound on Equation (1.7), one faces the challenge of counting, for each divisor
$\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
leads to a rather challenging counting problem. In order to get a sharp bound on Equation (1.7), one faces the challenge of counting, for each divisor
![]() $\ell $
of N and each T with
$\ell $
of N and each T with
![]() $\ell ^{-1/2} \ll T \ll 1$
, the sextuples of integers
$\ell ^{-1/2} \ll T \ll 1$
, the sextuples of integers
![]() $(a_1,b_1,c_1,a_2,b_2,c_2)$
satisfying
$(a_1,b_1,c_1,a_2,b_2,c_2)$
satisfying
We would need to know that the number of such sextuples is roughly
![]() $O(\ell T^2)$
in the range
$O(\ell T^2)$
in the range
![]() ${N^{-1} \ll y \ll N^{-1/2}}$
and
${N^{-1} \ll y \ll N^{-1/2}}$
and
![]() $|x| \le \frac {1}{2}$
. We do not know how to establish such a bound directly when, for instance,
$|x| \le \frac {1}{2}$
. We do not know how to establish such a bound directly when, for instance,
![]() $\ell = N$
. On the other hand, when
$\ell = N$
. On the other hand, when
![]() $\ell = 1$
, the congruence condition is void and, using arguments of Harcos–Templier, we can prove the required bound with some room to spare, namely, for T up to
$\ell = 1$
, the congruence condition is void and, using arguments of Harcos–Templier, we can prove the required bound with some room to spare, namely, for T up to
![]() $N^{1/2}$
. Our solution to this dichotomy is thus to decrease the size of the Siegel domains associated to larger
$N^{1/2}$
. Our solution to this dichotomy is thus to decrease the size of the Siegel domains associated to larger
![]() $\ell $
at the expense of increasing those associated to smaller
$\ell $
at the expense of increasing those associated to smaller
![]() $\ell $
. This solution may be implemented most simply by applying an Atkin–Lehner involution to the covering of
$\ell $
. This solution may be implemented most simply by applying an Atkin–Lehner involution to the covering of
![]() $\Gamma _0(N) \backslash \mathbb {H}$
by
$\Gamma _0(N) \backslash \mathbb {H}$
by
![]() $\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
-translates of the standard fundamental domain for
$\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
-translates of the standard fundamental domain for
![]() $\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
. With this maneuver, we reduce to considering the range
$\operatorname {\mathrm {SL}}_2(\mathbb {Z})$
. With this maneuver, we reduce to considering the range
![]() $T \ll N^{\frac {1}{2}} \ell ^{-1}$
. We are then able to prove the required bound by forgoing the congruence condition, reducing the problem to counting triples of integers
$T \ll N^{\frac {1}{2}} \ell ^{-1}$
. We are then able to prove the required bound by forgoing the congruence condition, reducing the problem to counting triples of integers
![]() $(a_i,b_i,c_i)$
satisfying Equation (1.10), which we carry out using geometry of numbers techniques. We refer subsequently to this type of counting problem, where we count traceless matrices
$(a_i,b_i,c_i)$
satisfying Equation (1.10), which we carry out using geometry of numbers techniques. We refer subsequently to this type of counting problem, where we count traceless matrices
![]() $\gamma \in R(\ell )^0$
with a bound on the entries of
$\gamma \in R(\ell )^0$
with a bound on the entries of
![]() $\sigma _{z}^{-1}\gamma \sigma _z$
, as ‘Type I’.
$\sigma _{z}^{-1}\gamma \sigma _z$
, as ‘Type I’.
In the case of equal trace, we need to count sextuples of integers
![]() $(a_1,b_1,c_1,a_2,b_2,c_2)$
satisfying Equation (1.10) and
$(a_1,b_1,c_1,a_2,b_2,c_2)$
satisfying Equation (1.10) and
We need to bound this count by
![]() $O(\ell T)$
in the same ranges as before. We refer to this type of counting problem as ‘Type II’. The key observation is that
$O(\ell T)$
in the same ranges as before. We refer to this type of counting problem as ‘Type II’. The key observation is that
![]() $(a_1,b_1,c_1)$
turns out to determine
$(a_1,b_1,c_1)$
turns out to determine
![]() $(a_2,b_2,c_2)$
up to a small number of possibilities. This allows us to reduce Type II estimates to Type I estimates.
$(a_2,b_2,c_2)$
up to a small number of possibilities. This allows us to reduce Type II estimates to Type I estimates.
The above arguments suffice for noncompact quotients, that is, for the proof of Theorem 1.1. They rely on the use of matrix coordinates
![]() $\left (\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}\right )$
with respect to which the lattices
$\left (\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}\right )$
with respect to which the lattices
![]() $\Gamma _0(N)$
are described by the simple congruence condition
$\Gamma _0(N)$
are described by the simple congruence condition
![]() $c \equiv 0\ \ \pod {N}$
. We were unable to find an analogously straightforward way to separate the variables in the compact setting (e.g., using fixed quadratic subalgebras of B). In the case that B is definite, the Type I counts were treated in a coordinate-free way by Blomer–Michel [Reference Blomer and MichelBM11, Reference Blomer and MichelBM13], who controlled the successive minima of the ternary quadratic lattice underlying
$c \equiv 0\ \ \pod {N}$
. We were unable to find an analogously straightforward way to separate the variables in the compact setting (e.g., using fixed quadratic subalgebras of B). In the case that B is definite, the Type I counts were treated in a coordinate-free way by Blomer–Michel [Reference Blomer and MichelBM11, Reference Blomer and MichelBM13], who controlled the successive minima of the ternary quadratic lattice underlying
![]() $\Gamma _0^B(N)$
in terms of only the content, level and discriminant of that lattice. We extend their arguments to the case that B is indefinite by defining analogous Archimedean quantities that control the disparity of the reduced norm and a majorant, such as the square of the Frobenius norm of
$\Gamma _0^B(N)$
in terms of only the content, level and discriminant of that lattice. We extend their arguments to the case that B is indefinite by defining analogous Archimedean quantities that control the disparity of the reduced norm and a majorant, such as the square of the Frobenius norm of
![]() $\sigma _z^{-1} \gamma \sigma _z$
for
$\sigma _z^{-1} \gamma \sigma _z$
for
![]() $\gamma \in R(\ell )^0$
.
$\gamma \in R(\ell )^0$
.
Following the same strategy as in the noncompact case, it remains then only to reduce Type II estimates to Type I estimates. This reduction is perhaps the most subtle part of our counting arguments. It requires us to establish the analogue in the compact setting of the key observation noted following Equation (1.12). For example, in case that B is definite, writing R for an Eichler order of level N, we need to show that for each
![]() $n \ll V$
, the number of elements
$n \ll V$
, the number of elements
![]() $\gamma \in R$
with trace
$\gamma \in R$
with trace
![]() $0$
and norm n is essentially
$0$
and norm n is essentially
![]() $O(1)$
, uniformly in N and B. We eventually managed to do so through a delicate argument involving commutators and representations of binary quadratic forms.
$O(1)$
, uniformly in N and B. We eventually managed to do so through a delicate argument involving commutators and representations of binary quadratic forms.
1.4. Organization of the paper
The complete statements of our results may be found in Section §2. In Section §3, we reduce the proofs to those of two auxiliary collections of results:
-
∘ those concerning matrix counting, and
-
∘ those reducing the required estimates for theta functions to matrix counting.
The latter, including the appropriate splicing of a fundamental domain into Siegel sets, may be found in Section §4. In Section §5, we summarize the required properties of the theta functions. The proofs of said properties are deferred to Appendix A.
Sections §7 and §8 are dedicated to the anisotropic extension of the lattice counting argument of Blomer–Michel, which we subsequently apply to the Type I counting problem in Section §9.
The final section, §10, treats the crucial Type II counting problem.
2. Statement of results
2.1. Setup
Let B be a quaternion algebra over
![]() $\mathbb {Q}$
. We denote by
$\mathbb {Q}$
. We denote by
![]() $d_B$
its reduced discriminant, or equivalently, the product of the primes at which B ramifies. We write G for the linear algebraic group over
$d_B$
its reduced discriminant, or equivalently, the product of the primes at which B ramifies. We write G for the linear algebraic group over
![]() $\mathbb {Q}$
given by
$\mathbb {Q}$
given by ![]() for any
for any
![]() $\mathbb {Q}$
-algebra L. Then G is an inner form of
$\mathbb {Q}$
-algebra L. Then G is an inner form of
![]() $\operatorname {PGL}_2$
, and all rational forms of
$\operatorname {PGL}_2$
, and all rational forms of
![]() $\operatorname {PGL}_2$
arise in this way. Denote by
$\operatorname {PGL}_2$
arise in this way. Denote by
![]() $[G]$
the adelic quotient
$[G]$
the adelic quotient
![]() $G(\mathbb {Q}) \backslash G(\mathbb {A})$
. We fix the probability Haar measure on
$G(\mathbb {Q}) \backslash G(\mathbb {A})$
. We fix the probability Haar measure on
![]() $[G]$
. Let
$[G]$
. Let
![]() $K_\infty $
be a compact maximal torus of
$K_\infty $
be a compact maximal torus of
![]() $G(\mathbb {R})$
. We assume that
$G(\mathbb {R})$
. We assume that
![]() $K_\infty $
comes equipped with a choice of isomorphism
$K_\infty $
comes equipped with a choice of isomorphism
![]() $\kappa : \mathbb {R} / \pi \mathbb {Z} \xrightarrow {\sim } K_\infty $
. In the split case
$\kappa : \mathbb {R} / \pi \mathbb {Z} \xrightarrow {\sim } K_\infty $
. In the split case
![]() $B=\operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {Q})$
, we identify
$B=\operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {Q})$
, we identify
![]() $G=\operatorname {PGL}_2$
and set
$G=\operatorname {PGL}_2$
and set
![]() $\kappa (\theta )=\left (\begin {smallmatrix} \cos (\theta ) & \sin (\theta ) \\ -\sin (\theta ) & \cos (\theta ) \end {smallmatrix}\right )$
.
$\kappa (\theta )=\left (\begin {smallmatrix} \cos (\theta ) & \sin (\theta ) \\ -\sin (\theta ) & \cos (\theta ) \end {smallmatrix}\right )$
.
Let R be an Eichler order in B, that is, an intersection of two maximal orders. We denote by N the level of R. It is a natural number, coprime to
![]() $d_B$
, characterized as follows: For each prime
$d_B$
, characterized as follows: For each prime
![]() $p \nmid d_B$
, there is an isomorphism
$p \nmid d_B$
, there is an isomorphism ![]() under which
under which ![]() maps to the order
maps to the order
![]() $\left ( \begin {smallmatrix} \mathbb {Z}_p &\mathbb {Z}_p \\ N \mathbb {Z}_p& \mathbb {Z}_p \end {smallmatrix} \right )$
. We may then identify
$\left ( \begin {smallmatrix} \mathbb {Z}_p &\mathbb {Z}_p \\ N \mathbb {Z}_p& \mathbb {Z}_p \end {smallmatrix} \right )$
. We may then identify
![]() $G(\mathbb {Q}_p)$
with
$G(\mathbb {Q}_p)$
with
![]() $\operatorname {PGL}_2(\mathbb {Q}_p)$
and the image of
$\operatorname {PGL}_2(\mathbb {Q}_p)$
and the image of
![]() $R_p^\times $
with a finite index subgroup of
$R_p^\times $
with a finite index subgroup of
![]() $\operatorname {PGL}_2(\mathbb {Z}_p)$
. We assume that N is squarefree so that
$\operatorname {PGL}_2(\mathbb {Z}_p)$
. We assume that N is squarefree so that
![]() $d_B N$
is likewise squarefree. We denote by
$d_B N$
is likewise squarefree. We denote by
![]() $K_R$
the compact open subgroup of
$K_R$
the compact open subgroup of
![]() $G(\mathbb {A}_f)=\prod _p ' G(\mathbb {Q}_p)$
given by the image of
$G(\mathbb {A}_f)=\prod _p ' G(\mathbb {Q}_p)$
given by the image of
![]() $\prod _p R_p^\times $
.
$\prod _p R_p^\times $
.
Fix
![]() $k \in 2\mathbb {Z}$
. Let
$k \in 2\mathbb {Z}$
. Let
![]() $\mathcal {A}$
denote the set of cusp forms
$\mathcal {A}$
denote the set of cusp forms
![]() $\varphi : [G] \rightarrow \mathbb {C}$
having the following properties:
$\varphi : [G] \rightarrow \mathbb {C}$
having the following properties:
-
∘
 $\varphi (g \kappa (\theta )) = e^{i k \theta } \varphi (g)$
for all
$\varphi (g \kappa (\theta )) = e^{i k \theta } \varphi (g)$
for all
 $\theta $
.
$\theta $
. -
∘
 $\varphi $
is an eigenfunction for some fixed Casimir operator for
$\varphi $
is an eigenfunction for some fixed Casimir operator for
 $G(\mathbb {R})$
, with eigenvalue
$G(\mathbb {R})$
, with eigenvalue
 $\lambda _{\varphi }$
. For the sake of concreteness, we scale the Casimir operator such that it agrees with the standard Laplace operator on the locally symmetric space
$\lambda _{\varphi }$
. For the sake of concreteness, we scale the Casimir operator such that it agrees with the standard Laplace operator on the locally symmetric space
 $G(\mathbb {R}) / K_{\infty }$
, which identifies with either
$G(\mathbb {R}) / K_{\infty }$
, which identifies with either
 $\mathbb {H}$
or
$\mathbb {H}$
or
 $S^2$
.
$S^2$
. -
∘
 $\varphi $
is
$\varphi $
is
 $K_R$
-invariant:
$K_R$
-invariant:
 $\varphi (g k) = \varphi (g)$
for
$\varphi (g k) = \varphi (g)$
for
 $k \in K_R$
.
$k \in K_R$
. -
∘
 $\varphi $
belongs to the newspace for R, that is,
$\varphi $
belongs to the newspace for R, that is,
 $K_R$
is the largest subgroup of
$K_R$
is the largest subgroup of
 $G(\mathbb {A}_f)$
keeping
$G(\mathbb {A}_f)$
keeping
 $\varphi $
invariant. Equivalently,
$\varphi $
invariant. Equivalently,
 $\varphi $
is orthogonal the space of
$\varphi $
is orthogonal the space of
 $K_{R'}$
-invariant cusp forms for every Eichler order
$K_{R'}$
-invariant cusp forms for every Eichler order
 $R'$
strictly containing R.
$R'$
strictly containing R. -
∘
 $\varphi $
is an eigenform for almost all Hecke operators.
$\varphi $
is an eigenform for almost all Hecke operators.
If
![]() $k \ge 2$
, then we write
$k \ge 2$
, then we write
![]() $\mathcal {A}^{\operatorname {hol}} \subseteq \mathcal {A}$
for the subspace of automorphic lifts of holomorphic forms or, equivalently, the kernel of the raising (resp. lowering) operator attached to
$\mathcal {A}^{\operatorname {hol}} \subseteq \mathcal {A}$
for the subspace of automorphic lifts of holomorphic forms or, equivalently, the kernel of the raising (resp. lowering) operator attached to
![]() $K_\infty $
if B is definite (resp. indefinite).
$K_\infty $
if B is definite (resp. indefinite).
Denote by
![]() $\mathcal {F}$
a maximal orthonormal subset of
$\mathcal {F}$
a maximal orthonormal subset of
![]() $\mathcal {A}$
. Analogously, we define
$\mathcal {A}$
. Analogously, we define
![]() $\mathcal {F}^{\operatorname {hol}} \subseteq \mathcal {A}^{\operatorname {hol}}$
if
$\mathcal {F}^{\operatorname {hol}} \subseteq \mathcal {A}^{\operatorname {hol}}$
if
![]() $k \ge 2$
. Because of the multiplicity-one theorem for
$k \ge 2$
. Because of the multiplicity-one theorem for
![]() $\operatorname {GL}_2$
and its inner forms, the bases
$\operatorname {GL}_2$
and its inner forms, the bases
![]() $\mathcal {F}, \mathcal {F}^{\operatorname {hol}}$
are unique up to rescaling each element by a scalar of unit magnitude. We note that the sets
$\mathcal {F}, \mathcal {F}^{\operatorname {hol}}$
are unique up to rescaling each element by a scalar of unit magnitude. We note that the sets
![]() $\mathcal {A}$
,
$\mathcal {A}$
,
![]() $\mathcal {A}^{\operatorname {hol}}$
,
$\mathcal {A}^{\operatorname {hol}}$
,
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {F}^{\operatorname {hol}}$
depend on k; while we suppress this dependence from the notation, k is one of the main parameters of interest.
$\mathcal {F}^{\operatorname {hol}}$
depend on k; while we suppress this dependence from the notation, k is one of the main parameters of interest.
We will consider several subfamilies of
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $\mathcal {F}^{\operatorname {hol}}$
. Here, a minus sign in the exponent signifies the indefinite case, a plus sign the definite case.
$\mathcal {F}^{\operatorname {hol}}$
. Here, a minus sign in the exponent signifies the indefinite case, a plus sign the definite case.
-
∘ If B is indefinite and
 $k=0$
, then we take
$k=0$
, then we take  and let
and let
 $\mathcal {F}^{-}_{\lambda }$
(resp.
$\mathcal {F}^{-}_{\lambda }$
(resp.
 $\mathcal {F}^{-}_{\le L}$
) denote the subsets defined by taking the Casimir eigenvalue equal to
$\mathcal {F}^{-}_{\le L}$
) denote the subsets defined by taking the Casimir eigenvalue equal to
 $- \lambda $
(respectively at most L in magnitude).
$- \lambda $
(respectively at most L in magnitude). -
∘ If B is indefinite and
 $k \ge 2$
, then we take
$k \ge 2$
, then we take  .
. -
∘ If B is definite and
 $k=0$
, then we let
$k=0$
, then we let
 $\mathcal {F}^{+}_m \subset \mathcal {F}$
be the subset of forms, whose associated automorphic representation at infinity is isomorphic to the unique irreducible unitary representation of
$\mathcal {F}^{+}_m \subset \mathcal {F}$
be the subset of forms, whose associated automorphic representation at infinity is isomorphic to the unique irreducible unitary representation of
 $\operatorname {\mathrm {SU}}_2(\mathbb {C})$
of degree
$\operatorname {\mathrm {SU}}_2(\mathbb {C})$
of degree
 $m+1$
. In other words, their eigenvalue with respect to the Casimir operator equals to
$m+1$
. In other words, their eigenvalue with respect to the Casimir operator equals to
 $-m(m+1)$
.
$-m(m+1)$
. -
∘ If B is definite and
 $k \ge 2$
, then we let
$k \ge 2$
, then we let
 $\mathcal {F}^{+, \operatorname {hol}}=\mathcal {F}^{\operatorname {hol}}$
.
$\mathcal {F}^{+, \operatorname {hol}}=\mathcal {F}^{\operatorname {hol}}$
.
2.2. The split case
Assume for the moment that B is split. We may suppose then that
 $$ \begin{align} B = \operatorname{\mathrm{Mat}}_{2 \times 2}(\mathbb{Q}), \quad G = \operatorname{PGL}_2, \quad R = \begin{pmatrix} \mathbb{Z} & \mathbb{Z} \\ N \mathbb{Z} & \mathbb{Z} \end{pmatrix}, \end{align} $$
$$ \begin{align} B = \operatorname{\mathrm{Mat}}_{2 \times 2}(\mathbb{Q}), \quad G = \operatorname{PGL}_2, \quad R = \begin{pmatrix} \mathbb{Z} & \mathbb{Z} \\ N \mathbb{Z} & \mathbb{Z} \end{pmatrix}, \end{align} $$
 $$ \begin{align} K_\infty = \operatorname{PSO}_2(\mathbb{R}), \quad \kappa(\theta) = \begin{pmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{pmatrix} \end{align} $$
$$ \begin{align} K_\infty = \operatorname{PSO}_2(\mathbb{R}), \quad \kappa(\theta) = \begin{pmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{pmatrix} \end{align} $$
and may identify
We define
as follows. Let
![]() $A_0(N)<\operatorname {GL}_2(\mathbb {Q})^+$
denote the group generated by
$A_0(N)<\operatorname {GL}_2(\mathbb {Q})^+$
denote the group generated by
![]() $\Gamma _0(N)$
and all Atkin–Lehner operators. If
$\Gamma _0(N)$
and all Atkin–Lehner operators. If
![]() $g \in [G] / K_\infty K_R$
identifies with
$g \in [G] / K_\infty K_R$
identifies with
![]() $z \in \Gamma _0(N) \backslash \mathbb {H}$
, then we set
$z \in \Gamma _0(N) \backslash \mathbb {H}$
, then we set
Since the Atkin–Lehner operators constitute scaling matrices for the various cusps of
![]() $\Gamma _0(N)$
(cf. §4.3.1), the function H may be understood as a normalized height or as quantifying closeness to the cusps. Let
$\Gamma _0(N)$
(cf. §4.3.1), the function H may be understood as a normalized height or as quantifying closeness to the cusps. Let
![]() $\mathfrak {a} \in P^{1}(\mathbb {Z})$
be a cusp of
$\mathfrak {a} \in P^{1}(\mathbb {Z})$
be a cusp of
![]() $\Gamma _0(N)$
, and let
$\Gamma _0(N)$
, and let
![]() $\sigma _{\mathfrak {a}}\in \operatorname {\mathrm {SL}}_2(\mathbb {Z})$
such that
$\sigma _{\mathfrak {a}}\in \operatorname {\mathrm {SL}}_2(\mathbb {Z})$
such that
![]() $\sigma _{\mathfrak {a}} \infty = \mathfrak {a}$
. Then,
$\sigma _{\mathfrak {a}} \infty = \mathfrak {a}$
. Then,
where
![]() $\mathfrak {a}$
runs over all cusps of
$\mathfrak {a}$
runs over all cusps of
![]() $\Gamma _0(N)$
,
$\Gamma _0(N)$
,
![]() $z_{\mathfrak {a}}= \sigma _{\mathfrak {a}}^{-1} z$
and
$z_{\mathfrak {a}}= \sigma _{\mathfrak {a}}^{-1} z$
and
![]() $w_{\mathfrak {a}}$
is the cusp width of
$w_{\mathfrak {a}}$
is the cusp width of
![]() $\mathfrak {a}$
.
$\mathfrak {a}$
.
2.3. Results on forms
We adopt the following asymptotic notation
![]() $\preccurlyeq $
:
$\preccurlyeq $
:
where
![]() $\mu $
is a quantity relating to the eigenvalues with respect to the Casimir operator of the automorphic forms of relevance to the inequality. Concretely, when talking about the families
$\mu $
is a quantity relating to the eigenvalues with respect to the Casimir operator of the automorphic forms of relevance to the inequality. Concretely, when talking about the families
![]() $\mathcal {F}^{-}_{\lambda },\mathcal {F}^{-}_{\le L}, \mathcal {F}^{+}_m, \mathcal {F}^{\pm ,\operatorname {hol}}$
we mean
$\mathcal {F}^{-}_{\lambda },\mathcal {F}^{-}_{\le L}, \mathcal {F}^{+}_m, \mathcal {F}^{\pm ,\operatorname {hol}}$
we mean
![]() $\mu =|\lambda |,L,m, k$
, respectively.
$\mu =|\lambda |,L,m, k$
, respectively.
Theorem 2.1. Let
![]() $g_1,g_2 \in [G]$
. If B is indefinite, then
$g_1,g_2 \in [G]$
. If B is indefinite, then
 $$ \begin{align} \sum _{\varphi \in \mathcal{F}^{-}_{\le L} } (|\varphi(g_1)|^2-|\varphi(g_2)|^2)^2 \preccurlyeq_{L} d_B N \left( 1+ d_BN \left[H(g_1)^2+H(g_2)^2 \right] \right), \end{align} $$
$$ \begin{align} \sum _{\varphi \in \mathcal{F}^{-}_{\le L} } (|\varphi(g_1)|^2-|\varphi(g_2)|^2)^2 \preccurlyeq_{L} d_B N \left( 1+ d_BN \left[H(g_1)^2+H(g_2)^2 \right] \right), \end{align} $$
for
![]() $L> 0$
, and
$L> 0$
, and
 $$ \begin{align} \nonumber & \sum _{\varphi \in \mathcal{F}^{-,\operatorname{hol}} } (|\varphi(g_1)|^2-|\varphi(g_2)|^2)^2 \\ &\qquad\qquad\quad\qquad \preccurlyeq d_B N k \left( 1+(d_BN)^{\frac{1}{2}} \left[H(g_1)+H(g_2)\right]+ d_B N k^{-\frac{1}{2}} \left[H(g_1)^2+H(g_2)^2 \right] \right), \end{align} $$
$$ \begin{align} \nonumber & \sum _{\varphi \in \mathcal{F}^{-,\operatorname{hol}} } (|\varphi(g_1)|^2-|\varphi(g_2)|^2)^2 \\ &\qquad\qquad\quad\qquad \preccurlyeq d_B N k \left( 1+(d_BN)^{\frac{1}{2}} \left[H(g_1)+H(g_2)\right]+ d_B N k^{-\frac{1}{2}} \left[H(g_1)^2+H(g_2)^2 \right] \right), \end{align} $$
for
![]() $k \ge 2$
even. In both cases, the term involving
$k \ge 2$
even. In both cases, the term involving
![]() $H(g_{1,2})$
is only present if B is split.
$H(g_{1,2})$
is only present if B is split.
If B is definite, then
 $$ \begin{align} \sum _{\varphi \in \mathcal{F}^{+}_{m} } (|\varphi(g_1)|^2-|\varphi(g_2)|^2)^2 \preccurlyeq d_B N(m+1)^2, \end{align} $$
$$ \begin{align} \sum _{\varphi \in \mathcal{F}^{+}_{m} } (|\varphi(g_1)|^2-|\varphi(g_2)|^2)^2 \preccurlyeq d_B N(m+1)^2, \end{align} $$
for
![]() $m \in \mathbb {N}_0$
, and
$m \in \mathbb {N}_0$
, and
 $$ \begin{align} \sum _{\varphi \in \mathcal{F}^{+,\operatorname{hol}} } |\varphi(g_1)|^4 \preccurlyeq d_B N k, \end{align} $$
$$ \begin{align} \sum _{\varphi \in \mathcal{F}^{+,\operatorname{hol}} } |\varphi(g_1)|^4 \preccurlyeq d_B N k, \end{align} $$
for
![]() $k \in 2 \mathbb {N}$
.
$k \in 2 \mathbb {N}$
.
Remark 2.2. In the indefinite holomorphic case (2.5), one may have the same bound for the fourth moment rather than the squared difference under the assumption that the weight satisfies
![]() $k \gg _{\eta } (d_BN)^{\eta }$
for some
$k \gg _{\eta } (d_BN)^{\eta }$
for some
![]() $\eta>0$
, in which case the implied constant also depends on
$\eta>0$
, in which case the implied constant also depends on
![]() $\eta $
and the implied constant in the assumed lower bound for the weight.
$\eta $
and the implied constant in the assumed lower bound for the weight.
Corollary 2.3. For
![]() $k \ge 2$
and
$k \ge 2$
and
![]() $\varphi \in \mathcal {F}^{\operatorname {hol}}$
, we have
$\varphi \in \mathcal {F}^{\operatorname {hol}}$
, we have
For
![]() $k=0$
and
$k=0$
and
![]() $\varphi \in \mathcal {F}$
, we have
$\varphi \in \mathcal {F}$
, we have
If B is definite, then we have more precisely
By a well-known procedure, these statements may be translated into the classical language, thus giving rise to the theorems in the introduction. For further details; see, for example, [Reference BumpBum97, §3.2 & §3.6] for the indefinite case and [Reference Blomer and MichelBM13] for the definite case.
2.4. Counting problems: setup
2.4.1. Lattices locally dual to R
Let
![]() $\ell $
be a divisor of the squarefree number
$\ell $
be a divisor of the squarefree number
![]() $d_B N$
. We denote by
$d_B N$
. We denote by
![]() $R(\ell )$
the lattice in B whose local components
$R(\ell )$
the lattice in B whose local components
![]() $R(\ell )_p$
are given
$R(\ell )_p$
are given
-
∘ for p dividing
 $\ell $
, by the lattice
$\ell $
, by the lattice
 $R_p^\vee \subseteq B_p$
dual to
$R_p^\vee \subseteq B_p$
dual to
 $R_p$
, and
$R_p$
, and -
∘ otherwise, by
 $R_p$
.
$R_p$
.
2.4.2. Reduced trace and norm
We denote by
![]() $\operatorname {\mathrm {tr}}$
and
$\operatorname {\mathrm {tr}}$
and
![]() $\det $
the reduced trace and reduced norm on B, and also on its completions. We use a superscripted
$\det $
the reduced trace and reduced norm on B, and also on its completions. We use a superscripted
![]() $0$
, as in
$0$
, as in
![]() $R^0$
or
$R^0$
or
![]() $R(\ell )^0$
, to denote the kernel of the reduced trace.
$R(\ell )^0$
, to denote the kernel of the reduced trace.
2.4.3. Coordinates tailored to
 $K_\infty $
$K_\infty $
Define ![]() . If B is indefinite, then
. If B is indefinite, then
![]() $B_\infty \cong \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {R})$
is split; otherwise,
$B_\infty \cong \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {R})$
is split; otherwise,
![]() $B_\infty $
is isomorphic to the real Hamilton quaternions. The exponential series identifies
$B_\infty $
is isomorphic to the real Hamilton quaternions. The exponential series identifies
![]() $B_\infty ^0$
with the Lie algebra of
$B_\infty ^0$
with the Lie algebra of
![]() $G(\mathbb {R})$
. We write
$G(\mathbb {R})$
. We write
![]() ${\mathbf{i}} \in B_\infty ^0$
for the derivative at the identity of
${\mathbf{i}} \in B_\infty ^0$
for the derivative at the identity of
![]() $\kappa $
so that
$\kappa $
so that
![]() $\kappa (\theta ) = \exp ( \theta {\mathbf{i}} )$
. Then,
$\kappa (\theta ) = \exp ( \theta {\mathbf{i}} )$
. Then,
![]() ${\mathbf{i}} ^2 = -1$
. We may find
${\mathbf{i}} ^2 = -1$
. We may find
![]() ${\mathbf{j}} \in B_\infty ^0$
with
${\mathbf{j}} \in B_\infty ^0$
with
![]() ${\mathbf{j}} ^2 = \pm 1$
(
${\mathbf{j}} ^2 = \pm 1$
(
![]() $+1$
if B is indefinite,
$+1$
if B is indefinite,
![]() $-1$
if B is definite) so that
$-1$
if B is definite) so that
![]() $B_\infty = \mathbb {R}({\mathbf{i}} ) \oplus \mathbb {R}({\mathbf{i}} ) {\mathbf{j}} $
. We note that
$B_\infty = \mathbb {R}({\mathbf{i}} ) \oplus \mathbb {R}({\mathbf{i}} ) {\mathbf{j}} $
. We note that
![]() ${\mathbf{j}} $
is not uniquely determined, but any two choices differ by multiplication by a norm one element of
${\mathbf{j}} $
is not uniquely determined, but any two choices differ by multiplication by a norm one element of
![]() $\mathbb {R}({\mathbf{i}} )$
. We set
$\mathbb {R}({\mathbf{i}} )$
. We set
![]() ${\mathbf{k}} = {\mathbf{i}} {\mathbf{j}} $
. Then,
${\mathbf{k}} = {\mathbf{i}} {\mathbf{j}} $
. Then,
![]() ${\mathbf{i}} ,{\mathbf{j}} ,{\mathbf{k}} $
give an
${\mathbf{i}} ,{\mathbf{j}} ,{\mathbf{k}} $
give an
![]() $\mathbb {R}$
-basis of
$\mathbb {R}$
-basis of
![]() $B_\infty ^0$
. For real numbers
$B_\infty ^0$
. For real numbers
![]() $a,b,c$
, we set
$a,b,c$
, we set ![]() . A general element of
. A general element of
![]() $B_\infty $
may then be written
$B_\infty $
may then be written
![]() $[a,b,c] + d$
, where we identify the real number d with a scalar element of
$[a,b,c] + d$
, where we identify the real number d with a scalar element of
![]() $B_\infty $
. In these coordinates,
$B_\infty $
. In these coordinates,
Example 2.4. Suppose that
![]() $B_\infty = \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {R})$
and that
$B_\infty = \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {R})$
and that
![]() $\kappa $
is as in Equation (2.2). Then, with suitable choices,
$\kappa $
is as in Equation (2.2). Then, with suitable choices,
 $$\begin{align*}[a,b,c] + d = \begin{pmatrix} d + c & b + a \\ b- a & d-c \end{pmatrix}. \end{align*}$$
$$\begin{align*}[a,b,c] + d = \begin{pmatrix} d + c & b + a \\ b- a & d-c \end{pmatrix}. \end{align*}$$
2.4.4. Archimedean regions
For
![]() $T> 0$
and
$T> 0$
and
![]() $\delta \in (0,1]$
, we denote by
$\delta \in (0,1]$
, we denote by
![]() $\Omega (\delta ,T)$
the set of all elements
$\Omega (\delta ,T)$
the set of all elements
![]() $[a,b,c] + d$
of
$[a,b,c] + d$
of
![]() $B_\infty $
for which
$B_\infty $
for which
With
![]() $\Omega ^{\star }(\delta ,T)$
, we denote the subset of nonzero elements of
$\Omega ^{\star }(\delta ,T)$
, we denote the subset of nonzero elements of
![]() $\Omega (\delta ,T)$
. Likewise, for
$\Omega (\delta ,T)$
. Likewise, for
![]() $T>0$
and
$T>0$
and
![]() $\delta \in (0,1]$
, we let
$\delta \in (0,1]$
, we let
![]() $\Psi (\delta ,T)$
denote the set of all elements
$\Psi (\delta ,T)$
denote the set of all elements
![]() $[a,b,c]+d$
of
$[a,b,c]+d$
of
![]() $B_{\infty }$
for which
$B_{\infty }$
for which
and
![]() $\Psi ^{\star }(\delta ,T)$
its subset consisting of nonzero elements.
$\Psi ^{\star }(\delta ,T)$
its subset consisting of nonzero elements.
2.5. Counting problems: results
We adopt the following asymptotic notation for counting estimates (compare with the notation
![]() $\preccurlyeq $
introduced in §2.3):
$\preccurlyeq $
introduced in §2.3):
Recall from §2.2 the height function H defined in the split case. In the nonsplit case, we adopt the convention in the following results that any terms involving H (in minima or sums) should be omitted.
Theorem 2.5 (Type I estimates).
Let
![]() $g \in G(\mathbb {R})$
. Then, the first successive minima (see Definition 6.1) of
$g \in G(\mathbb {R})$
. Then, the first successive minima (see Definition 6.1) of
![]() $g^{-1} R(\ell )^0 g$
with respect to
$g^{-1} R(\ell )^0 g$
with respect to
![]() $\Omega (\delta , 1)\cap B_{\infty }^0$
is
$\Omega (\delta , 1)\cap B_{\infty }^0$
is
![]() $\gg \min \left \{ \ell ^{-\frac {1}{2}} , \ell ^{-1} \delta ^{-\frac {1}{2}} H(g)^{-1} \right \}$
. Furthermore, we have
$\gg \min \left \{ \ell ^{-\frac {1}{2}} , \ell ^{-1} \delta ^{-\frac {1}{2}} H(g)^{-1} \right \}$
. Furthermore, we have
 $$\begin{align*}|g^{-1} R(\ell)^0 g \cap \Omega(\delta, T)| \prec 1 + \left(\ell^{\frac{1}{2}} +\ell \delta^{\frac{1}{2}} H(g) \right) T + \left( \frac{\ell^{\frac{3}{2}} \delta^{\frac{1}{2}} }{(d_B N)^{\frac{1}{2}}} + \ell \delta H(g) \right) T^2 + \frac{\ell^2 \delta}{d_B N} T^{3}. \end{align*}$$
$$\begin{align*}|g^{-1} R(\ell)^0 g \cap \Omega(\delta, T)| \prec 1 + \left(\ell^{\frac{1}{2}} +\ell \delta^{\frac{1}{2}} H(g) \right) T + \left( \frac{\ell^{\frac{3}{2}} \delta^{\frac{1}{2}} }{(d_B N)^{\frac{1}{2}}} + \ell \delta H(g) \right) T^2 + \frac{\ell^2 \delta}{d_B N} T^{3}. \end{align*}$$
If B is nonsplit, we further have that the first successive minima of
![]() $g^{-1} R(\ell )^0 g$
with respect to
$g^{-1} R(\ell )^0 g$
with respect to
![]() $\Psi (\delta , 1)\cap B_{\infty }^0$
is at least
$\Psi (\delta , 1)\cap B_{\infty }^0$
is at least
![]() $\gg \ell ^{-\frac {1}{2}}$
and
$\gg \ell ^{-\frac {1}{2}}$
and
 $$\begin{align*}|g^{-1} R(\ell)^0 g \cap \Psi(\delta, T)| \prec 1 + \ell^{\frac{1}{2}} T + \frac{\ell^{\frac{3}{2}} }{(d_B N)^{\frac{1}{2}}} T^2 + \frac{\ell^2 \delta^{\frac{1}{2}}}{d_B N} T^{3}. \end{align*}$$
$$\begin{align*}|g^{-1} R(\ell)^0 g \cap \Psi(\delta, T)| \prec 1 + \ell^{\frac{1}{2}} T + \frac{\ell^{\frac{3}{2}} }{(d_B N)^{\frac{1}{2}}} T^2 + \frac{\ell^2 \delta^{\frac{1}{2}}}{d_B N} T^{3}. \end{align*}$$
Theorem 2.6 (Type II estimates).
Let
![]() $g \in G(\mathbb {R})$
and
$g \in G(\mathbb {R})$
and
![]() $n \in \frac {1}{\ell } \mathbb {Z}$
. We have
$n \in \frac {1}{\ell } \mathbb {Z}$
. We have
 $$\begin{align*}|g^{-1} R(\ell)^0 g \cap \Omega(\delta, T) \cap \det{}^{-1}(\{n\})| \prec 1 + \ell \delta^{\frac{1}{2}} H(g) T +\frac{\ell^2}{d_B N} \delta T^2. \end{align*}$$
$$\begin{align*}|g^{-1} R(\ell)^0 g \cap \Omega(\delta, T) \cap \det{}^{-1}(\{n\})| \prec 1 + \ell \delta^{\frac{1}{2}} H(g) T +\frac{\ell^2}{d_B N} \delta T^2. \end{align*}$$
The proof of these results occupies §7 onwards. In §3, we explain how these results imply our main fourth moment bound, Theorem 2.1.
3. Division and reduction of the proof
3.1. Traversing the genus
Recall that
![]() $K_R$
is defined as the image of the subgroup
$K_R$
is defined as the image of the subgroup
![]() $\prod _p R_p^{\times }$
in
$\prod _p R_p^{\times }$
in
![]() $G(\mathbb {A}_f)$
; it is a compact open subgroup of
$G(\mathbb {A}_f)$
; it is a compact open subgroup of
![]() $G(\mathbb {A}_f)$
. In due course, we will consider the conjugated sets
$G(\mathbb {A}_f)$
. In due course, we will consider the conjugated sets
![]() $h_f K_R h_f^{-1}$
, for
$h_f K_R h_f^{-1}$
, for
![]() $h_f \in G(\mathbb {A}_f)$
. These are precisely the compact open subgroups
$h_f \in G(\mathbb {A}_f)$
. These are precisely the compact open subgroups
![]() $K_{R'}$
associated to the Eichler orders
$K_{R'}$
associated to the Eichler orders
![]() $R'$
in the genus of R. We note that
$R'$
in the genus of R. We note that
![]() $R'$
has the same level as R and may be given explicitly by the following intersection:
$R'$
has the same level as R and may be given explicitly by the following intersection:
where
![]() $\widehat {\mathbb {Z}}$
denotes the closure of
$\widehat {\mathbb {Z}}$
denotes the closure of
![]() $\mathbb {Z}$
inside
$\mathbb {Z}$
inside
![]() $\mathbb {A}_f$
. We further note that the action of
$\mathbb {A}_f$
. We further note that the action of
![]() $G(\mathbb {A}_f)$
on the genus of R commutes with partial dualization in the sense that
$G(\mathbb {A}_f)$
on the genus of R commutes with partial dualization in the sense that
This observation permits us to formulate the required
![]() $L^2$
-estimates for our differences of theta kernels in terms of integration over Archimedean, rather than adelic, arguments. To that end, we introduce the notation
$L^2$
-estimates for our differences of theta kernels in terms of integration over Archimedean, rather than adelic, arguments. To that end, we introduce the notation
for
![]() $h=(h_\infty ,h_f) \in G(\mathbb {A})$
. We note that for
$h=(h_\infty ,h_f) \in G(\mathbb {A})$
. We note that for
![]() $h \in G(\mathbb {R})$
(i.e.,
$h \in G(\mathbb {R})$
(i.e.,
![]() $h_f = 1$
), the set
$h_f = 1$
), the set
![]() $R(\ell; h)$
is just
$R(\ell; h)$
is just
![]() $h^{-1}R(\ell )h$
. Since taking the trace commutes with conjugation, we may extend the notation to kernels of the reduced trace without concern for confusion regarding the order of operation, that is,
$h^{-1}R(\ell )h$
. Since taking the trace commutes with conjugation, we may extend the notation to kernels of the reduced trace without concern for confusion regarding the order of operation, that is,
If B is split, then the class number of R is one and we have fixed the representative as in Equation (2.1). In this case, we find for
![]() $h \in G(\mathbb {A})$
that
$h \in G(\mathbb {A})$
that
![]() $h^{-1}R h=h^{\prime -1}Rh'$
, where
$h^{-1}R h=h^{\prime -1}Rh'$
, where
![]() $h' \in G(\mathbb {R})$
has the same image under the isomorphism
$h' \in G(\mathbb {R})$
has the same image under the isomorphism
![]() $[G]/ K_{\infty }K_R \cong \Gamma _0(N) \backslash \mathbb {H}$
as h does. In particular, we have the equality of height functions (see §2.2)
$[G]/ K_{\infty }K_R \cong \Gamma _0(N) \backslash \mathbb {H}$
as h does. In particular, we have the equality of height functions (see §2.2)
![]() $H(h)=H(h')$
.
$H(h)=H(h')$
.
Remark 3.1. By considering a right translate of
![]() $\varphi \in \mathcal {F}$
and thereby moving the maximal compact
$\varphi \in \mathcal {F}$
and thereby moving the maximal compact
![]() $K_{\infty }$
and the Eichler order R around, one could reduce the statement of the main Corollary 2.3 to the case that g is the identity. However, in the split case, our counting arguments do depend on the particular order in the genus. Moreover, our method relies on a difference of theta kernels defined relative to different g. Such a reduction would thus be premature.
$K_{\infty }$
and the Eichler order R around, one could reduce the statement of the main Corollary 2.3 to the case that g is the identity. However, in the split case, our counting arguments do depend on the particular order in the genus. Moreover, our method relies on a difference of theta kernels defined relative to different g. Such a reduction would thus be premature.
3.2. Estimating fourth moments via lattice sums
In §5, we introduce certain theta kernels. A spectral expansion of their
![]() $L^2$
-norms will yield the fourth moments of interest, while a ‘geometric’ expansion, using Siegel domains and Fourier expansions, bounds those
$L^2$
-norms will yield the fourth moments of interest, while a ‘geometric’ expansion, using Siegel domains and Fourier expansions, bounds those
![]() $L^2$
-norms in terms of certain lattice sums. We now state the latter bounds.
$L^2$
-norms in terms of certain lattice sums. We now state the latter bounds.
Proposition 3.2. Suppose B is indefinite. Then, for
![]() $g_1, g_2 \in [G]$
, there exists
$g_1, g_2 \in [G]$
, there exists
![]() $\ell |d_BN$
,
$\ell |d_BN$
,
![]() $g \in \{g_1, g_2\}$
, and
$g \in \{g_1, g_2\}$
, and
![]() $0< T \preccurlyeq \frac {(d_B N(k+1))^{\frac {1}{2}}}{\ell }$
(here, the notation
$0< T \preccurlyeq \frac {(d_B N(k+1))^{\frac {1}{2}}}{\ell }$
(here, the notation
![]() $\preccurlyeq $
is as in §2.3) so that, for
$\preccurlyeq $
is as in §2.3) so that, for
![]() $k=0$
,
$k=0$
,
 $$ \begin{align} \sum _{\varphi \in \mathcal{F}^{-}_{\le L} } (|\varphi(g_1)|^2 - |\varphi(g_2)|^2)^2 \preccurlyeq_{L} 1+ \frac{d _B N}{\ell T^2} \sum _{\substack{ \gamma_1, \gamma_2 \in R(\ell;g) \cap \Omega^{\star}(1, T): \\ \det(\gamma_1) = \det(\gamma_2) } } 1, \end{align} $$
$$ \begin{align} \sum _{\varphi \in \mathcal{F}^{-}_{\le L} } (|\varphi(g_1)|^2 - |\varphi(g_2)|^2)^2 \preccurlyeq_{L} 1+ \frac{d _B N}{\ell T^2} \sum _{\substack{ \gamma_1, \gamma_2 \in R(\ell;g) \cap \Omega^{\star}(1, T): \\ \det(\gamma_1) = \det(\gamma_2) } } 1, \end{align} $$
while for
![]() $k> 0$
,
$k> 0$
,
 $$ \begin{align} \sum _{\varphi \in \mathcal{F^{-,\operatorname{hol}}} } (|\varphi(g_1)|^2 - |\varphi(g_2)|^2)^2 \preccurlyeq 1+ \frac{d _B N k}{\ell T^2} \sum _{\substack{ \gamma_1, \gamma_2 \in R(\ell;g) \cap \Omega^{\star}(1, T): \\ \det(\gamma_1) = \det(\gamma_2) } } 1. \end{align} $$
$$ \begin{align} \sum _{\varphi \in \mathcal{F^{-,\operatorname{hol}}} } (|\varphi(g_1)|^2 - |\varphi(g_2)|^2)^2 \preccurlyeq 1+ \frac{d _B N k}{\ell T^2} \sum _{\substack{ \gamma_1, \gamma_2 \in R(\ell;g) \cap \Omega^{\star}(1, T): \\ \det(\gamma_1) = \det(\gamma_2) } } 1. \end{align} $$
Proposition 3.3. Suppose B is indefinite. Let
![]() $g \in [G]$
, and assume that
$g \in [G]$
, and assume that
![]() $k \gg (d_BN)^{\eta }$
for some arbitrarily small
$k \gg (d_BN)^{\eta }$
for some arbitrarily small
![]() $\eta>0$
. Then, there exists
$\eta>0$
. Then, there exists
![]() $\ell |d_BN$
and
$\ell |d_BN$
and
![]() $ 0<T \preccurlyeq \frac {(d_B N k)^{\frac {1}{2}}}{\ell }$
so that
$ 0<T \preccurlyeq \frac {(d_B N k)^{\frac {1}{2}}}{\ell }$
so that
 $$ \begin{align} \sum _{\varphi \in \mathcal{F}^{-,\operatorname{hol}} } |\varphi(g)|^4 \preccurlyeq_{\eta} 1+ \frac{d _B N k}{\ell T^2} \sum _{\substack{ \gamma_1, \gamma_2 \in R(\ell;g) \cap \Omega^{\star}(k^{-1+\varepsilon}, T): \\ \det(\gamma_1) = \det(\gamma_2)>0 } } 1. \end{align} $$
$$ \begin{align} \sum _{\varphi \in \mathcal{F}^{-,\operatorname{hol}} } |\varphi(g)|^4 \preccurlyeq_{\eta} 1+ \frac{d _B N k}{\ell T^2} \sum _{\substack{ \gamma_1, \gamma_2 \in R(\ell;g) \cap \Omega^{\star}(k^{-1+\varepsilon}, T): \\ \det(\gamma_1) = \det(\gamma_2)>0 } } 1. \end{align} $$
Proposition 3.4. Suppose B is definite and the weight is
![]() $k=0$
. Then, for
$k=0$
. Then, for
![]() $g_1,g_2 \in [G]$
and
$g_1,g_2 \in [G]$
and
![]() $m \in \mathbb {N}_0$
, there exists
$m \in \mathbb {N}_0$
, there exists
![]() $\ell |d_BN$
,
$\ell |d_BN$
,
![]() $ 0< T \preccurlyeq \frac {(d_B N (m+1))^{\frac {1}{2}}}{\ell }$
and
$ 0< T \preccurlyeq \frac {(d_B N (m+1))^{\frac {1}{2}}}{\ell }$
and
![]() $\frac {1}{m^2+1} \preccurlyeq \delta \le 1$
so that
$\frac {1}{m^2+1} \preccurlyeq \delta \le 1$
so that
 $$ \begin{align} \sum _{\varphi \in \mathcal{F}^{+}_{m}} \left(|\varphi(g_1)|^2-|\varphi(g_2)|^2\right)^2 \preccurlyeq 1+ \frac{d_B N}{\ell \delta^{\frac{1}{2}} T^2} \sum _{\substack{ \gamma_1, \gamma_2 \in R(\ell;g) \\ \gamma_1, \gamma_2 \in \Omega^{\star}(\delta, T)\cup \Psi^{\star}(\delta, T): \\ \det(\gamma_1) = \det(\gamma_2) } } 1. \end{align} $$
$$ \begin{align} \sum _{\varphi \in \mathcal{F}^{+}_{m}} \left(|\varphi(g_1)|^2-|\varphi(g_2)|^2\right)^2 \preccurlyeq 1+ \frac{d_B N}{\ell \delta^{\frac{1}{2}} T^2} \sum _{\substack{ \gamma_1, \gamma_2 \in R(\ell;g) \\ \gamma_1, \gamma_2 \in \Omega^{\star}(\delta, T)\cup \Psi^{\star}(\delta, T): \\ \det(\gamma_1) = \det(\gamma_2) } } 1. \end{align} $$
Proposition 3.5. Suppose B is definite. Then, for
![]() $g \in [G]$
, there exists
$g \in [G]$
, there exists
![]() $\ell |d_BN$
and
$\ell |d_BN$
and
![]() $ 0< T \preccurlyeq \frac {(d_B N k)^{\frac {1}{2}}}{\ell }$
so that
$ 0< T \preccurlyeq \frac {(d_B N k)^{\frac {1}{2}}}{\ell }$
so that
 $$ \begin{align} \sum _{\varphi \in \mathcal{F}^{+,\operatorname{hol}}} |\varphi(g)|^4 \preccurlyeq 1+\frac{d _B N k}{\ell T^2}\left( \sum _{\substack{ \gamma_1, \gamma_2 \in R(\ell;g) \cap \Omega^{\star}(k^{-1+\varepsilon}, T): \\ \det(\gamma_1) = \det(\gamma_2) } }1 + \sum _{\substack{ \gamma_1, \gamma_2 \in R(\ell;g) \cap \Omega^{\star}(1, T): \\ \det(\gamma_1) = \det(\gamma_2) } } k^{-2027}\right). \end{align} $$
$$ \begin{align} \sum _{\varphi \in \mathcal{F}^{+,\operatorname{hol}}} |\varphi(g)|^4 \preccurlyeq 1+\frac{d _B N k}{\ell T^2}\left( \sum _{\substack{ \gamma_1, \gamma_2 \in R(\ell;g) \cap \Omega^{\star}(k^{-1+\varepsilon}, T): \\ \det(\gamma_1) = \det(\gamma_2) } }1 + \sum _{\substack{ \gamma_1, \gamma_2 \in R(\ell;g) \cap \Omega^{\star}(1, T): \\ \det(\gamma_1) = \det(\gamma_2) } } k^{-2027}\right). \end{align} $$
3.3. Reduction to ternary lattices
In this section, we reduce the vital counting problem involving quaternary quadratic form to problems involving only ternary quadratic forms. The key observation is that we may orthogonally decompose the quaternion algebra
![]() $B_{\infty }$
into its trace part and its traceless part
$B_{\infty }$
into its trace part and its traceless part
![]() $B_{\infty }^{0}$
. Thus, for any
$B_{\infty }^{0}$
. Thus, for any
![]() $\alpha = \frac {1}{2}\operatorname {\mathrm {tr}}(\alpha ) + \alpha ^0 \in \mathbb {R} \oplus B_{\infty }^{0}$
, we have
$\alpha = \frac {1}{2}\operatorname {\mathrm {tr}}(\alpha ) + \alpha ^0 \in \mathbb {R} \oplus B_{\infty }^{0}$
, we have
We further note that the trace is invariant under conjugation. Hence, we have
![]() $\operatorname {\mathrm {tr}}(R(\ell ;g)) \subseteq \mathbb {Z}$
. We conclude that
$\operatorname {\mathrm {tr}}(R(\ell ;g)) \subseteq \mathbb {Z}$
. We conclude that
is a sublattice of the direct sum of the lattices
![]() $\frac {1}{2}\mathbb {Z}$
in
$\frac {1}{2}\mathbb {Z}$
in
![]() $\mathbb {R}$
and
$\mathbb {R}$
and
![]() $\tfrac {1}{2} R(\ell ;g)^{0}$
in
$\tfrac {1}{2} R(\ell ;g)^{0}$
in
![]() $B_{\infty }^0$
. Using this decomposition, we deduce
$B_{\infty }^0$
. Using this decomposition, we deduce
 $$ \begin{align} \sum_{\substack{\gamma_1,\gamma_2 \in R(\ell;g) \cap\Omega^{\star}(\delta,T) \\ \det(\gamma_1) = \det(\gamma_2)}} 1 \ll_{\varepsilon} T^{\varepsilon} \left|R(\ell;g)^0 \cap \Omega(\delta,2T) \right|{}^2 + T \sum_{\substack{\gamma_1,\gamma_2 \in R(\ell;g)^0 \cap\Omega(\delta,2T) \\ \det(\gamma_1) = \det(\gamma_2)}}1 \end{align} $$
$$ \begin{align} \sum_{\substack{\gamma_1,\gamma_2 \in R(\ell;g) \cap\Omega^{\star}(\delta,T) \\ \det(\gamma_1) = \det(\gamma_2)}} 1 \ll_{\varepsilon} T^{\varepsilon} \left|R(\ell;g)^0 \cap \Omega(\delta,2T) \right|{}^2 + T \sum_{\substack{\gamma_1,\gamma_2 \in R(\ell;g)^0 \cap\Omega(\delta,2T) \\ \det(\gamma_1) = \det(\gamma_2)}}1 \end{align} $$
by distinguishing the two cases of equal and nonequal trace and applying the divisor bound to the equality
We remark that we have forfeited the congruence condition
![]() $\det (\gamma _1^0) \equiv \det (\gamma _2^0) \ \mathrm {mod}\,(1)$
, and this forfeiture will be reflected in the suboptimality of our final counting estimates on larger scales when
$\det (\gamma _1^0) \equiv \det (\gamma _2^0) \ \mathrm {mod}\,(1)$
, and this forfeiture will be reflected in the suboptimality of our final counting estimates on larger scales when
![]() $\ell>1$
. We circumnavigate these larger scales by an appropriate choice of a covering domain (cf. Lemma 4.1).
$\ell>1$
. We circumnavigate these larger scales by an appropriate choice of a covering domain (cf. Lemma 4.1).
Note that we may further bound the diagonal contribution by considering its largest fiber:
 $$ \begin{align} \sum_{\substack{\gamma_1,\gamma_2 \in R(\ell;g)^0 \cap\Omega(\delta,2T) \\ \det(\gamma_1) = \det(\gamma_2)}}1 \le |R(\ell;g)^0 \cap\Omega(\delta,2T)| \times \max_{\substack{n \in \frac{1}{\ell} \mathbb{Z} \\ |n|\le 4T^2}} |R(\ell;g)^0 \cap\Omega(\delta,2T) \cap \det{}^{-1}(\{n\})|. \end{align} $$
$$ \begin{align} \sum_{\substack{\gamma_1,\gamma_2 \in R(\ell;g)^0 \cap\Omega(\delta,2T) \\ \det(\gamma_1) = \det(\gamma_2)}}1 \le |R(\ell;g)^0 \cap\Omega(\delta,2T)| \times \max_{\substack{n \in \frac{1}{\ell} \mathbb{Z} \\ |n|\le 4T^2}} |R(\ell;g)^0 \cap\Omega(\delta,2T) \cap \det{}^{-1}(\{n\})|. \end{align} $$
Arguing along the same lines, we also arrive at
 $$ \begin{align} \sum_{\substack{\gamma_1,\gamma_2 \in R(\ell;g) \cap\Psi^\star(\delta,T) \\ \det(\gamma_1) = \det(\gamma_2)}} 1 \ll_{\varepsilon} T^{\varepsilon} \left|R(\ell;g)^0 \cap \Psi(\delta,2T) \right|{}^2 + \delta^{\frac{1}{2}}T \sum_{\substack{\gamma_1,\gamma_2 \in R(\ell;g)^0 \cap\Psi(\delta,2T) \\ \det(\gamma_1) = \det(\gamma_2)}}1 \end{align} $$
$$ \begin{align} \sum_{\substack{\gamma_1,\gamma_2 \in R(\ell;g) \cap\Psi^\star(\delta,T) \\ \det(\gamma_1) = \det(\gamma_2)}} 1 \ll_{\varepsilon} T^{\varepsilon} \left|R(\ell;g)^0 \cap \Psi(\delta,2T) \right|{}^2 + \delta^{\frac{1}{2}}T \sum_{\substack{\gamma_1,\gamma_2 \in R(\ell;g)^0 \cap\Psi(\delta,2T) \\ \det(\gamma_1) = \det(\gamma_2)}}1 \end{align} $$
and
 $$ \begin{align} \sum_{\substack{\gamma_1,\gamma_2 \in R(\ell;g)^0 \cap\Psi(\delta,2T) \\ \det(\gamma_1) = \det(\gamma_2)}}1 \le |R(\ell;g)^0 \cap\Psi(\delta,2T)| \times \max_{\substack{n \in \frac{1}{\ell} \mathbb{Z} \\ |n|\le 4T^2}} |R(\ell;g)^0 \cap\Omega(1,2T) \cap \det{}^{-1}(\{n\})|. \end{align} $$
$$ \begin{align} \sum_{\substack{\gamma_1,\gamma_2 \in R(\ell;g)^0 \cap\Psi(\delta,2T) \\ \det(\gamma_1) = \det(\gamma_2)}}1 \le |R(\ell;g)^0 \cap\Psi(\delta,2T)| \times \max_{\substack{n \in \frac{1}{\ell} \mathbb{Z} \\ |n|\le 4T^2}} |R(\ell;g)^0 \cap\Omega(1,2T) \cap \det{}^{-1}(\{n\})|. \end{align} $$
Note that in this last inequality, we have passed from
![]() $\Psi (\delta ,2T)$
to the larger set
$\Psi (\delta ,2T)$
to the larger set
![]() $\Omega (1,2T)=\Psi (1,2T)$
; the resulting bound remains adequate for us thanks to the additional saving of
$\Omega (1,2T)=\Psi (1,2T)$
; the resulting bound remains adequate for us thanks to the additional saving of
![]() $\delta ^{\frac {1}{2}}$
in Equation (3.10).
$\delta ^{\frac {1}{2}}$
in Equation (3.10).
3.4. Proof of Theorem 2.1
Theorem 2.1 is an immediate consequence of the following pair of lemmas together with Propositions 3.2 through 3.5.
Lemma 3.6. We have
 $$ \begin{align} \nonumber \sum_{\substack{\gamma_1,\gamma_2 \in R(\ell;g) \cap\Omega^{\star}(\delta,T) \\ \det(\gamma_1) = \det(\gamma_2)}} 1 \prec \ell T^2 \left(1 + \ell^{\frac{1}{2}} \delta^{\frac{1}{2}} H(g) + \ell^{\frac{1}{2}} \delta H(g) T + \frac{\ell^2 }{d_B N} \delta T^2 \right) \\ \times \left(1 + \ell^{\frac{1}{2}} \delta^{\frac{1}{2}} H(g) + \ell^{\frac{1}{2}} \delta^{\frac{1}{2}} H(g) T + \frac{\ell^2 }{d_B N} \delta T^2 \right). \end{align} $$
$$ \begin{align} \nonumber \sum_{\substack{\gamma_1,\gamma_2 \in R(\ell;g) \cap\Omega^{\star}(\delta,T) \\ \det(\gamma_1) = \det(\gamma_2)}} 1 \prec \ell T^2 \left(1 + \ell^{\frac{1}{2}} \delta^{\frac{1}{2}} H(g) + \ell^{\frac{1}{2}} \delta H(g) T + \frac{\ell^2 }{d_B N} \delta T^2 \right) \\ \times \left(1 + \ell^{\frac{1}{2}} \delta^{\frac{1}{2}} H(g) + \ell^{\frac{1}{2}} \delta^{\frac{1}{2}} H(g) T + \frac{\ell^2 }{d_B N} \delta T^2 \right). \end{align} $$
Proof. Recall, from the discussion of Section §3.1, that we may express
![]() $R(\ell ;g)^0$
, for
$R(\ell ;g)^0$
, for
![]() $g \in G(\mathbb {A})$
, as
$g \in G(\mathbb {A})$
, as
![]() $(g')^{-1}R'(\ell )^0g'$
, where
$(g')^{-1}R'(\ell )^0g'$
, where
![]() $R'$
is an Eichler order of the same level and
$R'$
is an Eichler order of the same level and
![]() $g' \in G(\mathbb {R})$
, with
$g' \in G(\mathbb {R})$
, with
![]() $H(g)=H(g')$
in the case that B is split. We may thus apply the results of Section §2.5.
$H(g)=H(g')$
in the case that B is split. We may thus apply the results of Section §2.5.
Since
![]() $\operatorname {\mathrm {tr}}(R(\ell ;g)) \subseteq \mathbb {Z}$
, we find that the first successive minimum of
$\operatorname {\mathrm {tr}}(R(\ell ;g)) \subseteq \mathbb {Z}$
, we find that the first successive minimum of
![]() $R(\ell ;g)$
with respect to
$R(\ell ;g)$
with respect to
![]() $\Omega (\delta ,1)$
is at least the minimum of
$\Omega (\delta ,1)$
is at least the minimum of
![]() $1$
and the first successive minimum of
$1$
and the first successive minimum of
![]() $R(\ell ;g)^0$
with respect to
$R(\ell ;g)^0$
with respect to
![]() $\Omega (\delta ,1)\cap B_{\infty }^{0}$
. The latter is
$\Omega (\delta ,1)\cap B_{\infty }^{0}$
. The latter is
![]() $\gg \min \{ \ell ^{-\frac {1}{2}}, \ell ^{-1} \delta ^{-\frac {1}{2}} H(g)^{-1} \} =: \Lambda $
by Theorem 2.5, where the term involving
$\gg \min \{ \ell ^{-\frac {1}{2}}, \ell ^{-1} \delta ^{-\frac {1}{2}} H(g)^{-1} \} =: \Lambda $
by Theorem 2.5, where the term involving
![]() $H(g)$
is to be omitted if B is nonsplit. Thus, we find that
$H(g)$
is to be omitted if B is nonsplit. Thus, we find that
![]() $R(\ell ;g) \cap \Omega ^{\star }(\delta ,T)$
is empty for
$R(\ell ;g) \cap \Omega ^{\star }(\delta ,T)$
is empty for
![]() $T \ll \Lambda $
, in which case there is nothing to show. Next, assume instead that
$T \ll \Lambda $
, in which case there is nothing to show. Next, assume instead that
![]() $T \gg \Lambda $
. Then, by Theorem 2.5, we have
$T \gg \Lambda $
. Then, by Theorem 2.5, we have
 $$ \begin{align} \begin{aligned} |g^{-1} R(\ell)^0 g \cap \Omega(\delta, 2T)| &\prec 1 + \left(\ell^{\frac{1}{2}} +\ell \delta^{\frac{1}{2}} H(g) \right) T + \left( \frac{\ell^{\frac{3}{2}} \delta^{\frac{1}{2}} }{(d_B N)^{\frac{1}{2}}} + \ell \delta H(g) \right) T^2 + \frac{\ell^2 }{d_B N} \delta T^{3} \\ &\prec \ell^{\frac{1}{2}} T \left( 1 +\ell^{\frac{1}{2}} \delta^{\frac{1}{2}} H(g) + \frac{\ell }{(d_B N)^{\frac{1}{2}}} \delta^{\frac{1}{2}} T + \ell^{\frac{1}{2}} \delta H(g) T + \frac{\ell^{2} }{d_B N} \delta T^{2} \right), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} |g^{-1} R(\ell)^0 g \cap \Omega(\delta, 2T)| &\prec 1 + \left(\ell^{\frac{1}{2}} +\ell \delta^{\frac{1}{2}} H(g) \right) T + \left( \frac{\ell^{\frac{3}{2}} \delta^{\frac{1}{2}} }{(d_B N)^{\frac{1}{2}}} + \ell \delta H(g) \right) T^2 + \frac{\ell^2 }{d_B N} \delta T^{3} \\ &\prec \ell^{\frac{1}{2}} T \left( 1 +\ell^{\frac{1}{2}} \delta^{\frac{1}{2}} H(g) + \frac{\ell }{(d_B N)^{\frac{1}{2}}} \delta^{\frac{1}{2}} T + \ell^{\frac{1}{2}} \delta H(g) T + \frac{\ell^{2} }{d_B N} \delta T^{2} \right), \end{aligned} \end{align} $$
where we have used
![]() $1 \ll \ell ^{\frac {1}{2}}T+\ell \delta ^{\frac {1}{2}}H(g)T$
and
$1 \ll \ell ^{\frac {1}{2}}T+\ell \delta ^{\frac {1}{2}}H(g)T$
and
![]() $\ell ^{\frac {3}{2}} \le \ell ^{2}$
. Further note that the middle term in the bracket is dominated by the sum of the first and last term in the bracket. We also find by Theorem 2.6 that
$\ell ^{\frac {3}{2}} \le \ell ^{2}$
. Further note that the middle term in the bracket is dominated by the sum of the first and last term in the bracket. We also find by Theorem 2.6 that
 $$ \begin{align} \begin{aligned} \max_{n \in \frac{1}{\ell} \mathbb{Z}} |g^{-1} R(\ell)^0 g \cap \Omega(\delta, 2T) \cap \det{}^{-1}(\{n\})| &\prec 1 + \ell \delta^{\frac{1}{2}} H(g) T +\frac{\ell^2}{d_B N} \delta T^2 \\ &\prec \ell^{\frac{1}{2}} \left( 1 + \ell^{\frac{1}{2}} \delta^{\frac{1}{2}}H(g)T+\frac{\ell^{2}}{d_BN}\delta T^2 \right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \max_{n \in \frac{1}{\ell} \mathbb{Z}} |g^{-1} R(\ell)^0 g \cap \Omega(\delta, 2T) \cap \det{}^{-1}(\{n\})| &\prec 1 + \ell \delta^{\frac{1}{2}} H(g) T +\frac{\ell^2}{d_B N} \delta T^2 \\ &\prec \ell^{\frac{1}{2}} \left( 1 + \ell^{\frac{1}{2}} \delta^{\frac{1}{2}}H(g)T+\frac{\ell^{2}}{d_BN}\delta T^2 \right). \end{aligned} \end{align} $$
We conclude the Lemma by further appealing to the inequalities (3.8) and (3.9).
Lemma 3.7. Assume that B is nonsplit. Then
 $$ \begin{align} \sum_{\substack{\gamma_1,\gamma_2 \in R(\ell;g) \cap\Psi^{\star}(\delta,T) \\ \det(\gamma_1) = \det(\gamma_2)}} 1 \prec \ell T^2 \left(1 + \frac{\ell}{(d_BN)^{\frac{1}{2}}} T + \frac{\ell^2 }{d_B N} \delta^{\frac{1}{2}} T^2 \right)^2. \end{align} $$
$$ \begin{align} \sum_{\substack{\gamma_1,\gamma_2 \in R(\ell;g) \cap\Psi^{\star}(\delta,T) \\ \det(\gamma_1) = \det(\gamma_2)}} 1 \prec \ell T^2 \left(1 + \frac{\ell}{(d_BN)^{\frac{1}{2}}} T + \frac{\ell^2 }{d_B N} \delta^{\frac{1}{2}} T^2 \right)^2. \end{align} $$
Proof. As in the proof of Lemma 3.6, we find that the first successive minimum of
![]() $R(\ell ;g)$
with respect to
$R(\ell ;g)$
with respect to
![]() $\Psi (\delta ,1)$
is at least the minimum of
$\Psi (\delta ,1)$
is at least the minimum of
![]() $\delta ^{-\frac {1}{2}}$
and the first successive minimum of
$\delta ^{-\frac {1}{2}}$
and the first successive minimum of
![]() $R(\ell ;g)^0$
with respect to
$R(\ell ;g)^0$
with respect to
![]() $\Psi (\delta ,1)\cap B_{\infty }^{0}$
. The latter is
$\Psi (\delta ,1)\cap B_{\infty }^{0}$
. The latter is
![]() $\gg \ell ^{-\frac {1}{2}}$
by Theorem 2.5. Therefore,
$\gg \ell ^{-\frac {1}{2}}$
by Theorem 2.5. Therefore,
![]() $R(\ell ;g) \cap \Psi ^{\star }(\delta ,T)$
is empty for
$R(\ell ;g) \cap \Psi ^{\star }(\delta ,T)$
is empty for
![]() $T \ll \ell ^{-\frac {1}{2}} \le 1 \le \delta ^{-\frac {1}{2}}$
, in which case there is nothing to show. If
$T \ll \ell ^{-\frac {1}{2}} \le 1 \le \delta ^{-\frac {1}{2}}$
, in which case there is nothing to show. If
![]() $T \gg \ell ^{-\frac {1}{2}}$
, then, by Theorem 2.5, we have
$T \gg \ell ^{-\frac {1}{2}}$
, then, by Theorem 2.5, we have
 $$ \begin{align} \begin{aligned} |g^{-1} R(\ell)^0 g \cap \Psi(\delta, 2T)| &\prec 1 + \ell^{\frac{1}{2}} T + \frac{\ell^{\frac{3}{2}} }{(d_B N)^{\frac{1}{2}}} T^2 + \frac{\ell^2 }{d_B N} \delta^{\frac{1}{2}} T^{3} \\ &\prec \ell^{\frac{1}{2}} T \left( 1 + \frac{\ell }{(d_B N)^{\frac{1}{2}}} T + \frac{\ell^2 }{d_B N} \delta^{\frac{1}{2}} T^{2} \right), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} |g^{-1} R(\ell)^0 g \cap \Psi(\delta, 2T)| &\prec 1 + \ell^{\frac{1}{2}} T + \frac{\ell^{\frac{3}{2}} }{(d_B N)^{\frac{1}{2}}} T^2 + \frac{\ell^2 }{d_B N} \delta^{\frac{1}{2}} T^{3} \\ &\prec \ell^{\frac{1}{2}} T \left( 1 + \frac{\ell }{(d_B N)^{\frac{1}{2}}} T + \frac{\ell^2 }{d_B N} \delta^{\frac{1}{2}} T^{2} \right), \end{aligned} \end{align} $$
where we have used
![]() $1 \ll \ell ^{\frac {1}{2}}T$
and
$1 \ll \ell ^{\frac {1}{2}}T$
and
![]() $\ell ^{\frac {3}{2}} \le \ell ^{2}$
. Furthermore, by Theorem 2.6, we have
$\ell ^{\frac {3}{2}} \le \ell ^{2}$
. Furthermore, by Theorem 2.6, we have
 $$ \begin{align} \max_{n \in \frac{1}{\ell} \mathbb{Z}} |g^{-1} R(\ell)^0 g \cap \Omega(1, 2T) \cap \det{}^{-1}(\{n\})| \prec 1 +\frac{\ell^2}{d_B N} T^2 \prec \ell^{\frac{1}{2}} \delta^{-\frac{1}{2}} \left( 1 + \frac{\ell^2 }{d_B N} \delta^{\frac{1}{2}} T^{2} \right), \end{align} $$
$$ \begin{align} \max_{n \in \frac{1}{\ell} \mathbb{Z}} |g^{-1} R(\ell)^0 g \cap \Omega(1, 2T) \cap \det{}^{-1}(\{n\})| \prec 1 +\frac{\ell^2}{d_B N} T^2 \prec \ell^{\frac{1}{2}} \delta^{-\frac{1}{2}} \left( 1 + \frac{\ell^2 }{d_B N} \delta^{\frac{1}{2}} T^{2} \right), \end{align} $$
where we have used
![]() $1 \le \ell ^{\frac {1}{2}}$
and
$1 \le \ell ^{\frac {1}{2}}$
and
![]() $1 \le \delta ^{-\frac {1}{2}}$
. We conclude the lemma by further appealing to the inequalities (3.10) and (3.11).
$1 \le \delta ^{-\frac {1}{2}}$
. We conclude the lemma by further appealing to the inequalities (3.10) and (3.11).
3.5. Proof of Corollary 2.3
Let
![]() $\varphi \in \mathcal {F}$
, respectively
$\varphi \in \mathcal {F}$
, respectively
![]() $\mathcal {F}^{\operatorname {hol}}$
, be
$\mathcal {F}^{\operatorname {hol}}$
, be
![]() $L^2$
-normalized. Assume first that B is nonsplit. Then, since
$L^2$
-normalized. Assume first that B is nonsplit. Then, since
![]() $[G] / K_{\infty } K_{R}$
is compact and equipped with a probability measure, we may find
$[G] / K_{\infty } K_{R}$
is compact and equipped with a probability measure, we may find
![]() $g_2$
in
$g_2$
in
![]() $[G]$
such that
$[G]$
such that
![]() $|\varphi (g_2)| \le 1$
. Hence, Corollary 2.3 follows immediately from Theorem 2.1 by positivity and the particular choice of
$|\varphi (g_2)| \le 1$
. Hence, Corollary 2.3 follows immediately from Theorem 2.1 by positivity and the particular choice of
![]() $g_2$
.
$g_2$
.
We now turn our attention to the case that B is split, in other words when
![]() $d_B=1$
. Here, we need to supplement Theorem 2.1 with the additional information that for
$d_B=1$
. Here, we need to supplement Theorem 2.1 with the additional information that for
![]() $H(g) \ge N^{-\frac {1}{2}}$
, we have
$H(g) \ge N^{-\frac {1}{2}}$
, we have
The former is recorded in [Reference TemplierTem15, Prop. 3.1 & 3.2], for example, and the latter may be deduced from the Fourier expansion along the lines of Xia [Reference XiaXia07]. We include a brief proof here for the sake of completeness.
Lemma 3.8. Assume B is split, and let
![]() $\varphi \in \mathcal {F}^{-,\mathrm {hol}}$
be an
$\varphi \in \mathcal {F}^{-,\mathrm {hol}}$
be an
![]() $L^2$
-normalized holomorphic cuspidal newform of squarefree level N and even weight
$L^2$
-normalized holomorphic cuspidal newform of squarefree level N and even weight
![]() $k \ge 2$
. Then, we have for all
$k \ge 2$
. Then, we have for all
![]() $g \in [G]$
,
$g \in [G]$
,
If
![]() $H(g) \ge \frac {k}{2 \pi }$
, then we have the stronger bound
$H(g) \ge \frac {k}{2 \pi }$
, then we have the stronger bound
Proof. Suppose that g corresponds to
![]() $z=x+iy \in \Gamma _0(N) \backslash \mathbb {H}$
. As
$z=x+iy \in \Gamma _0(N) \backslash \mathbb {H}$
. As
![]() $|\varphi (g)|$
is further invariant under the Atkin–Lehner operators we may further assume that z has maximal imaginary part under the action of the group
$|\varphi (g)|$
is further invariant under the Atkin–Lehner operators we may further assume that z has maximal imaginary part under the action of the group
![]() $A_0(N)$
generated by the Atkin–Lehner operators and
$A_0(N)$
generated by the Atkin–Lehner operators and
![]() $\Gamma _0(N)$
, thus
$\Gamma _0(N)$
, thus
![]() $H(g)=y$
. We shall subsequently make use of the Fourier expansion of
$H(g)=y$
. We shall subsequently make use of the Fourier expansion of
![]() $\varphi $
at
$\varphi $
at
![]() $\infty $
:
$\infty $
:
 $$ \begin{align*} |\varphi(g)| = \left| y^{\frac{k}{2}} \sum_{n=1}^{\infty} a_n e(n(x+iy)) \right |. \end{align*} $$
$$ \begin{align*} |\varphi(g)| = \left| y^{\frac{k}{2}} \sum_{n=1}^{\infty} a_n e(n(x+iy)) \right |. \end{align*} $$
We may bound the Fourier coefficients by appealing to Deligne’s bound for the Hecke eigenvalues [Reference DeligneDel71, Reference DeligneDel74]. This implies
![]() $|a_n| \ll _{\varepsilon } n^{\frac {k-1}{2}+\varepsilon } |a_1|$
.Footnote 1 We find
$|a_n| \ll _{\varepsilon } n^{\frac {k-1}{2}+\varepsilon } |a_1|$
.Footnote 1 We find
 $$ \begin{align*} |\varphi(g)| \ll_{\varepsilon} |a_1| (2\pi)^{-\frac{k}{2}} y^{\frac{1}{2}-\varepsilon} \sum_{n=1}^{\infty} (2 \pi n y)^{\frac{k-1}{2}+\varepsilon} e^{-2 \pi n y}. \end{align*} $$
$$ \begin{align*} |\varphi(g)| \ll_{\varepsilon} |a_1| (2\pi)^{-\frac{k}{2}} y^{\frac{1}{2}-\varepsilon} \sum_{n=1}^{\infty} (2 \pi n y)^{\frac{k-1}{2}+\varepsilon} e^{-2 \pi n y}. \end{align*} $$
The above sum, we may bound by comparison to the corresponding integral. For this manner, we note that the function
![]() $x^{\alpha }e^{-x}$
increases up to
$x^{\alpha }e^{-x}$
increases up to
![]() $x= \alpha $
and then decreases. We may also bound the first Fourier coefficient
$x= \alpha $
and then decreases. We may also bound the first Fourier coefficient
![]() $a_1$
by a result of Hoffstein–Lockhart [Reference Hoffstein and LockhartHL94] (cf. [Reference Harcos and MichelHM06, Eq. (31)]Footnote 2). The bound reads
$a_1$
by a result of Hoffstein–Lockhart [Reference Hoffstein and LockhartHL94] (cf. [Reference Harcos and MichelHM06, Eq. (31)]Footnote 2). The bound reads
![]() $|a_1| \ll _{\varepsilon } (Nk)^{\varepsilon } (4\pi )^{\frac {k}{2}} \Gamma (k)^{-\frac {1}{2}}$
. We thus arrive at
$|a_1| \ll _{\varepsilon } (Nk)^{\varepsilon } (4\pi )^{\frac {k}{2}} \Gamma (k)^{-\frac {1}{2}}$
. We thus arrive at
 $$ \begin{align*}\begin{aligned} |\varphi(g)| &\ll_{\varepsilon} (Nk)^{\varepsilon}y^{-\varepsilon} \frac{2^{\frac{k}{2}}y^{\frac{1}{2}}}{\Gamma(k)^{\frac{1}{2}}} \left( \frac{1}{y} \Gamma\left( \frac{k+1}{2} \right) + \left(\frac{k-1}{2}\right)^{\frac{k-1}{2}+\varepsilon}e^{-\frac{k-1}{2}} \right) \\ &\ll_{\varepsilon} (Nk)^{\varepsilon} y^{-\varepsilon} \left( k^{\frac{1}{4}}y^{-\frac{1}{2}}+ k^{-\frac{1}{4}}y^{\frac{1}{2}} \right), \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} |\varphi(g)| &\ll_{\varepsilon} (Nk)^{\varepsilon}y^{-\varepsilon} \frac{2^{\frac{k}{2}}y^{\frac{1}{2}}}{\Gamma(k)^{\frac{1}{2}}} \left( \frac{1}{y} \Gamma\left( \frac{k+1}{2} \right) + \left(\frac{k-1}{2}\right)^{\frac{k-1}{2}+\varepsilon}e^{-\frac{k-1}{2}} \right) \\ &\ll_{\varepsilon} (Nk)^{\varepsilon} y^{-\varepsilon} \left( k^{\frac{1}{4}}y^{-\frac{1}{2}}+ k^{-\frac{1}{4}}y^{\frac{1}{2}} \right), \end{aligned}\end{align*} $$
where we have made use of Stirling’s approximation. If
![]() $y \ge \frac {k}{2 \pi }$
, then the maximum summand occurs when
$y \ge \frac {k}{2 \pi }$
, then the maximum summand occurs when
![]() $n=1$
and we may derive the improved bound
$n=1$
and we may derive the improved bound
 $$ \begin{align*}|\varphi(g)| &\ll_{\varepsilon} (Nk)^{\varepsilon} y^{-\varepsilon} \frac{2^{\frac{k}{2}}y^{\frac{1}{2}}}{\Gamma(k)^{\frac{1}{2}}} \left( \frac{1}{y} \Gamma\left( \frac{k+1}{2} \right) + \left(2 \pi y\right)^{\frac{k-1}{2}+\varepsilon}e^{-2 \pi y } \right) \\ & \ll_{\varepsilon} (Nk)^{\varepsilon} y^{-\varepsilon}.\\[-38pt] \end{align*} $$
$$ \begin{align*}|\varphi(g)| &\ll_{\varepsilon} (Nk)^{\varepsilon} y^{-\varepsilon} \frac{2^{\frac{k}{2}}y^{\frac{1}{2}}}{\Gamma(k)^{\frac{1}{2}}} \left( \frac{1}{y} \Gamma\left( \frac{k+1}{2} \right) + \left(2 \pi y\right)^{\frac{k-1}{2}+\varepsilon}e^{-2 \pi y } \right) \\ & \ll_{\varepsilon} (Nk)^{\varepsilon} y^{-\varepsilon}.\\[-38pt] \end{align*} $$
To deduce Equation (3.19) from the lemma, we consider separately the cases
![]() $N^{-\frac {1}{2}} \le H(g) \le \frac {k}{ 2 \pi }$
and
$N^{-\frac {1}{2}} \le H(g) \le \frac {k}{ 2 \pi }$
and
![]() $H(g) \ge \frac {k}{2 \pi }$
, applying Equation (3.20) in the former case and Equation (3.21) in the latter.
$H(g) \ge \frac {k}{2 \pi }$
, applying Equation (3.20) in the former case and Equation (3.21) in the latter.
We may now deduce the split case of Corollary 2.3, as follows. Our task is to bound
![]() $\varphi (g_1)$
suitably for
$\varphi (g_1)$
suitably for
![]() $g_1 \in [G]$
. We may assume that
$g_1 \in [G]$
. We may assume that
![]() $H(g_1) \le N^{-\frac {1}{2}}$
, as otherwise the estimates (3.18) and (3.19) are adequate. In that case, we choose another point
$H(g_1) \le N^{-\frac {1}{2}}$
, as otherwise the estimates (3.18) and (3.19) are adequate. In that case, we choose another point
![]() $g_2 \in [G]$
arbitrarily with
$g_2 \in [G]$
arbitrarily with
![]() $H(g_2) = N^{-\frac {1}{2}}$
such that
$H(g_2) = N^{-\frac {1}{2}}$
such that
![]() $|\varphi (g_2)| \preccurlyeq _{\lambda _{\varphi }} N^{\frac {1}{4}}$
, respectively
$|\varphi (g_2)| \preccurlyeq _{\lambda _{\varphi }} N^{\frac {1}{4}}$
, respectively
![]() $|\varphi (g_2)| \preccurlyeq (kN)^{\frac {1}{4}}$
, by Equation (3.18), respectively Equation (3.19). We apply Theorem 2.1 with these choices of
$|\varphi (g_2)| \preccurlyeq (kN)^{\frac {1}{4}}$
, by Equation (3.18), respectively Equation (3.19). We apply Theorem 2.1 with these choices of
![]() $g_1$
and
$g_1$
and
![]() $g_2$
. Upon recalling that
$g_2$
. Upon recalling that
![]() $d_B=1$
in the split case, we find by positivity that Equation (2.4), respectively Equation (2.5), yield
$d_B=1$
in the split case, we find by positivity that Equation (2.4), respectively Equation (2.5), yield
 $$ \begin{align*} \left| |\varphi(g_1)|^2- |\varphi(g_2)|^2 \right| &\preccurlyeq_{\lambda_{\varphi}} N^{\frac{1}{2}}, \quad \text{respectively} \\ \left| |\varphi(g_1)|^2- |\varphi(g_2)|^2 \right| &\preccurlyeq (kN)^{\frac{1}{2}}. \end{align*} $$
$$ \begin{align*} \left| |\varphi(g_1)|^2- |\varphi(g_2)|^2 \right| &\preccurlyeq_{\lambda_{\varphi}} N^{\frac{1}{2}}, \quad \text{respectively} \\ \left| |\varphi(g_1)|^2- |\varphi(g_2)|^2 \right| &\preccurlyeq (kN)^{\frac{1}{2}}. \end{align*} $$
We conclude by the triangle inequality and taking square roots:
4. Arithmetic quotients as real manifolds
4.1. Measure normalizations
For indefinite B, we fix an isomorphism
![]() $G(\mathbb {R})\cong \operatorname {PGL}_2(\mathbb {R})$
sending
$G(\mathbb {R})\cong \operatorname {PGL}_2(\mathbb {R})$
sending
![]() $K_\infty $
to
$K_\infty $
to
![]() $\operatorname {PSO}_2(\mathbb {R})$
. We fix the Haar measure
$\operatorname {PSO}_2(\mathbb {R})$
. We fix the Haar measure
![]() $\,\mathrm {d} g = \frac {\,\mathrm {d} y \,\mathrm {d} x}{y^2}\frac {\,\mathrm {d} \theta }{2 \pi }$
for
$\,\mathrm {d} g = \frac {\,\mathrm {d} y \,\mathrm {d} x}{y^2}\frac {\,\mathrm {d} \theta }{2 \pi }$
for
![]() $g=\left (\begin {smallmatrix} y^{1/2} & xy^{-1/2} \\ 0 & y^{-1/2} \end {smallmatrix}\right ) \kappa (\theta )$
on
$g=\left (\begin {smallmatrix} y^{1/2} & xy^{-1/2} \\ 0 & y^{-1/2} \end {smallmatrix}\right ) \kappa (\theta )$
on
![]() $\operatorname {SL}_2(\mathbb {R})$
. The push-forward of this measure to the hyperbolic plane
$\operatorname {SL}_2(\mathbb {R})$
. The push-forward of this measure to the hyperbolic plane ![]() is then the measure
is then the measure
![]() $\frac {\,\mathrm {d} x \,\mathrm {d} y}{y^2}$
. The Haar measure on
$\frac {\,\mathrm {d} x \,\mathrm {d} y}{y^2}$
. The Haar measure on
![]() $\operatorname {PGL}_2(\mathbb {R})$
is fixed so that its restriction to
$\operatorname {PGL}_2(\mathbb {R})$
is fixed so that its restriction to
![]() $\operatorname {PSL}_2(\mathbb {R})$
coincides with the push-forward of the Haar measure from
$\operatorname {PSL}_2(\mathbb {R})$
coincides with the push-forward of the Haar measure from
![]() $\operatorname {SL}_2(\mathbb {R})$
.
$\operatorname {SL}_2(\mathbb {R})$
.
If B is definite, we fix an isomorphism
![]() $G(\mathbb {R})\cong \operatorname {SO}_3(\mathbb {R})$
sending
$G(\mathbb {R})\cong \operatorname {SO}_3(\mathbb {R})$
sending
![]() $K_\infty $
to
$K_\infty $
to
![]() $\operatorname {SO}_2(\mathbb {R})$
. We fix a Haar measure on
$\operatorname {SO}_2(\mathbb {R})$
. We fix a Haar measure on
![]() $\operatorname {SO}_3(\mathbb {R})$
so that the measure of the
$\operatorname {SO}_3(\mathbb {R})$
so that the measure of the
![]() $2$
-sphere
$2$
-sphere ![]() is
is
![]() $4\pi $
.
$4\pi $
.
4.2. Volumes
Recall, that we fixed the measure on
![]() $[G]$
to be the probability Haar measure. Hence, the volume of the quotient
$[G]$
to be the probability Haar measure. Hence, the volume of the quotient
![]() $[G]/K_R$
is
$[G]/K_R$
is
![]() $1$
. In due course, we shall also require the volume of said quotient when viewed as a real manifold with respect to our fixed Haar measure on
$1$
. In due course, we shall also require the volume of said quotient when viewed as a real manifold with respect to our fixed Haar measure on
![]() $G(\mathbb {R})$
. More specifically, we will need the volume with respect to the measure on
$G(\mathbb {R})$
. More specifically, we will need the volume with respect to the measure on
![]() $G'(\mathbb {R})$
, where
$G'(\mathbb {R})$
, where
![]() $G'$
is the linear algebraic group defined over
$G'$
is the linear algebraic group defined over
![]() $\mathbb {Q}$
whose rational points are the proper unit quaternions
$\mathbb {Q}$
whose rational points are the proper unit quaternions
![]() $B^1$
. There is an obvious isogeny map
$B^1$
. There is an obvious isogeny map
![]() $G'\to G$
, where
$G'\to G$
, where
![]() $G'$
is the simply connected form and G is the adjoint one. Define
$G'$
is the simply connected form and G is the adjoint one. Define
![]() $R_p^1=R_p\cap G'(\mathbb {Q}_p)$
to be the proper unit quaternions in the local order
$R_p^1=R_p\cap G'(\mathbb {Q}_p)$
to be the proper unit quaternions in the local order
![]() $R_p$
, and set
$R_p$
, and set
![]() $K_R^1=\prod _{p} R_p^1$
. Then, the map
$K_R^1=\prod _{p} R_p^1$
. Then, the map
![]() $[G']/K_R^{1}\to [G]/K_R$
is a homeomorphism that pushes forward the probability Haar measure on
$[G']/K_R^{1}\to [G]/K_R$
is a homeomorphism that pushes forward the probability Haar measure on
![]() $[G']/K_R^{1}$
to the probability Haar measure on
$[G']/K_R^{1}$
to the probability Haar measure on
![]() $[G]/K_R$
; see Lemma A.2. In general, this map is not bijective if
$[G]/K_R$
; see Lemma A.2. In general, this map is not bijective if
![]() $K_R$
is replaced by a general compact open subgroup of
$K_R$
is replaced by a general compact open subgroup of
![]() $G(\mathbb {A}_f)$
and the fact that the map is indeed a homeomorphism is due to
$G(\mathbb {A}_f)$
and the fact that the map is indeed a homeomorphism is due to
![]() $K_R$
being the projectivized group of units of an Eichler order.
$K_R$
being the projectivized group of units of an Eichler order.
By Borel’s finiteness of class numbers [Reference BorelBor63],
![]() $[G']/K_R^1$
is a finite collection of
$[G']/K_R^1$
is a finite collection of
![]() $G'(\mathbb {R})$
-orbits with representatives
$G'(\mathbb {R})$
-orbits with representatives
![]() $\delta _1,\ldots ,\delta _h\in G'(\mathbb {A})$
. Define
$\delta _1,\ldots ,\delta _h\in G'(\mathbb {A})$
. Define
![]() $\Gamma _i=G'(\mathbb {Q})\cap \delta _i K_R^1 \delta _i^{-1}$
; the intersection is taken in
$\Gamma _i=G'(\mathbb {Q})\cap \delta _i K_R^1 \delta _i^{-1}$
; the intersection is taken in
![]() $G'(\mathbb {A}_f)$
but regarded as a subset of
$G'(\mathbb {A}_f)$
but regarded as a subset of
![]() $G'(\mathbb {Q})$
and hence also of
$G'(\mathbb {Q})$
and hence also of
![]() $G'(\mathbb {R})$
. In particular,
$G'(\mathbb {R})$
. In particular,
![]() $\Gamma _i$
is a lattice in
$\Gamma _i$
is a lattice in
![]() $G'(\mathbb {R})$
. It follows that
$G'(\mathbb {R})$
. It follows that
 $$ \begin{align*} [G]/K_R\cong [G']/K_R^{1}=\bigsqcup_{i=1}^h {\Gamma_i}\backslash{G'(\mathbb{R})}. \end{align*} $$
$$ \begin{align*} [G]/K_R\cong [G']/K_R^{1}=\bigsqcup_{i=1}^h {\Gamma_i}\backslash{G'(\mathbb{R})}. \end{align*} $$
This is a finite disjoint union of finite-volume homogeneous spaces for the real Lie group
![]() $G'(\mathbb {R})$
. We define
$G'(\mathbb {R})$
. We define
![]() $\operatorname {covol}(\Gamma _i)$
to be the measure of a fundamental domain for the action of
$\operatorname {covol}(\Gamma _i)$
to be the measure of a fundamental domain for the action of
![]() $\Gamma _i$
on
$\Gamma _i$
on
![]() $G'(\mathbb {R})$
with respect to the fixed Haar measure on
$G'(\mathbb {R})$
with respect to the fixed Haar measure on
![]() $G'(\mathbb {R})$
, either
$G'(\mathbb {R})$
, either
![]() $\frac {\,\mathrm {d} x \,\mathrm {d} y}{y^2} \frac {\,\mathrm {d} \theta }{2\pi }$
in the indefinite case or the measure giving volume
$\frac {\,\mathrm {d} x \,\mathrm {d} y}{y^2} \frac {\,\mathrm {d} \theta }{2\pi }$
in the indefinite case or the measure giving volume
![]() $4\pi $
to
$4\pi $
to ![]() in the definite case. We finally set
in the definite case. We finally set
 $$ \begin{align*} V = V_{d_B,N}=\sum_{i=1}^h \operatorname{covol}(\Gamma_i). \end{align*} $$
$$ \begin{align*} V = V_{d_B,N}=\sum_{i=1}^h \operatorname{covol}(\Gamma_i). \end{align*} $$
If B is indefinite, then
![]() $G'(\mathbb {R})\cong \operatorname {SL}_2(\mathbb {R})$
is noncompact and strong approximation implies that
$G'(\mathbb {R})\cong \operatorname {SL}_2(\mathbb {R})$
is noncompact and strong approximation implies that
![]() $h=1$
and we can write
$h=1$
and we can write
![]() $[G]/K_R\cong \Gamma \backslash \operatorname {SL}_2(\mathbb {R})$
. In this case, V is the volume of the hyperbolic surface
$[G]/K_R\cong \Gamma \backslash \operatorname {SL}_2(\mathbb {R})$
. In this case, V is the volume of the hyperbolic surface ![]() with respect to the volume form
with respect to the volume form
![]() $\frac {\,\mathrm {d} x \,\mathrm {d} y}{y^2}$
. If B is definite, then in general h can be large and
$\frac {\,\mathrm {d} x \,\mathrm {d} y}{y^2}$
. If B is definite, then in general h can be large and
![]() $[G]/K_\infty K_R$
is a finite collection of quotients of
$[G]/K_\infty K_R$
is a finite collection of quotients of
![]() $2$
-spheres by discrete rotation groups.
$2$
-spheres by discrete rotation groups.
Recall that we have denoted by
![]() $d_B$
the reduced discriminant of B and by N the squarefree level of the Eichler order R. The volume is given in both cases by
$d_B$
the reduced discriminant of B and by N the squarefree level of the Eichler order R. The volume is given in both cases by
 $$ \begin{align} V = V_{d_B,N} = \frac{\pi}{3} d_BN \prod_{p | d_B} \left(1-\frac{1}{p}\right) \prod_{p | N} \left(1+\frac{1}{p} \right) = (d_BN)^{1+o(1)}. \end{align} $$
$$ \begin{align} V = V_{d_B,N} = \frac{\pi}{3} d_BN \prod_{p | d_B} \left(1-\frac{1}{p}\right) \prod_{p | N} \left(1+\frac{1}{p} \right) = (d_BN)^{1+o(1)}. \end{align} $$
This follows from a corresponding mass formula; see [Reference VoightVoi18, Thm 39.1.8] in the indefinite case and [Reference VoightVoi18, Thm 25.1.1 & Thm 25.3.18] in the definite one. The space is furthermore compact if and only if B nonsplit, that is,
![]() $d_B> 1$
.
$d_B> 1$
.
4.3. Siegel domains
The main purpose of this section is to provide a specific Siegel-domain covering in order to bound the
![]() $L^2$
-norm of the (difference of) theta kernels in §5.2. Let M be a squarefree natural number and set
$L^2$
-norm of the (difference of) theta kernels in §5.2. Let M be a squarefree natural number and set
![]() $U = \left (\begin {smallmatrix} \widehat {\mathbb {Z}} & \widehat {\mathbb {Z}} \\ M \widehat {\mathbb {Z}} & \widehat {\mathbb {Z}} \end {smallmatrix}\right ) \cap \operatorname {\mathrm {SL}}_{2}(\mathbb {A}_f)$
. The theta functions of interest will turn out to be right invariant in the symplectic variable under U with
$U = \left (\begin {smallmatrix} \widehat {\mathbb {Z}} & \widehat {\mathbb {Z}} \\ M \widehat {\mathbb {Z}} & \widehat {\mathbb {Z}} \end {smallmatrix}\right ) \cap \operatorname {\mathrm {SL}}_{2}(\mathbb {A}_f)$
. The theta functions of interest will turn out to be right invariant in the symplectic variable under U with
![]() $M = d_B N$
, but the present discussion applies to any squarefree M.
$M = d_B N$
, but the present discussion applies to any squarefree M.
4.3.1. Cusps and Atkin–Lehner operators
Since M is squarefree, a representative set of cusps for
![]() $\Gamma _0(M)$
is given by the ratios
$\Gamma _0(M)$
is given by the ratios
![]() $\frac {\ell }{M}$
, where
$\frac {\ell }{M}$
, where
![]() $\ell $
runs through the positive divisors of M. The width of the cusp
$\ell $
runs through the positive divisors of M. The width of the cusp
![]() $\frac {\ell }{M}$
(understood here as with respect to the group
$\frac {\ell }{M}$
(understood here as with respect to the group
![]() $\Gamma _0(M)$
) is given by
$\Gamma _0(M)$
) is given by
![]() $\ell $
[Reference IwaniecIwa97, §2.4]. For each
$\ell $
[Reference IwaniecIwa97, §2.4]. For each
![]() $\ell |M$
, we choose an element
$\ell |M$
, we choose an element
![]() $\tau _{\ell } \in \operatorname {\mathrm {SL}}_2(\mathbb {Z})$
satisfying
$\tau _{\ell } \in \operatorname {\mathrm {SL}}_2(\mathbb {Z})$
satisfying
 $$ \begin{align} \tau_{\ell} \equiv \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \mathrm{mod}\,{\ell}, \quad \tau_{\ell} \equiv \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \mathrm{mod}\,{ M / \ell}. \end{align} $$
$$ \begin{align} \tau_{\ell} \equiv \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix} \mathrm{mod}\,{\ell}, \quad \tau_{\ell} \equiv \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \mathrm{mod}\,{ M / \ell}. \end{align} $$
Then, the cusp
![]() $\tau _{\ell } \infty $
is
$\tau _{\ell } \infty $
is
![]() $\Gamma _0(M)$
-equivalent to the cusp
$\Gamma _0(M)$
-equivalent to the cusp
![]() $\frac {\ell }{M}$
. Hence, writing
$\frac {\ell }{M}$
. Hence, writing
![]() $n(x)=\left (\begin {smallmatrix} 1 & x\\ & 1 \end {smallmatrix}\right )$
, we see that the elements
$n(x)=\left (\begin {smallmatrix} 1 & x\\ & 1 \end {smallmatrix}\right )$
, we see that the elements
![]() $\tau _{\ell }n(j)$
, where
$\tau _{\ell }n(j)$
, where
![]() $j=0,\dots ,\ell -1$
and
$j=0,\dots ,\ell -1$
and
![]() $\ell |M$
, give a complete system of representatives for
$\ell |M$
, give a complete system of representatives for
![]() $\Gamma _0(M) \backslash \operatorname {\mathrm {SL}}_{2}(\mathbb {Z})$
. The normalized matrices
$\Gamma _0(M) \backslash \operatorname {\mathrm {SL}}_{2}(\mathbb {Z})$
. The normalized matrices ![]() , where
, where
![]() $a(y)= \operatorname {\mathrm {diag}}(y^{\frac {1}{2}},y^{-\frac {1}{2}})$
, are scaling matrices for the respective cusps. Furthermore, the matrices
$a(y)= \operatorname {\mathrm {diag}}(y^{\frac {1}{2}},y^{-\frac {1}{2}})$
, are scaling matrices for the respective cusps. Furthermore, the matrices
![]() $\tilde {\tau _{\ell }}$
are Atkin–Lehner operators for
$\tilde {\tau _{\ell }}$
are Atkin–Lehner operators for
![]() $\Gamma _0(M)$
and give a set of representatives for
$\Gamma _0(M)$
and give a set of representatives for
![]() $A_0(M) / \Gamma _0(M)$
[Reference Atkin and LehnerAL70, Lemma 9].
$A_0(M) / \Gamma _0(M)$
[Reference Atkin and LehnerAL70, Lemma 9].
4.3.2. Coverings
The basic idea of the following lemma is to apply the Fricke involution to the tiling of
![]() $\Gamma _0(M) \backslash \mathbb {H}$
by translates of the standard fundamental domain for
$\Gamma _0(M) \backslash \mathbb {H}$
by translates of the standard fundamental domain for
![]() $\operatorname {\mathrm {SL}}_2(\mathbb {Z}) \backslash \mathbb {H}$
.
$\operatorname {\mathrm {SL}}_2(\mathbb {Z}) \backslash \mathbb {H}$
.
Lemma 4.1. Let
![]() $F : [\operatorname {\mathrm {SL}}_2] \rightarrow \mathbb {R}_{\ge 0}$
be a measurable function that is right U invariant and of weight
$F : [\operatorname {\mathrm {SL}}_2] \rightarrow \mathbb {R}_{\ge 0}$
be a measurable function that is right U invariant and of weight
![]() $0$
. Then,
$0$
. Then,
 $$ \begin{align*} \int_{[\operatorname{\mathrm{SL}}_2]} F(g) dg \le \frac{1}{V_{1,M}} \sum_{\ell|M} \int_{\frac{\sqrt{3}}{2} \frac{l^2}{M}}^{\infty} \int_0^{\ell} F \left( (\tau_{\ell})_{\infty} \left(\begin{smallmatrix} y^{1/2} & x y^{-1/2} \\ & y^{-1/2} \end{smallmatrix}\right) K_{\infty} U) \right) dx \frac{dy}{y^2}. \end{align*} $$
$$ \begin{align*} \int_{[\operatorname{\mathrm{SL}}_2]} F(g) dg \le \frac{1}{V_{1,M}} \sum_{\ell|M} \int_{\frac{\sqrt{3}}{2} \frac{l^2}{M}}^{\infty} \int_0^{\ell} F \left( (\tau_{\ell})_{\infty} \left(\begin{smallmatrix} y^{1/2} & x y^{-1/2} \\ & y^{-1/2} \end{smallmatrix}\right) K_{\infty} U) \right) dx \frac{dy}{y^2}. \end{align*} $$
Here,
![]() $(\tau )_{\infty }$
denotes the image of
$(\tau )_{\infty }$
denotes the image of
![]() $\tau $
in the Archimedean coordinate of
$\tau $
in the Archimedean coordinate of
![]() $\operatorname {\mathrm {SL}}_{2}(\mathbb {A})$
.
$\operatorname {\mathrm {SL}}_{2}(\mathbb {A})$
.
Proof. Let
![]() $f: \mathbb {H} \to \mathbb {R}_{\ge 0}$
be given by
$f: \mathbb {H} \to \mathbb {R}_{\ge 0}$
be given by
Then, f is
![]() $\Gamma _0(M)$
invariant on the left and we have
$\Gamma _0(M)$
invariant on the left and we have
 $$ \begin{align*} \int_{[\operatorname{\mathrm{SL}}_2]} F(g) dg = \frac{1}{V_{1,M}} \int_{\Gamma_0(M)\backslash \mathbb{H}} f(z) \frac{dxdy}{y^2} = \frac{1}{V_{1,M}} \int_{\Gamma_0(M)\backslash \mathbb{H}} f( \tilde \tau_{M}z) \frac{dxdy}{y^2}. \end{align*} $$
$$ \begin{align*} \int_{[\operatorname{\mathrm{SL}}_2]} F(g) dg = \frac{1}{V_{1,M}} \int_{\Gamma_0(M)\backslash \mathbb{H}} f(z) \frac{dxdy}{y^2} = \frac{1}{V_{1,M}} \int_{\Gamma_0(M)\backslash \mathbb{H}} f( \tilde \tau_{M}z) \frac{dxdy}{y^2}. \end{align*} $$
The standard Siegel set
![]() $\{z \in \mathbb {H} | \ 0\le \Re (x)\le 1 \text { and } \Im (z) \ge \frac {\sqrt {3}}{2}\}$
contains a fundamental domain for
$\{z \in \mathbb {H} | \ 0\le \Re (x)\le 1 \text { and } \Im (z) \ge \frac {\sqrt {3}}{2}\}$
contains a fundamental domain for
![]() $\operatorname {\mathrm {SL}}_2({\mathbb {Z}})$
. Using that the
$\operatorname {\mathrm {SL}}_2({\mathbb {Z}})$
. Using that the
![]() $\tau _{\ell }n(j)$
, for
$\tau _{\ell }n(j)$
, for
![]() $j=0,\dots ,\ell -1$
and
$j=0,\dots ,\ell -1$
and
![]() $\ell |M$
, form a representative set for
$\ell |M$
, form a representative set for
![]() $\Gamma _0(M) \backslash \operatorname {\mathrm {SL}}_2(\mathbb {Z})$
and that f is nonnegative, we may bound
$\Gamma _0(M) \backslash \operatorname {\mathrm {SL}}_2(\mathbb {Z})$
and that f is nonnegative, we may bound
 $$ \begin{align*}\int_{\Gamma_0(M)\backslash \mathbb{H}} f( \tilde \tau_{M}z) \frac{dxdy}{y^2} \le \sum_{\ell|M} \int_{\frac{\sqrt{3}}{2}}^{\infty} \int_0^{\ell} f( \tilde{\tau}_{M}\tau_{\ell} z) dx \frac{dy}{y^2}. \end{align*} $$
$$ \begin{align*}\int_{\Gamma_0(M)\backslash \mathbb{H}} f( \tilde \tau_{M}z) \frac{dxdy}{y^2} \le \sum_{\ell|M} \int_{\frac{\sqrt{3}}{2}}^{\infty} \int_0^{\ell} f( \tilde{\tau}_{M}\tau_{\ell} z) dx \frac{dy}{y^2}. \end{align*} $$
Since
![]() $\tilde {\tau }_{M} \tilde {\tau }_{\ell } = \gamma \tilde {\tau }_{\frac {M}{\ell }}$
for some
$\tilde {\tau }_{M} \tilde {\tau }_{\ell } = \gamma \tilde {\tau }_{\frac {M}{\ell }}$
for some
![]() $\gamma \in \Gamma _0(M)$
, we have the identity
$\gamma \in \Gamma _0(M)$
, we have the identity
Substituting this identity above and applying the change of variables
![]() $\frac {M}{l^2}z \mapsto z$
gives the desired result.
$\frac {M}{l^2}z \mapsto z$
gives the desired result.
5. Theta kernels and their
 $L^2$
-norms
$L^2$
-norms
5.1. Theta kernels and lifts
In this section, we summarize the required results on theta kernels and their lifts. The necessary theory is developed in Appendix A.
5.1.1. Theta functions
The theta kernels constructed in Appendix A are modular functions on
![]() $\operatorname {O}_{\det }(\mathbb {A})\times \operatorname {\mathrm {SL}}_2(\mathbb {A})$
. The group G acts by conjugation on the quadratic space
$\operatorname {O}_{\det }(\mathbb {A})\times \operatorname {\mathrm {SL}}_2(\mathbb {A})$
. The group G acts by conjugation on the quadratic space
![]() $(B,\det )$
, preserving the quadratic form. This gives an embedding
$(B,\det )$
, preserving the quadratic form. This gives an embedding
![]() $G\hookrightarrow \operatorname {O}_{\det }$
. We are mainly concerned here with the pullback of the theta kernels to
$G\hookrightarrow \operatorname {O}_{\det }$
. We are mainly concerned here with the pullback of the theta kernels to
![]() $G(\mathbb {A})\times \operatorname {\mathrm {SL}}_2(\mathbb {A})$
. We denote that pullback by
$G(\mathbb {A})\times \operatorname {\mathrm {SL}}_2(\mathbb {A})$
. We denote that pullback by
![]() $\Theta (g,s)$
. The function
$\Theta (g,s)$
. The function
![]() $\Theta (g,s)$
is right
$\Theta (g,s)$
is right
![]() $K_R \times U_R^1$
invariant, where
$K_R \times U_R^1$
invariant, where ![]() and of moderate growth. We caution that it is not a theta kernel for the Howe dual pair of the orthogonal group of the traceless quaternions and
and of moderate growth. We caution that it is not a theta kernel for the Howe dual pair of the orthogonal group of the traceless quaternions and
![]() $\operatorname {\mathrm {SL}}_2$
.
$\operatorname {\mathrm {SL}}_2$
.
We shall require several explicit expressions of the theta kernels
![]() $\Theta $
. Define functions
$\Theta $
. Define functions
![]() $P, u, X$
on
$P, u, X$
on
![]() $B_\infty $
by setting, for
$B_\infty $
by setting, for
![]() $\gamma = [a,b,c] + d \in B_\infty $
,
$\gamma = [a,b,c] + d \in B_\infty $
,
In other words, by identifying
![]() ${\mathbf{i}} \in B_{\infty }$
with
${\mathbf{i}} \in B_{\infty }$
with
![]() $i \in \mathbb {C}$
, we have that
$i \in \mathbb {C}$
, we have that
-
∘ X is the projection from
 $B_\infty = \mathbb {C} \oplus \mathbb {C} {\mathbf{j}} $
to the summand
$B_\infty = \mathbb {C} \oplus \mathbb {C} {\mathbf{j}} $
to the summand
 $\mathbb {C}$
,
$\mathbb {C}$
, -
∘ u is the squared magnitude of the projection onto the other summand
 $\mathbb {C} {\mathbf{j}} $
and
$\mathbb {C} {\mathbf{j}} $
and -
∘ P is the sum of the squared magnitudes of the two projections.
Upon recalling the notation
![]() $R(\ell ;g)$
from Section §3.1, we define for
$R(\ell ;g)$
from Section §3.1, we define for
![]() $g \in G(\mathbb {A})$
and
$g \in G(\mathbb {A})$
and
![]() $z=x+iy \in \mathbb {H}$
the theta functions
$z=x+iy \in \mathbb {H}$
the theta functions

if
![]() $k \ge 6$
$k \ge 6$



where
![]() $P_{m}$
is the m-th Legendre polynomial. When
$P_{m}$
is the m-th Legendre polynomial. When
![]() $\ell = 1$
, we abbreviate by dropping the subscript, for example,
$\ell = 1$
, we abbreviate by dropping the subscript, for example, ![]() . We are now ready to express
. We are now ready to express
![]() $\Theta $
by means of strong approximation. Set
$\Theta $
by means of strong approximation. Set
Then,
![]() $\Theta (g, s_{\infty }U_R^1) = \theta _g(z) e^{i \kappa \theta }$
for some
$\Theta (g, s_{\infty }U_R^1) = \theta _g(z) e^{i \kappa \theta }$
for some
![]() $\kappa \in 2\mathbb {Z}$
and a choice of
$\kappa \in 2\mathbb {Z}$
and a choice of
![]() $\theta _{g}$
from Equations (5.2)–(5.5). The precise choice and value of
$\theta _{g}$
from Equations (5.2)–(5.5). The precise choice and value of
![]() $\kappa $
depends on the family
$\kappa $
depends on the family
![]() $\mathcal {G}$
under consideration and may be read off Table 1. (For our study of
$\mathcal {G}$
under consideration and may be read off Table 1. (For our study of
![]() $\mathcal {F}^{-,\operatorname {hol}}$
, the precise choice of
$\mathcal {F}^{-,\operatorname {hol}}$
, the precise choice of
![]() $\Theta $
depends upon the size of k.)
$\Theta $
depends upon the size of k.)
Table 1 Families and the choice of
![]() $\Theta $
.
$\Theta $
.

Antipating the application of Lemma 4.1, we further require Fourier–Whittaker expansions of
![]() $\Theta $
at all of the cusps. They are expressable in terms of the
$\Theta $
at all of the cusps. They are expressable in terms of the
![]() $\theta _{g,\ell }$
from Equations (5.2)–(5.5) and a weight
$\theta _{g,\ell }$
from Equations (5.2)–(5.5) and a weight
![]() $\kappa $
, the choice of which are given by the Table 1 as before. We have
$\kappa $
, the choice of which are given by the Table 1 as before. We have
for
![]() $\ell | d_B N$
with
$\ell | d_B N$
with
![]() $\mu $
the Möbius function,
$\mu $
the Möbius function,
![]() $\tau _{\ell }$
as in Equation (4.2), and where
$\tau _{\ell }$
as in Equation (4.2), and where
![]() $(\tau _{\ell })_{\infty }$
denotes the image of
$(\tau _{\ell })_{\infty }$
denotes the image of
![]() $\tau _{\ell }$
in the Archimedean coordinate of
$\tau _{\ell }$
in the Archimedean coordinate of
![]() $\operatorname {\mathrm {SL}}_{2}(\mathbb {A})$
.
$\operatorname {\mathrm {SL}}_{2}(\mathbb {A})$
.
5.1.2. Jacquet–Langlands lifts
Set
![]() $U_R$
to be the image of
$U_R$
to be the image of
in
![]() $\operatorname {PGL}_2(\mathbb {A}_f)$
. This is a compact open subgroup of
$\operatorname {PGL}_2(\mathbb {A}_f)$
. This is a compact open subgroup of
![]() $\operatorname {PGL}_2(\mathbb {A}_f)$
. For each
$\operatorname {PGL}_2(\mathbb {A}_f)$
. For each
![]() $\varphi $
in the families
$\varphi $
in the families
![]() $\mathcal {F}^{-}, \mathcal {F}^{-,\operatorname {hol}}, \mathcal {F}^{+}_m, \mathcal {F}^{+,\operatorname {hol}}$
, we consider the Jacquet–Langlands transfer
$\mathcal {F}^{-}, \mathcal {F}^{-,\operatorname {hol}}, \mathcal {F}^{+}_m, \mathcal {F}^{+,\operatorname {hol}}$
, we consider the Jacquet–Langlands transfer
![]() $\pi ^{\operatorname {\mathrm {JL}}}$
to
$\pi ^{\operatorname {\mathrm {JL}}}$
to
![]() $[\operatorname {PGL}_2]$
of the representation
$[\operatorname {PGL}_2]$
of the representation
![]() $\pi $
generated by
$\pi $
generated by
![]() $\varphi $
. In the case that G is split, we let
$\varphi $
. In the case that G is split, we let
![]() $\pi ^{\operatorname {\mathrm {JL}}}=\pi $
. The space of vectors in
$\pi ^{\operatorname {\mathrm {JL}}}=\pi $
. The space of vectors in
![]() $\pi ^{\operatorname {\mathrm {JL}}}$
that are
$\pi ^{\operatorname {\mathrm {JL}}}$
that are
![]() $U_R$
-invariant and
$U_R$
-invariant and
![]() $K_{\infty }$
-isotypical of minimal nonnegative weight is one-dimensional [Reference Jacquet and LanglandsJL70, Reference CasselmanCas73]. We define the arithmetically normalized Jacquet–Langlands lift
$K_{\infty }$
-isotypical of minimal nonnegative weight is one-dimensional [Reference Jacquet and LanglandsJL70, Reference CasselmanCas73]. We define the arithmetically normalized Jacquet–Langlands lift
![]() $\varphi ^{\operatorname {\mathrm {JL}}}\in L^2([\operatorname {\mathrm {SL}}_2])$
of
$\varphi ^{\operatorname {\mathrm {JL}}}\in L^2([\operatorname {\mathrm {SL}}_2])$
of
![]() $\varphi $
to be the
$\varphi $
to be the
![]() $U_R^1$
-invariant restrictionFootnote 3 to
$U_R^1$
-invariant restrictionFootnote 3 to
![]() $[\operatorname {\mathrm {SL}}_2]$
of a vector in this one-dimensional space, that has a Whittaker function at
$[\operatorname {\mathrm {SL}}_2]$
of a vector in this one-dimensional space, that has a Whittaker function at
![]() $\left (\begin {smallmatrix} y^{1/2} & xy^{-1/2} \\ & y^{-1/2} \end {smallmatrix}\right ) \in \operatorname {\mathrm {SL}}_2(\mathbb {R}) \hookrightarrow \operatorname {\mathrm {SL}}_2(\mathbb {A})$
given by
$\left (\begin {smallmatrix} y^{1/2} & xy^{-1/2} \\ & y^{-1/2} \end {smallmatrix}\right ) \in \operatorname {\mathrm {SL}}_2(\mathbb {R}) \hookrightarrow \operatorname {\mathrm {SL}}_2(\mathbb {A})$
given by
-
∘
 $2 \sqrt {y} K_{it}(2 \pi y)e(x) \text { if } \varphi \in \mathcal {F}^{-}_{\frac {1}{4}+t^2}$
, and
$2 \sqrt {y} K_{it}(2 \pi y)e(x) \text { if } \varphi \in \mathcal {F}^{-}_{\frac {1}{4}+t^2}$
, and -
∘
 $y^{\frac {\kappa }{2}} e(x+iy)$
if
$y^{\frac {\kappa }{2}} e(x+iy)$
if
 $\varphi $
is in either of the families
$\varphi $
is in either of the families
 $\mathcal {F}^{-,\operatorname {hol}}$
,
$\mathcal {F}^{-,\operatorname {hol}}$
,
 $ \mathcal {F}^{+}_m$
,
$ \mathcal {F}^{+}_m$
,
 $\mathcal {F}^{+,\operatorname {hol}}$
, where
$\mathcal {F}^{+,\operatorname {hol}}$
, where
 $\kappa =k$
,
$\kappa =k$
,
 $2m+2$
,
$2m+2$
,
 $k+2$
depends on the family as before.
$k+2$
depends on the family as before.
The bounds by Hoffstein–Lockhart [Reference Hoffstein and LockhartHL94] and Iwaniec [Reference IwaniecIwa90] then imply the following bounds for the
![]() $L^2$
-norm of the arithmetically normalized Jacquet–Langlands lift (cf. [Reference Harcos and MichelHM06, (30), (31)]Footnote 4). One may also compare with the geometric normalization in [Reference Petrow and YoungPY19, Thm. 6.1]. If B is indefinite and
$L^2$
-norm of the arithmetically normalized Jacquet–Langlands lift (cf. [Reference Harcos and MichelHM06, (30), (31)]Footnote 4). One may also compare with the geometric normalization in [Reference Petrow and YoungPY19, Thm. 6.1]. If B is indefinite and
![]() $\varphi \in \mathcal {F}^{-}_{\frac {1}{4}+t^2}$
, we have
$\varphi \in \mathcal {F}^{-}_{\frac {1}{4}+t^2}$
, we have
In the other cases, that is, when
![]() $\varphi $
lies in either of the families
$\varphi $
lies in either of the families
![]() $\mathcal {F}^{-,\operatorname {hol}}$
,
$\mathcal {F}^{-,\operatorname {hol}}$
,
![]() $ \mathcal {F}^{+}_m$
or
$ \mathcal {F}^{+}_m$
or
![]() $\mathcal {F}^{+,\operatorname {hol}}$
, we have
$\mathcal {F}^{+,\operatorname {hol}}$
, we have
where
![]() $\kappa $
depends on the family in accord with Table 1.
$\kappa $
depends on the family in accord with Table 1.
5.1.3. Explicit theta lifting
The key identity is summarized in the following proposition.
Proposition 5.1. Let
![]() $g \in [G]$
. Let
$g \in [G]$
. Let
![]() $\mathcal {G}$
,
$\mathcal {G}$
,
![]() $\Theta $
and
$\Theta $
and
![]() $\kappa $
according to Table 1. Then, for
$\kappa $
according to Table 1. Then, for
![]() $\varphi \in \mathcal {G}$
, we have
$\varphi \in \mathcal {G}$
, we have
 $$ \begin{align} \frac { \langle \Theta(g,\cdot), \varphi^{ \operatorname{\mathrm{JL}}} \rangle } { \langle \varphi^{\operatorname{\mathrm{JL}}}, \varphi^{\operatorname{\mathrm{JL}}} \rangle } = \frac{|\varphi(g)|^2}{V_{d_B,N}}. \end{align} $$
$$ \begin{align} \frac { \langle \Theta(g,\cdot), \varphi^{ \operatorname{\mathrm{JL}}} \rangle } { \langle \varphi^{\operatorname{\mathrm{JL}}}, \varphi^{\operatorname{\mathrm{JL}}} \rangle } = \frac{|\varphi(g)|^2}{V_{d_B,N}}. \end{align} $$
Proof. The proof is carried out in the appendix. In short, Proposition A.16 implies that for
![]() $\varphi \in \mathcal {G}$
, the theta lift
$\varphi \in \mathcal {G}$
, the theta lift
![]() $\varphi _{\Phi }$
of
$\varphi _{\Phi }$
of
![]() $\varphi $
– defined in Equation (A.5), depending upon the precise family
$\varphi $
– defined in Equation (A.5), depending upon the precise family
![]() $\mathcal {G}$
– satisfies
$\mathcal {G}$
– satisfies
![]() $\varphi _{\Phi }=(V_{d_B,N})^{-1}\varphi ^{\mathrm {JL}}$
. The claim then follows from Propositions A.15 and A.12.
$\varphi _{\Phi }=(V_{d_B,N})^{-1}\varphi ^{\mathrm {JL}}$
. The claim then follows from Propositions A.15 and A.12.
5.2.
 $L^2$
-norms of theta kernels
$L^2$
-norms of theta kernels
5.2.1. Proofs of Propositions 3.2 through 3.5
The proofs are similar, so we discuss the first in detail and then explain the nonoverlapping parts of the rest. Recall the notation
![]() $\preccurlyeq $
from §2.3. We denote by
$\preccurlyeq $
from §2.3. We denote by
![]() $\Theta ^-, \Theta ^{-,\operatorname {hol}}, \Theta ^{+,m}, \Theta ^{+,\operatorname {hol}}$
the various functions ‘
$\Theta ^-, \Theta ^{-,\operatorname {hol}}, \Theta ^{+,m}, \Theta ^{+,\operatorname {hol}}$
the various functions ‘
![]() $\Theta $
’ defined as in §5.1.1.
$\Theta $
’ defined as in §5.1.1.
Proof of Proposition 3.2.
Let
![]() $\mathcal {G}$
denote either
$\mathcal {G}$
denote either
![]() $\mathcal {F}^{-}_{\le L}$
or
$\mathcal {F}^{-}_{\le L}$
or
![]() $\mathcal {F}^{-,\operatorname {hol}}$
according to whether
$\mathcal {F}^{-,\operatorname {hol}}$
according to whether
![]() $k=0$
or
$k=0$
or
![]() $k \ge 2$
. By Proposition 5.1, we may write
$k \ge 2$
. By Proposition 5.1, we may write
 $$ \begin{align*} \frac{\|\varphi^{\operatorname{\mathrm{JL}}}\|^2}{V_{d_B,N}} \left( |\varphi(g_1)|^2 - |\varphi(g_2)|^2 \right) = \langle \Theta^-(g_1,\cdot) - \Theta^-(g_2,\cdot), \varphi^{\operatorname{\mathrm{JL}}} \rangle. \end{align*} $$
$$ \begin{align*} \frac{\|\varphi^{\operatorname{\mathrm{JL}}}\|^2}{V_{d_B,N}} \left( |\varphi(g_1)|^2 - |\varphi(g_2)|^2 \right) = \langle \Theta^-(g_1,\cdot) - \Theta^-(g_2,\cdot), \varphi^{\operatorname{\mathrm{JL}}} \rangle. \end{align*} $$
By Bessel’s inequality, it follows that
 $$ \begin{align} \sum_{\varphi \in \mathcal{G}} \frac{\|\varphi^{\operatorname{\mathrm{JL}}}\|^2}{(V_{d_B,N})^2} \left(|\varphi(g_1)|^2-|\varphi(g_2)|^2\right)^2 \le \|\Theta^{-}(g_1,\cdot)-\Theta^{-}(g_2,\cdot)\|_2^2. \end{align} $$
$$ \begin{align} \sum_{\varphi \in \mathcal{G}} \frac{\|\varphi^{\operatorname{\mathrm{JL}}}\|^2}{(V_{d_B,N})^2} \left(|\varphi(g_1)|^2-|\varphi(g_2)|^2\right)^2 \le \|\Theta^{-}(g_1,\cdot)-\Theta^{-}(g_2,\cdot)\|_2^2. \end{align} $$
We now bound the right-hand side of Equation (5.10) (and in particular, verify that it is finite). Since
![]() $\Theta ^{-}(g,\cdot )$
is
$\Theta ^{-}(g,\cdot )$
is
![]() $K_{\infty }$
-isotypical, Lemma 4.1 and Equation (5.6) give the bound
$K_{\infty }$
-isotypical, Lemma 4.1 and Equation (5.6) give the bound
 $$ \begin{align} \ll \frac{1}{V_{1,d_BN}} \sum_{\ell|d_BN} \int_{\frac{\sqrt{3}}{2} \frac{\ell^2}{d_BN}}^{\infty} \int_0^{\ell} \frac{1}{\ell^2} |\theta_{g_1,\ell}^{-}(z)-\theta_{g_2,\ell}^{-}(z)|^2 dx \frac{dy}{y^2}. \end{align} $$
$$ \begin{align} \ll \frac{1}{V_{1,d_BN}} \sum_{\ell|d_BN} \int_{\frac{\sqrt{3}}{2} \frac{\ell^2}{d_BN}}^{\infty} \int_0^{\ell} \frac{1}{\ell^2} |\theta_{g_1,\ell}^{-}(z)-\theta_{g_2,\ell}^{-}(z)|^2 dx \frac{dy}{y^2}. \end{align} $$
We insert the definition (5.2) into the inner integral and evaluate, giving
 $$ \begin{align*} \frac{1}{\ell^2} \int_0^{\ell} |\theta_{g_1,\ell}^{-}(z)-\theta_{g_2,\ell}^{-}(z)|^2 dx = \frac{1}{\ell} y^{2+k} \sum_{n \in \frac{1}{\ell} \mathbb{Z}} \left| \sum_{i=1}^{2} (-1)^{i} \sum_{\substack{\gamma \in R(\ell;g_i) \\ \det(\gamma)=n}} X(\gamma)^k e^{-2\pi y P(\gamma)} \right|^2. \end{align*} $$
$$ \begin{align*} \frac{1}{\ell^2} \int_0^{\ell} |\theta_{g_1,\ell}^{-}(z)-\theta_{g_2,\ell}^{-}(z)|^2 dx = \frac{1}{\ell} y^{2+k} \sum_{n \in \frac{1}{\ell} \mathbb{Z}} \left| \sum_{i=1}^{2} (-1)^{i} \sum_{\substack{\gamma \in R(\ell;g_i) \\ \det(\gamma)=n}} X(\gamma)^k e^{-2\pi y P(\gamma)} \right|^2. \end{align*} $$
Note that the sum over i kills the contribution from
![]() $\gamma = 0$
, so we may omit that contribution in what follows. We separate the two sums by Cauchy–Schwarz and bound
$\gamma = 0$
, so we may omit that contribution in what follows. We separate the two sums by Cauchy–Schwarz and bound
![]() $X(\alpha )$
by
$X(\alpha )$
by
![]() $P(\alpha )^{\frac {1}{2}}$
, giving
$P(\alpha )^{\frac {1}{2}}$
, giving
 $$ \begin{align} \frac{1}{\ell^2} \int_0^{\ell} |\theta_{g_1,\ell}^{-}(z)-\theta_{g_2,\ell}^{-}(z)|^2 dx \ll \sum_{i=1}^{2} \frac{1}{\ell} \sum_{n \in \frac{1}{\ell} \mathbb{Z}} \left| \sum_{\substack{ 0 \neq\gamma \in R(\ell;g_i) \\ \det(\gamma)=n}} P(\gamma)^{\frac{k}{2}} e^{-2\pi y P(\gamma)} \right|^2 y^{2+k}. \end{align} $$
$$ \begin{align} \frac{1}{\ell^2} \int_0^{\ell} |\theta_{g_1,\ell}^{-}(z)-\theta_{g_2,\ell}^{-}(z)|^2 dx \ll \sum_{i=1}^{2} \frac{1}{\ell} \sum_{n \in \frac{1}{\ell} \mathbb{Z}} \left| \sum_{\substack{ 0 \neq\gamma \in R(\ell;g_i) \\ \det(\gamma)=n}} P(\gamma)^{\frac{k}{2}} e^{-2\pi y P(\gamma)} \right|^2 y^{2+k}. \end{align} $$
We now treat the contributions from
![]() $i=1,2$
individually. We commence with the integral in the variable y. Let
$i=1,2$
individually. We commence with the integral in the variable y. Let
denote the normalized incomplete gamma function. Setting ![]() , we find
, we find
 $$ \begin{align} \nonumber \frac{(4 \pi)^{k+1}}{\Gamma(k+1)} & \int_{Y}^{\infty} \left| \sum_{\substack{0 \neq \gamma \in R(\ell;g) \\ \det(\gamma)=n}} P(\gamma)^{\frac{k}{2}} e^{-2\pi y P(\gamma)} \right|^2 y^{2+k} \frac{dy}{y^2} \\ &\nonumber = \sum_{\substack{0 \neq\gamma_1,\gamma_2 \in R(\ell;g) \\ \det(\gamma_1)=\det(\gamma_2)=n}} \frac{2}{P(\gamma_1)+P(\gamma_2)} \left( \frac{2\sqrt{P(\gamma_1)P(\gamma_2)}}{P(\gamma_1)+P(\gamma_2)} \right)^{k} Q\left(k+1, 2\pi Y (P(\gamma_1)+P(\gamma_2) ) \right) \\ &\qquad\ \qquad\qquad \le \sum_{\substack{0 \neq \gamma_1,\gamma_2 \in R(\ell;g) \\ \det(\gamma_1)=\det(\gamma_2)=n}} \frac{2}{P(\gamma_1)+P(\gamma_2)} Q\left(k+1, 2\pi Y (P(\gamma_1)+P(\gamma_2)) \right). \end{align} $$
$$ \begin{align} \nonumber \frac{(4 \pi)^{k+1}}{\Gamma(k+1)} & \int_{Y}^{\infty} \left| \sum_{\substack{0 \neq \gamma \in R(\ell;g) \\ \det(\gamma)=n}} P(\gamma)^{\frac{k}{2}} e^{-2\pi y P(\gamma)} \right|^2 y^{2+k} \frac{dy}{y^2} \\ &\nonumber = \sum_{\substack{0 \neq\gamma_1,\gamma_2 \in R(\ell;g) \\ \det(\gamma_1)=\det(\gamma_2)=n}} \frac{2}{P(\gamma_1)+P(\gamma_2)} \left( \frac{2\sqrt{P(\gamma_1)P(\gamma_2)}}{P(\gamma_1)+P(\gamma_2)} \right)^{k} Q\left(k+1, 2\pi Y (P(\gamma_1)+P(\gamma_2) ) \right) \\ &\qquad\ \qquad\qquad \le \sum_{\substack{0 \neq \gamma_1,\gamma_2 \in R(\ell;g) \\ \det(\gamma_1)=\det(\gamma_2)=n}} \frac{2}{P(\gamma_1)+P(\gamma_2)} Q\left(k+1, 2\pi Y (P(\gamma_1)+P(\gamma_2)) \right). \end{align} $$
Since
![]() $Q(s,x)$
is superpolynomially small in both s and x as soon as
$Q(s,x)$
is superpolynomially small in both s and x as soon as
![]() $x \gg s$
, we see by dyadically partitioning
$x \gg s$
, we see by dyadically partitioning
![]() $\max _i\{P(\gamma _i)^{\frac {1}{2}}\}$
that Equation (5.13) is further bounded by
$\max _i\{P(\gamma _i)^{\frac {1}{2}}\}$
that Equation (5.13) is further bounded by
 $$ \begin{align*} \ll_{A} \sum_{j} \frac{1}{T_j^2} \left(1+\frac{T_j^2Y}{k+1} \right)^{-A} \sum _{\substack{ \gamma_1, \gamma_2 \in R(\ell;g) \cap \Omega^{\star}(1, T_j) \\ \det(\gamma_1) = \det(\gamma_2)=n}} 1 \end{align*} $$
$$ \begin{align*} \ll_{A} \sum_{j} \frac{1}{T_j^2} \left(1+\frac{T_j^2Y}{k+1} \right)^{-A} \sum _{\substack{ \gamma_1, \gamma_2 \in R(\ell;g) \cap \Omega^{\star}(1, T_j) \\ \det(\gamma_1) = \det(\gamma_2)=n}} 1 \end{align*} $$
for any
![]() $A \ge 0$
, where
$A \ge 0$
, where
![]() $T_j=2^j, j \in \mathbb {Z}$
. By putting all of these estimates together, we arrive at
$T_j=2^j, j \in \mathbb {Z}$
. By putting all of these estimates together, we arrive at
 $$ \begin{align*} \frac{1}{(V_{d_B,N})^2}\sum_{\varphi \in \mathcal{G}} & \|\varphi^{\operatorname{\mathrm{JL}}}\|^2 \left(|\varphi(g_1)|^2-|\varphi(g_2)|^2\right)^2 \\ & \preccurlyeq_{A} \frac{\Gamma(k+1)(4\pi)^{-k}}{V_{1,d_BN}} \sum_{i=1}^{2} \sum_{\ell|d_B N} \frac{1}{\ell} \sum_j \frac{1}{T_j^2} \left(1+ \frac{\ell^2}{d_BN} \frac{T_j^2}{k+1} \right)^{-A} \sum _{\substack{ \gamma_1, \gamma_2 \in R(\ell;g_i) \cap \Omega^{\star}(1, T_j) \\ \det(\gamma_1) = \det(\gamma_2)}} 1 \end{align*} $$
$$ \begin{align*} \frac{1}{(V_{d_B,N})^2}\sum_{\varphi \in \mathcal{G}} & \|\varphi^{\operatorname{\mathrm{JL}}}\|^2 \left(|\varphi(g_1)|^2-|\varphi(g_2)|^2\right)^2 \\ & \preccurlyeq_{A} \frac{\Gamma(k+1)(4\pi)^{-k}}{V_{1,d_BN}} \sum_{i=1}^{2} \sum_{\ell|d_B N} \frac{1}{\ell} \sum_j \frac{1}{T_j^2} \left(1+ \frac{\ell^2}{d_BN} \frac{T_j^2}{k+1} \right)^{-A} \sum _{\substack{ \gamma_1, \gamma_2 \in R(\ell;g_i) \cap \Omega^{\star}(1, T_j) \\ \det(\gamma_1) = \det(\gamma_2)}} 1 \end{align*} $$
for any
![]() $A \ge 0$
. Let us recall from Equation (4.1) that
$A \ge 0$
. Let us recall from Equation (4.1) that
![]() $V_{d_B,N}, V_{1,d_BN} = (d_BN)^{1+o(1)}$
and that for
$V_{d_B,N}, V_{1,d_BN} = (d_BN)^{1+o(1)}$
and that for
![]() $\varphi \in \mathcal {F}^{-}_{\le L}$
we have
$\varphi \in \mathcal {F}^{-}_{\le L}$
we have
![]() $\|\varphi ^{\operatorname {\mathrm {JL}}}\| \succcurlyeq _{L} 1$
(see Equation (5.7)). In order to conclude the first part of the proposition, we note that the range of T may be limited from above to
$\|\varphi ^{\operatorname {\mathrm {JL}}}\| \succcurlyeq _{L} 1$
(see Equation (5.7)). In order to conclude the first part of the proposition, we note that the range of T may be limited from above to
![]() $\preccurlyeq (d_BN)^{\frac {1}{2}} \ell ^{-1}$
by the superpolynomial decay and any polynomial bound on the second moment matrix count, which was noted in §3.4 and is the subject of the remaining sections §6 through §10. The second part of the proposition follows along the same lines, but we need to use the bound
$\preccurlyeq (d_BN)^{\frac {1}{2}} \ell ^{-1}$
by the superpolynomial decay and any polynomial bound on the second moment matrix count, which was noted in §3.4 and is the subject of the remaining sections §6 through §10. The second part of the proposition follows along the same lines, but we need to use the bound
![]() $\|\varphi ^{\operatorname {\mathrm {JL}}}\|^2 \succcurlyeq \Gamma (k) (4 \pi )^{-k}$
for
$\|\varphi ^{\operatorname {\mathrm {JL}}}\|^2 \succcurlyeq \Gamma (k) (4 \pi )^{-k}$
for
![]() $\varphi \in \mathcal {F}^{-,\operatorname {hol}}$
instead (see Equation (5.8)).
$\varphi \in \mathcal {F}^{-,\operatorname {hol}}$
instead (see Equation (5.8)).
Proof of Proposition 3.3.
We follow the recipe of the previous proof, only this time for the family
![]() $\mathcal {F}^{-,\operatorname {hol}}$
to which the theta function
$\mathcal {F}^{-,\operatorname {hol}}$
to which the theta function
![]() $\Theta ^{-,\operatorname {hol}}$
corresponds. As we shall see, the latter already possesses a finite
$\Theta ^{-,\operatorname {hol}}$
corresponds. As we shall see, the latter already possesses a finite
![]() $L^2$
-norm. Hence, we need not consider a difference of theta functions. After the initial steps, we arrive at
$L^2$
-norm. Hence, we need not consider a difference of theta functions. After the initial steps, we arrive at
 $$ \begin{align} \nonumber \sum_{\varphi \in \mathcal{F}^{-,\operatorname{hol}}} \frac{\|\varphi^{\operatorname{\mathrm{JL}}}\|^2}{(V_{d_B,N})^2} |\varphi(g)|^4 & \ll \frac{1}{V_{1,d_BN}} \frac{k^2 \Gamma(k-1)}{(4 \pi )^k} \\ & \times \sum_{\ell |d_BN} \frac{1}{\ell} \sum_{n \in \frac{1}{\ell} \mathbb{N}} \frac{1}{n} \left| \sum_{\substack{\gamma \in R(\ell;g)\\ \det(\gamma)=n}} \left( \frac{\det(\gamma)^{\frac{1}{2}}}{\overline{X(\gamma)}} \right)^k \right|^2 Q(k-1, 2 \sqrt{3} \pi n \tfrac{\ell^2}{d_BN}). \end{align} $$
$$ \begin{align} \nonumber \sum_{\varphi \in \mathcal{F}^{-,\operatorname{hol}}} \frac{\|\varphi^{\operatorname{\mathrm{JL}}}\|^2}{(V_{d_B,N})^2} |\varphi(g)|^4 & \ll \frac{1}{V_{1,d_BN}} \frac{k^2 \Gamma(k-1)}{(4 \pi )^k} \\ & \times \sum_{\ell |d_BN} \frac{1}{\ell} \sum_{n \in \frac{1}{\ell} \mathbb{N}} \frac{1}{n} \left| \sum_{\substack{\gamma \in R(\ell;g)\\ \det(\gamma)=n}} \left( \frac{\det(\gamma)^{\frac{1}{2}}}{\overline{X(\gamma)}} \right)^k \right|^2 Q(k-1, 2 \sqrt{3} \pi n \tfrac{\ell^2}{d_BN}). \end{align} $$
We further simplify using the lower bound
![]() $\|\varphi ^{\operatorname {\mathrm {JL}}}\|^2 \succcurlyeq \Gamma (k) (4 \pi )^{-k}$
(see Equation (5.8)), the approximations
$\|\varphi ^{\operatorname {\mathrm {JL}}}\|^2 \succcurlyeq \Gamma (k) (4 \pi )^{-k}$
(see Equation (5.8)), the approximations
![]() $V_{d_B,N}, V_{1,d_BN} = (d_B N)^{1+o(1)}$
and the superpolynomial decay of normalized incomplete gamma function, as well as the identities
$V_{d_B,N}, V_{1,d_BN} = (d_B N)^{1+o(1)}$
and the superpolynomial decay of normalized incomplete gamma function, as well as the identities
We obtain
 $$ \begin{align} \frac{1}{d_B N k}\sum_{\varphi \in \mathcal{F}^{-,\operatorname{hol}}} |\varphi(g)|^4 \preccurlyeq_A \sum_{\ell|d_BN} \frac{1}{\ell} \sum_{n \in \frac{1}{\ell}\mathbb{N}} \frac{1}{n} \left(1+ \frac{\ell^2}{d_BN} \frac{n}{k} \right)^{-A} \left|\sum_{\substack{\gamma \in R(\ell;g) \\ \det(\gamma)=n}} \left(1+ \frac{u(\gamma)}{n} \right)^{-\frac{k}{2}} \right|^2, \end{align} $$
$$ \begin{align} \frac{1}{d_B N k}\sum_{\varphi \in \mathcal{F}^{-,\operatorname{hol}}} |\varphi(g)|^4 \preccurlyeq_A \sum_{\ell|d_BN} \frac{1}{\ell} \sum_{n \in \frac{1}{\ell}\mathbb{N}} \frac{1}{n} \left(1+ \frac{\ell^2}{d_BN} \frac{n}{k} \right)^{-A} \left|\sum_{\substack{\gamma \in R(\ell;g) \\ \det(\gamma)=n}} \left(1+ \frac{u(\gamma)}{n} \right)^{-\frac{k}{2}} \right|^2, \end{align} $$
for any
![]() $A \ge 0$
. By the triangle inequality, we reduce to estimating similar expressions but with the sum over
$A \ge 0$
. By the triangle inequality, we reduce to estimating similar expressions but with the sum over
![]() $\gamma $
restricted by one of the following conditions:
$\gamma $
restricted by one of the following conditions:
-
(i)
 $u(\gamma ) \le k^{-1+\varepsilon } \det (\gamma )$
,
$u(\gamma ) \le k^{-1+\varepsilon } \det (\gamma )$
, -
(ii)
 $k^{-1+\varepsilon }\det (\gamma ) \le u(\gamma ) \le \det (\gamma )$
or
$k^{-1+\varepsilon }\det (\gamma ) \le u(\gamma ) \le \det (\gamma )$
or -
(iii)
 $\det (\gamma ) \le u(\gamma )$
.
$\det (\gamma ) \le u(\gamma )$
.
In Case (i), we bound
![]() $(1+u(\gamma )/n)^{-\frac {k}{2}} \le 1$
. Furthermore, we have
$(1+u(\gamma )/n)^{-\frac {k}{2}} \le 1$
. Furthermore, we have
![]() $\det (\gamma ) \asymp P(\gamma )$
and
$\det (\gamma ) \asymp P(\gamma )$
and
![]() $u(\gamma ) \ll k^{-1+\epsilon } P(\gamma )$
. Hence, after dyadically partitioning the range of
$u(\gamma ) \ll k^{-1+\epsilon } P(\gamma )$
. Hence, after dyadically partitioning the range of
![]() $P(\gamma )^{\frac {1}{2}}$
, we arrive at
$P(\gamma )^{\frac {1}{2}}$
, we arrive at
 $$ \begin{align*} \preccurlyeq_A \sum_{\ell|d_BN} \frac{1}{\ell} \sum_j \frac{1}{T_j^2} \left(1+ \frac{\ell^2}{d_BN} \frac{T_j^2}{k} \right)^{-A} \sum _{\substack{\gamma_1, \gamma_2 \in R(\ell;g) \cap \Omega^{\star}(k^{-1+\varepsilon}, T_j) \\ \det(\gamma_1) = \det(\gamma_2)>0}} 1. \end{align*} $$
$$ \begin{align*} \preccurlyeq_A \sum_{\ell|d_BN} \frac{1}{\ell} \sum_j \frac{1}{T_j^2} \left(1+ \frac{\ell^2}{d_BN} \frac{T_j^2}{k} \right)^{-A} \sum _{\substack{\gamma_1, \gamma_2 \in R(\ell;g) \cap \Omega^{\star}(k^{-1+\varepsilon}, T_j) \\ \det(\gamma_1) = \det(\gamma_2)>0}} 1. \end{align*} $$
In Case (ii), we use that
![]() $(1+u(\gamma )/n)^{-\frac {k}{2}}\le (1+k^{\varepsilon -1})^{-\frac {k}{2}}$
has superpolynomial decay in k (and hence also in
$(1+u(\gamma )/n)^{-\frac {k}{2}}\le (1+k^{\varepsilon -1})^{-\frac {k}{2}}$
has superpolynomial decay in k (and hence also in
![]() $(d_BN)$
as
$(d_BN)$
as
![]() $k \gg _{\eta } (d_BN)^{\eta }$
by assumption). As in Case (i), we have
$k \gg _{\eta } (d_BN)^{\eta }$
by assumption). As in Case (i), we have
![]() $ \det (\gamma ) \asymp P(\gamma )$
, but this time only
$ \det (\gamma ) \asymp P(\gamma )$
, but this time only
![]() $u(\gamma )\le P(\gamma )$
. We arrive at a contribution of
$u(\gamma )\le P(\gamma )$
. We arrive at a contribution of
 $$ \begin{align*} \preccurlyeq_{A,\eta} (kd_BN)^{-A} \sum_{\ell|d_BN} \frac{1}{\ell} \sum_j \frac{1}{T_j^2} \left(1+ \frac{\ell^2}{d_BN} \frac{T_j^2}{k} \right)^{-A} \sum _{\substack{\gamma_1, \gamma_2 \in R(\ell;g) \cap \Omega^{\star}(1, T_j) \\ \det(\gamma_1) = \det(\gamma_2)>0}} 1. \end{align*} $$
$$ \begin{align*} \preccurlyeq_{A,\eta} (kd_BN)^{-A} \sum_{\ell|d_BN} \frac{1}{\ell} \sum_j \frac{1}{T_j^2} \left(1+ \frac{\ell^2}{d_BN} \frac{T_j^2}{k} \right)^{-A} \sum _{\substack{\gamma_1, \gamma_2 \in R(\ell;g) \cap \Omega^{\star}(1, T_j) \\ \det(\gamma_1) = \det(\gamma_2)>0}} 1. \end{align*} $$
In Case (iii), we bound
 $$ \begin{align*} \left(1 + \frac{u(\gamma)}{n} \right)^{-\frac{k}{2}} \le 2^{-\frac{k}{4}} \left(1 + \frac{u(\gamma)}{n} \right)^{-\frac{k}{4}}. \end{align*} $$
$$ \begin{align*} \left(1 + \frac{u(\gamma)}{n} \right)^{-\frac{k}{2}} \le 2^{-\frac{k}{4}} \left(1 + \frac{u(\gamma)}{n} \right)^{-\frac{k}{4}}. \end{align*} $$
The factor
![]() $2^{-\frac {k}{4}}$
we use for superpolynomial decay in
$2^{-\frac {k}{4}}$
we use for superpolynomial decay in
![]() $(kd_BN)$
as before. The other factor we use as follows
$(kd_BN)$
as before. The other factor we use as follows
 $$ \begin{align*} \frac{1}{n} \left(1+\frac{u(\gamma)}{n}\right)^{-1} \left(1+\frac{\ell^2}{d_BN}\frac{n}{k}\right)^{-\frac{k}{4}+1} \left(1+\frac{u(\gamma)}{n} \right)^{-\frac{k}{4}+1} \le \frac{1}{u(\gamma)} \left(1+\frac{\ell^2}{d_BN}\frac{u(\gamma)}{k}\right)^{-\frac{k}{4}+1}. \end{align*} $$
$$ \begin{align*} \frac{1}{n} \left(1+\frac{u(\gamma)}{n}\right)^{-1} \left(1+\frac{\ell^2}{d_BN}\frac{n}{k}\right)^{-\frac{k}{4}+1} \left(1+\frac{u(\gamma)}{n} \right)^{-\frac{k}{4}+1} \le \frac{1}{u(\gamma)} \left(1+\frac{\ell^2}{d_BN}\frac{u(\gamma)}{k}\right)^{-\frac{k}{4}+1}. \end{align*} $$
Hence, Equation (5.15) is bounded by
 $$ \begin{align*}\preccurlyeq_{A,\eta} (kd_BN)^{-A} \sum_{\ell|d_BN} \frac{1}{\ell} \sum_{\substack{\gamma_1, \gamma_2 \in R(\ell;g)\\ \det(\gamma_1)=\det(\gamma_2)}} \frac{1}{u(\gamma_1)+u(\gamma_2)} \left(1+ \frac{\ell^2}{d_BN} \frac{u(\gamma_1)+u(\gamma_2)}{k} \right)^{-\frac{k}{4}+1} \\ \preccurlyeq_{A,\eta} (kd_BN)^{-A} \sum_{\ell|d_BN} \frac{1}{\ell} \sum_j \frac{1}{T_j^2} \left(1+\frac{\ell^2}{d_BN} \frac{T_j^2}{k} \right)^{-\frac{k}{4}+1} \sum _{\substack{\gamma_1, \gamma_2 \in R(\ell;g) \cap \Omega^{\star}(1, T_j) \\ \det(\gamma_1) = \det(\gamma_2)>0}} 1, \end{align*} $$
$$ \begin{align*}\preccurlyeq_{A,\eta} (kd_BN)^{-A} \sum_{\ell|d_BN} \frac{1}{\ell} \sum_{\substack{\gamma_1, \gamma_2 \in R(\ell;g)\\ \det(\gamma_1)=\det(\gamma_2)}} \frac{1}{u(\gamma_1)+u(\gamma_2)} \left(1+ \frac{\ell^2}{d_BN} \frac{u(\gamma_1)+u(\gamma_2)}{k} \right)^{-\frac{k}{4}+1} \\ \preccurlyeq_{A,\eta} (kd_BN)^{-A} \sum_{\ell|d_BN} \frac{1}{\ell} \sum_j \frac{1}{T_j^2} \left(1+\frac{\ell^2}{d_BN} \frac{T_j^2}{k} \right)^{-\frac{k}{4}+1} \sum _{\substack{\gamma_1, \gamma_2 \in R(\ell;g) \cap \Omega^{\star}(1, T_j) \\ \det(\gamma_1) = \det(\gamma_2)>0}} 1, \end{align*} $$
where we have dyadically partitioned
![]() $\max _i\{P(\gamma _i)^{\frac {1}{2}}\} \asymp \sqrt {u(\gamma _1)+u(\gamma _2)}$
. The proof of the proposition is now concluded as in the previous case.
$\max _i\{P(\gamma _i)^{\frac {1}{2}}\} \asymp \sqrt {u(\gamma _1)+u(\gamma _2)}$
. The proof of the proposition is now concluded as in the previous case.
Proof of Proposition 3.4.
We treat the definite spherical case in the same spirit as the indefinite spherical case. We readily arrive at the estimate
 $$ \begin{align} &\nonumber \sum_{\varphi \in \mathcal{F}^{+}_{m}} \frac{\|\varphi^{\operatorname{\mathrm{JL}}}\|^2}{(V_{d_B,N})^2} \left( |\varphi(g_1)|^2 - |\varphi(g_2)|^2 \right)^2 \ll \frac{1}{V_{1,d_BN}} \frac{(2m+1)^2 \Gamma(2m+1)}{(4 \pi )^{2m+2}} \\ &\qquad\qquad\times \sum_{i=1}^2 \sum_{\ell |d_BN} \frac{1}{\ell} \sum_{n \in \frac{1}{\ell} \mathbb{N}} \frac{1}{n} \left| \sum_{\substack{\gamma \in R(\ell;g_i)\\ \det(\gamma)=n}} P_m\left( \frac{|X(\gamma)|^2-u(\gamma)}{n} \right) \right|^2 Q(2m+1, 2 \sqrt{3} \pi n \tfrac{\ell^2}{d_BN}). \end{align} $$
$$ \begin{align} &\nonumber \sum_{\varphi \in \mathcal{F}^{+}_{m}} \frac{\|\varphi^{\operatorname{\mathrm{JL}}}\|^2}{(V_{d_B,N})^2} \left( |\varphi(g_1)|^2 - |\varphi(g_2)|^2 \right)^2 \ll \frac{1}{V_{1,d_BN}} \frac{(2m+1)^2 \Gamma(2m+1)}{(4 \pi )^{2m+2}} \\ &\qquad\qquad\times \sum_{i=1}^2 \sum_{\ell |d_BN} \frac{1}{\ell} \sum_{n \in \frac{1}{\ell} \mathbb{N}} \frac{1}{n} \left| \sum_{\substack{\gamma \in R(\ell;g_i)\\ \det(\gamma)=n}} P_m\left( \frac{|X(\gamma)|^2-u(\gamma)}{n} \right) \right|^2 Q(2m+1, 2 \sqrt{3} \pi n \tfrac{\ell^2}{d_BN}). \end{align} $$
We simplify the inequality by using the lower bound
![]() $\|\varphi ^{\operatorname {\mathrm {JL}}}\|^2 \succcurlyeq \Gamma (2m+2) (4 \pi )^{-2m-2}$
(see Equation (5.8)), the approximations
$\|\varphi ^{\operatorname {\mathrm {JL}}}\|^2 \succcurlyeq \Gamma (2m+2) (4 \pi )^{-2m-2}$
(see Equation (5.8)), the approximations
![]() $V_{d_B,N}, V_{1,d_BN}=(d_BN)^{1+o(1)}$
and the superpolynomial decay of the normalized incomplete Gamma function Q. We obtain
$V_{d_B,N}, V_{1,d_BN}=(d_BN)^{1+o(1)}$
and the superpolynomial decay of the normalized incomplete Gamma function Q. We obtain
 $$ \begin{align} \nonumber \frac{1}{d_BN (m+1)} & \sum_{\varphi \in \mathcal{F}^{+}_{m}} \left( |\varphi(g_1)|^2 - |\varphi(g_2)|^2 \right)^2 \\ & \preccurlyeq_A \sum_{i=1}^2 \sum_{\ell |d_BN} \frac{1}{\ell} \sum_{n \in \frac{1}{\ell} \mathbb{N}} \frac{1}{n} \left(1+\frac{\ell^2}{d_BN} \frac{n}{m+1} \right)^{-A} \left| \sum_{\substack{\gamma \in R(\ell;g_i)\\ \det(\gamma)=n}} P_m\left( \frac{|X(\gamma)|^2-u(\gamma)}{n} \right) \right|^2, \end{align} $$
$$ \begin{align} \nonumber \frac{1}{d_BN (m+1)} & \sum_{\varphi \in \mathcal{F}^{+}_{m}} \left( |\varphi(g_1)|^2 - |\varphi(g_2)|^2 \right)^2 \\ & \preccurlyeq_A \sum_{i=1}^2 \sum_{\ell |d_BN} \frac{1}{\ell} \sum_{n \in \frac{1}{\ell} \mathbb{N}} \frac{1}{n} \left(1+\frac{\ell^2}{d_BN} \frac{n}{m+1} \right)^{-A} \left| \sum_{\substack{\gamma \in R(\ell;g_i)\\ \det(\gamma)=n}} P_m\left( \frac{|X(\gamma)|^2-u(\gamma)}{n} \right) \right|^2, \end{align} $$
for any
![]() $A \ge 0$
. We proceed further by appealing to the Bernstein inequality [Reference BernsteinBer31] for the Legendre polynomials:
$A \ge 0$
. We proceed further by appealing to the Bernstein inequality [Reference BernsteinBer31] for the Legendre polynomials:
 $$ \begin{align} P_m(t) \le \min\left\{1 , \sqrt{\frac{2}{\pi m}} \frac{1}{(1-t^2)^{\frac{1}{4}}} \right\}, \quad \text{for } |t| \le 1. \end{align} $$
$$ \begin{align} P_m(t) \le \min\left\{1 , \sqrt{\frac{2}{\pi m}} \frac{1}{(1-t^2)^{\frac{1}{4}}} \right\}, \quad \text{for } |t| \le 1. \end{align} $$
We recall that
![]() $\det (\gamma )= |X(\gamma )|^2 + u(\gamma )$
so that, with
$\det (\gamma )= |X(\gamma )|^2 + u(\gamma )$
so that, with
![]() $\gamma $
and n as in the above sum,
$\gamma $
and n as in the above sum,
 $$ \begin{align*} t := \frac{|X(\gamma)|^2 - u(\gamma)}{n} = \frac{|X(\gamma)|^2 - u(\gamma)}{|X(\gamma)|^2 + u(\gamma) }, \quad 1 - t^2 = \frac{4 |X(\gamma)|^2 \cdot u (\gamma) }{n^2} \ge 0. \end{align*} $$
$$ \begin{align*} t := \frac{|X(\gamma)|^2 - u(\gamma)}{n} = \frac{|X(\gamma)|^2 - u(\gamma)}{|X(\gamma)|^2 + u(\gamma) }, \quad 1 - t^2 = \frac{4 |X(\gamma)|^2 \cdot u (\gamma) }{n^2} \ge 0. \end{align*} $$
Dyadically partitioning
![]() $P(\gamma )^{\frac {1}{2}}=\det (\gamma )^{\frac {1}{2}}$
, we conclude that Equation (5.17) is bounded by
$P(\gamma )^{\frac {1}{2}}=\det (\gamma )^{\frac {1}{2}}$
, we conclude that Equation (5.17) is bounded by
 $$ \begin{align} \nonumber \preccurlyeq_{A} \sum_{i=1}^2 \sum_{\ell|d_BN} \frac{1}{\ell} & \sum_{j} \frac{1}{T_j^2} \left(1+\frac{\ell^2}{d_BN} \frac{T_j^2}{m+1} \right)^{-A} \\ & \times \sum_{T_j^2 \le n < 4T_j^2} \left( \sum_{\substack{\gamma \in R(\ell;g_i) \\ \gamma \in \Omega^{\star}(1,2T_j)-\Omega^{\star}(1,T_j) \\ \det(\gamma)=n}} \min\left\{1, \frac{1}{(m+1)^{\frac{1}{2}}} \frac{T_j}{(|X(\gamma)|^2\cdot u(\gamma))^{\frac{1}{4}}} \right\} \right)^2, \end{align} $$
$$ \begin{align} \nonumber \preccurlyeq_{A} \sum_{i=1}^2 \sum_{\ell|d_BN} \frac{1}{\ell} & \sum_{j} \frac{1}{T_j^2} \left(1+\frac{\ell^2}{d_BN} \frac{T_j^2}{m+1} \right)^{-A} \\ & \times \sum_{T_j^2 \le n < 4T_j^2} \left( \sum_{\substack{\gamma \in R(\ell;g_i) \\ \gamma \in \Omega^{\star}(1,2T_j)-\Omega^{\star}(1,T_j) \\ \det(\gamma)=n}} \min\left\{1, \frac{1}{(m+1)^{\frac{1}{2}}} \frac{T_j}{(|X(\gamma)|^2\cdot u(\gamma))^{\frac{1}{4}}} \right\} \right)^2, \end{align} $$
where
![]() $T_j = 2^j$
as before. The minimum in Equation (5.19) lies between
$T_j = 2^j$
as before. The minimum in Equation (5.19) lies between
![]() $\asymp (m+1)^{-\frac {1}{2}}$
and
$\asymp (m+1)^{-\frac {1}{2}}$
and
![]() $1$
. Let us consider the
$1$
. Let us consider the
![]() $\gamma \in \Omega ^{\star }(1,2T_j)-\Omega ^{\star }(1,T_j)$
for which
$\gamma \in \Omega ^{\star }(1,2T_j)-\Omega ^{\star }(1,T_j)$
for which
 $$ \begin{align} \min\left\{1, \frac{1}{(m+1)^{\frac{1}{2}}} \frac{T_j}{(|X(\gamma)|^2\cdot u(\gamma))^{\frac{1}{4}}} \right\} \asymp \frac{1}{(m+1)^{\frac{1}{2}}} \frac{1}{\delta^{\frac{1}{4}}}, \end{align} $$
$$ \begin{align} \min\left\{1, \frac{1}{(m+1)^{\frac{1}{2}}} \frac{T_j}{(|X(\gamma)|^2\cdot u(\gamma))^{\frac{1}{4}}} \right\} \asymp \frac{1}{(m+1)^{\frac{1}{2}}} \frac{1}{\delta^{\frac{1}{4}}}, \end{align} $$
for some given
![]() $\delta $
with
$\delta $
with
![]() $1/(m+1)^2 \ll \delta \le 1$
. In particular,
$1/(m+1)^2 \ll \delta \le 1$
. In particular,
![]() $|X(\gamma )|^2 \cdot u(\gamma ) \ll \delta T_j^4$
. Since
$|X(\gamma )|^2 \cdot u(\gamma ) \ll \delta T_j^4$
. Since
![]() $|X(\gamma )|^2+u(\gamma )=P(\gamma ) \asymp T_j^2$
, both cannot be simultaneously small. Hence,
$|X(\gamma )|^2+u(\gamma )=P(\gamma ) \asymp T_j^2$
, both cannot be simultaneously small. Hence,
 $$ \begin{align*} \min \{|X(\gamma)|^2, u(\gamma)\} = \frac{|X(\gamma)|^2 \cdot u(\gamma)}{ \max\{|X(\gamma)|^2, u(\gamma)\}} \ll \delta T_j^2. \end{align*} $$
$$ \begin{align*} \min \{|X(\gamma)|^2, u(\gamma)\} = \frac{|X(\gamma)|^2 \cdot u(\gamma)}{ \max\{|X(\gamma)|^2, u(\gamma)\}} \ll \delta T_j^2. \end{align*} $$
Thus, after replacing
![]() $\delta $
with its multiple by a scalar of the form
$\delta $
with its multiple by a scalar of the form
![]() $\asymp 1$
if needed (which has no affect on Equation (5.20)), we may assume that
$\asymp 1$
if needed (which has no affect on Equation (5.20)), we may assume that
![]() $\min \{|X(\gamma )|^2, u(\gamma )\} \le \delta (2T_j)^2$
, that is, that
$\min \{|X(\gamma )|^2, u(\gamma )\} \le \delta (2T_j)^2$
, that is, that
![]() $\gamma $
lies in either
$\gamma $
lies in either
![]() $\Omega ^{\star }(\delta ,2T_j)$
or
$\Omega ^{\star }(\delta ,2T_j)$
or
![]() $\Psi ^{\star }(\delta ,2T_j)$
. We now consider dyadic scales
$\Psi ^{\star }(\delta ,2T_j)$
. We now consider dyadic scales
![]() $\delta _a$
of
$\delta _a$
of
![]() $\delta $
’s between
$\delta $
’s between
![]() $\asymp 1/(m^2+1)$
and
$\asymp 1/(m^2+1)$
and
![]() $1$
. The just mentioned arguments then allow us to bound second line in Equation (5.19) by
$1$
. The just mentioned arguments then allow us to bound second line in Equation (5.19) by
 $$ \begin{align*} \sum_{T_j^2 \le n < 4T_j^2} \Biggl( \sum_{a} \sum_{\substack{\gamma \in R(\ell;g_i) \\ \gamma \in \Omega^{\star}(\delta_a,2T_j)\cup \Psi^{\star}(\delta_a,2T_j) \\ \det(\gamma)=n}} (m+1)^{-\frac{1}{2}}\delta_a^{-\frac{1}{4}} \Biggr)^2. \end{align*} $$
$$ \begin{align*} \sum_{T_j^2 \le n < 4T_j^2} \Biggl( \sum_{a} \sum_{\substack{\gamma \in R(\ell;g_i) \\ \gamma \in \Omega^{\star}(\delta_a,2T_j)\cup \Psi^{\star}(\delta_a,2T_j) \\ \det(\gamma)=n}} (m+1)^{-\frac{1}{2}}\delta_a^{-\frac{1}{4}} \Biggr)^2. \end{align*} $$
There are at most
![]() $ \preccurlyeq 1$
dyadic scales in the range
$ \preccurlyeq 1$
dyadic scales in the range
![]() $1/(m^2+1) \ll \delta \le 1$
. Thus, after applying Cauchy–Schwarz in order to pull out the sum over
$1/(m^2+1) \ll \delta \le 1$
. Thus, after applying Cauchy–Schwarz in order to pull out the sum over
![]() $\delta _a$
, we bound Equation (5.19) by
$\delta _a$
, we bound Equation (5.19) by
 $$ \begin{align} \preccurlyeq_{A} \sum_{i=1}^2 \sum_{\ell|d_BN} \frac{1}{\ell} \sum_{j} \frac{1}{T_j^2} \left(1+\frac{\ell^2}{d_BN} \frac{T_j^2}{m+1} \right)^{-A} \sum_a \sum_{\substack{\gamma_1,\gamma_2 \in R(\ell;g_i) \\ \gamma_1,\gamma_2 \in \Omega^{\star}(\delta_a,2T_j) \cup \Psi^{\star}(\delta_a,2T_j))\\ \det(\gamma_1)=\det(\gamma_2)}} (m+1)^{-1} \delta_a^{-\frac{1}{2}}. \end{align} $$
$$ \begin{align} \preccurlyeq_{A} \sum_{i=1}^2 \sum_{\ell|d_BN} \frac{1}{\ell} \sum_{j} \frac{1}{T_j^2} \left(1+\frac{\ell^2}{d_BN} \frac{T_j^2}{m+1} \right)^{-A} \sum_a \sum_{\substack{\gamma_1,\gamma_2 \in R(\ell;g_i) \\ \gamma_1,\gamma_2 \in \Omega^{\star}(\delta_a,2T_j) \cup \Psi^{\star}(\delta_a,2T_j))\\ \det(\gamma_1)=\det(\gamma_2)}} (m+1)^{-1} \delta_a^{-\frac{1}{2}}. \end{align} $$
The proof is once more concluded as it was for the first proposition.
Proof of Proposition 3.5.
One final time we iterate the initial steps for the holomorphic family
![]() $\mathcal {F}^{\operatorname {hol}}$
in the definite case. We are again in the situation where the theta kernel
$\mathcal {F}^{\operatorname {hol}}$
in the definite case. We are again in the situation where the theta kernel
![]() $\Theta ^{+,\operatorname {hol}}$
has finite
$\Theta ^{+,\operatorname {hol}}$
has finite
![]() $L^2$
-norm, so we obtain, without having to take differences,
$L^2$
-norm, so we obtain, without having to take differences,
 $$ \begin{align} \nonumber \sum_{\varphi \in \mathcal{F}^{+,\operatorname{hol}}} \frac{\|\varphi^{\operatorname{\mathrm{JL}}}\|^2}{(V_{d_B,N})^2} |\varphi(g)|^4 & \ll \frac{1}{V_{1,d_BN}} \frac{(k+1)^2 \Gamma(k+1)}{(4 \pi )^{k+2}} \\ & \times \sum_{\ell |d_BN} \frac{1}{\ell} \sum_{n \in \frac{1}{\ell} \mathbb{N}} \frac{1}{n} \left| \sum_{\substack{\gamma \in R(\ell;g)\\ \det(\gamma)=n}} \left( \frac{X(\gamma)^2}{n} \right)^{\frac{k}{2}} \right|^2 Q(k+1, 2 \sqrt{3} \pi n \tfrac{\ell^2}{d_BN}). \end{align} $$
$$ \begin{align} \nonumber \sum_{\varphi \in \mathcal{F}^{+,\operatorname{hol}}} \frac{\|\varphi^{\operatorname{\mathrm{JL}}}\|^2}{(V_{d_B,N})^2} |\varphi(g)|^4 & \ll \frac{1}{V_{1,d_BN}} \frac{(k+1)^2 \Gamma(k+1)}{(4 \pi )^{k+2}} \\ & \times \sum_{\ell |d_BN} \frac{1}{\ell} \sum_{n \in \frac{1}{\ell} \mathbb{N}} \frac{1}{n} \left| \sum_{\substack{\gamma \in R(\ell;g)\\ \det(\gamma)=n}} \left( \frac{X(\gamma)^2}{n} \right)^{\frac{k}{2}} \right|^2 Q(k+1, 2 \sqrt{3} \pi n \tfrac{\ell^2}{d_BN}). \end{align} $$
We simplify this estimate using the lower bound
![]() $\|\varphi ^{\operatorname {\mathrm {JL}}}\|^2 \succcurlyeq \Gamma (k+2) (4 \pi )^{-k-2}$
(see Equation (5.8)), the approximations
$\|\varphi ^{\operatorname {\mathrm {JL}}}\|^2 \succcurlyeq \Gamma (k+2) (4 \pi )^{-k-2}$
(see Equation (5.8)), the approximations
![]() $V_{d_B,N}, V_{1,d_BN}=(d_BN)^{1+o(1)}$
, the superpolynomial decay of the normalized incomplete gamma function Q and the identity
$V_{d_B,N}, V_{1,d_BN}=(d_BN)^{1+o(1)}$
, the superpolynomial decay of the normalized incomplete gamma function Q and the identity
![]() $|X(\gamma )|^2=\det (\gamma )-u(\gamma )$
. We thereby obtain
$|X(\gamma )|^2=\det (\gamma )-u(\gamma )$
. We thereby obtain
 $$ \begin{align} \frac{1}{d_BN k} \sum_{\varphi \in \mathcal{F}^{+,\operatorname{hol}}} |\varphi(g)|^4 \preccurlyeq_A \sum_{\ell |d_BN} \frac{1}{\ell} \sum_{n \in \frac{1}{\ell} \mathbb{N}} \frac{1}{n} \left(1+\frac{\ell^2}{d_BN} \frac{n}{k} \right)^{-A} \left| \sum_{\substack{\gamma \in R(\ell;g)\\ \det(\gamma)=n}} \left( 1- \frac{u(\gamma)}{n} \right)^{\frac{k}{2}} \right|^2, \end{align} $$
$$ \begin{align} \frac{1}{d_BN k} \sum_{\varphi \in \mathcal{F}^{+,\operatorname{hol}}} |\varphi(g)|^4 \preccurlyeq_A \sum_{\ell |d_BN} \frac{1}{\ell} \sum_{n \in \frac{1}{\ell} \mathbb{N}} \frac{1}{n} \left(1+\frac{\ell^2}{d_BN} \frac{n}{k} \right)^{-A} \left| \sum_{\substack{\gamma \in R(\ell;g)\\ \det(\gamma)=n}} \left( 1- \frac{u(\gamma)}{n} \right)^{\frac{k}{2}} \right|^2, \end{align} $$
for any
![]() $A \ge 0$
. We dyadically partition
$A \ge 0$
. We dyadically partition
![]() $P(\gamma )^{\frac {1}{2}}=\det (\gamma )^{\frac {1}{2}}$
and distinguish the two cases:
$P(\gamma )^{\frac {1}{2}}=\det (\gamma )^{\frac {1}{2}}$
and distinguish the two cases:
-
(i)
 $u(\gamma ) \le k^{-1+\varepsilon } \det (\gamma )$
, and
$u(\gamma ) \le k^{-1+\varepsilon } \det (\gamma )$
, and -
(ii)
 $k^{-1+\varepsilon }\det (\gamma ) \le u(\gamma )$
.
$k^{-1+\varepsilon }\det (\gamma ) \le u(\gamma )$
.
We separate them by the triangle inequality. Using the inequality
![]() $(1-u(\gamma )/n)\le 1$
, we see that the contribution of the first case is bounded by
$(1-u(\gamma )/n)\le 1$
, we see that the contribution of the first case is bounded by
 $$ \begin{align*} \preccurlyeq_A \sum_{\ell|d_BN} \frac{1}{\ell} \sum_j \frac{1}{T_j^2} \left(1+ \frac{\ell^2}{d_BN} \frac{T_j^2}{k} \right)^{-A} \sum _{\substack{\gamma_1, \gamma_2 \in R(\ell;g) \cap \Omega^{\star}(k^{-1+\varepsilon}, T_j) \\ \det(\gamma_1) = \det(\gamma_2)}} 1, \end{align*} $$
$$ \begin{align*} \preccurlyeq_A \sum_{\ell|d_BN} \frac{1}{\ell} \sum_j \frac{1}{T_j^2} \left(1+ \frac{\ell^2}{d_BN} \frac{T_j^2}{k} \right)^{-A} \sum _{\substack{\gamma_1, \gamma_2 \in R(\ell;g) \cap \Omega^{\star}(k^{-1+\varepsilon}, T_j) \\ \det(\gamma_1) = \det(\gamma_2)}} 1, \end{align*} $$
where
![]() $T_j=2^j, j \in \mathbb {Z}$
. In the second case, we see that
$T_j=2^j, j \in \mathbb {Z}$
. In the second case, we see that
![]() $(1-k^{\varepsilon -1})^{\frac {k}{2}}$
enjoys superpolynomial decay in k. The contribution of the second case is thus bounded by
$(1-k^{\varepsilon -1})^{\frac {k}{2}}$
enjoys superpolynomial decay in k. The contribution of the second case is thus bounded by
 $$ \begin{align*} \preccurlyeq_{A} k^{-A} \sum_{\ell|d_BN} \frac{1}{\ell} \sum_j \frac{1}{T_j^2} \left(1+ \frac{\ell^2}{d_BN} \frac{T_j^2}{k} \right)^{-A} \sum _{\substack{\gamma_1, \gamma_2 \in R(\ell; g )\cap \Omega^{\star}(1, T_j) \\ \det(\gamma_1) = \det(\gamma_2)}} 1. \end{align*} $$
$$ \begin{align*} \preccurlyeq_{A} k^{-A} \sum_{\ell|d_BN} \frac{1}{\ell} \sum_j \frac{1}{T_j^2} \left(1+ \frac{\ell^2}{d_BN} \frac{T_j^2}{k} \right)^{-A} \sum _{\substack{\gamma_1, \gamma_2 \in R(\ell; g )\cap \Omega^{\star}(1, T_j) \\ \det(\gamma_1) = \det(\gamma_2)}} 1. \end{align*} $$
The proof is now concluded as it was for the previous propositions.
6. Preliminaries on the geometry of numbers
6.1. Bounds on successive minima
Definition 6.1. Let V be an n-dimensional real vector space. Let
![]() $L \subseteq V$
be a lattice (i.e., a cocompact discrete subgroup). Given a compact convex
$L \subseteq V$
be a lattice (i.e., a cocompact discrete subgroup). Given a compact convex
![]() $0$
-symmetric subset
$0$
-symmetric subset
![]() $\mathcal {K}$
of V with nonempty interior, we define a function
$\mathcal {K}$
of V with nonempty interior, we define a function
![]() $N : V \rightarrow \mathbb {R}_{\ge 0}$
by
$N : V \rightarrow \mathbb {R}_{\ge 0}$
by
![]() $N(v) := \inf \{t> 0 : v \in t \mathcal {K} \}$
. Given a positive-definite quadratic form Q on V, we define such a function by
$N(v) := \inf \{t> 0 : v \in t \mathcal {K} \}$
. Given a positive-definite quadratic form Q on V, we define such a function by
![]() $N(v) := Q(v)^{1/2}$
, or equivalently, by applying the previous definition with
$N(v) := Q(v)^{1/2}$
, or equivalently, by applying the previous definition with
![]() $\mathcal {K}$
the unit ball for Q. In either case, we define the successive minima
$\mathcal {K}$
the unit ball for Q. In either case, we define the successive minima
![]() $\lambda _1 \le \dotsb \le \lambda _n$
of
$\lambda _1 \le \dotsb \le \lambda _n$
of
![]() $\mathcal {K}$
on L (or of Q on L) as:
$\mathcal {K}$
on L (or of Q on L) as:
![]() $\lambda _k$
is the smallest positive real for which there is a linearly independent subset
$\lambda _k$
is the smallest positive real for which there is a linearly independent subset
![]() $\{v_1,\dotsc ,v_k\}$
of L for which
$\{v_1,\dotsc ,v_k\}$
of L for which
![]() $N(v_j) \le \lambda _k$
for each
$N(v_j) \le \lambda _k$
for each
![]() $1 \le j \le k$
.
$1 \le j \le k$
.
Lemma 6.2. Let
![]() $z\in \mathbb {H}$
with maximal imaginary part under the orbit of the Atkin–Lehner operators
$z\in \mathbb {H}$
with maximal imaginary part under the orbit of the Atkin–Lehner operators
![]() $A_0(N)$
of
$A_0(N)$
of
![]() $\Gamma _0(N)$
with N squarefree. Then, we have
$\Gamma _0(N)$
with N squarefree. Then, we have
for any
![]() $(c,d) \in \mathbb {Z}^2$
distinct from
$(c,d) \in \mathbb {Z}^2$
distinct from
![]() $(0,0)$
.
$(0,0)$
.
Proof. This is essentially [Reference Harcos and TemplierHT12, Lemma 1]. That reference gives the slightly weaker bound obtained by omitting the factor
![]() $(c,N)$
, but the stronger bound that we have stated follows from their proof, keeping track of
$(c,N)$
, but the stronger bound that we have stated follows from their proof, keeping track of
![]() $(c,N)$
at each step rather than bounding it from below by
$(c,N)$
at each step rather than bounding it from below by
![]() $1$
.
$1$
.
6.2. Lattice counting
Lemma 6.3. Let
![]() $f_{\mathcal {K}}$
be the distance function of a closed convex
$f_{\mathcal {K}}$
be the distance function of a closed convex
![]() $0$
-symmetric set
$0$
-symmetric set
![]() $\mathcal {K}\subseteq \mathbb {R}^n$
of positive volume. Let
$\mathcal {K}\subseteq \mathbb {R}^n$
of positive volume. Let
![]() $\Lambda \subset \mathbb {R}^n$
be a lattice, and let
$\Lambda \subset \mathbb {R}^n$
be a lattice, and let
![]() $ \lambda _1 \le \lambda _2 \le \dots \le \lambda _n$
denote the successive minima (see Definition 6.1) of
$ \lambda _1 \le \lambda _2 \le \dots \le \lambda _n$
denote the successive minima (see Definition 6.1) of
![]() $\mathcal {K}$
on
$\mathcal {K}$
on
![]() $\Lambda $
. Then, there is a basis
$\Lambda $
. Then, there is a basis
![]() $v_1,\dots ,v_n$
of
$v_1,\dots ,v_n$
of
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $f_{\mathcal {K}}(v_i) \asymp _n \lambda _i$
.
$f_{\mathcal {K}}(v_i) \asymp _n \lambda _i$
.
Proof. This is [Reference Gruber and LekkerkerkerGL87, Thm. 2, p. 66].
Lemma 6.4. Let
![]() $\mathcal {K}\subseteq \mathbb {R}^n$
be a closed convex
$\mathcal {K}\subseteq \mathbb {R}^n$
be a closed convex
![]() $0$
-symmetric set of positive volume. Let
$0$
-symmetric set of positive volume. Let
![]() $\Lambda \subset \mathbb {R}^n$
be a lattice, and let
$\Lambda \subset \mathbb {R}^n$
be a lattice, and let
![]() $ \lambda _1 \le \lambda _2 \le \dots \le \lambda _n$
denote the successive minima of
$ \lambda _1 \le \lambda _2 \le \dots \le \lambda _n$
denote the successive minima of
![]() $\mathcal {K}$
on
$\mathcal {K}$
on
![]() $\Lambda $
. Then
$\Lambda $
. Then
 $$ \begin{align*} |\mathcal{K} \cap \Lambda| \asymp_n \prod_{i=1}^n \left( 1+\frac{1}{\lambda_i} \right). \end{align*} $$
$$ \begin{align*} |\mathcal{K} \cap \Lambda| \asymp_n \prod_{i=1}^n \left( 1+\frac{1}{\lambda_i} \right). \end{align*} $$
Proof. The lower bound follows from van der Corput’s generalization of Minkowski’s first theorem [Reference van der CorputvdC36]. It states that for
![]() $\mathcal {K}' \subset \mathbb {R}^d$
a closed convex
$\mathcal {K}' \subset \mathbb {R}^d$
a closed convex
![]() $0$
-symmetric set and
$0$
-symmetric set and
![]() $\Lambda \subset \mathbb {R}^d$
a lattice, one has
$\Lambda \subset \mathbb {R}^d$
a lattice, one has
 $$ \begin{align} |\mathcal{K}'\cap \Lambda'|+1 \ge |\mathrm{int}\,\mathcal{K}'\cap \Lambda'|+1 \ge 2^{1-d} \frac{\operatorname{\mathrm{vol}}(\mathcal{K}')}{\operatorname{\mathrm{vol}}(\mathbb{R}^d / \Lambda')}. \end{align} $$
$$ \begin{align} |\mathcal{K}'\cap \Lambda'|+1 \ge |\mathrm{int}\,\mathcal{K}'\cap \Lambda'|+1 \ge 2^{1-d} \frac{\operatorname{\mathrm{vol}}(\mathcal{K}')}{\operatorname{\mathrm{vol}}(\mathbb{R}^d / \Lambda')}. \end{align} $$
Let d be the largest integer such that
![]() $\lambda _d \le 1$
. Let
$\lambda _d \le 1$
. Let
![]() $v_i\in \Lambda $
, for
$v_i\in \Lambda $
, for
![]() $i=1,\dots ,d$
, be a set of linearly independent vectors such that
$i=1,\dots ,d$
, be a set of linearly independent vectors such that
![]() $\lambda _i^{-1}v_i \in \mathcal {K}$
. Let
$\lambda _i^{-1}v_i \in \mathcal {K}$
. Let
![]() $\mathcal {K}'$
be the convex hull of the vectors
$\mathcal {K}'$
be the convex hull of the vectors
![]() $\pm \lambda _i^{-1}v_i$
and
$\pm \lambda _i^{-1}v_i$
and
![]() $\Lambda '$
the span of the vectors
$\Lambda '$
the span of the vectors
![]() $v_i$
. In particular,
$v_i$
. In particular,
![]() $\mathcal {K} '$
is nonempty, hence
$\mathcal {K} '$
is nonempty, hence
![]() $0 \in \mathcal {K}' \cap \Lambda '$
, and so
$0 \in \mathcal {K}' \cap \Lambda '$
, and so
Using Equation (6.1), it follows now that
 $$ \begin{align*} |\mathcal{K}\cap \Lambda| \ge |\mathcal{K}'\cap \Lambda'| \ge 2^{-d} \frac{\operatorname{\mathrm{vol}}(\mathcal{K}')}{\operatorname{\mathrm{vol}}(\mathbb{R}^d / \Lambda')} = \frac{1}{d!} \prod_{i=1}^d \frac{1}{\lambda_i}. \end{align*} $$
$$ \begin{align*} |\mathcal{K}\cap \Lambda| \ge |\mathcal{K}'\cap \Lambda'| \ge 2^{-d} \frac{\operatorname{\mathrm{vol}}(\mathcal{K}')}{\operatorname{\mathrm{vol}}(\mathbb{R}^d / \Lambda')} = \frac{1}{d!} \prod_{i=1}^d \frac{1}{\lambda_i}. \end{align*} $$
For the upper bound, we refer to [Reference Betke, Henk and WillsBHW93, Prop. 2.1].
Lemma 6.5. Let
![]() $\Lambda \subset \mathbb {R}^2$
be a lattice of rank
$\Lambda \subset \mathbb {R}^2$
be a lattice of rank
![]() $2$
and
$2$
and
![]() $B\subseteq \mathbb {R}^2$
a ball of radius R (not necessarily centred at
$B\subseteq \mathbb {R}^2$
a ball of radius R (not necessarily centred at
![]() $0$
). If
$0$
). If
![]() $\lambda _1 \le \lambda _2$
are the successive minima of
$\lambda _1 \le \lambda _2$
are the successive minima of
![]() $\Lambda $
, then
$\Lambda $
, then
 $$ \begin{align*} |B \cap \Lambda| \ll 1+\frac{R}{\lambda_1}+\frac{R^2}{\lambda_1\lambda_2}. \end{align*} $$
$$ \begin{align*} |B \cap \Lambda| \ll 1+\frac{R}{\lambda_1}+\frac{R^2}{\lambda_1\lambda_2}. \end{align*} $$
Proof. See [Reference Harcos and TemplierHT13, Lemma 2.1].
7. Local preliminaries on orders
7.1. Quadratic preliminaries
Let F be a non-Archimedean local field of characteristic
![]() $\neq 2$
. Let
$\neq 2$
. Let
![]() $E/F$
be a separable quadratic extension, thus E is either the split quadratic extension
$E/F$
be a separable quadratic extension, thus E is either the split quadratic extension
![]() $F \oplus F$
or a quadratic field extension. We write
$F \oplus F$
or a quadratic field extension. We write
![]() $\mathfrak {o}$
(resp.
$\mathfrak {o}$
(resp.
![]() $\mathfrak {o}_E$
) for the ring of integers in F (resp. E),
$\mathfrak {o}_E$
) for the ring of integers in F (resp. E),
![]() $x \mapsto \bar {x}$
for the canonical involution on E and
$x \mapsto \bar {x}$
for the canonical involution on E and
for the norm and trace. Recall that the different ideal
![]() $\mathfrak {d}$
for this extension is the smallest
$\mathfrak {d}$
for this extension is the smallest
![]() $\mathfrak {o}_E$
-ideal for which
$\mathfrak {o}_E$
-ideal for which
![]() $\operatorname {\mathrm {tr}}(\mathfrak {d}^{-1}) \subseteq \mathfrak {o}$
, and in fact
$\operatorname {\mathrm {tr}}(\mathfrak {d}^{-1}) \subseteq \mathfrak {o}$
, and in fact
![]() $\mathfrak {d}^{-1} = \{ x \in E: \operatorname {\mathrm {tr}}(x \mathfrak {o}_E) \subseteq \mathfrak {o} \}$
. If
$\mathfrak {d}^{-1} = \{ x \in E: \operatorname {\mathrm {tr}}(x \mathfrak {o}_E) \subseteq \mathfrak {o} \}$
. If
![]() $E/F$
is split or unramified, then
$E/F$
is split or unramified, then
![]() $\mathfrak {d} = \mathfrak {o}_E$
.
$\mathfrak {d} = \mathfrak {o}_E$
.
We may regard E as a two-dimensional vector space over F.
Let
![]() $q : E \rightarrow F$
be a nondegenerate binary quadratic form with the property that for all
$q : E \rightarrow F$
be a nondegenerate binary quadratic form with the property that for all
![]() $e,x \in E$
, we have
$e,x \in E$
, we have
![]() $q(e x) =\operatorname {\mathrm {nr}}(e) q(x)$
. In other words, q is an F-multiple of
$q(e x) =\operatorname {\mathrm {nr}}(e) q(x)$
. In other words, q is an F-multiple of
![]() $\operatorname {\mathrm {nr}}$
, specifically
$\operatorname {\mathrm {nr}}$
, specifically
![]() $q = q(1)\operatorname {\mathrm {nr}}$
.
$q = q(1)\operatorname {\mathrm {nr}}$
.
For
![]() $x,y \in E$
, we set
$x,y \in E$
, we set ![]() so that
so that
![]() $q(x) = \langle x, x \rangle /2$
.
$q(x) = \langle x, x \rangle /2$
.
Let
![]() $\mathfrak {a} \subset E$
be a fractional
$\mathfrak {a} \subset E$
be a fractional
![]() $\mathfrak {o}_E$
-ideal. Write
$\mathfrak {o}_E$
-ideal. Write
![]() $\mathfrak {a}^\vee $
for the dual of
$\mathfrak {a}^\vee $
for the dual of
![]() $\mathfrak {a}$
with respect to the quadratic form q, that is,
$\mathfrak {a}$
with respect to the quadratic form q, that is, ![]() .
.
Let
![]() $\mathfrak {n}$
denote the fractional
$\mathfrak {n}$
denote the fractional
![]() $\mathfrak {o}$
-ideal generated by
$\mathfrak {o}$
-ideal generated by
![]() $q(\mathfrak {a})$
.
$q(\mathfrak {a})$
.
Lemma 7.1. We have
![]() $\mathfrak {a} = \mathfrak {d} \mathfrak {n} \mathfrak {a}^\vee $
.
$\mathfrak {a} = \mathfrak {d} \mathfrak {n} \mathfrak {a}^\vee $
.
Proof. Let
![]() $\alpha $
be a generator of
$\alpha $
be a generator of
![]() $\mathfrak {a}$
. Then
$\mathfrak {a}$
. Then
![]() $\mathfrak {n} = q(1)\operatorname {\mathrm {nr}}(\mathfrak {a}) = \mathfrak {o} q(1) \alpha \bar {\alpha }$
,
$\mathfrak {n} = q(1)\operatorname {\mathrm {nr}}(\mathfrak {a}) = \mathfrak {o} q(1) \alpha \bar {\alpha }$
,
![]() $\mathfrak {a}^\vee = \{ q(1)^{-1} x: x \in E, \operatorname {\mathrm {tr}}(x \bar {\mathfrak {a}}) \subseteq \mathfrak {o} \} = q(1)^{-1} \bar {\alpha }^{-1} \mathfrak {d}^{-1}$
. Multiplying through, the conclusion follows.
$\mathfrak {a}^\vee = \{ q(1)^{-1} x: x \in E, \operatorname {\mathrm {tr}}(x \bar {\mathfrak {a}}) \subseteq \mathfrak {o} \} = q(1)^{-1} \bar {\alpha }^{-1} \mathfrak {d}^{-1}$
. Multiplying through, the conclusion follows.
Corollary 7.2. Suppose that
![]() $E/F$
is unramified and that q is integral on
$E/F$
is unramified and that q is integral on
![]() $\mathfrak {a}$
so that
$\mathfrak {a}$
so that
![]() $\mathfrak {a} \subseteq \mathfrak {a}^\vee $
. Then the elementary divisors for the
$\mathfrak {a} \subseteq \mathfrak {a}^\vee $
. Then the elementary divisors for the
![]() $\mathfrak {o}$
-module inclusion
$\mathfrak {o}$
-module inclusion
![]() $\mathfrak {a} \hookrightarrow \mathfrak {a}^\vee $
are
$\mathfrak {a} \hookrightarrow \mathfrak {a}^\vee $
are
![]() $(\mathfrak {n}, \mathfrak {n})$
.
$(\mathfrak {n}, \mathfrak {n})$
.
Proof. Our hypotheses imply that
![]() $\mathfrak {d} = \mathfrak {o}$
and that
$\mathfrak {d} = \mathfrak {o}$
and that
![]() $\mathfrak {n}$
is an integral ideal. The lemma implies that there is an isomorphism (first of
$\mathfrak {n}$
is an integral ideal. The lemma implies that there is an isomorphism (first of
![]() $\mathfrak {o}_E$
-modules, then of
$\mathfrak {o}_E$
-modules, then of
![]() $\mathfrak {o}$
-modules)
$\mathfrak {o}$
-modules)
![]() $\mathfrak {a}^\vee / \mathfrak {a} \cong \mathfrak {o}_E / \mathfrak {n} \mathfrak {o}_E \cong (\mathfrak {o}/\mathfrak {n})^2$
, whence the conclusion.
$\mathfrak {a}^\vee / \mathfrak {a} \cong \mathfrak {o}_E / \mathfrak {n} \mathfrak {o}_E \cong (\mathfrak {o}/\mathfrak {n})^2$
, whence the conclusion.
Remark 7.3. Under the hypotheses of the corollary, the discriminant ideal of the binary quadratic form
![]() $(q,\mathfrak {a})$
is
$(q,\mathfrak {a})$
is
![]() $\mathfrak {n}^2$
. More generally, under the hypotheses of the lemma, the discriminant ideal is
$\mathfrak {n}^2$
. More generally, under the hypotheses of the lemma, the discriminant ideal is
![]() $\mathfrak {D} \mathfrak {n}^2$
, with
$\mathfrak {D} \mathfrak {n}^2$
, with
![]() $\mathfrak {D} =\operatorname {\mathrm {nr}} (\mathfrak {d})$
. Conversely, given the discriminant ideal, we may compute
$\mathfrak {D} =\operatorname {\mathrm {nr}} (\mathfrak {d})$
. Conversely, given the discriminant ideal, we may compute
![]() $\mathfrak {n}$
as its square root.
$\mathfrak {n}$
as its square root.
7.2. Quaternionic preliminaries: general case
Let F be a non-Archimedean local field, let B be a quaternion F-algebra and let E be a separable quadratic F-subalgebra of B. We equip B with the quadratic form
![]() $q : B \rightarrow F$
given by the reduced norm, whose bilinearization
$q : B \rightarrow F$
given by the reduced norm, whose bilinearization
![]() $\langle \, , \rangle $
as above is described by the reduced trace and the main involution on B via the formula
$\langle \, , \rangle $
as above is described by the reduced trace and the main involution on B via the formula
![]() $\langle x, y \rangle = \operatorname {\mathrm {tr}}(x \bar {y})$
. We have a canonical decomposition
$\langle x, y \rangle = \operatorname {\mathrm {tr}}(x \bar {y})$
. We have a canonical decomposition
![]() $B = E \oplus E^\perp $
, where
$B = E \oplus E^\perp $
, where
![]() $E^\perp = \{ x \in B : \langle x, y \rangle = 0 \text { for all } y \in E \}$
.
$E^\perp = \{ x \in B : \langle x, y \rangle = 0 \text { for all } y \in E \}$
.
Let
![]() $\mathfrak {o}$
and
$\mathfrak {o}$
and
![]() $\mathfrak {o}_E$
denote the respective maximal orders of F and E. We write
$\mathfrak {o}_E$
denote the respective maximal orders of F and E. We write
![]() $\mathfrak {d}$
for the different ideal, as before.
$\mathfrak {d}$
for the different ideal, as before.
Let us say that an order R in B is E-adapted if it is of the form
![]() $R = \mathfrak {o}_E \oplus \mathfrak {a}$
for some
$R = \mathfrak {o}_E \oplus \mathfrak {a}$
for some
![]() $\mathfrak {o}_E$
-submodule
$\mathfrak {o}_E$
-submodule
![]() $\mathfrak {a}$
of
$\mathfrak {a}$
of
![]() $E^\perp $
(for the action by either left or right multiplication – it doesn’t matter which because they are conjugates of each other).
$E^\perp $
(for the action by either left or right multiplication – it doesn’t matter which because they are conjugates of each other).
Consider such an order R. Its traceless submodule is given by
We aim to compute the dual lattice
![]() $(R^0)^\vee $
with respect to q. To that end, it suffices to dualize each summand in the above decomposition because
$(R^0)^\vee $
with respect to q. To that end, it suffices to dualize each summand in the above decomposition because
![]() $(R^0)^\vee = (\mathfrak {o}_E^0)^\vee \oplus \mathfrak {a}^\vee $
. We generally have
$(R^0)^\vee = (\mathfrak {o}_E^0)^\vee \oplus \mathfrak {a}^\vee $
. We generally have
![]() ${(\mathfrak {d}^{-1})^0 \subseteq (\mathfrak {o}_E^0)^\vee \subseteq \frac {1}{2} (\mathfrak {d}^{-1})^0}$
. If E is unramified or split, then
${(\mathfrak {d}^{-1})^0 \subseteq (\mathfrak {o}_E^0)^\vee \subseteq \frac {1}{2} (\mathfrak {d}^{-1})^0}$
. If E is unramified or split, then
![]() $(\mathfrak {o}_E^0)^\vee = \frac {1}{2} \mathfrak {o}_E^0 = \frac {1}{2} (\mathfrak {d}^{-1})^0$
. On the other hand, we can compute
$(\mathfrak {o}_E^0)^\vee = \frac {1}{2} \mathfrak {o}_E^0 = \frac {1}{2} (\mathfrak {d}^{-1})^0$
. On the other hand, we can compute
![]() $\mathfrak {a}^\vee $
using the results of the previous section. Indeed, the choice of any invertible element
$\mathfrak {a}^\vee $
using the results of the previous section. Indeed, the choice of any invertible element
![]() $j \in E^\perp $
defines an isomorphism
$j \in E^\perp $
defines an isomorphism
![]() $E \rightarrow E^\perp $
,
$E \rightarrow E^\perp $
,
![]() $x \mapsto x j$
. Transporting q and
$x \mapsto x j$
. Transporting q and
![]() $\mathfrak {a}$
via the inverse of this isomorphism gives us a fractional ideal in E and a quadratic form on E that satisfy the hypotheses of that section. We obtain
$\mathfrak {a}$
via the inverse of this isomorphism gives us a fractional ideal in E and a quadratic form on E that satisfy the hypotheses of that section. We obtain
where
![]() $\mathfrak {n}$
is the integral
$\mathfrak {n}$
is the integral
![]() $\mathfrak {o}$
-ideal characterized by either of the following properties:
$\mathfrak {o}$
-ideal characterized by either of the following properties:
-
∘
 $\mathfrak {n}$
is generated by
$\mathfrak {n}$
is generated by
 $q(\mathfrak {a})$
.
$q(\mathfrak {a})$
. -
∘
 $\mathfrak {D} \mathfrak {n}^2$
is the discriminant ideal of
$\mathfrak {D} \mathfrak {n}^2$
is the discriminant ideal of
 $(q,\mathfrak {a})$
.
$(q,\mathfrak {a})$
.
Let
![]() $\mathcal {D}$
denote the discriminant ideal of R. The discriminant ideal of the summand
$\mathcal {D}$
denote the discriminant ideal of R. The discriminant ideal of the summand
![]() $(q,\mathfrak {o}_E)$
is
$(q,\mathfrak {o}_E)$
is
![]() $\mathfrak {D}$
. Since the discriminant ideal is multiplicative with respect to direct sums, we obtain
$\mathfrak {D}$
. Since the discriminant ideal is multiplicative with respect to direct sums, we obtain
We may regard this last identity as a formula for
![]() $\mathfrak {n}$
.
$\mathfrak {n}$
.
7.3. Quaternionic preliminaries: unramified case
Let us restrict henceforth to the case that
![]() $E/F$
is unramified. (The ramified case would be relevant for studying, for example, the ‘minimal vectors’ considered in [Reference Hu, Nelson and SahaHNS19, Reference Hu and NelsonHN18, Reference SahaSah20].)
$E/F$
is unramified. (The ramified case would be relevant for studying, for example, the ‘minimal vectors’ considered in [Reference Hu, Nelson and SahaHNS19, Reference Hu and NelsonHN18, Reference SahaSah20].)
The above formula then simplifies to
and we obtain
There are three possibilities for
![]() $F \subset E \subset B$
, up to isomorphism:
$F \subset E \subset B$
, up to isomorphism:
-
(i) B is split and
 $E \cong F \oplus F$
. We may then find an isomorphism
$E \cong F \oplus F$
. We may then find an isomorphism
 $B \cong \operatorname {\mathrm {Mat}}_{2 \times 2}(F)$
under which E identifies with the diagonal subalgebra.
$B \cong \operatorname {\mathrm {Mat}}_{2 \times 2}(F)$
under which E identifies with the diagonal subalgebra. -
(ii) B is split and
 $E/F$
is the unique unramified quadratic field extension.
$E/F$
is the unique unramified quadratic field extension. -
(iii) B is nonsplit and
 $E/F$
is the unique unramified quadratic field extension.
$E/F$
is the unique unramified quadratic field extension.
In Case (i), the E-adapted orders R are just the Eichler orders. An Eichler order of level
![]() $\mathfrak {q}$
has discriminant
$\mathfrak {q}$
has discriminant
![]() $\mathfrak {q}^2$
(cf. [Reference VoightVoi18, §23.4]), hence the ideal
$\mathfrak {q}^2$
(cf. [Reference VoightVoi18, §23.4]), hence the ideal
![]() $\mathfrak {n}$
defined above is
$\mathfrak {n}$
defined above is
![]() $\mathfrak {q}$
.
$\mathfrak {q}$
.
Case (ii) corresponds to another type of ‘minimal vectors’, which we do not consider in this paper.
In Case (iii), the maximal order R is E-adapted and has discriminant ideal
![]() $\mathfrak {p}^2$
(cf. [Reference VoightVoi18, §15.2.11, §23.4]), hence
$\mathfrak {p}^2$
(cf. [Reference VoightVoi18, §15.2.11, §23.4]), hence
![]() $\mathfrak {n} = \mathfrak {p}$
.
$\mathfrak {n} = \mathfrak {p}$
.
7.4. Bounds for commutators of elements of
 $R^0$
$R^0$
Lemma 7.4. Let
![]() $E / F$
unramified and R be an E-adapted order. Let
$E / F$
unramified and R be an E-adapted order. Let
![]() $[\gamma _1,\gamma _2] = \gamma _1\gamma _2-\gamma _2\gamma _1$
denote the commutator for two elements
$[\gamma _1,\gamma _2] = \gamma _1\gamma _2-\gamma _2\gamma _1$
denote the commutator for two elements
![]() $\gamma _1,\gamma _2$
in B. Then, we have
$\gamma _1,\gamma _2$
in B. Then, we have
-
(i)
 $q([\gamma _1,\gamma _2]) \in \mathfrak {n}$
for all
$q([\gamma _1,\gamma _2]) \in \mathfrak {n}$
for all
 $\gamma _1,\gamma _2 \in R$
,
$\gamma _1,\gamma _2 \in R$
, -
(ii)
 $[\gamma _1,\gamma _2] \in \mathfrak {n}^{-1}R$
for all
$[\gamma _1,\gamma _2] \in \mathfrak {n}^{-1}R$
for all
 $\gamma _1,\gamma _2 \in R^{\vee }$
,
$\gamma _1,\gamma _2 \in R^{\vee }$
, -
(iii)
 $q([\gamma _1,\gamma _2]) \in \mathfrak {n}^{-2}$
for all
$q([\gamma _1,\gamma _2]) \in \mathfrak {n}^{-2}$
for all
 $\gamma _1,\gamma _2 \in R^{\vee }$
.
$\gamma _1,\gamma _2 \in R^{\vee }$
.
Proof. By the previous discussion, we may write
![]() $\gamma _i=\alpha _i+\beta _i$
with
$\gamma _i=\alpha _i+\beta _i$
with
![]() $\alpha _i \in \mathfrak {o}_E$
and
$\alpha _i \in \mathfrak {o}_E$
and
![]() $\beta _i \in \mathfrak {a}$
if
$\beta _i \in \mathfrak {a}$
if
![]() $\gamma _i \in R$
, respectively
$\gamma _i \in R$
, respectively
![]() $\mathfrak {n}^{-1}\mathfrak {a}$
if
$\mathfrak {n}^{-1}\mathfrak {a}$
if
![]() $\gamma _i \in R^{\vee }$
. We have
$\gamma _i \in R^{\vee }$
. We have
![]() $[\alpha _1,\alpha _2]=0$
and
$[\alpha _1,\alpha _2]=0$
and
![]() $[\alpha _1,\beta _2] = 2\alpha _1\beta _2 \in \mathfrak {a}$
, respectively
$[\alpha _1,\beta _2] = 2\alpha _1\beta _2 \in \mathfrak {a}$
, respectively
![]() $\in \mathfrak {n}^{-1}\mathfrak {a}$
. Lastly, we have
$\in \mathfrak {n}^{-1}\mathfrak {a}$
. Lastly, we have
![]() $\mathfrak {a}^2=\mathfrak {n} \mathfrak {a}^{\vee } \mathfrak {a} = \mathfrak {n}$
and
$\mathfrak {a}^2=\mathfrak {n} \mathfrak {a}^{\vee } \mathfrak {a} = \mathfrak {n}$
and
![]() $(\mathfrak {a}^{\vee })^2=\mathfrak {n}^{-1} \mathfrak {a} \mathfrak {a}^{\vee } = \mathfrak {n}^{-1}$
. Hence,
$(\mathfrak {a}^{\vee })^2=\mathfrak {n}^{-1} \mathfrak {a} \mathfrak {a}^{\vee } = \mathfrak {n}^{-1}$
. Hence,
By the bilinearity of the commutator, we obtain Claim (ii) and subsequently Claim (iii). Similarly, we have
![]() $q([\beta _1,\beta _2]) \in \mathfrak {n}^2$
for
$q([\beta _1,\beta _2]) \in \mathfrak {n}^2$
for
![]() $\beta _i \in \mathfrak {a}$
. Thus, by orthogonality, we have
$\beta _i \in \mathfrak {a}$
. Thus, by orthogonality, we have
for
![]() $\gamma _i \in R$
, which gives Claim (i).
$\gamma _i \in R$
, which gives Claim (i).
8. Invariants of rational quadratic forms
Let V be an n-dimensional
![]() $\mathbb {Q}$
-vector space and
$\mathbb {Q}$
-vector space and
![]() $q : V \rightarrow \mathbb {Q}$
a nondegenerate quadratic form. We normalize the polarization
$q : V \rightarrow \mathbb {Q}$
a nondegenerate quadratic form. We normalize the polarization
![]() $\langle \,, \rangle $
of q such that
$\langle \,, \rangle $
of q such that
![]() $\langle x,x \rangle = 2 q(x)$
.
$\langle x,x \rangle = 2 q(x)$
.
Given a lattice
![]() $L \subseteq V$
and a positive-definite quadratic form Q on
$L \subseteq V$
and a positive-definite quadratic form Q on
![]() $V \otimes _{\mathbb {Q}} \mathbb {R}$
, one can define the successive minima of the pair
$V \otimes _{\mathbb {Q}} \mathbb {R}$
, one can define the successive minima of the pair
![]() $(L,Q)$
. Our aim in this section is to provide certain estimates for those successive minima in terms of other invariants of
$(L,Q)$
. Our aim in this section is to provide certain estimates for those successive minima in terms of other invariants of
![]() $(L,Q)$
. Our results may be understood as a generalization of those of Blomer–Michel [Reference Blomer and MichelBM13, §3, §4], who treated the special case that q is definite and
$(L,Q)$
. Our results may be understood as a generalization of those of Blomer–Michel [Reference Blomer and MichelBM13, §3, §4], who treated the special case that q is definite and
![]() $Q = q$
. We mention also the work of Saha [Reference SahaSah20, §2].
$Q = q$
. We mention also the work of Saha [Reference SahaSah20, §2].
8.1. Non-Archimedean invariants
Let
![]() $L \subseteq V$
be a lattice, that is, a
$L \subseteq V$
be a lattice, that is, a
![]() $\mathbb {Z}$
-submodule whose rank is the dimension of V. Define
$\mathbb {Z}$
-submodule whose rank is the dimension of V. Define
-
∘ the content C of L to be the greatest common divisor of
 $q(L)$
,
$q(L)$
, -
∘ the level N of L to be the reciprocal of the content of the dual lattice
 $L^\vee $
and
$L^\vee $
and -
∘ the (unsigned) discriminant
 $\Delta $
of L to be the absolute value of the determinant of the Gram matrix of q on L. (The discriminant of a quadratic form is traditionally defined without taking absolute values, but the sign will not matter for us.)
$\Delta $
of L to be the absolute value of the determinant of the Gram matrix of q on L. (The discriminant of a quadratic form is traditionally defined without taking absolute values, but the sign will not matter for us.)
Remark 8.1. In general, the content of L does not agree with the content of the Gram matrix of q on L, that is, the greatest common divisor of the entries. However, if q is integral on L, then the level of L agrees with the level of the Gram matrix of q.
Remark 8.2. For our purposes, the content, respectively level, may be replaced by the first, respectively last, elementary divisor of the Gram matrix of q as these quantities differ by a bounded power of
![]() $2$
.
$2$
.
To get acquainted with these quantities, consider for instance the case that L admits a basis
![]() $e_1, \dotsc , e_n$
with respect to which q is given by the diagonal quadratic form
$e_1, \dotsc , e_n$
with respect to which q is given by the diagonal quadratic form
![]() $q(\sum x_i e_i) = \frac {1}{2} \sum a_i x_i^2$
for some nonzero rational numbers
$q(\sum x_i e_i) = \frac {1}{2} \sum a_i x_i^2$
for some nonzero rational numbers
![]() $a_1,\dotsc ,a_n$
. Then
$a_1,\dotsc ,a_n$
. Then
We may relate the invariants attached to homothetic lattices: the effect of the substitution
![]() $L \mapsto m L$
for a nonzero rational scalar m is
$L \mapsto m L$
for a nonzero rational scalar m is
8.2. Archimedean invariants
Next, write
![]() $V_{\mathbb {R}} := V \otimes _{\mathbb {Q}} \mathbb {R}$
and let
$V_{\mathbb {R}} := V \otimes _{\mathbb {Q}} \mathbb {R}$
and let
![]() $Q : V_{ \mathbb {R} } \rightarrow \mathbb {R}$
be a positive-definite quadratic form. We may find a basis
$Q : V_{ \mathbb {R} } \rightarrow \mathbb {R}$
be a positive-definite quadratic form. We may find a basis
![]() $e_1,\dotsc ,e_n$
of
$e_1,\dotsc ,e_n$
of
![]() $V _{ \mathbb {R} }$
so that, writing
$V _{ \mathbb {R} }$
so that, writing
![]() $x = \sum x_i e_i$
, we have
$x = \sum x_i e_i$
, we have
![]() $Q(x) = \frac {1}{2}\sum x_i^2$
and
$Q(x) = \frac {1}{2}\sum x_i^2$
and
![]() $q(x) = \frac {1}{2} \sum a_i x_i^2$
for some nonzero real numbers
$q(x) = \frac {1}{2} \sum a_i x_i^2$
for some nonzero real numbers
![]() $a_1,\dotsc ,a_n$
. The dual
$a_1,\dotsc ,a_n$
. The dual
![]() $Q^\vee $
of Q with respect to q may be defined by
$Q^\vee $
of Q with respect to q may be defined by
![]() $Q^{\vee }(x) = \frac {1}{2} \sum a_i^2 x_i^2$
. We note that in the scaled coordinates
$Q^{\vee }(x) = \frac {1}{2} \sum a_i^2 x_i^2$
. We note that in the scaled coordinates
![]() $y = \sum a_i^{-1} y_i e_i$
, we have
$y = \sum a_i^{-1} y_i e_i$
, we have
![]() $Q^{\vee }(y) = \frac {1}{2} \sum y_i^2$
and
$Q^{\vee }(y) = \frac {1}{2} \sum y_i^2$
and
![]() $q(y) = \frac {1}{2} \sum a_i^{-1} y_i^2$
. The Gram matrix relative to q of Q is defined to be the diagonal matrix with entries
$q(y) = \frac {1}{2} \sum a_i^{-1} y_i^2$
. The Gram matrix relative to q of Q is defined to be the diagonal matrix with entries
![]() $(a_1,\dotsc ,a_n)$
.
$(a_1,\dotsc ,a_n)$
.
Define
-
∘ the content C of Q to be the infimum of the ratio
 $Q/|q|$
over the set where
$Q/|q|$
over the set where
 $q \neq 0$
,
$q \neq 0$
, -
∘ the level N of Q to be the reciprocal of the content of the dual
 $Q^{\vee }$
of Q and
$Q^{\vee }$
of Q and -
∘ the discriminant
 $\Delta $
of Q to be the absolute value of the reciprocal of the determinant of the Gram matrix relative to q of Q.
$\Delta $
of Q to be the absolute value of the reciprocal of the determinant of the Gram matrix relative to q of Q.
The invariants of Q may be described in terms of coordinates as above by
These again behave predictably under homotheties: If we substitute ![]() ] for some nonzero real scalar m (which has the effect of multiplying the Q-unit ball by m), then the coefficients transform like
] for some nonzero real scalar m (which has the effect of multiplying the Q-unit ball by m), then the coefficients transform like
![]() $a_i \mapsto m^2 a_i$
and hence the invariants like
$a_i \mapsto m^2 a_i$
and hence the invariants like
For later reference, it will be convenient to explicate the definition of ‘level’ in terms of matrices. To that end, we note first that for any basis
![]() $e_1,\dotsc ,e_n$
of V, we may find symmetric matrices S and P that represent q and Q in the sense that, for example,
$e_1,\dotsc ,e_n$
of V, we may find symmetric matrices S and P that represent q and Q in the sense that, for example,
![]() $q(\sum x_i e_i) = \frac {1}{2} \sum \sum x_i S_{i j} x_j$
. By singular value decomposition, we may find nonsingular matrices A and D, with D diagonal, so that
$q(\sum x_i e_i) = \frac {1}{2} \sum \sum x_i S_{i j} x_j$
. By singular value decomposition, we may find nonsingular matrices A and D, with D diagonal, so that
The level of Q is then the operator norm of the matrix
![]() $D^{-1}$
. For instance, if we choose our basis so that
$D^{-1}$
. For instance, if we choose our basis so that
![]() $Q(\sum x_i e_i) = \frac {1}{2} \sum x_i^2$
and
$Q(\sum x_i e_i) = \frac {1}{2} \sum x_i^2$
and
![]() $q(\sum x_i e_i) = \frac {1}{2} \sum d_i x_i^2$
, then the level of Q is
$q(\sum x_i e_i) = \frac {1}{2} \sum d_i x_i^2$
, then the level of Q is
![]() $\max |d_i|^{-1}$
.
$\max |d_i|^{-1}$
.
Remark 8.3. We may relate the above definition of level to more standard notions. We recall that the form Q is a majorant of q if
![]() $P S^{-1} P = S$
, or equivalently, if
$P S^{-1} P = S$
, or equivalently, if
![]() $D^2 = 1$
. Suppose that
$D^2 = 1$
. Suppose that
![]() $|q| \le Q$
. Then the level of Q is always at least
$|q| \le Q$
. Then the level of Q is always at least
![]() $1$
, and it is equal to
$1$
, and it is equal to
![]() $1$
if and only if Q is a majorant of q. Indeed, the assumption
$1$
if and only if Q is a majorant of q. Indeed, the assumption
![]() $|q| \le Q$
implies that
$|q| \le Q$
implies that
![]() $|d_i| \le 1$
for each i, with equality precisely when
$|d_i| \le 1$
for each i, with equality precisely when
![]() $D^2 = 1$
.
$D^2 = 1$
.
8.3. Duality
We note that replacing L (resp. Q) with its dual
![]() $L^\vee $
(resp.
$L^\vee $
(resp.
![]() $Q^\vee $
) has the following effect on the invariants:
$Q^\vee $
) has the following effect on the invariants:
In what follows, this relation allows us to reduce slightly the number of computations required. For instance, we can read off the invariants of the dual of an Eichler order (or its traceless submodule) from those of the Eichler order itself.
8.4. Adelic invariants
Let
![]() $(Q,L)$
be a pair consisting of a positive-definite quadratic form Q and a lattice L as above. We define the content (resp. level, discriminant) of the pair to be the product of the corresponding invariants of Q and L.
$(Q,L)$
be a pair consisting of a positive-definite quadratic form Q and a lattice L as above. We define the content (resp. level, discriminant) of the pair to be the product of the corresponding invariants of Q and L.
We note that the invariants
![]() $C, N, \Delta $
assigned to the pair
$C, N, \Delta $
assigned to the pair
![]() $(Q,L)$
are invariant by rational homotheties, that is, replacing L by
$(Q,L)$
are invariant by rational homotheties, that is, replacing L by
![]() $m L$
and Q by
$m L$
and Q by
![]() $Q_m$
for the same nonzero rational scalar m, and also under automorphisms of V that preserve q.
$Q_m$
for the same nonzero rational scalar m, and also under automorphisms of V that preserve q.
Furthermore, the discriminant of the pair
![]() $(Q,L)$
is the same as the determinant of the Gram matrix of Q with respect to a
$(Q,L)$
is the same as the determinant of the Gram matrix of Q with respect to a
![]() $\mathbb {Z}$
-basis of L, as the discriminant of Q is nothing but the inverse of the determinant of the matrix D in the singular value decomposition (8.1).
$\mathbb {Z}$
-basis of L, as the discriminant of Q is nothing but the inverse of the determinant of the matrix D in the singular value decomposition (8.1).
8.5. Statement of result
Proposition 8.4. Let V be an n-dimensional
![]() $\mathbb {Q}$
-vector space. Let
$\mathbb {Q}$
-vector space. Let
![]() $q : V \rightarrow \mathbb {Q}$
be an anisotropic quadratic form. Let
$q : V \rightarrow \mathbb {Q}$
be an anisotropic quadratic form. Let
![]() $L \subset V$
be a lattice. Let
$L \subset V$
be a lattice. Let
![]() $Q : V_{\mathbb {R}} \rightarrow \mathbb {R}$
be a positive-definite quadratic form. Let
$Q : V_{\mathbb {R}} \rightarrow \mathbb {R}$
be a positive-definite quadratic form. Let
![]() $\lambda _1 \le \dotsb \le \lambda _n$
denote the successive minima of Q on L (see Definition 6.1). Let
$\lambda _1 \le \dotsb \le \lambda _n$
denote the successive minima of Q on L (see Definition 6.1). Let
![]() $C, N, \Delta $
denote the content, level and discriminant of the pair
$C, N, \Delta $
denote the content, level and discriminant of the pair
![]() $(Q,L)$
. Then,
$(Q,L)$
. Then,
-
(i)
 $\lambda _1 \ge C^{1/2}$
,
$\lambda _1 \ge C^{1/2}$
, -
(ii)
 $\lambda _1 \dotsb \lambda _n \asymp \Delta ^{1/2}$
and
$\lambda _1 \dotsb \lambda _n \asymp \Delta ^{1/2}$
and -
(iii)
 $\lambda _1 \dotsb \lambda _{n-1} \gg (\Delta / N)^{1/2}$
.
$\lambda _1 \dotsb \lambda _{n-1} \gg (\Delta / N)^{1/2}$
.
In particular, for
![]() $n = 3$
, we have for all
$n = 3$
, we have for all
![]() $X> 0$
that
$X> 0$
that
 $$\begin{align*}| \{ v \in L : Q(v) \le X^2 \}| \ll 1 + \frac{X}{\sqrt{C}} + \frac{X^2}{\sqrt{\Delta/N}} + \frac{X^3}{\sqrt{\Delta}}.\end{align*}$$
$$\begin{align*}| \{ v \in L : Q(v) \le X^2 \}| \ll 1 + \frac{X}{\sqrt{C}} + \frac{X^2}{\sqrt{\Delta/N}} + \frac{X^3}{\sqrt{\Delta}}.\end{align*}$$
Remark 8.5. This last estimate is scale-invariant in the sense that replacing
![]() $(Q,L)$
with
$(Q,L)$
with
![]() $(Q_m, m L)$
for a positive rational scalar m has no effect on the right-hand side. This feature is not surprising in view of the multiplication-by-m bijection
$(Q_m, m L)$
for a positive rational scalar m has no effect on the right-hand side. This feature is not surprising in view of the multiplication-by-m bijection
![]() $\{ v \in L : Q(v) \le X^2 \} \cong \{ v \in m L : Q_m(v) \le X^2\}$
. The estimate is likewise invariant under replacing
$\{ v \in L : Q(v) \le X^2 \} \cong \{ v \in m L : Q_m(v) \le X^2\}$
. The estimate is likewise invariant under replacing
![]() $(Q,X)$
by
$(Q,X)$
by
![]() $(Q_m, X/m^2)$
for some nonzero real number m, as one might expect for similar reasons.
$(Q_m, X/m^2)$
for some nonzero real number m, as one might expect for similar reasons.
Proof. We follow the basic strategy of Blomer–Michel [Reference Blomer and MichelBM13, §3, §4], who established the corresponding result for q positive-definite and
![]() $Q=q$
.
$Q=q$
.
Let v be a nonzero element of L. Since L is anisotropic, we have
![]() $q(v) \neq 0$
. Let
$q(v) \neq 0$
. Let
![]() $C_Q, C_L$
denote the content of Q, respectively L. By the definition of the content, we have
$C_Q, C_L$
denote the content of Q, respectively L. By the definition of the content, we have
![]() $C_L|q(v)$
and
$C_L|q(v)$
and
![]() $Q \ge C_Q |q|$
. Thus,
$Q \ge C_Q |q|$
. Thus,
![]() $Q(v) \ge C_Q |q(v)| \ge C_QC_L = C$
, giving Claim (i).
$Q(v) \ge C_Q |q(v)| \ge C_QC_L = C$
, giving Claim (i).
By Lemma 6.3, we may find a basis
![]() $e_1,\dotsc ,e_n$
of L so that the submodules
$e_1,\dotsc ,e_n$
of L so that the submodules ![]() have covolume
have covolume
![]() $\asymp \prod _{j \le m} \lambda _j$
in their real span, with volume defined using the restriction of Q. On the other hand, that covolume is the square root of the Gram determinant of Q on
$\asymp \prod _{j \le m} \lambda _j$
in their real span, with volume defined using the restriction of Q. On the other hand, that covolume is the square root of the Gram determinant of Q on
![]() $L_m$
. Write
$L_m$
. Write
![]() $\det (Q,L_m)$
and
$\det (Q,L_m)$
and
![]() $\det (q,L_m)$
for the respective Gram determinants of Q and q. Then
$\det (q,L_m)$
for the respective Gram determinants of Q and q. Then
 $$ \begin{align} \prod_{j \le m} \lambda_j \asymp \det(Q,L_m)^{\frac{1}{2}}. \end{align} $$
$$ \begin{align} \prod_{j \le m} \lambda_j \asymp \det(Q,L_m)^{\frac{1}{2}}. \end{align} $$
Since
![]() $\det (Q,L_n) = \Delta $
by the remark in §8.4, the case
$\det (Q,L_n) = \Delta $
by the remark in §8.4, the case
![]() $m=n$
of this estimate gives Claim (ii).
$m=n$
of this estimate gives Claim (ii).
For the proof of Claim (iii), observe first that in view of Claim (ii), it is equivalent to check that
![]() $\lambda _n \ll (N_L N_Q)^{1/2}$
, where
$\lambda _n \ll (N_L N_Q)^{1/2}$
, where
![]() $N_L$
, respectively
$N_L$
, respectively
![]() $N_Q$
, is the level of L, respectively Q. To that end, write
$N_Q$
, is the level of L, respectively Q. To that end, write
![]() $P = A^t A$
and
$P = A^t A$
and
![]() $S = A^t D A$
for the matrices of Q and q, as in §8.2, and consider the final matrix entry
$S = A^t D A$
for the matrices of Q and q, as in §8.2, and consider the final matrix entry
![]() $(P^{-1})_{n n}$
of the inverse of P. Cramer’s rule expresses
$(P^{-1})_{n n}$
of the inverse of P. Cramer’s rule expresses
![]() $(P^{-1})_{n n} = \det (Q,L_{n-1}) / \det (Q, L_n)$
, so by the cases
$(P^{-1})_{n n} = \det (Q,L_{n-1}) / \det (Q, L_n)$
, so by the cases
![]() $m=n-1,n$
of Equation (8.3), we have
$m=n-1,n$
of Equation (8.3), we have
![]() $(P^{-1})_{n n} \asymp 1/\lambda _n^2$
. On the other hand, since
$(P^{-1})_{n n} \asymp 1/\lambda _n^2$
. On the other hand, since
![]() $N_Q$
bounds the operator norm of
$N_Q$
bounds the operator norm of
![]() $D^{-1}$
, we have
$D^{-1}$
, we have
Cramer’s rule likewise expresses
![]() $(S^{-1})_{n n} = \det (q,L_{n-1}) / \det (q,L_n)$
as a ratio of Gram determinants. Since q is anisotropic, both determinants are nonzero. Since
$(S^{-1})_{n n} = \det (q,L_{n-1}) / \det (q,L_n)$
as a ratio of Gram determinants. Since q is anisotropic, both determinants are nonzero. Since
![]() $2N_L (S^{-1})_{n n} \in \mathbb {Z}$
, it follows that
$2N_L (S^{-1})_{n n} \in \mathbb {Z}$
, it follows that
![]() $1/(2N_L) \le |(S^{-1})_{n n}|$
. Thus,
$1/(2N_L) \le |(S^{-1})_{n n}|$
. Thus,
![]() $1 / \lambda _n^2 \asymp (P^{-1})_{n n} \ge 1/(2N_L N_Q)$
, giving the required estimate.
$1 / \lambda _n^2 \asymp (P^{-1})_{n n} \ge 1/(2N_L N_Q)$
, giving the required estimate.
9. Type I estimates
The local computations of Section §7, together with the behavior of invariants under duality recorded in §8.2, imply that the elementary divisors of the Gram matrix of the reduced trace form on
![]() $g^{-1}R(\ell )^0g$
are given by
$g^{-1}R(\ell )^0g$
are given by
 $$ \begin{align} \begin{cases} \left(\frac{1}{\ell},\frac{d_B N}{\ell^2},\frac{2d_B N}{\ell}\right), & 2 \nmid d_BN, \\ \left(\frac{2}{\ell},\frac{d_BN}{\ell^2},\frac{d_BN}{\ell}\right), & 2 | d_BN, 2 \nmid \ell, \\ \left(\frac{1}{\ell},\frac{d_BN}{\ell^2},\frac{d_BN}{2\ell}\right), & 2 | d_BN, 2 | \ell. \end{cases} \end{align} $$
$$ \begin{align} \begin{cases} \left(\frac{1}{\ell},\frac{d_B N}{\ell^2},\frac{2d_B N}{\ell}\right), & 2 \nmid d_BN, \\ \left(\frac{2}{\ell},\frac{d_BN}{\ell^2},\frac{d_BN}{\ell}\right), & 2 | d_BN, 2 \nmid \ell, \\ \left(\frac{1}{\ell},\frac{d_BN}{\ell^2},\frac{d_BN}{2\ell}\right), & 2 | d_BN, 2 | \ell. \end{cases} \end{align} $$
Hence, the content, level and discriminant of
![]() $g^{-1}R(\ell )^0g$
with respect to the reduced norm are comparable to
$g^{-1}R(\ell )^0g$
with respect to the reduced norm are comparable to
![]() $1/\ell $
,
$1/\ell $
,
![]() $d_BN/\ell $
and
$d_BN/\ell $
and
![]() $(d_BN)^2/\ell ^4$
respectively. Here, ‘comparable to’ means the ratios are bounded from above and below by positive constants. Suppose that the reduced norm on R is anisotropic. In this case, we wish to apply Proposition 8.4 to the lattice
$(d_BN)^2/\ell ^4$
respectively. Here, ‘comparable to’ means the ratios are bounded from above and below by positive constants. Suppose that the reduced norm on R is anisotropic. In this case, we wish to apply Proposition 8.4 to the lattice
![]() $g^{-1}R(\ell )^0g$
with q given by the reduced norm. Recall the notation P, u and X from Equation (5.1). As a first choice, we let
$g^{-1}R(\ell )^0g$
with q given by the reduced norm. Recall the notation P, u and X from Equation (5.1). As a first choice, we let
![]() $Q=P+\delta ^{-1}u$
, whose content, level and discriminant are comparable to
$Q=P+\delta ^{-1}u$
, whose content, level and discriminant are comparable to
![]() $1,\delta ^{-1}$
and
$1,\delta ^{-1}$
and
![]() $\delta ^{-2}$
, respectively. This yields that the first successive minima of
$\delta ^{-2}$
, respectively. This yields that the first successive minima of
![]() $g^{-1}R(\ell )^0g$
with respect to
$g^{-1}R(\ell )^0g$
with respect to
![]() $P+\delta ^{-1}u$
is
$P+\delta ^{-1}u$
is
![]() $\gg \ell ^{-\frac {1}{2}}$
, and hence also with respect to
$\gg \ell ^{-\frac {1}{2}}$
, and hence also with respect to
![]() $\Omega (\delta ,1) \cap B_{\infty }^0$
. Furthermore,
$\Omega (\delta ,1) \cap B_{\infty }^0$
. Furthermore,
 $$ \begin{align*} |g^{-1} R(\ell)^0 g \cap \Omega(\delta, T)| \prec 1 + \ell^{\frac{1}{2}} T + \frac{\ell^{\frac{3}{2}} \delta^{\frac{1}{2}} }{(d_B N)^{\frac{1}{2}}} T^2 + \frac{\ell^2 \delta}{d_B N} T^{3}. \end{align*} $$
$$ \begin{align*} |g^{-1} R(\ell)^0 g \cap \Omega(\delta, T)| \prec 1 + \ell^{\frac{1}{2}} T + \frac{\ell^{\frac{3}{2}} \delta^{\frac{1}{2}} }{(d_B N)^{\frac{1}{2}}} T^2 + \frac{\ell^2 \delta}{d_B N} T^{3}. \end{align*} $$
This proves the first half of Theorem 2.5. Similarly, we have for the choice
![]() $Q=P+\delta ^{-1} |X|^2$
that the content, level and discriminant Q are comparable to
$Q=P+\delta ^{-1} |X|^2$
that the content, level and discriminant Q are comparable to
![]() $1,\delta ^{-1}$
and
$1,\delta ^{-1}$
and
![]() $\delta ^{-1}$
, respectively. Thus, the first successive minima of
$\delta ^{-1}$
, respectively. Thus, the first successive minima of
![]() $g^{-1}R(\ell )^0g$
with respect to
$g^{-1}R(\ell )^0g$
with respect to
![]() $\Psi (\delta ,1)\cap B_{\infty }^0$
is
$\Psi (\delta ,1)\cap B_{\infty }^0$
is
![]() $\gg \ell ^{-\frac {1}{2}}$
and
$\gg \ell ^{-\frac {1}{2}}$
and
 $$ \begin{align*} |g^{-1} R(\ell)^0 g \cap \Psi(\delta, T)| \prec 1 + \ell^{\frac{1}{2}} T + \frac{\ell^{\frac{3}{2}}}{(d_B N)^{\frac{1}{2}}} T^2 + \frac{\ell^2 \delta^{\frac{1}{2}}}{d_B N} T^{3}, \end{align*} $$
$$ \begin{align*} |g^{-1} R(\ell)^0 g \cap \Psi(\delta, T)| \prec 1 + \ell^{\frac{1}{2}} T + \frac{\ell^{\frac{3}{2}}}{(d_B N)^{\frac{1}{2}}} T^2 + \frac{\ell^2 \delta^{\frac{1}{2}}}{d_B N} T^{3}, \end{align*} $$
which is the second half of Theorem 2.5.
We now turn to the case that the quaternion algebra B is split. Here, we proceed in a more ad hoc manner. First, we note that
![]() $R(\ell )^0$
is normalized by the Atkin–Lehner operators. Thus, we need only consider
$R(\ell )^0$
is normalized by the Atkin–Lehner operators. Thus, we need only consider
![]() $g \in G(\mathbb {R})$
such that
$g \in G(\mathbb {R})$
such that
![]() $g \cdot i =x+iy$
has maximal imaginary part under the action of the Atkin–Lehner operators. In particular, we have
$g \cdot i =x+iy$
has maximal imaginary part under the action of the Atkin–Lehner operators. In particular, we have
![]() $H(g)=y$
. Let
$H(g)=y$
. Let
![]() $\lambda _1\le \lambda _2 \le \lambda _3$
be the successive minima (Definition 6.1) of the closed convex
$\lambda _1\le \lambda _2 \le \lambda _3$
be the successive minima (Definition 6.1) of the closed convex
![]() $0$
-symmetric set
$0$
-symmetric set
![]() $\Omega (\delta ,1)\cap B_{\infty }^0$
with respect to the lattice
$\Omega (\delta ,1)\cap B_{\infty }^0$
with respect to the lattice
![]() $g^{-1}R(\ell )^0g$
. Since
$g^{-1}R(\ell )^0g$
. Since
![]() $\Omega (\delta ,1)$
is both left and right
$\Omega (\delta ,1)$
is both left and right
![]() $K_{\infty }$
-invariant, we may further assume that
$K_{\infty }$
-invariant, we may further assume that
![]() $g=\left (\begin {smallmatrix} 1 & x \\ & 1 \end {smallmatrix}\right ) \operatorname {\mathrm {diag}}(y^{\frac {1}{2}} , y^{-\frac {1}{2}})$
. By Lemma 6.4, we have
$g=\left (\begin {smallmatrix} 1 & x \\ & 1 \end {smallmatrix}\right ) \operatorname {\mathrm {diag}}(y^{\frac {1}{2}} , y^{-\frac {1}{2}})$
. By Lemma 6.4, we have
 $$ \begin{align*} |g^{-1}R(\ell)^0g \cap \Omega(\delta,T) | = |g^{-1}R(\ell)^0g \cap T\Omega(\delta,1)| \asymp 1+\frac{T}{\lambda_1}+\frac{T^2}{\lambda_1\lambda_2}+\frac{T^3}{\lambda_1\lambda_2\lambda_3}. \end{align*} $$
$$ \begin{align*} |g^{-1}R(\ell)^0g \cap \Omega(\delta,T) | = |g^{-1}R(\ell)^0g \cap T\Omega(\delta,1)| \asymp 1+\frac{T}{\lambda_1}+\frac{T^2}{\lambda_1\lambda_2}+\frac{T^3}{\lambda_1\lambda_2\lambda_3}. \end{align*} $$
Let
![]() $\beta _0 = \left (\begin {smallmatrix} a & b \\ c & -a \end {smallmatrix}\right ) \in R(\ell )^0$
, thus
$\beta _0 = \left (\begin {smallmatrix} a & b \\ c & -a \end {smallmatrix}\right ) \in R(\ell )^0$
, thus
![]() $a \in \mathbb {Z}, b \in \frac {1}{\ell }\mathbb {Z}, c \in \frac {N}{\ell }\mathbb {Z}$
. Let
$a \in \mathbb {Z}, b \in \frac {1}{\ell }\mathbb {Z}, c \in \frac {N}{\ell }\mathbb {Z}$
. Let
 $$ \begin{align*} \alpha_0= g^{-1} \beta_0 g = \begin{pmatrix} a-cx & \frac{1}{y}(2ax+b-cx^2) \\ cy & cx-a \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \alpha_0= g^{-1} \beta_0 g = \begin{pmatrix} a-cx & \frac{1}{y}(2ax+b-cx^2) \\ cy & cx-a \end{pmatrix}. \end{align*} $$
Suppose
![]() $\beta _0 \neq 0$
. If
$\beta _0 \neq 0$
. If
![]() $(a,c)\neq (0,0)$
, then by Lemma 6.2 we have
$(a,c)\neq (0,0)$
, then by Lemma 6.2 we have
![]() $P(\alpha _0) \ge \frac {1}{2}|cz-a|^2 \ge \frac {1}{2\ell }$
. Otherwise, we have
$P(\alpha _0) \ge \frac {1}{2}|cz-a|^2 \ge \frac {1}{2\ell }$
. Otherwise, we have
![]() $u(\alpha _0)= (\frac {b}{y})^2 \ge \frac {1}{2(\ell y)^2}$
. Hence, we have
$u(\alpha _0)= (\frac {b}{y})^2 \ge \frac {1}{2(\ell y)^2}$
. Hence, we have
![]() $\lambda _1 \gg \min \{ \ell ^{-\frac {1}{2}} , \ell ^{-1} y^{-1} \delta ^{-\frac {1}{2}} \}$
. In order to get a lower bound on
$\lambda _1 \gg \min \{ \ell ^{-\frac {1}{2}} , \ell ^{-1} y^{-1} \delta ^{-\frac {1}{2}} \}$
. In order to get a lower bound on
![]() $\lambda _1\lambda _2$
and
$\lambda _1\lambda _2$
and
![]() $\lambda _1\lambda _2\lambda _3$
, we shall give an upper bound on
$\lambda _1\lambda _2\lambda _3$
, we shall give an upper bound on
![]() $|g^{-1}R(\ell )^0g \cap \Omega (\delta ,T)|$
along the lines of Harcos–Templier [Reference Harcos and TemplierHT13]. First, we bound the number of choices of c by
$|g^{-1}R(\ell )^0g \cap \Omega (\delta ,T)|$
along the lines of Harcos–Templier [Reference Harcos and TemplierHT13]. First, we bound the number of choices of c by
![]() $\ll 1+\frac {\ell T}{Ny}$
as
$\ll 1+\frac {\ell T}{Ny}$
as
![]() $|cy| \le P(\alpha _0)^{\frac {1}{2}} \le T$
. For each such choice of c, the equation
$|cy| \le P(\alpha _0)^{\frac {1}{2}} \le T$
. For each such choice of c, the equation
defines a circle of radius
![]() $\delta ^{\frac {1}{2}}T y$
and center
$\delta ^{\frac {1}{2}}T y$
and center
![]() $cz^2$
in which we need to count lattice points of the lattice generated by
$cz^2$
in which we need to count lattice points of the lattice generated by
![]() $2z$
and
$2z$
and
![]() $\frac {1}{\ell }$
. This lattice has covolume
$\frac {1}{\ell }$
. This lattice has covolume
![]() $2y/\ell $
and first successive minima
$2y/\ell $
and first successive minima
![]() $\ge (\ell N)^{-\frac {1}{2}}$
by Lemma 6.2. We may thus apply Lemma 6.5 to bound the number of
$\ge (\ell N)^{-\frac {1}{2}}$
by Lemma 6.2. We may thus apply Lemma 6.5 to bound the number of
![]() $(a,b)$
by
$(a,b)$
by
![]() $\ll 1+\ell ^{\frac {1}{2}}N^{\frac {1}{2}}\delta ^{\frac {1}{2}}T y + \ell \delta T^2 y$
. We obtain
$\ll 1+\ell ^{\frac {1}{2}}N^{\frac {1}{2}}\delta ^{\frac {1}{2}}T y + \ell \delta T^2 y$
. We obtain
 $$ \begin{align*} \frac{T^2}{\lambda_1\lambda_2} + \frac{T^{3}}{\lambda_1\lambda_2\lambda_3} \ll \left( 1+\frac{\ell T}{Ny} \right)\left( 1+\ell^{\frac{1}{2}}N^{\frac{1}{2}}\delta^{\frac{1}{2}}Ty + \ell\delta T^2 y \right). \end{align*} $$
$$ \begin{align*} \frac{T^2}{\lambda_1\lambda_2} + \frac{T^{3}}{\lambda_1\lambda_2\lambda_3} \ll \left( 1+\frac{\ell T}{Ny} \right)\left( 1+\ell^{\frac{1}{2}}N^{\frac{1}{2}}\delta^{\frac{1}{2}}Ty + \ell\delta T^2 y \right). \end{align*} $$
By letting T tend to
![]() $\infty $
, it follows that
$\infty $
, it follows that
![]() $\lambda _1\lambda _2\lambda _3 \gg N \ell ^{-2}\delta ^{-1}$
. By taking
$\lambda _1\lambda _2\lambda _3 \gg N \ell ^{-2}\delta ^{-1}$
. By taking
![]() $T=N^{\frac {1}{2}}/(\ell \delta )^{\frac {1}{2}}$
, we obtain
$T=N^{\frac {1}{2}}/(\ell \delta )^{\frac {1}{2}}$
, we obtain
 $$ \begin{align*} \frac{1}{\lambda_1\lambda_2} \ll \frac{\ell\delta}{N}+\frac{\ell^{\frac{3}{2}}\delta^{\frac{1}{2}}}{N^{\frac{3}{2}}y}+\ell\delta y + \frac{\ell^{\frac{3}{2}}\delta^{\frac{1}{2}}}{N^{\frac{1}{2}}} \ll \frac{\ell^{\frac{3}{2}}\delta^{\frac{1}{2}}}{N^{\frac{1}{2}}} + \ell \delta y. \end{align*} $$
$$ \begin{align*} \frac{1}{\lambda_1\lambda_2} \ll \frac{\ell\delta}{N}+\frac{\ell^{\frac{3}{2}}\delta^{\frac{1}{2}}}{N^{\frac{3}{2}}y}+\ell\delta y + \frac{\ell^{\frac{3}{2}}\delta^{\frac{1}{2}}}{N^{\frac{1}{2}}} \ll \frac{\ell^{\frac{3}{2}}\delta^{\frac{1}{2}}}{N^{\frac{1}{2}}} + \ell \delta y. \end{align*} $$
We thereby conclude the proof of the final case of Theorem 2.5.
10. Type II estimates
10.1. Bounds for representation numbers of binary quadratic forms
Lemma 10.1. Let M be a free
![]() $\mathbb {Z}$
-module of rank
$\mathbb {Z}$
-module of rank
![]() $2$
. Let
$2$
. Let
![]() $q : M \rightarrow \mathbb {Z}$
be a nondegenerate integral binary quadratic form. Let Q be a positive-definite quadratic form on
$q : M \rightarrow \mathbb {Z}$
be a nondegenerate integral binary quadratic form. Let Q be a positive-definite quadratic form on
![]() $M \otimes \mathbb {R}$
such that
$M \otimes \mathbb {R}$
such that
![]() $|q| \le Q$
. Let n be a nonzero integer and let
$|q| \le Q$
. Let n be a nonzero integer and let
![]() $X \ge 1$
. Set
$X \ge 1$
. Set
Then,
Proof. We begin with a preliminary reduction. Suppose we can find a lattice
![]() $M'$
in
$M'$
in
![]() $M \otimes \mathbb {Q}$
that contains M and on which the
$M \otimes \mathbb {Q}$
that contains M and on which the
![]() $\mathbb {Q}$
-bilinear extension of q is integral. It suffices then to verify the lemma after replacing M with
$\mathbb {Q}$
-bilinear extension of q is integral. It suffices then to verify the lemma after replacing M with
![]() $M'$
. Indeed, doing so enlarges the set S. In particular, we may assume that the quadratic form M is primitive.
$M'$
. Indeed, doing so enlarges the set S. In particular, we may assume that the quadratic form M is primitive.
Suppose now that M is primitive and anisotropic. Without loss of generality, M is either positive-definite or indefinite. By the form-ideal correspondence, we may assume then that M is an invertible ideal of an order
![]() $\mathfrak {o}$
in a quadratic field, with q given by the element norm
$\mathfrak {o}$
in a quadratic field, with q given by the element norm
![]() $\nu $
divided by the ideal norm
$\nu $
divided by the ideal norm
![]() $\nu (M)$
of M:
$\nu (M)$
of M:
We will establish the estimate
which suffices in view of the divisor bound. Let
![]() $\mathfrak {o}_{\max }$
denote the maximal order in the quadratic field containing
$\mathfrak {o}_{\max }$
denote the maximal order in the quadratic field containing
![]() $\mathfrak {o}$
. For each
$\mathfrak {o}$
. For each
![]() $\beta \in S$
, the
$\beta \in S$
, the
![]() $\mathfrak {o}$
-ideal
$\mathfrak {o}$
-ideal
![]() $M^{-1} \beta $
has norm
$M^{-1} \beta $
has norm
![]() $|n|$
, as does the
$|n|$
, as does the
![]() $\mathfrak {o}_{\max }$
-ideal
$\mathfrak {o}_{\max }$
-ideal
![]() $\mathfrak {o}_{\max } M^{-1} \beta $
. The number of
$\mathfrak {o}_{\max } M^{-1} \beta $
. The number of
![]() $\mathfrak {o}_{\max }$
-ideals of norm
$\mathfrak {o}_{\max }$
-ideals of norm
![]() $|n|$
is at most
$|n|$
is at most
![]() $\tau (n)$
. Suppose two elements
$\tau (n)$
. Suppose two elements
![]() $\beta _0, \beta \in S$
give rise to the same
$\beta _0, \beta \in S$
give rise to the same
![]() $\mathfrak {o}_{\max }$
-ideal. Then,
$\mathfrak {o}_{\max }$
-ideal. Then,
![]() $\beta /\beta _0$
is a norm one unit in
$\beta /\beta _0$
is a norm one unit in
![]() $\mathfrak {o}_{\max }^{\times }$
. The required estimate follows in the imaginary quadratic case (without the logarithmic factor) because
$\mathfrak {o}_{\max }^{\times }$
. The required estimate follows in the imaginary quadratic case (without the logarithmic factor) because
![]() $| \mathfrak {o}_{\max }^{\times }| \le 6$
. In the real quadratic case, we fix a positive generator
$| \mathfrak {o}_{\max }^{\times }| \le 6$
. In the real quadratic case, we fix a positive generator
![]() $\eta $
for the group
$\eta $
for the group
![]() $\cong \mathbb {Z}$
of non-root-of-unity norm one units in
$\cong \mathbb {Z}$
of non-root-of-unity norm one units in
![]() $\mathfrak {o}_{\max }$
and write
$\mathfrak {o}_{\max }$
and write
![]() $\beta = \pm \beta _0 \eta ^{\ell }$
for some
$\beta = \pm \beta _0 \eta ^{\ell }$
for some
![]() $\ell \in \mathbb {Z}$
. It will suffice then to verify that
$\ell \in \mathbb {Z}$
. It will suffice then to verify that
![]() $\ell \ll \log (2 + X^2/|n|)$
. To that end, we estimate
$\ell \ll \log (2 + X^2/|n|)$
. To that end, we estimate
![]() $q(\beta _0 + \beta )$
in two ways. On the one hand, the triangle inequality for the Euclidean norm defined by Q gives the upper bound
$q(\beta _0 + \beta )$
in two ways. On the one hand, the triangle inequality for the Euclidean norm defined by Q gives the upper bound
![]() $|q(\beta _0 + \beta )| \le Q(\beta _0 + \beta ) \ll Q(\beta _0) + Q(\beta ) \ll X^2$
. On the other hand, the multiplicativity of
$|q(\beta _0 + \beta )| \le Q(\beta _0 + \beta ) \ll Q(\beta _0) + Q(\beta ) \ll X^2$
. On the other hand, the multiplicativity of
![]() $\nu $
gives the identity
$\nu $
gives the identity
![]() $q(\beta _0 + \beta ) = n \nu (1 \pm \eta ^{\ell })$
. The lower bound
$q(\beta _0 + \beta ) = n \nu (1 \pm \eta ^{\ell })$
. The lower bound
![]() $\nu (1 \pm \eta ^{\ell }) \ge \frac {1}{4} \cdot 1.618^{\ell }$
for fundamental units now yields the required estimate for
$\nu (1 \pm \eta ^{\ell }) \ge \frac {1}{4} \cdot 1.618^{\ell }$
for fundamental units now yields the required estimate for
![]() $\ell $
.
$\ell $
.
It remains to consider the case that M is isotropic and q nondegenerate. In that case, after applying our preliminary reduction to enlarge M if necessary, we may assume that
![]() $M = \mathbb {Z}^2$
and
$M = \mathbb {Z}^2$
and
![]() $q(x,y) = x y$
. Indeed, we may choose a basis
$q(x,y) = x y$
. Indeed, we may choose a basis
![]() $e_1, e_2$
for M with
$e_1, e_2$
for M with
![]() $e_1$
isotropic. Then, q is given with respect to the coordinates
$e_1$
isotropic. Then, q is given with respect to the coordinates
![]() $x e_1 + y e_2$
by
$x e_1 + y e_2$
by
![]() $q(x,y) = a x y + b y^2$
for some
$q(x,y) = a x y + b y^2$
for some
![]() $a,b \in \mathbb {Z}$
, with
$a,b \in \mathbb {Z}$
, with
![]() $a \neq 0$
. Then
$a \neq 0$
. Then
![]() $q (\tfrac {x - b y}{a}, y) = x y$
and
$q (\tfrac {x - b y}{a}, y) = x y$
and
![]() $M \subseteq M' := \{ \tfrac {x - b y}{a} e_1 + y e_2 : x, y \in \mathbb {Z} \}$
, so
$M \subseteq M' := \{ \tfrac {x - b y}{a} e_1 + y e_2 : x, y \in \mathbb {Z} \}$
, so
![]() $(M',q)$
gives the required enlargement. Now, since
$(M',q)$
gives the required enlargement. Now, since
![]() $n \neq 0$
, the divisor bound gives
$n \neq 0$
, the divisor bound gives
![]() $|S| = 2 \tau (n) \ll _{\varepsilon } |n|^{\varepsilon }$
.
$|S| = 2 \tau (n) \ll _{\varepsilon } |n|^{\varepsilon }$
.
10.2. Local quaternionic preliminaries
Let B be a quaternion algebra over the rationals. We write
![]() $d_B$
for its reduced discriminant and q for its reduced norm.
$d_B$
for its reduced discriminant and q for its reduced norm.
10.2.1. Non-Archimedean preliminaries
Let
![]() $R \subset B$
be an Eichler order of level N, with N coprime to
$R \subset B$
be an Eichler order of level N, with N coprime to
![]() $d_B$
.
$d_B$
.
Lemma 10.2. For
![]() $x,y \in R(\ell )^0$
, we have
$x,y \in R(\ell )^0$
, we have
![]() $[x,y] \in \frac {1}{\ell } R^0$
and
$[x,y] \in \frac {1}{\ell } R^0$
and
![]() $q([x,y]) \in \frac {d_B N}{\ell ^3} \mathbb {Z}$
.
$q([x,y]) \in \frac {d_B N}{\ell ^3} \mathbb {Z}$
.
Proof. This follows from the local computations in Lemma 7.4 together with the fact that the trace of a commutator is zero.
10.2.2. Archimedean preliminaries
Recall the notation ‘
![]() $\Omega $
’ from §2.4.4 and ‘P’ from Equation (5.1).
$\Omega $
’ from §2.4.4 and ‘P’ from Equation (5.1).
Lemma 10.3. For
![]() $0 < \delta \le 1$
and
$0 < \delta \le 1$
and
![]() $x, y \in \Omega (\delta ,T)$
, we have
$x, y \in \Omega (\delta ,T)$
, we have
and
Proof. For
![]() $\delta = 1$
, the required estimates reduce via homogeneity to the compactness of the unit ball and the continuity of multiplication. We turn to the case
$\delta = 1$
, the required estimates reduce via homogeneity to the compactness of the unit ball and the continuity of multiplication. We turn to the case
![]() $0 < \delta < 1$
. We embed
$0 < \delta < 1$
. We embed
![]() $B_{\infty } \hookrightarrow \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {C})$
by
$B_{\infty } \hookrightarrow \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {C})$
by
![]() ${\mathbf{i}} \mapsto \left (\begin {smallmatrix} i & 0 \\ 0 & -i \end {smallmatrix}\right )$
,
${\mathbf{i}} \mapsto \left (\begin {smallmatrix} i & 0 \\ 0 & -i \end {smallmatrix}\right )$
,
![]() ${\mathbf{j}} \mapsto \left (\begin {smallmatrix} 0 & 1 \\ \pm 1 & 0 \end {smallmatrix}\right )$
. Then, P is asymptotic to the restriction of the squared Euclidean norm on the matrix entries, while q is the restriction of the determinant. We may assume that
${\mathbf{j}} \mapsto \left (\begin {smallmatrix} 0 & 1 \\ \pm 1 & 0 \end {smallmatrix}\right )$
. Then, P is asymptotic to the restriction of the squared Euclidean norm on the matrix entries, while q is the restriction of the determinant. We may assume that
![]() $x=[a_1,b_1,c_1]$
and
$x=[a_1,b_1,c_1]$
and
![]() $y=[a_2,b_2,c_2]$
are nonzero. We may assume (by the known
$y=[a_2,b_2,c_2]$
are nonzero. We may assume (by the known
![]() $\delta = 1$
case) that
$\delta = 1$
case) that
![]() $\delta $
is sufficiently small. The required conclusion then reduces via homogeneity to the following assertion: The commutator of any two matrices of the form
$\delta $
is sufficiently small. The required conclusion then reduces via homogeneity to the following assertion: The commutator of any two matrices of the form
 $$ \begin{align*} \begin{pmatrix} a_1 i & O(\delta^{1/2}) \\ O(\delta^{1/2}) & - a_1 i \end{pmatrix} \quad \text{and}\quad \begin{pmatrix} a_2 i & O(\delta^{1/2}) \\ O(\delta^{1/2}) & - a_2 i \end{pmatrix} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} a_1 i & O(\delta^{1/2}) \\ O(\delta^{1/2}) & - a_1 i \end{pmatrix} \quad \text{and}\quad \begin{pmatrix} a_2 i & O(\delta^{1/2}) \\ O(\delta^{1/2}) & - a_2 i \end{pmatrix} \end{align*} $$
is of the form
![]() $\left (\begin {smallmatrix} O(\delta ) & O(\delta ^{1/2}) \\ O(\delta ^{1/2}) & O(\delta ) \end {smallmatrix}\right )$
, and in particular has Euclidean norm
$\left (\begin {smallmatrix} O(\delta ) & O(\delta ^{1/2}) \\ O(\delta ^{1/2}) & O(\delta ) \end {smallmatrix}\right )$
, and in particular has Euclidean norm
![]() $O(\delta ^{1/2})$
and determinant
$O(\delta ^{1/2})$
and determinant
![]() $O(\delta )$
. Indeed, the product of any two matrices of the indicated form is readily computed to be of the form
$O(\delta )$
. Indeed, the product of any two matrices of the indicated form is readily computed to be of the form
![]() $\left (\begin {smallmatrix} -a_1a_2 + O(\delta ) & O(\delta ^{1/2}) \\ O(\delta ^{1/2}) & -a_1a_2 + O(\delta ) \end {smallmatrix}\right )$
, hence the commutator of two such matrices, being a difference of such products, has the required form.
$\left (\begin {smallmatrix} -a_1a_2 + O(\delta ) & O(\delta ^{1/2}) \\ O(\delta ^{1/2}) & -a_1a_2 + O(\delta ) \end {smallmatrix}\right )$
, hence the commutator of two such matrices, being a difference of such products, has the required form.
10.3. The nonsplit case
We retain the above setting and further assume that B is nonsplit and that the level N of the Eichler order R is squarefree.
The following estimate is, in some sense, the most intricate one in the paper. It requires us to bound certain matrix counts in the critical range (see Remark 10.5 below) by essentially
![]() $O(1)$
, uniformly in the discriminant and level. To achieve such uniformity seems to require the delicate argument involving commutators recorded below.
$O(1)$
, uniformly in the discriminant and level. To achieve such uniformity seems to require the delicate argument involving commutators recorded below.
Proposition 10.4. Let n be a nonzero integer, let
![]() $0 < \delta \le 1$
and let
$0 < \delta \le 1$
and let
![]() $T \ge \ell ^{-\frac {1}{2}}$
. Then the set
$T \ge \ell ^{-\frac {1}{2}}$
. Then the set ![]() has cardinality
has cardinality
 $$\begin{align*}|S| \ll_{\varepsilon} (\ell T)^\varepsilon \tau(d_B N) \left( 1 + \frac{\ell^2}{d_B N} \min\left\{\delta^{\frac{1}{2}} T^2 , \frac{\delta T^4}{|n|} \right\} \right).\end{align*}$$
$$\begin{align*}|S| \ll_{\varepsilon} (\ell T)^\varepsilon \tau(d_B N) \left( 1 + \frac{\ell^2}{d_B N} \min\left\{\delta^{\frac{1}{2}} T^2 , \frac{\delta T^4}{|n|} \right\} \right).\end{align*}$$
Remark 10.5. The critical range is when
![]() $n \asymp T^2 \asymp d_B N(1+k) / \ell ^2$
and
$n \asymp T^2 \asymp d_B N(1+k) / \ell ^2$
and
![]() $\delta \asymp (1+k)^{-1}$
; in that range, we obtain
$\delta \asymp (1+k)^{-1}$
; in that range, we obtain
![]() $|S| \ll _{\varepsilon } (d_B N (1+k) )^\varepsilon $
.
$|S| \ll _{\varepsilon } (d_B N (1+k) )^\varepsilon $
.
Proof. Suppose S is not empty, and let
![]() $\gamma _1, \gamma _2 \in S$
. Our strategy will be to bound for each
$\gamma _1, \gamma _2 \in S$
. Our strategy will be to bound for each
![]() $\gamma _1$
the number of possibilities for
$\gamma _1$
the number of possibilities for
![]() $\gamma _2$
.
$\gamma _2$
.
Set ![]() and
and ![]() . Then,
. Then,
![]() $2 \gamma _1 \gamma _2 = a + \beta $
,
$2 \gamma _1 \gamma _2 = a + \beta $
,
![]() $4 n^2 = a^2 + q(\beta )$
. In particular,
$4 n^2 = a^2 + q(\beta )$
. In particular,
![]() $\gamma _2 = (a + \beta ) / 2 \gamma _1$
, so it suffices to bound the number of possibilities for a and
$\gamma _2 = (a + \beta ) / 2 \gamma _1$
, so it suffices to bound the number of possibilities for a and
![]() $\beta $
.
$\beta $
.
Lemmas 10.2 and 10.3 give
![]() $q(\beta ) \ll \delta T^4$
and
$q(\beta ) \ll \delta T^4$
and
![]() $q(\beta ) \in \frac {d_B N}{\ell ^3} \mathbb {Z}$
, that is,
$q(\beta ) \in \frac {d_B N}{\ell ^3} \mathbb {Z}$
, that is,
thus
 $$\begin{align*}a = \pm 2 n + O\left(\min\left\{\delta^{\frac{1}{2}} T^2 , \frac{\delta T^4}{|n|} \right\} \right),\end{align*}$$
$$\begin{align*}a = \pm 2 n + O\left(\min\left\{\delta^{\frac{1}{2}} T^2 , \frac{\delta T^4}{|n|} \right\} \right),\end{align*}$$
for some sign
![]() $\pm $
and some residue class
$\pm $
and some residue class
![]() $a_0$
modulo
$a_0$
modulo
![]() $d_B N/ \ell ^2$
with
$d_B N/ \ell ^2$
with
![]() $a_0^2 \equiv 4 n^2\ \, \pod{\tfrac {d_B N}{\ell ^2}}$
. Since
$a_0^2 \equiv 4 n^2\ \, \pod{\tfrac {d_B N}{\ell ^2}}$
. Since
![]() $d_B N$
is squarefree, there are at most
$d_B N$
is squarefree, there are at most
![]() $\tau (d_B N)$
such classes. For each
$\tau (d_B N)$
such classes. For each
![]() $a_0$
, the number of possibilities for a is
$a_0$
, the number of possibilities for a is
![]() $O(1 + (\ell ^2 / d_B N) \cdot \min \{\delta ^{\frac {1}{2}} T^2, \delta T^4 /|n|\})$
.
$O(1 + (\ell ^2 / d_B N) \cdot \min \{\delta ^{\frac {1}{2}} T^2, \delta T^4 /|n|\})$
.
We now bound for each a the number of possibilities for
![]() $\beta $
. Let M denote the orthogonal complement in
$\beta $
. Let M denote the orthogonal complement in
![]() $\frac {1}{\ell } R^0$
of
$\frac {1}{\ell } R^0$
of
![]() $\gamma _1$
, thus
$\gamma _1$
, thus
![]() $M = \{ \gamma \in \frac {1}{\ell }R^0 : \operatorname {\mathrm {tr}}(\gamma \gamma _1) = 0 \}$
. By restricting q to M, we obtain an integral binary quadratic form. Since B is nonsplit, M is anisotropic. Since
$M = \{ \gamma \in \frac {1}{\ell }R^0 : \operatorname {\mathrm {tr}}(\gamma \gamma _1) = 0 \}$
. By restricting q to M, we obtain an integral binary quadratic form. Since B is nonsplit, M is anisotropic. Since
![]() $\operatorname {\mathrm {tr}}(\gamma _1 \gamma _2 \gamma _1) = \operatorname {\mathrm {tr}}(\gamma _2 \gamma _1 \gamma _1)$
, we have
$\operatorname {\mathrm {tr}}(\gamma _1 \gamma _2 \gamma _1) = \operatorname {\mathrm {tr}}(\gamma _2 \gamma _1 \gamma _1)$
, we have
![]() $\beta \in M$
. From Lemma 10.3, we obtain
$\beta \in M$
. From Lemma 10.3, we obtain
![]() $P(\beta ) \ll T^4$
. Thus,
$P(\beta ) \ll T^4$
. Thus,
![]() $\beta $
satisfies the system
$\beta $
satisfies the system
Since
![]() $q(M) \subseteq \frac {1}{\ell ^2} \mathbb {Z}$
and
$q(M) \subseteq \frac {1}{\ell ^2} \mathbb {Z}$
and
![]() $4 n ^2 - a^2 \ll \delta T^4$
, we see by Lemma 10.1 that the number of possibilities for
$4 n ^2 - a^2 \ll \delta T^4$
, we see by Lemma 10.1 that the number of possibilities for
![]() $\beta $
is
$\beta $
is
![]() $\ll _{\varepsilon } ( \ell T)^\varepsilon $
.
$\ll _{\varepsilon } ( \ell T)^\varepsilon $
.
By multiplying together the number of possibilities for
![]() $\pm , a_0, a$
and
$\pm , a_0, a$
and
![]() $\beta $
, we achieve the required bound.
$\beta $
, we achieve the required bound.
10.4. Extension to the split case
Recall from §2.2, that we may assume our Eichler order of level N in the split quaternion algebra
![]() $B = \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {Q})$
to be of the shape
$B = \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {Q})$
to be of the shape
![]() $g^{-1}Rg$
, where
$g^{-1}Rg$
, where
![]() $R=\left (\begin {smallmatrix} \mathbb {Z} & \mathbb {Z}\\ N\mathbb {Z} & \mathbb {Z} \end {smallmatrix}\right )$
and
$R=\left (\begin {smallmatrix} \mathbb {Z} & \mathbb {Z}\\ N\mathbb {Z} & \mathbb {Z} \end {smallmatrix}\right )$
and
![]() $g \in G(\mathbb {R})$
. Our aim is to bound the cardinality of the set
$g \in G(\mathbb {R})$
. Our aim is to bound the cardinality of the set
In the nonsplit case, we had verified that
where

We extend this to the split case as follows.
Proposition 10.6. Let n be an integer. If
![]() $-n$
is not a square, then
$-n$
is not a square, then
![]() $|S| \ll _{\varepsilon } C$
. If
$|S| \ll _{\varepsilon } C$
. If
![]() $-n$
is a square, then
$-n$
is a square, then
![]() $|S| \ll _{\varepsilon } C + \delta ^{1/2} T \ell H(g)$
, where H denotes the normalized height function defined in §2.2.
$|S| \ll _{\varepsilon } C + \delta ^{1/2} T \ell H(g)$
, where H denotes the normalized height function defined in §2.2.
Proof. We proceed as in the original argument, aiming to bound for fixed
![]() $\gamma _1 \in gSg^{-1}$
the number of possible
$\gamma _1 \in gSg^{-1}$
the number of possible
![]() $\gamma _2 \in gSg^{-1}$
. As before, we write
$\gamma _2 \in gSg^{-1}$
. As before, we write
so that
Since
![]() $\gamma _1 = (\alpha + \beta )/2 \gamma _2$
, it suffices to count the number of possible pairs
$\gamma _1 = (\alpha + \beta )/2 \gamma _2$
, it suffices to count the number of possible pairs
![]() $(\alpha ,\beta )$
. The pairs with
$(\alpha ,\beta )$
. The pairs with
![]() $q(\beta ) \neq 0$
may be counted as before after noting that the restriction of q to the orthogonal complement of
$q(\beta ) \neq 0$
may be counted as before after noting that the restriction of q to the orthogonal complement of
![]() $\gamma _1$
is nondegenerate. There are at most two pairs with
$\gamma _1$
is nondegenerate. There are at most two pairs with
![]() $\beta = 0$
, since then
$\beta = 0$
, since then
![]() $\alpha = \pm 2n$
. We thereby reduce to counting the number of pairs for which
$\alpha = \pm 2n$
. We thereby reduce to counting the number of pairs for which
Recall the notation of §4.3.1. We note that for each cusp
![]() $\mathfrak {a}$
, we may and shall choose
$\mathfrak {a}$
, we may and shall choose
![]() $\sigma _{\mathfrak {a}} \in \Gamma _0(N) \tau _{t}$
for some
$\sigma _{\mathfrak {a}} \in \Gamma _0(N) \tau _{t}$
for some
![]() $t | N$
. With this choice, we have
$t | N$
. With this choice, we have
 $$ \begin{align} \sigma_{\mathfrak{a}}^{-1} R \sigma_{\mathfrak{a}} = \begin{pmatrix} \mathbb{Z} & w_{\mathfrak{a}}\mathbb{Z} \\ \frac{N}{w_{\mathfrak{a}}}\mathbb{Z} & \mathbb{Z} \end{pmatrix}, \end{align} $$
$$ \begin{align} \sigma_{\mathfrak{a}}^{-1} R \sigma_{\mathfrak{a}} = \begin{pmatrix} \mathbb{Z} & w_{\mathfrak{a}}\mathbb{Z} \\ \frac{N}{w_{\mathfrak{a}}}\mathbb{Z} & \mathbb{Z} \end{pmatrix}, \end{align} $$
where
![]() $w_{\mathfrak {a}}$
is the cusp width of the cusp
$w_{\mathfrak {a}}$
is the cusp width of the cusp
![]() $\mathfrak {a}$
. This is easily verified locally. We further introduce the following notation: For
$\mathfrak {a}$
. This is easily verified locally. We further introduce the following notation: For
![]() $\mathfrak {a} \in \mathbb {P}^1(\mathbb {Z})$
and
$\mathfrak {a} \in \mathbb {P}^1(\mathbb {Z})$
and
![]() $\kappa \in B^0$
, we set
$\kappa \in B^0$
, we set ![]() .
.
We observe, by Equation (10.2), that
![]() $\ell \beta $
is a nonzero element of
$\ell \beta $
is a nonzero element of
![]() $R^0 \subseteq \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {Z})^0$
. There is thus a unique (up to sign) primitive element
$R^0 \subseteq \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {Z})^0$
. There is thus a unique (up to sign) primitive element
![]() $\beta _0$
of
$\beta _0$
of
![]() $\operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {Z})^0$
that generates
$\operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {Z})^0$
that generates
![]() $\mathbb {Q} \ell \beta \cap \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {Z})^0$
. We then have
$\mathbb {Q} \ell \beta \cap \operatorname {\mathrm {Mat}}_{2 \times 2}(\mathbb {Z})^0$
. We then have
![]() $\beta \in \frac {1}{\ell } \mathbb {Z} \beta _0$
.
$\beta \in \frac {1}{\ell } \mathbb {Z} \beta _0$
.
We may and shall choose
![]() $\mathfrak {a}$
so that
$\mathfrak {a}$
so that
![]() $\beta _0^{\mathfrak {a}} = \left (\begin {smallmatrix} 0 & \pm 1 \\ 0 & 0 \end {smallmatrix}\right )$
. Note that
$\beta _0^{\mathfrak {a}} = \left (\begin {smallmatrix} 0 & \pm 1 \\ 0 & 0 \end {smallmatrix}\right )$
. Note that
![]() $\beta $
(equivalently,
$\beta $
(equivalently,
![]() $\beta _0$
) is orthogonal not only to
$\beta _0$
) is orthogonal not only to
![]() $\gamma _1$
(as was used in the original argument), but also to
$\gamma _1$
(as was used in the original argument), but also to
![]() $\gamma _2$
. From this, we deduce that
$\gamma _2$
. From this, we deduce that
 $$\begin{align*}\gamma_2^{\mathfrak{a}} = \begin{pmatrix} a & b \\ 0 & -a \end{pmatrix}\end{align*}$$
$$\begin{align*}\gamma_2^{\mathfrak{a}} = \begin{pmatrix} a & b \\ 0 & -a \end{pmatrix}\end{align*}$$
for some
![]() $a \in \mathbb {Z}$
and
$a \in \mathbb {Z}$
and
![]() $b \in \frac {1}{\ell } \mathbb {Z}$
. We have
$b \in \frac {1}{\ell } \mathbb {Z}$
. We have
![]() $n = q(\gamma _2) = -a^2$
, which shows that
$n = q(\gamma _2) = -a^2$
, which shows that
![]() $-n$
must be a square and also that there are at most two possibilities for a. It remains to verify that the number of possibilities for b is
$-n$
must be a square and also that there are at most two possibilities for a. It remains to verify that the number of possibilities for b is
![]() $O(1+\delta ^{1/2} T \ell H(g))$
. We will show in fact that the number of b is
$O(1+\delta ^{1/2} T \ell H(g))$
. We will show in fact that the number of b is
where
![]() $\sigma _{\mathfrak {a}}^{-1}z=z_{\mathfrak {a}}=x_{\mathfrak {a}}+iy_{\mathfrak {a}}$
. To see this, observe first that the condition
$\sigma _{\mathfrak {a}}^{-1}z=z_{\mathfrak {a}}=x_{\mathfrak {a}}+iy_{\mathfrak {a}}$
. To see this, observe first that the condition
![]() $\gamma _2 \in R(\ell )^0 \subseteq \frac {1}{\ell } R^0 \Leftrightarrow \gamma _2^{\mathfrak {a}} \in \sigma _{\mathfrak {a}}^{-1}R(\ell )^0\sigma _{\mathfrak {a}} \subseteq \frac {1}{\ell } \sigma _{\mathfrak {a}}^{-1}R^0\sigma _{\mathfrak {a}}$
yields the congruence
$\gamma _2 \in R(\ell )^0 \subseteq \frac {1}{\ell } R^0 \Leftrightarrow \gamma _2^{\mathfrak {a}} \in \sigma _{\mathfrak {a}}^{-1}R(\ell )^0\sigma _{\mathfrak {a}} \subseteq \frac {1}{\ell } \sigma _{\mathfrak {a}}^{-1}R^0\sigma _{\mathfrak {a}}$
yields the congruence
![]() $b \equiv 0\ \,\pod {\tfrac {w_{\mathfrak {a}}}{\ell }}$
; see Equation (10.3). The condition
$b \equiv 0\ \,\pod {\tfrac {w_{\mathfrak {a}}}{\ell }}$
; see Equation (10.3). The condition
![]() $\gamma _2 \in g\Omega (\delta ,T)g^{-1}$
may be restated as
$\gamma _2 \in g\Omega (\delta ,T)g^{-1}$
may be restated as
Let
![]() $g'$
be an upper-triangular element of
$g'$
be an upper-triangular element of
![]() $G(\mathbb {R})$
for which
$G(\mathbb {R})$
for which
![]() $g' \cdot i = \sigma _{\mathfrak {a}}^{-1}g i=\sigma _{\mathfrak {a}}^{-1} z = z_{\mathfrak {a}}$
. Then, by the
$g' \cdot i = \sigma _{\mathfrak {a}}^{-1}g i=\sigma _{\mathfrak {a}}^{-1} z = z_{\mathfrak {a}}$
. Then, by the
![]() $K_{\infty }$
invariance of
$K_{\infty }$
invariance of
![]() $\Omega (\delta ,T)$
on the left and right, we have
$\Omega (\delta ,T)$
on the left and right, we have
![]() $\gamma _2^{\mathfrak {a}} \in g' \Omega (\delta , T) (g')^{-1}$
. We compute
$\gamma _2^{\mathfrak {a}} \in g' \Omega (\delta , T) (g')^{-1}$
. We compute
 $$\begin{align*}(g')^{-1} \gamma_2^{\mathfrak{a}} g' = \begin{pmatrix} a & y_{\mathfrak{a}}^{-1} (b + 2 a x_{\mathfrak{a}}) \\ 0 & -a \end{pmatrix} \in \Omega(\delta,T).\end{align*}$$
$$\begin{align*}(g')^{-1} \gamma_2^{\mathfrak{a}} g' = \begin{pmatrix} a & y_{\mathfrak{a}}^{-1} (b + 2 a x_{\mathfrak{a}}) \\ 0 & -a \end{pmatrix} \in \Omega(\delta,T).\end{align*}$$
This last condition forces b to lie in an interval of length
![]() $O(\delta ^{1/2} T y_{\mathfrak {a}})$
. We thereby obtain the required bound for the number of possible b’s.
$O(\delta ^{1/2} T y_{\mathfrak {a}})$
. We thereby obtain the required bound for the number of possible b’s.
10.5. Proof of Theorem 2.6
We may split the set
![]() $\Omega (\delta , T)$
into
$\Omega (\delta , T)$
into
![]() $\Omega (1/16, 4\delta ^{\frac {1}{2}} T)$
and the dyadic sets which are comprised of the elements
$\Omega (1/16, 4\delta ^{\frac {1}{2}} T)$
and the dyadic sets which are comprised of the elements
![]() $[a,b,c] +d\in B_{\infty }$
for which
$[a,b,c] +d\in B_{\infty }$
for which
for some
![]() $16 \delta \le \delta _j \le 1$
. We note that these are contained in
$16 \delta \le \delta _j \le 1$
. We note that these are contained in
![]() $\Omega (\delta \delta _j^{-1} , \delta _j^{\frac {1}{2}} T)$
. In order for the dyadic sets to contain an element of trace
$\Omega (\delta \delta _j^{-1} , \delta _j^{\frac {1}{2}} T)$
. In order for the dyadic sets to contain an element of trace
![]() $0$
and norm n, one must have
$0$
and norm n, one must have
![]() $|n| \asymp a^2 \asymp \delta _j T^2$
. Hence, if we apply Propositions 10.4 and 10.6, we get
$|n| \asymp a^2 \asymp \delta _j T^2$
. Hence, if we apply Propositions 10.4 and 10.6, we get
 $$ \begin{align*} |g^{-1} R(\ell)^0 g \cap \Omega(\delta \delta_j^{-1}, \delta_j^{\frac{1}{2}}T) \cap \det{}^{-1}(\{n\})| \prec 1+ \ell \delta^{\frac{1}{2}}H(g)T +\frac{\ell^2}{d_BN} \delta T^2, \end{align*} $$
$$ \begin{align*} |g^{-1} R(\ell)^0 g \cap \Omega(\delta \delta_j^{-1}, \delta_j^{\frac{1}{2}}T) \cap \det{}^{-1}(\{n\})| \prec 1+ \ell \delta^{\frac{1}{2}}H(g)T +\frac{\ell^2}{d_BN} \delta T^2, \end{align*} $$
where we used
![]() $|n|\asymp \delta _jT^2$
, and
$|n|\asymp \delta _jT^2$
, and
 $$ \begin{align*} |g^{-1} R(\ell)^0 g \cap \Omega(\tfrac{1}{16}, 4 \delta^{\frac{1}{2}}T) \cap \det{}^{-1}(\{n\})| \prec 1+ \ell \delta^{\frac{1}{2}}H(g)T +\frac{\ell^2}{d_BN} \delta T^2. \end{align*} $$
$$ \begin{align*} |g^{-1} R(\ell)^0 g \cap \Omega(\tfrac{1}{16}, 4 \delta^{\frac{1}{2}}T) \cap \det{}^{-1}(\{n\})| \prec 1+ \ell \delta^{\frac{1}{2}}H(g)T +\frac{\ell^2}{d_BN} \delta T^2. \end{align*} $$
If
![]() $\delta $
happens to be very small, say, if
$\delta $
happens to be very small, say, if
![]() $\delta \le (16 d_BNT^2)^{-1}$
, then it suffices to consider only
$\delta \le (16 d_BNT^2)^{-1}$
, then it suffices to consider only
![]() $\delta _j \ge (d_BNT^2)^{-1}$
and the final set
$\delta _j \ge (d_BNT^2)^{-1}$
and the final set
![]() $\Omega (\delta d_B N T^2,(d_BN)^{-\frac {1}{2}})$
. This avoids a factor
$\Omega (\delta d_B N T^2,(d_BN)^{-\frac {1}{2}})$
. This avoids a factor
![]() $\delta ^{-o(1)}$
for a too small
$\delta ^{-o(1)}$
for a too small
![]() $\delta $
. We conclude Theorem 2.6.
$\delta $
. We conclude Theorem 2.6.
A The theta lift
In this section, we use the theta correspondence for the reductive dual pair (
![]() $\operatorname {O}_{\det }$
,
$\operatorname {O}_{\det }$
,
![]() $\operatorname {SL}_2$
) to derive the necessary properties of the theta kernels in use. The group
$\operatorname {SL}_2$
) to derive the necessary properties of the theta kernels in use. The group
![]() $\operatorname {O}_{\det }$
is the affine algebraic group over
$\operatorname {O}_{\det }$
is the affine algebraic group over
![]() $\mathbb {Q}$
representing the orthogonal group of
$\mathbb {Q}$
representing the orthogonal group of
![]() $(B, \det )$
. Recall that G is the linear algebraic group defined over
$(B, \det )$
. Recall that G is the linear algebraic group defined over
![]() $\mathbb {Q}$
satisfying
$\mathbb {Q}$
satisfying ![]() for any
for any
![]() $\mathbb {Q}$
-algebra L. Denote by M the algebraic group representing the functor
$\mathbb {Q}$
-algebra L. Denote by M the algebraic group representing the functor
for any
![]() $\mathbb {Q}$
-algebra L. Then, M is defined over
$\mathbb {Q}$
-algebra L. Then, M is defined over
![]() $\mathbb {Q}$
and it is isomorphic to the special orthogonal group
$\mathbb {Q}$
and it is isomorphic to the special orthogonal group
![]() $\operatorname {SO}_{\det }$
via the action
$\operatorname {SO}_{\det }$
via the action
![]() $(g_1,g_2).x=g_1 x g_2^{-1}$
. We also define the algebraic group
$(g_1,g_2).x=g_1 x g_2^{-1}$
. We also define the algebraic group
![]() $G'$
over
$G'$
over
![]() $\mathbb {Q}$
to be the simply connected form of G, that is,
$\mathbb {Q}$
to be the simply connected form of G, that is,
![]() $G'(L)=\operatorname {SL}_1(B\otimes L)$
for any
$G'(L)=\operatorname {SL}_1(B\otimes L)$
for any
![]() $\mathbb {Q}$
-algebra L. The natural map
$\mathbb {Q}$
-algebra L. The natural map
![]() $G'\times G' \to M$
is an isogeny. The left-hand side is the simply connected form, that is, the Spin group, and the right-hand side the adjoint one.
$G'\times G' \to M$
is an isogeny. The left-hand side is the simply connected form, that is, the Spin group, and the right-hand side the adjoint one.
The determinant map provides two exact sequences

A.1 Restriction of automorphic representations
We would like to understand the behavior of irreducible cuspidal representation under pull-back by
![]() $\iota ^{(1)}$
and
$\iota ^{(1)}$
and
![]() $\iota '$
. We proceed to discuss some generalities that apply to these isogenies. Let H be a semisimple algebraic group defined over
$\iota '$
. We proceed to discuss some generalities that apply to these isogenies. Let H be a semisimple algebraic group defined over
![]() $\mathbb {Q}$
, and fix a maximal compact open subgroup
$\mathbb {Q}$
, and fix a maximal compact open subgroup
![]() $K_f=\prod _{v<\infty } K_v<H(\mathbb {A}_f)$
. Let
$K_f=\prod _{v<\infty } K_v<H(\mathbb {A}_f)$
. Let
![]() $K_\infty <H(\mathbb {R})$
a maximal compact real subgroup and set
$K_\infty <H(\mathbb {R})$
a maximal compact real subgroup and set
![]() $K=K_\infty K_f$
. For an automorphic representation
$K=K_\infty K_f$
. For an automorphic representation
![]() $\Pi $
of
$\Pi $
of
![]() $H(\mathbb {A})$
, we denote by
$H(\mathbb {A})$
, we denote by
![]() $\Pi ^\infty \subset \Pi $
the dense subset of K-finite vectors. That is, every
$\Pi ^\infty \subset \Pi $
the dense subset of K-finite vectors. That is, every
![]() $v\in \Pi ^\infty $
is invariant under a finite-index subgroup of
$v\in \Pi ^\infty $
is invariant under a finite-index subgroup of
![]() $K_f$
and its
$K_f$
and its
![]() $K_\infty $
-orbit spans a finite-dimensional subspace. Then,
$K_\infty $
-orbit spans a finite-dimensional subspace. Then,
![]() $\Pi ^\infty $
is an admissible
$\Pi ^\infty $
is an admissible
![]() $H(\mathbb {A})$
representation.
$H(\mathbb {A})$
representation.
Assume
![]() $\jmath \colon H'\to H$
is a homomorphism of algebraic groups satisfying the following conditions:
$\jmath \colon H'\to H$
is a homomorphism of algebraic groups satisfying the following conditions:
-
(i)
 $\ker \jmath $
is a finite central subgroup of
$\ker \jmath $
is a finite central subgroup of
 $H'$
,
$H'$
, -
(ii)
 ${{\Im}} \jmath $
is a normal subgroup of H and
${{\Im}} \jmath $
is a normal subgroup of H and
 $\operatorname {coker} \jmath $
is a finite abelian group.
$\operatorname {coker} \jmath $
is a finite abelian group. -
(iii)
 $H(\mathbb {Q}_p) = K_p j(H'(\mathbb {Q}_p))$
for almost all primes p.
$H(\mathbb {Q}_p) = K_p j(H'(\mathbb {Q}_p))$
for almost all primes p.
In particular, the Lie algebras of H and
![]() $H'$
are isomorphic, hence
$H'$
are isomorphic, hence
![]() $H'$
is semisimple. These assumptions are satisfied when
$H'$
is semisimple. These assumptions are satisfied when
![]() $\jmath $
is an isogeny of semisimple algebraic groups and for the inclusion map
$\jmath $
is an isogeny of semisimple algebraic groups and for the inclusion map
![]() $\operatorname {SO}_{\det }\to \operatorname {O}_{\det }$
. The group
$\operatorname {SO}_{\det }\to \operatorname {O}_{\det }$
. The group ![]() is a compact abelian group, that is often infinite. In particular,
is a compact abelian group, that is often infinite. In particular,
![]() $j(H'(\mathbb {A}))$
-orbits on
$j(H'(\mathbb {A}))$
-orbits on
![]() $[H]$
can have measure zero and the operation of restricting a function in
$[H]$
can have measure zero and the operation of restricting a function in
![]() $L^2([H])$
to an orbit of
$L^2([H])$
to an orbit of
![]() $j(H'(\mathbb {A}))$
is ill-defined. Nevertheless, we have the following.
$j(H'(\mathbb {A}))$
is ill-defined. Nevertheless, we have the following.
Lemma A.1. The pullback
![]() $\jmath ^*\colon \operatorname {\mathrm {Res}}^{H(\mathbb {A})}_{H'(\mathbb {A})} L^2([H])^\infty \to L^2([H'])^\infty $
is a well-defined operator that restricts to an intertwining operator of the cuspidal spectrum
$\jmath ^*\colon \operatorname {\mathrm {Res}}^{H(\mathbb {A})}_{H'(\mathbb {A})} L^2([H])^\infty \to L^2([H'])^\infty $
is a well-defined operator that restricts to an intertwining operator of the cuspidal spectrum
![]() $\jmath ^*\colon \operatorname {\mathrm {Res}}^{H(\mathbb {A})}_{H'(\mathbb {A})} L^2_{\mathrm {cusp}}([H])^\infty \to L_{\mathrm {cusp}}^2([H'])^\infty $
. Moreover,
$\jmath ^*\colon \operatorname {\mathrm {Res}}^{H(\mathbb {A})}_{H'(\mathbb {A})} L^2_{\mathrm {cusp}}([H])^\infty \to L_{\mathrm {cusp}}^2([H'])^\infty $
. Moreover,
![]() $f\in L^2([H])^\infty $
is cuspidal if and only if for any class
$f\in L^2([H])^\infty $
is cuspidal if and only if for any class
![]() $[h]\in H_{\mathrm {char}}$
, the vector
$[h]\in H_{\mathrm {char}}$
, the vector
![]() $\jmath ^*R_h f$
is cuspidal for some representative
$\jmath ^*R_h f$
is cuspidal for some representative
![]() $h\in [h]\subset H(\mathbb {A})$
.
$h\in [h]\subset H(\mathbb {A})$
.
Remark. Notice that
![]() $\jmath ^*$
does not preserve inner products.
$\jmath ^*$
does not preserve inner products.
Proof. Restricting to a
![]() $j(H'(\mathbb {A}))$
-orbit is a well-defined operation on
$j(H'(\mathbb {A}))$
-orbit is a well-defined operation on
![]() $L^2([H])^\infty $
because every vector
$L^2([H])^\infty $
because every vector
![]() $v_0\in L^2([H])^\infty $
is invariant under some compact-open subgoup
$v_0\in L^2([H])^\infty $
is invariant under some compact-open subgoup
![]() $K_0<H(\mathbb {A}_f)$
and
$K_0<H(\mathbb {A}_f)$
and ![]() is finite. We now show that the
is finite. We now show that the
![]() $L^2$
-norm of
$L^2$
-norm of
![]() $\jmath ^* v_0$
is finite. The push-forward of the probability Haar measure on
$\jmath ^* v_0$
is finite. The push-forward of the probability Haar measure on
![]() $[H]$
to
$[H]$
to
![]() $H_{\mathrm {char}}$
is invariant under the action of
$H_{\mathrm {char}}$
is invariant under the action of
![]() $H(\mathbb {A})$
, hence it is the probability Haar measure on
$H(\mathbb {A})$
, hence it is the probability Haar measure on
![]() $H_{\mathrm {char}}$
. If we disintegrate the Haar measure on
$H_{\mathrm {char}}$
. If we disintegrate the Haar measure on
![]() $[H]$
under the factor map
$[H]$
under the factor map
![]() $[H]\to H_{\mathrm {char}}$
, then the atoms are exactly the
$[H]\to H_{\mathrm {char}}$
, then the atoms are exactly the
![]() $\jmath (H'(\mathbb {A}))$
-orbits and the conditional measure on a.e. atom is
$\jmath (H'(\mathbb {A}))$
-orbits and the conditional measure on a.e. atom is
![]() $\jmath (H'(\mathbb {A}))$
-invariant, hence it is the push-forward of the probability Haar measure on
$\jmath (H'(\mathbb {A}))$
-invariant, hence it is the push-forward of the probability Haar measure on
![]() $[H']$
to the atom. We can now deduce that
$[H']$
to the atom. We can now deduce that
 $$ \begin{align*} \|v_0\|_2^2=|H_{\mathrm{char}}/ K_0|^{-1} \sum_{h\in H_{\mathrm{char}}/ K_0} \| \jmath^*(R_h v_0) \|_{2,[H']}^2. \end{align*} $$
$$ \begin{align*} \|v_0\|_2^2=|H_{\mathrm{char}}/ K_0|^{-1} \sum_{h\in H_{\mathrm{char}}/ K_0} \| \jmath^*(R_h v_0) \|_{2,[H']}^2. \end{align*} $$
Hence,
![]() $ \| \jmath ^*(v_0) \|_{2,[H']}\le \sqrt {|H_{\mathrm {char}}/ K_0|} \|v_0\|_2<\infty $
.
$ \| \jmath ^*(v_0) \|_{2,[H']}\le \sqrt {|H_{\mathrm {char}}/ K_0|} \|v_0\|_2<\infty $
.
We show next that the image of a cuspidal vector is cuspidal. Fix
![]() $v_0\in L^2([H])^\infty $
. Let
$v_0\in L^2([H])^\infty $
. Let
![]() $P<H'$
be a parabolic subgroup defined over
$P<H'$
be a parabolic subgroup defined over
![]() $\mathbb {Q}$
, and let
$\mathbb {Q}$
, and let
![]() $N_P$
be its unipotent radical. The kernel
$N_P$
be its unipotent radical. The kernel
![]() $\ker \jmath $
is a central subgroup, hence it is diagonalizable and its intersection with
$\ker \jmath $
is a central subgroup, hence it is diagonalizable and its intersection with
![]() $N_P$
is trivial. Then,
$N_P$
is trivial. Then,
![]() $\jmath\!\! \restriction _{N_P}$
is an isomorphism onto its image
$\jmath\!\! \restriction _{N_P}$
is an isomorphism onto its image
![]() $N_{\tilde {P}}$
, which is the unipotent radical of a parabolic
$N_{\tilde {P}}$
, which is the unipotent radical of a parabolic
![]() $\tilde {P}<H$
. Specifically,
$\tilde {P}<H$
. Specifically,
![]() $\tilde {P}$
is the parabolic associated to the same root data as P. For every
$\tilde {P}$
is the parabolic associated to the same root data as P. For every
![]() $g\in H'(\mathbb {A})$
, we have, writing
$g\in H'(\mathbb {A})$
, we have, writing
![]() $c_P$
and
$c_P$
and
![]() $c_{\tilde {P}}$
for the maps assigning to a function its corresponding constant term,
$c_{\tilde {P}}$
for the maps assigning to a function its corresponding constant term,
 $$ \begin{align*} c_P \jmath^* v_0(g)=\int_{[N_P]} \jmath^*(v_0)( n g) \,\mathrm{d} n=\int_{[N_{\tilde{P}} ]}v_0(n \jmath(g)) \,\mathrm{d} n =c_{\tilde{P}} v_0(\jmath(g)). \end{align*} $$
$$ \begin{align*} c_P \jmath^* v_0(g)=\int_{[N_P]} \jmath^*(v_0)( n g) \,\mathrm{d} n=\int_{[N_{\tilde{P}} ]}v_0(n \jmath(g)) \,\mathrm{d} n =c_{\tilde{P}} v_0(\jmath(g)). \end{align*} $$
Hence, the constant term of the push-forward of a cuspidal vector vanishes. This formula also establishes the last claim.
Next, we describe the transformation of the Haar measure. If
![]() $K<H(\mathbb {A})$
is a compact subgroup, we denote by
$K<H(\mathbb {A})$
is a compact subgroup, we denote by
![]() $[H]_K$
the double quotient
$[H]_K$
the double quotient ![]() .
.
Lemma A.2. Fix compact open subgroups
![]() $K^{\prime }_f<H'(\mathbb {A}_f)$
and
$K^{\prime }_f<H'(\mathbb {A}_f)$
and
![]() $K_f<H(\mathbb {A}_f)$
satisfying
$K_f<H(\mathbb {A}_f)$
satisfying
![]() $\jmath ^{-1}(K_f)=K^{\prime }_f$
. Assume the following conditions:
$\jmath ^{-1}(K_f)=K^{\prime }_f$
. Assume the following conditions:
-
(i)
 .
. -
(ii) The preimage of
 $K_f \bmod \jmath (H'(\mathbb {A}))$
under the map
$K_f \bmod \jmath (H'(\mathbb {A}))$
under the map
 $\operatorname {\mathrm {coker}} \jmath (\mathbb {Q})\to \operatorname {\mathrm {coker}}\jmath (\mathbb {A})$
is trivial.
$\operatorname {\mathrm {coker}} \jmath (\mathbb {Q})\to \operatorname {\mathrm {coker}}\jmath (\mathbb {A})$
is trivial. -
(iii)
 $\ker \jmath \restriction _{H'(\mathbb {A})}< \operatorname {Z}_{H'}(\mathbb {Q}) \cdot K^{\prime }_f$
.
$\ker \jmath \restriction _{H'(\mathbb {A})}< \operatorname {Z}_{H'}(\mathbb {Q}) \cdot K^{\prime }_f$
.
Then, the induced map
![]() $\jmath \colon [H']_{K^{\prime }_f}\to [H]_{K_f}$
is a homeomorphism and an isomorphism of Borel measure spaces when each space is endowed with the respective probability Haar measure.
$\jmath \colon [H']_{K^{\prime }_f}\to [H]_{K_f}$
is a homeomorphism and an isomorphism of Borel measure spaces when each space is endowed with the respective probability Haar measure.
Proof. To show the map
![]() $[H']_{K^{\prime }_f}\to [H]_{K_f}$
is surjective, we need to find for every
$[H']_{K^{\prime }_f}\to [H]_{K_f}$
is surjective, we need to find for every
![]() $x\in H(\mathbb {A})$
elements
$x\in H(\mathbb {A})$
elements
![]() $\gamma \in H(\mathbb {Q})$
,
$\gamma \in H(\mathbb {Q})$
,
![]() $k\in K_f$
and
$k\in K_f$
and
![]() $x'\in H'(\mathbb {A})$
such that
$x'\in H'(\mathbb {A})$
such that
![]() $x=\gamma \jmath (x') k$
. Equivalently, we need the class of
$x=\gamma \jmath (x') k$
. Equivalently, we need the class of
![]() $[\gamma ^{-1} x k^{-1}]=[x k^{-1}]$
in
$[\gamma ^{-1} x k^{-1}]=[x k^{-1}]$
in
![]() $H_{\mathrm {char}}$
to be trivial and this follows from the assumption that
$H_{\mathrm {char}}$
to be trivial and this follows from the assumption that ![]() .
.
To verify the map is injective, we consider
![]() $x^{\prime }_1,x^{\prime }_2\in H'(\mathbb {A})$
satisfying
$x^{\prime }_1,x^{\prime }_2\in H'(\mathbb {A})$
satisfying
![]() $\jmath (x^{\prime }_1)= \gamma \jmath (x^{\prime }_2) k$
, with
$\jmath (x^{\prime }_1)= \gamma \jmath (x^{\prime }_2) k$
, with
![]() $\gamma \in H(\mathbb {Q})$
and
$\gamma \in H(\mathbb {Q})$
and
![]() $k\in K_f$
. We first demonstrate that
$k\in K_f$
. We first demonstrate that
![]() $\gamma \in \jmath (H'(\mathbb {Q}))$
. Because
$\gamma \in \jmath (H'(\mathbb {Q}))$
. Because
![]() $\gamma =\jmath (x^{\prime }_{1,\infty }) k^{-1}\jmath ({x^{\prime }_{2,\infty }}^{-1})$
and
$\gamma =\jmath (x^{\prime }_{1,\infty }) k^{-1}\jmath ({x^{\prime }_{2,\infty }}^{-1})$
and
![]() $\operatorname {\mathrm {coker}} \jmath $
is abelian, we see that the class of
$\operatorname {\mathrm {coker}} \jmath $
is abelian, we see that the class of
![]() $\gamma $
in
$\gamma $
in ![]() is the same as the class of k. The second assumption then implies that the class of
is the same as the class of k. The second assumption then implies that the class of
![]() $\gamma $
in
$\gamma $
in ![]() is trivial as claimed. Hence,
is trivial as claimed. Hence,
![]() $\gamma =\jmath (\gamma _0)$
for some
$\gamma =\jmath (\gamma _0)$
for some
![]() $\gamma _0\in H'(\mathbb {Q})$
. We can now write
$\gamma _0\in H'(\mathbb {Q})$
. We can now write
![]() $k=\jmath ({x^{\prime }_2}^{-1}\gamma _0^{-1}x^{\prime }_1)\in \jmath (H'(\mathbb {A}))\cap K_f$
. Because we assumed
$k=\jmath ({x^{\prime }_2}^{-1}\gamma _0^{-1}x^{\prime }_1)\in \jmath (H'(\mathbb {A}))\cap K_f$
. Because we assumed
![]() $\jmath ^{-1}(K_f)=K^{\prime }_f$
, we can write
$\jmath ^{-1}(K_f)=K^{\prime }_f$
, we can write
![]() $k=\jmath (k')$
for
$k=\jmath (k')$
for
![]() $k'\in K^{\prime }_f$
and
$k'\in K^{\prime }_f$
and
![]() $\jmath ({x^{\prime }_1}^{-1}\gamma _0 x^{\prime }_2 k')=1$
. Thus,
$\jmath ({x^{\prime }_1}^{-1}\gamma _0 x^{\prime }_2 k')=1$
. Thus,
![]() ${x^{\prime }_1}^{-1}\gamma _0 x^{\prime }_2 k'=z k^{\prime }_0$
for some z in the center of
${x^{\prime }_1}^{-1}\gamma _0 x^{\prime }_2 k'=z k^{\prime }_0$
for some z in the center of
![]() $H'(\mathbb {Q})$
and
$H'(\mathbb {Q})$
and
![]() $k^{\prime }_0\in K^{\prime }_f$
. Because the center of
$k^{\prime }_0\in K^{\prime }_f$
. Because the center of
![]() $H'(\mathbb {Q})$
is contained in the center of
$H'(\mathbb {Q})$
is contained in the center of
![]() $H'(\mathbb {A})$
, we deduce
$H'(\mathbb {A})$
, we deduce
![]() $x^{\prime }_1=z^{-1}\gamma _0 x^{\prime }_2 k' {k^{\prime }_0}^{-1}\in H'(\mathbb {Q}) x^{\prime }_2 K^{\prime }_f$
as required.
$x^{\prime }_1=z^{-1}\gamma _0 x^{\prime }_2 k' {k^{\prime }_0}^{-1}\in H'(\mathbb {Q}) x^{\prime }_2 K^{\prime }_f$
as required.
We have established that
![]() $\jmath \colon [H']_{K^{\prime }_f}\to [H]_{K_f}$
is a continuous bijection. It is a homeomorphism because it is also a smooth function between two real manifolds with everywhere nonvanishing differential. The probability Haar measure on
$\jmath \colon [H']_{K^{\prime }_f}\to [H]_{K_f}$
is a continuous bijection. It is a homeomorphism because it is also a smooth function between two real manifolds with everywhere nonvanishing differential. The probability Haar measure on
![]() $[H]_{K_f}$
is the unique
$[H]_{K_f}$
is the unique
![]() $H(\mathbb {R})$
-invariant Borel probability measure that gives equal mass to each of the finitely many
$H(\mathbb {R})$
-invariant Borel probability measure that gives equal mass to each of the finitely many
![]() $H(\mathbb {R})$
-orbits. The same holds for
$H(\mathbb {R})$
-orbits. The same holds for
![]() $[H']_{K^{\prime }_f}$
and
$[H']_{K^{\prime }_f}$
and
![]() $H'(\mathbb {R})$
. Using this characterization, it is easy to check that the push-forward of the probability Haar measure from
$H'(\mathbb {R})$
. Using this characterization, it is easy to check that the push-forward of the probability Haar measure from
![]() $[H]_{K_f}$
to
$[H]_{K_f}$
to
![]() $[H']_{K^{\prime }_f}$
under
$[H']_{K^{\prime }_f}$
under
![]() $\jmath ^{-1}$
is the probability Haar measure.
$\jmath ^{-1}$
is the probability Haar measure.
A.2 The theta transfer
We now revert to our setting of interest, as described at the start of §A. Recall that
![]() $R\subset B$
is an Eichler order. For a finite rational place v, we define
$R\subset B$
is an Eichler order. For a finite rational place v, we define
![]() $R_v=R\otimes _{\mathbb {Z}} \mathbb {Z}_v$
and
$R_v=R\otimes _{\mathbb {Z}} \mathbb {Z}_v$
and
![]() $\widetilde {K}_{R_v}=R_v^\times $
. Define
$\widetilde {K}_{R_v}=R_v^\times $
. Define
![]() $K_{R_v}$
to be the image of
$K_{R_v}$
to be the image of
![]() $\tilde {K}_{R_v}$
under the map
$\tilde {K}_{R_v}$
under the map
![]() $B_v^\times \to G(\mathbb {Q}_v)$
. Finally, set
$B_v^\times \to G(\mathbb {Q}_v)$
. Finally, set
![]() $\widetilde {K}_R=\prod _{v<\infty } \widetilde {K}_{R_v}$
,
$\widetilde {K}_R=\prod _{v<\infty } \widetilde {K}_{R_v}$
,
![]() $K_R=\prod _{v<\infty } K_{R_v}$
, and let
$K_R=\prod _{v<\infty } K_{R_v}$
, and let
![]() $K_M$
denote the preimage of
$K_M$
denote the preimage of
![]() $K_R\times K_R$
under
$K_R\times K_R$
under
![]() $\iota ^{(1)}$
. Then,
$\iota ^{(1)}$
. Then,
![]() $K_R$
is a compact and open subgroup of
$K_R$
is a compact and open subgroup of
![]() $G(\mathbb {A}_f)$
. We also assume that R is of squarefree level N (see §2.1).
$G(\mathbb {A}_f)$
. We also assume that R is of squarefree level N (see §2.1).
We verify now that the hypotheses of Lemma A.2 hold for both of the maps
Indeed:
-
(i) We have
 $\det \left (\frac {\bullet }{\bullet }\right )(K_R\times K_R)=\widehat {\mathbb {Z}}^\times $
and
$\det \left (\frac {\bullet }{\bullet }\right )(K_R\times K_R)=\widehat {\mathbb {Z}}^\times $
and
 $\det \left (K_M\right )= \widehat {\mathbb {Z}}^\times $
. Because
$\det \left (K_M\right )= \widehat {\mathbb {Z}}^\times $
. Because  the equality
the equality  holds.
holds. -
(ii) This condition is easy to verify by applying the maps
 $\det \left (\frac {\bullet }{\bullet }\right )$
and
$\det \left (\frac {\bullet }{\bullet }\right )$
and
 $\det $
, and the fact that a rational number is a square if and only if it is positive and has even valuation at each finite place.
$\det $
, and the fact that a rational number is a square if and only if it is positive and has even valuation at each finite place. -
(iii) Consider the case
 $\jmath =\iota ^{(1)}$
. The last condition can be checked locally at each finite place to see that
$\jmath =\iota ^{(1)}$
. The last condition can be checked locally at each finite place to see that
 $(I,-I)_v\in (K_{R_v}\times K_{R_v})^{(1)}$
for all
$(I,-I)_v\in (K_{R_v}\times K_{R_v})^{(1)}$
for all
 $v<\infty $
. At the Archimedean place, we use the diagonal embedding of
$v<\infty $
. At the Archimedean place, we use the diagonal embedding of
 $(I,-I)$
in
$(I,-I)$
in
 $M(\mathbb {A})$
to arrive at
$M(\mathbb {A})$
to arrive at
 $(I,-I)_\infty \in Z_{M}(\mathbb {Q})\cdot K_M$
. The argument for
$(I,-I)_\infty \in Z_{M}(\mathbb {Q})\cdot K_M$
. The argument for
 $\jmath =\iota '$
follows mutatis mutandis.
$\jmath =\iota '$
follows mutatis mutandis.
Lemma A.2 now implies that the following maps are measure preserving homeomorphisms.
We get isomorphisms of Hilbert spaces
By Lemma A.1, these restrict to isomorphisms of the respective spaces of cusp forms.
Set
![]() $\tilde {U_0}(p^n)=\left (\begin {smallmatrix} \mathbb {Z}_p & \mathbb {Z}_p \\ p^n \mathbb {Z}_p & \mathbb {Z}_p \end {smallmatrix}\right ) \cap \operatorname {GL}_2(\mathbb {Z}_p)$
– a compact and open subgroup of
$\tilde {U_0}(p^n)=\left (\begin {smallmatrix} \mathbb {Z}_p & \mathbb {Z}_p \\ p^n \mathbb {Z}_p & \mathbb {Z}_p \end {smallmatrix}\right ) \cap \operatorname {GL}_2(\mathbb {Z}_p)$
– a compact and open subgroup of
![]() $\operatorname {GL}_2(\mathbb {Q}_p)$
. Let
$\operatorname {GL}_2(\mathbb {Q}_p)$
. Let
![]() ${\tilde {U}_R=\prod _{p}{\tilde {U}_p}<\operatorname {GL}_2(\mathbb {A}_f)}$
to be defined by
${\tilde {U}_R=\prod _{p}{\tilde {U}_p}<\operatorname {GL}_2(\mathbb {A}_f)}$
to be defined by
![]() $\tilde {U}_p=\tilde {U_0}(1)=\operatorname {GL}_2(\mathbb {Z}_p)$
for all primes p where G is unramified and
$\tilde {U}_p=\tilde {U_0}(1)=\operatorname {GL}_2(\mathbb {Z}_p)$
for all primes p where G is unramified and
![]() $R_p$
is maximal. If G ramifies at p or
$R_p$
is maximal. If G ramifies at p or
![]() $R_p$
is not maximal, then define
$R_p$
is not maximal, then define
![]() $\tilde {U}_p=\tilde {U}_0(p)$
. Note that we assume that R has squarefree level. Finally, set
$\tilde {U}_p=\tilde {U}_0(p)$
. Note that we assume that R has squarefree level. Finally, set
![]() $U^1_R=\tilde {U}_R\cap \operatorname {SL}_2(\mathbb {A}_f)$
and let
$U^1_R=\tilde {U}_R\cap \operatorname {SL}_2(\mathbb {A}_f)$
and let
![]() $U_R$
be the projection of
$U_R$
be the projection of
![]() $\tilde {U}_R$
to
$\tilde {U}_R$
to
![]() $\operatorname {PGL}_2(\mathbb {A}_f)$
. Similarly to the previous discussion, the natural map
$\operatorname {PGL}_2(\mathbb {A}_f)$
. Similarly to the previous discussion, the natural map
![]() $\iota _0\colon [\operatorname {SL}_2]_{U_R^1}\to [\operatorname {PGL}_2]_{U_R}$
is a homeomorphism that sends the probability Haar measure on the left-hand side to the probability Haar measure on the right-hand side. This induces an isomorphism of Hilbert spaces
$\iota _0\colon [\operatorname {SL}_2]_{U_R^1}\to [\operatorname {PGL}_2]_{U_R}$
is a homeomorphism that sends the probability Haar measure on the left-hand side to the probability Haar measure on the right-hand side. This induces an isomorphism of Hilbert spaces
that descends to an isomorphism of the cuspidal subspaces.
Recall that
![]() $B_p=B\otimes \mathbb {Q}_p$
. We also denote
$B_p=B\otimes \mathbb {Q}_p$
. We also denote ![]() . We denote by
. We denote by
![]() $\rho $
the Weil representation of the reductive dual pair
$\rho $
the Weil representation of the reductive dual pair
![]() $(\operatorname {O}_{\det },\operatorname {SL}_2)$
associated to the quadratic space
$(\operatorname {O}_{\det },\operatorname {SL}_2)$
associated to the quadratic space
![]() $(B, \det )$
. We refrain at the moment from specifying the exact space of test functions on
$(B, \det )$
. We refrain at the moment from specifying the exact space of test functions on ![]() on which we let
on which we let
![]() $\rho $
act. If
$\rho $
act. If
![]() ${\Phi }\colon B_{\mathbb {A}}\to \mathbb {C}$
is a test function, then the group
${\Phi }\colon B_{\mathbb {A}}\to \mathbb {C}$
is a test function, then the group
![]() $M(\mathbb {A})\cong \operatorname {SO}_{\det }$
acts by determinant preserving transformations,
$M(\mathbb {A})\cong \operatorname {SO}_{\det }$
acts by determinant preserving transformations,
![]() $\rho (l,r;e).{\Phi }(x)={\Phi }(l^{-1}xr)$
and the action of the group
$\rho (l,r;e).{\Phi }(x)={\Phi }(l^{-1}xr)$
and the action of the group
![]() $\operatorname {SL}_2(\mathbb {A})$
is described in [Reference WeilWei64, Reference ShimizuShi72]. Specifically, the definition of the
$\operatorname {SL}_2(\mathbb {A})$
is described in [Reference WeilWei64, Reference ShimizuShi72]. Specifically, the definition of the
![]() $\operatorname {SL}_2(\mathbb {A})$
-action depends on a global character
$\operatorname {SL}_2(\mathbb {A})$
-action depends on a global character ![]() . We fix
. We fix
![]() $\psi =\prod _v \psi _v$
with
$\psi =\prod _v \psi _v$
with
![]() $\psi _v$
everywhere unramified and
$\psi _v$
everywhere unramified and
![]() $\psi _\infty (x)=\exp (2\pi i x)$
.
$\psi _\infty (x)=\exp (2\pi i x)$
.
Let
![]() ${\Phi }=\prod _v {\Phi }_v \colon B_{\mathbb {A}}\to \mathbb {C}$
be a test function with
${\Phi }=\prod _v {\Phi }_v \colon B_{\mathbb {A}}\to \mathbb {C}$
be a test function with
![]() ${\Phi }_\infty \colon B_\infty \to \mathbb {C}$
the Bergman test function from [Reference Khayutin and SteinerKS20, §6] or a Schwartz function. Assume for
${\Phi }_\infty \colon B_\infty \to \mathbb {C}$
the Bergman test function from [Reference Khayutin and SteinerKS20, §6] or a Schwartz function. Assume for
![]() $v<\infty $
that
$v<\infty $
that
![]() ${\Phi }_v$
is Schwartz–Bruhat and that
${\Phi }_v$
is Schwartz–Bruhat and that ![]() for almost all v. If
for almost all v. If
![]() ${\Phi }_\infty $
is the Bergman test function, we let
${\Phi }_\infty $
is the Bergman test function, we let
![]() $\rho $
act on the space of functions defined in [Reference Khayutin and SteinerKS20, §3], otherwise we let
$\rho $
act on the space of functions defined in [Reference Khayutin and SteinerKS20, §3], otherwise we let
![]() $\rho $
act on the space of Schwartz–Bruhat functions as usual. The theta kernel associated to
$\rho $
act on the space of Schwartz–Bruhat functions as usual. The theta kernel associated to
![]() ${\Phi }$
is the function
${\Phi }$
is the function
![]() $\Theta _{\Phi }\colon M(\mathbb {A})\times \operatorname {SL}_2(\mathbb {A})\to \mathbb {C}$
defined by
$\Theta _{\Phi }\colon M(\mathbb {A})\times \operatorname {SL}_2(\mathbb {A})\to \mathbb {C}$
defined by
 $$ \begin{align} \Theta_{\Phi}(l,r;s)=\sum_{\xi\in B} (\rho(l,r;s).{\Phi})(\xi). \end{align} $$
$$ \begin{align} \Theta_{\Phi}(l,r;s)=\sum_{\xi\in B} (\rho(l,r;s).{\Phi})(\xi). \end{align} $$
The series defining
![]() $\Theta _{\Phi }(l,r;s)$
is absolutely convergent, [Reference Khayutin and SteinerKS20, §3.6], and is of moderate growth on
$\Theta _{\Phi }(l,r;s)$
is absolutely convergent, [Reference Khayutin and SteinerKS20, §3.6], and is of moderate growth on
![]() $M(\mathbb {A})\times \operatorname {SL}_2(\mathbb {A})$
, [Reference Rallis and SchiffmannRS75]. Moreover, it is
$M(\mathbb {A})\times \operatorname {SL}_2(\mathbb {A})$
, [Reference Rallis and SchiffmannRS75]. Moreover, it is
![]() $M(\mathbb {Q})\times \operatorname {SL}_2(\mathbb {Q})$
invariant on the left, cf. [Reference WeilWei64], [Reference ShimizuShi72, Proposition 1], [Reference Khayutin and SteinerKS20, §3.6].
$M(\mathbb {Q})\times \operatorname {SL}_2(\mathbb {Q})$
invariant on the left, cf. [Reference WeilWei64], [Reference ShimizuShi72, Proposition 1], [Reference Khayutin and SteinerKS20, §3.6].
Definition A.3. Let
![]() $\varphi ,\varphi '\in L^2_{\mathrm {cusp}}\left ([G]\right )^\infty $
and
$\varphi ,\varphi '\in L^2_{\mathrm {cusp}}\left ([G]\right )^\infty $
and
![]() $\varphi ^*\in L^2_{\mathrm {cusp}}\left ([\operatorname {SL}_2]\right )^\infty $
. Fix a test function
$\varphi ^*\in L^2_{\mathrm {cusp}}\left ([\operatorname {SL}_2]\right )^\infty $
. Fix a test function
![]() ${\Phi }$
as above. Then, the theta transfer of
${\Phi }$
as above. Then, the theta transfer of
![]() $\varphi \otimes \varphi '$
and
$\varphi \otimes \varphi '$
and
![]() $\varphi ^*$
relative to
$\varphi ^*$
relative to
![]() ${\Phi }$
is defined by
${\Phi }$
is defined by
 $$ \begin{align*} (\varphi\otimes \varphi')_{\Phi}(s)&=\int_{[M]} \Theta_{\Phi}(l,r;s) \varphi(l) \varphi'(r)\,\mathrm{d}(l,r)\\ &= \int_{[M]} \Theta_{\Phi}(l,r;s) {\iota^{(1)}}^*(\varphi \otimes \varphi')(l,r)\,\mathrm{d}(l,r),\\ {\varphi^*}^{\Phi}(l,r)&= \int_{[\operatorname{SL}_2]} \Theta_{\Phi}(l,r;s) \varphi^*(s) \,\mathrm{d} s. \end{align*} $$
$$ \begin{align*} (\varphi\otimes \varphi')_{\Phi}(s)&=\int_{[M]} \Theta_{\Phi}(l,r;s) \varphi(l) \varphi'(r)\,\mathrm{d}(l,r)\\ &= \int_{[M]} \Theta_{\Phi}(l,r;s) {\iota^{(1)}}^*(\varphi \otimes \varphi')(l,r)\,\mathrm{d}(l,r),\\ {\varphi^*}^{\Phi}(l,r)&= \int_{[\operatorname{SL}_2]} \Theta_{\Phi}(l,r;s) \varphi^*(s) \,\mathrm{d} s. \end{align*} $$
The former is a complex-valued function on
![]() $\operatorname {SL}_2(\mathbb {A})$
, and the latter is a function on
$\operatorname {SL}_2(\mathbb {A})$
, and the latter is a function on
![]() $M(\mathbb {A})$
. Both integrals converge absolutely because
$M(\mathbb {A})$
. Both integrals converge absolutely because
![]() $\Theta _{\Phi }$
is of moderate growth and
$\Theta _{\Phi }$
is of moderate growth and
![]() $\varphi $
,
$\varphi $
,
![]() $\varphi '$
,
$\varphi '$
,
![]() $\varphi ^*$
are of rapid decay. By abuse of notation, we will also denote
$\varphi ^*$
are of rapid decay. By abuse of notation, we will also denote
Note also that the modularity of the theta kernel
![]() $\Theta _{\Phi }$
implies that
$\Theta _{\Phi }$
implies that
![]() $(\varphi \otimes \varphi ')_{\Phi }$
is left
$(\varphi \otimes \varphi ')_{\Phi }$
is left
![]() $\operatorname {SL}_2(\mathbb {Q})$
-invariant, and
$\operatorname {SL}_2(\mathbb {Q})$
-invariant, and
![]() ${\varphi ^*}^{\Phi }$
is left
${\varphi ^*}^{\Phi }$
is left
![]() $M(\mathbb {Q})$
-invariant.
$M(\mathbb {Q})$
-invariant.
If, moreover,
![]() $\varphi $
is
$\varphi $
is
![]() $K_R$
-invariant and
$K_R$
-invariant and
![]() ${\Phi }$
is both left and right
${\Phi }$
is both left and right
![]() $\widetilde {K}_R$
-invariant then, because the maps in Equation (A.1) are isomorphisms of measure spaces, we have
$\widetilde {K}_R$
-invariant then, because the maps in Equation (A.1) are isomorphisms of measure spaces, we have
We will need the following lemma. It is mostly a corollary of [Reference RallisRal84, Reference MœglinMœg97, Reference Kudla and RallisKR94].
Lemma A.4. Let
![]() $\varphi ,\varphi '\in L^2_{\mathrm {cusp}}\left ([G]\right )^\infty $
and
$\varphi ,\varphi '\in L^2_{\mathrm {cusp}}\left ([G]\right )^\infty $
and
![]() $\varphi ^*\in L^2_{\mathrm {cusp}}\left ([\operatorname {SL}_2]\right )^\infty $
. Assume that
$\varphi ^*\in L^2_{\mathrm {cusp}}\left ([\operatorname {SL}_2]\right )^\infty $
. Assume that
![]() $\varphi ,\varphi '$
are
$\varphi ,\varphi '$
are
![]() $K_R$
-invariant and that
$K_R$
-invariant and that
![]() ${\Phi }$
is both left and right
${\Phi }$
is both left and right
![]() $\widetilde {K}_R$
-invariant. Then,
$\widetilde {K}_R$
-invariant. Then,
![]() $(\varphi \otimes \varphi ')_{\Phi }\in L^2_{\mathrm {cusp}}\left ([\operatorname {SL}_2]\right )$
and
$(\varphi \otimes \varphi ')_{\Phi }\in L^2_{\mathrm {cusp}}\left ([\operatorname {SL}_2]\right )$
and
![]() ${\varphi ^*}^{\Phi }\in L^2_{\mathrm {cusp}}\left ([M]\right )$
.
${\varphi ^*}^{\Phi }\in L^2_{\mathrm {cusp}}\left ([M]\right )$
.
Proof. The fact that
![]() ${\varphi ^*}^{\Phi }$
is square-integrable and cuspidal is trivial whenever G is anisotropic. If
${\varphi ^*}^{\Phi }$
is square-integrable and cuspidal is trivial whenever G is anisotropic. If
![]() $G\cong \operatorname {PGL}_2$
is split, then this follows from Rallis’ tower property [Reference RallisRal84, Reference MœglinMœg97] and the fact that the theta transfer of any cuspidal automorphic representation of
$G\cong \operatorname {PGL}_2$
is split, then this follows from Rallis’ tower property [Reference RallisRal84, Reference MœglinMœg97] and the fact that the theta transfer of any cuspidal automorphic representation of
![]() $\operatorname {SL}_2\cong \operatorname {Sp}_2$
to the orthogonal group of the hyperbolic plane
$\operatorname {SL}_2\cong \operatorname {Sp}_2$
to the orthogonal group of the hyperbolic plane
![]() $\operatorname {O}(1,1)$
vanishes.Footnote 5
$\operatorname {O}(1,1)$
vanishes.Footnote 5
That the lift of
![]() $\varphi \otimes \varphi '$
is cuspidal follows similarly, except that we need to use the theta transfer from
$\varphi \otimes \varphi '$
is cuspidal follows similarly, except that we need to use the theta transfer from
![]() $\operatorname {O}_{\det }$
to
$\operatorname {O}_{\det }$
to
![]() $\operatorname {SL}_2$
, that is, we need first to lift
$\operatorname {SL}_2$
, that is, we need first to lift
![]() ${\iota ^{(1)}}^*\varphi \otimes \varphi '$
to
${\iota ^{(1)}}^*\varphi \otimes \varphi '$
to
![]() $\operatorname {O}_{\det }$
. For that purpose, we use the homomorphism
$\operatorname {O}_{\det }$
. For that purpose, we use the homomorphism
![]() $\iota \colon M\to \operatorname {O}_{\det }$
, which is the composition of the isomorphism
$\iota \colon M\to \operatorname {O}_{\det }$
, which is the composition of the isomorphism
![]() $M\cong \operatorname {SO}_{\det }$
with the embedding
$M\cong \operatorname {SO}_{\det }$
with the embedding
![]() $\operatorname {SO}_{\det }\hookrightarrow \operatorname {O}_{\det }$
. This map satisfies the assumptions of §A.1. For every finite place v, let
$\operatorname {SO}_{\det }\hookrightarrow \operatorname {O}_{\det }$
. This map satisfies the assumptions of §A.1. For every finite place v, let
![]() $\operatorname {O}_{\det }(R_v)$
to be the group of orthogonal transformations of
$\operatorname {O}_{\det }(R_v)$
to be the group of orthogonal transformations of
![]() $B_v$
that send
$B_v$
that send
![]() $R_v$
to itself and define
$R_v$
to itself and define
![]() $\operatorname {O}_{\det }(\hat {R})=\prod _{v<\infty } \operatorname {O}_{\det }(R_v)$
. Then, the conditions of Lemma A.2 are easily verified and we deduce that the pull-back
$\operatorname {O}_{\det }(\hat {R})=\prod _{v<\infty } \operatorname {O}_{\det }(R_v)$
. Then, the conditions of Lemma A.2 are easily verified and we deduce that the pull-back
![]() $\iota ^*$
induces an isomorphism of
$\iota ^*$
induces an isomorphism of
![]() $L^2([\operatorname {O}_{\det }])^{\operatorname {O}_{\det }(\hat {R})}$
and
$L^2([\operatorname {O}_{\det }])^{\operatorname {O}_{\det }(\hat {R})}$
and
![]() $L^2([M])^{K_M}$
. We deduce from Lemma A.1 that
$L^2([M])^{K_M}$
. We deduce from Lemma A.1 that
![]() $(\iota ^{*})^{-1}{\iota ^{(1)}}^* \varphi \otimes \varphi '$
is cuspidal and
$(\iota ^{*})^{-1}{\iota ^{(1)}}^* \varphi \otimes \varphi '$
is cuspidal and
Here, we have extended the definition of
![]() $\Theta _{\Phi }$
in Equation (A.4) to
$\Theta _{\Phi }$
in Equation (A.4) to
![]() $\operatorname {O}_{\det }(\mathbb {A})\times \operatorname {SL}_2(\mathbb {A})$
in the obvious way. The integral in Equation (A.6) is a theta lift of a cuspidal function in
$\operatorname {O}_{\det }(\mathbb {A})\times \operatorname {SL}_2(\mathbb {A})$
in the obvious way. The integral in Equation (A.6) is a theta lift of a cuspidal function in
![]() $L^2([\operatorname {O}_{\det }])^\infty $
to
$L^2([\operatorname {O}_{\det }])^\infty $
to
![]() $L^2([\operatorname {SL}_2])^\infty $
. In this case, [Reference RallisRal84] verifies that the theta lift of a cuspidal function to
$L^2([\operatorname {SL}_2])^\infty $
. In this case, [Reference RallisRal84] verifies that the theta lift of a cuspidal function to
![]() $\operatorname {SL}_2$
is cuspidal.
$\operatorname {SL}_2$
is cuspidal.
Lemma A.5. Let
![]() $\varphi ^*\in L^2_{\mathrm {cusp}}([\operatorname {SL}_2])^\infty $
and
$\varphi ^*\in L^2_{\mathrm {cusp}}([\operatorname {SL}_2])^\infty $
and
![]() $\varphi ,\varphi ' \in L^2_{\mathrm {cusp}}([G])^\infty $
. Assume that
$\varphi ,\varphi ' \in L^2_{\mathrm {cusp}}([G])^\infty $
. Assume that
![]() $\varphi ,\varphi '$
are
$\varphi ,\varphi '$
are
![]() $K_R$
-invariant and that
$K_R$
-invariant and that
![]() ${\Phi }$
is both left and right
${\Phi }$
is both left and right
![]() $\widetilde {K}_R$
-invariant. Then
$\widetilde {K}_R$
-invariant. Then
Proof. This follows from Fubini and the fact that cusp forms are of rapid decay.
Proposition A.6. Assume
![]() $\varphi ,\varphi '\in L^2_{\mathrm {cusp}}([G])^{\infty }$
are
$\varphi ,\varphi '\in L^2_{\mathrm {cusp}}([G])^{\infty }$
are
![]() $K_R$
-invariant and that
$K_R$
-invariant and that
![]() ${\Phi }$
is both left and right
${\Phi }$
is both left and right
![]() $\widetilde {K}_R$
-invariant. For
$\widetilde {K}_R$
-invariant. For
![]() $s\in \operatorname {GL}_2(\mathbb {A}),$
define
$s\in \operatorname {GL}_2(\mathbb {A}),$
define
![]() $s_1=\left (\begin {smallmatrix} (\det s)^{-1} & 0 \\ 0 & 1 \end {smallmatrix}\right ) s$
. The Whittaker function of the theta lift satisfies
$s_1=\left (\begin {smallmatrix} (\det s)^{-1} & 0 \\ 0 & 1 \end {smallmatrix}\right ) s$
. The Whittaker function of the theta lift satisfies
where
 $$ \begin{align*} \left(T^{\Phi}_s \varphi\right)(r)= \begin{cases} \int_{G'(\mathbb{A})} \varphi(rl^{-1}) \left(\rho\left(s_1\right).{\Phi}\right)(l \alpha_{\det s}) \,\mathrm{d} l & \det s \in \det B_{\mathbb{A}} \\ 0 & \det s \not \in \det B_{\mathbb{A}} \end{cases}\ \end{align*} $$
$$ \begin{align*} \left(T^{\Phi}_s \varphi\right)(r)= \begin{cases} \int_{G'(\mathbb{A})} \varphi(rl^{-1}) \left(\rho\left(s_1\right).{\Phi}\right)(l \alpha_{\det s}) \,\mathrm{d} l & \det s \in \det B_{\mathbb{A}} \\ 0 & \det s \not \in \det B_{\mathbb{A}} \end{cases}\ \end{align*} $$
and
![]() $\alpha _{\det s}\in B_{\mathbb {A}}$
is any element satisfying
$\alpha _{\det s}\in B_{\mathbb {A}}$
is any element satisfying
![]() $\det \alpha _{\det s}=\det s$
. Moreover, we can replace the inner product in
$\det \alpha _{\det s}=\det s$
. Moreover, we can replace the inner product in
![]() $L^2([G'])$
in the formula above by an inner product in
$L^2([G'])$
in the formula above by an inner product in
![]() $L^2([G])$
.
$L^2([G])$
.
Proof. First, observe
 $$ \begin{align*} {\iota_0^*}^{-1}(\varphi\otimes \varphi')_{\Phi}(s) = |\det s |_{\mathbb{A}} \int_{[G']}\int_{[G']} \sum_{\xi \in B} (\rho(s_1).{\Phi})(l^{-1}\xi r \alpha_{\det s}) \varphi(l)\varphi'(r \alpha_{\det s}) \,\mathrm{d} l \,\mathrm{d} r. \end{align*} $$
$$ \begin{align*} {\iota_0^*}^{-1}(\varphi\otimes \varphi')_{\Phi}(s) = |\det s |_{\mathbb{A}} \int_{[G']}\int_{[G']} \sum_{\xi \in B} (\rho(s_1).{\Phi})(l^{-1}\xi r \alpha_{\det s}) \varphi(l)\varphi'(r \alpha_{\det s}) \,\mathrm{d} l \,\mathrm{d} r. \end{align*} $$
Consider both sides of the first equality as functions on
![]() $\operatorname {GL}_2(\mathbb {A})^\dagger =\{x\in \operatorname {GL}_2(\mathbb {A})\colon \det x\in \det B_{\mathbb {A}}\}$
. Set
$\operatorname {GL}_2(\mathbb {A})^\dagger =\{x\in \operatorname {GL}_2(\mathbb {A})\colon \det x\in \det B_{\mathbb {A}}\}$
. Set
![]() $\operatorname {GL}_2(\mathbb {Q})^\dagger =\{x\in \operatorname {GL}_2(\mathbb {Q})\colon \det x\in \det B\}$
and note that
$\operatorname {GL}_2(\mathbb {Q})^\dagger =\{x\in \operatorname {GL}_2(\mathbb {Q})\colon \det x\in \det B\}$
and note that ![]() because
because
![]() ${\operatorname {GL}_2(\mathbb {Q})}{\operatorname {GL}_2(\mathbb {A})^\dagger }=\operatorname {GL}_2(\mathbb {A})$
. The first equality then follows from Equation (A.5) by noticing that both sides are
${\operatorname {GL}_2(\mathbb {Q})}{\operatorname {GL}_2(\mathbb {A})^\dagger }=\operatorname {GL}_2(\mathbb {A})$
. The first equality then follows from Equation (A.5) by noticing that both sides are
![]() $\operatorname {GL}_2(\mathbb {Q})^\dagger $
-invariant on the left,
$\operatorname {GL}_2(\mathbb {Q})^\dagger $
-invariant on the left,
![]() $Z_{\operatorname {GL}_2}(\mathbb {A})$
-invariant,
$Z_{\operatorname {GL}_2}(\mathbb {A})$
-invariant,
![]() $U_R$
-invariant on the right and coincide on
$U_R$
-invariant on the right and coincide on
![]() $\operatorname {SL}_2(\mathbb {A})$
. A standard unfolding argument in the l variable (see [Reference ShimizuShi72, Reference Khayutin and SteinerKS20]) applied to the last expression shows for
$\operatorname {SL}_2(\mathbb {A})$
. A standard unfolding argument in the l variable (see [Reference ShimizuShi72, Reference Khayutin and SteinerKS20]) applied to the last expression shows for
![]() $\det s \in \det B_{\mathbb {A}}$
$\det s \in \det B_{\mathbb {A}}$
and
![]() $W_{{\iota _0^*}^{-1}(\varphi \otimes \varphi ')_{\Phi }}(s)=0$
if
$W_{{\iota _0^*}^{-1}(\varphi \otimes \varphi ')_{\Phi }}(s)=0$
if
![]() $\det s \not \in \det B_{\mathbb {A}}$
. Using the change of variables
$\det s \not \in \det B_{\mathbb {A}}$
. Using the change of variables
![]() $l^{-1}r\mapsto l$
, we can write
$l^{-1}r\mapsto l$
, we can write
This establishes the first formula.
The last formula extends naturally to any
![]() $r\in G(\mathbb {A}),$
and the result is left
$r\in G(\mathbb {A}),$
and the result is left
![]() $G(\mathbb {Q})$
-invariant. If
$G(\mathbb {Q})$
-invariant. If
![]() $\det s\not \in \det G(\mathbb {A}),$
then we extend
$\det s\not \in \det G(\mathbb {A}),$
then we extend
![]() $T^{\Phi }_s \varphi $
by zero to
$T^{\Phi }_s \varphi $
by zero to
![]() $G(\mathbb {A})$
. For any
$G(\mathbb {A})$
. For any
![]() $k\in K_R$
, using the invariance properties of
$k\in K_R$
, using the invariance properties of
![]() ${\Phi }$
and
${\Phi }$
and
![]() $\varphi $
, we can apply the change of variables
$\varphi $
, we can apply the change of variables
![]() $k l \alpha _{\det s}^{-1} k^{-1} \alpha _{\det s} \mapsto l$
to see that
$k l \alpha _{\det s}^{-1} k^{-1} \alpha _{\det s} \mapsto l$
to see that
![]() $T_s^{\Phi }\varphi $
is right
$T_s^{\Phi }\varphi $
is right
![]() $\alpha _{\det s}^{-1} K_R \alpha _{\det s}$
-invariant. The same holds for
$\alpha _{\det s}^{-1} K_R \alpha _{\det s}$
-invariant. The same holds for
![]() $\varphi '(\bullet \alpha _{\det s})$
. Because the groups
$\varphi '(\bullet \alpha _{\det s})$
. Because the groups
![]() $\alpha _{\det s} K_R \alpha _{\det s}^{-1}$
,
$\alpha _{\det s} K_R \alpha _{\det s}^{-1}$
,
![]() $\alpha _{\det s} K_R^1 \alpha _{\det s}^{-1}$
and the isogeny
$\alpha _{\det s} K_R^1 \alpha _{\det s}^{-1}$
and the isogeny
![]() $G'\to G$
satisfy the assumptions of Lemma A.2, we see that we can replace the inner product in
$G'\to G$
satisfy the assumptions of Lemma A.2, we see that we can replace the inner product in
![]() $[G']$
by an inner product in
$[G']$
by an inner product in
![]() $[G]$
.
$[G]$
.
Corollary A.7. Assume
![]() ${\Phi }$
is both left and right
${\Phi }$
is both left and right
![]() $\widetilde {K}_R$
-invariant. Let
$\widetilde {K}_R$
-invariant. Let
![]() $\varphi ,\varphi '\in L^2_{\mathrm {cusp}}([G])^{\infty }$
be
$\varphi ,\varphi '\in L^2_{\mathrm {cusp}}([G])^{\infty }$
be
![]() $K_R$
-invariant, and denote by
$K_R$
-invariant, and denote by
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
the cuspidal automorphic representations generated by
$\pi '$
the cuspidal automorphic representations generated by
![]() $\varphi $
and
$\varphi $
and
![]() $\varphi '$
, respectively. If
$\varphi '$
, respectively. If
![]() $\pi $
is disjoint from
$\pi $
is disjoint from
![]() $\pi ^{\prime \vee }$
, then
$\pi ^{\prime \vee }$
, then
![]() $(\varphi \otimes \varphi ')_{\Phi }=0$
.
$(\varphi \otimes \varphi ')_{\Phi }=0$
.
Proof. In this case, we see that
![]() ${\iota _0^*}^{-1}(\varphi \otimes \varphi ')_{\Phi }$
is cuspidal with a vanishing Whittaker function.
${\iota _0^*}^{-1}(\varphi \otimes \varphi ')_{\Phi }$
is cuspidal with a vanishing Whittaker function.
Corollary A.8. Assume
![]() ${\Phi }$
is invariant under the conjugation action of
${\Phi }$
is invariant under the conjugation action of
![]() $K_R$
. Let
$K_R$
. Let
![]() $\pi \subset L^2_{\mathrm {cusp}}([G])^{\infty }$
be an irreducible representation. Assume
$\pi \subset L^2_{\mathrm {cusp}}([G])^{\infty }$
be an irreducible representation. Assume
![]() $\varphi ,\overline {\varphi '}\in \pi $
are
$\varphi ,\overline {\varphi '}\in \pi $
are
![]() $K_R$
-invariant decomposable vectors, that is,
$K_R$
-invariant decomposable vectors, that is,
![]() $\varphi ,\overline {\varphi '}\mapsto \otimes \varphi _v, \otimes \overline {\varphi ^{\prime }_v}$
in
$\varphi ,\overline {\varphi '}\mapsto \otimes \varphi _v, \otimes \overline {\varphi ^{\prime }_v}$
in
![]() $\pi \cong \bigotimes '\pi _v$
. Then
$\pi \cong \bigotimes '\pi _v$
. Then
where V is the volume of the (possibly disconnected) real manifold ![]() with respect to the Haar measure of
with respect to the Haar measure of
![]() $G'(\mathbb {R})$
(see §4.2), and we normalize the Haar measure on
$G'(\mathbb {R})$
(see §4.2), and we normalize the Haar measure on
![]() $G'(\mathbb {Q}_p)$
so that
$G'(\mathbb {Q}_p)$
so that
![]() $R_p^1$
has unit volume.
$R_p^1$
has unit volume.
Proof. This follows directly from Proposition A.6. The constant
![]() $V^{-1}$
arises as a measure normalization constant. Specifically, denote by
$V^{-1}$
arises as a measure normalization constant. Specifically, denote by
![]() $m_{G'(\mathbb {Q}_p)}$
the Haar measure on
$m_{G'(\mathbb {Q}_p)}$
the Haar measure on
![]() $G'(\mathbb {Q}_p)$
satisfying
$G'(\mathbb {Q}_p)$
satisfying
![]() $m_{G'(\mathbb {Q})_p}(R_p^1)=1$
. The Haar measure on
$m_{G'(\mathbb {Q})_p}(R_p^1)=1$
. The Haar measure on
![]() $G'(\mathbb {A})$
satisfies
$G'(\mathbb {A})$
satisfies
![]() $m_{G'}=c \bigotimes _v m_{G'(\mathbb {Q}_v)}$
with some measure normalization constant
$m_{G'}=c \bigotimes _v m_{G'(\mathbb {Q}_v)}$
with some measure normalization constant
![]() $c>0$
. Specifically, this equality holds for linear combinations of standard test functions
$c>0$
. Specifically, this equality holds for linear combinations of standard test functions
![]() $\prod _v f_v$
with
$\prod _v f_v$
with ![]() for a.e. p. To compute c, we write
for a.e. p. To compute c, we write ![]() and denote by
and denote by
![]() $\mathcal {F}_i\subset G'(\mathbb {R})$
a fundamental domain for the right action of
$\mathcal {F}_i\subset G'(\mathbb {R})$
a fundamental domain for the right action of
![]() $\Gamma _i=G(\mathbb {Q}) \cap \delta _i K_R^1 \delta _i^{-1}$
on
$\Gamma _i=G(\mathbb {Q}) \cap \delta _i K_R^1 \delta _i^{-1}$
on
![]() $G'(\mathbb {R})$
. Then
$G'(\mathbb {R})$
. Then
![]() $\bigsqcup _{i=1}^h \delta _i \mathcal {F}_i K_R^1\subset G(\mathbb {A})$
is a fundamental domain for the left action of
$\bigsqcup _{i=1}^h \delta _i \mathcal {F}_i K_R^1\subset G(\mathbb {A})$
is a fundamental domain for the left action of
![]() $G(\mathbb {Q})$
on
$G(\mathbb {Q})$
on
![]() $G(\mathbb {A})$
, and we deduce
$G(\mathbb {A})$
, and we deduce
 $$ \begin{align*} 1=m_G\left(\bigsqcup_{i=1}^h \delta_i \mathcal{F}_i K_R^1\right)=c\sum_{i=1}^h m_{G'(\mathbb{R})}\left(\mathcal{F}_i\right) =cV.\\[-47pt] \end{align*} $$
$$ \begin{align*} 1=m_G\left(\bigsqcup_{i=1}^h \delta_i \mathcal{F}_i K_R^1\right)=c\sum_{i=1}^h m_{G'(\mathbb{R})}\left(\mathcal{F}_i\right) =cV.\\[-47pt] \end{align*} $$
Lemma A.9. Fix ![]() for all finite places
for all finite places
![]() $v<\infty $
, and let
$v<\infty $
, and let
![]() ${\Phi }_\infty $
be a Schwartz function or the Bergman test function from [Reference Khayutin and SteinerKS20]. Fix
${\Phi }_\infty $
be a Schwartz function or the Bergman test function from [Reference Khayutin and SteinerKS20]. Fix
![]() $s=(\iota _0(s_\infty ),u_f)$
with
$s=(\iota _0(s_\infty ),u_f)$
with
![]() $s_\infty \in \operatorname {SL}_2(\mathbb {R})$
and
$s_\infty \in \operatorname {SL}_2(\mathbb {R})$
and
![]() $u_f\in U_R$
. Assume that
$u_f\in U_R$
. Assume that
![]() $\varphi \in L^2_{\mathrm {cusp}}([G])^\infty $
has weight m and is a
$\varphi \in L^2_{\mathrm {cusp}}([G])^\infty $
has weight m and is a
![]() $K_R$
-invariant newvector in an irreducible cuspidal automorphic representation
$K_R$
-invariant newvector in an irreducible cuspidal automorphic representation
![]() $\pi $
. If
$\pi $
. If
![]() $\rho (\bullet , \bullet ;s){\Phi }_\infty $
is
$\rho (\bullet , \bullet ;s){\Phi }_\infty $
is
![]() $K_\infty \times K_\infty $
-isotypical of weight
$K_\infty \times K_\infty $
-isotypical of weight
![]() $(-m,m)$
, then
$(-m,m)$
, then
 $$ \begin{align*} W_{{\iota_0^*}^{-1}\varphi_{\Phi}}(s)&=\frac{\|\varphi\|_2^2}{V} \operatorname{\mathrm{Tr}} \left(\operatorname{\mathrm{Res}}^{G(\mathbb{R})}_{G'(\mathbb{R})}\pi_\infty\right)\left({\rho(s_\infty).{\Phi}_\infty}\restriction_{G'(\mathbb{R})}\right)\\ &=\frac{\|\varphi\|_2^2}{V} \overline{\left\langle f_{\varphi_\infty, \varphi_\infty} , (\rho(s_\infty).{\Phi}_\infty) \right\rangle}_{G'(\mathbb{R})}, \end{align*} $$
$$ \begin{align*} W_{{\iota_0^*}^{-1}\varphi_{\Phi}}(s)&=\frac{\|\varphi\|_2^2}{V} \operatorname{\mathrm{Tr}} \left(\operatorname{\mathrm{Res}}^{G(\mathbb{R})}_{G'(\mathbb{R})}\pi_\infty\right)\left({\rho(s_\infty).{\Phi}_\infty}\restriction_{G'(\mathbb{R})}\right)\\ &=\frac{\|\varphi\|_2^2}{V} \overline{\left\langle f_{\varphi_\infty, \varphi_\infty} , (\rho(s_\infty).{\Phi}_\infty) \right\rangle}_{G'(\mathbb{R})}, \end{align*} $$
where
![]() $f_{\varphi _\infty , \varphi _\infty }(g)=\langle \pi (g).\varphi _\infty , \varphi _\infty \rangle $
is the matrix coefficient attached to the Archimedean component of
$f_{\varphi _\infty , \varphi _\infty }(g)=\langle \pi (g).\varphi _\infty , \varphi _\infty \rangle $
is the matrix coefficient attached to the Archimedean component of
![]() $\varphi $
in
$\varphi $
in
![]() $\bigotimes ^{\prime }_v \pi _v$
, normalized so that
$\bigotimes ^{\prime }_v \pi _v$
, normalized so that
![]() $\|\varphi _\infty \|_2=1$
.
$\|\varphi _\infty \|_2=1$
.
Proof. It is sufficient to establish the claim when
![]() $\|\varphi \|_2=1$
. By [Reference Khayutin and SteinerKS20, §4], the theta transfer
$\|\varphi \|_2=1$
. By [Reference Khayutin and SteinerKS20, §4], the theta transfer
![]() $\varphi _{\Phi }$
is
$\varphi _{\Phi }$
is
![]() $U_R^1$
-invariant, thus
$U_R^1$
-invariant, thus
![]() ${\iota _0^*}^{-1}\varphi _{\Phi }$
is
${\iota _0^*}^{-1}\varphi _{\Phi }$
is
![]() $U_R$
-invariant and we can assume without loss of generality that
$U_R$
-invariant and we can assume without loss of generality that
![]() $u_f=e$
. Then
$u_f=e$
. Then
![]() $\det s=1$
and we take
$\det s=1$
and we take
![]() $\alpha _{\det s}=e$
.
$\alpha _{\det s}=e$
.
The newvector
![]() $\varphi $
decomposes as
$\varphi $
decomposes as
![]() $\varphi \mapsto \otimes \varphi _v$
in
$\varphi \mapsto \otimes \varphi _v$
in
![]() $\pi \cong \bigotimes ' \pi _v$
. We normalize
$\pi \cong \bigotimes ' \pi _v$
. We normalize
![]() $\varphi _\infty $
to have norm
$\varphi _\infty $
to have norm
![]() $1$
, then
$1$
, then
![]() $\prod _p \|\varphi _p\|_2=1$
as well. We also normalize the measure on
$\prod _p \|\varphi _p\|_2=1$
as well. We also normalize the measure on
![]() $G'(\mathbb {Q}_p)$
so that
$G'(\mathbb {Q}_p)$
so that
![]() $R_p^1=K_p^1$
has unit volume. Corollary A.8 now implies
$R_p^1=K_p^1$
has unit volume. Corollary A.8 now implies
![]() $W_{{\iota _0^*}^{-1}\varphi _{\Phi }}(s)= V^{-1} \prod _v\left \langle \varphi _v\star _{G'(\mathbb {Q}_v)} \left (\rho (s_v).{\Phi }_v\right ),\varphi _v \right \rangle $
. For a finite place p, we have
$W_{{\iota _0^*}^{-1}\varphi _{\Phi }}(s)= V^{-1} \prod _v\left \langle \varphi _v\star _{G'(\mathbb {Q}_v)} \left (\rho (s_v).{\Phi }_v\right ),\varphi _v \right \rangle $
. For a finite place p, we have
![]() $s_p=e$
and
$s_p=e$
and
![]() $\varphi _p$
is
$\varphi _p$
is
![]() $K_p$
-invariant, hence
$K_p$
-invariant, hence ![]() . We conclude
. We conclude
This expression coincides with the trace if the convolution operator
![]() $\star _{G'(\mathbb {R})}(\rho (s_\infty ).{\Phi }_\infty )$
annihilates the orthogonal complement to
$\star _{G'(\mathbb {R})}(\rho (s_\infty ).{\Phi }_\infty )$
annihilates the orthogonal complement to
![]() $\varphi _\infty $
in
$\varphi _\infty $
in
![]() $\pi _\infty $
. This follows from the facts that every
$\pi _\infty $
. This follows from the facts that every
![]() $K_\infty $
-isotypical component of the admissible unitary representation
$K_\infty $
-isotypical component of the admissible unitary representation
![]() $\pi _\infty $
is at most one-dimensional and the assumption that
$\pi _\infty $
is at most one-dimensional and the assumption that
![]() $\rho (\bullet , \bullet ;s){\Phi }_\infty $
is
$\rho (\bullet , \bullet ;s){\Phi }_\infty $
is
![]() $K_\infty \times K_\infty $
-isotypical.
$K_\infty \times K_\infty $
-isotypical.
To show the formula in terms of a matrix coefficient, we use Fubini to deduce
 $$ \begin{align*} \langle \varphi_\infty \star (\rho(s_\infty).{\Phi}_\infty)\restriction_{G'(\mathbb{R})}, \varphi_\infty \rangle &=\int_{G'(\mathbb{R})} \int_{G(\mathbb{R})} \varphi_\infty(g h^{-1}) (\rho(s_\infty).{\Phi}_\infty)(h) \overline{\varphi_\infty (g)} \,\mathrm{d} h \,\mathrm{d} g\\ &=\int_{G'(\mathbb{R})} \int_{G(\mathbb{R})} \varphi_\infty(g) \overline{\varphi_\infty (gh)} (\rho(s_\infty).{\Phi}_\infty)(h) \,\mathrm{d} g \,\mathrm{d} h\\ &=\left\langle \overline{f_{\varphi_\infty,\varphi_\infty}} , \overline{\rho(s_\infty).{\Phi}_\infty} \right\rangle_{G'(\mathbb{R})}. \end{align*} $$
$$ \begin{align*} \langle \varphi_\infty \star (\rho(s_\infty).{\Phi}_\infty)\restriction_{G'(\mathbb{R})}, \varphi_\infty \rangle &=\int_{G'(\mathbb{R})} \int_{G(\mathbb{R})} \varphi_\infty(g h^{-1}) (\rho(s_\infty).{\Phi}_\infty)(h) \overline{\varphi_\infty (g)} \,\mathrm{d} h \,\mathrm{d} g\\ &=\int_{G'(\mathbb{R})} \int_{G(\mathbb{R})} \varphi_\infty(g) \overline{\varphi_\infty (gh)} (\rho(s_\infty).{\Phi}_\infty)(h) \,\mathrm{d} g \,\mathrm{d} h\\ &=\left\langle \overline{f_{\varphi_\infty,\varphi_\infty}} , \overline{\rho(s_\infty).{\Phi}_\infty} \right\rangle_{G'(\mathbb{R})}. \end{align*} $$
The conditions of Fubini’s theorem are satisfied because the test function
![]() ${\Phi }_\infty \restriction _{G'(\mathbb {R})}$
is in
${\Phi }_\infty \restriction _{G'(\mathbb {R})}$
is in
![]() $L^q(G'(\mathbb {R}))$
for all
$L^q(G'(\mathbb {R}))$
for all
![]() $q\ge 1$
and
$q\ge 1$
and
![]() $f_{\varphi _\infty ,\varphi _\infty }\in L^p(G'(\mathbb {R}))$
for some
$f_{\varphi _\infty ,\varphi _\infty }\in L^p(G'(\mathbb {R}))$
for some
![]() $p\ge 2$
.
$p\ge 2$
.
Proposition A.10. Fix ![]() for all finite places
for all finite places
![]() $v<\infty $
. Let
$v<\infty $
. Let
![]() $\pi \subset L^2_{\mathrm {cusp}}([G])^\infty $
be an irreducible cuspidal automorphic representation, and denote by
$\pi \subset L^2_{\mathrm {cusp}}([G])^\infty $
be an irreducible cuspidal automorphic representation, and denote by
![]() $\pi ^{\mathrm {JL}}$
its Jacquet–Langlands transfer to
$\pi ^{\mathrm {JL}}$
its Jacquet–Langlands transfer to
![]() $L^2_{\mathrm {cusp}}([\operatorname {PGL}_2])^\infty $
. In case G is split, we define
$L^2_{\mathrm {cusp}}([\operatorname {PGL}_2])^\infty $
. In case G is split, we define
![]() $\pi ^{\mathrm {JL}}=\pi $
. Assume
$\pi ^{\mathrm {JL}}=\pi $
. Assume
![]() $\varphi \in \pi $
,
$\varphi \in \pi $
,
![]() $\varphi '\in \pi ^\vee $
are nonvanishing
$\varphi '\in \pi ^\vee $
are nonvanishing
![]() $K_R$
-invariant vectors, then
$K_R$
-invariant vectors, then
![]() ${\iota _0^*}^{-1}(\varphi \otimes \varphi ')_{\Phi }\in \pi ^{\mathrm {JL}}$
.
${\iota _0^*}^{-1}(\varphi \otimes \varphi ')_{\Phi }\in \pi ^{\mathrm {JL}}$
.
Moreover, if
![]() ${\Phi }_\infty $
is
${\Phi }_\infty $
is
![]() $\rho \left (K_\infty ,K_\infty ;\operatorname {SO}_2(\mathbb {R})\right )$
-isotypical with weight
$\rho \left (K_\infty ,K_\infty ;\operatorname {SO}_2(\mathbb {R})\right )$
-isotypical with weight
![]() $(-m,m,\kappa )$
,
$(-m,m,\kappa )$
,
![]() $\pi $
has conductor
$\pi $
has conductor
![]() $K_R$
and
$K_R$
and
![]() $\varphi $
is a newvector of weight m, then either
$\varphi $
is a newvector of weight m, then either
![]() $\varphi _{\Phi }$
vanishes or
$\varphi _{\Phi }$
vanishes or
![]() ${\iota _0^*}^{-1}\varphi _{\Phi }$
is a newvector of weight
${\iota _0^*}^{-1}\varphi _{\Phi }$
is a newvector of weight
![]() $\kappa $
in the Jacquet–Langlands transfer
$\kappa $
in the Jacquet–Langlands transfer
![]() $\pi ^{\mathrm {JL}}$
.
$\pi ^{\mathrm {JL}}$
.
Proof. Any smooth vector in
![]() $\pi ^{K_R}$
is a linear combination of
$\pi ^{K_R}$
is a linear combination of
![]() $K_R$
-invariant factorizable vectors in the representation
$K_R$
-invariant factorizable vectors in the representation
![]() $\pi \cong \bigotimes ^{\prime }_v \pi _v$
. Thus, we assume without loss of generality that
$\pi \cong \bigotimes ^{\prime }_v \pi _v$
. Thus, we assume without loss of generality that
![]() $\varphi $
and
$\varphi $
and
![]() $\varphi '$
are factorizable in
$\varphi '$
are factorizable in
![]() $\pi $
and
$\pi $
and
![]() $\pi ^\vee $
, respectively.
$\pi ^\vee $
, respectively.
The function
![]() ${\iota _0^*}^{-1}(\varphi \otimes \varphi ')_{\Phi }$
is cuspidal by Lemma A.4. Because
${\iota _0^*}^{-1}(\varphi \otimes \varphi ')_{\Phi }$
is cuspidal by Lemma A.4. Because
![]() $\varphi \mapsto \otimes _v \varphi _v$
and
$\varphi \mapsto \otimes _v \varphi _v$
and
![]() $\varphi '\mapsto \otimes _v \varphi ^{\prime }_v$
are factorizable, Corollary A.8 implies that the Whittaker function of
$\varphi '\mapsto \otimes _v \varphi ^{\prime }_v$
are factorizable, Corollary A.8 implies that the Whittaker function of
![]() ${\iota _0^*}^{-1}(\varphi \otimes \varphi ')_{\Phi }$
decomposes into a product.
${\iota _0^*}^{-1}(\varphi \otimes \varphi ')_{\Phi }$
decomposes into a product.
Assume
![]() $(\varphi \otimes \varphi ')_{\Phi }$
does not vanish. Let S be a finite set of rational places containing the Archimedean place, all places where G ramifies, all places where
$(\varphi \otimes \varphi ')_{\Phi }$
does not vanish. Let S be a finite set of rational places containing the Archimedean place, all places where G ramifies, all places where
![]() $\pi $
ramifies and all places where either
$\pi $
ramifies and all places where either
![]() $\varphi _v$
or
$\varphi _v$
or
![]() $\varphi ^{\prime }_v$
is not spherical. Shimizu [Reference ShimizuShi72] computes the local Whittaker function
$\varphi ^{\prime }_v$
is not spherical. Shimizu [Reference ShimizuShi72] computes the local Whittaker function
![]() $|\det s|_v\langle \varphi _v\star _{G'(\mathbb {Q}_v)} {\Phi }_v(\bullet \alpha _{\det s,v}), \pi _v(\alpha _{\det s ,v}).\overline {\varphi ^{\prime }_v} \rangle _{\pi _v}$
for every place
$|\det s|_v\langle \varphi _v\star _{G'(\mathbb {Q}_v)} {\Phi }_v(\bullet \alpha _{\det s,v}), \pi _v(\alpha _{\det s ,v}).\overline {\varphi ^{\prime }_v} \rangle _{\pi _v}$
for every place
![]() $v\not \in S$
and it coincides with the Whittaker function of a spherical newvector in
$v\not \in S$
and it coincides with the Whittaker function of a spherical newvector in
![]() $\pi ^{\mathrm {JL}}_v$
. Hence, every irreducible component
$\pi ^{\mathrm {JL}}_v$
. Hence, every irreducible component
![]() $\sigma \cong \bigotimes ^{\prime }_v \sigma _v$
of the representation generated by
$\sigma \cong \bigotimes ^{\prime }_v \sigma _v$
of the representation generated by
![]() ${\iota _0^*}^{-1}(\varphi \otimes \varphi ')_{\Phi }$
satisfies
${\iota _0^*}^{-1}(\varphi \otimes \varphi ')_{\Phi }$
satisfies
![]() $\sigma _v\cong \pi ^{\mathrm {JL}}_v$
for all
$\sigma _v\cong \pi ^{\mathrm {JL}}_v$
for all
![]() $v\not \in S$
. Using the strong multiplicity one property for
$v\not \in S$
. Using the strong multiplicity one property for
![]() $\operatorname {PGL}_2$
, we deduce that
$\operatorname {PGL}_2$
, we deduce that
![]() $\sigma =\pi ^{\mathrm {JL}}$
for every irreducible component
$\sigma =\pi ^{\mathrm {JL}}$
for every irreducible component
![]() $\sigma $
as above. Hence, the representation generated by
$\sigma $
as above. Hence, the representation generated by
![]() ${\iota _0^*}^{-1}(\varphi \otimes \varphi ')_{\Phi }$
is
${\iota _0^*}^{-1}(\varphi \otimes \varphi ')_{\Phi }$
is
![]() $\pi ^{\mathrm {JL}}$
.
$\pi ^{\mathrm {JL}}$
.
Assume next that
![]() $\pi $
has conductor
$\pi $
has conductor
![]() $K_R$
and that
$K_R$
and that
![]() $\varphi $
is a newvector of weight m. Then, the assumption that
$\varphi $
is a newvector of weight m. Then, the assumption that
![]() ${\Phi }_\infty $
has weight
${\Phi }_\infty $
has weight
![]() $(-m,m,\kappa )$
implies that
$(-m,m,\kappa )$
implies that
![]() $\varphi _{\Phi }$
has weight
$\varphi _{\Phi }$
has weight
![]() $\kappa $
. By [Reference Khayutin and SteinerKS20, §4], the theta transfer
$\kappa $
. By [Reference Khayutin and SteinerKS20, §4], the theta transfer
![]() $\varphi _{\Phi }$
is
$\varphi _{\Phi }$
is
![]() $U_R^1$
-invariant. Because the conductor of the Jacquet–Langlands transfer is exactly
$U_R^1$
-invariant. Because the conductor of the Jacquet–Langlands transfer is exactly
![]() $U_R$
and
$U_R$
and
![]() ${\iota _0^*}^{-1}\varphi _{\Phi }={\iota _0^*}^{-1}(\varphi \otimes \overline {\varphi })_{\Phi }\in \pi ^{\mathrm {JL}}$
, we deduce that
${\iota _0^*}^{-1}\varphi _{\Phi }={\iota _0^*}^{-1}(\varphi \otimes \overline {\varphi })_{\Phi }\in \pi ^{\mathrm {JL}}$
, we deduce that
![]() ${\iota _0^*}^{-1}\varphi _{\Phi }$
is a newvector as claimed.
${\iota _0^*}^{-1}\varphi _{\Phi }$
is a newvector as claimed.
Corollary A.11. Assume
![]() $\varphi ,\varphi '\in L^2_{\mathrm {cusp}}([G])^\infty $
are
$\varphi ,\varphi '\in L^2_{\mathrm {cusp}}([G])^\infty $
are
![]() $K_R$
-invariant and generate disjoint automorphic cuspidal representations, then
$K_R$
-invariant and generate disjoint automorphic cuspidal representations, then
![]() $\langle \varphi _{\Phi }, \varphi ^{\prime }_{\Phi } \rangle =0$
.
$\langle \varphi _{\Phi }, \varphi ^{\prime }_{\Phi } \rangle =0$
.
Proof. The Jacquet–Langlands transfers of disjoint automorphic representations are disjoint. Hence, Proposition A.10 above implies that
![]() ${\iota _0^*}^{-1}\varphi _{\Phi }$
,
${\iota _0^*}^{-1}\varphi _{\Phi }$
,
![]() ${\iota _0^*}^{-1}\varphi ^{\prime }_{\Phi }$
generate mutually orthogonal subrepresentations of
${\iota _0^*}^{-1}\varphi ^{\prime }_{\Phi }$
generate mutually orthogonal subrepresentations of
![]() $L^2_{\mathrm {cusp}}([\operatorname {PGL}_2])^\infty $
.
$L^2_{\mathrm {cusp}}([\operatorname {PGL}_2])^\infty $
.
Proposition A.12. Fix ![]() for all finite places
for all finite places
![]() $v<\infty $
, and assume that
$v<\infty $
, and assume that
![]() ${\Phi }_\infty $
is
${\Phi }_\infty $
is
![]() $\rho \left (K_\infty ,K_\infty ;\mathbf {SO}_2(\mathbb {R})\right )$
-isotypical with weight
$\rho \left (K_\infty ,K_\infty ;\mathbf {SO}_2(\mathbb {R})\right )$
-isotypical with weight
![]() $(-m,m,\kappa )$
. Let
$(-m,m,\kappa )$
. Let
![]() $\pi \subset L^2_{\mathrm {cusp}}([G])^\infty $
be an irreducible cuspidal automorphic representation with conductor
$\pi \subset L^2_{\mathrm {cusp}}([G])^\infty $
be an irreducible cuspidal automorphic representation with conductor
![]() $K_R$
. Assume
$K_R$
. Assume
![]() $0\neq \varphi \in \pi $
is a newvector of weight m. Then
$0\neq \varphi \in \pi $
is a newvector of weight m. Then
 $$ \begin{align} \left(\varphi_{\Phi}\right)^{\overline{{\Phi}}}=\left(\frac{\|\varphi_{\Phi}\|_2}{\|\varphi\|_2^2}\right)^2{\iota^{(1)}}^* \left(\varphi \otimes \overline{\varphi}\right). \end{align} $$
$$ \begin{align} \left(\varphi_{\Phi}\right)^{\overline{{\Phi}}}=\left(\frac{\|\varphi_{\Phi}\|_2}{\|\varphi\|_2^2}\right)^2{\iota^{(1)}}^* \left(\varphi \otimes \overline{\varphi}\right). \end{align} $$
Proof. Assume that
for some
![]() $\alpha \in \mathbb {C}$
. Then,
$\alpha \in \mathbb {C}$
. Then,
![]() $\alpha \|\varphi \|_2^4=\langle \left (\varphi _{\Phi }\right )^{\overline {{\Phi }}}, {\iota ^{(1)}}^* \left (\varphi \otimes \overline {\varphi }\right ) \rangle $
and Lemma A.5 implies that
$\alpha \|\varphi \|_2^4=\langle \left (\varphi _{\Phi }\right )^{\overline {{\Phi }}}, {\iota ^{(1)}}^* \left (\varphi \otimes \overline {\varphi }\right ) \rangle $
and Lemma A.5 implies that
![]() $\alpha =\|\varphi _{\Phi }\|_2^2/\|\varphi \|_2^4$
.
$\alpha =\|\varphi _{\Phi }\|_2^2/\|\varphi \|_2^4$
.
Because
![]() $\left (\varphi _{\Phi }\right )^{\overline {{\Phi }}}$
is continuous and cuspidal by Lemma A.4, to establish Equation (A.8) it is enough to show that
$\left (\varphi _{\Phi }\right )^{\overline {{\Phi }}}$
is continuous and cuspidal by Lemma A.4, to establish Equation (A.8) it is enough to show that
![]() ${\iota ^{(1)}}^{*-1}\left (\varphi _{\Phi }\right )^{\overline {{\Phi }}}$
is orthogonal to the orthogonal complement of
${\iota ^{(1)}}^{*-1}\left (\varphi _{\Phi }\right )^{\overline {{\Phi }}}$
is orthogonal to the orthogonal complement of
![]() $\mathbb {C}\left (\varphi \otimes \overline {\varphi }\right )$
in
$\mathbb {C}\left (\varphi \otimes \overline {\varphi }\right )$
in
![]() $L^2_{\mathrm {cusp}}([G\times G])^{K_R\times K_R}$
. Both
$L^2_{\mathrm {cusp}}([G\times G])^{K_R\times K_R}$
. Both
![]() $\left (\varphi \otimes \overline {\varphi }\right )$
and
$\left (\varphi \otimes \overline {\varphi }\right )$
and
![]() ${\iota ^{(1)}}^{*-1}\left (\varphi _{\Phi }\right )^{\overline {{\Phi }}}$
transform with weight
${\iota ^{(1)}}^{*-1}\left (\varphi _{\Phi }\right )^{\overline {{\Phi }}}$
transform with weight
![]() $(m,-m)$
under
$(m,-m)$
under
![]() $K_\infty \times K_\infty $
. Hence, it is enough to check orthogonality in the
$K_\infty \times K_\infty $
. Hence, it is enough to check orthogonality in the
![]() $(m,-m)$
isotypical subspace
$(m,-m)$
isotypical subspace
Denote by
![]() $V_m^0$
the orthogonal compliment of
$V_m^0$
the orthogonal compliment of
![]() $\mathbb {C}\left (\varphi \otimes \overline {\varphi }\right )$
in
$\mathbb {C}\left (\varphi \otimes \overline {\varphi }\right )$
in
![]() $V_m$
. We can choose an orthonormal basis for
$V_m$
. We can choose an orthonormal basis for
![]() $V_m^0$
consisting of vectors
$V_m^0$
consisting of vectors
![]() $\psi \otimes \psi '$
with
$\psi \otimes \psi '$
with
![]() $\psi ,\overline {\psi '}\in L^2_{\mathrm {cusp}}([G])^{(K_\infty ,m)\cdot K_R}$
and
$\psi ,\overline {\psi '}\in L^2_{\mathrm {cusp}}([G])^{(K_\infty ,m)\cdot K_R}$
and
![]() $\psi $
,
$\psi $
,
![]() $\psi '$
generate irreducible cuspidal automorphic representations of
$\psi '$
generate irreducible cuspidal automorphic representations of
![]() $G(\mathbb {A})$
. Because
$G(\mathbb {A})$
. Because
![]() $\pi $
has conductor
$\pi $
has conductor
![]() $K_R$
, either the representation generated by
$K_R$
, either the representation generated by
![]() $\psi $
is disjoint from
$\psi $
is disjoint from
![]() $\pi $
or the representation generated by
$\pi $
or the representation generated by
![]() $\psi '$
is disjoint from
$\psi '$
is disjoint from
![]() $\pi ^\vee $
. Fix
$\pi ^\vee $
. Fix
![]() $\psi $
,
$\psi $
,
![]() $\psi '$
as above. We need to show
$\psi '$
as above. We need to show
![]() $\left \langle {\iota ^{(1)}}^{*-1}\left (\varphi _{\Phi }\right )^{\Phi }, \psi \otimes \psi '\right \rangle =0$
. Denote by
$\left \langle {\iota ^{(1)}}^{*-1}\left (\varphi _{\Phi }\right )^{\Phi }, \psi \otimes \psi '\right \rangle =0$
. Denote by
![]() $\sigma $
,
$\sigma $
,
![]() $\sigma '$
the irreducible automorphic representations generated by
$\sigma '$
the irreducible automorphic representations generated by
![]() $\psi $
,
$\psi $
,
![]() $\psi '$
, respectively. We apply Lemma A.5 to deduce
$\psi '$
, respectively. We apply Lemma A.5 to deduce
![]() $\left \langle {\iota ^{(1)}}^{*-1}\left (\varphi _{\Phi }\right )^{\overline {{\Phi }}}, \psi \otimes \psi '\right \rangle = \left \langle \varphi _{\Phi }, \left (\psi \otimes \psi '\right )_{\Phi }\right \rangle $
. If
$\left \langle {\iota ^{(1)}}^{*-1}\left (\varphi _{\Phi }\right )^{\overline {{\Phi }}}, \psi \otimes \psi '\right \rangle = \left \langle \varphi _{\Phi }, \left (\psi \otimes \psi '\right )_{\Phi }\right \rangle $
. If
![]() $\sigma '\neq \sigma ^\vee $
, then
$\sigma '\neq \sigma ^\vee $
, then
![]() $\left (\psi \otimes \psi '\right )_{\Phi }=0$
by Corollary A.7. If
$\left (\psi \otimes \psi '\right )_{\Phi }=0$
by Corollary A.7. If
![]() $\sigma '=\sigma ^\vee $
, then
$\sigma '=\sigma ^\vee $
, then
![]() $\sigma $
is disjoint from
$\sigma $
is disjoint from
![]() $\pi $
, and
$\pi $
, and
![]() $(\iota _0^*)^{-1}\left (\psi \otimes \psi '\right )_{\Phi }\in \sigma ^{\mathrm {JL}}$
by Proposition A.10. The Jacquet–Langlands transfers of disjoint representations are disjoint. Hence,
$(\iota _0^*)^{-1}\left (\psi \otimes \psi '\right )_{\Phi }\in \sigma ^{\mathrm {JL}}$
by Proposition A.10. The Jacquet–Langlands transfers of disjoint representations are disjoint. Hence,
![]() $\pi ^{\mathrm {JL}}\perp \sigma ^{\mathrm {JL}}$
and
$\pi ^{\mathrm {JL}}\perp \sigma ^{\mathrm {JL}}$
and
![]() $\left \langle \varphi _{\Phi }, \left (\psi \otimes \psi '\right )_{\Phi }\right \rangle =0$
as claimed.
$\left \langle \varphi _{\Phi }, \left (\psi \otimes \psi '\right )_{\Phi }\right \rangle =0$
as claimed.
A.3 Explicit theta kernels
Definition A.13. We now define the Archimedean test functions on
![]() $B_\infty $
that give rise to the theta series from §5.1.1.
$B_\infty $
that give rise to the theta series from §5.1.1.
 $$ \begin{align*} {\Phi}_\infty^{-,k}(g)&= {X(g)}^k e^{-2\pi P(g)},\\ {\Phi}_\infty^{-,\mathrm{hol}}(g)&=\frac{k-1}{4\pi}\begin{cases} (\det g)^{k-1}\overline{X(g)}^{(-k)} e^{-2\pi \det g} & \det g> 0\\ 0 & \det g \le 0 \end{cases},\\ {\Phi}_\infty^{+,m}(g)&=(2m+1)(\det g)^m P_m\left(\frac{|X(g)|^2-u(g)}{\det g}\right)e^{-2\pi \det g},\\ {\Phi}_\infty^{+,\mathrm{hol}}(g)&=(k+1) X(g)^k e^{-2\pi \det g}. \end{align*} $$
$$ \begin{align*} {\Phi}_\infty^{-,k}(g)&= {X(g)}^k e^{-2\pi P(g)},\\ {\Phi}_\infty^{-,\mathrm{hol}}(g)&=\frac{k-1}{4\pi}\begin{cases} (\det g)^{k-1}\overline{X(g)}^{(-k)} e^{-2\pi \det g} & \det g> 0\\ 0 & \det g \le 0 \end{cases},\\ {\Phi}_\infty^{+,m}(g)&=(2m+1)(\det g)^m P_m\left(\frac{|X(g)|^2-u(g)}{\det g}\right)e^{-2\pi \det g},\\ {\Phi}_\infty^{+,\mathrm{hol}}(g)&=(k+1) X(g)^k e^{-2\pi \det g}. \end{align*} $$
The first two test functions are defined when
![]() $G(\mathbb {R})$
is split, and the last two are defined when
$G(\mathbb {R})$
is split, and the last two are defined when
![]() $G(\mathbb {R})$
is ramified.
$G(\mathbb {R})$
is ramified.
Lemma A.14. Let
![]() ${\Phi }_\infty $
be one of the kernels in Definition A.13 above, and set
${\Phi }_\infty $
be one of the kernels in Definition A.13 above, and set
![]() $\kappa =k,k,2m+2,k+2$
for the different kernels respectively. Then,
$\kappa =k,k,2m+2,k+2$
for the different kernels respectively. Then,
![]() $\rho (k_\theta ).{\Phi }_\infty =e^{i\kappa \theta } {\Phi }_\infty $
for all
$\rho (k_\theta ).{\Phi }_\infty =e^{i\kappa \theta } {\Phi }_\infty $
for all
![]() $k_\theta \in \operatorname {SO}_2(\mathbb {R})$
.
$k_\theta \in \operatorname {SO}_2(\mathbb {R})$
.
Proof. This is verified by Vignéras’ method [Reference VignérasVig77]. In all cases under consideration except
![]() ${\Phi }_\infty ^{-,\mathrm {hol}}$
, the test function is Schwartz, hence it is enough to check that
${\Phi }_\infty ^{-,\mathrm {hol}}$
, the test function is Schwartz, hence it is enough to check that
![]() ${\Phi }_\infty $
satisfies the partial differential equation in [Reference Khayutin and SteinerKS20, §3.3] and then use Lemma 3.4, op. cit.. In case
${\Phi }_\infty $
satisfies the partial differential equation in [Reference Khayutin and SteinerKS20, §3.3] and then use Lemma 3.4, op. cit.. In case
![]() ${\Phi }_\infty ={\Phi }_\infty ^{-,\mathrm {hol}}$
, the test function is not Schwartz and a technical argument is required to circumvent this issue. This case is treated [Reference Khayutin and SteinerKS20, §6]. We proceed to verify the three other cases.
${\Phi }_\infty ={\Phi }_\infty ^{-,\mathrm {hol}}$
, the test function is not Schwartz and a technical argument is required to circumvent this issue. This case is treated [Reference Khayutin and SteinerKS20, §6]. We proceed to verify the three other cases.
Recall the notation
![]() $x=[a,b,c]+d \in B_{\infty }$
from §2.4.3. The Laplace operator with Fourier multiplier
$x=[a,b,c]+d \in B_{\infty }$
from §2.4.3. The Laplace operator with Fourier multiplier
![]() $-4\pi ^2 \det (x)$
is then given by
$-4\pi ^2 \det (x)$
is then given by
![]() $\Delta = \frac {1}{4} ( \frac {\partial ^2}{\partial a^2} \mp (\frac {\partial ^2}{\partial b^2}+\frac {\partial ^2}{\partial c^2})+\frac {\partial ^2}{\partial d^2})$
, where the sign is
$\Delta = \frac {1}{4} ( \frac {\partial ^2}{\partial a^2} \mp (\frac {\partial ^2}{\partial b^2}+\frac {\partial ^2}{\partial c^2})+\frac {\partial ^2}{\partial d^2})$
, where the sign is
![]() $-$
if B is indefinite and
$-$
if B is indefinite and
![]() $+$
otherwise. The differential equation in §3.3 of [Reference Khayutin and SteinerKS20] for the test function
$+$
otherwise. The differential equation in §3.3 of [Reference Khayutin and SteinerKS20] for the test function
![]() ${\Phi }_{\infty }$
is equivalent to
${\Phi }_{\infty }$
is equivalent to
We note that for each of the remaining test functions, we may write
![]() ${\Phi }_{\infty }(x) = Q(x) e^{-2 \pi P(x)}$
, where
${\Phi }_{\infty }(x) = Q(x) e^{-2 \pi P(x)}$
, where
![]() $P(x)=a^2+b^2+c^2+d^2$
and Q a harmonic polynomial of homogeneous degree. For the first and last test function, this may be seen by a well-known criteria (c.f. [Reference IwaniecIwa97, Thm 9.1]) noting that
$P(x)=a^2+b^2+c^2+d^2$
and Q a harmonic polynomial of homogeneous degree. For the first and last test function, this may be seen by a well-known criteria (c.f. [Reference IwaniecIwa97, Thm 9.1]) noting that
![]() $[i,0,0]+1 \in B_{\infty } \otimes \mathbb {C} $
is an isotropic vector. For the third test function, this follows from [Reference Lubotzky, Phillips and SarnakLPS87, p. 405]. With this in mind, we have
$[i,0,0]+1 \in B_{\infty } \otimes \mathbb {C} $
is an isotropic vector. For the third test function, this follows from [Reference Lubotzky, Phillips and SarnakLPS87, p. 405]. With this in mind, we have
![]() $\Delta Q = 0$
and
$\Delta Q = 0$
and
![]() $(a\frac {\partial }{\partial a}+b\frac {\partial }{\partial b}+c\frac {\partial }{\partial c}+d\frac {\partial }{\partial d})Q=\deg (Q)Q$
, which allows one to easily verify that
$(a\frac {\partial }{\partial a}+b\frac {\partial }{\partial b}+c\frac {\partial }{\partial c}+d\frac {\partial }{\partial d})Q=\deg (Q)Q$
, which allows one to easily verify that
![]() ${\Phi }_{\infty }$
satisfies Equation (A.9) in the remaining cases.
${\Phi }_{\infty }$
satisfies Equation (A.9) in the remaining cases.
Proposition A.15. Let ![]() , where
, where
![]() ${\Phi }_\infty $
is any one of the test functions in Definition A.13 above. Set
${\Phi }_\infty $
is any one of the test functions in Definition A.13 above. Set
![]() $\kappa =k,k,2m+2,k+2$
for the different kernels, respectively. Denote by
$\kappa =k,k,2m+2,k+2$
for the different kernels, respectively. Denote by
![]() $\theta _g$
the matching classical theta function from §5.1.1. For
$\theta _g$
the matching classical theta function from §5.1.1. For
![]() $\tau \in \operatorname {SL}_2(\mathbb {Q})$
, we denote by
$\tau \in \operatorname {SL}_2(\mathbb {Q})$
, we denote by
![]() $(\tau )_\infty $
the image of
$(\tau )_\infty $
the image of
![]() $\tau $
in the Archimedean coordinate of
$\tau $
in the Archimedean coordinate of
![]() $\operatorname {SL}_2(\mathbb {A})$
. Then, for every
$\operatorname {SL}_2(\mathbb {A})$
. Then, for every
![]() $l\mid d_B N$
and
$l\mid d_B N$
and
![]() $g\in G(\mathbb {A})$
$g\in G(\mathbb {A})$
where
![]() $\mu $
is the Möbius function,
$\mu $
is the Möbius function,
![]() $s_\infty =\left (\begin {smallmatrix} y^{1/2} & xy^{-1/2} \\ 0 & y^{-1/2} \end {smallmatrix}\right ) \left (\begin {smallmatrix} \cos \theta &\sin \theta \\ -\sin \theta & \cos \theta \end {smallmatrix}\right )$
and
$s_\infty =\left (\begin {smallmatrix} y^{1/2} & xy^{-1/2} \\ 0 & y^{-1/2} \end {smallmatrix}\right ) \left (\begin {smallmatrix} \cos \theta &\sin \theta \\ -\sin \theta & \cos \theta \end {smallmatrix}\right )$
and
![]() $z=x+iy$
, that is,
$z=x+iy$
, that is,
![]() $s_\infty .i =z$
. Moreover,
$s_\infty .i =z$
. Moreover,
![]() $\theta _{g,\ell }(z)$
is a
$\theta _{g,\ell }(z)$
is a
![]() $\Gamma _0(d_B N)$
-invariant function on
$\Gamma _0(d_B N)$
-invariant function on
![]() $\mathbb {H}$
of moderate growth at the cusps.
$\mathbb {H}$
of moderate growth at the cusps.
Proof. We already know
![]() $\Theta _{\Phi }$
has weight
$\Theta _{\Phi }$
has weight
![]() $\kappa $
in the Archimedean symplectic variable
$\kappa $
in the Archimedean symplectic variable
![]() $s_\infty $
. Moreover, in [Reference Khayutin and SteinerKS20, §3.5] it is shown that
$s_\infty $
. Moreover, in [Reference Khayutin and SteinerKS20, §3.5] it is shown that
![]() $\Theta _{\Phi }$
is
$\Theta _{\Phi }$
is
![]() $U_R^1$
invariant. Denote by
$U_R^1$
invariant. Denote by
![]() $(\tau _{\ell })_f$
the diagonal image of
$(\tau _{\ell })_f$
the diagonal image of
![]() $\tau _{\ell }$
in
$\tau _{\ell }$
in
![]() $\operatorname {SL}_2(\mathbb {A}_f)$
. The left
$\operatorname {SL}_2(\mathbb {A}_f)$
. The left
![]() $\operatorname {SL}_2(\mathbb {Q})$
-invariance of the theta kernel implies
$\operatorname {SL}_2(\mathbb {Q})$
-invariance of the theta kernel implies
![]() $\Theta _{\Phi }(g,g; (\tau _{\ell })_\infty s_\infty )=\Theta _{\Phi }(g,g; s_\infty (\tau _{\ell })_f^{-1})$
. For every prime
$\Theta _{\Phi }(g,g; (\tau _{\ell })_\infty s_\infty )=\Theta _{\Phi }(g,g; s_\infty (\tau _{\ell })_f^{-1})$
. For every prime
![]() $p\nmid d_B N$
, we have
$p\nmid d_B N$
, we have
![]() $\tau _{\ell }\in \operatorname {SL}_2(\mathbb {Z})\subset \operatorname {SL}(\mathbb {Z}_p)= U_p^1$
. If
$\tau _{\ell }\in \operatorname {SL}_2(\mathbb {Z})\subset \operatorname {SL}(\mathbb {Z}_p)= U_p^1$
. If
![]() $p\mid l$
, then
$p\mid l$
, then
![]() $\tau _{\ell } \equiv w \bmod p$
, where
$\tau _{\ell } \equiv w \bmod p$
, where
![]() $w=\left (\begin {smallmatrix} 0 & 1 \\ -1 & 0 \end {smallmatrix}\right )$
, hence
$w=\left (\begin {smallmatrix} 0 & 1 \\ -1 & 0 \end {smallmatrix}\right )$
, hence
![]() $\tau _{\ell } \in w U_p^1$
. If
$\tau _{\ell } \in w U_p^1$
. If
![]() $p\mid \frac {d_B N}{l}$
, then
$p\mid \frac {d_B N}{l}$
, then
![]() $\tau _{\ell }\equiv e \bmod p$
, hence
$\tau _{\ell }\equiv e \bmod p$
, hence
![]() $\tau _{\ell }\in U_p^1$
. Because
$\tau _{\ell }\in U_p^1$
. Because ![]() , we can write
, we can write

The Weil action of w is by the Fourier transform for
![]() $p\nmid d_B$
and it is by the negative of the Fourier transform for
$p\nmid d_B$
and it is by the negative of the Fourier transform for
![]() $p \mid d_B$
. Specifically, it is shown in [Reference Khayutin and SteinerKS20, Section §4] that for
$p \mid d_B$
. Specifically, it is shown in [Reference Khayutin and SteinerKS20, Section §4] that for
![]() $p\mid d_B N$
$p\mid d_B N$
where
![]() $\gamma _p=1$
if
$\gamma _p=1$
if
![]() $B_p$
is split and
$B_p$
is split and
![]() $\gamma _p=-1$
if
$\gamma _p=-1$
if
![]() $B_p$
is ramified. We conclude that
$B_p$
is ramified. We conclude that

Because
![]() $\bigcap _{p\nmid \ell } g_p R_p g_p^{-1}\bigcap _{p\mid \ell } g_p R_p^\vee g_p^{-1}=R(\ell ;g_f)$
, we have for
$\bigcap _{p\nmid \ell } g_p R_p g_p^{-1}\bigcap _{p\mid \ell } g_p R_p^\vee g_p^{-1}=R(\ell ;g_f)$
, we have for
![]() $\xi \in B$
that
$\xi \in B$
that

and we can write
 $$ \begin{align*} \Theta_{\Phi}(g,g; (\tau_{\ell})_\infty s_\infty U_R^1)&=\frac{\mu(\gcd(l,d_B))}{\ell}\sum_{\xi\in R(\ell;g_f)} \left(\rho(s_\infty).{\Phi}_\infty\right)(g_\infty^{-1}\xi g_\infty)\\ &=\frac{\mu(\gcd(l,d_B))}{\ell}\sum_{x\in R(\ell;g)} \left(\rho(s_\infty).{\Phi}_\infty\right)(x). \end{align*} $$
$$ \begin{align*} \Theta_{\Phi}(g,g; (\tau_{\ell})_\infty s_\infty U_R^1)&=\frac{\mu(\gcd(l,d_B))}{\ell}\sum_{\xi\in R(\ell;g_f)} \left(\rho(s_\infty).{\Phi}_\infty\right)(g_\infty^{-1}\xi g_\infty)\\ &=\frac{\mu(\gcd(l,d_B))}{\ell}\sum_{x\in R(\ell;g)} \left(\rho(s_\infty).{\Phi}_\infty\right)(x). \end{align*} $$
The last equality holds because
![]() $g_\infty ^{-1} R(\ell ;g_f) g_\infty =R(\ell ;g)$
. The claim now follows from Lemma A.14 above and the formulæ for the Weil action of the diagonal and unipotent subgroups. The moderate growth of
$g_\infty ^{-1} R(\ell ;g_f) g_\infty =R(\ell ;g)$
. The claim now follows from Lemma A.14 above and the formulæ for the Weil action of the diagonal and unipotent subgroups. The moderate growth of
![]() $\theta _{g,\ell }$
now follows from the moderate growth of
$\theta _{g,\ell }$
now follows from the moderate growth of
![]() $\Theta _{\Phi }$
in the symplectic variable s. The
$\Theta _{\Phi }$
in the symplectic variable s. The
![]() $\Gamma _0(d_B N)$
-modularity of
$\Gamma _0(d_B N)$
-modularity of
![]() $\theta _{g,\ell }$
follows from the left
$\theta _{g,\ell }$
follows from the left
![]() $\operatorname {SL}_2(\mathbb {Q})$
-invariance and right
$\operatorname {SL}_2(\mathbb {Q})$
-invariance and right
![]() $U_R^1$
-invariance of
$U_R^1$
-invariance of
![]() $\Theta _{\Phi }$
in the symplectic variable, and the fact that
$\Theta _{\Phi }$
in the symplectic variable, and the fact that
![]() $\tau _{\ell }$
normalizes
$\tau _{\ell }$
normalizes
![]() $\Gamma _0(d_B N)$
.
$\Gamma _0(d_B N)$
.
Proposition A.16. Let ![]() , with
, with
![]() ${\Phi }_{\infty }$
given by any of test functions listed in Definition A.13. Let
${\Phi }_{\infty }$
given by any of test functions listed in Definition A.13. Let
![]() $\mathcal {G}$
be any of the families of automorphic forms corresponding to
$\mathcal {G}$
be any of the families of automorphic forms corresponding to
![]() $\Theta _{\Phi }$
according to Table 1. Then, for any
$\Theta _{\Phi }$
according to Table 1. Then, for any
![]() $\varphi \in \mathcal {G} \subseteq L^2([G])^{\infty }$
, a
$\varphi \in \mathcal {G} \subseteq L^2([G])^{\infty }$
, a
![]() $K_R$
-invariant Hecke eigenform, we have
$K_R$
-invariant Hecke eigenform, we have
![]() $\varphi _{\Phi }=V^{-1} \varphi ^{\mathrm {JL}}$
, where
$\varphi _{\Phi }=V^{-1} \varphi ^{\mathrm {JL}}$
, where
![]() $\varphi ^{\mathrm {JL}}$
is the arithmetically normalized Jacquet–Langlands lift of
$\varphi ^{\mathrm {JL}}$
is the arithmetically normalized Jacquet–Langlands lift of
![]() $\varphi $
, as defined in §5.1.2.
$\varphi $
, as defined in §5.1.2.
Proof. Let
![]() $\kappa $
be the entry of Table 1 corresponding to
$\kappa $
be the entry of Table 1 corresponding to
![]() $\mathcal {G}$
and
$\mathcal {G}$
and
![]() $\Theta _{\Phi }$
. Lemma A.14 shows that
$\Theta _{\Phi }$
. Lemma A.14 shows that
![]() $\varphi _{\Phi }$
is of weight
$\varphi _{\Phi }$
is of weight
![]() $\kappa $
and Proposition A.10 that
$\kappa $
and Proposition A.10 that
![]() ${\iota _0^*}^{-1}\varphi _{\Phi }$
is newvector (or zero) of level
${\iota _0^*}^{-1}\varphi _{\Phi }$
is newvector (or zero) of level
![]() $U_R$
of the Jacquet–Langlands transfer
$U_R$
of the Jacquet–Langlands transfer
![]() $\pi ^{\operatorname {\mathrm {JL}}}$
of the representation
$\pi ^{\operatorname {\mathrm {JL}}}$
of the representation
![]() $\pi $
generated by
$\pi $
generated by
![]() $\varphi $
. The subspace of vectors in
$\varphi $
. The subspace of vectors in
![]() $\pi ^{\operatorname {\mathrm {JL}}}$
satisfying these two properties is one-dimensional. This implies that
$\pi ^{\operatorname {\mathrm {JL}}}$
satisfying these two properties is one-dimensional. This implies that
![]() $\varphi _{\Phi }$
is proportional to
$\varphi _{\Phi }$
is proportional to
![]() $\varphi ^{\operatorname {\mathrm {JL}}}$
. In order to find the constant of proportionality
$\varphi ^{\operatorname {\mathrm {JL}}}$
. In order to find the constant of proportionality
![]() $\rho _1$
, we compute and compare the Whittaker functions at the identity. The Whittaker function of
$\rho _1$
, we compute and compare the Whittaker functions at the identity. The Whittaker function of
![]() $\varphi ^{\operatorname {\mathrm {JL}}}$
is recorded in §5.1.2 and those of
$\varphi ^{\operatorname {\mathrm {JL}}}$
is recorded in §5.1.2 and those of
![]() $\varphi _{\Phi }$
we shall compute with the aid of Lemma A.9.
$\varphi _{\Phi }$
we shall compute with the aid of Lemma A.9.
The case
![]() $\boldsymbol{\mathcal {G}}\boldsymbol{=}\boldsymbol{\mathcal {F}}^{\boldsymbol{-}}, \boldsymbol{{\Phi }}_{\boldsymbol\infty }\boldsymbol{=}\boldsymbol{\Phi }_{\boldsymbol{\infty} }^{\boldsymbol{-,0}}, \boldsymbol{\kappa =0:}$
$\boldsymbol{\mathcal {G}}\boldsymbol{=}\boldsymbol{\mathcal {F}}^{\boldsymbol{-}}, \boldsymbol{{\Phi }}_{\boldsymbol\infty }\boldsymbol{=}\boldsymbol{\Phi }_{\boldsymbol{\infty} }^{\boldsymbol{-,0}}, \boldsymbol{\kappa =0:}$
Suppose that
![]() $\varphi \in \mathcal {F}^{-}_{\frac {1}{4}+t^2} \subseteq \mathcal {F}^{-}$
. Then, the representation
$\varphi \in \mathcal {F}^{-}_{\frac {1}{4}+t^2} \subseteq \mathcal {F}^{-}$
. Then, the representation
![]() $\pi _\infty $
is a principal series representation obtained by normalized induction of the character
$\pi _\infty $
is a principal series representation obtained by normalized induction of the character
![]() $\left (\begin {smallmatrix} \lambda & \ast \\ 0 & \mu \end {smallmatrix}\right )\mapsto \operatorname {\mathrm {sgn}}(\lambda /\mu )^\alpha |\lambda / \mu |^{it}$
for some
$\left (\begin {smallmatrix} \lambda & \ast \\ 0 & \mu \end {smallmatrix}\right )\mapsto \operatorname {\mathrm {sgn}}(\lambda /\mu )^\alpha |\lambda / \mu |^{it}$
for some
![]() $\alpha \in \{0,1\}$
. The equality of Whittaker functions yields the following equation for the constant of proportionality
$\alpha \in \{0,1\}$
. The equality of Whittaker functions yields the following equation for the constant of proportionality
![]() $\rho _1$
:
$\rho _1$
:
Because
![]() ${\Phi }_\infty ^{-,0}\restriction _{G'(\mathbb {R})}$
is bi-
${\Phi }_\infty ^{-,0}\restriction _{G'(\mathbb {R})}$
is bi-
![]() $K_\infty $
-invariant, the trace is the Fourier transform of the Abel–Satake transform of
$K_\infty $
-invariant, the trace is the Fourier transform of the Abel–Satake transform of
![]() ${\Phi }_\infty ^{-,0}\restriction _{G'(\mathbb {R})}$
. Compute first the Abel–Satake transform
${\Phi }_\infty ^{-,0}\restriction _{G'(\mathbb {R})}$
. Compute first the Abel–Satake transform
 $$ \begin{align*} \mathcal{S}{\Phi}_\infty^{-,0}\restriction_{G'(\mathbb{R})} (\tau)&=e^{\tau/2}\int_{-\infty}^\infty {\Phi}_\infty^{-,0}\left( \begin{pmatrix} e^{\tau/2} & 0 \\ 0 & e^{-\tau/2} \end{pmatrix} \begin{pmatrix} 1 & n \\ 0 & 1 \end{pmatrix} \right) \,\mathrm{d} n\\ &= e^{\tau/2}\int_{-\infty}^\infty e^{-\pi (2\cosh \tau+e^\tau n^2)} \,\mathrm{d} n=e^{-2\pi \cosh \tau}. \end{align*} $$
$$ \begin{align*} \mathcal{S}{\Phi}_\infty^{-,0}\restriction_{G'(\mathbb{R})} (\tau)&=e^{\tau/2}\int_{-\infty}^\infty {\Phi}_\infty^{-,0}\left( \begin{pmatrix} e^{\tau/2} & 0 \\ 0 & e^{-\tau/2} \end{pmatrix} \begin{pmatrix} 1 & n \\ 0 & 1 \end{pmatrix} \right) \,\mathrm{d} n\\ &= e^{\tau/2}\int_{-\infty}^\infty e^{-\pi (2\cosh \tau+e^\tau n^2)} \,\mathrm{d} n=e^{-2\pi \cosh \tau}. \end{align*} $$
The trace is proportional to the Fourier transform of
![]() $\mathcal {S}{\Phi }_\infty ^{-,0}\restriction _{G'(\mathbb {R})} $
. Using our measure normalization this becomes
$\mathcal {S}{\Phi }_\infty ^{-,0}\restriction _{G'(\mathbb {R})} $
. Using our measure normalization this becomes
Hence,
![]() $\rho _1=V^{-1}$
.
$\rho _1=V^{-1}$
.
The case
![]() $\boldsymbol{\mathcal {G}}\boldsymbol{=}\boldsymbol{\mathcal {F}}^{\boldsymbol{-}, \mathbf{{hol}}}, \boldsymbol{\Phi }_{\boldsymbol{\infty}}\boldsymbol{=}\boldsymbol{\Phi }_{\boldsymbol{\infty}}^{\boldsymbol{-,k}}, \boldsymbol{\kappa =k{:}}$
$\boldsymbol{\mathcal {G}}\boldsymbol{=}\boldsymbol{\mathcal {F}}^{\boldsymbol{-}, \mathbf{{hol}}}, \boldsymbol{\Phi }_{\boldsymbol{\infty}}\boldsymbol{=}\boldsymbol{\Phi }_{\boldsymbol{\infty}}^{\boldsymbol{-,k}}, \boldsymbol{\kappa =k{:}}$
The equality of Whittaker functions, yields the following equation for the constant of proportionality
![]() $\rho _1$
:
$\rho _1$
:
The representation
![]() $\pi _\infty $
is the discrete series representation with parameter k, and
$\pi _\infty $
is the discrete series representation with parameter k, and
![]() $\varphi _\infty \in \pi _\infty $
is the
$\varphi _\infty \in \pi _\infty $
is the
![]() $L^2$
-normalized minimal weight vector. The matrix coefficient in this case is exactlyFootnote 6
$L^2$
-normalized minimal weight vector. The matrix coefficient in this case is exactlyFootnote 6
![]() $ f_{\varphi _\infty , \varphi _\infty }(g)=\overline {X(g)}^{(-k)}$
and we compute
$ f_{\varphi _\infty , \varphi _\infty }(g)=\overline {X(g)}^{(-k)}$
and we compute
 $$ \begin{align*} \rho_1e^{-2\pi}&=V^{-1}\int_{G'(\mathbb{R})} e^{-2\pi P(g)} \,\mathrm{d} g =V^{-1}2\pi\int_0^\infty e^{-2\pi \cosh \tau} \sinh \tau \,\mathrm{d} \tau\\ &= V^{-1} 2\pi \int_1^\infty e^{-2\pi \xi} \,\mathrm{d} \xi=V^{-1} e^{-2\pi}. \end{align*} $$
$$ \begin{align*} \rho_1e^{-2\pi}&=V^{-1}\int_{G'(\mathbb{R})} e^{-2\pi P(g)} \,\mathrm{d} g =V^{-1}2\pi\int_0^\infty e^{-2\pi \cosh \tau} \sinh \tau \,\mathrm{d} \tau\\ &= V^{-1} 2\pi \int_1^\infty e^{-2\pi \xi} \,\mathrm{d} \xi=V^{-1} e^{-2\pi}. \end{align*} $$
The remaining cases:
Here, we verifyFootnote 7 that the matrix coefficient satisfies
![]() $f_{\varphi _\infty , \varphi _\infty }=e^{2\pi }d_{\pi _{\infty }}^{-1} {\Phi }_\infty $
, where
$f_{\varphi _\infty , \varphi _\infty }=e^{2\pi }d_{\pi _{\infty }}^{-1} {\Phi }_\infty $
, where
![]() $\varphi _{\infty } \in \pi _{\infty }$
is the Archimedean component of
$\varphi _{\infty } \in \pi _{\infty }$
is the Archimedean component of
![]() $\varphi $
,
$\varphi $
,
![]() $L^2$
-normalized and
$L^2$
-normalized and
![]() $d_{\pi _{\infty }}$
the (formal) degree of
$d_{\pi _{\infty }}$
the (formal) degree of
![]() $\pi _{\infty }$
. The equality of Whittaker functions, then yields the following equation for the constant of proportionality
$\pi _{\infty }$
. The equality of Whittaker functions, then yields the following equation for the constant of proportionality
![]() $\rho _1$
:
$\rho _1$
:
 $$ \begin{align*}\begin{aligned} \rho_1e^{-2\pi}&=V^{-1} \overline{\left\langle f_{\varphi_\infty, \varphi_\infty} , {{\Phi}_\infty} \right\rangle}_{G'(\mathbb{R})} = V^{-1}e^{-2\pi} d_{\pi_{\infty}} \overline{\left\langle f_{\varphi_\infty, \varphi_\infty}, f_{\varphi_\infty, \varphi_\infty} \right\rangle}_{G'(\mathbb{R})} \\ &= V^{-1}e^{-2\pi} \|\varphi_\infty\|_2^4=V^{-1}e^{-2\pi}, \end{aligned}\end{align*} $$
$$ \begin{align*}\begin{aligned} \rho_1e^{-2\pi}&=V^{-1} \overline{\left\langle f_{\varphi_\infty, \varphi_\infty} , {{\Phi}_\infty} \right\rangle}_{G'(\mathbb{R})} = V^{-1}e^{-2\pi} d_{\pi_{\infty}} \overline{\left\langle f_{\varphi_\infty, \varphi_\infty}, f_{\varphi_\infty, \varphi_\infty} \right\rangle}_{G'(\mathbb{R})} \\ &= V^{-1}e^{-2\pi} \|\varphi_\infty\|_2^4=V^{-1}e^{-2\pi}, \end{aligned}\end{align*} $$
where we have used Schur–Weyl orthogonality for matrix coefficients.
Acknowledgements
We would like to thank E. Assing, V. Blomer, F. Brumley, G. Harcos, Y. Hu, S. Marshall, A. Saha, W. Sawin and R. Toma for their helpful feedback on an earlier draft. We would also like to thank P. Sarnak for fruitful discussions on this and surrounding topics as well as his continued encouragement and support. We also thank the referee for their careful read-through of the manuscript and their valuable comments.
Funding statement
I.K. is deeply grateful for support of the AMS Centennial fellowship and the Sloan Research Fellowship.
This paper was completed while P.N. was at the Institute for Advanced Study during the academic year 2021–2022, where he was supported by the National Science Foundation under Grant No. DMS-1926686. Some work on this project also occurred during a short-term visit of P.N. to the Institute for Advanced Study in February 2020. Whilst the paper was revised for publication in April 2024, P.N. was supported by the research grant (VIL54509) from VILLUM FONDEN .
R.S. wishes to extend his gratitude to the Institute for Advanced Study, where he was supported by the National Science Foundation Grant No. DMS – 1638352 and the Giorgio and Elena Petronio Fellowship Fund II and the Institute for Mathematical Research (FIM) at ETH Zürich, where this research was conducted. During revision for publication in April 2024, R.S. was employed at the Huawei Research Center in Zurich, whom he also thanks.
Competing interest
The authors have no competing interest to declare.
Data availability statement
Not applicable.
Ethical standards
No ethical standards were required in the pursuit of this research.
Author contributions
All authors contributed equally.