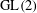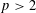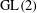Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gao, Hui
2017.
Crystalline liftings and the weight part of Serre’s conjecture.
Israel Journal of Mathematics,
Vol. 221,
Issue. 1,
p.
117.
Morra, Stefano
and
Park, Chol
2017.
Serre weights for three-dimensional ordinary Galois representations.
Journal of the London Mathematical Society,
Vol. 96,
Issue. 2,
p.
394.
Barnet-Lamb, Thomas
Gee, Toby
and
Geraghty, David
2018.
Serre weights for U(n){U(n)}.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2018,
Issue. 735,
p.
199.
Le, Daniel
Le Hung, Bao V.
Levin, Brandon
and
Morra, Stefano
2018.
Potentially crystalline deformation rings and Serre weight conjectures: shapes and shadows.
Inventiones mathematicae,
Vol. 212,
Issue. 1,
p.
1.
Le, Daniel
Morra, Stefano
and
Park, Chol
2018.
On mod p local-global compatibility for GL3(Qp) in the non-ordinary case.
Proceedings of the London Mathematical Society,
Vol. 117,
Issue. 4,
p.
790.
Le, Daniel
Le Hung, Bao V.
and
Levin, Brandon
2019.
Weight elimination in Serre-type conjectures.
Duke Mathematical Journal,
Vol. 168,
Issue. 13,
Bellovin, Rebecca
and
Gee, Toby
2019.
G-valued local deformation rings and global
lifts.
Algebra & Number Theory,
Vol. 13,
Issue. 2,
p.
333.
Hendel, Yotam I.
2019.
On the universal mod p supersingular quotients for GL2(F) over F‾p for a general F/Qp.
Journal of Algebra,
Vol. 519,
Issue. ,
p.
1.
BARTLETT, ROBIN
2020.
ON THE IRREDUCIBLE COMPONENTS OF SOME CRYSTALLINE DEFORMATION RINGS.
Forum of Mathematics, Sigma,
Vol. 8,
Issue. ,
Manning, Jeffrey
and
Shotton, Jack
2021.
Ihara’s Lemma for Shimura curves over totally real fields via patching.
Mathematische Annalen,
Vol. 379,
Issue. 1-2,
p.
187.
Dotto, Andrea
and
Le, Daniel
2021.
Diagrams in the mod p cohomology of Shimura curves.
Compositio Mathematica,
Vol. 157,
Issue. 8,
p.
1653.
Baldi, Gregorio
and
Grossi, Giada
2021.
Finite descent obstruction for Hilbert modular varieties.
Canadian Mathematical Bulletin,
Vol. 64,
Issue. 2,
p.
452.
Steinmetz, Misja
2022.
Explicit Serre weights for two-dimensional Galois representations over a ramified base.
Transactions of the American Mathematical Society,
Vol. 375,
Issue. 12,
p.
8739.
Bartlett, Robin
2024.
Degenerating products of flag varieties and applications to the Breuil–Mézard conjecture.
Selecta Mathematica,
Vol. 30,
Issue. 1,
Caraiani, Ana
Emerton, Matthew
Gee, Toby
and
Savitt, David
2024.
Components of moduli stacks of two-dimensional Galois representations.
Forum of Mathematics, Sigma,
Vol. 12,
Issue. ,
Bellovin, Rebecca
Borade, Neelima
Hilado, Anton
Kansal, Kalyani
Lee, Heejong
Levin, Brandon
Savitt, David
and
Wiersema, Hanneke
2024.
Irregular loci in the Emerton–Gee stack for GL2
.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2024,
Issue. 814,
p.
9.
Zhao, Luming
2025.
Herr complex of (φ,τ)-modules.
Journal of Number Theory,
Vol. 271,
Issue. ,
p.
66.
Boxer, George
Calegari, Frank
Gee, Toby
Newton, James
and
Thorne, Jack A.
2025.
The Ramanujan and Sato–Tate Conjectures for Bianchi modular forms.
Forum of Mathematics, Pi,
Vol. 13,
Issue. ,
Caraiani, Ana
Emerton, Matthew
Gee, Toby
and
Savitt, David
2025.
The geometric Breuil–Mézard conjecture for
two-dimensional potentially Barsotti–Tate Galois representations.
Algebra & Number Theory,
Vol. 19,
Issue. 2,
p.
287.