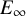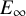1. Introduction
For any topological space
![]() $\mathfrak {X}$
, its complex of simplicial or cubical singular chains
$\mathfrak {X}$
, its complex of simplicial or cubical singular chains
![]() $\operatorname {\mathrm {S}}(\mathfrak {X})$
– regarded as a differential graded (dg) abelian group – encodes the homology of
$\operatorname {\mathrm {S}}(\mathfrak {X})$
– regarded as a differential graded (dg) abelian group – encodes the homology of
![]() $\mathfrak {X}$
in its quasi-isomorphism type. More homotopical information can be stored in the quasi-isomorphism type of this chain complex if considered as a (coassociative) coalgebra, which we will denote
$\mathfrak {X}$
in its quasi-isomorphism type. More homotopical information can be stored in the quasi-isomorphism type of this chain complex if considered as a (coassociative) coalgebra, which we will denote
![]() $\operatorname {S_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X})$
, where the coproduct comes from a natural choice of chain approximation to the diagonal
$\operatorname {S_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X})$
, where the coproduct comes from a natural choice of chain approximation to the diagonal
![]() $\mathfrak {X} \to \mathfrak {X} \times \mathfrak {X}$
. For instance, the cohomology ring of
$\mathfrak {X} \to \mathfrak {X} \times \mathfrak {X}$
. For instance, the cohomology ring of
![]() $\mathfrak {X}$
is retained, but the action of the Steenrod algebra on its mod p cohomology is not.
$\mathfrak {X}$
is retained, but the action of the Steenrod algebra on its mod p cohomology is not.
In Mandell’s seminal work [Reference Mandell23], it is shown that, when
![]() $\mathfrak {X}$
is nilpotent and finite type, the entire homotopy type of
$\mathfrak {X}$
is nilpotent and finite type, the entire homotopy type of
![]() $\mathfrak {X}$
can be encoded in the quasi-isomorphism type of this complex if considered as an
$\mathfrak {X}$
can be encoded in the quasi-isomorphism type of this complex if considered as an
![]() $E_\infty $
-coalgebra, a structure providing
$E_\infty $
-coalgebra, a structure providing
![]() $\operatorname {S_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X})$
with coherent homotopies witnessing the derived cocommutativity of the coproduct coming from the strict symmetry of the diagonal map.
$\operatorname {S_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X})$
with coherent homotopies witnessing the derived cocommutativity of the coproduct coming from the strict symmetry of the diagonal map.
The first contribution of this paper is to explicitly endow the cubical singular chains of the based loop space
![]() ${\Omega }_x \mathfrak {X}$
, with the structure of a monoidal
${\Omega }_x \mathfrak {X}$
, with the structure of a monoidal
![]() $E_\infty $
-coalgebra extending the Serre diagonal. More specifically, we verify that the monoid structure induced on
$E_\infty $
-coalgebra extending the Serre diagonal. More specifically, we verify that the monoid structure induced on
![]() $\operatorname {S^{\square }}({\Omega }_x \mathfrak {X})$
by the concatenation of loops is compatible with a natural
$\operatorname {S^{\square }}({\Omega }_x \mathfrak {X})$
by the concatenation of loops is compatible with a natural
![]() $E_\infty $
-coalgebra structure on cubical singular chains, similar to the one defined in [Reference Kaufmann and Medina-Mardones21].
$E_\infty $
-coalgebra structure on cubical singular chains, similar to the one defined in [Reference Kaufmann and Medina-Mardones21].
Applying Adams’ cobar construction to the coalgebra of simplicial singular chains of
![]() $(\mathfrak {X}, x)$
, one obtains another monoidal algebraic model
$(\mathfrak {X}, x)$
, one obtains another monoidal algebraic model
![]() $\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X}, x)$
of
$\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X}, x)$
of
![]() ${\Omega }_x \mathfrak {X}$
[Reference Adams1]. More precisely, Adams constructed a natural monoidal chain map
${\Omega }_x \mathfrak {X}$
[Reference Adams1]. More precisely, Adams constructed a natural monoidal chain map
![]() $\theta $
from
$\theta $
from
![]() $\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X}, x)$
to
$\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X}, x)$
to
![]() $\operatorname {S^{\square }}({\Omega }_x \mathfrak {X})$
and proved it to be a quasi-isomorphism if
$\operatorname {S^{\square }}({\Omega }_x \mathfrak {X})$
and proved it to be a quasi-isomorphism if
![]() $\mathfrak {X}$
is simply connected, a statement that also holds true for path-connected spaces after [Reference Rivera and Zeinalian31]. The model
$\mathfrak {X}$
is simply connected, a statement that also holds true for path-connected spaces after [Reference Rivera and Zeinalian31]. The model
![]() $\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X}, x)$
is smaller than
$\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X}, x)$
is smaller than
![]() $\operatorname {S^{\square }}({\Omega }_x \mathfrak {X})$
and unlocks effective analysis of quantitative and qualitative properties of
$\operatorname {S^{\square }}({\Omega }_x \mathfrak {X})$
and unlocks effective analysis of quantitative and qualitative properties of
![]() ${\Omega }_x \mathfrak {X}$
, as illustrated for instance in [Reference Adams and Hilton2] and [Reference Félix, Halperin and Thomas10].
${\Omega }_x \mathfrak {X}$
, as illustrated for instance in [Reference Adams and Hilton2] and [Reference Félix, Halperin and Thomas10].
The second main contribution of this paper is to make Adams model into a monoidal
![]() $E_\infty $
-coalgebra and to prove that
$E_\infty $
-coalgebra and to prove that
respects this higher structure. Although not pursued in the present article, we remark that the explicit nature of our
![]() $E_\infty $
-extension invites the study of primary and secondary operations for loops spaces using Adams’ model and the tools developed in [Reference Kaufmann and Medina-Mardones20], [Reference Medina-Mardones26], [Reference Brumfiel, Medina-Mardones and Morgan8] and [Reference Medina-Mardones28].
$E_\infty $
-extension invites the study of primary and secondary operations for loops spaces using Adams’ model and the tools developed in [Reference Kaufmann and Medina-Mardones20], [Reference Medina-Mardones26], [Reference Brumfiel, Medina-Mardones and Morgan8] and [Reference Medina-Mardones28].
Our starting point is groundbreaking work by Baues, which imply statements similar to those in this work but in the category of (coassociative) coalgebras. Baues reinterpreted Adams’ algebraic construction at a deeper geometric level [Reference Baues4], which allowed him to endow
![]() $\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X}, x)$
with the structure of a monoidal coalgebra and to show that
$\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X}, x)$
with the structure of a monoidal coalgebra and to show that
![]() $\theta $
preserves this structure. To prove our statement we interpret Adams’ construction at an even deeper categorical level. We interpret Baues’ geometric cobar construction, originally defined for
$\theta $
preserves this structure. To prove our statement we interpret Adams’ construction at an even deeper categorical level. We interpret Baues’ geometric cobar construction, originally defined for
![]() $1$
-reduced simplicial sets, as a functor
$1$
-reduced simplicial sets, as a functor
from the category of
![]() $0$
-reduced simplicial sets to that of monoidal cubical sets. The key difference with Baues’ original work is the use of connections to obtain a natural construction before geometric realization.
$0$
-reduced simplicial sets to that of monoidal cubical sets. The key difference with Baues’ original work is the use of connections to obtain a natural construction before geometric realization.
Additionally, we need a suitable model of the
![]() $E_\infty $
-operad endowing cubical chains with a natural
$E_\infty $
-operad endowing cubical chains with a natural
![]() $E_\infty $
-coalgebra extending the Serre diagonal. For this we take the operad
$E_\infty $
-coalgebra extending the Serre diagonal. For this we take the operad
![]() ${\operatorname {\mathrm {U}}(\mathcal {M})}$
introduced in [Reference Medina-Mardones27]. After proving that its coalgebras form a monoidal category, we show that the functor
${\operatorname {\mathrm {U}}(\mathcal {M})}$
introduced in [Reference Medina-Mardones27]. After proving that its coalgebras form a monoidal category, we show that the functor
![]() $\operatorname {N^{\square }_{{\operatorname {\mathrm {U}}(\mathcal {M})}}} \colon \mathsf {cSet} \to \mathsf {coAlg}_{\operatorname {\mathrm {U}}(\mathcal {M})}$
– defined in [Reference Kaufmann and Medina-Mardones21] with a different sign convention – is monoidal. This allows us to construct the following extension of Adams and Baues’ structures.
$\operatorname {N^{\square }_{{\operatorname {\mathrm {U}}(\mathcal {M})}}} \colon \mathsf {cSet} \to \mathsf {coAlg}_{\operatorname {\mathrm {U}}(\mathcal {M})}$
– defined in [Reference Kaufmann and Medina-Mardones21] with a different sign convention – is monoidal. This allows us to construct the following extension of Adams and Baues’ structures.
Theorem. The following diagram commutes up to natural isomorphisms:

where the unlabeled arrows are forgetful functors.
In the diagram of the above theorem, the arrow from
![]() $\mathsf {sSet}^0$
to
$\mathsf {sSet}^0$
to
![]() $\mathsf {Mon}_{\mathsf {Ch}}$
is Adams’ cobar construction, the one from
$\mathsf {Mon}_{\mathsf {Ch}}$
is Adams’ cobar construction, the one from
![]() $\mathsf {sSet}^0$
to
$\mathsf {sSet}^0$
to
![]() $\mathsf {Mon}_{\mathsf {coAlg}}$
is Baues’ enhancement and the one from
$\mathsf {Mon}_{\mathsf {coAlg}}$
is Baues’ enhancement and the one from
![]() $\mathsf {sSet}^0$
to
$\mathsf {sSet}^0$
to
![]() $\mathsf {Mon}_{\mathsf {coAlg}_{{\operatorname {\mathrm {U}}(\mathcal {M})}}}$
is our lift. Additionally, we prove the following statement about Adams’s map.
$\mathsf {Mon}_{\mathsf {coAlg}_{{\operatorname {\mathrm {U}}(\mathcal {M})}}}$
is our lift. Additionally, we prove the following statement about Adams’s map.
Theorem. For any pointed space
![]() $(\mathfrak {X}, x)$
,
$(\mathfrak {X}, x)$
,
is a quasi-isomorphism of monoidal
![]() ${\operatorname {\mathrm {U}}(\mathcal {M})}$
-coalgebras.
${\operatorname {\mathrm {U}}(\mathcal {M})}$
-coalgebras.
The fact that
![]() $\theta $
respects the monoid structure in
$\theta $
respects the monoid structure in
![]() $\mathsf {Ch}$
was proven by Adams, whereas the compatibility of the monoid structure with the Serre coalgebra structure was established by Baues. Our contribution is the compatibility of the monoid structure with a full
$\mathsf {Ch}$
was proven by Adams, whereas the compatibility of the monoid structure with the Serre coalgebra structure was established by Baues. Our contribution is the compatibility of the monoid structure with a full
![]() $E_\infty $
-coalgebra extension of Serre’s coalgebra. We also remark that, whereas both Adams and Baues worked in the setting where the underlying space is simply connected, the above theorem does not require any connectivity or finiteness hypotheses.
$E_\infty $
-coalgebra extension of Serre’s coalgebra. We also remark that, whereas both Adams and Baues worked in the setting where the underlying space is simply connected, the above theorem does not require any connectivity or finiteness hypotheses.
Related work
Kadeishvili [Reference Kadeishvili17, Reference Kadeishvili18] explicitly described monoidal cup-i coproducts on
![]() $\operatorname {\mathbf {\Omega }} \operatorname {N^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(X)$
extending Baues coalgebra. Kadeishvili, as Baues, used cubical methods to define these coproducts and to compare them, in the
$\operatorname {\mathbf {\Omega }} \operatorname {N^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(X)$
extending Baues coalgebra. Kadeishvili, as Baues, used cubical methods to define these coproducts and to compare them, in the
![]() $1$
-connected setting, to cup-i coproducts extending the Serre coalgebra structure on the cubical singular chains of the based loop space. Additionally, there are several papers [Reference Kadeishvili and Saneblidze19, Reference Smirnov32, Reference Smith33, Reference Smith34] that predict the existence of, but do not construct, an
$1$
-connected setting, to cup-i coproducts extending the Serre coalgebra structure on the cubical singular chains of the based loop space. Additionally, there are several papers [Reference Kadeishvili and Saneblidze19, Reference Smirnov32, Reference Smith33, Reference Smith34] that predict the existence of, but do not construct, an
![]() $E_\infty $
-structure on the cobar construction on the chains of simply connected simplicial sets.
$E_\infty $
-structure on the cobar construction on the chains of simply connected simplicial sets.
On the dual side, Fresse [Reference Fresse11] provided the bar construction of an algebra over the surjection operad with the structure of a comonoid in the category of algebras over the Barratt–Eccles operad. Additionally, in [Reference Fresse12] he used a model category structure on reduced operads [Reference Berger and Moerdijk7, Reference Hinich16] to iterate the bar construction on algebras over cofibrant
![]() $E_\infty $
-operads.
$E_\infty $
-operads.
The use of coalgebras instead of algebras allows us to relate the cobar construction to the based loop space directly – via the Adams map – without imposing restrictions on the underlying homotopy type, as done by Fresse. Furthermore, by grounding our approach on the cubical perspective at the heart of Adams’ and Baues’ seminal papers, we are able to preserve the natural monoidal structures when defining our
![]() $E_\infty $
-enhancements.
$E_\infty $
-enhancements.
2. Conventions and preliminaries
2.1. Coalgebras
Throughout this article,
![]() $\Bbbk $
denotes a commutative and unital ring and we work over its associated symmetric monoidal category of (homologically) graded chain complexes of
$\Bbbk $
denotes a commutative and unital ring and we work over its associated symmetric monoidal category of (homologically) graded chain complexes of
![]() $\Bbbk $
-modules
$\Bbbk $
-modules
![]() $(\mathsf {Ch}, \otimes , \Bbbk )$
.
$(\mathsf {Ch}, \otimes , \Bbbk )$
.
A coalgebra consists of a chain complex C and chain maps
![]() $\Delta \colon C \to C \otimes C$
and
$\Delta \colon C \to C \otimes C$
and
![]() $\varepsilon \colon C \to \Bbbk $
satisfying the usual coassociativity and counitality relations. Denote by
$\varepsilon \colon C \to \Bbbk $
satisfying the usual coassociativity and counitality relations. Denote by
![]() $\mathsf {coAlg}$
the category of coalgebras with morphisms being structure preserving chain maps. The category
$\mathsf {coAlg}$
the category of coalgebras with morphisms being structure preserving chain maps. The category
![]() $\mathsf {coAlg}$
is symmetric monoidal, with braiding induced from
$\mathsf {coAlg}$
is symmetric monoidal, with braiding induced from
![]() $\mathsf {Ch}$
and structure maps of a product
$\mathsf {Ch}$
and structure maps of a product
![]() $C \otimes C^\prime $
given by
$C \otimes C^\prime $
given by
 $$ \begin{gather*} C \otimes C^\prime \xrightarrow{\Delta \otimes \Delta^\prime} (C \otimes C) \otimes (C^\prime \otimes C^\prime) \xrightarrow{(23)} (C \otimes C^\prime) \otimes (C \otimes C^\prime), \\ C \otimes C^\prime \xrightarrow{\varepsilon \otimes \varepsilon^\prime} \Bbbk \otimes \Bbbk \xrightarrow{\cong} \Bbbk. \end{gather*} $$
$$ \begin{gather*} C \otimes C^\prime \xrightarrow{\Delta \otimes \Delta^\prime} (C \otimes C) \otimes (C^\prime \otimes C^\prime) \xrightarrow{(23)} (C \otimes C^\prime) \otimes (C \otimes C^\prime), \\ C \otimes C^\prime \xrightarrow{\varepsilon \otimes \varepsilon^\prime} \Bbbk \otimes \Bbbk \xrightarrow{\cong} \Bbbk. \end{gather*} $$
A coaugmentation on a coalgebra C is a coalgebra map
![]() $\nu \colon \Bbbk \to C$
. A coalgebra is said to be coaugmented if it is equipped with a coaugmentation. We denote by
$\nu \colon \Bbbk \to C$
. A coalgebra is said to be coaugmented if it is equipped with a coaugmentation. We denote by
![]() $\mathsf {coAlg}^\ast $
the category of coaugmented coalgebras with morphisms being coaugmentation preserving coalgebra maps. A coaugmented coalgebra is a connected coalgebra if it is
$\mathsf {coAlg}^\ast $
the category of coaugmented coalgebras with morphisms being coaugmentation preserving coalgebra maps. A coaugmented coalgebra is a connected coalgebra if it is
![]() $0$
in negative degrees and the coaugmentation induces an isomorphism
$0$
in negative degrees and the coaugmentation induces an isomorphism
![]() $\Bbbk \cong C_0$
of
$\Bbbk \cong C_0$
of
![]() $\Bbbk $
-modules. We denote by
$\Bbbk $
-modules. We denote by
![]() $\mathsf {coAlg}^0$
the full subcategory of
$\mathsf {coAlg}^0$
the full subcategory of
![]() $\mathsf {coAlg}^\ast $
defined by these.
$\mathsf {coAlg}^\ast $
defined by these.
2.2. Monoids
A monoidal object in a monoidal category
![]() $(\mathsf {C}, \otimes , \mathbb{1})$
is an object M together with morphisms
$(\mathsf {C}, \otimes , \mathbb{1})$
is an object M together with morphisms
![]() $\mu \colon M \otimes M \to M$
and
$\mu \colon M \otimes M \to M$
and
![]() $\eta \colon \mathbb{1} \to M$
satisfying the usual associativity and unital relations. The category of these together with structure preserving morphisms, referred to as monoidal morphisms, is denoted
$\eta \colon \mathbb{1} \to M$
satisfying the usual associativity and unital relations. The category of these together with structure preserving morphisms, referred to as monoidal morphisms, is denoted
![]() ${\mathsf {Mon}}_{\mathsf {C}}$
. We remark that a lax monoidal functor
${\mathsf {Mon}}_{\mathsf {C}}$
. We remark that a lax monoidal functor
![]() $\mathsf {C} \to \mathsf {C}^\prime $
induces a functor between their categories of monoids
$\mathsf {C} \to \mathsf {C}^\prime $
induces a functor between their categories of monoids
![]() $\mathsf {Mon}_{\mathsf {C}} \to \mathsf {Mon}_{\mathsf {C}^\prime }$
. For example, the forgetful functor from
$\mathsf {Mon}_{\mathsf {C}} \to \mathsf {Mon}_{\mathsf {C}^\prime }$
. For example, the forgetful functor from
![]() $\mathsf {coAlg}$
to
$\mathsf {coAlg}$
to
![]() $\mathsf {Ch}$
is monoidal and so, it induces a forgetful functor from monoidal coalgebras to monoidal chain complexes, which are more commonly known as bialgebras and algebras respectively, but this terminology is not well suited for our purposes.
$\mathsf {Ch}$
is monoidal and so, it induces a forgetful functor from monoidal coalgebras to monoidal chain complexes, which are more commonly known as bialgebras and algebras respectively, but this terminology is not well suited for our purposes.
2.3. Simplicial theory
The simplex category is denoted by
![]() $\triangle $
and its objects by
$\triangle $
and its objects by
![]() $[n]$
. The morphisms in
$[n]$
. The morphisms in
![]() $\triangle $
are generated by coface maps, denoted by
$\triangle $
are generated by coface maps, denoted by
![]() $\partial ^{j}_n \colon [n-1] \to [n]$
for
$\partial ^{j}_n \colon [n-1] \to [n]$
for
![]() $0\leq j \leq n$
, and codegeneracy maps, denoted by
$0\leq j \leq n$
, and codegeneracy maps, denoted by
![]() $\xi ^{j}_n \colon [n+1] \to [n]$
for
$\xi ^{j}_n \colon [n+1] \to [n]$
for
![]() $0 \leq j \leq n+1$
. These satisfy the usual cosimplicial identities. For simplicity, we omit the subscript in the notation when there is no risk of confusion and simply denote these maps by
$0 \leq j \leq n+1$
. These satisfy the usual cosimplicial identities. For simplicity, we omit the subscript in the notation when there is no risk of confusion and simply denote these maps by
![]() $\partial ^{j} \colon [n-1] \to [n]$
and
$\partial ^{j} \colon [n-1] \to [n]$
and
![]() $\xi ^{j} \colon [n+1] \to [n]$
.
$\xi ^{j} \colon [n+1] \to [n]$
.
The category of simplicial sets
![]() $\mathsf {Fun}(\triangle ^{\mathrm {op}}, \mathsf {Set})$
is denoted by
$\mathsf {Fun}(\triangle ^{\mathrm {op}}, \mathsf {Set})$
is denoted by
![]() $\mathsf {sSet}$
and the standard n-simplex
$\mathsf {sSet}$
and the standard n-simplex
![]() $\triangle (-, [n])$
by
$\triangle (-, [n])$
by
![]() $\triangle ^n$
. For any simplicial set X we write, as usual,
$\triangle ^n$
. For any simplicial set X we write, as usual,
![]() $X_n$
instead of
$X_n$
instead of
![]() $X[n]$
and identify the elements of
$X[n]$
and identify the elements of
![]() $\triangle ^n_m$
with increasing tuples
$\triangle ^n_m$
with increasing tuples
![]() $[v_0, \dots , v_m]$
where
$[v_0, \dots , v_m]$
where
![]() $v_i \in \{0, \dots , n\}$
.
$v_i \in \{0, \dots , n\}$
.
If X is such that
![]() $X_0$
is a singleton set, we say that X is reduced. We denote the full subcategory of reduced simplicial sets by
$X_0$
is a singleton set, we say that X is reduced. We denote the full subcategory of reduced simplicial sets by
![]() $\mathsf {sSet}^0$
.
$\mathsf {sSet}^0$
.
We consider the topological n-simplex
![]() $\mathbb {\Delta }^n$
embedded in
$\mathbb {\Delta }^n$
embedded in
![]() $\mathbb {R}^{n+1}$
as
$\mathbb {R}^{n+1}$
as
so that the i-th vertex is given by the standard basis vector
![]() $v_i=(0,\ldots ,1, \ldots ,0) \in \mathbb {R}^{n+1}$
with
$v_i=(0,\ldots ,1, \ldots ,0) \in \mathbb {R}^{n+1}$
with
![]() $1$
in the i-th entry and
$1$
in the i-th entry and
![]() $0$
in all other entries. Consider the usual adjunction pair formed by the geometric realization and singular complex
$0$
in all other entries. Consider the usual adjunction pair formed by the geometric realization and singular complex
determined by the spaces
![]() $\mathbb {\Delta }^n$
and usual coface inclusions
$\mathbb {\Delta }^n$
and usual coface inclusions
![]() $\delta ^i \colon \mathbb {\Delta }^{n-1} \to \mathbb {\Delta }^n$
and codegeneracy projections
$\delta ^i \colon \mathbb {\Delta }^{n-1} \to \mathbb {\Delta }^n$
and codegeneracy projections
![]() $\sigma ^j \colon \mathbb {\Delta }^n \to \mathbb {\Delta }^{n-1}$
.
$\sigma ^j \colon \mathbb {\Delta }^n \to \mathbb {\Delta }^{n-1}$
.
The functor of (normalized) simplicial chains
![]() $\operatorname {N^{\triangle }} \colon \mathsf {sSet} \to \mathsf {Ch}$
is defined on any simplicial set X by first considering the chain complex
$\operatorname {N^{\triangle }} \colon \mathsf {sSet} \to \mathsf {Ch}$
is defined on any simplicial set X by first considering the chain complex
![]() $(\Bbbk [X], \partial )$
, given on degree n by the free
$(\Bbbk [X], \partial )$
, given on degree n by the free
![]() $\Bbbk $
-module generated by the n-simplices of X with differential given by the alternating sum of face maps, and then modding out by the subchain complex of degenerate elements. We remark that this functor is naturally equivalent to the composition of the geometric realization functor and that of cellular chains with respect to the standard CW structure. When no confusion arises from doing so, we write
$\Bbbk $
-module generated by the n-simplices of X with differential given by the alternating sum of face maps, and then modding out by the subchain complex of degenerate elements. We remark that this functor is naturally equivalent to the composition of the geometric realization functor and that of cellular chains with respect to the standard CW structure. When no confusion arises from doing so, we write
![]() $\operatorname {\mathrm {N}}$
instead of
$\operatorname {\mathrm {N}}$
instead of
![]() $\operatorname {N^{\triangle }}$
and refer to it simply as the functor of chains. We will denote the functor of (simplicial) singular chains
$\operatorname {N^{\triangle }}$
and refer to it simply as the functor of chains. We will denote the functor of (simplicial) singular chains
![]() $\operatorname {N^{\triangle }} \circ \operatorname {Sing^{\triangle }} \colon \mathsf {Top} \to \mathsf {Ch}$
by
$\operatorname {N^{\triangle }} \circ \operatorname {Sing^{\triangle }} \colon \mathsf {Top} \to \mathsf {Ch}$
by
![]() $\operatorname {S^{\triangle }}$
, where
$\operatorname {S^{\triangle }}$
, where
![]() $\operatorname {Sing^{\triangle }} \colon \mathsf {Top} \to \mathsf {sSet}$
denotes the singular complex functor. We modify this construction for a pointed topological space
$\operatorname {Sing^{\triangle }} \colon \mathsf {Top} \to \mathsf {sSet}$
denotes the singular complex functor. We modify this construction for a pointed topological space
![]() $(\mathfrak {X},x)$
by only considering maps
$(\mathfrak {X},x)$
by only considering maps
![]() $\mathbb {\Delta }^n \to \mathfrak {X}$
sending all vertices to x. This produces a reduced simplicial set
$\mathbb {\Delta }^n \to \mathfrak {X}$
sending all vertices to x. This produces a reduced simplicial set
![]() $\operatorname {Sing^{\triangle }}(\mathfrak {X},x)$
whose normalized chains we denote by
$\operatorname {Sing^{\triangle }}(\mathfrak {X},x)$
whose normalized chains we denote by
![]() $\operatorname {S^{\triangle }}(\mathfrak {X},x)$
.
$\operatorname {S^{\triangle }}(\mathfrak {X},x)$
.
We now recall a classical chain approximation of the diagonal map on the chains of a simplicial set, that is, a lift of the functor of chains to coalgebras:

It suffices to define this functor
![]() $\operatorname {N^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}$
on standard simplices. For any
$\operatorname {N^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}$
on standard simplices. For any
![]() $n \in \mathbb {N}$
, define
$n \in \mathbb {N}$
, define
![]() $\Delta \colon \operatorname {\mathrm {N}}(\triangle ^n) \to \operatorname {\mathrm {N}}(\triangle ^n)^{\otimes 2}$
by
$\Delta \colon \operatorname {\mathrm {N}}(\triangle ^n) \to \operatorname {\mathrm {N}}(\triangle ^n)^{\otimes 2}$
by
 $$\begin{align*}\Delta \big( [v_0, \dots, v_q] \big) = \sum_{i=0}^q \ [v_0, \dots, v_i] \otimes [v_i, \dots, v_q] \end{align*}$$
$$\begin{align*}\Delta \big( [v_0, \dots, v_q] \big) = \sum_{i=0}^q \ [v_0, \dots, v_i] \otimes [v_i, \dots, v_q] \end{align*}$$
and
![]() $\epsilon \colon \operatorname {\mathrm {N}}(\triangle ^n) \to \Bbbk $
by
$\epsilon \colon \operatorname {\mathrm {N}}(\triangle ^n) \to \Bbbk $
by
 $$\begin{align*}\epsilon \big( [v_0, \dots, v_q] \big) = \begin{cases} 1 & \text{ if } q = 0, \\ 0 & \text{ if } q>0. \end{cases} \end{align*}$$
$$\begin{align*}\epsilon \big( [v_0, \dots, v_q] \big) = \begin{cases} 1 & \text{ if } q = 0, \\ 0 & \text{ if } q>0. \end{cases} \end{align*}$$
We referred to this lift as the Alexander–Whitney coalgebra structure on simplicial chains.
If X is a reduced simplicial set, then
![]() $\operatorname {N^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(X)$
becomes a connected coalgebra with the coaugmentation
$\operatorname {N^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(X)$
becomes a connected coalgebra with the coaugmentation
![]() $\nu \colon \Bbbk \to \operatorname {N^{\triangle }}(X)$
induced by sending
$\nu \colon \Bbbk \to \operatorname {N^{\triangle }}(X)$
induced by sending
![]() $1$
to the basis element represented by the unique
$1$
to the basis element represented by the unique
![]() $0$
-simplex of X. Hence, the functor
$0$
-simplex of X. Hence, the functor
![]() $\operatorname {N^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}$
restricts to a functor
$\operatorname {N^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}$
restricts to a functor
2.4. Cubical theory
We include an abridged presentation of cubical sets parallel to the our treatment of simplicial sets in the previous section. For more details, we refer the reader to any of [Reference Friedman, Medina-Mardones and Sinha13, Reference Grandis and Mauri15, Reference Kaufmann and Medina-Mardones21].
The cube category (with a connection)
![]() $\square $
is the subcategory of
$\square $
is the subcategory of
![]() $\mathsf {Set}$
whose objects are
$\mathsf {Set}$
whose objects are
![]() $2^n = \{0, 1\}^n$
for
$2^n = \{0, 1\}^n$
for
![]() $n \in \mathbb {N}$
with
$n \in \mathbb {N}$
with
![]() $2^0 = \{0\}$
. We will denote
$2^0 = \{0\}$
. We will denote
![]() $2^1$
by
$2^1$
by
![]() $2$
and
$2$
and
![]() $2^0$
by
$2^0$
by
![]() $1$
, which is the unit of the monoidal structure of
$1$
, which is the unit of the monoidal structure of
![]() $\square $
given by
$\square $
given by
![]() $2^n \times 2^m = 2^{n+m}$
. The morphisms of
$2^n \times 2^m = 2^{n+m}$
. The morphisms of
![]() $\square $
are monoidally generated by
$\square $
are monoidally generated by

defined by
for
![]() $p,q \in \{0,1\}$
. We remark that the cube category without connections will not be considered in this work.
$p,q \in \{0,1\}$
. We remark that the cube category without connections will not be considered in this work.
The category of cubical sets
![]() $\mathsf {Fun}(\square ^{\mathrm {op}}, \mathsf {Set})$
is denoted by
$\mathsf {Fun}(\square ^{\mathrm {op}}, \mathsf {Set})$
is denoted by
![]() $\mathsf {cSet}$
and the standard n-cube
$\mathsf {cSet}$
and the standard n-cube
![]() $\square (-, 2^n)$
by
$\square (-, 2^n)$
by
![]() $\square ^n$
. For any cubical set Y we write, as usual,
$\square ^n$
. For any cubical set Y we write, as usual,
![]() $Y_n$
instead of
$Y_n$
instead of
![]() $Y(2^n)$
. The monoidal structure on
$Y(2^n)$
. The monoidal structure on
![]() $\square $
induces one on
$\square $
induces one on
![]() $\mathsf {cSet}$
. More explicitly, for two cubical sets we have
$\mathsf {cSet}$
. More explicitly, for two cubical sets we have
Consider the monoidal functor
![]() $\square \to \mathsf {Top}$
defined by assigning
$\square \to \mathsf {Top}$
defined by assigning
![]() $2$
to the usual interval
$2$
to the usual interval
![]() $\mathbb {I}^1$
and Equation (2.1) to the continuous maps
$\mathbb {I}^1$
and Equation (2.1) to the continuous maps

where
![]() $\delta _i$
and
$\delta _i$
and
![]() $\sigma $
are the canonical cubical coface and codegeneracy maps, respectively, and
$\sigma $
are the canonical cubical coface and codegeneracy maps, respectively, and
![]() $\gamma (s,t)=\text {max}(s,t)$
.
$\gamma (s,t)=\text {max}(s,t)$
.
From this functor, we obtain the usual adjunction pair formed by the geometric realization and singular complex
Notice that
![]() $\operatorname {Sing^{\square }}$
is lax monoidal
$\operatorname {Sing^{\square }}$
is lax monoidal
The functor of (normalized) cubical chains
![]() $\operatorname {N^{\square }} \colon \mathsf {cSet} \to \mathsf {Ch}$
is the unique monoidal functor defined by assigning to
$\operatorname {N^{\square }} \colon \mathsf {cSet} \to \mathsf {Ch}$
is the unique monoidal functor defined by assigning to
![]() $\square ^1$
the usual cellular chains of the interval
$\square ^1$
the usual cellular chains of the interval
![]() $\mathbb {I}^1$
. Explicitly, it is defined on any cubical set Y by first considering the chain complex
$\mathbb {I}^1$
. Explicitly, it is defined on any cubical set Y by first considering the chain complex
![]() $(\Bbbk [Y], \delta )$
, given on degree n by the free
$(\Bbbk [Y], \delta )$
, given on degree n by the free
![]() $\Bbbk $
-module generated by the n-cubes of Y with differential
$\Bbbk $
-module generated by the n-cubes of Y with differential
![]() $\delta $
given on any n-cube
$\delta $
given on any n-cube
![]() $y \in Y_n$
by
$y \in Y_n$
by
 $$\begin{align*}\delta(y) = \sum_{i=1}^n (-1)^i \big( Y(\text{id}_2^{i-1} \times \delta_1 \times \text{id}_2^{n-i})(y) - Y(\text{id}_2^{i-1} \times \delta_0 \times \text{id}_2^{n-i})(y) \big) \end{align*}$$
$$\begin{align*}\delta(y) = \sum_{i=1}^n (-1)^i \big( Y(\text{id}_2^{i-1} \times \delta_1 \times \text{id}_2^{n-i})(y) - Y(\text{id}_2^{i-1} \times \delta_0 \times \text{id}_2^{n-i})(y) \big) \end{align*}$$
and then modding out by the subcomplex of degenerate cubes. When no confusion arises from doing so, we write
![]() $\operatorname {\mathrm {N}}$
instead of
$\operatorname {\mathrm {N}}$
instead of
![]() $\operatorname {N^{\square }}$
and refer to it simply as the functor of chains. We remark that
$\operatorname {N^{\square }}$
and refer to it simply as the functor of chains. We remark that
![]() $\operatorname {N^{\square }}$
is naturally equivalent to the composition of the geometric realization and cellular chains functors with respect to the canonical CW structure. We will denote the functor of (cubical) singular chains
$\operatorname {N^{\square }}$
is naturally equivalent to the composition of the geometric realization and cellular chains functors with respect to the canonical CW structure. We will denote the functor of (cubical) singular chains
![]() $\operatorname {N^{\square }} \circ \operatorname {Sing^{\square }} \colon \mathsf {Top} \to \mathsf {Ch}$
by
$\operatorname {N^{\square }} \circ \operatorname {Sing^{\square }} \colon \mathsf {Top} \to \mathsf {Ch}$
by
![]() $\operatorname {S^{\square }}$
.
$\operatorname {S^{\square }}$
.
Since
![]() $\operatorname {\mathrm {N}}(\square ^1)$
is a coalgebra and the category of coalgebras is monoidal, there is a unique monoidal functor
$\operatorname {\mathrm {N}}(\square ^1)$
is a coalgebra and the category of coalgebras is monoidal, there is a unique monoidal functor
![]() $\operatorname {N^{\square }_{\!{\mathcal {A}\mathsf {s}}}}$
lifting the functor of chains
$\operatorname {N^{\square }_{\!{\mathcal {A}\mathsf {s}}}}$
lifting the functor of chains

We refer to this lift as the Serre coalgebra structure on cubical chains and to the coproduct
![]() $\Delta $
as the Serre diagonal.
$\Delta $
as the Serre diagonal.
3. Adams’s model of the based loop space
In this section, we revisit Adams’s classical cobar construction as a model for the based loop space. A deeper exploration of Adams’s comparison map from the cobar construction of the simplicial singular chains on a space to the cubical chains on the based loop space naturally leads us to the framework of necklical sets, a notion related to both simplicial sets and cubical sets. We use this framework to construct a functorial cubical model for the based loop space. Similar constructions and results may be found in [Reference Baues3], [Reference Berger5], [Reference Baues4], [Reference Dugger and Spivak9], [Reference Gálvez-Carrillo, Kaufmann and Tonks14] and [Reference Rivera and Saneblidze30, Reference Rivera and Zeinalian31].
3.1. The based loop space
The path space functor
assigns to
![]() $\mathfrak {X}$
the space
$\mathfrak {X}$
the space
equipped with the compact-open topology. For any
![]() $x,x' \in \mathfrak {X}$
, the subspace
$x,x' \in \mathfrak {X}$
, the subspace
![]() $P(\mathfrak {X};x,x')$
consists of those paths starting and ending at x and
$P(\mathfrak {X};x,x')$
consists of those paths starting and ending at x and
![]() $x'$
, respectively. The points of
$x'$
, respectively. The points of
![]() $P(\mathfrak {X})$
are often referred to as Moore paths on
$P(\mathfrak {X})$
are often referred to as Moore paths on
![]() $\mathfrak {X}$
. We will think of this construction as a functor on bipointed spaces in the obvious way. There is a composition structure
$\mathfrak {X}$
. We will think of this construction as a functor on bipointed spaces in the obvious way. There is a composition structure
 $$ \begin{align} P(\mathfrak{X};x,x') \times P(\mathfrak{X};x',x") &\to P(\mathfrak{X};x,x") \nonumber\\ (\alpha, \beta) &\mapsto \alpha \cdot \beta \end{align} $$
$$ \begin{align} P(\mathfrak{X};x,x') \times P(\mathfrak{X};x',x") &\to P(\mathfrak{X};x,x") \nonumber\\ (\alpha, \beta) &\mapsto \alpha \cdot \beta \end{align} $$
given by concatenation of paths with addition of parameters, whose identities are constant paths with
![]() $r=0$
. We may assemble these data into a topologically enriched category
$r=0$
. We may assemble these data into a topologically enriched category
![]() $\mathcal {P}(\mathfrak {X})$
that has the points of
$\mathcal {P}(\mathfrak {X})$
that has the points of
![]() $\mathfrak {X}$
as objects, the spaces
$\mathfrak {X}$
as objects, the spaces
![]() $P(\mathfrak {X};x,x')$
as morphisms from x to
$P(\mathfrak {X};x,x')$
as morphisms from x to
![]() $x'$
, concatenation of paths as composition and constant paths with
$x'$
, concatenation of paths as composition and constant paths with
![]() $r=0$
as identity morphisms.
$r=0$
as identity morphisms.
Denote by
![]() $\mathsf {Top}^\ast $
the category of pointed topological spaces, which we think of as a full subcategory of that of bipointed spaces in the obvious way. The based loop space functor
$\mathsf {Top}^\ast $
the category of pointed topological spaces, which we think of as a full subcategory of that of bipointed spaces in the obvious way. The based loop space functor
associates to a pointed space
![]() $(\mathfrak {X},x)$
the space
$(\mathfrak {X},x)$
the space
of loops in
![]() $\mathfrak {X}$
based at x with the monoid structure induced from the composition structure (3.1).
$\mathfrak {X}$
based at x with the monoid structure induced from the composition structure (3.1).
Since
![]() $\operatorname {Sing^{\square }}$
is lax monoidal,
$\operatorname {Sing^{\square }}$
is lax monoidal,
![]() $\operatorname {Sing^{\square }}({\Omega }_x \mathfrak {X})$
is a monoid in
$\operatorname {Sing^{\square }}({\Omega }_x \mathfrak {X})$
is a monoid in
![]() $\mathsf {cSet}$
, and, since
$\mathsf {cSet}$
, and, since
![]() $\operatorname {N^{\square }}$
is monoidal,
$\operatorname {N^{\square }}$
is monoidal,
![]() $\operatorname {S^{\square }}(\mathfrak {X},x)$
is a monoid in
$\operatorname {S^{\square }}(\mathfrak {X},x)$
is a monoid in
![]() $\mathsf {Ch}$
.
$\mathsf {Ch}$
.
3.2. The cobar construction
We now describe an algebraic analogue of the based loop space introduced by Adams [Reference Adams1]. The cobar construction is the functor
defined on objects as follows. Let
![]() $(C, \Delta , \varepsilon , \nu )$
be a coaugmented coalgebra. Denote by
$(C, \Delta , \varepsilon , \nu )$
be a coaugmented coalgebra. Denote by
![]() $\overline {C}$
the cokernel of the coaugmentation
$\overline {C}$
the cokernel of the coaugmentation
![]() $\nu \colon \Bbbk \to C$
, and recall that
$\nu \colon \Bbbk \to C$
, and recall that ![]() is the suspension functor. The cobar construction
is the suspension functor. The cobar construction
![]() $\operatorname {\mathbf {\Omega }} C$
of this coaugmented coalgebra is the graded module
$\operatorname {\mathbf {\Omega }} C$
of this coaugmented coalgebra is the graded module
regarded as a monoid in
![]() $\mathsf {Ch}$
with free associative product
$\mathsf {Ch}$
with free associative product ![]() given by concatenation, unit map
given by concatenation, unit map ![]() by the obvious inclusion, and differential constructed by extending the linear map
by the obvious inclusion, and differential constructed by extending the linear map
as a derivation using the freeness of the underlying graded monoid. On morphisms, the functor
![]() $\operatorname {\mathbf {\Omega }}$
is defined using the functoriality of the free graded monoid construction. For any
$\operatorname {\mathbf {\Omega }}$
is defined using the functoriality of the free graded monoid construction. For any
![]() $x_1, \dots , x_k \in \overline {C}$
, we denote
$x_1, \dots , x_k \in \overline {C}$
, we denote
3.3. Adams’s map
Adams made precise the sense in which the cobar functor may be understood as an algebraic analogue of the based loop space functor. This was achieved by constructing a natural monoidal chain map
for any pointed topological space
![]() $(\mathfrak {X},x)$
and showing it to be a quasi-isomorphism for simply connected spaces in [Reference Adams1], a hypothesis removed in [Reference Rivera and Zeinalian31] and, using a different argument, in [Reference Rivera and Saneblidze30]. Here,
$(\mathfrak {X},x)$
and showing it to be a quasi-isomorphism for simply connected spaces in [Reference Adams1], a hypothesis removed in [Reference Rivera and Zeinalian31] and, using a different argument, in [Reference Rivera and Saneblidze30]. Here,
![]() $\operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
denotes the coalgebra
$\operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
denotes the coalgebra
![]() $\operatorname {N^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\operatorname {Sing^{\triangle }}(\mathfrak {X},x))$
(using the notation introduced in 2.3) of (pointed) normalized singular chains.
$\operatorname {N^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\operatorname {Sing^{\triangle }}(\mathfrak {X},x))$
(using the notation introduced in 2.3) of (pointed) normalized singular chains.
We now describe the construction of Adams’ map, whose combinatorial essence is the observation that the set of ascending chains in
![]() $0 < \dots < n$
containing
$0 < \dots < n$
containing
![]() $0$
and n, with the inclusion order, is isomorphic to the
$0$
and n, with the inclusion order, is isomorphic to the
![]() $(n-1)^{\mathrm {th}}$
cubical lattice. To define Adams’ map one uses a collection of continuous maps
$(n-1)^{\mathrm {th}}$
cubical lattice. To define Adams’ map one uses a collection of continuous maps
satisfying for each j the following conditions:
-
1.
 $\theta _1(0)\colon [0,\sqrt {2}] \to \mathbb {\Delta }^1$
is the path
$\theta _1(0)\colon [0,\sqrt {2}] \to \mathbb {\Delta }^1$
is the path
 $\theta _1(0)(s) = v_0 + \frac {s}{\sqrt {2}}(v_1-v_0)$
,
$\theta _1(0)(s) = v_0 + \frac {s}{\sqrt {2}}(v_1-v_0)$
, -
2.
 $\theta _n \circ \delta _0^j = P(\delta ^j) \circ \theta _{n-1}$
and
$\theta _n \circ \delta _0^j = P(\delta ^j) \circ \theta _{n-1}$
and -
3.
 $\theta _n \circ \delta _1^j = \big (P(\delta ^{f^n_j}) \circ \theta _j\big ) \cdot \big (P(\delta ^{\ell ^n_{n-j}}) \circ \theta _{n-j}\big )$
,
$\theta _n \circ \delta _1^j = \big (P(\delta ^{f^n_j}) \circ \theta _j\big ) \cdot \big (P(\delta ^{\ell ^n_{n-j}}) \circ \theta _{n-j}\big )$
,
where, for
![]() $\epsilon \in \{0,1\}$
,
$\epsilon \in \{0,1\}$
,
and
 $$ \begin{align*} \delta^{f^n_j} = \delta^n \circ \dotsb \circ \delta^{n-j+1} &\,\colon\ \mathbb{\Delta}^j \to \mathbb{\Delta}^n, \\ \delta^{\ell^n_{n-j}} = \delta^{n-j-1} \circ \dotsb \circ \delta^{0} &\, \colon\ \mathbb{\Delta}^{n-j} \to \mathbb{\Delta}^n, \end{align*} $$
$$ \begin{align*} \delta^{f^n_j} = \delta^n \circ \dotsb \circ \delta^{n-j+1} &\,\colon\ \mathbb{\Delta}^j \to \mathbb{\Delta}^n, \\ \delta^{\ell^n_{n-j}} = \delta^{n-j-1} \circ \dotsb \circ \delta^{0} &\, \colon\ \mathbb{\Delta}^{n-j} \to \mathbb{\Delta}^n, \end{align*} $$
are, respectively, the inclusions into the first and last faces of
![]() $\mathbb {\Delta }^n$
.
$\mathbb {\Delta }^n$
.
Adams showed the existence of a (nonunique) collection of such maps by induction, using the contractibility of
![]() $P(\mathbb {\Delta }^n;v_0,v_n)$
. He then defined
$P(\mathbb {\Delta }^n;v_0,v_n)$
. He then defined
![]() $\theta _{\mathfrak {X}}$
as follows. For any singular
$\theta _{\mathfrak {X}}$
as follows. For any singular
![]() $1$
-simplex
$1$
-simplex
![]() $\sigma \in \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
, let
$\sigma \in \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
, let
where
![]() $(c_x \colon \mathbb {I}^0 \to {\Omega }_x \mathfrak {X}) \in \operatorname {S^{\square }}({\Omega }_x \mathfrak {X})$
is the singular
$(c_x \colon \mathbb {I}^0 \to {\Omega }_x \mathfrak {X}) \in \operatorname {S^{\square }}({\Omega }_x \mathfrak {X})$
is the singular
![]() $0$
-cube determined by the constant loop (with
$0$
-cube determined by the constant loop (with
![]() $r=0$
) at
$r=0$
) at
![]() $x \in \mathfrak {X}$
. For any singular n-simplex
$x \in \mathfrak {X}$
. For any singular n-simplex
![]() $\sigma \in \operatorname {S^{\triangle }}(\mathfrak {X},x)$
with
$\sigma \in \operatorname {S^{\triangle }}(\mathfrak {X},x)$
with
![]() $n>1$
, let
$n>1$
, let
Since the underlying graded monoid structure of
![]() $\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
is free, we may extend the above to a monoidal chain map
$\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
is free, we may extend the above to a monoidal chain map
![]() $\theta _{\mathfrak {X}} \colon \operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x) \to \operatorname {S^{\square }}({\Omega }_x \mathfrak {X})$
. Conditions (1), (2) and (3) then imply that
$\theta _{\mathfrak {X}} \colon \operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x) \to \operatorname {S^{\square }}({\Omega }_x \mathfrak {X})$
. Conditions (1), (2) and (3) then imply that
![]() $\theta _{\mathfrak {X}}$
is a chain map.
$\theta _{\mathfrak {X}}$
is a chain map.
Remark 3.1. Adams originally worked with the subcoalgebra
![]() $\operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)^1$
of
$\operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)^1$
of
![]() $\operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
generated by singular simplices
$\operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
generated by singular simplices
![]() $\sigma \colon \mathbb {\Delta }^n \to \mathfrak {X}$
collapsing the
$\sigma \colon \mathbb {\Delta }^n \to \mathfrak {X}$
collapsing the
![]() $1$
-skeleton of
$1$
-skeleton of
![]() $\mathbb {\Delta }^n$
to
$\mathbb {\Delta }^n$
to
![]() $x \in \mathfrak {X}$
. If
$x \in \mathfrak {X}$
. If
![]() $\mathfrak {X}$
is simply connected, the inclusion map
$\mathfrak {X}$
is simply connected, the inclusion map
![]() $\operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)^1 \hookrightarrow \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
induces a quasi-isomorphism on homology. In this case, the degree
$\operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)^1 \hookrightarrow \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
induces a quasi-isomorphism on homology. In this case, the degree
![]() $1$
module in
$1$
module in
![]() $\operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)^1$
is trivial so that
$\operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)^1$
is trivial so that
![]() $\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)^1$
is connected, that is, isomorphic to the underlying ring
$\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)^1$
is connected, that is, isomorphic to the underlying ring
![]() $\Bbbk $
in degree
$\Bbbk $
in degree
![]() $0$
. The cobar construction does not preserve quasi-isomorphisms in general. It does preserve quasi-isomorphisms between coaugmented coalgebras that are trivial in degree
$0$
. The cobar construction does not preserve quasi-isomorphisms in general. It does preserve quasi-isomorphisms between coaugmented coalgebras that are trivial in degree
![]() $1$
.
$1$
.
3.4. An explicit choice
We now construct an explicit collection of maps
satisfying the conditions in §3.3.
Given
![]() $v,w \in \mathbb {R}^{n+1}$
denote by
$v,w \in \mathbb {R}^{n+1}$
denote by
the straight line path from v to w parameterized by arc length, that is,
For any
![]() $\mathbf {t}=(t_1, \dots , t_{n-1}) \in \mathbb {I}^{n-1}$
, we define
$\mathbf {t}=(t_1, \dots , t_{n-1}) \in \mathbb {I}^{n-1}$
, we define
![]() $p_1(\mathbf {t}), \dots , p_{n-1}(\mathbf {t})$
in
$p_1(\mathbf {t}), \dots , p_{n-1}(\mathbf {t})$
in
![]() $\mathbb {\Delta }^n$
inductively by
$\mathbb {\Delta }^n$
inductively by
 $$ \begin{align*} p_1(\mathbf{t}) &= v_0+ t_1(v_1-v_0), \\ p_j(\mathbf{t}) &= p_{j-1}(\mathbf{t}) + t_j(v_j-p_{j-1}(\mathbf{t})). \end{align*} $$
$$ \begin{align*} p_1(\mathbf{t}) &= v_0+ t_1(v_1-v_0), \\ p_j(\mathbf{t}) &= p_{j-1}(\mathbf{t}) + t_j(v_j-p_{j-1}(\mathbf{t})). \end{align*} $$
We may now define
where
as the piecewise linear path given by concatenating the straight line segments connecting the ordered sequence of points
![]() $v_0, p_1(\mathbf {t}), \dots , p_n(\mathbf {t}), v_n$
, that is,
$v_0, p_1(\mathbf {t}), \dots , p_n(\mathbf {t}), v_n$
, that is,
Please consult Figure 1 for an example illustrating this construction.

Figure 1 In red, the path
![]() $\theta _3(\mathbf {t}) \in P(\mathbb {\Delta }^3, v_0, v_3)$
associated to a
$\theta _3(\mathbf {t}) \in P(\mathbb {\Delta }^3, v_0, v_3)$
associated to a
![]() $\mathbf {t} \in \mathbb {I}^2$
.
$\mathbf {t} \in \mathbb {I}^2$
.

Figure 2 The faces of the
![]() $2$
-cube in blue, labeled by a red element in their corresponding family of paths.
$2$
-cube in blue, labeled by a red element in their corresponding family of paths.
A straightforward computation proves that the conditions in §3.3 are satisfied by this collection. A diagrammatical verification in low dimensions is provided in Figure 2. We can extend this collection
![]() $\{\theta _n \colon \mathbb {I}^{n-1} \to P(\mathbb {\Delta }^n;v_0,v_n)\}$
to one of the form
$\{\theta _n \colon \mathbb {I}^{n-1} \to P(\mathbb {\Delta }^n;v_0,v_n)\}$
to one of the form
where the topological necklace
![]() $\mathbb {\Delta }^{n_1} \vee \cdots \vee \mathbb {\Delta }^{n_k}$
is obtained by identifying the last vertex of
$\mathbb {\Delta }^{n_1} \vee \cdots \vee \mathbb {\Delta }^{n_k}$
is obtained by identifying the last vertex of
![]() $\mathbb {\Delta }^{n_i}$
with the first vertex of
$\mathbb {\Delta }^{n_i}$
with the first vertex of
![]() $\mathbb {\Delta }^{n_{i+1}}$
for each
$\mathbb {\Delta }^{n_{i+1}}$
for each
![]() $i = 1, \dots , k-1$
assuming each
$i = 1, \dots , k-1$
assuming each
![]() $n_i> 0$
. We do so by setting
$n_i> 0$
. We do so by setting
 $$ \begin{align*} \theta_{(n_1, \ldots, n_k)}(t_1, \ldots, t_{n_1+ \cdots + n_k-k})& \\ &\quad = \theta_{n_1}(t_1, \ldots, t_{n_1-1}) \cdot\ \dots\ \cdot \theta_{n_k}(t_{n_1+ \cdots n_{k-1}-k},\ldots,t_{n_1 + \cdots +n_k-k}). \end{align*} $$
$$ \begin{align*} \theta_{(n_1, \ldots, n_k)}(t_1, \ldots, t_{n_1+ \cdots + n_k-k})& \\ &\quad = \theta_{n_1}(t_1, \ldots, t_{n_1-1}) \cdot\ \dots\ \cdot \theta_{n_k}(t_{n_1+ \cdots n_{k-1}-k},\ldots,t_{n_1 + \cdots +n_k-k}). \end{align*} $$
Thus, we can think of the topological necklace
![]() $\mathbb {\Delta }^{n_1} \vee \cdots \vee \mathbb {\Delta }^{n_k}$
as a space parameterizing a
$\mathbb {\Delta }^{n_1} \vee \cdots \vee \mathbb {\Delta }^{n_k}$
as a space parameterizing a
![]() $(n_1+ \cdots + n_k-k)$
-dimensional family of paths between the first and last vertices. Please consult Figure 3 for an example illustrating this construction.
$(n_1+ \cdots + n_k-k)$
-dimensional family of paths between the first and last vertices. Please consult Figure 3 for an example illustrating this construction.

Figure 3 In red, the path
![]() $\theta _{(2,1,3,2)}(\mathbf {t})$
in
$\theta _{(2,1,3,2)}(\mathbf {t})$
in
![]() $P(\mathbb {\Delta }^2 \vee \mathbb {\Delta }^1 \vee \mathbb {\Delta }^3 \vee \mathbb {\Delta }^2)$
associated to an element
$P(\mathbb {\Delta }^2 \vee \mathbb {\Delta }^1 \vee \mathbb {\Delta }^3 \vee \mathbb {\Delta }^2)$
associated to an element
![]() $\mathbf {t}$
in
$\mathbf {t}$
in
![]() $\mathbb {I}^{4}$
.
$\mathbb {I}^{4}$
.
3.5. Necklaces
We now present a categorical viewpoint on the necklaces encountered in the previous subsection and their intimate relationship with Adams’ cobar construction. For any pointed space
![]() $(\mathfrak {X},x)$
, the underlying graded
$(\mathfrak {X},x)$
, the underlying graded
![]() $\Bbbk $
-module of
$\Bbbk $
-module of
![]() $\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
can be described as the graded
$\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
can be described as the graded
![]() $\Bbbk $
-module freely generated by finite ordered sequences
$\Bbbk $
-module freely generated by finite ordered sequences
of simplices
![]() $\sigma _i \in \operatorname {Sing^{\triangle }}(\mathfrak {X},x)$
, with degree
$\sigma _i \in \operatorname {Sing^{\triangle }}(\mathfrak {X},x)$
, with degree
![]() $ \left \lvert {T} \right \rvert = \left \lvert {\sigma _1} \right \rvert +\dots + \left \lvert {\sigma _k} \right \rvert - k$
, modulo the sub
$ \left \lvert {T} \right \rvert = \left \lvert {\sigma _1} \right \rvert +\dots + \left \lvert {\sigma _k} \right \rvert - k$
, modulo the sub
![]() $\Bbbk $
-module generated by those sequences with at least one degenerate simplex. The differential of
$\Bbbk $
-module generated by those sequences with at least one degenerate simplex. The differential of
![]() $\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
on a generator T of degree n can be expressed as a signed signed sum of all generators
$\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
on a generator T of degree n can be expressed as a signed signed sum of all generators
![]() $T'$
of degree
$T'$
of degree
![]() $n-1$
. The simplices in the ordered sequence corresponding to each of these
$n-1$
. The simplices in the ordered sequence corresponding to each of these
![]() $T'$
are all faces of simplices in the ordered sequence corresponding to T. Note that two types of generators
$T'$
are all faces of simplices in the ordered sequence corresponding to T. Note that two types of generators
![]() $T'$
appear in this differential: Those that have the same length as T and those that have exactly one more simplex. The first type corresponds to terms in the differential of
$T'$
appear in this differential: Those that have the same length as T and those that have exactly one more simplex. The first type corresponds to terms in the differential of
![]() $\operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
and the second type to terms in the Alexander–Whitney coproduct. Furthermore, the monoid structure of
$\operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
and the second type to terms in the Alexander–Whitney coproduct. Furthermore, the monoid structure of
![]() $\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
is induced by simply concatenating these ordered sequences of simplices. This perspective suggests that
$\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
is induced by simply concatenating these ordered sequences of simplices. This perspective suggests that
![]() $\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
may be obtained by applying a normalized chains functor to certain cellular monoid, naturally associated to
$\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
may be obtained by applying a normalized chains functor to certain cellular monoid, naturally associated to
![]() $(\mathfrak {X},x)$
, with cells labeled by finite ordered sequences of simplices in
$(\mathfrak {X},x)$
, with cells labeled by finite ordered sequences of simplices in
![]() $\operatorname {Sing^{\triangle }}(\mathfrak {X},x)$
. A geometric construction reflecting this idea was described in [Reference Baues3]. We instead take a categorical approach and make this discussion precise through the framework of necklaces and necklical sets as we now discuss.
$\operatorname {Sing^{\triangle }}(\mathfrak {X},x)$
. A geometric construction reflecting this idea was described in [Reference Baues3]. We instead take a categorical approach and make this discussion precise through the framework of necklaces and necklical sets as we now discuss.
Consider the subcategory
![]() $\triangle _{*,*}$
of the simplex category
$\triangle _{*,*}$
of the simplex category
![]() $\triangle $
with the same objects and morphisms given by functors
$\triangle $
with the same objects and morphisms given by functors
![]() $f \colon [n] \to [m]$
satisfying
$f \colon [n] \to [m]$
satisfying
![]() $f(0) = 0$
and
$f(0) = 0$
and
![]() $f(n) = m$
. It is a strict monoidal category when equipped with the monoidal structure
$f(n) = m$
. It is a strict monoidal category when equipped with the monoidal structure
![]() $[n] \otimes [m] = [n+m]$
, thought of as identifying the elements
$[n] \otimes [m] = [n+m]$
, thought of as identifying the elements
![]() $n \in [n]$
and
$n \in [n]$
and
![]() $0 \in [m]$
, and unit given by
$0 \in [m]$
, and unit given by
![]() $[0]$
. Heuristically, we may think of
$[0]$
. Heuristically, we may think of
![]() $\triangle _{*,*}$
as a category of models for cells parameterizing families of paths with fixed endpoints inside a simplex.
$\triangle _{*,*}$
as a category of models for cells parameterizing families of paths with fixed endpoints inside a simplex.
The necklace category
![]() $\mathsf {Nec}$
is obtained from
$\mathsf {Nec}$
is obtained from
![]() $\triangle _{*,*}$
as follows. Thinking of
$\triangle _{*,*}$
as follows. Thinking of
![]() $\triangle _{*,*}$
as a monoid in
$\triangle _{*,*}$
as a monoid in
![]() $\mathsf {Cat}$
, we first apply the bar construction to it and produce a simplicial object in
$\mathsf {Cat}$
, we first apply the bar construction to it and produce a simplicial object in
![]() $\mathsf {Mon}_{\mathsf {Cat}}$
which, after realization, defines the strict monoidal category
$\mathsf {Mon}_{\mathsf {Cat}}$
which, after realization, defines the strict monoidal category
![]() $\mathsf {Nec}$
. We denote the monoidal structure by
$\mathsf {Nec}$
. We denote the monoidal structure by
We describe
![]() $(\mathsf {Nec}, \vee )$
in more explicit terms. The objects of
$(\mathsf {Nec}, \vee )$
in more explicit terms. The objects of
![]() $\mathsf {Nec}$
, called necklaces, are freely generated by the objects of
$\mathsf {Nec}$
, called necklaces, are freely generated by the objects of
![]() $\triangle _{*,*}$
through the monoidal structure
$\triangle _{*,*}$
through the monoidal structure
![]() $\vee $
. Namely, the set of objects of
$\vee $
. Namely, the set of objects of
![]() $\mathsf {Nec}$
is the set of monomials
$\mathsf {Nec}$
is the set of monomials
together with
![]() $[0]$
serving as the monoidal unit.
$[0]$
serving as the monoidal unit.
The morphisms of
![]() $\mathsf {Nec}$
are generated through the monoidal structure by the following four types of morphisms for all
$\mathsf {Nec}$
are generated through the monoidal structure by the following four types of morphisms for all
![]() $n \in \mathbb {N}_{>0}$
$n \in \mathbb {N}_{>0}$
-
1.
 $\partial ^j \colon [n-1] \to [n]$
for
$\partial ^j \colon [n-1] \to [n]$
for
 $j = 1, \dots , n-1$
,
$j = 1, \dots , n-1$
, -
2.
 $\Delta _{[j], [n-j]} \colon [j] \vee [n-j] \to [n]$
for
$\Delta _{[j], [n-j]} \colon [j] \vee [n-j] \to [n]$
for
 $j = 1, \dots , n-1$
,
$j = 1, \dots , n-1$
, -
3.
 $\xi ^j \colon [n+1] \to [n]$
for
$\xi ^j \colon [n+1] \to [n]$
for
 $j = 0, \dots , n$
and
$j = 0, \dots , n$
and
 $n>0$
and
$n>0$
and -
4.
 $\xi ^0 \colon [1] \to [0]$
.
$\xi ^0 \colon [1] \to [0]$
.
We may identify
![]() $\mathsf {Nec}$
with a full subcategory of the category of double pointed simplicial sets
$\mathsf {Nec}$
with a full subcategory of the category of double pointed simplicial sets
![]() $\mathsf {sSet}_{*,*}$
as follows. Consider the functor
$\mathsf {sSet}_{*,*}$
as follows. Consider the functor
induced by sending any necklace
![]() $T = [n_1] \vee \dots \vee [n_k]$
to the simplicial set
$T = [n_1] \vee \dots \vee [n_k]$
to the simplicial set
where the wedge symbol now means we identify the last vertex of
![]() $\triangle ^{n_i}$
with the first vertex of
$\triangle ^{n_i}$
with the first vertex of
![]() $\triangle ^{n_{i+1}}$
for
$\triangle ^{n_{i+1}}$
for
![]() $i = 1, \dots , k-1$
and the two base points are given by the first vertex of
$i = 1, \dots , k-1$
and the two base points are given by the first vertex of
![]() $\triangle ^{n_1}$
and the last vertex of
$\triangle ^{n_1}$
and the last vertex of
![]() $\triangle ^{n_k}$
. Then
$\triangle ^{n_k}$
. Then
![]() $\mathcal {S}$
is a fully faithful functor, so
$\mathcal {S}$
is a fully faithful functor, so
![]() $\mathsf {Nec}$
may be identified with the full subcategory of
$\mathsf {Nec}$
may be identified with the full subcategory of
![]() $\mathsf {sSet}_{*,*}$
having as objects those double pointed simplicial sets of the form
$\mathsf {sSet}_{*,*}$
having as objects those double pointed simplicial sets of the form
![]() $\triangle ^{n_1} \vee \dots \vee \triangle ^{n_k}$
. The dimension of a necklace
$\triangle ^{n_1} \vee \dots \vee \triangle ^{n_k}$
. The dimension of a necklace
![]() $T = [n_1] \vee \dots \vee [n_k]$
is defined by
$T = [n_1] \vee \dots \vee [n_k]$
is defined by
![]() $\dim (T) = n_1 + \dots + n_k-k$
. Note there is a canonical homeomorphism
$\dim (T) = n_1 + \dots + n_k-k$
. Note there is a canonical homeomorphism
The category of necklical sets
![]() $\mathsf {Fun}(\mathsf {Nec}^{\mathrm {op}}, \mathsf {Set})$
becomes a (nonsymmetric) monoidal category with monoidal structure induced from
$\mathsf {Fun}(\mathsf {Nec}^{\mathrm {op}}, \mathsf {Set})$
becomes a (nonsymmetric) monoidal category with monoidal structure induced from
![]() $(\mathsf {Nec}, \vee )$
. We denote the monoidal category of necklical sets by
$(\mathsf {Nec}, \vee )$
. We denote the monoidal category of necklical sets by
![]() $\mathsf {nSet}$
.
$\mathsf {nSet}$
.
Remark. The category of necklaces was introduced in [Reference Dugger and Spivak9] to give an explicit description of the homotopy coherent nerve functor and its left adjoint.
3.6. From necklaces to cubes
In §3.4, we described an explicit way of decomposing a topological necklace
![]() $\mathbb {\Delta }^{n_1} \vee \cdots \vee \mathbb {\Delta }^{n_k}$
into a family of paths connecting the first and last vertices parameterized by an
$\mathbb {\Delta }^{n_1} \vee \cdots \vee \mathbb {\Delta }^{n_k}$
into a family of paths connecting the first and last vertices parameterized by an
![]() $(n_1 + \cdots + n_k-k)$
-dimensional cube. This construction satisfies conditions (1), (2) and (3) in §3.3. In particular, conditions (2) and (3) may be interpreted as saying that each face in the codimension
$(n_1 + \cdots + n_k-k)$
-dimensional cube. This construction satisfies conditions (1), (2) and (3) in §3.3. In particular, conditions (2) and (3) may be interpreted as saying that each face in the codimension
![]() $1$
boundary of such a cube of paths is in one-to-one correspondence with codimension
$1$
boundary of such a cube of paths is in one-to-one correspondence with codimension
![]() $1$
‘subnecklaces’ inside
$1$
‘subnecklaces’ inside
![]() $\mathbb {\Delta }^{n_1} \vee \cdots \vee \mathbb {\Delta }^{n_k}$
connecting the first and last vertices. Furthermore, subnecklaces in
$\mathbb {\Delta }^{n_1} \vee \cdots \vee \mathbb {\Delta }^{n_k}$
connecting the first and last vertices. Furthermore, subnecklaces in
![]() $\mathbb {\Delta }^{n_1} \vee \cdots \vee \mathbb {\Delta }^{n_k}$
are in one-to-one correspondence with the poset
$\mathbb {\Delta }^{n_1} \vee \cdots \vee \mathbb {\Delta }^{n_k}$
are in one-to-one correspondence with the poset
ordered by inclusion, which has a canonical cubical structure. We build upon this observation to describe a functorial relation between necklaces and cubes. This will be used to explain how Adams’ map is induced by a deeper categorical construction.
We begin by defining a monoidal functor
as follows. First, define
![]() $\mathcal {P}[0] = 2^0$
. On any other necklace
$\mathcal {P}[0] = 2^0$
. On any other necklace
![]() $T \in \mathsf {Nec}$
, define
$T \in \mathsf {Nec}$
, define
![]() $\mathcal {P}(T) = 2^{\dim (T)}$
. In order to define
$\mathcal {P}(T) = 2^{\dim (T)}$
. In order to define
![]() $\mathcal {P}$
on morphisms, it is sufficient to consider the following cases.
$\mathcal {P}$
on morphisms, it is sufficient to consider the following cases.
-
1. For any coface map
 $\partial ^j \colon [n] \to [n+1]$
such that
$\partial ^j \colon [n] \to [n+1]$
such that
 $0< j<{n+1}$
, define
$0< j<{n+1}$
, define
 $\mathcal {P}(\partial ^j) \colon 2^{n-1}\to 2^{n}$
to be the cubical coface functor
$\mathcal {P}(\partial ^j) \colon 2^{n-1}\to 2^{n}$
to be the cubical coface functor
 $\mathcal {P}(f)= \delta _0^{j}$
.
$\mathcal {P}(f)= \delta _0^{j}$
. -
2. For any
 $\Delta _{[j], [n+1-j]} \colon [j] \vee [n+1-j] \to [n+1]$
such that
$\Delta _{[j], [n+1-j]} \colon [j] \vee [n+1-j] \to [n+1]$
such that
 $0<j<n+1$
, define to be the cubical coface functor
$0<j<n+1$
, define to be the cubical coface functor $$\begin{align*}\mathcal{P}(\Delta_{[j], [n+1-j]}) \colon 2^{n-1}\to 2^{n} \end{align*}$$
$$\begin{align*}\mathcal{P}(\Delta_{[j], [n+1-j]}) \colon 2^{n-1}\to 2^{n} \end{align*}$$
 $\mathcal {P}(f)=\delta _1^{j}$
.
$\mathcal {P}(f)=\delta _1^{j}$
.
-
3. We now consider codegeneracy maps of the form
 $\xi ^j \colon [n+1] \to [n]$
for
$\xi ^j \colon [n+1] \to [n]$
for
 $n>0$
. If
$n>0$
. If
 $j=0$
or
$j=0$
or
 $j=n$
, define
$j=n$
, define
 $\mathcal {P}(f) \colon 2^n \to 2^{n-1}$
to be the cubical codegeneracy functor
$\mathcal {P}(f) \colon 2^n \to 2^{n-1}$
to be the cubical codegeneracy functor
 $\mathcal {P}(s^j)= \varepsilon ^{j}$
. If
$\mathcal {P}(s^j)= \varepsilon ^{j}$
. If
 $0<j<n$
, define
$0<j<n$
, define
 $\mathcal {P}(s^j) \colon 2^n \to 2^{n-1}$
to be the cubical coconnection functor
$\mathcal {P}(s^j) \colon 2^n \to 2^{n-1}$
to be the cubical coconnection functor
 $\gamma ^{j}$
.
$\gamma ^{j}$
. -
4. For
 $\xi ^0 \colon [1] \to [0]$
define
$\xi ^0 \colon [1] \to [0]$
define
 $\mathcal {P}(\xi ^0) \colon 2^0 \to 2^0$
to be the identity functor.
$\mathcal {P}(\xi ^0) \colon 2^0 \to 2^0$
to be the identity functor.
Remark. The functor
![]() $\mathcal {P}$
is neither faithful or full. However, for any necklace
$\mathcal {P}$
is neither faithful or full. However, for any necklace
![]() $T' \in \mathsf {Nec}$
with
$T' \in \mathsf {Nec}$
with
![]() $\dim (T')=n+1$
and any cubical coface functor
$\dim (T')=n+1$
and any cubical coface functor
![]() $\delta _{\epsilon }^j \colon 2^n \to 2^{n+1}$
for
$\delta _{\epsilon }^j \colon 2^n \to 2^{n+1}$
for
![]() $0 \leq j \leq n+1$
, there exists an map
$0 \leq j \leq n+1$
, there exists an map
![]() $f \colon T \hookrightarrow T'$
, where
$f \colon T \hookrightarrow T'$
, where
![]() $T \in \mathsf {Nec}$
with
$T \in \mathsf {Nec}$
with
![]() $\dim (T)=n$
such that
$\dim (T)=n$
such that
![]() $\mathcal {S}(f) \colon \mathcal {S}(T) \hookrightarrow \mathcal {S}(T')$
is an injective morphism in
$\mathcal {S}(f) \colon \mathcal {S}(T) \hookrightarrow \mathcal {S}(T')$
is an injective morphism in
![]() $\mathsf {Nec}$
and
$\mathsf {Nec}$
and
![]() $\mathcal {P}(f) = \delta _{\epsilon }^j$
.
$\mathcal {P}(f) = \delta _{\epsilon }^j$
.
The functor
![]() $\mathcal {P} \colon \mathsf {Nec} \to \square $
induces an adjunction between
$\mathcal {P} \colon \mathsf {Nec} \to \square $
induces an adjunction between
![]() $\mathsf {cSet}$
and
$\mathsf {cSet}$
and
![]() $\mathsf {nSet}$
with right and left adjoint functors given, respectively, by
$\mathsf {nSet}$
with right and left adjoint functors given, respectively, by
Explicitly, for a cubical set
![]() $Y \colon \square ^{\mathrm {op}} \to \mathsf {Set}$
,
$Y \colon \square ^{\mathrm {op}} \to \mathsf {Set}$
,
and for a necklical set
![]() $K \colon \mathsf {Nec}^{\mathrm {op}} \to \mathsf {Set}$
,
$K \colon \mathsf {Nec}^{\mathrm {op}} \to \mathsf {Set}$
,
where
![]() $\operatorname {\mathcal {Y}} \colon \mathsf {Nec} \to \mathsf {nSet}$
is the Yoneda embedding. Since
$\operatorname {\mathcal {Y}} \colon \mathsf {Nec} \to \mathsf {nSet}$
is the Yoneda embedding. Since
![]() $\mathcal {P}$
is a monoidal functor,
$\mathcal {P}$
is a monoidal functor,
![]() $\mathcal {P}_{!} \colon \mathsf {nSet} \to \mathsf {cSet}$
is monoidal as well.
$\mathcal {P}_{!} \colon \mathsf {nSet} \to \mathsf {cSet}$
is monoidal as well.
3.7. Cubical cobar construction
Using the framework of necklical sets, we may reinterpret Baues’ geometric cobar construction [Reference Baues3] as a functor
which we now define.
For any reduced simplicial set X, we define a necklical set
![]() ${\mathbb {\Omega }^{\mathrm {nec}}}(X) \colon \mathsf {Nec}^{\mathrm {op}} \to \mathsf {Set}$
having as necklical cells all necklaces inside X; namely,
${\mathbb {\Omega }^{\mathrm {nec}}}(X) \colon \mathsf {Nec}^{\mathrm {op}} \to \mathsf {Set}$
having as necklical cells all necklaces inside X; namely,
The monoidal structure
![]() $\vee \colon \mathsf {Nec} \times \mathsf {Nec} \to \mathsf {Nec}$
given by concatenation of necklaces induces a natural product
$\vee \colon \mathsf {Nec} \times \mathsf {Nec} \to \mathsf {Nec}$
given by concatenation of necklaces induces a natural product
making
![]() ${\mathbb {\Omega }^{\mathrm {nec}}}(X)$
into a monoid in
${\mathbb {\Omega }^{\mathrm {nec}}}(X)$
into a monoid in
![]() $\mathsf {nSet}$
.
$\mathsf {nSet}$
.
We may now define the cubical cobar construction
as the composition
Since
![]() $\mathcal {P}_!$
is monoidal,
$\mathcal {P}_!$
is monoidal,
![]() $\operatorname {\mathbb {\Omega }}(X)$
is a monoid in
$\operatorname {\mathbb {\Omega }}(X)$
is a monoid in
![]() $\mathsf {cSet}$
.
$\mathsf {cSet}$
.
Remark 3.2. This reinterpretation of Baues’ construction in terms of cubical sets was also studied in [Reference Rivera and Zeinalian31]. In this reference, it is also proven that the composition of functor
![]() $\mathcal {T} \circ \operatorname {\mathbb {\Omega }}$
, where
$\mathcal {T} \circ \operatorname {\mathbb {\Omega }}$
, where
![]() $\mathcal {T} \colon \mathsf {Mon}_{\mathsf {cSet}} \to \mathsf {Mon}_{\mathsf {sSet}}$
is the triangulation functor, coincides with the left adjoint of the homotopy coherent nerve functor restricted to
$\mathcal {T} \colon \mathsf {Mon}_{\mathsf {cSet}} \to \mathsf {Mon}_{\mathsf {sSet}}$
is the triangulation functor, coincides with the left adjoint of the homotopy coherent nerve functor restricted to
![]() $\mathsf {sSet}^0.$
$\mathsf {sSet}^0.$
3.8. Relation to the cobar construction
We now relate the cubical cobar functor
![]() $\operatorname {\mathbb {\Omega }} \colon \mathsf {sSet}^0 \to \mathsf {Mon}_{\mathsf {cSet}}$
to the cobar construction
$\operatorname {\mathbb {\Omega }} \colon \mathsf {sSet}^0 \to \mathsf {Mon}_{\mathsf {cSet}}$
to the cobar construction
![]() $\operatorname {\mathbf {\Omega }} \colon \mathsf {coAlg}^\ast \to \mathsf {Mon}_{\mathsf {Ch}}$
(§3.2).
$\operatorname {\mathbf {\Omega }} \colon \mathsf {coAlg}^\ast \to \mathsf {Mon}_{\mathsf {Ch}}$
(§3.2).
Theorem 3.3. There is a natural isomorphisms of functors
Proof. Denote by
![]() $\iota _n \in (\square ^n)_n$
the top dimensional nondegenerate element of the standard n-cube
$\iota _n \in (\square ^n)_n$
the top dimensional nondegenerate element of the standard n-cube
![]() $\square ^n$
. Note that for a reduced simplicial set X, we may represent any nondegenerate n-cube
$\square ^n$
. Note that for a reduced simplicial set X, we may represent any nondegenerate n-cube
![]() $\alpha \in (\mathcal {P}_!({\mathbb {\Omega }^{\mathrm {nec}}}(X)))_n$
as a pair
$\alpha \in (\mathcal {P}_!({\mathbb {\Omega }^{\mathrm {nec}}}(X)))_n$
as a pair
![]() $\alpha = [\sigma \colon \operatorname {\mathcal {Y}}(T) \to X, \iota _n]$
for some
$\alpha = [\sigma \colon \operatorname {\mathcal {Y}}(T) \to X, \iota _n]$
for some
![]() $T = [n_1] \vee \dots \vee [n_k] \in \mathsf {Nec}$
with
$T = [n_1] \vee \dots \vee [n_k] \in \mathsf {Nec}$
with
![]() $\dim (T) = n_1 + \dots + n_k - k = n$
.
$\dim (T) = n_1 + \dots + n_k - k = n$
.
To define a monoidal chain map
it suffices to define it on any generator of the form
![]() $\alpha =[\sigma \colon \triangle ^{n+1} \to X, \iota _{n}]$
, that is, when T is of the form
$\alpha =[\sigma \colon \triangle ^{n+1} \to X, \iota _{n}]$
, that is, when T is of the form
![]() $T = [n+1]$
, for some
$T = [n+1]$
, for some
![]() $n \geq 0$
. If
$n \geq 0$
. If
![]() $n = 0$
, let
$n = 0$
, let
![]() $\varphi _X(\alpha )= [\overline {\sigma }] + 1_\Bbbk $
, where
$\varphi _X(\alpha )= [\overline {\sigma }] + 1_\Bbbk $
, where ![]() denotes the (length
denotes the (length
![]() $1$
) generator in the cobar construction of
$1$
) generator in the cobar construction of
![]() $\operatorname {N^{\triangle }}(X)$
determined by
$\operatorname {N^{\triangle }}(X)$
determined by
![]() $\sigma \in X_{n+1}$
and
$\sigma \in X_{n+1}$
and
![]() $1_\Bbbk $
denotes the unit of the underlying ring
$1_\Bbbk $
denotes the unit of the underlying ring
![]() $\Bbbk $
. If
$\Bbbk $
. If
![]() $n> 0$
, we let
$n> 0$
, we let
![]() $\varphi _X(\alpha )=[\overline {\sigma }]$
. A straightforward computation yields that this gives rise to a well-defined isomorphism of algebras, which is compatible with the differentials, and natural with respect to maps of simplicial sets.
$\varphi _X(\alpha )=[\overline {\sigma }]$
. A straightforward computation yields that this gives rise to a well-defined isomorphism of algebras, which is compatible with the differentials, and natural with respect to maps of simplicial sets.
A similar result to Theorem 3.3 was observed in the case of
![]() $1$
-reduced simplicial sets in [5, Section 3.5].
$1$
-reduced simplicial sets in [5, Section 3.5].
3.9. Factorization of Adams’s map
Adams’s comparison map can be factored as a composition
The first map is the monoidal isomorphism induced by Theorem 3.3. The second map is given by applying chains
![]() $\operatorname {N^{\square }} \colon \mathsf {Mon}_{\mathsf {cSet}} \to \mathsf {Mon}_{\mathsf {Ch}}$
to the map of monoidal cubical sets
$\operatorname {N^{\square }} \colon \mathsf {Mon}_{\mathsf {cSet}} \to \mathsf {Mon}_{\mathsf {Ch}}$
to the map of monoidal cubical sets
determined through the monoid structure by sending an n-simplex
![]() $(\sigma \colon \mathbb {\Delta }^n \to \mathfrak {X})$
to the singular
$(\sigma \colon \mathbb {\Delta }^n \to \mathfrak {X})$
to the singular
![]() $(n-1)$
-cube
$(n-1)$
-cube
where the maps
![]() $\theta _n \colon \mathbb {I}^{n-1} \to P(\mathbb {\Delta }^n;0,n)$
are discussed in §3.3.
$\theta _n \colon \mathbb {I}^{n-1} \to P(\mathbb {\Delta }^n;0,n)$
are discussed in §3.3.
3.10. A monoidal coalgebra structure on the cobar construction
We follow [Reference Baues4] to construct a coalgebra structure on
![]() $\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
, compatible with both the differential and monoid structure, such that Adams’s map becomes a map of monoids in the category of coalgebras.
$\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
, compatible with both the differential and monoid structure, such that Adams’s map becomes a map of monoids in the category of coalgebras.
Recall the Serre coalgebra lift
![]() $\operatorname {N^{\square }_{\!{\mathcal {A}\mathsf {s}}}} \colon \mathsf {cSet} \to \mathsf {coAlg}$
of
$\operatorname {N^{\square }_{\!{\mathcal {A}\mathsf {s}}}} \colon \mathsf {cSet} \to \mathsf {coAlg}$
of
![]() $\operatorname {N^{\square }} \colon \mathsf {cSet} \to \mathsf {Ch}$
, the unique monoidal functor defined by the coalgebra structure on
$\operatorname {N^{\square }} \colon \mathsf {cSet} \to \mathsf {Ch}$
, the unique monoidal functor defined by the coalgebra structure on
![]() $\operatorname {\mathrm {N}}(\square ^1)$
. Since
$\operatorname {\mathrm {N}}(\square ^1)$
. Since
![]() $\operatorname {N^{\square }_{\!{\mathcal {A}\mathsf {s}}}}$
is monoidal and
$\operatorname {N^{\square }_{\!{\mathcal {A}\mathsf {s}}}}$
is monoidal and
![]() $\operatorname {\mathbb {\Omega }}(\operatorname {Sing^{\triangle }}(\mathfrak {X},x))$
is a monoid,
$\operatorname {\mathbb {\Omega }}(\operatorname {Sing^{\triangle }}(\mathfrak {X},x))$
is a monoid,
![]() $\operatorname {N^{\square }_{\!{\mathcal {A}\mathsf {s}}}}(\operatorname {\mathbb {\Omega }}(\operatorname {Sing^{\triangle }}(\mathfrak {X},x)))$
is a monoid in
$\operatorname {N^{\square }_{\!{\mathcal {A}\mathsf {s}}}}(\operatorname {\mathbb {\Omega }}(\operatorname {Sing^{\triangle }}(\mathfrak {X},x)))$
is a monoid in
![]() $\mathsf {coAlg}$
. Similarly, the lift
$\mathsf {coAlg}$
. Similarly, the lift
![]() $\operatorname {N^{\square }_{\!{\mathcal {A}\mathsf {s}}}}$
equips
$\operatorname {N^{\square }_{\!{\mathcal {A}\mathsf {s}}}}$
equips
![]() $\operatorname {Sing^{\square }}({\Omega }_x \mathfrak {X})$
with a natural monoidal coalgebra structure as well. Consequently, the isomorphism in (3.3) endows
$\operatorname {Sing^{\square }}({\Omega }_x \mathfrak {X})$
with a natural monoidal coalgebra structure as well. Consequently, the isomorphism in (3.3) endows
![]() $\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
with a natural monoidal coalgebra structure making
$\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
with a natural monoidal coalgebra structure making
![]() $\theta _{\mathfrak {X}}$
into natural map of monoidal coalgebras.
$\theta _{\mathfrak {X}}$
into natural map of monoidal coalgebras.
4. Monoidal
 ${E_\infty }$
-structures
${E_\infty }$
-structures
In this section, we recall the model
![]() ${\operatorname {\mathrm {U}}(\mathcal {M})}$
of the
${\operatorname {\mathrm {U}}(\mathcal {M})}$
of the
![]() $E_\infty $
-operad, whose category of coalgebras we show to be monoidal. We use this structure to construct a monoidal functor
$E_\infty $
-operad, whose category of coalgebras we show to be monoidal. We use this structure to construct a monoidal functor
![]() $\operatorname {N^{\square }_{{\operatorname {\mathrm {U}}(\mathcal {M})}}} \colon \mathsf {cSet} \to \mathsf {coAlg}_{\operatorname {\mathrm {U}}(\mathcal {M})}$
extending the Serre coalgebra structure. This endows for any pointed topological space both
$\operatorname {N^{\square }_{{\operatorname {\mathrm {U}}(\mathcal {M})}}} \colon \mathsf {cSet} \to \mathsf {coAlg}_{\operatorname {\mathrm {U}}(\mathcal {M})}$
extending the Serre coalgebra structure. This endows for any pointed topological space both
![]() $\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
and
$\operatorname {\mathbf {\Omega }} \operatorname {S^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}(\mathfrak {X},x)$
and
![]() $\operatorname {S^{\square }_{\!{\mathcal {A}\mathsf {s}}}}({\Omega }_x \mathfrak {X})$
with the structure of a monoidal
$\operatorname {S^{\square }_{\!{\mathcal {A}\mathsf {s}}}}({\Omega }_x \mathfrak {X})$
with the structure of a monoidal
![]() $E_\infty $
-coalgebra which is preserved by Adams’ map.
$E_\infty $
-coalgebra which is preserved by Adams’ map.
4.1.
 ${E_\infty }$
-operads
${E_\infty }$
-operads
Recall that operads control algebraic structures with either one input and multiple outputs or vice versa. In this article, we work with dg operads, that is, operads in the monoidal category
![]() $(\mathsf {Ch}, \otimes , \mathbb{1})$
; we refer to [Reference Loday and Vallette22] for more details.
$(\mathsf {Ch}, \otimes , \mathbb{1})$
; we refer to [Reference Loday and Vallette22] for more details.
For example, coalgebras, as defined in §2.1, are controlled by the operad
![]() ${\mathcal {A}\mathsf {s}}$
generated by two elements in degree
${\mathcal {A}\mathsf {s}}$
generated by two elements in degree
![]() $0$
$0$
modulo the relations
Let
![]() $\sigma \in \mathbb {S}_2$
be the nonidentity transposition. The operad
$\sigma \in \mathbb {S}_2$
be the nonidentity transposition. The operad
![]() $\mathcal {C}{om}$
controlling cocommutative coalgebras is obtained by adding the relation
$\mathcal {C}{om}$
controlling cocommutative coalgebras is obtained by adding the relation
to this presentation. We are interested in compatibly resolving the (trivial) symmetric group actions on
![]() $\mathcal {C}{om}$
associated to the permutation of factors. An
$\mathcal {C}{om}$
associated to the permutation of factors. An
![]() $E_\infty $
-operad is an operad
$E_\infty $
-operad is an operad
![]() $\mathcal {O}$
quasi-isomorphic to
$\mathcal {O}$
quasi-isomorphic to
![]() $\mathcal {C}{om}$
for which the action of
$\mathcal {C}{om}$
for which the action of
![]() $\mathbb {S}_r$
on
$\mathbb {S}_r$
on
![]() $\mathcal {O}(r)$
is free for each
$\mathcal {O}(r)$
is free for each
![]() $r \in \mathbb {N}$
. An
$r \in \mathbb {N}$
. An
![]() $E_\infty $
-coalgebra structure on a chain complex C is an operad morphism
$E_\infty $
-coalgebra structure on a chain complex C is an operad morphism
4.2. A finitely presented
 ${E_\infty }$
-prop
${E_\infty }$
-prop
A prop is an object controlling algebraic structures with multiple inputs and outputs. We refer to [Reference Markl24] for a detailed exposition. We recall the following construction from [Reference Medina-Mardones27]. The prop
![]() $\mathcal {M}$
is generated by adding to the presentation of
$\mathcal {M}$
is generated by adding to the presentation of
![]() ${\mathcal {A}\mathsf {s}}$
a generator and a relation. More specifically, a generator in degree
${\mathcal {A}\mathsf {s}}$
a generator and a relation. More specifically, a generator in degree
![]() $1$
with boundary
$1$
with boundary
and the relation
The importance of this construction is that the operad
![]() ${\operatorname {\mathrm {U}}(\mathcal {M})} = \{\mathcal {M}(1,r)\}_{r\in \mathbb {N}}$
obtained by restriction of structure is an
${\operatorname {\mathrm {U}}(\mathcal {M})} = \{\mathcal {M}(1,r)\}_{r\in \mathbb {N}}$
obtained by restriction of structure is an
![]() $E_\infty $
-operad.
$E_\infty $
-operad.
4.3.
 ${\mathcal {M}}$
-bialgebras
${\mathcal {M}}$
-bialgebras
An
![]() $\mathcal {M}$
-bialgebra structure on C is a prop morphism
$\mathcal {M}$
-bialgebra structure on C is a prop morphism
More explicitly, is a coalgebra
![]() $(C, \Delta , \operatorname {\mathrm {\varepsilon }})$
together with a degree 1 product satisfying for any
$(C, \Delta , \operatorname {\mathrm {\varepsilon }})$
together with a degree 1 product satisfying for any
![]() $a,b \in C$
that:
$a,b \in C$
that:
The signs appearing in identity (4.2) are a result of the Koszul sign convention.
Any
![]() $\mathcal {M}$
-bialgebra structure induces an
$\mathcal {M}$
-bialgebra structure induces an
![]() $E_\infty $
-coalgebra structure. More explicitly, let
$E_\infty $
-coalgebra structure. More explicitly, let
![]() $(C, \Delta , \operatorname {\mathrm {\varepsilon }}, \ast )$
be an
$(C, \Delta , \operatorname {\mathrm {\varepsilon }}, \ast )$
be an
![]() $\mathcal {M}$
-bialgebra. The collection of all maps
$\mathcal {M}$
-bialgebra. The collection of all maps
![]() $\{C \to C^{\otimes r}\}_{r \in \mathbb {N}}$
generated by
$\{C \to C^{\otimes r}\}_{r \in \mathbb {N}}$
generated by
![]() $\Delta $
,
$\Delta $
,
![]() $\operatorname {\mathrm {\varepsilon }}$
and
$\operatorname {\mathrm {\varepsilon }}$
and
![]() $\ast $
makes C into an
$\ast $
makes C into an
![]() $E_\infty $
-coalgebra, specifically into an
$E_\infty $
-coalgebra, specifically into an
![]() ${\operatorname {\mathrm {U}}(\mathcal {M})}$
-coalgebra.
${\operatorname {\mathrm {U}}(\mathcal {M})}$
-coalgebra.
4.4.
 ${E_\infty }$
-structure on simplicial chains
${E_\infty }$
-structure on simplicial chains
We recall the construction of an
![]() $E_\infty $
-extension of the Alexander–Whitney coalgebra structure on simplicial chains introduced in [Reference Medina-Mardones27]. Let us start by considering the representable simplicial sets. The coalgebra
$E_\infty $
-extension of the Alexander–Whitney coalgebra structure on simplicial chains introduced in [Reference Medina-Mardones27]. Let us start by considering the representable simplicial sets. The coalgebra
![]() $\operatorname {\mathrm {N}}(\triangle ^n)$
can be made into a natural
$\operatorname {\mathrm {N}}(\triangle ^n)$
can be made into a natural
![]() $\mathcal {M}$
-bialgebra considering an algebraic version of the join product defined by
$\mathcal {M}$
-bialgebra considering an algebraic version of the join product defined by
 $$ \begin{align*} \left[v_0, \dots, v_p \right] \ast \left[v_{p+1}, \dots, v_q\right] = \begin{cases} (-1)^{p} \operatorname{\mathrm{sign}}(\pi) \left[v_{\pi(0)}, \dots, v_{\pi(q)}\right] & \text{ if } v_i \neq v_j \text{ for } i \neq j, \\ \hfil 0 & \text{ if not}, \end{cases} \end{align*} $$
$$ \begin{align*} \left[v_0, \dots, v_p \right] \ast \left[v_{p+1}, \dots, v_q\right] = \begin{cases} (-1)^{p} \operatorname{\mathrm{sign}}(\pi) \left[v_{\pi(0)}, \dots, v_{\pi(q)}\right] & \text{ if } v_i \neq v_j \text{ for } i \neq j, \\ \hfil 0 & \text{ if not}, \end{cases} \end{align*} $$
where
![]() $\pi $
is the permutation that orders the vertices. A Kan extension of the induced
$\pi $
is the permutation that orders the vertices. A Kan extension of the induced
![]() ${\operatorname {\mathrm {U}}(\mathcal {M})}$
-coalgebra structure on
${\operatorname {\mathrm {U}}(\mathcal {M})}$
-coalgebra structure on
![]() $\operatorname {\mathrm {N}}(\triangle ^n)$
defines a lift
$\operatorname {\mathrm {N}}(\triangle ^n)$
defines a lift
![]() $\operatorname {N^{\triangle }_{{\operatorname {\mathrm {U}}(\mathcal {M})}}}$
of the Alexander–Whitney coalgebra to the category of
$\operatorname {N^{\triangle }_{{\operatorname {\mathrm {U}}(\mathcal {M})}}}$
of the Alexander–Whitney coalgebra to the category of
![]() $E_\infty $
-coalgebras defined by
$E_\infty $
-coalgebras defined by
![]() ${\operatorname {\mathrm {U}}(\mathcal {M})}$
. That is to say, these functors fit in a commutative diagram
${\operatorname {\mathrm {U}}(\mathcal {M})}$
. That is to say, these functors fit in a commutative diagram

where the vertical arrow is the obvious forgetful functor.
We remark that this
![]() $E_\infty $
-structure generalizes those previously introduced in [Reference Berger and Fresse6,Reference McClure and Smith25] in the sense that any cooperation
$E_\infty $
-structure generalizes those previously introduced in [Reference Berger and Fresse6,Reference McClure and Smith25] in the sense that any cooperation
![]() $\operatorname {\mathrm {N}} \to \operatorname {\mathrm {N}}^{\otimes r}$
arising from the action of the Barratt-Eccles or surjection operad can be expressed as a cooperation arising from the action of
$\operatorname {\mathrm {N}} \to \operatorname {\mathrm {N}}^{\otimes r}$
arising from the action of the Barratt-Eccles or surjection operad can be expressed as a cooperation arising from the action of
![]() ${\operatorname {\mathrm {U}}(\mathcal {M})}$
.
${\operatorname {\mathrm {U}}(\mathcal {M})}$
.
4.5.
 ${E_\infty }$
-structure on cubical chains
${E_\infty }$
-structure on cubical chains
We recall the construction of an
![]() $E_\infty $
-extension of the Serre coalgebra structure on cubical chains introduced in [Reference Kaufmann and Medina-Mardones21]. Let us first consider representable cubical sets. The coalgebra structure on
$E_\infty $
-extension of the Serre coalgebra structure on cubical chains introduced in [Reference Kaufmann and Medina-Mardones21]. Let us first consider representable cubical sets. The coalgebra structure on
![]() $\operatorname {\mathrm {N}}(\square ^n)$
can be made into a natural
$\operatorname {\mathrm {N}}(\square ^n)$
can be made into a natural
![]() $\mathcal {M}$
-bialgebra considering a product defined using the following notation. For a basis element
$\mathcal {M}$
-bialgebra considering a product defined using the following notation. For a basis element
![]() $x = x_1 \otimes \dotsb \otimes x_n$
of
$x = x_1 \otimes \dotsb \otimes x_n$
of
![]() $\operatorname {\mathrm {N}}(\square ^n)$
and an integer
$\operatorname {\mathrm {N}}(\square ^n)$
and an integer
![]() $\ell \in \{1,\dots ,n\}$
, we write
$\ell \in \{1,\dots ,n\}$
, we write
with the convention
![]() $x_{<1} = x_{>n} = 1 \in \mathbb {Z}$
. Then, for two such basis elements x and y we set
$x_{<1} = x_{>n} = 1 \in \mathbb {Z}$
. Then, for two such basis elements x and y we set
 $$ \begin{align} (x_1 \otimes \dotsb \otimes x_n) \ast (y_1 \otimes \dotsb \otimes y_n) = \sum_{i=1}^n x_{<i}\, \epsilon(y_{<i}) \otimes (x_i \ast y_i) \otimes \epsilon(x_{>i}) \, y_{>i}, \end{align} $$
$$ \begin{align} (x_1 \otimes \dotsb \otimes x_n) \ast (y_1 \otimes \dotsb \otimes y_n) = \sum_{i=1}^n x_{<i}\, \epsilon(y_{<i}) \otimes (x_i \ast y_i) \otimes \epsilon(x_{>i}) \, y_{>i}, \end{align} $$
where the only nonzero values of
![]() $x_i \ast y_i$
are
$x_i \ast y_i$
are
A Kan extension of the induced
![]() ${\operatorname {\mathrm {U}}(\mathcal {M})}$
-coalgebra structure on
${\operatorname {\mathrm {U}}(\mathcal {M})}$
-coalgebra structure on
![]() $\operatorname {\mathrm {N}}(\square ^n)$
defines a lift
$\operatorname {\mathrm {N}}(\square ^n)$
defines a lift
![]() $\operatorname {N^{\square }_{{\operatorname {\mathrm {U}}(\mathcal {M})}}}$
of the Serre coalgebra structure to the category of
$\operatorname {N^{\square }_{{\operatorname {\mathrm {U}}(\mathcal {M})}}}$
of the Serre coalgebra structure to the category of
![]() $E_\infty $
-coalgebras defined by
$E_\infty $
-coalgebras defined by
![]() ${\operatorname {\mathrm {U}}(\mathcal {M})}$
. That is, a commutative diagram
${\operatorname {\mathrm {U}}(\mathcal {M})}$
. That is, a commutative diagram

Remark. The product defined above in Equation (4.3) differs from the one defined in [Reference Kaufmann and Medina-Mardones21] by the sign
![]() $(-1)^x$
. The convention used here is more natural as we will see in §4.7.
$(-1)^x$
. The convention used here is more natural as we will see in §4.7.
4.6. Monoidal structure
In this subsection, we describe an extension of the tensor product of coalgebras to
![]() $\mathcal {M}$
-bialgebras and
$\mathcal {M}$
-bialgebras and
![]() ${\operatorname {\mathrm {U}}(\mathcal {M})}$
-coalgebras.
${\operatorname {\mathrm {U}}(\mathcal {M})}$
-coalgebras.
Lemma 4.1. Let C and
![]() $C'$
be
$C'$
be
![]() $\mathcal {M}$
-bialgebras. The coalgebra
$\mathcal {M}$
-bialgebras. The coalgebra
![]() $C \otimes C'$
is a natural
$C \otimes C'$
is a natural
![]() $\mathcal {M}$
-bialgebra with
$\mathcal {M}$
-bialgebra with
for any
![]() $a,c \in C$
and
$a,c \in C$
and
![]() $b,d \in C'$
.
$b,d \in C'$
.
Proof. We verify identity (4.1) using that
![]() $\operatorname {\mathrm {\varepsilon }}(b \ast d) = \operatorname {\mathrm {\varepsilon }}(a \ast c) = 0$
,
$\operatorname {\mathrm {\varepsilon }}(b \ast d) = \operatorname {\mathrm {\varepsilon }}(a \ast c) = 0$
,
 $$ \begin{align*} \operatorname{\mathrm{\varepsilon}}\big((a \otimes b) \ast (c \otimes d)\big) =& \operatorname{\mathrm{\varepsilon}}\big(a \operatorname{\mathrm{\varepsilon}}(c) \otimes (b \ast d)\big) + \operatorname{\mathrm{\varepsilon}}\big((a \ast c) \otimes \operatorname{\mathrm{\varepsilon}}(b) d\big) \\ =& \operatorname{\mathrm{\varepsilon}}(a) \operatorname{\mathrm{\varepsilon}}(c) \otimes \operatorname{\mathrm{\varepsilon}}(b \ast d) + \operatorname{\mathrm{\varepsilon}}(a \ast c) \otimes \operatorname{\mathrm{\varepsilon}}(b) \operatorname{\mathrm{\varepsilon}}(d) \\ =& \ 0. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{\varepsilon}}\big((a \otimes b) \ast (c \otimes d)\big) =& \operatorname{\mathrm{\varepsilon}}\big(a \operatorname{\mathrm{\varepsilon}}(c) \otimes (b \ast d)\big) + \operatorname{\mathrm{\varepsilon}}\big((a \ast c) \otimes \operatorname{\mathrm{\varepsilon}}(b) d\big) \\ =& \operatorname{\mathrm{\varepsilon}}(a) \operatorname{\mathrm{\varepsilon}}(c) \otimes \operatorname{\mathrm{\varepsilon}}(b \ast d) + \operatorname{\mathrm{\varepsilon}}(a \ast c) \otimes \operatorname{\mathrm{\varepsilon}}(b) \operatorname{\mathrm{\varepsilon}}(d) \\ =& \ 0. \end{align*} $$
To verify identity (4.2), we need to show that
 $$ \begin{align} \operatorname{\mathrm{\partial}} \big((a \otimes b) \ast (c \otimes d)\big) & = \operatorname{\mathrm{\partial}} (a \otimes b) \ast (c \otimes d) - (-1)^{a+b} (a \otimes b) \ast \operatorname{\mathrm{\partial}} (c \otimes d) \nonumber\\ &\quad + \operatorname{\mathrm{\varepsilon}}(a \otimes b) (c \otimes b) - (-1)^{a+b} (a \otimes b) \operatorname{\mathrm{\varepsilon}}(c \otimes d). \end{align} $$
$$ \begin{align} \operatorname{\mathrm{\partial}} \big((a \otimes b) \ast (c \otimes d)\big) & = \operatorname{\mathrm{\partial}} (a \otimes b) \ast (c \otimes d) - (-1)^{a+b} (a \otimes b) \ast \operatorname{\mathrm{\partial}} (c \otimes d) \nonumber\\ &\quad + \operatorname{\mathrm{\varepsilon}}(a \otimes b) (c \otimes b) - (-1)^{a+b} (a \otimes b) \operatorname{\mathrm{\varepsilon}}(c \otimes d). \end{align} $$
Let us start computing the left-hand side of the above expression.
 $$ \begin{align*} \operatorname{\mathrm{\partial}}\big((a \otimes b) \ast (c \otimes d)\big) & = \operatorname{\mathrm{\partial}}\big(a \operatorname{\mathrm{\varepsilon}}(c) \otimes (b \ast d) + (a \ast c) \otimes \operatorname{\mathrm{\varepsilon}}(b) d\big) \\ & = \operatorname{\mathrm{\partial}} a \operatorname{\mathrm{\varepsilon}}(c) \otimes (b \ast d) \,+\, (-1)^{a} a \operatorname{\mathrm{\varepsilon}}(c) \otimes \operatorname{\mathrm{\partial}}(b \ast d) \\ &\quad + \operatorname{\mathrm{\partial}} (a \ast c) \otimes \operatorname{\mathrm{\varepsilon}}(b) d \,+\, (-1)^{a+c+1} (a \ast c) \otimes \operatorname{\mathrm{\varepsilon}}(b) \operatorname{\mathrm{\partial}} d. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{\partial}}\big((a \otimes b) \ast (c \otimes d)\big) & = \operatorname{\mathrm{\partial}}\big(a \operatorname{\mathrm{\varepsilon}}(c) \otimes (b \ast d) + (a \ast c) \otimes \operatorname{\mathrm{\varepsilon}}(b) d\big) \\ & = \operatorname{\mathrm{\partial}} a \operatorname{\mathrm{\varepsilon}}(c) \otimes (b \ast d) \,+\, (-1)^{a} a \operatorname{\mathrm{\varepsilon}}(c) \otimes \operatorname{\mathrm{\partial}}(b \ast d) \\ &\quad + \operatorname{\mathrm{\partial}} (a \ast c) \otimes \operatorname{\mathrm{\varepsilon}}(b) d \,+\, (-1)^{a+c+1} (a \ast c) \otimes \operatorname{\mathrm{\varepsilon}}(b) \operatorname{\mathrm{\partial}} d. \end{align*} $$
Using that C and
![]() $C'$
satisfy identity (4.2), we have that
$C'$
satisfy identity (4.2), we have that
 $$ \begin{align*} \operatorname{\mathrm{\partial}}\big((a \otimes b) \ast (c \otimes d)\big) & = \operatorname{\mathrm{\partial}} a \operatorname{\mathrm{\varepsilon}}(c) \otimes (b \ast d) \\ &\quad + (-1)^a a \operatorname{\mathrm{\varepsilon}}(c) \otimes \big(\operatorname{\mathrm{\partial}} b \ast d + (-1)^{b+1} b \ast \operatorname{\mathrm{\partial}} d + \operatorname{\mathrm{\varepsilon}}(b) d + (-1)^{b+1} b \operatorname{\mathrm{\varepsilon}}(d)\big) \\ &\quad + \big(\operatorname{\mathrm{\partial}} a \ast c + (-1)^{a+1} a \ast \operatorname{\mathrm{\partial}} c + \operatorname{\mathrm{\varepsilon}}(a) c + (-1)^{a+1} a \operatorname{\mathrm{\varepsilon}}(c)\big) \otimes \operatorname{\mathrm{\varepsilon}}(b) d \\ &\quad + (-1)^{a+c+1} (a \ast c) \otimes \operatorname{\mathrm{\varepsilon}}(b) \operatorname{\mathrm{\partial}} d. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{\partial}}\big((a \otimes b) \ast (c \otimes d)\big) & = \operatorname{\mathrm{\partial}} a \operatorname{\mathrm{\varepsilon}}(c) \otimes (b \ast d) \\ &\quad + (-1)^a a \operatorname{\mathrm{\varepsilon}}(c) \otimes \big(\operatorname{\mathrm{\partial}} b \ast d + (-1)^{b+1} b \ast \operatorname{\mathrm{\partial}} d + \operatorname{\mathrm{\varepsilon}}(b) d + (-1)^{b+1} b \operatorname{\mathrm{\varepsilon}}(d)\big) \\ &\quad + \big(\operatorname{\mathrm{\partial}} a \ast c + (-1)^{a+1} a \ast \operatorname{\mathrm{\partial}} c + \operatorname{\mathrm{\varepsilon}}(a) c + (-1)^{a+1} a \operatorname{\mathrm{\varepsilon}}(c)\big) \otimes \operatorname{\mathrm{\varepsilon}}(b) d \\ &\quad + (-1)^{a+c+1} (a \ast c) \otimes \operatorname{\mathrm{\varepsilon}}(b) \operatorname{\mathrm{\partial}} d. \end{align*} $$
Inspecting this expression, we label terms which sum to
![]() $\operatorname {\mathrm {\partial }}\big ((a \otimes b) \ast (c \otimes d)\big )$
:
$\operatorname {\mathrm {\partial }}\big ((a \otimes b) \ast (c \otimes d)\big )$
:

Additionally, since
the following labeled terms sum to
![]() $\operatorname {\mathrm {\partial }} (a \otimes b) \ast (c \otimes d)$
:
$\operatorname {\mathrm {\partial }} (a \otimes b) \ast (c \otimes d)$
:
Similarly, since
the following labeled terms sum to
![]() $(-1)^{a+b+1}(a \otimes b) \ast \operatorname {\mathrm {\partial }} (c \otimes d)$
:
$(-1)^{a+b+1}(a \otimes b) \ast \operatorname {\mathrm {\partial }} (c \otimes d)$
:
We have the following matching pairs of labeled summands.
(4.7)-(4.17) : (4.8)-(4.19) : (4.9)-(4.21) : (4.10)-(4.15) : (4.12)-(4.18) : (4.13)-(4.20) : (4.16)-(4.22).
Additionally, the sum of the unmatched terms (4.14) and (4.11) correspond to
which concludes the verification of both identity (4.6) and the lemma.
We now give a more conceptual description of the monoidal structure on
![]() $\mathsf {biAlg}_{\mathcal {M}}$
, which generalizes to
$\mathsf {biAlg}_{\mathcal {M}}$
, which generalizes to
![]() $\mathsf {coAlg}_{\operatorname {\mathrm {U}}(\mathcal {M})}$
. The prop
$\mathsf {coAlg}_{\operatorname {\mathrm {U}}(\mathcal {M})}$
. The prop
![]() $\mathcal {M}$
is obtained by applying the functor of cellular chains to a CW prop [Reference Medina-Mardones29]. These cells are in fact cubical, generated through compositions by the generators
$\mathcal {M}$
is obtained by applying the functor of cellular chains to a CW prop [Reference Medina-Mardones29]. These cells are in fact cubical, generated through compositions by the generators

The Serre diagonal defines a diagonal
![]() $\Delta _{\mathcal {M}}$
on
$\Delta _{\mathcal {M}}$
on
![]() $\mathcal {M}$
compatible with its prop structure. More specifically, for any basis element
$\mathcal {M}$
compatible with its prop structure. More specifically, for any basis element
![]() $\mu $
in
$\mu $
in
![]() $\mathcal {M}$
we have a chain map
$\mathcal {M}$
we have a chain map
![]() $\phi _\mu \colon \operatorname {\mathrm {N}}(\square ^n) \to \mathcal {M}$
with
$\phi _\mu \colon \operatorname {\mathrm {N}}(\square ^n) \to \mathcal {M}$
with
![]() $\phi _\mu (2^n) = \mu $
, and
$\phi _\mu (2^n) = \mu $
, and
![]() $\Delta _{\mathcal {M}}(\mu )$
is set to be
$\Delta _{\mathcal {M}}(\mu )$
is set to be
![]() $\phi _D^{\otimes 2} \circ \Delta (2^n)$
. Crucially,
$\phi _D^{\otimes 2} \circ \Delta (2^n)$
. Crucially,
![]() $\Delta _{\mathcal {M}}$
acts on the generators by
$\Delta _{\mathcal {M}}$
acts on the generators by

which recovers the statement of Lemma 4.1. The structure preserving diagonal on the prop
![]() $\mathcal {M}$
induces one on the operad
$\mathcal {M}$
induces one on the operad
![]() ${\operatorname {\mathrm {U}}(\mathcal {M})}$
and defines, as usual for so-called Hopf operads, a monoidal structure on
${\operatorname {\mathrm {U}}(\mathcal {M})}$
and defines, as usual for so-called Hopf operads, a monoidal structure on
![]() $\mathsf {coAlg}_{\operatorname {\mathrm {U}}(\mathcal {M})}$
.
$\mathsf {coAlg}_{\operatorname {\mathrm {U}}(\mathcal {M})}$
.
4.7. Revisiting the
 ${E_\infty }$
-coalgebra structure on cubical chains
${E_\infty }$
-coalgebra structure on cubical chains
We show that the monoidal structure on
![]() ${\operatorname {\mathrm {U}}(\mathcal {M})}$
-coalgebras recover the
${\operatorname {\mathrm {U}}(\mathcal {M})}$
-coalgebras recover the
![]() $E_\infty $
-structure on cubical chains defined in §4.5. In fact, we have the following stronger statement at the level of
$E_\infty $
-structure on cubical chains defined in §4.5. In fact, we have the following stronger statement at the level of
![]() $\mathcal {M}$
-bialgebras.
$\mathcal {M}$
-bialgebras.
Theorem 4.2. For any
![]() $n \in \mathbb {N}$
, the
$n \in \mathbb {N}$
, the
![]() $\mathcal {M}$
-bialgebra structure on
$\mathcal {M}$
-bialgebra structure on
![]() $\operatorname {\mathrm {N}}(\square ^n)$
agrees with the monoidal extension of the
$\operatorname {\mathrm {N}}(\square ^n)$
agrees with the monoidal extension of the
![]() $\mathcal {M}$
-bialgebra structure on
$\mathcal {M}$
-bialgebra structure on
![]() $\operatorname {\mathrm {N}}(\square ^1)$
.
$\operatorname {\mathrm {N}}(\square ^1)$
.
Proof. Since the coalgebra part agrees by definition, we focus on the product. We will proceed by induction with the base case holding trivially. Let
![]() $x = x_1 \otimes \dotsb \otimes x_n$
and
$x = x_1 \otimes \dotsb \otimes x_n$
and
![]() $y = y_1 \otimes \dotsb \otimes y_n$
be two elements in
$y = y_1 \otimes \dotsb \otimes y_n$
be two elements in
![]() $\operatorname {\mathrm {N}}(\square ^n)$
. The following straightforward computation verifies that
$\operatorname {\mathrm {N}}(\square ^n)$
. The following straightforward computation verifies that
![]() $x \ast y$
in
$x \ast y$
in
![]() $\operatorname {\mathrm {N}}(\square ^n)$
corresponds to
$\operatorname {\mathrm {N}}(\square ^n)$
corresponds to
![]() $(x_{<n} \otimes x_n) \ast (y_{<n} \otimes y_n)$
in
$(x_{<n} \otimes x_n) \ast (y_{<n} \otimes y_n)$
in
![]() $\operatorname {\mathrm {N}}(\square ^{n-1}) \otimes \operatorname {\mathrm {N}}(\square ^1)$
:
$\operatorname {\mathrm {N}}(\square ^{n-1}) \otimes \operatorname {\mathrm {N}}(\square ^1)$
:
 $$ \begin{align*} x \ast y &= \sum_{i=1}^n x_{<i}\, \epsilon(y_{<i}) \otimes x_i \ast y_i \otimes \epsilon(x_{>i}) \, y_{>i} \\ &= \sum_{i=1}^{n-1} x_{<i}\, \epsilon(y_{<i}) \otimes x_i \ast y_i \otimes \epsilon(x_{>i}) \, y_{>i} \ +\ x_{<n}\, \epsilon(y_{<n}) \otimes x_n \ast y_n \\ &= x_{<n} \ast y_{<n} \otimes \operatorname{\mathrm{\varepsilon}}(x_n)\, y_n \ +\ x_{<n}\, \epsilon(y_{<n}) \otimes x_n \ast y_n \\ &= (x_{<n} \otimes x_n) \ast (y_{<n} \otimes y_n), \end{align*} $$
$$ \begin{align*} x \ast y &= \sum_{i=1}^n x_{<i}\, \epsilon(y_{<i}) \otimes x_i \ast y_i \otimes \epsilon(x_{>i}) \, y_{>i} \\ &= \sum_{i=1}^{n-1} x_{<i}\, \epsilon(y_{<i}) \otimes x_i \ast y_i \otimes \epsilon(x_{>i}) \, y_{>i} \ +\ x_{<n}\, \epsilon(y_{<n}) \otimes x_n \ast y_n \\ &= x_{<n} \ast y_{<n} \otimes \operatorname{\mathrm{\varepsilon}}(x_n)\, y_n \ +\ x_{<n}\, \epsilon(y_{<n}) \otimes x_n \ast y_n \\ &= (x_{<n} \otimes x_n) \ast (y_{<n} \otimes y_n), \end{align*} $$
which concludes the proof.
4.8. A monoidal
 ${E_\infty }$
-coalgebra structure on the cobar construction
${E_\infty }$
-coalgebra structure on the cobar construction
Using Theorem 4.2 and the natural equivalence of functors
![]() $\operatorname {N^{\square }} \operatorname {\mathbb {\Omega }} \cong \operatorname {\mathbf {\Omega }} \operatorname {N^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}$
proven in Theorem 3.3, we can transfer a monoidal
$\operatorname {N^{\square }} \operatorname {\mathbb {\Omega }} \cong \operatorname {\mathbf {\Omega }} \operatorname {N^{\triangle }_{\!{\mathcal {A}\mathsf {s}}}}$
proven in Theorem 3.3, we can transfer a monoidal
![]() $E_\infty $
-structure to the Adams’ cobar construction of any reduced simplicial set, extending the monoidal coalgebra structure defined by Baues. This is summarized by the following diagram commuting up to isomorphisms:
$E_\infty $
-structure to the Adams’ cobar construction of any reduced simplicial set, extending the monoidal coalgebra structure defined by Baues. This is summarized by the following diagram commuting up to isomorphisms:

Furthermore, using the factorization of Adams’ map described in §3.9 and the naturality of our monoidal
![]() $E_\infty $
-structure, we conclude that for any pointed topological space
$E_\infty $
-structure, we conclude that for any pointed topological space
![]() $\mathfrak {X}$
,
$\mathfrak {X}$
,
is a monoidal quasi-isomorphism of
![]() $E_{\infty }$
-coalgebras, as announced in the introduction. x
$E_{\infty }$
-coalgebras, as announced in the introduction. x
Acknowledgements
We would like to thank Clemens Berger, Matthias Franz, Kathryn Hess, Ralph Kaufmann, Emilio Minichello, Viet-Cuong Pham, Dennis Sullivan and Mahmoud Zeinalian for insightful discussions related to this project.
Competing interest
The authors have no competing interest to declare.
Funding statement
Both authors are grateful for the support and excellent working conditions of the Max Planck Institute for Mathematics in Bonn and LAGA at Université Sorbonne Paris Nord. A.M. acknowledges support from Innosuisse grant 32875.1 IP-ICT-1 and ANR 20 CE40 0016 01 PROJET HighAGT. M.R. acknowledges support from NSF Grant DMS 210554 and the Karen EDGE Fellowship.