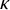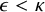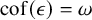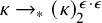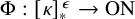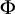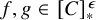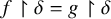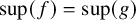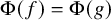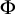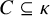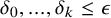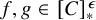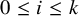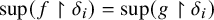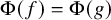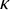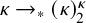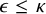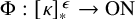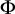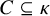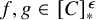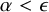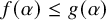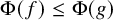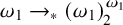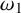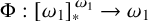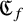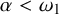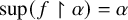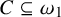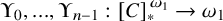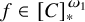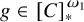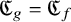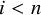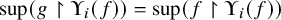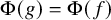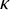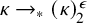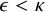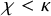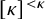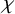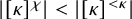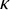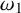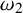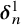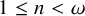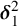1 Introduction
Partition relations appear frequently in combinatorics. Ramsey showed that the set of natural numbers,
![]() $\omega $
, satisfies the finite partition relations
$\omega $
, satisfies the finite partition relations
![]() $\omega \rightarrow (\omega )^k_2$
for each
$\omega \rightarrow (\omega )^k_2$
for each
![]() $k < \omega $
. The infinite exponent partition relation
$k < \omega $
. The infinite exponent partition relation
![]() $\omega \rightarrow (\omega )^\omega _2$
(also called the Ramsey property for all partitions) is a natural generalization which is not compatible with the axiom of choice. However, simply definable partitions such as Borel or analytic partitions always satisfy the Ramsey property by results of Galvin and Prikry [Reference Galvin and Prikry7] and Silver [Reference Silver17]. Mathias [Reference Mathias15] produced many important results concerning the Ramsey property including the technique of Mathias forcing which is used to verify
$\omega \rightarrow (\omega )^\omega _2$
(also called the Ramsey property for all partitions) is a natural generalization which is not compatible with the axiom of choice. However, simply definable partitions such as Borel or analytic partitions always satisfy the Ramsey property by results of Galvin and Prikry [Reference Galvin and Prikry7] and Silver [Reference Silver17]. Mathias [Reference Mathias15] produced many important results concerning the Ramsey property including the technique of Mathias forcing which is used to verify
![]() $\omega \rightarrow (\omega )^\omega _2$
in the Solovay model and Woodin’s extension
$\omega \rightarrow (\omega )^\omega _2$
in the Solovay model and Woodin’s extension
![]() $\mathsf {AD}^+$
of the axiom of determinacy,
$\mathsf {AD}^+$
of the axiom of determinacy,
![]() $\mathsf {AD}$
. Mathias also studied the Ramsey almost everywhere behavior of functions on the Ramsey space
$\mathsf {AD}$
. Mathias also studied the Ramsey almost everywhere behavior of functions on the Ramsey space
![]() $[\omega ]^\omega $
such as when every function
$[\omega ]^\omega $
such as when every function
![]() $\Phi : [\omega ]^\omega \rightarrow \mathbb {R}$
is Ramsey almost everywhere continuous or every relation
$\Phi : [\omega ]^\omega \rightarrow \mathbb {R}$
is Ramsey almost everywhere continuous or every relation
![]() $R \subseteq [\omega ]^\omega \times \mathbb {R}$
has a Ramsey almost everywhere uniformization. Recently, these two properties have been used by Schritteser and Törnquist [Reference Schrittesser and Törnquist16] to show that
$R \subseteq [\omega ]^\omega \times \mathbb {R}$
has a Ramsey almost everywhere uniformization. Recently, these two properties have been used by Schritteser and Törnquist [Reference Schrittesser and Törnquist16] to show that
![]() $\omega \rightarrow (\omega )^\omega _2$
implies there are no maximal almost disjoint families on
$\omega \rightarrow (\omega )^\omega _2$
implies there are no maximal almost disjoint families on
![]() $\omega $
. Finite exponent partition relations on uncountable cardinals are important in set theory and motivate large cardinal axioms such as the weakly compact and Ramsey cardinals. Martin, Kunen [Reference Solovay18], Jackson [Reference Jackson8], Kechris, Kleinberg, Moschovakis and Woodin [Reference Kechris, Kleinberg, Moschovakis and Hugh Woodin12] showed that the axiom of determinacy is a natural theory in which
$\omega $
. Finite exponent partition relations on uncountable cardinals are important in set theory and motivate large cardinal axioms such as the weakly compact and Ramsey cardinals. Martin, Kunen [Reference Solovay18], Jackson [Reference Jackson8], Kechris, Kleinberg, Moschovakis and Woodin [Reference Kechris, Kleinberg, Moschovakis and Hugh Woodin12] showed that the axiom of determinacy is a natural theory in which
![]() ${\omega _1}$
and many other cardinals
${\omega _1}$
and many other cardinals
![]() $\kappa $
possess even the strong partition relation:
$\kappa $
possess even the strong partition relation:
![]() $\kappa \rightarrow (\kappa )^\kappa _2$
. Kleinberg [Reference Kleinberg14], Martin and Paris studied functions on the finite partition spaces of
$\kappa \rightarrow (\kappa )^\kappa _2$
. Kleinberg [Reference Kleinberg14], Martin and Paris studied functions on the finite partition spaces of
![]() ${\omega _1}$
and produced ultrapower representations for
${\omega _1}$
and produced ultrapower representations for
![]() $\omega _n$
, showed
$\omega _n$
, showed
![]() $\omega _2$
has weak partition property and established combinatorial properties such as Jónssonness for
$\omega _2$
has weak partition property and established combinatorial properties such as Jónssonness for
![]() $\omega _n$
, for all
$\omega _n$
, for all
![]() $n \in \omega $
. Under the axiom of determinacy, the authors ([Reference Chan and Jackson4], [Reference Chan2], [Reference Chan, Jackson and Trang6] and [Reference Chan, Jackson and Trang5]) studied variations of almost everywhere continuity properties for functions on the partition spaces of
$n \in \omega $
. Under the axiom of determinacy, the authors ([Reference Chan and Jackson4], [Reference Chan2], [Reference Chan, Jackson and Trang6] and [Reference Chan, Jackson and Trang5]) studied variations of almost everywhere continuity properties for functions on the partition spaces of
![]() ${\omega _1}$
and
${\omega _1}$
and
![]() $\omega _2$
according to suitable partition measures and applied these results to distinguish the cardinalities below
$\omega _2$
according to suitable partition measures and applied these results to distinguish the cardinalities below
![]() ${\mathscr {P}({\omega _1})}$
and
${\mathscr {P}({\omega _1})}$
and
![]() ${\mathscr {P}(\omega _2)}$
. There,
${\mathscr {P}(\omega _2)}$
. There,
![]() $\mathsf {AD}$
provided useful motivation and elegant arguments, but the techniques have severe limitations. Here, the authors will prove stronger almost everywhere behaviors for functions on partition spaces (such as continuity and monotonicity) from pure combinatorial principles, and these results will be applied to distinguish important cardinalities below the power set of partition cardinals. This will lead to new results about the most important weak and strong partition cardinals of determinacy.
$\mathsf {AD}$
provided useful motivation and elegant arguments, but the techniques have severe limitations. Here, the authors will prove stronger almost everywhere behaviors for functions on partition spaces (such as continuity and monotonicity) from pure combinatorial principles, and these results will be applied to distinguish important cardinalities below the power set of partition cardinals. This will lead to new results about the most important weak and strong partition cardinals of determinacy.
A basic question of infinitary combinatorics is the computation of the size of infinite sets. Cantor formalized the notion of size and the comparison of sizes. Let X and Y be two sets. One says X and Y have the same cardinality (denoted
![]() $|X| = |Y|$
) if and only if there is a bijection
$|X| = |Y|$
) if and only if there is a bijection
![]() $\Phi : X \rightarrow Y$
. The cardinality of X is the (proper) class of sets Y which are in bijection with X. The cardinality of X is less than or equal the cardinality of Y (denoted
$\Phi : X \rightarrow Y$
. The cardinality of X is the (proper) class of sets Y which are in bijection with X. The cardinality of X is less than or equal the cardinality of Y (denoted
![]() $|X| \leq |Y|$
) if and only if there is an injection
$|X| \leq |Y|$
) if and only if there is an injection
![]() $\Phi : X \rightarrow Y$
. The cardinality of X is strictly smaller than the cardinality of Y (denoted
$\Phi : X \rightarrow Y$
. The cardinality of X is strictly smaller than the cardinality of Y (denoted
![]() $|X| < |Y|$
) if and only if
$|X| < |Y|$
) if and only if
![]() $|X| \leq |Y|$
but
$|X| \leq |Y|$
but
![]() $\neg (|Y| \leq |X|)$
.
$\neg (|Y| \leq |X|)$
.
The axiom of choice,
![]() $\mathsf {AC}$
, implies every set is wellorderable. Thus, the class of cardinalities forms a wellordered class under the injection relation. Each cardinality class has a canonical wellordered member (an ordinal) called the cardinal of the class. Wellorderings of sets (even
$\mathsf {AC}$
, implies every set is wellorderable. Thus, the class of cardinalities forms a wellordered class under the injection relation. Each cardinality class has a canonical wellordered member (an ordinal) called the cardinal of the class. Wellorderings of sets (even
![]() $\mathbb {R}$
) are incompatible with certain definability perspectives. This is usually the consequence of definable sets possessing combinatorial regularity properties.
$\mathbb {R}$
) are incompatible with certain definability perspectives. This is usually the consequence of definable sets possessing combinatorial regularity properties.
Let
![]() $\omega $
denote the set of natural numbers or the first infinite cardinal. Cantor showed that
$\omega $
denote the set of natural numbers or the first infinite cardinal. Cantor showed that
![]() $\omega $
does not surject onto
$\omega $
does not surject onto
![]() ${\mathscr {P}(\omega )}$
. Thus,
${\mathscr {P}(\omega )}$
. Thus,
![]() $\omega < |{\mathscr {P}(\omega )}|$
. Let
$\omega < |{\mathscr {P}(\omega )}|$
. Let
![]() ${\omega _1}$
denote the first uncountable cardinal. With the axiom of choice,
${\omega _1}$
denote the first uncountable cardinal. With the axiom of choice,
![]() ${\omega _1} \leq |{\mathscr {P}(\omega )}|$
using a wellordering of
${\omega _1} \leq |{\mathscr {P}(\omega )}|$
using a wellordering of
![]() ${\mathscr {P}(\omega )}$
or
${\mathscr {P}(\omega )}$
or
![]() $\mathbb {R}$
. However, if the axiom of choice is omitted and instead
$\mathbb {R}$
. However, if the axiom of choice is omitted and instead
![]() $\mathbb {R}$
is assumed to satisfy the perfect set property and the property of Baire, then a classical argument involving the Kuratowski–Ulam theorem would show that there is no injection of
$\mathbb {R}$
is assumed to satisfy the perfect set property and the property of Baire, then a classical argument involving the Kuratowski–Ulam theorem would show that there is no injection of
![]() ${\omega _1}$
into
${\omega _1}$
into
![]() $\mathbb {R}$
or
$\mathbb {R}$
or
![]() ${\mathscr {P}(\omega )}$
. Thus,
${\mathscr {P}(\omega )}$
. Thus,
![]() ${\omega _1}$
and
${\omega _1}$
and
![]() $|{\mathscr {P}(\omega )}| = |\mathbb {R}|$
are incompatible cardinalities. Moreover, the perfect set property completely characterizes the structure of the cardinalities below
$|{\mathscr {P}(\omega )}| = |\mathbb {R}|$
are incompatible cardinalities. Moreover, the perfect set property completely characterizes the structure of the cardinalities below
![]() $|{\mathscr {P}(\omega )}|$
in a manner which satisfies a choiceless continuum hypothesis: The only uncountable cardinality below
$|{\mathscr {P}(\omega )}|$
in a manner which satisfies a choiceless continuum hypothesis: The only uncountable cardinality below
![]() $|{\mathscr {P}(\omega )}|$
is
$|{\mathscr {P}(\omega )}|$
is
![]() $|{\mathscr {P}(\omega )}|$
.
$|{\mathscr {P}(\omega )}|$
.
With the perfect set property and the Baire property, the structure of the cardinalities below
![]() ${\mathscr {P}({\omega _1})}$
is nonlinear since
${\mathscr {P}({\omega _1})}$
is nonlinear since
![]() ${\omega _1}$
and
${\omega _1}$
and
![]() $|\mathbb {R}| = |{\mathscr {P}(\omega )}|$
are two incompatible cardinalities below
$|\mathbb {R}| = |{\mathscr {P}(\omega )}|$
are two incompatible cardinalities below
![]() $|{\mathscr {P}({\omega _1})}|$
. For each
$|{\mathscr {P}({\omega _1})}|$
. For each
![]() $\epsilon \leq {\omega _1}$
, let
$\epsilon \leq {\omega _1}$
, let
![]() $[{\omega _1}]^\epsilon $
be the increasing sequence space consisting of increasing functions
$[{\omega _1}]^\epsilon $
be the increasing sequence space consisting of increasing functions
![]() $f : \epsilon \rightarrow {\omega _1}$
.
$f : \epsilon \rightarrow {\omega _1}$
.
![]() ${\mathscr {P}({\omega _1})}$
and
${\mathscr {P}({\omega _1})}$
and
![]() $[{\omega _1}]^{\omega _1}$
are in bijection. Therefore, sequence spaces represent natural combinatorial cardinalities below
$[{\omega _1}]^{\omega _1}$
are in bijection. Therefore, sequence spaces represent natural combinatorial cardinalities below
![]() $|{\mathscr {P}({\omega _1})}| = |[{\omega _1}]^{\omega _1}|$
. Another important example is
$|{\mathscr {P}({\omega _1})}| = |[{\omega _1}]^{\omega _1}|$
. Another important example is
![]() $[{\omega _1}]^{<{\omega _1}} = \bigcup _{\epsilon < {\omega _1}} [{\omega _1}]^\epsilon _*$
, which is the set of countable length increasing sequences of countable ordinals. A natural question is to distinguish
$[{\omega _1}]^{<{\omega _1}} = \bigcup _{\epsilon < {\omega _1}} [{\omega _1}]^\epsilon _*$
, which is the set of countable length increasing sequences of countable ordinals. A natural question is to distinguish
![]() $|[{\omega _1}]^\omega |$
,
$|[{\omega _1}]^\omega |$
,
![]() $|[{\omega _1}]^{<{\omega _1}}|$
and
$|[{\omega _1}]^{<{\omega _1}}|$
and
![]() $|{\mathscr {P}({\omega _1})}| = |[{\omega _1}]^{\omega _1}|$
under suitable regularity properties. A helpful combinatorial property possessed by
$|{\mathscr {P}({\omega _1})}| = |[{\omega _1}]^{\omega _1}|$
under suitable regularity properties. A helpful combinatorial property possessed by
![]() ${\omega _1}$
(in some natural theories) is the strong partition property,
${\omega _1}$
(in some natural theories) is the strong partition property,
![]() ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
.
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
.
Partition properties will be discussed in detail in Section 2. Let
![]() $\kappa $
be a cardinal,
$\kappa $
be a cardinal,
![]() $\epsilon \leq \kappa $
and
$\epsilon \leq \kappa $
and
![]() $A \subseteq \kappa $
. Let
$A \subseteq \kappa $
. Let
![]() $[A]^\epsilon _*$
be the collection of increasing functions
$[A]^\epsilon _*$
be the collection of increasing functions
![]() $f : \epsilon \rightarrow A$
of the correct type (i.e., discontinuous everywhere and has uniform cofinality
$f : \epsilon \rightarrow A$
of the correct type (i.e., discontinuous everywhere and has uniform cofinality
![]() $\omega $
). The partition relation
$\omega $
). The partition relation
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _2$
is the assertion that for all
$\kappa \rightarrow _* (\kappa )^\epsilon _2$
is the assertion that for all
![]() $P : [\kappa ]^\epsilon _* \rightarrow 2$
, there is a closed and unbounded (club)
$P : [\kappa ]^\epsilon _* \rightarrow 2$
, there is a closed and unbounded (club)
![]() $C \subseteq {\omega _1}$
and
$C \subseteq {\omega _1}$
and
![]() $i \in 2$
so that for all
$i \in 2$
so that for all
![]() $f \in [C]^\epsilon _*$
,
$f \in [C]^\epsilon _*$
,
![]() $P(f) = i$
. If for all
$P(f) = i$
. If for all
![]() $\epsilon < \kappa $
,
$\epsilon < \kappa $
,
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _2$
holds, then
$\kappa \rightarrow _* (\kappa )^\epsilon _2$
holds, then
![]() $\kappa $
is called a weak partition cardinal. If
$\kappa $
is called a weak partition cardinal. If
![]() $\kappa \rightarrow _* (\kappa )^\kappa _2$
, then
$\kappa \rightarrow _* (\kappa )^\kappa _2$
, then
![]() $\kappa $
is called a strong partition cardinal. If
$\kappa $
is called a strong partition cardinal. If
![]() $\epsilon \leq \kappa $
and
$\epsilon \leq \kappa $
and
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _2$
holds, then the partition filter
$\kappa \rightarrow _* (\kappa )^\epsilon _2$
holds, then the partition filter
![]() $\mu ^\kappa _\epsilon $
on
$\mu ^\kappa _\epsilon $
on
![]() $[\kappa ]^\epsilon _*$
defined by
$[\kappa ]^\epsilon _*$
defined by
![]() $X \in \mu ^\kappa _\epsilon $
if and only if there is a club
$X \in \mu ^\kappa _\epsilon $
if and only if there is a club
![]() $C \subseteq \kappa $
so that
$C \subseteq \kappa $
so that
![]() $[C]^\epsilon _* \subseteq X$
is an ultrafilter.
$[C]^\epsilon _* \subseteq X$
is an ultrafilter.
If
![]() $\kappa $
satisfies suitable partition relations, then the partition spaces
$\kappa $
satisfies suitable partition relations, then the partition spaces
![]() $[\kappa ]^\epsilon _*$
for
$[\kappa ]^\epsilon _*$
for
![]() $\epsilon < \kappa $
,
$\epsilon < \kappa $
,
![]() $[\kappa ]^{<\kappa }_*$
and
$[\kappa ]^{<\kappa }_*$
and
![]() $[\kappa ]^\kappa _*$
represent important cardinalities below
$[\kappa ]^\kappa _*$
represent important cardinalities below
![]() ${\mathscr {P}(\kappa )}$
. Distinguishing the cardinality of these partition spaces involve understanding the possible injections that exist between these partition spaces. To answer such questions, this paper will use partition properties to obtain very deep understandings of the behavior of functions
${\mathscr {P}(\kappa )}$
. Distinguishing the cardinality of these partition spaces involve understanding the possible injections that exist between these partition spaces. To answer such questions, this paper will use partition properties to obtain very deep understandings of the behavior of functions
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
on measure one sets according to the relevant partition measure,
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
on measure one sets according to the relevant partition measure,
![]() $\mu ^\kappa _\epsilon $
. The following will summarize and motivate the main results of the paper concerning these almost everywhere behaviors of functions.
$\mu ^\kappa _\epsilon $
. The following will summarize and motivate the main results of the paper concerning these almost everywhere behaviors of functions.
In [Reference Chan2], it is shown that if
![]() $\kappa \rightarrow _* (\kappa )^\kappa _2$
, then every function
$\kappa \rightarrow _* (\kappa )^\kappa _2$
, then every function
![]() $\Lambda : [\kappa ]^\kappa _* \rightarrow \mathrm {ON}$
, there is an ordinal
$\Lambda : [\kappa ]^\kappa _* \rightarrow \mathrm {ON}$
, there is an ordinal
![]() $\alpha $
so that
$\alpha $
so that
![]() $\Lambda ^{-1}[\{\alpha \}]| = |[\kappa ]^\kappa _*|$
. This asserts that
$\Lambda ^{-1}[\{\alpha \}]| = |[\kappa ]^\kappa _*|$
. This asserts that
![]() $|[\kappa ]^\kappa _*| = |{\mathscr {P}(\kappa )}|$
satisfies a regularity property with respect to wellordered decompositions. The set
$|[\kappa ]^\kappa _*| = |{\mathscr {P}(\kappa )}|$
satisfies a regularity property with respect to wellordered decompositions. The set
![]() $[\kappa ]^{<\kappa }_*$
does not satisfy such regularity. This is used in [Reference Chan2] to show that
$[\kappa ]^{<\kappa }_*$
does not satisfy such regularity. This is used in [Reference Chan2] to show that
![]() $|[\kappa ]^{<\kappa }_*| < |[\kappa ]^\kappa _*|= |{\mathscr {P}(\kappa )}|$
. This paper is motivated by the question of distinguishing the cardinality of
$|[\kappa ]^{<\kappa }_*| < |[\kappa ]^\kappa _*|= |{\mathscr {P}(\kappa )}|$
. This paper is motivated by the question of distinguishing the cardinality of
![]() $[\kappa ]^\epsilon $
for
$[\kappa ]^\epsilon $
for
![]() $\epsilon < \kappa $
and
$\epsilon < \kappa $
and
![]() $[\kappa ]^{<\kappa }_*$
. For these computations, it will be important to understand functions
$[\kappa ]^{<\kappa }_*$
. For these computations, it will be important to understand functions
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \kappa $
through continuity properties.
$\Phi : [\kappa ]^\epsilon _* \rightarrow \kappa $
through continuity properties.
To motivate continuity, suppose
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
. Given
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
. Given
![]() $f \in [\kappa ]^\epsilon _*$
,
$f \in [\kappa ]^\epsilon _*$
,
![]() $\Phi $
can be considered as an abstract procedure which uses information about f to assign an ordinal value. Examples of such information include specific values of
$\Phi $
can be considered as an abstract procedure which uses information about f to assign an ordinal value. Examples of such information include specific values of
![]() $f(\alpha )$
for
$f(\alpha )$
for
![]() $\alpha < \epsilon $
, initial segments
$\alpha < \epsilon $
, initial segments
![]() $f \upharpoonright \alpha $
for
$f \upharpoonright \alpha $
for
![]() $\alpha < \epsilon $
or possibly the entirety of f or the values of f on some unbounded subsets of
$\alpha < \epsilon $
or possibly the entirety of f or the values of f on some unbounded subsets of
![]() $\epsilon $
. An almost everywhere continuity property intuitively asserts that for
$\epsilon $
. An almost everywhere continuity property intuitively asserts that for
![]() $\mu ^\kappa _\epsilon $
-almost all f,
$\mu ^\kappa _\epsilon $
-almost all f,
![]() $\Phi $
can assign an ordinal to f using only information from f which comes from a well-defined bounded subset of
$\Phi $
can assign an ordinal to f using only information from f which comes from a well-defined bounded subset of
![]() $\epsilon $
.
$\epsilon $
.
One appealing continuity property for a function
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \kappa $
(with
$\Phi : [\kappa ]^\epsilon _* \rightarrow \kappa $
(with
![]() $\epsilon < \kappa $
) would be that for
$\epsilon < \kappa $
) would be that for
![]() $\mu ^\kappa _\epsilon $
-almost all f, there exists a
$\mu ^\kappa _\epsilon $
-almost all f, there exists a
![]() $\delta < \epsilon $
so that
$\delta < \epsilon $
so that
![]() $\Phi (f)$
only depends on
$\Phi (f)$
only depends on
![]() $f \upharpoonright \delta $
. However, such a property is impossible by the following illustrative example. If
$f \upharpoonright \delta $
. However, such a property is impossible by the following illustrative example. If
![]() $\kappa $
satisfies
$\kappa $
satisfies
![]() $\kappa \rightarrow _* (\kappa )^2_2$
, then
$\kappa \rightarrow _* (\kappa )^2_2$
, then
![]() $\kappa $
is a regular cardinal. Thus, the function
$\kappa $
is a regular cardinal. Thus, the function
![]() $\Psi : [\kappa ]^\epsilon _* \rightarrow \kappa $
defined by
$\Psi : [\kappa ]^\epsilon _* \rightarrow \kappa $
defined by
![]() $\Psi (f) = \sup (f)$
is well defined and it depends on more than any initial segment. This suggests that perhaps a general function
$\Psi (f) = \sup (f)$
is well defined and it depends on more than any initial segment. This suggests that perhaps a general function
![]() $\Phi : [\kappa ]^\epsilon \rightarrow \kappa $
might have a fixed
$\Phi : [\kappa ]^\epsilon \rightarrow \kappa $
might have a fixed
![]() $\delta < \epsilon $
so that for
$\delta < \epsilon $
so that for
![]() $\mu ^\kappa _\epsilon $
-almost all f,
$\mu ^\kappa _\epsilon $
-almost all f,
![]() $\Phi (f)$
depends only on the initial segment
$\Phi (f)$
depends only on the initial segment
![]() $f \upharpoonright \delta $
and
$f \upharpoonright \delta $
and
![]() $\sup (f)$
. Under suitable partition properties, such a continuity will be true more generally for functions
$\sup (f)$
. Under suitable partition properties, such a continuity will be true more generally for functions
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
with
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
with
![]() ${\mathrm {cof}}(\epsilon ) = \omega $
(and this cofinality assumption is generally necessary).
${\mathrm {cof}}(\epsilon ) = \omega $
(and this cofinality assumption is generally necessary).
Fix
![]() $\epsilon < \kappa $
a limit ordinal with
$\epsilon < \kappa $
a limit ordinal with
![]() ${\mathrm {cof}}(\epsilon ) = \omega $
. Define an equivalence relation
${\mathrm {cof}}(\epsilon ) = \omega $
. Define an equivalence relation
![]() $E_0$
on
$E_0$
on
![]() $[\kappa ]^\epsilon $
by
$[\kappa ]^\epsilon $
by
![]() $f \ E_0 \ g$
if and only if there exists an
$f \ E_0 \ g$
if and only if there exists an
![]() $\alpha < \epsilon $
so that for all
$\alpha < \epsilon $
so that for all
![]() $\beta $
with
$\beta $
with
![]() $\alpha < \beta < \epsilon $
,
$\alpha < \beta < \epsilon $
,
![]() $f(\beta ) = g(\beta )$
. A function
$f(\beta ) = g(\beta )$
. A function
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
is
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
is
![]() $E_0$
-invariant if and only if whenever
$E_0$
-invariant if and only if whenever
![]() $f \ E_0 \ g$
,
$f \ E_0 \ g$
,
![]() $\Phi (f) = \Phi (g)$
. The first step is the following independently interesting result that functions which are
$\Phi (f) = \Phi (g)$
. The first step is the following independently interesting result that functions which are
![]() $E_0$
-invariant
$E_0$
-invariant
![]() $\mu ^\kappa _\epsilon $
-almost everywhere depend only on the supremum
$\mu ^\kappa _\epsilon $
-almost everywhere depend only on the supremum
![]() $\mu ^\kappa _\epsilon $
-almost everywhere under suitable partition relations.
$\mu ^\kappa _\epsilon $
-almost everywhere under suitable partition relations.
Theorem 3.6. Suppose
![]() $\kappa $
is a cardinal,
$\kappa $
is a cardinal,
![]() $\epsilon < \kappa $
is a limit ordinal with
$\epsilon < \kappa $
is a limit ordinal with
![]() ${\mathrm {cof}}(\epsilon ) = \omega $
and
${\mathrm {cof}}(\epsilon ) = \omega $
and
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon \cdot \epsilon }_2$
holds. Let
$\kappa \rightarrow _* (\kappa )^{\epsilon \cdot \epsilon }_2$
holds. Let
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
be a function which is
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
be a function which is
![]() $E_0$
-invariant
$E_0$
-invariant
![]() $\mu ^\kappa _\epsilon $
-almost everywhere. Then there is a club
$\mu ^\kappa _\epsilon $
-almost everywhere. Then there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if
$f,g \in [C]^\epsilon _*$
, if
![]() $\sup (f) = \sup (g)$
, then
$\sup (f) = \sup (g)$
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
Using this theorem, the desired almost everywhere short length continuity result is established.
Theorem 3.7. Suppose
![]() $\kappa $
is a cardinal,
$\kappa $
is a cardinal,
![]() $\epsilon < \kappa $
is a limit ordinal with
$\epsilon < \kappa $
is a limit ordinal with
![]() ${\mathrm {cof}}(\epsilon ) = \omega $
and
${\mathrm {cof}}(\epsilon ) = \omega $
and
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon \cdot \epsilon }_2$
holds. For any function
$\kappa \rightarrow _* (\kappa )^{\epsilon \cdot \epsilon }_2$
holds. For any function
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, there is a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, there is a club
![]() $C \subseteq \kappa $
and a
$C \subseteq \kappa $
and a
![]() $\delta < \epsilon $
so that for all
$\delta < \epsilon $
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if
$f,g \in [C]^\epsilon _*$
, if
![]() $f \upharpoonright \delta = g \upharpoonright \delta $
and
$f \upharpoonright \delta = g \upharpoonright \delta $
and
![]() $\sup (f) = \sup (g)$
, then
$\sup (f) = \sup (g)$
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
The almost everywhere short length continuity of Theorem 3.7 is used to show that if
![]() $\kappa $
is a weak partition cardinal, then for any
$\kappa $
is a weak partition cardinal, then for any
![]() $\chi < \kappa $
,
$\chi < \kappa $
,
![]() ${}^{<\kappa }\kappa $
does not inject into
${}^{<\kappa }\kappa $
does not inject into
![]() ${}^\chi \kappa $
or even
${}^\chi \kappa $
or even
![]() ${}^\chi \delta $
for any ordinal
${}^\chi \delta $
for any ordinal
![]() $\delta $
by providing a sufficiently complete analysis of potential injections.
$\delta $
by providing a sufficiently complete analysis of potential injections.
Theorem 4.4. Suppose
![]() $\kappa $
is a cardinal so that
$\kappa $
is a cardinal so that
![]() $\kappa \rightarrow _* (\kappa )^{<\kappa }_2$
. Then for all
$\kappa \rightarrow _* (\kappa )^{<\kappa }_2$
. Then for all
![]() $\chi < \kappa $
, there is no injection of
$\chi < \kappa $
, there is no injection of
![]() ${}^{<\kappa }\kappa $
into
${}^{<\kappa }\kappa $
into
![]() ${}^\chi \mathrm {ON}$
, the class of
${}^\chi \mathrm {ON}$
, the class of
![]() $\chi $
-length sequences of ordinals. In particular, for all
$\chi $
-length sequences of ordinals. In particular, for all
![]() $\chi < \kappa $
,
$\chi < \kappa $
,
![]() $|{}^\chi \kappa | < |{}^{<\kappa }\kappa |$
.
$|{}^\chi \kappa | < |{}^{<\kappa }\kappa |$
.
A stronger continuity notion would assert that a function
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
(with
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
(with
![]() $\epsilon < \kappa $
) has finitely many locations in
$\epsilon < \kappa $
) has finitely many locations in
![]() $\epsilon $
depending solely on
$\epsilon $
depending solely on
![]() $\Phi $
so that
$\Phi $
so that
![]() $\Phi (f)$
depends only on the behavior of f at these finitely many locations. (By the previous example, one of these locations must be allowed to be the supremum of f.) The next result states that if
$\Phi (f)$
depends only on the behavior of f at these finitely many locations. (By the previous example, one of these locations must be allowed to be the supremum of f.) The next result states that if
![]() $\epsilon $
is countable and
$\epsilon $
is countable and
![]() $\kappa $
satisfies a suitable partition relation, then
$\kappa $
satisfies a suitable partition relation, then
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
will satisfy a strong almost everywhere short length continuity.
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
will satisfy a strong almost everywhere short length continuity.
Theorem 3.9. Suppose
![]() $\kappa $
is a cardinal,
$\kappa $
is a cardinal,
![]() $\epsilon < \omega _1$
and
$\epsilon < \omega _1$
and
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon \cdot \epsilon }_2$
holds. Let
$\kappa \rightarrow _* (\kappa )^{\epsilon \cdot \epsilon }_2$
holds. Let
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
. Then there is a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
. Then there is a club
![]() $C \subseteq \kappa $
and finitely many ordinals
$C \subseteq \kappa $
and finitely many ordinals
![]() $\delta _0, ..., \delta _k \leq \epsilon $
so that for all
$\delta _0, ..., \delta _k \leq \epsilon $
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if for all
$f,g \in [C]^\epsilon _*$
, if for all
![]() $0 \leq i \leq k$
,
$0 \leq i \leq k$
,
![]() $\sup (f \upharpoonright \delta _i) = \sup (g \upharpoonright \delta _i)$
, then
$\sup (f \upharpoonright \delta _i) = \sup (g \upharpoonright \delta _i)$
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
Suppose
![]() $\epsilon \leq \kappa $
and
$\epsilon \leq \kappa $
and
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
. A natural question is that, if one increases the information stored in f by increasing the values of f, could the value of
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
. A natural question is that, if one increases the information stored in f by increasing the values of f, could the value of
![]() $\Phi $
possibly decrease? An almost everywhere monotonicity property for
$\Phi $
possibly decrease? An almost everywhere monotonicity property for
![]() $\Phi $
would assert that for
$\Phi $
would assert that for
![]() $\mu ^\kappa _\epsilon $
almost all
$\mu ^\kappa _\epsilon $
almost all
![]() $f,g \in [\kappa ]^\epsilon _*$
, if for all
$f,g \in [\kappa ]^\epsilon _*$
, if for all
![]() $\alpha < \epsilon $
,
$\alpha < \epsilon $
,
![]() $f(\alpha ) \leq g(\alpha )$
, then
$f(\alpha ) \leq g(\alpha )$
, then
![]() $\Phi (f) \leq \Phi (g)$
. By Fact 5.1, for all functions of the form
$\Phi (f) \leq \Phi (g)$
. By Fact 5.1, for all functions of the form
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
to satisfy this almost everywhere monotonicity property, one must at least have the partition relation
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
to satisfy this almost everywhere monotonicity property, one must at least have the partition relation
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _2$
. If
$\kappa \rightarrow _* (\kappa )^\epsilon _2$
. If
![]() $\epsilon $
is countable, then the strong almost everywhere short length continuity of Theorem 3.9 implies the following almost everywhere monotonicity result.
$\epsilon $
is countable, then the strong almost everywhere short length continuity of Theorem 3.9 implies the following almost everywhere monotonicity result.
Theorem 4.8. Suppose
![]() $\kappa $
is a cardinal,
$\kappa $
is a cardinal,
![]() $\epsilon < {\omega _1}$
,
$\epsilon < {\omega _1}$
,
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon \cdot \epsilon }_2$
holds and
$\kappa \rightarrow _* (\kappa )^{\epsilon \cdot \epsilon }_2$
holds and
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
. Then there is a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
. Then there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if for all
$f,g \in [C]^\epsilon _*$
, if for all
![]() $\alpha < \epsilon $
,
$\alpha < \epsilon $
,
![]() $f(\alpha ) \leq g(\alpha )$
, then
$f(\alpha ) \leq g(\alpha )$
, then
![]() $\Phi (f) \leq \Phi (g)$
.
$\Phi (f) \leq \Phi (g)$
.
When
![]() ${\mathrm {cof}}(\epsilon ) = \omega $
, one only has the weaker almost everywhere short length continuity property of Theorem 3.7. Moreover, there are functions on partition spaces of high dimension which do not satisfy a recognizable continuity property. Regardless, almost everywhere monotonicity still holds for functions on partition spaces assuming the appropriate partition relation.
${\mathrm {cof}}(\epsilon ) = \omega $
, one only has the weaker almost everywhere short length continuity property of Theorem 3.7. Moreover, there are functions on partition spaces of high dimension which do not satisfy a recognizable continuity property. Regardless, almost everywhere monotonicity still holds for functions on partition spaces assuming the appropriate partition relation.
Theorem 5.3. Suppose
![]() $\kappa $
is a cardinal satisfying
$\kappa $
is a cardinal satisfying
![]() $\kappa \rightarrow _* (\kappa )^\kappa _2$
. For any function
$\kappa \rightarrow _* (\kappa )^\kappa _2$
. For any function
![]() $\Phi : [\kappa ]^\kappa _* \rightarrow \mathrm {ON}$
, there is a club
$\Phi : [\kappa ]^\kappa _* \rightarrow \mathrm {ON}$
, there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f,g \in [C]^\kappa _*$
, if for all
$f,g \in [C]^\kappa _*$
, if for all
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $f(\alpha ) \leq g(\alpha )$
, then
$f(\alpha ) \leq g(\alpha )$
, then
![]() $\Phi (f) \leq \Phi (g)$
.
$\Phi (f) \leq \Phi (g)$
.
Adapting this argument, one can also show monotonicity for
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
when
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
when
![]() $\epsilon < \kappa $
.
$\epsilon < \kappa $
.
Theorem 5.7. Suppose
![]() $\kappa $
is a weak partition cardinal. For any
$\kappa $
is a weak partition cardinal. For any
![]() $\epsilon < \kappa $
and function
$\epsilon < \kappa $
and function
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, there is a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f, g \in [\kappa ]^\epsilon _*$
, if for all
$f, g \in [\kappa ]^\epsilon _*$
, if for all
![]() $\alpha < \epsilon $
,
$\alpha < \epsilon $
,
![]() $f(\alpha ) \leq g(\alpha )$
, then
$f(\alpha ) \leq g(\alpha )$
, then
![]() $\Phi (f) \leq \Phi (g)$
.
$\Phi (f) \leq \Phi (g)$
.
The last section will establish the strongest known continuity result for functions of the form
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
from the strong partition relation on
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
from the strong partition relation on
![]() ${\omega _1}$
and a certain club selection principle. A certain club uniformization principle will be an important tool. Let
${\omega _1}$
and a certain club selection principle. A certain club uniformization principle will be an important tool. Let
![]() ${\mathsf {club}}_{\omega _1}$
denote the set of club subset of
${\mathsf {club}}_{\omega _1}$
denote the set of club subset of
![]() ${\omega _1}$
. The almost everywhere short length club uniformization principle at
${\omega _1}$
. The almost everywhere short length club uniformization principle at
![]() ${\omega _1}$
is the assertion that for all
${\omega _1}$
is the assertion that for all
![]() $R \subseteq [{\omega _1}]^{<{\omega _1}}_* \times {\mathsf {club}}_{\omega _1}$
which is
$R \subseteq [{\omega _1}]^{<{\omega _1}}_* \times {\mathsf {club}}_{\omega _1}$
which is
![]() $\subseteq $
-downward closed (in the sense that for all
$\subseteq $
-downward closed (in the sense that for all
![]() $\ell \in [{\omega _1}]^{<{\omega _1}}_*$
, for all clubs
$\ell \in [{\omega _1}]^{<{\omega _1}}_*$
, for all clubs
![]() $C \subseteq D$
, if
$C \subseteq D$
, if
![]() $R(\ell ,D)$
holds, then
$R(\ell ,D)$
holds, then
![]() $R(\sigma ,C)$
holds), there is a club
$R(\sigma ,C)$
holds), there is a club
![]() $C \subseteq {\omega _1}$
and a function
$C \subseteq {\omega _1}$
and a function
![]() $\Lambda : [C]^{<{\omega _1}}_* \cap \mathrm {dom}(R) \rightarrow {\mathsf {club}}_{\omega _1}$
so that for all
$\Lambda : [C]^{<{\omega _1}}_* \cap \mathrm {dom}(R) \rightarrow {\mathsf {club}}_{\omega _1}$
so that for all
![]() $\ell \in [C]^{<{\omega _1}}_* \cap \mathrm {dom}(R)$
,
$\ell \in [C]^{<{\omega _1}}_* \cap \mathrm {dom}(R)$
,
![]() $R(\ell ,\Lambda (\ell ))$
.
$R(\ell ,\Lambda (\ell ))$
.
Consider a function
![]() $\Phi : [{\omega _1}]^{\omega _1} \rightarrow {\omega _1}$
. Asking that there exists a
$\Phi : [{\omega _1}]^{\omega _1} \rightarrow {\omega _1}$
. Asking that there exists a
![]() $\delta < {\omega _1}$
so that
$\delta < {\omega _1}$
so that
![]() $\Phi (f)$
only depending on
$\Phi (f)$
only depending on
![]() $f \upharpoonright \delta $
for
$f \upharpoonright \delta $
for
![]() $\mu ^{\omega _1}_{\omega _1}$
-almost
$\mu ^{\omega _1}_{\omega _1}$
-almost
![]() $f \in [{\omega _1}]^{\omega _1}_*$
is impossible in general. (For instance, consider
$f \in [{\omega _1}]^{\omega _1}_*$
is impossible in general. (For instance, consider
![]() $\Phi (f) = f(f(0))$
. See Example 6.1.) Using the almost everywhere short length club uniformization at
$\Phi (f) = f(f(0))$
. See Example 6.1.) Using the almost everywhere short length club uniformization at
![]() ${\omega _1}$
, [Reference Chan and Jackson4] showed that functions
${\omega _1}$
, [Reference Chan and Jackson4] showed that functions
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
do satisfy
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
do satisfy
![]() $\mu ^{\omega _1}_{\omega _1}$
-almost everywhere continuity where
$\mu ^{\omega _1}_{\omega _1}$
-almost everywhere continuity where
![]() $[{\omega _1}]^{\omega _1}_*$
is endowed with the topology generated by
$[{\omega _1}]^{\omega _1}_*$
is endowed with the topology generated by
![]() $\{N_\ell : \ell \in [{\omega _1}]^{\omega _1}_*\}$
as a basis, where
$\{N_\ell : \ell \in [{\omega _1}]^{\omega _1}_*\}$
as a basis, where
![]() $N_\ell = \{f \in [{\omega _1}]^{\omega _1}_* : \ell \subseteq f\}$
for each
$N_\ell = \{f \in [{\omega _1}]^{\omega _1}_* : \ell \subseteq f\}$
for each
![]() $\ell \in [{\omega _1}]^{<{\omega _1}}_*$
and
$\ell \in [{\omega _1}]^{<{\omega _1}}_*$
and
![]() ${\omega _1}$
is given the discrete topology. Explicitly, there is a club
${\omega _1}$
is given the discrete topology. Explicitly, there is a club
![]() $C \subseteq {\omega _1}$
so that for all
$C \subseteq {\omega _1}$
so that for all
![]() $f \in [C]^{\omega _1}_*$
, there exists an
$f \in [C]^{\omega _1}_*$
, there exists an
![]() $\alpha < {\omega _1}$
so that for all
$\alpha < {\omega _1}$
so that for all
![]() $g \in [C]^{\omega _1}_*$
, if
$g \in [C]^{\omega _1}_*$
, if
![]() $f \upharpoonright \alpha = g \upharpoonright \alpha $
, then
$f \upharpoonright \alpha = g \upharpoonright \alpha $
, then
![]() $\Phi (f) = \Phi (g)$
. [Reference Chan2] showed that the almost everywhere short length club uniformization at
$\Phi (f) = \Phi (g)$
. [Reference Chan2] showed that the almost everywhere short length club uniformization at
![]() ${\omega _1}$
can be used to get an even finer continuity result which asserts that there is a club
${\omega _1}$
can be used to get an even finer continuity result which asserts that there is a club
![]() $C \subseteq {\omega _1}$
so that for all
$C \subseteq {\omega _1}$
so that for all
![]() $f \in [C]^{\omega _1}_*$
and all
$f \in [C]^{\omega _1}_*$
and all
![]() $\alpha < {\omega _1}$
, if
$\alpha < {\omega _1}$
, if
![]() $\Phi (f) < f(\alpha )$
, then
$\Phi (f) < f(\alpha )$
, then
![]() $f \upharpoonright \alpha $
is a continuity point for
$f \upharpoonright \alpha $
is a continuity point for
![]() $\Phi $
relative to C. (For these results, the condition that
$\Phi $
relative to C. (For these results, the condition that
![]() $\Phi $
maps into
$\Phi $
maps into
![]() ${\omega _1}$
is generally necessary.)
${\omega _1}$
is generally necessary.)
A natural question is whether
![]() $\Phi : [{\omega _1}]^{\omega _1} \rightarrow {\omega _1}$
satisfies any form of continuity in which
$\Phi : [{\omega _1}]^{\omega _1} \rightarrow {\omega _1}$
satisfies any form of continuity in which
![]() $\Phi (f)$
depends only on the behavior of f at finitely many locations on
$\Phi (f)$
depends only on the behavior of f at finitely many locations on
![]() ${\omega _1}$
. By the function from Example 6.1, it is impossible to have finitely many ordinals
${\omega _1}$
. By the function from Example 6.1, it is impossible to have finitely many ordinals
![]() $\delta _0, ..., \delta _{n - 1} < {\omega _1}$
which are independent of any input f so that
$\delta _0, ..., \delta _{n - 1} < {\omega _1}$
which are independent of any input f so that
![]() $\Phi (f)$
depends only on the behavior of f at these finitely many points. One can conjecture if there are finitely many continuity locations for
$\Phi (f)$
depends only on the behavior of f at these finitely many points. One can conjecture if there are finitely many continuity locations for
![]() $\Phi $
which do depend on f. That is, are there finitely many functions
$\Phi $
which do depend on f. That is, are there finitely many functions
![]() $\Upsilon _0, ..., \Upsilon _{n - 1}$
so that there is a club
$\Upsilon _0, ..., \Upsilon _{n - 1}$
so that there is a club
![]() $C \subseteq {\omega _1}$
with the property that for all
$C \subseteq {\omega _1}$
with the property that for all
![]() $f \in [C]^{\omega _1}$
, for all
$f \in [C]^{\omega _1}$
, for all
![]() $g \in [C]^{\omega _1}_*$
, if for all
$g \in [C]^{\omega _1}_*$
, if for all
![]() $i < n$
,
$i < n$
,
![]() $\sup (g \upharpoonright \Upsilon _i(f)) = \sup (f \upharpoonright \Upsilon _i(f))$
, then
$\sup (g \upharpoonright \Upsilon _i(f)) = \sup (f \upharpoonright \Upsilon _i(f))$
, then
![]() $\Phi (f) = \Phi (g)$
? This is also not possible. For each
$\Phi (f) = \Phi (g)$
? This is also not possible. For each
![]() $f \in [{\omega _1}]^{\omega _1}_*$
, call an ordinal
$f \in [{\omega _1}]^{\omega _1}_*$
, call an ordinal
![]() $\alpha $
a closure point of f if and only if for all
$\alpha $
a closure point of f if and only if for all
![]() $\beta < \alpha $
,
$\beta < \alpha $
,
![]() $f(\beta ) < \alpha $
or equivalently
$f(\beta ) < \alpha $
or equivalently
![]() $\sup (f \upharpoonright \alpha ) = \alpha $
. Let
$\sup (f \upharpoonright \alpha ) = \alpha $
. Let
![]() $\mathfrak {C}_f$
denote the club set of closure points of f. Let
$\mathfrak {C}_f$
denote the club set of closure points of f. Let
![]() $\Psi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
be defined by
$\Psi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
be defined by
![]() $\Psi (f) = \min (\mathfrak {C}_f)$
, that is, the smallest closure point of f. Example 6.3 shows that there is no collection of finite functions
$\Psi (f) = \min (\mathfrak {C}_f)$
, that is, the smallest closure point of f. Example 6.3 shows that there is no collection of finite functions
![]() $\Upsilon _0, ..., \Upsilon _{n - 1}$
which satisfies the proposed continuity property with respect to
$\Upsilon _0, ..., \Upsilon _{n - 1}$
which satisfies the proposed continuity property with respect to
![]() $\Psi $
. Closure points necessarily contain infinite information concerning f. The next result shows that closure points are the only obstruction to a
$\Psi $
. Closure points necessarily contain infinite information concerning f. The next result shows that closure points are the only obstruction to a
![]() $\mu ^{\omega _1}_{\omega _1}$
-almost everywhere continuity property asserting finite dependence:
$\mu ^{\omega _1}_{\omega _1}$
-almost everywhere continuity property asserting finite dependence:
Theorem 6.18. Assume
![]() $\mathsf {DC}$
,
$\mathsf {DC}$
,
![]() ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
and that the almost everywhere short length club uniformization principle holds at
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
and that the almost everywhere short length club uniformization principle holds at
![]() ${\omega _1}$
. Let
${\omega _1}$
. Let
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
. There is a club
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
. There is a club
![]() $C \subseteq {\omega _1}$
and finitely many functions
$C \subseteq {\omega _1}$
and finitely many functions
![]() $\Upsilon _0,...,\Upsilon _{n - 1}$
so that for all
$\Upsilon _0,...,\Upsilon _{n - 1}$
so that for all
![]() $f \in [C]^{\omega _1}_*$
, for all
$f \in [C]^{\omega _1}_*$
, for all
![]() $g \in [C]^{\omega _1}_*$
, if
$g \in [C]^{\omega _1}_*$
, if
![]() $\mathfrak {C}_g = \mathfrak {C}_f$
and for all
$\mathfrak {C}_g = \mathfrak {C}_f$
and for all
![]() $i < n$
,
$i < n$
,
![]() $\sup (g \upharpoonright \Upsilon _i(f)) = \sup (f \upharpoonright \Upsilon _i(f))$
, then
$\sup (g \upharpoonright \Upsilon _i(f)) = \sup (f \upharpoonright \Upsilon _i(f))$
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
To put these results in context and discuss examples, one needs to consider the natural theories which possess combinatorially regular properties. Let
![]() $A \subseteq {{}^\omega \omega }$
. Consider a game
$A \subseteq {{}^\omega \omega }$
. Consider a game
![]() $G_A$
where two players take turns picking natural numbers to jointly produce an infinite sequence f. Player 1 is said to win
$G_A$
where two players take turns picking natural numbers to jointly produce an infinite sequence f. Player 1 is said to win
![]() $G_A$
if and only if
$G_A$
if and only if
![]() $f \in A$
. The axiom of determinacy, denoted
$f \in A$
. The axiom of determinacy, denoted
![]() $\mathsf {AD}$
, asserts that, for all
$\mathsf {AD}$
, asserts that, for all
![]() $A \subseteq {{}^\omega \omega }$
, one of the two players has a winning strategy for
$A \subseteq {{}^\omega \omega }$
, one of the two players has a winning strategy for
![]() $G_A$
. Under
$G_A$
. Under
![]() $\mathsf {AD}$
, the perfect set property and the Baire property hold for all sets of reals, and
$\mathsf {AD}$
, the perfect set property and the Baire property hold for all sets of reals, and
![]() ${\omega _1}$
and many other cardinals possess partition properties. Many weak versions of the continuity results mentioned here have been previously established for
${\omega _1}$
and many other cardinals possess partition properties. Many weak versions of the continuity results mentioned here have been previously established for
![]() ${\omega _1}$
and
${\omega _1}$
and
![]() $\omega _2$
under
$\omega _2$
under
![]() $\mathsf {AD}$
. This paper evolved from attempts to establish continuity properties and cardinality computations at the most important weak and strong partition cardinals of determinacy.
$\mathsf {AD}$
. This paper evolved from attempts to establish continuity properties and cardinality computations at the most important weak and strong partition cardinals of determinacy.
See Section 2 for a summary of partition properties under
![]() $\mathsf {AD}$
. Martin showed under
$\mathsf {AD}$
. Martin showed under
![]() $\mathsf {AD}$
that
$\mathsf {AD}$
that
![]() ${\omega _1}$
is a strong partition cardinal and
${\omega _1}$
is a strong partition cardinal and
![]() $\omega _2$
is a weak partition cardinal which is not a strong partition cardinal. Jackson [Reference Jackson8] showed under
$\omega _2$
is a weak partition cardinal which is not a strong partition cardinal. Jackson [Reference Jackson8] showed under
![]() $\mathsf {AD}$
that for all
$\mathsf {AD}$
that for all
![]() $n \in \omega $
,
$n \in \omega $
,
![]() $\boldsymbol {\delta }_{2n + 1}^1$
is a strong partition cardinal and
$\boldsymbol {\delta }_{2n + 1}^1$
is a strong partition cardinal and
![]() $\boldsymbol {\delta }_{2n + 2}^1$
is a weak partition cardinal which is not a strong partition cardinal. The next strong partition cardinal after
$\boldsymbol {\delta }_{2n + 2}^1$
is a weak partition cardinal which is not a strong partition cardinal. The next strong partition cardinal after
![]() ${\omega _1}$
is
${\omega _1}$
is
![]() $\boldsymbol {\delta }_3^1 = \omega _{\omega + 1}$
. Kechris, Kleinberg, Moschovakis and Woodin [Reference Kechris, Kleinberg, Moschovakis and Hugh Woodin12] showed that
$\boldsymbol {\delta }_3^1 = \omega _{\omega + 1}$
. Kechris, Kleinberg, Moschovakis and Woodin [Reference Kechris, Kleinberg, Moschovakis and Hugh Woodin12] showed that
![]() $\boldsymbol {\delta }^2_1$
and the
$\boldsymbol {\delta }^2_1$
and the
![]() $\Sigma _1$
-stable ordinals
$\Sigma _1$
-stable ordinals
![]() $\boldsymbol {\delta }_A$
of
$\boldsymbol {\delta }_A$
of
![]() $L(A,\mathbb {R})$
for any
$L(A,\mathbb {R})$
for any
![]() $A \subseteq \mathbb {R}$
are strong partition cardinals under
$A \subseteq \mathbb {R}$
are strong partition cardinals under
![]() $\mathsf {AD}$
.
$\mathsf {AD}$
.
Previously known continuity results at
![]() ${\omega _1}$
and
${\omega _1}$
and
![]() $\omega _2$
heavily used determinacy methods. For instance, Kunen trees and Kunen functions ([Reference Jackson9] and [Reference Chan3]) are very important for many combinatorial questions at
$\omega _2$
heavily used determinacy methods. For instance, Kunen trees and Kunen functions ([Reference Jackson9] and [Reference Chan3]) are very important for many combinatorial questions at
![]() ${\omega _1}$
and for the description analysis below
${\omega _1}$
and for the description analysis below
![]() $\omega _\omega $
which leads to the strong partition property for
$\omega _\omega $
which leads to the strong partition property for
![]() $\boldsymbol {\delta }_3^1 = \omega _{\omega + 1}$
. [Reference Chan, Jackson and Trang6] and [Reference Chan, Jackson and Trang5] Fact 2.5 used these Kunen functions to provide a very simple argument that every function
$\boldsymbol {\delta }_3^1 = \omega _{\omega + 1}$
. [Reference Chan, Jackson and Trang6] and [Reference Chan, Jackson and Trang5] Fact 2.5 used these Kunen functions to provide a very simple argument that every function
![]() $\Phi : [{\omega _1}]^\epsilon \rightarrow {\omega _1}$
with
$\Phi : [{\omega _1}]^\epsilon \rightarrow {\omega _1}$
with
![]() $\epsilon < {\omega _1}$
satisfies the almost everywhere short length continuity expressed in Theorem 3.7 and even the stronger version expressed in Theorem 3.9 (but only when the range of the function goes into
$\epsilon < {\omega _1}$
satisfies the almost everywhere short length continuity expressed in Theorem 3.7 and even the stronger version expressed in Theorem 3.9 (but only when the range of the function goes into
![]() ${\omega _1}$
). [Reference Chan, Jackson and Trang6] used this result to show that
${\omega _1}$
). [Reference Chan, Jackson and Trang6] used this result to show that
![]() $|[{\omega _1}]^\omega | < |[{\omega _1}]^{<{\omega _1}}|$
under
$|[{\omega _1}]^\omega | < |[{\omega _1}]^{<{\omega _1}}|$
under
![]() $\mathsf {AD}$
. Using Martin’s ultrapower representation of
$\mathsf {AD}$
. Using Martin’s ultrapower representation of ![]() for each
for each
![]() $1 \leq n < \omega $
, [Reference Chan, Jackson and Trang5] showed that
$1 \leq n < \omega $
, [Reference Chan, Jackson and Trang5] showed that
![]() $[{\omega _1}]^{<{\omega _1}}$
does not inject into
$[{\omega _1}]^{<{\omega _1}}$
does not inject into
![]() ${}^\omega (\omega _\omega )$
. Using a variety of determinacy specific techniques (the full wellordered additivity of the meager ideal, generic coding arguments, Banach–Mazur games, Wadge theory and Steel’s Suslin bounding), [Reference Chan, Jackson and Trang5] showed that
${}^\omega (\omega _\omega )$
. Using a variety of determinacy specific techniques (the full wellordered additivity of the meager ideal, generic coding arguments, Banach–Mazur games, Wadge theory and Steel’s Suslin bounding), [Reference Chan, Jackson and Trang5] showed that
![]() $[{\omega _1}]^{<{\omega _1}}$
does not inject into
$[{\omega _1}]^{<{\omega _1}}$
does not inject into
![]() ${}^\omega \mathrm {ON}$
under
${}^\omega \mathrm {ON}$
under
![]() $\mathsf {AD}$
and
$\mathsf {AD}$
and
![]() $\mathsf {DC}_{\mathbb {R}}$
. (Note that Theorem 4.4 improved this result to just the hypothesis
$\mathsf {DC}_{\mathbb {R}}$
. (Note that Theorem 4.4 improved this result to just the hypothesis
![]() $\mathsf {AD}$
without
$\mathsf {AD}$
without
![]() $\mathsf {DC}_{\mathbb {R}}$
.) Extending these methods to studying the next strong partition cardinal
$\mathsf {DC}_{\mathbb {R}}$
.) Extending these methods to studying the next strong partition cardinal
![]() $\boldsymbol {\delta }_3^1 = \omega _{\omega + 1}$
seems difficult. Although
$\boldsymbol {\delta }_3^1 = \omega _{\omega + 1}$
seems difficult. Although
![]() $\omega _{\omega + 1}$
has analogs of Kunen functions and generic coding functions ([Reference Kechris and Woodin13]) using supercompactness measures, there is no analog of the full wellordered additivity of the meager ideal which can be a major obstacle to generalizing results to
$\omega _{\omega + 1}$
has analogs of Kunen functions and generic coding functions ([Reference Kechris and Woodin13]) using supercompactness measures, there is no analog of the full wellordered additivity of the meager ideal which can be a major obstacle to generalizing results to
![]() $\omega _{\omega + 1}$
as observed by Becker at the end of [Reference Becker1]. Moreover,
$\omega _{\omega + 1}$
as observed by Becker at the end of [Reference Becker1]. Moreover,
![]() $\boldsymbol {\delta }^2_1$
and the
$\boldsymbol {\delta }^2_1$
and the
![]() $\Sigma _1$
-stable ordinals
$\Sigma _1$
-stable ordinals
![]() $\boldsymbol {\delta }_A$
(
$\boldsymbol {\delta }_A$
(
![]() $A \subseteq \mathbb {R}$
) are strong partition cardinals which are limit cardinals and cannot possess analogs of the desired Kunen functions. The methods for
$A \subseteq \mathbb {R}$
) are strong partition cardinals which are limit cardinals and cannot possess analogs of the desired Kunen functions. The methods for
![]() ${\omega _1}$
are much less applicable here. Although,
${\omega _1}$
are much less applicable here. Although,
![]() $\boldsymbol {\delta }_3^1$
,
$\boldsymbol {\delta }_3^1$
,
![]() $\boldsymbol {\delta }^2_1$
and
$\boldsymbol {\delta }^2_1$
and
![]() $\boldsymbol {\delta }_A$
are important cardinals of determinacy possessing numerous scales and reflection properties, unlike
$\boldsymbol {\delta }_A$
are important cardinals of determinacy possessing numerous scales and reflection properties, unlike
![]() ${\omega _1}$
, these properties do not seem to facilitate the analysis of cardinality. The pure combinatorial methods of Theorem 3.7, 4.4, 3.9, 5.3 and 5.7 are the only known method for establishing these properties for these important strong partition cardinals of determinacy.
${\omega _1}$
, these properties do not seem to facilitate the analysis of cardinality. The pure combinatorial methods of Theorem 3.7, 4.4, 3.9, 5.3 and 5.7 are the only known method for establishing these properties for these important strong partition cardinals of determinacy.
Corollary 3.10. Assume
![]() $\mathsf {AD}$
. Suppose
$\mathsf {AD}$
. Suppose
![]() $\kappa $
is
$\kappa $
is
![]() ${\omega _1}$
,
${\omega _1}$
,
![]() $\omega _2$
,
$\omega _2$
,
![]() $\boldsymbol {\delta }_n^1$
for
$\boldsymbol {\delta }_n^1$
for
![]() $1 \leq n < \omega $
,
$1 \leq n < \omega $
,
![]() $\boldsymbol {\delta }_A$
where
$\boldsymbol {\delta }_A$
where
![]() $A \subseteq \mathbb {R}$
or
$A \subseteq \mathbb {R}$
or
![]() $\boldsymbol {\delta }^2_1$
(assuming
$\boldsymbol {\delta }^2_1$
(assuming
![]() $\mathsf {DC}_{\mathbb {R}}$
). If
$\mathsf {DC}_{\mathbb {R}}$
). If
![]() $\epsilon < {\omega _1}$
and
$\epsilon < {\omega _1}$
and
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, then there is a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, then there is a club
![]() $C \subseteq \kappa $
and finitely many ordinals
$C \subseteq \kappa $
and finitely many ordinals
![]() $\beta _0 < \beta _1 < ... < \beta _{p - 1} \leq \epsilon $
(where
$\beta _0 < \beta _1 < ... < \beta _{p - 1} \leq \epsilon $
(where
![]() $p \in \omega $
) so that for all
$p \in \omega $
) so that for all
![]() $f,g \in [C]^\epsilon _*$
, if for all
$f,g \in [C]^\epsilon _*$
, if for all
![]() $i < p$
,
$i < p$
,
![]() $\sup (f \upharpoonright \beta _i) = \sup (g \upharpoonright \beta _i)$
, then
$\sup (f \upharpoonright \beta _i) = \sup (g \upharpoonright \beta _i)$
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
Assume
![]() $\mathsf {AD}$
. Suppose
$\mathsf {AD}$
. Suppose
![]() $\kappa $
is
$\kappa $
is
![]() ${\omega _1}$
,
${\omega _1}$
,
![]() $\omega _2$
,
$\omega _2$
,
![]() $\boldsymbol {\delta }_n^1$
for
$\boldsymbol {\delta }_n^1$
for
![]() $1 \leq n < \omega $
,
$1 \leq n < \omega $
,
![]() $\boldsymbol {\delta }_A$
, where
$\boldsymbol {\delta }_A$
, where
![]() $A \subseteq \mathbb {R}$
or
$A \subseteq \mathbb {R}$
or
![]() $\boldsymbol {\delta }^2_1$
(assuming
$\boldsymbol {\delta }^2_1$
(assuming
![]() $\mathsf {DC}_{\mathbb {R}}$
). If
$\mathsf {DC}_{\mathbb {R}}$
). If
![]() $\epsilon < \kappa $
with
$\epsilon < \kappa $
with
![]() ${\mathrm {cof}}(\epsilon ) = \omega $
and
${\mathrm {cof}}(\epsilon ) = \omega $
and
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, then there is a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, then there is a club
![]() $C \subseteq \kappa $
and a
$C \subseteq \kappa $
and a
![]() $\delta < \epsilon $
so that for all
$\delta < \epsilon $
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if
$f,g \in [C]^\epsilon _*$
, if
![]() $\sup (f) = \sup (g)$
and
$\sup (f) = \sup (g)$
and
![]() $f \upharpoonright \delta = g \upharpoonright \delta $
, then
$f \upharpoonright \delta = g \upharpoonright \delta $
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
Corollary 4.6. Assume
![]() $\mathsf {AD}$
. Suppose
$\mathsf {AD}$
. Suppose
![]() $\kappa $
is
$\kappa $
is
![]() ${\omega _1}$
,
${\omega _1}$
,
![]() $\omega _2$
,
$\omega _2$
,
![]() $\boldsymbol {\delta }_n^1$
for
$\boldsymbol {\delta }_n^1$
for
![]() $1 \leq n < \omega $
,
$1 \leq n < \omega $
,
![]() $\boldsymbol {\delta }_A$
, where
$\boldsymbol {\delta }_A$
, where
![]() $A \subseteq \mathbb {R}$
or
$A \subseteq \mathbb {R}$
or
![]() $\boldsymbol {\delta }^2_1$
(assuming
$\boldsymbol {\delta }^2_1$
(assuming
![]() $\mathsf {DC}_{\mathbb {R}}$
). Then for any
$\mathsf {DC}_{\mathbb {R}}$
). Then for any
![]() $\chi < \kappa $
,
$\chi < \kappa $
,
![]() $|{}^\chi \kappa | < |{}^{<\kappa }\kappa |$
and
$|{}^\chi \kappa | < |{}^{<\kappa }\kappa |$
and
![]() ${}^{<\kappa }\kappa $
does not inject into
${}^{<\kappa }\kappa $
does not inject into
![]() ${}^\chi \mathrm {ON}$
.
${}^\chi \mathrm {ON}$
.
Corollary 5.5. Assume
![]() $\mathsf {AD}$
. Suppose
$\mathsf {AD}$
. Suppose
![]() $\kappa $
is
$\kappa $
is
![]() ${\omega _1}$
,
${\omega _1}$
,
![]() $\boldsymbol {\delta }_{2n + 1}^1$
for
$\boldsymbol {\delta }_{2n + 1}^1$
for
![]() $1 \leq n < \omega $
,
$1 \leq n < \omega $
,
![]() $\boldsymbol {\delta }_A$
where
$\boldsymbol {\delta }_A$
where
![]() $A \subseteq \mathbb {R}$
or
$A \subseteq \mathbb {R}$
or
![]() $\boldsymbol {\delta }^2_1$
(assuming
$\boldsymbol {\delta }^2_1$
(assuming
![]() $\mathsf {DC}_{\mathbb {R}}$
). For any
$\mathsf {DC}_{\mathbb {R}}$
). For any
![]() $\epsilon \leq \kappa $
and any function
$\epsilon \leq \kappa $
and any function
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, there is a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if for all
$f,g \in [C]^\epsilon _*$
, if for all
![]() $\alpha < \epsilon $
,
$\alpha < \epsilon $
,
![]() $f(\alpha ) \leq g(\alpha )$
, then
$f(\alpha ) \leq g(\alpha )$
, then
![]() $\Phi (f) \leq \Phi (g)$
.
$\Phi (f) \leq \Phi (g)$
.
Corollary 5.8. Assume
![]() $\mathsf {AD}$
. Suppose
$\mathsf {AD}$
. Suppose
![]() $\kappa $
is
$\kappa $
is
![]() ${\omega _1}$
,
${\omega _1}$
,
![]() $\omega _2$
,
$\omega _2$
,
![]() $\boldsymbol {\delta }_n^1$
for
$\boldsymbol {\delta }_n^1$
for
![]() $1 \leq n < \omega $
,
$1 \leq n < \omega $
,
![]() $\boldsymbol {\delta }_A$
where
$\boldsymbol {\delta }_A$
where
![]() $A \subseteq \mathbb {R}$
or
$A \subseteq \mathbb {R}$
or
![]() $\boldsymbol {\delta }^2_1$
(assuming
$\boldsymbol {\delta }^2_1$
(assuming
![]() $\mathsf {DC}_{\mathbb {R}}$
). For any
$\mathsf {DC}_{\mathbb {R}}$
). For any
![]() $\epsilon < \kappa $
and
$\epsilon < \kappa $
and
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, there is a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if for all
$f,g \in [C]^\epsilon _*$
, if for all
![]() $\alpha < \epsilon $
,
$\alpha < \epsilon $
,
![]() $f(\alpha ) \leq g(\alpha )$
, then
$f(\alpha ) \leq g(\alpha )$
, then
![]() $\Phi (f) \leq \Phi (g)$
.
$\Phi (f) \leq \Phi (g)$
.
Determinacy provides examples to show that the hypothesis in Theorem 3.7 and Theorem 3.9 are generally necessary. Let
![]() $\Psi : [\omega _2]^{\omega _1} \rightarrow \omega _3$
be defined by
$\Psi : [\omega _2]^{\omega _1} \rightarrow \omega _3$
be defined by
![]() $\Phi (f) = [f]_{\mu ^{\omega _1}_1}$
, that is, the ordinal represented by f in the ultrapower
$\Phi (f) = [f]_{\mu ^{\omega _1}_1}$
, that is, the ordinal represented by f in the ultrapower ![]() of
of
![]() $\omega _2$
by the club measure on
$\omega _2$
by the club measure on
![]() ${\omega _1}$
.
${\omega _1}$
.
![]() $\Psi $
will not satisfy the weak or strong version of the almost everywhere short length continuity. (See Example 3.13.) Letting
$\Psi $
will not satisfy the weak or strong version of the almost everywhere short length continuity. (See Example 3.13.) Letting
![]() $\Upsilon : [\omega _2]^{{\omega _1} + \omega } \rightarrow \omega _3$
defined by
$\Upsilon : [\omega _2]^{{\omega _1} + \omega } \rightarrow \omega _3$
defined by
![]() $\Upsilon (f) = \Psi (f \upharpoonright {\omega _1})$
is an example of a function satisfying the weak short length continuity of Theorem 3.7 (note
$\Upsilon (f) = \Psi (f \upharpoonright {\omega _1})$
is an example of a function satisfying the weak short length continuity of Theorem 3.7 (note
![]() ${\mathrm {cof}}({\omega _1} + \omega ) = \omega $
) and does not satisfy the strong short length continuity of Theorem 3.9 (note that
${\mathrm {cof}}({\omega _1} + \omega ) = \omega $
) and does not satisfy the strong short length continuity of Theorem 3.9 (note that
![]() ${\omega _1} < {\omega _1} + \omega $
). In the two examples above, the range goes into
${\omega _1} < {\omega _1} + \omega $
). In the two examples above, the range goes into
![]() $\omega _3$
. Curiously, it is shown in [Reference Chan, Jackson and Trang6] that every function
$\omega _3$
. Curiously, it is shown in [Reference Chan, Jackson and Trang6] that every function
![]() $\Phi : [\omega _2]^{\omega _1}_* \rightarrow \omega _2$
satisfies even the strong almost everywhere short length continuity property (despite
$\Phi : [\omega _2]^{\omega _1}_* \rightarrow \omega _2$
satisfies even the strong almost everywhere short length continuity property (despite
![]() ${\mathrm {cof}}({\omega _1})> \omega $
). This remarkable property is unique only to
${\mathrm {cof}}({\omega _1})> \omega $
). This remarkable property is unique only to
![]() $\omega _2$
and is made possible by Martin’s ultrapower representation of
$\omega _2$
and is made possible by Martin’s ultrapower representation of
![]() $\omega _2$
under
$\omega _2$
under
![]() $\mathsf {AD}$
.
$\mathsf {AD}$
.
[Reference Chan and Jackson4] shows the almost everywhere short length club uniformization holds for
![]() ${\omega _1}$
under
${\omega _1}$
under
![]() $\mathsf {AD}$
. (By a more general argument, [Reference Chan2] shows that nearly all known strong partition cardinals of
$\mathsf {AD}$
. (By a more general argument, [Reference Chan2] shows that nearly all known strong partition cardinals of
![]() $\mathsf {AD}$
also satisfies this club uniformization principle.) By absorbing functions
$\mathsf {AD}$
also satisfies this club uniformization principle.) By absorbing functions
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
into the inner model
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
into the inner model
![]() $L(\mathbb {R})$
which satisfies
$L(\mathbb {R})$
which satisfies
![]() $\mathsf {AD}$
and
$\mathsf {AD}$
and
![]() $\mathsf {DC}$
, Theorem 6.18 implies the following holds in
$\mathsf {DC}$
, Theorem 6.18 implies the following holds in
![]() $\mathsf {AD}$
.
$\mathsf {AD}$
.
Theorem 6.22. Assume
![]() $\mathsf {AD}$
. Let
$\mathsf {AD}$
. Let
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
. There is a club
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
. There is a club
![]() $C \subseteq {\omega _1}$
and finitely many function
$C \subseteq {\omega _1}$
and finitely many function
![]() $\Gamma _0,...,\Gamma _{n - 1}$
so that for all
$\Gamma _0,...,\Gamma _{n - 1}$
so that for all
![]() $f \in [C]^{\omega _1}_*$
, for all
$f \in [C]^{\omega _1}_*$
, for all
![]() $g \in [C]^{\omega _1}_*$
, if
$g \in [C]^{\omega _1}_*$
, if
![]() $\mathfrak {C}_g = \mathfrak {C}_f$
and for all
$\mathfrak {C}_g = \mathfrak {C}_f$
and for all
![]() $i < n$
,
$i < n$
,
![]() $\sup (g \upharpoonright \Gamma _i(f)) = \sup (f \upharpoonright \Gamma _i(f))$
, then
$\sup (g \upharpoonright \Gamma _i(f)) = \sup (f \upharpoonright \Gamma _i(f))$
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
In this result, it is necessary that the range goes into
![]() ${\omega _1}$
. For example under
${\omega _1}$
. For example under
![]() $\mathsf {AD}$
, the function
$\mathsf {AD}$
, the function
![]() $\Phi : [{\omega _1}]_*^{\omega _1} \rightarrow \omega _2$
defined by
$\Phi : [{\omega _1}]_*^{\omega _1} \rightarrow \omega _2$
defined by
![]() $\Psi (f) = [f]_{\mu ^{\omega _1}_1}$
(f is mapped to the ordinal below
$\Psi (f) = [f]_{\mu ^{\omega _1}_1}$
(f is mapped to the ordinal below
![]() $\omega _2$
represented by f in the ultrapower of
$\omega _2$
represented by f in the ultrapower of
![]() ${\omega _1}$
by the club measure on
${\omega _1}$
by the club measure on
![]() ${\omega _1}$
) does not satisfy any recognizable continuity property.
${\omega _1}$
) does not satisfy any recognizable continuity property.
2 Partition properties
![]() $\mathrm {ON}$
will denote the class of ordinals.
$\mathrm {ON}$
will denote the class of ordinals.
Definition 2.1. Suppose
![]() $\epsilon \in \mathrm {ON}$
and
$\epsilon \in \mathrm {ON}$
and
![]() $f : \epsilon \rightarrow \mathrm {ON}$
is a function. The function f is discontinuous everywhere if and only if for all
$f : \epsilon \rightarrow \mathrm {ON}$
is a function. The function f is discontinuous everywhere if and only if for all
![]() $\alpha < \epsilon $
,
$\alpha < \epsilon $
,
![]() $\sup (f \upharpoonright \alpha ) = \sup \{f(\beta ) : \beta < \alpha \} < f(\alpha )$
.
$\sup (f \upharpoonright \alpha ) = \sup \{f(\beta ) : \beta < \alpha \} < f(\alpha )$
.
The function f has uniform cofinality
![]() $\omega $
if and only if there is a function
$\omega $
if and only if there is a function
![]() $F : \epsilon \times \omega \rightarrow \mathrm {ON}$
with the following properties:
$F : \epsilon \times \omega \rightarrow \mathrm {ON}$
with the following properties:
-
1. For all
 $\alpha < \epsilon $
, for all
$\alpha < \epsilon $
, for all
 $n \in \omega $
,
$n \in \omega $
,
 $F(\alpha ,n) < F(\alpha ,n + 1)$
.
$F(\alpha ,n) < F(\alpha ,n + 1)$
. -
2. For all
 $\alpha < \epsilon $
,
$\alpha < \epsilon $
,
 $f(\alpha ) = \sup \{F(\alpha ,n) : n \in \omega \}$
.
$f(\alpha ) = \sup \{F(\alpha ,n) : n \in \omega \}$
.
The function f has the correct type if and only if f is both discontinuous everywhere and has uniform cofinality
![]() $\omega $
.
$\omega $
.
Definition 2.2. If A and B are two sets, then
![]() ${}^A B$
denote the set of functions
${}^A B$
denote the set of functions
![]() $f : A \rightarrow B$
.
$f : A \rightarrow B$
.
Let
![]() $\epsilon \in \mathrm {ON}$
and X be a class of ordinals. Let
$\epsilon \in \mathrm {ON}$
and X be a class of ordinals. Let
![]() $[X]^\epsilon $
be the class of increasing functions
$[X]^\epsilon $
be the class of increasing functions
![]() $f : \epsilon \rightarrow X$
. Let
$f : \epsilon \rightarrow X$
. Let
![]() $[X]^\epsilon _*$
be the class of increasing functions
$[X]^\epsilon _*$
be the class of increasing functions
![]() $f : \epsilon \rightarrow X$
of the correct type.
$f : \epsilon \rightarrow X$
of the correct type.
Definition 2.3. (Ordinary partition relation) Suppose
![]() $\kappa $
is a cardinal and
$\kappa $
is a cardinal and
![]() $\epsilon \leq \kappa $
, then let
$\epsilon \leq \kappa $
, then let
![]() $\kappa \rightarrow (\kappa )^\epsilon _2$
state that for all
$\kappa \rightarrow (\kappa )^\epsilon _2$
state that for all
![]() $P : [\kappa ]^\epsilon \rightarrow 2$
, there is an
$P : [\kappa ]^\epsilon \rightarrow 2$
, there is an
![]() $A \subseteq \kappa $
with
$A \subseteq \kappa $
with
![]() $|A| = \kappa $
and an
$|A| = \kappa $
and an
![]() $i \in 2$
so that for all
$i \in 2$
so that for all
![]() $f \in [A]^\epsilon $
,
$f \in [A]^\epsilon $
,
![]() $P(f) = i$
.
$P(f) = i$
.
Definition 2.4. (Correct type partition relations) Suppose
![]() $\kappa $
is a cardinal,
$\kappa $
is a cardinal,
![]() $\epsilon \leq \kappa $
and
$\epsilon \leq \kappa $
and
![]() $\gamma < \kappa $
, let
$\gamma < \kappa $
, let
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _\gamma $
assert that for all
$\kappa \rightarrow _* (\kappa )^\epsilon _\gamma $
assert that for all
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \gamma $
, there is a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \gamma $
, there is a club
![]() $C \subseteq \kappa $
and an
$C \subseteq \kappa $
and an
![]() $\eta < \gamma $
so that for all
$\eta < \gamma $
so that for all
![]() $f \in [C]^\epsilon _*$
,
$f \in [C]^\epsilon _*$
,
![]() $\Phi (f) = \eta $
.
$\Phi (f) = \eta $
.
![]() $\kappa $
is a strong partition cardinal if and only if
$\kappa $
is a strong partition cardinal if and only if
![]() $\kappa \rightarrow _* (\kappa )^\kappa _2$
.
$\kappa \rightarrow _* (\kappa )^\kappa _2$
.
![]() $\kappa $
is a very strong partition cardinal if and only if
$\kappa $
is a very strong partition cardinal if and only if
![]() $\kappa \rightarrow _* (\kappa )^\kappa _{<\kappa }$
.
$\kappa \rightarrow _* (\kappa )^\kappa _{<\kappa }$
.
![]() $\kappa $
is a weak partition cardinal if and only if
$\kappa $
is a weak partition cardinal if and only if
![]() $\kappa \rightarrow (\kappa )^{<\kappa }_2$
.
$\kappa \rightarrow (\kappa )^{<\kappa }_2$
.
The correct type partition relations will be used in this paper. Under the axiom of determinacy, partition relations are often established by proving the correct type partition relation and many applications directly involve the correct type partition relation. The ordinary and correct type partition relations are nearly equivalent by the following result.
Fact 2.5. ([Reference Chan3] Fact 2.6)
Suppose
![]() $\kappa $
is a cardinal and
$\kappa $
is a cardinal and
![]() $\epsilon \leq \kappa $
.
$\epsilon \leq \kappa $
.
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _2$
implies
$\kappa \rightarrow _* (\kappa )^\epsilon _2$
implies
![]() $\kappa \rightarrow (\kappa )^\epsilon _2$
.
$\kappa \rightarrow (\kappa )^\epsilon _2$
.
![]() $\kappa \rightarrow (\kappa )^{\omega \cdot \epsilon }_2$
implies
$\kappa \rightarrow (\kappa )^{\omega \cdot \epsilon }_2$
implies
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _2$
.
$\kappa \rightarrow _* (\kappa )^\epsilon _2$
.
It is not known if
![]() $\kappa \rightarrow _* (\kappa )^\kappa _2$
implies
$\kappa \rightarrow _* (\kappa )^\kappa _2$
implies
![]() $\kappa \rightarrow (\kappa )^\kappa _{<\kappa }$
, that is, whether a strong partition cardinal is a very strong partition cardinal. (Although all known strong partition cardinals are very strong partition cardinals.) However, one does have the following related results for weak partition cardinals. The first follows from an induction argument.
$\kappa \rightarrow (\kappa )^\kappa _{<\kappa }$
, that is, whether a strong partition cardinal is a very strong partition cardinal. (Although all known strong partition cardinals are very strong partition cardinals.) However, one does have the following related results for weak partition cardinals. The first follows from an induction argument.
Fact 2.6. Suppose
![]() $\kappa $
is a cardinal and
$\kappa $
is a cardinal and
![]() $\epsilon \leq \kappa $
.
$\epsilon \leq \kappa $
.
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _2$
implies
$\kappa \rightarrow _* (\kappa )^\epsilon _2$
implies
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _n$
for all
$\kappa \rightarrow _* (\kappa )^\epsilon _n$
for all
![]() $n \in \omega $
.
$n \in \omega $
.
Fact 2.7. ([Reference Chan3] Fact 2.13)
Suppose
![]() $\kappa $
is a cardinal and
$\kappa $
is a cardinal and
![]() $\epsilon < \kappa $
. Then
$\epsilon < \kappa $
. Then
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon + \epsilon }_2$
implies
$\kappa \rightarrow _* (\kappa )^{\epsilon + \epsilon }_2$
implies
![]() $\kappa \rightarrow (\kappa )^\epsilon _{<\kappa }$
.
$\kappa \rightarrow (\kappa )^\epsilon _{<\kappa }$
.
Thus,
![]() $\kappa \rightarrow _* (\kappa )^{<\kappa }_2$
implies
$\kappa \rightarrow _* (\kappa )^{<\kappa }_2$
implies
![]() $\kappa \rightarrow _* (\kappa )^{<\kappa }_{<\kappa }$
.
$\kappa \rightarrow _* (\kappa )^{<\kappa }_{<\kappa }$
.
Definition 2.8. If
![]() $\kappa $
is a cardinal and
$\kappa $
is a cardinal and
![]() $\epsilon \leq \kappa $
, then let
$\epsilon \leq \kappa $
, then let
![]() $\mu ^\kappa _\epsilon $
be the filter on
$\mu ^\kappa _\epsilon $
be the filter on
![]() $[\kappa ]^\epsilon _*$
defined by
$[\kappa ]^\epsilon _*$
defined by
![]() $X \in \mu ^\kappa _\epsilon $
if and only if there is a club
$X \in \mu ^\kappa _\epsilon $
if and only if there is a club
![]() $C \subseteq \kappa $
so that
$C \subseteq \kappa $
so that
![]() $[C]^\epsilon _* \subseteq X$
.
$[C]^\epsilon _* \subseteq X$
.
If
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _2$
holds, then
$\kappa \rightarrow _* (\kappa )^\epsilon _2$
holds, then
![]() $\mu ^\kappa _\epsilon $
is an ultrafilter and is called the
$\mu ^\kappa _\epsilon $
is an ultrafilter and is called the
![]() $\epsilon $
-partition measure on
$\epsilon $
-partition measure on
![]() $\kappa $
. If
$\kappa $
. If
![]() $\kappa \rightarrow _* (\kappa )^\kappa _2$
holds, then
$\kappa \rightarrow _* (\kappa )^\kappa _2$
holds, then
![]() $\mu ^\kappa _\kappa $
is called the strong partition measure on
$\mu ^\kappa _\kappa $
is called the strong partition measure on
![]() $\kappa $
.
$\kappa $
.
Note that
![]() $\mu ^\kappa _\epsilon $
is
$\mu ^\kappa _\epsilon $
is
![]() $\kappa $
-complete if and only if
$\kappa $
-complete if and only if
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _{<\kappa }$
holds. Thus, if
$\kappa \rightarrow _* (\kappa )^\epsilon _{<\kappa }$
holds. Thus, if
![]() $\epsilon < \kappa $
and
$\epsilon < \kappa $
and
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon + \epsilon }_2$
holds, then
$\kappa \rightarrow _* (\kappa )^{\epsilon + \epsilon }_2$
holds, then
![]() $\mu ^\kappa _\epsilon $
is
$\mu ^\kappa _\epsilon $
is
![]() $\kappa $
-complete by Fact 2.7.
$\kappa $
-complete by Fact 2.7.
Definition 2.9. Suppose A is a set of ordinals. Let
![]() $\xi = {\mathrm {ot}}(A)$
. Let
$\xi = {\mathrm {ot}}(A)$
. Let
![]() ${\mathsf {enum}}_A : \xi \rightarrow A$
denote the increasing enumeration of A.
${\mathsf {enum}}_A : \xi \rightarrow A$
denote the increasing enumeration of A.
Suppose
![]() $\kappa $
be a regular cardinal. Let
$\kappa $
be a regular cardinal. Let
![]() $X \subseteq \kappa $
be an unbounded subset of
$X \subseteq \kappa $
be an unbounded subset of
![]() $\kappa $
. Let
$\kappa $
. Let
![]() ${\mathsf {next}}_{X} : \kappa \rightarrow X$
be defined by
${\mathsf {next}}_{X} : \kappa \rightarrow X$
be defined by
![]() ${\mathsf {next}}_{X}(\alpha )$
is the least element of X greater than
${\mathsf {next}}_{X}(\alpha )$
is the least element of X greater than
![]() $\alpha $
. Let
$\alpha $
. Let
![]() ${\mathsf {next}}_X^0 : \kappa \rightarrow \kappa $
be the identity function. For each
${\mathsf {next}}_X^0 : \kappa \rightarrow \kappa $
be the identity function. For each
![]() $0 < \gamma < \kappa $
, let
$0 < \gamma < \kappa $
, let
![]() ${\mathsf {next}}_{X}^{\gamma } : \kappa \rightarrow X$
be defined by
${\mathsf {next}}_{X}^{\gamma } : \kappa \rightarrow X$
be defined by
![]() ${\mathsf {next}}_X^\gamma (\alpha )$
is the
${\mathsf {next}}_X^\gamma (\alpha )$
is the
![]() $\gamma ^{\text {th}}$
-element of X strictly greater than
$\gamma ^{\text {th}}$
-element of X strictly greater than
![]() $\alpha $
. (Note that
$\alpha $
. (Note that
![]() ${\mathsf {next}}_X(\alpha ) = {\mathsf {next}}_X^1(\alpha )$
.)
${\mathsf {next}}_X(\alpha ) = {\mathsf {next}}_X^1(\alpha )$
.)
Suppose
![]() $\kappa $
is a cardinal,
$\kappa $
is a cardinal,
![]() $\epsilon \leq \kappa $
and
$\epsilon \leq \kappa $
and
![]() $f : \epsilon \rightarrow \kappa $
. Let
$f : \epsilon \rightarrow \kappa $
. Let
![]() $\mathcal {C}_f$
denote the closure of
$\mathcal {C}_f$
denote the closure of
![]() $f[\epsilon ]$
in
$f[\epsilon ]$
in
![]() $\kappa $
.
$\kappa $
.
If
![]() $\epsilon \in \mathrm {ON}$
,
$\epsilon \in \mathrm {ON}$
,
![]() $f : \epsilon \rightarrow \mathrm {ON}$
and
$f : \epsilon \rightarrow \mathrm {ON}$
and
![]() $\alpha < \epsilon $
, then let
$\alpha < \epsilon $
, then let
![]() ${\mathsf {drop}}(f,\alpha ) : (\epsilon - \alpha ) \rightarrow \mathrm {ON}$
be defined by
${\mathsf {drop}}(f,\alpha ) : (\epsilon - \alpha ) \rightarrow \mathrm {ON}$
be defined by
![]() ${\mathsf {drop}}(f,\alpha )(\beta ) = f(\alpha + \beta )$
.
${\mathsf {drop}}(f,\alpha )(\beta ) = f(\alpha + \beta )$
.
Fact 2.10. Suppose
![]() $\kappa $
is a cardinal,
$\kappa $
is a cardinal,
![]() $\epsilon \leq \kappa $
and
$\epsilon \leq \kappa $
and
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _{<\kappa }$
holds. (By Fact 2.7, if
$\kappa \rightarrow _* (\kappa )^\epsilon _{<\kappa }$
holds. (By Fact 2.7, if
![]() $\epsilon < \kappa $
, then
$\epsilon < \kappa $
, then
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon + \epsilon }_2$
is enough to ensure this condition.) Let
$\kappa \rightarrow _* (\kappa )^{\epsilon + \epsilon }_2$
is enough to ensure this condition.) Let
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \kappa $
have the property that for
$\Phi : [\kappa ]^\epsilon _* \rightarrow \kappa $
have the property that for
![]() $\mu ^\kappa _\epsilon $
-almost all f,
$\mu ^\kappa _\epsilon $
-almost all f,
![]() $\Phi (f) < f(0)$
. Then there is a club
$\Phi (f) < f(0)$
. Then there is a club
![]() $C \subseteq \kappa $
and a
$C \subseteq \kappa $
and a
![]() $\zeta < \kappa $
so that for all
$\zeta < \kappa $
so that for all
![]() $f \in [C]^\epsilon _*$
,
$f \in [C]^\epsilon _*$
,
![]() $\Phi (f) = \zeta $
.
$\Phi (f) = \zeta $
.
Proof. Let
![]() $C_0 \subseteq \kappa $
be such that for all
$C_0 \subseteq \kappa $
be such that for all
![]() $f \in [C_0]^\epsilon _*$
,
$f \in [C_0]^\epsilon _*$
,
![]() $\Phi (f) < f(0)$
. Define
$\Phi (f) < f(0)$
. Define
![]() $P : [\kappa ]^{1 + \epsilon }_* \rightarrow 2$
by
$P : [\kappa ]^{1 + \epsilon }_* \rightarrow 2$
by
![]() $P(g) = 0$
if and only if
$P(g) = 0$
if and only if
![]() $\Phi ({\mathsf {drop}}(g,1)) < g(0)$
. By
$\Phi ({\mathsf {drop}}(g,1)) < g(0)$
. By
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _2$
, there is a club
$\kappa \rightarrow _* (\kappa )^\epsilon _2$
, there is a club
![]() $C_1 \subseteq C_0$
which is homogeneous for P. Let
$C_1 \subseteq C_0$
which is homogeneous for P. Let
![]() $C_2 \subseteq C_1$
be the club of limit points of
$C_2 \subseteq C_1$
be the club of limit points of
![]() $C_1$
. Take any
$C_1$
. Take any
![]() $f \in [C_2]^\epsilon _*$
. By the stated property of
$f \in [C_2]^\epsilon _*$
. By the stated property of
![]() $C_0$
,
$C_0$
,
![]() $\Phi (f) < f(0)$
. Since
$\Phi (f) < f(0)$
. Since
![]() $f(0) \in C_2$
, there is a
$f(0) \in C_2$
, there is a
![]() $\gamma \in C_1$
so that
$\gamma \in C_1$
so that
![]() $\Phi (f) < \gamma < f(0)$
. Let
$\Phi (f) < \gamma < f(0)$
. Let
![]() $g \in [C_1]^{1 + \epsilon }_*$
be defined by
$g \in [C_1]^{1 + \epsilon }_*$
be defined by
![]() $g(0) = \gamma $
and
$g(0) = \gamma $
and
![]() ${\mathsf {drop}}(g,1) = f$
. Then
${\mathsf {drop}}(g,1) = f$
. Then
![]() $\Phi ({\mathsf {drop}}(g,1)) = \Phi (f) < \gamma = g(0)$
and hence
$\Phi ({\mathsf {drop}}(g,1)) = \Phi (f) < \gamma = g(0)$
and hence
![]() $P(g) = 0$
. This shows that
$P(g) = 0$
. This shows that
![]() $C_1$
must be homogeneous for P taking value
$C_1$
must be homogeneous for P taking value
![]() $0$
. Let
$0$
. Let
![]() $f \in [C_2]^\epsilon _*$
. Since
$f \in [C_2]^\epsilon _*$
. Since
![]() $f(0) \in C_2$
,
$f(0) \in C_2$
,
![]() $\min (C_1) < f(0)$
. Let
$\min (C_1) < f(0)$
. Let
![]() $g \in [C_1]^{1 + \epsilon }_*$
be defined so that
$g \in [C_1]^{1 + \epsilon }_*$
be defined so that
![]() ${\mathsf {drop}}(g,1) = f$
and
${\mathsf {drop}}(g,1) = f$
and
![]() $g(0) = \min (C_1)$
. Then
$g(0) = \min (C_1)$
. Then
![]() $P(g) = 0$
implies that
$P(g) = 0$
implies that
![]() $\Phi (f) = \Phi ({\mathsf {drop}}(g,1)) < g(0) = \min (C_1)$
. Since f was arbitrary, it has been shown that for all
$\Phi (f) = \Phi ({\mathsf {drop}}(g,1)) < g(0) = \min (C_1)$
. Since f was arbitrary, it has been shown that for all
![]() $f \in [C_2]^\epsilon _*$
,
$f \in [C_2]^\epsilon _*$
,
![]() $\Phi (f) < \min (C_1)$
. Since
$\Phi (f) < \min (C_1)$
. Since
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon }_{<\kappa }$
implies that
$\kappa \rightarrow _* (\kappa )^{\epsilon }_{<\kappa }$
implies that
![]() $\mu ^\kappa _\epsilon $
is
$\mu ^\kappa _\epsilon $
is
![]() $\kappa $
-complete, there is a
$\kappa $
-complete, there is a
![]() $C_3 \subseteq C_2$
and a
$C_3 \subseteq C_2$
and a
![]() $\zeta < \kappa $
so that for all
$\zeta < \kappa $
so that for all
![]() $f \in [C_3]^\epsilon _*$
,
$f \in [C_3]^\epsilon _*$
,
![]() $\Phi (f) = \zeta $
.
$\Phi (f) = \zeta $
.
Fact 2.11. Assume
![]() $\kappa \rightarrow _* (\kappa )^{2}_2$
. Then
$\kappa \rightarrow _* (\kappa )^{2}_2$
. Then
![]() $\mu ^\kappa _1$
(i.e., the
$\mu ^\kappa _1$
(i.e., the
![]() $\omega $
-club filter on
$\omega $
-club filter on
![]() $\kappa $
) is a normal
$\kappa $
) is a normal
![]() $\kappa $
-complete ultrafilter.
$\kappa $
-complete ultrafilter.
Proof. Let
![]() $\Phi : \kappa \rightarrow \kappa $
be a
$\Phi : \kappa \rightarrow \kappa $
be a
![]() $\mu ^\kappa _1$
-almost everywhere regressive function. Then there is a club
$\mu ^\kappa _1$
-almost everywhere regressive function. Then there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $\alpha \in [C]^1_*$
,
$\alpha \in [C]^1_*$
,
![]() $\Phi (\alpha ) < \alpha $
. By Fact 2.10, there is a club
$\Phi (\alpha ) < \alpha $
. By Fact 2.10, there is a club
![]() $D \subseteq \kappa $
and a
$D \subseteq \kappa $
and a
![]() $\zeta < \kappa $
so that for all
$\zeta < \kappa $
so that for all
![]() $\alpha \in [D]^1_*$
,
$\alpha \in [D]^1_*$
,
![]() $\Phi (\alpha ) = \zeta $
. So
$\Phi (\alpha ) = \zeta $
. So
![]() $\Phi $
is
$\Phi $
is
![]() $\mu ^\kappa _1$
-almost everywhere constant.
$\mu ^\kappa _1$
-almost everywhere constant.
An ordinal
![]() $\gamma $
is additively indecomposable if and only if for all
$\gamma $
is additively indecomposable if and only if for all
![]() $\alpha < \gamma $
and
$\alpha < \gamma $
and
![]() $\beta < \gamma $
,
$\beta < \gamma $
,
![]() $\alpha + \beta < \gamma $
. An ordinal
$\alpha + \beta < \gamma $
. An ordinal
![]() $\gamma $
is multiplicatively indecomposable if and only if for all
$\gamma $
is multiplicatively indecomposable if and only if for all
![]() $\alpha < \gamma $
and
$\alpha < \gamma $
and
![]() $\beta < \gamma $
,
$\beta < \gamma $
,
![]() $\alpha \cdot \beta < \gamma $
. An ordinal is indecomposable if and only if it is additively and multiplicatively indecomposable. In all discussions,
$\alpha \cdot \beta < \gamma $
. An ordinal is indecomposable if and only if it is additively and multiplicatively indecomposable. In all discussions,
![]() $0$
and
$0$
and
![]() $1$
will be excluded and hence additively indecomposable ordinals will always be limit ordinals. For every limit ordinal
$1$
will be excluded and hence additively indecomposable ordinals will always be limit ordinals. For every limit ordinal
![]() $\epsilon $
, there exists
$\epsilon $
, there exists
![]() $\epsilon _0 < \epsilon $
and
$\epsilon _0 < \epsilon $
and
![]() $\epsilon _1 \leq \epsilon $
so that
$\epsilon _1 \leq \epsilon $
so that
![]() $\epsilon = \epsilon _0 + \epsilon _1$
and
$\epsilon = \epsilon _0 + \epsilon _1$
and
![]() $\epsilon _1$
is additively indecomposable. Because of this decomposition, it will be useful to establish results for sequences whose lengths are additively indecomposable (but possibly not multiplicatively indecomposable) before deducing the general result. One will frequently assume club subsets consists entirely of (additively and multiplicatively) indecomposable ordinals.
$\epsilon _1$
is additively indecomposable. Because of this decomposition, it will be useful to establish results for sequences whose lengths are additively indecomposable (but possibly not multiplicatively indecomposable) before deducing the general result. One will frequently assume club subsets consists entirely of (additively and multiplicatively) indecomposable ordinals.
Fact 2.12. Let
![]() $C_0 \subseteq \kappa $
be a club subset of
$C_0 \subseteq \kappa $
be a club subset of
![]() $\kappa $
consisting entirely of indecomposable ordinals. Let
$\kappa $
consisting entirely of indecomposable ordinals. Let
![]() $C_1 = \{\alpha \in C_0 : {\mathsf {enum}}_{C_0}(\alpha ) = \alpha \}$
. Then
$C_1 = \{\alpha \in C_0 : {\mathsf {enum}}_{C_0}(\alpha ) = \alpha \}$
. Then
![]() $C_1 \subseteq C_0$
is a club subset of
$C_1 \subseteq C_0$
is a club subset of
![]() $\kappa $
consisting entirely of indecomposable ordinals. For any
$\kappa $
consisting entirely of indecomposable ordinals. For any
![]() $\gamma < \kappa $
,
$\gamma < \kappa $
,
![]() $\alpha < \gamma $
and
$\alpha < \gamma $
and
![]() $\beta < \gamma $
with
$\beta < \gamma $
with
![]() $\gamma \in C_1$
,
$\gamma \in C_1$
,
![]() ${\mathsf {next}}^{\beta }_{C_0}(\alpha ) < \gamma $
and in particular,
${\mathsf {next}}^{\beta }_{C_0}(\alpha ) < \gamma $
and in particular,
![]() ${\mathsf {next}}_{C_0}^{\omega \cdot (\beta + 1)}(\alpha ) < \gamma $
.
${\mathsf {next}}_{C_0}^{\omega \cdot (\beta + 1)}(\alpha ) < \gamma $
.
Proof. Fix
![]() $\gamma \in C_1$
and
$\gamma \in C_1$
and
![]() $\alpha < \gamma $
. Let
$\alpha < \gamma $
. Let
![]() $\zeta = \sup \{\eta < \kappa : {\mathsf {enum}}_{C_0}(\eta ) \leq \alpha \}$
. Note that
$\zeta = \sup \{\eta < \kappa : {\mathsf {enum}}_{C_0}(\eta ) \leq \alpha \}$
. Note that
![]() ${\mathsf {next}}_{C_0}^0(\alpha ) = \alpha $
and if
${\mathsf {next}}_{C_0}^0(\alpha ) = \alpha $
and if
![]() $0 < \beta < \gamma $
,
$0 < \beta < \gamma $
,
![]() ${\mathsf {next}}_{C_0}^\beta (\alpha ) = {\mathsf {enum}}_{C_0}(\zeta + \beta )$
. Since
${\mathsf {next}}_{C_0}^\beta (\alpha ) = {\mathsf {enum}}_{C_0}(\zeta + \beta )$
. Since
![]() $\alpha < \gamma $
and
$\alpha < \gamma $
and
![]() $\gamma \in C_1$
,
$\gamma \in C_1$
,
![]() $\zeta < {\mathsf {enum}}_{C_0}^{-1}(\gamma ) = \gamma $
. Because
$\zeta < {\mathsf {enum}}_{C_0}^{-1}(\gamma ) = \gamma $
. Because
![]() $\gamma $
is additively indecomposable,
$\gamma $
is additively indecomposable,
![]() $\zeta + \beta < \gamma $
. Thus,
$\zeta + \beta < \gamma $
. Thus,
![]() ${\mathsf {next}}_{C_0}^\beta (\alpha ) = {\mathsf {enum}}_{C_0}(\zeta + \beta ) < {\mathsf {enum}}_{C_0}(\gamma ) = \gamma $
. The last statement follows from the first statement and the fact that since
${\mathsf {next}}_{C_0}^\beta (\alpha ) = {\mathsf {enum}}_{C_0}(\zeta + \beta ) < {\mathsf {enum}}_{C_0}(\gamma ) = \gamma $
. The last statement follows from the first statement and the fact that since
![]() $\gamma $
is additively and multiplicatively indecomposable and for all
$\gamma $
is additively and multiplicatively indecomposable and for all
![]() $\beta < \gamma $
,
$\beta < \gamma $
,
![]() $\omega \cdot (\beta + 1) < \gamma $
.
$\omega \cdot (\beta + 1) < \gamma $
.
Fact 2.13. (Almost everywhere fixed length measure witness uniformization) Let
![]() $\kappa $
be a cardinal,
$\kappa $
be a cardinal,
![]() $1 \leq \delta < \kappa $
and
$1 \leq \delta < \kappa $
and
![]() $1 \leq \epsilon \leq \kappa $
. Suppose
$1 \leq \epsilon \leq \kappa $
. Suppose
![]() $\kappa \rightarrow _* (\kappa )^{\delta + \epsilon }_2$
holds. Let
$\kappa \rightarrow _* (\kappa )^{\delta + \epsilon }_2$
holds. Let
![]() $R \subseteq [\kappa ]^{\delta }_* \times [\kappa ]^{\epsilon }_*$
be such that for all
$R \subseteq [\kappa ]^{\delta }_* \times [\kappa ]^{\epsilon }_*$
be such that for all
![]() $f \in [\kappa ]^{\delta }_*$
,
$f \in [\kappa ]^{\delta }_*$
,
![]() $R_f = \{g \in [\kappa ]^{\epsilon }_* : R(f,g)\} \in \mu ^\kappa _{\epsilon }$
. Then there is a club
$R_f = \{g \in [\kappa ]^{\epsilon }_* : R(f,g)\} \in \mu ^\kappa _{\epsilon }$
. Then there is a club
![]() $C \subseteq \kappa $
so that for
$C \subseteq \kappa $
so that for
![]() $f \in [C]^{\delta }_*$
,
$f \in [C]^{\delta }_*$
,
![]() $[C \setminus \sup (f) + 1]^{\epsilon }_* \subseteq R_f$
.
$[C \setminus \sup (f) + 1]^{\epsilon }_* \subseteq R_f$
.
Proof. If
![]() $h \in [\kappa ]^{\delta + \epsilon }_*$
, then let
$h \in [\kappa ]^{\delta + \epsilon }_*$
, then let
![]() $h^0 \in [\kappa ]^\delta _*$
and
$h^0 \in [\kappa ]^\delta _*$
and
![]() $h^1 \in [\kappa ]^\epsilon _*$
be defined by
$h^1 \in [\kappa ]^\epsilon _*$
be defined by
![]() $h^0 = h \upharpoonright \delta $
and
$h^0 = h \upharpoonright \delta $
and
![]() $h^1 = {\mathsf {drop}}(h,\delta )$
. Define a partition
$h^1 = {\mathsf {drop}}(h,\delta )$
. Define a partition
![]() $P : [\kappa ]^{\delta + \epsilon }_* \rightarrow 2$
by
$P : [\kappa ]^{\delta + \epsilon }_* \rightarrow 2$
by
![]() $P(h) = 0$
if and only if
$P(h) = 0$
if and only if
![]() $R(h^0,h^1)$
. By
$R(h^0,h^1)$
. By
![]() $\kappa \rightarrow _* (\kappa )^{\delta + \epsilon }_2$
, there is a club
$\kappa \rightarrow _* (\kappa )^{\delta + \epsilon }_2$
, there is a club
![]() $C \subseteq {\omega _1}$
which is homogeneous for P. Fix an
$C \subseteq {\omega _1}$
which is homogeneous for P. Fix an
![]() $f \in [C]^\delta _*$
. Since
$f \in [C]^\delta _*$
. Since
![]() $R_f \in \mu ^\kappa _\epsilon $
, there is a club
$R_f \in \mu ^\kappa _\epsilon $
, there is a club
![]() $D \subseteq C$
so that for all
$D \subseteq C$
so that for all
![]() $g \in [D]^\epsilon _*$
,
$g \in [D]^\epsilon _*$
,
![]() $R(f,g)$
holds. Pick a
$R(f,g)$
holds. Pick a
![]() $g \in [D]^\epsilon _*$
with
$g \in [D]^\epsilon _*$
with
![]() $\sup (f) < g(0)$
, and let
$\sup (f) < g(0)$
, and let
![]() $h \in [C]^{\delta + \epsilon }_*$
be defined so that
$h \in [C]^{\delta + \epsilon }_*$
be defined so that
![]() $h^0 = f$
and
$h^0 = f$
and
![]() $h^1 = g$
. Then
$h^1 = g$
. Then
![]() $P(h) = 0$
. Thus, C is homogeneous for P taking value
$P(h) = 0$
. Thus, C is homogeneous for P taking value
![]() $0$
. Now, fix an
$0$
. Now, fix an
![]() $f \in [C]^\delta _*$
. Take any
$f \in [C]^\delta _*$
. Take any
![]() $g \in [C \setminus \sup (f) + 1]^\epsilon _*$
. Let
$g \in [C \setminus \sup (f) + 1]^\epsilon _*$
. Let
![]() $h \in [C]^{\delta + \epsilon }_*$
be defined so that
$h \in [C]^{\delta + \epsilon }_*$
be defined so that
![]() $h^0 = f$
and
$h^0 = f$
and
![]() $h^1 = g$
.
$h^1 = g$
.
![]() $P(h) = 0$
implies that
$P(h) = 0$
implies that
![]() $R(f,g)$
. Thus,
$R(f,g)$
. Thus,
![]() $[C \setminus \sup (f) + 1]^\epsilon _* \subseteq R_f$
.
$[C \setminus \sup (f) + 1]^\epsilon _* \subseteq R_f$
.
If
![]() $\kappa $
is a cardinal, then let
$\kappa $
is a cardinal, then let
![]() ${\mathsf {club}}_\kappa $
denote the collection of club subsets of
${\mathsf {club}}_\kappa $
denote the collection of club subsets of
![]() $\kappa $
.
$\kappa $
.
Fact 2.14. ([Reference Chan2])
Let
![]() $\kappa $
be a cardinal satisfying
$\kappa $
be a cardinal satisfying
![]() $\kappa \rightarrow _* (\kappa )^{\kappa }_2$
and
$\kappa \rightarrow _* (\kappa )^{\kappa }_2$
and
![]() $1 \leq \epsilon < \kappa $
. Suppose
$1 \leq \epsilon < \kappa $
. Suppose
![]() $R \subseteq [\kappa ]^\epsilon _* \times {\mathsf {club}}_\kappa $
is a relation which is
$R \subseteq [\kappa ]^\epsilon _* \times {\mathsf {club}}_\kappa $
is a relation which is
![]() $\subseteq $
-downward closed in the club coordinate in the sense that for all
$\subseteq $
-downward closed in the club coordinate in the sense that for all
![]() $\ell \in [\kappa ]^\epsilon $
and all clubs
$\ell \in [\kappa ]^\epsilon $
and all clubs
![]() $C \subseteq D$
, if
$C \subseteq D$
, if
![]() $R(\ell ,D)$
, then
$R(\ell ,D)$
, then
![]() $R(\ell ,C)$
. Then there is a club
$R(\ell ,C)$
. Then there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $\ell \in [C]^\epsilon _* \cap \mathrm {dom}(R)$
,
$\ell \in [C]^\epsilon _* \cap \mathrm {dom}(R)$
,
![]() $R(\ell , C \setminus (\sup (\ell + 1))$
.
$R(\ell , C \setminus (\sup (\ell + 1))$
.
Fact 2.14 will not be used here. Fact 2.14 implies Fact 2.13; however, it requires
![]() $\kappa \rightarrow _* (\kappa )^\kappa _2$
. Fact 2.14 is generally not true for weak partition cardinals which are not strong partition cardinals. For instance, under
$\kappa \rightarrow _* (\kappa )^\kappa _2$
. Fact 2.14 is generally not true for weak partition cardinals which are not strong partition cardinals. For instance, under
![]() $\mathsf {AD}$
, Fact 2.14 fails at
$\mathsf {AD}$
, Fact 2.14 fails at
![]() $\omega _2$
. Fact 2.14 gives slightly easier proof in the case of strong partition cardinals, but the paper seeks to prove these results for weak partition cardinals so Fact 2.13 must be used in a more indirect way.
$\omega _2$
. Fact 2.14 gives slightly easier proof in the case of strong partition cardinals, but the paper seeks to prove these results for weak partition cardinals so Fact 2.13 must be used in a more indirect way.
Fact 2.15. (Everywhere wellordered measure witness uniformization) Let
![]() $\kappa $
be a cardinal,
$\kappa $
be a cardinal,
![]() $\epsilon < \kappa $
and assume
$\epsilon < \kappa $
and assume
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon + \epsilon }_2$
. If
$\kappa \rightarrow _* (\kappa )^{\epsilon + \epsilon }_2$
. If
![]() $R \subseteq \kappa \times [\kappa ]^\epsilon _*$
has the property that for all
$R \subseteq \kappa \times [\kappa ]^\epsilon _*$
has the property that for all
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $R_\alpha \in \mu ^\kappa _\epsilon $
, then there is a club
$R_\alpha \in \mu ^\kappa _\epsilon $
, then there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $[C \setminus {\mathsf {next}}^\omega _C(\alpha ) + 1]^\epsilon _* \subseteq R_\alpha $
.
$[C \setminus {\mathsf {next}}^\omega _C(\alpha ) + 1]^\epsilon _* \subseteq R_\alpha $
.
Proof. Define a new relation
![]() $S \subseteq \kappa \times [\kappa ]^\epsilon _*$
by
$S \subseteq \kappa \times [\kappa ]^\epsilon _*$
by
![]() $S(\alpha ,f)$
if and only if for all
$S(\alpha ,f)$
if and only if for all
![]() $\beta \leq \alpha $
,
$\beta \leq \alpha $
,
![]() $R(\beta ,f)$
. Note that
$R(\beta ,f)$
. Note that
![]() $S_\alpha \in \mu ^\kappa _\epsilon $
since
$S_\alpha \in \mu ^\kappa _\epsilon $
since
![]() $S_\alpha = \bigcap _{\beta \leq \alpha } R_\beta $
,
$S_\alpha = \bigcap _{\beta \leq \alpha } R_\beta $
,
![]() $R_\beta \in \mu ^\kappa _\epsilon $
for each
$R_\beta \in \mu ^\kappa _\epsilon $
for each
![]() $\beta \leq \alpha $
, and
$\beta \leq \alpha $
, and
![]() $\mu ^\kappa _\epsilon $
is
$\mu ^\kappa _\epsilon $
is
![]() $\kappa $
-complete by Fact 2.7. Applying Theorem 2.13, there is a club
$\kappa $
-complete by Fact 2.7. Applying Theorem 2.13, there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $\alpha \in [C]^1_*$
,
$\alpha \in [C]^1_*$
,
![]() $[C \setminus \alpha + 1]^\epsilon _* \subseteq S_\alpha $
.
$[C \setminus \alpha + 1]^\epsilon _* \subseteq S_\alpha $
.
Let
![]() $\alpha < \kappa $
. Note that
$\alpha < \kappa $
. Note that
![]() ${\mathsf {next}}^\omega _C(\alpha )$
is an element of C of cofinality
${\mathsf {next}}^\omega _C(\alpha )$
is an element of C of cofinality
![]() $\omega $
and thus
$\omega $
and thus
![]() ${\mathsf {next}}^\omega _C(\alpha ) \in [C]^1_*$
. Thus,
${\mathsf {next}}^\omega _C(\alpha ) \in [C]^1_*$
. Thus,
![]() $[C \setminus {\mathsf {next}}^\omega _C(\alpha ) + 1]^\epsilon _* \subseteq S_{{\mathsf {next}}^\omega _C(\alpha )}$
. Since
$[C \setminus {\mathsf {next}}^\omega _C(\alpha ) + 1]^\epsilon _* \subseteq S_{{\mathsf {next}}^\omega _C(\alpha )}$
. Since
![]() $S_{{\mathsf {next}}^\omega _C(\alpha )} \subseteq R_\alpha $
,
$S_{{\mathsf {next}}^\omega _C(\alpha )} \subseteq R_\alpha $
,
![]() $[C \setminus {\mathsf {next}}^\omega _C(\alpha ) + 1]^\epsilon _* \subseteq R_\alpha $
.
$[C \setminus {\mathsf {next}}^\omega _C(\alpha ) + 1]^\epsilon _* \subseteq R_\alpha $
.
The axiom of determinacy
![]() $\mathsf {AD}$
provides a rich theory with an abundance of partition cardinals possessing desirable structures. For each
$\mathsf {AD}$
provides a rich theory with an abundance of partition cardinals possessing desirable structures. For each
![]() $n \in \omega $
, let
$n \in \omega $
, let
![]() $\boldsymbol {\delta }_n^1$
be the supremum of the ranks of prewellorderings on
$\boldsymbol {\delta }_n^1$
be the supremum of the ranks of prewellorderings on
![]() $\mathbb {R}$
which belong to the pointclass
$\mathbb {R}$
which belong to the pointclass
![]() $\mathbf {\Delta }_n^1$
. Under
$\mathbf {\Delta }_n^1$
. Under
![]() $\mathsf {AD}$
,
$\mathsf {AD}$
,
![]() $\boldsymbol {\delta }_1^1 = {\omega _1}$
,
$\boldsymbol {\delta }_1^1 = {\omega _1}$
,
![]() $\boldsymbol {\delta }_2^1 = \omega _2$
,
$\boldsymbol {\delta }_2^1 = \omega _2$
,
![]() $\boldsymbol {\delta }_3^1 = \omega _{\omega + 1}$
,
$\boldsymbol {\delta }_3^1 = \omega _{\omega + 1}$
,
![]() $\boldsymbol {\delta }_4^1 = \omega _{\omega + 2}$
. Similarly, let
$\boldsymbol {\delta }_4^1 = \omega _{\omega + 2}$
. Similarly, let
![]() $\boldsymbol {\delta }^2_1$
be the supremum of the ranks of prewellorderings on
$\boldsymbol {\delta }^2_1$
be the supremum of the ranks of prewellorderings on
![]() $\mathbb {R}$
which belong to the pointclass
$\mathbb {R}$
which belong to the pointclass
![]() $\mathbf {\Delta }^2_1$
. If
$\mathbf {\Delta }^2_1$
. If
![]() $A \subseteq \mathbb {R}$
, then let
$A \subseteq \mathbb {R}$
, then let
![]() $\boldsymbol {\delta }_A$
be the least
$\boldsymbol {\delta }_A$
be the least
![]() $\Sigma _1$
-stable ordinals of
$\Sigma _1$
-stable ordinals of
![]() $L(A,\mathbb {R})$
, which is the least ordinal
$L(A,\mathbb {R})$
, which is the least ordinal
![]() $\delta $
so that
$\delta $
so that
![]() $L_\delta (A,\mathbb {R}) \prec _1 L(A,\mathbb {R})$
. It is the case that
$L_\delta (A,\mathbb {R}) \prec _1 L(A,\mathbb {R})$
. It is the case that
![]() $(\boldsymbol {\delta }^2_1)^{L(\mathbb {R})} = \boldsymbol {\delta }_\emptyset $
.
$(\boldsymbol {\delta }^2_1)^{L(\mathbb {R})} = \boldsymbol {\delta }_\emptyset $
.
Fact 2.16. Assume
![]() $\mathsf {AD}$
.
$\mathsf {AD}$
.
-
1. (Martin; [Reference Kechris10] Theorem 12.2, [Reference Chan3] Corollary 4.27)
 ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_{<{\omega _1}}$
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_{<{\omega _1}}$
-
2. (Martin–Paris; [Reference Kechris10] Corollary 13.5, [Reference Chan3] Theorem 5.19 and Corollary 6.17)
 $\omega _2 \rightarrow _* (\omega _2)^{<\omega _2}_2$
.
$\omega _2 \rightarrow _* (\omega _2)^{<\omega _2}_2$
.
 $\neg (\omega _2 \rightarrow _* (\omega _2)^{\omega _2}_2)$
.
$\neg (\omega _2 \rightarrow _* (\omega _2)^{\omega _2}_2)$
. -
3. (Martin; [Reference Kechris10] Theorem 11.2; Theorem [Reference Jackson9] 2.36) For any
 $n \in \omega $
,
$n \in \omega $
,
 $\boldsymbol {\delta }_{2n + 1}^1 \rightarrow _* (\boldsymbol {\delta }^1_{2n + 1})^{<{\omega _1}}_2$
.
$\boldsymbol {\delta }_{2n + 1}^1 \rightarrow _* (\boldsymbol {\delta }^1_{2n + 1})^{<{\omega _1}}_2$
. -
4. ([Reference Jackson8])
 $\boldsymbol {\delta }^1_{2n + 1} \rightarrow _* (\boldsymbol {\delta }^1_{2n + 1})^{\boldsymbol {\delta }_{2n + 1}^1}_{<\boldsymbol {\delta }^1_{2n + 1}}$
.
$\boldsymbol {\delta }^1_{2n + 1} \rightarrow _* (\boldsymbol {\delta }^1_{2n + 1})^{\boldsymbol {\delta }_{2n + 1}^1}_{<\boldsymbol {\delta }^1_{2n + 1}}$
. -
5. (Kunen; [Reference Kechris10] Theorem 15.3) For all
 $n \in \omega $
,
$n \in \omega $
,
 $\boldsymbol {\delta }^1_{2n + 2} \rightarrow _* (\boldsymbol {\delta }^1_{2n + 2})^{<{\omega _1}}_2$
.
$\boldsymbol {\delta }^1_{2n + 2} \rightarrow _* (\boldsymbol {\delta }^1_{2n + 2})^{<{\omega _1}}_2$
. -
6. ([Reference Jackson8])
 $\boldsymbol {\delta }^1_{2n + 2} \rightarrow _* (\boldsymbol {\delta }^1_{2n + 2})^{<\boldsymbol {\delta }^1_{2n + 2}}_2$
.
$\boldsymbol {\delta }^1_{2n + 2} \rightarrow _* (\boldsymbol {\delta }^1_{2n + 2})^{<\boldsymbol {\delta }^1_{2n + 2}}_2$
.
 $\neg (\boldsymbol {\delta }_{2n + 2}^1 \rightarrow _* (\boldsymbol {\delta }^1_{2n + 2})^{\boldsymbol {\delta }_{2n + 2}^1}_2)$
.
$\neg (\boldsymbol {\delta }_{2n + 2}^1 \rightarrow _* (\boldsymbol {\delta }^1_{2n + 2})^{\boldsymbol {\delta }_{2n + 2}^1}_2)$
. -
7. ([Reference Kechris, Kleinberg, Moschovakis and Hugh Woodin12]) For any
 $A \subseteq \mathbb {R}$
,
$A \subseteq \mathbb {R}$
,
 $\boldsymbol {\delta }_A \rightarrow _* (\boldsymbol {\delta }_A)^{\boldsymbol {\delta }_A}_{<\boldsymbol {\delta }_A}$
.
$\boldsymbol {\delta }_A \rightarrow _* (\boldsymbol {\delta }_A)^{\boldsymbol {\delta }_A}_{<\boldsymbol {\delta }_A}$
. -
8. ([Reference Kechris, Kleinberg, Moschovakis and Hugh Woodin12]) Assuming
 $\mathsf {DC}_{\mathbb {R}}$
,
$\mathsf {DC}_{\mathbb {R}}$
,
 $\boldsymbol {\delta }^2_1 \rightarrow _* (\boldsymbol {\delta }^2_1)^{\boldsymbol {\delta }^2_1}_{<\boldsymbol {\delta }^2_1}$
.
$\boldsymbol {\delta }^2_1 \rightarrow _* (\boldsymbol {\delta }^2_1)^{\boldsymbol {\delta }^2_1}_{<\boldsymbol {\delta }^2_1}$
.
Remark 2.17. Jackson [Reference Jackson8] established the partition relations for the projective ordinals
![]() $\boldsymbol {\delta }^1_n$
for
$\boldsymbol {\delta }^1_n$
for
![]() $1 \leq n < \omega $
by first analyzing the measures on the odd projective ordinals
$1 \leq n < \omega $
by first analyzing the measures on the odd projective ordinals
![]() $\boldsymbol {\delta }^1_{2n + 1}$
which seem to require
$\boldsymbol {\delta }^1_{2n + 1}$
which seem to require
![]() $\mathsf {AD} + \mathsf {DC}_{\mathbb {R}}$
. Kechris [Reference Kechris11] showed that if
$\mathsf {AD} + \mathsf {DC}_{\mathbb {R}}$
. Kechris [Reference Kechris11] showed that if
![]() $\mathsf {AD}$
holds, then
$\mathsf {AD}$
holds, then
![]() $L(\mathbb {R}) \models \mathsf {AD} + \mathsf {DC}$
. Thus, Jackson argument of [Reference Jackson8] applied in
$L(\mathbb {R}) \models \mathsf {AD} + \mathsf {DC}$
. Thus, Jackson argument of [Reference Jackson8] applied in
![]() $L(\mathbb {R})$
gives a good coding system for
$L(\mathbb {R})$
gives a good coding system for
![]() $(\boldsymbol {\delta }^1_{2n + 1})^{L(\mathbb {R})}$
which belongs to
$(\boldsymbol {\delta }^1_{2n + 1})^{L(\mathbb {R})}$
which belongs to
![]() $L(\mathbb {R})$
.
$L(\mathbb {R})$
.
![]() $\boldsymbol {\delta }^1_{2n + 1} = (\boldsymbol {\delta }^1_{2n + 1})^{L(\mathbb {R})}$
and a good coding system in
$\boldsymbol {\delta }^1_{2n + 1} = (\boldsymbol {\delta }^1_{2n + 1})^{L(\mathbb {R})}$
and a good coding system in
![]() $L(\mathbb {R})$
is still a good coding system in the original determinacy universe by the Moschovakis coding lemma. This shows that
$L(\mathbb {R})$
is still a good coding system in the original determinacy universe by the Moschovakis coding lemma. This shows that
![]() $\boldsymbol {\delta }^1_{2n + 1}$
is a strong partition cardinal using only the assumption of
$\boldsymbol {\delta }^1_{2n + 1}$
is a strong partition cardinal using only the assumption of
![]() $\mathsf {AD}$
.
$\mathsf {AD}$
.
3 Almost everywhere short length continuity
Definition 3.1. Let
![]() $\kappa $
be a cardinal and
$\kappa $
be a cardinal and
![]() $\epsilon \leq \kappa $
. Define an equivalence relation on
$\epsilon \leq \kappa $
. Define an equivalence relation on
![]() ${}^\epsilon \kappa $
by
${}^\epsilon \kappa $
by
![]() $f \ E_0 \ g$
if and only if there is an
$f \ E_0 \ g$
if and only if there is an
![]() $\alpha < \epsilon $
so that for all
$\alpha < \epsilon $
so that for all
![]() $\beta $
with
$\beta $
with
![]() $\alpha \leq \beta < \epsilon $
,
$\alpha \leq \beta < \epsilon $
,
![]() $f(\beta ) = g(\beta )$
.
$f(\beta ) = g(\beta )$
.
Suppose
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
is a function.
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
is a function.
![]() $\Phi $
is
$\Phi $
is
![]() $E_0$
-invariant
$E_0$
-invariant
![]() $\mu ^\kappa _\epsilon $
-almost everywhere if and only if there is a club
$\mu ^\kappa _\epsilon $
-almost everywhere if and only if there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if
$f,g \in [C]^\epsilon _*$
, if
![]() $f \ E_0 \ g$
, then
$f \ E_0 \ g$
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
Definition 3.2. Let
![]() $\kappa $
be a cardinal and
$\kappa $
be a cardinal and
![]() $\epsilon \leq \kappa $
. Define
$\epsilon \leq \kappa $
. Define
![]() $\sqsubseteq $
on
$\sqsubseteq $
on
![]() $[\kappa ]^\epsilon _*$
by
$[\kappa ]^\epsilon _*$
by
![]() $g \sqsubseteq f$
if and only if
$g \sqsubseteq f$
if and only if
![]() $g \in [\mathcal {C}_f]^\epsilon _*$
.
$g \in [\mathcal {C}_f]^\epsilon _*$
.
(This notion depends on
![]() $\kappa $
and
$\kappa $
and
![]() $\epsilon $
. Implicitly,
$\epsilon $
. Implicitly,
![]() $g \sqsubseteq f$
implies f and g are functions of the correct type.)
$g \sqsubseteq f$
implies f and g are functions of the correct type.)
Lemma 3.3. Suppose
![]() $\kappa $
is a cardinal,
$\kappa $
is a cardinal,
![]() $\epsilon < \kappa $
is an additively indecomposable ordinal with
$\epsilon < \kappa $
is an additively indecomposable ordinal with
![]() ${\mathrm {cof}}(\epsilon ) = \omega $
, and
${\mathrm {cof}}(\epsilon ) = \omega $
, and
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon \cdot \epsilon }_2$
holds. Let
$\kappa \rightarrow _* (\kappa )^{\epsilon \cdot \epsilon }_2$
holds. Let
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
be a function which is
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
be a function which is
![]() $E_0$
-invariant
$E_0$
-invariant
![]() $\mu ^\kappa _\epsilon $
-almost everywhere. Then there is a club
$\mu ^\kappa _\epsilon $
-almost everywhere. Then there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if
$f,g \in [C]^\epsilon _*$
, if
![]() $\sup (f) = \sup (g)$
, then
$\sup (f) = \sup (g)$
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
Proof. Since
![]() $\Phi $
is
$\Phi $
is
![]() $E_0$
-invariant
$E_0$
-invariant
![]() $\mu _\epsilon ^\kappa $
-almost everywhere, let
$\mu _\epsilon ^\kappa $
-almost everywhere, let
![]() $C_0 \subseteq \kappa $
be a club so that for all
$C_0 \subseteq \kappa $
be a club so that for all
![]() $f,g \in [C_0]^\epsilon _*$
, if
$f,g \in [C_0]^\epsilon _*$
, if
![]() $f \ E_0 \ g$
, then
$f \ E_0 \ g$
, then
![]() $\Phi (f) = \Phi (g)$
. Define
$\Phi (f) = \Phi (g)$
. Define
![]() $P_0 : [C_0]^\epsilon _* \rightarrow 2$
by
$P_0 : [C_0]^\epsilon _* \rightarrow 2$
by
![]() $P(f) = 0$
if and only if for all
$P(f) = 0$
if and only if for all
![]() $g \sqsubseteq f$
,
$g \sqsubseteq f$
,
![]() $\Phi (g) = \Phi (f)$
. By
$\Phi (g) = \Phi (f)$
. By
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon \cdot \epsilon }_2$
, there is a club
$\kappa \rightarrow _* (\kappa )^{\epsilon \cdot \epsilon }_2$
, there is a club
![]() $C_1 \subseteq C_0$
which is homogeneous for
$C_1 \subseteq C_0$
which is homogeneous for
![]() $P_0$
.
$P_0$
.
The claim is that
![]() $C_1$
is homogeneous for
$C_1$
is homogeneous for
![]() $P_0$
taking value
$P_0$
taking value
![]() $0$
. For the sake of obtaining a contradiction, suppose
$0$
. For the sake of obtaining a contradiction, suppose
![]() $C_1$
is homogeneous for
$C_1$
is homogeneous for
![]() $P_0$
taking value
$P_0$
taking value
![]() $1$
. Define
$1$
. Define
![]() $P_1 : [C_1]^\epsilon _* \rightarrow 2$
by
$P_1 : [C_1]^\epsilon _* \rightarrow 2$
by
![]() $P_1(f) = 0$
if and only if there exists a
$P_1(f) = 0$
if and only if there exists a
![]() $g \sqsubseteq f$
so that
$g \sqsubseteq f$
so that
![]() $\Phi (g)> \Phi (f)$
. By
$\Phi (g)> \Phi (f)$
. By
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _2$
, there is a club
$\kappa \rightarrow _* (\kappa )^\epsilon _2$
, there is a club
![]() $C_2 \subseteq C_1$
which is homogeneous for
$C_2 \subseteq C_1$
which is homogeneous for
![]() $P_1$
.
$P_1$
.
Case 1: Suppose
![]() $C_2$
is homogeneous for
$C_2$
is homogeneous for
![]() $P_1$
taking value
$P_1$
taking value
![]() $1$
. Let
$1$
. Let
![]() $Z = \{\Phi (f) : f \in [C_2]^\epsilon _*\}$
. Z has a minimal element since Z is a nonempty set of ordinals. Pick
$Z = \{\Phi (f) : f \in [C_2]^\epsilon _*\}$
. Z has a minimal element since Z is a nonempty set of ordinals. Pick
![]() $f \in [C_2]^\epsilon _*$
with
$f \in [C_2]^\epsilon _*$
with
![]() $\Phi (f) = \min (Z)$
. Note that
$\Phi (f) = \min (Z)$
. Note that
![]() $P_0(f) = 1$
and
$P_0(f) = 1$
and
![]() $P_1(f) = 1$
imply that there exists a
$P_1(f) = 1$
imply that there exists a
![]() $g \sqsubseteq f$
so that
$g \sqsubseteq f$
so that
![]() $\Phi (g) < \Phi (f)$
. However, because
$\Phi (g) < \Phi (f)$
. However, because
![]() $g \in [C_2]^\epsilon _*$
since
$g \in [C_2]^\epsilon _*$
since
![]() $C_2$
is a club,
$C_2$
is a club,
![]() $\Phi (g) \in Z$
and
$\Phi (g) \in Z$
and
![]() $\Phi (g) < \Phi (f) = \min (Z)$
which is a contradiction.
$\Phi (g) < \Phi (f) = \min (Z)$
which is a contradiction.
Case 2: Suppose
![]() $C_2$
is homogeneous for
$C_2$
is homogeneous for
![]() $P_1$
taking value
$P_1$
taking value
![]() $0$
. For any function
$0$
. For any function
![]() $h : \epsilon \cdot \epsilon \rightarrow \kappa $
, define
$h : \epsilon \cdot \epsilon \rightarrow \kappa $
, define
![]() ${\mathsf {main}}(h) : \epsilon \rightarrow \kappa $
by
${\mathsf {main}}(h) : \epsilon \rightarrow \kappa $
by
![]() ${\mathsf {main}}(h)(\alpha ) = \sup \{h(\epsilon \cdot \alpha + \beta ) : \beta < \epsilon \}$
. Define
${\mathsf {main}}(h)(\alpha ) = \sup \{h(\epsilon \cdot \alpha + \beta ) : \beta < \epsilon \}$
. Define
![]() $P_2 : [C_2]^{\epsilon \cdot \epsilon }_* \rightarrow 2$
by
$P_2 : [C_2]^{\epsilon \cdot \epsilon }_* \rightarrow 2$
by
![]() $P_2(h) = 0$
if and only if there is an
$P_2(h) = 0$
if and only if there is an
![]() $f \in [\mathcal {C}_h]^\epsilon _*$
so that
$f \in [\mathcal {C}_h]^\epsilon _*$
so that
![]() ${\mathsf {main}}(h) \sqsubseteq f$
and
${\mathsf {main}}(h) \sqsubseteq f$
and
![]() $\Phi (f) < \Phi ({\mathsf {main}}(h))$
. (Recall
$\Phi (f) < \Phi ({\mathsf {main}}(h))$
. (Recall
![]() $\mathcal {C}_h$
is the closure
$\mathcal {C}_h$
is the closure
![]() $f[\epsilon \cdot \epsilon )]$
.) By
$f[\epsilon \cdot \epsilon )]$
.) By
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon \cdot \epsilon }_2$
, there is a club
$\kappa \rightarrow _* (\kappa )^{\epsilon \cdot \epsilon }_2$
, there is a club
![]() $C_3 \subseteq C_2$
which is homogeneous for
$C_3 \subseteq C_2$
which is homogeneous for
![]() $P_2$
and consists entirely of indecomposable ordinals. Let
$P_2$
and consists entirely of indecomposable ordinals. Let
![]() $C_3^1 = \{\alpha \in C_3 : {\mathsf {enum}}_{C_3}(\alpha ) = \alpha \}$
. Let
$C_3^1 = \{\alpha \in C_3 : {\mathsf {enum}}_{C_3}(\alpha ) = \alpha \}$
. Let
![]() $f \in [C_3^1]^\epsilon _*$
with
$f \in [C_3^1]^\epsilon _*$
with
![]() $f(0)> \epsilon $
. Since
$f(0)> \epsilon $
. Since
![]() $P_1(f) = 0$
, there exists some
$P_1(f) = 0$
, there exists some
![]() $g \sqsubseteq f$
such that
$g \sqsubseteq f$
such that
![]() $\Phi (f) < \Phi (g)$
. As
$\Phi (f) < \Phi (g)$
. As
![]() $C_3^1$
is a club,
$C_3^1$
is a club,
![]() $g \in [C_3^1]^\epsilon _*$
. Because g has the correct type, let
$g \in [C_3^1]^\epsilon _*$
. Because g has the correct type, let
![]() $G : \epsilon \times \omega \rightarrow \mathrm {ON}$
witness that g has uniform cofinality
$G : \epsilon \times \omega \rightarrow \mathrm {ON}$
witness that g has uniform cofinality
![]() $\omega $
. Since g is discontinuous everywhere, by modifying G if necessary, one may assume that for all
$\omega $
. Since g is discontinuous everywhere, by modifying G if necessary, one may assume that for all
![]() $\alpha < \epsilon $
,
$\alpha < \epsilon $
,
![]() $\sup (g \upharpoonright \alpha ) < G(\alpha ,0)$
. Since
$\sup (g \upharpoonright \alpha ) < G(\alpha ,0)$
. Since
![]() ${\mathrm {cof}}(\epsilon ) = \omega $
, let
${\mathrm {cof}}(\epsilon ) = \omega $
, let
![]() $\rho : \omega \rightarrow \epsilon $
be an increasing cofinal sequence through
$\rho : \omega \rightarrow \epsilon $
be an increasing cofinal sequence through
![]() $\epsilon $
. For each
$\epsilon $
. For each
![]() $\eta < \epsilon $
, let
$\eta < \epsilon $
, let
![]() $\varpi (\eta )$
be the least n so that
$\varpi (\eta )$
be the least n so that
![]() $\eta < \rho (n)$
.
$\eta < \rho (n)$
.
Fix
![]() $\alpha < \epsilon $
. Let
$\alpha < \epsilon $
. Let
![]() $\iota ^\alpha _0 = G(\alpha ,0)$
. Let
$\iota ^\alpha _0 = G(\alpha ,0)$
. Let
![]() $\iota ^\alpha _{n + 1} = \max \{{\mathsf {next}}_{C_3}^{\omega \cdot (\rho (n) + 1)}(\iota ^\alpha _n), G(\alpha ,n + 1)\}$
. Suppose inductively, one has shown
$\iota ^\alpha _{n + 1} = \max \{{\mathsf {next}}_{C_3}^{\omega \cdot (\rho (n) + 1)}(\iota ^\alpha _n), G(\alpha ,n + 1)\}$
. Suppose inductively, one has shown
![]() $\iota ^\alpha _n < g(\alpha )$
. Then since
$\iota ^\alpha _n < g(\alpha )$
. Then since
![]() $\iota ^\alpha _n < g(\alpha )$
and
$\iota ^\alpha _n < g(\alpha )$
and
![]() $\omega \cdot (\rho (n) + 1) < g(\alpha )$
, Fact 2.12 implies that
$\omega \cdot (\rho (n) + 1) < g(\alpha )$
, Fact 2.12 implies that
![]() $\iota ^\alpha _{n + 1} < g(\alpha )$
. For each
$\iota ^\alpha _{n + 1} < g(\alpha )$
. For each
![]() $\eta < \epsilon $
, let
$\eta < \epsilon $
, let
![]() $r^\alpha (\eta ) = {\mathsf {next}}_{C_3}^{\omega \cdot (\eta + 1)}(\iota ^\alpha _{\varpi (\eta )})$
. Note that
$r^\alpha (\eta ) = {\mathsf {next}}_{C_3}^{\omega \cdot (\eta + 1)}(\iota ^\alpha _{\varpi (\eta )})$
. Note that
![]() $\iota ^\alpha _{\varpi (\eta )} < {\mathsf {next}}_{C_3}^{\omega \cdot (\eta + 1)}(\iota ^\alpha _{\varpi (\eta )}) = r^\alpha (\eta ) < {\mathsf {next}}_{C_3}^{\omega \cdot (\rho (\varpi (\eta )) + 1)}(\iota ^\alpha _{\varpi (\eta )}) \leq \iota ^\alpha _{\varpi (\eta ) + 1}$
,
$\iota ^\alpha _{\varpi (\eta )} < {\mathsf {next}}_{C_3}^{\omega \cdot (\eta + 1)}(\iota ^\alpha _{\varpi (\eta )}) = r^\alpha (\eta ) < {\mathsf {next}}_{C_3}^{\omega \cdot (\rho (\varpi (\eta )) + 1)}(\iota ^\alpha _{\varpi (\eta )}) \leq \iota ^\alpha _{\varpi (\eta ) + 1}$
,
![]() $r^\alpha \in [C_3]^\epsilon _*$
and
$r^\alpha \in [C_3]^\epsilon _*$
and
![]() $\sup (r^\alpha ) = \sup \{\iota ^\alpha _n : n \in \omega \} = g(\alpha )$
. Let
$\sup (r^\alpha ) = \sup \{\iota ^\alpha _n : n \in \omega \} = g(\alpha )$
. Let
![]() $F_\alpha $
be the collection of
$F_\alpha $
be the collection of
![]() $\gamma \in f[\epsilon ]$
such that
$\gamma \in f[\epsilon ]$
such that
![]() $\sup (g \upharpoonright \alpha ) < \gamma < g(\alpha )$
and there is no ordinal
$\sup (g \upharpoonright \alpha ) < \gamma < g(\alpha )$
and there is no ordinal
![]() $\eta < \epsilon $
so that
$\eta < \epsilon $
so that
![]() $\sup (r^\alpha \upharpoonright \eta ) = \gamma $
. Note that
$\sup (r^\alpha \upharpoonright \eta ) = \gamma $
. Note that
![]() ${\mathrm {ot}}(F_\alpha ) < \epsilon $
since
${\mathrm {ot}}(F_\alpha ) < \epsilon $
since
![]() $g \sqsubseteq f$
. Thus,
$g \sqsubseteq f$
. Thus,
![]() ${\mathrm {ot}}(r^\alpha [\epsilon ] \cup F_\alpha ) = \epsilon $
since
${\mathrm {ot}}(r^\alpha [\epsilon ] \cup F_\alpha ) = \epsilon $
since
![]() $\epsilon $
is additively indecomposable,
$\epsilon $
is additively indecomposable,
![]() ${\mathrm {ot}}(F_\alpha ) < \epsilon $
and
${\mathrm {ot}}(F_\alpha ) < \epsilon $
and
![]() $\sup (F_\alpha ) \leq g(\alpha ) = \sup (r^\alpha )$
. Let
$\sup (F_\alpha ) \leq g(\alpha ) = \sup (r^\alpha )$
. Let
![]() $s^\alpha : \epsilon \rightarrow (r^\alpha [\epsilon ] \cup F_\alpha )$
be the unique increasing function which enumerates
$s^\alpha : \epsilon \rightarrow (r^\alpha [\epsilon ] \cup F_\alpha )$
be the unique increasing function which enumerates
![]() $r[\epsilon ] \cup F_\alpha $
. Note that
$r[\epsilon ] \cup F_\alpha $
. Note that
![]() $s^\alpha $
has the correct type and
$s^\alpha $
has the correct type and
![]() $\sup (s^\alpha ) = g(\alpha )$
. Define
$\sup (s^\alpha ) = g(\alpha )$
. Define
![]() $h : \epsilon \cdot \epsilon \rightarrow C_3$
by
$h : \epsilon \cdot \epsilon \rightarrow C_3$
by
![]() $h(\epsilon \cdot \alpha + \eta ) = s^\alpha (\eta )$
whenever
$h(\epsilon \cdot \alpha + \eta ) = s^\alpha (\eta )$
whenever
![]() $\alpha ,\eta < \epsilon $
. Note that
$\alpha ,\eta < \epsilon $
. Note that
![]() $h \in [C_3]^{\epsilon \cdot \epsilon }_*$
,
$h \in [C_3]^{\epsilon \cdot \epsilon }_*$
,
![]() $f \in [\mathcal {C}_h]^\epsilon _*$
,
$f \in [\mathcal {C}_h]^\epsilon _*$
,
![]() ${\mathsf {main}}(h) = g \sqsubseteq f$
and
${\mathsf {main}}(h) = g \sqsubseteq f$
and
![]() $\Phi ({\mathsf {main}}(h)) = \Phi (g)> \Phi (f)$
. So
$\Phi ({\mathsf {main}}(h)) = \Phi (g)> \Phi (f)$
. So
![]() $P_2(h) = 0$
and thus
$P_2(h) = 0$
and thus
![]() $C_3$
is homogeneous for
$C_3$
is homogeneous for
![]() $P_2$
taking value
$P_2$
taking value
![]() $0$
.
$0$
.
Let
![]() $C_3^0 = C_3$
. If
$C_3^0 = C_3$
. If
![]() $C_3^n$
has been defined, then let
$C_3^n$
has been defined, then let
![]() $C_3^{n + 1} = \{\alpha \in C_3^n : {\mathsf {enum}}_{C_3^n}(\alpha ) = \alpha \}$
. For
$C_3^{n + 1} = \{\alpha \in C_3^n : {\mathsf {enum}}_{C_3^n}(\alpha ) = \alpha \}$
. For
![]() $\alpha \in C_3$
, let
$\alpha \in C_3$
, let
![]() $\varsigma (\alpha ) = \sup \{n \leq \varpi (\alpha ) + 1 : \alpha \in C_3^n\}$
. Let Y be the collection of
$\varsigma (\alpha ) = \sup \{n \leq \varpi (\alpha ) + 1 : \alpha \in C_3^n\}$
. Let Y be the collection of
![]() $f \in [C_3^1]^\epsilon _*$
with the property that for all
$f \in [C_3^1]^\epsilon _*$
with the property that for all
![]() $1 \leq n < \omega $
, there exists an
$1 \leq n < \omega $
, there exists an
![]() $\alpha < \epsilon $
so that for all
$\alpha < \epsilon $
so that for all
![]() $\beta \geq \alpha $
,
$\beta \geq \alpha $
,
![]() $\varsigma (f(\beta )) \geq n$
. Let
$\varsigma (f(\beta )) \geq n$
. Let
![]() $Z = \{\Phi (f) : f \in Y\}$
. Since Z is a nonempty set of ordinals, Z has a minimal element. Let
$Z = \{\Phi (f) : f \in Y\}$
. Since Z is a nonempty set of ordinals, Z has a minimal element. Let
![]() $g \in Y$
be such that
$g \in Y$
be such that
![]() $\Phi (g) = \min (Z)$
. Since g is of the correct type, let
$\Phi (g) = \min (Z)$
. Since g is of the correct type, let
![]() $G : \epsilon \times \omega \rightarrow \kappa $
witness that g has uniform cofinality
$G : \epsilon \times \omega \rightarrow \kappa $
witness that g has uniform cofinality
![]() $\omega $
. Since g is discontinuous, one may assume that for all
$\omega $
. Since g is discontinuous, one may assume that for all
![]() $\alpha < \epsilon $
,
$\alpha < \epsilon $
,
![]() $\sup (g \upharpoonright \alpha ) < G(\alpha ,0)$
.
$\sup (g \upharpoonright \alpha ) < G(\alpha ,0)$
.
Fix
![]() $\alpha < \epsilon $
. Let
$\alpha < \epsilon $
. Let
![]() $\iota ^\alpha _0 = G(\alpha ,0)$
. Let
$\iota ^\alpha _0 = G(\alpha ,0)$
. Let
![]() $\iota ^\alpha _{n + 1} = \max \{{\mathsf {next}}_{C_3^{\varsigma (g(\alpha )) - 1}}^{\omega \cdot (\rho (n) + 1)}(\iota ^\alpha _n), G(\alpha , n + 1)\}\}$
. Suppose inductively it has been shown that
$\iota ^\alpha _{n + 1} = \max \{{\mathsf {next}}_{C_3^{\varsigma (g(\alpha )) - 1}}^{\omega \cdot (\rho (n) + 1)}(\iota ^\alpha _n), G(\alpha , n + 1)\}\}$
. Suppose inductively it has been shown that
![]() $\iota ^\alpha _n < g(\alpha )$
. Then since
$\iota ^\alpha _n < g(\alpha )$
. Then since
![]() $\iota ^\alpha _{n} < g(\alpha )$
,
$\iota ^\alpha _{n} < g(\alpha )$
,
![]() $\omega \cdot (\rho (n) + 1) < g(\alpha )$
and
$\omega \cdot (\rho (n) + 1) < g(\alpha )$
and
![]() $g(\alpha ) \in C^{\varsigma (g(\alpha ))}_3 = \{\gamma \in C_3^{\varsigma (g(\alpha )) - 1} : {\mathsf {enum}}_{C^{\varsigma (g(\alpha )) - 1}_3}(\gamma ) = \gamma \}$
, Fact 2.12 implies that
$g(\alpha ) \in C^{\varsigma (g(\alpha ))}_3 = \{\gamma \in C_3^{\varsigma (g(\alpha )) - 1} : {\mathsf {enum}}_{C^{\varsigma (g(\alpha )) - 1}_3}(\gamma ) = \gamma \}$
, Fact 2.12 implies that
![]() $\iota ^\alpha _{n + 1} < g(\alpha )$
. For each
$\iota ^\alpha _{n + 1} < g(\alpha )$
. For each
![]() $\eta < \epsilon $
, let
$\eta < \epsilon $
, let
![]() $r^\alpha (\eta ) = {\mathsf {next}}^{\omega \cdot (\eta + 1)}_{C^{\varsigma (g(\alpha )) - 1}_3}(\iota ^\alpha _{\varpi (\eta )})$
. Note that
$r^\alpha (\eta ) = {\mathsf {next}}^{\omega \cdot (\eta + 1)}_{C^{\varsigma (g(\alpha )) - 1}_3}(\iota ^\alpha _{\varpi (\eta )})$
. Note that
![]() $\iota ^\alpha _{\varpi (\eta )} < r^\alpha (\eta ) < \iota ^{\alpha }_{\varpi (\eta ) + 1}$
,
$\iota ^\alpha _{\varpi (\eta )} < r^\alpha (\eta ) < \iota ^{\alpha }_{\varpi (\eta ) + 1}$
,
![]() $r^\alpha \in [C^{\varsigma (g(\alpha )) - 1}_3]^\epsilon _*$
and
$r^\alpha \in [C^{\varsigma (g(\alpha )) - 1}_3]^\epsilon _*$
and
![]() $\sup (r^\alpha ) = \sup \{\iota _n^\alpha : n \in \omega \} = g(\alpha )$
. Let
$\sup (r^\alpha ) = \sup \{\iota _n^\alpha : n \in \omega \} = g(\alpha )$
. Let
![]() $h : \epsilon \cdot \epsilon \rightarrow C_3$
be defined by
$h : \epsilon \cdot \epsilon \rightarrow C_3$
be defined by
![]() $h(\epsilon \cdot \alpha + \eta ) = r^\alpha (\eta )$
whenever
$h(\epsilon \cdot \alpha + \eta ) = r^\alpha (\eta )$
whenever
![]() $\alpha ,\eta < \epsilon $
. Note that
$\alpha ,\eta < \epsilon $
. Note that
![]() $h \in [C_3]^{\epsilon \cdot \epsilon }_*$
and
$h \in [C_3]^{\epsilon \cdot \epsilon }_*$
and
![]() ${\mathsf {main}}(h) = g$
. Since
${\mathsf {main}}(h) = g$
. Since
![]() $P_2(h) = 0$
, there is an
$P_2(h) = 0$
, there is an
![]() $f \in [\mathcal {C}_h]^\epsilon _*$
so that
$f \in [\mathcal {C}_h]^\epsilon _*$
so that
![]() $g = {\mathsf {main}}(h) \sqsubseteq f$
and
$g = {\mathsf {main}}(h) \sqsubseteq f$
and
![]() $\Phi (f) < \Phi ({\mathsf {main}}(h)) = \Phi (g)$
. For each
$\Phi (f) < \Phi ({\mathsf {main}}(h)) = \Phi (g)$
. For each
![]() $n \in \omega $
, let
$n \in \omega $
, let
![]() $\delta _n < \epsilon $
be least ordinal
$\delta _n < \epsilon $
be least ordinal
![]() $\delta $
so that for all
$\delta $
so that for all
![]() $\alpha $
with
$\alpha $
with
![]() $\delta \leq \alpha < \epsilon $
,
$\delta \leq \alpha < \epsilon $
,
![]() $\varsigma (g(\alpha )) - 1 \geq n$
. For each
$\varsigma (g(\alpha )) - 1 \geq n$
. For each
![]() $n \in \omega $
, let
$n \in \omega $
, let
![]() $\eta _n < \epsilon $
be the least
$\eta _n < \epsilon $
be the least
![]() $\eta $
so that
$\eta $
so that
![]() $f(\eta ) \geq g(\delta _n)$
which exists since
$f(\eta ) \geq g(\delta _n)$
which exists since
![]() $g = {\mathsf {main}}(h) \sqsubseteq f$
. For all
$g = {\mathsf {main}}(h) \sqsubseteq f$
. For all
![]() $\eta \geq \eta _n$
, since
$\eta \geq \eta _n$
, since
![]() $f \in [\mathcal {C}_h]^\epsilon _*$
, there is a unique
$f \in [\mathcal {C}_h]^\epsilon _*$
, there is a unique
![]() $\alpha \geq \delta _n$
so that
$\alpha \geq \delta _n$
so that
![]() $f(\eta ) \in \mathcal {C}_{r^\alpha } \subseteq C_3^{\varsigma (g(\alpha )) - 1} \subseteq C_3^{n}$
. Thus, it has been shown that for all
$f(\eta ) \in \mathcal {C}_{r^\alpha } \subseteq C_3^{\varsigma (g(\alpha )) - 1} \subseteq C_3^{n}$
. Thus, it has been shown that for all
![]() $n \in \omega $
, there is a
$n \in \omega $
, there is a
![]() $\eta _n < \epsilon $
so that for all
$\eta _n < \epsilon $
so that for all
![]() $\eta $
with
$\eta $
with
![]() $\eta _n \leq \eta < \epsilon $
,
$\eta _n \leq \eta < \epsilon $
,
![]() $\varsigma (f(\eta )) \geq n$
. In particular,
$\varsigma (f(\eta )) \geq n$
. In particular,
![]() $\varsigma (f(\eta _2)) \in C^2_3$
. (There is a possibility that
$\varsigma (f(\eta _2)) \in C^2_3$
. (There is a possibility that
![]() $f \notin Y$
since
$f \notin Y$
since
![]() $f \notin [C_3^1]^\epsilon _*$
because an initial segment of f takes value in
$f \notin [C_3^1]^\epsilon _*$
because an initial segment of f takes value in
![]() $C^0_3 \setminus C^1_3$
. However, an initial segment of f can be swapped to obtain an element
$C^0_3 \setminus C^1_3$
. However, an initial segment of f can be swapped to obtain an element
![]() $k \in Y$
. The details follow.) Let
$k \in Y$
. The details follow.) Let
![]() $\sigma \in [C_3^1]^{\eta _2}_*$
be defined by
$\sigma \in [C_3^1]^{\eta _2}_*$
be defined by
![]() $\sigma (\nu ) = {\mathsf {next}}_{C_3^1}^{\omega \cdot (\nu + 1)}(0)$
for each
$\sigma (\nu ) = {\mathsf {next}}_{C_3^1}^{\omega \cdot (\nu + 1)}(0)$
for each
![]() $\nu < \eta _2$
. Note that
$\nu < \eta _2$
. Note that
![]() $\sup (\sigma ) \leq {\mathsf {next}}^{\omega \cdot (\eta _2 + 1)}_{C_3^1}(0) < f(\eta _2)$
by Fact 2.12 since
$\sup (\sigma ) \leq {\mathsf {next}}^{\omega \cdot (\eta _2 + 1)}_{C_3^1}(0) < f(\eta _2)$
by Fact 2.12 since
![]() $\omega \cdot (\eta _2 + 1) < f(\eta _2)$
,
$\omega \cdot (\eta _2 + 1) < f(\eta _2)$
,
![]() $f(\eta _2) \in C^2_3$
and
$f(\eta _2) \in C^2_3$
and
![]() $C^2_3 = \{\alpha \in C_3^1 : {\mathsf {enum}}_{C_3^1}(\alpha ) = \alpha \}$
. Let
$C^2_3 = \{\alpha \in C_3^1 : {\mathsf {enum}}_{C_3^1}(\alpha ) = \alpha \}$
. Let
![]() $k \in [C_3^1]^\epsilon _*$
be defined as
$k \in [C_3^1]^\epsilon _*$
be defined as
![]() $k = \sigma \hat {\ }{\mathsf {drop}}(f,\eta _2)$
. Note that k also has the property that for all
$k = \sigma \hat {\ }{\mathsf {drop}}(f,\eta _2)$
. Note that k also has the property that for all
![]() $1 \leq n < \omega $
, there is an
$1 \leq n < \omega $
, there is an
![]() $\eta < \epsilon $
so that for all
$\eta < \epsilon $
so that for all
![]() $\alpha $
with
$\alpha $
with
![]() $\eta \leq \alpha < \epsilon $
,
$\eta \leq \alpha < \epsilon $
,
![]() $\varsigma (k(\alpha )) \geq n$
. Thus,
$\varsigma (k(\alpha )) \geq n$
. Thus,
![]() $k \in Y$
and
$k \in Y$
and
![]() $\Phi (k) \in Z$
. Since
$\Phi (k) \in Z$
. Since
![]() $k \ E_0 \ f$
, one has that
$k \ E_0 \ f$
, one has that
![]() $\Phi (k) = \Phi (f) < \Phi (g) = \min (Z)$
. Contradiction.
$\Phi (k) = \Phi (f) < \Phi (g) = \min (Z)$
. Contradiction.
Since Case 1 and Case 2 both lead to contradictions,
![]() $P_1$
is a partition with no homogeneous club which is impossible since
$P_1$
is a partition with no homogeneous club which is impossible since
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _2$
holds. Thus,
$\kappa \rightarrow _* (\kappa )^\epsilon _2$
holds. Thus,
![]() $C_1$
must be homogeneous for
$C_1$
must be homogeneous for
![]() $P_0$
taking value
$P_0$
taking value
![]() $0$
.
$0$
.
Now, suppose
![]() $f,g \in [C_1]^\epsilon _*$
with
$f,g \in [C_1]^\epsilon _*$
with
![]() $\sup (f) = \sup (g)$
. Since
$\sup (f) = \sup (g)$
. Since
![]() $\epsilon $
is additively indecomposable,
$\epsilon $
is additively indecomposable,
![]() ${\mathrm {ot}}(f[\epsilon ] \cup g[\epsilon ]) = \epsilon $
. Define
${\mathrm {ot}}(f[\epsilon ] \cup g[\epsilon ]) = \epsilon $
. Define
![]() $h \in [C_1]^\epsilon _*$
by recursion as follows: Let
$h \in [C_1]^\epsilon _*$
by recursion as follows: Let
![]() $h(0) = \min (f[\epsilon ] \cup g[\epsilon ])$
. If
$h(0) = \min (f[\epsilon ] \cup g[\epsilon ])$
. If
![]() $\beta < \epsilon $
and
$\beta < \epsilon $
and
![]() $h \upharpoonright \beta $
has been defined, then let
$h \upharpoonright \beta $
has been defined, then let
![]() $h(\beta )$
be the least element of
$h(\beta )$
be the least element of
![]() $f[\epsilon ] \cup g[\epsilon ]$
greater than
$f[\epsilon ] \cup g[\epsilon ]$
greater than
![]() $\sup (h \upharpoonright \beta ) + 1$
. Note that h is increasing, discontinuous and can be shown to have uniform cofinality
$\sup (h \upharpoonright \beta ) + 1$
. Note that h is increasing, discontinuous and can be shown to have uniform cofinality
![]() $\omega $
using the witnesses to f and g having uniform cofinality
$\omega $
using the witnesses to f and g having uniform cofinality
![]() $\omega $
. Observe that
$\omega $
. Observe that
![]() $P_1(h) = 0$
,
$P_1(h) = 0$
,
![]() $f \sqsubseteq h$
and
$f \sqsubseteq h$
and
![]() $g \sqsubseteq h$
imply that
$g \sqsubseteq h$
imply that
![]() $\Phi (f) = \Phi (h) = \Phi (g)$
. The proof is complete.
$\Phi (f) = \Phi (h) = \Phi (g)$
. The proof is complete.
Definition 3.4. Let
![]() $\kappa $
be cardinal,
$\kappa $
be cardinal,
![]() $\epsilon < \kappa $
,
$\epsilon < \kappa $
,
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _2$
holds,
$\kappa \rightarrow _* (\kappa )^\epsilon _2$
holds,
![]() $C \subseteq \kappa $
be a club and
$C \subseteq \kappa $
be a club and
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
be a function. Say that
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
be a function. Say that
![]() $\Phi $
depends only on the supremum relative to C if and only if for all
$\Phi $
depends only on the supremum relative to C if and only if for all
![]() $f,g \in [C]^\epsilon _*$
, if
$f,g \in [C]^\epsilon _*$
, if
![]() $\sup (f) = \sup (g)$
, then
$\sup (f) = \sup (g)$
, then
![]() $\Phi (f) = \Phi (g)$
. Say that
$\Phi (f) = \Phi (g)$
. Say that
![]() $\Phi $
is
$\Phi $
is
![]() $\sqsubseteq $
-constant on
$\sqsubseteq $
-constant on
![]() $[C]^\epsilon _*$
if and only if for all
$[C]^\epsilon _*$
if and only if for all
![]() $f \in [C]^\epsilon _*$
, for all
$f \in [C]^\epsilon _*$
, for all
![]() $g \sqsubseteq f$
,
$g \sqsubseteq f$
,
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
A property
![]() $\varphi (f)$
on
$\varphi (f)$
on
![]() $[\kappa ]^\epsilon _*$
holds
$[\kappa ]^\epsilon _*$
holds
![]() $\mu ^\kappa _\epsilon $
-almost everywhere if and only if there is a club
$\mu ^\kappa _\epsilon $
-almost everywhere if and only if there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f \in [C]^\epsilon _*$
,
$f \in [C]^\epsilon _*$
,
![]() $\varphi (f)$
holds. To express
$\varphi (f)$
holds. To express
![]() $\Phi $
is
$\Phi $
is
![]() $\sqsubseteq $
-constant
$\sqsubseteq $
-constant
![]() $\mu ^\kappa _\epsilon $
-almost everywhere involves a formula
$\mu ^\kappa _\epsilon $
-almost everywhere involves a formula
![]() $\varphi _0(f)$
which only involves f. To express
$\varphi _0(f)$
which only involves f. To express
![]() $\Phi $
depends only on the supremum relative to C requires a formula
$\Phi $
depends only on the supremum relative to C requires a formula
![]() $\varphi _1(f)$
which has C itself as a parameter. This causes some technical difficulties which can easily be resolved using the club uniformization principle, Fact 2.14, if
$\varphi _1(f)$
which has C itself as a parameter. This causes some technical difficulties which can easily be resolved using the club uniformization principle, Fact 2.14, if
![]() $\kappa \rightarrow _* (\kappa )^\kappa _2$
. However, at weak partition cardinals which are not strong partition cardinals, Fact 2.13 will need to be used together with the next result.
$\kappa \rightarrow _* (\kappa )^\kappa _2$
. However, at weak partition cardinals which are not strong partition cardinals, Fact 2.13 will need to be used together with the next result.
Fact 3.5. Suppose
![]() $\kappa $
is a cardinal,
$\kappa $
is a cardinal,
![]() $\epsilon < \kappa $
is an additively indecomposable ordinal,
$\epsilon < \kappa $
is an additively indecomposable ordinal,
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _2$
and
$\kappa \rightarrow _* (\kappa )^\epsilon _2$
and
![]() $C \subseteq \kappa $
is a club.
$C \subseteq \kappa $
is a club.
![]() $\Phi $
depends on supremum relative to C if and only if
$\Phi $
depends on supremum relative to C if and only if
![]() $\Phi $
is
$\Phi $
is
![]() $\sqsubseteq $
-constant on
$\sqsubseteq $
-constant on
![]() $[C]^\epsilon _*$
.
$[C]^\epsilon _*$
.
Proof. Suppose
![]() $\Phi $
depends only on the supremum relative to C. Suppose
$\Phi $
depends only on the supremum relative to C. Suppose
![]() $f \in [C]^\epsilon _*$
and
$f \in [C]^\epsilon _*$
and
![]() $g \sqsubseteq f$
. Then
$g \sqsubseteq f$
. Then
![]() $\sup (f) = \sup (g)$
and thus
$\sup (f) = \sup (g)$
and thus
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
Suppose
![]() $\Phi $
is
$\Phi $
is
![]() $\sqsubseteq $
-constant on
$\sqsubseteq $
-constant on
![]() $[C]^\epsilon _*$
. Let
$[C]^\epsilon _*$
. Let
![]() $f,g \in [C]^\epsilon _*$
be such that
$f,g \in [C]^\epsilon _*$
be such that
![]() $\sup (f) = \sup (g)$
. Since
$\sup (f) = \sup (g)$
. Since
![]() $\epsilon < \kappa $
is an additively indecomposable ordinal and
$\epsilon < \kappa $
is an additively indecomposable ordinal and
![]() $\sup (f) = \sup (g)$
,
$\sup (f) = \sup (g)$
,
![]() ${\mathrm {ot}}(f[\epsilon ] \cup g[\epsilon ]) = \epsilon $
. Let
${\mathrm {ot}}(f[\epsilon ] \cup g[\epsilon ]) = \epsilon $
. Let
![]() $h : \epsilon \rightarrow C$
be defined by induction as follows: Let
$h : \epsilon \rightarrow C$
be defined by induction as follows: Let
![]() $h(0) = \min (f[\epsilon ] \cup g[\epsilon ])$
. If
$h(0) = \min (f[\epsilon ] \cup g[\epsilon ])$
. If
![]() $\beta < \epsilon $
and
$\beta < \epsilon $
and
![]() $h \upharpoonright \beta $
has been defined, then let
$h \upharpoonright \beta $
has been defined, then let
![]() $h(\beta )$
be the least element of
$h(\beta )$
be the least element of
![]() $f[\epsilon ] \cup g[\epsilon ]$
greater than
$f[\epsilon ] \cup g[\epsilon ]$
greater than
![]() $\sup (h \upharpoonright \beta )$
. Then
$\sup (h \upharpoonright \beta )$
. Then
![]() $f \sqsubseteq h$
and
$f \sqsubseteq h$
and
![]() $g \sqsubseteq h$
. Since
$g \sqsubseteq h$
. Since
![]() $\Phi $
is
$\Phi $
is
![]() $\sqsubseteq $
-constant on
$\sqsubseteq $
-constant on
![]() $[C]^\epsilon _*$
, one has that
$[C]^\epsilon _*$
, one has that
![]() $\Phi (f) = \Phi (h) = \Phi (g)$
.
$\Phi (f) = \Phi (h) = \Phi (g)$
.
Theorem 3.6. Suppose
![]() $\kappa $
is a cardinal and
$\kappa $
is a cardinal and
![]() $\epsilon < \kappa $
is a limit ordinal with
$\epsilon < \kappa $
is a limit ordinal with
![]() ${\mathrm {cof}}(\epsilon ) = \omega $
. Let
${\mathrm {cof}}(\epsilon ) = \omega $
. Let
![]() $\epsilon _0 < \epsilon $
and
$\epsilon _0 < \epsilon $
and
![]() $\epsilon _1 \leq \epsilon $
be such that
$\epsilon _1 \leq \epsilon $
be such that
![]() $\epsilon = \epsilon _0 + \epsilon _1$
and
$\epsilon = \epsilon _0 + \epsilon _1$
and
![]() $\epsilon _1$
is an additively indecomposable ordinal. Suppose
$\epsilon _1$
is an additively indecomposable ordinal. Suppose
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon }_2$
and
$\kappa \rightarrow _* (\kappa )^{\epsilon }_2$
and
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon _1 \cdot \epsilon _1}_2$
hold. Let
$\kappa \rightarrow _* (\kappa )^{\epsilon _1 \cdot \epsilon _1}_2$
hold. Let
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
be a function which is
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
be a function which is
![]() $E_0$
-invariant
$E_0$
-invariant
![]() $\mu ^\kappa _\epsilon $
-almost everywhere. Then there is a club
$\mu ^\kappa _\epsilon $
-almost everywhere. Then there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if
$f,g \in [C]^\epsilon _*$
, if
![]() $\sup (f) = \sup (g)$
, then
$\sup (f) = \sup (g)$
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
Proof. Since
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
is
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
is
![]() $E_0$
-invariant
$E_0$
-invariant
![]() $\mu ^\kappa _\epsilon $
-almost everywhere, let
$\mu ^\kappa _\epsilon $
-almost everywhere, let
![]() $C_0 \subseteq \kappa $
be a club so that for all
$C_0 \subseteq \kappa $
be a club so that for all
![]() $f,g \in [C_0]^\epsilon _*$
, if
$f,g \in [C_0]^\epsilon _*$
, if
![]() $f \ E_0 \ g$
, then
$f \ E_0 \ g$
, then
![]() $\Phi (f) = \Phi (g)$
. For each
$\Phi (f) = \Phi (g)$
. For each
![]() $\sigma \in [C_0]^{\epsilon _0}_*$
, define
$\sigma \in [C_0]^{\epsilon _0}_*$
, define
![]() $\Phi _\sigma : [C_0 \setminus \sup (\sigma ) + 1]^{\epsilon _1}_* \rightarrow \mathrm {ON}$
by
$\Phi _\sigma : [C_0 \setminus \sup (\sigma ) + 1]^{\epsilon _1}_* \rightarrow \mathrm {ON}$
by
![]() $\Phi _\sigma (\ell ) = \Phi (\sigma \hat {\ }\ell )$
. Note that
$\Phi _\sigma (\ell ) = \Phi (\sigma \hat {\ }\ell )$
. Note that
![]() $\Phi _\sigma $
is
$\Phi _\sigma $
is
![]() $E_0$
-invariant on
$E_0$
-invariant on
![]() $[C_0 \setminus (\sup (\sigma ) + 1)]^{\epsilon _1}_*$
. Since
$[C_0 \setminus (\sup (\sigma ) + 1)]^{\epsilon _1}_*$
. Since
![]() ${\mathrm {cof}}(\epsilon ) = \omega $
implies that
${\mathrm {cof}}(\epsilon ) = \omega $
implies that
![]() ${\mathrm {cof}}(\epsilon _1) = \omega $
,
${\mathrm {cof}}(\epsilon _1) = \omega $
,
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon _1 \cdot \epsilon _1}_2$
and Lemma 3.3 imply there is a club
$\kappa \rightarrow _* (\kappa )^{\epsilon _1 \cdot \epsilon _1}_2$
and Lemma 3.3 imply there is a club
![]() $D \subseteq C_0 \setminus (\sup (\sigma ) + 1)$
so that for all
$D \subseteq C_0 \setminus (\sup (\sigma ) + 1)$
so that for all
![]() $\ell ,\iota \in [D]_*^{\epsilon _1}$
, if
$\ell ,\iota \in [D]_*^{\epsilon _1}$
, if
![]() $\sup (\ell ) = \sup (\iota )$
, then
$\sup (\ell ) = \sup (\iota )$
, then
![]() $\Phi _\sigma (\ell ) = \Phi _\sigma (\iota )$
.
$\Phi _\sigma (\ell ) = \Phi _\sigma (\iota )$
.
Define
![]() $R \subseteq [C_0]^{\epsilon _0}_* \times [\kappa ]^{\epsilon _1}_*$
by
$R \subseteq [C_0]^{\epsilon _0}_* \times [\kappa ]^{\epsilon _1}_*$
by
![]() $R(\sigma ,\ell )$
if and only if for all
$R(\sigma ,\ell )$
if and only if for all
![]() $\iota \sqsubseteq \ell $
,
$\iota \sqsubseteq \ell $
,
![]() $\Phi _\sigma (\iota ) = \Phi _\sigma (\ell )$
. By the observation of the previous paragraph, for each
$\Phi _\sigma (\iota ) = \Phi _\sigma (\ell )$
. By the observation of the previous paragraph, for each
![]() $\sigma \in [C_0]^{\epsilon _0}_*$
, there is a club D so that
$\sigma \in [C_0]^{\epsilon _0}_*$
, there is a club D so that
![]() $\Phi _\sigma $
depends only on supremum relative to D. By Fact 3.5,
$\Phi _\sigma $
depends only on supremum relative to D. By Fact 3.5,
![]() $\Phi _\sigma $
is
$\Phi _\sigma $
is
![]() $\sqsubseteq $
-constant on
$\sqsubseteq $
-constant on
![]() $[D]^{\epsilon _1}_*$
. Thus,
$[D]^{\epsilon _1}_*$
. Thus,
![]() $[D]^{\epsilon _1}_* \subseteq R_\sigma $
. This shows that for all
$[D]^{\epsilon _1}_* \subseteq R_\sigma $
. This shows that for all
![]() $\sigma \in [C_0]^{\epsilon _0}_*$
,
$\sigma \in [C_0]^{\epsilon _0}_*$
,
![]() $R_\sigma \in \mu ^\kappa _{\epsilon _1}$
. By
$R_\sigma \in \mu ^\kappa _{\epsilon _1}$
. By
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon }_2$
and Fact 2.13, there is a club
$\kappa \rightarrow _* (\kappa )^{\epsilon }_2$
and Fact 2.13, there is a club
![]() $C_1 \subseteq C_0$
so that for all
$C_1 \subseteq C_0$
so that for all
![]() $\sigma \in [C_1]^{\epsilon _0}_*$
,
$\sigma \in [C_1]^{\epsilon _0}_*$
,
![]() $[C_1 \setminus (\sup (\sigma ) + 1)]^{\epsilon _1}_* \subseteq R_\sigma $
.
$[C_1 \setminus (\sup (\sigma ) + 1)]^{\epsilon _1}_* \subseteq R_\sigma $
.
Let
![]() $\tau \in [C_1]^{\epsilon _0}_*$
be defined by
$\tau \in [C_1]^{\epsilon _0}_*$
be defined by
![]() $\tau (\alpha ) = {\mathsf {enum}}_{C_1}(\omega \cdot \alpha + \omega )$
for each
$\tau (\alpha ) = {\mathsf {enum}}_{C_1}(\omega \cdot \alpha + \omega )$
for each
![]() $\alpha < \epsilon _0$
. Let
$\alpha < \epsilon _0$
. Let
![]() $C_2 = C_1 \setminus \sup (\tau ) + 1$
. Now, suppose
$C_2 = C_1 \setminus \sup (\tau ) + 1$
. Now, suppose
![]() $f,g \in [C_2]^{\epsilon }_*$
and
$f,g \in [C_2]^{\epsilon }_*$
and
![]() $\sup (f) = \sup (g)$
. Let
$\sup (f) = \sup (g)$
. Let
![]() $\sigma _0,\sigma _1 \in [C_2]^{\epsilon _0}_*$
and
$\sigma _0,\sigma _1 \in [C_2]^{\epsilon _0}_*$
and
![]() $\ell _0,\ell _1 \in [C_2]^{\epsilon _1}_*$
be such that
$\ell _0,\ell _1 \in [C_2]^{\epsilon _1}_*$
be such that
![]() $f = \sigma _0\hat {\ }\ell _0$
and
$f = \sigma _0\hat {\ }\ell _0$
and
![]() $g = \sigma _1\hat {\ }\ell _1$
. Let
$g = \sigma _1\hat {\ }\ell _1$
. Let
![]() $f' = \tau \hat {\ }\ell _0$
and
$f' = \tau \hat {\ }\ell _0$
and
![]() $g' = \tau \hat {\ }\ell _1$
. Note that
$g' = \tau \hat {\ }\ell _1$
. Note that
![]() $f \ E_0 \ f'$
and
$f \ E_0 \ f'$
and
![]() $g \ E_0 \ g'$
. Since
$g \ E_0 \ g'$
. Since
![]() $\Phi $
is
$\Phi $
is
![]() $E_0$
-invariant,
$E_0$
-invariant,
![]() $\Phi (f) = \Phi (f')$
and
$\Phi (f) = \Phi (f')$
and
![]() $\Phi (g) = \Phi (g')$
. However,
$\Phi (g) = \Phi (g')$
. However,
![]() $\Phi _\tau $
is
$\Phi _\tau $
is
![]() $\sqsubseteq $
-constant on
$\sqsubseteq $
-constant on
![]() $[C_2]^{\epsilon _1}_*$
and so by Fact 3.5,
$[C_2]^{\epsilon _1}_*$
and so by Fact 3.5,
![]() $\Phi _\tau $
depends only on supremum relative to
$\Phi _\tau $
depends only on supremum relative to
![]() $C_2$
. Since
$C_2$
. Since
![]() $\sup (\ell _0) = \sup (\ell _1)$
,
$\sup (\ell _0) = \sup (\ell _1)$
,
![]() $\Phi _\tau (\ell _0) = \Phi _\tau (\ell _1)$
. In summary,
$\Phi _\tau (\ell _0) = \Phi _\tau (\ell _1)$
. In summary,
![]() $\Phi (f) = \Phi (f') = \Phi _\tau (\ell _0) = \Phi _\tau (\ell _1) = \Phi (g') = \Phi (g)$
. Thus,
$\Phi (f) = \Phi (f') = \Phi _\tau (\ell _0) = \Phi _\tau (\ell _1) = \Phi (g') = \Phi (g)$
. Thus,
![]() $C_2$
is the desired club which completes the proof.
$C_2$
is the desired club which completes the proof.
Theorem 3.7. Suppose
![]() $\kappa $
is a cardinal and
$\kappa $
is a cardinal and
![]() $\epsilon < \kappa $
with
$\epsilon < \kappa $
with
![]() ${\mathrm {cof}}(\epsilon ) = \omega $
. Let
${\mathrm {cof}}(\epsilon ) = \omega $
. Let
![]() $\epsilon _0 < \epsilon $
and
$\epsilon _0 < \epsilon $
and
![]() $\epsilon _1 \leq \epsilon $
be such that
$\epsilon _1 \leq \epsilon $
be such that
![]() $\epsilon = \epsilon _0 + \epsilon _1$
and
$\epsilon = \epsilon _0 + \epsilon _1$
and
![]() $\epsilon _1$
is an additively indecomposable ordinal. Suppose
$\epsilon _1$
is an additively indecomposable ordinal. Suppose
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon + \epsilon }_2$
and
$\kappa \rightarrow _* (\kappa )^{\epsilon + \epsilon }_2$
and
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon _1 \cdot \epsilon _1}_2$
hold. For any function
$\kappa \rightarrow _* (\kappa )^{\epsilon _1 \cdot \epsilon _1}_2$
hold. For any function
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, there is a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, there is a club
![]() $C \subseteq \kappa $
and a
$C \subseteq \kappa $
and a
![]() $\delta < \epsilon $
so that for all
$\delta < \epsilon $
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if
$f,g \in [C]^\epsilon _*$
, if
![]() $f \upharpoonright \delta = g \upharpoonright \delta $
and
$f \upharpoonright \delta = g \upharpoonright \delta $
and
![]() $\sup (f) = \sup (g)$
, then
$\sup (f) = \sup (g)$
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
Proof. Since
![]() ${\mathrm {cof}}(\epsilon ) = \omega $
, let
${\mathrm {cof}}(\epsilon ) = \omega $
, let
![]() $\rho : \omega \rightarrow \epsilon $
be a cofinal increasing sequence through
$\rho : \omega \rightarrow \epsilon $
be a cofinal increasing sequence through
![]() $\epsilon $
with
$\epsilon $
with
![]() $\rho (0) = \epsilon _0$
. For
$\rho (0) = \epsilon _0$
. For
![]() $n \in \omega $
, let
$n \in \omega $
, let
![]() $A^n = \{(0,0,\alpha ) : \alpha < \rho (n)\}$
and for each
$A^n = \{(0,0,\alpha ) : \alpha < \rho (n)\}$
and for each
![]() $1 \leq m < \omega $
,
$1 \leq m < \omega $
,
![]() $B^n_m = \{(m,i,\alpha ) : i \in 2 \wedge \rho (n + m - 1) \leq \alpha < \rho (n + m)\}$
. Let
$B^n_m = \{(m,i,\alpha ) : i \in 2 \wedge \rho (n + m - 1) \leq \alpha < \rho (n + m)\}$
. Let
![]() $L^n = A^n \cup \bigcup _{1 \leq m < \omega } B^n_m$
, and note that
$L^n = A^n \cup \bigcup _{1 \leq m < \omega } B^n_m$
, and note that
![]() $L^n \subseteq \omega \times 2 \times \epsilon $
. Let
$L^n \subseteq \omega \times 2 \times \epsilon $
. Let
![]() $\mathcal {L}^n = (L^n, \prec )$
where
$\mathcal {L}^n = (L^n, \prec )$
where
![]() $\prec $
is the lexicographic ordering on
$\prec $
is the lexicographic ordering on
![]() $\omega \times 2 \times \epsilon $
. Since
$\omega \times 2 \times \epsilon $
. Since
![]() $\rho (0) = \epsilon _0$
and
$\rho (0) = \epsilon _0$
and
![]() $\epsilon _1$
is additively indecomposable,
$\epsilon _1$
is additively indecomposable,
![]() ${\mathrm {ot}}(\mathcal {L}^n) = \epsilon _0 + \epsilon _1 = \epsilon $
. For any function
${\mathrm {ot}}(\mathcal {L}^n) = \epsilon _0 + \epsilon _1 = \epsilon $
. For any function
![]() $h \in [\kappa ]^{\mathcal {L}^n}_*$
and
$h \in [\kappa ]^{\mathcal {L}^n}_*$
and
![]() $i \in 2$
, let
$i \in 2$
, let
![]() $h^{n,i} \in [\kappa ]^\epsilon _*$
be defined by
$h^{n,i} \in [\kappa ]^\epsilon _*$
be defined by
 $$ \begin{align*}h^{n,i}(\alpha) = \begin{cases} h(m,0,\alpha) & \quad m = 0 \wedge \alpha < \rho(n) \\ h(m,i,\alpha) & \quad m = 1 \wedge \rho(n) \leq \alpha < \rho(n + 1) \\ h(m,1 - i, \alpha) & \quad m> 1 \wedge \rho(n + m - 1) \leq \alpha < \rho(n + m) \end{cases}.\end{align*} $$
$$ \begin{align*}h^{n,i}(\alpha) = \begin{cases} h(m,0,\alpha) & \quad m = 0 \wedge \alpha < \rho(n) \\ h(m,i,\alpha) & \quad m = 1 \wedge \rho(n) \leq \alpha < \rho(n + 1) \\ h(m,1 - i, \alpha) & \quad m> 1 \wedge \rho(n + m - 1) \leq \alpha < \rho(n + m) \end{cases}.\end{align*} $$
The following picture indicates the relation between h,
![]() $h^{n,0}$
and
$h^{n,0}$
and
![]() $h^{n,1}$
.
$h^{n,1}$
.

In other words,
![]() $h^{n,0}$
and
$h^{n,0}$
and
![]() $h^{n,1}$
are extracted from h in a manner so that
$h^{n,1}$
are extracted from h in a manner so that
![]() $h^{n,0}$
and
$h^{n,0}$
and
![]() $h^{n,1}$
share the same
$h^{n,1}$
share the same
![]() $k^{\text {th}}$
-block for
$k^{\text {th}}$
-block for
![]() $k < n$
(i.e., the functions agree before
$k < n$
(i.e., the functions agree before
![]() $\rho (n)$
), the
$\rho (n)$
), the
![]() $n^{\text {th}}$
-block of
$n^{\text {th}}$
-block of
![]() $h^{n,0}$
comes before the
$h^{n,0}$
comes before the
![]() $n^{\text {th}}$
-block of
$n^{\text {th}}$
-block of
![]() $h^{n,1}$
, and for
$h^{n,1}$
, and for
![]() $k> n$
, the
$k> n$
, the
![]() $k^{\text {th}}$
-block of
$k^{\text {th}}$
-block of
![]() $h^{n,1}$
comes before the
$h^{n,1}$
comes before the
![]() $k^{\text {th}}$
-block of
$k^{\text {th}}$
-block of
![]() $h^{n,0}$
.
$h^{n,0}$
.
If
![]() $f,g \in [\kappa ]^\epsilon _*$
, then say that the pair
$f,g \in [\kappa ]^\epsilon _*$
, then say that the pair
![]() $(f,g)$
has type n if and only if the following holds.
$(f,g)$
has type n if and only if the following holds.
-
• For all
 $\alpha < \rho (n)$
,
$\alpha < \rho (n)$
,
 $f(\alpha ) = g(\alpha )$
.
$f(\alpha ) = g(\alpha )$
. -
•
 $\sup (f \upharpoonright \rho (n + 1)) < g(\rho (n))$
.
$\sup (f \upharpoonright \rho (n + 1)) < g(\rho (n))$
. -
• For all
 $m \geq n + 1$
,
$m \geq n + 1$
,
 $\sup (g \upharpoonright \rho (m + 1)) < f(\rho (m))$
.
$\sup (g \upharpoonright \rho (m + 1)) < f(\rho (m))$
.
Observe that
![]() $(f,g)$
has type n if and only if there is an
$(f,g)$
has type n if and only if there is an
![]() $h \in [\kappa ]^{\mathcal {L}^n}_*$
so that
$h \in [\kappa ]^{\mathcal {L}^n}_*$
so that
![]() $h^{n,0} = f$
and
$h^{n,0} = f$
and
![]() $h^{n,1} = g$
.
$h^{n,1} = g$
.
For each
![]() $n \in \omega $
, let
$n \in \omega $
, let
![]() $P^n : [\kappa ]^{\mathcal {L}^n}_* \rightarrow 3$
be defined by
$P^n : [\kappa ]^{\mathcal {L}^n}_* \rightarrow 3$
be defined by
 $$ \begin{align*}P^n(h) = \begin{cases} 0 & \quad \Phi(h^{n,0}) = \Phi(h^{n,1}) \\ 1 & \quad \Phi(h^{n,0}) < \Phi(h^{n,1}) \\ 2 & \quad \Phi(h^{n,0})> \Phi(h^{n,1}) \end{cases}.\end{align*} $$
$$ \begin{align*}P^n(h) = \begin{cases} 0 & \quad \Phi(h^{n,0}) = \Phi(h^{n,1}) \\ 1 & \quad \Phi(h^{n,0}) < \Phi(h^{n,1}) \\ 2 & \quad \Phi(h^{n,0})> \Phi(h^{n,1}) \end{cases}.\end{align*} $$
By the fact that
![]() ${\mathrm {ot}}(\mathcal {L}^n) = \epsilon $
and Fact 2.6,
${\mathrm {ot}}(\mathcal {L}^n) = \epsilon $
and Fact 2.6,
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon }_3$
implies that for each
$\kappa \rightarrow _* (\kappa )^{\epsilon }_3$
implies that for each
![]() $n \in \omega $
, there is a club
$n \in \omega $
, there is a club
![]() $C \subseteq \kappa $
and an
$C \subseteq \kappa $
and an
![]() $i_n \in 3$
so that for all
$i_n \in 3$
so that for all
![]() $h \in [C]^{\mathcal {L}^n}_*$
,
$h \in [C]^{\mathcal {L}^n}_*$
,
![]() $P(h) = i_n$
. For each
$P(h) = i_n$
. For each
![]() $n \in \omega $
, let
$n \in \omega $
, let
![]() $K_n = \{h \in [\kappa ]^\epsilon _* : P^n(h) = i_n\}$
where
$K_n = \{h \in [\kappa ]^\epsilon _* : P^n(h) = i_n\}$
where
![]() $\mathcal {L}^n$
is identified with
$\mathcal {L}^n$
is identified with
![]() $\epsilon $
. For each
$\epsilon $
. For each
![]() $n \in \omega $
,
$n \in \omega $
,
![]() $K_n \in \mu ^\kappa _\epsilon $
. Since
$K_n \in \mu ^\kappa _\epsilon $
. Since
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon + \epsilon }_2$
implies
$\kappa \rightarrow _* (\kappa )^{\epsilon + \epsilon }_2$
implies
![]() $\mu ^\kappa _\epsilon $
is
$\mu ^\kappa _\epsilon $
is
![]() $\kappa $
-complete by Fact 2.7, there is a club
$\kappa $
-complete by Fact 2.7, there is a club
![]() $C \subseteq \kappa $
so that
$C \subseteq \kappa $
so that
![]() $[C]^\epsilon _* \subseteq K_n$
for all
$[C]^\epsilon _* \subseteq K_n$
for all
![]() $n \in \omega $
. Thus, for all
$n \in \omega $
. Thus, for all
![]() $n \in \omega $
and all
$n \in \omega $
and all
![]() $h \in [C]^\epsilon _*$
,
$h \in [C]^\epsilon _*$
,
![]() $P^n(h) = i_n$
. By thinning C, one may assume C consists entirely of indecomposable ordinals and
$P^n(h) = i_n$
. By thinning C, one may assume C consists entirely of indecomposable ordinals and
![]() $\omega \cdot \epsilon < \min (C)$
. Let
$\omega \cdot \epsilon < \min (C)$
. Let
![]() $C^0 = C$
. If
$C^0 = C$
. If
![]() $C^n$
has been defined, then let
$C^n$
has been defined, then let
![]() $C^{n + 1} = \{\alpha \in C^n : {\mathsf {enum}}_{C^n}(\alpha ) = \alpha \}$
. For each
$C^{n + 1} = \{\alpha \in C^n : {\mathsf {enum}}_{C^n}(\alpha ) = \alpha \}$
. For each
![]() $\alpha $
with
$\alpha $
with
![]() $\alpha \geq \epsilon _0 = \rho (0)$
, let
$\alpha \geq \epsilon _0 = \rho (0)$
, let
![]() $\varsigma (\alpha )$
be the unique n so that
$\varsigma (\alpha )$
be the unique n so that
![]() $\rho (n) \leq \alpha < \rho (n + 1)$
.
$\rho (n) \leq \alpha < \rho (n + 1)$
.
(Case 1) For all
![]() $m \in \omega $
, there exists an
$m \in \omega $
, there exists an
![]() $n \geq m$
so that
$n \geq m$
so that
![]() $i_n = 1$
.
$i_n = 1$
.
Let
![]() $\langle n_j : j \in \omega \rangle $
be an increasing enumeration of
$\langle n_j : j \in \omega \rangle $
be an increasing enumeration of
![]() $\{n \in \omega : i_n = 1\}$
. Let
$\{n \in \omega : i_n = 1\}$
. Let
![]() $\iota _n = {\mathsf {enum}}_{C^2}(n)$
, the
$\iota _n = {\mathsf {enum}}_{C^2}(n)$
, the
![]() $n^{\text {th}}$
-element of
$n^{\text {th}}$
-element of
![]() $C^2$
. Let
$C^2$
. Let
![]() $\tau \in [C]^{\epsilon _0}_*$
be defined by
$\tau \in [C]^{\epsilon _0}_*$
be defined by
![]() $\tau (\alpha ) = {\mathsf {next}}^{\omega \cdot (\alpha + 1)}_{C}(0)$
. Note that
$\tau (\alpha ) = {\mathsf {next}}^{\omega \cdot (\alpha + 1)}_{C}(0)$
. Note that
![]() $\sup (\tau ) < \iota _0$
since
$\sup (\tau ) < \iota _0$
since
![]() $\iota _0 \in C^2$
,
$\iota _0 \in C^2$
,
![]() $\omega \cdot (\epsilon _0 + 1) < \iota _0$
, and Fact 2.12. A sequence
$\omega \cdot (\epsilon _0 + 1) < \iota _0$
, and Fact 2.12. A sequence
![]() $\langle f_j : j \in \omega \rangle $
will be constructed so that all
$\langle f_j : j \in \omega \rangle $
will be constructed so that all
![]() $j \in \omega $
, the pair
$j \in \omega $
, the pair
![]() $(f_{j + 1},f_j)$
has type
$(f_{j + 1},f_j)$
has type
![]() $n_j$
. This will be accomplished by recursively constructing the sequence while maintaining the following properties:
$n_j$
. This will be accomplished by recursively constructing the sequence while maintaining the following properties:
-
1. For all
 $j \in \omega $
,
$j \in \omega $
,
 $f_j \in [C]^\epsilon _*$
.
$f_j \in [C]^\epsilon _*$
. -
2. For all
 $j \in \omega $
,
$j \in \omega $
,
 $f_j \upharpoonright \epsilon _0 = \tau $
.
$f_j \upharpoonright \epsilon _0 = \tau $
. -
3. For all
 $j,n \in \omega $
,
$j,n \in \omega $
,
 $\iota _n < f_j(\rho (n)) < \sup (f_j \upharpoonright \rho (n + 1)) < \iota _{n + 1}$
.
$\iota _n < f_j(\rho (n)) < \sup (f_j \upharpoonright \rho (n + 1)) < \iota _{n + 1}$
. -
4. For all
 $j \in \omega $
and
$j \in \omega $
and
 $\alpha < \rho (n_j)$
,
$\alpha < \rho (n_j)$
,
 $f_j(\alpha ) = f_{j + 1}(\alpha )$
.
$f_j(\alpha ) = f_{j + 1}(\alpha )$
. -
5. For all
 $j \in \omega $
,
$j \in \omega $
,
 $\sup (f_{j + 1} \upharpoonright \rho (n_j + 1)) < f_j(\rho (n_j))$
.
$\sup (f_{j + 1} \upharpoonright \rho (n_j + 1)) < f_j(\rho (n_j))$
. -
6. For all
 $j \in \omega $
and
$j \in \omega $
and
 $n> n_j$
,
$n> n_j$
,
 $\sup (f_j \upharpoonright \rho (n + 1)) < f_{j + 1}(\rho (n))$
.
$\sup (f_j \upharpoonright \rho (n + 1)) < f_{j + 1}(\rho (n))$
. -
7. For all
 $j \in \omega $
and
$j \in \omega $
and
 $\alpha \geq \rho (n_j)$
,
$\alpha \geq \rho (n_j)$
,
 $f_j(\alpha ) \in C^1$
.
$f_j(\alpha ) \in C^1$
.
Define
![]() $f_0$
by
$f_0$
by
![]() $f_0(\alpha ) = \tau (\alpha )$
if
$f_0(\alpha ) = \tau (\alpha )$
if
![]() $\alpha < \epsilon _0$
and
$\alpha < \epsilon _0$
and
![]() $f_0(\alpha ) = {\mathsf {next}}_{C^1}^{\omega \cdot (\alpha + 1)}(\iota _{\varsigma (\alpha )})$
if
$f_0(\alpha ) = {\mathsf {next}}_{C^1}^{\omega \cdot (\alpha + 1)}(\iota _{\varsigma (\alpha )})$
if
![]() $\epsilon _0 \leq \alpha < \epsilon $
. Since
$\epsilon _0 \leq \alpha < \epsilon $
. Since
![]() $\omega \cdot (\rho (n + 1) + 1) < \iota _{n + 1}$
,
$\omega \cdot (\rho (n + 1) + 1) < \iota _{n + 1}$
,
![]() $\iota _n < \iota _{n + 1}$
and
$\iota _n < \iota _{n + 1}$
and
![]() $C^2 = \{\alpha \in C_1 : {\mathsf {enum}}_{C^1}(\alpha ) = \alpha \}$
, Fact 2.12 implies that
$C^2 = \{\alpha \in C_1 : {\mathsf {enum}}_{C^1}(\alpha ) = \alpha \}$
, Fact 2.12 implies that
![]() $\sup (f_0 \upharpoonright \rho (n + 1)) < {\mathsf {next}}^{\omega \cdot (\rho (n + 1) + 1)}_{C^1}(\iota _n) < \iota _{n + 1}$
.
$\sup (f_0 \upharpoonright \rho (n + 1)) < {\mathsf {next}}^{\omega \cdot (\rho (n + 1) + 1)}_{C^1}(\iota _n) < \iota _{n + 1}$
.
Suppose
![]() $f_j$
has been defined. Define
$f_j$
has been defined. Define
![]() $f_{j + 1}$
as follows: If
$f_{j + 1}$
as follows: If
![]() $\alpha < \rho (n_j)$
, let
$\alpha < \rho (n_j)$
, let
![]() $f_{j + 1}(\alpha ) = f_j(\alpha )$
. If
$f_{j + 1}(\alpha ) = f_j(\alpha )$
. If
![]() $\rho (n_j) \leq \alpha < \rho (n_j + 1)$
, let
$\rho (n_j) \leq \alpha < \rho (n_j + 1)$
, let
![]() $f_{j + 1}(\alpha ) = {\mathsf {next}}_{C^0}^{\omega \cdot (\alpha + 1)}(\iota _{n_j})$
. Observe that since
$f_{j + 1}(\alpha ) = {\mathsf {next}}_{C^0}^{\omega \cdot (\alpha + 1)}(\iota _{n_j})$
. Observe that since
![]() $f_j(\rho (n_j)) \in C^1$
by (7),
$f_j(\rho (n_j)) \in C^1$
by (7),
![]() $\omega \cdot (\rho (n_j + 1)) < f_j(\rho (n_j))$
,
$\omega \cdot (\rho (n_j + 1)) < f_j(\rho (n_j))$
,
![]() $\iota _{n_j} < f_j(\rho (n_j))$
by (3) and
$\iota _{n_j} < f_j(\rho (n_j))$
by (3) and
![]() $C^1 = \{\alpha \in C^0 : {\mathsf {enum}}_{C^0}(\alpha ) = \alpha \}$
, Fact 2.12 implies that
$C^1 = \{\alpha \in C^0 : {\mathsf {enum}}_{C^0}(\alpha ) = \alpha \}$
, Fact 2.12 implies that
![]() $\sup (f_{j + 1} \upharpoonright \rho (n_j + 1)) < f_j(\rho (n_j))$
. For
$\sup (f_{j + 1} \upharpoonright \rho (n_j + 1)) < f_j(\rho (n_j))$
. For
![]() $\alpha $
with
$\alpha $
with
![]() $\rho (n_j + 1) \leq \alpha < \epsilon $
, let
$\rho (n_j + 1) \leq \alpha < \epsilon $
, let
![]() $f_{j + 1}(\alpha ) = {\mathsf {next}}_{C^1}^{\omega \cdot \alpha }(\sup (f_j \upharpoonright \rho (\varsigma (\alpha ) + 1)))$
. For all
$f_{j + 1}(\alpha ) = {\mathsf {next}}_{C^1}^{\omega \cdot \alpha }(\sup (f_j \upharpoonright \rho (\varsigma (\alpha ) + 1)))$
. For all
![]() $n> n_j$
,
$n> n_j$
,
![]() $\sup (f_j \upharpoonright \rho (n + 1)) < f_{j + 1}(\rho (n)) < \sup (f_{j + 1} \upharpoonright \rho (n + 1)) < \iota _{n + 1}$
since
$\sup (f_j \upharpoonright \rho (n + 1)) < f_{j + 1}(\rho (n)) < \sup (f_{j + 1} \upharpoonright \rho (n + 1)) < \iota _{n + 1}$
since
![]() $\sup (f_{j + 1} \upharpoonright \rho (n + 1)) < {\mathsf {next}}_{C^1}^{\omega \cdot (\rho (n + 1) + 1)}(\sup (f_j \upharpoonright \rho (n + 1))) < \iota _{n + 1}$
because
$\sup (f_{j + 1} \upharpoonright \rho (n + 1)) < {\mathsf {next}}_{C^1}^{\omega \cdot (\rho (n + 1) + 1)}(\sup (f_j \upharpoonright \rho (n + 1))) < \iota _{n + 1}$
because
![]() $\omega \cdot (\rho (n + 1) + 1) < \iota _{n + 1}$
,
$\omega \cdot (\rho (n + 1) + 1) < \iota _{n + 1}$
,
![]() $\sup (f_j \upharpoonright \rho (n + 1)) < \iota _{n + 1} \in C^2$
,
$\sup (f_j \upharpoonright \rho (n + 1)) < \iota _{n + 1} \in C^2$
,
![]() $C^2 = \{\alpha \in C_1 : {\mathsf {enum}}_{C^1}(\alpha ) = \alpha \}$
and Fact 2.12. This shows that
$C^2 = \{\alpha \in C_1 : {\mathsf {enum}}_{C^1}(\alpha ) = \alpha \}$
and Fact 2.12. This shows that
![]() $f_{j + 1}$
has been constructed with the desired relations between
$f_{j + 1}$
has been constructed with the desired relations between
![]() $f_j$
and
$f_j$
and
![]() $f_{j + 1}$
.
$f_{j + 1}$
.
By (1), (2), (4), (5) and (6),
![]() $f_j, f_{j + 1} \in [C]^\epsilon _*$
and
$f_j, f_{j + 1} \in [C]^\epsilon _*$
and
![]() $(f_{j + 1},f_j)$
has type
$(f_{j + 1},f_j)$
has type
![]() $n_j$
. Thus, for each
$n_j$
. Thus, for each
![]() $j \in \omega $
, there is a function
$j \in \omega $
, there is a function
![]() $h_j \in [C]^{\mathcal {L}^{n_j}}_*$
so that
$h_j \in [C]^{\mathcal {L}^{n_j}}_*$
so that
![]() $h_j^{n_j,0} = f_{j + 1}$
and
$h_j^{n_j,0} = f_{j + 1}$
and
![]() $h_j^{n_j,1} = f_j$
. Since for all
$h_j^{n_j,1} = f_j$
. Since for all
![]() $j \in \omega $
, C is homogeneous for
$j \in \omega $
, C is homogeneous for
![]() $P^{n_j}$
taking value
$P^{n_j}$
taking value
![]() $1$
,
$1$
,
![]() $P^{n_j}(h_j) = 1$
. This implies
$P^{n_j}(h_j) = 1$
. This implies
![]() $\Phi (f_{j + 1}) = \Phi (h_j^{n_j,0}) < \Phi (h^{n_j,1}_j) = \Phi (f_j)$
. Thus,
$\Phi (f_{j + 1}) = \Phi (h_j^{n_j,0}) < \Phi (h^{n_j,1}_j) = \Phi (f_j)$
. Thus,
![]() $\langle \Phi (f_j) : j \in \omega \rangle $
is an infinite descending sequence of ordinals. This shows Case 1 is impossible.
$\langle \Phi (f_j) : j \in \omega \rangle $
is an infinite descending sequence of ordinals. This shows Case 1 is impossible.
(Case 2) For all
![]() $m \in \omega $
, there exists an
$m \in \omega $
, there exists an
![]() $n \geq m$
so that
$n \geq m$
so that
![]() $i_n = 2$
.
$i_n = 2$
.
Let
![]() $\langle n_j : j \in \omega \rangle $
be an increasing enumeration of
$\langle n_j : j \in \omega \rangle $
be an increasing enumeration of
![]() $\{n \in \omega : i_n = 2\}$
. For each
$\{n \in \omega : i_n = 2\}$
. For each
![]() $k \in \omega $
, let
$k \in \omega $
, let
![]() $\varpi (k) = |\{n < k : i_n = 2\}$
. For
$\varpi (k) = |\{n < k : i_n = 2\}$
. For
![]() $\alpha < \epsilon _0 = \rho (0)$
, let
$\alpha < \epsilon _0 = \rho (0)$
, let
![]() $\tau _0(\alpha ) = {\mathsf {next}}_{C^0}^{\omega \cdot (\alpha + 1)}(0)$
. Let
$\tau _0(\alpha ) = {\mathsf {next}}_{C^0}^{\omega \cdot (\alpha + 1)}(0)$
. Let
![]() $\iota _0 = {\mathsf {next}}_{C^0}^\omega (\sup (\tau _0))$
. If
$\iota _0 = {\mathsf {next}}_{C^0}^\omega (\sup (\tau _0))$
. If
![]() $\iota _n$
has been defined, then let
$\iota _n$
has been defined, then let
![]() $\iota _{n + 1} = {\mathsf {next}}^{\omega \cdot (\rho (n + 1) + 1)}_{C^{\varpi (n + 1)}}(\iota _n)$
. A sequence
$\iota _{n + 1} = {\mathsf {next}}^{\omega \cdot (\rho (n + 1) + 1)}_{C^{\varpi (n + 1)}}(\iota _n)$
. A sequence
![]() $\langle f_j : j \in \omega \rangle $
will be constructed so that for all
$\langle f_j : j \in \omega \rangle $
will be constructed so that for all
![]() $j \in \omega $
, the pair
$j \in \omega $
, the pair
![]() $(f_j,f_{j + 1})$
has type
$(f_j,f_{j + 1})$
has type
![]() $n_j$
. This will be accomplished by maintaining the following properties throughout the construction:
$n_j$
. This will be accomplished by maintaining the following properties throughout the construction:
-
1. For all
 $j \in \omega $
,
$j \in \omega $
,
 $f_j \in [C]^\epsilon _*$
.
$f_j \in [C]^\epsilon _*$
. -
2. For all
 $j \in \omega $
,
$j \in \omega $
,
 $f_j \upharpoonright \epsilon _0 = \tau $
.
$f_j \upharpoonright \epsilon _0 = \tau $
. -
3. For all
 $j,n \in \omega $
,
$j,n \in \omega $
,
 $\iota _n < f_j(\rho (n)) < \sup (f_j \upharpoonright \rho (n + 1)) < \iota _{n + 1}$
.
$\iota _n < f_j(\rho (n)) < \sup (f_j \upharpoonright \rho (n + 1)) < \iota _{n + 1}$
. -
4. For all
 $j \in \omega $
and
$j \in \omega $
and
 $\alpha < \rho (n_j)$
,
$\alpha < \rho (n_j)$
,
 $f_j(\alpha ) = f_{j + 1}(\alpha )$
.
$f_j(\alpha ) = f_{j + 1}(\alpha )$
. -
5. For all
 $j \in \omega $
,
$j \in \omega $
,
 $\sup (f_j \upharpoonright \rho (n_j + 1)) < f_{j + 1}(\rho (n_j))$
.
$\sup (f_j \upharpoonright \rho (n_j + 1)) < f_{j + 1}(\rho (n_j))$
. -
6. For all
 $j \in \omega $
,
$j \in \omega $
,
 $n> n_j$
,
$n> n_j$
,
 $\sup (f_{j + 1} \upharpoonright \rho (n + 1)) < f_j(\rho (n))$
.
$\sup (f_{j + 1} \upharpoonright \rho (n + 1)) < f_j(\rho (n))$
. -
7. For all
 $j \in \omega $
and
$j \in \omega $
and
 $\alpha \geq \rho (n_j + 1)$
,
$\alpha \geq \rho (n_j + 1)$
,
 $f_j(\alpha ) \in C^{\varpi (\varsigma (\alpha )) - j}$
.
$f_j(\alpha ) \in C^{\varpi (\varsigma (\alpha )) - j}$
.
For
![]() $\alpha < \epsilon _0$
, let
$\alpha < \epsilon _0$
, let
![]() $f_0(\alpha ) = \tau (\alpha )$
. For
$f_0(\alpha ) = \tau (\alpha )$
. For
![]() $\alpha $
with
$\alpha $
with
![]() $\epsilon _0 = \rho (0) \leq \alpha < \epsilon $
, let
$\epsilon _0 = \rho (0) \leq \alpha < \epsilon $
, let
![]() $f_0(\alpha ) = {\mathsf {next}}_{C^{\varpi (\varsigma (\alpha ))}}^{\omega \cdot (\alpha + 1)}(\iota _{\varsigma (\alpha )})$
. Note that for each
$f_0(\alpha ) = {\mathsf {next}}_{C^{\varpi (\varsigma (\alpha ))}}^{\omega \cdot (\alpha + 1)}(\iota _{\varsigma (\alpha )})$
. Note that for each
![]() $n \in \omega $
,
$n \in \omega $
,
![]() $\sup (f_0 \upharpoonright \rho (n + 1)) \leq {\mathsf {next}}^{\omega \cdot (\rho (n + 1))}_{C^{\varpi (n)}}(\iota _n) \leq {\mathsf {next}}^{\omega \cdot (\rho (n + 1))}_{C^{\varpi (n + 1)}}(\iota _n) < {\mathsf {next}}^{\omega \cdot (\rho (n + 1) + 1)}_{C^{\varpi (n + 1)}}(\iota _n) = \iota _{n + 1}$
.
$\sup (f_0 \upharpoonright \rho (n + 1)) \leq {\mathsf {next}}^{\omega \cdot (\rho (n + 1))}_{C^{\varpi (n)}}(\iota _n) \leq {\mathsf {next}}^{\omega \cdot (\rho (n + 1))}_{C^{\varpi (n + 1)}}(\iota _n) < {\mathsf {next}}^{\omega \cdot (\rho (n + 1) + 1)}_{C^{\varpi (n + 1)}}(\iota _n) = \iota _{n + 1}$
.
Suppose
![]() $f_j$
has been defined. Define
$f_j$
has been defined. Define
![]() $f_{j + 1}$
as follows: If
$f_{j + 1}$
as follows: If
![]() $\alpha < \rho (n_j)$
, let
$\alpha < \rho (n_j)$
, let
![]() $f_{j + 1}(\alpha ) = f_j(\alpha )$
. If
$f_{j + 1}(\alpha ) = f_j(\alpha )$
. If
![]() $\rho (n_j) \leq \alpha < \rho (n_j + 1)$
, let
$\rho (n_j) \leq \alpha < \rho (n_j + 1)$
, let
![]() $f_{j + 1}(\alpha ) = {\mathsf {next}}^{\omega \cdot (\alpha + 1)}_{C^0}(\sup (f_j \upharpoonright \rho (n_j + 1)))$
. Observe that
$f_{j + 1}(\alpha ) = {\mathsf {next}}^{\omega \cdot (\alpha + 1)}_{C^0}(\sup (f_j \upharpoonright \rho (n_j + 1)))$
. Observe that
![]() $\sup (f_{j + 1} \upharpoonright \rho (n_j + 1)) < \iota _{n_j + 1}$
since
$\sup (f_{j + 1} \upharpoonright \rho (n_j + 1)) < \iota _{n_j + 1}$
since
![]() $\iota _{n_j + 1} \in C^{j + 1}$
,
$\iota _{n_j + 1} \in C^{j + 1}$
,
![]() $\sup (f_j \upharpoonright \rho (n_j + 1)) < \iota _{n_j + 1}$
by (3),
$\sup (f_j \upharpoonright \rho (n_j + 1)) < \iota _{n_j + 1}$
by (3),
![]() $\omega \cdot (\rho (n_j + 1) + 1) < \iota _{n_j + 1}$
and by Fact 2.12. For
$\omega \cdot (\rho (n_j + 1) + 1) < \iota _{n_j + 1}$
and by Fact 2.12. For
![]() $\alpha $
with
$\alpha $
with
![]() $\rho (n_j + 1) \leq \alpha < \epsilon $
, let
$\rho (n_j + 1) \leq \alpha < \epsilon $
, let
![]() $f_{j + 1}(\alpha ) = {\mathsf {next}}_{C^{\varpi (\varsigma (\alpha )) - j - 1}}^{\omega \cdot (\alpha + 1)}(\iota _{\varsigma (\alpha )})$
. (Observe for all
$f_{j + 1}(\alpha ) = {\mathsf {next}}_{C^{\varpi (\varsigma (\alpha )) - j - 1}}^{\omega \cdot (\alpha + 1)}(\iota _{\varsigma (\alpha )})$
. (Observe for all
![]() $\alpha $
with
$\alpha $
with
![]() $\rho (n_j + 1) \leq \alpha < \epsilon $
,
$\rho (n_j + 1) \leq \alpha < \epsilon $
,
![]() $\varpi (\varsigma (\alpha )) \geq j + 1$
.) Note that for each
$\varpi (\varsigma (\alpha )) \geq j + 1$
.) Note that for each
![]() $n> n_j$
,
$n> n_j$
,
![]() $\sup (f_{j + 1} \upharpoonright \rho (n + 1)) \leq {\mathsf {next}}^{\omega \cdot (\rho (n + 1) + 1)}_{C^{\varpi (n)} - j - 1}(\iota _n) < f_j(\rho (n))$
since
$\sup (f_{j + 1} \upharpoonright \rho (n + 1)) \leq {\mathsf {next}}^{\omega \cdot (\rho (n + 1) + 1)}_{C^{\varpi (n)} - j - 1}(\iota _n) < f_j(\rho (n))$
since
![]() $\omega \cdot (\rho (n + 1) + 1) < f_j(\rho (n))$
,
$\omega \cdot (\rho (n + 1) + 1) < f_j(\rho (n))$
,
![]() $\iota _n < f(\rho (n))$
,
$\iota _n < f(\rho (n))$
,
![]() $f_j(\rho (n)) \in C^{\varpi (n) - j}$
and by Fact 2.12. This completes the construction of
$f_j(\rho (n)) \in C^{\varpi (n) - j}$
and by Fact 2.12. This completes the construction of
![]() $f_{j + 1}$
with the desired relation between
$f_{j + 1}$
with the desired relation between
![]() $f_j$
and
$f_j$
and
![]() $f_{j + 1}$
.
$f_{j + 1}$
.
By (1), (2), (4), (5) and (6),
![]() $f_j,f_{j + 1} \in [C]^\epsilon _*$
and
$f_j,f_{j + 1} \in [C]^\epsilon _*$
and
![]() $(f_j,f_{j + 1})$
has type
$(f_j,f_{j + 1})$
has type
![]() $n_j$
. Thus, for each
$n_j$
. Thus, for each
![]() $j \in \omega $
, there is a function
$j \in \omega $
, there is a function
![]() $h_j \in [C]^{\mathcal {L}^{n_j}}_*$
so that
$h_j \in [C]^{\mathcal {L}^{n_j}}_*$
so that
![]() $h_j^{n_j,0} = f_j$
and
$h_j^{n_j,0} = f_j$
and
![]() $h_j^{n_j,1} = f_{j + 1}$
. Since for all
$h_j^{n_j,1} = f_{j + 1}$
. Since for all
![]() $j \in \omega $
, C is homogeneous for
$j \in \omega $
, C is homogeneous for
![]() $P^{n_j}$
taking value
$P^{n_j}$
taking value
![]() $2$
,
$2$
,
![]() $P^{n_j}(h_j) = 2$
. This implies
$P^{n_j}(h_j) = 2$
. This implies
![]() $\Phi (f_j) = \Phi (h^{n_j,0})> \Phi (h^{n_j,1}) = \Phi (f_{j + 1})$
.
$\Phi (f_j) = \Phi (h^{n_j,0})> \Phi (h^{n_j,1}) = \Phi (f_{j + 1})$
.
![]() $\langle \Phi (f_j) : j \in \omega \rangle $
is an infinite descending sequence of ordinals. This shows Case 2 is impossible.
$\langle \Phi (f_j) : j \in \omega \rangle $
is an infinite descending sequence of ordinals. This shows Case 2 is impossible.
The failure of both Case 1 and Case 2 implies that the following Case 3 must hold.
(Case 3) There exists an
![]() $m^* \in \omega $
so that for all
$m^* \in \omega $
so that for all
![]() $n \geq m^*$
,
$n \geq m^*$
,
![]() $i_n = 0$
.
$i_n = 0$
.
Fix
![]() $\ell \in [C]^{\rho (m^*)}_*$
. Define
$\ell \in [C]^{\rho (m^*)}_*$
. Define
![]() $\Phi _\ell : [C]^{\epsilon _1}_* \rightarrow \mathrm {ON}$
by
$\Phi _\ell : [C]^{\epsilon _1}_* \rightarrow \mathrm {ON}$
by
![]() $\Phi _\ell (v) = \Phi (\ell \hat {\ }v)$
. It will be shown that
$\Phi _\ell (v) = \Phi (\ell \hat {\ }v)$
. It will be shown that
![]() $\Phi _\ell $
is
$\Phi _\ell $
is
![]() $E_0$
-invariant
$E_0$
-invariant
![]() $\mu ^\kappa _{\epsilon _1}$
-almost everywhere. Suppose
$\mu ^\kappa _{\epsilon _1}$
-almost everywhere. Suppose
![]() $v,w \in [C^2]^{\epsilon _1}_*$
and
$v,w \in [C^2]^{\epsilon _1}_*$
and
![]() $v \ E_0 \ w$
. Let
$v \ E_0 \ w$
. Let
![]() $f_{m^*} = \ell \hat {\ }v$
and
$f_{m^*} = \ell \hat {\ }v$
and
![]() $g_{m^*} = \ell \hat {\ }w$
. Since
$g_{m^*} = \ell \hat {\ }w$
. Since
![]() $v \ E_0 \ w$
, let
$v \ E_0 \ w$
, let
![]() $n^* \geq m^*$
be such that for all
$n^* \geq m^*$
be such that for all
![]() $\alpha \geq \rho (n^*)$
,
$\alpha \geq \rho (n^*)$
,
![]() $f_{m^*}(\alpha ) = g_{m^*}(\alpha )$
. For
$f_{m^*}(\alpha ) = g_{m^*}(\alpha )$
. For
![]() $j \geq m^*$
, let
$j \geq m^*$
, let
![]() $\iota _j^f = f_{m^*}(\rho (j))$
and
$\iota _j^f = f_{m^*}(\rho (j))$
and
![]() $\iota _j^g = g_{m^*}(\rho (j))$
. Note that
$\iota _j^g = g_{m^*}(\rho (j))$
. Note that
![]() $\iota ^f_j,\iota ^g_j \in C^2$
for all
$\iota ^f_j,\iota ^g_j \in C^2$
for all
![]() $j \geq m^*$
. One will define two finite sequences
$j \geq m^*$
. One will define two finite sequences
![]() $\langle f_j : m^* \leq j \leq n^*\rangle $
and
$\langle f_j : m^* \leq j \leq n^*\rangle $
and
![]() $\langle g_j : m^* \leq j \leq n^*\rangle $
with the following properties:
$\langle g_j : m^* \leq j \leq n^*\rangle $
with the following properties:
-
1. For all
 $m^* \leq j \leq n^*$
,
$m^* \leq j \leq n^*$
,
 $f_j,g_j \in [C]^\epsilon _*$
. For all
$f_j,g_j \in [C]^\epsilon _*$
. For all
 $m^* \leq j \leq n^*$
and
$m^* \leq j \leq n^*$
and
 $\rho (j) \leq \alpha < \epsilon $
,
$\rho (j) \leq \alpha < \epsilon $
,
 $f_j(\alpha ),g_j(\alpha ) \in C^1$
.
$f_j(\alpha ),g_j(\alpha ) \in C^1$
. -
2. For all
 $m^* \leq j \leq n^*$
and
$m^* \leq j \leq n^*$
and
 $m^* \leq k < \omega $
,
$m^* \leq k < \omega $
,
 $\sup (f_j \upharpoonright \rho (k)) < \iota ^f_k$
and
$\sup (f_j \upharpoonright \rho (k)) < \iota ^f_k$
and
 $\sup (g_j \upharpoonright \rho (k)) < \iota ^g_{k}$
.
$\sup (g_j \upharpoonright \rho (k)) < \iota ^g_{k}$
. -
3. For all
 $m^* \leq j \leq n^*$
,
$m^* \leq j \leq n^*$
,
 $f_j \upharpoonright \rho (m^*) = \ell = g_j \upharpoonright \rho (m^*)$
.
$f_j \upharpoonright \rho (m^*) = \ell = g_j \upharpoonright \rho (m^*)$
. -
4. For all
 $m^* \leq j \leq n^*$
,
$m^* \leq j \leq n^*$
,
 $f_j \upharpoonright \rho (j) = g_j \upharpoonright \rho (j)$
.
$f_j \upharpoonright \rho (j) = g_j \upharpoonright \rho (j)$
. -
5. For all
 $m^* \leq j \leq n^*$
and
$m^* \leq j \leq n^*$
and
 $\alpha $
with
$\alpha $
with
 $\rho (n^*) \leq \alpha < \epsilon $
,
$\rho (n^*) \leq \alpha < \epsilon $
,
 $f_j(\alpha ) = g_j(\alpha )$
.
$f_j(\alpha ) = g_j(\alpha )$
. -
6. For all
 $m^* \leq j < n^*$
,
$m^* \leq j < n^*$
,
 $\sup (f_{j + 1} \upharpoonright \rho (j + 1)) < f_j(\rho (j))$
and
$\sup (f_{j + 1} \upharpoonright \rho (j + 1)) < f_j(\rho (j))$
and
 $\sup (g_{j + 1} \upharpoonright \rho (j + 1)) < g_j(\rho (j))$
.
$\sup (g_{j + 1} \upharpoonright \rho (j + 1)) < g_j(\rho (j))$
. -
7. For all
 $m^* \leq j < n^*$
and
$m^* \leq j < n^*$
and
 $j + 1 \leq k < \omega $
,
$j + 1 \leq k < \omega $
,
 $\sup (f_j \upharpoonright \rho (k + 1)) < f_{j + 1}(\rho (k))$
and
$\sup (f_j \upharpoonright \rho (k + 1)) < f_{j + 1}(\rho (k))$
and
 $\sup (g_j \upharpoonright \rho (k + 1)) < g_{j + 1}(\rho (k))$
.
$\sup (g_j \upharpoonright \rho (k + 1)) < g_{j + 1}(\rho (k))$
.
Note that
![]() $f_{m^*}$
and
$f_{m^*}$
and
![]() $g_{m^*}$
have already been defined above. Suppose
$g_{m^*}$
have already been defined above. Suppose
![]() $m^* \leq j < n^*$
and
$m^* \leq j < n^*$
and
![]() $f_j$
and
$f_j$
and
![]() $g_j$
have already been defined with the above properties. For
$g_j$
have already been defined with the above properties. For
![]() $\alpha < \rho (j)$
, let
$\alpha < \rho (j)$
, let
![]() $f_{j + 1}(\alpha )$
and
$f_{j + 1}(\alpha )$
and
![]() $g_{j + 1}(\alpha )$
be
$g_{j + 1}(\alpha )$
be
![]() $f_j(\alpha ) = g_{j}(\alpha )$
by (4) and therefore
$f_j(\alpha ) = g_{j}(\alpha )$
by (4) and therefore
![]() $\sup (f_{j + 1} \upharpoonright \rho (j)) = \sup (g_{j + 1} \upharpoonright \rho (j))$
. For
$\sup (f_{j + 1} \upharpoonright \rho (j)) = \sup (g_{j + 1} \upharpoonright \rho (j))$
. For
![]() $\rho (j) \leq \alpha < \rho (j + 1)$
, define
$\rho (j) \leq \alpha < \rho (j + 1)$
, define
![]() $f_{j + 1}(\alpha )$
and
$f_{j + 1}(\alpha )$
and
![]() $g_{j + 1}(\alpha )$
to be
$g_{j + 1}(\alpha )$
to be
![]() ${\mathsf {next}}^{\omega \cdot (\alpha + 1)}_{C^0}(\sup (f_{j + 1} \upharpoonright \rho (j))) = {\mathsf {next}}^{\omega \cdot (\alpha + 1)}_{C_0}(\sup (g_{j + 1} \upharpoonright \rho (j)))$
. Thus,
${\mathsf {next}}^{\omega \cdot (\alpha + 1)}_{C^0}(\sup (f_{j + 1} \upharpoonright \rho (j))) = {\mathsf {next}}^{\omega \cdot (\alpha + 1)}_{C_0}(\sup (g_{j + 1} \upharpoonright \rho (j)))$
. Thus,
![]() $f_{j + 1} \upharpoonright \rho (j + 1) = g_{j + 1}\upharpoonright \rho (j + 1)$
. Note that since
$f_{j + 1} \upharpoonright \rho (j + 1) = g_{j + 1}\upharpoonright \rho (j + 1)$
. Note that since
![]() $f_j(\rho (j)) \in C^1$
,
$f_j(\rho (j)) \in C^1$
,
![]() $g_j(\rho (j)) \in C^1$
and
$g_j(\rho (j)) \in C^1$
and
![]() $\omega \cdot (\rho (j + 1) + 1) < \min \{f_j(\rho (j)), g_j(\rho (j))\}$
, Fact 2.12 implies that
$\omega \cdot (\rho (j + 1) + 1) < \min \{f_j(\rho (j)), g_j(\rho (j))\}$
, Fact 2.12 implies that
![]() $\sup (f_{j + 1} \upharpoonright \rho (j + 1)) = \sup (g_{j + 1} \upharpoonright \rho (j + 1)) < \min \{f_j(\rho (j)), g_j(\rho (j))\}$
. For
$\sup (f_{j + 1} \upharpoonright \rho (j + 1)) = \sup (g_{j + 1} \upharpoonright \rho (j + 1)) < \min \{f_j(\rho (j)), g_j(\rho (j))\}$
. For
![]() $\alpha \geq \rho (j + 1)$
, let
$\alpha \geq \rho (j + 1)$
, let
![]() $f_{j + 1}(\alpha ) = {\mathsf {next}}^{\omega \cdot (\alpha + 1)}_{C^1}(\sup (f_j \upharpoonright \rho (\varsigma (\alpha ))))$
and
$f_{j + 1}(\alpha ) = {\mathsf {next}}^{\omega \cdot (\alpha + 1)}_{C^1}(\sup (f_j \upharpoonright \rho (\varsigma (\alpha ))))$
and
![]() $g_{j + 1}(\alpha ) = {\mathsf {next}}^{\omega \cdot (\alpha + 1)}_{C^1}(\sup (g_j \upharpoonright \rho (\varsigma (\alpha ))))$
. Since for all
$g_{j + 1}(\alpha ) = {\mathsf {next}}^{\omega \cdot (\alpha + 1)}_{C^1}(\sup (g_j \upharpoonright \rho (\varsigma (\alpha ))))$
. Since for all
![]() $k \geq j + 1$
,
$k \geq j + 1$
,
![]() $\sup (f_j \upharpoonright \rho (k)) < \iota _k^f$
and
$\sup (f_j \upharpoonright \rho (k)) < \iota _k^f$
and
![]() $\sup (g_j \upharpoonright \rho (k)) < \iota ^g_k$
by (2),
$\sup (g_j \upharpoonright \rho (k)) < \iota ^g_k$
by (2),
![]() $\omega \cdot (\rho (k) + 1) < \min \{\iota ^g_f,\iota ^f_k\}$
and
$\omega \cdot (\rho (k) + 1) < \min \{\iota ^g_f,\iota ^f_k\}$
and
![]() $\iota ^f_k,\iota ^g_k \in C^2$
, Fact 2.12 implies that
$\iota ^f_k,\iota ^g_k \in C^2$
, Fact 2.12 implies that
![]() $\sup (f_{j + 1} \upharpoonright \rho (k)) < \iota ^f_k$
and
$\sup (f_{j + 1} \upharpoonright \rho (k)) < \iota ^f_k$
and
![]() $\sup (g_{j + 1} \upharpoonright \rho (k)) < \iota ^f_k$
. By (5), for any
$\sup (g_{j + 1} \upharpoonright \rho (k)) < \iota ^f_k$
. By (5), for any
![]() $k \geq n^*$
,
$k \geq n^*$
,
![]() $\sup (f_j \upharpoonright \rho (k)) = \sup (g_j \upharpoonright \rho (k))$
. This implies that for all
$\sup (f_j \upharpoonright \rho (k)) = \sup (g_j \upharpoonright \rho (k))$
. This implies that for all
![]() $\alpha \geq \rho (n^*)$
,
$\alpha \geq \rho (n^*)$
,
![]() $f_{j + 1}(\alpha ) = g_{j + 1}(\alpha )$
. This completes the construction of
$f_{j + 1}(\alpha ) = g_{j + 1}(\alpha )$
. This completes the construction of
![]() $f_{j + 1}$
and
$f_{j + 1}$
and
![]() $g_{j + 1}$
.
$g_{j + 1}$
.
By (1), (3), (4), (5), (6) and (7),
![]() $(f_{j + 1}, f_j)$
and
$(f_{j + 1}, f_j)$
and
![]() $(g_{j + 1}, g_j)$
are of type j for each j such that
$(g_{j + 1}, g_j)$
are of type j for each j such that
![]() $m^* \leq j < n^*$
. For each j so that
$m^* \leq j < n^*$
. For each j so that
![]() $m^* \leq j < n^*$
, let
$m^* \leq j < n^*$
, let
![]() $h_j,p_j \in [C]^{\mathcal {L}^j}_*$
be such that
$h_j,p_j \in [C]^{\mathcal {L}^j}_*$
be such that
![]() $h_j^{j,0} = f_{j + 1}$
,
$h_j^{j,0} = f_{j + 1}$
,
![]() $h_j^{j,1} = f_j$
,
$h_j^{j,1} = f_j$
,
![]() $p_j^{j,0} = g_{j + 1}$
and
$p_j^{j,0} = g_{j + 1}$
and
![]() $p_j^{j,1} = g_j$
. Since for all
$p_j^{j,1} = g_j$
. Since for all
![]() $j \geq m^*$
, C is homogeneous for
$j \geq m^*$
, C is homogeneous for
![]() $P^j$
taking value
$P^j$
taking value
![]() $0$
, one has that for all
$0$
, one has that for all
![]() $m^* \leq j < n^*$
,
$m^* \leq j < n^*$
,
![]() $P^j(h_j) = 0$
and
$P^j(h_j) = 0$
and
![]() $P^j(p_j) = 0$
. Thus,
$P^j(p_j) = 0$
. Thus,
![]() $\Phi (f_{j + 1}) = \Phi (f_j)$
and
$\Phi (f_{j + 1}) = \Phi (f_j)$
and
![]() $\Phi (g_{j + 1}) = \Phi (g_j)$
. Also, by (3), (4) and (5),
$\Phi (g_{j + 1}) = \Phi (g_j)$
. Also, by (3), (4) and (5),
![]() $f_{n^*} = g_{n^*}$
. Putting these together, one has that
$f_{n^*} = g_{n^*}$
. Putting these together, one has that
It has been shown that for all
![]() $v,w \in [C]^{\epsilon _1}_*$
, if
$v,w \in [C]^{\epsilon _1}_*$
, if
![]() $v \ E_0 \ w$
, then
$v \ E_0 \ w$
, then
![]() $\Phi _\ell (v) = \Phi _\ell (w)$
. This shows that
$\Phi _\ell (v) = \Phi _\ell (w)$
. This shows that
![]() $\Phi _\ell $
is
$\Phi _\ell $
is
![]() $E_0$
-invariant
$E_0$
-invariant
![]() $\mu ^\kappa _{\epsilon _1}$
-almost everywhere.
$\mu ^\kappa _{\epsilon _1}$
-almost everywhere.
Define a relation
![]() $R \subseteq [C]^{\rho (m^*)}_* \times [\kappa ]^{\epsilon _1}_*$
by
$R \subseteq [C]^{\rho (m^*)}_* \times [\kappa ]^{\epsilon _1}_*$
by
![]() $R(\ell ,v)$
if and only if for all
$R(\ell ,v)$
if and only if for all
![]() $w \sqsubseteq v$
,
$w \sqsubseteq v$
,
![]() $\Phi _\ell (w) = \Phi _\ell (v)$
. Since it was shown above that for each
$\Phi _\ell (w) = \Phi _\ell (v)$
. Since it was shown above that for each
![]() $\ell \in [C]^{\rho (m^*)}$
,
$\ell \in [C]^{\rho (m^*)}$
,
![]() $\Phi _{\ell }$
is
$\Phi _{\ell }$
is
![]() $E_0$
-invariant
$E_0$
-invariant
![]() $\mu ^\kappa _{\epsilon _1}$
-almost everywhere and
$\mu ^\kappa _{\epsilon _1}$
-almost everywhere and
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon _1 \cdot \epsilon _1}$
holds, Theorem 3.7 implies that there is a club
$\kappa \rightarrow _* (\kappa )^{\epsilon _1 \cdot \epsilon _1}$
holds, Theorem 3.7 implies that there is a club
![]() $D \subseteq \kappa $
so that for all
$D \subseteq \kappa $
so that for all
![]() $v,w \in [D]^{\epsilon _1}_*$
, if
$v,w \in [D]^{\epsilon _1}_*$
, if
![]() $\sup (v) = \sup (w)$
, then
$\sup (v) = \sup (w)$
, then
![]() $\Phi _\ell (v) = \Phi _\ell (w)$
. In particular, for any
$\Phi _\ell (v) = \Phi _\ell (w)$
. In particular, for any
![]() $v \in [D]^{\epsilon _1}_*$
and any
$v \in [D]^{\epsilon _1}_*$
and any
![]() $w \sqsubseteq v$
,
$w \sqsubseteq v$
,
![]() $\sup (v) = \sup (w)$
and thus
$\sup (v) = \sup (w)$
and thus
![]() $\Phi _\ell (v) = \Phi _\ell (w)$
. This shows
$\Phi _\ell (v) = \Phi _\ell (w)$
. This shows
![]() $[D]^{\epsilon _1}_* \subseteq R_{\ell }$
. For all
$[D]^{\epsilon _1}_* \subseteq R_{\ell }$
. For all
![]() $\ell \in [C]^{\rho (m^*)}_*$
,
$\ell \in [C]^{\rho (m^*)}_*$
,
![]() $R_\ell \in \mu ^\kappa _{\epsilon _1}$
. By Fact 2.13, there is a club
$R_\ell \in \mu ^\kappa _{\epsilon _1}$
. By Fact 2.13, there is a club
![]() $E \subseteq C$
so that for all
$E \subseteq C$
so that for all
![]() $\ell \in [E]^{\rho (m^*)}$
,
$\ell \in [E]^{\rho (m^*)}$
,
![]() $[E \setminus (\sup (\ell ) + 1)]^{\epsilon _1}_* \subseteq R_\ell $
.
$[E \setminus (\sup (\ell ) + 1)]^{\epsilon _1}_* \subseteq R_\ell $
.
Let
![]() $\delta = \rho (m^*)$
. Suppose
$\delta = \rho (m^*)$
. Suppose
![]() $f,g \in [E]_*^\epsilon $
,
$f,g \in [E]_*^\epsilon $
,
![]() $\sup (f) = \sup (g)$
and
$\sup (f) = \sup (g)$
and
![]() $f \upharpoonright \delta = g \upharpoonright \delta $
. Let
$f \upharpoonright \delta = g \upharpoonright \delta $
. Let
![]() $\ell = f \upharpoonright \delta = g \upharpoonright \delta $
. There exists
$\ell = f \upharpoonright \delta = g \upharpoonright \delta $
. There exists
![]() $v,w \in [E]^{\epsilon _1}_*$
so that
$v,w \in [E]^{\epsilon _1}_*$
so that
![]() $f = \ell \hat {\ }v$
and
$f = \ell \hat {\ }v$
and
![]() $g = \ell \hat {\ }w$
.
$g = \ell \hat {\ }w$
.
![]() $\Phi _\ell $
is
$\Phi _\ell $
is
![]() $\sqsubseteq $
-constant on
$\sqsubseteq $
-constant on
![]() $[E \setminus (\sup (\ell ) + 1)]^{\epsilon _1}_*$
and so by Fact 3.5,
$[E \setminus (\sup (\ell ) + 1)]^{\epsilon _1}_*$
and so by Fact 3.5,
![]() $\Phi _\ell $
depends on supremum relative to
$\Phi _\ell $
depends on supremum relative to
![]() $E \setminus (\sup (\ell ) + 1)$
. Since
$E \setminus (\sup (\ell ) + 1)$
. Since
![]() $v,w \in [E \setminus (\sup (\ell ) + 1)]^{\epsilon _1}_*$
and
$v,w \in [E \setminus (\sup (\ell ) + 1)]^{\epsilon _1}_*$
and
![]() $\sup (v) = \sup (w)$
,
$\sup (v) = \sup (w)$
,
![]() $\Phi (f) = \Phi (\ell \hat {\ }v) = \Phi _\ell (v) = \Phi _\ell (w) = \Phi (\ell \hat {\ }w) = \Phi (g)$
. It has been shown that there is a
$\Phi (f) = \Phi (\ell \hat {\ }v) = \Phi _\ell (v) = \Phi _\ell (w) = \Phi (\ell \hat {\ }w) = \Phi (g)$
. It has been shown that there is a
![]() $\delta $
so that for all
$\delta $
so that for all
![]() $f,g \in [E]^\epsilon _*$
, if
$f,g \in [E]^\epsilon _*$
, if
![]() $\sup (f) = \sup (g)$
and
$\sup (f) = \sup (g)$
and
![]() $f \upharpoonright \delta = g \upharpoonright \delta $
, then
$f \upharpoonright \delta = g \upharpoonright \delta $
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
Corollary 3.8. Suppose
![]() $\kappa $
is a cardinal,
$\kappa $
is a cardinal,
![]() $\epsilon < \kappa $
is a limit ordinal with
$\epsilon < \kappa $
is a limit ordinal with
![]() ${\mathrm {cof}}(\epsilon ) = \omega $
and
${\mathrm {cof}}(\epsilon ) = \omega $
and
![]() $p \in \omega $
. Let
$p \in \omega $
. Let
![]() $\epsilon _0 < \epsilon $
and
$\epsilon _0 < \epsilon $
and
![]() $\epsilon _1 \leq \epsilon $
be such that
$\epsilon _1 \leq \epsilon $
be such that
![]() $\epsilon = \epsilon _0 + \epsilon _1$
and
$\epsilon = \epsilon _0 + \epsilon _1$
and
![]() $\epsilon _1$
is an additively indecomposable ordinal. Assume
$\epsilon _1$
is an additively indecomposable ordinal. Assume
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon + \epsilon + p}_2$
and
$\kappa \rightarrow _* (\kappa )^{\epsilon + \epsilon + p}_2$
and
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon _1 \cdot \epsilon _1 + p}_2$
. Let
$\kappa \rightarrow _* (\kappa )^{\epsilon _1 \cdot \epsilon _1 + p}_2$
. Let
![]() $\Phi : [\kappa ]^{\epsilon + p}_* \rightarrow \mathrm {ON}$
be a function. Then there is a club
$\Phi : [\kappa ]^{\epsilon + p}_* \rightarrow \mathrm {ON}$
be a function. Then there is a club
![]() $C \subseteq \kappa $
and a
$C \subseteq \kappa $
and a
![]() $\delta < \epsilon $
so that for all
$\delta < \epsilon $
so that for all
![]() $f,g \in [C]^{\epsilon + p}_*$
, if
$f,g \in [C]^{\epsilon + p}_*$
, if
![]() $f \upharpoonright \delta = g \upharpoonright \delta $
,
$f \upharpoonright \delta = g \upharpoonright \delta $
,
![]() $\sup (f \upharpoonright \epsilon ) = \sup (g \upharpoonright \epsilon )$
and for all
$\sup (f \upharpoonright \epsilon ) = \sup (g \upharpoonright \epsilon )$
and for all
![]() $i < p$
,
$i < p$
,
![]() $f(\epsilon + i) = g(\epsilon + i)$
, then
$f(\epsilon + i) = g(\epsilon + i)$
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
Proof. The argument is similar to Theorem 3.7 where all partitions now include p elements at the top.
Theorem 3.9. Suppose
![]() $\kappa $
is a cardinal,
$\kappa $
is a cardinal,
![]() $\epsilon < \omega _1$
and
$\epsilon < \omega _1$
and
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon \cdot \epsilon }_2$
holds. Let
$\kappa \rightarrow _* (\kappa )^{\epsilon \cdot \epsilon }_2$
holds. Let
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
. Then there is a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
. Then there is a club
![]() $C \subseteq \kappa $
and finitely many ordinals
$C \subseteq \kappa $
and finitely many ordinals
![]() $\delta _0, ..., \delta _k \leq \epsilon $
so that for all
$\delta _0, ..., \delta _k \leq \epsilon $
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if for all
$f,g \in [C]^\epsilon _*$
, if for all
![]() $0 \leq i \leq k$
,
$0 \leq i \leq k$
,
![]() $\sup (f \upharpoonright \delta _i) = \sup (g \upharpoonright \delta _i)$
, then
$\sup (f \upharpoonright \delta _i) = \sup (g \upharpoonright \delta _i)$
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
Proof. The sequences of ordinals
![]() $\delta _0, ..., \delta _k$
will be defined by recursion. Let
$\delta _0, ..., \delta _k$
will be defined by recursion. Let
![]() $\delta _0 = \epsilon $
. Suppose
$\delta _0 = \epsilon $
. Suppose
![]() $\epsilon = \delta _0> ... > \delta _i$
have been defined so that there exists a club
$\epsilon = \delta _0> ... > \delta _i$
have been defined so that there exists a club
![]() $D \subseteq \kappa $
with the property that for all
$D \subseteq \kappa $
with the property that for all
![]() $f,g \in [C]^\epsilon _*$
, if
$f,g \in [C]^\epsilon _*$
, if
![]() $f \upharpoonright \delta _i = g \upharpoonright \delta _i$
and for all
$f \upharpoonright \delta _i = g \upharpoonright \delta _i$
and for all
![]() $0 \leq j < i$
,
$0 \leq j < i$
,
![]() $\sup (f \upharpoonright \delta _j) = \sup (g \upharpoonright \delta _j)$
, then
$\sup (f \upharpoonright \delta _j) = \sup (g \upharpoonright \delta _j)$
, then
![]() $\Phi (f) = \Phi (g)$
. Fix such a club D. If
$\Phi (f) = \Phi (g)$
. Fix such a club D. If
![]() $\delta _i$
is a successor ordinal, then let
$\delta _i$
is a successor ordinal, then let
![]() $\delta _{i + 1}$
be the predecessor of
$\delta _{i + 1}$
be the predecessor of
![]() $\delta _i$
. If
$\delta _i$
. If
![]() $\delta _i$
is a limit, then
$\delta _i$
is a limit, then
![]() ${\mathrm {cof}}(\delta _i) = \omega $
since
${\mathrm {cof}}(\delta _i) = \omega $
since
![]() $\delta _i \leq \epsilon < {\omega _1}$
. Define
$\delta _i \leq \epsilon < {\omega _1}$
. Define
![]() $\Psi : [D]^{\delta _i + i} \rightarrow \mathrm {ON}$
as follows: Suppose
$\Psi : [D]^{\delta _i + i} \rightarrow \mathrm {ON}$
as follows: Suppose
![]() $\ell \in [D]^{\delta _i}$
and
$\ell \in [D]^{\delta _i}$
and
![]() $\gamma _0> ... > \gamma _{i - 1} > \sup (\ell )$
in D. Let
$\gamma _0> ... > \gamma _{i - 1} > \sup (\ell )$
in D. Let
![]() $\Psi (\ell ,\gamma _{i - 1}, ..., \gamma _0) = \Phi (f)$
where f is any element of
$\Psi (\ell ,\gamma _{i - 1}, ..., \gamma _0) = \Phi (f)$
where f is any element of
![]() $[D]^\epsilon _*$
so that
$[D]^\epsilon _*$
so that
![]() $\sup (f \upharpoonright \delta _i) = \ell $
,
$\sup (f \upharpoonright \delta _i) = \ell $
,
![]() $\sup (f \upharpoonright \delta _j) = \gamma _j$
for each
$\sup (f \upharpoonright \delta _j) = \gamma _j$
for each
![]() $j < i$
.
$j < i$
.
![]() $\Psi (\ell ,\gamma _{i - 1}, ..., \gamma _0)$
is well defined and independent of the choice of f with the above property by the induction hypothesis on
$\Psi (\ell ,\gamma _{i - 1}, ..., \gamma _0)$
is well defined and independent of the choice of f with the above property by the induction hypothesis on
![]() $\delta _0,...,\delta _i$
and D. By Corollary 3.8, there is a
$\delta _0,...,\delta _i$
and D. By Corollary 3.8, there is a
![]() $\delta < \delta _i$
and a club
$\delta < \delta _i$
and a club
![]() $C \subseteq D$
so that for all
$C \subseteq D$
so that for all
![]() $\ell , \iota \in [C]^{\delta _i}_*$
,
$\ell , \iota \in [C]^{\delta _i}_*$
,
![]() $\gamma _{i - 1} < ... < \gamma _0$
in C, if
$\gamma _{i - 1} < ... < \gamma _0$
in C, if
![]() $\sup (\ell ) = \sup (\iota ) < \gamma _{i - 1}$
and
$\sup (\ell ) = \sup (\iota ) < \gamma _{i - 1}$
and
![]() $\ell \upharpoonright \delta = \iota \upharpoonright \delta $
, then
$\ell \upharpoonright \delta = \iota \upharpoonright \delta $
, then
![]() $\Psi (\ell ,\gamma _{i - 1}, ..., \gamma _0) = \Psi (\iota ,\gamma _{i - 1}, ..., \gamma _0)$
. Let
$\Psi (\ell ,\gamma _{i - 1}, ..., \gamma _0) = \Psi (\iota ,\gamma _{i - 1}, ..., \gamma _0)$
. Let
![]() $\delta _{i + 1}$
be the least
$\delta _{i + 1}$
be the least
![]() $\delta $
with this property. By definition of
$\delta $
with this property. By definition of
![]() $\Psi $
, it has been shown that there is a club C and ordinals
$\Psi $
, it has been shown that there is a club C and ordinals
![]() $\epsilon = \delta _0> ... > \delta _{i + 1}$
so that for all
$\epsilon = \delta _0> ... > \delta _{i + 1}$
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if
$f,g \in [C]^\epsilon _*$
, if
![]() $f \upharpoonright \delta _{i + 1} = g \upharpoonright \delta _{i + 1}$
and for all
$f \upharpoonright \delta _{i + 1} = g \upharpoonright \delta _{i + 1}$
and for all
![]() $j < i + 1$
,
$j < i + 1$
,
![]() $\sup (f \upharpoonright \delta _j) = \sup (g \upharpoonright \delta _j)$
, then
$\sup (f \upharpoonright \delta _j) = \sup (g \upharpoonright \delta _j)$
, then
![]() $\Phi (f) = \Phi (g)$
. By the wellfoundedness of the ordinals, there is some k so that at stage k,
$\Phi (f) = \Phi (g)$
. By the wellfoundedness of the ordinals, there is some k so that at stage k,
![]() $\delta _k = 0$
. Then the finite sequence
$\delta _k = 0$
. Then the finite sequence
![]() $\epsilon = \delta _0> \delta _1 > ... > \delta _k = 0$
has the property that there is a club C so that for all
$\epsilon = \delta _0> \delta _1 > ... > \delta _k = 0$
has the property that there is a club C so that for all
![]() $f,g \in [C]^\epsilon _*$
, if for all
$f,g \in [C]^\epsilon _*$
, if for all
![]() $j \leq k$
,
$j \leq k$
,
![]() $\sup (f \upharpoonright \delta _j) = \sup (g \upharpoonright \delta _j)$
, then
$\sup (f \upharpoonright \delta _j) = \sup (g \upharpoonright \delta _j)$
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
The rest of this section will put the earlier result in context and provide some additional examples especially under
![]() $\mathsf {AD}$
.
$\mathsf {AD}$
.
Corollary 3.10. Assume
![]() $\mathsf {AD}$
. Suppose
$\mathsf {AD}$
. Suppose
![]() $\kappa $
is
$\kappa $
is
![]() ${\omega _1}$
,
${\omega _1}$
,
![]() $\omega _2$
,
$\omega _2$
,
![]() $\boldsymbol {\delta }_n^1$
for
$\boldsymbol {\delta }_n^1$
for
![]() $1 \leq n < \omega $
,
$1 \leq n < \omega $
,
![]() $\boldsymbol {\delta }_A$
where
$\boldsymbol {\delta }_A$
where
![]() $A \subseteq \mathbb {R}$
or
$A \subseteq \mathbb {R}$
or
![]() $\boldsymbol {\delta }^2_1$
(assuming
$\boldsymbol {\delta }^2_1$
(assuming
![]() $\mathsf {DC}_{\mathbb {R}}$
). If
$\mathsf {DC}_{\mathbb {R}}$
). If
![]() $\epsilon < {\omega _1}$
and
$\epsilon < {\omega _1}$
and
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, then there is a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, then there is a club
![]() $C \subseteq \kappa $
and finitely many ordinals
$C \subseteq \kappa $
and finitely many ordinals
![]() $\beta _0 < \beta _1 < ... < \beta _{p - 1} \leq \epsilon $
(where
$\beta _0 < \beta _1 < ... < \beta _{p - 1} \leq \epsilon $
(where
![]() $p \in \omega $
) so that for all
$p \in \omega $
) so that for all
![]() $f,g \in [C]^\epsilon _*$
, if for all
$f,g \in [C]^\epsilon _*$
, if for all
![]() $i < p$
,
$i < p$
,
![]() $\sup (f \upharpoonright \beta _i) = \sup (g \upharpoonright \beta _i)$
, then
$\sup (f \upharpoonright \beta _i) = \sup (g \upharpoonright \beta _i)$
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
Assume
![]() $\mathsf {AD}$
. Suppose
$\mathsf {AD}$
. Suppose
![]() $\kappa $
is
$\kappa $
is
![]() ${\omega _1}$
,
${\omega _1}$
,
![]() $\omega _2$
,
$\omega _2$
,
![]() $\boldsymbol {\delta }_n^1$
for
$\boldsymbol {\delta }_n^1$
for
![]() $1 \leq n < \omega $
,
$1 \leq n < \omega $
,
![]() $\boldsymbol {\delta }_A$
where
$\boldsymbol {\delta }_A$
where
![]() $A \subseteq \mathbb {R}$
or
$A \subseteq \mathbb {R}$
or
![]() $\boldsymbol {\delta }^2_1$
(assuming
$\boldsymbol {\delta }^2_1$
(assuming
![]() $\mathsf {DC}_{\mathbb {R}}$
). If
$\mathsf {DC}_{\mathbb {R}}$
). If
![]() $\epsilon < \kappa $
with
$\epsilon < \kappa $
with
![]() ${\mathrm {cof}}(\epsilon ) = \omega $
and
${\mathrm {cof}}(\epsilon ) = \omega $
and
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, then there is a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, then there is a club
![]() $C \subseteq \kappa $
and a
$C \subseteq \kappa $
and a
![]() $\delta < \epsilon $
so that for all
$\delta < \epsilon $
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if
$f,g \in [C]^\epsilon _*$
, if
![]() $\sup (f) = \sup (g)$
and
$\sup (f) = \sup (g)$
and
![]() $f \upharpoonright \delta = g \upharpoonright \delta $
, then
$f \upharpoonright \delta = g \upharpoonright \delta $
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
The next result shows that the assumption that
![]() ${\mathrm {cof}}(\epsilon ) = \omega $
is necessary in Theorem 3.7.
${\mathrm {cof}}(\epsilon ) = \omega $
is necessary in Theorem 3.7.
Fact 3.11. Suppose
![]() $\zeta < \kappa $
are two cardinals such that
$\zeta < \kappa $
are two cardinals such that
![]() $\zeta \rightarrow _* (\zeta )^2_2$
,
$\zeta \rightarrow _* (\zeta )^2_2$
,
![]() $\kappa \rightarrow _* (\kappa )^\zeta _2$
and
$\kappa \rightarrow _* (\kappa )^\zeta _2$
and
![]() $\mathsf {DC}_{[\kappa ]^\zeta }$
hold. Then the ultrapower
$\mathsf {DC}_{[\kappa ]^\zeta }$
hold. Then the ultrapower ![]() is a wellordering (and hence an ordinal) and there is a function
is a wellordering (and hence an ordinal) and there is a function ![]() so that for all clubs
so that for all clubs
![]() $C \subseteq \kappa $
and all
$C \subseteq \kappa $
and all
![]() $\delta < \zeta $
, there are functions
$\delta < \zeta $
, there are functions
![]() $f,g \in [C]^\zeta _*$
with
$f,g \in [C]^\zeta _*$
with
![]() $\sup (f) = \sup (g)$
,
$\sup (f) = \sup (g)$
,
![]() $f \upharpoonright \delta = g \upharpoonright \delta $
and
$f \upharpoonright \delta = g \upharpoonright \delta $
and
![]() $\Phi (f) \neq \Phi (g)$
.
$\Phi (f) \neq \Phi (g)$
.
Proof. The partition relation
![]() $\zeta \rightarrow _* (\zeta )^2_2$
implies that
$\zeta \rightarrow _* (\zeta )^2_2$
implies that
![]() $\mu ^\zeta _1$
is a
$\mu ^\zeta _1$
is a
![]() $\zeta $
-complete ultrafilter on
$\zeta $
-complete ultrafilter on
![]() $\zeta $
and thus
$\zeta $
and thus
![]() ${\mathrm {cof}}(\zeta ) = \zeta> \omega $
.
${\mathrm {cof}}(\zeta ) = \zeta> \omega $
.
![]() $\mathsf {DC}_{[\kappa ]^\zeta }$
implies that the ultrapower
$\mathsf {DC}_{[\kappa ]^\zeta }$
implies that the ultrapower ![]() is a wellordering which can be identified as an ordinal. If
is a wellordering which can be identified as an ordinal. If
![]() $f : \zeta \rightarrow \kappa $
, then let
$f : \zeta \rightarrow \kappa $
, then let
![]() $[f]_{\mu ^\zeta _1}$
denote the element of the ultrapower represented by the function f. Define
$[f]_{\mu ^\zeta _1}$
denote the element of the ultrapower represented by the function f. Define ![]() by
by
![]() $\Phi (f) = [f]_{\mu ^\zeta _1}$
. Let
$\Phi (f) = [f]_{\mu ^\zeta _1}$
. Let
![]() $\delta < \zeta $
and
$\delta < \zeta $
and
![]() $C \subseteq \kappa $
be a club. Let
$C \subseteq \kappa $
be a club. Let
![]() $\ell \in [C]^\delta _*$
. Let
$\ell \in [C]^\delta _*$
. Let
![]() $\iota _0,\iota _1 \in [C]^\zeta _*$
be defined by
$\iota _0,\iota _1 \in [C]^\zeta _*$
be defined by
![]() $\iota _0(\alpha ) = {\mathsf {next}}_C^{\omega \cdot (\alpha + 1)}(\sup (\ell ))$
and
$\iota _0(\alpha ) = {\mathsf {next}}_C^{\omega \cdot (\alpha + 1)}(\sup (\ell ))$
and
![]() $\iota _1(\alpha ) = {\mathsf {next}}_C^{\omega \cdot (\alpha + 2)}(\sup (\ell ))$
. Let
$\iota _1(\alpha ) = {\mathsf {next}}_C^{\omega \cdot (\alpha + 2)}(\sup (\ell ))$
. Let
![]() $f = \ell \hat {\ }\iota _0$
and
$f = \ell \hat {\ }\iota _0$
and
![]() $g = \ell \hat {\ }\iota _1$
. Then
$g = \ell \hat {\ }\iota _1$
. Then
![]() $f,g \in [C]^\zeta _*$
,
$f,g \in [C]^\zeta _*$
,
![]() $\sup (f) = \sup (g)$
,
$\sup (f) = \sup (g)$
,
![]() $f \upharpoonright \delta = \ell = g \upharpoonright \delta $
and
$f \upharpoonright \delta = \ell = g \upharpoonright \delta $
and
![]() $\Phi (f) < \Phi (g)$
since
$\Phi (f) < \Phi (g)$
since
![]() $\{\alpha < \zeta : f(\alpha ) < g(\alpha )\} \supseteq \{\alpha < \zeta : \alpha \geq \delta \} \in \mu ^\zeta _1$
.
$\{\alpha < \zeta : f(\alpha ) < g(\alpha )\} \supseteq \{\alpha < \zeta : \alpha \geq \delta \} \in \mu ^\zeta _1$
.
Fact 3.12. Assume
![]() $\mathsf {AD}$
. There is a function
$\mathsf {AD}$
. There is a function
![]() $\Phi : [\omega _2]^{\omega _1}_* \rightarrow \omega _3$
so that for all clubs
$\Phi : [\omega _2]^{\omega _1}_* \rightarrow \omega _3$
so that for all clubs
![]() $C \subseteq \kappa $
and
$C \subseteq \kappa $
and
![]() $\delta < {\omega _1}$
, there are functions
$\delta < {\omega _1}$
, there are functions
![]() $f,g \in [C]^{\omega _1}_*$
so that
$f,g \in [C]^{\omega _1}_*$
so that
![]() $\sup (f) = \sup (g)$
,
$\sup (f) = \sup (g)$
,
![]() $f \upharpoonright \delta = g \upharpoonright \delta $
and
$f \upharpoonright \delta = g \upharpoonright \delta $
and
![]() $\Phi (f) \neq \Phi (g)$
.
$\Phi (f) \neq \Phi (g)$
.
Proof. Under
![]() $\mathsf {AD}$
,
$\mathsf {AD}$
,
![]() ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
and
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
and ![]() . As in Fact 3.11, the map
. As in Fact 3.11, the map
![]() $\Phi : [\omega _2]^{\omega _1} \rightarrow \omega _3$
defined by
$\Phi : [\omega _2]^{\omega _1} \rightarrow \omega _3$
defined by
![]() $\Phi (f) = [f]_{\mu ^{\omega _1}_1}$
has the desired property.
$\Phi (f) = [f]_{\mu ^{\omega _1}_1}$
has the desired property.
The restriction that
![]() $\epsilon < {\omega _1}$
is also necessary in Theorem 3.9 according to the following example.
$\epsilon < {\omega _1}$
is also necessary in Theorem 3.9 according to the following example.
Example 3.13. Suppose
![]() $\zeta < \kappa $
are two cardinals such that
$\zeta < \kappa $
are two cardinals such that
![]() $\zeta \rightarrow _* (\zeta )^2_2$
,
$\zeta \rightarrow _* (\zeta )^2_2$
,
![]() $\kappa \rightarrow (\kappa )^\zeta _2$
and
$\kappa \rightarrow (\kappa )^\zeta _2$
and
![]() $\mathsf {DC}_{[\kappa ]^\zeta }$
hold. Then there is a function
$\mathsf {DC}_{[\kappa ]^\zeta }$
hold. Then there is a function ![]() so that for all clubs
so that for all clubs
![]() $C \subseteq \kappa $
and all finite set of ordinals
$C \subseteq \kappa $
and all finite set of ordinals
![]() $\beta _0 < ... < \beta _{p - 1} \leq \zeta + \omega $
(where
$\beta _0 < ... < \beta _{p - 1} \leq \zeta + \omega $
(where
![]() $p \in \omega $
), there are functions
$p \in \omega $
), there are functions
![]() $f,g \in [C]^{\zeta + \omega }_*$
so that for all
$f,g \in [C]^{\zeta + \omega }_*$
so that for all
![]() $i < p$
,
$i < p$
,
![]() $\sup (f \upharpoonright \beta _i) = \sup (g \upharpoonright \beta _i)$
and
$\sup (f \upharpoonright \beta _i) = \sup (g \upharpoonright \beta _i)$
and
![]() $\Psi (f) \neq \Psi (g)$
.
$\Psi (f) \neq \Psi (g)$
.
Assume
![]() $\mathsf {AD}$
. There is a function
$\mathsf {AD}$
. There is a function
![]() $\Psi : [\omega _2]^{{\omega _1} + \omega }_* \rightarrow \omega _3$
so that for all clubs
$\Psi : [\omega _2]^{{\omega _1} + \omega }_* \rightarrow \omega _3$
so that for all clubs
![]() $C \subseteq \omega _2$
and all finite sets of ordinals
$C \subseteq \omega _2$
and all finite sets of ordinals
![]() $\beta _0 < \beta _1 < ... < \beta _{p - 1} \leq {\omega _1} + \omega $
(where
$\beta _0 < \beta _1 < ... < \beta _{p - 1} \leq {\omega _1} + \omega $
(where
![]() $p \in \omega $
), there are functions
$p \in \omega $
), there are functions
![]() $f,g \in [C]^{{\omega _1} + \omega }_*$
so that for all
$f,g \in [C]^{{\omega _1} + \omega }_*$
so that for all
![]() $i < p$
,
$i < p$
,
![]() $\sup (f \upharpoonright \beta _i) = \sup (g \upharpoonright \beta _i)$
and
$\sup (f \upharpoonright \beta _i) = \sup (g \upharpoonright \beta _i)$
and
![]() $\Psi (f) \neq \Psi (g)$
.
$\Psi (f) \neq \Psi (g)$
.
Proof. For the first statement, let ![]() be defined by
be defined by
![]() $\Psi (f) = \Phi (f \upharpoonright \zeta )$
where
$\Psi (f) = \Phi (f \upharpoonright \zeta )$
where
![]() $\Phi $
is the function from the proof of Fact 3.11.
$\Phi $
is the function from the proof of Fact 3.11.
For the second statement, let
![]() $\Psi : [\omega _2]^{{\omega _1} + \omega }_* \rightarrow \omega _3$
be defined by
$\Psi : [\omega _2]^{{\omega _1} + \omega }_* \rightarrow \omega _3$
be defined by
![]() $\Psi (f) = \Phi (f \upharpoonright {\omega _1})$
where
$\Psi (f) = \Phi (f \upharpoonright {\omega _1})$
where
![]() $\Phi $
is the function from the proof of Fact 3.12. For a slightly more interesting example, one can also use
$\Phi $
is the function from the proof of Fact 3.12. For a slightly more interesting example, one can also use
![]() $\Upsilon (f) = \Psi (f) + \sup (f) = \Phi (f \upharpoonright {\omega _1}) + \sup (f)$
. Note that since
$\Upsilon (f) = \Psi (f) + \sup (f) = \Phi (f \upharpoonright {\omega _1}) + \sup (f)$
. Note that since
![]() ${\mathrm {cof}}({\omega _1} + \omega ) = \omega $
, Theorem 3.7 does apply to
${\mathrm {cof}}({\omega _1} + \omega ) = \omega $
, Theorem 3.7 does apply to
![]() $\Upsilon $
and indeed, for all
$\Upsilon $
and indeed, for all
![]() $f,g \in [\omega _2]^{{\omega _1} + \omega }_*$
, if
$f,g \in [\omega _2]^{{\omega _1} + \omega }_*$
, if
![]() $\sup (f) = \sup (g)$
and
$\sup (f) = \sup (g)$
and
![]() $f \upharpoonright {\omega _1} = g \upharpoonright {\omega _1}$
, then
$f \upharpoonright {\omega _1} = g \upharpoonright {\omega _1}$
, then
![]() $\Upsilon (f) = \Upsilon (g)$
.
$\Upsilon (f) = \Upsilon (g)$
.
Consider a function
![]() $\Phi : [\omega _2]^\epsilon \rightarrow \mathrm {ON}$
where
$\Phi : [\omega _2]^\epsilon \rightarrow \mathrm {ON}$
where
![]() ${\omega _1} \leq \epsilon < \omega _2$
but
${\omega _1} \leq \epsilon < \omega _2$
but
![]() ${\mathrm {cof}}(\epsilon )> \omega $
. Neither Theorem 3.7 nor Theorem 3.9 is applicable since
${\mathrm {cof}}(\epsilon )> \omega $
. Neither Theorem 3.7 nor Theorem 3.9 is applicable since
![]() $\epsilon \geq {\omega _1}$
and
$\epsilon \geq {\omega _1}$
and
![]() ${\mathrm {cof}}(\epsilon ) \neq \omega $
. Moreover, Fact 3.12 gives an example of a function
${\mathrm {cof}}(\epsilon ) \neq \omega $
. Moreover, Fact 3.12 gives an example of a function
![]() $\Phi : [\omega _2]^{\omega _1}_* \rightarrow \omega _3$
which fails to satisfy the short length continuity property under
$\Phi : [\omega _2]^{\omega _1}_* \rightarrow \omega _3$
which fails to satisfy the short length continuity property under
![]() $\mathsf {AD}$
. Remarkably under
$\mathsf {AD}$
. Remarkably under
![]() $\mathsf {AD}$
, if one demands the function
$\mathsf {AD}$
, if one demands the function
![]() $\Phi $
takes image in
$\Phi $
takes image in
![]() $\omega _2$
rather than
$\omega _2$
rather than
![]() $\omega _3$
, then the short length continuity properties do hold even if
$\omega _3$
, then the short length continuity properties do hold even if
![]() ${\mathrm {cof}}(\epsilon ) = {\omega _1}$
. This result is possible under
${\mathrm {cof}}(\epsilon ) = {\omega _1}$
. This result is possible under
![]() $\mathsf {AD}$
because
$\mathsf {AD}$
because
![]() $\omega _2$
has an ultrapower representation as
$\omega _2$
has an ultrapower representation as ![]() which can be studied using the Kunen tree analysis.
which can be studied using the Kunen tree analysis.
Fact 3.14. ([Reference Chan, Jackson and Trang6])
Assume
![]() $\mathsf {AD}$
. Suppose
$\mathsf {AD}$
. Suppose
![]() $\epsilon < \omega _2$
(including the possibility
$\epsilon < \omega _2$
(including the possibility
![]() ${\mathrm {cof}}(\epsilon ) = {\omega _1}$
) and
${\mathrm {cof}}(\epsilon ) = {\omega _1}$
) and
![]() $\Phi : [\omega _2]^\epsilon _* \rightarrow \omega _2$
. Then there is a club
$\Phi : [\omega _2]^\epsilon _* \rightarrow \omega _2$
. Then there is a club
![]() $C \subseteq \omega _2$
and finitely many ordinals
$C \subseteq \omega _2$
and finitely many ordinals
![]() $\beta _0 < \beta _1 < ... < \beta _{p - 1} \leq \epsilon $
(where
$\beta _0 < \beta _1 < ... < \beta _{p - 1} \leq \epsilon $
(where
![]() $p \in \omega $
) so that for all
$p \in \omega $
) so that for all
![]() $f,g \in [C]^\epsilon _*$
, if for all
$f,g \in [C]^\epsilon _*$
, if for all
![]() $i < p$
,
$i < p$
,
![]() $\sup (f \upharpoonright \beta _i) = \sup (g \upharpoonright \beta _i)$
, then
$\sup (f \upharpoonright \beta _i) = \sup (g \upharpoonright \beta _i)$
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
4 Applications of short length continuity
Fact 4.1. If
![]() $\kappa $
is a cardinal and
$\kappa $
is a cardinal and
![]() $\epsilon \leq \kappa $
with
$\epsilon \leq \kappa $
with
![]() ${\mathrm {cof}}(\kappa ) \geq \epsilon $
, then
${\mathrm {cof}}(\kappa ) \geq \epsilon $
, then
![]() $|{}^\epsilon \kappa | = |[\kappa ]^\epsilon | = |[\kappa ]^\epsilon _*|$
.
$|{}^\epsilon \kappa | = |[\kappa ]^\epsilon | = |[\kappa ]^\epsilon _*|$
.
Proof. For
![]() $f \in {}^\epsilon \kappa $
, define by recursion
$f \in {}^\epsilon \kappa $
, define by recursion
![]() $\Phi (f)$
as follows:
$\Phi (f)$
as follows:
![]() $\Phi (f)(0) = f(0)$
. If
$\Phi (f)(0) = f(0)$
. If
![]() $\beta < \epsilon $
and
$\beta < \epsilon $
and
![]() $\Phi (f) \upharpoonright \beta $
has been defined, then
$\Phi (f) \upharpoonright \beta $
has been defined, then
![]() $\sup (\Phi (f) \upharpoonright \beta ) < \kappa $
since
$\sup (\Phi (f) \upharpoonright \beta ) < \kappa $
since
![]() ${\mathrm {cof}}(\kappa ) \geq \epsilon $
and so let
${\mathrm {cof}}(\kappa ) \geq \epsilon $
and so let
![]() $\Phi (f)(\beta ) = \sup (\Phi (f) \upharpoonright \beta ) + f(\beta )$
.
$\Phi (f)(\beta ) = \sup (\Phi (f) \upharpoonright \beta ) + f(\beta )$
.
![]() $\Phi (f) \in [\kappa ]^\epsilon $
.
$\Phi (f) \in [\kappa ]^\epsilon $
.
![]() $\Phi : {}^\epsilon \kappa \rightarrow [\kappa ]^\epsilon $
is an injection and thus
$\Phi : {}^\epsilon \kappa \rightarrow [\kappa ]^\epsilon $
is an injection and thus
![]() $|{}^\epsilon \kappa | \leq |[\kappa ]^\epsilon | \leq |{}^\epsilon \kappa |$
.
$|{}^\epsilon \kappa | \leq |[\kappa ]^\epsilon | \leq |{}^\epsilon \kappa |$
.
Let
![]() $A = \{\omega \cdot (\alpha + 1): \alpha < \kappa \}$
. Suppose
$A = \{\omega \cdot (\alpha + 1): \alpha < \kappa \}$
. Suppose
![]() $f \in [A]^\epsilon $
. For each
$f \in [A]^\epsilon $
. For each
![]() $\alpha < \epsilon $
, let
$\alpha < \epsilon $
, let
![]() $\gamma _\alpha < \kappa $
be such that
$\gamma _\alpha < \kappa $
be such that
![]() $f(\alpha ) = \omega \cdot (\gamma _\alpha + 1)$
. Define
$f(\alpha ) = \omega \cdot (\gamma _\alpha + 1)$
. Define
![]() $F : \epsilon \times \omega \rightarrow \kappa $
by
$F : \epsilon \times \omega \rightarrow \kappa $
by
![]() $F(\alpha ,n) = \omega \cdot \gamma _\alpha + n$
. F witnesses that f has uniform cofinality
$F(\alpha ,n) = \omega \cdot \gamma _\alpha + n$
. F witnesses that f has uniform cofinality
![]() $\omega $
. Fix
$\omega $
. Fix
![]() $\beta < \epsilon $
. Let
$\beta < \epsilon $
. Let
![]() $\zeta = \sup \{\gamma _\alpha + 1 : \alpha < \beta \}$
. Note that
$\zeta = \sup \{\gamma _\alpha + 1 : \alpha < \beta \}$
. Note that
![]() $\zeta \leq \gamma _\beta $
. Then
$\zeta \leq \gamma _\beta $
. Then
![]() $\sup (f \upharpoonright \beta ) \leq \omega \cdot \zeta \leq \omega \cdot \gamma _\beta < \omega \cdot (\gamma _\beta + 1) = f(\beta )$
. This shows that f is discontinuous everywhere. Hence, f has the correct type. Thus, it has been shown that
$\sup (f \upharpoonright \beta ) \leq \omega \cdot \zeta \leq \omega \cdot \gamma _\beta < \omega \cdot (\gamma _\beta + 1) = f(\beta )$
. This shows that f is discontinuous everywhere. Hence, f has the correct type. Thus, it has been shown that
![]() $[A]^\epsilon = [A]^\epsilon _*$
. Since
$[A]^\epsilon = [A]^\epsilon _*$
. Since
![]() $|A| = \kappa $
,
$|A| = \kappa $
,
![]() $|[\kappa ]^\epsilon _*| \leq |[\kappa ]^\epsilon | = |[A]^\epsilon | = |[A]^\epsilon _*| \leq |[\kappa ]^\epsilon _*|$
.
$|[\kappa ]^\epsilon _*| \leq |[\kappa ]^\epsilon | = |[A]^\epsilon | = |[A]^\epsilon _*| \leq |[\kappa ]^\epsilon _*|$
.
The following application of the almost everywhere short length continuity shows that infinite exponent partition spaces are not wellorderable assuming suitable partition properties. (More optimal results are known. For instance, the correct type partition relation
![]() $\kappa \rightarrow _* (\kappa )^2_2$
implies
$\kappa \rightarrow _* (\kappa )^2_2$
implies
![]() $[\kappa ]^\omega $
is not wellorderable. The ordinary partition relation
$[\kappa ]^\omega $
is not wellorderable. The ordinary partition relation
![]() $\kappa \rightarrow (\kappa )^\omega _2$
also implies
$\kappa \rightarrow (\kappa )^\omega _2$
also implies
![]() $[\kappa ]^\omega $
is not wellorderable. It is not clear if
$[\kappa ]^\omega $
is not wellorderable. It is not clear if
![]() $\kappa \rightarrow _* (\kappa )^2_2$
implies
$\kappa \rightarrow _* (\kappa )^2_2$
implies
![]() $\kappa \rightarrow (\kappa )^\omega _2$
or
$\kappa \rightarrow (\kappa )^\omega _2$
or
![]() $\kappa \rightarrow (\kappa )^\omega _2$
implies
$\kappa \rightarrow (\kappa )^\omega _2$
implies
![]() $\kappa \rightarrow _* (\kappa )^2_2$
.)
$\kappa \rightarrow _* (\kappa )^2_2$
.)
Theorem 4.2. Suppose
![]() $\kappa $
is a cardinal so that
$\kappa $
is a cardinal so that
![]() $\kappa \rightarrow _* (\kappa )^{\omega \cdot \omega }_2$
.
$\kappa \rightarrow _* (\kappa )^{\omega \cdot \omega }_2$
.
![]() $[\kappa ]^\omega $
is not wellorderable and thus for all
$[\kappa ]^\omega $
is not wellorderable and thus for all
![]() $\epsilon , \delta \in \mathrm {ON}$
with
$\epsilon , \delta \in \mathrm {ON}$
with
![]() $\omega \leq \epsilon $
and
$\omega \leq \epsilon $
and
![]() $\kappa \leq \delta $
,
$\kappa \leq \delta $
,
![]() ${}^\epsilon \delta $
and
${}^\epsilon \delta $
and
![]() ${\mathscr {P}(\delta )}$
are not wellorderable.
${\mathscr {P}(\delta )}$
are not wellorderable.
Proof. Suppose
![]() $[\kappa ]^\omega $
was wellorderable. Then there is an injection
$[\kappa ]^\omega $
was wellorderable. Then there is an injection
![]() $\Phi : [\kappa ]^\omega _* \rightarrow \mathrm {ON}$
. By Theorem 3.7, there is a club
$\Phi : [\kappa ]^\omega _* \rightarrow \mathrm {ON}$
. By Theorem 3.7, there is a club
![]() $C \subseteq \kappa $
and an
$C \subseteq \kappa $
and an
![]() $n < \omega $
so that for all
$n < \omega $
so that for all
![]() $f,g \in [C]^\omega _*$
, if
$f,g \in [C]^\omega _*$
, if
![]() $f \upharpoonright n = g \upharpoonright n$
and
$f \upharpoonright n = g \upharpoonright n$
and
![]() $\sup (f) = \sup (g)$
, then
$\sup (f) = \sup (g)$
, then
![]() $\Phi (f) = \Phi (g)$
. Pick any
$\Phi (f) = \Phi (g)$
. Pick any
![]() $f,g \in [C]^\omega _*$
so that
$f,g \in [C]^\omega _*$
so that
![]() $f \upharpoonright n = g \upharpoonright n$
,
$f \upharpoonright n = g \upharpoonright n$
,
![]() $\sup (f) = \sup (g)$
and
$\sup (f) = \sup (g)$
and
![]() $f(n) \neq g(n)$
. Then
$f(n) \neq g(n)$
. Then
![]() $f \neq g$
and
$f \neq g$
and
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
![]() $\Phi $
is not an injection. Contradiction.
$\Phi $
is not an injection. Contradiction.
If
![]() $\omega \leq \epsilon $
and
$\omega \leq \epsilon $
and
![]() $\kappa \leq \delta $
, then
$\kappa \leq \delta $
, then
![]() $[\kappa ]^\omega $
injects to
$[\kappa ]^\omega $
injects to
![]() ${}^\epsilon \delta $
and
${}^\epsilon \delta $
and
![]() ${\mathscr {P}(\delta )}$
. Thus,
${\mathscr {P}(\delta )}$
. Thus,
![]() ${}^\epsilon \delta $
and
${}^\epsilon \delta $
and
![]() ${\mathscr {P}(\delta )}$
cannot be wellorderable.
${\mathscr {P}(\delta )}$
cannot be wellorderable.
The following cardinality computation was proved in [Reference Chan, Jackson and Trang5] for
![]() ${\omega _1}$
using
${\omega _1}$
using
![]() $\mathsf {AD}$
and
$\mathsf {AD}$
and
![]() $\mathsf {DC}_{\mathbb {R}}$
.
$\mathsf {DC}_{\mathbb {R}}$
.
Fact 4.3. ([Reference Chan, Jackson and Trang5] Theorem 2.9)
Assuming
![]() $\mathsf {AD}$
,
$\mathsf {AD}$
,
![]() $\neg (|{}^{<{\omega _1}}{\omega _1}| \leq |{}^\omega (\omega _\omega )|)$
.
$\neg (|{}^{<{\omega _1}}{\omega _1}| \leq |{}^\omega (\omega _\omega )|)$
.
([Reference Chan, Jackson and Trang5] Theorem 4.4) Assuming
![]() $\mathsf {AD}$
and
$\mathsf {AD}$
and
![]() $\mathsf {DC}_{\mathbb {R}}$
, there is no injection of
$\mathsf {DC}_{\mathbb {R}}$
, there is no injection of
![]() ${}^{<{\omega _1}}{\omega _1}$
into
${}^{<{\omega _1}}{\omega _1}$
into
![]() ${}^\omega \mathrm {ON}$
, the class of
${}^\omega \mathrm {ON}$
, the class of
![]() $\omega $
-sequences of ordinals.
$\omega $
-sequences of ordinals.
The arguments in [Reference Chan, Jackson and Trang5] used many techniques of determinacy (often specific to
![]() ${\omega _1}$
). The techniques seem difficult to generalize to the higher projective ordinals
${\omega _1}$
). The techniques seem difficult to generalize to the higher projective ordinals
![]() $\boldsymbol {\delta }^1_n$
and have no analog at strong partition cardinals which are limit cardinals like
$\boldsymbol {\delta }^1_n$
and have no analog at strong partition cardinals which are limit cardinals like
![]() $\boldsymbol {\delta }^2_1$
. The following result generalizes Fact 4.3 purely from the weak partition relation.
$\boldsymbol {\delta }^2_1$
. The following result generalizes Fact 4.3 purely from the weak partition relation.
Theorem 4.4. Suppose
![]() $\kappa $
is a cardinal so that
$\kappa $
is a cardinal so that
![]() $\kappa \rightarrow _* (\kappa )^{<\kappa }_2$
. Then for all
$\kappa \rightarrow _* (\kappa )^{<\kappa }_2$
. Then for all
![]() $\chi < \kappa $
, there is no injection of
$\chi < \kappa $
, there is no injection of
![]() ${}^{<\kappa }\kappa $
into
${}^{<\kappa }\kappa $
into
![]() ${}^\chi \mathrm {ON}$
, the class of
${}^\chi \mathrm {ON}$
, the class of
![]() $\chi $
-length sequences of ordinals. In particular, for all
$\chi $
-length sequences of ordinals. In particular, for all
![]() $\chi < \kappa $
,
$\chi < \kappa $
,
![]() $|{}^\chi \kappa | < |{}^{<\kappa }\kappa |$
.
$|{}^\chi \kappa | < |{}^{<\kappa }\kappa |$
.
Proof. Suppose there is an injection
![]() $\Phi ' : {}^{<\kappa }\kappa \rightarrow {}^\chi \mathrm {ON}$
. By Fact 4.1,
$\Phi ' : {}^{<\kappa }\kappa \rightarrow {}^\chi \mathrm {ON}$
. By Fact 4.1,
![]() $|{}^{<\kappa }\kappa | = |[\kappa ]_*^{<\kappa }|$
and thus one has an injection
$|{}^{<\kappa }\kappa | = |[\kappa ]_*^{<\kappa }|$
and thus one has an injection
![]() $\Phi : [\kappa ]^{<\kappa }_* \rightarrow {}^\chi \mathrm {ON}$
. For each
$\Phi : [\kappa ]^{<\kappa }_* \rightarrow {}^\chi \mathrm {ON}$
. For each
![]() $\epsilon < \kappa $
and
$\epsilon < \kappa $
and
![]() $\gamma < \chi $
, let
$\gamma < \chi $
, let
![]() $\Phi ^\epsilon _\gamma : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
be defined by
$\Phi ^\epsilon _\gamma : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
be defined by
![]() $\Phi ^\epsilon _\gamma (f) = \Phi (f)(\gamma )$
. By Theorem 3.7, for each
$\Phi ^\epsilon _\gamma (f) = \Phi (f)(\gamma )$
. By Theorem 3.7, for each
![]() $\gamma < \chi $
and
$\gamma < \chi $
and
![]() $\epsilon \in [\kappa ]^1_*$
(equivalently,
$\epsilon \in [\kappa ]^1_*$
(equivalently,
![]() $\epsilon < \kappa $
and
$\epsilon < \kappa $
and
![]() ${\mathrm {cof}}(\epsilon ) = \omega $
), there is a club C and a
${\mathrm {cof}}(\epsilon ) = \omega $
), there is a club C and a
![]() $\delta < \epsilon $
so that for all
$\delta < \epsilon $
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if
$f,g \in [C]^\epsilon _*$
, if
![]() $\sup (f) = \sup (g)$
and
$\sup (f) = \sup (g)$
and
![]() $f \upharpoonright \delta = g \upharpoonright \delta $
, then
$f \upharpoonright \delta = g \upharpoonright \delta $
, then
![]() $\Phi ^\epsilon _\gamma (f) = \Phi ^\epsilon _\gamma (g)$
. Let
$\Phi ^\epsilon _\gamma (f) = \Phi ^\epsilon _\gamma (g)$
. Let
![]() $\delta ^\epsilon _\gamma $
be the least such
$\delta ^\epsilon _\gamma $
be the least such
![]() $\delta < \epsilon $
. For each
$\delta < \epsilon $
. For each
![]() $\gamma < \chi $
, define
$\gamma < \chi $
, define
![]() $\Lambda _\gamma : [\kappa ]^1_* \rightarrow \kappa $
by
$\Lambda _\gamma : [\kappa ]^1_* \rightarrow \kappa $
by
![]() $\Lambda _\gamma (\epsilon ) = \delta ^\epsilon _\gamma $
. Note that for all
$\Lambda _\gamma (\epsilon ) = \delta ^\epsilon _\gamma $
. Note that for all
![]() $\epsilon \in [\kappa ]^1_*$
,
$\epsilon \in [\kappa ]^1_*$
,
![]() $\Lambda _\gamma (\epsilon ) < \epsilon $
and so by Fact 2.10 or Fact 2.11, there is a unique
$\Lambda _\gamma (\epsilon ) < \epsilon $
and so by Fact 2.10 or Fact 2.11, there is a unique
![]() $\delta _\gamma < \kappa $
so that
$\delta _\gamma < \kappa $
so that
![]() $\Lambda _{\gamma }^{-1}[\{\delta _\gamma \}] \in \mu ^\kappa _1$
. Since
$\Lambda _{\gamma }^{-1}[\{\delta _\gamma \}] \in \mu ^\kappa _1$
. Since
![]() $\kappa \rightarrow _* (\kappa )^2_2$
implies
$\kappa \rightarrow _* (\kappa )^2_2$
implies
![]() $\kappa $
is regular and
$\kappa $
is regular and
![]() $\chi < \kappa $
, let
$\chi < \kappa $
, let
![]() $\delta ^* = \sup \{\delta _\gamma + 1 : \gamma < \chi \}$
and observe
$\delta ^* = \sup \{\delta _\gamma + 1 : \gamma < \chi \}$
and observe
![]() $\delta ^* < \kappa $
.
$\delta ^* < \kappa $
.
Note that for all
![]() $\gamma < \chi $
,
$\gamma < \chi $
,
![]() $\Lambda _{\gamma }^{-1}[\delta ^*] \in \mu ^\kappa _1$
since
$\Lambda _{\gamma }^{-1}[\delta ^*] \in \mu ^\kappa _1$
since
![]() $\delta _\gamma \in \delta ^*$
. By Fact 2.11,
$\delta _\gamma \in \delta ^*$
. By Fact 2.11,
![]() $\mu ^\kappa _1$
is
$\mu ^\kappa _1$
is
![]() $\kappa $
-complete and thus
$\kappa $
-complete and thus
![]() $\bigcap _{\gamma < \chi } \Lambda _{\gamma }^{-1}[\delta ^*] \in \mu ^\kappa _1$
. There is a club
$\bigcap _{\gamma < \chi } \Lambda _{\gamma }^{-1}[\delta ^*] \in \mu ^\kappa _1$
. There is a club
![]() $E \subseteq \kappa $
with E consisting entirely of indecomposable ordinals so that
$E \subseteq \kappa $
with E consisting entirely of indecomposable ordinals so that
![]() $[E]^1_* \subseteq \bigcap _{\gamma < \chi } \Lambda _{\gamma }^{-1}[\delta ^*]$
. Fix an
$[E]^1_* \subseteq \bigcap _{\gamma < \chi } \Lambda _{\gamma }^{-1}[\delta ^*]$
. Fix an
![]() $\epsilon ^*> \delta ^*$
with
$\epsilon ^*> \delta ^*$
with
![]() $\epsilon ^* \in [E]^1_*$
and observe that
$\epsilon ^* \in [E]^1_*$
and observe that
![]() $\epsilon ^*$
is an additively indecomposable ordinal with
$\epsilon ^*$
is an additively indecomposable ordinal with
![]() ${\mathrm {cof}}(\epsilon ^*) = \omega $
.
${\mathrm {cof}}(\epsilon ^*) = \omega $
.
(See Remark 4.5 for some context for the argument of this next paragraph.) For any
![]() $\gamma < \chi $
and
$\gamma < \chi $
and
![]() $\iota \in [\kappa ]^{\delta ^*}_*$
, let
$\iota \in [\kappa ]^{\delta ^*}_*$
, let
![]() $\Phi ^{\epsilon ^*}_{\gamma ,\iota } : [\kappa ]^{\epsilon ^*}_* \rightarrow \kappa $
be defined by
$\Phi ^{\epsilon ^*}_{\gamma ,\iota } : [\kappa ]^{\epsilon ^*}_* \rightarrow \kappa $
be defined by
![]() $\Phi ^{\epsilon ^*}_{\gamma ,\iota }(\ell ) = \Phi ^{\epsilon ^*}_{\gamma }(\iota \hat {\ }\ell )$
. For each
$\Phi ^{\epsilon ^*}_{\gamma ,\iota }(\ell ) = \Phi ^{\epsilon ^*}_{\gamma }(\iota \hat {\ }\ell )$
. For each
![]() $\gamma < \chi $
, let
$\gamma < \chi $
, let
![]() $A_\gamma $
be the set of
$A_\gamma $
be the set of
![]() $f \in [\kappa ]^{\epsilon ^*}_*$
so that for all
$f \in [\kappa ]^{\epsilon ^*}_*$
so that for all
![]() $\ell \sqsubseteq {\mathsf {drop}}(f,\delta ^*)$
,
$\ell \sqsubseteq {\mathsf {drop}}(f,\delta ^*)$
,
![]() $\Phi ^{\epsilon ^*}_{\gamma }(f) = \Phi ^{\epsilon ^*}_{\gamma ,f\upharpoonright \delta ^*}(\ell )$
. Fix a
$\Phi ^{\epsilon ^*}_{\gamma }(f) = \Phi ^{\epsilon ^*}_{\gamma ,f\upharpoonright \delta ^*}(\ell )$
. Fix a
![]() $\gamma < \chi $
.
$\gamma < \chi $
.
![]() $\Lambda _\gamma (\epsilon ^*) = \delta _\gamma \leq \delta ^*$
implies that there is a club
$\Lambda _\gamma (\epsilon ^*) = \delta _\gamma \leq \delta ^*$
implies that there is a club
![]() $F \subseteq \kappa $
so that for all
$F \subseteq \kappa $
so that for all
![]() $f,g \in [F]^{\epsilon ^*}_*$
, if
$f,g \in [F]^{\epsilon ^*}_*$
, if
![]() $\sup (f) = \sup (g)$
and
$\sup (f) = \sup (g)$
and
![]() $f \upharpoonright \delta ^* = g \upharpoonright \delta ^*$
, then
$f \upharpoonright \delta ^* = g \upharpoonright \delta ^*$
, then
![]() $\Phi _\gamma ^{\epsilon ^*}(f) = \Phi ^{\epsilon ^*}_\gamma (g)$
. In particular, if
$\Phi _\gamma ^{\epsilon ^*}(f) = \Phi ^{\epsilon ^*}_\gamma (g)$
. In particular, if
![]() $f \in [F]^{\epsilon ^*}_*$
, then for any
$f \in [F]^{\epsilon ^*}_*$
, then for any
![]() $\ell \sqsubseteq {\mathsf {drop}}(f,\delta ^*)$
,
$\ell \sqsubseteq {\mathsf {drop}}(f,\delta ^*)$
,
![]() $\Phi ^{\epsilon ^*}_{\gamma ,f\upharpoonright \delta ^*}(\ell ) = \Phi _\gamma (f)$
. This shows that
$\Phi ^{\epsilon ^*}_{\gamma ,f\upharpoonright \delta ^*}(\ell ) = \Phi _\gamma (f)$
. This shows that
![]() $[F]^{\epsilon ^*}_* \subseteq A_\gamma $
and hence
$[F]^{\epsilon ^*}_* \subseteq A_\gamma $
and hence
![]() $A_\gamma \in \mu ^\kappa _{\epsilon ^*}$
. Since
$A_\gamma \in \mu ^\kappa _{\epsilon ^*}$
. Since
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon ^* + \epsilon ^*}_2$
implies
$\kappa \rightarrow _* (\kappa )^{\epsilon ^* + \epsilon ^*}_2$
implies
![]() $\mu ^\kappa _{\epsilon ^*}$
is
$\mu ^\kappa _{\epsilon ^*}$
is
![]() $\kappa $
-complete,
$\kappa $
-complete,
![]() $\bigcap _{\gamma < \chi } A_\gamma \in \mu ^\kappa _{\epsilon ^*}$
. Thus, there is a club
$\bigcap _{\gamma < \chi } A_\gamma \in \mu ^\kappa _{\epsilon ^*}$
. Thus, there is a club
![]() $G \subseteq \kappa $
so that
$G \subseteq \kappa $
so that
![]() $[G]^{\epsilon ^*}_* \subseteq \bigcap _{\gamma < \chi } A_\gamma $
. (Such a club G could also be obtain by an application of Fact 2.15.)
$[G]^{\epsilon ^*}_* \subseteq \bigcap _{\gamma < \chi } A_\gamma $
. (Such a club G could also be obtain by an application of Fact 2.15.)
Fix a
![]() $\gamma < \chi $
. Suppose
$\gamma < \chi $
. Suppose
![]() $f,g \in [G]^{\epsilon ^*}_*$
with
$f,g \in [G]^{\epsilon ^*}_*$
with
![]() $\sup (f) = \sup (g)$
and
$\sup (f) = \sup (g)$
and
![]() $f \upharpoonright \delta ^* = g \upharpoonright \delta ^*$
. Let
$f \upharpoonright \delta ^* = g \upharpoonright \delta ^*$
. Let
![]() $\iota = f \upharpoonright \delta ^* = g \upharpoonright \delta ^*$
. Note that
$\iota = f \upharpoonright \delta ^* = g \upharpoonright \delta ^*$
. Note that
![]() $\Phi ^{\epsilon ^*}_{\gamma ,\iota }$
is
$\Phi ^{\epsilon ^*}_{\gamma ,\iota }$
is
![]() $\sqsubseteq $
-constant on
$\sqsubseteq $
-constant on
![]() $[G]^{\epsilon ^*}_*$
. Fact 3.5 implies that
$[G]^{\epsilon ^*}_*$
. Fact 3.5 implies that
![]() $\Phi ^{\epsilon ^*}_{\gamma ,\iota }$
depends only on supremum relative to G. Thus,
$\Phi ^{\epsilon ^*}_{\gamma ,\iota }$
depends only on supremum relative to G. Thus,
![]() $\Phi ^{\epsilon ^*}_\gamma (f) = \Phi ^{\epsilon ^*}_{\gamma ,\iota }({\mathsf {drop}}(f,\delta ^*)) = \Phi ^{\epsilon ^*}_{\gamma ,\iota }({\mathsf {drop}}(g,\delta ^*)) = \Phi ^{\epsilon ^*}_{\gamma }(g)$
since
$\Phi ^{\epsilon ^*}_\gamma (f) = \Phi ^{\epsilon ^*}_{\gamma ,\iota }({\mathsf {drop}}(f,\delta ^*)) = \Phi ^{\epsilon ^*}_{\gamma ,\iota }({\mathsf {drop}}(g,\delta ^*)) = \Phi ^{\epsilon ^*}_{\gamma }(g)$
since
![]() $\sup ({\mathsf {drop}}(f,\delta ^*)) = \sup ({\mathsf {drop}}(g,\delta ^*))$
. So it has been shown that for all
$\sup ({\mathsf {drop}}(f,\delta ^*)) = \sup ({\mathsf {drop}}(g,\delta ^*))$
. So it has been shown that for all
![]() $\gamma < \chi $
, for all
$\gamma < \chi $
, for all
![]() $f,g \in [G]^{\epsilon ^*}_*$
, if
$f,g \in [G]^{\epsilon ^*}_*$
, if
![]() $\sup (f) = \sup (g)$
and
$\sup (f) = \sup (g)$
and
![]() $f \upharpoonright \delta ^* = g \upharpoonright \delta ^*$
, then
$f \upharpoonright \delta ^* = g \upharpoonright \delta ^*$
, then
![]() $\Phi ^{\epsilon ^*}_{\gamma }(f) = \Phi ^{\epsilon ^*}_\gamma (g)$
.
$\Phi ^{\epsilon ^*}_{\gamma }(f) = \Phi ^{\epsilon ^*}_\gamma (g)$
.
Let
![]() $f,g \in [G]^{\epsilon ^*}_*$
be such that
$f,g \in [G]^{\epsilon ^*}_*$
be such that
![]() $\sup (f) = \sup (g)$
,
$\sup (f) = \sup (g)$
,
![]() $f \upharpoonright \delta ^* = g \upharpoonright \delta ^*$
and
$f \upharpoonright \delta ^* = g \upharpoonright \delta ^*$
and
![]() $f \neq g$
. By the property of G from above, for all
$f \neq g$
. By the property of G from above, for all
![]() $\gamma < \chi $
,
$\gamma < \chi $
,
![]() $\Phi ^{\epsilon ^*}_\gamma (f) = \Phi ^{\epsilon ^*}_\gamma (g)$
. This implies
$\Phi ^{\epsilon ^*}_\gamma (f) = \Phi ^{\epsilon ^*}_\gamma (g)$
. This implies
![]() $\Phi (f) = \Phi (g)$
. This is impossible since
$\Phi (f) = \Phi (g)$
. This is impossible since
![]() $\Phi : [\kappa ]^{<\kappa }_* \rightarrow {}^\chi \mathrm {ON}$
was assumed to be an injection.
$\Phi : [\kappa ]^{<\kappa }_* \rightarrow {}^\chi \mathrm {ON}$
was assumed to be an injection.
Remark 4.5. In the proof of Theorem 4.4, an indirect argument was used to obtain the club G and establish its properties by appealing to the
![]() $\kappa $
-completeness of
$\kappa $
-completeness of
![]() $\mu ^\kappa _{\epsilon ^*}$
. This argument could be circumvented if one had the ability to make a
$\mu ^\kappa _{\epsilon ^*}$
. This argument could be circumvented if one had the ability to make a
![]() $\chi $
-length choice of clubs given by each instance of Theorem 3.7 applied to
$\chi $
-length choice of clubs given by each instance of Theorem 3.7 applied to
![]() $\Phi ^{\epsilon ^*}_\gamma $
with
$\Phi ^{\epsilon ^*}_\gamma $
with
![]() $\gamma < \chi $
.
$\gamma < \chi $
.
The short length continuity result is also used in [Reference Chan, Jackson and Trang6] to show
![]() $|[{\omega _1}]^\omega | < |[{\omega _1}]^{<{\omega _1}}|$
under
$|[{\omega _1}]^\omega | < |[{\omega _1}]^{<{\omega _1}}|$
under
![]() $\mathsf {AD}$
. There, this indirect argument was not necessary since
$\mathsf {AD}$
. There, this indirect argument was not necessary since
![]() $\omega $
-many clubs could be chosen by
$\omega $
-many clubs could be chosen by
![]() $\mathsf {AC}_\omega ^{\mathbb {R}}$
and the Moschovakis coding lemma, which follows from
$\mathsf {AC}_\omega ^{\mathbb {R}}$
and the Moschovakis coding lemma, which follows from
![]() $\mathsf {AD}$
. [Reference Chan2] investigated the everywhere wellordered club uniformization principle at
$\mathsf {AD}$
. [Reference Chan2] investigated the everywhere wellordered club uniformization principle at
![]() $\kappa $
, which is the assertion that for every relation
$\kappa $
, which is the assertion that for every relation
![]() $R \subseteq \kappa \times {\mathsf {club}}_\kappa $
which is
$R \subseteq \kappa \times {\mathsf {club}}_\kappa $
which is
![]() $\subseteq $
-downward closed in the
$\subseteq $
-downward closed in the
![]() ${\mathsf {club}}_\kappa $
-coordinate, there is a function
${\mathsf {club}}_\kappa $
-coordinate, there is a function
![]() $\Lambda : \mathrm {dom}(R) \rightarrow {\mathsf {club}}_\kappa $
so that for all
$\Lambda : \mathrm {dom}(R) \rightarrow {\mathsf {club}}_\kappa $
so that for all
![]() $\alpha \in \mathrm {dom}(R)$
,
$\alpha \in \mathrm {dom}(R)$
,
![]() $R(\alpha ,\Phi (\alpha ))$
. This selection principle would also suffice. [Reference Chan2] showed that this principle holds at
$R(\alpha ,\Phi (\alpha ))$
. This selection principle would also suffice. [Reference Chan2] showed that this principle holds at
![]() $\kappa $
under
$\kappa $
under
![]() $\mathsf {AD}$
if
$\mathsf {AD}$
if
![]() $\kappa $
is the prewellordering ordinal of a pointclass possessing suitable definable boundedness properties. [Reference Chan2] also showed that if
$\kappa $
is the prewellordering ordinal of a pointclass possessing suitable definable boundedness properties. [Reference Chan2] also showed that if
![]() $\kappa $
is a strong partition cardinal, then the everywhere wellordered club uniformization principle at
$\kappa $
is a strong partition cardinal, then the everywhere wellordered club uniformization principle at
![]() $\kappa $
is equivalent to
$\kappa $
is equivalent to
![]() $\kappa \rightarrow _* (\kappa )^{\kappa }_{<\kappa }$
. However, Theorem 4.4 does not presuppose that
$\kappa \rightarrow _* (\kappa )^{\kappa }_{<\kappa }$
. However, Theorem 4.4 does not presuppose that
![]() $\kappa $
is a strong partition cardinal,
$\kappa $
is a strong partition cardinal,
![]() $\mathsf {AD}$
or any other conditions beyond
$\mathsf {AD}$
or any other conditions beyond
![]() $\kappa $
being a weak partition cardinal.
$\kappa $
being a weak partition cardinal.
Corollary 4.6. Assume
![]() $\mathsf {AD}$
. Suppose
$\mathsf {AD}$
. Suppose
![]() $\kappa $
is
$\kappa $
is
![]() ${\omega _1}$
,
${\omega _1}$
,
![]() $\omega _2$
,
$\omega _2$
,
![]() $\boldsymbol {\delta }_n^1$
for
$\boldsymbol {\delta }_n^1$
for
![]() $1 \leq n < \omega $
,
$1 \leq n < \omega $
,
![]() $\boldsymbol {\delta }_A$
where
$\boldsymbol {\delta }_A$
where
![]() $A \subseteq \mathbb {R}$
or
$A \subseteq \mathbb {R}$
or
![]() $\boldsymbol {\delta }^2_1$
(assuming
$\boldsymbol {\delta }^2_1$
(assuming
![]() $\mathsf {DC}_{\mathbb {R}}$
). Then for any
$\mathsf {DC}_{\mathbb {R}}$
). Then for any
![]() $\chi < \kappa $
,
$\chi < \kappa $
,
![]() $|{}^\chi \kappa | < |{}^{<\kappa }\kappa |$
and
$|{}^\chi \kappa | < |{}^{<\kappa }\kappa |$
and
![]() ${}^{<\kappa }\kappa $
does not inject into
${}^{<\kappa }\kappa $
does not inject into
![]() ${}^\chi \mathrm {ON}$
.
${}^\chi \mathrm {ON}$
.
Section 5 will investigate almost everywhere monotonicity. The remainder of this section will establish almost everywhere monotonicity for functions
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
when
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
when
![]() $\epsilon < {\omega _1}$
and satisfies suitable partition relations. This will use Theorem 3.9 to reduce to the almost everywhere monotonicity of functions
$\epsilon < {\omega _1}$
and satisfies suitable partition relations. This will use Theorem 3.9 to reduce to the almost everywhere monotonicity of functions
![]() $\Phi : [\kappa ]^p_* \rightarrow \mathrm {ON}$
when p is finite which will be established next.
$\Phi : [\kappa ]^p_* \rightarrow \mathrm {ON}$
when p is finite which will be established next.
Fact 4.7. Suppose
![]() $\kappa $
is a cardinal,
$\kappa $
is a cardinal,
![]() $p \in \omega $
,
$p \in \omega $
,
![]() $\kappa \rightarrow _* (\kappa )^{p + 1}_2$
and
$\kappa \rightarrow _* (\kappa )^{p + 1}_2$
and
![]() $\Phi : [\kappa ]^p_* \rightarrow \mathrm {ON}$
is a function. Then there is a club
$\Phi : [\kappa ]^p_* \rightarrow \mathrm {ON}$
is a function. Then there is a club
![]() $C \subseteq \kappa $
so that for
$C \subseteq \kappa $
so that for
![]() $f,g \in [C]^p_*$
, if for all
$f,g \in [C]^p_*$
, if for all
![]() $n < p$
,
$n < p$
,
![]() $f(n) \leq g(n)$
, then
$f(n) \leq g(n)$
, then
![]() $\Phi (f) \leq \Phi (g)$
.
$\Phi (f) \leq \Phi (g)$
.
Proof. Let
![]() $k < p$
. For
$k < p$
. For
![]() $h \in [\kappa ]^{p + 1}_*$
, let
$h \in [\kappa ]^{p + 1}_*$
, let
![]() $h^{k,0},h^{k,1} \in [\kappa ]^p_*$
be defined by
$h^{k,0},h^{k,1} \in [\kappa ]^p_*$
be defined by
 $$ \begin{align*}h^{k,0}(n) = \begin{cases} h(n) & \quad n \leq k \\ h(n + 1) & \quad k < n < p \end{cases} \ \ \ h^{k,1}(n) = \begin{cases} h(n) & \quad n < k \\ h(n + 1) & \quad k \leq n < p \end{cases}.\end{align*} $$
$$ \begin{align*}h^{k,0}(n) = \begin{cases} h(n) & \quad n \leq k \\ h(n + 1) & \quad k < n < p \end{cases} \ \ \ h^{k,1}(n) = \begin{cases} h(n) & \quad n < k \\ h(n + 1) & \quad k \leq n < p \end{cases}.\end{align*} $$
Define
![]() $P^k : [\kappa ]^{p + 1}_* \rightarrow 2$
by
$P^k : [\kappa ]^{p + 1}_* \rightarrow 2$
by
![]() $P^k(h) = 0$
if and only if
$P^k(h) = 0$
if and only if
![]() $\Phi (h^{k,0}) \leq \Phi (h^{k,1})$
. By
$\Phi (h^{k,0}) \leq \Phi (h^{k,1})$
. By
![]() $\kappa \rightarrow _* (\kappa )^{p + 1}_2$
, let
$\kappa \rightarrow _* (\kappa )^{p + 1}_2$
, let
![]() $C \subseteq \kappa $
be homogeneous for
$C \subseteq \kappa $
be homogeneous for
![]() $P^k$
. Suppose C is homogeneous for P taking value
$P^k$
. Suppose C is homogeneous for P taking value
![]() $1$
. Fix
$1$
. Fix
![]() $\ell \in [C]^{\omega + (p - k - 1)}$
. Define
$\ell \in [C]^{\omega + (p - k - 1)}$
. Define
![]() $f_i \in [C]^p_*$
as follows.
$f_i \in [C]^p_*$
as follows.
 $$ \begin{align*}f_i(n) = \begin{cases} \ell(n) & \quad n < k \\ \ell(k + i) & \quad n = k \\ \ell(\omega + n - k - 1) & \quad k < n < p. \end{cases}\end{align*} $$
$$ \begin{align*}f_i(n) = \begin{cases} \ell(n) & \quad n < k \\ \ell(k + i) & \quad n = k \\ \ell(\omega + n - k - 1) & \quad k < n < p. \end{cases}\end{align*} $$
Note that for all
![]() $i \in \omega $
, there is an
$i \in \omega $
, there is an
![]() $h_i \in [C]^{p + 1}_*$
so that
$h_i \in [C]^{p + 1}_*$
so that
![]() $h^{k,0} = f_i$
and
$h^{k,0} = f_i$
and
![]() $h^{k,1} = f_{i + 1}$
.
$h^{k,1} = f_{i + 1}$
.
![]() $P(h_i) = 1$
implies that
$P(h_i) = 1$
implies that
![]() $\Phi (f_{i + 1}) = \Phi (h_i^{k,1}) < \Phi (h_i^{k,0}) = \Phi (f_i)$
. Thus,
$\Phi (f_{i + 1}) = \Phi (h_i^{k,1}) < \Phi (h_i^{k,0}) = \Phi (f_i)$
. Thus,
![]() $\langle \Phi (f_i) : i \in \omega \rangle $
is an infinite descending sequence of ordinals. Thus, C must be homogeneous for
$\langle \Phi (f_i) : i \in \omega \rangle $
is an infinite descending sequence of ordinals. Thus, C must be homogeneous for
![]() $P^k$
taking value
$P^k$
taking value
![]() $0$
.
$0$
.
For each
![]() $k < p$
, let
$k < p$
, let
![]() $C_k \subseteq \kappa $
be a club which is homogeneous for
$C_k \subseteq \kappa $
be a club which is homogeneous for
![]() $P^k$
taking value
$P^k$
taking value
![]() $0$
. Let
$0$
. Let
![]() $C = \bigcap _{k < p} C_k$
. Suppose
$C = \bigcap _{k < p} C_k$
. Suppose
![]() $f,g \in [C]^p_*$
is such that for all
$f,g \in [C]^p_*$
is such that for all
![]() $n < p$
,
$n < p$
,
![]() $f(n) \leq g(n)$
. If
$f(n) \leq g(n)$
. If
![]() $f = g$
, then it is clear that
$f = g$
, then it is clear that
![]() $\Phi (f) \leq \Phi (g)$
. Suppose
$\Phi (f) \leq \Phi (g)$
. Suppose
![]() $f \neq g$
. Let
$f \neq g$
. Let
![]() $k_0 < ... < k_q$
with
$k_0 < ... < k_q$
with
![]() $q < p$
enumerate
$q < p$
enumerate
![]() $\{k < p : f(k) < g(k)\}$
. For
$\{k < p : f(k) < g(k)\}$
. For
![]() $0 \leq i \leq q$
, let
$0 \leq i \leq q$
, let
 $$ \begin{align*}c_i(n) = \begin{cases} f(n) & \quad n < k_{q - i} \\ g(n) & \quad k_{q - i} \geq n \end{cases}.\end{align*} $$
$$ \begin{align*}c_i(n) = \begin{cases} f(n) & \quad n < k_{q - i} \\ g(n) & \quad k_{q - i} \geq n \end{cases}.\end{align*} $$
Observe the following hold.
-
1. For all
 $i \leq q$
,
$i \leq q$
,
 $c_i \in [C]^p_*$
.
$c_i \in [C]^p_*$
. -
2.
 $c_{q} = g$
.
$c_{q} = g$
. -
3. There is an
 $h_0 \in [C]^{p + 1}_*$
so that
$h_0 \in [C]^{p + 1}_*$
so that
 $h_0^{k_q,0} = f$
and
$h_0^{k_q,0} = f$
and
 $h_0^{k_q,1} = c_0$
.
$h_0^{k_q,1} = c_0$
. -
4. For each
 $0 < i \leq q$
, there is an
$0 < i \leq q$
, there is an
 $h_i \in [C]^{p + 1}_*$
so that
$h_i \in [C]^{p + 1}_*$
so that
 $h_i^{k_{q - i},0} = c_{i - 1}$
and
$h_i^{k_{q - i},0} = c_{i - 1}$
and
 $h_i^{k_{q - i},1} = c_i$
.
$h_i^{k_{q - i},1} = c_i$
.
These properties and the fact that
![]() $P^{k_{q - i}}(h_i) = 0$
for each
$P^{k_{q - i}}(h_i) = 0$
for each
![]() $i \leq q$
imply that
$i \leq q$
imply that
![]() $\Phi (f) \leq \Phi (c_0) \leq \Phi (c_1) \leq ... \leq \Phi (c_q) = \Phi (g)$
.
$\Phi (f) \leq \Phi (c_0) \leq \Phi (c_1) \leq ... \leq \Phi (c_q) = \Phi (g)$
.
The next result will be improved in Section 5.
Theorem 4.8. Suppose
![]() $\kappa $
is a cardinal,
$\kappa $
is a cardinal,
![]() $\epsilon < {\omega _1}$
,
$\epsilon < {\omega _1}$
,
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon \cdot \epsilon }_2$
holds and
$\kappa \rightarrow _* (\kappa )^{\epsilon \cdot \epsilon }_2$
holds and
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
. Then there is a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
. Then there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if for all
$f,g \in [C]^\epsilon _*$
, if for all
![]() $\alpha < \epsilon $
,
$\alpha < \epsilon $
,
![]() $f(\alpha ) \leq g(\alpha )$
, then
$f(\alpha ) \leq g(\alpha )$
, then
![]() $\Phi (f) \leq \Phi (g)$
.
$\Phi (f) \leq \Phi (g)$
.
Proof. By Theorem 3.9, there is a club
![]() $C_0$
and finitely many ordinals
$C_0$
and finitely many ordinals
![]() $\beta _0 < \beta _1 < ... < \beta _{p - 1} \leq \epsilon $
so that for all
$\beta _0 < \beta _1 < ... < \beta _{p - 1} \leq \epsilon $
so that for all
![]() $f,g \in [C_0]^\epsilon _*$
, if for all
$f,g \in [C_0]^\epsilon _*$
, if for all
![]() $i < p$
,
$i < p$
,
![]() $\sup (f \upharpoonright \beta _i) = \sup (g \upharpoonright \beta _i)$
, then
$\sup (f \upharpoonright \beta _i) = \sup (g \upharpoonright \beta _i)$
, then
![]() $\Phi (f) = \Phi (g)$
. Let
$\Phi (f) = \Phi (g)$
. Let
![]() $C_1$
be the club of limit points of
$C_1$
be the club of limit points of
![]() $C_0$
. Define
$C_0$
. Define
![]() $\Psi : [C_1]^p_* \rightarrow \mathrm {ON}$
by
$\Psi : [C_1]^p_* \rightarrow \mathrm {ON}$
by
![]() $\Psi (\ell ) = \Phi (f)$
for any
$\Psi (\ell ) = \Phi (f)$
for any
![]() $f \in [C_0]^\epsilon _*$
so that for all
$f \in [C_0]^\epsilon _*$
so that for all
![]() $i < p$
,
$i < p$
,
![]() $\sup (f \upharpoonright \beta _i) = \ell (i)$
. Note
$\sup (f \upharpoonright \beta _i) = \ell (i)$
. Note
![]() $\Psi (\ell )$
is well defined and independent of the choice of f. By Fact 4.7, there is a club
$\Psi (\ell )$
is well defined and independent of the choice of f. By Fact 4.7, there is a club
![]() $C_2 \subseteq C_1$
so that for all
$C_2 \subseteq C_1$
so that for all
![]() $\ell ,\iota \in [C_2]^p_*$
, if for all
$\ell ,\iota \in [C_2]^p_*$
, if for all
![]() $i < p$
,
$i < p$
,
![]() $\ell (i) \leq \iota (i)$
, then
$\ell (i) \leq \iota (i)$
, then
![]() $\Psi (\ell ) \leq \Psi (\iota )$
.
$\Psi (\ell ) \leq \Psi (\iota )$
.
Now, suppose
![]() $f,g \in [C_2]^\epsilon _*$
so that for all
$f,g \in [C_2]^\epsilon _*$
so that for all
![]() $\alpha < \epsilon $
,
$\alpha < \epsilon $
,
![]() $f(\alpha ) \leq g(\alpha )$
. Let
$f(\alpha ) \leq g(\alpha )$
. Let
![]() $\ell _f(i) = \sup (f \upharpoonright \beta _i)$
and
$\ell _f(i) = \sup (f \upharpoonright \beta _i)$
and
![]() $\ell _g(i) = \sup (g\upharpoonright \beta _i)$
. Note that
$\ell _g(i) = \sup (g\upharpoonright \beta _i)$
. Note that
![]() $\ell _f,\ell _g$
are discontinuous since p is finite and
$\ell _f,\ell _g$
are discontinuous since p is finite and
![]() $\beta _0 < ... < \beta _{p - 1}$
. Since
$\beta _0 < ... < \beta _{p - 1}$
. Since
![]() $\epsilon < {\omega _1}$
and
$\epsilon < {\omega _1}$
and
![]() $f,g \in [C_2]^\epsilon _*$
, it follows that
$f,g \in [C_2]^\epsilon _*$
, it follows that
![]() $\ell _f(i)$
and
$\ell _f(i)$
and
![]() $\ell _g(i)$
have cofinality
$\ell _g(i)$
have cofinality
![]() $\omega $
, and thus
$\omega $
, and thus
![]() $\ell _f,\ell _g \in [C_2]^p_*$
. By definition of
$\ell _f,\ell _g \in [C_2]^p_*$
. By definition of
![]() $\Psi $
,
$\Psi $
,
![]() $\Phi (f) = \Psi (\ell _f)$
and
$\Phi (f) = \Psi (\ell _f)$
and
![]() $\Phi (g) = \Psi (\ell _g)$
. Note that for all
$\Phi (g) = \Psi (\ell _g)$
. Note that for all
![]() $i < p$
,
$i < p$
,
![]() $\ell _f(i) \leq \ell _g(i)$
. By the choice of club
$\ell _f(i) \leq \ell _g(i)$
. By the choice of club
![]() $C_2$
,
$C_2$
,
![]() $\Psi (\ell _f) \leq \Psi (\ell _g)$
. Thus,
$\Psi (\ell _f) \leq \Psi (\ell _g)$
. Thus,
![]() $\Phi (f) = \Psi (\ell _f) \leq \Psi (\ell _g) = \Phi (g)$
.
$\Phi (f) = \Psi (\ell _f) \leq \Psi (\ell _g) = \Phi (g)$
.
Corollary 4.9. Assume
![]() $\mathsf {AD}$
. If
$\mathsf {AD}$
. If
![]() $\kappa $
is
$\kappa $
is
![]() ${\omega _1}$
,
${\omega _1}$
,
![]() $\omega _2$
,
$\omega _2$
,
![]() $\boldsymbol {\delta }_n^1$
for any
$\boldsymbol {\delta }_n^1$
for any
![]() $1 \leq n < \omega $
,
$1 \leq n < \omega $
,
![]() $\boldsymbol {\delta }_A$
for some
$\boldsymbol {\delta }_A$
for some
![]() $A \subseteq \mathbb {R}$
or
$A \subseteq \mathbb {R}$
or
![]() $\boldsymbol {\delta }^2_1$
(assuming
$\boldsymbol {\delta }^2_1$
(assuming
![]() $\mathsf {DC}_{\mathbb {R}}$
), then for any
$\mathsf {DC}_{\mathbb {R}}$
), then for any
![]() $\epsilon < {\omega _1}$
and function
$\epsilon < {\omega _1}$
and function
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, there exists a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, there exists a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if for all
$f,g \in [C]^\epsilon _*$
, if for all
![]() $\alpha < \epsilon $
,
$\alpha < \epsilon $
,
![]() $f(\alpha ) \leq g(\alpha )$
, then
$f(\alpha ) \leq g(\alpha )$
, then
![]() $\Phi (f) \leq \Phi (g)$
.
$\Phi (f) \leq \Phi (g)$
.
Proof. This follows from Theorem 4.8.
5 Almost everywhere monotonicity
The next result shows that if a partition relation fails at
![]() $\kappa $
, then there is a corresponding failure of almost everywhere monotonicity at
$\kappa $
, then there is a corresponding failure of almost everywhere monotonicity at
![]() $\kappa $
. Thus, partition relations are necessary for the almost everywhere monotonicity property.
$\kappa $
. Thus, partition relations are necessary for the almost everywhere monotonicity property.
Fact 5.1. Suppose
![]() $\kappa $
is a cardinal and
$\kappa $
is a cardinal and
![]() $\epsilon \leq \kappa $
is such that
$\epsilon \leq \kappa $
is such that
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _2$
fails. Then there is a function
$\kappa \rightarrow _* (\kappa )^\epsilon _2$
fails. Then there is a function
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
so that for all club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
so that for all club
![]() $C \subseteq \kappa $
, there exist
$C \subseteq \kappa $
, there exist
![]() $f,g \in [C]^\epsilon _*$
so that for all
$f,g \in [C]^\epsilon _*$
so that for all
![]() $\alpha \leq \epsilon $
,
$\alpha \leq \epsilon $
,
![]() $f(\alpha ) \leq g(\alpha )$
and
$f(\alpha ) \leq g(\alpha )$
and
![]() $\Phi (g) < \Phi (f)$
.
$\Phi (g) < \Phi (f)$
.
Proof. Let
![]() $P : [\kappa ]^\epsilon _* \rightarrow 2$
be such that for all club
$P : [\kappa ]^\epsilon _* \rightarrow 2$
be such that for all club
![]() $C \subseteq \kappa $
, there exists functions
$C \subseteq \kappa $
, there exists functions
![]() $h_0,h_1 \in [C]^\epsilon _*$
so that
$h_0,h_1 \in [C]^\epsilon _*$
so that
![]() $P(h_0) = 0$
and
$P(h_0) = 0$
and
![]() $P(h_1) = 1$
. P fails the monotonicity property.
$P(h_1) = 1$
. P fails the monotonicity property.
Suppose
![]() $C \subseteq \kappa $
is a club. As noted above, there is some
$C \subseteq \kappa $
is a club. As noted above, there is some
![]() $f \in [C]^\epsilon _*$
with
$f \in [C]^\epsilon _*$
with
![]() $P(f) = 1$
. Let
$P(f) = 1$
. Let
![]() $D \subseteq C$
be a club with the property that for all
$D \subseteq C$
be a club with the property that for all
![]() $h \in [D]^\kappa _*$
,
$h \in [D]^\kappa _*$
,
![]() $f(\alpha ) \leq h(\alpha )$
for all
$f(\alpha ) \leq h(\alpha )$
for all
![]() $\alpha < \epsilon $
. As noted above, there is some
$\alpha < \epsilon $
. As noted above, there is some
![]() $g \in [D]^\epsilon _*$
so that
$g \in [D]^\epsilon _*$
so that
![]() $\Phi (g) = 0$
. Then
$\Phi (g) = 0$
. Then
![]() $f,g \in [C]^\epsilon _*$
, for all
$f,g \in [C]^\epsilon _*$
, for all
![]() $\alpha < \epsilon $
,
$\alpha < \epsilon $
,
![]() $f(\alpha ) \leq g(\alpha )$
and
$f(\alpha ) \leq g(\alpha )$
and
![]() $\Phi (g) = 0 < 1 = \Phi (f)$
.
$\Phi (g) = 0 < 1 = \Phi (f)$
.
The following lemma considers pairs
![]() $(f,g)$
possessing property (2) and (3) stated below in order to simplify the construction of the relevant functions of the correct type. Theorem 5.3 will reduce the general case to this lemma.
$(f,g)$
possessing property (2) and (3) stated below in order to simplify the construction of the relevant functions of the correct type. Theorem 5.3 will reduce the general case to this lemma.
Lemma 5.2. Suppose
![]() $\kappa $
is a cardinal satisfying
$\kappa $
is a cardinal satisfying
![]() $\kappa \rightarrow _* (\kappa )^\kappa _2$
. For any function
$\kappa \rightarrow _* (\kappa )^\kappa _2$
. For any function
![]() $\Phi : [\kappa ]^\kappa _* \rightarrow \mathrm {ON}$
, there is a club
$\Phi : [\kappa ]^\kappa _* \rightarrow \mathrm {ON}$
, there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f,g \in [C]^\kappa _*$
, if f and g have the property that for all
$f,g \in [C]^\kappa _*$
, if f and g have the property that for all
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
-
1.
 $f(\alpha ) \leq g(\alpha )$
,
$f(\alpha ) \leq g(\alpha )$
, -
2. there is no limit ordinal
 $\beta < \kappa $
so that
$\beta < \kappa $
so that
 $\sup (f \upharpoonright \beta ) = g(\alpha )$
,
$\sup (f \upharpoonright \beta ) = g(\alpha )$
, -
3. and there is no limit ordinal
 $\beta < \kappa $
so that
$\beta < \kappa $
so that
 $\sup (g \upharpoonright \beta ) = f(\alpha )$
,
$\sup (g \upharpoonright \beta ) = f(\alpha )$
,
then
![]() $\Phi (f) \leq \Phi (g)$
.
$\Phi (f) \leq \Phi (g)$
.
Proof. Let
![]() $\mathcal {I} : \kappa \rightarrow \kappa $
be an increasing and discontinuous function whose image consists of indecomposable ordinals. For any
$\mathcal {I} : \kappa \rightarrow \kappa $
be an increasing and discontinuous function whose image consists of indecomposable ordinals. For any
![]() $h \in [\kappa ]^\kappa _*$
, let
$h \in [\kappa ]^\kappa _*$
, let
![]() ${\mathsf {main}}(h) \in [\kappa ]^\kappa _*$
be defined by
${\mathsf {main}}(h) \in [\kappa ]^\kappa _*$
be defined by
![]() ${\mathsf {main}}(h)(\alpha ) = h(\mathcal {I}(\alpha ))$
. (Observe that
${\mathsf {main}}(h)(\alpha ) = h(\mathcal {I}(\alpha ))$
. (Observe that
![]() ${\mathsf {main}}(h)$
is an increasing function of the correct type since h is an increasing function of the correct type.) Define
${\mathsf {main}}(h)$
is an increasing function of the correct type since h is an increasing function of the correct type.) Define
![]() $P : [\kappa ]^\kappa _* \rightarrow 2$
by
$P : [\kappa ]^\kappa _* \rightarrow 2$
by
![]() $P(h) = 0$
if and only if for all
$P(h) = 0$
if and only if for all
![]() $p \in [h[\kappa ]]^\kappa _*$
,
$p \in [h[\kappa ]]^\kappa _*$
,
![]() $\Phi ({\mathsf {main}}(h)) \leq \Phi ({\mathsf {main}}(p))$
. By
$\Phi ({\mathsf {main}}(h)) \leq \Phi ({\mathsf {main}}(p))$
. By
![]() $\kappa \rightarrow _* (\kappa )^\kappa _2$
, let
$\kappa \rightarrow _* (\kappa )^\kappa _2$
, let
![]() $C_0 \subseteq \kappa $
be a club homogeneous for P. Let
$C_0 \subseteq \kappa $
be a club homogeneous for P. Let
![]() $Z = \{\Phi ({\mathsf {main}}(h)) : h \in [C_0]^\kappa _*\}$
which has a minimal element since it is a nonempty set of ordinals. Let
$Z = \{\Phi ({\mathsf {main}}(h)) : h \in [C_0]^\kappa _*\}$
which has a minimal element since it is a nonempty set of ordinals. Let
![]() $h^* \in [C_0]^\kappa _*$
be such that
$h^* \in [C_0]^\kappa _*$
be such that
![]() $\Phi ({\mathsf {main}}(h^*)) = \min (Z)$
. If
$\Phi ({\mathsf {main}}(h^*)) = \min (Z)$
. If
![]() $p \in [h^*[\kappa ]]^\kappa _*$
, then
$p \in [h^*[\kappa ]]^\kappa _*$
, then
![]() $p \in [C_0]^\kappa _*$
and thus
$p \in [C_0]^\kappa _*$
and thus
![]() $\Phi ({\mathsf {main}}(p)) \in Z$
and
$\Phi ({\mathsf {main}}(p)) \in Z$
and
![]() $\Phi ({\mathsf {main}}(h^*)) = \min (Z) \leq \Phi ({\mathsf {main}}(p))$
. This shows
$\Phi ({\mathsf {main}}(h^*)) = \min (Z) \leq \Phi ({\mathsf {main}}(p))$
. This shows
![]() $P(h^*) = 0$
. Since
$P(h^*) = 0$
. Since
![]() $h^* \in [C_0]^\kappa _*$
,
$h^* \in [C_0]^\kappa _*$
,
![]() $C_0$
must be homogeneous for P taking value
$C_0$
must be homogeneous for P taking value
![]() $0$
. By choosing a subclub of
$0$
. By choosing a subclub of
![]() $C_0$
if necessary, one may assume that
$C_0$
if necessary, one may assume that
![]() $C_0$
consists entirely of indecomposable ordinals and for all
$C_0$
consists entirely of indecomposable ordinals and for all
![]() $f \in [C_0]^\kappa _*$
, for all
$f \in [C_0]^\kappa _*$
, for all
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $\mathcal {I}(\alpha ) < f(\alpha )$
(which is possible since
$\mathcal {I}(\alpha ) < f(\alpha )$
(which is possible since
![]() $\mathcal {I}$
and f are discontinuous). Let
$\mathcal {I}$
and f are discontinuous). Let
![]() $C_1 = \{\alpha \in C_0 : {\mathsf {enum}}_{C_0}(\alpha ) = \alpha \}$
. Since
$C_1 = \{\alpha \in C_0 : {\mathsf {enum}}_{C_0}(\alpha ) = \alpha \}$
. Since
![]() $C_1$
is a subclub of
$C_1$
is a subclub of
![]() $C_0$
,
$C_0$
,
![]() $C_1$
also consists entirely of indecomposable ordinals.
$C_1$
also consists entirely of indecomposable ordinals.
Now, fix
![]() $f,g \in [C_1]^\kappa _*$
with properties (1), (2) and (3). One will construct simultaneously by recursion two functions
$f,g \in [C_1]^\kappa _*$
with properties (1), (2) and (3). One will construct simultaneously by recursion two functions
![]() $h \in [C_0]^\kappa _*$
and
$h \in [C_0]^\kappa _*$
and
![]() $p \in [h[\kappa ]]^\kappa _*$
so that
$p \in [h[\kappa ]]^\kappa _*$
so that
![]() ${\mathsf {main}}(h) = f$
and
${\mathsf {main}}(h) = f$
and
![]() ${\mathsf {main}}(p) = g$
. The construction will recursively define at each stage longer initial segments of the final two objects, h and p.
${\mathsf {main}}(p) = g$
. The construction will recursively define at each stage longer initial segments of the final two objects, h and p.
Suppose
![]() $\alpha < \kappa $
and the following holds:
$\alpha < \kappa $
and the following holds:
-
(a) For each
 $\beta < \alpha $
,
$\beta < \alpha $
,
 $h \upharpoonright \mathcal {I}(\beta ) + 1$
has been defined, is a function of the correct type and
$h \upharpoonright \mathcal {I}(\beta ) + 1$
has been defined, is a function of the correct type and
 $h(\mathcal {I}(\beta )) = f(\beta )$
.
$h(\mathcal {I}(\beta )) = f(\beta )$
. -
(b) For each
 $\beta < \alpha $
,
$\beta < \alpha $
,
 $\sigma _\beta \leq \beta + 1$
has been defined. If
$\sigma _\beta \leq \beta + 1$
has been defined. If
 $\beta _0 \leq \beta _1 < \alpha $
, then
$\beta _0 \leq \beta _1 < \alpha $
, then
 $\sigma _{\beta _0} \leq \sigma _{\beta _1}$
.
$\sigma _{\beta _0} \leq \sigma _{\beta _1}$
. -
(c) For all
 $\beta < \alpha $
, for all
$\beta < \alpha $
, for all
 $\eta < \sigma _\beta $
,
$\eta < \sigma _\beta $
,
 $p \upharpoonright \mathcal {I}(\eta ) + 1$
has been defined, is a function of the correct type and
$p \upharpoonright \mathcal {I}(\eta ) + 1$
has been defined, is a function of the correct type and
 $p(\mathcal {I}(\eta )) = g(\eta )$
.
$p(\mathcal {I}(\eta )) = g(\eta )$
. -
(d) For all
 $\beta < \alpha $
, for all
$\beta < \alpha $
, for all
 $\eta < \sigma _\beta $
,
$\eta < \sigma _\beta $
,
 $g(\eta ) \leq f(\beta ) < g(\sigma _\beta )$
.
$g(\eta ) \leq f(\beta ) < g(\sigma _\beta )$
.
Let
![]() $\iota _\alpha = \sup \{\sigma _\beta : \beta < \alpha \}$
. Let
$\iota _\alpha = \sup \{\sigma _\beta : \beta < \alpha \}$
. Let
![]() $\delta _0 = \sup \{\mathcal {I}(\beta ) + 1 : \beta < \alpha \}$
and
$\delta _0 = \sup \{\mathcal {I}(\beta ) + 1 : \beta < \alpha \}$
and
![]() $\tau _0 = \sup \{\mathcal {I}(\beta ) + 1 : \beta < \iota _\alpha \}$
. Since
$\tau _0 = \sup \{\mathcal {I}(\beta ) + 1 : \beta < \iota _\alpha \}$
. Since
![]() $\iota _\alpha \leq \alpha $
, one has
$\iota _\alpha \leq \alpha $
, one has
![]() $\tau _0 \leq \delta _0$
. Note that, since
$\tau _0 \leq \delta _0$
. Note that, since
![]() $\mathcal {I}$
is discontinuous and takes value among indecomposable ordinals,
$\mathcal {I}$
is discontinuous and takes value among indecomposable ordinals,
![]() $\tau _0 \leq \delta _0 \leq \sup (\mathcal {I} \upharpoonright \alpha ) + 1 < \mathcal {I}(\alpha )$
. Properties (a) and (c) imply that
$\tau _0 \leq \delta _0 \leq \sup (\mathcal {I} \upharpoonright \alpha ) + 1 < \mathcal {I}(\alpha )$
. Properties (a) and (c) imply that
![]() $h \upharpoonright \delta _0$
and
$h \upharpoonright \delta _0$
and
![]() $p \upharpoonright \tau _0$
have been defined. Note
$p \upharpoonright \tau _0$
have been defined. Note
![]() $\sup (h \upharpoonright \delta _0) = \sup (f \upharpoonright \alpha ) < f(\alpha )$
since f is discontinuous. Also,
$\sup (h \upharpoonright \delta _0) = \sup (f \upharpoonright \alpha ) < f(\alpha )$
since f is discontinuous. Also,
![]() $\sup (p \upharpoonright \tau _0) = \sup (g \upharpoonright \iota _\alpha )$
.
$\sup (p \upharpoonright \tau _0) = \sup (g \upharpoonright \iota _\alpha )$
.
If
![]() $\alpha $
is a successor ordinal with
$\alpha $
is a successor ordinal with
![]() $\alpha = \alpha ^* + 1$
, then
$\alpha = \alpha ^* + 1$
, then
![]() $\iota _\alpha = \sigma _{\alpha *}$
. By property (d),
$\iota _\alpha = \sigma _{\alpha *}$
. By property (d),
![]() $\sup (g \upharpoonright \iota _\alpha ) = \sup (g \upharpoonright \sigma _{\alpha ^*}) \leq f(\alpha ^*) = \sup (f\upharpoonright \alpha ) < g(\sigma _{\alpha ^*}) = g(\iota _\alpha )$
. Suppose
$\sup (g \upharpoonright \iota _\alpha ) = \sup (g \upharpoonright \sigma _{\alpha ^*}) \leq f(\alpha ^*) = \sup (f\upharpoonright \alpha ) < g(\sigma _{\alpha ^*}) = g(\iota _\alpha )$
. Suppose
![]() $\alpha $
is a limit ordinal and
$\alpha $
is a limit ordinal and
![]() $\langle \sigma _\beta : \beta < \alpha \rangle $
is not eventually constant. Property (d) implies that
$\langle \sigma _\beta : \beta < \alpha \rangle $
is not eventually constant. Property (d) implies that
![]() $\sup (g \upharpoonright \iota _\alpha ) \leq \sup (f \upharpoonright \alpha ) \leq \sup \{g(\sigma _\beta ) : \beta < \alpha \} = \sup (g \upharpoonright \iota _\alpha ) < g(\iota _\alpha )$
by the discontinuity of g. Suppose
$\sup (g \upharpoonright \iota _\alpha ) \leq \sup (f \upharpoonright \alpha ) \leq \sup \{g(\sigma _\beta ) : \beta < \alpha \} = \sup (g \upharpoonright \iota _\alpha ) < g(\iota _\alpha )$
by the discontinuity of g. Suppose
![]() $\alpha $
is a limit ordinal and
$\alpha $
is a limit ordinal and
![]() $\langle \sigma _\beta : \beta < \alpha \rangle $
is eventually constant. Then
$\langle \sigma _\beta : \beta < \alpha \rangle $
is eventually constant. Then
![]() $\sup \{g(\sigma _\beta ) : \beta < \alpha \} = g(\iota _\alpha )$
. Then by property (d) and property (2) for the strict inequality,
$\sup \{g(\sigma _\beta ) : \beta < \alpha \} = g(\iota _\alpha )$
. Then by property (d) and property (2) for the strict inequality,
![]() $\sup (g \upharpoonright \iota _\alpha ) \leq \sup (f \upharpoonright \alpha ) < g(\iota _\alpha )$
. The following property
$\sup (g \upharpoonright \iota _\alpha ) \leq \sup (f \upharpoonright \alpha ) < g(\iota _\alpha )$
. The following property
![]() $(*)$
has been established in all cases:
$(*)$
has been established in all cases:
![]() $\sup (g \upharpoonright \iota _\alpha ) \leq \sup (f \upharpoonright \alpha ) < g(\iota _\alpha )$
.
$\sup (g \upharpoonright \iota _\alpha ) \leq \sup (f \upharpoonright \alpha ) < g(\iota _\alpha )$
.
Let
![]() $A = \{\beta < \alpha : \sup (f \upharpoonright \alpha ) < g(\beta ) < f(\alpha )\}$
.
$A = \{\beta < \alpha : \sup (f \upharpoonright \alpha ) < g(\beta ) < f(\alpha )\}$
.
(Case A) If
![]() $A = \emptyset $
.
$A = \emptyset $
.
Then let
![]() $\tau = \tau _0$
and
$\tau = \tau _0$
and
![]() $\delta = \delta _0$
.
$\delta = \delta _0$
.
(Case B)
![]() $A \neq \emptyset $
.
$A \neq \emptyset $
.
Note
![]() $\iota _\alpha < \alpha $
since if
$\iota _\alpha < \alpha $
since if
![]() $\iota _\alpha = \alpha $
, then by
$\iota _\alpha = \alpha $
, then by
![]() $(*)$
and the discontinuity of f,
$(*)$
and the discontinuity of f,
![]() $\sup (g \upharpoonright \alpha ) = \sup (g \upharpoonright \iota _\alpha ) \leq \sup (f \upharpoonright \alpha ) < f(\alpha )$
. However,
$\sup (g \upharpoonright \alpha ) = \sup (g \upharpoonright \iota _\alpha ) \leq \sup (f \upharpoonright \alpha ) < f(\alpha )$
. However,
![]() $\sup (g \upharpoonright \alpha ) < f(\alpha )$
implies
$\sup (g \upharpoonright \alpha ) < f(\alpha )$
implies
![]() $A = \emptyset $
which is a contradiction. Note that by
$A = \emptyset $
which is a contradiction. Note that by
![]() $(*)$
,
$(*)$
,
![]() $\iota _\alpha = \min (A)$
. Let
$\iota _\alpha = \min (A)$
. Let
![]() $\xi = {\mathrm {ot}}(A) \leq \alpha $
, and observe that
$\xi = {\mathrm {ot}}(A) \leq \alpha $
, and observe that
![]() $A = \{\iota _\alpha + \eta : \eta < \xi \}$
. Recall
$A = \{\iota _\alpha + \eta : \eta < \xi \}$
. Recall
![]() $\delta _0$
and
$\delta _0$
and
![]() $\tau _0$
have already been defined above. Note that
$\tau _0$
have already been defined above. Note that
![]() $\sup (h \upharpoonright \delta _0) = \sup (f \upharpoonright \alpha ) < g(\iota _\alpha )$
. For
$\sup (h \upharpoonright \delta _0) = \sup (f \upharpoonright \alpha ) < g(\iota _\alpha )$
. For
![]() $0 < \nu < \xi $
, suppose that for all
$0 < \nu < \xi $
, suppose that for all
![]() $\eta < \nu $
, the following holds:
$\eta < \nu $
, the following holds:
-
•
 $\epsilon _\eta = \delta _0 + \mathcal {I}(\iota _\alpha + \eta )$
and
$\epsilon _\eta = \delta _0 + \mathcal {I}(\iota _\alpha + \eta )$
and
 $\mu _\eta = \tau _0 + \mathcal {I}(\iota _\alpha + \eta )$
have been defined.
$\mu _\eta = \tau _0 + \mathcal {I}(\iota _\alpha + \eta )$
have been defined. -
•
 $h \upharpoonright \epsilon _\eta + 1$
and
$h \upharpoonright \epsilon _\eta + 1$
and
 $p \upharpoonright \mu _\eta + 1$
have been defined.
$p \upharpoonright \mu _\eta + 1$
have been defined. -
•
 $h(\epsilon _\eta ) = g(\iota _\alpha + \eta ) = p(\mu _\eta )$
.
$h(\epsilon _\eta ) = g(\iota _\alpha + \eta ) = p(\mu _\eta )$
.
Let
![]() $\delta _\nu = \sup \{\epsilon _\eta + 1 : \eta < \nu \}$
and
$\delta _\nu = \sup \{\epsilon _\eta + 1 : \eta < \nu \}$
and
![]() $\tau _\nu = \sup \{\mu _\eta + 1 : \eta < \nu \}$
. Note that
$\tau _\nu = \sup \{\mu _\eta + 1 : \eta < \nu \}$
. Note that
![]() $\delta _\nu = \sup \{\delta _0 + \mathcal {I}(\iota _\alpha + \eta ) + 1 : \eta < \nu \} < \delta _0 + \mathcal {I}(\iota _\alpha + \nu )$
and
$\delta _\nu = \sup \{\delta _0 + \mathcal {I}(\iota _\alpha + \eta ) + 1 : \eta < \nu \} < \delta _0 + \mathcal {I}(\iota _\alpha + \nu )$
and
![]() $\tau _\nu = \sup \{\tau _0 + \mathcal {I}(\iota _\alpha + \eta ) + 1 : \eta < \nu \} < \tau _0 + \mathcal {I}(\iota _\alpha + \nu )$
since
$\tau _\nu = \sup \{\tau _0 + \mathcal {I}(\iota _\alpha + \eta ) + 1 : \eta < \nu \} < \tau _0 + \mathcal {I}(\iota _\alpha + \nu )$
since
![]() $\mathcal {I}$
is discontinuous. The above assumptions imply that
$\mathcal {I}$
is discontinuous. The above assumptions imply that
![]() $h \upharpoonright \delta _\nu $
and
$h \upharpoonright \delta _\nu $
and
![]() $p \upharpoonright \tau _\nu $
are defined, and
$p \upharpoonright \tau _\nu $
are defined, and
![]() $\sup (h \upharpoonright \delta _\nu ) = \sup (g \upharpoonright (\iota _\alpha + \nu )) = \sup (p \upharpoonright \tau _\nu )$
.
$\sup (h \upharpoonright \delta _\nu ) = \sup (g \upharpoonright (\iota _\alpha + \nu )) = \sup (p \upharpoonright \tau _\nu )$
.
Fix
![]() $\nu $
with
$\nu $
with
![]() $0 \leq \nu < \xi $
. Let
$0 \leq \nu < \xi $
. Let
![]() $\epsilon _\nu = \delta _\nu + \mathcal {I}(\iota _\alpha + \nu )$
and
$\epsilon _\nu = \delta _\nu + \mathcal {I}(\iota _\alpha + \nu )$
and
![]() $\mu _\nu = \tau _\nu + \mathcal {I}(\iota _\alpha + \nu )$
. Since
$\mu _\nu = \tau _\nu + \mathcal {I}(\iota _\alpha + \nu )$
. Since
![]() $\delta _\nu < \delta _0 + \mathcal {I}(\iota _\alpha + \nu )$
,
$\delta _\nu < \delta _0 + \mathcal {I}(\iota _\alpha + \nu )$
,
![]() $\tau _\nu < \tau _0 + \mathcal {I}(\iota _\alpha + \nu )$
and
$\tau _\nu < \tau _0 + \mathcal {I}(\iota _\alpha + \nu )$
and
![]() $\mathcal {I}(\iota _\alpha + \nu )$
is indecomposable,
$\mathcal {I}(\iota _\alpha + \nu )$
is indecomposable,
![]() $\epsilon _\nu = \delta _\nu + \mathcal {I}(\iota _\alpha + \nu ) = \delta _0 + \mathcal {I}(\iota _\alpha + \nu )$
and
$\epsilon _\nu = \delta _\nu + \mathcal {I}(\iota _\alpha + \nu ) = \delta _0 + \mathcal {I}(\iota _\alpha + \nu )$
and
![]() $\mu _\nu = \tau _\nu + \mathcal {I}(\iota _\alpha + \nu ) = \tau _0 + \mathcal {I}(\iota _\alpha + \nu )$
. For
$\mu _\nu = \tau _\nu + \mathcal {I}(\iota _\alpha + \nu ) = \tau _0 + \mathcal {I}(\iota _\alpha + \nu )$
. For
![]() $\beta < \mathcal {I}(\iota _\alpha + \nu )$
, let
$\beta < \mathcal {I}(\iota _\alpha + \nu )$
, let
![]() $h(\delta _\nu + \beta ) = p(\tau _\nu + \beta ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\beta + 1)}(\sup (h \upharpoonright \delta _\nu ))$
. This defines
$h(\delta _\nu + \beta ) = p(\tau _\nu + \beta ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\beta + 1)}(\sup (h \upharpoonright \delta _\nu ))$
. This defines
![]() $h \upharpoonright \epsilon _\nu $
and
$h \upharpoonright \epsilon _\nu $
and
![]() $p \upharpoonright \mu _\nu $
with
$p \upharpoonright \mu _\nu $
with
![]() $\sup (h \upharpoonright \epsilon _\nu ) = \sup (p \upharpoonright \mu _\nu ) \leq {\mathsf {next}}_{C_0}^{\mathcal {I}(\iota _\alpha + \nu )}(\sup (h \upharpoonright \delta _\nu )) < g(\iota _\alpha + \nu )$
by Fact 2.12 since
$\sup (h \upharpoonright \epsilon _\nu ) = \sup (p \upharpoonright \mu _\nu ) \leq {\mathsf {next}}_{C_0}^{\mathcal {I}(\iota _\alpha + \nu )}(\sup (h \upharpoonright \delta _\nu )) < g(\iota _\alpha + \nu )$
by Fact 2.12 since
![]() $\sup (h \upharpoonright \delta _0) < g(\iota _\alpha )$
(in the case
$\sup (h \upharpoonright \delta _0) < g(\iota _\alpha )$
(in the case
![]() $\nu = 0$
),
$\nu = 0$
),
![]() $\sup (h \upharpoonright \delta _\nu ) = \sup (g \upharpoonright \tau _\nu ) = \sup (g \upharpoonright (\iota _\alpha + \nu )) < g(\iota _\alpha + \nu )$
(in the case
$\sup (h \upharpoonright \delta _\nu ) = \sup (g \upharpoonright \tau _\nu ) = \sup (g \upharpoonright (\iota _\alpha + \nu )) < g(\iota _\alpha + \nu )$
(in the case
![]() $0 < \nu < \xi )$
and
$0 < \nu < \xi )$
and
![]() $\mathcal {I}(\iota _\alpha + \nu ) < g(\iota _\alpha + \nu )$
. Let
$\mathcal {I}(\iota _\alpha + \nu ) < g(\iota _\alpha + \nu )$
. Let
![]() $h(\epsilon _\nu ) = p(\mu _\nu ) = g(\iota _\alpha + \nu )$
.
$h(\epsilon _\nu ) = p(\mu _\nu ) = g(\iota _\alpha + \nu )$
.
Let
![]() $\tau = \sup \{\mu _\nu + 1 : \nu < \xi \}$
and
$\tau = \sup \{\mu _\nu + 1 : \nu < \xi \}$
and
![]() $\delta = \sup \{\epsilon _\nu + 1 : \nu < \xi \}$
. Note
$\delta = \sup \{\epsilon _\nu + 1 : \nu < \xi \}$
. Note
![]() $p \upharpoonright \tau $
and
$p \upharpoonright \tau $
and
![]() $h \upharpoonright \delta $
have been defined so that
$h \upharpoonright \delta $
have been defined so that
![]() $\sup (p \upharpoonright \tau ) = \sup (h \upharpoonright \delta ) = \sup \{g(\gamma ) : \gamma \in A\} < f(\alpha )$
by property (3). Since
$\sup (p \upharpoonright \tau ) = \sup (h \upharpoonright \delta ) = \sup \{g(\gamma ) : \gamma \in A\} < f(\alpha )$
by property (3). Since
![]() $\mathcal {I}$
is discontinuous,
$\mathcal {I}$
is discontinuous,
![]() $\iota _\alpha + \nu < \alpha $
for all
$\iota _\alpha + \nu < \alpha $
for all
![]() $\nu < \xi $
,
$\nu < \xi $
,
![]() $\delta _0 < \mathcal {I}(\alpha )$
and
$\delta _0 < \mathcal {I}(\alpha )$
and
![]() $\mathcal {I}(\alpha )$
is indecomposable, one has
$\mathcal {I}(\alpha )$
is indecomposable, one has
![]() $\delta = \sup \{\epsilon _\nu + 1 : \nu < \xi \} = \sup \{\delta _0 + \mathcal {I}(\iota _\alpha + \nu ) + 1 : \nu < \xi \} \leq \delta _0 + \sup (\mathcal {I}\upharpoonright \alpha ) + 1 < \delta _0 + \mathcal {I}(\alpha ) = \mathcal {I}(\alpha )$
.
$\delta = \sup \{\epsilon _\nu + 1 : \nu < \xi \} = \sup \{\delta _0 + \mathcal {I}(\iota _\alpha + \nu ) + 1 : \nu < \xi \} \leq \delta _0 + \sup (\mathcal {I}\upharpoonright \alpha ) + 1 < \delta _0 + \mathcal {I}(\alpha ) = \mathcal {I}(\alpha )$
.
In either Case A or Case B, ordinals
![]() $\tau $
and
$\tau $
and
![]() $\delta $
have been defined with
$\delta $
have been defined with
![]() $\tau \leq \delta < \mathcal {I}(\alpha )$
and
$\tau \leq \delta < \mathcal {I}(\alpha )$
and
![]() $\sup (h \upharpoonright \delta ) < f(\alpha )$
. Let
$\sup (h \upharpoonright \delta ) < f(\alpha )$
. Let
![]() $\ell = \min (\kappa \setminus A)$
.
$\ell = \min (\kappa \setminus A)$
.
(Case I)
![]() $g(\ell )> f(\alpha )$
.
$g(\ell )> f(\alpha )$
.
Let
![]() $\sigma _\alpha = \iota _\alpha $
if Case A held, and let
$\sigma _\alpha = \iota _\alpha $
if Case A held, and let
![]() $\sigma _\alpha = \ell $
if Case B held. For
$\sigma _\alpha = \ell $
if Case B held. For
![]() $\beta < \mathcal {I}(\alpha )$
, let
$\beta < \mathcal {I}(\alpha )$
, let
![]() $h(\delta + \beta ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\beta + 1)}(\sup (h\upharpoonright \delta ))$
. Note that
$h(\delta + \beta ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\beta + 1)}(\sup (h\upharpoonright \delta ))$
. Note that
![]() $\sup (h \upharpoonright \mathcal {I}(\alpha )) \leq {\mathsf {next}}_{C_0}^{\mathcal {I}(\alpha )}(\sup (h\upharpoonright \delta )) < f(\alpha )$
by Fact 2.12 since
$\sup (h \upharpoonright \mathcal {I}(\alpha )) \leq {\mathsf {next}}_{C_0}^{\mathcal {I}(\alpha )}(\sup (h\upharpoonright \delta )) < f(\alpha )$
by Fact 2.12 since
![]() $f(\alpha ) \in C_1$
,
$f(\alpha ) \in C_1$
,
![]() $\sup (h \upharpoonright \delta ) < f(\alpha )$
and
$\sup (h \upharpoonright \delta ) < f(\alpha )$
and
![]() $\mathcal {I}(\alpha ) < f(\alpha )$
. Let
$\mathcal {I}(\alpha ) < f(\alpha )$
. Let
![]() $h(\mathcal {I}(\alpha )) = f(\alpha )$
.
$h(\mathcal {I}(\alpha )) = f(\alpha )$
.
(Case II)
![]() $g(\ell ) = f(\alpha )$
.
$g(\ell ) = f(\alpha )$
.
For
![]() $\beta < \mathcal {I}(\ell )$
, let
$\beta < \mathcal {I}(\ell )$
, let
![]() $h(\delta + \beta ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\beta + 1)}(\sup (h \upharpoonright \delta ))$
.
$h(\delta + \beta ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\beta + 1)}(\sup (h \upharpoonright \delta ))$
.
(Case II.1)
![]() $\ell = \alpha $
.
$\ell = \alpha $
.
Then
![]() $h \upharpoonright \mathcal {I}(\alpha )$
and
$h \upharpoonright \mathcal {I}(\alpha )$
and
![]() $p \upharpoonright \mathcal {I}(\alpha )$
have been defined with
$p \upharpoonright \mathcal {I}(\alpha )$
have been defined with
![]() $\sup (h \upharpoonright \mathcal {I}(\alpha )) = \sup (p \upharpoonright \mathcal {I}(\alpha )) \leq {\mathsf {next}}_{C_0}^{\mathcal {I}(\alpha )}(\sup (h \upharpoonright \delta )) < f(\alpha )$
by Fact 2.12 since
$\sup (h \upharpoonright \mathcal {I}(\alpha )) = \sup (p \upharpoonright \mathcal {I}(\alpha )) \leq {\mathsf {next}}_{C_0}^{\mathcal {I}(\alpha )}(\sup (h \upharpoonright \delta )) < f(\alpha )$
by Fact 2.12 since
![]() $f(\alpha ) \in C_1$
,
$f(\alpha ) \in C_1$
,
![]() $\sup (h \upharpoonright \delta ) < f(\alpha )$
and
$\sup (h \upharpoonright \delta ) < f(\alpha )$
and
![]() $\mathcal {I}(\alpha ) < f(\alpha )$
. Let
$\mathcal {I}(\alpha ) < f(\alpha )$
. Let
![]() $h(\mathcal {I}(\alpha )) = p(\mathcal {I}(\alpha )) = f(\alpha ) = g(\alpha )$
. Let
$h(\mathcal {I}(\alpha )) = p(\mathcal {I}(\alpha )) = f(\alpha ) = g(\alpha )$
. Let
![]() $\sigma _\alpha = \alpha + 1$
.
$\sigma _\alpha = \alpha + 1$
.
(Case II.2)
![]() $\ell < \alpha $
.
$\ell < \alpha $
.
Then
![]() $h \upharpoonright (\delta + \mathcal {I}(\ell ))$
and
$h \upharpoonright (\delta + \mathcal {I}(\ell ))$
and
![]() $p \upharpoonright (\delta + \mathcal {I}(\ell ))$
have been defined with
$p \upharpoonright (\delta + \mathcal {I}(\ell ))$
have been defined with
![]() $\sup (p \upharpoonright (\delta + \mathcal {I}(\ell ))) = \sup (h \upharpoonright (\delta + \mathcal {I}(\ell ))) < {\mathsf {next}}_{C_0}^{\mathcal {I}(\ell )}(\sup (h \upharpoonright \delta )) < f(\alpha )$
by Fact 2.12 since
$\sup (p \upharpoonright (\delta + \mathcal {I}(\ell ))) = \sup (h \upharpoonright (\delta + \mathcal {I}(\ell ))) < {\mathsf {next}}_{C_0}^{\mathcal {I}(\ell )}(\sup (h \upharpoonright \delta )) < f(\alpha )$
by Fact 2.12 since
![]() $f(\alpha ) \in C_1$
,
$f(\alpha ) \in C_1$
,
![]() $\sup (h \upharpoonright \mathcal {I}(\ell )) < f(\alpha )$
and
$\sup (h \upharpoonright \mathcal {I}(\ell )) < f(\alpha )$
and
![]() $\mathcal {I}(\ell ) < \mathcal {I}(\alpha ) < f(\alpha )$
. For
$\mathcal {I}(\ell ) < \mathcal {I}(\alpha ) < f(\alpha )$
. For
![]() $\beta < \mathcal {I}(\alpha )$
, let
$\beta < \mathcal {I}(\alpha )$
, let
![]() $h(\delta + \mathcal {I}(\ell ) + \beta ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\beta + 1)}(\sup (h \upharpoonright (\delta + \mathcal {I}(\ell ))))$
.
$h(\delta + \mathcal {I}(\ell ) + \beta ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\beta + 1)}(\sup (h \upharpoonright (\delta + \mathcal {I}(\ell ))))$
.
This defines
![]() $h \upharpoonright \mathcal {I}(\alpha )$
with
$h \upharpoonright \mathcal {I}(\alpha )$
with
![]() $\sup (h \upharpoonright \mathcal {I}(\alpha )) \leq {\mathsf {next}}_{C_0}^{\mathcal {I}(\alpha )}(\sup (h \upharpoonright (\delta + \mathcal {I}(\ell )))) < f(\alpha )$
by Fact 2.12 since
$\sup (h \upharpoonright \mathcal {I}(\alpha )) \leq {\mathsf {next}}_{C_0}^{\mathcal {I}(\alpha )}(\sup (h \upharpoonright (\delta + \mathcal {I}(\ell )))) < f(\alpha )$
by Fact 2.12 since
![]() $f(\alpha ) \in C_1$
,
$f(\alpha ) \in C_1$
,
![]() $\sup (f \upharpoonright (\delta + \mathcal {I}(\ell ))) < f(\alpha )$
and
$\sup (f \upharpoonright (\delta + \mathcal {I}(\ell ))) < f(\alpha )$
and
![]() $\mathcal {I}(\alpha ) < f(\alpha )$
. Let
$\mathcal {I}(\alpha ) < f(\alpha )$
. Let
![]() $h(\mathcal {I}(\alpha )) = f(\alpha )$
and
$h(\mathcal {I}(\alpha )) = f(\alpha )$
and
![]() $p(\mathcal {I}(\ell )) = g(\ell ) = f(\alpha )$
. Let
$p(\mathcal {I}(\ell )) = g(\ell ) = f(\alpha )$
. Let
![]() $\sigma _\alpha = \ell + 1$
.
$\sigma _\alpha = \ell + 1$
.
This completes the construction of the desired objects satisfying properties (a), (b), (c) and (d). Let
![]() $h = \bigcup \{h \upharpoonright \mathcal {I}(\alpha ) : \alpha < \kappa \}$
and
$h = \bigcup \{h \upharpoonright \mathcal {I}(\alpha ) : \alpha < \kappa \}$
and
![]() $p \in \bigcup \{p \upharpoonright \sigma _\alpha : \alpha < \kappa \}$
. By construction, h and p are increasing functions of the correct type. (To verify these functions have uniform cofinality
$p \in \bigcup \{p \upharpoonright \sigma _\alpha : \alpha < \kappa \}$
. By construction, h and p are increasing functions of the correct type. (To verify these functions have uniform cofinality
![]() $\omega $
, note that an ordinal of the form
$\omega $
, note that an ordinal of the form
![]() ${\mathsf {next}}^{\omega \cdot (\beta + 1)}_{C_0}(\gamma )$
with
${\mathsf {next}}^{\omega \cdot (\beta + 1)}_{C_0}(\gamma )$
with
![]() $\beta ,\gamma < \kappa $
is a uniform limit of an
$\beta ,\gamma < \kappa $
is a uniform limit of an
![]() $\omega $
-sequence from
$\omega $
-sequence from
![]() $C_0$
). Then
$C_0$
). Then
![]() $h \in [C_0]^\kappa _*$
,
$h \in [C_0]^\kappa _*$
,
![]() $p \in [h[\kappa ]]^\kappa _*$
,
$p \in [h[\kappa ]]^\kappa _*$
,
![]() ${\mathsf {main}}(h) = f$
and
${\mathsf {main}}(h) = f$
and
![]() ${\mathsf {main}}(p) = g$
. Since
${\mathsf {main}}(p) = g$
. Since
![]() $P(h) = 0$
, one has
$P(h) = 0$
, one has
![]() $\Phi (f) = \Phi ({\mathsf {main}}(h)) \leq \Phi ({\mathsf {main}}(p)) = \Phi (g)$
.
$\Phi (f) = \Phi ({\mathsf {main}}(h)) \leq \Phi ({\mathsf {main}}(p)) = \Phi (g)$
.
Theorem 5.3. Suppose
![]() $\kappa $
is a cardinal satisfying
$\kappa $
is a cardinal satisfying
![]() $\kappa \rightarrow _* (\kappa )^\kappa _2$
. For any function
$\kappa \rightarrow _* (\kappa )^\kappa _2$
. For any function
![]() $\Phi : [\kappa ]^\kappa _* \rightarrow \mathrm {ON}$
, there is a club
$\Phi : [\kappa ]^\kappa _* \rightarrow \mathrm {ON}$
, there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f,g \in [C]^\kappa _*$
, if for all
$f,g \in [C]^\kappa _*$
, if for all
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $f(\alpha ) \leq g(\alpha )$
, then
$f(\alpha ) \leq g(\alpha )$
, then
![]() $\Phi (f) \leq \Phi (g)$
.
$\Phi (f) \leq \Phi (g)$
.
Proof. Let
![]() $C_0 \subseteq \kappa $
be a club satisfying the property from Lemma 5.2. One may assume that
$C_0 \subseteq \kappa $
be a club satisfying the property from Lemma 5.2. One may assume that
![]() $C_0$
consists entirely of indecomposable ordinals. Let
$C_0$
consists entirely of indecomposable ordinals. Let
![]() $C_1 = \{\alpha \in C_0 : {\mathsf {enum}}_{C_0}(\alpha ) = \alpha \}$
. Suppose
$C_1 = \{\alpha \in C_0 : {\mathsf {enum}}_{C_0}(\alpha ) = \alpha \}$
. Suppose
![]() $f,g \in [C_1]^\kappa _*$
and for all
$f,g \in [C_1]^\kappa _*$
and for all
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $f(\alpha ) \leq g(\alpha )$
. Let conditions (1), (2) and (3) refer to the conditions from Lemma 5.2.
$f(\alpha ) \leq g(\alpha )$
. Let conditions (1), (2) and (3) refer to the conditions from Lemma 5.2.
First, one will construct a
![]() $k \in [C_1]^\kappa _*$
so that the pair
$k \in [C_1]^\kappa _*$
so that the pair
![]() $(f,k)$
satisfies condition (1) and (2) and the pair
$(f,k)$
satisfies condition (1) and (2) and the pair
![]() $(k,g)$
satisfies condition (1), (2) and (3). Let
$(k,g)$
satisfies condition (1), (2) and (3). Let
![]() $\zeta \leq \kappa $
and
$\zeta \leq \kappa $
and
![]() $\langle \eta _\xi : \xi < \zeta \rangle $
and
$\langle \eta _\xi : \xi < \zeta \rangle $
and
![]() $\langle \nu _\xi : \xi < \zeta \rangle $
be two increasing sequences so that the following holds.
$\langle \nu _\xi : \xi < \zeta \rangle $
be two increasing sequences so that the following holds.
-
(a) For all
 $\xi < \zeta $
,
$\xi < \zeta $
,
 $\nu _\xi $
is a limit ordinal.
$\nu _\xi $
is a limit ordinal. -
(b) For all
 $\xi < \zeta $
,
$\xi < \zeta $
,
 $\sup (f \upharpoonright \nu _\xi ) = g(\eta _\xi )$
.
$\sup (f \upharpoonright \nu _\xi ) = g(\eta _\xi )$
. -
(c) For all
 $\nu < \kappa $
and
$\nu < \kappa $
and
 $\eta < \kappa $
, if
$\eta < \kappa $
, if
 $\nu $
is a limit ordinal and
$\nu $
is a limit ordinal and
 $\sup (f \upharpoonright \nu ) = g(\eta )$
, then there is a
$\sup (f \upharpoonright \nu ) = g(\eta )$
, then there is a
 $\xi < \zeta $
so that
$\xi < \zeta $
so that
 $\nu = \nu _\xi $
and
$\nu = \nu _\xi $
and
 $\eta = \eta _\xi $
.
$\eta = \eta _\xi $
.
These objects refer to the areas in which the pair
![]() $(f,g)$
fails to satisfy condition (2). (Note
$(f,g)$
fails to satisfy condition (2). (Note
![]() $\zeta = 0$
if there are no failures.) Observe that for all
$\zeta = 0$
if there are no failures.) Observe that for all
![]() $\xi < \zeta $
,
$\xi < \zeta $
,
![]() $g(\eta _\xi ) < f(\nu _\xi )$
implies that
$g(\eta _\xi ) < f(\nu _\xi )$
implies that
![]() $\eta _\xi < \nu _\xi $
since for all
$\eta _\xi < \nu _\xi $
since for all
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $f(\alpha ) \leq g(\alpha )$
. For each
$f(\alpha ) \leq g(\alpha )$
. For each
![]() $\xi < \zeta $
, let
$\xi < \zeta $
, let
![]() $\mu _\xi $
be the least
$\mu _\xi $
be the least
![]() $\gamma $
so that
$\gamma $
so that
![]() $\sup (g \upharpoonright \eta _\xi ) \leq f(\gamma )$
. Note that
$\sup (g \upharpoonright \eta _\xi ) \leq f(\gamma )$
. Note that
![]() $\eta _\xi \leq \mu _\xi < \mu _\xi + 1 < \nu _\xi $
since for all
$\eta _\xi \leq \mu _\xi < \mu _\xi + 1 < \nu _\xi $
since for all
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $f(\alpha ) \leq g(\alpha )$
,
$f(\alpha ) \leq g(\alpha )$
,
![]() $\eta _\xi < \nu _\xi $
and
$\eta _\xi < \nu _\xi $
and
![]() $\nu _\xi $
is a limit ordinal.
$\nu _\xi $
is a limit ordinal.
Define
![]() $k : \kappa \rightarrow C_1$
as follows: Let
$k : \kappa \rightarrow C_1$
as follows: Let
![]() $\alpha < \kappa $
. If
$\alpha < \kappa $
. If
![]() $\alpha \neq \eta _\xi $
for any
$\alpha \neq \eta _\xi $
for any
![]() $\xi < \zeta $
, then let
$\xi < \zeta $
, then let
![]() $k(\alpha ) = g(\alpha )$
. If there is a
$k(\alpha ) = g(\alpha )$
. If there is a
![]() $\xi < \zeta $
so that
$\xi < \zeta $
so that
![]() $\alpha = \eta _\xi $
, then let
$\alpha = \eta _\xi $
, then let
![]() $k(\alpha ) = f(\mu _\xi + 1)$
. The following illustrates the construction.
$k(\alpha ) = f(\mu _\xi + 1)$
. The following illustrates the construction.

Since for all
![]() $\alpha $
,
$\alpha $
,
![]() $k(\alpha ) \in f[\kappa ] \cup g[\kappa ]$
, one can construct a witness
$k(\alpha ) \in f[\kappa ] \cup g[\kappa ]$
, one can construct a witness
![]() $K : \kappa \times \omega \rightarrow \kappa $
to k having uniform cofinality
$K : \kappa \times \omega \rightarrow \kappa $
to k having uniform cofinality
![]() $\omega $
by using witnesses
$\omega $
by using witnesses
![]() $F : \kappa \times \omega \rightarrow \kappa $
and
$F : \kappa \times \omega \rightarrow \kappa $
and
![]() $G : \kappa \times \omega \rightarrow \kappa $
to f and g, respectively, having uniform cofinality
$G : \kappa \times \omega \rightarrow \kappa $
to f and g, respectively, having uniform cofinality
![]() $\omega $
.
$\omega $
.
If for all
![]() $\xi < \zeta $
,
$\xi < \zeta $
,
![]() $\alpha \neq \eta _\xi $
, then
$\alpha \neq \eta _\xi $
, then
![]() $f(\alpha ) \leq g(\alpha ) = k(\alpha )$
. If
$f(\alpha ) \leq g(\alpha ) = k(\alpha )$
. If
![]() $\alpha = \eta _\xi $
for some
$\alpha = \eta _\xi $
for some
![]() $\xi < \zeta $
, then
$\xi < \zeta $
, then
![]() $f(\alpha ) = f(\eta _\xi ) \leq f(\mu _\xi ) < f(\mu _\xi + 1) = k(\alpha )$
. So for all
$f(\alpha ) = f(\eta _\xi ) \leq f(\mu _\xi ) < f(\mu _\xi + 1) = k(\alpha )$
. So for all
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $f(\alpha ) \leq k(\alpha )$
. The pair
$f(\alpha ) \leq k(\alpha )$
. The pair
![]() $(f,k)$
satisfies condition (1).
$(f,k)$
satisfies condition (1).
If for all
![]() $\alpha < \zeta $
,
$\alpha < \zeta $
,
![]() $\alpha \neq \eta _\xi $
, then
$\alpha \neq \eta _\xi $
, then
![]() $k(\alpha ) = g(\alpha )$
. If there is a
$k(\alpha ) = g(\alpha )$
. If there is a
![]() $\xi < \zeta $
so that
$\xi < \zeta $
so that
![]() $\alpha = \eta _\xi $
, then
$\alpha = \eta _\xi $
, then
![]() $k(\alpha ) = f(\mu _\xi + 1) < \sup (f \upharpoonright \nu _\xi ) = g(\eta _\xi ) = g(\alpha )$
. Thus, for all
$k(\alpha ) = f(\mu _\xi + 1) < \sup (f \upharpoonright \nu _\xi ) = g(\eta _\xi ) = g(\alpha )$
. Thus, for all
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $k(\alpha ) \leq g(\alpha )$
and hence condition (1) holds for the pair
$k(\alpha ) \leq g(\alpha )$
and hence condition (1) holds for the pair
![]() $(k,g)$
.
$(k,g)$
.
Let property
![]() $(*)$
for
$(*)$
for
![]() $(k,g)$
assert that for all
$(k,g)$
assert that for all
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $\sup (g \upharpoonright \alpha ) < k(\alpha )$
. If for all
$\sup (g \upharpoonright \alpha ) < k(\alpha )$
. If for all
![]() $\xi < \zeta $
,
$\xi < \zeta $
,
![]() $\alpha \neq \eta _\xi $
, then
$\alpha \neq \eta _\xi $
, then
![]() $\sup (g \upharpoonright \alpha ) < g(\alpha ) = k(\alpha )$
since g is discontinuous. If there is a
$\sup (g \upharpoonright \alpha ) < g(\alpha ) = k(\alpha )$
since g is discontinuous. If there is a
![]() $\xi < \zeta $
so that
$\xi < \zeta $
so that
![]() $\alpha = \eta _\xi $
, then
$\alpha = \eta _\xi $
, then
![]() $\sup (g \upharpoonright \alpha ) = \sup (g \upharpoonright \eta _\xi ) \leq f(\mu _\xi ) < f(\mu _\xi + 1) = k(\alpha )$
. It has been shown that property
$\sup (g \upharpoonright \alpha ) = \sup (g \upharpoonright \eta _\xi ) \leq f(\mu _\xi ) < f(\mu _\xi + 1) = k(\alpha )$
. It has been shown that property
![]() $(*)$
for
$(*)$
for
![]() $(k,g)$
holds.
$(k,g)$
holds.
By property
![]() $(*)$
for
$(*)$
for
![]() $(k,g)$
and condition (1) for the pair
$(k,g)$
and condition (1) for the pair
![]() $(k,g)$
, for any
$(k,g)$
, for any
![]() $\alpha < \beta < \kappa $
,
$\alpha < \beta < \kappa $
,
![]() $k(\alpha ) \leq g(\alpha ) \leq \sup (g \upharpoonright \beta ) < k(\beta )$
. This shows that k is increasing. Also, by property
$k(\alpha ) \leq g(\alpha ) \leq \sup (g \upharpoonright \beta ) < k(\beta )$
. This shows that k is increasing. Also, by property
![]() $(*)$
for
$(*)$
for
![]() $(k,g)$
and condition (1) for the pair
$(k,g)$
and condition (1) for the pair
![]() $(k,g)$
, for all
$(k,g)$
, for all
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $\sup (k \upharpoonright \alpha ) \leq \sup (g \upharpoonright \alpha ) < k(\alpha )$
. This shows that k is discontinuous. It has been shown that k is an increasing function of the correct type into
$\sup (k \upharpoonright \alpha ) \leq \sup (g \upharpoonright \alpha ) < k(\alpha )$
. This shows that k is discontinuous. It has been shown that k is an increasing function of the correct type into
![]() $C_1$
, that is,
$C_1$
, that is,
![]() $k \in [C_1]^\kappa _*$
.
$k \in [C_1]^\kappa _*$
.
If for all
![]() $\xi < \zeta $
,
$\xi < \zeta $
,
![]() $\alpha \neq \eta _\xi $
, then there is no limit ordinal
$\alpha \neq \eta _\xi $
, then there is no limit ordinal
![]() $\nu $
so that
$\nu $
so that
![]() $\sup (f \upharpoonright \nu ) = g(\alpha ) = k(\alpha )$
. If there is a
$\sup (f \upharpoonright \nu ) = g(\alpha ) = k(\alpha )$
. If there is a
![]() $\xi < \zeta $
so that
$\xi < \zeta $
so that
![]() $\alpha = \eta _\xi $
, then
$\alpha = \eta _\xi $
, then
![]() $k(\alpha ) = f(\mu _{\xi } + 1)$
and there is no limit ordinal
$k(\alpha ) = f(\mu _{\xi } + 1)$
and there is no limit ordinal
![]() $\nu $
so that
$\nu $
so that
![]() $\sup (f \upharpoonright \nu ) = k(\alpha ) = f(\mu _\xi + 1)$
since f is a strictly increasing function. The pair
$\sup (f \upharpoonright \nu ) = k(\alpha ) = f(\mu _\xi + 1)$
since f is a strictly increasing function. The pair
![]() $(f,k)$
satisfies condition (2).
$(f,k)$
satisfies condition (2).
Let property
![]() $(**)$
for
$(**)$
for
![]() $(k,g)$
assert that for all limit ordinals
$(k,g)$
assert that for all limit ordinals
![]() $\nu $
,
$\nu $
,
![]() $\sup (k \upharpoonright \nu ) = \sup (g \upharpoonright \nu )$
. Fix a limit ordinal
$\sup (k \upharpoonright \nu ) = \sup (g \upharpoonright \nu )$
. Fix a limit ordinal
![]() $\nu $
. By condition (1) for the pair
$\nu $
. By condition (1) for the pair
![]() $(k,g)$
,
$(k,g)$
,
![]() $\sup (k \upharpoonright \nu ) \leq \sup (g \upharpoonright \nu )$
. By property
$\sup (k \upharpoonright \nu ) \leq \sup (g \upharpoonright \nu )$
. By property
![]() $(*)$
for
$(*)$
for
![]() $(k,g)$
, for each
$(k,g)$
, for each
![]() $\eta < \nu $
,
$\eta < \nu $
,
![]() $\sup (g \upharpoonright \eta ) < k(\eta )$
. Thus, since
$\sup (g \upharpoonright \eta ) < k(\eta )$
. Thus, since
![]() $\nu $
is a limit ordinal,
$\nu $
is a limit ordinal,
![]() $\sup (g \upharpoonright \nu ) \leq \sup (k \upharpoonright \nu )$
. Property
$\sup (g \upharpoonright \nu ) \leq \sup (k \upharpoonright \nu )$
. Property
![]() $(**)$
for
$(**)$
for
![]() $(k,g)$
has been established.
$(k,g)$
has been established.
Suppose condition (2) for
![]() $(k,g)$
fails. Then there is an
$(k,g)$
fails. Then there is an
![]() $\alpha < \kappa $
and a limit ordinal
$\alpha < \kappa $
and a limit ordinal
![]() $\nu $
so that
$\nu $
so that
![]() $\sup (k \upharpoonright \nu ) = g(\alpha )$
. Then by property
$\sup (k \upharpoonright \nu ) = g(\alpha )$
. Then by property
![]() $(**)$
for
$(**)$
for
![]() $(k,g)$
,
$(k,g)$
,
![]() $\sup (g \upharpoonright \nu ) = \sup (k \upharpoonright \nu ) = g(\alpha )$
which is impossible since g is an increasing and discontinuous function. Condition (2) for the pair
$\sup (g \upharpoonright \nu ) = \sup (k \upharpoonright \nu ) = g(\alpha )$
which is impossible since g is an increasing and discontinuous function. Condition (2) for the pair
![]() $(k,g)$
has been shown.
$(k,g)$
has been shown.
Suppose condition (3) for the pair
![]() $(k,g)$
fails. Then there is ordinal
$(k,g)$
fails. Then there is ordinal
![]() $\alpha $
and a limit ordinal
$\alpha $
and a limit ordinal
![]() $\nu $
so that
$\nu $
so that
![]() $\sup (g \upharpoonright \nu ) = k(\alpha )$
. Then by property
$\sup (g \upharpoonright \nu ) = k(\alpha )$
. Then by property
![]() $(**)$
for
$(**)$
for
![]() $(k,g)$
,
$(k,g)$
,
![]() $\sup (k \upharpoonright \nu ) = \sup (g \upharpoonright \nu ) = k(\alpha )$
. This is impossible since k is an increasing and discontinuous function. Condition (3) for the pair
$\sup (k \upharpoonright \nu ) = \sup (g \upharpoonright \nu ) = k(\alpha )$
. This is impossible since k is an increasing and discontinuous function. Condition (3) for the pair
![]() $(k,g)$
has been shown.
$(k,g)$
has been shown.
Since
![]() $C_0$
has the property stated in Lemma 5.2,
$C_0$
has the property stated in Lemma 5.2,
![]() $(k,g)$
satisfies condition (1), (2) and (3) and
$(k,g)$
satisfies condition (1), (2) and (3) and
![]() $k,g \in [C_1]^\kappa _*$
, one has that
$k,g \in [C_1]^\kappa _*$
, one has that
![]() $\Phi (k) \leq \Phi (g)$
.
$\Phi (k) \leq \Phi (g)$
.
Next, one will construct an
![]() $h \in [C_0]^\kappa _*$
so that the pair
$h \in [C_0]^\kappa _*$
so that the pair
![]() $(f,h)$
satisfies condition (1), (2) and (3) and the pair
$(f,h)$
satisfies condition (1), (2) and (3) and the pair
![]() $(h,k)$
satisfies condition (1), (2) and (3). Let
$(h,k)$
satisfies condition (1), (2) and (3). Let
![]() $\zeta \leq \kappa $
and
$\zeta \leq \kappa $
and
![]() $\langle \eta _\xi : \xi < \zeta \rangle $
and
$\langle \eta _\xi : \xi < \zeta \rangle $
and
![]() $\langle \nu _\xi : \xi < \zeta \rangle $
be two increasing sequences so that the following holds.
$\langle \nu _\xi : \xi < \zeta \rangle $
be two increasing sequences so that the following holds.
-
(a) For all
 $\xi < \zeta $
,
$\xi < \zeta $
,
 $\eta _\xi $
is a limit ordinal.
$\eta _\xi $
is a limit ordinal. -
(b) For all
 $\xi < \zeta $
,
$\xi < \zeta $
,
 $\sup (k \upharpoonright \eta _\xi ) = f(\nu _\xi )$
.
$\sup (k \upharpoonright \eta _\xi ) = f(\nu _\xi )$
. -
(c) For all
 $\eta < \kappa $
and
$\eta < \kappa $
and
 $\nu < \kappa $
, if
$\nu < \kappa $
, if
 $\eta $
is a limit ordinal and
$\eta $
is a limit ordinal and
 $\sup (k \upharpoonright \eta ) = f(\nu )$
, then there is a
$\sup (k \upharpoonright \eta ) = f(\nu )$
, then there is a
 $\xi < \zeta $
so that
$\xi < \zeta $
so that
 $\eta = \eta _\xi $
and
$\eta = \eta _\xi $
and
 $\nu = \nu _\xi $
.
$\nu = \nu _\xi $
.
These objects refer to the areas in which the pair
![]() $(f,k)$
fails to satisfy condition (3). Note that
$(f,k)$
fails to satisfy condition (3). Note that
![]() $\eta _\xi \leq \nu _\xi $
because if
$\eta _\xi \leq \nu _\xi $
because if
![]() $\nu _\xi < \eta _\xi $
, then there is a
$\nu _\xi < \eta _\xi $
, then there is a
![]() $\gamma $
with
$\gamma $
with
![]() $\nu _\xi < \gamma < \eta _\xi $
since
$\nu _\xi < \gamma < \eta _\xi $
since
![]() $\eta _\xi $
is a limit and thus
$\eta _\xi $
is a limit and thus
![]() $f(\nu _\xi ) \leq k(\nu _\xi ) < k(\gamma ) < \sup (k \upharpoonright \eta _\xi ) = f(\nu _\xi )$
which is a contradiction. Let
$f(\nu _\xi ) \leq k(\nu _\xi ) < k(\gamma ) < \sup (k \upharpoonright \eta _\xi ) = f(\nu _\xi )$
which is a contradiction. Let
![]() $\mu _\xi $
be the least
$\mu _\xi $
be the least
![]() $\gamma < \eta _\xi $
so that
$\gamma < \eta _\xi $
so that
![]() $\sup (f \upharpoonright \nu _\xi ) < k(\gamma )$
.
$\sup (f \upharpoonright \nu _\xi ) < k(\gamma )$
.
Define
![]() $h : \kappa \rightarrow C_0$
as follows: If
$h : \kappa \rightarrow C_0$
as follows: If
![]() $\alpha < \kappa $
and there is no
$\alpha < \kappa $
and there is no
![]() $\xi < \zeta $
so that
$\xi < \zeta $
so that
![]() $\mu _\xi \leq \alpha < \eta _\xi $
, then let
$\mu _\xi \leq \alpha < \eta _\xi $
, then let
![]() $h(\alpha ) = k(\alpha )$
. If
$h(\alpha ) = k(\alpha )$
. If
![]() $\alpha < \kappa $
and there is a
$\alpha < \kappa $
and there is a
![]() $\xi < \zeta $
so that
$\xi < \zeta $
so that
![]() $\mu _\xi \leq \alpha < \eta _\xi $
, then let
$\mu _\xi \leq \alpha < \eta _\xi $
, then let
![]() $h(\alpha ) = {\mathsf {next}}_{C_0}^{\omega \cdot ((\alpha - \mu _\xi ) + 1)}(\sup (f \upharpoonright \nu _\xi ))$
. The following illustrates the construction.
$h(\alpha ) = {\mathsf {next}}_{C_0}^{\omega \cdot ((\alpha - \mu _\xi ) + 1)}(\sup (f \upharpoonright \nu _\xi ))$
. The following illustrates the construction.

Since k has the correct type, there is a function
![]() $K : \kappa \times \omega \rightarrow \kappa $
witnessing k has uniform cofinality
$K : \kappa \times \omega \rightarrow \kappa $
witnessing k has uniform cofinality
![]() $\omega $
. If
$\omega $
. If
![]() $\alpha < \kappa $
and there is no
$\alpha < \kappa $
and there is no
![]() $\xi < \zeta $
with
$\xi < \zeta $
with
![]() $\mu _\xi \leq \alpha < \eta _\xi $
, then
$\mu _\xi \leq \alpha < \eta _\xi $
, then
![]() $h(\alpha ) = k(\alpha )$
and K can be used to produce an
$h(\alpha ) = k(\alpha )$
and K can be used to produce an
![]() $\omega $
-sequence whose limit is
$\omega $
-sequence whose limit is
![]() $h(\alpha )$
. If
$h(\alpha )$
. If
![]() $\alpha < \kappa $
and there is a
$\alpha < \kappa $
and there is a
![]() $\xi < \zeta $
with
$\xi < \zeta $
with
![]() $\mu _\xi \leq \alpha < \nu _\xi $
, then
$\mu _\xi \leq \alpha < \nu _\xi $
, then
![]() $h(\alpha ) = {\mathsf {next}}_{C_0}^{\omega \cdot ((\alpha - \mu _\xi ) + 1)}(\sup (f \upharpoonright \nu _\xi )$
is a uniform limit of an
$h(\alpha ) = {\mathsf {next}}_{C_0}^{\omega \cdot ((\alpha - \mu _\xi ) + 1)}(\sup (f \upharpoonright \nu _\xi )$
is a uniform limit of an
![]() $\omega $
-sequence from
$\omega $
-sequence from
![]() $C_0$
. From these observations, a witness to h having uniform cofinality
$C_0$
. From these observations, a witness to h having uniform cofinality
![]() $\omega $
can be constructed.
$\omega $
can be constructed.
Note that for each
![]() $\xi < \zeta $
,
$\xi < \zeta $
,
![]() $\eta _\xi \leq \nu _\xi \leq \sup (f \upharpoonright \nu _\xi ) < k(\mu _\xi )$
. Since
$\eta _\xi \leq \nu _\xi \leq \sup (f \upharpoonright \nu _\xi ) < k(\mu _\xi )$
. Since
![]() $k(\mu _\xi )$
is indecomposable,
$k(\mu _\xi )$
is indecomposable,
![]() $\omega \cdot ((\eta _\xi - \mu _\xi ) + 1) < k(\mu _\xi )$
. By Fact 2.12, for all
$\omega \cdot ((\eta _\xi - \mu _\xi ) + 1) < k(\mu _\xi )$
. By Fact 2.12, for all
![]() $\alpha $
such that
$\alpha $
such that
![]() $\mu _\xi \leq \alpha < \eta _\xi $
,
$\mu _\xi \leq \alpha < \eta _\xi $
,
![]() $h(\alpha ) = {\mathsf {next}}_{C_0}^{\omega \cdot ((\alpha - \mu _\xi ) + 1)}(\sup (f \upharpoonright \nu _\xi )) < {\mathsf {next}}_{C_0}^{\omega \cdot ((\eta _\xi - \mu _\xi ) + 1)}(\sup (f \upharpoonright \nu _\xi )) < k(\mu _\xi )$
. In particular, the following property
$h(\alpha ) = {\mathsf {next}}_{C_0}^{\omega \cdot ((\alpha - \mu _\xi ) + 1)}(\sup (f \upharpoonright \nu _\xi )) < {\mathsf {next}}_{C_0}^{\omega \cdot ((\eta _\xi - \mu _\xi ) + 1)}(\sup (f \upharpoonright \nu _\xi )) < k(\mu _\xi )$
. In particular, the following property
![]() $(***)$
holds:
$(***)$
holds:
![]() $\sup (h \upharpoonright \eta _\xi ) \leq {\mathsf {next}}_{C_0}^{\omega \cdot ((\eta _\xi - \mu _\xi ) + 1)}(\sup (f \upharpoonright \nu _\xi )) < k(\mu _\xi )$
.
$\sup (h \upharpoonright \eta _\xi ) \leq {\mathsf {next}}_{C_0}^{\omega \cdot ((\eta _\xi - \mu _\xi ) + 1)}(\sup (f \upharpoonright \nu _\xi )) < k(\mu _\xi )$
.
If
![]() $\alpha $
is such that there is no
$\alpha $
is such that there is no
![]() $\xi < \zeta $
with
$\xi < \zeta $
with
![]() $\mu _\xi \leq \alpha < \eta _\xi $
, then
$\mu _\xi \leq \alpha < \eta _\xi $
, then
![]() $h(\alpha ) = k(\alpha )$
. If
$h(\alpha ) = k(\alpha )$
. If
![]() $\alpha < \kappa $
and there is a
$\alpha < \kappa $
and there is a
![]() $\xi < \zeta $
so that
$\xi < \zeta $
so that
![]() $\mu _\xi \leq \alpha < \eta _\xi $
, then
$\mu _\xi \leq \alpha < \eta _\xi $
, then
![]() $h(\alpha ) < k(\mu _\xi ) \leq k(\alpha )$
by
$h(\alpha ) < k(\mu _\xi ) \leq k(\alpha )$
by
![]() $(***)$
. It has been shown that for all
$(***)$
. It has been shown that for all
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $h(\alpha ) \leq k(\alpha )$
and thus condition (1) holds for the pair
$h(\alpha ) \leq k(\alpha )$
and thus condition (1) holds for the pair
![]() $(h,k)$
.
$(h,k)$
.
Suppose
![]() $\alpha < \beta < \kappa $
. If there are no
$\alpha < \beta < \kappa $
. If there are no
![]() $\xi _1 < \zeta $
and
$\xi _1 < \zeta $
and
![]() $\xi _2 < \zeta $
with
$\xi _2 < \zeta $
with
![]() $\mu _{\xi _1} \leq \alpha < \eta _{\xi _1}$
and
$\mu _{\xi _1} \leq \alpha < \eta _{\xi _1}$
and
![]() $\mu _{\xi _2} \leq \beta < \eta _{\xi _2}$
, then
$\mu _{\xi _2} \leq \beta < \eta _{\xi _2}$
, then
![]() $h(\alpha ) = k(\alpha ) < k(\beta ) = h(\beta )$
. Suppose there is a
$h(\alpha ) = k(\alpha ) < k(\beta ) = h(\beta )$
. Suppose there is a
![]() $\xi _1 < \zeta $
with
$\xi _1 < \zeta $
with
![]() $\mu _{\xi _1} \leq \alpha < \eta _{\xi _1}$
and no
$\mu _{\xi _1} \leq \alpha < \eta _{\xi _1}$
and no
![]() $\xi _2 < \zeta $
with
$\xi _2 < \zeta $
with
![]() $\mu _{\xi _2} \leq \beta < \eta _{\xi _2}$
. Then
$\mu _{\xi _2} \leq \beta < \eta _{\xi _2}$
. Then
![]() $\mu _{\xi _1} < \eta _{\xi _1} \leq \beta $
. By
$\mu _{\xi _1} < \eta _{\xi _1} \leq \beta $
. By
![]() $(***)$
,
$(***)$
,
![]() $h(\alpha ) < k(\mu _{\xi _1}) < k(\eta _{\xi _1}) \leq k(\beta ) = h(\beta )$
. Suppose there is no
$h(\alpha ) < k(\mu _{\xi _1}) < k(\eta _{\xi _1}) \leq k(\beta ) = h(\beta )$
. Suppose there is no
![]() $\xi _1 < \zeta $
with
$\xi _1 < \zeta $
with
![]() $\mu _{\xi _1} \leq \alpha < \eta _{\xi _1}$
and there is a
$\mu _{\xi _1} \leq \alpha < \eta _{\xi _1}$
and there is a
![]() $\xi _2 < \zeta $
with
$\xi _2 < \zeta $
with
![]() $\mu _{\xi _2} \leq \beta < \eta _{\xi _2}$
. Note that
$\mu _{\xi _2} \leq \beta < \eta _{\xi _2}$
. Note that
![]() $\alpha < \mu _{\xi _2}$
. Then by the definition of
$\alpha < \mu _{\xi _2}$
. Then by the definition of
![]() $\mu _{\xi _2}$
,
$\mu _{\xi _2}$
,
![]() $h(\alpha ) = k(\alpha ) < \sup (f \upharpoonright \nu _{\xi _2}) < h(\beta )$
. Now, suppose there exist
$h(\alpha ) = k(\alpha ) < \sup (f \upharpoonright \nu _{\xi _2}) < h(\beta )$
. Now, suppose there exist
![]() $\xi _1 < \zeta $
and
$\xi _1 < \zeta $
and
![]() $\xi _2 < \zeta $
so that
$\xi _2 < \zeta $
so that
![]() $\mu _{\xi _1} \leq \alpha < \eta _{\xi _1}$
and
$\mu _{\xi _1} \leq \alpha < \eta _{\xi _1}$
and
![]() $\mu _{\xi _2} \leq \beta < \eta _{\xi _2}$
. If
$\mu _{\xi _2} \leq \beta < \eta _{\xi _2}$
. If
![]() $\xi _1 = \xi _2$
, then let
$\xi _1 = \xi _2$
, then let
![]() $\xi = \xi _1 = \xi _1$
and observe
$\xi = \xi _1 = \xi _1$
and observe
![]() $h(\alpha ) = {\mathsf {next}}_{C_0}^{\omega \cdot ((\alpha - \mu _\xi ) + 1)}(\sup (f\upharpoonright \nu _{\xi })) < {\mathsf {next}}_{C_0}^{\omega \cdot ((\beta - \mu _\xi ) + 1)}(\sup (f\upharpoonright \nu _\xi )) = h(\beta )$
. Suppose
$h(\alpha ) = {\mathsf {next}}_{C_0}^{\omega \cdot ((\alpha - \mu _\xi ) + 1)}(\sup (f\upharpoonright \nu _{\xi })) < {\mathsf {next}}_{C_0}^{\omega \cdot ((\beta - \mu _\xi ) + 1)}(\sup (f\upharpoonright \nu _\xi )) = h(\beta )$
. Suppose
![]() $\xi _1 \neq \xi _2$
and thus
$\xi _1 \neq \xi _2$
and thus
![]() $\xi _1 < \xi _2$
. By
$\xi _1 < \xi _2$
. By
![]() $(***)$
and the definitions of
$(***)$
and the definitions of
![]() $\mu _\xi $
,
$\mu _\xi $
,
![]() $\eta _\xi $
and
$\eta _\xi $
and
![]() $\nu _\xi $
,
$\nu _\xi $
,
![]() $h(\alpha ) < k(\mu _{\xi _1}) < \sup (k \upharpoonright \eta _{\xi _1}) = f(\nu _{\xi _1}) \leq \sup (f \upharpoonright \nu _{\xi _2}) < h(\beta )$
. Thus, in all cases, it has been shown that if
$h(\alpha ) < k(\mu _{\xi _1}) < \sup (k \upharpoonright \eta _{\xi _1}) = f(\nu _{\xi _1}) \leq \sup (f \upharpoonright \nu _{\xi _2}) < h(\beta )$
. Thus, in all cases, it has been shown that if
![]() $\alpha < \beta < \kappa $
, then
$\alpha < \beta < \kappa $
, then
![]() $h(\alpha ) < h(\beta )$
and thus h is an increasing function.
$h(\alpha ) < h(\beta )$
and thus h is an increasing function.
Suppose
![]() $\alpha < \kappa $
is such that there is no
$\alpha < \kappa $
is such that there is no
![]() $\xi < \zeta $
with
$\xi < \zeta $
with
![]() $\mu _\xi \leq \alpha < \eta _\xi $
. Then by property (1) for the pair
$\mu _\xi \leq \alpha < \eta _\xi $
. Then by property (1) for the pair
![]() $(h,k)$
and the discontinuity of k,
$(h,k)$
and the discontinuity of k,
![]() $\sup (h \upharpoonright \alpha ) \leq \sup (k \upharpoonright \alpha ) < k(\alpha ) = h(\alpha )$
. Suppose there is a
$\sup (h \upharpoonright \alpha ) \leq \sup (k \upharpoonright \alpha ) < k(\alpha ) = h(\alpha )$
. Suppose there is a
![]() $\xi < \zeta $
with
$\xi < \zeta $
with
![]() $\mu _\xi \leq \alpha < \eta _\xi $
. First, suppose
$\mu _\xi \leq \alpha < \eta _\xi $
. First, suppose
![]() $\alpha = \mu _\xi $
. Then by condition (1) for the pair
$\alpha = \mu _\xi $
. Then by condition (1) for the pair
![]() $(h,k)$
and the definition of
$(h,k)$
and the definition of
![]() $\mu _\xi $
,
$\mu _\xi $
,
![]() $\sup (h \upharpoonright \alpha ) = \sup (h \upharpoonright \mu _\xi ) \leq \sup (k \upharpoonright \mu _\xi ) \leq \sup (f \upharpoonright \nu _\xi ) < h(\mu _\xi ) = h(\alpha )$
. Suppose
$\sup (h \upharpoonright \alpha ) = \sup (h \upharpoonright \mu _\xi ) \leq \sup (k \upharpoonright \mu _\xi ) \leq \sup (f \upharpoonright \nu _\xi ) < h(\mu _\xi ) = h(\alpha )$
. Suppose
![]() $\mu _\xi < \alpha < \eta _\xi $
. Then
$\mu _\xi < \alpha < \eta _\xi $
. Then
![]() $\sup (h \upharpoonright \alpha ) \leq {\mathsf {next}}_{C_0}^{\omega \cdot (\alpha - \mu _\xi )}(\sup (f\upharpoonright \nu _\xi )) < {\mathsf {next}}_{C_0}^{\omega \cdot ((\alpha - \mu _\xi ) + 1)}(\sup (f\upharpoonright \nu _\xi )) = h(\alpha )$
. Thus, in all cases,
$\sup (h \upharpoonright \alpha ) \leq {\mathsf {next}}_{C_0}^{\omega \cdot (\alpha - \mu _\xi )}(\sup (f\upharpoonright \nu _\xi )) < {\mathsf {next}}_{C_0}^{\omega \cdot ((\alpha - \mu _\xi ) + 1)}(\sup (f\upharpoonright \nu _\xi )) = h(\alpha )$
. Thus, in all cases,
![]() $\sup (h \upharpoonright \alpha ) < h(\alpha )$
. This shows h is discontinuous everywhere. It has been established that h is an increasing function of the correct type through
$\sup (h \upharpoonright \alpha ) < h(\alpha )$
. This shows h is discontinuous everywhere. It has been established that h is an increasing function of the correct type through
![]() $C_0$
(that is,
$C_0$
(that is,
![]() $h \in [C_0]^\kappa _*$
).
$h \in [C_0]^\kappa _*$
).
If
![]() $\alpha < \kappa $
and there is no
$\alpha < \kappa $
and there is no
![]() $\xi < \zeta $
with
$\xi < \zeta $
with
![]() $\mu _\xi \leq \alpha < \eta _\xi $
, then
$\mu _\xi \leq \alpha < \eta _\xi $
, then
![]() $\sup (h \upharpoonright \alpha ) < h(\alpha ) = k(\alpha )$
since h is discontinuous. Suppose
$\sup (h \upharpoonright \alpha ) < h(\alpha ) = k(\alpha )$
since h is discontinuous. Suppose
![]() $\alpha < \kappa $
and there is a
$\alpha < \kappa $
and there is a
![]() $\xi < \zeta $
with
$\xi < \zeta $
with
![]() $\mu _\xi \leq \alpha < \eta _\xi $
. Suppose there is no
$\mu _\xi \leq \alpha < \eta _\xi $
. Suppose there is no
![]() $\bar {\xi } < \zeta $
so that
$\bar {\xi } < \zeta $
so that
![]() $\mu _{\bar {\xi }} \leq \eta _\xi < \eta _{\bar \xi }$
, then
$\mu _{\bar {\xi }} \leq \eta _\xi < \eta _{\bar \xi }$
, then
![]() $\sup (h \upharpoonright \eta _\xi ) < k(\mu _\xi ) \leq k(\alpha ) < \sup (k \upharpoonright \eta _\xi ) = f(\nu _\xi ) < k(\eta _\xi ) = h(\eta _\xi )$
. In particular,
$\sup (h \upharpoonright \eta _\xi ) < k(\mu _\xi ) \leq k(\alpha ) < \sup (k \upharpoonright \eta _\xi ) = f(\nu _\xi ) < k(\eta _\xi ) = h(\eta _\xi )$
. In particular,
![]() $\sup (h \upharpoonright \eta _\xi ) < k(\alpha ) < h(\eta _\xi )$
. Suppose there is a
$\sup (h \upharpoonright \eta _\xi ) < k(\alpha ) < h(\eta _\xi )$
. Suppose there is a
![]() $\bar {\xi } < \zeta $
so that
$\bar {\xi } < \zeta $
so that
![]() $\mu _{\bar {\xi }} \leq \eta _\xi < \eta _{\bar {\xi }}$
. Then
$\mu _{\bar {\xi }} \leq \eta _\xi < \eta _{\bar {\xi }}$
. Then
![]() $\sup (h \upharpoonright \eta _\xi ) < k(\mu _\xi ) \leq k(\alpha ) < \sup (k \upharpoonright \eta _\xi ) = f(\nu _\xi ) \leq \sup (f \upharpoonright \nu _{\bar {\xi }}) < h(\mu _{\bar {\xi }}) \leq h(\eta _\xi )$
. (This implies that
$\sup (h \upharpoonright \eta _\xi ) < k(\mu _\xi ) \leq k(\alpha ) < \sup (k \upharpoonright \eta _\xi ) = f(\nu _\xi ) \leq \sup (f \upharpoonright \nu _{\bar {\xi }}) < h(\mu _{\bar {\xi }}) \leq h(\eta _\xi )$
. (This implies that
![]() $\mu _{\bar {\xi }} = \eta _\xi $
.) One has
$\mu _{\bar {\xi }} = \eta _\xi $
.) One has
![]() $\sup (h \upharpoonright \eta _\xi ) < k(\alpha ) < h(\eta _\xi )$
. This shows that for all
$\sup (h \upharpoonright \eta _\xi ) < k(\alpha ) < h(\eta _\xi )$
. This shows that for all
![]() $\alpha < \kappa $
, there is no limit ordinal
$\alpha < \kappa $
, there is no limit ordinal
![]() $\gamma $
so that
$\gamma $
so that
![]() $\sup (h \upharpoonright \gamma ) = k(\alpha )$
. Therefore, condition (2) holds for the pair
$\sup (h \upharpoonright \gamma ) = k(\alpha )$
. Therefore, condition (2) holds for the pair
![]() $(h,k)$
.
$(h,k)$
.
If
![]() $\alpha < \kappa $
and there is no
$\alpha < \kappa $
and there is no
![]() $\xi < \zeta $
with
$\xi < \zeta $
with
![]() $\mu _\xi \leq \alpha < \eta _\xi $
, then
$\mu _\xi \leq \alpha < \eta _\xi $
, then
![]() $\sup (k \upharpoonright \alpha ) < k(\alpha ) = h(\alpha ) < k(\alpha + 1)$
. If
$\sup (k \upharpoonright \alpha ) < k(\alpha ) = h(\alpha ) < k(\alpha + 1)$
. If
![]() $\alpha < \kappa $
and there is a
$\alpha < \kappa $
and there is a
![]() $\xi < \zeta $
with
$\xi < \zeta $
with
![]() $\mu _\xi \leq \alpha < \eta _\xi $
, then
$\mu _\xi \leq \alpha < \eta _\xi $
, then
![]() $\sup (k \upharpoonright \mu _\xi ) \leq \sup (f \upharpoonright \nu _\xi ) < h(\mu _\xi ) \leq h(\alpha ) < \sup (h \upharpoonright \eta _\xi ) < k(\mu _\xi )$
using
$\sup (k \upharpoonright \mu _\xi ) \leq \sup (f \upharpoonright \nu _\xi ) < h(\mu _\xi ) \leq h(\alpha ) < \sup (h \upharpoonright \eta _\xi ) < k(\mu _\xi )$
using
![]() $(***)$
. It has been shown that for all
$(***)$
. It has been shown that for all
![]() $\alpha < \kappa $
, there is no limit ordinal
$\alpha < \kappa $
, there is no limit ordinal
![]() $\gamma $
so that
$\gamma $
so that
![]() $\sup (k \upharpoonright \gamma ) = h(\alpha )$
. Condition (3) has been shown for the pair
$\sup (k \upharpoonright \gamma ) = h(\alpha )$
. Condition (3) has been shown for the pair
![]() $(h,k)$
.
$(h,k)$
.
Since
![]() $C_0$
has the property of Lemma 5.2,
$C_0$
has the property of Lemma 5.2,
![]() $(h,k)$
satisfies condition (1), (2) and (3) and
$(h,k)$
satisfies condition (1), (2) and (3) and
![]() $h,k \in [C_0]^\kappa _*$
, one has that
$h,k \in [C_0]^\kappa _*$
, one has that
![]() $\Phi (h) \leq \Phi (k)$
.
$\Phi (h) \leq \Phi (k)$
.
Suppose
![]() $\alpha < \kappa $
and there is no
$\alpha < \kappa $
and there is no
![]() $\xi < \zeta $
such that
$\xi < \zeta $
such that
![]() $\mu _\xi \leq \alpha < \eta _\xi $
. Then
$\mu _\xi \leq \alpha < \eta _\xi $
. Then
![]() $f(\alpha ) \leq k(\alpha ) = h(\alpha )$
since the pair
$f(\alpha ) \leq k(\alpha ) = h(\alpha )$
since the pair
![]() $(f,k)$
satisfies condition (1). Suppose
$(f,k)$
satisfies condition (1). Suppose
![]() $\alpha < \kappa $
and there is a
$\alpha < \kappa $
and there is a
![]() $\xi < \zeta $
such that
$\xi < \zeta $
such that
![]() $\mu _\xi \leq \alpha < \eta _\xi $
. Since
$\mu _\xi \leq \alpha < \eta _\xi $
. Since
![]() $\alpha < \eta _\xi \leq \nu _\xi $
, one has that
$\alpha < \eta _\xi \leq \nu _\xi $
, one has that
![]() $f(\alpha ) \leq \sup (f \upharpoonright \nu _\xi ) < h(\mu _\xi ) \leq h(\alpha )$
. It has been shown that for all
$f(\alpha ) \leq \sup (f \upharpoonright \nu _\xi ) < h(\mu _\xi ) \leq h(\alpha )$
. It has been shown that for all
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $f(\alpha ) \leq h(\alpha )$
and so condition (1) holds for the pair
$f(\alpha ) \leq h(\alpha )$
and so condition (1) holds for the pair
![]() $(f,h)$
.
$(f,h)$
.
Suppose
![]() $\alpha < \kappa $
and there is no
$\alpha < \kappa $
and there is no
![]() $\xi < \zeta $
such that
$\xi < \zeta $
such that
![]() $\mu _\xi \leq \alpha < \eta _\xi $
, then there is no limit ordinal
$\mu _\xi \leq \alpha < \eta _\xi $
, then there is no limit ordinal
![]() $\gamma $
so that
$\gamma $
so that
![]() $\sup (f \upharpoonright \gamma ) = k(\alpha ) = h(\alpha )$
since the pair
$\sup (f \upharpoonright \gamma ) = k(\alpha ) = h(\alpha )$
since the pair
![]() $(f,k)$
satisfies condition (2). Suppose
$(f,k)$
satisfies condition (2). Suppose
![]() $\alpha < \kappa $
and there is a
$\alpha < \kappa $
and there is a
![]() $\xi < \zeta $
such that
$\xi < \zeta $
such that
![]() $\mu _\xi \leq \alpha < \eta _\xi $
, then
$\mu _\xi \leq \alpha < \eta _\xi $
, then
![]() $\sup (f \upharpoonright \nu _\xi ) < h(\mu _\xi ) \leq h(\alpha ) < \sup (h \upharpoonright \eta _\xi ) < k(\mu _\xi ) < \sup (k \upharpoonright \eta _\xi ) = f(\nu _\xi )$
. So for all
$\sup (f \upharpoonright \nu _\xi ) < h(\mu _\xi ) \leq h(\alpha ) < \sup (h \upharpoonright \eta _\xi ) < k(\mu _\xi ) < \sup (k \upharpoonright \eta _\xi ) = f(\nu _\xi )$
. So for all
![]() $\alpha < \kappa $
, there is no limit ordinal
$\alpha < \kappa $
, there is no limit ordinal
![]() $\gamma $
so that
$\gamma $
so that
![]() $\sup (f \upharpoonright \gamma ) = h(\alpha )$
. Condition (2) holds for the pair
$\sup (f \upharpoonright \gamma ) = h(\alpha )$
. Condition (2) holds for the pair
![]() $(f,h)$
.
$(f,h)$
.
Suppose
![]() $\alpha < \kappa $
. First, suppose there is no
$\alpha < \kappa $
. First, suppose there is no
![]() $\xi < \zeta $
so that
$\xi < \zeta $
so that
![]() $\alpha = \nu _\xi $
. There is a unique
$\alpha = \nu _\xi $
. There is a unique
![]() $\rho $
so that
$\rho $
so that
![]() $\sup (k \upharpoonright \rho ) < f(\alpha ) \leq k(\rho )$
. Suppose there is no
$\sup (k \upharpoonright \rho ) < f(\alpha ) \leq k(\rho )$
. Suppose there is no
![]() $\bar {\xi } < \zeta $
so that
$\bar {\xi } < \zeta $
so that
![]() $\mu _{\bar {\xi }} \leq \rho < \eta _{\bar {\xi }}$
. Then
$\mu _{\bar {\xi }} \leq \rho < \eta _{\bar {\xi }}$
. Then
![]() $\sup (h \upharpoonright \rho ) \leq \sup (k \upharpoonright \rho ) < f(\alpha ) \leq k(\rho ) = h(\rho )$
. Suppose there is a
$\sup (h \upharpoonright \rho ) \leq \sup (k \upharpoonright \rho ) < f(\alpha ) \leq k(\rho ) = h(\rho )$
. Suppose there is a
![]() $\bar {\xi } < \zeta $
so that
$\bar {\xi } < \zeta $
so that
![]() $\mu _{\bar {\xi }} \leq \rho < \eta _{\bar {\xi }}$
. Then
$\mu _{\bar {\xi }} \leq \rho < \eta _{\bar {\xi }}$
. Then
![]() $f(\alpha ) \leq \sup (f \upharpoonright \nu _{\bar {\xi }})$
. Therefore,
$f(\alpha ) \leq \sup (f \upharpoonright \nu _{\bar {\xi }})$
. Therefore,
![]() $\sup (h \upharpoonright \rho ) \leq \sup (k \upharpoonright \rho ) < f(\alpha ) \leq \sup (f \upharpoonright \nu _{\bar {\xi }}) < h(\mu _{\bar {\xi }}) \leq h(\rho )$
. (This implies
$\sup (h \upharpoonright \rho ) \leq \sup (k \upharpoonright \rho ) < f(\alpha ) \leq \sup (f \upharpoonright \nu _{\bar {\xi }}) < h(\mu _{\bar {\xi }}) \leq h(\rho )$
. (This implies
![]() $\mu _{\bar {\xi }} = \rho $
.) Hence,
$\mu _{\bar {\xi }} = \rho $
.) Hence,
![]() $\sup (h \upharpoonright \rho ) < f(\alpha ) < h(\rho )$
. Now, suppose there is a
$\sup (h \upharpoonright \rho ) < f(\alpha ) < h(\rho )$
. Now, suppose there is a
![]() $\xi < \zeta $
so that
$\xi < \zeta $
so that
![]() $\alpha = \nu _\xi $
. Suppose that there is no
$\alpha = \nu _\xi $
. Suppose that there is no
![]() $\bar {\xi } < \zeta $
so that
$\bar {\xi } < \zeta $
so that
![]() $\mu _{\bar {\xi }} \leq \eta _\xi < \eta _{\bar {\xi }}$
. Then
$\mu _{\bar {\xi }} \leq \eta _\xi < \eta _{\bar {\xi }}$
. Then
![]() $\sup (h \upharpoonright \eta _\xi ) < k(\mu _\xi ) < \sup (k \upharpoonright \eta _\xi ) = f(\nu _\xi ) = f(\alpha ) < k(\eta _\xi ) = h(\eta _\xi )$
using
$\sup (h \upharpoonright \eta _\xi ) < k(\mu _\xi ) < \sup (k \upharpoonright \eta _\xi ) = f(\nu _\xi ) = f(\alpha ) < k(\eta _\xi ) = h(\eta _\xi )$
using
![]() $(***)$
here. Thus,
$(***)$
here. Thus,
![]() $\sup (h \upharpoonright \eta _\xi ) < f(\alpha ) < h(\eta _\xi )$
. Suppose there is a
$\sup (h \upharpoonright \eta _\xi ) < f(\alpha ) < h(\eta _\xi )$
. Suppose there is a
![]() $\bar {\xi }$
so that
$\bar {\xi }$
so that
![]() $\mu _{\bar {\xi }} \leq \eta _\xi < \eta _{\bar {\xi }}$
. Then
$\mu _{\bar {\xi }} \leq \eta _\xi < \eta _{\bar {\xi }}$
. Then
![]() $f(\alpha ) \leq \sup (f \upharpoonright \nu _{\bar {\xi }})$
. Therefore,
$f(\alpha ) \leq \sup (f \upharpoonright \nu _{\bar {\xi }})$
. Therefore,
![]() $\sup (h \upharpoonright \eta _\xi ) < k(\mu _{\xi }) \leq \sup (k \upharpoonright \eta _\xi ) = f(\nu _\xi ) = f(\alpha ) \leq \sup (f \upharpoonright \nu _{\bar {\xi }}) < h(\mu _{\bar {\xi }}) \leq h(\eta _\xi )$
. (This implies
$\sup (h \upharpoonright \eta _\xi ) < k(\mu _{\xi }) \leq \sup (k \upharpoonright \eta _\xi ) = f(\nu _\xi ) = f(\alpha ) \leq \sup (f \upharpoonright \nu _{\bar {\xi }}) < h(\mu _{\bar {\xi }}) \leq h(\eta _\xi )$
. (This implies
![]() $\mu _{\bar {\xi }} = \eta _\xi $
.) Hence,
$\mu _{\bar {\xi }} = \eta _\xi $
.) Hence,
![]() $\sup (h \upharpoonright \eta _\xi ) < f(\alpha ) < h(\eta _\xi )$
. In all cases, it has been shown that for all
$\sup (h \upharpoonright \eta _\xi ) < f(\alpha ) < h(\eta _\xi )$
. In all cases, it has been shown that for all
![]() $\alpha < \kappa $
, there is no limit ordinal
$\alpha < \kappa $
, there is no limit ordinal
![]() $\gamma $
so that
$\gamma $
so that
![]() $\sup (h \upharpoonright \gamma ) = f(\alpha )$
. The pair
$\sup (h \upharpoonright \gamma ) = f(\alpha )$
. The pair
![]() $(f,h)$
satisfies condition (3).
$(f,h)$
satisfies condition (3).
Since
![]() $C_0$
has the property of Lemma 5.2,
$C_0$
has the property of Lemma 5.2,
![]() $(f,h)$
satisfies condition (1), (2) and (3) and
$(f,h)$
satisfies condition (1), (2) and (3) and
![]() $f,h \in [C_0]^\kappa _*$
, one has that
$f,h \in [C_0]^\kappa _*$
, one has that
![]() $\Phi (f) \leq \Phi (h)$
.
$\Phi (f) \leq \Phi (h)$
.
In conclusion
![]() $\Phi (f) \leq \Phi (h) \leq \Phi (k) \leq \Phi (g)$
.
$\Phi (f) \leq \Phi (h) \leq \Phi (k) \leq \Phi (g)$
.
Corollary 5.4. Suppose
![]() $\kappa $
is a cardinal satisfying
$\kappa $
is a cardinal satisfying
![]() $\kappa \rightarrow _* (\kappa )^\kappa _2$
,
$\kappa \rightarrow _* (\kappa )^\kappa _2$
,
![]() $\epsilon \leq \kappa $
and
$\epsilon \leq \kappa $
and
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
. Then there is a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
. Then there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if for all
$f,g \in [C]^\epsilon _*$
, if for all
![]() $\alpha < \epsilon $
,
$\alpha < \epsilon $
,
![]() $f(\alpha ) \leq g(\alpha )$
, then
$f(\alpha ) \leq g(\alpha )$
, then
![]() $\Phi (f) \leq \Phi (g)$
.
$\Phi (f) \leq \Phi (g)$
.
Proof. Define
![]() $\Phi ' : [\kappa ]^\kappa _* \rightarrow \mathrm {ON}$
by
$\Phi ' : [\kappa ]^\kappa _* \rightarrow \mathrm {ON}$
by
![]() $\Phi '(f) = \Phi (f \upharpoonright \epsilon )$
. The result follows by applying Theorem 5.3 to
$\Phi '(f) = \Phi (f \upharpoonright \epsilon )$
. The result follows by applying Theorem 5.3 to
![]() $\Phi '$
.
$\Phi '$
.
Corollary 5.5. Assume
![]() $\mathsf {AD}$
. Suppose
$\mathsf {AD}$
. Suppose
![]() $\kappa $
is
$\kappa $
is
![]() ${\omega _1}$
,
${\omega _1}$
,
![]() $\boldsymbol {\delta }_{2n + 1}^1$
for
$\boldsymbol {\delta }_{2n + 1}^1$
for
![]() $1 \leq n < \omega $
,
$1 \leq n < \omega $
,
![]() $\boldsymbol {\delta }_A$
where
$\boldsymbol {\delta }_A$
where
![]() $A \subseteq \mathbb {R}$
or
$A \subseteq \mathbb {R}$
or
![]() $\boldsymbol {\delta }^2_1$
(assuming
$\boldsymbol {\delta }^2_1$
(assuming
![]() $\mathsf {DC}_{\mathbb {R}}$
). For any
$\mathsf {DC}_{\mathbb {R}}$
). For any
![]() $\epsilon \leq \kappa $
and any function
$\epsilon \leq \kappa $
and any function
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, there is a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if for all
$f,g \in [C]^\epsilon _*$
, if for all
![]() $\alpha < \epsilon $
,
$\alpha < \epsilon $
,
![]() $f(\alpha ) \leq g(\alpha )$
, then
$f(\alpha ) \leq g(\alpha )$
, then
![]() $\Phi (f) \leq \Phi (g)$
.
$\Phi (f) \leq \Phi (g)$
.
A suitable modification can be used to investigate almost everywhere monotonicity for weak partition cardinals which may not be strong partition cardinals.
Lemma 5.6. Suppose
![]() $\kappa $
is a cardinal satisfying
$\kappa $
is a cardinal satisfying
![]() $\kappa \rightarrow _* (\kappa )^{<\kappa }_2$
. For any
$\kappa \rightarrow _* (\kappa )^{<\kappa }_2$
. For any
![]() $\epsilon < \kappa $
and function
$\epsilon < \kappa $
and function
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, there is a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if f and g have the following properties:
$f,g \in [C]^\epsilon _*$
, if f and g have the following properties:
-
1. For all
 $\alpha < \epsilon $
,
$\alpha < \epsilon $
,
 $f(\alpha ) \leq g(\alpha )$
.
$f(\alpha ) \leq g(\alpha )$
. -
2. For all
 $\alpha < \epsilon $
, there is no limit ordinal
$\alpha < \epsilon $
, there is no limit ordinal
 $\beta \leq \epsilon $
so that
$\beta \leq \epsilon $
so that
 $\sup (f \upharpoonright \beta ) = g(\alpha )$
(where
$\sup (f \upharpoonright \beta ) = g(\alpha )$
(where
 $\sup (f \upharpoonright \epsilon ) = \sup (f)$
).
$\sup (f \upharpoonright \epsilon ) = \sup (f)$
). -
3. For all
 $\alpha < \epsilon $
, there is no limit ordinal
$\alpha < \epsilon $
, there is no limit ordinal
 $\beta < \epsilon $
so that
$\beta < \epsilon $
so that
 $\sup (g \upharpoonright \beta ) = f(\alpha )$
.
$\sup (g \upharpoonright \beta ) = f(\alpha )$
.
then
![]() $\Phi (f) \leq \Phi (g)$
.
$\Phi (f) \leq \Phi (g)$
.
Proof. Let
![]() $\mathcal {I} : \epsilon + \epsilon \rightarrow \kappa $
be an increasing and discontinuous function whose image consists of indecomposable ordinals. Let
$\mathcal {I} : \epsilon + \epsilon \rightarrow \kappa $
be an increasing and discontinuous function whose image consists of indecomposable ordinals. Let
![]() $\epsilon ^0 = \sup \{\mathcal {I}(\alpha ) + 1 : \alpha < \epsilon \}$
and
$\epsilon ^0 = \sup \{\mathcal {I}(\alpha ) + 1 : \alpha < \epsilon \}$
and
![]() $\epsilon ^1 = \sup \{\mathcal {I}(\alpha ) + 1 : \alpha < \epsilon + \epsilon \}$
. Note that
$\epsilon ^1 = \sup \{\mathcal {I}(\alpha ) + 1 : \alpha < \epsilon + \epsilon \}$
. Note that
![]() $\epsilon ^0 + \epsilon ^1 = \epsilon ^1$
. Suppose
$\epsilon ^0 + \epsilon ^1 = \epsilon ^1$
. Suppose
![]() $h \in [\kappa ]^{\epsilon ^1}_*$
. Let
$h \in [\kappa ]^{\epsilon ^1}_*$
. Let
![]() $h^0 \in [\kappa ]^{\epsilon ^0}_*$
be defined by
$h^0 \in [\kappa ]^{\epsilon ^0}_*$
be defined by
![]() $h^0 = h \upharpoonright \epsilon ^0$
. If
$h^0 = h \upharpoonright \epsilon ^0$
. If
![]() $\ell \in [\kappa ]^{\epsilon ^0}$
, then let
$\ell \in [\kappa ]^{\epsilon ^0}$
, then let
![]() ${\mathsf {main}}(\ell ) \in [\kappa ]^\epsilon $
be defined by
${\mathsf {main}}(\ell ) \in [\kappa ]^\epsilon $
be defined by
![]() ${\mathsf {main}}(\ell )(\alpha ) = \ell (\mathcal {I}(\alpha ))$
.
${\mathsf {main}}(\ell )(\alpha ) = \ell (\mathcal {I}(\alpha ))$
.
Define
![]() $P : [\kappa ]^{\epsilon ^1}_* \rightarrow 2$
by
$P : [\kappa ]^{\epsilon ^1}_* \rightarrow 2$
by
![]() $P(h) = 0$
if and only if for all
$P(h) = 0$
if and only if for all
![]() $p \in [h[\epsilon ^1]]^{\epsilon ^0}_*$
,
$p \in [h[\epsilon ^1]]^{\epsilon ^0}_*$
,
![]() $\Phi ({\mathsf {main}}(h^0)) \leq \Phi ({\mathsf {main}}(p))$
. By
$\Phi ({\mathsf {main}}(h^0)) \leq \Phi ({\mathsf {main}}(p))$
. By
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon ^1}_2$
, there is a club
$\kappa \rightarrow _* (\kappa )^{\epsilon ^1}_2$
, there is a club
![]() $C_0 \subseteq \kappa $
which is homogeneous for P. Let
$C_0 \subseteq \kappa $
which is homogeneous for P. Let
![]() $Z = \{\Phi ({\mathsf {main}}(\ell ))) : \ell \in [C_0]^{\epsilon ^0}_*\}$
which has a minimal element since it is a nonempty set of ordinals. Let
$Z = \{\Phi ({\mathsf {main}}(\ell ))) : \ell \in [C_0]^{\epsilon ^0}_*\}$
which has a minimal element since it is a nonempty set of ordinals. Let
![]() $\ell ^* \in [C_0]^{\epsilon ^0}_*$
be such that
$\ell ^* \in [C_0]^{\epsilon ^0}_*$
be such that
![]() $\Phi (\ell ^*) = \min (Z)$
. Let
$\Phi (\ell ^*) = \min (Z)$
. Let
![]() $\mathfrak {h} \in [C_0]^{\epsilon ^1}_*$
be defined by
$\mathfrak {h} \in [C_0]^{\epsilon ^1}_*$
be defined by
 $$ \begin{align*}\mathfrak{h}(\alpha) = \begin{cases} \ell^*(\alpha) & \quad \alpha < \epsilon^0 \\ {\mathsf{next}}^{\omega\cdot((\alpha - \epsilon^0) + 1)}_{C_0}(\sup(\ell^*)) & \quad \epsilon^0 \leq \alpha < \epsilon^1 \end{cases}.\end{align*} $$
$$ \begin{align*}\mathfrak{h}(\alpha) = \begin{cases} \ell^*(\alpha) & \quad \alpha < \epsilon^0 \\ {\mathsf{next}}^{\omega\cdot((\alpha - \epsilon^0) + 1)}_{C_0}(\sup(\ell^*)) & \quad \epsilon^0 \leq \alpha < \epsilon^1 \end{cases}.\end{align*} $$
Note that
![]() $\mathfrak {h} \in [C_0]^{\epsilon ^1}_*$
and
$\mathfrak {h} \in [C_0]^{\epsilon ^1}_*$
and
![]() $\mathfrak {h}^0 = \ell ^*$
. If
$\mathfrak {h}^0 = \ell ^*$
. If
![]() $p \in [h[\epsilon ^1]]^{\epsilon ^0}_*$
, then
$p \in [h[\epsilon ^1]]^{\epsilon ^0}_*$
, then
![]() $p \in [C_0]^{\epsilon ^0}_*$
. Thus,
$p \in [C_0]^{\epsilon ^0}_*$
. Thus,
![]() $\Phi ({\mathsf {main}}(p)) \in Z$
and
$\Phi ({\mathsf {main}}(p)) \in Z$
and
![]() $\Phi (\mathfrak {h}^0) = \Phi ({\mathsf {main}}(\ell ^*)) = \min (Z) \leq \Phi ({\mathsf {main}}(p))$
. This shows
$\Phi (\mathfrak {h}^0) = \Phi ({\mathsf {main}}(\ell ^*)) = \min (Z) \leq \Phi ({\mathsf {main}}(p))$
. This shows
![]() $P(\mathfrak {h}) = 0$
. Since
$P(\mathfrak {h}) = 0$
. Since
![]() $\mathfrak {h} \in [C_0]^{\epsilon ^1}_*$
,
$\mathfrak {h} \in [C_0]^{\epsilon ^1}_*$
,
![]() $C_0$
must be homogeneous for P taking value
$C_0$
must be homogeneous for P taking value
![]() $0$
. (Note only
$0$
. (Note only
![]() $\kappa \rightarrow _* (\kappa )^{\epsilon ^1}_2$
is needed rather than the full weak partition relation.) By choosing a subclub of
$\kappa \rightarrow _* (\kappa )^{\epsilon ^1}_2$
is needed rather than the full weak partition relation.) By choosing a subclub of
![]() $C_0$
, one may assume
$C_0$
, one may assume
![]() $C_0$
consists of indecomposable ordinals and
$C_0$
consists of indecomposable ordinals and
![]() $\epsilon ^1 < \min (C_0)$
. Let
$\epsilon ^1 < \min (C_0)$
. Let
![]() $C_1 = \{\alpha \in C_0 : {\mathsf {enum}}_{C_0}(\alpha ) = \alpha \}$
.
$C_1 = \{\alpha \in C_0 : {\mathsf {enum}}_{C_0}(\alpha ) = \alpha \}$
.
Fix
![]() $f,g \in [C_1]^\epsilon _*$
with properties (1), (2) and (3). One will construct by recursion two functions
$f,g \in [C_1]^\epsilon _*$
with properties (1), (2) and (3). One will construct by recursion two functions
![]() $h \in [C_0]^{\epsilon ^1}_*$
and
$h \in [C_0]^{\epsilon ^1}_*$
and
![]() $p \in [h[\epsilon ^1]]^{\epsilon ^0}_*$
so that
$p \in [h[\epsilon ^1]]^{\epsilon ^0}_*$
so that
![]() ${\mathsf {main}}(h^0) = f$
and
${\mathsf {main}}(h^0) = f$
and
![]() ${\mathsf {main}}(p) = g$
. The construction and verification are quite similar to Lemma 5.2, so some details of the verification will be omitted.
${\mathsf {main}}(p) = g$
. The construction and verification are quite similar to Lemma 5.2, so some details of the verification will be omitted.
Suppose
![]() $\alpha < \epsilon $
and the following holds:
$\alpha < \epsilon $
and the following holds:
-
(a) For each
 $\beta < \alpha $
,
$\beta < \alpha $
,
 $h \upharpoonright \mathcal {I}(\beta ) + 1$
has been defined, is a function of the correct type and
$h \upharpoonright \mathcal {I}(\beta ) + 1$
has been defined, is a function of the correct type and
 $h(\mathcal {I}(\beta )) = f(\beta )$
.
$h(\mathcal {I}(\beta )) = f(\beta )$
. -
(b) For each
 $\beta < \alpha $
,
$\beta < \alpha $
,
 $\sigma _\beta \leq \beta + 1$
has been defined. If
$\sigma _\beta \leq \beta + 1$
has been defined. If
 $\beta _0 \leq \beta _1 < \alpha $
, then
$\beta _0 \leq \beta _1 < \alpha $
, then
 $\sigma _{\beta _0} \leq \sigma _{\beta _1}$
.
$\sigma _{\beta _0} \leq \sigma _{\beta _1}$
. -
(c) For all
 $\beta < \alpha $
, for all
$\beta < \alpha $
, for all
 $\eta < \sigma _\beta $
,
$\eta < \sigma _\beta $
,
 $p \upharpoonright \mathcal {I}(\eta ) + 1$
has been defined, is a function of the correct type and
$p \upharpoonright \mathcal {I}(\eta ) + 1$
has been defined, is a function of the correct type and
 $p(\mathcal {I}(\eta )) = g(\eta )$
.
$p(\mathcal {I}(\eta )) = g(\eta )$
. -
(d) For all
 $\beta < \alpha $
, for all
$\beta < \alpha $
, for all
 $\eta < \sigma _\beta $
,
$\eta < \sigma _\beta $
,
 $g(\eta ) \leq f(\beta ) < g(\sigma _\beta )$
.
$g(\eta ) \leq f(\beta ) < g(\sigma _\beta )$
.
Let
![]() $\iota _\alpha = \sup \{\sigma _\beta : \beta < \alpha \}$
,
$\iota _\alpha = \sup \{\sigma _\beta : \beta < \alpha \}$
,
![]() $\delta _0 = \sup \{\mathcal {I}(\beta ) + 1 : \beta < \alpha \}$
and
$\delta _0 = \sup \{\mathcal {I}(\beta ) + 1 : \beta < \alpha \}$
and
![]() $\tau _0 = \sup \{\mathcal {I}(\beta ) + 1 : \beta < \iota _\alpha \}$
. Observe
$\tau _0 = \sup \{\mathcal {I}(\beta ) + 1 : \beta < \iota _\alpha \}$
. Observe
![]() $\sup (g \upharpoonright \iota _\alpha ) \leq \sup (f \upharpoonright \alpha ) < g(\iota _\alpha )$
.
$\sup (g \upharpoonright \iota _\alpha ) \leq \sup (f \upharpoonright \alpha ) < g(\iota _\alpha )$
.
Let
![]() $A = \{\beta < \alpha : \sup (f \upharpoonright \alpha ) < g(\beta ) < f(\alpha )\}$
.
$A = \{\beta < \alpha : \sup (f \upharpoonright \alpha ) < g(\beta ) < f(\alpha )\}$
.
(Case A) If
![]() $A = \emptyset $
.
$A = \emptyset $
.
Then let
![]() $\tau = \tau _0$
and
$\tau = \tau _0$
and
![]() $\delta = \delta _0$
.
$\delta = \delta _0$
.
(Case B)
![]() $A \neq \emptyset $
.
$A \neq \emptyset $
.
One must have
![]() $\iota _\alpha < \alpha $
and
$\iota _\alpha < \alpha $
and
![]() $\iota _\alpha = \min (A)$
. Let
$\iota _\alpha = \min (A)$
. Let
![]() $\xi = {\mathrm {ot}}(A) \leq \alpha $
, and observe that
$\xi = {\mathrm {ot}}(A) \leq \alpha $
, and observe that
![]() $A = \{\iota _\alpha + \eta : \eta < \xi \}$
.
$A = \{\iota _\alpha + \eta : \eta < \xi \}$
.
![]() $\delta _0$
and
$\delta _0$
and
![]() $\tau _0$
have already been defined above with
$\tau _0$
have already been defined above with
![]() $\sup (h \upharpoonright \delta _0) = \sup (f \upharpoonright \alpha ) < g(\iota _\alpha )$
. For
$\sup (h \upharpoonright \delta _0) = \sup (f \upharpoonright \alpha ) < g(\iota _\alpha )$
. For
![]() $0 < \nu < \xi $
, suppose that for all
$0 < \nu < \xi $
, suppose that for all
![]() $\eta < \nu $
, the following holds:
$\eta < \nu $
, the following holds:
-
•
 $\epsilon _\eta = \delta _0 + \mathcal {I}(\iota _\alpha + \eta )$
and
$\epsilon _\eta = \delta _0 + \mathcal {I}(\iota _\alpha + \eta )$
and
 $\mu _\eta = \tau _0 + \mathcal {I}(\iota _\alpha + \eta )$
have been defined.
$\mu _\eta = \tau _0 + \mathcal {I}(\iota _\alpha + \eta )$
have been defined. -
•
 $h \upharpoonright \epsilon _\eta + 1$
and
$h \upharpoonright \epsilon _\eta + 1$
and
 $p \upharpoonright \mu _\eta + 1$
have been defined.
$p \upharpoonright \mu _\eta + 1$
have been defined. -
•
 $h(\epsilon _\eta ) = g(\iota _\alpha + \eta ) = p(\mu _\eta )$
.
$h(\epsilon _\eta ) = g(\iota _\alpha + \eta ) = p(\mu _\eta )$
.
Let
![]() $\delta _\nu = \sup \{\epsilon _\eta + 1 : \eta < \nu \}$
and
$\delta _\nu = \sup \{\epsilon _\eta + 1 : \eta < \nu \}$
and
![]() $\tau _\nu = \sup \{\mu _\eta + 1 : \eta < \nu \}$
. Note that
$\tau _\nu = \sup \{\mu _\eta + 1 : \eta < \nu \}$
. Note that
![]() $\delta _\nu < \delta _0 + \mathcal {I}(\iota _\alpha + \nu )$
and
$\delta _\nu < \delta _0 + \mathcal {I}(\iota _\alpha + \nu )$
and
![]() $\tau _\nu < \tau _0 + \mathcal {I}(\iota _\alpha + \nu )$
.
$\tau _\nu < \tau _0 + \mathcal {I}(\iota _\alpha + \nu )$
.
![]() $h \upharpoonright \delta _\nu $
and
$h \upharpoonright \delta _\nu $
and
![]() $p \upharpoonright \tau _\nu $
are defined with
$p \upharpoonright \tau _\nu $
are defined with
![]() $\sup (h \upharpoonright \delta _\nu ) = \sup (g \upharpoonright (\iota _\alpha + \nu )) = \sup (g \upharpoonright \tau _\nu )$
.
$\sup (h \upharpoonright \delta _\nu ) = \sup (g \upharpoonright (\iota _\alpha + \nu )) = \sup (g \upharpoonright \tau _\nu )$
.
Fix
![]() $\nu $
with
$\nu $
with
![]() $0 \leq \nu < \xi $
. Let
$0 \leq \nu < \xi $
. Let
![]() $\epsilon _\nu = \delta _\nu + \mathcal {I}(\iota _\alpha + \nu ) = \delta _0 + \mathcal {I}(\iota _\alpha + \nu )$
and
$\epsilon _\nu = \delta _\nu + \mathcal {I}(\iota _\alpha + \nu ) = \delta _0 + \mathcal {I}(\iota _\alpha + \nu )$
and
![]() $\mu _\nu = \tau _\nu + \mathcal {I}(\iota _\alpha + \nu ) = \tau _0 + \mathcal {I}(\iota _\alpha + \nu )$
. For
$\mu _\nu = \tau _\nu + \mathcal {I}(\iota _\alpha + \nu ) = \tau _0 + \mathcal {I}(\iota _\alpha + \nu )$
. For
![]() $\beta < \mathcal {I}(\iota _\alpha + \nu )$
, let
$\beta < \mathcal {I}(\iota _\alpha + \nu )$
, let
![]() $h(\delta _\nu + \beta ) = p(\tau _\nu + \beta ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\beta + 1)}(\sup (h \upharpoonright \delta _\nu ))$
. Let
$h(\delta _\nu + \beta ) = p(\tau _\nu + \beta ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\beta + 1)}(\sup (h \upharpoonright \delta _\nu ))$
. Let
![]() $h(\epsilon _\nu ) = p(\mu _\nu ) = g(\iota _\alpha + \nu )$
.
$h(\epsilon _\nu ) = p(\mu _\nu ) = g(\iota _\alpha + \nu )$
.
Let
![]() $\tau = \sup \{\mu _\xi + 1 : \nu < \xi \}$
and
$\tau = \sup \{\mu _\xi + 1 : \nu < \xi \}$
and
![]() $\delta = \sup \{\epsilon _\nu + 1 : \nu < \xi \}$
. Note
$\delta = \sup \{\epsilon _\nu + 1 : \nu < \xi \}$
. Note
![]() $p \upharpoonright \tau $
and
$p \upharpoonright \tau $
and
![]() $h \upharpoonright \tau $
have been defined so that
$h \upharpoonright \tau $
have been defined so that
![]() $\sup (p \upharpoonright \tau ) = \sup (h \upharpoonright \delta ) = \sup (g(\gamma ) : \gamma \in A\} < f(\alpha )$
by property (3). Observe also that
$\sup (p \upharpoonright \tau ) = \sup (h \upharpoonright \delta ) = \sup (g(\gamma ) : \gamma \in A\} < f(\alpha )$
by property (3). Observe also that
![]() $\delta < \mathcal {I}(\alpha )$
.
$\delta < \mathcal {I}(\alpha )$
.
Now, in either Case A or Case B, ordinals
![]() $\tau $
and
$\tau $
and
![]() $\delta $
have been defined with
$\delta $
have been defined with
![]() $\tau \leq \delta < \mathcal {I}(\alpha )$
and
$\tau \leq \delta < \mathcal {I}(\alpha )$
and
![]() $\sup (h \upharpoonright \delta ) < f(\alpha )$
. Let
$\sup (h \upharpoonright \delta ) < f(\alpha )$
. Let
![]() $\ell = \min (\kappa \setminus A)$
.
$\ell = \min (\kappa \setminus A)$
.
(Case I)
![]() $g(\ell )> f(\alpha )$
.
$g(\ell )> f(\alpha )$
.
Let
![]() $\sigma _\alpha = \iota _\alpha $
if Case A held, and let
$\sigma _\alpha = \iota _\alpha $
if Case A held, and let
![]() $\sigma _\alpha = \ell $
if Case B held. For
$\sigma _\alpha = \ell $
if Case B held. For
![]() $\beta < \mathcal {I}(\alpha )$
, let
$\beta < \mathcal {I}(\alpha )$
, let
![]() $h(\delta + \beta ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\beta + 1)}(\sup (h \upharpoonright \delta ))$
. Let
$h(\delta + \beta ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\beta + 1)}(\sup (h \upharpoonright \delta ))$
. Let
![]() $h(\mathcal {I}(\alpha )) = f(\alpha )$
.
$h(\mathcal {I}(\alpha )) = f(\alpha )$
.
(Case II)
![]() $g(\ell ) = f(\alpha )$
.
$g(\ell ) = f(\alpha )$
.
For
![]() $\beta < \mathcal {I}(\ell )$
, let
$\beta < \mathcal {I}(\ell )$
, let
![]() $h(\delta + \beta ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\beta + 1)}(\sup (h \upharpoonright \delta ))$
.
$h(\delta + \beta ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\beta + 1)}(\sup (h \upharpoonright \delta ))$
.
(Case II.1)
![]() $\ell = \alpha $
.
$\ell = \alpha $
.
Let
![]() $h(\mathcal {I}(\alpha )) = p(\mathcal {I}(\alpha )) = f(\alpha ) = g(\alpha )$
. Let
$h(\mathcal {I}(\alpha )) = p(\mathcal {I}(\alpha )) = f(\alpha ) = g(\alpha )$
. Let
![]() $\sigma _\alpha = \alpha + 1$
.
$\sigma _\alpha = \alpha + 1$
.
(Case II.2)
![]() $\ell < \alpha $
.
$\ell < \alpha $
.
For
![]() $\beta < \mathcal {I}(\alpha )$
, let
$\beta < \mathcal {I}(\alpha )$
, let
![]() $h(\delta + \mathcal {I}(\ell ) + \beta ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\beta + 1)}(\sup (h \upharpoonright (\delta + \mathcal {I}(\ell ))))$
. Let
$h(\delta + \mathcal {I}(\ell ) + \beta ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\beta + 1)}(\sup (h \upharpoonright (\delta + \mathcal {I}(\ell ))))$
. Let
![]() $h(\mathcal {I}(\alpha )) = f(\alpha )$
and
$h(\mathcal {I}(\alpha )) = f(\alpha )$
and
![]() $p(\mathcal {I}(\ell )) = g(\ell ) = f(\alpha )$
. Let
$p(\mathcal {I}(\ell )) = g(\ell ) = f(\alpha )$
. Let
![]() $\sigma _\alpha = \ell + 1$
.
$\sigma _\alpha = \ell + 1$
.
Let
![]() $\varpi \leq \epsilon $
be largest such that
$\varpi \leq \epsilon $
be largest such that
![]() $\sup (g \upharpoonright \varpi ) \leq \sup (f)$
. Let
$\sup (g \upharpoonright \varpi ) \leq \sup (f)$
. Let
![]() $\varsigma = \sup \{\mathcal {I}(\alpha ) + 1 : \alpha < \varpi \}$
. After
$\varsigma = \sup \{\mathcal {I}(\alpha ) + 1 : \alpha < \varpi \}$
. After
![]() $\epsilon $
-many stages,
$\epsilon $
-many stages,
![]() $h \upharpoonright \epsilon ^0$
and
$h \upharpoonright \epsilon ^0$
and
![]() $p \upharpoonright \varsigma $
have been defined. Note
$p \upharpoonright \varsigma $
have been defined. Note
![]() ${\mathsf {main}}(h \upharpoonright \epsilon ^0) = f$
.
${\mathsf {main}}(h \upharpoonright \epsilon ^0) = f$
.
(Case 1)
![]() $\sup (f) = \sup (g)$
.
$\sup (f) = \sup (g)$
.
Then
![]() $\varpi = \epsilon $
,
$\varpi = \epsilon $
,
![]() $\varsigma = \epsilon ^0$
and
$\varsigma = \epsilon ^0$
and
![]() $p \in [C_0]^{\epsilon ^0}_*$
has been completely defined with
$p \in [C_0]^{\epsilon ^0}_*$
has been completely defined with
![]() ${\mathsf {main}}(p) = g$
.
${\mathsf {main}}(p) = g$
.
For
![]() $\alpha < \epsilon ^1$
, let
$\alpha < \epsilon ^1$
, let
![]() $h(\epsilon ^0 + \alpha ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\alpha + 1)}(\sup (h \upharpoonright \epsilon ^0))$
. This completes the construction of
$h(\epsilon ^0 + \alpha ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\alpha + 1)}(\sup (h \upharpoonright \epsilon ^0))$
. This completes the construction of
![]() $h \in [C_0]^{\epsilon ^1}_*$
.
$h \in [C_0]^{\epsilon ^1}_*$
.
(Case 2)
![]() $\sup (f) < \sup (g)$
.
$\sup (f) < \sup (g)$
.
Then
![]() $\varpi < \epsilon $
and
$\varpi < \epsilon $
and
![]() $\varsigma < \epsilon ^0$
. Suppose
$\varsigma < \epsilon ^0$
. Suppose
![]() $\nu < \epsilon $
and the following holds.
$\nu < \epsilon $
and the following holds.
-
(i) For all
 $\eta < \epsilon + \nu $
,
$\eta < \epsilon + \nu $
,
 $h \upharpoonright \mathcal {I}(\eta ) + 1$
has been defined and is a function of the correct type.
$h \upharpoonright \mathcal {I}(\eta ) + 1$
has been defined and is a function of the correct type. -
(ii) For all
 $\eta < \varpi + \nu $
,
$\eta < \varpi + \nu $
,
 $p \upharpoonright \mathcal {I}(\eta ) + 1$
has been defined and is a function of the correct type.
$p \upharpoonright \mathcal {I}(\eta ) + 1$
has been defined and is a function of the correct type. -
(iii) For
 $\eta < \epsilon $
,
$\eta < \epsilon $
,
 $h(\mathcal {I}(\epsilon + \eta )) = g(\varpi + \eta ) = p(\mathcal {I}(\varpi + \eta ))$
.
$h(\mathcal {I}(\epsilon + \eta )) = g(\varpi + \eta ) = p(\mathcal {I}(\varpi + \eta ))$
.
Suppose
![]() $\nu < \epsilon $
. Let
$\nu < \epsilon $
. Let
![]() $\lambda _\nu = \sup \{\mathcal {I}(\eta ) + 1 : \eta < \epsilon + \nu \}$
and
$\lambda _\nu = \sup \{\mathcal {I}(\eta ) + 1 : \eta < \epsilon + \nu \}$
and
![]() $\rho _\nu = \sup \{\mathcal {I}(\eta ) + 1 : \eta < \varpi + \nu \}$
. (Note that
$\rho _\nu = \sup \{\mathcal {I}(\eta ) + 1 : \eta < \varpi + \nu \}$
. (Note that
![]() $\lambda _0 = \epsilon ^0$
and
$\lambda _0 = \epsilon ^0$
and
![]() $\rho _0 = \varsigma $
.) These assumptions imply that
$\rho _0 = \varsigma $
.) These assumptions imply that
![]() $h \upharpoonright \lambda _\nu $
and
$h \upharpoonright \lambda _\nu $
and
![]() $p \upharpoonright \rho _\nu $
are defined. For
$p \upharpoonright \rho _\nu $
are defined. For
![]() $\alpha < \mathcal {I}(\varpi + \nu )$
, let
$\alpha < \mathcal {I}(\varpi + \nu )$
, let
![]() $h(\lambda _\nu + \alpha ) = p(\rho _\nu + \alpha ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\alpha + 1)}(\sup (h \upharpoonright \lambda _\nu ))$
. This defines
$h(\lambda _\nu + \alpha ) = p(\rho _\nu + \alpha ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\alpha + 1)}(\sup (h \upharpoonright \lambda _\nu ))$
. This defines
![]() $h \upharpoonright (\lambda _\nu + \mathcal {I}(\varpi + \nu ))$
and
$h \upharpoonright (\lambda _\nu + \mathcal {I}(\varpi + \nu ))$
and
![]() $p \upharpoonright \mathcal {I}(\varpi + \nu )$
. For all
$p \upharpoonright \mathcal {I}(\varpi + \nu )$
. For all
![]() $\alpha < \mathcal {I}(\epsilon + \nu )$
, let
$\alpha < \mathcal {I}(\epsilon + \nu )$
, let
![]() $h(\lambda _\nu + \mathcal {I}(\varpi + \nu ) + \alpha ) = {\mathsf {next}}^{\omega \cdot (\alpha + 1)}_{C_0}(\sup (h \upharpoonright (\lambda _\nu + \mathcal {I}(\varpi + \nu ))))$
. This defines
$h(\lambda _\nu + \mathcal {I}(\varpi + \nu ) + \alpha ) = {\mathsf {next}}^{\omega \cdot (\alpha + 1)}_{C_0}(\sup (h \upharpoonright (\lambda _\nu + \mathcal {I}(\varpi + \nu ))))$
. This defines
![]() $h \upharpoonright \mathcal {I}(\epsilon + \nu )$
since
$h \upharpoonright \mathcal {I}(\epsilon + \nu )$
since
![]() $\lambda _\nu + \mathcal {I}(\varpi + \nu ) + \mathcal {I}(\epsilon + \nu ) = \mathcal {I}(\epsilon + \nu )$
since
$\lambda _\nu + \mathcal {I}(\varpi + \nu ) + \mathcal {I}(\epsilon + \nu ) = \mathcal {I}(\epsilon + \nu )$
since
![]() $\mathcal {I}(\epsilon + \nu )$
is indecomposable. Let
$\mathcal {I}(\epsilon + \nu )$
is indecomposable. Let
![]() $h(\mathcal {I}(\epsilon + \nu )) = p(\mathcal {I}(\varpi + \nu )) = g(\varpi + \nu )$
. This defines
$h(\mathcal {I}(\epsilon + \nu )) = p(\mathcal {I}(\varpi + \nu )) = g(\varpi + \nu )$
. This defines
![]() $h \upharpoonright \mathcal {I}(\epsilon + \nu ) + 1$
and
$h \upharpoonright \mathcal {I}(\epsilon + \nu ) + 1$
and
![]() $p \upharpoonright \mathcal {I}(\varpi + \nu ) + 1$
.
$p \upharpoonright \mathcal {I}(\varpi + \nu ) + 1$
.
The construction of
![]() $h \in [C_0]^{\epsilon ^1}_*$
and
$h \in [C_0]^{\epsilon ^1}_*$
and
![]() $p \in [h[\epsilon ^1]]^{\epsilon ^0}_*$
has been completed so that
$p \in [h[\epsilon ^1]]^{\epsilon ^0}_*$
has been completed so that
![]() ${\mathsf {main}}(h^0) = f$
and
${\mathsf {main}}(h^0) = f$
and
![]() ${\mathsf {main}}(p) = g$
. Since
${\mathsf {main}}(p) = g$
. Since
![]() $h \in [C_0]^{\epsilon ^1}_*$
,
$h \in [C_0]^{\epsilon ^1}_*$
,
![]() $p \in [h[\epsilon ^1]]^{\epsilon _0}_*$
and
$p \in [h[\epsilon ^1]]^{\epsilon _0}_*$
and
![]() $P(h) = 0$
, one has
$P(h) = 0$
, one has
![]() $\Phi (f) = \Phi ({\mathsf {main}}(h^0)) \leq \Phi ({\mathsf {main}}(p)) = \Phi (g)$
.
$\Phi (f) = \Phi ({\mathsf {main}}(h^0)) \leq \Phi ({\mathsf {main}}(p)) = \Phi (g)$
.
Theorem 5.7. Suppose
![]() $\kappa $
is a cardinal satisfying
$\kappa $
is a cardinal satisfying
![]() $\kappa \rightarrow _* (\kappa )^{<\kappa }_2$
. For any
$\kappa \rightarrow _* (\kappa )^{<\kappa }_2$
. For any
![]() $\epsilon < \kappa $
and function
$\epsilon < \kappa $
and function
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, there is a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f, g \in [\kappa ]^\epsilon _*$
, if for all
$f, g \in [\kappa ]^\epsilon _*$
, if for all
![]() $\alpha < \epsilon $
,
$\alpha < \epsilon $
,
![]() $f(\alpha ) \leq g(\alpha )$
, then
$f(\alpha ) \leq g(\alpha )$
, then
![]() $\Phi (f) \leq \Phi (g)$
.
$\Phi (f) \leq \Phi (g)$
.
Proof. Let
![]() $C_0 \subseteq \kappa $
be a club consisting of indecomposable ordinals with the properties from Lemma 5.6. Let
$C_0 \subseteq \kappa $
be a club consisting of indecomposable ordinals with the properties from Lemma 5.6. Let
![]() $C_1 = \{\alpha \in C_0 : {\mathsf {enum}}_{C_0}(\alpha ) = \alpha \}$
.
$C_1 = \{\alpha \in C_0 : {\mathsf {enum}}_{C_0}(\alpha ) = \alpha \}$
.
Let
![]() $\zeta \leq \epsilon $
and
$\zeta \leq \epsilon $
and
![]() $\langle \eta _\xi : \xi < \zeta \rangle $
and
$\langle \eta _\xi : \xi < \zeta \rangle $
and
![]() $\langle \nu _\xi : \xi < \zeta \rangle $
be two increasing sequences with the following property.
$\langle \nu _\xi : \xi < \zeta \rangle $
be two increasing sequences with the following property.
-
(a) For all
 $\xi < \zeta $
,
$\xi < \zeta $
,
 $\nu _\xi $
is a limit ordinal.
$\nu _\xi $
is a limit ordinal. -
(b) For all
 $\xi < \zeta $
,
$\xi < \zeta $
,
 $\sup (f \upharpoonright \nu _\xi ) = g(\eta _\xi )$
.
$\sup (f \upharpoonright \nu _\xi ) = g(\eta _\xi )$
. -
(c) For all
 $\nu < \epsilon $
and
$\nu < \epsilon $
and
 $\eta < \epsilon $
, if
$\eta < \epsilon $
, if
 $\nu $
is a limit ordinal and
$\nu $
is a limit ordinal and
 $\sup (f \upharpoonright \nu ) = g(\eta )$
, then there is a
$\sup (f \upharpoonright \nu ) = g(\eta )$
, then there is a
 $\xi < \zeta $
so that
$\xi < \zeta $
so that
 $\nu = \nu _\xi $
and
$\nu = \nu _\xi $
and
 $\eta = \eta _\xi $
.
$\eta = \eta _\xi $
.
(Note it is possible that
![]() $\nu _\xi = \epsilon $
when
$\nu _\xi = \epsilon $
when
![]() $\sup (f \upharpoonright \epsilon ) = \sup (f) = g(\eta _\xi )$
.) These indicate the region in which the pair
$\sup (f \upharpoonright \epsilon ) = \sup (f) = g(\eta _\xi )$
.) These indicate the region in which the pair
![]() $(f,g)$
fails to satisfy condition (2) of Lemma 5.6. For each
$(f,g)$
fails to satisfy condition (2) of Lemma 5.6. For each
![]() $\xi < \zeta $
, let
$\xi < \zeta $
, let
![]() $\mu _\xi $
be the least
$\mu _\xi $
be the least
![]() $\gamma $
so that
$\gamma $
so that
![]() $\sup (g \upharpoonright \eta _\xi ) \leq f(\gamma )$
.
$\sup (g \upharpoonright \eta _\xi ) \leq f(\gamma )$
.
Define
![]() $k \in [C_1]^\epsilon _*$
as follows: If
$k \in [C_1]^\epsilon _*$
as follows: If
![]() $\alpha < \epsilon $
and there is no
$\alpha < \epsilon $
and there is no
![]() $\xi < \zeta $
so that
$\xi < \zeta $
so that
![]() $\alpha = \eta _\xi $
, then let
$\alpha = \eta _\xi $
, then let
![]() $k(\alpha ) = g(\alpha )$
. If
$k(\alpha ) = g(\alpha )$
. If
![]() $\alpha < \epsilon $
and there is a
$\alpha < \epsilon $
and there is a
![]() $\xi < \zeta $
so that
$\xi < \zeta $
so that
![]() $\alpha = \eta _\xi $
, then let
$\alpha = \eta _\xi $
, then let
![]() $k(\alpha ) = f(\mu _\xi + 1)$
. As in Theorem 5.3, the pair
$k(\alpha ) = f(\mu _\xi + 1)$
. As in Theorem 5.3, the pair
![]() $(f,k)$
satisfies conditions (1) and (2) and the pair
$(f,k)$
satisfies conditions (1) and (2) and the pair
![]() $(k,g)$
satisfies conditions (1), (2) and (3) of Lemma 5.6. Therefore,
$(k,g)$
satisfies conditions (1), (2) and (3) of Lemma 5.6. Therefore,
![]() $\Phi (k) \leq \Phi (g)$
.
$\Phi (k) \leq \Phi (g)$
.
Let
![]() $\zeta \leq \epsilon $
and
$\zeta \leq \epsilon $
and
![]() $\langle \eta _\xi : \xi < \zeta \rangle $
and
$\langle \eta _\xi : \xi < \zeta \rangle $
and
![]() $\langle \nu _\xi : \xi < \zeta \rangle $
be two increasing sequences so that the following hold.
$\langle \nu _\xi : \xi < \zeta \rangle $
be two increasing sequences so that the following hold.
-
(i) For all
 $\xi < \zeta $
,
$\xi < \zeta $
,
 $\eta _\xi $
is a limit ordinal.
$\eta _\xi $
is a limit ordinal. -
(ii) For all
 $\xi < \zeta $
,
$\xi < \zeta $
,
 $\sup (k \upharpoonright \eta _\xi ) = f(\nu _\xi )$
.
$\sup (k \upharpoonright \eta _\xi ) = f(\nu _\xi )$
. -
(iii) For all
 $\eta < \epsilon $
and
$\eta < \epsilon $
and
 $\nu < \epsilon $
, if
$\nu < \epsilon $
, if
 $\eta $
is a limit ordinal and
$\eta $
is a limit ordinal and
 $\sup (k \upharpoonright \eta ) = f(\nu )$
, then there is a
$\sup (k \upharpoonright \eta ) = f(\nu )$
, then there is a
 $\xi < \zeta $
so that
$\xi < \zeta $
so that
 $\eta = \eta _\xi $
and
$\eta = \eta _\xi $
and
 $\nu = \nu _\xi $
.
$\nu = \nu _\xi $
.
Let
![]() $\mu _\xi $
be the least
$\mu _\xi $
be the least
![]() $\gamma < \eta _\xi $
so that
$\gamma < \eta _\xi $
so that
![]() $\sup (f \upharpoonright \nu _\xi ) < k(\gamma )$
.
$\sup (f \upharpoonright \nu _\xi ) < k(\gamma )$
.
Define
![]() $h \in [C_0]^\epsilon _*$
as follows: If
$h \in [C_0]^\epsilon _*$
as follows: If
![]() $\alpha < \epsilon $
and there is no
$\alpha < \epsilon $
and there is no
![]() $\xi < \zeta $
so that
$\xi < \zeta $
so that
![]() $\mu _\xi \leq \alpha < \eta _\xi $
, then let
$\mu _\xi \leq \alpha < \eta _\xi $
, then let
![]() $h(\alpha ) = k(\alpha )$
. If
$h(\alpha ) = k(\alpha )$
. If
![]() $\alpha < \epsilon $
and there is a
$\alpha < \epsilon $
and there is a
![]() $\xi < \zeta $
so that
$\xi < \zeta $
so that
![]() $\mu _\xi \leq \alpha < \eta _\xi $
, then let
$\mu _\xi \leq \alpha < \eta _\xi $
, then let
![]() $h(\alpha ) = {\mathsf {next}}_{C_0}^{\omega \cdot ((\alpha - \mu _\xi ) + 1)}(\sup (f\upharpoonright \nu _\xi ))$
. As before, the pairs
$h(\alpha ) = {\mathsf {next}}_{C_0}^{\omega \cdot ((\alpha - \mu _\xi ) + 1)}(\sup (f\upharpoonright \nu _\xi ))$
. As before, the pairs
![]() $(f,h)$
and
$(f,h)$
and
![]() $(h,k)$
both satisfy conditions (1), (2) and (3) of Lemma 5.6. Thus,
$(h,k)$
both satisfy conditions (1), (2) and (3) of Lemma 5.6. Thus,
![]() $\Phi (f) \leq \Phi (h) \leq \Phi (k)$
.
$\Phi (f) \leq \Phi (h) \leq \Phi (k)$
.
This concludes that
![]() $\Phi (f) \leq \Phi (g)$
.
$\Phi (f) \leq \Phi (g)$
.
Corollary 5.8. Assume
![]() $\mathsf {AD}$
. Suppose
$\mathsf {AD}$
. Suppose
![]() $\kappa $
is
$\kappa $
is
![]() ${\omega _1}$
,
${\omega _1}$
,
![]() $\omega _2$
,
$\omega _2$
,
![]() $\boldsymbol {\delta }_n^1$
for
$\boldsymbol {\delta }_n^1$
for
![]() $1 \leq n < \omega $
,
$1 \leq n < \omega $
,
![]() $\boldsymbol {\delta }_A$
where
$\boldsymbol {\delta }_A$
where
![]() $A \subseteq \mathbb {R}$
or
$A \subseteq \mathbb {R}$
or
![]() $\boldsymbol {\delta }^2_1$
(assuming
$\boldsymbol {\delta }^2_1$
(assuming
![]() $\mathsf {DC}_{\mathbb {R}}$
). For any
$\mathsf {DC}_{\mathbb {R}}$
). For any
![]() $\epsilon < \kappa $
and
$\epsilon < \kappa $
and
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, there is a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
, there is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f,g \in [C]^\epsilon _*$
, if for all
$f,g \in [C]^\epsilon _*$
, if for all
![]() $\alpha < \epsilon $
,
$\alpha < \epsilon $
,
![]() $f(\alpha ) \leq g(\alpha )$
, then
$f(\alpha ) \leq g(\alpha )$
, then
![]() $\Phi (f) \leq \Phi (g)$
.
$\Phi (f) \leq \Phi (g)$
.
6 A finite continuity property for long functions on
 ${\omega _1}$
${\omega _1}$
Expecting a function
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
to satisfy an almost everywhere finite continuity in the sense that there are finitely many ordinals
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
to satisfy an almost everywhere finite continuity in the sense that there are finitely many ordinals
![]() $\delta _0, ..., \delta _k < {\omega _1}$
so that
$\delta _0, ..., \delta _k < {\omega _1}$
so that
![]() $\Phi (f)$
only depends on
$\Phi (f)$
only depends on
![]() $\sup (f \upharpoonright \delta _i)$
is impossible.
$\sup (f \upharpoonright \delta _i)$
is impossible.
Example 6.1. Let
![]() $\Psi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
be defined by
$\Psi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
be defined by
![]() $\Psi (f) = f(f(0))$
. For any finite set of ordinals
$\Psi (f) = f(f(0))$
. For any finite set of ordinals
![]() $\delta _0, ..., \delta _{k - 1} < {\omega _1}$
, for any club C, there are
$\delta _0, ..., \delta _{k - 1} < {\omega _1}$
, for any club C, there are
![]() $f,g \in [C]^{\omega _1}_*$
so that for all
$f,g \in [C]^{\omega _1}_*$
so that for all
![]() $i < k$
,
$i < k$
,
![]() $\sup (f \upharpoonright \delta _i) = \sup (g \upharpoonright \delta _i)$
and
$\sup (f \upharpoonright \delta _i) = \sup (g \upharpoonright \delta _i)$
and
![]() $\Psi (f) \neq \Psi (g)$
.
$\Psi (f) \neq \Psi (g)$
.
Proof. Let
![]() $\delta = \sup \{\delta _0,...,\delta _{k - 1}\}$
. Pick
$\delta = \sup \{\delta _0,...,\delta _{k - 1}\}$
. Pick
![]() $f,g \in [C]^{\omega _1}_*$
so that
$f,g \in [C]^{\omega _1}_*$
so that
![]() $f \upharpoonright \delta = g \upharpoonright \delta $
,
$f \upharpoonright \delta = g \upharpoonright \delta $
,
![]() $f(0) = g(0)> \delta $
and
$f(0) = g(0)> \delta $
and
![]() $f(f(0)) \neq g(g(0))$
. Then for all
$f(f(0)) \neq g(g(0))$
. Then for all
![]() $i < k$
,
$i < k$
,
![]() $\sup (f \upharpoonright \delta _i) = \sup (g \upharpoonright \delta _i)$
but
$\sup (f \upharpoonright \delta _i) = \sup (g \upharpoonright \delta _i)$
but
![]() $\Psi (f) = f(f(0)) \neq g(g(0)) = \Psi (g)$
.
$\Psi (f) = f(f(0)) \neq g(g(0)) = \Psi (g)$
.
Expecting a function
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
to have finitely many functions
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
to have finitely many functions
![]() $\Gamma _0,...,\Gamma _{k - 1}$
so that
$\Gamma _0,...,\Gamma _{k - 1}$
so that
![]() $\Phi (f)$
depends only on
$\Phi (f)$
depends only on
![]() $\sup (f \upharpoonright \Gamma _i(f))$
is also impossible by the following example. The concept of a closure point of a function will be very important in this section.
$\sup (f \upharpoonright \Gamma _i(f))$
is also impossible by the following example. The concept of a closure point of a function will be very important in this section.
Definition 6.2. Let
![]() $f \in [{\omega _1}]^{\omega _1}_*$
. An ordinal
$f \in [{\omega _1}]^{\omega _1}_*$
. An ordinal
![]() $\beta \in \omega $
is a closure point of f if and only if for all
$\beta \in \omega $
is a closure point of f if and only if for all
![]() $\alpha < \beta $
,
$\alpha < \beta $
,
![]() $f(\alpha ) < \beta $
(or equivalently) if and only if
$f(\alpha ) < \beta $
(or equivalently) if and only if
![]() $\sup (f \upharpoonright \beta ) = \beta $
. Let
$\sup (f \upharpoonright \beta ) = \beta $
. Let
![]() $\mathfrak {C}_f = \{\beta \in {\omega _1} : \sup (f \upharpoonright \beta ) = \beta \}$
be the collection of closure points of f.
$\mathfrak {C}_f = \{\beta \in {\omega _1} : \sup (f \upharpoonright \beta ) = \beta \}$
be the collection of closure points of f.
![]() $\mathfrak {C}_f$
is a club subset of
$\mathfrak {C}_f$
is a club subset of
![]() ${\omega _1}$
.
${\omega _1}$
.
Example 6.3. Let
![]() $\Psi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
be defined by
$\Psi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
be defined by
![]() $\Psi (f) = \min (\mathfrak {C}_f)$
, that is,
$\Psi (f) = \min (\mathfrak {C}_f)$
, that is,
![]() $\Psi (f)$
is the least closure point of f. Then for any club
$\Psi (f)$
is the least closure point of f. Then for any club
![]() $C \subseteq {\omega _1}$
and for any finite collection of functions
$C \subseteq {\omega _1}$
and for any finite collection of functions
![]() $\Gamma _0, ..., \Gamma _{k-1} : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
, there is an
$\Gamma _0, ..., \Gamma _{k-1} : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
, there is an
![]() $f \in [C]^{\omega _1}_*$
and a
$f \in [C]^{\omega _1}_*$
and a
![]() $g \in [C]^{\omega _1}_*$
so that for all
$g \in [C]^{\omega _1}_*$
so that for all
![]() $i < k$
,
$i < k$
,
![]() $\sup (f \upharpoonright \Gamma _i(f)) = \sup (g \upharpoonright \Gamma _i(f))$
and
$\sup (f \upharpoonright \Gamma _i(f)) = \sup (g \upharpoonright \Gamma _i(f))$
and
![]() $\Phi (f) \neq \Phi (g)$
.
$\Phi (f) \neq \Phi (g)$
.
Proof. Let
![]() $C_0 \subseteq C$
be a club consisting entirely of indecomposable ordinals. Let
$C_0 \subseteq C$
be a club consisting entirely of indecomposable ordinals. Let
![]() $C_1 = \{\alpha \in C_0 : {\mathsf {enum}}_{C_0}(\alpha ) = \alpha \}$
. Let
$C_1 = \{\alpha \in C_0 : {\mathsf {enum}}_{C_0}(\alpha ) = \alpha \}$
. Let
![]() $C_2$
be the club of limit points of
$C_2$
be the club of limit points of
![]() $C_1$
. Let
$C_1$
. Let
![]() $f \in [C_2]^{\omega _1}_*$
. Then
$f \in [C_2]^{\omega _1}_*$
. Then
![]() $\Psi (f) = \min (\mathfrak {C}_f) \in C_2$
. Let
$\Psi (f) = \min (\mathfrak {C}_f) \in C_2$
. Let
![]() $\gamma = \sup \{\Gamma _i(f) : i < k \wedge \Gamma _i(f) < \Psi (f)\}$
, and note that
$\gamma = \sup \{\Gamma _i(f) : i < k \wedge \Gamma _i(f) < \Psi (f)\}$
, and note that
![]() $\gamma = 0$
if there are no
$\gamma = 0$
if there are no
![]() $i < k$
with
$i < k$
with
![]() $\Gamma _i(f) < \Psi (f)$
. Since
$\Gamma _i(f) < \Psi (f)$
. Since
![]() $\Psi (f) \in C_2$
and
$\Psi (f) \in C_2$
and
![]() $\sup (f \upharpoonright \gamma ) < \sup (f \upharpoonright \Psi (f)) = \Psi (f)$
, there exists a
$\sup (f \upharpoonright \gamma ) < \sup (f \upharpoonright \Psi (f)) = \Psi (f)$
, there exists a
![]() $\delta \in C_1$
with
$\delta \in C_1$
with
![]() $\sup (f \upharpoonright \gamma ) < \delta < \Psi (f)$
. Define
$\sup (f \upharpoonright \gamma ) < \delta < \Psi (f)$
. Define
![]() $g \in [C_0]^{\omega _1}_*$
by
$g \in [C_0]^{\omega _1}_*$
by
 $$ \begin{align*}g(\alpha) = \begin{cases} f(\alpha) & \quad \alpha < \gamma \vee \alpha \geq \Psi(f) \\ {\mathsf{next}}_{C_0}^{\omega \cdot (\alpha + 1)}(\sup(f \upharpoonright \gamma)) & \quad \gamma \leq \alpha < \Psi(f) \\ \end{cases}.\end{align*} $$
$$ \begin{align*}g(\alpha) = \begin{cases} f(\alpha) & \quad \alpha < \gamma \vee \alpha \geq \Psi(f) \\ {\mathsf{next}}_{C_0}^{\omega \cdot (\alpha + 1)}(\sup(f \upharpoonright \gamma)) & \quad \gamma \leq \alpha < \Psi(f) \\ \end{cases}.\end{align*} $$
By Fact 2.12, g is indeed an increasing function. Moreover, since
![]() $\gamma < \delta $
and
$\gamma < \delta $
and
![]() $\sup (f \upharpoonright \gamma ) < \delta $
, Fact 2.12 also implies that
$\sup (f \upharpoonright \gamma ) < \delta $
, Fact 2.12 also implies that
![]() $\sup (g \upharpoonright \delta ) = \delta $
. Thus,
$\sup (g \upharpoonright \delta ) = \delta $
. Thus,
![]() $\delta \in \mathfrak {C}_g$
. Therefore,
$\delta \in \mathfrak {C}_g$
. Therefore,
![]() $\Psi (g) = \min (\mathfrak {C}_g) \leq \delta < \Psi (f)$
. However, for all
$\Psi (g) = \min (\mathfrak {C}_g) \leq \delta < \Psi (f)$
. However, for all
![]() $i < k$
,
$i < k$
,
![]() $\sup (g \upharpoonright \Gamma _i(f)) = \sup (f \upharpoonright \Gamma _i(f))$
.
$\sup (g \upharpoonright \Gamma _i(f)) = \sup (f \upharpoonright \Gamma _i(f))$
.
Motivated by this example, Theorem 6.18 will show that if one demands that closure points remains the same, then there will be finitely many functions
![]() $\Gamma _0,...,\Gamma _{k - 1}$
so that for
$\Gamma _0,...,\Gamma _{k - 1}$
so that for
![]() $\mu ^{\omega _1}_{\omega _1}$
-almost all f,
$\mu ^{\omega _1}_{\omega _1}$
-almost all f,
![]() $\Phi (f)$
depends only on
$\Phi (f)$
depends only on
![]() $\sup (f \upharpoonright \Gamma _i(f))$
.
$\sup (f \upharpoonright \Gamma _i(f))$
.
The results of this section will be proved using the strong partition relation
![]() ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_*$
and an additional combinatorial principle called the almost everywhere short length club uniformization for
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_*$
and an additional combinatorial principle called the almost everywhere short length club uniformization for
![]() ${\omega _1}$
. More specifically, a fine form of
${\omega _1}$
. More specifically, a fine form of
![]() $\mu ^{\omega _1}_{\omega _1}$
-almost everywhere continuity is needed.
$\mu ^{\omega _1}_{\omega _1}$
-almost everywhere continuity is needed.
Let
![]() ${\mathsf {club}}_{\omega _1}$
denote the collection of club subsets of
${\mathsf {club}}_{\omega _1}$
denote the collection of club subsets of
![]() ${\omega _1}$
. A relation
${\omega _1}$
. A relation
![]() $R \subseteq [{\omega _1}]^{<{\omega _1}}_* \times {\mathsf {club}}_{\omega _1}$
is said to
$R \subseteq [{\omega _1}]^{<{\omega _1}}_* \times {\mathsf {club}}_{\omega _1}$
is said to
![]() $\subseteq $
-downward closed in the
$\subseteq $
-downward closed in the
![]() ${\mathsf {club}}_{\omega _1}$
-coordinate if and only if for all
${\mathsf {club}}_{\omega _1}$
-coordinate if and only if for all
![]() $\ell \in [{\omega _1}]^{<{\omega _1}}_*$
, if
$\ell \in [{\omega _1}]^{<{\omega _1}}_*$
, if
![]() $R(\ell ,D)$
and
$R(\ell ,D)$
and
![]() $C \subseteq D$
, then
$C \subseteq D$
, then
![]() $R(\ell ,C)$
.
$R(\ell ,C)$
.
Definition 6.4. Almost everywhere short length club uniformization at
![]() ${\omega _1}$
is the asserting that for all
${\omega _1}$
is the asserting that for all
![]() $R \subseteq [{\omega _1}]^{<{\omega _1}}_* \times {\mathsf {club}}_{\omega _1}$
which is
$R \subseteq [{\omega _1}]^{<{\omega _1}}_* \times {\mathsf {club}}_{\omega _1}$
which is
![]() $\subseteq $
-downward closed in the
$\subseteq $
-downward closed in the
![]() ${\mathsf {club}}_{\omega _1}$
-coordinate, there is a club
${\mathsf {club}}_{\omega _1}$
-coordinate, there is a club
![]() $C \subseteq {\omega _1}$
and a function
$C \subseteq {\omega _1}$
and a function
![]() $\Lambda : (\mathrm {dom}(R) \cap [C]^{<{\omega _1}}_*) \rightarrow {\mathsf {club}}_{\omega _1}$
so that for all
$\Lambda : (\mathrm {dom}(R) \cap [C]^{<{\omega _1}}_*) \rightarrow {\mathsf {club}}_{\omega _1}$
so that for all
![]() $\ell \in \mathrm {dom}(R) \cap [C]^{<{\omega _1}}_*$
,
$\ell \in \mathrm {dom}(R) \cap [C]^{<{\omega _1}}_*$
,
![]() $R(\ell , \Lambda (\ell ))$
.
$R(\ell , \Lambda (\ell ))$
.
Almost everywhere short length club uniformization is established in [Reference Chan and Jackson4] Theorem 3.10 under
![]() $\mathsf {AD}$
using techniques which are specific to
$\mathsf {AD}$
using techniques which are specific to
![]() ${\omega _1}$
. [Reference Chan2] gives a more general argument which holds for many other known strong partition cardinals under
${\omega _1}$
. [Reference Chan2] gives a more general argument which holds for many other known strong partition cardinals under
![]() $\mathsf {AD}$
.
$\mathsf {AD}$
.
Fact 6.5. ([Reference Chan and Jackson4] Theorem 3.10, [Reference Chan2])
Assume
![]() $\mathsf {AD}$
. The almost everywhere short length club uniformization at
$\mathsf {AD}$
. The almost everywhere short length club uniformization at
![]() ${\omega _1}$
holds.
${\omega _1}$
holds.
The almost everywhere short length club uniformization at
![]() ${\omega _1}$
combined with the strong partition relation
${\omega _1}$
combined with the strong partition relation
![]() ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
gives a simpler form of the almost everywhere club uniformization principle stated below.
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
gives a simpler form of the almost everywhere club uniformization principle stated below.
Fact 6.6. ([Reference Chan2])
(Strong almost everywhere short length club uniformization for
![]() ${\omega _1}$
) Assume
${\omega _1}$
) Assume
![]() ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
and the almost everywhere short length club uniformization principle holds at
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
and the almost everywhere short length club uniformization principle holds at
![]() ${\omega _1}$
. For all
${\omega _1}$
. For all
![]() $R \subseteq [{\omega _1}]^{<{\omega _1}}_* \times {\mathsf {club}}_{\omega _1}$
, there exists a club
$R \subseteq [{\omega _1}]^{<{\omega _1}}_* \times {\mathsf {club}}_{\omega _1}$
, there exists a club
![]() $C \subseteq {\omega _1}$
so that for all
$C \subseteq {\omega _1}$
so that for all
![]() $\ell \in [C]^{<{\omega _1}}_* \cap \mathrm {dom}(R)$
,
$\ell \in [C]^{<{\omega _1}}_* \cap \mathrm {dom}(R)$
,
![]() $R(\ell , C \setminus \sup (\ell ) + 1)$
.
$R(\ell , C \setminus \sup (\ell ) + 1)$
.
[Reference Chan and Jackson4] used Fact 6.5 to show that every function
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
is continuous
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
is continuous
![]() $\mu ^{\omega _1}_{\omega _1}$
-almost everywhere.
$\mu ^{\omega _1}_{\omega _1}$
-almost everywhere.
Fact 6.7. Assume
![]() ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
and the almost everywhere short length club uniformization principle holds for
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
and the almost everywhere short length club uniformization principle holds for
![]() ${\omega _1}$
. Let
${\omega _1}$
. Let
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
. There is a club
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
. There is a club
![]() $C \subseteq {\omega _1}$
so that for all
$C \subseteq {\omega _1}$
so that for all
![]() $f \in [C]^{\omega _1}_*$
, there is an
$f \in [C]^{\omega _1}_*$
, there is an
![]() $\alpha < {\omega _1}$
so that for all
$\alpha < {\omega _1}$
so that for all
![]() $g \in [C]^{\omega _1}_*$
, if
$g \in [C]^{\omega _1}_*$
, if
![]() $g \upharpoonright \alpha = f \upharpoonright \alpha $
, then
$g \upharpoonright \alpha = f \upharpoonright \alpha $
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
Here, an even finer form of continuity established in [Reference Chan2] from Fact 6.6 will be needed.
Definition 6.8. Let
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
and
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
and
![]() $C \subseteq {\omega _1}$
be a club. One says that
$C \subseteq {\omega _1}$
be a club. One says that
![]() $\ell \in [C]^{<{\omega _1}}_*$
is a continuity point for
$\ell \in [C]^{<{\omega _1}}_*$
is a continuity point for
![]() $\Phi $
relative to C if and only if for all
$\Phi $
relative to C if and only if for all
![]() $f,g \in [C]^{\omega _1}_*$
so that
$f,g \in [C]^{\omega _1}_*$
so that
![]() $f \upharpoonright |\ell | = \ell = g \upharpoonright |\ell |$
,
$f \upharpoonright |\ell | = \ell = g \upharpoonright |\ell |$
,
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
Fact 6.9. ([Reference Chan2]) Assume
![]() ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
and the almost everywhere short length club uniformization principle holds for
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
and the almost everywhere short length club uniformization principle holds for
![]() ${\omega _1}$
. Suppose
${\omega _1}$
. Suppose
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
. Then there is a club
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
. Then there is a club
![]() $C \subseteq {\omega _1}$
so that for all
$C \subseteq {\omega _1}$
so that for all
![]() $f \in [C]^{\omega _1}_*$
and
$f \in [C]^{\omega _1}_*$
and
![]() $\alpha < {\omega _1}$
, if
$\alpha < {\omega _1}$
, if
![]() $\Phi (f) < f(\alpha )$
, then
$\Phi (f) < f(\alpha )$
, then
![]() $f \upharpoonright \alpha $
is a continuity point for
$f \upharpoonright \alpha $
is a continuity point for
![]() $\Phi $
relative to C.
$\Phi $
relative to C.
Lemma 6.10. Assume
![]() ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
and that the almost everywhere short length club uniformization principle holds at
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
and that the almost everywhere short length club uniformization principle holds at
![]() ${\omega _1}$
. Suppose
${\omega _1}$
. Suppose
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
is a function so that for
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
is a function so that for
![]() $\mu ^{\omega _1}_{\omega _1}$
-almost all f,
$\mu ^{\omega _1}_{\omega _1}$
-almost all f,
![]() $\Phi (f)$
is a successor ordinal. Then there is a club
$\Phi (f)$
is a successor ordinal. Then there is a club
![]() $C \subseteq {\omega _1}$
and a function
$C \subseteq {\omega _1}$
and a function
![]() $\Gamma ^\Phi : [C]^{\omega _1}_* \rightarrow {\omega _1}$
so that the following holds:
$\Gamma ^\Phi : [C]^{\omega _1}_* \rightarrow {\omega _1}$
so that the following holds:
-
1. For all
 $f \in [C]^{\omega _1}_*$
,
$f \in [C]^{\omega _1}_*$
,
 $\Gamma ^\Phi (f) < \Phi (f)$
.
$\Gamma ^\Phi (f) < \Phi (f)$
. -
2. For all
 $f \in [C]^{\omega _1}_*$
,
$f \in [C]^{\omega _1}_*$
,
 $\Gamma ^\Phi (f) + 1 = \Phi (f)$
.
$\Gamma ^\Phi (f) + 1 = \Phi (f)$
. -
3. For all
 $f \in [C]^{\omega _1}_*$
,
$f \in [C]^{\omega _1}_*$
,
 $f \upharpoonright \Gamma ^\Phi (f)$
is a continuity point for
$f \upharpoonright \Gamma ^\Phi (f)$
is a continuity point for
 $\Phi $
relative to C.
$\Phi $
relative to C.
Proof. Let
![]() $C_0 \subseteq {\omega _1}$
be a club consisting entirely of limit ordinals so that for all
$C_0 \subseteq {\omega _1}$
be a club consisting entirely of limit ordinals so that for all
![]() $f \in [C_0]^{\omega _1}_*$
,
$f \in [C_0]^{\omega _1}_*$
,
![]() $\Phi (f)$
is a successor ordinal. By Fact 6.9, there is a club
$\Phi (f)$
is a successor ordinal. By Fact 6.9, there is a club
![]() $C_1 \subseteq C_0$
so that for all
$C_1 \subseteq C_0$
so that for all
![]() $f \in [C_1]^{\omega _1}_*$
and
$f \in [C_1]^{\omega _1}_*$
and
![]() $\alpha < {\omega _1}$
, if
$\alpha < {\omega _1}$
, if
![]() $\Phi (f) < f(\alpha )$
, then
$\Phi (f) < f(\alpha )$
, then
![]() $f \upharpoonright \alpha $
is a continuity point for
$f \upharpoonright \alpha $
is a continuity point for
![]() $\Phi $
relative to
$\Phi $
relative to
![]() $C_1$
. Define
$C_1$
. Define
![]() $\Gamma ^\Phi : [C_1]^{\omega _1}_* \rightarrow {\omega _1}$
by letting
$\Gamma ^\Phi : [C_1]^{\omega _1}_* \rightarrow {\omega _1}$
by letting
![]() $\Gamma ^\Phi (f)$
be the predecessor of
$\Gamma ^\Phi (f)$
be the predecessor of
![]() $\Phi (f)$
. Note that
$\Phi (f)$
. Note that
![]() $\Gamma ^\Phi (f) \leq \sup (f \upharpoonright \Gamma ^\Phi (f)) < f(\Gamma ^\Phi (f))$
since
$\Gamma ^\Phi (f) \leq \sup (f \upharpoonright \Gamma ^\Phi (f)) < f(\Gamma ^\Phi (f))$
since
![]() $\sup (f \upharpoonright \Gamma ^\Phi (f)) \in C_1$
is a limit ordinal and by the discontinuity of f. Since
$\sup (f \upharpoonright \Gamma ^\Phi (f)) \in C_1$
is a limit ordinal and by the discontinuity of f. Since
![]() $\Phi (f) = \Gamma ^\Phi (f) + 1$
, this implies that
$\Phi (f) = \Gamma ^\Phi (f) + 1$
, this implies that
![]() $\Phi (f) \leq f(\Gamma ^\Phi (f))$
. However, since
$\Phi (f) \leq f(\Gamma ^\Phi (f))$
. However, since
![]() $f \in [C_1]^{\omega _1}_*$
and
$f \in [C_1]^{\omega _1}_*$
and
![]() $C_1$
consist entirely of limit ordinals,
$C_1$
consist entirely of limit ordinals,
![]() $\Phi (f) < f(\Gamma ^\Phi (f))$
since
$\Phi (f) < f(\Gamma ^\Phi (f))$
since
![]() $\Phi (f)$
is a successor ordinal. By Fact 6.9,
$\Phi (f)$
is a successor ordinal. By Fact 6.9,
![]() $f \upharpoonright \Gamma ^\Phi (f)$
is a continuity point for
$f \upharpoonright \Gamma ^\Phi (f)$
is a continuity point for
![]() $\Phi $
relative to
$\Phi $
relative to
![]() $C_1$
.
$C_1$
.
Lemma 6.11. Assume
![]() ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
and that the almost everywhere short length club uniformization principle holds at
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
and that the almost everywhere short length club uniformization principle holds at
![]() ${\omega _1}$
. Suppose
${\omega _1}$
. Suppose
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
is a function so that for
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
is a function so that for
![]() $\mu ^{\omega _1}_{\omega _1}$
-almost all f,
$\mu ^{\omega _1}_{\omega _1}$
-almost all f,
![]() $\Phi (f)$
is a nonzero limit ordinal and
$\Phi (f)$
is a nonzero limit ordinal and
![]() $\Phi (f) \notin \mathfrak {C}_f$
(i.e.,
$\Phi (f) \notin \mathfrak {C}_f$
(i.e.,
![]() $\Phi (f)$
is not a closure point of f). Then there is a club
$\Phi (f)$
is not a closure point of f). Then there is a club
![]() $C \subseteq {\omega _1}$
and a function
$C \subseteq {\omega _1}$
and a function
![]() $\Gamma ^\Phi : [C]^{\omega _1}_* \rightarrow {\omega _1}$
so that the following holds:
$\Gamma ^\Phi : [C]^{\omega _1}_* \rightarrow {\omega _1}$
so that the following holds:
-
1. For all
 $f \in [C]^{\omega _1}_*$
,
$f \in [C]^{\omega _1}_*$
,
 $\Gamma ^\Phi (f) < \Phi (f)$
.
$\Gamma ^\Phi (f) < \Phi (f)$
. -
2. For all
 $f \in [C]^{\omega _1}_*$
,
$f \in [C]^{\omega _1}_*$
,
 ${\mathrm {ot}}(\{\alpha : \Gamma ^\Phi (f) \leq \alpha < \Phi (f)\})$
is an additively indecomposable ordinal.
${\mathrm {ot}}(\{\alpha : \Gamma ^\Phi (f) \leq \alpha < \Phi (f)\})$
is an additively indecomposable ordinal. -
3. For all
 $f \in [C]^{\omega _1}_*$
,
$f \in [C]^{\omega _1}_*$
,
 $f \upharpoonright \Gamma ^\Phi (f)$
is a continuity point for
$f \upharpoonright \Gamma ^\Phi (f)$
is a continuity point for
 $\Phi $
relative to C.
$\Phi $
relative to C.
Proof. Let
![]() $C_0 \subseteq {\omega _1}$
be a club so that for all
$C_0 \subseteq {\omega _1}$
be a club so that for all
![]() $f \in [C_0]^{\omega _1}_*$
,
$f \in [C_0]^{\omega _1}_*$
,
![]() $\Phi (f)$
is a limit ordinal which is not a closure point of f. By Fact 6.9, let
$\Phi (f)$
is a limit ordinal which is not a closure point of f. By Fact 6.9, let
![]() $C_1 \subseteq C_0$
be a club so that for all
$C_1 \subseteq C_0$
be a club so that for all
![]() $\alpha < {\omega _1}$
, if
$\alpha < {\omega _1}$
, if
![]() $\Phi (f) < f(\alpha )$
, then
$\Phi (f) < f(\alpha )$
, then
![]() $f \upharpoonright \alpha $
is a continuity point of
$f \upharpoonright \alpha $
is a continuity point of
![]() $\Phi $
relative to
$\Phi $
relative to
![]() $C_1$
. Define
$C_1$
. Define
![]() $\Gamma : [C_1]^{\omega _1}_* \rightarrow {\omega _1}$
by
$\Gamma : [C_1]^{\omega _1}_* \rightarrow {\omega _1}$
by
![]() $\Gamma (f)$
is the unique
$\Gamma (f)$
is the unique
![]() $\beta $
such that
$\beta $
such that
![]() $\sup (f \upharpoonright \beta ) \leq \Phi (f) < f(\beta )$
. For all
$\sup (f \upharpoonright \beta ) \leq \Phi (f) < f(\beta )$
. For all
![]() $f \in [C_1]^{\omega _1}_*$
,
$f \in [C_1]^{\omega _1}_*$
,
![]() $f \upharpoonright \Gamma (f)$
is a continuity point for
$f \upharpoonright \Gamma (f)$
is a continuity point for
![]() $\Phi $
relative to
$\Phi $
relative to
![]() $C_1$
. Note that
$C_1$
. Note that
![]() $\Gamma (f) \leq \Phi (f)$
. If
$\Gamma (f) \leq \Phi (f)$
. If
![]() $\Gamma (f) = \Phi (f)$
, then since
$\Gamma (f) = \Phi (f)$
, then since
![]() $\Phi (f)$
is a limit ordinal,
$\Phi (f)$
is a limit ordinal,
![]() $\Phi (f) \leq \sup (f \upharpoonright \Phi (f)) = \sup (f \upharpoonright \Gamma (f)) \leq \Phi (f)$
. Thus,
$\Phi (f) \leq \sup (f \upharpoonright \Phi (f)) = \sup (f \upharpoonright \Gamma (f)) \leq \Phi (f)$
. Thus,
![]() $\Phi (f) \in \mathfrak {C}_f$
which contradicts the assumption. It has been shown that
$\Phi (f) \in \mathfrak {C}_f$
which contradicts the assumption. It has been shown that
![]() $\Gamma (f) < \Phi (f)$
for all
$\Gamma (f) < \Phi (f)$
for all
![]() $f \in [C_1]^{\omega _1}_*$
. For each
$f \in [C_1]^{\omega _1}_*$
. For each
![]() $f \in [C_1]^{\omega _1}_*$
, let
$f \in [C_1]^{\omega _1}_*$
, let
![]() $\delta _f = {\mathrm {ot}}(\{\alpha : \Gamma (f) \leq \alpha < \Phi (f)\})$
. Note that
$\delta _f = {\mathrm {ot}}(\{\alpha : \Gamma (f) \leq \alpha < \Phi (f)\})$
. Note that
![]() $\delta _f$
is a limit ordinal since
$\delta _f$
is a limit ordinal since
![]() $\Phi (f)$
is a limit ordinal. Let
$\Phi (f)$
is a limit ordinal. Let
![]() $\epsilon _f$
be the least ordinal so that there exists an additively indecomposable ordinal
$\epsilon _f$
be the least ordinal so that there exists an additively indecomposable ordinal
![]() $\nu _f$
with
$\nu _f$
with
![]() $\delta _f = \epsilon _f + \nu _f$
. Note that
$\delta _f = \epsilon _f + \nu _f$
. Note that
![]() $\epsilon _f < \delta _f$
. Define
$\epsilon _f < \delta _f$
. Define
![]() $\Gamma ^\Phi : [C_1]^{\omega _1}_* \rightarrow {\omega _1}$
by
$\Gamma ^\Phi : [C_1]^{\omega _1}_* \rightarrow {\omega _1}$
by
![]() $\Gamma ^\Phi (f) = \Gamma (f) + \epsilon _f$
. Then for all
$\Gamma ^\Phi (f) = \Gamma (f) + \epsilon _f$
. Then for all
![]() $f \in [C_1]^{\omega _1}_*$
,
$f \in [C_1]^{\omega _1}_*$
,
![]() $\Gamma ^\Phi (f) < \Phi (f)$
,
$\Gamma ^\Phi (f) < \Phi (f)$
,
![]() $f \upharpoonright \Gamma ^\Phi (f)$
is a continuity point for
$f \upharpoonright \Gamma ^\Phi (f)$
is a continuity point for
![]() $\Phi $
relative to
$\Phi $
relative to
![]() $C_1$
and
$C_1$
and
![]() ${\mathrm {ot}}(\{\alpha : \Gamma ^\Phi (f) \leq \alpha < \Phi (f)\}) = \nu _f$
which is an additively indecomposable ordinal.
${\mathrm {ot}}(\{\alpha : \Gamma ^\Phi (f) \leq \alpha < \Phi (f)\}) = \nu _f$
which is an additively indecomposable ordinal.
If
![]() $\Phi (f)$
is a function so that for
$\Phi (f)$
is a function so that for
![]() $\mu ^{\omega _1}_{\omega _1}$
-almost all f,
$\mu ^{\omega _1}_{\omega _1}$
-almost all f,
![]() $\Phi (f) \in \mathfrak {C}_f$
(such as the function from Example 6.3), then
$\Phi (f) \in \mathfrak {C}_f$
(such as the function from Example 6.3), then
![]() $\Phi (f)$
is the least
$\Phi (f)$
is the least
![]() $\beta $
so that
$\beta $
so that
![]() $f \upharpoonright \beta $
is a continuity point for
$f \upharpoonright \beta $
is a continuity point for
![]() $\Phi $
. For such a function, condition (3) must be weakened otherwise the crucial condition (1) will not hold.
$\Phi $
. For such a function, condition (3) must be weakened otherwise the crucial condition (1) will not hold.
Fact 6.12. Assume
![]() $\kappa $
is a cardinal,
$\kappa $
is a cardinal,
![]() $\epsilon \leq \kappa $
and
$\epsilon \leq \kappa $
and
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _2$
. Let
$\kappa \rightarrow _* (\kappa )^\epsilon _2$
. Let
![]() $\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
. There is a club
$\Phi : [\kappa ]^\epsilon _* \rightarrow \mathrm {ON}$
. There is a club
![]() $C \subseteq \kappa $
so that for all
$C \subseteq \kappa $
so that for all
![]() $f \in [C]^\epsilon _*$
, for all
$f \in [C]^\epsilon _*$
, for all
![]() $g \sqsubseteq f$
,
$g \sqsubseteq f$
,
![]() $\Phi (f) \leq \Phi (g)$
.
$\Phi (f) \leq \Phi (g)$
.
Proof. This follows from Theorem 5.3; however, in this particular instance, the argument is much simpler. Let
![]() $P : [\kappa ]^\epsilon _* \rightarrow 2$
be defined by
$P : [\kappa ]^\epsilon _* \rightarrow 2$
be defined by
![]() $P(f) = 0$
if and only if for all
$P(f) = 0$
if and only if for all
![]() $g \sqsubseteq f$
,
$g \sqsubseteq f$
,
![]() $\Phi (f) \leq \Phi (g)$
. By
$\Phi (f) \leq \Phi (g)$
. By
![]() $\kappa \rightarrow _* (\kappa )^\epsilon _2$
, there is a club
$\kappa \rightarrow _* (\kappa )^\epsilon _2$
, there is a club
![]() $C \subseteq \kappa $
which is homogeneous for P. Suppose C was homogeneous for P taking value
$C \subseteq \kappa $
which is homogeneous for P. Suppose C was homogeneous for P taking value
![]() $1$
. Let
$1$
. Let
![]() $Z = \{\Phi (f) : f \in [C]^\epsilon _*\}$
. Let
$Z = \{\Phi (f) : f \in [C]^\epsilon _*\}$
. Let
![]() $\beta = \min (Z)$
. Let
$\beta = \min (Z)$
. Let
![]() $f \in [C]^{\omega _1}_*$
be such that
$f \in [C]^{\omega _1}_*$
be such that
![]() $\Phi (f) = \beta $
. Since
$\Phi (f) = \beta $
. Since
![]() $P(f) = 1$
, there is a
$P(f) = 1$
, there is a
![]() $g \sqsubseteq f$
so that
$g \sqsubseteq f$
so that
![]() $\Phi (g) < \Phi (f)$
. Since
$\Phi (g) < \Phi (f)$
. Since
![]() $g \in [C]^\epsilon _*$
,
$g \in [C]^\epsilon _*$
,
![]() $\Phi (g) \in Z$
. Then
$\Phi (g) \in Z$
. Then
![]() $\Phi (g) < \beta = \min (Z)$
which is a contradiction. C must be homogeneous for P taking value
$\Phi (g) < \beta = \min (Z)$
which is a contradiction. C must be homogeneous for P taking value
![]() $0$
.
$0$
.
Definition 6.13. Suppose
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
and
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
and
![]() $f \in [{\omega _1}]^{\omega _1}_*$
. Let
$f \in [{\omega _1}]^{\omega _1}_*$
. Let
![]() $A^{\Phi ,\beta }_f = \{g \in [{\omega _1}]^{\omega _1}_* : g \sqsubseteq f \wedge \mathfrak {C}_g = \mathfrak {C}_f \wedge g \upharpoonright \beta = f \upharpoonright \beta \}$
. Let
$A^{\Phi ,\beta }_f = \{g \in [{\omega _1}]^{\omega _1}_* : g \sqsubseteq f \wedge \mathfrak {C}_g = \mathfrak {C}_f \wedge g \upharpoonright \beta = f \upharpoonright \beta \}$
. Let
![]() $\mathfrak {B}^{\Phi ,\beta }_f = \{\Phi (g) : g \in A^{\Phi ,\beta }_f\}$
. Note that if
$\mathfrak {B}^{\Phi ,\beta }_f = \{\Phi (g) : g \in A^{\Phi ,\beta }_f\}$
. Note that if
![]() $\beta _0 \leq \beta _1$
, then
$\beta _0 \leq \beta _1$
, then
![]() $A^{\Phi ,\beta _1}_f \subseteq A^{\Phi ,\beta _0}_f$
and
$A^{\Phi ,\beta _1}_f \subseteq A^{\Phi ,\beta _0}_f$
and
![]() $\mathfrak {B}^{\Phi ,\beta _1}_f \subseteq \mathfrak {B}^{\Phi ,\beta _0}_f$
.
$\mathfrak {B}^{\Phi ,\beta _1}_f \subseteq \mathfrak {B}^{\Phi ,\beta _0}_f$
.
Lemma 6.14. Suppose
![]() ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
. For all
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
. For all
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
, there is a club
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
, there is a club
![]() $C \subseteq {\omega _1}$
so that for all
$C \subseteq {\omega _1}$
so that for all
![]() $f \in [C]^{\omega _1}_*$
,
$f \in [C]^{\omega _1}_*$
,
![]() $\sup (\mathfrak {B}^{\Phi ,0}_f) < {\omega _1}$
.
$\sup (\mathfrak {B}^{\Phi ,0}_f) < {\omega _1}$
.
Proof. Suppose
![]() $h \in [{\omega _1}]^{\omega _1}_*$
and for all
$h \in [{\omega _1}]^{\omega _1}_*$
and for all
![]() $\alpha < {\omega _1}$
,
$\alpha < {\omega _1}$
,
![]() $h(\alpha )$
is an indecomposable ordinal. Let
$h(\alpha )$
is an indecomposable ordinal. Let
![]() $\langle \gamma ^h_\alpha : \alpha < {\omega _1}\rangle $
denote the increasing enumeration of
$\langle \gamma ^h_\alpha : \alpha < {\omega _1}\rangle $
denote the increasing enumeration of
![]() $\mathfrak {C}_h$
, the club of closure points of h, which are also indecomposable ordinals. Thus, for all
$\mathfrak {C}_h$
, the club of closure points of h, which are also indecomposable ordinals. Thus, for all
![]() $\alpha < \beta $
,
$\alpha < \beta $
,
![]() ${\mathrm {ot}}(\{\eta < {\omega _1} : \gamma ^h_{\alpha } \leq \eta < \gamma ^h_\beta \}) = \gamma ^h_\beta $
. For
${\mathrm {ot}}(\{\eta < {\omega _1} : \gamma ^h_{\alpha } \leq \eta < \gamma ^h_\beta \}) = \gamma ^h_\beta $
. For
![]() $\alpha < {\omega _1}$
, let
$\alpha < {\omega _1}$
, let
![]() $B^h_\alpha = \{(\eta ,\zeta ) : \gamma _{\alpha }^h \leq \eta < \gamma _{\alpha + 1}^h \wedge \zeta = h(\eta )\}$
. For
$B^h_\alpha = \{(\eta ,\zeta ) : \gamma _{\alpha }^h \leq \eta < \gamma _{\alpha + 1}^h \wedge \zeta = h(\eta )\}$
. For
![]() $i \in 2$
,
$i \in 2$
,
![]() $\bigcup _{\alpha < {\omega _1}} B^h_{2\alpha + i}$
is the graph of a partial function whose domain is a subset of
$\bigcup _{\alpha < {\omega _1}} B^h_{2\alpha + i}$
is the graph of a partial function whose domain is a subset of
![]() ${\omega _1}$
. Denote this partial function by
${\omega _1}$
. Denote this partial function by
![]() $\tilde h^i$
. Let
$\tilde h^i$
. Let
![]() $\mathfrak {m}_{\mathrm {dom}(\tilde h^i)} : \mathrm {dom}(\tilde h^i) \rightarrow {\omega _1}$
be the Mostowski collapse of
$\mathfrak {m}_{\mathrm {dom}(\tilde h^i)} : \mathrm {dom}(\tilde h^i) \rightarrow {\omega _1}$
be the Mostowski collapse of
![]() $\mathrm {dom}(\tilde h^i)$
. Define
$\mathrm {dom}(\tilde h^i)$
. Define
![]() $h^i(\alpha ) = \tilde h^i \circ \mathfrak {m}^{-1}_{\mathrm {dom}(\tilde h^i)}$
. Intuitively,
$h^i(\alpha ) = \tilde h^i \circ \mathfrak {m}^{-1}_{\mathrm {dom}(\tilde h^i)}$
. Intuitively,
![]() $h^0$
and
$h^0$
and
![]() $h^1$
are the concatenations of h restricted to the even and odd, respectively, blocks determined by the sequence
$h^1$
are the concatenations of h restricted to the even and odd, respectively, blocks determined by the sequence
![]() $\langle \gamma ^h_\alpha : \alpha < {\omega _1}\rangle $
of closure points of h. Note that
$\langle \gamma ^h_\alpha : \alpha < {\omega _1}\rangle $
of closure points of h. Note that
![]() $\gamma ^{h^i}_{\alpha + 1} = \gamma ^h_{2\alpha + 1 + i}$
and thus if
$\gamma ^{h^i}_{\alpha + 1} = \gamma ^h_{2\alpha + 1 + i}$
and thus if
![]() $\alpha $
is a limit ordinal
$\alpha $
is a limit ordinal
![]() $\gamma ^{h^i}_\alpha = \gamma ^h_\alpha $
.
$\gamma ^{h^i}_\alpha = \gamma ^h_\alpha $
.
Also, observe that if
![]() $f,g \in [{\omega _1}]^{\omega _1}_*$
have the property that for all
$f,g \in [{\omega _1}]^{\omega _1}_*$
have the property that for all
![]() $\alpha < {\omega _1}$
,
$\alpha < {\omega _1}$
,
![]() $f(\alpha )$
and
$f(\alpha )$
and
![]() $g(\alpha )$
are indecomposable ordinals,
$g(\alpha )$
are indecomposable ordinals,
![]() $\sup (B^f_\alpha ) < \min (B^g_\alpha )$
and
$\sup (B^f_\alpha ) < \min (B^g_\alpha )$
and
![]() $\sup (B^g_\alpha ) < \min (B^f_{\alpha + 1})$
, then there is an
$\sup (B^g_\alpha ) < \min (B^f_{\alpha + 1})$
, then there is an
![]() $h \in [{\omega _1}]^{\omega _1}_*$
so that
$h \in [{\omega _1}]^{\omega _1}_*$
so that
![]() $h^0 = f$
and
$h^0 = f$
and
![]() $h^1 = g$
. To see this: Let
$h^1 = g$
. To see this: Let
![]() $\langle \gamma ^*_\alpha : \alpha < {\omega _1}\rangle $
be the increasing enumeration of
$\langle \gamma ^*_\alpha : \alpha < {\omega _1}\rangle $
be the increasing enumeration of
![]() $\{\gamma ^f_\alpha : \alpha < {\omega _1}\} \cup \{\gamma ^g_\alpha : \alpha < {\omega _1}\}$
. Note that for all limit ordinals
$\{\gamma ^f_\alpha : \alpha < {\omega _1}\} \cup \{\gamma ^g_\alpha : \alpha < {\omega _1}\}$
. Note that for all limit ordinals
![]() $\alpha $
,
$\alpha $
,
![]() $\gamma ^*_{2\alpha } = \gamma ^*_\alpha = \gamma ^f_\alpha = \gamma ^g_\alpha $
. For each
$\gamma ^*_{2\alpha } = \gamma ^*_\alpha = \gamma ^f_\alpha = \gamma ^g_\alpha $
. For each
![]() $\alpha $
,
$\alpha $
,
![]() $\gamma ^*_{2\alpha + 1} = \gamma ^f_{\alpha + 1}$
and
$\gamma ^*_{2\alpha + 1} = \gamma ^f_{\alpha + 1}$
and
![]() $\gamma ^*_{2\alpha + 2} = \gamma ^g_{\alpha + 1}$
by the assumptions on f and g. Define h by recursion as follows. Suppose
$\gamma ^*_{2\alpha + 2} = \gamma ^g_{\alpha + 1}$
by the assumptions on f and g. Define h by recursion as follows. Suppose
![]() $h \upharpoonright \gamma ^*_{2\alpha }$
has been defined. For each
$h \upharpoonright \gamma ^*_{2\alpha }$
has been defined. For each
![]() $\xi < \gamma ^*_{2\alpha + 1} = \gamma ^f_{\alpha + 1}$
, let
$\xi < \gamma ^*_{2\alpha + 1} = \gamma ^f_{\alpha + 1}$
, let
![]() $h(\gamma ^*_{2\alpha } + \xi ) = f(\gamma ^f_\alpha + \xi )$
. This defines
$h(\gamma ^*_{2\alpha } + \xi ) = f(\gamma ^f_\alpha + \xi )$
. This defines
![]() $h \upharpoonright \gamma ^*_{2\alpha + 1}$
. For each
$h \upharpoonright \gamma ^*_{2\alpha + 1}$
. For each
![]() $\xi < \gamma ^*_{2\alpha + 2} = \gamma ^g_{\alpha + 1}$
, let
$\xi < \gamma ^*_{2\alpha + 2} = \gamma ^g_{\alpha + 1}$
, let
![]() $h(\gamma ^*_{2\alpha + 1} + \xi ) = g(\gamma ^g_\alpha + \xi )$
. This defines
$h(\gamma ^*_{2\alpha + 1} + \xi ) = g(\gamma ^g_\alpha + \xi )$
. This defines
![]() $h \upharpoonright \gamma ^*_{2\alpha + 2}$
. By recursion, this completes the definition of h. (The assumptions on f and g are needed to ensure h is an increasing and discontinuous function.) Note that for all
$h \upharpoonright \gamma ^*_{2\alpha + 2}$
. By recursion, this completes the definition of h. (The assumptions on f and g are needed to ensure h is an increasing and discontinuous function.) Note that for all
![]() $\alpha < {\omega _1}$
,
$\alpha < {\omega _1}$
,
![]() $\gamma ^h_\alpha = \gamma ^*_\alpha $
. Therefore,
$\gamma ^h_\alpha = \gamma ^*_\alpha $
. Therefore,
![]() $h^0 = f$
and
$h^0 = f$
and
![]() $h^1 = g$
.
$h^1 = g$
.
Define
![]() $P : [{\omega _1}]^{\omega _1}_* \rightarrow 2$
by
$P : [{\omega _1}]^{\omega _1}_* \rightarrow 2$
by
![]() $P(h) = 0$
if and only if
$P(h) = 0$
if and only if
![]() $\Phi (h^0) \leq \Phi (h^1)$
. By
$\Phi (h^0) \leq \Phi (h^1)$
. By
![]() ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
, there is a club
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
, there is a club
![]() $C_0 \subseteq {\omega _1}$
which is homogeneous for P and consists entirely of indecomposable ordinals. For the sake of contradiction, suppose
$C_0 \subseteq {\omega _1}$
which is homogeneous for P and consists entirely of indecomposable ordinals. For the sake of contradiction, suppose
![]() $C_0$
is homogeneous for P taking value
$C_0$
is homogeneous for P taking value
![]() $1$
. Pick any
$1$
. Pick any
![]() $h \in [C_0]^{\omega _1}_*$
. For each
$h \in [C_0]^{\omega _1}_*$
. For each
![]() $n \in \omega $
, let
$n \in \omega $
, let
![]() $\tilde g_n$
denote the partial function whose graph is
$\tilde g_n$
denote the partial function whose graph is
![]() $\bigcup _{\alpha < {\omega _1}} B^h_{\omega \cdot \alpha + n}$
. Let
$\bigcup _{\alpha < {\omega _1}} B^h_{\omega \cdot \alpha + n}$
. Let
![]() $\mathfrak {m}_{\mathrm {dom}(\tilde g_n)} : \mathrm {dom}(\tilde g_n) \rightarrow {\omega _1}$
be the Mostowski collapse of
$\mathfrak {m}_{\mathrm {dom}(\tilde g_n)} : \mathrm {dom}(\tilde g_n) \rightarrow {\omega _1}$
be the Mostowski collapse of
![]() $\mathrm {dom}(\tilde g_n)$
. Let
$\mathrm {dom}(\tilde g_n)$
. Let
![]() $g_n = \tilde g_n \circ \mathfrak {m}^{-1}_{\mathrm {dom}(\tilde g_n)}$
. Note that
$g_n = \tilde g_n \circ \mathfrak {m}^{-1}_{\mathrm {dom}(\tilde g_n)}$
. Note that
![]() $B^{g_n}_\alpha = B^h_{\omega \cdot \alpha + n}$
. Therefore,
$B^{g_n}_\alpha = B^h_{\omega \cdot \alpha + n}$
. Therefore,
 $\sup (B^{g_n}_\alpha ) = \gamma ^h_{\omega \cdot \alpha + n + 1} < h(\omega \cdot \alpha + n + 1) = \min (B^h_{\omega \cdot \alpha + n + 1}) = \min (B^{g_{n + 1}}_\alpha ) < \gamma _{\omega \cdot \alpha + \omega } = \min (B^{g_0}_{\alpha + 1}) \leq \min (B^{g_n}_{\alpha + 1})$
. By the previous observation, for each
$\sup (B^{g_n}_\alpha ) = \gamma ^h_{\omega \cdot \alpha + n + 1} < h(\omega \cdot \alpha + n + 1) = \min (B^h_{\omega \cdot \alpha + n + 1}) = \min (B^{g_{n + 1}}_\alpha ) < \gamma _{\omega \cdot \alpha + \omega } = \min (B^{g_0}_{\alpha + 1}) \leq \min (B^{g_n}_{\alpha + 1})$
. By the previous observation, for each
![]() $n \in \omega $
, there is an
$n \in \omega $
, there is an
![]() $h_n \in [C_0]^{\omega _1}_*$
so that
$h_n \in [C_0]^{\omega _1}_*$
so that
![]() $h_n^0 = g_n$
and
$h_n^0 = g_n$
and
![]() $h_n^1 = g_{n + 1}$
. However,
$h_n^1 = g_{n + 1}$
. However,
![]() $P(h_n) = 1$
implies that
$P(h_n) = 1$
implies that
![]() $\Phi (g_{n + 1}) = \Phi (h_n^1) < \Phi (h_n^0) = \Phi (g_n)$
.
$\Phi (g_{n + 1}) = \Phi (h_n^1) < \Phi (h_n^0) = \Phi (g_n)$
.
![]() $\langle \Phi (g_n) : n \in \omega \rangle $
is an infinite decreasing sequence of ordinals which is impossible. This shows that
$\langle \Phi (g_n) : n \in \omega \rangle $
is an infinite decreasing sequence of ordinals which is impossible. This shows that
![]() $C_0$
must be homogeneous for P taking value
$C_0$
must be homogeneous for P taking value
![]() $0$
.
$0$
.
Let
![]() $C_1 = \{\alpha \in C_0 : {\mathsf {enum}}_{C_0}(\alpha ) = \alpha \}$
. Let
$C_1 = \{\alpha \in C_0 : {\mathsf {enum}}_{C_0}(\alpha ) = \alpha \}$
. Let
![]() $C_2$
be the club of limit points of
$C_2$
be the club of limit points of
![]() $C_1$
. Let
$C_1$
. Let
![]() $f \in [C_2]^{\omega _1}_*$
. Let
$f \in [C_2]^{\omega _1}_*$
. Let
![]() $\gamma _0 = 0$
. If
$\gamma _0 = 0$
. If
![]() $\alpha $
is a limit ordinal and for all
$\alpha $
is a limit ordinal and for all
![]() $\beta < \alpha $
,
$\beta < \alpha $
,
![]() $\gamma _\beta $
has been defined, then let
$\gamma _\beta $
has been defined, then let
![]() $\gamma _\alpha = \sup \{\gamma _\beta : \beta < \alpha \}$
. If
$\gamma _\alpha = \sup \{\gamma _\beta : \beta < \alpha \}$
. If
![]() $\alpha $
is a successor ordinal, then let
$\alpha $
is a successor ordinal, then let
![]() $\gamma _\alpha = {\mathsf {next}}_{C_1}(\gamma ^f_\alpha )$
. Since
$\gamma _\alpha = {\mathsf {next}}_{C_1}(\gamma ^f_\alpha )$
. Since
![]() $f(\gamma _\alpha ^f) \in C_2$
and
$f(\gamma _\alpha ^f) \in C_2$
and
![]() $C_2$
consists of the limit points of
$C_2$
consists of the limit points of
![]() $C_1$
,
$C_1$
,
![]() $\gamma _\alpha < f(\gamma _\alpha ^f)$
. Define
$\gamma _\alpha < f(\gamma _\alpha ^f)$
. Define
![]() $k \in [C_0]^{\omega _1}_*$
by recursion as follow: Suppose
$k \in [C_0]^{\omega _1}_*$
by recursion as follow: Suppose
![]() $\delta < {\omega _1}$
and
$\delta < {\omega _1}$
and
![]() $k \upharpoonright \gamma _\delta $
has been defined. For each
$k \upharpoonright \gamma _\delta $
has been defined. For each
![]() $\alpha < \gamma _{\delta + 1}$
, let
$\alpha < \gamma _{\delta + 1}$
, let
![]() $k(\gamma _\delta + \alpha ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\alpha + 1)}(\gamma ^f_{\delta + 1})$
. Since
$k(\gamma _\delta + \alpha ) = {\mathsf {next}}_{C_0}^{\omega \cdot (\alpha + 1)}(\gamma ^f_{\delta + 1})$
. Since
![]() $\gamma _{\delta + 1}$
is indecomposable and
$\gamma _{\delta + 1}$
is indecomposable and
![]() $\gamma _{\delta + 1} \in C_1 = \{\alpha \in C_0 : {\mathsf {enum}}_{C_0}(\alpha ) = \alpha \}$
, Fact 2.12 implies that this defines
$\gamma _{\delta + 1} \in C_1 = \{\alpha \in C_0 : {\mathsf {enum}}_{C_0}(\alpha ) = \alpha \}$
, Fact 2.12 implies that this defines
![]() $k \upharpoonright \gamma _{\delta + 1}$
and
$k \upharpoonright \gamma _{\delta + 1}$
and
![]() $\sup (k \upharpoonright \gamma _{\delta + 1}) = \gamma _{\delta + 1}$
. Thus,
$\sup (k \upharpoonright \gamma _{\delta + 1}) = \gamma _{\delta + 1}$
. Thus,
![]() $\gamma ^k_{\alpha } = \gamma _\alpha $
for all
$\gamma ^k_{\alpha } = \gamma _\alpha $
for all
![]() $\alpha < {\omega _1}$
. Observe that for each
$\alpha < {\omega _1}$
. Observe that for each
![]() $\delta < {\omega _1}$
,
$\delta < {\omega _1}$
,
![]() $\gamma ^f_{\delta + 1} < {\mathsf {next}}^\omega _{C_0}(\gamma ^f_{\delta + 1}) = k(\gamma _{\delta }) = \min (B^k_\delta ) < \sup (B^k_\delta ) = \gamma ^k_{\delta + 1} < f(\gamma ^f_{\delta + 1}) = \min (B^f_{\delta + 1})$
. Now, suppose
$\gamma ^f_{\delta + 1} < {\mathsf {next}}^\omega _{C_0}(\gamma ^f_{\delta + 1}) = k(\gamma _{\delta }) = \min (B^k_\delta ) < \sup (B^k_\delta ) = \gamma ^k_{\delta + 1} < f(\gamma ^f_{\delta + 1}) = \min (B^f_{\delta + 1})$
. Now, suppose
![]() $g \sqsubseteq f$
and
$g \sqsubseteq f$
and
![]() $\mathfrak {C}_g = \mathfrak {C}_f$
(that is, for all
$\mathfrak {C}_g = \mathfrak {C}_f$
(that is, for all
![]() $\alpha < {\omega _1}$
,
$\alpha < {\omega _1}$
,
![]() $\gamma ^g_\alpha = \gamma ^f_\alpha $
). Then we have that for all
$\gamma ^g_\alpha = \gamma ^f_\alpha $
). Then we have that for all
![]() $\delta < {\omega _1}$
,
$\delta < {\omega _1}$
,
 $\sup (B^g_\delta ) = \gamma ^g_{\delta + 1} = \gamma ^f_{\delta + 1} < \min (B^k_\delta ) < \sup (B^k_\delta ) = \gamma ^k_{\delta + 1} < f(\gamma ^f_{\delta + 1}) \leq g(\gamma ^f_{\delta + 1}) = g(\gamma ^g_{\delta + 1}) = \min (B^g_{\delta + 1})$
. By the observation above, there is an
$\sup (B^g_\delta ) = \gamma ^g_{\delta + 1} = \gamma ^f_{\delta + 1} < \min (B^k_\delta ) < \sup (B^k_\delta ) = \gamma ^k_{\delta + 1} < f(\gamma ^f_{\delta + 1}) \leq g(\gamma ^f_{\delta + 1}) = g(\gamma ^g_{\delta + 1}) = \min (B^g_{\delta + 1})$
. By the observation above, there is an
![]() $h_g \in [C_0]^{\omega _1}_*$
so that
$h_g \in [C_0]^{\omega _1}_*$
so that
![]() $h_g^0 = g$
and
$h_g^0 = g$
and
![]() $h_g^1 = k$
. Then
$h_g^1 = k$
. Then
![]() $P(h_g) = 0$
implies that
$P(h_g) = 0$
implies that
![]() $\Phi (g) \leq \Phi (k)$
. It has been shown that for all
$\Phi (g) \leq \Phi (k)$
. It has been shown that for all
![]() $g \sqsubseteq f$
with
$g \sqsubseteq f$
with
![]() $\mathfrak {C}_g = \mathfrak {C}_f$
,
$\mathfrak {C}_g = \mathfrak {C}_f$
,
![]() $\Phi (g) \leq \Phi (k)$
. Hence,
$\Phi (g) \leq \Phi (k)$
. Hence,
![]() $\sup (\mathfrak {B}^{\Phi ,0}_f) \leq \Phi (k) < {\omega _1}$
.
$\sup (\mathfrak {B}^{\Phi ,0}_f) \leq \Phi (k) < {\omega _1}$
.
Lemma 6.15. Assume
![]() $\mathsf {DC}$
,
$\mathsf {DC}$
,
![]() ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
and that the almost everywhere short length club uniformization principle holds at
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
and that the almost everywhere short length club uniformization principle holds at
![]() ${\omega _1}$
. Suppose
${\omega _1}$
. Suppose
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
is a function so that for
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
is a function so that for
![]() $\mu ^{\omega _1}_{\omega _1}$
-almost all f,
$\mu ^{\omega _1}_{\omega _1}$
-almost all f,
![]() $\Phi (f) \in \mathfrak {C}_f$
. Then there is a club
$\Phi (f) \in \mathfrak {C}_f$
. Then there is a club
![]() $C \subseteq {\omega _1}$
and a function
$C \subseteq {\omega _1}$
and a function
![]() $\Gamma ^\Phi : [C]^{\omega _1}_* \rightarrow {\omega _1}$
so that that the following holds:
$\Gamma ^\Phi : [C]^{\omega _1}_* \rightarrow {\omega _1}$
so that that the following holds:
-
1. For all
 $f \in [C]^{\omega _1}_*$
,
$f \in [C]^{\omega _1}_*$
,
 $\Gamma ^\Phi (f) < \Phi (f)$
.
$\Gamma ^\Phi (f) < \Phi (f)$
. -
2. For all
 $f \in [C]^{\omega _1}_*$
,
$f \in [C]^{\omega _1}_*$
,
 ${\mathrm {ot}}(\{\alpha : \Gamma ^\Phi (f) \leq \alpha < \Phi (\alpha )\})$
is an additively indecomposable ordinal.
${\mathrm {ot}}(\{\alpha : \Gamma ^\Phi (f) \leq \alpha < \Phi (\alpha )\})$
is an additively indecomposable ordinal. -
3. For all
 $f \in [C]^{\omega _1}_*$
, for all
$f \in [C]^{\omega _1}_*$
, for all
 $g \sqsubseteq f$
with
$g \sqsubseteq f$
with
 $\mathfrak {C}_f = \mathfrak {C}_g$
and
$\mathfrak {C}_f = \mathfrak {C}_g$
and
 $g \upharpoonright \Gamma ^\Phi (f) = f \upharpoonright \Gamma ^\Phi (f)$
, then
$g \upharpoonright \Gamma ^\Phi (f) = f \upharpoonright \Gamma ^\Phi (f)$
, then
 $\Phi (g) = \Phi (f)$
.
$\Phi (g) = \Phi (f)$
.
Proof. By the assumption and Fact 6.9, there is a club
![]() $C_0$
so that the following holds.
$C_0$
so that the following holds.
-
(a) For all
 $f \in [C_0]^{\omega _1}_*$
, if
$f \in [C_0]^{\omega _1}_*$
, if
 $\Phi (f) < f(\alpha )$
, then
$\Phi (f) < f(\alpha )$
, then
 $f \upharpoonright \alpha $
is a continuity point for
$f \upharpoonright \alpha $
is a continuity point for
 $\Phi $
relative to
$\Phi $
relative to
 $C_0$
.
$C_0$
. -
(b)
 $\Phi (f) \in \mathfrak {C}_f$
.
$\Phi (f) \in \mathfrak {C}_f$
.
For
![]() $f \in [C_0]^{\omega _1}_*$
and
$f \in [C_0]^{\omega _1}_*$
and
![]() $\beta < {\omega _1}$
, let
$\beta < {\omega _1}$
, let
![]() $\Lambda (f,\beta ) = \sup (\mathfrak {B}^{\Phi ,\beta }_f) < {\omega _1}$
by Fact 6.14 (where
$\Lambda (f,\beta ) = \sup (\mathfrak {B}^{\Phi ,\beta }_f) < {\omega _1}$
by Fact 6.14 (where
![]() $\mathfrak {B}^{\Phi ,\beta }$
is defined in Definition 6.13). Observe that by condition (b),
$\mathfrak {B}^{\Phi ,\beta }$
is defined in Definition 6.13). Observe that by condition (b),
![]() $\Lambda (f,\beta ) \in \mathfrak {C}_f$
. Let
$\Lambda (f,\beta ) \in \mathfrak {C}_f$
. Let
![]() $Z_f = \{\Lambda (f,\beta ) : \beta < \Phi (f)\}$
. Let
$Z_f = \{\Lambda (f,\beta ) : \beta < \Phi (f)\}$
. Let
![]() $\Gamma (f) = \min \{\beta < \Phi (f) : \Lambda (f,\beta ) = \min (Z_f)\}$
. The main property of
$\Gamma (f) = \min \{\beta < \Phi (f) : \Lambda (f,\beta ) = \min (Z_f)\}$
. The main property of
![]() $\Gamma $
is that for all
$\Gamma $
is that for all
![]() $\beta $
with
$\beta $
with
![]() $\Gamma (f) \leq \beta < \Phi (f)$
,
$\Gamma (f) \leq \beta < \Phi (f)$
,
![]() $\Lambda (f,\beta ) = \Lambda (f,\Gamma (f))$
. Define
$\Lambda (f,\beta ) = \Lambda (f,\Gamma (f))$
. Define
![]() $\Sigma \colon [C_0]^{\omega _1}_* \rightarrow {\omega _1}$
by
$\Sigma \colon [C_0]^{\omega _1}_* \rightarrow {\omega _1}$
by
![]() $\Sigma (f) = \Lambda (f,\Gamma (f))$
. Again, for all
$\Sigma (f) = \Lambda (f,\Gamma (f))$
. Again, for all
![]() $f \in [C_0]^{\omega _1}_*$
,
$f \in [C_0]^{\omega _1}_*$
,
![]() $\Sigma (f) \in \mathfrak {C}_f$
. Applying Fact 6.12 to
$\Sigma (f) \in \mathfrak {C}_f$
. Applying Fact 6.12 to
![]() $\Sigma $
,
$\Sigma $
,
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Phi $
, there is a club
$\Phi $
, there is a club
![]() $C_1 \subseteq C_0$
on which
$C_1 \subseteq C_0$
on which
![]() $\Sigma $
,
$\Sigma $
,
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Phi $
are subsequence monotonic: that is, for all
$\Phi $
are subsequence monotonic: that is, for all
![]() $f \in [C_1]^{\omega _1}_*$
, for all
$f \in [C_1]^{\omega _1}_*$
, for all
![]() $g \sqsubseteq f$
,
$g \sqsubseteq f$
,
![]() $\Phi (f) \leq \Phi (g)$
,
$\Phi (f) \leq \Phi (g)$
,
![]() $\Sigma (f) \leq \Sigma (g)$
and
$\Sigma (f) \leq \Sigma (g)$
and
![]() $\Gamma (f) \leq \Gamma (g)$
.
$\Gamma (f) \leq \Gamma (g)$
.
Claim 1: For all
![]() $f \in [C_1]^{\omega _1}_*$
, for all
$f \in [C_1]^{\omega _1}_*$
, for all
![]() $g \sqsubseteq f$
with
$g \sqsubseteq f$
with
![]() $\mathfrak {C}_f = \mathfrak {C}_g$
and
$\mathfrak {C}_f = \mathfrak {C}_g$
and
![]() $g \upharpoonright \Gamma (f) = f \upharpoonright \Gamma (f)$
,
$g \upharpoonright \Gamma (f) = f \upharpoonright \Gamma (f)$
,
![]() $\Sigma (f) = \Sigma (g)$
and
$\Sigma (f) = \Sigma (g)$
and
![]() $\Gamma (f) = \Gamma (g)$
.
$\Gamma (f) = \Gamma (g)$
.
To see Claim 1: Because
![]() $g \sqsubseteq f$
and subsequence monotonicity of
$g \sqsubseteq f$
and subsequence monotonicity of
![]() $\Gamma $
,
$\Gamma $
,
![]() $\Gamma (f) \leq \Gamma (g)$
. Hence,
$\Gamma (f) \leq \Gamma (g)$
. Hence,
![]() $A^{\Phi ,\Gamma (g)}_g \subseteq A^{\Phi ,\Gamma (f)}_f$
and thus
$A^{\Phi ,\Gamma (g)}_g \subseteq A^{\Phi ,\Gamma (f)}_f$
and thus
![]() $\Sigma (g) \leq \Sigma (f)$
. However, subsequence monotonicity of
$\Sigma (g) \leq \Sigma (f)$
. However, subsequence monotonicity of
![]() $\Sigma $
and
$\Sigma $
and
![]() $g \sqsubseteq f$
imply
$g \sqsubseteq f$
imply
![]() $\Sigma (f) \leq \Sigma (g)$
. Thus,
$\Sigma (f) \leq \Sigma (g)$
. Thus,
![]() $\Sigma (f) = \Sigma (g)$
. Now, suppose
$\Sigma (f) = \Sigma (g)$
. Now, suppose
![]() $\Gamma (f) < \Gamma (g)$
. This implies that there is an
$\Gamma (f) < \Gamma (g)$
. This implies that there is an
![]() $h \sqsubseteq g$
with
$h \sqsubseteq g$
with
![]() $\mathfrak {C}_h = \mathfrak {C}_g$
,
$\mathfrak {C}_h = \mathfrak {C}_g$
,
![]() $h \upharpoonright \Gamma (f) = g \upharpoonright \Gamma (f) = f \upharpoonright \Gamma (f)$
and
$h \upharpoonright \Gamma (f) = g \upharpoonright \Gamma (f) = f \upharpoonright \Gamma (f)$
and
![]() $\Phi (h)> \Sigma (g) = \Sigma (f)$
. Thus,
$\Phi (h)> \Sigma (g) = \Sigma (f)$
. Thus,
![]() $h \in A^{\Phi ,\Gamma (f)}_f$
and therefore
$h \in A^{\Phi ,\Gamma (f)}_f$
and therefore
![]() $\Lambda (f,\Gamma (f)) \geq \Phi (h)> \Sigma (f) = \Lambda (f,\Gamma (f))$
, which is a contradiction. One must have that
$\Lambda (f,\Gamma (f)) \geq \Phi (h)> \Sigma (f) = \Lambda (f,\Gamma (f))$
, which is a contradiction. One must have that
![]() $\Gamma (g) \leq \Gamma (f)$
. Since it has already been observed above that
$\Gamma (g) \leq \Gamma (f)$
. Since it has already been observed above that
![]() $\Gamma (f) \leq \Gamma (g)$
,
$\Gamma (f) \leq \Gamma (g)$
,
![]() $\Gamma (f) = \Gamma (g)$
. This establishes Claim 1.
$\Gamma (f) = \Gamma (g)$
. This establishes Claim 1.
Define
![]() $P : [C_1]^{\omega _1}_* \rightarrow 2$
by
$P : [C_1]^{\omega _1}_* \rightarrow 2$
by
![]() $P(f) = 0$
if and only if
$P(f) = 0$
if and only if
![]() $\Phi (f) = \Sigma (f)$
. By
$\Phi (f) = \Sigma (f)$
. By
![]() ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
, there is a club
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
, there is a club
![]() $C_2 \subseteq C_1$
which is homogeneous for P.
$C_2 \subseteq C_1$
which is homogeneous for P.
Claim 2:
![]() $C_2$
is homogeneous for P taking value
$C_2$
is homogeneous for P taking value
![]() $0$
.
$0$
.
To see Claim 2: Pick
![]() $f \in [C_2]^{\omega _1}_*$
. Let
$f \in [C_2]^{\omega _1}_*$
. Let
![]() $\rho : \omega \rightarrow \Sigma (f)$
be an increasing cofinal sequence with
$\rho : \omega \rightarrow \Sigma (f)$
be an increasing cofinal sequence with
![]() $\rho (0) = \Gamma (f)$
. One will construct a sequence
$\rho (0) = \Gamma (f)$
. One will construct a sequence
![]() $\langle f_n : n \in \omega \rangle $
with the following properties:
$\langle f_n : n \in \omega \rangle $
with the following properties:
-
1.
 $f_0 = f$
. For all
$f_0 = f$
. For all
 $n \in \omega $
,
$n \in \omega $
,
 $f_n \in [C_2]^{\omega _1}_*$
,
$f_n \in [C_2]^{\omega _1}_*$
,
 $f_{n + 1} \sqsubseteq f_{n}$
and
$f_{n + 1} \sqsubseteq f_{n}$
and
 $\mathfrak {C}_{f_n} = \mathfrak {C}_{f_{n + 1}} = \mathfrak {C}_f$
.
$\mathfrak {C}_{f_n} = \mathfrak {C}_{f_{n + 1}} = \mathfrak {C}_f$
. -
2. For all
 $n \in \omega $
, for all
$n \in \omega $
, for all
 $\alpha \geq \Sigma (f)$
,
$\alpha \geq \Sigma (f)$
,
 $f_n(\alpha ) = f(\alpha )$
.
$f_n(\alpha ) = f(\alpha )$
. -
3. For all
 $n \in \omega $
,
$n \in \omega $
,
 $f_{n + 1} \upharpoonright \rho (n) = f_n \upharpoonright \rho (n)$
.
$f_{n + 1} \upharpoonright \rho (n) = f_n \upharpoonright \rho (n)$
. -
4. For all
 $n \in \omega $
,
$n \in \omega $
,
 $\rho (n) < \Phi (f_n) \leq \Sigma (f)$
.
$\rho (n) < \Phi (f_n) \leq \Sigma (f)$
.
Let
![]() $f_0 = f$
and note that
$f_0 = f$
and note that
![]() $\rho (0) = \Gamma (f) < \Phi (f) = \Phi (f_0)$
. Suppose
$\rho (0) = \Gamma (f) < \Phi (f) = \Phi (f_0)$
. Suppose
![]() $f_n$
has been constructed satisfying the above four properties. Since
$f_n$
has been constructed satisfying the above four properties. Since
![]() $f_n \sqsubseteq f$
, Claim 1 implies
$f_n \sqsubseteq f$
, Claim 1 implies
![]() $\Sigma (f_n) = \Sigma (f)$
and
$\Sigma (f_n) = \Sigma (f)$
and
![]() $\Gamma (f_n) = \Gamma (f) \leq \rho (n)$
. By condition (4),
$\Gamma (f_n) = \Gamma (f) \leq \rho (n)$
. By condition (4),
![]() $\rho (n) < \Phi (f_n)$
and therefore by the main property of
$\rho (n) < \Phi (f_n)$
and therefore by the main property of
![]() $\Gamma $
,
$\Gamma $
,
![]() $\Lambda (f_n,\rho (n)) = \Lambda (f_n,\Gamma (f_n)) = \Sigma (f_n) = \Sigma (f)$
. Since
$\Lambda (f_n,\rho (n)) = \Lambda (f_n,\Gamma (f_n)) = \Sigma (f_n) = \Sigma (f)$
. Since
![]() $\rho (n + 1) < \Sigma (f)$
, there exists an
$\rho (n + 1) < \Sigma (f)$
, there exists an
![]() $h \sqsubseteq f_n$
with
$h \sqsubseteq f_n$
with
![]() $\mathfrak {C}_{h} = \mathfrak {C}_{f_n}$
,
$\mathfrak {C}_{h} = \mathfrak {C}_{f_n}$
,
![]() $h \upharpoonright \rho (n) = f_n \upharpoonright \rho (n)$
and
$h \upharpoonright \rho (n) = f_n \upharpoonright \rho (n)$
and
![]() $\rho (n + 1) < \Phi (h) \leq \Sigma (h) = \Sigma (f)$
by Claim 1. Since
$\rho (n + 1) < \Phi (h) \leq \Sigma (h) = \Sigma (f)$
by Claim 1. Since
![]() $\Phi (h) \in \mathfrak {C}_{h}$
(is a closure point of h) by the assumptions,
$\Phi (h) \in \mathfrak {C}_{h}$
(is a closure point of h) by the assumptions,
![]() $\Phi (h)$
is a limit ordinal and therefore,
$\Phi (h)$
is a limit ordinal and therefore,
![]() $\Phi (h) \leq \sup (h \upharpoonright \Phi (h)) < h(\Phi (h))$
. Since
$\Phi (h) \leq \sup (h \upharpoonright \Phi (h)) < h(\Phi (h))$
. Since
![]() $\Phi (h) \leq \Sigma (f)$
,
$\Phi (h) \leq \Sigma (f)$
,
![]() $h \upharpoonright \Sigma (f)$
is a continuity point for
$h \upharpoonright \Sigma (f)$
is a continuity point for
![]() $\Phi $
relative to
$\Phi $
relative to
![]() $C_2$
. Define
$C_2$
. Define
![]() $f_{n + 1} \in [C_2]^{\omega _1}_*$
by
$f_{n + 1} \in [C_2]^{\omega _1}_*$
by
 $$ \begin{align*}f_{n + 1}(\alpha) = \begin{cases} h(\alpha) & \quad \alpha < \Sigma(f) \\ f(\alpha) & \quad \Sigma(f) \leq \alpha \end{cases}.\end{align*} $$
$$ \begin{align*}f_{n + 1}(\alpha) = \begin{cases} h(\alpha) & \quad \alpha < \Sigma(f) \\ f(\alpha) & \quad \Sigma(f) \leq \alpha \end{cases}.\end{align*} $$
Note that
![]() $f_{n + 1}$
is indeed an increasing and discontinuous function since
$f_{n + 1}$
is indeed an increasing and discontinuous function since
![]() $\Sigma (f) \in \mathfrak {C}_f$
and
$\Sigma (f) \in \mathfrak {C}_f$
and
![]() $\mathfrak {C}_{h} = \mathfrak {C}_f$
imply that
$\mathfrak {C}_{h} = \mathfrak {C}_f$
imply that
![]() $\sup (f_{n + 1} \upharpoonright \Sigma (f)) = \sup (h \upharpoonright \Sigma (f)) = \Sigma (f) < f(\Sigma (f)) = f_{n + 1}(\Sigma (f))$
. Since
$\sup (f_{n + 1} \upharpoonright \Sigma (f)) = \sup (h \upharpoonright \Sigma (f)) = \Sigma (f) < f(\Sigma (f)) = f_{n + 1}(\Sigma (f))$
. Since
![]() $h \upharpoonright \Sigma (f)$
is a continuity point for
$h \upharpoonright \Sigma (f)$
is a continuity point for
![]() $\Phi $
relative to
$\Phi $
relative to
![]() $C_2$
,
$C_2$
,
![]() $\Phi (f_{n + 1}) = \Phi (h)$
. This function
$\Phi (f_{n + 1}) = \Phi (h)$
. This function
![]() $f_{n + 1}$
satisfies all the required properties relative to the previous
$f_{n + 1}$
satisfies all the required properties relative to the previous
![]() $f_n$
.
$f_n$
.
By
![]() $\mathsf {DC}$
, there is a sequence
$\mathsf {DC}$
, there is a sequence
![]() $\langle f_n : n \in \omega \rangle $
with all the required properties. Define
$\langle f_n : n \in \omega \rangle $
with all the required properties. Define
![]() $f_\omega \in [C_2]^{\omega _1}_*$
by
$f_\omega \in [C_2]^{\omega _1}_*$
by
![]() $f_\omega (\alpha ) = \sup \{f_n(\alpha ) : n < \omega \}$
. Note that for all n,
$f_\omega (\alpha ) = \sup \{f_n(\alpha ) : n < \omega \}$
. Note that for all n,
![]() $f_\omega \sqsubseteq f_n$
,
$f_\omega \sqsubseteq f_n$
,
![]() $\mathfrak {C}_{f_\omega } = \mathfrak {C}_f$
and
$\mathfrak {C}_{f_\omega } = \mathfrak {C}_f$
and
![]() $f_\omega \upharpoonright \rho (n) = f_n \upharpoonright \rho (n)$
. (Note that
$f_\omega \upharpoonright \rho (n) = f_n \upharpoonright \rho (n)$
. (Note that
![]() $\Sigma (f) \in \mathfrak {C}_{f_\omega }$
since
$\Sigma (f) \in \mathfrak {C}_{f_\omega }$
since
![]() $\Sigma (f) \in \mathfrak {C}_{f_n}$
for all
$\Sigma (f) \in \mathfrak {C}_{f_n}$
for all
![]() $n \in \omega $
.) Since
$n \in \omega $
.) Since
![]() $\Phi $
satisfies subsequence monotonicity on
$\Phi $
satisfies subsequence monotonicity on
![]() $C_2$
,
$C_2$
,
![]() $f_\omega \sqsubseteq f_n$
implies that
$f_\omega \sqsubseteq f_n$
implies that
![]() $\rho (n) < \Phi (f_n) \leq \Phi (f_\omega )$
. Thus,
$\rho (n) < \Phi (f_n) \leq \Phi (f_\omega )$
. Thus,
![]() $\Sigma (f) \leq \Phi (f_\omega )$
. Since
$\Sigma (f) \leq \Phi (f_\omega )$
. Since
![]() $f_\omega \sqsubseteq f$
and
$f_\omega \sqsubseteq f$
and
![]() $f_\omega \upharpoonright \Gamma (f) = f \upharpoonright \Gamma (f)$
, Claim 1 implies that
$f_\omega \upharpoonright \Gamma (f) = f \upharpoonright \Gamma (f)$
, Claim 1 implies that
![]() $\Sigma (f) = \Sigma (f_\omega )$
. By definition,
$\Sigma (f) = \Sigma (f_\omega )$
. By definition,
![]() $\Phi (f_\omega ) \leq \Sigma (f_\omega )$
. Hence,
$\Phi (f_\omega ) \leq \Sigma (f_\omega )$
. Hence,
![]() $\Sigma (f_\omega ) = \Phi (f_\omega )$
. Since
$\Sigma (f_\omega ) = \Phi (f_\omega )$
. Since
![]() $f_\omega \in [C_2]^{\omega _1}_*$
,
$f_\omega \in [C_2]^{\omega _1}_*$
,
![]() $P(f_\omega ) = 0$
and
$P(f_\omega ) = 0$
and
![]() $C_2$
is homogeneous for P, one must have that
$C_2$
is homogeneous for P, one must have that
![]() $C_2$
is homogeneous for P taking value
$C_2$
is homogeneous for P taking value
![]() $0$
. This completes the argument for Claim 2.
$0$
. This completes the argument for Claim 2.
For each
![]() $f \in [C_2]^{\omega _1}_*$
,
$f \in [C_2]^{\omega _1}_*$
,
![]() $\Phi (f) = \Sigma (f) = \Lambda (f,\Gamma (f))$
. This implies the club
$\Phi (f) = \Sigma (f) = \Lambda (f,\Gamma (f))$
. This implies the club
![]() $C_2$
and the function
$C_2$
and the function
![]() $\Gamma $
satisfy condition (1) and (3). For each
$\Gamma $
satisfy condition (1) and (3). For each
![]() $f \in [C_2]^{\omega _1}_*$
, let
$f \in [C_2]^{\omega _1}_*$
, let
![]() $\delta _f = {\mathrm {ot}}(\{\alpha : \Gamma (f) \leq \alpha < \Phi (f)\})$
. Let
$\delta _f = {\mathrm {ot}}(\{\alpha : \Gamma (f) \leq \alpha < \Phi (f)\})$
. Let
![]() $\epsilon _f$
be the least ordinal so that there exists an additively indecomposable ordinal
$\epsilon _f$
be the least ordinal so that there exists an additively indecomposable ordinal
![]() $\nu _f$
with
$\nu _f$
with
![]() $\delta _f = \epsilon _f + \nu _f$
. Let
$\delta _f = \epsilon _f + \nu _f$
. Let
![]() $\Gamma ^\Phi (f) = \Gamma (f) + \epsilon _f$
. Now,
$\Gamma ^\Phi (f) = \Gamma (f) + \epsilon _f$
. Now,
![]() $\Gamma ^\Phi $
satisfies all the desired properties.
$\Gamma ^\Phi $
satisfies all the desired properties.
Definition 6.16. Let
![]() $n \in \omega $
,
$n \in \omega $
,
![]() $C \subseteq {\omega _1}$
be a club and
$C \subseteq {\omega _1}$
be a club and
![]() $\Gamma _0, ..., \Gamma _{n - 1} : [C]^{\omega _1}_* \rightarrow {\omega _1}$
be a sequence of functions.
$\Gamma _0, ..., \Gamma _{n - 1} : [C]^{\omega _1}_* \rightarrow {\omega _1}$
be a sequence of functions.
![]() $\langle C, \Gamma _0,...,\Gamma _{n - 1}\rangle $
is a good sequence if and only if the following holds.
$\langle C, \Gamma _0,...,\Gamma _{n - 1}\rangle $
is a good sequence if and only if the following holds.
-
1. For all
 $f \in [C]^{\omega _1}_*$
and for all
$f \in [C]^{\omega _1}_*$
and for all
 $k < n - 1$
,
$k < n - 1$
,
 $\Gamma _{k + 1}(f) < \Gamma _k(f)$
.
$\Gamma _{k + 1}(f) < \Gamma _k(f)$
. -
2. For each
 $i < n - 1$
,
$i < n - 1$
,
 ${\mathrm {ot}}(\{\alpha : \Gamma _{i + 1}(f) \leq \alpha < \Gamma _i(f)\})$
is an additively indecomposable ordinals or the ordinal
${\mathrm {ot}}(\{\alpha : \Gamma _{i + 1}(f) \leq \alpha < \Gamma _i(f)\})$
is an additively indecomposable ordinals or the ordinal
 $1$
.
$1$
. -
3. For all
 $j < n - 1$
, for all
$j < n - 1$
, for all
 $f \in [C]^{\omega _1}_*$
, for all
$f \in [C]^{\omega _1}_*$
, for all
 $g \in [C]^{\omega _1}_*$
, if
$g \in [C]^{\omega _1}_*$
, if-
•
 $g \sqsubseteq f$
and
$g \sqsubseteq f$
and
 $\mathfrak {C}_g = \mathfrak {C}_f$
,
$\mathfrak {C}_g = \mathfrak {C}_f$
, -
• for all
 $j < k < n - 1$
,
$j < k < n - 1$
,
 $\sup (g \upharpoonright \Gamma _k(f)) = \sup (f \upharpoonright \Gamma _k(f))$
,
$\sup (g \upharpoonright \Gamma _k(f)) = \sup (f \upharpoonright \Gamma _k(f))$
, -
• and
 $g \upharpoonright \Gamma _{n - 1}(f) = f \upharpoonright \Gamma _{n - 1}(f)$
,
$g \upharpoonright \Gamma _{n - 1}(f) = f \upharpoonright \Gamma _{n - 1}(f)$
,
then
 $\Gamma _j(f) = \Gamma _j(g)$
.
$\Gamma _j(f) = \Gamma _j(g)$
. -
Lemma 6.17. Assume
![]() $\mathsf {DC}$
,
$\mathsf {DC}$
,
![]() ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
and that the almost everywhere short length club uniformization principle holds at
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
and that the almost everywhere short length club uniformization principle holds at
![]() ${\omega _1}$
. If
${\omega _1}$
. If
![]() $\langle D, \Gamma _0,...,\Gamma _{n - 1}\rangle $
is a good sequence so that
$\langle D, \Gamma _0,...,\Gamma _{n - 1}\rangle $
is a good sequence so that
![]() $\Gamma _{n - 1}$
is not
$\Gamma _{n - 1}$
is not
![]() $\mu ^{\omega _1}_{\omega _1}$
-almost everywhere the constant
$\mu ^{\omega _1}_{\omega _1}$
-almost everywhere the constant
![]() $0$
function, then there is a
$0$
function, then there is a
![]() $C \subseteq D$
and a function
$C \subseteq D$
and a function
![]() $\Gamma _n$
so that
$\Gamma _n$
so that
![]() $\langle C, \Gamma _0,...,\Gamma _{n - 1},\Gamma _n\rangle $
is a good sequence.
$\langle C, \Gamma _0,...,\Gamma _{n - 1},\Gamma _n\rangle $
is a good sequence.
Proof. It will be shown by induction on the length
![]() $n \geq 1$
of the good sequence. Suppose
$n \geq 1$
of the good sequence. Suppose
![]() $\langle D, \Gamma _0\rangle $
is a good sequence so that
$\langle D, \Gamma _0\rangle $
is a good sequence so that
![]() $\Gamma _0$
is not
$\Gamma _0$
is not
![]() $\mu ^{\omega _1}_{\omega _1}$
-almost everywhere constantly
$\mu ^{\omega _1}_{\omega _1}$
-almost everywhere constantly
![]() $0$
. Depending on whether for
$0$
. Depending on whether for
![]() $\mu ^{\omega _1}_{\omega _1}$
-almost all f,
$\mu ^{\omega _1}_{\omega _1}$
-almost all f,
![]() $\Gamma _0(f)$
is a successor ordinal, a limit ordinal which is not a closure point of f or a closure point of f, let
$\Gamma _0(f)$
is a successor ordinal, a limit ordinal which is not a closure point of f or a closure point of f, let
![]() $C \subseteq D$
and
$C \subseteq D$
and
![]() $\Gamma _1 = \Gamma ^{\Gamma _0}$
be given by Lemma 6.10, Lemma 6.11 or Lemma 6.15.
$\Gamma _1 = \Gamma ^{\Gamma _0}$
be given by Lemma 6.10, Lemma 6.11 or Lemma 6.15.
![]() $\langle C,\Gamma _0,\Gamma _1\rangle $
is the desired extension.
$\langle C,\Gamma _0,\Gamma _1\rangle $
is the desired extension.
Now, suppose that
![]() $n> 1$
and that any length
$n> 1$
and that any length
![]() $n - 1$
good sequence where the last function is not
$n - 1$
good sequence where the last function is not
![]() $\mu ^{\omega _1}_{\omega _1}$
-almost everywhere constantly
$\mu ^{\omega _1}_{\omega _1}$
-almost everywhere constantly
![]() $0$
can be extended. Let
$0$
can be extended. Let
![]() $\langle D, \Gamma _0,...,\Gamma _{n - 1}\rangle $
be a good sequence of length n with
$\langle D, \Gamma _0,...,\Gamma _{n - 1}\rangle $
be a good sequence of length n with
![]() $\Gamma _{n - 1}$
not
$\Gamma _{n - 1}$
not
![]() $\mu ^{\omega _1}_{\omega _1}$
-almost everywhere constantly
$\mu ^{\omega _1}_{\omega _1}$
-almost everywhere constantly
![]() $0$
. The restriction
$0$
. The restriction
![]() $\langle D,\Gamma _1,...,\Gamma _{n - 1}\rangle $
is a length
$\langle D,\Gamma _1,...,\Gamma _{n - 1}\rangle $
is a length
![]() $n - 1$
good sequence. Applying the induction hypothesis to this sequence, there is a
$n - 1$
good sequence. Applying the induction hypothesis to this sequence, there is a
![]() $D_0 \subseteq D$
and a function
$D_0 \subseteq D$
and a function
![]() $\Gamma $
so that
$\Gamma $
so that
![]() $\langle D_0,\Gamma _1,,...,\Gamma _{n - 1},\Gamma \rangle $
is a length n good sequence and by applying Fact 6.9 to
$\langle D_0,\Gamma _1,,...,\Gamma _{n - 1},\Gamma \rangle $
is a length n good sequence and by applying Fact 6.9 to
![]() $\Gamma $
, one may also assume that for all
$\Gamma $
, one may also assume that for all
![]() $f \in [D_0]^{\omega _1}_*$
and
$f \in [D_0]^{\omega _1}_*$
and
![]() $\alpha < {\omega _1}$
, if
$\alpha < {\omega _1}$
, if
![]() $\Gamma (f) < f(\alpha )$
, then
$\Gamma (f) < f(\alpha )$
, then
![]() $f \upharpoonright \alpha $
is a continuity point for
$f \upharpoonright \alpha $
is a continuity point for
![]() $\Gamma $
relative to
$\Gamma $
relative to
![]() $D_0$
.
$D_0$
.
(Case 1) For all
![]() $f \in [D_0]^{\omega _1}_*$
,
$f \in [D_0]^{\omega _1}_*$
,
![]() ${\mathrm {ot}}(\{\alpha : \Gamma (f) \leq \alpha < \Gamma _{n - 1}(f)\}) = 1$
.
${\mathrm {ot}}(\{\alpha : \Gamma (f) \leq \alpha < \Gamma _{n - 1}(f)\}) = 1$
.
Setting
![]() $C = D_0$
and
$C = D_0$
and
![]() $\Gamma _n = \Gamma $
,
$\Gamma _n = \Gamma $
,
![]() $\langle C,\Gamma _0,...,\Gamma _{n - 1},\Gamma _n\rangle $
is the desired extension.
$\langle C,\Gamma _0,...,\Gamma _{n - 1},\Gamma _n\rangle $
is the desired extension.
(Case 2) For all
![]() $f \in [D_0]^{\omega _1}_*$
,
$f \in [D_0]^{\omega _1}_*$
,
![]() ${\mathrm {ot}}\{(\alpha : \Gamma (f) \leq \alpha < \Gamma _{n - 1}(f)\})$
is an indecomposable ordinal.
${\mathrm {ot}}\{(\alpha : \Gamma (f) \leq \alpha < \Gamma _{n - 1}(f)\})$
is an indecomposable ordinal.
For all
![]() $\beta $
such that
$\beta $
such that
![]() $\Gamma (f) \leq \beta < \Gamma _{n - 1}(f)$
, let
$\Gamma (f) \leq \beta < \Gamma _{n - 1}(f)$
, let
Let
![]() $\mathfrak {E}^\beta _f = \{\Gamma _0(g) : g \in T_f^\beta \}$
. Let
$\mathfrak {E}^\beta _f = \{\Gamma _0(g) : g \in T_f^\beta \}$
. Let
![]() $\Lambda (f,\beta ) = \sup (\mathfrak {E}_f^{\beta })$
which is an ordinal less than
$\Lambda (f,\beta ) = \sup (\mathfrak {E}_f^{\beta })$
which is an ordinal less than
![]() ${\omega _1}$
by Fact 6.14 since
${\omega _1}$
by Fact 6.14 since
![]() $T^f_\beta \subseteq A^{\Gamma _0,0}_f$
and hence
$T^f_\beta \subseteq A^{\Gamma _0,0}_f$
and hence
![]() $\mathfrak {E}^\beta _f \subseteq \mathfrak {B}^{\Gamma _0,0}_f$
(recall that
$\mathfrak {E}^\beta _f \subseteq \mathfrak {B}^{\Gamma _0,0}_f$
(recall that
![]() $A^{\Gamma _0,0}_f$
and
$A^{\Gamma _0,0}_f$
and
![]() $\mathfrak {B}^{\Gamma _0,0}_f$
were defined in Definition 6.13). Note that if
$\mathfrak {B}^{\Gamma _0,0}_f$
were defined in Definition 6.13). Note that if
![]() $\Gamma (f) \leq \beta _0 \leq \beta _1 < \Gamma _{n - 1}(f)$
, then
$\Gamma (f) \leq \beta _0 \leq \beta _1 < \Gamma _{n - 1}(f)$
, then
![]() $\Lambda (f,\beta _1) \leq \Lambda (f,\beta _0)$
. Let
$\Lambda (f,\beta _1) \leq \Lambda (f,\beta _0)$
. Let
![]() $Z_f = \{\Lambda (f,\beta ) : \Gamma (f) \leq \beta < \Gamma _{n - 1}(f)\}$
. Define
$Z_f = \{\Lambda (f,\beta ) : \Gamma (f) \leq \beta < \Gamma _{n - 1}(f)\}$
. Define
![]() $\Gamma _n : [D_0]^{\omega _1}_* \rightarrow {\omega _1}$
by
$\Gamma _n : [D_0]^{\omega _1}_* \rightarrow {\omega _1}$
by
![]() $\Gamma _n(f) = \min \{\beta : \Gamma (f) \leq \beta < \Gamma _{n - 1}(f) \wedge \min (Z_f) = \Lambda (f,\beta )\}$
. Define
$\Gamma _n(f) = \min \{\beta : \Gamma (f) \leq \beta < \Gamma _{n - 1}(f) \wedge \min (Z_f) = \Lambda (f,\beta )\}$
. Define
![]() $\Sigma : [D_0]^{\omega _1}_* \rightarrow {\omega _1}$
by
$\Sigma : [D_0]^{\omega _1}_* \rightarrow {\omega _1}$
by
![]() $\Sigma (f) = \Lambda (f,\Gamma _n(f))$
. The main property is that for all
$\Sigma (f) = \Lambda (f,\Gamma _n(f))$
. The main property is that for all
![]() $\beta $
with
$\beta $
with
![]() $\Gamma _n(f) \leq \beta < \Gamma _{n - 1}(f)$
,
$\Gamma _n(f) \leq \beta < \Gamma _{n - 1}(f)$
,
![]() $\Lambda (f,\beta ) = \Lambda (f,\Gamma _n(f)) = \Sigma (f)$
. Applying Fact 6.12 to
$\Lambda (f,\beta ) = \Lambda (f,\Gamma _n(f)) = \Sigma (f)$
. Applying Fact 6.12 to
![]() $\Sigma $
,
$\Sigma $
,
![]() $\Gamma _n$
and
$\Gamma _n$
and
![]() $\Gamma _0$
, there is a club
$\Gamma _0$
, there is a club
![]() $D_1 \subseteq D_0$
so that
$D_1 \subseteq D_0$
so that
![]() $\Sigma $
,
$\Sigma $
,
![]() $\Gamma _n$
and
$\Gamma _n$
and
![]() $\Gamma _0$
are subsequence monotonic on
$\Gamma _0$
are subsequence monotonic on
![]() $D_1$
.
$D_1$
.
Claim 1: For all
![]() $f \in [D_1]^{\omega _1}_*$
, if
$f \in [D_1]^{\omega _1}_*$
, if
![]() $g \in [D_1]^{\omega _1}_*$
has the property that
$g \in [D_1]^{\omega _1}_*$
has the property that
![]() $g \sqsubseteq f$
,
$g \sqsubseteq f$
,
![]() $\mathfrak {C}_g = \mathfrak {C}_f$
, for all
$\mathfrak {C}_g = \mathfrak {C}_f$
, for all
![]() $1 \leq i \leq n - 1$
,
$1 \leq i \leq n - 1$
,
![]() $\sup (g \upharpoonright \Gamma _i(f)) = \sup (f \upharpoonright \Gamma _i(f))$
and
$\sup (g \upharpoonright \Gamma _i(f)) = \sup (f \upharpoonright \Gamma _i(f))$
and
![]() $f \upharpoonright \Gamma _n(f) = g \upharpoonright \Gamma _n(f)$
, then
$f \upharpoonright \Gamma _n(f) = g \upharpoonright \Gamma _n(f)$
, then
![]() $\Sigma (f) = \Sigma (g)$
and
$\Sigma (f) = \Sigma (g)$
and
![]() $\Gamma _n(f) = \Gamma _n(g)$
.
$\Gamma _n(f) = \Gamma _n(g)$
.
To see Claim 1: Since
![]() $g \sqsubseteq f$
, subsequence monotonicity implies that
$g \sqsubseteq f$
, subsequence monotonicity implies that
![]() $\Gamma _n(f) \leq \Gamma _n(g)$
. Since
$\Gamma _n(f) \leq \Gamma _n(g)$
. Since
![]() $\Gamma (f) \leq \Gamma _n(f)$
and
$\Gamma (f) \leq \Gamma _n(f)$
and
![]() $\langle D_0, \Gamma _1,...,\Gamma _{n - 1}, \Gamma \rangle $
is a good sequence, one has by Definition 6.16 condition (3) that for all
$\langle D_0, \Gamma _1,...,\Gamma _{n - 1}, \Gamma \rangle $
is a good sequence, one has by Definition 6.16 condition (3) that for all
![]() $1 \leq i \leq n - 1$
,
$1 \leq i \leq n - 1$
,
![]() $\Gamma _i(f) = \Gamma _i(g)$
. Hence, one has that
$\Gamma _i(f) = \Gamma _i(g)$
. Hence, one has that
![]() $T^{\Gamma _n(g)}_g \subseteq T^{\Gamma _n(f)}_f$
and hence
$T^{\Gamma _n(g)}_g \subseteq T^{\Gamma _n(f)}_f$
and hence
![]() $\Sigma (g) \leq \Sigma (f)$
. However, by subsequence monotonocity, one has
$\Sigma (g) \leq \Sigma (f)$
. However, by subsequence monotonocity, one has
![]() $\Sigma (f) \leq \Sigma (g)$
. Hence,
$\Sigma (f) \leq \Sigma (g)$
. Hence,
![]() $\Sigma (f) = \Sigma (g)$
. Suppose for sake of contradiction that
$\Sigma (f) = \Sigma (g)$
. Suppose for sake of contradiction that
![]() $\Gamma _n(f) < \Gamma _n(g)$
. Since
$\Gamma _n(f) < \Gamma _n(g)$
. Since
![]() $\Gamma $
satisfies the fine continuity property of Fact 6.9 relative to
$\Gamma $
satisfies the fine continuity property of Fact 6.9 relative to
![]() $D_0$
,
$D_0$
,
![]() $\Gamma (g) = \Gamma (f)$
. Now, since
$\Gamma (g) = \Gamma (f)$
. Now, since
![]() $\Gamma (g) = \Gamma (f) < \Gamma _n(f) < \Gamma _n(g)$
, the definition of
$\Gamma (g) = \Gamma (f) < \Gamma _n(f) < \Gamma _n(g)$
, the definition of
![]() $\Gamma _n(g)$
implies there is an h with
$\Gamma _n(g)$
implies there is an h with
![]() $\mathfrak {C}_h = \mathfrak {C}_g$
,
$\mathfrak {C}_h = \mathfrak {C}_g$
,
![]() $h \upharpoonright \Gamma _n(f) = g \upharpoonright \Gamma _n(f) = f \upharpoonright \Gamma _n(f)$
, for all
$h \upharpoonright \Gamma _n(f) = g \upharpoonright \Gamma _n(f) = f \upharpoonright \Gamma _n(f)$
, for all
![]() $1 \leq i \leq n - 1$
,
$1 \leq i \leq n - 1$
,
![]() $\sup (h \upharpoonright \Gamma _i(f)) = \sup (g \upharpoonright \Gamma _i(f)) = \sup (f \upharpoonright \Gamma _i(h))$
and
$\sup (h \upharpoonright \Gamma _i(f)) = \sup (g \upharpoonright \Gamma _i(f)) = \sup (f \upharpoonright \Gamma _i(h))$
and
![]() $\Gamma _0(h)> \Sigma (g) = \Sigma (f)$
. However,
$\Gamma _0(h)> \Sigma (g) = \Sigma (f)$
. However,
![]() $h \in T^{\Gamma _n(f)}_f$
and thus
$h \in T^{\Gamma _n(f)}_f$
and thus
![]() $\Lambda (f,\Gamma (f)) \geq \Gamma _0(h)> \Sigma (f) = \Lambda (f,\Gamma (f))$
which is a contradiction. This shows that one must have
$\Lambda (f,\Gamma (f)) \geq \Gamma _0(h)> \Sigma (f) = \Lambda (f,\Gamma (f))$
which is a contradiction. This shows that one must have
![]() $\Gamma _n(f) = \Gamma _n(g)$
. The proof of Claim 1 is complete.
$\Gamma _n(f) = \Gamma _n(g)$
. The proof of Claim 1 is complete.
Define
![]() $P : [D_1]^{\omega _1}_* \rightarrow 2$
by
$P : [D_1]^{\omega _1}_* \rightarrow 2$
by
![]() $P(f) = 0$
if and only if
$P(f) = 0$
if and only if
![]() $\Gamma _0(f) = \Sigma (f)$
. By
$\Gamma _0(f) = \Sigma (f)$
. By
![]() ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
, there is a club
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
, there is a club
![]() $D_2 \subseteq D_1$
which is homogeneous for P.
$D_2 \subseteq D_1$
which is homogeneous for P.
Claim 2:
![]() $D_2$
is homogeneous for P taking value
$D_2$
is homogeneous for P taking value
![]() $0$
.
$0$
.
First, if there is an
![]() $f \in [D_2]^{\omega _1}_*$
such that
$f \in [D_2]^{\omega _1}_*$
such that
![]() $\Sigma (f)$
is a successor, then the supremum in the definition of
$\Sigma (f)$
is a successor, then the supremum in the definition of
![]() $\Sigma (f) = \Lambda (f,\Gamma _n(f))$
is obtained. That is, there is a
$\Sigma (f) = \Lambda (f,\Gamma _n(f))$
is obtained. That is, there is a
![]() $g \sqsubseteq f$
with
$g \sqsubseteq f$
with
![]() $\mathfrak {C}_g = \mathfrak {C}_f$
,
$\mathfrak {C}_g = \mathfrak {C}_f$
,
![]() $g \upharpoonright \Gamma _n(f) = f \upharpoonright \Gamma _n(f)$
, for all
$g \upharpoonright \Gamma _n(f) = f \upharpoonright \Gamma _n(f)$
, for all
![]() $1 \leq i \leq n - 1$
,
$1 \leq i \leq n - 1$
,
![]() $\sup (g \upharpoonright \Gamma _i(f)) = \sup (f \upharpoonright \Gamma _i(f))$
and
$\sup (g \upharpoonright \Gamma _i(f)) = \sup (f \upharpoonright \Gamma _i(f))$
and
![]() $\Gamma _0(g) = \Sigma (f)$
. By Claim 1,
$\Gamma _0(g) = \Sigma (f)$
. By Claim 1,
![]() $\Sigma (g) = \Sigma (f)$
. Thus,
$\Sigma (g) = \Sigma (f)$
. Thus,
![]() $P(g) = 0$
and since
$P(g) = 0$
and since
![]() $g \in [D_2]^{\omega _1}_*$
,
$g \in [D_2]^{\omega _1}_*$
,
![]() $D_2$
must be homogeneous for C taking value
$D_2$
must be homogeneous for C taking value
![]() $0$
.
$0$
.
Thus, assume that for all
![]() $f \in [D_2]^{\omega _1}_*$
,
$f \in [D_2]^{\omega _1}_*$
,
![]() $\Sigma (f)$
is a limit ordinal. Pick any
$\Sigma (f)$
is a limit ordinal. Pick any
![]() $f \in [D_2]^{\omega _1}_*$
. Let
$f \in [D_2]^{\omega _1}_*$
. Let
![]() $\rho : \omega \rightarrow \Gamma _{n - 1}(f)$
be an increasing cofinal sequence through
$\rho : \omega \rightarrow \Gamma _{n - 1}(f)$
be an increasing cofinal sequence through
![]() $\Gamma _{n - 1}(f)$
with
$\Gamma _{n - 1}(f)$
with
![]() $\rho (0) = \Gamma _n(f)$
. Let
$\rho (0) = \Gamma _n(f)$
. Let
![]() $\tau : \omega \rightarrow \Sigma (f)$
be an increasing sequence through
$\tau : \omega \rightarrow \Sigma (f)$
be an increasing sequence through
![]() $\Sigma (f)$
. One will construct a sequence
$\Sigma (f)$
. One will construct a sequence
![]() $\langle f_k : k \in \omega \rangle $
with the following properties:
$\langle f_k : k \in \omega \rangle $
with the following properties:
-
1.
 $f_0 = f$
. For all
$f_0 = f$
. For all
 $k \in \omega $
,
$k \in \omega $
,
 $f_k \in [D_2]^{\omega _1}_*$
,
$f_k \in [D_2]^{\omega _1}_*$
,
 $f_{k + 1} \sqsubseteq f_k$
and
$f_{k + 1} \sqsubseteq f_k$
and
 $\mathfrak {C}_{f_{k + 1}} = \mathfrak {C}_{f_k} = \mathfrak {C}_{f}$
.
$\mathfrak {C}_{f_{k + 1}} = \mathfrak {C}_{f_k} = \mathfrak {C}_{f}$
. -
2. For all
 $k \in \omega $
, for all
$k \in \omega $
, for all
 $\alpha \geq \Gamma _{n - 1}(f)$
,
$\alpha \geq \Gamma _{n - 1}(f)$
,
 $f_k(\alpha ) = f(\alpha )$
.
$f_k(\alpha ) = f(\alpha )$
. -
3. For all
 $k \in \omega $
,
$k \in \omega $
,
 $f_{k + 1} \upharpoonright \rho (k) = f_k \upharpoonright \rho (k)$
.
$f_{k + 1} \upharpoonright \rho (k) = f_k \upharpoonright \rho (k)$
. -
4. For all
 $k \in \omega $
,
$k \in \omega $
,
 $\tau (k) < \Gamma _0(f_{k + 1}) \leq \Sigma (f)$
.
$\tau (k) < \Gamma _0(f_{k + 1}) \leq \Sigma (f)$
.
Let
![]() $f_0 = f$
. Suppose
$f_0 = f$
. Suppose
![]() $f_k$
has been constructed satisfying the above properties. Claim 1 implies that
$f_k$
has been constructed satisfying the above properties. Claim 1 implies that
![]() $\Sigma (f_k) = \Sigma (f)$
and
$\Sigma (f_k) = \Sigma (f)$
and
![]() $\Gamma _n(f_k) = \Gamma _n(f)$
. The main property above and the fact that
$\Gamma _n(f_k) = \Gamma _n(f)$
. The main property above and the fact that
![]() $\rho (k) \geq \rho (0) = \Gamma _n(f_k)$
give that
$\rho (k) \geq \rho (0) = \Gamma _n(f_k)$
give that
![]() $\Lambda (f_k,\rho (k)) = \Lambda (f_k,\Gamma _n(f_k)) = \Sigma (f_k) = \Sigma (f)$
. Thus, there is an
$\Lambda (f_k,\rho (k)) = \Lambda (f_k,\Gamma _n(f_k)) = \Sigma (f_k) = \Sigma (f)$
. Thus, there is an
![]() $h \sqsubseteq f_k$
with
$h \sqsubseteq f_k$
with
![]() $\mathfrak {C}_h = \mathfrak {C}_{f_k}$
,
$\mathfrak {C}_h = \mathfrak {C}_{f_k}$
,
![]() $h \upharpoonright \rho (k) = f_k \upharpoonright \rho (k)$
, for all
$h \upharpoonright \rho (k) = f_k \upharpoonright \rho (k)$
, for all
![]() $1 \leq i \leq n - 1$
,
$1 \leq i \leq n - 1$
,
![]() $\sup (h \upharpoonright \Gamma _i(f_k)) = \sup (f_k \upharpoonright \Gamma _i(f_k))$
and
$\sup (h \upharpoonright \Gamma _i(f_k)) = \sup (f_k \upharpoonright \Gamma _i(f_k))$
and
![]() $\tau (k) < \Gamma _0(h) \leq \Sigma (f_k)$
. Now, define
$\tau (k) < \Gamma _0(h) \leq \Sigma (f_k)$
. Now, define
![]() $f_{k + 1}$
by
$f_{k + 1}$
by
 $$ \begin{align*}f_{k + 1}(\alpha) = \begin{cases} h(\alpha) & \quad \alpha < \Gamma_{n - 1}(f) \\ f(\alpha) & \quad \Gamma_{n - 1}(f) \leq \alpha \end{cases}.\end{align*} $$
$$ \begin{align*}f_{k + 1}(\alpha) = \begin{cases} h(\alpha) & \quad \alpha < \Gamma_{n - 1}(f) \\ f(\alpha) & \quad \Gamma_{n - 1}(f) \leq \alpha \end{cases}.\end{align*} $$
Since
![]() $\langle D_0, \Gamma _1, ..., \Gamma _{n - 1}, \Gamma \rangle $
is a good sequence and
$\langle D_0, \Gamma _1, ..., \Gamma _{n - 1}, \Gamma \rangle $
is a good sequence and
![]() $h \upharpoonright \Gamma (f) = f \upharpoonright \Gamma (f)$
, one has that
$h \upharpoonright \Gamma (f) = f \upharpoonright \Gamma (f)$
, one has that
![]() $\Gamma _i(h) = \Gamma _i(f)$
for all
$\Gamma _i(h) = \Gamma _i(f)$
for all
![]() $1 \leq i \leq n - 1$
. (In particular,
$1 \leq i \leq n - 1$
. (In particular,
![]() $\Gamma _{n - 1}(h) = \Gamma _{n - 1}(f)$
.) Since
$\Gamma _{n - 1}(h) = \Gamma _{n - 1}(f)$
.) Since
![]() $f_{k + 1} \upharpoonright \Gamma _{n - 1}(h) = h \upharpoonright \Gamma _{n - 1}(h)$
, for all
$f_{k + 1} \upharpoonright \Gamma _{n - 1}(h) = h \upharpoonright \Gamma _{n - 1}(h)$
, for all
![]() $i < n - 1$
,
$i < n - 1$
,
![]() $\sup (f_{k + 1} \upharpoonright \Gamma _i(h)) = \sup (h \upharpoonright \Gamma _i(h))$
and
$\sup (f_{k + 1} \upharpoonright \Gamma _i(h)) = \sup (h \upharpoonright \Gamma _i(h))$
and
![]() $\langle D, \Gamma _0,...,\Gamma _{n - 1}\rangle $
is a good sequence, one has that
$\langle D, \Gamma _0,...,\Gamma _{n - 1}\rangle $
is a good sequence, one has that
![]() $\Gamma _0(f_{k + 1}) = \Gamma _0(h)> \tau (k)$
. Thus,
$\Gamma _0(f_{k + 1}) = \Gamma _0(h)> \tau (k)$
. Thus,
![]() $f_{k + 1}$
satisfies the required properties.
$f_{k + 1}$
satisfies the required properties.
By
![]() $\mathsf {DC}$
, there is a sequence
$\mathsf {DC}$
, there is a sequence
![]() $\langle f_k : k \in \omega \rangle $
with the desired properties. Define
$\langle f_k : k \in \omega \rangle $
with the desired properties. Define
![]() $f_\omega \in [D_2]^{\omega _1}_*$
by
$f_\omega \in [D_2]^{\omega _1}_*$
by
![]() $f_\omega (\alpha ) = \sup \{f_k(\alpha ) : k < \omega \}$
. Since
$f_\omega (\alpha ) = \sup \{f_k(\alpha ) : k < \omega \}$
. Since
![]() $f_\omega \sqsubseteq f_{k + 1}$
, the subsequence monotonicity of
$f_\omega \sqsubseteq f_{k + 1}$
, the subsequence monotonicity of
![]() $\Gamma _0$
implies that
$\Gamma _0$
implies that
![]() $\tau (k) < \Gamma _0(f_{k + 1}) \leq \Gamma _0(f_\omega )$
. Hence,
$\tau (k) < \Gamma _0(f_{k + 1}) \leq \Gamma _0(f_\omega )$
. Hence,
![]() $\Sigma (f) \leq \Gamma _0(f_\omega )$
. Claim 1 implies that
$\Sigma (f) \leq \Gamma _0(f_\omega )$
. Claim 1 implies that
![]() $\Sigma (f) = \Sigma (f_\omega )$
. Therefore,
$\Sigma (f) = \Sigma (f_\omega )$
. Therefore,
![]() $\Sigma (f_\omega ) \leq \Gamma _0(f_\omega )$
. Since
$\Sigma (f_\omega ) \leq \Gamma _0(f_\omega )$
. Since
![]() $\Gamma _0(f_\omega ) \leq \Sigma (f_\omega )$
by definition, one has shown that
$\Gamma _0(f_\omega ) \leq \Sigma (f_\omega )$
by definition, one has shown that
![]() $\Gamma _0(f_\omega ) = \Sigma (f_\omega )$
. Since
$\Gamma _0(f_\omega ) = \Sigma (f_\omega )$
. Since
![]() $P(f_\omega ) = 0$
and
$P(f_\omega ) = 0$
and
![]() $f_\omega \in [D_2]^{\omega _1}_*$
, one must have that
$f_\omega \in [D_2]^{\omega _1}_*$
, one must have that
![]() $D_2$
is homogeneous for P taking value
$D_2$
is homogeneous for P taking value
![]() $0$
. This completes the proof of Claim 2.
$0$
. This completes the proof of Claim 2.
Claim 2 implies that
![]() $\langle C, \Gamma _0, ..., \Gamma _{n - 1}, \Gamma _n\rangle $
is a good sequence where
$\langle C, \Gamma _0, ..., \Gamma _{n - 1}, \Gamma _n\rangle $
is a good sequence where
![]() $C = D_2$
. This completes the argument.
$C = D_2$
. This completes the argument.
Theorem 6.18. Assume
![]() $\mathsf {DC}$
,
$\mathsf {DC}$
,
![]() ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
and that the almost everywhere short length club uniformization principle holds at
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
and that the almost everywhere short length club uniformization principle holds at
![]() ${\omega _1}$
. Let
${\omega _1}$
. Let
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
. There is a club
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
. There is a club
![]() $C \subseteq {\omega _1}$
and finitely many functions
$C \subseteq {\omega _1}$
and finitely many functions
![]() $\Upsilon _0,...,\Upsilon _{n - 1}$
so that for all
$\Upsilon _0,...,\Upsilon _{n - 1}$
so that for all
![]() $f \in [C]^{\omega _1}_*$
, for all
$f \in [C]^{\omega _1}_*$
, for all
![]() $g \in [C]^{\omega _1}_*$
, if
$g \in [C]^{\omega _1}_*$
, if
![]() $\mathfrak {C}_g = \mathfrak {C}_f$
and for all
$\mathfrak {C}_g = \mathfrak {C}_f$
and for all
![]() $i < n$
,
$i < n$
,
![]() $\sup (g \upharpoonright \Upsilon _i(f)) = \sup (f \upharpoonright \Upsilon _i(f))$
, then
$\sup (g \upharpoonright \Upsilon _i(f)) = \sup (f \upharpoonright \Upsilon _i(f))$
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
Proof. Fix
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
. Let
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
. Let
![]() $\mathcal {T}$
consists of good sequences
$\mathcal {T}$
consists of good sequences
![]() $\langle C, \Gamma _0, ..., \Gamma _{n - 1}\rangle $
with
$\langle C, \Gamma _0, ..., \Gamma _{n - 1}\rangle $
with
![]() $\Gamma _0(f) = \Phi (f)$
for all
$\Gamma _0(f) = \Phi (f)$
for all
![]() $f \in C$
. Define an ordering on
$f \in C$
. Define an ordering on
![]() $\prec $
on
$\prec $
on
![]() $\mathcal {T}$
by
$\mathcal {T}$
by
![]() $\langle D, \Psi _0, ..., \Psi _{m - 1}\rangle \prec \langle C, \Gamma _0, ..., \Gamma _{n - 1}\rangle $
if and only if
$\langle D, \Psi _0, ..., \Psi _{m - 1}\rangle \prec \langle C, \Gamma _0, ..., \Gamma _{n - 1}\rangle $
if and only if
![]() $n < m$
,
$n < m$
,
![]() $D \subseteq C$
and for all
$D \subseteq C$
and for all
![]() $f \in [D]^{\omega _1}_*$
, for all
$f \in [D]^{\omega _1}_*$
, for all
![]() $i < n$
,
$i < n$
,
![]() $\Gamma _i(f) = \Psi _i(f)$
.
$\Gamma _i(f) = \Psi _i(f)$
.
Claim 1: There is a
![]() $\langle C, \Gamma _0, ..., \Gamma _{n - 1}\rangle \in \mathcal {T}$
so that
$\langle C, \Gamma _0, ..., \Gamma _{n - 1}\rangle \in \mathcal {T}$
so that
![]() $\Gamma _{n - 1}$
is
$\Gamma _{n - 1}$
is
![]() $\mu ^{\omega _1}_{\omega _1}$
-almost everywhere constantly
$\mu ^{\omega _1}_{\omega _1}$
-almost everywhere constantly
![]() $0$
.
$0$
.
To see Claim 1: Suppose not. Then Lemma 6.17 implies that
![]() $(\mathcal {T},\prec )$
is a tree with no dead branches.
$(\mathcal {T},\prec )$
is a tree with no dead branches.
![]() $\mathsf {DC}$
implies there is an infinite
$\mathsf {DC}$
implies there is an infinite
![]() $\prec $
-descending sequence
$\prec $
-descending sequence
![]() $\langle \langle C_j, \Gamma _0^j, ..., \Gamma _{j}^j \rangle : j \in \omega \rangle $
. Let
$\langle \langle C_j, \Gamma _0^j, ..., \Gamma _{j}^j \rangle : j \in \omega \rangle $
. Let
![]() $C = \bigcap _{j < \omega } C_j$
. Pick
$C = \bigcap _{j < \omega } C_j$
. Pick
![]() $f \in [C]^{\omega _1}_*$
. Then
$f \in [C]^{\omega _1}_*$
. Then
![]() $\langle \Gamma ^i_i(f) : i \in \omega \rangle $
is an infinite descending sequence of ordinals. Contradiction. This completes the proof of Claim 1.
$\langle \Gamma ^i_i(f) : i \in \omega \rangle $
is an infinite descending sequence of ordinals. Contradiction. This completes the proof of Claim 1.
Let
![]() $\langle C,\Gamma _0, ..., \Gamma _{n - 1}\rangle $
be a good sequence so that for all
$\langle C,\Gamma _0, ..., \Gamma _{n - 1}\rangle $
be a good sequence so that for all
![]() $f \in [C]^{\omega _1}_*$
,
$f \in [C]^{\omega _1}_*$
,
![]() $\Gamma _0(f) = \Phi (f)$
and
$\Gamma _0(f) = \Phi (f)$
and
![]() $\Gamma _{n - 1}(f) = 0$
. Now, suppose
$\Gamma _{n - 1}(f) = 0$
. Now, suppose
![]() $f,g \in [C]^{\omega _1}_*$
with the property that
$f,g \in [C]^{\omega _1}_*$
with the property that
![]() $\mathfrak {C}_g = \mathfrak {C}_f$
and for all
$\mathfrak {C}_g = \mathfrak {C}_f$
and for all
![]() $0 < i < n$
,
$0 < i < n$
,
![]() $\sup (g \upharpoonright \Gamma _i(f)) = \sup (f \upharpoonright \Gamma _i(f))$
. Let
$\sup (g \upharpoonright \Gamma _i(f)) = \sup (f \upharpoonright \Gamma _i(f))$
. Let
![]() $h : {\omega _1} \rightarrow {\omega _1}$
be defined by
$h : {\omega _1} \rightarrow {\omega _1}$
be defined by
![]() $h(0) = \min \{f[{\omega _1}] \cup g[{\omega _1}]\}$
. Suppose
$h(0) = \min \{f[{\omega _1}] \cup g[{\omega _1}]\}$
. Suppose
![]() $h \upharpoonright \alpha $
has been defined. Let
$h \upharpoonright \alpha $
has been defined. Let
![]() $h(\alpha )$
be the least element of
$h(\alpha )$
be the least element of
![]() $f[{\omega _1}] \cup g[{\omega _1}]$
greater than
$f[{\omega _1}] \cup g[{\omega _1}]$
greater than
![]() $\sup (h \upharpoonright \alpha )$
. Note that
$\sup (h \upharpoonright \alpha )$
. Note that
![]() $h \in [C]^{\omega _1}_*$
, that is, is increasing, discontinuous, and has uniform cofinality
$h \in [C]^{\omega _1}_*$
, that is, is increasing, discontinuous, and has uniform cofinality
![]() $\omega $
. For each
$\omega $
. For each
![]() $0 < i < n - 1$
, let
$0 < i < n - 1$
, let
![]() $K_i = \{\alpha : \Gamma _{i + 1}(f) \leq \alpha < \Gamma _i(f)\}$
and
$K_i = \{\alpha : \Gamma _{i + 1}(f) \leq \alpha < \Gamma _i(f)\}$
and
![]() $\nu _i = {\mathrm {ot}}(K_i)$
which is either an additively indecomposable ordinal or
$\nu _i = {\mathrm {ot}}(K_i)$
which is either an additively indecomposable ordinal or
![]() $1$
. Therefore, for each
$1$
. Therefore, for each
![]() $0 < i < n - 1$
,
$0 < i < n - 1$
,
![]() ${\mathrm {ot}}(\{f(\alpha ) : \alpha \in K_i\}) = {\mathrm {ot}}(\{g(\alpha ) : \alpha \in K_i\}) = {\mathrm {ot}}(\{f(\alpha ),g(\alpha ) : \alpha \in K_i\}) = \nu _i$
since
${\mathrm {ot}}(\{f(\alpha ) : \alpha \in K_i\}) = {\mathrm {ot}}(\{g(\alpha ) : \alpha \in K_i\}) = {\mathrm {ot}}(\{f(\alpha ),g(\alpha ) : \alpha \in K_i\}) = \nu _i$
since
![]() $\nu _i$
is an additively indecomposable ordinal or
$\nu _i$
is an additively indecomposable ordinal or
![]() $1$
. Hence, for each
$1$
. Hence, for each
![]() $0 < i < n$
,
$0 < i < n$
,
![]() $\sup (f \upharpoonright \Gamma _i(f)) = \sup (g \upharpoonright \Gamma _i(f)) = \sup (h \upharpoonright \Gamma _i(f))$
,
$\sup (f \upharpoonright \Gamma _i(f)) = \sup (g \upharpoonright \Gamma _i(f)) = \sup (h \upharpoonright \Gamma _i(f))$
,
![]() $\mathfrak {C}_f = \mathfrak {C}_g =\mathfrak {C}_h$
,
$\mathfrak {C}_f = \mathfrak {C}_g =\mathfrak {C}_h$
,
![]() $f \sqsubseteq h$
and
$f \sqsubseteq h$
and
![]() $g \sqsubseteq h$
.
$g \sqsubseteq h$
.
Claim 2: For all
![]() $k < n$
,
$k < n$
,
![]() $\Gamma _{n - 1 - k}(h) = \Gamma _{n - 1 - k}(f) = \Gamma _{n - 1 - k}(g)$
.
$\Gamma _{n - 1 - k}(h) = \Gamma _{n - 1 - k}(f) = \Gamma _{n - 1 - k}(g)$
.
To see Claim 2: This will be shown by induction on k. If
![]() $k = 0$
, then
$k = 0$
, then
![]() $\Gamma _{n - 1}(h) = \Gamma _{n - 1}(f) = \Gamma _{n - 1}(h) = 0$
. Now, suppose
$\Gamma _{n - 1}(h) = \Gamma _{n - 1}(f) = \Gamma _{n - 1}(h) = 0$
. Now, suppose
![]() $k < n$
and for all
$k < n$
and for all
![]() $j < k$
, it has been shown that
$j < k$
, it has been shown that
![]() $\Gamma _{n - 1 - j}(h) = \Gamma _{n - 1 - j}(f) = \Gamma _{n - 1 - j}(g)$
. Since it was shown above that
$\Gamma _{n - 1 - j}(h) = \Gamma _{n - 1 - j}(f) = \Gamma _{n - 1 - j}(g)$
. Since it was shown above that
![]() $f \sqsubseteq h$
,
$f \sqsubseteq h$
,
![]() $\mathfrak {C}_f = \mathfrak {C}_h$
,
$\mathfrak {C}_f = \mathfrak {C}_h$
,
![]() $\sup (f \upharpoonright \Gamma _{n - 1 - j}(h)) = \sup (f \upharpoonright \Gamma _{n - 1 - j}(f)) = \sup (h \upharpoonright \Gamma _{n - 1 - j}(f)) = \sup (h \upharpoonright \Gamma _{n - 1 - j}(h))$
for each
$\sup (f \upharpoonright \Gamma _{n - 1 - j}(h)) = \sup (f \upharpoonright \Gamma _{n - 1 - j}(f)) = \sup (h \upharpoonright \Gamma _{n - 1 - j}(f)) = \sup (h \upharpoonright \Gamma _{n - 1 - j}(h))$
for each
![]() $j < k$
, Definition 6.16 condition (3) for the pair
$j < k$
, Definition 6.16 condition (3) for the pair
![]() $(f,h)$
at
$(f,h)$
at
![]() $\Gamma _{n - 1 - k}$
implies that
$\Gamma _{n - 1 - k}$
implies that
![]() $\Gamma _{n - 1 - k}(f) = \Gamma _{n - 1 - k}(h)$
. The same argument for the pair
$\Gamma _{n - 1 - k}(f) = \Gamma _{n - 1 - k}(h)$
. The same argument for the pair
![]() $(g,h)$
implies
$(g,h)$
implies
![]() $\Gamma _{n - 1 - k}(g) = \Gamma _{n - 1 - k}(h)$
. This concludes the proof of Claim 2.
$\Gamma _{n - 1 - k}(g) = \Gamma _{n - 1 - k}(h)$
. This concludes the proof of Claim 2.
Applying Claim 2 for
![]() $k = n - 1$
, one has that
$k = n - 1$
, one has that
![]() $\Phi (f) = \Gamma _0(f) = \Gamma _0(h) = \Gamma _0(g) = \Phi (g)$
. For each
$\Phi (f) = \Gamma _0(f) = \Gamma _0(h) = \Gamma _0(g) = \Phi (g)$
. For each
![]() $i < n - 2$
, let
$i < n - 2$
, let
![]() $\Upsilon _i = \Gamma _{i + 1}$
. Then C and the function
$\Upsilon _i = \Gamma _{i + 1}$
. Then C and the function
![]() $\Upsilon _0, ..., \Upsilon _{n - 2}$
are the desired objects. (This just removes
$\Upsilon _0, ..., \Upsilon _{n - 2}$
are the desired objects. (This just removes
![]() $\Gamma _0 = \Phi $
which is redundant.)
$\Gamma _0 = \Phi $
which is redundant.)
Next, one will show that the continuity property expressed in Theorem 6.18 holds under the axiom of determinacy. The following is a consequence of the Moschovakis coding lemma.
Fact 6.19. Assume
![]() $\mathsf {AD}$
.
$\mathsf {AD}$
.
![]() ${\mathscr {P}({\omega _1})} = ({\mathscr {P}({\omega _1})})^{L(\mathbb {R})}$
.
${\mathscr {P}({\omega _1})} = ({\mathscr {P}({\omega _1})})^{L(\mathbb {R})}$
.
The next fact asserts that every function
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
is equal to a function in
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
is equal to a function in
![]() $L(\mathbb {R}) \mu ^{\omega _1}_{\omega _1}$
-almost everywhere.
$L(\mathbb {R}) \mu ^{\omega _1}_{\omega _1}$
-almost everywhere.
Fact 6.20. ([Reference Chan2])
Assume
![]() $\mathsf {AD}$
. Suppose
$\mathsf {AD}$
. Suppose
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
. Then there is a club
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
. Then there is a club
![]() $C \subseteq {\omega _1}$
so that
$C \subseteq {\omega _1}$
so that
![]() $\Phi \upharpoonright [C]^{\omega _1}_* \in L(\mathbb {R})$
.
$\Phi \upharpoonright [C]^{\omega _1}_* \in L(\mathbb {R})$
.
It is not known if
![]() $\mathsf {AD}$
implies
$\mathsf {AD}$
implies
![]() $\mathsf {DC}_{\mathbb {R}}$
; however, Kechris showed that
$\mathsf {DC}_{\mathbb {R}}$
; however, Kechris showed that
![]() $L(\mathbb {R})$
satisfies
$L(\mathbb {R})$
satisfies
![]() $\mathsf {DC}$
.
$\mathsf {DC}$
.
Fact 6.21. ([Reference Kechris11])
Assume
![]() $\mathsf {AD}$
. Then
$\mathsf {AD}$
. Then
![]() $L(\mathbb {R}) \models \mathsf {AD} + \mathsf {DC}$
.
$L(\mathbb {R}) \models \mathsf {AD} + \mathsf {DC}$
.
Theorem 6.22. Assume
![]() $\mathsf {AD}$
. Let
$\mathsf {AD}$
. Let
![]() $\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
. There is a club
$\Phi : [{\omega _1}]^{\omega _1}_* \rightarrow {\omega _1}$
. There is a club
![]() $C \subseteq {\omega _1}$
and finitely many function
$C \subseteq {\omega _1}$
and finitely many function
![]() $\Gamma _0,...,\Gamma _{n - 1}$
so that for all
$\Gamma _0,...,\Gamma _{n - 1}$
so that for all
![]() $f \in [C]^{\omega _1}_*$
, for all
$f \in [C]^{\omega _1}_*$
, for all
![]() $g \in [C]^{\omega _1}_*$
, if
$g \in [C]^{\omega _1}_*$
, if
![]() $\mathfrak {C}_g = \mathfrak {C}_f$
and for all
$\mathfrak {C}_g = \mathfrak {C}_f$
and for all
![]() $i < n$
,
$i < n$
,
![]() $\sup (g \upharpoonright \Gamma _i(f)) = \sup (f \upharpoonright \Gamma _i(f))$
, then
$\sup (g \upharpoonright \Gamma _i(f)) = \sup (f \upharpoonright \Gamma _i(f))$
, then
![]() $\Phi (f) = \Phi (g)$
.
$\Phi (f) = \Phi (g)$
.
Proof. By Fact 6.20, there is a club
![]() $C_0 \subseteq {\omega _1}$
so that
$C_0 \subseteq {\omega _1}$
so that
![]() $\Phi \upharpoonright [C_0]^{\omega _1}_* \in L(\mathbb {R})$
. By Fact 6.21,
$\Phi \upharpoonright [C_0]^{\omega _1}_* \in L(\mathbb {R})$
. By Fact 6.21,
![]() $L(\mathbb {R})$
satisfies
$L(\mathbb {R})$
satisfies
![]() $\mathsf {AD}$
and
$\mathsf {AD}$
and
![]() $\mathsf {DC}$
.
$\mathsf {DC}$
.
![]() $\mathsf {AD}$
implies
$\mathsf {AD}$
implies
![]() ${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
by Fact 2.16. The almost everywhere short length club uniformization for
${\omega _1} \rightarrow _* ({\omega _1})^{\omega _1}_2$
by Fact 2.16. The almost everywhere short length club uniformization for
![]() ${\omega _1}$
holds by Fact 6.5. Fact 6.19 implies
${\omega _1}$
holds by Fact 6.5. Fact 6.19 implies
![]() ${\omega _1} = ({\omega _1})^{L(\mathbb {R})}$
. Theorem 6.18 applied inside
${\omega _1} = ({\omega _1})^{L(\mathbb {R})}$
. Theorem 6.18 applied inside
![]() $L(\mathbb {R})$
for
$L(\mathbb {R})$
for
![]() $\Phi \upharpoonright [C_0]^{\omega _1}_*$
will provide a club
$\Phi \upharpoonright [C_0]^{\omega _1}_*$
will provide a club
![]() $C_1 \subseteq C$
and functions
$C_1 \subseteq C$
and functions
![]() $\Gamma _0, ..., \Gamma _{n - 1}$
which satisfies the required property in
$\Gamma _0, ..., \Gamma _{n - 1}$
which satisfies the required property in
![]() $L(\mathbb {R})$
. Fact 6.19 will imply that these objects continue to have the desired property in the original universe satisfying determinacy.
$L(\mathbb {R})$
. Fact 6.19 will imply that these objects continue to have the desired property in the original universe satisfying determinacy.
Competing interest
The authors have no competing interest to declare.
Financial support
The first author was supported by NSF grant DMS-1703708. The second author was supported by NSF grant DMS-1800323. The third author was supported by NSF grant DMS-1855757 and DMS-1945592.