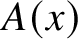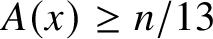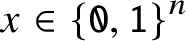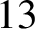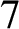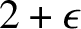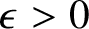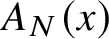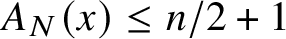1. Introduction
Kolmogorov’s structure function for a word x is intended to provide a statistical explanation for x. We focus here on a computable version, the automatic structure function
![]() $h_x$
. For definiteness, suppose x is a word over the alphabet
$h_x$
. For definiteness, suppose x is a word over the alphabet
![]() $\{\mathtt {0},\mathtt {1}\}$
. By definition,
$\{\mathtt {0},\mathtt {1}\}$
. By definition,
![]() $h_x(m)$
is the minimum number of states of a finite automaton that accepts x and accepts at most
$h_x(m)$
is the minimum number of states of a finite automaton that accepts x and accepts at most
![]() $2^m$
many words of length
$2^m$
many words of length
![]() $\left \lvert x\right \rvert $
. The best explanation for the word x is then an automaton witnessing a value of
$\left \lvert x\right \rvert $
. The best explanation for the word x is then an automaton witnessing a value of
![]() $h_x$
that is unusually low, compared to values of
$h_x$
that is unusually low, compared to values of
![]() $h_y$
for most other words y of the same length. To find such explanations we would like to know the distribution of
$h_y$
for most other words y of the same length. To find such explanations we would like to know the distribution of
![]() $h_x$
for random x. In the present paper we take a step in this direction by studying the case
$h_x$
for random x. In the present paper we take a step in this direction by studying the case
![]() $h_x(0)$
, known as the automatic complexity of x.
$h_x(0)$
, known as the automatic complexity of x.
The automatic complexity of Shallit and Wang [Reference Shallit and Wang9] is the minimal number of states of an automaton accepting only a given word among its equal-length peers. Finding such an automaton is analogous to the protein-folding problem, where one looks for a minimum-energy configuration. The protein-folding problem may be NP-complete [Reference Fraenkel2], depending on how one formalises it as a mathematical problem. For automatic complexity, the computational complexity is not known, but a certain generalisation to equivalence relations gives an NP-complete decision problem [Reference Kjos-Hanssen4].
Here we show (Theorem 18) that automatic complexity has a similar incompressibility phenomenon as that of Kolmogorov complexity for Turing machines, first studied in [Reference Kolmogorov6, Reference Kolmogorov7, Reference Solomonoff11, Reference Solomonoff12].
1.1. Incompressibility
Let C denote Kolmogorov complexity, so that
![]() $C(\sigma )$
is the length of the shortest program, for a fixed universal Turing machine, that outputs
$C(\sigma )$
is the length of the shortest program, for a fixed universal Turing machine, that outputs
![]() $\sigma $
on empty input. Let
$\sigma $
on empty input. Let
![]() $\omega =\{0,1,2,\dotsc \}$
be the set of nonnegative integers and let
$\omega =\{0,1,2,\dotsc \}$
be the set of nonnegative integers and let
![]() $\omega ^{<\omega }=\omega ^*$
be the set of finite words over
$\omega ^{<\omega }=\omega ^*$
be the set of finite words over
![]() $\omega $
.
$\omega $
.
As Solomonoff and Kolmogorov observed, for each n there is a word
![]() $\sigma \in \{\mathtt {0},\mathtt {1}\}^n$
with
$\sigma \in \{\mathtt {0},\mathtt {1}\}^n$
with
![]() $C(\sigma )\ge n$
. Indeed, each word with
$C(\sigma )\ge n$
. Indeed, each word with
![]() $C(\sigma )<n$
uses up a description of length
$C(\sigma )<n$
uses up a description of length
![]() $<n$
, and there are at most
$<n$
, and there are at most
 $\sum _{k=0}^{n-1} 2^k=2^n-1<2^n=\left \lvert \{\mathtt {0},\mathtt {1}\}^n\right \rvert $
of those.
$\sum _{k=0}^{n-1} 2^k=2^n-1<2^n=\left \lvert \{\mathtt {0},\mathtt {1}\}^n\right \rvert $
of those.
Similarly, we have the following:
Lemma 1 Solomonoff, Kolmogorov
For each nonnegative integer n, there are at least
![]() $2^n-\left (2^{n-k}-1\right )$
binary words
$2^n-\left (2^{n-k}-1\right )$
binary words
![]() $\sigma $
of length n such that
$\sigma $
of length n such that
![]() $C(\sigma )\ge n-k$
.
$C(\sigma )\ge n-k$
.
Proof. For each word with
![]() $C(\sigma )< n-k$
, we use up at least one of the at most
$C(\sigma )< n-k$
, we use up at least one of the at most
![]() $2^{n-k}-1$
many possible descriptions of length less than
$2^{n-k}-1$
many possible descriptions of length less than
![]() $n-k$
, leaving at least
$n-k$
, leaving at least
 $$ \begin{align*} \left\lvert\{\mathtt{0},\mathtt{1}\}^n\right\rvert - \left(2^{n-k} - 1\right) \end{align*} $$
$$ \begin{align*} \left\lvert\{\mathtt{0},\mathtt{1}\}^n\right\rvert - \left(2^{n-k} - 1\right) \end{align*} $$
words
![]() $\sigma $
that must have
$\sigma $
that must have
![]() $C(\sigma )\ge n-k$
.
$C(\sigma )\ge n-k$
.
1.2. Almost all words of a given length
Shallit and Wang connected their automatic complexity
![]() $A(x)$
with Kolmogorov complexity in the following theorem:
$A(x)$
with Kolmogorov complexity in the following theorem:
Theorem 2 Shallit and Wang [Reference Shallit and Wang9, proof of Theorem 8]
For all binary words x,
They mention ([Reference Shallit and Wang9, proof of Theorem 8]), without singling it out as a lemma, the result that is our Lemma 4. Since they used, but did not give a definition of, the notion of almost all, we give a definition here. The notion is also known by the phrase natural density 1.
Definition 3. A set of strings
![]() $S\subseteq \{\mathtt {0},\mathtt {1}\}^*$
contains almost all
$S\subseteq \{\mathtt {0},\mathtt {1}\}^*$
contains almost all
![]() $x\in \{\mathtt {0},\mathtt {1}\}^n$
if
$x\in \{\mathtt {0},\mathtt {1}\}^n$
if
 $$ \begin{align*} \lim_{n\to\infty} \frac{\left\lvert S\cap \{\mathtt{0},\mathtt{1}\}^n\right\rvert}{2^n}=1. \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty} \frac{\left\lvert S\cap \{\mathtt{0},\mathtt{1}\}^n\right\rvert}{2^n}=1. \end{align*} $$
Lemma 4.
![]() $C(x)\ge \left \lvert x\right \rvert -\log _2 \left \lvert x\right \rvert $
for almost all x.
$C(x)\ge \left \lvert x\right \rvert -\log _2 \left \lvert x\right \rvert $
for almost all x.
Proof. Let
![]() $S=\{x\in \{\mathtt {0},\mathtt {1}\}^*: C(x)\ge \left \lvert x\right \rvert -\log _2\left \lvert x\right \rvert \}$
. By Lemma 1,
$S=\{x\in \{\mathtt {0},\mathtt {1}\}^*: C(x)\ge \left \lvert x\right \rvert -\log _2\left \lvert x\right \rvert \}$
. By Lemma 1,
 $$ \begin{align*} \lim_{n\to\infty}\frac{\left\lvert S\cap \{\mathtt{0},\mathtt{1}\}^n\right\rvert}{2^n} \ge \lim_{n\to\infty}\frac{2^n-\left(2^{n-\log_2 n} - 1\right)}{2^n} = \lim_{n\to\infty} 1 - \left(\frac1n - \frac1{2^n}\right) = 1. \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty}\frac{\left\lvert S\cap \{\mathtt{0},\mathtt{1}\}^n\right\rvert}{2^n} \ge \lim_{n\to\infty}\frac{2^n-\left(2^{n-\log_2 n} - 1\right)}{2^n} = \lim_{n\to\infty} 1 - \left(\frac1n - \frac1{2^n}\right) = 1. \end{align*} $$
Shallit and Wang then deduced the following:
Theorem 5 [Reference Shallit and Wang9, Theorem 8]
For almost all
![]() $x\in \{\mathtt {0},\mathtt {1}\}^n$
, we have A(x)
$x\in \{\mathtt {0},\mathtt {1}\}^n$
, we have A(x)
![]() $\geq$
n/13.
$\geq$
n/13.
Proof. By Lemma 4 and Theorem 2, there is a constant C such that for almost all x,
Let
![]() $C'=C/12$
. By taking n large enough, we have
$C'=C/12$
. By taking n large enough, we have
 $$ \begin{align*} \frac{n}{13}\le \frac{n}{12} -\frac13\log_2 n-C' \le A(x). \end{align*} $$
$$ \begin{align*} \frac{n}{13}\le \frac{n}{12} -\frac13\log_2 n-C' \le A(x). \end{align*} $$
Our main result (Theorem 18) implies that for all
![]() $\epsilon>0$
,
$\epsilon>0$
,
![]() $A(x)\ge n/(2+\epsilon )$
for almost all words
$A(x)\ge n/(2+\epsilon )$
for almost all words
![]() $x\in \{\mathtt {0},\mathtt {1}\}^n$
. Analogously, one way of expressing the Solomonoff–Kolmogorov result is as follows:
$x\in \{\mathtt {0},\mathtt {1}\}^n$
. Analogously, one way of expressing the Solomonoff–Kolmogorov result is as follows:
Proposition 6. For each
![]() $\epsilon>0$
, the following statement holds:
$\epsilon>0$
, the following statement holds:
![]() $C(x)\ge \left \lvert x\right \rvert (1-\epsilon )$
for almost all
$C(x)\ge \left \lvert x\right \rvert (1-\epsilon )$
for almost all
![]() $x\in \{\mathtt {0},\mathtt {1}\}^n$
.
$x\in \{\mathtt {0},\mathtt {1}\}^n$
.
The core idea for Theorem 18 is as follows. Consider an automaton processing a word x of length n over
![]() $n+1$
points in time. We show that there exist powers
$n+1$
points in time. We show that there exist powers
![]() $x_i^{\alpha _i}$
within x with
$x_i^{\alpha _i}$
within x with
![]() $\alpha _i\ge 2$
, and all distinct base lengths
$\alpha _i\ge 2$
, and all distinct base lengths
![]() $\left \lvert x_i\right \rvert $
, that in total occupy
$\left \lvert x_i\right \rvert $
, that in total occupy
![]() $\sum 1+\alpha _i\left \lvert x_i\right \rvert $
time, and such that all other states are visited at most twice. Since most words do not contain any long powers, this forces the number of states to be large.
$\sum 1+\alpha _i\left \lvert x_i\right \rvert $
time, and such that all other states are visited at most twice. Since most words do not contain any long powers, this forces the number of states to be large.
Automatic complexity, introduced by [Reference Shallit and Wang9], is an automaton-based and length-conditional analogue of
![]() $CD$
complexity [Reference Sipser10].
$CD$
complexity [Reference Sipser10].
![]() $CD$
complexity is in turn a computable analogue of the noncomputable Kolmogorov complexity.
$CD$
complexity is in turn a computable analogue of the noncomputable Kolmogorov complexity.
![]() $CD$
stands for ‘complexity of distinguishing’. Buhrman and Fortnow [Reference Buhrman, Fortnow and Laplante1] call it
$CD$
stands for ‘complexity of distinguishing’. Buhrman and Fortnow [Reference Buhrman, Fortnow and Laplante1] call it
![]() $CD$
, whereas Sipser called it
$CD$
, whereas Sipser called it
![]() $KD$
.
$KD$
.
![]() $KD^t(x)$
is the minimum length of a program for a fixed universal Turing machine that accepts x, rejects all other strings and runs in at most
$KD^t(x)$
is the minimum length of a program for a fixed universal Turing machine that accepts x, rejects all other strings and runs in at most
![]() $t(\left \lvert y\right \rvert )$
steps for all strings y.
$t(\left \lvert y\right \rvert )$
steps for all strings y.
The nondeterministic case of automatic complexity was studied in [Reference Hyde and Kjos-Hanssen3]. Among other results, that paper gave a table of the number of words of length n of nondeterministic automatic complexity
![]() $A_N$
equal to a given number q for
$A_N$
equal to a given number q for
![]() $n\le 23$
, and showed the following:
$n\le 23$
, and showed the following:
Theorem 7 Hyde [Reference Shallit and Wang9, Theorem 8], [Reference Hyde and Kjos-Hanssen3]
For all x,
![]() $A_N(x)\le \lfloor n/2\rfloor + 1$
.
$A_N(x)\le \lfloor n/2\rfloor + 1$
.
In this article we shall use
![]() $\langle a_1,\dotsc ,a_k\rangle $
to denote a k-tuple and denote concatenation by
$\langle a_1,\dotsc ,a_k\rangle $
to denote a k-tuple and denote concatenation by
![]() ${}^\frown $
. Thus, for example,
${}^\frown $
. Thus, for example,
![]() $\langle 3,6\rangle {}^\frown \langle 4,4\rangle =\langle 3,6,4,4\rangle $
. When no confusion is likely, we may also denote concatenation by juxtaposition. For example, instead of
$\langle 3,6\rangle {}^\frown \langle 4,4\rangle =\langle 3,6,4,4\rangle $
. When no confusion is likely, we may also denote concatenation by juxtaposition. For example, instead of
![]() $U{}^\frown V{}^\frown U{}^\frown C{}^\frown C{}^\frown V$
we may write simply
$U{}^\frown V{}^\frown U{}^\frown C{}^\frown C{}^\frown V$
we may write simply
![]() $UVUCCV$
.
$UVUCCV$
.
Definition 8. Let
![]() $\Sigma $
be finite a set called the alphabet and let Q be a finite set whose elements are called states. A nondeterministic finite automaton (NFA) is a
$\Sigma $
be finite a set called the alphabet and let Q be a finite set whose elements are called states. A nondeterministic finite automaton (NFA) is a
![]() $5$
-tuple M = (Q,
$5$
-tuple M = (Q,
![]() $\varSigma$
,
$\varSigma$
,
![]() $\delta$
, q
0, F). The transition function
$\delta$
, q
0, F). The transition function
![]() $\delta :Q\times \Sigma \to \mathcal P(Q)$
maps each
$\delta :Q\times \Sigma \to \mathcal P(Q)$
maps each
![]() $(q,b)\in Q\times \Sigma $
to a subset of Q. Within Q we find the initial state
$(q,b)\in Q\times \Sigma $
to a subset of Q. Within Q we find the initial state
![]() $q_0\in Q$
and the set of final states
$q_0\in Q$
and the set of final states
![]() $F\subseteq Q$
. As usual,
$F\subseteq Q$
. As usual,
![]() $\delta $
is extended to a function
$\delta $
is extended to a function
![]() $\delta ^*:Q\times \Sigma ^*\to \mathcal P(Q)$
by
$\delta ^*:Q\times \Sigma ^*\to \mathcal P(Q)$
by
 $$ \begin{align*} \delta^*\left(q,\sigma{}^\frown i\right)=\bigcup_{s\in \delta^*\left(q,\sigma\right)}\delta(s,i). \end{align*} $$
$$ \begin{align*} \delta^*\left(q,\sigma{}^\frown i\right)=\bigcup_{s\in \delta^*\left(q,\sigma\right)}\delta(s,i). \end{align*} $$
Overloading notation, we also write
![]() $\delta =\delta ^*$
. The set of words accepted by M is
$\delta =\delta ^*$
. The set of words accepted by M is
A deterministic finite automaton is also a
![]() $5$
-tuple M = (Q,
$5$
-tuple M = (Q,
![]() $\varSigma$
,
$\varSigma$
,
![]() $\delta$
, q
0, F). In this case,
$\delta$
, q
0, F). In this case,
![]() $\delta :Q\times \Sigma \to Q$
is a total function and is extended to
$\delta :Q\times \Sigma \to Q$
is a total function and is extended to
![]() $\delta ^*$
by
$\delta ^*$
by
![]() $\delta ^*\left (q,\sigma {}^\frown i\right )=\delta (\delta ^*(q,\sigma ),i)$
. Finally, the set of words accepted by M is
$\delta ^*\left (q,\sigma {}^\frown i\right )=\delta (\delta ^*(q,\sigma ),i)$
. Finally, the set of words accepted by M is
We now formally recall our basic notions.
Definition 9 [Reference Hyde and Kjos-Hanssen3, Reference Shallit and Wang9]
The nondeterministic automatic complexity
![]() $A_{N}(x)$
of a word
$A_{N}(x)$
of a word
![]() $x\in \Sigma ^n$
is the minimal number of states of an NFA M accepting x such that there is only one accepting walk in M of length n.
$x\in \Sigma ^n$
is the minimal number of states of an NFA M accepting x such that there is only one accepting walk in M of length n.
The automatic complexity
![]() $A(x)$
of a word
$A(x)$
of a word
![]() $x\in \Sigma ^n$
is the minimal number of states of a deterministic finite automaton M accepting x such that
$x\in \Sigma ^n$
is the minimal number of states of a deterministic finite automaton M accepting x such that
![]() $L(M)\cap \Sigma ^n=\{x\}$
.
$L(M)\cap \Sigma ^n=\{x\}$
.
Insisting that there be only one accepting walk enforces a kind of unambiguity at a fixed length. This appears to reduce the computational complexity of
![]() $A_N(x)$
, compared to requiring that there be only one accepted word, since one can use matrix exponentiation. It is not known whether these are equivalent definitions [Reference Kjos-Hanssen5].
$A_N(x)$
, compared to requiring that there be only one accepted word, since one can use matrix exponentiation. It is not known whether these are equivalent definitions [Reference Kjos-Hanssen5].
Clearly,
![]() $A_N(x)\le A(x)$
. Thus our lower bounds in this paper for
$A_N(x)\le A(x)$
. Thus our lower bounds in this paper for
![]() $A_N(x)$
apply to
$A_N(x)$
apply to
![]() $A(x)$
as well.
$A(x)$
as well.
2. The power–complexity connection
The reader may note that in the context of automatic complexity, Definition 8 can without loss of generality be simplified as follows:
-
1. We may assume that the set of final states is a singleton.
-
2. We may assume that whenever
 $q,r\in Q$
and
$q,r\in Q$
and
 $b_1,b_2\in \Sigma $
, if
$b_1,b_2\in \Sigma $
, if
 $r\in {\delta (q,b_1)}\cap {\delta (q,b_2)}$
, then
$r\in {\delta (q,b_1)}\cap {\delta (q,b_2)}$
, then
 $b_1=b_2$
. Indeed, having multiple edges from q to r in an automaton witnessing the automatic complexity of a word would would violate uniqueness.
$b_1=b_2$
. Indeed, having multiple edges from q to r in an automaton witnessing the automatic complexity of a word would would violate uniqueness. -
3. Each automaton M may be assumed to be generated by a witnessing walk. That is, only edges used by a walk taken when processing x along the unique accepting walk need to be included in M.
Let us call an NFA M witness generated if there is some
![]() $x\in \Sigma ^*$
such that x is the only word of length
$x\in \Sigma ^*$
such that x is the only word of length
![]() $\left \lvert x\right \rvert $
that is accepted by M, and M accepts x along only one walk and every state and transition of M is visited during this one walk. In this case we also say that M is witness generated by x. When studying nondeterministic automatic complexity, we may without loss of generality restrict attention to witness-generated NFAs.
$\left \lvert x\right \rvert $
that is accepted by M, and M accepts x along only one walk and every state and transition of M is visited during this one walk. In this case we also say that M is witness generated by x. When studying nondeterministic automatic complexity, we may without loss of generality restrict attention to witness-generated NFAs.
Definition 10. Two occurrences of words a (starting at position i) and b (starting at position j) in a word x are disjoint if
![]() $x=uavbw$
, where
$x=uavbw$
, where
![]() $u,v,w$
are words and
$u,v,w$
are words and
![]() $\left \lvert u\right \rvert =i$
,
$\left \lvert u\right \rvert =i$
,
![]() $\left \lvert uav\right \rvert =j$
.
$\left \lvert uav\right \rvert =j$
.
Definition 11. A digraph
![]() $D=(V,E)$
consists of a set of vertices V and a set of edges
$D=(V,E)$
consists of a set of vertices V and a set of edges
![]() $E\subseteq V^2$
. Set
$E\subseteq V^2$
. Set
![]() $s,t\in V$
. Set
$s,t\in V$
. Set
![]() $n\ge 0$
,
$n\ge 0$
,
![]() $n\in \mathbb Z$
. A walk of length n from s to t is a function
$n\in \mathbb Z$
. A walk of length n from s to t is a function
![]() $\Delta :\{0,1,\dotsc ,n\}\to V$
such that
$\Delta :\{0,1,\dotsc ,n\}\to V$
such that
![]() $\Delta (0)=s$
,
$\Delta (0)=s$
,
![]() $\Delta (n)=t$
and
$\Delta (n)=t$
and
![]() $(\Delta (k),\Delta (k+1))\in E$
for each
$(\Delta (k),\Delta (k+1))\in E$
for each
![]() $0\le k<n$
.
$0\le k<n$
.
A cycle of length
![]() $n=\left \lvert \Delta \right \rvert \ge 1$
in D is a walk from s to s, for some
$n=\left \lvert \Delta \right \rvert \ge 1$
in D is a walk from s to s, for some
![]() $s\in V$
, such that
$s\in V$
, such that
 $\Delta (t_1)=\Delta (t_2), t_1\ne t_2,\implies \{t_1,t_2\}=\{0, n\}$
. Two cycles are disjoint if their ranges are disjoint.
$\Delta (t_1)=\Delta (t_2), t_1\ne t_2,\implies \{t_1,t_2\}=\{0, n\}$
. Two cycles are disjoint if their ranges are disjoint.
Theorem 12. Let n be a positive integer. Let
![]() $D=(V,E)$
be a digraph and set
$D=(V,E)$
be a digraph and set
![]() $s,t\in V$
. Suppose that there is a unique walk
$s,t\in V$
. Suppose that there is a unique walk
![]() $\Delta $
on D from s to t of length n, and that for each
$\Delta $
on D from s to t of length n, and that for each
![]() $e\in E$
there is a t with
$e\in E$
there is a t with
![]() $(\Delta (t),\Delta (t+1))=e$
. Then there is a set of disjoint cycles
$(\Delta (t),\Delta (t+1))=e$
. Then there is a set of disjoint cycles
![]() $\mathcal C$
such that
$\mathcal C$
such that
 $$ \begin{align*} v\in V \mathbin{\big\backslash} \bigcup_{C\in\mathcal C} \mathrm{range}(C) \implies \left\lvert\{t:\Delta(t)=v\}\right\rvert\le 2, \end{align*} $$
$$ \begin{align*} v\in V \mathbin{\big\backslash} \bigcup_{C\in\mathcal C} \mathrm{range}(C) \implies \left\lvert\{t:\Delta(t)=v\}\right\rvert\le 2, \end{align*} $$
and such that for each
![]() $C\in \mathcal C$
there exist
$C\in \mathcal C$
there exist
![]() $\mu _C\ge 2\left \lvert C\right \rvert $
and
$\mu _C\ge 2\left \lvert C\right \rvert $
and
![]() $t_C$
such that
$t_C$
such that
 $$ \begin{align} \{t: \Delta(t)&\in\mathrm{range}(C)\} = [t_C, t_C + \mu_C],\notag\\\Delta(t_C+k)&=C(k \bmod \left\lvert C\right\rvert) \quad\text{for all}\ 0\le k\le \mu_C. \end{align} $$
$$ \begin{align} \{t: \Delta(t)&\in\mathrm{range}(C)\} = [t_C, t_C + \mu_C],\notag\\\Delta(t_C+k)&=C(k \bmod \left\lvert C\right\rvert) \quad\text{for all}\ 0\le k\le \mu_C. \end{align} $$
Proof. Suppose
![]() $v\in V$
with
$v\in V$
with
 $\left \{t:\Delta \left (t_j\right )=v\right \}=\{t_1<t_2<\dotsb < t_k\}$
and
$\left \{t:\Delta \left (t_j\right )=v\right \}=\{t_1<t_2<\dotsb < t_k\}$
and
![]() $k\ge 3$
. Let us write
$k\ge 3$
. Let us write
![]() $\Delta _{\left [a,b\right ]}$
for the sequence
$\Delta _{\left [a,b\right ]}$
for the sequence
![]() $(\Delta (a),\dotsc ,\Delta (b))$
for any
$(\Delta (a),\dotsc ,\Delta (b))$
for any
![]() $a,b$
.
$a,b$
.
Claim. The vertex sequence
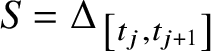 $S= \Delta _{\left [t_j,t_{j+1}\right ]}$
does not depend on j.
$S= \Delta _{\left [t_j,t_{j+1}\right ]}$
does not depend on j.
Proof Proof of claim
For
![]() $k=3$
,
$k=3$
,
![]() $v\in V$
with
$v\in V$
with
![]() $\Delta (t_1)=\Delta (t_2)=\Delta (t_3)$
for some
$\Delta (t_1)=\Delta (t_2)=\Delta (t_3)$
for some
![]() $t_1<t_2<t_3$
. Then the same vertex sequence must have appeared in
$t_1<t_2<t_3$
. Then the same vertex sequence must have appeared in
![]() $[t_1,t_2]$
and
$[t_1,t_2]$
and
![]() $[t_2,t_3]$
,
$[t_2,t_3]$
,
or else the uniqueness of the path would be violated, since
would be a second walk on D from s to t of length n. For
![]() $k>3$
, the only difference in the argument is notational.
$k>3$
, the only difference in the argument is notational.
By definition of the
![]() $t_j$
s, S is a cycle except for reindexing. Thus, let
$t_j$
s, S is a cycle except for reindexing. Thus, let
![]() $C(r)=S(t_1+r)$
for all r, let
$C(r)=S(t_1+r)$
for all r, let
![]() $t_{C}=t_1$
and let
$t_{C}=t_1$
and let
![]() $\mu =\mu _{C}$
be defined by equation (1). We have
$\mu =\mu _{C}$
be defined by equation (1). We have
 $$ \begin{align*} t_C+\mu_C\ge t_k=t_1+\sum_{j=1}^{k-1} t_{j+1}-t_j=t_1 + (k-1)\left\lvert C\right\rvert, \end{align*} $$
$$ \begin{align*} t_C+\mu_C\ge t_k=t_1+\sum_{j=1}^{k-1} t_{j+1}-t_j=t_1 + (k-1)\left\lvert C\right\rvert, \end{align*} $$
and hence
![]() $\mu _C \ge (k-1)\left \lvert C\right \rvert \ge 2\left \lvert C\right \rvert $
.
$\mu _C \ge (k-1)\left \lvert C\right \rvert \ge 2\left \lvert C\right \rvert $
.
3. Main theorem from power–complexity connection
Definition 13. Let
![]() $\mathbf {w}$
be an infinite word over the alphabet
$\mathbf {w}$
be an infinite word over the alphabet
![]() $\Sigma $
, and let x be a finite word over
$\Sigma $
, and let x be a finite word over
![]() $\Sigma $
. Let
$\Sigma $
. Let
![]() $\alpha>0$
be a rational number. The word x is said to occur in
$\alpha>0$
be a rational number. The word x is said to occur in
![]() $\mathbf {w}$
with exponent
$\mathbf {w}$
with exponent
![]() $\alpha $
if there is a subword y of
$\alpha $
if there is a subword y of
![]() $\mathbf {w}$
with
$\mathbf {w}$
with
![]() $y = x^a x_0$
, where
$y = x^a x_0$
, where
![]() $x_0$
is a prefix of x, a is the integer part of
$x_0$
is a prefix of x, a is the integer part of
![]() $\alpha $
and
$\alpha $
and
![]() $\left \lvert y\right \rvert =\alpha \left \lvert x\right \rvert $
. We say that y is an
$\left \lvert y\right \rvert =\alpha \left \lvert x\right \rvert $
. We say that y is an
![]() $\alpha $
-power. The word
$\alpha $
-power. The word
![]() $\mathbf {w}$
is
$\mathbf {w}$
is
![]() $\alpha $
-power-free if it contains no subwords which are
$\alpha $
-power-free if it contains no subwords which are
![]() $\alpha $
-powers.
$\alpha $
-powers.
Here in Section 3 we show how to establish our main theorem (Theorem 18).
Definition 14. Let M be an NFA. The directed graph
![]() $D(M)$
has the set of states Q as its set of vertices and has edges
$D(M)$
has the set of states Q as its set of vertices and has edges
![]() $(s,t)$
whenever
$(s,t)$
whenever
![]() $t\in \delta (s,b)$
for some
$t\in \delta (s,b)$
for some
![]() $b\in \Sigma $
.
$b\in \Sigma $
.
Theorem 15. Set
![]() $q\ge 1$
and
$q\ge 1$
and
![]() $n\ge 0$
, and let x be a word of length n such that
$n\ge 0$
, and let x be a word of length n such that
![]() $A_N(x)= q$
. Then x contains a set of powers
$A_N(x)= q$
. Then x contains a set of powers
![]() $x_i^{\alpha _i}$
,
$x_i^{\alpha _i}$
,
![]() $\alpha _i\ge 2$
,
$\alpha _i\ge 2$
,
![]() $1\le i\le m$
, satisfying the following equations with
$1\le i\le m$
, satisfying the following equations with
![]() $\beta _i=\left \lfloor \alpha _i\right \rfloor $
:
$\beta _i=\left \lfloor \alpha _i\right \rfloor $
:
 $$ \begin{align} \sum_{i=1}^m \beta_i \left\lvert x_i\right\rvert = \sum_{i=1}^m \gamma_i \left\lvert x_i\right\rvert,\quad \gamma_i\in\mathbb Z, \gamma_i\ge 0 \implies \gamma_i=\beta_i \text{ for each } i, \end{align} $$
$$ \begin{align} \sum_{i=1}^m \beta_i \left\lvert x_i\right\rvert = \sum_{i=1}^m \gamma_i \left\lvert x_i\right\rvert,\quad \gamma_i\in\mathbb Z, \gamma_i\ge 0 \implies \gamma_i=\beta_i \text{ for each } i, \end{align} $$
 $$ \begin{align} n+1-m-\sum_{i=1}^m (\alpha_i-2) \left\lvert x_i\right\rvert\le 2q. \end{align} $$
$$ \begin{align} n+1-m-\sum_{i=1}^m (\alpha_i-2) \left\lvert x_i\right\rvert\le 2q. \end{align} $$
Proof. Let M be an NFA witnessing that
![]() $A_N(x)\le q$
. Let D be the digraph
$A_N(x)\le q$
. Let D be the digraph
![]() $D(M)$
. Let
$D(M)$
. Let
![]() $\mathcal C$
be a set of disjoint cycles in D as guaranteed by Theorem 12. Let
$\mathcal C$
be a set of disjoint cycles in D as guaranteed by Theorem 12. Let
![]() $m=\left \lvert \mathcal C\right \rvert $
and write
$m=\left \lvert \mathcal C\right \rvert $
and write
![]() $\mathcal C=\{C_1,\dotsc ,C_m\}$
. Let
$\mathcal C=\{C_1,\dotsc ,C_m\}$
. Let
![]() $x_i$
be the word read by M while traversing
$x_i$
be the word read by M while traversing
![]() $C_i$
and let
$C_i$
and let
![]() $\alpha _i=\mu _{C_i}$
from Theorem 12.
$\alpha _i=\mu _{C_i}$
from Theorem 12.
Since the
![]() $C_i$
are disjoint, there are
$C_i$
are disjoint, there are
![]() $\Omega := q-\sum _{i=1}^m \left \lvert x_i\right \rvert $
vertices not in
$\Omega := q-\sum _{i=1}^m \left \lvert x_i\right \rvert $
vertices not in
![]() $\bigcup _i C_i$
. Let
$\bigcup _i C_i$
. Let
![]() $P=\left \lvert \{t:\Delta (t)\in C_i, \text { for some }i\}\right \rvert $
and let
$P=\left \lvert \{t:\Delta (t)\in C_i, \text { for some }i\}\right \rvert $
and let
![]() $N=n+1-P$
. By Theorem 12,
$N=n+1-P$
. By Theorem 12,
![]() $N\le 2\Omega $
, and so
$N\le 2\Omega $
, and so
![]() $P=n+1-N\ge n+1-2\Omega $
. On the other hand,
$P=n+1-N\ge n+1-2\Omega $
. On the other hand,
![]() $P = \sum _{i=1}^m (1+\alpha _i \left \lvert x_i\right \rvert )$
, since a walk of length k is the range of a function with domain of cardinality
$P = \sum _{i=1}^m (1+\alpha _i \left \lvert x_i\right \rvert )$
, since a walk of length k is the range of a function with domain of cardinality
![]() $k+1$
. Substituting back into the inequality
$k+1$
. Substituting back into the inequality
![]() $P\ge n+1-2\Omega $
now yields
$P\ge n+1-2\Omega $
now yields
 $$ \begin{align*} \sum_{i=1}^m (1+\alpha_i \left\lvert x_i\right\rvert) \ge n+1 - 2\left(q-\sum_{i=1}^m \left\lvert x_i\right\rvert\right) \end{align*} $$
$$ \begin{align*} \sum_{i=1}^m (1+\alpha_i \left\lvert x_i\right\rvert) \ge n+1 - 2\left(q-\sum_{i=1}^m \left\lvert x_i\right\rvert\right) \end{align*} $$
and hence formula (3).
Theorem 16. Set
![]() $q\ge 1$
and let x be a word such that
$q\ge 1$
and let x be a word such that
![]() $A_N(x)\le q$
. Then x contains a set of powers
$A_N(x)\le q$
. Then x contains a set of powers
![]() $x_i^{\alpha _i}$
,
$x_i^{\alpha _i}$
,
![]() $\alpha _i\ge 2$
,
$\alpha _i\ge 2$
,
![]() $1\le i\le m$
, such that all the
$1\le i\le m$
, such that all the
![]() $\left \lvert x_i\right \rvert , 1\le i\le m$
, are distinct and nonzero, and satisfying formula (3).
$\left \lvert x_i\right \rvert , 1\le i\le m$
, are distinct and nonzero, and satisfying formula (3).
Proof. This follows from Theorem 15 once we note that unique solvability of equation (2) implies that all the lengths are distinct.
The unique solution is
![]() $\beta _k=\lfloor \alpha _k\rfloor \ge 1$
. Suppose
$\beta _k=\lfloor \alpha _k\rfloor \ge 1$
. Suppose
 $\left \lvert x_i\right \rvert =\left \lvert x_j\right \rvert $
,
$\left \lvert x_i\right \rvert =\left \lvert x_j\right \rvert $
,
![]() $i\ne j$
. Then another solution is
$i\ne j$
. Then another solution is
![]() $\gamma _k = \beta _k$
for
$\gamma _k = \beta _k$
for
![]() $k\not \in \{i,j\}$
,
$k\not \in \{i,j\}$
,
![]() $\gamma _i=\beta _i-1, \gamma _j = \beta _j+1$
.
$\gamma _i=\beta _i-1, \gamma _j = \beta _j+1$
.
For a word
![]() $x=x_1\dotsm x_n$
with each
$x=x_1\dotsm x_n$
with each
![]() $x_i\in \{\mathtt 0,\mathtt 1\}$
, we write
$x_i\in \{\mathtt 0,\mathtt 1\}$
, we write
![]() $x_{\left [a,b\right ]}=x_ax_{a+1}\dotsm x_b$
.
$x_{\left [a,b\right ]}=x_ax_{a+1}\dotsm x_b$
.
Definition 17. Let
![]() $x=x_1\dotsm x_n$
with each
$x=x_1\dotsm x_n$
with each
![]() $x_i\in \{\mathtt 0,\mathtt 1\}$
.
$x_i\in \{\mathtt 0,\mathtt 1\}$
.
![]() $\operatorname {\mathrm {Lookback}}(m,k,t,x)$
is the statement that
$\operatorname {\mathrm {Lookback}}(m,k,t,x)$
is the statement that
![]() $x_{m+1+u}=x_{m+1+u-k}$
for each
$x_{m+1+u}=x_{m+1+u-k}$
for each
![]() $0\le u<t$
– that is,
$0\le u<t$
– that is,
We can read
![]() $\operatorname {\mathrm {Lookback}}(m,k,t,x)$
as ‘position m starts a continued run with lookback amount k of length t in x’.
$\operatorname {\mathrm {Lookback}}(m,k,t,x)$
as ‘position m starts a continued run with lookback amount k of length t in x’.
Theorem 18. Let
![]() $\mathbb P_n$
denote the uniform probability measure on words
$\mathbb P_n$
denote the uniform probability measure on words
![]() $x\in \Gamma ^n$
, where
$x\in \Gamma ^n$
, where
![]() $\Gamma $
is a finite alphabet of cardinality at least
$\Gamma $
is a finite alphabet of cardinality at least
![]() $2$
. For all
$2$
. For all
![]() $\epsilon>0$
,
$\epsilon>0$
,
 $$ \begin{align*} \lim_{n\to\infty}\mathbb P_n\left(\left\lvert\frac{A_N(x)}{n/2}-1\right\rvert<\epsilon\right)=1. \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty}\mathbb P_n\left(\left\lvert\frac{A_N(x)}{n/2}-1\right\rvert<\epsilon\right)=1. \end{align*} $$
Proof. Let us write
![]() $\log =\log _{\left \lvert \Gamma \right \rvert }$
in this proof. Let
$\log =\log _{\left \lvert \Gamma \right \rvert }$
in this proof. Let
![]() $d=3$
, although any fixed real number
$d=3$
, although any fixed real number
![]() $d>2$
will do for the proof. For
$d>2$
will do for the proof. For
![]() $1\le m\le n$
and
$1\le m\le n$
and
![]() $1\le k\le m$
, let
$1\le k\le m$
, let
![]() $R_{m,k}=\{x\in \Gamma ^n: \operatorname {\mathrm {Lookback}}(m,k,\lceil d\log n\rceil ,x)\}$
. By the union bound,Footnote
1
$R_{m,k}=\{x\in \Gamma ^n: \operatorname {\mathrm {Lookback}}(m,k,\lceil d\log n\rceil ,x)\}$
. By the union bound,Footnote
1
 $$ \begin{align} \mathbb P_n\left(\bigcup_{m=1}^n\bigcup_{k=1}^m R_{m,k}\right)\le \sum_{m=1}^n \sum_{k=1}^m \left\lvert\Gamma\right\rvert^{-d\log n}= n^{-d}\sum_{m=1}^n m =\frac{n(n+1)}2\cdot n^{-d} =: \epsilon_{n,d}. \end{align} $$
$$ \begin{align} \mathbb P_n\left(\bigcup_{m=1}^n\bigcup_{k=1}^m R_{m,k}\right)\le \sum_{m=1}^n \sum_{k=1}^m \left\lvert\Gamma\right\rvert^{-d\log n}= n^{-d}\sum_{m=1}^n m =\frac{n(n+1)}2\cdot n^{-d} =: \epsilon_{n,d}. \end{align} $$
By Theorem 16, if
![]() $A_N(x)\le q$
then x contains powers
$A_N(x)\le q$
then x contains powers
![]() $x_i^{\alpha _i}$
with all
$x_i^{\alpha _i}$
with all
![]() $\alpha _i\ge 2$
and all
$\alpha _i\ge 2$
and all
![]() $\left \lvert x_i\right \rvert $
distinct and nonzero such that formula (3) holds:
$\left \lvert x_i\right \rvert $
distinct and nonzero such that formula (3) holds:
 $$ \begin{align*} n+1-m-\sum_{i=1}^m (\alpha_i-2) \left\lvert x_i\right\rvert\le 2q. \end{align*} $$
$$ \begin{align*} n+1-m-\sum_{i=1}^m (\alpha_i-2) \left\lvert x_i\right\rvert\le 2q. \end{align*} $$
Applying this with
![]() $q=A_N(x)$
,
$q=A_N(x)$
,
 $$ \begin{align} n+1-m-\sum_{i=1}^m (\alpha_i-2) \left\lvert x_i\right\rvert\le 2A_N(x). \end{align} $$
$$ \begin{align} n+1-m-\sum_{i=1}^m (\alpha_i-2) \left\lvert x_i\right\rvert\le 2A_N(x). \end{align} $$
Let
![]() $S_i=(\alpha _i-1) \left \lvert x_i\right \rvert $
and
$S_i=(\alpha _i-1) \left \lvert x_i\right \rvert $
and
![]() $S=\sum _{i=1}^m S_i$
. Using
$S=\sum _{i=1}^m S_i$
. Using
![]() $\left \lvert x_i\right \rvert \ge 1$
and formula (5), we have
$\left \lvert x_i\right \rvert \ge 1$
and formula (5), we have
 $$ \begin{align} n+1-S \le n+1-S - m + \sum_{i=1}^m \left\lvert x_i\right\rvert \le 2A_N(x). \end{align} $$
$$ \begin{align} n+1-S \le n+1-S - m + \sum_{i=1}^m \left\lvert x_i\right\rvert \le 2A_N(x). \end{align} $$
Using
![]() $\alpha _i\ge 2$
, and the observation that if m many distinct positive integers
$\alpha _i\ge 2$
, and the observation that if m many distinct positive integers
![]() $\left \lvert x_i\right \rvert $
are all bounded by
$\left \lvert x_i\right \rvert $
are all bounded by
![]() $\lceil d\log n\rceil $
, then it follows that
$\lceil d\log n\rceil $
, then it follows that
![]() $m\le \lceil d\log n\rceil $
, we have
$m\le \lceil d\log n\rceil $
, we have
 $$ \begin{align} \left\{x:\max_{i=1}^m S_i\le \lceil d\log n\rceil\right\} \subseteq \left\{x:\max_{i=1}^m\left\lvert x_i\right\rvert\le \lceil d\log n\rceil)\right\} \subseteq \{x: m \le \lfloor d\log n\rfloor\}. \end{align} $$
$$ \begin{align} \left\{x:\max_{i=1}^m S_i\le \lceil d\log n\rceil\right\} \subseteq \left\{x:\max_{i=1}^m\left\lvert x_i\right\rvert\le \lceil d\log n\rceil)\right\} \subseteq \{x: m \le \lfloor d\log n\rfloor\}. \end{align} $$
By equation (4) (since
![]() $S_i$
is the length of a continued run in x), we have
$S_i$
is the length of a continued run in x), we have
 $$ \begin{align} \mathbb P_n\left(\max_{i=1}^m S_i\le \lceil d\log n\rceil\right) \ge 1-\epsilon_{n,d}. \end{align} $$
$$ \begin{align} \mathbb P_n\left(\max_{i=1}^m S_i\le \lceil d\log n\rceil\right) \ge 1-\epsilon_{n,d}. \end{align} $$
Using
![]() $S \le m \max _{i=1}^m S_i$
and formulas (7) and (8),
$S \le m \max _{i=1}^m S_i$
and formulas (7) and (8),
 $$ \begin{align*} \mathbb P_n\left(S\le (\lceil d\log n\rceil)^2\right) &\ge \mathbb P_n\left(m \max_i S_i\le (\lceil d\log n\rceil)^2\right)\\ &\ge \mathbb P_n\left(\max_{i=1}^m S_i\le \lceil d\log n\rceil\right) \ge 1-\epsilon_{n,d}. \end{align*} $$
$$ \begin{align*} \mathbb P_n\left(S\le (\lceil d\log n\rceil)^2\right) &\ge \mathbb P_n\left(m \max_i S_i\le (\lceil d\log n\rceil)^2\right)\\ &\ge \mathbb P_n\left(\max_{i=1}^m S_i\le \lceil d\log n\rceil\right) \ge 1-\epsilon_{n,d}. \end{align*} $$
So by formula (6),
 $$ \begin{align} \mathbb P_n \left(A_N(x)\ge \frac{n+1}2-\frac12(\lceil d\log n\rceil)^2\right) \ge 1-\epsilon_{n,d}. \end{align} $$
$$ \begin{align} \mathbb P_n \left(A_N(x)\ge \frac{n+1}2-\frac12(\lceil d\log n\rceil)^2\right) \ge 1-\epsilon_{n,d}. \end{align} $$
Letting
![]() $n\to \infty $
completes the proof.
$n\to \infty $
completes the proof.
Acknowledgments
This work was partially supported a grant from the Simons Foundation (#704836).
Conflicts of Interest
None.