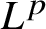1 Introduction
1.1 Boundedness of spectral projectors on Riemannian manifolds
1.1.1 A general problem
Given a Riemannian manifold M with Laplace-Beltrami operator ![]() $\Delta $, and for
$\Delta $, and for ![]() $\lambda \geq 1$,
$\lambda \geq 1$, ![]() $0<\delta <1$, let
$0<\delta <1$, let
 $$ \begin{align*}P_{\lambda,\delta} = P_{\lambda,\delta}^{\chi} = \chi \left( \frac{\sqrt{-\Delta} - \lambda}{\delta} \right), \end{align*} $$
$$ \begin{align*}P_{\lambda,\delta} = P_{\lambda,\delta}^{\chi} = \chi \left( \frac{\sqrt{-\Delta} - \lambda}{\delta} \right), \end{align*} $$where ![]() $\chi $ is a non-negative cutoff function supported in
$\chi $ is a non-negative cutoff function supported in ![]() $[-1,1]$, equal to
$[-1,1]$, equal to ![]() $1$ on
$1$ on  $[-\frac {1}{2},\frac {1}{2}]$.
$[-\frac {1}{2},\frac {1}{2}]$.
A general question is to estimate
 $$ \begin{align*}{ \| P_{\lambda,\delta}^{\chi} \|_{L^{2} \to L^{p}}, \qquad \mbox{where }p \in [2,\infty]}. \end{align*} $$
$$ \begin{align*}{ \| P_{\lambda,\delta}^{\chi} \|_{L^{2} \to L^{p}}, \qquad \mbox{where }p \in [2,\infty]}. \end{align*} $$ Using self-adjointness of  $P_{\lambda ,\delta }^{\chi }$ and a
$P_{\lambda ,\delta }^{\chi }$ and a ![]() $TT^{*}$ argument, it follows that
$TT^{*}$ argument, it follows that
 $$ \begin{align} \| P^{\chi^{2}}_{\lambda,\delta} \|_{L^{p^{\prime}} \to L^{p}} = \| P_{\lambda,\delta}^{\chi} \|_{L^{p^{\prime}} \to L^{2}}^{2} = \| P_{\lambda,\delta}^{\chi} \|_{L^{2} \to L^{p}}^{2}. \end{align} $$
$$ \begin{align} \| P^{\chi^{2}}_{\lambda,\delta} \|_{L^{p^{\prime}} \to L^{p}} = \| P_{\lambda,\delta}^{\chi} \|_{L^{p^{\prime}} \to L^{2}}^{2} = \| P_{\lambda,\delta}^{\chi} \|_{L^{2} \to L^{p}}^{2}. \end{align} $$Furthermore, given two cutoff functions ![]() $\chi $ and
$\chi $ and ![]() $\widetilde {\chi }$, the boundedness of
$\widetilde {\chi }$, the boundedness of  $P_{\lambda ,\delta }^{\chi }$ on
$P_{\lambda ,\delta }^{\chi }$ on ![]() $L^{2}$ implies the following: if
$L^{2}$ implies the following: if  $\| P_{\lambda ,\delta }^{\chi } \|_{L^{2} \to L^{p}}$ obeys, say, a polynomial bound of the type
$\| P_{\lambda ,\delta }^{\chi } \|_{L^{2} \to L^{p}}$ obeys, say, a polynomial bound of the type ![]() $\lambda ^{\alpha } \delta ^{\beta }$, so does
$\lambda ^{\alpha } \delta ^{\beta }$, so does  $\| P_{\lambda ,\delta }^{\widetilde \chi } \|_{L^{2} \to L^{p}}$, with a different constant. Therefore, it will be equivalent to estimate either of the three quantities appearing in equation (1.1), and the result is essentially independent of the cutoff function, which might even be taken to be a sharp cutoff.
$\| P_{\lambda ,\delta }^{\widetilde \chi } \|_{L^{2} \to L^{p}}$, with a different constant. Therefore, it will be equivalent to estimate either of the three quantities appearing in equation (1.1), and the result is essentially independent of the cutoff function, which might even be taken to be a sharp cutoff.
Up to possibly logarithmic factors, this question is essentially equivalent to that of estimating the ![]() $L^{2} \to L^{p}$ norm of the resolvent
$L^{2} \to L^{p}$ norm of the resolvent ![]() $R((x+iy)^{2}) = (\Delta + (x+iy)^{2})^{-1}$; this is the point of view taken in Dos Santos Ferreira-Kenig-Salo [Reference Ferreira, Kenig and Salo12] and Bourgain-Shao-Sogge-Yao [Reference Bourgain, Shao, Sogge and Yao8]. Essentially, one can think of
$R((x+iy)^{2}) = (\Delta + (x+iy)^{2})^{-1}$; this is the point of view taken in Dos Santos Ferreira-Kenig-Salo [Reference Ferreira, Kenig and Salo12] and Bourgain-Shao-Sogge-Yao [Reference Bourgain, Shao, Sogge and Yao8]. Essentially, one can think of ![]() $R((x+iy)^{2})$ as a variant of
$R((x+iy)^{2})$ as a variant of  $\frac {1}{xy} P_{x,y}$.
$\frac {1}{xy} P_{x,y}$.
1.1.2 The case of Euclidean space
We will denote the Stein-Tomas exponent
 $$ \begin{align*} p_{ST} = \frac{2(d+1)}{d-1}. \end{align*} $$
$$ \begin{align*} p_{ST} = \frac{2(d+1)}{d-1}. \end{align*} $$As will become clear, it often plays the role of a critical point when estimating the norm of ![]() $P_{\lambda ,\delta }$.
$P_{\lambda ,\delta }$.
On ![]() $\mathbb {R}^{d}$ (with the Euclidean metric), there holds
$\mathbb {R}^{d}$ (with the Euclidean metric), there holds
 $$ \begin{align} \| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} \lesssim \left\{ \begin{array}{ll} \lambda^{\sigma(p)/2} \delta^{1/2} & \mbox{if }p \geq p_{ST} \\ \lambda^{\frac{d-1}{2} \left( \frac{1}{2} - \frac{1}{p} \right)} \delta^{\frac{(d+1)}{2}\left( \frac{1}{2} - \frac{1}{p} \right)} & \mbox{if }2 \leq p \leq p_{ST}, \end{array} \right. \end{align} $$
$$ \begin{align} \| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} \lesssim \left\{ \begin{array}{ll} \lambda^{\sigma(p)/2} \delta^{1/2} & \mbox{if }p \geq p_{ST} \\ \lambda^{\frac{d-1}{2} \left( \frac{1}{2} - \frac{1}{p} \right)} \delta^{\frac{(d+1)}{2}\left( \frac{1}{2} - \frac{1}{p} \right)} & \mbox{if }2 \leq p \leq p_{ST}, \end{array} \right. \end{align} $$where
 $$ \begin{align*}\sigma(p) = d - 1 - \frac{2d}{p} \qquad \mbox{so that} \qquad \sigma(p_{ST}) = \frac{d-1}{d+1}; \end{align*} $$
$$ \begin{align*}\sigma(p) = d - 1 - \frac{2d}{p} \qquad \mbox{so that} \qquad \sigma(p_{ST}) = \frac{d-1}{d+1}; \end{align*} $$see the appendix for a proof of the above bounds. For more general second-order operators in the resolvent formulation, we refer to Kenig-Ruiz-Sogge [Reference Kenig, Ruiz and Sogge18]. Finally, the case of the hyperbolic space was recently treated by the first author and Léger [Reference Germain and Leger13].
1.1.3 The case of a compact manifold
On a compact manifold of dimension d, as was proved by Sogge [Reference Sogge23],
 $$ \begin{align*}\| P_{\lambda,1} \|_{L^{2} \to L^{p}} \lesssim \left\{ \begin{array}{ll} \lambda^{\sigma(p)/2} & \mbox{if }p \geq p_{ST} \\ \lambda^{\frac{d-1}{2} \left( \frac{1}{2} - \frac{1}{p} \right)} & \mbox{if }2 \leq p \leq p_{ST}, \end{array} \right. \end{align*} $$
$$ \begin{align*}\| P_{\lambda,1} \|_{L^{2} \to L^{p}} \lesssim \left\{ \begin{array}{ll} \lambda^{\sigma(p)/2} & \mbox{if }p \geq p_{ST} \\ \lambda^{\frac{d-1}{2} \left( \frac{1}{2} - \frac{1}{p} \right)} & \mbox{if }2 \leq p \leq p_{ST}, \end{array} \right. \end{align*} $$where ![]() $\sigma (p)$ is as above. For any given compact manifold, this estimate is optimal for
$\sigma (p)$ is as above. For any given compact manifold, this estimate is optimal for ![]() $\delta = 1$. In the case of the sphere
$\delta = 1$. In the case of the sphere ![]() $ \mathbb {S}^{d}$ (or more generally of a Zoll manifold), it does not improve if
$ \mathbb {S}^{d}$ (or more generally of a Zoll manifold), it does not improve if ![]() $\delta $ decreases, since the eigenvalues of the sphere Laplacian are essentially distributed like squared integers. However, for ‘most’ manifolds, the estimates above are expected to improve as
$\delta $ decreases, since the eigenvalues of the sphere Laplacian are essentially distributed like squared integers. However, for ‘most’ manifolds, the estimates above are expected to improve as ![]() $\delta $ decreases. It is the aim of this article to examine this question in the case of the torus.
$\delta $ decreases. It is the aim of this article to examine this question in the case of the torus.
If the manifold M is negatively curved, then logarithmic improvements are possible over the allowed range of ![]() $\delta $, as in Bourgain-Shao-Sogge-Yao [Reference Bourgain, Shao, Sogge and Yao8] and Blair-Sogge [Reference Blair and Sogge1]. The work of Sogge-Toth-Zelditch [Reference Sogge, Toth and Zelditch24] shows that generic manifolds also allow improvements.
$\delta $, as in Bourgain-Shao-Sogge-Yao [Reference Bourgain, Shao, Sogge and Yao8] and Blair-Sogge [Reference Blair and Sogge1]. The work of Sogge-Toth-Zelditch [Reference Sogge, Toth and Zelditch24] shows that generic manifolds also allow improvements.
1.2 Spectral projectors on tori
1.2.1 Formulating the problem
From now on, we focus on the case of tori given by the quotient ![]() $\mathbb {R}^{d} / (\mathbb {Z} e_{1} + \dots + \mathbb {Z} e_{1})$, where
$\mathbb {R}^{d} / (\mathbb {Z} e_{1} + \dots + \mathbb {Z} e_{1})$, where ![]() $e_{1},\dots ,e_{d}$ is a basis of
$e_{1},\dots ,e_{d}$ is a basis of ![]() $\mathbb {R}^{d}$, with the standard metric. This is equivalent to considering the operators
$\mathbb {R}^{d}$, with the standard metric. This is equivalent to considering the operators
 $$ \begin{align*}P_{\lambda,\delta} = \chi \left( \frac{\sqrt{-Q(\nabla)} - \lambda}{\delta} \right) \qquad \mbox{on} \;\; \mathbb{T}^{d} = \mathbb{R}^{d} / \mathbb{Z}^{d}, \end{align*} $$
$$ \begin{align*}P_{\lambda,\delta} = \chi \left( \frac{\sqrt{-Q(\nabla)} - \lambda}{\delta} \right) \qquad \mbox{on} \;\; \mathbb{T}^{d} = \mathbb{R}^{d} / \mathbb{Z}^{d}, \end{align*} $$where ![]() $\nabla $ is the standard gradient operator, and Q is a positive definite quadratic form on
$\nabla $ is the standard gradient operator, and Q is a positive definite quadratic form on ![]() $\mathbb {R}^{d}$, with coefficients
$\mathbb {R}^{d}$, with coefficients ![]() $\beta _{ij}$:
$\beta _{ij}$:
 $$ \begin{align*}Q(x) = \sum_{i=1}^{d} \beta_{ij} x^{i} x^{j} \qquad \implies \qquad Q(\nabla) = - \sum_{i=1}^{d} \beta_{ij} \partial_{i} \partial_{j}. \end{align*} $$
$$ \begin{align*}Q(x) = \sum_{i=1}^{d} \beta_{ij} x^{i} x^{j} \qquad \implies \qquad Q(\nabla) = - \sum_{i=1}^{d} \beta_{ij} \partial_{i} \partial_{j}. \end{align*} $$Dispensing with factors of ![]() $2\pi $, which can be absorbed in Q, the associated Fourier multiplier has the symbol
$2\pi $, which can be absorbed in Q, the associated Fourier multiplier has the symbol
 $$ \begin{align*}\chi \left( \frac{\sqrt{Q(k)} - \lambda}{\delta} \right). \end{align*} $$
$$ \begin{align*}\chi \left( \frac{\sqrt{Q(k)} - \lambda}{\delta} \right). \end{align*} $$1.2.2 Known results for  $p = \infty $: counting lattice points
$p = \infty $: counting lattice points
Abusing notations by writing ![]() $P_{\lambda ,\delta }(z)$ for the convolution kernel giving
$P_{\lambda ,\delta }(z)$ for the convolution kernel giving ![]() $P_{\lambda ,\delta }$, we have the formula
$P_{\lambda ,\delta }$, we have the formula
 $$ \begin{align*}P_{\lambda,\delta}(z) = \sum_{n} \chi \left( \frac{\sqrt{Q(n)} - \lambda}{\delta} \right) e^{2\pi i n \cdot z}. \end{align*} $$
$$ \begin{align*}P_{\lambda,\delta}(z) = \sum_{n} \chi \left( \frac{\sqrt{Q(n)} - \lambda}{\delta} \right) e^{2\pi i n \cdot z}. \end{align*} $$It is easy to see that
 $$ \begin{align*}\| P_{\lambda,\delta} \|_{L^{1} \to L^{\infty}} = \| P_{\lambda,\delta}(z) \|_{L^{\infty}_{z}} = \sum_{n} \chi \left( \frac{\sqrt{Q(n)} - \lambda}{\delta} \right). \end{align*} $$
$$ \begin{align*}\| P_{\lambda,\delta} \|_{L^{1} \to L^{\infty}} = \| P_{\lambda,\delta}(z) \|_{L^{\infty}_{z}} = \sum_{n} \chi \left( \frac{\sqrt{Q(n)} - \lambda}{\delta} \right). \end{align*} $$If ![]() $\chi = \mathbf {1}_{[-1,1]}$, this can be expressed as
$\chi = \mathbf {1}_{[-1,1]}$, this can be expressed as
where ![]() $N(\lambda )$ is the counting function associated to the quadratic form Q: namely, it denotes the number of lattice points
$N(\lambda )$ is the counting function associated to the quadratic form Q: namely, it denotes the number of lattice points ![]() $n \in \mathbb {Z}^{d}$ such that
$n \in \mathbb {Z}^{d}$ such that ![]() $Q(n) < \lambda ^{2}$. To leading order,
$Q(n) < \lambda ^{2}$. To leading order, ![]() $N(\lambda )$ equals
$N(\lambda )$ equals ![]() $\operatorname {Vol}(B_{1}) \lambda ^{d}$, where
$\operatorname {Vol}(B_{1}) \lambda ^{d}$, where ![]() $\operatorname {Vol}(B_{1})$ is the volume of the ellipsoid
$\operatorname {Vol}(B_{1})$ is the volume of the ellipsoid ![]() $\{Q(x) < 1\}.$ We denote the error term by
$\{Q(x) < 1\}.$ We denote the error term by ![]() $P(\lambda )$, thus:
$P(\lambda )$, thus:
For a general quadratic form Q, it was showed by Landau [Reference Landau20, Section 4] that  $P(\lambda ) = O( \lambda ^{d - \frac {2d}{d+1}})$. Consequently, we have
$P(\lambda ) = O( \lambda ^{d - \frac {2d}{d+1}})$. Consequently, we have
 $$ \begin{align} \| P_{\lambda,\delta} \|_{L^{1} \to L^{\infty}} &\ll \delta\lambda^{d-1} &\text{for }\delta&> \lambda^{-\frac{d-1}{d+1}}. \end{align} $$
$$ \begin{align} \| P_{\lambda,\delta} \|_{L^{1} \to L^{\infty}} &\ll \delta\lambda^{d-1} &\text{for }\delta&> \lambda^{-\frac{d-1}{d+1}}. \end{align} $$Landau’s result, and hence the range for ![]() $\delta $ in equation (1.3), has been improved for every dimension d. Nonetheless, equation (1.3) is a useful point of comparison since our approach is, in a sense, a refinement of a proof of Landau’s theorem (see the comments after Theorem 4.1). Regarding lower bounds for P, when
$\delta $ in equation (1.3), has been improved for every dimension d. Nonetheless, equation (1.3) is a useful point of comparison since our approach is, in a sense, a refinement of a proof of Landau’s theorem (see the comments after Theorem 4.1). Regarding lower bounds for P, when  $Q(x)=|x|_{2}^{2}$, one can show that
$Q(x)=|x|_{2}^{2}$, one can show that  $P(\lambda _{i})\gg \lambda _{i}^{d-2}$ for some sequence
$P(\lambda _{i})\gg \lambda _{i}^{d-2}$ for some sequence ![]() $\lambda _{i} \to \infty $. The present state of the art is as follows:
$\lambda _{i} \to \infty $. The present state of the art is as follows:
• If
 $d=2$, then estimating
$d=2$, then estimating  $P(\lambda )$ is a variation on the celebrated Gauss circle problem. One conjectures
$P(\lambda )$ is a variation on the celebrated Gauss circle problem. One conjectures  $P(\lambda )=O_{\epsilon }(\lambda ^{\frac {1}{2}+\epsilon })$, and the best known result is
$P(\lambda )=O_{\epsilon }(\lambda ^{\frac {1}{2}+\epsilon })$, and the best known result is  $O(\lambda ^{\frac {131}{208}}\log ^{\frac {18627}{8320}}\lambda )$; see Huxley [Reference Huxley17].
$O(\lambda ^{\frac {131}{208}}\log ^{\frac {18627}{8320}}\lambda )$; see Huxley [Reference Huxley17].• If
 $d=3$, then one conjectures
$d=3$, then one conjectures  $P(\lambda )=O_{\epsilon }(\lambda ^{1+\epsilon })$; see Nowak [Reference Nowak21, §§1.1-1.2]. We have
$P(\lambda )=O_{\epsilon }(\lambda ^{1+\epsilon })$; see Nowak [Reference Nowak21, §§1.1-1.2]. We have  $O(\lambda ^{\frac {231}{158}})$ by Guo [Reference Guo15]. If moreover Q has rational coefficients, then
$O(\lambda ^{\frac {231}{158}})$ by Guo [Reference Guo15]. If moreover Q has rational coefficients, then  $P(\lambda )=O(\lambda ^{\frac {21}{16}})$ by Chamizo-Cristobál-Ubis [Reference Chamizo, Cristóbal and Ubis10].
$P(\lambda )=O(\lambda ^{\frac {21}{16}})$ by Chamizo-Cristobál-Ubis [Reference Chamizo, Cristóbal and Ubis10].• If
 $d=4$, then
$d=4$, then  $P(\lambda )= O(\lambda ^{2} \log ^{\frac {2}{3}}\lambda )$ by Walfisz [Reference Walfisz28]. The case
$P(\lambda )= O(\lambda ^{2} \log ^{\frac {2}{3}}\lambda )$ by Walfisz [Reference Walfisz28]. The case  $Q(x)=|x|_{2}^{2}$ shows that up the log power this is best-possible.
$Q(x)=|x|_{2}^{2}$ shows that up the log power this is best-possible.• If
 $d>4$, then we have
$d>4$, then we have  $P(\lambda ) = O( \lambda ^{d - 2})$, see Krätzel [Reference Krätzel19]. This is best-possible if Q is a multiple of a form with rational coefficients, and if not then
$P(\lambda ) = O( \lambda ^{d - 2})$, see Krätzel [Reference Krätzel19]. This is best-possible if Q is a multiple of a form with rational coefficients, and if not then  $P(\lambda ) = o( \lambda ^{d - 2})$ by Götze [Reference Götze14].
$P(\lambda ) = o( \lambda ^{d - 2})$ by Götze [Reference Götze14].
1.2.3 Known results on standard tori: eigenfunctions of the Laplacian
It was conjectured by Bourgain [Reference Bourgain2] that an eigenfunction f of the Laplacian on the standard torus with eigenvalue ![]() $\lambda ^{2}$ satisfies
$\lambda ^{2}$ satisfies
 $$ \begin{align*} \| f \|_{L^{p}} \lesssim_{\epsilon} \lambda^{\frac{d-2}{2} - \frac{d}{p} + \epsilon} \| f \|_{L^{2}} \qquad \mbox{for }p \geq p^{*}, \;\;\;\mbox{where} \; p^{*} = \frac{2d}{d-2}, \end{align*} $$
$$ \begin{align*} \| f \|_{L^{p}} \lesssim_{\epsilon} \lambda^{\frac{d-2}{2} - \frac{d}{p} + \epsilon} \| f \|_{L^{2}} \qquad \mbox{for }p \geq p^{*}, \;\;\;\mbox{where} \; p^{*} = \frac{2d}{d-2}, \end{align*} $$which can be reformulated as
 $$ \begin{align*} \| P_{\lambda,\frac{1}{\lambda}} \|_{L^{2} \to L^{p}} \lesssim_{\epsilon} \lambda^{\frac{d-2}{2} - \frac{d}{p} + \epsilon} \qquad \mbox{for }p \geq p^{*}\mbox{.} \end{align*} $$
$$ \begin{align*} \| P_{\lambda,\frac{1}{\lambda}} \|_{L^{2} \to L^{p}} \lesssim_{\epsilon} \lambda^{\frac{d-2}{2} - \frac{d}{p} + \epsilon} \qquad \mbox{for }p \geq p^{*}\mbox{.} \end{align*} $$Progress toward this conjecture [Reference Bourgain3, Reference Bourgain and Demeter5, Reference Bourgain and Demeter6] culminated in the work of Bourgain and Demeter on ![]() $\ell ^{2}$-decoupling [Reference Bourgain and Demeter7], where the above conjecture is proved for
$\ell ^{2}$-decoupling [Reference Bourgain and Demeter7], where the above conjecture is proved for ![]() $d \geq 4$ and
$d \geq 4$ and  $p \geq \frac {2(d-1)}{d-3}$.
$p \geq \frac {2(d-1)}{d-3}$.
1.2.4 Known results on standard tori: uniform resolvent bounds
It was proved in Dos Santos Ferreira-Kenig-Salo [Reference Ferreira, Kenig and Salo12] that, for general compact manifolds, each ![]() $x,y \in \mathbb {R}$, and writing
$x,y \in \mathbb {R}$, and writing  $ p^{*} = \frac {2d}{d-2}$, we have
$ p^{*} = \frac {2d}{d-2}$, we have
In terms of spectral projectors, this is equivalent (see Cuenin [Reference Cuenin11]) to the bound
It was also asked whether this bound could be extended to a broader range of y, or equivalently a broader range of ![]() $\delta $. Bourgain-Shao-Sogge-Yao [Reference Bourgain, Shao, Sogge and Yao8] showed that on the sphere, the range above is optimal. In the case of the standard d-dimensional torus
$\delta $. Bourgain-Shao-Sogge-Yao [Reference Bourgain, Shao, Sogge and Yao8] showed that on the sphere, the range above is optimal. In the case of the standard d-dimensional torus ![]() $\mathbb R^{d}/\mathbb Z^{d}$, they could improve earlier results of Shen [Reference Shen22]. The results of Shen and Bourgain-Shao-Sogge-Yao were then sharpened by Hickman [Reference Hickman16], who extended the range for the standard d-dimensional torus further to
$\mathbb R^{d}/\mathbb Z^{d}$, they could improve earlier results of Shen [Reference Shen22]. The results of Shen and Bourgain-Shao-Sogge-Yao were then sharpened by Hickman [Reference Hickman16], who extended the range for the standard d-dimensional torus further to  $|\delta |> \lambda ^{-\frac {1}{3} -\frac {d}{3(21d^{2}-d-24)} + \epsilon }$.
$|\delta |> \lambda ^{-\frac {1}{3} -\frac {d}{3(21d^{2}-d-24)} + \epsilon }$.
1.2.5 Known results in dimension 2
The classical estimate of Zygmund corresponds, in our language, to a sharp result for ![]() $d=2$,
$d=2$, ![]() $p=4$,
$p=4$, ![]() $\delta = \lambda ^{-1}$. It was showed by Bourgain-Burq-Zworski [Reference Bourgain, Burq and Zworski4] that it can be extended to
$\delta = \lambda ^{-1}$. It was showed by Bourgain-Burq-Zworski [Reference Bourgain, Burq and Zworski4] that it can be extended to ![]() $\delta> \lambda ^{-1}$. A striking feature of the estimates in [Reference Bourgain, Burq and Zworski4] is that they entail no subpolynomial loss (
$\delta> \lambda ^{-1}$. A striking feature of the estimates in [Reference Bourgain, Burq and Zworski4] is that they entail no subpolynomial loss (![]() $\epsilon $ power in the exponent), which has important consequences for control theory in particular, as explained in that paper.
$\epsilon $ power in the exponent), which has important consequences for control theory in particular, as explained in that paper.
1.3 Conjecture and results
Based on two specific examples, developed in Section 3, we conjecture that
 $$ \begin{align} \boxed{ \| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} \lesssim (\lambda \delta)^{\frac{(d-1)}{2} \left( \frac{1}{2} - \frac{1}{p} \right)} + \lambda^{\sigma(p)/2} \delta^{1/2},} \end{align} $$
$$ \begin{align} \boxed{ \| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} \lesssim (\lambda \delta)^{\frac{(d-1)}{2} \left( \frac{1}{2} - \frac{1}{p} \right)} + \lambda^{\sigma(p)/2} \delta^{1/2},} \end{align} $$where ![]() $\delta> \lambda ^{-1}$, and
$\delta> \lambda ^{-1}$, and  $\sigma (p) = d - 1 - \frac {2d}{p}$, for any fixed torus. We show there that this bound would be optimal and describe when each term in the conjecture dominates.
$\sigma (p) = d - 1 - \frac {2d}{p}$, for any fixed torus. We show there that this bound would be optimal and describe when each term in the conjecture dominates.
The methods developed in the present paper give improvements on the range of validity of this conjecture. The precise statement is Theorem 6.1 below. As this is a rather cumbersome formula, we choose to state some simpler results in fairly natural cases of interest, namely ![]() $p<p_{ST}$,
$p<p_{ST}$, ![]() $\delta $ large and
$\delta $ large and ![]() $d=3$. Here we have
$d=3$. Here we have  $p_{ST} = \frac {2(d+1)}{d-1}$; in Sections 1.2.3 and 1.2.4, we saw that
$p_{ST} = \frac {2(d+1)}{d-1}$; in Sections 1.2.3 and 1.2.4, we saw that  $p^{*} = \frac {2d}{d-2}$ has some special significance, so we will also state a result in this case.
$p^{*} = \frac {2d}{d-2}$ has some special significance, so we will also state a result in this case.
Theorem 1.1 The case  $p<p_{ST}$
$p<p_{ST}$
For any positive definite quadratic form Q, the conjecture in equation (1.4) is verified, up to subpolynomial losses, if ![]() $\lambda>1$,
$\lambda>1$, ![]() $\delta \geq \lambda ^{-1}$ and
$\delta \geq \lambda ^{-1}$ and ![]() $1<p<p_{ST}$.
$1<p<p_{ST}$.
Here, subpolynomial losses mean that the conjecture holds true with an additional ![]() $\lambda ^{\epsilon }$ factor on the right-hand side, where the implicit constant depends on
$\lambda ^{\epsilon }$ factor on the right-hand side, where the implicit constant depends on ![]() $\epsilon $, but
$\epsilon $, but ![]() $\epsilon $ can be chosen arbitrarily small.
$\epsilon $ can be chosen arbitrarily small.
Theorem 1.2 The case of large  $\delta $
$\delta $
For any positive definite quadratic form Q, the conjecture in equation (1.4) is verified, up to subpolynomial losses, if ![]() $\lambda>1$,
$\lambda>1$, ![]() $p\geq p_{ST}$ and
$p\geq p_{ST}$ and
 $$ \begin{align*} \delta> \lambda^{-\frac{(d-1)p-dp_{ST}+2}{(d+1)p-dp_{ST}-2}}. \end{align*} $$
$$ \begin{align*} \delta> \lambda^{-\frac{(d-1)p-dp_{ST}+2}{(d+1)p-dp_{ST}-2}}. \end{align*} $$ By substituting ![]() $p=2d/(d-2)$ and performing a brief computation, we obtain:
$p=2d/(d-2)$ and performing a brief computation, we obtain:
Corollary 1.3 The case  $p = p^{*}$
$p = p^{*}$
Let  $p^{*}=\frac {2d}{d-2}$. For any positive definite quadratic form Q, the conjecture in equation (1.4) is verified, up to subpolynomial losses, for
$p^{*}=\frac {2d}{d-2}$. For any positive definite quadratic form Q, the conjecture in equation (1.4) is verified, up to subpolynomial losses, for ![]() $p=p^{*}$, if
$p=p^{*}$, if ![]() $\lambda>1$ and
$\lambda>1$ and ![]() $\delta \geq \lambda ^{-\frac {1}{2 d - 1}}$.
$\delta \geq \lambda ^{-\frac {1}{2 d - 1}}$.
In Theorems 1.2 and Corollary 1.3, we have aimed to provide simple statements, which are consequently somewhat weaker than Theorem 6.1 below. For any particular d, these last results can be improved by a short computation. We present the following as a representative example.
Theorem 1.4 The case  $d=3$
$d=3$
For any positive definite quadratic form Q, the conjecture in equation (1.4) is verified, up to subpolynomial losses, if ![]() $d=3$, whenever
$d=3$, whenever ![]() $\lambda>1$,
$\lambda>1$,  $\delta \geq \min \{\lambda ^{-\frac {3p-8}{5p-8}}, \lambda ^{-\frac {8-p}{5p-16}}\}$ and also
$\delta \geq \min \{\lambda ^{-\frac {3p-8}{5p-8}}, \lambda ^{-\frac {8-p}{5p-16}}\}$ and also ![]() $\delta \geq \lambda ^{-1/2}$.
$\delta \geq \lambda ^{-1/2}$.
In the proofs of the results above, the value ![]() $\delta = \lambda ^{-\frac {d-1}{d+1}}$ will emerge as playing a special role. In particular, to prove our conjecture in even a single case with
$\delta = \lambda ^{-\frac {d-1}{d+1}}$ will emerge as playing a special role. In particular, to prove our conjecture in even a single case with ![]() $p>p_{ST}$ and
$p>p_{ST}$ and ![]() $\delta \ll \lambda ^{-\frac {d-1}{d+1}}$ needs a different approach. This threshold also appears in the classical result in equation (1.3), and more generally when counting lattice points in a
$\delta \ll \lambda ^{-\frac {d-1}{d+1}}$ needs a different approach. This threshold also appears in the classical result in equation (1.3), and more generally when counting lattice points in a ![]() $\delta $-thick shell around a manifold with curvature
$\delta $-thick shell around a manifold with curvature ![]() $\sim \lambda ^{-1}$ using, for example, Poisson summation. Substituting
$\sim \lambda ^{-1}$ using, for example, Poisson summation. Substituting ![]() $d=3$ into the last theorem does, however, yield the full range
$d=3$ into the last theorem does, however, yield the full range ![]() $\delta> \lambda ^{-\frac {d-1}{d+1}}$, as well as the the full range
$\delta> \lambda ^{-\frac {d-1}{d+1}}$, as well as the the full range ![]() $p>2$, in the following setting:
$p>2$, in the following setting:
Corollary 1.5. If ![]() $d=3$, then for any positive definite quadratic form Q the conjecture holds for all
$d=3$, then for any positive definite quadratic form Q the conjecture holds for all ![]() $\delta \geq \lambda ^{-\frac {d-1}{d+1}} = \lambda ^{-1/2}$ if
$\delta \geq \lambda ^{-\frac {d-1}{d+1}} = \lambda ^{-1/2}$ if  $p\leq p_{ST}+\frac {4}{7}$ or
$p\leq p_{ST}+\frac {4}{7}$ or ![]() $p\geq p_{ST}+4$, and it holds for all
$p\geq p_{ST}+4$, and it holds for all ![]() $p>2$ if
$p>2$ if ![]() $\delta> \lambda ^{-2/5}$.
$\delta> \lambda ^{-2/5}$.
The proof of the above results will combine a number theoretical argument, which allows one to count the number of caps in a spherical shell that contain many lattice points, with a harmonic analysis approach, relying in particular on the ![]() $\ell ^{2}$ decoupling theorem of Bourgain and Demeter.
$\ell ^{2}$ decoupling theorem of Bourgain and Demeter.
In order to understand better the statement of these theorems, it is helpful to spell out what they imply for each of the classical problems presented in Sections 1.2.2, 1.2.3 and 1.2.4.
• For the problem of counting points in thin spherical shells (Subsection 1.2.2), we recover the bound in equation (1.3) of Landau [Reference Landau20]; see also the comments after Theorem 4.1.
• The problem of bounding
 $L^{p}$ norms of eigenfunctions was previously considered for rational tori: that is,
$L^{p}$ norms of eigenfunctions was previously considered for rational tori: that is,  $\mathbb R^{d}/A\mathbb Z^{d}$, where
$\mathbb R^{d}/A\mathbb Z^{d}$, where  $A\in \operatorname {GL}_{d}(\mathbb Q)$. Our results do not improve the bounds of Bourgain-Demeter [Reference Bourgain and Demeter7] in this case. For generic tori, eigenfunction bounds are trivial; the natural analogue of bounding the
$A\in \operatorname {GL}_{d}(\mathbb Q)$. Our results do not improve the bounds of Bourgain-Demeter [Reference Bourgain and Demeter7] in this case. For generic tori, eigenfunction bounds are trivial; the natural analogue of bounding the  $L^{p}$ norms of eigenfunctions is to bound the operator norm of
$L^{p}$ norms of eigenfunctions is to bound the operator norm of  $P_{\lambda ,\frac {1}{\lambda }}$, and this question does not appear to have been considered before. For any torus, that is any
$P_{\lambda ,\frac {1}{\lambda }}$, and this question does not appear to have been considered before. For any torus, that is any  $\mathbb R^{d}/B\mathbb Z^{d}$ with
$\mathbb R^{d}/B\mathbb Z^{d}$ with  $B\in \operatorname {GL}_{d}(\mathbb R)$, we obtain from Theorem 6.1 below the bound
$B\in \operatorname {GL}_{d}(\mathbb R)$, we obtain from Theorem 6.1 below the bound  $$ \begin{align*} \| P_{\lambda,\frac{1}{\lambda}} \|_{L^{2} \to L^{p}} &\lesssim_{\epsilon} \lambda^{\epsilon} (\lambda^{\frac{d}{d+1}})^{\frac{1}{2}(1-\frac{2}{p})+\frac{d}{2}(1- \frac{p_{ST}}{p})-\sqrt{(1 - \frac{2}{p}) (1- \frac{p_{ST}}{p})}} & (p&\geq p_{ST}). \end{align*} $$
$$ \begin{align*} \| P_{\lambda,\frac{1}{\lambda}} \|_{L^{2} \to L^{p}} &\lesssim_{\epsilon} \lambda^{\epsilon} (\lambda^{\frac{d}{d+1}})^{\frac{1}{2}(1-\frac{2}{p})+\frac{d}{2}(1- \frac{p_{ST}}{p})-\sqrt{(1 - \frac{2}{p}) (1- \frac{p_{ST}}{p})}} & (p&\geq p_{ST}). \end{align*} $$• For the problem of proving uniform resolvent bounds (Subsection 1.2.4), it proves the desired estimate up to a subpolynomial loss
if $$ \begin{align*}\| P_{\lambda,\delta} \|_{L^{(p^{*})^{\prime}} \to L^{p^{*}}} \lesssim_{\epsilon} \lambda^{1+\epsilon} \delta, \qquad \end{align*} $$
$$ \begin{align*}\| P_{\lambda,\delta} \|_{L^{(p^{*})^{\prime}} \to L^{p^{*}}} \lesssim_{\epsilon} \lambda^{1+\epsilon} \delta, \qquad \end{align*} $$ $d=3$ and
$d=3$ and  $\delta > \lambda^{-5/11}$, improving over Hickman’s [Reference Hickman16] result that
$\delta > \lambda^{-5/11}$, improving over Hickman’s [Reference Hickman16] result that  $\lambda^{-\frac{1}{3} -\frac{d}{3(21d^2-d-24)}}$.
$\lambda^{-\frac{1}{3} -\frac{d}{3(21d^2-d-24)}}$.
2 Notation
Throughout,  $p_{ST} = \frac {2(d+1)}{d-1},$ and
$p_{ST} = \frac {2(d+1)}{d-1},$ and  $\sigma (p) = d - 1 - \frac {2d}{p}$ will be as in Section 1.1.2, and
$\sigma (p) = d - 1 - \frac {2d}{p}$ will be as in Section 1.1.2, and  $p^{*} = \frac {2d}{d-2}$ as in Section 1.2.3. We adopt the following normalizations for the Fourier series on
$p^{*} = \frac {2d}{d-2}$ as in Section 1.2.3. We adopt the following normalizations for the Fourier series on ![]() $\mathbb {T}^{d}$ and Fourier transform on
$\mathbb {T}^{d}$ and Fourier transform on ![]() $\mathbb {R}^{d}$, respectively:
$\mathbb {R}^{d}$, respectively:
 $$ \begin{align*} & f(x) = \sum_{k \in \mathbb{Z}^{d}} \widehat{f}_{k} e^{2\pi i k \cdot x}, \qquad \qquad \widehat{f}_{k} = \int_{\mathbb{T}^{d}} f(x) e^{-2\pi i k \cdot x} \,dx \\ & f(x) = \int_{\mathbb{R}^{d}} \widehat{f}(\xi) e^{2\pi ix \cdot \xi} \,dx, \qquad \qquad \widehat{f}(\xi) = \int_{\mathbb{R}^{d}} f(x) e^{-2\pi ix \cdot \xi} \,dx. \end{align*} $$
$$ \begin{align*} & f(x) = \sum_{k \in \mathbb{Z}^{d}} \widehat{f}_{k} e^{2\pi i k \cdot x}, \qquad \qquad \widehat{f}_{k} = \int_{\mathbb{T}^{d}} f(x) e^{-2\pi i k \cdot x} \,dx \\ & f(x) = \int_{\mathbb{R}^{d}} \widehat{f}(\xi) e^{2\pi ix \cdot \xi} \,dx, \qquad \qquad \widehat{f}(\xi) = \int_{\mathbb{R}^{d}} f(x) e^{-2\pi ix \cdot \xi} \,dx. \end{align*} $$The Poisson summation formula is then given by
 $$ \begin{align*} \sum_{n \in \mathbb{Z}^{d}} f(n) = \sum_{k \in \mathbb{Z}^{d}} \widehat{f}(k). \end{align*} $$
$$ \begin{align*} \sum_{n \in \mathbb{Z}^{d}} f(n) = \sum_{k \in \mathbb{Z}^{d}} \widehat{f}(k). \end{align*} $$ We write ![]() $(\vec {v}^{(1)}|\cdots |\vec {v}^{(k)})$ for the matrix with columns
$(\vec {v}^{(1)}|\cdots |\vec {v}^{(k)})$ for the matrix with columns ![]() $\vec {v}^{(i)}$.
$\vec {v}^{(i)}$.
Given two quantities A and B, we write ![]() $A \lesssim B$ or equivalently
$A \lesssim B$ or equivalently ![]() $A = O(B)$ if there exists a constant C such that
$A = O(B)$ if there exists a constant C such that ![]() $A \leq CB$, and
$A \leq CB$, and ![]() $A \lesssim _{a,b,c} B$ if the constant C is allowed to depend on
$A \lesssim _{a,b,c} B$ if the constant C is allowed to depend on ![]() $a,b,c$. We always allow C to depend on the dimension d. In the following, it will often be the case that the implicit constant will depend on
$a,b,c$. We always allow C to depend on the dimension d. In the following, it will often be the case that the implicit constant will depend on ![]() $\beta $ and an arbitrarily small power of
$\beta $ and an arbitrarily small power of ![]() $\lambda $:
$\lambda $: ![]() $A \lesssim _{\beta ,\epsilon } \lambda ^{\epsilon } B$. When this is clear from the context, we simply write
$A \lesssim _{\beta ,\epsilon } \lambda ^{\epsilon } B$. When this is clear from the context, we simply write ![]() $A \lesssim \lambda ^{\epsilon } B$. When we are assuming that the implicit constant is sufficiently small, we will write
$A \lesssim \lambda ^{\epsilon } B$. When we are assuming that the implicit constant is sufficiently small, we will write ![]() $A\ll B$.
$A\ll B$.
If both ![]() $A\lesssim B$ and
$A\lesssim B$ and ![]() $B\lesssim A$, then we write
$B\lesssim A$, then we write ![]() $A\sim B$.
$A\sim B$.
3 Lower bounds and conjecture
3.1 The discrete Knapp example
Lemma 3.1. For any ![]() $n \in \mathbb {N}$, there exists
$n \in \mathbb {N}$, there exists ![]() $\lambda \sim |n|$ such that if
$\lambda \sim |n|$ such that if ![]() $\delta \in (0,1)$,
$\delta \in (0,1)$,
 $$ \begin{align*} \| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} \gtrsim (1 + \lambda \delta)^{\frac{(d-1)}{2} \left( \frac{1}{2} - \frac{1}{p} \right)}. \end{align*} $$
$$ \begin{align*} \| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} \gtrsim (1 + \lambda \delta)^{\frac{(d-1)}{2} \left( \frac{1}{2} - \frac{1}{p} \right)}. \end{align*} $$Proof. Consider the ellipse ![]() $\{ \xi \in \mathbb {R}^{d}, \; Q(\xi ) = 1\}$. Its normal vector is colinear to
$\{ \xi \in \mathbb {R}^{d}, \; Q(\xi ) = 1\}$. Its normal vector is colinear to ![]() $e_{d} = (0,\dots ,0,1)$ at the point
$e_{d} = (0,\dots ,0,1)$ at the point ![]() $\xi _{0}$. We now dilate this ellipse by a factor
$\xi _{0}$. We now dilate this ellipse by a factor ![]() $\lambda $ such that
$\lambda $ such that  $\lambda \xi ^{d}_{0} = n \in \mathbb {N}$, smear it to a thickness
$\lambda \xi ^{d}_{0} = n \in \mathbb {N}$, smear it to a thickness ![]() $\delta $, and observe that, around the point
$\delta $, and observe that, around the point ![]() $\lambda \xi _{0}$, it contains many lattice points of
$\lambda \xi _{0}$, it contains many lattice points of ![]() $\mathbb {Z}^{d}$. More precisely, the cuboid
$\mathbb {Z}^{d}$. More precisely, the cuboid ![]() $C \subset \mathbb {R}^{d}$ defined by
$C \subset \mathbb {R}^{d}$ defined by
 $$ \begin{align*} C = \{ |\xi^{i} - \lambda \xi^{i}_{0}| < c \sqrt{\lambda \delta} \;\; \mbox{for }i = 1,\dots,d-1 \quad \mbox{and} \quad |\xi^{d} - \lambda \xi^{d}_{0}| < c\delta \} \end{align*} $$
$$ \begin{align*} C = \{ |\xi^{i} - \lambda \xi^{i}_{0}| < c \sqrt{\lambda \delta} \;\; \mbox{for }i = 1,\dots,d-1 \quad \mbox{and} \quad |\xi^{d} - \lambda \xi^{d}_{0}| < c\delta \} \end{align*} $$(where the constant c is chosen to be sufficiently small) is such that
 $$ \begin{align*} C \subset \left\{ \xi \in \mathbb{R}^{d}, \,\lambda-\frac{\delta}{2} < \sqrt{Q(\xi)} < \lambda + \frac{\delta}{2} \right\}. \end{align*} $$
$$ \begin{align*} C \subset \left\{ \xi \in \mathbb{R}^{d}, \,\lambda-\frac{\delta}{2} < \sqrt{Q(\xi)} < \lambda + \frac{\delta}{2} \right\}. \end{align*} $$Furthermore, for ![]() $\lambda \in \mathbb {Z}$, C will contain
$\lambda \in \mathbb {Z}$, C will contain  $\sim (1 + \lambda \delta )^{\frac {d-1}{2}}$ points in
$\sim (1 + \lambda \delta )^{\frac {d-1}{2}}$ points in ![]() $\mathbb {Z}^{d}$. Writing
$\mathbb {Z}^{d}$. Writing ![]() $\xi = (\xi ^{\prime },\xi ^{d})$ and
$\xi = (\xi ^{\prime },\xi ^{d})$ and ![]() $x=(x^{\prime },x^{d})$, let
$x=(x^{\prime },x^{d})$, let
 $$ \begin{align*} f(x) = e^{2\pi i\lambda \xi_{0}^{d} x^{d}}\sum_{\xi^{\prime} \in \mathbb{Z}^{d-1}} \phi \left( \frac{\xi^{\prime}- \lambda \xi_{0}^{\prime}}{\sqrt{\lambda \delta}} \right) e^{2\pi i \xi^{\prime} \cdot x^{\prime}}, \end{align*} $$
$$ \begin{align*} f(x) = e^{2\pi i\lambda \xi_{0}^{d} x^{d}}\sum_{\xi^{\prime} \in \mathbb{Z}^{d-1}} \phi \left( \frac{\xi^{\prime}- \lambda \xi_{0}^{\prime}}{\sqrt{\lambda \delta}} \right) e^{2\pi i \xi^{\prime} \cdot x^{\prime}}, \end{align*} $$where  $\phi \in \mathcal {C}_{0}^{\infty } (\mathbb {R}^{d-1})$ is such that
$\phi \in \mathcal {C}_{0}^{\infty } (\mathbb {R}^{d-1})$ is such that ![]() $\widehat {\phi } \geq 0$ and
$\widehat {\phi } \geq 0$ and ![]() $\operatorname {Supp} \widehat {\phi } \subset C$. By the Poisson summation formula, f can be written
$\operatorname {Supp} \widehat {\phi } \subset C$. By the Poisson summation formula, f can be written
 $$ \begin{align*} f(x) = e^{2\pi i\lambda x^{d} \xi_{0}^{d}} (\lambda \delta)^{\frac{d-1}{2}} \sum_{n \in \mathbb{Z}^{d-1}} \widehat{\phi}( \sqrt{\lambda \delta}(x^{\prime}-n)) e^{2 \pi i \lambda \xi_{0}^{\prime} \cdot (x^{\prime}-n)}, \end{align*} $$
$$ \begin{align*} f(x) = e^{2\pi i\lambda x^{d} \xi_{0}^{d}} (\lambda \delta)^{\frac{d-1}{2}} \sum_{n \in \mathbb{Z}^{d-1}} \widehat{\phi}( \sqrt{\lambda \delta}(x^{\prime}-n)) e^{2 \pi i \lambda \xi_{0}^{\prime} \cdot (x^{\prime}-n)}, \end{align*} $$which implies
 $$ \begin{align*} \| f \|_{L^{p}} \sim (1 + \lambda \delta)^{\frac{d-1}{2} \left( 1 - \frac{1}{p} \right)}. \end{align*} $$
$$ \begin{align*} \| f \|_{L^{p}} \sim (1 + \lambda \delta)^{\frac{d-1}{2} \left( 1 - \frac{1}{p} \right)}. \end{align*} $$Since ![]() $P_{\lambda ,\delta } f = f$, we find that
$P_{\lambda ,\delta } f = f$, we find that
 $$ \begin{align*} \| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} \geq \frac{\| f \|_{L^{p}}}{\| f \|_{L^{2}}} \sim (1 + \lambda \delta)^{\frac{(d-1)}{2} \left( \frac{1}{2} - \frac{1}{p} \right)}. \end{align*} $$
$$ \begin{align*} \| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} \geq \frac{\| f \|_{L^{p}}}{\| f \|_{L^{2}}} \sim (1 + \lambda \delta)^{\frac{(d-1)}{2} \left( \frac{1}{2} - \frac{1}{p} \right)}. \end{align*} $$3.2 The radial example
Lemma 3.2. For any ![]() $n \in \mathbb {N}$ and
$n \in \mathbb {N}$ and ![]() $\delta \in (0,1)$, there exists
$\delta \in (0,1)$, there exists ![]() $\lambda $ such that
$\lambda $ such that ![]() $|n-\lambda | \lesssim 1$ and
$|n-\lambda | \lesssim 1$ and
 $$ \begin{align*} \| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} \gtrsim \lambda^{\sigma(p)/2} \sqrt \delta. \end{align*} $$
$$ \begin{align*} \| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} \gtrsim \lambda^{\sigma(p)/2} \sqrt \delta. \end{align*} $$Proof. For any ![]() $n \in \mathbb {N}$, there exists
$n \in \mathbb {N}$, there exists ![]() $\lambda $ with
$\lambda $ with ![]() $|n-\lambda | \lesssim 1$, and such that the corona
$|n-\lambda | \lesssim 1$, and such that the corona
 $$ \begin{align*} \mathcal{C} = \{ \lambda -\frac{\delta}{2} < Q(x) < \lambda + \frac{\delta}{2} \} \end{align*} $$
$$ \begin{align*} \mathcal{C} = \{ \lambda -\frac{\delta}{2} < Q(x) < \lambda + \frac{\delta}{2} \} \end{align*} $$contains ![]() $N \gtrsim \lambda ^{d-1} \delta $ points in
$N \gtrsim \lambda ^{d-1} \delta $ points in ![]() $\mathbb {Z}^{d}$. Define
$\mathbb {Z}^{d}$. Define
 $$ \begin{align*} f(x) = \sum_{\xi \in \mathcal{C} \cap \mathbb{Z}^{d-1}} e^{2\pi i \xi \cdot x}. \end{align*} $$
$$ \begin{align*} f(x) = \sum_{\xi \in \mathcal{C} \cap \mathbb{Z}^{d-1}} e^{2\pi i \xi \cdot x}. \end{align*} $$It is clear that
By Bernstein’s inequality, for ![]() $p\geq 2$,
$p\geq 2$,
 $$ \begin{align*} \| f \|_{L^{p}} \gtrsim \|f\|_{L^{\infty}} \lambda^{-\frac{d}{p}} \sim \lambda^{-\frac{d}{p}} N. \end{align*} $$
$$ \begin{align*} \| f \|_{L^{p}} \gtrsim \|f\|_{L^{\infty}} \lambda^{-\frac{d}{p}} \sim \lambda^{-\frac{d}{p}} N. \end{align*} $$Therefore,
 $$ \begin{align*} \| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} \geq \frac{\|f\|_{L^{p}}}{\|f\|_{L^{2}}} \gtrsim \lambda^{\sigma(p)/2} \sqrt \delta. \end{align*} $$
$$ \begin{align*} \| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} \geq \frac{\|f\|_{L^{p}}}{\|f\|_{L^{2}}} \gtrsim \lambda^{\sigma(p)/2} \sqrt \delta. \end{align*} $$3.3 The conjecture
Based on Lemmas 3.1 and 3.2, it is reasonable to conjecture that
 $$ \begin{align*} \boxed{\| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} \lesssim (\lambda \delta)^{\frac{(d-1)}{2} \left( \frac{1}{2} - \frac{1}{p} \right)} + \lambda^{\sigma(p)/2} \delta^{1/2}.} \end{align*} $$
$$ \begin{align*} \boxed{\| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} \lesssim (\lambda \delta)^{\frac{(d-1)}{2} \left( \frac{1}{2} - \frac{1}{p} \right)} + \lambda^{\sigma(p)/2} \delta^{1/2}.} \end{align*} $$The next question is: how small can ![]() $\delta $ be taken? In full generality, the limitation is
$\delta $ be taken? In full generality, the limitation is
 $$ \begin{align*} \delta \geq \frac{1}{\lambda}, \end{align*} $$
$$ \begin{align*} \delta \geq \frac{1}{\lambda}, \end{align*} $$as this is best-possible for rational tori; this will be the range we consider here.
We now describe the different regimes involved in the above conjecture.
![]() $\underline {\mbox {If} \ d=2}$, the conjecture can be formulated as
$\underline {\mbox {If} \ d=2}$, the conjecture can be formulated as
•
 $\| P_{\lambda ,\delta } \|_{L^{2} \to L^{p}} \lesssim (\lambda \delta )^{\frac {1}{4} - \frac {1}{2p} }$ if
$\| P_{\lambda ,\delta } \|_{L^{2} \to L^{p}} \lesssim (\lambda \delta )^{\frac {1}{4} - \frac {1}{2p} }$ if  $\left \{ \begin {array}{l} 2 \leq p \leq 6\; \mbox {and} \; \delta> \lambda ^{-1} \\ \mbox {or} \; p \geq 6 \; \mbox {and} \; \lambda ^{-1} < \delta < \lambda ^{\frac {6-p}{2+p}} \end {array} \right.$.
$\left \{ \begin {array}{l} 2 \leq p \leq 6\; \mbox {and} \; \delta> \lambda ^{-1} \\ \mbox {or} \; p \geq 6 \; \mbox {and} \; \lambda ^{-1} < \delta < \lambda ^{\frac {6-p}{2+p}} \end {array} \right.$.•
 $\| P_{\lambda ,\delta } \|_{L^{2} \to L^{p}} \lesssim \lambda ^{\frac 1 2 - \frac {2}{p}} \delta $ if
$\| P_{\lambda ,\delta } \|_{L^{2} \to L^{p}} \lesssim \lambda ^{\frac 1 2 - \frac {2}{p}} \delta $ if  $p \geq 6$ and
$p \geq 6$ and  $\delta> \lambda ^{\frac {6-p}{2+p}}$.
$\delta> \lambda ^{\frac {6-p}{2+p}}$.
![]() $\underline {\mbox {If} \ d\geq 3}$, let
$\underline {\mbox {If} \ d\geq 3}$, let
 $$ \begin{align*}p_{ST} = \frac{2(d+1)}{d-1}, \qquad p^{*} = \frac{2d}{d-2}, \qquad \widetilde p = \frac{2(d-1)}{d-3} \end{align*} $$
$$ \begin{align*}p_{ST} = \frac{2(d+1)}{d-1}, \qquad p^{*} = \frac{2d}{d-2}, \qquad \widetilde p = \frac{2(d-1)}{d-3} \end{align*} $$and define
 $$ \begin{align*}e(p) = \frac{d+1}{d-1} \cdot \frac{\frac{1}{p} - \frac{1}{p_{ST}}}{\frac{1}{p} - \frac{1}{\widetilde{p}}}. \end{align*} $$
$$ \begin{align*}e(p) = \frac{d+1}{d-1} \cdot \frac{\frac{1}{p} - \frac{1}{p_{ST}}}{\frac{1}{p} - \frac{1}{\widetilde{p}}}. \end{align*} $$We have
Keeping in mind that ![]() $\delta> \lambda ^{-1}$, the above conjecture becomes
$\delta> \lambda ^{-1}$, the above conjecture becomes
•
 $\| P_{\lambda ,\delta } \|_{L^{2} \to L^{p}} \lesssim (\lambda \delta )^{\frac {(d-1)}{2} \left ( \frac {1}{2} - \frac {1}{p} \right )}$ if
$\| P_{\lambda ,\delta } \|_{L^{2} \to L^{p}} \lesssim (\lambda \delta )^{\frac {(d-1)}{2} \left ( \frac {1}{2} - \frac {1}{p} \right )}$ if  $\left \{ \begin {array}{l} 2 \leq p \leq p_{ST} \\ \mbox {or} \; p_{ST} \leq p \leq p^{*} \; \mbox {and} \; \delta < \lambda ^{e(p)} \end {array} \right.$;
$\left \{ \begin {array}{l} 2 \leq p \leq p_{ST} \\ \mbox {or} \; p_{ST} \leq p \leq p^{*} \; \mbox {and} \; \delta < \lambda ^{e(p)} \end {array} \right.$;•
 $\| P_{\lambda ,\delta } \|_{L^{2} \to L^{p}} \lesssim \lambda ^{\sigma (p)/2} \delta ^{1/2}$ if
$\| P_{\lambda ,\delta } \|_{L^{2} \to L^{p}} \lesssim \lambda ^{\sigma (p)/2} \delta ^{1/2}$ if  $\displaystyle \left \{ \begin {array}{l} p_{ST} \leq p \leq p^{*} \; \mbox {and} \; \delta> \lambda ^{e(p)} \\ \mbox {or} \; p \geq p^{*} \end {array} \right.$.
$\displaystyle \left \{ \begin {array}{l} p_{ST} \leq p \leq p^{*} \; \mbox {and} \; \delta> \lambda ^{e(p)} \\ \mbox {or} \; p \geq p^{*} \end {array} \right.$.
4 Caps containing many points
We split the spherical shell
 $$ \begin{align*} S_{\lambda,\delta} = \{ x \in \mathbb{R}^{d}, \, \left| \sqrt{Q(x)}-\lambda \right| < \delta \} \end{align*} $$
$$ \begin{align*} S_{\lambda,\delta} = \{ x \in \mathbb{R}^{d}, \, \left| \sqrt{Q(x)}-\lambda \right| < \delta \} \end{align*} $$into a collection ![]() $\mathcal {C}$ of almost disjoint caps
$\mathcal {C}$ of almost disjoint caps ![]() $\theta $:
$\theta $:
 $$ \begin{align*} S_{\lambda,\delta} = \bigcup_{\theta \in \mathcal{C}} \theta, \end{align*} $$
$$ \begin{align*} S_{\lambda,\delta} = \bigcup_{\theta \in \mathcal{C}} \theta, \end{align*} $$where each cap is of the form
 $$ \begin{align*} \theta = \{ x \in \mathbb{R}^{d}, \, | x - x_{\theta}| < \sqrt{\lambda \delta} \} \cap S_{\lambda,\delta} \qquad \mbox{for some }x_{\theta} \in S_{\lambda,\delta}. \end{align*} $$
$$ \begin{align*} \theta = \{ x \in \mathbb{R}^{d}, \, | x - x_{\theta}| < \sqrt{\lambda \delta} \} \cap S_{\lambda,\delta} \qquad \mbox{for some }x_{\theta} \in S_{\lambda,\delta}. \end{align*} $$Each cap fits into a rectangular box with dimensions ![]() $\sim \delta \times \sqrt {\lambda \delta } \times \dots \times \sqrt {\lambda \delta }$. We call
$\sim \delta \times \sqrt {\lambda \delta } \times \dots \times \sqrt {\lambda \delta }$. We call  $\vec {n}_{\theta } = \frac {x_{\theta }}{|\vec {x}_{\theta }|_{2}}$ the normal vector to
$\vec {n}_{\theta } = \frac {x_{\theta }}{|\vec {x}_{\theta }|_{2}}$ the normal vector to ![]() $\theta $; observe that as
$\theta $; observe that as ![]() $\theta $ varies over caps, the normal vector
$\theta $ varies over caps, the normal vector ![]() $\vec {n}_{\theta }$ varies over a
$\vec {n}_{\theta }$ varies over a  $\sqrt {\delta /\lambda }$-spaced set.
$\sqrt {\delta /\lambda }$-spaced set.
Denote ![]() $N_{\theta }$ for the number of points in
$N_{\theta }$ for the number of points in ![]() $\mathbb {Z}^{d} \cap \theta $. On the one hand, it is clear that
$\mathbb {Z}^{d} \cap \theta $. On the one hand, it is clear that ![]() $N_{\theta } \lesssim (\sqrt {\lambda \delta })^{d-1}$. On the other hand, one expects that the average cap will contain a number of points comparable to its volume, in other words
$N_{\theta } \lesssim (\sqrt {\lambda \delta })^{d-1}$. On the other hand, one expects that the average cap will contain a number of points comparable to its volume, in other words ![]() $N_{\theta } \sim (\sqrt {\lambda \delta })^{d-1} \delta $ (provided this quantity is
$N_{\theta } \sim (\sqrt {\lambda \delta })^{d-1} \delta $ (provided this quantity is ![]() $>1$, which occurs if
$>1$, which occurs if ![]() $\delta> \lambda ^{-\frac {d-1}{d+1}}$).
$\delta> \lambda ^{-\frac {d-1}{d+1}}$).
This leads naturally to defining the following sets, which gather caps containing comparable numbers of points
 $$ \begin{align*} & \mathcal{C}_{0} = \{ \theta \in \mathcal{C}, \, N_{\theta} < (\sqrt{\lambda \delta})^{d-1} \delta \} \\ & \mathcal{C}_{j} = \{ \theta \in \mathcal{C}, \, (\sqrt{\lambda \delta})^{d-1} \delta 2^{j-1}<N_{\theta}\leq (\sqrt{\lambda \delta})^{d-1} \delta 2^{j}\} , \qquad \mbox{for }1\leq 2^{j} \lesssim \delta^{-1}\mbox{ }. \end{align*} $$
$$ \begin{align*} & \mathcal{C}_{0} = \{ \theta \in \mathcal{C}, \, N_{\theta} < (\sqrt{\lambda \delta})^{d-1} \delta \} \\ & \mathcal{C}_{j} = \{ \theta \in \mathcal{C}, \, (\sqrt{\lambda \delta})^{d-1} \delta 2^{j-1}<N_{\theta}\leq (\sqrt{\lambda \delta})^{d-1} \delta 2^{j}\} , \qquad \mbox{for }1\leq 2^{j} \lesssim \delta^{-1}\mbox{ }. \end{align*} $$Theorem 4.1. There is a constant ![]() $K > 0$, depending only on d, as follows. Let
$K > 0$, depending only on d, as follows. Let ![]() $ k \in \{ 1, \dotsc , d-1 \} $. If
$ k \in \{ 1, \dotsc , d-1 \} $. If ![]() $ 2^{ j }>K $ and
$ 2^{ j }>K $ and ![]() $(\sqrt { \delta \lambda })^{ k } \delta 2^{ j }>K$, then
$(\sqrt { \delta \lambda })^{ k } \delta 2^{ j }>K$, then
 $$ \begin{align*} \# \mathcal{ C }_{ j } \lesssim ( 2^{ j / k } \delta )^{ - d }. \end{align*} $$
$$ \begin{align*} \# \mathcal{ C }_{ j } \lesssim ( 2^{ j / k } \delta )^{ - d }. \end{align*} $$Remark 4.2. There is an integer ![]() $k \in \{ 1, \dotsc , d-1 \}$ satisfying
$k \in \{ 1, \dotsc , d-1 \}$ satisfying ![]() $(\sqrt { \delta \lambda })^{ k } \delta 2^{ j }>K$ whenever
$(\sqrt { \delta \lambda })^{ k } \delta 2^{ j }>K$ whenever ![]() $\delta> \lambda ^{-\frac {d-1}{d+1}}$, which in practise we will assume whenever we apply the theorem above.
$\delta> \lambda ^{-\frac {d-1}{d+1}}$, which in practise we will assume whenever we apply the theorem above.
By summing over the caps in each ![]() $ \mathcal {C}_{j} $, we find that
$ \mathcal {C}_{j} $, we find that  $ \#(S_{\lambda ,\delta }\cap \mathbb Z^{d}) \ll \delta \lambda ^{d-1} +\sqrt {\lambda /\delta }^{d-1} $, and in particular
$ \#(S_{\lambda ,\delta }\cap \mathbb Z^{d}) \ll \delta \lambda ^{d-1} +\sqrt {\lambda /\delta }^{d-1} $, and in particular ![]() $ \#(S_{\lambda ,\delta }\cap \mathbb Z^{d}) \ll \delta \lambda ^{d-1}$ for
$ \#(S_{\lambda ,\delta }\cap \mathbb Z^{d}) \ll \delta \lambda ^{d-1}$ for ![]() $\delta> \lambda ^{-\frac {d-1}{d+1}}$. This recovers the classical result in equation (1.3). As explained in Section 1.2.2, the range
$\delta> \lambda ^{-\frac {d-1}{d+1}}$. This recovers the classical result in equation (1.3). As explained in Section 1.2.2, the range ![]() $\delta> \lambda ^{-\frac {d-1}{d+1}}$ has now been improved in every dimension. Thus Theorem 4.1 is certainly suboptimal if
$\delta> \lambda ^{-\frac {d-1}{d+1}}$ has now been improved in every dimension. Thus Theorem 4.1 is certainly suboptimal if ![]() $\delta \ll \lambda ^{-\frac {d-1}{d+1}}$.
$\delta \ll \lambda ^{-\frac {d-1}{d+1}}$.
To further gauge the strength of this theorem, we can compare it to the trivial bounds
 $$ \begin{align} \# \mathcal{C}_{0} &\lesssim ( \lambda \delta^{-1})^{\frac{d-1}{2}}, \end{align} $$
$$ \begin{align} \# \mathcal{C}_{0} &\lesssim ( \lambda \delta^{-1})^{\frac{d-1}{2}}, \end{align} $$ $$ \begin{align} \# \mathcal{C}_{j} &=0\qquad( 2^{j} \gg \delta^{-1}). \end{align} $$
$$ \begin{align} \# \mathcal{C}_{j} &=0\qquad( 2^{j} \gg \delta^{-1}). \end{align} $$If ![]() $\delta = \lambda ^{-\frac {d-1}{d+1}}$, then the theorem interpolates between these bounds. For it reduces, on the one hand, to
$\delta = \lambda ^{-\frac {d-1}{d+1}}$, then the theorem interpolates between these bounds. For it reduces, on the one hand, to  $\#\mathcal {C}_{j} \lesssim ( \lambda \delta ^{-1})^{\frac {d-1}{2}}$ for
$\#\mathcal {C}_{j} \lesssim ( \lambda \delta ^{-1})^{\frac {d-1}{2}}$ for ![]() $2^{j}\sim 1$, and on the other, to
$2^{j}\sim 1$, and on the other, to ![]() $\# \mathcal {C}_{j} \lesssim (\delta 2^{j})^{-d}$ for
$\# \mathcal {C}_{j} \lesssim (\delta 2^{j})^{-d}$ for ![]() $\delta 2^{j} \gg (\sqrt {\lambda \delta })^{-1}$.
$\delta 2^{j} \gg (\sqrt {\lambda \delta })^{-1}$.
If ![]() $\delta> \lambda ^{-\frac {d-1}{d+1}}$, then the theorem shows that for some constant
$\delta> \lambda ^{-\frac {d-1}{d+1}}$, then the theorem shows that for some constant ![]() $C_{d}>0$, all but
$C_{d}>0$, all but  $\frac {C_{d}}{\delta (\sqrt {\lambda \delta })^{d-1}}\%$ of the caps
$\frac {C_{d}}{\delta (\sqrt {\lambda \delta })^{d-1}}\%$ of the caps ![]() $\theta $ satisfy
$\theta $ satisfy ![]() $N_{\theta } \lesssim \delta (\sqrt {\lambda \delta })^{d-1}$, and interpolates between this bound and in equation (4.2). Inspecting the proof, we could strengthen the former bound: if
$N_{\theta } \lesssim \delta (\sqrt {\lambda \delta })^{d-1}$, and interpolates between this bound and in equation (4.2). Inspecting the proof, we could strengthen the former bound: if ![]() $\delta> \lambda ^{-\frac {d-1}{d+1}}$, then all but
$\delta> \lambda ^{-\frac {d-1}{d+1}}$, then all but  $\frac {C_{d}}{\delta (\sqrt {\lambda \delta })^{d-1}}\%$ of the caps
$\frac {C_{d}}{\delta (\sqrt {\lambda \delta })^{d-1}}\%$ of the caps ![]() $\theta $ contain a fundamental region for
$\theta $ contain a fundamental region for ![]() $\mathbb Z^{d}$.
$\mathbb Z^{d}$.
If ![]() $\delta < \lambda ^{-\frac {d-1}{d+1}}$ then the theorem shows that all but
$\delta < \lambda ^{-\frac {d-1}{d+1}}$ then the theorem shows that all but  $(C^{\prime }_{d}\sqrt {\lambda }(\sqrt {\delta })^{\frac {d+1}{d-1}})\%$ of the caps
$(C^{\prime }_{d}\sqrt {\lambda }(\sqrt {\delta })^{\frac {d+1}{d-1}})\%$ of the caps ![]() $\theta $ satisfy
$\theta $ satisfy ![]() $N_{\theta } \lesssim 1$, and interpolates between this bound and in equation (4.1). Again, by inspecting the proof, we could strengthen first part: if
$N_{\theta } \lesssim 1$, and interpolates between this bound and in equation (4.1). Again, by inspecting the proof, we could strengthen first part: if ![]() $\delta> \lambda ^{-\frac {d-1}{d+1}}$, then all but
$\delta> \lambda ^{-\frac {d-1}{d+1}}$, then all but  $(C^{\prime }_{d}\sqrt {\lambda }(\sqrt {\delta })^{\frac {d+1}{d-1}})\%$ of the caps
$(C^{\prime }_{d}\sqrt {\lambda }(\sqrt {\delta })^{\frac {d+1}{d-1}})\%$ of the caps ![]() $\theta $ satisfy
$\theta $ satisfy ![]() $N_{\theta } \leq 1$. In this regime, most caps should have
$N_{\theta } \leq 1$. In this regime, most caps should have ![]() $N_{\theta }=0$.
$N_{\theta }=0$.
Proof of Theorem 4.1.
Let ![]() $\theta $ be any cap. Let
$\theta $ be any cap. Let ![]() $R_{\theta }$ be a rectangular box, centred at the origin, containing
$R_{\theta }$ be a rectangular box, centred at the origin, containing ![]() $\theta -\theta $ and having dimensions
$\theta -\theta $ and having dimensions ![]() $\sim \delta \times \sqrt {\lambda \delta } \times \dots \times \sqrt {\lambda \delta }$.
$\sim \delta \times \sqrt {\lambda \delta } \times \dots \times \sqrt {\lambda \delta }$.
Define a norm ![]() $|\,\cdot \,|_{\theta }$ on
$|\,\cdot \,|_{\theta }$ on ![]() $\mathbb R^{d}$ by
$\mathbb R^{d}$ by
so that ![]() $R_{\theta }$ is the unit ball in this norm, with
$R_{\theta }$ is the unit ball in this norm, with
Because ![]() $R_{\theta }$ is contained in a slab of the form
$R_{\theta }$ is contained in a slab of the form ![]() $\{\vec {x}\in \mathbb R^{d}:\vec {n}_{\theta }\cdot \vec {x}\lesssim \delta \}$, we also have
$\{\vec {x}\in \mathbb R^{d}:\vec {n}_{\theta }\cdot \vec {x}\lesssim \delta \}$, we also have
Morally, the idea of the proof is to fix the lattice generated by ![]() $R_{\theta }\cap \mathbb Z^{d}$ and count the number of caps with a given lattice. Carrying out this programme in a literal fashion seems possible but technically complex. We take advantage of a trick: we will construct a small integer vector
$R_{\theta }\cap \mathbb Z^{d}$ and count the number of caps with a given lattice. Carrying out this programme in a literal fashion seems possible but technically complex. We take advantage of a trick: we will construct a small integer vector ![]() $\vec {v}$ that is orthogonal to all the integer vectors in
$\vec {v}$ that is orthogonal to all the integer vectors in ![]() $R_{\theta }\cap \mathbb Z^{d}$ and approximately perpendicular to
$R_{\theta }\cap \mathbb Z^{d}$ and approximately perpendicular to ![]() $\vec {n}_{\theta }$, and it is this vector, rather than the lattice itself, that we will fix. The outline of the proof is as follows: after some further definitions, we set out some basic results from the geometry of numbers in Step 1 below; we then construct
$\vec {n}_{\theta }$, and it is this vector, rather than the lattice itself, that we will fix. The outline of the proof is as follows: after some further definitions, we set out some basic results from the geometry of numbers in Step 1 below; we then construct ![]() $\vec {v}$ in Step 2 and complete the proof in Step 3.
$\vec {v}$ in Step 2 and complete the proof in Step 3.
Define ![]() $r_{\theta }$ to be the dimension of the span (over
$r_{\theta }$ to be the dimension of the span (over ![]() $\mathbb R$, say) of the vectors in
$\mathbb R$, say) of the vectors in ![]() $R_{\theta }\cap \mathbb Z^{d}$. The hypotheses of the theorem imply that we cannot have
$R_{\theta }\cap \mathbb Z^{d}$. The hypotheses of the theorem imply that we cannot have ![]() $r_{\theta } =d$, since then
$r_{\theta } =d$, since then  $N_{\theta }\lesssim \delta (\sqrt {\lambda /\delta })^{d-1}$.
$N_{\theta }\lesssim \delta (\sqrt {\lambda /\delta })^{d-1}$.
Step 1: We show that there is a basis ![]() $\vec {x}^{(1)},\dotsc ,\vec {x}^{(d)}$ of
$\vec {x}^{(1)},\dotsc ,\vec {x}^{(d)}$ of ![]() $\mathbb Z^{d}$ with
$\mathbb Z^{d}$ with
 $$ \begin{align} \delta (\sqrt{\delta\lambda})^{d-1} \sim \prod_{i=1}^{d} |\vec{x}^{(i)}|_{\theta}^{-1}, \qquad \#(\mathbb Z^{d}\cap R_{\theta}) \sim \prod_{i=1}^{r_{\theta}} |\vec{x}^{(i)}|_{\theta}^{-1}. \end{align} $$
$$ \begin{align} \delta (\sqrt{\delta\lambda})^{d-1} \sim \prod_{i=1}^{d} |\vec{x}^{(i)}|_{\theta}^{-1}, \qquad \#(\mathbb Z^{d}\cap R_{\theta}) \sim \prod_{i=1}^{r_{\theta}} |\vec{x}^{(i)}|_{\theta}^{-1}. \end{align} $$This is more or less a standard result from the geometry of numbers.
In this step only, let A be the matrix with ![]() $AR_{\theta }=[-1,1]^{d}$, and for
$AR_{\theta }=[-1,1]^{d}$, and for ![]() $1\leq i \leq d$, let
$1\leq i \leq d$, let ![]() $M_{i}$ be minimal such that there are i linearly independent vectors
$M_{i}$ be minimal such that there are i linearly independent vectors ![]() $\vec {x}\in \mathbb Z^{d}$ with
$\vec {x}\in \mathbb Z^{d}$ with ![]() $|\vec {x}|_{\theta }\leq M_{i}$, or equivalently there are i linearly independent vectors
$|\vec {x}|_{\theta }\leq M_{i}$, or equivalently there are i linearly independent vectors ![]() $\vec {y}\in A\mathbb Z^{d}$ with
$\vec {y}\in A\mathbb Z^{d}$ with ![]() $|A\vec {y}|_{\infty } \leq M_{i}$. In particular,
$|A\vec {y}|_{\infty } \leq M_{i}$. In particular,
By Theorem V in Section VIII.4.3 of Cassels [Reference Cassels9], we have
 $$ \begin{align} \prod_{i=1}^{d} M_{i} \sim \det A \sim \frac{1}{\delta(\sqrt{\delta\lambda})^{d-1}}. \end{align} $$
$$ \begin{align} \prod_{i=1}^{d} M_{i} \sim \det A \sim \frac{1}{\delta(\sqrt{\delta\lambda})^{d-1}}. \end{align} $$Also, by Lemma 2 in Section VIII.1.2 of Cassels, there is a basis ![]() $\vec {y}^{(1)},\dotsc ,\vec {y}^{(d)}$ of
$\vec {y}^{(1)},\dotsc ,\vec {y}^{(d)}$ of ![]() $A\mathbb Z^{d}$ such that
$A\mathbb Z^{d}$ such that
Let ![]() $\vec {z}^{(i)}$ be the dual basis, so that
$\vec {z}^{(i)}$ be the dual basis, so that
for all ![]() $\vec {y}\in A\mathbb Z^{d}$. Note that we must have
$\vec {y}\in A\mathbb Z^{d}$. Note that we must have ![]() $ M_{i}\leq |\vec {y}^{(i)}|_{\infty }$ from the definition of
$ M_{i}\leq |\vec {y}^{(i)}|_{\infty }$ from the definition of ![]() $M_{i}$. By the Corollary to Theorem VIII in Section VIII.5.2 of Cassels, we may choose the
$M_{i}$. By the Corollary to Theorem VIII in Section VIII.5.2 of Cassels, we may choose the ![]() $\vec {y}^{(i)}$ such that
$\vec {y}^{(i)}$ such that
 $$ \begin{align} M_{i}\leq |\vec{y}^{(i)}|_{\infty} \leq \max\{1,i/2\} M_{i}, \qquad |\vec{z}^{(i)}| \leq (\tfrac{1}{2})^{n-1}(n!)^{2}/ |\vec{y}^{(i)}|_{\infty}. \end{align} $$
$$ \begin{align} M_{i}\leq |\vec{y}^{(i)}|_{\infty} \leq \max\{1,i/2\} M_{i}, \qquad |\vec{z}^{(i)}| \leq (\tfrac{1}{2})^{n-1}(n!)^{2}/ |\vec{y}^{(i)}|_{\infty}. \end{align} $$We now let ![]() $\vec {x}^{(i)}=A^{-1}\vec {y}^{(i)}$ be our basis of
$\vec {x}^{(i)}=A^{-1}\vec {y}^{(i)}$ be our basis of ![]() $\mathbb Z^{d}$. We then have
$\mathbb Z^{d}$. We then have
 $$ \begin{align} |\vec{x}^{(i)}|_{\theta} =|\vec{y}^{(i)}|_{\infty}\sim M_{i}^{-1}, \end{align} $$
$$ \begin{align} |\vec{x}^{(i)}|_{\theta} =|\vec{y}^{(i)}|_{\infty}\sim M_{i}^{-1}, \end{align} $$by equation (4.8). Now equations (4.9) and (4.6) together imply the first part of equation (4.5). It also follows from equation (4.8) that for some ![]() $c>0$ depending only on d, we have
$c>0$ depending only on d, we have
 $$ \begin{align*} |c_{i}|\leq c M_{i}^{-1}\;(1\leq i\leq r_{\theta}) &\implies |c_{1}\vec{x}^{(1)}+\dotsb+c_{r_{\theta}} \vec{x}^{(r_{\theta})}|\leq 1, \end{align*} $$
$$ \begin{align*} |c_{i}|\leq c M_{i}^{-1}\;(1\leq i\leq r_{\theta}) &\implies |c_{1}\vec{x}^{(1)}+\dotsb+c_{r_{\theta}} \vec{x}^{(r_{\theta})}|\leq 1, \end{align*} $$and combining equation (4.7) with equation (4.8) shows that there is a constant ![]() $C>0$ depending only on d such that
$C>0$ depending only on d such that
 $$ \begin{align*} |c_{1}\vec{x}^{(1)}+\dotsb+c_{d} \vec{x}^{(d)}|\leq 1 &\implies |c_{i}|\leq CM_{i}^{-1}\;(1\leq i\leq r_{\theta}),\; c_{i}=0\;(i>r_{\theta} ). \end{align*} $$
$$ \begin{align*} |c_{1}\vec{x}^{(1)}+\dotsb+c_{d} \vec{x}^{(d)}|\leq 1 &\implies |c_{i}|\leq CM_{i}^{-1}\;(1\leq i\leq r_{\theta}),\; c_{i}=0\;(i>r_{\theta} ). \end{align*} $$The last two displays yield
 $$ \begin{align*} \#(\mathbb Z^{d}\cap R_{\theta}) = \#([-1,1]^{d}\cap A\mathbb Z^{d})\sim \frac{ 1}{\prod_{i=1}^{r_{\theta}} M_{i}} \sim\frac{ 1}{\prod_{i=1}^{r_{\theta}} |\vec{y}^{(i)}|_{\infty}}, \end{align*} $$
$$ \begin{align*} \#(\mathbb Z^{d}\cap R_{\theta}) = \#([-1,1]^{d}\cap A\mathbb Z^{d})\sim \frac{ 1}{\prod_{i=1}^{r_{\theta}} M_{i}} \sim\frac{ 1}{\prod_{i=1}^{r_{\theta}} |\vec{y}^{(i)}|_{\infty}}, \end{align*} $$and the last part of equation (4.5) follows by equation (4.9).
Step 2: We claim that if ![]() $1\leq r_{\theta }<d$ and
$1\leq r_{\theta }<d$ and ![]() $\vec {n}_{\theta }$ is the normal vector to
$\vec {n}_{\theta }$ is the normal vector to ![]() $\theta $, then there is
$\theta $, then there is  $\vec {v}\in \mathbb Z^{d}\setminus \{\vec {0}\}$ such that
$\vec {v}\in \mathbb Z^{d}\setminus \{\vec {0}\}$ such that
 $$ \begin{align*} |\vec{v}|_{2}\lesssim\delta^{-1} \left( \frac{\delta(\sqrt{\lambda\delta})^{d-1}}{\#(\mathbb Z^{d}\cap R_{\theta})} \right)^{\frac{1}{d-r_{\theta}},}\qquad \left| \vec{n}_{\theta}- \vec{v}/|\vec{v}|_{2} \right| \lesssim (\sqrt{\lambda\delta})^{-1} |\vec{v}|_{2} {}^{-1} \left(\frac{ \delta(\sqrt{\lambda\delta})^{d-1} }{\#(\mathbb Z^{d}\cap R_{\theta}) }\right)^{\frac{1}{d-r_{\theta}}}. \end{align*} $$
$$ \begin{align*} |\vec{v}|_{2}\lesssim\delta^{-1} \left( \frac{\delta(\sqrt{\lambda\delta})^{d-1}}{\#(\mathbb Z^{d}\cap R_{\theta})} \right)^{\frac{1}{d-r_{\theta}},}\qquad \left| \vec{n}_{\theta}- \vec{v}/|\vec{v}|_{2} \right| \lesssim (\sqrt{\lambda\delta})^{-1} |\vec{v}|_{2} {}^{-1} \left(\frac{ \delta(\sqrt{\lambda\delta})^{d-1} }{\#(\mathbb Z^{d}\cap R_{\theta}) }\right)^{\frac{1}{d-r_{\theta}}}. \end{align*} $$ For the proof, let ![]() $\vec {x}^{(i)}$ be as in Step 1. Recall the notation
$\vec {x}^{(i)}$ be as in Step 1. Recall the notation ![]() $(\vec {v}^{(1)}|\cdots |\vec {v}^{(k)})$ for the matrix with columns
$(\vec {v}^{(1)}|\cdots |\vec {v}^{(k)})$ for the matrix with columns ![]() $\vec {v}^{(i)}$. We let
$\vec {v}^{(i)}$. We let
By equation (4.4), we have
 $$ \begin{align} \bigg\lvert\vec{n}_{\theta}^{T}\left(\frac{\vec{x}^{(1)}}{|\vec{x}^{(1)}|_{\theta}} \,\middle|\, \cdots \,\middle|\, \frac{\vec{x}^{(d-1)}}{|\vec{x}^{(d-1)}|_{\theta}}\right) \bigg\rvert_{\infty}\lesssim \delta. \end{align} $$
$$ \begin{align} \bigg\lvert\vec{n}_{\theta}^{T}\left(\frac{\vec{x}^{(1)}}{|\vec{x}^{(1)}|_{\theta}} \,\middle|\, \cdots \,\middle|\, \frac{\vec{x}^{(d-1)}}{|\vec{x}^{(d-1)}|_{\theta}}\right) \bigg\rvert_{\infty}\lesssim \delta. \end{align} $$Now every ![]() $\vec {x}^{(i)}$ satisfies
$\vec {x}^{(i)}$ satisfies  $ \frac {\lvert \vec {x}^{(1)}\rvert _{\infty } }{|\vec {x}^{(1)}|_{\theta }}\lesssim \sqrt {\lambda \delta }$ by equation (4.3). Therefore
$ \frac {\lvert \vec {x}^{(1)}\rvert _{\infty } }{|\vec {x}^{(1)}|_{\theta }}\lesssim \sqrt {\lambda \delta }$ by equation (4.3). Therefore
 $$ \begin{align} \left(\frac{\vec{x}^{(1)}}{|\vec{x}^{(1)}|_{\theta}} \,\middle|\, \cdots \,\middle|\, \frac{\vec{x}^{(d-1)}}{|\vec{x}^{(d-1)}|_{\theta}}\right) = U \begin{pmatrix} \operatorname{diag}(d_{1},\dotsc,d_{d-1})\\ O_{1\times (d-1)} \end{pmatrix} V, \end{align} $$
$$ \begin{align} \left(\frac{\vec{x}^{(1)}}{|\vec{x}^{(1)}|_{\theta}} \,\middle|\, \cdots \,\middle|\, \frac{\vec{x}^{(d-1)}}{|\vec{x}^{(d-1)}|_{\theta}}\right) = U \begin{pmatrix} \operatorname{diag}(d_{1},\dotsc,d_{d-1})\\ O_{1\times (d-1)} \end{pmatrix} V, \end{align} $$where O is a matrix of zeroes, ![]() $U,V$ are orthogonal, and
$U,V$ are orthogonal, and ![]() $d_{i}\lesssim \sqrt {\lambda \delta }$. It follows that
$d_{i}\lesssim \sqrt {\lambda \delta }$. It follows that
 $$ \begin{align} |\vec{v}|_{2} \sim \prod_{i=1}^{d-1} d_{i} |\vec{x}^{(i)}|_{\theta} \lesssim \delta^{-1}|\vec{x}^{(d)}|^{-1}_{\theta}. \end{align} $$
$$ \begin{align} |\vec{v}|_{2} \sim \prod_{i=1}^{d-1} d_{i} |\vec{x}^{(i)}|_{\theta} \lesssim \delta^{-1}|\vec{x}^{(d)}|^{-1}_{\theta}. \end{align} $$Now equations (4.10) and (4.11) together yield
 $$ \begin{align*} \bigg\lvert\vec{n}_{\theta}^{T} U \left(\begin{smallmatrix} 1 \\&\ddots\\&&1\\&&&0 \end{smallmatrix}\right)\bigg\rvert_{\infty} \lesssim \delta (\min_{i} |d_{i}|)^{-1}. \end{align*} $$
$$ \begin{align*} \bigg\lvert\vec{n}_{\theta}^{T} U \left(\begin{smallmatrix} 1 \\&\ddots\\&&1\\&&&0 \end{smallmatrix}\right)\bigg\rvert_{\infty} \lesssim \delta (\min_{i} |d_{i}|)^{-1}. \end{align*} $$For any vector with ![]() $|\vec {m}|_{2}= 1$, we have
$|\vec {m}|_{2}= 1$, we have
 $$ \begin{align*} |m_{d}|-1 \lesssim \bigg\lvert\vec{m}^{T} \left(\begin{smallmatrix} 1\\&\ddots\\&&1\\&&&0 \end{smallmatrix}\right)\bigg\rvert_{2}^{2}, \end{align*} $$
$$ \begin{align*} |m_{d}|-1 \lesssim \bigg\lvert\vec{m}^{T} \left(\begin{smallmatrix} 1\\&\ddots\\&&1\\&&&0 \end{smallmatrix}\right)\bigg\rvert_{2}^{2}, \end{align*} $$and so
 $$ \begin{align*} \min\{ |\vec{m}-\vec{e}^{(d)}|_{2}, |\vec{m}+\vec{e}^{(d)}|_{2} \} \lesssim\bigg\lvert\vec{m}^{T} \left(\begin{smallmatrix} 1 \\&\ddots\\&&1\\&&&0 \end{smallmatrix}\right)\bigg\rvert_{\infty}. \end{align*} $$
$$ \begin{align*} \min\{ |\vec{m}-\vec{e}^{(d)}|_{2}, |\vec{m}+\vec{e}^{(d)}|_{2} \} \lesssim\bigg\lvert\vec{m}^{T} \left(\begin{smallmatrix} 1 \\&\ddots\\&&1\\&&&0 \end{smallmatrix}\right)\bigg\rvert_{\infty}. \end{align*} $$It follows that for some choice of sign,
 $$ \begin{align*} |\vec{n}_{\theta}\pm U\vec{e}^{(d)}|_{2} = |U^{T}\vec{n}_{\theta}\pm \vec{e}^{(d)}|_{2} \lesssim \delta (\min_{i} |d_{i}|)^{-1}. \end{align*} $$
$$ \begin{align*} |\vec{n}_{\theta}\pm U\vec{e}^{(d)}|_{2} = |U^{T}\vec{n}_{\theta}\pm \vec{e}^{(d)}|_{2} \lesssim \delta (\min_{i} |d_{i}|)^{-1}. \end{align*} $$By our definition ![]() $\vec {v}= \vec {x}^{(1)}\wedge \dotsb \wedge \vec {x}^{(d-1)}$, we have
$\vec {v}= \vec {x}^{(1)}\wedge \dotsb \wedge \vec {x}^{(d-1)}$, we have
 $$ \begin{align*} \vec{v}^{T} \left(\frac{\vec{x}^{(1)}}{|\vec{x}^{(1)}|_{\theta}} \,\middle|\, \cdots \,\middle|\, \frac{\vec{x}^{(d-1)}}{|\vec{x}^{(d-1)}|_{\theta}} \right) =(0,\dotsc,0), \end{align*} $$
$$ \begin{align*} \vec{v}^{T} \left(\frac{\vec{x}^{(1)}}{|\vec{x}^{(1)}|_{\theta}} \,\middle|\, \cdots \,\middle|\, \frac{\vec{x}^{(d-1)}}{|\vec{x}^{(d-1)}|_{\theta}} \right) =(0,\dotsc,0), \end{align*} $$so that ![]() $U\vec {e}^{(d)}=\vec {v}/|\vec {v}|_{2}$. It follows that, possibly after replacing
$U\vec {e}^{(d)}=\vec {v}/|\vec {v}|_{2}$. It follows that, possibly after replacing ![]() $\vec {v}$ with
$\vec {v}$ with ![]() $-\vec {v}$ if necessary, we have
$-\vec {v}$ if necessary, we have
 $$ \begin{align} \left| \vec{n}_{\theta}- \vec{v}/|\vec{v}|_{2} \right| \lesssim \frac{ \delta(\sqrt{\lambda\delta})^{d-2} \prod_{i=1}^{d-1} |\vec{x}^{(i)}|_{\theta} }{ |\vec{v}|_{2} } \sim \frac{ 1 }{ \sqrt{\lambda\delta} |\vec{x}^{(d)}|_{\theta} |\vec{v}|_{2} }, \end{align} $$
$$ \begin{align} \left| \vec{n}_{\theta}- \vec{v}/|\vec{v}|_{2} \right| \lesssim \frac{ \delta(\sqrt{\lambda\delta})^{d-2} \prod_{i=1}^{d-1} |\vec{x}^{(i)}|_{\theta} }{ |\vec{v}|_{2} } \sim \frac{ 1 }{ \sqrt{\lambda\delta} |\vec{x}^{(d)}|_{\theta} |\vec{v}|_{2} }, \end{align} $$where the last part follows by Step 1. It remains to observe that, again by Step 1, we have
 $$ \begin{align*} |\vec{x}^{(d)}|_{\theta}^{d-r_{\theta}} \geq \prod_{i=r_{\theta}+1}^{d} |\vec{x}^{(i)}|_{\theta} \sim \frac{\#(\mathbb Z^{d}\cap R_{\theta})}{\delta (\sqrt{\delta\lambda})^{d-1}}, \end{align*} $$
$$ \begin{align*} |\vec{x}^{(d)}|_{\theta}^{d-r_{\theta}} \geq \prod_{i=r_{\theta}+1}^{d} |\vec{x}^{(i)}|_{\theta} \sim \frac{\#(\mathbb Z^{d}\cap R_{\theta})}{\delta (\sqrt{\delta\lambda})^{d-1}}, \end{align*} $$and the result follows from this bound together with equations (4.12) and (4.13).
Step 3: By Step 2, the number of ![]() $\theta \in \mathcal {C}$ with
$\theta \in \mathcal {C}$ with ![]() $r_{\theta }=r$ and
$r_{\theta }=r$ and ![]() $\#(\mathbb Z^{d}\cap R_{\theta }) \sim 2^{J}\delta (\sqrt {\delta \lambda })^{d-1}$ is
$\#(\mathbb Z^{d}\cap R_{\theta }) \sim 2^{J}\delta (\sqrt {\delta \lambda })^{d-1}$ is
 $$ \begin{align*} \lesssim \sum_{ \substack{\vec{v}\in \mathbb Z^{d}\setminus\{\vec{0}\}\\ |\vec{v}|_{2} \leq \delta^{-1} 2^{ {-J/(d-r)} }}} \left(1+ \delta^{-1} |\vec{v}|_{2} {}^{-1}2^{-J/(d-r)}\right)^{d-1} \lesssim \left(\delta 2^{J/(d-r)}\right)^{-d}. \end{align*} $$
$$ \begin{align*} \lesssim \sum_{ \substack{\vec{v}\in \mathbb Z^{d}\setminus\{\vec{0}\}\\ |\vec{v}|_{2} \leq \delta^{-1} 2^{ {-J/(d-r)} }}} \left(1+ \delta^{-1} |\vec{v}|_{2} {}^{-1}2^{-J/(d-r)}\right)^{d-1} \lesssim \left(\delta 2^{J/(d-r)}\right)^{-d}. \end{align*} $$ Let ![]() $2^{j}$ be as in the theorem, and suppose
$2^{j}$ be as in the theorem, and suppose ![]() $\theta \in \mathcal {C}_{j}$. Then
$\theta \in \mathcal {C}_{j}$. Then
and it follows that  $\#(\mathbb Z^{d}\cap R_{\theta })>{\color {black}{\frac {1}{2}}}K(\sqrt {\delta \lambda })^{d-k-1}$.
$\#(\mathbb Z^{d}\cap R_{\theta })>{\color {black}{\frac {1}{2}}}K(\sqrt {\delta \lambda })^{d-k-1}$.
Recall that ![]() $R_{\theta }\cap \mathbb Z^{d}$ is contained in a box of size
$R_{\theta }\cap \mathbb Z^{d}$ is contained in a box of size ![]() $\sim \delta \times \sqrt {\lambda \delta } \times \dots \times \sqrt {\lambda \delta }$, intersected with a linear space of dimension
$\sim \delta \times \sqrt {\lambda \delta } \times \dots \times \sqrt {\lambda \delta }$, intersected with a linear space of dimension ![]() $r_{\theta }<d$, and so
$r_{\theta }<d$, and so
 $$ \begin{align*} \#(\mathbb Z^{d}\cap R_{\theta})\ll \sqrt{\delta\lambda}^{r_{\theta}}. \end{align*} $$
$$ \begin{align*} \#(\mathbb Z^{d}\cap R_{\theta})\ll \sqrt{\delta\lambda}^{r_{\theta}}. \end{align*} $$Hence ![]() $r_{\theta }\geq d-k$ since K may be taken arbitrarily large. So the number of possible
$r_{\theta }\geq d-k$ since K may be taken arbitrarily large. So the number of possible ![]() $\theta $ is
$\theta $ is ![]() $\lesssim (\delta 2^{j/k})^{-d}$.
$\lesssim (\delta 2^{j/k})^{-d}$.
5 Application of the  $\ell ^{2}$ decoupling theorem
$\ell ^{2}$ decoupling theorem
We decompose ![]() $P_{\lambda ,\delta }$ into projectors
$P_{\lambda ,\delta }$ into projectors  $P_{\lambda ,\delta }^{j}$, which are supported on the union of caps in
$P_{\lambda ,\delta }^{j}$, which are supported on the union of caps in ![]() $\mathcal {C}_{j}$. To be more specific, we choose a partition of unity
$\mathcal {C}_{j}$. To be more specific, we choose a partition of unity ![]() $(\chi _{\theta })$ adapted to the caps defined in the previous section:
$(\chi _{\theta })$ adapted to the caps defined in the previous section:
 $$ \begin{align*} \operatorname{Supp} \chi_{\theta} \subset \theta \qquad \mbox{and} \qquad \sum_{\theta} \chi_{\theta} = 1 \quad \mbox{on }S_{\lambda, \delta}, \end{align*} $$
$$ \begin{align*} \operatorname{Supp} \chi_{\theta} \subset \theta \qquad \mbox{and} \qquad \sum_{\theta} \chi_{\theta} = 1 \quad \mbox{on }S_{\lambda, \delta}, \end{align*} $$and let
 $$ \begin{align*} & \chi_{j} = \sum_{\theta \in \mathcal{C}_{j}} \chi_{\theta} \\ & P_{\lambda,\delta}^{j} = P_{\lambda,\delta}\, \chi_{j}(D) \end{align*} $$
$$ \begin{align*} & \chi_{j} = \sum_{\theta \in \mathcal{C}_{j}} \chi_{\theta} \\ & P_{\lambda,\delta}^{j} = P_{\lambda,\delta}\, \chi_{j}(D) \end{align*} $$(where ![]() $\chi _{j}(D)$ is the Fourier multiplier with symbol
$\chi _{j}(D)$ is the Fourier multiplier with symbol ![]() $\chi _{j}(k)$). Using the
$\chi _{j}(k)$). Using the ![]() $\ell ^{2}$ decoupling theorem of Bourgain and Demeter [Reference Bourgain and Demeter7], we can estimate the operator norm of
$\ell ^{2}$ decoupling theorem of Bourgain and Demeter [Reference Bourgain and Demeter7], we can estimate the operator norm of  $P_{\lambda ,\delta }^{j}$ from
$P_{\lambda ,\delta }^{j}$ from ![]() $L^{2}$ to
$L^{2}$ to ![]() $L^{p}$:
$L^{p}$:
Proposition 5.1. For any Q, for any ![]() $\epsilon>0$, for
$\epsilon>0$, for ![]() $p \geq p_{ST}$, and for
$p \geq p_{ST}$, and for ![]() $\delta> \lambda ^{-1}$,
$\delta> \lambda ^{-1}$,
 $$ \begin{align*} \| P_{\lambda,\delta}^{j} \|_{L^{2} \to L^{p}} \lesssim_{\epsilon} \lambda^{\frac{\sigma(p)}{2} +\epsilon} \delta^{1/2} 2^{j \left( \frac{1}{2} - \frac{1}{p} \right)}. \end{align*} $$
$$ \begin{align*} \| P_{\lambda,\delta}^{j} \|_{L^{2} \to L^{p}} \lesssim_{\epsilon} \lambda^{\frac{\sigma(p)}{2} +\epsilon} \delta^{1/2} 2^{j \left( \frac{1}{2} - \frac{1}{p} \right)}. \end{align*} $$Proof. For simplicity in the notation, we only consider the case ![]() $Q = \operatorname {Id}$. Let
$Q = \operatorname {Id}$. Let ![]() $a_{k}$ be an arbitrary sequence in
$a_{k}$ be an arbitrary sequence in ![]() $\ell ^{2}(\mathbb {Z}^{d})$ or, in other words, the Fourier series associated to an arbitrary function in
$\ell ^{2}(\mathbb {Z}^{d})$ or, in other words, the Fourier series associated to an arbitrary function in ![]() $L^{2}(\mathbb {T}^{d})$. Changing variables to
$L^{2}(\mathbb {T}^{d})$. Changing variables to ![]() $X = \lambda x$ and
$X = \lambda x$ and ![]() $K = k/ \lambda $, and taking advantage of the periodicity of Fourier series, we get
$K = k/ \lambda $, and taking advantage of the periodicity of Fourier series, we get
 $$ \begin{align*} & \left\| \sum_{k \in \mathbb{Z}^{d}} \chi_{j}(k) \chi\left( \frac{|k|-\lambda}{\delta} \right) a_{k} e^{2\pi i k\cdot x} \right\|_{L^{p}(\mathbb{T}^{d})} \\ & \qquad \qquad \lesssim \left( \frac{\delta}{\lambda} \right)^{d/p} \left\| \phi \left( \frac{\delta X}{\lambda} \right) \sum_{K \in \mathbb{Z}^{d}/\lambda} \chi_{j}(\lambda K)\chi\left( \frac{|K|-1}{(\delta/\lambda)} \right) a_{\lambda K} e^{2\pi i K \cdot X} \right\|_{L^{p}(\mathbb{R}^{d})}, \end{align*} $$
$$ \begin{align*} & \left\| \sum_{k \in \mathbb{Z}^{d}} \chi_{j}(k) \chi\left( \frac{|k|-\lambda}{\delta} \right) a_{k} e^{2\pi i k\cdot x} \right\|_{L^{p}(\mathbb{T}^{d})} \\ & \qquad \qquad \lesssim \left( \frac{\delta}{\lambda} \right)^{d/p} \left\| \phi \left( \frac{\delta X}{\lambda} \right) \sum_{K \in \mathbb{Z}^{d}/\lambda} \chi_{j}(\lambda K)\chi\left( \frac{|K|-1}{(\delta/\lambda)} \right) a_{\lambda K} e^{2\pi i K \cdot X} \right\|_{L^{p}(\mathbb{R}^{d})}, \end{align*} $$where the cutoff function ![]() $\phi $ can be chosen to have compactly supported Fourier transform. As a result, the Fourier transform of the function on the right-hand side is supported on a
$\phi $ can be chosen to have compactly supported Fourier transform. As a result, the Fourier transform of the function on the right-hand side is supported on a ![]() $\delta /\lambda $-neighborhood of
$\delta /\lambda $-neighborhood of ![]() $\mathbb {S}^{d-1}$. Using the
$\mathbb {S}^{d-1}$. Using the ![]() $\ell ^{2}$ decoupling theorem of Bourgain and Demeter Footnote 1, this is
$\ell ^{2}$ decoupling theorem of Bourgain and Demeter Footnote 1, this is
 $$ \begin{align*} \dots \lesssim_{\epsilon} \left( \frac{\delta}{\lambda} \right)^{\frac{d}{p}- \frac{d-1}{4} + \frac{d+1}{2p} - \epsilon} \left( \sum_{\theta \in \mathcal{C}_{j}} \left\| \phi \left( \frac{\delta X}{\lambda} \right) \sum_{K \in \mathbb{Z}^{d} / \lambda} \chi_{\theta}(\lambda K) \chi \left( \frac{|K|-1}{(\delta/\lambda)} \right) a_{\lambda K} e^{2\pi i K \cdot X}\right\|_{L^{p}(\mathbb{R}^{d})}^{2} \right)^{1/2} \end{align*} $$
$$ \begin{align*} \dots \lesssim_{\epsilon} \left( \frac{\delta}{\lambda} \right)^{\frac{d}{p}- \frac{d-1}{4} + \frac{d+1}{2p} - \epsilon} \left( \sum_{\theta \in \mathcal{C}_{j}} \left\| \phi \left( \frac{\delta X}{\lambda} \right) \sum_{K \in \mathbb{Z}^{d} / \lambda} \chi_{\theta}(\lambda K) \chi \left( \frac{|K|-1}{(\delta/\lambda)} \right) a_{\lambda K} e^{2\pi i K \cdot X}\right\|_{L^{p}(\mathbb{R}^{d})}^{2} \right)^{1/2} \end{align*} $$(notice that ![]() $\theta /\lambda $ has dimensions
$\theta /\lambda $ has dimensions  $\sim \frac {\delta }{\lambda } \times \frac {\delta ^{1/2}}{\lambda ^{1/2}} \dots \times \frac {\delta ^{1/2}}{\lambda ^{1/2}}$). At this point, we use the inequality
$\sim \frac {\delta }{\lambda } \times \frac {\delta ^{1/2}}{\lambda ^{1/2}} \dots \times \frac {\delta ^{1/2}}{\lambda ^{1/2}}$). At this point, we use the inequality
 $$ \begin{align*} \mbox{if }p \geq 2, \qquad \| f \|_{L^{p}(\mathbb{R}^{d})} \lesssim \| f \|_{L^{2}} | \operatorname{Supp} \widehat{f} |^{\frac{1}{2} - \frac{1}{p}}, \end{align*} $$
$$ \begin{align*} \mbox{if }p \geq 2, \qquad \| f \|_{L^{p}(\mathbb{R}^{d})} \lesssim \| f \|_{L^{2}} | \operatorname{Supp} \widehat{f} |^{\frac{1}{2} - \frac{1}{p}}, \end{align*} $$which follows by applying successively the Hausdorff-Young and Hölder inequalities, and finally the Plancherel equality. We use this inequality for  $f = \phi \left ( \frac {\delta X}{\lambda } \right ) \sum _{K} \chi \left ( \frac {|K|-1}{(\delta /\lambda )} \right ) \chi _{\theta }(\lambda K) a_{\lambda K} e^{2\pi i K \cdot X}$. Since
$f = \phi \left ( \frac {\delta X}{\lambda } \right ) \sum _{K} \chi \left ( \frac {|K|-1}{(\delta /\lambda )} \right ) \chi _{\theta }(\lambda K) a_{\lambda K} e^{2\pi i K \cdot X}$. Since ![]() $\theta \in \mathcal {C}_{j}$, its Fourier transform is supported on the union of at most
$\theta \in \mathcal {C}_{j}$, its Fourier transform is supported on the union of at most  $O((\delta \lambda )^{\frac {d-1}{2}}\delta 2^{j})$ balls of radius
$O((\delta \lambda )^{\frac {d-1}{2}}\delta 2^{j})$ balls of radius ![]() $O( \delta / \lambda ) $, giving
$O( \delta / \lambda ) $, giving  $| \operatorname {Supp} \widehat {f} | \lesssim \delta ^{\frac {3d+1}{2}} \lambda ^{-\frac {d+1}{2}} 2^{j}$. Coming back to the quantity we want to bound, it is
$| \operatorname {Supp} \widehat {f} | \lesssim \delta ^{\frac {3d+1}{2}} \lambda ^{-\frac {d+1}{2}} 2^{j}$. Coming back to the quantity we want to bound, it is
 $$ \begin{align*} & \lesssim \left( \frac{\delta}{\lambda} \right)^{\frac{d}{p}- \frac{d-1}{4} + \frac{d+1}{2p} - \epsilon} \left(\delta^{\frac{3d+1}{2}} \lambda^{-\frac{d+1}{2}} 2^{j} \right)^{\frac{1}{2} - \frac{1}{p}} \\ & \qquad \qquad \qquad \qquad \left( \sum_{\theta \in \mathcal{C}_{j}} \left\| \phi \left( \frac{\delta X}{\lambda} \right) \sum_{K \in \mathbb{Z}^{d} / \lambda} \chi_{\theta}(\lambda K) \chi \left( \frac{|K|-1}{(\delta/\lambda)} \right) a_{\lambda K} e^{2\pi i K \cdot X}\right\|_{L^{2}(\mathbb{R}^{d})}^{2} \right)^{1/2} \\ & \lesssim \left( \frac{\delta}{\lambda} \right)^{\frac{d}{p} - \frac{d-1}{4} + \frac{d+1}{2p} - \epsilon}\left( \delta^{\frac{3d+1}{2}} \lambda^{-\frac{d+1}{2}} 2^{j}\right)^{\frac{1}{2} - \frac{1}{p}} \left\| \phi \left( \frac{\delta X}{\lambda} \right) \sum_{K \in \mathbb{Z}^{d}/\lambda} \chi_{j}(\lambda K)\chi\left( \frac{|K|-1}{(\delta/\lambda)} \right) a_{\lambda K} e^{2\pi i K \cdot X} \right\|_{L^{2}(\mathbb{R}^{d})}, \end{align*} $$
$$ \begin{align*} & \lesssim \left( \frac{\delta}{\lambda} \right)^{\frac{d}{p}- \frac{d-1}{4} + \frac{d+1}{2p} - \epsilon} \left(\delta^{\frac{3d+1}{2}} \lambda^{-\frac{d+1}{2}} 2^{j} \right)^{\frac{1}{2} - \frac{1}{p}} \\ & \qquad \qquad \qquad \qquad \left( \sum_{\theta \in \mathcal{C}_{j}} \left\| \phi \left( \frac{\delta X}{\lambda} \right) \sum_{K \in \mathbb{Z}^{d} / \lambda} \chi_{\theta}(\lambda K) \chi \left( \frac{|K|-1}{(\delta/\lambda)} \right) a_{\lambda K} e^{2\pi i K \cdot X}\right\|_{L^{2}(\mathbb{R}^{d})}^{2} \right)^{1/2} \\ & \lesssim \left( \frac{\delta}{\lambda} \right)^{\frac{d}{p} - \frac{d-1}{4} + \frac{d+1}{2p} - \epsilon}\left( \delta^{\frac{3d+1}{2}} \lambda^{-\frac{d+1}{2}} 2^{j}\right)^{\frac{1}{2} - \frac{1}{p}} \left\| \phi \left( \frac{\delta X}{\lambda} \right) \sum_{K \in \mathbb{Z}^{d}/\lambda} \chi_{j}(\lambda K)\chi\left( \frac{|K|-1}{(\delta/\lambda)} \right) a_{\lambda K} e^{2\pi i K \cdot X} \right\|_{L^{2}(\mathbb{R}^{d})}, \end{align*} $$where the last inequality is a consequence of almost orthogonality. Finally, undoing the change of variables, this is
 $$ \begin{align*} & \lesssim \left( \frac{\delta}{\lambda} \right)^{\frac{d}{p}-\frac{d}{2} - \frac{d-1}{4} + \frac{d+1}{2p} - \epsilon} \left( \delta^{\frac{3d+1}{2}} \lambda^{-\frac{d+1}{2}} 2^{j} \right)^{\frac{1}{2} - \frac{1}{p}} \left\| \sum_{k \in \mathbb{Z}^{d}} \chi_{j}(k) \chi\left( \frac{|k|-\lambda}{\delta} \right) a_{k} e^{2\pi i k\cdot x} \right\|_{L^{2}(\mathbb{T}^{d})} \\ & \leq \left( \frac{\delta}{\lambda} \right)^{-\epsilon} \lambda^{\sigma(p)/2} \delta^{1/2} 2^{j \left( \frac{1}{2} - \frac{1}{p} \right)} \left\| \sum_{k \in \mathbb{Z}^{d}} a_{k} e^{2\pi i k\cdot x} \right\|_{L^{2}(\mathbb{T}^{d})}. \end{align*} $$
$$ \begin{align*} & \lesssim \left( \frac{\delta}{\lambda} \right)^{\frac{d}{p}-\frac{d}{2} - \frac{d-1}{4} + \frac{d+1}{2p} - \epsilon} \left( \delta^{\frac{3d+1}{2}} \lambda^{-\frac{d+1}{2}} 2^{j} \right)^{\frac{1}{2} - \frac{1}{p}} \left\| \sum_{k \in \mathbb{Z}^{d}} \chi_{j}(k) \chi\left( \frac{|k|-\lambda}{\delta} \right) a_{k} e^{2\pi i k\cdot x} \right\|_{L^{2}(\mathbb{T}^{d})} \\ & \leq \left( \frac{\delta}{\lambda} \right)^{-\epsilon} \lambda^{\sigma(p)/2} \delta^{1/2} 2^{j \left( \frac{1}{2} - \frac{1}{p} \right)} \left\| \sum_{k \in \mathbb{Z}^{d}} a_{k} e^{2\pi i k\cdot x} \right\|_{L^{2}(\mathbb{T}^{d})}. \end{align*} $$6 Proof of the main theorems
6.1 The case  $p<p_{ST}$: proof of Theorem 1.1
$p<p_{ST}$: proof of Theorem 1.1
Proposition 5.1 gives the bounds
 $$ \begin{align*} \| P_{\lambda,\delta} \|_{L^{2} \to L^{p_{ST}}} \leq \sum_{j=0}^{\infty} \| P_{\lambda,\delta}^{j} \|_{L^{2} \to L^{p_{ST}}} \lesssim \lambda^{\epsilon} (\delta \lambda)^{\frac{d-1}{2(d+1)}}. \end{align*} $$
$$ \begin{align*} \| P_{\lambda,\delta} \|_{L^{2} \to L^{p_{ST}}} \leq \sum_{j=0}^{\infty} \| P_{\lambda,\delta}^{j} \|_{L^{2} \to L^{p_{ST}}} \lesssim \lambda^{\epsilon} (\delta \lambda)^{\frac{d-1}{2(d+1)}}. \end{align*} $$Interpolating with the trivial ![]() $L^{2} \to L^{2}$ bound, this gives the conjecture for
$L^{2} \to L^{2}$ bound, this gives the conjecture for ![]() $2 \leq p \leq p_{ST}$.
$2 \leq p \leq p_{ST}$.
6.2 An exact but involved statement
The theorems in the introduction are deduced from the following result. The first bound, equation (6.2), in this next theorem is precisely the result of interpolating between the bounds obtained above. The last part of the theorem allows for the concise result in Theorem 1.2 but, as we will see in the proof, it is slightly weaker.
Theorem 6.1. Assume ![]() $p_{ST} \leq p \leq \infty $, and write
$p_{ST} \leq p \leq \infty $, and write
 $$ \begin{align} \alpha(p) &=1-\frac{2}{p}, &\beta(p) &= 1- \frac{p_{ST}}{p}. \end{align} $$
$$ \begin{align} \alpha(p) &=1-\frac{2}{p}, &\beta(p) &= 1- \frac{p_{ST}}{p}. \end{align} $$Assume further that ![]() $\delta> \lambda ^{-\frac {d-1}{d+1}}$. Then
$\delta> \lambda ^{-\frac {d-1}{d+1}}$. Then
 $$ \begin{align} \begin{aligned} \| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} \lesssim \lambda^{\sigma(p)/2} \delta^{1/2} + \lambda^{\epsilon} (\lambda\delta)^{\frac{d}{4}\alpha(p)} ( \lambda/\delta)^{\frac{d}{4}\beta(p)} &\sum_{\substack{ 1\leq k\leq d-1 \\ (\delta \lambda)^{(k-1)/2} \delta<1 }} (\delta \lambda)^{-\frac{k}{4}\alpha(p)} (\lambda/\delta)^{\frac{-1}{2k}\frac{d}{2}\beta(p)} \\ & +\lambda^{\epsilon}(\lambda\delta)^{\frac{d}{4}\alpha({p})}(\lambda/\delta)^{-\frac{1}{4}\alpha({p})} \delta^{-\frac{d}{2}\beta({p})}, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} \lesssim \lambda^{\sigma(p)/2} \delta^{1/2} + \lambda^{\epsilon} (\lambda\delta)^{\frac{d}{4}\alpha(p)} ( \lambda/\delta)^{\frac{d}{4}\beta(p)} &\sum_{\substack{ 1\leq k\leq d-1 \\ (\delta \lambda)^{(k-1)/2} \delta<1 }} (\delta \lambda)^{-\frac{k}{4}\alpha(p)} (\lambda/\delta)^{\frac{-1}{2k}\frac{d}{2}\beta(p)} \\ & +\lambda^{\epsilon}(\lambda\delta)^{\frac{d}{4}\alpha({p})}(\lambda/\delta)^{-\frac{1}{4}\alpha({p})} \delta^{-\frac{d}{2}\beta({p})}, \end{aligned} \end{align} $$and it follows that
 $$ \begin{align*} \| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} &\lesssim \lambda^{\sigma(p)/2} \delta^{1/2} + \lambda^{\epsilon} (\lambda\delta)^{\frac{d}{4}\alpha({p})}(\lambda/\delta)^{-\frac{1}{4}\alpha({p})} \delta^{-\frac{d}{2}\beta({p})} \\ &\quad +\lambda^{\epsilon} (\lambda\delta)^{\frac{d}{4}\alpha(p)}( \lambda/\delta)^{\frac{d}{4}\beta(p)} e^{-\frac{1}{2}\sqrt{d\alpha(p) \beta(p)\log (\delta \lambda)\log ( \lambda/\delta)}}, \end{align*} $$
$$ \begin{align*} \| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} &\lesssim \lambda^{\sigma(p)/2} \delta^{1/2} + \lambda^{\epsilon} (\lambda\delta)^{\frac{d}{4}\alpha({p})}(\lambda/\delta)^{-\frac{1}{4}\alpha({p})} \delta^{-\frac{d}{2}\beta({p})} \\ &\quad +\lambda^{\epsilon} (\lambda\delta)^{\frac{d}{4}\alpha(p)}( \lambda/\delta)^{\frac{d}{4}\beta(p)} e^{-\frac{1}{2}\sqrt{d\alpha(p) \beta(p)\log (\delta \lambda)\log ( \lambda/\delta)}}, \end{align*} $$where the final term may be omitted if  $\delta> \lambda ^{\frac {\alpha (p)-d\beta (p)}{\alpha (p)+d\beta (p)}}$.
$\delta> \lambda ^{\frac {\alpha (p)-d\beta (p)}{\alpha (p)+d\beta (p)}}$.
In order to prove the theorem, we need a brief lemma.
Lemma 6.2. We introduce the notation ![]() $k_{0}$ for the optimal index in Theorem 4.1 given
$k_{0}$ for the optimal index in Theorem 4.1 given ![]() $\delta ,\lambda , 2^{j}$. Namely, assume that
$\delta ,\lambda , 2^{j}$. Namely, assume that ![]() $\delta> \lambda ^{-\frac {d-1}{d+1}}$. Then let
$\delta> \lambda ^{-\frac {d-1}{d+1}}$. Then let ![]() $k_{0} = k_{0}(\delta ,\lambda ,2^{j})$ be the smallest
$k_{0} = k_{0}(\delta ,\lambda ,2^{j})$ be the smallest ![]() $k\in \mathbb Z$ such that
$k\in \mathbb Z$ such that
If ![]() $1< 2^{j}<K\delta ^{-1}$, then
$1< 2^{j}<K\delta ^{-1}$, then ![]() $k_{0}(\delta ,\lambda ,2^{j})\in \{ 1 ,\dots ,d-1\}$.
$k_{0}(\delta ,\lambda ,2^{j})\in \{ 1 ,\dots ,d-1\}$.
Proof. Let ![]() $1< 2^{j}<K\delta ^{-1}$, then
$1< 2^{j}<K\delta ^{-1}$, then
and so it suffices to observe that as ![]() $\delta> \lambda ^{-\frac {d-1}{d+1}}$, we have
$\delta> \lambda ^{-\frac {d-1}{d+1}}$, we have ![]() $(\delta \lambda )^{-(d-1)/2} \delta ^{-1}< 1$.
$(\delta \lambda )^{-(d-1)/2} \delta ^{-1}< 1$.
Proof of Theorem 6.1.
Throughout the proof, ![]() $k_{0}$ will be as in Lemma 6.2. We begin by bounding
$k_{0}$ will be as in Lemma 6.2. We begin by bounding  $P^{0}_{\lambda ,\delta }$, by interpolating between
$P^{0}_{\lambda ,\delta }$, by interpolating between
 $$ \begin{align*} \| P^{0}_{\lambda,\delta} \|_{L^{2} \to L^{p_{ST}}} \lesssim \lambda^{\frac{d-1}{2(d+1)}} \delta^{1/2}, \end{align*} $$
$$ \begin{align*} \| P^{0}_{\lambda,\delta} \|_{L^{2} \to L^{p_{ST}}} \lesssim \lambda^{\frac{d-1}{2(d+1)}} \delta^{1/2}, \end{align*} $$which is a consequence of Proposition 5.1, and
 $$ \begin{align*} \| P^{0}_{\lambda,\delta} \|_{L^{2} \to L^{\infty}} \lesssim {\bigg\lvert\bigcup_{\theta \in \mathcal{C}_{0}} \mathbb Z^{d}\cap \theta\bigg\rvert^{1/2}} \leq \sqrt{|\mathcal{C}|(\sqrt{\lambda \delta})^{d-1} \delta } \lesssim (\lambda^{d-1} \delta)^{1/2}. \end{align*} $$
$$ \begin{align*} \| P^{0}_{\lambda,\delta} \|_{L^{2} \to L^{\infty}} \lesssim {\bigg\lvert\bigcup_{\theta \in \mathcal{C}_{0}} \mathbb Z^{d}\cap \theta\bigg\rvert^{1/2}} \leq \sqrt{|\mathcal{C}|(\sqrt{\lambda \delta})^{d-1} \delta } \lesssim (\lambda^{d-1} \delta)^{1/2}. \end{align*} $$Interpolating between these two estimates gives
 $$ \begin{align*} \| P^{0}_{\lambda,\delta} \|_{L^{2} \to L^{p}} \lesssim \lambda^{\sigma(p)/2} \delta^{1/2}. \end{align*} $$
$$ \begin{align*} \| P^{0}_{\lambda,\delta} \|_{L^{2} \to L^{p}} \lesssim \lambda^{\sigma(p)/2} \delta^{1/2}. \end{align*} $$ If ![]() $2^{j}\geq K\delta ^{-1}$, then we can assume
$2^{j}\geq K\delta ^{-1}$, then we can assume ![]() $\mathcal {C}_{j}=\emptyset $ by equation (4.2), by increasing the size of the constant K if necessary. It follows that
$\mathcal {C}_{j}=\emptyset $ by equation (4.2), by increasing the size of the constant K if necessary. It follows that  $P^{j}_{\lambda ,\delta }=0$ for such j.
$P^{j}_{\lambda ,\delta }=0$ for such j.
Next let ![]() $1< 2^{j}<K\delta ^{-1}$. Now, on the one hand, Proposition 5.1 gives
$1< 2^{j}<K\delta ^{-1}$. Now, on the one hand, Proposition 5.1 gives
 $$ \begin{align*} \| P^{j}_{\lambda,\delta} \|_{L^{2} \to L^{p_{ST}}} \lesssim \lambda^{\frac{1}{p_{ST}}} \delta^{1/2} 2^{\frac{j}{d+1}}. \end{align*} $$
$$ \begin{align*} \| P^{j}_{\lambda,\delta} \|_{L^{2} \to L^{p_{ST}}} \lesssim \lambda^{\frac{1}{p_{ST}}} \delta^{1/2} 2^{\frac{j}{d+1}}. \end{align*} $$On the other hand, bounding the number of points in ![]() $\cup _{\mathcal {C}_{j}} \theta $ through Lemma 6.2 and Theorem 4.1 gives
$\cup _{\mathcal {C}_{j}} \theta $ through Lemma 6.2 and Theorem 4.1 gives
 $$ \begin{align*} \| P^{j}_{\lambda,\delta}\|_{L^{2} \to L^{\infty}} \lesssim \left( \# \mathcal{C}_{j} (\lambda \delta)^{\frac{d-1}{2}} \delta 2^{j} \right)^{1/2} \lesssim \left( (2^{j/k_{0}} \delta)^{-d} (\lambda \delta)^{\frac{d-1}{2}} \delta 2^{j} \right)^{1/2}. \end{align*} $$
$$ \begin{align*} \| P^{j}_{\lambda,\delta}\|_{L^{2} \to L^{\infty}} \lesssim \left( \# \mathcal{C}_{j} (\lambda \delta)^{\frac{d-1}{2}} \delta 2^{j} \right)^{1/2} \lesssim \left( (2^{j/k_{0}} \delta)^{-d} (\lambda \delta)^{\frac{d-1}{2}} \delta 2^{j} \right)^{1/2}. \end{align*} $$Interpolating between the last two bounds gives
 $$ \begin{align*} \| P^{j}_{\lambda,\delta}\|_{L^{2} \to L^{p}} &\lesssim \lambda^{\frac{d-1}{4} - \frac{d-1}{2p}} \delta^{\frac{d+1}{4} - \frac{d+1}{2p}} 2^{\frac{j}{2} - \frac{j}{p}} (2^{j/k_{0}} \delta)^{-\frac{d}{2} + \frac{d(d+1)}{d-1} \frac{1}{p}} \\ &= (\lambda\delta)^{\frac{d}{4}(1- \frac{2}{p})}(\lambda/\delta)^{-\frac{1}{4}(1- \frac{2}{p})} 2^{\frac{j}{2}(1- \frac{2}{p})} (2^{j/k_{0}} \delta)^{-\frac{d}{2}(1- \frac{p_{ST}}{p})}. \end{align*} $$
$$ \begin{align*} \| P^{j}_{\lambda,\delta}\|_{L^{2} \to L^{p}} &\lesssim \lambda^{\frac{d-1}{4} - \frac{d-1}{2p}} \delta^{\frac{d+1}{4} - \frac{d+1}{2p}} 2^{\frac{j}{2} - \frac{j}{p}} (2^{j/k_{0}} \delta)^{-\frac{d}{2} + \frac{d(d+1)}{d-1} \frac{1}{p}} \\ &= (\lambda\delta)^{\frac{d}{4}(1- \frac{2}{p})}(\lambda/\delta)^{-\frac{1}{4}(1- \frac{2}{p})} 2^{\frac{j}{2}(1- \frac{2}{p})} (2^{j/k_{0}} \delta)^{-\frac{d}{2}(1- \frac{p_{ST}}{p})}. \end{align*} $$From this point on it will simplify matters to write  $\alpha (p)=1-\frac {2}{p},\beta (p)=1-\frac {p_{ST}}{p}$ as in equation (6.1). On summing over j, we obtain
$\alpha (p)=1-\frac {2}{p},\beta (p)=1-\frac {p_{ST}}{p}$ as in equation (6.1). On summing over j, we obtain
 $$ \begin{align} \| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} \lesssim \lambda^{\sigma(p)/2} \delta^{1/2} + (\lambda\delta)^{\frac{d}{4}\alpha({p})}(\lambda/\delta)^{-\frac{1}{4}\alpha({p})} \sum_{1< 2^{j} < K\delta^{-1}} 2^{\frac{j}{2}\alpha({p})} (2^{j/k_{0}}\delta )^{-\frac{d}{2}\beta({p})}. \end{align} $$
$$ \begin{align} \| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} \lesssim \lambda^{\sigma(p)/2} \delta^{1/2} + (\lambda\delta)^{\frac{d}{4}\alpha({p})}(\lambda/\delta)^{-\frac{1}{4}\alpha({p})} \sum_{1< 2^{j} < K\delta^{-1}} 2^{\frac{j}{2}\alpha({p})} (2^{j/k_{0}}\delta )^{-\frac{d}{2}\beta({p})}. \end{align} $$Recall that ![]() $k_{0}$ is minimal such that
$k_{0}$ is minimal such that ![]() $(\delta \lambda )^{-k/2} \delta ^{-1} <2^{j} $, and that
$(\delta \lambda )^{-k/2} \delta ^{-1} <2^{j} $, and that ![]() $1\leq k_{0}\leq d-1$ by Lemma 6.2. Hence
$1\leq k_{0}\leq d-1$ by Lemma 6.2. Hence
 $$ \begin{align*} \sum_{1< 2^{j} < K\delta^{-1}} 2^{\frac{j}{2}\alpha({p})} (2^{j/k_{0}}\delta )^{-\frac{d}{2}\beta({p})} &\leq \sum_{1\leq k\leq d-1} \sum_{\substack{j\in\mathbb N \\ (\delta \lambda)^{-k/2} \delta^{-1} <2^{j} \\ (\delta \lambda)^{(1-k)/2} \delta^{-1} \geq 2^{j} \\ 1< 2^{j} < K\delta^{-1} }} 2^{\frac{j}{2}\alpha({p})} (2^{j/k} \delta)^{-\frac{d}{2}\beta({p})} \\ & \lesssim_{\epsilon} \sum_{1\leq k\leq d-1}\lambda^{\epsilon} \sum_{\substack{j \in\mathbb R \\ 2^{j}=\max\{1,(\delta \lambda)^{-\ell/2} \delta^{-1}\} \\\ell\in\{k-1,k\}}} 2^{\frac{j}{2}\alpha({p})} (2^{j/k} \delta)^{-\frac{d}{2}\beta({p})}, \end{align*} $$
$$ \begin{align*} \sum_{1< 2^{j} < K\delta^{-1}} 2^{\frac{j}{2}\alpha({p})} (2^{j/k_{0}}\delta )^{-\frac{d}{2}\beta({p})} &\leq \sum_{1\leq k\leq d-1} \sum_{\substack{j\in\mathbb N \\ (\delta \lambda)^{-k/2} \delta^{-1} <2^{j} \\ (\delta \lambda)^{(1-k)/2} \delta^{-1} \geq 2^{j} \\ 1< 2^{j} < K\delta^{-1} }} 2^{\frac{j}{2}\alpha({p})} (2^{j/k} \delta)^{-\frac{d}{2}\beta({p})} \\ & \lesssim_{\epsilon} \sum_{1\leq k\leq d-1}\lambda^{\epsilon} \sum_{\substack{j \in\mathbb R \\ 2^{j}=\max\{1,(\delta \lambda)^{-\ell/2} \delta^{-1}\} \\\ell\in\{k-1,k\}}} 2^{\frac{j}{2}\alpha({p})} (2^{j/k} \delta)^{-\frac{d}{2}\beta({p})}, \end{align*} $$and exchanging order of summation, this is
 $$ \begin{align*} & = \lambda^{\epsilon} \sum_{\substack{j \in\mathbb R \\ 2^{j}=\max\{1,(\delta \lambda)^{-\ell/2} \delta^{-1}\} \\ 0\leq \ell\leq d-1}} \sum_{\substack{ k\in\{\ell,\ell+1\} \\ 1\leq k\leq d-1}} 2^{\frac{j}{2}\alpha({p})} (2^{j/k} \delta)^{-\frac{d}{2}\beta({p})}. \end{align*} $$
$$ \begin{align*} & = \lambda^{\epsilon} \sum_{\substack{j \in\mathbb R \\ 2^{j}=\max\{1,(\delta \lambda)^{-\ell/2} \delta^{-1}\} \\ 0\leq \ell\leq d-1}} \sum_{\substack{ k\in\{\ell,\ell+1\} \\ 1\leq k\leq d-1}} 2^{\frac{j}{2}\alpha({p})} (2^{j/k} \delta)^{-\frac{d}{2}\beta({p})}. \end{align*} $$On recalling that ![]() $p\geq p_{ST}$ and so
$p\geq p_{ST}$ and so ![]() $\beta (p)\geq 0$, we see that when
$\beta (p)\geq 0$, we see that when ![]() $\ell \leq d-2$, we can obtain an upper bound for the inner sum in the last line above by substituting
$\ell \leq d-2$, we can obtain an upper bound for the inner sum in the last line above by substituting ![]() $k= \ell +1$. Thus
$k= \ell +1$. Thus
 $$ \begin{align*} \sum_{1< 2^{j} < K\delta^{-1}} 2^{\frac{j}{2}\alpha({p})} (2^{j/k_{0}}\delta )^{-\frac{d}{2}\beta({p})} &\lesssim_{\epsilon} \lambda^{\epsilon} \sum_{\substack{j \in\mathbb R \\ 2^{j}=\max\{1,(\delta \lambda)^{-\ell/2} \delta^{-1}\} \\0\leq \ell\leq d-2}} 2^{\frac{j}{2}\alpha({p})} (2^{\frac{j}{\ell+1}} \delta)^{-\frac{d}{2}\beta({p})} \\ &\hphantom{{}\leq{}}+ \lambda^{\epsilon} \max\left\{1,(\delta \lambda)^{-(d-1)/2} \delta^{-1}\right\}^{\frac{1}{2}\alpha({p})-\frac{d}{2(d-1)}\beta({p})} \delta^{-\frac{d}{2}\beta({p})} \\ &= \lambda^{\epsilon} \sum_{\substack{ 1\leq k\leq d-1 \\ (\delta \lambda)^{(k-1)/2} \delta<1 }} \left((\delta \lambda)^{-(k-1)/2} \delta^{-1}\right)^{\frac{1}{2}\alpha({p})-\frac{d}{2k}\beta({p})} \delta^{-\frac{d}{2}\beta({p})} \\ &\hphantom{{}={}} + \lambda^{\epsilon} \delta^{-\frac{d}{2}\beta({p})}, \end{align*} $$
$$ \begin{align*} \sum_{1< 2^{j} < K\delta^{-1}} 2^{\frac{j}{2}\alpha({p})} (2^{j/k_{0}}\delta )^{-\frac{d}{2}\beta({p})} &\lesssim_{\epsilon} \lambda^{\epsilon} \sum_{\substack{j \in\mathbb R \\ 2^{j}=\max\{1,(\delta \lambda)^{-\ell/2} \delta^{-1}\} \\0\leq \ell\leq d-2}} 2^{\frac{j}{2}\alpha({p})} (2^{\frac{j}{\ell+1}} \delta)^{-\frac{d}{2}\beta({p})} \\ &\hphantom{{}\leq{}}+ \lambda^{\epsilon} \max\left\{1,(\delta \lambda)^{-(d-1)/2} \delta^{-1}\right\}^{\frac{1}{2}\alpha({p})-\frac{d}{2(d-1)}\beta({p})} \delta^{-\frac{d}{2}\beta({p})} \\ &= \lambda^{\epsilon} \sum_{\substack{ 1\leq k\leq d-1 \\ (\delta \lambda)^{(k-1)/2} \delta<1 }} \left((\delta \lambda)^{-(k-1)/2} \delta^{-1}\right)^{\frac{1}{2}\alpha({p})-\frac{d}{2k}\beta({p})} \delta^{-\frac{d}{2}\beta({p})} \\ &\hphantom{{}={}} + \lambda^{\epsilon} \delta^{-\frac{d}{2}\beta({p})}, \end{align*} $$where to deal with the maximum we use the assumption ![]() $\delta>\lambda ^{-\frac {d-1}{d+1}}$ from the theorem. Upon writing
$\delta>\lambda ^{-\frac {d-1}{d+1}}$ from the theorem. Upon writing ![]() $(\delta \lambda )^{-(k-1)/2} \delta ^{-1} = (\delta \lambda )^{-k/2} (\lambda /\delta )^{1/2}$, it now follows by equation (6.3) that
$(\delta \lambda )^{-(k-1)/2} \delta ^{-1} = (\delta \lambda )^{-k/2} (\lambda /\delta )^{1/2}$, it now follows by equation (6.3) that
 $$ \begin{align*} &\| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} \lesssim \lambda^{\sigma(p)/2} \delta^{1/2} + \\ &\lambda^{\epsilon} (\lambda\delta)^{\frac{d}{4}\alpha({p})}(\lambda/\delta)^{-\frac{1}{4}\alpha({p})} \sum_{\substack{ 1\leq k\leq d-1 \\ (\delta \lambda)^{(k-1)/2} \delta<1 }} (\delta\lambda)^{-\frac{k}{2}\big(\frac{1}{2}\alpha({p})-\frac{d}{2k}\beta({p})\big)-\frac{d}{4}\beta(p)} (\lambda/\delta)^{\frac{1}{2}\big(\frac{1}{2}\alpha({p})-\frac{d}{2k}\beta({p})\big)+\frac{d}{4}\beta(p)} \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad +\lambda^{\epsilon} (\lambda\delta)^{\frac{d}{4}\alpha({p})}(\lambda/\delta)^{-\frac{1}{4}\alpha({p})} \delta^{-\frac{d}{2}\beta({p})}. \end{align*} $$
$$ \begin{align*} &\| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} \lesssim \lambda^{\sigma(p)/2} \delta^{1/2} + \\ &\lambda^{\epsilon} (\lambda\delta)^{\frac{d}{4}\alpha({p})}(\lambda/\delta)^{-\frac{1}{4}\alpha({p})} \sum_{\substack{ 1\leq k\leq d-1 \\ (\delta \lambda)^{(k-1)/2} \delta<1 }} (\delta\lambda)^{-\frac{k}{2}\big(\frac{1}{2}\alpha({p})-\frac{d}{2k}\beta({p})\big)-\frac{d}{4}\beta(p)} (\lambda/\delta)^{\frac{1}{2}\big(\frac{1}{2}\alpha({p})-\frac{d}{2k}\beta({p})\big)+\frac{d}{4}\beta(p)} \\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad +\lambda^{\epsilon} (\lambda\delta)^{\frac{d}{4}\alpha({p})}(\lambda/\delta)^{-\frac{1}{4}\alpha({p})} \delta^{-\frac{d}{2}\beta({p})}. \end{align*} $$This proves equation (6.2), and we now proceed to deduce the last part of the theorem. If ![]() $A,B>0$, then
$A,B>0$, then
and moreover
 $$ \begin{align*} \sum_{\substack{ 1\leq k\leq d-1 \\ k < k_{1} }} \exp(-kA-B/k)\lesssim \exp(-k_{1}A-B/k_{1}) \qquad\text{if } k_{1}\leq \sqrt{B/A}. \end{align*} $$
$$ \begin{align*} \sum_{\substack{ 1\leq k\leq d-1 \\ k < k_{1} }} \exp(-kA-B/k)\lesssim \exp(-k_{1}A-B/k_{1}) \qquad\text{if } k_{1}\leq \sqrt{B/A}. \end{align*} $$We apply this with
so that ![]() $ (\delta \lambda )^{(k_{1}-1)/2} \delta =1$. Noting that
$ (\delta \lambda )^{(k_{1}-1)/2} \delta =1$. Noting that
 $$ \begin{align*} \exp( -k_{1}A-B/k_{1}) = \exp\Big( - \tfrac{1}{4}\alpha(p)\log(\lambda/\delta) - \tfrac{d}{4}\beta(p) \log (\delta \lambda)\Big) = \delta^{-\frac{d}{2}\beta(p)}(\lambda/\delta)^{-\frac{d}{4} \beta(p)-\frac{1}{4}\alpha(p) } , \end{align*} $$
$$ \begin{align*} \exp( -k_{1}A-B/k_{1}) = \exp\Big( - \tfrac{1}{4}\alpha(p)\log(\lambda/\delta) - \tfrac{d}{4}\beta(p) \log (\delta \lambda)\Big) = \delta^{-\frac{d}{2}\beta(p)}(\lambda/\delta)^{-\frac{d}{4} \beta(p)-\frac{1}{4}\alpha(p) } , \end{align*} $$we deduce from equation (6.2) that
 $$ \begin{align*} \| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} &\lesssim \lambda^{\sigma(p)/2} \delta^{1/2} +\lambda^{\epsilon} (\lambda\delta)^{\frac{d}{4}\alpha({p})}(\lambda/\delta)^{-\frac{1}{4}\alpha({p})} \delta^{-\frac{d}{2}\beta({p})} \\ &\quad + \lambda^{\epsilon} (\lambda\delta)^{\frac{d}{4}\alpha(p)}( \lambda/\delta)^{\frac{d}{4}\beta(p)} e^{-\frac{1}{2}\sqrt{d\alpha(p) \beta(p)\log (\delta \lambda)\log ( \lambda/\delta)}}, \end{align*} $$
$$ \begin{align*} \| P_{\lambda,\delta} \|_{L^{2} \to L^{p}} &\lesssim \lambda^{\sigma(p)/2} \delta^{1/2} +\lambda^{\epsilon} (\lambda\delta)^{\frac{d}{4}\alpha({p})}(\lambda/\delta)^{-\frac{1}{4}\alpha({p})} \delta^{-\frac{d}{2}\beta({p})} \\ &\quad + \lambda^{\epsilon} (\lambda\delta)^{\frac{d}{4}\alpha(p)}( \lambda/\delta)^{\frac{d}{4}\beta(p)} e^{-\frac{1}{2}\sqrt{d\alpha(p) \beta(p)\log (\delta \lambda)\log ( \lambda/\delta)}}, \end{align*} $$where the last term is omitted if  $k_{1} <\sqrt {B/A}$. This is the remaining bound in Theorem 6.1.
$k_{1} <\sqrt {B/A}$. This is the remaining bound in Theorem 6.1.
6.3 From Theorem 6.1 to Theorems 1.2 and 1.4
Proof of Theorem 1.2.
We use throughout the proof the notation  $\alpha (p)=1-\frac {2}{p},\beta (p)=1-\frac {p_{ST}}{p}$ from equation (6.1). As in the theorem, we assume
$\alpha (p)=1-\frac {2}{p},\beta (p)=1-\frac {p_{ST}}{p}$ from equation (6.1). As in the theorem, we assume  $\delta> \lambda ^{\frac {\alpha (p)-d\beta (p)}{\alpha (p)+d\beta (p)}}$. We claim that
$\delta> \lambda ^{\frac {\alpha (p)-d\beta (p)}{\alpha (p)+d\beta (p)}}$. We claim that ![]() $\delta \geq \lambda ^{-\frac {d-1}{d+1}}$, that is to say
$\delta \geq \lambda ^{-\frac {d-1}{d+1}}$, that is to say
 $$ \begin{align*} \frac{1-\beta(p)\alpha(p)^{-1}d}{1-\beta(p)\alpha(p)^{-1}d}>\frac{1-d}{1+d}, \end{align*} $$
$$ \begin{align*} \frac{1-\beta(p)\alpha(p)^{-1}d}{1-\beta(p)\alpha(p)^{-1}d}>\frac{1-d}{1+d}, \end{align*} $$which is true since ![]() $\beta (p)\alpha (p)^{-1} < 1$ and
$\beta (p)\alpha (p)^{-1} < 1$ and  $\frac {1-dx}{1+dx}$ is an increasing function of x.
$\frac {1-dx}{1+dx}$ is an increasing function of x.
The last bound in Theorem 6.1 will now agree with Conjecture 1.4 if
 $$ \begin{align} (\lambda\delta)^{\frac{d}{4}\alpha({p})}(\lambda/\delta)^{-\frac{1}{4}\alpha({p})} \delta^{-\frac{d}{2}\beta({p})} &\leq\lambda^{\frac{d-1}{2}-\frac{d}{p}} \delta^{1/2}. \end{align} $$
$$ \begin{align} (\lambda\delta)^{\frac{d}{4}\alpha({p})}(\lambda/\delta)^{-\frac{1}{4}\alpha({p})} \delta^{-\frac{d}{2}\beta({p})} &\leq\lambda^{\frac{d-1}{2}-\frac{d}{p}} \delta^{1/2}. \end{align} $$Grouping all the terms with a ![]() $1/p$ and without a
$1/p$ and without a ![]() $1/p$ in their exponent, the bound in equation (6.4) is exactly
$1/p$ in their exponent, the bound in equation (6.4) is exactly
 $$ \begin{align*} \lambda^{ \frac{d+1}{2p} } \delta^{\frac{(d+1)^{2}}{2(d-1)p}} \leq \lambda^{\frac{d-1}{4}} \delta^{\frac{d+1}{4}}, \end{align*} $$
$$ \begin{align*} \lambda^{ \frac{d+1}{2p} } \delta^{\frac{(d+1)^{2}}{2(d-1)p}} \leq \lambda^{\frac{d-1}{4}} \delta^{\frac{d+1}{4}}, \end{align*} $$which is to say  $(\lambda \delta ^{\frac {d+1}{d-1}})^{-\frac {d-1}{4}\beta (p)}\leq 1 $, and this is true since
$(\lambda \delta ^{\frac {d+1}{d-1}})^{-\frac {d-1}{4}\beta (p)}\leq 1 $, and this is true since ![]() $\delta \geq \lambda ^{-\frac {d-1}{d+1}}$ and
$\delta \geq \lambda ^{-\frac {d-1}{d+1}}$ and ![]() $p>p_{ST}$.
$p>p_{ST}$.
Proof of Theorem 1.4.
As in the last proof, we use throughout the notation  $\alpha (p)=1-\frac {2}{p},\beta (p)=1-\frac {p_{ST}}{p}$ from equation (6.1), noting that since
$\alpha (p)=1-\frac {2}{p},\beta (p)=1-\frac {p_{ST}}{p}$ from equation (6.1), noting that since ![]() $d=3$, we have
$d=3$, we have ![]() $p_{ST}=4$ and
$p_{ST}=4$ and  $\beta (p)=1-\frac {4}{p}$. If
$\beta (p)=1-\frac {4}{p}$. If ![]() $d=3$, the first bound in Theorem 6.1 agrees with the conjecture when
$d=3$, the first bound in Theorem 6.1 agrees with the conjecture when
 $$ \begin{align*} (\lambda\delta)^{\frac{3}{4}\alpha(p)} & ( \lambda/\delta)^{\frac{3}{4}\beta(p)}(\delta \lambda)^{-\frac{1}{4}\alpha(p)} ( \lambda/\delta)^{-\frac{3}{4}\beta(p)} \\ &\quad +(\lambda\delta)^{\frac{3}{4}\alpha(p)} ( \lambda/\delta)^{\frac{3}{4}\beta(p)} (\delta \lambda)^{-\frac{2}{4}\alpha(p)}( \lambda/\delta)^{-\frac{3}{8}\beta(p)} \leq (\lambda\delta)^{\frac{3}{4}\alpha(p)} (\lambda/\delta)^{\frac{1}{4}-\frac{3}{2p}} +(\lambda\delta)^{\frac{1}{2}\alpha(p)}, \end{align*} $$
$$ \begin{align*} (\lambda\delta)^{\frac{3}{4}\alpha(p)} & ( \lambda/\delta)^{\frac{3}{4}\beta(p)}(\delta \lambda)^{-\frac{1}{4}\alpha(p)} ( \lambda/\delta)^{-\frac{3}{4}\beta(p)} \\ &\quad +(\lambda\delta)^{\frac{3}{4}\alpha(p)} ( \lambda/\delta)^{\frac{3}{4}\beta(p)} (\delta \lambda)^{-\frac{2}{4}\alpha(p)}( \lambda/\delta)^{-\frac{3}{8}\beta(p)} \leq (\lambda\delta)^{\frac{3}{4}\alpha(p)} (\lambda/\delta)^{\frac{1}{4}-\frac{3}{2p}} +(\lambda\delta)^{\frac{1}{2}\alpha(p)}, \end{align*} $$that is
 $$ \begin{align*} (\lambda\delta)^{\alpha(p)} + (\lambda\delta)^{\frac{1}{4}\alpha(p)} ( \lambda/\delta)^{\frac{3}{8}\beta(p)} \leq (\lambda\delta)^{\frac{3}{4}\alpha(p)} (\lambda/\delta)^{\frac{1}{4}-\frac{3}{2p}} +(\lambda\delta)^{\frac{1}{2}\alpha(p)}. \end{align*} $$
$$ \begin{align*} (\lambda\delta)^{\alpha(p)} + (\lambda\delta)^{\frac{1}{4}\alpha(p)} ( \lambda/\delta)^{\frac{3}{8}\beta(p)} \leq (\lambda\delta)^{\frac{3}{4}\alpha(p)} (\lambda/\delta)^{\frac{1}{4}-\frac{3}{2p}} +(\lambda\delta)^{\frac{1}{2}\alpha(p)}. \end{align*} $$The first term on the left-hand side is clearly bounded by the last term. The second term on the left-hand side is bounded by the right-hand side if
 $$ \begin{align*} ( \lambda/\delta)^{\frac{1}{8}} \leq (\lambda\delta)^{\frac{1}{2}\alpha(p)} \qquad\text{or}\qquad ( \lambda/\delta)^{\frac{3}{8}\beta(p)} \leq (\lambda\delta)^{\frac{1}{4}\alpha(p)}. \end{align*} $$
$$ \begin{align*} ( \lambda/\delta)^{\frac{1}{8}} \leq (\lambda\delta)^{\frac{1}{2}\alpha(p)} \qquad\text{or}\qquad ( \lambda/\delta)^{\frac{3}{8}\beta(p)} \leq (\lambda\delta)^{\frac{1}{4}\alpha(p)}. \end{align*} $$This is  $\delta \geq \min \{\lambda ^{-\frac {3p-8}{5p-8}}\, \lambda ^{-\frac {8-p}{5p-16}}\}$, and recalling our standing assumption
$\delta \geq \min \{\lambda ^{-\frac {3p-8}{5p-8}}\, \lambda ^{-\frac {8-p}{5p-16}}\}$, and recalling our standing assumption ![]() $\delta \geq \lambda ^{-(d-1)/(d+1)}$ from Theorem 6.1, this gives the result.
$\delta \geq \lambda ^{-(d-1)/(d+1)}$ from Theorem 6.1, this gives the result.
A The Euclidean case
We prove here the estimate in equation (1.2) and show its optimality; the arguments are classical and elementary, but we give them here for ease of reference.
First notice the scaling relation  $\| P_{\lambda ,\delta } \|_{L^{2} \to L^{p}} = \lambda ^{\frac {d}{2} - \frac {d}{p}} \| P_{1,\delta /\lambda } \|_{L^{2} \to L^{p}}$, which reduces matters to
$\| P_{\lambda ,\delta } \|_{L^{2} \to L^{p}} = \lambda ^{\frac {d}{2} - \frac {d}{p}} \| P_{1,\delta /\lambda } \|_{L^{2} \to L^{p}}$, which reduces matters to ![]() $\lambda = 1$: it suffices to prove that
$\lambda = 1$: it suffices to prove that
 $$ \begin{align*} \| P_{1,\delta} \|_{L^{2} \to L^{p}} \lesssim \left\{ \begin{array}{ll} \delta^{1/2} & \mbox{if }p \geq p_{ST} \\ \delta^{\frac{(d+1)}{2}\left( \frac{1}{2} - \frac{1}{p} \right)} & \mbox{if }2 \leq p \leq p_{ST} \end{array}. \right. \end{align*} $$
$$ \begin{align*} \| P_{1,\delta} \|_{L^{2} \to L^{p}} \lesssim \left\{ \begin{array}{ll} \delta^{1/2} & \mbox{if }p \geq p_{ST} \\ \delta^{\frac{(d+1)}{2}\left( \frac{1}{2} - \frac{1}{p} \right)} & \mbox{if }2 \leq p \leq p_{ST} \end{array}. \right. \end{align*} $$This is achieved by interpolating between the following points:
•
 $p=2$, which is trivial by Plancherel’s theorem;
$p=2$, which is trivial by Plancherel’s theorem;•
 $p=\infty $, which follows from the Hausdorff-Young and Cauchy-Schwarz inequality, as well as Plancherel’s theorem:
$p=\infty $, which follows from the Hausdorff-Young and Cauchy-Schwarz inequality, as well as Plancherel’s theorem:  $$ \begin{align*} \| P_{1, \delta} f \|_{L^{\infty}} \lesssim \left\| \chi \left( \frac{|\xi| - 1}{\delta} \right) \widehat{f} \right\|_{L^{1}} \lesssim \left\| \chi \left( \frac{|\xi| - 1}{\delta} \right) \right\|_{L^{2}} \| \widehat f \|_{L^{2}} \lesssim \delta^{1/2} \| f \|_{L^{2}}; \end{align*} $$
$$ \begin{align*} \| P_{1, \delta} f \|_{L^{\infty}} \lesssim \left\| \chi \left( \frac{|\xi| - 1}{\delta} \right) \widehat{f} \right\|_{L^{1}} \lesssim \left\| \chi \left( \frac{|\xi| - 1}{\delta} \right) \right\|_{L^{2}} \| \widehat f \|_{L^{2}} \lesssim \delta^{1/2} \| f \|_{L^{2}}; \end{align*} $$•
 $p = p_{ST}$, for which we will use the formula where
$p = p_{ST}$, for which we will use the formula where $$ \begin{align*} P_{1,\delta} f = \int_{0}^{\infty} \chi \left( \frac{r - 1}{\delta} \right) \int_{\mathbb{R}^{d}} \widehat{f}(\xi) e^{ix\cdot \xi}\, d\sigma_{r}(\xi) \,dr, \end{align*} $$
$$ \begin{align*} P_{1,\delta} f = \int_{0}^{\infty} \chi \left( \frac{r - 1}{\delta} \right) \int_{\mathbb{R}^{d}} \widehat{f}(\xi) e^{ix\cdot \xi}\, d\sigma_{r}(\xi) \,dr, \end{align*} $$ $d\sigma _{r}$ is the surface measure on the sphere
$d\sigma _{r}$ is the surface measure on the sphere  $S_{r}$ with center at the origin and radius r. We can then apply successively the Minkowski inequality, the Stein-Tomas theorem [Reference Tomas27, Reference Stein25], the Cauchy-Schwarz inequality and the Plancherel theorem to obtain
$S_{r}$ with center at the origin and radius r. We can then apply successively the Minkowski inequality, the Stein-Tomas theorem [Reference Tomas27, Reference Stein25], the Cauchy-Schwarz inequality and the Plancherel theorem to obtain  $$ \begin{align*} \| P_{1, \delta} f \|_{L^{p_{ST}}(\mathbb{R}^{d})} & \leq \int_{0}^{\infty} \chi \left( \frac{r - 1}{\delta} \right) \left\| \int \widehat{f}(\xi) e^{ix\cdot \xi} \, d\sigma_{r}(\xi) \right\|_{L^{p_{ST}}(\mathbb{R}^{d})} \,dr \\ & \leq \int_{0}^{\infty} \chi \left( \frac{r - 1}{\delta} \right) \| \widehat{f} \|_{L^{2}(S_{r})}\,dr \lesssim \delta^{1/2} \|f\|_{L^{2}(\mathbb{R}^{d})}. \end{align*} $$
$$ \begin{align*} \| P_{1, \delta} f \|_{L^{p_{ST}}(\mathbb{R}^{d})} & \leq \int_{0}^{\infty} \chi \left( \frac{r - 1}{\delta} \right) \left\| \int \widehat{f}(\xi) e^{ix\cdot \xi} \, d\sigma_{r}(\xi) \right\|_{L^{p_{ST}}(\mathbb{R}^{d})} \,dr \\ & \leq \int_{0}^{\infty} \chi \left( \frac{r - 1}{\delta} \right) \| \widehat{f} \|_{L^{2}(S_{r})}\,dr \lesssim \delta^{1/2} \|f\|_{L^{2}(\mathbb{R}^{d})}. \end{align*} $$
Finally, there remains to check optimality. It follows from two examples:
• The Knapp example is a function
 $\widehat {f}$, which is a cutoff function adapted to a rectangular box of size
$\widehat {f}$, which is a cutoff function adapted to a rectangular box of size  $\sim \delta $ in one direction, and
$\sim \delta $ in one direction, and  $\sim \delta ^{1/2}$ in
$\sim \delta ^{1/2}$ in  $d-1$ directions; this box is furthermore chosen to be contained in
$d-1$ directions; this box is furthermore chosen to be contained in  $B(0,r+\delta ) \setminus B(0,r-\delta )$. Such a function is easily seen to achieve
$B(0,r+\delta ) \setminus B(0,r-\delta )$. Such a function is easily seen to achieve  $$ \begin{align*} \frac{\| P_{1,\delta} f \|_{L^{p}}}{\| f \|_{L^{2}}} \sim \delta^{\frac{(d+1)}{2}\left( \frac{1}{2} - \frac{1}{p} \right)}. \end{align*} $$
$$ \begin{align*} \frac{\| P_{1,\delta} f \|_{L^{p}}}{\| f \|_{L^{2}}} \sim \delta^{\frac{(d+1)}{2}\left( \frac{1}{2} - \frac{1}{p} \right)}. \end{align*} $$• The radial example is
 $\widehat {g}(\xi ) = \chi \left ( \frac {|\xi | - \lambda }{\delta } \right ) $. Using the fact that the Fourier transform of the surface measure on the unit sphere decays like
$\widehat {g}(\xi ) = \chi \left ( \frac {|\xi | - \lambda }{\delta } \right ) $. Using the fact that the Fourier transform of the surface measure on the unit sphere decays like  $|\xi |^{-\frac {d-1}{2}}$ as
$|\xi |^{-\frac {d-1}{2}}$ as  $|\xi | \to \infty $, one can check that
$|\xi | \to \infty $, one can check that  $$ \begin{align*} \frac{\| P_{1,\delta} f \|_{L^{p}}}{\| f \|_{L^{2}}} \sim \delta^{1/2} \qquad \mbox{for }p>\frac{2d}{d-1}. \end{align*} $$
$$ \begin{align*} \frac{\| P_{1,\delta} f \|_{L^{p}}}{\| f \|_{L^{2}}} \sim \delta^{1/2} \qquad \mbox{for }p>\frac{2d}{d-1}. \end{align*} $$
Acknowledgments
The authors are grateful to the anonymous referee for a careful reading of their manuscript and pointing out an error in an earlier version; they are also thankful to Yu Deng for insightful discussions at an early stage of this project.
While working on this project, SLRM was supported by German Research Foundation (DFG) project number 255083470 and by a Leverhulme Early Career Fellowship. PG was supported by the NSF grant DMS-1501019, by the Simons collaborative grant on weak turbulence and by the Center for Stability, Instability and Turbulence (NYUAD).
Conflicts of Interest
None.