Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T16:23:36.767Z Has data issue: false hasContentIssue false
  • English
  • Français

CALDERÓN’S INVERSE PROBLEM WITH A FINITE NUMBER OF MEASUREMENTS

Part of: Nontrigonometric harmonic analysis Communication, information Miscellaneous topics - Partial differential equations

Published online by Cambridge University Press:  08 October 2019

GIOVANNI S. ALBERTI Open the ORCID record for GIOVANNI S. ALBERTI [Opens in a new window]  and
MATTEO SANTACESARIA Open the ORCID record for MATTEO SANTACESARIA [Opens in a new window]
GIOVANNI S. ALBERTI
Affiliation:
Department of Mathematics, University of Genoa, Via Dodecaneso 35, 16146 Genova, Italy; giovanni.alberti@unige.it, matteo.santacesaria@unige.it
MATTEO SANTACESARIA
Affiliation:
Department of Mathematics, University of Genoa, Via Dodecaneso 35, 16146 Genova, Italy; giovanni.alberti@unige.it, matteo.santacesaria@unige.it

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

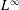We prove that an $L^{\infty }$ potential in the Schrödinger equation in three and higher dimensions can be uniquely determined from a finite number of boundary measurements, provided it belongs to a known finite dimensional subspace 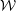${\mathcal{W}}$. As a corollary, we obtain a similar result for Calderón’s inverse conductivity problem. Lipschitz stability estimates and a globally convergent nonlinear reconstruction algorithm for both inverse problems are also presented. These are the first results on global uniqueness, stability and reconstruction for nonlinear inverse boundary value problems with finitely many measurements. We also discuss a few relevant examples of finite dimensional subspaces 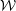${\mathcal{W}}$, including bandlimited and piecewise constant potentials, and explicitly compute the number of required measurements as a function of $\dim {\mathcal{W}}$.

MSC classification

Primary: 35R30: Inverse problems
Secondary: 42C40: Wavelets and other special systems 94A20: Sampling theory
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e35
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Adcock, B. and Hansen, A. C., ‘Generalized sampling and infinite-dimensional compressed sensing’, Found. Comput. Math. 16 (2016), 1263–1323.Google Scholar
Adcock, B., Hansen, A. C. and Poon, C., ‘On optimal wavelet reconstructions from Fourier samples: linearity and universality of the stable sampling rate’, Appl. Comput. Harmon. Anal. 36 (2014), 387–415.Google Scholar
Adcock, B., Hansen, A. C., Poon, C. and Roman, B., ‘Breaking the coherence barrier: a new theory for compressed sensing’, Forum Math. Sigma 5 (2017), e4, 84.Google Scholar
Alberti, G. S. and Santacesaria, M., ‘Infinite dimensional compressed sensing from anisotropic measurements and applications to inverse problems in PDE’, Appl. Comput. Harmon. Anal. (2019), doi:10.1016/j.acha.2019.08.002.Google Scholar
Alberti, G. S. and Santacesaria, M., ‘Infinite-dimensional inverse problems with finite measurements’. Preprint, 2019, arXiv:1906.10028.Google Scholar
Alessandrini, G., ‘Stable determination of conductivity by boundary measurements’, Appl. Anal. 27 (1988), 153–172.Google Scholar
Alessandrini, G., De Hoop, M. V. and Gaburro, R., ‘Uniqueness for the electrostatic inverse boundary value problem with piecewise constant anisotropic conductivities’, Inverse Problems 33 125013 (2017).Google Scholar
Alessandrini, G., de Hoop, M. V., Gaburro, R. and Sincich, E., ‘Lipschitz stability for the electrostatic inverse boundary value problem with piecewise linear conductivities’, J. Math. Pures Appl. 107(9) (2017), 638–664.Google Scholar
Alessandrini, G. and Vessella, S., ‘Lipschitz stability for the inverse conductivity problem’, Adv. Appl. Math. 35 (2005), 207–241.Google Scholar
Astala, K. and Päivärinta, L., ‘Calderón’s inverse conductivity problem in the plane’, Ann. of Math. (2) 163(1) (2006), 265–299.Google Scholar
Beretta, E., de Hoop, M. V., Francini, E. and Vessella, S., ‘Stable determination of polyhedral interfaces from boundary data for the Helmholtz equation’, Comm. Partial Differential Equations 40 (2015), 1365–1392.Google Scholar
Beretta, E., de Hoop, M. V., Francini, E., Vessella, S. and Zhai, J., ‘Uniqueness and Lipschitz stability of an inverse boundary value problem for time-harmonic elastic waves’, Inverse Problems 33 (2017), 035013, 27.Google Scholar
Beretta, E., de Hoop, M. V. and Qiu, L., ‘Lipschitz stability of an inverse boundary value problem for a Schrödinger-type equation’, SIAM J. Math. Anal. 45 (2013), 679–699.Google Scholar
Beretta, E. and Francini, E., ‘Lipschitz stability for the electrical impedance tomography problem: the complex case’, Comm. Partial Differential Equations 36 (2011), 1723–1749.Google Scholar
Blåsten, E., Imanuvilov, O. Y. and Yamamoto, M., ‘Stability and uniqueness for a two-dimensional inverse boundary value problem for less regular potentials’, Inverse Probl. Imaging 9 (2015), 709–723.Google Scholar
Blåsten, E. and Liu, H., ‘Recovering piecewise constant refractive indices by a single far-field pattern’. Preprint, 2017, arXiv:1705.00815.Google Scholar
Bukhgeim, A. L., ‘Recovering a potential from Cauchy data in the two-dimensional case’, J. Inverse Ill-Posed Probl. 16 (2008), 19–33.Google Scholar
Calderón, A. P., ‘On an inverse boundary value problem’, inSeminar on Numerical Analysis and its Applications to Continuum Physics (Rio de Janeiro, 1980) (Soc. Brasil. Mat., Rio de Janeiro, 1980), 65–73.Google Scholar
Caro, P. and Rogers, K. M., ‘Global uniqueness for the calderón problem with lipschitz conductivities’, Forum of Mathematics, Pi 4 (2016), E2. doi:10.1017/fmp.2015.9.Google Scholar
Clop, A., Faraco, D. and Ruiz, A., ‘Stability of Calderón’s inverse conductivity problem in the plane for discontinuous conductivities’, Inverse Probl. Imaging 4 (2010), 49–91.Google Scholar
Di Cristo, M. and Rondi, L., ‘Examples of exponential instability for inverse inclusion and scattering problems’, Inverse Problems 19 (2003), 685.Google Scholar
Ding, Z., ‘A proof of the trace theorem of Sobolev spaces on Lipschitz domains’, Proc. Amer. Math. Soc. 124 (1996), 591–600.Google Scholar
Faddeev, L. D., ‘Increasing solutions of the Schrödinger equation’, Sov. Phys. Dok. 10 (1966), 1033–1035.Google Scholar
Friedman, A. and Isakov, V., ‘On the uniqueness in the inverse conductivity problem with one measurement’, Indiana Univ. Math. J. 38 (1989), 563–579.Google Scholar
Gaburro, R. and Sincich, E., ‘Lipschitz stability for the inverse conductivity problem for a conformal class of anisotropic conductivities’, Inverse Problems 31 (2015), 015008, 26.Google Scholar
Haberman, B., ‘Uniqueness in calderón’s problem for conductivities with unbounded gradient’, Commun. Math. Phys. 340 (2015), 639–659.Google Scholar
Harrach, B., ‘Uniqueness and Lipschitz stability in electrical impedance tomography with finitely many electrodes’, Inverse Problems 35 (2019), 024005, 19.Google Scholar
Isaev, M. I., ‘Exponential instability in the Gel’fand inverse problem on the energy intervals’, J. Inverse Ill-Posed Probl. 19 (2011), 453–472.Google Scholar
Isaev, M. and Novikov, R., ‘Reconstruction of a potential from the impedance boundary map’, Eur. J. Math. Comput. Appl. 1 (2013), 5–28.Google Scholar
Jones, A. D., Adcock, B. and Hansen, A. C., ‘Analyzing the structure of multidimensional compressed sensing problems through coherence’, Preprint, 2016, arXiv:1610.07497.Google Scholar
Lakshtanov, E. L., Novikov, R. G. and Vainberg, B. R., ‘A global Riemann–Hilbert problem for two-dimensional inverse scattering at fixed energy’, Rend. Istit. Mat. Univ. Trieste 48 (2016), 21–47.Google Scholar
Lakshtanov, E. L., Tejero, J. and Vainberg, B. R., ‘Uniqueness in the inverse conductivity problem for complex-valued Lipschitz conductivities in the plane’, SIAM J. Math. Anal. 49 (2017), 3766–3775.Google Scholar
Mandache, N., ‘Exponential instability in an inverse problem for the Schrödinger equation’, Inverse Problems 17 (2001), 1435.Google Scholar
Mueller, J. L. and Siltanen, S., Linear and Nonlinear Inverse Problems with Practical Applications, Computational Science & Engineering, 10 (Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 2012).Google Scholar
Nachman, A. I., ‘Reconstructions from boundary measurements’, Ann. of Math. (2) 128 (1988), 531–576.Google Scholar
Nachman, A. I., ‘Global uniqueness for a two-dimensional inverse boundary value problem’, Ann. of Math. (2) 143 (1996), 71–96.Google Scholar
Novikov, R. G., ‘A multidimensional inverse spectral problem for the equation -𝛥𝜓 + (v (x) - Eu (x))𝜓 = 0’, Funct. Anal. Appl. 22 (1988), 263–272.Google Scholar
Novikov, R. G., ‘Formulae and equations for finding scattering data from the Dirichlet-to-Neumann map with nonzero background potential’, Inverse Problems 21 (2004), 257.Google Scholar
Novikov, R. G. and Santacesaria, M., ‘A global stability estimate for the Gel’fand–Calderón inverse problem in two dimensions’, J. Inverse Ill-Posed Probl. 18 (2010), 765–785.Google Scholar
Päivärinta, L., ‘Analytic methods for inverse scattering theory’, inNew Analytic and Geometric Methods in Inverse Problems (Springer, Berlin, 2004), 165–185.Google Scholar
Poon, C., ‘A consistent and stable approach to generalized sampling’, J. Fourier Anal. Appl. 20 (2014), 985–1019.Google Scholar
Rondi, L., ‘A remark on a paper by G. Alessandrini and S. Vessella: “Lipschitz stability for the inverse conductivity problem”’, Adv. Appl. Math. 35(2) (2005), 207–241. mr2152888, Adv. in Appl. Math., 36 (2006), 67–69.Google Scholar
Serov, V., ‘Inverse fixed energy scattering problem for the generalized nonlinear Schrödinger operator’, Inverse Problems 28 (2012), 025002, 11.Google Scholar
Sylvester, J. and Uhlmann, G., ‘A global uniqueness theorem for an inverse boundary value problem’, Ann. of Math. (2) 125 (1987), 153–169.Google Scholar