CANONICAL REPRESENTATIVES FOR DIVISOR CLASSES ON TROPICAL CURVES AND THE MATRIX–TREE THEOREM

Abstract

Let 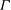$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\Gamma $ be a compact tropical curve (or metric graph) of genus 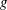$g$. Using the theory of tropical theta functions, Mikhalkin and Zharkov proved that there is a canonical effective representative (called a break divisor) for each linear equivalence class of divisors of degree 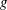$g$ on 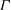$\Gamma $. We present a new combinatorial proof of the fact that there is a unique break divisor in each equivalence class, establishing in the process an ‘integral’ version of this result which is of independent interest. As an application, we provide a ‘geometric proof’ of (a dual version of) Kirchhoff’s celebrated matrix–tree theorem. Indeed, we show that each weighted graph model 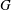$G$ for 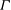$\Gamma $ gives rise to a canonical polyhedral decomposition of the 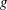$g$-dimensional real torus 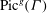$\mathrm{Pic}^g(\Gamma )$ into parallelotopes 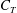$C_T$, one for each spanning tree 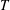$T$ of 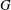$G$, and the dual Kirchhoff theorem becomes the statement that the volume of 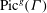$\mathrm{Pic}^g(\Gamma )$ is the sum of the volumes of the cells in the decomposition.