Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T04:40:41.507Z Has data issue: false hasContentIssue false
  • English
  • Français

The cohomology of Torelli groups is algebraic

Part of: Modules, bimodules and ideals Rings and algebras with additional structure

Published online by Cambridge University Press:  16 December 2020

Alexander Kupers Open the ORCID record for Alexander Kupers [Opens in a new window]  and
Oscar Randal-Williams
Alexander Kupers
Affiliation:
Department of Computer and Mathematical Sciences, University of Toronto Scarborough, 1265 Military Trail, Toronto, ON M1C 1A4, Canada; E-mail: a.kupers@utoronto.ca
Oscar Randal-Williams
Affiliation:
Centre for Mathematical Sciences, Wilberforce Road, CambridgeCB3 0WB, UK; E-mail: o.randal-williams@dpmms.cam.ac.uk

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Torelli group of 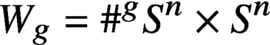$W_g = \#^g S^n \times S^n$ is the group of diffeomorphisms of 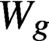$W_g$ fixing a disc that act trivially on 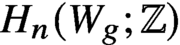$H_n(W_g;\mathbb{Z} )$ . The rational cohomology groups of the Torelli group are representations of an arithmetic subgroup of 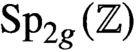$\text{Sp}_{2g}(\mathbb{Z} )$ or 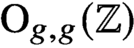$\text{O}_{g,g}(\mathbb{Z} )$ . In this article we prove that for 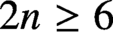$2n \geq 6$ and 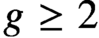$g \geq 2$ , they are in fact algebraic representations. Combined with previous work, this determines the rational cohomology of the Torelli group in a stable range. We further prove that the classifying space of the Torelli group is nilpotent.

MSC classification

Primary: 16W10: Rings with involution; Lie, Jordan and other nonassociative structures
Secondary: 16D50: Injective modules, self-injective rings
Type
Topology
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e64
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Boardman, J. M., ‘Conditionally convergent spectral sequences’, in Homotopy Invariant Algebraic Structures, Vol. 239 of Contemporary Mathematics (American Mathematical Society, Providence, RI, 1999), 49–84.CrossRefGoogle Scholar
de Brito, P. Boavida and Weiss, M., ‘Manifold calculus and homotopy sheaves’, Homology Homotopy Appl. 15 (2013), 361–383.CrossRefGoogle Scholar
de Brito, P. Boavida and Weiss, M., ‘Spaces of smooth embeddings and configuration categories’, J. Topol. 11 (2018), 65–143.CrossRefGoogle Scholar
Borel, A., ‘Density properties for certain subgroups of semi-simple groups without compact components’, Ann. Math. 2 (1960), 179–188.CrossRefGoogle Scholar
Borel, A., ‘Stable real cohomology of arithmetic groups’, Ann. Sci. École Norm. 7 (1974), 235–272.CrossRefGoogle Scholar
Borel, A., ‘Stable real cohomology of arithmetic groups. II’, in Manifolds and Lie Groups , Vol. 14 of Progress in Mathematics (Birkhäuser, Boston, 1981), 21–55.CrossRefGoogle Scholar
Borel, A. and Harish-Chandra, , ‘Arithmetic subgroups of algebraic groups’, Ann. Math. 75 (1962), 485–535.CrossRefGoogle Scholar
Bott, R., ‘The stable homotopy of the classical groups’, Ann. of Math. (2) 70 (1959), 313–337.CrossRefGoogle Scholar
Bousfield, A. K., ‘Homotopy spectral sequences and obstructions’, Isr. J. Math. 66 (1989), 54–104.CrossRefGoogle Scholar
Bousfield, A. K. and Kan, D. M., Homotopy Limits, Completions and Localizations , Vol. 34 of Lecture Notes in Mathematics (Springer-Verlag, Berlin, 1972).Google Scholar
Brown, K. S., Cohomology of Groups , Vol. 87 of Graduate Texts in Mathematics, (Springer-Verlag, New York, 1994).Google Scholar
Burghelea, D. and Lashof, R., ‘The homotopy type of the space of diffeomorphisms. I. Trans. Amer. Math. Soc. 196 (1974), 1–36.CrossRefGoogle Scholar
Burghelea, D. and Lashof, R., ‘The homotopy type of the space of diffeomorphisms. II. Trans. Amer. Math. Soc. 196 (1974), 37–50.CrossRefGoogle Scholar
Cerf, J., ‘La stratification naturelle des espaces de fonctions différentiables réelles et le théorème de la pseudo-isotopie’, Inst. Hautes Études Sci. Publ. Math. 39 (1970), 5–173.CrossRefGoogle Scholar
Dress, A., ‘Zur Spectralsequenz von Faserungen’, Invent. Math. 3 (1967), 172–178.CrossRefGoogle Scholar
Dwyer, W. G. and Kan, D. M., ‘Function complexes in homotopical algebra’, Topology 19 (1980), 427–440.CrossRefGoogle Scholar
Dwyer, W. G. and Kan, D. M., ‘An obstruction theory for diagrams of simplicial sets’, Nederl. Akad. Wetensch. Indag. Math. 46 (1984), 139–146.CrossRefGoogle Scholar
Federer, H., ‘A study of function spaces by spectral sequences’, Trans. Amer. Math. Soc. 82 (1956), 340–361.CrossRefGoogle Scholar
Galatius, S. and Randal-Williams, O., ‘Monoids of moduli spaces of manifolds’, Geom. Topol. 14 (2010), 1243–1302.CrossRefGoogle Scholar
Galatius, S. and Randal-Williams, O., ‘Homological stability for moduli spaces of high dimensional manifolds. I’, J. Amer. Math. Soc. 31 (2018), 215–264.CrossRefGoogle Scholar
Goodwillie, T. G., ‘A multiple disjunction lemma for smooth concordance embeddings’, Mem. Amer. Math. Soc. 86 (1990), viii $+$ 317.Google Scholar
Goodwillie, T. G. and Klein, J. R., ‘Multiple disjunction for spaces of smooth embeddings’, J. Topol. 8 (2015), 651–674.CrossRefGoogle Scholar
Goodwillie, T. G., Klein, J. R. and Weiss, M. S., ‘A Haefliger style description of the embedding calculus tower’, Topology 42 (2003), 509–524.CrossRefGoogle Scholar
Goodwillie, T. G. and Weiss, M., ‘Embeddings from the point of view of immersion theory. II’, Geom. Topol. 3 (1999), 103–118 (electronic).CrossRefGoogle Scholar
Haefliger, A., ‘Plongements différentiables de variétés dans variétés’, Comment. Math. Helv. 36 (1961), 47–82.CrossRefGoogle Scholar
Hain, R. M., ‘The Hodge de Rham theory of relative Malcev completion’, Ann. Sci. École Norm. 31 (1998), 47–92.CrossRefGoogle Scholar
Kervaire, M. A., ‘Some nonstable homotopy groups of Lie groups’, Illinois J. Math. 4 (1960), 161–169.CrossRefGoogle Scholar
Kirby, R. C. and Siebenmann, L. C., Foundational Essays on Topological Manifolds, Smoothings, and Triangulations , Vol. 88 of Annals of Mathematics Studies (Princeton University Press, Princeton, NJ, 1977).Google Scholar
Kosiński, A., ‘On the inertia group of $\pi$ -manifolds’, Amer. J. Math. 89 (1967), 227–248.CrossRefGoogle Scholar
Krannich, M., ‘Homological stability of topological moduli spaces’, Geom. Topol. 23 (2019), 2397–2474.CrossRefGoogle Scholar
Krannich, M., ‘Mapping class groups of highly connected $\left(4k+2\right)$ -manifolds’, 2019, http://arxiv.org/abs/1902.10097. Selecta Mathematica, to appear.CrossRefGoogle Scholar
Kreck, M., ‘Isotopy classes of diffeomorphisms of $\left(k-1\right)$ -connected almost-parallelizable $2k$ -manifolds’, in Algebraic Topology, Aarhus 1978, Vol. 763 of Lecture Notes in Mathematics (Springer, Berlin, Germany, 1979), 643–663.CrossRefGoogle Scholar
Kupers, A., ‘Some finiteness results for groups of automorphisms of manifolds’, Geom. Topol. 23 (2019), 2277–2333 (electronic).CrossRefGoogle Scholar
Kupers, A. and Randal-Williams, O., ‘On the cohomology of Torelli groups’, Forum of Mathematics, Pi 8 (2020), e7.CrossRefGoogle Scholar
Levine, J. P., ‘Lectures on groups of homotopy spheres’, in Algebraic and Geometric Topology, Vol. 1126 of Lecture Notes in Mathematics (Springer, Berlin, 1985), 62–95.CrossRefGoogle Scholar
Lillig, J., ‘A union theorem for cofibrations’, Arch. Math. (Basel) 24 (1973), 410–415.CrossRefGoogle Scholar
Margulis, G. A., Discrete Subgroups of Semisimple Lie Groups , Vol. 17 of Ergebnisse der Mathematik und ihrer Grenzgebiete (Springer-Verlag, Berlin, 1991).Google Scholar
May, J. P. and Ponto, K., More Concise Algebraic Topology, Chicago Lectures in Mathematics (University of Chicago Press, Chicago, IL, 2012).Google Scholar
Munson, B. A. and Volić, I., Cubical Homotopy Theory , Vol. 25 of New Mathematical Monographs (Cambridge University Press, Cambridge, United Kingdom, 2015).Google Scholar
Riehl, E. and Verity, D., ‘The theory and practice of Reedy categories’, Theory Appl. Categ. 29 (2014), 256–301.Google Scholar
Schultz, R., ‘Homotopy decompositions of equivariant function spaces. I’, Math. Z. 131 (1973), 49–75.CrossRefGoogle Scholar
Serre, J.-P., ‘Arithmetic groups’, in Homological Group Theory, Vol. 36 of London Mathematical Society Lecture Note Series (Cambridge University Press, Cambridge, United Kingdom, 1979), 105–136.CrossRefGoogle Scholar
Sinha, D. P., ‘Manifold-theoretic compactifications of configuration spaces’, Selecta Math. (N.S.) 10 (2004), 391–428.CrossRefGoogle Scholar
Spanier, E. H., Algebraic Topology (Springer-Verlag, New York, 1994).Google Scholar
Totaro, B., ‘Configuration spaces of algebraic varieties’, Topology 35 (1996), 1057–1067.CrossRefGoogle Scholar
Tshishiku, B., ‘Borel’s stable range for the cohomology of arithmetic groups’, J. Lie Theory 29 (2019), 1093–1102.Google Scholar
Turchin, V., ‘Context-free manifold calculus and the Fulton-MacPherson operad’, Algebr. Geom. Topol. 13 (2013), 1243–1271.CrossRefGoogle Scholar
Wall, C. T. C., ‘The action of ${\Gamma}_{2n}$ on $\left(n-1\right)$ -connected $2n$ -manifolds’, Proc. Amer. Math. Soc. 13 (1962), 943–944.Google Scholar
Wall, C. T. C., ‘Classification problems in differential topology. II. Diffeomorphisms of handlebodies’, Topology 2 (1963), 263–272.Google Scholar
Wall, C. T. C., Surgery on compact manifolds , second ed., Vol. 69 of Mathematical Surveys and Monographs (American Mathematical Society, Providence, RI, 1999). Edited and with a foreword by Ranicki, A. A..CrossRefGoogle Scholar
Weiss, M., ‘Embeddings from the point of view of immersion theory. I’, Geom. Topol. 3 (1999), 67–101 (electronic).CrossRefGoogle Scholar
Weiss, M., ‘Erratum to the article Embeddings from the point of view of immersion theory: Part I’, Geom. Topol. 15 (2011), 407–409.CrossRefGoogle Scholar
Weiss, M., ‘Dalian notes on Pontryagin classes’, Preprint 2015, http://arxiv.org/abs/1507.00153.Google Scholar