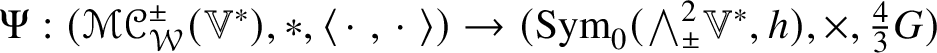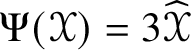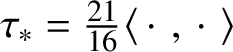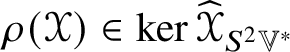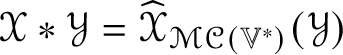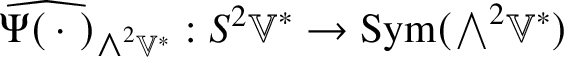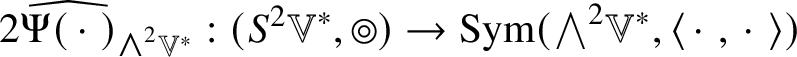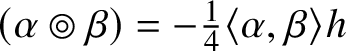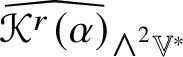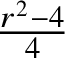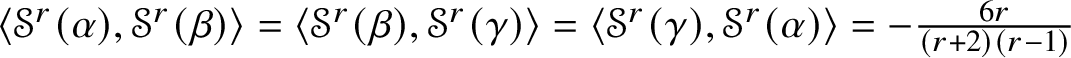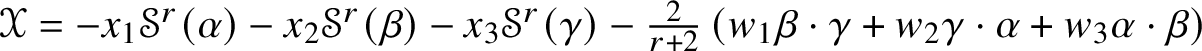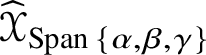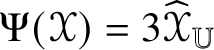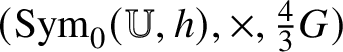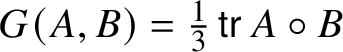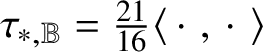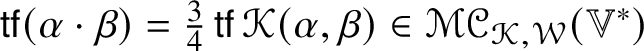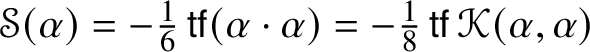1 Introduction
Let ![]() $\mathbb {V}$ be an n-dimensional real vector space equipped with a metric
$\mathbb {V}$ be an n-dimensional real vector space equipped with a metric ![]() $h_{ij}$. Let
$h_{ij}$. Let ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$
$\mathscr {MC}(\mathbb {V}^{\ast })$
 $$ \begin{align} \mathscr{MC}(\mathbb{V}^{\ast}) = \{\mathscr{Y}_{ijkl} \in \otimes^{4}\mathbb{V}^{\ast}: \mathscr{Y}_{[ij]kl} = \mathscr{Y}_{ijkl} = \mathscr{Y}_{ij[kl]}, \mathscr{Y}_{[ijk]l} = 0\} \end{align} $$
$$ \begin{align} \mathscr{MC}(\mathbb{V}^{\ast}) = \{\mathscr{Y}_{ijkl} \in \otimes^{4}\mathbb{V}^{\ast}: \mathscr{Y}_{[ij]kl} = \mathscr{Y}_{ijkl} = \mathscr{Y}_{ij[kl]}, \mathscr{Y}_{[ijk]l} = 0\} \end{align} $$be the ![]() $n^{2}(n^{2} \,{-}\, 1)/12$-dimensional vector space of metric curvature tensors. Any
$n^{2}(n^{2} \,{-}\, 1)/12$-dimensional vector space of metric curvature tensors. Any ![]() $\mathscr {Y}_{ijkl} \in \mathscr {MC}(\mathbb {V}^{\ast })$ satisfies
$\mathscr {Y}_{ijkl} \in \mathscr {MC}(\mathbb {V}^{\ast })$ satisfies ![]() $\mathscr {Y}_{klij} = \mathscr {Y}_{ijkl}$ and
$\mathscr {Y}_{klij} = \mathscr {Y}_{ijkl}$ and ![]() $\mathscr {Y}_{i(jk)l}$ is symmetric in i and l. The metric curvature tensors of n type
$\mathscr {Y}_{i(jk)l}$ is symmetric in i and l. The metric curvature tensors of n type ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ comprise the kernel of the Ricci trace
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ comprise the kernel of the Ricci trace ![]() $\operatorname {\rho }:\mathscr {MC}(\mathbb {V}^{\ast }) \to S^{2}(\mathbb {V}^{\ast })$ defined by
$\operatorname {\rho }:\mathscr {MC}(\mathbb {V}^{\ast }) \to S^{2}(\mathbb {V}^{\ast })$ defined by ![]() $\operatorname {\rho }(\mathscr {Y})_{ij} = \mathscr {Y}_{pij}{}^{p}$. Note that
$\operatorname {\rho }(\mathscr {Y})_{ij} = \mathscr {Y}_{pij}{}^{p}$. Note that ![]() $\operatorname {\rho }(\mathscr {Y})_{ij}$ is symmetric because
$\operatorname {\rho }(\mathscr {Y})_{ij}$ is symmetric because 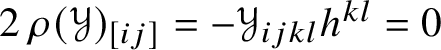 $2\operatorname {\rho }(\mathscr {Y})_{[ij]} = -\mathscr {Y}_{ijkl}h^{kl} = 0$. The trace
$2\operatorname {\rho }(\mathscr {Y})_{[ij]} = -\mathscr {Y}_{ijkl}h^{kl} = 0$. The trace ![]() $\operatorname {s}(\mathscr {Y}) = \operatorname {\mathsf {tr}} \operatorname {\rho }(\mathscr {Y}) = h^{ij}\operatorname {\rho }(\mathscr {Y})_{ij}$ is the scalar curvature of
$\operatorname {s}(\mathscr {Y}) = \operatorname {\mathsf {tr}} \operatorname {\rho }(\mathscr {Y}) = h^{ij}\operatorname {\rho }(\mathscr {Y})_{ij}$ is the scalar curvature of ![]() $\mathscr {Y}$. (Here, and when convenient, the abstract index conventions [Reference Penrose and Rindler30, chapter
$\mathscr {Y}$. (Here, and when convenient, the abstract index conventions [Reference Penrose and Rindler30, chapter ![]() $2$] are used.) These definitions are consistent with the conventions in which the curvature tensor of the round metric
$2$] are used.) These definitions are consistent with the conventions in which the curvature tensor of the round metric ![]() $g_{ij}$ on the sphere has the form
$g_{ij}$ on the sphere has the form ![]() $-2g_{k[i}g_{j]l}$ (see Remark 5.10 for detailed discussion of signs).
$-2g_{k[i}g_{j]l}$ (see Remark 5.10 for detailed discussion of signs).
By [Reference Hamilton17, Theorem ![]() $7.1$] the curvature tensor
$7.1$] the curvature tensor ![]() $\mathscr {R}_{ijkl}$ of a family of metrics
$\mathscr {R}_{ijkl}$ of a family of metrics ![]() $g(t)_{ij}$ solving the Ricci flow
$g(t)_{ij}$ solving the Ricci flow 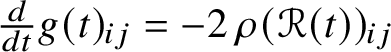 $\tfrac {d}{dt}g(t)_{ij} = -2\operatorname {\rho }(\mathscr {R}(t))_{ij}$ evolves according to
$\tfrac {d}{dt}g(t)_{ij} = -2\operatorname {\rho }(\mathscr {R}(t))_{ij}$ evolves according to
 $$ \begin{align} \tfrac{d}{dt}\mathscr{R}_{ijkl} = \Delta\mathscr{R}_{ijkl} + 2(\mathscr{R}\ast \mathscr{R})_{ijkl} + 2\mathscr{R}_{p[i}\mathscr{R}_{j]}{}^{p}{}_{kl} + 2\mathscr{R}_{p[k}\mathscr{R}_{l]}{}^{p}{}_{ij}, \end{align} $$
$$ \begin{align} \tfrac{d}{dt}\mathscr{R}_{ijkl} = \Delta\mathscr{R}_{ijkl} + 2(\mathscr{R}\ast \mathscr{R})_{ijkl} + 2\mathscr{R}_{p[i}\mathscr{R}_{j]}{}^{p}{}_{kl} + 2\mathscr{R}_{p[k}\mathscr{R}_{l]}{}^{p}{}_{ij}, \end{align} $$where ![]() $\mathscr {R}\ast \mathscr {R}$ is some quadratic form on
$\mathscr {R}\ast \mathscr {R}$ is some quadratic form on ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$. The polarization of the quadratic form appearing in (1.2) can be viewed as a commutative multiplication
$\mathscr {MC}(\mathbb {V}^{\ast })$. The polarization of the quadratic form appearing in (1.2) can be viewed as a commutative multiplication ![]() $\ast $ on
$\ast $ on ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$. Here,
$\mathscr {MC}(\mathbb {V}^{\ast })$. Here, ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ is studied as an interesting example in the general context of commutative nonassociative algebras that exhibits some special structural properties. Although they did not explicitly use this algebraic perspective, it was R. Hamilton [Reference Hamilton17, Reference Hamilton18, Reference Hamilton19] and G. Huisken [Reference Huisken21] who first emphasized the importance of
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ is studied as an interesting example in the general context of commutative nonassociative algebras that exhibits some special structural properties. Although they did not explicitly use this algebraic perspective, it was R. Hamilton [Reference Hamilton17, Reference Hamilton18, Reference Hamilton19] and G. Huisken [Reference Huisken21] who first emphasized the importance of ![]() $\ast $ and discovered its basic properties.
$\ast $ and discovered its basic properties.
The class of commutative not necessarily associative algebras with no additional structure is too general to admit a good theory. In many interesting examples the commutative algebra ![]() $(\mathbb {A}, \circ )$ satisfies the further condition that it is metrized, meaning it is equipped with a nondegenerate bilinear form h that is invariant in the sense that the cubic form
$(\mathbb {A}, \circ )$ satisfies the further condition that it is metrized, meaning it is equipped with a nondegenerate bilinear form h that is invariant in the sense that the cubic form ![]() $h(x\circ y, z)$ is completely symmetric in
$h(x\circ y, z)$ is completely symmetric in ![]() $x, y, z \in \mathbb {A}$ (in this case h is also often called a Frobenius form). For various perspectives on metrized commutative algebras, see [Reference Bordemann3, Reference Fox10, Reference Griess12, Reference Griess13, Reference Hall14, Reference Hall, Rehren and Shpectorov16, Reference Ivanov22, Reference Nadirashvili, Tkachev and Vlăduţ29, Reference Tkachev37].
$x, y, z \in \mathbb {A}$ (in this case h is also often called a Frobenius form). For various perspectives on metrized commutative algebras, see [Reference Bordemann3, Reference Fox10, Reference Griess12, Reference Griess13, Reference Hall14, Reference Hall, Rehren and Shpectorov16, Reference Ivanov22, Reference Nadirashvili, Tkachev and Vlăduţ29, Reference Tkachev37].
The definition of ![]() $\ast $ and its basic properties are described in Section 5 and are based on Theorem 5.4, which yields two different new constructions of
$\ast $ and its basic properties are described in Section 5 and are based on Theorem 5.4, which yields two different new constructions of ![]() $\ast $.
$\ast $.
By Lemma 4.2, for ![]() $k \geq 2$ there is an
$k \geq 2$ there is an ![]() $O(n)$-equivariant linear map
$O(n)$-equivariant linear map 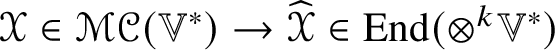 $\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast }) \to \widehat {\mathscr {X}} \in \operatorname {End}(\otimes ^{k}\mathbb {V}^{\ast })$ such that
$\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast }) \to \widehat {\mathscr {X}} \in \operatorname {End}(\otimes ^{k}\mathbb {V}^{\ast })$ such that ![]() $\widehat {\mathscr {X}}$ is self-adjoint and preserves the type (by symmetries) of tensors. If
$\widehat {\mathscr {X}}$ is self-adjoint and preserves the type (by symmetries) of tensors. If ![]() $\widehat {\mathscr {X}}$ preserves the
$\widehat {\mathscr {X}}$ preserves the ![]() $O(n)$-submodule
$O(n)$-submodule ![]() $\mathbb {W} \subset \otimes ^{k}\mathbb {V}^{\ast }$, it restriction to
$\mathbb {W} \subset \otimes ^{k}\mathbb {V}^{\ast }$, it restriction to ![]() $\mathbb {W}$ is written
$\mathbb {W}$ is written ![]() $\widehat {\mathscr {X}}_{\mathbb {W}}$. If
$\widehat {\mathscr {X}}_{\mathbb {W}}$. If ![]() $\mathscr {X} \to \widehat {\mathscr {X}}_{\mathbb {W}}$ is injective, the pullback of the projection onto the image of
$\mathscr {X} \to \widehat {\mathscr {X}}_{\mathbb {W}}$ is injective, the pullback of the projection onto the image of ![]() $\widehat {\,\cdot \,\,}_{\mathbb {W}}$ of the Jordan product
$\widehat {\,\cdot \,\,}_{\mathbb {W}}$ of the Jordan product ![]() $\widehat {\mathscr {X}}_{\mathbb {W}}\circledcirc \widehat {\mathscr {Y}}_{\mathbb {W}}$ yields a commutative multiplication on
$\widehat {\mathscr {X}}_{\mathbb {W}}\circledcirc \widehat {\mathscr {Y}}_{\mathbb {W}}$ yields a commutative multiplication on ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$ on which
$\mathscr {MC}(\mathbb {V}^{\ast })$ on which ![]() $O(n)$ acts by automorphisms.
$O(n)$ acts by automorphisms.
For example, ![]() $\widehat {\mathscr {X}}$ preserves
$\widehat {\mathscr {X}}$ preserves ![]() ${\bigwedge }^{2}\mathbb {V}^{\ast }$ and
${\bigwedge }^{2}\mathbb {V}^{\ast }$ and ![]() $S^{2}\mathbb {V}^{\ast }$ and the induced maps
$S^{2}\mathbb {V}^{\ast }$ and the induced maps 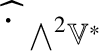 $\widehat {\,\cdot \,\,}_{{\bigwedge }^{2}\mathbb {V}^{\ast }}$ and
$\widehat {\,\cdot \,\,}_{{\bigwedge }^{2}\mathbb {V}^{\ast }}$ and ![]() $\widehat {\,\cdot \,\,}_{S^{2}\mathbb {V}^{\ast }}$ are injective by Corollary 4.5. By Lemma 5.2, the linear combinations of the pullbacks of the projections onto their images of the Jordan products of endomorphisms,
$\widehat {\,\cdot \,\,}_{S^{2}\mathbb {V}^{\ast }}$ are injective by Corollary 4.5. By Lemma 5.2, the linear combinations of the pullbacks of the projections onto their images of the Jordan products of endomorphisms, 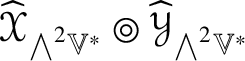 $\widehat {\mathscr {X}}_{{\bigwedge }^{2}\mathbb {V}^{\ast }}\circledcirc \widehat {\mathscr {Y}}_{{\bigwedge }^{2}\mathbb {V}^{\ast }}$ and
$\widehat {\mathscr {X}}_{{\bigwedge }^{2}\mathbb {V}^{\ast }}\circledcirc \widehat {\mathscr {Y}}_{{\bigwedge }^{2}\mathbb {V}^{\ast }}$ and  $\widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}\circledcirc \widehat {\mathscr {Y}}_{S^{2}\mathbb {V}^{\ast }}$, yield a two-parameter family
$\widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}\circledcirc \widehat {\mathscr {Y}}_{S^{2}\mathbb {V}^{\ast }}$, yield a two-parameter family ![]() $s\ast _{A} + t\ast _{S}$ of commutative multiplications on
$s\ast _{A} + t\ast _{S}$ of commutative multiplications on ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$ that are metrized by the metric
$\mathscr {MC}(\mathbb {V}^{\ast })$ that are metrized by the metric ![]() $\langle \mathscr {X}, \mathscr {Y} \rangle = \mathscr {X}_{ijkl}\mathscr {Y}^{ijkl}$ on
$\langle \mathscr {X}, \mathscr {Y} \rangle = \mathscr {X}_{ijkl}\mathscr {Y}^{ijkl}$ on ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$ and on which
$\mathscr {MC}(\mathbb {V}^{\ast })$ and on which ![]() $O(n)$ acts isometrically by algebra automorphisms. Moreover, a specific linear combination recovers
$O(n)$ acts isometrically by algebra automorphisms. Moreover, a specific linear combination recovers ![]() $\ast $ as follows. As
$\ast $ as follows. As ![]() $\mathscr {X}\in \mathscr {MC}(\mathbb {V}^{\ast })$ determines an endomorphism
$\mathscr {X}\in \mathscr {MC}(\mathbb {V}^{\ast })$ determines an endomorphism 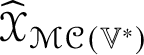 $\widehat {\mathscr {X}}_{\mathscr {MC}(\mathbb {V}^{\ast })}$ of
$\widehat {\mathscr {X}}_{\mathscr {MC}(\mathbb {V}^{\ast })}$ of ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$, it makes sense to define a multiplication on
$\mathscr {MC}(\mathbb {V}^{\ast })$, it makes sense to define a multiplication on ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$ by
$\mathscr {MC}(\mathbb {V}^{\ast })$ by 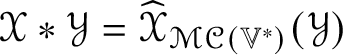 $\mathscr {X} \ast \mathscr {Y} = \widehat {\mathscr {X}}_{\mathscr {MC}(\mathbb {V}^{\ast })}(\mathscr {Y})$. It turns out that the multiplication
$\mathscr {X} \ast \mathscr {Y} = \widehat {\mathscr {X}}_{\mathscr {MC}(\mathbb {V}^{\ast })}(\mathscr {Y})$. It turns out that the multiplication ![]() $\ast $ so defined is commutative, for Theorem 5.4 shows that
$\ast $ so defined is commutative, for Theorem 5.4 shows that 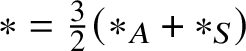 $\ast = \tfrac {3}{2}(\ast _{A} + \ast _{S})$ and that it recovers the multiplication of (1.2), for it shows that
$\ast = \tfrac {3}{2}(\ast _{A} + \ast _{S})$ and that it recovers the multiplication of (1.2), for it shows that ![]() $\ast $ has the explicit form (5.14) found by Hamilton. Because
$\ast $ has the explicit form (5.14) found by Hamilton. Because 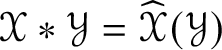 $\mathscr {X} \ast \mathscr {Y} = \widehat {\mathscr {X}}(\mathscr {Y})$, an immediate consequence of the self-adjointness of
$\mathscr {X} \ast \mathscr {Y} = \widehat {\mathscr {X}}(\mathscr {Y})$, an immediate consequence of the self-adjointness of 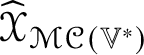 $\widehat {\mathscr {X}}_{\mathscr {MC}(\mathbb {V}^{\ast })}$ with respect to
$\widehat {\mathscr {X}}_{\mathscr {MC}(\mathbb {V}^{\ast })}$ with respect to ![]() $\langle \,\cdot \,\,, \,\cdot \,\, \rangle $ is that
$\langle \,\cdot \,\,, \,\cdot \,\, \rangle $ is that ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ is metrized by
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ is metrized by ![]() $\langle \,\cdot \,\,, \,\cdot \,\, \rangle $, a fact due to Huisken.
$\langle \,\cdot \,\,, \,\cdot \,\, \rangle $, a fact due to Huisken.
Remark 1.1. For any metrized commutative algebra ![]() $(\mathbb {A}, \circ , h)$ and any
$(\mathbb {A}, \circ , h)$ and any ![]() $t \in \mathbb {R}^{\times }$,
$t \in \mathbb {R}^{\times }$, ![]() $t\operatorname {Id}_{\mathbb {A}} \in \operatorname {End}(\mathbb {A})$ is an isometric algebra isomorphism from
$t\operatorname {Id}_{\mathbb {A}} \in \operatorname {End}(\mathbb {A})$ is an isometric algebra isomorphism from ![]() $(\mathbb {A}, \circ _{t}, t^{2}h)$ to
$(\mathbb {A}, \circ _{t}, t^{2}h)$ to ![]() $(\mathbb {A}, \circ , h)$ where
$(\mathbb {A}, \circ , h)$ where ![]() $x\circ _{t} y = t x \circ y$. For this reason, the family
$x\circ _{t} y = t x \circ y$. For this reason, the family ![]() $s\ast _{A} + t\ast _{S}$ should be regarded as associated with
$s\ast _{A} + t\ast _{S}$ should be regarded as associated with ![]() $[s:t] \in \mathbb {P}^{1}(\mathbb R)$, and it is any one of the multiplications corresponding with
$[s:t] \in \mathbb {P}^{1}(\mathbb R)$, and it is any one of the multiplications corresponding with ![]() $[1:1] \in \mathbb {P}^{1}(\mathbb R)$ that arises in the Ricci flow, the choice of which amounting to a normalization that is inconsequential from a purely algebraic perspective. However, considerations related to geometric applications motivate a particular choice. Concretely, the choice of
$[1:1] \in \mathbb {P}^{1}(\mathbb R)$ that arises in the Ricci flow, the choice of which amounting to a normalization that is inconsequential from a purely algebraic perspective. However, considerations related to geometric applications motivate a particular choice. Concretely, the choice of ![]() $\ast = \ast _{1}$ over
$\ast = \ast _{1}$ over ![]() $\ast _{-1}$ is made by requiring that a positive multiple of the curvature tensor of the round sphere be idempotent. See Remark 5.10 for further discussion.
$\ast _{-1}$ is made by requiring that a positive multiple of the curvature tensor of the round sphere be idempotent. See Remark 5.10 for further discussion.
Remark 1.2. Some authors [Reference Böhm and Wilking2, Reference Richard32, Reference Richard and Seshadri34] define ![]() $\ast $ directly in terms of curvature operators on
$\ast $ directly in terms of curvature operators on ![]() ${\bigwedge }^{2}\mathbb {V}^{\ast }$. Here
${\bigwedge }^{2}\mathbb {V}^{\ast }$. Here ![]() $\ast $ is defined on curvature tensors, and the two definitions involve curvature operators on
$\ast $ is defined on curvature tensors, and the two definitions involve curvature operators on ![]() $S^{2}\mathbb {V}^{\ast }$ and
$S^{2}\mathbb {V}^{\ast }$ and ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$ itself. Although there seems to be no good notion of representation of a commutative nonassociative algebra (at least not without embedding it in a vertex operator algebra), it is convenient to think of curvature operators on different tensor modules such as
$\mathscr {MC}(\mathbb {V}^{\ast })$ itself. Although there seems to be no good notion of representation of a commutative nonassociative algebra (at least not without embedding it in a vertex operator algebra), it is convenient to think of curvature operators on different tensor modules such as ![]() $S^{2}\mathbb {V}^{\ast }$ and
$S^{2}\mathbb {V}^{\ast }$ and ![]() ${\bigwedge }^{2}\mathbb {V}^{\ast }$ as different representations of
${\bigwedge }^{2}\mathbb {V}^{\ast }$ as different representations of ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$, Theorem 5.4 shows that the multiplication itself is determined by
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$, Theorem 5.4 shows that the multiplication itself is determined by ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$ somehow viewed as a module over itself.
$\mathscr {MC}(\mathbb {V}^{\ast })$ somehow viewed as a module over itself.
The irreducible submodules of ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$ under the action of certain groups of orthogonal transformations are subalgebras. Lemma 5.7 shows that the space
$\mathscr {MC}(\mathbb {V}^{\ast })$ under the action of certain groups of orthogonal transformations are subalgebras. Lemma 5.7 shows that the space ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ of metric curvature tensors of Weyl type is a subalgebra of
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ of metric curvature tensors of Weyl type is a subalgebra of ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$. If
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$. If ![]() $(\mathbb {V}, h)$ carries an almost complex structure compatible with h it makes sense to speak of the submodule of Kähler curvature tensors (see Section 11 for the definition),
$(\mathbb {V}, h)$ carries an almost complex structure compatible with h it makes sense to speak of the submodule of Kähler curvature tensors (see Section 11 for the definition), ![]() $\mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast })$ and its submodule of Kähler Weyl curvature tensor
$\mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast })$ and its submodule of Kähler Weyl curvature tensor ![]() $\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }) = \mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast }) \cap \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, and Lemma 11.1 shows that
$\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }) = \mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast }) \cap \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, and Lemma 11.1 shows that ![]() $\mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast })$ and
$\mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast })$ and ![]() $\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$ are subalgebras of
$\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$ are subalgebras of ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$. The 1-dimensional submodule of
$\mathscr {MC}(\mathbb {V}^{\ast })$. The 1-dimensional submodule of ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$ generated by the metric is also a subalgebra (isomorphic to the real field), but the irreducible submodule generated by the Kulkarni–Nomizu products of the metric with trace-free symmetric two-tensors (the submodule comprising curvature tensors of pure trace-free Ricci type) is not a subalgebra. The fusion rules (in the sense of [Reference Hall, Rehren and Shpectorov16]) describing the interactions of the irreducible summands of
$\mathscr {MC}(\mathbb {V}^{\ast })$ generated by the metric is also a subalgebra (isomorphic to the real field), but the irreducible submodule generated by the Kulkarni–Nomizu products of the metric with trace-free symmetric two-tensors (the submodule comprising curvature tensors of pure trace-free Ricci type) is not a subalgebra. The fusion rules (in the sense of [Reference Hall, Rehren and Shpectorov16]) describing the interactions of the irreducible summands of ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$ are given in Table 1. They follow from Theorem 7.12, which gives more information than do the fusion rules alone because it asserts the equalities of products of subspaces, rather than simply containment relations. The proofs of these relations are based on detailed calculations of products in
$\mathscr {MC}(\mathbb {V}^{\ast })$ are given in Table 1. They follow from Theorem 7.12, which gives more information than do the fusion rules alone because it asserts the equalities of products of subspaces, rather than simply containment relations. The proofs of these relations are based on detailed calculations of products in ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$, given in Section 6, that, while technical, should be useful in further study of
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$, given in Section 6, that, while technical, should be useful in further study of ![]() $\ast $. The ingredients of the proof of Theorem 7.12 also yield a conceptually simple proof of the Böhm–Wilking theorem (see Section 7) used in the construction of curvature cones. The fusion rules for the unitary irreducible subspaces of the subalgebra
$\ast $. The ingredients of the proof of Theorem 7.12 also yield a conceptually simple proof of the Böhm–Wilking theorem (see Section 7) used in the construction of curvature cones. The fusion rules for the unitary irreducible subspaces of the subalgebra ![]() $\mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast })$ and the corresponding analogue of the Böhm–Wilking theorem are described in the companion paper [Reference Fox11].
$\mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast })$ and the corresponding analogue of the Böhm–Wilking theorem are described in the companion paper [Reference Fox11].
Table 1 Fusion rules for ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$
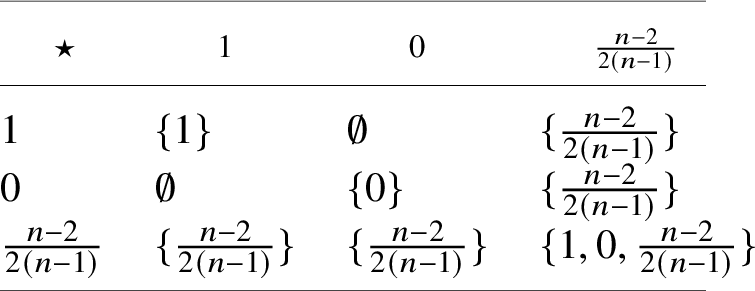
A commutative algebra ![]() $(\mathbb {A}, \circ )$ is exact (called harmonic in [Reference Nadirashvili, Tkachev and Vlăduţ29]) if its multiplication endomorphisms
$(\mathbb {A}, \circ )$ is exact (called harmonic in [Reference Nadirashvili, Tkachev and Vlăduţ29]) if its multiplication endomorphisms ![]() $L_{\circ }:\mathbb {A} \to \operatorname {End}(\mathbb {A})$ defined by
$L_{\circ }:\mathbb {A} \to \operatorname {End}(\mathbb {A})$ defined by ![]() $L_{\circ }(x) = x\circ y$ satisfy
$L_{\circ }(x) = x\circ y$ satisfy ![]() $\operatorname {\mathsf {tr}} L_{\circ }(x) = 0$ for all
$\operatorname {\mathsf {tr}} L_{\circ }(x) = 0$ for all ![]() $x \in \mathbb {A}$. Note that an exact algebra is nonunital. A commutative algebra
$x \in \mathbb {A}$. Note that an exact algebra is nonunital. A commutative algebra ![]() $(\mathbb {A}, \circ )$ is Killing metrized if the Killing type trace-form
$(\mathbb {A}, \circ )$ is Killing metrized if the Killing type trace-form ![]() $\tau _{\circ }(x, y) = \operatorname {\mathsf {tr}} L_{\circ }(x)L_{\circ }(y)$ is nondegenerate and invariant. The multiplication of a Killing metrized commutative algebra is necessarily faithful, meaning that
$\tau _{\circ }(x, y) = \operatorname {\mathsf {tr}} L_{\circ }(x)L_{\circ }(y)$ is nondegenerate and invariant. The multiplication of a Killing metrized commutative algebra is necessarily faithful, meaning that ![]() $L_{\circ }$ is injective.
$L_{\circ }$ is injective.
Important structural features of the subalgebra ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ shown in Theorem 1.3 are that it is exact and Killing metrized and is simple when
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ shown in Theorem 1.3 are that it is exact and Killing metrized and is simple when ![]() $\dim \mathbb {V}^{\ast }> 4$.
$\dim \mathbb {V}^{\ast }> 4$.
Theorem 1.3. Let ![]() $(\mathbb {V}, h)$ be a Euclidean vector space of dimension at least
$(\mathbb {V}, h)$ be a Euclidean vector space of dimension at least ![]() $4$. The algebra
$4$. The algebra ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is exact and Killing metrized. Moreover:
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is exact and Killing metrized. Moreover:
1. The Killing form
 $\tau _{\ast }(\mathscr {X}, \mathscr {Y}) = \operatorname {\mathsf {tr}} L_{\ast }(\mathscr {X})L_{\ast }(\mathscr {Y})$ is a nonzero multiple of
$\tau _{\ast }(\mathscr {X}, \mathscr {Y}) = \operatorname {\mathsf {tr}} L_{\ast }(\mathscr {X})L_{\ast }(\mathscr {Y})$ is a nonzero multiple of  $\langle \,\cdot \,\,, \,\cdot \,\, \rangle $.
$\langle \,\cdot \,\,, \,\cdot \,\, \rangle $.2. If
 $\dim \mathbb {V}> 4$, then
$\dim \mathbb {V}> 4$, then  $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is simple.
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is simple.
Proof of Theorem 1.3.
Let ![]() $(\mathbb {V}, h)$ be a Euclidean vector space with
$(\mathbb {V}, h)$ be a Euclidean vector space with ![]() $\dim \mathbb {V} = n \geq 4$. The group
$\dim \mathbb {V} = n \geq 4$. The group ![]() $O(n) = O(\mathbb {V}, h)$ acts on
$O(n) = O(\mathbb {V}, h)$ acts on ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ isometrically and irreducibly. By Theorem 5.4,
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ isometrically and irreducibly. By Theorem 5.4, ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is metrized by the pairing
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is metrized by the pairing ![]() $\langle \,\cdot \,\,, \,\cdot \,\, \rangle $ and
$\langle \,\cdot \,\,, \,\cdot \,\, \rangle $ and ![]() $O(n)$ acts on
$O(n)$ acts on ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ by algebra automorphisms. By Lemma 10.1 there is a nontrivial idempotent
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ by algebra automorphisms. By Lemma 10.1 there is a nontrivial idempotent ![]() $\mathscr {E} \in (\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$. Because
$\mathscr {E} \in (\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$. Because ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ contains a nontrivial idempotent, its multiplication is nontrivial. Theorem 3.2 implies
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ contains a nontrivial idempotent, its multiplication is nontrivial. Theorem 3.2 implies ![]() $\operatorname {\mathsf {tr}} L_{\ast }(\mathscr {X}) = 0$, and
$\operatorname {\mathsf {tr}} L_{\ast }(\mathscr {X}) = 0$, and ![]() $\tau _{\ast }(\mathscr {X}, \mathscr {Y}) = \operatorname {\mathsf {tr}} L_{\ast }(\mathscr {X})L_{\ast }(\mathscr {Y})$ equals
$\tau _{\ast }(\mathscr {X}, \mathscr {Y}) = \operatorname {\mathsf {tr}} L_{\ast }(\mathscr {X})L_{\ast }(\mathscr {Y})$ equals ![]() $\kappa \langle \,\cdot \,\,, \,\cdot \,\, \rangle $ for some nonzero
$\kappa \langle \,\cdot \,\,, \,\cdot \,\, \rangle $ for some nonzero ![]() $\kappa $ which must be positive because both
$\kappa $ which must be positive because both ![]() $\tau _{\ast }$ and
$\tau _{\ast }$ and ![]() $\langle \,\cdot \,\,, \,\cdot \,\, \rangle $ are positive definite. If
$\langle \,\cdot \,\,, \,\cdot \,\, \rangle $ are positive definite. If ![]() $\dim \mathbb {V}> 4$, the action by automorphisms of the connected simple Lie group
$\dim \mathbb {V}> 4$, the action by automorphisms of the connected simple Lie group ![]() $SO(n)$ on
$SO(n)$ on ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is irreducible, so Theorem 3.1 implies
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is irreducible, so Theorem 3.1 implies ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is simple.
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is simple.
When ![]() $\dim \mathbb {V} = 4$, a choice of orientation determines an orthogonal decomposition
$\dim \mathbb {V} = 4$, a choice of orientation determines an orthogonal decomposition ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) = \mathscr {MC}^{+}_{\mathscr {W}}(\mathbb {V}^{\ast }) \oplus \mathscr {MC}^{-}_{\mathscr {W}}(\mathbb {V}^{\ast })$ where
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) = \mathscr {MC}^{+}_{\mathscr {W}}(\mathbb {V}^{\ast }) \oplus \mathscr {MC}^{-}_{\mathscr {W}}(\mathbb {V}^{\ast })$ where ![]() $\mathscr {MC}^{\pm }_{\mathscr {W}}(\mathbb {V}^{\ast })$ are the subspaces of self-dual and anti-self-dual curvature tensors. Theorem 1.5, discussed in more detail later in the introduction, shows that these are mutually isomorphic subalgebras that are simple, exact, and Killing metrized with Killing form equal to
$\mathscr {MC}^{\pm }_{\mathscr {W}}(\mathbb {V}^{\ast })$ are the subspaces of self-dual and anti-self-dual curvature tensors. Theorem 1.5, discussed in more detail later in the introduction, shows that these are mutually isomorphic subalgebras that are simple, exact, and Killing metrized with Killing form equal to 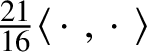 $\tfrac {21}{16}\langle \,\cdot \,\,, \,\cdot \,\, \rangle $. Alternatively, this is a consequence of Theorem 11.3, which is the analogue of Theorem 1.3 for the algebra of Kähler–Weyl tensors. It shows that if
$\tfrac {21}{16}\langle \,\cdot \,\,, \,\cdot \,\, \rangle $. Alternatively, this is a consequence of Theorem 11.3, which is the analogue of Theorem 1.3 for the algebra of Kähler–Weyl tensors. It shows that if ![]() $(\mathbb {V}, h, J)$ is a
$(\mathbb {V}, h, J)$ is a ![]() $2n$-dimensional Kähler vector space, then
$2n$-dimensional Kähler vector space, then ![]() $(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is a simple, exact, Killing metrized algebra with Killing form a positive multiple of
$(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is a simple, exact, Killing metrized algebra with Killing form a positive multiple of ![]() $\langle \,\cdot \,\,, \,\cdot \,\, \rangle $. When
$\langle \,\cdot \,\,, \,\cdot \,\, \rangle $. When ![]() $\dim \mathbb {V} = 4$, a choice of compatible almost complex structure J determines an orientation of
$\dim \mathbb {V} = 4$, a choice of compatible almost complex structure J determines an orientation of ![]() $\mathbb {V}$ and Lemma 11.2 shows
$\mathbb {V}$ and Lemma 11.2 shows ![]() $\mathscr {MC}^{-}_{\mathscr {W}}(\mathbb {V}^{\ast }) = \mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$.
$\mathscr {MC}^{-}_{\mathscr {W}}(\mathbb {V}^{\ast }) = \mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$.
Remark 1.4. When ![]() $\dim \mathbb {V}> 4$, Theorem 1.3 does not give the value of the positive constant
$\dim \mathbb {V}> 4$, Theorem 1.3 does not give the value of the positive constant ![]() $\kappa $ such that
$\kappa $ such that ![]() $\tau _{\ast } = \kappa \langle \,\cdot \,\,, \,\cdot \,\, \rangle $. To calculate
$\tau _{\ast } = \kappa \langle \,\cdot \,\,, \,\cdot \,\, \rangle $. To calculate ![]() $\kappa $ it would suffice to calculate the eigenvalues on
$\kappa $ it would suffice to calculate the eigenvalues on ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ of the operator
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ of the operator ![]() $\widehat {\mathscr {E}}$ associated with a nonzero idempotent, as this suffices to calculate its
$\widehat {\mathscr {E}}$ associated with a nonzero idempotent, as this suffices to calculate its ![]() $\tau _{\ast }$-norm. When
$\tau _{\ast }$-norm. When ![]() $\dim \mathbb {V} = 4$, the explicit calculations used to prove Theorem 1.5 make it possible to calculate
$\dim \mathbb {V} = 4$, the explicit calculations used to prove Theorem 1.5 make it possible to calculate ![]() $\kappa = 21/16$ for
$\kappa = 21/16$ for ![]() $(\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast }), \ast )$ (and so also for
$(\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast }), \ast )$ (and so also for ![]() $(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$).
$(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$).
A basic problem is to describe ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$, or its subalgebras more explicitly, in terms of known algebras. As mentioned already, when
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$, or its subalgebras more explicitly, in terms of known algebras. As mentioned already, when ![]() $\dim \mathbb {V} = 2$, the 1-dimensional algebra
$\dim \mathbb {V} = 2$, the 1-dimensional algebra ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ is isometrically isomorphic to the field of real numbers with its Euclidean inner product. When
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ is isometrically isomorphic to the field of real numbers with its Euclidean inner product. When ![]() $\dim \mathbb {V}$ is
$\dim \mathbb {V}$ is ![]() $3$ or
$3$ or ![]() $4$, explicit results are obtained relating
$4$, explicit results are obtained relating ![]() $\ast $ to the usual Jordan product of symmetric endomorphisms.
$\ast $ to the usual Jordan product of symmetric endomorphisms.
V. L. Popov [Reference Popov31] discussed invariants of algebras constructed from traces of products of powers of their multiplication operators, addressing questions such as when does a module for a group G admit a nontrivial G-invariant multiplication that is simple or have automorphism group equal to G. Specific instances of this last question are addressed in [Reference Dixmier6] for ![]() $G = SL(2)$ and [Reference Èlashvili8] for certain exceptional Lie groups. In this context, metrizability by some particular trace-form, for example, Killing metrizability, appears as a structurally important condition. Its importance has been explicitly indicated in work of A. Ryba, for example [Reference Ryba35], constructing commutative nonassociative algebras on which certain finite simple groups act by automorphisms (see, in particular, [Reference Ryba35, Lemma
$G = SL(2)$ and [Reference Èlashvili8] for certain exceptional Lie groups. In this context, metrizability by some particular trace-form, for example, Killing metrizability, appears as a structurally important condition. Its importance has been explicitly indicated in work of A. Ryba, for example [Reference Ryba35], constructing commutative nonassociative algebras on which certain finite simple groups act by automorphisms (see, in particular, [Reference Ryba35, Lemma ![]() $9.1$] and see also [Reference Ivanov22]), and in the work of V. G. Tkachev and collaborators dedicated to a general program, detailed in [Reference Nadirashvili, Tkachev and Vlăduţ29], of constructing homogeneous solutions to certain geometrically motivated linear and fully nonlinear elliptic partial differential equations, for example, those describing minimal cones, by studying the algebras associated with completely symmetric cubic forms. An interesting class of examples of exact Killing metrized commutative nonassociative algebras, relevant here also for the statement of Theorem 1.5, are the deunitalizations of the finite-dimensional simple real Euclidean Jordan algebras.
$9.1$] and see also [Reference Ivanov22]), and in the work of V. G. Tkachev and collaborators dedicated to a general program, detailed in [Reference Nadirashvili, Tkachev and Vlăduţ29], of constructing homogeneous solutions to certain geometrically motivated linear and fully nonlinear elliptic partial differential equations, for example, those describing minimal cones, by studying the algebras associated with completely symmetric cubic forms. An interesting class of examples of exact Killing metrized commutative nonassociative algebras, relevant here also for the statement of Theorem 1.5, are the deunitalizations of the finite-dimensional simple real Euclidean Jordan algebras.
The vector space ![]() $\operatorname {Sym}(\mathbb {W}, g)$ of g-self-adjoint endomorphisms of the n-dimensional Euclidean vector space
$\operatorname {Sym}(\mathbb {W}, g)$ of g-self-adjoint endomorphisms of the n-dimensional Euclidean vector space ![]() $(\mathbb {W}, g)$ equipped with the multiplication
$(\mathbb {W}, g)$ equipped with the multiplication ![]() $\circledcirc $ that is the symmetric part of the ordinary composition of endomorphisms is an
$\circledcirc $ that is the symmetric part of the ordinary composition of endomorphisms is an ![]() $n(n+1)/2$-dimensional simple real Euclidean Jordan algebra with unit. Its deunitalization is the
$n(n+1)/2$-dimensional simple real Euclidean Jordan algebra with unit. Its deunitalization is the ![]() $(n+2)(n-1)/2$-dimensional commutative, nonassociative, nonunital algebra obtained by retraction along the unit. Precisely, this is the algebra
$(n+2)(n-1)/2$-dimensional commutative, nonassociative, nonunital algebra obtained by retraction along the unit. Precisely, this is the algebra ![]() $\operatorname {Sym}_{0}(\mathbb {W}, g) = \{A \in \operatorname {Sym}(\mathbb {W}, g): \operatorname {\mathsf {tr}} A = 0\}$ of trace-free symmetric endomorphisms of
$\operatorname {Sym}_{0}(\mathbb {W}, g) = \{A \in \operatorname {Sym}(\mathbb {W}, g): \operatorname {\mathsf {tr}} A = 0\}$ of trace-free symmetric endomorphisms of ![]() $(\mathbb {W}, g)$ equipped with the multiplication
$(\mathbb {W}, g)$ equipped with the multiplication
 $$ \begin{align} A \times B = A \circledcirc B + B \circ A - \tfrac{1}{2n}\operatorname{\mathsf{tr}}(A \circ B + B \circ A)\operatorname{Id}_{\mathbb{W}} \end{align} $$
$$ \begin{align} A \times B = A \circledcirc B + B \circ A - \tfrac{1}{2n}\operatorname{\mathsf{tr}}(A \circ B + B \circ A)\operatorname{Id}_{\mathbb{W}} \end{align} $$and the invariant metric 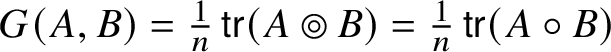 $G(A, B) = \tfrac {1}{n}\operatorname {\mathsf {tr}}(A \circledcirc B) = \tfrac {1}{n}\operatorname {\mathsf {tr}}(A\circ B)$. When
$G(A, B) = \tfrac {1}{n}\operatorname {\mathsf {tr}}(A \circledcirc B) = \tfrac {1}{n}\operatorname {\mathsf {tr}}(A\circ B)$. When ![]() $\dim \mathbb {W} = 3$,
$\dim \mathbb {W} = 3$, 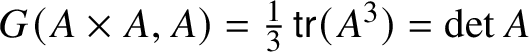 $G(A \times A, A) = \tfrac {1}{3}\operatorname {\mathsf {tr}}(A^{3}) = \det A$. (These claims follow from standard formulas as in [Reference Faraut and Korányi9] and are demonstrated more or less explicitly in [Reference Fox10] and [Reference Tkachev38, section
$G(A \times A, A) = \tfrac {1}{3}\operatorname {\mathsf {tr}}(A^{3}) = \det A$. (These claims follow from standard formulas as in [Reference Faraut and Korányi9] and are demonstrated more or less explicitly in [Reference Fox10] and [Reference Tkachev38, section ![]() $10$].)
$10$].)
Section 8 treats the case ![]() $\dim \mathbb {V} = 3$. In this case the
$\dim \mathbb {V} = 3$. In this case the ![]() $6$-dimensional algebra
$6$-dimensional algebra ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ is linearly isomorphic to
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ is linearly isomorphic to ![]() $S^{2}\mathbb {V}^{\ast }$. The map sending
$S^{2}\mathbb {V}^{\ast }$. The map sending ![]() $\alpha \in S^{2}\mathbb {V}^{\ast }$ to
$\alpha \in S^{2}\mathbb {V}^{\ast }$ to ![]() $\alpha ^{\sharp } \in \operatorname {Sym}(\mathbb {V}, h)$ defined by
$\alpha ^{\sharp } \in \operatorname {Sym}(\mathbb {V}, h)$ defined by ![]() $h(\alpha ^{\sharp }(x), y) = \alpha (x, y)$ for
$h(\alpha ^{\sharp }(x), y) = \alpha (x, y)$ for ![]() $x, y \in \mathbb {V}^{\ast }$ is a linear isomorphism. Transported from
$x, y \in \mathbb {V}^{\ast }$ is a linear isomorphism. Transported from ![]() $S^{2}\mathbb {V}^{\ast }$ to
$S^{2}\mathbb {V}^{\ast }$ to ![]() $\operatorname {Sym}(\mathbb {V}, h)$ via
$\operatorname {Sym}(\mathbb {V}, h)$ via ![]() $\sharp $, the product
$\sharp $, the product ![]() $\ast $ can be expressed in terms of familiar operations on symmetric endomorphisms. Lemma 8.2 and Theorem 8.5 describe the product on
$\ast $ can be expressed in terms of familiar operations on symmetric endomorphisms. Lemma 8.2 and Theorem 8.5 describe the product on ![]() $\operatorname {Sym}(\mathbb {V}, h)$ corresponding to
$\operatorname {Sym}(\mathbb {V}, h)$ corresponding to ![]() $\ast $ as
$\ast $ as
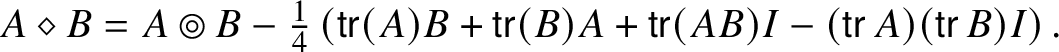 $$ \begin{align} A\diamond B = A\circledcirc B - \tfrac{1}{4}\left(\operatorname{\mathsf{tr}}(A)B + \operatorname{\mathsf{tr}}(B)A + \operatorname{\mathsf{tr}}(AB)I- (\operatorname{\mathsf{tr}} A)(\operatorname{\mathsf{tr}} B)I\right). \end{align} $$
$$ \begin{align} A\diamond B = A\circledcirc B - \tfrac{1}{4}\left(\operatorname{\mathsf{tr}}(A)B + \operatorname{\mathsf{tr}}(B)A + \operatorname{\mathsf{tr}}(AB)I- (\operatorname{\mathsf{tr}} A)(\operatorname{\mathsf{tr}} B)I\right). \end{align} $$In particular, this product is nonunital and it is not the Jordan product ![]() $\circledcirc $. Identify
$\circledcirc $. Identify 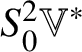 $S^{2}_{0}\mathbb {V}^{\ast }$ with
$S^{2}_{0}\mathbb {V}^{\ast }$ with ![]() $\operatorname {Sym}_{0}(\mathbb {V}, h)$ and equip it with the trace-free Jordan product
$\operatorname {Sym}_{0}(\mathbb {V}, h)$ and equip it with the trace-free Jordan product ![]() $\times $ defined in (1.3). More precisely, Lemma 8.2 shows that
$\times $ defined in (1.3). More precisely, Lemma 8.2 shows that ![]() $\operatorname {Sym}_{0}(\mathbb {V}, h) \oplus \mathbb R$ equipped with the multiplication
$\operatorname {Sym}_{0}(\mathbb {V}, h) \oplus \mathbb R$ equipped with the multiplication
 $$ \begin{align} (A, r)\bullet (B, s) = \left(A \times B + \tfrac{1}{4}(rB + sA), rs + \tfrac{1}{12}\langle A, B \rangle\right) \end{align} $$
$$ \begin{align} (A, r)\bullet (B, s) = \left(A \times B + \tfrac{1}{4}(rB + sA), rs + \tfrac{1}{12}\langle A, B \rangle\right) \end{align} $$is isomorphic to ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ via the linear map
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ via the linear map 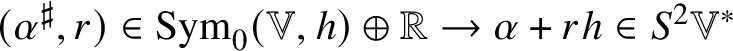 $(\alpha ^{\sharp }, r) \in \operatorname {Sym}_{0}(\mathbb {V}, h) \oplus \mathbb R \to \alpha + rh \in S^{2}\mathbb {V}^{\ast }$.
$(\alpha ^{\sharp }, r) \in \operatorname {Sym}_{0}(\mathbb {V}, h) \oplus \mathbb R \to \alpha + rh \in S^{2}\mathbb {V}^{\ast }$.
What is more interesting is Theorem 8.5, which characterizes ![]() $\diamond $ in terms in intrinsic algebraic terms (for Euclidean h). The situation can be summarized informally as that
$\diamond $ in terms in intrinsic algebraic terms (for Euclidean h). The situation can be summarized informally as that ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ is the most symmetric
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ is the most symmetric ![]() $O(3)$-invariant metrized commutative algebra structure on
$O(3)$-invariant metrized commutative algebra structure on ![]() $S^{2}\mathbb {V}^{\ast }$, in that the number of orbits of its idempotents is the smallest possible, two, and the spectra of their multiplication endomorphisms have the maximal redundancy. Up to isomorphism there is a one-parameter family of
$S^{2}\mathbb {V}^{\ast }$, in that the number of orbits of its idempotents is the smallest possible, two, and the spectra of their multiplication endomorphisms have the maximal redundancy. Up to isomorphism there is a one-parameter family of ![]() $O(3)$-invariant commutative algebra structures on
$O(3)$-invariant commutative algebra structures on ![]() $S^{2}\mathbb {V}^{\ast }$ each metrized by an
$S^{2}\mathbb {V}^{\ast }$ each metrized by an ![]() $O(3)$-invariant inner product and each of which contains a rank 1 idempotent and contains no square-zero element. The additional condition that there be only two orbits of idempotents, one generated by a multiple of h and the other by a rank 1 idempotent, distinguishes two such algebras. One of them is Killing metrized and the other is
$O(3)$-invariant inner product and each of which contains a rank 1 idempotent and contains no square-zero element. The additional condition that there be only two orbits of idempotents, one generated by a multiple of h and the other by a rank 1 idempotent, distinguishes two such algebras. One of them is Killing metrized and the other is ![]() $(S^{2}\mathbb {V}^{\ast }, \diamond )$. Alternatively, they are distinguished by the multiplicity of the eigenvalue
$(S^{2}\mathbb {V}^{\ast }, \diamond )$. Alternatively, they are distinguished by the multiplicity of the eigenvalue ![]() $1/2$ of the multiplication endomorphism of a rank 1 idempotent, which is always at least
$1/2$ of the multiplication endomorphism of a rank 1 idempotent, which is always at least ![]() $2$, as a consequence of
$2$, as a consequence of ![]() $O(3)$-invariance, but is
$O(3)$-invariance, but is ![]() $3$ uniquely for
$3$ uniquely for ![]() $(S^{2}\mathbb {V}^{\ast }, \diamond )$. The proof yields as corollaries that
$(S^{2}\mathbb {V}^{\ast }, \diamond )$. The proof yields as corollaries that ![]() $\diamond $ is simple and its automorphism group is exactly the image of
$\diamond $ is simple and its automorphism group is exactly the image of ![]() $O(3)$ in its induced action on
$O(3)$ in its induced action on ![]() $S^{2}\mathbb {V}^{\ast }$. Corollary 8.10 summarizes precisely all that is proved.
$S^{2}\mathbb {V}^{\ast }$. Corollary 8.10 summarizes precisely all that is proved.
When ![]() $\dim \mathbb {V} = 4$, Lemma 9.7 shows that the
$\dim \mathbb {V} = 4$, Lemma 9.7 shows that the ![]() $5$-dimensional subspaces
$5$-dimensional subspaces ![]() $\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast })$ are orthogonal ideals of
$\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast })$ are orthogonal ideals of ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$. Theorem 1.5 shows that each of these subalgebras is isometrically isomorphic to the deunitalization of the 6-dimensional rank
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$. Theorem 1.5 shows that each of these subalgebras is isometrically isomorphic to the deunitalization of the 6-dimensional rank ![]() $3$ simple real Euclidean Jordan algebra of symmetric endomorphisms of a
$3$ simple real Euclidean Jordan algebra of symmetric endomorphisms of a ![]() $3$-dimensional vector space. The linear maps assigning to
$3$-dimensional vector space. The linear maps assigning to ![]() $\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ endomorphisms
$\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ endomorphisms 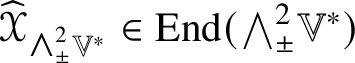 $\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}_{\pm }\mathbb {V}^{\ast }} \in \operatorname {End}({\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast })$ of the spaces
$\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}_{\pm }\mathbb {V}^{\ast }} \in \operatorname {End}({\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast })$ of the spaces ![]() ${\bigwedge }^{2}_{\pm } \mathbb {V}^{\ast }$ of self-dual and anti-self-dual
${\bigwedge }^{2}_{\pm } \mathbb {V}^{\ast }$ of self-dual and anti-self-dual ![]() $2$-forms induce
$2$-forms induce ![]() $SO(4)$-module isomorphisms
$SO(4)$-module isomorphisms 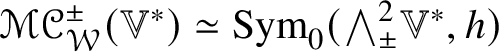 $\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast }) \simeq \operatorname {Sym}_{0}({\bigwedge }^{2}_{\pm } \mathbb {V}^{\ast }, h)$ [Reference Besse1, Section
$\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast }) \simeq \operatorname {Sym}_{0}({\bigwedge }^{2}_{\pm } \mathbb {V}^{\ast }, h)$ [Reference Besse1, Section ![]() $1.127$]. The content of Theorem 1.5 is that a suitable multiple of
$1.127$]. The content of Theorem 1.5 is that a suitable multiple of  $\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}_{\pm }\mathbb {V}^{\ast }}$ is an algebra isomorphism.
$\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}_{\pm }\mathbb {V}^{\ast }}$ is an algebra isomorphism.
Theorem 1.5. Let ![]() $(\mathbb {V}, h)$ be a
$(\mathbb {V}, h)$ be a ![]() $4$-dimensional oriented Euclidean vector space. Consider the deunitalization
$4$-dimensional oriented Euclidean vector space. Consider the deunitalization 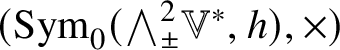 $(\operatorname {Sym}_{0}({\bigwedge }^{2}_{\pm } \mathbb {V}^{\ast }, h), \times )$ of the
$(\operatorname {Sym}_{0}({\bigwedge }^{2}_{\pm } \mathbb {V}^{\ast }, h), \times )$ of the ![]() $6$-dimensional rank
$6$-dimensional rank ![]() $3$ simple real Euclidean Jordan algebra
$3$ simple real Euclidean Jordan algebra ![]() $(\operatorname {Sym}({\bigwedge }^{2}_{\pm } \mathbb {V}^{\ast }, h), \circledcirc )$ of symmetric endomorphisms of the
$(\operatorname {Sym}({\bigwedge }^{2}_{\pm } \mathbb {V}^{\ast }, h), \circledcirc )$ of symmetric endomorphisms of the ![]() $3$-dimensional space
$3$-dimensional space ![]() ${\bigwedge }^{2}_{\pm } \mathbb {V}^{\ast }$, equipped with the product
${\bigwedge }^{2}_{\pm } \mathbb {V}^{\ast }$, equipped with the product ![]() $\times $ equal to the traceless part of the usual Jordan product
$\times $ equal to the traceless part of the usual Jordan product ![]() $\circledcirc $ of endomorphisms and the metric
$\circledcirc $ of endomorphisms and the metric 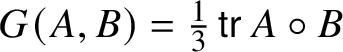 $G(A, B) = \tfrac {1}{3}\operatorname {\mathsf {tr}} A \circ B$.
$G(A, B) = \tfrac {1}{3}\operatorname {\mathsf {tr}} A \circ B$.
1. The map
 $\Psi :(\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast }), \ast , \langle \,\cdot \,\,, \,\cdot \,\, \rangle )\to (\operatorname {Sym}_{0}({\bigwedge }^{2}_{\pm } \mathbb {V}^{\ast }, h), \times , \tfrac {4}{3}G)$ defined by
$\Psi :(\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast }), \ast , \langle \,\cdot \,\,, \,\cdot \,\, \rangle )\to (\operatorname {Sym}_{0}({\bigwedge }^{2}_{\pm } \mathbb {V}^{\ast }, h), \times , \tfrac {4}{3}G)$ defined by  $\Psi (\mathscr {X}) = 3\widehat {\mathscr {X}}$ is an
$\Psi (\mathscr {X}) = 3\widehat {\mathscr {X}}$ is an  $SO(4)$-equivariant isometric algebra isomorphism.
$SO(4)$-equivariant isometric algebra isomorphism.2. The Killing form
 $\tau _{\ast }(\mathscr {X}, \mathscr {Y}) = \operatorname {\mathsf {tr}} L_{\ast }(\mathscr {X})L_{\ast }(\mathscr {Y})$ on
$\tau _{\ast }(\mathscr {X}, \mathscr {Y}) = \operatorname {\mathsf {tr}} L_{\ast }(\mathscr {X})L_{\ast }(\mathscr {Y})$ on  $(\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast }), \ast )$ satisfies
$(\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast }), \ast )$ satisfies  $\tau _{\ast } = \tfrac {21}{16}\langle \,\cdot \,\,, \,\cdot \,\, \rangle $, where
$\tau _{\ast } = \tfrac {21}{16}\langle \,\cdot \,\,, \,\cdot \,\, \rangle $, where  $\langle \,\cdot \,\,, \,\cdot \,\, \rangle $ is the metric on
$\langle \,\cdot \,\,, \,\cdot \,\, \rangle $ is the metric on  $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ given by complete contraction with
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ given by complete contraction with  $h_{ij}$.
$h_{ij}$.3.
 $(\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast }), \ast , \langle \,\cdot \,\,, \,\cdot \,\, \rangle )$ is simple and contains no nontrivial square-zero elements.
$(\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast }), \ast , \langle \,\cdot \,\,, \,\cdot \,\, \rangle )$ is simple and contains no nontrivial square-zero elements.
Theorem 1.5 is proved twice, at the end of Section 9 and again in Section 10 (Section 12 sketches still another proof). The isomorphism is described both conceptually and explicitly. The explicit isomorphism is based on the construction of a convenient basis of ![]() $\mathscr {MC}_{\mathscr {W}}^{+}(\mathbb {V}^{\ast })$ and the calculation of the multiplication table for its elements. See Lemma 10.8. The conceptual proof is based on a calculation relating the endomorphisms of
$\mathscr {MC}_{\mathscr {W}}^{+}(\mathbb {V}^{\ast })$ and the calculation of the multiplication table for its elements. See Lemma 10.8. The conceptual proof is based on a calculation relating the endomorphisms of ![]() ${\bigwedge }^{2}\mathbb {V}^{\ast }$ given by
${\bigwedge }^{2}\mathbb {V}^{\ast }$ given by 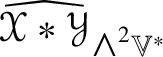 $\widehat {\mathscr {X} \ast \mathscr {Y}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ and
$\widehat {\mathscr {X} \ast \mathscr {Y}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ and 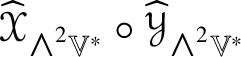 $\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}\circ \widehat {\mathscr {Y}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$, where
$\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}\circ \widehat {\mathscr {Y}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$, where ![]() $\circ $ denotes composition of endomorphisms, which shows
$\circ $ denotes composition of endomorphisms, which shows
 $$ \begin{align} \begin{split} \tfrac{1}{3}\widehat{\mathscr{X} \ast \mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}& = \widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}- \tfrac{1}{6}\operatorname{\mathsf{tr}}(\widehat{\star \mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} \circ \widehat{ \mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}) \star - \tfrac{1}{6}\operatorname{\mathsf{tr}}( \widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} \circ \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}) \operatorname{Id}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}, \end{split} \end{align} $$
$$ \begin{align} \begin{split} \tfrac{1}{3}\widehat{\mathscr{X} \ast \mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}& = \widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}- \tfrac{1}{6}\operatorname{\mathsf{tr}}(\widehat{\star \mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} \circ \widehat{ \mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}) \star - \tfrac{1}{6}\operatorname{\mathsf{tr}}( \widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} \circ \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}) \operatorname{Id}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}, \end{split} \end{align} $$in which ![]() $\circ $ is composition of endomorphisms and
$\circ $ is composition of endomorphisms and ![]() $\star $ denotes both the Hodge star operator on
$\star $ denotes both the Hodge star operator on ![]() ${\bigwedge }^{2}\mathbb {V}^{\ast }$ and the involution it induces on
${\bigwedge }^{2}\mathbb {V}^{\ast }$ and the involution it induces on ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$; see Lemma 9.7 for details.
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$; see Lemma 9.7 for details.
For ![]() $\mathbb {V}$ of dimension greater than
$\mathbb {V}$ of dimension greater than ![]() $4$, it would be interesting to obtain a formula like (1.6) for the difference
$4$, it would be interesting to obtain a formula like (1.6) for the difference 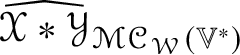 $\widehat {\mathscr {X} \ast \mathscr {Y}}_{\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })}$ in terms of the Jordan product
$\widehat {\mathscr {X} \ast \mathscr {Y}}_{\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })}$ in terms of the Jordan product 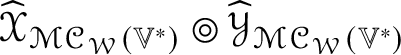 $\widehat {\mathscr {X}}_{\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })}\circledcirc \widehat {\mathscr {Y}}_{\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })}$ and expressions like those on the right side of (1.6).
$\widehat {\mathscr {X}}_{\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })}\circledcirc \widehat {\mathscr {Y}}_{\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })}$ and expressions like those on the right side of (1.6).
Part of claim 3 of Theorem 1.5 depends strongly on the assumption of Euclidean signature. It shows that in Euclidean signature ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ contains no square-zero element if
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ contains no square-zero element if ![]() $\dim \mathbb {V} = 4$, while Lemma 7.3 shows that if
$\dim \mathbb {V} = 4$, while Lemma 7.3 shows that if ![]() $\dim \mathbb {V} \geq 4$ and h has indefinite signature, then
$\dim \mathbb {V} \geq 4$ and h has indefinite signature, then ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is spanned by square-zero elements (see also Example 12.4). It would be interesting to know if
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is spanned by square-zero elements (see also Example 12.4). It would be interesting to know if ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ contains a nonzero square-zero element when h is Euclidean and
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ contains a nonzero square-zero element when h is Euclidean and ![]() $\dim \mathbb {V}> 4$. Theorem 7.10 shows the weaker result that the multiplication
$\dim \mathbb {V}> 4$. Theorem 7.10 shows the weaker result that the multiplication ![]() $\ast $ is faithful if h is Euclidean and
$\ast $ is faithful if h is Euclidean and ![]() $\dim \mathbb {V} \geq 4$; equivalently,
$\dim \mathbb {V} \geq 4$; equivalently, ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ contains no zero divisors.
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ contains no zero divisors.
The simplicity of the algebras ![]() $(\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast }), \ast )$ and
$(\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast }), \ast )$ and ![]() $(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ could perhaps appear unremarkable in light of a result of Popov showing that, over an algebraically closed field
$(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ could perhaps appear unremarkable in light of a result of Popov showing that, over an algebraically closed field ![]() $\mathbb {k}$ of characteristic zero, a generic algebra is simple. Precisely, [Reference Popov31, Theorem
$\mathbb {k}$ of characteristic zero, a generic algebra is simple. Precisely, [Reference Popov31, Theorem ![]() $4$] shows that the set of structure tensors of simple algebras over
$4$] shows that the set of structure tensors of simple algebras over ![]() $\mathbb {k}$ is open and dense. However, the first Theorem
$\mathbb {k}$ is open and dense. However, the first Theorem ![]() $3$ of [Reference Popov31]Footnote 1 shows that a generic (in the same sense) algebra has trivial automorphism group, whereas
$3$ of [Reference Popov31]Footnote 1 shows that a generic (in the same sense) algebra has trivial automorphism group, whereas ![]() $(\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast }), \ast , \langle \,\cdot \,\,, \,\cdot \,\, \rangle )$,
$(\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast }), \ast , \langle \,\cdot \,\,, \,\cdot \,\, \rangle )$, ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$, and
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$, and ![]() $(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ have large automorphism groups that contain respectively the Lie groups
$(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ have large automorphism groups that contain respectively the Lie groups ![]() $SO(4)$,
$SO(4)$, ![]() $O(n)$, and
$O(n)$, and ![]() $U(n)$ and so are atypical from this point of view. Nonetheless, [Reference Popov31, Theorem
$U(n)$ and so are atypical from this point of view. Nonetheless, [Reference Popov31, Theorem ![]() $5$] shows that if the automorphism group of a finite-dimensional algebra with nontrivial multiplication over
$5$] shows that if the automorphism group of a finite-dimensional algebra with nontrivial multiplication over ![]() $\mathbb {k}$ contains a connected algebraic subgroup that acts irreducibly on the algebra, then the algebra is simple. Although the algebras considered here are defined over
$\mathbb {k}$ contains a connected algebraic subgroup that acts irreducibly on the algebra, then the algebra is simple. Although the algebras considered here are defined over ![]() $\mathbb R$, Popov’s argument can be used essentially as written to show that
$\mathbb R$, Popov’s argument can be used essentially as written to show that ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ and
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ and ![]() $(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ are simple when
$(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ are simple when ![]() $\dim \mathbb {V}^{\ast }> 4$. A precise statement of a more general result is given here as Theorem 3.1 and Theorem 1.3 records its application to
$\dim \mathbb {V}^{\ast }> 4$. A precise statement of a more general result is given here as Theorem 3.1 and Theorem 1.3 records its application to ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$.
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$.
Among metrized commutative algebras, those that have large automorphism groups are somewhat exceptional. That a Lie group G acts on a metrized commutative algbera by automorphisms has the consequence that the orbit of an idempotent is a G homogeneous space. It would be interesting to describe completely the G-orbits of idempotents in subalgebras of ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$. For
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$. For ![]() $\dim \mathbb {V}^{\ast } = 3$, Corollary 8.10 gives such a description, while for
$\dim \mathbb {V}^{\ast } = 3$, Corollary 8.10 gives such a description, while for ![]() $\dim \mathbb {V}^{\ast } = 4$, such a description can be deduced from Theorem 1.5 and the computations used to prove Theorem 7.12. In this direction, Lemma 10.4 shows that when
$\dim \mathbb {V}^{\ast } = 4$, such a description can be deduced from Theorem 1.5 and the computations used to prove Theorem 7.12. In this direction, Lemma 10.4 shows that when ![]() $\dim \mathbb {V}^{\ast } = 2n \geq 4$, certain of the idempotents produced by Lemma 10.1 constitute an orbit of
$\dim \mathbb {V}^{\ast } = 2n \geq 4$, certain of the idempotents produced by Lemma 10.1 constitute an orbit of ![]() $O(2n)$ acting in
$O(2n)$ acting in ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ identified with the space
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ identified with the space ![]() $SO(2n)/U(n)$ of orthogonal complex structures on
$SO(2n)/U(n)$ of orthogonal complex structures on ![]() $\mathbb {V}$ inducing a given orientation on
$\mathbb {V}$ inducing a given orientation on ![]() $\mathbb {V}$.
$\mathbb {V}$.
Since all claims in the article are pure linear algebra, they extend straightforwardly to sections of tensor bundles over smooth manifolds. Although no application to Ricci flow is immediately available, it is reasonable to hope that the results obtained here will be useful for studying curvature conditions on manifolds. A different, Lie theoretic, point of view on the structure of the multiplication ![]() $\ast $ has been used profitably in [Reference Böhm and Wilking2, Reference Wilking41]. For background on the definition of
$\ast $ has been used profitably in [Reference Böhm and Wilking2, Reference Wilking41]. For background on the definition of ![]() $\ast $ as in (5.14), its properties, and its role in the study of the Ricci flow, see also [Reference Hopper and Andrews20]. Some features of the algebra
$\ast $ as in (5.14), its properties, and its role in the study of the Ricci flow, see also [Reference Hopper and Andrews20]. Some features of the algebra ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ are used implicitly in the study of the Ricci flow [Reference Böhm and Wilking2, Reference Brendle4, Reference Brendle5, Reference Hamilton17, Reference Hamilton18, Reference Huisken21, Reference Richard32, Reference Richard33, Reference Richard and Seshadri34, Reference Wilking41]. The algebraic perspective makes some of the manipulations used in such studies appear more natural and focuses attention on certain structural features, namely, the invariance and nondegeneracy of the Killing type trace-form and the identification of idempotent elements and the spectra of their left multiplication operators that are not self-evidently relevant from the geometric perspective.
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ are used implicitly in the study of the Ricci flow [Reference Böhm and Wilking2, Reference Brendle4, Reference Brendle5, Reference Hamilton17, Reference Hamilton18, Reference Huisken21, Reference Richard32, Reference Richard33, Reference Richard and Seshadri34, Reference Wilking41]. The algebraic perspective makes some of the manipulations used in such studies appear more natural and focuses attention on certain structural features, namely, the invariance and nondegeneracy of the Killing type trace-form and the identification of idempotent elements and the spectra of their left multiplication operators that are not self-evidently relevant from the geometric perspective.
It would be interesting to extend results obtained here, for example, Theorem 1.5, to pseudo-Euclidean real vector spaces and to vector spaces over general base fields.
2 Notation and conventions
All vector spaces considered here are finite-dimensional over ![]() $\mathbb R$. The abstract index conventions in the sense of Penrose [Reference Penrose and Rindler30, chapter
$\mathbb R$. The abstract index conventions in the sense of Penrose [Reference Penrose and Rindler30, chapter ![]() $2$] are used when convenient. Given a vector space
$2$] are used when convenient. Given a vector space ![]() $\mathbb {V}$,
$\mathbb {V}$,  $\alpha _{i_{1}\dots i_{l}}^{j_{1}\dots j_{k}}$ indicates an element of
$\alpha _{i_{1}\dots i_{l}}^{j_{1}\dots j_{k}}$ indicates an element of ![]() $\otimes ^{k}\mathbb {V} \otimes \otimes ^{l}\mathbb {V}^{\ast }$. The indices are labels indicating tensor valencies and symmetries and do not refer to any choice of reference frame. Enclosure of indices in square brackets or parentheses indicates complete antisymmetrization or complete symmetrization over the enclosed indices; indices delimited by vertical bars are omitted from such (anti)symmetrizations. For example,
$\otimes ^{k}\mathbb {V} \otimes \otimes ^{l}\mathbb {V}^{\ast }$. The indices are labels indicating tensor valencies and symmetries and do not refer to any choice of reference frame. Enclosure of indices in square brackets or parentheses indicates complete antisymmetrization or complete symmetrization over the enclosed indices; indices delimited by vertical bars are omitted from such (anti)symmetrizations. For example, ![]() $2a_{ijk} = a_{[i|j|k} + a_{(i|j|k)}$ is the decomposition of
$2a_{ijk} = a_{[i|j|k} + a_{(i|j|k)}$ is the decomposition of ![]() $a_{ijk}$ into its parts antisymmetric and symmetric in the first and last indices. The symmetric product
$a_{ijk}$ into its parts antisymmetric and symmetric in the first and last indices. The symmetric product ![]() $\alpha \odot \beta \in S^{k+l}\mathbb {V}^{\ast }$ of symmetric tensors
$\alpha \odot \beta \in S^{k+l}\mathbb {V}^{\ast }$ of symmetric tensors ![]() $\alpha \in S^{k}\mathbb {V}^{\ast }$ and
$\alpha \in S^{k}\mathbb {V}^{\ast }$ and ![]() $\beta \in S^{l}\mathbb {V}^{\ast }$ is defined by complete symmetrization,
$\beta \in S^{l}\mathbb {V}^{\ast }$ is defined by complete symmetrization, ![]() $(\alpha \odot \beta )_{i_{1}\dots i_{k+l}} = \alpha _{(i_{1}\dots i_{k}}\beta _{i_{k+1}\dots i_{k+l})}$, whereas the wedge product
$(\alpha \odot \beta )_{i_{1}\dots i_{k+l}} = \alpha _{(i_{1}\dots i_{k}}\beta _{i_{k+1}\dots i_{k+l})}$, whereas the wedge product ![]() $\alpha \wedge \beta $ of antisymmetric tensors
$\alpha \wedge \beta $ of antisymmetric tensors ![]() $\alpha \in {\bigwedge }^{k}\mathbb {V}^{\ast }$ and
$\alpha \in {\bigwedge }^{k}\mathbb {V}^{\ast }$ and ![]() $\beta \in {\bigwedge }^{l}\mathbb {V}^{\ast }$ is defined as a multiple of the complete antisymmetrization of their tensor product, by
$\beta \in {\bigwedge }^{l}\mathbb {V}^{\ast }$ is defined as a multiple of the complete antisymmetrization of their tensor product, by 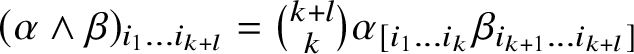 $(\alpha \wedge \beta )_{i_{1}\dots i_{k+l}} = \binom {k+l}{k}\alpha _{[i_{1}\dots i_{k}}\beta _{i_{k+1}\dots i_{k+l}]}$.
$(\alpha \wedge \beta )_{i_{1}\dots i_{k+l}} = \binom {k+l}{k}\alpha _{[i_{1}\dots i_{k}}\beta _{i_{k+1}\dots i_{k+l}]}$.
Indices are raised and lowered, respecting horizontal position, using a nondegenerate symmetric bilinear form ![]() $h_{ij}$ (called a metric) and the inverse symmetric bivector
$h_{ij}$ (called a metric) and the inverse symmetric bivector ![]() $h^{ij}$ satisfying
$h^{ij}$ satisfying ![]() $h^{ip}h_{pj} = \delta _{j}{\kern2pt}^{i}$. The pair
$h^{ip}h_{pj} = \delta _{j}{\kern2pt}^{i}$. The pair ![]() $(\mathbb {V}, h)$ is called a metric vector space. The metric h is Euclidean if it is positive definite and in this case
$(\mathbb {V}, h)$ is called a metric vector space. The metric h is Euclidean if it is positive definite and in this case ![]() $(\mathbb {V}, h)$ is called a Euclidean vector space. Throughout the article the norms used on tensor modules are those given by complete contraction with the metric (and not those induced from the standard
$(\mathbb {V}, h)$ is called a Euclidean vector space. Throughout the article the norms used on tensor modules are those given by complete contraction with the metric (and not those induced from the standard ![]() $O(h)$-representation). A subspace
$O(h)$-representation). A subspace ![]() $\mathbb {M} \subset \otimes ^{k}\mathbb {V}^{\ast } \otimes \otimes ^{l}\mathbb {V}$ is a metric vector space with the metric
$\mathbb {M} \subset \otimes ^{k}\mathbb {V}^{\ast } \otimes \otimes ^{l}\mathbb {V}$ is a metric vector space with the metric ![]() $\langle \,\cdot \,\,, \,\cdot \,\, \rangle $ defined via complete contraction with
$\langle \,\cdot \,\,, \,\cdot \,\, \rangle $ defined via complete contraction with ![]() $h_{ij}$ and
$h_{ij}$ and ![]() $h^{ij}$ by
$h^{ij}$ by  $\langle \alpha , \beta \rangle = \alpha _{i_{1}\dots i_{k}}^{j_{1}\dots j_{l}}\beta _{a_{1}\dots a_{k}}^{b_{1}\dots b_{l}}h^{i_{1}a_{1}}\dots h^{i_{k}a_{k}}h_{j_{1}b_{1}}\dots h_{j_{l}b_{l}}$.
$\langle \alpha , \beta \rangle = \alpha _{i_{1}\dots i_{k}}^{j_{1}\dots j_{l}}\beta _{a_{1}\dots a_{k}}^{b_{1}\dots b_{l}}h^{i_{1}a_{1}}\dots h^{i_{k}a_{k}}h_{j_{1}b_{1}}\dots h_{j_{l}b_{l}}$.
Let ![]() $(\mathbb {V}, h)$ be an n-dimensional metric vector space. When Euclidean h is fixed, the abstract orthogonal group
$(\mathbb {V}, h)$ be an n-dimensional metric vector space. When Euclidean h is fixed, the abstract orthogonal group ![]() $O(n)$ is identified with the orthogonal group
$O(n)$ is identified with the orthogonal group ![]() $O(h)$ of linear automorphisms of
$O(h)$ of linear automorphisms of ![]() $\mathbb {V}$ preserving h. The action of
$\mathbb {V}$ preserving h. The action of ![]() $GL(\mathbb {V})$ on
$GL(\mathbb {V})$ on ![]() $\mathbb {V}$ given by
$\mathbb {V}$ given by ![]() $(g\cdot x)^{i} = x^{p}g_{p}{}^{i}$ induces the cogredient action on
$(g\cdot x)^{i} = x^{p}g_{p}{}^{i}$ induces the cogredient action on ![]() $\mathbb {V}^{\ast }$ given by
$\mathbb {V}^{\ast }$ given by ![]() $(g\cdot \mu )_{i} = (g^{-1})_{i}{}^{p}\mu _{p}$ and these actions extend in the usual way to
$(g\cdot \mu )_{i} = (g^{-1})_{i}{}^{p}\mu _{p}$ and these actions extend in the usual way to ![]() $\otimes ^{k}\mathbb {V} \otimes \otimes ^{l}\mathbb {V}^{\ast }$. By definition,
$\otimes ^{k}\mathbb {V} \otimes \otimes ^{l}\mathbb {V}^{\ast }$. By definition, ![]() $g_{i}{}^{j} \in GL(\mathbb {V})$ is in
$g_{i}{}^{j} \in GL(\mathbb {V})$ is in ![]() $O(h)$ if and only if
$O(h)$ if and only if ![]() $g_{i}{}^{p}g_{jp} = h_{ij}$ or, similarly,
$g_{i}{}^{p}g_{jp} = h_{ij}$ or, similarly, ![]() $(g^{-1})_{i}{}^{j} = g^{j}{}_{i}$. This implies the action of
$(g^{-1})_{i}{}^{j} = g^{j}{}_{i}$. This implies the action of ![]() $O(h)$ commutes with taking traces. For example, for
$O(h)$ commutes with taking traces. For example, for ![]() $\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$ and
$\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$ and ![]() $g \in O(h)$,
$g \in O(h)$, ![]() $\operatorname {\rho }(g\cdot \mathscr {X}) = g \cdot \operatorname {\rho }(\mathscr {X})$, so
$\operatorname {\rho }(g\cdot \mathscr {X}) = g \cdot \operatorname {\rho }(\mathscr {X})$, so ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is an
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is an ![]() $O(h)$-submodule of
$O(h)$-submodule of ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$.
$\mathscr {MC}(\mathbb {V}^{\ast })$.
The space ![]() $\operatorname {End}(\mathbb {V})$ of linear endomorphisms of
$\operatorname {End}(\mathbb {V})$ of linear endomorphisms of ![]() $\mathbb {V}$ is regarded as an algebra with multiplication
$\mathbb {V}$ is regarded as an algebra with multiplication ![]() $\circ $ given by composition. The adjoint involution
$\circ $ given by composition. The adjoint involution ![]() $\sigma _{h}:(\operatorname {End}(\mathbb {V}), \circ )\to (\operatorname {End}(\mathbb {V}), \circ )$ of the metric h on
$\sigma _{h}:(\operatorname {End}(\mathbb {V}), \circ )\to (\operatorname {End}(\mathbb {V}), \circ )$ of the metric h on ![]() $\mathbb {V}$ is the real linear antiautomorphism defined by
$\mathbb {V}$ is the real linear antiautomorphism defined by ![]() $h(\sigma _{h}(\phi )x, y) = h(x, \phi (y))$ for all
$h(\sigma _{h}(\phi )x, y) = h(x, \phi (y))$ for all ![]() $x, y \in \mathbb {V}$ and
$x, y \in \mathbb {V}$ and ![]() $\phi \in \operatorname {End}(\mathbb {V})$. For a metrized vector space
$\phi \in \operatorname {End}(\mathbb {V})$. For a metrized vector space ![]() $(\mathbb {V}, h)$, the subspace
$(\mathbb {V}, h)$, the subspace ![]() $\operatorname {Sym}(\mathbb {V}, h) = \operatorname {Sym}(\operatorname {End}(\mathbb {V}), \sigma _{h}) = \{\phi \in \operatorname {End}(\mathbb {V}): \sigma _{h}(\phi ) = \phi \}$ of h-self-adjoint endormorphisms is a Jordan algebra with the product
$\operatorname {Sym}(\mathbb {V}, h) = \operatorname {Sym}(\operatorname {End}(\mathbb {V}), \sigma _{h}) = \{\phi \in \operatorname {End}(\mathbb {V}): \sigma _{h}(\phi ) = \phi \}$ of h-self-adjoint endormorphisms is a Jordan algebra with the product  $\phi \circledcirc \psi = \tfrac {1}{2}(\phi \circ \psi + \psi \circ \phi )$ for
$\phi \circledcirc \psi = \tfrac {1}{2}(\phi \circ \psi + \psi \circ \phi )$ for ![]() $\phi , \psi \in \operatorname {Sym}(\mathbb {V}, h)$. (When h is clear from context there is written simply
$\phi , \psi \in \operatorname {Sym}(\mathbb {V}, h)$. (When h is clear from context there is written simply ![]() $\operatorname {Sym}(\mathbb {V})$ for brevity.) There holds
$\operatorname {Sym}(\mathbb {V})$ for brevity.) There holds 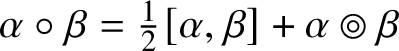 $\alpha \circ \beta = \tfrac {1}{2}[\alpha , \beta ] + \alpha \circledcirc \beta $, where
$\alpha \circ \beta = \tfrac {1}{2}[\alpha , \beta ] + \alpha \circledcirc \beta $, where 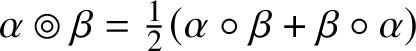 $\alpha \circledcirc \beta = \tfrac {1}{2}(\alpha \circ \beta + \beta \circ \alpha )$.
$\alpha \circledcirc \beta = \tfrac {1}{2}(\alpha \circ \beta + \beta \circ \alpha )$.
Via metric duality, ![]() $\alpha _{ij} \in \otimes ^{2}(\mathbb {V}^{\ast })$ is identified with the endomorphism
$\alpha _{ij} \in \otimes ^{2}(\mathbb {V}^{\ast })$ is identified with the endomorphism ![]() $x^{j} \to x^{i}\alpha _{i}{}^{j}$ of
$x^{j} \to x^{i}\alpha _{i}{}^{j}$ of ![]() $\mathbb {V}$, and the composition of the endomorphisms of
$\mathbb {V}$, and the composition of the endomorphisms of ![]() $\mathbb {V}$ determined by raising the second indices of
$\mathbb {V}$ determined by raising the second indices of ![]() $\alpha _{ij} , \beta _{ij} \in \otimes ^{2}\mathbb {V}^{\ast }$ is given by
$\alpha _{ij} , \beta _{ij} \in \otimes ^{2}\mathbb {V}^{\ast }$ is given by ![]() $(\alpha \circ \beta )_{i}{}^{j} = \alpha _{p}{}^{j}\beta _{i}{}^{p}$. These conventions are such that, for
$(\alpha \circ \beta )_{i}{}^{j} = \alpha _{p}{}^{j}\beta _{i}{}^{p}$. These conventions are such that, for ![]() $x, y, z, w \in \mathbb {V}^{\ast }$,
$x, y, z, w \in \mathbb {V}^{\ast }$,
The pullback to ![]() $\otimes ^{2}\mathbb {V}^{\ast }$ of the Lie bracket of endomorphisms yields the Lie bracket
$\otimes ^{2}\mathbb {V}^{\ast }$ of the Lie bracket of endomorphisms yields the Lie bracket ![]() $[\,\cdot \,\,, \,\cdot \,\,]:\otimes ^{2}(\mathbb {V}^{\ast }) \times \otimes ^{2}(\mathbb {V}^{\ast }) \to \otimes ^{2}(\mathbb {V}^{\ast })$ given by
$[\,\cdot \,\,, \,\cdot \,\,]:\otimes ^{2}(\mathbb {V}^{\ast }) \times \otimes ^{2}(\mathbb {V}^{\ast }) \to \otimes ^{2}(\mathbb {V}^{\ast })$ given by ![]() $[\alpha , \beta ] = \alpha \circ \beta - \beta \circ \alpha $. Similarly, the multiplication induced via metric duality on
$[\alpha , \beta ] = \alpha \circ \beta - \beta \circ \alpha $. Similarly, the multiplication induced via metric duality on ![]() $\otimes ^{2}\mathbb {V}^{\ast }$ by the usual Jordan product of endomorphisms is denoted by
$\otimes ^{2}\mathbb {V}^{\ast }$ by the usual Jordan product of endomorphisms is denoted by ![]() $\circledcirc $. The subspace
$\circledcirc $. The subspace ![]() ${\bigwedge }^{2}\mathbb {V}^{\ast }$ is a subalgebra of
${\bigwedge }^{2}\mathbb {V}^{\ast }$ is a subalgebra of ![]() $(\otimes ^{2}\mathbb {V}^{\ast }, [\,\cdot \,\,, \,\cdot \,\,])$ and
$(\otimes ^{2}\mathbb {V}^{\ast }, [\,\cdot \,\,, \,\cdot \,\,])$ and ![]() $({\bigwedge }^{2}\mathbb {V}^{\ast }, [\,\cdot \,\,, \,\cdot \,\,])$ is isomorphic to the Lie algebra
$({\bigwedge }^{2}\mathbb {V}^{\ast }, [\,\cdot \,\,, \,\cdot \,\,])$ is isomorphic to the Lie algebra ![]() $\mathfrak {so}(\mathbb {V}, h)$.
$\mathfrak {so}(\mathbb {V}, h)$.
3 General results about commutative algebras
As explained in the introduction, the argument proving [Reference Popov31, Theorem ![]() $5$] adapts almost without change to the present setting to prove Theorem 3.1. For the reader’s convenience, it is reproduced here with modifications appropriate to the current setting.
$5$] adapts almost without change to the present setting to prove Theorem 3.1. For the reader’s convenience, it is reproduced here with modifications appropriate to the current setting.
Theorem 3.1. Let ![]() $(\mathbb {A}, \circ , h)$ be a nontrivial finite-dimensional commutative algebra. If a connected simple real Lie group G acts on
$(\mathbb {A}, \circ , h)$ be a nontrivial finite-dimensional commutative algebra. If a connected simple real Lie group G acts on ![]() $(\mathbb {A}, \circ )$ irreducibly by automorphisms, then
$(\mathbb {A}, \circ )$ irreducibly by automorphisms, then ![]() $(\mathbb {A}, \circ )$ is simple.
$(\mathbb {A}, \circ )$ is simple.
Proof. Since the action is irreducible, a nontrivial G-invariant ideal equals ![]() $\mathbb {A}$. Assume
$\mathbb {A}$. Assume ![]() $(\mathbb {A}, \circ )$ is not simple and let
$(\mathbb {A}, \circ )$ is not simple and let ![]() $\mathbb {I} \subset \mathbb {A}$ be a minimal proper ideal. Then
$\mathbb {I} \subset \mathbb {A}$ be a minimal proper ideal. Then ![]() $g\cdot \mathbb {I}$ is again a minimal proper ideal for all
$g\cdot \mathbb {I}$ is again a minimal proper ideal for all ![]() $g \in G$. Since the sum of the ideals
$g \in G$. Since the sum of the ideals ![]() $g\cdot \mathbb {I}$ as g ranges over G is a nontrivial G-invariant ideal, it equals
$g\cdot \mathbb {I}$ as g ranges over G is a nontrivial G-invariant ideal, it equals ![]() $\mathbb {A}$. For
$\mathbb {A}$. For ![]() $g, \bar {g} \in G$, the ideals
$g, \bar {g} \in G$, the ideals ![]() $g\cdot \mathbb {I}$ and
$g\cdot \mathbb {I}$ and ![]() $\bar {g}\cdot \mathbb {I}$ either are equal or have intersection
$\bar {g}\cdot \mathbb {I}$ either are equal or have intersection ![]() $\{0\}$, and it follows that there are
$\{0\}$, and it follows that there are ![]() $g_{1}, \dots , g_{r} \in G$ such that
$g_{1}, \dots , g_{r} \in G$ such that ![]() $\mathbb {A} = \oplus _{i = 1}^{r}g_{i}\cdot \mathbb {I}$ is a direct sum of vector spaces. Since the product of distinct minimal ideals is the zero ideal, this sum is in fact a direct sum of algebras. If
$\mathbb {A} = \oplus _{i = 1}^{r}g_{i}\cdot \mathbb {I}$ is a direct sum of vector spaces. Since the product of distinct minimal ideals is the zero ideal, this sum is in fact a direct sum of algebras. If ![]() $\mathbb {J} \subset \mathbb {A}$ is a minimal proper ideal not equal to
$\mathbb {J} \subset \mathbb {A}$ is a minimal proper ideal not equal to ![]() $g_{i}\cdot I$ for any
$g_{i}\cdot I$ for any ![]() $1 \leq i \leq r$, then its product with each
$1 \leq i \leq r$, then its product with each ![]() $g_{i}\cdot \mathbb {I}$ is the zero ideal, so its product with
$g_{i}\cdot \mathbb {I}$ is the zero ideal, so its product with ![]() $\mathbb {A}$ is the zero ideal. Applying the preceding argument with
$\mathbb {A}$ is the zero ideal. Applying the preceding argument with ![]() $\mathbb {J}$ in place of
$\mathbb {J}$ in place of ![]() $\mathbb {I}$ shows that the multiplication on
$\mathbb {I}$ shows that the multiplication on ![]() $\mathbb {A}$ is trivial, contrary to hypothesis. The preceding shows that any minimal proper ideal of
$\mathbb {A}$ is trivial, contrary to hypothesis. The preceding shows that any minimal proper ideal of ![]() $(\mathbb {A}, \circ )$ has the form
$(\mathbb {A}, \circ )$ has the form ![]() $g_{i}\cdot \mathbb {I}$ for some
$g_{i}\cdot \mathbb {I}$ for some ![]() $1 \leq i \leq r$, and so G permutes the set
$1 \leq i \leq r$, and so G permutes the set ![]() $\{g_{1}\cdot \mathbb {I}, \dots , g_{r}\cdot \mathbb {I}\}$. Since G is connected with simple Lie algebra, any proper normal subgroup of G must be discrete, so this permutation action must be trivial. Consequently, each
$\{g_{1}\cdot \mathbb {I}, \dots , g_{r}\cdot \mathbb {I}\}$. Since G is connected with simple Lie algebra, any proper normal subgroup of G must be discrete, so this permutation action must be trivial. Consequently, each ![]() $g_{i}\cdot \mathbb {I}$ is a G-invariant linear subspace of
$g_{i}\cdot \mathbb {I}$ is a G-invariant linear subspace of ![]() $\mathbb {A}$, contradicting the G-irreducibility of
$\mathbb {A}$, contradicting the G-irreducibility of ![]() $\mathbb {A}$.
$\mathbb {A}$.
Theorem 3.2. A nontrivial finite-dimensional Euclidean metrized commutative algebra ![]() $(\mathbb {A}, \circ , h)$ on which a real Lie group G acts irreducibly by isometric automorphisms is exact and Killing metrized with Killing form
$(\mathbb {A}, \circ , h)$ on which a real Lie group G acts irreducibly by isometric automorphisms is exact and Killing metrized with Killing form ![]() $\tau _{\circ }(x, y) = \operatorname {\mathsf {tr}} L_{\circ }(x)L_{\circ }(y)$ equal to a nonzero multiple of the metric h.
$\tau _{\circ }(x, y) = \operatorname {\mathsf {tr}} L_{\circ }(x)L_{\circ }(y)$ equal to a nonzero multiple of the metric h.
Proof. Since G acts on ![]() $(\mathbb {A}, \circ )$ by automorphisms, the linear form
$(\mathbb {A}, \circ )$ by automorphisms, the linear form ![]() $x \to \operatorname {\mathsf {tr}} L_{\circ }(x)$ is G-invariant and so, because
$x \to \operatorname {\mathsf {tr}} L_{\circ }(x)$ is G-invariant and so, because ![]() $\mathbb {A}$ is G-irreducible,
$\mathbb {A}$ is G-irreducible, ![]() $\ker \operatorname {\mathsf {tr}} L_{\circ } = \mathbb {A}$. Likewise,
$\ker \operatorname {\mathsf {tr}} L_{\circ } = \mathbb {A}$. Likewise, ![]() $\tau _{\circ }$ is G-invariant, and because both h and
$\tau _{\circ }$ is G-invariant, and because both h and ![]() $\tau _{\circ }$ are G-invariant, the endomorphism
$\tau _{\circ }$ are G-invariant, the endomorphism ![]() $A \in \operatorname {End}(\mathbb {A})$ defined by
$A \in \operatorname {End}(\mathbb {A})$ defined by ![]() $\tau _{\circ }(x, y) = h(Ax, y)$ for
$\tau _{\circ }(x, y) = h(Ax, y)$ for ![]() $x, y, \in \mathbb {A}$ is G-invariant as well. Because both h and
$x, y, \in \mathbb {A}$ is G-invariant as well. Because both h and ![]() $\tau _{\circ }$ are symmetric, A is h-self-adjoint and so is semisimple with real eigenvalues. Since
$\tau _{\circ }$ are symmetric, A is h-self-adjoint and so is semisimple with real eigenvalues. Since ![]() $\mathbb {A}$ is G-irreducible and A is h-self-adjoint, by the Schur Lemma,
$\mathbb {A}$ is G-irreducible and A is h-self-adjoint, by the Schur Lemma, ![]() $A = \kappa \operatorname {Id}_{\mathbb {A}}$ for some
$A = \kappa \operatorname {Id}_{\mathbb {A}}$ for some ![]() $\kappa \in \mathbb R$, so
$\kappa \in \mathbb R$, so ![]() $\tau _{\circ } =\kappa h$. Because
$\tau _{\circ } =\kappa h$. Because 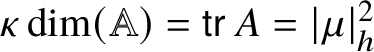 $\kappa \dim (\mathbb {A}) = \operatorname {\mathsf {tr}} A = |\mu |^{2}_{h}$ where
$\kappa \dim (\mathbb {A}) = \operatorname {\mathsf {tr}} A = |\mu |^{2}_{h}$ where ![]() $\mu (x, y, z) = h(x\circ y, z)$, were
$\mu (x, y, z) = h(x\circ y, z)$, were ![]() $\kappa $ zero, then
$\kappa $ zero, then ![]() $\mu $ would be identically zero. However, because
$\mu $ would be identically zero. However, because ![]() $(\mathbb {A}, \circ )$ is assumed nontrivial there exist
$(\mathbb {A}, \circ )$ is assumed nontrivial there exist ![]() $x, y \in \mathbb {A}$ such that
$x, y \in \mathbb {A}$ such that ![]() $x \circ y \neq 0$, so, by the nondegeneracy of h there is
$x \circ y \neq 0$, so, by the nondegeneracy of h there is ![]() $z \in \mathbb {A}$ such that
$z \in \mathbb {A}$ such that ![]() $h(x\circ y, z) \neq 0$.
$h(x\circ y, z) \neq 0$.
The following alternative argument shows ![]() $\kappa \neq 0$. By [Reference Tkachev36, Lemma
$\kappa \neq 0$. By [Reference Tkachev36, Lemma ![]() $2.1$], a nontrivial finite-dimensional Euclidean metrized commutative real algebra
$2.1$], a nontrivial finite-dimensional Euclidean metrized commutative real algebra ![]() $(\mathbb {A}, \circ )$ contains a nonzero idempotent, for, if y is an extremum of the restriction to the h-unit sphere of the cubic polynomial
$(\mathbb {A}, \circ )$ contains a nonzero idempotent, for, if y is an extremum of the restriction to the h-unit sphere of the cubic polynomial ![]() $h(x\circ x, x)$, then
$h(x\circ x, x)$, then ![]() $e =h(y\circ y, y)^{-1}y$ is a nonzero idempotent. By the invariance of h,
$e =h(y\circ y, y)^{-1}y$ is a nonzero idempotent. By the invariance of h, ![]() $L_{\circ }(e)$ is a self-adjoint endomorphism of
$L_{\circ }(e)$ is a self-adjoint endomorphism of ![]() $\mathbb {A}$ that preserves the orthogonal complement of the span of e. Hence, it is diagonalizable with (possibly repeated) real eigenvalues
$\mathbb {A}$ that preserves the orthogonal complement of the span of e. Hence, it is diagonalizable with (possibly repeated) real eigenvalues ![]() $1, \lambda _{1}, \dots , \lambda _{n-1}$, and
$1, \lambda _{1}, \dots , \lambda _{n-1}$, and 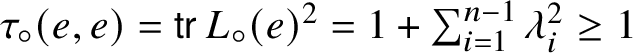 $\tau _{\circ }(e, e) = \operatorname {\mathsf {tr}} L_{\circ }(e)^{2} = 1 + \sum _{i = 1}^{n-1}\lambda _{i}^{2} \geq 1$. Since
$\tau _{\circ }(e, e) = \operatorname {\mathsf {tr}} L_{\circ }(e)^{2} = 1 + \sum _{i = 1}^{n-1}\lambda _{i}^{2} \geq 1$. Since ![]() $\langle e, e\rangle \neq 0$, it follows that
$\langle e, e\rangle \neq 0$, it follows that ![]() $\kappa = \tau _{\circ }(e, e)h(e, e)^{-1} \neq 0$.
$\kappa = \tau _{\circ }(e, e)h(e, e)^{-1} \neq 0$.
4 Action of metric curvature tensors on tensors
Let ![]() $(\mathbb {V}, h)$ be a metric vector space. Note that
$(\mathbb {V}, h)$ be a metric vector space. Note that 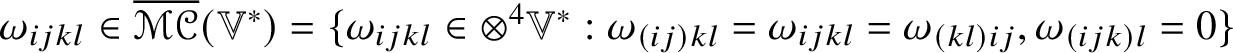 $\omega _{ijkl} \in \overline {\mathscr {MC}}(\mathbb {V}^{\ast }) = \{\omega _{ijkl} \in \otimes ^{4}\mathbb {V}^{\ast }: \omega _{(ij)kl} = \omega _{ijkl} = \omega _{(kl)ij}, \omega _{(ijk)l} = 0\}$ satisfies
$\omega _{ijkl} \in \overline {\mathscr {MC}}(\mathbb {V}^{\ast }) = \{\omega _{ijkl} \in \otimes ^{4}\mathbb {V}^{\ast }: \omega _{(ij)kl} = \omega _{ijkl} = \omega _{(kl)ij}, \omega _{(ijk)l} = 0\}$ satisfies ![]() $\omega _{klij} = \omega _{ijkl}$ and
$\omega _{klij} = \omega _{ijkl}$ and ![]() $\omega _{k[ij]l}$ is antisymmetric in k and l. A straightforward calculation proves that the linear map
$\omega _{k[ij]l}$ is antisymmetric in k and l. A straightforward calculation proves that the linear map ![]() $\mathcal {T}:\overline {\mathscr {MC}}(\mathbb {V}^{\ast }) \to \mathscr {MC}(\mathbb {V}^{\ast })$ defined by
$\mathcal {T}:\overline {\mathscr {MC}}(\mathbb {V}^{\ast }) \to \mathscr {MC}(\mathbb {V}^{\ast })$ defined by  $\mathcal {T}(\mu )_{ijkl} = \tfrac {2}{\sqrt {3}}\mu _{k[ij]l}$ is an isometric isomorphism with inverse given by
$\mathcal {T}(\mu )_{ijkl} = \tfrac {2}{\sqrt {3}}\mu _{k[ij]l}$ is an isometric isomorphism with inverse given by  $\mathcal {T}^{-1}(\nu )_{ijkl} = -\tfrac {2}{\sqrt {3}}\nu _{k(ij)l}$.
$\mathcal {T}^{-1}(\nu )_{ijkl} = -\tfrac {2}{\sqrt {3}}\nu _{k(ij)l}$.
It is convenient to abuse notation by identifying ![]() $S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$ and
$S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$ and ![]() $S^{2}(S^{2}\mathbb {V}^{\ast })$ with the subspaces
$S^{2}(S^{2}\mathbb {V}^{\ast })$ with the subspaces 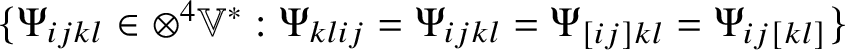 $\{\Psi _{ijkl} \in \otimes ^{4}\mathbb {V}^{\ast }: \Psi _{klij} = \Psi _{ijkl} = \Psi _{[ij]kl} = \Psi _{ij[kl]}\}$ and
$\{\Psi _{ijkl} \in \otimes ^{4}\mathbb {V}^{\ast }: \Psi _{klij} = \Psi _{ijkl} = \Psi _{[ij]kl} = \Psi _{ij[kl]}\}$ and  $\{\Phi _{ijkl} \in \otimes ^{4}\mathbb {V}^{\ast }: \Phi _{klij} = \Phi _{ijkl} = \Phi _{(ij)kl} = \Phi _{ij(kl)}\}$. As
$\{\Phi _{ijkl} \in \otimes ^{4}\mathbb {V}^{\ast }: \Phi _{klij} = \Phi _{ijkl} = \Phi _{(ij)kl} = \Phi _{ij(kl)}\}$. As 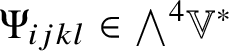 $\Psi _{ijkl} \in {\bigwedge }^{4}\mathbb {V}^{\ast }$ satisfies
$\Psi _{ijkl} \in {\bigwedge }^{4}\mathbb {V}^{\ast }$ satisfies ![]() $\Psi _{klij} = \Psi _{ijkl}$,
$\Psi _{klij} = \Psi _{ijkl}$, ![]() ${\bigwedge }^{4}\mathbb {V}^{\ast }$ can be viewed as a subspace of
${\bigwedge }^{4}\mathbb {V}^{\ast }$ can be viewed as a subspace of ![]() $S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$ and, likewise,
$S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$ and, likewise, ![]() $S^{4}\mathbb {V}^{\ast }$ can be regarded as a subspace of
$S^{4}\mathbb {V}^{\ast }$ can be regarded as a subspace of ![]() $S^{2}(S^{2}\mathbb {V}^{\ast })$. The Bianchi identity implies
$S^{2}(S^{2}\mathbb {V}^{\ast })$. The Bianchi identity implies ![]() ${\bigwedge }^{4}\mathbb {V}^{\ast }$ and
${\bigwedge }^{4}\mathbb {V}^{\ast }$ and ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$ are orthogonal subspaces of
$\mathscr {MC}(\mathbb {V}^{\ast })$ are orthogonal subspaces of ![]() $S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$ with trivial intersection and, similarly,
$S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$ with trivial intersection and, similarly, ![]() $S^{4}\mathbb {V}^{\ast }$ and
$S^{4}\mathbb {V}^{\ast }$ and ![]() $\overline {\mathscr {MC}}(\mathbb {V}^{\ast })$ are orthogonal subspaces of
$\overline {\mathscr {MC}}(\mathbb {V}^{\ast })$ are orthogonal subspaces of ![]() $S^{2}(S^{2}\mathbb {V}^{\ast })$ with trivial intersection. Comparing dimensions shows
$S^{2}(S^{2}\mathbb {V}^{\ast })$ with trivial intersection. Comparing dimensions shows ![]() $S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast }) \simeq \mathscr {MC}(\mathbb {V}^{\ast })\oplus {\bigwedge }^{4}\mathbb {V}^{\ast }$ and
$S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast }) \simeq \mathscr {MC}(\mathbb {V}^{\ast })\oplus {\bigwedge }^{4}\mathbb {V}^{\ast }$ and ![]() $S^{2}(S^{2}\mathbb {V}^{\ast }) \simeq \overline {\mathscr {MC}}(\mathbb {V}^{\ast })\oplus S^{4}\mathbb {V}^{\ast }$.
$S^{2}(S^{2}\mathbb {V}^{\ast }) \simeq \overline {\mathscr {MC}}(\mathbb {V}^{\ast })\oplus S^{4}\mathbb {V}^{\ast }$.
For ![]() $\Psi \in S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$,
$\Psi \in S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$, ![]() $\Psi _{[ijkl]} = \Psi _{[ijk]l}$ and the orthogonal projection
$\Psi _{[ijkl]} = \Psi _{[ijk]l}$ and the orthogonal projection ![]() $\mathscr {M}:S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast }) \to \mathscr {MC}(\mathbb {V}^{\ast })$ is given by
$\mathscr {M}:S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast }) \to \mathscr {MC}(\mathbb {V}^{\ast })$ is given by ![]() $\mathscr {M}(\Psi )_{ijkl} = \Psi _{ijkl} - \Psi _{[ijk]l}$, so
$\mathscr {M}(\Psi )_{ijkl} = \Psi _{ijkl} - \Psi _{[ijk]l}$, so  $\mathscr {M} \oplus (\operatorname {Id}_{S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })} - \mathscr {M}): S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast }) \to \mathscr {MC}(\mathbb {V}^{\ast })\oplus {\bigwedge }^{4}\mathbb {V}^{\ast }$ is an isometric isomorphism. Similarly, the orthogonal projection
$\mathscr {M} \oplus (\operatorname {Id}_{S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })} - \mathscr {M}): S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast }) \to \mathscr {MC}(\mathbb {V}^{\ast })\oplus {\bigwedge }^{4}\mathbb {V}^{\ast }$ is an isometric isomorphism. Similarly, the orthogonal projection ![]() $\mathscr {S}:S^{2}(S^{2}\mathbb {V}^{\ast }) \to \overline {\mathscr {MC}}(\mathbb {V}^{\ast })$ is given by
$\mathscr {S}:S^{2}(S^{2}\mathbb {V}^{\ast }) \to \overline {\mathscr {MC}}(\mathbb {V}^{\ast })$ is given by ![]() $\mathscr {S}(\Psi )_{ijkl} = \Psi _{ijkl} - \Psi _{(ijk)l}$, so
$\mathscr {S}(\Psi )_{ijkl} = \Psi _{ijkl} - \Psi _{(ijk)l}$, so  $(\mathcal {T}\circ \mathscr {S}) \oplus (\operatorname {Id}_{S^{2}(S^{2}\mathbb {V}^{\ast })} - \mathscr {S}): S^{2}(S^{2}\mathbb {V}^{\ast }) \to \mathscr {MC}(\mathbb {V}^{\ast })\oplus S^{4}\mathbb {V}^{\ast }$ is an isometric isomorphism, where, for
$(\mathcal {T}\circ \mathscr {S}) \oplus (\operatorname {Id}_{S^{2}(S^{2}\mathbb {V}^{\ast })} - \mathscr {S}): S^{2}(S^{2}\mathbb {V}^{\ast }) \to \mathscr {MC}(\mathbb {V}^{\ast })\oplus S^{4}\mathbb {V}^{\ast }$ is an isometric isomorphism, where, for ![]() $\omega _{ijkl} \in S^{2}(S^{2}\mathbb {V}^{\ast })$,
$\omega _{ijkl} \in S^{2}(S^{2}\mathbb {V}^{\ast })$,
 $$ \begin{align} (\mathcal{T} \circ \mathscr{S})(\omega)_{ijkl} = \tfrac{2}{\sqrt{3}}\omega_{k[ij]l}. \end{align} $$
$$ \begin{align} (\mathcal{T} \circ \mathscr{S})(\omega)_{ijkl} = \tfrac{2}{\sqrt{3}}\omega_{k[ij]l}. \end{align} $$Lemma 4.1. Let ![]() $(\mathbb {V}, h)$ be a finite-dimensional metric vector space and let
$(\mathbb {V}, h)$ be a finite-dimensional metric vector space and let ![]() $k \geq 2$. For
$k \geq 2$. For ![]() $\alpha , \beta \in \otimes ^{k}\mathbb {V}^{\ast }$, setting
$\alpha , \beta \in \otimes ^{k}\mathbb {V}^{\ast }$, setting ![]() $\varrho (\alpha , \beta )$ equal to the h-orthogonal projection
$\varrho (\alpha , \beta )$ equal to the h-orthogonal projection ![]() $\mathscr {M}(\pi (\alpha , \beta )) \in \mathscr {MC}(\mathbb {V}^{\ast })$ of
$\mathscr {M}(\pi (\alpha , \beta )) \in \mathscr {MC}(\mathbb {V}^{\ast })$ of  $\pi (\alpha , \beta )_{abcd} = \Psi (\alpha , \beta )_{[ab][cd]} \in S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$ where
$\pi (\alpha , \beta )_{abcd} = \Psi (\alpha , \beta )_{[ab][cd]} \in S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$ where
 $$ \begin{align} \Psi(\alpha, \beta)_{abcd} = \tfrac{1}{k}\sum_{r \neq s}\alpha_{i_{1}\dots i_{r-1}b i_{r+1}\dots i_{s-1} c i_{s+1}\dots i_{k}}\beta^{i_{1}\dots i_{r-1}}{}_{a}{}^{i_{r+1}\dots i_{s-1}}{}_{d}{}^{i_{s+1}\dots i_{k}} \end{align} $$
$$ \begin{align} \Psi(\alpha, \beta)_{abcd} = \tfrac{1}{k}\sum_{r \neq s}\alpha_{i_{1}\dots i_{r-1}b i_{r+1}\dots i_{s-1} c i_{s+1}\dots i_{k}}\beta^{i_{1}\dots i_{r-1}}{}_{a}{}^{i_{r+1}\dots i_{s-1}}{}_{d}{}^{i_{s+1}\dots i_{k}} \end{align} $$defines a symmetric ![]() $O(h)$-equivariant bilinear map
$O(h)$-equivariant bilinear map ![]() $\varrho :\otimes ^{k}\mathbb {V}^{\ast } \times \otimes ^{k}\mathbb {V}^{\ast } \to \mathscr {MC}(\mathbb {V}^{\ast })$.
$\varrho :\otimes ^{k}\mathbb {V}^{\ast } \times \otimes ^{k}\mathbb {V}^{\ast } \to \mathscr {MC}(\mathbb {V}^{\ast })$.
Proof. It needs to be checked only that ![]() $\varrho (\beta , \alpha ) = \varrho (\alpha , \beta )$. The definition (4.2) implies
$\varrho (\beta , \alpha ) = \varrho (\alpha , \beta )$. The definition (4.2) implies ![]() $\Psi (\beta , \alpha )_{abcd} = \Psi (\alpha , \beta )_{badc}$ and there follows
$\Psi (\beta , \alpha )_{abcd} = \Psi (\alpha , \beta )_{badc}$ and there follows
 $$ \begin{align} \begin{split} \pi(\beta, \alpha)_{abcd} &=\Psi(\beta, \alpha)_{[ab][cd]} \\ &= \tfrac{1}{4}\left(\Psi(\beta, \alpha)_{abcd} -\Psi(\beta, \alpha)_{bacd} -\Psi(\beta, \alpha)_{abdc} + \Psi(\beta, \alpha)_{badc}\right) \\ &= \tfrac{1}{4}\left(\Psi(\alpha, \beta)_{badc} -\Psi(\alpha, \beta)_{abdc} -\Psi(\alpha, \beta)_{bacd} + \Psi(\alpha, \beta)_{abcd}\right) \\ &= \Psi(\alpha, \beta)_{[ab][cd]} = \pi(\alpha, \beta)_{abcd}, \end{split} \end{align} $$
$$ \begin{align} \begin{split} \pi(\beta, \alpha)_{abcd} &=\Psi(\beta, \alpha)_{[ab][cd]} \\ &= \tfrac{1}{4}\left(\Psi(\beta, \alpha)_{abcd} -\Psi(\beta, \alpha)_{bacd} -\Psi(\beta, \alpha)_{abdc} + \Psi(\beta, \alpha)_{badc}\right) \\ &= \tfrac{1}{4}\left(\Psi(\alpha, \beta)_{badc} -\Psi(\alpha, \beta)_{abdc} -\Psi(\alpha, \beta)_{bacd} + \Psi(\alpha, \beta)_{abcd}\right) \\ &= \Psi(\alpha, \beta)_{[ab][cd]} = \pi(\alpha, \beta)_{abcd}, \end{split} \end{align} $$so that ![]() $\varrho (\beta , \alpha ) = \mathscr {M}(\pi (\beta , \alpha )) = \mathscr {M}(\pi (\alpha , \beta )) = \varrho (\alpha , \beta )$. That
$\varrho (\beta , \alpha ) = \mathscr {M}(\pi (\beta , \alpha )) = \mathscr {M}(\pi (\alpha , \beta )) = \varrho (\alpha , \beta )$. That ![]() $\varrho $ is
$\varrho $ is ![]() $O(h)$-equivariant means that
$O(h)$-equivariant means that ![]() $\varrho (g\cdot \alpha , g \cdot \beta ) = g \cdot \varrho (\alpha , \beta )$ for all
$\varrho (g\cdot \alpha , g \cdot \beta ) = g \cdot \varrho (\alpha , \beta )$ for all ![]() $\alpha , \beta \in \otimes ^{k}\mathbb {V}^{\ast }$ and
$\alpha , \beta \in \otimes ^{k}\mathbb {V}^{\ast }$ and ![]() $g \in O(h)$, and this is apparent from the manifest
$g \in O(h)$, and this is apparent from the manifest ![]() $O(h)$-equivariance of the construction of
$O(h)$-equivariance of the construction of ![]() $\varrho $.
$\varrho $.
Because ![]() $\varrho $ is
$\varrho $ is ![]() $O(h)$-equivariant, its restriction to
$O(h)$-equivariant, its restriction to ![]() $\mathbb {W} \times \mathbb {W}$ where
$\mathbb {W} \times \mathbb {W}$ where ![]() $\mathbb {W}$ is any
$\mathbb {W}$ is any ![]() $O(h)$-submodule
$O(h)$-submodule ![]() $\mathbb {W} \subset \otimes ^{k}\mathbb {V}^{\ast }$ takes values in some
$\mathbb {W} \subset \otimes ^{k}\mathbb {V}^{\ast }$ takes values in some ![]() $O(h)$-submodule of
$O(h)$-submodule of ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$.
$\mathscr {MC}(\mathbb {V}^{\ast })$.
The symmetric group on k elements, ![]() $S_{k}$, acts on the left on
$S_{k}$, acts on the left on ![]() $\otimes ^{k}\mathbb {V}^{\ast }$ by
$\otimes ^{k}\mathbb {V}^{\ast }$ by 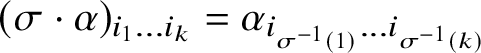 $(\sigma \cdot \alpha )_{i_{1}\dots i_{k}} = \alpha _{i_{\sigma ^{-1}(1)}\dots i_{\sigma ^{-1}(k)}}$ for
$(\sigma \cdot \alpha )_{i_{1}\dots i_{k}} = \alpha _{i_{\sigma ^{-1}(1)}\dots i_{\sigma ^{-1}(k)}}$ for ![]() $\sigma \in S_{k}$. A filling of a k box Young diagram by distinct indices
$\sigma \in S_{k}$. A filling of a k box Young diagram by distinct indices ![]() $i_{1},\dots , i_{k}$ determines the submodule of
$i_{1},\dots , i_{k}$ determines the submodule of ![]() $\otimes ^{k}\mathbb {V}^{\ast }$ comprising tensors antisymmetric in the indices in any column of the filled Young diagram and such that there vanishes the antisymmetrization over a subset of indices comprising the indices in any given column plus any index from any column to the right of the given column. The tensors in such a submodule are said to have the type given by the filled Young diagram. By [Reference Weyl40, Theorems
$\otimes ^{k}\mathbb {V}^{\ast }$ comprising tensors antisymmetric in the indices in any column of the filled Young diagram and such that there vanishes the antisymmetrization over a subset of indices comprising the indices in any given column plus any index from any column to the right of the given column. The tensors in such a submodule are said to have the type given by the filled Young diagram. By [Reference Weyl40, Theorems ![]() $5.7.$A and
$5.7.$A and ![]() $5.7.$C], an
$5.7.$C], an ![]() $O(n)$-module of covariant trace-free tensors on an n-dimensional vector space having symmetries corresponding to a Young diagram is nontrivial if and only if the sum of the lengths of the first two columns is no greater than n, and by [Reference Weyl40, Theorem
$O(n)$-module of covariant trace-free tensors on an n-dimensional vector space having symmetries corresponding to a Young diagram is nontrivial if and only if the sum of the lengths of the first two columns is no greater than n, and by [Reference Weyl40, Theorem ![]() $5.7$G] all irreducible finite-dimensional
$5.7$G] all irreducible finite-dimensional ![]() $O(n)$-modules correspond to some such Young diagram. For example,
$O(n)$-modules correspond to some such Young diagram. For example, ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) = \ker \operatorname {\rho } \subset \mathscr {MC}(\mathbb {V}^{\ast })$ corresponds with a filling of a
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) = \ker \operatorname {\rho } \subset \mathscr {MC}(\mathbb {V}^{\ast })$ corresponds with a filling of a ![]() $2\times 2$ square array of boxes, so
$2\times 2$ square array of boxes, so ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) = \{0\}$ if
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) = \{0\}$ if ![]() $\dim \mathbb {V} < 4$. If
$\dim \mathbb {V} < 4$. If ![]() $n = \dim \mathbb {V} \geq 4$,
$n = \dim \mathbb {V} \geq 4$, ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is a nontrivial irreducible
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is a nontrivial irreducible ![]() $O(n)$-module. When
$O(n)$-module. When ![]() $\dim \mathbb {V} = 4$, it decomposes as an
$\dim \mathbb {V} = 4$, it decomposes as an ![]() $SO(n)$-module into two 5-dimensional submodules (see Section 9). A linear endomorphism is said to preserve the type of tensors if it maps tensors with the symmetries determined by a given filled Young diagram into tensors with the same symmetries.
$SO(n)$-module into two 5-dimensional submodules (see Section 9). A linear endomorphism is said to preserve the type of tensors if it maps tensors with the symmetries determined by a given filled Young diagram into tensors with the same symmetries.
Lemma 4.2. Let ![]() $(\mathbb {V}, h)$ be a finite-dimensional metric vector space and let
$(\mathbb {V}, h)$ be a finite-dimensional metric vector space and let ![]() $k \geq 2$. The linear map
$k \geq 2$. The linear map ![]() $\mathscr {MC}(\mathbb {V}^{\ast }) \to \operatorname {End}(\otimes ^{k}\mathbb {V}^{\ast })$ associating with
$\mathscr {MC}(\mathbb {V}^{\ast }) \to \operatorname {End}(\otimes ^{k}\mathbb {V}^{\ast })$ associating with ![]() $\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$ the operator
$\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$ the operator 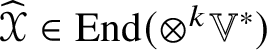 $\widehat {\mathscr {X}} \in \operatorname {End}(\otimes ^{k}\mathbb {V}^{\ast })$ defined by
$\widehat {\mathscr {X}} \in \operatorname {End}(\otimes ^{k}\mathbb {V}^{\ast })$ defined by
 $$ \begin{align} \widehat{\mathscr{X}}(\alpha)_{i_{1}\dots i_{k}} = \tfrac{1}{k}\sum_{r \neq s}\mathscr{X}^{p}{}_{i_{r}i_{s}}{}^{q}\alpha_{i_{1}\dots i_{r-1}pi_{r+1}\dots i_{s-1} q i_{s+1}\dots i_{k}} \end{align} $$
$$ \begin{align} \widehat{\mathscr{X}}(\alpha)_{i_{1}\dots i_{k}} = \tfrac{1}{k}\sum_{r \neq s}\mathscr{X}^{p}{}_{i_{r}i_{s}}{}^{q}\alpha_{i_{1}\dots i_{r-1}pi_{r+1}\dots i_{s-1} q i_{s+1}\dots i_{k}} \end{align} $$commutes with the action of ![]() $S_{k}$ on
$S_{k}$ on ![]() $\otimes ^{k}\mathbb {V}^{\ast }$ and so preserves the type of tensors; is
$\otimes ^{k}\mathbb {V}^{\ast }$ and so preserves the type of tensors; is ![]() $O(h)$-equivariant, meaning
$O(h)$-equivariant, meaning 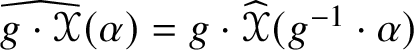 $\widehat {g \cdot \mathscr {X}}(\alpha ) = g\cdot \widehat {\mathscr {X}}(g^{-1}\cdot \alpha )$ for all
$\widehat {g \cdot \mathscr {X}}(\alpha ) = g\cdot \widehat {\mathscr {X}}(g^{-1}\cdot \alpha )$ for all ![]() $\alpha \in \otimes ^{k}\mathbb {V}^{\ast }$ and
$\alpha \in \otimes ^{k}\mathbb {V}^{\ast }$ and ![]() $g \in O(h)$; and has image in the self-adjoint endomorphisms, meaning
$g \in O(h)$; and has image in the self-adjoint endomorphisms, meaning 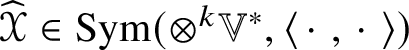 $\widehat {\mathscr {X}} \in \operatorname {Sym}(\otimes ^{k}\mathbb {V}^{\ast }, \langle \,\cdot \,\,, \,\cdot \,\, \rangle )$ for all
$\widehat {\mathscr {X}} \in \operatorname {Sym}(\otimes ^{k}\mathbb {V}^{\ast }, \langle \,\cdot \,\,, \,\cdot \,\, \rangle )$ for all ![]() $\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$.
$\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$.
Proof. That ![]() $\widehat {\mathscr {X}}$ preserves the type of tensors follows from
$\widehat {\mathscr {X}}$ preserves the type of tensors follows from  $\widehat {\mathscr {X}}(\sigma \cdot \alpha ) = \sigma \cdot \widehat {\mathscr {X}}(\alpha )$ for
$\widehat {\mathscr {X}}(\sigma \cdot \alpha ) = \sigma \cdot \widehat {\mathscr {X}}(\alpha )$ for ![]() $\sigma \in S_{k}$ and
$\sigma \in S_{k}$ and ![]() $\alpha \in \otimes ^{k}\mathbb {V}^{\ast }$. This is immediate from the definition (4.4) and the symmetries of
$\alpha \in \otimes ^{k}\mathbb {V}^{\ast }$. This is immediate from the definition (4.4) and the symmetries of ![]() $\mathscr {X}_{ijkl}$. The relation
$\mathscr {X}_{ijkl}$. The relation 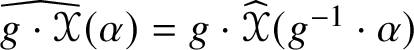 $\widehat {g \cdot \mathscr {X}}(\alpha ) = g\cdot \widehat {\mathscr {X}}(g^{-1}\cdot \alpha )$ likewise follows from a straightforward computation (for this relation to hold it is necessary that g be orthogonal because the metric is used in (4.4) where indices are contracted). It follows from (4.4) that
$\widehat {g \cdot \mathscr {X}}(\alpha ) = g\cdot \widehat {\mathscr {X}}(g^{-1}\cdot \alpha )$ likewise follows from a straightforward computation (for this relation to hold it is necessary that g be orthogonal because the metric is used in (4.4) where indices are contracted). It follows from (4.4) that
 $$ \begin{align} \begin{split} \langle \widehat{\mathscr{X}}(\alpha), \beta \rangle = \langle \mathscr{X}, \varrho(\alpha, \beta)\rangle \end{split} \end{align} $$
$$ \begin{align} \begin{split} \langle \widehat{\mathscr{X}}(\alpha), \beta \rangle = \langle \mathscr{X}, \varrho(\alpha, \beta)\rangle \end{split} \end{align} $$where ![]() $\varrho (\alpha , \beta )$ is as in Lemma 4.1. By Lemma 4.1,
$\varrho (\alpha , \beta )$ is as in Lemma 4.1. By Lemma 4.1, ![]() $\varrho (\alpha , \beta )$ is symmetric in
$\varrho (\alpha , \beta )$ is symmetric in ![]() $\alpha $ and
$\alpha $ and ![]() $\beta $ and by (4.5) this implies that
$\beta $ and by (4.5) this implies that 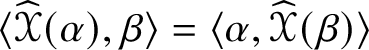 $\langle \widehat {\mathscr {X}}(\alpha ), \beta \rangle = \langle \alpha , \widehat {\mathscr {X}}(\beta )\rangle $ for all
$\langle \widehat {\mathscr {X}}(\alpha ), \beta \rangle = \langle \alpha , \widehat {\mathscr {X}}(\beta )\rangle $ for all ![]() $\alpha , \beta \in \otimes ^{k}\mathbb {V}^{\ast }$, so
$\alpha , \beta \in \otimes ^{k}\mathbb {V}^{\ast }$, so ![]() $\widehat {\mathscr {X}}$ is self-adjoint.
$\widehat {\mathscr {X}}$ is self-adjoint.
When it is known that ![]() $\widehat {\mathscr {X}}$ preserves a subspace
$\widehat {\mathscr {X}}$ preserves a subspace ![]() $\mathbb {W} \subset \otimes ^{k}\mathbb {V}^{\ast }$,
$\mathbb {W} \subset \otimes ^{k}\mathbb {V}^{\ast }$, ![]() $\widehat {\mathscr {X}}_{\mathbb {W}}$ is written instead of
$\widehat {\mathscr {X}}_{\mathbb {W}}$ is written instead of ![]() $\widehat {\mathscr {X}}$ when helpful for clarity. By Lemma 4.2, for
$\widehat {\mathscr {X}}$ when helpful for clarity. By Lemma 4.2, for ![]() $\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$ and
$\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$ and ![]() $k \geq 2$,
$k \geq 2$, ![]() $\widehat {\mathscr {X}}$ preserves
$\widehat {\mathscr {X}}$ preserves ![]() ${\bigwedge }^{k}\mathbb {V}^{\ast }$ and
${\bigwedge }^{k}\mathbb {V}^{\ast }$ and ![]() $S^{k}\mathbb {V}^{\ast }$, so
$S^{k}\mathbb {V}^{\ast }$, so  $\widehat {\mathscr {X}}_{{\textstyle \wedge }^{k}\mathbb {V}^{\ast }} \in \operatorname {Sym}({\bigwedge }^{k}\mathbb {V}^{\ast })$ and
$\widehat {\mathscr {X}}_{{\textstyle \wedge }^{k}\mathbb {V}^{\ast }} \in \operatorname {Sym}({\bigwedge }^{k}\mathbb {V}^{\ast })$ and 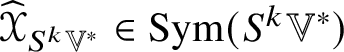 $\widehat {\mathscr {X}}_{S^{k}\mathbb {V}^{\ast }} \in \operatorname {Sym}(S^{k}\mathbb {V}^{\ast })$ are written for the restrictions of
$\widehat {\mathscr {X}}_{S^{k}\mathbb {V}^{\ast }} \in \operatorname {Sym}(S^{k}\mathbb {V}^{\ast })$ are written for the restrictions of ![]() $\widehat {\mathscr {X}}$ to
$\widehat {\mathscr {X}}$ to ![]() ${\bigwedge }^{k}\mathbb {V}^{\ast }, S^{k}\mathbb {V}^{\ast } \subset \otimes ^{k}\mathbb {V}^{\ast }$. By Lemma 4.2,
${\bigwedge }^{k}\mathbb {V}^{\ast }, S^{k}\mathbb {V}^{\ast } \subset \otimes ^{k}\mathbb {V}^{\ast }$. By Lemma 4.2, 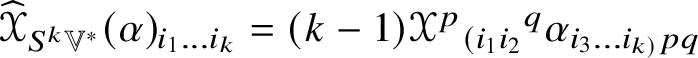 $\widehat {\mathscr {X}}_{S^{k}\mathbb {V}^{\ast }}(\alpha )_{i_{1}\dots i_{k}} = (k-1)\mathscr {X}^{p}{}_{(i_{1}i_{2}}{}^{q}\alpha _{i_{3}\dots i_{k)}pq}$ for
$\widehat {\mathscr {X}}_{S^{k}\mathbb {V}^{\ast }}(\alpha )_{i_{1}\dots i_{k}} = (k-1)\mathscr {X}^{p}{}_{(i_{1}i_{2}}{}^{q}\alpha _{i_{3}\dots i_{k)}pq}$ for ![]() $\alpha \in S^{k}\mathbb {V}^{\ast }$ and
$\alpha \in S^{k}\mathbb {V}^{\ast }$ and 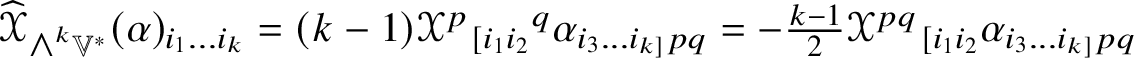 $\widehat {\mathscr {X}}_{{\textstyle \wedge }^{k}\mathbb {V}^{\ast }}(\alpha )_{i_{1}\dots i_{k}} = (k-1)\mathscr {X}^{p}{}_{[i_{1}i_{2}}{}^{q}\alpha _{i_{3}\dots i_{k]}pq} = -\tfrac {k-1}{2}\mathscr {X}^{pq}{}_{[i_{1}i_{2}}\alpha _{i_{3}\dots i_{k]}pq}$ for
$\widehat {\mathscr {X}}_{{\textstyle \wedge }^{k}\mathbb {V}^{\ast }}(\alpha )_{i_{1}\dots i_{k}} = (k-1)\mathscr {X}^{p}{}_{[i_{1}i_{2}}{}^{q}\alpha _{i_{3}\dots i_{k]}pq} = -\tfrac {k-1}{2}\mathscr {X}^{pq}{}_{[i_{1}i_{2}}\alpha _{i_{3}\dots i_{k]}pq}$ for ![]() $\alpha \in {\bigwedge }^{k}\mathbb {V}^{\ast }$. In particular, when
$\alpha \in {\bigwedge }^{k}\mathbb {V}^{\ast }$. In particular, when ![]() $k = 2$,
$k = 2$, 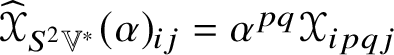 $\widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}(\alpha )_{ij} = \alpha ^{pq}\mathscr {X}_{ipqj}$ and
$\widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}(\alpha )_{ij} = \alpha ^{pq}\mathscr {X}_{ipqj}$ and 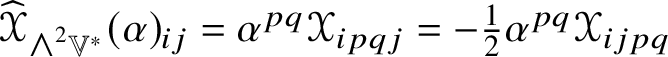 $\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\alpha )_{ij} = \alpha ^{pq}\mathscr {X}_{ipqj} = -\tfrac {1}{2}\alpha ^{pq}\mathscr {X}_{ijpq}$. For example,
$\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\alpha )_{ij} = \alpha ^{pq}\mathscr {X}_{ipqj} = -\tfrac {1}{2}\alpha ^{pq}\mathscr {X}_{ijpq}$. For example, 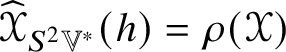 $\widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}(h) = \operatorname {\rho }(\mathscr {X})$. For
$\widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}(h) = \operatorname {\rho }(\mathscr {X})$. For ![]() $\sigma _{ij} \in \otimes ^{2}\mathbb {V}^{\ast }$, write
$\sigma _{ij} \in \otimes ^{2}\mathbb {V}^{\ast }$, write ![]() $(\mathsf {Sym}\, \sigma )_{ij} = \sigma _{(ij)}$ and
$(\mathsf {Sym}\, \sigma )_{ij} = \sigma _{(ij)}$ and ![]() $(\mathsf {Skew}\,\sigma )_{ij} = \sigma _{[ij]}$. For
$(\mathsf {Skew}\,\sigma )_{ij} = \sigma _{[ij]}$. For ![]() $\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$, by Lemma 4.2,
$\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$, by Lemma 4.2,  $\widehat {\mathscr {X}}_{\otimes ^{2}\mathbb {V}^{\ast }}(\sigma )= \widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}(\mathsf {Sym}\, \sigma ) + \widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\mathsf {Skew}\, \sigma )$. This means that if
$\widehat {\mathscr {X}}_{\otimes ^{2}\mathbb {V}^{\ast }}(\sigma )= \widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}(\mathsf {Sym}\, \sigma ) + \widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\mathsf {Skew}\, \sigma )$. This means that if ![]() $\otimes ^{2}\mathbb {V}^{\ast }$ is regarded as the orthogonal direct sum
$\otimes ^{2}\mathbb {V}^{\ast }$ is regarded as the orthogonal direct sum ![]() $S^{2}\mathbb {V}^{\ast } \oplus {\bigwedge }^{2}\mathbb {V}^{\ast }$ via
$S^{2}\mathbb {V}^{\ast } \oplus {\bigwedge }^{2}\mathbb {V}^{\ast }$ via ![]() $\sigma _{ij} = \sigma _{(ij)} + \sigma _{[ij]}$, then
$\sigma _{ij} = \sigma _{(ij)} + \sigma _{[ij]}$, then 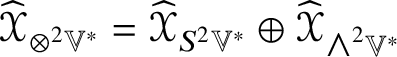 $\widehat {\mathscr {X}}_{\otimes ^{2}\mathbb {V}^{\ast }} = \widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}\oplus \widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ is an orthogonal direct sum too.
$\widehat {\mathscr {X}}_{\otimes ^{2}\mathbb {V}^{\ast }} = \widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}\oplus \widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ is an orthogonal direct sum too.
Example 4.3. Because ![]() satisfies
satisfies ![]() for
for ![]() $g \in O(h)$, when
$g \in O(h)$, when ![]() $\mathbb {W}$ is an irreducible
$\mathbb {W}$ is an irreducible ![]() $O(n)$-submodule preserved by
$O(n)$-submodule preserved by ![]() , it follows from Lemma 4.2 and the Schur Lemma that
, it follows from Lemma 4.2 and the Schur Lemma that ![]() is a constant multiple of
is a constant multiple of ![]() $\operatorname {Id}_{\mathbb {W}}$. For example,
$\operatorname {Id}_{\mathbb {W}}$. For example, 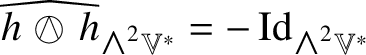 .
.
Transferring the canonical isomorphisms ![]() $\operatorname {End}({\bigwedge }^{2}\mathbb {V}^{\ast }) \simeq {\bigwedge }^{2}\mathbb {V}^{\ast } \otimes ({\bigwedge }^{2}\mathbb {V}^{\ast })^{\ast }$ and
$\operatorname {End}({\bigwedge }^{2}\mathbb {V}^{\ast }) \simeq {\bigwedge }^{2}\mathbb {V}^{\ast } \otimes ({\bigwedge }^{2}\mathbb {V}^{\ast })^{\ast }$ and ![]() $\operatorname {End}(S^{2}\mathbb {V}^{\ast }) \simeq S^{2}\mathbb {V}^{\ast } \otimes (S^{2}\mathbb {V}^{\ast })^{\ast }$ via metric duality yields linear isomorphisms
$\operatorname {End}(S^{2}\mathbb {V}^{\ast }) \simeq S^{2}\mathbb {V}^{\ast } \otimes (S^{2}\mathbb {V}^{\ast })^{\ast }$ via metric duality yields linear isomorphisms
 $$ \begin{align} \begin{split} &\sharp:\otimes^{2}({\textstyle\bigwedge}^{2}\mathbb{V}^{\ast}) = \{\Psi_{ijkl} \in \otimes^{4}\mathbb{V}^{\ast}: \Psi_{ijkl} = \Psi_{[ij]kl} = \Psi_{ij[kl]}\} \to \operatorname{End}({\textstyle\bigwedge}^{2}\mathbb{V}^{\ast}),\\ &\sharp:\otimes^{2}(S^{2}\mathbb{V}^{\ast}) = \{\Phi_{ijkl} \in \otimes^{4}\mathbb{V}^{\ast}: \Phi_{ijkl} = \Phi_{(ij)kl} = \Phi_{ij(kl)}\} \to {\operatorname{End}}(S^{2}\mathbb{V}^{\ast}), \end{split} \end{align} $$
$$ \begin{align} \begin{split} &\sharp:\otimes^{2}({\textstyle\bigwedge}^{2}\mathbb{V}^{\ast}) = \{\Psi_{ijkl} \in \otimes^{4}\mathbb{V}^{\ast}: \Psi_{ijkl} = \Psi_{[ij]kl} = \Psi_{ij[kl]}\} \to \operatorname{End}({\textstyle\bigwedge}^{2}\mathbb{V}^{\ast}),\\ &\sharp:\otimes^{2}(S^{2}\mathbb{V}^{\ast}) = \{\Phi_{ijkl} \in \otimes^{4}\mathbb{V}^{\ast}: \Phi_{ijkl} = \Phi_{(ij)kl} = \Phi_{ij(kl)}\} \to {\operatorname{End}}(S^{2}\mathbb{V}^{\ast}), \end{split} \end{align} $$defined by sending ![]() $\Psi \in \otimes ^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$ to
$\Psi \in \otimes ^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$ to 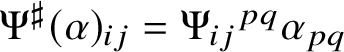 $\Psi ^{\sharp }(\alpha )_{ij} = \Psi _{ij}{}^{pq}\alpha _{pq}$ and
$\Psi ^{\sharp }(\alpha )_{ij} = \Psi _{ij}{}^{pq}\alpha _{pq}$ and ![]() $\Phi \in \otimes ^{2}(S^{2}\mathbb {V}^{\ast }) $ to
$\Phi \in \otimes ^{2}(S^{2}\mathbb {V}^{\ast }) $ to  $\Phi ^{\sharp }(\sigma )_{ij} = \Phi _{ij}{}^{pq}\sigma _{pq}$. Note that, for
$\Phi ^{\sharp }(\sigma )_{ij} = \Phi _{ij}{}^{pq}\sigma _{pq}$. Note that, for ![]() $\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$, the tensor identified in this way with
$\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$, the tensor identified in this way with 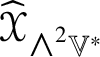 $\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ is
$\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ is 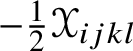 $-\tfrac {1}{2}\mathscr {X}_{ijkl}$. Said otherwise, for
$-\tfrac {1}{2}\mathscr {X}_{ijkl}$. Said otherwise, for ![]() $\mathscr {X}$ viewed as an element of
$\mathscr {X}$ viewed as an element of ![]() $S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$,
$S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$, 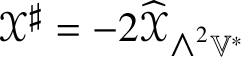 $\mathscr {X}^{\sharp } = -2\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$.
$\mathscr {X}^{\sharp } = -2\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$.
Lemma 4.4. Let ![]() $(\mathbb {V},h)$ be a Euclidean vector space. For
$(\mathbb {V},h)$ be a Euclidean vector space. For ![]() $\Psi \in \otimes ^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$ and
$\Psi \in \otimes ^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$ and ![]() $\Phi \in \otimes ^{2}(S^{2}\mathbb {V}^{\ast })$,
$\Phi \in \otimes ^{2}(S^{2}\mathbb {V}^{\ast })$, 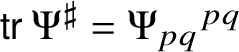 $\operatorname {\mathsf {tr}} \Psi ^{\sharp } = \Psi _{pq}{}^{pq}$ and
$\operatorname {\mathsf {tr}} \Psi ^{\sharp } = \Psi _{pq}{}^{pq}$ and 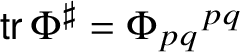 $\operatorname {\mathsf {tr}} \Phi ^{\sharp } = \Phi _{pq}{}^{pq}$.
$\operatorname {\mathsf {tr}} \Phi ^{\sharp } = \Phi _{pq}{}^{pq}$.
Proof. For an orthonormal basis  $\{E^{(1)}_{i}, \dots , E^{(n)}_{i}\}$ of
$\{E^{(1)}_{i}, \dots , E^{(n)}_{i}\}$ of ![]() $\mathbb {V}^{\ast }$,
$\mathbb {V}^{\ast }$, 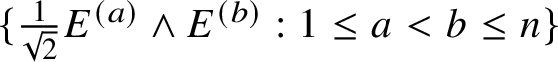 $\{\tfrac {1}{\sqrt {2}} E^{(a)}\wedge E^{(b)}: 1 \leq a < b \leq n\}$ is an orthonormal basis of
$\{\tfrac {1}{\sqrt {2}} E^{(a)}\wedge E^{(b)}: 1 \leq a < b \leq n\}$ is an orthonormal basis of ![]() ${\bigwedge }^{2}\mathbb {V}^{\ast }$ and
${\bigwedge }^{2}\mathbb {V}^{\ast }$ and ![]() $\{\sqrt {2} E^{(a)}\odot E^{(b)} : 1 \leq a < b \leq n\}\cup \{E^{(a)}\odot E^{(a)}:1 \leq a \leq n\}$ is an orthonormal basis of
$\{\sqrt {2} E^{(a)}\odot E^{(b)} : 1 \leq a < b \leq n\}\cup \{E^{(a)}\odot E^{(a)}:1 \leq a \leq n\}$ is an orthonormal basis of ![]() $S^{2}\mathbb {V}^{\ast }$, so
$S^{2}\mathbb {V}^{\ast }$, so
 $$ \begin{align} \begin{aligned} \operatorname{\mathsf{tr}} \Psi^{\sharp} & = \tfrac{1}{2}\sum_{1 \leq a < b \leq n}\langle\Psi^{\sharp}(E^{(a)}\wedge E^{(b)}), E^{(a)}\wedge E^{(b)}\rangle \\ &= \sum_{a = 1}^{n}\sum_{b = 1}^{n}\Psi^{ijkl}E^{(a)}_{i}E^{(b)}_{j}E^{(a)}_{k}E^{(b)}_{l} = \Psi_{pq}{}^{pq},\\ \operatorname{\mathsf{tr}} \Phi^{\sharp} & = 2\sum_{1 \leq a < b \leq n}\langle\Phi^{\sharp}(E^{(a)}\odot E^{(b)}), E^{(a)}\odot E^{(b)}\rangle + \sum_{1 \leq a \leq n}\langle\Phi^{\sharp}(E^{(a)}\odot E^{(a)}), E^{(a)}\odot E^{(a)}\rangle \\ &= \sum_{a = 1}^{n}\sum_{b = 1}^{n}\Phi^{ijkl}E^{(a)}_{i}E^{(b)}_{j}E^{(a)}_{k}E^{(b)}_{l} = \Phi_{pq}{}^{pq}. \end{aligned} \\[-2.2pc] \nonumber \end{align} $$
$$ \begin{align} \begin{aligned} \operatorname{\mathsf{tr}} \Psi^{\sharp} & = \tfrac{1}{2}\sum_{1 \leq a < b \leq n}\langle\Psi^{\sharp}(E^{(a)}\wedge E^{(b)}), E^{(a)}\wedge E^{(b)}\rangle \\ &= \sum_{a = 1}^{n}\sum_{b = 1}^{n}\Psi^{ijkl}E^{(a)}_{i}E^{(b)}_{j}E^{(a)}_{k}E^{(b)}_{l} = \Psi_{pq}{}^{pq},\\ \operatorname{\mathsf{tr}} \Phi^{\sharp} & = 2\sum_{1 \leq a < b \leq n}\langle\Phi^{\sharp}(E^{(a)}\odot E^{(b)}), E^{(a)}\odot E^{(b)}\rangle + \sum_{1 \leq a \leq n}\langle\Phi^{\sharp}(E^{(a)}\odot E^{(a)}), E^{(a)}\odot E^{(a)}\rangle \\ &= \sum_{a = 1}^{n}\sum_{b = 1}^{n}\Phi^{ijkl}E^{(a)}_{i}E^{(b)}_{j}E^{(a)}_{k}E^{(b)}_{l} = \Phi_{pq}{}^{pq}. \end{aligned} \\[-2.2pc] \nonumber \end{align} $$ For example, Lemma 4.4 implies that 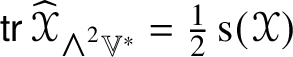 $\operatorname {\mathsf {tr}}\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} = \tfrac {1}{2}\operatorname {s}(\mathscr {X})$ for
$\operatorname {\mathsf {tr}}\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} = \tfrac {1}{2}\operatorname {s}(\mathscr {X})$ for ![]() $\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$.
$\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$.
When 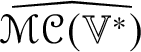 $\widehat {\mathscr {MC}(\mathbb {V}^{\ast })}$ preserves
$\widehat {\mathscr {MC}(\mathbb {V}^{\ast })}$ preserves ![]() $\mathbb {W} \subset \otimes ^{k}\mathbb {V}^{\ast }$, Lemma 4.2 does not affirm that the linear map
$\mathbb {W} \subset \otimes ^{k}\mathbb {V}^{\ast }$, Lemma 4.2 does not affirm that the linear map ![]() $\mathscr {X} \to \widehat {\mathscr {X}}_{\mathbb {W}}$ is injective. From (4.5) it is apparent that this is true if and only if
$\mathscr {X} \to \widehat {\mathscr {X}}_{\mathbb {W}}$ is injective. From (4.5) it is apparent that this is true if and only if ![]() $\{\varrho (\alpha , \beta ): \alpha , \beta \in \mathbb {W}\}$ spans
$\{\varrho (\alpha , \beta ): \alpha , \beta \in \mathbb {W}\}$ spans ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$. Corollary 4.5 shows that
$\mathscr {MC}(\mathbb {V}^{\ast })$. Corollary 4.5 shows that 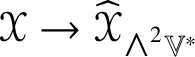 $\mathscr {X} \to \widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ and
$\mathscr {X} \to \widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ and 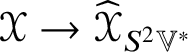 $\mathscr {X} \to \widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}$ are injective. It is used in the proof of Theorem 1.5. Note that viewing
$\mathscr {X} \to \widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}$ are injective. It is used in the proof of Theorem 1.5. Note that viewing ![]() $\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$ as an element of
$\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$ as an element of ![]() $\mathcal {T}(S^{2}(S^{2}\mathbb {V}^{\ast }))$ yields
$\mathcal {T}(S^{2}(S^{2}\mathbb {V}^{\ast }))$ yields 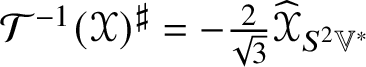 $\mathcal {T}^{-1}(\mathscr {X})^{\sharp } = -\tfrac {2}{\sqrt {3}}\widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}$.
$\mathcal {T}^{-1}(\mathscr {X})^{\sharp } = -\tfrac {2}{\sqrt {3}}\widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}$.
Corollary 4.5. Let ![]() $(\mathbb {V},h)$ be an n-dimensional Euclidean vector space. For
$(\mathbb {V},h)$ be an n-dimensional Euclidean vector space. For ![]() $\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$,
$\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$,
 $$ \begin{align} &\operatorname{\mathsf{tr}}(\widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}) = \tfrac{1}{4}\langle \mathscr{X}, \mathscr{Y}\rangle, && \operatorname{\mathsf{tr}}(\widehat{\mathscr{X}}_{S^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{Y}}_{S^{2}\mathbb{V}^{\ast}}) = \tfrac{3}{4}\langle \mathscr{X}, \mathscr{Y}\rangle. \end{align} $$
$$ \begin{align} &\operatorname{\mathsf{tr}}(\widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}) = \tfrac{1}{4}\langle \mathscr{X}, \mathscr{Y}\rangle, && \operatorname{\mathsf{tr}}(\widehat{\mathscr{X}}_{S^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{Y}}_{S^{2}\mathbb{V}^{\ast}}) = \tfrac{3}{4}\langle \mathscr{X}, \mathscr{Y}\rangle. \end{align} $$The ![]() $O(n)$-equivariant linear maps
$O(n)$-equivariant linear maps ![]() $\mathscr {MC}(\mathbb {V}^{\ast }) \to \operatorname {Sym}({\bigwedge }^{2}\mathbb {V}^{\ast })$,
$\mathscr {MC}(\mathbb {V}^{\ast }) \to \operatorname {Sym}({\bigwedge }^{2}\mathbb {V}^{\ast })$, ![]() $\mathscr {MC}(\mathbb {V}^{\ast }) \to \operatorname {Sym}(S^{2}\mathbb {V}^{\ast })$, and
$\mathscr {MC}(\mathbb {V}^{\ast }) \to \operatorname {Sym}(S^{2}\mathbb {V}^{\ast })$, and ![]() $\mathscr {MC}(\mathbb {V}^{\ast }) \to \operatorname {Sym}(\otimes ^{2}\mathbb {V}^{\ast })$ given by
$\mathscr {MC}(\mathbb {V}^{\ast }) \to \operatorname {Sym}(\otimes ^{2}\mathbb {V}^{\ast })$ given by  $\mathscr {X} \to 2\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} = -\mathscr {X}^{\sharp }$,
$\mathscr {X} \to 2\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} = -\mathscr {X}^{\sharp }$, 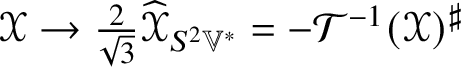 $\mathscr {X} \to \tfrac {2}{\sqrt {3}}\widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }} = - \mathcal {T}^{-1}(\mathscr {X})^{\sharp }$, and
$\mathscr {X} \to \tfrac {2}{\sqrt {3}}\widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }} = - \mathcal {T}^{-1}(\mathscr {X})^{\sharp }$, and 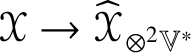 $\mathscr {X} \to \widehat {\mathscr {X}}_{\otimes ^{2}\mathbb {V}^{\ast }}$ are isometric with respect to the trace-norms on
$\mathscr {X} \to \widehat {\mathscr {X}}_{\otimes ^{2}\mathbb {V}^{\ast }}$ are isometric with respect to the trace-norms on ![]() $\operatorname {Sym}({\bigwedge }^{2}\mathbb {V}^{\ast })$,
$\operatorname {Sym}({\bigwedge }^{2}\mathbb {V}^{\ast })$, ![]() $\operatorname {Sym}(S^{2}\mathbb {V}^{\ast })$, and
$\operatorname {Sym}(S^{2}\mathbb {V}^{\ast })$, and ![]() $\operatorname {Sym}(\otimes ^{2}\mathbb {V}^{\ast })$ and injective.
$\operatorname {Sym}(\otimes ^{2}\mathbb {V}^{\ast })$ and injective.
Proof. Via ![]() $\sharp $, the endomorphisms
$\sharp $, the endomorphisms 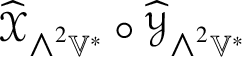 $\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} \circ \widehat {\mathscr {Y}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ and
$\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} \circ \widehat {\mathscr {Y}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ and 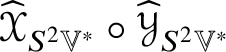 $\widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }} \circ \widehat {\mathscr {Y}}_{S^{2}\mathbb {V}^{\ast }}$ are identified with the tensors
$\widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }} \circ \widehat {\mathscr {Y}}_{S^{2}\mathbb {V}^{\ast }}$ are identified with the tensors 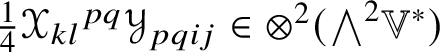 $\tfrac {1}{4}\mathscr {X}_{kl}{}^{pq}\mathscr {Y}_{pqij} \in \otimes ^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$ and
$\tfrac {1}{4}\mathscr {X}_{kl}{}^{pq}\mathscr {Y}_{pqij} \in \otimes ^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$ and 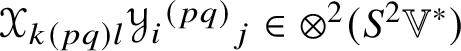 $\mathscr {X}_{k(pq)l}\mathscr {Y}_{i}{}^{(pq)}{}_{j} \in \otimes ^{2}(S^{2}\mathbb {V}^{\ast })$, so (4.8) follows from Lemma 4.4 and
$\mathscr {X}_{k(pq)l}\mathscr {Y}_{i}{}^{(pq)}{}_{j} \in \otimes ^{2}(S^{2}\mathbb {V}^{\ast })$, so (4.8) follows from Lemma 4.4 and 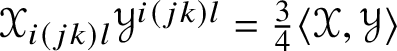 $\mathscr {X}_{i(jk)l}\mathscr {Y}^{i(jk)l} = \tfrac {3}{4}\langle \mathscr {X}, \mathscr {Y}\rangle $. The injectivity follows from the nondegeneracy of the pairing
$\mathscr {X}_{i(jk)l}\mathscr {Y}^{i(jk)l} = \tfrac {3}{4}\langle \mathscr {X}, \mathscr {Y}\rangle $. The injectivity follows from the nondegeneracy of the pairing ![]() $\langle \,\cdot \,\,, \,\cdot \,\, \rangle $.
$\langle \,\cdot \,\,, \,\cdot \,\, \rangle $.
5 Algebra structures on the space of metric curvature tensors
This section defines the multiplication ![]() $\ast $ and derives its basic properties.
$\ast $ and derives its basic properties.
The injectivity of ![]() $\widehat {\,\cdot \,\,}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ and
$\widehat {\,\cdot \,\,}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ and ![]() $\widehat {\,\cdot \,\,}_{S^{2}\mathbb {V}^{\ast }}$ shown in Corollary 4.5 means that commutative algebra structures
$\widehat {\,\cdot \,\,}_{S^{2}\mathbb {V}^{\ast }}$ shown in Corollary 4.5 means that commutative algebra structures ![]() $\ast _{A}$ and
$\ast _{A}$ and ![]() $\ast _{S}$ on
$\ast _{S}$ on ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$ can be constructed as follows. By the injectivity there are unique
$\mathscr {MC}(\mathbb {V}^{\ast })$ can be constructed as follows. By the injectivity there are unique ![]() $\mathscr {X} \ast _{A} \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$ and
$\mathscr {X} \ast _{A} \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$ and ![]() $\mathscr {X} \ast _{S} \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$ such that
$\mathscr {X} \ast _{S} \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$ such that 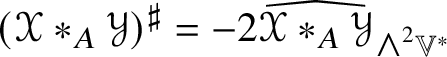 $(\mathscr {X}\ast _{A} \mathscr {Y})^{\sharp } = -2\widehat {\mathscr {X} \ast _{A} \mathscr {Y} }_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ equals the orthogonal projection on
$(\mathscr {X}\ast _{A} \mathscr {Y})^{\sharp } = -2\widehat {\mathscr {X} \ast _{A} \mathscr {Y} }_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ equals the orthogonal projection on 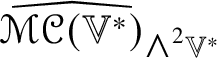 $\widehat {\mathscr {MC}(\mathbb {V}^{\ast })}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ of the Jordan product
$\widehat {\mathscr {MC}(\mathbb {V}^{\ast })}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ of the Jordan product 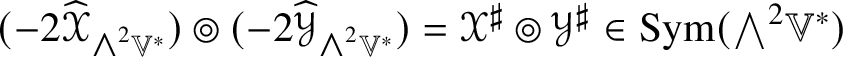 $(-2\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }})\circledcirc (-2\widehat {\mathscr {Y}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}) = \mathscr {X}^{\sharp }\circledcirc \mathscr {Y}^{\sharp }\in \operatorname {Sym}({\bigwedge }^{2}\mathbb {V}^{\ast }) $ and
$(-2\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }})\circledcirc (-2\widehat {\mathscr {Y}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}) = \mathscr {X}^{\sharp }\circledcirc \mathscr {Y}^{\sharp }\in \operatorname {Sym}({\bigwedge }^{2}\mathbb {V}^{\ast }) $ and  $\mathcal {T}^{-1}(\mathscr {X}\ast _{S} \mathscr {Y})^{\sharp } = -\tfrac {2}{\sqrt {3}}\widehat {\mathscr {X} \ast _{S} \mathscr {Y} }_{S^{2}\mathbb {V}^{\ast }}$ equals the orthogonal projection on
$\mathcal {T}^{-1}(\mathscr {X}\ast _{S} \mathscr {Y})^{\sharp } = -\tfrac {2}{\sqrt {3}}\widehat {\mathscr {X} \ast _{S} \mathscr {Y} }_{S^{2}\mathbb {V}^{\ast }}$ equals the orthogonal projection on 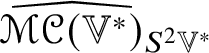 $\widehat {\mathscr {MC}(\mathbb {V}^{\ast })}_{S^{2}\mathbb {V}^{\ast }}$ of the Jordan product
$\widehat {\mathscr {MC}(\mathbb {V}^{\ast })}_{S^{2}\mathbb {V}^{\ast }}$ of the Jordan product 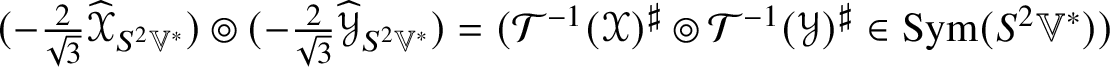 $(-\tfrac {2}{\sqrt {3}}\widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }})\circledcirc (-\tfrac {2}{\sqrt {3}}\widehat {\mathscr {Y}}_{S^{2}\mathbb {V}^{\ast }}) = (\mathcal {T}^{-1}(\mathscr {X})^{\sharp }\circledcirc \mathcal {T}^{-1}(\mathscr {Y})^{\sharp } \in \operatorname {Sym}(S^{2}\mathbb {V}^{\ast }))$. More precisely:
$(-\tfrac {2}{\sqrt {3}}\widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }})\circledcirc (-\tfrac {2}{\sqrt {3}}\widehat {\mathscr {Y}}_{S^{2}\mathbb {V}^{\ast }}) = (\mathcal {T}^{-1}(\mathscr {X})^{\sharp }\circledcirc \mathcal {T}^{-1}(\mathscr {Y})^{\sharp } \in \operatorname {Sym}(S^{2}\mathbb {V}^{\ast }))$. More precisely:
 $$ \begin{align} &\mathscr{X}\ast_{A} \mathscr{Y} = -2\mathscr{M}\left(\left(\widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\right)^{\flat}\right),&& &\mathscr{X}\ast_{S} \mathscr{Y} = -\tfrac{2}{\sqrt{3}}\mathcal{T}\circ \mathscr{S}\left(\left(\widehat{\mathscr{X}}_{S^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{S^{2}\mathbb{V}^{\ast}}\right)^{\flat}\right), \end{align} $$
$$ \begin{align} &\mathscr{X}\ast_{A} \mathscr{Y} = -2\mathscr{M}\left(\left(\widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\right)^{\flat}\right),&& &\mathscr{X}\ast_{S} \mathscr{Y} = -\tfrac{2}{\sqrt{3}}\mathcal{T}\circ \mathscr{S}\left(\left(\widehat{\mathscr{X}}_{S^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{S^{2}\mathbb{V}^{\ast}}\right)^{\flat}\right), \end{align} $$where ![]() $\flat $ is the inverse of
$\flat $ is the inverse of ![]() $\sharp $.
$\sharp $.
Lemma 5.1. Let ![]() $(\mathbb {V}, h)$ be a metric vector space. For
$(\mathbb {V}, h)$ be a metric vector space. For ![]() $\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$, the commutative multiplications
$\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$, the commutative multiplications ![]() $\ast _{A}$ and
$\ast _{A}$ and ![]() $\ast _{S}$ on
$\ast _{S}$ on ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$ are given by
$\mathscr {MC}(\mathbb {V}^{\ast })$ are given by
 $$ \begin{align} (\mathscr{X} \ast_{A} \mathscr{Y})_{ijkl} & =- \tfrac{1}{4}\left(\mathscr{X}_{ij}{}^{pq}\mathscr{Y}_{klpq} + \mathscr{Y}_{ij}{}^{pq}\mathscr{X}_{klpq} - 2\mathscr{X}_{[ij}{}^{pq}\mathscr{Y}_{kl]pq}\right), \end{align} $$
$$ \begin{align} (\mathscr{X} \ast_{A} \mathscr{Y})_{ijkl} & =- \tfrac{1}{4}\left(\mathscr{X}_{ij}{}^{pq}\mathscr{Y}_{klpq} + \mathscr{Y}_{ij}{}^{pq}\mathscr{X}_{klpq} - 2\mathscr{X}_{[ij}{}^{pq}\mathscr{Y}_{kl]pq}\right), \end{align} $$ $$ \begin{align} (\mathscr{X} \ast_{S} \mathscr{Y})_{ijkl} & =-\tfrac{1}{3}\left(\mathscr{X}_{k(pq)i}\mathscr{Y}_{j}{}^{(pq)}{}_{l}-\mathscr{X}_{k(pq)j}\mathscr{Y}_{i}{}^{(pq)}{}_{l} + \mathscr{X}_{j(pq)l}\mathscr{Y}_{k}{}^{(pq)}{}_{i}- \mathscr{X}_{i(pq)l}\mathscr{Y}_{k}{}^{(pq)}{}_{j}\right). \end{align} $$
$$ \begin{align} (\mathscr{X} \ast_{S} \mathscr{Y})_{ijkl} & =-\tfrac{1}{3}\left(\mathscr{X}_{k(pq)i}\mathscr{Y}_{j}{}^{(pq)}{}_{l}-\mathscr{X}_{k(pq)j}\mathscr{Y}_{i}{}^{(pq)}{}_{l} + \mathscr{X}_{j(pq)l}\mathscr{Y}_{k}{}^{(pq)}{}_{i}- \mathscr{X}_{i(pq)l}\mathscr{Y}_{k}{}^{(pq)}{}_{j}\right). \end{align} $$The Ricci and scalar traces are
 $$ \begin{align} \begin{aligned} {} &\operatorname{\rho}(\mathscr{X} \ast_{A} \mathscr{Y})_{ij} = \tfrac{1}{2}\mathscr{X}_{(i}{}^{abc}\mathscr{Y}_{j)abc}, \qquad \operatorname{s}(\mathscr{X} \ast_{A} \mathscr{Y}) = \tfrac{1}{2}\langle \mathscr{X}, \mathscr{Y}\rangle, &\\ &\operatorname{\rho}(\mathscr{X} \ast_{S} \mathscr{Y})_{ij} = -\tfrac{1}{2}\mathscr{X}_{(i}{}^{abc}\mathscr{Y}_{j)abc} + \tfrac{1}{3}\left(\widehat{\mathscr{X}}_{S^{2}\mathbb{V}^{\ast}}(\operatorname{\rho}(\mathscr{Y}))_{ij} + \widehat{\mathscr{Y}}_{S^{2}\mathbb{V}^{\ast}}(\operatorname{\rho}(\mathscr{X}))_{ij} \right), \\ &\operatorname{s}(\mathscr{X} \ast_{S} \mathscr{Y}) = -\tfrac{1}{2}\langle \mathscr{X}, \mathscr{Y}\rangle + \tfrac{2}{3}\langle \operatorname{\rho}(\mathscr{X}), \operatorname{\rho}(\mathscr{Y})\rangle. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {} &\operatorname{\rho}(\mathscr{X} \ast_{A} \mathscr{Y})_{ij} = \tfrac{1}{2}\mathscr{X}_{(i}{}^{abc}\mathscr{Y}_{j)abc}, \qquad \operatorname{s}(\mathscr{X} \ast_{A} \mathscr{Y}) = \tfrac{1}{2}\langle \mathscr{X}, \mathscr{Y}\rangle, &\\ &\operatorname{\rho}(\mathscr{X} \ast_{S} \mathscr{Y})_{ij} = -\tfrac{1}{2}\mathscr{X}_{(i}{}^{abc}\mathscr{Y}_{j)abc} + \tfrac{1}{3}\left(\widehat{\mathscr{X}}_{S^{2}\mathbb{V}^{\ast}}(\operatorname{\rho}(\mathscr{Y}))_{ij} + \widehat{\mathscr{Y}}_{S^{2}\mathbb{V}^{\ast}}(\operatorname{\rho}(\mathscr{X}))_{ij} \right), \\ &\operatorname{s}(\mathscr{X} \ast_{S} \mathscr{Y}) = -\tfrac{1}{2}\langle \mathscr{X}, \mathscr{Y}\rangle + \tfrac{2}{3}\langle \operatorname{\rho}(\mathscr{X}), \operatorname{\rho}(\mathscr{Y})\rangle. \end{aligned} \end{align} $$Proof. Each of (5.2) and (5.3) is just a matter of unraveling the notation in (5.1). Straightforward computations using (5.2) and (5.3) show (5.4).
Lemma 5.2. Let ![]() $(\mathbb {V}, h)$ be a metric vector space. For
$(\mathbb {V}, h)$ be a metric vector space. For ![]() $s, t \in \mathbb R$ and
$s, t \in \mathbb R$ and ![]() $\ast _{s, t} = s\ast _{A} + t \ast _{S}$, the commutative algebra
$\ast _{s, t} = s\ast _{A} + t \ast _{S}$, the commutative algebra ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast _{s, t})$ is metrized by
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast _{s, t})$ is metrized by ![]() $\langle \,\cdot \,\,, \,\cdot \,\,\rangle $ and
$\langle \,\cdot \,\,, \,\cdot \,\,\rangle $ and ![]() $O(h)$ acts on it by isometric algebra automorphisms.
$O(h)$ acts on it by isometric algebra automorphisms.
Proof. By (5.1), Lemma 4.5, and using  $\mathscr {Z}^{\sharp } = -2\widehat {\mathscr {Z}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ and
$\mathscr {Z}^{\sharp } = -2\widehat {\mathscr {Z}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ and 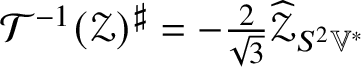 $\mathcal {T}^{-1}(\mathscr {Z})^{\sharp } = -\tfrac {2}{\sqrt {3}}\widehat {\mathscr {Z}}_{S^{2}\mathbb {V}^{\ast }}$,
$\mathcal {T}^{-1}(\mathscr {Z})^{\sharp } = -\tfrac {2}{\sqrt {3}}\widehat {\mathscr {Z}}_{S^{2}\mathbb {V}^{\ast }}$,
 $$ \begin{align} \begin{aligned} \langle \mathscr{X} \ast_{A} \mathscr{Y}, \mathscr{Z}\rangle &= -2\left\langle\mathscr{M}\left(\left(\widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\right)^{\flat}\right), \mathscr{Z} \right\rangle = 4\left\langle \left(\widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\right)^{\flat}, \widehat{\mathscr{Z}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}^{\flat} \right\rangle\\ &= 2\operatorname{\mathsf{tr}}\left(\widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{Z}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} + \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{Z}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} \right),\\ \langle \mathscr{X} \ast_{S} \mathscr{Y}, \mathscr{Z}\rangle &=-\tfrac{2}{\sqrt{3}}\left\langle\mathcal{T}\circ \mathscr{S}\left(\left(\widehat{\mathscr{X}}_{S^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{S^{2}\mathbb{V}^{\ast}}\right)^{\flat}\right), \mathscr{Z} \right\rangle = \tfrac{4}{3}\left\langle \left(\widehat{\mathscr{X}}_{S^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{S^{2}\mathbb{V}^{\ast}}\right)^{\flat}, \widehat{\mathscr{Z}}_{S^{2}\mathbb{V}^{\ast}}^{\flat} \right\rangle \\ &= \tfrac{2}{3}\operatorname{\mathsf{tr}}\left(\widehat{\mathscr{X}}_{S^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{Y}}_{S^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{Z}}_{S^{2}\mathbb{V}^{\ast}} + \widehat{\mathscr{Y}}_{S^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{X}}_{S^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{Z}}_{S^{2}\mathbb{V}^{\ast}} \right). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \langle \mathscr{X} \ast_{A} \mathscr{Y}, \mathscr{Z}\rangle &= -2\left\langle\mathscr{M}\left(\left(\widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\right)^{\flat}\right), \mathscr{Z} \right\rangle = 4\left\langle \left(\widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\right)^{\flat}, \widehat{\mathscr{Z}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}^{\flat} \right\rangle\\ &= 2\operatorname{\mathsf{tr}}\left(\widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{Z}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} + \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{Z}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} \right),\\ \langle \mathscr{X} \ast_{S} \mathscr{Y}, \mathscr{Z}\rangle &=-\tfrac{2}{\sqrt{3}}\left\langle\mathcal{T}\circ \mathscr{S}\left(\left(\widehat{\mathscr{X}}_{S^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{S^{2}\mathbb{V}^{\ast}}\right)^{\flat}\right), \mathscr{Z} \right\rangle = \tfrac{4}{3}\left\langle \left(\widehat{\mathscr{X}}_{S^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{S^{2}\mathbb{V}^{\ast}}\right)^{\flat}, \widehat{\mathscr{Z}}_{S^{2}\mathbb{V}^{\ast}}^{\flat} \right\rangle \\ &= \tfrac{2}{3}\operatorname{\mathsf{tr}}\left(\widehat{\mathscr{X}}_{S^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{Y}}_{S^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{Z}}_{S^{2}\mathbb{V}^{\ast}} + \widehat{\mathscr{Y}}_{S^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{X}}_{S^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{Z}}_{S^{2}\mathbb{V}^{\ast}} \right). \end{aligned} \end{align} $$The right-hand sides of (5.5) are completely symmetric in ![]() $\mathscr {X}$,
$\mathscr {X}$, ![]() $\mathscr {Y}$, and
$\mathscr {Y}$, and ![]() $\mathscr {Z}$, and this shows the invariance with respect to
$\mathscr {Z}$, and this shows the invariance with respect to ![]() $\langle \,\cdot \,\,, \,\cdot \,\,\rangle $ of
$\langle \,\cdot \,\,, \,\cdot \,\,\rangle $ of ![]() $\ast _{A}$ and
$\ast _{A}$ and ![]() $\ast _{S}$ and so also of any linear combination
$\ast _{S}$ and so also of any linear combination ![]() $s\ast _{A} + t \ast _{S}$. That
$s\ast _{A} + t \ast _{S}$. That ![]() $O(h)$ acts on
$O(h)$ acts on ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast _{s, t})$ by isometric algebra automorphisms follows from the manifest
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast _{s, t})$ by isometric algebra automorphisms follows from the manifest ![]() $O(h)$ invariance of the construction of
$O(h)$ invariance of the construction of ![]() $\ast _{A}$ and
$\ast _{A}$ and ![]() $\ast _{S}$.
$\ast _{S}$.
Because rescaling the multiplication of a commutative algebra yields an isomorphic algebra, the products ![]() $\ast _{s, t}$ are best viewed as parametrized by
$\ast _{s, t}$ are best viewed as parametrized by ![]() $[s:t] \in \mathbb {P}(\mathbb R)$.
$[s:t] \in \mathbb {P}(\mathbb R)$.
For ![]() $\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$ define
$\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$ define ![]() $B_{ijkl} = B(\mathscr {X}, \mathscr {Y})_{ijkl} \in S^{2}(\otimes ^{2}\mathbb {V}^{\ast })$ by
$B_{ijkl} = B(\mathscr {X}, \mathscr {Y})_{ijkl} \in S^{2}(\otimes ^{2}\mathbb {V}^{\ast })$ by
 $$ \begin{align} B(\mathscr{X}, \mathscr{Y})^{\sharp} = \widehat{\mathscr{X}}_{\otimes^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{\otimes^{2}\mathbb{V}^{\ast}} = \widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} + \widehat{\mathscr{X}}_{S^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{S^{2}\mathbb{V}^{\ast}}, \end{align} $$
$$ \begin{align} B(\mathscr{X}, \mathscr{Y})^{\sharp} = \widehat{\mathscr{X}}_{\otimes^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{\otimes^{2}\mathbb{V}^{\ast}} = \widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} + \widehat{\mathscr{X}}_{S^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{S^{2}\mathbb{V}^{\ast}}, \end{align} $$the second equality by Lemma 4.2, so that
 $$ \begin{align} B_{ijkl} = B(\mathscr{X}, \mathscr{Y})_{ijkl} &= \tfrac{1}{2}\left(\mathscr{X}_{ipjq}\mathscr{Y}_{k}{}^{p}{}_{l}{}^{q} + \mathscr{Y}_{ipjq}\mathscr{X}_{k}{}^{p}{}_{l}{}^{q} \right) = \left(\widehat{\mathscr{X}}_{\otimes^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{\otimes^{2}\mathbb{V}^{\ast}}\right)^{\flat}_{ijkl}. \end{align} $$
$$ \begin{align} B_{ijkl} = B(\mathscr{X}, \mathscr{Y})_{ijkl} &= \tfrac{1}{2}\left(\mathscr{X}_{ipjq}\mathscr{Y}_{k}{}^{p}{}_{l}{}^{q} + \mathscr{Y}_{ipjq}\mathscr{X}_{k}{}^{p}{}_{l}{}^{q} \right) = \left(\widehat{\mathscr{X}}_{\otimes^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{\otimes^{2}\mathbb{V}^{\ast}}\right)^{\flat}_{ijkl}. \end{align} $$Lemma 5.3. Let ![]() $(\mathbb {V}, h)$ be a metric vector space. For
$(\mathbb {V}, h)$ be a metric vector space. For ![]() $\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$, the commutative multiplications
$\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$, the commutative multiplications ![]() $\ast _{A}$ and
$\ast _{A}$ and ![]() $\ast _{S}$ on
$\ast _{S}$ on ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$ are given by
$\mathscr {MC}(\mathbb {V}^{\ast })$ are given by
 $$ \begin{align} (\mathscr{X} \ast_{A} \mathscr{Y})_{ijkl} & = -2(B_{[ij]kl} - B_{[ijkl]}) = -\tfrac{2}{3}\left(2B_{[ij]kl} - B_{k[ijl]} + B_{[i|k|j]l}\right), \end{align} $$
$$ \begin{align} (\mathscr{X} \ast_{A} \mathscr{Y})_{ijkl} & = -2(B_{[ij]kl} - B_{[ijkl]}) = -\tfrac{2}{3}\left(2B_{[ij]kl} - B_{k[ijl]} + B_{[i|k|j]l}\right), \end{align} $$ $$ \begin{align} (\mathscr{X} \ast_{S} \mathscr{Y})_{ijkl} & = -\tfrac{2}{3}\left(B_{k[ij]l} + B_{[i|k|j]l} \right) = -\tfrac{2}{3}\left(B_{[ij]kl} + 2B_{k[ij]l} - 3B_{[ijkl]} \right). \end{align} $$
$$ \begin{align} (\mathscr{X} \ast_{S} \mathscr{Y})_{ijkl} & = -\tfrac{2}{3}\left(B_{k[ij]l} + B_{[i|k|j]l} \right) = -\tfrac{2}{3}\left(B_{[ij]kl} + 2B_{k[ij]l} - 3B_{[ijkl]} \right). \end{align} $$Proof. That ![]() $B_{ijkl}$ is contained in
$B_{ijkl}$ is contained in ![]() $S^{2}(\otimes ^{2}\mathbb {V}^{\ast })$ is equivalent to the symmetry
$S^{2}(\otimes ^{2}\mathbb {V}^{\ast })$ is equivalent to the symmetry ![]() $B_{klij} = B_{ijkl}$, which is apparent from (5.7). There holds
$B_{klij} = B_{ijkl}$, which is apparent from (5.7). There holds
Hence, ![]() $2B_{[ij]kl} = B_{ijkl} - B_{jikl} = B_{ijkl} - B_{ijlk} = 2B_{ij[kl]}$. It follows that
$2B_{[ij]kl} = B_{ijkl} - B_{jikl} = B_{ijkl} - B_{ijlk} = 2B_{ij[kl]}$. It follows that ![]() $2B_{[ij][kl]} = B_{ij[kl]} - B_{ji[kl]} = B_{[ij]kl} - B_{[ji]kl} = 2B_{[ij]kl}$. This means that
$2B_{[ij][kl]} = B_{ij[kl]} - B_{ji[kl]} = B_{[ij]kl} - B_{[ji]kl} = 2B_{[ij]kl}$. This means that ![]() $B_{[ij]kl} = B_{[ij][kl]} = B_{ij[kl]}$ is the orthogonal projection of
$B_{[ij]kl} = B_{[ij][kl]} = B_{ij[kl]}$ is the orthogonal projection of ![]() $B_{ijkl}$ onto
$B_{ijkl}$ onto ![]() $S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$. It follows that
$S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$. It follows that ![]() $B_{ij(kl)} = B_{(ij)kl} = B_{(ij)(kl)} = B_{(kl)(ij)}$ is the orthogonal projection of
$B_{ij(kl)} = B_{(ij)kl} = B_{(ij)(kl)} = B_{(kl)(ij)}$ is the orthogonal projection of ![]() $B_{ijkl}$ onto
$B_{ijkl}$ onto ![]() $S^{2}(S^{2}\mathbb {V}^{\ast })$. From the second equality of (5.7) it follows that
$S^{2}(S^{2}\mathbb {V}^{\ast })$. From the second equality of (5.7) it follows that ![]() $(\mathscr {X} \ast _{A} \mathscr {Y})_{ijkl}$ and
$(\mathscr {X} \ast _{A} \mathscr {Y})_{ijkl}$ and ![]() $(\mathscr {X} \ast _{S} \mathscr {Y})_{ijkl}$ are given by applying
$(\mathscr {X} \ast _{S} \mathscr {Y})_{ijkl}$ are given by applying ![]() $-2\mathscr {M}$ to
$-2\mathscr {M}$ to ![]() $B_{[ij]kl}$ and
$B_{[ij]kl}$ and 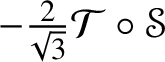 $-\tfrac {2}{\sqrt {3}} \mathcal {T}\circ \mathscr {S}$ to
$-\tfrac {2}{\sqrt {3}} \mathcal {T}\circ \mathscr {S}$ to ![]() $B_{(ij)kl}$, respectively, and doing so yields the first equalities of (5.8) and (5.9). The second equalities of (5.2) and (5.9) follow from
$B_{(ij)kl}$, respectively, and doing so yields the first equalities of (5.8) and (5.9). The second equalities of (5.2) and (5.9) follow from ![]() $3B_{[ijkl]} = B_{[ij]kl} + B_{k[ij]l} - B_{[i|k|j]l}$.
$3B_{[ijkl]} = B_{[ij]kl} + B_{k[ij]l} - B_{[i|k|j]l}$.
Since, by Lemma 4.2, the operator ![]() $\widehat {\mathscr {X}}$ preserves type, if
$\widehat {\mathscr {X}}$ preserves type, if ![]() $\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$, then
$\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$, then 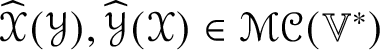 $\widehat {\mathscr {X}}(\mathscr {Y}), \widehat {\mathscr {Y}}(\mathscr {X}) \in \mathscr {MC}(\mathbb {V}^{\ast })$. Theorem 5.4 shows that, remarkably,
$\widehat {\mathscr {X}}(\mathscr {Y}), \widehat {\mathscr {Y}}(\mathscr {X}) \in \mathscr {MC}(\mathbb {V}^{\ast })$. Theorem 5.4 shows that, remarkably, 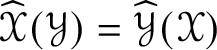 $\widehat {\mathscr {X}}(\mathscr {Y}) = \widehat {\mathscr {Y}}(\mathscr {X})$, so that a commutative multiplication of curvature tensors can be defined by
$\widehat {\mathscr {X}}(\mathscr {Y}) = \widehat {\mathscr {Y}}(\mathscr {X})$, so that a commutative multiplication of curvature tensors can be defined by 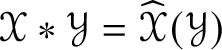 $\mathscr {X} \ast \mathscr {Y} = \widehat {\mathscr {X}}(\mathscr {Y})$, and, moreover,
$\mathscr {X} \ast \mathscr {Y} = \widehat {\mathscr {X}}(\mathscr {Y})$, and, moreover, 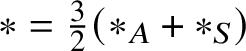 $\ast = \tfrac {3}{2}(\ast _{A} + \ast _{S})$.
$\ast = \tfrac {3}{2}(\ast _{A} + \ast _{S})$.
Theorem 5.4. Let ![]() $(\mathbb {V}, h)$ be a metric vector space. The bilinear map
$(\mathbb {V}, h)$ be a metric vector space. The bilinear map ![]() $\ast :\mathscr {MC}(\mathbb {V}^{\ast }) \times \mathscr {MC}(\mathbb {V}^{\ast }) \to \mathscr {MC}(\mathbb {V}^{\ast })$ defined by
$\ast :\mathscr {MC}(\mathbb {V}^{\ast }) \times \mathscr {MC}(\mathbb {V}^{\ast }) \to \mathscr {MC}(\mathbb {V}^{\ast })$ defined by  $\mathscr {X} \ast \mathscr {Y} =\widehat {\mathscr {X}}(\mathscr {Y})$ for
$\mathscr {X} \ast \mathscr {Y} =\widehat {\mathscr {X}}(\mathscr {Y})$ for ![]() $\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$ is
$\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$ is ![]() $O(h)$-equivariant and symmetric and so determines a commutative algebra structure
$O(h)$-equivariant and symmetric and so determines a commutative algebra structure ![]() $\ast $ on
$\ast $ on ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$ metrized by the pairing
$\mathscr {MC}(\mathbb {V}^{\ast })$ metrized by the pairing ![]() $\langle \,\cdot \,\,, \,\cdot \,\,\rangle $ given by complete contraction with h and on which
$\langle \,\cdot \,\,, \,\cdot \,\,\rangle $ given by complete contraction with h and on which ![]() $O(h)$ acts by algebra automorphisms. Moreover,
$O(h)$ acts by algebra automorphisms. Moreover, 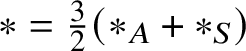 $\ast = \tfrac {3}{2}(\ast _{A} + \ast _{S})$ and
$\ast = \tfrac {3}{2}(\ast _{A} + \ast _{S})$ and ![]() $\ast $ equals that multiplication given by polarizing the quadratic term of the expression (1.2) for the evolution of the curvature tensor under the Ricci flow.
$\ast $ equals that multiplication given by polarizing the quadratic term of the expression (1.2) for the evolution of the curvature tensor under the Ricci flow.
Proof. Evaluation of 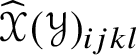 $\widehat {\mathscr {X}}(\mathscr {Y})_{ijkl}$ using (4.4) and
$\widehat {\mathscr {X}}(\mathscr {Y})_{ijkl}$ using (4.4) and ![]() $\varrho (\mathscr {X}, \mathscr {Y})_{ijkl}$ using (4.2) and (4.3) yields
$\varrho (\mathscr {X}, \mathscr {Y})_{ijkl}$ using (4.2) and (4.3) yields
 $$ \begin{align} 4\widehat{\mathscr{X}}(\mathscr{Y})_{ijkl} &= - 2\mathscr{X}_{i}{}^{p}{}_{k}{}^{q}\mathscr{Y}_{jplq}- 2\mathscr{Y}_{i}{}^{p}{}_{k}{}^{q}\mathscr{X}_{jplq} + 2\mathscr{X}_{i}{}^{p}{}_{l}{}^{q}\mathscr{Y}_{jpkq} + 2\mathscr{Y}_{i}{}^{p}{}_{k}{}^{q}\mathscr{X}_{jpkq} \nonumber\\ &\qquad - \mathscr{X}_{ij}{}^{pq}\mathscr{Y}_{pqkl} - \mathscr{X}_{kl}{}^{pq}\mathscr{Y}_{pqij} = 4\varrho(\mathscr{X}, \mathscr{Y})_{ijkl}, \end{align} $$
$$ \begin{align} 4\widehat{\mathscr{X}}(\mathscr{Y})_{ijkl} &= - 2\mathscr{X}_{i}{}^{p}{}_{k}{}^{q}\mathscr{Y}_{jplq}- 2\mathscr{Y}_{i}{}^{p}{}_{k}{}^{q}\mathscr{X}_{jplq} + 2\mathscr{X}_{i}{}^{p}{}_{l}{}^{q}\mathscr{Y}_{jpkq} + 2\mathscr{Y}_{i}{}^{p}{}_{k}{}^{q}\mathscr{X}_{jpkq} \nonumber\\ &\qquad - \mathscr{X}_{ij}{}^{pq}\mathscr{Y}_{pqkl} - \mathscr{X}_{kl}{}^{pq}\mathscr{Y}_{pqij} = 4\varrho(\mathscr{X}, \mathscr{Y})_{ijkl}, \end{align} $$which is evidently symmetric in ![]() $\mathscr {X}$ and
$\mathscr {X}$ and ![]() $\mathscr {Y}$, showing that
$\mathscr {Y}$, showing that 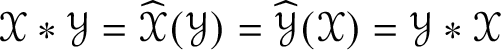 $\mathscr {X}\ast \mathscr {Y} = \widehat {\mathscr {X}}(\mathscr {Y}) = \widehat {\mathscr {Y}}(\mathscr {X})= \mathscr {Y} \ast \mathscr {X}$. By Lemma 4.2,
$\mathscr {X}\ast \mathscr {Y} = \widehat {\mathscr {X}}(\mathscr {Y}) = \widehat {\mathscr {Y}}(\mathscr {X})= \mathscr {Y} \ast \mathscr {X}$. By Lemma 4.2, ![]() $\widehat {\mathscr {Y}}$ is self-adjoint, so, for
$\widehat {\mathscr {Y}}$ is self-adjoint, so, for ![]() $\mathscr {X}, \mathscr {Y}, \mathscr {Z} \in \mathscr {MC}(\mathbb {V}^{\ast })$,
$\mathscr {X}, \mathscr {Y}, \mathscr {Z} \in \mathscr {MC}(\mathbb {V}^{\ast })$,
 $$ \begin{align} \langle \mathscr{X} &\ast \mathscr{Y}, \mathscr{Z}\rangle =\langle \widehat{\mathscr{Y}}(\mathscr{X}), \mathscr{Z}\rangle = \langle \mathscr{X}, \widehat{\mathscr{Y}}(\mathscr{Z})\rangle = \langle \mathscr{X}, \mathscr{Y} \ast \mathscr{Z}\rangle. \end{align} $$
$$ \begin{align} \langle \mathscr{X} &\ast \mathscr{Y}, \mathscr{Z}\rangle =\langle \widehat{\mathscr{Y}}(\mathscr{X}), \mathscr{Z}\rangle = \langle \mathscr{X}, \widehat{\mathscr{Y}}(\mathscr{Z})\rangle = \langle \mathscr{X}, \mathscr{Y} \ast \mathscr{Z}\rangle. \end{align} $$This shows the complete symmetry of ![]() $\langle \mathscr {X} \ast \mathscr {Y}, \mathscr {Z}\rangle $. That
$\langle \mathscr {X} \ast \mathscr {Y}, \mathscr {Z}\rangle $. That ![]() $O(h)$ acts by algebra automorphisms follows from (5.11) and the
$O(h)$ acts by algebra automorphisms follows from (5.11) and the ![]() $O(h)$-equivariance of
$O(h)$-equivariance of ![]() $\varrho $ established in Lemma 4.1.
$\varrho $ established in Lemma 4.1.
From the symmetries of ![]() $B_{ijkl} = B(\mathscr {X}, \mathscr {Y})_{ijkl}$ it follows that
$B_{ijkl} = B(\mathscr {X}, \mathscr {Y})_{ijkl}$ it follows that
 $$ \begin{align} \tfrac{1}{2}\left(\mathscr{X}_{ij}{}^{pq}\mathscr{Y}_{pqkl} \right.&\left. + \mathscr{Y}_{ij}{}^{pq}\mathscr{X}_{pqkl}\right) \nonumber\\ &= \left(\mathscr{X}_{jpiq} + \mathscr{X}_{pijq} \right)\left(\mathscr{Y}^{q}{}_{k}{}^{p}{}_{l} + \mathscr{Y}_{k}{}^{pq}{}_{l} \right) + \left(\mathscr{Y}_{jpiq} + \mathscr{Y}_{pijq} \right)\left(\mathscr{X}^{q}{}_{k}{}^{p}{}_{l} + \mathscr{X}_{k}{}^{pq}{}_{l} \right) \nonumber\\ & = B_{ijkl} + B_{jilk} - B_{ijlk} - B_{jikl} = 4B_{[ij][kl]} = 4B_{ij[kl]} = 4B_{[ij]kl}. \end{align} $$
$$ \begin{align} \tfrac{1}{2}\left(\mathscr{X}_{ij}{}^{pq}\mathscr{Y}_{pqkl} \right.&\left. + \mathscr{Y}_{ij}{}^{pq}\mathscr{X}_{pqkl}\right) \nonumber\\ &= \left(\mathscr{X}_{jpiq} + \mathscr{X}_{pijq} \right)\left(\mathscr{Y}^{q}{}_{k}{}^{p}{}_{l} + \mathscr{Y}_{k}{}^{pq}{}_{l} \right) + \left(\mathscr{Y}_{jpiq} + \mathscr{Y}_{pijq} \right)\left(\mathscr{X}^{q}{}_{k}{}^{p}{}_{l} + \mathscr{X}_{k}{}^{pq}{}_{l} \right) \nonumber\\ & = B_{ijkl} + B_{jilk} - B_{ijlk} - B_{jikl} = 4B_{[ij][kl]} = 4B_{ij[kl]} = 4B_{[ij]kl}. \end{align} $$Combining (5.11) and (5.13) shows
That 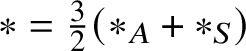 $\ast = \tfrac {3}{2}(\ast _{A} + \ast _{S})$ follows from (5.8), (5.9), and (5.14). By [Reference Hamilton18, section
$\ast = \tfrac {3}{2}(\ast _{A} + \ast _{S})$ follows from (5.8), (5.9), and (5.14). By [Reference Hamilton18, section ![]() $7$] the polarization of the quadratic term of the expression (1.2) for the evolution of the curvature tensor under the Ricci flow equals the right-hand side of (5.14).
$7$] the polarization of the quadratic term of the expression (1.2) for the evolution of the curvature tensor under the Ricci flow equals the right-hand side of (5.14).
Remark 5.5. It is not self-evident that the right-hand side of (5.14) determines an element of ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$. Here this is seen as following from the construction of
$\mathscr {MC}(\mathbb {V}^{\ast })$. Here this is seen as following from the construction of ![]() $\ast $. It also can be checked directly using the symmetries of
$\ast $. It also can be checked directly using the symmetries of ![]() $B_{ijkl}$ as in [Reference Hamilton17, Reference Hamilton18]. The invariance of
$B_{ijkl}$ as in [Reference Hamilton17, Reference Hamilton18]. The invariance of ![]() $\langle \,\cdot \,\,, \,\cdot \,\, \rangle $ with respect to
$\langle \,\cdot \,\,, \,\cdot \,\, \rangle $ with respect to ![]() $\ast $ is attributed to G. Huisken in [Reference Böhm and Wilking2]. The proof given here is conceptually different than the usual proofs by direct computation or as in [Reference Böhm and Wilking2, section
$\ast $ is attributed to G. Huisken in [Reference Böhm and Wilking2]. The proof given here is conceptually different than the usual proofs by direct computation or as in [Reference Böhm and Wilking2, section ![]() $1$].
$1$].
A metrized commutative ![]() $\mathbb R$-algebra
$\mathbb R$-algebra ![]() $(\mathbb {A}, \circ , h)$ is determined up to isometric isomorphism by the
$(\mathbb {A}, \circ , h)$ is determined up to isometric isomorphism by the ![]() $O(h)$-orbit of the associated homogeneous cubic polynomial,
$O(h)$-orbit of the associated homogeneous cubic polynomial, ![]() $P_{(\mathbb {A}, \circ )}(x)= (1/6)h(x\circ x, x)$, because P and the metric h determine the multiplication
$P_{(\mathbb {A}, \circ )}(x)= (1/6)h(x\circ x, x)$, because P and the metric h determine the multiplication ![]() $\circ $ via polarization.
$\circ $ via polarization.
Corollary 5.6. The cubic polynomial of ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ has the form
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ has the form
 $$ \begin{align} P_{(\mathscr{MC}(\mathbb{V}^{\ast}), \ast)}(\mathscr{X}) = \operatorname{\mathsf{tr}} \widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}^{3} + \tfrac{1}{3}\operatorname{\mathsf{tr}} \widehat{\mathscr{X}}_{S^{2}\mathbb{V}^{\ast}}^{3}. \end{align} $$
$$ \begin{align} P_{(\mathscr{MC}(\mathbb{V}^{\ast}), \ast)}(\mathscr{X}) = \operatorname{\mathsf{tr}} \widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}^{3} + \tfrac{1}{3}\operatorname{\mathsf{tr}} \widehat{\mathscr{X}}_{S^{2}\mathbb{V}^{\ast}}^{3}. \end{align} $$Lemma 5.7. Let ![]() $(\mathbb {V}, h)$ be a metric vector space. For
$(\mathbb {V}, h)$ be a metric vector space. For ![]() $\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$,
$\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$,
 $$ \begin{align} & \operatorname{\rho}(\mathscr{X} \ast \mathscr{Y}) = \tfrac{1}{2}\left( \widehat{\mathscr{X}}_{S^{2}\mathbb{V}^{\ast}}(\operatorname{\rho}(\mathscr{Y})) + \widehat{\mathscr{Y}}_{S^{2}\mathbb{V}^{\ast}}(\operatorname{\rho}(\mathscr{X}))\right),&& \operatorname{s}(\mathscr{X} \ast \mathscr{Y}) = \langle \operatorname{\rho}(\mathscr{X}), \operatorname{\rho}(\mathscr{Y})\rangle. \end{align} $$
$$ \begin{align} & \operatorname{\rho}(\mathscr{X} \ast \mathscr{Y}) = \tfrac{1}{2}\left( \widehat{\mathscr{X}}_{S^{2}\mathbb{V}^{\ast}}(\operatorname{\rho}(\mathscr{Y})) + \widehat{\mathscr{Y}}_{S^{2}\mathbb{V}^{\ast}}(\operatorname{\rho}(\mathscr{X}))\right),&& \operatorname{s}(\mathscr{X} \ast \mathscr{Y}) = \langle \operatorname{\rho}(\mathscr{X}), \operatorname{\rho}(\mathscr{Y})\rangle. \end{align} $$In particular, the subspace ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) = \ker \operatorname {\rho } \subset \mathscr {MC}(\mathbb {V}^{\ast })$ is a subalgebra of
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) = \ker \operatorname {\rho } \subset \mathscr {MC}(\mathbb {V}^{\ast })$ is a subalgebra of ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }),\ast )$.
$(\mathscr {MC}(\mathbb {V}^{\ast }),\ast )$.
Lemma 5.8. Let ![]() $(\mathbb {V}, h)$ be a Euclidean vector space.
$(\mathbb {V}, h)$ be a Euclidean vector space.
1. (Due to [Reference Richard32]) For all
 $\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$,
$\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$,  $\operatorname {s}(\mathscr {X}\ast \mathscr {X}) \geq 0$ with equality if and only if
$\operatorname {s}(\mathscr {X}\ast \mathscr {X}) \geq 0$ with equality if and only if  $\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$.
$\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$.2. If
 $\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$ is such that
$\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$ is such that  $\widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}$ is nonnegative, then
$\widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}$ is nonnegative, then  $\operatorname {s}((\mathscr {X} \ast \mathscr {X})\ast \mathscr {X}) \geq 0$, with equality if and only if
$\operatorname {s}((\mathscr {X} \ast \mathscr {X})\ast \mathscr {X}) \geq 0$, with equality if and only if  $\operatorname {\rho }(\mathscr {X}) \in \ker \widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}$.
$\operatorname {\rho }(\mathscr {X}) \in \ker \widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}$.3. If
 $\mathscr {Y} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, then
$\mathscr {Y} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, then  $\operatorname {s}((\mathscr {X} \ast \mathscr {Y})\ast \mathscr {Z} - \mathscr {X} \ast (\mathscr {Y} \ast \mathscr {Z})) = 0$ for all
$\operatorname {s}((\mathscr {X} \ast \mathscr {Y})\ast \mathscr {Z} - \mathscr {X} \ast (\mathscr {Y} \ast \mathscr {Z})) = 0$ for all  $\mathscr {X}, \mathscr {Z} \in \mathscr {MC}(\mathbb {V}^{\ast })$.
$\mathscr {X}, \mathscr {Z} \in \mathscr {MC}(\mathbb {V}^{\ast })$.
Proof. If ![]() $\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$ satisfies
$\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$ satisfies ![]() $\operatorname {s}(\mathscr {X} \ast \mathscr {X}) =0$, then, by (5.16),
$\operatorname {s}(\mathscr {X} \ast \mathscr {X}) =0$, then, by (5.16), ![]() $0 = \operatorname {s}(\mathscr {X} \ast \mathscr {X}) = |\operatorname {\rho }(\mathscr {X})|^{2}$, so
$0 = \operatorname {s}(\mathscr {X} \ast \mathscr {X}) = |\operatorname {\rho }(\mathscr {X})|^{2}$, so ![]() $\operatorname {\rho }(\mathscr {X}) = 0$ and
$\operatorname {\rho }(\mathscr {X}) = 0$ and ![]() $\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. By (5.16),
$\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. By (5.16), 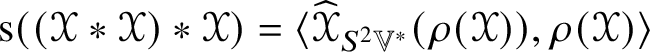 $\operatorname {s}((\mathscr {X} \ast \mathscr {X})\ast \mathscr {X}) = \langle \widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}(\operatorname {\rho }(\mathscr {X})), \operatorname {\rho }(\mathscr {X})\rangle $, from which 2 follows. From (5.16) and the self-adjointness of
$\operatorname {s}((\mathscr {X} \ast \mathscr {X})\ast \mathscr {X}) = \langle \widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}(\operatorname {\rho }(\mathscr {X})), \operatorname {\rho }(\mathscr {X})\rangle $, from which 2 follows. From (5.16) and the self-adjointness of  $\widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}$ and
$\widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}$ and 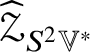 $\widehat {\mathscr {Z}}_{S^{2}\mathbb {V}^{\ast }}$ it follows that
$\widehat {\mathscr {Z}}_{S^{2}\mathbb {V}^{\ast }}$ it follows that 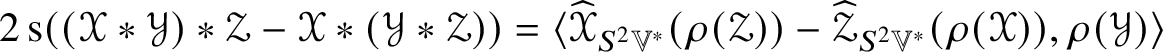 $2\operatorname {s}((\mathscr {X} \ast \mathscr {Y})\ast \mathscr {Z} - \mathscr {X} \ast (\mathscr {Y} \ast \mathscr {Z})) = \langle \widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}(\operatorname {\rho }(\mathscr {Z})) - \widehat {\mathscr {Z}}_{S^{2}\mathbb {V}^{\ast }}(\operatorname {\rho }(\mathscr {X})) , \operatorname {\rho }(\mathscr {Y})\rangle $ for all
$2\operatorname {s}((\mathscr {X} \ast \mathscr {Y})\ast \mathscr {Z} - \mathscr {X} \ast (\mathscr {Y} \ast \mathscr {Z})) = \langle \widehat {\mathscr {X}}_{S^{2}\mathbb {V}^{\ast }}(\operatorname {\rho }(\mathscr {Z})) - \widehat {\mathscr {Z}}_{S^{2}\mathbb {V}^{\ast }}(\operatorname {\rho }(\mathscr {X})) , \operatorname {\rho }(\mathscr {Y})\rangle $ for all ![]() $\mathscr {X}, \mathscr {Y}, \mathscr {Z} \in \mathscr {MC}(\mathbb {V}^{\ast })$. Claim 3 follows.
$\mathscr {X}, \mathscr {Y}, \mathscr {Z} \in \mathscr {MC}(\mathbb {V}^{\ast })$. Claim 3 follows.
In particular, Lemma 5.8 shows that, in Euclidean signature, if ![]() $\mathscr {X} \ast \mathscr {X} = 0$, then
$\mathscr {X} \ast \mathscr {X} = 0$, then ![]() $\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. That is, a square-zero element of
$\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. That is, a square-zero element of ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ must be contained in
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ must be contained in ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. The first claim of Lemma 5.8 is an example of a claim that depends on the assumption that h have definite signature. In other signatures the same proof shows only that
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. The first claim of Lemma 5.8 is an example of a claim that depends on the assumption that h have definite signature. In other signatures the same proof shows only that ![]() $\operatorname {\rho }(\mathscr {X})$ is null.
$\operatorname {\rho }(\mathscr {X})$ is null.
Lemma 5.9. Let ![]() $(\mathbb {V}, h)$ be a Euclidean vector space and let
$(\mathbb {V}, h)$ be a Euclidean vector space and let ![]() $\Pi \in \operatorname {End}(\mathbb {V})$ be the h-orthogonal projection onto the subspace
$\Pi \in \operatorname {End}(\mathbb {V})$ be the h-orthogonal projection onto the subspace ![]() $\mathbb {W} \subset \mathbb {V}$. The linear map
$\mathbb {W} \subset \mathbb {V}$. The linear map ![]() $\iota :\otimes ^{4}\mathbb {W}^{\ast } \to \otimes ^{4}\mathbb {V}^{\ast }$ defined by
$\iota :\otimes ^{4}\mathbb {W}^{\ast } \to \otimes ^{4}\mathbb {V}^{\ast }$ defined by ![]() $\iota (\mathscr {X})(A, B, C, D) = \mathscr {X}(\Pi A, \Pi B,\Pi C,\Pi D)$ restricts to an injective algebra homomorphism that maps
$\iota (\mathscr {X})(A, B, C, D) = \mathscr {X}(\Pi A, \Pi B,\Pi C,\Pi D)$ restricts to an injective algebra homomorphism that maps ![]() $(\mathscr {MC}(\mathbb {W}^{\ast }), \ast )$ into
$(\mathscr {MC}(\mathbb {W}^{\ast }), \ast )$ into ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ and
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ and ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {W}^{\ast }), \ast )$ into
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {W}^{\ast }), \ast )$ into ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$.
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$.
Proof. Straightforward calculations show that ![]() $B(\iota (\mathscr {X}), \iota (\mathscr {Y})) = \iota (B(\mathscr {X}, \mathscr {Y}))$ for
$B(\iota (\mathscr {X}), \iota (\mathscr {Y})) = \iota (B(\mathscr {X}, \mathscr {Y}))$ for ![]() $\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {W})$. Since
$\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {W})$. Since ![]() $\iota :\otimes ^{4}\mathbb {W}^{\ast } \to \otimes ^{4}\mathbb {V}^{\ast }$ commutes with permutations of the factors, this suffices to show
$\iota :\otimes ^{4}\mathbb {W}^{\ast } \to \otimes ^{4}\mathbb {V}^{\ast }$ commutes with permutations of the factors, this suffices to show ![]() $\iota (\mathscr {X})\ast \iota (\mathscr {Y}) = \iota (\mathscr {X} \ast \mathscr {Y})$ for
$\iota (\mathscr {X})\ast \iota (\mathscr {Y}) = \iota (\mathscr {X} \ast \mathscr {Y})$ for ![]() $\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {W}^{\ast })$. Similarly,
$\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {W}^{\ast })$. Similarly, ![]() $\operatorname {\rho }(\iota (\mathscr {X})) = \iota (\operatorname {\rho }(\mathscr {X}))$ (where
$\operatorname {\rho }(\iota (\mathscr {X})) = \iota (\operatorname {\rho }(\mathscr {X}))$ (where ![]() $\iota $ is defined on
$\iota $ is defined on ![]() $\otimes ^{2}\mathbb {W}$) and so
$\otimes ^{2}\mathbb {W}$) and so ![]() $\iota (\mathscr {MC}_{\mathscr {W}}(\mathbb {W}^{\ast })) \subset \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$.
$\iota (\mathscr {MC}_{\mathscr {W}}(\mathbb {W}^{\ast })) \subset \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$.
Remark 5.10. As commented in Remark 1.1, there is no purely algebraic reason to prefer ![]() $\ast $ to its pullback
$\ast $ to its pullback ![]() $\ast _{t}$ via rescaling by
$\ast _{t}$ via rescaling by ![]() $t \in \mathbb {R}^{\times }$, as these algebras are isomorphic. In particular, there is no algebraic reason to prefer
$t \in \mathbb {R}^{\times }$, as these algebras are isomorphic. In particular, there is no algebraic reason to prefer ![]() $\ast $ to
$\ast $ to ![]() $-\ast = \ast _{-1}$. However, there are at least three aesthetic and geometric reasons for preferring
$-\ast = \ast _{-1}$. However, there are at least three aesthetic and geometric reasons for preferring ![]() $\ast $ to
$\ast $ to ![]() $-\ast $:
$-\ast $:
• (geometric) By Lemma 7.8, a positive multiple of the curvature tensor of the round metric on the sphere is an
 $\ast $-idempotent.
$\ast $-idempotent.• (aesthetic) By Lemma 5.8, the scalar curvature of an
 $\ast $-square is nonnegative. (Morally, squares should be positive.)
$\ast $-square is nonnegative. (Morally, squares should be positive.)• (aesthetic) For the induced curvature operator on
 $\mathscr {MC}(\mathbb {V}^{\ast })$,
$\mathscr {MC}(\mathbb {V}^{\ast })$,  $\mathscr {X} \ast \mathscr {Y} = \widehat {\mathscr {X}}_{\mathscr {MC}(\mathbb {V}^{\ast })}(\mathscr {Y})$.
$\mathscr {X} \ast \mathscr {Y} = \widehat {\mathscr {X}}_{\mathscr {MC}(\mathbb {V}^{\ast })}(\mathscr {Y})$.
When comparing with the literature, care has to be taken. For example, that some signs in [Reference Richard32] at first glance appear inconsistent with those here is because [Reference Richard32] works directly with curvature operators, essentially with what is here called  $\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$, which is the image under the map here called
$\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$, which is the image under the map here called ![]() $\sharp $ of the tensor
$\sharp $ of the tensor 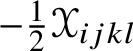 $-\tfrac {1}{2}\mathscr {X}_{ijkl}$, whereas here results are stated directly in terms of the tensor
$-\tfrac {1}{2}\mathscr {X}_{ijkl}$, whereas here results are stated directly in terms of the tensor ![]() $\mathscr {X}_{ijkl}$.
$\mathscr {X}_{ijkl}$.
6 Calculation of products in  $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$
There are two ways to construct curvature tensors from simpler objects, a commutative product ![]() of symmetric two-tensors and a commutative product
of symmetric two-tensors and a commutative product ![]() $\cdot $ of antisymmetric two-tensors. Lemma 6.1 records the
$\cdot $ of antisymmetric two-tensors. Lemma 6.1 records the ![]() $\ast $ products of curvature tensors obtained in these ways. They are used later in the construction of idempotents in
$\ast $ products of curvature tensors obtained in these ways. They are used later in the construction of idempotents in ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$. Although the full strength of these computations is not needed in this article, their proofs illustrate the use of
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$. Although the full strength of these computations is not needed in this article, their proofs illustrate the use of ![]() $\ast _{A}$ and
$\ast _{A}$ and ![]() $\ast _{S}$ in the computation of
$\ast _{S}$ in the computation of ![]() $\ast $.
$\ast $.
By straightforward computations using (4.2), Lemma 4.1, and (4.1),

defines a symmetric bilinear map ![]() . When
. When ![]() $k = 2$,
$k = 2$, ![]() is half what is usually called the Kulkarni–Nomizu product. Again by (4.2), for
is half what is usually called the Kulkarni–Nomizu product. Again by (4.2), for ![]() $\alpha , \beta \in {\bigwedge }^{2}\mathbb {V}^{\ast }$,
$\alpha , \beta \in {\bigwedge }^{2}\mathbb {V}^{\ast }$, 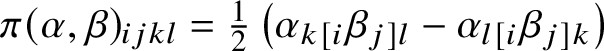 $\pi (\alpha , \beta )_{ijkl} = \tfrac {1}{2}\left ( \alpha _{k[i}\beta _{j]l} - \alpha _{l[i}\beta _{j]k}\right )$, so that, by Lemma 4.1, an
$\pi (\alpha , \beta )_{ijkl} = \tfrac {1}{2}\left ( \alpha _{k[i}\beta _{j]l} - \alpha _{l[i}\beta _{j]k}\right )$, so that, by Lemma 4.1, an ![]() $O(h)$-equivariant symmetric bilinear map
$O(h)$-equivariant symmetric bilinear map ![]() $\cdot :{\bigwedge }^{2}(\mathbb {V}^{\ast }) \times {\bigwedge }^{2}(\mathbb {V}^{\ast }) \to \mathscr {MC}(\mathbb {V}^{\ast })$ is defined by
$\cdot :{\bigwedge }^{2}(\mathbb {V}^{\ast }) \times {\bigwedge }^{2}(\mathbb {V}^{\ast }) \to \mathscr {MC}(\mathbb {V}^{\ast })$ is defined by
 $$ \begin{align} \alpha \cdot \beta &= -6\varrho(\alpha, \beta)_{ijkl} = -6\mathscr{M}(\pi(\alpha, \beta))_{ijkl} = -3\left( \alpha_{k[i}\beta_{j]l} - \alpha_{l[i}\beta_{j]k} - 2\alpha_{[ij}\beta_{kl]}\right)\nonumber\\ &= \tfrac{3}{2}(\alpha_{ij}\beta_{kl} + \alpha_{kl}\beta_{ij}) - \tfrac{1}{2}(\alpha \wedge \beta)_{ijkl} = \tfrac{3}{2}\mathscr{M}(\alpha \otimes \beta + \beta \otimes \alpha)_{ijkl}. \end{align} $$
$$ \begin{align} \alpha \cdot \beta &= -6\varrho(\alpha, \beta)_{ijkl} = -6\mathscr{M}(\pi(\alpha, \beta))_{ijkl} = -3\left( \alpha_{k[i}\beta_{j]l} - \alpha_{l[i}\beta_{j]k} - 2\alpha_{[ij}\beta_{kl]}\right)\nonumber\\ &= \tfrac{3}{2}(\alpha_{ij}\beta_{kl} + \alpha_{kl}\beta_{ij}) - \tfrac{1}{2}(\alpha \wedge \beta)_{ijkl} = \tfrac{3}{2}\mathscr{M}(\alpha \otimes \beta + \beta \otimes \alpha)_{ijkl}. \end{align} $$For a commutative algebra ![]() $(\mathbb {A}, \circ )$ define
$(\mathbb {A}, \circ )$ define
For a Jordan algebra, ![]() $Q_{\circ }(x)$ is what is usually called the quadratic representation [Reference Jacobson23, Reference Koecher24]. For the special case of
$Q_{\circ }(x)$ is what is usually called the quadratic representation [Reference Jacobson23, Reference Koecher24]. For the special case of ![]() $\alpha , \beta , \gamma \in \otimes ^{2}\mathbb {V}^{\ast }$,
$\alpha , \beta , \gamma \in \otimes ^{2}\mathbb {V}^{\ast }$,
 $$ \begin{align} &Q_{\circledcirc}(\alpha, \beta)(\gamma) = \tfrac{1}{2}(\alpha \circ \gamma \circ \beta + \beta \circ \gamma \circ \alpha), && Q_{\circledcirc}(\alpha)(\gamma) = \alpha \circ \gamma \circ \alpha. \end{align} $$
$$ \begin{align} &Q_{\circledcirc}(\alpha, \beta)(\gamma) = \tfrac{1}{2}(\alpha \circ \gamma \circ \beta + \beta \circ \gamma \circ \alpha), && Q_{\circledcirc}(\alpha)(\gamma) = \alpha \circ \gamma \circ \alpha. \end{align} $$The following identities relate ![]() $Q_{\circledcirc }$ with
$Q_{\circledcirc }$ with ![]() $\circledcirc $ and
$\circledcirc $ and ![]() $[\,\cdot \,\,, \,\cdot \,\,]$.
$[\,\cdot \,\,, \,\cdot \,\,]$.
 $$ \begin{align} \begin{aligned} Q_{\circledcirc}(\alpha \circledcirc \beta) &+ \tfrac{1}{4}Q_{\circledcirc}([\alpha, \beta]) = \tfrac{1}{2}Q_{\circledcirc}(\alpha\circ \beta) + \tfrac{1}{2}Q_{\circledcirc}(\beta \circ\alpha),\\ Q_{\circledcirc}(\alpha \circledcirc \beta) &- \tfrac{1}{4}Q_{\circledcirc}([\alpha, \beta]) =Q_{\circledcirc}(\alpha) \circledcirc Q_{\circledcirc}(\beta). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} Q_{\circledcirc}(\alpha \circledcirc \beta) &+ \tfrac{1}{4}Q_{\circledcirc}([\alpha, \beta]) = \tfrac{1}{2}Q_{\circledcirc}(\alpha\circ \beta) + \tfrac{1}{2}Q_{\circledcirc}(\beta \circ\alpha),\\ Q_{\circledcirc}(\alpha \circledcirc \beta) &- \tfrac{1}{4}Q_{\circledcirc}([\alpha, \beta]) =Q_{\circledcirc}(\alpha) \circledcirc Q_{\circledcirc}(\beta). \end{aligned} \end{align} $$Define ![]() $\operatorname {\mathsf {tr}}:S^{k}\mathbb {V}^{\ast } \to S^{k-2}\mathbb {V}^{\ast }$ by
$\operatorname {\mathsf {tr}}:S^{k}\mathbb {V}^{\ast } \to S^{k-2}\mathbb {V}^{\ast }$ by ![]() $\operatorname {\mathsf {tr}}(\omega )_{i_{1}\dots i_{k-2}} = \omega _{i_{1}\dots i_{k-2}p}{}^{p}$. For
$\operatorname {\mathsf {tr}}(\omega )_{i_{1}\dots i_{k-2}} = \omega _{i_{1}\dots i_{k-2}p}{}^{p}$. For ![]() $\alpha \in \otimes ^{2}\mathbb {V}^{\ast }$, let
$\alpha \in \otimes ^{2}\mathbb {V}^{\ast }$, let ![]() $\alpha ^{\sharp } = \langle \alpha , \,\cdot \,\,\rangle \in \otimes ^{2}\mathbb {V}$, so that, in the notation of (4.6),
$\alpha ^{\sharp } = \langle \alpha , \,\cdot \,\,\rangle \in \otimes ^{2}\mathbb {V}$, so that, in the notation of (4.6), ![]() $2(\alpha \odot \beta )^{\sharp } = \alpha \otimes \beta ^{\sharp } + \beta \otimes \alpha ^{\sharp }$, where
$2(\alpha \odot \beta )^{\sharp } = \alpha \otimes \beta ^{\sharp } + \beta \otimes \alpha ^{\sharp }$, where ![]() $\odot $ is the symmetrized tensor product of elements of
$\odot $ is the symmetrized tensor product of elements of ![]() $\otimes ^{2}\mathbb {V}^{\ast }$. From the definitions there follow
$\otimes ^{2}\mathbb {V}^{\ast }$. From the definitions there follow



By (4.5), (6.1), and (6.2), for ![]() $\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$,
$\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$, ![]() $\gamma , \sigma \in S^{2}\mathbb {V}^{\ast }$, and
$\gamma , \sigma \in S^{2}\mathbb {V}^{\ast }$, and ![]() $\alpha , \beta \in {\bigwedge }^{2}\mathbb {V}^{\ast }$,
$\alpha , \beta \in {\bigwedge }^{2}\mathbb {V}^{\ast }$,

 $$ \begin{align} \langle \alpha \cdot \beta , \mathscr{X}\rangle & = -6 \langle \varrho(\alpha, \beta), \mathscr{X}\rangle = -6\langle \widehat{\mathscr{X}}(\alpha), \beta \rangle = -6\langle \alpha, \widehat{\mathscr{X}}(\beta)\rangle. \end{align} $$
$$ \begin{align} \langle \alpha \cdot \beta , \mathscr{X}\rangle & = -6 \langle \varrho(\alpha, \beta), \mathscr{X}\rangle = -6\langle \widehat{\mathscr{X}}(\alpha), \beta \rangle = -6\langle \alpha, \widehat{\mathscr{X}}(\beta)\rangle. \end{align} $$For ![]() $\alpha , \beta , \gamma , \sigma \in {\bigwedge }^{2}(\mathbb {V}^{\ast })$, by (6.10) and (6.7),
$\alpha , \beta , \gamma , \sigma \in {\bigwedge }^{2}(\mathbb {V}^{\ast })$, by (6.10) and (6.7),
 $$ \begin{align} \langle \alpha \cdot \beta, \gamma \cdot \sigma \rangle& = - 6\langle \widehat{\alpha\cdot \beta}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(\gamma), \sigma\rangle \nonumber\\ & = 3\left(\langle \alpha, \gamma \rangle\langle \beta, \sigma \rangle + \langle \alpha, \sigma \rangle \langle \beta, \gamma \rangle + \operatorname{\mathsf{tr}}(\alpha\circ \gamma \circ \beta \circ \sigma+ \alpha\circ \sigma \circ \beta \circ \gamma)\right). \end{align} $$
$$ \begin{align} \langle \alpha \cdot \beta, \gamma \cdot \sigma \rangle& = - 6\langle \widehat{\alpha\cdot \beta}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(\gamma), \sigma\rangle \nonumber\\ & = 3\left(\langle \alpha, \gamma \rangle\langle \beta, \sigma \rangle + \langle \alpha, \sigma \rangle \langle \beta, \gamma \rangle + \operatorname{\mathsf{tr}}(\alpha\circ \gamma \circ \beta \circ \sigma+ \alpha\circ \sigma \circ \beta \circ \gamma)\right). \end{align} $$For ![]() $\alpha , \beta , \gamma , \sigma \in S^{2}\mathbb {V}^{\ast }$, by (6.9) and (6.6),
$\alpha , \beta , \gamma , \sigma \in S^{2}\mathbb {V}^{\ast }$, by (6.9) and (6.6),

For ![]() $\alpha , \beta \in {\bigwedge }^{2}\mathbb {V}^{\ast }$ and
$\alpha , \beta \in {\bigwedge }^{2}\mathbb {V}^{\ast }$ and ![]() $\gamma , \sigma \in S^{2}\mathbb {V}^{\ast }$, by (6.8) together with (6.9) or (6.10),
$\gamma , \sigma \in S^{2}\mathbb {V}^{\ast }$, by (6.8) together with (6.9) or (6.10),
Using (4.1) it is straightforward to check that, for ![]() $\sigma \in S^{2}\mathbb {V}^{\ast }$ and
$\sigma \in S^{2}\mathbb {V}^{\ast }$ and ![]() $\tau \in {\bigwedge }^{2}\mathbb {V}^{\ast }$, there hold
$\tau \in {\bigwedge }^{2}\mathbb {V}^{\ast }$, there hold

 $$ \begin{align} \hspace{-12pt}\tau_{i[k}\tau_{l]j} - \tau_{[ik}\tau_{lj]} = -\tfrac{1}{6}(\tau\cdot \tau)_{ijkl}, \phantom{sssss.ss}&\implies -2\mathscr{M}((Q_{\circledcirc}(\tau)_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}})^{\flat}) = \tfrac{1}{3}\tau \cdot \tau, \quad \ \, \end{align} $$
$$ \begin{align} \hspace{-12pt}\tau_{i[k}\tau_{l]j} - \tau_{[ik}\tau_{lj]} = -\tfrac{1}{6}(\tau\cdot \tau)_{ijkl}, \phantom{sssss.ss}&\implies -2\mathscr{M}((Q_{\circledcirc}(\tau)_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}})^{\flat}) = \tfrac{1}{3}\tau \cdot \tau, \quad \ \, \end{align} $$
 $$ \begin{align} \hspace{-30pt}\tau_{i(k}\tau_{l)j} =-\tfrac{\sqrt{3}}{6}\mathcal{T}^{-1}(\tau \cdot \tau)_{ijkl},\phantom{ssssss.sssss}&\implies -\tfrac{2}{\sqrt{3}}\mathcal{T} \circ \mathscr{S}((Q_{\circledcirc}(\tau)_{S^{2}\mathbb{V}^{\ast}})^{\flat}) =\tfrac{1}{3}\tau \cdot \tau. \end{align} $$
$$ \begin{align} \hspace{-30pt}\tau_{i(k}\tau_{l)j} =-\tfrac{\sqrt{3}}{6}\mathcal{T}^{-1}(\tau \cdot \tau)_{ijkl},\phantom{ssssss.sssss}&\implies -\tfrac{2}{\sqrt{3}}\mathcal{T} \circ \mathscr{S}((Q_{\circledcirc}(\tau)_{S^{2}\mathbb{V}^{\ast}})^{\flat}) =\tfrac{1}{3}\tau \cdot \tau. \end{align} $$Lemma 6.1. Let ![]() $(\mathbb {V}, h)$ be a metric vector space. For
$(\mathbb {V}, h)$ be a metric vector space. For ![]() $\alpha , \beta , \gamma , \sigma \in S^{2}(\mathbb {V}^{\ast })$,
$\alpha , \beta , \gamma , \sigma \in S^{2}(\mathbb {V}^{\ast })$,

For ![]() $\alpha , \beta \in {\bigwedge }^{2}\mathbb {V}^{\ast }$ and
$\alpha , \beta \in {\bigwedge }^{2}\mathbb {V}^{\ast }$ and ![]() $\gamma , \sigma \in S^{2}(\mathbb {V}^{\ast })$,
$\gamma , \sigma \in S^{2}(\mathbb {V}^{\ast })$,

For ![]() $\alpha , \beta , \gamma , \sigma \in {\bigwedge }^{2}(\mathbb {V}^{\ast })$,
$\alpha , \beta , \gamma , \sigma \in {\bigwedge }^{2}(\mathbb {V}^{\ast })$,

Proof. For ![]() $\alpha , \beta \in S^{2}\mathbb {V}^{\ast }$, by (6.8), (6.6), and (6.5),
$\alpha , \beta \in S^{2}\mathbb {V}^{\ast }$, by (6.8), (6.6), and (6.5),


By (5.1), applying ![]() $-2\mathscr {M}$ to (6.21) and
$-2\mathscr {M}$ to (6.21) and  $-\tfrac {2}{\sqrt {3}}\mathcal {T} \circ \mathscr {S}$ to (6.22), and using (6.2) and (6.14)–(6.17) with
$-\tfrac {2}{\sqrt {3}}\mathcal {T} \circ \mathscr {S}$ to (6.22), and using (6.2) and (6.14)–(6.17) with ![]() $\sigma = \alpha \circledcirc \beta $ and
$\sigma = \alpha \circledcirc \beta $ and ![]() $\tau = [\alpha , \beta ]$ to simplify the results yields
$\tau = [\alpha , \beta ]$ to simplify the results yields

Using 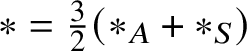 $\ast = \tfrac {3}{2}(\ast _{A} + \ast _{S})$ and (6.23) to evaluate
$\ast = \tfrac {3}{2}(\ast _{A} + \ast _{S})$ and (6.23) to evaluate ![]() yields
yields

Polarizing (6.24) first in ![]() $\alpha $ and then in
$\alpha $ and then in ![]() $\beta $ yields (6.18).
$\beta $ yields (6.18).
For ![]() $\alpha \in {\bigwedge }^{2}\mathbb {V}^{\ast }$ and
$\alpha \in {\bigwedge }^{2}\mathbb {V}^{\ast }$ and ![]() $\gamma \in S^{2}\mathbb {V}^{\ast }$, by (6.7), (6.8), (6.6), and (6.5),
$\gamma \in S^{2}\mathbb {V}^{\ast }$, by (6.7), (6.8), (6.6), and (6.5),


By (5.1), applying ![]() $-2\mathscr {M}$ to (6.25) and
$-2\mathscr {M}$ to (6.25) and 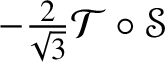 $-\tfrac {2}{\sqrt {3}}\mathcal {T} \circ \mathscr {S}$ to (6.26), and using (6.2), (6.1), and (6.14)–(6.17) with
$-\tfrac {2}{\sqrt {3}}\mathcal {T} \circ \mathscr {S}$ to (6.26), and using (6.2), (6.1), and (6.14)–(6.17) with ![]() $\sigma = [\alpha , \gamma ]$ and
$\sigma = [\alpha , \gamma ]$ and ![]() $\tau = \alpha \circledcirc \gamma $ to simplify the results yields
$\tau = \alpha \circledcirc \gamma $ to simplify the results yields

Using 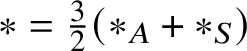 $\ast = \tfrac {3}{2}(\ast _{A} + \ast _{S})$ and (6.27) to evaluate
$\ast = \tfrac {3}{2}(\ast _{A} + \ast _{S})$ and (6.27) to evaluate ![]() yields
yields

Polarizing (6.28) first in ![]() $\alpha $ and then in
$\alpha $ and then in ![]() $\gamma $ yields (6.19).
$\gamma $ yields (6.19).
For ![]() $\alpha , \beta \in {\bigwedge }^{2}\mathbb {V}^{\ast }$, by (6.7), (6.8), and (6.5),
$\alpha , \beta \in {\bigwedge }^{2}\mathbb {V}^{\ast }$, by (6.7), (6.8), and (6.5),
 $$ \begin{align} \begin{split} &\widehat{\alpha \cdot \alpha}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\beta \cdot \beta}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} = (Q_{\circledcirc}(\alpha) - (\alpha \otimes \alpha)^{\sharp})\circledcirc(Q_{\circledcirc}(\beta) - (\beta \otimes \beta)^{\sharp})\\ & = Q_{\circledcirc}(\alpha \circledcirc \beta) - \tfrac{1}{4}Q_{\circledcirc}([\alpha, \beta]) + \langle \alpha, \beta \rangle \left(\alpha \odot \beta\right)^{\sharp} -\left( Q_{\circledcirc}(\beta)(\alpha) \odot \alpha\right)^{\sharp} -\left( Q_{\circledcirc}(\alpha)(\beta) \odot \beta\right)^{\sharp} , \end{split} \end{align} $$
$$ \begin{align} \begin{split} &\widehat{\alpha \cdot \alpha}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\beta \cdot \beta}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} = (Q_{\circledcirc}(\alpha) - (\alpha \otimes \alpha)^{\sharp})\circledcirc(Q_{\circledcirc}(\beta) - (\beta \otimes \beta)^{\sharp})\\ & = Q_{\circledcirc}(\alpha \circledcirc \beta) - \tfrac{1}{4}Q_{\circledcirc}([\alpha, \beta]) + \langle \alpha, \beta \rangle \left(\alpha \odot \beta\right)^{\sharp} -\left( Q_{\circledcirc}(\beta)(\alpha) \odot \alpha\right)^{\sharp} -\left( Q_{\circledcirc}(\alpha)(\beta) \odot \beta\right)^{\sharp} , \end{split} \end{align} $$ $$ \begin{align} \begin{split} &\widehat{\alpha \cdot \alpha}_{S^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\beta \cdot \beta}_{S^{2}\mathbb{V}^{\ast}} = 9Q_{\circledcirc}(\alpha)\circledcirc Q_{\circledcirc}(\beta) = 9Q_{\circledcirc}(\alpha \circledcirc \beta) - \tfrac{9}{4}Q_{\circledcirc}([\alpha, \beta]). \end{split} \end{align} $$
$$ \begin{align} \begin{split} &\widehat{\alpha \cdot \alpha}_{S^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\beta \cdot \beta}_{S^{2}\mathbb{V}^{\ast}} = 9Q_{\circledcirc}(\alpha)\circledcirc Q_{\circledcirc}(\beta) = 9Q_{\circledcirc}(\alpha \circledcirc \beta) - \tfrac{9}{4}Q_{\circledcirc}([\alpha, \beta]). \end{split} \end{align} $$By (5.1), applying ![]() $-2\mathscr {M}$ to (6.29) and
$-2\mathscr {M}$ to (6.29) and 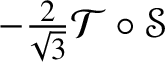 $-\tfrac {2}{\sqrt {3}}\mathcal {T} \circ \mathscr {S}$ to (6.30), and using (6.2) and (6.14)–(6.17) with
$-\tfrac {2}{\sqrt {3}}\mathcal {T} \circ \mathscr {S}$ to (6.30), and using (6.2) and (6.14)–(6.17) with ![]() $\tau = [\alpha , \beta ]$ and
$\tau = [\alpha , \beta ]$ and ![]() $\sigma = \alpha \circledcirc \beta $ to simplify the results yields
$\sigma = \alpha \circledcirc \beta $ to simplify the results yields

Using  $\ast = \tfrac {3}{2}(\ast _{A} + \ast _{S})$ and (6.31) to evaluate
$\ast = \tfrac {3}{2}(\ast _{A} + \ast _{S})$ and (6.31) to evaluate ![]() $(\alpha \cdot \alpha ) \ast (\beta \cdot \beta )$ yields
$(\alpha \cdot \alpha ) \ast (\beta \cdot \beta )$ yields

Polarizing (6.32) first in ![]() $\alpha $ and then in
$\alpha $ and then in ![]() $\beta $ yields (6.20).
$\beta $ yields (6.20).
Remark 6.2. Taking ![]() $\beta = \alpha \in S^{2}\mathbb {V}^{\ast }$ in (6.24) yields
$\beta = \alpha \in S^{2}\mathbb {V}^{\ast }$ in (6.24) yields
Taking ![]() $\gamma = \alpha \in S^{2}\mathbb {V}^{\ast }$ and
$\gamma = \alpha \in S^{2}\mathbb {V}^{\ast }$ and ![]() $\sigma = \beta \in S^{2}\mathbb {V}^{\ast }$ in (6.18) yields
$\sigma = \beta \in S^{2}\mathbb {V}^{\ast }$ in (6.18) yields

The identities (6.33) and (6.34) suggest that, with further conditions on ![]() $\alpha $ and
$\alpha $ and ![]() $\beta $,
$\beta $, ![]() $\ast $-idempotents can be constructed from
$\ast $-idempotents can be constructed from ![]() ,
, ![]() , and
, and ![]() . This is shown to be the case in Lemma 7.4. Similarly, taking
. This is shown to be the case in Lemma 7.4. Similarly, taking ![]() $\alpha = \beta = \gamma = \sigma \in {\bigwedge }^{2}\mathbb {V}^{\ast }$ in (6.20) yields
$\alpha = \beta = \gamma = \sigma \in {\bigwedge }^{2}\mathbb {V}^{\ast }$ in (6.20) yields
The identity (6.35) suggests that with some further condition on ![]() $\alpha $, the element
$\alpha $, the element ![]() $\alpha \cdot \alpha $ or its trace-free part
$\alpha \cdot \alpha $ or its trace-free part ![]() $\operatorname {\mathsf {tf}}(\alpha \cdot \alpha )$ might be a
$\operatorname {\mathsf {tf}}(\alpha \cdot \alpha )$ might be a ![]() $\ast $-idempotent. Corollary 7.5 and Lemma 10.1 show that this works. In this regard, see also Lemma 7.3, which uses (6.32) and (6.35) to construct square-zero elements in
$\ast $-idempotent. Corollary 7.5 and Lemma 10.1 show that this works. In this regard, see also Lemma 7.3, which uses (6.32) and (6.35) to construct square-zero elements in ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ when h has indefinite signature.
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ when h has indefinite signature.
7 Simplicity of  $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ and fusion rules for
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ and fusion rules for  $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$
Lemma 5.7 shows that the Weyl curvature tensors constitute a subalgebra of ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$. The first part of the section is dedicated to constructing idempotents in
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$. The first part of the section is dedicated to constructing idempotents in ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$. This is used in the proof of Theorem 1.3 and to show the nontriviality of the subalgebra
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$. This is used in the proof of Theorem 1.3 and to show the nontriviality of the subalgebra ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$, which in turn yields Corollary 7.6, showing the simplicity of
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$, which in turn yields Corollary 7.6, showing the simplicity of ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ when
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ when ![]() $\dim \mathbb {V}> 4$, but is also interesting in its own right, as experience with Jordan and axial algebras suggests that detailed information about idempotents and the spectra of their multiplication endomorphisms is useful for understanding the internal structure of an algebra such as
$\dim \mathbb {V}> 4$, but is also interesting in its own right, as experience with Jordan and axial algebras suggests that detailed information about idempotents and the spectra of their multiplication endomorphisms is useful for understanding the internal structure of an algebra such as ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$.
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$.
Next, explicit formulas for products in ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ are deduced and these are used to deduce the main result of this section, Theorem 7.12, that describes the interaction of the subspaces
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ are deduced and these are used to deduce the main result of this section, Theorem 7.12, that describes the interaction of the subspaces ![]() $\mathscr {MC}_{\mathscr {S}}(\mathbb {V}^{\ast })$,
$\mathscr {MC}_{\mathscr {S}}(\mathbb {V}^{\ast })$, ![]() $\mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast })$, and
$\mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast })$, and ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ with respect to
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ with respect to ![]() $\ast $.
$\ast $.
Lemma 7.1. Let ![]() $(\mathbb {V}, h)$ be an n-dimensional Euclidean vector space. For an
$(\mathbb {V}, h)$ be an n-dimensional Euclidean vector space. For an ![]() $O(n)$-module of tensors
$O(n)$-module of tensors ![]() $\mathbb {W}$, let
$\mathbb {W}$, let ![]() $\operatorname {\mathsf {tf}}\in \operatorname {End}(\mathbb {W})$ denote the orthogonal projection onto the
$\operatorname {\mathsf {tf}}\in \operatorname {End}(\mathbb {W})$ denote the orthogonal projection onto the ![]() $O(n)$-submodule
$O(n)$-submodule ![]() $\mathbb {W}_{0} \subset \mathbb {W}$ comprising trace-free elements. Define
$\mathbb {W}_{0} \subset \mathbb {W}$ comprising trace-free elements. Define 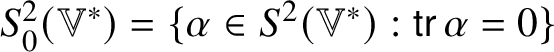 $S^{2}_{0}(\mathbb {V}^{\ast }) = \{\alpha \in S^{2}(\mathbb {V}^{\ast }): \operatorname {\mathsf {tr}}\alpha = 0\}$,
$S^{2}_{0}(\mathbb {V}^{\ast }) = \{\alpha \in S^{2}(\mathbb {V}^{\ast }): \operatorname {\mathsf {tr}}\alpha = 0\}$, 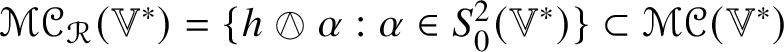 , and
, and ![]() . The orthogonal projections
. The orthogonal projections ![]() $\mathscr {P}_{\mathscr {R}}, \mathscr {P}_{\mathscr {S}} \in \operatorname {End}(\mathscr {MC}(\mathbb {V}^{\ast }))$ on
$\mathscr {P}_{\mathscr {R}}, \mathscr {P}_{\mathscr {S}} \in \operatorname {End}(\mathscr {MC}(\mathbb {V}^{\ast }))$ on ![]() $\mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast })$ and
$\mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast })$ and ![]() $\mathscr {MC}_{\mathscr {S}}(\mathbb {V}^{\ast })$ are given by
$\mathscr {MC}_{\mathscr {S}}(\mathbb {V}^{\ast })$ are given by

where 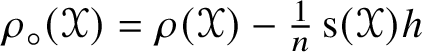 $\operatorname {\rho }_{\circ }(\mathscr {X}) = \operatorname {\rho }(\mathscr {X}) - \tfrac {1}{n}\operatorname {s}(\mathscr {X})h$, and the trace-free part
$\operatorname {\rho }_{\circ }(\mathscr {X}) = \operatorname {\rho }(\mathscr {X}) - \tfrac {1}{n}\operatorname {s}(\mathscr {X})h$, and the trace-free part ![]() $\operatorname {\mathsf {tf}}(\mathscr {X})$ of
$\operatorname {\mathsf {tf}}(\mathscr {X})$ of ![]() $\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$ is given by
$\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$ is given by

Proof. For ![]() $\alpha , \beta \in S^{2}(\mathbb {V}^{\ast })$, computations using the definitions show
$\alpha , \beta \in S^{2}(\mathbb {V}^{\ast })$, computations using the definitions show


When ![]() $n>2$,
$n>2$, ![]() $\mathscr {MC}(\mathbb {V}^{\ast }) = \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) \oplus \mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast }) \oplus \mathscr {MC}_{\mathscr {S}}(\mathbb {V}^{\ast })$ is an orthogonal decomposition into irreducible
$\mathscr {MC}(\mathbb {V}^{\ast }) = \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) \oplus \mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast }) \oplus \mathscr {MC}_{\mathscr {S}}(\mathbb {V}^{\ast })$ is an orthogonal decomposition into irreducible ![]() $O(n)$-modules (although
$O(n)$-modules (although ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is trivial if
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is trivial if ![]() $\dim \mathbb {V} = 3$). By (7.4), if
$\dim \mathbb {V} = 3$). By (7.4), if ![]() $n> 2$, the map
$n> 2$, the map ![]() is a linear isomorphism from
is a linear isomorphism from 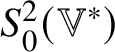 $S^{2}_{0}(\mathbb {V}^{\ast })$ onto its image in
$S^{2}_{0}(\mathbb {V}^{\ast })$ onto its image in ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$, which is
$\mathscr {MC}(\mathbb {V}^{\ast })$, which is ![]() $\mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast })$. The expressions (7.1) and (7.2) follow from (7.4) and (7.5).
$\mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast })$. The expressions (7.1) and (7.2) follow from (7.4) and (7.5).
Example 7.2. For ![]() $\alpha , \beta \in S^{2}\mathbb {V}^{\ast }$, taking
$\alpha , \beta \in S^{2}\mathbb {V}^{\ast }$, taking ![]() in (7.2) and using (7.3) yields
in (7.2) and using (7.3) yields

Similarly, by (7.2) and (7.7), for ![]() $\alpha , \beta \in {\bigwedge }^{2}(\mathbb {V}^{\ast })$,
$\alpha , \beta \in {\bigwedge }^{2}(\mathbb {V}^{\ast })$,

Since, by (6.9), ![]() for any
for any ![]() $\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$, by (7.7) there holds
$\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$, by (7.7) there holds ![]() . Alternatively, this is a special case of (6.10) or a special case of (6.13).
. Alternatively, this is a special case of (6.10) or a special case of (6.13).
Lemma 7.3. Let ![]() $(\mathbb {V}, h)$ be a metric vector space of dimension
$(\mathbb {V}, h)$ be a metric vector space of dimension ![]() $n> 3$. If h has indefinite signature with minimal inertial index
$n> 3$. If h has indefinite signature with minimal inertial index ![]() $k \geq 1$, then
$k \geq 1$, then ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is spanned by square-zero elements and contains a trivial subalgebra of dimension
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is spanned by square-zero elements and contains a trivial subalgebra of dimension ![]() $n- 2k - 1$.
$n- 2k - 1$.
Proof. By assumption there are a nonzero h-isotropic ![]() $w \in \mathbb {V}^{\ast }$ and a unimodular h-orthogonal basis
$w \in \mathbb {V}^{\ast }$ and a unimodular h-orthogonal basis ![]() $\{z^{(\alpha )}:0 \leq \alpha \leq n-2k-1\}$ of a codimension
$\{z^{(\alpha )}:0 \leq \alpha \leq n-2k-1\}$ of a codimension ![]() $2k$ subspace of
$2k$ subspace of ![]() $\mathbb {V}^{\ast }$ orthogonal to w and on which h has definite signature. Concretely, there is
$\mathbb {V}^{\ast }$ orthogonal to w and on which h has definite signature. Concretely, there is ![]() $\epsilon \in \{\pm 1\}$ such that
$\epsilon \in \{\pm 1\}$ such that ![]() $h(w, z^{(\alpha )}) = 0$ and
$h(w, z^{(\alpha )}) = 0$ and ![]() $h(z^{(\alpha )}, z^{(\alpha )}) = \epsilon $ for
$h(z^{(\alpha )}, z^{(\alpha )}) = \epsilon $ for ![]() $0 \leq \alpha \leq n-2k-1$. For
$0 \leq \alpha \leq n-2k-1$. For ![]() $1 \leq \alpha \leq n- 2k-1$, the tensor
$1 \leq \alpha \leq n- 2k-1$, the tensor ![]() $\mathscr {Z}^{(\alpha )} = (w \wedge z^{(0)})\cdot (w \wedge z^{(0)}) - (w \wedge z^{(\alpha )})\cdot (w \wedge z^{(\alpha )})$ is nontrivial. Suppose
$\mathscr {Z}^{(\alpha )} = (w \wedge z^{(0)})\cdot (w \wedge z^{(0)}) - (w \wedge z^{(\alpha )})\cdot (w \wedge z^{(\alpha )})$ is nontrivial. Suppose ![]() $1 \leq \alpha < \beta \leq n - 2k -1$. Because
$1 \leq \alpha < \beta \leq n - 2k -1$. Because ![]() $(w\wedge z^{(\alpha )}) \circ (w\wedge z^{(\alpha )}) = -\epsilon w \otimes w = (w \wedge z^{(\beta )})\otimes (w \wedge z^{(\beta )})$, by (7.7),
$(w\wedge z^{(\alpha )}) \circ (w\wedge z^{(\alpha )}) = -\epsilon w \otimes w = (w \wedge z^{(\beta )})\otimes (w \wedge z^{(\beta )})$, by (7.7), ![]() $\operatorname {\rho }(\mathscr {Z}^{(\alpha )}) =0$, so
$\operatorname {\rho }(\mathscr {Z}^{(\alpha )}) =0$, so ![]() $\mathscr {Z}^{(\alpha )} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. Because
$\mathscr {Z}^{(\alpha )} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. Because ![]() $(w \wedge z^{(\alpha )})\circ (w \wedge z^{(\alpha )}) \circ (w\wedge z^{(\alpha )}) = 0$ and
$(w \wedge z^{(\alpha )})\circ (w \wedge z^{(\alpha )}) \circ (w\wedge z^{(\alpha )}) = 0$ and ![]() , by (6.35),
, by (6.35),  $((w \wedge z^{(\alpha )})\otimes (w \wedge z^{(\alpha )}))\ast ((w \wedge z^{(\alpha )})\otimes (w \wedge z^{(\alpha )})) = 0 = ((w \wedge z^{(\beta )})\otimes (w \wedge z^{(\beta )}))\ast ((w \wedge z^{(\beta )})\otimes (w \wedge z^{(\beta )}))$ and, because
$((w \wedge z^{(\alpha )})\otimes (w \wedge z^{(\alpha )}))\ast ((w \wedge z^{(\alpha )})\otimes (w \wedge z^{(\alpha )})) = 0 = ((w \wedge z^{(\beta )})\otimes (w \wedge z^{(\beta )}))\ast ((w \wedge z^{(\beta )})\otimes (w \wedge z^{(\beta )}))$ and, because ![]() $(w \wedge z^{(\alpha )})\circ (w \wedge z^{(\beta )}) = 0$, by (6.32),
$(w \wedge z^{(\alpha )})\circ (w \wedge z^{(\beta )}) = 0$, by (6.32), ![]() $((w \wedge z^{(\alpha )})\otimes (w \wedge z^{(\alpha )}))\ast ((w \wedge z^{(\beta )})\otimes (w \wedge z^{(\beta )})) = 0$, so
$((w \wedge z^{(\alpha )})\otimes (w \wedge z^{(\alpha )}))\ast ((w \wedge z^{(\beta )})\otimes (w \wedge z^{(\beta )})) = 0$, so ![]() $\mathscr {Z}^{(\alpha )} \ast \mathscr {Z}^{(\alpha )} = 0$ and
$\mathscr {Z}^{(\alpha )} \ast \mathscr {Z}^{(\alpha )} = 0$ and ![]() $\mathscr {Z}^{(\alpha )} \ast \mathscr {Z}^{(\beta )} = 0$. It follows that
$\mathscr {Z}^{(\alpha )} \ast \mathscr {Z}^{(\beta )} = 0$. It follows that ![]() $\text {Span}\,\{\mathscr {Z}^{(\alpha )}:1 \leq \alpha \leq n-2k-1\}$ is a trivial subalgebra of
$\text {Span}\,\{\mathscr {Z}^{(\alpha )}:1 \leq \alpha \leq n-2k-1\}$ is a trivial subalgebra of ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$.
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$.
Since ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ contains a nonzero square-zero element
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ contains a nonzero square-zero element ![]() $\mathscr {Z}$, the span of the
$\mathscr {Z}$, the span of the ![]() $O(h)$-orbit of
$O(h)$-orbit of ![]() $\mathscr {Z}$ is a nontrivial
$\mathscr {Z}$ is a nontrivial ![]() $O(h)$-invariant subspace of the irreducible
$O(h)$-invariant subspace of the irreducible ![]() $O(h)$-module
$O(h)$-module ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ and so equals
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ and so equals ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, and hence
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, and hence ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is spanned by square-zero elements.
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is spanned by square-zero elements.
Let ![]() denote the set of idempotent elements in the algebra
denote the set of idempotent elements in the algebra ![]() $(\mathbb {A}, \circ )$. Two idempotents
$(\mathbb {A}, \circ )$. Two idempotents ![]() are orthogonal if
are orthogonal if ![]() $e\circ f = 0 = f\circ e$.
$e\circ f = 0 = f\circ e$.
If ![]() , then
, then ![]() $\operatorname {\mathsf {tr}} \alpha = |\alpha |^{2}$ is the rank of the orthogonal proejction
$\operatorname {\mathsf {tr}} \alpha = |\alpha |^{2}$ is the rank of the orthogonal proejction ![]() $\alpha _{i}{}^{j}$, so
$\alpha _{i}{}^{j}$, so ![]() $\operatorname {\mathsf {tr}} \alpha $ is said to be the rank of
$\operatorname {\mathsf {tr}} \alpha $ is said to be the rank of ![]() $\alpha $. If
$\alpha $. If ![]() are orthogonal idempotents, then
are orthogonal idempotents, then ![]() $\alpha \circ \beta = 0 = \beta \circ \alpha $, for
$\alpha \circ \beta = 0 = \beta \circ \alpha $, for ![]() $\alpha \circ \beta = \alpha \circ \alpha \circ \beta \circ \beta = \beta \circ \beta \circ \alpha \circ \alpha = \beta \circ \alpha = -\alpha \circ \beta $.
$\alpha \circ \beta = \alpha \circ \alpha \circ \beta \circ \beta = \beta \circ \beta \circ \alpha \circ \alpha = \beta \circ \alpha = -\alpha \circ \beta $.
Lemma 7.4. Let ![]() $(\mathbb {V}, h)$ be an n-dimensional Euclidean vector space. For orthogonal idempotents
$(\mathbb {V}, h)$ be an n-dimensional Euclidean vector space. For orthogonal idempotents ![]() with
with ![]() $a = \operatorname {\mathsf {tr}} \alpha $ and
$a = \operatorname {\mathsf {tr}} \alpha $ and ![]() $b =\operatorname {\mathsf {tr}} \beta$ there hold
$b =\operatorname {\mathsf {tr}} \beta$ there hold

Moreover, ![]() , so
, so ![]() if and only if
if and only if ![]() $b \neq 1$. In this case
$b \neq 1$. In this case  . If
. If ![]() $a \neq 1$ and
$a \neq 1$ and ![]() $b \neq 1$, then
$b \neq 1$, then  and
and 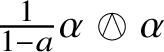 are orthogonal idempotents in
are orthogonal idempotents in ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$.
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$.
Proof. That ![]() follows from (6.12). (Note that
follows from (6.12). (Note that ![]() $b = 1$ if and only if
$b = 1$ if and only if ![]() $\beta = u\otimes u$ for a unit norm
$\beta = u\otimes u$ for a unit norm ![]() $u \in \mathbb {V}^{\ast }$, in which case
$u \in \mathbb {V}^{\ast }$, in which case ![]() .) Specializing (6.18), (6.33), and (6.34) yields (7.9) and the remaining claims.
.) Specializing (6.18), (6.33), and (6.34) yields (7.9) and the remaining claims.
Corollary 7.5. Let ![]() $(\mathbb {V}, h)$ be a Euclidean vector space of dimension
$(\mathbb {V}, h)$ be a Euclidean vector space of dimension ![]() $n> 2$. If orthogonal idempotents
$n> 2$. If orthogonal idempotents ![]() satisfy
satisfy ![]() $a = \operatorname {\mathsf {tr}} \alpha \neq 1$ and
$a = \operatorname {\mathsf {tr}} \alpha \neq 1$ and ![]() $b = \operatorname {\mathsf {tr}} \beta \neq 1$, then
$b = \operatorname {\mathsf {tr}} \beta \neq 1$, then

is an idempotent in ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ satisfying
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ satisfying  $|\mathscr {B}(\alpha , \beta )|^{2} = \tfrac {2(a + b -2)ab}{(a + b -1)(a - 1)(b - 1)}$. In particular, if
$|\mathscr {B}(\alpha , \beta )|^{2} = \tfrac {2(a + b -2)ab}{(a + b -1)(a - 1)(b - 1)}$. In particular, if ![]() $b \notin \{1, n-1\}$,
$b \notin \{1, n-1\}$, ![]() $\hat {\beta } = h - \beta $, and
$\hat {\beta } = h - \beta $, and ![]() $\hat {b} = \operatorname {\mathsf {tr}} \hat {\beta }$, then
$\hat {b} = \operatorname {\mathsf {tr}} \hat {\beta }$, then

is an idempotent in ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ satisfying
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ satisfying  $|\mathscr {B}(\beta )|^{2} = \tfrac {2(n-2)(n-b)b}{(n-1)(n-1 - b)(b - 1)}$.
$|\mathscr {B}(\beta )|^{2} = \tfrac {2(n-2)(n-b)b}{(n-1)(n-1 - b)(b - 1)}$.
Proof. That ![]() $\mathscr {B}(\alpha , \beta )$ defined by the first equality of (7.11) is an idempotent follows from (7.9). That
$\mathscr {B}(\alpha , \beta )$ defined by the first equality of (7.11) is an idempotent follows from (7.9). That ![]() $\operatorname {\rho }(\mathscr {B}(\alpha , \beta )) =0$ follows from (7.3). The claimed value of
$\operatorname {\rho }(\mathscr {B}(\alpha , \beta )) =0$ follows from (7.3). The claimed value of ![]() $|\mathscr {B}(\alpha , \beta )|^{2}$ follows from (7.10) and (6.12) by straightforward computations. Because
$|\mathscr {B}(\alpha , \beta )|^{2}$ follows from (7.10) and (6.12) by straightforward computations. Because ![]() $(h - \beta ) \circ \beta = 0$ and
$(h - \beta ) \circ \beta = 0$ and ![]() $\operatorname {\mathsf {tr}}(h - \beta ) = n - \operatorname {\mathsf {tr}}\beta $, that (7.11) is an idempotent in
$\operatorname {\mathsf {tr}}(h - \beta ) = n - \operatorname {\mathsf {tr}}\beta $, that (7.11) is an idempotent in ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ with
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ with ![]() $|\mathscr {B}(\beta )|^{2}$ having the claimed value is a special case of the preceding. The first equality of (7.11) follows upon substituting
$|\mathscr {B}(\beta )|^{2}$ having the claimed value is a special case of the preceding. The first equality of (7.11) follows upon substituting ![]() $\hat {\beta } = h - \beta $ in (7.10). Specializing (7.6) yields the second equality of (7.11). Finally,
$\hat {\beta } = h - \beta $ in (7.10). Specializing (7.6) yields the second equality of (7.11). Finally, ![]() because
because ![]() .
.
Corollary 7.6. Let ![]() $(\mathbb {V}, h)$ be an n-dimensional Euclidean vector space. If
$(\mathbb {V}, h)$ be an n-dimensional Euclidean vector space. If ![]() $n> 3$, then
$n> 3$, then ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) \ast \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) = \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, and if
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) \ast \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) = \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, and if ![]() $n> 4$, then
$n> 4$, then ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is a simple algebra.
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is a simple algebra.
Proof. By Lemma 5.7, ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is a subalgebra of
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is a subalgebra of ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$. Let
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$. Let ![]() $x, y \in \mathbb {V}^{\ast }$ be orthogonal unit norm vectors. Because
$x, y \in \mathbb {V}^{\ast }$ be orthogonal unit norm vectors. Because ![]() $\beta = x\otimes x + y \otimes y$ satisfies
$\beta = x\otimes x + y \otimes y$ satisfies ![]() $\beta \circ \beta = \beta $ and
$\beta \circ \beta = \beta $ and ![]() $\operatorname {\mathsf {tr}} \beta = 2$, by Corollary 7.5,
$\operatorname {\mathsf {tr}} \beta = 2$, by Corollary 7.5,  $|\mathscr {B}(\beta )|^{2} = \tfrac {4(n-2)^{2}}{(n-1)(n-3)} \neq 0$, so
$|\mathscr {B}(\beta )|^{2} = \tfrac {4(n-2)^{2}}{(n-1)(n-3)} \neq 0$, so ![]() $\mathscr {B}(\beta )$ is a nontrivial idempotent in (
$\mathscr {B}(\beta )$ is a nontrivial idempotent in (![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$. If
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$. If ![]() $n> 3$, this shows
$n> 3$, this shows ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is a nontrivial algebra and
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is a nontrivial algebra and ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) \ast \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is a nontrivial
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) \ast \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is a nontrivial ![]() $O(n)$-submodule of the irreducible
$O(n)$-submodule of the irreducible ![]() $O(n)$-module
$O(n)$-module ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ and so must equal
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ and so must equal ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. If
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. If ![]() $n> 4$,
$n> 4$, ![]() $SO(n)$ acts on
$SO(n)$ acts on ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ irreducibly by automorphisms, so, by Theorem 3.1,
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ irreducibly by automorphisms, so, by Theorem 3.1, ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is simple.
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is simple.
Lemma 7.7. Let ![]() $(\mathbb {V}, h)$ be a metric vector space. For
$(\mathbb {V}, h)$ be a metric vector space. For ![]() $\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$ and
$\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$ and ![]() $\alpha \in S^{2}(\mathbb {V}^{\ast })$,
$\alpha \in S^{2}(\mathbb {V}^{\ast })$,

Proof. For ![]() $\alpha \in S^{2}\mathbb {V}^{\ast }$ and
$\alpha \in S^{2}\mathbb {V}^{\ast }$ and ![]() $\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$,
$\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$,

the first equality by the invariance of ![]() $\langle \,\cdot \,\,, \,\cdot \,\,\rangle $, the second equality by (6.9), the third and fourth equalities because
$\langle \,\cdot \,\,, \,\cdot \,\,\rangle $, the second equality by (6.9), the third and fourth equalities because 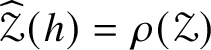 $\widehat {\mathscr {Z}}(h) = \operatorname {\rho }(\mathscr {Z})$ for any
$\widehat {\mathscr {Z}}(h) = \operatorname {\rho }(\mathscr {Z})$ for any ![]() $\mathscr {Z} \in \mathscr {MC}(\mathbb {V}^{\ast })$, the fifth equality again by (6.9), and the last equality by (5.16). By the nondegeneracy of
$\mathscr {Z} \in \mathscr {MC}(\mathbb {V}^{\ast })$, the fifth equality again by (6.9), and the last equality by (5.16). By the nondegeneracy of ![]() $\langle \,\cdot \,\,, \,\cdot \,\, \rangle $, (7.13) implies the first equality of (7.12). Because
$\langle \,\cdot \,\,, \,\cdot \,\, \rangle $, (7.13) implies the first equality of (7.12). Because  $\widehat {\mathscr {X}}(h) = \operatorname {\rho }(\mathscr {X})$, taking
$\widehat {\mathscr {X}}(h) = \operatorname {\rho }(\mathscr {X})$, taking ![]() $\alpha = h$ in the first equality of (7.12) yields its second equality.
$\alpha = h$ in the first equality of (7.12) yields its second equality.
Lemma 7.8. Let ![]() $(\mathbb {V}, h)$ be an n-dimensional metric vector space. For
$(\mathbb {V}, h)$ be an n-dimensional metric vector space. For ![]() $\alpha , \beta \in S^{2}(\mathbb {V}^{\ast })$,
$\alpha , \beta \in S^{2}(\mathbb {V}^{\ast })$,


Proof. Taking ![]() in (7.12) and simplifying using (7.4) and (6.6) yields (7.14), and (7.15) and (7.16) are special cases of (7.14). Alternatively, (7.14)–(7.16) are special cases of (6.18).
in (7.12) and simplifying using (7.4) and (6.6) yields (7.14), and (7.15) and (7.16) are special cases of (7.14). Alternatively, (7.14)–(7.16) are special cases of (6.18).
Lemma 7.9. Let ![]() $(\mathbb {V}, h)$ be a Euclidean vector space of dimension
$(\mathbb {V}, h)$ be a Euclidean vector space of dimension ![]() $n \geq 4$. Let
$n \geq 4$. Let

Then ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) = \mathbb {W}_{1} = \mathbb {W}_{2} = \mathbb {W}_{3} = \mathbb {W}_{4}$.
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) = \mathbb {W}_{1} = \mathbb {W}_{2} = \mathbb {W}_{3} = \mathbb {W}_{4}$.
Proof. By (7.3) and (7.7), ![]() $\mathbb {W}_{2}, \mathbb {W}_{4} \subset \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. By (6.11) and (6.12),
$\mathbb {W}_{2}, \mathbb {W}_{4} \subset \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. By (6.11) and (6.12), ![]() and
and ![]() $|(x\wedge y) \cdot (z \wedge w)|^{2} = 12$, so
$|(x\wedge y) \cdot (z \wedge w)|^{2} = 12$, so ![]() $\mathbb {W}_{1}$ and
$\mathbb {W}_{1}$ and ![]() $\mathbb {W}_{3}$ are nontrivial. If
$\mathbb {W}_{3}$ are nontrivial. If ![]() $x, y, z, w$ are pairwise orthogonal, then
$x, y, z, w$ are pairwise orthogonal, then 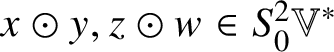 $x \odot y, z \odot w \in S^{2}_{0}\mathbb {V}^{\ast }$ satisfy
$x \odot y, z \odot w \in S^{2}_{0}\mathbb {V}^{\ast }$ satisfy ![]() $(x\odot y)\circ (z \odot w) = 0$, so
$(x\odot y)\circ (z \odot w) = 0$, so ![]() $\mathbb {W}_{1} \subset \mathbb {W}_{2}$, and
$\mathbb {W}_{1} \subset \mathbb {W}_{2}$, and ![]() $x \wedge y, z \wedge w\in {\bigwedge }^{2}\mathbb {V}^{\ast }$ satisfy
$x \wedge y, z \wedge w\in {\bigwedge }^{2}\mathbb {V}^{\ast }$ satisfy ![]() $(x\wedge y)\circ (z \wedge w) = 0$, so
$(x\wedge y)\circ (z \wedge w) = 0$, so ![]() $\mathbb {W}_{3} \subset \mathbb {W}_{4}$. Since
$\mathbb {W}_{3} \subset \mathbb {W}_{4}$. Since ![]() $\mathbb {W}_{1}$ and
$\mathbb {W}_{1}$ and ![]() $\mathbb {W}_{3}$ are nontrivial
$\mathbb {W}_{3}$ are nontrivial ![]() $O(n)$-submodules of the
$O(n)$-submodules of the ![]() $O(n)$-irreducible module
$O(n)$-irreducible module ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, they equal
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, they equal ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$.
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$.
Theorem 7.10. Let ![]() $(\mathbb {V}, h)$ be a Euclidean vector space of dimension
$(\mathbb {V}, h)$ be a Euclidean vector space of dimension ![]() $n \geq 4$. If
$n \geq 4$. If ![]() $\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$ satisfies
$\mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$ satisfies ![]() $\mathscr {X} \ast \mathscr {Y} = 0$ for all
$\mathscr {X} \ast \mathscr {Y} = 0$ for all ![]() $\mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$, then
$\mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$, then ![]() $\mathscr {X} = 0$.
$\mathscr {X} = 0$.
Proof. Because 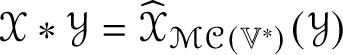 $\mathscr {X} \ast \mathscr {Y} = \widehat {\mathscr {X}}_{\mathscr {MC}(\mathbb {V}^{\ast })}(\mathscr {Y})$, an equivalent claim is that the map
$\mathscr {X} \ast \mathscr {Y} = \widehat {\mathscr {X}}_{\mathscr {MC}(\mathbb {V}^{\ast })}(\mathscr {Y})$, an equivalent claim is that the map ![]() $\widehat {\,\cdot \,\,}_{\mathscr {MC}(\mathbb {V}^{\ast })}:\mathscr {MC}(\mathbb {V}^{\ast }) \to \operatorname {End}(\mathscr {MC}(\mathbb {V}^{\ast }))$ is injective. If
$\widehat {\,\cdot \,\,}_{\mathscr {MC}(\mathbb {V}^{\ast })}:\mathscr {MC}(\mathbb {V}^{\ast }) \to \operatorname {End}(\mathscr {MC}(\mathbb {V}^{\ast }))$ is injective. If ![]() $\mathscr {X} \ast \mathscr {Y} = 0$ for all
$\mathscr {X} \ast \mathscr {Y} = 0$ for all ![]() $\mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$, then
$\mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$, then ![]() $0 = \langle \mathscr {X} \ast \mathscr {Y}, \mathscr {Z} \rangle = \langle \mathscr {X}, \mathscr {Y} \ast \mathscr {Z}\rangle $ for all
$0 = \langle \mathscr {X} \ast \mathscr {Y}, \mathscr {Z} \rangle = \langle \mathscr {X}, \mathscr {Y} \ast \mathscr {Z}\rangle $ for all ![]() $\mathscr {Y}, \mathscr {Z} \in \mathscr {MC}(\mathbb {V}^{\ast })$. With
$\mathscr {Y}, \mathscr {Z} \in \mathscr {MC}(\mathbb {V}^{\ast })$. With ![]() , by (7.16) and (6.9) this yields
, by (7.16) and (6.9) this yields ![]() . Taking
. Taking ![]() and
and ![]() for
for 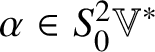 $\alpha \in S^{2}_{0}\mathbb {V}^{\ast }$, by (7.15) and (6.9) this yields
$\alpha \in S^{2}_{0}\mathbb {V}^{\ast }$, by (7.15) and (6.9) this yields  . Since
. Since 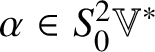 $\alpha \in S^{2}_{0}\mathbb {V}^{\ast }$ is arbitrary, this shows
$\alpha \in S^{2}_{0}\mathbb {V}^{\ast }$ is arbitrary, this shows ![]() $\operatorname {\rho }(\mathscr {X}) = 0$, so
$\operatorname {\rho }(\mathscr {X}) = 0$, so ![]() $\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. Finally, if
$\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. Finally, if 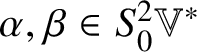 $\alpha , \beta \in S^{2}_{0}\mathbb {V}^{\ast }$, then, by (7.14) and the preceding,
$\alpha , \beta \in S^{2}_{0}\mathbb {V}^{\ast }$, then, by (7.14) and the preceding, ![]() . Because the set
. Because the set ![]() $\mathbb {W}_{2}$ of Lemma 7.9 spans
$\mathbb {W}_{2}$ of Lemma 7.9 spans ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, this shows that
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, this shows that ![]() $\mathscr {X}$ is orthogonal to
$\mathscr {X}$ is orthogonal to ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, so
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, so ![]() $\mathscr {X} = 0$.
$\mathscr {X} = 0$.
Lemma 7.11. Let ![]() $(\mathbb {V}, h)$ be an n-dimensional Euclidean vector space. The projections onto the
$(\mathbb {V}, h)$ be an n-dimensional Euclidean vector space. The projections onto the ![]() $O(h)$-irreducible summands of
$O(h)$-irreducible summands of ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$ of
$\mathscr {MC}(\mathbb {V}^{\ast })$ of ![]() $\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$ satisfy
$\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$ satisfy



Proof. The identities (7.18)–(7.20) follow from (7.12), (7.15), and (7.16) and the definitions (7.1) of ![]() $\mathscr {P}_{\mathscr {R}}$ and
$\mathscr {P}_{\mathscr {R}}$ and ![]() $\mathscr {P}_{\mathscr {S}}$. By (7.1) and (7.12),
$\mathscr {P}_{\mathscr {S}}$. By (7.1) and (7.12), 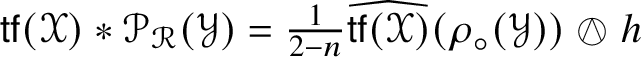 . By (5.16),
. By (5.16), 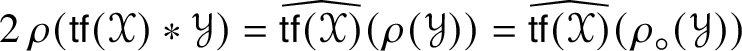 $2\operatorname {\rho }(\operatorname {\mathsf {tf}}(\mathscr {X})\ast \mathscr {Y}) = \widehat {\operatorname {\mathsf {tf}}(\mathscr {X})}(\operatorname {\rho }(\mathscr {Y})) =\widehat {\operatorname {\mathsf {tf}}(\mathscr {X})}(\operatorname {\rho }_{\circ }(\mathscr {Y}))$, the last equality because
$2\operatorname {\rho }(\operatorname {\mathsf {tf}}(\mathscr {X})\ast \mathscr {Y}) = \widehat {\operatorname {\mathsf {tf}}(\mathscr {X})}(\operatorname {\rho }(\mathscr {Y})) =\widehat {\operatorname {\mathsf {tf}}(\mathscr {X})}(\operatorname {\rho }_{\circ }(\mathscr {Y}))$, the last equality because 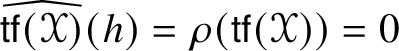 $\widehat {\operatorname {\mathsf {tf}}(\mathscr {X})}(h) = \operatorname {\rho }(\operatorname {\mathsf {tf}}(\mathscr {X})) = 0$. Combining the preceding observations yields (7.21). Finally, (7.22) follows straightforwardly from (7.14), using
$\widehat {\operatorname {\mathsf {tf}}(\mathscr {X})}(h) = \operatorname {\rho }(\operatorname {\mathsf {tf}}(\mathscr {X})) = 0$. Combining the preceding observations yields (7.21). Finally, (7.22) follows straightforwardly from (7.14), using ![]() and
and ![]() .
.
An irreducible ![]() $O(n)$-submodule of
$O(n)$-submodule of ![]() $\otimes ^{k}\mathbb {V}^{\ast }$ comprises the completely trace-free tensors of a given type (this statement is false for even
$\otimes ^{k}\mathbb {V}^{\ast }$ comprises the completely trace-free tensors of a given type (this statement is false for even ![]() $k = n$ if
$k = n$ if ![]() $O(n)$ is replaced by
$O(n)$ is replaced by ![]() $SO(n)$). By Lemma 4.2, if
$SO(n)$). By Lemma 4.2, if ![]() $G \subset O(n)$ is a Lie subgroup and
$G \subset O(n)$ is a Lie subgroup and ![]() $\mathbb {U} \subset \mathscr {MC}(\mathbb {V}^{\ast })$ and
$\mathbb {U} \subset \mathscr {MC}(\mathbb {V}^{\ast })$ and ![]() $\mathbb {W} \subset \otimes ^{k}\mathbb {V}^{\ast }$ are G-submodules, then
$\mathbb {W} \subset \otimes ^{k}\mathbb {V}^{\ast }$ are G-submodules, then ![]() $\widehat {\mathbb {U}}(\mathbb {W})$ is a G-submodule of
$\widehat {\mathbb {U}}(\mathbb {W})$ is a G-submodule of ![]() $\otimes ^{k}\mathbb {V}^{\ast }$, for if
$\otimes ^{k}\mathbb {V}^{\ast }$, for if ![]() $g \in O(n)$,
$g \in O(n)$, ![]() $\mathscr {X} \in \mathbb {U}$ and
$\mathscr {X} \in \mathbb {U}$ and ![]() $\mathscr {Y} \in \mathbb {W}$,
$\mathscr {Y} \in \mathbb {W}$, 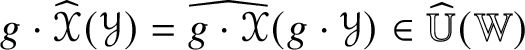 $g\cdot \widehat {\mathscr {X}}(\mathscr {Y}) = \widehat {g\cdot \mathscr {X}}(g\cdot \mathscr {Y}) \in \widehat {\mathbb {U}}(\mathbb {W})$. In particular, because
$g\cdot \widehat {\mathscr {X}}(\mathscr {Y}) = \widehat {g\cdot \mathscr {X}}(g\cdot \mathscr {Y}) \in \widehat {\mathbb {U}}(\mathbb {W})$. In particular, because ![]() $\widehat {\mathscr {X}}$ preserves type, if
$\widehat {\mathscr {X}}$ preserves type, if ![]() $\mathbb {U}_{1}, \mathbb {U}_{2} \subset \mathscr {MC}(\mathbb {V}^{\ast })$ are G-submodules, then
$\mathbb {U}_{1}, \mathbb {U}_{2} \subset \mathscr {MC}(\mathbb {V}^{\ast })$ are G-submodules, then ![]() $\widehat {\mathbb {U}_{1}}(\mathbb {U}_{2})$ is a G-submodule of
$\widehat {\mathbb {U}_{1}}(\mathbb {U}_{2})$ is a G-submodule of ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$. By Theorem 5.4,
$\mathscr {MC}(\mathbb {V}^{\ast })$. By Theorem 5.4, ![]() $\widehat {\mathbb {U}_{2}}(\mathbb {U}_{1}) = \mathbb {U}_{2}\ast \mathbb {U}_{1} = \mathbb {U}_{1}\ast \mathbb {U}_{2}= \widehat {\mathbb {U}_{1}}(\mathbb {U}_{2})$. For example, Corollary 7.6 shows that
$\widehat {\mathbb {U}_{2}}(\mathbb {U}_{1}) = \mathbb {U}_{2}\ast \mathbb {U}_{1} = \mathbb {U}_{1}\ast \mathbb {U}_{2}= \widehat {\mathbb {U}_{1}}(\mathbb {U}_{2})$. For example, Corollary 7.6 shows that ![]() $\widehat {\mathbb {U}}(\mathbb {U}) = \mathbb {U} \ast \mathbb {U} = \mathbb {U}$ for
$\widehat {\mathbb {U}}(\mathbb {U}) = \mathbb {U} \ast \mathbb {U} = \mathbb {U}$ for ![]() $\mathbb {U} = \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. Theorem 7.12 describes completely the submodules
$\mathbb {U} = \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. Theorem 7.12 describes completely the submodules ![]() $\mathbb {U}_{1}\ast \mathbb {U}_{2}$ for
$\mathbb {U}_{1}\ast \mathbb {U}_{2}$ for ![]() $\mathbb {U}_{1}, \mathbb {U}_{2}$ among the
$\mathbb {U}_{1}, \mathbb {U}_{2}$ among the ![]() $O(n)$-irreducible summands of
$O(n)$-irreducible summands of ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$.
$\mathscr {MC}(\mathbb {V}^{\ast })$.
Theorem 7.12. Let ![]() $(\mathbb {V}, h)$ be an n-dimensional Euclidean vector space. The products of the
$(\mathbb {V}, h)$ be an n-dimensional Euclidean vector space. The products of the ![]() $O(n)$-irreducible submodules of
$O(n)$-irreducible submodules of ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$ satisfy:
$\mathscr {MC}(\mathbb {V}^{\ast })$ satisfy:
Proof. The containments in (7.23)–(7.27) of subspaces are consequences of polarizing (7.18)–(7.22). The equalities require further justification. The product (7.25) is immediate from (7.20). By (7.15), multiplication by ![]() , which spans
, which spans ![]() $\mathscr {MC}_{\mathscr {S}}(\mathbb {V}^{\ast })$, is invertible on
$\mathscr {MC}_{\mathscr {S}}(\mathbb {V}^{\ast })$, is invertible on ![]() $\mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast })$ when
$\mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast })$ when ![]() $n> 2$ and on
$n> 2$ and on ![]() $\mathscr {MC}_{\mathscr {S}}(\mathbb {V}^{\ast })$ when
$\mathscr {MC}_{\mathscr {S}}(\mathbb {V}^{\ast })$ when ![]() $n> 1$, and this suffices to show the equalities (7.23) and (7.24).
$n> 1$, and this suffices to show the equalities (7.23) and (7.24).
Let ![]() $\alpha \in S^{2}(\mathbb {V}^{\ast })$. If
$\alpha \in S^{2}(\mathbb {V}^{\ast })$. If ![]() $\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, then
$\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, then 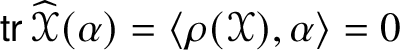 $\operatorname {\mathsf {tr}} \widehat {\mathscr {X}}(\alpha ) = \langle \operatorname {\rho }(\mathscr {X}), \alpha \rangle = 0$, so, by (7.12),
$\operatorname {\mathsf {tr}} \widehat {\mathscr {X}}(\alpha ) = \langle \operatorname {\rho }(\mathscr {X}), \alpha \rangle = 0$, so, by (7.12),  . This shows the containment of
. This shows the containment of ![]() $O(n)$-modules,
$O(n)$-modules, ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) \ast \mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast }) \subset \mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast })$. By the irreducibility of
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) \ast \mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast }) \subset \mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast })$. By the irreducibility of ![]() $\mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast })$, to show equality it suffices to exhibit a nonzero element of
$\mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast })$, to show equality it suffices to exhibit a nonzero element of ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) \ast \mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast })$. Let
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) \ast \mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast })$. Let ![]() $u, v \in \mathbb {V}$ be such that
$u, v \in \mathbb {V}$ be such that ![]() $|u|^{2} = 2 = |v|^{2}$ and
$|u|^{2} = 2 = |v|^{2}$ and ![]() $\langle u, v \rangle = 0$. Then
$\langle u, v \rangle = 0$. Then 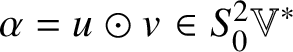 $\alpha = u\odot v \in S^{2}_{0}\mathbb {V}^{\ast }$ satisfies
$\alpha = u\odot v \in S^{2}_{0}\mathbb {V}^{\ast }$ satisfies ![]() $|\alpha |^{2} = 2$,
$|\alpha |^{2} = 2$, ![]() $2 \alpha \circ \alpha = u \otimes u + v \otimes v$,
$2 \alpha \circ \alpha = u \otimes u + v \otimes v$, ![]() $\langle \alpha , \alpha \circ \alpha \rangle = 0$, and
$\langle \alpha , \alpha \circ \alpha \rangle = 0$, and ![]() $\alpha \circ \alpha \circ \alpha = \alpha $. From these and
$\alpha \circ \alpha \circ \alpha = \alpha $. From these and ![]() there follow
there follow ![]() ,
, ![]() ,
, 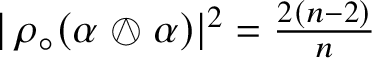 , and
, and ![]() . By (7.6),
. By (7.6), 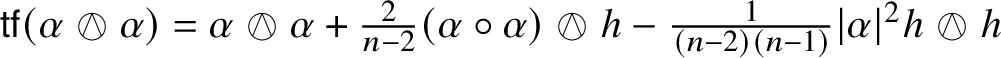 , and by (6.6) and the preceding observations,
, and by (6.6) and the preceding observations, 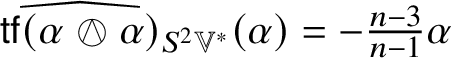 , so, by (7.12),
, so, by (7.12),

which shows that ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) \ast \mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast })$ is nontrivial if
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) \ast \mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast })$ is nontrivial if ![]() $n> 3$ and so proves the equality in (7.26).
$n> 3$ and so proves the equality in (7.26).
Suppose ![]() $\dim \mathbb {V}^{\ast }> 3$. Let
$\dim \mathbb {V}^{\ast }> 3$. Let ![]() $x, y, z, w \in \mathbb {V}^{\ast }$ be pairwise orthogonal unit norm vectors. Then
$x, y, z, w \in \mathbb {V}^{\ast }$ be pairwise orthogonal unit norm vectors. Then ![]() $\alpha = x \odot y$ and
$\alpha = x \odot y$ and ![]() $\beta = z \odot w$ are in
$\beta = z \odot w$ are in 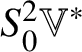 $S^{2}_{0}\mathbb {V}^{\ast }$, so
$S^{2}_{0}\mathbb {V}^{\ast }$, so ![]() . Because
. Because ![]() $\alpha \circledcirc \beta = 0$ and
$\alpha \circledcirc \beta = 0$ and ![]() $\langle \alpha , \beta \rangle = 0$, by (7.14),
$\langle \alpha , \beta \rangle = 0$, by (7.14), ![]() . By (7.3),
. By (7.3), ![]() , so
, so ![]() . Since, by Lemma 7.9,
. Since, by Lemma 7.9, ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is spanned by elements of the form
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is spanned by elements of the form ![]() , this shows the equality in (7.27). The equality (7.28) is Corollary 7.6.
, this shows the equality in (7.27). The equality (7.28) is Corollary 7.6.
Remark 7.13. Lemma 7.11 and Theorem 7.12 give fusion rules (in the sense of [Reference Hall, Rehren and Shpectorov16]) for ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$. Precisely, for the idempotent
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$. Precisely, for the idempotent  , the subspaces
, the subspaces ![]() $\mathscr {MC}_{\mathscr {S}}(\mathbb {V}^{\ast })$,
$\mathscr {MC}_{\mathscr {S}}(\mathbb {V}^{\ast })$, ![]() $\mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast })$, and
$\mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast })$, and ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ are the eigenspaces of
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ are the eigenspaces of ![]() $L_{\ast }(\mathscr {H})$ with eigenvalues
$L_{\ast }(\mathscr {H})$ with eigenvalues ![]() $1$,
$1$, 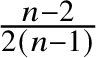 $\tfrac {n-2}{2(n-1)}$, and
$\tfrac {n-2}{2(n-1)}$, and ![]() $0$. Lemma 7.11 shows that their products satisfy the fusion rule
$0$. Lemma 7.11 shows that their products satisfy the fusion rule ![]() $\star : \Phi \times \Phi \to 2^{\Phi }$ indicated in Table 1, where
$\star : \Phi \times \Phi \to 2^{\Phi }$ indicated in Table 1, where 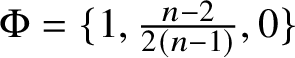 $\Phi = \{1, \tfrac {n-2}{2(n-1)}, 0\}$. A subset of
$\Phi = \{1, \tfrac {n-2}{2(n-1)}, 0\}$. A subset of ![]() $\Phi $ indicates the sum of the eigenspaces corresponding to this subset and an entry in the table means that the
$\Phi $ indicates the sum of the eigenspaces corresponding to this subset and an entry in the table means that the ![]() $\ast $ product of the eigenspaces corresponding with
$\ast $ product of the eigenspaces corresponding with ![]() $\alpha , \beta \in \Phi $ is contained in the sum of the eigenspaces corresponding with elements of
$\alpha , \beta \in \Phi $ is contained in the sum of the eigenspaces corresponding with elements of ![]() $\alpha \star \beta $.
$\alpha \star \beta $.
Note that Theorem 7.12 gives more information than Table 1 because it asserts the equalities of the products of subspaces, rather than mere containment relations.
As an application of Lemma 7.11 there is given a simple proof of [Reference Böhm and Wilking2, Theorem ![]() $2$]. For
$2$]. For ![]() $\alpha , \beta \in \mathbb R$ define an
$\alpha , \beta \in \mathbb R$ define an ![]() $O(n)$-equivariant endomorphism
$O(n)$-equivariant endomorphism ![]() $\Phi _{\alpha , \beta } \in \operatorname {End}(\mathscr {MC}(\mathbb {V}^{\ast }))$ by
$\Phi _{\alpha , \beta } \in \operatorname {End}(\mathscr {MC}(\mathbb {V}^{\ast }))$ by
For example, (7.22) can be rewritten as ![]() .
.
Note that ![]() $\Phi _{1, 1} = \operatorname {Id}_{\mathscr {MC}(\mathbb {V}^{\ast })}$. Because
$\Phi _{1, 1} = \operatorname {Id}_{\mathscr {MC}(\mathbb {V}^{\ast })}$. Because ![]() $\Phi _{\alpha , \beta }\circ \Phi _{\bar {\alpha }, \bar {\beta }} = \Phi _{\alpha \bar {\alpha }, \beta \bar {\beta }}$,
$\Phi _{\alpha , \beta }\circ \Phi _{\bar {\alpha }, \bar {\beta }} = \Phi _{\alpha \bar {\alpha }, \beta \bar {\beta }}$, ![]() $\Phi _{\alpha , \beta }$ is invertible if and only if
$\Phi _{\alpha , \beta }$ is invertible if and only if ![]() $\alpha \neq 0$ and
$\alpha \neq 0$ and ![]() $\beta \neq 0$, in which case
$\beta \neq 0$, in which case  $\Phi _{\alpha , \beta }^{-1} = \Phi _{\alpha ^{-1}, \beta ^{-1}}$. If
$\Phi _{\alpha , \beta }^{-1} = \Phi _{\alpha ^{-1}, \beta ^{-1}}$. If ![]() $\alpha = 1 + 2(n-1)a$ and
$\alpha = 1 + 2(n-1)a$ and ![]() $\beta = 1 + (n-2)b$, then
$\beta = 1 + (n-2)b$, then ![]() $\Phi _{\alpha , \beta }$ equals the endomorphism called
$\Phi _{\alpha , \beta }$ equals the endomorphism called ![]() $l_{a, b}$ introduced by C. Böhm and B. Wilking in [Reference Böhm and Wilking2]. The reason for working with the parameters
$l_{a, b}$ introduced by C. Böhm and B. Wilking in [Reference Böhm and Wilking2]. The reason for working with the parameters ![]() $\alpha $ and
$\alpha $ and ![]() $\beta $ is that the map
$\beta $ is that the map ![]() $(\alpha , \beta ) \in \mathbb {R}^{\times } \times \mathbb {R}^{\times } \to \Phi _{\alpha , \beta } \in \operatorname {End}(\mathscr {MC}(\mathbb {V}^{\ast }))$ is an injective group homomorphism.
$(\alpha , \beta ) \in \mathbb {R}^{\times } \times \mathbb {R}^{\times } \to \Phi _{\alpha , \beta } \in \operatorname {End}(\mathscr {MC}(\mathbb {V}^{\ast }))$ is an injective group homomorphism.
The key point of Theorem 7.14 for its applications is that (7.31) does not depend on ![]() $\operatorname {\mathsf {tf}}(\mathscr {X})$.
$\operatorname {\mathsf {tf}}(\mathscr {X})$.
Theorem 7.14 C. Böhm and B. Wilking [Reference Böhm and Wilking2, Theorem  $2$].
$2$].
Let ![]() $(\mathbb {V}, h)$ be an n-dimensional Euclidean vector space. If
$(\mathbb {V}, h)$ be an n-dimensional Euclidean vector space. If ![]() $\alpha , \beta \in \mathbb R\setminus \{0\}$ and
$\alpha , \beta \in \mathbb R\setminus \{0\}$ and 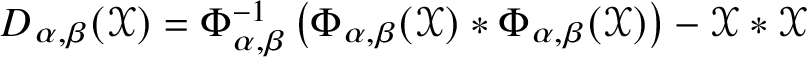 $D_{\alpha , \beta }(\mathscr {X}) = \Phi _{\alpha , \beta }^{-1}\left (\Phi _{\alpha , \beta }(\mathscr {X}) \ast \Phi _{\alpha , \beta }(\mathscr {X}) \right ) - \mathscr {X} \ast \mathscr {X}$, where
$D_{\alpha , \beta }(\mathscr {X}) = \Phi _{\alpha , \beta }^{-1}\left (\Phi _{\alpha , \beta }(\mathscr {X}) \ast \Phi _{\alpha , \beta }(\mathscr {X}) \right ) - \mathscr {X} \ast \mathscr {X}$, where ![]() $\Phi _{\alpha , \beta } \in \operatorname {End}(\mathscr {MC}(\mathbb {V}^{\ast }))$ is defined in (7.30), then
$\Phi _{\alpha , \beta } \in \operatorname {End}(\mathscr {MC}(\mathbb {V}^{\ast }))$ is defined in (7.30), then

Proof. Straightforward calculations using (7.18)–(7.22) yield

The special case ![]() $\alpha = 1 = \beta $ yields
$\alpha = 1 = \beta $ yields

Combining (7.32) and (7.33) yields (7.31). After rewriting (7.31) in terms of the parameters a and b and a bit of computation it can be seen that (7.31) recovers the conclusion of [Reference Böhm and Wilking2, Theorem ![]() $2$].
$2$].
8 Characterization of  $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ when
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ when  $\dim \mathbb {V} = 3$
$\dim \mathbb {V} = 3$
If ![]() $\dim \mathbb {V} = 2$, the
$\dim \mathbb {V} = 2$, the ![]() $1$-dimensional algebra
$1$-dimensional algebra ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ is generated by
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ is generated by ![]() and, by (7.16), it is isomorphic to the field
and, by (7.16), it is isomorphic to the field ![]() $\mathbb R$ of real numbers by the map sending
$\mathbb R$ of real numbers by the map sending ![]() to
to ![]() $1 \in \mathbb R$. This section identifies
$1 \in \mathbb R$. This section identifies ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ in a similarly explicit manner when
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ in a similarly explicit manner when ![]() $(\mathbb {V}, h)$ is a
$(\mathbb {V}, h)$ is a ![]() $3$-dimensional Euclidean vector space. Pulling the multiplication
$3$-dimensional Euclidean vector space. Pulling the multiplication ![]() $\ast $ back via an
$\ast $ back via an ![]() $O(3)$-equivariant linear isomorphisms
$O(3)$-equivariant linear isomorphisms ![]() $\Psi : S^{2}\mathbb {V}^{\ast } \to \mathscr {MC}(\mathbb {V}^{\ast })$ yields an
$\Psi : S^{2}\mathbb {V}^{\ast } \to \mathscr {MC}(\mathbb {V}^{\ast })$ yields an ![]() $O(3)$-equivariant commutative multiplication
$O(3)$-equivariant commutative multiplication ![]() $\diamond $ on
$\diamond $ on ![]() $S^{2}\mathbb {V}^{\ast }$. By Lemma 8.1, requiring that the associated map
$S^{2}\mathbb {V}^{\ast }$. By Lemma 8.1, requiring that the associated map  $\alpha \in S^{2}\mathbb {V}^{\ast } \to 2\widehat {\Psi (\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} \in \operatorname {Sym}({\bigwedge }^{2}\mathbb {V}^{\ast }, \langle \,\cdot \,\,, \,\cdot \,\, \rangle )$ be a Jordan algebra isomorphism determines
$\alpha \in S^{2}\mathbb {V}^{\ast } \to 2\widehat {\Psi (\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} \in \operatorname {Sym}({\bigwedge }^{2}\mathbb {V}^{\ast }, \langle \,\cdot \,\,, \,\cdot \,\, \rangle )$ be a Jordan algebra isomorphism determines ![]() $\Psi $ uniquely, and this determines a standard model
$\Psi $ uniquely, and this determines a standard model ![]() $(S^{2}\mathbb {V}^{\ast }, \diamond )$ of
$(S^{2}\mathbb {V}^{\ast }, \diamond )$ of ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ realizing it as a deformation of Jordan product
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ realizing it as a deformation of Jordan product ![]() $\circledcirc $ on
$\circledcirc $ on ![]() $S^{2}\mathbb {V}^{\ast }$ by terms built from the metric and the trace. Most of the section is devoted to formulating and proving Theorem 8.5, which specifies algebraic conditions that characterize the resulting algebra
$S^{2}\mathbb {V}^{\ast }$ by terms built from the metric and the trace. Most of the section is devoted to formulating and proving Theorem 8.5, which specifies algebraic conditions that characterize the resulting algebra ![]() $(S^{2}\mathbb {V}^{\ast }, \diamond )$ up to isomorphism.
$(S^{2}\mathbb {V}^{\ast }, \diamond )$ up to isomorphism.
Because 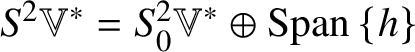 $S^{2}\mathbb {V}^{\ast } = S^{2}_{0}\mathbb {V}^{\ast } \oplus \text {Span}\, \{h\}$ and
$S^{2}\mathbb {V}^{\ast } = S^{2}_{0}\mathbb {V}^{\ast } \oplus \text {Span}\, \{h\}$ and ![]() $\mathscr {MC}(\mathbb {V}^{\ast }) = \mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast })\oplus \mathscr {MC}_{\mathscr {S}}(\mathbb {V}^{\ast })$ are decompositions into
$\mathscr {MC}(\mathbb {V}^{\ast }) = \mathscr {MC}_{\mathscr {R}}(\mathbb {V}^{\ast })\oplus \mathscr {MC}_{\mathscr {S}}(\mathbb {V}^{\ast })$ are decompositions into ![]() $O(3)$-irreducible submodules, by the Schur Lemma the most general
$O(3)$-irreducible submodules, by the Schur Lemma the most general ![]() $O(3)$-equivariant linear map
$O(3)$-equivariant linear map ![]() $S^{2}\mathbb {V}^{\ast } \to \mathscr {MC}(\mathbb {V}^{\ast })$ has the form
$S^{2}\mathbb {V}^{\ast } \to \mathscr {MC}(\mathbb {V}^{\ast })$ has the form ![]() for some
for some ![]() $p,\tau \in \mathbb R$ and
$p,\tau \in \mathbb R$ and ![]() $\psi _{p, \tau } \in \operatorname {End}(S^{2}\mathbb {V}^{\ast })$ defined by
$\psi _{p, \tau } \in \operatorname {End}(S^{2}\mathbb {V}^{\ast })$ defined by 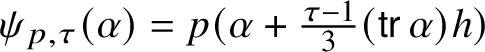 $\psi _{p, \tau }(\alpha )= p(\alpha +\tfrac {\tau - 1}{3} (\operatorname {\mathsf {tr}} \alpha )h)$. Because
$\psi _{p, \tau }(\alpha )= p(\alpha +\tfrac {\tau - 1}{3} (\operatorname {\mathsf {tr}} \alpha )h)$. Because ![]() $\psi _{p, \tau }\circ \psi _{\bar {p}, \bar {\tau }} = \psi _{p\bar {p}, \tau \bar {\tau }}$,
$\psi _{p, \tau }\circ \psi _{\bar {p}, \bar {\tau }} = \psi _{p\bar {p}, \tau \bar {\tau }}$, ![]() $\psi _{p, \tau }$ is invertible if and only if
$\psi _{p, \tau }$ is invertible if and only if ![]() $p\tau \neq 0$, in which case
$p\tau \neq 0$, in which case  $\psi _{p, \tau }^{-1} = \psi _{p^{-1}, \tau ^{-1}}$, and
$\psi _{p, \tau }^{-1} = \psi _{p^{-1}, \tau ^{-1}}$, and ![]() $\Psi _{p, \tau }\circ \psi _{\bar {p}, \bar {\tau }} = \Psi _{p\bar {p}, \tau \bar {\tau }}$. By (7.3),
$\Psi _{p, \tau }\circ \psi _{\bar {p}, \bar {\tau }} = \Psi _{p\bar {p}, \tau \bar {\tau }}$. By (7.3),
 $$ \begin{align} &\operatorname{\rho}(\Psi_{p, \tau}(\alpha)) = -\tfrac{p}{2}\left(\alpha + \tfrac{4\tau - 1}{3}(\operatorname{\mathsf{tr}} \alpha)h\right) = \psi_{-p/2, 4\tau}(\alpha),&& \operatorname{s}(\Psi_{p, \tau}(\alpha)) = -2p\tau\operatorname{\mathsf{tr}} \alpha, \end{align} $$
$$ \begin{align} &\operatorname{\rho}(\Psi_{p, \tau}(\alpha)) = -\tfrac{p}{2}\left(\alpha + \tfrac{4\tau - 1}{3}(\operatorname{\mathsf{tr}} \alpha)h\right) = \psi_{-p/2, 4\tau}(\alpha),&& \operatorname{s}(\Psi_{p, \tau}(\alpha)) = -2p\tau\operatorname{\mathsf{tr}} \alpha, \end{align} $$so, if ![]() $p\tau \neq 0$,
$p\tau \neq 0$,
 $$ \begin{align} \Psi_{p, \tau}^{-1}(\mathscr{X}) =- \tfrac{2}{p}\left(\operatorname{\rho}(\mathscr{X}) + \tfrac{1 -4\tau}{12\tau}\operatorname{s}(\mathscr{X})h\right) =- \tfrac{2}{p}\left(\operatorname{\rho}_{\circ}(\mathscr{X}) + \tfrac{1}{12\tau}\operatorname{s}(\mathscr{X})h\right)= \psi_{-2/p, 1/4\tau}(\operatorname{\rho}(\mathscr{X})). \end{align} $$
$$ \begin{align} \Psi_{p, \tau}^{-1}(\mathscr{X}) =- \tfrac{2}{p}\left(\operatorname{\rho}(\mathscr{X}) + \tfrac{1 -4\tau}{12\tau}\operatorname{s}(\mathscr{X})h\right) =- \tfrac{2}{p}\left(\operatorname{\rho}_{\circ}(\mathscr{X}) + \tfrac{1}{12\tau}\operatorname{s}(\mathscr{X})h\right)= \psi_{-2/p, 1/4\tau}(\operatorname{\rho}(\mathscr{X})). \end{align} $$That ![]() $\Psi _{p, \tau }\circ \psi _{\bar {p}, \bar {\tau }} = \Psi _{p\bar {p}, \tau \bar {\tau }}$ means that the pullbacks of
$\Psi _{p, \tau }\circ \psi _{\bar {p}, \bar {\tau }} = \Psi _{p\bar {p}, \tau \bar {\tau }}$ means that the pullbacks of ![]() $\ast $ via any
$\ast $ via any ![]() $\Psi _{p, \tau }$ with
$\Psi _{p, \tau }$ with ![]() $p\tau \neq 0$ yield isomorphic algebras. Lemma 8.1 shows that certain natural conditions determine a unique choice. For its statement, observe that
$p\tau \neq 0$ yield isomorphic algebras. Lemma 8.1 shows that certain natural conditions determine a unique choice. For its statement, observe that ![]() $\Psi _{p, \tau }$ determines a linear isomorphism
$\Psi _{p, \tau }$ determines a linear isomorphism ![]() $S^{2}\mathbb {V}^{\ast } \to \operatorname {Sym}({\bigwedge }^{2}\mathbb {V}^{\ast }, \langle \,\cdot \,\,, \,\cdot \,\, \rangle )$ by
$S^{2}\mathbb {V}^{\ast } \to \operatorname {Sym}({\bigwedge }^{2}\mathbb {V}^{\ast }, \langle \,\cdot \,\,, \,\cdot \,\, \rangle )$ by  $\alpha \to \widehat {\Psi _{p, \tau }(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$, so it makes sense to say that
$\alpha \to \widehat {\Psi _{p, \tau }(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$, so it makes sense to say that ![]() $\Psi _{p, \tau }$ maps rank one elements to rank 1 elements if
$\Psi _{p, \tau }$ maps rank one elements to rank 1 elements if 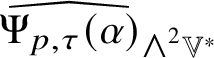 $\widehat {\Psi _{p, \tau }(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ has rank 1 whenever
$\widehat {\Psi _{p, \tau }(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ has rank 1 whenever ![]() $\alpha $ has rank 1, where the rank of an element of
$\alpha $ has rank 1, where the rank of an element of ![]() $S^{2}\mathbb {V}^{\ast }$ means its rank as a bilinear form.
$S^{2}\mathbb {V}^{\ast }$ means its rank as a bilinear form.
Lemma 8.1. Let ![]() $(\mathbb {V}, h)$ be a
$(\mathbb {V}, h)$ be a ![]() $3$-dimensional Euclidean vector space. For an
$3$-dimensional Euclidean vector space. For an ![]() $O(3)$-equivariant linear isomorphism
$O(3)$-equivariant linear isomorphism ![]() $\Psi :S^{2}\mathbb {V}^{\ast } \to \mathscr {MC}(\mathbb {V}^{\ast })$, the following are equivalent:
$\Psi :S^{2}\mathbb {V}^{\ast } \to \mathscr {MC}(\mathbb {V}^{\ast })$, the following are equivalent:
1.
 $\Psi $ has the form
$\Psi $ has the form  $\Psi _{1, -1/2}$.
$\Psi _{1, -1/2}$.2.
 $\Psi $ is isometric,
$\Psi $ is isometric,  $\Psi $ maps h to an idempotent in
$\Psi $ maps h to an idempotent in  $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ and
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ and  $\widehat {\Psi (\,\cdot \,\,)}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}: S^{2}\mathbb {V}^{\ast } \to \operatorname {Sym}({\bigwedge }^{2}\mathbb {V}^{\ast })$ maps rank 1 elements to rank 1 elements.
$\widehat {\Psi (\,\cdot \,\,)}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}: S^{2}\mathbb {V}^{\ast } \to \operatorname {Sym}({\bigwedge }^{2}\mathbb {V}^{\ast })$ maps rank 1 elements to rank 1 elements.3.
 $2\widehat {\Psi (\,\cdot \,\,)}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}: (S^{2}\mathbb {V}^{\ast }, \circledcirc ) \to \operatorname {Sym}({\bigwedge }^{2}\mathbb {V}^{\ast }, \langle \,\cdot \,\,, \,\cdot \,\, \rangle )$ is a Jordan algebra isomorphism.
$2\widehat {\Psi (\,\cdot \,\,)}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}: (S^{2}\mathbb {V}^{\ast }, \circledcirc ) \to \operatorname {Sym}({\bigwedge }^{2}\mathbb {V}^{\ast }, \langle \,\cdot \,\,, \,\cdot \,\, \rangle )$ is a Jordan algebra isomorphism.
Proof. For ![]() $\alpha , \beta \in S^{2}\mathbb {V}^{\ast }$, by (6.12),
$\alpha , \beta \in S^{2}\mathbb {V}^{\ast }$, by (6.12),
 $$ \begin{align} \begin{split} \langle \Psi_{p, \mu}(\alpha), \Psi_{p, \mu}(\beta)\rangle & = \langle \psi_{p, \tau}(\alpha), \psi_{p, \tau}(\beta)\rangle + \operatorname{\mathsf{tr}} \psi_{p,\tau}(\alpha)\operatorname{\mathsf{tr}} \psi_{p, \tau}(\beta) \\&= p^{2}\left(\langle \alpha, \beta \rangle + \left(\tfrac{4\tau^{2} - 1}{3}\right)\operatorname{\mathsf{tr}} \alpha \operatorname{\mathsf{tr}} \beta \right)\!, \end{split} \end{align} $$
$$ \begin{align} \begin{split} \langle \Psi_{p, \mu}(\alpha), \Psi_{p, \mu}(\beta)\rangle & = \langle \psi_{p, \tau}(\alpha), \psi_{p, \tau}(\beta)\rangle + \operatorname{\mathsf{tr}} \psi_{p,\tau}(\alpha)\operatorname{\mathsf{tr}} \psi_{p, \tau}(\beta) \\&= p^{2}\left(\langle \alpha, \beta \rangle + \left(\tfrac{4\tau^{2} - 1}{3}\right)\operatorname{\mathsf{tr}} \alpha \operatorname{\mathsf{tr}} \beta \right)\!, \end{split} \end{align} $$from which it follows that ![]() $ \langle \Psi _{p, \mu }(\alpha ), \Psi _{p, \mu }(\beta )\rangle = \langle \alpha , \beta \rangle $ if and only if
$ \langle \Psi _{p, \mu }(\alpha ), \Psi _{p, \mu }(\beta )\rangle = \langle \alpha , \beta \rangle $ if and only if ![]() $p, 2\tau \in \{\pm 1\}$. As
$p, 2\tau \in \{\pm 1\}$. As ![]() , by (7.16),
, by (7.16), ![]() $\Psi _{p, \tau }(h)$ is idempotent in
$\Psi _{p, \tau }(h)$ is idempotent in ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ if and only if
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ if and only if ![]() $2p\tau = -1$, in which case
$2p\tau = -1$, in which case ![]() $\Psi $ has the form
$\Psi $ has the form ![]() $\Psi _{1, -1/2}$ or
$\Psi _{1, -1/2}$ or ![]() $\Psi _{-1, 1/2}$.
$\Psi _{-1, 1/2}$.
For ![]() $\alpha \in S^{2}\mathbb {V}^{\ast }$ define
$\alpha \in S^{2}\mathbb {V}^{\ast }$ define ![]() $\alpha ^{\sharp } \in \operatorname {End}(\mathbb {V}^{\ast })$ by
$\alpha ^{\sharp } \in \operatorname {End}(\mathbb {V}^{\ast })$ by ![]() $\alpha (u)_{i} = \alpha _{i}{}^{p}u_{p}$ for
$\alpha (u)_{i} = \alpha _{i}{}^{p}u_{p}$ for ![]() $u \in \mathbb {V}^{\ast }$. If
$u \in \mathbb {V}^{\ast }$. If ![]() $u, v \in \mathbb {V}^{\ast }$, then
$u, v \in \mathbb {V}^{\ast }$, then 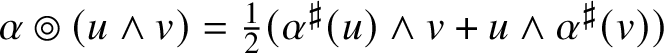 $\alpha \circledcirc (u\wedge v) = \tfrac {1}{2}(\alpha ^{\sharp }(u)\wedge v + u \wedge \alpha ^{\sharp }(v))$. By (6.8),
$\alpha \circledcirc (u\wedge v) = \tfrac {1}{2}(\alpha ^{\sharp }(u)\wedge v + u \wedge \alpha ^{\sharp }(v))$. By (6.8), 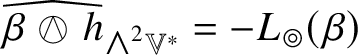 for
for ![]() $\beta \in S^{2}\mathbb {V}^{\ast }$, so
$\beta \in S^{2}\mathbb {V}^{\ast }$, so
 $$ \begin{align} \widehat{\Psi_{p, \tau}(\alpha)}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} = - p(L_{\circledcirc}(\alpha) + \tfrac{\tau-1}{3}\operatorname{\mathsf{tr}}(\alpha)\operatorname{Id}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}) \end{align} $$
$$ \begin{align} \widehat{\Psi_{p, \tau}(\alpha)}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} = - p(L_{\circledcirc}(\alpha) + \tfrac{\tau-1}{3}\operatorname{\mathsf{tr}}(\alpha)\operatorname{Id}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}) \end{align} $$and, hence,
 $$ \begin{align} \widehat{\Psi_{p, \tau}(\alpha)}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(u\wedge v) = -\tfrac{p}{2}\left(\alpha^{\sharp}(u)\wedge v + u \wedge \alpha^{\sharp}(v) + \tfrac{2(\tau-1)}{3}\operatorname{\mathsf{tr}}(\alpha)u\wedge v\right)\!. \end{align} $$
$$ \begin{align} \widehat{\Psi_{p, \tau}(\alpha)}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(u\wedge v) = -\tfrac{p}{2}\left(\alpha^{\sharp}(u)\wedge v + u \wedge \alpha^{\sharp}(v) + \tfrac{2(\tau-1)}{3}\operatorname{\mathsf{tr}}(\alpha)u\wedge v\right)\!. \end{align} $$Let ![]() $\{u_{1}, u_{2}, u_{3}\}$ be an orthonormal basis of
$\{u_{1}, u_{2}, u_{3}\}$ be an orthonormal basis of ![]() $\mathbb {V}^{\ast }$ comprising eigenvectors of
$\mathbb {V}^{\ast }$ comprising eigenvectors of ![]() $\alpha ^{\sharp }$ with respective eigenvalues
$\alpha ^{\sharp }$ with respective eigenvalues ![]() $\mu _{1}$,
$\mu _{1}$, ![]() $\mu _{2}$, and
$\mu _{2}$, and ![]() $\mu _{3}$. By (8.5),
$\mu _{3}$. By (8.5), ![]() $u_{2}\wedge u_{3}$ is an eigenvector of
$u_{2}\wedge u_{3}$ is an eigenvector of  $\widehat {\Psi _{p, \tau }(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ with eigenvalue
$\widehat {\Psi _{p, \tau }(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ with eigenvalue ![]() $-\tfrac {p}{6}((2\tau +1)(\mu _{2} + \mu _{3}) + (2\tau -2)\mu _{1})$ and similarly for permutations of the indices. If
$-\tfrac {p}{6}((2\tau +1)(\mu _{2} + \mu _{3}) + (2\tau -2)\mu _{1})$ and similarly for permutations of the indices. If ![]() $\alpha $ has rank 1, then it can be supposed that
$\alpha $ has rank 1, then it can be supposed that ![]() $\mu _{2} = \mu _{3} = 0$ and
$\mu _{2} = \mu _{3} = 0$ and ![]() $\mu _{1} \neq 0$ and it results that the eigenvalues of
$\mu _{1} \neq 0$ and it results that the eigenvalues of 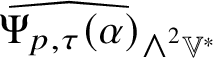 $\widehat {\Psi _{p, \tau }(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ are
$\widehat {\Psi _{p, \tau }(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ are ![]() $-\tfrac {p}{3}(\tau -1)\mu _{1}$ with multiplicity
$-\tfrac {p}{3}(\tau -1)\mu _{1}$ with multiplicity ![]() $1$ and
$1$ and ![]() $-\tfrac {p}{6}(2\tau + 1)\mu _{1}$ with multiplicity
$-\tfrac {p}{6}(2\tau + 1)\mu _{1}$ with multiplicity ![]() $2$. Consequently, that
$2$. Consequently, that 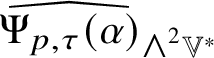 $\widehat {\Psi _{p, \tau }(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ have rank 1 is possible if and only if
$\widehat {\Psi _{p, \tau }(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ have rank 1 is possible if and only if ![]() $\tau = -1/2$, and in this case
$\tau = -1/2$, and in this case  $\widehat {\Psi _{p, -1/2}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ has rank 1 for any
$\widehat {\Psi _{p, -1/2}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ has rank 1 for any ![]() $\alpha \in S^{2}\mathbb {V}^{\ast }$ having rank 1, for any
$\alpha \in S^{2}\mathbb {V}^{\ast }$ having rank 1, for any ![]() $p \neq 0$. This completes the proof of the equivalence of 1 and 2.
$p \neq 0$. This completes the proof of the equivalence of 1 and 2.
Because ![]() $\dim \mathbb {V} = 3$,
$\dim \mathbb {V} = 3$, ![]() for
for ![]() $\alpha , \beta \in S^{2}\mathbb {V}^{\ast }$, so, by (7.6),
$\alpha , \beta \in S^{2}\mathbb {V}^{\ast }$, so, by (7.6),


Combining (8.4) and (8.7) yields
 $$ \begin{align} \begin{split} \widehat{\Psi_{p, \tau}(\alpha)}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}&\circledcirc\widehat{\Psi_{p, \tau}(\beta)}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} - \tfrac{p}{2}\widehat{\Psi_{p, \tau}(\alpha \circledcirc \beta)}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\\ & = \tfrac{p^{2}(2\tau + 1)}{6}L_{\circledcirc} \left(\operatorname{\mathsf{tr}}(\alpha)\beta + \operatorname{\mathsf{tr}}(\beta)\alpha + \tfrac{2\tau - 5}{6}\operatorname{\mathsf{tr}}(\alpha)\operatorname{\mathsf{tr}}(\beta)h + \tfrac{1}{2}\langle \alpha, \beta \rangle h \right)\!. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \widehat{\Psi_{p, \tau}(\alpha)}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}&\circledcirc\widehat{\Psi_{p, \tau}(\beta)}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} - \tfrac{p}{2}\widehat{\Psi_{p, \tau}(\alpha \circledcirc \beta)}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\\ & = \tfrac{p^{2}(2\tau + 1)}{6}L_{\circledcirc} \left(\operatorname{\mathsf{tr}}(\alpha)\beta + \operatorname{\mathsf{tr}}(\beta)\alpha + \tfrac{2\tau - 5}{6}\operatorname{\mathsf{tr}}(\alpha)\operatorname{\mathsf{tr}}(\beta)h + \tfrac{1}{2}\langle \alpha, \beta \rangle h \right)\!. \end{split} \end{align} $$It follows that 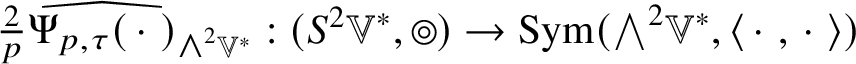 $\tfrac {2}{p}\widehat {\Psi _{p, \tau }(\,\cdot \,\,)}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}: (S^{2}\mathbb {V}^{\ast }, \circledcirc ) \to \operatorname {Sym}({\bigwedge }^{2}\mathbb {V}^{\ast }, \langle \,\cdot \,\,, \,\cdot \,\, \rangle )$ is a Jordan algebra isomorphism if and only if
$\tfrac {2}{p}\widehat {\Psi _{p, \tau }(\,\cdot \,\,)}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}: (S^{2}\mathbb {V}^{\ast }, \circledcirc ) \to \operatorname {Sym}({\bigwedge }^{2}\mathbb {V}^{\ast }, \langle \,\cdot \,\,, \,\cdot \,\, \rangle )$ is a Jordan algebra isomorphism if and only if ![]() $\tau = -1/2$. This shows the equivalence of 1 and 3.
$\tau = -1/2$. This shows the equivalence of 1 and 3.
Lemma 8.2. Let ![]() $(\mathbb {V}, h)$ be a
$(\mathbb {V}, h)$ be a ![]() $3$-dimensional Euclidean vector space. The pullback of
$3$-dimensional Euclidean vector space. The pullback of ![]() $\ast $ via
$\ast $ via ![]() $\Psi _{1, -1/2}$ yields on
$\Psi _{1, -1/2}$ yields on ![]() $S^{2}\mathbb {V}^{\ast }$ an
$S^{2}\mathbb {V}^{\ast }$ an ![]() $O(3)$-invariant commutative multiplication
$O(3)$-invariant commutative multiplication ![]() $\diamond $ having the form
$\diamond $ having the form
 $$ \begin{align} \begin{split} \alpha \diamond \beta &= \alpha \circledcirc \beta - \tfrac{1}{4}\left((\operatorname{\mathsf{tr}}\alpha)\beta + (\operatorname{\mathsf{tr}} \beta)\alpha + \langle \alpha, \beta \rangle h- (\operatorname{\mathsf{tr}} \alpha \operatorname{\mathsf{tr}} \beta) h\right)\!. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \alpha \diamond \beta &= \alpha \circledcirc \beta - \tfrac{1}{4}\left((\operatorname{\mathsf{tr}}\alpha)\beta + (\operatorname{\mathsf{tr}} \beta)\alpha + \langle \alpha, \beta \rangle h- (\operatorname{\mathsf{tr}} \alpha \operatorname{\mathsf{tr}} \beta) h\right)\!. \end{split} \end{align} $$Proof. Let ![]() $p, \tau \in \mathbb R$ satisfy
$p, \tau \in \mathbb R$ satisfy ![]() $p\tau \neq 0$. Write
$p\tau \neq 0$. Write ![]() $\Psi = \Psi _{p, \tau }$. Using (7.14), (7.15), (7.16), and (8.6) yields
$\Psi = \Psi _{p, \tau }$. Using (7.14), (7.15), (7.16), and (8.6) yields

 $$ \begin{align} \begin{split} \operatorname{\rho}(&\Psi(\alpha)\ast \Psi(\beta))\\ & = -\tfrac{p^{2}}{2}\left(\alpha \circledcirc \beta - \left(\tfrac{\tau + 2}{6}\right)\left((\operatorname{\mathsf{tr}}\alpha)\beta + (\operatorname{\mathsf{tr}}\beta)\alpha\right) -\left( \tfrac{1}{2}\langle \alpha, \beta\rangle + (\tfrac{(8\tau - 5)(2\tau + 1)}{18})(\operatorname{\mathsf{tr}}\alpha)(\operatorname{\mathsf{tr}}\beta) \right)h\right)\!. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \operatorname{\rho}(&\Psi(\alpha)\ast \Psi(\beta))\\ & = -\tfrac{p^{2}}{2}\left(\alpha \circledcirc \beta - \left(\tfrac{\tau + 2}{6}\right)\left((\operatorname{\mathsf{tr}}\alpha)\beta + (\operatorname{\mathsf{tr}}\beta)\alpha\right) -\left( \tfrac{1}{2}\langle \alpha, \beta\rangle + (\tfrac{(8\tau - 5)(2\tau + 1)}{18})(\operatorname{\mathsf{tr}}\alpha)(\operatorname{\mathsf{tr}}\beta) \right)h\right)\!. \end{split} \end{align} $$Tracing (8.11) yields 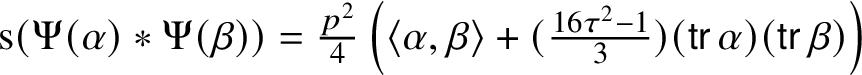 $\operatorname {s}(\Psi (\alpha )\ast \Psi (\beta )) = \tfrac {p^{2}}{4}\left (\langle \alpha , \beta \rangle + (\tfrac {16\tau ^{2} - 1}{3})(\operatorname {\mathsf {tr}}\alpha )(\operatorname {\mathsf {tr}}\beta ) \right )$. Substituting this and (8.11) in (8.2) shows that the pullback
$\operatorname {s}(\Psi (\alpha )\ast \Psi (\beta )) = \tfrac {p^{2}}{4}\left (\langle \alpha , \beta \rangle + (\tfrac {16\tau ^{2} - 1}{3})(\operatorname {\mathsf {tr}}\alpha )(\operatorname {\mathsf {tr}}\beta ) \right )$. Substituting this and (8.11) in (8.2) shows that the pullback 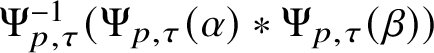 $\Psi _{p, \tau }^{-1}(\Psi _{p, \tau }(\alpha )\ast \Psi _{p, \tau }(\beta ))$ equals
$\Psi _{p, \tau }^{-1}(\Psi _{p, \tau }(\alpha )\ast \Psi _{p, \tau }(\beta ))$ equals
 $$ \begin{align} \begin{split} p\left( \alpha \diamond \beta - \tfrac{(2\tau + 1)}{12}\left((\operatorname{\mathsf{tr}}\alpha)\beta + (\operatorname{\mathsf{tr}} \beta)\alpha + \tfrac{1}{2\tau}\left(\langle \alpha, \beta \rangle + \tfrac{4\tau - 1}{3}\operatorname{\mathsf{tr}} \alpha \operatorname{\mathsf{tr}} \beta\right)h \right)\right)\!. \end{split} \end{align} $$
$$ \begin{align} \begin{split} p\left( \alpha \diamond \beta - \tfrac{(2\tau + 1)}{12}\left((\operatorname{\mathsf{tr}}\alpha)\beta + (\operatorname{\mathsf{tr}} \beta)\alpha + \tfrac{1}{2\tau}\left(\langle \alpha, \beta \rangle + \tfrac{4\tau - 1}{3}\operatorname{\mathsf{tr}} \alpha \operatorname{\mathsf{tr}} \beta\right)h \right)\right)\!. \end{split} \end{align} $$Specializing ![]() $(p, \tau ) = (1, -1/2)$ yields (8.9).
$(p, \tau ) = (1, -1/2)$ yields (8.9).
Lemma 8.3. Let ![]() $(\mathbb {V}, h)$ be a
$(\mathbb {V}, h)$ be a ![]() $3$-dimensional Euclidean vector space. The multiplication
$3$-dimensional Euclidean vector space. The multiplication ![]() $\diamond $ on
$\diamond $ on ![]() $S^{2}\mathbb {V}^{\ast }$ defined in (8.9) is not unital. In particular,
$S^{2}\mathbb {V}^{\ast }$ defined in (8.9) is not unital. In particular, ![]() $\diamond $ is not isomorphic to the Jordan product on
$\diamond $ is not isomorphic to the Jordan product on ![]() $S^{2}\mathbb {V}^{\ast }$.
$S^{2}\mathbb {V}^{\ast }$.
Proof. Were ![]() $\alpha \in S^{2}\mathbb {V}^{\ast }$ a unit, then
$\alpha \in S^{2}\mathbb {V}^{\ast }$ a unit, then ![]() $4h = 4\alpha \diamond h = \alpha + (\operatorname {\mathsf {tr}} \alpha )h$. Tracing this yields
$4h = 4\alpha \diamond h = \alpha + (\operatorname {\mathsf {tr}} \alpha )h$. Tracing this yields ![]() $\operatorname {\mathsf {tr}} \alpha = 3$, so
$\operatorname {\mathsf {tr}} \alpha = 3$, so ![]() $4h = \alpha + 3h$, implying that
$4h = \alpha + 3h$, implying that ![]() $\alpha = h$. However, h is not a unit, for, if
$\alpha = h$. However, h is not a unit, for, if 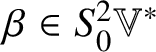 $\beta \in S^{2}_{0}\mathbb {V}^{\ast }$, then
$\beta \in S^{2}_{0}\mathbb {V}^{\ast }$, then 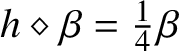 $h\diamond \beta = \tfrac {1}{4}\beta $.
$h\diamond \beta = \tfrac {1}{4}\beta $.
Remark 8.4. If ![]() $\alpha \in S^{2}\mathbb {V}^{\ast }$ satisfies
$\alpha \in S^{2}\mathbb {V}^{\ast }$ satisfies ![]() $\alpha \circ \alpha = \alpha $ and
$\alpha \circ \alpha = \alpha $ and ![]() $\operatorname {\mathsf {tr}} \alpha = 1$, then, by Lemma 7.4,
$\operatorname {\mathsf {tr}} \alpha = 1$, then, by Lemma 7.4, ![]() is idempotent in
is idempotent in ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$. By the proof of Lemma 7.4,
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$. By the proof of Lemma 7.4, ![]() , so
, so ![]() , so, by Lemma 8.2,
, so, by Lemma 8.2, ![]() $2\alpha $ is idempotent in
$2\alpha $ is idempotent in ![]() $(S^{2}\mathbb {V}^{\ast }, \diamond )$. This observation motivates motivates formulating a Characterization of
$(S^{2}\mathbb {V}^{\ast }, \diamond )$. This observation motivates motivates formulating a Characterization of ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ in terms of rank 1 idempotents in
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ in terms of rank 1 idempotents in ![]() $S^{2}\mathbb {V}^{\ast }$.
$S^{2}\mathbb {V}^{\ast }$.
Theorem 8.5. Let ![]() $(\mathbb {V}, h)$ be a
$(\mathbb {V}, h)$ be a ![]() $3$-dimensional Euclidean vector space and let
$3$-dimensional Euclidean vector space and let ![]() $O(3) = O(h)$. On
$O(3) = O(h)$. On ![]() $S^{2}\mathbb {V}^{\ast }$ there is up to algebra isomorphism a unique commutative multiplication
$S^{2}\mathbb {V}^{\ast }$ there is up to algebra isomorphism a unique commutative multiplication ![]() $\square $ satisfying:
$\square $ satisfying:
1.
 $O(3)$ acts on
$O(3)$ acts on  $(S^{2}\mathbb {V}^{\ast }, \square )$ by algebra automorphisms.
$(S^{2}\mathbb {V}^{\ast }, \square )$ by algebra automorphisms.2.
 $(S^{2}\mathbb {V}^{\ast }, \square )$ is metrized by an
$(S^{2}\mathbb {V}^{\ast }, \square )$ is metrized by an  $O(3)$-invariant inner product.
$O(3)$-invariant inner product.3.
 $(S^{2}\mathbb {V}^{\ast }, \square )$ contains no nonzero square-zero element.
$(S^{2}\mathbb {V}^{\ast }, \square )$ contains no nonzero square-zero element.4. There is an idempotent in
 $(S^{2}\mathbb {V}^{\ast }, \square )$ having rank 1.
$(S^{2}\mathbb {V}^{\ast }, \square )$ having rank 1.5. Any idempotent in
 $(S^{2}\mathbb {V}^{\ast }, \square )$ not a multiple of h has rank 1.
$(S^{2}\mathbb {V}^{\ast }, \square )$ not a multiple of h has rank 1.6. For a rank 1 idempotent e in
 $(S^{2}\mathbb {V}^{\ast }, \square )$,
$(S^{2}\mathbb {V}^{\ast }, \square )$,  $1/2$ is a multiplicity
$1/2$ is a multiplicity  $3$ eigenvalue of
$3$ eigenvalue of  $L_{\square }(e)$.
$L_{\square }(e)$.
The algebra ![]() $(S^{2}\mathbb {V}^{\ast }, \square )$ is isomorphic to
$(S^{2}\mathbb {V}^{\ast }, \square )$ is isomorphic to ![]() $(S^{2}\mathbb {V}^{\ast }, \diamond )$, where
$(S^{2}\mathbb {V}^{\ast }, \diamond )$, where ![]() $\diamond $ is defined in (8.9).
$\diamond $ is defined in (8.9).
Proof. Let g be an ![]() $O(3)$-invariant inner product on
$O(3)$-invariant inner product on ![]() $S^{2}\mathbb {V}^{\ast }$. By the Schur Lemma, an
$S^{2}\mathbb {V}^{\ast }$. By the Schur Lemma, an ![]() $O(3)$-invariant bilinear form on
$O(3)$-invariant bilinear form on ![]() $S^{2}\mathbb {V}^{\ast }$ has the form
$S^{2}\mathbb {V}^{\ast }$ has the form ![]() $k(\alpha , \beta ) = A\langle \alpha , \beta \rangle + B\operatorname {\mathsf {tr}}(\alpha )\operatorname {\mathsf {tr}}(\beta )$ for all
$k(\alpha , \beta ) = A\langle \alpha , \beta \rangle + B\operatorname {\mathsf {tr}}(\alpha )\operatorname {\mathsf {tr}}(\beta )$ for all ![]() $\alpha , \beta \in S^{2}\mathbb {V}^{\ast }$. It is positive definite if and only if
$\alpha , \beta \in S^{2}\mathbb {V}^{\ast }$. It is positive definite if and only if ![]() $A> 0$ and
$A> 0$ and ![]() $A + 3B> 0$. A calculation shows
$A + 3B> 0$. A calculation shows
 $$ \begin{align} k(\psi_{p, \tau}(\alpha), \psi_{p, \tau}(\beta)) = p^{2}\left(A\langle \alpha, \beta\rangle + \left(\tfrac{\tau^{2} - 1}{3}A + \tau^{2}B\right)\operatorname{\mathsf{tr}}(\alpha)\operatorname{\mathsf{tr}}(\beta)\right)\!. \end{align} $$
$$ \begin{align} k(\psi_{p, \tau}(\alpha), \psi_{p, \tau}(\beta)) = p^{2}\left(A\langle \alpha, \beta\rangle + \left(\tfrac{\tau^{2} - 1}{3}A + \tau^{2}B\right)\operatorname{\mathsf{tr}}(\alpha)\operatorname{\mathsf{tr}}(\beta)\right)\!. \end{align} $$Taking ![]() $p^{2} = 1/A$ and
$p^{2} = 1/A$ and ![]() $\tau ^{2} = A/(A+3B)$ yields
$\tau ^{2} = A/(A+3B)$ yields ![]() $k(\psi _{p, \tau }(\alpha ), \psi _{p, \tau }(\beta )) = \langle \alpha , \beta \rangle $. Hence, it can and will be assumed that the
$k(\psi _{p, \tau }(\alpha ), \psi _{p, \tau }(\beta )) = \langle \alpha , \beta \rangle $. Hence, it can and will be assumed that the ![]() $O(3)$-invariant inner product metrizing
$O(3)$-invariant inner product metrizing ![]() $(S^{2}\mathbb {V}^{\ast }, \square )$ is
$(S^{2}\mathbb {V}^{\ast }, \square )$ is ![]() $\langle \,\cdot \,\,, \,\cdot \,\, \rangle $.
$\langle \,\cdot \,\,, \,\cdot \,\, \rangle $.
Decomposing ![]() $S^{2}(S^{2}\mathbb {V})\otimes S^{2}\mathbb {V}^{\ast }$ into its irreducible components, it can be seen that the most general
$S^{2}(S^{2}\mathbb {V})\otimes S^{2}\mathbb {V}^{\ast }$ into its irreducible components, it can be seen that the most general ![]() $O(3)$-equivariant commutative bilinear map
$O(3)$-equivariant commutative bilinear map ![]() $\square :S^{2}\mathbb {V}^{\ast } \times S^{2}\mathbb {V}^{\ast } \to S^{2}\mathbb {V}^{\ast }$ has the form
$\square :S^{2}\mathbb {V}^{\ast } \times S^{2}\mathbb {V}^{\ast } \to S^{2}\mathbb {V}^{\ast }$ has the form
for some ![]() $r, s, t, u \in \mathbb R$. Because
$r, s, t, u \in \mathbb R$. Because ![]() $\langle \alpha \square \beta , \gamma \rangle - \langle \alpha , \beta \square \gamma \rangle = (s- t)((\operatorname {\mathsf {tr}}\alpha )\langle \beta , \gamma \rangle - (\operatorname {\mathsf {tr}} \gamma )\langle \alpha , \beta \rangle )$, the invariance of
$\langle \alpha \square \beta , \gamma \rangle - \langle \alpha , \beta \square \gamma \rangle = (s- t)((\operatorname {\mathsf {tr}}\alpha )\langle \beta , \gamma \rangle - (\operatorname {\mathsf {tr}} \gamma )\langle \alpha , \beta \rangle )$, the invariance of ![]() $\langle \,\cdot \,\,, \,\cdot \,\,\rangle $ with respect to
$\langle \,\cdot \,\,, \,\cdot \,\,\rangle $ with respect to ![]() $\square $ is equivalent to
$\square $ is equivalent to ![]() $t = s$.
$t = s$.
By assumption, ![]() $O(h)$ stabilizes
$O(h)$ stabilizes ![]() $h\square h$ so there is
$h\square h$ so there is ![]() $c \in \mathbb R$ such that
$c \in \mathbb R$ such that ![]() $h \square h = ch$. The assumption that there is no nonzero square-zero element implies
$h \square h = ch$. The assumption that there is no nonzero square-zero element implies ![]() $c \neq 0$. By (8.14),
$c \neq 0$. By (8.14), ![]() $ch = h \square h = (r + 6s + 3t + 9u)h = (6 + 9s + 9u)h$, so
$ch = h \square h = (r + 6s + 3t + 9u)h = (6 + 9s + 9u)h$, so ![]() $r + 9s + 9u = c$.
$r + 9s + 9u = c$.
Suppose there is a rank 1 element of ![]() $S^{2}\mathbb {V}^{\ast }$ that is a
$S^{2}\mathbb {V}^{\ast }$ that is a ![]() $\square $-idempotent. Then there is
$\square $-idempotent. Then there is ![]() $\sigma \in S^{2}\mathbb {V}^{\ast }$ satisfying
$\sigma \in S^{2}\mathbb {V}^{\ast }$ satisfying ![]() $\sigma \circ \sigma = \sigma $,
$\sigma \circ \sigma = \sigma $, ![]() $\operatorname {\mathsf {tr}}(\sigma ) = 1 = |\sigma |^{2}$, and
$\operatorname {\mathsf {tr}}(\sigma ) = 1 = |\sigma |^{2}$, and ![]() $\sigma \square \sigma = \lambda \sigma $ for some
$\sigma \square \sigma = \lambda \sigma $ for some ![]() $\lambda \in \mathbb {R}^{\times }$ (so the rank 1 idempotent is
$\lambda \in \mathbb {R}^{\times }$ (so the rank 1 idempotent is ![]() $\lambda ^{-1}\sigma $). For
$\lambda ^{-1}\sigma $). For 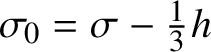 $\sigma _{0} =\sigma - \tfrac {1}{3}h$, there holds
$\sigma _{0} =\sigma - \tfrac {1}{3}h$, there holds
 $$ \begin{align} \lambda\sigma_{0} + \tfrac{\lambda}{3}h = \lambda \sigma = \sigma \square \sigma = (c + 2s)\sigma + (s+ u)h = (c+ 2s)\sigma_{0} + \tfrac{1}{3}(c + 5s + 3u)h, \end{align} $$
$$ \begin{align} \lambda\sigma_{0} + \tfrac{\lambda}{3}h = \lambda \sigma = \sigma \square \sigma = (c + 2s)\sigma + (s+ u)h = (c+ 2s)\sigma_{0} + \tfrac{1}{3}(c + 5s + 3u)h, \end{align} $$so ![]() $c + 2s = \lambda = c + 5s + 3u$, which imply
$c + 2s = \lambda = c + 5s + 3u$, which imply ![]() $s = (\lambda - c)/2$ and
$s = (\lambda - c)/2$ and ![]() $u = -s$. This shows
$u = -s$. This shows ![]() $\square $ has the form
$\square $ has the form
 $$ \begin{align} \alpha \square_{\lambda, c} \beta =c \alpha \circledcirc \beta + \tfrac{\lambda - c}{2}\left((\operatorname{\mathsf{tr}}\alpha)\beta + (\operatorname{\mathsf{tr}} \beta)\alpha + \langle \alpha, \beta \rangle h- (\operatorname{\mathsf{tr}} \alpha \operatorname{\mathsf{tr}} \beta) h\right)\!. \end{align} $$
$$ \begin{align} \alpha \square_{\lambda, c} \beta =c \alpha \circledcirc \beta + \tfrac{\lambda - c}{2}\left((\operatorname{\mathsf{tr}}\alpha)\beta + (\operatorname{\mathsf{tr}} \beta)\alpha + \langle \alpha, \beta \rangle h- (\operatorname{\mathsf{tr}} \alpha \operatorname{\mathsf{tr}} \beta) h\right)\!. \end{align} $$Pulling ![]() $\square $ back via the dilation by
$\square $ back via the dilation by ![]() $c^{-1}$ yields the product
$c^{-1}$ yields the product ![]() $\square _{\lambda } = \square _{\lambda , 1}$ on
$\square _{\lambda } = \square _{\lambda , 1}$ on ![]() $S^{2}\mathbb {V}^{\ast }$ defined by
$S^{2}\mathbb {V}^{\ast }$ defined by
 $$ \begin{align} &\alpha \square_{\lambda} \beta = \alpha \circledcirc \beta + \tfrac{\lambda - 1}{2}\left((\operatorname{\mathsf{tr}}\alpha)\beta + (\operatorname{\mathsf{tr}} \beta)\alpha + \langle \alpha, \beta \rangle h- (\operatorname{\mathsf{tr}} \alpha \operatorname{\mathsf{tr}} \beta) h\right)\!, &&\alpha, \beta \in S^{2}\mathbb{V}^{\ast}. \end{align} $$
$$ \begin{align} &\alpha \square_{\lambda} \beta = \alpha \circledcirc \beta + \tfrac{\lambda - 1}{2}\left((\operatorname{\mathsf{tr}}\alpha)\beta + (\operatorname{\mathsf{tr}} \beta)\alpha + \langle \alpha, \beta \rangle h- (\operatorname{\mathsf{tr}} \alpha \operatorname{\mathsf{tr}} \beta) h\right)\!, &&\alpha, \beta \in S^{2}\mathbb{V}^{\ast}. \end{align} $$This establishes that if ![]() $(S^{2}\mathbb {V}^{\ast }, \square )$ satisfies conditions 1–4, then there is
$(S^{2}\mathbb {V}^{\ast }, \square )$ satisfies conditions 1–4, then there is ![]() $\lambda \in \mathbb {R}^{\times }$ such that
$\lambda \in \mathbb {R}^{\times }$ such that ![]() $(S^{2}\mathbb {V}^{\ast }, \square )$ is isomorphic as an algebra to
$(S^{2}\mathbb {V}^{\ast }, \square )$ is isomorphic as an algebra to ![]() $(S^{2}\mathbb {V}^{\ast }, \square _{\lambda })$. For example,
$(S^{2}\mathbb {V}^{\ast }, \square _{\lambda })$. For example, ![]() $\lambda = 1$ yields the usual Jordan algebra structure
$\lambda = 1$ yields the usual Jordan algebra structure ![]() $\diamond _{1} = \circledcirc $. However, a nontrivial
$\diamond _{1} = \circledcirc $. However, a nontrivial ![]() $\circledcirc $-idempotent can have rank
$\circledcirc $-idempotent can have rank ![]() $1$,
$1$, ![]() $2$, or
$2$, or ![]() $3$.
$3$.
For an h-orthonormal basis ![]() $\{u_{1}, u_{2}, u_{3}\}$ of
$\{u_{1}, u_{2}, u_{3}\}$ of ![]() $\mathbb {V}^{\ast }$, define
$\mathbb {V}^{\ast }$, define ![]() $\gamma = (2\lambda - 1)(u_{1}\otimes u_{1} + u_{2}\otimes u_{2}) + (1 - \lambda )(u_{3}\otimes u_{3})$. Observe that
$\gamma = (2\lambda - 1)(u_{1}\otimes u_{1} + u_{2}\otimes u_{2}) + (1 - \lambda )(u_{3}\otimes u_{3})$. Observe that ![]() $\gamma $ does not have rank
$\gamma $ does not have rank ![]() $1$ provided that
$1$ provided that ![]() $2\lambda \neq 1$ and
$2\lambda \neq 1$ and ![]() $\gamma $ is not a multiple of h provided that
$\gamma $ is not a multiple of h provided that ![]() $3\lambda \ne 2$. A straightforward calculation using (8.17) shows that
$3\lambda \ne 2$. A straightforward calculation using (8.17) shows that ![]() $\gamma \square _{\lambda } \gamma = (3\lambda ^{2} - 3\lambda + 1)\gamma $. Since
$\gamma \square _{\lambda } \gamma = (3\lambda ^{2} - 3\lambda + 1)\gamma $. Since ![]() $3\lambda ^{2} - 3\lambda + 1 \geq 1/4> 0$ for all
$3\lambda ^{2} - 3\lambda + 1 \geq 1/4> 0$ for all ![]() $\lambda \in \mathbb R$, this shows that
$\lambda \in \mathbb R$, this shows that ![]() $(S^{2}\mathbb {V}^{\ast }, \square _{\lambda })$ contains an idempotent that is neither rank 1 nor a multiple of h provided that
$(S^{2}\mathbb {V}^{\ast }, \square _{\lambda })$ contains an idempotent that is neither rank 1 nor a multiple of h provided that ![]() $(2\lambda - 1)(3\lambda - 2) \neq 0$.
$(2\lambda - 1)(3\lambda - 2) \neq 0$.
Next it is shown that for ![]() $\lambda \in \{1/2, 2/3\}$ the algebra
$\lambda \in \{1/2, 2/3\}$ the algebra ![]() $(S^{2}\mathbb {V}^{\ast }, \square _{\lambda })$ contains no nonzero square-zero element and satisfies 5. Suppose
$(S^{2}\mathbb {V}^{\ast }, \square _{\lambda })$ contains no nonzero square-zero element and satisfies 5. Suppose ![]() $(\alpha _{0} + zh)\square _{\lambda } (\alpha _{0} + z h) = \epsilon (\alpha _{0} + zh)$ for
$(\alpha _{0} + zh)\square _{\lambda } (\alpha _{0} + z h) = \epsilon (\alpha _{0} + zh)$ for ![]() $\epsilon \in \{0, 1\}$ and
$\epsilon \in \{0, 1\}$ and 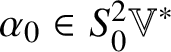 $\alpha _{0} \in S^{2}_{0}\mathbb {V}^{\ast }$ and
$\alpha _{0} \in S^{2}_{0}\mathbb {V}^{\ast }$ and ![]() $z \in \mathbb R$. Separating
$z \in \mathbb R$. Separating ![]() $(\alpha _{0} + zh)\diamond (\alpha _{0} + z h) - \epsilon (\alpha _{0} + zh)$ into its trace-free and pure trace parts yields the equations
$(\alpha _{0} + zh)\diamond (\alpha _{0} + z h) - \epsilon (\alpha _{0} + zh)$ into its trace-free and pure trace parts yields the equations
 $$ \begin{align} \begin{aligned} {} &\alpha_{0} \circ \alpha_{0} - \tfrac{1}{3}|\alpha_{0}|^{2}h + ((3\lambda - 1)z - \epsilon)\alpha_{0} =0,& &z^{2} - \epsilon z + \tfrac{3\lambda - 1}{6}|\alpha_{0}|^{2} = 0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {} &\alpha_{0} \circ \alpha_{0} - \tfrac{1}{3}|\alpha_{0}|^{2}h + ((3\lambda - 1)z - \epsilon)\alpha_{0} =0,& &z^{2} - \epsilon z + \tfrac{3\lambda - 1}{6}|\alpha_{0}|^{2} = 0. \end{aligned} \end{align} $$If ![]() $\epsilon =0$ and
$\epsilon =0$ and ![]() $\lambda> 1/3$, the second equation of (8.18) implies
$\lambda> 1/3$, the second equation of (8.18) implies ![]() $z =0$ and
$z =0$ and ![]() $\alpha _{0} = 0$; this shows
$\alpha _{0} = 0$; this shows ![]() $(S^{2}\mathbb {V}^{\ast }, \square _{\lambda })$ contains no nonzero square-zero element if
$(S^{2}\mathbb {V}^{\ast }, \square _{\lambda })$ contains no nonzero square-zero element if ![]() $\lambda \in \{1/2, 2/3\}$. Henceforth assume
$\lambda \in \{1/2, 2/3\}$. Henceforth assume ![]() $\epsilon = 1$. There are h-orthonormal
$\epsilon = 1$. There are h-orthonormal ![]() $u_{1}, u_{2}, u_{3} \in \mathbb {V}^{\ast }$ and
$u_{1}, u_{2}, u_{3} \in \mathbb {V}^{\ast }$ and ![]() $x_{1}, x_{2} \in \mathbb R$ such that
$x_{1}, x_{2} \in \mathbb R$ such that ![]() $\alpha _{0}= x_{1}u_{1}\otimes u_{1} + x_{2}u_{2}\otimes u_{2} - (x_{1} + x_{2})u_{3}\otimes u_{3}$ and
$\alpha _{0}= x_{1}u_{1}\otimes u_{1} + x_{2}u_{2}\otimes u_{2} - (x_{1} + x_{2})u_{3}\otimes u_{3}$ and 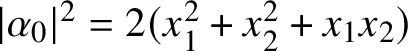 $|\alpha _{0}|^{2}= 2(x_{1}^{2} + x_{2}^{2} +x_{1}x_{2})$. Contracting the first equation of (8.18) with each of
$|\alpha _{0}|^{2}= 2(x_{1}^{2} + x_{2}^{2} +x_{1}x_{2})$. Contracting the first equation of (8.18) with each of ![]() $u_{1}\otimes u_{1}$ and
$u_{1}\otimes u_{1}$ and ![]() $u_{2}\otimes u_{2}$ yields the equations
$u_{2}\otimes u_{2}$ yields the equations
 $$ \begin{align} \begin{aligned} {} &0 = x_{1}^{2} - 2x_{2}^{2} - 2x_{1}x_{2} + 3((3\lambda -1)z - 1)x_{1},&\\& 0 = -2x_{1}^{2} +x_{2}^{2} - 2x_{1}x_{2} + 3((3\lambda -1)z - 1)x_{2}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {} &0 = x_{1}^{2} - 2x_{2}^{2} - 2x_{1}x_{2} + 3((3\lambda -1)z - 1)x_{1},&\\& 0 = -2x_{1}^{2} +x_{2}^{2} - 2x_{1}x_{2} + 3((3\lambda -1)z - 1)x_{2}. \end{aligned} \end{align} $$Appropriate linear combinations of the equations (8.19) yield
while the second equation of (8.18) becomes
 $$ \begin{align} 0 & = z^{2} - z + \tfrac{3\lambda - 1}{3}(x_{1}^{2} + x_{2}^{2} + x_{1}x_{2}). \end{align} $$
$$ \begin{align} 0 & = z^{2} - z + \tfrac{3\lambda - 1}{3}(x_{1}^{2} + x_{2}^{2} + x_{1}x_{2}). \end{align} $$If ![]() $x_{1} = x_{2}$, the second equation of (8.20) yields
$x_{1} = x_{2}$, the second equation of (8.20) yields ![]() $x_{1}((3\lambda - 1)z -1 - x_{1}) = 0$, so either
$x_{1}((3\lambda - 1)z -1 - x_{1}) = 0$, so either ![]() $x_{1} = 0$, in which case
$x_{1} = 0$, in which case ![]() $z \in \{0, 1\}$ and
$z \in \{0, 1\}$ and ![]() $\gamma $ is a multiple of h, or
$\gamma $ is a multiple of h, or ![]() $x_{1} = (3\lambda - 1)z - 1$. In the latter case, (8.21) yields
$x_{1} = (3\lambda - 1)z - 1$. In the latter case, (8.21) yields
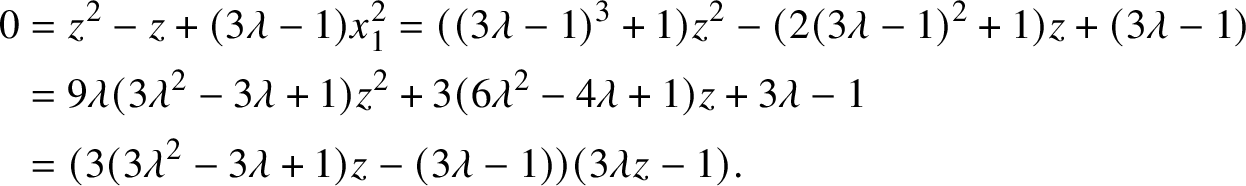 $$ \begin{align} \begin{split} 0 &=z^{2} - z + (3\lambda - 1)x_{1}^{2} = ((3\lambda - 1)^{3} + 1)z^{2} - (2(3\lambda - 1)^{2} + 1)z + (3\lambda -1)\\ & = 9\lambda(3\lambda^{2} - 3\lambda + 1)z^{2} + 3(6\lambda^{2} - 4\lambda + 1)z + 3\lambda - 1\\ & = (3(3\lambda^{2} - 3\lambda + 1)z - (3\lambda - 1))(3\lambda z - 1). \end{split} \end{align} $$
$$ \begin{align} \begin{split} 0 &=z^{2} - z + (3\lambda - 1)x_{1}^{2} = ((3\lambda - 1)^{3} + 1)z^{2} - (2(3\lambda - 1)^{2} + 1)z + (3\lambda -1)\\ & = 9\lambda(3\lambda^{2} - 3\lambda + 1)z^{2} + 3(6\lambda^{2} - 4\lambda + 1)z + 3\lambda - 1\\ & = (3(3\lambda^{2} - 3\lambda + 1)z - (3\lambda - 1))(3\lambda z - 1). \end{split} \end{align} $$If ![]() $z = 1/(3\lambda )$ there results
$z = 1/(3\lambda )$ there results ![]() $\alpha _{0} + zh = \lambda ^{-1}u_{3}\otimes u_{3}$, which has rank
$\alpha _{0} + zh = \lambda ^{-1}u_{3}\otimes u_{3}$, which has rank ![]() $1$. If
$1$. If  $z = \tfrac {3\lambda - 1}{3(3\lambda ^{2} - 3\lambda + 1)}$ there results
$z = \tfrac {3\lambda - 1}{3(3\lambda ^{2} - 3\lambda + 1)}$ there results
 $$ \begin{align} \alpha_{0} + z h = \tfrac{1}{(3\lambda^{2} - 3\lambda + 1)}\left((2\lambda - 1)(u_{1}\otimes u_{1} + u_{2}\otimes u_{2}) + (1 - \lambda)u_{3}\otimes u_{3}\right)\!. \end{align} $$
$$ \begin{align} \alpha_{0} + z h = \tfrac{1}{(3\lambda^{2} - 3\lambda + 1)}\left((2\lambda - 1)(u_{1}\otimes u_{1} + u_{2}\otimes u_{2}) + (1 - \lambda)u_{3}\otimes u_{3}\right)\!. \end{align} $$As observed before, this element is idempotent, but it has rank 1 if ![]() $\lambda = 1/2$ and is a multiple of h if
$\lambda = 1/2$ and is a multiple of h if ![]() $\lambda = 2/3$.
$\lambda = 2/3$.
If ![]() $x_{1} \neq x_{2}$, the first equation of (8.20) yields
$x_{1} \neq x_{2}$, the first equation of (8.20) yields ![]() $(3\lambda - 1)z = 1 - x_{1} - x_{2}$ and the second equation of (8.20) becomes
$(3\lambda - 1)z = 1 - x_{1} - x_{2}$ and the second equation of (8.20) becomes ![]() $0 = (2x_{2} + x_{1})(2x_{1} + x_{2})$. Without loss of generality, it can be assumed that
$0 = (2x_{2} + x_{1})(2x_{1} + x_{2})$. Without loss of generality, it can be assumed that ![]() $x_{2} = -2x_{1}$ (otherwise, interchange the indices
$x_{2} = -2x_{1}$ (otherwise, interchange the indices ![]() $1$ and
$1$ and ![]() $2$), in which case
$2$), in which case ![]() $(3\lambda - 1)z - 1 = - x_{1} - x_{2} = x_{1}$. As in (8.22), in (8.21) this yields
$(3\lambda - 1)z - 1 = - x_{1} - x_{2} = x_{1}$. As in (8.22), in (8.21) this yields
 $$ \begin{align} \begin{split} 0 &=z^{2} - z + \tfrac{(3\lambda - 1)}{3}(x_{1}^{2} + 4x_{1}^{2} - x_{1}^{2})= z^{2} - z + (3\lambda - 1)x_{1}^{2}\\&= (3(3\lambda^{2} - 3\lambda + 1)z - (3\lambda - 1))(3\lambda z - 1). \end{split} \end{align} $$
$$ \begin{align} \begin{split} 0 &=z^{2} - z + \tfrac{(3\lambda - 1)}{3}(x_{1}^{2} + 4x_{1}^{2} - x_{1}^{2})= z^{2} - z + (3\lambda - 1)x_{1}^{2}\\&= (3(3\lambda^{2} - 3\lambda + 1)z - (3\lambda - 1))(3\lambda z - 1). \end{split} \end{align} $$If ![]() $z = 1/(3\lambda )$, there results
$z = 1/(3\lambda )$, there results ![]() $x_{1} = -1/(3\lambda )$ and
$x_{1} = -1/(3\lambda )$ and ![]() $x_{2} = 2/(3\lambda )$ so that
$x_{2} = 2/(3\lambda )$ so that ![]() $\alpha _{0} + zh = \lambda ^{-1}u_{2}\otimes u_{2}$, which has rank
$\alpha _{0} + zh = \lambda ^{-1}u_{2}\otimes u_{2}$, which has rank ![]() $1$. If
$1$. If 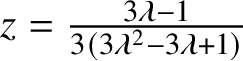 $z = \tfrac {3\lambda - 1}{3(3\lambda ^{2} - 3\lambda + 1)}$ and
$z = \tfrac {3\lambda - 1}{3(3\lambda ^{2} - 3\lambda + 1)}$ and ![]() $\lambda = 1/2$, then
$\lambda = 1/2$, then ![]() $z = 2/3$,
$z = 2/3$, ![]() $x_{1} = -2/3$, and
$x_{1} = -2/3$, and ![]() $x_{2} = 4/3$, which yields
$x_{2} = 4/3$, which yields ![]() $\alpha _{0} + zh = 2u_{2}\otimes u_{2}$, which has rank 1, while if
$\alpha _{0} + zh = 2u_{2}\otimes u_{2}$, which has rank 1, while if ![]() $\lambda = 2/3$, then
$\lambda = 2/3$, then ![]() $z = 1$,
$z = 1$, ![]() $x_{1} = 0$, and
$x_{1} = 0$, and ![]() $x_{2} =0$, which yields
$x_{2} =0$, which yields ![]() $\alpha _{0} + zh = h$. This shows that
$\alpha _{0} + zh = h$. This shows that ![]() $\square _{\lambda }$ satisfies 5 for
$\square _{\lambda }$ satisfies 5 for ![]() $\lambda \in \{1/2, 2/3\}$.
$\lambda \in \{1/2, 2/3\}$.
For an h-orthonormal basis ![]() $\{u_{1}, u_{2}, u_{3}\}$ of
$\{u_{1}, u_{2}, u_{3}\}$ of ![]() $\mathbb {V}^{\ast }$, define
$\mathbb {V}^{\ast }$, define ![]() $e_{i} = u_{i}\otimes u_{i} \in S^{2}\mathbb {V}^{\ast }$ and
$e_{i} = u_{i}\otimes u_{i} \in S^{2}\mathbb {V}^{\ast }$ and 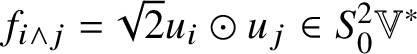 $f_{i\wedge j} = \sqrt {2}u_{i}\odot u_{j} \in S^{2}_{0}\mathbb {V}^{\ast }$, where distinct indices take distinct values from
$f_{i\wedge j} = \sqrt {2}u_{i}\odot u_{j} \in S^{2}_{0}\mathbb {V}^{\ast }$, where distinct indices take distinct values from ![]() $\{1, 2, 3\}$ and
$\{1, 2, 3\}$ and ![]() $i\wedge j$ is the complement of
$i\wedge j$ is the complement of ![]() $\{i, j\}$ in
$\{i, j\}$ in ![]() $\{1, 2, 3\}$ (so
$\{1, 2, 3\}$ (so ![]() $1 \wedge 2 = 3$ and
$1 \wedge 2 = 3$ and ![]() $i\wedge (i\wedge j) = j$). Then
$i\wedge (i\wedge j) = j$). Then ![]() $\{e_{i}, f_{i}: 1 \leq i \leq 3\}$ is an orthonormal basis of
$\{e_{i}, f_{i}: 1 \leq i \leq 3\}$ is an orthonormal basis of ![]() $S^{2}\mathbb {V}^{\ast }$. Calculations using (8.16) show
$S^{2}\mathbb {V}^{\ast }$. Calculations using (8.16) show
 $$ \begin{align} \begin{aligned} {} &e_{i}\square_{\lambda} e_{i} = \lambda e_{i},&& e_{i}\square_{\lambda} e_{j} = \tfrac{1-\lambda}{2}e_{i\wedge j},&& e_{i}\square_{\lambda} f_{i} = \tfrac{\lambda - 1}{2}f_{i},&\\ & e_{i}\square_{\lambda} f_{j} = \tfrac{\lambda}{2}f_{j},&& f_{i}\square_{\lambda} f_{i} = \tfrac{\lambda}{2}h - \tfrac{1}{2}e_{i}, &&f_{i}\square_{\lambda} f_{j} = \tfrac{1}{2\sqrt{2}}f_{i\wedge j}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {} &e_{i}\square_{\lambda} e_{i} = \lambda e_{i},&& e_{i}\square_{\lambda} e_{j} = \tfrac{1-\lambda}{2}e_{i\wedge j},&& e_{i}\square_{\lambda} f_{i} = \tfrac{\lambda - 1}{2}f_{i},&\\ & e_{i}\square_{\lambda} f_{j} = \tfrac{\lambda}{2}f_{j},&& f_{i}\square_{\lambda} f_{i} = \tfrac{\lambda}{2}h - \tfrac{1}{2}e_{i}, &&f_{i}\square_{\lambda} f_{j} = \tfrac{1}{2\sqrt{2}}f_{i\wedge j}. \end{aligned} \end{align} $$By (8.25), the basis ![]() $e_{i}$,
$e_{i}$, ![]() $f_{j}$,
$f_{j}$, ![]() $f_{i \wedge j}$,
$f_{i \wedge j}$, ![]() $e_{j} + e_{i\wedge j}$,
$e_{j} + e_{i\wedge j}$, ![]() $f_{i}$, and
$f_{i}$, and ![]() $e_{j} - e_{i\wedge j}$ comprises eigenvectors of of
$e_{j} - e_{i\wedge j}$ comprises eigenvectors of of ![]() $L_{\square _{\lambda }}(\lambda ^{-1}e_{i})$ having respective eigenvalues
$L_{\square _{\lambda }}(\lambda ^{-1}e_{i})$ having respective eigenvalues ![]() $1$,
$1$, ![]() $1/2$,
$1/2$, ![]() $1/2$,
$1/2$,  $\tfrac {1-\lambda }{2\lambda }$,
$\tfrac {1-\lambda }{2\lambda }$, 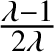 $\tfrac {\lambda - 1}{2\lambda }$, and
$\tfrac {\lambda - 1}{2\lambda }$, and 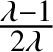 $\tfrac {\lambda - 1}{2\lambda }$. The four values
$\tfrac {\lambda - 1}{2\lambda }$. The four values ![]() $1$,
$1$, ![]() $1/2$,
$1/2$, 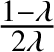 $\tfrac {1-\lambda }{2\lambda }$, and
$\tfrac {1-\lambda }{2\lambda }$, and  $\tfrac {\lambda - 1}{2\lambda }$ are pairwise distinct if
$\tfrac {\lambda - 1}{2\lambda }$ are pairwise distinct if ![]() $\lambda \notin \{-1, 1/3, 1/2\}$. The
$\lambda \notin \{-1, 1/3, 1/2\}$. The ![]() $1/2$ eigenspace always contains
$1/2$ eigenspace always contains ![]() $f_{j}$ and
$f_{j}$ and ![]() $f_{i \wedge j}$, and the multiplicity of the eigenvalue
$f_{i \wedge j}$, and the multiplicity of the eigenvalue ![]() $1/2$ is greater than
$1/2$ is greater than ![]() $2$ if and only if
$2$ if and only if ![]() $(1 - \lambda )/(2\lambda ) = 1/2$, which occurs if and only if
$(1 - \lambda )/(2\lambda ) = 1/2$, which occurs if and only if ![]() $\lambda = 1/2$. The eigenvalues of
$\lambda = 1/2$. The eigenvalues of ![]() $L_{\square _{1/2}}(2e_{i})$ are
$L_{\square _{1/2}}(2e_{i})$ are ![]() $1$ with eigenspace spanned by
$1$ with eigenspace spanned by ![]() $e_{i}$;
$e_{i}$; ![]() $1/2$ with eigenspace spanned by
$1/2$ with eigenspace spanned by ![]() $f_{j}$,
$f_{j}$, ![]() $f_{i \wedge j}$, and
$f_{i \wedge j}$, and ![]() $e_{j} + e_{i\wedge j}$; and
$e_{j} + e_{i\wedge j}$; and ![]() $-1/2$ with eigenspace spanned by
$-1/2$ with eigenspace spanned by ![]() $f_{i}$ and
$f_{i}$ and ![]() $e_{j} - e_{i\wedge j}$. Because any rank 1 idempotent is in the
$e_{j} - e_{i\wedge j}$. Because any rank 1 idempotent is in the ![]() $O(3)$ orbit of a multiple of
$O(3)$ orbit of a multiple of ![]() $e_{1}$, this proves 6 and completes the proof.
$e_{1}$, this proves 6 and completes the proof.
Remark 8.6. That ![]() $1/2$ is an eigenvalue of multiplicity at least
$1/2$ is an eigenvalue of multiplicity at least ![]() $2$ of
$2$ of ![]() $L_{\square _{\lambda }}(\lambda ^{-1}e_{i})$ is a consequence of the
$L_{\square _{\lambda }}(\lambda ^{-1}e_{i})$ is a consequence of the ![]() $O(3)$-invariance of
$O(3)$-invariance of ![]() $\square _{\lambda }$. Differentiating along a one-parameter family of rank 1 idempotents passing through
$\square _{\lambda }$. Differentiating along a one-parameter family of rank 1 idempotents passing through ![]() $\lambda ^{-1}e_{i}$ shows that a vector tangent to the
$\lambda ^{-1}e_{i}$ shows that a vector tangent to the ![]() $O(3)$-orbit passing through
$O(3)$-orbit passing through ![]() $\lambda ^{-1}e_{i}$ is an eigenvector of
$\lambda ^{-1}e_{i}$ is an eigenvector of ![]() $L_{\square _{\lambda }}(\lambda ^{-1}e_{i})$ with eigenvalue
$L_{\square _{\lambda }}(\lambda ^{-1}e_{i})$ with eigenvalue ![]() $1/2$. The content of 6 of Theorem 8.5 is that, for
$1/2$. The content of 6 of Theorem 8.5 is that, for ![]() $\lambda = 1/2$, the
$\lambda = 1/2$, the ![]() $1/2$ eigenspace of
$1/2$ eigenspace of ![]() $L_{\square _{1/2}}(2e_{i})$ has an extra third dimension.
$L_{\square _{1/2}}(2e_{i})$ has an extra third dimension.
Remark 8.7. The conditions in Theorem 8.5 are all necessary and serve to exclude certain particularly symmetric ![]() $O(3)$-invariant algebra structures on
$O(3)$-invariant algebra structures on ![]() $S^{2}\mathbb {V}^{\ast }$.
$S^{2}\mathbb {V}^{\ast }$.
As mentioned in the proof, the algebra ![]() $\operatorname {Sym}(\mathbb {V}, h)$ satisfies conditions 1–4 of Theorem 8.5 but fails 5 (and also 6) because it contains rank 2 idempotents.
$\operatorname {Sym}(\mathbb {V}, h)$ satisfies conditions 1–4 of Theorem 8.5 but fails 5 (and also 6) because it contains rank 2 idempotents.
Consider ![]() $S^{2}\mathbb {V}^{\ast }$ with the
$S^{2}\mathbb {V}^{\ast }$ with the ![]() $O(3)$-invariant multiplication
$O(3)$-invariant multiplication
 $$ \begin{align} \alpha \bar{\times} \beta = \alpha \circledcirc \beta - \tfrac{5}{12}\left(\operatorname{\mathsf{tr}}(\alpha)\beta + \operatorname{\mathsf{tr}}(\beta)\alpha + \langle \alpha, \beta\rangle h\right) + \tfrac{4}{9}\operatorname{\mathsf{tr}}(\alpha)\operatorname{\mathsf{tr}}(\beta)h. \end{align} $$
$$ \begin{align} \alpha \bar{\times} \beta = \alpha \circledcirc \beta - \tfrac{5}{12}\left(\operatorname{\mathsf{tr}}(\alpha)\beta + \operatorname{\mathsf{tr}}(\beta)\alpha + \langle \alpha, \beta\rangle h\right) + \tfrac{4}{9}\operatorname{\mathsf{tr}}(\alpha)\operatorname{\mathsf{tr}}(\beta)h. \end{align} $$It can be checked that ![]() $(S^{2}\mathbb {V}^{\ast }, \bar {\times })$ is exact and Killing metrized with
$(S^{2}\mathbb {V}^{\ast }, \bar {\times })$ is exact and Killing metrized with 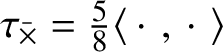 $\tau _{\bar {\times }} = \tfrac {5}{8}\langle \,\cdot \,\,, \,\cdot \,\, \rangle $, so that
$\tau _{\bar {\times }} = \tfrac {5}{8}\langle \,\cdot \,\,, \,\cdot \,\, \rangle $, so that ![]() $\operatorname {\mathrm {Aut}}(S^{2}\mathbb {V}^{\ast }, \bar {\times }) = O(3)$ (modulo inconsequential scalar factors, this algebra is what is in [Reference Fox10] called the conformal extension of
$\operatorname {\mathrm {Aut}}(S^{2}\mathbb {V}^{\ast }, \bar {\times }) = O(3)$ (modulo inconsequential scalar factors, this algebra is what is in [Reference Fox10] called the conformal extension of ![]() $(\operatorname {Sym}_{0}(\mathbb {V}, h), \times )$). That
$(\operatorname {Sym}_{0}(\mathbb {V}, h), \times )$). That ![]() $(S^{2}\mathbb {V}^{\ast }, \bar {\times })$ contains no square-zero element can be checked directly or follows from results in [Reference Fox10]. However,
$(S^{2}\mathbb {V}^{\ast }, \bar {\times })$ contains no square-zero element can be checked directly or follows from results in [Reference Fox10]. However, ![]() $(S^{2}\mathbb {V}^{\ast }, \bar {\times })$ contains no rank 1 idempotent, for if
$(S^{2}\mathbb {V}^{\ast }, \bar {\times })$ contains no rank 1 idempotent, for if ![]() $\sigma \in S^{2}\mathbb {V}^{\ast }$ has rank
$\sigma \in S^{2}\mathbb {V}^{\ast }$ has rank ![]() $1$, then
$1$, then ![]() $36 \sigma \bar {\times } \sigma = 6\operatorname {\mathsf {tr}}(\sigma )\sigma + \operatorname {\mathsf {tr}}(\sigma )^{2}h$.
$36 \sigma \bar {\times } \sigma = 6\operatorname {\mathsf {tr}}(\sigma )\sigma + \operatorname {\mathsf {tr}}(\sigma )^{2}h$.
As the proof of Theorem 8.5 shows, 6 excludes ![]() $(S^{2}\mathbb {V}^{\ast }, \square _{2/3})$, which is an interesting algebra because, in addition to satisfying 1–5, it is Killing metrized, as follows from Lemma 8.8.
$(S^{2}\mathbb {V}^{\ast }, \square _{2/3})$, which is an interesting algebra because, in addition to satisfying 1–5, it is Killing metrized, as follows from Lemma 8.8.
Lemma 8.8. Let ![]() $(\mathbb {V}, h)$ be a
$(\mathbb {V}, h)$ be a ![]() $3$-dimensional Euclidean vector space. For
$3$-dimensional Euclidean vector space. For ![]() $\lambda \in \mathbb {R}^{\times }$, let
$\lambda \in \mathbb {R}^{\times }$, let ![]() $\square _{\lambda }$ be as in (8.17).
$\square _{\lambda }$ be as in (8.17).
1.
 $(S^{2}\mathbb {V}^{\ast }, \square _{\lambda })$ is simple if
$(S^{2}\mathbb {V}^{\ast }, \square _{\lambda })$ is simple if  $\lambda \notin \{1, 1/3\}$.
$\lambda \notin \{1, 1/3\}$.2. There holds
 $\operatorname {\mathsf {tr}} L_{\square _{\lambda }} = \tfrac {5\lambda - 1}{2}\langle h, \,\cdot \,\, \rangle $. In particular,
$\operatorname {\mathsf {tr}} L_{\square _{\lambda }} = \tfrac {5\lambda - 1}{2}\langle h, \,\cdot \,\, \rangle $. In particular,  $\square _{\lambda }$ is exact if and only if
$\square _{\lambda }$ is exact if and only if  $\lambda = 1/5$.
$\lambda = 1/5$.3. For all
 $\alpha , \beta \in S^{2}\mathbb {V}^{\ast }$, there hold (8.27)In particular,
$\alpha , \beta \in S^{2}\mathbb {V}^{\ast }$, there hold (8.27)In particular, $$ \begin{align} \begin{aligned} 4(5\lambda - 1)\operatorname{\mathsf{tr}} L_{\square_{\lambda}}(\alpha \square_{\lambda} \beta) + 4(\lambda - 1)\operatorname{\mathsf{tr}} L_{\square_{\lambda}}(\alpha)\operatorname{\mathsf{tr}} L_{\square_{\lambda}}(\beta) = (5\lambda - 1)^{2}(3\lambda - 1)\langle \alpha, \beta \rangle,\\ 4(5\lambda - 1)^{2}\tau_{\square_{\lambda}}(\alpha , \beta) -4\lambda (3\lambda - 2)\operatorname{\mathsf{tr}} L_{\square_{\lambda}}(\alpha)\operatorname{\mathsf{tr}} L_{\square_{\lambda}}(\beta) = (5\lambda - 1)^{2}(6\lambda^{2} - 4\lambda + 3)\langle \alpha, \beta \rangle. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} 4(5\lambda - 1)\operatorname{\mathsf{tr}} L_{\square_{\lambda}}(\alpha \square_{\lambda} \beta) + 4(\lambda - 1)\operatorname{\mathsf{tr}} L_{\square_{\lambda}}(\alpha)\operatorname{\mathsf{tr}} L_{\square_{\lambda}}(\beta) = (5\lambda - 1)^{2}(3\lambda - 1)\langle \alpha, \beta \rangle,\\ 4(5\lambda - 1)^{2}\tau_{\square_{\lambda}}(\alpha , \beta) -4\lambda (3\lambda - 2)\operatorname{\mathsf{tr}} L_{\square_{\lambda}}(\alpha)\operatorname{\mathsf{tr}} L_{\square_{\lambda}}(\beta) = (5\lambda - 1)^{2}(6\lambda^{2} - 4\lambda + 3)\langle \alpha, \beta \rangle. \end{aligned} \end{align} $$ $(S^{2}\mathbb {V}^{\ast }, \square _{\lambda })$ is Killing metrized if and only if
$(S^{2}\mathbb {V}^{\ast }, \square _{\lambda })$ is Killing metrized if and only if  $\lambda = 2/3$.
$\lambda = 2/3$.4. If
 $\lambda \neq 1/5$, the automorphism group
$\lambda \neq 1/5$, the automorphism group  $\operatorname {\mathrm {Aut}}(S^{2}\mathbb {V}^{\ast }, \square _{\lambda })$ is isomorphic to
$\operatorname {\mathrm {Aut}}(S^{2}\mathbb {V}^{\ast }, \square _{\lambda })$ is isomorphic to  $SO(3)$ in its induced action on
$SO(3)$ in its induced action on  $S^{2}\mathbb {V}^{\ast }$.
$S^{2}\mathbb {V}^{\ast }$.
Proof. Suppose ![]() $\mathbb {I} \subset S^{2}\mathbb {V}^{\ast }$ is a
$\mathbb {I} \subset S^{2}\mathbb {V}^{\ast }$ is a ![]() $\square _{\lambda }$-ideal and there are
$\square _{\lambda }$-ideal and there are 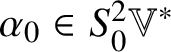 $\alpha _{0} \in S^{2}_{0}\mathbb {V}^{\ast }$ and
$\alpha _{0} \in S^{2}_{0}\mathbb {V}^{\ast }$ and ![]() $z \in \mathbb R$ such that
$z \in \mathbb R$ such that ![]() $0 \neq \alpha _{0} + zh \in \mathbb {I}$. Suppose
$0 \neq \alpha _{0} + zh \in \mathbb {I}$. Suppose ![]() $\lambda \notin \{1, 1/3\}$. Then
$\lambda \notin \{1, 1/3\}$. Then 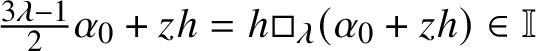 $\tfrac {3\lambda - 1}{2}\alpha _{0} + zh = h\square _{\lambda }(\alpha _{0} + zh) \in \mathbb {I}$, so
$\tfrac {3\lambda - 1}{2}\alpha _{0} + zh = h\square _{\lambda }(\alpha _{0} + zh) \in \mathbb {I}$, so 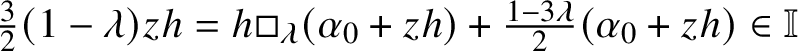 $\tfrac {3}{2}(1 - \lambda )zh = h\square _{\lambda }(\alpha _{0} + zh) + \tfrac {1 - 3\lambda }{2}(\alpha _{0} + zh) \in \mathbb {I}$. If
$\tfrac {3}{2}(1 - \lambda )zh = h\square _{\lambda }(\alpha _{0} + zh) + \tfrac {1 - 3\lambda }{2}(\alpha _{0} + zh) \in \mathbb {I}$. If ![]() $z \neq 0$, this implies
$z \neq 0$, this implies ![]() $h \in \mathbb {I}$. Otherwise, there is
$h \in \mathbb {I}$. Otherwise, there is 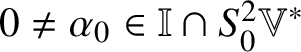 $0 \neq \alpha _{0} \in \mathbb {I} \cap S^{2}_{0}\mathbb {V}^{\ast }$. As
$0 \neq \alpha _{0} \in \mathbb {I} \cap S^{2}_{0}\mathbb {V}^{\ast }$. As ![]() $4h\square _{\lambda }(\alpha _{0}\square _{\lambda }\alpha _{0}) = 2(3\lambda - 1)\alpha _{0}\square _{\lambda }\alpha _{0} - (\lambda - 1)(3\lambda - 1)|\alpha _{0}|^{2}h$, in this case,
$4h\square _{\lambda }(\alpha _{0}\square _{\lambda }\alpha _{0}) = 2(3\lambda - 1)\alpha _{0}\square _{\lambda }\alpha _{0} - (\lambda - 1)(3\lambda - 1)|\alpha _{0}|^{2}h$, in this case, ![]() $(1-\lambda )(3\lambda - 1)|\alpha _{0}|^{2}h = 4h\square _{\lambda }(\alpha _{0}\square _{\lambda }\alpha _{0}) + 2(1 - 3\lambda )\alpha _{0}\square _{\lambda }\alpha _{0} \in \mathbb {I}$. Because
$(1-\lambda )(3\lambda - 1)|\alpha _{0}|^{2}h = 4h\square _{\lambda }(\alpha _{0}\square _{\lambda }\alpha _{0}) + 2(1 - 3\lambda )\alpha _{0}\square _{\lambda }\alpha _{0} \in \mathbb {I}$. Because ![]() $|\alpha _{0}|^{2} \neq 0$, this implies
$|\alpha _{0}|^{2} \neq 0$, this implies ![]() $h \in \mathbb {I}$. In either case, because
$h \in \mathbb {I}$. In either case, because ![]() $L_{\square _{\lambda }}(h)$ is invertible, that
$L_{\square _{\lambda }}(h)$ is invertible, that ![]() $h \in \mathbb {I}$ implies
$h \in \mathbb {I}$ implies ![]() $\mathbb {I} = S^{2}\mathbb {V}^{\ast }$. This shows
$\mathbb {I} = S^{2}\mathbb {V}^{\ast }$. This shows ![]() $(S^{2}\mathbb {V}^{\ast }, \square _{\lambda })$ is simple if
$(S^{2}\mathbb {V}^{\ast }, \square _{\lambda })$ is simple if ![]() $\lambda \notin \{1, 1/3\}$. (When
$\lambda \notin \{1, 1/3\}$. (When ![]() $\lambda = 1/3$,
$\lambda = 1/3$, ![]() $L_{\square _{1/3}}(h)$ annihilates
$L_{\square _{1/3}}(h)$ annihilates  $S^{2}_{0}\mathbb {V}^{\ast }$, so h generates a proper ideal, while when
$S^{2}_{0}\mathbb {V}^{\ast }$, so h generates a proper ideal, while when ![]() $\lambda = 1$,
$\lambda = 1$, ![]() $\square _{1} = \circledcirc $ and
$\square _{1} = \circledcirc $ and  $S^{2}_{0}\mathbb {V}^{\ast }$ is a proper ideal.)
$S^{2}_{0}\mathbb {V}^{\ast }$ is a proper ideal.)
Claims 2 and 3 can be proved by straightforward through tedious calculations using (8.25). Their principal relevance here is to prove 4. An alternative approach is the following. Identify 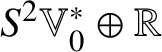 $S^{2}\mathbb {V}^{\ast }_{0} \oplus \mathbb R$ with
$S^{2}\mathbb {V}^{\ast }_{0} \oplus \mathbb R$ with ![]() $S^{2}\mathbb {V}^{\ast }$ via the map
$S^{2}\mathbb {V}^{\ast }$ via the map ![]() $(\alpha _{0}, a) \to \alpha _{0} + a h$. With respect to this identification the multiplication endomorphism
$(\alpha _{0}, a) \to \alpha _{0} + a h$. With respect to this identification the multiplication endomorphism ![]() $L_{\square _{\lambda }}(\alpha _{0}, a)$ has the block form
$L_{\square _{\lambda }}(\alpha _{0}, a)$ has the block form
 $$ \begin{align} L_{\square_{\lambda}}(\alpha_{0}, a) = \begin{pmatrix} L_{\times}(\alpha_{0}) + \tfrac{3\lambda - 1}{2}a\operatorname{Id}_{S^{2}_{0}\mathbb{V}^{\ast}} & \tfrac{3\lambda - 1}{2}\alpha_{0}\\ \tfrac{3\lambda - 1}{6}\langle \alpha_{0}, \,\cdot\,\,\rangle & a \end{pmatrix}, \end{align} $$
$$ \begin{align} L_{\square_{\lambda}}(\alpha_{0}, a) = \begin{pmatrix} L_{\times}(\alpha_{0}) + \tfrac{3\lambda - 1}{2}a\operatorname{Id}_{S^{2}_{0}\mathbb{V}^{\ast}} & \tfrac{3\lambda - 1}{2}\alpha_{0}\\ \tfrac{3\lambda - 1}{6}\langle \alpha_{0}, \,\cdot\,\,\rangle & a \end{pmatrix}, \end{align} $$in which ![]() $\times $ is the trace-free Jordan product
$\times $ is the trace-free Jordan product 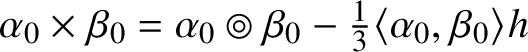 $\alpha _{0}\times \beta _{0} = \alpha _{0}\circledcirc \beta _{0} - \tfrac {1}{3}\langle \alpha _{0}, \beta _{0}\rangle h$. Claim 2 follows by tracing (8.28), while (8.27) follow by straightforward computations using (8.28) and the fact that
$\alpha _{0}\times \beta _{0} = \alpha _{0}\circledcirc \beta _{0} - \tfrac {1}{3}\langle \alpha _{0}, \beta _{0}\rangle h$. Claim 2 follows by tracing (8.28), while (8.27) follow by straightforward computations using (8.28) and the fact that  $\tau _{\times }(\alpha _{0}, \beta _{0}) = \tfrac {7}{12}\langle \alpha _{0}, \beta _{0}\rangle $, which is proved in [Reference Fox10].
$\tau _{\times }(\alpha _{0}, \beta _{0}) = \tfrac {7}{12}\langle \alpha _{0}, \beta _{0}\rangle $, which is proved in [Reference Fox10].
Suppose ![]() $\lambda \neq 1/5$. By 3, an algebra automorphism
$\lambda \neq 1/5$. By 3, an algebra automorphism ![]() $\phi $ of
$\phi $ of ![]() $\square _{\lambda }$ preserves
$\square _{\lambda }$ preserves ![]() $\langle \,\cdot \,\,, \,\cdot \,\, \rangle $. By 2,
$\langle \,\cdot \,\,, \,\cdot \,\, \rangle $. By 2, 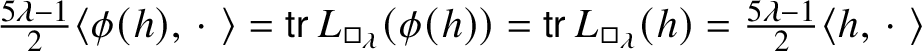 $\tfrac {5\lambda - 1}{2}\langle \phi (h), \,\cdot \,\, \rangle = \operatorname {\mathsf {tr}} L_{\square _{\lambda }}(\phi (h)) = \operatorname {\mathsf {tr}} L_{\square _{\lambda }}(h)= \tfrac {5\lambda - 1}{2}\langle h, \,\cdot \,\, \rangle $, so
$\tfrac {5\lambda - 1}{2}\langle \phi (h), \,\cdot \,\, \rangle = \operatorname {\mathsf {tr}} L_{\square _{\lambda }}(\phi (h)) = \operatorname {\mathsf {tr}} L_{\square _{\lambda }}(h)= \tfrac {5\lambda - 1}{2}\langle h, \,\cdot \,\, \rangle $, so ![]() $\phi (h) = h$. It follows that
$\phi (h) = h$. It follows that ![]() $0 = \phi (\alpha )\square _{\lambda }\phi (\beta ) - \phi (\alpha \square _{\lambda }\beta ) = \phi (\alpha )\circledcirc \phi (\beta ) - \phi (\alpha \circledcirc \beta )$, so that
$0 = \phi (\alpha )\square _{\lambda }\phi (\beta ) - \phi (\alpha \square _{\lambda }\beta ) = \phi (\alpha )\circledcirc \phi (\beta ) - \phi (\alpha \circledcirc \beta )$, so that ![]() $\phi $ is an automorphism of the Jordan algebra
$\phi $ is an automorphism of the Jordan algebra ![]() $(S^{2}\mathbb {V}^{\ast }, \circledcirc )$. Every automorphism of
$(S^{2}\mathbb {V}^{\ast }, \circledcirc )$. Every automorphism of ![]() $(S^{2}\mathbb {V}^{\ast }, \circledcirc )$ is given by the action of an element of
$(S^{2}\mathbb {V}^{\ast }, \circledcirc )$ is given by the action of an element of ![]() $O(3)$ [Reference Koecher24, Theorem VII.13]. This proves 4.
$O(3)$ [Reference Koecher24, Theorem VII.13]. This proves 4.
Remark 8.9. The ![]() $\lambda = 1$ case of 2 and 3 of Lemma 8.8 recovers identities for the Jordan algebra
$\lambda = 1$ case of 2 and 3 of Lemma 8.8 recovers identities for the Jordan algebra ![]() $(\operatorname {Sym}(\mathbb {V}, h), \circledcirc )$ that can be found in [Reference Faraut and Korányi9, Proposition III.4.2 and Lemma VI.1.1].
$(\operatorname {Sym}(\mathbb {V}, h), \circledcirc )$ that can be found in [Reference Faraut and Korányi9, Proposition III.4.2 and Lemma VI.1.1].
Corollary 8.10 summarizes the result of combining Theorem 8.5 and Lemma 8.8 for ![]() $\diamond $.
$\diamond $.
Corollary 8.10. Let ![]() $(\mathbb {V}, h)$ be a
$(\mathbb {V}, h)$ be a ![]() $3$-dimensional Euclidean vector space. The map
$3$-dimensional Euclidean vector space. The map ![]() $\Psi : (S^{2}\mathbb {V}^{\ast }, \diamond ) \to (\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ defined by
$\Psi : (S^{2}\mathbb {V}^{\ast }, \diamond ) \to (\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ defined by  is an algebra isomorphism, where the commutative multiplication
is an algebra isomorphism, where the commutative multiplication ![]() $\diamond $ on
$\diamond $ on ![]() $S^{2}\mathbb {V}^{\ast }$ is defined by
$S^{2}\mathbb {V}^{\ast }$ is defined by
 $$ \begin{align} \alpha \diamond \beta &= \alpha \circledcirc \beta - \tfrac{1}{4}\left((\operatorname{\mathsf{tr}}\alpha)\beta + (\operatorname{\mathsf{tr}} \beta)\alpha + \langle \alpha, \beta \rangle h- (\operatorname{\mathsf{tr}} \alpha \operatorname{\mathsf{tr}} \beta) h\right) \end{align} $$
$$ \begin{align} \alpha \diamond \beta &= \alpha \circledcirc \beta - \tfrac{1}{4}\left((\operatorname{\mathsf{tr}}\alpha)\beta + (\operatorname{\mathsf{tr}} \beta)\alpha + \langle \alpha, \beta \rangle h- (\operatorname{\mathsf{tr}} \alpha \operatorname{\mathsf{tr}} \beta) h\right) \end{align} $$and is characterized as the unique, up to algebra isomorphism, commutative multiplication on ![]() $S^{2}\mathbb {V}^{\ast }$ satisfying:
$S^{2}\mathbb {V}^{\ast }$ satisfying:
1.
 $O(3)$ acts on
$O(3)$ acts on  $(S^{2}\mathbb {V}^{\ast }, \diamond )$ by algebra automorphisms.
$(S^{2}\mathbb {V}^{\ast }, \diamond )$ by algebra automorphisms.2.
 $(S^{2}\mathbb {V}^{\ast }, \diamond )$ is metrized by an
$(S^{2}\mathbb {V}^{\ast }, \diamond )$ is metrized by an  $O(3)$-invariant inner product.
$O(3)$-invariant inner product.3.
 $(S^{2}\mathbb {V}^{\ast }, \diamond )$ contains no nonzero square-zero element.
$(S^{2}\mathbb {V}^{\ast }, \diamond )$ contains no nonzero square-zero element.4. There is an idempotent in
 $(S^{2}\mathbb {V}^{\ast }, \diamond )$ having rank 1.
$(S^{2}\mathbb {V}^{\ast }, \diamond )$ having rank 1.5. Any idempotent in
 $(S^{2}\mathbb {V}^{\ast }, \diamond )$ not a multiple of h has rank 1.
$(S^{2}\mathbb {V}^{\ast }, \diamond )$ not a multiple of h has rank 1.6. For a rank 1 idempotent e in
 $(S^{2}\mathbb {V}^{\ast }, \diamond )$, the spectrum of
$(S^{2}\mathbb {V}^{\ast }, \diamond )$, the spectrum of  $L_{\diamond }(e)$ contains
$L_{\diamond }(e)$ contains  $1/2$ with multiplicity
$1/2$ with multiplicity  $3$.
$3$.
Moreover, the multiplication ![]() $\diamond $ has the following properties:
$\diamond $ has the following properties:
1. An idempotent in
 $(S^{2}\mathbb {V}^{\ast }, \diamond )$ distinct from h has the form
$(S^{2}\mathbb {V}^{\ast }, \diamond )$ distinct from h has the form  $\alpha = 2u \otimes u$ for a unit norm
$\alpha = 2u \otimes u$ for a unit norm  $u \in \mathbb {V}^{\ast }$.
$u \in \mathbb {V}^{\ast }$.2. For an idempotent
 $\alpha $ as in 5, the eigenvalues of
$\alpha $ as in 5, the eigenvalues of  $L_{\diamond }(\alpha )$ are
$L_{\diamond }(\alpha )$ are  $1$ with multiplicity
$1$ with multiplicity  $1$,
$1$,  $1/2$ with multiplicity
$1/2$ with multiplicity  $3$, and
$3$, and  $-1/2$ with multiplicity
$-1/2$ with multiplicity  $2$.
$2$.3.
 $(S^{2}\mathbb {V}^{\ast }, \diamond )$ is simple.
$(S^{2}\mathbb {V}^{\ast }, \diamond )$ is simple.4. For all
 $\alpha , \beta \in S^{2}\mathbb {V}^{\ast }$, (8.30)
$\alpha , \beta \in S^{2}\mathbb {V}^{\ast }$, (8.30) $$ \begin{align} \tfrac{16}{3}\left(\operatorname{\mathsf{tr}} L_{\diamond}(\alpha \diamond \beta) - \tfrac{1}{3}\operatorname{\mathsf{tr}} L_{\diamond}(\alpha)\operatorname{\mathsf{tr}} L_{\diamond}(\beta)\right) = \langle \alpha, \beta \rangle = \tfrac{8}{5}\left(\tau_{\diamond}(\alpha, \beta) + \operatorname{\mathsf{tr}} L_{\diamond}(\alpha)\operatorname{\mathsf{tr}} L_{\diamond}(\beta)\right)\!. \end{align} $$
$$ \begin{align} \tfrac{16}{3}\left(\operatorname{\mathsf{tr}} L_{\diamond}(\alpha \diamond \beta) - \tfrac{1}{3}\operatorname{\mathsf{tr}} L_{\diamond}(\alpha)\operatorname{\mathsf{tr}} L_{\diamond}(\beta)\right) = \langle \alpha, \beta \rangle = \tfrac{8}{5}\left(\tau_{\diamond}(\alpha, \beta) + \operatorname{\mathsf{tr}} L_{\diamond}(\alpha)\operatorname{\mathsf{tr}} L_{\diamond}(\beta)\right)\!. \end{align} $$5. The full automorphism group of
 $(S^{2}\mathbb {V}^{\ast }, \diamond )$ is
$(S^{2}\mathbb {V}^{\ast }, \diamond )$ is  $O(3)$ in its induced action on
$O(3)$ in its induced action on  $S^{2}\mathbb {V}^{\ast }$.
$S^{2}\mathbb {V}^{\ast }$.
The idempotents in ![]() $(S^{2}\mathbb {V}^{\ast }, \diamond )$ are parametrized by the disjoint union of a point, corresponding with h, and a projective plane, corresponding with the
$(S^{2}\mathbb {V}^{\ast }, \diamond )$ are parametrized by the disjoint union of a point, corresponding with h, and a projective plane, corresponding with the ![]() $O(3)$-orbit of a rank 1 symmetric bilinear form having norm
$O(3)$-orbit of a rank 1 symmetric bilinear form having norm ![]() $2$.
$2$.
9 Characterization of the subalgebra of anti-self-dual Weyl tensors when  $\dim \mathbb {V} = 4$
$\dim \mathbb {V} = 4$
This section proves Theorem 1.5, that shows that, when ![]() $\dim \mathbb {V} = 4$, the subalgebra of anti-self-dual Weyl tensors is isomorphic to the space of trace-free endomorphisms of a
$\dim \mathbb {V} = 4$, the subalgebra of anti-self-dual Weyl tensors is isomorphic to the space of trace-free endomorphisms of a ![]() $3$-dimensional vector space equipped with the trace-free Jordan product. The proof is conceptual in the sense that it relies on the description of
$3$-dimensional vector space equipped with the trace-free Jordan product. The proof is conceptual in the sense that it relies on the description of ![]() $\ast $ in terms of curvature operators. On the other hand, the approach is special to
$\ast $ in terms of curvature operators. On the other hand, the approach is special to ![]() $\dim \mathbb {V} = 4$. Lemma 10.8 yields an alternative proof that, while more computational, is based on an approach viable in all dimensions.
$\dim \mathbb {V} = 4$. Lemma 10.8 yields an alternative proof that, while more computational, is based on an approach viable in all dimensions.
Let ![]() $(\mathbb {V}, h)$ be an n-dimensional Euclidean vector space. Let
$(\mathbb {V}, h)$ be an n-dimensional Euclidean vector space. Let ![]() $\epsilon _{i_{1}\dots i_{n}}$ be the volume n-form determined by choice of orientation of
$\epsilon _{i_{1}\dots i_{n}}$ be the volume n-form determined by choice of orientation of ![]() $\mathbb {V}$ and evaluating to
$\mathbb {V}$ and evaluating to ![]() $1$ when paired with the wedge product of the vectors of an ordered h-orthonormal basis consistent with the chosen orientation. The polyvector
$1$ when paired with the wedge product of the vectors of an ordered h-orthonormal basis consistent with the chosen orientation. The polyvector ![]() $\epsilon ^{i_{1}\dots i_{n}}$ obtained by raising indices satisfies
$\epsilon ^{i_{1}\dots i_{n}}$ obtained by raising indices satisfies  $\epsilon _{i_{1}\dots i_{p}k_{1}\dots k_{n-p}}\epsilon ^{j_{1}\dots j_{p}k_{1}\dots k_{n-p}} = p!(n-p)!\delta _{[i_{1}}{}^{[j_{1}}\delta _{i_{2}}{}^{j_{2}}\dots \delta _{i_{p-1}}{}^{j_{p-1}} \delta _{i_{p}]}{}^{j_{p}]}$. Suppose
$\epsilon _{i_{1}\dots i_{p}k_{1}\dots k_{n-p}}\epsilon ^{j_{1}\dots j_{p}k_{1}\dots k_{n-p}} = p!(n-p)!\delta _{[i_{1}}{}^{[j_{1}}\delta _{i_{2}}{}^{j_{2}}\dots \delta _{i_{p-1}}{}^{j_{p-1}} \delta _{i_{p}]}{}^{j_{p}]}$. Suppose ![]() $\dim \mathbb {V} = 4$. Then this yields the identities
$\dim \mathbb {V} = 4$. Then this yields the identities
 $$ \begin{align} \begin{aligned} {} &\epsilon_{abcd}\epsilon^{abcd} = 4!,&& \epsilon_{iabc}\epsilon^{jabc} = 6\delta_{i}{}^{j}, &\\ &\epsilon_{ijab}\epsilon^{klab} = 4\delta_{[i}{}^{[k}\delta_{j]}{}^{l]},&& \epsilon_{ijkp}\epsilon^{abcp} = 6\delta_{[i}{}^{[a}\delta_{j}{}^{b}\delta_{k]}{}^{c]}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {} &\epsilon_{abcd}\epsilon^{abcd} = 4!,&& \epsilon_{iabc}\epsilon^{jabc} = 6\delta_{i}{}^{j}, &\\ &\epsilon_{ijab}\epsilon^{klab} = 4\delta_{[i}{}^{[k}\delta_{j]}{}^{l]},&& \epsilon_{ijkp}\epsilon^{abcp} = 6\delta_{[i}{}^{[a}\delta_{j}{}^{b}\delta_{k]}{}^{c]}. \end{aligned} \end{align} $$The Hodge star operator ![]() $\star \in \operatorname {End}({\bigwedge }^{2}\mathbb {V}^{\ast })$ is defined by
$\star \in \operatorname {End}({\bigwedge }^{2}\mathbb {V}^{\ast })$ is defined by  $(\star \alpha )_{ij} = \tfrac {1}{2}\epsilon _{ij}{}^{pq}\alpha _{pq}$. By (9.1),
$(\star \alpha )_{ij} = \tfrac {1}{2}\epsilon _{ij}{}^{pq}\alpha _{pq}$. By (9.1), ![]() $\star \circ \star = \operatorname {Id}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$, so
$\star \circ \star = \operatorname {Id}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$, so ![]() ${\bigwedge }^{2}\mathbb {V}^{\ast }$ decomposes into the two 3-dimensional
${\bigwedge }^{2}\mathbb {V}^{\ast }$ decomposes into the two 3-dimensional ![]() $\star $-eigenspaces
$\star $-eigenspaces ![]() ${\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast }$, denominated the self-dual and anti-self-dual two-forms on
${\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast }$, denominated the self-dual and anti-self-dual two-forms on ![]() $\mathbb {V}$. Note that, with the conventions used here,
$\mathbb {V}$. Note that, with the conventions used here, 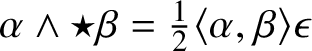 $\alpha \wedge \star \beta = \tfrac {1}{2}\langle \alpha , \beta \rangle \epsilon $.
$\alpha \wedge \star \beta = \tfrac {1}{2}\langle \alpha , \beta \rangle \epsilon $.
Lemma 9.1. Let ![]() $(\mathbb {V}, h, \epsilon )$ be an oriented
$(\mathbb {V}, h, \epsilon )$ be an oriented ![]() $4$-dimensional Euclidean vector space.
$4$-dimensional Euclidean vector space.
1. If
 $\alpha , \beta \in {\bigwedge }^{2}_{+}\mathbb {V}^{\ast }$ or
$\alpha , \beta \in {\bigwedge }^{2}_{+}\mathbb {V}^{\ast }$ or  $\alpha , \beta \in {\bigwedge }^{2}_{-}\mathbb {V}^{\ast }$, then
$\alpha , \beta \in {\bigwedge }^{2}_{-}\mathbb {V}^{\ast }$, then  $ (\alpha \circledcirc \beta ) = -\tfrac {1}{4}\langle \alpha , \beta \rangle h$.
$ (\alpha \circledcirc \beta ) = -\tfrac {1}{4}\langle \alpha , \beta \rangle h$.2. For
 $\alpha , \beta \in {\bigwedge }^{2}\mathbb {V}^{\ast }$,
$\alpha , \beta \in {\bigwedge }^{2}\mathbb {V}^{\ast }$,  $[\star \alpha , \star \beta ] = [\alpha , \beta ]$ and
$[\star \alpha , \star \beta ] = [\alpha , \beta ]$ and  $\star [\alpha , \beta ] = [\star \alpha , \beta ]$. In particular,
$\star [\alpha , \beta ] = [\star \alpha , \beta ]$. In particular,  $[{\bigwedge }^{2}_{+}\mathbb {V}^{\ast }, {\bigwedge }^{2}_{-}\mathbb {V}^{\ast }] =\{0\}$ and
$[{\bigwedge }^{2}_{+}\mathbb {V}^{\ast }, {\bigwedge }^{2}_{-}\mathbb {V}^{\ast }] =\{0\}$ and  $\langle {\bigwedge }^{2}_{+}\mathbb {V}^{\ast }, {\bigwedge }^{2}_{-}\mathbb {V}^{\ast }\rangle = \{0\}$. Under the identification of
$\langle {\bigwedge }^{2}_{+}\mathbb {V}^{\ast }, {\bigwedge }^{2}_{-}\mathbb {V}^{\ast }\rangle = \{0\}$. Under the identification of  $({\bigwedge }^{2}\mathbb {V}^{\ast }, [\,\cdot \,\,, \,\cdot \,\,])$ with
$({\bigwedge }^{2}\mathbb {V}^{\ast }, [\,\cdot \,\,, \,\cdot \,\,])$ with  $\mathfrak {so}(4)$, the subspaces
$\mathfrak {so}(4)$, the subspaces  ${\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast }$ are commuting Lie ideals identified with commuting ideals of
${\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast }$ are commuting Lie ideals identified with commuting ideals of  $\mathfrak {so}(4)$ isomorphic to
$\mathfrak {so}(4)$ isomorphic to  $\mathfrak {so}(3)$.
$\mathfrak {so}(3)$.
Proof. For ![]() $\alpha , \beta \in {\bigwedge }^{2}\mathbb {V}^{\ast }$, using (9.1) yields
$\alpha , \beta \in {\bigwedge }^{2}\mathbb {V}^{\ast }$, using (9.1) yields
 $$ \begin{align} \begin{split} ((\star \beta)\circ (\star \alpha))_{ij} & = -(\star \alpha)_{pi}(\star \beta)^{pk}h_{kj} = -\tfrac{1}{4}\epsilon_{iabp}\epsilon^{kcdp}\alpha^{ab}\beta_{cd}h_{kj}\\ &= -\tfrac{3}{2}\delta_{[i}{}^{[k}\delta_{a}{}^{c}\delta_{b]}{}^{d]}\alpha^{ab}\beta_{cd}h_{kj} = -\tfrac{1}{2}\langle \alpha, \beta \rangle h_{ij} - (\alpha \circ \beta)_{ij}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} ((\star \beta)\circ (\star \alpha))_{ij} & = -(\star \alpha)_{pi}(\star \beta)^{pk}h_{kj} = -\tfrac{1}{4}\epsilon_{iabp}\epsilon^{kcdp}\alpha^{ab}\beta_{cd}h_{kj}\\ &= -\tfrac{3}{2}\delta_{[i}{}^{[k}\delta_{a}{}^{c}\delta_{b]}{}^{d]}\alpha^{ab}\beta_{cd}h_{kj} = -\tfrac{1}{2}\langle \alpha, \beta \rangle h_{ij} - (\alpha \circ \beta)_{ij}. \end{split} \end{align} $$Symmetrizing (9.2) in ![]() $\alpha $ and
$\alpha $ and ![]() $\beta $ yields 1. Antisymmetrizing (9.2) in
$\beta $ yields 1. Antisymmetrizing (9.2) in ![]() $\alpha $ and
$\alpha $ and ![]() $\beta $ yields
$\beta $ yields ![]() $[\star \alpha , \star \beta ] = [\alpha , \beta ]$. Because
$[\star \alpha , \star \beta ] = [\alpha , \beta ]$. Because ![]() $\star $ is self-adjoint and
$\star $ is self-adjoint and ![]() $\operatorname {ad}(\alpha ) = [\alpha , \,\cdot \,\,]$ is anti-self-adjoint, for any
$\operatorname {ad}(\alpha ) = [\alpha , \,\cdot \,\,]$ is anti-self-adjoint, for any ![]() $\gamma \in {\bigwedge }^{2}\mathbb {V}^{\ast }$,
$\gamma \in {\bigwedge }^{2}\mathbb {V}^{\ast }$,
showing that ![]() $\star [\alpha , \beta ] = [\star \alpha , \beta ]$. It follows that
$\star [\alpha , \beta ] = [\star \alpha , \beta ]$. It follows that ![]() ${\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast }$ are commuting Lie ideals in
${\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast }$ are commuting Lie ideals in ![]() ${\bigwedge }^{2}\mathbb {V}^{\ast }$. This shows the first part of 2. The claimed isomorphisms with
${\bigwedge }^{2}\mathbb {V}^{\ast }$. This shows the first part of 2. The claimed isomorphisms with ![]() $\mathfrak {so}(4)$ and
$\mathfrak {so}(4)$ and ![]() $\mathfrak {so}(3)$ follow from standard representation theory and are omitted.
$\mathfrak {so}(3)$ follow from standard representation theory and are omitted.
Lemma 9.2. Let ![]() $(\mathbb {V}, h, \epsilon )$ be an oriented
$(\mathbb {V}, h, \epsilon )$ be an oriented ![]() $4$-dimensional Euclidean vector space. For
$4$-dimensional Euclidean vector space. For ![]() $\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, define
$\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, define 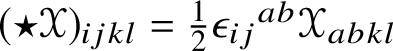 $(\star \mathscr {X})_{ijkl} = \tfrac {1}{2}\epsilon _{ij}{}^{ab}\mathscr {X}_{abkl}$. Then
$(\star \mathscr {X})_{ijkl} = \tfrac {1}{2}\epsilon _{ij}{}^{ab}\mathscr {X}_{abkl}$. Then ![]() $(\star \mathscr {X})_{ijkl} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, and
$(\star \mathscr {X})_{ijkl} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, and ![]() $\star :\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) \to \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is a linear involution satisfying
$\star :\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }) \to \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is a linear involution satisfying 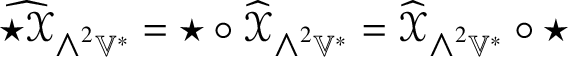 $\widehat {\star \mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} = \star \circ \widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} = \widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}\circ \star $.
$\widehat {\star \mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} = \star \circ \widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} = \widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}\circ \star $.
Proof. By definition ![]() $(\star \mathscr {X})_{ijkl} = (\star \mathscr {X})_{[ij]kl} = (\star \mathscr {X})_{ij[kl]}$, so
$(\star \mathscr {X})_{ijkl} = (\star \mathscr {X})_{[ij]kl} = (\star \mathscr {X})_{ij[kl]}$, so ![]() $\star \mathscr {X} \in S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$. To show
$\star \mathscr {X} \in S^{2}({\bigwedge }^{2}\mathbb {V}^{\ast })$. To show ![]() $\star \mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$ it suffices to show that
$\star \mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$ it suffices to show that ![]() $(\star \mathscr {X})_{[ijk]l}$ vanishes. For
$(\star \mathscr {X})_{[ijk]l}$ vanishes. For ![]() $\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, if
$\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, if ![]() $n = \dim \mathbb {V}$, tracing
$n = \dim \mathbb {V}$, tracing 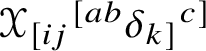 $\mathscr {X}_{[ij}{}^{[ab}\delta _{k]}{}^{c]}$ in k and c yields a multiple of
$\mathscr {X}_{[ij}{}^{[ab}\delta _{k]}{}^{c]}$ in k and c yields a multiple of ![]() $(n-4)\mathscr {X}_{ij}{}^{ab}$. Since this vanishes if
$(n-4)\mathscr {X}_{ij}{}^{ab}$. Since this vanishes if ![]() $n = 4$ and, by [Reference Weyl40, Theorem
$n = 4$ and, by [Reference Weyl40, Theorem ![]() $5.7.$A], an
$5.7.$A], an ![]() $O(n)$-module of covariant trace-free tensors on an n-dimensional vector space having symmetries corresponding to a Young diagram for which the sum of the lengths of the first two columns is greater than n is trivial, when
$O(n)$-module of covariant trace-free tensors on an n-dimensional vector space having symmetries corresponding to a Young diagram for which the sum of the lengths of the first two columns is greater than n is trivial, when ![]() $\dim \mathbb {V} = 4$,
$\dim \mathbb {V} = 4$,
 $$ \begin{align} \mathscr{X}_{[ij}{}^{[ab}\delta_{k]}{}^{c]} = 0 \end{align} $$
$$ \begin{align} \mathscr{X}_{[ij}{}^{[ab}\delta_{k]}{}^{c]} = 0 \end{align} $$for any ![]() $\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. (The identity is sometimes called a Lovelock identity because similar identities generalizing it are discussed in [Reference Lovelock25].) Contracting (9.4) with
$\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. (The identity is sometimes called a Lovelock identity because similar identities generalizing it are discussed in [Reference Lovelock25].) Contracting (9.4) with ![]() $\epsilon _{abcl}$ yields
$\epsilon _{abcl}$ yields 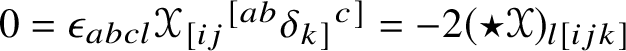 $0 = \epsilon _{abcl}\mathscr {X}_{[ij}{}^{[ab}\delta _{k]}{}^{c]} = -2(\star \mathscr {X})_{l[ijk]}$, so
$0 = \epsilon _{abcl}\mathscr {X}_{[ij}{}^{[ab}\delta _{k]}{}^{c]} = -2(\star \mathscr {X})_{l[ijk]}$, so ![]() $\star \mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$. There holds
$\star \mathscr {X} \in \mathscr {MC}(\mathbb {V}^{\ast })$. There holds 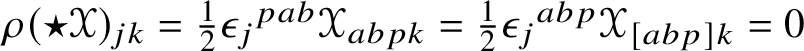 $\operatorname {\rho }(\star \mathscr {X})_{jk} = \tfrac {1}{2}\epsilon _{j}{}^{pab}\mathscr {X}_{abpk} = \tfrac {1}{2}\epsilon _{j}{}^{abp}\mathscr {X}_{[abp]k} = 0$, so
$\operatorname {\rho }(\star \mathscr {X})_{jk} = \tfrac {1}{2}\epsilon _{j}{}^{pab}\mathscr {X}_{abpk} = \tfrac {1}{2}\epsilon _{j}{}^{abp}\mathscr {X}_{[abp]k} = 0$, so ![]() $\star \mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. For
$\star \mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. For 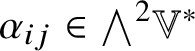 $\alpha _{ij} \in {\bigwedge }^{2}\mathbb {V}^{\ast }$,
$\alpha _{ij} \in {\bigwedge }^{2}\mathbb {V}^{\ast }$,
 $$ \begin{align} \begin{split} (\star \widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(\alpha))_{ij} &= \tfrac{1}{2}\epsilon_{ij}{}^{ab}\widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(\alpha)_{ab} = -\tfrac{1}{4}\epsilon_{ij}{}^{ab}\alpha^{pq}\mathscr{X}_{abpq} \\ &= -\tfrac{1}{2}\alpha^{pq}(\star \mathscr{X})_{ijpq} = \widehat{\star \mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(\alpha)_{ij}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} (\star \widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(\alpha))_{ij} &= \tfrac{1}{2}\epsilon_{ij}{}^{ab}\widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(\alpha)_{ab} = -\tfrac{1}{4}\epsilon_{ij}{}^{ab}\alpha^{pq}\mathscr{X}_{abpq} \\ &= -\tfrac{1}{2}\alpha^{pq}(\star \mathscr{X})_{ijpq} = \widehat{\star \mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(\alpha)_{ij}. \end{split} \end{align} $$That ![]() $\star \mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ implies
$\star \mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ implies ![]() $(\star \mathscr {X})_{ijkl}$ has all the other symmetries that this inclusion implies; for example,
$(\star \mathscr {X})_{ijkl}$ has all the other symmetries that this inclusion implies; for example, 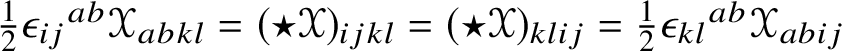 $\tfrac {1}{2}\epsilon _{ij}{}^{ab}\mathscr {X}_{abkl} = (\star \mathscr {X})_{ijkl} = (\star \mathscr {X})_{klij} = \tfrac {1}{2}\epsilon _{kl}{}^{ab}\mathscr {X}_{abij}$. It follows that
$\tfrac {1}{2}\epsilon _{ij}{}^{ab}\mathscr {X}_{abkl} = (\star \mathscr {X})_{ijkl} = (\star \mathscr {X})_{klij} = \tfrac {1}{2}\epsilon _{kl}{}^{ab}\mathscr {X}_{abij}$. It follows that
 $$ \begin{align} \begin{split} \widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(\star \alpha)_{ij} &= -\tfrac{1}{2}(\star \alpha)^{ab}\mathscr{X}_{ijab} = -\tfrac{1}{4}\epsilon^{abpq}\alpha_{pq}\mathscr{X}_{ijab}= -\tfrac{1}{4}\alpha^{pq}\epsilon_{pq}{}^{ab}\mathscr{X}_{abij}\\ &= -\tfrac{1}{4}\alpha^{pq}\epsilon_{ij}{}^{ab}\mathscr{X}_{abpq} = -\tfrac{1}{2}\alpha^{pq}(\star \mathscr{X})_{ijpq} = \widehat{\star\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(\alpha)_{ij}, \end{split} \end{align} $$
$$ \begin{align} \begin{split} \widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(\star \alpha)_{ij} &= -\tfrac{1}{2}(\star \alpha)^{ab}\mathscr{X}_{ijab} = -\tfrac{1}{4}\epsilon^{abpq}\alpha_{pq}\mathscr{X}_{ijab}= -\tfrac{1}{4}\alpha^{pq}\epsilon_{pq}{}^{ab}\mathscr{X}_{abij}\\ &= -\tfrac{1}{4}\alpha^{pq}\epsilon_{ij}{}^{ab}\mathscr{X}_{abpq} = -\tfrac{1}{2}\alpha^{pq}(\star \mathscr{X})_{ijpq} = \widehat{\star\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(\alpha)_{ij}, \end{split} \end{align} $$which, with (9.5), shows that 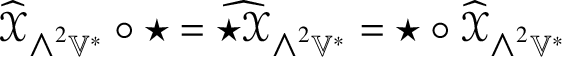 $\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} \circ \star = \widehat {\star \mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} = \star \circ \widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$.
$\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} \circ \star = \widehat {\star \mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} = \star \circ \widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$.
For a ![]() $4$-dimensional oriented Euclidean vector space
$4$-dimensional oriented Euclidean vector space ![]() $(\mathbb {V}, h, \epsilon )$, define
$(\mathbb {V}, h, \epsilon )$, define ![]() $\mathscr {MC}^{\pm }_{\mathscr {W}}(\mathbb {V}^{\ast }) = \{\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }): \star \mathscr {X} = \pm \mathscr {X}\}$. Because
$\mathscr {MC}^{\pm }_{\mathscr {W}}(\mathbb {V}^{\ast }) = \{\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }): \star \mathscr {X} = \pm \mathscr {X}\}$. Because ![]() $\langle \star \mathscr {X}, \mathscr {Y} \rangle = \langle \mathscr {X}, \star \mathscr {Y} \rangle $,
$\langle \star \mathscr {X}, \mathscr {Y} \rangle = \langle \mathscr {X}, \star \mathscr {Y} \rangle $, ![]() $\mathscr {MC}^{+}_{\mathscr {W}}(\mathbb {V}^{\ast })$ and
$\mathscr {MC}^{+}_{\mathscr {W}}(\mathbb {V}^{\ast })$ and ![]() $\mathscr {MC}^{-}_{\mathscr {W}}(\mathbb {V}^{\ast })$ are orthogonal complements.
$\mathscr {MC}^{-}_{\mathscr {W}}(\mathbb {V}^{\ast })$ are orthogonal complements.
Lemma 9.3. Let ![]() $(\mathbb {V}, h, \epsilon )$ be an oriented
$(\mathbb {V}, h, \epsilon )$ be an oriented ![]() $4$-dimensional Euclidean vector space. Write
$4$-dimensional Euclidean vector space. Write ![]() $\alpha = \alpha ^{+} + \alpha ^{-}$ for the decomposition of
$\alpha = \alpha ^{+} + \alpha ^{-}$ for the decomposition of ![]() $\alpha $ into its self-dual and anti-self-dual parts
$\alpha $ into its self-dual and anti-self-dual parts ![]() $\alpha ^{\pm } \in {\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast }$. For
$\alpha ^{\pm } \in {\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast }$. For ![]() $\alpha , \beta \in {\bigwedge }^{2}\mathbb {V}^{\ast }$,
$\alpha , \beta \in {\bigwedge }^{2}\mathbb {V}^{\ast }$,

In particular, ![]() $\operatorname {\mathsf {tf}}(\alpha ^{+}\cdot \beta ^{+}) \in \mathscr {MC}^{+}_{\mathscr {W}}(\mathbb {V}^{\ast })$,
$\operatorname {\mathsf {tf}}(\alpha ^{+}\cdot \beta ^{+}) \in \mathscr {MC}^{+}_{\mathscr {W}}(\mathbb {V}^{\ast })$, ![]() $\operatorname {\mathsf {tf}}(\alpha ^{-}\cdot \beta ^{-}) \in \mathscr {MC}^{-}_{\mathscr {W}}(\mathbb {V}^{\ast })$ and
$\operatorname {\mathsf {tf}}(\alpha ^{-}\cdot \beta ^{-}) \in \mathscr {MC}^{-}_{\mathscr {W}}(\mathbb {V}^{\ast })$ and ![]() $\operatorname {\mathsf {tf}}(\alpha ^{+}\cdot \beta ^{-}) = 0$ so that
$\operatorname {\mathsf {tf}}(\alpha ^{+}\cdot \beta ^{-}) = 0$ so that
Proof. By (6.10) and Lemma 9.2, for ![]() $\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ and
$\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ and ![]() $\alpha , \beta \in {\bigwedge }^{2}\mathbb {V}^{\ast }$,
$\alpha , \beta \in {\bigwedge }^{2}\mathbb {V}^{\ast }$,
 $$ \begin{align} \begin{split} \langle \operatorname{\mathsf{tf}}(\star \alpha \cdot \star \beta), \mathscr{X}\rangle& =\langle \star \alpha \cdot \star \beta, \mathscr{X}\rangle = -6\langle \widehat{\mathscr{X}}(\star \alpha), \star \beta \rangle \\&= -6\langle \star \widehat{\mathscr{X}}(\alpha), \star \beta \rangle = -6\langle \widehat{\mathscr{X}}(\alpha), \beta \rangle = \langle \alpha \cdot \beta, \mathscr{X}\rangle =\langle \operatorname{\mathsf{tf}}(\alpha \cdot \beta), \mathscr{X}\rangle ,\\ \langle \star \operatorname{\mathsf{tf}}((\star \alpha)\cdot \beta), \mathscr{X} \rangle & = \langle \operatorname{\mathsf{tf}}((\star \alpha) \cdot \beta), \star \mathscr{X}\rangle = \langle (\star\alpha) \cdot \beta, \star \mathscr{X}\rangle = -6\langle \star \alpha, \widehat{\star\mathscr{X}}(\beta)\rangle \\&= -6\langle \star \alpha ,\star \widehat{\mathscr{X}}(\beta)\rangle = -6\langle \alpha, \widehat{\mathscr{X}}(\beta)\rangle = \langle \alpha\cdot \beta, \mathscr{X}\rangle = \langle \operatorname{\mathsf{tf}}(\alpha\cdot \beta), \mathscr{X}\rangle, \end{split} \end{align} $$
$$ \begin{align} \begin{split} \langle \operatorname{\mathsf{tf}}(\star \alpha \cdot \star \beta), \mathscr{X}\rangle& =\langle \star \alpha \cdot \star \beta, \mathscr{X}\rangle = -6\langle \widehat{\mathscr{X}}(\star \alpha), \star \beta \rangle \\&= -6\langle \star \widehat{\mathscr{X}}(\alpha), \star \beta \rangle = -6\langle \widehat{\mathscr{X}}(\alpha), \beta \rangle = \langle \alpha \cdot \beta, \mathscr{X}\rangle =\langle \operatorname{\mathsf{tf}}(\alpha \cdot \beta), \mathscr{X}\rangle ,\\ \langle \star \operatorname{\mathsf{tf}}((\star \alpha)\cdot \beta), \mathscr{X} \rangle & = \langle \operatorname{\mathsf{tf}}((\star \alpha) \cdot \beta), \star \mathscr{X}\rangle = \langle (\star\alpha) \cdot \beta, \star \mathscr{X}\rangle = -6\langle \star \alpha, \widehat{\star\mathscr{X}}(\beta)\rangle \\&= -6\langle \star \alpha ,\star \widehat{\mathscr{X}}(\beta)\rangle = -6\langle \alpha, \widehat{\mathscr{X}}(\beta)\rangle = \langle \alpha\cdot \beta, \mathscr{X}\rangle = \langle \operatorname{\mathsf{tf}}(\alpha\cdot \beta), \mathscr{X}\rangle, \end{split} \end{align} $$which show (9.7). By (7.2) and (7.7),

By (9.10) and Lemma 9.1, 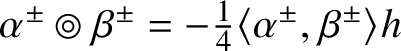 $\alpha ^{\pm } \circledcirc \beta ^{\pm } = -\tfrac {1}{4}\langle \alpha ^{\pm }, \beta ^{\pm }\rangle h$, and in (9.10) this yields (9.7). By (9.7),
$\alpha ^{\pm } \circledcirc \beta ^{\pm } = -\tfrac {1}{4}\langle \alpha ^{\pm }, \beta ^{\pm }\rangle h$, and in (9.10) this yields (9.7). By (9.7), ![]() $\star \operatorname {\mathsf {tf}}(\alpha \cdot \beta ) = \operatorname {\mathsf {tf}}((\star \alpha )\cdot \beta ) = \operatorname {\mathsf {tf}}(\alpha ^{+}\cdot \beta ^{+}) - \operatorname {\mathsf {tf}}(\alpha ^{-}\cdot \beta ^{-})$, and it follows that
$\star \operatorname {\mathsf {tf}}(\alpha \cdot \beta ) = \operatorname {\mathsf {tf}}((\star \alpha )\cdot \beta ) = \operatorname {\mathsf {tf}}(\alpha ^{+}\cdot \beta ^{+}) - \operatorname {\mathsf {tf}}(\alpha ^{-}\cdot \beta ^{-})$, and it follows that ![]() $\operatorname {\mathsf {tf}}(\alpha ^{\pm }\cdot \beta ^{\pm }) \in \mathscr {MC}^{\pm }_{\mathscr {W}}(\mathbb {V}^{\ast })$ and
$\operatorname {\mathsf {tf}}(\alpha ^{\pm }\cdot \beta ^{\pm }) \in \mathscr {MC}^{\pm }_{\mathscr {W}}(\mathbb {V}^{\ast })$ and ![]() $\operatorname {\mathsf {tf}}(\alpha ^{+}\cdot \beta ^{-}) =0$. Substituting the last identity in (9.10) yields (9.8).
$\operatorname {\mathsf {tf}}(\alpha ^{+}\cdot \beta ^{-}) =0$. Substituting the last identity in (9.10) yields (9.8).
Example 9.4. Given an oriented ![]() $4$-dimensional Euclidean vector space
$4$-dimensional Euclidean vector space ![]() $(\mathbb {V}, h, \epsilon )$, let
$(\mathbb {V}, h, \epsilon )$, let ![]() $\omega \in {\bigwedge }^{2}\mathbb {V}^{\ast }$ satisfy
$\omega \in {\bigwedge }^{2}\mathbb {V}^{\ast }$ satisfy ![]() $\omega \circ \omega = -h$, so that
$\omega \circ \omega = -h$, so that ![]() $\omega _{i}{}^{j}$ is a compatible almost complex structure and
$\omega _{i}{}^{j}$ is a compatible almost complex structure and ![]() $(\mathbb {V}, h, \omega )$ is a Kähler structure. Then
$(\mathbb {V}, h, \omega )$ is a Kähler structure. Then ![]() $\omega \in {\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast }$ as
$\omega \in {\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast }$ as  $\tfrac {1}{2}\omega \wedge \omega = \pm \epsilon $ and, by Lemma 9.3, the idempotent
$\tfrac {1}{2}\omega \wedge \omega = \pm \epsilon $ and, by Lemma 9.3, the idempotent 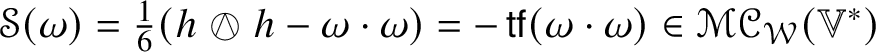 defined in (10.2) satisfies
defined in (10.2) satisfies ![]() $\mathscr {S}(\omega ) \in \mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast })$.
$\mathscr {S}(\omega ) \in \mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast })$.
Lemma 9.5 gives another expression for ![]() $\mathscr {X} \ast \mathscr {Y}$ that is used in the proof of Lemma 9.6.
$\mathscr {X} \ast \mathscr {Y}$ that is used in the proof of Lemma 9.6.
Lemma 9.5. Let ![]() $(\mathbb {V}, h)$ be a metric vector space. For
$(\mathbb {V}, h)$ be a metric vector space. For ![]() $\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$,
$\mathscr {X}, \mathscr {Y} \in \mathscr {MC}(\mathbb {V}^{\ast })$,
 $$ \begin{align} \begin{split} (\mathscr{X}\ast \mathscr{Y})_{ijkl} & = -4B(\mathscr{X}, \mathscr{Y})_{[ij]kl} - 2B(\mathscr{X}, \mathscr{Y})_{k[ij]l} + 6B(\mathscr{X}, \mathscr{Y})_{[ijkl]} \\ & = -\tfrac{1}{2}\left( \mathscr{X}_{ij}{}^{pq}\mathscr{Y}_{pqkl} + \mathscr{Y}_{ij}{}^{pq}\mathscr{X}_{pqkl}\right) + \tfrac{3}{2}\mathscr{X}_{[ij}{}^{pq}\mathscr{Y}_{kl]pq} - 2B(\mathscr{X}, \mathscr{Y})_{k[ij]l}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} (\mathscr{X}\ast \mathscr{Y})_{ijkl} & = -4B(\mathscr{X}, \mathscr{Y})_{[ij]kl} - 2B(\mathscr{X}, \mathscr{Y})_{k[ij]l} + 6B(\mathscr{X}, \mathscr{Y})_{[ijkl]} \\ & = -\tfrac{1}{2}\left( \mathscr{X}_{ij}{}^{pq}\mathscr{Y}_{pqkl} + \mathscr{Y}_{ij}{}^{pq}\mathscr{X}_{pqkl}\right) + \tfrac{3}{2}\mathscr{X}_{[ij}{}^{pq}\mathscr{Y}_{kl]pq} - 2B(\mathscr{X}, \mathscr{Y})_{k[ij]l}. \end{split} \end{align} $$Proof. The first equality of (9.11) follows from (5.8), (5.9), and Theorem 5.4. The second equality of (9.11) follows from (5.13).
Lemma 9.6. Let ![]() $(\mathbb {V}, h)$ be a
$(\mathbb {V}, h)$ be a ![]() $4$-dimensional Euclidean vector space. For
$4$-dimensional Euclidean vector space. For ![]() $\mathscr {X}, \mathscr {Y} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$,
$\mathscr {X}, \mathscr {Y} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$,
 $$ \begin{align} \kern-183.5pt \mathscr{X}_{(i}{}^{abc}\mathscr{Y}_{j)abc} = \tfrac{1}{4}\langle \mathscr{X}, \mathscr{Y}\rangle h_{ij}, \kern70pt \end{align} $$
$$ \begin{align} \kern-183.5pt \mathscr{X}_{(i}{}^{abc}\mathscr{Y}_{j)abc} = \tfrac{1}{4}\langle \mathscr{X}, \mathscr{Y}\rangle h_{ij}, \kern70pt \end{align} $$

Proof. By (9.4), 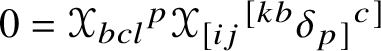 $0 = \mathscr {X}_{bcl}{}^{p}\mathscr {X}_{[ij}{}^{[kb}\delta _{p]}{}^{c]}$. Lowering the index k and simplifying this expression yields
$0 = \mathscr {X}_{bcl}{}^{p}\mathscr {X}_{[ij}{}^{[kb}\delta _{p]}{}^{c]}$. Lowering the index k and simplifying this expression yields
 $$ \begin{align} \mathscr{X}_{ij}{}^{pq}\mathscr{X}_{pqkl} = - 2\mathscr{X}_{iplq}\mathscr{X}_{k}{}^{p}{}_{j}{}^{q} + 2\mathscr{X}_{jplq}\mathscr{X}_{k}{}^{p}{}_{i}{}^{q} + \mathscr{X}_{labc}\mathscr{X}_{j}{}^{abc}h_{ik} - \mathscr{X}_{labc}\mathscr{X}_{i}{}^{abc}h_{jk}. \end{align} $$
$$ \begin{align} \mathscr{X}_{ij}{}^{pq}\mathscr{X}_{pqkl} = - 2\mathscr{X}_{iplq}\mathscr{X}_{k}{}^{p}{}_{j}{}^{q} + 2\mathscr{X}_{jplq}\mathscr{X}_{k}{}^{p}{}_{i}{}^{q} + \mathscr{X}_{labc}\mathscr{X}_{j}{}^{abc}h_{ik} - \mathscr{X}_{labc}\mathscr{X}_{i}{}^{abc}h_{jk}. \end{align} $$Tracing (9.15) in ![]() $jl$ and relabeling the result yields
$jl$ and relabeling the result yields  $\mathscr {X}_{iabc}\mathscr {X}_{j}{}^{abc} = \tfrac {1}{4}|\mathscr {X}|^{2}h_{ij}$. Polarizing this yields (9.12). Substituting (9.12) into (9.15) and using (5.13) yields
$\mathscr {X}_{iabc}\mathscr {X}_{j}{}^{abc} = \tfrac {1}{4}|\mathscr {X}|^{2}h_{ij}$. Polarizing this yields (9.12). Substituting (9.12) into (9.15) and using (5.13) yields

Polarizing (9.16) yields (9.13). Because ![]() $\dim {\bigwedge }^{4}\mathbb {V}^{\ast } = 1$,
$\dim {\bigwedge }^{4}\mathbb {V}^{\ast } = 1$, ![]() $\mathscr {X}_{[ij}{}^{pq}\mathscr {Y}_{kl]pq} = c \epsilon _{ijkl}$ for some
$\mathscr {X}_{[ij}{}^{pq}\mathscr {Y}_{kl]pq} = c \epsilon _{ijkl}$ for some ![]() $c \in \mathbb R$. Contracting this equality with
$c \in \mathbb R$. Contracting this equality with ![]() $\epsilon ^{ijkl}$ yields
$\epsilon ^{ijkl}$ yields ![]() $24c = 2\langle \star \mathscr {X}, \mathscr {Y} \rangle $, so that
$24c = 2\langle \star \mathscr {X}, \mathscr {Y} \rangle $, so that ![]() $12\mathscr {X}_{[ij}{}^{pq}\mathscr {Y}_{kl]pq} = \langle \star \mathscr {X}, \mathscr {Y} \rangle \epsilon _{ijkl}$. Substituting this and (9.13) into (9.11) of Lemma 9.5 yields (9.14).
$12\mathscr {X}_{[ij}{}^{pq}\mathscr {Y}_{kl]pq} = \langle \star \mathscr {X}, \mathscr {Y} \rangle \epsilon _{ijkl}$. Substituting this and (9.13) into (9.11) of Lemma 9.5 yields (9.14).
Lemma 9.7. Let ![]() $(\mathbb {V}, h, \epsilon )$ be a
$(\mathbb {V}, h, \epsilon )$ be a ![]() $4$-dimensional oriented Euclidean vector space. There hold
$4$-dimensional oriented Euclidean vector space. There hold
 $$ \begin{align} \begin{split} \tfrac{1}{3}\widehat{\mathscr{X} \ast \mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}& = \widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} - \tfrac{1}{3}\operatorname{\mathsf{tr}}( \widehat{\mathscr{X}} _{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}) \mathscr{P}_{{\textstyle\wedge}^{2}_{\pm}\mathbb{V}^{\ast}} \quad \text{if} \quad \mathscr{X}, \mathscr{Y} \in \mathscr{MC}_{\mathscr{W}}^{\pm}(\mathbb{V}^{\ast}),\\ \widehat{\mathscr{X} \ast \mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}& = 0 \quad \text{if} \quad \mathscr{X} \in \mathscr{MC}_{\mathscr{W}}^{+}(\mathbb{V}^{\ast}), \mathscr{Y} \in \mathscr{MC}_{\mathscr{W}}^{-}(\mathbb{V}^{\ast}), \end{split} \end{align} $$
$$ \begin{align} \begin{split} \tfrac{1}{3}\widehat{\mathscr{X} \ast \mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}& = \widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} - \tfrac{1}{3}\operatorname{\mathsf{tr}}( \widehat{\mathscr{X}} _{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circ \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}) \mathscr{P}_{{\textstyle\wedge}^{2}_{\pm}\mathbb{V}^{\ast}} \quad \text{if} \quad \mathscr{X}, \mathscr{Y} \in \mathscr{MC}_{\mathscr{W}}^{\pm}(\mathbb{V}^{\ast}),\\ \widehat{\mathscr{X} \ast \mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}& = 0 \quad \text{if} \quad \mathscr{X} \in \mathscr{MC}_{\mathscr{W}}^{+}(\mathbb{V}^{\ast}), \mathscr{Y} \in \mathscr{MC}_{\mathscr{W}}^{-}(\mathbb{V}^{\ast}), \end{split} \end{align} $$where 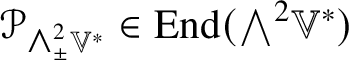 $\mathscr {P}_{{\textstyle \wedge }^{2}_{\pm }\mathbb {V}^{\ast }} \in \operatorname {End}({\bigwedge }^{2}\mathbb {V}^{\ast })$ are the orthogonal projections onto
$\mathscr {P}_{{\textstyle \wedge }^{2}_{\pm }\mathbb {V}^{\ast }} \in \operatorname {End}({\bigwedge }^{2}\mathbb {V}^{\ast })$ are the orthogonal projections onto ![]() ${\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast }$. Consequently,
${\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast }$. Consequently,
Proof. For ![]() $\mathscr {X}, \mathscr {Y} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, rewriting (9.14) in terms of
$\mathscr {X}, \mathscr {Y} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, rewriting (9.14) in terms of ![]() $\,\widehat {\,\,}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ and using Corollary 4.5 yields
$\,\widehat {\,\,}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ and using Corollary 4.5 yields
 $$ \begin{align} \begin{split} \tfrac{1}{3}\widehat{\mathscr{X} \ast \mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}& = \widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} - \tfrac{1}{6}\operatorname{\mathsf{tr}}(\widehat{\star \mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} \circ \widehat{ \mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}) \star - \tfrac{1}{6}\operatorname{\mathsf{tr}}( \widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} \circ \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} ) \operatorname{Id}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \tfrac{1}{3}\widehat{\mathscr{X} \ast \mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}& = \widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}\circledcirc \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} - \tfrac{1}{6}\operatorname{\mathsf{tr}}(\widehat{\star \mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} \circ \widehat{ \mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}) \star - \tfrac{1}{6}\operatorname{\mathsf{tr}}( \widehat{\mathscr{X}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} \circ \widehat{\mathscr{Y}}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} ) \operatorname{Id}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}. \end{split} \end{align} $$Because, by Lemma 9.2, ![]() $\star $ commutes with
$\star $ commutes with ![]() $\widehat {\mathscr {X}}$ and
$\widehat {\mathscr {X}}$ and ![]() $\widehat {\mathscr {Y}}$, (9.19) implies the equality
$\widehat {\mathscr {Y}}$, (9.19) implies the equality ![]() $\star \mathscr {X} \ast \star \mathscr {Y} = \mathscr {X} \ast \mathscr {Y}$, which shows
$\star \mathscr {X} \ast \star \mathscr {Y} = \mathscr {X} \ast \mathscr {Y}$, which shows ![]() $\mathscr {MC}^{+}_{\mathscr {W}}(\mathbb {V}^{\ast }) \ast \mathscr {MC}^{-}_{\mathscr {W}}(\mathbb {V}^{\ast }) = \{0\}$. Since
$\mathscr {MC}^{+}_{\mathscr {W}}(\mathbb {V}^{\ast }) \ast \mathscr {MC}^{-}_{\mathscr {W}}(\mathbb {V}^{\ast }) = \{0\}$. Since 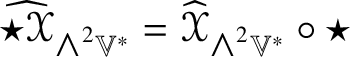 $\widehat {\star \mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} = \widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}\circ \star $, if
$\widehat {\star \mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} = \widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}\circ \star $, if ![]() $\mathscr {X} = \mathscr {X}^{+} + \mathscr {X}^{-}$ with
$\mathscr {X} = \mathscr {X}^{+} + \mathscr {X}^{-}$ with ![]() $\mathscr {X}^{\pm } \in \mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast })$, then
$\mathscr {X}^{\pm } \in \mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast })$, then 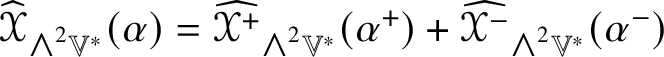 $\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\alpha ) = \widehat {\mathscr {X}^{+}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\alpha ^{+}) + \widehat {\mathscr {X}^{-}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\alpha ^{-})$ where
$\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\alpha ) = \widehat {\mathscr {X}^{+}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\alpha ^{+}) + \widehat {\mathscr {X}^{-}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\alpha ^{-})$ where ![]() $\alpha = \alpha ^{+} + \alpha ^{-}$ is the decomposition of
$\alpha = \alpha ^{+} + \alpha ^{-}$ is the decomposition of ![]() $\alpha \in {\bigwedge }^{2}\mathbb {V}^{\ast }$ into its self-dual and anti-self-dual parts. In particular,
$\alpha \in {\bigwedge }^{2}\mathbb {V}^{\ast }$ into its self-dual and anti-self-dual parts. In particular, 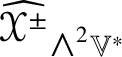 $\widehat {\mathscr {X}^{\pm }}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ annihilates
$\widehat {\mathscr {X}^{\pm }}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ annihilates ![]() ${\bigwedge }^{2}_{\mp }\mathbb {V}^{\ast }$ and
${\bigwedge }^{2}_{\mp }\mathbb {V}^{\ast }$ and  $\widehat {\mathscr {X}^{+}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ and
$\widehat {\mathscr {X}^{+}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ and  $\widehat {\mathscr {Y}^{-}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ anticommute. In (9.19) these observations yield (9.17), which implies the containments in (9.18). Because, by Example 9.4, each of
$\widehat {\mathscr {Y}^{-}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ anticommute. In (9.19) these observations yield (9.17), which implies the containments in (9.18). Because, by Example 9.4, each of ![]() $\mathscr {MC}^{+}_{\mathscr {W}}(\mathbb {V}^{\ast })$ contains a nontrivial idempotent, the
$\mathscr {MC}^{+}_{\mathscr {W}}(\mathbb {V}^{\ast })$ contains a nontrivial idempotent, the ![]() $SO(4)$-submodules
$SO(4)$-submodules ![]() $\mathscr {MC}^{\pm }_{\mathscr {W}}(\mathbb {V}^{\ast }) \ast \mathscr {MC}^{\pm }_{\mathscr {W}}(\mathbb {V}^{\ast })$ are nontrivial
$\mathscr {MC}^{\pm }_{\mathscr {W}}(\mathbb {V}^{\ast }) \ast \mathscr {MC}^{\pm }_{\mathscr {W}}(\mathbb {V}^{\ast })$ are nontrivial ![]() $SO(4)$-submodules of the irreducible
$SO(4)$-submodules of the irreducible ![]() $SO(4)$-modules
$SO(4)$-modules ![]() $\mathscr {MC}^{+}_{\mathscr {W}}(\mathbb {V}^{\ast })$, so equality holds in (9.18).
$\mathscr {MC}^{+}_{\mathscr {W}}(\mathbb {V}^{\ast })$, so equality holds in (9.18).
Remark 9.8. Reversing the orientation of ![]() $\mathbb {V}$ interchanges the subspaces
$\mathbb {V}$ interchanges the subspaces ![]() $\mathscr {MC}^{\pm }_{\mathscr {W}}(\mathbb {V}^{\ast })$, but the orthogonal decomposition remains; all that changes is the labeling as
$\mathscr {MC}^{\pm }_{\mathscr {W}}(\mathbb {V}^{\ast })$, but the orthogonal decomposition remains; all that changes is the labeling as ![]() $+$ or
$+$ or ![]() $-$. Hence, the relations (9.18) make sense independent of any choice of orientation, in the sense that
$-$. Hence, the relations (9.18) make sense independent of any choice of orientation, in the sense that ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ decomposes as an orthogonal direct sum of two
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ decomposes as an orthogonal direct sum of two ![]() $5$-dimensional
$5$-dimensional ![]() $\ast $-subalgebras whose product is
$\ast $-subalgebras whose product is ![]() $\{0\}$.
$\{0\}$.
Lemma 9.9. The deunitalization ![]() $(\operatorname {Sym}_{0}(3, \mathbb R), \times )$ of the
$(\operatorname {Sym}_{0}(3, \mathbb R), \times )$ of the ![]() $6$-dimensional rank
$6$-dimensional rank ![]() $3$ simple real Euclidean Jordan algebra
$3$ simple real Euclidean Jordan algebra ![]() $\operatorname {Sym}(3, \mathbb R)$ is simple and contains no nontrivial square-zero elements.
$\operatorname {Sym}(3, \mathbb R)$ is simple and contains no nontrivial square-zero elements.
Proof. Consider the representation of ![]() $\operatorname {Sym}_{0}(3, \mathbb R)$ as trace-free
$\operatorname {Sym}_{0}(3, \mathbb R)$ as trace-free ![]() $3 \times 3$ symmetric matrices. Let
$3 \times 3$ symmetric matrices. Let ![]() $\mathbb {D} \subset \operatorname {Sym}_{0}(3, \mathbb R)$ be the
$\mathbb {D} \subset \operatorname {Sym}_{0}(3, \mathbb R)$ be the ![]() $2$-dimensional subalgebra comprising the diagonal matrices. First it is shown that the subalgebra
$2$-dimensional subalgebra comprising the diagonal matrices. First it is shown that the subalgebra ![]() $(\mathbb {D}, \times )$ is simple. Let
$(\mathbb {D}, \times )$ is simple. Let ![]() $\gamma _{1} = E_{11} - E_{33}, \gamma _{2} = E_{22} - E_{33}, \gamma _{3} = E_{33} - E_{11} \in \mathbb {D}$ where
$\gamma _{1} = E_{11} - E_{33}, \gamma _{2} = E_{22} - E_{33}, \gamma _{3} = E_{33} - E_{11} \in \mathbb {D}$ where ![]() $E_{ij}$ is the matrix with
$E_{ij}$ is the matrix with ![]() $1$ in the
$1$ in the ![]() $ij$ component and
$ij$ component and ![]() $0$ in all other components. Then
$0$ in all other components. Then ![]() $\{\gamma _{i}:1 \leq i \leq 3\}$ are idempotents satisfying
$\{\gamma _{i}:1 \leq i \leq 3\}$ are idempotents satisfying ![]() $\gamma _{i}\circ \gamma _{j} = -\gamma _{i} - \gamma _{j}$. Let
$\gamma _{i}\circ \gamma _{j} = -\gamma _{i} - \gamma _{j}$. Let ![]() $\mathbb {I}$ be an ideal of
$\mathbb {I}$ be an ideal of ![]() $\mathbb {D}$ and let
$\mathbb {D}$ and let ![]() $a = a_{1}\gamma _{1} + a_{2}\gamma _{2} \in \mathbb {I}$. Then
$a = a_{1}\gamma _{1} + a_{2}\gamma _{2} \in \mathbb {I}$. Then ![]() $a\times \gamma _{1} + a = (2a_{1} - a_{2})\gamma _{1}$ and
$a\times \gamma _{1} + a = (2a_{1} - a_{2})\gamma _{1}$ and ![]() $a\times \gamma _{2} + a = (2a_{2} - a_{1})\gamma _{2}$. If
$a\times \gamma _{2} + a = (2a_{2} - a_{1})\gamma _{2}$. If ![]() $2a_{1} = a_{2}$ and
$2a_{1} = a_{2}$ and ![]() $2a_{2} = a_{1}$, then
$2a_{2} = a_{1}$, then ![]() $4a_{1} = a_{1}$, so
$4a_{1} = a_{1}$, so ![]() $a_{1} = 0$ and
$a_{1} = 0$ and ![]() $a_{2} = 0$, so
$a_{2} = 0$, so ![]() $a = 0$. Otherwise, if
$a = 0$. Otherwise, if ![]() $2a_{1} \neq a_{2}$, then
$2a_{1} \neq a_{2}$, then ![]() $\gamma _{1} \in \mathbb {I}$, in which case
$\gamma _{1} \in \mathbb {I}$, in which case ![]() $\gamma _{2} = \gamma _{1} + \gamma _{1}\times \gamma _{2} \in \mathbb {I}$, so
$\gamma _{2} = \gamma _{1} + \gamma _{1}\times \gamma _{2} \in \mathbb {I}$, so ![]() $\mathbb {I} = \mathbb {D}$, while, if
$\mathbb {I} = \mathbb {D}$, while, if ![]() $a_{1} \neq 2a_{2}$, then
$a_{1} \neq 2a_{2}$, then ![]() $\gamma _{2} \in \mathbb {I}$, so
$\gamma _{2} \in \mathbb {I}$, so ![]() $\gamma _{1} = \gamma _{2} + \gamma _{1}\times \gamma _{2} \in \mathbb {I}$, so
$\gamma _{1} = \gamma _{2} + \gamma _{1}\times \gamma _{2} \in \mathbb {I}$, so ![]() $\mathbb {I} = \mathbb {D}$. This shows
$\mathbb {I} = \mathbb {D}$. This shows ![]() $\mathbb {D}$ is simple.
$\mathbb {D}$ is simple.
Now let ![]() $\mathbb {I}$ be a nonzero ideal in
$\mathbb {I}$ be a nonzero ideal in ![]() $\operatorname {Sym}_{0}(3, \mathbb R, \times )$. By the principal axis theorem, every element of
$\operatorname {Sym}_{0}(3, \mathbb R, \times )$. By the principal axis theorem, every element of ![]() $\operatorname {Sym}_{0}(3, \mathbb R, \times )$ is equivalent via an automorphism of
$\operatorname {Sym}_{0}(3, \mathbb R, \times )$ is equivalent via an automorphism of ![]() $(\operatorname {Sym}_{0}(3, \mathbb R), \times )$ to an element of
$(\operatorname {Sym}_{0}(3, \mathbb R), \times )$ to an element of ![]() $\mathbb {D}$, so it can be assumed that
$\mathbb {D}$, so it can be assumed that ![]() $\mathbb {I}$ contains a nonzero element. Since
$\mathbb {I}$ contains a nonzero element. Since ![]() $E_{ii} + E_{jj} - 2E_{kk} \in \mathbb {D} \subset \mathbb {I}$,
$E_{ii} + E_{jj} - 2E_{kk} \in \mathbb {D} \subset \mathbb {I}$, ![]() $E_{ij} + E_{ji} = (E_{ij} + E_{ji})\times (E_{ii} + E_{jj} - 2E_{kk}) \in \mathbb {I}$ for all
$E_{ij} + E_{ji} = (E_{ij} + E_{ji})\times (E_{ii} + E_{jj} - 2E_{kk}) \in \mathbb {I}$ for all ![]() $i \neq j \in \{1, 2, 3\}$. Since together
$i \neq j \in \{1, 2, 3\}$. Since together ![]() $\mathbb {D}$ and the elements
$\mathbb {D}$ and the elements ![]() $E_{ij} + E_{ji}$ with
$E_{ij} + E_{ji}$ with ![]() $i \neq j$ span
$i \neq j$ span ![]() $\operatorname {Sym}_{0}(3, \mathbb R)$, this shows
$\operatorname {Sym}_{0}(3, \mathbb R)$, this shows ![]() $\mathbb {I} = \operatorname {Sym}_{0}(3, \mathbb R)$.
$\mathbb {I} = \operatorname {Sym}_{0}(3, \mathbb R)$.
By the principal axis theorem, any square-zero element of ![]() $(\operatorname {Sym}_{0}(3, \mathbb R), \times )$ is equivalent via an automorphism to an element of
$(\operatorname {Sym}_{0}(3, \mathbb R), \times )$ is equivalent via an automorphism to an element of ![]() $\mathbb {D}$. If
$\mathbb {D}$. If ![]() $a = a_{1}\gamma _{1} + a_{2}\gamma _{2} \in \mathbb {D}$ is square-zero, then
$a = a_{1}\gamma _{1} + a_{2}\gamma _{2} \in \mathbb {D}$ is square-zero, then ![]() $a_{1}(a_{1} - 2a_{2}) = 0 = a_{2}(a_{2}- 2a_{1})$ and the unique solution is
$a_{1}(a_{1} - 2a_{2}) = 0 = a_{2}(a_{2}- 2a_{1})$ and the unique solution is ![]() $a_{1}= 0 = a_{2}$.
$a_{1}= 0 = a_{2}$.
Remark 9.10. Essentially the same argument shows that the deunitalization of a simple real Euclidean Jordan algebra of rank at least ![]() $3$ is simple. However, that there are no nontrivial square-zero elements is true if and only if the rank is odd. See [Reference Fox10] for details.
$3$ is simple. However, that there are no nontrivial square-zero elements is true if and only if the rank is odd. See [Reference Fox10] for details.
Proof of Theorem 1.5.
Let ![]() $(\mathbb {V}, h)$ be a
$(\mathbb {V}, h)$ be a ![]() $4$-dimensional Euclidean vector space. By Lemma 9.2, for any
$4$-dimensional Euclidean vector space. By Lemma 9.2, for any ![]() $\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$,
$\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, 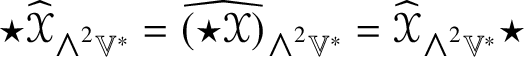 $\star \widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} = \widehat {(\star \mathscr {X})}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} = \widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}\star $, so, if
$\star \widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} = \widehat {(\star \mathscr {X})}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} = \widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}\star $, so, if ![]() $\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast })$, then
$\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast })$, then ![]() $\mathscr {X}$ preserves
$\mathscr {X}$ preserves ![]() ${\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast }$ and annihilates
${\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast }$ and annihilates ![]() ${\bigwedge }^{2}_{\mp }\mathbb {V}^{\ast }$ and so induces a symmetric endomorphism of
${\bigwedge }^{2}_{\mp }\mathbb {V}^{\ast }$ and so induces a symmetric endomorphism of ![]() ${\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast }$. By Example 9.4, if
${\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast }$. By Example 9.4, if ![]() $\omega \in {\bigwedge }^{2}\mathbb {V}^{\ast }$ satisfies
$\omega \in {\bigwedge }^{2}\mathbb {V}^{\ast }$ satisfies ![]() $\omega \circ \omega = -h$, then
$\omega \circ \omega = -h$, then ![]() $\omega \in {\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast }$ as
$\omega \in {\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast }$ as  $\tfrac {1}{2}\omega \wedge \omega = \pm \epsilon $, and
$\tfrac {1}{2}\omega \wedge \omega = \pm \epsilon $, and ![]() $\mathscr {S}(\omega ) \in \mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast })$. By (6.7),
$\mathscr {S}(\omega ) \in \mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast })$. By (6.7), ![]() $\widehat {\omega \cdot \omega }_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\omega ) = -5\omega $, so
$\widehat {\omega \cdot \omega }_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\omega ) = -5\omega $, so  . Since this shows that
. Since this shows that 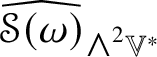 $\widehat {\mathscr {S}(\omega )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ acts nontrivially on
$\widehat {\mathscr {S}(\omega )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ acts nontrivially on ![]() ${\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast }$, it follows from the Schur Lemma that the
${\bigwedge }^{2}_{\pm }\mathbb {V}^{\ast }$, it follows from the Schur Lemma that the ![]() $SO(4)$-equivariant map
$SO(4)$-equivariant map  $\Psi :\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast }) \to \operatorname {Sym}_{0}({\bigwedge }^{2}_{\pm } \mathbb {V}^{\ast }, h)$ sending
$\Psi :\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast }) \to \operatorname {Sym}_{0}({\bigwedge }^{2}_{\pm } \mathbb {V}^{\ast }, h)$ sending ![]() $\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast })$ to
$\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast })$ to 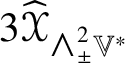 $3\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}_{\pm }\mathbb {V}^{\ast }}$ is a linear isomorphism. It follows from (9.17) of Lemma 9.7 that
$3\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}_{\pm }\mathbb {V}^{\ast }}$ is a linear isomorphism. It follows from (9.17) of Lemma 9.7 that 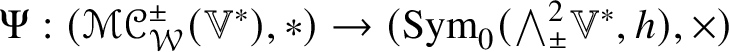 $\Psi : (\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast }), \ast ) \to (\operatorname {Sym}_{0}({\bigwedge }^{2}_{\pm } \mathbb {V}^{\ast }, h), \times )$ is an algebra isomorphism. By the definition of G and Corollary 4.5, for
$\Psi : (\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast }), \ast ) \to (\operatorname {Sym}_{0}({\bigwedge }^{2}_{\pm } \mathbb {V}^{\ast }, h), \times )$ is an algebra isomorphism. By the definition of G and Corollary 4.5, for ![]() $\mathscr {X}, \mathscr {Y} \in \mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast })$,
$\mathscr {X}, \mathscr {Y} \in \mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast })$,  $\Psi ^{\ast }(G)(\mathscr {X}, \mathscr {Y}) = 9 G(\widehat {\mathscr {X}}, \widehat {\mathscr {Y}}) = 3\operatorname {\mathsf {tr}}(\widehat {\mathscr {X}} \circ \widehat {\mathscr {Y}}) = \tfrac {3}{4}\langle \mathscr {X}, \mathscr {Y}\rangle $. That the trace-form
$\Psi ^{\ast }(G)(\mathscr {X}, \mathscr {Y}) = 9 G(\widehat {\mathscr {X}}, \widehat {\mathscr {Y}}) = 3\operatorname {\mathsf {tr}}(\widehat {\mathscr {X}} \circ \widehat {\mathscr {Y}}) = \tfrac {3}{4}\langle \mathscr {X}, \mathscr {Y}\rangle $. That the trace-form ![]() $\tau _{\ast }$ is the stated multiple of h follows from the corresponding statement in the algebra
$\tau _{\ast }$ is the stated multiple of h follows from the corresponding statement in the algebra  $(\operatorname {Sym}_{0}({\bigwedge }^{2}_{\pm } \mathbb {V}^{\ast }, h), \times , \tfrac {4}{3}G)$ and the fact that
$(\operatorname {Sym}_{0}({\bigwedge }^{2}_{\pm } \mathbb {V}^{\ast }, h), \times , \tfrac {4}{3}G)$ and the fact that ![]() $\Psi $ is an isometric isomorphism. That
$\Psi $ is an isometric isomorphism. That ![]() $(\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast }), \ast , \langle \,\cdot \,\,, \,\cdot \,\, \rangle )$ is simple and contains no square-zero elements follows from the preceding in conjunction with Lemma 9.9.
$(\mathscr {MC}_{\mathscr {W}}^{\pm }(\mathbb {V}^{\ast }), \ast , \langle \,\cdot \,\,, \,\cdot \,\, \rangle )$ is simple and contains no square-zero elements follows from the preceding in conjunction with Lemma 9.9.
10 Idempotents in the subalgebra of Weyl curvature tensors
In this section some idempotents in ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ are constructed and some of their products are calculated. This provides more detailed information about the internal structure of
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ are constructed and some of their products are calculated. This provides more detailed information about the internal structure of ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ and yields an alternative proof of Theorem 1.5 along lines viable when
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ and yields an alternative proof of Theorem 1.5 along lines viable when ![]() $\dim \mathbb {V}> 4$.
$\dim \mathbb {V}> 4$.
Let ![]() $(\mathbb {V}, h)$ be a Euclidean vector space of dimension
$(\mathbb {V}, h)$ be a Euclidean vector space of dimension ![]() $n> 2$. A subspace
$n> 2$. A subspace ![]() $\mathbb {W} \subset \mathbb {V}$ determines
$\mathbb {W} \subset \mathbb {V}$ determines ![]() such that
such that ![]() $\mathbb {W}$ equals the image of the endomorphism
$\mathbb {W}$ equals the image of the endomorphism ![]() $g_{i}{}^{j}$, in which case
$g_{i}{}^{j}$, in which case ![]() $\operatorname {\mathsf {tr}} g = \dim \mathbb {W}$. The space of orthogonal almost complex structures on
$\operatorname {\mathsf {tr}} g = \dim \mathbb {W}$. The space of orthogonal almost complex structures on ![]() $\mathbb {W}$ is identified with
$\mathbb {W}$ is identified with
By construction, ![]() $\alpha \in \mathscr {OC}(\mathbb {W}, h)$ satisfies
$\alpha \in \mathscr {OC}(\mathbb {W}, h)$ satisfies ![]() $\dim \mathbb {W} = \operatorname {\mathsf {tr}} g = |g|^{2} = |\alpha |^{2}$. It will be said that
$\dim \mathbb {W} = \operatorname {\mathsf {tr}} g = |g|^{2} = |\alpha |^{2}$. It will be said that ![]() $\alpha \in \mathscr {OC}(\mathbb {W}, h)$ determines an orthogonal almost complex structure on
$\alpha \in \mathscr {OC}(\mathbb {W}, h)$ determines an orthogonal almost complex structure on ![]() $\mathbb {W}$.
$\mathbb {W}$.
For even r satisfying ![]() $2 \leq r \leq n$, there is r-dimensional
$2 \leq r \leq n$, there is r-dimensional ![]() $\mathbb {W} \subset \mathbb {V}$ such that
$\mathbb {W} \subset \mathbb {V}$ such that ![]() $\mathscr {OC}(\mathbb {W}, h)$ is nonempty. Let
$\mathscr {OC}(\mathbb {W}, h)$ is nonempty. Let ![]() $\{\epsilon (1), \dots , \epsilon (n)\}$ be an h-orthonormal basis of
$\{\epsilon (1), \dots , \epsilon (n)\}$ be an h-orthonormal basis of ![]() $\mathbb {V}^{\ast }$ such that
$\mathbb {V}^{\ast }$ such that ![]() $\{\epsilon (1), \dots , \epsilon (r)\}$ spans
$\{\epsilon (1), \dots , \epsilon (r)\}$ spans ![]() $\mathbb {W}^{\ast }$ and
$\mathbb {W}^{\ast }$ and ![]() $\{\epsilon (r+1), \dots , \epsilon (n)\}$ spans the h-orthogonal complement
$\{\epsilon (r+1), \dots , \epsilon (n)\}$ spans the h-orthogonal complement ![]() $\mathbb {W}^{\ast \,\perp }$. The endomorphism associated with
$\mathbb {W}^{\ast \,\perp }$. The endomorphism associated with 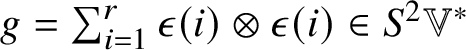 $g = \sum _{i = 1}^{r}\epsilon (i)\otimes \epsilon (i) \in S^{2}\mathbb {V}^{\ast }$ is the orthogonal projection on
$g = \sum _{i = 1}^{r}\epsilon (i)\otimes \epsilon (i) \in S^{2}\mathbb {V}^{\ast }$ is the orthogonal projection on ![]() $\mathbb {W}$ and
$\mathbb {W}$ and 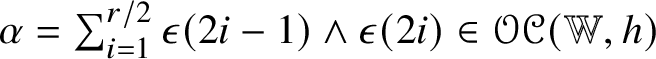 $\alpha = \sum _{i = 1}^{r/2}\epsilon (2i-1)\wedge \epsilon (2i) \in \mathscr {OC}(\mathbb {W}, h)$.
$\alpha = \sum _{i = 1}^{r/2}\epsilon (2i-1)\wedge \epsilon (2i) \in \mathscr {OC}(\mathbb {W}, h)$.
Lemma 10.1. Let ![]() $(\mathbb {V}, h)$ be a Euclidean vector space of dimension
$(\mathbb {V}, h)$ be a Euclidean vector space of dimension ![]() $n> 2$. Let r be even and satisfy
$n> 2$. Let r be even and satisfy ![]() $2 \leq r \leq n$, let
$2 \leq r \leq n$, let ![]() $\mathbb {W} \subset \mathbb {V}$ have dimension r, let
$\mathbb {W} \subset \mathbb {V}$ have dimension r, let ![]() $\alpha \in \mathscr {OC}(\mathbb {W}, h)$, and let
$\alpha \in \mathscr {OC}(\mathbb {W}, h)$, and let ![]() $g = -\alpha \circ \alpha $. The elements of
$g = -\alpha \circ \alpha $. The elements of ![]() $\mathscr {MC}(\mathbb {V}^{\ast })$ defined by
$\mathscr {MC}(\mathbb {V}^{\ast })$ defined by

are idempotents in ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ that are nontrivial and linearly independent when
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ that are nontrivial and linearly independent when ![]() $r \geq 4$, while, when
$r \geq 4$, while, when ![]() $r = 2$,
$r = 2$, ![]() $\mathscr {S}^{2}(\alpha )$ is trivial and
$\mathscr {S}^{2}(\alpha )$ is trivial and ![]() $\mathscr {K}^{2}(\alpha ) = \mathscr {H}(g)$. They satisfy the relations
$\mathscr {K}^{2}(\alpha ) = \mathscr {H}(g)$. They satisfy the relations
 $$ \begin{align} \begin{aligned} {} &\langle \mathscr{K}^{r}(\alpha), \mathscr{S}^{r}(\alpha)\rangle = |\mathscr{S}^{r}(\alpha)|^{2}_{h} = \tfrac{6r(r-2)}{(r+2)(r-1)} ,&& |\mathscr{K}^{r}(\alpha)|^{2}_{h} = \tfrac{8r}{r+2},\\ &\langle \mathscr{K}^{r}(\alpha), \mathscr{H}(g)\rangle =|\mathscr{H}(g)|^{2}_{h} = \tfrac{2r}{r-1},&& \langle\mathscr{S}^{r}(\alpha), \mathscr{H}(g) \rangle = 0. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {} &\langle \mathscr{K}^{r}(\alpha), \mathscr{S}^{r}(\alpha)\rangle = |\mathscr{S}^{r}(\alpha)|^{2}_{h} = \tfrac{6r(r-2)}{(r+2)(r-1)} ,&& |\mathscr{K}^{r}(\alpha)|^{2}_{h} = \tfrac{8r}{r+2},\\ &\langle \mathscr{K}^{r}(\alpha), \mathscr{H}(g)\rangle =|\mathscr{H}(g)|^{2}_{h} = \tfrac{2r}{r-1},&& \langle\mathscr{S}^{r}(\alpha), \mathscr{H}(g) \rangle = 0. \end{aligned} \end{align} $$Moreover:
1.
 $\mathscr {S}^{r}(\alpha ) \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, while
$\mathscr {S}^{r}(\alpha ) \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, while  $\mathscr {K}^{r}(\alpha )\notin \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ because
$\mathscr {K}^{r}(\alpha )\notin \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ because  $\operatorname {\rho }(\mathscr {K}^{r}(\alpha )) = g$.
$\operatorname {\rho }(\mathscr {K}^{r}(\alpha )) = g$.2. If
 $r \in \{n-1, n\}$,
$r \in \{n-1, n\}$,  $\mathscr {S}^{r}(\alpha ) = -\tfrac {1}{r+2}\operatorname {\mathsf {tf}}(\alpha \cdot \alpha )$.
$\mathscr {S}^{r}(\alpha ) = -\tfrac {1}{r+2}\operatorname {\mathsf {tf}}(\alpha \cdot \alpha )$.
Proof. By (6.35), (6.19), and Lemma 7.4,

Combining the identities (10.5) yields

That (10.6) vanish yields the equations ![]() $A^{2}(r+2) = -A$ and
$A^{2}(r+2) = -A$ and ![]() $(r-1)B^{2} + (6A + 1)B - 3A^{2} = 0$. These equations have the three nontrivial solutions
$(r-1)B^{2} + (6A + 1)B - 3A^{2} = 0$. These equations have the three nontrivial solutions 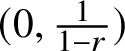 $(0, \tfrac {1}{1-r})$,
$(0, \tfrac {1}{1-r})$, 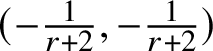 $(-\tfrac {1}{r+2}, -\tfrac {1}{r+2})$, and
$(-\tfrac {1}{r+2}, -\tfrac {1}{r+2})$, and 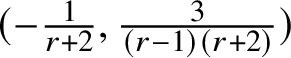 $(-\tfrac {1}{r+2}, \tfrac {3}{(r-1)(r+2)})$ for
$(-\tfrac {1}{r+2}, \tfrac {3}{(r-1)(r+2)})$ for ![]() $(A, B)$ that yield, respectively, the idempotents
$(A, B)$ that yield, respectively, the idempotents ![]() $\mathscr {H}(g)$,
$\mathscr {H}(g)$, ![]() $\mathscr {K}^{r}(\omega )$, and
$\mathscr {K}^{r}(\omega )$, and ![]() $\mathscr {S}^{r}(\omega )$. The relations (10.3) follow from (10.5) by computations similar to those showing (10.6).
$\mathscr {S}^{r}(\omega )$. The relations (10.3) follow from (10.5) by computations similar to those showing (10.6).
By (7.7), ![]() $\operatorname {\rho }(\alpha \cdot \alpha ) = 3\alpha \circ \alpha = -3g$, and by (7.3),
$\operatorname {\rho }(\alpha \cdot \alpha ) = 3\alpha \circ \alpha = -3g$, and by (7.3), ![]() , from which there follow
, from which there follow ![]() $\operatorname {\rho }(\mathscr {S}^{r}(\alpha )) = 0$ and
$\operatorname {\rho }(\mathscr {S}^{r}(\alpha )) = 0$ and ![]() $\operatorname {\rho }(\mathscr {K}^{r}(\alpha )) = g$, so that
$\operatorname {\rho }(\mathscr {K}^{r}(\alpha )) = g$, so that ![]() $\mathscr {S}^{r}(\alpha ) \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ but
$\mathscr {S}^{r}(\alpha ) \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ but ![]() $\mathscr {K}^{r}(\alpha ) \notin \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$.
$\mathscr {K}^{r}(\alpha ) \notin \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$.
From (6.11), (6.13), and (6.12) there follow 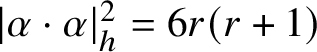 $|\alpha \cdot \alpha |^{2}_{h} =6r(r+1)$,
$|\alpha \cdot \alpha |^{2}_{h} =6r(r+1)$, ![]() , and
, and ![]() , which yield (10.4). By (10.4),
, which yield (10.4). By (10.4), ![]() $\mathscr {H}(g)$,
$\mathscr {H}(g)$, ![]() $\mathscr {K}^{r}(\alpha )$, and
$\mathscr {K}^{r}(\alpha )$, and ![]() $\mathscr {S}^{r}(\alpha )$ are nontrivial and linearly independent when
$\mathscr {S}^{r}(\alpha )$ are nontrivial and linearly independent when ![]() $r \geq 4$, while when
$r \geq 4$, while when ![]() $r = 2$,
$r = 2$, ![]() $\mathscr {S}^{2}(\alpha )$ is trivial and
$\mathscr {S}^{2}(\alpha )$ is trivial and ![]() $\mathscr {K}^{2}(\alpha ) = \mathscr {H}(g)$.
$\mathscr {K}^{2}(\alpha ) = \mathscr {H}(g)$.
A straightforward computation using (7.8) shows

where ![]() $\mathscr {H}(g)$ is as in (7.11). If
$\mathscr {H}(g)$ is as in (7.11). If ![]() $r = n$, then
$r = n$, then ![]() $h = g$ and
$h = g$ and ![]() $\mathscr {H}(g) = 0$, so if
$\mathscr {H}(g) = 0$, so if ![]() $r \in \{n-1, n\}$, by (10.7),
$r \in \{n-1, n\}$, by (10.7), ![]() $(r+2)\mathscr {S}^{r}(\alpha ) = -\operatorname {\mathsf {tf}}(\alpha \cdot \alpha )$.
$(r+2)\mathscr {S}^{r}(\alpha ) = -\operatorname {\mathsf {tf}}(\alpha \cdot \alpha )$.
Remark 10.2. From Lemma 5.9 it follows that, if ![]() $\mathbb {W}^{\ast }$ is a subspace of
$\mathbb {W}^{\ast }$ is a subspace of ![]() $\mathbb {V}^{\ast }$, the inclusion of an idempotent of
$\mathbb {V}^{\ast }$, the inclusion of an idempotent of ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {W}^{\ast })$ is an idempotent in
$\mathscr {MC}_{\mathscr {W}}(\mathbb {W}^{\ast })$ is an idempotent in ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. In particular, the
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. In particular, the ![]() $r < m$ cases of Lemma 10.1 follow from the
$r < m$ cases of Lemma 10.1 follow from the ![]() $r = m$ case of Lemma 10.1 in conjunction with Lemma 5.9.
$r = m$ case of Lemma 10.1 in conjunction with Lemma 5.9.
Lemma 10.4 shows that when ![]() $\dim \mathbb {V}^{\ast } = 2n \geq 4$, certain of the idempotents produced by Lemma 10.1 constitute an orbit of
$\dim \mathbb {V}^{\ast } = 2n \geq 4$, certain of the idempotents produced by Lemma 10.1 constitute an orbit of ![]() $O(2n)$ acting in
$O(2n)$ acting in ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ that can be identified with the space of orthogonal complex structures on
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ that can be identified with the space of orthogonal complex structures on ![]() $\mathbb {V}$ inducing a given orientation on
$\mathbb {V}$ inducing a given orientation on ![]() $\mathbb {V}$. The proof uses Lemma 10.3.
$\mathbb {V}$. The proof uses Lemma 10.3.
Lemma 10.3. Let ![]() $(\mathbb {V}, h)$ be a Euclidean vector space of dimension n. Let r be even and satisfy
$(\mathbb {V}, h)$ be a Euclidean vector space of dimension n. Let r be even and satisfy ![]() $4 \leq r \leq n$. Let
$4 \leq r \leq n$. Let ![]() $\mathbb {W} \subset \mathbb {V}$ have dimension r, let
$\mathbb {W} \subset \mathbb {V}$ have dimension r, let ![]() $\alpha \in \mathscr {OC}(\mathbb {W}, h)$, and let
$\alpha \in \mathscr {OC}(\mathbb {W}, h)$, and let ![]() $g = -\alpha \circ \alpha $.
$g = -\alpha \circ \alpha $.
1. The eigenvalues of
 $\widehat {\mathscr {S}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ are
$\widehat {\mathscr {S}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ are  $\tfrac {r-2}{r-1}$, with 1-dimensional eigenspace spanned by
$\tfrac {r-2}{r-1}$, with 1-dimensional eigenspace spanned by  $\alpha $;
$\alpha $;  $\tfrac {1}{1-r}$, with
$\tfrac {1}{1-r}$, with  $\tfrac {r(r-2)}{4}$-dimensional eigenspace contained in
$\tfrac {r(r-2)}{4}$-dimensional eigenspace contained in  ${\bigwedge }^{2}\mathbb {W}^{\ast }$;
${\bigwedge }^{2}\mathbb {W}^{\ast }$;  $\tfrac {r-4}{(r+2)(r-1)}$, with
$\tfrac {r-4}{(r+2)(r-1)}$, with  $\tfrac {r^{2} - 4}{4}$-dimensional eigenspace contained in
$\tfrac {r^{2} - 4}{4}$-dimensional eigenspace contained in  ${\bigwedge }^{2}\mathbb {W}^{\ast }$; and
${\bigwedge }^{2}\mathbb {W}^{\ast }$; and  $0$, with eigenspace equal to
$0$, with eigenspace equal to  ${\bigwedge }^{2}\mathbb {W}^{\perp \,\ast } \oplus \mathbb {W}^{\perp \,\ast }\wedge \mathbb {W}^{\ast }$.
${\bigwedge }^{2}\mathbb {W}^{\perp \,\ast } \oplus \mathbb {W}^{\perp \,\ast }\wedge \mathbb {W}^{\ast }$.2. The nonzero eigenvalues of
 $\widehat {\mathscr {K}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ are
$\widehat {\mathscr {K}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ are  $1$, with 1-dimensional eigenspace spanned by
$1$, with 1-dimensional eigenspace spanned by  $\alpha $, and
$\alpha $, and  $-\tfrac {2}{r+2}$, with
$-\tfrac {2}{r+2}$, with  $\tfrac {r^{2} - 4}{4}$-dimensional eigenspace contained in
$\tfrac {r^{2} - 4}{4}$-dimensional eigenspace contained in  ${\bigwedge }^{2}\mathbb {W}^{\ast }$.
${\bigwedge }^{2}\mathbb {W}^{\ast }$.
Proof. Write ![]() $\mathcal {A} = Q_{\circledcirc }(\alpha ) \in \operatorname {End}({\bigwedge }^{2}\mathbb {V}^{\ast })$. By (6.5),
$\mathcal {A} = Q_{\circledcirc }(\alpha ) \in \operatorname {End}({\bigwedge }^{2}\mathbb {V}^{\ast })$. By (6.5), ![]() $\mathcal {A}^{2} = Q_{\circledcirc }(\alpha )\circledcirc Q_{\circledcirc }(\alpha ) = Q_{\circledcirc }(g)$ and
$\mathcal {A}^{2} = Q_{\circledcirc }(\alpha )\circledcirc Q_{\circledcirc }(\alpha ) = Q_{\circledcirc }(g)$ and ![]() $\mathcal {A}^{3} = Q_{\circledcirc }(\alpha )\circledcirc Q_{\circledcirc }(g) = Q_{\circledcirc }(\alpha ) = \mathcal {A}$. By (6.7) and (6.8),
$\mathcal {A}^{3} = Q_{\circledcirc }(\alpha )\circledcirc Q_{\circledcirc }(g) = Q_{\circledcirc }(\alpha ) = \mathcal {A}$. By (6.7) and (6.8),
 $$ \begin{align} \begin{aligned} \widehat{\mathscr{S}^{r}(\alpha)}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} &= \tfrac{1}{r+2}\left(\alpha \otimes \alpha^{\sharp} - \mathcal{A} - \tfrac{3}{r-1}\mathcal{A}^{2}\right)\!. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \widehat{\mathscr{S}^{r}(\alpha)}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}} &= \tfrac{1}{r+2}\left(\alpha \otimes \alpha^{\sharp} - \mathcal{A} - \tfrac{3}{r-1}\mathcal{A}^{2}\right)\!. \end{aligned} \end{align} $$Since ![]() $\mathcal {A}(\alpha ) = -\alpha $, by (10.8),
$\mathcal {A}(\alpha ) = -\alpha $, by (10.8), 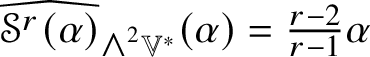 $\widehat {\mathscr {S}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\alpha ) = \tfrac {r-2}{r-1}\alpha $. Because
$\widehat {\mathscr {S}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\alpha ) = \tfrac {r-2}{r-1}\alpha $. Because  $\widehat {\mathscr {S}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ is self-adjoint, it preserves the orthogonal complement
$\widehat {\mathscr {S}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ is self-adjoint, it preserves the orthogonal complement ![]() $\langle \alpha \rangle ^{\perp }\subset {\bigwedge }^{2}\mathbb {V}^{\ast }$. Because
$\langle \alpha \rangle ^{\perp }\subset {\bigwedge }^{2}\mathbb {V}^{\ast }$. Because ![]() $\langle \mathcal {A}(\gamma ), \alpha \rangle = -\langle \alpha , \gamma \rangle $,
$\langle \mathcal {A}(\gamma ), \alpha \rangle = -\langle \alpha , \gamma \rangle $, ![]() $\mathcal {A}$ preserves
$\mathcal {A}$ preserves ![]() $\langle \alpha \rangle ^{\perp }$ as well. A straightforward computation using
$\langle \alpha \rangle ^{\perp }$ as well. A straightforward computation using ![]() $\mathcal {A}^{3} =\mathcal {A}$ shows that the minimal polynomial of the restriction
$\mathcal {A}^{3} =\mathcal {A}$ shows that the minimal polynomial of the restriction 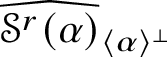 $\widehat {\mathscr {S}^{r}(\alpha )}_{\langle \alpha \rangle ^{\perp }}$ is
$\widehat {\mathscr {S}^{r}(\alpha )}_{\langle \alpha \rangle ^{\perp }}$ is 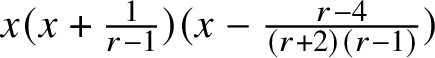 $x(x + \tfrac {1}{r-1})(x - \tfrac {r-4}{(r+2)(r-1)})$. It follows that
$x(x + \tfrac {1}{r-1})(x - \tfrac {r-4}{(r+2)(r-1)})$. It follows that 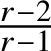 $\tfrac {r-2}{r-1}$ has multiplicity 1 as an eigenvalue of
$\tfrac {r-2}{r-1}$ has multiplicity 1 as an eigenvalue of 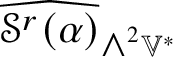 $\widehat {\mathscr {S}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$. It is convenient to identify
$\widehat {\mathscr {S}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$. It is convenient to identify ![]() $\mathbb {W}^{\ast }$ and
$\mathbb {W}^{\ast }$ and ![]() $\mathbb {W}^{\perp \,\ast }$ with orthogonal subspaces of
$\mathbb {W}^{\perp \,\ast }$ with orthogonal subspaces of ![]() $\mathbb {V}^{\ast }$. If
$\mathbb {V}^{\ast }$. If ![]() $\nu \in \mathbb {W}^{\perp \,\ast }$, then
$\nu \in \mathbb {W}^{\perp \,\ast }$, then ![]() $\nu ^{p}g _{pi} =0$, so
$\nu ^{p}g _{pi} =0$, so ![]() $\nu ^{p}\alpha _{pi} = \nu ^{p}g _{p}{}^{q}\alpha _{q}{}^{i} = 0$, and it follows that, for all
$\nu ^{p}\alpha _{pi} = \nu ^{p}g _{p}{}^{q}\alpha _{q}{}^{i} = 0$, and it follows that, for all ![]() $\mu \in \mathbb {V}^{\ast }$,
$\mu \in \mathbb {V}^{\ast }$, ![]() $\mathcal {A}(\mu \wedge \nu ) = 0$, so
$\mathcal {A}(\mu \wedge \nu ) = 0$, so 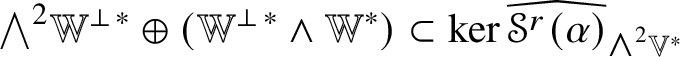 ${\bigwedge }^{2}\mathbb {W}^{\perp \,\ast } \oplus (\mathbb {W}^{\perp \,\ast }\wedge \mathbb {W}^{\ast }) \subset \ker \widehat {\mathscr {S}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$. Because it commutes with
${\bigwedge }^{2}\mathbb {W}^{\perp \,\ast } \oplus (\mathbb {W}^{\perp \,\ast }\wedge \mathbb {W}^{\ast }) \subset \ker \widehat {\mathscr {S}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$. Because it commutes with ![]() $g _{i}{}^{j}$, the endomorphism
$g _{i}{}^{j}$, the endomorphism ![]() $\alpha _{i}{}^{j}$ preserves
$\alpha _{i}{}^{j}$ preserves ![]() $\mathbb {W}$ and its restriction to
$\mathbb {W}$ and its restriction to ![]() $\mathbb {W}$ is an almost complex structure compatible with the restriction of h to
$\mathbb {W}$ is an almost complex structure compatible with the restriction of h to ![]() $\mathbb {W}$. Consequently, both
$\mathbb {W}$. Consequently, both ![]() $\mathcal {A}$ and
$\mathcal {A}$ and 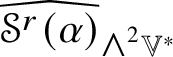 $\widehat {\mathscr {S}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ preserve
$\widehat {\mathscr {S}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ preserve ![]() ${\bigwedge }^{2}\mathbb {W}^{\ast }$ and their eigenvalues on
${\bigwedge }^{2}\mathbb {W}^{\ast }$ and their eigenvalues on ![]() ${\bigwedge }^{2}\mathbb {W}^{\ast }$ are nonzero. In addition to forcing the equality
${\bigwedge }^{2}\mathbb {W}^{\ast }$ are nonzero. In addition to forcing the equality 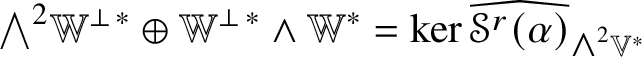 ${\bigwedge }^{2}\mathbb {W}^{\perp \,\ast } \oplus \mathbb {W}^{\perp \,\ast }\wedge \mathbb {W}^{\ast } = \ker \widehat {\mathscr {S}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$, this observation implies that the nonzero eigenspaces of
${\bigwedge }^{2}\mathbb {W}^{\perp \,\ast } \oplus \mathbb {W}^{\perp \,\ast }\wedge \mathbb {W}^{\ast } = \ker \widehat {\mathscr {S}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$, this observation implies that the nonzero eigenspaces of 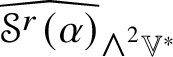 $\widehat {\mathscr {S}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ on
$\widehat {\mathscr {S}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ on ![]() ${\bigwedge }^{2}\mathbb {W}^{\ast } \cap \langle \alpha \rangle ^{\perp }$ are the
${\bigwedge }^{2}\mathbb {W}^{\ast } \cap \langle \alpha \rangle ^{\perp }$ are the ![]() $\pm 1$-eigenspaces of
$\pm 1$-eigenspaces of ![]() $\mathcal {A}$ on
$\mathcal {A}$ on ![]() ${\bigwedge }^{2}\mathbb {W}^{\ast } \cap \langle \alpha \rangle ^{\perp }$. The dimensions of these eigenspaces can be computed using the observation that these subspaces comprise the real parts of forms of type
${\bigwedge }^{2}\mathbb {W}^{\ast } \cap \langle \alpha \rangle ^{\perp }$. The dimensions of these eigenspaces can be computed using the observation that these subspaces comprise the real parts of forms of type ![]() $(2,0)$ and
$(2,0)$ and ![]() $(1,1)$ with respect to the almost complex structure given by
$(1,1)$ with respect to the almost complex structure given by ![]() $\alpha _{i}{}^{j}$ (see [Reference Fox11] for details). This proves 1. Claim 2 follows from the preceding and
$\alpha _{i}{}^{j}$ (see [Reference Fox11] for details). This proves 1. Claim 2 follows from the preceding and 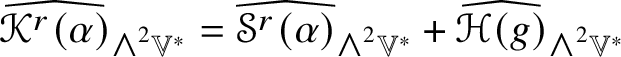 $\widehat {\mathscr {K}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} = \widehat {\mathscr {S}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} + \widehat {\mathscr {H}(g)}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$. Further details are omitted.
$\widehat {\mathscr {K}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} = \widehat {\mathscr {S}^{r}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }} + \widehat {\mathscr {H}(g)}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$. Further details are omitted.
For a Euclidean vector space ![]() $(\mathbb {V}, h)$ of even dimension
$(\mathbb {V}, h)$ of even dimension ![]() $n = 2m$, the space
$n = 2m$, the space 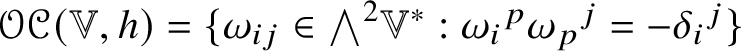 $\mathscr {OC}(\mathbb {V}, h) = \{\omega _{ij} \in {\bigwedge }^{2}\mathbb {V}^{\ast }: \omega _{i}{}^{p}\omega _{p}{}^{j} = -\delta _{i}{}^{j}\}$ is identified with the homogeneous space
$\mathscr {OC}(\mathbb {V}, h) = \{\omega _{ij} \in {\bigwedge }^{2}\mathbb {V}^{\ast }: \omega _{i}{}^{p}\omega _{p}{}^{j} = -\delta _{i}{}^{j}\}$ is identified with the homogeneous space ![]() $O(2m)/U(m)$. The action of
$O(2m)/U(m)$. The action of ![]() $O(2m)$ on
$O(2m)$ on ![]() ${\bigwedge }^{2}\mathbb {V}^{\ast }$ preserves
${\bigwedge }^{2}\mathbb {V}^{\ast }$ preserves ![]() $\mathscr {OC}(\mathbb {V}, h)$. Given
$\mathscr {OC}(\mathbb {V}, h)$. Given ![]() $\omega \in \mathscr {OC}(\mathbb {V}, h)$ with associated almost complex structure
$\omega \in \mathscr {OC}(\mathbb {V}, h)$ with associated almost complex structure ![]() $J_{i}{}^{j} = \omega _{i}{}^{j}$ there exists an orthonormal basis of
$J_{i}{}^{j} = \omega _{i}{}^{j}$ there exists an orthonormal basis of ![]() $\mathbb {V}$ of the form
$\mathbb {V}$ of the form ![]() $\{e_{1}, \dots , e_{n}, J(e_{1}), \dots , J(e_{n})\}$, and this suffices to show that
$\{e_{1}, \dots , e_{n}, J(e_{1}), \dots , J(e_{n})\}$, and this suffices to show that ![]() $O(2m)$ acts transitively on
$O(2m)$ acts transitively on ![]() $\mathscr {OC}(\mathbb {V}, h)$. The stabilizer of
$\mathscr {OC}(\mathbb {V}, h)$. The stabilizer of ![]() $\omega \in \mathscr {OC}(\mathbb {V}, h)$ is
$\omega \in \mathscr {OC}(\mathbb {V}, h)$ is ![]() $U(m) = O(2m) \cap Sp(n, \mathbb R)$, where
$U(m) = O(2m) \cap Sp(n, \mathbb R)$, where ![]() $Sp(n, \mathbb R)$ is the symplectic group fixing
$Sp(n, \mathbb R)$ is the symplectic group fixing ![]() $\omega $ and
$\omega $ and ![]() $U(m)$ the unitary group preserving
$U(m)$ the unitary group preserving ![]() $(h, J)$. Thus,
$(h, J)$. Thus, ![]() $\mathscr {OC}(\mathbb {V}, h)$ is identified with
$\mathscr {OC}(\mathbb {V}, h)$ is identified with ![]() $O(2m)/U(m)$ for any
$O(2m)/U(m)$ for any ![]() $\omega \in \mathscr {OC}(\mathbb {V}, h)$.
$\omega \in \mathscr {OC}(\mathbb {V}, h)$.
Since ![]() $O(2m)$ has two connected components, comprising orthogonal transformations preserving opposite orientations of
$O(2m)$ has two connected components, comprising orthogonal transformations preserving opposite orientations of ![]() $\mathbb {V}$, and
$\mathbb {V}$, and ![]() $U(m)$ is connected, the space
$U(m)$ is connected, the space ![]() $\mathscr {OC}(\mathbb {V}, h)$ has two connected components
$\mathscr {OC}(\mathbb {V}, h)$ has two connected components ![]() $\mathscr {OC}^{\pm }(\mathbb {V}, h)$, each identified with
$\mathscr {OC}^{\pm }(\mathbb {V}, h)$, each identified with ![]() $SO(2m)/U(m)$, and the complex structures of
$SO(2m)/U(m)$, and the complex structures of ![]() $\mathscr {OC}^{+}(\mathbb {V}, h)$ induce the orientation opposite that induced by the complex structures of
$\mathscr {OC}^{+}(\mathbb {V}, h)$ induce the orientation opposite that induced by the complex structures of ![]() $\mathscr {OC}^{-}(\mathbb {V}, h)$. If
$\mathscr {OC}^{-}(\mathbb {V}, h)$. If ![]() $\omega \in \mathscr {OC}(\mathbb {V}, h)$ is fixed and
$\omega \in \mathscr {OC}(\mathbb {V}, h)$ is fixed and ![]() $F \in O(2m)$ is the orthogonal reflection through the
$F \in O(2m)$ is the orthogonal reflection through the ![]() $+1$ eigenspace of the endomorphism
$+1$ eigenspace of the endomorphism ![]() $\omega _{i}{}^{j}$, then the action of F interchanges
$\omega _{i}{}^{j}$, then the action of F interchanges ![]() $\mathscr {OC}^{\pm }(\mathbb {V}, h)$. Let
$\mathscr {OC}^{\pm }(\mathbb {V}, h)$. Let ![]() $\hat {U}(m) \subset O(2m)$ be the subgroup generated by
$\hat {U}(m) \subset O(2m)$ be the subgroup generated by ![]() $U(m)$ and F. Then
$U(m)$ and F. Then ![]() $O(2m)/\hat {U}(m)$ is identified with the quotient space
$O(2m)/\hat {U}(m)$ is identified with the quotient space ![]() $\mathscr {OC}(\mathbb {V}, h)/\sim $ where
$\mathscr {OC}(\mathbb {V}, h)/\sim $ where ![]() $\omega \sim - \omega = F\cdot \omega $. Since
$\omega \sim - \omega = F\cdot \omega $. Since ![]() $U(m)$ and
$U(m)$ and ![]() $FU(m)$ lie in different connected components of
$FU(m)$ lie in different connected components of ![]() $O(2m)$, this quotient space is identified with
$O(2m)$, this quotient space is identified with ![]() $SO(2m)/U(m)$.
$SO(2m)/U(m)$.
Lemma 10.4. Let ![]() $(\mathbb {V}, h)$ be a Euclidean vector space of even dimension
$(\mathbb {V}, h)$ be a Euclidean vector space of even dimension ![]() $n = 2m$. The map
$n = 2m$. The map ![]() defined by
defined by

is an ![]() $O(2m)$-equivariant double cover of its image
$O(2m)$-equivariant double cover of its image ![]() $\mathscr {S}(\mathscr {OC}(\mathbb {V}, h))) = \{\mathscr {S}(\omega ): \omega \in \mathscr {OC}(\mathbb {V}, h)\}$, injective on either connected component
$\mathscr {S}(\mathscr {OC}(\mathbb {V}, h))) = \{\mathscr {S}(\omega ): \omega \in \mathscr {OC}(\mathbb {V}, h)\}$, injective on either connected component ![]() $\mathscr {OC}^{\pm }(\mathbb {V}, h) \simeq SO(2m)/U(m)$, with image equal to
$\mathscr {OC}^{\pm }(\mathbb {V}, h) \simeq SO(2m)/U(m)$, with image equal to ![]() $O(2m)/\hat {U}(m) \simeq SO(2m)/U(m)$, realized as the
$O(2m)/\hat {U}(m) \simeq SO(2m)/U(m)$, realized as the ![]() $O(2m)$ orbit of
$O(2m)$ orbit of ![]() $\mathscr {S}(\omega )$ for any
$\mathscr {S}(\omega )$ for any ![]() $\omega \in \mathscr {OC}(\mathbb {V}, h)$, and spanning
$\omega \in \mathscr {OC}(\mathbb {V}, h)$, and spanning ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$.
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$.
Proof. Because the map ![]() $\operatorname {\mathsf {tf}}$ and the product
$\operatorname {\mathsf {tf}}$ and the product ![]() $\cdot $ are
$\cdot $ are ![]() $O(2m)$-equivariant, so is the map
$O(2m)$-equivariant, so is the map ![]() $\mathscr {S}$. By Lemma 10.1, for
$\mathscr {S}$. By Lemma 10.1, for ![]() $g \in O(2m)$,
$g \in O(2m)$, ![]() $\mathscr {S}(g\cdot \omega )= g \cdot \mathscr {S}(\omega )$ is an idempotent in
$\mathscr {S}(g\cdot \omega )= g \cdot \mathscr {S}(\omega )$ is an idempotent in ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$, and so
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$, and so ![]() $\mathscr {S}$ is a map from the homogeneous space
$\mathscr {S}$ is a map from the homogeneous space ![]() $O(2m)/U(m) \simeq \mathscr {OC}(\mathbb {V}, h)$ to the
$O(2m)/U(m) \simeq \mathscr {OC}(\mathbb {V}, h)$ to the ![]() $O(2m)$ orbit of
$O(2m)$ orbit of ![]() $\mathscr {S}(\omega )$ in
$\mathscr {S}(\omega )$ in ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ whose image comprises idempotents. By definition,
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ whose image comprises idempotents. By definition, ![]() $\mathscr {S}(-\omega ) = \mathscr {S}(\omega )$. If
$\mathscr {S}(-\omega ) = \mathscr {S}(\omega )$. If ![]() $\mathscr {S}(g \cdot \omega ) = \mathscr {S}(\omega )$ for
$\mathscr {S}(g \cdot \omega ) = \mathscr {S}(\omega )$ for ![]() $g \in O(2n)$, then, by Lemmas 4.2, and 10.3 and the
$g \in O(2n)$, then, by Lemmas 4.2, and 10.3 and the ![]() $O(2n)$-equivariance of
$O(2n)$-equivariance of ![]() $\mathscr {S}$,
$\mathscr {S}$,
 $$ \begin{align} \begin{split} \widehat{\mathscr{S}(\omega)}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(g\cdot \omega) &= \widehat{\mathscr{S}(g\cdot \omega)}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(g\cdot \omega)\\ &=\widehat{g\cdot\mathscr{S}(\omega)}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(g\cdot \omega) = g\cdot \widehat{\mathscr{S}(\omega)}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(\omega) = \tfrac{n-2}{n-1} g\cdot \omega. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \widehat{\mathscr{S}(\omega)}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(g\cdot \omega) &= \widehat{\mathscr{S}(g\cdot \omega)}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(g\cdot \omega)\\ &=\widehat{g\cdot\mathscr{S}(\omega)}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(g\cdot \omega) = g\cdot \widehat{\mathscr{S}(\omega)}_{{\textstyle\wedge}^{2}\mathbb{V}^{\ast}}(\omega) = \tfrac{n-2}{n-1} g\cdot \omega. \end{split} \end{align} $$By Lemma 10.3, ![]() $\omega $ spans the
$\omega $ spans the 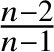 $\tfrac {n-2}{n-1}$-eigenspace of
$\tfrac {n-2}{n-1}$-eigenspace of 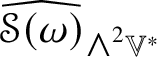 $\widehat {\mathscr {S}(\omega )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$, so (10.10) shows
$\widehat {\mathscr {S}(\omega )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$, so (10.10) shows ![]() $g\cdot \omega $ is a multiple of
$g\cdot \omega $ is a multiple of ![]() $\omega $. Since
$\omega $. Since ![]() $(g\cdot \omega )\circ (g\cdot \omega ) = -h$, this forces
$(g\cdot \omega )\circ (g\cdot \omega ) = -h$, this forces ![]() $g\cdot \omega = \pm \omega $, and hence
$g\cdot \omega = \pm \omega $, and hence ![]() $g \in \hat {U}(m)$. It follows that
$g \in \hat {U}(m)$. It follows that ![]() $\mathscr {S}$ is two-to-one, with image equal to the
$\mathscr {S}$ is two-to-one, with image equal to the ![]() $O(2m)$ orbit of
$O(2m)$ orbit of ![]() $\mathscr {S}(\omega )$ for any
$\mathscr {S}(\omega )$ for any ![]() $\omega \in \mathscr {OC}(\mathbb {V}, h)$, and that this orbit is identified with
$\omega \in \mathscr {OC}(\mathbb {V}, h)$, and that this orbit is identified with ![]() $O(2m)/\hat {U}(m)$ in such a way that
$O(2m)/\hat {U}(m)$ in such a way that ![]() $\mathscr {S}$ maps either connected component
$\mathscr {S}$ maps either connected component ![]() $\mathscr {OC}^{\pm }(\omega , h)$ onto it bijectively. By the
$\mathscr {OC}^{\pm }(\omega , h)$ onto it bijectively. By the ![]() $O(2m)$-irreducibility of
$O(2m)$-irreducibility of ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, because the
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$, because the ![]() $O(2m)$-invariant subspace
$O(2m)$-invariant subspace ![]() $\text {Span}\,\{\mathscr {S}(\omega ): \omega \in \mathscr {OC}(\mathbb {V}, h)\} \subset \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is nonempty, it equals
$\text {Span}\,\{\mathscr {S}(\omega ): \omega \in \mathscr {OC}(\mathbb {V}, h)\} \subset \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is nonempty, it equals ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$.
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$.
Lemma 10.5. For ![]() $m \times m$ anti-Hermitian complex matrices A and B such that
$m \times m$ anti-Hermitian complex matrices A and B such that ![]() $A^{2} = -I = B^{2}$,
$A^{2} = -I = B^{2}$,
 $$ \begin{align} -2m \leq 2m - 4 \operatorname{\mathsf{tr}} \overline{A\circledcirc B}^{t}A\circledcirc B= -2\operatorname{\mathsf{tr}}(ABAB) = -2m + \operatorname{\mathsf{tr}} \overline{[A, B]}^{t}[A, B] \leq 2m, \end{align} $$
$$ \begin{align} -2m \leq 2m - 4 \operatorname{\mathsf{tr}} \overline{A\circledcirc B}^{t}A\circledcirc B= -2\operatorname{\mathsf{tr}}(ABAB) = -2m + \operatorname{\mathsf{tr}} \overline{[A, B]}^{t}[A, B] \leq 2m, \end{align} $$with equality in the upper bound if and only if A and B anticommute and equality in the lower bound if and only if A and B commute. In the latter case there is ![]() $q \in \mathbb {Z}$ such that
$q \in \mathbb {Z}$ such that ![]() $0 \leq q \leq m$ such that
$0 \leq q \leq m$ such that ![]() $\operatorname {\mathsf {tr}} AB = 2q- m$ with
$\operatorname {\mathsf {tr}} AB = 2q- m$ with ![]() $\operatorname {\mathsf {tr}} AB = \pm m$ if and only if
$\operatorname {\mathsf {tr}} AB = \pm m$ if and only if ![]() $B = \pm A$; moreover, if A and B are real matrices, then q must be even.
$B = \pm A$; moreover, if A and B are real matrices, then q must be even.
Proof. The equalities in (10.11) are always valid. If ![]() $A\circledcirc B = 0$, then
$A\circledcirc B = 0$, then 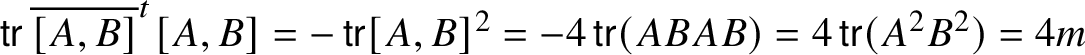 $\operatorname {\mathsf {tr}} \overline {[A, B]}^{t}[A, B] = -\operatorname {\mathsf {tr}} [A, B]^{2} = -4\operatorname {\mathsf {tr}}(ABAB) = 4\operatorname {\mathsf {tr}}(A^{2}B^{2}) = 4m$, so equality holds in the upper bound in (10.11). It is immediate that equality holds in the lower bound in (10.11) if and only if A and B commute. In this case,
$\operatorname {\mathsf {tr}} \overline {[A, B]}^{t}[A, B] = -\operatorname {\mathsf {tr}} [A, B]^{2} = -4\operatorname {\mathsf {tr}}(ABAB) = 4\operatorname {\mathsf {tr}}(A^{2}B^{2}) = 4m$, so equality holds in the upper bound in (10.11). It is immediate that equality holds in the lower bound in (10.11) if and only if A and B commute. In this case, ![]() $iA$ and
$iA$ and ![]() $iB$ are commuting Hermitian matrices and so are simultaneously unitarily diagonalizable. If
$iB$ are commuting Hermitian matrices and so are simultaneously unitarily diagonalizable. If ![]() $m-q$ is the dimension of their joint
$m-q$ is the dimension of their joint ![]() $1$ eigenspace, then
$1$ eigenspace, then ![]() $-\operatorname {\mathsf {tr}} AB \operatorname {\mathsf {tr}} (\mathsf {i} A)(\mathsf {i} B)= (m-q) - q = m - 2q$ and
$-\operatorname {\mathsf {tr}} AB \operatorname {\mathsf {tr}} (\mathsf {i} A)(\mathsf {i} B)= (m-q) - q = m - 2q$ and ![]() $\operatorname {\mathsf {tr}} AB = \pm m$ if and only if
$\operatorname {\mathsf {tr}} AB = \pm m$ if and only if ![]() $q \in \{0, m\}$, in which case
$q \in \{0, m\}$, in which case ![]() $B = \pm A$. If A and B are, moreover, real, then their eigenvalues
$B = \pm A$. If A and B are, moreover, real, then their eigenvalues ![]() $\pm \mathsf {i}$ have the same multiplicities, so q must be even. Now suppose A and B are anti-Hermitian and
$\pm \mathsf {i}$ have the same multiplicities, so q must be even. Now suppose A and B are anti-Hermitian and ![]() $A^{2} = -I = B^{2}$. There is an
$A^{2} = -I = B^{2}$. There is an ![]() $m \times m$ unitary matrix U such that
$m \times m$ unitary matrix U such that ![]() $C = UA\bar {U}^{t}$ is diagonal with diagonal entries
$C = UA\bar {U}^{t}$ is diagonal with diagonal entries ![]() $c_{1}, \dots , c_{m} \in \{\pm \mathsf {i}\}$. Define
$c_{1}, \dots , c_{m} \in \{\pm \mathsf {i}\}$. Define ![]() $D = UB\bar {U}^{t}$. The components of
$D = UB\bar {U}^{t}$. The components of ![]() $[C, D]$ with respect to a basis satisfy
$[C, D]$ with respect to a basis satisfy ![]() $[C, D]_{ij} = (c_{i} - c_{j})D_{ij}$ and
$[C, D]_{ij} = (c_{i} - c_{j})D_{ij}$ and ![]() $\overline {c_{i} - c_{j}} = -(c_{i} - c_{j})$, so
$\overline {c_{i} - c_{j}} = -(c_{i} - c_{j})$, so
 $$ \begin{align} \begin{aligned} 0 & \leq \operatorname{\mathsf{tr}} \overline{[A, B]}^{t}[A, B] = \operatorname{\mathsf{tr}} \overline{[C, D]}^{t}[C, D] = -\sum_{ i \neq j} (c_{i} - c_{j})^{2}|D_{ij}|^{2} &\\ &\leq 2\sum_{i \neq j}(|c_{i}|^{2} + |c_{j}|^{2})|D_{ij}|^{2} \leq 4\sum_{i \neq j}|D_{ij}|^{2} \leq -4\operatorname{\mathsf{tr}} D^{2} = -4\operatorname{\mathsf{tr}} B^{2} = 4m. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} 0 & \leq \operatorname{\mathsf{tr}} \overline{[A, B]}^{t}[A, B] = \operatorname{\mathsf{tr}} \overline{[C, D]}^{t}[C, D] = -\sum_{ i \neq j} (c_{i} - c_{j})^{2}|D_{ij}|^{2} &\\ &\leq 2\sum_{i \neq j}(|c_{i}|^{2} + |c_{j}|^{2})|D_{ij}|^{2} \leq 4\sum_{i \neq j}|D_{ij}|^{2} \leq -4\operatorname{\mathsf{tr}} D^{2} = -4\operatorname{\mathsf{tr}} B^{2} = 4m. \end{aligned} \end{align} $$By (10.12), 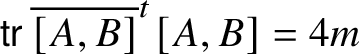 $\operatorname {\mathsf {tr}} \overline {[A, B]}^{t}[A, B] = 4m$ if and only if
$\operatorname {\mathsf {tr}} \overline {[A, B]}^{t}[A, B] = 4m$ if and only if ![]() $(c_{i} + c_{j})|D_{ij}|^{2}= 0$ for all
$(c_{i} + c_{j})|D_{ij}|^{2}= 0$ for all ![]() $1\leq i \neq j \leq m$ and
$1\leq i \neq j \leq m$ and ![]() $D_{ii} = 0$ for all
$D_{ii} = 0$ for all ![]() $1 \leq i \leq m$. This means
$1 \leq i \leq m$. This means ![]() $c_{i} + c_{j} = 0$ or
$c_{i} + c_{j} = 0$ or ![]() $D_{ij} = 0$ for all
$D_{ij} = 0$ for all ![]() $1\leq i \neq j \leq m$, so
$1\leq i \neq j \leq m$, so 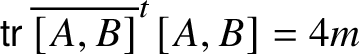 $\operatorname {\mathsf {tr}} \overline {[A, B]}^{t}[A, B] = 4m$ if and only if
$\operatorname {\mathsf {tr}} \overline {[A, B]}^{t}[A, B] = 4m$ if and only if ![]() $(c_{i} + c_{j})D_{ij} = 0$ for all
$(c_{i} + c_{j})D_{ij} = 0$ for all ![]() $1 \leq i,j \leq m$. Equivalently,
$1 \leq i,j \leq m$. Equivalently,  $\operatorname {\mathsf {tr}} \overline {[A, B]}^{t}[A, B] = 4m$ if and only if
$\operatorname {\mathsf {tr}} \overline {[A, B]}^{t}[A, B] = 4m$ if and only if ![]() $CD + DC =0$ or, similarly, if and only if A and B anticommute.
$CD + DC =0$ or, similarly, if and only if A and B anticommute.
Lemma 10.6. Let ![]() $(\mathbb {V}, h)$ be a Euclidean vector space of dimension n. Let
$(\mathbb {V}, h)$ be a Euclidean vector space of dimension n. Let ![]() $\mathbb {W} \subset \mathbb {V}$ have dimension
$\mathbb {W} \subset \mathbb {V}$ have dimension ![]() $r \in 2\mathbb {Z}$ satisfying
$r \in 2\mathbb {Z}$ satisfying ![]() $4 \leq r \leq n$, let
$4 \leq r \leq n$, let ![]() $\alpha , \beta \in \mathscr {OC}(\mathbb {W}, h)$ and let
$\alpha , \beta \in \mathscr {OC}(\mathbb {W}, h)$ and let ![]() $g = -\alpha \circ \alpha = -\beta \circ \beta $. There holds
$g = -\alpha \circ \alpha = -\beta \circ \beta $. There holds
 $$ \begin{align} \langle \mathscr{S}^{r}(\alpha), \mathscr{S}^{r}(\beta)\rangle = \tfrac{6}{(r+2)^{2}}\left(\langle \alpha, \beta\rangle^{2} + \operatorname{\mathsf{tr}} (\alpha\circ \beta \circ \alpha\circ \beta) - \tfrac{3r}{r-1}\right) \geq - \tfrac{6r}{(r+2)(r-1)}, \end{align} $$
$$ \begin{align} \langle \mathscr{S}^{r}(\alpha), \mathscr{S}^{r}(\beta)\rangle = \tfrac{6}{(r+2)^{2}}\left(\langle \alpha, \beta\rangle^{2} + \operatorname{\mathsf{tr}} (\alpha\circ \beta \circ \alpha\circ \beta) - \tfrac{3r}{r-1}\right) \geq - \tfrac{6r}{(r+2)(r-1)}, \end{align} $$so that
 $$ \begin{align} \tfrac{\langle \mathscr{S}^{r}(\alpha), \mathscr{S}^{r}(\beta)\rangle}{|\mathscr{S}^{r}(\alpha)||\mathscr{S}^{r}(\beta)|} = \tfrac{r-1}{r(r-2)(r+2)}\left(\langle \alpha, \beta\rangle^{2} + \operatorname{\mathsf{tr}}(\alpha\circ \beta \circ \alpha\circ \beta) - r(r+1)\right) + 1 \geq -\tfrac{1}{r-2}. \end{align} $$
$$ \begin{align} \tfrac{\langle \mathscr{S}^{r}(\alpha), \mathscr{S}^{r}(\beta)\rangle}{|\mathscr{S}^{r}(\alpha)||\mathscr{S}^{r}(\beta)|} = \tfrac{r-1}{r(r-2)(r+2)}\left(\langle \alpha, \beta\rangle^{2} + \operatorname{\mathsf{tr}}(\alpha\circ \beta \circ \alpha\circ \beta) - r(r+1)\right) + 1 \geq -\tfrac{1}{r-2}. \end{align} $$1. There holds equality in the lower bounds in (10.13) and (10.14) if and only if
 $\alpha \circ \beta + \beta \circ \alpha = 0$.
$\alpha \circ \beta + \beta \circ \alpha = 0$.2. If
 $[\alpha , \beta ] = 0$, then there is
$[\alpha , \beta ] = 0$, then there is  $k \in \{4p - r: 0 \leq p \leq r/2\}$ such that
$k \in \{4p - r: 0 \leq p \leq r/2\}$ such that  $\langle \alpha , \beta \rangle = -k$ and
$\langle \alpha , \beta \rangle = -k$ and  $\langle \mathscr {S}^{r}(\alpha ), \mathscr {S}^{r}(\beta )\rangle = \tfrac {6r(r-4)}{(r-1)(r+2)^{2}} + \tfrac {6k^{2}}{(r+2)^{2}}$. Moreover,
$\langle \mathscr {S}^{r}(\alpha ), \mathscr {S}^{r}(\beta )\rangle = \tfrac {6r(r-4)}{(r-1)(r+2)^{2}} + \tfrac {6k^{2}}{(r+2)^{2}}$. Moreover,  $k = \pm r$ if and only if
$k = \pm r$ if and only if  $\beta = \pm \alpha $. In particular,
$\beta = \pm \alpha $. In particular,  $\langle \mathscr {S}^{4}(\alpha ), \mathscr {S}^{4}(\beta )\rangle =0$ if and only if
$\langle \mathscr {S}^{4}(\alpha ), \mathscr {S}^{4}(\beta )\rangle =0$ if and only if  $r = 4$ and
$r = 4$ and  $\beta \neq \pm \alpha $.
$\beta \neq \pm \alpha $.
Proof. Let ![]() $\beta \in \mathscr {OC}(\mathbb {V}, h)$ and note that this means
$\beta \in \mathscr {OC}(\mathbb {V}, h)$ and note that this means ![]() $\beta \circ \beta = -g$. By (6.11),
$\beta \circ \beta = -g$. By (6.11), 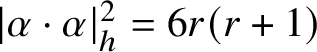 $|\alpha \cdot \alpha |^{2}_{h} =6r(r+1)$ and
$|\alpha \cdot \alpha |^{2}_{h} =6r(r+1)$ and ![]() $\langle \alpha \cdot \alpha , \beta \cdot \beta \rangle = 6\langle \alpha , \beta \rangle ^{2} + 6\operatorname {\mathsf {tr}} (\alpha \circ \beta \circ \alpha \circ \beta )$. By (6.12),
$\langle \alpha \cdot \alpha , \beta \cdot \beta \rangle = 6\langle \alpha , \beta \rangle ^{2} + 6\operatorname {\mathsf {tr}} (\alpha \circ \beta \circ \alpha \circ \beta )$. By (6.12), 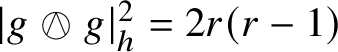 and
and
and, similarly, ![]() . There result the equality in (10.13) and (10.14). Equality holds in the lower bounds of (10.13) and (10.14) when
. There result the equality in (10.13) and (10.14). Equality holds in the lower bounds of (10.13) and (10.14) when ![]() $\alpha \circ \beta = -\beta \circ \alpha $ because in this case
$\alpha \circ \beta = -\beta \circ \alpha $ because in this case ![]() $\langle \alpha , \beta \rangle = 0$ and
$\langle \alpha , \beta \rangle = 0$ and ![]() $\operatorname {\mathsf {tr}} \alpha \circ \beta \circ \alpha \circ \beta = -r$. By Lemma 10.5 applied to the matrices of
$\operatorname {\mathsf {tr}} \alpha \circ \beta \circ \alpha \circ \beta = -r$. By Lemma 10.5 applied to the matrices of ![]() $\alpha _{i}{}^{j}$ and
$\alpha _{i}{}^{j}$ and ![]() $\beta _{i}{}^{j}$ in some basis,
$\beta _{i}{}^{j}$ in some basis, ![]() $2r - 2\operatorname {\mathsf {tr}}(\alpha \circ \beta \circ \alpha \circ \beta ) = -\operatorname {\mathsf {tr}}([\alpha , \beta ]\circ [\alpha , \beta ]) \leq 4r$, with equality if and only if
$2r - 2\operatorname {\mathsf {tr}}(\alpha \circ \beta \circ \alpha \circ \beta ) = -\operatorname {\mathsf {tr}}([\alpha , \beta ]\circ [\alpha , \beta ]) \leq 4r$, with equality if and only if ![]() $\alpha \circledcirc \beta = 0$, so that
$\alpha \circledcirc \beta = 0$, so that ![]() $\operatorname {\mathsf {tr}}(\alpha \circ \beta \circ \alpha \circ \beta ) \geq -r$, with equality if and only if
$\operatorname {\mathsf {tr}}(\alpha \circ \beta \circ \alpha \circ \beta ) \geq -r$, with equality if and only if ![]() $\alpha \circledcirc \beta = 0$. There follow the lower bounds in (10.13) and (10.14), with equality if and only if
$\alpha \circledcirc \beta = 0$. There follow the lower bounds in (10.13) and (10.14), with equality if and only if ![]() $\alpha \circledcirc \beta = 0$. If
$\alpha \circledcirc \beta = 0$. If ![]() $[\alpha , \beta ] = 0$, then
$[\alpha , \beta ] = 0$, then ![]() $\alpha \circ \beta $ is self-adjoint and
$\alpha \circ \beta $ is self-adjoint and ![]() $\alpha \circ \beta \circ \alpha \circ \beta = g$, so
$\alpha \circ \beta \circ \alpha \circ \beta = g$, so ![]() $-\langle \alpha , \beta \rangle = \operatorname {\mathsf {tr}}(\alpha \circ \beta )$ is an integer k such that
$-\langle \alpha , \beta \rangle = \operatorname {\mathsf {tr}}(\alpha \circ \beta )$ is an integer k such that ![]() $-r \leq k \leq r$. By Lemma 10.5,
$-r \leq k \leq r$. By Lemma 10.5, ![]() $k = 4p - r$ for some
$k = 4p - r$ for some ![]() $0 \leq p \leq r/2$. In (10.13) this yields 2.
$0 \leq p \leq r/2$. In (10.13) this yields 2.
A hypercomplex structure on a real vector space ![]() $\mathbb {V}$ is a pair of anticommuting almost complex structures
$\mathbb {V}$ is a pair of anticommuting almost complex structures ![]() $I, J \in \operatorname {End}(\mathbb {V})$ such that
$I, J \in \operatorname {End}(\mathbb {V})$ such that ![]() $K = I\circ J$ is an almost complex structure. Because it is a module over the quaternions, a hypercomplex vector space has dimension divisible by
$K = I\circ J$ is an almost complex structure. Because it is a module over the quaternions, a hypercomplex vector space has dimension divisible by ![]() $4$. A hyper-Kähler structure on a Euclidean vector space
$4$. A hyper-Kähler structure on a Euclidean vector space ![]() $(\mathbb {V}, h)$ equipped with a hypercomplex structure
$(\mathbb {V}, h)$ equipped with a hypercomplex structure ![]() $\{I, J, K\}$ and a metric h such that each of I, J, and K is compatible with h. By definition this means that
$\{I, J, K\}$ and a metric h such that each of I, J, and K is compatible with h. By definition this means that ![]() $\alpha _{ij} = I_{i}{}^{p}h_{pj}$,
$\alpha _{ij} = I_{i}{}^{p}h_{pj}$, ![]() $\beta _{ij} = J_{i}{}^{p}h_{pj}$, and
$\beta _{ij} = J_{i}{}^{p}h_{pj}$, and ![]() $\gamma _{ij} = K_{i}{}^{p}h_{pj}$ are symplectic forms. Given a subspace
$\gamma _{ij} = K_{i}{}^{p}h_{pj}$ are symplectic forms. Given a subspace ![]() $\mathbb {W} \subset \mathbb {V}$, it will be said that an ordered pair
$\mathbb {W} \subset \mathbb {V}$, it will be said that an ordered pair ![]() $(\alpha , \beta )\in \mathscr {OC}(\mathbb {W}, h)^{2}$ determines a hyper-Kähler structure on
$(\alpha , \beta )\in \mathscr {OC}(\mathbb {W}, h)^{2}$ determines a hyper-Kähler structure on ![]() $\mathbb {W}$ if
$\mathbb {W}$ if ![]() $\alpha $ and
$\alpha $ and ![]() $\beta $ anticommute, meaning
$\beta $ anticommute, meaning ![]() $\alpha \circledcirc \beta = 0$. In this case,
$\alpha \circledcirc \beta = 0$. In this case, ![]() $\gamma = \alpha \circ \beta \in \mathscr {OC}(\mathbb {W}, h)$,
$\gamma = \alpha \circ \beta \in \mathscr {OC}(\mathbb {W}, h)$, ![]() $\mathbb {W}$ is the image of the endomorphism
$\mathbb {W}$ is the image of the endomorphism ![]() $g_{i}{}^{j}$ where
$g_{i}{}^{j}$ where ![]() $-g = \alpha \circ \alpha = \beta \circ \beta = \gamma \circ \gamma $,
$-g = \alpha \circ \alpha = \beta \circ \beta = \gamma \circ \gamma $, ![]() $\alpha \circ g= \alpha = g \circ g$,
$\alpha \circ g= \alpha = g \circ g$, ![]() $\beta \circ g = \beta = g \circ \beta $, and
$\beta \circ g = \beta = g \circ \beta $, and ![]() $\gamma \circ g = \gamma = g \circ \gamma $, and
$\gamma \circ g = \gamma = g \circ \gamma $, and ![]() $\operatorname {\mathsf {tr}} g = |g|^{2}= |\alpha |^{2} = |\beta |^{2} = \dim \mathbb {W}$.
$\operatorname {\mathsf {tr}} g = |g|^{2}= |\alpha |^{2} = |\beta |^{2} = \dim \mathbb {W}$.
Lemma 10.7. Let ![]() $(\mathbb {V}, h)$ be a Euclidean vector space. Let
$(\mathbb {V}, h)$ be a Euclidean vector space. Let ![]() $\mathbb {W} \subset \mathbb {V}$ be a subspace of dimension r divisible by
$\mathbb {W} \subset \mathbb {V}$ be a subspace of dimension r divisible by ![]() $4$, suppose
$4$, suppose ![]() $(\alpha , \beta ) \in \mathscr {OC}(\mathbb {W}, h)^{2}$ determines a hyper-Kähler structure on
$(\alpha , \beta ) \in \mathscr {OC}(\mathbb {W}, h)^{2}$ determines a hyper-Kähler structure on ![]() $\mathbb {W}$ and let
$\mathbb {W}$ and let ![]() $\mathscr {S}^{r}(\alpha ), \mathscr {S}^{r}(\beta ), \mathscr {S}^{r}(\gamma ) \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ be the idempotents defined as in (10.2) (where
$\mathscr {S}^{r}(\alpha ), \mathscr {S}^{r}(\beta ), \mathscr {S}^{r}(\gamma ) \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ be the idempotents defined as in (10.2) (where ![]() $\gamma = \alpha \circ \beta $).
$\gamma = \alpha \circ \beta $).
1. There hold the relations
(10.16) $$ \begin{align} \begin{aligned} {} &\mathscr{S}^{r}(\alpha) \ast \mathscr{S}^{r}(\beta) = -\tfrac{1}{r+2}\left(\mathscr{S}^{r}(\alpha) +\mathscr{S}^{r}(\beta) -5 \mathscr{S}^{r}(\gamma)\right)\!,&\\ &\mathscr{S}^{r}(\alpha)\ast(\alpha \cdot \beta) = \tfrac{1}{2}\alpha \cdot \beta,& &\mathscr{S}^{r}(\alpha)\ast(\beta \cdot \gamma) = -\tfrac{6}{r+2}\beta \cdot \gamma,& \end{aligned} \end{align} $$(10.17)and those obtained from them by permuting
$$ \begin{align} \begin{aligned} {} &\mathscr{S}^{r}(\alpha) \ast \mathscr{S}^{r}(\beta) = -\tfrac{1}{r+2}\left(\mathscr{S}^{r}(\alpha) +\mathscr{S}^{r}(\beta) -5 \mathscr{S}^{r}(\gamma)\right)\!,&\\ &\mathscr{S}^{r}(\alpha)\ast(\alpha \cdot \beta) = \tfrac{1}{2}\alpha \cdot \beta,& &\mathscr{S}^{r}(\alpha)\ast(\beta \cdot \gamma) = -\tfrac{6}{r+2}\beta \cdot \gamma,& \end{aligned} \end{align} $$(10.17)and those obtained from them by permuting $$ \begin{align} \begin{aligned} {} &(\alpha \cdot \beta) \ast (\alpha \cdot \beta)=(r+2)\left(\tfrac{(r+4)}{4}(\mathscr{S}^{r}(\alpha) + \mathscr{S}^{r}(\beta)) - \tfrac{5}{2}\mathscr{S}^{r}(\gamma)\right)\!,&\\ &(\alpha \cdot \beta) \ast (\alpha \cdot \gamma) = -\tfrac{r+14}{4}\beta \cdot \gamma& \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {} &(\alpha \cdot \beta) \ast (\alpha \cdot \beta)=(r+2)\left(\tfrac{(r+4)}{4}(\mathscr{S}^{r}(\alpha) + \mathscr{S}^{r}(\beta)) - \tfrac{5}{2}\mathscr{S}^{r}(\gamma)\right)\!,&\\ &(\alpha \cdot \beta) \ast (\alpha \cdot \gamma) = -\tfrac{r+14}{4}\beta \cdot \gamma& \end{aligned} \end{align} $$ $\alpha $,
$\alpha $,  $\beta $, and
$\beta $, and  $\gamma $.
$\gamma $.2.
 $\langle \mathscr {S}^{r}(\alpha ), \mathscr {S}^{r}(\beta )\rangle = \langle \mathscr {S}^{r}(\beta ), \mathscr {S}^{r}(\gamma )\rangle = \langle \mathscr {S}^{r}(\gamma ), \mathscr {S}^{r}(\alpha )\rangle =-\tfrac {6r}{(r+2)(r-1)}$, so the cosine of the angle between any two of
$\langle \mathscr {S}^{r}(\alpha ), \mathscr {S}^{r}(\beta )\rangle = \langle \mathscr {S}^{r}(\beta ), \mathscr {S}^{r}(\gamma )\rangle = \langle \mathscr {S}^{r}(\gamma ), \mathscr {S}^{r}(\alpha )\rangle =-\tfrac {6r}{(r+2)(r-1)}$, so the cosine of the angle between any two of  $\mathscr {S}^{r}(\alpha )$,
$\mathscr {S}^{r}(\alpha )$,  $\mathscr {S}^{r}(\beta )$, and
$\mathscr {S}^{r}(\beta )$, and  $\mathscr {S}^{r}(\gamma )$ is
$\mathscr {S}^{r}(\gamma )$ is  $1/(2-r)$.
$1/(2-r)$.3. The elements
 $\alpha \cdot \beta $,
$\alpha \cdot \beta $,  $\beta \cdot \gamma $, and
$\beta \cdot \gamma $, and  $\gamma \cdot \alpha $ are pairwise orthogonal of norm
$\gamma \cdot \alpha $ are pairwise orthogonal of norm  $\sqrt {3r(r+2)}$ and each is orthogonal to
$\sqrt {3r(r+2)}$ and each is orthogonal to  $\text {Span}\,\{\mathscr {S}^{r}(\alpha ), \mathscr {S}^{r}(\beta ), \mathscr {S}^{r}(\gamma )\}$.
$\text {Span}\,\{\mathscr {S}^{r}(\alpha ), \mathscr {S}^{r}(\beta ), \mathscr {S}^{r}(\gamma )\}$.4. Let
 $\mathbb {B} = \text {Span}\,\{\mathscr {S}^{4}(\alpha ),\mathscr {S}^{4}(\beta ), \mathscr {S}^{4}(\gamma ), \alpha \cdot \beta , \beta \cdot \gamma , \gamma \cdot \alpha \}$.
$\mathbb {B} = \text {Span}\,\{\mathscr {S}^{4}(\alpha ),\mathscr {S}^{4}(\beta ), \mathscr {S}^{4}(\gamma ), \alpha \cdot \beta , \beta \cdot \gamma , \gamma \cdot \alpha \}$.(a) If
 $r = 4$,
$r = 4$,  $\mathscr {S}^{4}(\alpha ) + \mathscr {S}^{4}(\beta ) + \mathscr {S}^{4}(\gamma ) = 0$, and
$\mathscr {S}^{4}(\alpha ) + \mathscr {S}^{4}(\beta ) + \mathscr {S}^{4}(\gamma ) = 0$, and  $\mathbb {B} \subset (\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is a
$\mathbb {B} \subset (\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is a  $5$-dimensional subalgebra.
$5$-dimensional subalgebra.(b) If
 $r \geq 8$,
$r \geq 8$,  $\mathbb {B}$ is a
$\mathbb {B}$ is a  $6$-dimensional subalgebra of
$6$-dimensional subalgebra of  $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$.
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$.
5. For
 $\mathscr {X} \in \text {Span}\,\{\mathscr {S}^{r}(\alpha ), \mathscr {S}^{r}(\beta ), \mathscr {S}^{r}(\gamma ), \beta \cdot \gamma , \gamma \cdot \alpha , \alpha \cdot \beta \}$,
$\mathscr {X} \in \text {Span}\,\{\mathscr {S}^{r}(\alpha ), \mathscr {S}^{r}(\beta ), \mathscr {S}^{r}(\gamma ), \beta \cdot \gamma , \gamma \cdot \alpha , \alpha \cdot \beta \}$,  $\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ preserves
$\widehat {\mathscr {X}}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}$ preserves  $\text {Span}\, \{\alpha , \beta , \gamma \} \subset {\bigwedge }^{2}\mathbb {V}^{\ast }$.
$\text {Span}\, \{\alpha , \beta , \gamma \} \subset {\bigwedge }^{2}\mathbb {V}^{\ast }$.6. For
 $\mathscr {X} = -x_{1}\mathscr {S}^{r}(\alpha ) - x_{2}\mathscr {S}^{r}(\beta ) - x_{3}\mathscr {S}^{r}(\gamma ) - \tfrac {2}{r+2}\left (w_{1}\beta \cdot \gamma + w_{2}\gamma \cdot \alpha + w_{3}\alpha \cdot \beta \right )$, the matrix of
$\mathscr {X} = -x_{1}\mathscr {S}^{r}(\alpha ) - x_{2}\mathscr {S}^{r}(\beta ) - x_{3}\mathscr {S}^{r}(\gamma ) - \tfrac {2}{r+2}\left (w_{1}\beta \cdot \gamma + w_{2}\gamma \cdot \alpha + w_{3}\alpha \cdot \beta \right )$, the matrix of  $\widehat {\mathscr {X}}_{\text {Span}\,\{\alpha , \beta , \gamma \}}$ with respect to the equal-norm orthogonal basis
$\widehat {\mathscr {X}}_{\text {Span}\,\{\alpha , \beta , \gamma \}}$ with respect to the equal-norm orthogonal basis  $\{\alpha , \beta , \gamma \}$ is (10.18)
$\{\alpha , \beta , \gamma \}$ is (10.18) $$ \begin{align} \begin{pmatrix} \tfrac{(2-r)x_{1} + x_{2} + x_{3}}{r-1} & w_{3} & w_{2} \\ w_{3} &\tfrac{x_{1}+ (2-r)x_{2} + x_{3}}{r-1} & w_{1}\\ w_{2} & w_{1} &\tfrac{x_{1} + x_{2} + (2-r)x_{3}}{r-1} \end{pmatrix}. \end{align} $$
$$ \begin{align} \begin{pmatrix} \tfrac{(2-r)x_{1} + x_{2} + x_{3}}{r-1} & w_{3} & w_{2} \\ w_{3} &\tfrac{x_{1}+ (2-r)x_{2} + x_{3}}{r-1} & w_{1}\\ w_{2} & w_{1} &\tfrac{x_{1} + x_{2} + (2-r)x_{3}}{r-1} \end{pmatrix}. \end{align} $$
Proof. The two-forms ![]() $\alpha , \beta , \gamma $ are pairwise orthogonal. Specializing (6.20) yields (10.17) and the identities obtained from them by permuting
$\alpha , \beta , \gamma $ are pairwise orthogonal. Specializing (6.20) yields (10.17) and the identities obtained from them by permuting ![]() $\alpha $,
$\alpha $, ![]() $\beta $, and
$\beta $, and ![]() $\gamma $. By (6.18), (6.19), and (6.20) there hold
$\gamma $. By (6.18), (6.19), and (6.20) there hold

and the identities obtained from them by permuting ![]() $\alpha $,
$\alpha $, ![]() $\beta $, and
$\beta $, and ![]() $\gamma $. The identities (10.16) follow from (10.19). By (10.16) and (10.4),
$\gamma $. The identities (10.16) follow from (10.19). By (10.16) and (10.4),
 $$ \begin{align} \begin{split} \langle \mathscr{S}^{r}(\alpha),\mathscr{S}^{r}(\beta)\rangle & = \langle \mathscr{S}^{r}(\alpha)\ast \mathscr{S}^{r}(\alpha),\mathscr{S}^{r}(\beta)\rangle = \langle \mathscr{S}^{r}(\alpha), \mathscr{S}^{r}(\alpha)\ast \mathscr{S}^{r}(\beta)\rangle \\ &= -\tfrac{1}{r+2}|\mathscr{S}^{r}(\alpha)|^{2} - \tfrac{1}{r+2} \langle \mathscr{S}^{r}(\alpha),\mathscr{S}^{r}(\beta)\rangle + \tfrac{5}{r+2}\langle \mathscr{S}^{r}(\alpha),\mathscr{S}^{r}(\gamma)\rangle \\ &= -\tfrac{6r(r-2)}{(r+2)^{2}(r-1)} + \tfrac{4}{r+2}\langle \mathscr{S}^{r}(\alpha),\mathscr{S}^{r}(\beta)\rangle, \end{split} \end{align} $$
$$ \begin{align} \begin{split} \langle \mathscr{S}^{r}(\alpha),\mathscr{S}^{r}(\beta)\rangle & = \langle \mathscr{S}^{r}(\alpha)\ast \mathscr{S}^{r}(\alpha),\mathscr{S}^{r}(\beta)\rangle = \langle \mathscr{S}^{r}(\alpha), \mathscr{S}^{r}(\alpha)\ast \mathscr{S}^{r}(\beta)\rangle \\ &= -\tfrac{1}{r+2}|\mathscr{S}^{r}(\alpha)|^{2} - \tfrac{1}{r+2} \langle \mathscr{S}^{r}(\alpha),\mathscr{S}^{r}(\beta)\rangle + \tfrac{5}{r+2}\langle \mathscr{S}^{r}(\alpha),\mathscr{S}^{r}(\gamma)\rangle \\ &= -\tfrac{6r(r-2)}{(r+2)^{2}(r-1)} + \tfrac{4}{r+2}\langle \mathscr{S}^{r}(\alpha),\mathscr{S}^{r}(\beta)\rangle, \end{split} \end{align} $$so that 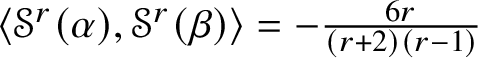 $\langle \mathscr {S}^{r}(\alpha ),\mathscr {S}^{r}(\beta )\rangle = -\tfrac {6r}{(r+2)(r-1)}$. Combined with (10.4) this shows that the cosine of the angle between
$\langle \mathscr {S}^{r}(\alpha ),\mathscr {S}^{r}(\beta )\rangle = -\tfrac {6r}{(r+2)(r-1)}$. Combined with (10.4) this shows that the cosine of the angle between ![]() $\mathscr {S}^{r}(\alpha )$ and
$\mathscr {S}^{r}(\alpha )$ and ![]() $\mathscr {S}^{r}(\beta )$ is
$\mathscr {S}^{r}(\beta )$ is ![]() $1/(2-r)$. The preceding claims remain true when
$1/(2-r)$. The preceding claims remain true when ![]() $\alpha $,
$\alpha $, ![]() $\beta $, and
$\beta $, and ![]() $\gamma $ are permuted cyclically. The identities (10.19) show
$\gamma $ are permuted cyclically. The identities (10.19) show ![]() $\mathbb {B}$ as in 4 is a subalgebra. By (10.4) and 2,
$\mathbb {B}$ as in 4 is a subalgebra. By (10.4) and 2,
 $$ \begin{align} \begin{split} \left|c_{1}\mathscr{S}^{r}(\alpha) + c_{2}\mathscr{S}^{r}(\beta) + c_{3}\mathscr{S}^{r}(\gamma)\right|{}^{2} = \tfrac{6r\left( (r-4)(c_{1}^{2} + c_{2}^{2} + c_{3}^{2}) + (c_{1} - c_{2})^{2} + (c_{2} - c_{3})^{2} + (c_{3} - c_{1})^{2}\right)}{(r+2)(r-1)}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \left|c_{1}\mathscr{S}^{r}(\alpha) + c_{2}\mathscr{S}^{r}(\beta) + c_{3}\mathscr{S}^{r}(\gamma)\right|{}^{2} = \tfrac{6r\left( (r-4)(c_{1}^{2} + c_{2}^{2} + c_{3}^{2}) + (c_{1} - c_{2})^{2} + (c_{2} - c_{3})^{2} + (c_{3} - c_{1})^{2}\right)}{(r+2)(r-1)}. \end{split} \end{align} $$It follows that ![]() $c_{1}\mathscr {S}^{r}(\alpha ) + c_{2}\mathscr {S}^{r}(\beta ) + c_{3}\mathscr {S}^{r}(\gamma ) = 0$ for
$c_{1}\mathscr {S}^{r}(\alpha ) + c_{2}\mathscr {S}^{r}(\beta ) + c_{3}\mathscr {S}^{r}(\gamma ) = 0$ for ![]() $c_{i}$ not all zero if and only if
$c_{i}$ not all zero if and only if ![]() $r = 4$ and
$r = 4$ and ![]() $c_{1} = c_{2} = c_{3}$. Together with (10.4), 2, and 3 this implies both claims of 4 straightforwardly.
$c_{1} = c_{2} = c_{3}$. Together with (10.4), 2, and 3 this implies both claims of 4 straightforwardly.
By (6.7) and (6.8), there hold ![]() $\widehat {\alpha \cdot \alpha }_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\alpha ) = -(r\,{+}\,1)\alpha $,
$\widehat {\alpha \cdot \alpha }_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\alpha ) = -(r\,{+}\,1)\alpha $, 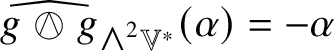 ,
, 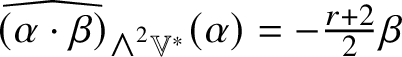 $\widehat {(\alpha \cdot \beta )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\alpha ) = -\tfrac {r+2}{2}\beta $,
$\widehat {(\alpha \cdot \beta )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\alpha ) = -\tfrac {r+2}{2}\beta $, 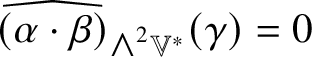 $\widehat {(\alpha \cdot \beta )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\gamma ) = 0$, and the identities obtained from these by permuting
$\widehat {(\alpha \cdot \beta )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\gamma ) = 0$, and the identities obtained from these by permuting ![]() $\alpha $,
$\alpha $, ![]() $\beta $, and
$\beta $, and ![]() $\gamma $. Combining these identities with the definition of
$\gamma $. Combining these identities with the definition of ![]() $\mathscr {S}(\alpha )$ yields
$\mathscr {S}(\alpha )$ yields  $\widehat {\mathscr {S}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\alpha ) = \tfrac {r-2}{r-1}\alpha $ and
$\widehat {\mathscr {S}(\alpha )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\alpha ) = \tfrac {r-2}{r-1}\alpha $ and 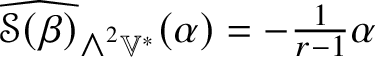 $\widehat {\mathscr {S}(\beta )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\alpha ) = -\tfrac {1}{r-1}\alpha $. Claims 5 and 6 follow from these identities.
$\widehat {\mathscr {S}(\beta )}_{{\textstyle \wedge }^{2}\mathbb {V}^{\ast }}(\alpha ) = -\tfrac {1}{r-1}\alpha $. Claims 5 and 6 follow from these identities.
Lemma 10.8 identifies the ![]() $5$-dimensional subalgebra of (4a) of Lemma 10.7.
$5$-dimensional subalgebra of (4a) of Lemma 10.7.
Lemma 10.8. Let ![]() $(\mathbb {V}, h)$ be a Euclidean vector space of dimension at least
$(\mathbb {V}, h)$ be a Euclidean vector space of dimension at least ![]() $4$. Let
$4$. Let ![]() $\mathbb {W} \subset \mathbb {V}$ be a 4-dimensional subspace and suppose
$\mathbb {W} \subset \mathbb {V}$ be a 4-dimensional subspace and suppose ![]() $(\alpha , \beta ) \in \mathscr {OC}(\mathbb {W}, h)^{2}$ determines a hyper-Kähler structure on
$(\alpha , \beta ) \in \mathscr {OC}(\mathbb {W}, h)^{2}$ determines a hyper-Kähler structure on ![]() $\mathbb {W}$. Define
$\mathbb {W}$. Define ![]() $\mathscr {S}(\alpha ) = \mathscr {S}^{4}(\alpha ), \mathscr {S}(\beta ) = \mathscr {S}^{4}(\beta ), \mathscr {S}(\gamma ) = \mathscr {S}^{4}(\gamma ) \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ as in (10.2) (where
$\mathscr {S}(\alpha ) = \mathscr {S}^{4}(\alpha ), \mathscr {S}(\beta ) = \mathscr {S}^{4}(\beta ), \mathscr {S}(\gamma ) = \mathscr {S}^{4}(\gamma ) \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ as in (10.2) (where ![]() $\gamma = \alpha \circ \beta $).
$\gamma = \alpha \circ \beta $).
1. For
 $\mathscr {X}$ contained in the
$\mathscr {X}$ contained in the  $5$-dimensional subalgebra
$5$-dimensional subalgebra  $\mathbb {B} = \text {Span}\,\{\mathscr {S}(\alpha ), \mathscr {S}(\beta ), \mathscr {S}(\gamma ), \alpha \cdot \beta , \beta \cdot \gamma , \gamma \cdot \alpha \}$,
$\mathbb {B} = \text {Span}\,\{\mathscr {S}(\alpha ), \mathscr {S}(\beta ), \mathscr {S}(\gamma ), \alpha \cdot \beta , \beta \cdot \gamma , \gamma \cdot \alpha \}$,  $\widehat {\mathscr {X}}$ preserves
$\widehat {\mathscr {X}}$ preserves  $\mathbb {U} = \text {Span}\,\{\alpha , \beta , \gamma \} \subset {\bigwedge }^{2}\mathbb {V}^{\ast }$.
$\mathbb {U} = \text {Span}\,\{\alpha , \beta , \gamma \} \subset {\bigwedge }^{2}\mathbb {V}^{\ast }$.2. The map
 $\Psi :\mathbb {B} \to \operatorname {End}(\mathbb {U})$ defined by
$\Psi :\mathbb {B} \to \operatorname {End}(\mathbb {U})$ defined by  $\Psi (\mathscr {X}) = 3\widehat {\mathscr {X}}_{\mathbb {U}}$ is an isometric algebra isomorphism from
$\Psi (\mathscr {X}) = 3\widehat {\mathscr {X}}_{\mathbb {U}}$ is an isometric algebra isomorphism from  $(\mathbb {B}, \ast , h)$ to the deunitalization
$(\mathbb {B}, \ast , h)$ to the deunitalization  $(\operatorname {Sym}_{0}(\mathbb {U}, h), \times , \tfrac {4}{3}G)$ of the
$(\operatorname {Sym}_{0}(\mathbb {U}, h), \times , \tfrac {4}{3}G)$ of the  $6$-dimensional rank
$6$-dimensional rank  $3$ simple real Euclidean Jordan algebra
$3$ simple real Euclidean Jordan algebra  $(\operatorname {Sym}(\mathbb {U}, h), \circledcirc )$, in its realization as the trace-free symmetric endomorphisms of
$(\operatorname {Sym}(\mathbb {U}, h), \circledcirc )$, in its realization as the trace-free symmetric endomorphisms of  $\mathbb {U}$ equipped with the product
$\mathbb {U}$ equipped with the product  $\times $ equal to the traceless part of the usual Jordan product
$\times $ equal to the traceless part of the usual Jordan product  $\circledcirc $ of endomorphisms and the metric
$\circledcirc $ of endomorphisms and the metric  $G(A, B) = \tfrac {1}{3}\operatorname {\mathsf {tr}} A \circ B$.
$G(A, B) = \tfrac {1}{3}\operatorname {\mathsf {tr}} A \circ B$.3. The Killing form
 $\tau _{\ast , \mathbb {B}}(\mathscr {X}, \mathscr {Y}) = \operatorname {\mathsf {tr}} L_{\ast , \mathbb {B}}(\mathscr {X})L_{\ast , \mathbb {B}}(\mathscr {Y})$ on
$\tau _{\ast , \mathbb {B}}(\mathscr {X}, \mathscr {Y}) = \operatorname {\mathsf {tr}} L_{\ast , \mathbb {B}}(\mathscr {X})L_{\ast , \mathbb {B}}(\mathscr {Y})$ on  $(\mathbb {B}, \ast )$ satisfies
$(\mathbb {B}, \ast )$ satisfies  $\tau _{\ast , \mathbb {B}} = \tfrac {21}{16}\langle \,\cdot \,\,, \,\cdot \,\, \rangle $.
$\tau _{\ast , \mathbb {B}} = \tfrac {21}{16}\langle \,\cdot \,\,, \,\cdot \,\, \rangle $.4. The subalgebra
 $(\mathbb {B}, \ast , h)$ is simple.
$(\mathbb {B}, \ast , h)$ is simple.
Proof. By 4 of Lemma 10.7, ![]() $\mathscr {S}(\gamma ) = -\mathscr {S}(\alpha ) -\mathscr {S}(\beta )$. In (10.16) and (10.17) this yields the relations
$\mathscr {S}(\gamma ) = -\mathscr {S}(\alpha ) -\mathscr {S}(\beta )$. In (10.16) and (10.17) this yields the relations
 $$ \begin{align} \begin{aligned} {} &\mathscr{S}(\alpha) \ast \mathscr{S}(\beta) = -\mathscr{S}(\alpha) -\mathscr{S}(\beta),& &\mathscr{S}(\alpha)\ast (\mathscr{S}(\beta) - \mathscr{S}(\gamma)) = -(\mathscr{S}(\beta) - \mathscr{S}(\gamma)),&\\ &(\alpha \cdot \gamma) \ast (\beta \cdot \gamma) = -\tfrac{9}{2}\alpha \cdot \beta, & &(\alpha \cdot \beta) \ast (\alpha \cdot \beta) = 27(\mathscr{S}(\alpha) + \mathscr{S}(\beta)),&\\ &\mathscr{S}(\alpha)\ast(\alpha \cdot \beta) = \tfrac{1}{2}\alpha \cdot \beta,& &\mathscr{S}(\alpha)\ast(\beta \cdot \gamma) = -\beta \cdot \gamma,& \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {} &\mathscr{S}(\alpha) \ast \mathscr{S}(\beta) = -\mathscr{S}(\alpha) -\mathscr{S}(\beta),& &\mathscr{S}(\alpha)\ast (\mathscr{S}(\beta) - \mathscr{S}(\gamma)) = -(\mathscr{S}(\beta) - \mathscr{S}(\gamma)),&\\ &(\alpha \cdot \gamma) \ast (\beta \cdot \gamma) = -\tfrac{9}{2}\alpha \cdot \beta, & &(\alpha \cdot \beta) \ast (\alpha \cdot \beta) = 27(\mathscr{S}(\alpha) + \mathscr{S}(\beta)),&\\ &\mathscr{S}(\alpha)\ast(\alpha \cdot \beta) = \tfrac{1}{2}\alpha \cdot \beta,& &\mathscr{S}(\alpha)\ast(\beta \cdot \gamma) = -\beta \cdot \gamma,& \end{aligned} \end{align} $$and those obtained from them by permuting ![]() $\alpha $,
$\alpha $, ![]() $\beta $, and
$\beta $, and ![]() $\gamma $. By 6 of Lemma 10.7, for
$\gamma $. By 6 of Lemma 10.7, for
 $$ \begin{align} \begin{split} \mathscr{X} &= (2x_{1} + x_{2})\mathscr{S}(\alpha) + (x_{1} + 2x_{2})\mathscr{S}(\beta) - \tfrac{1}{3}\left(z_{1}\beta \cdot \gamma + z_{2}\alpha \cdot \gamma + z_{3}\alpha \cdot \beta\right)\!, \end{split} \end{align} $$
$$ \begin{align} \begin{split} \mathscr{X} &= (2x_{1} + x_{2})\mathscr{S}(\alpha) + (x_{1} + 2x_{2})\mathscr{S}(\beta) - \tfrac{1}{3}\left(z_{1}\beta \cdot \gamma + z_{2}\alpha \cdot \gamma + z_{3}\alpha \cdot \beta\right)\!, \end{split} \end{align} $$the matrix of ![]() $\widehat {\mathscr {X}}_{\mathbb {U}}$ with respect to the equal-norm orthogonal ordered basis
$\widehat {\mathscr {X}}_{\mathbb {U}}$ with respect to the equal-norm orthogonal ordered basis ![]() $\{\alpha , \beta , \gamma \}$ of
$\{\alpha , \beta , \gamma \}$ of ![]() $\mathbb {U}$ is
$\mathbb {U}$ is
 $$ \begin{align} \mathbb{X} = \begin{pmatrix}[c] x_{1} & z_{3} & z_{2} \\ z_{3} & x_{2}& z_{1}\\ z_{2} & z_{1} & - x_{1} - x_{2} \end{pmatrix}\in \operatorname{Sym}_{0}(\mathbb{U}, h). \end{align} $$
$$ \begin{align} \mathbb{X} = \begin{pmatrix}[c] x_{1} & z_{3} & z_{2} \\ z_{3} & x_{2}& z_{1}\\ z_{2} & z_{1} & - x_{1} - x_{2} \end{pmatrix}\in \operatorname{Sym}_{0}(\mathbb{U}, h). \end{align} $$From (10.24) it is apparent that ![]() $\Psi : \mathbb {B} \to \operatorname {Sym}_{0}(\mathbb {U}, h)$ defined by
$\Psi : \mathbb {B} \to \operatorname {Sym}_{0}(\mathbb {U}, h)$ defined by 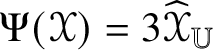 $\Psi (\mathscr {X}) = 3\widehat {\mathscr {X}}_{\mathbb {U}}$ is a linear isomorphism. Because
$\Psi (\mathscr {X}) = 3\widehat {\mathscr {X}}_{\mathbb {U}}$ is a linear isomorphism. Because ![]() $\ast $ and
$\ast $ and ![]() $\times $ are commutative, by polarization, to check that
$\times $ are commutative, by polarization, to check that ![]() $\Psi $ is an algebra homomorphism it suffices to check that
$\Psi $ is an algebra homomorphism it suffices to check that ![]() $\Psi (\mathscr {X} \ast \mathscr {X}) = \Psi (\mathscr {X})\times \Psi (\mathscr {X})$. By (10.22),
$\Psi (\mathscr {X} \ast \mathscr {X}) = \Psi (\mathscr {X})\times \Psi (\mathscr {X})$. By (10.22),
 $$ \begin{align} \begin{split} \mathscr{X} \ast \mathscr{X} & = -3(2x_{1}x_{2} + x_{2}^{2} + z_{1}^{2} - z_{3}^{2})\mathscr{S}(\alpha) -3(2x_{1}x_{2} + x_{1}^{2} + z_{2}^{2} - z_{3}^{2})\mathscr{S}(\beta)\\ &\quad - (z_{1}z_{2} + (x_{1} + x_{2})z_{3})\alpha \cdot \beta + (z_{2}z_{3} - x_{1}z_{1})\beta \cdot \gamma + (z_{1}z_{3} - x_{2}z_{2})\gamma \cdot \alpha. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \mathscr{X} \ast \mathscr{X} & = -3(2x_{1}x_{2} + x_{2}^{2} + z_{1}^{2} - z_{3}^{2})\mathscr{S}(\alpha) -3(2x_{1}x_{2} + x_{1}^{2} + z_{2}^{2} - z_{3}^{2})\mathscr{S}(\beta)\\ &\quad - (z_{1}z_{2} + (x_{1} + x_{2})z_{3})\alpha \cdot \beta + (z_{2}z_{3} - x_{1}z_{1})\beta \cdot \gamma + (z_{1}z_{3} - x_{2}z_{2})\gamma \cdot \alpha. \end{split} \end{align} $$Comparing (10.25) with
 $$ \begin{align} \begin{split} \mathbb{X} \times \mathbb{X}= \begin{pmatrix}[c] \tfrac{x_{1}^{2} - 2x_{2}^{2} - 2x_{1}x_{2} - 2z_{1}^{2} + z_{2}^{2} + z_{3}^{2}}{3} & z_{1}z_{2} + (x_{1} + x_{2})z_{3} &z_{1}z_{3} - x_{2}z_{2}\\ z_{1}z_{2} + (x_{1} + x_{2})z_{3} &\tfrac{-2x_{1}^{2} +x_{2}^{2} - 2x_{1}x_{2} +z_{1}^{2} -2 z_{2}^{2} + z_{3}^{2} }{3}& z_{2}z_{3} - x_{1}z_{1}\\ z_{1}z_{3} - x_{2}z_{2} &z_{2}z_{3} - x_{1}z_{1} &\tfrac{x_{1}^{2} + x_{2}^{2} + 4x_{1}x_{2} + z_{1}^{2} + z_{2}^{2} - 2z_{3}^{2}}{3} \end{pmatrix} \end{split} \end{align} $$
$$ \begin{align} \begin{split} \mathbb{X} \times \mathbb{X}= \begin{pmatrix}[c] \tfrac{x_{1}^{2} - 2x_{2}^{2} - 2x_{1}x_{2} - 2z_{1}^{2} + z_{2}^{2} + z_{3}^{2}}{3} & z_{1}z_{2} + (x_{1} + x_{2})z_{3} &z_{1}z_{3} - x_{2}z_{2}\\ z_{1}z_{2} + (x_{1} + x_{2})z_{3} &\tfrac{-2x_{1}^{2} +x_{2}^{2} - 2x_{1}x_{2} +z_{1}^{2} -2 z_{2}^{2} + z_{3}^{2} }{3}& z_{2}z_{3} - x_{1}z_{1}\\ z_{1}z_{3} - x_{2}z_{2} &z_{2}z_{3} - x_{1}z_{1} &\tfrac{x_{1}^{2} + x_{2}^{2} + 4x_{1}x_{2} + z_{1}^{2} + z_{2}^{2} - 2z_{3}^{2}}{3} \end{pmatrix} \end{split} \end{align} $$shows that ![]() $\Psi (\mathscr {X} \ast \mathscr {X}) = \Psi (\mathscr {X})\times \Psi (\mathscr {X})$.
$\Psi (\mathscr {X} \ast \mathscr {X}) = \Psi (\mathscr {X})\times \Psi (\mathscr {X})$.
By claims 2 and 3 of Lemma 10.7 with ![]() $r = 4$,
$r = 4$,
 $$ \begin{align} \left\{\tfrac{\sqrt{3}}{2\sqrt{2}}(\mathscr{S}(\alpha) + \mathscr{S}(\beta)), -\tfrac{1}{2\sqrt{2}}(\mathscr{S}(\alpha) - \mathscr{S}(\beta)), \tfrac{1}{6\sqrt{2}}\beta \cdot \gamma, \tfrac{1}{6\sqrt{2}}\gamma \cdot \alpha, \tfrac{1}{6\sqrt{2}}\alpha \cdot \beta\right\} \end{align} $$
$$ \begin{align} \left\{\tfrac{\sqrt{3}}{2\sqrt{2}}(\mathscr{S}(\alpha) + \mathscr{S}(\beta)), -\tfrac{1}{2\sqrt{2}}(\mathscr{S}(\alpha) - \mathscr{S}(\beta)), \tfrac{1}{6\sqrt{2}}\beta \cdot \gamma, \tfrac{1}{6\sqrt{2}}\gamma \cdot \alpha, \tfrac{1}{6\sqrt{2}}\alpha \cdot \beta\right\} \end{align} $$is an orthonormal basis of ![]() $\mathbb {B}$. By definition of G, (10.24), and the orthonormality of (10.27) (used to compute the norm of (10.23)),
$\mathbb {B}$. By definition of G, (10.24), and the orthonormality of (10.27) (used to compute the norm of (10.23)),
 $$ \begin{align} \begin{split} \Psi^{\ast}(G)(\mathscr{X}, \mathscr{X}) &= \tfrac{1}{3}\operatorname{\mathsf{tr}}\Psi(\mathscr{X})^2 = 3\operatorname{\mathsf{tr}} \mathbb{X}^{2} = 6\left(x_{1}^{2} + x_{1}x_{2} + x_{2}^{2} + z_{1}^{2} + z_{2}^{2} + z_{3}^{2}\right) = \tfrac{3}{4}|\mathscr{X}|^{2}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \Psi^{\ast}(G)(\mathscr{X}, \mathscr{X}) &= \tfrac{1}{3}\operatorname{\mathsf{tr}}\Psi(\mathscr{X})^2 = 3\operatorname{\mathsf{tr}} \mathbb{X}^{2} = 6\left(x_{1}^{2} + x_{1}x_{2} + x_{2}^{2} + z_{1}^{2} + z_{2}^{2} + z_{3}^{2}\right) = \tfrac{3}{4}|\mathscr{X}|^{2}. \end{split} \end{align} $$Slightly tedious calculations using (10.22) show that the matrix of the restriction to ![]() $\mathbb {B}$ of
$\mathbb {B}$ of ![]() $L_{\ast , \mathbb {B}}(\mathscr {X})$ with respect to the ordered orthonormal basis (10.27) is
$L_{\ast , \mathbb {B}}(\mathscr {X})$ with respect to the ordered orthonormal basis (10.27) is
 $$ \begin{align} M= \begin{pmatrix}[c] -\tfrac{3}{2}(x_{1} + x_{2}) & -\tfrac{\sqrt{3}}{2}(x_{1} - x_{2}) & \tfrac{\sqrt{3}}{2}z_{1} & \tfrac{\sqrt{3}}{2}z_{2} & -\sqrt{3}z_{3}\\ -\tfrac{\sqrt{3}}{2}(x_{1} - x_{2}) & \tfrac{3}{2}(x_{1} + x_{1}) & -\tfrac{3}{2}z_{1} & \tfrac{3}{2}z_{2} & 0\\ \tfrac{\sqrt{3}}{2}z_{1} & -\tfrac{3}{2}z_{1} & -\tfrac{3}{2}x_{1} & \tfrac{3}{2}z_{3} & \tfrac{3}{2}z_{2}\\ \tfrac{\sqrt{3}}{2}z_{2} & \tfrac{3}{2}z_{2} & \tfrac{3}{2}z_{3} & -\tfrac{3}{2}x_{2} & \tfrac{3}{2}z_{1}\\ -\sqrt{3}z_{3} & 0 & \tfrac{3}{2}z_{2} & \tfrac{3}{2}z_{1} & \tfrac{3}{2}(x_{1} + x_{2}) \end{pmatrix}. \end{align} $$
$$ \begin{align} M= \begin{pmatrix}[c] -\tfrac{3}{2}(x_{1} + x_{2}) & -\tfrac{\sqrt{3}}{2}(x_{1} - x_{2}) & \tfrac{\sqrt{3}}{2}z_{1} & \tfrac{\sqrt{3}}{2}z_{2} & -\sqrt{3}z_{3}\\ -\tfrac{\sqrt{3}}{2}(x_{1} - x_{2}) & \tfrac{3}{2}(x_{1} + x_{1}) & -\tfrac{3}{2}z_{1} & \tfrac{3}{2}z_{2} & 0\\ \tfrac{\sqrt{3}}{2}z_{1} & -\tfrac{3}{2}z_{1} & -\tfrac{3}{2}x_{1} & \tfrac{3}{2}z_{3} & \tfrac{3}{2}z_{2}\\ \tfrac{\sqrt{3}}{2}z_{2} & \tfrac{3}{2}z_{2} & \tfrac{3}{2}z_{3} & -\tfrac{3}{2}x_{2} & \tfrac{3}{2}z_{1}\\ -\sqrt{3}z_{3} & 0 & \tfrac{3}{2}z_{2} & \tfrac{3}{2}z_{1} & \tfrac{3}{2}(x_{1} + x_{2}) \end{pmatrix}. \end{align} $$Comparing (10.29) with (10.28) shows
 $$ \begin{align} \begin{split} \tau_{\mathbb{B}, \ast} &= \operatorname{\mathsf{tr}} L_{\ast, \mathbb{B}}(\mathscr{X})L_{\ast, \mathbb{B}}(\mathscr{X}) = \operatorname{\mathsf{tr}} M^{2} = \tfrac{21}{2}\left(x_{1}^{2} + x_{1}x_{2} + x_{2}^{2} + z_{1}^{2} + z_{2}^{2} + z_{3}^{2} \right) = \tfrac{21}{16}|\mathscr{X}|^{2}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \tau_{\mathbb{B}, \ast} &= \operatorname{\mathsf{tr}} L_{\ast, \mathbb{B}}(\mathscr{X})L_{\ast, \mathbb{B}}(\mathscr{X}) = \operatorname{\mathsf{tr}} M^{2} = \tfrac{21}{2}\left(x_{1}^{2} + x_{1}x_{2} + x_{2}^{2} + z_{1}^{2} + z_{2}^{2} + z_{3}^{2} \right) = \tfrac{21}{16}|\mathscr{X}|^{2}. \end{split} \end{align} $$That ![]() $(\mathbb {B}, \ast , h)$ is simple follows from 2 and Lemma 9.9.
$(\mathbb {B}, \ast , h)$ is simple follows from 2 and Lemma 9.9.
11 Subalgebra of Kähler–Weyl tensors and the  $4$-dimensional case revisited
$4$-dimensional case revisited
A ![]() $2n$-dimensional Kähler vector space
$2n$-dimensional Kähler vector space ![]() $(\mathbb {V}, h, J, \omega )$ is a Euclidean vector space
$(\mathbb {V}, h, J, \omega )$ is a Euclidean vector space ![]() $(\mathbb {V}, h)$ of dimension
$(\mathbb {V}, h)$ of dimension ![]() $m = 2n$ equipped with a compatible complex structure
$m = 2n$ equipped with a compatible complex structure ![]() $J_{i}{}^{j}$, meaning that
$J_{i}{}^{j}$, meaning that ![]() $J_{i}{}^{p}J_{j}{}^{q}h_{pq} = h_{ij}$ and
$J_{i}{}^{p}J_{j}{}^{q}h_{pq} = h_{ij}$ and ![]() $\omega _{ij} = J_{i}{}^{p}h_{pj}$ is a symplectic form. When a Kähler vector space is fixed, the abstract unitary group
$\omega _{ij} = J_{i}{}^{p}h_{pj}$ is a symplectic form. When a Kähler vector space is fixed, the abstract unitary group ![]() $U(n)$ is identified with the unitary group
$U(n)$ is identified with the unitary group ![]() $U(h, J)$ of linear automorphisms of
$U(h, J)$ of linear automorphisms of ![]() $\mathbb {V}$ preserving h and J.
$\mathbb {V}$ preserving h and J.
Lemma 11.1. Let ![]() $(\mathbb {V}, h, J, \omega )$ be a
$(\mathbb {V}, h, J, \omega )$ be a ![]() $2n$-dimensional Kähler vector space. The
$2n$-dimensional Kähler vector space. The ![]() $U(n)$-submodules
$U(n)$-submodules
 $$ \begin{align} \begin{split} \mathscr{MC}_{\mathscr{K}}(\mathbb{V}^{\ast}) &= \{\mathscr{X} \in \mathscr{MC}(\mathbb{V}^{\ast}): J_{i}{}^{a}J_{j}{}^{b}\mathscr{X}_{abkl} = \mathscr{X}_{ijkl}\} = \{\mathscr{X} \in \mathscr{MC}(\mathbb{V}^{\ast}):J_{[i}{}^{p}\mathscr{X}_{j]pkl} = 0\} \end{split} \end{align} $$
$$ \begin{align} \begin{split} \mathscr{MC}_{\mathscr{K}}(\mathbb{V}^{\ast}) &= \{\mathscr{X} \in \mathscr{MC}(\mathbb{V}^{\ast}): J_{i}{}^{a}J_{j}{}^{b}\mathscr{X}_{abkl} = \mathscr{X}_{ijkl}\} = \{\mathscr{X} \in \mathscr{MC}(\mathbb{V}^{\ast}):J_{[i}{}^{p}\mathscr{X}_{j]pkl} = 0\} \end{split} \end{align} $$of curvature tensors of Kähler type and ![]() $\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }) = \mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast }) \cap \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ of Kähler-Weyl curvature tensors are subalgebras of
$\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }) = \mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast }) \cap \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ of Kähler-Weyl curvature tensors are subalgebras of ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ on which
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ on which ![]() $U(n)$ acts by automorphisms.
$U(n)$ acts by automorphisms.
Proof. Let ![]() $\mathscr {X}, \mathscr {Y} \in \mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast })$. Write
$\mathscr {X}, \mathscr {Y} \in \mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast })$. Write ![]() $B_{ijkl} = B(\mathscr {X}, \mathscr {Y})_{ijkl}$. By (5.13),
$B_{ijkl} = B(\mathscr {X}, \mathscr {Y})_{ijkl}$. By (5.13),
 $$ \begin{align} \begin{split} 8J_{i}{}^{a}J_{j}{}^{b}B_{ab[kl]} &= J_{i}{}^{a}J_{j}{}^{b}(\mathscr{X}_{ab}{}^{pq}\mathscr{Y}_{pqkl} + \mathscr{Y}_{ab}{}^{pq}\mathscr{X}_{pqkl}) \\ &= \mathscr{X}_{ij}{}^{pq}\mathscr{Y}_{pqkl} + \mathscr{Y}_{ij}{}^{pq}\mathscr{X}_{pqkl} = 8B_{ij[kl]}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} 8J_{i}{}^{a}J_{j}{}^{b}B_{ab[kl]} &= J_{i}{}^{a}J_{j}{}^{b}(\mathscr{X}_{ab}{}^{pq}\mathscr{Y}_{pqkl} + \mathscr{Y}_{ab}{}^{pq}\mathscr{X}_{pqkl}) \\ &= \mathscr{X}_{ij}{}^{pq}\mathscr{Y}_{pqkl} + \mathscr{Y}_{ij}{}^{pq}\mathscr{X}_{pqkl} = 8B_{ij[kl]}. \end{split} \end{align} $$Similarly,
 $$ \begin{align} \begin{split} 2J_{j}{}^{a}J_{l}{}^{b}B_{iakb} &= J_{j}{}^{a}J_{l}{}^{b}\mathscr{X}_{ipaq}\mathscr{Y}_{k}{}^{p}{}_{b}{}^{q} + J_{j}{}^{a}J_{l}{}^{b}\mathscr{Y}_{ipaq}\mathscr{X}_{k}{}^{p}{}_{b}{}^{q}\\ & = J_{q}{}^{a}J_{bl}\mathscr{X}_{ipja}\mathscr{Y}_{k}{}^{pbq} + J_{q}{}^{a}J_{bl}\mathscr{Y}_{ipja}\mathscr{X}_{k}{}^{pbq} \\ & = - J_{q}{}^{a}J_{b}{}^{q}\mathscr{X}_{ipja}\mathscr{Y}_{k}{}^{p}{}_{l}{}^{b}- J_{q}{}^{a}J_{b}{}^{q}\mathscr{Y}_{ipja}\mathscr{X}_{k}{}^{p}{}_{l}{}^{b}\\ & = \mathscr{X}_{ipjb}\mathscr{Y}_{k}{}^{p}{}_{l}{}^{b} + \mathscr{Y}_{ipjb}\mathscr{X}_{k}{}^{p}{}_{l}{}^{b} = 2B_{ijkl}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} 2J_{j}{}^{a}J_{l}{}^{b}B_{iakb} &= J_{j}{}^{a}J_{l}{}^{b}\mathscr{X}_{ipaq}\mathscr{Y}_{k}{}^{p}{}_{b}{}^{q} + J_{j}{}^{a}J_{l}{}^{b}\mathscr{Y}_{ipaq}\mathscr{X}_{k}{}^{p}{}_{b}{}^{q}\\ & = J_{q}{}^{a}J_{bl}\mathscr{X}_{ipja}\mathscr{Y}_{k}{}^{pbq} + J_{q}{}^{a}J_{bl}\mathscr{Y}_{ipja}\mathscr{X}_{k}{}^{pbq} \\ & = - J_{q}{}^{a}J_{b}{}^{q}\mathscr{X}_{ipja}\mathscr{Y}_{k}{}^{p}{}_{l}{}^{b}- J_{q}{}^{a}J_{b}{}^{q}\mathscr{Y}_{ipja}\mathscr{X}_{k}{}^{p}{}_{l}{}^{b}\\ & = \mathscr{X}_{ipjb}\mathscr{Y}_{k}{}^{p}{}_{l}{}^{b} + \mathscr{Y}_{ipjb}\mathscr{X}_{k}{}^{p}{}_{l}{}^{b} = 2B_{ijkl}. \end{split} \end{align} $$Together (5.14), (11.2), and (11.3) yield
 $$ \begin{align} \begin{split} J_{i}{}^{a}J_{j}{}^{b}(\mathscr{X} \ast\mathscr{Y})_{abkl} &= J_{i}{}^{a}J_{j}{}^{b}\left(-2B_{ab[kl]} - B_{akbl} + B_{alkb}\right) \\& = -2B_{ij[kl]} - 2B_{i[k|j|l]} = (\mathscr{X} \ast \mathscr{Y})_{ijkl}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} J_{i}{}^{a}J_{j}{}^{b}(\mathscr{X} \ast\mathscr{Y})_{abkl} &= J_{i}{}^{a}J_{j}{}^{b}\left(-2B_{ab[kl]} - B_{akbl} + B_{alkb}\right) \\& = -2B_{ij[kl]} - 2B_{i[k|j|l]} = (\mathscr{X} \ast \mathscr{Y})_{ijkl}. \end{split} \end{align} $$This shows ![]() $\mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast })$ is a subalgebra of
$\mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast })$ is a subalgebra of ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$. By Lemmas 5.7 and 11.1,
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$. By Lemmas 5.7 and 11.1, ![]() $\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }) = \mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast }) \cap \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is a subalgebra of
$\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }) = \mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast }) \cap \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is a subalgebra of ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$. That
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$. That ![]() $U(n)$ acts by automorphisms on these subalgebras follows from the containment
$U(n)$ acts by automorphisms on these subalgebras follows from the containment ![]() $U(n) \subset O(2n)$.
$U(n) \subset O(2n)$.
A Kähler vector space is canonically oriented by the Euclidean volume form 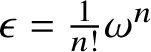 $\epsilon = \tfrac {1}{n!}\omega ^{n}$. Lemma 11.2 shows that, for a
$\epsilon = \tfrac {1}{n!}\omega ^{n}$. Lemma 11.2 shows that, for a ![]() $4$-dimensional Kähler vector space, the space of Weyl curvature tensors anti-self-dual with respect to the orientation determined by the complex structure coincides with the space of Kähler–Weyl curvature tensors. As is explained subsequently, this has the consequence of showing that the subalgebra
$4$-dimensional Kähler vector space, the space of Weyl curvature tensors anti-self-dual with respect to the orientation determined by the complex structure coincides with the space of Kähler–Weyl curvature tensors. As is explained subsequently, this has the consequence of showing that the subalgebra ![]() $(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is nontrivial whenever
$(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is nontrivial whenever ![]() $\dim \mathbb {V}^{\ast } \geq 4$.
$\dim \mathbb {V}^{\ast } \geq 4$.
Lemma 11.2. Let ![]() $(\mathbb {V}, h, J, \omega )$ be a
$(\mathbb {V}, h, J, \omega )$ be a ![]() $4$-dimensional Kähler vector space oriented by
$4$-dimensional Kähler vector space oriented by 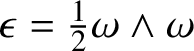 $\epsilon = \tfrac {1}{2}\omega \wedge \omega $.
$\epsilon = \tfrac {1}{2}\omega \wedge \omega $.
1. For
 $\alpha , \beta \in {\bigwedge }^{2}_{-}\mathbb {V}^{\ast }$,
$\alpha , \beta \in {\bigwedge }^{2}_{-}\mathbb {V}^{\ast }$,  is contained in
is contained in  $\mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast })$.
$\mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast })$.2. If
 $\alpha , \beta \in {\bigwedge }^{2}_{-}\mathbb {V}^{\ast }$, then
$\alpha , \beta \in {\bigwedge }^{2}_{-}\mathbb {V}^{\ast }$, then  $\operatorname {\mathsf {tf}}(\alpha \cdot \beta ) = \tfrac {3}{4}\operatorname {\mathsf {tf}} \mathscr {K}(\alpha , \beta ) \in \mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$.
$\operatorname {\mathsf {tf}}(\alpha \cdot \beta ) = \tfrac {3}{4}\operatorname {\mathsf {tf}} \mathscr {K}(\alpha , \beta ) \in \mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$.3. If
 $\alpha \in {\bigwedge }^{2}_{-}(\mathbb {V}^{\ast })$ satisfies
$\alpha \in {\bigwedge }^{2}_{-}(\mathbb {V}^{\ast })$ satisfies  $|\alpha |^{2}_{h} = 4$, then
$|\alpha |^{2}_{h} = 4$, then  $\mathscr {S}(\alpha ) = -\tfrac {1}{6}\operatorname {\mathsf {tf}}(\alpha \cdot \alpha ) = -\tfrac {1}{8}\operatorname {\mathsf {tf}} \mathscr {K}(\alpha , \alpha )$, where
$\mathscr {S}(\alpha ) = -\tfrac {1}{6}\operatorname {\mathsf {tf}}(\alpha \cdot \alpha ) = -\tfrac {1}{8}\operatorname {\mathsf {tf}} \mathscr {K}(\alpha , \alpha )$, where  $\mathscr {S}(\alpha )$ is as defined in (10.2), is a nontrivial idempotent in
$\mathscr {S}(\alpha )$ is as defined in (10.2), is a nontrivial idempotent in  $(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ satisfying
$(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ satisfying  $|\mathscr {S}(\alpha )|^{2} = \tfrac {8}{3}$.
$|\mathscr {S}(\alpha )|^{2} = \tfrac {8}{3}$.4.
 $\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }) = \mathscr {MC}_{\mathscr {W}}^{-}(\mathbb {V}^{\ast })$.
$\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }) = \mathscr {MC}_{\mathscr {W}}^{-}(\mathbb {V}^{\ast })$.
Proof. The operator ![]() $\star \in \operatorname {End}({\bigwedge }^{2}\mathbb {V}^{\ast })$ can be expressed
$\star \in \operatorname {End}({\bigwedge }^{2}\mathbb {V}^{\ast })$ can be expressed 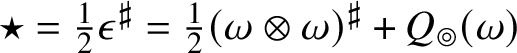 $\star = \tfrac {1}{2}\epsilon ^{\sharp } = \tfrac {1}{2}(\omega \otimes \omega )^{\sharp } + Q_{\circledcirc }(\omega )$ (recall from (4.6) the isomorphism
$\star = \tfrac {1}{2}\epsilon ^{\sharp } = \tfrac {1}{2}(\omega \otimes \omega )^{\sharp } + Q_{\circledcirc }(\omega )$ (recall from (4.6) the isomorphism ![]() $\sharp $ and its inverse
$\sharp $ and its inverse ![]() $\flat $). It follows that
$\flat $). It follows that ![]() $\alpha \in {\bigwedge }^{2}\mathbb {V}^{\ast }$ is contained in
$\alpha \in {\bigwedge }^{2}\mathbb {V}^{\ast }$ is contained in ![]() ${\bigwedge }^{2}_{-}\mathbb {V}^{\ast }$ if and only if
${\bigwedge }^{2}_{-}\mathbb {V}^{\ast }$ if and only if ![]() $\langle \alpha , \omega \rangle =0$ and
$\langle \alpha , \omega \rangle =0$ and ![]() $Q_{\circledcirc }(\omega )(\alpha ) = -\alpha $. The latter condition is equivalent to
$Q_{\circledcirc }(\omega )(\alpha ) = -\alpha $. The latter condition is equivalent to ![]() $\alpha \circ \omega = \omega \circ \alpha \in S^{2}\mathbb {V}^{\ast }$, and this shows that the element
$\alpha \circ \omega = \omega \circ \alpha \in S^{2}\mathbb {V}^{\ast }$, and this shows that the element ![]() $\mathscr {K}(\alpha , \beta )$ of 1 is correctly defined.
$\mathscr {K}(\alpha , \beta )$ of 1 is correctly defined.
Suppose ![]() $\alpha , \beta \in {\bigwedge }^{2}\mathbb {V}^{\ast }$. Substituting
$\alpha , \beta \in {\bigwedge }^{2}\mathbb {V}^{\ast }$. Substituting 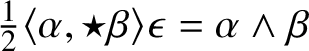 $\tfrac {1}{2}\langle \alpha , \star \beta \rangle \epsilon = \alpha \wedge \beta $ into (6.2) yields the alternative expressions
$\tfrac {1}{2}\langle \alpha , \star \beta \rangle \epsilon = \alpha \wedge \beta $ into (6.2) yields the alternative expressions
 $$ \begin{align} \begin{split} \alpha \cdot \beta &= \tfrac{3}{2}(\alpha \otimes \beta + \beta \otimes \alpha) - \tfrac{1}{4}\langle \alpha, \star \beta \rangle \epsilon= \tfrac{3}{2}(\alpha \otimes \beta + \beta \otimes \alpha) - \tfrac{1}{8}\langle \alpha, \star \beta \rangle \omega \wedge \omega. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \alpha \cdot \beta &= \tfrac{3}{2}(\alpha \otimes \beta + \beta \otimes \alpha) - \tfrac{1}{4}\langle \alpha, \star \beta \rangle \epsilon= \tfrac{3}{2}(\alpha \otimes \beta + \beta \otimes \alpha) - \tfrac{1}{8}\langle \alpha, \star \beta \rangle \omega \wedge \omega. \end{split} \end{align} $$Taking ![]() $\alpha = \beta = \omega $ in (11.5) yields
$\alpha = \beta = \omega $ in (11.5) yields
 $$ \begin{align} \omega \cdot \omega = 3\omega\otimes \omega - \tfrac{1}{2} \omega \wedge \omega = 3\omega\otimes \omega -\epsilon. \end{align} $$
$$ \begin{align} \omega \cdot \omega = 3\omega\otimes \omega - \tfrac{1}{2} \omega \wedge \omega = 3\omega\otimes \omega -\epsilon. \end{align} $$By Example 4.3, 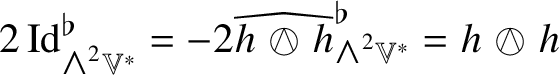 , so
, so

Combining  $\alpha \wedge \beta = \tfrac {1}{2}\langle \alpha , \star \beta \rangle \epsilon $ with (11.7) and noting
$\alpha \wedge \beta = \tfrac {1}{2}\langle \alpha , \star \beta \rangle \epsilon $ with (11.7) and noting ![]() $(\alpha \wedge \beta )^{\sharp } = (\alpha \otimes \beta + \beta \otimes \alpha )^{\sharp } + 4Q_{\circledcirc }(\alpha ,\beta )$ yields
$(\alpha \wedge \beta )^{\sharp } = (\alpha \otimes \beta + \beta \otimes \alpha )^{\sharp } + 4Q_{\circledcirc }(\alpha ,\beta )$ yields

Now suppose ![]() $\alpha , \beta \in {\bigwedge }^{2}_{-}\mathbb {V}^{\ast }$. In this case, by (6.8),
$\alpha , \beta \in {\bigwedge }^{2}_{-}\mathbb {V}^{\ast }$. In this case, by (6.8),

and, because 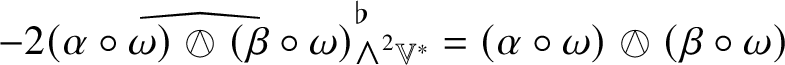 , substituting this into (11.8) yields
, substituting this into (11.8) yields

Substituting (11.5) and (11.6) into (11.10) and simplifying the result using (11.7) yields

A straightforward calculation using the last equality of (11.11) shows ![]() $Q_{\circledcirc }(\omega )\circ \mathscr {K}(\alpha , \beta )^{\sharp } = - \mathscr {K}(\alpha , \beta )^{\sharp }$, so
$Q_{\circledcirc }(\omega )\circ \mathscr {K}(\alpha , \beta )^{\sharp } = - \mathscr {K}(\alpha , \beta )^{\sharp }$, so ![]() $\mathscr {K}(\alpha , \beta ) \in \mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast })$. By (11.11), (7.8), and 1 of Lemma 9.1,
$\mathscr {K}(\alpha , \beta ) \in \mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast })$. By (11.11), (7.8), and 1 of Lemma 9.1,

This shows 2. If ![]() $\alpha \in {\bigwedge }^{2}_{-}(\mathbb {V}^{\ast })$, then
$\alpha \in {\bigwedge }^{2}_{-}(\mathbb {V}^{\ast })$, then 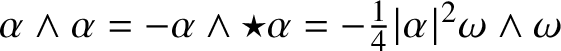 $\alpha \wedge \alpha = -\alpha \wedge \star \alpha = -\tfrac {1}{4}|\alpha |^{2}\omega \wedge \omega $, so if
$\alpha \wedge \alpha = -\alpha \wedge \star \alpha = -\tfrac {1}{4}|\alpha |^{2}\omega \wedge \omega $, so if 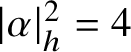 $|\alpha |^{2}_{h} = 4$, then
$|\alpha |^{2}_{h} = 4$, then ![]() $\alpha \wedge \alpha = - \omega \wedge \omega $. Hence,
$\alpha \wedge \alpha = - \omega \wedge \omega $. Hence, ![]() $0 = (\alpha \wedge \alpha + \omega \wedge \omega )^{\sharp }(\omega ) = 4(Q_{\circledcirc }(\alpha )(\omega ) + \omega )$, so
$0 = (\alpha \wedge \alpha + \omega \wedge \omega )^{\sharp }(\omega ) = 4(Q_{\circledcirc }(\alpha )(\omega ) + \omega )$, so ![]() $\alpha \circ \omega \circ \alpha = -\omega $. This implies
$\alpha \circ \omega \circ \alpha = -\omega $. This implies ![]() $\alpha \circ \alpha = - \alpha \circ \omega \circ \omega \circ \alpha = -\alpha \circ \omega \circ \alpha \circ \omega = \omega \circ \omega = -h$, showing
$\alpha \circ \alpha = - \alpha \circ \omega \circ \omega \circ \alpha = -\alpha \circ \omega \circ \alpha \circ \omega = \omega \circ \omega = -h$, showing ![]() $\alpha $ satisfies the hypotheses of Lemma 10.1. Taking
$\alpha $ satisfies the hypotheses of Lemma 10.1. Taking ![]() $\beta = \alpha $ in (11.12) yields 3.
$\beta = \alpha $ in (11.12) yields 3.
For ![]() $\mathscr {X} \in \mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast })$, pairing
$\mathscr {X} \in \mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast })$, pairing ![]() $J_{i}{}^{p}\mathscr {X}_{pjkl} = J_{j}{}^{p}\mathscr {X}_{ipkl}$ with
$J_{i}{}^{p}\mathscr {X}_{pjkl} = J_{j}{}^{p}\mathscr {X}_{ipkl}$ with ![]() $h^{il}$ yields
$h^{il}$ yields ![]() $\omega ^{pq}\mathscr {X}_{pqjk} = -2\omega ^{pq}\mathscr {X}_{pjkq} = J_{j}{}^{p}\operatorname {\rho }(\mathscr {X})_{pk}$, so, because
$\omega ^{pq}\mathscr {X}_{pqjk} = -2\omega ^{pq}\mathscr {X}_{pjkq} = J_{j}{}^{p}\operatorname {\rho }(\mathscr {X})_{pk}$, so, because ![]() $\mathscr {X} \in \mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$,
$\mathscr {X} \in \mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$, 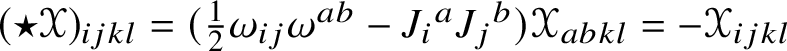 $(\star \mathscr {X})_{ijkl} = (\tfrac {1}{2}\omega _{ij}\omega ^{ab} - J_{i}{}^{a}J_{j}{}^{b})\mathscr {X}_{abkl} = -\mathscr {X}_{ijkl}$. This shows that
$(\star \mathscr {X})_{ijkl} = (\tfrac {1}{2}\omega _{ij}\omega ^{ab} - J_{i}{}^{a}J_{j}{}^{b})\mathscr {X}_{abkl} = -\mathscr {X}_{ijkl}$. This shows that ![]() $\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }) \subset \mathscr {MC}_{\mathscr {W}}^{-}(\mathbb {V}^{\ast })$. Since both
$\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }) \subset \mathscr {MC}_{\mathscr {W}}^{-}(\mathbb {V}^{\ast })$. Since both ![]() $\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$ and
$\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$ and ![]() $\mathscr {MC}_{\mathscr {W}}^{-}(\mathbb {V}^{\ast })$ are
$\mathscr {MC}_{\mathscr {W}}^{-}(\mathbb {V}^{\ast })$ are ![]() $SU(2)$-modules and
$SU(2)$-modules and ![]() $\mathscr {MC}_{\mathscr {W}}^{-}(\mathbb {V}^{\ast })$ is an irreducible
$\mathscr {MC}_{\mathscr {W}}^{-}(\mathbb {V}^{\ast })$ is an irreducible ![]() $SU(2)$-module, to prove equality it suffices to show that
$SU(2)$-module, to prove equality it suffices to show that ![]() $\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$ has dimension at least
$\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$ has dimension at least ![]() $1$. By the preceding paragraph there exists
$1$. By the preceding paragraph there exists ![]() $\alpha \in {\bigwedge }^{2}_{-}\mathbb {V}^{\ast }$ such that
$\alpha \in {\bigwedge }^{2}_{-}\mathbb {V}^{\ast }$ such that ![]() $\operatorname {\mathsf {tf}}(\alpha \cdot \alpha )$ is nontrivial and is contained in
$\operatorname {\mathsf {tf}}(\alpha \cdot \alpha )$ is nontrivial and is contained in ![]() $\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$. This proves claim 4.
$\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$. This proves claim 4.
Theorem 11.3. Let ![]() $(\mathbb {V}, h, J, \omega )$ be a Kähler vector space of dimension
$(\mathbb {V}, h, J, \omega )$ be a Kähler vector space of dimension ![]() $m = 2n \geq 4$. The subspace
$m = 2n \geq 4$. The subspace ![]() $\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$ is a simple subalgebra of
$\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$ is a simple subalgebra of ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ that is exact and Killing metrized, with Killing form equal to a positive multiple of the metric
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ that is exact and Killing metrized, with Killing form equal to a positive multiple of the metric ![]() $\langle \,\cdot \,\,, \,\cdot \,\, \rangle $ and on which
$\langle \,\cdot \,\,, \,\cdot \,\, \rangle $ and on which ![]() $U(n) = U(\mathbb {V}, J, h)$ acts irreducibly by automorphisms.
$U(n) = U(\mathbb {V}, J, h)$ acts irreducibly by automorphisms.
Proof. The group ![]() $U(n)$ acts irreducibly on
$U(n)$ acts irreducibly on ![]() $\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$ [Reference Tricerri and Vanhecke39, Theorem
$\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$ [Reference Tricerri and Vanhecke39, Theorem ![]() $6.4$]. It is straightforward to check that when, in the setting of Lemma 5.9,
$6.4$]. It is straightforward to check that when, in the setting of Lemma 5.9, ![]() $\mathbb {V}$ is equipped with a Kähler structure and
$\mathbb {V}$ is equipped with a Kähler structure and ![]() $\mathbb {W} \subset \mathbb {V}$ is a Kähler subspace, the map
$\mathbb {W} \subset \mathbb {V}$ is a Kähler subspace, the map ![]() $\iota $ of Lemma 5.9 is an injective algebra homomorphism from
$\iota $ of Lemma 5.9 is an injective algebra homomorphism from ![]() $(\mathscr {MC}_{\mathscr {K}}(\mathbb {W}^{\ast }), \ast )$ and
$(\mathscr {MC}_{\mathscr {K}}(\mathbb {W}^{\ast }), \ast )$ and ![]() $(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {W}^{\ast }), \ast )$ to
$(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {W}^{\ast }), \ast )$ to ![]() $(\mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast }), \ast )$ and
$(\mathscr {MC}_{\mathscr {K}}(\mathbb {V}^{\ast }), \ast )$ and ![]() $(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$, respectively. Consequently, by Lemmas 5.9 and 11.2,
$(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$, respectively. Consequently, by Lemmas 5.9 and 11.2, ![]() $(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ contains a nontrivial idempotent, so its multiplication is nontrivial. The group
$(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ contains a nontrivial idempotent, so its multiplication is nontrivial. The group ![]() $U(n)$ acts on
$U(n)$ acts on ![]() $(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ by isometric automorphisms because it is a subgroup of
$(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ by isometric automorphisms because it is a subgroup of ![]() $O(2n)$, which acts on
$O(2n)$, which acts on ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ by algebra automorphisms. By Theorem 3.2,
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ by algebra automorphisms. By Theorem 3.2, ![]() $(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is exact and Killing metrized, with Killing form equal to a positive multiple of the metric
$(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is exact and Killing metrized, with Killing form equal to a positive multiple of the metric ![]() $\langle \,\cdot \,\,, \,\cdot \,\, \rangle $. Because every finite-dimensional irreducible representation of
$\langle \,\cdot \,\,, \,\cdot \,\, \rangle $. Because every finite-dimensional irreducible representation of ![]() $U(n)$ restricts to an irreducible representation of
$U(n)$ restricts to an irreducible representation of ![]() $SU(n)$,
$SU(n)$, ![]() $\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$ is irreducible as an
$\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$ is irreducible as an ![]() $SU(n)$-module. Since the action by automorphisms of
$SU(n)$-module. Since the action by automorphisms of ![]() $SU(n)$ on
$SU(n)$ on ![]() $\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$ is irreducible, the simplicity of
$\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast })$ is irreducible, the simplicity of ![]() $(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ follows from Theorem 3.1.
$(\mathscr {MC}_{\mathscr {K},\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ follows from Theorem 3.1.
12 Examples related with idempotents
This final section shows the viability of making explicit computations in ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ and describes some relations among the idempotents constructed earlier that are suggestive both with respect to the structure of
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ and describes some relations among the idempotents constructed earlier that are suggestive both with respect to the structure of ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ and in the context of developing a structure theory for commutative algebras metrized by a trace-form. It is indicated how this yields an alternative proof of Theorem 1.5. Theorem 12.3 shows that
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ and in the context of developing a structure theory for commutative algebras metrized by a trace-form. It is indicated how this yields an alternative proof of Theorem 1.5. Theorem 12.3 shows that ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ contains many 2-dimensional unital associative subalgebras isomorphic to the paracomplex numbers and exhibits zeros of its cubic polynomial. The final Example 12.5 shows that when
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ contains many 2-dimensional unital associative subalgebras isomorphic to the paracomplex numbers and exhibits zeros of its cubic polynomial. The final Example 12.5 shows that when ![]() $\dim \mathbb {V} \geq 6$,
$\dim \mathbb {V} \geq 6$, ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ contains subalgebras isomorphic to Matsuo algebras.
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ contains subalgebras isomorphic to Matsuo algebras.
Lemma 12.1. Let ![]() $(\mathbb {V}, h)$ be a Euclidean vector space. For
$(\mathbb {V}, h)$ be a Euclidean vector space. For ![]() $x, y, z, w \in \mathbb {V}^{\ast }$,
$x, y, z, w \in \mathbb {V}^{\ast }$,

Proof. The identities (12.1) follow from the definitions (6.1) and (6.2); precisely, summing ![]() $(x\odot y)\odot (z \odot w)$ and
$(x\odot y)\odot (z \odot w)$ and ![]() $(x \wedge y)\odot (z \wedge w)$ cyclically over x, y, and z yields elements in
$(x \wedge y)\odot (z \wedge w)$ cyclically over x, y, and z yields elements in ![]() $\ker \mathscr {S}$ and
$\ker \mathscr {S}$ and ![]() $\ker \mathscr {M}$, respectively. By the definitions, (6.1) and (6.2),
$\ker \mathscr {M}$, respectively. By the definitions, (6.1) and (6.2),

Polarizing (12.4) first in x and then in y and using (12.1) yields (12.2). Using (12.2) and (12.1) to evaluate the right-hand side of (12.3) yields the left-hand side of (12.3).
Example 12.2. Let ![]() $(\mathbb {V}, h)$ be a Euclidean vector space. Let
$(\mathbb {V}, h)$ be a Euclidean vector space. Let ![]() $x, y \in \mathbb {V}^{\ast }$ be orthogonal unit norm vectors. Let
$x, y \in \mathbb {V}^{\ast }$ be orthogonal unit norm vectors. Let ![]() $\sigma = x \wedge y$, so that
$\sigma = x \wedge y$, so that ![]() $\sigma \circ \sigma = -\alpha $ where
$\sigma \circ \sigma = -\alpha $ where ![]() $\alpha = x \otimes x + y \otimes y$. Then
$\alpha = x \otimes x + y \otimes y$. Then ![]() $\alpha $ satisfies
$\alpha $ satisfies ![]() $\alpha \circ \alpha = \alpha $,
$\alpha \circ \alpha = \alpha $, ![]() $\operatorname {\mathsf {tr}} \alpha = 2$ and, by (12.4),
$\operatorname {\mathsf {tr}} \alpha = 2$ and, by (12.4), ![]() , so that
, so that ![]() . On the other hand, by (6.35), Lemma 10.1, and (12.4),
. On the other hand, by (6.35), Lemma 10.1, and (12.4), ![]() is an idempotent in
is an idempotent in ![]() $(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ satisfying
$(\mathscr {MC}(\mathbb {V}^{\ast }), \ast )$ satisfying ![]() . Similarly, if
. Similarly, if ![]() $\{x, y, z, w\}\subset \mathbb {V}^{\ast } $ is an orthonormal set,
$\{x, y, z, w\}\subset \mathbb {V}^{\ast } $ is an orthonormal set,
 $$ \begin{align} \begin{split} \left((x\wedge y)\otimes (x \wedge y)\right)\ast\left((y\wedge z)\otimes (y \wedge z)\right) &=- \tfrac{1}{2}(x\wedge z)\otimes (x\wedge z),\\ \left((x\wedge y)\otimes (x \wedge y)\right)\ast\left((z\wedge w)\otimes (z \wedge w)\right) &= 0. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \left((x\wedge y)\otimes (x \wedge y)\right)\ast\left((y\wedge z)\otimes (y \wedge z)\right) &=- \tfrac{1}{2}(x\wedge z)\otimes (x\wedge z),\\ \left((x\wedge y)\otimes (x \wedge y)\right)\ast\left((z\wedge w)\otimes (z \wedge w)\right) &= 0. \end{split} \end{align} $$These are most easily computed using (6.18) or (6.20) in conjunction with (12.4). By Corollary 7.5, as the idempotents ![]() are orthogonal,
are orthogonal,
 $$ \begin{align} \begin{split} \mathscr{B}&(x, y, z, w) = \mathscr{B}(\alpha, \beta) = -\tfrac{2}{3}\left((x\wedge y)\otimes (x \wedge y) + (z\wedge w)\otimes(z \wedge w)\right) \\ &\quad + \tfrac{1}{3}\left((x\wedge z)\otimes (x \wedge z) + (x\wedge w)\otimes (x \wedge w)+ (y\wedge z)\otimes (y \wedge z)+ (y\wedge w)\otimes (y \wedge w) \right) \end{split} \end{align} $$
$$ \begin{align} \begin{split} \mathscr{B}&(x, y, z, w) = \mathscr{B}(\alpha, \beta) = -\tfrac{2}{3}\left((x\wedge y)\otimes (x \wedge y) + (z\wedge w)\otimes(z \wedge w)\right) \\ &\quad + \tfrac{1}{3}\left((x\wedge z)\otimes (x \wedge z) + (x\wedge w)\otimes (x \wedge w)+ (y\wedge z)\otimes (y \wedge z)+ (y\wedge w)\otimes (y \wedge w) \right) \end{split} \end{align} $$is an idempotent in ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ satisfying
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ satisfying ![]() $|\mathscr {B}(x, y, z, w)|^{2} = 16/3$. The symmetries
$|\mathscr {B}(x, y, z, w)|^{2} = 16/3$. The symmetries ![]() $\mathscr {B}(y, x, z, w) =\mathscr {B}(x, y, z, w) = \mathscr {B}(x, y, w, z) = \mathscr {B}(z, w, x, y)$, evident from (12.6), show that (12.6) yields only three distinct idempotents, namely,
$\mathscr {B}(y, x, z, w) =\mathscr {B}(x, y, z, w) = \mathscr {B}(x, y, w, z) = \mathscr {B}(z, w, x, y)$, evident from (12.6), show that (12.6) yields only three distinct idempotents, namely, ![]() $\mathscr {B}(x, y, z, w)$,
$\mathscr {B}(x, y, z, w)$, ![]() $\mathscr {B}(y, z, x, w)$, and
$\mathscr {B}(y, z, x, w)$, and ![]() $\mathscr {B}(z, x, y, w)$. From (12.6) it is apparent that
$\mathscr {B}(z, x, y, w)$. From (12.6) it is apparent that ![]() $\mathscr {B}(x, y, z, w) + \mathscr {B}(y, z, x, w) + \mathscr {B}(z, x, y, w) =0$. This shows
$\mathscr {B}(x, y, z, w) + \mathscr {B}(y, z, x, w) + \mathscr {B}(z, x, y, w) =0$. This shows ![]() $-\mathscr {B}(x, y, z, w) - \mathscr {B}(y, z, x, w)$ is idempotent, which implies
$-\mathscr {B}(x, y, z, w) - \mathscr {B}(y, z, x, w)$ is idempotent, which implies
This shows ![]() $\mathscr {B}(x, y, z, w)$,
$\mathscr {B}(x, y, z, w)$, ![]() $\mathscr {B}(y, z, x, w)$, and
$\mathscr {B}(y, z, x, w)$, and ![]() $\mathscr {B}(z, x, y, w)$ span a
$\mathscr {B}(z, x, y, w)$ span a ![]() $2$-dimensional subalgebra isomorphic to the algebra
$2$-dimensional subalgebra isomorphic to the algebra ![]() $\mathbb {E}^{2}(\mathbb R)$ called the simplicial algebra in [Reference Fox10]; it is the unique
$\mathbb {E}^{2}(\mathbb R)$ called the simplicial algebra in [Reference Fox10]; it is the unique ![]() $2$-dimensional metrized commutative algebra with automorphism group
$2$-dimensional metrized commutative algebra with automorphism group ![]() $S_{3}$.
$S_{3}$.
Theorem 12.3. Let ![]() $(\mathbb {V}, h)$ be a Euclidean vector space of dimension
$(\mathbb {V}, h)$ be a Euclidean vector space of dimension ![]() $n \geq 4$. For an h-orthonormal set
$n \geq 4$. For an h-orthonormal set ![]() $\{x, y, z, w\} \subset \mathbb {V}^{\ast }$,
$\{x, y, z, w\} \subset \mathbb {V}^{\ast }$,
 $$ \begin{align} \mathscr{E} = \mathscr{E}(x, y, z, w) = \tfrac{2}{3}(x \wedge y)\cdot (z \wedge w) \in \mathscr{MC}_{\mathscr{W}}(\mathbb{V}^{\ast}) \end{align} $$
$$ \begin{align} \mathscr{E} = \mathscr{E}(x, y, z, w) = \tfrac{2}{3}(x \wedge y)\cdot (z \wedge w) \in \mathscr{MC}_{\mathscr{W}}(\mathbb{V}^{\ast}) \end{align} $$is a zero of the cubic polynomial ![]() $P_{\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast }$ that satisfies:
$P_{\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast }$ that satisfies:
1.
 $\mathscr {E}\ast (\mathscr {E} \ast \mathscr {E}) = \mathscr {E}$ and
$\mathscr {E}\ast (\mathscr {E} \ast \mathscr {E}) = \mathscr {E}$ and  $\mathscr {E} \ast \mathscr {E} = \mathscr {B}(x, y, z, w)$ is idempotent.
$\mathscr {E} \ast \mathscr {E} = \mathscr {B}(x, y, z, w)$ is idempotent.2. The subspace
 $\text {Span}\,\{\mathscr {E}, \mathscr {E}\ast \mathscr {E}\} \subset \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is an associative subalgebra isomorphic to the algebra
$\text {Span}\,\{\mathscr {E}, \mathscr {E}\ast \mathscr {E}\} \subset \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is an associative subalgebra isomorphic to the algebra  $\mathbb R[t]/(t^{2} - 1)$ of paracomplex numbers via the linear map
$\mathbb R[t]/(t^{2} - 1)$ of paracomplex numbers via the linear map  $a\mathscr {E}\ast \mathscr {E} + b \mathscr {E} \to a + bt$.
$a\mathscr {E}\ast \mathscr {E} + b \mathscr {E} \to a + bt$.
Proof. The two-forms ![]() $\alpha ^{\pm }(x, y, z, w) = \alpha ^{\pm } = x\wedge y \pm z \wedge w$ satisfy
$\alpha ^{\pm }(x, y, z, w) = \alpha ^{\pm } = x\wedge y \pm z \wedge w$ satisfy ![]() $\alpha ^{\pm } \circ \alpha ^{\pm } = -g$ for
$\alpha ^{\pm } \circ \alpha ^{\pm } = -g$ for ![]() $g = x\otimes x + y\otimes y + z \otimes z + w\otimes w$ and
$g = x\otimes x + y\otimes y + z \otimes z + w\otimes w$ and ![]() $[\alpha ^{+}, \alpha ^{-}] = 0$. Because
$[\alpha ^{+}, \alpha ^{-}] = 0$. Because ![]() $\langle \alpha ^{+}, \alpha ^{-}\rangle = 0$ and
$\langle \alpha ^{+}, \alpha ^{-}\rangle = 0$ and ![]() $\alpha ^{+}\circ \alpha ^{-}\circ \alpha ^{+}\circ \alpha ^{-} = g$, by (10.13),
$\alpha ^{+}\circ \alpha ^{-}\circ \alpha ^{+}\circ \alpha ^{-} = g$, by (10.13), ![]() $\langle \mathscr {S}^{4}(\alpha ^{+}), \mathscr {S}^{4}(\alpha ^{-})\rangle = 0$. Define
$\langle \mathscr {S}^{4}(\alpha ^{+}), \mathscr {S}^{4}(\alpha ^{-})\rangle = 0$. Define ![]() $\mathscr {S}^{\pm }(x, y, z, w) = \mathscr {S}^{4}(\alpha ^{\pm })$. By (12.4),
$\mathscr {S}^{\pm }(x, y, z, w) = \mathscr {S}^{4}(\alpha ^{\pm })$. By (12.4),

By (12.2), (12.3), and (12.9),
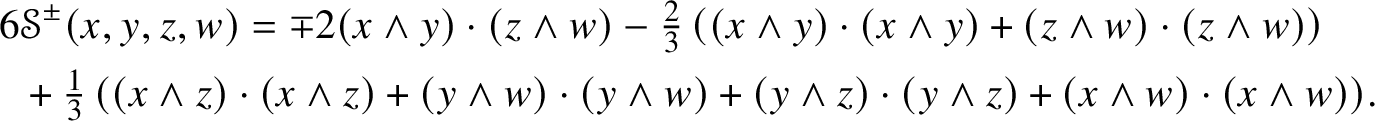 $$ \begin{align} \begin{split} 6&\mathscr{S}^{\pm}(x, y, z, w) = \mp 2(x \wedge y)\cdot (z \wedge w) - \tfrac{2}{3}\left((x\wedge y) \cdot (x \wedge y) + (z\wedge w) \cdot (z \wedge w)\right)\\ &+\tfrac{1}{3}\left( (x\wedge z) \cdot (x \wedge z)+ (y\wedge w) \cdot (y \wedge w) +(y\wedge z) \cdot (y \wedge z)+ (x\wedge w) \cdot (x \wedge w) \right)\!. \end{split} \end{align} $$
$$ \begin{align} \begin{split} 6&\mathscr{S}^{\pm}(x, y, z, w) = \mp 2(x \wedge y)\cdot (z \wedge w) - \tfrac{2}{3}\left((x\wedge y) \cdot (x \wedge y) + (z\wedge w) \cdot (z \wedge w)\right)\\ &+\tfrac{1}{3}\left( (x\wedge z) \cdot (x \wedge z)+ (y\wedge w) \cdot (y \wedge w) +(y\wedge z) \cdot (y \wedge z)+ (x\wedge w) \cdot (x \wedge w) \right)\!. \end{split} \end{align} $$Comparing (12.6) and (12.8) with (12.10) shows that
 $$ \begin{align} \begin{split} \mathscr{S}^{+}(x, y, z, w) + \mathscr{S}^{-}(x, y, z, w) &= \mathscr{B}(x, y, z, w),\\ \mathscr{S}^{-}(x, y, z, w) - \mathscr{S}^{+}(x, y, z, w) &= \mathscr{E}(x, y, z, w). \end{split} \end{align} $$
$$ \begin{align} \begin{split} \mathscr{S}^{+}(x, y, z, w) + \mathscr{S}^{-}(x, y, z, w) &= \mathscr{B}(x, y, z, w),\\ \mathscr{S}^{-}(x, y, z, w) - \mathscr{S}^{+}(x, y, z, w) &= \mathscr{E}(x, y, z, w). \end{split} \end{align} $$Write ![]() $\mathscr {S}^{\pm } = \mathscr {S}^{\pm }(x, y, z, w)$ and
$\mathscr {S}^{\pm } = \mathscr {S}^{\pm }(x, y, z, w)$ and ![]() $\mathscr {B} = \mathscr {B}(x, y, z, w)$. Because
$\mathscr {B} = \mathscr {B}(x, y, z, w)$. Because ![]() $\mathscr {S}^{+}$,
$\mathscr {S}^{+}$, ![]() $\mathscr {S}^{-}$, and
$\mathscr {S}^{-}$, and ![]() $\mathscr {B}(x, y, z, w)$ are idempotents in
$\mathscr {B}(x, y, z, w)$ are idempotents in ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$, (12.11) implies
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$, (12.11) implies ![]() $\mathscr {S}^{+}\ast \mathscr {S}^{-} = 0$ and
$\mathscr {S}^{+}\ast \mathscr {S}^{-} = 0$ and ![]() $\langle \mathscr {S}^{+}, \mathscr {S}^{-}\rangle = 0$. By (12.11),
$\langle \mathscr {S}^{+}, \mathscr {S}^{-}\rangle = 0$. By (12.11), ![]() $\mathscr {E}\ast \mathscr {E} = \mathscr {S}^{-} + \mathscr {S}^{+} = \mathscr {B}$. This shows
$\mathscr {E}\ast \mathscr {E} = \mathscr {S}^{-} + \mathscr {S}^{+} = \mathscr {B}$. This shows ![]() $\mathscr {E}\ast \mathscr {E}$ is idempotent and
$\mathscr {E}\ast \mathscr {E}$ is idempotent and ![]() $\langle \mathscr {E}, \mathscr {E}\ast \mathscr {E}\rangle = \langle \mathscr {S}^{-} - \mathscr {S}^{+}, \mathscr {S}^{-} + \mathscr {S}^{+}\rangle = |\mathscr {S}^{-}|^{2} - |\mathscr {S}^{+}|^{2} = 0$, the last equality because
$\langle \mathscr {E}, \mathscr {E}\ast \mathscr {E}\rangle = \langle \mathscr {S}^{-} - \mathscr {S}^{+}, \mathscr {S}^{-} + \mathscr {S}^{+}\rangle = |\mathscr {S}^{-}|^{2} - |\mathscr {S}^{+}|^{2} = 0$, the last equality because ![]() $|\mathscr {S}^{\pm }(x, y, z, w)|^{2} = 8/3$ by Lemma 10.6 or direct computation using (12.10). Finally,
$|\mathscr {S}^{\pm }(x, y, z, w)|^{2} = 8/3$ by Lemma 10.6 or direct computation using (12.10). Finally, ![]() $\mathscr {E} \ast (\mathscr {E} \ast \mathscr {E}) = \mathscr {E} \ast \mathscr {B} = (\mathscr {S}^{-} - \mathscr {S}^{+})\ast (\mathscr {S}^{-} +\mathscr {S}^{+}) = \mathscr {S}^{-} - \mathscr {S}^{+} = \mathscr {E}$. The final claim follows.
$\mathscr {E} \ast (\mathscr {E} \ast \mathscr {E}) = \mathscr {E} \ast \mathscr {B} = (\mathscr {S}^{-} - \mathscr {S}^{+})\ast (\mathscr {S}^{-} +\mathscr {S}^{+}) = \mathscr {S}^{-} - \mathscr {S}^{+} = \mathscr {E}$. The final claim follows.
For an h-orthonormal set ![]() $\{x, y, z, w\} \subset \mathbb {V}^{\ast }$, by (12.10) and (12.1),
$\{x, y, z, w\} \subset \mathbb {V}^{\ast }$, by (12.10) and (12.1),
The symmetries ![]() $\mathscr {S}^{\pm }(x, y, z, w) = \mathscr {S}^{\pm }(z, w, x, y) = \mathscr {S}^{\pm }(y, x, w, z) = \mathscr {S}^{\pm }(w, z, y, x)$ and
$\mathscr {S}^{\pm }(x, y, z, w) = \mathscr {S}^{\pm }(z, w, x, y) = \mathscr {S}^{\pm }(y, x, w, z) = \mathscr {S}^{\pm }(w, z, y, x)$ and ![]() $\mathscr {S}^{+}(y, x, z, w) = \mathscr {S}^{-}(x, y, z, w)$, evident from (12.10), show that, under the action of
$\mathscr {S}^{+}(y, x, z, w) = \mathscr {S}^{-}(x, y, z, w)$, evident from (12.10), show that, under the action of ![]() $S_{4}$ permuting
$S_{4}$ permuting ![]() $\{x, y, z, w\}$, (12.10) yields only six distinct idempotents, namely,
$\{x, y, z, w\}$, (12.10) yields only six distinct idempotents, namely, ![]() $\mathscr {S}^{\pm }(x, y, z, w)$,
$\mathscr {S}^{\pm }(x, y, z, w)$, ![]() $\mathscr {S}^{\pm }(y, z, x, w)$ and
$\mathscr {S}^{\pm }(y, z, x, w)$ and ![]() $\mathscr {S}^{\pm }(z, x, y, w)$. By (12.12),
$\mathscr {S}^{\pm }(z, x, y, w)$. By (12.12), ![]() $-\mathscr {S}^{\pm }(x, y, z, w) - \mathscr {S}^{\pm }(y, z, x, w)$ is idempotent, which implies
$-\mathscr {S}^{\pm }(x, y, z, w) - \mathscr {S}^{\pm }(y, z, x, w)$ is idempotent, which implies
(Alternatively, (12.13) follows from Lemma 10.7.) This shows ![]() $\mathscr {S}^{\pm }(x, y, z, w)$,
$\mathscr {S}^{\pm }(x, y, z, w)$, ![]() $\mathscr {S}^{\pm }(y, z, x, w)$, and
$\mathscr {S}^{\pm }(y, z, x, w)$, and ![]() $\mathscr {S}^{\pm }(z, x, y, w)$ span a
$\mathscr {S}^{\pm }(z, x, y, w)$ span a ![]() $2$-dimensional subalgebra isomorphic to
$2$-dimensional subalgebra isomorphic to ![]() $\mathbb {E}^{2}(\mathbb R)$. Computations using (6.11)–(6.13), as in the proof of Lemma 10.1, or computations using
$\mathbb {E}^{2}(\mathbb R)$. Computations using (6.11)–(6.13), as in the proof of Lemma 10.1, or computations using ![]() $\alpha ^{+}(x, y, z, w)\circledcirc \alpha ^{+}(y, z, x, w) = 0$ and
$\alpha ^{+}(x, y, z, w)\circledcirc \alpha ^{+}(y, z, x, w) = 0$ and ![]() $[\alpha ^{+}(x, y, z, w), \alpha ^{-}(y, z, x, w)] = 0$ and those relations obtained from them via the action of
$[\alpha ^{+}(x, y, z, w), \alpha ^{-}(y, z, x, w)] = 0$ and those relations obtained from them via the action of ![]() $S_{4}$ on
$S_{4}$ on ![]() $\{x, y, z, w\}$ together with (10.13) of Lemma 10.6, show that
$\{x, y, z, w\}$ together with (10.13) of Lemma 10.6, show that ![]() $ \mathscr {S}^{\pm }(x, y, z, w)$ is orthogonal to the span of
$ \mathscr {S}^{\pm }(x, y, z, w)$ is orthogonal to the span of ![]() $\mathscr {S}^{\mp }(x, y, z, w)$ and
$\mathscr {S}^{\mp }(x, y, z, w)$ and ![]() $\mathscr {S}^{\mp }(y, z, x, w)$ while
$\mathscr {S}^{\mp }(y, z, x, w)$ while ![]() $|\mathscr {S}^{\pm }(x, y, z, w)|^{2} = 8/3$ and
$|\mathscr {S}^{\pm }(x, y, z, w)|^{2} = 8/3$ and ![]() $\langle \mathscr {S}^{\pm }(x, y, z, w), \mathscr {S}^{\pm }(y,z, x, w)\rangle = -4/3$. The last identity gives an example where equality holds in (10.13).
$\langle \mathscr {S}^{\pm }(x, y, z, w), \mathscr {S}^{\pm }(y,z, x, w)\rangle = -4/3$. The last identity gives an example where equality holds in (10.13).
Define ![]() $\mathscr {Y}(x, y, z, w) = (x\wedge z)\cdot (z \wedge z) - (y\wedge w)\cdot (y \wedge w)$. By Lemma 10.8 the element
$\mathscr {Y}(x, y, z, w) = (x\wedge z)\cdot (z \wedge z) - (y\wedge w)\cdot (y \wedge w)$. By Lemma 10.8 the element
 $$ \begin{align} \begin{split} \mathscr{C}^{\pm}(x, y, z, w) &= \alpha^{\pm}(x, y, z, w) \cdot \alpha^{\pm}(y, z, x, w) \\&= \mathscr{Y}(x, z, w, y) \pm \mathscr{Y}(y, w, x, z) = \alpha^{\mp}(z, y, x, w) \cdot \alpha^{\mp}(y, x, z, w) \end{split} \end{align} $$
$$ \begin{align} \begin{split} \mathscr{C}^{\pm}(x, y, z, w) &= \alpha^{\pm}(x, y, z, w) \cdot \alpha^{\pm}(y, z, x, w) \\&= \mathscr{Y}(x, z, w, y) \pm \mathscr{Y}(y, w, x, z) = \alpha^{\mp}(z, y, x, w) \cdot \alpha^{\mp}(y, x, z, w) \end{split} \end{align} $$and its cyclic permutations in x, y, and z are orthogonal eigenvectors of ![]() $L_{\ast }(\mathscr {S}^{\pm }(x, y, z, w))$. By definition
$L_{\ast }(\mathscr {S}^{\pm }(x, y, z, w))$. By definition ![]() $\mathscr {S}^{\pm }(x, y, z, w) = \mathscr {S}^{4}(\alpha ^{\pm })$,
$\mathscr {S}^{\pm }(x, y, z, w) = \mathscr {S}^{4}(\alpha ^{\pm })$, ![]() $\mathscr {S}^{\pm }(y, z, x, w) = \mathscr {S}^{4}(\beta ^{\pm })$, and
$\mathscr {S}^{\pm }(y, z, x, w) = \mathscr {S}^{4}(\beta ^{\pm })$, and ![]() $\mathscr {S}^{\pm }(z, x, y, w) = \mathscr {S}^{4}(\gamma ^{\pm })$, where
$\mathscr {S}^{\pm }(z, x, y, w) = \mathscr {S}^{4}(\gamma ^{\pm })$, where ![]() $\alpha ^{\pm } = \alpha ^{\pm }(x, y, z, w)$,
$\alpha ^{\pm } = \alpha ^{\pm }(x, y, z, w)$, ![]() $\beta ^{\pm } = \alpha ^{\pm }(y, z, x, w)$, and
$\beta ^{\pm } = \alpha ^{\pm }(y, z, x, w)$, and ![]() $\gamma ^{\pm } = \alpha ^{\pm }(z, x, y, w)$. There hold
$\gamma ^{\pm } = \alpha ^{\pm }(z, x, y, w)$. There hold ![]() $\alpha ^{\pm } \circ \alpha ^{\pm } = \beta ^{\pm } \circ \beta ^{\pm } = \gamma ^{\pm } \circ \gamma ^{\pm } = -g$ and
$\alpha ^{\pm } \circ \alpha ^{\pm } = \beta ^{\pm } \circ \beta ^{\pm } = \gamma ^{\pm } \circ \gamma ^{\pm } = -g$ and ![]() $\alpha ^{\pm } \circ \beta ^{\pm } = \gamma ^{\pm } = -\beta ^{\pm } \circ \alpha ^{\pm }$ and its cyclic permutations. Computations using
$\alpha ^{\pm } \circ \beta ^{\pm } = \gamma ^{\pm } = -\beta ^{\pm } \circ \alpha ^{\pm }$ and its cyclic permutations. Computations using ![]() $\alpha ^{+}\circ \alpha ^{-} = \alpha ^{-}\circ \alpha ^{+} = -x\otimes x - y\otimes y + z\otimes z + w \otimes w$;
$\alpha ^{+}\circ \alpha ^{-} = \alpha ^{-}\circ \alpha ^{+} = -x\otimes x - y\otimes y + z\otimes z + w \otimes w$; ![]() $\alpha ^{\pm }\circ \beta ^{\mp } = \beta ^{\mp }\circ \alpha ^{\pm } = 2x\odot z \pm 2y \odot w$;
$\alpha ^{\pm }\circ \beta ^{\mp } = \beta ^{\mp }\circ \alpha ^{\pm } = 2x\odot z \pm 2y \odot w$; ![]() $\alpha ^{+}\circ \gamma ^{-} = \gamma ^{-}\circ \alpha ^{+} = 2y\odot z - 2x \odot w$; that, by (6.28),
$\alpha ^{+}\circ \gamma ^{-} = \gamma ^{-}\circ \alpha ^{+} = 2y\odot z - 2x \odot w$; that, by (6.28), ![]() and
and ![]() ; (6.32); (12.4); and (12.2) yield
; (6.32); (12.4); and (12.2) yield ![]() ,
, ![]() ,
, ![]() $(\alpha ^{+}\cdot \alpha ^{+})\ast (\alpha ^{-}\cdot \beta ^{-})=0$,
$(\alpha ^{+}\cdot \alpha ^{+})\ast (\alpha ^{-}\cdot \beta ^{-})=0$, ![]() $(\alpha ^{+}\cdot \alpha ^{+})\ast (\beta ^{-}\cdot \gamma ^{-}) =0$,
$(\alpha ^{+}\cdot \alpha ^{+})\ast (\beta ^{-}\cdot \gamma ^{-}) =0$, ![]() $(\alpha ^{+}\cdot \beta ^{+})\ast (\alpha ^{-}\cdot \beta ^{-}) =0$, and
$(\alpha ^{+}\cdot \beta ^{+})\ast (\alpha ^{-}\cdot \beta ^{-}) =0$, and ![]() $(\alpha ^{+}\cdot \beta ^{+})\ast (\alpha ^{-}\cdot \gamma ^{-}) =0$. Together these imply
$(\alpha ^{+}\cdot \beta ^{+})\ast (\alpha ^{-}\cdot \gamma ^{-}) =0$. Together these imply ![]() ,
, ![]() ,
, ![]() $6\mathscr {S}^{4}(\alpha ^{+})\ast \mathscr {C}^{-}(x, y, z, w) = - (\alpha ^{+}\cdot \alpha ^{+})\ast (\alpha ^{-}\cdot \beta ^{-}) = 0$, and
$6\mathscr {S}^{4}(\alpha ^{+})\ast \mathscr {C}^{-}(x, y, z, w) = - (\alpha ^{+}\cdot \alpha ^{+})\ast (\alpha ^{-}\cdot \beta ^{-}) = 0$, and ![]() $6\mathscr {S}^{4}(\alpha ^{+})\ast \mathscr {C}^{-}( y, z, x, w) = - (\alpha ^{+}\cdot \alpha ^{+})\ast (\beta ^{-}\cdot \gamma ^{-}) = 0$. In particular,
$6\mathscr {S}^{4}(\alpha ^{+})\ast \mathscr {C}^{-}( y, z, x, w) = - (\alpha ^{+}\cdot \alpha ^{+})\ast (\beta ^{-}\cdot \gamma ^{-}) = 0$. In particular, ![]() $\mathscr {S}^{+}(x, y, z, w) \ast \mathscr {S}^{-}(y, z, x, w) =0$. It follows that
$\mathscr {S}^{+}(x, y, z, w) \ast \mathscr {S}^{-}(y, z, x, w) =0$. It follows that
are orthogonal ![]() $5$-dimensional subalgebras of
$5$-dimensional subalgebras of ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast , h)$ that satisfy
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast , h)$ that satisfy ![]() $\mathbb {B}^{+}\ast \mathbb {B}^{-} = \{0\}$ and each of which is as in Lemma 10.8. The two nonisomorphic structures of a
$\mathbb {B}^{+}\ast \mathbb {B}^{-} = \{0\}$ and each of which is as in Lemma 10.8. The two nonisomorphic structures of a ![]() $Cl_{2}$-module on
$Cl_{2}$-module on ![]() $\mathbb {V}$ are represented by the hyper-Kähler structures determined by the pairs
$\mathbb {V}$ are represented by the hyper-Kähler structures determined by the pairs ![]() $(\alpha ^{\pm }, \beta ^{\pm }) \in \mathscr {OC}(\mathbb {V}, h)^{2}$.
$(\alpha ^{\pm }, \beta ^{\pm }) \in \mathscr {OC}(\mathbb {V}, h)^{2}$.
Example 12.4. Let ![]() $(\mathbb {V}, h)$ be a Euclidean vector space of dimension
$(\mathbb {V}, h)$ be a Euclidean vector space of dimension ![]() $n> 3$. Let
$n> 3$. Let ![]() $x, y \in \mathbb {V}^{\ast }$ be orthogonal unit norm vectors. Since
$x, y \in \mathbb {V}^{\ast }$ be orthogonal unit norm vectors. Since ![]() $\alpha = x\otimes x + y \otimes y$ satisfies
$\alpha = x\otimes x + y \otimes y$ satisfies ![]() $\alpha \circ \alpha = \alpha $ and
$\alpha \circ \alpha = \alpha $ and ![]() $\operatorname {\mathsf {tr}} \alpha = 2$, by Lemma 7.5,
$\operatorname {\mathsf {tr}} \alpha = 2$, by Lemma 7.5, ![]() $\mathscr {B}(\alpha )$ defined by (7.11) satisfies
$\mathscr {B}(\alpha )$ defined by (7.11) satisfies 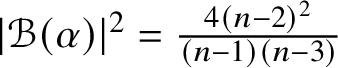 $|\mathscr {B}(\alpha )|^{2} = \tfrac {4(n-2)^{2}}{(n-1)(n-3)}$. Let
$|\mathscr {B}(\alpha )|^{2} = \tfrac {4(n-2)^{2}}{(n-1)(n-3)}$. Let ![]() $\hat {\alpha } = h - \alpha $ and write
$\hat {\alpha } = h - \alpha $ and write 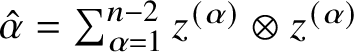 $\hat {\alpha } = \sum _{\alpha = 1}^{n-2}z^{(\alpha )}\otimes z^{(\alpha )}$ where
$\hat {\alpha } = \sum _{\alpha = 1}^{n-2}z^{(\alpha )}\otimes z^{(\alpha )}$ where ![]() $\{z^{(1)}, \dots , z^{(n-2)}\}$ is an orthonormal basis of the orthocomplement of
$\{z^{(1)}, \dots , z^{(n-2)}\}$ is an orthonormal basis of the orthocomplement of ![]() $\text {Span}\,\{x, y\}$. (Note that
$\text {Span}\,\{x, y\}$. (Note that ![]() $n> 3$ is assumed because
$n> 3$ is assumed because ![]() if
if ![]() $n = 3$.) By (7.6),
$n = 3$.) By (7.6),

By Corollary 7.5, if ![]() $n> 3$,
$n> 3$, ![]() $\mathscr {B}(\alpha )$ is a nontrivial idempotent in
$\mathscr {B}(\alpha )$ is a nontrivial idempotent in ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$.
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$.
Let ![]() $(\mathbb {V}, h)$ be a metric vector space of dimension
$(\mathbb {V}, h)$ be a metric vector space of dimension ![]() $n \geq 4$. In accord with [Reference Doubrov and The7, Definition
$n \geq 4$. In accord with [Reference Doubrov and The7, Definition ![]() $1.2$], a nonzero
$1.2$], a nonzero ![]() $\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is maximally degenerate if the stabilizer
$\mathscr {X} \in \mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is maximally degenerate if the stabilizer ![]() $O(h)_{[\mathscr {X}]}$ in
$O(h)_{[\mathscr {X}]}$ in ![]() $O(h)$ of
$O(h)$ of ![]() $[\mathscr {X}] \in \mathbb {P}(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }))$ has maximal dimension among subgroups of
$[\mathscr {X}] \in \mathbb {P}(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }))$ has maximal dimension among subgroups of ![]() $O(h)$ stabilizing a point in
$O(h)$ stabilizing a point in ![]() $\mathbb {P}(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }))$. Equivalently, the
$\mathbb {P}(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }))$. Equivalently, the ![]() $O(h)$-orbit of
$O(h)$-orbit of ![]() $\mathscr {X}$ has the minimal dimension possible among nontrivial
$\mathscr {X}$ has the minimal dimension possible among nontrivial ![]() $O(h)$-orbits in
$O(h)$-orbits in ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. By [Reference Doubrov and The7, Equation
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$. By [Reference Doubrov and The7, Equation ![]() $(3.2)$and Appendix B], when h is Euclidean, if
$(3.2)$and Appendix B], when h is Euclidean, if ![]() $n = 5$ or
$n = 5$ or ![]() $n \geq 7$ the tensor
$n \geq 7$ the tensor ![]() $\mathscr {B}(\alpha )$ of (12.16) is maximally degenerate with
$\mathscr {B}(\alpha )$ of (12.16) is maximally degenerate with 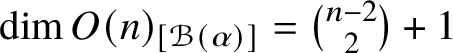 $\dim O(n)_{[\mathscr {B}(\alpha )]} = \binom {n-2}{2} + 1$ and
$\dim O(n)_{[\mathscr {B}(\alpha )]} = \binom {n-2}{2} + 1$ and ![]() $O(n)$-orbit of dimension
$O(n)$-orbit of dimension ![]() $2n-4$. Moreover, by [Reference Doubrov and The7, Theorem
$2n-4$. Moreover, by [Reference Doubrov and The7, Theorem ![]() $1.3$], if
$1.3$], if ![]() $n \geq 7$, any maximally degenerate element of
$n \geq 7$, any maximally degenerate element of ![]() $\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is in the
$\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast })$ is in the ![]() $O(n)$-orbit of a nonzero multiple of
$O(n)$-orbit of a nonzero multiple of ![]() $\mathscr {B}(\alpha )$ and any element of
$\mathscr {B}(\alpha )$ and any element of ![]() $\mathbb {P}(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }))$ stabilized by
$\mathbb {P}(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }))$ stabilized by ![]() $\dim O(n)_{[\mathscr {B}(\alpha )]}$ equals
$\dim O(n)_{[\mathscr {B}(\alpha )]}$ equals ![]() $[\mathscr {B}(\alpha )]$ (this gives an alternative proof that some multiple of
$[\mathscr {B}(\alpha )]$ (this gives an alternative proof that some multiple of ![]() $\mathscr {B}(\alpha )$ is idempotent, for
$\mathscr {B}(\alpha )$ is idempotent, for ![]() $[\mathscr {B}(\alpha )\ast \mathscr {B}(\alpha )]$ is stabilized by
$[\mathscr {B}(\alpha )\ast \mathscr {B}(\alpha )]$ is stabilized by ![]() $\dim O(n)_{[\mathscr {B}(\alpha )]}$ and so must equal
$\dim O(n)_{[\mathscr {B}(\alpha )]}$ and so must equal ![]() $[\mathscr {B}(\alpha )]$). The cases
$[\mathscr {B}(\alpha )]$). The cases ![]() $n \in \{4, 5, 6\}$ require special treatment; if
$n \in \{4, 5, 6\}$ require special treatment; if ![]() $n = 5$, there are maximally degenerate tensors not orthogonally equivalent to a multiple of
$n = 5$, there are maximally degenerate tensors not orthogonally equivalent to a multiple of ![]() $\mathscr {B}(\alpha )$, while if
$\mathscr {B}(\alpha )$, while if ![]() $n \in \{4, 6\}$,
$n \in \{4, 6\}$, ![]() $\mathscr {B}(\alpha )$ is not maximally degenerate. In these cases the maximally degenerate tensors can be built from Kähler–Weyl tensors; see [Reference Doubrov and The7].
$\mathscr {B}(\alpha )$ is not maximally degenerate. In these cases the maximally degenerate tensors can be built from Kähler–Weyl tensors; see [Reference Doubrov and The7].
If both inertial indices of h are least ![]() $2$, there are x and y spanning a
$2$, there are x and y spanning a ![]() $2$-dimensional h-null subspace of
$2$-dimensional h-null subspace of ![]() $\mathbb {V}^{\ast }$, and it follows from (6.35) that
$\mathbb {V}^{\ast }$, and it follows from (6.35) that ![]() $(x\wedge y)\otimes (x \wedge y)$ is a nontrivial square-zero element in
$(x\wedge y)\otimes (x \wedge y)$ is a nontrivial square-zero element in ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$. By [Reference Doubrov and The7], any maximally degenerate Weyl tensor is in the
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$. By [Reference Doubrov and The7], any maximally degenerate Weyl tensor is in the ![]() $O(h)$ orbit of a nonzero multiple of this tensor. Its stabilizer in
$O(h)$ orbit of a nonzero multiple of this tensor. Its stabilizer in ![]() $O(h)$ has dimension
$O(h)$ has dimension 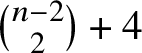 $\binom {n-2}{2} + 4$.
$\binom {n-2}{2} + 4$.
If h has negative inertial index 1, for ![]() $\mathscr {Z}^{(\alpha )}$ as in the proof of Lemma 7.3,
$\mathscr {Z}^{(\alpha )}$ as in the proof of Lemma 7.3, ![]() $\mathscr {Z}^{A} = \sum _{\alpha \in A}\mathscr {Z}^{(\alpha )}$ is square-zero for any nonempty subset
$\mathscr {Z}^{A} = \sum _{\alpha \in A}\mathscr {Z}^{(\alpha )}$ is square-zero for any nonempty subset ![]() $A \subset \{1, \dots , n-3\}$. The elements
$A \subset \{1, \dots , n-3\}$. The elements ![]() $\mathscr {Z}^{A}$ and
$\mathscr {Z}^{A}$ and ![]() $\mathscr {Z}^{B}$ are orthogonally equivalent if and only if A and B have the same cardinality, and by [Reference Doubrov and The7, Theorem
$\mathscr {Z}^{B}$ are orthogonally equivalent if and only if A and B have the same cardinality, and by [Reference Doubrov and The7, Theorem ![]() $4.2$],
$4.2$], ![]() $\mathscr {Z}^{\{1, \dots , n-3\}}$ is maximally degenerate having stabilizer of dimension
$\mathscr {Z}^{\{1, \dots , n-3\}}$ is maximally degenerate having stabilizer of dimension 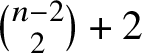 $\binom {n-2}{2} + 2$.
$\binom {n-2}{2} + 2$.
Example 12.5. This example shows that, when ![]() $\dim \mathbb {V} \geq 6$,
$\dim \mathbb {V} \geq 6$, ![]() $(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ contains subalgebras isomorphic to
$(\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ contains subalgebras isomorphic to ![]() $3$-dimensional Matsuo algebras.
$3$-dimensional Matsuo algebras.
Straightforward computations using (6.12), (6.18), and (7.10) show that if ![]() are pairwise orthogonal idempotents of ranks
are pairwise orthogonal idempotents of ranks ![]() $a_{1}$,
$a_{1}$, ![]() $a_{2}$, and
$a_{2}$, and ![]() $a_{3}$, each at least
$a_{3}$, each at least ![]() $2$, and
$2$, and ![]() $\mathscr {B}_{ij} = \mathscr {B}(\alpha (i), \alpha (j))$ for
$\mathscr {B}_{ij} = \mathscr {B}(\alpha (i), \alpha (j))$ for ![]() $1 \leq i < j \leq 3$, there hold
$1 \leq i < j \leq 3$, there hold
 $$ \begin{align} \begin{split} 2&(a_{1} + a_{2}-1)(a + a_{3} - 1)\mathscr{B}_{12}\ast \mathscr{B}_{13} \\ &= (a_{3}(a_{1}+a_{2}-1)\mathscr{B}_{12} + a_{2}(a_{1} + a_{3} - 1)\mathscr{B}_{13} - a_{1}(a_{2}+a_{3}-1)\mathscr{B}_{23},\\ \langle&\mathscr{B}_{12}, \mathscr{B}_{13}\rangle = \tfrac{2a_{1}a_{2}a_{3}}{(a_{1} + a_{2} - 1)(a_{1} + a_{3} - 1)(a_{1} - 1)}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} 2&(a_{1} + a_{2}-1)(a + a_{3} - 1)\mathscr{B}_{12}\ast \mathscr{B}_{13} \\ &= (a_{3}(a_{1}+a_{2}-1)\mathscr{B}_{12} + a_{2}(a_{1} + a_{3} - 1)\mathscr{B}_{13} - a_{1}(a_{2}+a_{3}-1)\mathscr{B}_{23},\\ \langle&\mathscr{B}_{12}, \mathscr{B}_{13}\rangle = \tfrac{2a_{1}a_{2}a_{3}}{(a_{1} + a_{2} - 1)(a_{1} + a_{3} - 1)(a_{1} - 1)}. \end{split} \end{align} $$Note that there must hold ![]() $n \geq a + a_{2} + a_{3} \geq 6$.
$n \geq a + a_{2} + a_{3} \geq 6$.
Suppose that ![]() $a_{1} = a_{2} = a_{3} = 2$. Then (12.17) becomes
$a_{1} = a_{2} = a_{3} = 2$. Then (12.17) becomes 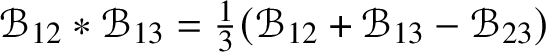 $\mathscr {B}_{12}\ast \mathscr {B}_{13} = \tfrac {1}{3}(\mathscr {B}_{12} + \mathscr {B}_{13} - \mathscr {B}_{23})$. Using this relation it is straightforward to check that the elements
$\mathscr {B}_{12}\ast \mathscr {B}_{13} = \tfrac {1}{3}(\mathscr {B}_{12} + \mathscr {B}_{13} - \mathscr {B}_{23})$. Using this relation it is straightforward to check that the elements 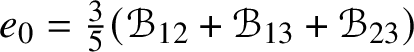 $e_{0} = \tfrac {3}{5}(\mathscr {B}_{12} + \mathscr {B}_{13} + \mathscr {B}_{23})$,
$e_{0} = \tfrac {3}{5}(\mathscr {B}_{12} + \mathscr {B}_{13} + \mathscr {B}_{23})$,  $e_{1} = \tfrac {3}{5}(\mathscr {B}_{12} + \mathscr {B}_{13} -\tfrac {2}{3} \mathscr {B}_{23})$,
$e_{1} = \tfrac {3}{5}(\mathscr {B}_{12} + \mathscr {B}_{13} -\tfrac {2}{3} \mathscr {B}_{23})$, 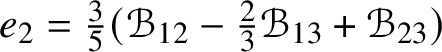 $e_{2} = \tfrac {3}{5}(\mathscr {B}_{12} -\tfrac {2}{3} \mathscr {B}_{13} + \mathscr {B}_{23})$, and
$e_{2} = \tfrac {3}{5}(\mathscr {B}_{12} -\tfrac {2}{3} \mathscr {B}_{13} + \mathscr {B}_{23})$, and  $e_{3} = \tfrac {3}{5}(-\tfrac {2}{3}\mathscr {B}_{12} + \mathscr {B}_{13} + \mathscr {B}_{23})$ are idempotents satisfying
$e_{3} = \tfrac {3}{5}(-\tfrac {2}{3}\mathscr {B}_{12} + \mathscr {B}_{13} + \mathscr {B}_{23})$ are idempotents satisfying ![]() $3(e_{1} + e_{2} + e_{2}) = 4e_{0}$ and the relations
$3(e_{1} + e_{2} + e_{2}) = 4e_{0}$ and the relations
 $$ \begin{align} \begin{aligned} {} &e_{0}\ast e_{i} = e_{i},& &e_{i}\ast e_{j} = \tfrac{1}{6}(e_{i} + e_{j}- e_{i\wedge j}), & &1\leq i \neq j \leq 3,& \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {} &e_{0}\ast e_{i} = e_{i},& &e_{i}\ast e_{j} = \tfrac{1}{6}(e_{i} + e_{j}- e_{i\wedge j}), & &1\leq i \neq j \leq 3,& \end{aligned} \end{align} $$where ![]() $i \wedge j$ is the unique element of
$i \wedge j$ is the unique element of ![]() $\{1, 2, 3\}$ distinct from i and j. From (12.17) it follows that
$\{1, 2, 3\}$ distinct from i and j. From (12.17) it follows that ![]() $\langle \mathscr {B}_{ij}, \mathscr {B}_{ik}\rangle = 16/9$ and so, for
$\langle \mathscr {B}_{ij}, \mathscr {B}_{ik}\rangle = 16/9$ and so, for ![]() $1 \leq i \neq j \leq 3$,
$1 \leq i \neq j \leq 3$, ![]() $|e_{0}|^{2} = 48/5$,
$|e_{0}|^{2} = 48/5$, ![]() $|e_{i}|^{2} = 64/15 = \langle e_{0}, e_{i}\rangle $, and
$|e_{i}|^{2} = 64/15 = \langle e_{0}, e_{i}\rangle $, and ![]() $\langle e_{i}, e_{j}\rangle = 32/45$. These norm calculations together with the relations (12.18) show that the subalgebra
$\langle e_{i}, e_{j}\rangle = 32/45$. These norm calculations together with the relations (12.18) show that the subalgebra ![]() $\text {Span}\,\{e_{1}, e_{2}, e_{3}\} \subset (\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is the
$\text {Span}\,\{e_{1}, e_{2}, e_{3}\} \subset (\mathscr {MC}_{\mathscr {W}}(\mathbb {V}^{\ast }), \ast )$ is the ![]() $3$-dimensional algebra based on the Fischer space with one line
$3$-dimensional algebra based on the Fischer space with one line ![]() $\{1, 2, 3\}$ and having parameters
$\{1, 2, 3\}$ and having parameters ![]() $\gamma = 512/15$ and
$\gamma = 512/15$ and ![]() $\delta = 2/3$ defined by Matsuo in [Reference Matsuo26, Sections
$\delta = 2/3$ defined by Matsuo in [Reference Matsuo26, Sections ![]() $3.2$and
$3.2$and ![]() $3.3$]Footnote 2; this algebra is denoted
$3.3$]Footnote 2; this algebra is denoted 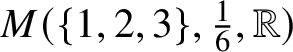 $M(\{1, 2, 3\}, \tfrac {1}{6}, \mathbb R)$ in the notations of [Reference Hall, Rehren and Shpectorov15].
$M(\{1, 2, 3\}, \tfrac {1}{6}, \mathbb R)$ in the notations of [Reference Hall, Rehren and Shpectorov15].
Acknowledgements
I thank Vladimir Tkachev for his interest in this work, for helpful comments on the first version and for giving me access to related work in preparation. I thank Mamuka Jibladze for comments (unrelated to this article) that brought to my attention [Reference Èlashvili8] and [Reference Popov31].
Conflicts of interest
None.