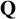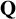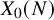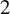1 Introduction
1.1 Background
The Conjecture of Birch and Swinnerton-Dyer (‘BSD’ for short), originally formulated based on extensive computations by Birch and Swinnerton-Dyer [Reference Birch and Swinnerton-Dyer8] in the 1960s for elliptic curves over
![]() ${\mathbf {Q}}$
, is one of the most important open conjectures in number theory. For example, it is one of the seven ‘Millennium Problems’, for whose solution the Clay Foundation is offering a million dollars each. It relates in a surprising way analytic invariants of an elliptic curve E, which are obtained via its L-series from its local properties (essentially the number of points modulo p on E, for all prime numbers p), to global arithmetic invariants like the rank of the Mordell–Weil group
${\mathbf {Q}}$
, is one of the most important open conjectures in number theory. For example, it is one of the seven ‘Millennium Problems’, for whose solution the Clay Foundation is offering a million dollars each. It relates in a surprising way analytic invariants of an elliptic curve E, which are obtained via its L-series from its local properties (essentially the number of points modulo p on E, for all prime numbers p), to global arithmetic invariants like the rank of the Mordell–Weil group
![]() $E({\mathbf {Q}})$
, its regulator, and the rather mysterious Tate–Shafarevich group
$E({\mathbf {Q}})$
, its regulator, and the rather mysterious Tate–Shafarevich group ![]() . The conjecture has been generalized to cover all abelian varieties over all algebraic number fields. It consists of two parts, which we will explain for the case of an abelian variety A of dimension g over
. The conjecture has been generalized to cover all abelian varieties over all algebraic number fields. It consists of two parts, which we will explain for the case of an abelian variety A of dimension g over
![]() ${\mathbf {Q}}$
.
${\mathbf {Q}}$
.
One attaches to A its L-function
![]() $L(A/{\mathbf {Q}},s)$
, which is defined by an Euler product over all prime numbers p. If A is the Jacobian variety of a curve X of genus g, the Euler factor at p for a prime p of good reduction is determined by the number of
$L(A/{\mathbf {Q}},s)$
, which is defined by an Euler product over all prime numbers p. If A is the Jacobian variety of a curve X of genus g, the Euler factor at p for a prime p of good reduction is determined by the number of
![]() ${\mathbf {F}}_{p^n}$
-points on the mod p reduction of X for
${\mathbf {F}}_{p^n}$
-points on the mod p reduction of X for
![]() $n \leq g$
. It follows from the Weil conjectures for varieties over finite fields that the Euler product converges for
$n \leq g$
. It follows from the Weil conjectures for varieties over finite fields that the Euler product converges for
![]() $\operatorname {Re}(s)> \frac {3}{2}$
to a holomorphic function. A standard conjecture predicts that
$\operatorname {Re}(s)> \frac {3}{2}$
to a holomorphic function. A standard conjecture predicts that
![]() $L(A/{\mathbf {Q}},s)$
extends to an entire function; this is known when A is modular (i.e., occurs as an isogeny factor of the Jacobian
$L(A/{\mathbf {Q}},s)$
extends to an entire function; this is known when A is modular (i.e., occurs as an isogeny factor of the Jacobian
![]() $J_0(N)$
of one of the modular curves
$J_0(N)$
of one of the modular curves
![]() $X_0(N)$
). By the Modularity Theorem of Wiles and others [Reference Breuil, Conrad, Diamond and Taylor15, Reference Taylor and Wiles114, Reference Wiles116], this is always the case when A is an elliptic curve over
$X_0(N)$
). By the Modularity Theorem of Wiles and others [Reference Breuil, Conrad, Diamond and Taylor15, Reference Taylor and Wiles114, Reference Wiles116], this is always the case when A is an elliptic curve over
![]() ${\mathbf {Q}}$
(this is now a special case of Serre’s Modularity Conjecture [Reference Khare and Wintenberger61]).
${\mathbf {Q}}$
(this is now a special case of Serre’s Modularity Conjecture [Reference Khare and Wintenberger61]).
We now introduce the relevant global invariants of A. By the Mordell–Weil Theorem, the abelian group
![]() $A({\mathbf {Q}})$
of rational points on A is finitely generated, so it splits as
$A({\mathbf {Q}})$
of rational points on A is finitely generated, so it splits as
![]() $A({\mathbf {Q}}) \cong A({\mathbf {Q}})_{\mathrm {tors}} \oplus {\mathbf {Z}}^r$
, where
$A({\mathbf {Q}}) \cong A({\mathbf {Q}})_{\mathrm {tors}} \oplus {\mathbf {Z}}^r$
, where
![]() $A({\mathbf {Q}})_{\mathrm {tors}}$
is the finite torsion subgroup and r is a nonnegative integer, the rank of
$A({\mathbf {Q}})_{\mathrm {tors}}$
is the finite torsion subgroup and r is a nonnegative integer, the rank of
![]() $A({\mathbf {Q}})$
. There is a natural positive definite quadratic form
$A({\mathbf {Q}})$
. There is a natural positive definite quadratic form
![]() $\hat {h}$
on
$\hat {h}$
on
![]() $A({\mathbf {Q}}) \otimes _{\mathbf {Z}} {\mathbf {R}} \cong {\mathbf {R}}^r$
, the canonical height, turning
$A({\mathbf {Q}}) \otimes _{\mathbf {Z}} {\mathbf {R}} \cong {\mathbf {R}}^r$
, the canonical height, turning
![]() $A({\mathbf {Q}})/A({\mathbf {Q}})_{\mathrm {tors}}$
into a lattice in a euclidean vector space. The squared covolume of this lattice (equivalently, the determinant of the Gram matrix of
$A({\mathbf {Q}})/A({\mathbf {Q}})_{\mathrm {tors}}$
into a lattice in a euclidean vector space. The squared covolume of this lattice (equivalently, the determinant of the Gram matrix of
![]() $\hat {h}$
with respect to a lattice basis) is the regulator
$\hat {h}$
with respect to a lattice basis) is the regulator
![]() $\operatorname {Reg}_{A/{\mathbf {Q}}}$
. The final global arithmetic invariant of A that we need is the Tate–Shafarevich group
$\operatorname {Reg}_{A/{\mathbf {Q}}}$
. The final global arithmetic invariant of A that we need is the Tate–Shafarevich group ![]() . It can be defined as the localization kernel
. It can be defined as the localization kernel
in Galois cohomology; here,
![]() ${\mathbf {Q}}_v$
denotes the completion of
${\mathbf {Q}}_v$
denotes the completion of
![]() ${\mathbf {Q}}$
with respect to a place v, and the direct sum is over all places of
${\mathbf {Q}}$
with respect to a place v, and the direct sum is over all places of
![]() ${\mathbf {Q}}$
. Geometrically,
${\mathbf {Q}}$
. Geometrically, ![]() is the group of equivalence classes of everywhere locally trivial
is the group of equivalence classes of everywhere locally trivial
![]() $A/{\mathbf {Q}}$
-torsors. This group is conjectured to be finite, but this is not known in general; for example, it is not known for a single elliptic curve with (algebraic or analytic) rank at least
$A/{\mathbf {Q}}$
-torsors. This group is conjectured to be finite, but this is not known in general; for example, it is not known for a single elliptic curve with (algebraic or analytic) rank at least
![]() $2$
.
$2$
.
We also need some local invariants. To each prime p, one associates the Tamagawa number
![]() $c_p(A)$
; this is the number of connected components of the special fiber at p of the Néron model
$c_p(A)$
; this is the number of connected components of the special fiber at p of the Néron model
![]() $\mathscr {A}/{\mathbf {Z}}$
of A that are fixed by Frobenius and equals
$\mathscr {A}/{\mathbf {Z}}$
of A that are fixed by Frobenius and equals
![]() $1$
for all primes of good reduction. Let
$1$
for all primes of good reduction. Let
![]() $(\omega _1, \ldots , \omega _g)$
be the pullback to
$(\omega _1, \ldots , \omega _g)$
be the pullback to
![]() ${\operatorname {H}}^0(A, \Omega ^1)$
of a basis of the free
${\operatorname {H}}^0(A, \Omega ^1)$
of a basis of the free
![]() ${\mathbf {Z}}$
-module
${\mathbf {Z}}$
-module
![]() ${\operatorname {H}}^0(\mathscr {A}, \Omega ^1)$
of rank g. Then the real period of A is the volume of
${\operatorname {H}}^0(\mathscr {A}, \Omega ^1)$
of rank g. Then the real period of A is the volume of
![]() $A({\mathbf {R}})$
measured using
$A({\mathbf {R}})$
measured using
![]() $|\omega _1 \wedge \dots \wedge \omega _g|$
:
$|\omega _1 \wedge \dots \wedge \omega _g|$
:
![]() $\Omega _A = \int _{A({\mathbf {R}})} |\omega _1 \wedge \dots \wedge \omega _g|$
.
$\Omega _A = \int _{A({\mathbf {R}})} |\omega _1 \wedge \dots \wedge \omega _g|$
.
The weak BSD or BSD rank conjecture says that
![]() $L(A/{\mathbf {Q}},s)$
has an analytic continuation to a neighborhood of
$L(A/{\mathbf {Q}},s)$
has an analytic continuation to a neighborhood of
![]() $s = 1$
and
$s = 1$
and
The order of vanishing of
![]() $L(A/{\mathbf {Q}}, s)$
at
$L(A/{\mathbf {Q}}, s)$
at
![]() $s = 1$
is also called the analytic rank of
$s = 1$
is also called the analytic rank of
![]() $A/{\mathbf {Q}}$
.
$A/{\mathbf {Q}}$
.
We will from now on assume that A is principally polarized – for example, the Jacobian variety of a curve. In particular,
![]() $A \cong A^{\vee }$
, where
$A \cong A^{\vee }$
, where
![]() $A^{\vee }$
is the dual abelian variety. Then the strong BSD conjecture says that in addition
$A^{\vee }$
is the dual abelian variety. Then the strong BSD conjecture says that in addition ![]() is finite and
is finite and

Since all the other invariants of A can (usually) be computed at least numerically, we define the analytic order of Sha to be

Assuming the BSD rank conjecture, strong BSD can then be phrased as ‘![]() is finite and
is finite and ![]() ’,
’,
Even the weak BSD conjecture for elliptic curves over
![]() ${\mathbf {Q}}$
is wide open in general (this is the Clay Millennium Problem mentioned above). However, the strong BSD conjecture has been verified for many ‘small’ elliptic curves; see below. In this article, we verify the strong BSD conjecture for the first time in dimension greater than
${\mathbf {Q}}$
is wide open in general (this is the Clay Millennium Problem mentioned above). However, the strong BSD conjecture has been verified for many ‘small’ elliptic curves; see below. In this article, we verify the strong BSD conjecture for the first time in dimension greater than
![]() $1$
– namely, for a number of abelian surfaces
$1$
– namely, for a number of abelian surfaces
![]() $A/{\mathbf {Q}}$
, in a situation where it cannot be reduced to BSD for some elliptic curves. Concretely, this means that A is absolutely simple.
$A/{\mathbf {Q}}$
, in a situation where it cannot be reduced to BSD for some elliptic curves. Concretely, this means that A is absolutely simple.
Recall that an abelian variety A of positive dimension over
![]() ${\mathbf {Q}}$
is absolutely simple if
${\mathbf {Q}}$
is absolutely simple if
![]() $A_{{\overline {{\mathbf {Q}}}}}$
is not isogenous to a product of at least two abelian varieties of positive dimension. An abelian variety of dimension g whose endomorphism ring
$A_{{\overline {{\mathbf {Q}}}}}$
is not isogenous to a product of at least two abelian varieties of positive dimension. An abelian variety of dimension g whose endomorphism ring
![]() $\mathrm {End}_{\mathbf {Q}}(A)$
is isomorphic to an order
$\mathrm {End}_{\mathbf {Q}}(A)$
is isomorphic to an order
![]() $\mathcal {O}$
in a totally real number field F of degree
$\mathcal {O}$
in a totally real number field F of degree
![]() $[F:{\mathbf {Q}}] = g$
is said to have real multiplication (RM).
$[F:{\mathbf {Q}}] = g$
is said to have real multiplication (RM).
Absolutely simple abelian varieties with real multiplication over
![]() ${\mathbf {Q}}$
are modular (see theorem 2.1 for references). This means that A can be obtained as an isogeny factor of some
${\mathbf {Q}}$
are modular (see theorem 2.1 for references). This means that A can be obtained as an isogeny factor of some
![]() $J_0(N)$
, where
$J_0(N)$
, where
![]() $J_0(N)$
denotes the Jacobian variety of the modular curve
$J_0(N)$
denotes the Jacobian variety of the modular curve
![]() $X_0(N)$
. These isogeny factors correspond to (Galois orbits of) newforms in
$X_0(N)$
. These isogeny factors correspond to (Galois orbits of) newforms in
![]() $S_2(\Gamma _0(N))$
; see theorem 2.1 below. (Note that we reserve the term ‘modular’ for
$S_2(\Gamma _0(N))$
; see theorem 2.1 below. (Note that we reserve the term ‘modular’ for
![]() $\mathrm {GL}_2$
-type abelian varieties here as opposed to the more general property of being ‘automorphic’; see [Reference Boxer, Calegari, Gee and Pilloni14, § 9.1].)
$\mathrm {GL}_2$
-type abelian varieties here as opposed to the more general property of being ‘automorphic’; see [Reference Boxer, Calegari, Gee and Pilloni14, § 9.1].)
1.2 General results
While the BSD conjecture is wide open in general, there are some cases where parts of it are known to be true. Assume that
![]() $A/{\mathbf {Q}}$
is an absolutely simple abelian variety of dimension g with real multiplication by an order
$A/{\mathbf {Q}}$
is an absolutely simple abelian variety of dimension g with real multiplication by an order
![]() $\mathcal {O}$
in a totally real number field of degree g. Then A is of
$\mathcal {O}$
in a totally real number field of degree g. Then A is of
![]() $\mathrm {GL}_2$
-type; in particular, for each prime ideal
$\mathrm {GL}_2$
-type; in particular, for each prime ideal
![]() $\mathfrak {p}$
of
$\mathfrak {p}$
of
![]() $\mathcal {O}$
, the common kernel
$\mathcal {O}$
, the common kernel
![]() $A[\mathfrak {p}]$
of all elements of
$A[\mathfrak {p}]$
of all elements of
![]() $\mathfrak {p}$
acting on A is a
$\mathfrak {p}$
acting on A is a
![]() $2$
-dimensional vector space over
$2$
-dimensional vector space over
![]() $\mathcal {O}/\mathfrak {p}$
, and hence induces a Galois representation into
$\mathcal {O}/\mathfrak {p}$
, and hence induces a Galois representation into
![]() $\mathrm {GL}_2(\mathcal {O}/\mathfrak {p})$
. In this situation, there is a newform f of weight
$\mathrm {GL}_2(\mathcal {O}/\mathfrak {p})$
. In this situation, there is a newform f of weight
![]() $2$
and some level N with q-expansion coefficients that generate an order commensurable with
$2$
and some level N with q-expansion coefficients that generate an order commensurable with
![]() $\mathcal {O}$
and such that A is an isogeny factor of
$\mathcal {O}$
and such that A is an isogeny factor of
![]() $J_0(N)$
; furthermore,
$J_0(N)$
; furthermore,
where
![]() $\sigma $
acts on the q-expansion coefficients. Since it is known that
$\sigma $
acts on the q-expansion coefficients. Since it is known that
![]() $L(f^\sigma , s)$
is an entire function, the same is true for
$L(f^\sigma , s)$
is an entire function, the same is true for
![]() $L(A/{\mathbf {Q}}, s)$
. So for
$L(A/{\mathbf {Q}}, s)$
. So for
![]() $A/{\mathbf {Q}}$
with RM, we can at least speak of the analytic rank
$A/{\mathbf {Q}}$
with RM, we can at least speak of the analytic rank
![]() $r_{\mathrm {an}}$
and the leading coefficient
$r_{\mathrm {an}}$
and the leading coefficient
![]() $L^*(A/{\mathbf {Q}},1)$
of the L-function at
$L^*(A/{\mathbf {Q}},1)$
of the L-function at
![]() $s = 1$
. The parity of the order of vanishing of
$s = 1$
. The parity of the order of vanishing of
![]() $L(f^\sigma , s)$
at
$L(f^\sigma , s)$
at
![]() $s = 1$
does not depend on
$s = 1$
does not depend on
![]() $\sigma $
(it is determined by the eigenvalue
$\sigma $
(it is determined by the eigenvalue
![]() $\varepsilon _N$
of
$\varepsilon _N$
of
![]() $f^\sigma $
under the Fricke involution, which is the same for all
$f^\sigma $
under the Fricke involution, which is the same for all
![]() $f^\sigma $
), and the order of vanishing itself does not depend on
$f^\sigma $
), and the order of vanishing itself does not depend on
![]() $\sigma $
when
$\sigma $
when
![]() $ {\mathrm {ord}}_{s=1} L(f^\sigma ,s) \le 1$
for some
$ {\mathrm {ord}}_{s=1} L(f^\sigma ,s) \le 1$
for some
![]() $\sigma $
, so in this case, we have that
$\sigma $
, so in this case, we have that
![]() $r_{\mathrm {an}} = g \cdot {\mathrm {ord}}_{s=1} L(f,s)$
, where
$r_{\mathrm {an}} = g \cdot {\mathrm {ord}}_{s=1} L(f,s)$
, where
![]() $ {\mathrm {ord}}_{s=1} L(f,s) := {\mathrm {ord}}_{s=1} L(f^\sigma ,s)$
for any
$ {\mathrm {ord}}_{s=1} L(f,s) := {\mathrm {ord}}_{s=1} L(f^\sigma ,s)$
for any
![]() $\sigma $
; see [Reference Gross and Zagier52, Cor. V.1.3]. We call
$\sigma $
; see [Reference Gross and Zagier52, Cor. V.1.3]. We call
![]() $ {\mathrm {ord}}_{s=1} L(f,s)$
the L-rank of A in this case and abbreviate it as
$ {\mathrm {ord}}_{s=1} L(f,s)$
the L-rank of A in this case and abbreviate it as
![]() $L\!\operatorname {-rk} A$
. If the BSD rank conjecture holds for A, then the L-rank of A is the same as the rank of
$L\!\operatorname {-rk} A$
. If the BSD rank conjecture holds for A, then the L-rank of A is the same as the rank of
![]() $A({\mathbf {Q}})$
as an
$A({\mathbf {Q}})$
as an
![]() $\mathcal {O}$
-module.
$\mathcal {O}$
-module.
Based on work of Gross–Zagier [Reference Gross and Zagier52] relating the canonical height of Heegner points to
![]() $L^{(g)}(A/K,1)$
for suitable imaginary quadratic fields K, Kolyvagin [Reference Kolyvagin63] (for modular elliptic curves) and Kolyvagin–Logachëv [Reference Kolyvagin and Logachëv64] (for modular abelian varieties in general) were able to show that the BSD rank conjecture holds under the assumption that the L-rank is
$L^{(g)}(A/K,1)$
for suitable imaginary quadratic fields K, Kolyvagin [Reference Kolyvagin63] (for modular elliptic curves) and Kolyvagin–Logachëv [Reference Kolyvagin and Logachëv64] (for modular abelian varieties in general) were able to show that the BSD rank conjecture holds under the assumption that the L-rank is
![]() $0$
or
$0$
or
![]() $1$
, that in this case,
$1$
, that in this case, ![]() is finite (this is the only case where we know finiteness), and that
is finite (this is the only case where we know finiteness), and that ![]() is a rational number.
is a rational number.
The rational number ![]() can be computed when A is an elliptic curve, and we show in this paper how to do that when A is a modular abelian surface. To complete the verification of the strong BSD Conjecture for A, it remains to determine
can be computed when A is an elliptic curve, and we show in this paper how to do that when A is a modular abelian surface. To complete the verification of the strong BSD Conjecture for A, it remains to determine ![]() and to check that the two numbers agree.
and to check that the two numbers agree.
This involves showing that ![]() is trivial for all primes
is trivial for all primes
![]() $p \notin S$
, where S is an explicit finite set of primes, and then determining
$p \notin S$
, where S is an explicit finite set of primes, and then determining ![]() for the finitely many
for the finitely many
![]() $p \in S$
. When A is an elliptic curve, a suitable set S (or even an explicit annihilator of
$p \in S$
. When A is an elliptic curve, a suitable set S (or even an explicit annihilator of ![]() ) can be extracted from Kolyvagin’s work and subsequent refinements; see below. We show in this paper how to obtain a suitable set S when A is a modular abelian surface.
) can be extracted from Kolyvagin’s work and subsequent refinements; see below. We show in this paper how to obtain a suitable set S when A is a modular abelian surface.
The remaining task is to determine ![]() for a given prime p. This is always possible in theory (assuming that
for a given prime p. This is always possible in theory (assuming that ![]() is finite), since one can compute the
is finite), since one can compute the
![]() $p^n$
-Selmer group of A for
$p^n$
-Selmer group of A for
![]() $n = 1,2,\ldots $
, which is defined as
$n = 1,2,\ldots $
, which is defined as
and sits in an exact sequence
Since we know
![]() $A({\mathbf {Q}})$
, this gives us
$A({\mathbf {Q}})$
, this gives us ![]() , and as soon as
, and as soon as ![]() , we have determined
, we have determined ![]() (and if
(and if ![]() , then
, then ![]() as well). For the computability of the Selmer group in theory, see [Reference Stoll110] for elliptic curves and [Reference Bruin, Poonen and Stoll16] in general. In practice, there are fairly tight limits on
as well). For the computability of the Selmer group in theory, see [Reference Stoll110] for elliptic curves and [Reference Bruin, Poonen and Stoll16] in general. In practice, there are fairly tight limits on
![]() $p^n$
, since the computation requires the knowledge of the class and unit groups of number fields of degree growing quickly with
$p^n$
, since the computation requires the knowledge of the class and unit groups of number fields of degree growing quickly with
![]() $p^n$
, for which no really efficient algorithms are available so far.
$p^n$
, for which no really efficient algorithms are available so far.
If one has a conjecturally tight bound on ![]() , then another approach is to try and get a lower bound that agrees with the upper bound. If the upper bound is nontrivial, this involves showing the existence of nontrivial elements of
, then another approach is to try and get a lower bound that agrees with the upper bound. If the upper bound is nontrivial, this involves showing the existence of nontrivial elements of ![]() in some way. One possibility for this is ‘visibility’, which uses another related abelian variety B, for which one can construct a nontrivial map
in some way. One possibility for this is ‘visibility’, which uses another related abelian variety B, for which one can construct a nontrivial map
![]() $B({\mathbf {Q}}) \to {\operatorname {H}}^1({\mathbf {Q}}, A)$
, whose image one can show to contain nontrivial elements of
$B({\mathbf {Q}}) \to {\operatorname {H}}^1({\mathbf {Q}}, A)$
, whose image one can show to contain nontrivial elements of ![]() under suitable conditions. This is used for the example in Appendix A.
under suitable conditions. This is used for the example in Appendix A.
We now give a short overview of what has been done so far regarding the verification of the strong BSD Conjecture in concrete cases.
1.3 Exact verification of strong BSD for elliptic curves
In the case of elliptic curves, the various ingredients mentioned above have been worked out, made explicit and been improved to an extent that it was possible to verify the strong BSD conjecture for all elliptic curves E over
![]() ${\mathbf {Q}}$
of rank
${\mathbf {Q}}$
of rank
![]() $\le 1$
and conductor
$\le 1$
and conductor
![]() $N < 5000$
; see [Reference Creutz and Miller34, Reference Grigorov, Jorza, Patrikis, Stein and Tarniţǎ50, Reference Lawson and Wuthrich67, Reference Miller74, Reference Miller and Stoll75].
$N < 5000$
; see [Reference Creutz and Miller34, Reference Grigorov, Jorza, Patrikis, Stein and Tarniţǎ50, Reference Lawson and Wuthrich67, Reference Miller74, Reference Miller and Stoll75].
An explicit finite set S of primes such that ![]() for
for
![]() $p \notin S$
can be obtained using Kolyvagin’s work and refinements building on it [Reference Cha23, Reference Jetchev56]. The size of
$p \notin S$
can be obtained using Kolyvagin’s work and refinements building on it [Reference Cha23, Reference Jetchev56]. The size of ![]() for
for
![]() $p \in S$
can be obtained by several methods – for example, using Iwasawa theory and p-adic L-functions [Reference Stein and Wuthrich109] or by performing descents [Reference Bruin, Poonen and Stoll16, Reference Cremona, Fisher, O’Neil, Simon and Stoll27, Reference Cremona, Fisher, O’Neil, Simon and Stoll28, Reference Cremona, Fisher, O’Neil, Simon and Stoll29, Reference Cremona31, Reference Creutz33, Reference Creutz and Miller34, Reference Miller and Stoll75, Reference Schaefer and Stoll93, Reference Stoll110].
$p \in S$
can be obtained by several methods – for example, using Iwasawa theory and p-adic L-functions [Reference Stein and Wuthrich109] or by performing descents [Reference Bruin, Poonen and Stoll16, Reference Cremona, Fisher, O’Neil, Simon and Stoll27, Reference Cremona, Fisher, O’Neil, Simon and Stoll28, Reference Cremona, Fisher, O’Neil, Simon and Stoll29, Reference Cremona31, Reference Creutz33, Reference Creutz and Miller34, Reference Miller and Stoll75, Reference Schaefer and Stoll93, Reference Stoll110].
1.4 Numerical verification of strong BSD for higher-dimensional abelian varieties
Compared to the case of elliptic curves, considerably less has been done regarding the verification of the BSD conjectures for higher-dimensional abelian varieties A over
![]() ${\mathbf {Q}}$
. If A is not absolutely simple, then A splits up to isogeny (and possibly after base-change to an algebraic number field) as a product of abelian varieties of lower dimension. Since the validity of strong BSD is invariant under isogenies [Reference Tate113] and Weil restriction [Reference Milne77], this reduces the verification of strong BSD for A to cases of lower dimension. We will therefore assume that A is absolutely simple in the following.
${\mathbf {Q}}$
. If A is not absolutely simple, then A splits up to isogeny (and possibly after base-change to an algebraic number field) as a product of abelian varieties of lower dimension. Since the validity of strong BSD is invariant under isogenies [Reference Tate113] and Weil restriction [Reference Milne77], this reduces the verification of strong BSD for A to cases of lower dimension. We will therefore assume that A is absolutely simple in the following.
In [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and Wetherell45], all factors in the BSD formula except for the order of the Tate–Shafarevich group (only its
![]() $2$
-torsion is computed) and the analytic order of Sha are determined exactly in the L-rank
$2$
-torsion is computed) and the analytic order of Sha are determined exactly in the L-rank
![]() $0$
cases and numerically to high precision in the L-rank
$0$
cases and numerically to high precision in the L-rank
![]() $1$
cases for the Jacobian varieties of
$1$
cases for the Jacobian varieties of
![]() $29$
genus
$29$
genus
![]() $2$
curves over
$2$
curves over
![]() ${\mathbf {Q}}$
such that the Jacobians are absolutely simple, of
${\mathbf {Q}}$
such that the Jacobians are absolutely simple, of
![]() $\mathrm {GL}_2$
-type and have level
$\mathrm {GL}_2$
-type and have level
![]() $N \le 200$
. This work also includes results on three curves whose Jacobians are Weil restrictions of elliptic curves over
$N \le 200$
. This work also includes results on three curves whose Jacobians are Weil restrictions of elliptic curves over
![]() ${\mathbf {Q}}(\sqrt {-3})$
.
${\mathbf {Q}}(\sqrt {-3})$
.
More recently, van Bommel [Reference van Bommel11] has done computations similar to those in [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and Wetherell45] for various (in general non-modular) Jacobians of hyperelliptic curves of genus
![]() $\leq 5$
. He did not provably compute the regulator or the torsion subgroup, which means that the approximate value of
$\leq 5$
. He did not provably compute the regulator or the torsion subgroup, which means that the approximate value of ![]() that he computes may be off by a square rational factor. Van Bommel also provides an algorithm for the computation of the real period, which corrects the version described in [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and Wetherell45] in the case when some of the special fibers of a minimal regular model of the curve have multiple components.
that he computes may be off by a square rational factor. Van Bommel also provides an algorithm for the computation of the real period, which corrects the version described in [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and Wetherell45] in the case when some of the special fibers of a minimal regular model of the curve have multiple components.
However, it was still an open problem to provably compute ![]() as an exact rational number when A has positive rank and to determine
as an exact rational number when A has positive rank and to determine ![]() . See, for example, William Stein’s blog post [Reference Stein108] for the former.
. See, for example, William Stein’s blog post [Reference Stein108] for the former.
We now verify the strong BSD Conjecture unconditionally and exactly for all the curves in [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and Wetherell45] with absolutely simple Jacobian and all genus
![]() $2$
curves in the LMFDB [68] with absolutely simple modular Jacobian.
$2$
curves in the LMFDB [68] with absolutely simple modular Jacobian.
1.5 New general results in this paper
We note that, compared to elliptic curves, a number of additional difficulties show up when trying to verify strong BSD for higher-dimensional modular abelian varieties. By the Modularity Theorem, every elliptic curve E over
![]() ${\mathbf {Q}}$
of conductor N is the target of a nontrivial morphism
${\mathbf {Q}}$
of conductor N is the target of a nontrivial morphism
![]() $X_0(N) \to E$
. This makes it fairly easy to compute Heegner points on E. Also, elliptic curves are given explicitly by a Weierstrass equation, and a variety of algorithms are available for them. There is no comparable explicit representation of a general (modular) abelian variety of higher dimension. We can, however, work with curves X and their Jacobians. In particular, for hyperelliptic curves, a variety of algorithms exist. However, in general, there is only a dominant homomorphism from
$X_0(N) \to E$
. This makes it fairly easy to compute Heegner points on E. Also, elliptic curves are given explicitly by a Weierstrass equation, and a variety of algorithms are available for them. There is no comparable explicit representation of a general (modular) abelian variety of higher dimension. We can, however, work with curves X and their Jacobians. In particular, for hyperelliptic curves, a variety of algorithms exist. However, in general, there is only a dominant homomorphism from
![]() $J_0(N)$
to the Jacobian in question and no nontrivial morphism from
$J_0(N)$
to the Jacobian in question and no nontrivial morphism from
![]() $X_0(N)$
to the curve X. When there is such a morphism, the relevant computations are much simpler; we have dealt with this case for surfaces first, and the results are described in [Reference Keller and Stoll59]. In the other cases, the required arguments are much more subtle; for example, it is quite nontrivial to obtain a formula for the canonical height of a Heegner point on the Jacobian J of X from the Gross–Zagier formula.
$X_0(N)$
to the curve X. When there is such a morphism, the relevant computations are much simpler; we have dealt with this case for surfaces first, and the results are described in [Reference Keller and Stoll59]. In the other cases, the required arguments are much more subtle; for example, it is quite nontrivial to obtain a formula for the canonical height of a Heegner point on the Jacobian J of X from the Gross–Zagier formula.
In this paper, we overcome these difficulties and devise general methods to verify strong BSD exactly for absolutely simple modular Jacobians
![]() $J/{\mathbf {Q}}$
of L-rank
$J/{\mathbf {Q}}$
of L-rank
![]() $0$
and
$0$
and
![]() $1$
and apply them to several examples. Many of our results and algorithms apply to any dimension or at least to hyperelliptic Jacobians. We note that an abelian variety (assumed to be absolutely simple) is automatically a Jacobian when it is principally polarized and its dimension is
$1$
and apply them to several examples. Many of our results and algorithms apply to any dimension or at least to hyperelliptic Jacobians. We note that an abelian variety (assumed to be absolutely simple) is automatically a Jacobian when it is principally polarized and its dimension is
![]() $2$
or
$2$
or
![]() $3$
.
$3$
.
More specifically, given such a Jacobian J and/or an attached newform f, we do the following. (The numbers link to the corresponding sections.)
-
(2) We determine the (projective) images of the associated mod-
 $\mathfrak {p}$
Galois representations for all maximal ideals
$\mathfrak {p}$
Galois representations for all maximal ideals
 $\mathfrak {p}$
of the endomorphism ring; in particular, we determine which of them are reducible.
$\mathfrak {p}$
of the endomorphism ring; in particular, we determine which of them are reducible. -
(3) We develop an efficient algorithm for the computation of Heegner points, their canonical heights and Heegner indices. This involves the computation of Petersson norms of newforms of weight
 $2$
. We also provide the refined information of the Heegner index as a characteristic ideal of the endomorphism ring.
$2$
. We also provide the refined information of the Heegner index as a characteristic ideal of the endomorphism ring. -
(4) We derive explicit formulas for
 and
and  (where K is a Heegner field). When the L-rank is
(where K is a Heegner field). When the L-rank is
 $1$
, this involves some fairly nontrivial arguments.
$1$
, this involves some fairly nontrivial arguments. -
(5) We give an explicit upper bound for the set of primes dividing
 and for the primes dividing
and for the primes dividing  , where K is a Heegner field.
, where K is a Heegner field. -
(6) We perform
 $\mathfrak {p}$
-isogeny descents in some cases where the mod-
$\mathfrak {p}$
-isogeny descents in some cases where the mod-
 $\mathfrak {p}$
Galois representation is reducible to get an upper bound on the
$\mathfrak {p}$
Galois representation is reducible to get an upper bound on the
 $\mathfrak {p}$
-Selmer group and thus show that
$\mathfrak {p}$
-Selmer group and thus show that  .
. -
(7) We provide a feasible algorithm for the computation of p-adic L-functions in our setting.
-
(8) We provide an algorithm that, combining the above algorithms, verifies strong BSD for the Jacobian J (absolutely simple and modular) of a given genus
 $2$
curve X of level N or returns at least a small finite set of primes
$2$
curve X of level N or returns at least a small finite set of primes
 $\mathfrak {p}$
for which
$\mathfrak {p}$
for which  needs to be computed to finish the verification.
needs to be computed to finish the verification.
We also improve van Bommel’s algorithm for the determination of the real period so that it does not rely on a gcd computation with real numbers; see lemma 3.7.
Our methods and algorithms generalize to RM abelian varieties over
![]() ${\mathbf {Q}}$
of arbitrary dimension, provided one can compute Mordell–Weil groups and canonical heights and one has an analogue of algorithm 2.44. In joint work in progress with Pip Goodman and John Voight, we are planning to treat modular abelian varieties over totally real number fields.
${\mathbf {Q}}$
of arbitrary dimension, provided one can compute Mordell–Weil groups and canonical heights and one has an analogue of algorithm 2.44. In joint work in progress with Pip Goodman and John Voight, we are planning to treat modular abelian varieties over totally real number fields.
We then use the algorithms we developed to verify strong BSD exactly for the first time for a number of absolutely simple abelian surfaces. The specific examples are described below.
1.6 Examples
All computations were carried out with Magma [Reference Bosma, Cannon and Playoust13]. The code to reproduce our computations can be found at
The README.md file contains short descriptions of the Magma files and which sections in this paper they belong to.
Using the methods and algorithms developed in this paper, we verified strong BSD completely for the Jacobians of the following genus
![]() $2$
curves over
$2$
curves over
![]() ${\mathbf {Q}}$
(whose Jacobians are modular and absolutely simple).
${\mathbf {Q}}$
(whose Jacobians are modular and absolutely simple).
-
(a) The LMFDB [68] currently (as of September 2024) lists exactly
 $97$
genus
$97$
genus
 $2$
curves with absolutely simple Jacobian of
$2$
curves with absolutely simple Jacobian of
 $\mathrm {GL}_2$
-type; they all have level
$\mathrm {GL}_2$
-type; they all have level
 $\leq 1000$
. By their completeness statement, this comprises all such examples with absolute value of their discriminant at most
$\leq 1000$
. By their completeness statement, this comprises all such examples with absolute value of their discriminant at most
 $10^6$
and ‘small’ coefficients. We will refer to these as the LMFDB examples. Note that there are more newforms of weight
$10^6$
and ‘small’ coefficients. We will refer to these as the LMFDB examples. Note that there are more newforms of weight
 $2$
with real quadratic coefficients of level
$2$
with real quadratic coefficients of level
 $\leq 1000$
contained in the LMFDB; our algorithms would at least give an upper bound on the size of the Tate–Shafarevich group of their associated modular abelian variety given a Jacobian in their isogeny class. Some of the examples mentioned below provide such a Jacobian for additional newforms.
$\leq 1000$
contained in the LMFDB; our algorithms would at least give an upper bound on the size of the Tate–Shafarevich group of their associated modular abelian variety given a Jacobian in their isogeny class. Some of the examples mentioned below provide such a Jacobian for additional newforms. -
(b) The
 $28$
‘Hasegawa curves’ from [Reference Hasegawa54] that have absolutely simple Jacobian. These are all quotients of
$28$
‘Hasegawa curves’ from [Reference Hasegawa54] that have absolutely simple Jacobian. These are all quotients of
 $X_0(N)$
by a subgroup of Atkin–Lehner involutions. Because of this, these examples are easier to deal with (compare corollary 3.17, which shows that the computation of Heegner points is simpler in this case), which is why we treated them first, before extending the theory and algorithms to the general case. See [Reference Keller and Stoll59] for an overview of the results. Note that
$X_0(N)$
by a subgroup of Atkin–Lehner involutions. Because of this, these examples are easier to deal with (compare corollary 3.17, which shows that the computation of Heegner points is simpler in this case), which is why we treated them first, before extending the theory and algorithms to the general case. See [Reference Keller and Stoll59] for an overview of the results. Note that
 $X_0(161)/\langle {w_7, w_{23}}\rangle $
is the only curve on this list whose Jacobian is not isogenous to the Jacobian of one of the LMFDB examples. (We check this by comparing the associated newforms.) Hence, strong BSD for the other
$X_0(161)/\langle {w_7, w_{23}}\rangle $
is the only curve on this list whose Jacobian is not isogenous to the Jacobian of one of the LMFDB examples. (We check this by comparing the associated newforms.) Hence, strong BSD for the other
 $27$
Hasegawa curves follows from isogeny invariance and the validity of strong BSD for the LMFDB examples.
$27$
Hasegawa curves follows from isogeny invariance and the validity of strong BSD for the LMFDB examples. -
(c) The four ‘Wang curves’ from [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and Wetherell45] that are neither Hasegawa curves nor have Jacobian isogenous to that of a curve in the LMFDB. They are the curves labeled 65A, 117B, 125B and 175 in [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and Wetherell45].
-
(d) Sam Frengley’s example of a curve with
 $N = 3200$
and
$N = 3200$
and  .
.
Note that there is some overlap between the first two sets:
![]() $21$
of the Hasegawa curves are in the LMFDB. In total, the LMFDB, Hasegawa, and Wang examples comprise the Jacobians of
$21$
of the Hasegawa curves are in the LMFDB. In total, the LMFDB, Hasegawa, and Wang examples comprise the Jacobians of
![]() $108$
isomorphism classes of curves, whose Jacobians fall into
$108$
isomorphism classes of curves, whose Jacobians fall into
![]() $95$
distinct isogeny classes. Including the last example, we therefore have verified the strong BSD conjecture completely for
$95$
distinct isogeny classes. Including the last example, we therefore have verified the strong BSD conjecture completely for
![]() $96$
isogeny classes of absolutely simple modular abelian surfaces. The distribution of the L-ranks in our examples is as follows:
$96$
isogeny classes of absolutely simple modular abelian surfaces. The distribution of the L-ranks in our examples is as follows:
-
(a) There are
 $36$
isomorphism classes of L-rank
$36$
isomorphism classes of L-rank
 $0$
and
$0$
and
 $61$
of L-rank
$61$
of L-rank
 $1$
. These belong to
$1$
. These belong to
 $31$
and
$31$
and
 $59$
isogeny classes, respectively.
$59$
isogeny classes, respectively. -
(b) There are
 $6$
isomorphism classes of L-rank
$6$
isomorphism classes of L-rank
 $0$
and
$0$
and
 $22$
of L-rank
$22$
of L-rank
 $1$
. Out of the
$1$
. Out of the
 $7$
Hasegawa non-LMFDB examples, there are
$7$
Hasegawa non-LMFDB examples, there are
 $4$
isomorphism classes of L-rank
$4$
isomorphism classes of L-rank
 $0$
and
$0$
and
 $3$
of L-rank
$3$
of L-rank
 $1$
. The latter include the single isogeny class not represented by LMFDB curves. All these examples belong to distinct isogeny classes. The abundance of L-rank
$1$
. The latter include the single isogeny class not represented by LMFDB curves. All these examples belong to distinct isogeny classes. The abundance of L-rank
 $1$
examples is explained by the fact that one often quotients out by the Fricke involution
$1$
examples is explained by the fact that one often quotients out by the Fricke involution
 $w_N$
; hence, the sign in the functional equation shows that the L-rank is odd.
$w_N$
; hence, the sign in the functional equation shows that the L-rank is odd. -
(c) All
 $4$
isogeny classes have L-rank
$4$
isogeny classes have L-rank
 $0$
.
$0$
.
In total, there are
![]() $44$
isomorphism classes and
$44$
isomorphism classes and
![]() $35$
isogeny classes of L-rank
$35$
isogeny classes of L-rank
![]() $0$
and
$0$
and
![]() $64$
isomorphism classes and
$64$
isomorphism classes and
![]() $60$
isogeny classes of L-rank
$60$
isogeny classes of L-rank
![]() $1$
.
$1$
.
Completeness of our data
We consider all the Hasegawa examples (already contained in [Reference Keller and Stoll59]) and all Wang-only examples from [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and Wetherell45]. The LMFDB examples comprise all absolutely simple modular genus
![]() $2$
Jacobians of curves with ‘small’ coefficients and of level
$2$
Jacobians of curves with ‘small’ coefficients and of level
![]() $N \le 1000$
. The smallest level for which there exists a pair of conjugate newforms that is not related to one of these examples is 43. There is an ongoing project that attempts to produce, for a given weight
$N \le 1000$
. The smallest level for which there exists a pair of conjugate newforms that is not related to one of these examples is 43. There is an ongoing project that attempts to produce, for a given weight
![]() $2$
newform f with real quadratic coefficients, a genus-
$2$
newform f with real quadratic coefficients, a genus-
![]() $2$
curve over
$2$
curve over
![]() ${\mathbf {Q}}$
with Jacobian isogenous to
${\mathbf {Q}}$
with Jacobian isogenous to
![]() $A_f$
. Our code can prove strong BSD for many of these examples automatically, especially by using [Reference Keller and Yin60] to skip many descent computations.
$A_f$
. Our code can prove strong BSD for many of these examples automatically, especially by using [Reference Keller and Yin60] to skip many descent computations.
1.7 Structure of the paper
We give an overview of the paper; more details are given at the beginning of each section. In Section 2, we give algorithms to determine whether the residual Galois representations attached to f are irreducible or not. In Section 3, we compute (a multiple of) the Heegner index, which is used in the following two sections: In Section 4, we compute ![]() exactly. In Section 5, we give a description of a finite set S of prime ideals
exactly. In Section 5, we give a description of a finite set S of prime ideals
![]() $\mathfrak {p}$
such that
$\mathfrak {p}$
such that ![]() for
for
![]() $\mathfrak {p} \notin S$
; this strongly depends on the determination of the residual Galois representations and the Heegner index. In Section 6, we perform isogeny descents to prove
$\mathfrak {p} \notin S$
; this strongly depends on the determination of the residual Galois representations and the Heegner index. In Section 6, we perform isogeny descents to prove ![]() for several
for several
![]() $\mathfrak {p} \in S$
. In Section 7, we show how results from Iwasawa theory and the computation of p-adic L-functions can be used to prove an upper bound on
$\mathfrak {p} \in S$
. In Section 7, we show how results from Iwasawa theory and the computation of p-adic L-functions can be used to prove an upper bound on ![]() . In Appendix A, we prove strong BSD for an example of Sam Frengley, where
. In Appendix A, we prove strong BSD for an example of Sam Frengley, where ![]() . In all our other examples,
. In all our other examples, ![]() . We also exhibit examples
. We also exhibit examples
![]() $J/{\mathbf {Q}}$
for which
$J/{\mathbf {Q}}$
for which ![]() with
with
![]() $p \in \{3,5,7\}$
and prove the
$p \in \{3,5,7\}$
and prove the
![]() $\ell $
-part of strong BSD for them except for
$\ell $
-part of strong BSD for them except for
![]() $\ell \in \{2,p\}$
, where we only get an upper bound. These examples are obtained as quadratic twists
$\ell \in \{2,p\}$
, where we only get an upper bound. These examples are obtained as quadratic twists
![]() $J^K$
of some of our main examples, where K is a suitable Heegner field.
$J^K$
of some of our main examples, where K is a suitable Heegner field.
1.8 Terms and notation
We denote canonical isomorphisms by
![]() $\simeq $
and arbitrary, not necessarily canonical isomorphisms by
$\simeq $
and arbitrary, not necessarily canonical isomorphisms by
![]() $\cong $
. We fix an embedding
$\cong $
. We fix an embedding
![]() ${\overline {{\mathbf {Q}}}} \hookrightarrow {\mathbf {C}}$
once and for all.
${\overline {{\mathbf {Q}}}} \hookrightarrow {\mathbf {C}}$
once and for all.
We use boldface
![]() $\boldsymbol {\pi }$
to denote the area of the unit disk to avoid confusion with our use of the letter
$\boldsymbol {\pi }$
to denote the area of the unit disk to avoid confusion with our use of the letter
![]() $\pi $
to denote an isogeny in most of the paper.
$\pi $
to denote an isogeny in most of the paper.
2 Computation of the residual Galois representations
The purpose of this section is to generalize several results on the image of mod-p Galois representations of elliptic curves over
![]() ${\mathbf {Q}}$
(mainly from [Reference Serre98] and [Reference Cojocaru26]) to modular abelian varieties over
${\mathbf {Q}}$
(mainly from [Reference Serre98] and [Reference Cojocaru26]) to modular abelian varieties over
![]() ${\mathbf {Q}}$
of higher dimension.
${\mathbf {Q}}$
of higher dimension.
Let A be an abelian variety of dimension
![]() $g \ge 1$
. Let
$g \ge 1$
. Let
![]() $\mathcal {O}$
be an order in a totally real number field F of degree g over
$\mathcal {O}$
be an order in a totally real number field F of degree g over
![]() ${\mathbf {Q}}$
. Recall that A has real multiplication by
${\mathbf {Q}}$
. Recall that A has real multiplication by
![]() $\mathcal {O}$
over
$\mathcal {O}$
over
![]() ${\mathbf {Q}}$
if
${\mathbf {Q}}$
if
![]() $\mathrm {End}_{\mathbf {Q}}(A) \cong \mathcal {O}$
, where
$\mathrm {End}_{\mathbf {Q}}(A) \cong \mathcal {O}$
, where
![]() $\mathrm {End}_{\mathbf {Q}}(A)$
denotes the ring of
$\mathrm {End}_{\mathbf {Q}}(A)$
denotes the ring of
![]() ${\mathbf {Q}}$
-defined endomorphisms of A. Then A is of
${\mathbf {Q}}$
-defined endomorphisms of A. Then A is of
![]() $\mathrm {GL}_2$
-type in the following sense. Let
$\mathrm {GL}_2$
-type in the following sense. Let
![]() $\mathfrak {p}$
be a nonzero prime ideal of
$\mathfrak {p}$
be a nonzero prime ideal of
![]() $\mathcal {O}$
lying above a rational prime p. We denote its finite residue field
$\mathcal {O}$
lying above a rational prime p. We denote its finite residue field
![]() $\mathcal {O}/\mathfrak {p}$
by
$\mathcal {O}/\mathfrak {p}$
by
![]() ${\mathbf {F}}_{\mathfrak {p}}$
and call
${\mathbf {F}}_{\mathfrak {p}}$
and call
![]() $[{\mathbf {F}}_{\mathfrak {p}} : {\mathbf {F}}_p]$
the degree
$[{\mathbf {F}}_{\mathfrak {p}} : {\mathbf {F}}_p]$
the degree
![]() $\deg \mathfrak {p}$
of
$\deg \mathfrak {p}$
of
![]() $\mathfrak {p}$
;
$\mathfrak {p}$
;
![]() ${\mathbf {F}}_{\mathfrak {p}}$
is isomorphic to
${\mathbf {F}}_{\mathfrak {p}}$
is isomorphic to
![]() ${\mathbf {F}}_{p^{\deg \mathfrak {p}}}$
. If
${\mathbf {F}}_{p^{\deg \mathfrak {p}}}$
. If
![]() $\mathfrak {p}$
is regular – that is, its local ring is a discrete valuation ring, or equivalently,
$\mathfrak {p}$
is regular – that is, its local ring is a discrete valuation ring, or equivalently,
![]() $\mathfrak {p}$
does not divide the conductor ideal
$\mathfrak {p}$
does not divide the conductor ideal
![]() $\mathfrak {f}(\mathcal {O}_F/\mathcal {O}) = \{a \in \mathcal {O} : a \mathcal {O}_F \subseteq \mathcal {O}\}$
of
$\mathfrak {f}(\mathcal {O}_F/\mathcal {O}) = \{a \in \mathcal {O} : a \mathcal {O}_F \subseteq \mathcal {O}\}$
of
![]() $\mathcal {O}$
in
$\mathcal {O}$
in
![]() $\mathcal {O}_F$
– then
$\mathcal {O}_F$
– then
![]() $A[\mathfrak {p}^n]({\overline {{\mathbf {Q}}}})$
is free of rank
$A[\mathfrak {p}^n]({\overline {{\mathbf {Q}}}})$
is free of rank
![]() $2$
over
$2$
over
![]() $\mathcal {O}/\mathfrak {p}^n$
for all
$\mathcal {O}/\mathfrak {p}^n$
for all
![]() $n \ge 1$
.
$n \ge 1$
.
We then obtain
![]() $2$
-dimensional Galois representations
$2$
-dimensional Galois representations
In a similar way, we have
![]() $2g$
-dimensional Galois representations
$2g$
-dimensional Galois representations
Since the Galois action preserves the Weil pairing, the image of
![]() $\rho _{p,A}$
lies in the general symplectic group
$\rho _{p,A}$
lies in the general symplectic group
![]() $\operatorname {GSp}_{2g}({\mathbf {F}}_p)$
.
$\operatorname {GSp}_{2g}({\mathbf {F}}_p)$
.
We define the
![]() $\mathfrak {p}$
-adic Tate module
$\mathfrak {p}$
-adic Tate module
![]() $T_{\mathfrak {p}} A := \varprojlim _n A[\mathfrak {p}^n]({\overline {{\mathbf {Q}}}})$
; it is free of rank
$T_{\mathfrak {p}} A := \varprojlim _n A[\mathfrak {p}^n]({\overline {{\mathbf {Q}}}})$
; it is free of rank
![]() $2$
over the completion
$2$
over the completion
![]() $\mathcal {O}_{\mathfrak {p}}$
. We also define
$\mathcal {O}_{\mathfrak {p}}$
. We also define
![]() $V_{\mathfrak {p}} A = F_{\mathfrak {p}} \otimes _{\mathcal {O}_{\mathfrak {p}}} T_{\mathfrak {p}} A$
; this is a
$V_{\mathfrak {p}} A = F_{\mathfrak {p}} \otimes _{\mathcal {O}_{\mathfrak {p}}} T_{\mathfrak {p}} A$
; this is a
![]() $2$
-dimensional vector space over
$2$
-dimensional vector space over
![]() $F_{\mathfrak {p}}$
. There is also the standard p-adic Tate-module
$F_{\mathfrak {p}}$
. There is also the standard p-adic Tate-module
![]() $T_p A$
, which is a free module of rank
$T_p A$
, which is a free module of rank
![]() $2g$
over
$2g$
over
![]() ${\mathbf {Z}}_p$
and the associated vector space
${\mathbf {Z}}_p$
and the associated vector space
![]() $V_p A = {\mathbf {Q}}_p \otimes _{{\mathbf {Z}}_p} T_p A$
. We obtain the
$V_p A = {\mathbf {Q}}_p \otimes _{{\mathbf {Z}}_p} T_p A$
. We obtain the
![]() $\mathfrak {p}$
-adic Galois representation
$\mathfrak {p}$
-adic Galois representation
and the p-adic Galois representation
As before, the image of
![]() $\rho _{p^\infty ,A}$
is contained in
$\rho _{p^\infty ,A}$
is contained in
![]() $\operatorname {GSp}_{2g}({\mathbf {Q}}_p)$
.
$\operatorname {GSp}_{2g}({\mathbf {Q}}_p)$
.
If A is understood, we omit it from the notation and write
![]() $\rho _{\mathfrak {p}}$
etc.
$\rho _{\mathfrak {p}}$
etc.
We heavily exploit that we can work with
![]() $2$
-dimensional Galois representations instead of
$2$
-dimensional Galois representations instead of
![]() $2g$
-dimensional ones in the following. For example, there is an easy classification of (maximal) subgroups of
$2g$
-dimensional ones in the following. For example, there is an easy classification of (maximal) subgroups of
![]() $\mathrm {GL}_2({\mathbf {F}}_{\mathfrak {p}})$
, whereas the subgroups of
$\mathrm {GL}_2({\mathbf {F}}_{\mathfrak {p}})$
, whereas the subgroups of
![]() $\operatorname {GSp}_{2g}({\mathbf {F}}_p)$
are more complicated.
$\operatorname {GSp}_{2g}({\mathbf {F}}_p)$
are more complicated.
The goal of this section is to determine the image
![]() $G_{\mathfrak {p}}$
of the mod-
$G_{\mathfrak {p}}$
of the mod-
![]() $\mathfrak {p}$
Galois representation
$\mathfrak {p}$
Galois representation
in the case when
![]() $g = 2$
, so
$g = 2$
, so
![]() $\mathcal {O}$
is an order in a real quadratic number field. In particular, we want to decide whether
$\mathcal {O}$
is an order in a real quadratic number field. In particular, we want to decide whether
![]() $\rho _{\mathfrak {p}}$
is irreducible as an
$\rho _{\mathfrak {p}}$
is irreducible as an
![]() ${\mathbf {F}}_{\mathfrak {p}}[{ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})}]$
- or
${\mathbf {F}}_{\mathfrak {p}}[{ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})}]$
- or
![]() ${\mathbf {F}}_p[{ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})}]$
-representation and whether its image in
${\mathbf {F}}_p[{ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})}]$
-representation and whether its image in
![]() $\mathrm {GL}_2({\mathbf {F}}_{\mathfrak {p}})$
is as large as allowed by the extra endomorphisms coming from
$\mathrm {GL}_2({\mathbf {F}}_{\mathfrak {p}})$
is as large as allowed by the extra endomorphisms coming from
![]() $\mathcal {O}$
.
$\mathcal {O}$
.
We will state our results for general g if this is easily possible, but in some cases, we assume
![]() $g = 2$
to simplify the statements and algorithms.
$g = 2$
to simplify the statements and algorithms.
Let
![]() $f \in S_2(\Gamma _0(N))$
be a newform (i.e., a normalized eigenform for the action of the Hecke algebra
$f \in S_2(\Gamma _0(N))$
be a newform (i.e., a normalized eigenform for the action of the Hecke algebra
![]() ${\mathbf {T}}_{\mathbf {Z}}$
on the new subspace of
${\mathbf {T}}_{\mathbf {Z}}$
on the new subspace of
![]() $S_2(\Gamma _0(N))$
). The Fourier coefficients of f generate an order
$S_2(\Gamma _0(N))$
). The Fourier coefficients of f generate an order
![]() ${\mathbf {Z}}[f]$
in a totally real number field
${\mathbf {Z}}[f]$
in a totally real number field
![]() ${\mathbf {Q}}(f)$
. Let
${\mathbf {Q}}(f)$
. Let
![]() $I_f := \operatorname {Ann}_{{\mathbf {T}}_{\mathbf {Z}}}(f)$
be the annihilator of f; then
$I_f := \operatorname {Ann}_{{\mathbf {T}}_{\mathbf {Z}}}(f)$
be the annihilator of f; then
![]() ${\mathbf {T}}_{\mathbf {Z}}/I_f \simeq {\mathbf {Z}}[f]$
, where the Hecke operator
${\mathbf {T}}_{\mathbf {Z}}/I_f \simeq {\mathbf {Z}}[f]$
, where the Hecke operator
![]() $T_n$
is mapped to the Fourier coefficient
$T_n$
is mapped to the Fourier coefficient
![]() $a_n(f)$
. The Hecke algebra also acts via
$a_n(f)$
. The Hecke algebra also acts via
![]() ${\mathbf {Q}}$
-defined endomorphisms on
${\mathbf {Q}}$
-defined endomorphisms on
![]() $J_0(N)$
, and so we can define an abelian variety
$J_0(N)$
, and so we can define an abelian variety
![]() $A_f$
over
$A_f$
over
![]() ${\mathbf {Q}}$
as
${\mathbf {Q}}$
as
![]() $A_f := J_0(N)/I_f J_0(N)$
. Then
$A_f := J_0(N)/I_f J_0(N)$
. Then
![]() $\dim A_f = [{\mathbf {Q}}(f) : {\mathbf {Q}}]$
and
$\dim A_f = [{\mathbf {Q}}(f) : {\mathbf {Q}}]$
and
![]() $\mathrm {End}_{\mathbf {Q}}(A_f) \simeq {\mathbf {T}}_{\mathbf {Z}}/I_f \simeq {\mathbf {Z}}[f]$
. Acting by
$\mathrm {End}_{\mathbf {Q}}(A_f) \simeq {\mathbf {T}}_{\mathbf {Z}}/I_f \simeq {\mathbf {Z}}[f]$
. Acting by
![]() ${ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})}$
on the Fourier coefficients of f, we obtain a Galois orbit of conjugate newforms
${ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})}$
on the Fourier coefficients of f, we obtain a Galois orbit of conjugate newforms
![]() $f^\sigma $
, which has size
$f^\sigma $
, which has size
![]() $[{\mathbf {Q}}(f) : {\mathbf {Q}}]$
. More generally, if
$[{\mathbf {Q}}(f) : {\mathbf {Q}}]$
. More generally, if
![]() $\alpha \colon {\mathbf {Z}}[f] \hookrightarrow {\mathbf {R}}$
is an embedding of
$\alpha \colon {\mathbf {Z}}[f] \hookrightarrow {\mathbf {R}}$
is an embedding of
![]() ${\mathbf {Z}}[f]$
into
${\mathbf {Z}}[f]$
into
![]() ${\mathbf {R}}$
, then
${\mathbf {R}}$
, then
![]() $f^\alpha $
denotes the newform with (real) coefficients
$f^\alpha $
denotes the newform with (real) coefficients
![]() $\alpha (a_n(f))$
. The abelian variety
$\alpha (a_n(f))$
. The abelian variety
![]() $A_f$
only depends on the Galois orbit of f.
$A_f$
only depends on the Galois orbit of f.
We give a short summary of the contents of this section. After recalling basic results about modular abelian varieties and their Galois representations in Section 2.1, we determine the maximal possible image of
![]() $\rho _{\mathfrak {p}}$
in Section 2.3 and state the classification of its maximal subgroups in Section 2.4. This is eventually used to show that
$\rho _{\mathfrak {p}}$
in Section 2.3 and state the classification of its maximal subgroups in Section 2.4. This is eventually used to show that
![]() $\rho _{\mathfrak {p}}$
has maximal image for all
$\rho _{\mathfrak {p}}$
has maximal image for all
![]() $\mathfrak {p}$
outside an explicit finite set by excluding the possibility that the image is contained in one of the maximal subgroups. For fixed
$\mathfrak {p}$
outside an explicit finite set by excluding the possibility that the image is contained in one of the maximal subgroups. For fixed
![]() $\mathfrak {p}$
, we give an algorithm that returns a set of types of maximal subgroups that could contain the image of
$\mathfrak {p}$
, we give an algorithm that returns a set of types of maximal subgroups that could contain the image of
![]() $\rho _{\mathfrak {p}}$
in Section 2.5. In Section 2.6, we show how
$\rho _{\mathfrak {p}}$
in Section 2.5. In Section 2.6, we show how
![]() $\rho _{\mathfrak {p}}$
can be determined explicitly for a given prime ideal
$\rho _{\mathfrak {p}}$
can be determined explicitly for a given prime ideal
![]() $\mathfrak {p}$
. We then give some criteria for when the image of the decomposition group at p is contained in a Cartan subgroup in Section 2.7. Together with some results on the image of inertia at primes
$\mathfrak {p}$
. We then give some criteria for when the image of the decomposition group at p is contained in a Cartan subgroup in Section 2.7. Together with some results on the image of inertia at primes
![]() $\ell \neq p$
, which we recall in Section 2.8, this provides the input for an algorithm that determines a (small and explicit) finite set S of prime ideals
$\ell \neq p$
, which we recall in Section 2.8, this provides the input for an algorithm that determines a (small and explicit) finite set S of prime ideals
![]() $\mathfrak {p}$
such that
$\mathfrak {p}$
such that
![]() $\rho _{\mathfrak {p}}$
is irreducible for all
$\rho _{\mathfrak {p}}$
is irreducible for all
![]() $\mathfrak {p} \notin S$
in Section 2.9. To approach the goal of determining an analogous set with respect to
$\mathfrak {p} \notin S$
in Section 2.9. To approach the goal of determining an analogous set with respect to
![]() $\rho _{\mathfrak {p}}$
with maximal image, we first describe a method that allows us to eliminate two further types of maximal subgroups (other than Borel subgroups, which correspond to reducible representations) in Section 2.10. To deal with maximal images, we need to exclude that the given newform f has complex multiplication, so we provide an algorithm that checks that in Section 2.11. We then derive an algorithm that computes a small explicit finite set of prime ideals
$\rho _{\mathfrak {p}}$
with maximal image, we first describe a method that allows us to eliminate two further types of maximal subgroups (other than Borel subgroups, which correspond to reducible representations) in Section 2.10. To deal with maximal images, we need to exclude that the given newform f has complex multiplication, so we provide an algorithm that checks that in Section 2.11. We then derive an algorithm that computes a small explicit finite set of prime ideals
![]() $\mathfrak {p}$
such that
$\mathfrak {p}$
such that
![]() $\rho _{\mathfrak {p}}$
has maximal image for all
$\rho _{\mathfrak {p}}$
has maximal image for all
![]() $\mathfrak {p}$
not in this set in Section 2.12. Finally, we provide a table giving the types of all representations
$\mathfrak {p}$
not in this set in Section 2.12. Finally, we provide a table giving the types of all representations
![]() $\rho _{\mathfrak {p}}$
attached to our LMFDB examples.
$\rho _{\mathfrak {p}}$
attached to our LMFDB examples.
2.1 Preliminaries
We begin by stating the correspondence between (absolutely simple) abelian varieties with real multiplication over
![]() ${\mathbf {Q}}$
and weight-
${\mathbf {Q}}$
and weight-
![]() $2$
newforms for
$2$
newforms for
![]() $\Gamma _0(N)$
.
$\Gamma _0(N)$
.
Recall that
![]() $L(A/{\mathbf {Q}}, s)$
denotes the L-series of A and
$L(A/{\mathbf {Q}}, s)$
denotes the L-series of A and
![]() $L(f, s)$
denotes the L-series of f and that
$L(f, s)$
denotes the L-series of f and that
![]() $L(A/{\mathbf {Q}},s)$
is defined as
$L(A/{\mathbf {Q}},s)$
is defined as
 $$ \begin{align*} L(A/{\mathbf{Q}},s) &= \prod_p\frac{1}{\det(1 - \operatorname{Frob}_p^{-1} p^{-s} \mid {\operatorname{H}}_{\mathrm{\acute{e}t}}^1(A \otimes {\overline{{\mathbf{Q}}}}, {\mathbf{Q}}_\ell)^{I_p})}, \end{align*} $$
$$ \begin{align*} L(A/{\mathbf{Q}},s) &= \prod_p\frac{1}{\det(1 - \operatorname{Frob}_p^{-1} p^{-s} \mid {\operatorname{H}}_{\mathrm{\acute{e}t}}^1(A \otimes {\overline{{\mathbf{Q}}}}, {\mathbf{Q}}_\ell)^{I_p})}, \end{align*} $$
where for each Euler factor at p, one chooses a prime
![]() $\ell \neq p$
for the
$\ell \neq p$
for the
![]() $\ell $
-adic cohomology group; this is well-defined because the Euler factors are independent of
$\ell $
-adic cohomology group; this is well-defined because the Euler factors are independent of
![]() $\ell $
. The product converges for
$\ell $
. The product converges for
![]() $\operatorname {Re}(s)> \frac {3}{2}$
to a holomorphic function. The L-function associated to
$\operatorname {Re}(s)> \frac {3}{2}$
to a holomorphic function. The L-function associated to
![]() $f = \sum _n a_n q^n$
with coefficients
$f = \sum _n a_n q^n$
with coefficients
![]() $a_n \in {\mathbf {C}}$
is
$a_n \in {\mathbf {C}}$
is
 $$ \begin{align*} L(f,s) &= \sum_{n \ge 1}\frac{a_n}{n^s} = \prod_p\frac{1}{1 - a_pp^{-s} + \varepsilon(p)p^{1-2s}}, \end{align*} $$
$$ \begin{align*} L(f,s) &= \sum_{n \ge 1}\frac{a_n}{n^s} = \prod_p\frac{1}{1 - a_pp^{-s} + \varepsilon(p)p^{1-2s}}, \end{align*} $$
where
![]() $\varepsilon (p)$
is
$\varepsilon (p)$
is
![]() $1$
if
$1$
if
![]() $p \nmid N$
and
$p \nmid N$
and
![]() $0$
otherwise. Since
$0$
otherwise. Since
![]() $L(f,s)$
is the Mellin transform of f and f is a cusp form,
$L(f,s)$
is the Mellin transform of f and f is a cusp form,
![]() $L(f, s)$
is holomorphic on the whole complex plane.
$L(f, s)$
is holomorphic on the whole complex plane.
Theorem 2.1 (Characterization of modular abelian varieties over
 ${\mathbf {Q}}$
)
${\mathbf {Q}}$
)
Let
![]() $A/{\mathbf {Q}}$
be an absolutely simple abelian variety. The following are equivalent.
$A/{\mathbf {Q}}$
be an absolutely simple abelian variety. The following are equivalent.
-
(i) A has real multiplication over
 ${\mathbf {Q}}$
.
${\mathbf {Q}}$
. -
(ii) There is some N such that A is an isogeny factor of
 $J_0(N)$
.
$J_0(N)$
. -
(iii) There is some N and a newform
 $f \in S_2(\Gamma _0(N))$
such that
$f \in S_2(\Gamma _0(N))$
such that  $$\begin{align*}L(A/{\mathbf{Q}},s) = \prod_{\alpha \colon {\mathbf{Z}}[f] \hookrightarrow {\mathbf{R}}} L(f^\alpha,s) \,. \end{align*}$$
$$\begin{align*}L(A/{\mathbf{Q}},s) = \prod_{\alpha \colon {\mathbf{Z}}[f] \hookrightarrow {\mathbf{R}}} L(f^\alpha,s) \,. \end{align*}$$
The number N in (iii) is uniquely determined; we call it the level
![]() $N_A$
of
$N_A$
of
![]() $A/{\mathbf {Q}}$
. The statement in (ii) holds for the same N and its multiples. If these equivalences hold, then
$A/{\mathbf {Q}}$
. The statement in (ii) holds for the same N and its multiples. If these equivalences hold, then
![]() $\mathrm {End}_{\mathbf {Q}}^0(A) := \mathrm {End}_{\mathbf {Q}}(A) \otimes _{\mathbf {Z}} {\mathbf {Q}}$
is isomorphic to
$\mathrm {End}_{\mathbf {Q}}^0(A) := \mathrm {End}_{\mathbf {Q}}(A) \otimes _{\mathbf {Z}} {\mathbf {Q}}$
is isomorphic to
![]() ${\mathbf {Q}}(f)$
and the conductor of
${\mathbf {Q}}(f)$
and the conductor of
![]() $A/{\mathbf {Q}}$
equals
$A/{\mathbf {Q}}$
equals
![]() $N_A^{\dim {A}}$
. Furthermore, A is of
$N_A^{\dim {A}}$
. Furthermore, A is of
![]() $\mathrm {GL}_2$
-type (i.e., the p-adic Tate modules
$\mathrm {GL}_2$
-type (i.e., the p-adic Tate modules
![]() $V_p A$
are free modules of rank
$V_p A$
are free modules of rank
![]() $2$
over the completion of
$2$
over the completion of
![]() ${\mathbf {Q}}(f)$
at p); if
${\mathbf {Q}}(f)$
at p); if
![]() $\mathfrak {p}$
is a prime ideal of
$\mathfrak {p}$
is a prime ideal of
![]() ${\mathbf {Q}}(f)$
above the rational prime p, then
${\mathbf {Q}}(f)$
above the rational prime p, then
![]() $V_{\mathfrak {p}} A$
is a vector space of dimension
$V_{\mathfrak {p}} A$
is a vector space of dimension
![]() $2$
over the completion
$2$
over the completion
![]() ${\mathbf {Q}}(f)_{\mathfrak {p}}$
, a local field.
${\mathbf {Q}}(f)_{\mathfrak {p}}$
, a local field.
Proof. The equivalence of (ii) and (iii) is a well-known characterization of modular abelian varieties following from the Eichler–Shimura relation and Faltings’ Isogeny Theorem. The equivalence of (i) and (ii) can be found as [Reference Serre97, Thm. 5] as a consequence of Serre’s Modularity Conjecture for absolutely simple
![]() $2$
-dimensional residual odd Galois representations (which is formulated in the same paper); this conjecture is now a theorem [Reference Khare and Wintenberger61]. See also [Reference Ribet91]. The remaining statements are well-known.
$2$
-dimensional residual odd Galois representations (which is formulated in the same paper); this conjecture is now a theorem [Reference Khare and Wintenberger61]. See also [Reference Ribet91]. The remaining statements are well-known.
We will use these equivalences tacitly. Note that in the literature, sometimes more general modular abelian varieties are considered, which are quotients of
![]() $J_1(N)$
and which can have complex multiplication.
$J_1(N)$
and which can have complex multiplication.
However, when A is an absolutely simple abelian surface with CM, then A cannot be of
![]() $\mathrm {GL}_2$
-type over
$\mathrm {GL}_2$
-type over
![]() ${\mathbf {Q}}$
, as the following result shows. We thank Pip Goodman for pointing it out to us.
${\mathbf {Q}}$
, as the following result shows. We thank Pip Goodman for pointing it out to us.
Proposition 2.2. Let
![]() $A/{\mathbf {Q}}$
be an absolutely simple abelian surface with CM. Then
$A/{\mathbf {Q}}$
be an absolutely simple abelian surface with CM. Then
![]() $\mathrm {End}_{\mathbf {Q}}^0(A) ={\mathbf {Q}}$
; in particular,
$\mathrm {End}_{\mathbf {Q}}^0(A) ={\mathbf {Q}}$
; in particular,
![]() $A/{\mathbf {Q}}$
is not of
$A/{\mathbf {Q}}$
is not of
![]() $\mathrm {GL}_2$
-type.
$\mathrm {GL}_2$
-type.
Proof. Let
![]() $E = \mathrm {End}_{{\overline {{\mathbf {Q}}}}}^0(A) = \mathrm {End}_{{\overline {{\mathbf {Q}}}}}(A) \otimes _{\mathbf {Z}} {\mathbf {Q}}$
be the geometric endomorphism algebra of A. By [Reference Shimura101, Proposition 30], the minimal field over which the endomorphisms of A are defined is
$E = \mathrm {End}_{{\overline {{\mathbf {Q}}}}}^0(A) = \mathrm {End}_{{\overline {{\mathbf {Q}}}}}(A) \otimes _{\mathbf {Z}} {\mathbf {Q}}$
be the geometric endomorphism algebra of A. By [Reference Shimura101, Proposition 30], the minimal field over which the endomorphisms of A are defined is
![]() $E^*$
, the reflex field of E (note that the base field is just
$E^*$
, the reflex field of E (note that the base field is just
![]() ${\mathbf {Q}}$
here). In particular,
${\mathbf {Q}}$
here). In particular,
![]() $E^*|{\mathbf {Q}}$
is Galois, and the absolute Galois group
$E^*|{\mathbf {Q}}$
is Galois, and the absolute Galois group
![]() ${ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})}$
acts on
${ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})}$
acts on
![]() $\mathrm {End}_{{\overline {{\mathbf {Q}}}}}^0(A)$
through
$\mathrm {End}_{{\overline {{\mathbf {Q}}}}}^0(A)$
through
![]() $ {\mathrm {Gal}}(E^*|{\mathbf {Q}})$
, so we obtain an embedding
$ {\mathrm {Gal}}(E^*|{\mathbf {Q}})$
, so we obtain an embedding
We now consult Examples 8.4 (2) in loc. cit. In Example (C), there the reflex field is not Galois, and in Example (A), the CM-type is not primitive, which means that A is not absolutely simple. So both these cases cannot occur, and by Example (B), it follows that
![]() $E^* = E$
; in particular, the map i above is an isomorphism. This finally implies that
$E^* = E$
; in particular, the map i above is an isomorphism. This finally implies that
Remark 2.3. In the situation of theorem 2.1, A is isogenous to
![]() $A_f$
(by Faltings’ Isogeny Theorem), and therefore, the Galois representations on
$A_f$
(by Faltings’ Isogeny Theorem), and therefore, the Galois representations on
![]() $V_{\mathfrak {p}} A$
and on
$V_{\mathfrak {p}} A$
and on
![]() $V_{\mathfrak {p}} A_f$
are isomorphic (similarly for
$V_{\mathfrak {p}} A_f$
are isomorphic (similarly for
![]() $V_p A$
and
$V_p A$
and
![]() $V_p A_f$
). When A and/or f are clear from the context, we write
$V_p A_f$
). When A and/or f are clear from the context, we write
![]() $\rho _{\mathfrak {p}^\infty }$
and
$\rho _{\mathfrak {p}^\infty }$
and
![]() $\rho _{p^\infty }$
for these representations, which depend only on the Galois orbit of f. The fact that A and
$\rho _{p^\infty }$
for these representations, which depend only on the Galois orbit of f. The fact that A and
![]() $A_f$
are isogenous also implies that the semi-simplifications of
$A_f$
are isogenous also implies that the semi-simplifications of
![]() $\rho _{\mathfrak {p},A}$
and of
$\rho _{\mathfrak {p},A}$
and of
![]() $\rho _{\mathfrak {p},f} := \rho _{\mathfrak {p},A_f}$
are isomorphic when
$\rho _{\mathfrak {p},f} := \rho _{\mathfrak {p},A_f}$
are isomorphic when
![]() $\mathfrak {p}$
is a regular prime of both
$\mathfrak {p}$
is a regular prime of both
![]() ${\mathbf {Z}}[f] \simeq \mathrm {End}_{{\mathbf {Q}}}(A_f)$
and
${\mathbf {Z}}[f] \simeq \mathrm {End}_{{\mathbf {Q}}}(A_f)$
and
![]() $\mathrm {End}_{{\mathbf {Q}}}(A)$
(and similarly for
$\mathrm {End}_{{\mathbf {Q}}}(A)$
(and similarly for
![]() $\rho _{p,A}$
and
$\rho _{p,A}$
and
![]() $\rho _{p,f}$
).
$\rho _{p,f}$
).
Note that the canonical isomorphism
![]() ${\mathbf {Z}}[f] \simeq {\mathbf {T}}_{\mathbf {Z}}/I_f \simeq \mathrm {End}_{{\mathbf {Q}}}(A_f)$
induces a canonical identification of
${\mathbf {Z}}[f] \simeq {\mathbf {T}}_{\mathbf {Z}}/I_f \simeq \mathrm {End}_{{\mathbf {Q}}}(A_f)$
induces a canonical identification of
![]() ${\mathbf {Q}}(f)$
with
${\mathbf {Q}}(f)$
with
![]() $\mathrm {End}^0_{{\mathbf {Q}}}(A_f)$
, which in turn is isomorphic to
$\mathrm {End}^0_{{\mathbf {Q}}}(A_f)$
, which in turn is isomorphic to
![]() $\mathrm {End}^0_{{\mathbf {Q}}}(A)$
via the isogeny between A and
$\mathrm {End}^0_{{\mathbf {Q}}}(A)$
via the isogeny between A and
![]() $A_f$
. Fixing the isogeny, this identifies
$A_f$
. Fixing the isogeny, this identifies
![]() $\mathcal {O} = \mathrm {End}_{{\mathbf {Q}}}(A)$
with an order in the totally real number field
$\mathcal {O} = \mathrm {End}_{{\mathbf {Q}}}(A)$
with an order in the totally real number field
![]() ${\mathbf {Q}}(f)$
. If
${\mathbf {Q}}(f)$
. If
![]() ${\mathbf {Z}}[f]$
is contained in
${\mathbf {Z}}[f]$
is contained in
![]() $\mathcal {O}$
under this identification (e.g., when
$\mathcal {O}$
under this identification (e.g., when
![]() $\mathcal {O}$
is the maximal order), then the Fourier coefficient
$\mathcal {O}$
is the maximal order), then the Fourier coefficient
![]() $a_n$
of f, which is the image of the Hecke operator
$a_n$
of f, which is the image of the Hecke operator
![]() $T_n \in {\mathbf {T}}_{{\mathbf {Z}}}$
in
$T_n \in {\mathbf {T}}_{{\mathbf {Z}}}$
in
![]() ${\mathbf {Z}}[f]$
, can be interpreted as an element of
${\mathbf {Z}}[f]$
, can be interpreted as an element of
![]() $\mathcal {O}$
(i.e., an endomorphism of A). We make use of this to get the correct identifications of
$\mathcal {O}$
(i.e., an endomorphism of A). We make use of this to get the correct identifications of
![]() $\sigma $
-isotypic components when dealing with the Gross–Zagier formula for the height of a Heegner point in Section 3.7.
$\sigma $
-isotypic components when dealing with the Gross–Zagier formula for the height of a Heegner point in Section 3.7.
Write
![]() $F = {\mathbf {Q}}(f)$
and
$F = {\mathbf {Q}}(f)$
and
![]() $\mathcal {O}_F$
for the maximal order of F, and let
$\mathcal {O}_F$
for the maximal order of F, and let
![]() $\mathcal {O} \subseteq \mathcal {O}_F$
be any order in F. Recall the conductor ideal of
$\mathcal {O} \subseteq \mathcal {O}_F$
be any order in F. Recall the conductor ideal of
![]() $\mathcal {O}$
in
$\mathcal {O}$
in
![]() $\mathcal {O}_F$
,
$\mathcal {O}_F$
,
it is the largest ideal of
![]() $\mathcal {O}$
that is also an ideal of
$\mathcal {O}$
that is also an ideal of
![]() $\mathcal {O}_F$
. If A is an abelian variety such that
$\mathcal {O}_F$
. If A is an abelian variety such that
![]() $\mathrm {End}_{\mathbf {Q}}(A) \cong \mathcal {O}$
, then one can check that the isogenous abelian variety
$\mathrm {End}_{\mathbf {Q}}(A) \cong \mathcal {O}$
, then one can check that the isogenous abelian variety
![]() $A' := A/A[\mathfrak {f}(\mathcal {O}_F/\mathcal {O})]$
has
$A' := A/A[\mathfrak {f}(\mathcal {O}_F/\mathcal {O})]$
has
![]() $\mathrm {End}_{\mathbf {Q}}(A') \cong \mathcal {O}_F$
. So by working with
$\mathrm {End}_{\mathbf {Q}}(A') \cong \mathcal {O}_F$
. So by working with
![]() $A'$
instead of with A (or
$A'$
instead of with A (or
![]() $A_f$
), we can assume that the endomorphism ring is the maximal order.
$A_f$
), we can assume that the endomorphism ring is the maximal order.
Definition 2.4. Let p be a prime. We write
for the mod-
![]() $p^n$
cyclotomic character and
$p^n$
cyclotomic character and
for the p-adic cyclotomic character.
Definition 2.5. If
![]() $\mathfrak {p}$
is a maximal ideal in an order
$\mathfrak {p}$
is a maximal ideal in an order
![]() $\mathcal {O}$
of a number field, we write
$\mathcal {O}$
of a number field, we write
![]() $p(\mathfrak {p})$
for the characteristic of the finite field
$p(\mathfrak {p})$
for the characteristic of the finite field
![]() ${\mathbf {F}}_{\mathfrak {p}} = \mathcal {O}/\mathfrak {p}$
.
${\mathbf {F}}_{\mathfrak {p}} = \mathcal {O}/\mathfrak {p}$
.
Theorem 2.6 (Characteristic polynomials of Frobenii of a modular Galois representation)
Let
![]() $f \in S_2(\Gamma _0(N))$
be a newform with Fourier coefficients
$f \in S_2(\Gamma _0(N))$
be a newform with Fourier coefficients
![]() $a_\ell $
and coefficient field
$a_\ell $
and coefficient field
![]() ${\mathbf {Q}}(f)$
a totally real field of degree g.
${\mathbf {Q}}(f)$
a totally real field of degree g.
Associated to f, there is a strictly compatible system of
![]() $\mathfrak {p}$
-adic Galois representations
$\mathfrak {p}$
-adic Galois representations
![]() $\rho _{\mathfrak {p}^\infty }$
, unramified outside
$\rho _{\mathfrak {p}^\infty }$
, unramified outside
![]() $N p(\mathfrak {p})$
. For all
$N p(\mathfrak {p})$
. For all
![]() $\ell \nmid N p(\mathfrak {p})$
, the characteristic polynomial of
$\ell \nmid N p(\mathfrak {p})$
, the characteristic polynomial of
![]() $\rho _{\mathfrak {p}^\infty }(\operatorname {Frob}_\ell )$
equals
$\rho _{\mathfrak {p}^\infty }(\operatorname {Frob}_\ell )$
equals
One has
for
![]() $\mathfrak {p} \nmid N$
. In particular,
$\mathfrak {p} \nmid N$
. In particular,
![]() $\rho _{\mathfrak {p}^\infty }$
is odd. The determinant of the p-adic Galois representation
$\rho _{\mathfrak {p}^\infty }$
is odd. The determinant of the p-adic Galois representation
is
![]() $\chi _{p^\infty }^g$
.
$\chi _{p^\infty }^g$
.
Proof. This is well-known and shown more generally for weight
![]() $k \geq 2$
in [Reference Deligne37] (and for weight
$k \geq 2$
in [Reference Deligne37] (and for weight
![]() $2$
earlier by Shimura).
$2$
earlier by Shimura).
If
![]() $\mathfrak {p}$
is a regular prime of
$\mathfrak {p}$
is a regular prime of
![]() ${\mathbf {Z}}[f]$
(or
${\mathbf {Z}}[f]$
(or
![]() $\mathcal {O}$
) not dividing
$\mathcal {O}$
) not dividing
![]() $N\ell $
, then we write
$N\ell $
, then we write
![]() $\operatorname {charpol}(f, \ell , \mathfrak {p}; T)$
for the characteristic polynomial of the image of
$\operatorname {charpol}(f, \ell , \mathfrak {p}; T)$
for the characteristic polynomial of the image of
![]() $\operatorname {Frob}_\ell $
under
$\operatorname {Frob}_\ell $
under
![]() $\rho _{\mathfrak {p},f}$
(or
$\rho _{\mathfrak {p},f}$
(or
![]() $\rho _{\mathfrak {p},A}$
); it is the image of
$\rho _{\mathfrak {p},A}$
); it is the image of
![]() $\operatorname {charpol}(f, \ell; T)$
in
$\operatorname {charpol}(f, \ell; T)$
in
![]() ${\mathbf {F}}_{\mathfrak {p}}[T]$
.
${\mathbf {F}}_{\mathfrak {p}}[T]$
.
Magma can compute the Fourier coefficients
![]() $a_\ell $
of a newform f and its coefficient ring
$a_\ell $
of a newform f and its coefficient ring
![]() ${\mathbf {Z}}[f]$
efficiently. This will be crucial for computing the image of
${\mathbf {Z}}[f]$
efficiently. This will be crucial for computing the image of
![]() $\rho _{\mathfrak {p}}$
, because the only access to elements of the absolute Galois group of
$\rho _{\mathfrak {p}}$
, because the only access to elements of the absolute Galois group of
![]() ${\mathbf {Q}}$
we have is via Frobenius elements, and we can reconstruct the characteristic polynomials of the Frobenii acting on
${\mathbf {Q}}$
we have is via Frobenius elements, and we can reconstruct the characteristic polynomials of the Frobenii acting on
![]() $A[\mathfrak {p}]({\mathbf {Q}})$
, which uniquely determine their semi-simple part. The fact that we know only the characteristic polynomials also means that we do not have direct access to the unipotent part of
$A[\mathfrak {p}]({\mathbf {Q}})$
, which uniquely determine their semi-simple part. The fact that we know only the characteristic polynomials also means that we do not have direct access to the unipotent part of
![]() $\rho _p(\operatorname {Frob}_\ell )$
via
$\rho _p(\operatorname {Frob}_\ell )$
via
![]() $a_\ell $
alone.
$a_\ell $
alone.
Let p be a prime. We fix an embedding of
![]() ${\overline {{\mathbf {Q}}}}$
into
${\overline {{\mathbf {Q}}}}$
into
![]() ${\overline {{\mathbf {Q}}}}_p$
; this determines a decomposition group
${\overline {{\mathbf {Q}}}}_p$
; this determines a decomposition group
![]() $D_p = { {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)} \hookrightarrow { {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})}$
and its inertia subgroup
$D_p = { {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)} \hookrightarrow { {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})}$
and its inertia subgroup
![]() $I_p = {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p^{\mathrm {nr}})$
. The inertia subgroup has a descending filtration by its (normal) higher ramification subgroups, the first of which is the wild ramification subgroup
$I_p = {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p^{\mathrm {nr}})$
. The inertia subgroup has a descending filtration by its (normal) higher ramification subgroups, the first of which is the wild ramification subgroup
![]() $I_p^{\mathrm {w}}$
, the unique (hence normal) Sylow pro-p subgroup of
$I_p^{\mathrm {w}}$
, the unique (hence normal) Sylow pro-p subgroup of
![]() $I_p$
. The quotient
$I_p$
. The quotient
![]() $I_p/I_p^{\mathrm {w}}$
is the tame inertia group
$I_p/I_p^{\mathrm {w}}$
is the tame inertia group
![]() $I_p^{\mathrm {t}}$
, which is canonically isomorphic to the pro-cyclic
$I_p^{\mathrm {t}}$
, which is canonically isomorphic to the pro-cyclic
![]() $p'$
-group
$p'$
-group
 $$\begin{align*}\varprojlim_{\mathbf{N}_{{\mathbf{F}}|}} {\mathbf{F}}^\times \cong {\hat{{\mathbf{Z}}}}^{(p')}(1) \simeq \prod_{\ell \neq p} {\mathbf{Z}}_\ell(1), \end{align*}$$
$$\begin{align*}\varprojlim_{\mathbf{N}_{{\mathbf{F}}|}} {\mathbf{F}}^\times \cong {\hat{{\mathbf{Z}}}}^{(p')}(1) \simeq \prod_{\ell \neq p} {\mathbf{Z}}_\ell(1), \end{align*}$$
where the limit is taken over all finite fields
![]() ${\mathbf {F}}$
of characteristic p, the transition maps in the projective limit are the field norms and
${\mathbf {F}}$
of characteristic p, the transition maps in the projective limit are the field norms and
![]() ${\mathbf {Z}}_\ell (1)$
is the Galois module
${\mathbf {Z}}_\ell (1)$
is the Galois module
![]() $\varprojlim _n \mu _{\ell ^n}({\overline {{\mathbf {Q}}}}_p)$
. (See [Reference Serre98, § 1.3]. Note that Serre uses
$\varprojlim _n \mu _{\ell ^n}({\overline {{\mathbf {Q}}}}_p)$
. (See [Reference Serre98, § 1.3]. Note that Serre uses
![]() $I_p$
to denote
$I_p$
to denote
![]() $I_p^{\mathrm {w}}$
,
$I_p^{\mathrm {w}}$
,
![]() $I_t$
to denote
$I_t$
to denote
![]() $I_p^{\mathrm {t}}$
and I to denote
$I_p^{\mathrm {t}}$
and I to denote
![]() $I_p$
.)
$I_p$
.)
Lemma 2.7. The absolute Galois group of the residue field
![]() ${\mathbf {F}}_p$
, which is canonically isomorphic to
${\mathbf {F}}_p$
, which is canonically isomorphic to
![]() ${\hat {{\mathbf {Z}}}}\operatorname {Frob}_p$
, acts on
${\hat {{\mathbf {Z}}}}\operatorname {Frob}_p$
, acts on
![]() $I_p^{\mathrm {t}}$
via conjugation. One has
$I_p^{\mathrm {t}}$
via conjugation. One has
Note that we have written
![]() $I_p^{\mathrm {t}}$
multiplicatively here.
$I_p^{\mathrm {t}}$
multiplicatively here.
Proof. See [Reference Neukirch, Schmidt and Wingberg81, Theorem 7.5.3].
See [Reference Serre98, § 1.7] for the following definition.
Definition 2.8. Let
![]() $k \ge 1$
. We define the character
$k \ge 1$
. We define the character
![]() $\psi _k$
of
$\psi _k$
of
![]() $I_p^{\mathrm {t}}$
via the canonical projection from the projective limit as
$I_p^{\mathrm {t}}$
via the canonical projection from the projective limit as
One has
![]() $\mathbf {N}_{{\mathbf {F}}_{p^k}|{\mathbf {F}}_p} \circ \psi _k = \psi _1 = \chi _p$
.
$\mathbf {N}_{{\mathbf {F}}_{p^k}|{\mathbf {F}}_p} \circ \psi _k = \psi _1 = \chi _p$
.
The k fundamental characters of level k are the powers
![]() $\psi _k^{p^n}$
for
$\psi _k^{p^n}$
for
![]() $0 \le n < k$
(equivalently,
$0 \le n < k$
(equivalently,
![]() $\psi _k$
followed by the k automorphisms of
$\psi _k$
followed by the k automorphisms of
![]() ${\mathbf {F}}_{p^k}$
).
${\mathbf {F}}_{p^k}$
).
2.2 General set-up and notation
In the following, f will always denote a newform of weight
![]() $2$
, level N and trivial nebentypus. We let
$2$
, level N and trivial nebentypus. We let
![]() $\mathcal {N}(N)$
denote the set of such newforms;
$\mathcal {N}(N)$
denote the set of such newforms;
![]() $\mathcal {N}(N, g)$
denotes the subset consisting of forms whose Galois orbit has size g. The Fourier coefficients of f will be denoted
$\mathcal {N}(N, g)$
denotes the subset consisting of forms whose Galois orbit has size g. The Fourier coefficients of f will be denoted
![]() $a_n$
(or
$a_n$
(or
![]() $a_n(f)$
if we want to make the dependence on f explicit); they generate the coefficient ring
$a_n(f)$
if we want to make the dependence on f explicit); they generate the coefficient ring
![]() ${\mathbf {Z}}[f]$
, which is an order in a totally real number field
${\mathbf {Z}}[f]$
, which is an order in a totally real number field
![]() $F = {\mathbf {Q}}(f)$
(of degree g when
$F = {\mathbf {Q}}(f)$
(of degree g when
![]() $f \in \mathcal {N}(N, g)$
).
$f \in \mathcal {N}(N, g)$
).
Further, A will denote an abelian variety over
![]() ${\mathbf {Q}}$
that is
${\mathbf {Q}}$
that is
![]() ${\mathbf {Q}}$
-isogenous to
${\mathbf {Q}}$
-isogenous to
![]() $A_f$
(e.g.,
$A_f$
(e.g.,
![]() $A = A_f$
or
$A = A_f$
or
![]() $A = A' = A_f/A_f[\mathfrak {f}(\mathcal {O}_F/{\mathbf {Z}}[f])]$
as in remark 2.3) and has endomorphism ring
$A = A' = A_f/A_f[\mathfrak {f}(\mathcal {O}_F/{\mathbf {Z}}[f])]$
as in remark 2.3) and has endomorphism ring
![]() $\mathcal {O}$
. Let
$\mathcal {O}$
. Let
![]() $\mathfrak {p}$
be a regular prime ideal of
$\mathfrak {p}$
be a regular prime ideal of
![]() $\mathcal {O}$
; then
$\mathcal {O}$
; then
![]() $\mathfrak {p}$
is a maximal ideal of
$\mathfrak {p}$
is a maximal ideal of
![]() $\mathcal {O}$
; we write
$\mathcal {O}$
; we write
![]() ${\mathbf {F}}_{\mathfrak {p}} = \mathcal {O}/\mathfrak {p}$
for its residue class field and
${\mathbf {F}}_{\mathfrak {p}} = \mathcal {O}/\mathfrak {p}$
for its residue class field and
![]() $p(\mathfrak {p})$
for the residue characteristic (i.e., the characteristic of
$p(\mathfrak {p})$
for the residue characteristic (i.e., the characteristic of
![]() ${\mathbf {F}}_{\mathfrak {p}}$
). Then
${\mathbf {F}}_{\mathfrak {p}}$
). Then
![]() $\rho _{\mathfrak {p}} = \rho _{\mathfrak {p},A}$
is the Galois representation on
$\rho _{\mathfrak {p}} = \rho _{\mathfrak {p},A}$
is the Galois representation on
![]() $A[\mathfrak {p}]$
; its semi-simplification
$A[\mathfrak {p}]$
; its semi-simplification
![]() $\rho _{\mathfrak {p}}^{\mathrm {ss}}$
is independent of the choice of A (as long as
$\rho _{\mathfrak {p}}^{\mathrm {ss}}$
is independent of the choice of A (as long as
![]() $\mathfrak {p}$
is regular). Since we are mostly interested in determining when
$\mathfrak {p}$
is regular). Since we are mostly interested in determining when
![]() $\rho _{\mathfrak {p}}$
is irreducible (or has maximal image), knowing
$\rho _{\mathfrak {p}}$
is irreducible (or has maximal image), knowing
![]() $\rho _{\mathfrak {p}}^{\mathrm {ss}}$
is usually enough, and so we suppress the dependency on A in the notation. (Note that when
$\rho _{\mathfrak {p}}^{\mathrm {ss}}$
is usually enough, and so we suppress the dependency on A in the notation. (Note that when
![]() $\mathfrak {p}$
is a prime ideal of
$\mathfrak {p}$
is a prime ideal of
![]() $\mathcal {O}_F$
that does not correspond to a regular prime ideal of
$\mathcal {O}_F$
that does not correspond to a regular prime ideal of
![]() $\mathcal {O}$
, then
$\mathcal {O}$
, then
![]() $\rho _{\mathfrak {p},A'}$
will be reducible, since there is an isogeny
$\rho _{\mathfrak {p},A'}$
will be reducible, since there is an isogeny
![]() $A' \to A$
whose kernel has nontrivial intersection with
$A' \to A$
whose kernel has nontrivial intersection with
![]() $A'[\mathfrak {p}]$
.)
$A'[\mathfrak {p}]$
.)
2.3 Determination of the maximal image
One of our goals is to show that the image of
![]() $\rho _{\mathfrak {p}}$
is as large as possible for all but finitely many prime ideals
$\rho _{\mathfrak {p}}$
is as large as possible for all but finitely many prime ideals
![]() $\mathfrak {p}$
(with a small explicit set of possible exceptions). The first step is to determine what this maximal image is. Then we will show that it suffices to consider the image in
$\mathfrak {p}$
(with a small explicit set of possible exceptions). The first step is to determine what this maximal image is. Then we will show that it suffices to consider the image in
![]() $\operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
.
$\operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
.
To show that the projective image is maximal, we have to exclude the possibility that it is contained in one of the maximal subgroups of the maximal projective image, so we need a classification of these maximal subgroups. This will be done in Section 2.4 below.
Definition 2.9. We write
![]() $G_{\mathfrak {p}} := \rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})}) \subseteq \mathrm {GL}_2({\mathbf {F}}_{\mathfrak {p}})$
for the image of
$G_{\mathfrak {p}} := \rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})}) \subseteq \mathrm {GL}_2({\mathbf {F}}_{\mathfrak {p}})$
for the image of
![]() $\rho _{\mathfrak {p}}$
. theorem 2.6 implies that
$\rho _{\mathfrak {p}}$
. theorem 2.6 implies that
![]() $\det (G_{\mathfrak {p}}) = {\mathbf {F}}_p^\times $
, since
$\det (G_{\mathfrak {p}}) = {\mathbf {F}}_p^\times $
, since
![]() $\det \circ \rho _{\mathfrak {p}}$
is the mod-p cyclotomic character. We set
$\det \circ \rho _{\mathfrak {p}}$
is the mod-p cyclotomic character. We set
then
![]() $G_{\mathfrak {p}} \subseteq G_{\mathfrak {p}}^{{\operatorname {max}}}$
.
$G_{\mathfrak {p}} \subseteq G_{\mathfrak {p}}^{{\operatorname {max}}}$
.
Definition 2.10. We write
![]() ${\mathbf {P}} \colon \mathrm {GL}_2({\mathbf {F}}_{\mathfrak {p}}) \to \operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
for the canonical surjection. For a subgroup G of
${\mathbf {P}} \colon \mathrm {GL}_2({\mathbf {F}}_{\mathfrak {p}}) \to \operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
for the canonical surjection. For a subgroup G of
![]() $\mathrm {GL}_2({\mathbf {F}}_{\mathfrak {p}})$
, we write
$\mathrm {GL}_2({\mathbf {F}}_{\mathfrak {p}})$
, we write
![]() ${\mathbf {P}} G$
for its image in
${\mathbf {P}} G$
for its image in
![]() $\operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
. We call
$\operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
. We call
![]() ${\mathbf {P}} G$
the projective image of G. We also say that
${\mathbf {P}} G$
the projective image of G. We also say that
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
is the projective image of
${\mathbf {P}}{G_{\mathfrak {p}}}$
is the projective image of
![]() $\rho _{\mathfrak {p}}$
. We write
$\rho _{\mathfrak {p}}$
. We write
![]() $\overline {\det } \colon \operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}}) \to {\mathbf {F}}_{\mathfrak {p}}^\times /{\mathbf {F}}_{\mathfrak {p}}^{\times 2}$
for the homomorphism induced by the determinant.
$\overline {\det } \colon \operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}}) \to {\mathbf {F}}_{\mathfrak {p}}^\times /{\mathbf {F}}_{\mathfrak {p}}^{\times 2}$
for the homomorphism induced by the determinant.
We write
![]() $\operatorname {PSL}_2({\mathbf {F}}_{\mathfrak {p}}) := {\mathbf {P}} {\mathrm {SL}}_2({\mathbf {F}}_{\mathfrak {p}})$
for the quotient of
$\operatorname {PSL}_2({\mathbf {F}}_{\mathfrak {p}}) := {\mathbf {P}} {\mathrm {SL}}_2({\mathbf {F}}_{\mathfrak {p}})$
for the quotient of
![]() $ {\mathrm {SL}}_2({\mathbf {F}}_{\mathfrak {p}})$
by its center
$ {\mathrm {SL}}_2({\mathbf {F}}_{\mathfrak {p}})$
by its center
![]() $\{\pm I_2\}$
. Note that this is not the same as the group of
$\{\pm I_2\}$
. Note that this is not the same as the group of
![]() ${\mathbf {F}}_{\mathfrak {p}}$
-points of the algebraic group
${\mathbf {F}}_{\mathfrak {p}}$
-points of the algebraic group
![]() $\operatorname {PSL}_2$
. When p is odd,
$\operatorname {PSL}_2$
. When p is odd,
![]() $\operatorname {PSL}_2({\mathbf {F}}_{\mathfrak {p}})$
has index
$\operatorname {PSL}_2({\mathbf {F}}_{\mathfrak {p}})$
has index
![]() $2$
in
$2$
in
![]() $\operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
and is the kernel of
$\operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
and is the kernel of
![]() $\overline {\det }$
.
$\overline {\det }$
.
Lemma 2.11. We have that
![]() ${\mathbf {P}} G_{\mathfrak {p}}^{{\operatorname {max}}} = \operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
when
${\mathbf {P}} G_{\mathfrak {p}}^{{\operatorname {max}}} = \operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
when
![]() $\deg \mathfrak {p}$
is odd and
$\deg \mathfrak {p}$
is odd and
![]() ${\mathbf {P}} G_{\mathfrak {p}}^{{\operatorname {max}}} = \operatorname {PSL}_2({\mathbf {F}}_{\mathfrak {p}})$
when
${\mathbf {P}} G_{\mathfrak {p}}^{{\operatorname {max}}} = \operatorname {PSL}_2({\mathbf {F}}_{\mathfrak {p}})$
when
![]() $\deg \mathfrak {p}$
is even.
$\deg \mathfrak {p}$
is even.
Proof. The image of
![]() $G_{\mathfrak {p}}^{{\operatorname {max}}}$
in
$G_{\mathfrak {p}}^{{\operatorname {max}}}$
in
![]() $\operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
consists of the elements
$\operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
consists of the elements
![]() $\gamma \in \operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
such that
$\gamma \in \operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
such that
![]() $\overline {\det }(\gamma )$
is in the image of
$\overline {\det }(\gamma )$
is in the image of
![]() ${\mathbf {F}}_p^\times $
. The latter is trivial if and only if
${\mathbf {F}}_p^\times $
. The latter is trivial if and only if
![]() $\deg \mathfrak {p}$
is even (or
$\deg \mathfrak {p}$
is even (or
![]() $p = 2$
, in which case
$p = 2$
, in which case
![]() $\operatorname {PSL}_2({\mathbf {F}}_{\mathfrak {p}}) = \operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
). (See also [Reference Ribet89, § 5.2].)
$\operatorname {PSL}_2({\mathbf {F}}_{\mathfrak {p}}) = \operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
). (See also [Reference Ribet89, § 5.2].)
Proposition 2.12. Let
![]() $G \le G_{\mathfrak {p}}^{{\operatorname {max}}}$
be a subgroup such that
$G \le G_{\mathfrak {p}}^{{\operatorname {max}}}$
be a subgroup such that
![]() $\det (G) = {\mathbf {F}}_p^\times $
and
$\det (G) = {\mathbf {F}}_p^\times $
and
![]() ${\mathbf {P}} G = {\mathbf {P}} G_{\mathfrak {p}}^{{\operatorname {max}}}$
. Then
${\mathbf {P}} G = {\mathbf {P}} G_{\mathfrak {p}}^{{\operatorname {max}}}$
. Then
![]() $G = G_{\mathfrak {p}}^{{\operatorname {max}}}$
.
$G = G_{\mathfrak {p}}^{{\operatorname {max}}}$
.
Proof. First assume that
![]() $\#{\mathbf {F}}_{\mathfrak {p}}> 3$
and let
$\#{\mathbf {F}}_{\mathfrak {p}}> 3$
and let
![]() ${{\mathscr {D}H}}$
denote the derived subgroup of a group H. Since the center of
${{\mathscr {D}H}}$
denote the derived subgroup of a group H. Since the center of
![]() $\mathrm {GL}_2({\mathbf {F}}_{\mathfrak {p}})$
is abelian, the assumption
$\mathrm {GL}_2({\mathbf {F}}_{\mathfrak {p}})$
is abelian, the assumption
![]() ${\mathbf {P}} G = {\mathbf {P}} G_{\mathfrak {p}}^{{\operatorname {max}}}$
implies that
${\mathbf {P}} G = {\mathbf {P}} G_{\mathfrak {p}}^{{\operatorname {max}}}$
implies that
![]() ${{\mathscr {D}G}} = {{\mathscr {D}G}}_{\mathfrak {p}}^{{\operatorname {max}}} = {\mathrm {SL}}_2({\mathbf {F}}_{\mathfrak {p}})$
, so
${{\mathscr {D}G}} = {{\mathscr {D}G}}_{\mathfrak {p}}^{{\operatorname {max}}} = {\mathrm {SL}}_2({\mathbf {F}}_{\mathfrak {p}})$
, so
![]() $ {\mathrm {SL}}_2({\mathbf {F}}_{\mathfrak {p}}) \le G$
. The second equality follows from
$ {\mathrm {SL}}_2({\mathbf {F}}_{\mathfrak {p}}) \le G$
. The second equality follows from
where the first equality follows from the fact that
![]() $\operatorname {PSL}_2({\mathbf {F}}_{\mathfrak {p}})$
is nonsolvable simple (since nonabelian when
$\operatorname {PSL}_2({\mathbf {F}}_{\mathfrak {p}})$
is nonsolvable simple (since nonabelian when
![]() $\#{\mathbf {F}}_{\mathfrak {p}}> 3$
) by [Reference Lang65, Theorem 8.4]. Since both groups map onto
$\#{\mathbf {F}}_{\mathfrak {p}}> 3$
) by [Reference Lang65, Theorem 8.4]. Since both groups map onto
![]() ${\mathbf {F}}_p^\times $
under the determinant, we then have exact sequences
${\mathbf {F}}_p^\times $
under the determinant, we then have exact sequences
so
![]() $\#G = \# {\mathrm {SL}}_2({\mathbf {F}}_{\mathfrak {p}}) \#{\mathbf {F}}_p^\times = \#G_{\mathfrak {p}}^{{\operatorname {max}}}$
, whence the claim.
$\#G = \# {\mathrm {SL}}_2({\mathbf {F}}_{\mathfrak {p}}) \#{\mathbf {F}}_p^\times = \#G_{\mathfrak {p}}^{{\operatorname {max}}}$
, whence the claim.
The two cases
![]() ${\mathbf {F}}_{\mathfrak {p}} = {\mathbf {F}}_2$
or
${\mathbf {F}}_{\mathfrak {p}} = {\mathbf {F}}_2$
or
![]() ${\mathbf {F}}_3$
can be checked by an easy computation.
${\mathbf {F}}_3$
can be checked by an easy computation.
2.4 Classification of the maximal subgroups of
 ${\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}}$
${\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}}$
By lemma 2.11,
![]() ${\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}} = \operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
when
${\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}} = \operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
when
![]() $\deg \mathfrak {p}$
is odd, and
$\deg \mathfrak {p}$
is odd, and
![]() ${\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}} = \operatorname {PSL}_2({\mathbf {F}}_{\mathfrak {p}})$
when
${\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}} = \operatorname {PSL}_2({\mathbf {F}}_{\mathfrak {p}})$
when
![]() $\deg \mathfrak {p}$
is even. By proposition 2.12, we know that
$\deg \mathfrak {p}$
is even. By proposition 2.12, we know that
![]() $G_{\mathfrak {p}} = G_{\mathfrak {p}}^{\operatorname {max}}$
if and only if
$G_{\mathfrak {p}} = G_{\mathfrak {p}}^{\operatorname {max}}$
if and only if
![]() ${\mathbf {P}}{G_{\mathfrak {p}}} = {\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}}$
, which is equivalent to
${\mathbf {P}}{G_{\mathfrak {p}}} = {\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}}$
, which is equivalent to
![]() ${\mathbf {P}}{G_{\mathfrak {p}}} \not \subseteq \Gamma $
for every maximal subgroup
${\mathbf {P}}{G_{\mathfrak {p}}} \not \subseteq \Gamma $
for every maximal subgroup
![]() $\Gamma $
of
$\Gamma $
of
![]() ${\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}}$
. In this section, we recall the classification of these maximal subgroups.
${\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}}$
. In this section, we recall the classification of these maximal subgroups.
We begin with the case
![]() $\deg \mathfrak {p}$
even, where
$\deg \mathfrak {p}$
even, where
![]() ${\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}} = \operatorname {PSL}_2({\mathbf {F}}_{\mathfrak {p}})$
.
${\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}} = \operatorname {PSL}_2({\mathbf {F}}_{\mathfrak {p}})$
.
Theorem 2.13 (Maximal subgroups of
 ${\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}}$
,
${\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}}$
,
 $\deg \mathfrak {p}$
even)
$\deg \mathfrak {p}$
even)
Let p be a prime and let
![]() $q = p^{2e}$
be an even power of p. The maximal subgroups of
$q = p^{2e}$
be an even power of p. The maximal subgroups of
![]() $\operatorname {PSL}_2({\mathbf {F}}_q)$
are as follows.
$\operatorname {PSL}_2({\mathbf {F}}_q)$
are as follows.
-
(i) (Borel) The stabilizer of a point of
 ${\mathbf {P}}^1({\mathbf {F}}_q)$
. It has order
${\mathbf {P}}^1({\mathbf {F}}_q)$
. It has order
 $q (q-1)/2$
when q is odd and
$q (q-1)/2$
when q is odd and
 $q(q-1)$
when q is even.
$q(q-1)$
when q is even. -
(ii) (Sub-line) The stabilizer
 $\operatorname {PGL}_2({\mathbf {F}}_{q'}) \cap \operatorname {PSL}_2({\mathbf {F}}_q)$
of a sub-line
$\operatorname {PGL}_2({\mathbf {F}}_{q'}) \cap \operatorname {PSL}_2({\mathbf {F}}_q)$
of a sub-line
 ${\mathbf {P}}^1({\mathbf {F}}_{q'})$
, where
${\mathbf {P}}^1({\mathbf {F}}_{q'})$
, where
 $q = {q'}^\ell $
with a prime
$q = {q'}^\ell $
with a prime
 $\ell $
(in particular,
$\ell $
(in particular,
 $\ell \mid 2e$
).
$\ell \mid 2e$
). -
(iii) (Dihedral) Stabilizers of a pair of points in
 ${\mathbf {P}}^1({\mathbf {F}}_q)$
(normalizer of a split Cartan subgroup, order
${\mathbf {P}}^1({\mathbf {F}}_q)$
(normalizer of a split Cartan subgroup, order
 $q-1$
for
$q-1$
for
 $q \neq 9$
odd and
$q \neq 9$
odd and
 $2(q-1)$
for q even) or of a pair of
$2(q-1)$
for q even) or of a pair of
 ${\mathbf {F}}_q$
-conjugate points in
${\mathbf {F}}_q$
-conjugate points in
 ${\mathbf {P}}^1({\mathbf {F}}_{q^2})$
(normalizer of a nonsplit Cartan subgroup, order
${\mathbf {P}}^1({\mathbf {F}}_{q^2})$
(normalizer of a nonsplit Cartan subgroup, order
 $q+1$
for
$q+1$
for
 $q \neq 9$
odd and
$q \neq 9$
odd and
 $2(q+1)$
for q even).
$2(q+1)$
for q even). -
(iv) (Exceptional) Subgroups isomorphic to
 $S_4$
(when
$S_4$
(when
 $e = 1$
and
$e = 1$
and
 $3 < p \equiv \pm 3 \bmod 8$
), or
$3 < p \equiv \pm 3 \bmod 8$
), or
 $A_5$
(when
$A_5$
(when
 $e = 1$
and
$e = 1$
and
 $p \equiv \pm 3 \bmod 10$
).
$p \equiv \pm 3 \bmod 10$
).
Proof. See [Reference King62, Corollary 2.2], taking into account that q is an even power of p.
When
![]() $q = 4$
, the sub-line and normalizer of a split Cartan case are in the same conjugacy class. When
$q = 4$
, the sub-line and normalizer of a split Cartan case are in the same conjugacy class. When
![]() $q = 9$
, the normalizers of split Cartan subgroups are contained in exceptional subgroups of type
$q = 9$
, the normalizers of split Cartan subgroups are contained in exceptional subgroups of type
![]() $A_5$
, and the normalizers of nonsplit Cartan subgroups are contained in sub-line stabilizers.
$A_5$
, and the normalizers of nonsplit Cartan subgroups are contained in sub-line stabilizers.
When
![]() $\deg \mathfrak {p}$
is odd, we have
$\deg \mathfrak {p}$
is odd, we have
![]() ${\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}} = \operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
. Since
${\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}} = \operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
. Since
![]() $\det (G_{\mathfrak {p}}) = {\mathbf {F}}_p^\times $
contains elements of
$\det (G_{\mathfrak {p}}) = {\mathbf {F}}_p^\times $
contains elements of
![]() ${\mathbf {F}}_{\mathfrak {p}}^\times $
that are non-squares in this case, we also know that
${\mathbf {F}}_{\mathfrak {p}}^\times $
that are non-squares in this case, we also know that
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
is not contained in
${\mathbf {P}}{G_{\mathfrak {p}}}$
is not contained in
![]() $\operatorname {PSL}_2({\mathbf {F}}_{\mathfrak {p}})$
.
$\operatorname {PSL}_2({\mathbf {F}}_{\mathfrak {p}})$
.
Theorem 2.14 (Maximal subgroups of
 ${\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}}$
,
${\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}}$
,
 $\deg \mathfrak {p}$
odd)
$\deg \mathfrak {p}$
odd)
Let
![]() $p \neq 2$
be a prime and let
$p \neq 2$
be a prime and let
![]() $q = p^{2e+1}$
be an odd power of p. The maximal subgroups of
$q = p^{2e+1}$
be an odd power of p. The maximal subgroups of
![]() $\operatorname {PGL}_2({\mathbf {F}}_q)$
different from
$\operatorname {PGL}_2({\mathbf {F}}_q)$
different from
![]() $\operatorname {PSL}_2({\mathbf {F}}_q)$
are as follows.
$\operatorname {PSL}_2({\mathbf {F}}_q)$
are as follows.
-
(i) (Borel) The stabilizer of a point of
 ${\mathbf {P}}^1({\mathbf {F}}_q)$
. It has order
${\mathbf {P}}^1({\mathbf {F}}_q)$
. It has order
 $q (q-1)$
.
$q (q-1)$
. -
(ii) (Sub-line) The stabilizer
 $\operatorname {PGL}_2({\mathbf {F}}_{q'})$
of a sub-line
$\operatorname {PGL}_2({\mathbf {F}}_{q'})$
of a sub-line
 ${\mathbf {P}}^1({\mathbf {F}}_{q'})$
, where
${\mathbf {P}}^1({\mathbf {F}}_{q'})$
, where
 $q = {q'}^\ell $
with a prime
$q = {q'}^\ell $
with a prime
 $\ell $
(in particular,
$\ell $
(in particular,
 $\ell \mid 2e+1$
).
$\ell \mid 2e+1$
). -
(iii) (Dihedral) Stabilizers of a pair of points in
 ${\mathbf {P}}^1({\mathbf {F}}_q)$
(normalizer of a split Cartan subgroup, order
${\mathbf {P}}^1({\mathbf {F}}_q)$
(normalizer of a split Cartan subgroup, order
 $2(q-1)$
, when
$2(q-1)$
, when
 $q> 5$
) or of a pair of
$q> 5$
) or of a pair of
 ${\mathbf {F}}_q$
-conjugate points in
${\mathbf {F}}_q$
-conjugate points in
 ${\mathbf {P}}^1({\mathbf {F}}_{q^2})$
(normalizer of a nonsplit Cartan subgroup, order
${\mathbf {P}}^1({\mathbf {F}}_{q^2})$
(normalizer of a nonsplit Cartan subgroup, order
 $2(q+1)$
).
$2(q+1)$
). -
(iv) (Exceptional) Subgroups isomorphic to
 $S_4$
(when
$S_4$
(when
 $e = 0$
and
$e = 0$
and
 $3 < p \equiv \pm 3 \bmod 8$
), and if
$3 < p \equiv \pm 3 \bmod 8$
), and if
 $q = 3$
,
$q = 3$
,
 $A_4$
.
$A_4$
.
Proof. See [Reference King62, Corollary 2.3], which excludes
![]() $q = 3$
. For
$q = 3$
. For
![]() $q = 3$
, Magma computes that
$q = 3$
, Magma computes that
![]() $\operatorname {PGL}_2({\mathbf {F}}_3) \cong S_4$
has
$\operatorname {PGL}_2({\mathbf {F}}_3) \cong S_4$
has
![]() $3$
maximal subgroups,
$3$
maximal subgroups,
![]() $S_3, D_4, A_4$
, which correspond to the Borel, normalizer of nonsplit Cartan and exceptional maximal subgroup case, respectively.
$S_3, D_4, A_4$
, which correspond to the Borel, normalizer of nonsplit Cartan and exceptional maximal subgroup case, respectively.
Definition 2.15. We say that
![]() $\rho _{\mathfrak {p}}$
or
$\rho _{\mathfrak {p}}$
or
![]() $G_{\mathfrak {p}}$
is Borel, sub-line, dihedral or exceptional when
$G_{\mathfrak {p}}$
is Borel, sub-line, dihedral or exceptional when
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
is contained in a maximal subgroup of
${\mathbf {P}}{G_{\mathfrak {p}}}$
is contained in a maximal subgroup of
![]() ${\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}}$
of the corresponding type. In the dihedral case, we distinguish between split and nonsplit, according to the Cartan subgroup involved. We say that
${\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}}$
of the corresponding type. In the dihedral case, we distinguish between split and nonsplit, according to the Cartan subgroup involved. We say that
![]() $\rho _{\mathfrak {p}}$
or
$\rho _{\mathfrak {p}}$
or
![]() $G_{\mathfrak {p}}$
is reducible or irreducible if the action of
$G_{\mathfrak {p}}$
is reducible or irreducible if the action of
![]() $G_{\mathfrak {p}}$
on
$G_{\mathfrak {p}}$
on
![]() ${\mathbf {F}}_{\mathfrak {p}}^2$
is, and we say that it is maximal if
${\mathbf {F}}_{\mathfrak {p}}^2$
is, and we say that it is maximal if
![]() $G_{\mathfrak {p}} = G_{\mathfrak {p}}^{\operatorname {max}}$
.
$G_{\mathfrak {p}} = G_{\mathfrak {p}}^{\operatorname {max}}$
.
The action of
![]() $G_{\mathfrak {p}}$
is reducible if and only if
$G_{\mathfrak {p}}$
is reducible if and only if
![]() $\rho _{\mathfrak {p}}$
is Borel. In the sub-line case, the invariant sub-line can be the image of a nontrivial invariant subspace of
$\rho _{\mathfrak {p}}$
is Borel. In the sub-line case, the invariant sub-line can be the image of a nontrivial invariant subspace of
![]() $A[\mathfrak {p}]$
considered as an
$A[\mathfrak {p}]$
considered as an
![]() ${\mathbf {F}}_p$
-vector space. In this case (if
${\mathbf {F}}_p$
-vector space. In this case (if
![]() $\rho _{\mathfrak {p}}$
is not also Borel),
$\rho _{\mathfrak {p}}$
is not also Borel),
![]() $\rho _{\mathfrak {p}}$
is irreducible as a
$\rho _{\mathfrak {p}}$
is irreducible as a
![]() $2$
-dimensional
$2$
-dimensional
![]() ${\mathbf {F}}_{\mathfrak {p}}$
-representation, but reducible as a
${\mathbf {F}}_{\mathfrak {p}}$
-representation, but reducible as a
![]() $2 (\deg \mathfrak {p})$
-dimensional
$2 (\deg \mathfrak {p})$
-dimensional
![]() ${\mathbf {F}}_p$
-representation. See Section 2.10 below for a more detailed discussion.
${\mathbf {F}}_p$
-representation. See Section 2.10 below for a more detailed discussion.
2.5 Irreducibility and maximality criteria for fixed
 $\mathfrak {p}$
$\mathfrak {p}$
In this section, we collect some criteria that allow us to verify that
![]() $\rho _{\mathfrak {p}}$
is irreducible or maximal for a given prime ideal
$\rho _{\mathfrak {p}}$
is irreducible or maximal for a given prime ideal
![]() $\mathfrak {p}$
, using information from the characteristic polynomials of
$\mathfrak {p}$
, using information from the characteristic polynomials of
![]() $\rho _{\mathfrak {p}}(\operatorname {Frob}_\ell )$
for
$\rho _{\mathfrak {p}}(\operatorname {Frob}_\ell )$
for
![]() $\ell \nmid Np$
. Recall from theorem 2.6 that the characteristic polynomial of
$\ell \nmid Np$
. Recall from theorem 2.6 that the characteristic polynomial of
![]() $\rho _{\mathfrak {p}}(\operatorname {Frob}_\ell )$
has the form
$\rho _{\mathfrak {p}}(\operatorname {Frob}_\ell )$
has the form
where
![]() $x \mapsto \bar {x}$
denotes the reduction homomorphism
$x \mapsto \bar {x}$
denotes the reduction homomorphism
![]() ${\mathbf {Z}}[f] \to {\mathbf {F}}_{\mathfrak {p}}$
.
${\mathbf {Z}}[f] \to {\mathbf {F}}_{\mathfrak {p}}$
.
We define some invariants associated to elements of
![]() $\operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
; see [Reference Serre98, § 2]. For
$\operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
; see [Reference Serre98, § 2]. For
![]() ${\mathbf {F}}$
a finite field of odd characteristic, we define the Legendre symbol for
${\mathbf {F}}$
a finite field of odd characteristic, we define the Legendre symbol for
![]() $a \in {\mathbf {F}}$
as usual:
$a \in {\mathbf {F}}$
as usual:
 $$\begin{align*}\Bigl(\frac{a}{{\mathbf{F}}}\Bigr) = \begin{cases} 0 & \text{if }a = 0, \\ 1 & \text{if } a = b^2 \text{ for some } b \in {\mathbf{F}}^\times, \\ -1 & \text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}\Bigl(\frac{a}{{\mathbf{F}}}\Bigr) = \begin{cases} 0 & \text{if }a = 0, \\ 1 & \text{if } a = b^2 \text{ for some } b \in {\mathbf{F}}^\times, \\ -1 & \text{otherwise.} \end{cases} \end{align*}$$
Lemma 2.16. Let
![]() ${\mathbf {F}}$
be a finite field.
${\mathbf {F}}$
be a finite field.
-
(1) The function
descends to a function $$\begin{align*}\mathrm{GL}_2({\mathbf{F}}) \to {\mathbf{F}}, \quad M \mapsto \frac{\operatorname{Tr}(M)^2}{\det(M)} \end{align*}$$
$$\begin{align*}\mathrm{GL}_2({\mathbf{F}}) \to {\mathbf{F}}, \quad M \mapsto \frac{\operatorname{Tr}(M)^2}{\det(M)} \end{align*}$$
 $u \colon \operatorname {PGL}_2({\mathbf {F}}) \to {\mathbf {F}}$
.
$u \colon \operatorname {PGL}_2({\mathbf {F}}) \to {\mathbf {F}}$
.
-
(2) Assume that
 ${\mathbf {F}}$
has characteristic
${\mathbf {F}}$
has characteristic
 $p \neq 2$
. The function descends to
$p \neq 2$
. The function descends to $$\begin{align*}\mathrm{GL}_2({\mathbf{F}}) \to \{0,1,-1\}, \quad M \mapsto \Bigl(\frac{\operatorname{Tr}(M)^2 - 4 \det(M)}{{\mathbf{F}}}\Bigr) \end{align*}$$
$$\begin{align*}\mathrm{GL}_2({\mathbf{F}}) \to \{0,1,-1\}, \quad M \mapsto \Bigl(\frac{\operatorname{Tr}(M)^2 - 4 \det(M)}{{\mathbf{F}}}\Bigr) \end{align*}$$
 $\Delta \colon \operatorname {PGL}_2({\mathbf {F}}) \to \{0,1,-1\}$
.
$\Delta \colon \operatorname {PGL}_2({\mathbf {F}}) \to \{0,1,-1\}$
.
Proof. Since
![]() $\operatorname {Tr}^2$
and
$\operatorname {Tr}^2$
and
![]() $\det $
are both homogeneous of degree
$\det $
are both homogeneous of degree
![]() $2$
and
$2$
and
![]() $\det (M) \neq 0$
, the existence of u follows. Similarly,
$\det (M) \neq 0$
, the existence of u follows. Similarly,
![]() $\operatorname {Tr}(M)^2 - 4 \det (M)$
is well-defined up to multiplication with a nonzero square, so the Legendre symbol is well-defined.
$\operatorname {Tr}(M)^2 - 4 \det (M)$
is well-defined up to multiplication with a nonzero square, so the Legendre symbol is well-defined.
We now assume that the characteristic of
![]() ${\mathbf {F}}$
is odd.
${\mathbf {F}}$
is odd.
If
![]() $u(g) \neq 0$
(equivalently,
$u(g) \neq 0$
(equivalently,
![]() $\operatorname {Tr}(M) \neq 0$
, where M is a lift of g to
$\operatorname {Tr}(M) \neq 0$
, where M is a lift of g to
![]() $\mathrm {GL}_2({\mathbf {F}})$
), then
$\mathrm {GL}_2({\mathbf {F}})$
), then
![]() $\Delta (g) = \left (\frac {u(g)(u(g)-4)}{{\mathbf {F}}}\right )$
. If
$\Delta (g) = \left (\frac {u(g)(u(g)-4)}{{\mathbf {F}}}\right )$
. If
![]() $u(g) = 0$
, then
$u(g) = 0$
, then
![]() $\Delta (g) = \left (\frac {-\det (M)}{{\mathbf {F}}}\right ) \neq 0$
, so
$\Delta (g) = \left (\frac {-\det (M)}{{\mathbf {F}}}\right ) \neq 0$
, so
![]() $\Delta (g) = 0$
is equivalent to
$\Delta (g) = 0$
is equivalent to
![]() $u(g) = 4$
.
$u(g) = 4$
.
We note that
![]() $\Delta (g)$
gives the square class of the discriminant of the characteristic polynomial of any lift M of g to
$\Delta (g)$
gives the square class of the discriminant of the characteristic polynomial of any lift M of g to
![]() $\mathrm {GL}_2({\mathbf {F}})$
. This implies that
$\mathrm {GL}_2({\mathbf {F}})$
. This implies that
![]() $\Delta (g) \neq 0$
if and only if M has distinct eigenvalues (and hence is semi-simple). The eigenvalues are in
$\Delta (g) \neq 0$
if and only if M has distinct eigenvalues (and hence is semi-simple). The eigenvalues are in
![]() ${\mathbf {F}}$
when
${\mathbf {F}}$
when
![]() $\Delta (g) = 1$
and in the quadratic extension of
$\Delta (g) = 1$
and in the quadratic extension of
![]() ${\mathbf {F}}$
and conjugate when
${\mathbf {F}}$
and conjugate when
![]() $\Delta (g) = -1$
. It follows that the elements of any Borel subgroup of
$\Delta (g) = -1$
. It follows that the elements of any Borel subgroup of
![]() $\operatorname {PGL}_2({\mathbf {F}})$
have
$\operatorname {PGL}_2({\mathbf {F}})$
have
![]() $\Delta \neq -1$
. We therefore obtain the following.
$\Delta \neq -1$
. We therefore obtain the following.
Corollary 2.17. Let
![]() $\mathfrak {p}$
be a prime ideal of odd residue characteristic. If
$\mathfrak {p}$
be a prime ideal of odd residue characteristic. If
![]() $\Delta (g) = -1$
for some
$\Delta (g) = -1$
for some
![]() $g \in {\mathbf {P}}{G_{\mathfrak {p}}}$
, then
$g \in {\mathbf {P}}{G_{\mathfrak {p}}}$
, then
![]() $\rho _{\mathfrak {p}}$
is irreducible.
$\rho _{\mathfrak {p}}$
is irreducible.
Proof. If
![]() $\rho _{\mathfrak {p}}$
were reducible, then
$\rho _{\mathfrak {p}}$
were reducible, then
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
would be contained in a Borel subgroup, and so
${\mathbf {P}}{G_{\mathfrak {p}}}$
would be contained in a Borel subgroup, and so
![]() $\Delta ({\mathbf {P}}{G_{\mathfrak {p}}}) \subseteq \{0, 1\}$
, contradicting the assumption.
$\Delta ({\mathbf {P}}{G_{\mathfrak {p}}}) \subseteq \{0, 1\}$
, contradicting the assumption.
This gives a method to prove the irreducibility of
![]() $\rho _{\mathfrak {p}}$
by computing
$\rho _{\mathfrak {p}}$
by computing
 $$\begin{align*}\Delta({\mathbf{P}} \rho_{\mathfrak{p}}(\operatorname{Frob}_\ell)) = \Bigl(\frac{a_\ell^2 - 4 \ell}{{\mathbf{F}}_{\mathfrak{p}}}\Bigr) \end{align*}$$
$$\begin{align*}\Delta({\mathbf{P}} \rho_{\mathfrak{p}}(\operatorname{Frob}_\ell)) = \Bigl(\frac{a_\ell^2 - 4 \ell}{{\mathbf{F}}_{\mathfrak{p}}}\Bigr) \end{align*}$$
for a number of primes
![]() $\ell \nmid N p(\mathfrak {p})$
. If we obtain the value
$\ell \nmid N p(\mathfrak {p})$
. If we obtain the value
![]() $-1$
for one such
$-1$
for one such
![]() $\ell $
, this shows that
$\ell $
, this shows that
![]() $\rho _{\mathfrak {p}}$
is irreducible.
$\rho _{\mathfrak {p}}$
is irreducible.
We can use the invariant
![]() $u(g)$
to obtain information on the order of g. (See [Reference Serre98, § 2.6 iii].)
$u(g)$
to obtain information on the order of g. (See [Reference Serre98, § 2.6 iii].)
Proposition 2.18. Let
![]() ${\mathbf {F}}$
be a finite field of characteristic p and let
${\mathbf {F}}$
be a finite field of characteristic p and let
![]() $g \in \operatorname {PGL}_2({\mathbf {F}})$
.
$g \in \operatorname {PGL}_2({\mathbf {F}})$
.
-
(1) g is unipotent
 $\iff u(g) = 4 \iff \Delta (g) = 0$
.
$\iff u(g) = 4 \iff \Delta (g) = 0$
. -
(2) If
 $p \neq 2$
:
$p \neq 2$
:
 $ {\mathrm {ord}}(g) = 2 \iff u(g) = 0$
.
$ {\mathrm {ord}}(g) = 2 \iff u(g) = 0$
. -
(3) If
 $p \neq 3$
:
$p \neq 3$
:
 $ {\mathrm {ord}}(g) = 3 \iff u(g) = 1$
.
$ {\mathrm {ord}}(g) = 3 \iff u(g) = 1$
. -
(4) If
 $p \neq 2$
:
$p \neq 2$
:
 $ {\mathrm {ord}}(g) = 4 \iff u(g) = 2$
.
$ {\mathrm {ord}}(g) = 4 \iff u(g) = 2$
. -
(5) If
 $p \neq 5$
:
$p \neq 5$
:
 $ {\mathrm {ord}}(g) = 5 \iff u(g)^2 - 3 u(g) + 1 = 0$
.
$ {\mathrm {ord}}(g) = 5 \iff u(g)^2 - 3 u(g) + 1 = 0$
.
Proof. Let
![]() $g = {\mathbf {P}} M$
for some
$g = {\mathbf {P}} M$
for some
![]() $M \in \mathrm {GL}_2({\mathbf {F}})$
. If
$M \in \mathrm {GL}_2({\mathbf {F}})$
. If
![]() $\Delta (g) \neq 0$
(equivalently,
$\Delta (g) \neq 0$
(equivalently,
![]() $u(g) \neq 4$
), then M is semi-simple by the discussion above, and so, up to scaling, we can diagonalize M over
$u(g) \neq 4$
), then M is semi-simple by the discussion above, and so, up to scaling, we can diagonalize M over
![]() $\bar {{\mathbf {F}}}$
as
$\bar {{\mathbf {F}}}$
as
![]() $M \sim \operatorname {diag}(1, \zeta )$
, where
$M \sim \operatorname {diag}(1, \zeta )$
, where
![]() $\zeta $
is some root of unity of order
$\zeta $
is some root of unity of order
![]() $ {\mathrm {ord}}(g)$
. Then
$ {\mathrm {ord}}(g)$
. Then
![]() $u(g) = (1 + \zeta )^2/\zeta = \zeta + 2 + \zeta ^{-1}$
. Two values of u agree if and only if the corresponding values of
$u(g) = (1 + \zeta )^2/\zeta = \zeta + 2 + \zeta ^{-1}$
. Two values of u agree if and only if the corresponding values of
![]() $\zeta $
are either equal or inverses of each other. Claim (1) follows from the discussion above, and the others follow by observing that the condition on p ensures that the corresponding
$\zeta $
are either equal or inverses of each other. Claim (1) follows from the discussion above, and the others follow by observing that the condition on p ensures that the corresponding
![]() $u(g)$
is not equal to
$u(g)$
is not equal to
![]() $4$
and by matching roots of unity
$4$
and by matching roots of unity
![]() $\zeta $
with u:
$\zeta $
with u:
![]() $\zeta = -1 \iff u = 0$
,
$\zeta = -1 \iff u = 0$
,
![]() $ {\mathrm {ord}}(\zeta ) = 3 \iff \zeta + \zeta ^{-1} = -1 \iff u = 1$
,
$ {\mathrm {ord}}(\zeta ) = 3 \iff \zeta + \zeta ^{-1} = -1 \iff u = 1$
,
![]() $ {\mathrm {ord}}(\zeta ) = 4 \iff \zeta + \zeta ^{-1} = 0 \iff u = 2$
, and the two values of
$ {\mathrm {ord}}(\zeta ) = 4 \iff \zeta + \zeta ^{-1} = 0 \iff u = 2$
, and the two values of
![]() $\zeta + 2 + \zeta ^{-1}$
for a fifth root of unity
$\zeta + 2 + \zeta ^{-1}$
for a fifth root of unity
![]() $\zeta $
are the roots of
$\zeta $
are the roots of
![]() $u^2 - 3 u + 1$
.
$u^2 - 3 u + 1$
.
We can use this to show that
![]() $\rho _{\mathfrak {p}}$
is not exceptional since the elements of
$\rho _{\mathfrak {p}}$
is not exceptional since the elements of
![]() $S_4$
have order at most
$S_4$
have order at most
![]() $4$
and the elements of
$4$
and the elements of
![]() $A_5$
have order
$A_5$
have order
![]() $5$
or at most
$5$
or at most
![]() $3$
. So if we can find an element
$3$
. So if we can find an element
![]() $g \in {\mathbf {P}}{G_{\mathfrak {p}}}$
of order at least
$g \in {\mathbf {P}}{G_{\mathfrak {p}}}$
of order at least
![]() $5$
, then
$5$
, then
![]() ${\mathbf {P}}{G_{\mathfrak {p}}} \not \subseteq S_4$
, and if we can find an element of order
${\mathbf {P}}{G_{\mathfrak {p}}} \not \subseteq S_4$
, and if we can find an element of order
![]() $4$
or at least
$4$
or at least
![]() $6$
, then
$6$
, then
![]() ${\mathbf {P}}{G_{\mathfrak {p}}} \not \subseteq A_5$
.
${\mathbf {P}}{G_{\mathfrak {p}}} \not \subseteq A_5$
.
We now want to rule out the other possible maximal subgroups.
If
![]() $\rho _{\mathfrak {p}}$
is dihedral, then
$\rho _{\mathfrak {p}}$
is dihedral, then
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
is contained in the normalizer
${\mathbf {P}}{G_{\mathfrak {p}}}$
is contained in the normalizer
![]() $N(C)$
either of a split or of a nonsplit Cartan subgroup C. The elements of
$N(C)$
either of a split or of a nonsplit Cartan subgroup C. The elements of
![]() $N(C) \setminus C$
have order
$N(C) \setminus C$
have order
![]() $2$
; hence,
$2$
; hence,
![]() $u = 0$
. If C is split, then the nontrivial elements of C have
$u = 0$
. If C is split, then the nontrivial elements of C have
![]() $\Delta = 1$
; if C is nonsplit, its nontrivial elements have
$\Delta = 1$
; if C is nonsplit, its nontrivial elements have
![]() $\Delta = -1$
. So if we find elements in
$\Delta = -1$
. So if we find elements in
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
with
${\mathbf {P}}{G_{\mathfrak {p}}}$
with
![]() $\Delta = 1$
and
$\Delta = 1$
and
![]() $u \neq 0$
and also elements with
$u \neq 0$
and also elements with
![]() $\Delta = -1$
and
$\Delta = -1$
and
![]() $u \neq 0$
, then
$u \neq 0$
, then
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
cannot be dihedral.
${\mathbf {P}}{G_{\mathfrak {p}}}$
cannot be dihedral.
For the sub-line case, we restrict to
![]() $\deg \mathfrak {p} \le 2$
. If
$\deg \mathfrak {p} \le 2$
. If
![]() $\rho _{\mathfrak {p}}$
is sub-line, we must then have
$\rho _{\mathfrak {p}}$
is sub-line, we must then have
![]() $\deg \mathfrak {p} = 2$
, and
$\deg \mathfrak {p} = 2$
, and
![]() ${\mathbf {P}}{G_{\mathfrak {p}}} \subseteq \operatorname {PGL}_2({\mathbf {F}}_p)$
(up to conjugation in
${\mathbf {P}}{G_{\mathfrak {p}}} \subseteq \operatorname {PGL}_2({\mathbf {F}}_p)$
(up to conjugation in
![]() $\operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
). Since clearly
$\operatorname {PGL}_2({\mathbf {F}}_{\mathfrak {p}})$
). Since clearly
![]() $u(g) \in {\mathbf {F}}_p$
for each element
$u(g) \in {\mathbf {F}}_p$
for each element
![]() $g \in \operatorname {PGL}_2({\mathbf {F}}_p) \subset \operatorname {PSL}_2({\mathbf {F}}_{\mathfrak {p}})$
, we can exclude the sub-line case when we find an element
$g \in \operatorname {PGL}_2({\mathbf {F}}_p) \subset \operatorname {PSL}_2({\mathbf {F}}_{\mathfrak {p}})$
, we can exclude the sub-line case when we find an element
![]() $g \in {\mathbf {P}}{G_{\mathfrak {p}}}$
such that
$g \in {\mathbf {P}}{G_{\mathfrak {p}}}$
such that
![]() $u(g) \in {\mathbf {F}}_{\mathfrak {p}} \setminus {\mathbf {F}}_p$
. Without the restriction on
$u(g) \in {\mathbf {F}}_{\mathfrak {p}} \setminus {\mathbf {F}}_p$
. Without the restriction on
![]() $\deg \mathfrak {p}$
, we can similarly exclude the sub-line case when we find
$\deg \mathfrak {p}$
, we can similarly exclude the sub-line case when we find
![]() $g \in {\mathbf {P}}{G_{\mathfrak {p}}}$
such that
$g \in {\mathbf {P}}{G_{\mathfrak {p}}}$
such that
![]() ${\mathbf {F}}_p(u(g)) = {\mathbf {F}}_{\mathfrak {p}}$
. It is also the case that the discriminant of the characteristic polynomial of any element is in
${\mathbf {F}}_p(u(g)) = {\mathbf {F}}_{\mathfrak {p}}$
. It is also the case that the discriminant of the characteristic polynomial of any element is in
![]() ${\mathbf {F}}_p$
(up to squares in
${\mathbf {F}}_p$
(up to squares in
![]() ${\mathbf {F}}_{\mathfrak {p}}^\times $
) and therefore a square in
${\mathbf {F}}_{\mathfrak {p}}^\times $
) and therefore a square in
![]() ${\mathbf {F}}_{\mathfrak {p}}$
, so that
${\mathbf {F}}_{\mathfrak {p}}$
, so that
![]() $\Delta \in \{0, 1\}$
. So, similar to the Borel case, this case can also be ruled out as soon as we find an element with
$\Delta \in \{0, 1\}$
. So, similar to the Borel case, this case can also be ruled out as soon as we find an element with
![]() $\Delta = -1$
. (This last argument is specific to
$\Delta = -1$
. (This last argument is specific to
![]() $\deg \mathfrak {p} = 2^n$
for some n.)
$\deg \mathfrak {p} = 2^n$
for some n.)
Assuming that we already know that the image is not exceptional, we can therefore prove that it is maximal by considering primes
![]() $\ell \nmid Np$
, computing
$\ell \nmid Np$
, computing
 $$\begin{align*}\Delta(\ell) := \Delta({\mathbf{P}}\rho_{\mathfrak{p}}(\operatorname{Frob}_\ell)) = \Bigl(\frac{a_\ell^2 - 4 \ell}{{\mathbf{F}}_{\mathfrak{p}}}\Bigr) \end{align*}$$
$$\begin{align*}\Delta(\ell) := \Delta({\mathbf{P}}\rho_{\mathfrak{p}}(\operatorname{Frob}_\ell)) = \Bigl(\frac{a_\ell^2 - 4 \ell}{{\mathbf{F}}_{\mathfrak{p}}}\Bigr) \end{align*}$$
until we have found one
![]() $\ell $
such that
$\ell $
such that
![]() $\Delta (\ell ) = -1$
and
$\Delta (\ell ) = -1$
and
![]() $\mathfrak {p} \nmid a_\ell $
and another
$\mathfrak {p} \nmid a_\ell $
and another
![]() $\ell $
such that
$\ell $
such that
![]() $\Delta (\ell ) = 1$
and
$\Delta (\ell ) = 1$
and
![]() $\mathfrak {p} \nmid a_\ell $
. (Recall that
$\mathfrak {p} \nmid a_\ell $
. (Recall that
![]() $u({\mathbf {P}}\rho _{\mathfrak {p}}(\operatorname {Frob}_\ell )) \neq 0 \iff \mathfrak {p} \nmid a_\ell $
).
$u({\mathbf {P}}\rho _{\mathfrak {p}}(\operatorname {Frob}_\ell )) \neq 0 \iff \mathfrak {p} \nmid a_\ell $
).
We obtain the following algorithm that returns a set of possible types of subgroups of
![]() ${\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}}$
that can contain
${\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}}$
that can contain
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
. If this set is empty, then
${\mathbf {P}}{G_{\mathfrak {p}}}$
. If this set is empty, then
![]() $\rho _{\mathfrak {p}}$
has maximal image. We assume
$\rho _{\mathfrak {p}}$
has maximal image. We assume
![]() $g = 2$
here since the discussion of the sub-line case above was assuming
$g = 2$
here since the discussion of the sub-line case above was assuming
![]() $\deg \mathfrak {p} \le 2$
, and
$\deg \mathfrak {p} \le 2$
, and
![]() $g = 2$
is our main case of interest. The algorithm can be modified to work for general g if desired.
$g = 2$
is our main case of interest. The algorithm can be modified to work for general g if desired.
We use the symbols
![]() $S_4$
and
$S_4$
and
![]() $A_5$
to denote subgroups isomorphic to the respective groups, R (‘reducible’) for a Borel subgroup, L for a sub-line stabilizer, and
$A_5$
to denote subgroups isomorphic to the respective groups, R (‘reducible’) for a Borel subgroup, L for a sub-line stabilizer, and
![]() $N_s$
and
$N_s$
and
![]() $N_{ns}$
for the normalizers of a split or nonsplit Cartan subgroup.
$N_{ns}$
for the normalizers of a split or nonsplit Cartan subgroup.
Algorithm 2.19.


The correctness of the algorithm follows from the classification results in Section 2.4 and the discussion in this section. The fact that
![]() $N_{ns}$
can be excluded when
$N_{ns}$
can be excluded when
![]() $\deg \mathfrak {p} = 2$
in Step 3c follows from corollary 2.24 below.
$\deg \mathfrak {p} = 2$
in Step 3c follows from corollary 2.24 below.
If the image is indeed maximal, then
![]() ${\mathbf {P}}{G_{\mathfrak {p}}} = {\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}}$
contains elements with
${\mathbf {P}}{G_{\mathfrak {p}}} = {\mathbf {P}}{G_{\mathfrak {p}}^{\operatorname {max}}}$
contains elements with
![]() $u \neq 0$
and
$u \neq 0$
and
![]() $\Delta = 1$
, with
$\Delta = 1$
, with
![]() $u \neq 0$
and
$u \neq 0$
and
![]() $\Delta = -1$
, of order
$\Delta = -1$
, of order
![]() $\ge 6$
(when
$\ge 6$
(when
![]() $p \ge 5$
) and of order
$p \ge 5$
) and of order
![]() $4$
. Chebotarëv’s density theorem then guarantees that suitable primes
$4$
. Chebotarëv’s density theorem then guarantees that suitable primes
![]() $\ell $
exist to rule out all the possible types. Using an effective version of the density theorem would give an explicit bound B for the primes
$\ell $
exist to rule out all the possible types. Using an effective version of the density theorem would give an explicit bound B for the primes
![]() $\ell $
that have to be considered in the algorithm to be able to decide whether
$\ell $
that have to be considered in the algorithm to be able to decide whether
![]() $\rho _{\mathfrak {p}}$
has maximal image. This bound will be too large to be useful in practice, however.
$\rho _{\mathfrak {p}}$
has maximal image. This bound will be too large to be useful in practice, however.
2.6 Explicit computation
When algorithm 2.19 returns a nonempty set of types, we can try to determine the image explicitly as follows. We assume that we have given a curve X of genus
![]() $2$
over
$2$
over
![]() ${\mathbf {Q}}$
whose Jacobian J is isogenous to
${\mathbf {Q}}$
whose Jacobian J is isogenous to
![]() $A_f$
; we will determine the image of
$A_f$
; we will determine the image of
![]() $\rho _{J,\mathfrak {p}}$
(which has the same semi-simplification as
$\rho _{J,\mathfrak {p}}$
(which has the same semi-simplification as
![]() $\rho _{\mathfrak {p},f}$
), assuming that
$\rho _{\mathfrak {p},f}$
), assuming that
![]() $\mathfrak {p}$
is a regular prime of
$\mathfrak {p}$
is a regular prime of
![]() $\mathrm {End}_{{\mathbf {Q}}}(J)$
.
$\mathrm {End}_{{\mathbf {Q}}}(J)$
.
We compute (using Magma, say) the big period matrix associated to J, which allows us to write
![]() $J({\mathbf {C}}) = {\mathbf {C}}^2/\Lambda $
for some (numerically) explicit lattice
$J({\mathbf {C}}) = {\mathbf {C}}^2/\Lambda $
for some (numerically) explicit lattice
![]() $\Lambda $
. We can also determine the action of
$\Lambda $
. We can also determine the action of
![]() $\mathrm {End}(J)$
on
$\mathrm {End}(J)$
on
![]() ${\mathbf {C}}^2$
, and so we can approximate numerically the points in
${\mathbf {C}}^2$
, and so we can approximate numerically the points in
![]() $J({\mathbf {C}})[\mathfrak {p}]$
. We represent these points by (numerical) divisors on X, which we then recognize as divisors supported in algebraic points (this will work when the precision is sufficiently large). We then verify that the algebraic points on J we obtain are indeed in
$J({\mathbf {C}})[\mathfrak {p}]$
. We represent these points by (numerical) divisors on X, which we then recognize as divisors supported in algebraic points (this will work when the precision is sufficiently large). We then verify that the algebraic points on J we obtain are indeed in
![]() $J[\mathfrak {p}]$
. Knowing the points explicitly as algebraic points allows us to determine the Galois action.
$J[\mathfrak {p}]$
. Knowing the points explicitly as algebraic points allows us to determine the Galois action.
Since Magma can easily determine the torsion subgroup of
![]() $J({\mathbf {Q}})$
using the algorithm described in [Reference Stoll111, § 11], we can at least deduce that the representation associated to some prime ideal
$J({\mathbf {Q}})$
using the algorithm described in [Reference Stoll111, § 11], we can at least deduce that the representation associated to some prime ideal
![]() $\mathfrak {p}$
with
$\mathfrak {p}$
with
![]() $p(\mathfrak {p}) = p$
is reducible if
$p(\mathfrak {p}) = p$
is reducible if
![]() $J({\mathbf {Q}})[p]$
is nontrivial.
$J({\mathbf {Q}})[p]$
is nontrivial.
Examples 2.20. We give two examples for such an explicit computation.
-
(1)
 $A = J_0(125)^+$
with endomorphism ring the maximal order of
$A = J_0(125)^+$
with endomorphism ring the maximal order of
 ${\mathbf {Q}}(\sqrt {5})$
. The representation
${\mathbf {Q}}(\sqrt {5})$
. The representation
 $\rho _{\langle {\sqrt {5}}\rangle }$
is reducible.
$\rho _{\langle {\sqrt {5}}\rangle }$
is reducible.
 $A[\sqrt {5}]$
has constituents
$A[\sqrt {5}]$
has constituents
 $\mu _5^{\otimes 2}$
and
$\mu _5^{\otimes 2}$
and
 $\mu _5^{\otimes 3}$
. In this case,
$\mu _5^{\otimes 3}$
. In this case,
 $5 \nmid [{\mathbf {Q}}(A[\sqrt {5}]) : {\mathbf {Q}}]$
, so
$5 \nmid [{\mathbf {Q}}(A[\sqrt {5}]) : {\mathbf {Q}}]$
, so  $$\begin{align*}A[\sqrt{5}] \cong \mu_5^{\otimes 2} \oplus \mu_5^{\otimes 3} \,. \end{align*}$$
$$\begin{align*}A[\sqrt{5}] \cong \mu_5^{\otimes 2} \oplus \mu_5^{\otimes 3} \,. \end{align*}$$
-
(2)
 $A = J_0(147)^{\langle w_3,w_{49} \rangle }$
with endomorphism ring the maximal order of
$A = J_0(147)^{\langle w_3,w_{49} \rangle }$
with endomorphism ring the maximal order of
 ${\mathbf {Q}}(\sqrt {2})$
. There is a prime
${\mathbf {Q}}(\sqrt {2})$
. There is a prime
 $\mathfrak {p} \mid 7$
in
$\mathfrak {p} \mid 7$
in
 $\mathrm {End}(A)$
such that
$\mathrm {End}(A)$
such that
 $\rho _{\mathfrak {p}}$
is reducible. We find that its irreducible constituents are
$\rho _{\mathfrak {p}}$
is reducible. We find that its irreducible constituents are
 $\mu _7^{\otimes 3}$
and
$\mu _7^{\otimes 3}$
and
 $\mu _7^{\otimes 4}$
. As
$\mu _7^{\otimes 4}$
. As
 $[{\mathbf {Q}}(A[\mathfrak {p}]) : {\mathbf {Q}}] = 7 \cdot (7-1)$
and
$[{\mathbf {Q}}(A[\mathfrak {p}]) : {\mathbf {Q}}] = 7 \cdot (7-1)$
and
 $A[7]({\mathbf {Q}}(\sqrt {-7})) = A[7]({\mathbf {Q}}(\mu _7^{\otimes 3})) = 0$
, one has a nonsplit short exact sequence of Galois modules
$A[7]({\mathbf {Q}}(\sqrt {-7})) = A[7]({\mathbf {Q}}(\mu _7^{\otimes 3})) = 0$
, one has a nonsplit short exact sequence of Galois modules  $$\begin{align*}0 \to \mu_7^{\otimes 4} \to A[\mathfrak{p}] \to \mu_7^{\otimes 3} \to 0 \,.\end{align*}$$
$$\begin{align*}0 \to \mu_7^{\otimes 4} \to A[\mathfrak{p}] \to \mu_7^{\otimes 3} \to 0 \,.\end{align*}$$
2.7 The image of inertia at p
Our next goal will be to prove that
![]() $\rho _{\mathfrak {p}}$
is irreducible (or even maximal) for all but finitely many
$\rho _{\mathfrak {p}}$
is irreducible (or even maximal) for all but finitely many
![]() $\mathfrak {p}$
, with a small explicit set of possible exceptions. To this end, we need to study the representations
$\mathfrak {p}$
, with a small explicit set of possible exceptions. To this end, we need to study the representations
![]() $\rho _{\mathfrak {p}}$
more carefully, so that we can extract some uniform statements. We begin by considering the action of the inertia group at the prime p. Recall the definitions and the notations
$\rho _{\mathfrak {p}}$
more carefully, so that we can extract some uniform statements. We begin by considering the action of the inertia group at the prime p. Recall the definitions and the notations
![]() $I_p$
,
$I_p$
,
![]() $I_p^{\mathrm {w}}$
,
$I_p^{\mathrm {w}}$
,
![]() $I_p^{\mathrm {t}}$
from Section 2.1. Also recall the fundamental characters
$I_p^{\mathrm {t}}$
from Section 2.1. Also recall the fundamental characters
![]() $\psi _k$
from definition 2.8. In the following, g is arbitrary again.
$\psi _k$
from definition 2.8. In the following, g is arbitrary again.
We now consider
![]() $\rho _{\mathfrak {p}}|_{I_p}$
, where
$\rho _{\mathfrak {p}}|_{I_p}$
, where
![]() $p = p(\mathfrak {p})$
is the residue characteristic of
$p = p(\mathfrak {p})$
is the residue characteristic of
![]() $\mathfrak {p}$
. We have the following result.
$\mathfrak {p}$
. We have the following result.
Theorem 2.21. Assume
![]() $p^2 \nmid N$
. Exactly one of the following two statements is true.
$p^2 \nmid N$
. Exactly one of the following two statements is true.
-
(i)
 $\rho _{\mathfrak {p}}|_{I_p}$
has, up to conjugation, the form for some
$\rho _{\mathfrak {p}}|_{I_p}$
has, up to conjugation, the form for some $$\begin{align*}\begin{pmatrix} \chi_p^n & * \\ 0 & \chi_p^{1-n} \end{pmatrix} \end{align*}$$
$$\begin{align*}\begin{pmatrix} \chi_p^n & * \\ 0 & \chi_p^{1-n} \end{pmatrix} \end{align*}$$
 $n \in \{0, 1\}$
.
$n \in \{0, 1\}$
.
-
(ii) After extending to the quadratic extension of
 ${\mathbf {F}}_{\mathfrak {p}}$
when
${\mathbf {F}}_{\mathfrak {p}}$
when
 $\deg \mathfrak {p}$
is odd,
$\deg \mathfrak {p}$
is odd,
 $\rho _{\mathfrak {p}}|_{I_p}$
has, up to conjugation, the form
$\rho _{\mathfrak {p}}|_{I_p}$
has, up to conjugation, the form  $$\begin{align*}\begin{pmatrix} \psi_2 & 0 \\ 0 & \psi_2^{p} \end{pmatrix} \,. \end{align*}$$
$$\begin{align*}\begin{pmatrix} \psi_2 & 0 \\ 0 & \psi_2^{p} \end{pmatrix} \,. \end{align*}$$
Proof. By [Reference Serre97, Prop. 1], the claim is true up to the exponents of the characters. (Note that according to loc. cit., fundamental characters of level
![]() $> 2$
cannot occur.) By [Reference Raynaud87, Cor. 3.4.4], as extended via [Reference Larson and Vaintrob66, Lemma 4.9] to the semistable case, the characters must be among
$> 2$
cannot occur.) By [Reference Raynaud87, Cor. 3.4.4], as extended via [Reference Larson and Vaintrob66, Lemma 4.9] to the semistable case, the characters must be among
![]() $\chi _p^0$
and
$\chi _p^0$
and
![]() $\chi _p^1$
in the first case, and among
$\chi _p^1$
in the first case, and among
![]() $\psi _2^0$
,
$\psi _2^0$
,
![]() $\psi _2^1$
,
$\psi _2^1$
,
![]() $\psi _2^p$
and
$\psi _2^p$
and
![]() $\psi _2^{p+1}$
in the second case. The condition that
$\psi _2^{p+1}$
in the second case. The condition that
![]() $\det \circ \rho _{\mathfrak {p}} = \chi _p = \psi _2^{p+1}$
, together with the fact that the characters are conjugate in the second case, then fixes the exponents. See also [Reference Lombardo69, Thm. 3.6].
$\det \circ \rho _{\mathfrak {p}} = \chi _p = \psi _2^{p+1}$
, together with the fact that the characters are conjugate in the second case, then fixes the exponents. See also [Reference Lombardo69, Thm. 3.6].
Definition 2.22. In case (i), we say that
![]() $\rho _{\mathfrak {p}}|_{I_p}$
has level 1, and in case (ii),
$\rho _{\mathfrak {p}}|_{I_p}$
has level 1, and in case (ii),
![]() $\rho _{\mathfrak {p}}|_{I_p}$
has level 2.
$\rho _{\mathfrak {p}}|_{I_p}$
has level 2.
Corollary 2.23. Assume
![]() $p^2 \nmid N$
. When
$p^2 \nmid N$
. When
![]() $\rho _{\mathfrak {p}}|_{I_p}$
has level 1, then
$\rho _{\mathfrak {p}}|_{I_p}$
has level 1, then
![]() ${\mathbf {P}}{\rho _{\mathfrak {p}}(I_p)}$
contains a cyclic subgroup of order
${\mathbf {P}}{\rho _{\mathfrak {p}}(I_p)}$
contains a cyclic subgroup of order
![]() $p-1$
of a split Cartan subgroup. In the case of level 2,
$p-1$
of a split Cartan subgroup. In the case of level 2,
![]() ${\mathbf {P}}{\rho _{\mathfrak {p}}(I_p)}$
is cyclic of order
${\mathbf {P}}{\rho _{\mathfrak {p}}(I_p)}$
is cyclic of order
![]() $p+1$
.
$p+1$
.
Proof. This follows immediately from theorem 2.21.
Corollary 2.24. If
![]() $\deg \mathfrak {p}$
is even and
$\deg \mathfrak {p}$
is even and
![]() $p> 3$
with
$p> 3$
with
![]() $p^2 \nmid N$
, then
$p^2 \nmid N$
, then
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
cannot be contained in the normalizer of a nonsplit Cartan subgroup.
${\mathbf {P}}{G_{\mathfrak {p}}}$
cannot be contained in the normalizer of a nonsplit Cartan subgroup.
Proof. By corollary 2.23,
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
contains elements of order
${\mathbf {P}}{G_{\mathfrak {p}}}$
contains elements of order
![]() $\ge p - 1> 2$
. Since
$\ge p - 1> 2$
. Since
![]() $\deg \mathfrak {p}$
is even, no quadratic extension is necessary in theorem 2.21 in the level
$\deg \mathfrak {p}$
is even, no quadratic extension is necessary in theorem 2.21 in the level
![]() $2$
case, so in all cases, we find elements of order
$2$
case, so in all cases, we find elements of order
![]() $> 2$
in a split Cartan subgroup. Since such elements lie in a unique Cartan subgroup (which is the centralizer of the element) and the normalizer of a nonsplit Cartan subgroup contains only one Cartan subgroup, the claim follows.
$> 2$
in a split Cartan subgroup. Since such elements lie in a unique Cartan subgroup (which is the centralizer of the element) and the normalizer of a nonsplit Cartan subgroup contains only one Cartan subgroup, the claim follows.
Lemma 2.25. Let
![]() $\chi \colon { {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)} \to {\mathbf {F}}^\times $
be a one-dimensional character of order prime to p. Then
$\chi \colon { {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)} \to {\mathbf {F}}^\times $
be a one-dimensional character of order prime to p. Then
![]() $\chi |_{I_p}$
is a power of
$\chi |_{I_p}$
is a power of
![]() $\chi _p$
.
$\chi _p$
.
Proof. Since
![]() $\chi $
has order prime to p and
$\chi $
has order prime to p and
![]() $I_p^{\mathrm {w}}$
is a pro-p group, its image under
$I_p^{\mathrm {w}}$
is a pro-p group, its image under
![]() $\chi $
must be trivial, so
$\chi $
must be trivial, so
![]() $\chi $
is at most tamely ramified. Since
$\chi $
is at most tamely ramified. Since
![]() ${\mathbf {Q}}_p^{\mathrm {nr}}(\mu _p)$
is the maximal abelian tamely ramified extension of
${\mathbf {Q}}_p^{\mathrm {nr}}(\mu _p)$
is the maximal abelian tamely ramified extension of
![]() ${\mathbf {Q}}_p^{\mathrm {nr}}$
,
${\mathbf {Q}}_p^{\mathrm {nr}}$
,
![]() $\chi |_{I_p}$
must factor through
$\chi |_{I_p}$
must factor through
![]() $I_p \to I_p^{\mathrm {t}} \to {\mathbf {F}}_p^\times $
, which implies the claim.
$I_p \to I_p^{\mathrm {t}} \to {\mathbf {F}}_p^\times $
, which implies the claim.
Corollary 2.26. Let
![]() $\mathfrak {p}$
be a regular prime of
$\mathfrak {p}$
be a regular prime of
![]() ${\mathbf {Z}}[f]$
of residue characteristic p and assume that
${\mathbf {Z}}[f]$
of residue characteristic p and assume that
![]() $\rho _{\mathfrak {p}}$
is reducible and
$\rho _{\mathfrak {p}}$
is reducible and
![]() $p^2 \nmid N$
. Then there is a character
$p^2 \nmid N$
. Then there is a character
![]() $\varepsilon $
of
$\varepsilon $
of
![]() ${ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})}$
with values in
${ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})}$
with values in
![]() ${\mathbf {F}}_{\mathfrak {p}}^\times $
and conductor d such that
${\mathbf {F}}_{\mathfrak {p}}^\times $
and conductor d such that
![]() $d^2 \mid N$
and (with respect to a suitable basis)
$d^2 \mid N$
and (with respect to a suitable basis)
 $$\begin{align*}\rho_{\mathfrak{p}} = \begin{pmatrix} \varepsilon \chi_p^n & * \\ 0 & \varepsilon^{-1} \chi_p^{1-n} \end{pmatrix} \end{align*}$$
$$\begin{align*}\rho_{\mathfrak{p}} = \begin{pmatrix} \varepsilon \chi_p^n & * \\ 0 & \varepsilon^{-1} \chi_p^{1-n} \end{pmatrix} \end{align*}$$
with
![]() $n = 0$
or
$n = 0$
or
![]() $n = 1$
.
$n = 1$
.
Proof. The semi-simplification of
![]() $\rho _{\mathfrak {p}}$
splits as a direct sum
$\rho _{\mathfrak {p}}$
splits as a direct sum
![]() $\pi _1 \oplus \pi _2$
of one-dimensional characters
$\pi _1 \oplus \pi _2$
of one-dimensional characters
![]() $\pi _1, \pi _2 \colon { {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})} \to {\mathbf {F}}_{\mathfrak {p}}^\times $
. By lemma 2.25,
$\pi _1, \pi _2 \colon { {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})} \to {\mathbf {F}}_{\mathfrak {p}}^\times $
. By lemma 2.25,
![]() $\pi _1|_{I_p} = \chi _p^n$
for some n, and so
$\pi _1|_{I_p} = \chi _p^n$
for some n, and so
![]() $\pi _2|_{I_p} = \chi _p^{1-n}$
. We can therefore write
$\pi _2|_{I_p} = \chi _p^{1-n}$
. We can therefore write
![]() $\pi _1 = \varepsilon \chi _p^n$
with some character
$\pi _1 = \varepsilon \chi _p^n$
with some character
![]() $\varepsilon $
that is unramified at p. Since
$\varepsilon $
that is unramified at p. Since
![]() $\chi _p = \det \circ \rho _{\mathfrak {p}} = \pi _1 \cdot \pi _2$
, it follows that
$\chi _p = \det \circ \rho _{\mathfrak {p}} = \pi _1 \cdot \pi _2$
, it follows that
![]() $\pi _2 = \varepsilon ^{-1} \chi _p^{1-n}$
. We then have
$\pi _2 = \varepsilon ^{-1} \chi _p^{1-n}$
. We then have
Since
![]() $p^2 \nmid N$
, we have
$p^2 \nmid N$
, we have
![]() $n \in \{0, 1\}$
by theorem 2.21.
$n \in \{0, 1\}$
by theorem 2.21.
Remark 2.27. One can use this to refine algorithm 2.19 by potentially eliminating type R in more cases. For each prime
![]() $\ell \nmid Np$
, compare the reduction of
$\ell \nmid Np$
, compare the reduction of
![]() $a_\ell $
mod
$a_\ell $
mod
![]() $\mathfrak {p}$
with all elements of the form
$\mathfrak {p}$
with all elements of the form
![]() $\varepsilon (\ell ) \ell ^n + \varepsilon (\ell )^{-1} \ell ^{1-n}$
for the finitely many possible characters
$\varepsilon (\ell ) \ell ^n + \varepsilon (\ell )^{-1} \ell ^{1-n}$
for the finitely many possible characters
![]() $\varepsilon $
and
$\varepsilon $
and
![]() $n \in \{0, 1\}$
, and let
$n \in \{0, 1\}$
, and let
![]() $S_\ell $
be the set of compatible pairs
$S_\ell $
be the set of compatible pairs
![]() $(\varepsilon , n)$
. Then one takes the intersection of the sets
$(\varepsilon , n)$
. Then one takes the intersection of the sets
![]() $S_\ell $
for several
$S_\ell $
for several
![]() $\ell $
. If the intersection is empty, then
$\ell $
. If the intersection is empty, then
![]() $\rho _{\mathfrak {p}}$
must be irreducible.
$\rho _{\mathfrak {p}}$
must be irreducible.
Examples 2.28. We give two examples that illustrate corollary 2.26. In order to determine whether
![]() $G_{\mathfrak {p}}$
has a nontrivial unipotent part, we determine explicit generators of
$G_{\mathfrak {p}}$
has a nontrivial unipotent part, we determine explicit generators of
![]() $A[\mathfrak {p}]({\overline {{\mathbf {Q}}}})$
, which allows us to find
$A[\mathfrak {p}]({\overline {{\mathbf {Q}}}})$
, which allows us to find
![]() $[{\mathbf {Q}}(A[\mathfrak {p}]) : {\mathbf {Q}}]$
(and, in fact, to determine the Galois action); see Section 2.6.
$[{\mathbf {Q}}(A[\mathfrak {p}]) : {\mathbf {Q}}]$
(and, in fact, to determine the Galois action); see Section 2.6.
-
(1)
 $A = J_0(39)^{w_{13}}$
with endomorphism ring the maximal order of
$A = J_0(39)^{w_{13}}$
with endomorphism ring the maximal order of
 ${\mathbf {Q}}(\sqrt {2})$
. There is exactly one prime
${\mathbf {Q}}(\sqrt {2})$
. There is exactly one prime
 $\mathfrak {p} \mid 7$
such that
$\mathfrak {p} \mid 7$
such that
 $\rho _{\mathfrak {p}}$
is reducible. Since
$\rho _{\mathfrak {p}}$
is reducible. Since
 $39$
is squarefree,
$39$
is squarefree,
 $\rho _{\mathfrak {p}}^{\mathrm {ss}} \cong 1 \oplus \chi _7$
. We find that
$\rho _{\mathfrak {p}}^{\mathrm {ss}} \cong 1 \oplus \chi _7$
. We find that
 $A[\mathfrak {p}]({\mathbf {Q}}) \cong {\mathbf {Z}}/7{\mathbf {Z}}$
, so we have a short exact sequence which turns out to be nonsplit since
$A[\mathfrak {p}]({\mathbf {Q}}) \cong {\mathbf {Z}}/7{\mathbf {Z}}$
, so we have a short exact sequence which turns out to be nonsplit since $$\begin{align*}0 \to {\mathbf{Z}}/7{\mathbf{Z}} \to A[\mathfrak{p}] \to \mu_7 \to 0, \end{align*}$$
$$\begin{align*}0 \to {\mathbf{Z}}/7{\mathbf{Z}} \to A[\mathfrak{p}] \to \mu_7 \to 0, \end{align*}$$
 $[{\mathbf {Q}}(A[\mathfrak {p}]) : {\mathbf {Q}}]$
is divisible by
$[{\mathbf {Q}}(A[\mathfrak {p}]) : {\mathbf {Q}}]$
is divisible by
 $7$
.
$7$
.
-
(2)
 $A = J_0(87)^{w_{29}}$
with endomorphism ring the maximal order of
$A = J_0(87)^{w_{29}}$
with endomorphism ring the maximal order of
 ${\mathbf {Q}}(\sqrt {5})$
. The representation
${\mathbf {Q}}(\sqrt {5})$
. The representation
 $\rho _{\langle {\sqrt {5}}\rangle }$
is reducible. Similarly as in Example (1), the constituents are
$\rho _{\langle {\sqrt {5}}\rangle }$
is reducible. Similarly as in Example (1), the constituents are
 ${\mathbf {Z}}/5{\mathbf {Z}}$
and
${\mathbf {Z}}/5{\mathbf {Z}}$
and
 $\mu _5$
. Since
$\mu _5$
. Since
 $A[\sqrt {5}]({\mathbf {Q}}) \cong {\mathbf {Z}}/5{\mathbf {Z}}$
, we have the exact sequence which is again nonsplit.
$A[\sqrt {5}]({\mathbf {Q}}) \cong {\mathbf {Z}}/5{\mathbf {Z}}$
, we have the exact sequence which is again nonsplit. $$\begin{align*}0 \to {\mathbf{Z}}/5{\mathbf{Z}} \to A[\mathfrak{p}] \to \mu_5 \to 0, \end{align*}$$
$$\begin{align*}0 \to {\mathbf{Z}}/5{\mathbf{Z}} \to A[\mathfrak{p}] \to \mu_5 \to 0, \end{align*}$$
We now consider the case that
![]() $\rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)})$
is contained in the normalizer of a Cartan subgroup of
$\rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)})$
is contained in the normalizer of a Cartan subgroup of
![]() $\mathrm {GL}_2({\mathbf {F}}_{\mathfrak {p}})$
.
$\mathrm {GL}_2({\mathbf {F}}_{\mathfrak {p}})$
.
Lemma 2.29. Assume
![]() $\mathfrak {p}$
is a regular prime ideal lying above a rational prime
$\mathfrak {p}$
is a regular prime ideal lying above a rational prime
![]() $p> 3$
such that
$p> 3$
such that
![]() $p^2 \nmid N$
and that
$p^2 \nmid N$
and that
![]() $\rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)})$
is contained in the normalizer
$\rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)})$
is contained in the normalizer
![]() $N(C)$
of a Cartan subgroup C of
$N(C)$
of a Cartan subgroup C of
![]() $\mathrm {GL}_2({\mathbf {F}}_{\mathfrak {p}})$
. Then the following are equivalent:
$\mathrm {GL}_2({\mathbf {F}}_{\mathfrak {p}})$
. Then the following are equivalent:
-
(i)
 $\rho _{\mathfrak {p}}|_{I_p}$
has level 1.
$\rho _{\mathfrak {p}}|_{I_p}$
has level 1. -
(ii)
 $\rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)}) \subseteq C$
.
$\rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)}) \subseteq C$
. -
(iii)
 ${\mathbf {P}}\rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)}) \subseteq {\mathbf {P}} C$
has order
${\mathbf {P}}\rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)}) \subseteq {\mathbf {P}} C$
has order
 $p-1$
and C is split.
$p-1$
and C is split.
Proof. Clearly, (iii) implies (ii) (since
![]() ${\mathbf {P}}^{-1} ({\mathbf {P}} C) = C$
). If (ii) holds, then
${\mathbf {P}}^{-1} ({\mathbf {P}} C) = C$
). If (ii) holds, then
![]() $\rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)})$
is abelian of order prime to p, so lemma 2.25 implies that
$\rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)})$
is abelian of order prime to p, so lemma 2.25 implies that
![]() $\rho _{\mathfrak {p}}|_{I_p}$
has level 1.
$\rho _{\mathfrak {p}}|_{I_p}$
has level 1.
To show that (i) implies (iii), first note that the image of the wild inertia group
![]() $I_p^{\mathrm {w}}$
must be trivial since
$I_p^{\mathrm {w}}$
must be trivial since
![]() $I_p^{\mathrm {w}}$
is a pro-p group and the order of
$I_p^{\mathrm {w}}$
is a pro-p group and the order of
![]() $N(C)$
is prime to p (since
$N(C)$
is prime to p (since
![]() $p> 2$
). So
$p> 2$
). So
![]() $\rho _{\mathfrak {p}}|_{I_p}$
factors through
$\rho _{\mathfrak {p}}|_{I_p}$
factors through
![]() $I_p^{\mathrm {t}}$
, which is pro-cyclic, and hence,
$I_p^{\mathrm {t}}$
, which is pro-cyclic, and hence,
![]() $\rho _{\mathfrak {p}}(I_p)$
is a cyclic group, which has order
$\rho _{\mathfrak {p}}(I_p)$
is a cyclic group, which has order
![]() $p-1$
since
$p-1$
since
![]() $\rho _{\mathfrak {p}}|_{I_p}$
has level 1 and
$\rho _{\mathfrak {p}}|_{I_p}$
has level 1 and
![]() $p^2 \nmid N$
. Let
$p^2 \nmid N$
. Let
![]() $\operatorname {Frob}_p$
be any lift of the p-Frobenius on
$\operatorname {Frob}_p$
be any lift of the p-Frobenius on
![]() $\overline {{\mathbf {F}}}_p$
to
$\overline {{\mathbf {F}}}_p$
to
![]() ${ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)}$
. lemma 2.7 implies that conjugating by
${ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)}$
. lemma 2.7 implies that conjugating by
![]() $\rho _{\mathfrak {p}}(\operatorname {Frob}_p)$
has the effect of taking pth powers on
$\rho _{\mathfrak {p}}(\operatorname {Frob}_p)$
has the effect of taking pth powers on
![]() $\rho _{\mathfrak {p}}(I_p)$
. Since
$\rho _{\mathfrak {p}}(I_p)$
. Since
![]() $p \equiv 1 \bmod \#\rho _{\mathfrak {p}}(I_p)$
, this action is trivial, so the image of
$p \equiv 1 \bmod \#\rho _{\mathfrak {p}}(I_p)$
, this action is trivial, so the image of
![]() $\operatorname {Frob}_p$
commutes with the image of
$\operatorname {Frob}_p$
commutes with the image of
![]() $I_p$
. This shows that
$I_p$
. This shows that
![]() $\rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)})$
is abelian. Since
$\rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)})$
is abelian. Since
![]() $\#\rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)})$
contains elements of order
$\#\rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)})$
contains elements of order
![]() $p - 1> 3$
, this implies that
$p - 1> 3$
, this implies that
![]() $\rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)}) \le C$
. (This is where we use that
$\rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)}) \le C$
. (This is where we use that
![]() $\rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)}) \le N(C)$
: all the abelian subgroups of
$\rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)}) \le N(C)$
: all the abelian subgroups of
![]() $N(C)$
containing elements of order
$N(C)$
containing elements of order
![]() $\ge 3$
are contained in C.) From the discussion above, it follows that
$\ge 3$
are contained in C.) From the discussion above, it follows that
![]() $\mathbf{P}{\rho_\mathfrak{p}(I_p)}$
has order
$\mathbf{P}{\rho_\mathfrak{p}(I_p)}$
has order
![]() $p - 1$
; both statements together imply (iii).
$p - 1$
; both statements together imply (iii).
Corollary 2.30. Assume
![]() $\mathfrak {p}$
is a regular prime ideal lying above a rational prime
$\mathfrak {p}$
is a regular prime ideal lying above a rational prime
![]() $p> 3$
such that
$p> 3$
such that
![]() $p^2 \nmid N$
and that
$p^2 \nmid N$
and that
![]() $G_{\mathfrak {p}}$
is contained in a Cartan subgroup C. Then C is split; in particular,
$G_{\mathfrak {p}}$
is contained in a Cartan subgroup C. Then C is split; in particular,
![]() $\rho _{\mathfrak {p}}$
is reducible.
$\rho _{\mathfrak {p}}$
is reducible.
Proof. The assumption implies that
![]() $\rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)}) \subseteq G_{\mathfrak {p}} \subseteq C$
. The claim then follows from the implication ‘(ii)
$\rho _{\mathfrak {p}}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_p|{\mathbf {Q}}_p)}) \subseteq G_{\mathfrak {p}} \subseteq C$
. The claim then follows from the implication ‘(ii)
![]() $\Rightarrow $
(iii)’ in lemma 2.29.
$\Rightarrow $
(iii)’ in lemma 2.29.
Corollary 2.31. Assume
![]() $p> 3$
and
$p> 3$
and
![]() $p^2 \nmid N$
. If
$p^2 \nmid N$
. If
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
is dihedral, then
${\mathbf {P}}{G_{\mathfrak {p}}}$
is dihedral, then
![]() ${\mathbf {P}}{\rho _{\mathfrak {p}}(I_p)}$
is cyclic and contained in the corresponding Cartan subgroup C.
${\mathbf {P}}{\rho _{\mathfrak {p}}(I_p)}$
is cyclic and contained in the corresponding Cartan subgroup C.
Proof. The first statement follows as in the proof of lemma 2.29. The second statement follows from the classification of
![]() $\rho _{\mathfrak {p}}(I_p)$
.
$\rho _{\mathfrak {p}}(I_p)$
.
2.8 The image of inertia at a prime
 $\ell \neq p$
$\ell \neq p$
We now consider the image
![]() $\rho _{\mathfrak {p}}(I_\ell )$
of the inertia subgroup at a prime
$\rho _{\mathfrak {p}}(I_\ell )$
of the inertia subgroup at a prime
![]() $\ell \neq p$
.
$\ell \neq p$
.
Lemma 2.32. Let
![]() $\mathfrak {p}$
be a regular prime ideal of
$\mathfrak {p}$
be a regular prime ideal of
![]() ${\mathbf {Z}}[f]$
of residue characteristic p and let
${\mathbf {Z}}[f]$
of residue characteristic p and let
![]() $\ell \neq p$
be a prime. If
$\ell \neq p$
be a prime. If
![]() $\ell ^2 \nmid N$
, then the image
$\ell ^2 \nmid N$
, then the image
![]() $\rho _{\mathfrak {p}}(I_\ell )$
of the inertia subgroup at
$\rho _{\mathfrak {p}}(I_\ell )$
of the inertia subgroup at
![]() $\ell $
consists of unipotent elements.
$\ell $
consists of unipotent elements.
Proof. If
![]() $\ell \nmid N$
, then
$\ell \nmid N$
, then
![]() $\rho _{\mathfrak {p}}$
is unramified at
$\rho _{\mathfrak {p}}$
is unramified at
![]() $\ell $
, and so the image of inertia is trivial. Otherwise, since the prime-to-p part of the Artin conductor of
$\ell $
, and so the image of inertia is trivial. Otherwise, since the prime-to-p part of the Artin conductor of
![]() $\rho _{\mathfrak {p}}$
divides the prime-to-p part of N, it follows from
$\rho _{\mathfrak {p}}$
divides the prime-to-p part of N, it follows from
![]() $v_\ell (N) = 1$
that the image of wild inertia is trivial and that the image of inertia has a one-dimensional fixed subspace; see [Reference Serre97, p. 181]. So
$v_\ell (N) = 1$
that the image of wild inertia is trivial and that the image of inertia has a one-dimensional fixed subspace; see [Reference Serre97, p. 181]. So
 $$\begin{align*}\rho_{\mathfrak{p}}|_{I_\ell} \sim \begin{pmatrix} 1 & * \\ 0 & \chi_p \end{pmatrix} \,. \end{align*}$$
$$\begin{align*}\rho_{\mathfrak{p}}|_{I_\ell} \sim \begin{pmatrix} 1 & * \\ 0 & \chi_p \end{pmatrix} \,. \end{align*}$$
Since
![]() $\chi _p$
is unramified at
$\chi _p$
is unramified at
![]() $\ell $
, this implies that
$\ell $
, this implies that
![]() $\rho _{\mathfrak {p}}(I_\ell )$
is unipotent. (See also [Reference Ribet90, Section 2]; note that the definition of the conductor is purely local.)
$\rho _{\mathfrak {p}}(I_\ell )$
is unipotent. (See also [Reference Ribet90, Section 2]; note that the definition of the conductor is purely local.)
Corollary 2.33. Let
![]() $\mathfrak {p}$
be a regular prime ideal of
$\mathfrak {p}$
be a regular prime ideal of
![]() ${\mathbf {Z}}[f]$
of residue characteristic p and assume that
${\mathbf {Z}}[f]$
of residue characteristic p and assume that
![]() $G_{\mathfrak {p}}$
is contained in the normalizer
$G_{\mathfrak {p}}$
is contained in the normalizer
![]() $N(C)$
of a Cartan subgroup C. Then
$N(C)$
of a Cartan subgroup C. Then
![]() $\rho _{\mathfrak {p}}$
is unramified at all primes
$\rho _{\mathfrak {p}}$
is unramified at all primes
![]() $\ell \neq p$
such that
$\ell \neq p$
such that
![]() $\ell ^2 \nmid N$
.
$\ell ^2 \nmid N$
.
Proof. This follows from lemma 2.32 since
![]() $N(C)$
contains no nontrivial unipotent elements.
$N(C)$
contains no nontrivial unipotent elements.
Corollary 2.34. Let
![]() $\mathfrak {p}$
be a regular prime ideal of
$\mathfrak {p}$
be a regular prime ideal of
![]() ${\mathbf {Z}}[f]$
of residue characteristic
${\mathbf {Z}}[f]$
of residue characteristic
![]() $p> 3$
and assume that
$p> 3$
and assume that
![]() $G_{\mathfrak {p}}$
is contained in the normalizer
$G_{\mathfrak {p}}$
is contained in the normalizer
![]() $N(C)$
of a Cartan subgroup C. Since C has index
$N(C)$
of a Cartan subgroup C. Since C has index
![]() $2$
in
$2$
in
![]() $N(C)$
, we obtain a quadratic character (which can be trivial)
$N(C)$
, we obtain a quadratic character (which can be trivial)
let d be its conductor. Then the odd part of
![]() $d^2$
divides N. Moreover, if
$d^2$
divides N. Moreover, if
![]() $4 \nmid N$
, then
$4 \nmid N$
, then
![]() $d^2 \mid N$
.
$d^2 \mid N$
.
Proof. Note that the odd part of d is squarefree. Let
![]() $\ell \neq p$
be an odd prime. If
$\ell \neq p$
be an odd prime. If
![]() $\ell ^2 \nmid N$
, then
$\ell ^2 \nmid N$
, then
![]() $\rho _{\mathfrak {p}}$
is unramified at
$\rho _{\mathfrak {p}}$
is unramified at
![]() $\ell $
by corollary 2.33, and so
$\ell $
by corollary 2.33, and so
![]() $\ell \nmid d$
. This shows the claim except for powers of
$\ell \nmid d$
. This shows the claim except for powers of
![]() $2$
or p. If
$2$
or p. If
![]() $p^2 \nmid N$
, then
$p^2 \nmid N$
, then
![]() $\rho _{\mathfrak {p}}(I_p) \subseteq C$
by corollary 2.31 (here, we use
$\rho _{\mathfrak {p}}(I_p) \subseteq C$
by corollary 2.31 (here, we use
![]() $p> 3$
), and so
$p> 3$
), and so
![]() $\varepsilon _{\mathfrak {p}}$
is unramified at p. This takes care of the power of p. If
$\varepsilon _{\mathfrak {p}}$
is unramified at p. This takes care of the power of p. If
![]() $4 \nmid N$
, corollary 2.33 applies as well to show that
$4 \nmid N$
, corollary 2.33 applies as well to show that
![]() $2 \nmid d$
. This completes the proof.
$2 \nmid d$
. This completes the proof.
Question 2.35. Can the stronger statement be extended to the case
![]() $4 \mid N$
?
$4 \mid N$
?
Corollary 2.36. Let
![]() $p> 2$
be prime and let
$p> 2$
be prime and let
![]() $K|{\mathbf {Q}}$
be an imaginary quadratic extension such that N and
$K|{\mathbf {Q}}$
be an imaginary quadratic extension such that N and
![]() $D_K$
are coprime and K is not equal to
$D_K$
are coprime and K is not equal to
![]() ${\mathbf {Q}}(\sqrt {-1})$
,
${\mathbf {Q}}(\sqrt {-1})$
,
![]() ${\mathbf {Q}}(\sqrt {-2})$
, or
${\mathbf {Q}}(\sqrt {-2})$
, or
![]() ${\mathbf {Q}}(\sqrt {-3})$
. If
${\mathbf {Q}}(\sqrt {-3})$
. If
![]() $\rho _{\mathfrak {p}}$
is irreducible, then the restriction
$\rho _{\mathfrak {p}}$
is irreducible, then the restriction
![]() $\rho _{\mathfrak {p}}|_{G_K}$
is still irreducible.
$\rho _{\mathfrak {p}}|_{G_K}$
is still irreducible.
Proof. Suppose that
![]() $\rho _{\mathfrak {p}}$
is irreducible, but
$\rho _{\mathfrak {p}}$
is irreducible, but
![]() $\rho _{\mathfrak {p}}|_{G_K}$
is reducible. Then the quadratic character on
$\rho _{\mathfrak {p}}|_{G_K}$
is reducible. Then the quadratic character on
![]() $G_{\mathbf {Q}}$
associated to
$G_{\mathbf {Q}}$
associated to
![]() $K|{\mathbf {Q}}$
induces a nontrivial quadratic character
$K|{\mathbf {Q}}$
induces a nontrivial quadratic character
![]() $\varepsilon $
on the image of
$\varepsilon $
on the image of
![]() $\rho _{\mathfrak {p}}$
:
$\rho _{\mathfrak {p}}$
:
![]() $G_K$
fixes a one-dimensional subspace V, and
$G_K$
fixes a one-dimensional subspace V, and
![]() $\varepsilon $
is given by the action on
$\varepsilon $
is given by the action on
![]() $\{V, \rho _{\mathfrak {p}}(\sigma ) V\}$
for
$\{V, \rho _{\mathfrak {p}}(\sigma ) V\}$
for
![]() $\sigma \in G_{\mathbf {Q}} \setminus G_K$
. Since
$\sigma \in G_{\mathbf {Q}} \setminus G_K$
. Since
![]() $\rho _{\mathfrak {p}}$
is ramified only at primes dividing
$\rho _{\mathfrak {p}}$
is ramified only at primes dividing
![]() $Np$
and
$Np$
and
![]() $K|{\mathbf {Q}}$
is ramified exactly at the primes dividing
$K|{\mathbf {Q}}$
is ramified exactly at the primes dividing
![]() $D_K$
, it follows from the condition that N and
$D_K$
, it follows from the condition that N and
![]() $D_K$
are coprime that the conductor
$D_K$
are coprime that the conductor
![]() $|D_K|$
of
$|D_K|$
of
![]() $\varepsilon $
is a power of p. Since
$\varepsilon $
is a power of p. Since
![]() $D_K \neq -3, -4, -8$
, we must have
$D_K \neq -3, -4, -8$
, we must have
![]() $p> 3$
and
$p> 3$
and
![]() $D_K = -p$
.
$D_K = -p$
.
Since
![]() $\rho _{\mathfrak {p}}$
fixes an unordered pair of complementary one-dimensional subspaces but does not fix the two subspaces individually, it must be dihedral (compare theorems 2.13 and 2.14). Then
$\rho _{\mathfrak {p}}$
fixes an unordered pair of complementary one-dimensional subspaces but does not fix the two subspaces individually, it must be dihedral (compare theorems 2.13 and 2.14). Then
![]() $\varepsilon $
is the character as in corollary 2.34, so corollary 2.34 implies that
$\varepsilon $
is the character as in corollary 2.34, so corollary 2.34 implies that
![]() $|D_K|^2 = p^2 \mid N$
(here, we use that
$|D_K|^2 = p^2 \mid N$
(here, we use that
![]() $p> 3$
), contradicting again the coprimality of N and
$p> 3$
), contradicting again the coprimality of N and
![]() $D_K$
.
$D_K$
.
2.9 Explicit irreducibility for almost all
 $\mathfrak {p}$
$\mathfrak {p}$
It is known that
![]() $\rho _{\mathfrak {p}}$
is irreducible for all but finitely many
$\rho _{\mathfrak {p}}$
is irreducible for all but finitely many
![]() $\mathfrak {p}$
. Lombardo [Reference Lombardo69, Thm. 1.4] gives an explicit (but very large) bound for the reducible primes (actually, for the primes such that the image is not maximal). What we need, however, is to determine as exactly as possible the finite set of primes
$\mathfrak {p}$
. Lombardo [Reference Lombardo69, Thm. 1.4] gives an explicit (but very large) bound for the reducible primes (actually, for the primes such that the image is not maximal). What we need, however, is to determine as exactly as possible the finite set of primes
![]() $\mathfrak {p}$
such that
$\mathfrak {p}$
such that
![]() $\rho _{\mathfrak {p}}$
is reducible in each concrete case.
$\rho _{\mathfrak {p}}$
is reducible in each concrete case.
In view of corollary 2.26, we make the following definition.
Definition 2.37. We write
![]() $d_{\operatorname {max}}$
for the largest positive integer d such that
$d_{\operatorname {max}}$
for the largest positive integer d such that
![]() $d^2 \mid N$
.
$d^2 \mid N$
.
We then obtain the following criterion. (Compare [Reference Dieulefait38, § 3.1], where similar criteria are used to show that the mod-p Galois representations associated to an abelian surface with minimal endomorphism ring are maximal for almost all primes p.)
Proposition 2.38. Let
![]() $\ell \nmid N$
be a prime and let
$\ell \nmid N$
be a prime and let
![]() $m(\ell )$
be the order of
$m(\ell )$
be the order of
![]() $\ell $
in
$\ell $
in
![]() $({\mathbf {Z}}/d_{\operatorname {max}}{\mathbf {Z}})^\times $
. Let
$({\mathbf {Z}}/d_{\operatorname {max}}{\mathbf {Z}})^\times $
. Let
![]() $\mathfrak {p}$
be a regular prime of
$\mathfrak {p}$
be a regular prime of
![]() ${\mathbf {Z}}[f]$
of residue characteristic p. If
${\mathbf {Z}}[f]$
of residue characteristic p. If
![]() $p^2 \nmid N$
and
$p^2 \nmid N$
and
then
![]() $\rho _{\mathfrak {p}}$
is irreducible.
$\rho _{\mathfrak {p}}$
is irreducible.
We note that when
![]() $\varphi (d_{\operatorname {max}}) = 1$
(which is the case, for example, when N is squarefree) or
$\varphi (d_{\operatorname {max}}) = 1$
(which is the case, for example, when N is squarefree) or
![]() $\ell \equiv 1 \bmod d_{\operatorname {max}}$
, the resultant simplifies to
$\ell \equiv 1 \bmod d_{\operatorname {max}}$
, the resultant simplifies to
![]() $\ell + 1 - a_\ell $
.
$\ell + 1 - a_\ell $
.
Proof. Let us prove the contrapositive. Thus, suppose that
![]() $\rho _{\mathfrak {p}}$
is reducible. Let
$\rho _{\mathfrak {p}}$
is reducible. Let
![]() $\varepsilon $
be the character in corollary 2.26. It can be considered as a Dirichlet character of conductor
$\varepsilon $
be the character in corollary 2.26. It can be considered as a Dirichlet character of conductor
![]() $d \mid d_{\operatorname {max}}$
with values in
$d \mid d_{\operatorname {max}}$
with values in
![]() ${\mathbf {F}}_{\mathfrak {p}}^\times $
. Since
${\mathbf {F}}_{\mathfrak {p}}^\times $
. Since
![]() $p^2 \nmid N$
, we have
$p^2 \nmid N$
, we have
![]() $n = 0$
or
$n = 0$
or
![]() $n = 1$
in corollary 2.26, and by symmetry (and since what we do depends only on the semi-simplification of
$n = 1$
in corollary 2.26, and by symmetry (and since what we do depends only on the semi-simplification of
![]() $\rho _{\mathfrak {p}}$
), we can assume
$\rho _{\mathfrak {p}}$
), we can assume
![]() $n = 0$
. If
$n = 0$
. If
![]() $\ell = p$
, then
$\ell = p$
, then
![]() $\mathfrak {p} \mid \ell $
, and we are done. Hence, suppose
$\mathfrak {p} \mid \ell $
, and we are done. Hence, suppose
![]() $\ell \nmid Np$
. Then
$\ell \nmid Np$
. Then
![]() $\rho _{\mathfrak {p}}(\operatorname {Frob}_\ell )$
is well-defined and has
$\rho _{\mathfrak {p}}(\operatorname {Frob}_\ell )$
is well-defined and has
![]() $\varepsilon (\ell )$
as an eigenvalue, which is also a root of unity of order dividing
$\varepsilon (\ell )$
as an eigenvalue, which is also a root of unity of order dividing
![]() $m(\ell )$
. So the characteristic polynomial
$m(\ell )$
. So the characteristic polynomial
![]() $T^2 - \bar {a}_\ell T + \bar {\ell } \in {\mathbf {F}}_{\mathfrak {p}}[T]$
of
$T^2 - \bar {a}_\ell T + \bar {\ell } \in {\mathbf {F}}_{\mathfrak {p}}[T]$
of
![]() $\rho _{\mathfrak {p}}(\operatorname {Frob}_\ell )$
has at least one root in common with
$\rho _{\mathfrak {p}}(\operatorname {Frob}_\ell )$
has at least one root in common with
![]() $T^{m(\ell )} - 1$
. This is equivalent to
$T^{m(\ell )} - 1$
. This is equivalent to
Since the resultant is compatible with ring homomorphisms, this implies that
![]() $\mathfrak {p}$
divides the resultant in the statement.
$\mathfrak {p}$
divides the resultant in the statement.
Remark 2.39. One can alternatively consider the condition
with the same
![]() $m(\ell )$
as above. Using the fact that the resultant is the product of all differences of roots of the first and of the second polynomial, together with the Weil conjectures for the characteristic polynomial of
$m(\ell )$
as above. Using the fact that the resultant is the product of all differences of roots of the first and of the second polynomial, together with the Weil conjectures for the characteristic polynomial of
![]() $\operatorname {Frob}_\ell $
on
$\operatorname {Frob}_\ell $
on
![]() $T_p A$
, we see that the resultant above is an integer R satisfying
$T_p A$
, we see that the resultant above is an integer R satisfying
In particular, it is nonzero, so taking just one
![]() $\ell \nmid N$
gives a relatively small bound for the set of primes p such that
$\ell \nmid N$
gives a relatively small bound for the set of primes p such that
![]() $\rho _{\mathfrak {p}}$
is reducible for some
$\rho _{\mathfrak {p}}$
is reducible for some
![]() $\mathfrak {p} \mid p$
. In practice, one takes several
$\mathfrak {p} \mid p$
. In practice, one takes several
![]() $\ell $
and uses the gcd of the resultants to obtain reasonably sharp bounds.
$\ell $
and uses the gcd of the resultants to obtain reasonably sharp bounds.
This leads to the following algorithm. Recall the notation
![]() $p(\mathfrak {p})$
for the residue characteristic of the prime ideal
$p(\mathfrak {p})$
for the residue characteristic of the prime ideal
![]() $\mathfrak {p}$
.
$\mathfrak {p}$
.
Algorithm 2.40.

We can then use algorithm 2.19 on the regular odd primes in S to try to show that
![]() $\rho _{\mathfrak {p}}$
is irreducible even though algorithm 2.40 was unable to prove that. One can also use the idea from remark 2.27.
$\rho _{\mathfrak {p}}$
is irreducible even though algorithm 2.40 was unable to prove that. One can also use the idea from remark 2.27.
Remark 2.41. If we take B sufficiently large in algorithm 2.40, then by the Chebotarëv density theorem, the set S that the algorithm returns will contain only the prime ideals
![]() $\mathfrak {p}$
such that
$\mathfrak {p}$
such that
![]() $p(\mathfrak {p})^2 \mid N$
or that the image of
$p(\mathfrak {p})^2 \mid N$
or that the image of
![]() $\rho _{\mathfrak {p}}$
consists of elements with one eigenvalue in the image of a character of conductor dividing
$\rho _{\mathfrak {p}}$
consists of elements with one eigenvalue in the image of a character of conductor dividing
![]() $d_{\operatorname {max}}$
. This is compatible with the image being contained in the normalizer of a split Cartan subgroup (but not in the Cartan subgroup itself).
$d_{\operatorname {max}}$
. This is compatible with the image being contained in the normalizer of a split Cartan subgroup (but not in the Cartan subgroup itself).
Example 2.42. Let
![]() $A = J_0(35)^{w_7}$
be the Jacobian of the modular curve quotient
$A = J_0(35)^{w_7}$
be the Jacobian of the modular curve quotient
![]() $X_0(35)/\langle w_7 \rangle $
, where
$X_0(35)/\langle w_7 \rangle $
, where
![]() $w_7$
denotes the Atkin–Lehner involution. A corresponds to the Galois orbit of size 2 of newforms of level 35, weight
$w_7$
denotes the Atkin–Lehner involution. A corresponds to the Galois orbit of size 2 of newforms of level 35, weight
![]() $2$
and trivial nebentypus. Let f be one of these two newforms. Then
$2$
and trivial nebentypus. Let f be one of these two newforms. Then
![]() ${\mathbf {Z}}[f]$
is the maximal order of
${\mathbf {Z}}[f]$
is the maximal order of
![]() ${\mathbf {Q}}(\sqrt {17})$
. Since the level
${\mathbf {Q}}(\sqrt {17})$
. Since the level
![]() $N = 35$
is squarefree,
$N = 35$
is squarefree,
![]() $d_{\operatorname {max}} = 1$
.
$d_{\operatorname {max}} = 1$
.
Let
![]() $\beta = (1 + \sqrt {17})/2$
be a generator of
$\beta = (1 + \sqrt {17})/2$
be a generator of
![]() ${\mathbf {Z}}[f]$
. We then have
${\mathbf {Z}}[f]$
. We then have
![]() $a_2 = -\beta $
(for one of the two conjugate newforms), so the resultant is
$a_2 = -\beta $
(for one of the two conjugate newforms), so the resultant is
which is an element of norm
![]() $2^3$
. This shows that
$2^3$
. This shows that
![]() $\rho _{\mathfrak {p}}$
is irreducible for all prime ideals
$\rho _{\mathfrak {p}}$
is irreducible for all prime ideals
![]() $\mathfrak {p}$
with odd residue characteristic. We also have
$\mathfrak {p}$
with odd residue characteristic. We also have
![]() $a_3 = \beta - 1$
, and the corresponding resultant is
$a_3 = \beta - 1$
, and the corresponding resultant is
whose norm is
![]() $2^4$
and which is not divisible by
$2^4$
and which is not divisible by
![]() $2$
, so it generates a power of one of the two prime ideals above
$2$
, so it generates a power of one of the two prime ideals above
![]() $2$
in
$2$
in
![]() ${\mathbf {Z}}[f]$
; explicitly,
${\mathbf {Z}}[f]$
; explicitly,
Write
![]() $\langle 2 \rangle = \mathfrak {p} \mathfrak {p}'$
. Then we can deduce that
$\langle 2 \rangle = \mathfrak {p} \mathfrak {p}'$
. Then we can deduce that
![]() $\rho _{\mathfrak {p}'}$
is irreducible.
$\rho _{\mathfrak {p}'}$
is irreducible.
Magma computes that
![]() $A({\mathbf {Q}})_{\mathrm {tors}} \cong {\mathbf {Z}}/16{\mathbf {Z}}$
. This shows that
$A({\mathbf {Q}})_{\mathrm {tors}} \cong {\mathbf {Z}}/16{\mathbf {Z}}$
. This shows that
![]() $\rho _{\mathfrak {p}}$
must be reducible (and that it is nontrivial since
$\rho _{\mathfrak {p}}$
must be reducible (and that it is nontrivial since
![]() $A[\mathfrak {p}]({\mathbf {Q}}) \cong {\mathbf {Z}}/2{\mathbf {Z}}$
and not
$A[\mathfrak {p}]({\mathbf {Q}}) \cong {\mathbf {Z}}/2{\mathbf {Z}}$
and not
![]() $({\mathbf {Z}}/2{\mathbf {Z}})^2$
).
$({\mathbf {Z}}/2{\mathbf {Z}})^2$
).
Example 2.43. We now consider
![]() $A = J_0(125)^+$
, which corresponds to a Galois orbit of newforms with coefficient ring the maximal order of
$A = J_0(125)^+$
, which corresponds to a Galois orbit of newforms with coefficient ring the maximal order of
![]() ${\mathbf {Q}}(\sqrt {5})$
. Let
${\mathbf {Q}}(\sqrt {5})$
. Let
![]() $\alpha = (1 + \sqrt {5})/2$
. Then we can pick one of the newforms f such that
$\alpha = (1 + \sqrt {5})/2$
. Then we can pick one of the newforms f such that
![]() $a_2 = -\alpha $
and
$a_2 = -\alpha $
and
![]() $a_3 = \alpha - 2$
. Here,
$a_3 = \alpha - 2$
. Here,
![]() $d_{\operatorname {max}} = 5$
and so
$d_{\operatorname {max}} = 5$
and so
![]() $m(2) = m(3) = 4$
. We find that
$m(2) = m(3) = 4$
. We find that
The ideal of
![]() ${\mathbf {Z}}[f]$
generated by
${\mathbf {Z}}[f]$
generated by
![]() $2 r_2$
and
$2 r_2$
and
![]() $3 r_3$
has norm
$3 r_3$
has norm
![]() $5^2$
. So the algorithm shows that
$5^2$
. So the algorithm shows that
![]() $\rho _{\mathfrak {p}}$
is irreducible for all primes
$\rho _{\mathfrak {p}}$
is irreducible for all primes
![]() $\mathfrak {p} \neq \langle \sqrt {5} \rangle $
. An explicit computation shows that
$\mathfrak {p} \neq \langle \sqrt {5} \rangle $
. An explicit computation shows that
![]() $\rho _{\langle \sqrt {5} \rangle }$
is reducible; see example 2.20, (1).
$\rho _{\langle \sqrt {5} \rangle }$
is reducible; see example 2.20, (1).
2.10 Excluding the sub-line and exceptional cases for almost all
 $\mathfrak {p}$
$\mathfrak {p}$
In the following, we require that the coefficient field of the newform is of degree
![]() $2$
, and so
$2$
, and so
![]() $\dim A = 2$
as well. This simplifies the discussion of the sub-line case.
$\dim A = 2$
as well. This simplifies the discussion of the sub-line case.
Our next goal will be to show that
![]() $\rho _{\mathfrak {p}}$
has maximal image for all
$\rho _{\mathfrak {p}}$
has maximal image for all
![]() $\mathfrak {p}$
outside a small explicit finite set. Starting from the result of the previous subsection, it remains to show that for all but a few explicit
$\mathfrak {p}$
outside a small explicit finite set. Starting from the result of the previous subsection, it remains to show that for all but a few explicit
![]() $\mathfrak {p}$
,
$\mathfrak {p}$
,
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
is not contained in the stabilizer of a sub-line (when
${\mathbf {P}}{G_{\mathfrak {p}}}$
is not contained in the stabilizer of a sub-line (when
![]() $\deg \mathfrak {p} = 2$
), in a maximal subgroup of type
$\deg \mathfrak {p} = 2$
), in a maximal subgroup of type
![]() $S_4$
or
$S_4$
or
![]() $A_5$
, or in the normalizer of a Cartan subgroup.
$A_5$
, or in the normalizer of a Cartan subgroup.
We begin with the sub-line case and assume that
![]() $\rho _{\mathfrak {p}}$
is irreducible and
$\rho _{\mathfrak {p}}$
is irreducible and
![]() $p(\mathfrak {p})$
is odd. In this case,
$p(\mathfrak {p})$
is odd. In this case,
![]() $G_{\mathfrak {p}} \subseteq {\mathbf {P}}^{-1}(\operatorname {PGL}_2({\mathbf {F}}_p)) \cap G_{\mathfrak {p}}^{\operatorname {max}}$
, which is a group containing
$G_{\mathfrak {p}} \subseteq {\mathbf {P}}^{-1}(\operatorname {PGL}_2({\mathbf {F}}_p)) \cap G_{\mathfrak {p}}^{\operatorname {max}}$
, which is a group containing
![]() $\mathrm {GL}_2({\mathbf {F}}_p)$
with index
$\mathrm {GL}_2({\mathbf {F}}_p)$
with index
![]() $2$
. More precisely, let
$2$
. More precisely, let
![]() $\alpha \in {\mathbf {F}}_{\mathfrak {p}}^\times \setminus {\mathbf {F}}_p^\times $
be such that
$\alpha \in {\mathbf {F}}_{\mathfrak {p}}^\times \setminus {\mathbf {F}}_p^\times $
be such that
![]() $\alpha ^2 \in {\mathbf {F}}_p^\times $
; then the group is the union of
$\alpha ^2 \in {\mathbf {F}}_p^\times $
; then the group is the union of
![]() $\mathrm {GL}_2({\mathbf {F}}_p)$
and
$\mathrm {GL}_2({\mathbf {F}}_p)$
and
![]() $\alpha \mathrm {GL}_2({\mathbf {F}}_p)$
. So
$\alpha \mathrm {GL}_2({\mathbf {F}}_p)$
. So
![]() $G_{\mathfrak {p}}$
stabilizes the union of a
$G_{\mathfrak {p}}$
stabilizes the union of a
![]() $2$
-dimensional
$2$
-dimensional
![]() ${\mathbf {F}}_p$
-subspace U (that is not a
${\mathbf {F}}_p$
-subspace U (that is not a
![]() $1$
-dimensional
$1$
-dimensional
![]() ${\mathbf {F}}_{\mathfrak {p}}$
-subspace) of
${\mathbf {F}}_{\mathfrak {p}}$
-subspace) of
![]() $A[p]$
and
$A[p]$
and
![]() $\alpha U$
. If
$\alpha U$
. If
![]() $G_{\mathfrak {p}} \subseteq \mathrm {GL}_2({\mathbf {F}}_p)$
(for some choice of
$G_{\mathfrak {p}} \subseteq \mathrm {GL}_2({\mathbf {F}}_p)$
(for some choice of
![]() ${\mathbf {F}}_{\mathfrak {p}}$
-basis of
${\mathbf {F}}_{\mathfrak {p}}$
-basis of
![]() $A[p]$
), then these two
$A[p]$
), then these two
![]() ${\mathbf {F}}_p$
-subspaces are fixed individually, and so
${\mathbf {F}}_p$
-subspaces are fixed individually, and so
![]() $\rho _p$
is the direct sum of two copies of a
$\rho _p$
is the direct sum of two copies of a
![]() $2$
-dimensional
$2$
-dimensional
![]() ${ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})}$
-representation over
${ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})}$
-representation over
![]() ${\mathbf {F}}_p$
; in particular,
${\mathbf {F}}_p$
; in particular,
![]() $\rho _p$
is reducible. Conversely, if
$\rho _p$
is reducible. Conversely, if
![]() $\rho _p$
is reducible (but
$\rho _p$
is reducible (but
![]() $\rho _{\mathfrak {p}}$
is not), then
$\rho _{\mathfrak {p}}$
is not), then
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
must be contained in the stabilizer of the sub-line that is the image of a
${\mathbf {P}}{G_{\mathfrak {p}}}$
must be contained in the stabilizer of the sub-line that is the image of a
![]() $2$
-dimensional
$2$
-dimensional
![]() ${\mathbf {F}}_p$
-subspace fixed by
${\mathbf {F}}_p$
-subspace fixed by
![]() $G_{\mathfrak {p}}$
. So, by showing that
$G_{\mathfrak {p}}$
. So, by showing that
![]() $\rho _{\mathfrak {p}}$
is irreducible and
$\rho _{\mathfrak {p}}$
is irreducible and
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
is not contained in the stabilizer of a sub-line, we also show that A has no nontrivial isogenies of degree a power of p.
${\mathbf {P}}{G_{\mathfrak {p}}}$
is not contained in the stabilizer of a sub-line, we also show that A has no nontrivial isogenies of degree a power of p.
In any case, we know from the discussion in Section 2.5 that the element
![]() $u({\mathbf {P}}\rho _{\mathfrak {p}}(\operatorname {Frob}_\ell )) = a_\ell ^2/\ell \in {\mathbf {F}}_{\mathfrak {p}}$
must be in
$u({\mathbf {P}}\rho _{\mathfrak {p}}(\operatorname {Frob}_\ell )) = a_\ell ^2/\ell \in {\mathbf {F}}_{\mathfrak {p}}$
must be in
![]() ${\mathbf {F}}_p$
for all
${\mathbf {F}}_p$
for all
![]() $\ell \nmid Np$
if
$\ell \nmid Np$
if
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
is contained in the stabilizer of a sub-line. This is equivalent to
${\mathbf {P}}{G_{\mathfrak {p}}}$
is contained in the stabilizer of a sub-line. This is equivalent to
![]() $p \mid a_\ell ^2 - {a_\ell ^\sigma }^2$
, where
$p \mid a_\ell ^2 - {a_\ell ^\sigma }^2$
, where
![]() $\sigma $
denotes the nontrivial automorphism of
$\sigma $
denotes the nontrivial automorphism of
![]() ${\mathbf {Z}}[f]$
. Since in our setting, there always are
${\mathbf {Z}}[f]$
. Since in our setting, there always are
![]() $\mathfrak {p}$
of degree
$\mathfrak {p}$
of degree
![]() $2$
such that
$2$
such that
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
does not consist entirely of elements g such that
${\mathbf {P}}{G_{\mathfrak {p}}}$
does not consist entirely of elements g such that
![]() $u(g) \in {\mathbf {F}}_p$
, there will be a set of primes
$u(g) \in {\mathbf {F}}_p$
, there will be a set of primes
![]() $\ell \nmid N$
of positive density such that
$\ell \nmid N$
of positive density such that
![]() $a_\ell ^2 \neq {a_\ell ^\sigma }^2$
. (If f has an inner twist by a quadratic character, then
$a_\ell ^2 \neq {a_\ell ^\sigma }^2$
. (If f has an inner twist by a quadratic character, then
![]() $a_\ell = \pm a_\ell ^\sigma $
for almost all
$a_\ell = \pm a_\ell ^\sigma $
for almost all
![]() $\ell $
. But in this case,
$\ell $
. But in this case,
![]() $A_f$
is isogenous to the Weil restriction of an elliptic curve over the quadratic field associated to the character, and so
$A_f$
is isogenous to the Weil restriction of an elliptic curve over the quadratic field associated to the character, and so
![]() $A_f$
is not absolutely simple.) We can replace
$A_f$
is not absolutely simple.) We can replace
![]() $a_\ell ^2 - {a_\ell ^\sigma }^2$
by
$a_\ell ^2 - {a_\ell ^\sigma }^2$
by
![]() $(a_\ell ^2 - {a_\ell ^\sigma }^2)/\sqrt {\operatorname {disc}({\mathbf {Z}}[f])} \in {\mathbf {Z}}$
(note that the prime divisors of
$(a_\ell ^2 - {a_\ell ^\sigma }^2)/\sqrt {\operatorname {disc}({\mathbf {Z}}[f])} \in {\mathbf {Z}}$
(note that the prime divisors of
![]() $\operatorname {disc}({\mathbf {Z}}[f])$
are always ramified, so the corresponding primes of
$\operatorname {disc}({\mathbf {Z}}[f])$
are always ramified, so the corresponding primes of
![]() ${\mathbf {Z}}[f]$
have degree
${\mathbf {Z}}[f]$
have degree
![]() $1$
). This leads to the following algorithm.
$1$
). This leads to the following algorithm.
Algorithm 2.44.

By the discussion above, the algorithm will not return ‘failure’ when B is sufficiently large.
We now consider the case of exceptional image. Our analysis of the projective image of the inertia group
![]() $I_p$
allows us to find elements of order at least
$I_p$
allows us to find elements of order at least
![]() $6$
in
$6$
in
![]() ${\mathbf {P}}{\rho _{\mathfrak {p}}(I_p)} \leq {\mathbf {P}}{G_{\mathfrak {p}}}$
in most cases, which implies that
${\mathbf {P}}{\rho _{\mathfrak {p}}(I_p)} \leq {\mathbf {P}}{G_{\mathfrak {p}}}$
in most cases, which implies that
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
is not contained in
${\mathbf {P}}{G_{\mathfrak {p}}}$
is not contained in
![]() $S_4$
or
$S_4$
or
![]() $A_5$
.
$A_5$
.
Proposition 2.45. If
![]() $p \ge 7$
is a prime such that
$p \ge 7$
is a prime such that
![]() $p^2 \nmid N$
, then
$p^2 \nmid N$
, then
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
is not exceptional for all
${\mathbf {P}}{G_{\mathfrak {p}}}$
is not exceptional for all
![]() $\mathfrak {p} \mid p$
.
$\mathfrak {p} \mid p$
.
Proof. Since we assume
![]() $p^2 \nmid N$
, it follows from corollary 2.23 that
$p^2 \nmid N$
, it follows from corollary 2.23 that
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
contains elements of order
${\mathbf {P}}{G_{\mathfrak {p}}}$
contains elements of order
![]() $p-1$
or
$p-1$
or
![]() $p+1$
. So if
$p+1$
. So if
![]() $p \ge 7$
, there are always elements of order at least
$p \ge 7$
, there are always elements of order at least
![]() $6$
in
$6$
in
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
, which implies that
${\mathbf {P}}{G_{\mathfrak {p}}}$
, which implies that
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
cannot be contained in a group isomorphic to
${\mathbf {P}}{G_{\mathfrak {p}}}$
cannot be contained in a group isomorphic to
![]() $S_4$
or to
$S_4$
or to
![]() $A_5$
.
$A_5$
.
So we only have to consider prime ideals
![]() $\mathfrak {p}$
of residue characteristic p such that
$\mathfrak {p}$
of residue characteristic p such that
![]() $p \le 5$
or
$p \le 5$
or
![]() $p^2 \mid N$
. By the classification in Section 2.4, we can also exclude
$p^2 \mid N$
. By the classification in Section 2.4, we can also exclude
![]() $p = 3$
when
$p = 3$
when
![]() $\deg \mathfrak {p} = 1$
and
$\deg \mathfrak {p} = 1$
and
![]() $p = 2$
. We can then run algorithm 2.19 on these finitely many
$p = 2$
. We can then run algorithm 2.19 on these finitely many
![]() $\mathfrak {p}$
to reduce the set of possibly exceptional primes further.
$\mathfrak {p}$
to reduce the set of possibly exceptional primes further.
2.11 Proving non-CM
Recall that our goal is to show that
![]() $G_{\mathfrak {p}} = G_{\mathfrak {p}}^{\operatorname {max}}$
for all
$G_{\mathfrak {p}} = G_{\mathfrak {p}}^{\operatorname {max}}$
for all
![]() $\mathfrak {p}$
outside an explicit small finite set. Now if f has CM, then
$\mathfrak {p}$
outside an explicit small finite set. Now if f has CM, then
![]() $G_{\mathfrak {p}}$
will always be contained in the normalizer of a Cartan subgroup, so in this case, our task is impossible. Note that by proposition 2.2, in our case of interest when
$G_{\mathfrak {p}}$
will always be contained in the normalizer of a Cartan subgroup, so in this case, our task is impossible. Note that by proposition 2.2, in our case of interest when
![]() $g = 2$
, if the associated abelian surface is absolutely simple, f cannot have CM. However, since it may be of interest in other situations, we describe a suitable algorithm.
$g = 2$
, if the associated abelian surface is absolutely simple, f cannot have CM. However, since it may be of interest in other situations, we describe a suitable algorithm.
We recall the relevant definition (see [Reference Ribet88, § 3], specialized to the case of interest).
Definition 2.46. Let f be a newform of weight
![]() $2$
, level N and trivial nebentypus, and let
$2$
, level N and trivial nebentypus, and let
![]() $\varepsilon $
be a Dirichlet character. We say that f has CM by
$\varepsilon $
be a Dirichlet character. We say that f has CM by
![]() $\varepsilon $
, if
$\varepsilon $
, if
![]() $f \otimes \varepsilon = f$
. We say that f has CM, if f has CM by some nontrivial Dirichlet character
$f \otimes \varepsilon = f$
. We say that f has CM, if f has CM by some nontrivial Dirichlet character
![]() $\varepsilon $
.
$\varepsilon $
.
Remark 2.47. The Dirichlet character
![]() $\varepsilon $
is then necessarily quadratic: Since f has totally real coefficients,
$\varepsilon $
is then necessarily quadratic: Since f has totally real coefficients,
![]() $\varepsilon $
has to take real values.
$\varepsilon $
has to take real values.
If f has CM by
![]() $\varepsilon $
, then
$\varepsilon $
, then
![]() $\varepsilon (\ell ) a_\ell = a_\ell $
for all
$\varepsilon (\ell ) a_\ell = a_\ell $
for all
![]() $\ell \nmid N \operatorname {cond}(\varepsilon )$
, so
$\ell \nmid N \operatorname {cond}(\varepsilon )$
, so
![]() $a_\ell = 0$
whenever
$a_\ell = 0$
whenever
![]() $\varepsilon (\ell ) = -1$
. This can be used to show that f does not have CM by
$\varepsilon (\ell ) = -1$
. This can be used to show that f does not have CM by
![]() $\varepsilon $
, by exhibiting a prime
$\varepsilon $
, by exhibiting a prime
![]() $\ell \nmid N$
such that
$\ell \nmid N$
such that
![]() $\varepsilon (\ell ) = -1$
and
$\varepsilon (\ell ) = -1$
and
![]() $a_\ell \neq 0$
.
$a_\ell \neq 0$
.
The idea is then to first determine a finite set of possibilities for the conductor D of
![]() $\varepsilon $
and then to check for each of the finitely many possible characters
$\varepsilon $
and then to check for each of the finitely many possible characters
![]() $\varepsilon $
of conductor D that f does not have CM by
$\varepsilon $
of conductor D that f does not have CM by
![]() $\varepsilon $
using this approach.
$\varepsilon $
using this approach.
Theorem 2.48. Let f be a newform of weight
![]() $2$
, level N and trivial nebentypus, and let
$2$
, level N and trivial nebentypus, and let
![]() $\varepsilon $
be a quadratic Dirichlet character of conductor D. Then the twist
$\varepsilon $
be a quadratic Dirichlet character of conductor D. Then the twist
![]() $f \otimes \varepsilon $
of f by
$f \otimes \varepsilon $
of f by
![]() $\varepsilon $
is a normalized eigenform of level dividing
$\varepsilon $
is a normalized eigenform of level dividing
![]() $\operatorname {lcm}(N,D^2)$
and trivial nebentypus.
$\operatorname {lcm}(N,D^2)$
and trivial nebentypus.
Proof. See [Reference Shimura102, Proposition 3.64], using that
![]() $\varepsilon ^2$
is trivial.
$\varepsilon ^2$
is trivial.
Proposition 2.49. If f is a CM form of level N, it is the newform associated to a Hecke character
![]() $\psi $
of some conductor
$\psi $
of some conductor
![]() ${\mathfrak {m}}$
of an imaginary quadratic number field K of discriminant
${\mathfrak {m}}$
of an imaginary quadratic number field K of discriminant
![]() $-\Delta _K$
. One has
$-\Delta _K$
. One has
![]() $N = \Delta _K M$
with M the absolute norm
$N = \Delta _K M$
with M the absolute norm
![]() $\mathscr {N}({\mathfrak {m}}) := \#\mathcal {O}_K/{\mathfrak {m}}$
and
$\mathscr {N}({\mathfrak {m}}) := \#\mathcal {O}_K/{\mathfrak {m}}$
and
![]() $\langle \Delta _K \rangle \mid {\mathfrak {m}}$
. In particular,
$\langle \Delta _K \rangle \mid {\mathfrak {m}}$
. In particular,
![]() $\Delta _K^2 \mid N$
.
$\Delta _K^2 \mid N$
.
Proof. [Reference Schütt96, Theorem 1.4 and Corollary 1.5]
In the situation of proposition 2.49, the CM character
![]() $\varepsilon $
is the quadratic character associated to K.
$\varepsilon $
is the quadratic character associated to K.
This leads to the following algorithm.
Algorithm 2.50.

Remark 2.51. If f does have CM, then this algorithm will eventually return ‘no result’. Then one has a candidate character
![]() $\varepsilon $
(the character associated to
$\varepsilon $
(the character associated to
![]() $-\Delta $
), and one can try to verify that
$-\Delta $
), and one can try to verify that
![]() $f \otimes \varepsilon = f$
(this is a finite computation, as the space of cusp forms of weight
$f \otimes \varepsilon = f$
(this is a finite computation, as the space of cusp forms of weight
![]() $2$
, level
$2$
, level
![]() $\operatorname {lcm}(N, \Delta ^2)$
and trivial nebentypus is of finite dimension and can be computed).
$\operatorname {lcm}(N, \Delta ^2)$
and trivial nebentypus is of finite dimension and can be computed).
The following result guarantees that there will be enough primes
![]() $\ell $
as above when f has no CM.
$\ell $
as above when f has no CM.
Theorem 2.52. Let f be a non-CM form. The set of primes
![]() $\ell $
such that
$\ell $
such that
![]() $a_\ell = 0$
has density
$a_\ell = 0$
has density
![]() $0$
.
$0$
.
Proof. See [Reference Serre99, p. 174].
Example 2.53. If N is squarefree, then proposition 2.49 implies that f has no CM since the only possible value of
![]() $\Delta $
would lead to
$\Delta $
would lead to
![]() $-\Delta _K = -1$
, which is not a discriminant of an imaginary quadratic number field.
$-\Delta _K = -1$
, which is not a discriminant of an imaginary quadratic number field.
Remark 2.54. The newforms of weight
![]() $2$
, level
$2$
, level
![]() $800$
, trivial nebentypus and with coefficients in
$800$
, trivial nebentypus and with coefficients in
![]() ${\mathbf {Q}}(\sqrt {5})$
in the Galois orbit with LMFDB label 800.2.a.j have CM by
${\mathbf {Q}}(\sqrt {5})$
in the Galois orbit with LMFDB label 800.2.a.j have CM by
![]() ${\mathbf {Q}}(\sqrt {-5})$
. Computing its endomorphism ring using Magma, we see that it has nontrivial idempotents, so
${\mathbf {Q}}(\sqrt {-5})$
. Computing its endomorphism ring using Magma, we see that it has nontrivial idempotents, so
![]() $A_f$
is not absolutely simple as predicted by proposition 2.2.
$A_f$
is not absolutely simple as predicted by proposition 2.2.
2.12 Maximal image for almost all
 $\mathfrak {p}$
$\mathfrak {p}$
Let f as usual be a newform of weight
![]() $2$
, level N and trivial nebentypus. We now assume that f does not have CM. In this section, we will describe an algorithm inspired by [Reference Cojocaru26] that finds a small finite set of primes
$2$
, level N and trivial nebentypus. We now assume that f does not have CM. In this section, we will describe an algorithm inspired by [Reference Cojocaru26] that finds a small finite set of primes
![]() $\mathfrak {p}$
such that for all
$\mathfrak {p}$
such that for all
![]() $\mathfrak {p} \notin S$
, the representation
$\mathfrak {p} \notin S$
, the representation
![]() $\rho _{\mathfrak {p}}$
has maximal image.
$\rho _{\mathfrak {p}}$
has maximal image.
Using the algorithms we have described so far (and assuming
![]() $g = 2$
, as that is required for some of these algorithms), we can determine a finite set S of prime ideals such that for all
$g = 2$
, as that is required for some of these algorithms), we can determine a finite set S of prime ideals such that for all
![]() $\mathfrak {p} \notin S$
, the representation
$\mathfrak {p} \notin S$
, the representation
![]() $\rho _{\mathfrak {p}}$
is either maximal or irreducible and dihedral. So if
$\rho _{\mathfrak {p}}$
is either maximal or irreducible and dihedral. So if
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
is not maximal for
${\mathbf {P}}{G_{\mathfrak {p}}}$
is not maximal for
![]() $\mathfrak {p} \notin S$
, it is contained in the normalizer
$\mathfrak {p} \notin S$
, it is contained in the normalizer
![]() $N(C)$
of a Cartan subgroup C. It therefore remains to find a finite set of prime ideals such that
$N(C)$
of a Cartan subgroup C. It therefore remains to find a finite set of prime ideals such that
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
is not dihedral for
${\mathbf {P}}{G_{\mathfrak {p}}}$
is not dihedral for
![]() $\mathfrak {p}$
outside this set.
$\mathfrak {p}$
outside this set.
So assume that
![]() $\rho _{\mathfrak {p}}$
is irreducible and dihedral, with
$\rho _{\mathfrak {p}}$
is irreducible and dihedral, with
![]() ${\mathbf {P}}{G_{\mathfrak {p}}} \subseteq N(C)$
as above. We can also assume that
${\mathbf {P}}{G_{\mathfrak {p}}} \subseteq N(C)$
as above. We can also assume that
![]() $p^2 \nmid N$
, as this excludes only finitely many p, which we can consider separately. By corollary 2.30,
$p^2 \nmid N$
, as this excludes only finitely many p, which we can consider separately. By corollary 2.30,
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
is not contained in C. So the character
${\mathbf {P}}{G_{\mathfrak {p}}}$
is not contained in C. So the character
![]() $\varepsilon _{\mathfrak {p}}$
defined in corollary 2.34 is nontrivial.
$\varepsilon _{\mathfrak {p}}$
defined in corollary 2.34 is nontrivial.
Proposition 2.55. If N is squarefree, the residue characteristic of
![]() $\mathfrak {p}$
is not
$\mathfrak {p}$
is not
![]() $2$
and
$2$
and
![]() $\rho _{\mathfrak {p}}$
is irreducible, then
$\rho _{\mathfrak {p}}$
is irreducible, then
![]() $\rho _{\mathfrak {p}}$
is not dihedral.
$\rho _{\mathfrak {p}}$
is not dihedral.
Proof. Let us prove the contrapositive. Thus, suppose that
![]() $\rho _{\mathfrak {p}}$
is dihedral. Then by the discussion above,
$\rho _{\mathfrak {p}}$
is dihedral. Then by the discussion above,
![]() $\varepsilon _{\mathfrak {p}}$
is nontrivial. By Corollary 2.34, the conductor
$\varepsilon _{\mathfrak {p}}$
is nontrivial. By Corollary 2.34, the conductor
![]() $d> 1$
of
$d> 1$
of
![]() $\epsilon_\mathfrak{p}$
satisfies
$\epsilon_\mathfrak{p}$
satisfies
![]() $d^2\, {\mid}\, N$
. Thus, N is not squarefree.
$d^2\, {\mid}\, N$
. Thus, N is not squarefree.
So in the semi-stable case, we already know that
![]() $\rho _{\mathfrak {p}}$
is maximal for all
$\rho _{\mathfrak {p}}$
is maximal for all
![]() $\mathfrak {p} \notin S$
. If N is not squarefree, then corollary 2.34 provides us with a finite set of possibilities for
$\mathfrak {p} \notin S$
. If N is not squarefree, then corollary 2.34 provides us with a finite set of possibilities for
![]() $\varepsilon _{\mathfrak {p}}$
, and we can try to rule each of them out for all prime ideals outside a finite set.
$\varepsilon _{\mathfrak {p}}$
, and we can try to rule each of them out for all prime ideals outside a finite set.
Lemma 2.56. Assume that
![]() $\mathfrak {p}$
has odd residue characteristic p and that
$\mathfrak {p}$
has odd residue characteristic p and that
![]() $\rho _{\mathfrak {p}}$
is dihedral, with associated character
$\rho _{\mathfrak {p}}$
is dihedral, with associated character
![]() $\varepsilon _{\mathfrak {p}}$
. If
$\varepsilon _{\mathfrak {p}}$
. If
![]() $\ell \nmid Np$
is a prime such that
$\ell \nmid Np$
is a prime such that
![]() $\varepsilon _{\mathfrak {p}}(\ell ) = -1$
, then
$\varepsilon _{\mathfrak {p}}(\ell ) = -1$
, then
![]() $\mathfrak {p} \mid a_\ell $
.
$\mathfrak {p} \mid a_\ell $
.
Proof. Since
![]() $\varepsilon _{\mathfrak {p}}(\ell ) = -1$
by assumption, we have
$\varepsilon _{\mathfrak {p}}(\ell ) = -1$
by assumption, we have
![]() $\rho _{\mathfrak {p}}(\operatorname {Frob}_\ell ) \in N(C) \setminus C$
. Then
$\rho _{\mathfrak {p}}(\operatorname {Frob}_\ell ) \in N(C) \setminus C$
. Then
![]() ${\mathbf {P}}\rho _{\mathfrak {p}}(\operatorname {Frob}_\ell )$
has order
${\mathbf {P}}\rho _{\mathfrak {p}}(\operatorname {Frob}_\ell )$
has order
![]() $2$
, which implies that
$2$
, which implies that
![]() $a_\ell \equiv \operatorname {Tr}(\rho _{\mathfrak {p}}(\operatorname {Frob}_\ell )) = 0 \bmod \mathfrak {p}$
.
$a_\ell \equiv \operatorname {Tr}(\rho _{\mathfrak {p}}(\operatorname {Frob}_\ell )) = 0 \bmod \mathfrak {p}$
.
We make use of this as follows. For each quadratic character
![]() $\varepsilon $
of conductor d such that
$\varepsilon $
of conductor d such that
![]() $d^2 \mid N$
(or
$d^2 \mid N$
(or
![]() $d \mid 8 d_0$
with
$d \mid 8 d_0$
with
![]() $d_0$
odd such that
$d_0$
odd such that
![]() $d_0^2 \mid N$
if
$d_0^2 \mid N$
if
![]() $4 \mid N$
), find some prime
$4 \mid N$
), find some prime
![]() $\ell = \ell (\varepsilon ) \nmid N$
such that
$\ell = \ell (\varepsilon ) \nmid N$
such that
![]() $a_\ell \neq 0$
and
$a_\ell \neq 0$
and
![]() $\varepsilon (\ell ) = -1$
(there are many such primes by theorem 2.52). Then for all
$\varepsilon (\ell ) = -1$
(there are many such primes by theorem 2.52). Then for all
![]() $\mathfrak {p}$
such that
$\mathfrak {p}$
such that
![]() $\mathfrak {p} \nmid \ell a_\ell $
(which are all but finitely many), it follows that
$\mathfrak {p} \nmid \ell a_\ell $
(which are all but finitely many), it follows that
![]() $\varepsilon _{\mathfrak {p}} \neq \varepsilon $
. (In practice, it makes sense to use several such primes
$\varepsilon _{\mathfrak {p}} \neq \varepsilon $
. (In practice, it makes sense to use several such primes
![]() $\ell $
to cut the set of possible exceptions down further.) So replacing S by the union of S with the finitely many finite sets
$\ell $
to cut the set of possible exceptions down further.) So replacing S by the union of S with the finitely many finite sets
![]() $S_\varepsilon = \{\mathfrak {p} : \mathfrak {p} \mid \ell a_{\ell (\varepsilon )}\}$
, we obtain the desired finite set S of prime ideals such that for
$S_\varepsilon = \{\mathfrak {p} : \mathfrak {p} \mid \ell a_{\ell (\varepsilon )}\}$
, we obtain the desired finite set S of prime ideals such that for
![]() $\mathfrak {p} \notin S$
,
$\mathfrak {p} \notin S$
,
![]() $\rho _{\mathfrak {p}}$
has maximal image.
$\rho _{\mathfrak {p}}$
has maximal image.
Algorithm 2.57.

If B is sufficiently large, then the algorithm will not return ‘failure’, and by the discussion above, S will satisfy the specification.
We can use the information obtained from the various algorithms to provide a list of possible types of maximal subgroups that could contain
![]() $G_{\mathfrak {p}}$
for those primes
$G_{\mathfrak {p}}$
for those primes
![]() $\mathfrak {p}$
that are in the set returned by algorithm 2.57.
$\mathfrak {p}$
that are in the set returned by algorithm 2.57.
2.13 The image of the
 $\mathfrak {p}$
-adic Galois representation
$\mathfrak {p}$
-adic Galois representation
For theorem 7.7, we also need information about the image of
![]() $\rho _{\mathfrak {p}^\infty }|_{ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}}(\mu _{p^\infty }))}$
, and for theorem 5.10, about the image of
$\rho _{\mathfrak {p}^\infty }|_{ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}}(\mu _{p^\infty }))}$
, and for theorem 5.10, about the image of
![]() $\rho _{\mathfrak {p}^\infty }$
.
$\rho _{\mathfrak {p}^\infty }$
.
Proposition 2.58. Let
![]() $\mathcal {O}$
be the ring of integers of an unramified extension of
$\mathcal {O}$
be the ring of integers of an unramified extension of
![]() ${\mathbf {Z}}_p$
. Let
${\mathbf {Z}}_p$
. Let
![]() $G \subseteq {\mathrm {SL}}_2(\mathcal {O})$
be a closed subgroup.
$G \subseteq {\mathrm {SL}}_2(\mathcal {O})$
be a closed subgroup.
-
(i) If
 $p> 3$
and G surjects onto
$p> 3$
and G surjects onto
 $ {\mathrm {SL}}_2(\mathcal {O}/p)$
, then
$ {\mathrm {SL}}_2(\mathcal {O}/p)$
, then
 $G = {\mathrm {SL}}_2(\mathcal {O})$
.
$G = {\mathrm {SL}}_2(\mathcal {O})$
. -
(ii) If
 $p = 3$
and G surjects onto
$p = 3$
and G surjects onto
 $ {\mathrm {SL}}_2(\mathcal {O}/3^2)$
, then
$ {\mathrm {SL}}_2(\mathcal {O}/3^2)$
, then
 $G = {\mathrm {SL}}_2(\mathcal {O})$
.
$G = {\mathrm {SL}}_2(\mathcal {O})$
.
Proof. See [Reference Serre100, Lemma IV.23.3], noting that the proof works for
![]() $\mathcal {O}$
instead of
$\mathcal {O}$
instead of
![]() ${\mathbf {Z}}_p$
; for
${\mathbf {Z}}_p$
; for
![]() $p = 3$
, our claim follows from the proof given there.
$p = 3$
, our claim follows from the proof given there.
Proposition 2.59. Assume that
![]() $\mathcal {O}/3 \in \{{\mathbf {F}}_3,{\mathbf {F}}_{3^2}\}$
. Let
$\mathcal {O}/3 \in \{{\mathbf {F}}_3,{\mathbf {F}}_{3^2}\}$
. Let
![]() $\rho \colon { {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})} \to \mathrm {GL}_2(\mathcal {O})$
be a continuous homomorphism with mod-
$\rho \colon { {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})} \to \mathrm {GL}_2(\mathcal {O})$
be a continuous homomorphism with mod-
![]() $3^n$
reduction
$3^n$
reduction
![]() $\rho _{3^n}$
. If
$\rho _{3^n}$
. If
![]() $\rho _{3}$
is surjective and the number of characteristic polynomials of elements of
$\rho _{3}$
is surjective and the number of characteristic polynomials of elements of
![]() $\rho _{3^2}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})})$
with constant term
$\rho _{3^2}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})})$
with constant term
![]() $1$
is larger than the number of characteristic polynomials of elements of
$1$
is larger than the number of characteristic polynomials of elements of
![]() $\rho _{3}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})})$
with constant term
$\rho _{3}({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})})$
with constant term
![]() $1$
, then
$1$
, then
![]() $\rho _{3^2}$
is surjective.
$\rho _{3^2}$
is surjective.
Proof. This is a Magma computation, looping over all subgroups of
![]() $ {\mathrm {SL}}_2(\mathcal {O}/3^2)$
that surject onto
$ {\mathrm {SL}}_2(\mathcal {O}/3^2)$
that surject onto
![]() $ {\mathrm {SL}}_2(\mathcal {O}/3)$
and computing characteristic polynomials.
$ {\mathrm {SL}}_2(\mathcal {O}/3)$
and computing characteristic polynomials.
Proposition 2.60. Let
![]() $\mathcal {O}$
be the ring of integers of an unramified extension of
$\mathcal {O}$
be the ring of integers of an unramified extension of
![]() ${\mathbf {Z}}_p$
. Let
${\mathbf {Z}}_p$
. Let
be a closed subgroup with
![]() $\det (G) = {\mathbf {Z}}_p^\times $
.
$\det (G) = {\mathbf {Z}}_p^\times $
.
If
![]() $p> 3$
and the image of G in
$p> 3$
and the image of G in
![]() $\mathrm {GL}_2({\mathbf {F}}_{\mathfrak {p}})$
contains
$\mathrm {GL}_2({\mathbf {F}}_{\mathfrak {p}})$
contains
![]() $ {\mathrm {SL}}_2({\mathbf {F}}_p)$
, then
$ {\mathrm {SL}}_2({\mathbf {F}}_p)$
, then
![]() $G = G_{\mathfrak {p}^\infty }^{\operatorname {max}}$
.
$G = G_{\mathfrak {p}^\infty }^{\operatorname {max}}$
.
Proof. This follows from the proof of [Reference Lombardo69, Theorem 4.22].
We do not need proposition 2.60 for the examples in this article, but it is useful for further examples.
2.14 Examples
The following table contains the result of running our algorithms on all absolutely simple Jacobians with real multiplication of genus
![]() $2$
curves over
$2$
curves over
![]() ${\mathbf {Q}}$
that are contained in the LMFDB. (The genus
${\mathbf {Q}}$
that are contained in the LMFDB. (The genus
![]() $2$
curves in the LMFDB have discriminant bounded by
$2$
curves in the LMFDB have discriminant bounded by
![]() $10^6$
; since the conductor of the Jacobian is the square of the level N and divides the discriminant, this implies that
$10^6$
; since the conductor of the Jacobian is the square of the level N and divides the discriminant, this implies that
![]() $N \le 1000$
.) We add information on the isogeny classes coming from Hasegawa or Wang curves that are not also represented by an LMFDB curve.
$N \le 1000$
.) We add information on the isogeny classes coming from Hasegawa or Wang curves that are not also represented by an LMFDB curve.
The entry ‘N’ gives the level and the letter x of the isogeny class of the curve in the LMFDB (the LMFDB label of the isogeny class is then
![]() $N^2.x\dots $
). For the Hasegawa and Wang curves not representing an isogeny class of an LMFDB curve, we use the label from [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and Wetherell45]. The entry ‘
$N^2.x\dots $
). For the Hasegawa and Wang curves not representing an isogeny class of an LMFDB curve, we use the label from [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and Wetherell45]. The entry ‘
![]() $p^2 \mid N$
’ lists the primes at which the Jacobian does not have semi-stable reduction. The third entry ‘
$p^2 \mid N$
’ lists the primes at which the Jacobian does not have semi-stable reduction. The third entry ‘
![]() $\operatorname {disc}(\mathcal {O})$
’ gives the discriminant of the endomorphism ring of the Jacobian. The next entry lists the prime ideals
$\operatorname {disc}(\mathcal {O})$
’ gives the discriminant of the endomorphism ring of the Jacobian. The next entry lists the prime ideals
![]() $\mathfrak {p}$
such that
$\mathfrak {p}$
such that
![]() $\rho _{\mathfrak {p}}$
is reducible and gives the splitting of
$\rho _{\mathfrak {p}}$
is reducible and gives the splitting of
![]() $\rho _{\mathfrak {p}}^{{\mathrm {ss}}}$
into characters. We use
$\rho _{\mathfrak {p}}^{{\mathrm {ss}}}$
into characters. We use
![]() $\varepsilon _d$
to denote the quadratic character associated to the quadratic extension of discriminant d. Since
$\varepsilon _d$
to denote the quadratic character associated to the quadratic extension of discriminant d. Since
![]() $\rho _{\mathfrak {p}}^{{\mathrm {ss}}}$
is the same for isogenous Jacobians, we list each isogeny class only once. The primes are given as ‘p’ when
$\rho _{\mathfrak {p}}^{{\mathrm {ss}}}$
is the same for isogenous Jacobians, we list each isogeny class only once. The primes are given as ‘p’ when
![]() $\mathfrak {p} = \langle p \rangle $
is of degree
$\mathfrak {p} = \langle p \rangle $
is of degree
![]() $2$
, as ‘
$2$
, as ‘
![]() $\mathfrak {p}_p'$
’ or ‘
$\mathfrak {p}_p'$
’ or ‘
![]() $\mathfrak {p}_p"$
’ when
$\mathfrak {p}_p"$
’ when
![]() $p = p(\mathfrak {p})$
is split and as ‘
$p = p(\mathfrak {p})$
is split and as ‘
![]() $\mathfrak {p}_p$
’ when p is ramified. The last entry lists the prime ideals
$\mathfrak {p}_p$
’ when p is ramified. The last entry lists the prime ideals
![]() $\mathfrak {p}$
such that
$\mathfrak {p}$
such that
![]() $\rho _{\mathfrak {p}}$
is irreducible, but algorithm 2.57 does not prove that
$\rho _{\mathfrak {p}}$
is irreducible, but algorithm 2.57 does not prove that
![]() $\rho _{\mathfrak {p}}$
is maximal. In these cases, we have determined the isomorphism type of
$\rho _{\mathfrak {p}}$
is maximal. In these cases, we have determined the isomorphism type of
![]() ${\mathbf {P}}{G_{\mathfrak {p}}}$
by a direct computation; we give it in the table.
${\mathbf {P}}{G_{\mathfrak {p}}}$
by a direct computation; we give it in the table.

3 Computation of Heegner points and the Heegner index
For this section, we fix the following setup. Let
![]() $f \in \mathcal {N}(N, g)$
be a newform of level N with Galois orbit of size g, so that its coefficient ring
$f \in \mathcal {N}(N, g)$
be a newform of level N with Galois orbit of size g, so that its coefficient ring
![]() ${\mathbf {Z}}[f]$
is an order in the totally real number field
${\mathbf {Z}}[f]$
is an order in the totally real number field
![]() ${\mathbf {Q}}(f)$
of degree g. Its Fourier coefficients are
${\mathbf {Q}}(f)$
of degree g. Its Fourier coefficients are
![]() $a_n = a_n(f) \in {\mathbf {Z}}[f]$
. We denote the set of embeddings
$a_n = a_n(f) \in {\mathbf {Z}}[f]$
. We denote the set of embeddings
![]() ${\mathbf {Q}}(f) \hookrightarrow {\mathbf {R}}$
by
${\mathbf {Q}}(f) \hookrightarrow {\mathbf {R}}$
by
![]() $\Sigma $
, and we write
$\Sigma $
, and we write
![]() $f^\sigma $
for the modular form with real coefficients obtained from f by applying
$f^\sigma $
for the modular form with real coefficients obtained from f by applying
![]() $\sigma \in \Sigma $
to its coefficients. Recall that
$\sigma \in \Sigma $
to its coefficients. Recall that
![]() $I_f$
denotes the annihilator of f in the integral Hecke algebra
$I_f$
denotes the annihilator of f in the integral Hecke algebra
![]() $\mathbf {T}$
, and that we have morphisms of abelian varieties
$\mathbf {T}$
, and that we have morphisms of abelian varieties
the composition
![]() $\lambda _f = \pi _f \circ \iota _f \colon A_f^{\vee } \to A_f$
is a polarization of
$\lambda _f = \pi _f \circ \iota _f \colon A_f^{\vee } \to A_f$
is a polarization of
![]() $A_f^{\vee }$
; it is the polarization induced by the canonical principal polarization of
$A_f^{\vee }$
; it is the polarization induced by the canonical principal polarization of
![]() $J_0(N)$
as the Jacobian of
$J_0(N)$
as the Jacobian of
![]() $X_0(N)$
. (If
$X_0(N)$
. (If
![]() $\lambda \colon A \to A^{\vee }$
is the polarization coming from
$\lambda \colon A \to A^{\vee }$
is the polarization coming from
![]() $L \in {\mathrm {NS}}(A)$
and
$L \in {\mathrm {NS}}(A)$
and
![]() $\varphi \colon B \subseteq A$
is an abelian subvariety, then
$\varphi \colon B \subseteq A$
is an abelian subvariety, then
![]() $\varphi ^{\vee } \circ \lambda \circ \varphi \colon B \to B^{\vee }$
is the polarization on B coming from
$\varphi ^{\vee } \circ \lambda \circ \varphi \colon B \to B^{\vee }$
is the polarization on B coming from
![]() $\varphi ^* L$
. See [Reference Birkenhake and Lange9, Cor. 2.4.6 (d)].) Note that
$\varphi ^* L$
. See [Reference Birkenhake and Lange9, Cor. 2.4.6 (d)].) Note that
![]() $\iota _f$
is the composition of
$\iota _f$
is the composition of
![]() $\pi _f^{\vee }$
with the inverse of the canonical polarization of
$\pi _f^{\vee }$
with the inverse of the canonical polarization of
![]() $J_0(N)$
. We write
$J_0(N)$
. We write
where
![]() $(d_1, \ldots , d_g)$
is the type of
$(d_1, \ldots , d_g)$
is the type of
![]() $\lambda _f$
; then
$\lambda _f$
; then
![]() $\deg \lambda _f = d_f^2$
(see [Reference Birkenhake and Lange9, Thm. 3.6.1 and Cor. 3.6.2]). The number
$\deg \lambda _f = d_f^2$
(see [Reference Birkenhake and Lange9, Thm. 3.6.1 and Cor. 3.6.2]). The number
![]() $d_f$
is sometimes called the modular degree of
$d_f$
is sometimes called the modular degree of
![]() $A_f$
; see, for example, [Reference Agashe and Stein3, § 3.3].
$A_f$
; see, for example, [Reference Agashe and Stein3, § 3.3].
We further assume that we are given a (nice) curve X whose Jacobian J is isogenous to
![]() $A_f$
via an isogeny
$A_f$
via an isogeny
![]() $\pi \colon A_f \to J$
. We denote
$\pi \colon A_f \to J$
. We denote
![]() $\mathrm {End}_{\mathbf {Q}}(J)$
by
$\mathrm {End}_{\mathbf {Q}}(J)$
by
![]() $\mathcal {O}$
. The isogeny
$\mathcal {O}$
. The isogeny
![]() $\pi $
induces an isomorphism of endomorphism algebras (where
$\pi $
induces an isomorphism of endomorphism algebras (where
![]() $\mathrm {End}^0_{\mathbf {Q}}(A) := \mathrm {End}_{\mathbf {Q}}(A) \otimes _{\mathbf {Z}} {\mathbf {Q}}$
)
$\mathrm {End}^0_{\mathbf {Q}}(A) := \mathrm {End}_{\mathbf {Q}}(A) \otimes _{\mathbf {Z}} {\mathbf {Q}}$
)
which we use to identify
![]() $\mathrm {End}^0_{\mathbf {Q}}(J) = {\mathbf {Q}}(f)$
. In particular,
$\mathrm {End}^0_{\mathbf {Q}}(J) = {\mathbf {Q}}(f)$
. In particular,
![]() $\mathcal {O}$
is identified with an order of
$\mathcal {O}$
is identified with an order of
![]() ${\mathbf {Q}}(f)$
. Then for any
${\mathbf {Q}}(f)$
. Then for any
![]() $\gamma \in {\mathbf {Z}}[f] \cap \mathcal {O}$
, it follows that
$\gamma \in {\mathbf {Z}}[f] \cap \mathcal {O}$
, it follows that
We write
![]() $\pi _J = \pi \circ \pi _f \colon J_0(N) \to J$
. We then have a commutative diagram
$\pi _J = \pi \circ \pi _f \colon J_0(N) \to J$
. We then have a commutative diagram

with a polarization
![]() $\lambda = \pi \circ \lambda _f \circ \pi ^{\vee } = \pi _J \circ \pi _J^{\vee }$
of
$\lambda = \pi \circ \lambda _f \circ \pi ^{\vee } = \pi _J \circ \pi _J^{\vee }$
of
![]() $J^{\vee }$
. Then by pre-composing
$J^{\vee }$
. Then by pre-composing
![]() $\lambda $
with the canonical principal polarization
$\lambda $
with the canonical principal polarization
![]() $\lambda _J$
of J, we obtain an element
$\lambda _J$
of J, we obtain an element
By [Reference Milne76, Prop. 12.12],
![]() $(\deg \pi )^2 (\deg \lambda _f) = \deg \alpha = \mathbf {N}(\alpha )^2$
, which implies that
$(\deg \pi )^2 (\deg \lambda _f) = \deg \alpha = \mathbf {N}(\alpha )^2$
, which implies that
In practice, we start with the curve X of genus g, and we know that its Jacobian J has real multiplication (and is absolutely simple). We then need to find the corresponding newform
![]() $f \in \mathcal {N}(N, g)$
. We first determine N. When X is a quotient of
$f \in \mathcal {N}(N, g)$
. We first determine N. When X is a quotient of
![]() $X_0(N)$
, then we know N by construction. In general, we find N as the square root of the conductor of J, which can be computed up to finitely many choices of power of
$X_0(N)$
, then we know N by construction. In general, we find N as the square root of the conductor of J, which can be computed up to finitely many choices of power of
![]() $2$
at worst; in our LMFDB examples, the conductor has been determined exactly and is available in the LMFDB. Given N, we then compare the traces of the Fourier coefficients at primes
$2$
at worst; in our LMFDB examples, the conductor has been determined exactly and is available in the LMFDB. Given N, we then compare the traces of the Fourier coefficients at primes
![]() $\ell \nmid N$
of the various candidate f with the corresponding coefficient of the L-function of J. This quickly leaves only one candidate, which must then be the correct f (up to the Galois action). We now assume that f is fixed.
$\ell \nmid N$
of the various candidate f with the corresponding coefficient of the L-function of J. This quickly leaves only one candidate, which must then be the correct f (up to the Galois action). We now assume that f is fixed.
One of the ingredients we need in order to prove that ![]() for all except an explicit finite set of prime ideals
for all except an explicit finite set of prime ideals
![]() $\mathfrak {p}$
of
$\mathfrak {p}$
of
![]() $\mathcal {O}$
is the Heegner index, whose definition we now recall. (See Sections 4 and 5 below for why the Heegner index is important.) Let K be a Heegner field for f; this is an imaginary quadratic field such that all prime divisors of N split in K and such that the L-series
$\mathcal {O}$
is the Heegner index, whose definition we now recall. (See Sections 4 and 5 below for why the Heegner index is important.) Let K be a Heegner field for f; this is an imaginary quadratic field such that all prime divisors of N split in K and such that the L-series
![]() $L(f/K, s) = L(f, s) L(f \otimes \varepsilon _K, s)$
(with
$L(f/K, s) = L(f, s) L(f \otimes \varepsilon _K, s)$
(with
![]() $\varepsilon _K$
the quadratic character corresponding to K) vanishes to first order at
$\varepsilon _K$
the quadratic character corresponding to K) vanishes to first order at
![]() $s = 1$
. The first condition implies that
$s = 1$
. The first condition implies that
![]() $\mathcal {O}_K$
contains ideals
$\mathcal {O}_K$
contains ideals
![]() $\mathfrak {n}$
of norm N such that
$\mathfrak {n}$
of norm N such that
![]() $\mathcal {O}_K/\mathfrak {n}$
is a cyclic group of order N. Then the natural map
$\mathcal {O}_K/\mathfrak {n}$
is a cyclic group of order N. Then the natural map
![]() ${\mathbf {C}}/\mathcal {O}_K \to {\mathbf {C}}/\mathfrak {n}^{-1}$
corresponds to a cyclic isogeny of degree N between two elliptic curves with CM by
${\mathbf {C}}/\mathcal {O}_K \to {\mathbf {C}}/\mathfrak {n}^{-1}$
corresponds to a cyclic isogeny of degree N between two elliptic curves with CM by
![]() $\mathcal {O}_K$
and so defines a point in
$\mathcal {O}_K$
and so defines a point in
![]() $X_0(N)$
, which is known to be defined over the Hilbert class field H of K. More generally, let
$X_0(N)$
, which is known to be defined over the Hilbert class field H of K. More generally, let
![]() $\mathfrak {a}$
be some ideal of
$\mathfrak {a}$
be some ideal of
![]() $\mathcal {O}$
; then we can consider
$\mathcal {O}$
; then we can consider
![]() ${\mathbf {C}}/\mathfrak {a} \to {\mathbf {C}}/\mathfrak {a} \mathfrak {n}^{-1}$
. We obtain
${\mathbf {C}}/\mathfrak {a} \to {\mathbf {C}}/\mathfrak {a} \mathfrak {n}^{-1}$
. We obtain
![]() $h_K$
points
$h_K$
points
![]() $x_{[\mathfrak {a}]} \in X_0(N)(H)$
in this way, where
$x_{[\mathfrak {a}]} \in X_0(N)(H)$
in this way, where
![]() $h_K$
denotes the class number of K and the point depends only on the ideal class of
$h_K$
denotes the class number of K and the point depends only on the ideal class of
![]() $\mathfrak {a}$
. These points form an orbit under
$\mathfrak {a}$
. These points form an orbit under
![]() $ {\mathrm {Gal}}(H|K)$
; their formal sum
$ {\mathrm {Gal}}(H|K)$
; their formal sum
![]() $\mathbf {x}_K$
is the Heegner cycle on
$\mathbf {x}_K$
is the Heegner cycle on
![]() $X_0(N)$
associated to K and
$X_0(N)$
associated to K and
![]() $\mathfrak {n}$
; it is defined over K. Let
$\mathfrak {n}$
; it is defined over K. Let
![]() $\infty \in X_0(N)({\mathbf {Q}})$
denote the cusp at infinity. Then
$\infty \in X_0(N)({\mathbf {Q}})$
denote the cusp at infinity. Then
![]() $y_K = [\mathbf {x}_K - h_K \cdot (\infty )] \in J_0(N)(K)$
is a Heegner point associated to K. By varying
$y_K = [\mathbf {x}_K - h_K \cdot (\infty )] \in J_0(N)(K)$
is a Heegner point associated to K. By varying
![]() $\mathfrak {n}$
in the construction, we may get different Heegner points, but they all agree up to sign and adding a torsion point. (See also [Reference Gross51].) So in the following, we will consider Heegner points up to sign and modulo torsion.
$\mathfrak {n}$
in the construction, we may get different Heegner points, but they all agree up to sign and adding a torsion point. (See also [Reference Gross51].) So in the following, we will consider Heegner points up to sign and modulo torsion.
We then obtain a point
![]() $y_{K,\pi } = \pi _J(y_K) \in J(K)$
. By [Reference Gross and Zagier52], the
$y_{K,\pi } = \pi _J(y_K) \in J(K)$
. By [Reference Gross and Zagier52], the
![]() $\mathcal {O}$
-span of
$\mathcal {O}$
-span of
![]() $y_{K,\pi } \in J(K)$
is a rank
$y_{K,\pi } \in J(K)$
is a rank
![]() $g = \dim {J}$
subgroup of finite index of
$g = \dim {J}$
subgroup of finite index of
![]() $J(K)$
(which does not depend on the choice of the Heegner point). This index is the Heegner index; we denote it by
$J(K)$
(which does not depend on the choice of the Heegner point). This index is the Heegner index; we denote it by
Considering the characteristic ideal
![]() $\mathcal {I}_{K,\pi } := {\mathrm {Char}}_{\mathcal {O}}(J(K)/\mathcal {O} y_{K,\pi })$
gives refined information; this refinement is helpful for our intended application because we can study the summands of
$\mathcal {I}_{K,\pi } := {\mathrm {Char}}_{\mathcal {O}}(J(K)/\mathcal {O} y_{K,\pi })$
gives refined information; this refinement is helpful for our intended application because we can study the summands of ![]() individually. In the same way, we have
individually. In the same way, we have
![]() $y_{K,A_f} = \pi _f(y_K) \in A_f(K)$
, and we set
$y_{K,A_f} = \pi _f(y_K) \in A_f(K)$
, and we set
![]() $I_K := (A_f(K) : {\mathbf {Z}}[f] y_{K,A_f})$
and
$I_K := (A_f(K) : {\mathbf {Z}}[f] y_{K,A_f})$
and
![]() $\mathcal {I}_K := {\mathrm {Char}}_{{\mathbf {Z}}[f]}(A_f(K)/{\mathbf {Z}}[f] y_{K,A_f})$
.
$\mathcal {I}_K := {\mathrm {Char}}_{{\mathbf {Z}}[f]}(A_f(K)/{\mathbf {Z}}[f] y_{K,A_f})$
.
For an abelian variety
![]() $A/{\mathbf {Q}}$
and a quadratic number field K, we denote the quadratic twist of A by the quadratic character associated to K by
$A/{\mathbf {Q}}$
and a quadratic number field K, we denote the quadratic twist of A by the quadratic character associated to K by
![]() $A^K$
. Then
$A^K$
. Then
![]() $A^K$
is isomorphic to A over K. The natural map
$A^K$
is isomorphic to A over K. The natural map
![]() $A({\mathbf {Q}}) \times A^K({\mathbf {Q}}) \to A(K)$
has finite kernel and cokernel killed by
$A({\mathbf {Q}}) \times A^K({\mathbf {Q}}) \to A(K)$
has finite kernel and cokernel killed by
![]() $2$
: The kernel is the diagonally embedded
$2$
: The kernel is the diagonally embedded
![]() $A({\mathbf {Q}})[2]$
, and the image contains
$A({\mathbf {Q}})[2]$
, and the image contains
![]() $2 A(K)$
.
$2 A(K)$
.
When
![]() $L\!\operatorname {-rk} J = 0$
, then
$L\!\operatorname {-rk} J = 0$
, then
![]() $J(K)$
is essentially
$J(K)$
is essentially
![]() $J^K({\mathbf {Q}})$
; more precisely, the image of
$J^K({\mathbf {Q}})$
; more precisely, the image of
![]() $J^K({\mathbf {Q}})$
in
$J^K({\mathbf {Q}})$
in
![]() $J(K)$
contains
$J(K)$
contains
![]() $2 J(K)$
up to torsion, and so we can identify
$2 J(K)$
up to torsion, and so we can identify
![]() $2 y_{K,\pi }$
up to torsion with a rational point on
$2 y_{K,\pi }$
up to torsion with a rational point on
![]() $J^K$
. When
$J^K$
. When
![]() $L\!\operatorname {-rk} J = 1$
, then
$L\!\operatorname {-rk} J = 1$
, then
![]() $2 J(K)$
is contained in
$2 J(K)$
is contained in
![]() $J({\mathbf {Q}})$
up to torsion, and we can identify
$J({\mathbf {Q}})$
up to torsion, and we can identify
![]() $2 y_{K,\pi }$
up to torsion with a rational point on J. (See also [Reference Miller73, Lemma 2.1].) This simplifies the computations since certain algorithms (for example, computing canonical heights on J) are so far only implemented when the base field is
$2 y_{K,\pi }$
up to torsion with a rational point on J. (See also [Reference Miller73, Lemma 2.1].) This simplifies the computations since certain algorithms (for example, computing canonical heights on J) are so far only implemented when the base field is
![]() ${\mathbf {Q}}$
.
${\mathbf {Q}}$
.
The aim of this section is to explain how we can compute the Heegner index
![]() $I_{K,\pi }$
(or the corresponding ideal
$I_{K,\pi }$
(or the corresponding ideal
![]() $\mathcal {I}_{K,\pi })$
.
$\mathcal {I}_{K,\pi })$
.
The first step is to determine a Heegner field K. This is explained in Section 3.2. In order to determine the
![]() $\mathcal {O}$
-span of
$\mathcal {O}$
-span of
![]() $y_{K,\pi }$
, we need to determine
$y_{K,\pi }$
, we need to determine
![]() $\mathcal {O} = \mathrm {End}_{\mathbf {Q}}(J)$
and its action on
$\mathcal {O} = \mathrm {End}_{\mathbf {Q}}(J)$
and its action on
![]() $J(K)$
(we can determine generators of
$J(K)$
(we can determine generators of
![]() $J(K)$
from generators of
$J(K)$
from generators of
![]() $J({\mathbf {Q}})$
and of
$J({\mathbf {Q}})$
and of
![]() $J^K({\mathbf {Q}})$
, which Magma can usually compute). Section 3.3 explains how to do that. Then, of course, we need to find the Heegner point
$J^K({\mathbf {Q}})$
, which Magma can usually compute). Section 3.3 explains how to do that. Then, of course, we need to find the Heegner point
![]() $y_{K,\pi }$
on J.
$y_{K,\pi }$
on J.
One approach is to compute the j-invariant morphism
![]() $X_0(N) \to \mathbf {P}^1_{\mathbf {Q}}$
given by sending the point representing an isogeny
$X_0(N) \to \mathbf {P}^1_{\mathbf {Q}}$
given by sending the point representing an isogeny
![]() $E \to E'$
to
$E \to E'$
to
![]() $j(E)$
as an algebraic map. Then, given the
$j(E)$
as an algebraic map. Then, given the
![]() $h_K$
different j-invariants of elliptic curves with CM by
$h_K$
different j-invariants of elliptic curves with CM by
![]() $\mathcal {O}_K$
, we can lift them to the corresponding points in
$\mathcal {O}_K$
, we can lift them to the corresponding points in
![]() $X_0(N)(H)$
and thus get an algebraic description of the Heegner cycle. However, this turns out to be too slow even for moderately large N. Therefore, we do not give more details here.
$X_0(N)(H)$
and thus get an algebraic description of the Heegner cycle. However, this turns out to be too slow even for moderately large N. Therefore, we do not give more details here.
Instead, we use an analytic approach. We start with the
![]() $h_K$
reduced integral binary quadratic forms whose roots with positive imaginary part map to the points in the support of the Heegner cycle on
$h_K$
reduced integral binary quadratic forms whose roots with positive imaginary part map to the points in the support of the Heegner cycle on
![]() $X_0(N)$
under the uniformization map
$X_0(N)$
under the uniformization map
![]() $\mathbf {H} \to X_0(N)({\mathbf {C}})$
, where
$\mathbf {H} \to X_0(N)({\mathbf {C}})$
, where
![]() $\mathbf {H}$
denotes the upper half plane. These quadratic forms can easily be determined using the built-in Magma function HeegnerForms. Via the uniformization map
$\mathbf {H}$
denotes the upper half plane. These quadratic forms can easily be determined using the built-in Magma function HeegnerForms. Via the uniformization map
![]() $\mathbf {H} \to X_0(N)({\mathbf {C}})$
, we obtain the set of
$\mathbf {H} \to X_0(N)({\mathbf {C}})$
, we obtain the set of
![]() $h_K$
points in the Heegner cycle. If the curve X is a quotient of
$h_K$
points in the Heegner cycle. If the curve X is a quotient of
![]() $X_0(N)$
, we can then map the Heegner cycle directly to X and try to recognize it as a divisor defined over K. We can then obtain the point on J given by the Heegner cycle. If X is not a quotient of
$X_0(N)$
, we can then map the Heegner cycle directly to X and try to recognize it as a divisor defined over K. We can then obtain the point on J given by the Heegner cycle. If X is not a quotient of
![]() $X_0(N)$
, we do the following. We first use the Abel–Jacobi map
$X_0(N)$
, we do the following. We first use the Abel–Jacobi map
![]() $X_0(N)({\mathbf {C}}) \to J_0(N)({\mathbf {C}})$
and the map
$X_0(N)({\mathbf {C}}) \to J_0(N)({\mathbf {C}})$
and the map
![]() $\pi _{f,{\mathbf {C}}} \colon J_0(N)({\mathbf {C}}) \to A_f({\mathbf {C}}) \cong {\mathbf {C}}/\Lambda _f$
to map the Heegner cycle to
$\pi _{f,{\mathbf {C}}} \colon J_0(N)({\mathbf {C}}) \to A_f({\mathbf {C}}) \cong {\mathbf {C}}/\Lambda _f$
to map the Heegner cycle to
![]() $A_f({\mathbf {C}})$
. We then compute the point
$A_f({\mathbf {C}})$
. We then compute the point
![]() $y_K \in A_f({\mathbf {C}})$
(by taking a sum in
$y_K \in A_f({\mathbf {C}})$
(by taking a sum in
![]() ${\mathbf {C}}/\Lambda _f$
). Then we use an explicit numerical representation of the isogeny
${\mathbf {C}}/\Lambda _f$
). Then we use an explicit numerical representation of the isogeny
![]() $\pi _{\mathbf {C}} \colon A_f({\mathbf {C}}) \to J({\mathbf {C}})$
to map the Heegner point from
$\pi _{\mathbf {C}} \colon A_f({\mathbf {C}}) \to J({\mathbf {C}})$
to map the Heegner point from
![]() $A_f({\mathbf {C}})$
to
$A_f({\mathbf {C}})$
to
![]() $J({\mathbf {C}})$
. Finally, we recognize the image as a point defined over the Heegner field K. This is explained in Section 3.4. However,
$J({\mathbf {C}})$
. Finally, we recognize the image as a point defined over the Heegner field K. This is explained in Section 3.4. However,
![]() $J(K) \subset J({\mathbf {C}})$
is dense. Hence, we must prove that we have found the correct point. We do this by determining its canonical height (which is well-defined since it does not change when adding a torsion point or changing the sign) via the Gross–Zagier formula. Since there are only finitely many points with bounded height, knowing the height is sufficient to cut the possibilities down to finitely many candidates up to sign and torsion; in practice, there is only one candidate. So we check that the point we have computed has the correct height and that no other point (up to sign and torsion) has the same height up to the numerical precision used in the computation. In principle, we could use this approach to bypass the analytic computation of the Heegner point altogether and just recognize it from its height, but using both approaches provides an additional level of confirmation that our results are correct. A further benefit of computing the Heegner point (and its image under a generator of the endomorphism ring of J) is that this provides us with generators of a finite-index subgroup of
$J(K) \subset J({\mathbf {C}})$
is dense. Hence, we must prove that we have found the correct point. We do this by determining its canonical height (which is well-defined since it does not change when adding a torsion point or changing the sign) via the Gross–Zagier formula. Since there are only finitely many points with bounded height, knowing the height is sufficient to cut the possibilities down to finitely many candidates up to sign and torsion; in practice, there is only one candidate. So we check that the point we have computed has the correct height and that no other point (up to sign and torsion) has the same height up to the numerical precision used in the computation. In principle, we could use this approach to bypass the analytic computation of the Heegner point altogether and just recognize it from its height, but using both approaches provides an additional level of confirmation that our results are correct. A further benefit of computing the Heegner point (and its image under a generator of the endomorphism ring of J) is that this provides us with generators of a finite-index subgroup of
![]() $J(K)$
. So in order to determine
$J(K)$
. So in order to determine
![]() $J(K)$
(which is necessary for the computation of the Heegner index
$J(K)$
(which is necessary for the computation of the Heegner index
![]() $I_{K,\pi }$
), it then suffices to saturate the known subgroup, which means that we do not have to search for points first. This can save a considerable amount of time.
$I_{K,\pi }$
), it then suffices to saturate the known subgroup, which means that we do not have to search for points first. This can save a considerable amount of time.
Since the Gross–Zagier formula involves the Petersson norm of
![]() $f^\sigma $
for the various embeddings
$f^\sigma $
for the various embeddings
![]() $\sigma \colon {\mathbf {Z}}[f] \hookrightarrow {\mathbf {R}}$
, we need a way to compute these Petersson norms; see Section 3.5. To apply the Gross–Zagier formula, we project
$\sigma \colon {\mathbf {Z}}[f] \hookrightarrow {\mathbf {R}}$
, we need a way to compute these Petersson norms; see Section 3.5. To apply the Gross–Zagier formula, we project
![]() $y_K$
, viewed as an element of
$y_K$
, viewed as an element of
![]() $J_0(N)(K) \otimes _{\mathbf {Z}} {\mathbf {R}}$
, to its various
$J_0(N)(K) \otimes _{\mathbf {Z}} {\mathbf {R}}$
, to its various
![]() $\sigma $
-components
$\sigma $
-components
![]() $y_{K,\sigma }$
(which have the property that
$y_{K,\sigma }$
(which have the property that
![]() ${\mathbf {Q}}(f)$
acts on them via the embedding
${\mathbf {Q}}(f)$
acts on them via the embedding
![]() $\sigma $
). The formula then gives an expression for
$\sigma $
). The formula then gives an expression for
![]() ${\hat {h}}(y_{K,\sigma })$
, where
${\hat {h}}(y_{K,\sigma })$
, where
![]() ${\hat {h}} \colon J_0(N)(K) \otimes _{\mathbf {Z}} {\mathbf {R}} \to {\mathbf {R}}$
is the normalized canonical height on
${\hat {h}} \colon J_0(N)(K) \otimes _{\mathbf {Z}} {\mathbf {R}} \to {\mathbf {R}}$
is the normalized canonical height on
![]() $J_0(N)$
associated to twice the theta divisor. This is discussed in Section 3.7. Finally, we have to relate the height
$J_0(N)$
associated to twice the theta divisor. This is discussed in Section 3.7. Finally, we have to relate the height
![]() ${\hat {h}}_J(y_{K,\pi })$
with respect to twice the theta divisor on J to the heights
${\hat {h}}_J(y_{K,\pi })$
with respect to twice the theta divisor on J to the heights
![]() ${\hat {h}}(y_{K,\sigma })$
; this is done in Section 3.8.
${\hat {h}}(y_{K,\sigma })$
; this is done in Section 3.8.
3.1 Computational representation of Diagram (3.4)
For our computations, we need to represent
![]() $A_f^{\vee }$
,
$A_f^{\vee }$
,
![]() $A_f$
, J as complex tori and the isogenies between them. This is done as follows.
$A_f$
, J as complex tori and the isogenies between them. This is done as follows.
Definition 3.1. Let A be an arbitrary abelian variety over
![]() ${\mathbf {C}}$
, of dimension g. Associated to a
${\mathbf {C}}$
, of dimension g. Associated to a
![]() ${\mathbf {C}}$
-basis
${\mathbf {C}}$
-basis
![]() $\underline {\omega } = (\omega _1, \ldots , \omega _g)$
of
$\underline {\omega } = (\omega _1, \ldots , \omega _g)$
of
![]() ${\operatorname {H}}^0(A, \Omega ^1)$
and a
${\operatorname {H}}^0(A, \Omega ^1)$
and a
![]() ${\mathbf {Z}}$
-basis
${\mathbf {Z}}$
-basis
![]() $\underline {\gamma } = (\gamma _1\, \ldots , \gamma _{2g})$
of the integral homology
$\underline {\gamma } = (\gamma _1\, \ldots , \gamma _{2g})$
of the integral homology
![]() ${\operatorname {H}}_1(A({\mathbf {C}}), {\mathbf {Z}})$
, there is the period matrix
${\operatorname {H}}_1(A({\mathbf {C}}), {\mathbf {Z}})$
, there is the period matrix
 $$\begin{align*}\Pi_A := \Pi_{A,\underline{\omega},\underline{\gamma}} := \Bigl(\int_{\gamma_j} \omega_i\Bigr)_{i,j} \in {\mathbf{C}}^{g \times 2g} . \end{align*}$$
$$\begin{align*}\Pi_A := \Pi_{A,\underline{\omega},\underline{\gamma}} := \Bigl(\int_{\gamma_j} \omega_i\Bigr)_{i,j} \in {\mathbf{C}}^{g \times 2g} . \end{align*}$$
Its
![]() $2g$
columns generate a lattice
$2g$
columns generate a lattice
![]() $\Lambda $
, and
$\Lambda $
, and
![]() $A({\mathbf {C}}) \cong {\mathbf {C}}/\Lambda $
via
$A({\mathbf {C}}) \cong {\mathbf {C}}/\Lambda $
via
![]() $x \mapsto \bigl (\int _0^x \omega _i\bigr )_i + \Lambda $
. We also write
$x \mapsto \bigl (\int _0^x \omega _i\bigr )_i + \Lambda $
. We also write
![]() $\Lambda _A$
for
$\Lambda _A$
for
![]() $\Lambda $
to indicate the associated abelian variety.
$\Lambda $
to indicate the associated abelian variety.
Definition 3.2. Let A and B be two abelian varieties over
![]() ${\mathbf {C}}$
of the same dimension g, and let
${\mathbf {C}}$
of the same dimension g, and let
![]() $\Pi _A$
and
$\Pi _A$
and
![]() $\Pi _B$
be associated period matrices. If
$\Pi _B$
be associated period matrices. If
![]() $\varphi \colon A \to B$
is an isogeny, then there are uniquely determined matrices
$\varphi \colon A \to B$
is an isogeny, then there are uniquely determined matrices
![]() $\alpha _\varphi \in \mathrm {GL}_g({\mathbf {C}})$
and
$\alpha _\varphi \in \mathrm {GL}_g({\mathbf {C}})$
and
![]() $M_\varphi \in {\mathbf {Z}}^{2g \times 2g}$
such that
$M_\varphi \in {\mathbf {Z}}^{2g \times 2g}$
such that
We call
![]() $(\alpha _\varphi , M_\varphi )$
the pair of matrices associated to
$(\alpha _\varphi , M_\varphi )$
the pair of matrices associated to
![]() $\varphi $
.
$\varphi $
.
We observe that, given
![]() $\Pi _A$
and
$\Pi _A$
and
![]() $\Pi _B$
, each of
$\Pi _B$
, each of
![]() $M_\varphi $
and
$M_\varphi $
and
![]() $\alpha _\varphi $
can be determined from the other.
$\alpha _\varphi $
can be determined from the other.
Note that
![]() $\alpha _\varphi $
is the matrix of the
$\alpha _\varphi $
is the matrix of the
![]() ${\mathbf {C}}$
-linear map
${\mathbf {C}}$
-linear map
![]() $\omega \mapsto \varphi ^* \omega $
with respect to the bases of the spaces of holomorphic differentials used for
$\omega \mapsto \varphi ^* \omega $
with respect to the bases of the spaces of holomorphic differentials used for
![]() $\Pi _A$
and
$\Pi _A$
and
![]() $\Pi _B$
, and
$\Pi _B$
, and
![]() $M_\varphi $
is the matrix of the
$M_\varphi $
is the matrix of the
![]() ${\mathbf {Z}}$
-linear map
${\mathbf {Z}}$
-linear map
![]() $\gamma \mapsto \varphi _* \gamma $
on the homology bases.
$\gamma \mapsto \varphi _* \gamma $
on the homology bases.
If A, B and
![]() $\varphi $
are defined over
$\varphi $
are defined over
![]() ${\mathbf {Q}}$
and we use
${\mathbf {Q}}$
and we use
![]() ${\mathbf {Q}}$
-bases of
${\mathbf {Q}}$
-bases of
![]() ${\operatorname {H}}^0(A, \Omega ^1)$
and
${\operatorname {H}}^0(A, \Omega ^1)$
and
![]() ${\operatorname {H}}^0(B, \Omega ^1)$
, then
${\operatorname {H}}^0(B, \Omega ^1)$
, then
![]() $\alpha _\varphi \in \mathrm {GL}_g({\mathbf {Q}})$
(since
$\alpha _\varphi \in \mathrm {GL}_g({\mathbf {Q}})$
(since
![]() $\varphi ^*$
is a
$\varphi ^*$
is a
![]() ${\mathbf {Q}}$
-linear map). Similarly, if we use
${\mathbf {Q}}$
-linear map). Similarly, if we use
![]() ${\mathbf {Z}}$
-bases of
${\mathbf {Z}}$
-bases of
![]() ${\operatorname {H}}^0(\mathscr {A}, \Omega ^1)$
and
${\operatorname {H}}^0(\mathscr {A}, \Omega ^1)$
and
![]() ${\operatorname {H}}^0(\mathscr {B}, \Omega ^1)$
, where
${\operatorname {H}}^0(\mathscr {B}, \Omega ^1)$
, where
![]() $\mathscr {A}$
and
$\mathscr {A}$
and
![]() $\mathscr {B}$
are the Néron models of A and B over
$\mathscr {B}$
are the Néron models of A and B over
![]() ${\mathbf {Z}}$
, then
${\mathbf {Z}}$
, then
![]() $\alpha _\varphi \in {\mathbf {Z}}^{g \times g} \cap \mathrm {GL}_g({\mathbf {Q}})$
.
$\alpha _\varphi \in {\mathbf {Z}}^{g \times g} \cap \mathrm {GL}_g({\mathbf {Q}})$
.
Definition 3.3. Let A and B be abelian varieties defined over
![]() ${\mathbf {Q}}$
, with Néron models
${\mathbf {Q}}$
, with Néron models
![]() $\mathscr {A}$
and
$\mathscr {A}$
and
![]() $\mathscr {B}$
over
$\mathscr {B}$
over
![]() ${\mathbf {Z}}$
, respectively. Let
${\mathbf {Z}}$
, respectively. Let
![]() $\varphi \colon A \to B$
be an isogeny defined over
$\varphi \colon A \to B$
be an isogeny defined over
![]() ${\mathbf {Q}}$
. Then we set
${\mathbf {Q}}$
. Then we set
If
![]() $\Pi _A$
and
$\Pi _A$
and
![]() $\Pi _B$
are computed using
$\Pi _B$
are computed using
![]() ${\mathbf {Z}}$
-bases of
${\mathbf {Z}}$
-bases of
![]() ${\operatorname {H}}^0(\mathscr {A}, \Omega ^1)$
and
${\operatorname {H}}^0(\mathscr {A}, \Omega ^1)$
and
![]() ${\operatorname {H}}^0(\mathscr {B}, \Omega ^1)$
, then
${\operatorname {H}}^0(\mathscr {B}, \Omega ^1)$
, then
![]() $c_\varphi = |\det \alpha _\varphi |$
.
$c_\varphi = |\det \alpha _\varphi |$
.
Definition 3.4. Let
![]() $f \in \mathcal {N}(N, g)$
. We define
$f \in \mathcal {N}(N, g)$
. We define
![]() $S_2(f, {\mathbf {Z}})$
to be the
$S_2(f, {\mathbf {Z}})$
to be the
![]() ${\mathbf {Z}}$
-sublattice of the
${\mathbf {Z}}$
-sublattice of the
![]() ${\mathbf {C}}$
-span of f and its Galois conjugates in
${\mathbf {C}}$
-span of f and its Galois conjugates in
![]() $S_2(\Gamma _0(N))$
that consists of forms whose q-expansions have integral coefficients. Under the natural identification of
$S_2(\Gamma _0(N))$
that consists of forms whose q-expansions have integral coefficients. Under the natural identification of
![]() $S_2(\Gamma _0(N))$
with
$S_2(\Gamma _0(N))$
with
![]() ${\operatorname {H}}^0(X_0(N), \Omega ^1) \simeq {\operatorname {H}}^0(J_0(N), \Omega ^1)$
, the image of
${\operatorname {H}}^0(X_0(N), \Omega ^1) \simeq {\operatorname {H}}^0(J_0(N), \Omega ^1)$
, the image of
![]() $S_2(f, {\mathbf {Z}})$
contains
$S_2(f, {\mathbf {Z}})$
contains
![]() $\pi _f^* {\operatorname {H}}^0(\mathscr {A}_f,\Omega ^1)$
(where
$\pi _f^* {\operatorname {H}}^0(\mathscr {A}_f,\Omega ^1)$
(where
![]() $\mathscr {A}_f$
is the Néron model of
$\mathscr {A}_f$
is the Néron model of
![]() $A_f$
over
$A_f$
over
![]() ${\mathbf {Z}}$
). The index
${\mathbf {Z}}$
). The index
is the Manin constant of
![]() $\pi _f$
.
$\pi _f$
.
See [Reference Agashe, Ribet and Stein1, Def. 3.3 and Thm. 3.4].
Proposition 3.5. The Manin constant
![]() $c_f$
is divisible only by primes p such that
$c_f$
is divisible only by primes p such that
![]() $p^2 \mid N$
or
$p^2 \mid N$
or
![]() $p = 2$
, and the conductor of
$p = 2$
, and the conductor of
![]() ${\mathbf {Z}}[f]$
is even.
${\mathbf {Z}}[f]$
is even.
In particular,
![]() $c_f = 1$
if N is squarefree and the conductor of
$c_f = 1$
if N is squarefree and the conductor of
![]() ${\mathbf {Z}}[f]$
is odd.
${\mathbf {Z}}[f]$
is odd.
Proof. This is [Reference Agashe, Ribet and Stein1, Cor. 3.7] for odd primes and [Reference Česnavičius22, Thm. 5.19] for
![]() $p = 2$
.
$p = 2$
.
It has been conjectured (see [Reference Česnavičius22, Conj. 5.2] and the text preceding it) that
![]() $c_f$
is always
$c_f$
is always
![]() $1$
, but [Reference Česnavičius22, Thm. 5.10] gives a counterexample in dimension
$1$
, but [Reference Česnavičius22, Thm. 5.10] gives a counterexample in dimension
![]() $24$
(with
$24$
(with
![]() $N = 431$
odd and
$N = 431$
odd and
![]() $2 \mid c_f$
).
$2 \mid c_f$
).
Magma can compute a period matrix
![]() $\Pi _{A_f^{\vee }}$
of
$\Pi _{A_f^{\vee }}$
of
![]() $A_f^{\vee }$
with respect to a
$A_f^{\vee }$
with respect to a
![]() ${\mathbf {Z}}$
-basis of
${\mathbf {Z}}$
-basis of
![]() $S_2(f, {\mathbf {Z}})$
and some homology basis. Magma also computes the matrix I of the intersection pairing (inside the homology of
$S_2(f, {\mathbf {Z}})$
and some homology basis. Magma also computes the matrix I of the intersection pairing (inside the homology of
![]() $J_0(N)({\mathbf {C}})$
) on the first homology of
$J_0(N)({\mathbf {C}})$
) on the first homology of
![]() $A_f^{\vee }({\mathbf {C}})$
. Then
$A_f^{\vee }({\mathbf {C}})$
. Then
![]() $\Pi _{A_f} := \Pi _{A_f^{\vee }} \cdot I^{-1}$
is a period matrix for
$\Pi _{A_f} := \Pi _{A_f^{\vee }} \cdot I^{-1}$
is a period matrix for
![]() $A_f$
(with respect to the same basis of
$A_f$
(with respect to the same basis of
![]() $S_2(f, {\mathbf {Z}})$
), and
$S_2(f, {\mathbf {Z}})$
), and
![]() $(I_g, I)$
is the pair of matrices associated to the polarization
$(I_g, I)$
is the pair of matrices associated to the polarization
![]() $\lambda _f$
. Let now J be the Jacobian of a curve of genus
$\lambda _f$
. Let now J be the Jacobian of a curve of genus
![]() $2$
over
$2$
over
![]() ${\mathbf {Q}}$
such that there is an isogeny
${\mathbf {Q}}$
such that there is an isogeny
![]() $\pi \colon A_f \to J$
as in (3.4). Magma can compute a period matrix
$\pi \colon A_f \to J$
as in (3.4). Magma can compute a period matrix
![]() $\Pi _J$
for J with respect to a certain
$\Pi _J$
for J with respect to a certain
![]() ${\mathbf {Q}}$
-basis B of
${\mathbf {Q}}$
-basis B of
![]() ${\operatorname {H}}^0(J, \Omega ^1)$
(if J is the Jacobian of a genus
${\operatorname {H}}^0(J, \Omega ^1)$
(if J is the Jacobian of a genus
![]() $2$
curve
$2$
curve
![]() $y^2 = f(x)$
, then B corresponds to the differentials
$y^2 = f(x)$
, then B corresponds to the differentials
![]() $dx/y$
and
$dx/y$
and
![]() $x\,dx/y$
on the curve) and a symplectic homology basis. We can then find the associated pair of matrices
$x\,dx/y$
on the curve) and a symplectic homology basis. We can then find the associated pair of matrices
![]() $(\alpha _\pi , M_\pi )$
. The algorithm [Reference van Bommel11, Algorithm 13] determines the ‘compensation factor’ (called W in loc. cit.)
$(\alpha _\pi , M_\pi )$
. The algorithm [Reference van Bommel11, Algorithm 13] determines the ‘compensation factor’ (called W in loc. cit.)
(where
![]() $\mathscr {J}$
is the Néron model of J over
$\mathscr {J}$
is the Néron model of J over
![]() ${\mathbf {Z}}$
and the index of two commensurable
${\mathbf {Z}}$
and the index of two commensurable
![]() ${\mathbf {Z}}$
-lattices in
${\mathbf {Z}}$
-lattices in
![]() ${\operatorname {H}}^0(J, \Omega ^1)$
is in general a positive rational number). Combining these computations gives the following.
${\operatorname {H}}^0(J, \Omega ^1)$
is in general a positive rational number). Combining these computations gives the following.
Lemma 3.6.
In our LMFDB examples, the compensation factor C (with respect to a minimal Weierstrass model) is always
![]() $1$
, and
$1$
, and
![]() $c_f c_\pi $
divides the degree of the isogeny
$c_f c_\pi $
divides the degree of the isogeny
![]() $\pi $
.
$\pi $
.
For later applications, we want to compute the sizes of the kernel and cokernel of the map
![]() $\pi _{\mathbf {R}} \colon A_f({\mathbf {R}}) \to J({\mathbf {R}})$
induced by the isogeny
$\pi _{\mathbf {R}} \colon A_f({\mathbf {R}}) \to J({\mathbf {R}})$
induced by the isogeny
![]() $\pi $
on the groups of real points. We note that we can obtain the action of complex conjugation
$\pi $
on the groups of real points. We note that we can obtain the action of complex conjugation
![]() $\tau $
on
$\tau $
on
![]() $A({\mathbf {C}}) \cong {\operatorname {H}}_1(A({\mathbf {C}}), {\mathbf {Z}}) \otimes {\mathbf {R}}/{\mathbf {Z}}$
by solving
$A({\mathbf {C}}) \cong {\operatorname {H}}_1(A({\mathbf {C}}), {\mathbf {Z}}) \otimes {\mathbf {R}}/{\mathbf {Z}}$
by solving
![]() $\overline {\Pi _A} = \Pi _A \cdot M_{A,\tau }$
for
$\overline {\Pi _A} = \Pi _A \cdot M_{A,\tau }$
for
![]() $M_{A,\tau } \in {\mathbf {Z}}^{2g \times 2g}$
. We obtain
$M_{A,\tau } \in {\mathbf {Z}}^{2g \times 2g}$
. We obtain
![]() $\mathrm {ker} \pi \cong M_\pi ^{-1} {\mathbf {Z}}^{2g}/{\mathbf {Z}}^{2g} \simeq {\mathbf {Z}}^{2g}/M_\pi {\mathbf {Z}}^{2g}$
, and we can find its
$\mathrm {ker} \pi \cong M_\pi ^{-1} {\mathbf {Z}}^{2g}/{\mathbf {Z}}^{2g} \simeq {\mathbf {Z}}^{2g}/M_\pi {\mathbf {Z}}^{2g}$
, and we can find its
![]() $\tau $
-invariant part
$\tau $
-invariant part
![]() $\mathrm {ker} \pi _{\mathbf {R}}$
using
$\mathrm {ker} \pi _{\mathbf {R}}$
using
![]() $M_{A_f,\tau }$
. The group
$M_{A_f,\tau }$
. The group
![]() $\pi _0(J({\mathbf {R}}))$
of connected components of
$\pi _0(J({\mathbf {R}}))$
of connected components of
![]() $J({\mathbf {R}})$
is isomorphic to
$J({\mathbf {R}})$
is isomorphic to
and similarly for
![]() $A_f$
, so
$A_f$
, so
 $$\begin{align*}\operatorname{\mathrm{coker}} \pi_{\mathbf{R}} \cong \frac{\mathrm{ker}(I_{2g} + M_{J,\tau} \mid {\mathbf{Z}}^{2g})} {(I_{2g} - M_{J,\tau}) {\mathbf{Z}}^{2g} + \mathrm{ker}(I_{2g} + M_{J,\tau} \mid M_\pi {\mathbf{Z}}^{2g})}. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{coker}} \pi_{\mathbf{R}} \cong \frac{\mathrm{ker}(I_{2g} + M_{J,\tau} \mid {\mathbf{Z}}^{2g})} {(I_{2g} - M_{J,\tau}) {\mathbf{Z}}^{2g} + \mathrm{ker}(I_{2g} + M_{J,\tau} \mid M_\pi {\mathbf{Z}}^{2g})}. \end{align*}$$
When considering the quadratic twist
![]() $\pi ^K$
for an imaginary quadratic field K, then we have to replace
$\pi ^K$
for an imaginary quadratic field K, then we have to replace
![]() $M_{J,\tau }$
by
$M_{J,\tau }$
by
![]() $-M_{J,\tau }$
to obtain the twisted action of
$-M_{J,\tau }$
to obtain the twisted action of
![]() $\tau $
on
$\tau $
on
![]() $J^K({\mathbf {C}}) \cong J({\mathbf {C}})$
.
$J^K({\mathbf {C}}) \cong J({\mathbf {C}})$
.
We can use a similar idea to compute
![]() $\Omega _J$
from the period matrix
$\Omega _J$
from the period matrix
![]() $\Pi _J$
and the compensation factor C from (3.8), as follows.
$\Pi _J$
and the compensation factor C from (3.8), as follows.
Lemma 3.7. Let
![]() $T \in \mathrm {GL}_{2g}({\mathbf {Z}})$
be such that
$T \in \mathrm {GL}_{2g}({\mathbf {Z}})$
be such that
![]() $(M_{J,\tau } + I_{2g}) \cdot T = (\tilde {M} \mid 0)$
with
$(M_{J,\tau } + I_{2g}) \cdot T = (\tilde {M} \mid 0)$
with
![]() $\tilde {M} \in {\mathbf {Z}}^{2g \times g}$
. Then
$\tilde {M} \in {\mathbf {Z}}^{2g \times g}$
. Then
Proof. It is well-known that
![]() $\Omega _J$
is the covolume of the lattice given by integrating a Néron basis over the
$\Omega _J$
is the covolume of the lattice given by integrating a Néron basis over the
![]() ${\mathbf {C}}|{\mathbf {R}}$
-trace of
${\mathbf {C}}|{\mathbf {R}}$
-trace of
![]() ${\operatorname {H}}_1(X({\mathbf {C}}), {\mathbf {Z}})$
(see [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and Wetherell45, § 3.5] or [Reference van Bommel11, Def. 11]). The
${\operatorname {H}}_1(X({\mathbf {C}}), {\mathbf {Z}})$
(see [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and Wetherell45, § 3.5] or [Reference van Bommel11, Def. 11]). The
![]() ${\mathbf {Z}}$
-lattice generated by the columns of the matrix
${\mathbf {Z}}$
-lattice generated by the columns of the matrix
![]() $M_{J,\tau } + I_{2g}$
corresponds to the
$M_{J,\tau } + I_{2g}$
corresponds to the
![]() ${\mathbf {C}}|{\mathbf {R}}$
-trace of
${\mathbf {C}}|{\mathbf {R}}$
-trace of
![]() ${\operatorname {H}}_1(X({\mathbf {C}}), {\mathbf {Z}})$
(w.r.t. the homology basis used to compute
${\operatorname {H}}_1(X({\mathbf {C}}), {\mathbf {Z}})$
(w.r.t. the homology basis used to compute
![]() $\Pi _J$
). This lattice is known to have rank g, so there exists a unimodular matrix T as in the statement, and multiplying on the right by T preserves the lattice. So the columns of
$\Pi _J$
). This lattice is known to have rank g, so there exists a unimodular matrix T as in the statement, and multiplying on the right by T preserves the lattice. So the columns of
![]() $\tilde {M}$
give a basis of the
$\tilde {M}$
give a basis of the
![]() ${\mathbf {C}}|{\mathbf {R}}$
-trace of
${\mathbf {C}}|{\mathbf {R}}$
-trace of
![]() ${\operatorname {H}}_1(X({\mathbf {C}}), {\mathbf {Z}})$
, and the result follows (taking into account the factor C arising from changing the basis of differentials used in the computation of
${\operatorname {H}}_1(X({\mathbf {C}}), {\mathbf {Z}})$
, and the result follows (taking into account the factor C arising from changing the basis of differentials used in the computation of
![]() $\Pi _J$
to a Néron basis).
$\Pi _J$
to a Néron basis).
This improves over the method currently implemented in Magma (which is based on [Reference van Bommel11, Algorithm 13]) in that it uses an exact computation to find the correct integral linear combination of
![]() $g \times g$
minors of
$g \times g$
minors of
![]() $\Pi _J$
instead of relying on a ‘real gcd’ computation with numerical approximations. (The approximation step is in the computation of
$\Pi _J$
instead of relying on a ‘real gcd’ computation with numerical approximations. (The approximation step is in the computation of
![]() $M_{J,\tau }$
, but here we know that the entries are integers, so we can simply round.)
$M_{J,\tau }$
, but here we know that the entries are integers, so we can simply round.)
We now want to determine the endomorphism
![]() $\alpha \in \mathcal {O} = \mathrm {End} J$
that was defined in (3.5). Since
$\alpha \in \mathcal {O} = \mathrm {End} J$
that was defined in (3.5). Since
![]() $\Pi _J$
is computed with respect to a symplectic homology basis, we obtain the M-matrix of the canonical polarization of J as the matrix
$\Pi _J$
is computed with respect to a symplectic homology basis, we obtain the M-matrix of the canonical polarization of J as the matrix
![]() $I'$
of the standard symplectic pairing. Then
$I'$
of the standard symplectic pairing. Then
![]() $M := M_\pi \cdot I \cdot M_\pi ^\top \cdot I'$
gives the action of
$M := M_\pi \cdot I \cdot M_\pi ^\top \cdot I'$
gives the action of
![]() $\alpha \in \mathcal {O}$
on the lattice associated to J, and its action on the tangent space can be recovered from that. (Recall that I denotes the matrix of the intersection pairing for
$\alpha \in \mathcal {O}$
on the lattice associated to J, and its action on the tangent space can be recovered from that. (Recall that I denotes the matrix of the intersection pairing for
![]() $A_f^{\vee }({\mathbf {C}})$
.) We can (and do) ‘optimize’
$A_f^{\vee }({\mathbf {C}})$
.) We can (and do) ‘optimize’
![]() $\alpha $
by post-composing
$\alpha $
by post-composing
![]() $\pi $
with an automorphism
$\pi $
with an automorphism
![]() $\varepsilon \in \mathrm {End}_{\mathbf {Q}}(J)^\times $
(this has the effect of multiplying
$\varepsilon \in \mathrm {End}_{\mathbf {Q}}(J)^\times $
(this has the effect of multiplying
![]() $\alpha $
by
$\alpha $
by
![]() $\varepsilon ^2$
) in the sense that we minimize the images
$\varepsilon ^2$
) in the sense that we minimize the images
![]() $\alpha ^\sigma \in {\mathbf {R}}_{>0}$
under the real embeddings of
$\alpha ^\sigma \in {\mathbf {R}}_{>0}$
under the real embeddings of
![]() $\mathcal {O}$
(in practice, we minimize the trace of
$\mathcal {O}$
(in practice, we minimize the trace of
![]() $\alpha $
). This leads to potentially smaller Heegner points on J, which simplifies some of the computations.
$\alpha $
). This leads to potentially smaller Heegner points on J, which simplifies some of the computations.
3.2 Determining Heegner fields
To be able to use the results of [Reference Gross and Zagier52] and some other results that require the discriminant of the Heegner field to be odd, we restrict to odd discriminants in the following.
We find a Heegner field K by enumerating the odd discriminants
![]() $-D$
of imaginary quadratic number fields with the property that all prime divisors of N split completely in
$-D$
of imaginary quadratic number fields with the property that all prime divisors of N split completely in
![]() $\mathcal {O}_K$
(this can be checked easily by computing Legendre symbols). The condition
$\mathcal {O}_K$
(this can be checked easily by computing Legendre symbols). The condition
![]() $ {\mathrm {ord}}_{s=1} L(f/K, s) = 1$
is equivalent to
$ {\mathrm {ord}}_{s=1} L(f/K, s) = 1$
is equivalent to
![]() $L(f \otimes \varepsilon _K, 1) \neq 0$
when
$L(f \otimes \varepsilon _K, 1) \neq 0$
when
![]() $L\!\operatorname {-rk} J = 1$
and to
$L\!\operatorname {-rk} J = 1$
and to
![]() $L'(f \otimes \varepsilon _K, 1) \neq 0$
when
$L'(f \otimes \varepsilon _K, 1) \neq 0$
when
![]() $L\!\operatorname {-rk} J = 0$
. Using modular symbols as described in [Reference Cremona31, § 2.8], we can decide whether
$L\!\operatorname {-rk} J = 0$
. Using modular symbols as described in [Reference Cremona31, § 2.8], we can decide whether
![]() $L(f \otimes \varepsilon _K, 1) = 0$
or not. The nonvanishing of
$L(f \otimes \varepsilon _K, 1) = 0$
or not. The nonvanishing of
![]() $L'(f \otimes \varepsilon _K, 1)$
can be proved by computing it to a high enough precision using Dokchitser’s Magma implementation [Reference Dokchitser40]. Alternatively and in practice (because the evaluation of the twisted L-value can take fairly long when N is large), we can compute the Heegner point for a given K; if it is non-torsion, then K is a suitable Heegner field.
$L'(f \otimes \varepsilon _K, 1)$
can be proved by computing it to a high enough precision using Dokchitser’s Magma implementation [Reference Dokchitser40]. Alternatively and in practice (because the evaluation of the twisted L-value can take fairly long when N is large), we can compute the Heegner point for a given K; if it is non-torsion, then K is a suitable Heegner field.
3.3 Computing the endomorphism ring and its action on Mordell–Weil groups
We need to determine the endomorphism ring
![]() $\mathcal {O}$
of the Jacobian J and how it acts on the Mordell–Weil group
$\mathcal {O}$
of the Jacobian J and how it acts on the Mordell–Weil group
![]() $J({\mathbf {Q}})$
or
$J({\mathbf {Q}})$
or
![]() $J^K({\mathbf {Q}})$
, or, more generally, on
$J^K({\mathbf {Q}})$
, or, more generally, on
![]() $J(L)$
for some number field L. For this, we compute a numerical approximation to the big period matrix as in Section 3.1; potential endomorphisms can be guessed from this information. To verify that the presumed endomorphism ring is the correct one, we can use data from the LMFDB [68]. (Alternatively, one could use [Reference Lombardo70].) This shows that the numerical endomorphisms are close to actual endomorphisms and thus gives us a representation of
$J(L)$
for some number field L. For this, we compute a numerical approximation to the big period matrix as in Section 3.1; potential endomorphisms can be guessed from this information. To verify that the presumed endomorphism ring is the correct one, we can use data from the LMFDB [68]. (Alternatively, one could use [Reference Lombardo70].) This shows that the numerical endomorphisms are close to actual endomorphisms and thus gives us a representation of
![]() $\mathcal {O}$
as a subring of a matrix algebra over
$\mathcal {O}$
as a subring of a matrix algebra over
![]() ${\mathbf {Z}}$
, together with its action on the complex torus
${\mathbf {Z}}$
, together with its action on the complex torus
![]() ${\mathbf {C}}^2/\Lambda \cong J({\mathbf {C}})$
. To compute the action of
${\mathbf {C}}^2/\Lambda \cong J({\mathbf {C}})$
. To compute the action of
![]() $\mathcal {O}$
on
$\mathcal {O}$
on
![]() $J(L)$
, we use an improved version of Magma’s (To/From)AnalyticJacobian to convert between points in
$J(L)$
, we use an improved version of Magma’s (To/From)AnalyticJacobian to convert between points in
![]() $J({\mathbf {C}})$
in Mumford representation and representatives in
$J({\mathbf {C}})$
in Mumford representation and representatives in
![]() ${\mathbf {C}}^2$
. (The improvement also handles points at infinity and Weierstrass points.) For a generator
${\mathbf {C}}^2$
. (The improvement also handles points at infinity and Weierstrass points.) For a generator
![]() $\gamma $
of
$\gamma $
of
![]() $\mathcal {O}$
and each generator x of
$\mathcal {O}$
and each generator x of
![]() $J(L)$
, we map x to
$J(L)$
, we map x to
![]() ${\mathbf {C}}^2/\Lambda $
, apply
${\mathbf {C}}^2/\Lambda $
, apply
![]() $\gamma $
to the image, and map back to
$\gamma $
to the image, and map back to
![]() $J({\mathbf {C}})$
. We then recognize the coefficients of the Mumford representation as elements of L using Magma’s MinimalPolynomial and check that the coefficients we recognize really define a point in
$J({\mathbf {C}})$
. We then recognize the coefficients of the Mumford representation as elements of L using Magma’s MinimalPolynomial and check that the coefficients we recognize really define a point in
![]() $J(L)$
. We then write the resulting point as a linear combination of the generators of
$J(L)$
. We then write the resulting point as a linear combination of the generators of
![]() $J(L)$
. In this way, we obtain a matrix giving the action of
$J(L)$
. In this way, we obtain a matrix giving the action of
![]() $\gamma $
on
$\gamma $
on
![]() $J(L)$
with respect to the chosen generators. We can bound the height of
$J(L)$
with respect to the chosen generators. We can bound the height of
![]() $\gamma \cdot x$
by
$\gamma \cdot x$
by
![]() ${\operatorname {max}}_\sigma |\gamma ^\sigma |^2$
times the height of x, so there are only finitely many candidates for
${\operatorname {max}}_\sigma |\gamma ^\sigma |^2$
times the height of x, so there are only finitely many candidates for
![]() $\gamma \cdot x$
, which allows us to determine
$\gamma \cdot x$
, which allows us to determine
![]() $\gamma \cdot x$
exactly by computing with sufficient precision. As an additional check, we verify that the matrix we obtain has the same minimal polynomial as
$\gamma \cdot x$
exactly by computing with sufficient precision. As an additional check, we verify that the matrix we obtain has the same minimal polynomial as
![]() $\gamma $
.
$\gamma $
.
3.4 Computing Heegner points analytically
Recall that
![]() $\pi $
denotes the isogeny
$\pi $
denotes the isogeny
![]() $A_f \to J$
and that we want to compute the Heegner point
$A_f \to J$
and that we want to compute the Heegner point
In this section, we explain how to find
![]() $y_{K,\pi }$
explicitly. Also recall that
$y_{K,\pi }$
explicitly. Also recall that
![]() $\boldsymbol {\pi }$
denotes the real number giving the area of the unit disk, to avoid confusion with the isogeny
$\boldsymbol {\pi }$
denotes the real number giving the area of the unit disk, to avoid confusion with the isogeny
![]() $\pi $
.
$\pi $
.
We obtain a computational representation of the isogeny
![]() $\pi \colon A_f \to J$
as described in Section 3.1. Since we know that an isogeny has to exist, we can be sure that what we obtain indeed describes an actual isogeny.
$\pi \colon A_f \to J$
as described in Section 3.1. Since we know that an isogeny has to exist, we can be sure that what we obtain indeed describes an actual isogeny.
To find the Heegner point on J, we first determine the integral binary quadratic ‘Heegner forms’ associated to K and N. These are representatives of the
![]() $h_K$
classes of positive definite binary quadratic forms of discriminant
$h_K$
classes of positive definite binary quadratic forms of discriminant
![]() $D_K$
such that their roots
$D_K$
such that their roots
![]() $\tau \in \mathbf {H}$
map to the points in the Heegner cycle
$\tau \in \mathbf {H}$
map to the points in the Heegner cycle
![]() $\mathbf {x}_K$
. Let
$\mathbf {x}_K$
. Let
![]() $(f_1, \ldots , f_g)$
be the
$(f_1, \ldots , f_g)$
be the
![]() ${\mathbf {Z}}$
-basis of
${\mathbf {Z}}$
-basis of
![]() $S_2(f, {\mathbf {Z}})$
that is used for the computation of the big period matrix of
$S_2(f, {\mathbf {Z}})$
that is used for the computation of the big period matrix of
![]() $A_f$
(it can be obtained via the Magma function qIntegralBasis). We then compute the period integrals
$A_f$
(it can be obtained via the Magma function qIntegralBasis). We then compute the period integrals
 $$\begin{align*}P(\tau, j) := 2 \boldsymbol{\pi} i \int_{i \infty}^\tau f_{j}(z)\,dz = \int_0^{e^{2 \boldsymbol{\pi} i \tau}} \sum_{n \ge 1} a_n(f_j) q^n \, \frac{dq}{q} = \sum_{n \geq 1} \frac{a_n(f_j)}{n} e^{2 \boldsymbol{\pi} i \tau n} \in {\mathbf{C}} \end{align*}$$
$$\begin{align*}P(\tau, j) := 2 \boldsymbol{\pi} i \int_{i \infty}^\tau f_{j}(z)\,dz = \int_0^{e^{2 \boldsymbol{\pi} i \tau}} \sum_{n \ge 1} a_n(f_j) q^n \, \frac{dq}{q} = \sum_{n \geq 1} \frac{a_n(f_j)}{n} e^{2 \boldsymbol{\pi} i \tau n} \in {\mathbf{C}} \end{align*}$$
for each of these roots
![]() $\tau $
and each
$\tau $
and each
![]() $1 \le j \le g$
to the desired precision. (We pick our Heegner forms in such a way that
$1 \le j \le g$
to the desired precision. (We pick our Heegner forms in such a way that
![]() $\tau $
has imaginary part as large as possible. We can use the bound
$\tau $
has imaginary part as large as possible. We can use the bound
![]() $|a_n^\sigma | \le \sqrt {3} n$
(see [Reference Grigorov, Jorza, Patrikis, Stein and Tarniţǎ50, Lemma 2.9], where a bound
$|a_n^\sigma | \le \sqrt {3} n$
(see [Reference Grigorov, Jorza, Patrikis, Stein and Tarniţǎ50, Lemma 2.9], where a bound
![]() $|a_n^\sigma | \le n$
is claimed, but their argument bounding
$|a_n^\sigma | \le n$
is claimed, but their argument bounding
![]() $|a_{p^m}^\sigma |$
is not correct for powers of
$|a_{p^m}^\sigma |$
is not correct for powers of
![]() $2$
or
$2$
or
![]() $3$
) and the representation of
$3$
) and the representation of
![]() $f_j$
as a linear combination of the
$f_j$
as a linear combination of the
![]() $f^\sigma $
to determine the number of terms we need. The points
$f^\sigma $
to determine the number of terms we need. The points
![]() $y_\tau = \bigl (P(\tau , j)\bigr )_{j} \in {\mathbf {C}}^g/\Lambda _f \simeq A_f({\mathbf {C}})$
then are of the form
$y_\tau = \bigl (P(\tau , j)\bigr )_{j} \in {\mathbf {C}}^g/\Lambda _f \simeq A_f({\mathbf {C}})$
then are of the form
![]() $[x_\tau - (\infty )]$
projected to
$[x_\tau - (\infty )]$
projected to
![]() $A_f$
, where
$A_f$
, where
![]() $\infty $
is the cusp at infinity and
$\infty $
is the cusp at infinity and
![]() $x_\tau $
runs through the points in the support of the Heegner cycle
$x_\tau $
runs through the points in the support of the Heegner cycle
![]() $\mathbf {x}_K$
. In particular, we have
$\mathbf {x}_K$
. In particular, we have
![]() $\sum _\tau y_\tau = y_{K,A_f}$
.
$\sum _\tau y_\tau = y_{K,A_f}$
.
We then use the matrix
![]() $\alpha _\pi $
associated to the isogeny
$\alpha _\pi $
associated to the isogeny
![]() $\pi $
to map
$\pi $
to map
![]() $y_K$
or all the points
$y_K$
or all the points
![]() $y_\tau $
to
$y_\tau $
to
![]() ${\mathbf {C}}^g/\Lambda \cong J({\mathbf {C}})$
. We apply the numerical inverse of the Abel–Jacobi map to find the Mumford representation of this or these points as points on J. We then try to recognize the coefficients in the Mumford representation as elements of K (for
${\mathbf {C}}^g/\Lambda \cong J({\mathbf {C}})$
. We apply the numerical inverse of the Abel–Jacobi map to find the Mumford representation of this or these points as points on J. We then try to recognize the coefficients in the Mumford representation as elements of K (for
![]() $\pi (y_{K, A_f}) = y_{K,\pi }$
) or of H (for
$\pi (y_{K, A_f}) = y_{K,\pi }$
) or of H (for
![]() $\pi (y_\tau )$
) and check that this really gives rise to a point in
$\pi (y_\tau )$
) and check that this really gives rise to a point in
![]() $J(K)$
or
$J(K)$
or
![]() $J(H)$
.
$J(H)$
.
Using the action of
![]() $\mathcal {O}$
on
$\mathcal {O}$
on
![]() $J(K)$
that we have determined in Section 3.3, we can then determine the
$J(K)$
that we have determined in Section 3.3, we can then determine the
![]() $\mathcal {O}$
-span of
$\mathcal {O}$
-span of
![]() $y_{K,\pi }$
and from it the ideal
$y_{K,\pi }$
and from it the ideal
and the index
![]() $I_{K,\pi } = (J(K) : \mathcal {O} y_{K,\pi })$
. The corresponding index for
$I_{K,\pi } = (J(K) : \mathcal {O} y_{K,\pi })$
. The corresponding index for
![]() $A_f$
is
$A_f$
is
![]() $I_K = (A_f(K) : {\mathbf {Z}}[f] \cdot y_{K,A_f})$
. We can express it in terms of
$I_K = (A_f(K) : {\mathbf {Z}}[f] \cdot y_{K,A_f})$
. We can express it in terms of
![]() $I_{K,\pi }$
via
$I_{K,\pi }$
via
 $$\begin{align*}I_K = \frac{(\mathcal{O}_{{\mathbf{Q}}(f)} : {\mathbf{Z}}[f])}{(\mathcal{O}_{{\mathbf{Q}}(f)} : \mathcal{O})} \cdot \frac{\#A_f[\pi](K)}{\#\bigl(J(K)/\pi(A_f(K))\bigr)} \cdot I_{K,\pi} . \end{align*}$$
$$\begin{align*}I_K = \frac{(\mathcal{O}_{{\mathbf{Q}}(f)} : {\mathbf{Z}}[f])}{(\mathcal{O}_{{\mathbf{Q}}(f)} : \mathcal{O})} \cdot \frac{\#A_f[\pi](K)}{\#\bigl(J(K)/\pi(A_f(K))\bigr)} \cdot I_{K,\pi} . \end{align*}$$
The first factor on the right takes care of the fact that
![]() ${\mathbf {Z}}[f]$
and
${\mathbf {Z}}[f]$
and
![]() $\mathcal {O} = \mathrm {End}_{{\mathbf {Q}}}(J)$
can be different orders in
$\mathcal {O} = \mathrm {End}_{{\mathbf {Q}}}(J)$
can be different orders in
![]() ${\mathbf {Q}}(f)$
; it can be computed easily as
${\mathbf {Q}}(f)$
; it can be computed easily as
![]() $\sqrt {\operatorname {disc} {\mathbf {Z}}[f]/\operatorname {disc} \mathcal {O}}$
. The second factor captures the effect of the isogeny
$\sqrt {\operatorname {disc} {\mathbf {Z}}[f]/\operatorname {disc} \mathcal {O}}$
. The second factor captures the effect of the isogeny
![]() $\pi $
. Note that the second factor can be multiplicatively bounded from above by
$\pi $
. Note that the second factor can be multiplicatively bounded from above by
![]() $\#A_f[\pi ](K) \mid \deg \pi $
, which gives a multiplicative upper bound for
$\#A_f[\pi ](K) \mid \deg \pi $
, which gives a multiplicative upper bound for
![]() $I_K$
as well. (We may get a better bound than
$I_K$
as well. (We may get a better bound than
![]() $\deg \pi $
from bounding
$\deg \pi $
from bounding
![]() $\#A_f(K)_{\mathrm {tors}}$
using the coefficients of the L-series of
$\#A_f(K)_{\mathrm {tors}}$
using the coefficients of the L-series of
![]() $A_f/K$
.)
$A_f/K$
.)
We will need
![]() $I_{K,\pi }$
in Section 4.4 for the computation of
$I_{K,\pi }$
in Section 4.4 for the computation of ![]() when
when
![]() $L\!\operatorname {-rk} J = 1$
and in Section 5.2 for the determination of an explicit finite support of
$L\!\operatorname {-rk} J = 1$
and in Section 5.2 for the determination of an explicit finite support of ![]() . We will need (a multiplicative upper bound for)
. We will need (a multiplicative upper bound for)
![]() $I_K$
in Section 7.
$I_K$
in Section 7.
3.5 Computing the Petersson norm of a newform
Let
![]() $\sigma \colon {\mathbf {Q}}(f) \hookrightarrow {\mathbf {R}}$
be an embedding. For the Gross–Zagier formula, we need the Petersson norms of the conjugates
$\sigma \colon {\mathbf {Q}}(f) \hookrightarrow {\mathbf {R}}$
be an embedding. For the Gross–Zagier formula, we need the Petersson norms of the conjugates
![]() $f^\sigma $
for the various possible
$f^\sigma $
for the various possible
![]() $\sigma $
. We identify
$\sigma $
. We identify
![]() $X_0(N)({\mathbf {C}})$
with
$X_0(N)({\mathbf {C}})$
with
![]() $\Gamma _0(N) \backslash \mathbf {H}^*$
(where
$\Gamma _0(N) \backslash \mathbf {H}^*$
(where
![]() $\mathbf {H}^* = \mathbf {H} \cup \mathbf {P}^1({\mathbf {Q}})$
is the upper half-plane together with the cusps) and use the normalization
$\mathbf {H}^* = \mathbf {H} \cup \mathbf {P}^1({\mathbf {Q}})$
is the upper half-plane together with the cusps) and use the normalization
 $$\begin{align*}\|f^\sigma\|^2 = \int_{X_0(N)({\mathbf{C}})} |f^\sigma(x + yi)|^2\, dx \wedge dy \end{align*}$$
$$\begin{align*}\|f^\sigma\|^2 = \int_{X_0(N)({\mathbf{C}})} |f^\sigma(x + yi)|^2\, dx \wedge dy \end{align*}$$
for the Petersson norm of
![]() $f^\sigma \in S_2(\Gamma _0(N), {\mathbf {C}})$
as in [Reference Gross and Zagier52, (5.1)]. (Sometimes this is normalized differently by dividing by the volume
$f^\sigma \in S_2(\Gamma _0(N), {\mathbf {C}})$
as in [Reference Gross and Zagier52, (5.1)]. (Sometimes this is normalized differently by dividing by the volume
![]() $\mu (X_0(N)({\mathbf {C}}))$
to make it independent of the choice of N.) We compute the Petersson norm by relating it to the symmetric square L-function
$\mu (X_0(N)({\mathbf {C}}))$
to make it independent of the choice of N.) We compute the Petersson norm by relating it to the symmetric square L-function
![]() $L(\operatorname {Sym}^2 f^\sigma , s)$
.
$L(\operatorname {Sym}^2 f^\sigma , s)$
.
If an L-function
![]() $L(\mathcal {X}, s)$
has an Euler product expansion, we write it as
$L(\mathcal {X}, s)$
has an Euler product expansion, we write it as
where
![]() $L_\ell (\mathcal {X}, T) \in R[T]$
(with R the coefficient ring of the L-function) is the Euler polynomial at
$L_\ell (\mathcal {X}, T) \in R[T]$
(with R the coefficient ring of the L-function) is the Euler polynomial at
![]() $\ell $
.
$\ell $
.
We define the symmetric square L-function
![]() $L(\operatorname {Sym}^2 f, s)$
as the L-function associated to the strictly compatible system
$L(\operatorname {Sym}^2 f, s)$
as the L-function associated to the strictly compatible system
![]() $(\operatorname {Sym}^2 \rho _{\mathfrak {p}^\infty , f})$
of
$(\operatorname {Sym}^2 \rho _{\mathfrak {p}^\infty , f})$
of
![]() $\mathfrak {p}$
-adic Galois representations. For a prime
$\mathfrak {p}$
-adic Galois representations. For a prime
![]() $\ell \nmid N$
, write
$\ell \nmid N$
, write
then
 $$ \begin{align} \begin{array}{r@{{}={}}l} L_\ell(\operatorname{Sym}^2 f, T) & (1 - \alpha_\ell^2 T) (1 - \alpha_\ell \beta_\ell T) (1 - \beta_\ell^2 T) \\[6pt] & (1 - \ell T) \bigl((1 + \ell T)^2 - a_\ell^2 T\bigr). \end{array} \end{align} $$
$$ \begin{align} \begin{array}{r@{{}={}}l} L_\ell(\operatorname{Sym}^2 f, T) & (1 - \alpha_\ell^2 T) (1 - \alpha_\ell \beta_\ell T) (1 - \beta_\ell^2 T) \\[6pt] & (1 - \ell T) \bigl((1 + \ell T)^2 - a_\ell^2 T\bigr). \end{array} \end{align} $$
We define the imprimitive symmetric square L-function
![]() $\tilde {L}(\operatorname {Sym}^2 f, s)$
by this formula for the Euler polynomial at all primes (then we take
$\tilde {L}(\operatorname {Sym}^2 f, s)$
by this formula for the Euler polynomial at all primes (then we take
![]() $\alpha _\ell = a_\ell $
and
$\alpha _\ell = a_\ell $
and
![]() $\beta _\ell = 0$
when
$\beta _\ell = 0$
when
![]() $\ell \mid N$
); compare [Reference Coates and Schmidt24, p. 110]. (The difference is whether we take
$\ell \mid N$
); compare [Reference Coates and Schmidt24, p. 110]. (The difference is whether we take
![]() $I_\ell $
-coinvariants before (
$I_\ell $
-coinvariants before (
![]() $\tilde {L}(\operatorname {Sym}^2 f, s)$
) or after (
$\tilde {L}(\operatorname {Sym}^2 f, s)$
) or after (
![]() $L(\operatorname {Sym}^2 f, s)$
) applying
$L(\operatorname {Sym}^2 f, s)$
) applying
![]() $\operatorname {Sym}^2$
when defining the Euler polynomials.) This imprimitive version is what Shimura denotes
$\operatorname {Sym}^2$
when defining the Euler polynomials.) This imprimitive version is what Shimura denotes
![]() $D(s)$
in [Reference Shimura103].
$D(s)$
in [Reference Shimura103].
We thank user334725 on MathOverflow [115] for pointers to the relevant literature.
Proposition 3.8. Let
![]() $f \in S_2(\Gamma _0(N), {\mathbf {C}})$
be a normalized eigenform. Then the Petersson norm of f is given by
$f \in S_2(\Gamma _0(N), {\mathbf {C}})$
be a normalized eigenform. Then the Petersson norm of f is given by
Proof. Denote the Fourier coefficients of f by
![]() $a_n$
. We set
$a_n$
. We set
 $$\begin{align*}D(f, s) := \sum_{n \ge 1} \frac{a_n^2}{n^s} . \end{align*}$$
$$\begin{align*}D(f, s) := \sum_{n \ge 1} \frac{a_n^2}{n^s} . \end{align*}$$
By [Reference Petersson83, Satz 6] (and taking into account the different normalization (compare also [Reference Shimura104, Eq. (2.5)])),
 $$ \begin{align} \|f\|^2 &= [\Gamma(1) : \Gamma_0(N)] \, \frac{\boldsymbol{\pi}}{3} \, \frac{1}{(4\boldsymbol{\pi})^2} \, \operatorname{\mathrm{res}}_{s=2} D(f, s) \nonumber \\ &= N \prod_{\ell \mid N} \Bigl(1 + \frac{1}{\ell}\Bigr) \frac{1}{48 \boldsymbol{\pi}} \, \operatorname{\mathrm{res}}_{s=2} D(f, s). \end{align} $$
$$ \begin{align} \|f\|^2 &= [\Gamma(1) : \Gamma_0(N)] \, \frac{\boldsymbol{\pi}}{3} \, \frac{1}{(4\boldsymbol{\pi})^2} \, \operatorname{\mathrm{res}}_{s=2} D(f, s) \nonumber \\ &= N \prod_{\ell \mid N} \Bigl(1 + \frac{1}{\ell}\Bigr) \frac{1}{48 \boldsymbol{\pi}} \, \operatorname{\mathrm{res}}_{s=2} D(f, s). \end{align} $$
By [Reference Shimura103, Eq. (0.4)] (see [Reference Shimura104, Lemma 1] for the relation between the Euler factors), we have the following equality, where the superscript N means that we leave out the Euler factors coming from prime divisors of N.
 $$\begin{align*}D(f, s) = \frac{\zeta^N(s-1)}{\zeta^N(2s - 2)} \, \tilde{L}(\operatorname{Sym}^2 f, s) . \end{align*}$$
$$\begin{align*}D(f, s) = \frac{\zeta^N(s-1)}{\zeta^N(2s - 2)} \, \tilde{L}(\operatorname{Sym}^2 f, s) . \end{align*}$$
Taking the residue at
![]() $s = 2$
on both sides, we obtain
$s = 2$
on both sides, we obtain
 $$\begin{align*}\operatorname{\mathrm{res}}_{s=2} D(f, s) = \frac{6}{\boldsymbol{\pi}^2} \prod_{\ell \mid N} \Bigl(1 + \frac{1}{\ell}\Bigr)^{-1} \, \tilde{L}(\operatorname{Sym}^2 f, 2), \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{res}}_{s=2} D(f, s) = \frac{6}{\boldsymbol{\pi}^2} \prod_{\ell \mid N} \Bigl(1 + \frac{1}{\ell}\Bigr)^{-1} \, \tilde{L}(\operatorname{Sym}^2 f, 2), \end{align*}$$
which gives the desired result when used in (3.10).
So we need to compute
![]() $\tilde {L}(\operatorname {Sym}^2 f, 2)$
. However, we cannot directly do that since
$\tilde {L}(\operatorname {Sym}^2 f, 2)$
. However, we cannot directly do that since
![]() $\tilde {L}(\operatorname {Sym}^2 f, 2)$
does not in general satisfy a suitable functional equation (which is needed to obtain a reasonably fast converging series for the value via a Mellin transform). We can, however, compute
$\tilde {L}(\operatorname {Sym}^2 f, 2)$
does not in general satisfy a suitable functional equation (which is needed to obtain a reasonably fast converging series for the value via a Mellin transform). We can, however, compute
![]() $L(\operatorname {Sym}^2 f, 2)$
if we know its Euler factors at primes dividing N. So we need to determine these Euler factors; combining this with (3.9) will also tell us what the correction factor
$L(\operatorname {Sym}^2 f, 2)$
if we know its Euler factors at primes dividing N. So we need to determine these Euler factors; combining this with (3.9) will also tell us what the correction factor
![]() $\tilde {L}(\operatorname {Sym}^2 f, 2)/L(\operatorname {Sym}^2 f, 2)$
is.
$\tilde {L}(\operatorname {Sym}^2 f, 2)/L(\operatorname {Sym}^2 f, 2)$
is.
For a prime
![]() $\ell $
, we set
$\ell $
, we set
 $$\begin{align*}C_\ell := \frac{L_\ell(\operatorname{Sym}^2 f, \ell^{-2})}{\tilde{L}_\ell(\operatorname{Sym}^2 f, \ell^{-2})} . \end{align*}$$
$$\begin{align*}C_\ell := \frac{L_\ell(\operatorname{Sym}^2 f, \ell^{-2})}{\tilde{L}_\ell(\operatorname{Sym}^2 f, \ell^{-2})} . \end{align*}$$
Corollary 3.9. Let f and
![]() $C_\ell $
be as above. Then
$C_\ell $
be as above. Then
 $$\begin{align*}\|f\|^2 = \frac{N}{8 \boldsymbol{\pi}^3} \prod_{\ell^2 \mid N} C_\ell \cdot L(\operatorname{Sym}^2 f, 2) . \end{align*}$$
$$\begin{align*}\|f\|^2 = \frac{N}{8 \boldsymbol{\pi}^3} \prod_{\ell^2 \mid N} C_\ell \cdot L(\operatorname{Sym}^2 f, 2) . \end{align*}$$
In particular,
when the level N is squarefree.
Proof. This follows from proposition 3.8 and the definition of
![]() $C_\ell $
, together with the fact that
$C_\ell $
, together with the fact that
![]() $C_\ell = 1$
unless
$C_\ell = 1$
unless
![]() $\ell ^2 \mid N$
, which will be shown in lemma 3.10 below.
$\ell ^2 \mid N$
, which will be shown in lemma 3.10 below.
Alternative algorithms for computing the Petersson inner product are described in [Reference Cohen25] and have been implemented in Pari.
Using the formula in corollary 3.9, we can compute
![]() $\|f^\sigma \|^2$
using [Reference Dokchitser40] for all
$\|f^\sigma \|^2$
using [Reference Dokchitser40] for all
![]() $\sigma \in \Sigma $
if we can determine the Euler factors
$\sigma \in \Sigma $
if we can determine the Euler factors
![]() $L_\ell (\operatorname {Sym}^2 f, T)$
for the primes
$L_\ell (\operatorname {Sym}^2 f, T)$
for the primes
![]() $\ell \mid N$
. We will do that in the following subsection.
$\ell \mid N$
. We will do that in the following subsection.
3.6 Euler factors of the symmetric square L-function
In this section, we explain how to find the Euler factors of
![]() $L(\operatorname {Sym}^2 f, s)$
at primes
$L(\operatorname {Sym}^2 f, s)$
at primes
![]() $\ell $
dividing the level N of f. In [Reference Coates and Schmidt24, § 1], analogous statements are shown for the L-function of an elliptic curve, and [Reference Schmidt94] has similar results stated in a somewhat different language.
$\ell $
dividing the level N of f. In [Reference Coates and Schmidt24, § 1], analogous statements are shown for the L-function of an elliptic curve, and [Reference Schmidt94] has similar results stated in a somewhat different language.
Recall that when
![]() $\ell \nmid N$
,
$\ell \nmid N$
,
![]() $L_\ell (\operatorname {Sym}^2 f, T) = \tilde {L}_\ell (\operatorname {Sym}^2 f, T)$
(and hence
$L_\ell (\operatorname {Sym}^2 f, T) = \tilde {L}_\ell (\operatorname {Sym}^2 f, T)$
(and hence
![]() $C_\ell = 1$
), and we can write down
$C_\ell = 1$
), and we can write down
![]() $\tilde {L}_\ell (\operatorname {Sym}^2 f, T)$
easily in terms of
$\tilde {L}_\ell (\operatorname {Sym}^2 f, T)$
easily in terms of
![]() $L_\ell (f, T)$
. We now consider the case
$L_\ell (f, T)$
. We now consider the case
![]() $v_\ell (N) = 1$
.
$v_\ell (N) = 1$
.
Lemma 3.10. Assume that
![]() $v_\ell (N) = 1$
. Then
$v_\ell (N) = 1$
. Then
In particular,
![]() $C_\ell = 1$
whenever
$C_\ell = 1$
whenever
![]() $\ell ^2 \nmid N$
.
$\ell ^2 \nmid N$
.
Proof. Fix some
![]() $\mathfrak {p} \nmid N \ell $
and set
$\mathfrak {p} \nmid N \ell $
and set
![]() $p = p(\mathfrak {p})$
and
$p = p(\mathfrak {p})$
and
![]() $V_{\mathfrak {p}} = V_{\mathfrak {p}}(A_f)$
. Since
$V_{\mathfrak {p}} = V_{\mathfrak {p}}(A_f)$
. Since
![]() $v_\ell (N) = 1$
,
$v_\ell (N) = 1$
,
![]() $V_{\mathfrak {p}}$
has a one-dimensional quotient of
$V_{\mathfrak {p}}$
has a one-dimensional quotient of
![]() $I_\ell $
-coinvariants. Since
$I_\ell $
-coinvariants. Since
![]() $\chi _{p^\infty } = \det \circ \rho _{\mathfrak {p}^\infty }$
is trivial on
$\chi _{p^\infty } = \det \circ \rho _{\mathfrak {p}^\infty }$
is trivial on
![]() $I_\ell $
, it follows that
$I_\ell $
, it follows that
![]() $\rho _{\mathfrak {p}^\infty }(I_\ell )$
lands in a unipotent subgroup (compare lemma 2.32). The image is nontrivial, since otherwise,
$\rho _{\mathfrak {p}^\infty }(I_\ell )$
lands in a unipotent subgroup (compare lemma 2.32). The image is nontrivial, since otherwise,
![]() $\ell \nmid N$
. Since
$\ell \nmid N$
. Since
![]() $\ell \neq p$
and the unipotent subgroups of
$\ell \neq p$
and the unipotent subgroups of
![]() $\mathrm {GL}_2({\mathbf {Q}}(f)_{\mathfrak {p}})$
are pro-p groups, whereas the wild inertia at
$\mathrm {GL}_2({\mathbf {Q}}(f)_{\mathfrak {p}})$
are pro-p groups, whereas the wild inertia at
![]() $\ell $
is a pro-
$\ell $
is a pro-
![]() $\ell $
group, it follows that
$\ell $
group, it follows that
![]() $\rho _{\mathfrak {p}^\infty }|_{I_\ell }$
factors through the tame inertia group
$\rho _{\mathfrak {p}^\infty }|_{I_\ell }$
factors through the tame inertia group
![]() $I_\ell ^{\mathrm {t}}$
. By lemma 2.7, conjugating by any lift
$I_\ell ^{\mathrm {t}}$
. By lemma 2.7, conjugating by any lift
![]() $\operatorname {Frob}_\ell $
of the Frobenius automorphism to
$\operatorname {Frob}_\ell $
of the Frobenius automorphism to
![]() $I_\ell ^{\mathrm {t}}$
has the effect of raising to the
$I_\ell ^{\mathrm {t}}$
has the effect of raising to the
![]() $\ell $
th power. Using that
$\ell $
th power. Using that
![]() $\det \rho _{\mathfrak {p}^\infty }(\operatorname {Frob}_\ell ) = \chi _{p^\infty }(\operatorname {Frob}_\ell ) = \ell $
, it follows that (with respect to a suitable
$\det \rho _{\mathfrak {p}^\infty }(\operatorname {Frob}_\ell ) = \chi _{p^\infty }(\operatorname {Frob}_\ell ) = \ell $
, it follows that (with respect to a suitable
![]() ${\mathbf {Q}}(f)_{\mathfrak {p}}$
-basis),
${\mathbf {Q}}(f)_{\mathfrak {p}}$
-basis),
![]() $\rho _{\mathfrak {p}^\infty }(\operatorname {Frob}_\ell ) = \pm \left (\begin {smallmatrix} \ell & 0 \\ 0 & 1 \end {smallmatrix}\right )$
and
$\rho _{\mathfrak {p}^\infty }(\operatorname {Frob}_\ell ) = \pm \left (\begin {smallmatrix} \ell & 0 \\ 0 & 1 \end {smallmatrix}\right )$
and
![]() $\rho _{\mathfrak {p}^\infty }|_{I_\ell } \subseteq \left (\begin {smallmatrix} 1 & * \\ 0 & 1 \end {smallmatrix}\right )$
. This implies that
$\rho _{\mathfrak {p}^\infty }|_{I_\ell } \subseteq \left (\begin {smallmatrix} 1 & * \\ 0 & 1 \end {smallmatrix}\right )$
. This implies that
![]() $L_\ell (f, T) = 1 \mp T$
, and so
$L_\ell (f, T) = 1 \mp T$
, and so
![]() $\tilde {L}_\ell (\operatorname {Sym}^2 f, T) = 1 - T$
. We also see that
$\tilde {L}_\ell (\operatorname {Sym}^2 f, T) = 1 - T$
. We also see that
 $$\begin{align*}\operatorname{Sym}^2 \rho_{\mathfrak{p}^\infty}|_{{\operatorname{\mathrm{Gal}}({\overline{{\mathbf{Q}}}}_\ell|{\mathbf{Q}}_\ell)}} = \begin{pmatrix} \chi_{p^\infty}^2 & * & * \\ 0 & \chi_{p^\infty} & * \\ 0 & 0 & 1 \end{pmatrix} \end{align*}$$
$$\begin{align*}\operatorname{Sym}^2 \rho_{\mathfrak{p}^\infty}|_{{\operatorname{\mathrm{Gal}}({\overline{{\mathbf{Q}}}}_\ell|{\mathbf{Q}}_\ell)}} = \begin{pmatrix} \chi_{p^\infty}^2 & * & * \\ 0 & \chi_{p^\infty} & * \\ 0 & 0 & 1 \end{pmatrix} \end{align*}$$
with a one-dimensional
![]() $I_\ell $
-coinvariant quotient, on which
$I_\ell $
-coinvariant quotient, on which
![]() $\operatorname {Frob}_\ell $
acts trivially. This shows that
$\operatorname {Frob}_\ell $
acts trivially. This shows that
![]() $L_\ell (\operatorname {Sym}^2 f, T) = 1 - T$
as well. (This is analogous to [Reference Coates and Schmidt24, Lemma 1.2].)
$L_\ell (\operatorname {Sym}^2 f, T) = 1 - T$
as well. (This is analogous to [Reference Coates and Schmidt24, Lemma 1.2].)
In particular,
![]() $C_\ell = 1$
, which, together with the discussion preceding this lemma, gives the last claim.
$C_\ell = 1$
, which, together with the discussion preceding this lemma, gives the last claim.
We now consider the case
![]() $\ell ^2 \mid N$
. We first note that
$\ell ^2 \mid N$
. We first note that
![]() $L(\operatorname {Sym}^2 f, s)$
does not change under quadratic twists.
$L(\operatorname {Sym}^2 f, s)$
does not change under quadratic twists.
Lemma 3.11. Let
![]() $\tilde {f}$
be a quadratic twist of f. Then
$\tilde {f}$
be a quadratic twist of f. Then
Proof. We consider the Euler factor at
![]() $\ell $
. Fix some
$\ell $
. Fix some
![]() $\mathfrak {p} \nmid N \ell $
and set
$\mathfrak {p} \nmid N \ell $
and set
![]() $p = p(\mathfrak {p})$
and
$p = p(\mathfrak {p})$
and
![]() $V_{\mathfrak {p}} = V_{\mathfrak {p}}(A_f)$
. Let
$V_{\mathfrak {p}} = V_{\mathfrak {p}}(A_f)$
. Let
![]() $\varepsilon $
be the quadratic character such that
$\varepsilon $
be the quadratic character such that
![]() $\tilde {f} = f \otimes \varepsilon $
. Since the canonical group homomorphism
$\tilde {f} = f \otimes \varepsilon $
. Since the canonical group homomorphism
![]() $\mathrm {GL}(V_{\mathfrak {p}}) \to \mathrm {GL}(\operatorname {Sym}^2 V_{\mathfrak {p}})$
is trivial on
$\mathrm {GL}(V_{\mathfrak {p}}) \to \mathrm {GL}(\operatorname {Sym}^2 V_{\mathfrak {p}})$
is trivial on
![]() $\pm {\mathrm {id}}$
, it follows that
$\pm {\mathrm {id}}$
, it follows that
![]() $\operatorname {Sym}^2 (\rho _{\mathfrak {p}^\infty } \otimes \varepsilon ) = \operatorname {Sym}^2 \rho _{\mathfrak {p}^\infty }$
, which, upon restricting to
$\operatorname {Sym}^2 (\rho _{\mathfrak {p}^\infty } \otimes \varepsilon ) = \operatorname {Sym}^2 \rho _{\mathfrak {p}^\infty }$
, which, upon restricting to
![]() ${ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_\ell |{\mathbf {Q}}_\ell )}$
, directly translates into
${ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_\ell |{\mathbf {Q}}_\ell )}$
, directly translates into
![]() $L_\ell (\operatorname {Sym}^2 \tilde {f}, T) = L_\ell (\operatorname {Sym}^2 f, T)$
. The claim follows.
$L_\ell (\operatorname {Sym}^2 \tilde {f}, T) = L_\ell (\operatorname {Sym}^2 f, T)$
. The claim follows.
The argument in the proof together with the fact that
![]() $\rho _{\mathfrak {p}^\infty }(I_\ell ) \subseteq {\mathrm {SL}}(V_{\mathfrak {p}})$
shows that the action of
$\rho _{\mathfrak {p}^\infty }(I_\ell ) \subseteq {\mathrm {SL}}(V_{\mathfrak {p}})$
shows that the action of
![]() $I_\ell $
on
$I_\ell $
on
![]() $\operatorname {Sym}^2 V_{\mathfrak {p}}$
depends only on the projective image
$\operatorname {Sym}^2 V_{\mathfrak {p}}$
depends only on the projective image
![]() ${\mathbf {P}} \rho _{\mathfrak {p}^\infty }(I_\ell ) \subseteq \operatorname {PSL}(V_{\mathfrak {p}})$
. We will see that the dimension of the
${\mathbf {P}} \rho _{\mathfrak {p}^\infty }(I_\ell ) \subseteq \operatorname {PSL}(V_{\mathfrak {p}})$
. We will see that the dimension of the
![]() $I_\ell $
-coinvariants of
$I_\ell $
-coinvariants of
![]() $\operatorname {Sym}^2 V_{\mathfrak {p}}$
depends on whether this projective image is abelian or not.
$\operatorname {Sym}^2 V_{\mathfrak {p}}$
depends on whether this projective image is abelian or not.
Lemma 3.12. Let k be a field of characteristic zero and let V be a two-dimensional k-vector space. Let
![]() $G \subseteq {\mathrm {SL}}(V)$
be such that
$G \subseteq {\mathrm {SL}}(V)$
be such that
![]() ${\mathbf {P}} G$
is not unipotent.
${\mathbf {P}} G$
is not unipotent.
-
(1) If
 $\operatorname {Sym}^2 V$
has a nontrivial G-invariant quotient, then G is abelian.
$\operatorname {Sym}^2 V$
has a nontrivial G-invariant quotient, then G is abelian. -
(2) If
 ${\mathbf {P}} G$
is abelian, then
${\mathbf {P}} G$
is abelian, then
 $\bar {V} := V \otimes _k \bar {k}$
has a basis
$\bar {V} := V \otimes _k \bar {k}$
has a basis
 $e_1$
,
$e_1$
,
 $e_2$
consisting of simultaneous eigenvectors for the elements of G. The G-coinvariant space of
$e_2$
consisting of simultaneous eigenvectors for the elements of G. The G-coinvariant space of
 $\operatorname {Sym}^2 \bar {V} = \langle e_1^2, e_1 e_2, e_2^2 \rangle $
is one-dimensional and is isomorphic to the direct summand
$\operatorname {Sym}^2 \bar {V} = \langle e_1^2, e_1 e_2, e_2^2 \rangle $
is one-dimensional and is isomorphic to the direct summand
 $\bar {k} \cdot e_1 e_2$
.
$\bar {k} \cdot e_1 e_2$
.
Proof. We can assume without loss of generality that k is algebraically closed.
-
(1) If
 $\operatorname {Sym}^2 V$
has a nontrivial G-invariant quotient, then
$\operatorname {Sym}^2 V$
has a nontrivial G-invariant quotient, then
 $\operatorname {Sym}^2 V^*$
has a nonzero G-invariant element, which is a quadratic form q on V. Then G must fix the zero set of q in
$\operatorname {Sym}^2 V^*$
has a nonzero G-invariant element, which is a quadratic form q on V. Then G must fix the zero set of q in
 ${\mathbf {P}}^1(k)$
. This zero set can have either one or two elements.
${\mathbf {P}}^1(k)$
. This zero set can have either one or two elements.In the first case, G fixes a point in
 ${\mathbf {P}}^1$
, and hence is contained in a Borel subgroup, so, after fixing a suitable basis, the associated representation
${\mathbf {P}}^1$
, and hence is contained in a Borel subgroup, so, after fixing a suitable basis, the associated representation
 $\rho $
has the form
$\rho $
has the form
 $\left (\begin {smallmatrix} \chi & \alpha \\ 0 & \chi ^{-1} \end {smallmatrix}\right )$
with a character
$\left (\begin {smallmatrix} \chi & \alpha \\ 0 & \chi ^{-1} \end {smallmatrix}\right )$
with a character
 $\chi $
such that
$\chi $
such that
 $\chi ^2 \neq \mathbf {1}$
(recall that
$\chi ^2 \neq \mathbf {1}$
(recall that
 ${\mathbf {P}} G$
is not unipotent). Then (with the columns giving the action on
${\mathbf {P}} G$
is not unipotent). Then (with the columns giving the action on
 $X^2$
,
$X^2$
,
 $XY$
,
$XY$
,
 $Y^2$
, when
$Y^2$
, when
 $X, Y$
is the given basis with
$X, Y$
is the given basis with
 $\rho (g) X = \chi (g) X$
,
$\rho (g) X = \chi (g) X$
,
 $\rho (g) Y = \alpha (g) X + \chi ^{-1}(g) Y$
) and this has nontrivial G-coinvariants only when
$\rho (g) Y = \alpha (g) X + \chi ^{-1}(g) Y$
) and this has nontrivial G-coinvariants only when $$\begin{align*}\operatorname{Sym}^2 \rho = \begin{pmatrix} \chi^2 & \alpha \chi & \alpha^2 \\ 0 & \mathbf{1} & 2 \alpha \chi^{-1} \\ 0 & 0 & \chi^{-2} \end{pmatrix} , \end{align*}$$
$$\begin{align*}\operatorname{Sym}^2 \rho = \begin{pmatrix} \chi^2 & \alpha \chi & \alpha^2 \\ 0 & \mathbf{1} & 2 \alpha \chi^{-1} \\ 0 & 0 & \chi^{-2} \end{pmatrix} , \end{align*}$$
 $\alpha = 0$
, which implies that G is abelian.
$\alpha = 0$
, which implies that G is abelian.
In the second case, G is contained in the normalizer of a Cartan subgroup, so its elements are (with respect to a suitable basis
 $(e_1, e_2)$
) either of the form
$(e_1, e_2)$
) either of the form
 $\left (\begin {smallmatrix} a & 0 \\ 0 & a^{-1} \end {smallmatrix}\right )$
(which fix
$\left (\begin {smallmatrix} a & 0 \\ 0 & a^{-1} \end {smallmatrix}\right )$
(which fix
 $e_1 \cdot e_2$
) or of the form
$e_1 \cdot e_2$
) or of the form
 $\left (\begin {smallmatrix} 0 & -a \\ a^{-1} & 0 \end {smallmatrix}\right )$
. However, the elements of the second form send
$\left (\begin {smallmatrix} 0 & -a \\ a^{-1} & 0 \end {smallmatrix}\right )$
. However, the elements of the second form send
 $e_1 \cdot e_2$
to its negative, so (noting that there must be elements of the first form with
$e_1 \cdot e_2$
to its negative, so (noting that there must be elements of the first form with
 $a^2 \neq 1$
, again since
$a^2 \neq 1$
, again since
 ${\mathbf {P}} G$
is not unipotent, so that neither
${\mathbf {P}} G$
is not unipotent, so that neither
 $e_1^2$
nor
$e_1^2$
nor
 $e_2^2$
can be fixed by G) such elements cannot be present in G, which again implies that G is abelian.
$e_2^2$
can be fixed by G) such elements cannot be present in G, which again implies that G is abelian. -
(2) If
 ${\mathbf {P}} G$
is abelian, then so is G. The representation on V then splits as a sum of two characters
${\mathbf {P}} G$
is abelian, then so is G. The representation on V then splits as a sum of two characters
 $\chi $
and
$\chi $
and
 $\chi ^{-1}$
such that
$\chi ^{-1}$
such that
 $\chi ^2 \neq 1$
. Let
$\chi ^2 \neq 1$
. Let
 $e_1$
and
$e_1$
and
 $e_2$
be corresponding eigenvectors. Then
$e_2$
be corresponding eigenvectors. Then
 $\operatorname {Sym}^2 V$
splits as
$\operatorname {Sym}^2 V$
splits as
 $\chi ^2 \oplus \mathbf {1} \oplus \chi ^{-2}$
, with the G-action on
$\chi ^2 \oplus \mathbf {1} \oplus \chi ^{-2}$
, with the G-action on
 $e_1 e_2$
being trivial. This shows the claim.
$e_1 e_2$
being trivial. This shows the claim.
This leads to the following classification.
Lemma 3.13. Let
![]() $\ell $
be a prime such that
$\ell $
be a prime such that
![]() $\ell ^2 \mid N$
. Then
$\ell ^2 \mid N$
. Then
![]() $\tilde {L}_\ell (\operatorname {Sym}^2 f, T) = 1$
. Let
$\tilde {L}_\ell (\operatorname {Sym}^2 f, T) = 1$
. Let
![]() $\tilde {f}$
be a quadratic twist of f whose level
$\tilde {f}$
be a quadratic twist of f whose level
![]() $\tilde {N}$
is (multiplicatively) minimal. Fix a regular prime ideal
$\tilde {N}$
is (multiplicatively) minimal. Fix a regular prime ideal
![]() $\mathfrak {p} \nmid N \ell $
of
$\mathfrak {p} \nmid N \ell $
of
![]() ${\mathbf {Z}}[f]$
.
${\mathbf {Z}}[f]$
.
-
(1)
 ${\mathbf {P}} \rho _{\mathfrak {p}^\infty }(I_\ell )$
is trivial if and only if
${\mathbf {P}} \rho _{\mathfrak {p}^\infty }(I_\ell )$
is trivial if and only if
 $\ell \nmid \tilde {N}$
. In particular, using (3.9),
$\ell \nmid \tilde {N}$
. In particular, using (3.9),  $$\begin{align*}C_\ell = \frac{(\ell - 1)((\ell + 1)^2 - a_\ell(\tilde{f})^2)}{\ell^3} . \end{align*}$$
$$\begin{align*}C_\ell = \frac{(\ell - 1)((\ell + 1)^2 - a_\ell(\tilde{f})^2)}{\ell^3} . \end{align*}$$
-
(2)
 ${\mathbf {P}} \rho _{\mathfrak {p}^\infty }(I_\ell )$
is nontrivial and unipotent if and only if
${\mathbf {P}} \rho _{\mathfrak {p}^\infty }(I_\ell )$
is nontrivial and unipotent if and only if
 $v_\ell (\tilde {N}) = 1$
. In this case,
$v_\ell (\tilde {N}) = 1$
. In this case,
 $L_\ell (\operatorname {Sym}^2 f, T) = 1 - T$
and the conductor exponent of
$L_\ell (\operatorname {Sym}^2 f, T) = 1 - T$
and the conductor exponent of
 $\operatorname {Sym}^2 f$
at
$\operatorname {Sym}^2 f$
at
 $\ell $
is
$\ell $
is
 $2$
. In particular,
$2$
. In particular,
 $C_\ell = \frac {\ell ^2 - 1}{\ell ^2}$
.
$C_\ell = \frac {\ell ^2 - 1}{\ell ^2}$
. -
(3)
 ${\mathbf {P}} \rho _{\mathfrak {p}^\infty }(I_\ell )$
is abelian and not unipotent if and only if
${\mathbf {P}} \rho _{\mathfrak {p}^\infty }(I_\ell )$
is abelian and not unipotent if and only if
 $v_\ell (\tilde {N}) = 2$
. In this case,
$v_\ell (\tilde {N}) = 2$
. In this case,
 $L_\ell (\operatorname {Sym}^2 f, T) = 1 \mp \ell T$
, with the negative sign if and only if
$L_\ell (\operatorname {Sym}^2 f, T) = 1 \mp \ell T$
, with the negative sign if and only if
 $\rho _{\mathfrak {p}^\infty }({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_\ell |{\mathbf {Q}}_\ell )})$
is abelian, and the conductor exponent of
$\rho _{\mathfrak {p}^\infty }({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_\ell |{\mathbf {Q}}_\ell )})$
is abelian, and the conductor exponent of
 $\operatorname {Sym}^2 f$
at
$\operatorname {Sym}^2 f$
at
 $\ell $
is
$\ell $
is
 $2$
. In particular,
$2$
. In particular,
 $C_\ell = \frac {\ell \mp 1}{\ell }$
(with the same sign).
$C_\ell = \frac {\ell \mp 1}{\ell }$
(with the same sign). -
(4)
 ${\mathbf {P}} \rho _{\mathfrak {p}^\infty }(I_\ell )$
is nonabelian if and only if
${\mathbf {P}} \rho _{\mathfrak {p}^\infty }(I_\ell )$
is nonabelian if and only if
 $v_\ell (\tilde {N}) \ge 3$
. In this case, we have
$v_\ell (\tilde {N}) \ge 3$
. In this case, we have
 $L_\ell (\operatorname {Sym}^2 f, T) = 1$
, and the conductor exponent of
$L_\ell (\operatorname {Sym}^2 f, T) = 1$
, and the conductor exponent of
 $\operatorname {Sym}^2 f$
at
$\operatorname {Sym}^2 f$
at
 $\ell $
is at least
$\ell $
is at least
 $4$
and at most
$4$
and at most
 $2v_\ell (\tilde {N}) - 1$
. In particular,
$2v_\ell (\tilde {N}) - 1$
. In particular,
 $C_\ell = 1$
.
$C_\ell = 1$
.
Proof. When
![]() $\ell ^2 \mid N$
, then the space of
$\ell ^2 \mid N$
, then the space of
![]() $I_\ell $
-coinvariants is trivial, and hence, so is its symmetric square. This means that
$I_\ell $
-coinvariants is trivial, and hence, so is its symmetric square. This means that
![]() $\tilde {L}_\ell (\operatorname {Sym}^2 f, T) = 1$
. By lemma 3.11, we have that
$\tilde {L}_\ell (\operatorname {Sym}^2 f, T) = 1$
. By lemma 3.11, we have that
![]() $L(\operatorname {Sym}^2 f, s) = L(\operatorname {Sym}^2 \tilde {f}, s)$
. It suffices to show the ‘only if’ direction of the equivalences at the beginning of each statement since the consequences exhaust all possibilities disjointly.
$L(\operatorname {Sym}^2 f, s) = L(\operatorname {Sym}^2 \tilde {f}, s)$
. It suffices to show the ‘only if’ direction of the equivalences at the beginning of each statement since the consequences exhaust all possibilities disjointly.
-
(1) If
 ${\mathbf {P}} \rho _{\mathfrak {p}^\infty }(I_\ell )$
is trivial, then
${\mathbf {P}} \rho _{\mathfrak {p}^\infty }(I_\ell )$
is trivial, then
 $\rho _{\mathfrak {p}^\infty }|_{I_\ell }$
is of the form
$\rho _{\mathfrak {p}^\infty }|_{I_\ell }$
is of the form
 $(\mathbf {1} \oplus \mathbf {1}) \otimes \varepsilon $
with a quadratic character
$(\mathbf {1} \oplus \mathbf {1}) \otimes \varepsilon $
with a quadratic character
 $\varepsilon $
. Twisting by
$\varepsilon $
. Twisting by
 $\varepsilon $
makes the representation unramified at
$\varepsilon $
makes the representation unramified at
 $\ell $
, so
$\ell $
, so
 $\ell \nmid \tilde {N}$
(using that
$\ell \nmid \tilde {N}$
(using that
 $\tilde {N}$
is minimal). The statement on
$\tilde {N}$
is minimal). The statement on
 $C_\ell $
then follows.
$C_\ell $
then follows. -
(2) If the projective image is nontrivial and unipotent, then there is a quadratic character
 $\varepsilon $
such that
$\varepsilon $
such that
 $\rho _{\mathfrak {p}^\infty } \otimes \varepsilon |_{I_\ell }$
is unipotent and nontrivial, which implies that
$\rho _{\mathfrak {p}^\infty } \otimes \varepsilon |_{I_\ell }$
is unipotent and nontrivial, which implies that
 $v_\ell (\tilde {N}) = 1$
. The statement on the Euler factor then follows from lemma 3.10.
$v_\ell (\tilde {N}) = 1$
. The statement on the Euler factor then follows from lemma 3.10. -
(3) We assume that
 ${\mathbf {P}} \rho _{\mathfrak {p}^\infty }(I_\ell )$
is abelian, but not unipotent. By lemma 3.12,
${\mathbf {P}} \rho _{\mathfrak {p}^\infty }(I_\ell )$
is abelian, but not unipotent. By lemma 3.12,
 $\operatorname {Sym}^2 V_{\mathfrak {p}}$
has a one-dimensional
$\operatorname {Sym}^2 V_{\mathfrak {p}}$
has a one-dimensional
 $I_\ell $
-coinvariant space. Also, because
$I_\ell $
-coinvariant space. Also, because
 $\rho _{\mathfrak {p}^\infty }|_{I_\ell }$
is a sum of two characters of order coprime to
$\rho _{\mathfrak {p}^\infty }|_{I_\ell }$
is a sum of two characters of order coprime to
 $\ell $
, the representation factors through the tame inertia group, and hence, there is no wild part in the conductor. This shows that
$\ell $
, the representation factors through the tame inertia group, and hence, there is no wild part in the conductor. This shows that
 $v_\ell (\tilde {N}) = 2$
and that the conductor exponent of
$v_\ell (\tilde {N}) = 2$
and that the conductor exponent of
 $\operatorname {Sym}^2 f = \operatorname {Sym}^2 \tilde {f}$
is
$\operatorname {Sym}^2 f = \operatorname {Sym}^2 \tilde {f}$
is
 $3 - 1 = 2$
. Also by lemma 3.12, the coinvariant space corresponds to the tensor product of the two one-dimensional representations in the splitting of
$3 - 1 = 2$
. Also by lemma 3.12, the coinvariant space corresponds to the tensor product of the two one-dimensional representations in the splitting of
 $V_{\mathfrak {p}}$
. Frobenius either fixes each of these two one-dimensional spaces, in which case its action on the tensor product is by
$V_{\mathfrak {p}}$
. Frobenius either fixes each of these two one-dimensional spaces, in which case its action on the tensor product is by
 $\det (\rho _{\mathfrak {p}^\infty }(\operatorname {Frob}_\ell )) = \ell $
; then
$\det (\rho _{\mathfrak {p}^\infty }(\operatorname {Frob}_\ell )) = \ell $
; then
 $L_\ell (\operatorname {Sym}^2 f, T) = 1 - \ell T$
, and
$L_\ell (\operatorname {Sym}^2 f, T) = 1 - \ell T$
, and
 $\rho _{\mathfrak {p}^\infty }({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_\ell |{\mathbf {Q}}_\ell )})$
is abelian. Or else
$\rho _{\mathfrak {p}^\infty }({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_\ell |{\mathbf {Q}}_\ell )})$
is abelian. Or else
 $\operatorname {Frob}_\ell $
swaps the two spaces; then it acts by the negative of the determinant (compare the proof of lemma 3.12), so
$\operatorname {Frob}_\ell $
swaps the two spaces; then it acts by the negative of the determinant (compare the proof of lemma 3.12), so
 $L_\ell (\operatorname {Sym}^2 f, T) = 1 + \ell T$
, and
$L_\ell (\operatorname {Sym}^2 f, T) = 1 + \ell T$
, and
 $\rho _{\mathfrak {p}^\infty }({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_\ell |{\mathbf {Q}}_\ell )})$
is nonabelian.
$\rho _{\mathfrak {p}^\infty }({ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}_\ell |{\mathbf {Q}}_\ell )})$
is nonabelian. -
(4) We assume that
 ${\mathbf {P}} \rho _{\mathfrak {p}^\infty }(I_\ell )$
is nonabelian. This implies that it is not unipotent. By lemma 3.12, the
${\mathbf {P}} \rho _{\mathfrak {p}^\infty }(I_\ell )$
is nonabelian. This implies that it is not unipotent. By lemma 3.12, the
 $I_\ell $
-coinvariant space of
$I_\ell $
-coinvariant space of
 $\operatorname {Sym}^2 V_{\mathfrak {p}}$
is trivial. This shows that
$\operatorname {Sym}^2 V_{\mathfrak {p}}$
is trivial. This shows that
 $L_\ell (\operatorname {Sym}^2 f, T) = 1$
. Also,
$L_\ell (\operatorname {Sym}^2 f, T) = 1$
. Also,
 ${\mathbf {P}} \rho _{\mathfrak {p}^\infty }|_{I_\ell }$
cannot factor through the tame inertia group since the latter is abelian. So there must be wild ramification at
${\mathbf {P}} \rho _{\mathfrak {p}^\infty }|_{I_\ell }$
cannot factor through the tame inertia group since the latter is abelian. So there must be wild ramification at
 $\ell $
both in
$\ell $
both in
 ${\mathbf {P}} \rho _{\mathfrak {p}^\infty }$
and in
${\mathbf {P}} \rho _{\mathfrak {p}^\infty }$
and in
 $\operatorname {Sym}^2 \rho _{\mathfrak {p}_\infty }$
. As the tame parts of the conductor exponents of these two are given by
$\operatorname {Sym}^2 \rho _{\mathfrak {p}_\infty }$
. As the tame parts of the conductor exponents of these two are given by
 $\dim V_{\mathfrak {p}} = 2$
and
$\dim V_{\mathfrak {p}} = 2$
and
 $\dim \operatorname {Sym}^2 V_{\mathfrak {p}} = 3$
, respectively, it follows that
$\dim \operatorname {Sym}^2 V_{\mathfrak {p}} = 3$
, respectively, it follows that
 $\ell ^3 \mid \tilde {N}$
and the conductor exponent c of
$\ell ^3 \mid \tilde {N}$
and the conductor exponent c of
 $\operatorname {Sym}^2 f$
is at least
$\operatorname {Sym}^2 f$
is at least
 $4$
. To obtain the claimed upper bound, we observe that when
$4$
. To obtain the claimed upper bound, we observe that when
 $\rho \colon G \to \mathrm {GL}(V)$
is a
$\rho \colon G \to \mathrm {GL}(V)$
is a
 $2$
-dimensional representation, then the codimension of the invariant subspace of
$2$
-dimensional representation, then the codimension of the invariant subspace of
 $\operatorname {Sym}^2 \rho $
is at most twice the codimension of the invariant subspace of
$\operatorname {Sym}^2 \rho $
is at most twice the codimension of the invariant subspace of
 $\rho $
. Then [Reference Serre97, Eq. (1.2.1)] implies that the wild part
$\rho $
. Then [Reference Serre97, Eq. (1.2.1)] implies that the wild part
 $c - 3$
of c is at most twice the wild part
$c - 3$
of c is at most twice the wild part
 $v_\ell (\tilde {N}) - 2$
of the conductor exponent of
$v_\ell (\tilde {N}) - 2$
of the conductor exponent of
 $\tilde {f}$
. This gives the desired bound.
$\tilde {f}$
. This gives the desired bound.
Given f, a choice of
![]() $\tilde {f}$
can be obtained from the LMFDB. Alternatively, the conductor d of the twisting character
$\tilde {f}$
can be obtained from the LMFDB. Alternatively, the conductor d of the twisting character
![]() $\varepsilon $
must satisfy
$\varepsilon $
must satisfy
![]() $d^2 \mid N$
, so we can check the finitely many possibilities for
$d^2 \mid N$
, so we can check the finitely many possibilities for
![]() $\varepsilon $
and compare the resulting levels to find
$\varepsilon $
and compare the resulting levels to find
![]() $\tilde {f}$
.
$\tilde {f}$
.
Which of the two possibilities for the Euler factor in case (3) is correct and what the correct choice of conductor exponent is in case (4) can be checked by trying all possibilities and determining which one is compatible with the functional equation. Using the function SymmetricPower that Magma provides for constructing symmetric power L-functions seems to result in fairly slow code. Instead, we compute the relevant number of coefficients ourselves and use this coefficient sequence when constructing the L-series, which is then used for testing the functional equation and evaluating at
![]() $s = 2$
.
$s = 2$
.
3.7 Computing the height of a Heegner point using the Gross–Zagier formula
To state the Gross–Zagier formula, we need to introduce some more notation. Let K be a Heegner field for f. Recall that H denotes the Hilbert class field of K. The Heegner cycle
![]() $\mathbf {x}_K$
on
$\mathbf {x}_K$
on
![]() $X_0(N)$
and the Heegner point
$X_0(N)$
and the Heegner point
![]() $y_K = [\mathbf {x}_K - h_K \cdot (\infty )] \in J_0(N)(K)$
have been defined in the introduction to this section. Recall that
$y_K = [\mathbf {x}_K - h_K \cdot (\infty )] \in J_0(N)(K)$
have been defined in the introduction to this section. Recall that
![]() $I_f = \operatorname {Ann}_{\mathbf {T}}(f)$
.
$I_f = \operatorname {Ann}_{\mathbf {T}}(f)$
.
The action of
![]() $\mathbf {T}$
(or its quotient
$\mathbf {T}$
(or its quotient
![]() $\mathrm {End}_{\mathbf {Q}}(J_0(N))$
) on
$\mathrm {End}_{\mathbf {Q}}(J_0(N))$
) on
![]() $J_0(N)(K)$
extends to a linear action on the real vector space
$J_0(N)(K)$
extends to a linear action on the real vector space
![]() $J_0(N)(K) \otimes _{\mathbf {Z}} {\mathbf {R}}$
. Since the center Z of
$J_0(N)(K) \otimes _{\mathbf {Z}} {\mathbf {R}}$
. Since the center Z of
![]() $\mathrm {End}_{\mathbf {Q}}(J_0(N))$
is an order in a totally real étale
$\mathrm {End}_{\mathbf {Q}}(J_0(N))$
is an order in a totally real étale
![]() ${\mathbf {Q}}$
-algebra, we obtain a canonical decomposition
${\mathbf {Q}}$
-algebra, we obtain a canonical decomposition
into isotypical linear subspaces. If
![]() $\sigma $
factors through
$\sigma $
factors through
![]() ${\mathbf {Z}}[f]$
, then
${\mathbf {Z}}[f]$
, then
and by the Heegner hypothesis (which implies that
![]() $A_f^{\vee }(K)$
has rank
$A_f^{\vee }(K)$
has rank
![]() $1$
as a
$1$
as a
![]() ${\mathbf {Z}}[f]$
-module), it follows that
${\mathbf {Z}}[f]$
-module), it follows that
![]() $\dim J_0(N)(K)_\sigma = 1$
. We will abuse notation slightly and also write
$\dim J_0(N)(K)_\sigma = 1$
. We will abuse notation slightly and also write
![]() $J_0(N)(K)_\sigma $
when
$J_0(N)(K)_\sigma $
when
![]() $\sigma \in \Sigma $
, implicitly pre-composing with the projection
$\sigma \in \Sigma $
, implicitly pre-composing with the projection
![]() $Z \to {\mathbf {Z}}[f]$
. We write
$Z \to {\mathbf {Z}}[f]$
. We write
![]() $y_{K,\sigma } \in J_0(N)(K)_\sigma $
for the components of
$y_{K,\sigma } \in J_0(N)(K)_\sigma $
for the components of
![]() $y_K$
with respect to this composition and set
$y_K$
with respect to this composition and set
Then
![]() $\lambda _f(y_K^f) = y_{K,A_f}$
; compare the diagram (3.4). Note that
$\lambda _f(y_K^f) = y_{K,A_f}$
; compare the diagram (3.4). Note that
![]() $\omega \in {\mathbf {Q}}(f)$
acts on
$\omega \in {\mathbf {Q}}(f)$
acts on
![]() $y_{K,\sigma }$
as
$y_{K,\sigma }$
as
![]() $\omega \cdot y_{K,\sigma } = \omega ^\sigma y_{K,\sigma }$
. Explicitly, when
$\omega \cdot y_{K,\sigma } = \omega ^\sigma y_{K,\sigma }$
. Explicitly, when
![]() $(b_j)_{1 \le j \le g}$
is a
$(b_j)_{1 \le j \le g}$
is a
![]() ${\mathbf {Z}}$
-basis of
${\mathbf {Z}}$
-basis of
![]() ${\mathbf {Z}}[f]$
and
${\mathbf {Z}}[f]$
and
![]() $(b_j^*)_{1 \le j \le g}$
is its dual basis in
$(b_j^*)_{1 \le j \le g}$
is its dual basis in
![]() ${\mathbf {Z}}[f] \otimes _{{\mathbf {Z}}} {\mathbf {R}}$
with respect to the trace form, we have
${\mathbf {Z}}[f] \otimes _{{\mathbf {Z}}} {\mathbf {R}}$
with respect to the trace form, we have
 $$ \begin{align} y_{K,\sigma} = \sum_{j=1}^g (b_j \cdot y_K) \otimes {b_j^*}^\sigma. \end{align} $$
$$ \begin{align} y_{K,\sigma} = \sum_{j=1}^g (b_j \cdot y_K) \otimes {b_j^*}^\sigma. \end{align} $$
The normalized canonical height on
![]() $J_0(N)(K)$
(with respect to twice the theta divisor) induces a positive definite quadratic form on
$J_0(N)(K)$
(with respect to twice the theta divisor) induces a positive definite quadratic form on
![]() $J_0(N)(K) \otimes _{\mathbf {Z}} {\mathbf {R}}$
, which (by abuse of notation) we also denote
$J_0(N)(K) \otimes _{\mathbf {Z}} {\mathbf {R}}$
, which (by abuse of notation) we also denote
![]() ${\hat {h}}$
. Since the endomorphisms are self-adjoint with respect to the height pairing (this is because they are fixed under the Rosati involution; see [Reference Birkenhake and Lange9, Section 5.5] and recall that the endomorphism ring is totally real), it follows that the
${\hat {h}}$
. Since the endomorphisms are self-adjoint with respect to the height pairing (this is because they are fixed under the Rosati involution; see [Reference Birkenhake and Lange9, Section 5.5] and recall that the endomorphism ring is totally real), it follows that the
![]() $\sigma $
-components are pairwise orthogonal under the height pairing.
$\sigma $
-components are pairwise orthogonal under the height pairing.
Recall that we write
![]() $L(f/K, s)$
for the L-function of f base-changed to K. This is the same as
$L(f/K, s)$
for the L-function of f base-changed to K. This is the same as
![]() $L(f, \mathbf {1}, s)$
for the trivial character
$L(f, \mathbf {1}, s)$
for the trivial character
![]() $\mathbf {1} \colon {\mathrm {Gal}}(H|K) \to {\mathbf {C}}^\times $
in the notation of [Reference Gross and Zagier52].
$\mathbf {1} \colon {\mathrm {Gal}}(H|K) \to {\mathbf {C}}^\times $
in the notation of [Reference Gross and Zagier52].
Theorem 3.14 (Gross–Zagier formula)
With the notation introduced above and assuming that
![]() $D_K$
is odd, we have
$D_K$
is odd, we have
 $$\begin{align*}{\hat{h}}(y_{K,\sigma}) = L'(f^\sigma/K, 1) \frac{u_K^2 \sqrt{-D_K}}{16 \boldsymbol{\pi}^2 \|f^\sigma\|^2} . \end{align*}$$
$$\begin{align*}{\hat{h}}(y_{K,\sigma}) = L'(f^\sigma/K, 1) \frac{u_K^2 \sqrt{-D_K}}{16 \boldsymbol{\pi}^2 \|f^\sigma\|^2} . \end{align*}$$
Here,
![]() $u_K := \#\mathcal {O}_K^\times /{\mathbf {Z}}^\times $
, which equals
$u_K := \#\mathcal {O}_K^\times /{\mathbf {Z}}^\times $
, which equals
![]() $1$
for
$1$
for
![]() $D_K < -4$
,
$D_K < -4$
,
![]() $2$
for
$2$
for
![]() $D_K = -4$
and
$D_K = -4$
and
![]() $3$
for
$3$
for
![]() $D_K = -3$
.
$D_K = -3$
.
Proof. This is a reformulation of [Reference Gross and Zagier52, Theorem I.6.3], taking into account that our
![]() ${\hat {h}}$
is
${\hat {h}}$
is
![]() $1/2h_K$
times the height used there (see [Reference Gross and Zagier52, Eq. (I.6.4)]), where
$1/2h_K$
times the height used there (see [Reference Gross and Zagier52, Eq. (I.6.4)]), where
![]() $h_K$
is the class number of K. Note that Gross and Zagier assume that the Heegner discriminant is odd; see [Reference Gross and Zagier52, § I.3].
$h_K$
is the class number of K. Note that Gross and Zagier assume that the Heegner discriminant is odd; see [Reference Gross and Zagier52, § I.3].
To evaluate this formula, we need the Petersson norm from 3.5, and we need to evaluate
![]() $L'(f^\sigma /K, 1)$
. By the Artin formalism of L-functions,
$L'(f^\sigma /K, 1)$
. By the Artin formalism of L-functions,
with
![]() $f \otimes \varepsilon _K$
the twist of f by (the Kronecker character associated to) K. Its first derivative at
$f \otimes \varepsilon _K$
the twist of f by (the Kronecker character associated to) K. Its first derivative at
![]() $s = 1$
is
$s = 1$
is
Since K is a Heegner field by assumption,
![]() $L(f/K, s)$
vanishes to first order at
$L(f/K, s)$
vanishes to first order at
![]() $s = 1$
. This implies that exactly one of the two terms in the sum is nonzero; which one it is can be decided by considering the action of the Fricke involution
$s = 1$
. This implies that exactly one of the two terms in the sum is nonzero; which one it is can be decided by considering the action of the Fricke involution
![]() $w_N$
on f: if
$w_N$
on f: if
![]() $w_N \cdot f = f$
, then
$w_N \cdot f = f$
, then
![]() $L(f, 1) = 0$
; otherwise,
$L(f, 1) = 0$
; otherwise,
![]() $w_N \cdot f = -f$
, and
$w_N \cdot f = -f$
, and
![]() $L'(f, 1) = 0$
. The special values of the L-functions of newforms and their derivatives can be computed to arbitrary precision using Tim Dokchitser’s Magma implementation [Reference Dokchitser40]. It provides a TensorProduct function for L-functions, which, however, tends to be slow in our use case. So we construct the tensor product L-function
$L'(f, 1) = 0$
. The special values of the L-functions of newforms and their derivatives can be computed to arbitrary precision using Tim Dokchitser’s Magma implementation [Reference Dokchitser40]. It provides a TensorProduct function for L-functions, which, however, tends to be slow in our use case. So we construct the tensor product L-function
![]() $L(f \otimes \varepsilon _K, s)$
‘by hand’ for performance reasons, explicitly giving the Euler factors.
$L(f \otimes \varepsilon _K, s)$
‘by hand’ for performance reasons, explicitly giving the Euler factors.
We finally obtain a formula for
![]() ${\hat {h}}(y_K^f)$
.
${\hat {h}}(y_K^f)$
.
Corollary 3.15. Let K be a Heegner field for f and let
![]() $y_K^f \in A_f(K)^{\vee }$
be an associated Heegner point. Then
$y_K^f \in A_f(K)^{\vee }$
be an associated Heegner point. Then
 $$\begin{align*}{\hat{h}}(y_K^f) = \frac{u_K^2 \sqrt{-D_K} \boldsymbol{\pi}}{2 N \prod_{\ell^2 \mid N} C_\ell} \sum_{\sigma \in \Sigma} \frac{L'(f^\sigma/K, 1)}{L(\operatorname{Sym}^2 f^\sigma, 2)} . \end{align*}$$
$$\begin{align*}{\hat{h}}(y_K^f) = \frac{u_K^2 \sqrt{-D_K} \boldsymbol{\pi}}{2 N \prod_{\ell^2 \mid N} C_\ell} \sum_{\sigma \in \Sigma} \frac{L'(f^\sigma/K, 1)}{L(\operatorname{Sym}^2 f^\sigma, 2)} . \end{align*}$$
3.8 Comparing canonical heights
Our goal in this section is to determine
![]() ${\hat {h}}_J(y_{K,\pi })$
(so that we can either use that to identify
${\hat {h}}_J(y_{K,\pi })$
(so that we can either use that to identify
![]() $y_{K,\pi }$
up to a sign and adding torsion assuming there is an essentially unique point of that height, or to verify that our computation of
$y_{K,\pi }$
up to a sign and adding torsion assuming there is an essentially unique point of that height, or to verify that our computation of
![]() $y_{K,\pi }$
is correct). Recall the diagram (3.4) –in particular, the endomorphism
$y_{K,\pi }$
is correct). Recall the diagram (3.4) –in particular, the endomorphism
![]() $\alpha $
of J defined in (3.5). Note that
$\alpha $
of J defined in (3.5). Note that
![]() $\lambda = \pi _J \circ \pi _J^{\vee }$
equals
$\lambda = \pi _J \circ \pi _J^{\vee }$
equals
![]() $\alpha $
composed with the inverse of the canonical polarization
$\alpha $
composed with the inverse of the canonical polarization
![]() $\lambda _J$
of J induced by the theta divisor.
$\lambda _J$
of J induced by the theta divisor.
We freely use standard facts about height pairings on abelian varieties; see, for example, [Reference Bombieri and Gubler10, § 9]. We denote by
![]() $\langle {-}, {-} \rangle _J$
the height pairing on J (such that
$\langle {-}, {-} \rangle _J$
the height pairing on J (such that
![]() ${\hat {h}}_J(x) = \langle x, x \rangle _J$
). By [Reference Bombieri and Gubler10, Prop. 9.3.6] (noting that our
${\hat {h}}_J(x) = \langle x, x \rangle _J$
). By [Reference Bombieri and Gubler10, Prop. 9.3.6] (noting that our
![]() ${\hat {h}}_J$
is twice their
${\hat {h}}_J$
is twice their
![]() ${\hat {h}}_\theta $
), it satisfies
${\hat {h}}_\theta $
), it satisfies
where
![]() ${\hat {h}}_{\mathscr {P}}({-})$
is the canonical height on
${\hat {h}}_{\mathscr {P}}({-})$
is the canonical height on
![]() $J^{\vee } \times J$
associated to the Poincaré bundle
$J^{\vee } \times J$
associated to the Poincaré bundle
![]() $\mathscr {P}$
. Similarly, we obtain the canonical height associated to a polarization
$\mathscr {P}$
. Similarly, we obtain the canonical height associated to a polarization
![]() $\lambda \colon J^{\vee } \to J$
as
$\lambda \colon J^{\vee } \to J$
as
![]() ${\hat {h}}_\lambda (x) = {\hat {h}}_{\mathscr {P}}(x, \lambda (x))$
. If
${\hat {h}}_\lambda (x) = {\hat {h}}_{\mathscr {P}}(x, \lambda (x))$
. If
![]() $\varphi \colon A \to J$
is a homomorphism and
$\varphi \colon A \to J$
is a homomorphism and
![]() $\lambda _{A^{\vee }} \colon A^{\vee } \to A$
is a polarization such that
$\lambda _{A^{\vee }} \colon A^{\vee } \to A$
is a polarization such that
with
![]() $\alpha \in \mathrm {End}_{\mathbf {Q}}(J)$
, then by functoriality of heights, we have for
$\alpha \in \mathrm {End}_{\mathbf {Q}}(J)$
, then by functoriality of heights, we have for
![]() $x \in J({\overline {{\mathbf {Q}}}})$
$x \in J({\overline {{\mathbf {Q}}}})$
 $$ \begin{align*} {\hat{h}}_{\lambda_{A^{\vee}}}(\varphi^{\vee}(\lambda_J(x))) &= {\hat{h}}_{{\varphi^{\vee}}^* \lambda_{A^{\vee}}}(\lambda_J(x)) = {\hat{h}}_{\lambda}(\lambda_J(x)) = {\hat{h}}_{\mathscr{P}}(\lambda_J(x), \lambda(\lambda_J(x))) \\ &= {\hat{h}}_{\mathscr{P}}(\lambda_J(x), \alpha(x)) = \langle x, \alpha(x) \rangle_J. \end{align*} $$
$$ \begin{align*} {\hat{h}}_{\lambda_{A^{\vee}}}(\varphi^{\vee}(\lambda_J(x))) &= {\hat{h}}_{{\varphi^{\vee}}^* \lambda_{A^{\vee}}}(\lambda_J(x)) = {\hat{h}}_{\lambda}(\lambda_J(x)) = {\hat{h}}_{\mathscr{P}}(\lambda_J(x), \lambda(\lambda_J(x))) \\ &= {\hat{h}}_{\mathscr{P}}(\lambda_J(x), \alpha(x)) = \langle x, \alpha(x) \rangle_J. \end{align*} $$
Proposition 3.16. For each
![]() $\sigma \in \Sigma $
, write
$\sigma \in \Sigma $
, write
![]() $y_{K,\pi ,\sigma } = \pi _J(y_{K,\sigma }) \in J(K) \otimes _{\mathbf {Z}} {\mathbf {R}}$
for the
$y_{K,\pi ,\sigma } = \pi _J(y_{K,\sigma }) \in J(K) \otimes _{\mathbf {Z}} {\mathbf {R}}$
for the
![]() $\sigma $
-component of
$\sigma $
-component of
![]() $y_{K,\pi }$
. Then
$y_{K,\pi }$
. Then
![]() ${\hat {h}}_J(y_{K,\pi ,\sigma }) = \alpha ^\sigma {\hat {h}}(y_{K,\sigma })$
, and so
${\hat {h}}_J(y_{K,\pi ,\sigma }) = \alpha ^\sigma {\hat {h}}(y_{K,\sigma })$
, and so
Proof. Chasing
![]() $y_{K,\sigma }$
through the diagram (3.4) and taking into account the definition of
$y_{K,\sigma }$
through the diagram (3.4) and taking into account the definition of
![]() $\alpha \in \mathcal {O} \subseteq {\mathbf {Q}}(f)$
, we see that (identifying
$\alpha \in \mathcal {O} \subseteq {\mathbf {Q}}(f)$
, we see that (identifying
![]() $A_f^{\vee }(K)$
with its image under the inclusion
$A_f^{\vee }(K)$
with its image under the inclusion
![]() $\iota _f$
)
$\iota _f$
)
 $$ \begin{align*} \pi^{\vee}\bigl(\lambda_J(y_{K,\pi,\sigma})\bigr) &= \pi^{\vee}\bigl((\lambda_J \circ \pi_J)(y_{K,\sigma})\bigr) = \pi_J^{\vee}\bigl((\lambda_J \circ \pi_J)(y_{K,\sigma})\bigr) \\ &= \alpha \cdot y_{K,\sigma} = \alpha^\sigma y_{K,\sigma}. \end{align*} $$
$$ \begin{align*} \pi^{\vee}\bigl(\lambda_J(y_{K,\pi,\sigma})\bigr) &= \pi^{\vee}\bigl((\lambda_J \circ \pi_J)(y_{K,\sigma})\bigr) = \pi_J^{\vee}\bigl((\lambda_J \circ \pi_J)(y_{K,\sigma})\bigr) \\ &= \alpha \cdot y_{K,\sigma} = \alpha^\sigma y_{K,\sigma}. \end{align*} $$
By the discussion preceding the proposition, we have
 $$ \begin{align*} {\hat{h}}\bigl(\pi^{\vee}\bigl(\lambda_J(y_{K,\pi,\sigma})\bigr)\bigr) &= \langle y_{K,\pi,\sigma}, \alpha \cdot y_{K,\pi,\sigma} \rangle_J = \langle y_{K,\pi,\sigma}, \alpha^\sigma y_{K,\pi,\sigma} \rangle_J \\ &= \alpha^\sigma \langle y_{K,\pi,\sigma}, y_{K,\pi,\sigma} \rangle_J = \alpha^\sigma {\hat{h}}_J(y_{K,\pi,\sigma}). \end{align*} $$
$$ \begin{align*} {\hat{h}}\bigl(\pi^{\vee}\bigl(\lambda_J(y_{K,\pi,\sigma})\bigr)\bigr) &= \langle y_{K,\pi,\sigma}, \alpha \cdot y_{K,\pi,\sigma} \rangle_J = \langle y_{K,\pi,\sigma}, \alpha^\sigma y_{K,\pi,\sigma} \rangle_J \\ &= \alpha^\sigma \langle y_{K,\pi,\sigma}, y_{K,\pi,\sigma} \rangle_J = \alpha^\sigma {\hat{h}}_J(y_{K,\pi,\sigma}). \end{align*} $$
Therefore,
When X is a quotient of
![]() $X_0(N)$
, this gives a particularly simple formula.
$X_0(N)$
, this gives a particularly simple formula.
Corollary 3.17. Assume that
![]() $\pi _X \colon X_0(N) \to X$
is a finite covering of curves of degree n and that
$\pi _X \colon X_0(N) \to X$
is a finite covering of curves of degree n and that
![]() $\pi _J \colon J_0(N) \to J$
is induced by
$\pi _J \colon J_0(N) \to J$
is induced by
![]() $\pi _X$
via Albanese functoriality. Then
$\pi _X$
via Albanese functoriality. Then
Proof. In this case,
![]() $\alpha = \lambda _J \circ \pi _J \circ \pi _J^{\vee }$
is multiplication by
$\alpha = \lambda _J \circ \pi _J \circ \pi _J^{\vee }$
is multiplication by
![]() $\deg \pi _X = n$
, so
$\deg \pi _X = n$
, so
![]() $\alpha ^\sigma = n$
for all
$\alpha ^\sigma = n$
for all
![]() $\sigma \in \Sigma $
. Now use proposition 3.16.
$\sigma \in \Sigma $
. Now use proposition 3.16.
In the general case, we can determine
![]() $\alpha $
as described in Section 3.1. We record the final general formula for the height of
$\alpha $
as described in Section 3.1. We record the final general formula for the height of
![]() $y_{K,\pi }$
.
$y_{K,\pi }$
.
Corollary 3.18. With the notation introduced so far, we have
 $$\begin{align*}{\hat{h}}_J(y_{K,\pi}) = \frac{u_K^2 \sqrt{-D_K} \boldsymbol{\pi}}{2 N \prod_{\ell^2 \mid N} C_\ell} \sum_{\sigma \in \Sigma} \alpha^\sigma \frac{L'(f^\sigma/K, 1)}{L(\operatorname{Sym}^2 f^\sigma, 2)} . \end{align*}$$
$$\begin{align*}{\hat{h}}_J(y_{K,\pi}) = \frac{u_K^2 \sqrt{-D_K} \boldsymbol{\pi}}{2 N \prod_{\ell^2 \mid N} C_\ell} \sum_{\sigma \in \Sigma} \alpha^\sigma \frac{L'(f^\sigma/K, 1)}{L(\operatorname{Sym}^2 f^\sigma, 2)} . \end{align*}$$
Remark 3.19. In a similar way as in the proof of proposition 3.16, we obtain the formula
for arbitrary
![]() $\beta , \gamma \in \mathcal {O}$
. This allows us to compute the height pairing matrix M for a
$\beta , \gamma \in \mathcal {O}$
. This allows us to compute the height pairing matrix M for a
![]() ${\mathbf {Z}}$
-basis of
${\mathbf {Z}}$
-basis of
![]() $\mathcal {O} y_{K,\pi }$
and from this the regulator
$\mathcal {O} y_{K,\pi }$
and from this the regulator
![]() $\operatorname {Reg}_{\mathcal {O} y_{K,\pi }} = \det M$
. Then the Heegner index is given by
$\operatorname {Reg}_{\mathcal {O} y_{K,\pi }} = \det M$
. Then the Heegner index is given by
 $$\begin{align*}I_{K,\pi} = \#J(K)_{\mathrm{tors}} \sqrt{\frac{\operatorname{Reg}_{\mathcal{O} y_{K,\pi}}}{\operatorname{Reg}_{J(K)}}} . \end{align*}$$
$$\begin{align*}I_{K,\pi} = \#J(K)_{\mathrm{tors}} \sqrt{\frac{\operatorname{Reg}_{\mathcal{O} y_{K,\pi}}}{\operatorname{Reg}_{J(K)}}} . \end{align*}$$
4 Computing the analytic order of 
Recall that J is an absolutely simple and principally polarized abelian variety over
![]() ${\mathbf {Q}}$
of dimension g of
${\mathbf {Q}}$
of dimension g of
![]() $\mathrm {GL}_2$
-type with associated newform
$\mathrm {GL}_2$
-type with associated newform
![]() $f \in S_2(\Gamma _0(N))$
, and
$f \in S_2(\Gamma _0(N))$
, and
![]() $A_f$
is the modular abelian variety associated to f. In particular,
$A_f$
is the modular abelian variety associated to f. In particular,
![]() $A_f$
and J are isogenous.
$A_f$
and J are isogenous.
For an abelian variety J over a number field F, we define the Tamagawa product to be
where v runs through the finite places of F. When J is the Jacobian variety of an explicitly given curve, the Tamagawa numbers
![]() $c_v(C/F)$
(which are
$c_v(C/F)$
(which are
![]() $1$
for all places of good reduction) and hence the Tamagawa product
$1$
for all places of good reduction) and hence the Tamagawa product
![]() $ {\mathrm {Tam}}(J/F)$
can be computed. For Jacobians of genus
$ {\mathrm {Tam}}(J/F)$
can be computed. For Jacobians of genus
![]() $2$
curves in the LMFDB [68], this information is also available in the LMFDB. For the Tamagawa number at
$2$
curves in the LMFDB [68], this information is also available in the LMFDB. For the Tamagawa number at
![]() $2$
in the example in Appendix A, we compute a regular model by hand.
$2$
in the example in Appendix A, we compute a regular model by hand.
We now describe how to compute the analytic order of the Tate–Shafarevich group

as an exact positive rational number, assuming that
![]() $L\!\operatorname {-rk} J \in \{0,1\}$
.
$L\!\operatorname {-rk} J \in \{0,1\}$
.
Note that we can provably verify that
![]() $L\!\operatorname {-rk} J \in \{0, 1\}$
and determine
$L\!\operatorname {-rk} J \in \{0, 1\}$
and determine
![]() $L\!\operatorname {-rk} J$
in this case. The Fricke involution
$L\!\operatorname {-rk} J$
in this case. The Fricke involution
![]() $w_N$
sends f to f or
$w_N$
sends f to f or
![]() $-f$
. In the first case, the analytic order of
$-f$
. In the first case, the analytic order of
![]() $L(f,s)$
is odd, and in the second case, it is even. In the even case, we can show that
$L(f,s)$
is odd, and in the second case, it is even. In the even case, we can show that
![]() $L(f,1) \neq 0$
, and in the odd case that
$L(f,1) \neq 0$
, and in the odd case that
![]() $L'(f,1) \neq 0$
by computing the respective value numerically to a high enough precision.
$L'(f,1) \neq 0$
by computing the respective value numerically to a high enough precision.
4.1 Comparing the real periods of
 $A_f$
and J
$A_f$
and J
Let A be an abelian variety over
![]() ${\mathbf {Q}}$
of dimension g with Néron model
${\mathbf {Q}}$
of dimension g with Néron model
![]() $\mathscr {A}$
over
$\mathscr {A}$
over
![]() ${\mathbf {Z}}$
. We say that a
${\mathbf {Z}}$
. We say that a
![]() ${\mathbf {Q}}$
-basis of
${\mathbf {Q}}$
-basis of
![]() ${\operatorname {H}}^0(A, \Omega ^1)$
is a Néron basis for A if it is a
${\operatorname {H}}^0(A, \Omega ^1)$
is a Néron basis for A if it is a
![]() ${\mathbf {Z}}$
basis of the image of
${\mathbf {Z}}$
basis of the image of
![]() ${\operatorname {H}}^0(\mathscr {A}, \Omega ^1_{\mathscr {A}/{\mathbf {Z}}})$
. Let
${\operatorname {H}}^0(\mathscr {A}, \Omega ^1_{\mathscr {A}/{\mathbf {Z}}})$
. Let
![]() $(\omega _1, \ldots , \omega _g)$
be a Néron basis for A. Then
$(\omega _1, \ldots , \omega _g)$
be a Néron basis for A. Then
![]() $\omega _A := \omega _1 \wedge \dots \wedge \omega _g$
is a generator of the free
$\omega _A := \omega _1 \wedge \dots \wedge \omega _g$
is a generator of the free
![]() ${\mathbf {Z}}$
-module of rank
${\mathbf {Z}}$
-module of rank
![]() $1 {\operatorname {H}}^0(\mathscr {A}, \Omega ^g_{\mathscr {A}/{\mathbf {Z}}})$
. Recall that the real period of A is
$1 {\operatorname {H}}^0(\mathscr {A}, \Omega ^g_{\mathscr {A}/{\mathbf {Z}}})$
. Recall that the real period of A is
Let B be another abelian variety over
![]() ${\mathbf {Q}}$
of dimension g with Néron model
${\mathbf {Q}}$
of dimension g with Néron model
![]() $\mathscr {B}$
over
$\mathscr {B}$
over
![]() ${\mathbf {Z}}$
, and let
${\mathbf {Z}}$
, and let
![]() $\pi \colon A \to B$
be an isogeny. Since by the Néron mapping property,
$\pi \colon A \to B$
be an isogeny. Since by the Néron mapping property,
![]() $\pi $
uniquely extends to the Néron models, one has
$\pi $
uniquely extends to the Néron models, one has
![]() $\pi ^*\omega _B = n_\pi \cdot \omega _A$
with an integer
$\pi ^*\omega _B = n_\pi \cdot \omega _A$
with an integer
![]() $n_\pi $
. By the above,
$n_\pi $
. By the above,
![]() $|n_\pi | = c_\pi $
, where
$|n_\pi | = c_\pi $
, where
![]() $c_\pi $
is defined in definition 3.3. We now compare
$c_\pi $
is defined in definition 3.3. We now compare
![]() $\Omega _A$
and
$\Omega _A$
and
![]() $\Omega _B$
.
$\Omega _B$
.
Lemma 4.1. Let
![]() $\pi \colon A \to B$
be an isogeny of abelian varieties of dimension g over
$\pi \colon A \to B$
be an isogeny of abelian varieties of dimension g over
![]() ${\mathbf {Q}}$
. Denote by
${\mathbf {Q}}$
. Denote by
![]() $\pi _{\mathbf {R}}$
the induced morphism
$\pi _{\mathbf {R}}$
the induced morphism
![]() $A({\mathbf {R}}) \to B({\mathbf {R}})$
on the real Lie groups. Then
$A({\mathbf {R}}) \to B({\mathbf {R}})$
on the real Lie groups. Then
Here,
![]() $c_\pi $
divides
$c_\pi $
divides
![]() $e(\pi )^g$
, where
$e(\pi )^g$
, where
![]() $e(\pi )$
is the exponent of
$e(\pi )$
is the exponent of
![]() $\mathrm {ker} \pi $
,
$\mathrm {ker} \pi $
,
![]() $\#\mathrm {ker}\pi _{\mathbf {R}}$
divides
$\#\mathrm {ker}\pi _{\mathbf {R}}$
divides
![]() $\deg \pi $
, and
$\deg \pi $
, and
![]() $\# {\mathrm {coker}}\pi _{\mathbf {R}}$
divides the number
$\# {\mathrm {coker}}\pi _{\mathbf {R}}$
divides the number
![]() $\#\pi _0(B({\mathbf {R}}))$
of connected components of
$\#\pi _0(B({\mathbf {R}}))$
of connected components of
![]() $B({\mathbf {R}})$
, which divides
$B({\mathbf {R}})$
, which divides
![]() $2^g$
.
$2^g$
.
Proof. The isogeny
![]() $\pi $
induces a short exact sequence of real Lie groups
$\pi $
induces a short exact sequence of real Lie groups
This gives, for
![]() $\omega \in {\operatorname {H}}^0(B, \Omega ^g)$
,
$\omega \in {\operatorname {H}}^0(B, \Omega ^g)$
,
 $$\begin{align*}\int_{A({\mathbf{R}})} \pi^* \omega = \#\mathrm{ker} \pi_{\mathbf{R}} \cdot \int_{\operatorname{\mathrm{im}}(\pi_{\mathbf{R}})} \omega = \frac{\#\mathrm{ker} \pi_{\mathbf{R}}}{\#\operatorname{\mathrm{coker}} \pi_{\mathbf{R}}} \int_{B({\mathbf{R}})} \omega, \end{align*}$$
$$\begin{align*}\int_{A({\mathbf{R}})} \pi^* \omega = \#\mathrm{ker} \pi_{\mathbf{R}} \cdot \int_{\operatorname{\mathrm{im}}(\pi_{\mathbf{R}})} \omega = \frac{\#\mathrm{ker} \pi_{\mathbf{R}}}{\#\operatorname{\mathrm{coker}} \pi_{\mathbf{R}}} \int_{B({\mathbf{R}})} \omega, \end{align*}$$
where the second equality uses that
![]() $\omega $
is translation-invariant (compare [Reference Jorza57, Lemma 5.13]). Hence,
$\omega $
is translation-invariant (compare [Reference Jorza57, Lemma 5.13]). Hence,
 $$ \begin{align*} \frac{\Omega_B}{\Omega_A} &= \frac{\int_{B({\mathbf{R}})}|\omega_B|}{\int_{A({\mathbf{R}})}|\omega_A|} = \frac{c_\pi \cdot \int_{B({\mathbf{R}})}|\omega_B|}{\int_{A({\mathbf{R}})}|\pi^*\omega_B|} \\ &= \frac{c_\pi \cdot \#\operatorname{\mathrm{coker}} \pi_{\mathbf{R}} \cdot \int_{B({\mathbf{R}})}|\omega_B|}{\#\mathrm{ker} \pi_{\mathbf{R}} \cdot\int_{B({\mathbf{R}})}|\omega_B|} = \frac{c_\pi \cdot \#\operatorname{\mathrm{coker}} \pi_{\mathbf{R}}}{\#\mathrm{ker} \pi_{\mathbf{R}}}. \end{align*} $$
$$ \begin{align*} \frac{\Omega_B}{\Omega_A} &= \frac{\int_{B({\mathbf{R}})}|\omega_B|}{\int_{A({\mathbf{R}})}|\omega_A|} = \frac{c_\pi \cdot \int_{B({\mathbf{R}})}|\omega_B|}{\int_{A({\mathbf{R}})}|\pi^*\omega_B|} \\ &= \frac{c_\pi \cdot \#\operatorname{\mathrm{coker}} \pi_{\mathbf{R}} \cdot \int_{B({\mathbf{R}})}|\omega_B|}{\#\mathrm{ker} \pi_{\mathbf{R}} \cdot\int_{B({\mathbf{R}})}|\omega_B|} = \frac{c_\pi \cdot \#\operatorname{\mathrm{coker}} \pi_{\mathbf{R}}}{\#\mathrm{ker} \pi_{\mathbf{R}}}. \end{align*} $$
One has
![]() $\#\mathrm {ker}\pi _{\mathbf {R}} \mid \deg \pi $
because
$\#\mathrm {ker}\pi _{\mathbf {R}} \mid \deg \pi $
because
![]() $\mathrm {ker} \pi _{\mathbf {R}} \subseteq \mathrm {ker} \pi $
. Let
$\mathrm {ker} \pi _{\mathbf {R}} \subseteq \mathrm {ker} \pi $
. Let
![]() $\pi ' \colon B \xrightarrow {\sim } A/\mathrm {ker} \pi \to A/A[e(\pi )] \xrightarrow {\sim } A$
be the isogeny such that
$\pi ' \colon B \xrightarrow {\sim } A/\mathrm {ker} \pi \to A/A[e(\pi )] \xrightarrow {\sim } A$
be the isogeny such that
![]() $\pi ' \circ \pi $
is multiplication by
$\pi ' \circ \pi $
is multiplication by
![]() $e(\pi )$
. Then
$e(\pi )$
. Then
so
![]() $c_\pi = |n_\pi |$
divides
$c_\pi = |n_\pi |$
divides
![]() $e(\pi )^g$
.
$e(\pi )^g$
.
![]() $\pi _{\mathbf {R}}$
is a topological covering map, so its image is open and closed (i.e., a union of connected components). This implies that
$\pi _{\mathbf {R}}$
is a topological covering map, so its image is open and closed (i.e., a union of connected components). This implies that
![]() $\# {\mathrm {coker}} \pi _{\mathbf {R}}$
divides
$\# {\mathrm {coker}} \pi _{\mathbf {R}}$
divides
![]() $\#\pi _0(B({\mathbf {R}}))$
. Since the trace map
$\#\pi _0(B({\mathbf {R}}))$
. Since the trace map
![]() $B({\mathbf {C}}) \to B({\mathbf {R}})$
has image the connected component
$B({\mathbf {C}}) \to B({\mathbf {R}})$
has image the connected component
![]() $B({\mathbf {R}})^0$
of the origin, it follows that
$B({\mathbf {R}})^0$
of the origin, it follows that
![]() $\pi _0(B({\mathbf {R}}))$
is killed by
$\pi _0(B({\mathbf {R}}))$
is killed by
![]() $2$
. This implies that
$2$
. This implies that
![]() $\pi _0(B({\mathbf {R}}))$
is isomorphic to
$\pi _0(B({\mathbf {R}}))$
is isomorphic to
![]() $B({\mathbf {R}})[2]/B({\mathbf {R}})^0[2]$
of order dividing
$B({\mathbf {R}})[2]/B({\mathbf {R}})^0[2]$
of order dividing
![]() $4^g/2^g = 2^g$
[Reference Schaefer92, proof of Lemma 3.10].
$4^g/2^g = 2^g$
[Reference Schaefer92, proof of Lemma 3.10].
Note that we can determine
![]() $\#\mathrm {ker} \pi _{\mathbf {R}}$
and
$\#\mathrm {ker} \pi _{\mathbf {R}}$
and
![]() $\# {\mathrm {coker}} \pi _{\mathbf {R}}$
explicitly if we have a suitable computational representation of the isogeny
$\# {\mathrm {coker}} \pi _{\mathbf {R}}$
explicitly if we have a suitable computational representation of the isogeny
![]() $\pi $
; see Section 3.1.
$\pi $
; see Section 3.1.
Remark 4.2. See [Reference Jorza57, Lemma 5.13] for a similar statement over arbitrary completions of global fields.
4.2 Computing
 $L(J/{\mathbf {Q}}, 1)/\Omega _J$
$L(J/{\mathbf {Q}}, 1)/\Omega _J$
We now consider the isogeny
![]() $\pi \colon A_f \to J$
. The formula for
$\pi \colon A_f \to J$
. The formula for ![]() in the case of L-rank
in the case of L-rank
![]() $0$
contains the factor
$0$
contains the factor
![]() $L(J/{\mathbf {Q}}, 1)/\Omega _J$
. In this section, we explain how this quotient can be computed as a rational number. We will then also use this later applied to a rank
$L(J/{\mathbf {Q}}, 1)/\Omega _J$
. In this section, we explain how this quotient can be computed as a rational number. We will then also use this later applied to a rank
![]() $0$
quadratic twist of J when dealing with the L-rank
$0$
quadratic twist of J when dealing with the L-rank
![]() $1$
case. By lemma 4.1, we have
$1$
case. By lemma 4.1, we have
 $$\begin{align*}\frac{L(J/{\mathbf{Q}}, 1)}{\Omega_J} = \frac{L(A_f/{\mathbf{Q}}, 1)}{\Omega_{A_f}} \cdot \frac{\Omega_{A_f}}{\Omega_J} = \frac{L(A_f/{\mathbf{Q}}, 1)}{\Omega_{A_f}} \cdot \frac{1}{c_\pi} \cdot \frac{\#\mathrm{ker} \pi_{\mathbf{R}}}{\#\operatorname{\mathrm{coker}} \pi_{\mathbf{R}}}, \end{align*}$$
$$\begin{align*}\frac{L(J/{\mathbf{Q}}, 1)}{\Omega_J} = \frac{L(A_f/{\mathbf{Q}}, 1)}{\Omega_{A_f}} \cdot \frac{\Omega_{A_f}}{\Omega_J} = \frac{L(A_f/{\mathbf{Q}}, 1)}{\Omega_{A_f}} \cdot \frac{1}{c_\pi} \cdot \frac{\#\mathrm{ker} \pi_{\mathbf{R}}}{\#\operatorname{\mathrm{coker}} \pi_{\mathbf{R}}}, \end{align*}$$
and
![]() $\Omega _{A_f} = c_f \cdot \Omega ^{\prime }_{A_f}$
, where
$\Omega _{A_f} = c_f \cdot \Omega ^{\prime }_{A_f}$
, where
![]() $\Omega ^{\prime }_{A_f}$
is the volume computed with respect to a
$\Omega ^{\prime }_{A_f}$
is the volume computed with respect to a
![]() ${\mathbf {Z}}$
-basis of
${\mathbf {Z}}$
-basis of
![]() $S_2(f, {\mathbf {Z}})$
instead of a Néron basis. This gives
$S_2(f, {\mathbf {Z}})$
instead of a Néron basis. This gives
 $$ \begin{align} \frac{L(J/{\mathbf{Q}}, 1)}{\Omega_J} = \frac{L(A_f/{\mathbf{Q}}, 1)}{\Omega^{\prime}_{A_f}} \cdot \frac{1}{c_f c_\pi} \cdot \frac{\#\mathrm{ker} \pi_{\mathbf{R}}}{\#\operatorname{\mathrm{coker}} \pi_{\mathbf{R}}}. \end{align} $$
$$ \begin{align} \frac{L(J/{\mathbf{Q}}, 1)}{\Omega_J} = \frac{L(A_f/{\mathbf{Q}}, 1)}{\Omega^{\prime}_{A_f}} \cdot \frac{1}{c_f c_\pi} \cdot \frac{\#\mathrm{ker} \pi_{\mathbf{R}}}{\#\operatorname{\mathrm{coker}} \pi_{\mathbf{R}}}. \end{align} $$
The quotient
![]() $LR(A_f) := L(A_f/{\mathbf {Q}}, 1)/\Omega ^{\prime }_{A_f}$
is what Magma calls the LRatio of
$LR(A_f) := L(A_f/{\mathbf {Q}}, 1)/\Omega ^{\prime }_{A_f}$
is what Magma calls the LRatio of
![]() $A_f$
. This Magma function computes
$A_f$
. This Magma function computes
![]() $LR(A_f) \in {\mathbf {Q}}_{\ge 0}$
directly using modular symbols, but this computation is very slow and needs lots of memory when the level N of f is not very small (this seems to be caused by a computation of an integral homology basis of the ambient modular symbols space). The computation runs in reasonable time for
$LR(A_f) \in {\mathbf {Q}}_{\ge 0}$
directly using modular symbols, but this computation is very slow and needs lots of memory when the level N of f is not very small (this seems to be caused by a computation of an integral homology basis of the ambient modular symbols space). The computation runs in reasonable time for
![]() $N \le 1000$
, which is enough for the L-rank zero case, but becomes infeasible for example when
$N \le 1000$
, which is enough for the L-rank zero case, but becomes infeasible for example when
![]() $N = 67 \cdot 7^2$
, which is the first relevant level of a suitable quadratic twist in the L-rank one case.
$N = 67 \cdot 7^2$
, which is the first relevant level of a suitable quadratic twist in the L-rank one case.
So we use a numerical method instead. We compute numerical approximations to
![]() $L(A_f/{\mathbf {Q}}, 1)$
and to
$L(A_f/{\mathbf {Q}}, 1)$
and to
![]() $\Omega ^{\prime }_{A_f}$
or
$\Omega ^{\prime }_{A_f}$
or
![]() $\Omega _J$
and recognize the quotient as a rational number of small height. (See [Reference Wuthrich117] for a similar approach in the context of elliptic curves.) To do that reliably, we need a bound for the denominator of this quotient.
$\Omega _J$
and recognize the quotient as a rational number of small height. (See [Reference Wuthrich117] for a similar approach in the context of elliptic curves.) To do that reliably, we need a bound for the denominator of this quotient.
Proposition 4.3.
Proof. By [Reference Agashe and Stein3, Prop. 4.6], the denominator of
![]() $\#\pi _0(A_f({\mathbf {R}})) \cdot LR(A_f)$
divides the order n of the image in
$\#\pi _0(A_f({\mathbf {R}})) \cdot LR(A_f)$
divides the order n of the image in
![]() $A_f$
of the difference of the cusps represented by
$A_f$
of the difference of the cusps represented by
![]() $0$
and
$0$
and
![]() $\infty $
. This image is a rational torsion point, so
$\infty $
. This image is a rational torsion point, so
![]() $n \mid \#A_f({\mathbf {Q}})_{\mathrm {tors}}$
.
$n \mid \#A_f({\mathbf {Q}})_{\mathrm {tors}}$
.
Corollary 4.4. Let g denote the dimension of
![]() $A_f$
and of J. Then
$A_f$
and of J. Then
 $$\begin{align*}\frac{L(J/{\mathbf{Q}}, 1)}{\Omega_J} = \frac{m}{4^g \cdot c_f c_\pi \cdot \#J({\mathbf{Q}})_{\mathrm{tors}}} \qquad \text{for some } m \in {\mathbf{Z}}_{\ge 0}. \end{align*}$$
$$\begin{align*}\frac{L(J/{\mathbf{Q}}, 1)}{\Omega_J} = \frac{m}{4^g \cdot c_f c_\pi \cdot \#J({\mathbf{Q}})_{\mathrm{tors}}} \qquad \text{for some } m \in {\mathbf{Z}}_{\ge 0}. \end{align*}$$
Proof. Note that
![]() $\#A_f({\mathbf {Q}})_{\mathrm {tors}}$
divides
$\#A_f({\mathbf {Q}})_{\mathrm {tors}}$
divides
![]() $\#\mathrm {ker} \pi _{\mathbf {R}} \cdot \#J({\mathbf {Q}})_{\mathrm {tors}}$
and that
$\#\mathrm {ker} \pi _{\mathbf {R}} \cdot \#J({\mathbf {Q}})_{\mathrm {tors}}$
and that
![]() $\#\pi _0(A_f({\mathbf {R}}))$
and
$\#\pi _0(A_f({\mathbf {R}}))$
and
![]() $\# {\mathrm {coker}} \pi _{\mathbf {R}}$
both divide
$\# {\mathrm {coker}} \pi _{\mathbf {R}}$
both divide
![]() $2^g$
. The claim then follows from (4.2) and proposition 4.3.
$2^g$
. The claim then follows from (4.2) and proposition 4.3.
Since we can determine
![]() $\#J({\mathbf {Q}})_{\mathrm {tors}}$
(an upper bound obtained from the L-series coefficients as in [Reference Agashe and Stein3, § 3.5] would be enough) and we can compute
$\#J({\mathbf {Q}})_{\mathrm {tors}}$
(an upper bound obtained from the L-series coefficients as in [Reference Agashe and Stein3, § 3.5] would be enough) and we can compute
![]() $c_f c_\pi $
by lemma 3.6, it suffices to compute
$c_f c_\pi $
by lemma 3.6, it suffices to compute
![]() $L(J/{\mathbf {Q}}, 1)$
and
$L(J/{\mathbf {Q}}, 1)$
and
![]() $\Omega _J$
to sufficient precision so that the resulting approximation to
$\Omega _J$
to sufficient precision so that the resulting approximation to
![]() $4^g \cdot c_f c_\pi \cdot \#J({\mathbf {Q}})_{\mathrm {tors}} \cdot L(J/{\mathbf {Q}}, 1)/\Omega _J$
has error
$4^g \cdot c_f c_\pi \cdot \#J({\mathbf {Q}})_{\mathrm {tors}} \cdot L(J/{\mathbf {Q}}, 1)/\Omega _J$
has error
![]() $< 1/2$
. We then round to the nearest integer to obtain the numerator m in corollary 4.4. In practice, we use higher precision and check that the error is as small as can be expected.
$< 1/2$
. We then round to the nearest integer to obtain the numerator m in corollary 4.4. In practice, we use higher precision and check that the error is as small as can be expected.
4.3 The case of L-rank
 $0$
$0$
We obtain the following formula.
Proposition 4.5. Assume that
![]() $L(f, 1) \neq 0$
. Then
$L(f, 1) \neq 0$
. Then

Proof. This is (4.1) for
![]() $r = 0$
.
$r = 0$
.
Note that all quantities in the formula in theorem 4.5 can be computed explicitly: for the first factor, see Section 4.2, for the torsion subgroup, see [Reference Stoll111, § 11], and for the Tamagawa product, see the beginning of this section.
4.4 The case of L-rank
 $1$
: Computing
$1$
: Computing 
In the following, we keep assuming that J is a Jacobian. In particular, J is principally polarized.
When the L-rank is
![]() $1$
, we first find a Heegner field K and compute the analytic order of
$1$
, we first find a Heegner field K and compute the analytic order of ![]() for
for
![]() $J/K$
exactly from the BSD formula
$J/K$
exactly from the BSD formula

Here, the period
![]() $\Omega _{J/K}$
is defined as
$\Omega _{J/K}$
is defined as
where
![]() $\omega $
is a generator of the free rank
$\omega $
is a generator of the free rank
![]() $1 {\mathbf {Z}}$
-module of top Néron differentials on J (this works since
$1 {\mathbf {Z}}$
-module of top Néron differentials on J (this works since
![]() $J/K$
is base-changed from an abelian variety over
$J/K$
is base-changed from an abelian variety over
![]() ${\mathbf {Q}}$
). Note that this is
${\mathbf {Q}}$
). Note that this is
![]() $2^g$
times the covolume of the period lattice (which is generated by the columns of the big period matrix
$2^g$
times the covolume of the period lattice (which is generated by the columns of the big period matrix
![]() $\Pi _J$
, if it is computed with respect to a Néron basis of the invariant
$\Pi _J$
, if it is computed with respect to a Néron basis of the invariant
![]() $1$
-forms).
$1$
-forms).
The regulator
![]() $\operatorname {Reg}^{\prime }_{J/K}$
is computed with respect to heights over K. We will write
$\operatorname {Reg}^{\prime }_{J/K}$
is computed with respect to heights over K. We will write
![]() $\operatorname {Reg}_{J/K}$
to denote the regulator with respect to the normalized height; we then have that
$\operatorname {Reg}_{J/K}$
to denote the regulator with respect to the normalized height; we then have that
![]() $\operatorname {Reg}^{\prime }_{J/K} = [K : {\mathbf {Q}}]^{\operatorname {rk} J(K)} \cdot \operatorname {Reg}_{J/K}$
. See [Reference Tate113]. (In the literature, the formula is often stated without making precise what ‘the regulator’ and ‘the period’ are, which can lead to confusion. See the answers to the Math Overflow question at [Reference Dokchitser and Silverman41] and [Reference Cremona32] for a discussion.) We deduce that
$\operatorname {Reg}^{\prime }_{J/K} = [K : {\mathbf {Q}}]^{\operatorname {rk} J(K)} \cdot \operatorname {Reg}_{J/K}$
. See [Reference Tate113]. (In the literature, the formula is often stated without making precise what ‘the regulator’ and ‘the period’ are, which can lead to confusion. See the answers to the Math Overflow question at [Reference Dokchitser and Silverman41] and [Reference Cremona32] for a discussion.) We deduce that

 $$ \begin{align} &\qquad \qquad\qquad\quad = \frac{(\#J(K)_{\mathrm{tors}})^2}{\operatorname{\mathrm{Tam}}(J/K) \cdot u_K^{2g}} \cdot \frac{\prod_\sigma 8 \boldsymbol{\pi}^2 \|f^\sigma\|^2}{\Omega_{J/K}} \cdot \frac{\prod_\sigma {\hat{h}}(y_{K,\sigma})}{\operatorname{Reg}_{J/K}}, \end{align} $$
$$ \begin{align} &\qquad \qquad\qquad\quad = \frac{(\#J(K)_{\mathrm{tors}})^2}{\operatorname{\mathrm{Tam}}(J/K) \cdot u_K^{2g}} \cdot \frac{\prod_\sigma 8 \boldsymbol{\pi}^2 \|f^\sigma\|^2}{\Omega_{J/K}} \cdot \frac{\prod_\sigma {\hat{h}}(y_{K,\sigma})}{\operatorname{Reg}_{J/K}}, \end{align} $$
where
![]() $\sigma $
runs through the g embeddings
$\sigma $
runs through the g embeddings
![]() $\sigma \colon {\mathbf {Q}}(f) \hookrightarrow {\mathbf {R}}$
. The second equality follows from the Gross–Zagier formula theorem 3.14 with
$\sigma \colon {\mathbf {Q}}(f) \hookrightarrow {\mathbf {R}}$
. The second equality follows from the Gross–Zagier formula theorem 3.14 with
 $$\begin{align*}L^*(J/K, 1) = \frac{L^{(g)}(J/K,1)}{g!} = \prod_\sigma L'(f/K^\sigma,1), \end{align*}$$
$$\begin{align*}L^*(J/K, 1) = \frac{L^{(g)}(J/K,1)}{g!} = \prod_\sigma L'(f/K^\sigma,1), \end{align*}$$
where
![]() $L(f/K^\sigma , s) = L(f^\sigma , s) L(f^\sigma \otimes \varepsilon _K, s)$
with the quadratic character
$L(f/K^\sigma , s) = L(f^\sigma , s) L(f^\sigma \otimes \varepsilon _K, s)$
with the quadratic character
![]() $\varepsilon _K$
associated to
$\varepsilon _K$
associated to
![]() $K|{\mathbf {Q}}$
.
$K|{\mathbf {Q}}$
.
Note that all primes p of bad reduction for
![]() $J/{\mathbf {Q}}$
split as
$J/{\mathbf {Q}}$
split as
![]() $\mathfrak {p}\bar {\mathfrak {p}}$
in K by the Heegner condition. This implies that
$\mathfrak {p}\bar {\mathfrak {p}}$
in K by the Heegner condition. This implies that
![]() $K_{\mathfrak {p}} \simeq {\mathbf {Q}}_p \simeq K_{\bar {\mathfrak {p}}}$
and so in particular that
$K_{\mathfrak {p}} \simeq {\mathbf {Q}}_p \simeq K_{\bar {\mathfrak {p}}}$
and so in particular that
![]() $c_{\mathfrak {p}}(J/K) = c_p(J/{\mathbf {Q}}) = c_{\bar {\mathfrak {p}}}(J/K)$
. Therefore, the Tamagawa product over K is the square of the Tamagawa product over
$c_{\mathfrak {p}}(J/K) = c_p(J/{\mathbf {Q}}) = c_{\bar {\mathfrak {p}}}(J/K)$
. Therefore, the Tamagawa product over K is the square of the Tamagawa product over
![]() ${\mathbf {Q}}$
,
${\mathbf {Q}}$
,
We now describe in a series of lemmas how to determine the last two factors in (4.5). Combining the results gives the explicit formula in Corollary 4.13.
Lemma 4.6. Let
![]() $f \in \mathcal {N}(N,g)$
. Then the Petersson norm
$f \in \mathcal {N}(N,g)$
. Then the Petersson norm
![]() $\|f\|^2$
satisfies
$\|f\|^2$
satisfies
 $$\begin{align*}8\boldsymbol{\pi}^2\|f\|^2 = \|\omega_f\|^2 := \int_{X_0(N)({\mathbf{C}})}\omega_f \wedge \overline{i \omega_f} \end{align*}$$
$$\begin{align*}8\boldsymbol{\pi}^2\|f\|^2 = \|\omega_f\|^2 := \int_{X_0(N)({\mathbf{C}})}\omega_f \wedge \overline{i \omega_f} \end{align*}$$
with
![]() $\omega _f = 2\boldsymbol {\pi } i f(z) \,dz$
.
$\omega _f = 2\boldsymbol {\pi } i f(z) \,dz$
.
Proof. See [Reference Gross and Zagier52, § 1.6].
We now want to relate the product of the Petersson norms to the complex period of
![]() $A_f$
. Extending diagram (3.4) to the left, we obtain the following diagram, where
$A_f$
. Extending diagram (3.4) to the left, we obtain the following diagram, where
![]() $B_f = I_f J_0(N)$
is the kernel of
$B_f = I_f J_0(N)$
is the kernel of
![]() $\pi _f$
:
$\pi _f$
:

Also recall the definition of
![]() $d_f$
from (3.1).
$d_f$
from (3.1).
Lemma 4.7. Let
![]() $W_g$
be the image of
$W_g$
be the image of
![]() $\operatorname {Sym}^g X_0(N)$
in
$\operatorname {Sym}^g X_0(N)$
in
![]() $J_0(N)$
(with respect to some base divisor of degree g). Let
$J_0(N)$
(with respect to some base divisor of degree g). Let
![]() $B_f = I_f J_0(N) = \mathrm {ker} \pi _f$
. Then the intersection number
$B_f = I_f J_0(N) = \mathrm {ker} \pi _f$
. Then the intersection number
![]() $W_g \cdot B_f$
equals
$W_g \cdot B_f$
equals
![]() $d_f$
.
$d_f$
.
We thank Jakob Stix and Yusuf Mustopa for help with the proof.
Proof. Let
![]() $m := \dim J_0(N) = g(X_0(N))$
. By [Reference Arbarello, Cornalba, Griffiths and Harris4, Thm. V.1.3] (with
$m := \dim J_0(N) = g(X_0(N))$
. By [Reference Arbarello, Cornalba, Griffiths and Harris4, Thm. V.1.3] (with
![]() $(r, d, n) \leftarrow (0, g, m)$
), the class of
$(r, d, n) \leftarrow (0, g, m)$
), the class of
![]() $W_g$
is
$W_g$
is
![]() $1/(m-g)! \cdot \theta ^{m-g}$
, where
$1/(m-g)! \cdot \theta ^{m-g}$
, where
![]() $\theta $
is the class of the theta divisor on
$\theta $
is the class of the theta divisor on
![]() $J_0(N)$
. We write
$J_0(N)$
. We write
![]() $d_f'$
for the product
$d_f'$
for the product
![]() $d^{\prime }_1 \cdots d^{\prime }_g$
, where
$d^{\prime }_1 \cdots d^{\prime }_g$
, where
![]() $(d^{\prime }_1, \ldots , d^{\prime }_g)$
is the type of
$(d^{\prime }_1, \ldots , d^{\prime }_g)$
is the type of
![]() $\lambda _f'$
in diagram (4.7) above. Then
$\lambda _f'$
in diagram (4.7) above. Then
so
![]() $d_f' = d_f$
. This implies that the intersection number is (compare [Reference Birkenhake and Lange9, Thm. 3.6.3])
$d_f' = d_f$
. This implies that the intersection number is (compare [Reference Birkenhake and Lange9, Thm. 3.6.3])
 $$ \begin{align*} W_g \cdot B_f &= \frac{\theta|_{B_f}^{m-g}}{(m-g)!} = \frac{(m-g)! \cdot d_f'}{(m-g)!} = d_f' = d_f. \end{align*} $$
$$ \begin{align*} W_g \cdot B_f &= \frac{\theta|_{B_f}^{m-g}}{(m-g)!} = \frac{(m-g)! \cdot d_f'}{(m-g)!} = d_f' = d_f. \end{align*} $$
We denote the Abel–Jacobi morphism
![]() $X_0(N) \hookrightarrow J_0(N)$
with respect to the cusp
$X_0(N) \hookrightarrow J_0(N)$
with respect to the cusp
![]() $\infty $
by
$\infty $
by
![]() $\iota $
. Since
$\iota $
. Since
![]() $\iota ^* \colon {\operatorname {H}}^0(J_0(N), \Omega ^1) \xrightarrow {\sim } {\operatorname {H}}^0(X_0(N), \Omega ^1)$
is an isomorphism, we can identify the differentials
$\iota ^* \colon {\operatorname {H}}^0(J_0(N), \Omega ^1) \xrightarrow {\sim } {\operatorname {H}}^0(X_0(N), \Omega ^1)$
is an isomorphism, we can identify the differentials
![]() $\omega _{f^\sigma }$
with holomorphic (hence invariant)
$\omega _{f^\sigma }$
with holomorphic (hence invariant)
![]() $1$
-forms on
$1$
-forms on
![]() $J_0(N)$
, which we also denote by
$J_0(N)$
, which we also denote by
![]() $\omega _{f^\sigma }$
. The map
$\omega _{f^\sigma }$
. The map
![]() $\pi _f \colon J_0(N) \to A_f$
induces an injective homomorphism
$\pi _f \colon J_0(N) \to A_f$
induces an injective homomorphism
![]() $\pi _f^* \colon {\operatorname {H}}^0(A_f({\mathbf {C}}), \Omega ^1) \to {\operatorname {H}}^0(J_0(N)({\mathbf {C}}), \Omega ^1)$
whose image is the subspace spanned by the
$\pi _f^* \colon {\operatorname {H}}^0(A_f({\mathbf {C}}), \Omega ^1) \to {\operatorname {H}}^0(J_0(N)({\mathbf {C}}), \Omega ^1)$
whose image is the subspace spanned by the
![]() $\omega _{f^\sigma }$
. We write
$\omega _{f^\sigma }$
. We write
![]() $\omega _{A_f,\sigma }$
for the uniquely determined preimage of
$\omega _{A_f,\sigma }$
for the uniquely determined preimage of
![]() $\omega _{f^\sigma }$
under this map.
$\omega _{f^\sigma }$
under this map.
Lemma 4.8. With the notation introduced so far,
 $$\begin{align*}\prod_\sigma \|\omega_{f^\sigma}\|^2 = d_f \cdot \int_{A_f({\mathbf{C}})}\bigwedge_\sigma(\omega_{A_f,\sigma} \wedge \overline{i \omega_{A_f,\sigma}}) . \end{align*}$$
$$\begin{align*}\prod_\sigma \|\omega_{f^\sigma}\|^2 = d_f \cdot \int_{A_f({\mathbf{C}})}\bigwedge_\sigma(\omega_{A_f,\sigma} \wedge \overline{i \omega_{A_f,\sigma}}) . \end{align*}$$
Proof. To simplify notation, fix a numbering
![]() $\sigma _1, \ldots , \sigma _g$
of the embeddings
$\sigma _1, \ldots , \sigma _g$
of the embeddings
![]() $\sigma \colon {\mathbf {Q}}(f) \hookrightarrow {\mathbf {R}}$
and write
$\sigma \colon {\mathbf {Q}}(f) \hookrightarrow {\mathbf {R}}$
and write
![]() $\omega _j$
for
$\omega _j$
for
![]() $\omega _{f^{\sigma _j}}$
.
$\omega _{f^{\sigma _j}}$
.
We first show that
 $$\begin{align*}\prod_\sigma \|\omega_{f^\sigma}\|^2 = \int_{W_g({\mathbf{C}})} \omega_1 \wedge \overline{i \omega_1} \wedge \dots \wedge \omega_g \wedge \overline{i \omega_g}, \end{align*}$$
$$\begin{align*}\prod_\sigma \|\omega_{f^\sigma}\|^2 = \int_{W_g({\mathbf{C}})} \omega_1 \wedge \overline{i \omega_1} \wedge \dots \wedge \omega_g \wedge \overline{i \omega_g}, \end{align*}$$
where
![]() $W_g$
is as in theorem 4.7 with base divisor
$W_g$
is as in theorem 4.7 with base divisor
![]() $g \cdot \infty $
. Consider the composition
$g \cdot \infty $
. Consider the composition
![]() $X_0(N)^g \stackrel {\iota ^g}{\to } J_0(N)^g \stackrel {s}{\to } J_0(N)$
with the first morphism
$X_0(N)^g \stackrel {\iota ^g}{\to } J_0(N)^g \stackrel {s}{\to } J_0(N)$
with the first morphism
![]() $\iota \times \ldots \times \iota $
and s the summation morphism. This morphism has degree
$\iota \times \ldots \times \iota $
and s the summation morphism. This morphism has degree
![]() $g!$
above its image
$g!$
above its image
![]() $W_g$
since it factors through the g-fold symmetric power of
$W_g$
since it factors through the g-fold symmetric power of
![]() $X_0(N)$
, which is birational to
$X_0(N)$
, which is birational to
![]() $W_g$
via s. This gives
$W_g$
via s. This gives
 $$ \begin{align*} \int_{W_g({\mathbf{C}})} \omega_1 \wedge \overline{i \omega_1} \wedge \dots &\wedge \omega_g \wedge \overline{i \omega_g} = \frac{1}{g!} \int_{X_0(N)({\mathbf{C}})^g} (\iota^g)^* s^* (\omega_1 \wedge \overline{i \omega_1} \wedge \dots \wedge \omega_g \wedge \overline{i \omega_g}). \end{align*} $$
$$ \begin{align*} \int_{W_g({\mathbf{C}})} \omega_1 \wedge \overline{i \omega_1} \wedge \dots &\wedge \omega_g \wedge \overline{i \omega_g} = \frac{1}{g!} \int_{X_0(N)({\mathbf{C}})^g} (\iota^g)^* s^* (\omega_1 \wedge \overline{i \omega_1} \wedge \dots \wedge \omega_g \wedge \overline{i \omega_g}). \end{align*} $$
Now for any invariant
![]() $1$
-form
$1$
-form
![]() $\omega $
on an abelian variety, we have that
$\omega $
on an abelian variety, we have that
![]() $s^* \omega = \sum _{k=1}^g \operatorname {pr}_k^* \omega $
with
$s^* \omega = \sum _{k=1}^g \operatorname {pr}_k^* \omega $
with
![]() $\operatorname {pr}_k$
the kth projection
$\operatorname {pr}_k$
the kth projection
![]() $J_0(N)^g \to J_0(N)$
; see [Reference Birkenhake and Lange9, § 1.5 (9)]. This implies
$J_0(N)^g \to J_0(N)$
; see [Reference Birkenhake and Lange9, § 1.5 (9)]. This implies
 $$ \begin{align*} (\iota^g)^*s^*\Bigg(\bigwedge_{j=1}^g \omega_j \wedge \overline{i \omega_j}\Bigg) &= (\iota^g)^*\Bigg(\bigwedge_{j=1}^g \Big(\sum_{k=1}^g \operatorname{pr}_k^*\omega_j\Big) \wedge \Big(\sum_{k=1}^g \operatorname{pr}_k^* \overline{i \omega_j}\Big)\Bigg). \end{align*} $$
$$ \begin{align*} (\iota^g)^*s^*\Bigg(\bigwedge_{j=1}^g \omega_j \wedge \overline{i \omega_j}\Bigg) &= (\iota^g)^*\Bigg(\bigwedge_{j=1}^g \Big(\sum_{k=1}^g \operatorname{pr}_k^*\omega_j\Big) \wedge \Big(\sum_{k=1}^g \operatorname{pr}_k^* \overline{i \omega_j}\Big)\Bigg). \end{align*} $$
We expand the right-hand side. Terms containing two factors
![]() $\operatorname {pr}_k^* \omega _j$
or two factors
$\operatorname {pr}_k^* \omega _j$
or two factors
![]() $\operatorname {pr}_k^* \overline {i \omega _j}$
with the same k vanish since the wedge product of two holomorphic differentials on a curve vanishes. So we are left with a sum of terms of the form
$\operatorname {pr}_k^* \overline {i \omega _j}$
with the same k vanish since the wedge product of two holomorphic differentials on a curve vanishes. So we are left with a sum of terms of the form
 $$ \begin{align*} \pm \frac{1}{g!} \int_{X_0(N)({\mathbf{C}})^g} \operatorname{pr}_1^*(\omega_{j_1} \wedge \overline{i \omega_{j^{\prime}_1}}) &\wedge \dots \wedge \operatorname{pr}_g^*(\omega_{j_g} \wedge \overline{i \omega_{j^{\prime}_g}}) = \pm \frac{1}{g!} \prod_{k=1}^g \int_{X_0(N)({\mathbf{C}})} \omega_{j_k} \wedge \overline{i \omega_{j^{\prime}_k}} \end{align*} $$
$$ \begin{align*} \pm \frac{1}{g!} \int_{X_0(N)({\mathbf{C}})^g} \operatorname{pr}_1^*(\omega_{j_1} \wedge \overline{i \omega_{j^{\prime}_1}}) &\wedge \dots \wedge \operatorname{pr}_g^*(\omega_{j_g} \wedge \overline{i \omega_{j^{\prime}_g}}) = \pm \frac{1}{g!} \prod_{k=1}^g \int_{X_0(N)({\mathbf{C}})} \omega_{j_k} \wedge \overline{i \omega_{j^{\prime}_k}} \end{align*} $$
with
![]() $\{j_1, \ldots , j_g\} = \{j^{\prime }_1, \ldots , j^{\prime }_g\} = \{1, \ldots , g\}$
. Now when
$\{j_1, \ldots , j_g\} = \{j^{\prime }_1, \ldots , j^{\prime }_g\} = \{1, \ldots , g\}$
. Now when
![]() $j_k \neq j^{\prime }_k$
for some k, then the corresponding integral vanishes since the
$j_k \neq j^{\prime }_k$
for some k, then the corresponding integral vanishes since the
![]() $f^\sigma $
are pairwise orthogonal with respect to the Petersson inner product. All the remaining terms have a positive sign (all relevant permutations are even) and differ only in the ordering of the factors; in particular, there are exactly
$f^\sigma $
are pairwise orthogonal with respect to the Petersson inner product. All the remaining terms have a positive sign (all relevant permutations are even) and differ only in the ordering of the factors; in particular, there are exactly
![]() $g!$
such terms. So we obtain
$g!$
such terms. So we obtain
 $$ \begin{align*} \int_{W_g({\mathbf{C}})} \bigwedge_\sigma (\omega_{f^\sigma} \wedge \overline{i \omega_{f^\sigma}}) &= \int_{W_g({\mathbf{C}})} \omega_1 \wedge \overline{i \omega_1} \wedge \dots \wedge \omega_g \wedge \overline{i \omega_g} \\ &= \prod_{j=1}^g \int_{X_0(N)({\mathbf{C}})} \omega_{j} \wedge \overline{i \omega_{j}} = \prod_\sigma \|\omega_{f^\sigma}\|^2, \end{align*} $$
$$ \begin{align*} \int_{W_g({\mathbf{C}})} \bigwedge_\sigma (\omega_{f^\sigma} \wedge \overline{i \omega_{f^\sigma}}) &= \int_{W_g({\mathbf{C}})} \omega_1 \wedge \overline{i \omega_1} \wedge \dots \wedge \omega_g \wedge \overline{i \omega_g} \\ &= \prod_{j=1}^g \int_{X_0(N)({\mathbf{C}})} \omega_{j} \wedge \overline{i \omega_{j}} = \prod_\sigma \|\omega_{f^\sigma}\|^2, \end{align*} $$
as desired.
We now consider
![]() $\pi _f|_{W_g} \colon W_g \to A_f$
. Since
$\pi _f|_{W_g} \colon W_g \to A_f$
. Since
![]() $\dim W_g = \dim A_f = g$
and by theorem 4.7,
$\dim W_g = \dim A_f = g$
and by theorem 4.7,
![]() $W_g$
meets generic cosets of
$W_g$
meets generic cosets of
![]() $B_f = \mathrm {ker} \pi _f$
transversally in
$B_f = \mathrm {ker} \pi _f$
transversally in
![]() $W_g \cdot B_f = d_f$
points, we finally obtain that
$W_g \cdot B_f = d_f$
points, we finally obtain that
 $$ \begin{align*} \prod_\sigma \|\omega_{f^\sigma}\|^2 &= \int_{W_g({\mathbf{C}})} \omega_1 \wedge \overline{i \omega_1} \wedge \dots \wedge \omega_g \wedge \overline{i \omega_g} \\ &= \int_{W_g({\mathbf{C}})} \bigwedge_\sigma (\pi_f^* \omega_{A_f,\sigma} \wedge \overline{i \pi_f^* \omega_{A_f,\sigma}}) \\ &= d_f \cdot \int_{A_f({\mathbf{C}})} \bigwedge_\sigma (\omega_{A_f,\sigma} \wedge \overline{i \omega_{A_f,\sigma}}). \end{align*} $$
$$ \begin{align*} \prod_\sigma \|\omega_{f^\sigma}\|^2 &= \int_{W_g({\mathbf{C}})} \omega_1 \wedge \overline{i \omega_1} \wedge \dots \wedge \omega_g \wedge \overline{i \omega_g} \\ &= \int_{W_g({\mathbf{C}})} \bigwedge_\sigma (\pi_f^* \omega_{A_f,\sigma} \wedge \overline{i \pi_f^* \omega_{A_f,\sigma}}) \\ &= d_f \cdot \int_{A_f({\mathbf{C}})} \bigwedge_\sigma (\omega_{A_f,\sigma} \wedge \overline{i \omega_{A_f,\sigma}}). \end{align*} $$
We now relate the integral on the right-hand side in lemma 4.8 to the period
![]() $\Omega _{A_f/K}$
.
$\Omega _{A_f/K}$
.
Lemma 4.9. One has
 $$ \begin{align*} \int_{A_f({\mathbf{C}})} \bigwedge_\sigma (\omega_{A_f,\sigma} \wedge \overline{i \omega_{A_f,\sigma}}) &= \frac{\operatorname{disc} {\mathbf{Z}}[f]}{c_f^2} \cdot \int_{A_f({\mathbf{C}})}|\omega_{A_f} \wedge \overline{\omega_{A_f}}| \\ &= \frac{\operatorname{disc} {\mathbf{Z}}[f]}{c_f^2} \cdot \Omega_{A_f/K}, \end{align*} $$
$$ \begin{align*} \int_{A_f({\mathbf{C}})} \bigwedge_\sigma (\omega_{A_f,\sigma} \wedge \overline{i \omega_{A_f,\sigma}}) &= \frac{\operatorname{disc} {\mathbf{Z}}[f]}{c_f^2} \cdot \int_{A_f({\mathbf{C}})}|\omega_{A_f} \wedge \overline{\omega_{A_f}}| \\ &= \frac{\operatorname{disc} {\mathbf{Z}}[f]}{c_f^2} \cdot \Omega_{A_f/K}, \end{align*} $$
where
![]() $\omega _{A_f}$
is a top Néron differential on
$\omega _{A_f}$
is a top Néron differential on
![]() $A_f$
, that is, a generator of
$A_f$
, that is, a generator of
![]() ${\operatorname {H}}^0(\mathscr {A}_f,\Omega ^g)$
with
${\operatorname {H}}^0(\mathscr {A}_f,\Omega ^g)$
with
![]() $\mathscr {A}_f/{\mathbf {Z}}$
the Néron model of
$\mathscr {A}_f/{\mathbf {Z}}$
the Néron model of
![]() $A_f$
,
$A_f$
,
![]() $\Omega _{A_f/K} := \int _{A_f({\mathbf {C}})}|\omega _{A_f} \wedge \overline {\omega _{A_f}}|$
, and
$\Omega _{A_f/K} := \int _{A_f({\mathbf {C}})}|\omega _{A_f} \wedge \overline {\omega _{A_f}}|$
, and
![]() $c_f$
is the Manin constant from definition 3.4.
$c_f$
is the Manin constant from definition 3.4.
Over
![]() ${\mathbf {R}}$
, one has
${\mathbf {R}}$
, one has
 $$\begin{align*}\int_{A_f({\mathbf{R}})} \bigwedge_\sigma \omega_{A_f,\sigma} = \pm \frac{\sqrt{\operatorname{disc} {\mathbf{Z}}[f]}}{c_f} \cdot \Omega_{A_f/{\mathbf{Q}}} . \end{align*}$$
$$\begin{align*}\int_{A_f({\mathbf{R}})} \bigwedge_\sigma \omega_{A_f,\sigma} = \pm \frac{\sqrt{\operatorname{disc} {\mathbf{Z}}[f]}}{c_f} \cdot \Omega_{A_f/{\mathbf{Q}}} . \end{align*}$$
Proof. Let
![]() $(f_j)_{j=1}^g$
be a
$(f_j)_{j=1}^g$
be a
![]() ${\mathbf {Z}}$
-basis of
${\mathbf {Z}}$
-basis of
![]() $S_2(f, {\mathbf {Z}})$
. Then
$S_2(f, {\mathbf {Z}})$
. Then
![]() $f = \sum _j b_j f_j$
for some
$f = \sum _j b_j f_j$
for some
![]() $b_j \in {\mathbf {Z}}[f]$
, which form a
$b_j \in {\mathbf {Z}}[f]$
, which form a
![]() ${\mathbf {Z}}$
-basis of
${\mathbf {Z}}$
-basis of
![]() ${\mathbf {Z}}[f] = {\mathbf {Z}}[a_n(f) : n \ge 1]$
. The matrix
${\mathbf {Z}}[f] = {\mathbf {Z}}[a_n(f) : n \ge 1]$
. The matrix
![]() $A = (b_j^\sigma )_{\sigma ,j}$
then is such that
$A = (b_j^\sigma )_{\sigma ,j}$
then is such that
![]() $A \cdot (f_j)_j^\top = (f^\sigma )_\sigma ^\top $
, and it satisfies
$A \cdot (f_j)_j^\top = (f^\sigma )_\sigma ^\top $
, and it satisfies
By the definition of
![]() $c_f$
, we have that
$c_f$
, we have that
so
where
![]() $\pi _f^* \omega _{A,j} = \omega _{f_j}$
. We also have that
$\pi _f^* \omega _{A,j} = \omega _{f_j}$
. We also have that
Combining these gives the result.
The formula for
![]() $A_f({\mathbf {R}})$
follows in the same way, the only difference being that we do not take wedge products with conjugate differentials; hence, we get the square root of the factor.
$A_f({\mathbf {R}})$
follows in the same way, the only difference being that we do not take wedge products with conjugate differentials; hence, we get the square root of the factor.
We need to compare the periods
![]() $\Omega _{J/K}$
and
$\Omega _{J/K}$
and
![]() $\Omega _{A_f/K}$
.
$\Omega _{A_f/K}$
.
Lemma 4.10. One has
 $$\begin{align*}\frac{\Omega_{J/K}}{\Omega_{A_f/K}} = \frac{c_\pi^2}{\deg \pi}, \end{align*}$$
$$\begin{align*}\frac{\Omega_{J/K}}{\Omega_{A_f/K}} = \frac{c_\pi^2}{\deg \pi}, \end{align*}$$
where
![]() $c_\pi $
is as in definition 3.3.
$c_\pi $
is as in definition 3.3.
Proof. Note that the top Néron differentials
![]() $\omega _{A_f}$
and
$\omega _{A_f}$
and
![]() $\omega _J$
on
$\omega _J$
on
![]() $A_f$
and J are related by
$A_f$
and J are related by
![]() $\pi ^*\omega _J = \pm c_\pi \cdot \omega _{A_f}$
. Hence,
$\pi ^*\omega _J = \pm c_\pi \cdot \omega _{A_f}$
. Hence,
 $$ \begin{align*} \Omega_{J/K} &= \int_{J({\mathbf{C}})}|\omega_J \wedge \overline{\omega_J}| = \frac{1}{\deg \pi}\int_{A_f({\mathbf{C}})}|\pi^*(\omega_J \wedge \overline{\omega_J})| \\ &= \frac{1}{\deg \pi}\int_{A_f({\mathbf{C}})}|(c_\pi \cdot \omega_{A_f}) \wedge \overline{(c_\pi \cdot \omega_{A_f})}| = \frac{c_\pi^2}{\deg \pi} \Omega_{A_f/K}. \end{align*} $$
$$ \begin{align*} \Omega_{J/K} &= \int_{J({\mathbf{C}})}|\omega_J \wedge \overline{\omega_J}| = \frac{1}{\deg \pi}\int_{A_f({\mathbf{C}})}|\pi^*(\omega_J \wedge \overline{\omega_J})| \\ &= \frac{1}{\deg \pi}\int_{A_f({\mathbf{C}})}|(c_\pi \cdot \omega_{A_f}) \wedge \overline{(c_\pi \cdot \omega_{A_f})}| = \frac{c_\pi^2}{\deg \pi} \Omega_{A_f/K}. \end{align*} $$
Combining Lemmata 4.6 and 4.8 to 4.10 yields the following explicit expression for the second factor in (4.5).
Corollary 4.11. One has
 $$\begin{align*}\frac{\prod_\sigma 8\boldsymbol{\pi}^2\|f^\sigma\|^2}{\Omega_{J/K}} = \frac{\deg \pi \cdot d_f \cdot \operatorname{disc} {\mathbf{Z}}[f]}{(c_f c_\pi)^2} \in {\mathbf{Q}}_{>0} . \end{align*}$$
$$\begin{align*}\frac{\prod_\sigma 8\boldsymbol{\pi}^2\|f^\sigma\|^2}{\Omega_{J/K}} = \frac{\deg \pi \cdot d_f \cdot \operatorname{disc} {\mathbf{Z}}[f]}{(c_f c_\pi)^2} \in {\mathbf{Q}}_{>0} . \end{align*}$$
We now consider the third (and last) factor in (4.5).
Lemma 4.12. One has
 $$\begin{align*}\frac{\prod_\sigma{\hat{h}}(y_{K,\sigma})}{\operatorname{Reg}_{J/K}} = \frac{I_{K,\pi}^{2}}{(\#J(K)_{\mathrm{tors}})^2 \cdot \mathbf{N}(\alpha) \cdot \operatorname{disc}\mathrm{End}_{\mathbf{Q}}(J)} \in {\mathbf{Q}}_{>0}, \end{align*}$$
$$\begin{align*}\frac{\prod_\sigma{\hat{h}}(y_{K,\sigma})}{\operatorname{Reg}_{J/K}} = \frac{I_{K,\pi}^{2}}{(\#J(K)_{\mathrm{tors}})^2 \cdot \mathbf{N}(\alpha) \cdot \operatorname{disc}\mathrm{End}_{\mathbf{Q}}(J)} \in {\mathbf{Q}}_{>0}, \end{align*}$$
where
![]() $\alpha \in \mathrm {End}_{\mathbf {Q}} J$
is defined in (3.5) and
$\alpha \in \mathrm {End}_{\mathbf {Q}} J$
is defined in (3.5) and
![]() $I_{K,\pi }$
is the Heegner index of J with respect to the chosen isogeny
$I_{K,\pi }$
is the Heegner index of J with respect to the chosen isogeny
![]() $\pi \colon A_f \to J$
; see (3.7).
$\pi \colon A_f \to J$
; see (3.7).
Proof. Since
![]() $\alpha ^\sigma {\hat {h}}(y_{K,\sigma }) = {\hat {h}}_J((\pi \circ \lambda _f)(y_{K,\sigma }))$
(see proposition 3.16),
$\alpha ^\sigma {\hat {h}}(y_{K,\sigma }) = {\hat {h}}_J((\pi \circ \lambda _f)(y_{K,\sigma }))$
(see proposition 3.16),
Here,
![]() $\sigma $
runs through the embeddings
$\sigma $
runs through the embeddings
![]() $\mathrm {End}_{{\mathbf {Q}}}(J) \hookrightarrow {\mathbf {R}}$
. Now
$\mathrm {End}_{{\mathbf {Q}}}(J) \hookrightarrow {\mathbf {R}}$
. Now
with
![]() $(b_i)_{i=1}^g$
a
$(b_i)_{i=1}^g$
a
![]() ${\mathbf {Z}}$
-basis of
${\mathbf {Z}}$
-basis of
![]() $\mathrm {End}_{{\mathbf {Q}}}(J)$
.
$\mathrm {End}_{{\mathbf {Q}}}(J)$
.
But
![]() $(\pi \circ \lambda _f)(y_{K,\sigma }) = \sum _{j=1}^g b_j \cdot y_{K,\pi } \otimes b_j^{*,\sigma }$
, where
$(\pi \circ \lambda _f)(y_{K,\sigma }) = \sum _{j=1}^g b_j \cdot y_{K,\pi } \otimes b_j^{*,\sigma }$
, where
![]() $(b_j^*)_{j = 1}^g$
is the dual basis of
$(b_j^*)_{j = 1}^g$
is the dual basis of
![]() $\mathrm {End}_{{\mathbf {Q}}}(J) \otimes _{\mathbf {Z}} {\mathbf {R}}$
with respect to the trace pairing
$\mathrm {End}_{{\mathbf {Q}}}(J) \otimes _{\mathbf {Z}} {\mathbf {R}}$
with respect to the trace pairing
![]() $(a,b) \mapsto \operatorname {Tr}_{\mathrm {End}_{{\mathbf {Q}}}(J)/{\mathbf {Z}}}(ab)$
of
$(a,b) \mapsto \operatorname {Tr}_{\mathrm {End}_{{\mathbf {Q}}}(J)/{\mathbf {Z}}}(ab)$
of
![]() $\mathrm {End}_{{\mathbf {Q}}}(J)$
; see (3.11). Using this and the fact that the
$\mathrm {End}_{{\mathbf {Q}}}(J)$
; see (3.11). Using this and the fact that the
![]() $(\pi \circ \lambda _f)(y_{K,\sigma })$
are orthogonal in pairs with respect to the height pairing, we find that
$(\pi \circ \lambda _f)(y_{K,\sigma })$
are orthogonal in pairs with respect to the height pairing, we find that
 $$ \begin{align*} \prod_\sigma {\hat{h}}_J((\pi \circ \lambda_f)(y_{K,\sigma})) &= \det(\langle (\pi \circ \lambda_f)(y_{K,\sigma_1}), (\pi \circ \lambda_f)(y_{K,\sigma_2})\rangle_{J}) \\[-9pt] &= \operatorname{Reg}_J(\mathrm{End}_{{\mathbf{Q}}}(J)\cdot y_{K,\pi}) \cdot \det(b_j^{*,\sigma})^2 \\ &= \operatorname{Reg}_J(\mathrm{End}_{{\mathbf{Q}}}(J)\cdot y_{K,\pi}) \cdot \det(b_j^{\sigma})^{-2}\\ &= \operatorname{Reg}_J(\mathrm{End}_{{\mathbf{Q}}}(J)\cdot y_{K,\pi}) \cdot (\operatorname{disc}\mathrm{End}_{{\mathbf{Q}}}(J))^{-1}. \end{align*} $$
$$ \begin{align*} \prod_\sigma {\hat{h}}_J((\pi \circ \lambda_f)(y_{K,\sigma})) &= \det(\langle (\pi \circ \lambda_f)(y_{K,\sigma_1}), (\pi \circ \lambda_f)(y_{K,\sigma_2})\rangle_{J}) \\[-9pt] &= \operatorname{Reg}_J(\mathrm{End}_{{\mathbf{Q}}}(J)\cdot y_{K,\pi}) \cdot \det(b_j^{*,\sigma})^2 \\ &= \operatorname{Reg}_J(\mathrm{End}_{{\mathbf{Q}}}(J)\cdot y_{K,\pi}) \cdot \det(b_j^{\sigma})^{-2}\\ &= \operatorname{Reg}_J(\mathrm{End}_{{\mathbf{Q}}}(J)\cdot y_{K,\pi}) \cdot (\operatorname{disc}\mathrm{End}_{{\mathbf{Q}}}(J))^{-1}. \end{align*} $$
Using that
![]() $\operatorname {Reg}_J(\mathrm {End}_{{\mathbf {Q}}}(J)\cdot y_{K,\pi }) = I_{K,\pi }^2 \operatorname {Reg}_{J/K}/(\#J(K)_{\mathrm {tors}})^2$
, we finally obtain
$\operatorname {Reg}_J(\mathrm {End}_{{\mathbf {Q}}}(J)\cdot y_{K,\pi }) = I_{K,\pi }^2 \operatorname {Reg}_{J/K}/(\#J(K)_{\mathrm {tors}})^2$
, we finally obtain
 $$ \begin{align*} \frac{\prod_\sigma{\hat{h}}(y_{K,\sigma})}{\operatorname{Reg}_{J/K}} &= \frac{\prod_\sigma \hat{h}_J((\pi \circ \lambda_f)(y_{K,\sigma}))}{\mathbf{N}(\alpha) \cdot \operatorname{Reg}_{J/K}} = \frac{\operatorname{Reg}_J(\mathrm{End}_{{\mathbf{Q}}}(J)\cdot y_{K,\pi})}{\mathbf{N}(\alpha) \cdot \operatorname{Reg}_{J/K} \cdot \operatorname{disc}\mathrm{End}_{{\mathbf{Q}}}(J)} \\ &= \frac{I_{K,\pi}^2}{(\#J(K)_{\mathrm{tors}})^2 \cdot \mathbf{N}(\alpha) \cdot \operatorname{disc}\mathrm{End}_{{\mathbf{Q}}}(J)}. \end{align*} $$
$$ \begin{align*} \frac{\prod_\sigma{\hat{h}}(y_{K,\sigma})}{\operatorname{Reg}_{J/K}} &= \frac{\prod_\sigma \hat{h}_J((\pi \circ \lambda_f)(y_{K,\sigma}))}{\mathbf{N}(\alpha) \cdot \operatorname{Reg}_{J/K}} = \frac{\operatorname{Reg}_J(\mathrm{End}_{{\mathbf{Q}}}(J)\cdot y_{K,\pi})}{\mathbf{N}(\alpha) \cdot \operatorname{Reg}_{J/K} \cdot \operatorname{disc}\mathrm{End}_{{\mathbf{Q}}}(J)} \\ &= \frac{I_{K,\pi}^2}{(\#J(K)_{\mathrm{tors}})^2 \cdot \mathbf{N}(\alpha) \cdot \operatorname{disc}\mathrm{End}_{{\mathbf{Q}}}(J)}. \end{align*} $$
We can now compute ![]() exactly, as follows.
exactly, as follows.
Corollary 4.13.

Proof. This follows from using corollary 4.11 and lemma 4.12 in (4.5), noting that
![]() $\mathbf {N}(\alpha ) = d_f \cdot \deg \pi $
by (3.6).
$\mathbf {N}(\alpha ) = d_f \cdot \deg \pi $
by (3.6).
Since
![]() ${\mathbf {Z}}[f]$
and
${\mathbf {Z}}[f]$
and
![]() $\mathrm {End}_{\mathbf {Q}}(J)$
both are sub-orders of the ring of integers of
$\mathrm {End}_{\mathbf {Q}}(J)$
both are sub-orders of the ring of integers of
![]() ${\mathbf {Q}}(f)$
, the quotient of their discriminants is a square. So
${\mathbf {Q}}(f)$
, the quotient of their discriminants is a square. So ![]() is a square; this is consistent with the fact that J over K is even in the sense of [Reference Poonen and Stoll86] since the only bad places are primes that split in K, and the curve J is the Jacobian of is simultaneously deficient or not at both places above a bad prime p of J over
is a square; this is consistent with the fact that J over K is even in the sense of [Reference Poonen and Stoll86] since the only bad places are primes that split in K, and the curve J is the Jacobian of is simultaneously deficient or not at both places above a bad prime p of J over
![]() ${\mathbf {Q}}$
.
${\mathbf {Q}}$
.
Remark 4.14. Assuming
![]() ${\mathbf {Z}}[f] = \mathrm {End}_{{\mathbf {Q}}}(J)$
and
${\mathbf {Z}}[f] = \mathrm {End}_{{\mathbf {Q}}}(J)$
and
![]() $u_K = 1$
, all invariants on the right-hand side of Corollary 4.13 are orders of finite
$u_K = 1$
, all invariants on the right-hand side of Corollary 4.13 are orders of finite
![]() $\mathcal {O}$
-modules in a natural way. It is natural to ask for a refined BSD formula over
$\mathcal {O}$
-modules in a natural way. It is natural to ask for a refined BSD formula over
![]() $\mathcal {O}$
– namely, whether the element in the Grothendieck group of finite
$\mathcal {O}$
– namely, whether the element in the Grothendieck group of finite
![]() $\mathcal {O}$
-modules corresponding to the right-hand side of Corollary 4.13 equals that defined by
$\mathcal {O}$
-modules corresponding to the right-hand side of Corollary 4.13 equals that defined by ![]() .
.
4.5 Periods of quadratic twists
In order to compute ![]() in the L-rank
in the L-rank
![]() $1$
case, we also need to compute
$1$
case, we also need to compute ![]() . We can do this as described in Section 4.3. This requires the computation of the quotient
. We can do this as described in Section 4.3. This requires the computation of the quotient
![]() $L(J^K/{\mathbf {Q}}, 1)/\Omega _{J^K}$
. We do that as explained in Section 4.2. The computation of
$L(J^K/{\mathbf {Q}}, 1)/\Omega _{J^K}$
. We do that as explained in Section 4.2. The computation of
![]() $\Omega _{J^K}$
requires the period matrix of
$\Omega _{J^K}$
requires the period matrix of
![]() $J^K$
. We explain in this section how we can obtain this period matrix easily from that of J. See corollary 4.17 below for a slightly more general version. We also need to determine
$J^K$
. We explain in this section how we can obtain this period matrix easily from that of J. See corollary 4.17 below for a slightly more general version. We also need to determine
![]() $c_{f^K} c_{\pi ^K}$
to obtain the bound for the denominator. We show in corollary 4.20 that it is the same as
$c_{f^K} c_{\pi ^K}$
to obtain the bound for the denominator. We show in corollary 4.20 that it is the same as
![]() $c_f c_\pi $
.
$c_f c_\pi $
.
The following result is a generalization of [Reference Pal82, Lemma 3.1 and Cor. 2.6] from elliptic curves to more general abelian varieties. We first state a local version. We will frequently use the embedding
induced by the isomorphism
![]() $A^K_K \simeq A_K$
, where
$A^K_K \simeq A_K$
, where
![]() $\mathscr {A}^K$
is a Néron model of the quadratic twist
$\mathscr {A}^K$
is a Néron model of the quadratic twist
![]() $A^K$
.
$A^K$
.
Lemma 4.15. Let A be an abelian variety over
![]() ${\mathbf {Q}}_p$
, where p is an odd prime; assume that A has good reduction. Let
${\mathbf {Q}}_p$
, where p is an odd prime; assume that A has good reduction. Let
![]() $K|{\mathbf {Q}}_p$
be a ramified quadratic extension, given as
$K|{\mathbf {Q}}_p$
be a ramified quadratic extension, given as
![]() $K = {\mathbf {Q}}_p(\varpi )$
with
$K = {\mathbf {Q}}_p(\varpi )$
with
![]() $\varpi ^2 = u p$
, where
$\varpi ^2 = u p$
, where
![]() $u \in {\mathbf {Z}}_p^\times $
. Let
$u \in {\mathbf {Z}}_p^\times $
. Let
![]() $\mathscr {A}$
and
$\mathscr {A}$
and
![]() $\mathscr {A}^K$
denote the Néron models of A and of its quadratic twist
$\mathscr {A}^K$
denote the Néron models of A and of its quadratic twist
![]() $A^K$
over
$A^K$
over
![]() ${\mathbf {Z}}_p$
.
${\mathbf {Z}}_p$
.
Then the image of
![]() ${\operatorname {H}}^0(\mathscr {A}^K, \Omega ^1)$
in
${\operatorname {H}}^0(\mathscr {A}^K, \Omega ^1)$
in
![]() ${\operatorname {H}}^0(A_K, \Omega ^1)$
is
${\operatorname {H}}^0(A_K, \Omega ^1)$
is
![]() $1/\varpi $
times the image of
$1/\varpi $
times the image of
![]() ${\operatorname {H}}^0(\mathscr {A}, \Omega ^1)$
.
${\operatorname {H}}^0(\mathscr {A}, \Omega ^1)$
.
We thank Kęstutis Česnavicius for help with the proof.
Proof. We consider the images of
![]() ${\operatorname {H}}^0(\mathscr {A}, \Omega ^1)$
and of
${\operatorname {H}}^0(\mathscr {A}, \Omega ^1)$
and of
![]() ${\operatorname {H}}^0(\mathscr {A}^K, \Omega ^1)$
in
${\operatorname {H}}^0(\mathscr {A}^K, \Omega ^1)$
in
![]() $V := {\operatorname {H}}^0(A_K, \Omega ^1)$
, respectively; they are free
$V := {\operatorname {H}}^0(A_K, \Omega ^1)$
, respectively; they are free
![]() ${\mathbf {Z}}_p$
-submodules of V of rank
${\mathbf {Z}}_p$
-submodules of V of rank
![]() $g = \dim _K V = \dim A$
. The first image is the
$g = \dim _K V = \dim A$
. The first image is the
![]() ${\mathbf {Z}}_p$
-dual of
${\mathbf {Z}}_p$
-dual of
![]() $L := \operatorname {Lie}(\mathscr {A}) \hookrightarrow \operatorname {Lie}(A_K)$
(i.e., it consists of the differentials
$L := \operatorname {Lie}(\mathscr {A}) \hookrightarrow \operatorname {Lie}(A_K)$
(i.e., it consists of the differentials
![]() $\omega $
such that
$\omega $
such that
![]() $\langle \lambda , \omega \rangle \in {\mathbf {Z}}_p$
for all
$\langle \lambda , \omega \rangle \in {\mathbf {Z}}_p$
for all
![]() $\lambda \in L$
under the natural pairing between the Lie algebra (the tangent space at the origin) and V (its dual)), and similarly for
$\lambda \in L$
under the natural pairing between the Lie algebra (the tangent space at the origin) and V (its dual)), and similarly for
![]() $L^K := \operatorname {Lie}(\mathscr {A}^K) \hookrightarrow \operatorname {Lie}(A_K)$
and the second image. To see this, note first that
$L^K := \operatorname {Lie}(\mathscr {A}^K) \hookrightarrow \operatorname {Lie}(A_K)$
and the second image. To see this, note first that
![]() ${\operatorname {H}}^0(\mathscr {A}, \Omega ^1_{\mathscr {A}})$
is identified with
${\operatorname {H}}^0(\mathscr {A}, \Omega ^1_{\mathscr {A}})$
is identified with
![]() ${\operatorname {H}}^0( {\mathrm {Spec}} {\mathbf {Z}}_p, \varepsilon ^* \Omega ^1_{\mathscr {A}})$
, where
${\operatorname {H}}^0( {\mathrm {Spec}} {\mathbf {Z}}_p, \varepsilon ^* \Omega ^1_{\mathscr {A}})$
, where
![]() $\varepsilon $
is the zero section of
$\varepsilon $
is the zero section of
![]() $\mathscr {A}$
; see [Reference Bosch, Lütkebohmert and Raynaud12, § 4.2, Prop. 1]. Then by [Reference Bosch, Lütkebohmert and Raynaud12, § 2.2, Prop. 7(b)],
$\mathscr {A}$
; see [Reference Bosch, Lütkebohmert and Raynaud12, § 4.2, Prop. 1]. Then by [Reference Bosch, Lütkebohmert and Raynaud12, § 2.2, Prop. 7(b)],
![]() $\varepsilon ^* \Omega ^1_{\mathscr {A}} = \mathcal {I}/\mathcal {I}^2$
, where
$\varepsilon ^* \Omega ^1_{\mathscr {A}} = \mathcal {I}/\mathcal {I}^2$
, where
![]() $\mathcal {I}$
is the ideal sheaf of the zero section of
$\mathcal {I}$
is the ideal sheaf of the zero section of
![]() $\mathscr {A}$
. The functor of points definition of the Lie algebra then gives that
$\mathscr {A}$
. The functor of points definition of the Lie algebra then gives that
![]() $\operatorname {Lie}(\mathscr {A})$
is the
$\operatorname {Lie}(\mathscr {A})$
is the
![]() ${\mathbf {Z}}_p$
-dual of
${\mathbf {Z}}_p$
-dual of
![]() $\mathcal {I}/\mathcal {I}^2$
. These identifications are all compatible with base change to
$\mathcal {I}/\mathcal {I}^2$
. These identifications are all compatible with base change to
![]() ${\mathbf {Q}}_p$
, so the duality is compatible with what is happening on the generic fiber.
${\mathbf {Q}}_p$
, so the duality is compatible with what is happening on the generic fiber.
It therefore suffices to show that
![]() $L^K = \varpi \cdot L$
. By our assumptions,
$L^K = \varpi \cdot L$
. By our assumptions,
![]() $K|{\mathbf {Q}}_p$
is tamely ramified. By [Reference Edixhoven42, Thm. 4.2], the natural map induces an isomorphism of
$K|{\mathbf {Q}}_p$
is tamely ramified. By [Reference Edixhoven42, Thm. 4.2], the natural map induces an isomorphism of
![]() $\mathscr {A}^K$
with the subscheme of the restriction of scalars
$\mathscr {A}^K$
with the subscheme of the restriction of scalars
![]() $R_{{\mathbf {Z}}_p[\varpi ]/{\mathbf {Z}}_p} \mathscr {A}_{{\mathbf {Z}}_p[\varpi ]}$
fixed by the twisted action of
$R_{{\mathbf {Z}}_p[\varpi ]/{\mathbf {Z}}_p} \mathscr {A}_{{\mathbf {Z}}_p[\varpi ]}$
fixed by the twisted action of
![]() $ {\mathrm {Gal}}(K|{\mathbf {Q}}_p)$
. Taking the invariants under this action commutes with forming the Lie algebra, so we obtain that
$ {\mathrm {Gal}}(K|{\mathbf {Q}}_p)$
. Taking the invariants under this action commutes with forming the Lie algebra, so we obtain that
![]() $L^K$
is obtained by taking the invariants under this twisted action on
$L^K$
is obtained by taking the invariants under this twisted action on
![]() $\operatorname {Lie}(\mathscr {A}_{{\mathbf {Z}}_p[\varpi ]}) = L \otimes _{{\mathbf {Z}}_p} {\mathbf {Z}}_p[\varpi ]$
; this invariant space is exactly
$\operatorname {Lie}(\mathscr {A}_{{\mathbf {Z}}_p[\varpi ]}) = L \otimes _{{\mathbf {Z}}_p} {\mathbf {Z}}_p[\varpi ]$
; this invariant space is exactly
![]() $\varpi \cdot L$
.
$\varpi \cdot L$
.
Corollary 4.16. Let A be an abelian variety over
![]() ${\mathbf {Q}}$
and let K be a quadratic number field of odd discriminant
${\mathbf {Q}}$
and let K be a quadratic number field of odd discriminant
![]() $D_K$
such that all primes of bad reduction for A are unramified in K. Let
$D_K$
such that all primes of bad reduction for A are unramified in K. Let
![]() $\mathscr {A}$
and
$\mathscr {A}$
and
![]() $\mathscr {A}^K$
denote the Néron models of A and of its quadratic twist
$\mathscr {A}^K$
denote the Néron models of A and of its quadratic twist
![]() $A^K$
over
$A^K$
over
![]() ${\mathbf {Z}}$
. Then the image of
${\mathbf {Z}}$
. Then the image of
![]() ${\operatorname {H}}^0(\mathscr {A}^K, \Omega ^1)$
in
${\operatorname {H}}^0(\mathscr {A}^K, \Omega ^1)$
in
![]() ${\operatorname {H}}^0(A_K, \Omega ^1)$
is
${\operatorname {H}}^0(A_K, \Omega ^1)$
is
![]() $1/\sqrt {D_K}$
times the image of
$1/\sqrt {D_K}$
times the image of
![]() ${\operatorname {H}}^0(\mathscr {A}, \Omega ^1)$
.
${\operatorname {H}}^0(\mathscr {A}, \Omega ^1)$
.
Proof. Fix a Néron basis
![]() $(\omega _1, \ldots , \omega _g)$
for A, where
$(\omega _1, \ldots , \omega _g)$
for A, where
![]() $g = \dim A$
. Identifying invariant
$g = \dim A$
. Identifying invariant
![]() $1$
-forms on A and on
$1$
-forms on A and on
![]() $A^K$
with their images on
$A^K$
with their images on
![]() $A_K$
, we see that
$A_K$
, we see that
![]() $(\sqrt {D_K}^{-1} \omega _1, \ldots , \sqrt {D_K}^{-1} \omega _g)$
is a
$(\sqrt {D_K}^{-1} \omega _1, \ldots , \sqrt {D_K}^{-1} \omega _g)$
is a
![]() ${\mathbf {Q}}$
-basis of the space of invariant
${\mathbf {Q}}$
-basis of the space of invariant
![]() $1$
-forms on
$1$
-forms on
![]() $A^K$
. Since
$A^K$
. Since
![]() $K|{\mathbf {Q}}$
is unramified at all places of bad reduction of A, these
$K|{\mathbf {Q}}$
is unramified at all places of bad reduction of A, these
![]() $1$
-forms will form a local Néron basis at all these places, and also at all places of good reduction for A at which
$1$
-forms will form a local Néron basis at all these places, and also at all places of good reduction for A at which
![]() $K|{\mathbf {Q}}$
is unramified. Finally, lemma 4.15 (with
$K|{\mathbf {Q}}$
is unramified. Finally, lemma 4.15 (with
![]() $\varpi \leftarrow \sqrt {D_K}$
) shows that they also form a local Néron basis at all places where
$\varpi \leftarrow \sqrt {D_K}$
) shows that they also form a local Néron basis at all places where
![]() $K|{\mathbf {Q}}$
is ramified. So we have obtained a (global) Néron basis for
$K|{\mathbf {Q}}$
is ramified. So we have obtained a (global) Néron basis for
![]() $A^K$
, and the claim follows.
$A^K$
, and the claim follows.
Corollary 4.17. Let A be an abelian variety over
![]() ${\mathbf {Q}}$
and let K be a quadratic number field of odd discriminant such that all primes of bad reduction for A are unramified in K. Let
${\mathbf {Q}}$
and let K be a quadratic number field of odd discriminant such that all primes of bad reduction for A are unramified in K. Let
![]() $\Pi _A$
be a big period matrix for A with respect to a Néron basis of
$\Pi _A$
be a big period matrix for A with respect to a Néron basis of
![]() ${\operatorname {H}}^0(A, \Omega ^1)$
. Then
${\operatorname {H}}^0(A, \Omega ^1)$
. Then
![]() $\sqrt {D_K}^{-1} \Pi _A$
is a big period matrix for the quadratic twist
$\sqrt {D_K}^{-1} \Pi _A$
is a big period matrix for the quadratic twist
![]() $A^K$
with respect to a Néron basis of
$A^K$
with respect to a Néron basis of
![]() ${\operatorname {H}}^0(A^K, \Omega ^1)$
.
${\operatorname {H}}^0(A^K, \Omega ^1)$
.
Proof. We use the Néron bases described in the proof of corollary 4.16. Fixing an embedding
![]() $K \hookrightarrow {\mathbf {C}}$
and a symplectic basis of
$K \hookrightarrow {\mathbf {C}}$
and a symplectic basis of
![]() ${\operatorname {H}}_1(A({\mathbf {C}}), {\mathbf {Z}})$
, we see for the resulting period matrices that
${\operatorname {H}}_1(A({\mathbf {C}}), {\mathbf {Z}})$
, we see for the resulting period matrices that
![]() $\Pi _{A^K} = \sqrt {D_K}^{-1} \Pi _A$
.
$\Pi _{A^K} = \sqrt {D_K}^{-1} \Pi _A$
.
We can use this result, together with the following elementary statement about abelian groups with an involution, to relate the period of
![]() $A/K$
to the real periods of
$A/K$
to the real periods of
![]() $A/{\mathbf {Q}}$
and
$A/{\mathbf {Q}}$
and
![]() $A^K/{\mathbf {Q}}$
when K is an imaginary quadratic field.
$A^K/{\mathbf {Q}}$
when K is an imaginary quadratic field.
Lemma 4.18.
-
(1) Let V be a finite dimensional
 ${\mathbf {F}}_2$
-vector space and let
${\mathbf {F}}_2$
-vector space and let
 $\iota \in \mathrm {GL}(V)$
with
$\iota \in \mathrm {GL}(V)$
with
 $\iota ^2 = {\mathrm {id}}_V$
. Then
$\iota ^2 = {\mathrm {id}}_V$
. Then  $$\begin{align*}(V : (\operatorname{\mathrm{id}}+\iota)(V)) = \#V^{\langle \iota \rangle} . \end{align*}$$
$$\begin{align*}(V : (\operatorname{\mathrm{id}}+\iota)(V)) = \#V^{\langle \iota \rangle} . \end{align*}$$
-
(2) Let G be a finitely generated abelian group and let
 $\iota \in {\mathrm {Aut}}(G)$
with
$\iota \in {\mathrm {Aut}}(G)$
with
 $\iota ^2 = {\mathrm {id}}_G$
. Let
$\iota ^2 = {\mathrm {id}}_G$
. Let
 $G_1 = \{g + \iota (g) : g \in G\}$
and
$G_1 = \{g + \iota (g) : g \in G\}$
and
 $G_2 = \{g - \iota (g) : g \in G\}$
. Then
$G_2 = \{g - \iota (g) : g \in G\}$
. Then  $$\begin{align*}(G : G_1 + G_2) = \#\Bigl(\frac{G}{2G}\Bigr)^{\langle \iota \rangle} . \end{align*}$$
$$\begin{align*}(G : G_1 + G_2) = \#\Bigl(\frac{G}{2G}\Bigr)^{\langle \iota \rangle} . \end{align*}$$
Proof.
-
(1) The map
 $\varphi := {\mathrm {id}} + \iota = {\mathrm {id}} - \iota $
has kernel
$\varphi := {\mathrm {id}} + \iota = {\mathrm {id}} - \iota $
has kernel
 $V^{\langle \iota \rangle }$
. Since V is finite, we have
$V^{\langle \iota \rangle }$
. Since V is finite, we have  $$\begin{align*}(V : (\operatorname{\mathrm{id}}+\iota)(V)) = \#\operatorname{\mathrm{coker}} \varphi = \#\mathrm{ker} \varphi = \#V^{\langle \iota \rangle} . \end{align*}$$
$$\begin{align*}(V : (\operatorname{\mathrm{id}}+\iota)(V)) = \#\operatorname{\mathrm{coker}} \varphi = \#\mathrm{ker} \varphi = \#V^{\langle \iota \rangle} . \end{align*}$$
-
(2) Since for each
 $g \in G$
,
$g \in G$
,
 $2g = (g + \iota (g)) + (g - \iota (g)) \in G_1 + G_2$
, we have that
$2g = (g + \iota (g)) + (g - \iota (g)) \in G_1 + G_2$
, we have that
 $2G \subseteq G_1 + G_2$
. Therefore, using part (1),
$2G \subseteq G_1 + G_2$
. Therefore, using part (1),  $$\begin{align*}(G : G_1 + G_2) = \Bigl(\frac{G}{2G} : \frac{G_1 + G_2}{2G}\Bigr) = \Bigl(\frac{G}{2G} : (\operatorname{\mathrm{id}} + \iota)\Bigl(\frac{G}{2G}\Bigr)\Bigr) = \#\Bigl(\frac{G}{2G}\Bigr)^{\langle \iota \rangle} . \end{align*}$$
$$\begin{align*}(G : G_1 + G_2) = \Bigl(\frac{G}{2G} : \frac{G_1 + G_2}{2G}\Bigr) = \Bigl(\frac{G}{2G} : (\operatorname{\mathrm{id}} + \iota)\Bigl(\frac{G}{2G}\Bigr)\Bigr) = \#\Bigl(\frac{G}{2G}\Bigr)^{\langle \iota \rangle} . \end{align*}$$
Corollary 4.19. Let A and K be as in corollary 4.17, with
![]() $D_K < 0$
. Then
$D_K < 0$
. Then
 $$\begin{align*}\frac{\Omega_{A/{\mathbf{Q}}} \Omega_{A^K/{\mathbf{Q}}} \sqrt{|D_K|}^{g}}{\Omega_{A/K}} = \frac{\#A({\mathbf{R}})[2]}{2^g} = \#\pi_0(A({\mathbf{R}})) . \end{align*}$$
$$\begin{align*}\frac{\Omega_{A/{\mathbf{Q}}} \Omega_{A^K/{\mathbf{Q}}} \sqrt{|D_K|}^{g}}{\Omega_{A/K}} = \frac{\#A({\mathbf{R}})[2]}{2^g} = \#\pi_0(A({\mathbf{R}})) . \end{align*}$$
Proof. We use
![]() $\Pi _A$
and
$\Pi _A$
and
![]() $\Pi _{A^K}$
to denote big period matrices of A and
$\Pi _{A^K}$
to denote big period matrices of A and
![]() $A^K$
with respect to a Néron basis of the invariant
$A^K$
with respect to a Néron basis of the invariant
![]() $1$
-forms. The period
$1$
-forms. The period
![]() $\Omega _{A/K}$
is
$\Omega _{A/K}$
is
![]() $2^g$
times the covolume of the lattice
$2^g$
times the covolume of the lattice
![]() $\Lambda \subseteq {\mathbf {C}}^g$
(where, as usual,
$\Lambda \subseteq {\mathbf {C}}^g$
(where, as usual,
![]() $g = \dim A$
) generated by the columns of
$g = \dim A$
) generated by the columns of
![]() $\Pi _A$
(a Néron basis of
$\Pi _A$
(a Néron basis of
![]() ${\operatorname {H}}^0(A/{\mathbf {Q}}, \Omega ^1)$
gives a Néron basis of
${\operatorname {H}}^0(A/{\mathbf {Q}}, \Omega ^1)$
gives a Néron basis of
![]() ${\operatorname {H}}^0(A/K, \Omega ^1)$
, since at the bad places of A,
${\operatorname {H}}^0(A/K, \Omega ^1)$
, since at the bad places of A,
![]() $K|{\mathbf {Q}}$
is unramified and Néron models are preserved by unramified base extension). The real periods
$K|{\mathbf {Q}}$
is unramified and Néron models are preserved by unramified base extension). The real periods
![]() $\Omega _{A/{\mathbf {Q}}}$
and
$\Omega _{A/{\mathbf {Q}}}$
and
![]() $\Omega _{A^K/{\mathbf {Q}}}$
are the covolumes of the lattices in
$\Omega _{A^K/{\mathbf {Q}}}$
are the covolumes of the lattices in
![]() ${\mathbf {R}}^g$
generated by the
${\mathbf {R}}^g$
generated by the
![]() ${\mathbf {C}}|{\mathbf {R}}$
-traces of the columns of
${\mathbf {C}}|{\mathbf {R}}$
-traces of the columns of
![]() $\Pi _A$
and
$\Pi _A$
and
![]() $\Pi _{A^K}$
, respectively. The first lattice is
$\Pi _{A^K}$
, respectively. The first lattice is
![]() $\Lambda _1 = \{\lambda + \bar {\lambda } : \lambda \in \Lambda \}$
. By corollary 4.17,
$\Lambda _1 = \{\lambda + \bar {\lambda } : \lambda \in \Lambda \}$
. By corollary 4.17,
![]() $\Pi _{A^K} = D_K^{-1/2} \Pi _A$
(using suitable bases), which together with
$\Pi _{A^K} = D_K^{-1/2} \Pi _A$
(using suitable bases), which together with
![]() $D_K < 0$
implies that
$D_K < 0$
implies that
![]() $\Omega _{A^K/{\mathbf {Q}}}$
is
$\Omega _{A^K/{\mathbf {Q}}}$
is
![]() $\sqrt {|D_K|}^{-g}$
times the covolume of the lattice in
$\sqrt {|D_K|}^{-g}$
times the covolume of the lattice in
![]() ${\mathbf {R}}^g$
generated by the
${\mathbf {R}}^g$
generated by the
![]() ${\mathbf {C}}|{\mathbf {R}}$
-traces of the columns of
${\mathbf {C}}|{\mathbf {R}}$
-traces of the columns of
![]() $\sqrt {-1} \cdot \Pi _A$
. This is the same as the covolume of
$\sqrt {-1} \cdot \Pi _A$
. This is the same as the covolume of
![]() $\Lambda _2 \subseteq \sqrt {-1} \,{\mathbf {R}}^g$
, where
$\Lambda _2 \subseteq \sqrt {-1} \,{\mathbf {R}}^g$
, where
![]() $\Lambda _2 = \{\lambda - \bar {\lambda } : \lambda \in \Lambda \}$
. So
$\Lambda _2 = \{\lambda - \bar {\lambda } : \lambda \in \Lambda \}$
. So
![]() $\Omega _{A/{\mathbf {Q}}} \Omega _{A^K/{\mathbf {Q}}} \sqrt {|D_K|}^{g}$
is the covolume of
$\Omega _{A/{\mathbf {Q}}} \Omega _{A^K/{\mathbf {Q}}} \sqrt {|D_K|}^{g}$
is the covolume of
![]() $\Lambda _1 + \Lambda _2 \subseteq {\mathbf {C}}^g$
. Applying lemma 4.18 (2) with
$\Lambda _1 + \Lambda _2 \subseteq {\mathbf {C}}^g$
. Applying lemma 4.18 (2) with
![]() $G = \Lambda $
and
$G = \Lambda $
and
![]() $\iota $
the restriction of complex conjugation, we finally obtain
$\iota $
the restriction of complex conjugation, we finally obtain
 $$\begin{align*}\frac{\Omega_{A/{\mathbf{Q}}} \Omega_{A^K/{\mathbf{Q}}} \sqrt{|D_K|}^{g}}{\Omega_{A/K}} = \frac{(\Lambda : \Lambda_1 + \Lambda_2)}{2^g} = \frac{\#(\Lambda/2\Lambda)^+}{2^g} = \frac{\#A({\mathbf{R}})[2]}{2^g}, \end{align*}$$
$$\begin{align*}\frac{\Omega_{A/{\mathbf{Q}}} \Omega_{A^K/{\mathbf{Q}}} \sqrt{|D_K|}^{g}}{\Omega_{A/K}} = \frac{(\Lambda : \Lambda_1 + \Lambda_2)}{2^g} = \frac{\#(\Lambda/2\Lambda)^+}{2^g} = \frac{\#A({\mathbf{R}})[2]}{2^g}, \end{align*}$$
where
![]() $(\Lambda /2\Lambda )^+$
denotes the subgroup fixed under the induced action of complex conjugation. (Note that
$(\Lambda /2\Lambda )^+$
denotes the subgroup fixed under the induced action of complex conjugation. (Note that
![]() $A({\mathbf {C}})[2] \simeq \tfrac {1}{2} \Lambda /\Lambda \simeq \Lambda /2\Lambda $
as a
$A({\mathbf {C}})[2] \simeq \tfrac {1}{2} \Lambda /\Lambda \simeq \Lambda /2\Lambda $
as a
![]() $ {\mathrm {Gal}}({\mathbf {C}}|{\mathbf {R}})$
-module.) The last equality comes from the fact that
$ {\mathrm {Gal}}({\mathbf {C}}|{\mathbf {R}})$
-module.) The last equality comes from the fact that
![]() $\#A({\mathbf {R}})^0[2] = 2^g$
since the connected component of the identity is a g-dimensional real torus.
$\#A({\mathbf {R}})^0[2] = 2^g$
since the connected component of the identity is a g-dimensional real torus.
Corollary 4.20. Let
![]() $f \in \mathcal {N}(N, g)$
and let K be a quadratic number field such that
$f \in \mathcal {N}(N, g)$
and let K be a quadratic number field such that
![]() $D_K$
is coprime with
$D_K$
is coprime with
![]() $2N$
. Let further
$2N$
. Let further
![]() $\pi \colon A_f \to J$
be an isogeny defined over
$\pi \colon A_f \to J$
be an isogeny defined over
![]() ${\mathbf {Q}}$
. We write
${\mathbf {Q}}$
. We write
![]() $f^K$
and
$f^K$
and
![]() $\pi ^K$
for the corresponding quadratic twists of f and
$\pi ^K$
for the corresponding quadratic twists of f and
![]() $\pi $
, respectively. Then
$\pi $
, respectively. Then
![]() $c_{f^K} c_{\pi ^K} = c_f c_\pi $
.
$c_{f^K} c_{\pi ^K} = c_f c_\pi $
.
Proof. The map
![]() $\pi _f \colon J_0(N) \to A_f$
is geometrically defined, so
$\pi _f \colon J_0(N) \to A_f$
is geometrically defined, so
![]() $\pi _{f^K}$
is the same as the quadratic twist
$\pi _{f^K}$
is the same as the quadratic twist
![]() $\pi _f^K$
of
$\pi _f^K$
of
![]() $\pi _f$
. Note that
$\pi _f$
. Note that
![]() $c_f$
is the index of
$c_f$
is the index of
![]() $\pi _f^* {\operatorname {H}}^0(\mathscr {A}_f, \Omega ^1_{\mathscr {A}_f/{\mathbf {Z}}})$
in
$\pi _f^* {\operatorname {H}}^0(\mathscr {A}_f, \Omega ^1_{\mathscr {A}_f/{\mathbf {Z}}})$
in
![]() $\pi _f^*(A_f, \Omega ^1) \cap {\operatorname {H}}^0(\mathscr {J}_0(N), \Omega ^1_{\mathscr {J}_0(N)/{\mathbf {Z}}})$
(where, as usual,
$\pi _f^*(A_f, \Omega ^1) \cap {\operatorname {H}}^0(\mathscr {J}_0(N), \Omega ^1_{\mathscr {J}_0(N)/{\mathbf {Z}}})$
(where, as usual,
![]() $\mathscr {A}_f$
and
$\mathscr {A}_f$
and
![]() $\mathscr {J}_0(N)$
denote the Néron models of
$\mathscr {J}_0(N)$
denote the Néron models of
![]() $A_f$
and
$A_f$
and
![]() $J_0(N)$
over
$J_0(N)$
over
![]() ${\mathbf {Z}}$
). Applying corollary 4.16, we see that, considered inside
${\mathbf {Z}}$
). Applying corollary 4.16, we see that, considered inside
![]() ${\operatorname {H}}^0(J_0(N)_K, \Omega ^1)$
, the images of both spaces are multiplied by
${\operatorname {H}}^0(J_0(N)_K, \Omega ^1)$
, the images of both spaces are multiplied by
![]() $1/\sqrt {D_K}$
by twisting, so the index stays the same. This shows that
$1/\sqrt {D_K}$
by twisting, so the index stays the same. This shows that
![]() $c_{f^K} = c_f$
. An analogous argument shows that
$c_{f^K} = c_f$
. An analogous argument shows that
![]() $c_{\pi ^K} = c_\pi $
.
$c_{\pi ^K} = c_\pi $
.
4.6 The case of L-rank
 $1$
: Computing
$1$
: Computing 
We now show how we can compute ![]() from
from ![]() as determined in Section 4.4 and
as determined in Section 4.4 and ![]() , which we can compute as in Section 4.3 (and using Section 4.5 to make the computation of the ‘L-ratio’ for the quadratic twist feasible, which would otherwise be quite slow, as the level of the twisted newform tends to be fairly large) since the L-rank of
, which we can compute as in Section 4.3 (and using Section 4.5 to make the computation of the ‘L-ratio’ for the quadratic twist feasible, which would otherwise be quite slow, as the level of the twisted newform tends to be fairly large) since the L-rank of
![]() $J^K$
is zero by the Heegner hypothesis.
$J^K$
is zero by the Heegner hypothesis.
From the induction formula
![]() $L(J/K,s) = L(J/{\mathbf {Q}},s)L(J^K/{\mathbf {Q}},s)$
, we obtain
$L(J/K,s) = L(J/{\mathbf {Q}},s)L(J^K/{\mathbf {Q}},s)$
, we obtain
Then one computes ![]() from the relation
from the relation

that we obtain from (4.4) and its analogues for
![]() $J/{\mathbf {Q}}$
and
$J/{\mathbf {Q}}$
and
![]() $J^K/{\mathbf {Q}}$
.
$J^K/{\mathbf {Q}}$
.
As discussed at the beginning of Section 4.4, both regulators are defined in terms of the normalized canonical height. This implies that
 $$\begin{align*}\frac{\operatorname{Reg}_{J/{\mathbf{Q}}}}{(\#J({\mathbf{Q}})_{\mathrm{tors}})^2} \cdot \frac{(\#J(K)_{\mathrm{tors}})^2}{\operatorname{Reg}_{J/K}} = (J(K) : J({\mathbf{Q}}))^2 . \end{align*}$$
$$\begin{align*}\frac{\operatorname{Reg}_{J/{\mathbf{Q}}}}{(\#J({\mathbf{Q}})_{\mathrm{tors}})^2} \cdot \frac{(\#J(K)_{\mathrm{tors}})^2}{\operatorname{Reg}_{J/K}} = (J(K) : J({\mathbf{Q}}))^2 . \end{align*}$$
Since we have computed
![]() $J(K)$
already, we can easily determine this index. By corollary 4.19, the last factor is
$J(K)$
already, we can easily determine this index. By corollary 4.19, the last factor is
![]() $\#J({\mathbf {R}})[2]/2^g$
, assuming
$\#J({\mathbf {R}})[2]/2^g$
, assuming
![]() $D_K$
is odd.
$D_K$
is odd.
We can evaluate the factor involving Tamagawa numbers using the following result. This is not used in the proof of the formula in corollary 4.22 below but will be useful for the example in Appendix A.
Lemma 4.21. We have
and hence,
 $$\begin{align*}\frac{\operatorname{\mathrm{Tam}}(J/{\mathbf{Q}}) \operatorname{\mathrm{Tam}}(J^K/{\mathbf{Q}})}{\operatorname{\mathrm{Tam}}(J/K)} = \prod\limits_{p \mid D_K} c_p(J^K/{\mathbf{Q}}), \end{align*}$$
$$\begin{align*}\frac{\operatorname{\mathrm{Tam}}(J/{\mathbf{Q}}) \operatorname{\mathrm{Tam}}(J^K/{\mathbf{Q}})}{\operatorname{\mathrm{Tam}}(J/K)} = \prod\limits_{p \mid D_K} c_p(J^K/{\mathbf{Q}}), \end{align*}$$
where
![]() $c_p(J^K/{\mathbf {Q}}) = \#J({\mathbf {F}}_p)[2]$
when
$c_p(J^K/{\mathbf {Q}}) = \#J({\mathbf {F}}_p)[2]$
when
![]() $p \mid D_K$
is an odd prime.
$p \mid D_K$
is an odd prime.
Proof. Since all bad primes p of J split in K, the Tamagawa numbers of
![]() $J^K$
at these primes are the same as those of J and also agree with the two Tamagawa numbers of
$J^K$
at these primes are the same as those of J and also agree with the two Tamagawa numbers of
![]() $J/K$
at the primes dividing p. Since the only further primes of bad reduction for
$J/K$
at the primes dividing p. Since the only further primes of bad reduction for
![]() $J^K$
are those dividing
$J^K$
are those dividing
![]() $D_K$
, we obtain the stated equalities.
$D_K$
, we obtain the stated equalities.
The last claim follows from the fact that
![]() $J^K$
has totally unipotent reduction at p, which implies that there is no
$J^K$
has totally unipotent reduction at p, which implies that there is no
![]() $2$
-torsion in
$2$
-torsion in
![]() $\mathscr {J}^K({\mathbf {F}}_p)^0$
(where
$\mathscr {J}^K({\mathbf {F}}_p)^0$
(where
![]() $\mathscr {J}^K$
is the Néron model of
$\mathscr {J}^K$
is the Néron model of
![]() $J^K$
), together with the fact that the component group is killed by
$J^K$
), together with the fact that the component group is killed by
![]() $2$
since
$2$
since
![]() $J^K$
obtains good reduction after a quadratic extension (see [Reference Halle and Nicaise53, Cor. 5.3.3.2]). This gives an isomorphism between
$J^K$
obtains good reduction after a quadratic extension (see [Reference Halle and Nicaise53, Cor. 5.3.3.2]). This gives an isomorphism between
![]() $J({\mathbf {F}}_p)[2] \simeq \mathscr {J}^K({\mathbf {F}}_p)[2]$
and the
$J({\mathbf {F}}_p)[2] \simeq \mathscr {J}^K({\mathbf {F}}_p)[2]$
and the
![]() ${\mathbf {F}}_p$
-points of the component group.
${\mathbf {F}}_p$
-points of the component group.
Recall that
![]() $ {\mathrm {Tam}}(J/K) = {\mathrm {Tam}}(J/{\mathbf {Q}})^2$
by (4.6). We then obtain the following.
$ {\mathrm {Tam}}(J/K) = {\mathrm {Tam}}(J/{\mathbf {Q}})^2$
by (4.6). We then obtain the following.
Corollary 4.22. Keep the notations and assumptions introduced so far. If
![]() $D_K$
is odd, then
$D_K$
is odd, then

5 Bounding the support of the Tate–Shafarevich group
Let
![]() $A/{\mathbf {Q}}$
be an absolutely simple
$A/{\mathbf {Q}}$
be an absolutely simple
![]() $\mathrm {GL}_2$
-type abelian variety with associated newform f. In this section, we obtain an explicit bound on the support of the Tate–Shafarevich group coming from the Heegner point Euler system. This leads to an explicit description of a finite set of (regular) prime ideals
$\mathrm {GL}_2$
-type abelian variety with associated newform f. In this section, we obtain an explicit bound on the support of the Tate–Shafarevich group coming from the Heegner point Euler system. This leads to an explicit description of a finite set of (regular) prime ideals
![]() $\mathfrak {p}$
of
$\mathfrak {p}$
of
![]() ${\mathbf {Z}}[f]$
such that
${\mathbf {Z}}[f]$
such that ![]() for all
for all
![]() $\mathfrak {p}$
not in this set. In the L-rank
$\mathfrak {p}$
not in this set. In the L-rank
![]() $0$
case, we make the results of Kolyvagin–Logachëv [Reference Kolyvagin and Logachëv64] explicit and in the L-rank
$0$
case, we make the results of Kolyvagin–Logachëv [Reference Kolyvagin and Logachëv64] explicit and in the L-rank
![]() $1$
case those of Nekovář [Reference Nekovář80]. We first prove a result on the vanishing of the first Galois cohomology group for irreducible
$1$
case those of Nekovář [Reference Nekovář80]. We first prove a result on the vanishing of the first Galois cohomology group for irreducible
![]() $\rho _{\mathfrak {p}}$
in Section 5.1. Specializing to the case where
$\rho _{\mathfrak {p}}$
in Section 5.1. Specializing to the case where
![]() $A = J$
is a Jacobian for simplicity (so we do not have to deal with polarizations), we derive the explicit finite support for
$A = J$
is a Jacobian for simplicity (so we do not have to deal with polarizations), we derive the explicit finite support for ![]() in Section 5.2; see theorems 5.6, 5.7 and 5.10.
in Section 5.2; see theorems 5.6, 5.7 and 5.10.
In the following subsection, F will be a general number field and does not denote
![]() $\operatorname {Frac} {\mathbf {Z}}[f]$
.
$\operatorname {Frac} {\mathbf {Z}}[f]$
.
5.1 Vanishing of
 ${\operatorname {H}}^1(F(A[\mathfrak {p}])|F, A[\mathfrak {p}])$
${\operatorname {H}}^1(F(A[\mathfrak {p}])|F, A[\mathfrak {p}])$
We assume that
![]() $\mathfrak {p}$
is a regular prime ideal of
$\mathfrak {p}$
is a regular prime ideal of
![]() ${\mathbf {Z}}[f]$
and set
${\mathbf {Z}}[f]$
and set
![]() $p = p(\mathfrak {p})$
. The goal of this section is to show that the Galois cohomology group
$p = p(\mathfrak {p})$
. The goal of this section is to show that the Galois cohomology group
![]() ${\operatorname {H}}^1(F(A[\mathfrak {p}])|F, A[\mathfrak {p}])$
vanishes when the mod
${\operatorname {H}}^1(F(A[\mathfrak {p}])|F, A[\mathfrak {p}])$
vanishes when the mod
![]() $\mathfrak {p}$
Galois representation is irreducible (and
$\mathfrak {p}$
Galois representation is irreducible (and
![]() $p> 2$
); see proposition 5.4. The vanishing of this group is an important input for [Reference Kolyvagin and Logachëv64, Proposition 5.10].
$p> 2$
); see proposition 5.4. The vanishing of this group is an important input for [Reference Kolyvagin and Logachëv64, Proposition 5.10].
Let F be a number field. (This level of generality is needed later on and is also useful for further applications – for example, in our forthcoming work on the BSD conjecture over totally real fields with Pip Goodman.) Let
![]() $G := {\mathrm {Gal}}(F(A[\mathfrak {p}])|F) \hookrightarrow G_{\mathfrak {p}}^{\operatorname {max}}$
with
$G := {\mathrm {Gal}}(F(A[\mathfrak {p}])|F) \hookrightarrow G_{\mathfrak {p}}^{\operatorname {max}}$
with
![]() $G_{\mathfrak {p}}^{\operatorname {max}}$
defined as in definition 2.9.
$G_{\mathfrak {p}}^{\operatorname {max}}$
defined as in definition 2.9.
The main idea is that
![]() ${\operatorname {H}}^1(G,A[\mathfrak {p}]) = 0$
if G contains a nontrivial homothety. Our arguments are purely group cohomological, without much arithmetic input.
${\operatorname {H}}^1(G,A[\mathfrak {p}]) = 0$
if G contains a nontrivial homothety. Our arguments are purely group cohomological, without much arithmetic input.
Definition 5.1. A homothety in the automorphism group of a vector space V over a field K is a map of the form
![]() $v \mapsto \lambda v$
with
$v \mapsto \lambda v$
with
![]() $\lambda \in K^\times $
. It is nontrivial if
$\lambda \in K^\times $
. It is nontrivial if
![]() $\lambda \neq 1$
.
$\lambda \neq 1$
.
Lemma 5.2. Let V be a finite-dimensional vector space over a finite field
![]() ${\mathbf {F}}$
and let G be a subgroup of
${\mathbf {F}}$
and let G be a subgroup of
![]() $\mathrm {GL}(V)$
. If G contains a nontrivial homothety, then
$\mathrm {GL}(V)$
. If G contains a nontrivial homothety, then
![]() ${\operatorname {H}}^1(G, V) = 0$
.
${\operatorname {H}}^1(G, V) = 0$
.
Proof. (Compare [Reference Lawson and Wuthrich67, Lemma 3].) Let
![]() $g \in G$
be a nontrivial homothety; note that
$g \in G$
be a nontrivial homothety; note that
![]() $\langle {g}\rangle $
is a normal subgroup of G. Consider the associated inflation-restriction exact sequence:
$\langle {g}\rangle $
is a normal subgroup of G. Consider the associated inflation-restriction exact sequence:
The left-hand group is trivial since
![]() $V^{\langle {g}\rangle } = 0$
(a nontrivial scalar matrix fixes no nontrivial element of a vector space), and the right-hand group is trivial because
$V^{\langle {g}\rangle } = 0$
(a nontrivial scalar matrix fixes no nontrivial element of a vector space), and the right-hand group is trivial because
![]() $\#\langle {g}\rangle \mid \#{\mathbf {F}}^\times $
and
$\#\langle {g}\rangle \mid \#{\mathbf {F}}^\times $
and
![]() $\#V = \#{\mathbf {F}}^{\dim {V}}$
are coprime. So the middle group must be trivial as well.
$\#V = \#{\mathbf {F}}^{\dim {V}}$
are coprime. So the middle group must be trivial as well.
Lemma 5.3. Let
![]() ${\mathbf {F}}$
be a finite field of characteristic
${\mathbf {F}}$
be a finite field of characteristic
![]() $p \ge 3$
and let
$p \ge 3$
and let
![]() $G \subseteq \mathrm {GL}_2({\mathbf {F}})$
be such that G does not fix a unique line in
$G \subseteq \mathrm {GL}_2({\mathbf {F}})$
be such that G does not fix a unique line in
![]() ${\mathbf {F}}^2$
. Then
${\mathbf {F}}^2$
. Then
Proof. We proceed in a number of steps.
-
(1) If N is a normal subgroup in G and N fixes a unique line, then so does G. This is because G acts on the lines fixed by N.
-
(2) If N is a normal subgroup in G of index prime to p, then (by inflation-restriction and since
 ${\operatorname {H}}^1(G/N, V) = 0$
for
${\operatorname {H}}^1(G/N, V) = 0$
for
 $V = ({\mathbf {F}}^2)^N$
)
$V = ({\mathbf {F}}^2)^N$
)
 ${\operatorname {H}}^1(N, {\mathbf {F}}^2) = 0$
implies
${\operatorname {H}}^1(N, {\mathbf {F}}^2) = 0$
implies
 ${\operatorname {H}}^1(G, {\mathbf {F}}^2) = 0$
.
${\operatorname {H}}^1(G, {\mathbf {F}}^2) = 0$
. -
(3) By (1) and (2), we can restrict to subgroups of
 $ {\mathrm {SL}}_2({\mathbf {F}})$
, observing that
$ {\mathrm {SL}}_2({\mathbf {F}})$
, observing that
 $G \cap {\mathrm {SL}}_2({\mathbf {F}})$
is a normal subgroup of G of index dividing
$G \cap {\mathrm {SL}}_2({\mathbf {F}})$
is a normal subgroup of G of index dividing
 $\#{\mathbf {F}}^\times $
.
$\#{\mathbf {F}}^\times $
. -
(4) If
 $\#G$
is prime to p, then
$\#G$
is prime to p, then
 ${\operatorname {H}}^1(G, {\mathbf {F}}^2) = 0$
. We can therefore assume that p divides
${\operatorname {H}}^1(G, {\mathbf {F}}^2) = 0$
. We can therefore assume that p divides
 $\#G$
and therefore also
$\#G$
and therefore also
 $\#{\mathbf {P}} G$
.
$\#{\mathbf {P}} G$
. -
(5) If G contains
 $-I$
(the unique nontrivial homothety in
$-I$
(the unique nontrivial homothety in
 $ {\mathrm {SL}}_2({\mathbf {F}})$
; note
$ {\mathrm {SL}}_2({\mathbf {F}})$
; note
 $p \geq 3$
), then
$p \geq 3$
), then
 ${\operatorname {H}}^1(G, {\mathbf {F}}^2) = 0$
by lemma 5.2. Since
${\operatorname {H}}^1(G, {\mathbf {F}}^2) = 0$
by lemma 5.2. Since
 $-I$
is the unique element of order
$-I$
is the unique element of order
 $2$
in
$2$
in
 $ {\mathrm {SL}}_2({\mathbf {F}})$
, this is the case whenever
$ {\mathrm {SL}}_2({\mathbf {F}})$
, this is the case whenever
 $\#G$
is even, so in particular when
$\#G$
is even, so in particular when
 $\#{\mathbf {P}} G$
is even.
$\#{\mathbf {P}} G$
is even. -
(6) We consult [Reference King62, Thm. 2.1], which lists all subgroups of
 $\operatorname {PSL}_2({\mathbf {F}})$
. In cases (f), (i), (p) and (u),
$\operatorname {PSL}_2({\mathbf {F}})$
. In cases (f), (i), (p) and (u),
 $p = 2$
. In cases (b)–(e), (g), (h), (j) and (k), p does not divide
$p = 2$
. In cases (b)–(e), (g), (h), (j) and (k), p does not divide
 $\#{\mathbf {P}} G$
. In cases (n), (o), (q)–(t) and (v),
$\#{\mathbf {P}} G$
. In cases (n), (o), (q)–(t) and (v),
 $\#{\mathbf {P}} G$
is even. In the remaining cases (a), (l) and (m),
$\#{\mathbf {P}} G$
is even. In the remaining cases (a), (l) and (m),
 ${\mathbf {P}} G$
is contained in a Borel subgroup and has order divisible by p, so G fixes a unique line. In each case, either the assumptions are violated, or we can conclude using (4) or (5).
${\mathbf {P}} G$
is contained in a Borel subgroup and has order divisible by p, so G fixes a unique line. In each case, either the assumptions are violated, or we can conclude using (4) or (5).
Proposition 5.4 (Irreducible implies trivial cohomology)
Let A be an absolutely simple abelian variety over
![]() ${\mathbf {Q}}$
of
${\mathbf {Q}}$
of
![]() $\mathrm {GL}_2$
-type and let
$\mathrm {GL}_2$
-type and let
![]() $\mathfrak {p}$
be a regular prime ideal of
$\mathfrak {p}$
be a regular prime ideal of
![]() $\mathrm {End}_{\mathbf {Q}}(A)$
. Let F be a number field that is a Galois extension of
$\mathrm {End}_{\mathbf {Q}}(A)$
. Let F be a number field that is a Galois extension of
![]() ${\mathbf {Q}}$
. We assume that
${\mathbf {Q}}$
. We assume that
![]() $p(\mathfrak {p}) \ge 3$
and that
$p(\mathfrak {p}) \ge 3$
and that
![]() $\rho _{\mathfrak {p}}|_{G_F}$
is irreducible. Then
$\rho _{\mathfrak {p}}|_{G_F}$
is irreducible. Then
Proof. Let G be the image of
![]() $\rho _{\mathfrak {p}}$
and let
$\rho _{\mathfrak {p}}$
and let
![]() $G' := \rho _{\mathfrak {p}}(G_F)$
, which is a normal subgroup of G. Since
$G' := \rho _{\mathfrak {p}}(G_F)$
, which is a normal subgroup of G. Since
![]() $\rho _{\mathfrak {p}}$
is irreducible, G does not fix a unique line; by part (1) of the proof of lemma 5.3, this implies that
$\rho _{\mathfrak {p}}$
is irreducible, G does not fix a unique line; by part (1) of the proof of lemma 5.3, this implies that
![]() $G'$
also does not fix a unique line. Then lemma 5.3 says that
$G'$
also does not fix a unique line. Then lemma 5.3 says that
5.2 Bounding the support of 
Using our computations of
![]() $G_{\mathfrak {p}}$
from Section 2 and the Heegner index from Section 3, we can improve [Reference Kolyvagin and Logachëv64] and [Reference Nekovář80] to give an explicit finite bound for the support of
$G_{\mathfrak {p}}$
from Section 2 and the Heegner index from Section 3, we can improve [Reference Kolyvagin and Logachëv64] and [Reference Nekovář80] to give an explicit finite bound for the support of ![]() considered as a
considered as a
![]() ${\mathbf {Z}}$
- or an
${\mathbf {Z}}$
- or an
![]() $\mathcal {O}$
-module.
$\mathcal {O}$
-module.
We do not repeat the full proof; we only explain how to make the arguments explicit.
Assumption 5.5. Let A be a modular abelian variety of level N. We write
![]() $\mathcal {O} := \mathrm {End}_{\mathbf {Q}}(A)$
and assume that
$\mathcal {O} := \mathrm {End}_{\mathbf {Q}}(A)$
and assume that
![]() $\mathcal {O}$
is the maximal order of
$\mathcal {O}$
is the maximal order of
![]() ${\mathbf {Q}}(f)$
(via an isomorphism as in (3.2)). This is no essential restriction; compare remark 2.3 and note that the truth of the strong BSD Conjecture is an isogeny invariant by [Reference Milne78, Theorem I.7.3]. (However, the support of
${\mathbf {Q}}(f)$
(via an isomorphism as in (3.2)). This is no essential restriction; compare remark 2.3 and note that the truth of the strong BSD Conjecture is an isogeny invariant by [Reference Milne78, Theorem I.7.3]. (However, the support of ![]() can change under isogenies.) Let K be a Heegner field of odd Heegner discriminant
can change under isogenies.) Let K be a Heegner field of odd Heegner discriminant
![]() $D_K \neq -3$
(in particular,
$D_K \neq -3$
(in particular,
![]() $D_K \notin \{-3, -4, -8\}$
) (i.e., K is an imaginary quadratic field such that all primes dividing the level N split completely in K). Then
$D_K \notin \{-3, -4, -8\}$
) (i.e., K is an imaginary quadratic field such that all primes dividing the level N split completely in K). Then
![]() $y_{K,\pi } \in A(K)$
is a Heegner point, and we assume that
$y_{K,\pi } \in A(K)$
is a Heegner point, and we assume that
![]() $L\!\operatorname {-rk}(A/K) = 1$
(i.e.,
$L\!\operatorname {-rk}(A/K) = 1$
(i.e.,
![]() $y_{K,\pi }$
is non-torsion by the Gross–Zagier formula). Note that
$y_{K,\pi }$
is non-torsion by the Gross–Zagier formula). Note that
![]() $y_{K,\pi }$
satisfies the Euler system relations from [Reference Kolyvagin and Logachëv64, § 2] because the isogeny
$y_{K,\pi }$
satisfies the Euler system relations from [Reference Kolyvagin and Logachëv64, § 2] because the isogeny
![]() $\pi $
is equivariant with respect to the action of
$\pi $
is equivariant with respect to the action of
![]() ${\mathbf {Z}}[f] \subseteq \mathcal {O}$
; see (3.3).
${\mathbf {Z}}[f] \subseteq \mathcal {O}$
; see (3.3).
For several curves among our LMFDB examples, the endomorphism ring of the Jacobian is not maximal. However, in all these cases, there is another curve in the database whose Jacobian is isogenous with endomorphism ring the maximal order; it then suffices to consider these other curves.
In Table 1, we collect the most important objects and constants in [Reference Kolyvagin and Logachëv64]. We specialize to the case that A is the Jacobian J of a curve with its canonical principal polarization. In particular, since J has RM, the Rosati involution associated to the polarization is the identity on
![]() $\mathrm {End}_{\mathbf {Q}}(J) \otimes _{\mathbf {Z}} {\mathbf {R}}$
, which we need to use the results in [Reference Kolyvagin and Logachëv64, § 2.1]. This implies that the polarization
$\mathrm {End}_{\mathbf {Q}}(J) \otimes _{\mathbf {Z}} {\mathbf {R}}$
, which we need to use the results in [Reference Kolyvagin and Logachëv64, § 2.1]. This implies that the polarization
![]() $\varphi _\Lambda $
in Table 1 is principal. Recall that
$\varphi _\Lambda $
in Table 1 is principal. Recall that
![]() $ {\mathrm {Tam}}(J/{\mathbf {Q}}) = \prod _\ell c_\ell (J/{\mathbf {Q}})$
is the Tamagawa product of J. The component group
$ {\mathrm {Tam}}(J/{\mathbf {Q}}) = \prod _\ell c_\ell (J/{\mathbf {Q}})$
is the Tamagawa product of J. The component group
![]() $\pi _0(\mathscr {J})$
of the Néron model
$\pi _0(\mathscr {J})$
of the Néron model
![]() $\mathscr {J}/{\mathbf {Z}}$
of
$\mathscr {J}/{\mathbf {Z}}$
of
![]() $J/{\mathbf {Q}}$
is an
$J/{\mathbf {Q}}$
is an
![]() $\mathcal {O}$
-module. This allows us to consider its order
$\mathcal {O}$
-module. This allows us to consider its order
![]() $ {\mathrm {Tam}}(J/{\mathbf {Q}})$
as the corresponding characteristic ideal in
$ {\mathrm {Tam}}(J/{\mathbf {Q}})$
as the corresponding characteristic ideal in
![]() $\mathcal {O}$
in the following.
$\mathcal {O}$
in the following.
Table 1 The constants
![]() $m_k = m_k(\mathfrak {p}^{n})$
and important objects occurring in the proof of [Reference Kolyvagin and Logachëv64]. The notation ‘
$m_k = m_k(\mathfrak {p}^{n})$
and important objects occurring in the proof of [Reference Kolyvagin and Logachëv64]. The notation ‘
![]() $[m]$
’ denotes m when
$[m]$
’ denotes m when
![]() $p(\mathfrak {p}) = 2$
and
$p(\mathfrak {p}) = 2$
and
![]() $0$
otherwise.
$0$
otherwise.

Theorem 5.6 (Explicit finite support of  in the L-rank
in the L-rank
 $0$
case)
$0$
case)
Assume
![]() $L\!\operatorname {-rk} J = 0$
. Suppose that
$L\!\operatorname {-rk} J = 0$
. Suppose that
![]() $\mathfrak {p}$
is a maximal ideal of
$\mathfrak {p}$
is a maximal ideal of
![]() $\mathcal {O}$
such that
$\mathcal {O}$
such that
![]() $\rho _{\mathfrak {p}}$
is irreducible and
$\rho _{\mathfrak {p}}$
is irreducible and
where K runs through the Heegner fields for
![]() $J/{\mathbf {Q}}$
. Then
$J/{\mathbf {Q}}$
. Then
Proof. Note that the arguments in [Reference Kolyvagin and Logachëv64] (there for a prime
![]() $\ell $
) also work for prime ideals
$\ell $
) also work for prime ideals
![]() $\mathfrak {p}$
; this is explained in [Reference Dogra and Le Fourn39, § 7.1]: annihilation of modules under
$\mathfrak {p}$
; this is explained in [Reference Dogra and Le Fourn39, § 7.1]: annihilation of modules under
![]() $\mathcal {O}$
by p is translated to the annihilation under
$\mathcal {O}$
by p is translated to the annihilation under
![]() $\mathfrak {p} \mid p$
using the Chinese remainder theorem
$\mathfrak {p} \mid p$
using the Chinese remainder theorem
![]() $\mathcal {O}/p \xrightarrow {\sim } \bigoplus _{\mathfrak {p} \mid p}\mathcal {O}/\mathfrak {p}^{e_{\mathfrak {p}}}$
. We set
$\mathcal {O}/p \xrightarrow {\sim } \bigoplus _{\mathfrak {p} \mid p}\mathcal {O}/\mathfrak {p}^{e_{\mathfrak {p}}}$
. We set
![]() $p := p(\mathfrak {p})$
.
$p := p(\mathfrak {p})$
.
Looking at Table 1, all constants
![]() $m_i$
are
$m_i$
are
![]() $0$
for
$0$
for
![]() $\mathfrak {p}$
satisfying our hypotheses.
$\mathfrak {p}$
satisfying our hypotheses.
-
(i)
 $m_3 = 0$
because
$m_3 = 0$
because
 $\mathfrak {p} \nmid 2$
and the polarization is principal.
$\mathfrak {p} \nmid 2$
and the polarization is principal. -
(ii) If
 $\mathfrak {p} \nmid {\mathrm {Tam}}(J/{\mathbf {Q}})$
, then
$\mathfrak {p} \nmid {\mathrm {Tam}}(J/{\mathbf {Q}})$
, then
 $\mathfrak {p} \nmid A$
: Let
$\mathfrak {p} \nmid A$
: Let
 $p = p(\mathfrak {p})$
. Let
$p = p(\mathfrak {p})$
. Let
 $v \nmid p$
be a finite prime of K with residue field
$v \nmid p$
be a finite prime of K with residue field
 ${\mathbf {F}}_v$
. Let
${\mathbf {F}}_v$
. Let
 $\mathscr {J}$
be the Néron model of
$\mathscr {J}$
be the Néron model of
 $J/K$
. By [Reference Milne78, Proposition I.3.8],Footnote 1 as
$J/K$
. By [Reference Milne78, Proposition I.3.8],Footnote 1 as $$ \begin{align*} {\operatorname{H}}^1_{\mathrm{nr}}(K_v, J) &\simeq {\operatorname{H}}^1({\mathbf{F}}_v, \pi_0(\mathscr{J})(\overline{{\mathbf{F}}}_v)) \\ &\simeq \varinjlim_n{\operatorname{H}}^1({\mathbf{F}}_{v^n}|{\mathbf{F}}_v, \pi_0(\mathscr{J})({\mathbf{F}}_{v^n})) \end{align*} $$
$$ \begin{align*} {\operatorname{H}}^1_{\mathrm{nr}}(K_v, J) &\simeq {\operatorname{H}}^1({\mathbf{F}}_v, \pi_0(\mathscr{J})(\overline{{\mathbf{F}}}_v)) \\ &\simeq \varinjlim_n{\operatorname{H}}^1({\mathbf{F}}_{v^n}|{\mathbf{F}}_v, \pi_0(\mathscr{J})({\mathbf{F}}_{v^n})) \end{align*} $$
 $\mathcal {O}$
-modules. The last module is a subquotient of
$\mathcal {O}$
-modules. The last module is a subquotient of
 $\pi _0(\mathscr {J})({\mathbf {F}}_{v^n})$
since
$\pi _0(\mathscr {J})({\mathbf {F}}_{v^n})$
since
 ${\mathbf {F}}_{v^n}|{\mathbf {F}}_v$
is cyclic [Reference Neukirch, Schmidt and Wingberg81, Proposition 1.7.1]. (Note that conjecturally,
${\mathbf {F}}_{v^n}|{\mathbf {F}}_v$
is cyclic [Reference Neukirch, Schmidt and Wingberg81, Proposition 1.7.1]. (Note that conjecturally,
 $ {\mathrm {Tam}}(J/{\mathbf {Q}})$
divides all Heegner indices [Reference Gross and Zagier52, Conjecture V.(2.2)]; see also Corollary 4.13.)
$ {\mathrm {Tam}}(J/{\mathbf {Q}})$
divides all Heegner indices [Reference Gross and Zagier52, Conjecture V.(2.2)]; see also Corollary 4.13.)
-
(iii) If
 $\mathfrak {p} \mid B$
, then
$\mathfrak {p} \mid B$
, then
 $J({\mathbf {Q}})[\mathfrak {p}] \neq 0$
, so
$J({\mathbf {Q}})[\mathfrak {p}] \neq 0$
, so
 $\rho _{\mathfrak {p}}$
is reducible.
$\rho _{\mathfrak {p}}$
is reducible. -
(iv)
 $m_9 = 0$
if
$m_9 = 0$
if
 $\mathfrak {p} \nmid 2$
and
$\mathfrak {p} \nmid 2$
and
 $\rho _{\mathfrak {p}}$
is irreducible because the irreducibility implies that the p-isogeny graph is reduced to a point; see [Reference Kolyvagin and Logachëv64, Lemma 5.9].
$\rho _{\mathfrak {p}}$
is irreducible because the irreducibility implies that the p-isogeny graph is reduced to a point; see [Reference Kolyvagin and Logachëv64, Lemma 5.9]. -
(v)
 $\mathfrak {p} \nmid 2$
implies that
$\mathfrak {p} \nmid 2$
implies that
 $m_{10} = 0$
since
$m_{10} = 0$
since
 $\# {\mathrm {Gal}}(K|{\mathbf {Q}}) = 2$
is prime to
$\# {\mathrm {Gal}}(K|{\mathbf {Q}}) = 2$
is prime to
 $\#A[\mathfrak {p}]$
.
$\#A[\mathfrak {p}]$
. -
(vi)
 $\rho _{\mathfrak {p}}$
irreducible implies
$\rho _{\mathfrak {p}}$
irreducible implies
 $m_{11} = 0$
by proposition 5.4 with
$m_{11} = 0$
by proposition 5.4 with
 $F = K$
.
$F = K$
. -
(vii) One can take
 $m_{13}$
to be
$m_{13}$
to be  $$\begin{align*}v_{\mathfrak{p}}(\mathcal{I}_{K,\pi}) = v_{\mathfrak{p}}\big(\operatorname{\mathrm{Char}}_{\mathcal{O}}(J(K)/\mathcal{O} y_K)\big) . \end{align*}$$
$$\begin{align*}v_{\mathfrak{p}}(\mathcal{I}_{K,\pi}) = v_{\mathfrak{p}}\big(\operatorname{\mathrm{Char}}_{\mathcal{O}}(J(K)/\mathcal{O} y_K)\big) . \end{align*}$$
This is because this choice of
 $m_{13} = m_{13}(\mathfrak {p}^\infty )$
satisfies [Reference Kolyvagin and Logachëv64, Proposition 5.12].
$m_{13} = m_{13}(\mathfrak {p}^\infty )$
satisfies [Reference Kolyvagin and Logachëv64, Proposition 5.12].
Hence,
![]() $m_1 = 0$
, so
$m_1 = 0$
, so
![]() $\operatorname {Sel}_{\mathfrak {p}^\infty }(J/{\mathbf {Q}}) = 0$
.
$\operatorname {Sel}_{\mathfrak {p}^\infty }(J/{\mathbf {Q}}) = 0$
.
To simplify notation below, we write
![]() $\mathscr {K}_{\mathfrak {p}}(f)$
for the set of all Heegner fields K such that
$\mathscr {K}_{\mathfrak {p}}(f)$
for the set of all Heegner fields K such that
![]() $a_n(f) \not \equiv \varepsilon _K(n) a_n(f) \pmod {\mathfrak {p}}$
for some n coprime to N, where
$a_n(f) \not \equiv \varepsilon _K(n) a_n(f) \pmod {\mathfrak {p}}$
for some n coprime to N, where
![]() $\varepsilon _K$
is the nontrivial quadratic Dirichlet character associated with
$\varepsilon _K$
is the nontrivial quadratic Dirichlet character associated with
![]() $K|{\mathbf {Q}}$
. In practice, we find a Heegner field K such that
$K|{\mathbf {Q}}$
. In practice, we find a Heegner field K such that
![]() $K \in \mathscr {K}_{\mathfrak {p}}(f)$
for all
$K \in \mathscr {K}_{\mathfrak {p}}(f)$
for all
![]() $\mathfrak {p} \nmid 2$
by checking that for some small bound B the ideal
$\mathfrak {p} \nmid 2$
by checking that for some small bound B the ideal
of
![]() ${\mathbf {Z}}[f]$
has norm a power of
${\mathbf {Z}}[f]$
has norm a power of
![]() $2$
(note that the norm is always divisible by
$2$
(note that the norm is always divisible by
![]() $2$
). Note that this ideal is nonzero if f does not have CM by
$2$
). Note that this ideal is nonzero if f does not have CM by
![]() $\varepsilon _K$
in the terminology of definition 2.46.
$\varepsilon _K$
in the terminology of definition 2.46.
Theorem 5.7 (Explicit finite support of  in the L-rank
in the L-rank
 $1$
case)
$1$
case)
Assume that
![]() $L\!\operatorname {-rk} J = 1$
and
$L\!\operatorname {-rk} J = 1$
and
![]() $J/{\mathbf {Q}}$
is simple and does not have CM. Suppose that
$J/{\mathbf {Q}}$
is simple and does not have CM. Suppose that
![]() $\mathfrak {p}$
is a maximal ideal of
$\mathfrak {p}$
is a maximal ideal of
![]() $\mathcal {O}$
such that
$\mathcal {O}$
such that
![]() $\rho _{\mathfrak {p}}$
is irreducible,
$\rho _{\mathfrak {p}}$
is irreducible,
![]() $K \in \mathscr {K}_{\mathfrak {p}}(f)$
and
$K \in \mathscr {K}_{\mathfrak {p}}(f)$
and
Then
Proof. In the setting of [Reference Nekovář80],
![]() $F = {\mathbf {Q}}$
, K is a Heegner field for
$F = {\mathbf {Q}}$
, K is a Heegner field for
![]() $J/{\mathbf {Q}}$
and the character
$J/{\mathbf {Q}}$
and the character
![]() $\alpha $
is trivial (see the main theorem at the beginning of [Reference Nekovář80]); therefore,
$\alpha $
is trivial (see the main theorem at the beginning of [Reference Nekovář80]); therefore,
![]() $K(\alpha ) = K$
, and hence,
$K(\alpha ) = K$
, and hence,
![]() $\beta = 1$
by [Reference Nekovář80, (3.1)]. According to [Reference Nekovář80, 7.3, 7.5, 7.5.3], we have to show that our hypotheses imply
$\beta = 1$
by [Reference Nekovář80, (3.1)]. According to [Reference Nekovář80, 7.3, 7.5, 7.5.3], we have to show that our hypotheses imply
![]() $C_i(\mathfrak {p}) = 0$
for
$C_i(\mathfrak {p}) = 0$
for
![]() $i = 1, \ldots , 6, 0$
(with
$i = 1, \ldots , 6, 0$
(with
![]() $C_i(\mathfrak {p})$
as defined in [Reference Nekovář80]):
$C_i(\mathfrak {p})$
as defined in [Reference Nekovář80]):
-
(1) If
 $\mathfrak {p} \nmid {\mathrm {Tam}}(J/{\mathbf {Q}})$
, then
$\mathfrak {p} \nmid {\mathrm {Tam}}(J/{\mathbf {Q}})$
, then
 $C_1(\mathfrak {p}) = 0$
because of the definition of
$C_1(\mathfrak {p}) = 0$
because of the definition of
 $C_1(\mathfrak {p})$
in [Reference Nekovář80, Proposition 5.12] and by the argument in the proof of theorem 5.6.
$C_1(\mathfrak {p})$
in [Reference Nekovář80, Proposition 5.12] and by the argument in the proof of theorem 5.6. -
(2) If
 $\mathrm {ker}\big ({\operatorname {H}}^1(K,J[\mathfrak {p}]) \stackrel { {\mathrm {res}}}{\to } {\operatorname {H}}^1(K(J[\mathfrak {p}]),J[\mathfrak {p}])\big ) = 0$
, then
$\mathrm {ker}\big ({\operatorname {H}}^1(K,J[\mathfrak {p}]) \stackrel { {\mathrm {res}}}{\to } {\operatorname {H}}^1(K(J[\mathfrak {p}]),J[\mathfrak {p}])\big ) = 0$
, then
 $C_2(\mathfrak {p}) = 0$
[Reference Nekovář80, Proposition 6.1.2]. By proposition 5.4 with
$C_2(\mathfrak {p}) = 0$
[Reference Nekovář80, Proposition 6.1.2]. By proposition 5.4 with
 $F = K$
and the inflation-restriction sequence, this holds since
$F = K$
and the inflation-restriction sequence, this holds since
 $\rho _{\mathfrak {p}}|_{G_K}$
is irreducible by corollary 2.36 (here, we use
$\rho _{\mathfrak {p}}|_{G_K}$
is irreducible by corollary 2.36 (here, we use
 $D_K \neq -4, -8, -3$
; compare Assumption 5.5).
$D_K \neq -4, -8, -3$
; compare Assumption 5.5). -
(3) Since
 $\alpha $
is trivial,
$\alpha $
is trivial,
 $H = K(\alpha ) = K$
in [Reference Nekovář80, § 6]. Hence, there we only need to consider the Dirichlet character
$H = K(\alpha ) = K$
in [Reference Nekovář80, § 6]. Hence, there we only need to consider the Dirichlet character
 $\eta = \varepsilon _K \colon {\mathrm {Gal}}(K|{\mathbf {Q}}) \to \{\pm 1\}$
of
$\eta = \varepsilon _K \colon {\mathrm {Gal}}(K|{\mathbf {Q}}) \to \{\pm 1\}$
of
 $ {\mathrm {Gal}}(K|{\mathbf {Q}})$
in [Reference Nekovář80, Proposition 6.2.2]; thus,
$ {\mathrm {Gal}}(K|{\mathbf {Q}})$
in [Reference Nekovář80, Proposition 6.2.2]; thus,
 $C_3(\mathfrak {p}) = 0$
if
$C_3(\mathfrak {p}) = 0$
if
 $K \in \mathscr {K}_{\mathfrak {p}}(f)$
.
$K \in \mathscr {K}_{\mathfrak {p}}(f)$
. -
(4) We have
 $C_4(\mathfrak {p}) = 0$
because
$C_4(\mathfrak {p}) = 0$
because
 $\beta ^2 = 1$
.
$\beta ^2 = 1$
. -
(5) By definition [Reference Nekovář80, (7.4)],
 $C_5(\mathfrak {p}) = 0$
since
$C_5(\mathfrak {p}) = 0$
since
 $H = K(\alpha ) = K$
.
$H = K(\alpha ) = K$
. -
(6) One has
 $C_6(\mathfrak {p}) := {\mathrm {ord}}_{\mathfrak {p}} \deg \varphi $
with
$C_6(\mathfrak {p}) := {\mathrm {ord}}_{\mathfrak {p}} \deg \varphi $
with
 $\varphi \colon J \to J^{\vee }$
a polarization (for the Weil pairing) [Reference Nekovář80, (7.4)]. Hence,
$\varphi \colon J \to J^{\vee }$
a polarization (for the Weil pairing) [Reference Nekovář80, (7.4)]. Hence,
 $C_6(\mathfrak {p}) = 0$
because J is principally polarized.
$C_6(\mathfrak {p}) = 0$
because J is principally polarized. -
(0) Let
 $x \in J(K)$
be a Heegner point. One has see [Reference Nekovář80, (7.4)]. Hence,
$x \in J(K)$
be a Heegner point. One has see [Reference Nekovář80, (7.4)]. Hence, $$\begin{align*}C_0(\mathfrak{p}) := {\operatorname{max}}\{c \in {\mathbf{Z}}_{\geq 0} : x \in J(K)_{\mathrm{tors}} + \mathfrak{p}^c J(K)\} \,; \end{align*}$$
$$\begin{align*}C_0(\mathfrak{p}) := {\operatorname{max}}\{c \in {\mathbf{Z}}_{\geq 0} : x \in J(K)_{\mathrm{tors}} + \mathfrak{p}^c J(K)\} \,; \end{align*}$$
 $C_0(\mathfrak {p}) = 0$
if
$C_0(\mathfrak {p}) = 0$
if
 $\mathfrak {p} \nmid \mathcal {I}_{K,\pi }$
.
$\mathfrak {p} \nmid \mathcal {I}_{K,\pi }$
.
Note that these results imply ![]() . Since
. Since
![]() $\mathfrak {p} \nmid 2$
,
$\mathfrak {p} \nmid 2$
, ![]() follows.
follows.
We use the refined information that is provided by considering
![]() $ {\mathrm {Tam}}(J/{\mathbf {Q}})$
as an
$ {\mathrm {Tam}}(J/{\mathbf {Q}})$
as an
![]() $\mathcal {O}$
-ideal in the following way.
$\mathcal {O}$
-ideal in the following way.
Proposition 5.8. We assume that J is the Jacobian of a curve of genus
![]() $2$
. Fix an odd prime q. Let
$2$
. Fix an odd prime q. Let
![]() $\mathscr {J}/{\mathbf {Z}}$
be the Néron model of
$\mathscr {J}/{\mathbf {Z}}$
be the Néron model of
![]() $J/{\mathbf {Q}}$
. If
$J/{\mathbf {Q}}$
. If
-
(i) there is exactly one rational prime p with
 $v_q(c_p(J/{\mathbf {Q}})) \geq 1$
and we have
$v_q(c_p(J/{\mathbf {Q}})) \geq 1$
and we have
 $v_q(c_p(J/{\mathbf {Q}})) = 1$
(then
$v_q(c_p(J/{\mathbf {Q}})) = 1$
(then
 $a_p(f) \in \{\pm 1,0\}$
),
$a_p(f) \in \{\pm 1,0\}$
), -
(ii)
 $q \mathcal {O} = \mathfrak {q} \mathfrak {q}'$
is split in
$q \mathcal {O} = \mathfrak {q} \mathfrak {q}'$
is split in
 $\mathcal {O}$
with
$\mathcal {O}$
with
 $\rho _{\mathfrak {q}'}$
irreducible,
$\rho _{\mathfrak {q}'}$
irreducible, -
(iii)
 $v_q(\exp (J({\mathbf {Q}})_{\mathrm {tors}}))> v_q(p - a_p(f))$
, where
$v_q(\exp (J({\mathbf {Q}})_{\mathrm {tors}}))> v_q(p - a_p(f))$
, where
 $\exp (J({\mathbf {Q}})_{\mathrm {tors}})$
denotes the exponent of the rational torsion subgroup of J,
$\exp (J({\mathbf {Q}})_{\mathrm {tors}})$
denotes the exponent of the rational torsion subgroup of J,
then
![]() $v_{\mathfrak {q}'}( {\mathrm {Tam}}(J/{\mathbf {Q}})) = 0$
and
$v_{\mathfrak {q}'}( {\mathrm {Tam}}(J/{\mathbf {Q}})) = 0$
and
![]() $v_{\mathfrak {q}}( {\mathrm {Tam}}(J/{\mathbf {Q}})) = 1$
.
$v_{\mathfrak {q}}( {\mathrm {Tam}}(J/{\mathbf {Q}})) = 1$
.
Proof. Since q is odd, the q-primary part of
![]() $J({\mathbf {Q}})_{\mathrm {tors}}$
injects into
$J({\mathbf {Q}})_{\mathrm {tors}}$
injects into
![]() $\mathscr {J}({\mathbf {F}}_p)$
. The group of
$\mathscr {J}({\mathbf {F}}_p)$
. The group of
![]() ${\mathbf {F}}_p$
-points on the connected component of the identity of
${\mathbf {F}}_p$
-points on the connected component of the identity of
![]() $\mathscr {J}_{{\mathbf {F}}_p}$
has exponent
$\mathscr {J}_{{\mathbf {F}}_p}$
has exponent
![]() $p - a_p(f)$
since it is a product of two copies of
$p - a_p(f)$
since it is a product of two copies of
![]() ${\mathbf {F}}_p^\times $
(when
${\mathbf {F}}_p^\times $
(when
![]() $a_p(f) = 1$
) or of the norm
$a_p(f) = 1$
) or of the norm
![]() $1$
subgroup of
$1$
subgroup of
![]() ${\mathbf {F}}_{p^2}^\times $
(when
${\mathbf {F}}_{p^2}^\times $
(when
![]() $a_p(f) = -1$
) or of
$a_p(f) = -1$
) or of
![]() ${\mathbf {F}}_p$
(when
${\mathbf {F}}_p$
(when
![]() $a_p(f) = 0$
). So (iii) implies that the q-primary part of
$a_p(f) = 0$
). So (iii) implies that the q-primary part of
![]() $J({\mathbf {Q}})_{\mathrm {tors}}$
maps nontrivially into the q-primary part of the group of
$J({\mathbf {Q}})_{\mathrm {tors}}$
maps nontrivially into the q-primary part of the group of
![]() ${\mathbf {F}}_p$
-points of the component group,
${\mathbf {F}}_p$
-points of the component group,
![]() $\pi _0(\mathscr {J}_{{\mathbf {F}}_p})({\mathbf {F}}_p)$
. By (i), the latter is the same as the q-primary part of the ideal
$\pi _0(\mathscr {J}_{{\mathbf {F}}_p})({\mathbf {F}}_p)$
. By (i), the latter is the same as the q-primary part of the ideal
![]() $ {\mathrm {Tam}}(J/{\mathbf {Q}})$
, and it has order q, so by (ii), this q-primary part of
$ {\mathrm {Tam}}(J/{\mathbf {Q}})$
, and it has order q, so by (ii), this q-primary part of
![]() $ {\mathrm {Tam}}(J/{\mathbf {Q}})$
is either
$ {\mathrm {Tam}}(J/{\mathbf {Q}})$
is either
![]() $\mathfrak {q}$
or
$\mathfrak {q}$
or
![]() $\mathfrak {q}'$
. The map from the q-primary part of
$\mathfrak {q}'$
. The map from the q-primary part of
![]() $J({\mathbf {Q}})_{\mathrm {tors}}$
to
$J({\mathbf {Q}})_{\mathrm {tors}}$
to
![]() $\pi _0(\mathscr {J}_{{\mathbf {F}}_p})({\mathbf {F}}_p)$
respects the action of the endomorphism ring. Since
$\pi _0(\mathscr {J}_{{\mathbf {F}}_p})({\mathbf {F}}_p)$
respects the action of the endomorphism ring. Since
![]() $\rho _{\mathfrak {q}'}$
is irreducible, only
$\rho _{\mathfrak {q}'}$
is irreducible, only
![]() $\mathfrak {q}$
can occur in the characteristic ideal of
$\mathfrak {q}$
can occur in the characteristic ideal of
![]() $J({\mathbf {Q}})_{\mathrm {tors}}$
, so only
$J({\mathbf {Q}})_{\mathrm {tors}}$
, so only
![]() $\mathfrak {q}$
can occur in
$\mathfrak {q}$
can occur in
![]() $ {\mathrm {Tam}}(J/{\mathbf {Q}})$
.
$ {\mathrm {Tam}}(J/{\mathbf {Q}})$
.
Examples 5.9. There are three Jacobians of curves from the LMFDB for which we need to apply proposition 5.8 to show that the
![]() $\mathfrak {p}$
-primary part of
$\mathfrak {p}$
-primary part of ![]() is trivial for a degree
is trivial for a degree
![]() $1$
prime ideal
$1$
prime ideal
![]() $\mathfrak {p}$
such that
$\mathfrak {p}$
such that
![]() $\rho _{\mathfrak {p}}$
is irreducible. For one curve each at levels
$\rho _{\mathfrak {p}}$
is irreducible. For one curve each at levels
![]() $N = 39$
and
$N = 39$
and
![]() $123$
, the Tamagawa product is
$123$
, the Tamagawa product is
![]() $7$
and
$7$
and
![]() $7$
is split in the endomorphism ring. In both cases, there is rational
$7$
is split in the endomorphism ring. In both cases, there is rational
![]() $7$
-torsion and
$7$
-torsion and
![]() $c_3 = 7$
, so the proposition applies. In the last case,
$c_3 = 7$
, so the proposition applies. In the last case,
![]() $N = 133$
and the Tamagawa product is
$N = 133$
and the Tamagawa product is
![]() $3$
, with
$3$
, with
![]() $c_7 = 3$
. We have
$c_7 = 3$
. We have
![]() $a_7 = 1$
, so
$a_7 = 1$
, so
![]() $v_3(7 - a_7(f)) = 1$
, but luckily,
$v_3(7 - a_7(f)) = 1$
, but luckily,
![]() $J({\mathbf {Q}}) \cong {\mathbf {Z}}/9$
, so condition (iii) above is still satisfied.
$J({\mathbf {Q}}) \cong {\mathbf {Z}}/9$
, so condition (iii) above is still satisfied.
Under stronger assumptions on
![]() $\mathfrak {p}$
, we can even get an upper bound for
$\mathfrak {p}$
, we can even get an upper bound for ![]() .
.
Theorem 5.10. Assume that
![]() $L'(f/K,1) \neq 0$
. Let
$L'(f/K,1) \neq 0$
. Let
![]() $\mathfrak {p} \mid p> 2$
be a regular prime ideal of
$\mathfrak {p} \mid p> 2$
be a regular prime ideal of
![]() $\mathrm {End}_{\mathbf {Q}}(J)$
with
$\mathrm {End}_{\mathbf {Q}}(J)$
with
![]() $p \nmid h_K \cdot u_K \cdot N$
. Suppose
$p \nmid h_K \cdot u_K \cdot N$
. Suppose
![]() $ {\mathrm {im}}\rho _{\mathfrak {p}^\infty } = G_{\mathfrak {p}^\infty }^{\operatorname {max}}$
. Then
$ {\mathrm {im}}\rho _{\mathfrak {p}^\infty } = G_{\mathfrak {p}^\infty }^{\operatorname {max}}$
. Then
with M finite of order bounded by
![]() $\#\mathcal {O}_{\mathfrak {p}}/I_{K,\pi }$
. Here,
$\#\mathcal {O}_{\mathfrak {p}}/I_{K,\pi }$
. Here,
![]() $E_{\mathfrak {p}}$
is the completion of
$E_{\mathfrak {p}}$
is the completion of
![]() $E = \mathrm {End}^0_{\mathbf {Q}}(J)$
.
$E = \mathrm {End}^0_{\mathbf {Q}}(J)$
.
Proof. This is [Reference Howard55, Theorem A].
Note that this implies ![]() , so in particular,
, so in particular,
theorem 5.10 requires p to be a prime of good reduction and
![]() $\rho _{\mathfrak {p}^\infty }$
to be surjective, which theorems 5.6 and 5.7 do not.
$\rho _{\mathfrak {p}^\infty }$
to be surjective, which theorems 5.6 and 5.7 do not.
6 Computing  using descent
using descent
In this section, let J be the Jacobian of a curve of genus
![]() $2$
whose endomorphism ring
$2$
whose endomorphism ring
![]() $\mathcal {O} = \mathrm {End}_{\mathbf {Q}}(J)$
is an order in a real quadratic field. Let
$\mathcal {O} = \mathrm {End}_{\mathbf {Q}}(J)$
is an order in a real quadratic field. Let
![]() $\mathfrak {p}$
be a prime ideal of degree
$\mathfrak {p}$
be a prime ideal of degree
![]() $1$
of
$1$
of
![]() $\mathcal {O}$
of residue characteristic p. Then J is modular; let N be the level.
$\mathcal {O}$
of residue characteristic p. Then J is modular; let N be the level.
The results of the preceding section reduce the problem of showing that ![]() to the verification that
to the verification that
for finitely many primes p. The left-hand side can be computed by studying ![]() for the prime ideals
for the prime ideals
![]() $\mathfrak {p}$
of
$\mathfrak {p}$
of
![]() $\mathcal {O}$
dividing p. In most cases, we need to show that
$\mathcal {O}$
dividing p. In most cases, we need to show that ![]() , for which it is sufficient to show that
, for which it is sufficient to show that ![]() . We can compute (the size of)
. We can compute (the size of) ![]() in principle by doing a descent (i.e., by computing the
in principle by doing a descent (i.e., by computing the
![]() $\mathfrak {p}$
-Selmer group
$\mathfrak {p}$
-Selmer group
![]() $\operatorname {Sel}_{\mathfrak {p}}(J/{\mathbf {Q}})$
of
$\operatorname {Sel}_{\mathfrak {p}}(J/{\mathbf {Q}})$
of
![]() $J/{\mathbf {Q}}$
). Recall that
$J/{\mathbf {Q}}$
). Recall that
and that the Selmer group sits in the following exact sequence:
(There are analogous definitions with p in place of
![]() $\mathfrak {p}$
.) This implies that
$\mathfrak {p}$
.) This implies that
So to verify that ![]() , it is sufficient to show that
, it is sufficient to show that
6.1 Dealing with
 $p = 2$
$p = 2$
We always need to determine ![]() since primes dividing
since primes dividing
![]() $2$
are always excluded in theorems 5.6 and 5.7. Luckily, for Jacobians of hyperelliptic curves, the size of the
$2$
are always excluded in theorems 5.6 and 5.7. Luckily, for Jacobians of hyperelliptic curves, the size of the
![]() $2$
-Selmer group can be computed fairly easily. This is described in [Reference Stoll112] and is implemented in Magma. If this computation shows that
$2$
-Selmer group can be computed fairly easily. This is described in [Reference Stoll112] and is implemented in Magma. If this computation shows that ![]() , then we know that
, then we know that ![]() is odd.
is odd.
The
![]() $2$
-primary part of
$2$
-primary part of ![]() is somewhat special, as its cardinality can be twice a square (the odd part, if finite, is always the square of some group). Using results of [Reference Poonen and Stoll86], we can determine whether this is the case; in particular, the computation of
is somewhat special, as its cardinality can be twice a square (the odd part, if finite, is always the square of some group). Using results of [Reference Poonen and Stoll86], we can determine whether this is the case; in particular, the computation of
![]() $J({\mathbf {Q}})$
and the
$J({\mathbf {Q}})$
and the
![]() $2$
-Selmer group is sufficient to detect that
$2$
-Selmer group is sufficient to detect that ![]() . In all cases from our database where the
. In all cases from our database where the
![]() $2$
-part of
$2$
-part of ![]() is
is
![]() $1$
or
$1$
or
![]() $2$
, this computation shows that
$2$
, this computation shows that ![]() has the expected value.
has the expected value.
When ![]() , but
, but ![]() , then this can be verified by computing the Cassels–Tate pairing on
, then this can be verified by computing the Cassels–Tate pairing on
![]() $\operatorname {Sel}_2(J/{\mathbf {Q}})$
(this is a symmetric bilinear form on the
$\operatorname {Sel}_2(J/{\mathbf {Q}})$
(this is a symmetric bilinear form on the
![]() ${\mathbf {F}}_2$
-vector space
${\mathbf {F}}_2$
-vector space
![]() $\operatorname {Sel}_2(J/{\mathbf {Q}})$
whose kernel is the preimage of
$\operatorname {Sel}_2(J/{\mathbf {Q}})$
whose kernel is the preimage of ![]() ). A method for doing this is described in the recent preprint [Reference Fisher and Yan44] by Fisher and Yan, and an alternative approach will be detailed in forthcoming work by Shukla.
). A method for doing this is described in the recent preprint [Reference Fisher and Yan44] by Fisher and Yan, and an alternative approach will be detailed in forthcoming work by Shukla.
There are ten cases in our database where ![]() (in all cases,
(in all cases, ![]() ), corresponding to the levels and isogeny classes
), corresponding to the levels and isogeny classes
each of which occurs only once in the list. In each case, the
![]() $2$
-descent computation shows that
$2$
-descent computation shows that ![]() as expected. For the two curves at level
as expected. For the two curves at level
![]() $640$
(that are quadratic twists by
$640$
(that are quadratic twists by
![]() $-1$
of each other), there exists a Richelot isogenous Jacobian
$-1$
of each other), there exists a Richelot isogenous Jacobian
![]() $J'$
, for which a
$J'$
, for which a
![]() $2$
-descent shows that
$2$
-descent shows that ![]() . This shows that in both cases,
. This shows that in both cases, ![]() since elements of order
since elements of order
![]() $4$
would have to survive the isogeny.
$4$
would have to survive the isogeny.
To deal with the remaining eight cases, we need to compute the kernel of the Cassels–Tate pairing on ![]() and verify that this kernel is trivial. Fortunately, Fisher and Yan [Reference Fisher and Yan44] have computed the pairing on the
and verify that this kernel is trivial. Fortunately, Fisher and Yan [Reference Fisher and Yan44] have computed the pairing on the
![]() $2$
-Selmer groups of all Jacobians of genus
$2$
-Selmer groups of all Jacobians of genus
![]() $2$
curves in the LMFDB with even analytic order of
$2$
curves in the LMFDB with even analytic order of ![]() . In particular, they have verified that
. In particular, they have verified that ![]() in all cases where
in all cases where ![]() . This finishes the verification for the
. This finishes the verification for the
![]() $2$
-primary part of
$2$
-primary part of ![]() in our LMFDB examples. There is one of the ‘Wang only’ curves that also has
in our LMFDB examples. There is one of the ‘Wang only’ curves that also has ![]() (the curve with label 125B); Tom Fisher has kindly checked for us using the code from [Reference Fisher and Yan44] that
(the curve with label 125B); Tom Fisher has kindly checked for us using the code from [Reference Fisher and Yan44] that ![]() for this curve as well.
for this curve as well.
6.2 Odd primes
We will now assume that
![]() $\mathfrak {p}$
is a prime ideal of
$\mathfrak {p}$
is a prime ideal of
![]() $\mathcal {O}$
dividing an odd prime. We will also assume that
$\mathcal {O}$
dividing an odd prime. We will also assume that
![]() $\deg \mathfrak {p} = 1$
, as for primes of degree
$\deg \mathfrak {p} = 1$
, as for primes of degree
![]() $2$
, the computation tends to get fairly involved. The situation is then analogous to that of a full p-descent (where
$2$
, the computation tends to get fairly involved. The situation is then analogous to that of a full p-descent (where
![]() $p = p(\mathfrak {p})$
) on an elliptic curve: the kernel of the isogeny is isomorphic to
$p = p(\mathfrak {p})$
) on an elliptic curve: the kernel of the isogeny is isomorphic to
![]() ${\mathbf {Z}}/p \times {\mathbf {Z}}/p$
as a group, and it carries a Weil pairing. How to do a p-descent on an elliptic curve is analyzed in detail in [Reference Schaefer and Stoll93]; most of what is done below builds on this analysis. For the general theory of how to perform descent computations, see [Reference Bruin, Poonen and Stoll16]. We assume that the prime ideal
${\mathbf {Z}}/p \times {\mathbf {Z}}/p$
as a group, and it carries a Weil pairing. How to do a p-descent on an elliptic curve is analyzed in detail in [Reference Schaefer and Stoll93]; most of what is done below builds on this analysis. For the general theory of how to perform descent computations, see [Reference Bruin, Poonen and Stoll16]. We assume that the prime ideal
![]() $\mathfrak {p}$
is principal, generated by a prime element
$\mathfrak {p}$
is principal, generated by a prime element
![]() $\varpi $
. This ensures that
$\varpi $
. This ensures that
![]() $J/J[\mathfrak {p}] \cong J$
via the multiplication-by-
$J/J[\mathfrak {p}] \cong J$
via the multiplication-by-
![]() $\varpi $
map. This assumption is satisfied in all the examples that we have considered.
$\varpi $
map. This assumption is satisfied in all the examples that we have considered.
We now assume in addition that
![]() $\rho _{\mathfrak {p}}$
is reducible; this is the most common situation when the general results do not allow us to conclude that
$\rho _{\mathfrak {p}}$
is reducible; this is the most common situation when the general results do not allow us to conclude that ![]() . We then have an exact sequence of Galois modules
. We then have an exact sequence of Galois modules
where
![]() $M_1$
and
$M_1$
and
![]() $M_2$
are one-dimensional Galois modules corresponding to characters with values in
$M_2$
are one-dimensional Galois modules corresponding to characters with values in
![]() ${\mathbf {F}}_p^\times $
. A frequently occurring case is that
${\mathbf {F}}_p^\times $
. A frequently occurring case is that
![]() $J[\mathfrak {p}]$
contains a rational point of order p; then
$J[\mathfrak {p}]$
contains a rational point of order p; then
![]() $M_1 \cong {\mathbf {Z}}/p$
, and the action on
$M_1 \cong {\mathbf {Z}}/p$
, and the action on
![]() $M_2$
is via the cyclotomic character
$M_2$
is via the cyclotomic character
![]() $\chi _p$
. Let
$\chi _p$
. Let
![]() $A = J/M_1$
be the isogenous abelian surface; write
$A = J/M_1$
be the isogenous abelian surface; write
![]() $\varphi \colon J \to A$
for the corresponding isogeny and
$\varphi \colon J \to A$
for the corresponding isogeny and
![]() $\psi \colon A \to J$
for the isogeny such that
$\psi \colon A \to J$
for the isogeny such that
![]() $\psi \circ \varphi = \varpi $
; its kernel is
$\psi \circ \varphi = \varpi $
; its kernel is
![]() $\varphi (J[\mathfrak {p}]) \simeq M_2$
. Then we have the associated Selmer groups
$\varphi (J[\mathfrak {p}]) \simeq M_2$
. Then we have the associated Selmer groups
![]() $\operatorname {Sel}(\varphi ) \subseteq {\operatorname {H}}^1({\mathbf {Q}}, M_1)$
and
$\operatorname {Sel}(\varphi ) \subseteq {\operatorname {H}}^1({\mathbf {Q}}, M_1)$
and
![]() $\operatorname {Sel}(\psi ) \subseteq {\operatorname {H}}^1({\mathbf {Q}}, M_2)$
and an exact sequence (see [Reference Schaefer and Stoll93, Lemma 6.1])
$\operatorname {Sel}(\psi ) \subseteq {\operatorname {H}}^1({\mathbf {Q}}, M_2)$
and an exact sequence (see [Reference Schaefer and Stoll93, Lemma 6.1])
This allows us to bound
![]() $\dim _{{\mathbf {F}}_p} \operatorname {Sel}_{\mathfrak {p}}(J/{\mathbf {Q}})$
via
$\dim _{{\mathbf {F}}_p} \operatorname {Sel}_{\mathfrak {p}}(J/{\mathbf {Q}})$
via
Let S be a finite set of primes. For a finite Galois module M such that
![]() $pM = 0$
, we denote by
$pM = 0$
, we denote by
![]() ${\operatorname {H}}^1({\mathbf {Q}}, M; S)$
the subgroup of cohomology classes unramified outside S (i.e., mapping to zero in
${\operatorname {H}}^1({\mathbf {Q}}, M; S)$
the subgroup of cohomology classes unramified outside S (i.e., mapping to zero in
![]() ${\operatorname {H}}^1(I_q, M)$
for all primes
${\operatorname {H}}^1(I_q, M)$
for all primes
![]() $q \notin S$
, where
$q \notin S$
, where
![]() $I_q$
is the inertia group at q). (Since p is odd, we can ignore the infinite place.)
$I_q$
is the inertia group at q). (Since p is odd, we can ignore the infinite place.)
By Lemma 3.1 and the following text in [Reference Schaefer and Stoll93] (the arguments carry over from elliptic curves to abelian varieties), the Selmer group
![]() $\operatorname {Sel}(\theta )$
of an isogeny
$\operatorname {Sel}(\theta )$
of an isogeny
![]() $\theta \colon A_1 \to A_2$
is contained in
$\theta \colon A_1 \to A_2$
is contained in
![]() ${\operatorname {H}}^1({\mathbf {Q}}, \mathrm {ker} \theta; S)$
, where S is the set of primes q such that the Tamagawa number
${\operatorname {H}}^1({\mathbf {Q}}, \mathrm {ker} \theta; S)$
, where S is the set of primes q such that the Tamagawa number
![]() $c_q(A_2)$
is divisible by p, together with p. We set
$c_q(A_2)$
is divisible by p, together with p. We set
and define
![]() $S_A$
in a similar way. Then
$S_A$
in a similar way. Then
By considering the reduction type of J at q, we may be able to obtain a smaller upper bound for
![]() $S_A$
.
$S_A$
.
Now let M be a one-dimensional (over
![]() ${\mathbf {F}}_p$
) Galois representation given by the character
${\mathbf {F}}_p$
) Galois representation given by the character
![]() $\chi \colon { {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})} \to {\mathbf {F}}_p^\times $
. Let
$\chi \colon { {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})} \to {\mathbf {F}}_p^\times $
. Let
![]() $M^{\vee } := {\mathrm {Hom}}(M, \mu _p)$
be the Cartier dual, with character
$M^{\vee } := {\mathrm {Hom}}(M, \mu _p)$
be the Cartier dual, with character
![]() $\chi _p \chi ^{-1}$
. Let L be the fixed field of the kernel of
$\chi _p \chi ^{-1}$
. Let L be the fixed field of the kernel of
![]() $\chi _p \chi ^{-1}$
. The degree of
$\chi _p \chi ^{-1}$
. The degree of
![]() $L/{\mathbf {Q}}$
divides
$L/{\mathbf {Q}}$
divides
![]() $p-1$
, so is prime to p, so by inflation-restriction, we see that
$p-1$
, so is prime to p, so by inflation-restriction, we see that
where the superscript
![]() $(1)$
denotes the subspace on which the action of
$(1)$
denotes the subspace on which the action of
![]() $\sigma \in {\mathrm {Gal}}(L/{\mathbf {Q}})$
is given by multiplying by
$\sigma \in {\mathrm {Gal}}(L/{\mathbf {Q}})$
is given by multiplying by
![]() $a_\sigma $
/ raising to the
$a_\sigma $
/ raising to the
![]() $a_\sigma $
th power, where
$a_\sigma $
th power, where
![]() $a_\sigma = \chi _p \chi ^{-1}(\sigma ) \in {\mathbf {F}}_p^\times $
. We can restrict this isomorphism to the elements that are unramified outside S. Here,
$a_\sigma = \chi _p \chi ^{-1}(\sigma ) \in {\mathbf {F}}_p^\times $
. We can restrict this isomorphism to the elements that are unramified outside S. Here,
![]() $\alpha L^{\times p} \in L^\times /L^{\times p}$
is considered to be unramified outside S when the extension
$\alpha L^{\times p} \in L^\times /L^{\times p}$
is considered to be unramified outside S when the extension
![]() $L(\sqrt [p]{\alpha })/L$
is unramified outside places above primes in S; equivalently (when
$L(\sqrt [p]{\alpha })/L$
is unramified outside places above primes in S; equivalently (when
![]() $p \in S$
), p divides all valuations
$p \in S$
), p divides all valuations
![]() $v_{\mathfrak {q}}(\alpha )$
for
$v_{\mathfrak {q}}(\alpha )$
for
![]() $\mathfrak {q} \mid q \notin S$
. Denoting the subgroup of elements unramified outside S by
$\mathfrak {q} \mid q \notin S$
. Denoting the subgroup of elements unramified outside S by
![]() $L(S, p)$
, this shows that
$L(S, p)$
, this shows that
![]() $\operatorname {Sel}(\varphi ) \subseteq L_1(S_A, p)^{(1)}$
and
$\operatorname {Sel}(\varphi ) \subseteq L_1(S_A, p)^{(1)}$
and
![]() $\operatorname {Sel}(\psi ) \subseteq L_2(S_J, p)^{(1)}$
, where
$\operatorname {Sel}(\psi ) \subseteq L_2(S_J, p)^{(1)}$
, where
![]() $L_1$
and
$L_1$
and
![]() $L_2$
are the fields associated to
$L_2$
are the fields associated to
![]() $M_1$
and
$M_1$
and
![]() $M_2$
, respectively.
$M_2$
, respectively.
Since it occurs frequently, we give an explicit statement in the case that
![]() $J[\mathfrak {p}]$
contains a rational point of order p (then
$J[\mathfrak {p}]$
contains a rational point of order p (then
![]() $M_1 = {\mathbf {Z}}/p$
and
$M_1 = {\mathbf {Z}}/p$
and
![]() $M_2 = \mu _p$
). We will use the notation
$M_2 = \mu _p$
). We will use the notation
 $$\begin{align*}[\mathcal{A}] := \begin{cases} 1, & \text{if } \mathcal{A} \text{ is true} \\ 0, & \text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}[\mathcal{A}] := \begin{cases} 1, & \text{if } \mathcal{A} \text{ is true} \\ 0, & \text{otherwise.} \end{cases} \end{align*}$$
Proposition 6.1. Let J be the Jacobian of a curve of genus
![]() $2$
that has real multiplication; as before, let N be its level. Let
$2$
that has real multiplication; as before, let N be its level. Let
![]() $\mathfrak {p}$
be a prime ideal of degree
$\mathfrak {p}$
be a prime ideal of degree
![]() $1$
of
$1$
of
![]() $\mathcal {O} = \mathrm {End}_{\mathbf {Q}}(J)$
of residue characteristic
$\mathcal {O} = \mathrm {End}_{\mathbf {Q}}(J)$
of residue characteristic
![]() $p> 2$
. Assume that
$p> 2$
. Assume that
![]() $J[\mathfrak {p}]({\mathbf {Q}}) \cong {\mathbf {Z}}/p$
and that the class number of
$J[\mathfrak {p}]({\mathbf {Q}}) \cong {\mathbf {Z}}/p$
and that the class number of
![]() ${\mathbf {Q}}(\mu _p)$
is not divisible by p. Then
${\mathbf {Q}}(\mu _p)$
is not divisible by p. Then

If, in addition, there is a prime
![]() $\ell \equiv 1 \bmod p$
such that the natural map
$\ell \equiv 1 \bmod p$
such that the natural map
is nontrivial and the map
induced by any embedding
![]() ${\mathbf {Q}}(\mu _p) \to {\mathbf {Q}}_\ell $
is surjective, then the above inequality is strict.
${\mathbf {Q}}(\mu _p) \to {\mathbf {Q}}_\ell $
is surjective, then the above inequality is strict.
Proof. Since
![]() $M_1 = \langle P \rangle \cong {\mathbf {Z}}/p$
, we have
$M_1 = \langle P \rangle \cong {\mathbf {Z}}/p$
, we have
![]() $L_1 = {\mathbf {Q}}(\mu _p)$
. Similarly, since
$L_1 = {\mathbf {Q}}(\mu _p)$
. Similarly, since
![]() $M_2 \cong \mu _p$
, we have
$M_2 \cong \mu _p$
, we have
![]() $L_2 = {\mathbf {Q}}$
. Let
$L_2 = {\mathbf {Q}}$
. Let
![]() $F \in {\mathbf {Q}}(X)^\times $
be a function whose divisor is
$F \in {\mathbf {Q}}(X)^\times $
be a function whose divisor is
![]() $p D$
, where the linear equivalence class of D is P; then the ‘descent map’
$p D$
, where the linear equivalence class of D is P; then the ‘descent map’
![]() $\delta \colon J({\mathbf {Q}}) \to {\operatorname {H}}^1({\mathbf {Q}}, M_2) \simeq {\mathbf {Q}}^\times /{\mathbf {Q}}^{\times p}$
is given by evaluating F on a representative divisor whose support is disjoint from that of D. We have the analogous map
$\delta \colon J({\mathbf {Q}}) \to {\operatorname {H}}^1({\mathbf {Q}}, M_2) \simeq {\mathbf {Q}}^\times /{\mathbf {Q}}^{\times p}$
is given by evaluating F on a representative divisor whose support is disjoint from that of D. We have the analogous map
![]() $\delta _q \colon J({\mathbf {Q}}_q) \to {\mathbf {Q}}_q^\times /{\mathbf {Q}}_q^{\times p}$
for each prime q. By the above,
$\delta _q \colon J({\mathbf {Q}}_q) \to {\mathbf {Q}}_q^\times /{\mathbf {Q}}_q^{\times p}$
for each prime q. By the above,
![]() $\operatorname {Sel}(\psi \colon A \to J)$
is contained in the unramified outside
$\operatorname {Sel}(\psi \colon A \to J)$
is contained in the unramified outside
![]() $S_J$
part of
$S_J$
part of
![]() ${\mathbf {Q}}^\times /{\mathbf {Q}}^{\times p}$
, which is the subgroup generated by the classes of the primes in
${\mathbf {Q}}^\times /{\mathbf {Q}}^{\times p}$
, which is the subgroup generated by the classes of the primes in
![]() $S_J$
. When
$S_J$
. When
![]() $p \nmid N$
, so that J has good reduction at p, then we can choose F in such a way that its reduction mod p is well-defined. When evaluating
$p \nmid N$
, so that J has good reduction at p, then we can choose F in such a way that its reduction mod p is well-defined. When evaluating
![]() $\delta _p$
on a point
$\delta _p$
on a point
![]() $Q \in J({\mathbf {Q}}_p)$
, we can pick a representative divisor whose support is disjoint mod p from the support of D; this shows that
$Q \in J({\mathbf {Q}}_p)$
, we can pick a representative divisor whose support is disjoint mod p from the support of D; this shows that
![]() $F(Q)$
is in the image of
$F(Q)$
is in the image of
![]() ${\mathbf {Z}}_p^\times $
and hence that
${\mathbf {Z}}_p^\times $
and hence that
![]() $\operatorname {Sel}(\psi ) \subseteq \langle q : p \mid c_q(J) \rangle $
in this case. So in any case, we have
$\operatorname {Sel}(\psi ) \subseteq \langle q : p \mid c_q(J) \rangle $
in this case. So in any case, we have
We obtain a bound on
![]() $\operatorname {Sel}(\varphi )$
from the inclusion
$\operatorname {Sel}(\varphi )$
from the inclusion
![]() $\operatorname {Sel}(\varphi ) \subseteq L_1(S^{\prime }_J, p)^{(1)} = {\mathbf {Q}}(\mu _p)(S^{\prime }_J, p)^{(1)}$
. Since we assume that the class number of
$\operatorname {Sel}(\varphi ) \subseteq L_1(S^{\prime }_J, p)^{(1)} = {\mathbf {Q}}(\mu _p)(S^{\prime }_J, p)^{(1)}$
. Since we assume that the class number of
![]() ${\mathbf {Q}}(\mu _p)$
is not divisible by p, the group
${\mathbf {Q}}(\mu _p)$
is not divisible by p, the group
![]() ${\mathbf {Q}}(\mu _p)(S^{\prime }_J, p)$
is generated by the images of a primitive pth root of unity
${\mathbf {Q}}(\mu _p)(S^{\prime }_J, p)$
is generated by the images of a primitive pth root of unity
![]() $\zeta _p$
, a choice of fundamental units,
$\zeta _p$
, a choice of fundamental units,
![]() $1 - \zeta _p$
, and one element generating a suitable power of each prime ideal above a prime in
$1 - \zeta _p$
, and one element generating a suitable power of each prime ideal above a prime in
![]() $S^{\prime }_J$
. Of these, only
$S^{\prime }_J$
. Of these, only
![]() $\zeta _p$
and the totally split primes contribute to the relevant eigenspace (the fundamental units come, up to index prime to p, from the maximal real subfield, and the ideal
$\zeta _p$
and the totally split primes contribute to the relevant eigenspace (the fundamental units come, up to index prime to p, from the maximal real subfield, and the ideal
![]() $\langle 1 - \zeta _p \rangle $
and the nonsplit prime ideals have nontrivial stabilizer), and the contribution of each totally split prime q is exactly
$\langle 1 - \zeta _p \rangle $
and the nonsplit prime ideals have nontrivial stabilizer), and the contribution of each totally split prime q is exactly
![]() $1$
. Since q is totally split in
$1$
. Since q is totally split in
![]() ${\mathbf {Q}}(\mu _p)$
if and only if
${\mathbf {Q}}(\mu _p)$
if and only if
![]() $q \equiv 1 \bmod p$
, we obtain the bound
$q \equiv 1 \bmod p$
, we obtain the bound
 $$ \begin{align} \begin{array}{r@{\;}c@{\;}l} \dim_{{\mathbf{F}}_p} \operatorname{Sel}(\varphi) &\le& \dim_{{\mathbf{F}}_p} {\mathbf{Q}}(\mu_p)(S^{\prime}_J, p)^{(1)} \\[6pt] &=& 1 + \#\{q\ \text{prime} : q \mid N\ \text{and}\ q \equiv 1 \bmod p\}. \end{array} \end{align} $$
$$ \begin{align} \begin{array}{r@{\;}c@{\;}l} \dim_{{\mathbf{F}}_p} \operatorname{Sel}(\varphi) &\le& \dim_{{\mathbf{F}}_p} {\mathbf{Q}}(\mu_p)(S^{\prime}_J, p)^{(1)} \\[6pt] &=& 1 + \#\{q\ \text{prime} : q \mid N\ \text{and}\ q \equiv 1 \bmod p\}. \end{array} \end{align} $$
Finally, we have

where we have used
![]() $\dim J({\mathbf {Q}})/\mathfrak {p} J({\mathbf {Q}}) = \operatorname {rk}_{\mathcal {O}} J({\mathbf {Q}}) + \dim J({\mathbf {Q}})[\mathfrak {p}]$
and Equations (6.1) and (6.2).
$\dim J({\mathbf {Q}})/\mathfrak {p} J({\mathbf {Q}}) = \operatorname {rk}_{\mathcal {O}} J({\mathbf {Q}}) + \dim J({\mathbf {Q}})[\mathfrak {p}]$
and Equations (6.1) and (6.2).
To show the refinement, consider the kernel-cokernel exact sequence associated to
![]() $J({\mathbf {Q}}_\ell ) \stackrel {\varphi }{\longrightarrow } A({\mathbf {Q}}_\ell ) \stackrel {\psi }{\longrightarrow } J({\mathbf {Q}}_\ell )$
,
$J({\mathbf {Q}}_\ell ) \stackrel {\varphi }{\longrightarrow } A({\mathbf {Q}}_\ell ) \stackrel {\psi }{\longrightarrow } J({\mathbf {Q}}_\ell )$
,
 $$ \begin{align*} 0 &\longrightarrow {\mathbf{Z}}/p \longrightarrow J({\mathbf{Q}}_\ell)[\mathfrak{p}] \stackrel{\varphi}{\longrightarrow} \mu_p({\mathbf{Q}}_\ell) \longrightarrow \\ &\longrightarrow \frac{A({\mathbf{Q}}_\ell)}{\varphi(J({\mathbf{Q}}_\ell))} \stackrel{\psi}{\longrightarrow} \frac{J({\mathbf{Q}}_\ell)}{\mathfrak{p} J({\mathbf{Q}}_\ell)} \longrightarrow \frac{J({\mathbf{Q}}_\ell)}{\psi(A({\mathbf{Q}}_\ell))} \longrightarrow 0 . \end{align*} $$
$$ \begin{align*} 0 &\longrightarrow {\mathbf{Z}}/p \longrightarrow J({\mathbf{Q}}_\ell)[\mathfrak{p}] \stackrel{\varphi}{\longrightarrow} \mu_p({\mathbf{Q}}_\ell) \longrightarrow \\ &\longrightarrow \frac{A({\mathbf{Q}}_\ell)}{\varphi(J({\mathbf{Q}}_\ell))} \stackrel{\psi}{\longrightarrow} \frac{J({\mathbf{Q}}_\ell)}{\mathfrak{p} J({\mathbf{Q}}_\ell)} \longrightarrow \frac{J({\mathbf{Q}}_\ell)}{\psi(A({\mathbf{Q}}_\ell))} \longrightarrow 0 . \end{align*} $$
Since
![]() $\ell \equiv 1 \bmod p$
,
$\ell \equiv 1 \bmod p$
,
![]() $\dim \mu _p({\mathbf {Q}}_\ell ) = 1$
. Since
$\dim \mu _p({\mathbf {Q}}_\ell ) = 1$
. Since
![]() $p \nmid \ell $
,
$p \nmid \ell $
,
![]() $\dim J({\mathbf {Q}}_\ell )/\mathfrak {p} J({\mathbf {Q}}_\ell ) = \dim J({\mathbf {Q}}_\ell )[\mathfrak {p}]$
. These facts imply that
$\dim J({\mathbf {Q}}_\ell )/\mathfrak {p} J({\mathbf {Q}}_\ell ) = \dim J({\mathbf {Q}}_\ell )[\mathfrak {p}]$
. These facts imply that
We note that the elements of
![]() $\operatorname {Sel}(\varphi )$
(respectively,
$\operatorname {Sel}(\varphi )$
(respectively,
![]() $\operatorname {Sel}(\psi )$
) map into the image of
$\operatorname {Sel}(\psi )$
) map into the image of
![]() $A({\mathbf {Q}}_\ell )/\varphi (J({\mathbf {Q}}_\ell ))$
in
$A({\mathbf {Q}}_\ell )/\varphi (J({\mathbf {Q}}_\ell ))$
in
![]() ${\operatorname {H}}^1({\mathbf {Q}}_\ell , {\mathbf {Z}}/p) \cong {\mathbf {Q}}_\ell ^\times /{\mathbf {Q}}_\ell ^{\times p}$
(respectively, into the image of
${\operatorname {H}}^1({\mathbf {Q}}_\ell , {\mathbf {Z}}/p) \cong {\mathbf {Q}}_\ell ^\times /{\mathbf {Q}}_\ell ^{\times p}$
(respectively, into the image of
![]() $J({\mathbf {Q}}_\ell )/\psi (A({\mathbf {Q}}_\ell ))$
in
$J({\mathbf {Q}}_\ell )/\psi (A({\mathbf {Q}}_\ell ))$
in
![]() ${\operatorname {H}}^1({\mathbf {Q}}_\ell , \mu _p) \simeq {\mathbf {Q}}_\ell ^\times /{\mathbf {Q}}_\ell ^{\times p}$
) under
${\operatorname {H}}^1({\mathbf {Q}}_\ell , \mu _p) \simeq {\mathbf {Q}}_\ell ^\times /{\mathbf {Q}}_\ell ^{\times p}$
) under
![]() $r^{\prime }_\ell $
(respectively,
$r^{\prime }_\ell $
(respectively,
![]() $r_\ell $
). If
$r_\ell $
). If
![]() $\dim J({\mathbf {Q}}_\ell )/\psi (A({\mathbf {Q}}_\ell )) = 0$
, then
$\dim J({\mathbf {Q}}_\ell )/\psi (A({\mathbf {Q}}_\ell )) = 0$
, then
![]() $\operatorname {Sel}(\psi )$
is contained in the kernel of
$\operatorname {Sel}(\psi )$
is contained in the kernel of
![]() $r_\ell $
; since
$r_\ell $
; since
![]() $r_\ell $
is assumed to be nontrivial, this implies that the bound on
$r_\ell $
is assumed to be nontrivial, this implies that the bound on
![]() $\dim \operatorname {Sel}(\psi )$
can be reduced by
$\dim \operatorname {Sel}(\psi )$
can be reduced by
![]() $1$
. Otherwise,
$1$
. Otherwise,
![]() $\dim A({\mathbf {Q}}_\ell )/\varphi (J({\mathbf {Q}}_\ell )) \le 1 < 2 = \dim {\mathbf {Q}}_\ell ^\times /{\mathbf {Q}}_\ell ^{\times p}$
. Since
$\dim A({\mathbf {Q}}_\ell )/\varphi (J({\mathbf {Q}}_\ell )) \le 1 < 2 = \dim {\mathbf {Q}}_\ell ^\times /{\mathbf {Q}}_\ell ^{\times p}$
. Since
![]() $r^{\prime }_\ell $
is assumed to be surjective, this implies that the bound on
$r^{\prime }_\ell $
is assumed to be surjective, this implies that the bound on
![]() $\dim \operatorname {Sel}(\varphi )$
can be reduced by
$\dim \operatorname {Sel}(\varphi )$
can be reduced by
![]() $1$
. So in all cases, the bound on
$1$
. So in all cases, the bound on
![]() $\dim \operatorname {Sel}(\varphi ) + \dim \operatorname {Sel}(\psi )$
is reduced by
$\dim \operatorname {Sel}(\varphi ) + \dim \operatorname {Sel}(\psi )$
is reduced by
![]() $1$
, which gives a corresponding improvement for the bound on
$1$
, which gives a corresponding improvement for the bound on ![]() .
.
Remark 6.2. In some cases (for example in Examples 6.10 (iii)), we can improve the bound in proposition 6.1 by
![]() $1$
when
$1$
when
![]() $p \mid N$
. Assume that we can find enough ‘descent functions,
$p \mid N$
. Assume that we can find enough ‘descent functions,
![]() $F \in {\mathbf {Q}}(X)^\times $
(i.e., whose divisor is p times a divisor D such that
$F \in {\mathbf {Q}}(X)^\times $
(i.e., whose divisor is p times a divisor D such that
![]() $[D] \in J({\mathbf {Q}})$
generates
$[D] \in J({\mathbf {Q}})$
generates
![]() $J[\mathfrak {p}]$
) that reduce to well-defined functions
$J[\mathfrak {p}]$
) that reduce to well-defined functions
![]() $\bar {F}$
on
$\bar {F}$
on
![]() $X_{{\mathbf {F}}_p}$
and such that the support of
$X_{{\mathbf {F}}_p}$
and such that the support of
![]() $\bar {F}$
consists of smooth points on
$\bar {F}$
consists of smooth points on
![]() $X_{{\mathbf {F}}_p}$
and that the following holds: if D is a divisor of degree zero on X defined over
$X_{{\mathbf {F}}_p}$
and that the following holds: if D is a divisor of degree zero on X defined over
![]() ${\mathbf {Q}}$
with reduction
${\mathbf {Q}}$
with reduction
![]() $\bar {D}$
modulo p, then we can find some F such that the divisor of
$\bar {D}$
modulo p, then we can find some F such that the divisor of
![]() $\bar {F}$
has support disjoint from
$\bar {F}$
has support disjoint from
![]() $\bar {D}$
. Then the argument near the beginning of the proof of proposition 6.1 shows that
$\bar {D}$
. Then the argument near the beginning of the proof of proposition 6.1 shows that
![]() $F(D) \in {\mathbf {Z}}_p^\times $
; hence,
$F(D) \in {\mathbf {Z}}_p^\times $
; hence,
and so we can remove the term ‘
![]() $[p \mid N]$
’ in the final bound.
$[p \mid N]$
’ in the final bound.
We also note the following.
Lemma 6.3. If we assume additionally that
![]() $\operatorname {rk}_{\mathcal {O}} J({\mathbf {Q}}) \le 1$
in the situation above, then
$\operatorname {rk}_{\mathcal {O}} J({\mathbf {Q}}) \le 1$
in the situation above, then ![]() is even. In particular,
is even. In particular, ![]() implies that
implies that ![]() .
.
Proof. By the general results on abelian surfaces with RM, J is modular. The additional assumption then implies by [Reference Kolyvagin and Logachëv64] that ![]() is finite. Therefore, the Cassels–Tate pairing on
is finite. Therefore, the Cassels–Tate pairing on ![]() is perfect. It is also anti-symmetric, which implies (since p is odd) that its restriction to
is perfect. It is also anti-symmetric, which implies (since p is odd) that its restriction to ![]() is perfect and alternating. This in turn implies that
is perfect and alternating. This in turn implies that ![]() for some finite
for some finite
![]() $\mathcal {O}_{\mathfrak {p}}$
-module M. In particular,
$\mathcal {O}_{\mathfrak {p}}$
-module M. In particular, ![]() , and so
, and so ![]() .
.
Examples 6.4. For most pairs
![]() $(X, p)$
consisting of a curve X in our database of LMFDB curves and an odd prime p such that the table in Section 2.14 says that the semisimplification of
$(X, p)$
consisting of a curve X in our database of LMFDB curves and an odd prime p such that the table in Section 2.14 says that the semisimplification of
![]() $\rho _{\mathfrak {p}}$
splits as
$\rho _{\mathfrak {p}}$
splits as
![]() $\mathbf {1} \oplus \chi _p$
, where
$\mathbf {1} \oplus \chi _p$
, where
![]() $\mathfrak {p}$
is a prime ideal of the endomorphism ring of degree
$\mathfrak {p}$
is a prime ideal of the endomorphism ring of degree
![]() $1$
, the non-strict bound in proposition 6.1 together with lemma 6.3 show that
$1$
, the non-strict bound in proposition 6.1 together with lemma 6.3 show that ![]() . The exceptions are as follows. (We frequently indicate the isogeny class with a letter appended to the level N.)
. The exceptions are as follows. (We frequently indicate the isogeny class with a letter appended to the level N.)
-
(i) Two of the four curves at level
 $N = 31$
, where
$N = 31$
, where
 $p = 5$
(one has no rational point of order
$p = 5$
(one has no rational point of order
 $5$
, the other gives a bound
$5$
, the other gives a bound  ). This is unproblematic, since these Jacobians are isogenous to the Jacobians of the two other curves at that level, for which the simple bound proves that
). This is unproblematic, since these Jacobians are isogenous to the Jacobians of the two other curves at that level, for which the simple bound proves that  . By invariance of BSD in isogeny classes, it suffices to verify strong BSD for one of these Jacobians.
. By invariance of BSD in isogeny classes, it suffices to verify strong BSD for one of these Jacobians. -
(ii) The pairs
 $(N, p) = (73a, 3)$
and
$(N, p) = (73a, 3)$
and
 $(85b, 3)$
, where there is no rational point of order
$(85b, 3)$
, where there is no rational point of order
 $3$
.
$3$
. -
(iii) The curves at level
 $133d$
with
$133d$
with
 $p = 3$
and at level
$p = 3$
and at level
 $275a$
with
$275a$
with
 $p = 5$
, where the non-strict bound only gives
$p = 5$
, where the non-strict bound only gives  .
.
Examples 6.5. We consider the curves listed under (ii) above. In these cases, the
![]() $\mathfrak {p}$
-torsion (where
$\mathfrak {p}$
-torsion (where
![]() $\mathfrak {p}$
is an ideal of norm
$\mathfrak {p}$
is an ideal of norm
![]() $3$
) sits in an exact sequence
$3$
) sits in an exact sequence
Using the fact that
![]() $M_2({\mathbf {Q}})/\varphi (J[\mathfrak {p}]) \cong {\mathbf {Z}}/3{\mathbf {Z}}$
in these cases and that the Tamagawa numbers at all bad primes are not divisible by
$M_2({\mathbf {Q}})/\varphi (J[\mathfrak {p}]) \cong {\mathbf {Z}}/3{\mathbf {Z}}$
in these cases and that the Tamagawa numbers at all bad primes are not divisible by
![]() $3$
(and
$3$
(and
![]() $3$
is not a bad prime, which implies that
$3$
is not a bad prime, which implies that
![]() $\operatorname {Sel}(\psi ) \subseteq {\mathbf {Q}}(\{q \text {prime} : q \mid N\}, 3)$
), this leads to a general bound of the form
$\operatorname {Sel}(\psi ) \subseteq {\mathbf {Q}}(\{q \text {prime} : q \mid N\}, 3)$
), this leads to a general bound of the form

which evaluates to
![]() $1$
and
$1$
and
![]() $2$
, respectively, for
$2$
, respectively, for
![]() $N = 73$
and
$N = 73$
and
![]() $85$
. Using lemma 6.3, this already shows that
$85$
. Using lemma 6.3, this already shows that ![]() for
for
![]() $N = 73$
.
$N = 73$
.
To improve the bound for
![]() $N = 85$
, we note that in this case,
$N = 85$
, we note that in this case,
and that
![]() $\operatorname {Sel}(\psi ) \subseteq {\mathbf {Q}}(\{5, 17\}, 3)$
maps into the first factor by the obvious map. (Compare Section 6 of [Reference Schaefer and Stoll93]; one can check that the algebra that is called D there is a product of two copies of
$\operatorname {Sel}(\psi ) \subseteq {\mathbf {Q}}(\{5, 17\}, 3)$
maps into the first factor by the obvious map. (Compare Section 6 of [Reference Schaefer and Stoll93]; one can check that the algebra that is called D there is a product of two copies of
![]() ${\mathbf {Q}}(\sqrt [3]{5})$
.) Since any element involving
${\mathbf {Q}}(\sqrt [3]{5})$
.) Since any element involving
![]() $17$
will have image ramified at
$17$
will have image ramified at
![]() $17$
, this shows that actually,
$17$
, this shows that actually,
![]() $\operatorname {Sel}(\psi ) \subseteq {\mathbf {Q}}(\{5\}, 3)$
(we even have equality here, since we know the map to
$\operatorname {Sel}(\psi ) \subseteq {\mathbf {Q}}(\{5\}, 3)$
(we even have equality here, since we know the map to
![]() $\operatorname {Sel}_{\mathfrak {p}}(J/{\mathbf {Q}})$
has one-dimensional kernel), thus improving the bound by
$\operatorname {Sel}_{\mathfrak {p}}(J/{\mathbf {Q}})$
has one-dimensional kernel), thus improving the bound by
![]() $1$
, which is sufficient to conclude.
$1$
, which is sufficient to conclude.
Examples 6.6. We now consider the cases listed under (iii) above. For both pairs
![]() $(N, p)$
, we can use the strict bound in proposition 6.1. The non-strict bound for
$(N, p)$
, we can use the strict bound in proposition 6.1. The non-strict bound for ![]() is
is
![]() $2$
in both cases.
$2$
in both cases.
In the first case,
![]() $(7 \cdot 19, 3)$
for the curve in isogeny class 133d, we use
$(7 \cdot 19, 3)$
for the curve in isogeny class 133d, we use
![]() $\ell = 7$
. Here,
$\ell = 7$
. Here,
![]() $c_7 = 3$
and
$c_7 = 3$
and
![]() $c_{19} = 1$
, so the first condition is that
$c_{19} = 1$
, so the first condition is that
![]() ${\mathbf {Q}}(\{7\}, 3) \to {\mathbf {Q}}_7^\times /{\mathbf {Q}}_7^{\times 3}$
is nontrivial, which is clearly the case. The second condition is that
${\mathbf {Q}}(\{7\}, 3) \to {\mathbf {Q}}_7^\times /{\mathbf {Q}}_7^{\times 3}$
is nontrivial, which is clearly the case. The second condition is that
![]() ${\mathbf {Q}}(\mu _3)(\{3, 7, 19\}, 3)^{(1)} \to {\mathbf {Q}}_7^\times /{\mathbf {Q}}_7^{\times 3}$
is surjective, which follows from the fact that
${\mathbf {Q}}(\mu _3)(\{3, 7, 19\}, 3)^{(1)} \to {\mathbf {Q}}_7^\times /{\mathbf {Q}}_7^{\times 3}$
is surjective, which follows from the fact that
![]() ${\mathbf {Q}}_7$
does not contain a primitive ninth root of unity. So both conditions are satisfied, and the bound can be improved to
${\mathbf {Q}}_7$
does not contain a primitive ninth root of unity. So both conditions are satisfied, and the bound can be improved to ![]() , which is sufficient to conclude that
, which is sufficient to conclude that ![]() by lemma 6.3.
by lemma 6.3.
We now consider
![]() $(5^2 \cdot 11, 5)$
for the curve in isogeny class 275a. Here, we use
$(5^2 \cdot 11, 5)$
for the curve in isogeny class 275a. Here, we use
![]() $\ell = 11$
. Both Tamagawa numbers are
$\ell = 11$
. Both Tamagawa numbers are
![]() $1$
, so the first condition is that
$1$
, so the first condition is that
![]() ${\mathbf {Q}}(\{5\}, 5) \to {\mathbf {Q}}_{11}^\times /{\mathbf {Q}}_{11}^{\times 5}$
is nontrivial. This follows from the fact that
${\mathbf {Q}}(\{5\}, 5) \to {\mathbf {Q}}_{11}^\times /{\mathbf {Q}}_{11}^{\times 5}$
is nontrivial. This follows from the fact that
![]() $5$
is not a fifth power in
$5$
is not a fifth power in
![]() ${\mathbf {F}}_{11}$
. The second condition is that
${\mathbf {F}}_{11}$
. The second condition is that
![]() ${\mathbf {Q}}(\mu _5)(\{5, 11\}, 5)^{(1)} \to {\mathbf {Q}}_{11}^\times /{\mathbf {Q}}_{11}^{\times 5}$
is surjective. This follows in the same way as for the previous example. So we can again reduce the bound by
${\mathbf {Q}}(\mu _5)(\{5, 11\}, 5)^{(1)} \to {\mathbf {Q}}_{11}^\times /{\mathbf {Q}}_{11}^{\times 5}$
is surjective. This follows in the same way as for the previous example. So we can again reduce the bound by
![]() $1$
and obtain that
$1$
and obtain that ![]() .
.
We note that with some more work, one can show that in both these cases, we have
![]() $\operatorname {Sel}(\psi ) = 0$
.
$\operatorname {Sel}(\psi ) = 0$
.
The remaining cases (where
![]() $\rho _{\mathfrak {p}}^{{\mathrm {ss}}}$
splits into two nontrivial characters) come from the following pairs of level (+ isogeny class) and prime.
$\rho _{\mathfrak {p}}^{{\mathrm {ss}}}$
splits into two nontrivial characters) come from the following pairs of level (+ isogeny class) and prime.
 $$ \begin{align*} (125a, 5), \; (147a, 7), \; (245a, 7), \; (250a, 5), \; (275b, 3) \\ (289a, 3), \; (289a, 17), \; (375a, 5), \; (841a, 29). \end{align*} $$
$$ \begin{align*} (125a, 5), \; (147a, 7), \; (245a, 7), \; (250a, 5), \; (275b, 3) \\ (289a, 3), \; (289a, 17), \; (375a, 5), \; (841a, 29). \end{align*} $$
Examples 6.7. We consider the curve at level
![]() $N = 125 = 5^3$
and
$N = 125 = 5^3$
and
![]() $\mathfrak {p} = \langle \sqrt {5} \rangle $
. According to example 2.20, (1), we have
$\mathfrak {p} = \langle \sqrt {5} \rangle $
. According to example 2.20, (1), we have
![]() $\rho _{\mathfrak {p}} \cong \chi _5^2 \oplus \chi _5^3$
. This implies that
$\rho _{\mathfrak {p}} \cong \chi _5^2 \oplus \chi _5^3$
. This implies that
where the superscript
![]() $(m)$
indicates that the action is via
$(m)$
indicates that the action is via
![]() $\chi _5^m$
. One finds easily that the first summand is trivial and the second has dimension
$\chi _5^m$
. One finds easily that the first summand is trivial and the second has dimension
![]() $1$
. Since the
$1$
. Since the
![]() $\mathcal {O}$
-rank of
$\mathcal {O}$
-rank of
![]() $J({\mathbf {Q}})$
is
$J({\mathbf {Q}})$
is
![]() $1$
, we obtain the bound
$1$
, we obtain the bound
so ![]() .
.
Similarly, for the curves at levels
![]() $2 \cdot 5^3$
and
$2 \cdot 5^3$
and
![]() $3 \cdot 5^3$
, we have (for
$3 \cdot 5^3$
, we have (for
![]() $\mathfrak {p} = \langle \sqrt {5} \rangle $
) that
$\mathfrak {p} = \langle \sqrt {5} \rangle $
) that
![]() $\rho _{\mathfrak {p}}^{{\mathrm {ss}}} \cong \chi _5^2 \oplus \chi _5^3$
. Since
$\rho _{\mathfrak {p}}^{{\mathrm {ss}}} \cong \chi _5^2 \oplus \chi _5^3$
. Since
![]() $2$
and
$2$
and
![]() $3$
are primitive roots mod
$3$
are primitive roots mod
![]() $5$
, we still have that
$5$
, we still have that
![]() ${\mathbf {Q}}(\mu _5)(\{q, 5\}, 5)^{(-1)}$
is trivial and
${\mathbf {Q}}(\mu _5)(\{q, 5\}, 5)^{(-1)}$
is trivial and
![]() ${\mathbf {Q}}(\sqrt {5})(\{q, 5\}, 5)^{(1)}$
is one-dimensional, where
${\mathbf {Q}}(\sqrt {5})(\{q, 5\}, 5)^{(1)}$
is one-dimensional, where
![]() $q = 2$
or
$q = 2$
or
![]() $3$
. This gives the bound
$3$
. This gives the bound
(the rank is zero for the curve at level
![]() $2 \cdot 5^3$
and one for the curve at level
$2 \cdot 5^3$
and one for the curve at level
![]() $3 \cdot 5^3$
), which again suffices to conclude that
$3 \cdot 5^3$
), which again suffices to conclude that ![]() .
.
The two pairs
![]() $(N, p) = (17^2, 17)$
and
$(N, p) = (17^2, 17)$
and
![]() $(29^2, 29)$
can be dealt with in a similar way as
$(29^2, 29)$
can be dealt with in a similar way as
![]() $(N, p) = (5^3, 5)$
.
$(N, p) = (5^3, 5)$
.
Examples 6.8. We now consider
![]() $(N, p) = (3 \cdot 7^2, 7)$
and
$(N, p) = (3 \cdot 7^2, 7)$
and
![]() $(5 \cdot 7^2, 7)$
. In both cases,
$(5 \cdot 7^2, 7)$
. In both cases,
![]() $\mathcal {O} = {\mathbf {Z}}[\sqrt {2}]$
, and
$\mathcal {O} = {\mathbf {Z}}[\sqrt {2}]$
, and
![]() $\rho _{\mathfrak {p}}$
is reducible for exactly one of the two prime ideals above
$\rho _{\mathfrak {p}}$
is reducible for exactly one of the two prime ideals above
![]() $7$
, with
$7$
, with
![]() $\rho _{\mathfrak {p}}^{{\mathrm {ss}}} \cong \chi _7^3 \oplus \chi _7^4$
. The two relevant groups are
$\rho _{\mathfrak {p}}^{{\mathrm {ss}}} \cong \chi _7^3 \oplus \chi _7^4$
. The two relevant groups are
![]() ${\mathbf {Q}}(\mu _7)^+(\{q,7\}, 7)^{(4)}$
and
${\mathbf {Q}}(\mu _7)^+(\{q,7\}, 7)^{(4)}$
and
![]() ${\mathbf {Q}}(\sqrt {-7})(\{q,7\}, 7)^{(3)}$
, with
${\mathbf {Q}}(\sqrt {-7})(\{q,7\}, 7)^{(3)}$
, with
![]() $q = 3$
or
$q = 3$
or
![]() $q = 5$
. Since both are primitive roots mod
$q = 5$
. Since both are primitive roots mod
![]() $7$
, q does not contribute to the relevant eigenspaces, and it is easy to see that the first group has dimension
$7$
, q does not contribute to the relevant eigenspaces, and it is easy to see that the first group has dimension
![]() $1$
, whereas the second one is trivial. The
$1$
, whereas the second one is trivial. The
![]() $\mathcal {O}$
-rank is
$\mathcal {O}$
-rank is
![]() $1$
in both cases, which directly shows that
$1$
in both cases, which directly shows that ![]() .
.
Examples 6.9. For
![]() $(N, p) = (17^2, 3)$
, we have
$(N, p) = (17^2, 3)$
, we have
![]() $\rho _{\mathfrak {p}}^{{\mathrm {ss}}} \cong \varepsilon _{17} \oplus \varepsilon _{-3 \cdot 17}$
, where
$\rho _{\mathfrak {p}}^{{\mathrm {ss}}} \cong \varepsilon _{17} \oplus \varepsilon _{-3 \cdot 17}$
, where
![]() $\varepsilon _m$
denotes the quadratic character mod m. This is one of two cases in our examples where the two characters are not powers of
$\varepsilon _m$
denotes the quadratic character mod m. This is one of two cases in our examples where the two characters are not powers of
![]() $\chi _p$
. The two relevant groups are
$\chi _p$
. The two relevant groups are
![]() ${\mathbf {Q}}(\sqrt {-3 \cdot 17})(\{3, 17\}, 3)^-$
, which is trivial, and
${\mathbf {Q}}(\sqrt {-3 \cdot 17})(\{3, 17\}, 3)^-$
, which is trivial, and
![]() ${\mathbf {Q}}(\sqrt {17})(\{3, 17\}, 3)^-$
, which has dimension
${\mathbf {Q}}(\sqrt {17})(\{3, 17\}, 3)^-$
, which has dimension
![]() $1$
. The
$1$
. The
![]() $\mathcal {O}$
-rank is
$\mathcal {O}$
-rank is
![]() $1$
, which directly gives that
$1$
, which directly gives that ![]() .
.
The other similar case is
![]() $(N, p) = (5^2 \cdot 11, 3)$
, where
$(N, p) = (5^2 \cdot 11, 3)$
, where
![]() $\rho _{\mathfrak {p}}^{{\mathrm {ss}}} \cong \varepsilon _{5} \oplus \varepsilon _{-3 \cdot 5}$
, and we obtain the same bound with a similar argument. (Note that
$\rho _{\mathfrak {p}}^{{\mathrm {ss}}} \cong \varepsilon _{5} \oplus \varepsilon _{-3 \cdot 5}$
, and we obtain the same bound with a similar argument. (Note that
![]() $5$
and
$5$
and
![]() $11$
, like
$11$
, like
![]() $17$
, are primitive roots mod
$17$
, are primitive roots mod
![]() $3$
.)
$3$
.)
Examples 6.10. There are three ‘Wang only’ curves for which a
![]() $\mathfrak {p}$
-descent is necessary – namely,
$\mathfrak {p}$
-descent is necessary – namely,
-
(i) Curve 117B with
 $\mathfrak {p} \mid 7$
,
$\mathfrak {p} \mid 7$
, -
(ii) Curve 125B with
 $\mathfrak {p} \mid 5$
, and
$\mathfrak {p} \mid 5$
, and -
(iii) Curve 175 with
 $\mathfrak {p} \mid 5$
.
$\mathfrak {p} \mid 5$
.
In all cases, we have to show that ![]() .
.
In case (i), we have an exact sequence
This case can be dealt with in a similar way as in Examples 6.8; we obtain ![]() .
.
In case (ii),
![]() $J[\mathfrak {p}] \cong \mathbf {1} \oplus \chi _5$
is split. It can be dealt with similarly to Examples 6.7, leading again to
$J[\mathfrak {p}] \cong \mathbf {1} \oplus \chi _5$
is split. It can be dealt with similarly to Examples 6.7, leading again to ![]() .
.
Finally, in case (iii), we have a non-split exact sequence
and
![]() $\mathfrak {p} = \langle \sqrt {5} \rangle $
. The non-strict bound from proposition 6.1 gives us only
$\mathfrak {p} = \langle \sqrt {5} \rangle $
. The non-strict bound from proposition 6.1 gives us only ![]() : we have
: we have
![]() $\operatorname {Sel}(\varphi ) \subseteq {\mathbf {Q}}(\mu _5)(\{5, 7\}, 5)^{(1)} = {\mathbf {Q}}(\mu _5)(\emptyset , 5)^{(1)}$
, which has dimension
$\operatorname {Sel}(\varphi ) \subseteq {\mathbf {Q}}(\mu _5)(\{5, 7\}, 5)^{(1)} = {\mathbf {Q}}(\mu _5)(\emptyset , 5)^{(1)}$
, which has dimension
![]() $1$
, and
$1$
, and
![]() $\operatorname {Sel}(\psi ) \subseteq {\mathbf {Q}}(\{5, 7\}, 5)$
of dimension
$\operatorname {Sel}(\psi ) \subseteq {\mathbf {Q}}(\{5, 7\}, 5)$
of dimension
![]() $2$
. We can improve the bound using remark 6.2. The functions
$2$
. We can improve the bound using remark 6.2. The functions
 $$\begin{align*}\frac{(8 x^5 + 5 x^4 + 15 x^3 + 30 x^2 + 15 x + 4) \pm (6 x^2 + x - 2) y}{(x - a)^5} \end{align*}$$
$$\begin{align*}\frac{(8 x^5 + 5 x^4 + 15 x^3 + 30 x^2 + 15 x + 4) \pm (6 x^2 + x - 2) y}{(x - a)^5} \end{align*}$$
for
![]() $a \in \{0, \pm 1, \pm 2, \infty \}$
(where we set
$a \in \{0, \pm 1, \pm 2, \infty \}$
(where we set
![]() $1/(x - \infty )^5 := 1$
) form a suitable set of descent functions on the model
$1/(x - \infty )^5 := 1$
) form a suitable set of descent functions on the model
of the curve, so in fact,
![]() $\operatorname {Sel}(\psi ) \subseteq {\mathbf {Q}}(\{7\}, 5)$
has dimension at most
$\operatorname {Sel}(\psi ) \subseteq {\mathbf {Q}}(\{7\}, 5)$
has dimension at most
![]() $1$
, which is enough to conclude that
$1$
, which is enough to conclude that ![]() . (In fact,
. (In fact,
![]() $\dim \operatorname {Sel}(\psi ) = 1$
, since evaluating a suitable descent function on a point of order
$\dim \operatorname {Sel}(\psi ) = 1$
, since evaluating a suitable descent function on a point of order
![]() $5$
gives
$5$
gives
![]() $7^2$
, which is a fifth power in
$7^2$
, which is a fifth power in
![]() ${\mathbf {Q}}_5$
, but nontrivial in
${\mathbf {Q}}_5$
, but nontrivial in
![]() ${\mathbf {Q}}_7^\times /{\mathbf {Q}}_7^{\times 5}$
.)
${\mathbf {Q}}_7^\times /{\mathbf {Q}}_7^{\times 5}$
.)
7 Bounding  using Iwasawa Theory
using Iwasawa Theory
The Main Conjectures for modular forms in Iwasawa Theory imply the p-part of strong BSD under certain conditions when the L-rank is
![]() $0$
or
$0$
or
![]() $1$
; see theorem 7.3 below and [Reference Castella, Çiperiani, Skinner and Sprung21]. For fixed p of good ordinary reduction, we can also compute an approximation to the p-adic L-function and use the known results on the p-adic BSD conjecture (see theorem 7.6 below) to determine or at least bound the p-valuation of the order of
$1$
; see theorem 7.3 below and [Reference Castella, Çiperiani, Skinner and Sprung21]. For fixed p of good ordinary reduction, we can also compute an approximation to the p-adic L-function and use the known results on the p-adic BSD conjecture (see theorem 7.6 below) to determine or at least bound the p-valuation of the order of ![]() ; this works even for higher rank, assuming Schneider’s conjecture on the nonvanishing of the p-adic Schneider regulator (see [Reference Stein and Wuthrich109]).
; this works even for higher rank, assuming Schneider’s conjecture on the nonvanishing of the p-adic Schneider regulator (see [Reference Stein and Wuthrich109]).
As we will only need these results in the case that p is a prime of good ordinary reduction that is inert in
![]() ${\mathbf {Z}}[f]$
, we restrict to this situation in the following, although more general results are available, which apply more generally in the case when there is exactly one prime ideal of
${\mathbf {Z}}[f]$
, we restrict to this situation in the following, although more general results are available, which apply more generally in the case when there is exactly one prime ideal of
![]() ${\mathbf {Z}}[f]$
lying above p.
${\mathbf {Z}}[f]$
lying above p.
This section generalizes [Reference Stein and Wuthrich109] from elliptic curves to modular abelian varieties of arbitrary dimension. The results in Sections 7.1 and 7.2 are not fully used in this paper but can be used to extend the verification of strong BSD to examples not contained in our database.
Let f be a newform of level N with coefficient ring
![]() ${\mathbf {Z}}[f]$
. We assume that
${\mathbf {Z}}[f]$
. We assume that
![]() $a_p(f)$
is a p-adic unit (i.e., that p is ordinary for f). This implies that the Euler factor at p of f (equivalently, the characteristic polynomial of the Frobenius at p on the associated compatible system of
$a_p(f)$
is a p-adic unit (i.e., that p is ordinary for f). This implies that the Euler factor at p of f (equivalently, the characteristic polynomial of the Frobenius at p on the associated compatible system of
![]() $\ell $
-adic Galois representations) has exactly one root that is a p-adic unit; we denote this root by
$\ell $
-adic Galois representations) has exactly one root that is a p-adic unit; we denote this root by
![]() $\alpha $
. We use the following notation. Let f be a newform and
$\alpha $
. We use the following notation. Let f be a newform and
![]() $\mathfrak {p} \mid p$
a prime of
$\mathfrak {p} \mid p$
a prime of
![]() ${\mathbf {Z}}[f]$
. Let
${\mathbf {Z}}[f]$
. Let ![]() be the
be the
![]() $\mathfrak {p}$
-adic L-function of f constructed in [Reference Balakrishnan, Müller and Stein5, § 2.2]. If A is the abelian variety associated to f,
$\mathfrak {p}$
-adic L-function of f constructed in [Reference Balakrishnan, Müller and Stein5, § 2.2]. If A is the abelian variety associated to f,
![]() $\mathscr {L}_{\mathfrak {p}}(A,T) = \prod _{\sigma \colon {\mathbf {Z}}[f] \hookrightarrow {\mathbf {R}}} \mathscr {L}_{\mathfrak {p}}(f^\sigma , T)$
; see [Reference Balakrishnan, Müller and Stein5, § 2.3].
$\mathscr {L}_{\mathfrak {p}}(A,T) = \prod _{\sigma \colon {\mathbf {Z}}[f] \hookrightarrow {\mathbf {R}}} \mathscr {L}_{\mathfrak {p}}(f^\sigma , T)$
; see [Reference Balakrishnan, Müller and Stein5, § 2.3].
7.1 The Iwasawa–Greenberg Main Conjecture
We use the following known cases of the
![]() $\mathrm {GL}_2$
Iwasawa–Greenberg Main Conjecture.
$\mathrm {GL}_2$
Iwasawa–Greenberg Main Conjecture.
Theorem 7.1 (Skinner–Urban, Skinner)
Let
![]() $f \in S_2(\Gamma _0(N))$
be a newform and
$f \in S_2(\Gamma _0(N))$
be a newform and
![]() $p> 2$
be a prime with
$p> 2$
be a prime with
-
(ord)
 $v_p(N) \leq 1$
and
$v_p(N) \leq 1$
and
 $|a_p(f)|_p = 1$
.
$|a_p(f)|_p = 1$
.
Let
![]() $\mathfrak {p} \mid p$
be a finite place of
$\mathfrak {p} \mid p$
be a finite place of
![]() ${\mathbf {Q}}(f)$
and
${\mathbf {Q}}(f)$
and
![]() ${\mathbf {Q}}_\infty $
be the cyclotomic
${\mathbf {Q}}_\infty $
be the cyclotomic
![]() ${\mathbf {Z}}_p$
-extension of
${\mathbf {Z}}_p$
-extension of
![]() ${\mathbf {Q}}$
with Galois group
${\mathbf {Q}}$
with Galois group
![]() $\Gamma := {\mathrm {Gal}}({\mathbf {Q}}_\infty |{\mathbf {Q}})$
. Let
$\Gamma := {\mathrm {Gal}}({\mathbf {Q}}_\infty |{\mathbf {Q}})$
. Let ![]() be the Iwasawa algebra.
be the Iwasawa algebra.
Assume that
-
(irr)
 $\rho _{f,\mathfrak {p}}$
is irreducible and
$\rho _{f,\mathfrak {p}}$
is irreducible and -
(♠) that there exists a prime
 $q \neq p$
with
$q \neq p$
with
 $v_q(N) = 1$
such that
$v_q(N) = 1$
such that
 $\rho _{f,\mathfrak {p}}$
is ramified at q.
$\rho _{f,\mathfrak {p}}$
is ramified at q.
Then one has an equality
of ideals in
![]() $\Lambda $
. Here,
$\Lambda $
. Here,
![]() $ {\mathrm {Char}}_{{\mathbf {Q}}_\infty ,{\mathbf {Z}}[f]_{\mathfrak {p}}}(f)$
is the characteristic ideal of the
$ {\mathrm {Char}}_{{\mathbf {Q}}_\infty ,{\mathbf {Z}}[f]_{\mathfrak {p}}}(f)$
is the characteristic ideal of the
![]() $\mathfrak {p}$
-adic Selmer group of f over
$\mathfrak {p}$
-adic Selmer group of f over
![]() ${\mathbf {Q}}_\infty $
and
${\mathbf {Q}}_\infty $
and
![]() $\mathscr {L}_{\mathfrak {p}}(f,T)$
is the
$\mathscr {L}_{\mathfrak {p}}(f,T)$
is the
![]() $\mathfrak {p}$
-adic L-function of f; both are defined in [Reference Skinner and Urban107, § 1.1].
$\mathfrak {p}$
-adic L-function of f; both are defined in [Reference Skinner and Urban107, § 1.1].
Proof. See [Reference Skinner and Urban107, Theorem 1] in the case
![]() $v_p(N) = 0$
and [Reference Skinner106, Theorem A] in the case
$v_p(N) = 0$
and [Reference Skinner106, Theorem A] in the case
![]() $v_p(N) = 1$
(by reduction to [Reference Skinner and Urban107] using Hida theory). (Note the footnote 1 in [Reference Skinner106, p. 172], which says one can weaken the condition that there exists an
$v_p(N) = 1$
(by reduction to [Reference Skinner and Urban107] using Hida theory). (Note the footnote 1 in [Reference Skinner106, p. 172], which says one can weaken the condition that there exists an
![]() ${\mathbf {Z}}[f]_{\mathfrak {p}}$
-basis of
${\mathbf {Z}}[f]_{\mathfrak {p}}$
-basis of
![]() $T_f$
with respect to which the image of
$T_f$
with respect to which the image of
![]() $\rho _{f,\mathfrak {p}^\infty }$
contains
$\rho _{f,\mathfrak {p}^\infty }$
contains
![]() $ {\mathrm {SL}}_2({\mathbf {Z}}_p)$
to condition (
$ {\mathrm {SL}}_2({\mathbf {Z}}_p)$
to condition (
![]() $\spadesuit $
) for the Iwasawa Main Conjecture to hold integrally in [Reference Skinner and Urban107, Theorem 1].)
$\spadesuit $
) for the Iwasawa Main Conjecture to hold integrally in [Reference Skinner and Urban107, Theorem 1].)
Example 7.2. We expect that theorem 7.1 combined with the computation of
![]() $\mathscr {L}_{\mathfrak {p}}(f,T)$
can be used to verify strong BSD for the Jacobian J of level
$\mathscr {L}_{\mathfrak {p}}(f,T)$
can be used to verify strong BSD for the Jacobian J of level
![]() $145$
of the curve
$145$
of the curve
with
![]() $\mathrm {End}_{\mathbf {Q}}(J) \cong {\mathbf {Z}}[\sqrt {2}]$
. Our algorithm gives us that
$\mathrm {End}_{\mathbf {Q}}(J) \cong {\mathbf {Z}}[\sqrt {2}]$
. Our algorithm gives us that ![]() and
and ![]() except maybe for the two primes
except maybe for the two primes
![]() $\mathfrak {p}$
lying above
$\mathfrak {p}$
lying above
![]() $7$
. For them, one can compute the
$7$
. For them, one can compute the
![]() $\mathfrak {p}$
-adic L-function using Sage. (This curve is not contained in our dataset and is only an illustration of how the results in this section can be used in the verification of the p-part of BSD when descent methods are impractical. It came up in forthcoming work of Kaya–Masdeu–Müller–van der Put that computes Schneider regulators of Mumford curves. A verification the p-adic BSD conjecture for this example up to high precision is likely to be included in their article.)
$\mathfrak {p}$
-adic L-function using Sage. (This curve is not contained in our dataset and is only an illustration of how the results in this section can be used in the verification of the p-part of BSD when descent methods are impractical. It came up in forthcoming work of Kaya–Masdeu–Müller–van der Put that computes Schneider regulators of Mumford curves. A verification the p-adic BSD conjecture for this example up to high precision is likely to be included in their article.)
7.2 Results on the p-part of BSD from Main Conjectures in Iwasawa Theory
We state a result that follows from Iwasawa Theory and shows that the p-part of BSD holds in the L-rank
![]() $0$
case under fairly mild assumptions when p is inert in
$0$
case under fairly mild assumptions when p is inert in
![]() ${\mathbf {Z}}[f]$
. Note that an explicit descent computation is hard when p is inert and
${\mathbf {Z}}[f]$
. Note that an explicit descent computation is hard when p is inert and
![]() $\rho _{f,p}$
is irreducible, so this is useful to deal with such primes when our other methods do not show that
$\rho _{f,p}$
is irreducible, so this is useful to deal with such primes when our other methods do not show that ![]() is trivial.
is trivial.
Theorem 7.3 (p-part of BSD in the L-rank
 $0$
case)
$0$
case)
Let
![]() $A/{\mathbf {Q}}$
be a simple modular abelian variety associated to a newform f of level N. Let
$A/{\mathbf {Q}}$
be a simple modular abelian variety associated to a newform f of level N. Let
![]() $p> 2$
be a prime inert in
$p> 2$
be a prime inert in
![]() ${\mathbf {Z}}[f]$
with
${\mathbf {Z}}[f]$
with
-
(ord)
 $v_p(N) \leq 1$
and
$v_p(N) \leq 1$
and
 $|a_p(f)|_p = 1$
.
$|a_p(f)|_p = 1$
.
Assume that
-
(irr)
 $\rho _{f,p}$
is irreducible and
$\rho _{f,p}$
is irreducible and -
(♠) that there exists a prime
 $q \neq p$
with
$q \neq p$
with
 $v_q(N) = 1$
such that
$v_q(N) = 1$
such that
 $\rho _{f,p}$
is ramified at q.
$\rho _{f,p}$
is ramified at q.
If
![]() $L(A/{\mathbf {Q}},1) \neq 0$
, then the p-part of BSD holds for
$L(A/{\mathbf {Q}},1) \neq 0$
, then the p-part of BSD holds for
![]() $A/{\mathbf {Q}}$
; that is,
$A/{\mathbf {Q}}$
; that is,

Proof. This is [Reference Skinner106, Theorem C] (the proof generalizes from elliptic curves to modular abelian varieties because [Reference Skinner106, Theorem B] is for general newforms, and p is inert in
![]() ${\mathbf {Z}}[f]$
). Note that
${\mathbf {Z}}[f]$
). Note that
![]() $|\#A({\mathbf {Q}})_{\mathrm {tors}} \cdot \#A^{\vee }({\mathbf {Q}})_{\mathrm {tors}}|_p = 1$
since
$|\#A({\mathbf {Q}})_{\mathrm {tors}} \cdot \#A^{\vee }({\mathbf {Q}})_{\mathrm {tors}}|_p = 1$
since
![]() $\rho _{f,p}$
is irreducible.
$\rho _{f,p}$
is irreducible.
Remark 7.4.
-
(i) We have restricted ourselves to inert primes for simplicity. (The results hold more generally if there is exactly one prime above p.) The proofs for other primes
 $\mathfrak {p}$
would need to be adapted from the case of elliptic curves, and one would need to define the algebraic factors in the strong BSD formula as elements of
$\mathfrak {p}$
would need to be adapted from the case of elliptic curves, and one would need to define the algebraic factors in the strong BSD formula as elements of
 ${\mathbf {Z}}[f]_{\mathfrak {p}}$
up to units. (It is likely that one can even define them up to squares of units over the Heegner field as most terms are in fact squares.)
${\mathbf {Z}}[f]_{\mathfrak {p}}$
up to units. (It is likely that one can even define them up to squares of units over the Heegner field as most terms are in fact squares.) -
(ii) In the L-rank
 $1$
case, there is [Reference Zhang118, Theorem 10.3] for elliptic curves, which builds upon [Reference Zhang118, Theorem 9.3], which is for general newforms. These theorems have stronger assumptions than theorem 7.3.
$1$
case, there is [Reference Zhang118, Theorem 10.3] for elliptic curves, which builds upon [Reference Zhang118, Theorem 9.3], which is for general newforms. These theorems have stronger assumptions than theorem 7.3. -
(iii) [Reference Castella, Grossi, Lee and Skinner19] proves the p-part in the L-rank
 $1$
case for odd good ordinary primes p completely split in the Heegner field K with
$1$
case for odd good ordinary primes p completely split in the Heegner field K with
 $\rho _p$
reducible if
$\rho _p$
reducible if
 $\rho _p|_{G_K}^{\text {ss}} \cong \varphi \oplus \psi $
such that
$\rho _p|_{G_K}^{\text {ss}} \cong \varphi \oplus \psi $
such that
 $\varphi |_{G_{K_v}},\psi |_{G_{K_v}} \neq \mathbf {1}, \chi _p$
for the places
$\varphi |_{G_{K_v}},\psi |_{G_{K_v}} \neq \mathbf {1}, \chi _p$
for the places
 $v \mid p$
of K. For example, this excludes the case
$v \mid p$
of K. For example, this excludes the case
 $A(K)[p] \neq 0$
. The work of the first author and Mulun Yin [Reference Keller and Yin60] removes the restriction on
$A(K)[p] \neq 0$
. The work of the first author and Mulun Yin [Reference Keller and Yin60] removes the restriction on
 $\varphi $
and
$\varphi $
and
 $\psi $
. Depending on [Reference Castella, Grossi and Skinner20] and [Reference Burungale, Skinner, Tian and Wan17], it also treats the L-rank
$\psi $
. Depending on [Reference Castella, Grossi and Skinner20] and [Reference Burungale, Skinner, Tian and Wan17], it also treats the L-rank
 $0$
case and the case of bad multiplicative reduction. The introduction of [Reference Keller and Yin60] contains an example of a modular abelian surface over
$0$
case and the case of bad multiplicative reduction. The introduction of [Reference Keller and Yin60] contains an example of a modular abelian surface over
 ${\mathbf {Q}}$
that illustrates the use of the results proved there to make a descent computation for a torsion prime unnecessary.
${\mathbf {Q}}$
that illustrates the use of the results proved there to make a descent computation for a torsion prime unnecessary. -
(iv) The preprint [Reference Castella, Çiperiani, Skinner and Sprung21] proves the p-part of strong BSD in the L-rank
 $0$
and
$0$
and
 $1$
cases also for p good non-ordinary, but it assumes that the level N is squarefree.
$1$
cases also for p good non-ordinary, but it assumes that the level N is squarefree. -
(v) theorems 5.6 and 5.7 give
 under the assumptions there, but they do not prove the p-part of BSD. theorem 7.3 does this, but not for non-inert primes or supersingular or bad additive primes. Note that by the Sato–Tate conjecture, there are infinitely many p with
under the assumptions there, but they do not prove the p-part of BSD. theorem 7.3 does this, but not for non-inert primes or supersingular or bad additive primes. Note that by the Sato–Tate conjecture, there are infinitely many p with
 $a_p = 0$
, and they can be treated with [Reference Castella, Çiperiani, Skinner and Sprung21] only when N is squarefree.
$a_p = 0$
, and they can be treated with [Reference Castella, Çiperiani, Skinner and Sprung21] only when N is squarefree.
7.3 The p-adic BSD conjecture
We continue to assume that p is inert in
![]() ${\mathbf {Z}}[f]$
. The coefficient of the leading term of
${\mathbf {Z}}[f]$
. The coefficient of the leading term of
![]() $\mathscr {L}_p(A,T)$
at
$\mathscr {L}_p(A,T)$
at
![]() $T = 0$
is denoted by
$T = 0$
is denoted by
![]() $\mathscr {L}_p^*(A,0)$
. Recall from the introduction to this section that
$\mathscr {L}_p^*(A,0)$
. Recall from the introduction to this section that
![]() $\alpha \in {\mathbf {Z}}[f]_{\mathfrak {p}}^\times $
is the p-adic unit root of the Euler factor of f at p. As in [Reference Balakrishnan, Müller and Stein5], the p-adic multiplier is
$\alpha \in {\mathbf {Z}}[f]_{\mathfrak {p}}^\times $
is the p-adic unit root of the Euler factor of f at p. As in [Reference Balakrishnan, Müller and Stein5], the p-adic multiplier is
(Note that if
![]() $a_p = 1$
and
$a_p = 1$
and
![]() $p \mid N$
, then
$p \mid N$
, then
![]() $\alpha = 1$
and
$\alpha = 1$
and
![]() $\varepsilon _p(A/{\mathbf {Q}}) = 0$
, so conjecturally there will be an extra zero.) The p-adic regulator
$\varepsilon _p(A/{\mathbf {Q}}) = 0$
, so conjecturally there will be an extra zero.) The p-adic regulator
![]() $\operatorname {Reg}_p(A/{\mathbf {Q}})$
is the determinant of the p-adic height pairing on
$\operatorname {Reg}_p(A/{\mathbf {Q}})$
is the determinant of the p-adic height pairing on
![]() $A({\mathbf {Q}})$
defined in [Reference Balakrishnan, Müller and Stein5, Definition 3.3]. According to a Conjecture of Schneider,
$A({\mathbf {Q}})$
defined in [Reference Balakrishnan, Müller and Stein5, Definition 3.3]. According to a Conjecture of Schneider,
![]() $\operatorname {Reg}_p(A/{\mathbf {Q}})$
should be nonzero, but this is not known in general. Assume
$\operatorname {Reg}_p(A/{\mathbf {Q}})$
should be nonzero, but this is not known in general. Assume
![]() $p> 2$
. Let
$p> 2$
. Let
![]() $\gamma \in 1 + p{\mathbf {Z}}_p$
be a topological generator, the same as used in the construction of
$\gamma \in 1 + p{\mathbf {Z}}_p$
be a topological generator, the same as used in the construction of
![]() $\mathscr {L}_p(A,T)$
. We take
$\mathscr {L}_p(A,T)$
. We take
![]() $\gamma = 1 + p$
in our computations. Let
$\gamma = 1 + p$
in our computations. Let
![]() $\operatorname {Reg}_\gamma (A/{\mathbf {Q}}) := \operatorname {Reg}_p(A/{\mathbf {Q}})/\log _p(\gamma )^r$
, where
$\operatorname {Reg}_\gamma (A/{\mathbf {Q}}) := \operatorname {Reg}_p(A/{\mathbf {Q}})/\log _p(\gamma )^r$
, where
![]() $r = \operatorname {rk} A({\mathbf {Q}})$
. We then have the following p-adic version of the BSD conjecture; see [Reference Balakrishnan, Müller and Stein5, Conjecture 1.4], generalizing [Reference Mazur, Tate and Teitelbaum71].
$r = \operatorname {rk} A({\mathbf {Q}})$
. We then have the following p-adic version of the BSD conjecture; see [Reference Balakrishnan, Müller and Stein5, Conjecture 1.4], generalizing [Reference Mazur, Tate and Teitelbaum71].
Conjecture 7.5 (p-adic BSD conjecture)
Let
![]() $A/{\mathbf {Q}}$
be a principally polarized modular abelian variety and p a prime of good ordinary reduction for
$A/{\mathbf {Q}}$
be a principally polarized modular abelian variety and p a prime of good ordinary reduction for
![]() $A/{\mathbf {Q}}$
. Then
$A/{\mathbf {Q}}$
. Then
and

We are interested in the size of the p-part of ![]() , so it is sufficient to compare the p-adic valuations of both sides.
, so it is sufficient to compare the p-adic valuations of both sides.
The following result due to Schneider shows that the conjecture holds in some cases at least up to a p-adic unit, but with
![]() $\mathscr {L}_p(A/{\mathbf {Q}},T)$
replaced by the Iwasawa L-function
$\mathscr {L}_p(A/{\mathbf {Q}},T)$
replaced by the Iwasawa L-function
![]() $\mathscr {L}_p^{(1)}(A/{\mathbf {Q}},T)$
defined in [Reference Schneider95, § 2]. Note that the latter is defined without using modularity, but in a more algebraic way.
$\mathscr {L}_p^{(1)}(A/{\mathbf {Q}},T)$
defined in [Reference Schneider95, § 2]. Note that the latter is defined without using modularity, but in a more algebraic way.
Theorem 7.6. Let
![]() $A/{\mathbf {Q}}$
be a simple principally polarized modular abelian variety with associated newform f. If
$A/{\mathbf {Q}}$
be a simple principally polarized modular abelian variety with associated newform f. If
-
(i) p is a prime of good ordinary reduction,
-
(ii) such that the p-adic regulator
 $\operatorname {Reg}_\gamma (A/{\mathbf {Q}})$
is nonzero, and
$\operatorname {Reg}_\gamma (A/{\mathbf {Q}})$
is nonzero, and -
(iii)
 is finite,
is finite,
then the p-adic BSD conjecture holds (up to a p-adic unit) for
![]() $A/{\mathbf {Q}}$
and
$A/{\mathbf {Q}}$
and
![]() $\mathscr {L}_p^{(1)}(A/{\mathbf {Q}},T)$
:
$\mathscr {L}_p^{(1)}(A/{\mathbf {Q}},T)$
:
The Iwasawa L-function
![]() $\mathscr {L}_p^{(1)}(A/{\mathbf {Q}},T)$
vanishes to order
$\mathscr {L}_p^{(1)}(A/{\mathbf {Q}},T)$
vanishes to order
![]() $\operatorname {rk} A({\mathbf {Q}})$
at
$\operatorname {rk} A({\mathbf {Q}})$
at
![]() $T = 0$
, and its leading term has p-valuation equal to that of
$T = 0$
, and its leading term has p-valuation equal to that of

Proof. See [Reference Schneider95, Theorem
![]() ${2}^{\prime }$
].
${2}^{\prime }$
].
We need to compare the two L-functions
![]() $\mathscr {L}_p(A/{\mathbf {Q}},T)$
and
$\mathscr {L}_p(A/{\mathbf {Q}},T)$
and
![]() $\mathscr {L}_p^{(1)}(A/{\mathbf {Q}},T)$
.
$\mathscr {L}_p^{(1)}(A/{\mathbf {Q}},T)$
.
Theorem 7.7. Let
![]() $p> 2$
be a prime of good ordinary reduction for
$p> 2$
be a prime of good ordinary reduction for
![]() $A/{\mathbf {Q}}$
. Let
$A/{\mathbf {Q}}$
. Let
![]() $\mathfrak {p}$
be a prime ideal of
$\mathfrak {p}$
be a prime ideal of
![]() ${\mathbf {Z}}[f]$
lying above p. Assume that the image of
${\mathbf {Z}}[f]$
lying above p. Assume that the image of
![]() $ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}}(\mu _{p^\infty })) \to {\mathrm {Aut}}_{{\mathbf {Z}}[f]_{\mathfrak {p}}}(T_{\mathfrak {p}} A)$
contains
$ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}}(\mu _{p^\infty })) \to {\mathrm {Aut}}_{{\mathbf {Z}}[f]_{\mathfrak {p}}}(T_{\mathfrak {p}} A)$
contains
![]() $ {\mathrm {SL}}_2({\mathbf {Z}}_p)$
(see Section 2.13). Then
$ {\mathrm {SL}}_2({\mathbf {Z}}_p)$
(see Section 2.13). Then
Proof. See [Reference Kato58, Theorem 17.4 (3)].
Theorem 7.8. Let
![]() $p> 2$
such that
$p> 2$
such that
![]() $a_p(f) \in {\mathbf {Z}}[f]_p^\times $
. Then
$a_p(f) \in {\mathbf {Z}}[f]_p^\times $
. Then
Here, the corank
![]() $ {\mathrm {cork}}_{{\mathbf {Z}}[f]_p} M$
of a discrete torsion
$ {\mathrm {cork}}_{{\mathbf {Z}}[f]_p} M$
of a discrete torsion
![]() ${\mathbf {Z}}[f]_p$
-module is the
${\mathbf {Z}}[f]_p$
-module is the
![]() ${\mathbf {Z}}[f]_p$
-rank of its
${\mathbf {Z}}[f]_p$
-rank of its
![]() ${\mathbf {Z}}[f]_p$
-Pontrjagin dual.
${\mathbf {Z}}[f]_p$
-Pontrjagin dual.
Proof. See [Reference Kato58, Theorem 18.4].
Corollary 7.9. Let
![]() $A/{\mathbf {Q}}$
be a simple principally polarized modular abelian variety with associated newform f. If
$A/{\mathbf {Q}}$
be a simple principally polarized modular abelian variety with associated newform f. If
-
(i)
 $p> 2$
is a prime of good ordinary reduction
$p> 2$
is a prime of good ordinary reduction -
(i) such that the p-adic regulator
 $\operatorname {Reg}_\gamma (A/{\mathbf {Q}})$
is nonzero,
$\operatorname {Reg}_\gamma (A/{\mathbf {Q}})$
is nonzero, -
(iii)
 is finite,
is finite, -
(iv) the image of
 $ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}}(\mu _{p^\infty })) \to {\mathrm {Aut}}_{{\mathbf {Z}}[f]_p}(T_p A)$
contains
$ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}}(\mu _{p^\infty })) \to {\mathrm {Aut}}_{{\mathbf {Z}}[f]_p}(T_p A)$
contains
 $ {\mathrm {SL}}_2({\mathbf {Z}}_p)$
, and
$ {\mathrm {SL}}_2({\mathbf {Z}}_p)$
, and -
(v)
 $ {\mathrm {ord}}_{T=0} \mathscr {L}_p(f^\sigma ,T) \le \operatorname {rk}_{\mathcal {O}} A({\mathbf {Q}})$
for all
$ {\mathrm {ord}}_{T=0} \mathscr {L}_p(f^\sigma ,T) \le \operatorname {rk}_{\mathcal {O}} A({\mathbf {Q}})$
for all
 $\sigma $
,
$\sigma $
,
then equality holds in (7.9) and

Proof. Combine theorems 7.6 to 7.8 .
Note that [Reference Skinner106, Theorems A and B] (with the case of good ordinary reduction coming from [Reference Skinner and Urban107]) establishes equality up to units in ![]() in the ordinary case under some conditions like
in the ordinary case under some conditions like
![]() $\rho _p$
being surjective.
$\rho _p$
being surjective.
So if we can compute the p-adic valuations of
![]() $\mathscr {L}_p^*(A,0)$
and of
$\mathscr {L}_p^*(A,0)$
and of
![]() $\operatorname {Reg}_\gamma (A/{\mathbf {Q}})$
, this result allows us to bound the order of the p-part of
$\operatorname {Reg}_\gamma (A/{\mathbf {Q}})$
, this result allows us to bound the order of the p-part of ![]() from above. Note that we know by the results of Kolyvagin–Logachëv and their extensions that
from above. Note that we know by the results of Kolyvagin–Logachëv and their extensions that ![]() is finite in the cases of interest, so the main assumption is that p is a prime of good ordinary reduction. When the L-rank is zero, then the p-adic regulator is
is finite in the cases of interest, so the main assumption is that p is a prime of good ordinary reduction. When the L-rank is zero, then the p-adic regulator is
![]() $1$
, so it remains to compute
$1$
, so it remains to compute
![]() $\mathscr {L}_p(A,T)$
. We explain in the next subsection how to do this. When the L-rank is
$\mathscr {L}_p(A,T)$
. We explain in the next subsection how to do this. When the L-rank is
![]() $1$
, we also need to compute the p-adic height pairing. In the case that p is a prime of good ordinary reduction for the Jacobian of a genus
$1$
, we also need to compute the p-adic height pairing. In the case that p is a prime of good ordinary reduction for the Jacobian of a genus
![]() $2$
curve, this is accomplished in [Reference Balakrishnan, Müller and Stein5, § 3.4]; see also [Reference Gajović and Müller48].
$2$
curve, this is accomplished in [Reference Balakrishnan, Müller and Stein5, § 3.4]; see also [Reference Gajović and Müller48].
7.4 Computing approximations to p-adic L-functions
We use Greenberg’s improvement [Reference Greenberg49] of the Pollack–Stevens algorithm [Reference Pollack and Stevens84] to compute the p-adic L-function of a newform f with
![]() $a_p(f)$
a p-adic unit. Our Magma implementation is based on that of Darmon–Pollack [Reference Darmon and Pollack36] with their Magma code available at [Reference Darmon and Pollack35]. We modified the code so that it also works with newforms with arbitrary coefficient rings, accepts newforms as input and outputs the p-adic L-function as a p-adic power series to any specified precision for the uniformizer
$a_p(f)$
a p-adic unit. Our Magma implementation is based on that of Darmon–Pollack [Reference Darmon and Pollack36] with their Magma code available at [Reference Darmon and Pollack35]. We modified the code so that it also works with newforms with arbitrary coefficient rings, accepts newforms as input and outputs the p-adic L-function as a p-adic power series to any specified precision for the uniformizer
![]() $\pi $
of
$\pi $
of
![]() $\mathcal {O}_{\mathfrak {p}}$
and T. For performance reasons, we specialized to weight
$\mathcal {O}_{\mathfrak {p}}$
and T. For performance reasons, we specialized to weight
![]() $k = 2$
.
$k = 2$
.
7.4.1 Computing the p-stabilization of
 $\varphi _f$
if
$\varphi _f$
if
 $p \nmid N$
$p \nmid N$
The construction of the p-adic L-function via the overconvergent modular symbol algorithm of [Reference Greenberg49, Reference Pollack and Stevens84] needs
![]() $v_p(N) = 1$
. In the case that
$v_p(N) = 1$
. In the case that
![]() $p \nmid N$
is a good ordinary prime, one has to p-stabilize f to a form of level
$p \nmid N$
is a good ordinary prime, one has to p-stabilize f to a form of level
![]() $Np$
with the same
$Np$
with the same
![]() $T_\ell $
-eigenvalues as f and
$T_\ell $
-eigenvalues as f and
![]() $U_p$
-eigenvalue the unit root of
$U_p$
-eigenvalue the unit root of
![]() $T^2 - a_p(f)T + p$
. Note that the p-adic L-function is defined with respect to that (p-stabilized if
$T^2 - a_p(f)T + p$
. Note that the p-adic L-function is defined with respect to that (p-stabilized if
![]() $p \nmid N$
) lift; see [Reference Belabas and Perrin-Riou6, §§ 4.1, 4.2, 4.4].
$p \nmid N$
) lift; see [Reference Belabas and Perrin-Riou6, §§ 4.1, 4.2, 4.4].
Recall that
![]() $a_p(f) \in {\mathbf {Z}}[f]_{\mathfrak {p}}^\times $
. If
$a_p(f) \in {\mathbf {Z}}[f]_{\mathfrak {p}}^\times $
. If
![]() $p \nmid N$
, let
$p \nmid N$
, let
![]() $\alpha \in {\mathbf {Z}}[f]_{\mathfrak {p}}^\times $
be the unit root of
$\alpha \in {\mathbf {Z}}[f]_{\mathfrak {p}}^\times $
be the unit root of
![]() $T^2 - a_p(f)T + p$
. Let
$T^2 - a_p(f)T + p$
. Let
![]() $\beta $
be the other root. We then p-stabilize in the sense that we replace f by its p-stabilization
$\beta $
be the other root. We then p-stabilize in the sense that we replace f by its p-stabilization
![]() $f_\alpha (z) = f(z) - \beta f(pz)$
of level
$f_\alpha (z) = f(z) - \beta f(pz)$
of level
![]() $Np$
with the same Hecke eigenvalues away from p. Otherwise (i.e., if
$Np$
with the same Hecke eigenvalues away from p. Otherwise (i.e., if
![]() $v_p(N) = 1$
), we can directly use the algorithm of [Reference Greenberg49, Reference Pollack and Stevens84] to compute a lift. (The reason for the p-stabilization is that the distribution property for the modular symbol follows if it is an eigenvector under the
$v_p(N) = 1$
), we can directly use the algorithm of [Reference Greenberg49, Reference Pollack and Stevens84] to compute a lift. (The reason for the p-stabilization is that the distribution property for the modular symbol follows if it is an eigenvector under the
![]() $U_p$
-operator, but not under the
$U_p$
-operator, but not under the
![]() $T_p$
-operator.)
$T_p$
-operator.)
7.4.2 Modular symbols
Let
![]() $\Delta _0$
be the left
$\Delta _0$
be the left
![]() ${\mathbf {Z}}[\mathrm {GL}_2({\mathbf {Q}})]$
-module
${\mathbf {Z}}[\mathrm {GL}_2({\mathbf {Q}})]$
-module
![]() $\operatorname {Div}^0(\mathbf {P}^1({\mathbf {Q}}))$
, where
$\operatorname {Div}^0(\mathbf {P}^1({\mathbf {Q}}))$
, where
![]() $\mathrm {GL}_2({\mathbf {Q}})$
acts via fractional linear transformations on
$\mathrm {GL}_2({\mathbf {Q}})$
acts via fractional linear transformations on
![]() $\mathbf {P}^1({\mathbf {Q}})$
. We write an element
$\mathbf {P}^1({\mathbf {Q}})$
. We write an element
![]() $[s] - [r]$
of
$[s] - [r]$
of
![]() $\Delta _0$
with
$\Delta _0$
with
![]() $r,s \in \mathbf {P}^1({\mathbf {Q}})$
as
$r,s \in \mathbf {P}^1({\mathbf {Q}})$
as
![]() $\{r \to s\}$
.
$\{r \to s\}$
.
Consider the monoid
 $$\begin{align*}\Sigma_0(p) := \biggl\{\begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \operatorname{Mat}_2({\mathbf{Z}}) : (a,p) = 1, \; p \mid c, \; ad-bc \neq 0\biggr\} . \end{align*}$$
$$\begin{align*}\Sigma_0(p) := \biggl\{\begin{pmatrix} a & b \\ c & d \end{pmatrix} \in \operatorname{Mat}_2({\mathbf{Z}}) : (a,p) = 1, \; p \mid c, \; ad-bc \neq 0\biggr\} . \end{align*}$$
Note that because
![]() $p \mid N$
,
$p \mid N$
,
![]() $\Gamma _0(N) \subseteq \Sigma _0(p)$
. Let V be a right
$\Gamma _0(N) \subseteq \Sigma _0(p)$
. Let V be a right
![]() $\Sigma _0(p)$
-module with the action of
$\Sigma _0(p)$
-module with the action of
![]() $S \in \Sigma _0(p)$
on
$S \in \Sigma _0(p)$
on
![]() $v \in V$
denoted by
$v \in V$
denoted by
![]() $v|S$
. Then the Hecke operators
$v|S$
. Then the Hecke operators
 $$\begin{align*}T_\ell := \begin{pmatrix} \ell & 0 \\ 0 & 1 \end{pmatrix} + \sum_{a = 0}^{\ell-1} \begin{pmatrix} 1 & a \\ 0 & \ell \end{pmatrix} \in {\mathbf{Z}}[\Sigma_0(p)], \quad \ell \neq p \text{ prime,} \end{align*}$$
$$\begin{align*}T_\ell := \begin{pmatrix} \ell & 0 \\ 0 & 1 \end{pmatrix} + \sum_{a = 0}^{\ell-1} \begin{pmatrix} 1 & a \\ 0 & \ell \end{pmatrix} \in {\mathbf{Z}}[\Sigma_0(p)], \quad \ell \neq p \text{ prime,} \end{align*}$$
and
 $$\begin{align*}U_p := \sum_{a = 0}^{p-1} \begin{pmatrix} 1 & a \\ 0 & p \end{pmatrix} \in {\mathbf{Z}}[\Sigma_0(p)] \end{align*}$$
$$\begin{align*}U_p := \sum_{a = 0}^{p-1} \begin{pmatrix} 1 & a \\ 0 & p \end{pmatrix} \in {\mathbf{Z}}[\Sigma_0(p)] \end{align*}$$
act on V on the right, making it into a Hecke module. (The matrices constituting
![]() $T_\ell , U_\ell $
are in
$T_\ell , U_\ell $
are in
![]() $\Sigma _0(p)$
, but not in
$\Sigma _0(p)$
, but not in
![]() $\Gamma _0(N)$
.) In Magma, the elements of
$\Gamma _0(N)$
.) In Magma, the elements of
![]() $\Delta _0$
are called the modular symbols of
$\Delta _0$
are called the modular symbols of
![]() $\Gamma _0(N)$
, but we refer to the elements of the module
$\Gamma _0(N)$
, but we refer to the elements of the module
as the V-valued modular symbols. The abelian group
![]() $ {\mathrm {Hom}}_{{\mathbf {Z}}}(\Delta _0, V)$
is a right
$ {\mathrm {Hom}}_{{\mathbf {Z}}}(\Delta _0, V)$
is a right
![]() ${\mathbf {Z}}[\Gamma _0(N)]$
-module, and we write the action similarly as
${\mathbf {Z}}[\Gamma _0(N)]$
-module, and we write the action similarly as
![]() $\varphi |S$
. Spelled out explicitly, the
$\varphi |S$
. Spelled out explicitly, the
![]() $\Gamma _0(N)$
-equivariance means that for
$\Gamma _0(N)$
-equivariance means that for
![]() $\varphi \in {\mathrm {Symb}}_{\Gamma _0(N)}(V)$
one has
$\varphi \in {\mathrm {Symb}}_{\Gamma _0(N)}(V)$
one has
![]() $\varphi |S = \varphi $
(i.e.,
$\varphi |S = \varphi $
(i.e.,
![]() $\varphi (S\{r \to s\})|S = \varphi \{r \to s\}$
for
$\varphi (S\{r \to s\})|S = \varphi \{r \to s\}$
for
![]() $\{r \to s\} \in \Delta _0$
and
$\{r \to s\} \in \Delta _0$
and
![]() $S \in \Gamma _0(N)$
). Then
$S \in \Gamma _0(N)$
). Then
![]() $ {\mathrm {Symb}}_{\Gamma _0(N)}(V)$
is a right Hecke module via the left action on
$ {\mathrm {Symb}}_{\Gamma _0(N)}(V)$
is a right Hecke module via the left action on
![]() $\Delta _0$
and the right action on V.
$\Delta _0$
and the right action on V.
7.4.3 Computing the canonical periods
 $(\Omega _{f^\sigma }^\pm )_\sigma $
attached to f
$(\Omega _{f^\sigma }^\pm )_\sigma $
attached to f
We have to find canonical periods of
![]() $\{f^\sigma \}$
as defined in [Reference Balakrishnan, Müller and Stein5, § 2], unique up to
$\{f^\sigma \}$
as defined in [Reference Balakrishnan, Müller and Stein5, § 2], unique up to
![]() ${\mathbf {Z}}[f]^\times $
. We compute an approximation of the periods
${\mathbf {Z}}[f]^\times $
. We compute an approximation of the periods
![]() $(\Omega _{f^\sigma }^\pm )_\sigma $
with
$(\Omega _{f^\sigma }^\pm )_\sigma $
with
![]() $\sigma \colon {\mathbf {Q}}(f) \hookrightarrow {\mathbf {R}}$
as follows: We compute the period integrals
$\sigma \colon {\mathbf {Q}}(f) \hookrightarrow {\mathbf {R}}$
as follows: We compute the period integrals
 $$\begin{align*}p_{f^\sigma}^\pm(r) := \boldsymbol{\pi} i \Big(\int_r^{i\infty} f^\sigma(z) \,dz \pm \int_{-r}^{i\infty} f^\sigma(z) \,dz \Big) \end{align*}$$
$$\begin{align*}p_{f^\sigma}^\pm(r) := \boldsymbol{\pi} i \Big(\int_r^{i\infty} f^\sigma(z) \,dz \pm \int_{-r}^{i\infty} f^\sigma(z) \,dz \Big) \end{align*}$$
(i.e., over the path
![]() $\{r \to \infty \} \in {\operatorname {H}}_1(X_0(N)({\mathbf {C}}),\{\text {cusps}\};{\mathbf {Z}})$
) for a finite set of
$\{r \to \infty \} \in {\operatorname {H}}_1(X_0(N)({\mathbf {C}}),\{\text {cusps}\};{\mathbf {Z}})$
) for a finite set of
![]() $r \in {\mathbf {Q}}$
such that the
$r \in {\mathbf {Q}}$
such that the
![]() $\{r \to \infty \}$
generate
$\{r \to \infty \}$
generate
![]() $\Delta _0$
as a
$\Delta _0$
as a
![]() $\Gamma _0(N)$
-module to a high enough precision. By [Reference Balakrishnan, Müller and Stein5, § 2.1, Theorem 2.2 and 2.4], there are canonical periods
$\Gamma _0(N)$
-module to a high enough precision. By [Reference Balakrishnan, Müller and Stein5, § 2.1, Theorem 2.2 and 2.4], there are canonical periods
![]() $(\Omega _{f^\sigma }^\pm )_\sigma $
attached to f such that
$(\Omega _{f^\sigma }^\pm )_\sigma $
attached to f such that
![]() $p_{f^\sigma }^\pm /\Omega _{f^\sigma }^\pm \in {\mathbf {Q}}(f)$
and ‘being compatible with twists’, (for a precise formulation see [Reference Balakrishnan, Müller and Stein5, Theorem 2.2]).
$p_{f^\sigma }^\pm /\Omega _{f^\sigma }^\pm \in {\mathbf {Q}}(f)$
and ‘being compatible with twists’, (for a precise formulation see [Reference Balakrishnan, Müller and Stein5, Theorem 2.2]).
By [Reference Balakrishnan, Müller and Stein5, text after Remark 2.6], there is a
![]() $b \in {\mathbf {Q}}(f)^\times $
such that
$b \in {\mathbf {Q}}(f)^\times $
such that
![]() $(\Omega _{f^\sigma }^\pm )_\sigma = (\sigma (b) p_{f^\sigma }^\pm (r))_\sigma $
. We approximate a representative vector of an equivalence class
$(\Omega _{f^\sigma }^\pm )_\sigma = (\sigma (b) p_{f^\sigma }^\pm (r))_\sigma $
. We approximate a representative vector of an equivalence class
![]() $(\Omega _{f^\sigma }^\pm )_\sigma $
. To compute the period integrals
$(\Omega _{f^\sigma }^\pm )_\sigma $
. To compute the period integrals
![]() $p_{f^\sigma }^\pm (r)$
, we combine (4.2) (and the equation before it) and lemma 4.9 and get
$p_{f^\sigma }^\pm (r)$
, we combine (4.2) (and the equation before it) and lemma 4.9 and get
 $$ \begin{align} \Omega_{J/{\mathbf{Q}}} = \frac{c_fc_\pi}{\sqrt{\operatorname{disc}{\mathbf{Z}}[f]}} \cdot \frac{\#\operatorname{\mathrm{coker}}\pi_{\mathbf{R}}}{\#\mathrm{ker}\pi_{\mathbf{R}}} \cdot \Big|\prod_\sigma \Omega_{f^\sigma}^+\Big| . \end{align} $$
$$ \begin{align} \Omega_{J/{\mathbf{Q}}} = \frac{c_fc_\pi}{\sqrt{\operatorname{disc}{\mathbf{Z}}[f]}} \cdot \frac{\#\operatorname{\mathrm{coker}}\pi_{\mathbf{R}}}{\#\mathrm{ker}\pi_{\mathbf{R}}} \cdot \Big|\prod_\sigma \Omega_{f^\sigma}^+\Big| . \end{align} $$
We compute
![]() $\Omega _{J/{\mathbf {Q}}}$
as in lemma 3.7,
$\Omega _{J/{\mathbf {Q}}}$
as in lemma 3.7,
![]() $c_fc_\pi $
as in lemma 3.6, and
$c_fc_\pi $
as in lemma 3.6, and
![]() $\# {\mathrm {coker}}\pi _{\mathbf {R}}$
,
$\# {\mathrm {coker}}\pi _{\mathbf {R}}$
,
![]() $\#\mathrm {ker}\pi _{\mathbf {R}}$
as described in Section 3.1. In fact, since the latter two constants are powers of
$\#\mathrm {ker}\pi _{\mathbf {R}}$
as described in Section 3.1. In fact, since the latter two constants are powers of
![]() $2$
, we do not need to compute them if
$2$
, we do not need to compute them if
![]() $p \neq 2$
. Since we work with a
$p \neq 2$
. Since we work with a
![]() ${\mathbf {Z}}$
-basis
${\mathbf {Z}}$
-basis
![]() $(g_i)$
of
$(g_i)$
of
![]() $S_2(f, {\mathbf {Z}})$
, there is no factor
$S_2(f, {\mathbf {Z}})$
, there is no factor
![]() $\sqrt {\operatorname {disc}{\mathbf {Z}}[f]}$
when we replace
$\sqrt {\operatorname {disc}{\mathbf {Z}}[f]}$
when we replace
![]() $\prod _\sigma \Omega _{f^\sigma }^+$
by the corresponding product for the
$\prod _\sigma \Omega _{f^\sigma }^+$
by the corresponding product for the
![]() $(g_i)$
.
$(g_i)$
.
Assuming that Equation (7.1) holds, the canonical periods are unique up to
![]() $\sigma (b)$
for some
$\sigma (b)$
for some
![]() $b \in {\mathbf {Z}}[f]_{\mathfrak {p}}^\times $
. So the
$b \in {\mathbf {Z}}[f]_{\mathfrak {p}}^\times $
. So the
![]() $\mathfrak {p}$
-adic valuation of the leading term of the p-adic L-function is uniquely determined.
$\mathfrak {p}$
-adic valuation of the leading term of the p-adic L-function is uniquely determined.
7.4.4 The modular symbol
 $\varphi _f$
$\varphi _f$
The modular symbol associated with f is
![]() $\varphi _f \in {\mathrm {Hom}}_{{\mathbf {Z}}[\Gamma _0(N)]}(\Delta _0, {\mathbf {Q}}(f))$
, where
$\varphi _f \in {\mathrm {Hom}}_{{\mathbf {Z}}[\Gamma _0(N)]}(\Delta _0, {\mathbf {Q}}(f))$
, where
![]() ${\mathbf {Q}}(f)$
is a trivial
${\mathbf {Q}}(f)$
is a trivial
![]() $\Gamma _0(N)$
-module. It is defined as
$\Gamma _0(N)$
-module. It is defined as
![]() $\varphi _f\{r \to \infty \} = p_f^+(r)/\Omega _f^+ + p_f^-(r)/\Omega _f^- \in {\mathbf {Q}}(f)$
and by extension
$\varphi _f\{r \to \infty \} = p_f^+(r)/\Omega _f^+ + p_f^-(r)/\Omega _f^- \in {\mathbf {Q}}(f)$
and by extension
![]() $\varphi _f\{r \to s\} = \varphi _f\{r \to \infty \} - \varphi _f\{s \to \infty \}$
to all paths between cusps
$\varphi _f\{r \to s\} = \varphi _f\{r \to \infty \} - \varphi _f\{s \to \infty \}$
to all paths between cusps
![]() $r,s \in \mathbf {P}^1({\mathbf {Q}})$
. It is enough to know
$r,s \in \mathbf {P}^1({\mathbf {Q}})$
. It is enough to know
![]() $\varphi _f$
on a finite set of generators of
$\varphi _f$
on a finite set of generators of
![]() $\Delta _0$
as a
$\Delta _0$
as a
![]() ${\mathbf {Z}}[\Gamma _0(N)]$
-module, which can be obtained via Manin symbols [Reference Cremona31, §§ 2.2, 2.3].
${\mathbf {Z}}[\Gamma _0(N)]$
-module, which can be obtained via Manin symbols [Reference Cremona31, §§ 2.2, 2.3].
7.4.5 Overconvergent modular symbols and p-adic L-functions
Let
![]() $\mathfrak {p} \mid p$
be a prime ideal of
$\mathfrak {p} \mid p$
be a prime ideal of
![]() ${\mathbf {Z}}[f]$
inducing an embedding of
${\mathbf {Z}}[f]$
inducing an embedding of
![]() ${\mathbf {Q}}(f)$
into the completion
${\mathbf {Q}}(f)$
into the completion
![]() ${\mathbf {Q}}(f)_{\mathfrak {p}}$
. To approximate the distribution
${\mathbf {Q}}(f)_{\mathfrak {p}}$
. To approximate the distribution
![]() $L_{\mathfrak {p}}(f)$
(see [Reference Pollack and Stevens84, § 6.2]) and its associated power series
$L_{\mathfrak {p}}(f)$
(see [Reference Pollack and Stevens84, § 6.2]) and its associated power series
![]() $\mathscr {L}_{\mathfrak {p}}(f,T)$
, we implemented Greenberg’s improvement [Reference Greenberg49] of Pollack–Stevens’s computation of an overconvergent modular eigenlift of the modular symbol
$\mathscr {L}_{\mathfrak {p}}(f,T)$
, we implemented Greenberg’s improvement [Reference Greenberg49] of Pollack–Stevens’s computation of an overconvergent modular eigenlift of the modular symbol
![]() $\varphi _f \in {\mathrm {Symb}}_{\Gamma _0(N)}({\mathbf {Q}}(f))$
(see [Reference Pollack and Stevens84, § 6.3]).
$\varphi _f \in {\mathrm {Symb}}_{\Gamma _0(N)}({\mathbf {Q}}(f))$
(see [Reference Pollack and Stevens84, § 6.3]).
For the following, see [Reference Pollack and Stevens84, § 3.1] and [Reference Greenberg49, § 1]. For
![]() $r \in |{\mathbf {C}}_p^\times |_p$
, define
$r \in |{\mathbf {C}}_p^\times |_p$
, define
![]() $\mathscr {A}[r]({\mathbf {Q}}(f)_{\mathfrak {p}})$
to be the
$\mathscr {A}[r]({\mathbf {Q}}(f)_{\mathfrak {p}})$
to be the
![]() ${\mathbf {Q}}(f)_{\mathfrak {p}}$
-Banach space of
${\mathbf {Q}}(f)_{\mathfrak {p}}$
-Banach space of
![]() ${\mathbf {Q}}(f)_{\mathfrak {p}}$
-affinoid functions on
${\mathbf {Q}}(f)_{\mathfrak {p}}$
-affinoid functions on
endowed with the supremum norm. Let
endowed with the colimit topology, denote the algebra of
![]() ${\mathbf {Q}}(f)_{\mathfrak {p}}$
-overconvergent functions on
${\mathbf {Q}}(f)_{\mathfrak {p}}$
-overconvergent functions on
![]() $B[{\mathbf {Z}}_p,1]$
. The overconvergent distributions
$B[{\mathbf {Z}}_p,1]$
. The overconvergent distributions
![]() $\mathscr {D}^\dagger ({\mathbf {Q}}(f)_{\mathfrak {p}})$
are defined as its continuous
$\mathscr {D}^\dagger ({\mathbf {Q}}(f)_{\mathfrak {p}})$
are defined as its continuous
![]() ${\mathbf {Q}}(f)_{\mathfrak {p}}$
-linear dual endowed with the strong topology.
${\mathbf {Q}}(f)_{\mathfrak {p}}$
-linear dual endowed with the strong topology.
7.4.6 The strategy to compute the distribution
 $L_{\mathfrak {p}}(f)$
$L_{\mathfrak {p}}(f)$
We abbreviate
![]() $\Gamma _0(N)$
by
$\Gamma _0(N)$
by
![]() $\Gamma $
in the following. The method of constructing the
$\Gamma $
in the following. The method of constructing the
![]() $\mathfrak {p}$
-adic L-function
$\mathfrak {p}$
-adic L-function
![]() $L_{\mathfrak {p}}(f)$
of f as a distribution is summarized in the following diagram. Here,
$L_{\mathfrak {p}}(f)$
of f as a distribution is summarized in the following diagram. Here,
![]() $ {\mathrm {Symb}}_{\Gamma }({\mathbf {Q}}(f))[f]$
denotes the subspace of
$ {\mathrm {Symb}}_{\Gamma }({\mathbf {Q}}(f))[f]$
denotes the subspace of
![]() $ {\mathrm {Symb}}_{\Gamma }({\mathbf {Q}}(f))$
on which the Hecke operators
$ {\mathrm {Symb}}_{\Gamma }({\mathbf {Q}}(f))$
on which the Hecke operators
![]() $T_n$
with
$T_n$
with
![]() $p \nmid n$
act as multiplication by
$p \nmid n$
act as multiplication by
![]() $a_n(f)$
, and the superscript ‘
$a_n(f)$
, and the superscript ‘
![]() $U_p = \alpha $
’ means the subspace where the Hecke operator
$U_p = \alpha $
’ means the subspace where the Hecke operator
![]() $U_p$
acts as multiplication by the unit root eigenvalue
$U_p$
acts as multiplication by the unit root eigenvalue
![]() $\alpha $
of the characteristic polynomial at p.
$\alpha $
of the characteristic polynomial at p.

To compute the distribution
![]() $L_{\mathfrak {p}}(f)$
, we start with
$L_{\mathfrak {p}}(f)$
, we start with
![]() $\varphi _f$
in the lower left corner and lift it via the algorithm described below to a distribution valued modular symbol
$\varphi _f$
in the lower left corner and lift it via the algorithm described below to a distribution valued modular symbol
![]() $\Phi _f$
; this is the left vertical isomorphism. Then
$\Phi _f$
; this is the left vertical isomorphism. Then
![]() $L_{\mathfrak {p}}(f)$
is the evaluation
$L_{\mathfrak {p}}(f)$
is the evaluation
![]() $\Phi _f\{0 \to \infty \}$
(i.e., the image under the top horizontal morphism).
$\Phi _f\{0 \to \infty \}$
(i.e., the image under the top horizontal morphism).
7.4.7 Computing the modular symbol
 $\varphi _f^\pm $
attached to f
$\varphi _f^\pm $
attached to f
Knowing the canonical periods, we can compute
![]() $\varphi _f^\pm \{r \to s\}$
with
$\varphi _f^\pm \{r \to s\}$
with
![]() $r, s \in \mathbf {P}^1({\mathbf {Q}})$
as described in [Reference Wuthrich117] by computing the corresponding period integrals for all
$r, s \in \mathbf {P}^1({\mathbf {Q}})$
as described in [Reference Wuthrich117] by computing the corresponding period integrals for all
![]() $f^\sigma $
and dividing by
$f^\sigma $
and dividing by
![]() $\Omega _{f^\sigma }^\pm $
and recognizing the elements in
$\Omega _{f^\sigma }^\pm $
and recognizing the elements in
![]() ${\mathbf {Q}}(f)$
using that
${\mathbf {Q}}(f)$
using that
has rational coefficients with the denominator of the coefficient of
![]() $X^{[{\mathbf {Q}}(f):{\mathbf {Q}}]-n}$
bounded by
$X^{[{\mathbf {Q}}(f):{\mathbf {Q}}]-n}$
bounded by
![]() $(4^g \cdot c_fc_\pi \cdot \#J({\mathbf {Q}})_{\mathrm {tors}})^n$
; see Section 4.2 and [Reference Wuthrich117, Prop. 1].
$(4^g \cdot c_fc_\pi \cdot \#J({\mathbf {Q}})_{\mathrm {tors}})^n$
; see Section 4.2 and [Reference Wuthrich117, Prop. 1].
One can compute the modular symbol associated to f up to a factor in
![]() ${\mathbf {Q}}(f)$
with Magma. (Note that one has to take a suitable
${\mathbf {Q}}(f)$
with Magma. (Note that one has to take a suitable
![]() ${\mathbf {Q}}(f)$
-linear combination because Magma takes a basis of
${\mathbf {Q}}(f)$
-linear combination because Magma takes a basis of
![]() $S_2(f,{\mathbf {Z}})$
.) Hence, alternatively, one can compute this factor by comparing with our above computation for some
$S_2(f,{\mathbf {Z}})$
.) Hence, alternatively, one can compute this factor by comparing with our above computation for some
![]() $\varphi _f\{r \to s\} \neq 0$
and scale.
$\varphi _f\{r \to s\} \neq 0$
and scale.
7.4.8 Determining the required p-adic precision for the desired T-adic precision of
 $\mathscr {L}_p(f,T)$
$\mathscr {L}_p(f,T)$
Note that a distribution
![]() $\mu \in \mathscr {D}^\dagger ({\mathbf {Q}}(f)_{\mathfrak {p}})$
is uniquely determined by its moments
$\mu \in \mathscr {D}^\dagger ({\mathbf {Q}}(f)_{\mathfrak {p}})$
is uniquely determined by its moments
![]() $\mu (x^j)$
,
$\mu (x^j)$
,
![]() $j \geq 0$
. We represent a distribution in an approximation module
$j \geq 0$
. We represent a distribution in an approximation module
![]() $\mathbf {A}^M\mathscr {D}^\dagger ({\mathbf {Z}}[f]_{\mathfrak {p}})$
by storing its j-th moment up to precision
$\mathbf {A}^M\mathscr {D}^\dagger ({\mathbf {Z}}[f]_{\mathfrak {p}})$
by storing its j-th moment up to precision
![]() $M+1 - j$
(i.e., as an element of
$M+1 - j$
(i.e., as an element of
![]() ${\mathbf {Z}}[f]_{\mathfrak {p}}/\mathfrak {p}^{M+1-j}$
). To be able to compute lifts, we store the
${\mathbf {Z}}[f]_{\mathfrak {p}}/\mathfrak {p}^{M+1-j}$
). To be able to compute lifts, we store the
![]() $0$
-th moment up to the final precision.
$0$
-th moment up to the final precision.
To ensure the moments we consider are integral, we do the following: According to [Reference Pollack and Stevens84, Corollary 7.6, § 8.3 3], to obtain a precision of
![]() $n p$
-adic digits, one needs to compute with a precision M satisfying
$n p$
-adic digits, one needs to compute with a precision M satisfying
We take m minimal with
![]() $p^m> M+1$
and scale
$p^m> M+1$
and scale
![]() $\varphi _f$
by
$\varphi _f$
by
![]() $p^{m+1}$
. Then we perform M steps of the algorithm to obtain the approximation to
$p^{m+1}$
. Then we perform M steps of the algorithm to obtain the approximation to
![]() $p^{m+1} \Phi _f$
in
$p^{m+1} \Phi _f$
in
![]() $\mathbf {A}^M\mathscr {D}({\mathbf {Z}}[f]_{\mathfrak {p}})$
. Finally, we divide by
$\mathbf {A}^M\mathscr {D}({\mathbf {Z}}[f]_{\mathfrak {p}})$
. Finally, we divide by
![]() $p^{m+1}$
.
$p^{m+1}$
.
7.4.9 Computing the lift
 $\Phi $
of
$\Phi $
of
 $\varphi $
$\varphi $
This is the key step in the computation of the p-adic L-function and a simplification of [Reference Pollack and Stevens84] due to Greenberg [Reference Greenberg49], with the additional non-critical slope assumption, which is satisfied if there is a unit root of the characteristic polynomial of p-Frobenius.
Let
![]() $\varphi \in {\mathrm {Symb}}_{\Gamma }({\mathbf {Q}}(f))[f]^{U_p = \alpha }$
be a Hecke eigensymbol. The action of
$\varphi \in {\mathrm {Symb}}_{\Gamma }({\mathbf {Q}}(f))[f]^{U_p = \alpha }$
be a Hecke eigensymbol. The action of
![]() $\gamma = \left (\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}\right )$
with
$\gamma = \left (\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}\right )$
with
![]() $p \mid c$
and
$p \mid c$
and
![]() $p \nmid a$
on a distribution
$p \nmid a$
on a distribution
![]() $\mu $
is given by
$\mu $
is given by
![]() $(\mu | \gamma )(f) = \mu (\gamma \cdot f)$
, where
$(\mu | \gamma )(f) = \mu (\gamma \cdot f)$
, where
![]() $\gamma $
acts on the function f as
$\gamma $
acts on the function f as
![]() $(\gamma \cdot f)(z) = (a + cz)^2\cdot f(\frac {b+dz}{a+cz})$
.
$(\gamma \cdot f)(z) = (a + cz)^2\cdot f(\frac {b+dz}{a+cz})$
.
We start with
![]() $(\Phi )_0 := \varphi $
. To lift
$(\Phi )_0 := \varphi $
. To lift
![]() $(\Phi )_M$
from
$(\Phi )_M$
from
![]() $ {\mathrm {Symb}}_{\Gamma _0(N)}(\mathbf {A}^M\mathscr {D}^\dagger ({\mathbf {Z}}[f]_{\mathfrak {p}}))$
to precision
$ {\mathrm {Symb}}_{\Gamma _0(N)}(\mathbf {A}^M\mathscr {D}^\dagger ({\mathbf {Z}}[f]_{\mathfrak {p}}))$
to precision
![]() $M+1$
, we first lift all values on the finitely many generators of
$M+1$
, we first lift all values on the finitely many generators of
![]() $\Delta _0$
(computed using Manin symbols) arbitrarily to precision
$\Delta _0$
(computed using Manin symbols) arbitrarily to precision
![]() $M+1$
. The resulting function will usually not be additive,
$M+1$
. The resulting function will usually not be additive,
![]() $\Gamma _0(N)$
-equivariant or an
$\Gamma _0(N)$
-equivariant or an
![]() $U_p$
-eigensymbol anymore, but it will be after we apply the operator
$U_p$
-eigensymbol anymore, but it will be after we apply the operator
![]() $U_p$
.
$U_p$
.
We stop after we have reached the precision from 7.4.8.
7.4.10 Computing an approximation to the p-adic L-function from the distribution
 $L_{\mathfrak {p}}(f)$
$L_{\mathfrak {p}}(f)$
To go from an approximation of
![]() $L_{\mathfrak {p}}(f)$
to the power series
$L_{\mathfrak {p}}(f)$
to the power series
![]() $\mathscr {L}_{\mathfrak {p}}(f,T)$
, we use the formulas in [Reference Pollack and Stevens84, § 9]. The computation depends on the choice of a topological generator
$\mathscr {L}_{\mathfrak {p}}(f,T)$
, we use the formulas in [Reference Pollack and Stevens84, § 9]. The computation depends on the choice of a topological generator
![]() $\gamma \in 1 + p{\mathbf {Z}}_p$
. We take
$\gamma \in 1 + p{\mathbf {Z}}_p$
. We take
![]() $\gamma = 1 + p$
in our computations.
$\gamma = 1 + p$
in our computations.
7.5 Examples
The example below represents the only case where our other methods are not sufficient to compute ![]() , so that we need to use p-adic L-functions. (Note that a
, so that we need to use p-adic L-functions. (Note that a
![]() $\mathfrak {p}$
-descent would amount to a full
$\mathfrak {p}$
-descent would amount to a full
![]() $3$
-descent in this case, which is not really feasible with current methods.)
$3$
-descent in this case, which is not really feasible with current methods.)
Example 7.10. For the Jacobian J of the curve
X
of level 188 = 2
2
· 47 in our data set, the Tamagawa product is
![]() $9$
(we have
$9$
(we have
![]() $c_2 = 9$
and
$c_2 = 9$
and
![]() $c_{47} = 1$
); the prime
$c_{47} = 1$
); the prime
![]() $3$
is inert in the endomorphism ring
$3$
is inert in the endomorphism ring
![]() ${\mathbf {Z}}[(1+\sqrt {5})/2]$
. To show that
${\mathbf {Z}}[(1+\sqrt {5})/2]$
. To show that ![]() in this case, we therefore compute the
in this case, we therefore compute the
![]() $3$
-adic L-function. Since
$3$
-adic L-function. Since
![]() $3 \nmid N$
, we have to
$3 \nmid N$
, we have to
![]() $3$
-stabilize; see 7.4.1. Note that
$3$
-stabilize; see 7.4.1. Note that
![]() $a_3(f) = -\frac {3+\sqrt {5}}{2}$
is a
$a_3(f) = -\frac {3+\sqrt {5}}{2}$
is a
![]() $3$
-adic unit; hence, the reduction at
$3$
-adic unit; hence, the reduction at
![]() $3$
is good ordinary. Then
$3$
is good ordinary. Then
![]() $\varepsilon _3(J/{\mathbf {Q}})$
is a unit as well (since
$\varepsilon _3(J/{\mathbf {Q}})$
is a unit as well (since
![]() $\alpha \equiv a_3(f) \not \equiv 1 \bmod 3$
).
$\alpha \equiv a_3(f) \not \equiv 1 \bmod 3$
).
We verify using propositions 2.58 and 2.59 that
![]() $ {\mathrm {SL}}_2({\mathbf {Z}}_3)$
is contained in the image of
$ {\mathrm {SL}}_2({\mathbf {Z}}_3)$
is contained in the image of
![]() $\rho _{f,3^\infty }$
.
$\rho _{f,3^\infty }$
.
The L-rank is
![]() $1$
and
$1$
and
![]() $J({\mathbf {Q}}) \cong {\mathbf {Z}}^2$
. A computation of
$J({\mathbf {Q}}) \cong {\mathbf {Z}}^2$
. A computation of
![]() $3$
-adic heights shows that
$3$
-adic heights shows that
![]() $v_3(\operatorname {Reg}_3(J/{\mathbf {Q}})) = 0$
. Therefore, one has
$v_3(\operatorname {Reg}_3(J/{\mathbf {Q}})) = 0$
. Therefore, one has
We thank Steffen Müller for computing the
![]() $3$
-adic regulator for us using the code described in [Reference Gajović and Müller48]. Using the algorithm sketched above, we find that
$3$
-adic regulator for us using the code described in [Reference Gajović and Müller48]. Using the algorithm sketched above, we find that
 $$ \begin{align*} \mathscr{L}_3(J,T) &= \mathscr{L}_3(f,T) \cdot \mathscr{L}_3(f^\tau,T) \\ &= (O(3^3) + uT + O(T^2)) \cdot (O(3^3) + u'T + O(T^2)) \end{align*} $$
$$ \begin{align*} \mathscr{L}_3(J,T) &= \mathscr{L}_3(f,T) \cdot \mathscr{L}_3(f^\tau,T) \\ &= (O(3^3) + uT + O(T^2)) \cdot (O(3^3) + u'T + O(T^2)) \end{align*} $$
with
![]() $3$
-adic units
$3$
-adic units
![]() $u, u'$
, where
$u, u'$
, where
![]() $\tau $
is the nontrivial automorphism of
$\tau $
is the nontrivial automorphism of
![]() ${\mathbf {Z}}[f]$
. (The computation took 30 minutes and 214 MiB RAM on a AMD Ryzen 7 PRO 6850U.) Since
${\mathbf {Z}}[f]$
. (The computation took 30 minutes and 214 MiB RAM on a AMD Ryzen 7 PRO 6850U.) Since
![]() $\operatorname {rk} J({\mathbf {Q}}) = 2$
and
$\operatorname {rk} J({\mathbf {Q}}) = 2$
and ![]() is finite,
is finite,
![]() $ {\mathrm {cork}}_{{\mathbf {Z}}[f]_3} \operatorname {Sel}_{3^\infty }(J/{\mathbf {Q}}) = 1$
, so corollary 7.9 shows that the vanishing order of
$ {\mathrm {cork}}_{{\mathbf {Z}}[f]_3} \operatorname {Sel}_{3^\infty }(J/{\mathbf {Q}}) = 1$
, so corollary 7.9 shows that the vanishing order of
![]() $\mathscr {L}_3(J,T)$
at
$\mathscr {L}_3(J,T)$
at
![]() $T = 0$
must be exactly
$T = 0$
must be exactly
![]() $2$
and that
$2$
and that

hence, ![]() .
.
8 Examples
8.1 Jacobians of genus
 $2$
Atkin–Lehner quotients
$2$
Atkin–Lehner quotients
Tables displaying the results for the Hasegawa curves can be found in [Reference Keller and Stoll59].
8.2 All genus
 $2$
curves with absolutely simple modular Jacobian from the LMFDB
$2$
curves with absolutely simple modular Jacobian from the LMFDB
We compute the analytic order of ![]() using the results from Sections 3 and 4. It turns out that all of them are
using the results from Sections 3 and 4. It turns out that all of them are
![]() $1$
,
$1$
,
![]() $2$
or
$2$
or
![]() $4$
. We also discover some twists
$4$
. We also discover some twists
![]() $J^K$
which have analytic order of
$J^K$
which have analytic order of ![]() divisible by
divisible by
![]() $3^2$
,
$3^2$
,
![]() $5^2$
or
$5^2$
or
![]() $7^2$
.
$7^2$
.
It turns out that combining the information about the images of the residual Galois representations from Section 2 with the Heegner indices from Section 3 (for a few examples, we have to use two Heegner fields) and the Euler system from Section 5 prove that ![]() except in the following cases:
except in the following cases:
-
○
 $p(\mathfrak {p}) = 2$
: these are dealt with in Section 6.1.
$p(\mathfrak {p}) = 2$
: these are dealt with in Section 6.1. -
○ Odd primes
 $\mathfrak {p}$
with
$\mathfrak {p}$
with
 $\rho _{\mathfrak {p}}$
reducible: these are dealt with in Section 6.2.
$\rho _{\mathfrak {p}}$
reducible: these are dealt with in Section 6.2. -
○ One example with
 $N = 188$
for which
$N = 188$
for which
 $3 \mid {\mathrm {Tam}}(J/{\mathbf {Q}})$
and
$3 \mid {\mathrm {Tam}}(J/{\mathbf {Q}})$
and
 $\rho _3$
is irreducible: see example 7.10.
$\rho _3$
is irreducible: see example 7.10.
This completes the verification of strong BSD for all the
![]() $97$
absolutely simple modular Jacobians in the LMFDB.
$97$
absolutely simple modular Jacobians in the LMFDB.
The Heegner discriminants used in the computation were typically
![]() $\leq 51$
in absolute value. The largest Heegner discriminant used was
$\leq 51$
in absolute value. The largest Heegner discriminant used was
![]() $-131$
for the example of level
$-131$
for the example of level
![]() $165$
. We needed two Heegner discriminants in the examples of level
$165$
. We needed two Heegner discriminants in the examples of level
![]() $523$
and
$523$
and
![]() $621$
. The Heegner point used in one of the examples of level
$621$
. The Heegner point used in one of the examples of level
![]() $275$
has unusually large height (
$275$
has unusually large height (
![]() $\approx 83.863$
). Computing the Heegner point and the Mordell–Weil group of the Jacobian over the Heegner field are the most time-consuming computations in our verification.
$\approx 83.863$
). Computing the Heegner point and the Mordell–Weil group of the Jacobian over the Heegner field are the most time-consuming computations in our verification.
8.3 Jacobians of the four remaining Wang curves
The Jacobians J of the four Wang curves of levels 65A, 117B, 125B and 175 (in the notation of [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and Wetherell45]) also have analytic order of Sha in
![]() $\{1, 2, 4\}$
. The remaining descent computations that are necessary to finish the proof that
$\{1, 2, 4\}$
. The remaining descent computations that are necessary to finish the proof that ![]() in these cases are sketched in Examples 6.10.
in these cases are sketched in Examples 6.10.
A An example with
 $7$
-torsion in
$7$
-torsion in 
In this appendix, which heavily relies on contributions by Sam Frengley, we verify strong BSD for a genus
![]() $2$
Jacobian J such that
$2$
Jacobian J such that ![]() . This contrasts with the examples in our database, where we always have
. This contrasts with the examples in our database, where we always have ![]() .
.
A.1 Visibility
We first briefly recall some generalities about visibility of elements of Tate–Shafarevich groups of abelian varieties, following, for example, [Reference Agashe and Stein2, Reference Agashe and Stein3, Reference Cremona and Mazur30, Reference Fisher43].
Let
![]() $A_1/K$
and
$A_1/K$
and
![]() $A_2/K$
be abelian varieties defined over a number field K. Suppose that there exist finite
$A_2/K$
be abelian varieties defined over a number field K. Suppose that there exist finite
![]() $ {\mathrm {Gal}}(\overline {K}|K)$
-submodules
$ {\mathrm {Gal}}(\overline {K}|K)$
-submodules
![]() $\Delta _1 \subset A_1(\overline {K})$
and
$\Delta _1 \subset A_1(\overline {K})$
and
![]() $\Delta _2 \subset A_1(\overline {K})$
equipped with an isomorphism
$\Delta _2 \subset A_1(\overline {K})$
equipped with an isomorphism
![]() $\varphi \colon \Delta _1 \xrightarrow {\sim } \Delta _2$
of
$\varphi \colon \Delta _1 \xrightarrow {\sim } \Delta _2$
of
![]() $ {\mathrm {Gal}}(\overline {K}|K)$
-modules. Write
$ {\mathrm {Gal}}(\overline {K}|K)$
-modules. Write
![]() $A_1' = A_1/\Delta _1$
and
$A_1' = A_1/\Delta _1$
and
![]() $A_2' = A_2/\Delta _2$
and let
$A_2' = A_2/\Delta _2$
and let
![]() $\psi _1 \colon A_1 \to A_1'$
and
$\psi _1 \colon A_1 \to A_1'$
and
![]() $\psi _2 \colon A_2 \to A_2'$
be the quotient morphisms. The isomorphism
$\psi _2 \colon A_2 \to A_2'$
be the quotient morphisms. The isomorphism
![]() $\varphi $
induces an isomorphism on Galois cohomology
$\varphi $
induces an isomorphism on Galois cohomology
![]() ${\operatorname {H}}^1(K, \Delta _1) \xrightarrow {\sim } {\operatorname {H}}^1(K, \Delta _2)$
. We might hope that if enough ‘local coincidences’ occur at the bad primes, then the
${\operatorname {H}}^1(K, \Delta _1) \xrightarrow {\sim } {\operatorname {H}}^1(K, \Delta _2)$
. We might hope that if enough ‘local coincidences’ occur at the bad primes, then the
![]() $\psi _1$
and
$\psi _1$
and
![]() $\psi _2$
-Selmer groups
$\psi _2$
-Selmer groups
![]() $\operatorname {Sel}(\psi _1)$
and
$\operatorname {Sel}(\psi _1)$
and
![]() $\operatorname {Sel}(\psi _2)$
may be isomorphic. In this case, if the order of the group
$\operatorname {Sel}(\psi _2)$
may be isomorphic. In this case, if the order of the group
![]() $A_1(K) / \psi _1 A_1'(K)$
is smaller than the order of
$A_1(K) / \psi _1 A_1'(K)$
is smaller than the order of
![]() $A_2(K) / \psi _2 A_2'(K)$
, the latter will contribute to a discrepancy between the order of
$A_2(K) / \psi _2 A_2'(K)$
, the latter will contribute to a discrepancy between the order of
![]() $A_1(K) / \psi _1 A_1'(K)$
and
$A_1(K) / \psi _1 A_1'(K)$
and
![]() $\operatorname {Sel}(\psi _1)$
, thereby ‘explaining’ some nontrivial elements of
$\operatorname {Sel}(\psi _1)$
, thereby ‘explaining’ some nontrivial elements of ![]() .
.
To make this idea precise, let
![]() $\Delta \subset (A_1 \times A_2)(\overline {K})$
be the graph of the isomorphism
$\Delta \subset (A_1 \times A_2)(\overline {K})$
be the graph of the isomorphism
![]() $\varphi $
and consider the abelian variety
$\varphi $
and consider the abelian variety
![]() $B = (A_1 \times A_2)/\Delta $
. We have a pair of morphisms
$B = (A_1 \times A_2)/\Delta $
. We have a pair of morphisms
Definition A.1. We say that an element or subgroup of
![]() ${\operatorname {H}}^1(K, A_1)$
is visible in B if it is contained in the kernel of the homomorphism
${\operatorname {H}}^1(K, A_1)$
is visible in B if it is contained in the kernel of the homomorphism
![]() $\iota _* \colon {\operatorname {H}}^1(K, A_1) \to {\operatorname {H}}^1(K, B)$
. We write
$\iota _* \colon {\operatorname {H}}^1(K, A_1) \to {\operatorname {H}}^1(K, B)$
. We write
![]() $\operatorname {Vis}_B {\operatorname {H}}^1(K, A_1)$
(respectively
$\operatorname {Vis}_B {\operatorname {H}}^1(K, A_1)$
(respectively ![]() ) for the subgroup of
) for the subgroup of
![]() ${\operatorname {H}}^1(K, A_1)$
(respectively
${\operatorname {H}}^1(K, A_1)$
(respectively ![]() ) consisting of elements visible in B.
) consisting of elements visible in B.
We will use the following theorem (which is proved in [Reference Fisher43, Theorem 2.2] (see also [Reference Agashe and Stein2] and [Reference Agashe and Stein3, Appendix])), which we state in the case when
![]() $K = {\mathbf {Q}}$
.
$K = {\mathbf {Q}}$
.
Theorem A.2. If
![]() $A_1({\mathbf {Q}}) / \varphi _1 A_1'({\mathbf {Q}}) = 0$
, then the subgroup
$A_1({\mathbf {Q}}) / \varphi _1 A_1'({\mathbf {Q}}) = 0$
, then the subgroup
![]() $\operatorname {Vis}_B {\operatorname {H}}^1({\mathbf {Q}},A)$
is isomorphic to
$\operatorname {Vis}_B {\operatorname {H}}^1({\mathbf {Q}},A)$
is isomorphic to
![]() $A_2({\mathbf {Q}}) / \varphi _2 A_2'({\mathbf {Q}})$
. Moreover if
$A_2({\mathbf {Q}}) / \varphi _2 A_2'({\mathbf {Q}})$
. Moreover if
![]() $\#\Delta $
is odd, and
$\#\Delta $
is odd, and
-
(i) all Tamagawa numbers of
 $A_1/{\mathbf {Q}}$
and
$A_1/{\mathbf {Q}}$
and
 $A_2/{\mathbf {Q}}$
are coprime to
$A_2/{\mathbf {Q}}$
are coprime to
 $\#\Delta $
, and
$\#\Delta $
, and -
(ii) the abelian variety B has good reduction at all primes dividing
 $\#\Delta $
,
$\#\Delta $
,
then ![]() .
.
A.2 The example
Let
![]() $C/{\mathbf {Q}}$
be the genus
$C/{\mathbf {Q}}$
be the genus
![]() $2$
curve given by the Weierstrass equation
$2$
curve given by the Weierstrass equation
Its Jacobian J is of
![]() $\mathrm {GL}_2$
-type; the level is
$\mathrm {GL}_2$
-type; the level is
![]() $N = 3200$
. This genus
$N = 3200$
. This genus
![]() $2$
curve is obtained, up to quadratic twist, by specializing the family of genus
$2$
curve is obtained, up to quadratic twist, by specializing the family of genus
![]() $2$
curves with
$2$
curves with
![]() $\sqrt {2}$
-multiplication given by Bending [Reference Bending7, Theorem 4.1] at
$\sqrt {2}$
-multiplication given by Bending [Reference Bending7, Theorem 4.1] at
![]() $(A,P,Q) = (-10,1,-5)$
. This example was found by computing (for many such specializations) twists
$(A,P,Q) = (-10,1,-5)$
. This example was found by computing (for many such specializations) twists
![]() $X_{J[\mathfrak {p}]}^\pm (7)$
of the modular curve
$X_{J[\mathfrak {p}]}^\pm (7)$
of the modular curve
![]() $X(7)$
whose K-points parameterize elliptic curves E equipped with an isomorphism of
$X(7)$
whose K-points parameterize elliptic curves E equipped with an isomorphism of
![]() $ {\mathrm {Gal}}(\overline {K}|K)$
-modules
$ {\mathrm {Gal}}(\overline {K}|K)$
-modules
![]() $J[\mathfrak {p}] \cong E[7]$
(see, for example, [Reference Poonen, Schaefer and Stoll85, Section 4.4] for the construction of these twists). The details of these calculations and further examples appear in the PhD thesis of Sam Frengley [Reference Frengley46] and in [Reference Frengley47].
$J[\mathfrak {p}] \cong E[7]$
(see, for example, [Reference Poonen, Schaefer and Stoll85, Section 4.4] for the construction of these twists). The details of these calculations and further examples appear in the PhD thesis of Sam Frengley [Reference Frengley46] and in [Reference Frengley47].
We begin by showing that the support of ![]() is contained in
is contained in
![]() $\{7\}$
.
$\{7\}$
.
Proposition A.3. The Jacobian J has
![]() $\mathcal {O} := \mathrm {End}_{\mathbf {Q}}(J) \cong {\mathbf {Z}}[\sqrt {2}]$
and
$\mathcal {O} := \mathrm {End}_{\mathbf {Q}}(J) \cong {\mathbf {Z}}[\sqrt {2}]$
and
![]() $r_{\mathrm {an}} = 0 = r$
,
$r_{\mathrm {an}} = 0 = r$
,
![]() $J({\mathbf {Q}}) = 0$
,
$J({\mathbf {Q}}) = 0$
,
![]() $\operatorname {Sel}_2(J/{\mathbf {Q}}) = 0$
,
$\operatorname {Sel}_2(J/{\mathbf {Q}}) = 0$
,
![]() $c_2 = c_5 = 1$
, and
$c_2 = c_5 = 1$
, and
![]() $I_{{\mathbf {Q}}(\sqrt {-31}),\pi } = 7$
.
$I_{{\mathbf {Q}}(\sqrt {-31}),\pi } = 7$
.
In particular, ![]() , and
, and ![]() is a power of
is a power of
![]() $7$
.
$7$
.
Proof. The endomorphism ring contains
![]() ${\mathbf {Z}}[\sqrt {2}]$
by construction of the curve. Since
${\mathbf {Z}}[\sqrt {2}]$
by construction of the curve. Since
![]() ${\mathbf {Z}}[\sqrt {2}]$
is the maximal order of
${\mathbf {Z}}[\sqrt {2}]$
is the maximal order of
![]() ${\mathbf {Q}}(\sqrt {2})$
, it follows that
${\mathbf {Q}}(\sqrt {2})$
, it follows that
![]() $\mathcal {O} \cong {\mathbf {Z}}[\sqrt {2}]$
. A computation of the
$\mathcal {O} \cong {\mathbf {Z}}[\sqrt {2}]$
. A computation of the
![]() $2$
-Selmer group shows that
$2$
-Selmer group shows that
![]() $\operatorname {rk} J({\mathbf {Q}}) = 0$
and
$\operatorname {rk} J({\mathbf {Q}}) = 0$
and ![]() . We check that
. We check that
![]() $L(J/{\mathbf {Q}}, 1) \neq 0$
by computing
$L(J/{\mathbf {Q}}, 1) \neq 0$
by computing
![]() $L(J/{\mathbf {Q}}, 1)/\Omega _J$
as described in Section 4.2. The torsion subgroup of
$L(J/{\mathbf {Q}}, 1)/\Omega _J$
as described in Section 4.2. The torsion subgroup of
![]() $J({\mathbf {Q}})$
turns out to be trivial. The Tamagawa number at
$J({\mathbf {Q}})$
turns out to be trivial. The Tamagawa number at
![]() $5$
can be determined using van Bommel’s Magma code [Reference van Bommel11, § 4.4]. However, Magma is unable to compute a regular model at
$5$
can be determined using van Bommel’s Magma code [Reference van Bommel11, § 4.4]. However, Magma is unable to compute a regular model at
![]() $2$
. So we computed a regular model by hand (see Sha7-curve.m for the computation of
$2$
. So we computed a regular model by hand (see Sha7-curve.m for the computation of
![]() $c_2$
) and found that the reduction type is
$c_2$
) and found that the reduction type is
![]() $[\text {III}_2^*]$
in [Reference Namikawa and Ueno79]. Note that this is also needed to determine the power of
$[\text {III}_2^*]$
in [Reference Namikawa and Ueno79]. Note that this is also needed to determine the power of
![]() $2$
in the ‘compensation factor’ C in lemma 3.7, which we need for the computation of
$2$
in the ‘compensation factor’ C in lemma 3.7, which we need for the computation of ![]() . Using the approach in Section 3, we find that
. Using the approach in Section 3, we find that
![]() $I_{K,\pi } = 7$
for
$I_{K,\pi } = 7$
for
![]() $K = {\mathbf {Q}}(\sqrt {-31})$
. As all residual Galois representations are irreducible, the claim now follows from theorem 5.6.
$K = {\mathbf {Q}}(\sqrt {-31})$
. As all residual Galois representations are irreducible, the claim now follows from theorem 5.6.
Lemma A.4. We have that ![]() .
.
Proof. Note that
![]() $7$
is split in the endomorphism ring
$7$
is split in the endomorphism ring
![]() $\mathcal {O} \cong {\mathbf {Z}}[\sqrt {2}]$
, so the Heegner index as an ideal of
$\mathcal {O} \cong {\mathbf {Z}}[\sqrt {2}]$
, so the Heegner index as an ideal of
![]() $\mathcal {O}$
equals
$\mathcal {O}$
equals
![]() $\mathfrak {p}$
with
$\mathfrak {p}$
with
![]() $\mathfrak {p}$
one of the two prime ideals above
$\mathfrak {p}$
one of the two prime ideals above
![]() $7$
. Using proposition 2.58, we find that the
$7$
. Using proposition 2.58, we find that the
![]() $\mathfrak {p}$
-adic Galois representations for these two primes have image
$\mathfrak {p}$
-adic Galois representations for these two primes have image
![]() $\mathrm {GL}_2({\mathbf {Z}}_7)$
. Furthermore,
$\mathrm {GL}_2({\mathbf {Z}}_7)$
. Furthermore,
![]() $7 \nmid h_{{\mathbf {Q}}(\sqrt {-31})} N$
. Hence, theorem 5.10 shows
$7 \nmid h_{{\mathbf {Q}}(\sqrt {-31})} N$
. Hence, theorem 5.10 shows ![]() . Since
. Since
![]() $[K : {\mathbf {Q}}] = 2$
is coprime to
$[K : {\mathbf {Q}}] = 2$
is coprime to
![]() $7$
, we get
$7$
, we get ![]() .
.
Applying theorem A.2, we can show the following.
Proposition A.5 (Sam Frengley)
Let E be the elliptic curve with LMFDB label 3200.a1 and Weierstrass equation
There exists a prime
![]() $\mathfrak {p} \mid 7$
in
$\mathfrak {p} \mid 7$
in
![]() $\mathcal {O}$
such that
$\mathcal {O}$
such that
![]() $J[\mathfrak {p}] \cong E[7]$
as
$J[\mathfrak {p}] \cong E[7]$
as
![]() $ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})$
-modules. Moreover, if
$ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})$
-modules. Moreover, if
![]() $\Delta \subset J \times E$
is the graph of this isomorphism, then
$\Delta \subset J \times E$
is the graph of this isomorphism, then ![]() contains a subgroup isomorphic to
contains a subgroup isomorphic to
![]() $({\mathbf {Z}}/7)^2$
which is visible in the abelian threefold
$({\mathbf {Z}}/7)^2$
which is visible in the abelian threefold
![]() $(J \times E)/\Delta $
.
$(J \times E)/\Delta $
.
Proof. We first show that
![]() $J[\mathfrak {p}]$
is isomorphic to
$J[\mathfrak {p}]$
is isomorphic to
![]() $E[7]$
as a
$E[7]$
as a
![]() $ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})$
-module, following [Reference Fisher43, Theorem 6.3]. Let
$ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})$
-module, following [Reference Fisher43, Theorem 6.3]. Let
![]() $\mathcal {K} := J/\{\pm 1\}$
be the Kummer surface of J given by the model in [Reference Cassels and Flynn18, Chapter 3] and let
$\mathcal {K} := J/\{\pm 1\}$
be the Kummer surface of J given by the model in [Reference Cassels and Flynn18, Chapter 3] and let
![]() $x_J \colon J \to \mathcal {K}$
be the quotient morphism. Similarly, let
$x_J \colon J \to \mathcal {K}$
be the quotient morphism. Similarly, let
![]() $x_E \colon E \to E/\{\pm 1\} \cong \mathbf {P}^1$
be the x-coordinate morphism. Since the mod-
$x_E \colon E \to E/\{\pm 1\} \cong \mathbf {P}^1$
be the x-coordinate morphism. Since the mod-
![]() $7$
Galois representation attached to
$7$
Galois representation attached to
![]() $E/{\mathbf {Q}}$
is surjective, by [Reference Fisher43, Proposition 6.1] to show that there exists a quadratic twist
$E/{\mathbf {Q}}$
is surjective, by [Reference Fisher43, Proposition 6.1] to show that there exists a quadratic twist
![]() $E^d/{\mathbf {Q}}$
of
$E^d/{\mathbf {Q}}$
of
![]() $E/{\mathbf {Q}}$
such that
$E/{\mathbf {Q}}$
such that
![]() $J[\mathfrak {p}]$
is isomorphic to
$J[\mathfrak {p}]$
is isomorphic to
![]() $E^d[7]$
as a
$E^d[7]$
as a
![]() $ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}/{\mathbf {Q}})$
-module, it suffices to show that there exist points
$ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}/{\mathbf {Q}})$
-module, it suffices to show that there exist points
![]() $P \in J[\mathfrak {p}]$
and
$P \in J[\mathfrak {p}]$
and
![]() $Q \in E[7]$
such that
$Q \in E[7]$
such that
![]() ${\mathbf {Q}}(x_J(P))$
and
${\mathbf {Q}}(x_J(P))$
and
![]() ${\mathbf {Q}}(x_E(Q))$
are isomorphic. Using the approach detailed in [Reference Fisher43, Theorem 6.3], we give an explicit degree
${\mathbf {Q}}(x_E(Q))$
are isomorphic. Using the approach detailed in [Reference Fisher43, Theorem 6.3], we give an explicit degree
![]() $24$
number field
$24$
number field
![]() $L/{\mathbf {Q}}$
and equations for points
$L/{\mathbf {Q}}$
and equations for points
![]() $x_J(P) \in \mathcal {K}(L)$
and
$x_J(P) \in \mathcal {K}(L)$
and
![]() $x_E(Q) \in \mathbf {P}^1(L)$
which generate
$x_E(Q) \in \mathbf {P}^1(L)$
which generate
![]() $L/{\mathbf {Q}}$
. For the computations, see the file congruence.m.
$L/{\mathbf {Q}}$
. For the computations, see the file congruence.m.
Finally, if
![]() $d \in {\mathbf {Z}}$
is chosen to be squarefree, then d is divisible only by bad primes of E and C. As discussed in [Reference Fisher43, (5.2)], by [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and Wetherell45, Section 2.1] or [Reference Merriman and Smart72, Lemma 3], an isomorphism of Galois modules
$d \in {\mathbf {Z}}$
is chosen to be squarefree, then d is divisible only by bad primes of E and C. As discussed in [Reference Fisher43, (5.2)], by [Reference Flynn, Leprévost, Schaefer, Stein, Stoll and Wetherell45, Section 2.1] or [Reference Merriman and Smart72, Lemma 3], an isomorphism of Galois modules
![]() $J[\mathfrak {p}] \cong E^d[7]$
induces a congruence
$J[\mathfrak {p}] \cong E^d[7]$
induces a congruence
Here,
![]() $t_p = p + 1 - N_1 $
and
$t_p = p + 1 - N_1 $
and
![]() $n_p = (N_1^2 + N_2 )/2 - (p+1) N_1 - p$
, where
$n_p = (N_1^2 + N_2 )/2 - (p+1) N_1 - p$
, where
![]() $N_1 = \# C({\mathbf {F}}_p)$
and
$N_1 = \# C({\mathbf {F}}_p)$
and
![]() $N_2 = \# C({\mathbf {F}}_{p^2})$
. Note that E and C have bad reduction at
$N_2 = \# C({\mathbf {F}}_{p^2})$
. Note that E and C have bad reduction at
![]() $2$
and
$2$
and
![]() $5$
and good reduction at all other primes, and for each integer
$5$
and good reduction at all other primes, and for each integer
![]() $d \neq 1$
dividing
$d \neq 1$
dividing
![]() $10$
, the congruence in (A.1) fails to hold at one of
$10$
, the congruence in (A.1) fails to hold at one of
![]() $p = 11$
,
$p = 11$
,
![]() $17$
, or
$17$
, or
![]() $23$
. It follows that
$23$
. It follows that
![]() $J[\mathfrak {p}]$
and
$J[\mathfrak {p}]$
and
![]() $E[7]$
are isomorphic as
$E[7]$
are isomorphic as
![]() $ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})$
-modules.
$ {\mathrm {Gal}}({\overline {{\mathbf {Q}}}}|{\mathbf {Q}})$
-modules.
To show that ![]() contains a subgroup isomorphic to
contains a subgroup isomorphic to
![]() $({\mathbf {Z}}/7)^2$
, first note that the Tamagawa numbers of
$({\mathbf {Z}}/7)^2$
, first note that the Tamagawa numbers of
![]() $E/{\mathbf {Q}}$
are coprime to
$E/{\mathbf {Q}}$
are coprime to
![]() $7$
and by proposition A.3 so are the Tamagawa numbers of
$7$
and by proposition A.3 so are the Tamagawa numbers of
![]() $J/{\mathbf {Q}}$
. The torsion subgroups of
$J/{\mathbf {Q}}$
. The torsion subgroups of
![]() $E/{\mathbf {Q}}$
and
$E/{\mathbf {Q}}$
and
![]() $J/{\mathbf {Q}}$
are trivial, the rank of
$J/{\mathbf {Q}}$
are trivial, the rank of
![]() $E/{\mathbf {Q}}$
is
$E/{\mathbf {Q}}$
is
![]() $2$
, and the rank of
$2$
, and the rank of
![]() $J/{\mathbf {Q}}$
is
$J/{\mathbf {Q}}$
is
![]() $0$
, again by proposition A.3. It follows from Theorem A.2 that
$0$
, again by proposition A.3. It follows from Theorem A.2 that ![]() contains a subgroup isomorphic to
contains a subgroup isomorphic to
![]() $({\mathbf {Z}}/7)^2$
, which is visible in
$({\mathbf {Z}}/7)^2$
, which is visible in
![]() $(J \times E)/\Delta $
.
$(J \times E)/\Delta $
.
Combining these results, we obtain the following.
Theorem A.6. For J as above, we have ![]() .
.
The computations with precision 462 took 57 hours and
![]() $3.3$
GiB RAM on an MIT server running Magma V2.28-3 provided to us by Andrew Sutherland. The log of N3200.m can be found in 3200.log. The bottleneck was the computation of the Heegner point, which required 783700 Fourier coefficients of the newform. (The remaining computations take less than 2 minutes.) Note that one must use
$3.3$
GiB RAM on an MIT server running Magma V2.28-3 provided to us by Andrew Sutherland. The log of N3200.m can be found in 3200.log. The bottleneck was the computation of the Heegner point, which required 783700 Fourier coefficients of the newform. (The remaining computations take less than 2 minutes.) Note that one must use
![]() $c_2 = 1$
from proposition A.3 to obtain the correct value
$c_2 = 1$
from proposition A.3 to obtain the correct value ![]() ; Magma cannot compute a regular semistable model of the curve at
; Magma cannot compute a regular semistable model of the curve at
![]() $p = 2$
.
$p = 2$
.
A.3 Further examples
One expects the existence of elements of order p in ![]() in quadratic twists of
in quadratic twists of
![]() $A/\langle P \rangle $
, where
$A/\langle P \rangle $
, where
![]() $0 \neq P \in A[p](K)$
by [Reference Shnidman and Weiss105].
$0 \neq P \in A[p](K)$
by [Reference Shnidman and Weiss105].
Our computations of the analytic orders of Sha for the Jacobians J of the LMFDB examples with L-rank
![]() $1$
yield the following examples of twists of J by the first Heegner field such that there is nontrivial p-torsion in Sha for some
$1$
yield the following examples of twists of J by the first Heegner field such that there is nontrivial p-torsion in Sha for some
![]() $p \in \{3,5,7\}$
. The number in parentheses indicates the index of the curve in the list of LMFDB examples.
$p \in \{3,5,7\}$
. The number in parentheses indicates the index of the curve in the list of LMFDB examples.
-
(30) The twist of the second curve with
 $N = 133$
by
$N = 133$
by
 $D_K = -31$
has
$D_K = -31$
has
 $I_K = 3^2$
and
$I_K = 3^2$
and  .
. -
(55) The twist of the first curve with
 $N = 275$
by
$N = 275$
by
 $D_K = -19$
has
$D_K = -19$
has
 $I_K = 3$
and
$I_K = 3$
and  .
. -
(57) The twist of the curve with
 $N = 289$
by
$N = 289$
by
 $D_K = -15$
has
$D_K = -15$
has
 $I_K = 3$
and
$I_K = 3$
and  .
. -
(74) The twist of the curve with
 $N = 523$
by
$N = 523$
by
 $D_K = -35$
has
$D_K = -35$
has
 $I_K = 3^2$
and
$I_K = 3^2$
and  .
. -
(77) The twist of the first curve with
 $N = 621$
by
$N = 621$
by
 $D_K = -11$
has
$D_K = -11$
has
 $I_K = 7$
and
$I_K = 7$
and  .
. -
(82) The twist of the curve with
 $N = 647$
by
$N = 647$
by
 $D_K = -11$
has
$D_K = -11$
has
 $I_K = 5$
and
$I_K = 5$
and  .
.
To obtain these values, we computed ![]() for a Heegner field
for a Heegner field
![]() $K = {\mathbf {Q}}(\sqrt {D})$
and use that
$K = {\mathbf {Q}}(\sqrt {D})$
and use that ![]() is a power of
is a power of
![]() $2$
for the LMFDB examples; hence,
$2$
for the LMFDB examples; hence, ![]() and
and ![]() differ by a power of
differ by a power of
![]() $2$
. By corollary 2.36, the set of
$2$
. By corollary 2.36, the set of
![]() $\mathfrak {p} \nmid 2$
with
$\mathfrak {p} \nmid 2$
with
![]() $\rho _{J/{\mathbf {Q}},\mathfrak {p}}$
irreducible remains the same when
$\rho _{J/{\mathbf {Q}},\mathfrak {p}}$
irreducible remains the same when
![]() $\rho $
is restricted to
$\rho $
is restricted to
![]() $G_K$
. By lemma 4.21 and (4.6), the odd prime factors of
$G_K$
. By lemma 4.21 and (4.6), the odd prime factors of
![]() $ {\mathrm {Tam}}(J^K/{\mathbf {Q}})$
are those of
$ {\mathrm {Tam}}(J^K/{\mathbf {Q}})$
are those of
![]() $ {\mathrm {Tam}}(J/{\mathbf {Q}})$
.
$ {\mathrm {Tam}}(J/{\mathbf {Q}})$
.
To also show that ![]() agrees with the analytic order of Sha, one has to compute
agrees with the analytic order of Sha, one has to compute ![]() , which our computation predicts to be
, which our computation predicts to be
![]() $({\mathbf {Z}}/2)^2$
in all of the above cases except the curve with
$({\mathbf {Z}}/2)^2$
in all of the above cases except the curve with
![]() $N = 621$
. We verified this using the code from [Reference Fisher and Yan44]. Thus, using theorems 5.7 and 5.10, the remaining tasks for verifying strong BSD are as follows.
$N = 621$
. We verified this using the code from [Reference Fisher and Yan44]. Thus, using theorems 5.7 and 5.10, the remaining tasks for verifying strong BSD are as follows.
-
(30) Show that
 and
and
 $= 2$
for the two prime ideals
$= 2$
for the two prime ideals
 $\mathfrak {p} \mid 3$
, respectively.
$\mathfrak {p} \mid 3$
, respectively. -
(55) Show that
 for one of the two prime ideals
for one of the two prime ideals
 $\mathfrak {p} \mid 3$
. Since the Heegner index as an
$\mathfrak {p} \mid 3$
. Since the Heegner index as an
 $\mathcal {O}$
-ideal has norm
$\mathcal {O}$
-ideal has norm
 $3$
, this shows
$3$
, this shows  for the other
for the other
 $\mathfrak {p} \mid 3$
.
$\mathfrak {p} \mid 3$
. -
(57) Show that
 for one of the two prime ideals
for one of the two prime ideals
 $\mathfrak {p} \mid 3$
. Since the Heegner index as an
$\mathfrak {p} \mid 3$
. Since the Heegner index as an
 $\mathcal {O}$
-ideal has norm
$\mathcal {O}$
-ideal has norm
 $3$
, this shows
$3$
, this shows  for the other
for the other
 $\mathfrak {p} \mid 3$
. For one of them, one can perform an isogeny descent.
$\mathfrak {p} \mid 3$
. For one of them, one can perform an isogeny descent. -
(74) Show that
 has a subgroup isomorphic to
has a subgroup isomorphic to
 $({\mathbf {Z}}/3)^4$
; note that the prime
$({\mathbf {Z}}/3)^4$
; note that the prime
 $3$
is inert in
$3$
is inert in
 ${\mathbf {Z}}[f]$
.
${\mathbf {Z}}[f]$
. -
(77) Show that
 for one of the two prime ideals
for one of the two prime ideals
 $\mathfrak {p} \mid 7$
. Since the Heegner index as an
$\mathfrak {p} \mid 7$
. Since the Heegner index as an
 $\mathcal {O}$
-ideal has norm
$\mathcal {O}$
-ideal has norm
 $7$
, this shows
$7$
, this shows  for the other
for the other
 $\mathfrak {p} \mid 7$
.
$\mathfrak {p} \mid 7$
. -
(82) Show that
 for one of the two prime ideals
for one of the two prime ideals
 $\mathfrak {p} \mid 5$
.
$\mathfrak {p} \mid 5$
.
Acknowledgements
We thank Francesc Castella, Kęstutis Česnavicius, Maarten Derickx, Michael Dettweiler, Tom Fisher, Sam Frengley, Pip Goodman, Walter Gubler, Peter Humphries, David Loeffler, Steffen Müller, Yusuf Mustopa, Jakob Stix, Chris Williams and Chris Wuthrich for hints and helpful discussions. We thank the referee for their careful reading and suggestions to improve the article.
Competing interest
The authors have no competing interest to declare.
Financial Support
The authors were supported by the Deutsche Forschungsgemeinschaft (DFG), STO 299/18-1 (AOBJ: 667349) (MS and TK) and STO 299/18-2 (AOBJ: 686837) (MS) while working on this article. TK was partially supported by the 2021 MSCA Postdoctoral Fellowship 01064790 – ExplicitRatPoints. MS was supported by the National Science Foundation under Grant No. DMS-1928930 while he was in residence at the Simons Laufer Mathematical Sciences Institute in Berkeley, California, during the spring 2023 semester. This stay was also supported through DFG grants STO 299/13-1 (AOBJ: 635353) and STO 299/17-1 (AOBJ: 662415).