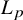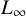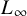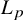1 Introduction
In numerical analysis, it matters how we measure errors. Change the metric we measure the perturbations with, and a well-conditioned input may turn badly conditioned (a remarkable example is in [Reference Cheung and Cucker22]). Because of this, a careful choice of how we measure errors is a fundamental step in the design and analysis of algorithms. A main example is numerical linear algebra, where it is commonplace to carefully choose a matrix norm depending on the problem at hand: the goal is to exploit the structure of the problem and optimise computational efficiency.
Unlike numerical linear algebra, a single norm – the Weyl norm – prevails in numerical algebraic geometry. The nice properties of the Weyl norm, ease of computing and unitary invariance, explain this prevalence. Nevertheless, the absence of complexity analyses using other norms in numerical algebraic geometry reflects badly on the theoretical strength of our analyses, which appear to rely on a specific choice of metric.
In this paper, we aim to show that using other norms is possible in numerical algebraic geometry. To do so, we consider an
![]() $L_\infty $
-norm in the space of polynomial systems and show how this leads to numerical algorithms and a complexity framework analogous to the one we have with the Weyl norm. Furthermore, we show that the change of norms leads to significant improvements in complexity bounds thanks to the better probabilistic behaviour of this
$L_\infty $
-norm in the space of polynomial systems and show how this leads to numerical algorithms and a complexity framework analogous to the one we have with the Weyl norm. Furthermore, we show that the change of norms leads to significant improvements in complexity bounds thanks to the better probabilistic behaviour of this
![]() $L_\infty $
norm with respect to the Weyl norm. We show this in three relevant cases: 1) computation of the homology of algebraic sets, 2) the Plantinga-Vegter algorithm and 3) the homotopy continuation method for quadratic polynomial systems.
$L_\infty $
norm with respect to the Weyl norm. We show this in three relevant cases: 1) computation of the homology of algebraic sets, 2) the Plantinga-Vegter algorithm and 3) the homotopy continuation method for quadratic polynomial systems.
We now discuss in more detail the aspects we have mentioned in passing to put our results in context within the wider setting of complexity theory for numerical algorithms and numerical algebraic geometry.
Complexity paradigm. The behaviour of numerical algorithms varies from input to input. This phenomenon is due not necessarily to the algorithms themselves but rather to the numerical sensitivity – how much the output varies with respect to a perturbation of the input – of the input we are processing. The numerical sensitivity of an input is captured by the so-called condition number. Then, in turn, condition numbers allow one to analyse numerical algorithms and explain why numerical algorithms handle some inputs faster than others.
Central to our paper is the fact that the choice of the metric under which we measure perturbations determines the condition number of the data. An example of this is given by the polynomial
![]() $X^d-1$
, which is well-conditioned (for the zero finding problem) with respect to the standard norm in equation (2.2) but badly conditioned with respect to the Weyl norm in equation (2.3) [Reference Bürgisser and Cucker14, Example 14.3].
$X^d-1$
, which is well-conditioned (for the zero finding problem) with respect to the standard norm in equation (2.2) but badly conditioned with respect to the Weyl norm in equation (2.3) [Reference Bürgisser and Cucker14, Example 14.3].
A drawback of condition-based complexity analyses is that, as we don’t know a priori the condition of the input at hand, we cannot foresee the running time for this input. We can nonetheless get an idea of how the algorithm behaves in general by randomising the input. This allows one to obtain probabilistic estimates for the practical performance of the numerical algorithm.
Again, we note that the metric we choose to measure perturbations affects the probabilistic models we consider. This is so because probabilistic parameters such as the variance are always given with respect to some metric, so when we change the metric, we change the values of these parameters.
We refer to [Reference Bürgisser and Cucker14] for a more detailed overview of this complexity paradigm based on condition numbers. In the rest of the paper, we will show how this complexity framework works for each of the three cases mentioned above.
Choice of the norm. Arguably, one disadvantage of the
![]() $L_\infty $
-norm is that we don’t have an efficient way to approximate
$L_\infty $
-norm is that we don’t have an efficient way to approximate
![]() $\|~\|_{\infty }$
. For polynomials in
$\|~\|_{\infty }$
. For polynomials in
![]() $n+1$
homogeneous variables whose degrees are bounded by
$n+1$
homogeneous variables whose degrees are bounded by
![]() $\mathbf {D}$
, our current fastest algorithm takes time polynomial in
$\mathbf {D}$
, our current fastest algorithm takes time polynomial in
![]() $\mathbf {D}$
and exponential in n. However, the computation of
$\mathbf {D}$
and exponential in n. However, the computation of
![]() $\|~\|_\infty $
amounts to a polynomial optimisation problem, and efficient algorithms exist for particular classes of polynomials. This is the case, for example, with sums of squares [Reference Laurent43, Reference Bhattiprolu, Guruswami and Lee10], sparse polynomials [Reference Dressler, Iliman and de Wolff31, Reference Chandrasekaran and Shah21] and other structures [Reference Barvinok5]. Unrestricted efficient algorithms are not expected to be designed because it is well-known that polynomial optimisation reduces to the feasibility problem over the reals, and the latter is
$\|~\|_\infty $
amounts to a polynomial optimisation problem, and efficient algorithms exist for particular classes of polynomials. This is the case, for example, with sums of squares [Reference Laurent43, Reference Bhattiprolu, Guruswami and Lee10], sparse polynomials [Reference Dressler, Iliman and de Wolff31, Reference Chandrasekaran and Shah21] and other structures [Reference Barvinok5]. Unrestricted efficient algorithms are not expected to be designed because it is well-known that polynomial optimisation reduces to the feasibility problem over the reals, and the latter is
![]() ${\mathrm {NP}_{\mathbb {R}}}$
-complete. Nonetheless, for most applications we only need a coarse approximation of
${\mathrm {NP}_{\mathbb {R}}}$
-complete. Nonetheless, for most applications we only need a coarse approximation of
![]() $\|~\|_{\infty }$
, which allows for some optimism.
$\|~\|_{\infty }$
, which allows for some optimism.
Our choice of the
![]() $L_\infty $
-norm is due to the inequalities shown in Kellogg’s theorem (Theorem 2.13), which we haven’t found for other
$L_\infty $
-norm is due to the inequalities shown in Kellogg’s theorem (Theorem 2.13), which we haven’t found for other
![]() $L_p$
-norms. A way around Kellogg’s theorem for general
$L_p$
-norms. A way around Kellogg’s theorem for general
![]() $L_p$
-norms would certainly lead to new results regarding the use of these norms in algorithm analysis.
$L_p$
-norms would certainly lead to new results regarding the use of these norms in algorithm analysis.
Despite the high cost of computing the
![]() $L_{\infty }$
norm, its use may yield substantially better cost bounds for some algorithms. This improvement rests on two facts:
$L_{\infty }$
norm, its use may yield substantially better cost bounds for some algorithms. This improvement rests on two facts:
-
1. For a homogeneous polynomial f with
 $n+1$
variables and degree
$n+1$
variables and degree
 $\mathbf {D}$
, we always have
$\mathbf {D}$
, we always have
 $ \left \lVert {f} \right \rVert _{\infty } \leq \left \lVert {f} \right \rVert _W$
, and for a random homogeneous polynomial
$ \left \lVert {f} \right \rVert _{\infty } \leq \left \lVert {f} \right \rVert _W$
, and for a random homogeneous polynomial
 $\mathfrak {f}$
, we have
$\mathfrak {f}$
, we have
 $ \left \lVert {\mathfrak {f}} \right \rVert _{\infty } \precsim \sqrt {n \log \mathbf {D}}$
, whereas
$ \left \lVert {\mathfrak {f}} \right \rVert _{\infty } \precsim \sqrt {n \log \mathbf {D}}$
, whereas
 $ \left \lVert {\mathfrak {f}} \right \rVert _W \sim \binom {n+\mathbf {D}}{n}^{\frac 12}$
. An analogous situation holds for polynomial systems (see Theorem 4.28 and Proposition 4.32).
$ \left \lVert {\mathfrak {f}} \right \rVert _W \sim \binom {n+\mathbf {D}}{n}^{\frac 12}$
. An analogous situation holds for polynomial systems (see Theorem 4.28 and Proposition 4.32). -
2. Condition numbers with respect to the
 $L_\infty $
-norm yield condition-based complexity estimates (i.e., cost bounds in terms of both n,
$L_\infty $
-norm yield condition-based complexity estimates (i.e., cost bounds in terms of both n,
 $\mathbf {D}$
and a condition number) almost identical to those obtained using the condition numbers with respect to the Weyl norm (see Section 3).
$\mathbf {D}$
and a condition number) almost identical to those obtained using the condition numbers with respect to the Weyl norm (see Section 3).
In this way, the reduction in the probabilistic estimates in passing to
![]() $ \left \lVert {~} \right \rVert _{\infty }$
from
$ \left \lVert {~} \right \rVert _{\infty }$
from
![]() $ \left \lVert {~} \right \rVert _W$
immediately translates to reductions in the magnitude of the corresponding condition numbers and, in turn, reductions in the complexity estimates.
$ \left \lVert {~} \right \rVert _W$
immediately translates to reductions in the magnitude of the corresponding condition numbers and, in turn, reductions in the complexity estimates.
Considered algorithms. We showcase three algorithms where despite the high cost of computing the
![]() $L_{\infty }$
-norm, the reductions in the total cost bounds remain significant.
$L_{\infty }$
-norm, the reductions in the total cost bounds remain significant.
Firstly, in Section 4.1, we consider a family of algorithms (we refer to them as grid-based) that solve various problems in real algebraic and semialgebraic geometry. The best numerical algorithms for these problems have exponential complexity. In Section 4.1, we replace the Weyl norm by
![]() $\|~\|_{\infty }$
in the design of one such algorithm (to compute Betti numbers); and in Section 4.3, we show a decrease in its cost bounds. We take advantage of the fact that there is only one norm computation, and it is done, so to speak, along the way. The gain in the reduction of the estimate for the number of iterations directly yields a reduction in the total cost bound (see Corollary 4.31).
$\|~\|_{\infty }$
in the design of one such algorithm (to compute Betti numbers); and in Section 4.3, we show a decrease in its cost bounds. We take advantage of the fact that there is only one norm computation, and it is done, so to speak, along the way. The gain in the reduction of the estimate for the number of iterations directly yields a reduction in the total cost bound (see Corollary 4.31).
Secondly, in Section 4.2, we consider the Plantinga-Vegter algorithm as it is described and analysed in [Reference Cucker, Ergür and Tonelli-Cueto23]. Again, we replace the Weyl norm by
![]() $\|~\|_{\infty }$
in the algorithm’s design results in improved cost bounds. And again, the computation of
$\|~\|_{\infty }$
in the algorithm’s design results in improved cost bounds. And again, the computation of
![]() $\|~\|_\infty $
is not a burden as it is done only once, and its cost is dominated by that of the rest of the algorithm. The Plantinga-Vegter algorithm is usually considered with
$\|~\|_\infty $
is not a burden as it is done only once, and its cost is dominated by that of the rest of the algorithm. The Plantinga-Vegter algorithm is usually considered with
![]() $n=2$
or
$n=2$
or
![]() $n=3$
. Remark 4.35 exhibits the improvement achieved on average complexity bounds for these two cases. For larger values of n, the improvement is more substantial.
$n=3$
. Remark 4.35 exhibits the improvement achieved on average complexity bounds for these two cases. For larger values of n, the improvement is more substantial.
Thirdly, in Section 5, we consider the problem of computing a zero of a system of complex quadratic equations. For this question, a particular case of Smale’s 17th problem, we consider the algorithms proposed in [Reference Beltrán and Pardo9, Reference Bürgisser and Cucker13] and, again, design versions of them where the Weyl norm is replaced by
![]() $\|~\|_{\infty }$
. Again, this results in a small but measurable reduction in the cost bounds (from
$\|~\|_{\infty }$
. Again, this results in a small but measurable reduction in the cost bounds (from
![]() $n^7$
to
$n^7$
to
![]() $n^{6.875}$
). A crucial fact in achieving this is that even though n is general, we can find an efficient way to compute
$n^{6.875}$
). A crucial fact in achieving this is that even though n is general, we can find an efficient way to compute
![]() $\|~\|_{\infty }$
using the fact that
$\|~\|_{\infty }$
using the fact that
![]() $\mathbf {D}=2$
.
$\mathbf {D}=2$
.
In all three cases, we are able to show that the use of
![]() $L_{\infty }$
-norm yields a clear reduction in the estimates for the expected number of iterations. We believe this is a common pattern. But in general, the reduction in the number of steps does not immediately translate into a reduction in total computational cost. This motivates the search for efficient algorithms that (roughly) approximate
$L_{\infty }$
-norm yields a clear reduction in the estimates for the expected number of iterations. We believe this is a common pattern. But in general, the reduction in the number of steps does not immediately translate into a reduction in total computational cost. This motivates the search for efficient algorithms that (roughly) approximate
![]() $\|~\|_{\infty }$
and for a better understanding of the complexity and accuracy of computing with
$\|~\|_{\infty }$
and for a better understanding of the complexity and accuracy of computing with
![]() $L_p$
-norms in polynomial spaces.
$L_p$
-norms in polynomial spaces.
Organisation of the paper. In Section 2, we define the norms that will be considered in this paper and work out several examples. We also recall basic properties of these norms and highlight their differences from the Weyl norm. Then, in Section 3, we define condition numbers
![]() $\mathsf {M}$
and
$\mathsf {M}$
and
![]() $\mathsf {K}$
that scale with the
$\mathsf {K}$
that scale with the
![]() $L_{\infty }$
-norm. These condition numbers are similar to their widely used Weyl versions
$L_{\infty }$
-norm. These condition numbers are similar to their widely used Weyl versions
![]() $\mu _{\mathrm {norm}}$
and
$\mu _{\mathrm {norm}}$
and
![]() $\kappa $
(for complex and real problems, respectively). We also prove in Section 3 that the main properties of
$\kappa $
(for complex and real problems, respectively). We also prove in Section 3 that the main properties of
![]() $\mu _{\mathrm {norm}}$
and
$\mu _{\mathrm {norm}}$
and
![]() $\kappa $
– those allowing them to feature in condition-based cost estimates – hold for
$\kappa $
– those allowing them to feature in condition-based cost estimates – hold for
![]() $\mathsf {M}$
and
$\mathsf {M}$
and
![]() $\mathsf {K}$
. Section 4.1, Section 4.2 and Section 5 are the home of three algorithms that are designed using
$\mathsf {K}$
. Section 4.1, Section 4.2 and Section 5 are the home of three algorithms that are designed using
![]() $L_{\infty }$
-scaled condition numbers. We compare the cost bounds of these algorithms to those of their Weyl counterparts and highlight computational gains.
$L_{\infty }$
-scaled condition numbers. We compare the cost bounds of these algorithms to those of their Weyl counterparts and highlight computational gains.
We conclude in Appendix A with a minor digression. Because a natural habitat for functional norms is spaces of continuous functions, we consider extensions of the real condition number
![]() $\kappa $
to the space
$\kappa $
to the space
![]() $C^1[q]:=C^1(\mathbb {S}^n,\mathbb {R}^q)$
, and we prove (somehow unexpectedly) Condition Number Theorems for these extensions. We do not analyse algorithms here. We nonetheless point out that substantial literature on algorithms on spaces of continuous functions exists [Reference Traub, Wasilkowski, Woźniakowski, Werschulz and Boult57, Reference Plaskota50, Reference Novak, Sloan, Traub and Woźniakowski48], where these theorems might be useful.
$C^1[q]:=C^1(\mathbb {S}^n,\mathbb {R}^q)$
, and we prove (somehow unexpectedly) Condition Number Theorems for these extensions. We do not analyse algorithms here. We nonetheless point out that substantial literature on algorithms on spaces of continuous functions exists [Reference Traub, Wasilkowski, Woźniakowski, Werschulz and Boult57, Reference Plaskota50, Reference Novak, Sloan, Traub and Woźniakowski48], where these theorems might be useful.
2 Norms for polynomials
Let
![]() $\mathbb {F}$
be either
$\mathbb {F}$
be either
![]() $\mathbb {R}$
or
$\mathbb {R}$
or
![]() $\mathbb {C}$
. Let also
$\mathbb {C}$
. Let also
![]() $n,d\in \mathbb {N}$
,
$n,d\in \mathbb {N}$
,
![]() $n,d\ge 1$
. We denote by
$n,d\ge 1$
. We denote by
![]() $\mathcal {H}^{\mathbb {F}}_d[1]$
the linear space of homogeneous polynomials of degree d in the
$\mathcal {H}^{\mathbb {F}}_d[1]$
the linear space of homogeneous polynomials of degree d in the
![]() $n+1$
variables
$n+1$
variables
![]() $X_0,X_1,\ldots ,X_n$
with coefficients in
$X_0,X_1,\ldots ,X_n$
with coefficients in
![]() $\mathbb {F}$
. Let
$\mathbb {F}$
. Let
![]() $\boldsymbol {d}=(d_1,\ldots ,d_q)\in \mathbb {N}^q$
and
$\boldsymbol {d}=(d_1,\ldots ,d_q)\in \mathbb {N}^q$
and
![]() $n\in \mathbb {N}$
as above. We denote by
$n\in \mathbb {N}$
as above. We denote by
![]() $\mathcal {H}_{\boldsymbol {d}}^{\mathbb {F}}[q]$
the space
$\mathcal {H}_{\boldsymbol {d}}^{\mathbb {F}}[q]$
the space
![]() $\mathcal {H}^{\mathbb {F}}_{d_1}[1]\times \cdots \times \mathcal {H}^{\mathbb {F}}_{d_q}[1]$
. If
$\mathcal {H}^{\mathbb {F}}_{d_1}[1]\times \cdots \times \mathcal {H}^{\mathbb {F}}_{d_q}[1]$
. If
![]() $\mathbb {F}$
is clear from the context, or if it is not relevant to the argument, we will omit the superscript. We will use the following conventions for dimension counting:
$\mathbb {F}$
is clear from the context, or if it is not relevant to the argument, we will omit the superscript. We will use the following conventions for dimension counting:
 $$ \begin{align*}N_i:=\binom{n+d_i}{d_i}=\dim_{\mathbb{F}}\mathcal{H}^{\mathbb{F}}_{d_i}[1] \quad \text{and}\quad N:=\sum_{i=1}^q\binom{n+d_i}{d_i}=\dim_{\mathbb{F}} \mathcal{H}_{\boldsymbol{d}}^{\mathbb{F}}[q].\end{align*} $$
$$ \begin{align*}N_i:=\binom{n+d_i}{d_i}=\dim_{\mathbb{F}}\mathcal{H}^{\mathbb{F}}_{d_i}[1] \quad \text{and}\quad N:=\sum_{i=1}^q\binom{n+d_i}{d_i}=\dim_{\mathbb{F}} \mathcal{H}_{\boldsymbol{d}}^{\mathbb{F}}[q].\end{align*} $$
We also use
![]() $\mathbf {D}:=\max \{d_1,\ldots ,d_q\}$
and denote by
$\mathbf {D}:=\max \{d_1,\ldots ,d_q\}$
and denote by
![]() $\Delta $
the
$\Delta $
the
![]() $q\times q$
diagonal matrix with
$q\times q$
diagonal matrix with
![]() $d_i$
in its ith diagonal entry.
$d_i$
in its ith diagonal entry.
In all that follows,
![]() $\mathbb {S}^n:=\{x\in \mathbb {R}^{n+1}\mid \|x\|_{2}=1\}$
will be the (real) n-sphere and
$\mathbb {S}^n:=\{x\in \mathbb {R}^{n+1}\mid \|x\|_{2}=1\}$
will be the (real) n-sphere and
![]() $\mathbb {P}^n:=\mathbb {C}^{n+1}/\mathbb {C}^*$
the complex projective space of dimension n. We note that there will be no ambiguity, as the sphere is the usual space to work with real polynomials and the projective space is the usual one for complex polynomials.
$\mathbb {P}^n:=\mathbb {C}^{n+1}/\mathbb {C}^*$
the complex projective space of dimension n. We note that there will be no ambiguity, as the sphere is the usual space to work with real polynomials and the projective space is the usual one for complex polynomials.
Remark 2.1. In what follows, we will write
![]() $z\in \mathbb {P}^n$
instead of
$z\in \mathbb {P}^n$
instead of
![]() $[z]\in \mathbb {P}^n$
, and we will assume that the representative
$[z]\in \mathbb {P}^n$
, and we will assume that the representative
![]() $z\in \mathbb {C}^{n+1}$
always satisfies
$z\in \mathbb {C}^{n+1}$
always satisfies
![]() $\|z\|_{2}=1$
. This simplifies the form of many of our definitions. This convention can be made without loss of generality as every point in
$\|z\|_{2}=1$
. This simplifies the form of many of our definitions. This convention can be made without loss of generality as every point in
![]() $\mathbb {P}^n$
has a representative of norm
$\mathbb {P}^n$
has a representative of norm
![]() $1$
.
$1$
.
2.1 Euclidean norms
The simplest norm considered on
![]() $\mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
is the one induced by the standard Euclidean inner product in a monomial basis. Every
$\mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
is the one induced by the standard Euclidean inner product in a monomial basis. Every
![]() $f\in \mathcal {H}^{\mathbb {F}}_d[1]$
can be uniquely represented as
$f\in \mathcal {H}^{\mathbb {F}}_d[1]$
can be uniquely represented as
where
![]() $\alpha =(\alpha _0,\ldots ,\alpha _n)\in {\mathbb {N}}^{n+1}$
and
$\alpha =(\alpha _0,\ldots ,\alpha _n)\in {\mathbb {N}}^{n+1}$
and
![]() $|\alpha |=\alpha _0+\cdots +\alpha _n$
. The norm induced by the standard Euclidean inner product is therefore
$|\alpha |=\alpha _0+\cdots +\alpha _n$
. The norm induced by the standard Euclidean inner product is therefore
 $$ \begin{align} \|f\|_{\mathrm{std}}:=\sqrt{\sum_{|\alpha|=d}|f_\alpha|^2}. \end{align} $$
$$ \begin{align} \|f\|_{\mathrm{std}}:=\sqrt{\sum_{|\alpha|=d}|f_\alpha|^2}. \end{align} $$
For
![]() $f=(f_1,\ldots ,f_q)\in \mathcal {H}_{\boldsymbol {d}}[q]$
, the norm extends as
$f=(f_1,\ldots ,f_q)\in \mathcal {H}_{\boldsymbol {d}}[q]$
, the norm extends as
![]() $\|f\|_{\mathrm {std}}^2:=\|f_1\|_{\mathrm {std}}^2+\cdots +\|f_q\|_{\mathrm {std}}^2$
.
$\|f\|_{\mathrm {std}}^2:=\|f_1\|_{\mathrm {std}}^2+\cdots +\|f_q\|_{\mathrm {std}}^2$
.
The most commonly used norm on
![]() $\mathcal {H}_{\boldsymbol {d}}[q]$
is the Weyl norm. For a polynomial as in equation (2.1), this is given by
$\mathcal {H}_{\boldsymbol {d}}[q]$
is the Weyl norm. For a polynomial as in equation (2.1), this is given by
 $$ \begin{align} \|f\|_W:=\sqrt{\sum_{|\alpha|=d}\binom{d}{\alpha}^{-1} |f_\alpha|^2}, \end{align} $$
$$ \begin{align} \|f\|_W:=\sqrt{\sum_{|\alpha|=d}\binom{d}{\alpha}^{-1} |f_\alpha|^2}, \end{align} $$
where
![]() $\binom {d}{\alpha }$
is the multinomial coefficient
$\binom {d}{\alpha }$
is the multinomial coefficient
![]() $\frac {d!}{\alpha _0!\ldots \alpha _n!}$
. Again, for
$\frac {d!}{\alpha _0!\ldots \alpha _n!}$
. Again, for
![]() $f\in \mathcal {H}_{\boldsymbol {d}}[q]$
, this extends by
$f\in \mathcal {H}_{\boldsymbol {d}}[q]$
, this extends by
![]() $\|f\|_W^2:=\|f_1\|_W^2+\cdots +\|f_q\|_W^2$
. The Weyl norm is also induced by an inner product, and this inner product is invariant under the action of the unitary group (respectively, the orthogonal group when the underlying field is
$\|f\|_W^2:=\|f_1\|_W^2+\cdots +\|f_q\|_W^2$
. The Weyl norm is also induced by an inner product, and this inner product is invariant under the action of the unitary group (respectively, the orthogonal group when the underlying field is
![]() $\mathbb {R}$
). It is straightforward to check that, for
$\mathbb {R}$
). It is straightforward to check that, for
![]() $f\in \mathcal {H}_{\boldsymbol {d}}[q]$
,
$f\in \mathcal {H}_{\boldsymbol {d}}[q]$
,
 $$ \begin{align*}\|f\|_W \le \|f\|_{\mathrm{std}}\le \max_{i\le q}\max_{|\alpha|=d_i}\binom{d_i}{\alpha} \|f\|_W. \end{align*} $$
$$ \begin{align*}\|f\|_W \le \|f\|_{\mathrm{std}}\le \max_{i\le q}\max_{|\alpha|=d_i}\binom{d_i}{\alpha} \|f\|_W. \end{align*} $$
Here, and in all that follows, for any
![]() $x\in \mathbb {S}^n$
and
$x\in \mathbb {S}^n$
and
![]() $f\in \mathcal {H}_{\boldsymbol {d}}[q]$
,
$f\in \mathcal {H}_{\boldsymbol {d}}[q]$
,
![]() $\mathrm {D}_xf:\mathrm {T}_x\mathbb {S}^n\to \mathbb {R}^q$
is the derivative of f at x restricted to the tangent space
$\mathrm {D}_xf:\mathrm {T}_x\mathbb {S}^n\to \mathbb {R}^q$
is the derivative of f at x restricted to the tangent space
![]() $\mathrm {T}_x\mathbb {S}^n$
of
$\mathrm {T}_x\mathbb {S}^n$
of
![]() $\mathbb {S}^n$
at x. A similar convention applies in the complex case replacing
$\mathbb {S}^n$
at x. A similar convention applies in the complex case replacing
![]() $\mathbb {S}^n$
and
$\mathbb {S}^n$
and
![]() $\mathrm {T}_x\mathbb {S}^n$
by
$\mathrm {T}_x\mathbb {S}^n$
by
![]() $\mathbb {P}^n$
and
$\mathbb {P}^n$
and
![]() $\mathrm {T}_{z}\mathbb {P}^n$
. The following property (see [Reference Bürgisser and Cucker14, Proposition 16.16]) is one of the most important properties of the Weyl norm from the viewpoint of the complexity of numerical algorithms.
$\mathrm {T}_{z}\mathbb {P}^n$
. The following property (see [Reference Bürgisser and Cucker14, Proposition 16.16]) is one of the most important properties of the Weyl norm from the viewpoint of the complexity of numerical algorithms.
Proposition 2.2. For all
![]() $x\in \mathbb {S}^n$
, the map
$x\in \mathbb {S}^n$
, the map
is an orthogonal projection from
![]() $\mathcal {H}_{\boldsymbol {d}}[q]$
endowed with the Weyl norm onto
$\mathcal {H}_{\boldsymbol {d}}[q]$
endowed with the Weyl norm onto
![]() $\mathbb {R}^{q}\times \mathrm {T}_x\mathbb {S}^n\simeq \mathbb {R}^{q+n}$
equipped with the standard Euclidean norm. An analogous statement holds in the complex case.
$\mathbb {R}^{q}\times \mathrm {T}_x\mathbb {S}^n\simeq \mathbb {R}^{q+n}$
equipped with the standard Euclidean norm. An analogous statement holds in the complex case.
2.2 Functional norms
We will consider functional norms that arise from evaluating polynomials at points on the sphere. One might consider other norms (as we do in Section A), but
![]() $L_p$
-norms suffice for obtaining the computational improvements we aim for. Although in the sequel we will only use the
$L_p$
-norms suffice for obtaining the computational improvements we aim for. Although in the sequel we will only use the
![]() $L_\infty $
-norm, we present the full family of
$L_\infty $
-norm, we present the full family of
![]() $L_p$
-norms since we consider that these norms will be useful in the future. Moreover, presenting the full family of
$L_p$
-norms since we consider that these norms will be useful in the future. Moreover, presenting the full family of
![]() $L_p$
-norms allows us to appreciate how the
$L_p$
-norms allows us to appreciate how the
![]() $L_\infty $
differs from and relates to these other norms.
$L_\infty $
differs from and relates to these other norms.
We will consider the two following classes of L-norms on
![]() $\mathcal {H}_{\boldsymbol {d}}[q]$
:
$\mathcal {H}_{\boldsymbol {d}}[q]$
:
-
 $(\mathbb {R})$
Real
$(\mathbb {R})$
Real
 $L_p$
-norm: For
$L_p$
-norm: For
 $p \in [1,\infty ]$
, where the expectations are taken over the uniform distribution of the n-dimensional sphere
$p \in [1,\infty ]$
, where the expectations are taken over the uniform distribution of the n-dimensional sphere $$ \begin{align*}\|f\|_{p}^{\mathbb{R}}:=\begin{cases} \displaystyle\max_{x\in\mathbb{S}^n}\|f(x)\|_{\infty}=\max_{x\in\mathbb{S}^n}\max_i|f_i(x)|&\text{if }p=\infty\\ \displaystyle\left(\mathop{\mathbb{E}}_{\mathfrak{x}\in\mathbb{S}^n}\|f(\mathfrak{x})\|_p^p\right)^{1/p}=\left(\mathop{\mathbb{E}}_{\mathfrak{x}\in\mathbb{S}^n}\left(\sum_{i=1}^q|f_i(\mathfrak{x})|^p\right)\right)^{1/p}&\text{otherwise},\end{cases}\end{align*} $$
$$ \begin{align*}\|f\|_{p}^{\mathbb{R}}:=\begin{cases} \displaystyle\max_{x\in\mathbb{S}^n}\|f(x)\|_{\infty}=\max_{x\in\mathbb{S}^n}\max_i|f_i(x)|&\text{if }p=\infty\\ \displaystyle\left(\mathop{\mathbb{E}}_{\mathfrak{x}\in\mathbb{S}^n}\|f(\mathfrak{x})\|_p^p\right)^{1/p}=\left(\mathop{\mathbb{E}}_{\mathfrak{x}\in\mathbb{S}^n}\left(\sum_{i=1}^q|f_i(\mathfrak{x})|^p\right)\right)^{1/p}&\text{otherwise},\end{cases}\end{align*} $$
 $\mathbb {S}^n\subseteq \mathbb {R}^{n+1}$
.
$\mathbb {S}^n\subseteq \mathbb {R}^{n+1}$
.
-
 $(\mathbb {C})$
Complex
$(\mathbb {C})$
Complex
 $L_p$
-norm: For
$L_p$
-norm: For
 $p \in [1,\infty ]$
, where the expectations are taken over the uniform distribution of the complex n-dimensional projective space
$p \in [1,\infty ]$
, where the expectations are taken over the uniform distribution of the complex n-dimensional projective space $$ \begin{align*}\|f\|_{p}^{\mathbb{C}}:=\begin{cases} \displaystyle\max_{z\in\mathbb{P}^n}\left\|f(z)\right\|_{\infty}=\max_{z\in\mathbb{P}^n}\max_i\left|f_i(z)\right|&\text{if }p=\infty\\ \displaystyle\left(\mathop{\mathbb{E}}_{\mathfrak{z}\in\mathbb{P}^n}\left\|f(\mathfrak{z})\right\|_p^p\right)^{1/p}=\left(\mathop{\mathbb{E}}_{\mathfrak{z}\in\mathbb{P}^n}\left(\sum_{i=1}^q\left|f_i(\mathfrak{z})\right|{}^p\right)\right)^{1/p}&\text{otherwise},\end{cases}\end{align*} $$
$$ \begin{align*}\|f\|_{p}^{\mathbb{C}}:=\begin{cases} \displaystyle\max_{z\in\mathbb{P}^n}\left\|f(z)\right\|_{\infty}=\max_{z\in\mathbb{P}^n}\max_i\left|f_i(z)\right|&\text{if }p=\infty\\ \displaystyle\left(\mathop{\mathbb{E}}_{\mathfrak{z}\in\mathbb{P}^n}\left\|f(\mathfrak{z})\right\|_p^p\right)^{1/p}=\left(\mathop{\mathbb{E}}_{\mathfrak{z}\in\mathbb{P}^n}\left(\sum_{i=1}^q\left|f_i(\mathfrak{z})\right|{}^p\right)\right)^{1/p}&\text{otherwise},\end{cases}\end{align*} $$
 $\mathbb {P}^n:=\mathbb {P}^n_{\mathbb {C}}$
.
$\mathbb {P}^n:=\mathbb {P}^n_{\mathbb {C}}$
.
Remark 2.3. In the case of a single polynomial, the definitions above become simpler. For
![]() $f\in \mathcal {H}_{\boldsymbol {d}}[1]$
,
$f\in \mathcal {H}_{\boldsymbol {d}}[1]$
,
 $$ \begin{align*} \|f\|_{p}^{\mathbb{R}}:=\begin{cases} \displaystyle\max_{x\in\mathbb{S}^n} \left\lvert {f(x)} \right\rvert &\text{if }p=\infty\\ \displaystyle\left(\mathop{\mathbb{E}}_{\mathfrak{x}\in\mathbb{S}^n}|f(\mathfrak{x})|^p\right)^{1/p}&\text{otherwise}\end{cases}~~\text{ and }~~\|f\|_{p}^{\mathbb{C}}:=\begin{cases} \displaystyle\max_{z\in\mathbb{P}^n}\left|f(z)\right|&\text{if }p=\infty\\ \displaystyle\left(\mathop{\mathbb{E}}_{\mathfrak{z}\in\mathbb{P}^n}\left|f(\mathfrak{z})\right|{}_p^p\right)^{1/p}&\text{otherwise},\end{cases} \end{align*} $$
$$ \begin{align*} \|f\|_{p}^{\mathbb{R}}:=\begin{cases} \displaystyle\max_{x\in\mathbb{S}^n} \left\lvert {f(x)} \right\rvert &\text{if }p=\infty\\ \displaystyle\left(\mathop{\mathbb{E}}_{\mathfrak{x}\in\mathbb{S}^n}|f(\mathfrak{x})|^p\right)^{1/p}&\text{otherwise}\end{cases}~~\text{ and }~~\|f\|_{p}^{\mathbb{C}}:=\begin{cases} \displaystyle\max_{z\in\mathbb{P}^n}\left|f(z)\right|&\text{if }p=\infty\\ \displaystyle\left(\mathop{\mathbb{E}}_{\mathfrak{z}\in\mathbb{P}^n}\left|f(\mathfrak{z})\right|{}_p^p\right)^{1/p}&\text{otherwise},\end{cases} \end{align*} $$
which amount to taking the p-mean of
![]() $|f|$
over, respectively,
$|f|$
over, respectively,
![]() $\mathbb {S}^n$
and
$\mathbb {S}^n$
and
![]() $\mathbb {P}^n$
.
$\mathbb {P}^n$
.
In general, we will omit the superscript when the context is clear. It will be common for us to work with the norms
![]() $\|~\|_{p}^{\mathbb {R}}$
in
$\|~\|_{p}^{\mathbb {R}}$
in
![]() $\mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
and the norms
$\mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
and the norms
![]() $\|~\|_{p}^{\mathbb {C}}$
in
$\|~\|_{p}^{\mathbb {C}}$
in
![]() $\mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[q]$
.Footnote
1
$\mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[q]$
.Footnote
1
Our definition has some arbitrary choices. These are motivated by the following two properties:
-
(D) For
 $p\in [1,\infty ]$
and
$p\in [1,\infty ]$
and
 $f\in \mathcal {H}_{\boldsymbol {d}}[q]$
,
$f\in \mathcal {H}_{\boldsymbol {d}}[q]$
,  $$ \begin{align*}\|f\|_p^{\mathbb{R}}=\left\|\left(\|f_1\|_p^{\mathbb{R}},\ldots,\|f_q\|_p^{\mathbb{R}}\right)\right\|_p~~\text{and}~~\|f\|_p^{\mathbb{C}} =\left\|\left(\|f_1\|_p^{\mathbb{C}},\ldots,\|f_q\|_p^{\mathbb{C}}\right)\right\|_p.\end{align*} $$
$$ \begin{align*}\|f\|_p^{\mathbb{R}}=\left\|\left(\|f_1\|_p^{\mathbb{R}},\ldots,\|f_q\|_p^{\mathbb{R}}\right)\right\|_p~~\text{and}~~\|f\|_p^{\mathbb{C}} =\left\|\left(\|f_1\|_p^{\mathbb{C}},\ldots,\|f_q\|_p^{\mathbb{C}}\right)\right\|_p.\end{align*} $$
This identity is why we take the p-mean of the p-norm of
 $f(x)$
instead of taking the p-mean of a fixed norm.
$f(x)$
instead of taking the p-mean of a fixed norm. -
(I) We have actions of the qth power of the (real) orthogonal group,
 $\mathscr {O}(n+1)^q$
, on
$\mathscr {O}(n+1)^q$
, on
 $\mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
, given by
$\mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
, given by
 $(A,f)\mapsto (f_i^{A_i}):=(f_i(A_iX))$
. Similarly, we have an action of the qth power of the unitary group,
$(A,f)\mapsto (f_i^{A_i}):=(f_i(A_iX))$
. Similarly, we have an action of the qth power of the unitary group,
 $\mathscr {U}(n+1)^q$
, on
$\mathscr {U}(n+1)^q$
, on
 $\mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[q]$
. The norms
$\mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[q]$
. The norms
 $\|~\|_{p}^{\mathbb {R}}$
and
$\|~\|_{p}^{\mathbb {R}}$
and
 $\|~\|_{p}^{\mathbb {C}}$
are invariant under these actions.
$\|~\|_{p}^{\mathbb {C}}$
are invariant under these actions.
We perform some simple computations to have a better grasp of the introduced norms.
Example 2.4 (Monomials).
We consider the value of the norms for a monomial
![]() $X^{\alpha }\in \mathcal {H}_d[1]$
of degree d. In this case, we have that for
$X^{\alpha }\in \mathcal {H}_d[1]$
of degree d. In this case, we have that for
![]() $p\in [1,\infty )$
,
$p\in [1,\infty )$
,
 $$ \begin{align*} \left\|X^\alpha\right\|_p^{\mathbb{R}}=\left(\frac{\Gamma\left(\frac{n+1}{2}\right)\prod_{i=0}^n\Gamma\left(\frac{p\alpha_i+1}{2}\right)}{\pi^{\frac{n+1}{2}}\Gamma\left(\frac{pd+n+1}{2}\right)}\right)^{\frac{1}{p}}~~\text{and}~~ \left\|X^\alpha\right\|_p^{\mathbb{C}}=\left(n!\frac{\prod_{i=0}^n\Gamma\left(\frac{p\alpha_i}{2}+1\right)}{\Gamma\left(\frac{pd}{2}+n+1\right)}\right)^{\frac{1}{p}}, \end{align*} $$
$$ \begin{align*} \left\|X^\alpha\right\|_p^{\mathbb{R}}=\left(\frac{\Gamma\left(\frac{n+1}{2}\right)\prod_{i=0}^n\Gamma\left(\frac{p\alpha_i+1}{2}\right)}{\pi^{\frac{n+1}{2}}\Gamma\left(\frac{pd+n+1}{2}\right)}\right)^{\frac{1}{p}}~~\text{and}~~ \left\|X^\alpha\right\|_p^{\mathbb{C}}=\left(n!\frac{\prod_{i=0}^n\Gamma\left(\frac{p\alpha_i}{2}+1\right)}{\Gamma\left(\frac{pd}{2}+n+1\right)}\right)^{\frac{1}{p}}, \end{align*} $$
where
![]() $\Gamma $
is Euler’s Gamma function, and that
$\Gamma $
is Euler’s Gamma function, and that
 $$ \begin{align*}\left\|X^\alpha\right\|_\infty^{\mathbb{R}}=\left\|X^\alpha\right\|_\infty^{\mathbb{C}}=\prod_{i=0}^n\left(\frac{\alpha_i}{d}\right)^{\frac{\alpha_i}{2}}=\sqrt{\frac{1}{d^d}\prod_{i=0}^n\alpha_i^{\alpha_i}}.\end{align*} $$
$$ \begin{align*}\left\|X^\alpha\right\|_\infty^{\mathbb{R}}=\left\|X^\alpha\right\|_\infty^{\mathbb{C}}=\prod_{i=0}^n\left(\frac{\alpha_i}{d}\right)^{\frac{\alpha_i}{2}}=\sqrt{\frac{1}{d^d}\prod_{i=0}^n\alpha_i^{\alpha_i}}.\end{align*} $$
For the calculations of
![]() $L_p$
-norms of monomials, we refer the reader to [Reference Folland36]. Although the calculation is only illustrated over the reals in the reference, the complex case is similar. For the second one, note that for monomials, real and complex
$L_p$
-norms of monomials, we refer the reader to [Reference Folland36]. Although the calculation is only illustrated over the reals in the reference, the complex case is similar. For the second one, note that for monomials, real and complex
![]() $\infty $
-norms are equivalent. Once this is clear, we are just using the method of Lagrange multipliers to compute the maximum over the sphere.
$\infty $
-norms are equivalent. Once this is clear, we are just using the method of Lagrange multipliers to compute the maximum over the sphere.
Example 2.5 (Linear functions).
Let
![]() and
and
![]() . Then f can be identified with a matrix A of size
. Then f can be identified with a matrix A of size
![]() $q\times (n+1)$
. We can see that
$q\times (n+1)$
. We can see that
where
![]() $\|~\|_{2,\infty }$
is the operator norm, where the domain vector space has the usual Euclidean norm
$\|~\|_{2,\infty }$
is the operator norm, where the domain vector space has the usual Euclidean norm
![]() $\|~\|_2$
and the codomain the
$\|~\|_2$
and the codomain the
![]() $\infty $
-norm
$\infty $
-norm
![]() $\|~\|_{\infty }$
.
$\|~\|_{\infty }$
.
For
![]() $p\in [1,\infty )$
,
$p\in [1,\infty )$
,
where
![]() $A^i$
is the ith row of A and
$A^i$
is the ith row of A and
![]() $X_0$
is a variable (and hence
$X_0$
is a variable (and hence
![]() $\|X_0\|^{\mathbb {F}}_p$
is given by the expressions in Example 2.4). Note that
$\|X_0\|^{\mathbb {F}}_p$
is given by the expressions in Example 2.4). Note that
![]() $\left \|\left (\|A^1\|_2,\ldots ,\|A^q\|_2\right )\right \|_p$
is just the p-norm of the vector of
$\left \|\left (\|A^1\|_2,\ldots ,\|A^q\|_2\right )\right \|_p$
is just the p-norm of the vector of
![]() $2$
-norms of the rows of A.
$2$
-norms of the rows of A.
Example 2.6 (Sum of squares).
Let
![]() $f:=\sum _{i=0}^nX_i^2\in \mathcal {H}_{2}[1]$
. As this function is constant on the real sphere, we have that for all
$f:=\sum _{i=0}^nX_i^2\in \mathcal {H}_{2}[1]$
. As this function is constant on the real sphere, we have that for all
![]() $p\in [1,\infty ]$
,
$p\in [1,\infty ]$
,
However, on
![]() $\mathbb {P}^n$
, f does not behave as a constant function as it has a positive dimensional zero set. Again, arguing as in [Reference Folland36], we can conclude that
$\mathbb {P}^n$
, f does not behave as a constant function as it has a positive dimensional zero set. Again, arguing as in [Reference Folland36], we can conclude that
 $$ \begin{align*} \|f\|_p^{\mathbb{C}}=\left(\frac{1}{\pi^{n+1}}\frac{n!}{(n+p)!}\int_{z\in\mathbb{C}^{n+1}}|f(z)|^p\mathrm{e}^{-|z|^2}\right)^{\frac{1}{p}} \end{align*} $$
$$ \begin{align*} \|f\|_p^{\mathbb{C}}=\left(\frac{1}{\pi^{n+1}}\frac{n!}{(n+p)!}\int_{z\in\mathbb{C}^{n+1}}|f(z)|^p\mathrm{e}^{-|z|^2}\right)^{\frac{1}{p}} \end{align*} $$
for
![]() $p\in [1,\infty )$
. Now, if p is even, we can obtain the expression
$p\in [1,\infty )$
. Now, if p is even, we can obtain the expression
 $$ \begin{align*} \|f\|_p^{\mathbb{C}}=\left(\binom{n+2}{2}^{-1}\sum_{\substack{\alpha\in\mathbb{N}^{n+1}\\|\alpha|=p/2}}\binom{p/2}{\alpha}^2\binom{p}{2\alpha}^{-1}\right)^{\frac{1}{p}} \end{align*} $$
$$ \begin{align*} \|f\|_p^{\mathbb{C}}=\left(\binom{n+2}{2}^{-1}\sum_{\substack{\alpha\in\mathbb{N}^{n+1}\\|\alpha|=p/2}}\binom{p/2}{\alpha}^2\binom{p}{2\alpha}^{-1}\right)^{\frac{1}{p}} \end{align*} $$
after writing
![]() $|f(z)|^p=f(z)^{\frac {p}{2}}\overline {f(z)}^{\kern1pt\frac {p}{2}}$
, expanding and using separation of variables. In particular, for
$|f(z)|^p=f(z)^{\frac {p}{2}}\overline {f(z)}^{\kern1pt\frac {p}{2}}$
, expanding and using separation of variables. In particular, for
![]() $p=2$
, we obtain that
$p=2$
, we obtain that
 $$ \begin{align*} \|f\|_2^{\mathbb{C}}=\sqrt{\frac{2}{n+2}}\neq 1. \end{align*} $$
$$ \begin{align*} \|f\|_2^{\mathbb{C}}=\sqrt{\frac{2}{n+2}}\neq 1. \end{align*} $$
This shows how the norms
![]() $\|~\|_p^{\mathbb {C}}$
may be smaller than their corresponding norm
$\|~\|_p^{\mathbb {C}}$
may be smaller than their corresponding norm
![]() $\|~\|_p^{\mathbb {R}}$
for
$\|~\|_p^{\mathbb {R}}$
for
![]() $p\in [1,\infty )$
.
$p\in [1,\infty )$
.
Example 2.7 (Cosine polynomials).
Let
![]() $d\geq 2$
, and consider the family of homogeneous polynomials
$d\geq 2$
, and consider the family of homogeneous polynomials
 $$ \begin{align*}c_d:=\sum_{k=0}^{\lfloor d/2\rfloor}\binom{d}{2k}(-1)^kX^{d-2k}Y^{2k}=\frac{1}{2}(X+iY)^d+\frac{1}{2}(X-iY)^d\in\mathcal{H}_d[1].\end{align*} $$
$$ \begin{align*}c_d:=\sum_{k=0}^{\lfloor d/2\rfloor}\binom{d}{2k}(-1)^kX^{d-2k}Y^{2k}=\frac{1}{2}(X+iY)^d+\frac{1}{2}(X-iY)^d\in\mathcal{H}_d[1].\end{align*} $$
Since
![]() $c_d(\cos \theta ,\sin \theta )=\cos d\theta $
, we have that
$c_d(\cos \theta ,\sin \theta )=\cos d\theta $
, we have that
Also,
![]() $c_d$
is unitarily equivalent to
$c_d$
is unitarily equivalent to
![]() $2^{\frac {d}{2}-1}(X^d+Y^d)$
. Hence
$2^{\frac {d}{2}-1}(X^d+Y^d)$
. Hence
since
![]() $\|X^d+Y^d\|_{\infty }^{\mathbb {C}}=1$
for
$\|X^d+Y^d\|_{\infty }^{\mathbb {C}}=1$
for
![]() $d\geq 2$
. This shows that for degrees
$d\geq 2$
. This shows that for degrees
![]() $d\geq 3$
, the norms
$d\geq 3$
, the norms
![]() $\|~\|_{\infty }^{\mathbb {R}}$
and
$\|~\|_{\infty }^{\mathbb {R}}$
and
![]() $\|~\|_{\infty }^{\mathbb {C}}$
disagree on real polynomials.
$\|~\|_{\infty }^{\mathbb {C}}$
disagree on real polynomials.
The following proposition lists simple inequalities between the functional norms. For a converse of some of the inequalities below, where the
![]() $L_\infty $
norm is bounded in terms of
$L_\infty $
norm is bounded in terms of
![]() $L_p$
norms, see [Reference Barvinok6].
$L_p$
norms, see [Reference Barvinok6].
Proposition 2.8. Let
![]() $1\leq p < p'<\infty $
and
$1\leq p < p'<\infty $
and
![]() $\mathbb {F}\in \{\mathbb {R},\mathbb {C}\}$
. Then for all
$\mathbb {F}\in \{\mathbb {R},\mathbb {C}\}$
. Then for all
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {F}}[q]$
, the following inequalities hold:
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {F}}[q]$
, the following inequalities hold:
 $$ \begin{align*}\frac{1}{q^{\frac{1}{p}}}\|f\|_p^{\mathbb{F}}\leq \frac{1}{q^{\frac{1}{p'}}}\|f\|_{p'}^{\mathbb{F}}\leq \|f\|_{\infty}^{\mathbb{F}}\leq \|f\|_{\infty}^{\mathbb{C}}.\end{align*} $$
$$ \begin{align*}\frac{1}{q^{\frac{1}{p}}}\|f\|_p^{\mathbb{F}}\leq \frac{1}{q^{\frac{1}{p'}}}\|f\|_{p'}^{\mathbb{F}}\leq \|f\|_{\infty}^{\mathbb{F}}\leq \|f\|_{\infty}^{\mathbb{C}}.\end{align*} $$
Sketch of proof.
It is a direct consequence of the inequalities between p-means.
![]() $\Box $
$\Box $
The Weyl norm is essentially a scaled version of the complex
![]() $L_2$
norm.
$L_2$
norm.
Proposition 2.9. Let
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[q]$
. Then
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[q]$
. Then
 $$ \begin{align*}\|f\|_W=\sqrt{\sum_{i=1}^qN_i \left(\|f_i\|_{2}^{\mathbb{C}}\right)^2}.\end{align*} $$
$$ \begin{align*}\|f\|_W=\sqrt{\sum_{i=1}^qN_i \left(\|f_i\|_{2}^{\mathbb{C}}\right)^2}.\end{align*} $$
In particular, for
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[1]$
,
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[1]$
,
Sketch of proof.
We only need to show this in the case
![]() $q=1$
. Now both the Weyl norm and the complex
$q=1$
. Now both the Weyl norm and the complex
![]() $L_2$
-norm are unitarily invariant Hermitian norms of
$L_2$
-norm are unitarily invariant Hermitian norms of
![]() $\mathcal {H}_d^{\mathbb {C}}$
. For the Weyl norm, see [Reference Bürgisser and Cucker14, Theorem 16.3]; for the complex
$\mathcal {H}_d^{\mathbb {C}}$
. For the Weyl norm, see [Reference Bürgisser and Cucker14, Theorem 16.3]; for the complex
![]() $L_2$
-norm, this is property (I). Since
$L_2$
-norm, this is property (I). Since
![]() $\mathcal {H}_d^{\mathbb {C}}$
is an irreducible representation of
$\mathcal {H}_d^{\mathbb {C}}$
is an irreducible representation of
![]() $\mathscr {U}(n+1)$
, this means the two norms are equal up to a constant. Using Example 2.4 with
$\mathscr {U}(n+1)$
, this means the two norms are equal up to a constant. Using Example 2.4 with
![]() $f=X_0^d$
, one can check that this constant is
$f=X_0^d$
, one can check that this constant is
![]() $\sqrt {N}$
.
$\sqrt {N}$
.
![]() $\Box $
$\Box $
From Proposition 2.2, we get the following result.
Proposition 2.10. Let
![]() $\mathbb {F}\in \{\mathbb {R},\mathbb {C}\}$
and
$\mathbb {F}\in \{\mathbb {R},\mathbb {C}\}$
and
![]() $f\in \mathcal {H}_{\boldsymbol {d}}[q]$
. Then for all
$f\in \mathcal {H}_{\boldsymbol {d}}[q]$
. Then for all
![]() $p\geq 2$
,
$p\geq 2$
,
Sketch of proof.
By Proposition 2.2,
![]() $f\mapsto f(x)$
is an orthogonal projection with respect to the Weyl norm, so
$f\mapsto f(x)$
is an orthogonal projection with respect to the Weyl norm, so
![]() $\|f(x)\|_2\leq \|f\|_W$
. Hence, for every
$\|f(x)\|_2\leq \|f\|_W$
. Hence, for every
![]() $x \in S^{n-1}$
,
$x \in S^{n-1}$
,
![]() $\|f(x)\|_p \leq \|f(x)\|_2\leq \|f\|_W$
, where the first inequality follows from Minkowski’s inequality.
$\|f(x)\|_p \leq \|f(x)\|_2\leq \|f\|_W$
, where the first inequality follows from Minkowski’s inequality.
![]() $\Box $
$\Box $
We finish this subsection by noting how the
![]() $L_\infty $
-norms relate to the Weyl norm. We note that this is related to the so-called best rank-one approximation of a symmetric tensor [Reference Agrachev, Kozhasov and Uschmajew1, Reference Zhang, Ling and Qi59]; the inequality for the real case below was already present in [Reference Zhang, Ling and Qi59, Theorem 2.4].
$L_\infty $
-norms relate to the Weyl norm. We note that this is related to the so-called best rank-one approximation of a symmetric tensor [Reference Agrachev, Kozhasov and Uschmajew1, Reference Zhang, Ling and Qi59]; the inequality for the real case below was already present in [Reference Zhang, Ling and Qi59, Theorem 2.4].
Proposition 2.11. Let
![]() $f\in \mathcal {H}_{\boldsymbol {d}}[q]$
. Then
$f\in \mathcal {H}_{\boldsymbol {d}}[q]$
. Then
If
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
, then
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
, then
Proof. The first part follows from Proposition 2.9 and 2.10. The left-hand side of the second part uses Proposition 2.10.
Now, for
![]() $f\in \mathcal {H}_d[1]$
, Corollary 2.20 implies that for each
$f\in \mathcal {H}_d[1]$
, Corollary 2.20 implies that for each
![]() $\alpha $
,
$\alpha $
,
![]() $|f_\alpha |=\left \|\frac {1}{\alpha !}\overline {\mathrm {D}}_xf\right \|\leq \binom {d}{\alpha }$
. The right-hand inequality follows from here.
$|f_\alpha |=\left \|\frac {1}{\alpha !}\overline {\mathrm {D}}_xf\right \|\leq \binom {d}{\alpha }$
. The right-hand inequality follows from here.
Example 2.12. Proposition 2.11 is almost optimal for
![]() $n=1$
. In [Reference Agrachev, Kozhasov and Uschmajew1], it was shown that for the cosine polynomials
$n=1$
. In [Reference Agrachev, Kozhasov and Uschmajew1], it was shown that for the cosine polynomials
![]() $c_d$
of Example 2.7, we have
$c_d$
of Example 2.7, we have
and that
![]() $c_d$
is the real polynomial of real
$c_d$
is the real polynomial of real
![]() $L_\infty $
norm 1 with largest Weyl norm. Curiously, in this case, the Weyl norm and the complex
$L_\infty $
norm 1 with largest Weyl norm. Curiously, in this case, the Weyl norm and the complex
![]() $L_\infty $
are almost equal, the former being the latter times
$L_\infty $
are almost equal, the former being the latter times
![]() $\sqrt {2}$
.
$\sqrt {2}$
.
2.3 Kellogg’s theorem
We will denote by
![]() $\overline {\mathrm {D}}$
the operation of taking all partial derivatives with respect to all variables: that is,
$\overline {\mathrm {D}}$
the operation of taking all partial derivatives with respect to all variables: that is,
![]() $f\mapsto \overline {\mathrm {D}} f$
is a linear map
$f\mapsto \overline {\mathrm {D}} f$
is a linear map
![]() , and for
, and for
![]() $x\in \mathbb {F}^{n+1}$
,
$x\in \mathbb {F}^{n+1}$
,
![]() $\overline {\mathrm {D}}_x f:\mathbb {F}^{n+1}\to \mathbb {F}^q$
is a linear map. We will write
$\overline {\mathrm {D}}_x f:\mathbb {F}^{n+1}\to \mathbb {F}^q$
is a linear map. We will write
![]() $\overline {\mathrm {D}}_Xf$
, with a capital X, to emphasise that we view
$\overline {\mathrm {D}}_Xf$
, with a capital X, to emphasise that we view
![]() $\overline {\mathrm {D}}_Xf$
as a polynomial tuple in
$\overline {\mathrm {D}}_Xf$
as a polynomial tuple in
![]() ; and we will write
; and we will write
![]() $\overline {\mathrm {D}}_xf$
, with a lowercase x, to emphasise that we view
$\overline {\mathrm {D}}_xf$
, with a lowercase x, to emphasise that we view
![]() $\overline {\mathrm {D}}_xf$
as the linear map
$\overline {\mathrm {D}}_xf$
as the linear map
![]() $\mathbb {F}^{n+1}\rightarrow \mathbb {F}^q$
defined at the point x. We also recall that
$\mathbb {F}^{n+1}\rightarrow \mathbb {F}^q$
defined at the point x. We also recall that
![]() $\mathrm {D}_xf$
is the tangent map
$\mathrm {D}_xf$
is the tangent map
![]() $\mathrm {T}_x\mathbb {S}^n\rightarrow \mathbb {R}^q$
in the real case and the tangent map
$\mathrm {T}_x\mathbb {S}^n\rightarrow \mathbb {R}^q$
in the real case and the tangent map
![]() $\mathrm {T}_x\mathbb {P}^n\rightarrow \mathbb {C}^q$
in the complex case.
$\mathrm {T}_x\mathbb {P}^n\rightarrow \mathbb {C}^q$
in the complex case.
The following result plays the role of Proposition 2.2 for the infinity norm instead of the Weyl one. It is a reformulation of a well-known inequality proved in [Reference Kellogg40].
Theorem 2.13 (Kellogg’s inequality).
Let
![]() $\mathbb {F}\in \{\mathbb {R},\mathbb {C}\}$
,
$\mathbb {F}\in \{\mathbb {R},\mathbb {C}\}$
,
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {F}}[q]$
and
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {F}}[q]$
and
![]() $v\in \mathbb {F}^{n+1}$
; then
$v\in \mathbb {F}^{n+1}$
; then
Corollary 2.14. Let
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {F}}[q]$
and
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {F}}[q]$
and
![]() $z\in \mathbb {S}^n$
(if
$z\in \mathbb {S}^n$
(if
![]() $\mathbb {F}=\mathbb {R}$
) or
$\mathbb {F}=\mathbb {R}$
) or
![]() $z\in \mathbb {P}^n$
(if
$z\in \mathbb {P}^n$
(if
![]() $\mathbb {F}=\mathbb {C}$
). Then
$\mathbb {F}=\mathbb {C}$
). Then
Before proving Theorem 2.13 and Corollary 2.14, we discuss some features of these results.
Remark 2.15. We note that the left-hand side in Corollary 2.14 is not optimal. In general, we have that
 $$ \begin{align*}\|\Delta^{-1}\overline{\mathrm{D}}_xf\|_{2,\infty}=\max_i \sqrt{|f_i(x)|^2+\frac{1}{d_i^2}\|\mathrm{D}_xf_i\|_{2,\infty}^2}.\end{align*} $$
$$ \begin{align*}\|\Delta^{-1}\overline{\mathrm{D}}_xf\|_{2,\infty}=\max_i \sqrt{|f_i(x)|^2+\frac{1}{d_i^2}\|\mathrm{D}_xf_i\|_{2,\infty}^2}.\end{align*} $$
The following examples show how the bound of Theorem 2.13 looks in a few particular cases.
Example 2.16. Consider the cosine polynomials
![]() $c_d$
of Example 2.7. A direct computation shows that
$c_d$
of Example 2.7. A direct computation shows that
where
![]() $s_{d-1}:=-\frac {i}{2}(X+iY)^{d-1}+\frac {i}{2}(X-iY)$
is the sine polynomial for which
$s_{d-1}:=-\frac {i}{2}(X+iY)^{d-1}+\frac {i}{2}(X-iY)$
is the sine polynomial for which
![]() $s_{d}(\cos \theta ,\sin \theta )=\sin d\theta $
.
$s_{d}(\cos \theta ,\sin \theta )=\sin d\theta $
.
In the real case, this gives
 $$ \begin{align*}\left\|\frac{1}{d}\overline{\mathrm{D}}_Xc_dv\right\|_{\infty}^{\mathbb{R}}=\|v\|_{2}=\|c_d\|_\infty^{\mathbb{R}}\|v\|_{2},\end{align*} $$
$$ \begin{align*}\left\|\frac{1}{d}\overline{\mathrm{D}}_Xc_dv\right\|_{\infty}^{\mathbb{R}}=\|v\|_{2}=\|c_d\|_\infty^{\mathbb{R}}\|v\|_{2},\end{align*} $$
using the Cauchy-Schwarz inequality. In the complex case,
![]() $\frac {1}{d}\mathrm {D}_Xc_dv=v_Xc_{d-1}-v_Ys_{d-1}$
is unitarily equivalent to
$\frac {1}{d}\mathrm {D}_Xc_dv=v_Xc_{d-1}-v_Ys_{d-1}$
is unitarily equivalent to
 $$ \begin{align*}\frac{2^{\frac{d-1}{2}}}{d}\left[(v_{X}-iv_Y) X^{d-1}+(v_{X}+iv_Y)Y^{d-1}\right].\end{align*} $$
$$ \begin{align*}\frac{2^{\frac{d-1}{2}}}{d}\left[(v_{X}-iv_Y) X^{d-1}+(v_{X}+iv_Y)Y^{d-1}\right].\end{align*} $$
Now,
![]() $\left \|(v_{X}-iv_Y)x^{d-1} +(v_{X}+iv_Y)y^{d-1}\right \| \leq \sqrt {2} \|v\|_{2}(|x|^{d-1}+|y|^{d-1}) \leq \|v\|_{2}$
for
$\left \|(v_{X}-iv_Y)x^{d-1} +(v_{X}+iv_Y)y^{d-1}\right \| \leq \sqrt {2} \|v\|_{2}(|x|^{d-1}+|y|^{d-1}) \leq \|v\|_{2}$
for
![]() $d\leq 3$
, and v real when
$d\leq 3$
, and v real when
![]() $|x|^2+|y|^2\leq 1$
. Thus
$|x|^2+|y|^2\leq 1$
. Thus
 $$ \begin{align*}\left\|\frac{1}{d}\overline{\mathrm{D}}_Xc_dv\right\|_{\infty}^{\mathbb{C}}=\frac{2^d}{d}\|v\|_{2}=\frac{\sqrt{2}}{d}\|c_d\|_\infty^{\mathbb{C}}\|v\|_{2}.\end{align*} $$
$$ \begin{align*}\left\|\frac{1}{d}\overline{\mathrm{D}}_Xc_dv\right\|_{\infty}^{\mathbb{C}}=\frac{2^d}{d}\|v\|_{2}=\frac{\sqrt{2}}{d}\|c_d\|_\infty^{\mathbb{C}}\|v\|_{2}.\end{align*} $$
This shows that the real version of Kellogg’s theorem is tight for
![]() $c_d$
, but the complex version is not.
$c_d$
, but the complex version is not.
Example 2.17. The reverse situation is true for the polynomial
![]() $X_{0}^d$
. One can see that
$X_{0}^d$
. One can see that
 $$ \begin{align*}\left\|\frac{1}{d}\overline{\mathrm{D}}_X X_{0}^d e_{0}\right\|_\infty^{\mathbb{C}} =\|X_{0}^d\|_\infty^{\mathbb{C}}.\end{align*} $$
$$ \begin{align*}\left\|\frac{1}{d}\overline{\mathrm{D}}_X X_{0}^d e_{0}\right\|_\infty^{\mathbb{C}} =\|X_{0}^d\|_\infty^{\mathbb{C}}.\end{align*} $$
Now it is the complex Kellogg’s theorem that is tight. We note, however, that one might still improve Corollary 2.14. For example, is it possible to substitute
![]() $\Delta $
by
$\Delta $
by
![]() $\Delta ^{\frac {1}{2}}$
in this corollary?
$\Delta ^{\frac {1}{2}}$
in this corollary?
Remark 2.18. Examples 2.16 and 2.17 motivate the search of a randomised Kellogg’s theorem that holds with high probability for random polynomials and has a tighter right-hand side.
Proof of Theorem 2.13.
We only prove the real case. The complex case is proven analogously (see [Reference Kellogg40, Section 8] for the complex version of the results we use in the real case).
By [Reference Kellogg40, Theorem IV], we have that for all i and all
![]() $x\in \mathbb {S}^n$
,
$x\in \mathbb {S}^n$
,
since
![]() $\overline {\mathrm {D}}_xf_iv$
is the directional derivative of f at x in the direction of v. Therefore, for all
$\overline {\mathrm {D}}_xf_iv$
is the directional derivative of f at x in the direction of v. Therefore, for all
![]() $x\in \mathbb {S}^n$
,
$x\in \mathbb {S}^n$
,
Now
![]() $\left \|\Delta ^{-1}\overline {\mathrm {D}}_{X}fv\right \|_{\infty }^{\mathbb {R}} =\max _{x\in \mathbb {S}^n}\|\Delta ^{-1}\overline {\mathrm {D}}_xfv\|_{\infty }$
by definition of
$\left \|\Delta ^{-1}\overline {\mathrm {D}}_{X}fv\right \|_{\infty }^{\mathbb {R}} =\max _{x\in \mathbb {S}^n}\|\Delta ^{-1}\overline {\mathrm {D}}_xfv\|_{\infty }$
by definition of
![]() $\|~\|_{\infty }^{\mathbb {R}}$
, so we are done.
$\|~\|_{\infty }^{\mathbb {R}}$
, so we are done.
Remark 2.19. We note that the application of [Reference Kellogg40, Theorem IV] using the scaling with the diagonal matrix was not used in [Reference Ergür, Paouris and Rojas33, Theorem 2.4] and [Reference Ergür, Paouris and Rojas34]. This can be used to improve by a factor of the degree some of the bounds there.
Proof of Corollary 2.14.
We only prove the real case, the proof for the complex case being essentially the same. Recall that by Euler’s formula for homogeneous functions,
In this way, for
![]() $x\in \mathbb {S}^n$
,
$x\in \mathbb {S}^n$
,
![]() $\lambda \in \mathbb {R}$
and
$\lambda \in \mathbb {R}$
and
![]() $w\in \mathrm {T}_x\mathbb {S}^n=x^{\perp }$
,
$w\in \mathrm {T}_x\mathbb {S}^n=x^{\perp }$
,
When
![]() $\lambda x+w=x$
, this expression yields
$\lambda x+w=x$
, this expression yields
![]() $f(x)$
; and when
$f(x)$
; and when
![]() $\lambda x+w=w$
, it yields
$\lambda x+w=w$
, it yields
![]() $\Delta ^{-1}\mathrm {D}_xfw$
. In this way,
$\Delta ^{-1}\mathrm {D}_xfw$
. In this way,
 $$ \begin{align*}\max_{\lambda x+w\neq 0}\frac{\|\Delta^{-1}\overline{\mathrm{D}}_xf(\lambda x+w)\|_{\infty}}{\sqrt{|\lambda|^2+\|w\|^2}}\geq \max\left\{\|f(x)\|_\infty,\max_{v\in\mathrm{T}_x\mathbb{S}^n\setminus 0}\frac{\|\Delta^{-1}\mathrm{D}_xv\|_{\infty}}{\|v\|}\right\}.\end{align*} $$
$$ \begin{align*}\max_{\lambda x+w\neq 0}\frac{\|\Delta^{-1}\overline{\mathrm{D}}_xf(\lambda x+w)\|_{\infty}}{\sqrt{|\lambda|^2+\|w\|^2}}\geq \max\left\{\|f(x)\|_\infty,\max_{v\in\mathrm{T}_x\mathbb{S}^n\setminus 0}\frac{\|\Delta^{-1}\mathrm{D}_xv\|_{\infty}}{\|v\|}\right\}.\end{align*} $$
The left-hand side is bounded by
![]() $\|f\|_\infty ^{\mathbb {R}}$
by Theorem 2.13, and the right-hand side equals
$\|f\|_\infty ^{\mathbb {R}}$
by Theorem 2.13, and the right-hand side equals
![]() $\max \{\|f(x)\|_{\infty },\|\Delta ^{-1}\mathrm {D}_xf\|_{2,\infty }\}$
. Thus the desired inequality follows.
$\max \{\|f(x)\|_{\infty },\|\Delta ^{-1}\mathrm {D}_xf\|_{2,\infty }\}$
. Thus the desired inequality follows.
Following the notations introduced above, we will write
![]() $\overline {\mathrm {D}}^k_xf$
to denote the kth derivative map of
$\overline {\mathrm {D}}^k_xf$
to denote the kth derivative map of
![]() $f\in \mathcal {H}_{\boldsymbol {d}}[q]$
at
$f\in \mathcal {H}_{\boldsymbol {d}}[q]$
at
![]() $x\in \mathbb {F}^{n+1}$
. This is the k-multilinear map
$x\in \mathbb {F}^{n+1}$
. This is the k-multilinear map
![]() $(\mathbb {F}^{n+1})^k\rightarrow \mathbb {F}^q$
given by the kth derivatives of f at x. Also,
$(\mathbb {F}^{n+1})^k\rightarrow \mathbb {F}^q$
given by the kth derivatives of f at x. Also,
![]() $\overline {\mathrm {D}}^k_Xf(v_1,\ldots ,v_k)$
, where
$\overline {\mathrm {D}}^k_Xf(v_1,\ldots ,v_k)$
, where
![]() $v_1,\ldots ,v_k\in \mathbb {F}^{n+1}$
will denote the corresponding polynomial tuple in
$v_1,\ldots ,v_k\in \mathbb {F}^{n+1}$
will denote the corresponding polynomial tuple in
![]() . For a real k-multilinear map
. For a real k-multilinear map
![]() $A:(\mathbb {R}^n)^k\rightarrow \mathbb {R}^q$
, we define
$A:(\mathbb {R}^n)^k\rightarrow \mathbb {R}^q$
, we define
 $$ \begin{align} \|A\|_{2,\infty}^{\mathbb{R}}:=\sup_{v_1,\ldots,v_k\neq 0}\frac{\|A(v_1,\ldots,v_k)\|_\infty}{\|v_1\|\cdots\|v_k\|}. \end{align} $$
$$ \begin{align} \|A\|_{2,\infty}^{\mathbb{R}}:=\sup_{v_1,\ldots,v_k\neq 0}\frac{\|A(v_1,\ldots,v_k)\|_\infty}{\|v_1\|\cdots\|v_k\|}. \end{align} $$
We define
![]() $\|A\|_{2,\infty }^{\mathbb {C}}$
for a complex k-multilinear map
$\|A\|_{2,\infty }^{\mathbb {C}}$
for a complex k-multilinear map
![]() $A:(\mathbb {C}^n)^k\rightarrow \mathbb {C}^q$
in a similar manner. Note that for
$A:(\mathbb {C}^n)^k\rightarrow \mathbb {C}^q$
in a similar manner. Note that for
![]() $k>2$
, by the following corollary and Example 2.7,
$k>2$
, by the following corollary and Example 2.7,
 $$ \begin{align*}\left\|\frac{1}{k!}\overline{\mathrm{D}}_{0}^kc_k\right\|_{2,\infty}^{\mathbb{C}} =\left\|c_k\right\|_\infty^{\mathbb{C}}=2^{\frac{k}{2}-1}>1 =\left\|c_k\right\|_\infty^{\mathbb{R}} =\left\|\frac{1}{k!}\overline{\mathrm{D}}_{0}^kc_k\right\|_{2,\infty}^{\mathbb{R}}, \end{align*} $$
$$ \begin{align*}\left\|\frac{1}{k!}\overline{\mathrm{D}}_{0}^kc_k\right\|_{2,\infty}^{\mathbb{C}} =\left\|c_k\right\|_\infty^{\mathbb{C}}=2^{\frac{k}{2}-1}>1 =\left\|c_k\right\|_\infty^{\mathbb{R}} =\left\|\frac{1}{k!}\overline{\mathrm{D}}_{0}^kc_k\right\|_{2,\infty}^{\mathbb{R}}, \end{align*} $$
so for real A,
![]() $\|A\|_{2,\infty }^{\mathbb {R}}$
and
$\|A\|_{2,\infty }^{\mathbb {R}}$
and
![]() $\|A\|_{2,\infty }^{\mathbb {C}}$
are not necessarily equal and can differ by a factor exponential in k. The following corollary (which is closely related to [Reference Zhang, Ling and Qi59, Theorem 2.1]) will be useful later.
$\|A\|_{2,\infty }^{\mathbb {C}}$
are not necessarily equal and can differ by a factor exponential in k. The following corollary (which is closely related to [Reference Zhang, Ling and Qi59, Theorem 2.1]) will be useful later.
Corollary 2.20. Let
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {F}}[q]$
and
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {F}}[q]$
and
![]() $z\in \mathbb {S}^n$
(if
$z\in \mathbb {S}^n$
(if
![]() $\mathbb {F}=\mathbb {R}$
) or
$\mathbb {F}=\mathbb {R}$
) or
![]() $z\in \mathbb {P}^n$
(if
$z\in \mathbb {P}^n$
(if
![]() $\mathbb {F}=\mathbb {C}$
). Then for all
$\mathbb {F}=\mathbb {C}$
). Then for all
![]() $k\geq 1$
and
$k\geq 1$
and
![]() $v_1,\ldots ,v_k\in \mathbb {F}^{n+1}$
,
$v_1,\ldots ,v_k\in \mathbb {F}^{n+1}$
,
 $$ \begin{align*} \left\|\frac{1}{k!}\Delta^{-1}\overline{\mathrm{D}}_X^kf(v_1,\ldots,v_k)\right\|_{\infty}\leq \frac{1}{k}\binom{\mathbf{D}-1}{k-1}\|f\|_{\infty}^{\mathbb{F}}\|v_1\|\cdots \|v_k\|. \end{align*} $$
$$ \begin{align*} \left\|\frac{1}{k!}\Delta^{-1}\overline{\mathrm{D}}_X^kf(v_1,\ldots,v_k)\right\|_{\infty}\leq \frac{1}{k}\binom{\mathbf{D}-1}{k-1}\|f\|_{\infty}^{\mathbb{F}}\|v_1\|\cdots \|v_k\|. \end{align*} $$
In particular,
![]() $\left \|\frac {1}{k!}\Delta ^{-1}\overline {\mathrm {D}}_z^kf\right \|_{2,\infty }\leq \frac {1}{k}\binom {\mathbf {D}-1}{k-1}\|f\|_{\infty }^{\mathbb {F}}$
.
$\left \|\frac {1}{k!}\Delta ^{-1}\overline {\mathrm {D}}_z^kf\right \|_{2,\infty }\leq \frac {1}{k}\binom {\mathbf {D}-1}{k-1}\|f\|_{\infty }^{\mathbb {F}}$
.
Remark 2.21. Although the results in this section were proved only for
![]() $\|~\|^{\mathbb {F}}_{\infty }$
, some of them can be generalised to other norms. For example, similar results can be obtained for
$\|~\|^{\mathbb {F}}_{\infty }$
, some of them can be generalised to other norms. For example, similar results can be obtained for
![]() $\|~\|^{\mathbb {R}}_2$
(see [Reference Seeley52]) and certainly for other norms. We defer to future work the application of these extensions to the analysis of numerical algorithms in algebraic geometry. We also note that Corollary 2.14 for
$\|~\|^{\mathbb {R}}_2$
(see [Reference Seeley52]) and certainly for other norms. We defer to future work the application of these extensions to the analysis of numerical algorithms in algebraic geometry. We also note that Corollary 2.14 for
![]() $\mathbb {F}=\mathbb {R}$
can be generalised to smooth real algebraic varieties other than the sphere (see [Reference Bos, Levenberg, Milman and Taylor11]).
$\mathbb {F}=\mathbb {R}$
can be generalised to smooth real algebraic varieties other than the sphere (see [Reference Bos, Levenberg, Milman and Taylor11]).
3 Condition numbers for the
 $L_\infty $
-norm
$L_\infty $
-norm
In this section, we will consider condition numbers that capture ‘how near to being singular’ a system
![]() $f\in \mathcal {H}_{\boldsymbol {d}}[q]$
is at a point
$f\in \mathcal {H}_{\boldsymbol {d}}[q]$
is at a point
![]() $x\in \mathbb {S}^n$
. We will define condition numbers and develop a geometric understanding of them for the
$x\in \mathbb {S}^n$
. We will define condition numbers and develop a geometric understanding of them for the
![]() $L_\infty $
-norms defined in the preceding section.
$L_\infty $
-norms defined in the preceding section.
Recall the local and global versions of the real condition number
![]() $\kappa $
used in [Reference Cucker, Krick, Malajovich and Wschebor25, Reference Cucker, Krick, Malajovich and Wschebor26, Reference Cucker, Krick, Malajovich and Wschebor27, Reference Cucker, Krick and Shub28]. For
$\kappa $
used in [Reference Cucker, Krick, Malajovich and Wschebor25, Reference Cucker, Krick, Malajovich and Wschebor26, Reference Cucker, Krick, Malajovich and Wschebor27, Reference Cucker, Krick and Shub28]. For
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
and
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
and
![]() $x\in \mathbb {S}^n$
, they are defined by
$x\in \mathbb {S}^n$
, they are defined by
 $$ \begin{align} \kappa(f,x):=\frac{\|f\|_W}{\sqrt{\|f(x)\|_2^2+\left\|\mathrm{D}_xf^\dagger\Delta^{1/2}\right\|^{-2}_{2,2}}}~\text{ and }~\kappa(f):=\sup_{y\in\mathbb{S}^n}\kappa(f,y). \end{align} $$
$$ \begin{align} \kappa(f,x):=\frac{\|f\|_W}{\sqrt{\|f(x)\|_2^2+\left\|\mathrm{D}_xf^\dagger\Delta^{1/2}\right\|^{-2}_{2,2}}}~\text{ and }~\kappa(f):=\sup_{y\in\mathbb{S}^n}\kappa(f,y). \end{align} $$
Here, for a surjective linear map A,
![]() $A^\dagger :=A^*(AA^*)^{-1}$
denotes its Moore-Penrose inverse [Reference Bürgisser and Cucker14, Section 1.6]. Also recall the
$A^\dagger :=A^*(AA^*)^{-1}$
denotes its Moore-Penrose inverse [Reference Bürgisser and Cucker14, Section 1.6]. Also recall the
![]() $\mu $
-condition number introduced by Shub and Smale [Reference Shub and Smale53]: for
$\mu $
-condition number introduced by Shub and Smale [Reference Shub and Smale53]: for
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[q]$
and
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[q]$
and
![]() $\zeta \in \mathbb {P}^n$
,
$\zeta \in \mathbb {P}^n$
,
![]() $\mu (f,\zeta )$
is defined by
$\mu (f,\zeta )$
is defined by
Remark 3.1. By convention, we assume that
![]() $\|A^\dagger \|_{2,2}=\infty $
when A is not surjective. We do this because for
$\|A^\dagger \|_{2,2}=\infty $
when A is not surjective. We do this because for
![]() $A\in \mathbb {C}^{q\times n}$
surjective,
$A\in \mathbb {C}^{q\times n}$
surjective,
where
![]() $\sigma _q$
is the qth singular value. As the latter is continuous, this choice guarantees that
$\sigma _q$
is the qth singular value. As the latter is continuous, this choice guarantees that
![]() $A\mapsto \|A^\dagger \|_{2,2}^{-1}$
is continuous.
$A\mapsto \|A^\dagger \|_{2,2}^{-1}$
is continuous.
Following these ideas, we define the real local condition number of
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
at
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
at
![]() $x\in \mathbb {S}^n$
as
$x\in \mathbb {S}^n$
as
 $$ \begin{align} \mathsf{K}(f,x):=\frac{\sqrt{q}\|f\|_\infty^{\mathbb{R}}} {\max\left\{\|f(x)\|,\left\|\mathrm{D}_xf^\dagger\Delta\right\|_{2,2}^{-1}\right\}} \end{align} $$
$$ \begin{align} \mathsf{K}(f,x):=\frac{\sqrt{q}\|f\|_\infty^{\mathbb{R}}} {\max\left\{\|f(x)\|,\left\|\mathrm{D}_xf^\dagger\Delta\right\|_{2,2}^{-1}\right\}} \end{align} $$
and the real global condition number of
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
as
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
as
And we define the complex local condition number of
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[q]$
at
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[q]$
at
![]() $\zeta \in \mathbb {P}^n$
as
$\zeta \in \mathbb {P}^n$
as
and the complex global condition number of
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[q]$
(with
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[q]$
(with
![]() $q\le n$
) as
$q\le n$
) as
We can see that
![]() $\mathsf {K}$
is a variant of
$\mathsf {K}$
is a variant of
![]() $\kappa $
and
$\kappa $
and
![]() $\mathsf {M}$
is a variant of
$\mathsf {M}$
is a variant of
![]() $\mu _{\mathrm {norm}}$
. We note that the main difference lies in the fact that we are substituting all occurrences of
$\mu _{\mathrm {norm}}$
. We note that the main difference lies in the fact that we are substituting all occurrences of
![]() $\|~\|_W$
with occurrences of
$\|~\|_W$
with occurrences of
![]() $\|~\|_\infty $
. The fact that we use a different scaling factor (
$\|~\|_\infty $
. The fact that we use a different scaling factor (
![]() $\Delta ^{1/2}$
instead of
$\Delta ^{1/2}$
instead of
![]() $\Delta $
) or different norms for vectors (
$\Delta $
) or different norms for vectors (
![]() $\|~\|_\infty $
instead of
$\|~\|_\infty $
instead of
![]() $\|~\|_2$
and so on) only affects these quantities up to a
$\|~\|_2$
and so on) only affects these quantities up to a
![]() $\sqrt {2q\mathbf {D}}$
factor. This has little consequence for complexity. We will be more explicit in Proposition 4.27. Note that despite these changes, we still have that the local condition numbers,
$\sqrt {2q\mathbf {D}}$
factor. This has little consequence for complexity. We will be more explicit in Proposition 4.27. Note that despite these changes, we still have that the local condition numbers,
![]() $\mathsf {K}$
and
$\mathsf {K}$
and
![]() $\mathsf {M}$
, become
$\mathsf {M}$
, become
![]() $\infty $
at a singular zero and that they are finite otherwise.
$\infty $
at a singular zero and that they are finite otherwise.
The remainder of this section is devoted to proving the main properties of
![]() $\mathsf {K}$
and
$\mathsf {K}$
and
![]() $\mathsf {M}$
, which are the reason we defined these numbers the way we did. The properties we will show are those needed for a condition-based complexity analyses of the algorithms in Sections 4 and 5 following the lines of the analyses in [Reference Cucker, Krick, Malajovich and Wschebor25, Reference Cucker, Krick and Shub28, Reference Bürgisser, Cucker and Lairez15, Reference Bürgisser, Cucker and Tonelli-Cueto16, Reference Bürgisser, Cucker and Tonelli-Cueto17] (see also [Reference Tonelli-Cueto55]) and [Reference Bürgisser and Cucker14, Chapter 17].
$\mathsf {M}$
, which are the reason we defined these numbers the way we did. The properties we will show are those needed for a condition-based complexity analyses of the algorithms in Sections 4 and 5 following the lines of the analyses in [Reference Cucker, Krick, Malajovich and Wschebor25, Reference Cucker, Krick and Shub28, Reference Bürgisser, Cucker and Lairez15, Reference Bürgisser, Cucker and Tonelli-Cueto16, Reference Bürgisser, Cucker and Tonelli-Cueto17] (see also [Reference Tonelli-Cueto55]) and [Reference Bürgisser and Cucker14, Chapter 17].
3.1 Properties of the real condition number
 $\mathsf {K}$
$\mathsf {K}$
Recall (see, e.g., [Reference Bürgisser and Cucker14, Definition 16.35]) that for
![]() $f\in \mathcal {H}_{\boldsymbol {d}}[q]$
and
$f\in \mathcal {H}_{\boldsymbol {d}}[q]$
and
![]() $x\in \mathbb {S}^n$
, the Smale’s projective gamma is given by
$x\in \mathbb {S}^n$
, the Smale’s projective gamma is given by
 $$ \begin{align*}\gamma(f,x):=\sup_{k\geq2} \left\|\frac{1}{k!}\mathrm{D}_xf^\dagger\overline{\mathrm{D}}_x^kf\right\|^{\frac{1}{k-1}},\end{align*} $$
$$ \begin{align*}\gamma(f,x):=\sup_{k\geq2} \left\|\frac{1}{k!}\mathrm{D}_xf^\dagger\overline{\mathrm{D}}_x^kf\right\|^{\frac{1}{k-1}},\end{align*} $$
where
![]() $\|~\|=\|~\|_{2,2}$
is the operator norm (with respect to Euclidean norms) of a multilinear map.
$\|~\|=\|~\|_{2,2}$
is the operator norm (with respect to Euclidean norms) of a multilinear map.
Theorem 3.2. Let
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
and
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
and
![]() $x\in \mathbb {S}^n$
. The following holds:
$x\in \mathbb {S}^n$
. The following holds:
-
• Regularity inequality: Either
In particular, if $$ \begin{align*}\frac{\|f(x)\|}{\sqrt{q}\|f\|_\infty^{\mathbb{R}}}\geq\frac{1}{\mathsf{K}(f,x)}\text{ or }\sqrt{q}\|f\|_\infty^{\mathbb{R}}\left\|\mathrm{D}_xf^\dagger\Delta\right\|_{2,2}\leq\mathsf{K}(f,x).\end{align*} $$
$$ \begin{align*}\frac{\|f(x)\|}{\sqrt{q}\|f\|_\infty^{\mathbb{R}}}\geq\frac{1}{\mathsf{K}(f,x)}\text{ or }\sqrt{q}\|f\|_\infty^{\mathbb{R}}\left\|\mathrm{D}_xf^\dagger\Delta\right\|_{2,2}\leq\mathsf{K}(f,x).\end{align*} $$
 $\mathsf {K}(f,x)\frac {\|f(x)\|}{\sqrt {q}\|f\|_\infty ^{\mathbb {R}}}<1$
, then
$\mathsf {K}(f,x)\frac {\|f(x)\|}{\sqrt {q}\|f\|_\infty ^{\mathbb {R}}}<1$
, then
 $\mathrm {D}_xf:\mathrm {T}_x\mathbb {S}^n\rightarrow \mathbb {R}^q$
is surjective and its pseudoinverse
$\mathrm {D}_xf:\mathrm {T}_x\mathbb {S}^n\rightarrow \mathbb {R}^q$
is surjective and its pseudoinverse
 $(\mathrm {D}_xf)^{\dagger }$
exists.
$(\mathrm {D}_xf)^{\dagger }$
exists.
-
• 1st Lipschitz property: The maps
are $$ \begin{align*} \begin{array}{rl}\mathcal{H}_{\boldsymbol{d}}^{\mathbb{R}}[q]&\rightarrow [0,\infty)\\ g&\mapsto \dfrac{\|g\|_\infty^{\mathbb{R}}}{\mathsf{K}(g,x)}\end{array}\qquad\qquad\textrm{and}\qquad\qquad\begin{array}{rl}\mathcal{H}_{\boldsymbol{d}}^{\mathbb{R}}[q]&\rightarrow [0,\infty)\\ g&\mapsto \dfrac{\|g\|_\infty^{\mathbb{R}}}{\mathsf{K}(g)}\end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{rl}\mathcal{H}_{\boldsymbol{d}}^{\mathbb{R}}[q]&\rightarrow [0,\infty)\\ g&\mapsto \dfrac{\|g\|_\infty^{\mathbb{R}}}{\mathsf{K}(g,x)}\end{array}\qquad\qquad\textrm{and}\qquad\qquad\begin{array}{rl}\mathcal{H}_{\boldsymbol{d}}^{\mathbb{R}}[q]&\rightarrow [0,\infty)\\ g&\mapsto \dfrac{\|g\|_\infty^{\mathbb{R}}}{\mathsf{K}(g)}\end{array} \end{align*} $$
 $1$
-Lipschitz with respect to the real
$1$
-Lipschitz with respect to the real
 $L_\infty $
-norm. In particular,
$L_\infty $
-norm. In particular,  $$ \begin{align*}\mathsf{K}(f,x)\geq 1~\text{ and }~\mathsf{K}(f)\geq 1.\end{align*} $$
$$ \begin{align*}\mathsf{K}(f,x)\geq 1~\text{ and }~\mathsf{K}(f)\geq 1.\end{align*} $$
-
• 2nd Lipschitz property: The map
is $$ \begin{align*} \mathbb{S}^n&\rightarrow [0,1]\\ y&\mapsto \frac{1}{\mathsf{K}(f,y)} \end{align*} $$
$$ \begin{align*} \mathbb{S}^n&\rightarrow [0,1]\\ y&\mapsto \frac{1}{\mathsf{K}(f,y)} \end{align*} $$
 $\mathbf {D}$
-Lipschitz with respect to the geodesic distance on
$\mathbf {D}$
-Lipschitz with respect to the geodesic distance on
 $\mathbb {S}^n$
.
$\mathbb {S}^n$
.
-
• Higher derivative estimate: If
 $\mathsf {K}(f,x)\frac {|f(x)|}{\|f\|_\infty ^{\mathbb {R}}}<1$
, then
$\mathsf {K}(f,x)\frac {|f(x)|}{\|f\|_\infty ^{\mathbb {R}}}<1$
, then  $$ \begin{align*} \gamma(f,x)\leq \frac{1}{2}(\mathbf{D}-1)\mathsf{K}(f,x). \end{align*} $$
$$ \begin{align*} \gamma(f,x)\leq \frac{1}{2}(\mathbf{D}-1)\mathsf{K}(f,x). \end{align*} $$
We now discuss the role of the above properties.
Regularity inequality. The regularity inequality guarantees that when
![]() $\mathsf {K}(f,x)<\infty $
, either x is far away from the zero set of f or
$\mathsf {K}(f,x)<\infty $
, either x is far away from the zero set of f or
![]() $\mathrm {D}_xf^\dagger $
exists and is well-defined. The latter is important because it allows us to do various geometric arguments that rely on this pseudoinverse being defined or, equivalently, on
$\mathrm {D}_xf^\dagger $
exists and is well-defined. The latter is important because it allows us to do various geometric arguments that rely on this pseudoinverse being defined or, equivalently, on
![]() $\mathrm {D}_x f$
being surjective. In the particular case of
$\mathrm {D}_x f$
being surjective. In the particular case of
![]() $\mathsf {K}$
, we could state it with equalities (see its proof below), but we leave the statement with inequalities as this is the one holding for
$\mathsf {K}$
, we could state it with equalities (see its proof below), but we leave the statement with inequalities as this is the one holding for
![]() $\kappa $
as well and it is enough for our purposes.
$\kappa $
as well and it is enough for our purposes.
1st Lipschitz property. The main use of the 1st Lipschitz inequality is to control the variation of
![]() $\mathsf {K}$
with respect to f. This property implies that
$\mathsf {K}$
with respect to f. This property implies that
 $$ \begin{align} \frac{1-\frac{\left\|f-\tilde{f}\right\|_\infty^{\mathbb{R}}}{\left\|f\right\|_\infty^{\mathbb{R}}}}{1+\mathsf{K}(f,x)\frac{\left\|f-\tilde{f}\right\|_\infty^{\mathbb{R}}}{\left\|f\right\|_\infty^{\mathbb{R}}}}\mathsf{K}(f,x) \leq\mathsf{K}\left(\tilde{f},x\right) \leq \frac{1+\frac{\left\|f-\tilde{f}\right\|_\infty^{\mathbb{R}}}{\left\|f\right\|_\infty^{\mathbb{R}}}}{1-\mathsf{K}(f,x)\frac{\left\|f-\tilde{f}\right\|_\infty^{\mathbb{R}}}{\left\|f\right\|_\infty^{\mathbb{R}}}}\mathsf{K}(f,x) \end{align} $$
$$ \begin{align} \frac{1-\frac{\left\|f-\tilde{f}\right\|_\infty^{\mathbb{R}}}{\left\|f\right\|_\infty^{\mathbb{R}}}}{1+\mathsf{K}(f,x)\frac{\left\|f-\tilde{f}\right\|_\infty^{\mathbb{R}}}{\left\|f\right\|_\infty^{\mathbb{R}}}}\mathsf{K}(f,x) \leq\mathsf{K}\left(\tilde{f},x\right) \leq \frac{1+\frac{\left\|f-\tilde{f}\right\|_\infty^{\mathbb{R}}}{\left\|f\right\|_\infty^{\mathbb{R}}}}{1-\mathsf{K}(f,x)\frac{\left\|f-\tilde{f}\right\|_\infty^{\mathbb{R}}}{\left\|f\right\|_\infty^{\mathbb{R}}}}\mathsf{K}(f,x) \end{align} $$
whenever
![]() $\mathsf {K}(f,x)\frac {\left \|f-\tilde {f}\right \|_\infty ^{\mathbb {R}}}{\left \|f\right \|_\infty ^{\mathbb {R}}}<1$
. This formula shows how the condition number of an approximation of f relates to that of f.
$\mathsf {K}(f,x)\frac {\left \|f-\tilde {f}\right \|_\infty ^{\mathbb {R}}}{\left \|f\right \|_\infty ^{\mathbb {R}}}<1$
. This formula shows how the condition number of an approximation of f relates to that of f.
2nd Lipschitz property. The 2nd Lipschitz property allows us to gauge the variation of
![]() $\mathsf {K}$
with respect to x. In this sense, it is very similar to the first Lipschitz property, and it implies that
$\mathsf {K}$
with respect to x. In this sense, it is very similar to the first Lipschitz property, and it implies that
whenever
![]() $\mathsf {K}(f,x)\mathrm {dist}_{\mathbb {S}}(x,\tilde {x})<1$
. Here
$\mathsf {K}(f,x)\mathrm {dist}_{\mathbb {S}}(x,\tilde {x})<1$
. Here
![]() $\mathrm {dist}_{\mathbb {S}}$
denotes the geodesic distance in
$\mathrm {dist}_{\mathbb {S}}$
denotes the geodesic distance in
![]() $\mathbb {S}^n$
.
$\mathbb {S}^n$
.
Higher derivative estimate. Smale’s projective gamma,
![]() $\gamma (f,\zeta )$
, controls many aspects of the local geometry around a zero
$\gamma (f,\zeta )$
, controls many aspects of the local geometry around a zero
![]() $\zeta $
of the function f, notably, in the case
$\zeta $
of the function f, notably, in the case
![]() $q=n$
, the radius of the basin of attraction at
$q=n$
, the radius of the basin of attraction at
![]() $\zeta $
of Newton’s operator
$\zeta $
of Newton’s operator
![]() $N_f$
associated with f. Recall (see [Reference Bürgisser and Cucker14, Definition 16.34]) that we say
$N_f$
associated with f. Recall (see [Reference Bürgisser and Cucker14, Definition 16.34]) that we say
![]() $x\in \mathbb {S}^n$
is an approximate zero of
$x\in \mathbb {S}^n$
is an approximate zero of
![]() $f\in \mathcal {H}_{\boldsymbol {d}}[n]$
with associated zero
$f\in \mathcal {H}_{\boldsymbol {d}}[n]$
with associated zero
![]() $\zeta \in \mathbb {S}^n$
when for all
$\zeta \in \mathbb {S}^n$
when for all
![]() $k\geq 1$
, the kth iteration
$k\geq 1$
, the kth iteration
![]() $N_f^k$
of
$N_f^k$
of
![]() $N_f$
satisfies
$N_f$
satisfies
 $$ \begin{align*}\mathrm{dist}_{\mathbb{S}}(N_f^k,x)\le \left(\frac12\right)^{2^k-1} \mathrm{dist}_{\mathbb{S}}(x,\zeta). \end{align*} $$
$$ \begin{align*}\mathrm{dist}_{\mathbb{S}}(N_f^k,x)\le \left(\frac12\right)^{2^k-1} \mathrm{dist}_{\mathbb{S}}(x,\zeta). \end{align*} $$
We have the following result (see [Reference Bürgisser and Cucker14, Theorem 16.38 and Table 16.1]).
Theorem 3.3. Let
![]() $f\in \mathcal {H}_{\boldsymbol {d}}[n]$
and
$f\in \mathcal {H}_{\boldsymbol {d}}[n]$
and
![]() $\zeta \in \mathbb {S}^n$
such that
$\zeta \in \mathbb {S}^n$
such that
![]() $f(\zeta )=0$
. Let
$f(\zeta )=0$
. Let
![]() $z\in \mathbb {S}^n$
be such that
$z\in \mathbb {S}^n$
be such that
![]() $\mathrm {dist}_{\mathbb {S}}(z,\zeta )\leq \frac {1}{45}$
and
$\mathrm {dist}_{\mathbb {S}}(z,\zeta )\leq \frac {1}{45}$
and
![]() $\mathrm {dist}_{\mathbb {S}}(z,\zeta )\gamma (f,\zeta )\le 0.17708$
. Then z is an approximate zero of f with associated zero
$\mathrm {dist}_{\mathbb {S}}(z,\zeta )\gamma (f,\zeta )\le 0.17708$
. Then z is an approximate zero of f with associated zero
![]() $\zeta $
.
$\zeta $
.
The computation of
![]() $\gamma (f,x)$
appears to require all the derivatives of f. The higher derivative estimate allows one to estimate
$\gamma (f,x)$
appears to require all the derivatives of f. The higher derivative estimate allows one to estimate
![]() $\gamma (f,x)$
in terms of the first derivative only.
$\gamma (f,x)$
in terms of the first derivative only.
Proof of Theorem 3.2.
Regularity inequality. By definition,
 $$ \begin{align*}\frac{1}{\mathsf{K}(f,x)}=\max\left\{\frac{\|f(x)\|}{\sqrt{q}\|f\|_\infty^{\mathbb{R}}},\frac{1}{\sqrt{q}\|f\|_\infty^{\mathbb{R}}\left\|\mathrm{D}_xf^\dagger\Delta\right\|_{2,2}}\right\}.\end{align*} $$
$$ \begin{align*}\frac{1}{\mathsf{K}(f,x)}=\max\left\{\frac{\|f(x)\|}{\sqrt{q}\|f\|_\infty^{\mathbb{R}}},\frac{1}{\sqrt{q}\|f\|_\infty^{\mathbb{R}}\left\|\mathrm{D}_xf^\dagger\Delta\right\|_{2,2}}\right\}.\end{align*} $$
Hence either
![]() $\frac {1}{\mathsf {K}(f,x)}=\frac {\|f(x)\|}{\sqrt {q}\|f\|_\infty ^{\mathbb {R}}}$
or
$\frac {1}{\mathsf {K}(f,x)}=\frac {\|f(x)\|}{\sqrt {q}\|f\|_\infty ^{\mathbb {R}}}$
or
![]() $\mathsf {K}(f,x)=\sqrt {q}\|f\|_\infty ^{\mathbb {R}}\left \|\mathrm {D}_xf^\dagger \Delta \right \|_{2,2}$
, which finishes the proof.
$\mathsf {K}(f,x)=\sqrt {q}\|f\|_\infty ^{\mathbb {R}}\left \|\mathrm {D}_xf^\dagger \Delta \right \|_{2,2}$
, which finishes the proof.
1st Lipschitz property. We have that
 $$ \begin{align*} \frac{\|g\|_\infty^{\mathbb{R}}}{\mathsf{K}(g,x)} =\max\left\{\frac{\|g(x)\|}{\sqrt{q}}, \frac{\sigma_q\left(\Delta^{-1}\mathrm{D}_xg\right)}{\sqrt{q}}\right\}. \end{align*} $$
$$ \begin{align*} \frac{\|g\|_\infty^{\mathbb{R}}}{\mathsf{K}(g,x)} =\max\left\{\frac{\|g(x)\|}{\sqrt{q}}, \frac{\sigma_q\left(\Delta^{-1}\mathrm{D}_xg\right)}{\sqrt{q}}\right\}. \end{align*} $$
Hence, we only need to show that
![]() $g\mapsto \|g(x)\|/\sqrt {q}$
and
$g\mapsto \|g(x)\|/\sqrt {q}$
and
![]() $g\mapsto \sigma _q\left (\Delta ^{-1}\mathrm {D}_xg\right )/\sqrt {q}$
are
$g\mapsto \sigma _q\left (\Delta ^{-1}\mathrm {D}_xg\right )/\sqrt {q}$
are
![]() $1$
-Lipschitz. Now,
$1$
-Lipschitz. Now,
 $$ \begin{align*} \left|\frac{\|g(x)\|}{\sqrt{q}}-\frac{\left\|\tilde{g}(x)\right\|}{\sqrt{q}}\right|\leq \frac{\left\|\left(g-\tilde{g}\right)(x)\right\|}{\sqrt{q}}\leq \left\|\left(g-\tilde{g}\right)(x)\right\|_{\infty}\leq \left\|g-\tilde{g}\right\|_\infty^{\mathbb{R}}, \end{align*} $$
$$ \begin{align*} \left|\frac{\|g(x)\|}{\sqrt{q}}-\frac{\left\|\tilde{g}(x)\right\|}{\sqrt{q}}\right|\leq \frac{\left\|\left(g-\tilde{g}\right)(x)\right\|}{\sqrt{q}}\leq \left\|\left(g-\tilde{g}\right)(x)\right\|_{\infty}\leq \left\|g-\tilde{g}\right\|_\infty^{\mathbb{R}}, \end{align*} $$
by the reverse triangle inequality,
![]() $\|~\|\leq \sqrt {q}\|~\|_\infty $
and the definition of the real
$\|~\|\leq \sqrt {q}\|~\|_\infty $
and the definition of the real
![]() $L_{\infty }$
-norm; and
$L_{\infty }$
-norm; and
 $$ \begin{align*} \left|\frac{\sigma_q\left(\Delta^{-1}\mathrm{D}_xg\right)}{\sqrt{q}}-\frac{\sigma_q\left(\Delta^{-1}\mathrm{D}_x\tilde{g}\right)}{\sqrt{q}}\right|\leq \frac{\left\|\Delta^{-1}\mathrm{D}_x\left(g-\tilde{g}\right)\right\|_{2,2}}{\sqrt{q}}\leq \left\|\Delta^{-1}\mathrm{D}_x\left(g-\tilde{g}\right)\right\|_{\infty,2}\left\|g-\tilde{g}\right\|_\infty^{\mathbb{R}}, \end{align*} $$
$$ \begin{align*} \left|\frac{\sigma_q\left(\Delta^{-1}\mathrm{D}_xg\right)}{\sqrt{q}}-\frac{\sigma_q\left(\Delta^{-1}\mathrm{D}_x\tilde{g}\right)}{\sqrt{q}}\right|\leq \frac{\left\|\Delta^{-1}\mathrm{D}_x\left(g-\tilde{g}\right)\right\|_{2,2}}{\sqrt{q}}\leq \left\|\Delta^{-1}\mathrm{D}_x\left(g-\tilde{g}\right)\right\|_{\infty,2}\left\|g-\tilde{g}\right\|_\infty^{\mathbb{R}}, \end{align*} $$
because
![]() $\sigma _q$
is
$\sigma _q$
is
![]() $1$
-Lipschitz with respect to
$1$
-Lipschitz with respect to
![]() $\|~\|_{2,2}$
,
$\|~\|_{2,2}$
,
![]() $\|~\|\leq \sqrt {q}\|~\|_\infty $
and Kellogg’s inequality (Theorem 2.13). Thus our claims follow.
$\|~\|\leq \sqrt {q}\|~\|_\infty $
and Kellogg’s inequality (Theorem 2.13). Thus our claims follow.
The claim for
![]() $g\mapsto \|g\|_\infty ^{\mathbb {R}}/\mathsf {K}(g)$
follows from the fact that the minimum of a family of
$g\mapsto \|g\|_\infty ^{\mathbb {R}}/\mathsf {K}(g)$
follows from the fact that the minimum of a family of
![]() $1$
-Lipschitz functions is
$1$
-Lipschitz functions is
![]() $1$
-Lipschitz and from
$1$
-Lipschitz and from
 $$ \begin{align*} \frac{\|g\|_\infty^{\mathbb{R}}}{\mathsf{K}(g)} =\min_{x\in\mathbb{S}^n}\frac{\|g\|_\infty^{\mathbb{R}}}{\mathsf{K}(g,x)}. \end{align*} $$
$$ \begin{align*} \frac{\|g\|_\infty^{\mathbb{R}}}{\mathsf{K}(g)} =\min_{x\in\mathbb{S}^n}\frac{\|g\|_\infty^{\mathbb{R}}}{\mathsf{K}(g,x)}. \end{align*} $$
For the lower bound, just note that
 $$ \begin{align*}\frac{\|f\|_\infty^{\mathbb{R}}}{\mathsf{K}(f,x)}=\left|\frac{\|f\|_\infty^{\mathbb{R}}}{\mathsf{K}(f,x)}-\frac{\|0\|_\infty^{\mathbb{R}}}{\mathsf{K}(0,x)}\right|\leq \|f-0\|_{\infty}^{\mathbb{R}}=\|f\|_\infty^{\mathbb{R}}\end{align*} $$
$$ \begin{align*}\frac{\|f\|_\infty^{\mathbb{R}}}{\mathsf{K}(f,x)}=\left|\frac{\|f\|_\infty^{\mathbb{R}}}{\mathsf{K}(f,x)}-\frac{\|0\|_\infty^{\mathbb{R}}}{\mathsf{K}(0,x)}\right|\leq \|f-0\|_{\infty}^{\mathbb{R}}=\|f\|_\infty^{\mathbb{R}}\end{align*} $$
by the proven Lipschitz property, so
![]() $\mathsf {K}(f,x)\geq 1$
. Similarly with
$\mathsf {K}(f,x)\geq 1$
. Similarly with
![]() $\mathsf {K}(f)$
.
$\mathsf {K}(f)$
.
2nd Lipschitz property. Without loss of generality, assume that
![]() $\|f\|_\infty ^{\mathbb {R}}=1$
after scaling f by an appropriate constant; note that this does not change the value of
$\|f\|_\infty ^{\mathbb {R}}=1$
after scaling f by an appropriate constant; note that this does not change the value of
![]() $\mathsf {K}$
. Let
$\mathsf {K}$
. Let
![]() $y,\tilde {y}\in \mathbb {S}^n$
and
$y,\tilde {y}\in \mathbb {S}^n$
and
![]() $u\in \mathscr {O}(n+1)$
be the planar rotation taking y into
$u\in \mathscr {O}(n+1)$
be the planar rotation taking y into
![]() $\tilde {y}$
. Then
$\tilde {y}$
. Then
 $$ \begin{align*} \left|\frac{1}{\mathsf{K}\left(f,y\right)}-\frac{1}{\mathsf{K}\left(f,\tilde{y}\right)}\right|=\left|\frac{1}{\mathsf{K}\left(f,y\right)}-\frac{1}{\mathsf{K}\left(f^u,y\right)}\right|\leq \|f-f^u\|_\infty^{\mathbb{R}}, \end{align*} $$
$$ \begin{align*} \left|\frac{1}{\mathsf{K}\left(f,y\right)}-\frac{1}{\mathsf{K}\left(f,\tilde{y}\right)}\right|=\left|\frac{1}{\mathsf{K}\left(f,y\right)}-\frac{1}{\mathsf{K}\left(f^u,y\right)}\right|\leq \|f-f^u\|_\infty^{\mathbb{R}}, \end{align*} $$
where
![]() $f^u:=f(uX)$
and where the equality follows from the fact that the
$f^u:=f(uX)$
and where the equality follows from the fact that the
![]() $L_\infty $
-norm is orthogonally invariant along with the inequality from the 1st Lipschitz property.
$L_\infty $
-norm is orthogonally invariant along with the inequality from the 1st Lipschitz property.
Now, arguing as when proving the 1st Lipschitz property, we have that for all
![]() $z\in \mathbb {S}^n$
,
$z\in \mathbb {S}^n$
,
By the choice of u, we have that
![]() $\mathrm {dist}_{\mathbb {S}}(z,uz)\leq \mathrm {dist}_{\mathbb {S}}(y,\tilde {y})$
. Therefore
$\mathrm {dist}_{\mathbb {S}}(z,uz)\leq \mathrm {dist}_{\mathbb {S}}(y,\tilde {y})$
. Therefore
![]() $\|f-f^u\|_\infty ^{\mathbb {R}}\leq \mathbf {D}\,\mathrm {dist}_{\mathbb {S}}(y,\tilde {y})$
, and we are done.
$\|f-f^u\|_\infty ^{\mathbb {R}}\leq \mathbf {D}\,\mathrm {dist}_{\mathbb {S}}(y,\tilde {y})$
, and we are done.
We note that a variational argument showing that both
![]() $y\mapsto \|g(y)\|/\sqrt {q}$
and
$y\mapsto \|g(y)\|/\sqrt {q}$
and
![]() $y\mapsto \sigma _q(\Delta ^{-1}\mathrm {D}_yf))/\sqrt {q}$
are Lipschitz is possible. This argument would be almost identical to the one used for proving the 1st Lipschitz property but varying the point in the sphere instead of the polynomial. We use the above argument since it is simpler and gives a slightly better bound.
$y\mapsto \sigma _q(\Delta ^{-1}\mathrm {D}_yf))/\sqrt {q}$
are Lipschitz is possible. This argument would be almost identical to the one used for proving the 1st Lipschitz property but varying the point in the sphere instead of the polynomial. We use the above argument since it is simpler and gives a slightly better bound.
Higher derivative estimate. Again, without loss of generality, we assume that
![]() $\|f\|_\infty ^{\mathbb {R}}=1$
, since multiplying f by a scalar affects neither the value of
$\|f\|_\infty ^{\mathbb {R}}=1$
, since multiplying f by a scalar affects neither the value of
![]() $\mathsf {K}$
nor Smale’s projective gamma. Then
$\mathsf {K}$
nor Smale’s projective gamma. Then
 $$ \begin{align*} \left\|\frac{1}{k!}\mathrm{D}_xf^\dagger\overline{\mathrm{D}}_x^kf\right\|&\leq \left\|\mathrm{D}_xf^\dagger\Delta\right\|_{2,2}\left\|\frac{\Delta^{-1}}{k!}\overline{\mathrm{D}}_x^kf\right\|_{2,2} &\text{(inequalities for operator norms)}\\ &\leq \sqrt{q}\left\|\mathrm{D}_xf^\dagger\Delta\right\|_{2,2}\left\|\frac{\Delta^{-1}}{k!}\overline{\mathrm{D}}_x^kf\right\|_{2,\infty} &\|~\|/\sqrt{q}\leq \|~\|_\infty\\ &\leq \mathsf{K}(f,x)\left\|\frac{\Delta^{-1}}{k!}\overline{\mathrm{D}}_x^kf\right\|_{2,\infty} &\text{(assumption + regularity inequality)}\\ &\leq \frac{1}{k}\binom{\mathbf{D}-1}{k-1}\mathsf{K}(f,x).&(\text{Corollary}~{2.20}) \end{align*} $$
$$ \begin{align*} \left\|\frac{1}{k!}\mathrm{D}_xf^\dagger\overline{\mathrm{D}}_x^kf\right\|&\leq \left\|\mathrm{D}_xf^\dagger\Delta\right\|_{2,2}\left\|\frac{\Delta^{-1}}{k!}\overline{\mathrm{D}}_x^kf\right\|_{2,2} &\text{(inequalities for operator norms)}\\ &\leq \sqrt{q}\left\|\mathrm{D}_xf^\dagger\Delta\right\|_{2,2}\left\|\frac{\Delta^{-1}}{k!}\overline{\mathrm{D}}_x^kf\right\|_{2,\infty} &\|~\|/\sqrt{q}\leq \|~\|_\infty\\ &\leq \mathsf{K}(f,x)\left\|\frac{\Delta^{-1}}{k!}\overline{\mathrm{D}}_x^kf\right\|_{2,\infty} &\text{(assumption + regularity inequality)}\\ &\leq \frac{1}{k}\binom{\mathbf{D}-1}{k-1}\mathsf{K}(f,x).&(\text{Corollary}~{2.20}) \end{align*} $$
Taking
![]() $(k-1)$
th roots, we have that
$(k-1)$
th roots, we have that
![]() $\mathsf {K}(f,x)^{\frac {1}{k-1}}\leq \mathsf {K}(f,x)$
, since
$\mathsf {K}(f,x)^{\frac {1}{k-1}}\leq \mathsf {K}(f,x)$
, since
![]() $\mathsf {K}(f,x)\geq 1$
by Corollary 2.14, and that
$\mathsf {K}(f,x)\geq 1$
by Corollary 2.14, and that
 $$ \begin{align*} \left(\frac{1}{k}\binom{\mathbf{D}-1}{k-1}\right)^{\frac{1}{k-1}}\leq \frac{\mathbf{D}-1}{2}, \end{align*} $$
$$ \begin{align*} \left(\frac{1}{k}\binom{\mathbf{D}-1}{k-1}\right)^{\frac{1}{k-1}}\leq \frac{\mathbf{D}-1}{2}, \end{align*} $$
using that
![]() $\frac {1}{k}\binom {\mathbf {D}-1}{k-1}\leq (\mathbf {D}-1)^{k-1}/2^{k-1}$
. Putting this together, we obtain the desired bound for Smale’s projective gamma.
$\frac {1}{k}\binom {\mathbf {D}-1}{k-1}\leq (\mathbf {D}-1)^{k-1}/2^{k-1}$
. Putting this together, we obtain the desired bound for Smale’s projective gamma.
The following proposition, which we state here for the sake of completeness, will be proved in Section A.
Proposition 3.4. Let
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
and
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
and
![]() $x\in \mathbb {S}^n$
. Then
$x\in \mathbb {S}^n$
. Then
 $$ \begin{align*} \frac{\|f\|_{\infty}^{\mathbb{R}}}{\mathrm{dist}_{\infty}^{\mathbb{R}}(f,\Sigma_{\boldsymbol{d},x}^{\mathbb{R}}[q])}\leq \mathsf{K}(f,x)\leq2\sqrt{\sum_{i=1}^qd_i^2}\,\frac{\|f\|_{\infty}^{\mathbb{R}}}{\mathrm{dist}_{\infty}^{\mathbb{R}}(f,\Sigma_{\boldsymbol{d},x}^{\mathbb{R}}[q])} \end{align*} $$
$$ \begin{align*} \frac{\|f\|_{\infty}^{\mathbb{R}}}{\mathrm{dist}_{\infty}^{\mathbb{R}}(f,\Sigma_{\boldsymbol{d},x}^{\mathbb{R}}[q])}\leq \mathsf{K}(f,x)\leq2\sqrt{\sum_{i=1}^qd_i^2}\,\frac{\|f\|_{\infty}^{\mathbb{R}}}{\mathrm{dist}_{\infty}^{\mathbb{R}}(f,\Sigma_{\boldsymbol{d},x}^{\mathbb{R}}[q])} \end{align*} $$
and
 $$ \begin{align*} \frac{\|f\|_{\infty}^{\mathbb{R}}}{\mathrm{dist}_{\infty}^{\mathbb{R}}(f,\Sigma_{\boldsymbol{d}}^{\mathbb{R}}[q])}\leq \mathsf{K}(f)\leq2\sqrt{\sum_{i=1}^qd_i^2}\,\frac{\|f\|_{\infty}^{\mathbb{R}}}{\mathrm{dist}_{\infty}^{\mathbb{R}}(f,\Sigma_{\boldsymbol{d}}^{\mathbb{R}}[q])}, \end{align*} $$
$$ \begin{align*} \frac{\|f\|_{\infty}^{\mathbb{R}}}{\mathrm{dist}_{\infty}^{\mathbb{R}}(f,\Sigma_{\boldsymbol{d}}^{\mathbb{R}}[q])}\leq \mathsf{K}(f)\leq2\sqrt{\sum_{i=1}^qd_i^2}\,\frac{\|f\|_{\infty}^{\mathbb{R}}}{\mathrm{dist}_{\infty}^{\mathbb{R}}(f,\Sigma_{\boldsymbol{d}}^{\mathbb{R}}[q])}, \end{align*} $$
where
![]() $\mathrm {dist}_\infty ^{\mathbb {R}}$
is the distance induced by
$\mathrm {dist}_\infty ^{\mathbb {R}}$
is the distance induced by
![]() $\|~\|_\infty ^{\mathbb {R}}$
,
$\|~\|_\infty ^{\mathbb {R}}$
,
3.2 Properties of the complex condition number
 $\mathsf {M}$
$\mathsf {M}$
In the complex case, Theorem 3.2 takes the form of the following result, whose proof is identical, so we omit it. We do not consider a regularity inequality for
![]() $\mathsf {M}$
since over complex numbers one usually considers
$\mathsf {M}$
since over complex numbers one usually considers
![]() $\mathsf {M}(f,\zeta )$
for a zero
$\mathsf {M}(f,\zeta )$
for a zero
![]() $\zeta $
of f (or a point nearby).
$\zeta $
of f (or a point nearby).
Theorem 3.5. Let
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[q]$
and
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[q]$
and
![]() $\zeta \in \mathbb {P}^n$
. The following holds:
$\zeta \in \mathbb {P}^n$
. The following holds:
-
• 1st Lipschitz property: The maps
are $$ \begin{align*} \begin{array}{rl}\mathcal{H}_{\boldsymbol{d}}^{\mathbb{C}}[q]&\rightarrow [0,\infty)\\ g&\mapsto \frac{\|g\|_\infty^{\mathbb{C}}}{\mathsf{M}(g,\zeta)}\end{array}\qquad\qquad\textrm{and}\qquad\qquad\begin{array}{rl}\mathcal{H}_{\boldsymbol{d}}^{\mathbb{C}}[q]&\rightarrow [0,\infty)\\ g&\mapsto \frac{\|g\|_\infty^{\mathbb{C}}}{\mathsf{M}(g)}\end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{rl}\mathcal{H}_{\boldsymbol{d}}^{\mathbb{C}}[q]&\rightarrow [0,\infty)\\ g&\mapsto \frac{\|g\|_\infty^{\mathbb{C}}}{\mathsf{M}(g,\zeta)}\end{array}\qquad\qquad\textrm{and}\qquad\qquad\begin{array}{rl}\mathcal{H}_{\boldsymbol{d}}^{\mathbb{C}}[q]&\rightarrow [0,\infty)\\ g&\mapsto \frac{\|g\|_\infty^{\mathbb{C}}}{\mathsf{M}(g)}\end{array} \end{align*} $$
 $1$
-Lipschitz with respect to the complex
$1$
-Lipschitz with respect to the complex
 $L_\infty $
-norm. In particular,
$L_\infty $
-norm. In particular,  $$ \begin{align*}\mathsf{M}(f,\zeta)\geq 1~\text{ and }~\mathsf{M}(f)\geq 1.\end{align*} $$
$$ \begin{align*}\mathsf{M}(f,\zeta)\geq 1~\text{ and }~\mathsf{M}(f)\geq 1.\end{align*} $$
-
• 2nd Lipschitz property: The map
is $$ \begin{align*} \mathbb{P}^n&\rightarrow [0,1]\\ \eta&\mapsto \frac{1}{\mathsf{M}(f,\eta)} \end{align*} $$
$$ \begin{align*} \mathbb{P}^n&\rightarrow [0,1]\\ \eta&\mapsto \frac{1}{\mathsf{M}(f,\eta)} \end{align*} $$
 $\mathbf {D}$
-Lipschitz with respect to the geodesic distance
$\mathbf {D}$
-Lipschitz with respect to the geodesic distance
 $\mathrm {dist}_{\mathbb {P}}$
on
$\mathrm {dist}_{\mathbb {P}}$
on
 $\mathbb {P}^n$
.
$\mathbb {P}^n$
.
-
• Higher derivative estimate: We have
 $$ \begin{align*} \gamma(f,\zeta)\leq \frac{1}{2}(\mathbf{D}-1)\mathsf{M}(f,\zeta). \end{align*} $$
$$ \begin{align*} \gamma(f,\zeta)\leq \frac{1}{2}(\mathbf{D}-1)\mathsf{M}(f,\zeta). \end{align*} $$
We finish with the following proposition, which combines the 1st and 2nd Lipschitz properties of
![]() $\mathsf {M}$
, as it will play a fundamental role in our analysis of linear homotopy in Section 5. We note that this proposition is to
$\mathsf {M}$
, as it will play a fundamental role in our analysis of linear homotopy in Section 5. We note that this proposition is to
![]() $\mathsf {M}$
what [Reference Bürgisser and Cucker14, Proposition 16.55] is to
$\mathsf {M}$
what [Reference Bürgisser and Cucker14, Proposition 16.55] is to
![]() $\mu _{\mathrm {norm}}$
.
$\mu _{\mathrm {norm}}$
.
Proposition 3.6. Let
![]() $f,\tilde {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[q]$
,
$f,\tilde {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[q]$
,
![]() $\zeta ,\tilde {\zeta }\in \mathbb {P}^n$
and
$\zeta ,\tilde {\zeta }\in \mathbb {P}^n$
and
![]() $\varepsilon \in (0,1)$
. If
$\varepsilon \in (0,1)$
. If
 $$ \begin{align*} \mathsf{M}(f,\zeta)\max\left\{\frac{2\|\tilde{f}-f\|_\infty^{\mathbb{R}}}{\|f\|_{\infty}^{\mathbb{C}}},\mathbf{D}\,\mathrm{dist}_{\mathbb{P}}(\zeta,\tilde{\zeta})\right\}\leq\frac{\varepsilon}{4}, \end{align*} $$
$$ \begin{align*} \mathsf{M}(f,\zeta)\max\left\{\frac{2\|\tilde{f}-f\|_\infty^{\mathbb{R}}}{\|f\|_{\infty}^{\mathbb{C}}},\mathbf{D}\,\mathrm{dist}_{\mathbb{P}}(\zeta,\tilde{\zeta})\right\}\leq\frac{\varepsilon}{4}, \end{align*} $$
then
Proof. Note that
 $$ \begin{align*} \left|\frac{1}{\mathsf{M}(f,\zeta)}- \frac{1}{\mathsf{M}\left(\tilde{f},\tilde{\zeta}\right)}\right| \leq \left|\frac{1}{\mathsf{M}(f,\zeta)} -\frac{1}{\mathsf{M}\left(\tilde{f},\zeta\right)}\right| +\left|\frac{1}{\mathsf{M}\left(\tilde{f},\zeta\right)} -\frac{1}{\mathsf{M}\left(\tilde{f},\tilde{\zeta}\right)}\right|. \end{align*} $$
$$ \begin{align*} \left|\frac{1}{\mathsf{M}(f,\zeta)}- \frac{1}{\mathsf{M}\left(\tilde{f},\tilde{\zeta}\right)}\right| \leq \left|\frac{1}{\mathsf{M}(f,\zeta)} -\frac{1}{\mathsf{M}\left(\tilde{f},\zeta\right)}\right| +\left|\frac{1}{\mathsf{M}\left(\tilde{f},\zeta\right)} -\frac{1}{\mathsf{M}\left(\tilde{f},\tilde{\zeta}\right)}\right|. \end{align*} $$
For the first term in the sum, we have
 $$ \begin{align*}\left|\frac{1}{\mathsf{M}\left(f,\zeta\right)} -\frac{1}{\mathsf{M}\left(\tilde{f},\zeta\right)}\right| =\left|\frac{1}{\mathsf{M}\left(\frac{f}{\|f\|_\infty^{\mathbb{C}}},\zeta\right)} -\frac{1}{\mathsf{M}\left(\frac{\tilde{f}} {\|\tilde{f}\|_\infty^{\mathbb{C}}},\zeta\right)}\right| \leq \left\|\frac{f}{\|f\|_\infty^{\mathbb{C}}} -\frac{\tilde{f}}{\|\tilde{f}\|_\infty^{\mathbb{C}}}\right\|_\infty^{\mathbb{C}} \end{align*} $$
$$ \begin{align*}\left|\frac{1}{\mathsf{M}\left(f,\zeta\right)} -\frac{1}{\mathsf{M}\left(\tilde{f},\zeta\right)}\right| =\left|\frac{1}{\mathsf{M}\left(\frac{f}{\|f\|_\infty^{\mathbb{C}}},\zeta\right)} -\frac{1}{\mathsf{M}\left(\frac{\tilde{f}} {\|\tilde{f}\|_\infty^{\mathbb{C}}},\zeta\right)}\right| \leq \left\|\frac{f}{\|f\|_\infty^{\mathbb{C}}} -\frac{\tilde{f}}{\|\tilde{f}\|_\infty^{\mathbb{C}}}\right\|_\infty^{\mathbb{C}} \end{align*} $$
by the 1st Lipschitz property of
![]() $\mathsf {M}$
(Theorem 3.5). Now,
$\mathsf {M}$
(Theorem 3.5). Now,
 $$ \begin{align*} \left\|\frac{f}{\|f\|_\infty^{\mathbb{C}}}-\frac{\tilde{f}}{\|\tilde{f}\|_\infty^{\mathbb{C}}}\right\|_\infty^{\mathbb{C}}\leq \left\|\frac{f}{\|f\|_\infty^{\mathbb{C}}}-\frac{\tilde{f}}{\|f\|_\infty^{\mathbb{C}}}\right\|_\infty^{\mathbb{C}}+\left\|\frac{\tilde{f}}{\|f\|_\infty^{\mathbb{C}}}-\frac{\tilde{f}}{\|\tilde{f}\|_\infty^{\mathbb{C}}}\right\|_\infty^{\mathbb{C}}\leq \frac{2\|\tilde{f}-f\|_\infty^{\mathbb{C}}}{\|f\|_\infty^{\mathbb{C}}}. \end{align*} $$
$$ \begin{align*} \left\|\frac{f}{\|f\|_\infty^{\mathbb{C}}}-\frac{\tilde{f}}{\|\tilde{f}\|_\infty^{\mathbb{C}}}\right\|_\infty^{\mathbb{C}}\leq \left\|\frac{f}{\|f\|_\infty^{\mathbb{C}}}-\frac{\tilde{f}}{\|f\|_\infty^{\mathbb{C}}}\right\|_\infty^{\mathbb{C}}+\left\|\frac{\tilde{f}}{\|f\|_\infty^{\mathbb{C}}}-\frac{\tilde{f}}{\|\tilde{f}\|_\infty^{\mathbb{C}}}\right\|_\infty^{\mathbb{C}}\leq \frac{2\|\tilde{f}-f\|_\infty^{\mathbb{C}}}{\|f\|_\infty^{\mathbb{C}}}. \end{align*} $$
For the second term, we have
 $$ \begin{align*} \left|\frac{1}{\mathsf{M}\left(\tilde{f},\zeta\right)}\right| +\left|\frac{1}{\mathsf{M}\left(\tilde{f},\zeta\right)} -\frac{1}{\mathsf{M}\left(\tilde{f},\tilde{\zeta}\right)}\right| \leq \mathbf{D}\,\mathrm{dist}_{\mathbb{P}}(\zeta,\tilde{\zeta}) \end{align*} $$
$$ \begin{align*} \left|\frac{1}{\mathsf{M}\left(\tilde{f},\zeta\right)}\right| +\left|\frac{1}{\mathsf{M}\left(\tilde{f},\zeta\right)} -\frac{1}{\mathsf{M}\left(\tilde{f},\tilde{\zeta}\right)}\right| \leq \mathbf{D}\,\mathrm{dist}_{\mathbb{P}}(\zeta,\tilde{\zeta}) \end{align*} $$
by the 2nd Lipschitz property of
![]() $\mathsf {M}$
(Theorem 3.5).
$\mathsf {M}$
(Theorem 3.5).
Hence, we have
 $$ \begin{align*} \left|\frac{1}{\mathsf{M}(f,\zeta)} -\frac{1}{\mathsf{M}\left(\tilde{f},\tilde{\zeta}\right)}\right| \leq \frac{2\|\tilde{f}-f\|_\infty^{\mathbb{C}}}{\|f\|_\infty^{\mathbb{C}}}+ \mathbf{D}\,\mathrm{dist}_{\mathbb{P}}(\zeta,\tilde{\zeta}). \end{align*} $$
$$ \begin{align*} \left|\frac{1}{\mathsf{M}(f,\zeta)} -\frac{1}{\mathsf{M}\left(\tilde{f},\tilde{\zeta}\right)}\right| \leq \frac{2\|\tilde{f}-f\|_\infty^{\mathbb{C}}}{\|f\|_\infty^{\mathbb{C}}}+ \mathbf{D}\,\mathrm{dist}_{\mathbb{P}}(\zeta,\tilde{\zeta}). \end{align*} $$
By assumption, after multiplying by
![]() $\mathsf {M}(f,\zeta )$
, we have
$\mathsf {M}(f,\zeta )$
, we have
 $$ \begin{align*} \left|1-\frac{\mathsf{M}(f,\zeta)}{\mathsf{M}\left(\tilde{f},\tilde{\zeta}\right)}\right|\leq \frac{\varepsilon}{2} \end{align*} $$
$$ \begin{align*} \left|1-\frac{\mathsf{M}(f,\zeta)}{\mathsf{M}\left(\tilde{f},\tilde{\zeta}\right)}\right|\leq \frac{\varepsilon}{2} \end{align*} $$
so, from
 $$ \begin{align*} 1-\frac{\mathsf{M}(f,\zeta)}{\mathsf{M}\left(\tilde{f},\tilde{\zeta}\right)}\leq \frac{\varepsilon}{2}~\text{ and }~\frac{\mathsf{M}(f,\zeta)}{\mathsf{M}\left(\tilde{f},\tilde{\zeta}\right)}-1\leq \frac{\varepsilon}{2}, \end{align*} $$
$$ \begin{align*} 1-\frac{\mathsf{M}(f,\zeta)}{\mathsf{M}\left(\tilde{f},\tilde{\zeta}\right)}\leq \frac{\varepsilon}{2}~\text{ and }~\frac{\mathsf{M}(f,\zeta)}{\mathsf{M}\left(\tilde{f},\tilde{\zeta}\right)}-1\leq \frac{\varepsilon}{2}, \end{align*} $$
we get
Since
![]() $\varepsilon <1$
, the desired inequalities follow.
$\varepsilon <1$
, the desired inequalities follow.
4 Numerical algorithms in real algebraic geometry
There is a growing literature on numerical algorithms that addresses basic computational tasks in real algebraic geometry, such as counting real zeros [Reference Cucker, Krick, Malajovich and Wschebor25, Reference Cucker, Krick, Malajovich and Wschebor26, Reference Cucker, Krick, Malajovich and Wschebor27], computing homology of algebraic [Reference Cucker, Krick and Shub28] and semialgebraic sets [Reference Bürgisser, Cucker and Lairez15, Reference Bürgisser, Cucker and Tonelli-Cueto16, Reference Bürgisser, Cucker and Tonelli-Cueto17], and meshing real curves and surfaces [Reference Plantinga and Vegter49, Reference Cucker, Ergür and Tonelli-Cueto23]. These works rely on condition numbers to control precision and estimate computational complexity.
In this section, we show how the complexity estimates in these works are improved by using the real
![]() $L_\infty $
-norm in the algorithm’s design. These improvements rely on three observations:
$L_\infty $
-norm in the algorithm’s design. These improvements rely on three observations:
-
1. The only properties of the real condition number
 $\kappa $
that are used in the complexity analyses are those stated in Theorem 3.2: the regularity inequality, the 1st and 2nd Lipschitz properties and the higher derivative estimate. As these properties hold as well for
$\kappa $
that are used in the complexity analyses are those stated in Theorem 3.2: the regularity inequality, the 1st and 2nd Lipschitz properties and the higher derivative estimate. As these properties hold as well for
 $\mathsf {K}$
, an almost identical condition-based cost analysis can be derived when we pass from the Weyl norm to the real
$\mathsf {K}$
, an almost identical condition-based cost analysis can be derived when we pass from the Weyl norm to the real
 $L_\infty $
-norm and from
$L_\infty $
-norm and from
 $\kappa $
to
$\kappa $
to
 $\mathsf {K}$
. We showcase this in Section 4.1 and Section 4.2.
$\mathsf {K}$
. We showcase this in Section 4.1 and Section 4.2. -
2. When we consider random input models, the gains in the complexity estimates become more evident. In Section 4.3, we show that the ratio of the new
 $\mathsf {K}$
to
$\mathsf {K}$
to
 $\kappa $
is typically of the order of
$\kappa $
is typically of the order of
 $\sqrt {n}/\sqrt {N}$
for a random polynomial system. Since
$\sqrt {n}/\sqrt {N}$
for a random polynomial system. Since
 $N \sim n^d$
for
$N \sim n^d$
for
 $n>d$
and
$n>d$
and
 $N \sim d^n$
for
$N \sim d^n$
for
 $d>n$
, this yields a significant reduction in the complexity estimates.
$d>n$
, this yields a significant reduction in the complexity estimates. -
3. Computing the Weyl norm is cheaper than computing the real
 $L_\infty $
-norm, but this does not affect the overall complexity: We only compute the
$L_\infty $
-norm, but this does not affect the overall complexity: We only compute the
 $L_\infty $
-norm once, and the cost of this computation is dominated by that of the remaining steps.
$L_\infty $
-norm once, and the cost of this computation is dominated by that of the remaining steps.
In what follows, we will focus on algorithms dealing with real algebraic sets. The algorithms we have in mind are the ones in [Reference Cucker, Krick, Malajovich and Wschebor25, Reference Cucker, Krick, Malajovich and Wschebor26, Reference Cucker, Krick, Malajovich and Wschebor27, Reference Cucker, Krick and Shub28] and the Plantinga-Vegter algorithm [Reference Plantinga and Vegter49] as described and analysed in [Reference Cucker, Ergür and Tonelli-Cueto24] (compare to [Reference Cucker, Ergür and Tonelli-Cueto23]). Our condition number
![]() $\mathsf {K}$
as defined in the preceding section will improve the overall computational complexity of these algorithms. Similar results can be obtained for the algorithms dealing with semialgebraic sets in [Reference Bürgisser, Cucker and Lairez15, Reference Bürgisser, Cucker and Tonelli-Cueto16, Reference Bürgisser, Cucker and Tonelli-Cueto17] (compare to [Reference Tonelli-Cueto55]) using natural extensions
$\mathsf {K}$
as defined in the preceding section will improve the overall computational complexity of these algorithms. Similar results can be obtained for the algorithms dealing with semialgebraic sets in [Reference Bürgisser, Cucker and Lairez15, Reference Bürgisser, Cucker and Tonelli-Cueto16, Reference Bürgisser, Cucker and Tonelli-Cueto17] (compare to [Reference Tonelli-Cueto55]) using natural extensions
![]() $\overline {\mathsf {K}}$
and
$\overline {\mathsf {K}}$
and
![]() $\mathsf {K}_*$
of the condition numbers
$\mathsf {K}_*$
of the condition numbers
![]() $\overline {\kappa }$
and
$\overline {\kappa }$
and
![]() $\kappa _*$
used in these papers.
$\kappa _*$
used in these papers.
4.1 A grid-based algorithm and its condition-based complexity
A grid-based algorithm is a subdivision-based method that constructs a grid to discretise the original problem and solves the latter by working on the grid points only (selecting and finding proximity relations between its points). The algorithms in [Reference Cucker, Krick, Malajovich and Wschebor25, Reference Cucker, Krick, Malajovich and Wschebor26, Reference Cucker, Krick, Malajovich and Wschebor27], [Reference Cucker, Krick and Shub28] and [Reference Bürgisser, Cucker and Lairez15, Reference Bürgisser, Cucker and Tonelli-Cueto16, Reference Bürgisser, Cucker and Tonelli-Cueto17] (compare to [Reference Tonelli-Cueto55]) are grid-based. Their basic structure is (simplifying to the extreme) the following:
-
1. Estimate the condition number of the problem (with a sequence of grids of increasing fineness).
-
2. Create an extra grid (if necessary) whose mesh is determined by the condition number.
-
3. Select points in the grid, and use them to obtain a solution to the problem.
In general, grid-based algorithms have complexity
![]() $\Omega (\mathbf {D}^n)$
. This fact allows us to estimate the norm
$\Omega (\mathbf {D}^n)$
. This fact allows us to estimate the norm
![]() $\|f\|_\infty ^{\mathbb {R}}$
of the data f without affecting the overall complexity of the algorithms. Moreover, the fact that
$\|f\|_\infty ^{\mathbb {R}}$
of the data f without affecting the overall complexity of the algorithms. Moreover, the fact that
![]() $\mathsf {K}$
is smaller than
$\mathsf {K}$
is smaller than
![]() $\kappa $
results in a cost reduction.
$\kappa $
results in a cost reduction.
In this subsection, we focus on an algorithm for the computation of the Betti numbers of a spherical algebraic set. This covers the case of counting zeros of a square polynomial system treated in [Reference Cucker, Krick, Malajovich and Wschebor25, Reference Cucker, Krick, Malajovich and Wschebor26, Reference Cucker, Krick, Malajovich and Wschebor27] and the computation of the Betti numbers of a projective real variety [Reference Cucker, Krick and Shub28]. For simplicity of exposition, we omit some computational aspects: 1) our presentation of the algorithms follows the construction-selection paradigm of [Reference Bürgisser, Cucker and Lairez15, Reference Bürgisser, Cucker and Tonelli-Cueto16, Reference Bürgisser, Cucker and Tonelli-Cueto17] instead of the inclusion-exclusion paradigm of [Reference Cucker, Krick, Malajovich and Wschebor25, Reference Cucker, Krick, Malajovich and Wschebor26, Reference Cucker, Krick, Malajovich and Wschebor27, Reference Cucker, Krick and Shub28]. This makes the exposition of the algorithms easier without compromising their computational complexity. 2) We focus on Betti numbers to avoid describing the more involved computation of torsion coefficients in the homology groups. 3) We deal with neither parallelisation nor finite precision. The interested reader can find details about these in the cited references.
The backbone of existing grid-based algorithms in numerical real algebraic geometry [Reference Cucker, Krick, Malajovich and Wschebor25, Reference Cucker, Krick, Malajovich and Wschebor26, Reference Cucker, Krick, Malajovich and Wschebor27, Reference Cucker, Krick and Shub28, Reference Bürgisser, Cucker and Lairez15, Reference Bürgisser, Cucker and Tonelli-Cueto16, Reference Bürgisser, Cucker and Tonelli-Cueto17] is an effective construction of spherical nets. The basic construction was done originally in [Reference Cucker, Krick, Malajovich and Wschebor25] and is based on projecting the uniform grid in the boundary of a unit cube onto the unit sphere.
Recall that a (spherical)
![]() $\delta $
-net is a finite subset
$\delta $
-net is a finite subset
![]() $\mathcal {G}\subset \mathbb {S}^n$
such that for all
$\mathcal {G}\subset \mathbb {S}^n$
such that for all
![]() $x\in \mathbb {S}^n$
,
$x\in \mathbb {S}^n$
,
![]() $\mathrm {dist}_{\mathbb {S}}(x,\mathcal {G})< \delta $
. We will omit the term ‘spherical’ as all nets we consider are so.
$\mathrm {dist}_{\mathbb {S}}(x,\mathcal {G})< \delta $
. We will omit the term ‘spherical’ as all nets we consider are so.
Proposition 4.1. There is an algorithm GRID that on input
![]() $(n,k)\in \mathbb {N}\times \mathbb {N}$
, outputs a
$(n,k)\in \mathbb {N}\times \mathbb {N}$
, outputs a
![]() $2^{-k}$
-net
$2^{-k}$
-net
![]() $\mathcal {G}_k\subset \mathbb {S}^n$
with
$\mathcal {G}_k\subset \mathbb {S}^n$
with
The cost of this algorithm is
![]() $\mathcal {O}\left (2^{n\log n+nk}\right )$
.
$\mathcal {O}\left (2^{n\log n+nk}\right )$
.
Remark 4.2. The grid construction in Proposition 4.1, which occurs in [Reference Cucker, Krick, Malajovich and Wschebor25, Reference Cucker, Krick, Malajovich and Wschebor26, Reference Cucker, Krick, Malajovich and Wschebor27, Reference Cucker, Krick and Shub28, Reference Bürgisser, Cucker and Lairez15, Reference Bürgisser, Cucker and Tonelli-Cueto16, Reference Bürgisser, Cucker and Tonelli-Cueto17], is not optimal. This is due to the
![]() $2^{n\log n}$
factor in the estimates, which can be decreased to
$2^{n\log n}$
factor in the estimates, which can be decreased to
![]() $2^{\mathcal {O}(n)}$
. An algorithm doing this – that is, constructing a spherical
$2^{\mathcal {O}(n)}$
. An algorithm doing this – that is, constructing a spherical
![]() $2^{-k}$
-net of size
$2^{-k}$
-net of size
![]() $2^{\mathcal {O}(n)}2^{k(n+1)}$
in
$2^{\mathcal {O}(n)}2^{k(n+1)}$
in
![]() $2^{\mathcal {O}(n)}2^{k(n+1)}$
-time – is given in [Reference Alon, Lee, Shraibman and Vempala2, Theorem 1.9(1)]. We use the suboptimal result of Proposition 4.1 to focus on the effect of just changing the norm when comparing the old and new versions of the algorithms. But we observe here that by using the nets in [Reference Alon, Lee, Shraibman and Vempala2], one can remove the
$2^{\mathcal {O}(n)}2^{k(n+1)}$
-time – is given in [Reference Alon, Lee, Shraibman and Vempala2, Theorem 1.9(1)]. We use the suboptimal result of Proposition 4.1 to focus on the effect of just changing the norm when comparing the old and new versions of the algorithms. But we observe here that by using the nets in [Reference Alon, Lee, Shraibman and Vempala2], one can remove the
![]() $\log (n)$
factors in the exponents.
$\log (n)$
factors in the exponents.
4.1.1 Computation of
 $\Vert~\Vert_\infty ^{\mathbb {R}}$
$\Vert~\Vert_\infty ^{\mathbb {R}}$
The following is an easy consequence of Kellogg’s theorem.
Proposition 4.3. Let
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
and
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
and
![]() $\mathcal {G}\subset \mathbb {S}^n$
be a
$\mathcal {G}\subset \mathbb {S}^n$
be a
![]() $\delta $
-net. If
$\delta $
-net. If
![]() $\mathbf {D} \delta <\sqrt {2}$
, then
$\mathbf {D} \delta <\sqrt {2}$
, then
 $$ \begin{align*} \max_{x\in\mathcal{G}}\|f(x)\|_\infty\leq \|f\|_\infty^{\mathbb{R}}\leq \frac{1}{1-\frac{\mathbf{D}^2}{2}\delta^2} \max_{x\in\mathcal{G}}\|f(x)\|_\infty. \end{align*} $$
$$ \begin{align*} \max_{x\in\mathcal{G}}\|f(x)\|_\infty\leq \|f\|_\infty^{\mathbb{R}}\leq \frac{1}{1-\frac{\mathbf{D}^2}{2}\delta^2} \max_{x\in\mathcal{G}}\|f(x)\|_\infty. \end{align*} $$
Proof. We only need to show the right-hand inequality, the other being trivial. Without loss of generality, assume that
![]() $q=1$
: that is, f is a homogeneous polynomial of degree
$q=1$
: that is, f is a homogeneous polynomial of degree
![]() $\mathbf {D}$
.
$\mathbf {D}$
.
Let
![]() $x_*$
be the maximum of
$x_*$
be the maximum of
![]() $|f|$
on
$|f|$
on
![]() $\mathbb {S}^n$
,
$\mathbb {S}^n$
,
![]() $x\in \mathcal {G}$
such that
$x\in \mathcal {G}$
such that
![]() $\mathrm {dist}_{\mathbb {S}}(x_\ast ,x)\leq \delta $
and
$\mathrm {dist}_{\mathbb {S}}(x_\ast ,x)\leq \delta $
and
![]() $[0,1]\ni t\mapsto x_t$
the geodesic on
$[0,1]\ni t\mapsto x_t$
the geodesic on
![]() $\mathbb {S}^n$
going from
$\mathbb {S}^n$
going from
![]() $x_*$
to x with constant speed. Then for the function
$x_*$
to x with constant speed. Then for the function
![]() $t\mapsto M(t):=f(x_t)$
, we have that
$t\mapsto M(t):=f(x_t)$
, we have that
![]() $|M(1)|\leq |M(0)|+| M'(0)|+\max _{s\in [0,1]}\frac {M"(s)}{2}$
by Taylor’s theorem. Furthermore,
$|M(1)|\leq |M(0)|+| M'(0)|+\max _{s\in [0,1]}\frac {M"(s)}{2}$
by Taylor’s theorem. Furthermore,
![]() $|M(0)|=|f(x_*)|=\|f\|_\infty ^{\mathbb {R}}$
,
$|M(0)|=|f(x_*)|=\|f\|_\infty ^{\mathbb {R}}$
,
![]() $|M(1)|=|f(x)|$
and
$|M(1)|=|f(x)|$
and
![]() $M'(0)=0$
. The latter is because
$M'(0)=0$
. The latter is because
![]() $x_*$
is an extremal point of f and so of M. Now
$x_*$
is an extremal point of f and so of M. Now
since
![]() $\ddot x_t=-\mathrm {dist}_{\mathbb {S}}(x_\ast ,x)^2x_t$
, as
$\ddot x_t=-\mathrm {dist}_{\mathbb {S}}(x_\ast ,x)^2x_t$
, as
![]() $x_t$
is a geodesic on
$x_t$
is a geodesic on
![]() $\mathbb {S}^n$
of constant speed
$\mathbb {S}^n$
of constant speed
![]() $\mathrm {dist}_{\mathbb {S}}(x_\ast ,x)$
and
$\mathrm {dist}_{\mathbb {S}}(x_\ast ,x)$
and
![]() $\overline {\mathrm {D}}_{x_t}f(x_t)=\mathbf {D} f(x_t)$
by Euler’s formula in equation (2.4). Then by Corollary 2.20,
$\overline {\mathrm {D}}_{x_t}f(x_t)=\mathbf {D} f(x_t)$
by Euler’s formula in equation (2.4). Then by Corollary 2.20,
 $$ \begin{align*} \max_{s\in [0,1]}\frac{|M"(s)|}{2}\leq \binom{\mathbf{D}}{2}\|f\|_\infty^{\mathbb{R}}+\frac{\mathbf{D}}{2}\|f\|_\infty^{\mathbb{R}} =\frac{\mathbf{D}^2}{2}\|f\|_\infty^{\mathbb{R}}. \end{align*} $$
$$ \begin{align*} \max_{s\in [0,1]}\frac{|M"(s)|}{2}\leq \binom{\mathbf{D}}{2}\|f\|_\infty^{\mathbb{R}}+\frac{\mathbf{D}}{2}\|f\|_\infty^{\mathbb{R}} =\frac{\mathbf{D}^2}{2}\|f\|_\infty^{\mathbb{R}}. \end{align*} $$
Thus
![]() $\|f\|_\infty ^{\mathbb {R}}\leq |f(x)|+\frac {\mathbf {D}^2}{2}\|f\|_\infty ^{\mathbb {R}}\delta ^2$
, and the desired inequality follows.
$\|f\|_\infty ^{\mathbb {R}}\leq |f(x)|+\frac {\mathbf {D}^2}{2}\|f\|_\infty ^{\mathbb {R}}\delta ^2$
, and the desired inequality follows.
Remark 4.4. Proposition 4.3 is a slight improvement of [Reference Ergür, Paouris and Rojas33, Lemma 2.5].
Proposition 4.3 suggests the following algorithm.

Proposition 4.5. Algorithm
![]() is correct. On input
is correct. On input
![]() $(f,k)\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]\times \mathbb {N}$
, its cost is bounded by
$(f,k)\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]\times \mathbb {N}$
, its cost is bounded by
Proof. This is a direct consequence of Propositions 4.1 and 4.3 and the fact that f can be evaluated at
![]() $x\in \mathbb {S}^n$
with
$x\in \mathbb {S}^n$
with
![]() $\mathcal {O}(N)$
arithmetic operations (see [Reference Bürgisser and Cucker14, Lemma 16.31]).
$\mathcal {O}(N)$
arithmetic operations (see [Reference Bürgisser and Cucker14, Lemma 16.31]).
Remark 4.6. The ideas here can also be applied to compute
![]() $\|f\|_\infty ^{\mathbb {C}}$
.
$\|f\|_\infty ^{\mathbb {C}}$
.
4.1.2 Estimation of
 $\mathsf {K}$
$\mathsf {K}$
In many grid-based algorithms, the estimation of condition numbers is done implicitly along the way; this does not affect the overall computational cost, and it makes for an easier understanding of these algorithms. The next proposition is the core of the estimation of
![]() $\mathsf {K}$
. Note that the mesh of the grid needed to estimate
$\mathsf {K}$
. Note that the mesh of the grid needed to estimate
![]() $\mathsf {K}$
depends on
$\mathsf {K}$
depends on
![]() $\mathsf {K}$
itself.
$\mathsf {K}$
itself.
Proposition 4.7. Let
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
and
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
and
![]() $\mathcal {G}\subset \mathbb {S}^n$
be a
$\mathcal {G}\subset \mathbb {S}^n$
be a
![]() $\delta $
-net. If
$\delta $
-net. If
then
Proof. We only have to prove the right-hand side inequality since the other one is obvious. Let
![]() $x_\ast \in \mathbb {S}^n$
such that
$x_\ast \in \mathbb {S}^n$
such that
![]() $\mathsf {K}(f)=\mathsf {K}(f,x_\ast )$
and
$\mathsf {K}(f)=\mathsf {K}(f,x_\ast )$
and
![]() $x\in \mathcal {G}$
such that
$x\in \mathcal {G}$
such that
![]() $\mathrm {dist}_{\mathbb {S}}(f,x)\leq \delta $
. Then by the 2nd Lipschitz property (Theorem 3.2), we have
$\mathrm {dist}_{\mathbb {S}}(f,x)\leq \delta $
. Then by the 2nd Lipschitz property (Theorem 3.2), we have
Hence
![]() $1/\mathsf {K}(f,x_\ast )\leq (1-\delta \,\mathbf {D}\,\mathsf {K}(f,x))/\mathsf {K}(f,x)$
, and the desired inequality follows from the hypothesis.
$1/\mathsf {K}(f,x_\ast )\leq (1-\delta \,\mathbf {D}\,\mathsf {K}(f,x))/\mathsf {K}(f,x)$
, and the desired inequality follows from the hypothesis.
Proposition 4.7 suggests the following algorithm, which involves only one
![]() $L_\infty $
-norm computation.
$L_\infty $
-norm computation.

Proposition 4.8. Algorithm
![]() is correct. On input
is correct. On input
![]() $(f,k,b)\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]\times \mathbb {N}\times (\mathbb {N}\cup \{\infty \})$
, its cost is bounded by
$(f,k,b)\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]\times \mathbb {N}\times (\mathbb {N}\cup \{\infty \})$
, its cost is bounded by
Proof. The correctness follows from Propositions 4.5 and 4.7 and
![]() $(1-2^{-(k+1)})^2>1-2^{-k}$
.
$(1-2^{-(k+1)})^2>1-2^{-k}$
.
The cost of the first line of the algorithm is bounded by Proposition 4.5. The number of evaluations of
in the
![]() $\ell $
th iteration of the loop is given by Proposition 4.1. We need
$\ell $
th iteration of the loop is given by Proposition 4.1. We need
![]() $\mathcal {O}(N+n^3)$
operations for each such evaluation, by [Reference Bürgisser and Cucker14, Proposition 16.32].
$\mathcal {O}(N+n^3)$
operations for each such evaluation, by [Reference Bürgisser and Cucker14, Proposition 16.32].
In this way, if the loop runs
![]() $\ell _0$
iterations, it performs a total of
$\ell _0$
iterations, it performs a total of
operations.
If the algorithm outputs
![]() $\mathcal {K}$
, then
$\mathcal {K}$
, then
![]() $\ell _0=\lceil k+\log \mathbf {D}+ \log \mathcal {K}-\log (1-2^{-k})\rceil $
. Moreover, from the correctness,
$\ell _0=\lceil k+\log \mathbf {D}+ \log \mathcal {K}-\log (1-2^{-k})\rceil $
. Moreover, from the correctness,
![]() $\log \mathcal {K}-\log (1-2^{-k})\leq \log \mathsf {K}(f)$
, so
$\log \mathcal {K}-\log (1-2^{-k})\leq \log \mathsf {K}(f)$
, so
![]() $\ell _0\leq k+1+\log \mathbf {D}+\log \mathsf {K}(f)$
.
$\ell _0\leq k+1+\log \mathbf {D}+\log \mathsf {K}(f)$
.
If the algorithm outputs fail, then the first criterion had to fail, so as long as the second criterion fails too, we have
So, in this case,
![]() $\ell _0\leq k+1+\log \mathbf {D}+\log b$
.
$\ell _0\leq k+1+\log \mathbf {D}+\log b$
.
We conclude from the bounds above and some straightforward computations.
By setting k to
![]() $7$
and
$7$
and
![]() $b=\infty $
, we have the following important corollary.
$b=\infty $
, we have the following important corollary.
Corollary 4.9. There is an algorithm
![]() $\mathsf {K}$
-Estimate
$\mathsf {K}$
-Estimate
![]() $^*$
that on input
$^*$
that on input
![]() $(f)\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
computes
$(f)\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
computes
![]() $\mathcal {K}\in [1,\infty )$
such that
$\mathcal {K}\in [1,\infty )$
such that
This algorithm halts if and only if
![]() $\mathsf {K}(f)<\infty $
, and its cost is bounded by
$\mathsf {K}(f)<\infty $
, and its cost is bounded by
4.1.3 Complexity analysis of grid-based algorithms using
 $\mathsf {K}$
$\mathsf {K}$
To get the grid method to work, we need two ingredients: a method for selecting the points in the grid near the geometric object of interest and a way of controlling distances between these two sets.
Theorem 4.10 (Construction-selection).
Let
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
and
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
and
![]() $\mathcal {G}\subseteq \mathbb {S}^n$
be a
$\mathcal {G}\subseteq \mathbb {S}^n$
be a
![]() $\delta $
-net. If
$\delta $
-net. If
and
![]() $Q\in \mathbb {R}$
is such that
$Q\in \mathbb {R}$
is such that
![]() $0.99Q\leq \|f\|_\infty ^{\mathbb {R}}\leq Q$
, then
$0.99Q\leq \|f\|_\infty ^{\mathbb {R}}\leq Q$
, then
 $$ \begin{align*} \mathrm{dist}_H\left(\left\{x\in \mathcal{G}\mid \frac{\|f(x)\|}{\sqrt{q}Q} < \mathbf{D}\,\delta\right\},\mathcal{Z}_{\mathbb{S}}(f)\right)< 2\mathbf{D}\mathsf{K}(f)\delta, \end{align*} $$
$$ \begin{align*} \mathrm{dist}_H\left(\left\{x\in \mathcal{G}\mid \frac{\|f(x)\|}{\sqrt{q}Q} < \mathbf{D}\,\delta\right\},\mathcal{Z}_{\mathbb{S}}(f)\right)< 2\mathbf{D}\mathsf{K}(f)\delta, \end{align*} $$
where
![]() $\mathrm {dist}_H(A,B):=\max \{\sup \{\mathrm {dist}(a,B)\mid a\in A\}, \sup \{\mathrm {dist}(b,A)\mid b\in B\}\}$
is the Hausdorff distance.
$\mathrm {dist}_H(A,B):=\max \{\sup \{\mathrm {dist}(a,B)\mid a\in A\}, \sup \{\mathrm {dist}(b,A)\mid b\in B\}\}$
is the Hausdorff distance.
Following [Reference Federer35], recall that the medial axis
![]() $\Delta _X$
of a closed set
$\Delta _X$
of a closed set
![]() $X\subset \mathbb {R}^n$
is the set
$X\subset \mathbb {R}^n$
is the set
consisting of those points for which there is more than one nearest point in X and that the reach
![]() $\tau (X)$
of X is the quantity
$\tau (X)$
of X is the quantity
measuring the size of the neighbourhood of X within which the nearest point projection is well-defined. If X is finite, then
![]() $\Delta _X$
is the union of the boundaries of the cells of the Voronoi diagram of X, and
$\Delta _X$
is the union of the boundaries of the cells of the Voronoi diagram of X, and
![]() $\tau (X)$
is half the minimum distance between two distinct points of X. Thus, when
$\tau (X)$
is half the minimum distance between two distinct points of X. Thus, when
![]() $\mathcal {Z}_{\mathbb {S}}(f)$
is zero-dimensional,
$\mathcal {Z}_{\mathbb {S}}(f)$
is zero-dimensional,
![]() $2\tau (\mathcal {Z}_{\mathbb {S}}(f))$
is the separation of the zeros of f in the sphere.
$2\tau (\mathcal {Z}_{\mathbb {S}}(f))$
is the separation of the zeros of f in the sphere.
Theorem 4.11. Let
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
. Then
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
. Then
Proof of Theorem 4.10.
Let
![]() $x_0\in \mathcal {Z}_{\mathbb {S}}(f)$
. Then there is some
$x_0\in \mathcal {Z}_{\mathbb {S}}(f)$
. Then there is some
![]() $x_1\in \mathcal {G}$
such that
$x_1\in \mathcal {G}$
such that
![]() $\mathrm {dist}_{\mathbb {S}}(x_0,x_1)\leq \delta $
. Let
$\mathrm {dist}_{\mathbb {S}}(x_0,x_1)\leq \delta $
. Let
![]() $[0,1]\ni t\mapsto x_t$
be the geodesic joining them. By Taylor’s theorem,
$[0,1]\ni t\mapsto x_t$
be the geodesic joining them. By Taylor’s theorem,
so, by Kellogg’s theorem (Corollary 2.14) and
![]() $f(x_0)=0$
, we have that
$f(x_0)=0$
, we have that
![]() $\frac {\|f(x_1)\|}{\sqrt {q}\|f\|_\infty ^{\mathbb {R}}}\leq \mathbf {D}\,\delta $
. Hence
$\frac {\|f(x_1)\|}{\sqrt {q}\|f\|_\infty ^{\mathbb {R}}}\leq \mathbf {D}\,\delta $
. Hence
![]() $\frac {\|f(x_1)\|}{\sqrt {q}Q}\leq \mathbf {D}\,\delta $
and
$\frac {\|f(x_1)\|}{\sqrt {q}Q}\leq \mathbf {D}\,\delta $
and
 $$ \begin{align*} \mathrm{dist}\left(x_0,\left\{x\in \mathcal{G}\mid \frac{\|f(x)\|}{\sqrt{q}Q}\leq \mathbf{D}\,\delta\right\}\right)\leq \mathrm{dist}(x_0,x_1)\le \mathrm{dist}_{\mathbb{S}}(x_0,x_1)\leq\delta. \end{align*} $$
$$ \begin{align*} \mathrm{dist}\left(x_0,\left\{x\in \mathcal{G}\mid \frac{\|f(x)\|}{\sqrt{q}Q}\leq \mathbf{D}\,\delta\right\}\right)\leq \mathrm{dist}(x_0,x_1)\le \mathrm{dist}_{\mathbb{S}}(x_0,x_1)\leq\delta. \end{align*} $$
Now let
![]() $x_2\in \mathcal {G}$
be such that
$x_2\in \mathcal {G}$
be such that
![]() $\frac {\|f(x_2)\|}{\sqrt {q}Q}< \mathbf {D}\,\delta $
. Then
$\frac {\|f(x_2)\|}{\sqrt {q}Q}< \mathbf {D}\,\delta $
. Then
 $$ \begin{align} \frac{\|f(x_2)\|}{\sqrt{q}\|f\|_\infty^{\mathbb{R}}} < 1.02\mathbf{D}\,\delta \le \frac{1}{4\mathbf{D}\mathsf{K}(f)^2} <\frac{1}{\mathsf{K}(f,x_2)}, \end{align} $$
$$ \begin{align} \frac{\|f(x_2)\|}{\sqrt{q}\|f\|_\infty^{\mathbb{R}}} < 1.02\mathbf{D}\,\delta \le \frac{1}{4\mathbf{D}\mathsf{K}(f)^2} <\frac{1}{\mathsf{K}(f,x_2)}, \end{align} $$
the second inequality by our hypothesis. Because of the regularity inequality (Theorem 3.2), we must then have
![]() $\sqrt {q}\|f\|^{\mathbb {R}}_{\infty }\|\mathrm {D}_{x_2}f^{\dagger }\Delta ^{1/2}\| \le \mathsf {K}(f,x_2)$
. It follows that
$\sqrt {q}\|f\|^{\mathbb {R}}_{\infty }\|\mathrm {D}_{x_2}f^{\dagger }\Delta ^{1/2}\| \le \mathsf {K}(f,x_2)$
. It follows that
 $$ \begin{align*} \|\mathrm{D}_{x_2}f^{\dagger}f(x_2)\|\gamma(f,x_2) &< \frac{\mathsf{K}(f,x_2)}{\sqrt{q}\|f\|^{\mathbb{R}}_{\infty}}\gamma(f,x_2) \le \frac{1}{2}\mathbf{D}\mathsf{K}(f)^2\frac{\|f(x_2)\|}{\sqrt{q}\|f\|_\infty^{\mathbb{R}}}\\ &< \frac{1.02}{2}\mathbf{D}^2\mathsf{K}(f)^2\delta< \frac{1.02}{8} < 0.13071\ldots \end{align*} $$
$$ \begin{align*} \|\mathrm{D}_{x_2}f^{\dagger}f(x_2)\|\gamma(f,x_2) &< \frac{\mathsf{K}(f,x_2)}{\sqrt{q}\|f\|^{\mathbb{R}}_{\infty}}\gamma(f,x_2) \le \frac{1}{2}\mathbf{D}\mathsf{K}(f)^2\frac{\|f(x_2)\|}{\sqrt{q}\|f\|_\infty^{\mathbb{R}}}\\ &< \frac{1.02}{2}\mathbf{D}^2\mathsf{K}(f)^2\delta< \frac{1.02}{8} < 0.13071\ldots \end{align*} $$
where we used the higher derivative estimate (Theorem 3.2) in the first line and equation (4.1) and the hypothesis in the second. This means Smale’s
![]() $\alpha $
-criterion holds for
$\alpha $
-criterion holds for
![]() $x_2$
and
$x_2$
and
![]() $f_{|\mathrm {T}_{x_0}\mathbb {S}^n}$
by [Reference Dedieu29, Théorème 128]. Hence there is
$f_{|\mathrm {T}_{x_0}\mathbb {S}^n}$
by [Reference Dedieu29, Théorème 128]. Hence there is
![]() $x_3\in \mathrm {T}_{x_2}\mathbb {S}^n$
such that
$x_3\in \mathrm {T}_{x_2}\mathbb {S}^n$
such that
![]() $f(x_3)=0$
and
$f(x_3)=0$
and
Since
![]() $\mathrm {dist}(x_2,x_3/\|x_3\|) =\arctan \mathrm {dist}(x_2,x_3)\leq \mathrm {dist}(x_2,x_3)$
, we are done.
$\mathrm {dist}(x_2,x_3/\|x_3\|) =\arctan \mathrm {dist}(x_2,x_3)\leq \mathrm {dist}(x_2,x_3)$
, we are done.
Remark 4.12. The proof also shows the convergence of Newton’s method associated with
![]() $f_{|\mathrm {T}_x\mathbb {S}^n}$
for every
$f_{|\mathrm {T}_x\mathbb {S}^n}$
for every
![]() $x\in \mathcal {G}$
such that
$x\in \mathcal {G}$
such that
![]() $\frac {\|f(x)\|}{\sqrt {q}\|f\|_\infty ^{\mathbb {R}}}\leq \mathbf {D}\,\delta $
. Hence, we can refine our approximations if needed.
$\frac {\|f(x)\|}{\sqrt {q}\|f\|_\infty ^{\mathbb {R}}}\leq \mathbf {D}\,\delta $
. Hence, we can refine our approximations if needed.
Sketch of proof of Theorem 4.11.
The proof is very similar to the one of [Reference Bürgisser, Cucker and Lairez15, Theorem 4.12]. By [Reference Bürgisser, Cucker and Lairez15, Lemma 2.7] and [Reference Bürgisser, Cucker and Lairez15, Theorem 3.3], we have that
 $$ \begin{align*} \tau(\mathcal{Z}_{\mathbb{S}}(f))\geq \min\left\{1,\frac{1}{14\max\{\gamma(f,x)\mid x\in \mathcal{Z}_{\mathbb{S}}(f)\}}\right\}. \end{align*} $$
$$ \begin{align*} \tau(\mathcal{Z}_{\mathbb{S}}(f))\geq \min\left\{1,\frac{1}{14\max\{\gamma(f,x)\mid x\in \mathcal{Z}_{\mathbb{S}}(f)\}}\right\}. \end{align*} $$
Hence, by the higher derivative estimate (Theorem 3.2), the desired bound follows.
![]() $\Box $
$\Box $
The following theorem is a variant of the so-called Niyogi-Smale-Weinberger theorem [Reference Niyogi, Smale and Weinberger47, Proposition 7.1].
Theorem 4.13. Let
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
,
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
,
![]() $\mathcal {G}\subset \mathbb {S}^n$
be a
$\mathcal {G}\subset \mathbb {S}^n$
be a
![]() $\delta $
-net and
$\delta $
-net and
![]() $Q\in \mathbb {R}$
be such that
$Q\in \mathbb {R}$
be such that
![]() $0.99Q\leq \|f\|_\infty ^{\mathbb {R}}\leq Q$
. If
$0.99Q\leq \|f\|_\infty ^{\mathbb {R}}\leq Q$
. If
![]() $90\mathbf {D}^2\mathsf {K}(f)^2\delta <1$
, then for every
$90\mathbf {D}^2\mathsf {K}(f)^2\delta <1$
, then for every
 $$ \begin{align*} \varepsilon\in \left(6\mathbf{D}\mathsf{K}(f)\delta,\frac{1}{14\mathbf{D}\mathsf{K}(f)}\right), \end{align*} $$
$$ \begin{align*} \varepsilon\in \left(6\mathbf{D}\mathsf{K}(f)\delta,\frac{1}{14\mathbf{D}\mathsf{K}(f)}\right), \end{align*} $$
the sets
![]() $\mathcal {Z}_{\mathbb {S}}(f)$
and
$\mathcal {Z}_{\mathbb {S}}(f)$
and
 $$ \begin{align*} \bigcup\left\{B(x,\varepsilon)\mid x\in\mathcal{G},\,\frac{\|f(x)\|}{\sqrt{q}Q}<\mathbf{D}\delta\right\} \end{align*} $$
$$ \begin{align*} \bigcup\left\{B(x,\varepsilon)\mid x\in\mathcal{G},\,\frac{\|f(x)\|}{\sqrt{q}Q}<\mathbf{D}\delta\right\} \end{align*} $$
are homotopically equivalent. In particular, they have the same Betti numbers.
Proof. This is just [Reference Bürgisser, Cucker and Lairez15, Theorem 2.8] combined with Theorems 4.10 and 4.11.
We can now describe the algorithm. We will call a black box Betti for computing the Betti numbers of a union of balls. This is a standard procedure in topological data analysis [Reference Edelsbrunner32].

Proposition 4.14. Algorithm
![]() is correct, and its cost is bounded by
is correct, and its cost is bounded by
Proof. Correctness is a consequence of Theorem 4.13 and the fact that the computed Q satisfies
![]() $0.99Q\leq \|f\|_\infty ^{\mathbb {R}}\leq Q$
by Proposition 4.5.
$0.99Q\leq \|f\|_\infty ^{\mathbb {R}}\leq Q$
by Proposition 4.5.
For the complexity, we apply Proposition 4.3 for the first line, Corollary 4.9 for the second line and Proposition 4.1 for the fourth and fifth lines. We know that
![]() has cost
has cost
![]() $\mathcal {O}\left (2^{\mathcal {O}(n\log n)}|\mathcal {X}|^{5n}\right )$
(see [Reference Cucker, Krick and Shub28, Section 5] for example) and that
$\mathcal {O}\left (2^{\mathcal {O}(n\log n)}|\mathcal {X}|^{5n}\right )$
(see [Reference Cucker, Krick and Shub28, Section 5] for example) and that
![]() $|\mathcal {X}|=\mathcal {O}(2^{n\log n}\mathbf {D}^{2n}\mathsf {K}(f)^{2n})$
, by Proposition 4.1. Note that we have eliminated N from the bounds. We have done so using the fact that as
$|\mathcal {X}|=\mathcal {O}(2^{n\log n}\mathbf {D}^{2n}\mathsf {K}(f)^{2n})$
, by Proposition 4.1. Note that we have eliminated N from the bounds. We have done so using the fact that as
![]() $q\le n$
(by the precondition of the input),
$q\le n$
(by the precondition of the input),
![]() $N\leq 2^{n\log n}\mathbf {D}^{n}$
.
$N\leq 2^{n\log n}\mathbf {D}^{n}$
.
We note that our bound uses
![]() $\mathcal {K}\leq 1.02\mathsf {K}(f)$
to get the cost dependent on
$\mathcal {K}\leq 1.02\mathsf {K}(f)$
to get the cost dependent on
![]() $\mathsf {K}(f)$
instead of on the computed estimate
$\mathsf {K}(f)$
instead of on the computed estimate
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
The complexity estimate in Proposition 4.14 does not differ much from those in other grid-based algorithms. We will see in Section 4.3, however, that the occurrence of
![]() $\mathsf {K}$
in the place of
$\mathsf {K}$
in the place of
![]() $\kappa $
leads to substantial improvements when one goes beyond the worst-case framework and considers random input models.
$\kappa $
leads to substantial improvements when one goes beyond the worst-case framework and considers random input models.
4.2 Complexity of the Plantinga-Vegter algorithm
The ideas above can also be applied to the Plantinga-Vegter algorithm [Reference Plantinga and Vegter49]. In a recent work [Reference Cucker, Ergür and Tonelli-Cueto24] (compare to [Reference Cucker, Ergür and Tonelli-Cueto23]), we performed an extensive analysis of this algorithm, including details for finite precision arithmetic. So we will be brief here, referring the reader to [Reference Cucker, Ergür and Tonelli-Cueto24] for details, and will only focus on the (exact) interval version of the algorithm.
4.2.1 The Plantinga-Vegter subdivision algorithm
Let
![]() $\mathcal {P}_{d}$
be the space of polynomials in
$\mathcal {P}_{d}$
be the space of polynomials in
![]() $X_1,\ldots ,X_n$
of degree at most d. The Plantinga-Vegter algorithm [Reference Plantinga and Vegter49]Footnote
2
is a subdivision-based algorithm for obtaining a piecewise linear approximation of the zero set of
$X_1,\ldots ,X_n$
of degree at most d. The Plantinga-Vegter algorithm [Reference Plantinga and Vegter49]Footnote
2
is a subdivision-based algorithm for obtaining a piecewise linear approximation of the zero set of
![]() $f\in \mathcal {P}_{d}$
inside
$f\in \mathcal {P}_{d}$
inside
![]() $[-a,a]^n$
. As customary, we will focus on the complexity analysis of the subdivision routine only. The idea is to iteratively subdivide some boxes – that is, sets of the form
$[-a,a]^n$
. As customary, we will focus on the complexity analysis of the subdivision routine only. The idea is to iteratively subdivide some boxes – that is, sets of the form
![]() $B=m(B)+[-w(B)/2,w(B)/2]^n$
(here
$B=m(B)+[-w(B)/2,w(B)/2]^n$
(here
![]() $m(B)\in \mathbb {R}^n$
is the centre of B and
$m(B)\in \mathbb {R}^n$
is the centre of B and
![]() $w(B)>0$
is its width) – in
$w(B)>0$
is its width) – in
![]() $[-a,a]^n$
until every box B in the subdivision satisfies the following condition:
$[-a,a]^n$
until every box B in the subdivision satisfies the following condition:
where
![]() $\langle ~,~\rangle $
is the standard inner product and
$\langle ~,~\rangle $
is the standard inner product and
![]() $\nabla f$
is the gradient vector of f. Once this criterion is satisfied by all boxes in the subdivision, the Plantinga-Vegter algorithm returns a topologically accurate approximation of the zero set of f in the region
$\nabla f$
is the gradient vector of f. Once this criterion is satisfied by all boxes in the subdivision, the Plantinga-Vegter algorithm returns a topologically accurate approximation of the zero set of f in the region
![]() $[a,-a]^n$
and halts (see [Reference Plantinga and Vegter49] (
$[a,-a]^n$
and halts (see [Reference Plantinga and Vegter49] (
![]() $n\leq 3$
) and [Reference Galehouse37] (arbitrary n) for details on how this is done).
$n\leq 3$
) and [Reference Galehouse37] (arbitrary n) for details on how this is done).
For
![]() $f\in \mathcal {P}_{d}$
, we define
$f\in \mathcal {P}_{d}$
, we define
where
![]() $f^{\mathsf {h}}\in \mathcal {H}_d[1]$
is the homogenisation of f. Taking the maps (2.3), (2.4), (2.5) in [Reference Cucker, Ergür and Tonelli-Cueto24] and substituting on them the Weyl norm by the real
$f^{\mathsf {h}}\in \mathcal {H}_d[1]$
is the homogenisation of f. Taking the maps (2.3), (2.4), (2.5) in [Reference Cucker, Ergür and Tonelli-Cueto24] and substituting on them the Weyl norm by the real
![]() $L_\infty $
-norm, we get
$L_\infty $
-norm, we get
together with
 $$ \begin{align} \widehat{f}:x\mapsto h(x)f(x)=\frac{f(x)}{\|f\|_\infty(1+\|x\|^2)^{(d-1)/2}} \end{align} $$
$$ \begin{align} \widehat{f}:x\mapsto h(x)f(x)=\frac{f(x)}{\|f\|_\infty(1+\|x\|^2)^{(d-1)/2}} \end{align} $$
and
 $$ \begin{align} \widehat{\nabla f}:x\mapsto h'(x)\mathrm{D} f(x) =\frac{\nabla f(x)}{d\|f\|_\infty(1+\|x\|^2)^{d/2-1}}. \end{align} $$
$$ \begin{align} \widehat{\nabla f}:x\mapsto h'(x)\mathrm{D} f(x) =\frac{\nabla f(x)}{d\|f\|_\infty(1+\|x\|^2)^{d/2-1}}. \end{align} $$
One can use these maps to produce interval approximations as we do in [Reference Cucker, Ergür and Tonelli-Cueto24]. For
![]() $X\subseteq \mathbb {R}^m$
, we denote by
$X\subseteq \mathbb {R}^m$
, we denote by
![]() $\square X$
the set of boxes contained in X. Recall that an interval approximation of
$\square X$
the set of boxes contained in X. Recall that an interval approximation of
![]() $f:\mathbb {R}^n\rightarrow \mathbb {R}^q$
is a function
$f:\mathbb {R}^n\rightarrow \mathbb {R}^q$
is a function
![]() $\square f:\square \mathbb {R}^n\rightarrow \square \mathbb {R}^q$
that maps boxes in
$\square f:\square \mathbb {R}^n\rightarrow \square \mathbb {R}^q$
that maps boxes in
![]() $\mathbb {R}^n$
to boxes in
$\mathbb {R}^n$
to boxes in
![]() $\mathbb {R}^q$
in such a way that
$\mathbb {R}^q$
in such a way that
![]() $f(B)\subseteq \square f(B)$
.
$f(B)\subseteq \square f(B)$
.
Proposition 4.15. Let
![]() $f\in \mathcal {P}_{d}$
. Then
$f\in \mathcal {P}_{d}$
. Then
 $$ \begin{align*}\square[hf]:B\mapsto \widehat{f}(m(B))+(1+d)\sqrt{n}\left[-\frac{w(B)}{2},\frac{w(B)}{2}\right] \end{align*} $$
$$ \begin{align*}\square[hf]:B\mapsto \widehat{f}(m(B))+(1+d)\sqrt{n}\left[-\frac{w(B)}{2},\frac{w(B)}{2}\right] \end{align*} $$
is an interval approximation of
![]() $hf$
and
$hf$
and
 $$ \begin{align*}\square[\|h'\mathrm{D} f\|]:B\mapsto \|\widehat{\nabla f}(m(B))\|+d\sqrt{n}\left[-\frac{w(B)}{2},\frac{w(B)}{2}\right]\end{align*} $$
$$ \begin{align*}\square[\|h'\mathrm{D} f\|]:B\mapsto \|\widehat{\nabla f}(m(B))\|+d\sqrt{n}\left[-\frac{w(B)}{2},\frac{w(B)}{2}\right]\end{align*} $$
is an interval approximation of
![]() $\|h'\mathrm {D} f\|$
.
$\|h'\mathrm {D} f\|$
.
Sketch of proof.
Using the bounds from Kellogg’s theorem (Theorem 2.13) and its corollaries, we can easily deduce (as is done in the proof of Theorem 3.2) that the maps
are d- and
![]() $(d-1)$
-Lipschitz (with respect to the geodesic distance) for
$(d-1)$
-Lipschitz (with respect to the geodesic distance) for
![]() $g\in \mathcal {H}_d^{\mathbb {R}}[1]$
.
$g\in \mathcal {H}_d^{\mathbb {R}}[1]$
.
![]() $\Box $
$\Box $
We now argue as in [Reference Cucker, Ergür and Tonelli-Cueto24, Section 4], but using these Lipschitz properties, to prove that
![]() $\hat f$
and
$\hat f$
and
![]() $\widehat {\nabla f}$
are
$\widehat {\nabla f}$
are
![]() $(1+d)$
- and d-Lipschitz, respectively. For the latter, we use the fact that for
$(1+d)$
- and d-Lipschitz, respectively. For the latter, we use the fact that for
![]() $v\in \mathbb {R}^n$
,
$v\in \mathbb {R}^n$
,
 $\overline {\mathrm {D}}_Xf^{\mathsf {h}}\begin {pmatrix}0\\v\end {pmatrix} =(\langle \nabla f,v\rangle )^{\mathsf {h}}$
and that
$\overline {\mathrm {D}}_Xf^{\mathsf {h}}\begin {pmatrix}0\\v\end {pmatrix} =(\langle \nabla f,v\rangle )^{\mathsf {h}}$
and that
![]() $\|\widehat {\nabla f}\|$
is d-Lipschitz if
$\|\widehat {\nabla f}\|$
is d-Lipschitz if
![]() $\langle \widehat {\nabla f},v\rangle $
is so for every
$\langle \widehat {\nabla f},v\rangle $
is so for every
![]() $v\in \mathbb {S}^{n-1}$
.
$v\in \mathbb {S}^{n-1}$
.
Using the interval approximations and their Lipschitz properties in Proposition 4.15, we can rewrite the condition
![]() $C_f(B)$
. We only need to use [Reference Cucker, Ergür and Tonelli-Cueto24, Lemma 4.2] for the second clause of the condition.
$C_f(B)$
. We only need to use [Reference Cucker, Ergür and Tonelli-Cueto24, Lemma 4.2] for the second clause of the condition.
Theorem 4.16. Let
![]() $B\in \square \mathbb {R}^n$
. If the condition
$B\in \square \mathbb {R}^n$
. If the condition
is satisfied, then
![]() $C_f(B)$
is true.
$C_f(B)$
is true.
The subdivision procedure of the Plantinga-Vegter algorithm thus takes the following form, where StandardSubdivision is a procedure that, given a box, divides it into
![]() $2^n$
equal boxes. Recall that
$2^n$
equal boxes. Recall that
![]() $\square [-a,a]^n$
is the set of boxes within
$\square [-a,a]^n$
is the set of boxes within
![]() $[-a,a]^n$
.
$[-a,a]^n$
.

4.2.2 Complexity of PV-Interval
 ${}_\infty $
${}_\infty $
Without much effort, [Reference Cucker, Ergür and Tonelli-Cueto24, Proposition 5.1] transforms into the following proposition. The essential step is multiplying the inequalities in that proposition by
![]() $\|f^{\mathsf {h}}\|_W/\|f\|_\infty $
.
$\|f^{\mathsf {h}}\|_W/\|f\|_\infty $
.
Proposition 4.17. Let
![]() $f\in \mathcal {P}_{d}$
and
$f\in \mathcal {P}_{d}$
and
![]() $x\in \mathbb {R}^n$
. Then either
$x\in \mathbb {R}^n$
. Then either

where

.
With Proposition 4.17 and the Lipschitz properties shown for
![]() $\hat f$
and
$\hat f$
and
![]() $\widehat {\nabla f}$
, one can produce a local size bound for
$\widehat {\nabla f}$
, one can produce a local size bound for
![]() $C^{\Box }_f(B)$
. This is a function that, evaluated at a point x, gives a lower bound on the volume of any possible box containing x and not satisfying the predicate
$C^{\Box }_f(B)$
. This is a function that, evaluated at a point x, gives a lower bound on the volume of any possible box containing x and not satisfying the predicate
![]() $C^{\prime }_f(B)$
.
$C^{\prime }_f(B)$
.
Then using the continuous amortisation of [Reference Burr, Krahmer and Yap20, Reference Burr18, Reference Burr, Gao and Tsigaridas19] (see [Reference Cucker, Ergür and Tonelli-Cueto24, Theorem 6.1]), we conclude the following, which takes into account the cost of calling NormApprox
![]() $\mathbb {R}$
(Proposition 4.3).
$\mathbb {R}$
(Proposition 4.3).
Theorem 4.19. The number of boxes in the final subdivision
![]() $\mathcal {S}$
of PV-Interval
$\mathcal {S}$
of PV-Interval
![]() ${}_\infty $
on input
${}_\infty $
on input
![]() $(f,a)$
is at most
$(f,a)$
is at most
The number of arithmetic operations performed by PV-Interval
![]() ${}_\infty $
on input
${}_\infty $
on input
![]() $(f,a)$
is at most
$(f,a)$
is at most

The condition-based estimates in Theorem 4.19 are very similar to those of [Reference Cucker, Ergür and Tonelli-Cueto24, Theorem 6.3]. It is important to observe that only one norm computation is performed by PV-Interval
![]() ${}_\infty $
(in its very first step) and that the cost of this computation is already included in the cost bound in Theorem 4.19. We will see in Section 4.3.3 that the occurrence of
${}_\infty $
(in its very first step) and that the cost of this computation is already included in the cost bound in Theorem 4.19. We will see in Section 4.3.3 that the occurrence of
![]() $\mathsf {K}$
in the place of
$\mathsf {K}$
in the place of
![]() $\kappa $
results in significant improvements in overall complexity when we consider average or smoothed analysis.
$\kappa $
results in significant improvements in overall complexity when we consider average or smoothed analysis.
4.3 Probabilistic analysis of algorithms
In the preceding sections, we have shown that existing grid-based and subdivision-based algorithms that use (in their design and/or analysis)
![]() $\kappa $
can be modified to use
$\kappa $
can be modified to use
![]() $\mathsf {K}$
instead. Moreover, we have shown that the condition-based complexity estimates in terms of
$\mathsf {K}$
instead. Moreover, we have shown that the condition-based complexity estimates in terms of
![]() $\mathsf {K}$
are similar to those in terms of
$\mathsf {K}$
are similar to those in terms of
![]() $\kappa $
. In this section, we will show that when we consider random inputs, in contrast, the cost (expected or in probability) substantially decreases.
$\kappa $
. In this section, we will show that when we consider random inputs, in contrast, the cost (expected or in probability) substantially decreases.
We first introduce the randomness model along with some useful probabilistic results. Then we prove a general comparison result showing that when substituting
![]() $\kappa $
by
$\kappa $
by
![]() $\mathsf {K}$
, one can expect to reduce the size of the condition number by a factor of
$\mathsf {K}$
, one can expect to reduce the size of the condition number by a factor of
![]() $\sqrt {N}$
. Finally, we apply these estimates to both PolyBetti and the Plantinga-Vegter algorithm and highlight the complexity improvements.
$\sqrt {N}$
. Finally, we apply these estimates to both PolyBetti and the Plantinga-Vegter algorithm and highlight the complexity improvements.
For most algorithms in real algebraic geometry, condition-based estimates show a dependence on either
![]() $\kappa ^n$
or
$\kappa ^n$
or
![]() $\mathsf {K}^n$
. When this occurs, the complexity estimates improve by a factor of the form
$\mathsf {K}^n$
. When this occurs, the complexity estimates improve by a factor of the form
![]() $N^{\frac {n}{2}}$
when we pass from
$N^{\frac {n}{2}}$
when we pass from
![]() $\kappa $
to
$\kappa $
to
![]() $\mathsf {K}$
. The final complexity estimates thus change from having an exponent quadratic in n to an exponent quasilinear in n.
$\mathsf {K}$
. The final complexity estimates thus change from having an exponent quadratic in n to an exponent quasilinear in n.
4.3.1 The randomness model: dobro random polynomials
Given a random variable
![]() $\mathfrak {x}\in \mathbb {R}$
, we say that:
$\mathfrak {x}\in \mathbb {R}$
, we say that:
-
(i)
 $\mathfrak {x}$
is centred if
$\mathfrak {x}$
is centred if
 $\mathop {\mathbb {E}}\mathfrak {x}=0$
.
$\mathop {\mathbb {E}}\mathfrak {x}=0$
. -
(ii)
 $\mathfrak {x}$
is subgaussian if there is a constant
$\mathfrak {x}$
is subgaussian if there is a constant
 $K>0$
such that for all
$K>0$
such that for all
 $p\geq 1$
,
$p\geq 1$
,  $$ \begin{align*} \left(\mathop{\mathbb{E}}|\mathfrak{x}|^p\right)^{\frac{1}{p}}\leq K\sqrt{p}. \end{align*} $$
$$ \begin{align*} \left(\mathop{\mathbb{E}}|\mathfrak{x}|^p\right)^{\frac{1}{p}}\leq K\sqrt{p}. \end{align*} $$
The smallest K satisfying this condition is called the
 $\psi _2$
-norm of
$\psi _2$
-norm of
 $\mathfrak {x}$
and is denoted
$\mathfrak {x}$
and is denoted
 $\|\mathfrak {x}\|_{\psi _2}$
.
$\|\mathfrak {x}\|_{\psi _2}$
. -
(iii)
 $\mathfrak {x}$
has the anti-concentration property with constant
$\mathfrak {x}$
has the anti-concentration property with constant
 $\rho $
if for all
$\rho $
if for all
 $u\in \mathbb {R}$
and
$u\in \mathbb {R}$
and
 $\varepsilon>0$
,
$\varepsilon>0$
,  $$ \begin{align*}\mathbb{P}(|\mathfrak{x}-u|<\varepsilon)\leq 2\rho\varepsilon.\end{align*} $$
$$ \begin{align*}\mathbb{P}(|\mathfrak{x}-u|<\varepsilon)\leq 2\rho\varepsilon.\end{align*} $$
Note that this is equivalent to
 $\mathfrak {x}$
having a density (with respect to the Lebesgue measure) bounded by
$\mathfrak {x}$
having a density (with respect to the Lebesgue measure) bounded by
 $\rho $
.
$\rho $
.
We now extend to tuples the class of real random polynomials introduced in [Reference Cucker, Ergür and Tonelli-Cueto23].
Definition 4.20. A dobro random polynomial tuple
![]() $\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
with parameters K and
$\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
with parameters K and
![]() $\rho $
is a tuple of random polynomials
$\rho $
is a tuple of random polynomials
 $$ \begin{align*} \left(\sum_{|\alpha|=d_1}\binom{d_1}{\alpha}^{\frac{1}{2}} \mathfrak{c}_{1,\alpha}X^\alpha,\ldots,\sum_{|\alpha|=d_q} \binom{d_q}{\alpha}^{\frac{1}{2}}\mathfrak{c}_{q,\alpha}X^\alpha\right) \end{align*} $$
$$ \begin{align*} \left(\sum_{|\alpha|=d_1}\binom{d_1}{\alpha}^{\frac{1}{2}} \mathfrak{c}_{1,\alpha}X^\alpha,\ldots,\sum_{|\alpha|=d_q} \binom{d_q}{\alpha}^{\frac{1}{2}}\mathfrak{c}_{q,\alpha}X^\alpha\right) \end{align*} $$
such that the
![]() $\mathfrak {c}_{i,\alpha }$
are independent centred subgaussian random variables with
$\mathfrak {c}_{i,\alpha }$
are independent centred subgaussian random variables with
![]() $\psi _2$
-norm at most K and anti-concentration property with constant
$\psi _2$
-norm at most K and anti-concentration property with constant
![]() $\rho $
.
$\rho $
.
Remark 4.21. Probabilistic estimates for a dobro polynomial
![]() $\mathfrak {f}$
will depend on
$\mathfrak {f}$
will depend on
![]() $K\rho $
. This product is invariant under scalar multiplication of
$K\rho $
. This product is invariant under scalar multiplication of
![]() $\mathfrak {f}$
since
$\mathfrak {f}$
since
![]() $\lambda \mathfrak {f}$
is dobro with parameters
$\lambda \mathfrak {f}$
is dobro with parameters
![]() $|\lambda |K$
and
$|\lambda |K$
and
![]() $\rho /|\lambda |$
. Moreover, note thatFootnote
3
$\rho /|\lambda |$
. Moreover, note thatFootnote
3
![]() $6K\rho \geq 1$
.
$6K\rho \geq 1$
.
Example 4.22. A dobro random polynomial tuple
![]() $\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
such that the
$\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
such that the
![]() $\mathfrak {c}_\alpha $
are are independent and identically distributed normal random variables of mean zero and variance one is called a KSS (real) polynomial tuple.Footnote
4
In this case, we can take
$\mathfrak {c}_\alpha $
are are independent and identically distributed normal random variables of mean zero and variance one is called a KSS (real) polynomial tuple.Footnote
4
In this case, we can take
![]() $K\rho =2/\sqrt {\pi }$
.
$K\rho =2/\sqrt {\pi }$
.
Example 4.23. A dobro random polynomial tuple
![]() $\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
such that the
$\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
such that the
![]() $\mathfrak {c}_\alpha $
are are independent and identically distributed uniform random variables in
$\mathfrak {c}_\alpha $
are are independent and identically distributed uniform random variables in
![]() $[-1,1]$
is a Weyl uniform (real) polynomial tuple. In this case, we can take
$[-1,1]$
is a Weyl uniform (real) polynomial tuple. In this case, we can take
![]() $K\rho =1/2$
.
$K\rho =1/2$
.
We now state and prove several probabilistic results that will be used later.
Proposition 4.24 (Subgaussian tail bounds).
Let
![]() $\mathfrak {x}\in \mathbb {R}$
be a random variable.
$\mathfrak {x}\in \mathbb {R}$
be a random variable.
-
1. If
 $\mathfrak {x}$
is subgaussian with
$\mathfrak {x}$
is subgaussian with
 $\psi _2$
-norm at most K, then for all
$\psi _2$
-norm at most K, then for all
 $t>0$
,
$t>0$
,
 $\mathbb {P}(|\mathfrak {x}|\geq t)\leq \mathrm {e}^{1-\frac {t^2}{6K^2}}$
.
$\mathbb {P}(|\mathfrak {x}|\geq t)\leq \mathrm {e}^{1-\frac {t^2}{6K^2}}$
. -
2. If there are
 $C\geq \mathrm {e}$
and
$C\geq \mathrm {e}$
and
 $K>0$
such that for all
$K>0$
such that for all
 $t>0$
,
$t>0$
,
 $\mathbb {P}(|\mathfrak {x}|\geq t)\leq C\mathrm {e}^{-\frac {t^2}{K^2}}$
, then
$\mathbb {P}(|\mathfrak {x}|\geq t)\leq C\mathrm {e}^{-\frac {t^2}{K^2}}$
, then
 $\mathfrak {x}$
is subgaussian with
$\mathfrak {x}$
is subgaussian with
 $\psi _2$
-norm at most
$\psi _2$
-norm at most
 $K\left (\sqrt {\pi /2}+\sqrt {2\ln C}\right )$
.
$K\left (\sqrt {\pi /2}+\sqrt {2\ln C}\right )$
.
Proposition 4.25 (Hoeffding inequality).
Let
![]() $\mathfrak {x}\in \mathbb {R}^N$
be a random vector such that its components
$\mathfrak {x}\in \mathbb {R}^N$
be a random vector such that its components
![]() $\mathfrak {x}_i$
are centred subgaussian random variables with
$\mathfrak {x}_i$
are centred subgaussian random variables with
![]() $\psi _2$
-norm at most K and
$\psi _2$
-norm at most K and
![]() $a\in \mathbb {S}^{N-1}$
. Then for all
$a\in \mathbb {S}^{N-1}$
. Then for all
![]() $t\geq 0$
,
$t\geq 0$
,
In particular,
![]() $a^*\mathfrak {x}$
is a subgaussian random variable with
$a^*\mathfrak {x}$
is a subgaussian random variable with
![]() $\psi _2$
-norm at most
$\psi _2$
-norm at most
![]() $5K$
.
$5K$
.
Proposition 4.26 (Anti-concentration bound).
Let
![]() $\mathfrak {x}\in \mathbb {R}^N$
be a random vector such that its components
$\mathfrak {x}\in \mathbb {R}^N$
be a random vector such that its components
![]() $\mathfrak {x}_i$
are independent random variables with anti-concentration property with constant
$\mathfrak {x}_i$
are independent random variables with anti-concentration property with constant
![]() $\rho $
. Then for every
$\rho $
. Then for every
![]() $A\in \mathbb {R}^{k\times N}$
with rank k and measurable
$A\in \mathbb {R}^{k\times N}$
with rank k and measurable
![]() $U\subseteq \mathbb {R}^k$
,
$U\subseteq \mathbb {R}^k$
,
 $$ \begin{align*}\mathbb{P}_{\mathfrak{x}}\left(A\mathfrak{x}\in U\right)\leq \frac{\operatorname{\mathrm{vol}}(U)(\sqrt{2}\rho)^k}{\sqrt{\det\left(AA^*\right)}}.\end{align*} $$
$$ \begin{align*}\mathbb{P}_{\mathfrak{x}}\left(A\mathfrak{x}\in U\right)\leq \frac{\operatorname{\mathrm{vol}}(U)(\sqrt{2}\rho)^k}{\sqrt{\det\left(AA^*\right)}}.\end{align*} $$
Proof of Proposition 4.24.
This is just [Reference Vershynin58, Proposition 2.5.2] with improved constants.
For the first part, we give a proof since we don’t explicitly use the constants in the proof of [Reference Vershynin58, Proposition 2.5.2]. Fix
![]() $\lambda>0$
. Then by Markov’s inequality and expanding the exponential as a power series,
$\lambda>0$
. Then by Markov’s inequality and expanding the exponential as a power series,
 $$ \begin{align*} \mathbb{P}(|\mathfrak{x}|\geq t) = \mathbb{P}\left(\mathrm{e}^{\lambda^2\mathfrak{x}^2}\geq \mathrm{e}^{\lambda^2t^2}\right) \leq \mathrm{e}^{-\lambda^2t^2}\sum_{p=0}^\infty \frac{\lambda^{2p}\mathop{\mathbb{E}} \mathfrak{x}^{\,2p}}{p!} \leq \mathrm{e}^{-\lambda^2t^2}\sum_{p=0}^\infty \frac{(\lambda^22pK^2)^p}{p!}. \end{align*} $$
$$ \begin{align*} \mathbb{P}(|\mathfrak{x}|\geq t) = \mathbb{P}\left(\mathrm{e}^{\lambda^2\mathfrak{x}^2}\geq \mathrm{e}^{\lambda^2t^2}\right) \leq \mathrm{e}^{-\lambda^2t^2}\sum_{p=0}^\infty \frac{\lambda^{2p}\mathop{\mathbb{E}} \mathfrak{x}^{\,2p}}{p!} \leq \mathrm{e}^{-\lambda^2t^2}\sum_{p=0}^\infty \frac{(\lambda^22pK^2)^p}{p!}. \end{align*} $$
Now, by setting the value of
![]() $\lambda $
to
$\lambda $
to
![]() $\frac {1}{\sqrt {6}K}$
,
$\frac {1}{\sqrt {6}K}$
,
![]() $ \mathbb {P}(|\mathfrak {x}|\geq t) \leq \mathrm {e}^{-\frac {t^2}{8K^2}}\sum _{p=0}^\infty \frac {(p/3)^p}{p!}. $
The right-hand series is convergent, and after adding the series numerically, we can see that
$ \mathbb {P}(|\mathfrak {x}|\geq t) \leq \mathrm {e}^{-\frac {t^2}{8K^2}}\sum _{p=0}^\infty \frac {(p/3)^p}{p!}. $
The right-hand series is convergent, and after adding the series numerically, we can see that
![]() $ \sum _{p=0}^\infty \frac {(p/3)^p}{p!}= 2.625\ldots \leq \mathrm {e}, $
which finishes the proof of the first part. Following the constants in the proof of [Reference Vershynin58, Proposition 2.5.2] directly seems to give
$ \sum _{p=0}^\infty \frac {(p/3)^p}{p!}= 2.625\ldots \leq \mathrm {e}, $
which finishes the proof of the first part. Following the constants in the proof of [Reference Vershynin58, Proposition 2.5.2] directly seems to give
![]() $4\mathrm {e}\simeq 10.8$
in the denominator of the exponent instead of
$4\mathrm {e}\simeq 10.8$
in the denominator of the exponent instead of
![]() $6$
.
$6$
.
For the second, note that
which follows from
 $$ \begin{align*} \mathbb{P}(|\mathfrak{x}|>u)\leq \begin{cases}1&\text{if }u\leq K\sqrt{2\ln C}\\ \mathrm{e}^{-\frac{u^2}{2K^2}}&\text{if }u\geq K\sqrt{2\ln C}, \end{cases} \end{align*} $$
$$ \begin{align*} \mathbb{P}(|\mathfrak{x}|>u)\leq \begin{cases}1&\text{if }u\leq K\sqrt{2\ln C}\\ \mathrm{e}^{-\frac{u^2}{2K^2}}&\text{if }u\geq K\sqrt{2\ln C}, \end{cases} \end{align*} $$
dividing the integration domain into
![]() $[0,K\sqrt {2\ln C}]$
and
$[0,K\sqrt {2\ln C}]$
and
![]() $[K\sqrt {2\ln C},\infty ]$
and applying some straightforward calculations and bounds.
$[K\sqrt {2\ln C},\infty ]$
and applying some straightforward calculations and bounds.
Now, applying the change of variables
![]() $t=\frac {u^2}{2K}$
, we obtain
$t=\frac {u^2}{2K}$
, we obtain
 $$ \begin{align*} \int_0^\infty pu^{p-1}\mathrm{e}^{-\frac{u^2}{2K}}\,\mathrm{d}u =pK^p2^{\frac{p}{2}-1}\Gamma\left(\frac{p}{2}\right) \leq K^p\left(\frac{\pi p}{2}\right)^{\frac{p}{2}}. \end{align*} $$
$$ \begin{align*} \int_0^\infty pu^{p-1}\mathrm{e}^{-\frac{u^2}{2K}}\,\mathrm{d}u =pK^p2^{\frac{p}{2}-1}\Gamma\left(\frac{p}{2}\right) \leq K^p\left(\frac{\pi p}{2}\right)^{\frac{p}{2}}. \end{align*} $$
Hence
 $$ \begin{align*} \mathop{\mathbb{E}}|\mathfrak{x}|^p\leq K^p\left(\left(2\ln C\right)^{\frac{p}{2}}+\left(\frac{\pi p}{2}\right)^{\frac{p}{2}}\right), \end{align*} $$
$$ \begin{align*} \mathop{\mathbb{E}}|\mathfrak{x}|^p\leq K^p\left(\left(2\ln C\right)^{\frac{p}{2}}+\left(\frac{\pi p}{2}\right)^{\frac{p}{2}}\right), \end{align*} $$
from which the second part follows.
Proof of Proposition 4.25.
This is a version of [Reference Vershynin58, Proposition 2.6.1]. Let us sketch a proof to see the values of the chosen constants.
Let
![]() $\mathfrak {y}\in \mathbb {R}$
be a centred random variable with
$\mathfrak {y}\in \mathbb {R}$
be a centred random variable with
![]() $\psi _2$
-norm at most K. Arguing as in part ‘ii
$\psi _2$
-norm at most K. Arguing as in part ‘ii
![]() $\Rightarrow $
iii’ of the proof of [Reference Vershynin58, Proposition 2.5.2], we have that for all
$\Rightarrow $
iii’ of the proof of [Reference Vershynin58, Proposition 2.5.2], we have that for all
![]() $\lambda \in [-1/\sqrt {2\mathrm {e}},1/\sqrt {2\mathrm {e}}]$
,
$\lambda \in [-1/\sqrt {2\mathrm {e}},1/\sqrt {2\mathrm {e}}]$
,
using
![]() $n!\geq \sqrt {2\pi }(n/e)^n$
and that for
$n!\geq \sqrt {2\pi }(n/e)^n$
and that for
![]() $x\in [-1/2,1/2]$
, we have
$x\in [-1/2,1/2]$
, we have
![]() $1+\frac {1}{\sqrt {2\pi }}\frac {x^2}{1-x^2}\leq \mathrm {e}^{x^2/2}$
. Then arguing as in part ‘iii
$1+\frac {1}{\sqrt {2\pi }}\frac {x^2}{1-x^2}\leq \mathrm {e}^{x^2/2}$
. Then arguing as in part ‘iii
![]() $\Rightarrow $
v’ of the proof of [Reference Vershynin58, Proposition 2.5.2], we get that for all
$\Rightarrow $
v’ of the proof of [Reference Vershynin58, Proposition 2.5.2], we get that for all
![]() $\lambda \in \mathbb {R}$
,
$\lambda \in \mathbb {R}$
,
In this way, we have that
 $$ \begin{align*} \mathbb{P}(|a^*\mathfrak{x}|\geq t)&\leq 2\mathbb{P}(a^*\mathfrak{x}\geq t)&\text{(symmetry)}\\ &=2\mathbb{P}(\mathrm{e}^{a^*\mathfrak{x}}\geq \mathrm{e}{t})&\\ &\leq 2\mathrm{e}^{-\lambda t}\mathop{\mathbb{E}}\mathrm{e}^{\lambda a^*\mathfrak{x}}&\text{(Markov's inequality)}\\ &= 2\mathrm{e}^{-\lambda t}\prod_{i=1}^N\mathop{\mathbb{E}}\mathrm{e}^{\lambda a_i\mathfrak{x}_i}&\text{(}a_1\mathfrak{x}_1,\ldots,a_N\mathfrak{x}_N\text{ independent)}\\ &\leq 2\mathrm{e}^{-\lambda t}\prod_{i=1}^N\mathrm{e}^{\mathrm{e} a_i^2K^2\lambda^2}&(4.5)\\ &= 2\mathrm{e}^{-\lambda t+\mathrm{e} K^2\lambda^2}&(\|a\|_2=1). \end{align*} $$
$$ \begin{align*} \mathbb{P}(|a^*\mathfrak{x}|\geq t)&\leq 2\mathbb{P}(a^*\mathfrak{x}\geq t)&\text{(symmetry)}\\ &=2\mathbb{P}(\mathrm{e}^{a^*\mathfrak{x}}\geq \mathrm{e}{t})&\\ &\leq 2\mathrm{e}^{-\lambda t}\mathop{\mathbb{E}}\mathrm{e}^{\lambda a^*\mathfrak{x}}&\text{(Markov's inequality)}\\ &= 2\mathrm{e}^{-\lambda t}\prod_{i=1}^N\mathop{\mathbb{E}}\mathrm{e}^{\lambda a_i\mathfrak{x}_i}&\text{(}a_1\mathfrak{x}_1,\ldots,a_N\mathfrak{x}_N\text{ independent)}\\ &\leq 2\mathrm{e}^{-\lambda t}\prod_{i=1}^N\mathrm{e}^{\mathrm{e} a_i^2K^2\lambda^2}&(4.5)\\ &= 2\mathrm{e}^{-\lambda t+\mathrm{e} K^2\lambda^2}&(\|a\|_2=1). \end{align*} $$
Taking
![]() $\lambda =\frac {t}{2\mathrm {e} K^2}$
, we get the desired tail bound. The last claim immediately follows from Proposition 4.24.
$\lambda =\frac {t}{2\mathrm {e} K^2}$
, we get the desired tail bound. The last claim immediately follows from Proposition 4.24.
Proof of Proposition 4.26.
This is a rewriting of [Reference Rudelson and Vershynin51, Theorem 1.1] using [Reference Livshyts, Paouris and Pivovarov44] to get explicit constants. This rewriting was first given in [Reference Tonelli-Cueto and Tsigaridas56, Proposition 2.5]. We provide the argument for the sake of completeness.
By the SVD, we have
![]() $A=P\Sigma Q$
, where P is an isometry,
$A=P\Sigma Q$
, where P is an isometry,
![]() $\Sigma \in \mathbb {R}^{k\times k}$
a positive diagonal matrix and Q an orthogonal projection. Hence
$\Sigma \in \mathbb {R}^{k\times k}$
a positive diagonal matrix and Q an orthogonal projection. Hence
and since
![]() $\operatorname {\mathrm {vol}}(\Sigma ^{-1}P^*U)=\operatorname {\mathrm {vol}}(U)/\det \Sigma =\operatorname {\mathrm {vol}}(U)/\sqrt {\det (AA^*)}$
, we only have to prove the claim for the case in which A is an orthogonal projection.
$\operatorname {\mathrm {vol}}(\Sigma ^{-1}P^*U)=\operatorname {\mathrm {vol}}(U)/\det \Sigma =\operatorname {\mathrm {vol}}(U)/\sqrt {\det (AA^*)}$
, we only have to prove the claim for the case in which A is an orthogonal projection.
Now, by [Reference Rudelson and Vershynin51, Theorem 1.1] (see [Reference Livshyts, Paouris and Pivovarov44, Theorem 1.1] for getting the constant), we have that
![]() $A\mathfrak {x}$
has density bounded by
$A\mathfrak {x}$
has density bounded by
![]() $\sqrt {2}\rho $
. Thus
$\sqrt {2}\rho $
. Thus
![]() $\mathbb {P}(A\mathfrak {x}\in U)\leq \operatorname {\mathrm {vol}}(U)(\sqrt {2}\rho )^k$
, as we wanted to show.
$\mathbb {P}(A\mathfrak {x}\in U)\leq \operatorname {\mathrm {vol}}(U)(\sqrt {2}\rho )^k$
, as we wanted to show.
4.3.2
 $\mathsf {K}$
vs.
$\mathsf {K}$
vs.
 $\kappa $
: Measuring the effect of the
$\kappa $
: Measuring the effect of the
 $L_\infty $
-norm on the grid method
$L_\infty $
-norm on the grid method
The condition-based complexity estimates we obtained in this section essentially substitute the
![]() $\kappa $
in the cost estimates of the original algorithm by
$\kappa $
in the cost estimates of the original algorithm by
![]() $\mathsf {K}$
. This way, the comparison between the two algorithms reduces to estimate
$\mathsf {K}$
. This way, the comparison between the two algorithms reduces to estimate
![]() $\mathsf {K}/\kappa $
. The following proposition shows that, in turn, this amounts to looking at the quotient
$\mathsf {K}/\kappa $
. The following proposition shows that, in turn, this amounts to looking at the quotient
![]() $\|f\|_\infty ^{\mathbb {R}}/\|f\|_W$
.
$\|f\|_\infty ^{\mathbb {R}}/\|f\|_W$
.
Proposition 4.27. Let
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
and
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
and
![]() $x\in \mathbb {S}^n$
. Then
$x\in \mathbb {S}^n$
. Then
 $$ \begin{align*} \frac{\|f\|_\infty^{\mathbb{R}}}{\|f\|_W}\leq \frac{\mathsf{K}(f,x)}{\kappa(f,x)}\leq \sqrt{2q\mathbf{D}}\frac{\|f\|_\infty^{\mathbb{R}}}{\|f\|_W} \end{align*} $$
$$ \begin{align*} \frac{\|f\|_\infty^{\mathbb{R}}}{\|f\|_W}\leq \frac{\mathsf{K}(f,x)}{\kappa(f,x)}\leq \sqrt{2q\mathbf{D}}\frac{\|f\|_\infty^{\mathbb{R}}}{\|f\|_W} \end{align*} $$
and
 $$ \begin{align*} \frac{\|f\|_\infty^{\mathbb{R}}}{\|f\|_W}\leq \frac{\mathsf{K}(f)}{\kappa(f)}\leq \sqrt{2q\mathbf{D}}\frac{\|f\|_\infty^{\mathbb{R}}}{\|f\|_W} .\end{align*} $$
$$ \begin{align*} \frac{\|f\|_\infty^{\mathbb{R}}}{\|f\|_W}\leq \frac{\mathsf{K}(f)}{\kappa(f)}\leq \sqrt{2q\mathbf{D}}\frac{\|f\|_\infty^{\mathbb{R}}}{\|f\|_W} .\end{align*} $$
Proof. It follows from
 $$ \begin{align*} \frac{\mathsf{K}(f,x)}{\kappa(f,x)}=\sqrt{q}\frac{\|f\|_\infty^{\mathbb{R}}}{\|f\|_W}\frac{\sqrt{\|f(x)\|^2+\sigma_q\left(\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right)^2}}{\max\left\{\|f(x)\|,\sigma_q\left(\Delta^{-1}\mathrm{D}_xf\right)\right\}} \end{align*} $$
$$ \begin{align*} \frac{\mathsf{K}(f,x)}{\kappa(f,x)}=\sqrt{q}\frac{\|f\|_\infty^{\mathbb{R}}}{\|f\|_W}\frac{\sqrt{\|f(x)\|^2+\sigma_q\left(\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right)^2}}{\max\left\{\|f(x)\|,\sigma_q\left(\Delta^{-1}\mathrm{D}_xf\right)\right\}} \end{align*} $$
and
In general, we have that
![]() $\frac {\|f\|_\infty ^{\mathbb {R}}}{\|f\|_W}\leq 1$
, so the corresponding quotient of condition numbers worsens by a factor of at most
$\frac {\|f\|_\infty ^{\mathbb {R}}}{\|f\|_W}\leq 1$
, so the corresponding quotient of condition numbers worsens by a factor of at most
![]() $\sqrt {2q\mathbf {D}}$
. Our main result derives from the fact that
$\sqrt {2q\mathbf {D}}$
. Our main result derives from the fact that
![]() $\frac {\|f\|_\infty ^{\mathbb {R}}}{\|f\|_W}$
is, for a substantial number of fs, much smaller than 1: we can expect it to be smaller than
$\frac {\|f\|_\infty ^{\mathbb {R}}}{\|f\|_W}$
is, for a substantial number of fs, much smaller than 1: we can expect it to be smaller than
![]() $\sqrt {n\ln (\mathrm {e}\mathbf {D})/N}$
with very high probability. Recall that
$\sqrt {n\ln (\mathrm {e}\mathbf {D})/N}$
with very high probability. Recall that
![]() $K \rho $
is a constant from the randomness model.
$K \rho $
is a constant from the randomness model.
Theorem 4.28. Let
![]() $q\leq n+1$
,
$q\leq n+1$
,
![]() $\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
be dobro with parameters K and
$\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
be dobro with parameters K and
![]() $\rho $
and
$\rho $
and
![]() $\ell \in \mathbb {N}$
. For any power
$\ell \in \mathbb {N}$
. For any power
![]() $\ell $
with
$\ell $
with
![]() $1 \leq \ell < \frac {N}{2}$
, we have
$1 \leq \ell < \frac {N}{2}$
, we have
 $$ \begin{align*} \mathop{\mathbb{E}}_{\mathfrak{f}}\left(\frac{\|\mathfrak{f}\|_\infty^{\mathbb{R}}}{\|\mathfrak{f}\|_W}\right)^\ell \leq \left(\frac{890\sqrt{2}K\rho\sqrt{n\ln(eD)\ell}}{\sqrt{N-2\ell}}\right)^\ell. \end{align*} $$
$$ \begin{align*} \mathop{\mathbb{E}}_{\mathfrak{f}}\left(\frac{\|\mathfrak{f}\|_\infty^{\mathbb{R}}}{\|\mathfrak{f}\|_W}\right)^\ell \leq \left(\frac{890\sqrt{2}K\rho\sqrt{n\ln(eD)\ell}}{\sqrt{N-2\ell}}\right)^\ell. \end{align*} $$
In particular,
 $$ \begin{align*} \mathop{\mathbb{E}}_{\mathfrak{f}} \frac{\|\mathfrak{f}\|_\infty^{\mathbb{R}}}{\|\mathfrak{f}\|_W} \leq \mathcal{O}\left(K\rho\sqrt{ \frac{n \ln(e \mathbf{D})}{N}} \right). \end{align*} $$
$$ \begin{align*} \mathop{\mathbb{E}}_{\mathfrak{f}} \frac{\|\mathfrak{f}\|_\infty^{\mathbb{R}}}{\|\mathfrak{f}\|_W} \leq \mathcal{O}\left(K\rho\sqrt{ \frac{n \ln(e \mathbf{D})}{N}} \right). \end{align*} $$
Remark 4.29. In the study of tensors, the quotients
![]() $\|\mathfrak {f}\|_\infty ^{\mathbb {R}}/\|\mathfrak {f}\|_W$
and their nonsymmetric analogue play an important role. Because of this, we can consider Theorem 4.28 a symmetric analogue of the results shown in [Reference Gross, Flammia and Eisert38] and [Reference Nguyen, Drineas and Tran46]. In a paper under preparation by Kozhasov and the third author [Reference Kozhasov and Tonelli-Cueto41], the probabilistic techniques introduced in this paper are developed further to study
$\|\mathfrak {f}\|_\infty ^{\mathbb {R}}/\|\mathfrak {f}\|_W$
and their nonsymmetric analogue play an important role. Because of this, we can consider Theorem 4.28 a symmetric analogue of the results shown in [Reference Gross, Flammia and Eisert38] and [Reference Nguyen, Drineas and Tran46]. In a paper under preparation by Kozhasov and the third author [Reference Kozhasov and Tonelli-Cueto41], the probabilistic techniques introduced in this paper are developed further to study
![]() $\|\mathfrak {f}\|_\infty ^{\mathbb {R}}/\|\mathfrak {f}\|_W$
in several settings.
$\|\mathfrak {f}\|_\infty ^{\mathbb {R}}/\|\mathfrak {f}\|_W$
in several settings.
Corollary 4.30. Let
![]() $q\leq n+1$
and
$q\leq n+1$
and
![]() $\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
be dobro with parameters K and
$\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
be dobro with parameters K and
![]() $\rho $
. Then for
$\rho $
. Then for
![]() $1 \leq \ell < \frac {N}{2}$
, we have
$1 \leq \ell < \frac {N}{2}$
, we have
 $$ \begin{align*} \mathop{\mathbb{E}}_{\mathfrak{f}}\left(\frac{\mathsf{K}(\mathfrak{f})}{\kappa(\mathfrak{f})}\right)^\ell \leq \left(\frac{1780}K\rho\sqrt{qn\mathbf{D}\ln(eD)\ell}{\sqrt{N-2\ell}}\right)^\ell. \end{align*} $$
$$ \begin{align*} \mathop{\mathbb{E}}_{\mathfrak{f}}\left(\frac{\mathsf{K}(\mathfrak{f})}{\kappa(\mathfrak{f})}\right)^\ell \leq \left(\frac{1780}K\rho\sqrt{qn\mathbf{D}\ln(eD)\ell}{\sqrt{N-2\ell}}\right)^\ell. \end{align*} $$
Let PolyBetti
![]() ${}_W$
be the version of
${}_W$
be the version of
using the Weyl norm and
![]() $\kappa $
. An analysis along the lines of [Reference Cucker, Krick and Shub28] (or [Reference Bürgisser, Cucker and Lairez15]) shows that the cost of PolyBetti
$\kappa $
. An analysis along the lines of [Reference Cucker, Krick and Shub28] (or [Reference Bürgisser, Cucker and Lairez15]) shows that the cost of PolyBetti
![]() ${}_W$
is
${}_W$
is
which is very similar to the cost bound for
in Proposition 4.14. Let us denote by
and
these cost bounds. It follows that

Using Corollary 4.30 and Markov’s inequality, it is easy to prove the following estimate.
Corollary 4.31. Let
![]() $q\leq n+1$
,
$q\leq n+1$
,
![]() $N>20n$
and
$N>20n$
and
![]() $\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
be dobro with parameters K and
$\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
be dobro with parameters K and
![]() $\rho $
,
$\rho $
,

with probability at least
![]() $1-1/N$
. Note that for fixed n and large
$1-1/N$
. Note that for fixed n and large
![]() $\mathbf {D}$
, the ratio in the right-hand side is of the order of
$\mathbf {D}$
, the ratio in the right-hand side is of the order of
 $$ \begin{align*} \left( \frac{ K\rho\sqrt{\ln(\mathrm{e}\mathbf{D})}}{\mathbf{D}}^{\frac{n-1}{2}} \right)^{10n}. \end{align*} $$
$$ \begin{align*} \left( \frac{ K\rho\sqrt{\ln(\mathrm{e}\mathbf{D})}}{\mathbf{D}}^{\frac{n-1}{2}} \right)^{10n}. \end{align*} $$
We proceed to prove Theorem 4.28.
Proposition 4.32. Let
![]() $\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
be dobro with parameters K and
$\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
be dobro with parameters K and
![]() $\rho $
. Then for all
$\rho $
. Then for all
![]() $t>0$
,
$t>0$
,
 $$ \begin{align*} \mathbb{P}\left(\|\mathfrak{f}\|_\infty^{\mathbb{R}}\geq t\right) \leq q\sqrt{2\pi}\sqrt{n+1}\left(\frac{\mathrm{e} \mathbf{D}}{2}\right)^n\mathrm{e}^{-\frac{t^2}{17K^2}}. \end{align*} $$
$$ \begin{align*} \mathbb{P}\left(\|\mathfrak{f}\|_\infty^{\mathbb{R}}\geq t\right) \leq q\sqrt{2\pi}\sqrt{n+1}\left(\frac{\mathrm{e} \mathbf{D}}{2}\right)^n\mathrm{e}^{-\frac{t^2}{17K^2}}. \end{align*} $$
In particular, if
![]() $q\leq n+1$
, for all
$q\leq n+1$
, for all
![]() $\ell \geq 1$
,
$\ell \geq 1$
,
![]() $\left (\mathop {\mathbb {E}}_{\mathfrak {f}}\left (\|\mathfrak {f}\|_\infty ^{\mathbb {R}}\right )^\ell \right )^{\frac {1}{\ell }} \leq 63K\sqrt {n\ln (\mathrm {e}\mathbf {D})\ell }$
.
$\left (\mathop {\mathbb {E}}_{\mathfrak {f}}\left (\|\mathfrak {f}\|_\infty ^{\mathbb {R}}\right )^\ell \right )^{\frac {1}{\ell }} \leq 63K\sqrt {n\ln (\mathrm {e}\mathbf {D})\ell }$
.
Proof of Theorem 4.28.
By the Cauchy-Schwarz inequality,
 $$ \begin{align*} \mathop{\mathbb{E}}_{\mathfrak{f}}\left(\frac{\|\mathfrak{f}\|_\infty^{\mathbb{R}}}{\|\mathfrak{f}\|_W}\right)^\ell &\leq \sqrt{\mathop{\mathbb{E}}_{\mathfrak{f}}\left(\|\mathfrak{f}\|_\infty^{\mathbb{R}}\right)^{2\ell}} \sqrt{\mathop{\mathbb{E}}_{\mathfrak{f}}\frac{1}{\|\mathfrak{f}\|_W^{2\ell}}}. \end{align*} $$
$$ \begin{align*} \mathop{\mathbb{E}}_{\mathfrak{f}}\left(\frac{\|\mathfrak{f}\|_\infty^{\mathbb{R}}}{\|\mathfrak{f}\|_W}\right)^\ell &\leq \sqrt{\mathop{\mathbb{E}}_{\mathfrak{f}}\left(\|\mathfrak{f}\|_\infty^{\mathbb{R}}\right)^{2\ell}} \sqrt{\mathop{\mathbb{E}}_{\mathfrak{f}}\frac{1}{\|\mathfrak{f}\|_W^{2\ell}}}. \end{align*} $$
The first term on the right is bounded by Proposition 4.32.
For the second term, we will use [Reference Mendelson and Paouris45, Theorem 1.11]. We note that
![]() $\mathfrak {x}\in \mathbb {R}^N$
satisfies the small ball assumption (SBA) with constant
$\mathfrak {x}\in \mathbb {R}^N$
satisfies the small ball assumption (SBA) with constant
![]() $\mathcal {L}$
[Reference Mendelson and Paouris45, Assumption 1.1.] if for every
$\mathcal {L}$
[Reference Mendelson and Paouris45, Assumption 1.1.] if for every
![]() $k\in \{1,\ldots ,N-1\}$
, every orthogonal projection
$k\in \{1,\ldots ,N-1\}$
, every orthogonal projection
![]() $P\in \mathbb {R}^{k\times N}$
, every
$P\in \mathbb {R}^{k\times N}$
, every
![]() $y\in \mathbb {R}^k$
and every
$y\in \mathbb {R}^k$
and every
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
By Proposition 4.26 (applied with coordinates orthogonal with respect to the Weyl inner product) and Stirling’s approximation, we have that
![]() $\mathfrak {f}$
has the SBA with constant
$\mathfrak {f}$
has the SBA with constant
![]() $2\sqrt {\pi e}\rho $
. Thus, by [Reference Mendelson and Paouris45, Theorem 1.11],
$2\sqrt {\pi e}\rho $
. Thus, by [Reference Mendelson and Paouris45, Theorem 1.11],
 $$ \begin{align*} \mathop{\mathbb{E}}_{\mathfrak{f}}\frac{1}{\|\mathfrak{f}\|_W^{2\ell}}\leq (14\rho)^{2\ell} \mathop{\mathbb{E}}_{\mathfrak{g}}\frac{1}{\|\mathfrak{g}\|_W^{2\ell}}, \end{align*} $$
$$ \begin{align*} \mathop{\mathbb{E}}_{\mathfrak{f}}\frac{1}{\|\mathfrak{f}\|_W^{2\ell}}\leq (14\rho)^{2\ell} \mathop{\mathbb{E}}_{\mathfrak{g}}\frac{1}{\|\mathfrak{g}\|_W^{2\ell}}, \end{align*} $$
where
![]() $\mathfrak {g}\in \mathcal {H}_{\boldsymbol {d}}[q]$
is KSS. Since
$\mathfrak {g}\in \mathcal {H}_{\boldsymbol {d}}[q]$
is KSS. Since
![]() $\mathfrak {g}$
is a Gaussian vector for all coordinate systems orthogonal with respect to the Weyl inner product,
$\mathfrak {g}$
is a Gaussian vector for all coordinate systems orthogonal with respect to the Weyl inner product,
![]() $\|\mathfrak {g}\|_W^{2}$
is distributed according to a
$\|\mathfrak {g}\|_W^{2}$
is distributed according to a
![]() $\chi ^2$
-distribution with N degrees of freedom. Therefore,
$\chi ^2$
-distribution with N degrees of freedom. Therefore,
 $$ \begin{align*} \mathop{\mathbb{E}}_{\mathfrak{g}}\frac{1}{\|\mathfrak{g}\|_W^{2\ell}} =\int_{0}^\infty t^{-\ell}\frac{1}{2^{\frac{N}{2}} \Gamma\left(\frac{N}{2}\right)}t^{\frac{N}{2}-1} \mathrm{e}^{-\frac{t}{2}}\,\mathrm{d}t =\frac{\Gamma\left(\frac{N}{2}-\ell\right)}{2^{\ell} \Gamma\left(\frac{N}{2}\right)}=\frac{1}{(N-2)(N-4)\cdots(N-2\ell)}. \end{align*} $$
$$ \begin{align*} \mathop{\mathbb{E}}_{\mathfrak{g}}\frac{1}{\|\mathfrak{g}\|_W^{2\ell}} =\int_{0}^\infty t^{-\ell}\frac{1}{2^{\frac{N}{2}} \Gamma\left(\frac{N}{2}\right)}t^{\frac{N}{2}-1} \mathrm{e}^{-\frac{t}{2}}\,\mathrm{d}t =\frac{\Gamma\left(\frac{N}{2}-\ell\right)}{2^{\ell} \Gamma\left(\frac{N}{2}\right)}=\frac{1}{(N-2)(N-4)\cdots(N-2\ell)}. \end{align*} $$
The desired claim now follows.
Proof of Proposition 4.32.
Fix
![]() $\delta \in [0,1/\mathbf {D}]$
. By the proof of Proposition 4.3, we have that
$\delta \in [0,1/\mathbf {D}]$
. By the proof of Proposition 4.3, we have that
![]() $\|\mathfrak {f}\|_\infty ^{\mathbb {R}}>t$
implies
$\|\mathfrak {f}\|_\infty ^{\mathbb {R}}>t$
implies
![]() $\operatorname {\mathrm {vol}}\left \{x\in \mathbb {S}^n\mid \|\mathfrak {f}(x)\|_\infty \geq \left (1-\frac {\mathbf {D}^2}{2}\delta ^2\right )t\right \} \geq \operatorname {\mathrm {vol}} B_{\mathbb {S}}(x_*,\delta )$
, where
$\operatorname {\mathrm {vol}}\left \{x\in \mathbb {S}^n\mid \|\mathfrak {f}(x)\|_\infty \geq \left (1-\frac {\mathbf {D}^2}{2}\delta ^2\right )t\right \} \geq \operatorname {\mathrm {vol}} B_{\mathbb {S}}(x_*,\delta )$
, where
![]() $x_*\in \mathbb {S}^n$
maximises
$x_*\in \mathbb {S}^n$
maximises
![]() $\|f(x)\|_\infty $
. Therefore,
$\|f(x)\|_\infty $
. Therefore,
 $$ \begin{align*} \mathbb{P}\left(\|\mathfrak{f}\|_\infty^{\mathbb{R}}\geq t\right)& \leq \mathbb{P}_{\mathfrak{f}}\left(\mathbb{P}_{\mathfrak{x}\in\mathbb{S}^n} \left(\|\mathfrak{f}(\mathfrak{x})\|_\infty\geq \left(1-\frac{\mathbf{D}^2}{2}\delta^2\right)t\right)\geq \operatorname{\mathrm{vol}} B_{\mathbb{S}}(x_*,\delta)/\operatorname{\mathrm{vol}}\mathbb{S}^n \right). \end{align*} $$
$$ \begin{align*} \mathbb{P}\left(\|\mathfrak{f}\|_\infty^{\mathbb{R}}\geq t\right)& \leq \mathbb{P}_{\mathfrak{f}}\left(\mathbb{P}_{\mathfrak{x}\in\mathbb{S}^n} \left(\|\mathfrak{f}(\mathfrak{x})\|_\infty\geq \left(1-\frac{\mathbf{D}^2}{2}\delta^2\right)t\right)\geq \operatorname{\mathrm{vol}} B_{\mathbb{S}}(x_*,\delta)/\operatorname{\mathrm{vol}}\mathbb{S}^n \right). \end{align*} $$
By [Reference Bürgisser and Cucker14, Lemma 2.25], [Reference Bürgisser and Cucker14, Lemma 2.31] and
![]() $\int _0^\delta \,n\sin ^{n-1}\theta \,\mathrm {d}\theta \geq (1-\delta ^2/6)^n\delta ^n$
, we have that
$\int _0^\delta \,n\sin ^{n-1}\theta \,\mathrm {d}\theta \geq (1-\delta ^2/6)^n\delta ^n$
, we have that
 $$ \begin{align*} \operatorname{\mathrm{vol}}_n B_{\mathbb{S}}(x_*,\delta)/\operatorname{\mathrm{vol}}_n\mathbb{S}^n\geq \frac{\left(1-\delta^2/6\right)^n}{\sqrt{2\pi}\sqrt{n+1}}\delta^n. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{vol}}_n B_{\mathbb{S}}(x_*,\delta)/\operatorname{\mathrm{vol}}_n\mathbb{S}^n\geq \frac{\left(1-\delta^2/6\right)^n}{\sqrt{2\pi}\sqrt{n+1}}\delta^n. \end{align*} $$
In this way,
 $$ \begin{align*} \mathbb{P}&\left(\|\mathfrak{f}\|_\infty^{\mathbb{R}}\geq t\right)\\ &\leq \mathbb{P}_{\mathfrak{f}}\left(\mathbb{P}_{\mathfrak{x}\in\mathbb{S}^n}\left(\|\mathfrak{f}(\mathfrak{x})\|_\infty \geq \left(1-\frac{\mathbf{D}^2}{2}\delta^2\right)t\right) \geq \frac{\left(1-\delta^2/6\right)^n}{\sqrt{2\pi}\sqrt{n+1}}\delta^n\right) \\ &\leq \frac{\sqrt{2\pi}\sqrt{n+1}}{\left(1-\delta^2/6\right)^n\delta^n}\, \mathop{\mathbb{E}}_{\mathfrak{f}} \mathbb{P}_{\mathfrak{x}\in\mathbb{S}^n}\left(\|\mathfrak{f}(\mathfrak{x})\|_\infty \geq \left(1-\frac{\mathbf{D}^2}{2}\delta^2\right)t\right)&\text{(Markov's inequality)}\\ &\leq \frac{\sqrt{2\pi}\sqrt{n+1}}{\left(1-\delta^2/6\right)^n\delta^n}\, \mathop{\mathbb{E}}_{\mathfrak{x}\in\mathbb{S}^n} \mathbb{P}_{\mathfrak{f}}\left(\|\mathfrak{f}(\mathfrak{x})\|_\infty \geq \left(1-\frac{\mathbf{D}^2}{2}\delta^2\right)t\right)&\text{(Tonelli's theorem)}\\ &\leq \frac{\sqrt{2\pi}\sqrt{n+1}}{\left(1-\delta^2/6\right)^n\delta^n}\, \max_{x\in\mathbb{S}^n} \mathbb{P}_{\mathfrak{f}}\left(\|\mathfrak{f}(x)\|_\infty \geq \left(1-\frac{\mathbf{D}^2}{2}\delta^2\right)t\right)\\ &\leq \frac{q\sqrt{2\pi}\sqrt{n+1}}{\left(1-\delta^2/6\right)^n\delta^n}\, \max_{i,x\in\mathbb{S}^n} \mathbb{P}_{\mathfrak{f}}\left(|\mathfrak{f}_i(x)|_\infty \geq \left(1-\frac{\mathbf{D}^2}{2}\delta^2\right)t\right)&\text{(Union bound)}. \end{align*} $$
$$ \begin{align*} \mathbb{P}&\left(\|\mathfrak{f}\|_\infty^{\mathbb{R}}\geq t\right)\\ &\leq \mathbb{P}_{\mathfrak{f}}\left(\mathbb{P}_{\mathfrak{x}\in\mathbb{S}^n}\left(\|\mathfrak{f}(\mathfrak{x})\|_\infty \geq \left(1-\frac{\mathbf{D}^2}{2}\delta^2\right)t\right) \geq \frac{\left(1-\delta^2/6\right)^n}{\sqrt{2\pi}\sqrt{n+1}}\delta^n\right) \\ &\leq \frac{\sqrt{2\pi}\sqrt{n+1}}{\left(1-\delta^2/6\right)^n\delta^n}\, \mathop{\mathbb{E}}_{\mathfrak{f}} \mathbb{P}_{\mathfrak{x}\in\mathbb{S}^n}\left(\|\mathfrak{f}(\mathfrak{x})\|_\infty \geq \left(1-\frac{\mathbf{D}^2}{2}\delta^2\right)t\right)&\text{(Markov's inequality)}\\ &\leq \frac{\sqrt{2\pi}\sqrt{n+1}}{\left(1-\delta^2/6\right)^n\delta^n}\, \mathop{\mathbb{E}}_{\mathfrak{x}\in\mathbb{S}^n} \mathbb{P}_{\mathfrak{f}}\left(\|\mathfrak{f}(\mathfrak{x})\|_\infty \geq \left(1-\frac{\mathbf{D}^2}{2}\delta^2\right)t\right)&\text{(Tonelli's theorem)}\\ &\leq \frac{\sqrt{2\pi}\sqrt{n+1}}{\left(1-\delta^2/6\right)^n\delta^n}\, \max_{x\in\mathbb{S}^n} \mathbb{P}_{\mathfrak{f}}\left(\|\mathfrak{f}(x)\|_\infty \geq \left(1-\frac{\mathbf{D}^2}{2}\delta^2\right)t\right)\\ &\leq \frac{q\sqrt{2\pi}\sqrt{n+1}}{\left(1-\delta^2/6\right)^n\delta^n}\, \max_{i,x\in\mathbb{S}^n} \mathbb{P}_{\mathfrak{f}}\left(|\mathfrak{f}_i(x)|_\infty \geq \left(1-\frac{\mathbf{D}^2}{2}\delta^2\right)t\right)&\text{(Union bound)}. \end{align*} $$
In the coordinates of a monomial basis orthogonal for the Weyl inner product, the following holds: (1) a dobro random polynomial
![]() $\mathfrak {f}$
looks like a random vector whose components are independent and subgaussian of
$\mathfrak {f}$
looks like a random vector whose components are independent and subgaussian of
![]() $\psi _2$
-norm at most K, and (2) evaluation at a point of the sphere,
$\psi _2$
-norm at most K, and (2) evaluation at a point of the sphere,
![]() $\mathfrak {f}(x)$
, becomes the inner product with a vector of norm 1 (by Proposition 2.2). Hence, by Proposition 4.24,
$\mathfrak {f}(x)$
, becomes the inner product with a vector of norm 1 (by Proposition 2.2). Hence, by Proposition 4.24,
 $$ \begin{align*} \mathbb{P}\left(\|\mathfrak{f}\|_\infty^{\mathbb{R}}\geq t\right) \leq \frac{q\sqrt{2\pi}\sqrt{n+1}}{\left(1-\delta^2/6\right)^n\delta^n}\, \exp\left(-\left(1-\frac{\mathbf{D}^2}{2}\delta^2\right)^2\frac{t^2}{11K^2}\right). \end{align*} $$
$$ \begin{align*} \mathbb{P}\left(\|\mathfrak{f}\|_\infty^{\mathbb{R}}\geq t\right) \leq \frac{q\sqrt{2\pi}\sqrt{n+1}}{\left(1-\delta^2/6\right)^n\delta^n}\, \exp\left(-\left(1-\frac{\mathbf{D}^2}{2}\delta^2\right)^2\frac{t^2}{11K^2}\right). \end{align*} $$
The claim follows taking
![]() $\delta =5/(6\mathbf {D})$
and
$\delta =5/(6\mathbf {D})$
and
 $\left (1-\frac {1}{2}\left (\frac {5}{6}\right )^2\right )\frac {1}{11}\geq \frac {1}{17}$
. For the other inequalities on the moments, use Proposition 4.24.
$\left (1-\frac {1}{2}\left (\frac {5}{6}\right )^2\right )\frac {1}{11}\geq \frac {1}{17}$
. For the other inequalities on the moments, use Proposition 4.24.
4.3.3 Complexity of the Plantinga-Vegter algorithm
In [Reference Cucker, Ergür and Tonelli-Cueto24] (compare to [Reference Cucker, Ergür and Tonelli-Cueto23]), we proved the following result (which we are just adapting to the notationFootnote 5 of this paper).
Theorem 4.33 [Reference Cucker, Ergür and Tonelli-Cueto24, Theorem 8.4 and Theorem 7.3].
Let
![]() $\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[1]$
be dobro with parameters K and
$\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[1]$
be dobro with parameters K and
![]() $\rho $
. For all
$\rho $
. For all
![]() $x\in \mathbb {S}^n$
and
$x\in \mathbb {S}^n$
and
![]() $t\geq e$
,
$t\geq e$
,
 $$ \begin{align*} \mathbb{P} \left(\kappa(\mathfrak{f},x) \geq t\right) \leq 2 \left(\frac{N} {n+1}\right)^{\frac{n+1}{2}}(30 K\rho)^{n+1} \frac{\ln^{\frac{n+1}{2}}t}{t^{n+1}}. \end{align*} $$
$$ \begin{align*} \mathbb{P} \left(\kappa(\mathfrak{f},x) \geq t\right) \leq 2 \left(\frac{N} {n+1}\right)^{\frac{n+1}{2}}(30 K\rho)^{n+1} \frac{\ln^{\frac{n+1}{2}}t}{t^{n+1}}. \end{align*} $$
In particular, for the Plantinga-Vegter algorithm with input
![]() $\mathfrak {f}$
over the domain
$\mathfrak {f}$
over the domain
![]() $[-a,a]^n$
, the expected number of hypercubes in the final subdivision is at most
$[-a,a]^n$
, the expected number of hypercubes in the final subdivision is at most
Our objective is the following theorem, which shows how the
![]() $N^{\frac {n+1}{2}}$
factor vanishes from these estimates when we pass from
$N^{\frac {n+1}{2}}$
factor vanishes from these estimates when we pass from
![]() $\kappa $
to
$\kappa $
to
![]() $\mathsf {K}$
. This shows that the version of Plantinga-Vegter using
$\mathsf {K}$
. This shows that the version of Plantinga-Vegter using
![]() $\mathsf {K}$
yields better cost bounds than the one using
$\mathsf {K}$
yields better cost bounds than the one using
![]() $\kappa $
: that is, the one in [Reference Cucker, Ergür and Tonelli-Cueto24].
$\kappa $
: that is, the one in [Reference Cucker, Ergür and Tonelli-Cueto24].
Theorem 4.34. Let
![]() $\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[1]$
be dobro with parameters K and
$\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[1]$
be dobro with parameters K and
![]() $\rho $
. For all
$\rho $
. For all
![]() $x\in \mathbb {S}^n$
and
$x\in \mathbb {S}^n$
and
![]() $t\geq e$
,
$t\geq e$
,
 $$ \begin{align*} \mathbb{P} \left(\mathsf{K}(\mathfrak{f},x) \geq t\right) \leq \mathbf{D}^{\frac{n}{2}}(\ln \mathrm{e}\mathbf{D})^{\frac{n+1}{2}}2^{6n+4}(K\rho)^{n+1} \frac{\ln^{\frac{n+1}{2}}t}{t^{n+1}}. \end{align*} $$
$$ \begin{align*} \mathbb{P} \left(\mathsf{K}(\mathfrak{f},x) \geq t\right) \leq \mathbf{D}^{\frac{n}{2}}(\ln \mathrm{e}\mathbf{D})^{\frac{n+1}{2}}2^{6n+4}(K\rho)^{n+1} \frac{\ln^{\frac{n+1}{2}}t}{t^{n+1}}. \end{align*} $$
It follows that for every compact
![]() $\Omega \subseteq \mathbb {S}^n$
,
$\Omega \subseteq \mathbb {S}^n$
,
In particular, for the Plantinga-Vegter algorithm with input
![]() $\mathfrak {f}$
over the domain
$\mathfrak {f}$
over the domain
![]() $[-a,a]^n$
, the expected number of hypercubes in the final subdivision is at most
$[-a,a]^n$
, the expected number of hypercubes in the final subdivision is at most
Remark 4.35. Theorem 4.34 allows us to compare the efficiency of Plantinga-Vegter for the versions based on the Weyl-norm and the
![]() $\infty $
-norm. One can observe that (in the region of interest
$\infty $
-norm. One can observe that (in the region of interest
![]() $\mathbf {D}> n$
) the term
$\mathbf {D}> n$
) the term
![]() $N^{\frac {n}{2}} \sim \mathbf {D}^{\frac {n^2}{2}}$
in the estimate for the Weyl-norm version is replaced with
$N^{\frac {n}{2}} \sim \mathbf {D}^{\frac {n^2}{2}}$
in the estimate for the Weyl-norm version is replaced with
![]() $(\mathbf {D} \log \mathbf {D})^{\frac {n}{2}} $
in the
$(\mathbf {D} \log \mathbf {D})^{\frac {n}{2}} $
in the
![]() $\infty $
-norm. Basically, the exponent of
$\infty $
-norm. Basically, the exponent of
![]() $\mathbf {D}$
goes from
$\mathbf {D}$
goes from
![]() $\mathcal {O}(n^2)$
to
$\mathcal {O}(n^2)$
to
![]() $\mathcal {O}(n)$
. If we focus on the original cases of interest (compare to [Reference Plantinga and Vegter49]) – that is,
$\mathcal {O}(n)$
. If we focus on the original cases of interest (compare to [Reference Plantinga and Vegter49]) – that is,
![]() $n=2$
and
$n=2$
and
![]() $n=3$
, with the average complexity analysis from [Reference Cucker, Ergür and Tonelli-Cueto24] – it is shown in Theorem 3.1 there that PV-Interval
$n=3$
, with the average complexity analysis from [Reference Cucker, Ergür and Tonelli-Cueto24] – it is shown in Theorem 3.1 there that PV-Interval
![]() ${}_W$
has an average complexity of
${}_W$
has an average complexity of
 $$ \begin{align*} \mathcal{O}\left(d^8\max\{1,a^2\}(K\rho)^3\right) &\qquad \text{for}\ n=2,\ \text{and}\\ \mathcal{O}\left(d^{13}\max\{1,a^3\}(K\rho)^4\right) &\qquad \text{for}\ n=3. \end{align*} $$
$$ \begin{align*} \mathcal{O}\left(d^8\max\{1,a^2\}(K\rho)^3\right) &\qquad \text{for}\ n=2,\ \text{and}\\ \mathcal{O}\left(d^{13}\max\{1,a^3\}(K\rho)^4\right) &\qquad \text{for}\ n=3. \end{align*} $$
It follows from Theorems 4.19 and 4.34 that the average complexity of PV-Interval
![]() ${}_\infty $
is
${}_\infty $
is
 $$ \begin{align*} \mathcal{O}\left(d^7\log^{1.5}(d)\max\{1,a^2\}(K\rho)^3\right) &\qquad \text{for}\ n=2,\ \text{and}\\ \mathcal{O}\left(d^{10}\log^2(d)\max\{1,a^3\}(K\rho)^4\right) &\qquad \text{for}\ n=3. \end{align*} $$
$$ \begin{align*} \mathcal{O}\left(d^7\log^{1.5}(d)\max\{1,a^2\}(K\rho)^3\right) &\qquad \text{for}\ n=2,\ \text{and}\\ \mathcal{O}\left(d^{10}\log^2(d)\max\{1,a^3\}(K\rho)^4\right) &\qquad \text{for}\ n=3. \end{align*} $$
We next proceed to prove Theorem 4.34.
Proof of Theorem 4.34.
Let
![]() $u,t\geq 0$
, then
$u,t\geq 0$
, then
 $$ \begin{align*} \mathbb{P}_{\mathfrak{f}}&\left(\mathsf{K}(\mathfrak{f},x)\geq t\right)\\ &\leq \mathbb{P}_{\mathfrak{f}}\left(\|f\|_\infty^{\mathbb{R}}\geq u\text{ or }\max\left\{|\mathfrak{f}(x)|,\frac{\|\mathrm{D}_x\mathfrak{f}\|}{\mathbf{D}}\right\}\leq \frac{u}{t}\right)&\text{(implication bound)}\\ &\leq \mathbb{P}_{\mathfrak{f}}\left(\|f\|_\infty^{\mathbb{R}}\geq u\right)+\mathbb{P}_{\mathfrak{f}}\left(\max\left\{|\mathfrak{f}(x)|,\frac{\|\mathrm{D}_x\mathfrak{f}\|}{\mathbf{D}}\right\}\leq \frac{u}{t}\right),&\text{(union bound)} \end{align*} $$
$$ \begin{align*} \mathbb{P}_{\mathfrak{f}}&\left(\mathsf{K}(\mathfrak{f},x)\geq t\right)\\ &\leq \mathbb{P}_{\mathfrak{f}}\left(\|f\|_\infty^{\mathbb{R}}\geq u\text{ or }\max\left\{|\mathfrak{f}(x)|,\frac{\|\mathrm{D}_x\mathfrak{f}\|}{\mathbf{D}}\right\}\leq \frac{u}{t}\right)&\text{(implication bound)}\\ &\leq \mathbb{P}_{\mathfrak{f}}\left(\|f\|_\infty^{\mathbb{R}}\geq u\right)+\mathbb{P}_{\mathfrak{f}}\left(\max\left\{|\mathfrak{f}(x)|,\frac{\|\mathrm{D}_x\mathfrak{f}\|}{\mathbf{D}}\right\}\leq \frac{u}{t}\right),&\text{(union bound)} \end{align*} $$
where we used the fact that for
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[1]$
,
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[1]$
,
![]() $\mathsf {K}(f,x)=\|f\|_\infty ^{\mathbb {R}}/\max \left \{|f(x)|,\|\mathrm {D}_xf\|/\mathbf {D}\right \}$
.
$\mathsf {K}(f,x)=\|f\|_\infty ^{\mathbb {R}}/\max \left \{|f(x)|,\|\mathrm {D}_xf\|/\mathbf {D}\right \}$
.
On the one hand,
![]() $\mathbb {P}_{\mathfrak {f}}\left (\|f\|_\infty ^{\mathbb {R}}\geq u\right )$
is bounded by Proposition 4.32. On the other hand, the map
$\mathbb {P}_{\mathfrak {f}}\left (\|f\|_\infty ^{\mathbb {R}}\geq u\right )$
is bounded by Proposition 4.32. On the other hand, the map
has singular values
![]() $1,1/\sqrt {\mathbf {D}},\ldots ,1/\sqrt {\mathbf {D}}$
in the coordinates of a monomial basis orthogonal with respect to the Weyl inner product. And since in such a basis, a dobro polynomial is a vector whose coefficients are independent and have the anti-concentration property with constant
$1,1/\sqrt {\mathbf {D}},\ldots ,1/\sqrt {\mathbf {D}}$
in the coordinates of a monomial basis orthogonal with respect to the Weyl inner product. And since in such a basis, a dobro polynomial is a vector whose coefficients are independent and have the anti-concentration property with constant
![]() $\rho $
, we deduce that
$\rho $
, we deduce that
 $$ \begin{align*} & \mathbb{P}_{\mathfrak{f}}\left(\max\left\{|\mathfrak{f}(x)|,\frac{\|\mathrm{D}_x\mathfrak{f}\|}{\mathbf{D}}\right\} \leq \frac{u}{t}\right)\leq \mathbf{D}^{\frac{n}{2}}\operatorname{\mathrm{vol}}\left\{(x_0,x)\in\mathbb{R}^{n+1}\mid |x_0|,\|x\| \leq u/t\right\}\left(\sqrt{2}\rho\right)^{n+1}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \leq \omega_n\mathbf{D}^{\frac{n}{2}}\left(\frac{\sqrt{2}\rho u}{t}\right)^{n+1} \leq 9^n\mathbf{D}^{\frac{n}{2}}\left(\frac{u\rho}{\sqrt{n}}\right)^{n+1} \frac{1}{t^{n+1}}, \end{align*} $$
$$ \begin{align*} & \mathbb{P}_{\mathfrak{f}}\left(\max\left\{|\mathfrak{f}(x)|,\frac{\|\mathrm{D}_x\mathfrak{f}\|}{\mathbf{D}}\right\} \leq \frac{u}{t}\right)\leq \mathbf{D}^{\frac{n}{2}}\operatorname{\mathrm{vol}}\left\{(x_0,x)\in\mathbb{R}^{n+1}\mid |x_0|,\|x\| \leq u/t\right\}\left(\sqrt{2}\rho\right)^{n+1}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \leq \omega_n\mathbf{D}^{\frac{n}{2}}\left(\frac{\sqrt{2}\rho u}{t}\right)^{n+1} \leq 9^n\mathbf{D}^{\frac{n}{2}}\left(\frac{u\rho}{\sqrt{n}}\right)^{n+1} \frac{1}{t^{n+1}}, \end{align*} $$
where
![]() $\omega _n$
is the volume of the unit n-ball, and we used Proposition 4.26 and Stirling’s estimation [Reference Bürgisser and Cucker14, Equation (2.14)].
$\omega _n$
is the volume of the unit n-ball, and we used Proposition 4.26 and Stirling’s estimation [Reference Bürgisser and Cucker14, Equation (2.14)].
Hence, combining the inequalities above,
 $$ \begin{align*} \mathbb{P}_{\mathfrak{f}}\left(\mathsf{K}(\mathfrak{f},x)\geq t\right)\leq \sqrt{2\pi(n+1)}\left(\frac{\mathrm{e}\mathbf{D}}{2}\right)^n\mathrm{e}^{-\frac{u^2}{17K^2}} +9^n\mathbf{D}^{\frac{n}{2}}\left(\frac{u\rho}{\sqrt{n}}\right)^{n+1} \frac{1}{t^{n+1}}. \end{align*} $$
$$ \begin{align*} \mathbb{P}_{\mathfrak{f}}\left(\mathsf{K}(\mathfrak{f},x)\geq t\right)\leq \sqrt{2\pi(n+1)}\left(\frac{\mathrm{e}\mathbf{D}}{2}\right)^n\mathrm{e}^{-\frac{u^2}{17K^2}} +9^n\mathbf{D}^{\frac{n}{2}}\left(\frac{u\rho}{\sqrt{n}}\right)^{n+1} \frac{1}{t^{n+1}}. \end{align*} $$
Taking
![]() $t\geq e$
and
$t\geq e$
and
![]() $u=\sqrt {17}K\sqrt {n\ln (\mathrm {e}^2\mathbf {D})\ln t}\geq \sqrt {17}K\sqrt {n\ln \mathbf {D}+(n+1)\ln t}$
, we get
$u=\sqrt {17}K\sqrt {n\ln (\mathrm {e}^2\mathbf {D})\ln t}\geq \sqrt {17}K\sqrt {n\ln \mathbf {D}+(n+1)\ln t}$
, we get
 $$ \begin{align*} \mathbb{P}_{\mathfrak{f}}\left(\mathsf{K}(\mathfrak{f},x)\geq t\right)\leq \frac{\sqrt{2\pi(n+1)}}{(2\mathrm{e})^n}\frac{1}{t^{n+1}}+9^n\mathbf{D}^{\frac{n}{2}}\left(\sqrt{17}K\rho\ln^{\frac{1}{2}(\mathrm{e}^2 \mathbf{D})}\right)^{n+1}\frac{\ln^{\frac{n+1}{2}}t}{t^{n+1}}. \end{align*} $$
$$ \begin{align*} \mathbb{P}_{\mathfrak{f}}\left(\mathsf{K}(\mathfrak{f},x)\geq t\right)\leq \frac{\sqrt{2\pi(n+1)}}{(2\mathrm{e})^n}\frac{1}{t^{n+1}}+9^n\mathbf{D}^{\frac{n}{2}}\left(\sqrt{17}K\rho\ln^{\frac{1}{2}(\mathrm{e}^2 \mathbf{D})}\right)^{n+1}\frac{\ln^{\frac{n+1}{2}}t}{t^{n+1}}. \end{align*} $$
This proves the first statement.
By Tonelli’s theorem, to prove the second statement, it is enough to bound
![]() $\mathop {\mathbb {E}}_{\mathfrak {f}}\mathsf {K}(\mathfrak {f},x)^n$
for a fixed
$\mathop {\mathbb {E}}_{\mathfrak {f}}\mathsf {K}(\mathfrak {f},x)^n$
for a fixed
![]() $x\in \mathbb {S}^n$
. Now,
$x\in \mathbb {S}^n$
. Now,
 $$ \begin{align*} &\mathop{\mathbb{E}}_{\mathfrak{f}}\mathsf{K}(\mathfrak{f},x)^n=\int_{0}^\infty\mathbb{P}_{\mathfrak{f}}\left(\mathsf{K}(\mathfrak{f},x) \geq t^{\frac{1}{n}}\right)\\ &\qquad\qquad\le \mathrm{e}^n+\int_{\mathrm{e}^n}^\infty\mathbb{P}_{\mathfrak{f}} \left(\mathsf{K}(\mathfrak{f},x)\geq t^{\frac{1}{n}}\right) \leq \mathrm{e}^n+\int_{\mathrm{e}^n}^\infty \mathbf{D}^{\frac{n}{2}}\ln^{\frac{n+1}{2}}(\mathrm{e}\mathbf{D})2^{6n+4}(K\rho)^{n+1} \frac{\ln(t^{\frac{1}{n}})^{\frac{n+1}{2}}}{t^{1+\frac{1}{n}}}\, \mathrm{d}t\\ &\qquad\qquad\qquad\qquad\qquad\qquad\leq \mathrm{e}^n+\mathbf{D}^{\frac{n}{2}}\ln^{\frac{n+1}{2}}(\mathrm{e}\mathbf{D})2^{6n+4}(K\rho)^{n+1} \int_{1}^\infty\frac{\ln(t^{\frac{1}{n}})^{\frac{n+1}{2}}} {t^{1+\frac{1}{n}}}\,\mathrm{d}t. \end{align*} $$
$$ \begin{align*} &\mathop{\mathbb{E}}_{\mathfrak{f}}\mathsf{K}(\mathfrak{f},x)^n=\int_{0}^\infty\mathbb{P}_{\mathfrak{f}}\left(\mathsf{K}(\mathfrak{f},x) \geq t^{\frac{1}{n}}\right)\\ &\qquad\qquad\le \mathrm{e}^n+\int_{\mathrm{e}^n}^\infty\mathbb{P}_{\mathfrak{f}} \left(\mathsf{K}(\mathfrak{f},x)\geq t^{\frac{1}{n}}\right) \leq \mathrm{e}^n+\int_{\mathrm{e}^n}^\infty \mathbf{D}^{\frac{n}{2}}\ln^{\frac{n+1}{2}}(\mathrm{e}\mathbf{D})2^{6n+4}(K\rho)^{n+1} \frac{\ln(t^{\frac{1}{n}})^{\frac{n+1}{2}}}{t^{1+\frac{1}{n}}}\, \mathrm{d}t\\ &\qquad\qquad\qquad\qquad\qquad\qquad\leq \mathrm{e}^n+\mathbf{D}^{\frac{n}{2}}\ln^{\frac{n+1}{2}}(\mathrm{e}\mathbf{D})2^{6n+4}(K\rho)^{n+1} \int_{1}^\infty\frac{\ln(t^{\frac{1}{n}})^{\frac{n+1}{2}}} {t^{1+\frac{1}{n}}}\,\mathrm{d}t. \end{align*} $$
By changing variables,
![]() $t=\mathrm {e}^{sn}$
, we can see that
$t=\mathrm {e}^{sn}$
, we can see that
 $$ \begin{align*} \int_{1}^\infty\frac{\ln(t^{\frac{1}{n}})^{\frac{n+1}{2}}} {t^{1+\frac{1}{n}}}\,\mathrm{d}t =n\Gamma\left(\frac{n+3}{2}\right) \leq \sqrt{2\pi\mathrm{e}}\,n\sqrt{n+1} \left(\frac{n+1}{2\mathrm{e}}\right)^{\frac{n+1}{2}}, \end{align*} $$
$$ \begin{align*} \int_{1}^\infty\frac{\ln(t^{\frac{1}{n}})^{\frac{n+1}{2}}} {t^{1+\frac{1}{n}}}\,\mathrm{d}t =n\Gamma\left(\frac{n+3}{2}\right) \leq \sqrt{2\pi\mathrm{e}}\,n\sqrt{n+1} \left(\frac{n+1}{2\mathrm{e}}\right)^{\frac{n+1}{2}}, \end{align*} $$
where the inequality comes from Stirling’s approximation [Reference Bürgisser and Cucker14, Equation (2.14)]. Hence, we get
 $$ \begin{align*} &\mathop{\mathbb{E}}_{\mathfrak{f}}\mathsf{K}(\mathfrak{f},x)^n\leq \mathrm{e}^n+\sqrt{2\pi\mathrm{e}}n\sqrt{n+1}\mathbf{D}^{\frac{n}{2}} \ln^{\frac{n+1}{2}}(\mathrm{e}\mathbf{D})\frac{2^{6n+4}}{(2\mathrm{e})^{\frac{n+1}{2}}}(\sqrt{n+1}K\rho)^{n+1}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\leq 8n\sqrt{n+1}\mathbf{D}^{\frac{n}{2}}\ln^{\frac{n+1}{2}} (\mathrm{e}\mathbf{D})\frac{2^{6n+4}}{(2\mathrm{e})^{\frac{n+1}{2}}}(\sqrt{n+1}K\rho)^{n+1}. \end{align*} $$
$$ \begin{align*} &\mathop{\mathbb{E}}_{\mathfrak{f}}\mathsf{K}(\mathfrak{f},x)^n\leq \mathrm{e}^n+\sqrt{2\pi\mathrm{e}}n\sqrt{n+1}\mathbf{D}^{\frac{n}{2}} \ln^{\frac{n+1}{2}}(\mathrm{e}\mathbf{D})\frac{2^{6n+4}}{(2\mathrm{e})^{\frac{n+1}{2}}}(\sqrt{n+1}K\rho)^{n+1}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\leq 8n\sqrt{n+1}\mathbf{D}^{\frac{n}{2}}\ln^{\frac{n+1}{2}} (\mathrm{e}\mathbf{D})\frac{2^{6n+4}}{(2\mathrm{e})^{\frac{n+1}{2}}}(\sqrt{n+1}K\rho)^{n+1}. \end{align*} $$
The second statement now follows after some easy bounds.
5 Linear homotopy for computing complex zeros
Smale’s 17th problem asks if a complex zero of n complex polynomial equations in
![]() $n+1$
homogeneous unknowns can be found on average polynomial time [Reference Smale, Arnold, Atiyah, Lax and Mazur54]. A probabilistic solution to Smale’s 17th problem was given by Beltrán and Pardo in 2009 [Reference Beltrán and Pardo7, Reference Beltrán and Pardo8]. The construction of Beltrán and Pardo was probabilistic in the sense that they exhibited a randomised algorithm.
$n+1$
homogeneous unknowns can be found on average polynomial time [Reference Smale, Arnold, Atiyah, Lax and Mazur54]. A probabilistic solution to Smale’s 17th problem was given by Beltrán and Pardo in 2009 [Reference Beltrán and Pardo7, Reference Beltrán and Pardo8]. The construction of Beltrán and Pardo was probabilistic in the sense that they exhibited a randomised algorithm.
The distribution underlying the average-case analysis for the Beltrán-Pardo algorithm is the complex version of the KSS distribution (see Example 4.22). Finally, the expected running time of Beltrán-Pardo’s algorithm is polynomial in
![]() $N=\dim _{\mathbb {C}}\mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]$
.
$N=\dim _{\mathbb {C}}\mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]$
.
A generic square system of equations with degrees
![]() $d_1,d_2,\ldots ,d_n$
has
$d_1,d_2,\ldots ,d_n$
has
![]() $\mathcal {D}:=d_1\cdot \cdots \cdot d_n$
many zeros, and Smale’s 17th problems asks to compute one of these zeros. Following the initial work by Shub and Smale [Reference Shub and Smale53], the hearth of Beltrán-Pardo solution is a linear homotopy: let’s call it ALH. It takes as input the system f for which a zero is sought, along with an initial pair
$\mathcal {D}:=d_1\cdot \cdots \cdot d_n$
many zeros, and Smale’s 17th problems asks to compute one of these zeros. Following the initial work by Shub and Smale [Reference Shub and Smale53], the hearth of Beltrán-Pardo solution is a linear homotopy: let’s call it ALH. It takes as input the system f for which a zero is sought, along with an initial pair
![]() $(g,\zeta )\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]\times {\mathbb {P}}^n$
satisfying
$(g,\zeta )\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]\times {\mathbb {P}}^n$
satisfying
![]() $g(\zeta )=0$
. If we define
$g(\zeta )=0$
. If we define
![]() $q_t:=tf+(1-t)g$
, for
$q_t:=tf+(1-t)g$
, for
![]() $t\in [0,1]$
, then generically, the segment
$t\in [0,1]$
, then generically, the segment
![]() $[g,f]$
in
$[g,f]$
in
![]() $\mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]$
lifts to a curve
$\mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]$
lifts to a curve
![]() $\{(q_t,\zeta _t)\mid t\in [0,1]\}$
in the solution variety
$\{(q_t,\zeta _t)\mid t\in [0,1]\}$
in the solution variety
The idea of ALH, in a nutshell, is to ‘follow’ this curve (for which we know its origin
![]() $(g,\zeta )$
) close enough that we end up with an approximation to the zero
$(g,\zeta )$
) close enough that we end up with an approximation to the zero
![]() $\zeta _1$
of
$\zeta _1$
of
![]() $f=q_1$
.
$f=q_1$
.
The breakthrough in [Reference Beltrán and Pardo7, Reference Beltrán and Pardo8] was to come up with a randomised algorithm to produce the (long-sought) initial pair
![]() $(g,\zeta )$
. To state this result, we endow
$(g,\zeta )$
. To state this result, we endow
![]() $\mathcal {V}$
with the standard distribution
$\mathcal {V}$
with the standard distribution
![]() $\rho _{\mathsf {std}}$
defined via the following procedure:
$\rho _{\mathsf {std}}$
defined via the following procedure:
-
• Draw a complex KSS system
 $\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]$
.
$\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]$
. -
• Draw
 $\zeta $
from the
$\zeta $
from the
 $\mathcal {D}$
zeros of
$\mathcal {D}$
zeros of
 $\mathfrak {f}$
with the uniform distribution.
$\mathfrak {f}$
with the uniform distribution.
For details on
![]() $\rho _{\mathsf {std}}$
, see [Reference Bürgisser and Cucker14, Section 17.5]. The description of
$\rho _{\mathsf {std}}$
, see [Reference Bürgisser and Cucker14, Section 17.5]. The description of
![]() $\rho _{\mathsf {std}}$
above is not constructive: it merely describes the distribution. It is remarkable, however, that it is possible to efficiently sample from
$\rho _{\mathsf {std}}$
above is not constructive: it merely describes the distribution. It is remarkable, however, that it is possible to efficiently sample from
![]() $\rho _{\mathsf {std}}$
.
$\rho _{\mathsf {std}}$
.
Proposition 5.1. ([Reference Bürgisser and Cucker14, Proposition 17.21]).
There is a randomised algorithm that, with input n and
![]() $\boldsymbol {d}$
, returns a pair
$\boldsymbol {d}$
, returns a pair
![]() $(g,\zeta )\in \mathcal {V}$
drawn from
$(g,\zeta )\in \mathcal {V}$
drawn from
![]() $\rho _{\mathsf {std}}$
. The algorithm performs
$\rho _{\mathsf {std}}$
. The algorithm performs
![]() $2(N+n^2+n+1)$
draws of random real numbers from the standard Gaussian distribution and
$2(N+n^2+n+1)$
draws of random real numbers from the standard Gaussian distribution and
![]() $O(\mathbf {D} nN+n^3)$
arithmetic operations.
$O(\mathbf {D} nN+n^3)$
arithmetic operations.
With this randomisation procedure at hand, the structure of the algorithm to compute approximate zeros is simple.

Here
![]() $\tilde {\Sigma }:=\{(f,\zeta )\in \mathcal {V}\mid \det \mathrm {D}_\zeta f=0\}$
. This set has complex codimension 1 in
$\tilde {\Sigma }:=\{(f,\zeta )\in \mathcal {V}\mid \det \mathrm {D}_\zeta f=0\}$
. This set has complex codimension 1 in
![]() $\mathcal {V}$
. Hence, because the lifting of the segment
$\mathcal {V}$
. Hence, because the lifting of the segment
![]() $[g,f]$
corresponding to
$[g,f]$
corresponding to
![]() $\zeta $
has real dimension 1, generically, it does not cut
$\zeta $
has real dimension 1, generically, it does not cut
![]() $\tilde {\Sigma }$
. That is, algorithm Solve almost surely terminates for almost all inputs
$\tilde {\Sigma }$
. That is, algorithm Solve almost surely terminates for almost all inputs
![]() $f\in \mathcal {H}_{\boldsymbol {d}}[n]$
.
$f\in \mathcal {H}_{\boldsymbol {d}}[n]$
.
Regarding complexity, the total cost of Solve is dominated by that of running ALH, which is given by the number of steps K performed by the homotopy times the cost of each step. In previous work ([Reference Shub and Smale53, Reference Beltrán and Pardo7, Reference Beltrán and Pardo8, Reference Bürgisser and Cucker13, Reference Armentano, Beltrán, Bürgisser, Cucker and Shub3] among others), the latter is essentially optimal as it is
![]() $O(N+n^3)$
(which is
$O(N+n^3)$
(which is
![]() $O(N)$
if
$O(N)$
if
![]() $d_i\ge 2$
for
$d_i\ge 2$
for
![]() $i=1,\ldots ,n$
). The former depends on the input at hand, and that is where average considerations play a role. In [Reference Beltrán and Pardo9, Reference Bürgisser and Cucker13], ALH was implemented using the Weyl norm to compute step lengths. Its average number of iterations is
$i=1,\ldots ,n$
). The former depends on the input at hand, and that is where average considerations play a role. In [Reference Beltrán and Pardo9, Reference Bürgisser and Cucker13], ALH was implemented using the Weyl norm to compute step lengths. Its average number of iterations is
![]() $O(n\mathbf {D}^{3/2}N)$
. The average total complexity of the resulting algorithm, let us call it Solve
$O(n\mathbf {D}^{3/2}N)$
. The average total complexity of the resulting algorithm, let us call it Solve
![]() ${}_W$
, is then
${}_W$
, is then
![]() $O(n\mathbf {D}^{3/2}N^2)$
.
$O(n\mathbf {D}^{3/2}N^2)$
.
The goal of this section is to analyse a version ALH
![]() ${}_\infty $
of ALH with step lengths based on
${}_\infty $
of ALH with step lengths based on
![]() $\|~\|_{\infty }$
. We show that this can be done in a straightforward manner and that, maybe surprisingly, the average number of iterations of ALH with step lengths based on our new condition number is
$\|~\|_{\infty }$
. We show that this can be done in a straightforward manner and that, maybe surprisingly, the average number of iterations of ALH with step lengths based on our new condition number is
![]() $\mathcal {O}(n^3\mathbf {D}^2\ln (n\mathbf {D}))$
: a bound independent of N. Unfortunately, this gain is not decisive for a general input model due to the high cost of computing
$\mathcal {O}(n^3\mathbf {D}^2\ln (n\mathbf {D}))$
: a bound independent of N. Unfortunately, this gain is not decisive for a general input model due to the high cost of computing
![]() $\|~\|_{\infty }$
norms.
$\|~\|_{\infty }$
norms.
Nonetheless, for the particular – but highly relevant – case of quadratic polynomials, we can efficiently compute the
![]() $\infty $
-norm. As a result, we derive bounds that show the expected complexity of Solve
$\infty $
-norm. As a result, we derive bounds that show the expected complexity of Solve
![]() ${}_\infty $
is smaller than the expected complexity of Solve
${}_\infty $
is smaller than the expected complexity of Solve
![]() ${}_W$
.
${}_W$
.
5.1 Description of the linear homotopy
The algorithm below is, essentially, the one in [Reference Bürgisser and Cucker13] and [Reference Bürgisser and Cucker14, Chapter 17]. The only change is in the computation of the step-length
![]() $\Delta _t$
, where we replace the original (here
$\Delta _t$
, where we replace the original (here
![]() $\mathrm {dist}_{\mathbb {S}}$
denotes angle)
$\mathrm {dist}_{\mathbb {S}}$
denotes angle)
 $$ \begin{align*}\frac{0.008535284}{\mathrm{dist}_{\mathbb{S}}(f,g) \mathbf{D}^{3/2}\mu_{\mathrm{norm}}^2(q,z)} \end{align*} $$
$$ \begin{align*}\frac{0.008535284}{\mathrm{dist}_{\mathbb{S}}(f,g) \mathbf{D}^{3/2}\mu_{\mathrm{norm}}^2(q,z)} \end{align*} $$
by
 $$ \begin{align} \frac{0.03\,\|q\|_{\infty}^{\mathbb{C}}} {\|f-g\|_{\infty}^{\mathbb{C}}\mathbf{D}\mathsf{M}^2(q,z)}. \end{align} $$
$$ \begin{align} \frac{0.03\,\|q\|_{\infty}^{\mathbb{C}}} {\|f-g\|_{\infty}^{\mathbb{C}}\mathbf{D}\mathsf{M}^2(q,z)}. \end{align} $$
This change amounts – leaving aside the difference in the constants and a smaller exponent in
![]() $\mathbf {D}$
– to the use of the
$\mathbf {D}$
– to the use of the
![]() $\infty $
-norm instead of the Weyl one and, consequently, the use of
$\infty $
-norm instead of the Weyl one and, consequently, the use of
![]() $\mathsf {M}$
instead of
$\mathsf {M}$
instead of
![]() $\mu _{\mathrm {norm}}$
. Recall that
$\mu _{\mathrm {norm}}$
. Recall that
![]() $N_q$
is the Newton operator associated to
$N_q$
is the Newton operator associated to
![]() $q\in \mathcal {H}_{\boldsymbol {d}}[n]$
.
$q\in \mathcal {H}_{\boldsymbol {d}}[n]$
.

5.2 A bound on the number of iterations
The analysis of ALH
![]() $_\infty $
closely follows the steps in [Reference Bürgisser and Cucker14]. It uses the properties of
$_\infty $
closely follows the steps in [Reference Bürgisser and Cucker14]. It uses the properties of
![]() $\mathsf {M}$
shown in Theorem 3.5 and one more result (we know for
$\mathsf {M}$
shown in Theorem 3.5 and one more result (we know for
![]() $\mu _{\mathrm {norm}}$
): namely, that
$\mu _{\mathrm {norm}}$
): namely, that
![]() $\mathsf {M}$
is a condition number in the standard sense of this expression – it measures how solutions change when data is perturbed (see Proposition 5.4 below). To simplify the notation, in the rest of this section, we will often omit the reference to the base field
$\mathsf {M}$
is a condition number in the standard sense of this expression – it measures how solutions change when data is perturbed (see Proposition 5.4 below). To simplify the notation, in the rest of this section, we will often omit the reference to the base field
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
Theorem 5.2. Suppose that the lifting of the segment
![]() $[g,f]$
in
$[g,f]$
in
![]() $\mathcal {V}$
corresponding to
$\mathcal {V}$
corresponding to
![]() $\zeta $
does not cut
$\zeta $
does not cut
![]() $\Sigma '$
. Then the algorithm ALH
$\Sigma '$
. Then the algorithm ALH
![]() $_\infty $
stops after at most K steps with
$_\infty $
stops after at most K steps with
 $$ \begin{align*}K\le 1+45\, \mathbf{D}\,\|f-g\|_{\infty} \int_0^1 \frac{\mathsf{M}^2(q_t,\zeta_t)}{\|q_t\|_{\infty}} {\mathrm d}t. \end{align*} $$
$$ \begin{align*}K\le 1+45\, \mathbf{D}\,\|f-g\|_{\infty} \int_0^1 \frac{\mathsf{M}^2(q_t,\zeta_t)}{\|q_t\|_{\infty}} {\mathrm d}t. \end{align*} $$
The returned point z is an approximate zero of f with associated zero
![]() $\zeta _1$
.
$\zeta _1$
.
Corollary 5.3. The bound K in Theorem 5.2 satisfies
 $$ \begin{align*}K\le 1+45\, n\,\mathbf{D} \int_0^1 (\| f \|_{\infty} + \| g \|_{\infty})^2 \|\mathrm{D}_{\zeta_t}q_t^{-1}\Delta\|^2 {\mathrm d}t. \end{align*} $$
$$ \begin{align*}K\le 1+45\, n\,\mathbf{D} \int_0^1 (\| f \|_{\infty} + \| g \|_{\infty})^2 \|\mathrm{D}_{\zeta_t}q_t^{-1}\Delta\|^2 {\mathrm d}t. \end{align*} $$
Proposition 5.4. Let
![]() $t\mapsto (f_t,\zeta _t)\in V$
be a smooth path. Then for all t,
$t\mapsto (f_t,\zeta _t)\in V$
be a smooth path. Then for all t,
 $$ \begin{align*}\|\dot{\zeta}_t\|\leq \mathsf{M}(f_t,\zeta_t) \frac{\|\dot{f_t}\|_{\infty}}{\|f_t\|_{\infty}}. \end{align*} $$
$$ \begin{align*}\|\dot{\zeta}_t\|\leq \mathsf{M}(f_t,\zeta_t) \frac{\|\dot{f_t}\|_{\infty}}{\|f_t\|_{\infty}}. \end{align*} $$
Proof in Theorem 5.2.
The proof follows the lines of [Reference Bürgisser and Cucker14, Theorem 17.3]. We will therefore only offer a brief sketch. Set
![]() $\varepsilon :=\frac {1}{4}$
and
$\varepsilon :=\frac {1}{4}$
and
![]() $C=\frac {\varepsilon }{4}=\frac 1{16}$
. Let
$C=\frac {\varepsilon }{4}=\frac 1{16}$
. Let
![]() $q_t:=tf+(1-t)g$
. Also let
$q_t:=tf+(1-t)g$
. Also let
![]() $0<t_1<\ldots <t_K=1$
and
$0<t_1<\ldots <t_K=1$
and
![]() $\zeta _0=z_0,\ldots ,z_K$
be the sequence of t-values and points in
$\zeta _0=z_0,\ldots ,z_K$
be the sequence of t-values and points in
![]() $\mathbb {P}^n$
, respectively, generated by the algorithm in its first K iterations. To simplify notation, we write
$\mathbb {P}^n$
, respectively, generated by the algorithm in its first K iterations. To simplify notation, we write
![]() $q_i$
and
$q_i$
and
![]() $\zeta _i$
instead of
$\zeta _i$
instead of
![]() $q_{t_i}$
and
$q_{t_i}$
and
![]() $\zeta _{t_i}$
.
$\zeta _{t_i}$
.
As in [Reference Bürgisser and Cucker14, Theorem 17.3], but using Proposition 3.6 in the place of [Reference Bürgisser and Cucker14, Proposition 16.2] and Theorem 3.5 in the place of [Reference Bürgisser and Cucker14, Theorem 16.1], one proves by induction the following statements for
![]() $i=0,\ldots ,K-1$
:
$i=0,\ldots ,K-1$
:
(a,i)
![]() $\mathrm {dist}_{\mathbb {P}}(z_i,\zeta _i)\le \frac {C}{\mathbf {D}\mathsf {M}(q_i,\zeta _i)}$
$\mathrm {dist}_{\mathbb {P}}(z_i,\zeta _i)\le \frac {C}{\mathbf {D}\mathsf {M}(q_i,\zeta _i)}$
(b,i)
![]() $\frac {\mathsf {M}(q_i,z_i)}{1+\varepsilon } \le \mathsf {M}(q_i,\zeta _i) \le (1+\varepsilon )\mathsf {M}(q_i,z_i)$
$\frac {\mathsf {M}(q_i,z_i)}{1+\varepsilon } \le \mathsf {M}(q_i,\zeta _i) \le (1+\varepsilon )\mathsf {M}(q_i,z_i)$
(c,i)
![]() $\|q_i-q_{i+1}\|_{\infty } \le \frac {C\|q_i\|_{\infty }}{\mathbf {D}\mathsf {M}(q_i,\zeta _i)}$
$\|q_i-q_{i+1}\|_{\infty } \le \frac {C\|q_i\|_{\infty }}{\mathbf {D}\mathsf {M}(q_i,\zeta _i)}$
(d,i)
![]() $\mathrm {dist}_{\mathbb {P}}(\zeta _i,\zeta _{i+1})\le \frac {C}{\mathbf {D}\mathsf {M}(q_i,\zeta _i)} \frac {1-\varepsilon }{1+\varepsilon }$
$\mathrm {dist}_{\mathbb {P}}(\zeta _i,\zeta _{i+1})\le \frac {C}{\mathbf {D}\mathsf {M}(q_i,\zeta _i)} \frac {1-\varepsilon }{1+\varepsilon }$
(e,i)
![]() $\mathrm {dist}_{\mathbb {P}}(z_i,\zeta _{i+1})\le \frac {2C}{(1+\varepsilon )\mathbf {D}\mathsf {M}(q_i,\zeta _i)}$
$\mathrm {dist}_{\mathbb {P}}(z_i,\zeta _{i+1})\le \frac {2C}{(1+\varepsilon )\mathbf {D}\mathsf {M}(q_i,\zeta _i)}$
(f,i)
![]() $z_i$
is an approximate zero of
$z_i$
is an approximate zero of
![]() $q_{i+1}$
with associated zero
$q_{i+1}$
with associated zero
![]() $\zeta _{i+1}$
.
$\zeta _{i+1}$
.
By Proposition 3.6,
![]() $(\mathrm {c},i)$
,
$(\mathrm {c},i)$
,
![]() $(\mathrm {d},i)$
and our choice of C and
$(\mathrm {d},i)$
and our choice of C and
![]() $\varepsilon $
, we have that for all
$\varepsilon $
, we have that for all
![]() $t\in [t_i,t_{i+1}]$
,
$t\in [t_i,t_{i+1}]$
,
And, by the triangle inequality and
![]() $(\mathrm {b},i)$
, for
$(\mathrm {b},i)$
, for
![]() $t\in [t_i,t_{i+1}]$
,
$t\in [t_i,t_{i+1}]$
,
The statement now easily follows. Consider any
![]() $i\in \{0,1,\ldots ,K-2\}$
. Then
$i\in \{0,1,\ldots ,K-2\}$
. Then
 $$ \begin{align*} \int_{t_i}^{t_{i+1}}\frac{\mathsf{M}^2(q_t,\zeta_t)}{\|q_t\|_\infty} \mathrm{d} t &\geq \frac{64}{85}\int_{t_i}^{t_{i+1}}\frac{\mathsf{M}^2(q_i,z_i)} {\|q_i\|_\infty} \mathrm{d} t=\frac{64}{85}\frac{\mathsf{M}^2(q_i,z_i)} {\|q_i\|_\infty}|t_{i+1}-t_i| & (({5.2})\ \text{and}\ ({5.3}))\\ & =\frac{64}{85}\frac{0.03}{\|f-g\|_\infty \mathbf{D}}.&\text{(choice of}\ \Delta t\text{)} \end{align*} $$
$$ \begin{align*} \int_{t_i}^{t_{i+1}}\frac{\mathsf{M}^2(q_t,\zeta_t)}{\|q_t\|_\infty} \mathrm{d} t &\geq \frac{64}{85}\int_{t_i}^{t_{i+1}}\frac{\mathsf{M}^2(q_i,z_i)} {\|q_i\|_\infty} \mathrm{d} t=\frac{64}{85}\frac{\mathsf{M}^2(q_i,z_i)} {\|q_i\|_\infty}|t_{i+1}-t_i| & (({5.2})\ \text{and}\ ({5.3}))\\ & =\frac{64}{85}\frac{0.03}{\|f-g\|_\infty \mathbf{D}}.&\text{(choice of}\ \Delta t\text{)} \end{align*} $$
Hence
 $$ \begin{align*}\int_{0}^1\frac{\mathsf{M}^2(q_t,z_t)}{\|q_t\|_{\infty}}\mathrm{d} t \ge \frac{192}{8500}\frac{K-1}{\|f-g\|_\infty \mathbf{D}} \ge \frac{K-1}{45\|f-g\|_{\infty}\mathbf{D}}, \end{align*} $$
$$ \begin{align*}\int_{0}^1\frac{\mathsf{M}^2(q_t,z_t)}{\|q_t\|_{\infty}}\mathrm{d} t \ge \frac{192}{8500}\frac{K-1}{\|f-g\|_\infty \mathbf{D}} \ge \frac{K-1}{45\|f-g\|_{\infty}\mathbf{D}}, \end{align*} $$
and the result follows.
Proof of Corollary 5.3.
It immediately follows from the definition of
![]() $\mathsf {M}(q_t,\zeta _t)$
and the inequality
$\mathsf {M}(q_t,\zeta _t)$
and the inequality
![]() $\|q_t\|_{\infty }\le \|f \|_{\infty } + \| g\|_{\infty }$
.
$\|q_t\|_{\infty }\le \|f \|_{\infty } + \| g\|_{\infty }$
.
Proof of Proposition 5.4.
Recall from [Reference Bürgisser and Cucker14, Section 14.3] that the zero
![]() $\zeta _t$
is given by
$\zeta _t$
is given by
![]() $\zeta _t=G(f_t)$
, where
$\zeta _t=G(f_t)$
, where
![]() $G:U\subset \mathcal {H}_{\boldsymbol {d}}[n]\to \mathbb {P}^n$
is a local inverse of the projection
$G:U\subset \mathcal {H}_{\boldsymbol {d}}[n]\to \mathbb {P}^n$
is a local inverse of the projection
![]() $\pi _1:\mathcal {V}\to \mathcal {H}_{\boldsymbol {d}}[n]$
. Hence, for all
$\pi _1:\mathcal {V}\to \mathcal {H}_{\boldsymbol {d}}[n]$
. Hence, for all
![]() $\dot {f_t}\in \mathcal {H}_{\boldsymbol {d}}[n]$
we have
$\dot {f_t}\in \mathcal {H}_{\boldsymbol {d}}[n]$
we have
where the second equality is shown in the course of the proof of [Reference Bürgisser and Cucker14, Proposition 16.10]. Using this equality along with the fact that
![]() $(\mathrm {D}_{\zeta _t} f_t)^{-1}=(\mathrm {D}_{\zeta _t} f_t)^{\dagger }$
(as
$(\mathrm {D}_{\zeta _t} f_t)^{-1}=(\mathrm {D}_{\zeta _t} f_t)^{\dagger }$
(as
![]() $q=n$
), we deduce that
$q=n$
), we deduce that
 $$ \begin{align*} \|\dot\zeta_t\| &= \max_{\|\dot{f_t}\|_{\infty}=1} \|(\mathrm{D}_{\zeta_t} f_t)^{-1}(\dot{f_t}(\zeta_t))\|&(\text{By}\ ({5.4}))\\ &\le \left(\max_{\|\dot{f_t}\|_{\infty}=1}\|\dot{f_t}(\zeta_t)\|\right)\|(\mathrm{D}_{\zeta_t} f_t)^{-1}\|&\text{(operator norm inequality)}\\ &\le \sqrt{n}\left(\max_{\|\dot{f_t}\|_{\infty}=1}\|\dot{f_t}(\zeta_t)\|_\infty\right)\|(\mathrm{D}_{\zeta_t} f_t)^{-1}\|&\|~\|\leq \sqrt{n}\|~\|_\infty\\ &\le \sqrt{n}\|(\mathrm{D}_{\zeta_t} f_t)^{-1}\|&\text{(definition of }\|~\|_\infty\text{)}\\ &= \frac{\sqrt{n}\|f_t\|_{\infty}\|(\Delta^{-1}\mathrm{D}_{\zeta_t} f_t)^{-1}\|}{\|f_t\|_{\infty}} \;=\; \frac{\mathsf{M}(f_t,\zeta_t)}{\|f_t\|_{\infty}}.&\text{(definition of }\mathsf{M})\text{} \end{align*} $$
$$ \begin{align*} \|\dot\zeta_t\| &= \max_{\|\dot{f_t}\|_{\infty}=1} \|(\mathrm{D}_{\zeta_t} f_t)^{-1}(\dot{f_t}(\zeta_t))\|&(\text{By}\ ({5.4}))\\ &\le \left(\max_{\|\dot{f_t}\|_{\infty}=1}\|\dot{f_t}(\zeta_t)\|\right)\|(\mathrm{D}_{\zeta_t} f_t)^{-1}\|&\text{(operator norm inequality)}\\ &\le \sqrt{n}\left(\max_{\|\dot{f_t}\|_{\infty}=1}\|\dot{f_t}(\zeta_t)\|_\infty\right)\|(\mathrm{D}_{\zeta_t} f_t)^{-1}\|&\|~\|\leq \sqrt{n}\|~\|_\infty\\ &\le \sqrt{n}\|(\mathrm{D}_{\zeta_t} f_t)^{-1}\|&\text{(definition of }\|~\|_\infty\text{)}\\ &= \frac{\sqrt{n}\|f_t\|_{\infty}\|(\Delta^{-1}\mathrm{D}_{\zeta_t} f_t)^{-1}\|}{\|f_t\|_{\infty}} \;=\; \frac{\mathsf{M}(f_t,\zeta_t)}{\|f_t\|_{\infty}}.&\text{(definition of }\mathsf{M})\text{} \end{align*} $$
We recall that the norms where we have omitted subscripts are the usual norm in the case of vectors and the usual operator norm in the case of linear maps.
5.3 Average complexity analysis of Solve
 ${}_\infty $
${}_\infty $
The execution of Solve
![]() ${}_\infty $
on an input
${}_\infty $
on an input
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]$
amounts to calling ALH
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]$
amounts to calling ALH
![]() $_\infty $
on input
$_\infty $
on input
![]() $(f,\mathfrak {g},\mathfrak {z})$
, where
$(f,\mathfrak {g},\mathfrak {z})$
, where
![]() $(\mathfrak {g},\mathfrak {z})\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]\times \mathbb {P}^n$
is a standard random pair. Consequently, the number of iterations of Solve
$(\mathfrak {g},\mathfrak {z})\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]\times \mathbb {P}^n$
is a standard random pair. Consequently, the number of iterations of Solve
![]() ${}_\infty $
amounts to the number of iterations done by ALH
${}_\infty $
amounts to the number of iterations done by ALH
![]() $_\infty $
. The latter is a random variable as
$_\infty $
. The latter is a random variable as
![]() $(\mathfrak {g},\mathfrak {z})$
is random. We will further consider f random and bound the average complexity of Solve
$(\mathfrak {g},\mathfrak {z})$
is random. We will further consider f random and bound the average complexity of Solve
![]() $_\infty $
by taking the expectation over both
$_\infty $
by taking the expectation over both
![]() $(\mathfrak {g},\mathfrak {z})$
and f. Recall that a KSS complex random polynomial system
$(\mathfrak {g},\mathfrak {z})$
and f. Recall that a KSS complex random polynomial system
![]() $\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]$
is a tuple of random polynomials
$\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]$
is a tuple of random polynomials
 $$ \begin{align*} \left(\sum_{|\alpha|=d_1}\binom{d_1}{\alpha}^{\frac{1}{2}}\mathfrak{c}_{1,\alpha}X^\alpha,\ldots,\sum_{|\alpha|=d_n}\binom{d_n}{\alpha}^{\frac{1}{2}}\mathfrak{c}_{n,\alpha}X^\alpha\right) \end{align*} $$
$$ \begin{align*} \left(\sum_{|\alpha|=d_1}\binom{d_1}{\alpha}^{\frac{1}{2}}\mathfrak{c}_{1,\alpha}X^\alpha,\ldots,\sum_{|\alpha|=d_n}\binom{d_n}{\alpha}^{\frac{1}{2}}\mathfrak{c}_{n,\alpha}X^\alpha\right) \end{align*} $$
such that the
![]() $\mathfrak {c}_{i,\alpha }$
are independent and identically distributed complex normal random variables of mean 0 and variance 1.
$\mathfrak {c}_{i,\alpha }$
are independent and identically distributed complex normal random variables of mean 0 and variance 1.
Our main result is the following.
Theorem 5.5. Let
![]() $\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]$
. On input
$\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]$
. On input
![]() $\mathfrak {f}$
, Algorithm Solve
$\mathfrak {f}$
, Algorithm Solve
![]() ${}_\infty $
halts with probability 1 and performs
${}_\infty $
halts with probability 1 and performs
iteration steps on average.
Remark 5.6. The bound in Theorem 5.5 is independent on N: it is a polynomial in n and
![]() $\mathbf {D}$
. The possibility of such a bound for the number of iterations of a linear homotopy was explored in [Reference Armentano, Beltrán, Bürgisser, Cucker and Shub3], where the dependence on N was reduced from linear to
$\mathbf {D}$
. The possibility of such a bound for the number of iterations of a linear homotopy was explored in [Reference Armentano, Beltrán, Bürgisser, Cucker and Shub3], where the dependence on N was reduced from linear to
![]() $\mathcal {O}(\sqrt {N})$
. Pierre Lairez subsequently exhibited one such bound but for a rigid homotopy [Reference Lairez42]. To the best of our knowledge, Theorem 5.5 is the first such bound for a linear homotopy.
$\mathcal {O}(\sqrt {N})$
. Pierre Lairez subsequently exhibited one such bound but for a rigid homotopy [Reference Lairez42]. To the best of our knowledge, Theorem 5.5 is the first such bound for a linear homotopy.
We will use the following two results. The first is the complex version of Proposition 4.32 and has an almost identical proof. The main difference lies in the needed volume computations, as the geometry of the complex projective space
![]() $\mathbb {P}^n$
is somewhat different from that of the real sphere
$\mathbb {P}^n$
is somewhat different from that of the real sphere
![]() $\mathbb {S}^n$
. The second is a known result on random complex Gaussian matrices.
$\mathbb {S}^n$
. The second is a known result on random complex Gaussian matrices.
Proposition 5.7. Let
![]() $\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]$
be a KSS complex random polynomial tuple. Then for all
$\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]$
be a KSS complex random polynomial tuple. Then for all
![]() $t>0$
,
$t>0$
,
 $$ \begin{align*} \mathbb{P}\left(\|\mathfrak{f}\|_\infty^{\mathbb{C}}\geq t\right)\leq 2n\left(\frac{3\mathbf{D}}{2}\right)^{2n}\mathrm{e}^{-(t/3)^2}. \end{align*} $$
$$ \begin{align*} \mathbb{P}\left(\|\mathfrak{f}\|_\infty^{\mathbb{C}}\geq t\right)\leq 2n\left(\frac{3\mathbf{D}}{2}\right)^{2n}\mathrm{e}^{-(t/3)^2}. \end{align*} $$
In particular, for all
![]() $\ell \geq 1$
,
$\ell \geq 1$
,
![]() $ \left (\mathop {\mathbb {E}}_{\mathfrak {f}}\left (\|\mathfrak {f}\|_\infty ^{\mathbb {C}}\right )^\ell \right )^{\frac {1}{\ell }}\leq 12\sqrt {\ell \,n\,\ln (eD)} $
.
$ \left (\mathop {\mathbb {E}}_{\mathfrak {f}}\left (\|\mathfrak {f}\|_\infty ^{\mathbb {C}}\right )^\ell \right )^{\frac {1}{\ell }}\leq 12\sqrt {\ell \,n\,\ln (eD)} $
.
Proposition 5.8 [Reference Bürgisser and Cucker14, Proposition 4.27].
Let
![]() $\mathfrak {A}\in \mathbb {C}^{n\times (n+1)}$
be a random complex matrix whose entries are independent and identically distributed complex normal Gaussian variables. Then for all
$\mathfrak {A}\in \mathbb {C}^{n\times (n+1)}$
be a random complex matrix whose entries are independent and identically distributed complex normal Gaussian variables. Then for all
![]() $t\geq 0$
,
$t\geq 0$
,
In particular, for
![]() $\ell \in [1,4)$
,
$\ell \in [1,4)$
,
![]() $\left (\mathop {\mathbb {E}}_{\mathfrak {A}}\|\mathfrak {A}^{\dagger }\|^{\ell }\right )^{\frac {1}{\ell }}\leq \frac {\sqrt {n}}{2}\left (\frac {4}{4-\ell }\right )^{\frac {1}{\ell }}$
.
$\left (\mathop {\mathbb {E}}_{\mathfrak {A}}\|\mathfrak {A}^{\dagger }\|^{\ell }\right )^{\frac {1}{\ell }}\leq \frac {\sqrt {n}}{2}\left (\frac {4}{4-\ell }\right )^{\frac {1}{\ell }}$
.
Proof of Theorem 5.5.
We are calling Algorithm ALH
![]() $_\infty $
with input
$_\infty $
with input
![]() $(\mathfrak {f},\mathfrak {g},\mathfrak {z})$
, where
$(\mathfrak {f},\mathfrak {g},\mathfrak {z})$
, where
![]() $\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]$
is a KSS complex polynomial system and
$\mathfrak {f}\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]$
is a KSS complex polynomial system and
![]() $(\mathfrak {g},\mathfrak {z})\in \mathcal {H}_{\boldsymbol {d}}[n]$
is a standard pair.
$(\mathfrak {g},\mathfrak {z})\in \mathcal {H}_{\boldsymbol {d}}[n]$
is a standard pair.
Let
![]() $\Sigma :=\{h\in \mathcal {H}_{\boldsymbol {d}}[n]\mid \exists \zeta \in \mathbb {P}^n \text { such that }(h,\zeta )\in \tilde {\Sigma }\}$
. By classic results in algebraic geometry, this set is a complex algebraic hypersurface, so it has real codimension
$\Sigma :=\{h\in \mathcal {H}_{\boldsymbol {d}}[n]\mid \exists \zeta \in \mathbb {P}^n \text { such that }(h,\zeta )\in \tilde {\Sigma }\}$
. By classic results in algebraic geometry, this set is a complex algebraic hypersurface, so it has real codimension
![]() $2$
. Hence, with probability one, the segment
$2$
. Hence, with probability one, the segment
![]() $[\mathfrak {g},\mathfrak {f}]$
does not intersect it, and for each zero
$[\mathfrak {g},\mathfrak {f}]$
does not intersect it, and for each zero
![]() $\zeta ^{(i)}$
of
$\zeta ^{(i)}$
of
![]() $\mathfrak {g}$
, we obtain a unique lifted path
$\mathfrak {g}$
, we obtain a unique lifted path
Here, for each t, the
![]() $\zeta _t^{(i)}$
cover all the
$\zeta _t^{(i)}$
cover all the
![]() $d_1\cdots d_n$
different zeros of
$d_1\cdots d_n$
different zeros of
![]() $\mathfrak {q}_t:=t\mathfrak {f}+(1-t)\mathfrak {g}$
. Recall that behind this lifting lies the fact that the map
$\mathfrak {q}_t:=t\mathfrak {f}+(1-t)\mathfrak {g}$
. Recall that behind this lifting lies the fact that the map
![]() $\mathcal {V}\setminus \tilde {\Sigma }\mapsto \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]\setminus \Sigma $
,
$\mathcal {V}\setminus \tilde {\Sigma }\mapsto \mathcal {H}_{\boldsymbol {d}}^{\mathbb {C}}[n]\setminus \Sigma $
,
![]() $(f,\eta )\mapsto f$
, is a regular covering map of degree
$(f,\eta )\mapsto f$
, is a regular covering map of degree
![]() $\mathcal {D}=d_1\cdots d_n$
.
$\mathcal {D}=d_1\cdots d_n$
.
In this way, the random zero
![]() $\mathfrak {z}$
of
$\mathfrak {z}$
of
![]() $\mathfrak {g}$
defines, following its lifted path, a zero
$\mathfrak {g}$
defines, following its lifted path, a zero
![]() $\mathfrak {z}_t$
of
$\mathfrak {z}_t$
of
![]() $\mathfrak {q}_t$
. Moreover, since the original
$\mathfrak {q}_t$
. Moreover, since the original
![]() $\mathfrak {z}$
is chosen uniformly from the
$\mathfrak {z}$
is chosen uniformly from the
![]() $\mathcal {D}$
zeros of
$\mathcal {D}$
zeros of
![]() $\mathfrak {g}$
, the
$\mathfrak {g}$
, the
![]() $\mathfrak {z}_t$
is a uniformly chosen zero of
$\mathfrak {z}_t$
is a uniformly chosen zero of
![]() $\mathfrak {q}_t$
. Hence
$\mathfrak {q}_t$
. Hence
 $$ \begin{align*} \left(\frac{\mathfrak{q}_t}{\sqrt{t^2+(1-t)^2}},\mathfrak{z}_t\right)\in\mathcal{V} \end{align*} $$
$$ \begin{align*} \left(\frac{\mathfrak{q}_t}{\sqrt{t^2+(1-t)^2}},\mathfrak{z}_t\right)\in\mathcal{V} \end{align*} $$
is a standard random pair, since
![]() $\frac {\mathfrak {q}_t}{\sqrt {t^2+(1-t)^2}}$
is a KSS complex random polynomial and
$\frac {\mathfrak {q}_t}{\sqrt {t^2+(1-t)^2}}$
is a KSS complex random polynomial and
![]() $\mathfrak {z}_t$
is a uniformly drawn zero of this system.
$\mathfrak {z}_t$
is a uniformly drawn zero of this system.
By Corollary 5.3, the expected number of iterations of Solve
![]() ${}_\infty $
with input
${}_\infty $
with input
![]() $\mathfrak {f}$
is bounded by
$\mathfrak {f}$
is bounded by
 $$ \begin{align} 45n\,\mathbf{D}\int_{0}^1\,\mathop{\mathbb{E}}_{(\mathfrak{f},\mathfrak{g},\mathfrak{z})} \left((\|\mathfrak{f}\|_\infty^2+\|\mathfrak{g}\|_\infty^2)^2 \|\mathrm{D}_{\mathfrak{z}_t}\mathfrak{q}_t^{-1}\Delta\|^2\right)\,\mathrm{d}t, \end{align} $$
$$ \begin{align} 45n\,\mathbf{D}\int_{0}^1\,\mathop{\mathbb{E}}_{(\mathfrak{f},\mathfrak{g},\mathfrak{z})} \left((\|\mathfrak{f}\|_\infty^2+\|\mathfrak{g}\|_\infty^2)^2 \|\mathrm{D}_{\mathfrak{z}_t}\mathfrak{q}_t^{-1}\Delta\|^2\right)\,\mathrm{d}t, \end{align} $$
where we have moved the expectation inside the integral using Tonelli’s theorem. Now, by Hölder’s inequality,
 $$ \begin{align} \mathop{\mathbb{E}}_{(\mathfrak{f},\mathfrak{g},\mathfrak{z})}\left((\|\mathfrak{f}\|_\infty^2+\|\mathfrak{g}\|_\infty^2)^2 \|\mathrm{D}_{\mathfrak{z}_t}\mathfrak{q}_t^{-1}\Delta\|^2\right)\leq \left(\mathop{\mathbb{E}}_{(\mathfrak{f},\mathfrak{g},\mathfrak{z})}(\|\mathfrak{f}\|_\infty^2 +\|\mathfrak{g}\|_\infty^2)^6\right)^{\frac{1}{3}}\left(\mathop{\mathbb{E}}_{(\mathfrak{f},\mathfrak{g},\mathfrak{z})} \|\mathrm{D}_{\mathfrak{z}_t}\mathfrak{q}_t^{-1}\Delta\|^3\right)^{\frac{2}{3}}. \end{align} $$
$$ \begin{align} \mathop{\mathbb{E}}_{(\mathfrak{f},\mathfrak{g},\mathfrak{z})}\left((\|\mathfrak{f}\|_\infty^2+\|\mathfrak{g}\|_\infty^2)^2 \|\mathrm{D}_{\mathfrak{z}_t}\mathfrak{q}_t^{-1}\Delta\|^2\right)\leq \left(\mathop{\mathbb{E}}_{(\mathfrak{f},\mathfrak{g},\mathfrak{z})}(\|\mathfrak{f}\|_\infty^2 +\|\mathfrak{g}\|_\infty^2)^6\right)^{\frac{1}{3}}\left(\mathop{\mathbb{E}}_{(\mathfrak{f},\mathfrak{g},\mathfrak{z})} \|\mathrm{D}_{\mathfrak{z}_t}\mathfrak{q}_t^{-1}\Delta\|^3\right)^{\frac{2}{3}}. \end{align} $$
By Proposition 5.7, we have that
 $$ \begin{align*} \left(\mathop{\mathbb{E}}_{(\mathfrak{f},\mathfrak{g},\mathfrak{z})}(\|\mathfrak{f}\|_\infty^2+\|\mathfrak{g}\|_\infty^2)^6\right)^{\frac{1}{3}}=\mathcal{O}(n\ln(\mathrm{e}\mathbf{D})). \end{align*} $$
$$ \begin{align*} \left(\mathop{\mathbb{E}}_{(\mathfrak{f},\mathfrak{g},\mathfrak{z})}(\|\mathfrak{f}\|_\infty^2+\|\mathfrak{g}\|_\infty^2)^6\right)^{\frac{1}{3}}=\mathcal{O}(n\ln(\mathrm{e}\mathbf{D})). \end{align*} $$
To apply the proposition, we expanded the binomial and used the fact that
![]() $\mathfrak {f}$
and
$\mathfrak {f}$
and
![]() $\mathfrak {g}$
are independent.
$\mathfrak {g}$
are independent.
Because
![]() $(\mathfrak {q}_t/\sqrt {t^2+(1-t)^2},\mathfrak {z}_t)$
is a random standard pair, we have that
$(\mathfrak {q}_t/\sqrt {t^2+(1-t)^2},\mathfrak {z}_t)$
is a random standard pair, we have that
 $$ \begin{align} \mathop{\mathbb{E}}_{(\mathfrak{f},\mathfrak{g},\mathfrak{z})}\|\mathrm{D}_{\mathfrak{z}_t}\mathfrak{q}_t^{-1}\Delta\|^3 =\left(t^2+(1-t)^2\right)^{\frac{3}{2}} \mathop{\mathbb{E}}_{(\mathfrak{h},\mathfrak{y})\sim\rho_{\mathsf{std}}}\|\mathrm{D}_{\mathfrak{y}}\mathfrak{h}^{-1}\Delta\|^3. \end{align} $$
$$ \begin{align} \mathop{\mathbb{E}}_{(\mathfrak{f},\mathfrak{g},\mathfrak{z})}\|\mathrm{D}_{\mathfrak{z}_t}\mathfrak{q}_t^{-1}\Delta\|^3 =\left(t^2+(1-t)^2\right)^{\frac{3}{2}} \mathop{\mathbb{E}}_{(\mathfrak{h},\mathfrak{y})\sim\rho_{\mathsf{std}}}\|\mathrm{D}_{\mathfrak{y}}\mathfrak{h}^{-1}\Delta\|^3. \end{align} $$
Now, since
![]() $(\mathfrak {h},\mathfrak {y})$
is a random standard pair, the matrix
$(\mathfrak {h},\mathfrak {y})$
is a random standard pair, the matrix
is a random complex Gaussian matrix. This is the so-called Beltrán-Pardo trick [Reference Bürgisser and Cucker14, Proposition 17.21(a)]. Moreover,
![]() $\|\mathrm {D}_{\mathfrak {y}}\mathfrak {h}^{-1}\Delta ^{\frac {1}{2}}\| =\|\overline {\mathrm {D}}_{\mathfrak {y}}\mathfrak {h}^{\dagger }\Delta ^{\frac {1}{2}}\|$
, since
$\|\mathrm {D}_{\mathfrak {y}}\mathfrak {h}^{-1}\Delta ^{\frac {1}{2}}\| =\|\overline {\mathrm {D}}_{\mathfrak {y}}\mathfrak {h}^{\dagger }\Delta ^{\frac {1}{2}}\|$
, since
![]() $\mathfrak {y}$
is a zero of
$\mathfrak {y}$
is a zero of
![]() $\mathfrak {h}$
and
$\mathfrak {h}$
and
![]() $\mathrm {D}_{\mathfrak {y}}\mathfrak {h}$
is just
$\mathrm {D}_{\mathfrak {y}}\mathfrak {h}$
is just
![]() $\overline {\mathrm {D}}_{\mathfrak {y}}\mathfrak {h}$
restricted to the orthogonal complement of
$\overline {\mathrm {D}}_{\mathfrak {y}}\mathfrak {h}$
restricted to the orthogonal complement of
![]() $\mathfrak {y}$
, which we can view as
$\mathfrak {y}$
, which we can view as
![]() $\mathrm {T}_{\mathfrak {y}}\mathbb {P}^n$
. Because of this, by Proposition 5.8,
$\mathrm {T}_{\mathfrak {y}}\mathbb {P}^n$
. Because of this, by Proposition 5.8,
 $$ \begin{align*} \mathop{\mathbb{E}}_{(\mathfrak{h},\mathfrak{y})\sim\rho_{\mathsf{std}}}\|\mathrm{D}_{\mathfrak{z}_t}\mathfrak{q}_t^{-1}\Delta\|^3 \leq \mathbf{D}^{\frac{3}{2}}\mathop{\mathbb{E}}_{(\mathfrak{h},\mathfrak{y})\sim\rho_{\mathsf{std}}} \left\|\left(\Delta^{-\frac{1}{2}}\overline{\mathrm{D}}_{\mathfrak{z}_t} \mathfrak{q}_t\right)^{\dagger}\right\|^3\leq \frac{1}{2}\mathbf{D}^{\frac{3}{2}}n^{\frac{3}{2}}. \end{align*} $$
$$ \begin{align*} \mathop{\mathbb{E}}_{(\mathfrak{h},\mathfrak{y})\sim\rho_{\mathsf{std}}}\|\mathrm{D}_{\mathfrak{z}_t}\mathfrak{q}_t^{-1}\Delta\|^3 \leq \mathbf{D}^{\frac{3}{2}}\mathop{\mathbb{E}}_{(\mathfrak{h},\mathfrak{y})\sim\rho_{\mathsf{std}}} \left\|\left(\Delta^{-\frac{1}{2}}\overline{\mathrm{D}}_{\mathfrak{z}_t} \mathfrak{q}_t\right)^{\dagger}\right\|^3\leq \frac{1}{2}\mathbf{D}^{\frac{3}{2}}n^{\frac{3}{2}}. \end{align*} $$
Hence, integrating equation (5.7),
 $$ \begin{align} \left(\int_0^1\,\mathop{\mathbb{E}}_{(\mathfrak{f},\mathfrak{g},\mathfrak{z})}\|\mathrm{D}_{\mathfrak{z}_t}\mathfrak{q}_t^{-1}\Delta\|^3 \,\mathrm{d}t\right)^{\frac{2}{3}}=\mathcal{O}(n\,\mathbf{D}). \end{align} $$
$$ \begin{align} \left(\int_0^1\,\mathop{\mathbb{E}}_{(\mathfrak{f},\mathfrak{g},\mathfrak{z})}\|\mathrm{D}_{\mathfrak{z}_t}\mathfrak{q}_t^{-1}\Delta\|^3 \,\mathrm{d}t\right)^{\frac{2}{3}}=\mathcal{O}(n\,\mathbf{D}). \end{align} $$
Putting together equations (5.5), (5.6) and (5.8), the desired result follows.
5.4 Systems of quadratic equations
Theorem 5.5 is an improvement over the average number of iterations of Solve
![]() ${}_W$
, which is
${}_W$
, which is
![]() $\mathcal {O}(nDN)$
. Furthermore, in the case of quadratic systems, we can compute each iteration with low cost, ensuring that the average total complexity remains smaller than the one for Solve
$\mathcal {O}(nDN)$
. Furthermore, in the case of quadratic systems, we can compute each iteration with low cost, ensuring that the average total complexity remains smaller than the one for Solve
![]() ${}_W$
, which is
${}_W$
, which is
![]() $\mathcal {O}(n^7)$
. The major task left, unsurprisingly, is to compute
$\mathcal {O}(n^7)$
. The major task left, unsurprisingly, is to compute
![]() $\|q\|_\infty ^{\mathbb {C}}$
in equation (5.1). But we can use that, for a quadratic polynomial
$\|q\|_\infty ^{\mathbb {C}}$
in equation (5.1). But we can use that, for a quadratic polynomial
![]() $q_i$
, we can write
$q_i$
, we can write
![]() $q_i(X)$
as
$q_i(X)$
as
![]() $X^TA_iX$
with
$X^TA_iX$
with
![]() $A_i$
complex symmetric and that
$A_i$
complex symmetric and that
![]() $\|q_i\|_\infty =\|A_i\|$
. We can then compute for a quadratic system
$\|q_i\|_\infty =\|A_i\|$
. We can then compute for a quadratic system
![]() $q\in \mathcal {H}_{\mathbf {2}}[n]$
the norm
$q\in \mathcal {H}_{\mathbf {2}}[n]$
the norm
![]() $\|q\|_\infty =\max \|q_i\|_{\infty }$
. A naive approach to compute each
$\|q\|_\infty =\max \|q_i\|_{\infty }$
. A naive approach to compute each
![]() $\|q_i\|_{\infty }$
leads to an
$\|q_i\|_{\infty }$
leads to an
![]() $\mathcal {O}(n^4)$
cost for the computation of
$\mathcal {O}(n^4)$
cost for the computation of
![]() $\|q\|_{\infty }$
as it uses
$\|q\|_{\infty }$
as it uses
![]() $\mathcal {O}(n^3)$
operations to compute each
$\mathcal {O}(n^3)$
operations to compute each
![]() $\|q_i\|_\infty $
. Proposition 5.10 below shows we can do better. All in all, we obtain the following result.
$\|q_i\|_\infty $
. Proposition 5.10 below shows we can do better. All in all, we obtain the following result.
Theorem 5.9 (Solving systems of quadratic equations).
Algorithm Solve
![]() ${}_\infty $
finds a common complex zero of a system of quadratic equations
${}_\infty $
finds a common complex zero of a system of quadratic equations
![]() $f\in \mathcal {H}_{\mathbf {2}}[n]$
within
$f\in \mathcal {H}_{\mathbf {2}}[n]$
within
![]() $\mathcal {O}(n^{4.5+\omega })$
time on average, where
$\mathcal {O}(n^{4.5+\omega })$
time on average, where
![]() $\omega $
is the exponent for the cost of matrix multiplication. We currently have
$\omega $
is the exponent for the cost of matrix multiplication. We currently have
![]() $\omega <2.375$
.
$\omega <2.375$
.
Proposition 5.10. Let
![]() $q\in \mathcal {H}_{\mathbf {2}}[n]$
be a quadratic system such that for each i,
$q\in \mathcal {H}_{\mathbf {2}}[n]$
be a quadratic system such that for each i,
![]() $q_i=X^TA_iX$
. Then
$q_i=X^TA_iX$
. Then
 $$ \begin{align*} \|q\|_\infty^{\mathbb{C}}\leq \sqrt{\left\|\sum_{i=1}^nA_i^*A_i\right\|}\leq \sqrt{n}\|q\|_\infty^{\mathbb{C}}, \end{align*} $$
$$ \begin{align*} \|q\|_\infty^{\mathbb{C}}\leq \sqrt{\left\|\sum_{i=1}^nA_i^*A_i\right\|}\leq \sqrt{n}\|q\|_\infty^{\mathbb{C}}, \end{align*} $$
where the norm
![]() $\|~\|$
in the middle formula is the usual operator norm. Moreover, the number
$\|~\|$
in the middle formula is the usual operator norm. Moreover, the number
![]() $\sqrt {\left \|\sum _{i=1}^nA_i^*A_i\right \|}$
can be computed with
$\sqrt {\left \|\sum _{i=1}^nA_i^*A_i\right \|}$
can be computed with
![]() $\mathcal {O}(n^{1+\omega })$
operations, where
$\mathcal {O}(n^{1+\omega })$
operations, where
![]() $\omega $
is the exponent of matrix multiplication.
$\omega $
is the exponent of matrix multiplication.
Proof of Theorem 5.9.
By Proposition 5.10, we can estimate the step length of our homotopy
 $$ \begin{align*} \frac{0.015\,\|q\|_{\infty}^{\mathbb{C}}} {\|f-g\|_{\infty}^{\mathbb{C}}\mathsf{M}^2(q,z)}=\frac{0.06} {\|f-g\|_{\infty}^{\mathbb{C}}\mathbf{D}\|q\|_{\infty}^{\mathbb{C}}\|\mathrm{D}_{z}q^{-1}\|^2} \end{align*} $$
$$ \begin{align*} \frac{0.015\,\|q\|_{\infty}^{\mathbb{C}}} {\|f-g\|_{\infty}^{\mathbb{C}}\mathsf{M}^2(q,z)}=\frac{0.06} {\|f-g\|_{\infty}^{\mathbb{C}}\mathbf{D}\|q\|_{\infty}^{\mathbb{C}}\|\mathrm{D}_{z}q^{-1}\|^2} \end{align*} $$
by the smaller
 $$ \begin{align*} \frac{0.06} {\|f-g\|_{\infty}^{\mathbb{C}}\sqrt{\left\|\sum_{i=1}^nA_i^*A_i\right\|}\,\|\mathrm{D}_{z}q^{-1}\|^2}, \end{align*} $$
$$ \begin{align*} \frac{0.06} {\|f-g\|_{\infty}^{\mathbb{C}}\sqrt{\left\|\sum_{i=1}^nA_i^*A_i\right\|}\,\|\mathrm{D}_{z}q^{-1}\|^2}, \end{align*} $$
where
![]() $q=(X^TA_iX)_i$
. In doing so, the algorithm still terminates but gets an extra factor of
$q=(X^TA_iX)_i$
. In doing so, the algorithm still terminates but gets an extra factor of
![]() $\sqrt {n}$
.
$\sqrt {n}$
.
Now
![]() $\|f-g\|_\infty $
can be computed in
$\|f-g\|_\infty $
can be computed in
![]() $\mathcal {O}(n^4)$
operations at the beginning of the algorithm a single time, so we don’t need to compute it in each iteration. By Proposition 5.10, we can compute
$\mathcal {O}(n^4)$
operations at the beginning of the algorithm a single time, so we don’t need to compute it in each iteration. By Proposition 5.10, we can compute
![]() $\sqrt {\left \|\sum _{i=1}^nA_i^*A_i\right \|}$
in
$\sqrt {\left \|\sum _{i=1}^nA_i^*A_i\right \|}$
in
![]() $\mathcal {O}(n^{1+\omega })$
operations, and by [Reference Bürgisser and Cucker14, Proposition 16.32], the remaining arithmetic operations can be done in
$\mathcal {O}(n^{1+\omega })$
operations, and by [Reference Bürgisser and Cucker14, Proposition 16.32], the remaining arithmetic operations can be done in
![]() $\mathcal {O}(n^3)$
operations. Combining this with the bound of Theorem 5.5 and adding the extra factor
$\mathcal {O}(n^3)$
operations. Combining this with the bound of Theorem 5.5 and adding the extra factor
![]() $\sqrt {n}$
gives the desired estimate.
$\sqrt {n}$
gives the desired estimate.
Proof of Proposition 5.10.
By the so-called Autonne–Takagi factorisation [Reference Horn and Johnson39, Problem 33], we have that
for some real diagonal matrix
![]() $D_i$
with nonnegative entries and some unitary matrix
$D_i$
with nonnegative entries and some unitary matrix
![]() $U_i$
. Now it is easy to check that
$U_i$
. Now it is easy to check that
 $$ \begin{align*} \|q_i\|_\infty^{\mathbb{C}}=\|D_i\|=\sqrt{\|D_i^*D_i\|}=\sqrt{\|A_i^*A_i\|}\leq \sqrt{\left\|\sum_{i=1}^nA_i^*A_i\right\|}, \end{align*} $$
$$ \begin{align*} \|q_i\|_\infty^{\mathbb{C}}=\|D_i\|=\sqrt{\|D_i^*D_i\|}=\sqrt{\|A_i^*A_i\|}\leq \sqrt{\left\|\sum_{i=1}^nA_i^*A_i\right\|}, \end{align*} $$
where the last inequality follows from the fact that the operator norm is nondecreasing with respect to the order of psd matrices. So
![]() $\|q\|_\infty ^{\mathbb {C}}\leq \sqrt {\left \|\sum _{i=1}^nA_i^*A_i\right \|}$
, as we wanted to show.
$\|q\|_\infty ^{\mathbb {C}}\leq \sqrt {\left \|\sum _{i=1}^nA_i^*A_i\right \|}$
, as we wanted to show.
For the other inequality, observe that
 $$ \begin{align*} \sqrt{\left\|\sum_{i=1}^nA_i^*A_i\right\|}\leq \sqrt{\sum_{i=1}^n\left\|A_i^*A_i\right\|} =\sqrt{\sum_{i=1}^n\left(\|q_i\|_\infty^{\mathbb{C}}\right)^2} \leq \sqrt{n}\|q\|_\infty^{\mathbb{C}}, \end{align*} $$
$$ \begin{align*} \sqrt{\left\|\sum_{i=1}^nA_i^*A_i\right\|}\leq \sqrt{\sum_{i=1}^n\left\|A_i^*A_i\right\|} =\sqrt{\sum_{i=1}^n\left(\|q_i\|_\infty^{\mathbb{C}}\right)^2} \leq \sqrt{n}\|q\|_\infty^{\mathbb{C}}, \end{align*} $$
where the equality follows from reversing the equalities in the previously displayed formula. This finishes the proof of the inequalities.
Regarding cost, note that computing
![]() $A_i^*A_i$
takes
$A_i^*A_i$
takes
![]() $\mathcal {O}(n^\omega )$
operations, so computing all the
$\mathcal {O}(n^\omega )$
operations, so computing all the
![]() $A_i^*A_i$
requires
$A_i^*A_i$
requires
![]() $\mathcal {O}(n^{1+\omega })$
operations. Then adding the
$\mathcal {O}(n^{1+\omega })$
operations. Then adding the
![]() $A_i^*A_i$
requires
$A_i^*A_i$
requires
![]() $\mathcal {O}(n^3)$
operations and computing
$\mathcal {O}(n^3)$
operations and computing
![]() $\left \|\sum _{i=1}^nA_i^*A_i\right \|$
another
$\left \|\sum _{i=1}^nA_i^*A_i\right \|$
another
![]() $\mathcal {O}(n^3)$
operations. We thus get
$\mathcal {O}(n^3)$
operations. We thus get
![]() $\mathcal {O}(n^{1+\omega })$
operations in total, as we wanted to show.
$\mathcal {O}(n^{1+\omega })$
operations in total, as we wanted to show.
Acknowledgements
The second author is grateful to Hakan and Bahadır Ergür for their cheerful response to his sudden all-day availability throughout the pandemic times. The third author is grateful to Evgenia Lagoda for moral support and Gato Suchen for useful suggestions for this paper. We are thankful to the reviewers of this paper for useful suggestions that helped improve the presentation and to Khazhgali Kozhasov for pointing out an error in a constant used in Proposition 4.24.
Conflict of Interest
The authors have no conflict of interest to declare.
Financial support
This work was supported by the Einstein Foundation Berlin. The first author was partially supported by GRF grant CityU 11300220. The second author was partially supported by NSF CCF 211 00 75. The last author was supported by a postdoctoral fellowship of the 2020 ‘Interaction’ program of the Fondation Sciences Mathématiques de Paris. Partially supported by the ANR JCJC GALOP (ANR-17-CE40-0009), the PGMO grant ALMA and the PHC GRAPE.
A Extension to spaces of
 $C^1$
-maps
$C^1$
-maps
In this appendix, we prove some condition number theorems for the space of
![]() $C^1$
-functions over
$C^1$
-functions over
![]() $\mathbb {S}^n$
,
$\mathbb {S}^n$
,
![]() $C^1[q]:=C^1(\mathbb {S}^n,\mathbb {R}^q)$
. Note that
$C^1[q]:=C^1(\mathbb {S}^n,\mathbb {R}^q)$
. Note that
![]() $C^1[q]$
is not complete with respect to
$C^1[q]$
is not complete with respect to
![]() $\|~\|_{\infty }$
. Consider instead, for
$\|~\|_{\infty }$
. Consider instead, for
![]() $f\in C^1[q]$
,
$f\in C^1[q]$
,
 $$ \begin{align*} \|f\|_{\overline{\infty}}:=\max_{x\in\mathbb{S}^n} \sqrt{\|f(x)\|^2_2+\|\mathrm{D}_xf\|^2_{2,2}} =\max_{\substack{x\in\mathbb{S}^n\\v\in\mathrm{T}_x\mathbb{S}^n}} \sqrt{\|f(x)\|^2+\frac{\|\mathrm{D}_xfv\|^2_2}{\|v\|_2^2}}. \end{align*} $$
$$ \begin{align*} \|f\|_{\overline{\infty}}:=\max_{x\in\mathbb{S}^n} \sqrt{\|f(x)\|^2_2+\|\mathrm{D}_xf\|^2_{2,2}} =\max_{\substack{x\in\mathbb{S}^n\\v\in\mathrm{T}_x\mathbb{S}^n}} \sqrt{\|f(x)\|^2+\frac{\|\mathrm{D}_xfv\|^2_2}{\|v\|_2^2}}. \end{align*} $$
This is a variant of the
![]() $C^1$
-norm, so one can show that
$C^1$
-norm, so one can show that
![]() $C^1[q]$
is complete with respect to
$C^1[q]$
is complete with respect to
![]() $\|~\|_{\overline {\infty }}$
. Let’s see how this norm looks like on an easy kind of
$\|~\|_{\overline {\infty }}$
. Let’s see how this norm looks like on an easy kind of
![]() $C^1$
-map.
$C^1$
-map.
Example A.1 (Linear functions).
Let
![]() $A\in q\times (n+1)$
be a linear matrix, and consider the map
$A\in q\times (n+1)$
be a linear matrix, and consider the map
![]() $\mathcal {A}\in C^1[q]$
given by
$\mathcal {A}\in C^1[q]$
given by
![]() $x\mapsto Ax$
. We can show that
$x\mapsto Ax$
. We can show that
where
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\sigma _2$
are, respectively, the first and second singular values. Recall that
$\sigma _2$
are, respectively, the first and second singular values. Recall that
![]() $\sigma _1$
is also the operator norm.
$\sigma _1$
is also the operator norm.
To see the above equality, note that
 $$ \begin{align*} \|\mathcal{A}\|_{\overline{\infty}}=\max_{\substack{v,w\in\mathbb{S}^n\\v\perp w}}\sqrt{\|Av\|_2^2+\|Aw\|_2^2}. \end{align*} $$
$$ \begin{align*} \|\mathcal{A}\|_{\overline{\infty}}=\max_{\substack{v,w\in\mathbb{S}^n\\v\perp w}}\sqrt{\|Av\|_2^2+\|Aw\|_2^2}. \end{align*} $$
Since
![]() $\begin {pmatrix}Av&Aw\end {pmatrix}$
has rank at most 2,
$\begin {pmatrix}Av&Aw\end {pmatrix}$
has rank at most 2,
and since
![]() $\begin {pmatrix}Av&Aw\end {pmatrix}$
is an orthogonal projection, by the interlacing theorem for singular values (compare to [Reference Horn and Johnson39, 3.1.3],
$\begin {pmatrix}Av&Aw\end {pmatrix}$
is an orthogonal projection, by the interlacing theorem for singular values (compare to [Reference Horn and Johnson39, 3.1.3],
Hence
![]() $\|\mathcal {A}\|_\infty \leq \sqrt {\sigma _1(A)^2+\sigma _2(A)^2}$
. And we actually have equality, as we can take v and w to be, respectively, the 1st and 2nd (right) singular vectors of A.
$\|\mathcal {A}\|_\infty \leq \sqrt {\sigma _1(A)^2+\sigma _2(A)^2}$
. And we actually have equality, as we can take v and w to be, respectively, the 1st and 2nd (right) singular vectors of A.
A.1 Condition number theorems for
 $C^1[q]$
$C^1[q]$
Given
![]() $x\in \mathbb {S}^n$
, we can consider the set of
$x\in \mathbb {S}^n$
, we can consider the set of
![]() $C^1$
-maps whose zero set in
$C^1$
-maps whose zero set in
![]() $\mathbb {S}^n$
have a singularity at x,
$\mathbb {S}^n$
have a singularity at x,
Similarly, we can consider the set of
![]() $C^1$
-maps having a singular zero,
$C^1$
-maps having a singular zero,
The following result shows a way to compute the distance of a
![]() $C^1$
-map to these sets.
$C^1$
-map to these sets.
Theorem A.2 (Condition number theorem).
Let
![]() $f\in C^1[q]$
and
$f\in C^1[q]$
and
![]() $x\in \mathbb {S}^n$
. Then
$x\in \mathbb {S}^n$
. Then
and
where
![]() $\mathrm {dist}_{\overline {\infty }}$
is the distance induced by
$\mathrm {dist}_{\overline {\infty }}$
is the distance induced by
![]() $\|~\|_{\overline {\infty }}$
and
$\|~\|_{\overline {\infty }}$
and
![]() $\sigma _q$
is the qth singular value.
$\sigma _q$
is the qth singular value.
We call this result the ‘condition number theorem’ as it is so for the following condition numbers for
![]() $C^1$
-maps:
$C^1$
-maps:
 $$ \begin{align*} \mathsf{K}_{\overline{\infty}}(f,x):=\frac{\|f\|_{\overline{\infty}}}{\sqrt{\|f(x)\|^2+\sigma_q\left(\mathrm{D}_xf\right)^2}} \end{align*} $$
$$ \begin{align*} \mathsf{K}_{\overline{\infty}}(f,x):=\frac{\|f\|_{\overline{\infty}}}{\sqrt{\|f(x)\|^2+\sigma_q\left(\mathrm{D}_xf\right)^2}} \end{align*} $$
and
These condition numbers are very similar to
![]() $\mathsf {K}$
, and one might try (but we won’t here) to prove an analogue of Theorem 3.2 for them when restricted to polynomial maps. For
$\mathsf {K}$
, and one might try (but we won’t here) to prove an analogue of Theorem 3.2 for them when restricted to polynomial maps. For
![]() $C^1$
-maps, instead, such a theorem would require dealing with multiple technical problems.
$C^1$
-maps, instead, such a theorem would require dealing with multiple technical problems.
For
![]() $\mathsf {K}_{\overline {\infty }}(f)$
, one has
$\mathsf {K}_{\overline {\infty }}(f)$
, one has
 $$ \begin{align*} \mathsf{K}_{\overline{\infty}}(f) = \frac{\max\left\{\sqrt{\|f(x)\|_2^2+\|a^*\mathrm{D}_xf\|^2_2}\mid x\in\mathbb{S}^n,\,a\in \mathbb{S}^{q-1}\right\}} {\min\left\{\sqrt{\|f(x)\|_2^2+\|a^*\mathrm{D}_xf\|^2_2}\mid x\in\mathbb{S}^n,\,a\in \mathbb{S}^{q-1}\right\}}. \end{align*} $$
$$ \begin{align*} \mathsf{K}_{\overline{\infty}}(f) = \frac{\max\left\{\sqrt{\|f(x)\|_2^2+\|a^*\mathrm{D}_xf\|^2_2}\mid x\in\mathbb{S}^n,\,a\in \mathbb{S}^{q-1}\right\}} {\min\left\{\sqrt{\|f(x)\|_2^2+\|a^*\mathrm{D}_xf\|^2_2}\mid x\in\mathbb{S}^n,\,a\in \mathbb{S}^{q-1}\right\}}. \end{align*} $$
This formula shows that
![]() $\mathsf {K}_{\overline {\infty }}(f)$
is similar to the condition number associated with an operator norm of a linear map.
$\mathsf {K}_{\overline {\infty }}(f)$
is similar to the condition number associated with an operator norm of a linear map.
Proof of Theorem A.2.
Using the triangular inequality and that
![]() $\sigma _q$
is Lipschitz with respect to the operator norm, we can see that for
$\sigma _q$
is Lipschitz with respect to the operator norm, we can see that for
![]() $f,g\in C^1[q]$
,
$f,g\in C^1[q]$
,
 $$ \begin{align*} \left| \sqrt{\|f(x)\|^2+\sigma_q(\mathrm{D}_xf)^2} -\sqrt{\|g(x)\|^2+\sigma_q(\mathrm{D}_xg)^2}\right| \leq \|f-g\|_{\overline{\infty}}. \end{align*} $$
$$ \begin{align*} \left| \sqrt{\|f(x)\|^2+\sigma_q(\mathrm{D}_xf)^2} -\sqrt{\|g(x)\|^2+\sigma_q(\mathrm{D}_xg)^2}\right| \leq \|f-g\|_{\overline{\infty}}. \end{align*} $$
From here, we deduce that
by taking
![]() $g\in \Sigma _x^1[q]$
and minimizing over the right-hand side. For the reversed inequality, let
$g\in \Sigma _x^1[q]$
and minimizing over the right-hand side. For the reversed inequality, let
 $$ \begin{align*} \mathrm{D}_x f=U\begin{pmatrix} \begin{matrix}s_1&&\\&\ddots&\\&&s_q\end{matrix} &{\Large\mathbf{0}}\end{pmatrix}V \end{align*} $$
$$ \begin{align*} \mathrm{D}_x f=U\begin{pmatrix} \begin{matrix}s_1&&\\&\ddots&\\&&s_q\end{matrix} &{\Large\mathbf{0}}\end{pmatrix}V \end{align*} $$
be the SVD of
![]() $D_xf$
, where U and V are orthogonal and
$D_xf$
, where U and V are orthogonal and
![]() $\mathbf {0}$
is the zero matrix.
$\mathbf {0}$
is the zero matrix.
Since orthogonal transformations leave invariant
![]() $\|~\|_{\overline {\infty }}$
, we can assume, without loss of generality, that
$\|~\|_{\overline {\infty }}$
, we can assume, without loss of generality, that
![]() $x=e_0$
and that V is the identity matrix. Consider now
$x=e_0$
and that V is the identity matrix. Consider now
We have then that
![]() $g\in \Sigma _{e_0}^1[q]$
, since
$g\in \Sigma _{e_0}^1[q]$
, since
![]() $g(e_0)=0$
and
$g(e_0)=0$
and
![]() $\sigma _q(\mathrm {D}_{e_0} g)=0$
, and that
$\sigma _q(\mathrm {D}_{e_0} g)=0$
, and that
By arguing as in Example 2.5 and noting that
![]() $f(e_0)X_0+s_qu_qX_q$
has rank at most 2, we have that
$f(e_0)X_0+s_qu_qX_q$
has rank at most 2, we have that
 $$ \begin{align*} & \|f(e_0)X_0+s_qu_qX_q\|_{\overline{\infty}}=\left\|\begin{pmatrix}f(e_0)&s_qu_q\end{pmatrix}\right\|_{F}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad =\sqrt{\|f(e_0)\|^2_2+\|s_qu_q\|^2_2}=\sqrt{\|f(e_0)\|^2+\sigma_q(\mathrm{D}_{e_0} f)^2}/ \end{align*} $$
$$ \begin{align*} & \|f(e_0)X_0+s_qu_qX_q\|_{\overline{\infty}}=\left\|\begin{pmatrix}f(e_0)&s_qu_q\end{pmatrix}\right\|_{F}\\ &\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad =\sqrt{\|f(e_0)\|^2_2+\|s_qu_q\|^2_2}=\sqrt{\|f(e_0)\|^2+\sigma_q(\mathrm{D}_{e_0} f)^2}/ \end{align*} $$
Hence
finishing the proof of the first equality.
The second equality follows immediately from the first one.
A.2 Structured condition number theorem for
 $C^1[q]$
$C^1[q]$
Recall that for
![]() $\boldsymbol {d}\in \mathbb {N}^q$
,
$\boldsymbol {d}\in \mathbb {N}^q$
,
![]() $\Delta $
is the diagonal
$\Delta $
is the diagonal
![]() $q\times q$
matrix whose diagonal is
$q\times q$
matrix whose diagonal is
![]() $\boldsymbol {d}$
. We consider the following variant of
$\boldsymbol {d}$
. We consider the following variant of
![]() $\|~\|_{\overline {\infty }}$
$\|~\|_{\overline {\infty }}$
 $$ \begin{align*} \|f\|_{\overline{\infty},\boldsymbol{d}}:=\max_{x\in\mathbb{S}^n} \sqrt{\|f(x)\|^2_2+\|\Delta^{-\frac{1}{2}}\mathrm{D}_xf\|^2_{2,2}} =\max_{\substack{x\in\mathbb{S}^n\\v\in\mathrm{T}_x\mathbb{S}^n}} \sqrt{\|f(x)\|^2+\frac{\|\Delta^{-\frac{1}{2}}\mathrm{D}_xfv\|^2_2}{\|v\|_2^2}} \end{align*} $$
$$ \begin{align*} \|f\|_{\overline{\infty},\boldsymbol{d}}:=\max_{x\in\mathbb{S}^n} \sqrt{\|f(x)\|^2_2+\|\Delta^{-\frac{1}{2}}\mathrm{D}_xf\|^2_{2,2}} =\max_{\substack{x\in\mathbb{S}^n\\v\in\mathrm{T}_x\mathbb{S}^n}} \sqrt{\|f(x)\|^2+\frac{\|\Delta^{-\frac{1}{2}}\mathrm{D}_xfv\|^2_2}{\|v\|_2^2}} \end{align*} $$
for
![]() $f\in C^1[q]$
. The following example shows a class of functions for which this norm can be computed exactly.
$f\in C^1[q]$
. The following example shows a class of functions for which this norm can be computed exactly.
Example A.3. Let
Then we can see that
Indeed, by Proposition 2.2, we have that for all
![]() $x\in \mathbb {S}^n$
,
$x\in \mathbb {S}^n$
,
 $$ \begin{align*} \sqrt{\|M_{a,b}(x)\|^2_2+\left\|\Delta^{-\frac{1}{2}}\mathrm{D}_x M_{a,b}\right\|^2_2}\leq \|M_{a,b}\|_W. \end{align*} $$
$$ \begin{align*} \sqrt{\|M_{a,b}(x)\|^2_2+\left\|\Delta^{-\frac{1}{2}}\mathrm{D}_x M_{a,b}\right\|^2_2}\leq \|M_{a,b}\|_W. \end{align*} $$
Thus
![]() $\|M_{a,b}\|_{\overline {\infty },\boldsymbol {d}}\leq \|M_{a,b}\|_W$
, where we have equality for
$\|M_{a,b}\|_{\overline {\infty },\boldsymbol {d}}\leq \|M_{a,b}\|_W$
, where we have equality for
![]() $x=e_0$
.
$x=e_0$
.
We can also associate to
![]() $\|~\|_{\overline {\infty },\boldsymbol {d}}$
, for
$\|~\|_{\overline {\infty },\boldsymbol {d}}$
, for
![]() $f\in C^1[q]$
and
$f\in C^1[q]$
and
![]() $x\in \mathbb {S}^n$
, the quantities
$x\in \mathbb {S}^n$
, the quantities
 $$ \begin{align*} \mathsf{K}_{\overline{\infty},\boldsymbol{d}}(f,x):=\frac{\|f\|_{\overline{\infty}}}{\sqrt{\|f(x)\|^2+\sigma_q\left(\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right)^2}} \end{align*} $$
$$ \begin{align*} \mathsf{K}_{\overline{\infty},\boldsymbol{d}}(f,x):=\frac{\|f\|_{\overline{\infty}}}{\sqrt{\|f(x)\|^2+\sigma_q\left(\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right)^2}} \end{align*} $$
and
For these variants of
![]() $\mathsf {K}_{\overline {\infty }}$
, we have the following structured condition number theorem for perturbations by homogeneous polynomials.
$\mathsf {K}_{\overline {\infty }}$
, we have the following structured condition number theorem for perturbations by homogeneous polynomials.
Theorem A.4 (Structured condition number theorem).
Let
![]() $f\in C^1[q]$
,
$f\in C^1[q]$
,
![]() $x\in \mathbb {S}^n$
and
$x\in \mathbb {S}^n$
and
![]() $\boldsymbol {d}\in \mathbb {N}^q$
. Then
$\boldsymbol {d}\in \mathbb {N}^q$
. Then
 $$ \begin{align*} \mathrm{dist}_{\overline{\infty},\boldsymbol{d}}\left(f,\Sigma_x^1[q]\cap (f+\mathcal{H}_{\boldsymbol{d}}^{\mathbb{R}}[q])\right) =\sqrt{\|f(x)\|^2+\sigma_q\left(\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right)^2} \end{align*} $$
$$ \begin{align*} \mathrm{dist}_{\overline{\infty},\boldsymbol{d}}\left(f,\Sigma_x^1[q]\cap (f+\mathcal{H}_{\boldsymbol{d}}^{\mathbb{R}}[q])\right) =\sqrt{\|f(x)\|^2+\sigma_q\left(\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right)^2} \end{align*} $$
and
 $$ \begin{align*}\mathrm{dist}_{\overline{\infty},\boldsymbol{d}}\left(f,\Sigma^1[q] \cap(f+\mathcal{H}_{\boldsymbol{d}}^{\mathbb{R}}[q])\right)=\min_{x\in\mathbb{S}^n}\sqrt{\|f(x)\|^2+\sigma_q\left(\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right)^2},\end{align*} $$
$$ \begin{align*}\mathrm{dist}_{\overline{\infty},\boldsymbol{d}}\left(f,\Sigma^1[q] \cap(f+\mathcal{H}_{\boldsymbol{d}}^{\mathbb{R}}[q])\right)=\min_{x\in\mathbb{S}^n}\sqrt{\|f(x)\|^2+\sigma_q\left(\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right)^2},\end{align*} $$
where
![]() $\mathrm {dist}_{\overline {\infty },\boldsymbol {d}}$
is the distance induced by
$\mathrm {dist}_{\overline {\infty },\boldsymbol {d}}$
is the distance induced by
![]() $\|~\|_{\overline {\infty },\boldsymbol {d}}$
and
$\|~\|_{\overline {\infty },\boldsymbol {d}}$
and
![]() $\sigma _q$
is the qth singular value.
$\sigma _q$
is the qth singular value.
Corollary A.5. Let
![]() $\boldsymbol {d}\in \mathbb {N}^d$
,
$\boldsymbol {d}\in \mathbb {N}^d$
,
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
and
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
and
![]() $x\in \mathbb {S}^n$
. Then
$x\in \mathbb {S}^n$
. Then
 $$ \begin{align*} \mathrm{dist}_{\overline{\infty},\boldsymbol{d}}(f,\Sigma_{\boldsymbol{d},x}[q]) =\sqrt{\|f(x)\|^2+\sigma_q\left(\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right)^2} =\mathrm{dist}_W(f,\Sigma_{\boldsymbol{d},x}[q]) \end{align*} $$
$$ \begin{align*} \mathrm{dist}_{\overline{\infty},\boldsymbol{d}}(f,\Sigma_{\boldsymbol{d},x}[q]) =\sqrt{\|f(x)\|^2+\sigma_q\left(\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right)^2} =\mathrm{dist}_W(f,\Sigma_{\boldsymbol{d},x}[q]) \end{align*} $$
and
 $$ \begin{align*} \mathrm{dist}_{\overline{\infty},\boldsymbol{d}}(f,\Sigma_{\boldsymbol{d}}[q]) =\min_{x\in\mathbb{S}^n}\sqrt{\|f(x)\|^2+\sigma_q \left(\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right)^2} =\mathrm{dist}_{W}(f,\Sigma_{\boldsymbol{d}}[q]), \end{align*} $$
$$ \begin{align*} \mathrm{dist}_{\overline{\infty},\boldsymbol{d}}(f,\Sigma_{\boldsymbol{d}}[q]) =\min_{x\in\mathbb{S}^n}\sqrt{\|f(x)\|^2+\sigma_q \left(\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right)^2} =\mathrm{dist}_{W}(f,\Sigma_{\boldsymbol{d}}[q]), \end{align*} $$
where
![]() $\mathrm {dist}_{\overline {\infty },\boldsymbol {d}}$
is the distance induced by
$\mathrm {dist}_{\overline {\infty },\boldsymbol {d}}$
is the distance induced by
![]() $\|~\|_{\overline {\infty },\boldsymbol {d}}$
and
$\|~\|_{\overline {\infty },\boldsymbol {d}}$
and
![]() $\sigma _q$
is the qth singular value.
$\sigma _q$
is the qth singular value.
Note that the adjective ‘structured’ refers to the fact that we only allow perturbations of f by
![]() $C^1$
-maps in
$C^1$
-maps in
![]() $\mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
. However, we might still be interested in general perturbations. If this is the case, we can get them using the relationship between
$\mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
. However, we might still be interested in general perturbations. If this is the case, we can get them using the relationship between
![]() $\|~\|_{\infty ,\boldsymbol {d}}$
and
$\|~\|_{\infty ,\boldsymbol {d}}$
and
![]() $\|~\|_{\overline {\infty }}$
. We will explore this in more detail in the next subsection.
$\|~\|_{\overline {\infty }}$
. We will explore this in more detail in the next subsection.
Proof of Theorem A.4.
This proof is almost the same as the one of Theorem A.2. We only have to modify the part where we find an explicit minimiser for the distance. Again, we write
 $$ \begin{align*}\Delta^{-\frac{1}{2}}\mathrm{D}_x f=U\begin{pmatrix}\begin{matrix}s_1&&\\&\ddots&\\&&s_q\end{matrix}&{\Large\mathbf{0}}\end{pmatrix}V,\end{align*} $$
$$ \begin{align*}\Delta^{-\frac{1}{2}}\mathrm{D}_x f=U\begin{pmatrix}\begin{matrix}s_1&&\\&\ddots&\\&&s_q\end{matrix}&{\Large\mathbf{0}}\end{pmatrix}V,\end{align*} $$
where
![]() $s_1,\ldots ,s_q>0$
, U and V are orthogonal and
$s_1,\ldots ,s_q>0$
, U and V are orthogonal and
![]() $\mathbf {0}$
is the zero matrix. Again, without loss of generality, we assume that
$\mathbf {0}$
is the zero matrix. Again, without loss of generality, we assume that
![]() $x=e_0$
and that V is the identity. We consider
$x=e_0$
and that V is the identity. We consider
so that
![]() $g\in \Sigma _{e_0}^1[q]$
, as
$g\in \Sigma _{e_0}^1[q]$
, as
![]() $g(e_0)=0$
and
$g(e_0)=0$
and
![]() $\sigma _q(\mathrm {D}_{e_0} g)=0$
, and
$\sigma _q(\mathrm {D}_{e_0} g)=0$
, and
Because of Example A.3, for
we have that
![]() $\|h\|_{\overline {\infty },\boldsymbol {d}}= \sqrt {\|a\|^2_2+\|b\|^2_2}$
. Hence,
$\|h\|_{\overline {\infty },\boldsymbol {d}}= \sqrt {\|a\|^2_2+\|b\|^2_2}$
. Hence,
and the first equality follows. The second equality immediately follows from the first one.
Proof of Corollary A.5.
This is Theorem A.4 together with [Reference Bürgisser, Cucker and Lairez15, Theorem 4.4].
A.3 Relationship between norms
As it happens with
![]() $\mathsf {K}$
and
$\mathsf {K}$
and
![]() $\kappa $
(see Section 4.3), the relations between the condition numbers
$\kappa $
(see Section 4.3), the relations between the condition numbers
![]() $\mathsf {K}$
,
$\mathsf {K}$
,
![]() $\kappa $
,
$\kappa $
,
![]() $\mathsf {K}_{\overline {\infty }}$
and
$\mathsf {K}_{\overline {\infty }}$
and
![]() $\mathsf {K}_{\overline {\infty },\boldsymbol {d}}$
reduces to the relations between the corresponding norms.
$\mathsf {K}_{\overline {\infty },\boldsymbol {d}}$
reduces to the relations between the corresponding norms.
We therefore prove the following propositions relating these norms. Note that for
![]() $C^1[q]$
, we compare
$C^1[q]$
, we compare
![]() $\|~\|_{\overline {\infty }}$
with
$\|~\|_{\overline {\infty }}$
with
![]() $\|~\|_{\overline {\infty },\boldsymbol {d}}$
, and for
$\|~\|_{\overline {\infty },\boldsymbol {d}}$
, and for
![]() $\mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
, we compare
$\mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
, we compare
![]() $\|~\|_{\infty }^{\mathbb {R}}$
,
$\|~\|_{\infty }^{\mathbb {R}}$
,
![]() $\|~\|_W$
,
$\|~\|_W$
,
![]() $\|~\|_{\overline {\infty }}$
and
$\|~\|_{\overline {\infty }}$
and
![]() $\|~\|_{\overline {\infty },\boldsymbol {d}}$
.
$\|~\|_{\overline {\infty },\boldsymbol {d}}$
.
Proposition A.6. Let
![]() $f\in C^1[q]$
. Then for all
$f\in C^1[q]$
. Then for all
![]() $\boldsymbol {d},\widetilde {\boldsymbol {d}}\in \mathbb {N}^q$
,
$\boldsymbol {d},\widetilde {\boldsymbol {d}}\in \mathbb {N}^q$
,
and
 $$ \begin{align*} \min\left\{1,\min_i\sqrt{\frac{\tilde{d_i}}{d_i}}\right\} \|f\|_{\overline{\infty},\widetilde{\boldsymbol{d}}}\leq \|f\|_{\overline{\infty},\boldsymbol{d}}\leq \max\left\{1,\max_i\sqrt{\frac{\tilde{d_i}}{d_i}}\right\} \|f\|_{\overline{\infty},\widetilde{\boldsymbol{d}}}. \end{align*} $$
$$ \begin{align*} \min\left\{1,\min_i\sqrt{\frac{\tilde{d_i}}{d_i}}\right\} \|f\|_{\overline{\infty},\widetilde{\boldsymbol{d}}}\leq \|f\|_{\overline{\infty},\boldsymbol{d}}\leq \max\left\{1,\max_i\sqrt{\frac{\tilde{d_i}}{d_i}}\right\} \|f\|_{\overline{\infty},\widetilde{\boldsymbol{d}}}. \end{align*} $$
Proposition A.7. Let
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
. Then the following inequalities hold:
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
. Then the following inequalities hold:
 $$ \begin{align} \frac{1}{\sqrt{2q}\,\mathbf{D}}\|f\|_{\overline{\infty}}&\leq \|f\|_\infty^{\mathbb{R}} \leq \|f\|_{\overline{\infty},\boldsymbol{d}}\leq \|f\|_{\overline{\infty}} \end{align} $$
$$ \begin{align} \frac{1}{\sqrt{2q}\,\mathbf{D}}\|f\|_{\overline{\infty}}&\leq \|f\|_\infty^{\mathbb{R}} \leq \|f\|_{\overline{\infty},\boldsymbol{d}}\leq \|f\|_{\overline{\infty}} \end{align} $$
 $$ \begin{align} \frac{1}{\sqrt{2q\mathbf{D}}}\|f\|_{\overline{\infty},\boldsymbol{d}}&\leq \|f\|_\infty^{\mathbb{R}} \leq \|f\|_{\overline{\infty},\boldsymbol{d}} \end{align} $$
$$ \begin{align} \frac{1}{\sqrt{2q\mathbf{D}}}\|f\|_{\overline{\infty},\boldsymbol{d}}&\leq \|f\|_\infty^{\mathbb{R}} \leq \|f\|_{\overline{\infty},\boldsymbol{d}} \end{align} $$
Proof of Proposition A.6.
It is enough to show that
 $$ \begin{align*} \|f\|_{\overline{\infty},\boldsymbol{d}}\leq \max\left\{1,\max_i\sqrt{\frac{\tilde{d_i}}{d_i}}\right\} \|f\|_{\overline{\infty},\tilde{\boldsymbol{d}}}, \end{align*} $$
$$ \begin{align*} \|f\|_{\overline{\infty},\boldsymbol{d}}\leq \max\left\{1,\max_i\sqrt{\frac{\tilde{d_i}}{d_i}}\right\} \|f\|_{\overline{\infty},\tilde{\boldsymbol{d}}}, \end{align*} $$
since the rest of the inequalities are derived from this claim in a straightforward way. For the latter, note that
![]() where
where
![]() .
.
Now one can easily check that for
![]() $A\in \mathbb {R}^{q\times n}$
,
$A\in \mathbb {R}^{q\times n}$
,
 $$ \begin{align*} \left\|\Delta^{-\frac{1}{2}}A\right\|_{2,2} =\left\|\Delta^{-\frac{1}{2}}\tilde{\Delta}^{\frac{1}{2}}\, \tilde{\Delta}^{-\frac{1}{2}}A\right\|_{2,2} \leq \left\|\Delta^{-\frac{1}{2}} \tilde{\Delta}^{\frac{1}{2}}\right\|_{2,2} \left\|\tilde{\Delta}^{-\frac{1}{2}}A\right\|_{2,2} = \max_i\sqrt{\frac{\tilde{d_i}}{d_i}} \left\|\tilde{\Delta}^{-\frac{1}{2}}\right\|_{2,2}, \end{align*} $$
$$ \begin{align*} \left\|\Delta^{-\frac{1}{2}}A\right\|_{2,2} =\left\|\Delta^{-\frac{1}{2}}\tilde{\Delta}^{\frac{1}{2}}\, \tilde{\Delta}^{-\frac{1}{2}}A\right\|_{2,2} \leq \left\|\Delta^{-\frac{1}{2}} \tilde{\Delta}^{\frac{1}{2}}\right\|_{2,2} \left\|\tilde{\Delta}^{-\frac{1}{2}}A\right\|_{2,2} = \max_i\sqrt{\frac{\tilde{d_i}}{d_i}} \left\|\tilde{\Delta}^{-\frac{1}{2}}\right\|_{2,2}, \end{align*} $$
and that, for
![]() $a,b,t\in \mathbb {R}^2$
,
$a,b,t\in \mathbb {R}^2$
,
Combining these bounds, we get
 $$ \begin{align*} \sqrt{\|f(x)\|^2+\left\|\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right\|_{2,2}^2}\leq \max\left\{1,\max_i\sqrt{\frac{\tilde{d_i}}{d_i}}\right\}\sqrt{\|f(x)\|^2+\left\|\tilde{\Delta}^{-\frac{1}{2}}\mathrm{D}_xf\right\|_{2,2}^2} \end{align*} $$
$$ \begin{align*} \sqrt{\|f(x)\|^2+\left\|\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right\|_{2,2}^2}\leq \max\left\{1,\max_i\sqrt{\frac{\tilde{d_i}}{d_i}}\right\}\sqrt{\|f(x)\|^2+\left\|\tilde{\Delta}^{-\frac{1}{2}}\mathrm{D}_xf\right\|_{2,2}^2} \end{align*} $$
and so the desired claim.
Proof of Proposition A.7.
Arguing as in Proposition A.6, we can prove that for all
![]() $x\in \mathbb {S}^n$
,
$x\in \mathbb {S}^n$
,
 $$ \begin{align*} \frac{1}{\sqrt{2q}\,\mathbf{D}}\sqrt{\|f(x)\|^2+\left\|\mathrm{D}_xf\right\|_{2,2}^2}\leq \max\left\{\|f(x)\|_{\infty},\left\|\tilde{\Delta}^{-1}\mathrm{D}_xf\right\|_{\infty,2}\right\}\leq \sqrt{\|f(x)\|^2+\left\|\mathrm{D}_xf\right\|_{2,2}^2} \end{align*} $$
$$ \begin{align*} \frac{1}{\sqrt{2q}\,\mathbf{D}}\sqrt{\|f(x)\|^2+\left\|\mathrm{D}_xf\right\|_{2,2}^2}\leq \max\left\{\|f(x)\|_{\infty},\left\|\tilde{\Delta}^{-1}\mathrm{D}_xf\right\|_{\infty,2}\right\}\leq \sqrt{\|f(x)\|^2+\left\|\mathrm{D}_xf\right\|_{2,2}^2} \end{align*} $$
and
 $$ \begin{align*} \frac{1}{\sqrt{2q\mathbf{D}}}\sqrt{\|f(x)\|^2 +\left\|\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right\|_{2,2}^2} &\leq \max\left\{\|f(x)\|_{\infty}, \left\|\tilde{\Delta}^{-1}\mathrm{D}_xf\right\|_{\infty,2}\right\}\\ &\leq \sqrt{\|f(x)\|^2 +\left\|\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right\|_{2,2}^2}. \end{align*} $$
$$ \begin{align*} \frac{1}{\sqrt{2q\mathbf{D}}}\sqrt{\|f(x)\|^2 +\left\|\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right\|_{2,2}^2} &\leq \max\left\{\|f(x)\|_{\infty}, \left\|\tilde{\Delta}^{-1}\mathrm{D}_xf\right\|_{\infty,2}\right\}\\ &\leq \sqrt{\|f(x)\|^2 +\left\|\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right\|_{2,2}^2}. \end{align*} $$
Maximizing over
![]() $z\in \mathbb {S}^n$
gives the inequalities in equations (A.1) and (A.2).
$z\in \mathbb {S}^n$
gives the inequalities in equations (A.1) and (A.2).
It only remains to prove
![]() $\|f\|_{\infty ,\boldsymbol {d}}\leq \|f\|_W$
in equation (A.3). To do this, note that by Proposition 2.2, for all
$\|f\|_{\infty ,\boldsymbol {d}}\leq \|f\|_W$
in equation (A.3). To do this, note that by Proposition 2.2, for all
![]() $x\in \mathbb {S}^n$
,
$x\in \mathbb {S}^n$
,
 $$ \begin{align*} \sqrt{\|f(x)\|^2+\left\|\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right\|_{2,2}^2}\leq \|f\|_W. \end{align*} $$
$$ \begin{align*} \sqrt{\|f(x)\|^2+\left\|\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right\|_{2,2}^2}\leq \|f\|_W. \end{align*} $$
The result follows from maximizing over
![]() $x\in \mathbb {S}^n$
.
$x\in \mathbb {S}^n$
.
We finish with the following theorem, similar in flavour to [Reference Diatta and Lerario30, Proposition 3] and [Reference Breiding, Keneshlou and Lerario12, Theorem 7], where it was shown that the distance of a polynomial tuple to polynomial tuples with singularities bounds the distance of this polynomial to
![]() $C^1$
-functions with singularities.
$C^1$
-functions with singularities.
Theorem A.8. Let
![]() $f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
and
$f\in \mathcal {H}_{\boldsymbol {d}}^{\mathbb {R}}[q]$
and
![]() $x\in \mathbb {S}^n$
. Then
$x\in \mathbb {S}^n$
. Then
and
where
![]() $\mathrm {dist}_{\overline {\infty }}$
and
$\mathrm {dist}_{\overline {\infty }}$
and
![]() $\mathrm {dist}_{\overline {\infty },\boldsymbol {d}}$
are, respectively, the distances induced by
$\mathrm {dist}_{\overline {\infty },\boldsymbol {d}}$
are, respectively, the distances induced by
![]() $\|~\|_{\overline {\infty }}$
and
$\|~\|_{\overline {\infty }}$
and
![]() $\|~\|_{\overline {\infty },\boldsymbol {d}}$
.
$\|~\|_{\overline {\infty },\boldsymbol {d}}$
.
Sketch of proof.
The proof is similar to that of Proposition A.6. Arguing as there, we can prove that for all
![]() $x\in \mathbb {S}^n$
,
$x\in \mathbb {S}^n$
,
 $$ \begin{align*} \frac{1}{\sqrt{\mathbf{D}}}\sqrt{\|f(x)\|_2^2+\sigma_q\left(\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right)^2}\leq \sqrt{\|f(x)\|_2^2+\sigma_q\left(\mathrm{D}_xf\right)^2}\leq \sqrt{\|f(x)\|_2^2+\sigma_q\left(\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right)^2}. \end{align*} $$
$$ \begin{align*} \frac{1}{\sqrt{\mathbf{D}}}\sqrt{\|f(x)\|_2^2+\sigma_q\left(\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right)^2}\leq \sqrt{\|f(x)\|_2^2+\sigma_q\left(\mathrm{D}_xf\right)^2}\leq \sqrt{\|f(x)\|_2^2+\sigma_q\left(\Delta^{-\frac{1}{2}}\mathrm{D}_xf\right)^2}. \end{align*} $$
Minimizing over
![]() $x\in \mathbb {S}^n$
and applying Theorems A.2 and Corollary A.5, we conclude.
$x\in \mathbb {S}^n$
and applying Theorems A.2 and Corollary A.5, we conclude.
![]() $\Box $
$\Box $