Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T04:46:33.192Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher rank K-theoretic Donaldson-Thomas Theory of points

Part of: Projective and enumerative geometry Cycles and subschemes

Published online by Cambridge University Press:  02 March 2021

Nadir Fasola Open the ORCID record for Nadir Fasola [Opens in a new window] ,
Sergej Monavari Open the ORCID record for Sergej Monavari [Opens in a new window]  and
Andrea T. Ricolfi Open the ORCID record for Andrea T. Ricolfi [Opens in a new window]
Nadir Fasola
Affiliation:
SISSA Trieste, Via Bonomea 265, 34136Trieste; E-mail: nfasola@sissa.it
Sergej Monavari
Affiliation:
Mathematical Institute, Utrecht University, 3584 CDUtrecht; E-mail: s.monavari@uu.nl
Andrea T. Ricolfi
Affiliation:
SISSA Trieste, Via Bonomea 265, 34136Trieste; E-mail: aricolfi@sissa.it

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We exploit the critical structure on the Quot scheme 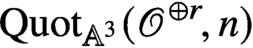$\text {Quot}_{{{\mathbb {A}}}^3}({\mathscr {O}}^{\oplus r}\!,n)$, in particular the associated symmetric obstruction theory, in order to study rank r K-theoretic Donaldson-Thomas (DT) invariants of the local Calabi-Yau 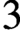$3$-fold 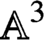${{\mathbb {A}}}^3$. We compute the associated partition function as a plethystic exponential, proving a conjecture proposed in string theory by Awata-Kanno and Benini-Bonelli-Poggi-Tanzini. A crucial step in the proof is the fact, nontrival if 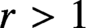$r>1$, that the invariants do not depend on the equivariant parameters of the framing torus 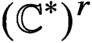$({{\mathbb {C}}}^\ast )^r$. Reducing from K-theoretic to cohomological invariants, we compute the corresponding DT invariants, proving a conjecture of Szabo. Reducing further to enumerative DT invariants, we solve the higher rank DT theory of a pair 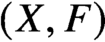$(X,F)$, where F is an equivariant exceptional locally free sheaf on a projective toric 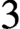$3$-fold X.

As a further refinement of the K-theoretic DT invariants, we formulate a mathematical definition of the chiral elliptic genus studied in physics. This allows us to define elliptic DT invariants of 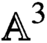${{\mathbb {A}}}^3$ in arbitrary rank, which we use to tackle a conjecture of Benini-Bonelli-Poggi-Tanzini.

MSC classification

Primary: 14N35: Gromov-Witten invariants, quantum cohomology, Gopakumar-Vafa invariants, Donaldson-Thomas invariants
Secondary: 14C05: Parametrization (Chow and Hilbert schemes)
Type
Mathematical Physics
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e15
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Arbesfeld, N., ‘K-theoretic Donaldson-Thomas theory and the Hilbert scheme of points on a surface’, 2019, arXiv:1905.04567.Google Scholar
Arbesfeld, N. and Kononov, Y., ‘Boxcounting and Quot schemes’, To appear.Google Scholar
Awata, H. and Kanno, H., ‘Quiver matrix model and topological partition function in six dimensions’, J. High Energy Phys. 2009(7) (2009), 23.CrossRefGoogle Scholar
Beentjes, S. and Ricolfi, A. T., ‘Virtual counts on Quot schemes and the higher rank local DT/PT correspondence’, 2018, arXiv:1811.09859, accepted for publication in Math. Res. Lett.Google Scholar
Behrend, K., ‘Donaldson-Thomas type invariants via microlocal geometry’, Ann. Math. 2(170) (2009), 1307–1338.CrossRefGoogle Scholar
Behrend, K., Bryan, J. and Szendrői, B., ‘Motivic degree zero Donaldson-Thomas invariants’, Invent. Math. 192(1) (2013), 111–160.Google Scholar
Behrend, K. and Fantechi, B., ‘The intrinsic normal cone’, Invent. Math. 128(1) (1997), 45–88.CrossRefGoogle Scholar
Behrend, K. and Fantechi, B., ‘Symmetric obstruction theories and Hilbert schemes of points on threefolds’, Algebra Number Theory 2 (2008), 313–345.CrossRefGoogle Scholar
Benini, F., Bonelli, G., Poggi, M. and Tanzini, A., ‘Elliptic non-abelian Donaldson-Thomas invariants of ${\mathbb{C}}^3$’, J. High Energy Phys. 2019(7) (2019), 41.Google Scholar
Bifet, E., ‘Sur les points fixes du schéma sous l’action du tore ${\textbf{G}}_{{m},{k}}^{{r}}$’, C. R. Acad. Sci. Paris Sér. I Math. 309(9) (1989), 609–612.Google Scholar
Bonelli, G., Fasola, N. and Tanzini, A., ‘Defects, nested instantons and comet shaped quivers’, 2019,arXiv:1907.02771.Google Scholar
Bonelli, G., Fasola, N. and Tanzini, A., ‘Flags of sheaves, quivers and symmetric polynomials’, 2019,arXiv:1911.12787.Google Scholar
Cao, Y., Kool, M. and Monavari, S., ‘K-theoretic DT/PT correspondence for toric Calabi-Yau 4-folds’, 2019,arXiv:1906.07856.Google Scholar
Cazzaniga, A., On Some Computations of Refined Donaldson-Thomas Invariants, PhD Thesis (University of Oxford, 2015).Google Scholar
Cazzaniga, A., Ralaivaosaona, D. and Ricolfi, A. T., ‘Higher rank motivic Donaldson-Thomas invariants of ${\text{A}}^3$via wall-crossing, and asymptotics’, 2020,arXiv:2004.07020.Google Scholar
Cazzaniga, A. and Ricolfi, A. T., ‘Framed motivic Donaldson-Thomas invariants of small crepant resolutions’, 2020,arXiv:2004.07837.Google Scholar
Cazzaniga, A. and Ricolfi, A. T., ‘Framed sheaves on projective space and Quot schemes’, 2020,arXiv:2004.13633.Google Scholar
Ciocan-Fontanine, I. and Kapranov, M., ‘Virtual fundamental classes via dg-manifolds’, Geom. Topol. 13(3) (2009), 1779–1804.CrossRefGoogle Scholar
Cirafici, M., Sinkovics, A. and Szabo, R. J., ‘Cohomological gauge theory, quiver matrix models and Donaldson-Thomas theory’, Nuclear Phys. B 809(3) (2009), 452–518.CrossRefGoogle Scholar
Davison, B. and Ricolfi, A. T., ‘The local motivic DT/PT correspondence’, 2019,arXiv:1905.12458.Google Scholar
Denef, J. and Loeser, F., Geometry on arc spaces of algebraic varieties, in 3rd European Congress of Mathematics (ECM), Barcelona, Spain, July 10–14, 2000, Vol. I (Birkhäuser, Basel, 2001), 327–348.Google Scholar
Dimofte, T. and Gukov, S., ‘Refined, motivic, and quantum’, Lett. Math. Phys. 91(1) (2010), 1–27.CrossRefGoogle Scholar
Fantechi, B. and Göttsche, L., ‘Riemann-Roch theorems and elliptic genus for virtually smooth schemes’, Geom. Topol. 14(1) (2010), 83–115.CrossRefGoogle Scholar
Franco, S., Ghim, D., Lee, S. and Seong, R.-K., ‘Elliptic genera of 2d (0, 2)gauge theories from brane brick models’, J. High Energy Phys. 2017(6) (2017), 46.CrossRefGoogle Scholar
Gholampour, A. and Kool, M., ‘Higher rank sheaves on threefolds and functional equations’, Épijournal de Géom. Algébrique 3 (2019), 29.Google Scholar
Gholampour, A., Kool, M. and Young, B., ‘Rank 2 sheaves on toric 3-folds: classical and virtual counts’, Int. Math. Res. Not. 2018(10) (2018), 2981–3069.Google Scholar
Graber, T. and Pandharipande, R., ‘Localization of virtual classes’, Invent. Math. 135(2) (1999), 487–518.CrossRefGoogle Scholar
Gulbrandsen, M. G. and Ricolfi, A. T., ‘The Euler characteristic of the generalized Kummer scheme of an abelian threefold’, Geom. Dedicata 182 (2016), 73–79.CrossRefGoogle Scholar
Hartshorne, R., Algebraic Geometry, Graduate Texts in Mathematics No. 52 (Springer-Verlag, New York–Heidelberg, 1977).Google Scholar
Illusie, L., Complexe cotangent et déformations. I, Lecture Notes in Mathematics, Vol. 239 (Springer-Verlag, Berlin–New York, 1971).CrossRefGoogle Scholar
Iqbal, A., Kozçaz, C. and Vafa, C., ‘The refined topological vertex’, J. High Energy Phys. 2009(10) (2009), 58.CrossRefGoogle Scholar
Johnson, D., Oprea, D. and Pandharipande, R., ‘Rationality of descendent series for Hilbert and Quot schemes of surfaces’, 2020,arXiv:2002.05861.Google Scholar
Kawai, T. and Mohri, K., ‘Geometry of $\left(0,2\right)$Landau-Ginzburg orbifolds’, Nuclear Phys. B 425(1–2) (1994), 191–216.CrossRefGoogle Scholar
Kontsevich, M., Enumeration of rational curves via torus actions, in The Moduli Space of Curves (Birkhäuser, Boston, 1995), 335–368.Google Scholar
Kontsevich, M. and Soibelman, Y., ‘Stability structures, motivic Donaldson-Thomas invariants and cluster transformations’, 2008,arXiv:0811.2435.Google Scholar
Kontsevich, M. and Soibelman, Y., ‘Cohomological Hall algebra, exponential Hodge structures and motivic Donaldson-Thomas invariants’, Commun. Number Theory Phys. 5(2) (2011), 231–352.CrossRefGoogle Scholar
Kool, M., ‘Fixed point loci of moduli spaces of sheaves on toric varieties’, Adv. Math. 227(4) (2011), 1700–1755.CrossRefGoogle Scholar
Levine, M. and Pandharipande, R., ‘Algebraic cobordism revisited’, Invent. Math. 176(1) (2009), 63–130.CrossRefGoogle Scholar
Li, J., ‘Zero dimensional Donaldson-Thomas invariants of threefolds’, Geom. Topol. 10 (2006), 2117–2171.CrossRefGoogle Scholar
Li, J. and Tian, G., ‘Virtual moduli cycles and Gromov-Witten invariants of algebraic varieties’, J. Amer. Math. Soc. 11(1) (1998), 119–174.CrossRefGoogle Scholar
Lim, W., ‘Virtual ${\chi}_{-\text{y}}$-genera of Quot schemes on surfaces’, 2020,arXiv:2003.04429.Google Scholar
Marian, A. and Oprea, D., ‘Virtual intersections on the Quot scheme and Vafa-Intriligator formulas’, Duke Math. J. 136(1) (2007), 81–113.CrossRefGoogle Scholar
Marian, A., Oprea, D. and Pandharipande, R., ‘Segre classes and Hilbert schemes of points’, Ann. Sci. Éc. Norm. Supér. (4) 50(1) (2017), 239–267.CrossRefGoogle Scholar
Maulik, D., Nekrasov, N., Okounkov, A. and Pandharipande, R., ‘Gromov-Witten theory and Donaldson-Thomas theory, I’, Compos. Math. 142(5) (2006), 1263–1285.CrossRefGoogle Scholar
Maulik, D., Nekrasov, N., Okounkov, A. and Pandharipande, R., ‘Gromov-Witten theory and Donaldson-Thomas theory, II’, Compos. Math. 142(5) (2006), 1286–1304.CrossRefGoogle Scholar
Nekrasov, N., ‘$\textbf{Z}$-theory: chasing $\text{m} / \text{f}$theory’, C. R. Physique 6(2) (2005), 261–269.CrossRefGoogle Scholar
Nekrasov, N., ‘Instanton partition functions and M-theory’, Jpn. J. Math. 4(1) (2009), 63–93.CrossRefGoogle Scholar
Nekrasov, N., ‘Magnificent four’, Ann. Inst. Henri Poincaré D 7(4) (2020), 505–534.CrossRefGoogle Scholar
Nekrasov, N. and Okounkov, A., ‘Membranes and sheaves’, Algebr. Geom. 3(3) (2016), 320–369.CrossRefGoogle Scholar
Nekrasov, N. and Piazzalunga, N., ‘Magnificent four with colors’, Commun. Math. Phys. 372(2) (2019), 573–597.CrossRefGoogle Scholar
Nori, M., ‘Appendix to the paper by C. S. Seshadri: Desingularisation of the moduli varieties of vector bundles over curves’, in Proceedings of the International Symposium on Algebraic Geometry (Kyoto Univ., Kyoto, 1977), pp. 155–184, Kinokuniya Book Store, Tokyo, 1978.Google Scholar
Okounkov, A., Lectures on K-Theoretic Computations in Enumerative Geometry, Geometry of Moduli Spaces and Representation Theory, IAS/Park City Math. Ser., Vol. 24 (American Mathematical Society, Providence, RI, 2017), 251–380.Google Scholar
Oprea, D. and Pandharipande, R., ‘Quot schemes of curves and surfaces: virtual classes, integrals, Euler characteristics’, 2019,arXiv:1903.08787.Google Scholar
Qu, F., ‘Virtual pullbacks in $\text{K}$-theory’, Ann. Inst. Fourier (Grenoble) 68(4) (2018), 1609–1641.CrossRefGoogle Scholar
Ricolfi, A. T., Local Donaldson-Thomas Invariants and Their Refinements, PhD Thesis (University of Stavanger, 2017).Google Scholar
Ricolfi, A. T., ‘The DT/PT correspondence for smooth curves’, Math. Z. 290(1–2) (2018), 699–710.CrossRefGoogle Scholar
Ricolfi, A. T., ‘Local contributions to Donaldson-Thomas invariants’, Int. Math. Res. Not. 2018(19) (2018), 5995–6025.CrossRefGoogle Scholar
Ricolfi, A. T., ‘On the motive of the Quot scheme of finite quotients of a locally free sheaf’, J. Math. Pure Appl. 144 (2020), 50–68.CrossRefGoogle Scholar
Ricolfi, A. T., ‘Virtual classes and virtual motives of Quot schemes on threefolds’, Adv. Math. 369 (2020), 107182.CrossRefGoogle Scholar
Ricolfi, A. T., ‘The equivariant Atiyah class’, 2020, arXiv:2003.05440, accepted for publication in C. R. Math. Acad. Sci. Paris.Google Scholar
Siebert, B., ‘Virtual fundamental classes, global normal cones and Fulton’s canonical classes’, in Frobenius Manifolds, Aspects Math., Vol. 36 (Friedr. Vieweg, Wiesbaden, 2004), 341–358.CrossRefGoogle Scholar
Szabo, R. J., ‘${\mathcal{N}}=2$gauge theories, instanton moduli spaces and geometric representation theory’, J. Geom. Phys. 109 (2016), 83–121.CrossRefGoogle Scholar
Szendrői, B., ‘Cohomological Donaldson-Thomas theory’, in String-Math 2014, Proc. Sympos. Pure Math., Vol. 93 (American Mathematical Society, Providence, RI, 2016), 363–396.Google Scholar
Thomas, R. P., ‘A holomorphic Casson invariant for Calabi-Yau 3-folds, and bundles on K3 fibrations’, J. Diff. Geom. 54(2) (2000), 367–438.CrossRefGoogle Scholar
Thomas, R. P., ‘A $\text{K}-$theoretic Fulton class’, 2018, arXiv:1810.00079, to appear in Facets of Algebraic Geometry: A Volume in Honour of William Fulton’s 80th Birthday (Cambridge University Press).Google Scholar
Thomas, R. P., ‘Equivariant $\text{K}$-theory and refined Vafa-Witten invariants’, Commun. Math. Phys. 378(2) (2020), 1451–1500.CrossRefGoogle Scholar
Toda, Y., ‘Hall algebras in the derived category and higher-rank DT invariants’, Algebr. Geom. 7(3) (2020), 240–262.CrossRefGoogle Scholar
Witten, E., ‘The index of the Dirac operator in loop space’, in Elliptic Curves and Modular Forms in Algebraic Topology (Princeton, NJ, 1986), Lecture Notes in Mathematics, Vol. 1326 (Springer, Berlin, 1988), 161–181.CrossRefGoogle Scholar