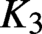Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hourong, Qin
2024.
Conjectures and problems on congruent numbers.
SCIENTIA SINICA Mathematica,
Vol. 54,
Issue. 8,
p.
1157.
El Boukhari, Saad
2025.
First order Stickelberger modules over imaginary quadratic fields.
Journal of Number Theory,
Vol. 269,
Issue. ,
p.
1.