Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T11:36:06.118Z Has data issue: false hasContentIssue false
  • English
  • Français

KAROUBI’S RELATIVE CHERN CHARACTER, THE RIGID SYNTOMIC REGULATOR, AND THE BLOCH–KATO EXPONENTIAL MAP

Part of: (Co)homology theory $K$-theory in number theory

Published online by Cambridge University Press:  20 August 2014

GEORG TAMME
GEORG TAMME*
Affiliation:
Fakultät für Mathematik, Universität Regensburg, 93040 Regensburg, Germany; georg.tamme@mathematik.uni-regensburg.de

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct a variant of Karoubi’s relative Chern character for smooth separated schemes over the ring of integers in a 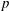$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}p$-adic field, and prove a comparison with the rigid syntomic regulator. For smooth projective schemes, we further relate the relative Chern character to the étale 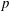$p$-adic regulator via the Bloch–Kato exponential map. This reproves a result of Huber and Kings for the spectrum of the ring of integers, and generalizes it to all smooth projective schemes as above.

MSC classification

Secondary: 19F27: Étale cohomology, higher regulators, zeta and $L$-functions 14F43: Other algebro-geometric (co)homologies (e.g., intersection, equivariant, Lawson, Deligne (co)homologies) 14F30: $p$-adic cohomology, crystalline cohomology
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 2 , 01 July 2014 , e20
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/3.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author 2014

References

Ayoub, J., Motifs des variétés analytiques rigides, preprint available athttp://user.math.uzh.ch/ayoub/.Google Scholar
Besser, A. and de Jeu, R., ‘The syntomic regulator for K 4of curves’, Pacific J. Math. 260 (2) (2012), 305–380.CrossRefGoogle Scholar
Beĭlinson, A., ‘Higher regulators and values of L-functions’, inCurrent Problems in Mathematics, Vol. 24 (Itogi Nauki i Tekhniki, Akad Nauk SSSR Vsesoyuz. Inst. Nauchn. i Tekhn. Inform., Moscow, 1984), 181–238.Google Scholar
Jon Berrick, A., An Approach to Algebraic K-Theory, Research Notes in Mathematics, 56 (Pitman (Advanced Publishing Program), Boston, MA, 1982).Google Scholar
Berthelot, P., Cohomologie rigide et cohomologie rigide à supports propres, Première partie (version provisoire 1991), Prépublication IRMAR 96-03, January 1996.Google Scholar
Berthelot, P., ‘Finitude et pureté cohomologique en cohomologie rigide’, Invent. Math. 128 (2) (1997), 329–377. With an appendix in English by Aise Johan de Jong.Google Scholar
Besser, A., ‘A generalization of Coleman’s p-adic integration theory’, Invent. Math. 142 (2) (2000), 397–434.Google Scholar
Besser, A., ‘Syntomic regulators and p-adic integration. I. Rigid syntomic regulators’, Israel J. Math. 120 (part B) (2000), 291–334.Google Scholar
Besser, A., ‘On the syntomic regulator for K 1of a surface’, Israel J. Math. 190 (2012), 29–66.Google Scholar
Borel, A., ‘Stable real cohomology of arithmetic groups’, Ann. Sci. Éc. Norm. Supér. (4) 7 (1974), 235–272. (1975).Google Scholar
Calvo, A., ‘ K-théorie des anneaux ultramétriques’, C. R. Acad. Sci. Paris Sér. I Math. 300 (14) (1985), 459–462.Google Scholar
Chiarellotto, B., Ciccioni, A. and Mazzari, N., ‘Cycle classes and the syntomic regulator’, Algebra Number Theory 7 (3) (2013), 533–566.CrossRefGoogle Scholar
Connes, A. and Karoubi, M., ‘Caractère multiplicatif d’un module de Fredholm’, K-Theory 2 (3) (1988), 431–463.CrossRefGoogle Scholar
Chiarellotto, B. and Le Stum, B., ‘Sur la pureté de la cohomologie cristalline’, C. R. Acad. Sci. Paris Sér. I Math. 326 (8) (1998), 961–963.Google Scholar
Choo, Z. and Snaith, V., ‘ p-adic cocycles and their regulator maps’, J. K-Theory 8 (2) (2011), 241–249.Google Scholar
Déglise, F. and Mazzari, N., The rigid syntomic ring spectrum, J. Inst. Math. Jussieu, available on CJO2014. doi:10.1017/S1474748014000152.Google Scholar
Deligne, P., ‘Théorie de Hodge, II’, Inst. Hautes Études Sci. Publ. Math. 40 (1971), 5–57.Google Scholar
Faltings, G., ‘Crystalline cohomology and p-adic Galois-representations’, inAlgebraic Analysis, Geometry, and Number Theory (Baltimore, MD, 1988) (John Hopkins University Press, Baltimore, MD, 1989), 25–80.Google Scholar
Gersten, S. M., ‘Higher K-theory of rings’, inAlgebraic K-Theory, I: Higher K-Theories (Proc. Conf. Seattle Res. Center, Battelle Memorial Inst., 1972), Lecture Notes in Mathematics, 341 (Springer, Berlin, 1973), 3–42.Google Scholar
Große-Klönne, E., de Rham–Komologie in der rigiden Analysis, Preprintreihe des SFB 478 – Geometrische Strukturen in der Mathematik, Münster, Heft 39, 1999.Google Scholar
Große-Klönne, E., ‘Rigid analytic spaces with overconvergent structure sheaf’, J. Reine Angew. Math. 519 (2000), 73–95.Google Scholar
Gros, M., ‘Régulateurs syntomiques et valeurs de fonctions L p-adiques II’, Invent. Math. 115 (1) (1994), 61–79.Google Scholar
Hamida, N., ‘Description explicite du régulateur de Borel’, C. R. Acad. Sci. Paris Sér. I Math. 330 (3) (2000), 169–172.Google Scholar
Hamida, N., ‘Le régulateur p-adique’, C. R. Math. Acad. Sci. Paris 342 (11) (2006), 807–812.CrossRefGoogle Scholar
Harder, G., ‘Die Kohomologie S-arithmetischer Gruppen über Funktionenkörpern’, Invent. Math. 42 (1977), 135–175.Google Scholar
Huber, A. and Kings, G., ‘A p-adic analogue of the Borel regulator and the Bloch–Kato exponential map’, J. Inst. Math. Jussieu 10 (1) (2011), 149–190.CrossRefGoogle Scholar
Huber, A., ‘Mixed motives and their realization in derived categories’, inLecture Notes in Mathematics, 1604 (Springer, Berlin, 1995).Google Scholar
Ivorra, F., Réalisations $\ell $ -adique des motifs mixtes, PhD Thesis, Université Paris VI - Pierre et Marie Curie, 2005.Google Scholar
Karoubi, M., ‘Connexions, courbures et classes caractéristiques en K-théorie algébrique’, inCurrent Trends in Algebraic Topology, Part 1, London, Ont., 1981, CMS Conf. Proc., 2 (American Mathematical Society, Providence, RI, 1982), 19–27.Google Scholar
Karoubi, M., ‘Homologie cyclique et régulateurs en K-théorie algébrique’, C. R. Acad. Sci. Paris Sér. I Math. 297 (10) (1983), 557–560.Google Scholar
Karoubi, M., ‘Homologie cyclique et K-théorie’, Astérisque (149) (1987), 1–147.Google Scholar
Karoubi, M. and Villamayor, O., ‘ K-théorie algébrique et K-théorie topologique I’, Math. Scand. 28 (1971), 265–307. (1972).Google Scholar
Meredith, D., ‘Weak formal schemes’, Nagoya Math. J. 45 (1972), 1–38.Google Scholar
Monsky, P. and Washnitzer, G., ‘Formal cohomology I’, Ann. of Math. (2) 88 (1968), 181–217.Google Scholar
Nizioł, W., ‘On the image of p-adic regulators’, Invent. Math. 127 (2) (1997), 375–400.Google Scholar
Nizioł, W., ‘Cohomology of crystalline smooth sheaves’, Compos. Math. 129 (2) (2001), 123–147.Google Scholar
Quillen, D., ‘On the cohomology and K-theory of the general linear groups over a finite field’, Ann. of Math. (2) 96 (1972), 552–586.Google Scholar
Tamme, G., The relative Chern character and regulators, PhD Thesis, Universität Regensburg, 2010, http://epub.uni-regensburg.de/15595/.Google Scholar
Tamme, G., ‘Comparison of Karoubi’s regulator and the p-adic Borel regulator’, J. K-Theory 9 (03) (2012), 579–600.Google Scholar
Tamme, G., ‘Karoubi’s relative Chern character and Beilinson’s regulator’, Ann. Sci. Éc. Norm. Supér. (4) 45 (4) (2012), 601–636.Google Scholar
Thomason, R. W., ‘Algebraic K-theory and étale cohomology’, Ann. Sci. Éc. Norm. Supér. (4) 18 (3) (1985), 437–552.Google Scholar
van der Put, M. and Schneider, P., ‘Points and topologies in rigid geometry’, Math. Ann. 302 (1) (1995), 81–103.CrossRefGoogle Scholar
Weibel, C., ‘Homotopy algebraic K-theory’, inAlgebraic K-Theory and Algebraic Number Theory (Honolulu, HI, 1987), Contemporary Mathematics, 83 (American Mathematical Society, Providence, RI, 1989), 461–488.Google Scholar
Weibel, C., An Introduction to Homological Algebra, Cambridge Studies in Advanced Mathematics, 38 (Cambridge University Press, Cambridge, 1994).Google Scholar
Weibel, C., ‘The Hodge filtration and cyclic homology’, K-Theory 12 (2) (1997), 145–164.Google Scholar