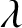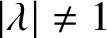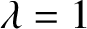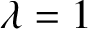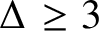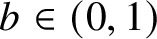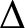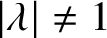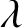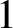1 Introduction
The Ising model is a classical model from statistical physics that arises in multiple sampling and inference tasks across computer science. The model has an edge interaction parameter b and a vertex parameter ![]() $\lambda $, known as the external field. For a graph
$\lambda $, known as the external field. For a graph ![]() $G=(V,E)$ (all graphs considered in this article are finite), configurations of the model are all possible assignments of two spins
$G=(V,E)$ (all graphs considered in this article are finite), configurations of the model are all possible assignments of two spins ![]() $\mathrm {\texttt {+}},\mathrm {\texttt {-}}$ to the vertices of G. Each configuration
$\mathrm {\texttt {+}},\mathrm {\texttt {-}}$ to the vertices of G. Each configuration ![]() $\sigma :V\rightarrow \{\mathrm {\texttt {+}},\mathrm {\texttt {-}} \}$ has weight
$\sigma :V\rightarrow \{\mathrm {\texttt {+}},\mathrm {\texttt {-}} \}$ has weight ![]() $\lambda ^{|n_{\mathrm {\texttt {+}}}(\sigma )|}b^{\delta (\sigma )}$, where
$\lambda ^{|n_{\mathrm {\texttt {+}}}(\sigma )|}b^{\delta (\sigma )}$, where ![]() $n_{\mathrm {\texttt {+}}}(\sigma )$ is the set of vertices that get the spin
$n_{\mathrm {\texttt {+}}}(\sigma )$ is the set of vertices that get the spin ![]() $\mathrm {\texttt {+}}$ under
$\mathrm {\texttt {+}}$ under ![]() $\sigma $ and
$\sigma $ and ![]() $\delta (\sigma )$ is the number of edges that get different spins.Footnote 1 The partition function is the aggregate weight of all configurations; that is,
$\delta (\sigma )$ is the number of edges that get different spins.Footnote 1 The partition function is the aggregate weight of all configurations; that is,
 $$ \begin{align*}Z_G(\lambda,b)=\sum_{\sigma:V\rightarrow\{\mathrm{\texttt{+}} ,\mathrm{\texttt{-}} \}}\lambda^{|n_{\mathrm{\texttt{+}}}(\sigma)|}b^{\delta(\sigma)}.\end{align*} $$
$$ \begin{align*}Z_G(\lambda,b)=\sum_{\sigma:V\rightarrow\{\mathrm{\texttt{+}} ,\mathrm{\texttt{-}} \}}\lambda^{|n_{\mathrm{\texttt{+}}}(\sigma)|}b^{\delta(\sigma)}.\end{align*} $$In this article, we consider the problem of approximating the partition function when ![]() $b\in (0,1]$, known as the ferromagnetic case, and when the parameter
$b\in (0,1]$, known as the ferromagnetic case, and when the parameter ![]() $\lambda $ is in the complex plane. Complex parameters for the Ising model have been studied in the computation of probability amplitudes of quantum circuits; see, for example, [Reference De las Cuevas, Dür, Van den Nest and Martin-Delgado12, Reference Mann and Bremner36, Reference Bremner, Montanaro and Shepherd8]. Somewhat surprising – and this is one of the main motivations behind this work – complex parameters are also fundamental in understanding the complexity of approximation even for real-valued parameters.
$\lambda $ is in the complex plane. Complex parameters for the Ising model have been studied in the computation of probability amplitudes of quantum circuits; see, for example, [Reference De las Cuevas, Dür, Van den Nest and Martin-Delgado12, Reference Mann and Bremner36, Reference Bremner, Montanaro and Shepherd8]. Somewhat surprising – and this is one of the main motivations behind this work – complex parameters are also fundamental in understanding the complexity of approximation even for real-valued parameters.
In particular, many of the recent advances on the development of approximation algorithms for counting problems have been based on viewing the partition function as a polynomial of the underlying parameters in the complex plane and using refined interpolation techniques from [Reference Barvinok1, Reference Patel and Regts39] to obtain fully polynomial time approximation schemes (![]() $\mathsf {FPTAS}$; see Subsection 1.1 below for the technical definition), even for real values [Reference Guo, Liao, Lu and Zhang23, Reference Guo, Liu and Lu24, Reference Liu, Sinclair and Srivastava33, Reference Bencs, Davies, Patel and Regts5, Reference Barvinok and Regts2, Reference Liu, Sinclair and Srivastava34, Reference Shao and Sun44, Reference Peters and Regts42, Reference Peters and Regts41]. The bottleneck of this approach is establishing zero-free regions in the complex plane of the polynomials, which in turn requires an in-depth understanding of the models with complex-valued parameters. This framework of designing approximation algorithms aligns with the classical statistical physics perspective on phase transitions, where zeros in the complex plane have long been studied in the context of phase transitions (see, e.g., [Reference Lee and Yang29, Reference Heilmann and Lieb25]), and several of these classical results have recently been used to obtain efficient approximation algorithms ([Reference Liu, Sinclair and Srivastava35, Reference Patel and Regts39]).
$\mathsf {FPTAS}$; see Subsection 1.1 below for the technical definition), even for real values [Reference Guo, Liao, Lu and Zhang23, Reference Guo, Liu and Lu24, Reference Liu, Sinclair and Srivastava33, Reference Bencs, Davies, Patel and Regts5, Reference Barvinok and Regts2, Reference Liu, Sinclair and Srivastava34, Reference Shao and Sun44, Reference Peters and Regts42, Reference Peters and Regts41]. The bottleneck of this approach is establishing zero-free regions in the complex plane of the polynomials, which in turn requires an in-depth understanding of the models with complex-valued parameters. This framework of designing approximation algorithms aligns with the classical statistical physics perspective on phase transitions, where zeros in the complex plane have long been studied in the context of phase transitions (see, e.g., [Reference Lee and Yang29, Reference Heilmann and Lieb25]), and several of these classical results have recently been used to obtain efficient approximation algorithms ([Reference Liu, Sinclair and Srivastava35, Reference Patel and Regts39]).
In particular, the celebrated Lee–Yang theorem [Reference Lee and Yang30] says that, when regarding the partition function of the ferromagnetic Ising model as a polynomial in the external field parameter ![]() $\lambda $, all of its zeros, referred to as Lee–Yang zeros, lie on the unit circle in the complex plane. (These Lee–Yang zeros have actually been observed in quantum experiments [Reference Peng, Zhou, Wei, Cui, Du and Liu40].) The Lee–Yang theorem was recently used by Liu, Sinclair and Srivastava [Reference Liu, Sinclair and Srivastava35] to obtain an
$\lambda $, all of its zeros, referred to as Lee–Yang zeros, lie on the unit circle in the complex plane. (These Lee–Yang zeros have actually been observed in quantum experiments [Reference Peng, Zhou, Wei, Cui, Du and Liu40].) The Lee–Yang theorem was recently used by Liu, Sinclair and Srivastava [Reference Liu, Sinclair and Srivastava35] to obtain an ![]() $\mathsf {FPTAS}$ for approximating the partition function for values
$\mathsf {FPTAS}$ for approximating the partition function for values ![]() $\lambda \in \mathbb {C}$ that do not lie on the unit circle. This result can be viewed as a derandomisation of the Markov chain–based randomised algorithm by Jerrum and Sinclair [Reference Jerrum and Sinclair26] for
$\lambda \in \mathbb {C}$ that do not lie on the unit circle. This result can be viewed as a derandomisation of the Markov chain–based randomised algorithm by Jerrum and Sinclair [Reference Jerrum and Sinclair26] for ![]() $\lambda>0$ (see also [Reference Guo and Jerrum22, Reference Collevecchio, Garoni, Hyndman and Tokarev11]), solving a longstanding problem.Footnote 2
$\lambda>0$ (see also [Reference Guo and Jerrum22, Reference Collevecchio, Garoni, Hyndman and Tokarev11]), solving a longstanding problem.Footnote 2
As noted in [Reference Liu, Sinclair and Srivastava35, Remark p. 290], the ‘no-field’ case ![]() $|\lambda |=1$ is unclear, since, on the one hand, we have the algorithm by [Reference Jerrum and Sinclair26] for
$|\lambda |=1$ is unclear, since, on the one hand, we have the algorithm by [Reference Jerrum and Sinclair26] for ![]() $\lambda =1$ and, on the other hand, it is known that Lee–Yang zeros are dense on the unit circle. The density picture was further explored in [Reference Peters and Regts42] for graphs of bounded maximum degree
$\lambda =1$ and, on the other hand, it is known that Lee–Yang zeros are dense on the unit circle. The density picture was further explored in [Reference Peters and Regts42] for graphs of bounded maximum degree ![]() $\Delta $, by establishing for each
$\Delta $, by establishing for each ![]() $b\in (0,1)$ a symmetric arc around
$b\in (0,1)$ a symmetric arc around ![]() $\lambda =1$ on the unit circle where the partition function does not vanish for all graphs of maximum degree at most
$\lambda =1$ on the unit circle where the partition function does not vanish for all graphs of maximum degree at most ![]() $\Delta $ and showing density of the Lee–Yang zeros on the complementary arc. See also [Reference Chio, He, Ji and Roeder10] for the density result.
$\Delta $ and showing density of the Lee–Yang zeros on the complementary arc. See also [Reference Chio, He, Ji and Roeder10] for the density result.
In this article, we resolve the complexity picture of the ferromagnetic Ising model. We show that for graphs of maximum degree ![]() $\Delta $, approximately computing the partition function is
$\Delta $, approximately computing the partition function is ![]() $\mathsf {\#P}$-hard,Footnote 3 on the arc of the unit circle where the Lee–Yang zeros are dense. See Theorem 1 for a precise statement of our main results. Since on the complementary arc there exists an
$\mathsf {\#P}$-hard,Footnote 3 on the arc of the unit circle where the Lee–Yang zeros are dense. See Theorem 1 for a precise statement of our main results. Since on the complementary arc there exists an ![]() $\mathsf {FPTAS}$, by the results of [Reference Peters and Regts42] (in combination with [Reference Barvinok1, Reference Patel and Regts39]), this gives a direct connection between hardness of approximation and the presence of Lee–Yang zeros. Combined with the results of [Reference Jerrum and Sinclair26, Reference Liu, Sinclair and Srivastava35], our work therefore classifies the complexity of approximating the partition function of the ferromagnetic Ising model on the complex plane.
$\mathsf {FPTAS}$, by the results of [Reference Peters and Regts42] (in combination with [Reference Barvinok1, Reference Patel and Regts39]), this gives a direct connection between hardness of approximation and the presence of Lee–Yang zeros. Combined with the results of [Reference Jerrum and Sinclair26, Reference Liu, Sinclair and Srivastava35], our work therefore classifies the complexity of approximating the partition function of the ferromagnetic Ising model on the complex plane.
It should be noted that the existence of zeros does not imply hardness in a straightforward manner.Footnote 4 We obtain the connection between the Lee–Yang zeros and computational complexity via tools from complex dynamical systems. The partition function on trees naturally gives rise to a dynamical system; cf. Subsection 2.1. Both the hardness of approximating the partition function as well as the density of the Lee–Yang zeros originate from chaotic behavior of the dynamics, while normal behavior is linked to absence of zeros and hence the existence of efficient approximation algorithms [Reference Peters and Regts42].
Our work falls into the broader context of showing how zeros in the complex plane actually relate to the existence and design of approximation algorithms. This connection has been well studied for general graphs, see, for example, [Reference Guo and Jerrum20, Reference Goldberg and Guo18, Reference Galanis, Goldberg and Herrera-Poyatos15]; for bounded-degree graphs, the picture is less clear, but the key seems to lie in understanding the underlying complex dynamical systems [Reference Bezáková, Galanis, Goldberg and Štefankovič6, Reference Buys9, Reference Chio, He, Ji and Roeder10, Reference Peters and Regts42, Reference Bencs, Buys, Guerini and Peters4, Reference Bezáková, Galanis, Goldberg and Štefankovič7]. A general theory is so far elusive, but it seems that the chaotic behavior of the underlying complex dynamical system is linked to the presence of zeros of the partition function and to the ![]() $\mathsf {\#P}$-hardness of approximation.
$\mathsf {\#P}$-hardness of approximation.
Establishing hardness results for ferromagnetic spin systems is notoriously challenging [Reference Liu, Lu and Zhang32, Reference Guo and Lu21]. We therefore expect our techniques to be applicable in a wider framework. We will explain in Section 2 the obstacles that arise relative to previous works for antiferromagnetic spin systems.
1.1 Our results
To state our inapproximability results, we first formally define the computational problems that we consider. For ![]() $z\in \mathbb {C}$, we let
$z\in \mathbb {C}$, we let ![]() $|z|$ be the norm of z,
$|z|$ be the norm of z, ![]() $\text {Arg}(z)$ be its argument in the interval
$\text {Arg}(z)$ be its argument in the interval ![]() $[0,2\pi )$ and
$[0,2\pi )$ and ![]() $\text {arg}(z)=\{\text {Arg}(z)+2k\pi \mid k\in \mathbb {Z}\}$ be the set of all of its arguments. We will consider the problems of approximating the norm of the partition function
$\text {arg}(z)=\{\text {Arg}(z)+2k\pi \mid k\in \mathbb {Z}\}$ be the set of all of its arguments. We will consider the problems of approximating the norm of the partition function ![]() $Z_G(\lambda ,b)$ within a rational factor
$Z_G(\lambda ,b)$ within a rational factor ![]() $K>1$ and its argument within an additive rational constant
$K>1$ and its argument within an additive rational constant ![]() $\rho>0$. For the computational problems, we moreover assume that
$\rho>0$. For the computational problems, we moreover assume that ![]() $b\in (0,1)$ is rational and
$b\in (0,1)$ is rational and ![]() $\lambda $ has rational real and imaginary parts. The rationality assumption is mainly for convenience (representation issues) and simplifies some of the proofs.
$\lambda $ has rational real and imaginary parts. The rationality assumption is mainly for convenience (representation issues) and simplifies some of the proofs.
Name
 $\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$.
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$.Instance A graph
 $G=(V,E)$ with maximum degree
$G=(V,E)$ with maximum degree  $\leq \Delta $.
$\leq \Delta $.Output If
 $Z_G(\lambda ,b)=0$, the algorithm may output any rational. Otherwise, it must return a rational
$Z_G(\lambda ,b)=0$, the algorithm may output any rational. Otherwise, it must return a rational  $\widehat {N}$ such that
$\widehat {N}$ such that  $\widehat {N}/K \leq |Z_{G}(\lambda ,b)|\leq K \widehat {N}$.
$\widehat {N}/K \leq |Z_{G}(\lambda ,b)|\leq K \widehat {N}$.
We remark here that the explicit constant ![]() $K>1$ in the problem definition above is only for convenience, having
$K>1$ in the problem definition above is only for convenience, having ![]() $K=2^{n^{1-\epsilon }}$ for any constant
$K=2^{n^{1-\epsilon }}$ for any constant ![]() $\epsilon>0$ and with n the number of vertices of the graph does not change the complexity of the problem using standard powering arguments.
$\epsilon>0$ and with n the number of vertices of the graph does not change the complexity of the problem using standard powering arguments.
Name
 $\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$.
$\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$.Instance A graph
 $G=(V,E)$ with maximum degree
$G=(V,E)$ with maximum degree  $\leq \Delta $.
$\leq \Delta $.Output If
 $Z_G(\lambda ,b)=0$, the algorithm may output any rational. Otherwise, it must return a rational
$Z_G(\lambda ,b)=0$, the algorithm may output any rational. Otherwise, it must return a rational  $\widehat {A}$ such that
$\widehat {A}$ such that  $|\widehat {A} - a| \leq \rho $ for some
$|\widehat {A} - a| \leq \rho $ for some  $a\in \text {arg}(Z_{G}(\lambda ,b))$.
$a\in \text {arg}(Z_{G}(\lambda ,b))$.
A fully polynomial time approximation scheme (![]() $\mathsf {FPTAS}$) for approximating
$\mathsf {FPTAS}$) for approximating ![]() $Z_G(\lambda ,b)$ for given
$Z_G(\lambda ,b)$ for given ![]() $\lambda $ and b and positive integer
$\lambda $ and b and positive integer ![]() $\Delta $ is an algorithm that for any n-vertex graph G of maximum degree at most
$\Delta $ is an algorithm that for any n-vertex graph G of maximum degree at most ![]() $\Delta $ and any rational
$\Delta $ and any rational ![]() $\varepsilon>0$ solves both probems
$\varepsilon>0$ solves both probems ![]() $\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,1+\varepsilon )$ and
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,1+\varepsilon )$ and ![]() $\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\varepsilon )$ in time polynomial in
$\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\varepsilon )$ in time polynomial in ![]() $n/\varepsilon $.
$n/\varepsilon $.
We use ![]() $\mathbb {Q}$ to denote the set of rational numbers and
$\mathbb {Q}$ to denote the set of rational numbers and ![]() $\mathbb {C}_{\mathbb {Q}}$ to denote the set of complex numbers with rational real and imaginary part. We denote by
$\mathbb {C}_{\mathbb {Q}}$ to denote the set of complex numbers with rational real and imaginary part. We denote by ![]() $\mathbb {S}$ the unit circle in the complex plane and
$\mathbb {S}$ the unit circle in the complex plane and ![]() $\mathbb {S}_{\mathbb {Q}}=\mathbb {S}\cap \mathbb {C}_{\mathbb {Q}}$. It is well-known that numbers in
$\mathbb {S}_{\mathbb {Q}}=\mathbb {S}\cap \mathbb {C}_{\mathbb {Q}}$. It is well-known that numbers in ![]() $\mathbb {S}_{\mathbb {Q}}$ are dense on the unit circle.Footnote 5 For
$\mathbb {S}_{\mathbb {Q}}$ are dense on the unit circle.Footnote 5 For ![]() $\theta \in (0,\pi )$ we denote
$\theta \in (0,\pi )$ we denote
For ![]() $\Delta \geq 3$ and
$\Delta \geq 3$ and  $b\in (\frac {\Delta -2}{\Delta },1)$ we denote by
$b\in (\frac {\Delta -2}{\Delta },1)$ we denote by ![]() $\theta _b\in (0,\pi )$ the angle from [Reference Peters and Regts42, Theorem A] for which the following hold:
$\theta _b\in (0,\pi )$ the angle from [Reference Peters and Regts42, Theorem A] for which the following hold:
(i) For any graph G of maximum degree at most
 $\Delta $ and any
$\Delta $ and any  $\lambda \in I(\theta _b)$,
$\lambda \in I(\theta _b)$,  $Z_G(\lambda ,b)\neq 0$.
$Z_G(\lambda ,b)\neq 0$.(ii) For each
 $\lambda \in \mathbb {S}\setminus I(\theta _b)$ there exists
$\lambda \in \mathbb {S}\setminus I(\theta _b)$ there exists  $\lambda '\in \mathbb {S}$ arbitrarily close to
$\lambda '\in \mathbb {S}$ arbitrarily close to  $\lambda $ and a tree T of maximum degree
$\lambda $ and a tree T of maximum degree  $\Delta $ for which
$\Delta $ for which  $Z_T(\lambda ',b)=0$.
$Z_T(\lambda ',b)=0$.
Our main result is as follows.
Theorem 1. Let ![]() $\Delta \geq 3$ be an integer and let
$\Delta \geq 3$ be an integer and let ![]() $K=1.001$ and
$K=1.001$ and ![]() $\rho =\pi /40$.
$\rho =\pi /40$.
(a) Let
 $b \in \big (0,\frac {\Delta -2}{\Delta }\big ]$ be a rational and
$b \in \big (0,\frac {\Delta -2}{\Delta }\big ]$ be a rational and  $\lambda \in \mathbb {S}_{\mathbb {Q}}$ such that
$\lambda \in \mathbb {S}_{\mathbb {Q}}$ such that  $\lambda \neq \pm 1$. Then the problems
$\lambda \neq \pm 1$. Then the problems  $\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ and
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ and  $\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$ are
$\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$ are  $\mathsf {\#P}$-hard.
$\mathsf {\#P}$-hard.(b) Let
 $b\in \big (\frac {\Delta -2}{\Delta },1\big )$ be a rational. Then the collection of complex numbers
$b\in \big (\frac {\Delta -2}{\Delta },1\big )$ be a rational. Then the collection of complex numbers  $\lambda \in \mathbb {S}_{\mathbb {Q}}$ for which
$\lambda \in \mathbb {S}_{\mathbb {Q}}$ for which  $\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ and
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ and  $\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$ are
$\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$ are  $\mathsf {\#P}$-hard is dense in the arc
$\mathsf {\#P}$-hard is dense in the arc  $\mathbb {S}\setminus I(\theta _b)$.
$\mathbb {S}\setminus I(\theta _b)$.
Combined with [Reference Liu, Sinclair and Srivastava35], part (a) of our main theorem completely classifies the hardness of approximating the partition function ![]() $Z_G(\lambda ,b)$ (as per the two computational problems stated above), for
$Z_G(\lambda ,b)$ (as per the two computational problems stated above), for  $b\in (0,\frac {\Delta -2}{\Delta }]$. Combined with [Reference Peters and Regts42, Corollary 1], part (b) of our main theorem ‘essentially’ classifies the hardness of approximating the partition function for
$b\in (0,\frac {\Delta -2}{\Delta }]$. Combined with [Reference Peters and Regts42, Corollary 1], part (b) of our main theorem ‘essentially’ classifies the hardness of approximating the partition function for  $b\in (\frac {\Delta -2}{\Delta },1)$ and answers a question from [Reference Peters and Regts42]. Technically, we do not rule out that there may be an efficient algorithm for these problems for some
$b\in (\frac {\Delta -2}{\Delta },1)$ and answers a question from [Reference Peters and Regts42]. Technically, we do not rule out that there may be an efficient algorithm for these problems for some ![]() $\lambda \in \mathbb {S}_{\mathbb {Q}}\setminus I(\theta _b)$, but such an algorithm must be specifically tailored to such a particular
$\lambda \in \mathbb {S}_{\mathbb {Q}}\setminus I(\theta _b)$, but such an algorithm must be specifically tailored to such a particular ![]() $\lambda $ (unless, of course,
$\lambda $ (unless, of course, ![]() $\mathsf {P}=\mathsf {\#P}$). We in fact conjecture that, when
$\mathsf {P}=\mathsf {\#P}$). We in fact conjecture that, when  $b\in (\frac {\Delta -2}{\Delta },1)$, approximating the partition function (as in Theorem 1) is
$b\in (\frac {\Delta -2}{\Delta },1)$, approximating the partition function (as in Theorem 1) is ![]() $\mathsf {\#P}$-hard for all non-real
$\mathsf {\#P}$-hard for all non-real ![]() $\lambda \in \mathbb {S}_{\mathbb {Q}}\setminus I(\theta _b)$. See Remark 2 for a discussion of the antipodal case
$\lambda \in \mathbb {S}_{\mathbb {Q}}\setminus I(\theta _b)$. See Remark 2 for a discussion of the antipodal case ![]() $\lambda =-1$.
$\lambda =-1$.
We should further remark that the open interval  $b\in \big (0,\frac {\Delta -2}{\Delta }\big )$ for positive
$b\in \big (0,\frac {\Delta -2}{\Delta }\big )$ for positive ![]() $\lambda $ corresponds to the so-called nonuniqueness region of the infinite
$\lambda $ corresponds to the so-called nonuniqueness region of the infinite ![]() $\Delta $-regular tree. For the antiferromagnetic Ising model and positive
$\Delta $-regular tree. For the antiferromagnetic Ising model and positive ![]() $\lambda $, nonuniqueness leads to computational intractability [Reference Sly and Sun46, Reference Galanis, Štefankovič and Vigoda17], in contrast to the ferromagnetic case. As we explain in Section 2, the phenomenon which underpins our proofs for
$\lambda $, nonuniqueness leads to computational intractability [Reference Sly and Sun46, Reference Galanis, Štefankovič and Vigoda17], in contrast to the ferromagnetic case. As we explain in Section 2, the phenomenon which underpins our proofs for ![]() $|\lambda |=1$ with
$|\lambda |=1$ with ![]() $\lambda \neq \pm 1$ is the chaotic behaviour of the underlying complex dynamical system, which resembles in rough terms a complex-plane analogue of nonuniqueness. Interestingly, at criticality – that is, when
$\lambda \neq \pm 1$ is the chaotic behaviour of the underlying complex dynamical system, which resembles in rough terms a complex-plane analogue of nonuniqueness. Interestingly, at criticality – that is, when  $b=\frac {\Delta -2}{\Delta }$ – while the model is in uniqueness for
$b=\frac {\Delta -2}{\Delta }$ – while the model is in uniqueness for ![]() $\lambda =1$, the chaotic behaviour is nevertheless present for non-real
$\lambda =1$, the chaotic behaviour is nevertheless present for non-real ![]() $\lambda $ and we show
$\lambda $ and we show ![]() $\mathsf {\#P}$-hardness for this case, too.
$\mathsf {\#P}$-hardness for this case, too.
Remark 2. We further discuss the real cases ![]() $\lambda =\pm 1$ which are not explicitly covered by Theorem 1. The case
$\lambda =\pm 1$ which are not explicitly covered by Theorem 1. The case ![]() $\lambda =1$ admits an
$\lambda =1$ admits an ![]() $\mathsf {FPRAS}$ [Reference Jerrum and Sinclair26, Reference Guo and Jerrum22, Reference Collevecchio, Garoni, Hyndman and Tokarev11], but the existence of a deterministic approximation scheme is open. We study the case
$\mathsf {FPRAS}$ [Reference Jerrum and Sinclair26, Reference Guo and Jerrum22, Reference Collevecchio, Garoni, Hyndman and Tokarev11], but the existence of a deterministic approximation scheme is open. We study the case ![]() $\lambda =-1$ in more detail in Section 9, where we show that the problem is not
$\lambda =-1$ in more detail in Section 9, where we show that the problem is not ![]() $\mathsf {\#P}$-hard (assuming
$\mathsf {\#P}$-hard (assuming ![]() $\mathsf {\#P}\neq \mathsf {NP}$): using the ‘high-temperature’ expansion of the model, we show an odd-subgraphs formulation of the partition function (Lemma 39), which is then used to conclude (Theorem 40) that the sign of the partition function can be determined trivially, while the problem of approximating the norm of the partition function for all
$\mathsf {\#P}\neq \mathsf {NP}$): using the ‘high-temperature’ expansion of the model, we show an odd-subgraphs formulation of the partition function (Lemma 39), which is then used to conclude (Theorem 40) that the sign of the partition function can be determined trivially, while the problem of approximating the norm of the partition function for all ![]() $\Delta \geq 3$ is equivalent to the problem of approximately counting the number of perfect matchings (even on unbounded-degree graphs); the complexity of the latter is an open problem in general, but it can be approximated with an NP-oracle [Reference Jerrum, Valiant and Vazirani27], therefore precluding
$\Delta \geq 3$ is equivalent to the problem of approximately counting the number of perfect matchings (even on unbounded-degree graphs); the complexity of the latter is an open problem in general, but it can be approximated with an NP-oracle [Reference Jerrum, Valiant and Vazirani27], therefore precluding ![]() $\mathsf {\#P}$-hardness.
$\mathsf {\#P}$-hardness.
In the next section, we give an outline of the key pieces to obtain our inapproximability results; the details of these pieces will be provided in the forthcoming sections (see also Subsection 2.5 for the organisation of the article).
2 Proof outline
Let ![]() $\Delta \geq 3$ be an integer,
$\Delta \geq 3$ be an integer,  $b\in (0,\frac {\Delta -2}{\Delta }]$ and
$b\in (0,\frac {\Delta -2}{\Delta }]$ and ![]() $\lambda \in \mathbb {S}_{\mathbb {Q}}$ with
$\lambda \in \mathbb {S}_{\mathbb {Q}}$ with ![]() $\lambda \neq \pm 1$. It will be convenient to work sometimes with
$\lambda \neq \pm 1$. It will be convenient to work sometimes with ![]() $d=\Delta -1$. For
$d=\Delta -1$. For ![]() $z_1, z_2 \in \mathbb {S}$, let
$z_1, z_2 \in \mathbb {S}$, let ![]() $\operatorname {\mathrm {Arc}}{[z_1,z_2]}$ and
$\operatorname {\mathrm {Arc}}{[z_1,z_2]}$ and ![]() $\operatorname {\mathrm {Arc}}{(z_1,z_2)}$ denote the counterclockwise arc in
$\operatorname {\mathrm {Arc}}{(z_1,z_2)}$ denote the counterclockwise arc in ![]() $\mathbb {S}$ from
$\mathbb {S}$ from ![]() $z_1$ to
$z_1$ to ![]() $z_2$ including and excluding the endpoints, respectively. For an arc A on the unit circle
$z_2$ including and excluding the endpoints, respectively. For an arc A on the unit circle ![]() $\mathbb {S}$, we let
$\mathbb {S}$, we let ![]() $\ell (A)$ denote the length of A. We use
$\ell (A)$ denote the length of A. We use ![]() $\overline {z}$ to denote the conjugate of z.
$\overline {z}$ to denote the conjugate of z.
2.1 Rooted-tree gadgets and complex dynamical systems
Our reductions are based on gadgets that are rooted trees, whose analysis will be based on understanding the dynamical behaviour of certain complex maps on the unit circle, given byFootnote 6
 $$ \begin{align} f_{\lambda,k}: z \mapsto \lambda \cdot \Big(\frac{z + b}{b z + 1}\Big)^k, \mbox{ for integers}\ k=1,\ldots, d. \end{align} $$
$$ \begin{align} f_{\lambda,k}: z \mapsto \lambda \cdot \Big(\frac{z + b}{b z + 1}\Big)^k, \mbox{ for integers}\ k=1,\ldots, d. \end{align} $$We will sometimes drop ![]() $\lambda $ when it is clear from the context. To connect these maps with rooted-tree gadgets, for a graph
$\lambda $ when it is clear from the context. To connect these maps with rooted-tree gadgets, for a graph ![]() $G=(V,E)$ and a vertex u of G, we let
$G=(V,E)$ and a vertex u of G, we let ![]() $Z_{G,\mathrm {\texttt {+}} u}$ be the contribution to the partition function from configurations with
$Z_{G,\mathrm {\texttt {+}} u}$ be the contribution to the partition function from configurations with ![]() $\sigma (u)=\mathrm {\texttt {+}}$; that is,
$\sigma (u)=\mathrm {\texttt {+}}$; that is,
 $$ \begin{align*}Z_{G,\mathrm{\texttt{+}} u}(\lambda,b):=\sum_{\sigma: V\rightarrow\{\mathrm{\texttt{+}},\mathrm{\texttt{-}} \}; \sigma(u)=\mathrm{\texttt{+}}} \lambda^{|n_{\mathrm{\texttt{+}}}(\sigma)|}b^{\delta(\sigma)},\end{align*} $$
$$ \begin{align*}Z_{G,\mathrm{\texttt{+}} u}(\lambda,b):=\sum_{\sigma: V\rightarrow\{\mathrm{\texttt{+}},\mathrm{\texttt{-}} \}; \sigma(u)=\mathrm{\texttt{+}}} \lambda^{|n_{\mathrm{\texttt{+}}}(\sigma)|}b^{\delta(\sigma)},\end{align*} $$and we define analogously ![]() $Z_{G,\mathrm {\texttt {-}} u}$.
$Z_{G,\mathrm {\texttt {-}} u}$.
Definition 3. Let ![]() $\lambda ,b$ be arbitrary numbers and T be a tree rooted at r. We say that T implements the field
$\lambda ,b$ be arbitrary numbers and T be a tree rooted at r. We say that T implements the field ![]() $\lambda '$ if
$\lambda '$ if ![]() $Z_{T,\mathrm {\texttt {-}} r}(\lambda ,b)\neq 0$ and
$Z_{T,\mathrm {\texttt {-}} r}(\lambda ,b)\neq 0$ and  $\lambda '=\tfrac {Z_{T,\mathrm {\texttt {+}} r}(\lambda ,b)}{Z_{T,\mathrm {\texttt {-}} r}(\lambda ,b)}$. We call
$\lambda '=\tfrac {Z_{T,\mathrm {\texttt {+}} r}(\lambda ,b)}{Z_{T,\mathrm {\texttt {-}} r}(\lambda ,b)}$. We call ![]() $\lambda '$ the field of T.
$\lambda '$ the field of T.
The next lemma explains the relevance of the maps ![]() $f_{\lambda ,1},\ldots , f_{\lambda ,d}$ for implementing fields.
$f_{\lambda ,1},\ldots , f_{\lambda ,d}$ for implementing fields.
Lemma 4. Let ![]() $b \in (0,1)$ and
$b \in (0,1)$ and ![]() $\lambda \in \mathbb {S}$. Let
$\lambda \in \mathbb {S}$. Let ![]() $T_1,T_2$ be rooted trees with roots
$T_1,T_2$ be rooted trees with roots ![]() $r_1,r_2$ and fields
$r_1,r_2$ and fields ![]() $\xi _1,\xi _2\in \mathbb {S}$, respectively. Then, the tree T rooted at
$\xi _1,\xi _2\in \mathbb {S}$, respectively. Then, the tree T rooted at ![]() $r_2$ consisting of
$r_2$ consisting of ![]() $T_2$ and k distinct copies of
$T_2$ and k distinct copies of ![]() $T_1$ which are attached to
$T_1$ which are attached to ![]() $r_2$ via an edge between
$r_2$ via an edge between ![]() $r_2$ and
$r_2$ and ![]() $r_1$ implements the field
$r_1$ implements the field ![]() $\xi =f_{\xi _2,k}(\xi _1)\in \mathbb {S}$.
$\xi =f_{\xi _2,k}(\xi _1)\in \mathbb {S}$.
Proof. Omitting for convenience the arguments ![]() $\lambda ,b$ from the partition functions, we have
$\lambda ,b$ from the partition functions, we have
 $$ \begin{align*} Z_{T,\mathrm{\texttt{+}} r_2}=Z_{T_2,\mathrm{\texttt{+}} r_2} ( Z_{T_1,\mathrm{\texttt{+}} r_1}+b Z_{T_1,\mathrm{\texttt{-}} r_1})^{k}, \quad Z_{T,\mathrm{\texttt{-}} r_2}=Z_{T_2,\mathrm{\texttt{-}} r_2} (b Z_{T_1,\mathrm{\texttt{+}} r_1}+ Z_{T_1,\mathrm{\texttt{-}} r_1})^{k}. \end{align*} $$
$$ \begin{align*} Z_{T,\mathrm{\texttt{+}} r_2}=Z_{T_2,\mathrm{\texttt{+}} r_2} ( Z_{T_1,\mathrm{\texttt{+}} r_1}+b Z_{T_1,\mathrm{\texttt{-}} r_1})^{k}, \quad Z_{T,\mathrm{\texttt{-}} r_2}=Z_{T_2,\mathrm{\texttt{-}} r_2} (b Z_{T_1,\mathrm{\texttt{+}} r_1}+ Z_{T_1,\mathrm{\texttt{-}} r_1})^{k}. \end{align*} $$Dividing these yields the result (note, ![]() $Z_{T_2,\mathrm {\texttt {-}} r_2}\neq 0$ and
$Z_{T_2,\mathrm {\texttt {-}} r_2}\neq 0$ and  $\xi _1=\tfrac {Z_{T_1,\mathrm {\texttt {+}} r_1}}{Z_{T_1,\mathrm {\texttt {-}} r_1}}\in \mathbb {S}$, so
$\xi _1=\tfrac {Z_{T_1,\mathrm {\texttt {+}} r_1}}{Z_{T_1,\mathrm {\texttt {-}} r_1}}\in \mathbb {S}$, so ![]() $Z_{T,\mathrm {\texttt {-}} r_2}\neq 0$); the fact that
$Z_{T,\mathrm {\texttt {-}} r_2}\neq 0$); the fact that ![]() $\xi \in \mathbb {S}$ follows from footnote 6.
$\xi \in \mathbb {S}$ follows from footnote 6.
Note, in particular, that all fields implemented by trees lie on the unit circle ![]() $\mathbb {S}$; cf. footnote (6). The following theorem, which lies at the heart of the construction of the gadgets, asserts that throughout the relevant range of the parameters we can in fact implement a field arbitrarily close to any number in
$\mathbb {S}$; cf. footnote (6). The following theorem, which lies at the heart of the construction of the gadgets, asserts that throughout the relevant range of the parameters we can in fact implement a field arbitrarily close to any number in ![]() $\mathbb {S}$. We use
$\mathbb {S}$. We use ![]() $\mathcal {T}_{d+1}$ to denote the set of all rooted trees with maximum degree
$\mathcal {T}_{d+1}$ to denote the set of all rooted trees with maximum degree ![]() $\leq d+1$ whose roots have degree
$\leq d+1$ whose roots have degree ![]() $\leq d$.
$\leq d$.
Definition 5. Given ![]() $b\in (0,1)$ and
$b\in (0,1)$ and ![]() $d\geq 2$, we denote by
$d\geq 2$, we denote by ![]() $\mathbb {S}_{\mathbb {Q}}(d,b)$ the collection of
$\mathbb {S}_{\mathbb {Q}}(d,b)$ the collection of ![]() $\lambda \in \mathbb {S}_{\mathbb {Q}}$ for which the set of fields implemented by trees in
$\lambda \in \mathbb {S}_{\mathbb {Q}}$ for which the set of fields implemented by trees in ![]() $\mathcal {T}_{d+1}$, whose roots have degree
$\mathcal {T}_{d+1}$, whose roots have degree ![]() $1$, is dense in
$1$, is dense in ![]() $\mathbb {S}$.
$\mathbb {S}$.
Theorem 6. Let ![]() $d\geq 2$ be an integer.
$d\geq 2$ be an integer.
(a) Let
 $b \in \big (0, \frac {d-1}{d+1}\big ]$ be a rational. Then
$b \in \big (0, \frac {d-1}{d+1}\big ]$ be a rational. Then  $\mathbb {S}_{\mathbb {Q}}(d,b)=\mathbb {S}_{\mathbb {Q}}\setminus \{\pm 1\}$.
$\mathbb {S}_{\mathbb {Q}}(d,b)=\mathbb {S}_{\mathbb {Q}}\setminus \{\pm 1\}$.(b) Let
 $b \in \big (\frac {d-1}{d+1},1\big )$ be a rational. Then
$b \in \big (\frac {d-1}{d+1},1\big )$ be a rational. Then  $\mathbb {S}_{\mathbb {Q}}(d,b)$ is dense in
$\mathbb {S}_{\mathbb {Q}}(d,b)$ is dense in  $\mathbb {S}\setminus I(\theta _b)$.
$\mathbb {S}\setminus I(\theta _b)$.
Theorem 6 (b) is in stark contrast to what happens for ![]() $\lambda \in I(\theta _b)$, where it is known that fields are confined in an arc around 1 [Reference Peters and Regts42]. We conjecture that in part (b) it is true that
$\lambda \in I(\theta _b)$, where it is known that fields are confined in an arc around 1 [Reference Peters and Regts42]. We conjecture that in part (b) it is true that ![]() $\mathbb {S}_{\mathbb {Q}}(d,b)=\mathbb {S}_{\mathbb {Q}}\setminus (I(\theta _b)\cup \{-1\})$. Moreover, while in Theorem 6 we focus on rational b, which is most relevant for our computational problems, we note that for any real
$\mathbb {S}_{\mathbb {Q}}(d,b)=\mathbb {S}_{\mathbb {Q}}\setminus (I(\theta _b)\cup \{-1\})$. Moreover, while in Theorem 6 we focus on rational b, which is most relevant for our computational problems, we note that for any real ![]() $b\in (0,1)$,
$b\in (0,1)$, ![]() $\mathbb {S}_{\mathbb {Q}}(d,b)$ is dense in
$\mathbb {S}_{\mathbb {Q}}(d,b)$ is dense in ![]() $\mathbb {S}$ in case (a) and dense in
$\mathbb {S}$ in case (a) and dense in ![]() $\mathbb {S}\setminus I(\theta _b)$ in case (b). We suspect that case (a) is true when
$\mathbb {S}\setminus I(\theta _b)$ in case (b). We suspect that case (a) is true when ![]() $\mathbb {S}_{\mathbb {Q}}$ is replaced by the collection of algebraic numbers on the unit circle and
$\mathbb {S}_{\mathbb {Q}}$ is replaced by the collection of algebraic numbers on the unit circle and  $b\in (0, \frac {d-1}{d+1}]$ is algebraic, but this seems to be challenging to prove.
$b\in (0, \frac {d-1}{d+1}]$ is algebraic, but this seems to be challenging to prove.
Later, in Section 7, we bootstrap Theorem 6 to obtain fast algorithms to implement fields with arbitrarily small error; see Lemma 32 for the exact statement. Roughly, these fields are then used as ‘probes’ in our reductions to compute exactly the ratio  $\tfrac {Z_{G,\mathrm {\texttt {+}} v}(\lambda ,b)}{Z_{G,\mathrm {\texttt {-}} v}(\lambda ,b)}$ for any graph G and vertex v; we say more about this in Subsection 2.4. For now, we focus on the key Theorem 6 and the ideas behind its proof.
$\tfrac {Z_{G,\mathrm {\texttt {+}} v}(\lambda ,b)}{Z_{G,\mathrm {\texttt {-}} v}(\lambda ,b)}$ for any graph G and vertex v; we say more about this in Subsection 2.4. For now, we focus on the key Theorem 6 and the ideas behind its proof.
2.2 Hardness via Julia-set density
To prove Theorem 6, we will be interested in the set of values obtained by successive composition of the maps ![]() $f_{\lambda ,k}$ in (1) starting from the point
$f_{\lambda ,k}$ in (1) starting from the point ![]() $z=1$; the main challenge in our setting is to prove that, for
$z=1$; the main challenge in our setting is to prove that, for ![]() $\lambda ,b$ as in Theorem 6, these values are dense on the unit circle
$\lambda ,b$ as in Theorem 6, these values are dense on the unit circle ![]() $\mathbb {S}$. Part (b) is relatively easy to prove, but the real challenge lies in proving part (a).
$\mathbb {S}$. Part (b) is relatively easy to prove, but the real challenge lies in proving part (a).
To understand the reason that this is challenging, let us consider the properties of the map ![]() $f_{\lambda ,k}$ for some root degree
$f_{\lambda ,k}$ for some root degree ![]() $k\geq 1$ viewed as a dynamical system; cf. the upcoming Lemmas 8 and 10 for details. Then, for all
$k\geq 1$ viewed as a dynamical system; cf. the upcoming Lemmas 8 and 10 for details. Then, for all ![]() $b\in (0,1)$ the following hold:
$b\in (0,1)$ the following hold:
1. The ‘well-behaved’ regime: When
 $b\in (\frac {k-1}{k+1},1)$, there exists
$b\in (\frac {k-1}{k+1},1)$, there exists  $\lambda _k=\lambda _k(b)\in \mathbb {S}$ with
$\lambda _k=\lambda _k(b)\in \mathbb {S}$ with  $\operatorname {\mathrm {Im}}{\lambda _k}>0$ such that for all
$\operatorname {\mathrm {Im}}{\lambda _k}>0$ such that for all  $\lambda $ in an arc around 1 given by
$\lambda $ in an arc around 1 given by  $\operatorname {\mathrm {Arc}}[\overline {\lambda _k},\lambda _k]$, the iterates of the point
$\operatorname {\mathrm {Arc}}[\overline {\lambda _k},\lambda _k]$, the iterates of the point  $z=1$ under the map
$z=1$ under the map  $f_{\lambda ,k}$ converge to a value
$f_{\lambda ,k}$ converge to a value  $R_k(\lambda )\in \mathbb {S}$. In fact, the map
$R_k(\lambda )\in \mathbb {S}$. In fact, the map  $f_{\lambda ,k}$ has nice convergence/contracting properties in an arc around
$f_{\lambda ,k}$ has nice convergence/contracting properties in an arc around  $z=1$: the iterates of any point in
$z=1$: the iterates of any point in  $\operatorname {\mathrm {Arc}}{[1,R_k(\lambda )]}$ converge to
$\operatorname {\mathrm {Arc}}{[1,R_k(\lambda )]}$ converge to  $R_k(\lambda )$.
$R_k(\lambda )$.2. The ‘chaotic’ regime: Instead, when
 $b\in (\frac {k-1}{k+1},1)$ and
$b\in (\frac {k-1}{k+1},1)$ and  $\lambda \in \operatorname {\mathrm {Arc}}(\lambda _k, \overline {\lambda _k})$ or
$\lambda \in \operatorname {\mathrm {Arc}}(\lambda _k, \overline {\lambda _k})$ or  $b\in (0,\frac {k-1}{k+1}]$, all points in
$b\in (0,\frac {k-1}{k+1}]$, all points in  $\mathbb {S}$ belong to the so-called Julia set of the map; roughly, this means that the iterates under
$\mathbb {S}$ belong to the so-called Julia set of the map; roughly, this means that the iterates under  $f_{\lambda ,k}$ of two distinct but arbitrarily close points in
$f_{\lambda ,k}$ of two distinct but arbitrarily close points in  $\mathbb {S}$ will be separated by some absolute constant infinitely many times. In other words, the map
$\mathbb {S}$ will be separated by some absolute constant infinitely many times. In other words, the map  $f_{\lambda ,k}$ has a chaotic behaviour on
$f_{\lambda ,k}$ has a chaotic behaviour on  $\mathbb {S}$.
$\mathbb {S}$.
For ![]() $b\in (0,1)$, we use
$b\in (0,1)$, we use ![]() $\Lambda _k(b)$ to denote the set of
$\Lambda _k(b)$ to denote the set of ![]() $\lambda \in \mathbb {S}$ where the degree-k map
$\lambda \in \mathbb {S}$ where the degree-k map ![]() $f_{\lambda ,k}$ exhibits the behaviour in (2); see the relevant Definition 7 and Lemma 8. Based on item (1), it was shown in [Reference Peters and Regts42] that the iterates of the point
$f_{\lambda ,k}$ exhibits the behaviour in (2); see the relevant Definition 7 and Lemma 8. Based on item (1), it was shown in [Reference Peters and Regts42] that the iterates of the point ![]() $z=1$ under the successive composition of the maps in (1) stay ‘trapped’ in a small arc around 1 when
$z=1$ under the successive composition of the maps in (1) stay ‘trapped’ in a small arc around 1 when  $b\in (\tfrac {d-1}{d+1},1)$ and
$b\in (\tfrac {d-1}{d+1},1)$ and ![]() $\lambda \in \operatorname {\mathrm {Arc}}(\overline {\lambda _d},\lambda _d)$.
$\lambda \in \operatorname {\mathrm {Arc}}(\overline {\lambda _d},\lambda _d)$.
Instead, our goal is to tame the chaotic behaviour in item (2) to get density on ![]() $\mathbb {S}$ for fixed
$\mathbb {S}$ for fixed  $b\in (0,\tfrac {d-1}{d+1}]$ and
$b\in (0,\tfrac {d-1}{d+1}]$ and ![]() $\lambda \in \mathbb {S}\backslash \{\pm 1\}$. We should emphasise here that, in the range of
$\lambda \in \mathbb {S}\backslash \{\pm 1\}$. We should emphasise here that, in the range of ![]() $b,\lambda $ we consider, the map
$b,\lambda $ we consider, the map ![]() $f_{\lambda ,d}$ has the chaotic behaviour described in item (2) throughout
$f_{\lambda ,d}$ has the chaotic behaviour described in item (2) throughout ![]() $\mathbb {S}$, so by default it is hopeless to aim for any fine analytical understanding, and this is the major technical obstacle we need to address.
$\mathbb {S}$, so by default it is hopeless to aim for any fine analytical understanding, and this is the major technical obstacle we need to address.
An analogous setting has been previously considered in [Reference Bezáková, Galanis, Goldberg and Štefankovič6], in the context of approximating the independent set polynomial. The bottleneck of showing the desired density is to first argue density around a point ![]() $x^*$ in the Julia set of the degree-d map. Once this is done, the chaotic behaviour of the degree-d map around the Julia-set point
$x^*$ in the Julia set of the degree-d map. Once this is done, the chaotic behaviour of the degree-d map around the Julia-set point ![]() $x^*$ can be utilised to bootstrap the density to the whole complex plane. The key challenge here is arguing the initial density around the Julia-set point of the degree-d map, since the degree-d map itself is useless for creating density in the Julia set. In [Reference Bezáková, Galanis, Goldberg and Štefankovič6], an auxiliary Fibonacci-style recursion was used to converge to such a point
$x^*$ can be utilised to bootstrap the density to the whole complex plane. The key challenge here is arguing the initial density around the Julia-set point of the degree-d map, since the degree-d map itself is useless for creating density in the Julia set. In [Reference Bezáková, Galanis, Goldberg and Štefankovič6], an auxiliary Fibonacci-style recursion was used to converge to such a point ![]() $x^*$; the density around
$x^*$; the density around ![]() $x^*$ was then achieved by utilising the convergence to further obtain a set of contracting maps around a neighbourhood N of
$x^*$ was then achieved by utilising the convergence to further obtain a set of contracting maps around a neighbourhood N of ![]() $x^*$, such that the images of N under the maps formed a covering of N.
$x^*$, such that the images of N under the maps formed a covering of N.
While the contracting/covering maps framework can be adapted to our setting (see Lemma 19), the bottleneck step of obtaining the initial density around the Julia-set point requires a radically different argument: the convergence of the recursion in [Reference Bezáková, Galanis, Goldberg and Štefankovič6] relies on a certain linearisation property, which is not present in the case of the ferromagnetic Ising model; even worse, the recursion does not converge for all the relevant range of ![]() $b,\lambda $.Footnote 7
$b,\lambda $.Footnote 7
2.3 Our approach to obtain density around a Julia-set point
We devise a new technique to tackle the problem of showing density around a point in the Julia set of ![]() $f_{\lambda ,d}$. The main idea is to exploit the chaotic behaviour of the iterates of
$f_{\lambda ,d}$. The main idea is to exploit the chaotic behaviour of the iterates of ![]() $f_{\lambda ,k}$ when
$f_{\lambda ,k}$ when ![]() $\lambda \in \Lambda _k(b)$ to obtain an iterate
$\lambda \in \Lambda _k(b)$ to obtain an iterate ![]() $\xi $ of 1 with an expanding derivative; that is,
$\xi $ of 1 with an expanding derivative; that is,  $|f_{\lambda ,k}'(\xi )|>1$. The existence of
$|f_{\lambda ,k}'(\xi )|>1$. The existence of ![]() $\xi $ follows by general arguments from the theory of complex dynamical systems; see the relevant Lemma 15. The lower bound on the derivative is then used in careful inductive constructions to obtain families of contracting maps that cover an appropriate arc of the circle.
$\xi $ follows by general arguments from the theory of complex dynamical systems; see the relevant Lemma 15. The lower bound on the derivative is then used in careful inductive constructions to obtain families of contracting maps that cover an appropriate arc of the circle.
To illustrate the main idea of this inductive construction, let us assume that the degree ![]() $d+1$ is odd. Then, using Lemma 15 and the fact that
$d+1$ is odd. Then, using Lemma 15 and the fact that ![]() $\lambda \in \Lambda _d(b)$, we obtain an iterate of the point
$\lambda \in \Lambda _d(b)$, we obtain an iterate of the point ![]() $z=1$ under the map
$z=1$ under the map ![]() $f_{\lambda ,d}$, say
$f_{\lambda ,d}$, say ![]() $\xi $, so that
$\xi $, so that  $|f_{\lambda ,d}'(\xi )|>1$. The key point is to consider the map
$|f_{\lambda ,d}'(\xi )|>1$. The key point is to consider the map ![]() $f_{\xi ,k}$ for
$f_{\xi ,k}$ for ![]() $k= d/2$. On one hand, if it happens that
$k= d/2$. On one hand, if it happens that ![]() $\xi \notin \Lambda _k(b)$ lies in the ‘well-behaved’ regime of the degree-k map, it can be shown that the maps
$\xi \notin \Lambda _k(b)$ lies in the ‘well-behaved’ regime of the degree-k map, it can be shown that the maps ![]() $f_{\xi ,k},f_{\xi ,k+1}$ are contracting/covering maps in an appropriate arc of
$f_{\xi ,k},f_{\xi ,k+1}$ are contracting/covering maps in an appropriate arc of ![]() $\mathbb {S}$, yielding the required density as needed (details of this argument can be found in Lemma 21). On the other hand, if
$\mathbb {S}$, yielding the required density as needed (details of this argument can be found in Lemma 21). On the other hand, if ![]() $\xi \in \Lambda _k(b)$ lies in the ‘chaotic’ regime of the degree-k map, then we can proceed inductively by finding an iterate
$\xi \in \Lambda _k(b)$ lies in the ‘chaotic’ regime of the degree-k map, then we can proceed inductively by finding an iterate ![]() $\nu $ of 1 under the map
$\nu $ of 1 under the map ![]() $f_{\xi ,k}$ with expanding derivative
$f_{\xi ,k}$ with expanding derivative  $|f_{\xi ,k}'(\nu )|>1$ and recurse.
$|f_{\xi ,k}'(\nu )|>1$ and recurse.
Technically, to carry out this inductive scheme we have to address the various integrality issues, while at the same time being careful to maintain the degrees of the trees bounded by ![]() $\Delta $. More important, we need to consider pairs/triples/quadruples of maps to ensure the contraction/covering property in the inductive step; to achieve this, we need to understand the dependence of the derivative at the fixpoint of the k-ary map with k. Here, things turn out to be surprisingly pleasant, since it turns out that
$\Delta $. More important, we need to consider pairs/triples/quadruples of maps to ensure the contraction/covering property in the inductive step; to achieve this, we need to understand the dependence of the derivative at the fixpoint of the k-ary map with k. Here, things turn out to be surprisingly pleasant, since it turns out that  $|f_{\lambda ,k}'(z)|$ depends linearly on the degree k and is independent of
$|f_{\lambda ,k}'(z)|$ depends linearly on the degree k and is independent of ![]() $\lambda $; see item (i) of Lemma 10. This fact is exploited in the arguments of Subsection 4.2. These considerations cover almost all cases, but a few small degrees d remain, which we cover by a Cantor-style construction; see Section 5.2 for details.
$\lambda $; see item (i) of Lemma 10. This fact is exploited in the arguments of Subsection 4.2. These considerations cover almost all cases, but a few small degrees d remain, which we cover by a Cantor-style construction; see Section 5.2 for details.
2.4 The reduction
The arguments discussed so far can be used to show that rooted trees in ![]() $\mathcal {T}_{d+1}$ implement any field
$\mathcal {T}_{d+1}$ implement any field ![]() $\xi $ on the unit circle
$\xi $ on the unit circle ![]() $\mathbb {S}$ within arbitrarily small error
$\mathbb {S}$ within arbitrarily small error ![]() $\epsilon>0$; see Lemma 32 for the form that we actually need. We now discuss in a bit more detail the high-level idea behind the final reduction argument in Section 8.
$\epsilon>0$; see Lemma 32 for the form that we actually need. We now discuss in a bit more detail the high-level idea behind the final reduction argument in Section 8.
The key observation to utilise the gadgets is that for any graph G and vertex v with ![]() $Z_{G,\mathrm {\texttt {-}} v}(\lambda ,b) \not = 0$, the ‘field’ at a vertex v satisfies
$Z_{G,\mathrm {\texttt {-}} v}(\lambda ,b) \not = 0$, the ‘field’ at a vertex v satisfies  $\tfrac {Z_{G,\mathrm {\texttt {+}} v}(\lambda ,b)}{Z_{G,\mathrm {\texttt {-}} v}(\lambda ,b)}\in \mathbb {S}$ (cf. Lemma 34), and hence we can use our rooted-tree gadgets as probes to compute exactly the ratio
$\tfrac {Z_{G,\mathrm {\texttt {+}} v}(\lambda ,b)}{Z_{G,\mathrm {\texttt {-}} v}(\lambda ,b)}\in \mathbb {S}$ (cf. Lemma 34), and hence we can use our rooted-tree gadgets as probes to compute exactly the ratio  $Q_{G,v}:=\tfrac {Z_{G,\mathrm {\texttt {+}} v}(\lambda ,b)}{Z_{G,\mathrm {\texttt {-}} v}(\lambda ,b)}$. The straightforward way to do this would be to attach a tree on v which implements a field
$Q_{G,v}:=\tfrac {Z_{G,\mathrm {\texttt {+}} v}(\lambda ,b)}{Z_{G,\mathrm {\texttt {-}} v}(\lambda ,b)}$. The straightforward way to do this would be to attach a tree on v which implements a field ![]() $x\in \mathbb {S}$ and use oracle calls to either
$x\in \mathbb {S}$ and use oracle calls to either ![]() $\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ and
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ and ![]() $\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$ and look for
$\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$ and look for ![]() $x=x^*$ that makes the partition function of the resulting graph equal to zero; from the key observation earlier, we know that such an
$x=x^*$ that makes the partition function of the resulting graph equal to zero; from the key observation earlier, we know that such an ![]() $x^*$ exists, namely,
$x^*$ exists, namely, ![]() $x^*=-1/Q_{G,v}$ and, to determine it, we can use binary search.
$x^*=-1/Q_{G,v}$ and, to determine it, we can use binary search.
This is the main idea behind the reduction, though there are a couple of caveats. First of all, there is no way to know whether the ratio ![]() $Q_{G,v}$ is well-defined; that is, whether
$Q_{G,v}$ is well-defined; that is, whether ![]() $Z_{G,\mathrm {\texttt {-}} v}(\lambda ,b)\neq 0$, even using oracle calls to the approximation problems we study:
$Z_{G,\mathrm {\texttt {-}} v}(\lambda ,b)\neq 0$, even using oracle calls to the approximation problems we study: ![]() $Z_{G,\mathrm {\texttt {-}} v}(\lambda ,b)$ is not a partition function of a graph (since v’s spin is fixed), and even if we managed to cast this as a partition function, the oracles cannot detect zeros (cf. Subsection 1.1). The second caveat is that attaching the tree increases the degree of v which is problematic when, for example, G is
$Z_{G,\mathrm {\texttt {-}} v}(\lambda ,b)$ is not a partition function of a graph (since v’s spin is fixed), and even if we managed to cast this as a partition function, the oracles cannot detect zeros (cf. Subsection 1.1). The second caveat is that attaching the tree increases the degree of v which is problematic when, for example, G is ![]() $\Delta $-regular and the peeling-vertices argument does not quite work since there is no simple way to utilise the oracles after the first step.
$\Delta $-regular and the peeling-vertices argument does not quite work since there is no simple way to utilise the oracles after the first step.
The first point is addressed by replacing the edges of G with paths of appropriate length, which has the effect of ‘changing’ the value of the parameter b to some value ![]() $\hat {b}$ close but not equal to
$\hat {b}$ close but not equal to ![]() $1$ where the partition function is zero-free (we actually need to attach to internal vertices of the paths rooted trees with fields close to
$1$ where the partition function is zero-free (we actually need to attach to internal vertices of the paths rooted trees with fields close to ![]() $1/\lambda $ so that the complex external field
$1/\lambda $ so that the complex external field ![]() $\lambda $ is almost cancelled). Then, using oracle calls to
$\lambda $ is almost cancelled). Then, using oracle calls to ![]() $\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ or
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ or ![]() $\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$, our algorithm aims to determine the value of
$\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$, our algorithm aims to determine the value of ![]() $Z_G(\lambda ,\hat {b})$, which is a
$Z_G(\lambda ,\hat {b})$, which is a ![]() $\mathsf {\#P}$-hard problem ([Reference Kowalczyk and Cai28], Theorem 1.1); the key point is that now we have zero-freeness of the partition function, which allows us to assert that the quantities we compute during the course of the algorithm are actually well-defined.
$\mathsf {\#P}$-hard problem ([Reference Kowalczyk and Cai28], Theorem 1.1); the key point is that now we have zero-freeness of the partition function, which allows us to assert that the quantities we compute during the course of the algorithm are actually well-defined.
The second point is addressed by doing the peeling argument at the level of edges by trying to figure out, for an edge e of G, the value of the ratio  $\hat {Q}_{G,e}=\tfrac {Z_{G}(\lambda ,\hat {b})}{Z_{G,\backslash e}(\lambda ,\hat {b})}$. We do this by subdividing the edge and use a field gadget on the middle vertex; this has the benefit that it does not increase the maximum degree of the graph, but certain complications arise since instead of
$\hat {Q}_{G,e}=\tfrac {Z_{G}(\lambda ,\hat {b})}{Z_{G,\backslash e}(\lambda ,\hat {b})}$. We do this by subdividing the edge and use a field gadget on the middle vertex; this has the benefit that it does not increase the maximum degree of the graph, but certain complications arise since instead of ![]() $\hat {Q}_{G,e}$, we retrieve a slightly different ratio (see Lemma 37 in Subsection 8.2), and some extra work is required to finish off the proof of Theorem 1; see Subsection 8.3 for details.
$\hat {Q}_{G,e}$, we retrieve a slightly different ratio (see Lemma 37 in Subsection 8.2), and some extra work is required to finish off the proof of Theorem 1; see Subsection 8.3 for details.
2.5 Outline
The next section details the dynamical properties of the maps ![]() $f_{\lambda ,k}$ and elaborates on the inductive proof of Theorem 6, which is based on the upcoming Lemma 17. Section 4 explains in more detail the contracting/covering maps framework and how we utilise the degree/derivative interplay to cover the bulk of the cases in Lemma 17. Section 5 contains the remaining pieces needed to complete the proof of Lemma 17, which is given in Section 6. In Section 7, we bootstrap Theorem 6 to obtain fast algorithms to implement fields on the unit circle with arbitrarily small precision error, which is used in the reduction arguments of Section 8, where the proof of Theorem 1 is completed. Finally, in Section 9, we study the case
$f_{\lambda ,k}$ and elaborates on the inductive proof of Theorem 6, which is based on the upcoming Lemma 17. Section 4 explains in more detail the contracting/covering maps framework and how we utilise the degree/derivative interplay to cover the bulk of the cases in Lemma 17. Section 5 contains the remaining pieces needed to complete the proof of Lemma 17, which is given in Section 6. In Section 7, we bootstrap Theorem 6 to obtain fast algorithms to implement fields on the unit circle with arbitrarily small precision error, which is used in the reduction arguments of Section 8, where the proof of Theorem 1 is completed. Finally, in Section 9, we study the case ![]() $\lambda =-1$ (cf. Remark 2) and show the equivalence with the problem of approximately counting perfect matchings.
$\lambda =-1$ (cf. Remark 2) and show the equivalence with the problem of approximately counting perfect matchings.
3 Complex Dynamics Preliminaries and the Inductive Step in Theorem 6
In this section, we set up some preliminaries about the maps ![]() $f_{\lambda ,k}$ in (1) that will be used to prove Theorem 6. We first consider the general case
$f_{\lambda ,k}$ in (1) that will be used to prove Theorem 6. We first consider the general case ![]() $k\geq 1$ in Subsection 3.1 and then further study the
$k\geq 1$ in Subsection 3.1 and then further study the ![]() $k = 1$ case separately in Subsection 3.2. In Subsection 3.3, we use these properties to obtain points with expanding derivatives using tools from complex dynamics. Then, in Subsection 3.4, we give the main lemma that lies at the heart of the inductive proof of Theorem 6 and conclude the proof of the latter.
$k = 1$ case separately in Subsection 3.2. In Subsection 3.3, we use these properties to obtain points with expanding derivatives using tools from complex dynamics. Then, in Subsection 3.4, we give the main lemma that lies at the heart of the inductive proof of Theorem 6 and conclude the proof of the latter.
3.1 Results on  $f_{\lambda ,k}$ for general k
$f_{\lambda ,k}$ for general k
This section contains relevant properties of the maps  $f_{\lambda ,k}: z \mapsto \lambda \cdot \big (\frac {z + b}{b z + 1}\big )^k$ that we will need; these were discussed informally in Subsection 2.2, and here we formalise them. Almost all results of this section follow from arguments in [Reference Peters and Regts42].
$f_{\lambda ,k}: z \mapsto \lambda \cdot \big (\frac {z + b}{b z + 1}\big )^k$ that we will need; these were discussed informally in Subsection 2.2, and here we formalise them. Almost all results of this section follow from arguments in [Reference Peters and Regts42].
We begin by formally defining the set ![]() $\Lambda _k(b)$.
$\Lambda _k(b)$.
Definition 7. Let ![]() $k\geq 1$ be an integer and
$k\geq 1$ be an integer and ![]() $b\in (0,1)$. We let
$b\in (0,1)$. We let ![]() $\Lambda _k(b)$ be the set of
$\Lambda _k(b)$ be the set of ![]() $\lambda \in \mathbb {S}$ such that all fixed points z of the map
$\lambda \in \mathbb {S}$ such that all fixed points z of the map ![]() $f_{\lambda ,k}$ with
$f_{\lambda ,k}$ with ![]() $z\in \mathbb {S}$ are repelling; that is,
$z\in \mathbb {S}$ are repelling; that is,  $|f^{\prime }_{\lambda ,k}(z)|>1$.
$|f^{\prime }_{\lambda ,k}(z)|>1$.
The following lemma gives a description of the set ![]() $\Lambda _k(b)$ and characterises the Julia set of
$\Lambda _k(b)$ and characterises the Julia set of ![]() $f_{\lambda ,k}$. We have described informally the dynamical properties of the map
$f_{\lambda ,k}$. We have described informally the dynamical properties of the map ![]() $f_{\lambda ,k}$ that the Julia set captures; see item (2) in Subsection 2.2. The reader is referred to [Reference Milnor38, Chapter 4] for more details on the general theory.
$f_{\lambda ,k}$ that the Julia set captures; see item (2) in Subsection 2.2. The reader is referred to [Reference Milnor38, Chapter 4] for more details on the general theory.
Lemma 8. Let ![]() $k\geq 1$ be an integer. Then,
$k\geq 1$ be an integer. Then,
• if
 $b\in (0,\frac {k-1}{k+1})$,
$b\in (0,\frac {k-1}{k+1})$,  $\Lambda _k(b)=\mathbb {S}$. For
$\Lambda _k(b)=\mathbb {S}$. For  $b=\frac {k-1}{k+1}$,
$b=\frac {k-1}{k+1}$,  $\Lambda _k(b)=\mathbb {S}\backslash \{+1\}$.
$\Lambda _k(b)=\mathbb {S}\backslash \{+1\}$.• if
 $b\in (\frac {k-1}{k+1}, 1)$, there is
$b\in (\frac {k-1}{k+1}, 1)$, there is  $\lambda _k=\lambda _k(b) \in \mathbb {S}$ with
$\lambda _k=\lambda _k(b) \in \mathbb {S}$ with  $\operatorname {\mathrm {Im}}{(\lambda _k)}> 0$ such that
$\operatorname {\mathrm {Im}}{(\lambda _k)}> 0$ such that  $\Lambda _k(b)=\operatorname {\mathrm {Arc}}(\lambda _k,\overline {\lambda _k})$.
$\Lambda _k(b)=\operatorname {\mathrm {Arc}}(\lambda _k,\overline {\lambda _k})$.
Moreover, if ![]() $k>1$, then for all
$k>1$, then for all ![]() $\lambda \in \Lambda _k(b)$, the Julia set of
$\lambda \in \Lambda _k(b)$, the Julia set of ![]() $f_{\lambda ,k}$ is equal to the unit circle
$f_{\lambda ,k}$ is equal to the unit circle ![]() $\mathbb {S}$.
$\mathbb {S}$.
Proof. For  $b\in (\frac {k-1}{k+1}, 1)$, the range of
$b\in (\frac {k-1}{k+1}, 1)$, the range of ![]() $\Lambda _k(b)$ follows from [Reference Peters and Regts42, Theorem 14]. For
$\Lambda _k(b)$ follows from [Reference Peters and Regts42, Theorem 14]. For  $b\in (0,\frac {k-1}{k+1}]$, the range of
$b\in (0,\frac {k-1}{k+1}]$, the range of ![]() $\Lambda _k(b)$ follows from item (i) in Lemma 10. The characterisation of the Julia set for
$\Lambda _k(b)$ follows from item (i) in Lemma 10. The characterisation of the Julia set for ![]() $\lambda \in \Lambda _k(b)$ is shown in [Reference Peters and Regts42, Proof of Proposition 17].
$\lambda \in \Lambda _k(b)$ is shown in [Reference Peters and Regts42, Proof of Proposition 17].
Remark 9. The ![]() $\lambda _k(b)$ of the lemma is equal to
$\lambda _k(b)$ of the lemma is equal to ![]() $e^{i\theta _b}$ from the statement of Theorem 1 (where we replace
$e^{i\theta _b}$ from the statement of Theorem 1 (where we replace ![]() $\Delta $ by
$\Delta $ by ![]() $k+1$).
$k+1$).
Let A be an arc of ![]() $\mathbb {S}$. A map
$\mathbb {S}$. A map ![]() $f:A\rightarrow \mathbb {S}$ is orientation-preserving if for any
$f:A\rightarrow \mathbb {S}$ is orientation-preserving if for any ![]() $z,z_1,z_2\in A$ with
$z,z_1,z_2\in A$ with ![]() $z\in \operatorname {\mathrm {Arc}}{[z_1,z_2]}$ it holds that
$z\in \operatorname {\mathrm {Arc}}{[z_1,z_2]}$ it holds that ![]() $f(z)\in \operatorname {\mathrm {Arc}}{[f(z_1),f(z_2)}]$. The orbit of a point
$f(z)\in \operatorname {\mathrm {Arc}}{[f(z_1),f(z_2)}]$. The orbit of a point ![]() $z_0\in \mathbb {S}$ under the map
$z_0\in \mathbb {S}$ under the map ![]() $f_{\lambda ,k}$ is the sequence of the iterates
$f_{\lambda ,k}$ is the sequence of the iterates  $\{f_{\lambda ,k}^n(z_0)\}_{n\geq 0}$. A fixed point z of the map
$\{f_{\lambda ,k}^n(z_0)\}_{n\geq 0}$. A fixed point z of the map ![]() $f_{\lambda ,k}$ is called attracting if
$f_{\lambda ,k}$ is called attracting if  $|f^{\prime }_{\lambda ,k}(z)|<1$ and parabolic if
$|f^{\prime }_{\lambda ,k}(z)|<1$ and parabolic if  $|f^{\prime }_{\lambda ,k}(z)|=1$.
$|f^{\prime }_{\lambda ,k}(z)|=1$.
The following lemma captures properties of the maps ![]() $f_{\lambda ,k}$ when
$f_{\lambda ,k}$ when ![]() $k\in \{1,\ldots ,d-1\}$ in the regime
$k\in \{1,\ldots ,d-1\}$ in the regime  $b \in \big (\frac {d-2}{d},\frac {d-1}{d+1}\big ]$, which turns out to be the hard part of the proof of Theorem 6 (the lemma is stated more generally for
$b \in \big (\frac {d-2}{d},\frac {d-1}{d+1}\big ]$, which turns out to be the hard part of the proof of Theorem 6 (the lemma is stated more generally for  $b \in \big (\frac {d-2}{d},1\big )$).
$b \in \big (\frac {d-2}{d},1\big )$).
Lemma 10. Let ![]() $d \in \mathbb {Z}_{\geq 2}$ and let
$d \in \mathbb {Z}_{\geq 2}$ and let  $b \in \big (\frac {d-2}{d},1\big )$. Then the following hold:
$b \in \big (\frac {d-2}{d},1\big )$. Then the following hold:
(i) For all
 $\lambda \in \mathbb {S}$ and
$\lambda \in \mathbb {S}$ and  $k \in \mathbb {Z}_{\geq 1}$, the map
$k \in \mathbb {Z}_{\geq 1}$, the map  $f_{\lambda ,k}: \mathbb {S} \to \mathbb {S}$ is orientation-preserving. Also, the magnitude of the derivative at a point
$f_{\lambda ,k}: \mathbb {S} \to \mathbb {S}$ is orientation-preserving. Also, the magnitude of the derivative at a point  $z \in \mathbb {S}$ does not depend on
$z \in \mathbb {S}$ does not depend on  $\lambda $ and equals
$\lambda $ and equals  $|f_{k}'(z)|$, where (2)
$|f_{k}'(z)|$, where (2) $$ \begin{align} \left| f_{k}'(z) \right| = k\cdot \left| f_{1}'(z) \right| = \frac{k(1-b^2)}{b^2 + 2b \cdot\operatorname{\mathrm{Re}}{(z)} + 1}. \end{align} $$
$$ \begin{align} \left| f_{k}'(z) \right| = k\cdot \left| f_{1}'(z) \right| = \frac{k(1-b^2)}{b^2 + 2b \cdot\operatorname{\mathrm{Re}}{(z)} + 1}. \end{align} $$(ii) For
 $k \in \{1,\dots , d-1\}$, let
$k \in \{1,\dots , d-1\}$, let  $\lambda _k=\lambda _k(b)\in \mathbb {S}$ be as in Lemma 8. Then,
$\lambda _k=\lambda _k(b)\in \mathbb {S}$ be as in Lemma 8. Then,• if
 $\lambda \in \operatorname {\mathrm {Arc}}{(\overline {\lambda _k},\lambda _k)}$, then
$\lambda \in \operatorname {\mathrm {Arc}}{(\overline {\lambda _k},\lambda _k)}$, then  $f_{\lambda ,k}$ has a unique attracting fixed point
$f_{\lambda ,k}$ has a unique attracting fixed point  $R_k(\lambda ) \in \mathbb {S}$.
$R_k(\lambda ) \in \mathbb {S}$.• if
 $\lambda =\overline {\lambda _k}$ or
$\lambda =\overline {\lambda _k}$ or  $\lambda _k$, then
$\lambda _k$, then  $f_{\lambda ,k}$ has a unique parabolic fixed point
$f_{\lambda ,k}$ has a unique parabolic fixed point  $R_k(\lambda ) \in \mathbb {S}$.
$R_k(\lambda ) \in \mathbb {S}$.
(iii) The fixed point maps
 $R_k: \operatorname {\mathrm {Arc}}{[\overline {\lambda _k},\lambda _k]} \to \mathbb {S}$ are continuously differentiable on
$R_k: \operatorname {\mathrm {Arc}}{[\overline {\lambda _k},\lambda _k]} \to \mathbb {S}$ are continuously differentiable on  $\operatorname {\mathrm {Arc}}{(\overline {\lambda _k},\lambda _k)}$ and orientation-preserving with the property that
$\operatorname {\mathrm {Arc}}{(\overline {\lambda _k},\lambda _k)}$ and orientation-preserving with the property that  $R_k(1) = 1$ and
$R_k(1) = 1$ and  $R_k(\overline {\lambda }) = \overline {R_k(\lambda )}$.
$R_k(\overline {\lambda }) = \overline {R_k(\lambda )}$.(iv) For
 $\lambda \in \operatorname {\mathrm {Arc}}{(1,\lambda _k]}$, the fixed point
$\lambda \in \operatorname {\mathrm {Arc}}{(1,\lambda _k]}$, the fixed point  $R_k(\lambda )$ is in the upper half-plane. For
$R_k(\lambda )$ is in the upper half-plane. For  $z_0 \in \operatorname {\mathrm {Arc}}{[1,R_k(\lambda )]}$, the orbit of
$z_0 \in \operatorname {\mathrm {Arc}}{[1,R_k(\lambda )]}$, the orbit of  $z_0$ under iteration of
$z_0$ under iteration of  $f_{\lambda ,k}$ converges to
$f_{\lambda ,k}$ converges to  $R_k(\lambda )$ and is contained in
$R_k(\lambda )$ and is contained in  $\operatorname {\mathrm {Arc}}{[z_0,R_k(\lambda )]}$.
$\operatorname {\mathrm {Arc}}{[z_0,R_k(\lambda )]}$.(v) The following inequalities hold:
while for $$ \begin{align*} \text{Arg}{(\lambda_{d-1})} < \text{Arg}{(\lambda_{d-2})} < \cdots < \text{Arg}{(\lambda_1)}, \end{align*} $$
$$ \begin{align*} \text{Arg}{(\lambda_{d-1})} < \text{Arg}{(\lambda_{d-2})} < \cdots < \text{Arg}{(\lambda_1)}, \end{align*} $$ $\lambda \in \operatorname {\mathrm {Arc}}{(1,\lambda _{m}]}$, with
$\lambda \in \operatorname {\mathrm {Arc}}{(1,\lambda _{m}]}$, with  $m\leq d-1$, we have with the additional property that, for
$m\leq d-1$, we have with the additional property that, for $$ \begin{align*} \text{Arg}{(R_1(\lambda))} < \text{Arg}{(R_2(\lambda))} < \cdots < \text{Arg}{(R_m(\lambda))}, \end{align*} $$
$$ \begin{align*} \text{Arg}{(R_1(\lambda))} < \text{Arg}{(R_2(\lambda))} < \cdots < \text{Arg}{(R_m(\lambda))}, \end{align*} $$ $i \in \{1, \dots , m-2\}$, (3)
$i \in \{1, \dots , m-2\}$, (3) $$ \begin{align} \ell\left(\operatorname{\mathrm{Arc}}{[R_{i}(\lambda),R_{i+1}(\lambda)]}\right) \leq \ell\left(\operatorname{\mathrm{Arc}}{[R_{i+1}(\lambda),R_{i+2}(\lambda)]}\right). \end{align} $$
$$ \begin{align} \ell\left(\operatorname{\mathrm{Arc}}{[R_{i}(\lambda),R_{i+1}(\lambda)]}\right) \leq \ell\left(\operatorname{\mathrm{Arc}}{[R_{i+1}(\lambda),R_{i+2}(\lambda)]}\right). \end{align} $$
Proof. We refer to [Reference Peters and Regts42] for proofs of items (i)–(iv). Specifically, item (i) follows from [Reference Peters and Regts42, Lemma 8 & Equation (3.1)], item (ii) from [Reference Peters and Regts42, Lemma 13, Theorem 14, Proof of Proposition 17], item (iii) from [Reference Peters and Regts42, Proof of Theorem 14] and item (iv) from [Reference Peters and Regts42, Theorem 14, Proof of Theorem 5(i)].
We will prove item (v). By taking the derivative of both sides of the equality ![]() $f_{\lambda ,k}(R_k(\lambda )) = R_k(\lambda )$ with respect to
$f_{\lambda ,k}(R_k(\lambda )) = R_k(\lambda )$ with respect to ![]() $\lambda $ and rewriting, we obtain
$\lambda $ and rewriting, we obtain
 $$ \begin{align*} R_k'(\lambda) = \frac{R_k(\lambda)}{\lambda\Big(1 - f_{\lambda,k}'\big(R_k(\lambda)\big)\Big)}. \end{align*} $$
$$ \begin{align*} R_k'(\lambda) = \frac{R_k(\lambda)}{\lambda\Big(1 - f_{\lambda,k}'\big(R_k(\lambda)\big)\Big)}. \end{align*} $$Using equation (2) for ![]() $z = R_m(1) = 1$, we obtain that
$z = R_m(1) = 1$, we obtain that ![]() $R_{i+1}'(1)> R_{i}'(1)$ for
$R_{i+1}'(1)> R_{i}'(1)$ for ![]() $i \in \{1, \dots , d-2\}$, and thus for
$i \in \{1, \dots , d-2\}$, and thus for ![]() $\lambda \in \mathbb {S}$ in the upper half-plane near
$\lambda \in \mathbb {S}$ in the upper half-plane near ![]() $1$ we find that
$1$ we find that ![]() $\text {Arg}{(R_{i+1}(\lambda ))}> \text {Arg}{(R_{i}(\lambda ))}$.
$\text {Arg}{(R_{i+1}(\lambda ))}> \text {Arg}{(R_{i}(\lambda ))}$.
The derivative at a fixed point of a map of the unit circle to itself is real (see also [Reference Peters and Regts42, Lemma 11]). Furthermore, if such a map is orientation-preserving, the derivative at a fixed point is positive. Because the map ![]() $f_{\lambda ,i}$ is orientation-preserving with attracting fixed point
$f_{\lambda ,i}$ is orientation-preserving with attracting fixed point ![]() $R_i(\lambda )$, we find that
$R_i(\lambda )$, we find that ![]() $f_{\lambda ,i}'(R_i(\lambda )) \in (0,1)$ for
$f_{\lambda ,i}'(R_i(\lambda )) \in (0,1)$ for ![]() $\lambda \in \operatorname {\mathrm {Arc}}{(\overline {\lambda _i}, \lambda _i)}$. From this, we deduce that we can write
$\lambda \in \operatorname {\mathrm {Arc}}{(\overline {\lambda _i}, \lambda _i)}$. From this, we deduce that we can write
 $$ \begin{align} \left|R_k'(\lambda)\right| = \frac{1}{1 - f_{\lambda,k}'\left(R_k(\lambda)\right)}. \end{align} $$
$$ \begin{align} \left|R_k'(\lambda)\right| = \frac{1}{1 - f_{\lambda,k}'\left(R_k(\lambda)\right)}. \end{align} $$From equation (2) it can be seen that  $\left |f_{i}'(z)\right |$ is increasing both with respect to
$\left |f_{i}'(z)\right |$ is increasing both with respect to ![]() $\text {Arg}{(z)}$ when
$\text {Arg}{(z)}$ when ![]() $\mathrm {Im}(z)>0$ and with respect to the index i and thus, as long as
$\mathrm {Im}(z)>0$ and with respect to the index i and thus, as long as ![]() $R_{i}(\lambda )$ and
$R_{i}(\lambda )$ and ![]() $R_{i+1}(\lambda )$ are both defined and
$R_{i+1}(\lambda )$ are both defined and ![]() $\text {Arg}(R_{i+1}(\lambda ))> \text {Arg}(R_{i}(\lambda ))$, we deduce that
$\text {Arg}(R_{i+1}(\lambda ))> \text {Arg}(R_{i}(\lambda ))$, we deduce that ![]() $|R_{i+1}'(\lambda )|> |R_{i}'(\lambda )|$. Since
$|R_{i+1}'(\lambda )|> |R_{i}'(\lambda )|$. Since ![]() $\text {Arg}(R_{i+1}(\lambda ))> \text {Arg}(R_{i}(\lambda ))$ for
$\text {Arg}(R_{i+1}(\lambda ))> \text {Arg}(R_{i}(\lambda ))$ for ![]() $\lambda $ in the upper half-plane close to
$\lambda $ in the upper half-plane close to ![]() $1$, we conclude that there cannot be any
$1$, we conclude that there cannot be any ![]() $\lambda $ in the upper half-plane such that
$\lambda $ in the upper half-plane such that ![]() $\text {Arg}(R_{i+1}(\lambda )) \leq \text {Arg}(R_{i}(\lambda ))$.
$\text {Arg}(R_{i+1}(\lambda )) \leq \text {Arg}(R_{i}(\lambda ))$.
Now suppose that there is some index i such that ![]() $\text {Arg}{(\lambda _i)} \leq \text {Arg}{(\lambda _{i+1})}$. Note that
$\text {Arg}{(\lambda _i)} \leq \text {Arg}{(\lambda _{i+1})}$. Note that ![]() $R_i(\lambda _i)$ is a parabolic fixed point of
$R_i(\lambda _i)$ is a parabolic fixed point of ![]() $f_{\lambda _i,i}$, which means that
$f_{\lambda _i,i}$, which means that  $f_{\lambda _i,i}'(R_i(\lambda _i)) = 1$. Because we assumed that
$f_{\lambda _i,i}'(R_i(\lambda _i)) = 1$. Because we assumed that ![]() $\text {Arg}{(\lambda _i)} \leq \text {Arg}{(\lambda _{i+1})}$, we see from item (ii) that
$\text {Arg}{(\lambda _i)} \leq \text {Arg}{(\lambda _{i+1})}$, we see from item (ii) that ![]() $R_{i+1}(\lambda _i)$ must be well-defined. We already deduced that
$R_{i+1}(\lambda _i)$ must be well-defined. We already deduced that ![]() $\text {Arg}{(R_{i+1}(\lambda _i))}> \text {Arg}{(R_{i}(\lambda _i))}$ and thus
$\text {Arg}{(R_{i+1}(\lambda _i))}> \text {Arg}{(R_{i}(\lambda _i))}$ and thus  $f_{\lambda _i,i+1}'(R_{i+1}(\lambda _i))> f_{\lambda _i,i}'(R_i(\lambda _i)) = 1$, which contradicts the fact that
$f_{\lambda _i,i+1}'(R_{i+1}(\lambda _i))> f_{\lambda _i,i}'(R_i(\lambda _i)) = 1$, which contradicts the fact that ![]() $R_{i+1}(\lambda _i)$ is an attracting fixed point of
$R_{i+1}(\lambda _i)$ is an attracting fixed point of ![]() $f_{\lambda _i,i+1}$. This concludes the proof of the first two claims of item (v).
$f_{\lambda _i,i+1}$. This concludes the proof of the first two claims of item (v).
Finally, we show the final claim of item (v). For indices ![]() $0\leq i\leq j\leq m$, it will be convenient to denote by
$0\leq i\leq j\leq m$, it will be convenient to denote by ![]() $A_{i,j,\lambda }$ the arc
$A_{i,j,\lambda }$ the arc ![]() $\operatorname {\mathrm {Arc}}{[R_{i}(\lambda ),R_{j}(\lambda )]}$, under the convention that
$\operatorname {\mathrm {Arc}}{[R_{i}(\lambda ),R_{j}(\lambda )]}$, under the convention that ![]() $R_0(\lambda )=1$. For
$R_0(\lambda )=1$. For ![]() $\lambda \in \operatorname {\mathrm {Arc}}{(1,\lambda _{m}]}$, our goal is hence to show that
$\lambda \in \operatorname {\mathrm {Arc}}{(1,\lambda _{m}]}$, our goal is hence to show that ![]() $\ell \left (A_{i,i+1,\lambda }\right ) \leq \ell \left (A_{i+1,i+2,\lambda }\right )$ for all
$\ell \left (A_{i,i+1,\lambda }\right ) \leq \ell \left (A_{i+1,i+2,\lambda }\right )$ for all ![]() $i\in \{1, \dots , m-2\}$.
$i\in \{1, \dots , m-2\}$.
For any ![]() $\lambda \in \operatorname {\mathrm {Arc}}{(1,\lambda _{k}]}$, we observe for
$\lambda \in \operatorname {\mathrm {Arc}}{(1,\lambda _{k}]}$, we observe for ![]() $i = 1, \dots , k$ that
$i = 1, \dots , k$ that
 $$ \begin{align*} \ell(A_{0,i,\lambda}) = \int_{\operatorname{\mathrm{Arc}}{[1,\lambda]}} |R_i'(z)| \,|dz|, \end{align*} $$
$$ \begin{align*} \ell(A_{0,i,\lambda}) = \int_{\operatorname{\mathrm{Arc}}{[1,\lambda]}} |R_i'(z)| \,|dz|, \end{align*} $$and thus for ![]() $i \in \{1, \dots , k-1\}$ we have
$i \in \{1, \dots , k-1\}$ we have  $\ell (A_{i,i+1,\lambda }) = \int _{\operatorname {\mathrm {Arc}}{[1,\lambda ]}} |R_{i+1}'(z)| - |R_{i}'(z)| \,|dz|$.
$\ell (A_{i,i+1,\lambda }) = \int _{\operatorname {\mathrm {Arc}}{[1,\lambda ]}} |R_{i+1}'(z)| - |R_{i}'(z)| \,|dz|$.
We first show item (v) for ![]() $\lambda $ near
$\lambda $ near ![]() $1$. As we let
$1$. As we let ![]() $\lambda $ approach
$\lambda $ approach ![]() $1$ along the circle, we obtain that
$1$ along the circle, we obtain that
 $$ \begin{align*} \lim_{\lambda \to 1} \frac{\ell(A_{i,i+1,\lambda}) }{\ell{\left(\operatorname{\mathrm{Arc}}{[1,\lambda]}\right)}} &= |R_{i+1}'(1)| - |R_{i}'(1)| = \frac{1}{1 - f_{\lambda,i+1}'(1)} - \frac{1}{1 - f_{\lambda,i}'(1)} \\ &=\frac{(1+b)/(1-b)}{\big(i - (1+b)/(1-b)\big)\big(i-2b/(1-b)\big)}. \end{align*} $$
$$ \begin{align*} \lim_{\lambda \to 1} \frac{\ell(A_{i,i+1,\lambda}) }{\ell{\left(\operatorname{\mathrm{Arc}}{[1,\lambda]}\right)}} &= |R_{i+1}'(1)| - |R_{i}'(1)| = \frac{1}{1 - f_{\lambda,i+1}'(1)} - \frac{1}{1 - f_{\lambda,i}'(1)} \\ &=\frac{(1+b)/(1-b)}{\big(i - (1+b)/(1-b)\big)\big(i-2b/(1-b)\big)}. \end{align*} $$The second equality can be obtained by using (4) and the third by using (2) and simplifying. If we denote this expression by ![]() $g(i)$, then it is not hard to see that
$g(i)$, then it is not hard to see that ![]() $g(i+1)> g(i)$ as long as
$g(i+1)> g(i)$ as long as ![]() $i + 1 < 2b/(1-b)$. Because
$i + 1 < 2b/(1-b)$. Because  $b\in (\tfrac {d-2}{d},1)$, we have
$b\in (\tfrac {d-2}{d},1)$, we have ![]() $2b/(1-b)>d-2$. So, indeed,
$2b/(1-b)>d-2$. So, indeed, ![]() $g(i+1)> g(i)$ for
$g(i+1)> g(i)$ for ![]() $i \in \{1, \dots , d-3\}$, which contains
$i \in \{1, \dots , d-3\}$, which contains ![]() $\{1, \dots , k-2\}$. This shows that the inequality in (3) is true for
$\{1, \dots , k-2\}$. This shows that the inequality in (3) is true for ![]() $\lambda $ near
$\lambda $ near ![]() $1$.
$1$.
Now suppose that there is ![]() $\lambda \in \mathbb {S}$ and index i for which the inequality in (3) does not hold. Then, by continuity, because the inequality does hold near
$\lambda \in \mathbb {S}$ and index i for which the inequality in (3) does not hold. Then, by continuity, because the inequality does hold near ![]() $1$, there is a
$1$, there is a ![]() $\lambda \in \mathbb {S}$ for which the inequality is an equality; that is,
$\lambda \in \mathbb {S}$ for which the inequality is an equality; that is,
For convenience, we will henceforth drop the subscript ![]() $\lambda $ from the notation for the arcs
$\lambda $ from the notation for the arcs ![]() $A_{i,j,\lambda }$ and simply write
$A_{i,j,\lambda }$ and simply write ![]() $A_{i,j}$. The maps
$A_{i,j}$. The maps ![]() $f_{\lambda ,j}$ are orientation-preserving for any j and thus
$f_{\lambda ,j}$ are orientation-preserving for any j and thus
 $$ \begin{align*} \ell{\left(\operatorname{\mathrm{Arc}}[\lambda,R_j(\lambda)]\right)} = \ell{\left(f_{\lambda,j}(A_{0,j})\right)} = \int_{A_{0,j}} |f_j'(z)|\, |dz|. \end{align*} $$
$$ \begin{align*} \ell{\left(\operatorname{\mathrm{Arc}}[\lambda,R_j(\lambda)]\right)} = \ell{\left(f_{\lambda,j}(A_{0,j})\right)} = \int_{A_{0,j}} |f_j'(z)|\, |dz|. \end{align*} $$Using this equality we can write
 $$ \begin{align*} \ell{\left(A_{j,j+1}\right)} = \int_{A_{0,j+1}} |f_{j+1}'(z)|\, |dz| - \int_{A_{0,j}}|f_j'(z)|\, |dz|. \end{align*} $$
$$ \begin{align*} \ell{\left(A_{j,j+1}\right)} = \int_{A_{0,j+1}} |f_{j+1}'(z)|\, |dz| - \int_{A_{0,j}}|f_j'(z)|\, |dz|. \end{align*} $$We use this equality for ![]() $j= i$ and
$j= i$ and ![]() $j= i+1$ and rearrange (5) to obtain
$j= i+1$ and rearrange (5) to obtain
 $$ \begin{align*} 2\int_{A_{0,i+1}} |f_{i+1}'(z)|\, |dz| = \int_{A_{0,i+2}} |f_{i+2}'(z)|\, |dz| + \int_{A_{0,i}} |f_i'(z)|\, |dz|. \end{align*} $$
$$ \begin{align*} 2\int_{A_{0,i+1}} |f_{i+1}'(z)|\, |dz| = \int_{A_{0,i+2}} |f_{i+2}'(z)|\, |dz| + \int_{A_{0,i}} |f_i'(z)|\, |dz|. \end{align*} $$We use (2) to rewrite the left-hand side of this equation as
 $$ \begin{align*} 2(i+1) \int_{A_{0,i}} |f_{1}'(z)|\, |dz| + 2 \int_{A_{i,i+1}} |f_{i+1}'(z)|\, |dz|, \end{align*} $$
$$ \begin{align*} 2(i+1) \int_{A_{0,i}} |f_{1}'(z)|\, |dz| + 2 \int_{A_{i,i+1}} |f_{i+1}'(z)|\, |dz|, \end{align*} $$and we rewrite the right-hand side as
 $$ \begin{align*} (i+2)\int_{A_{0,i}} |f_{1}'(z)|\, |dz| + \int_{A_{i,i+2}} |f_{i+2}'(z)|\, |dz| + i\cdot \int_{A_{0,i}} |f_{1}'(z)|\, |dz|. \end{align*} $$
$$ \begin{align*} (i+2)\int_{A_{0,i}} |f_{1}'(z)|\, |dz| + \int_{A_{i,i+2}} |f_{i+2}'(z)|\, |dz| + i\cdot \int_{A_{0,i}} |f_{1}'(z)|\, |dz|. \end{align*} $$These two being equal implies that
 $$ \begin{align*} 2 \int_{A_{i,i+1}} |f_{i+1}'(z)|\, |dz| = \int_{A_{i,i+2}} |f_{i+2}'(z)|\, |dz|. \end{align*} $$
$$ \begin{align*} 2 \int_{A_{i,i+1}} |f_{i+1}'(z)|\, |dz| = \int_{A_{i,i+2}} |f_{i+2}'(z)|\, |dz|. \end{align*} $$We will show that this yields a contradiction. We rewrite the right-hand side as
 $$ \begin{align*} \int_{A_{i,i+2}} |f_{i+2}'(z)|\, |dz| = \int_{A_{i,i+1}} |f_{i+2}'(z)|\, |dz| + \int_{A_{i+1,i+2}} |f_{i+2}'(z)|\, |dz|, \end{align*} $$
$$ \begin{align*} \int_{A_{i,i+2}} |f_{i+2}'(z)|\, |dz| = \int_{A_{i,i+1}} |f_{i+2}'(z)|\, |dz| + \int_{A_{i+1,i+2}} |f_{i+2}'(z)|\, |dz|, \end{align*} $$and we will show that both summands are greater than  $\int _{A_{i,i+1}} |f_{i+1}'(z)|\, |dz|$, which will yield the contradiction. The inequality for the first summand follows easily from the fact that
$\int _{A_{i,i+1}} |f_{i+1}'(z)|\, |dz|$, which will yield the contradiction. The inequality for the first summand follows easily from the fact that ![]() $|f_{i+2}'(z)|> |f_{i+1}'(z)|$ for all
$|f_{i+2}'(z)|> |f_{i+1}'(z)|$ for all ![]() $z \in \mathbb {S}$; cf. (2). The second inequality uses the fact that
$z \in \mathbb {S}$; cf. (2). The second inequality uses the fact that ![]() $|f_{i+2}'(z)|$ increases as
$|f_{i+2}'(z)|$ increases as ![]() $\text {Arg}(z)$ increases (when
$\text {Arg}(z)$ increases (when ![]() $\operatorname {\mathrm {Im}}{z}> 0$) and thus
$\operatorname {\mathrm {Im}}{z}> 0$) and thus
 $$ \begin{align*} \int_{A_{i+1,i+2}} |f_{i+2}'(z)|\, |dz| &> |f_{i+2}'(R_{i+1}(\lambda))| \cdot \ell{\left(A_{i+1,i+2}\right)} > |f_{i+1}'(R_{i+1}(\lambda))| \cdot \ell{\left(A_{i,i+1}\right)} \\ &> \int_{A_{i,i+1}} |f_{i+1}'(z)|\, |dz|. \end{align*} $$
$$ \begin{align*} \int_{A_{i+1,i+2}} |f_{i+2}'(z)|\, |dz| &> |f_{i+2}'(R_{i+1}(\lambda))| \cdot \ell{\left(A_{i+1,i+2}\right)} > |f_{i+1}'(R_{i+1}(\lambda))| \cdot \ell{\left(A_{i,i+1}\right)} \\ &> \int_{A_{i,i+1}} |f_{i+1}'(z)|\, |dz|. \end{align*} $$The second inequality of this derivation uses the assumed equality in (5). This yields the desired contradiction.
Remark 11. For any ![]() $\lambda \in \mathbb {S}$ and
$\lambda \in \mathbb {S}$ and ![]() $k \in \mathbb {Z}_{\geq 1}$ for which the fixed point
$k \in \mathbb {Z}_{\geq 1}$ for which the fixed point ![]() $R_k(\lambda )$ is defined, we have
$R_k(\lambda )$ is defined, we have ![]() $|f_k'(R_k(\lambda ))|> |f_k'(\lambda )|$. To see this when
$|f_k'(R_k(\lambda ))|> |f_k'(\lambda )|$. To see this when ![]() $\operatorname {\mathrm {Im}}{\lambda }>0$, note from item (iv) and the fact that the maps
$\operatorname {\mathrm {Im}}{\lambda }>0$, note from item (iv) and the fact that the maps ![]() $f_{\lambda ,k}$ are orientation-preserving that
$f_{\lambda ,k}$ are orientation-preserving that ![]() $\text {Arg}{(R_k(\lambda ))}\in (\text {Arg}{(\lambda )},\pi )$ and hence by (2) that
$\text {Arg}{(R_k(\lambda ))}\in (\text {Arg}{(\lambda )},\pi )$ and hence by (2) that ![]() $|f_k'(R_k(\lambda ))|> |f_k'(\lambda )|$. When
$|f_k'(R_k(\lambda ))|> |f_k'(\lambda )|$. When ![]() $\operatorname {\mathrm {Im}}{\lambda }<0$, the inequality follows from the above since
$\operatorname {\mathrm {Im}}{\lambda }<0$, the inequality follows from the above since ![]() $\overline {R_k(\lambda )}=R_k(\overline {\lambda })$ from item (iii) and the expression in (2) depends only the real part of z.
$\overline {R_k(\lambda )}=R_k(\overline {\lambda })$ from item (iii) and the expression in (2) depends only the real part of z.
3.2 Results on  $f_{\lambda ,1}$
$f_{\lambda ,1}$
Note that ![]() $f_{\lambda ,1}$ is a Möbius transformation; we will extract some relevant information about it using the theory of Möbius transformations, following [Reference Beardon3, Section 4.3].
$f_{\lambda ,1}$ is a Möbius transformation; we will extract some relevant information about it using the theory of Möbius transformations, following [Reference Beardon3, Section 4.3].
There is a natural way to relate each Möbius transformation g with a ![]() $2\times 2$ matrix A. Formally, let
$2\times 2$ matrix A. Formally, let ![]() $\textrm {GL}_2(\mathbb {C})$ be the group of
$\textrm {GL}_2(\mathbb {C})$ be the group of ![]() $2\,\times\, 2$ invertible matrices with complex entries (with the multiplication operation) and
$2\,\times\, 2$ invertible matrices with complex entries (with the multiplication operation) and ![]() $\mathcal {M}$ be the group of Möbius transformations (with the composition operation
$\mathcal {M}$ be the group of Möbius transformations (with the composition operation ![]() $\circ $). The following map gives a surjective homomorphism between the groups
$\circ $). The following map gives a surjective homomorphism between the groups ![]() $\textrm {GL}_2(\mathbb {C})$ and
$\textrm {GL}_2(\mathbb {C})$ and ![]() $\mathcal {M}$:
$\mathcal {M}$:
 $$ \begin{align*} \Phi:\textrm{GL}_2(\mathbb{C}) \to \mathcal{M},\quad \Big( \begin{array}{cc} a & b \\ c & d \\ \end{array} \Big) \mapsto (z \mapsto \frac{a z + b}{c z + d}). \end{align*} $$
$$ \begin{align*} \Phi:\textrm{GL}_2(\mathbb{C}) \to \mathcal{M},\quad \Big( \begin{array}{cc} a & b \\ c & d \\ \end{array} \Big) \mapsto (z \mapsto \frac{a z + b}{c z + d}). \end{align*} $$For ![]() $g \in \mathcal {M}$, let
$g \in \mathcal {M}$, let ![]() $A \in \textrm {GL}_2(\mathbb {C})$ such that
$A \in \textrm {GL}_2(\mathbb {C})$ such that ![]() $\Phi (A) = g$ and define
$\Phi (A) = g$ and define ![]() $\operatorname {\mathrm {tr}}^2(g) = \operatorname {\mathrm {tr}}(A)^2/\det (A)$. This value does not depend on the choice of preimage and, thus,
$\operatorname {\mathrm {tr}}^2(g) = \operatorname {\mathrm {tr}}(A)^2/\det (A)$. This value does not depend on the choice of preimage and, thus, ![]() $\operatorname {\mathrm {tr}}^2$ is a well-defined operator on
$\operatorname {\mathrm {tr}}^2$ is a well-defined operator on ![]() $\mathcal {M}$. In the following theorem, it is stated how this operator is used to classify Möbius transformations. We say that
$\mathcal {M}$. In the following theorem, it is stated how this operator is used to classify Möbius transformations. We say that ![]() $f,g\in \mathcal {M}$ are conjugate if there is
$f,g\in \mathcal {M}$ are conjugate if there is ![]() $h\in \mathcal {M}$ such that
$h\in \mathcal {M}$ such that ![]() $f=h\circ g\circ h^{-1}$.
$f=h\circ g\circ h^{-1}$.
Theorem 12 [Reference Beardon3, Theorem 4.3.4]
Let ![]() $g \in \mathcal {M}$ not equal to the identity; then g is conjugate to
$g \in \mathcal {M}$ not equal to the identity; then g is conjugate to
1. a rotation
 $z \mapsto e^{i \theta } z$ for some
$z \mapsto e^{i \theta } z$ for some  $\theta \in (0,\pi ]$ if and only if
$\theta \in (0,\pi ]$ if and only if  $\operatorname {\mathrm {tr}}^2(g) \in [0,4)$, in which case
$\operatorname {\mathrm {tr}}^2(g) \in [0,4)$, in which case  $\operatorname {\mathrm {tr}}^2(g) = 2 \cdot \left (\cos (\theta )+1\right );$
$\operatorname {\mathrm {tr}}^2(g) = 2 \cdot \left (\cos (\theta )+1\right );$2. a multiplication
 $z \mapsto e^{\theta } z$ for some
$z \mapsto e^{\theta } z$ for some  $\theta \in \mathbb {R}_{> 0}$ if and only if
$\theta \in \mathbb {R}_{> 0}$ if and only if  $\operatorname {\mathrm {tr}}^2(g) \in (4,\infty )$, in which case
$\operatorname {\mathrm {tr}}^2(g) \in (4,\infty )$, in which case  $\operatorname {\mathrm {tr}}^2(g) = 2 \cdot \left (\cosh (\theta )+1\right ).$
$\operatorname {\mathrm {tr}}^2(g) = 2 \cdot \left (\cosh (\theta )+1\right ).$
In case (1), g is said to be elliptic, while in case (2) g is called hyperbolic. If ![]() $\operatorname {\mathrm {tr}}^2(g) = 4$ the map is called parabolic.
$\operatorname {\mathrm {tr}}^2(g) = 4$ the map is called parabolic.
Corollary 13. Let ![]() $b \in (0,1)$, and let
$b \in (0,1)$, and let ![]() $\lambda _1=\lambda _1(b) \in \mathbb {S}$ be as in Lemma 8. The map
$\lambda _1=\lambda _1(b) \in \mathbb {S}$ be as in Lemma 8. The map ![]() $f_{\lambda ,1}$ is hyperbolic when
$f_{\lambda ,1}$ is hyperbolic when ![]() $\lambda \in \operatorname {\mathrm {Arc}}{(\overline {\lambda _1},\lambda _1)}$, and
$\lambda \in \operatorname {\mathrm {Arc}}{(\overline {\lambda _1},\lambda _1)}$, and ![]() $f_{\lambda ,1}$ is elliptic when
$f_{\lambda ,1}$ is elliptic when ![]() $\lambda \in \operatorname {\mathrm {Arc}}{(\lambda _1, \overline {\lambda _1})}$.
$\lambda \in \operatorname {\mathrm {Arc}}{(\lambda _1, \overline {\lambda _1})}$.
Proof. Write ![]() $\lambda = x + i y$ with
$\lambda = x + i y$ with ![]() $x,y \in \mathbb {R}$ such that
$x,y \in \mathbb {R}$ such that ![]() $x^2 + y^2 = 1$. A short calculation gives that
$x^2 + y^2 = 1$. A short calculation gives that
 $$ \begin{align*} \operatorname{\mathrm{tr}}^2(f_{\lambda,1}) = \frac{2 \left(x + 1\right)}{1 - b^2}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{tr}}^2(f_{\lambda,1}) = \frac{2 \left(x + 1\right)}{1 - b^2}. \end{align*} $$The value of ![]() $tr^2(f_{\lambda ,1})$ strictly increases from
$tr^2(f_{\lambda ,1})$ strictly increases from ![]() $0$ to
$0$ to ![]() $4/(1-b^2)$ as x increases from
$4/(1-b^2)$ as x increases from ![]() $-1$ to
$-1$ to ![]() $1$. It follows that there is a unique value
$1$. It follows that there is a unique value ![]() $x \in (-1,1)$ such that
$x \in (-1,1)$ such that ![]() $\operatorname {\mathrm {tr}}^2(f_{\lambda ,1}) = 4$. This value must coincide with
$\operatorname {\mathrm {tr}}^2(f_{\lambda ,1}) = 4$. This value must coincide with ![]() $\textrm {Re}(\lambda _1)$, where
$\textrm {Re}(\lambda _1)$, where ![]() $\lambda _1=\lambda _1(b) \in \mathbb {S}$ is as in Lemma 8, completing the proof.
$\lambda _1=\lambda _1(b) \in \mathbb {S}$ is as in Lemma 8, completing the proof.
Lemma 14. Let ![]() $b \in (0,1)$ be a rational. Suppose that
$b \in (0,1)$ be a rational. Suppose that ![]() $\xi \in \mathbb {S}_{\mathbb {Q}}$ with
$\xi \in \mathbb {S}_{\mathbb {Q}}$ with ![]() $\xi \neq \pm 1$ is such that
$\xi \neq \pm 1$ is such that ![]() $f_{\xi ,1}$ is elliptic. Then
$f_{\xi ,1}$ is elliptic. Then ![]() $f_{\xi ,1}$ is conjugate to an irrational rotation.
$f_{\xi ,1}$ is conjugate to an irrational rotation.
Proof. Let ![]() $\xi = x + i y$ with
$\xi = x + i y$ with ![]() $x,y \in \mathbb {Q}$ such that
$x,y \in \mathbb {Q}$ such that ![]() $x^2 + y^2 = 1$. Because
$x^2 + y^2 = 1$. Because ![]() $f_{\xi ,1}$ is elliptic, it is conjugate to a rotation
$f_{\xi ,1}$ is elliptic, it is conjugate to a rotation ![]() $z \mapsto e^{i \theta } z$ with
$z \mapsto e^{i \theta } z$ with
 $$ \begin{align} 2 \cdot \left(\cos (\theta )+1\right) = \frac{2 \left(x + 1\right)}{1 - b^2}. \end{align} $$
$$ \begin{align} 2 \cdot \left(\cos (\theta )+1\right) = \frac{2 \left(x + 1\right)}{1 - b^2}. \end{align} $$Let ![]() $t = 2 \cdot \left (\cos (\theta )+1\right )$. Suppose
$t = 2 \cdot \left (\cos (\theta )+1\right )$. Suppose ![]() $\theta $ is an angle corresponding to a rational rotation; that is, if we let
$\theta $ is an angle corresponding to a rational rotation; that is, if we let ![]() $z = e^{i \theta }$, then there is a natural number n such that
$z = e^{i \theta }$, then there is a natural number n such that ![]() $z^n = 1$. It follows that then
$z^n = 1$. It follows that then ![]() $\overline {z}^n = 1$ and thus both z and
$\overline {z}^n = 1$ and thus both z and ![]() $\overline {z}$ are also algebraic integers. Therefore,
$\overline {z}$ are also algebraic integers. Therefore, ![]() $z + \overline {z} = 2\cos (\theta )$ is an algebraic integer. It follows that t is an algebraic integer, while the right-hand side of (6) shows that t must also be rational. Because the only rational algebraic integers are integers, we can conclude that t must be an integer and thus
$z + \overline {z} = 2\cos (\theta )$ is an algebraic integer. It follows that t is an algebraic integer, while the right-hand side of (6) shows that t must also be rational. Because the only rational algebraic integers are integers, we can conclude that t must be an integer and thus ![]() $t \in \{0,1,2,3\}$. If
$t \in \{0,1,2,3\}$. If ![]() $t=0$, we see that
$t=0$, we see that ![]() $\xi = x = -1$, which we excluded, so only three possible values of t remain. Let
$\xi = x = -1$, which we excluded, so only three possible values of t remain. Let ![]() $X = t(1+b)/(1-b)$ and
$X = t(1+b)/(1-b)$ and ![]() $Y = 2ty/(1-b)^2$; then
$Y = 2ty/(1-b)^2$; then ![]() $(X,Y)$ is a rational point on the elliptic curve
$(X,Y)$ is a rational point on the elliptic curve ![]() $E_t$ given by the following equation:
$E_t$ given by the following equation:
The set of rational points of an elliptic curve together with an additional point has a group structure that is isomorphic to ![]() $\mathbb {Z}^r \times \mathbb {Z}/N\mathbb {Z}$. The number
$\mathbb {Z}^r \times \mathbb {Z}/N\mathbb {Z}$. The number ![]() $r \geq 0$ is called the rank of the curve and the subgroup isomorphic to
$r \geq 0$ is called the rank of the curve and the subgroup isomorphic to ![]() $\mathbb {Z}/N\mathbb {Z}$ is called the torsion subgroup. The rank and the torsion subgroup of a particular curve can be found using a computer algebra system. Using Sage, if the variable
$\mathbb {Z}/N\mathbb {Z}$ is called the torsion subgroup. The rank and the torsion subgroup of a particular curve can be found using a computer algebra system. Using Sage, if the variable ![]() $\texttt{t}$ is declared to be either
$\texttt{t}$ is declared to be either ![]() $1,2$ or
$1,2$ or ![]() $3$, the curve
$3$, the curve ![]() $E_t$ can be defined with the code
$E_t$ can be defined with the code ![]() $\texttt{Et = EllipticCurve([0, -(t-2)*t, 0, t**2, 0])}$. The rank and the torsion subgroup can subsequently be found with the commands
$\texttt{Et = EllipticCurve([0, -(t-2)*t, 0, t**2, 0])}$. The rank and the torsion subgroup can subsequently be found with the commands ![]() $\texttt{Et.rank()}$ and
$\texttt{Et.rank()}$ and ![]() $\texttt{Et.torsion\_subgroup()}$. We find that
$\texttt{Et.torsion\_subgroup()}$. We find that ![]() $E_t$ has rank
$E_t$ has rank ![]() $0$ for all
$0$ for all ![]() $t \in \{1,2,3\}$. For
$t \in \{1,2,3\}$. For ![]() $t \in \{1,3\}$ the torsion subgroup is isomorphic to
$t \in \{1,3\}$ the torsion subgroup is isomorphic to ![]() $\mathbb {Z}/2\mathbb {Z}$, and for
$\mathbb {Z}/2\mathbb {Z}$, and for ![]() $t=2$ it is isomorphic to
$t=2$ it is isomorphic to ![]() $\mathbb {Z}/4\mathbb {Z}$. This means that there is one rational point on
$\mathbb {Z}/4\mathbb {Z}$. This means that there is one rational point on ![]() $E_1$ and
$E_1$ and ![]() $E_3$, which we can see is the point
$E_3$, which we can see is the point ![]() $(0,0)$, and there are three rational points on
$(0,0)$, and there are three rational points on ![]() $E_2$, namely,
$E_2$, namely, ![]() $\{(0,0), (2, \pm 4)\}$. These points do not correspond to values of b within the interval
$\{(0,0), (2, \pm 4)\}$. These points do not correspond to values of b within the interval ![]() $(0,1)$, which means that
$(0,1)$, which means that ![]() $\theta $ cannot correspond to a rational rotation.
$\theta $ cannot correspond to a rational rotation.
3.3 Obtaining points with expanding derivatives
In this section, we use the dynamical study of the maps ![]() $f_{\lambda ,k}$ from previous sections to conclude the existence of points with expanding derivatives. More precisely, we show the following.
$f_{\lambda ,k}$ from previous sections to conclude the existence of points with expanding derivatives. More precisely, we show the following.
Lemma 15. Let ![]() $b \in (0,1)$,
$b \in (0,1)$, ![]() $k\geq 1$ be an integer, and
$k\geq 1$ be an integer, and ![]() $\xi \in \Lambda _k(b)$ with
$\xi \in \Lambda _k(b)$ with ![]() $\xi \neq -1$. Let
$\xi \neq -1$. Let ![]() $z_0 \in \mathbb {S}$ and let
$z_0 \in \mathbb {S}$ and let  $z_n = f_{\xi ,k}^n(z_0)$ for
$z_n = f_{\xi ,k}^n(z_0)$ for ![]() $n>0$. Then there is some index m such that
$n>0$. Then there is some index m such that  $|f_{\xi ,k}'(z_m)|> 1$.
$|f_{\xi ,k}'(z_m)|> 1$.
Proof. For ![]() $k = 1$ it follows from Corollary 13 that
$k = 1$ it follows from Corollary 13 that ![]() $f_{\xi ,1}$ is conjugate to a rotation. If
$f_{\xi ,1}$ is conjugate to a rotation. If ![]() $f_{\xi ,1}$ is conjugate to an irrational rotation, then the orbit of any initial point
$f_{\xi ,1}$ is conjugate to an irrational rotation, then the orbit of any initial point ![]() $z_0$ will get arbitrarily close to
$z_0$ will get arbitrarily close to ![]() $-1$ for which
$-1$ for which  $|f_{1}'(-1)| = \frac {1+b}{1-b}> 1$. Otherwise, if
$|f_{1}'(-1)| = \frac {1+b}{1-b}> 1$. Otherwise, if ![]() $f_{\xi ,1}$ is conjugate to a rational rotation, there is an integer
$f_{\xi ,1}$ is conjugate to a rational rotation, there is an integer ![]() $N> 1$ such that
$N> 1$ such that  $f_{\xi ,1}^N(z) = z$ for all z; consider the smallest such integer N. Let
$f_{\xi ,1}^N(z) = z$ for all z; consider the smallest such integer N. Let ![]() $\theta \in (0,\pi ]$ be the angle such that
$\theta \in (0,\pi ]$ be the angle such that ![]() $f_{\xi ,1}$ is conjugate to the rotation
$f_{\xi ,1}$ is conjugate to the rotation ![]() $z \mapsto e^{i\theta }\cdot z$. Equation (6) then states that
$z \mapsto e^{i\theta }\cdot z$. Equation (6) then states that
 $$ \begin{align*} 2 \cdot \left(\cos (\theta )+1\right) = \frac{2 \left(\operatorname{\mathrm{Re}}(\xi) + 1\right)}{1 - b^2}. \end{align*} $$
$$ \begin{align*} 2 \cdot \left(\cos (\theta )+1\right) = \frac{2 \left(\operatorname{\mathrm{Re}}(\xi) + 1\right)}{1 - b^2}. \end{align*} $$If ![]() $N=2$, then
$N=2$, then ![]() $\theta = \pi $ and thus
$\theta = \pi $ and thus ![]() $\operatorname {\mathrm {Re}}(\xi ) = -1$, contradicting
$\operatorname {\mathrm {Re}}(\xi ) = -1$, contradicting ![]() $\xi \neq -1$. Hence,
$\xi \neq -1$. Hence, ![]() $N>2$. From
$N>2$. From  $f_{\xi ,1}^N(z) = z$, we obtain
$f_{\xi ,1}^N(z) = z$, we obtain
 $$ \begin{align} \prod_{n=0}^{N-1} f_{\xi,1}'(z_n) = (f_{\xi,1}^N)'(z_0) = 1. \end{align} $$
$$ \begin{align} \prod_{n=0}^{N-1} f_{\xi,1}'(z_n) = (f_{\xi,1}^N)'(z_0) = 1. \end{align} $$From (2), there are precisely two values of ![]() $w\in \mathbb {S}$ such that
$w\in \mathbb {S}$ such that  $|f_{\xi ,1}'(w)| = 1$. Because
$|f_{\xi ,1}'(w)| = 1$. Because ![]() $N> 2$ and N is the smallest integer such that
$N> 2$ and N is the smallest integer such that  $f_{\xi ,1}^N(z_0) = z_0$, we conclude there is at least one term, say with index m, of the product in (7) for which
$f_{\xi ,1}^N(z_0) = z_0$, we conclude there is at least one term, say with index m, of the product in (7) for which  $|f_{\xi ,1}'(z_m)|> 1$.
$|f_{\xi ,1}'(z_m)|> 1$.
Consider now the case ![]() $k \geq 2$ and denote
$k \geq 2$ and denote ![]() $f = f_{\xi ,k}$. By Lemma 8, for
$f = f_{\xi ,k}$. By Lemma 8, for ![]() $\xi \in \Lambda _{k}(b)$ the Julia set of f is the circle
$\xi \in \Lambda _{k}(b)$ the Julia set of f is the circle ![]() $\mathbb {S}$. In [Reference Peters and Regts42, Proof of Proposition 17], it is shown that the two Fatou components of f, denoted by
$\mathbb {S}$. In [Reference Peters and Regts42, Proof of Proposition 17], it is shown that the two Fatou components of f, denoted by ![]() $\mathbb {D}$ and
$\mathbb {D}$ and ![]() $\overline {\mathbb {D}}^c$, are attracting basins and contain the critical points
$\overline {\mathbb {D}}^c$, are attracting basins and contain the critical points ![]() $-b$ and
$-b$ and ![]() $-1/b$. From [Reference Milnor38, Theorem 19.1], we therefore conclude that the map f is hyperbolic; that is, there exists a conformal metric
$-1/b$. From [Reference Milnor38, Theorem 19.1], we therefore conclude that the map f is hyperbolic; that is, there exists a conformal metric ![]() $\mu $ on a neighbourhood U of
$\mu $ on a neighbourhood U of ![]() $\mathbb {S}$ such that
$\mathbb {S}$ such that ![]() $||D f_z||_\mu \geq \kappa> 1$ for a constant
$||D f_z||_\mu \geq \kappa> 1$ for a constant ![]() $\kappa $ and all
$\kappa $ and all ![]() $z \in \mathbb {S}$. We will briefly expand on the meaning of this notation.
$z \in \mathbb {S}$. We will briefly expand on the meaning of this notation.
For any ![]() $z \in U$ the metric
$z \in U$ the metric ![]() $\mu $ induces a norm
$\mu $ induces a norm ![]() $||\cdot ||_\mu $ on the tangent space of U at z denoted by
$||\cdot ||_\mu $ on the tangent space of U at z denoted by ![]() $TU_z$. For
$TU_z$. For ![]() $z\in \mathbb {S}$ the map f induces a linear map, the derivative of f at z,
$z\in \mathbb {S}$ the map f induces a linear map, the derivative of f at z, ![]() $Df_z: TU_z \to TU_{f(z)}$. For nonzero
$Df_z: TU_z \to TU_{f(z)}$. For nonzero ![]() $v\in Df_z$, the ratio
$v\in Df_z$, the ratio ![]() $||D f_z(v)||_\mu /||v||_\mu $ is independent of the choice v and is denoted by
$||D f_z(v)||_\mu /||v||_\mu $ is independent of the choice v and is denoted by ![]() $||D f_z||_\mu $, the norm of
$||D f_z||_\mu $, the norm of ![]() $Df_z$.
$Df_z$.
Because ![]() $\mathbb {S}$ is compact and the metric
$\mathbb {S}$ is compact and the metric ![]() $\mu $ is conformal, there is a constant
$\mu $ is conformal, there is a constant ![]() $c> 0$ such that
$c> 0$ such that ![]() $|g'(z)|> c \cdot ||D g_z||_\mu $ for all
$|g'(z)|> c \cdot ||D g_z||_\mu $ for all ![]() $z \in \mathbb {S}$ and maps
$z \in \mathbb {S}$ and maps ![]() $g: \mathbb {S} \to \mathbb {S}$. It follows that for all
$g: \mathbb {S} \to \mathbb {S}$. It follows that for all ![]() $N> 0$,
$N> 0$,
 $$ \begin{align*} \prod_{n=0}^{N-1} |f'(z_n)| = |(f^N)'(z_0)|> c \cdot ||D f^N_{z_0}||_\mu \geq c \cdot \kappa^N. \end{align*} $$
$$ \begin{align*} \prod_{n=0}^{N-1} |f'(z_n)| = |(f^N)'(z_0)|> c \cdot ||D f^N_{z_0}||_\mu \geq c \cdot \kappa^N. \end{align*} $$There is an ![]() $N> 0$ such that the right-hand side of this equation is greater than
$N> 0$ such that the right-hand side of this equation is greater than ![]() $1$. The product on the left-hand side of the equation shows that for such an N there must be at least one index
$1$. The product on the left-hand side of the equation shows that for such an N there must be at least one index ![]() $m \in \{0,\dots ,N-1\}$ such that
$m \in \{0,\dots ,N-1\}$ such that ![]() $|f'(z_m)|> 1$.
$|f'(z_m)|> 1$.
Lemma 16. Let ![]() $b \in (0,1)$,
$b \in (0,1)$, ![]() $\lambda \in \mathbb {S}\setminus \{\pm 1\}$ and
$\lambda \in \mathbb {S}\setminus \{\pm 1\}$ and ![]() $d, k \in \mathbb {Z}_{\geq 1}$. Supppose there exists a rooted tree in
$d, k \in \mathbb {Z}_{\geq 1}$. Supppose there exists a rooted tree in ![]() $\mathcal {T}_{d+1}$ whose root degree m is at most
$\mathcal {T}_{d+1}$ whose root degree m is at most ![]() $d-k$ and which implements a field
$d-k$ and which implements a field ![]() $\xi \in \Lambda _k(b)\backslash \{-1\}$.
$\xi \in \Lambda _k(b)\backslash \{-1\}$.
Then there is ![]() $\sigma \in \mathbb {S}$ with
$\sigma \in \mathbb {S}$ with ![]() $|f_k'(\sigma )|> 1$ and a sequence of rooted trees
$|f_k'(\sigma )|> 1$ and a sequence of rooted trees ![]() $\{T_n\}_{n \geq 1}$ in
$\{T_n\}_{n \geq 1}$ in ![]() $\mathcal {T}_{d+1}$ with root degrees at most
$\mathcal {T}_{d+1}$ with root degrees at most ![]() $m+k$ which implement a sequence of fields
$m+k$ which implement a sequence of fields ![]() $\{\zeta _n\}_{n \geq 1}$ such that
$\{\zeta _n\}_{n \geq 1}$ such that ![]() $\zeta _n$ approaches
$\zeta _n$ approaches ![]() $\sigma $ without being equal to
$\sigma $ without being equal to ![]() $\sigma $.
$\sigma $.
Proof. Consider the orbit
 $$ \begin{align*} \mathcal{S} = \left\{f_{\lambda,1}^n(1): n \geq 1 \right\}. \end{align*} $$
$$ \begin{align*} \mathcal{S} = \left\{f_{\lambda,1}^n(1): n \geq 1 \right\}. \end{align*} $$Note that the elements of ![]() $\mathcal {S}$ are fields of paths. We have seen in Subsection 3.2 that either
$\mathcal {S}$ are fields of paths. We have seen in Subsection 3.2 that either ![]() $f_{\lambda ,1}$ is conjugate to an irrational rotation or the orbit of
$f_{\lambda ,1}$ is conjugate to an irrational rotation or the orbit of ![]() $1$ tends towards an attracting or a parabolic fixed point. In either case there is
$1$ tends towards an attracting or a parabolic fixed point. In either case there is ![]() $\sigma _0 \in \mathbb {S}$ such that
$\sigma _0 \in \mathbb {S}$ such that ![]() $\sigma _0 \not \in \mathcal {S}$ and the elements of
$\sigma _0 \not \in \mathcal {S}$ and the elements of ![]() $\mathcal {S}$ accumulate on
$\mathcal {S}$ accumulate on ![]() $\sigma _0$. It follows from Lemma 15 that there is a positive integer N such that
$\sigma _0$. It follows from Lemma 15 that there is a positive integer N such that  $\sigma := f_{\xi , k}^N(\sigma _0)$ has the property
$\sigma := f_{\xi , k}^N(\sigma _0)$ has the property ![]() $|f_{k}'(\sigma )|> 1$. Now define
$|f_{k}'(\sigma )|> 1$. Now define
 $$ \begin{align*} \mathcal{R} = \left\{f_{\xi, k}^N(s): s \in \mathcal{S} \right\}. \end{align*} $$
$$ \begin{align*} \mathcal{R} = \left\{f_{\xi, k}^N(s): s \in \mathcal{S} \right\}. \end{align*} $$By assumption, ![]() $\xi $ can be implemented by a rooted tree in
$\xi $ can be implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree
$\mathcal {T}_{d+1}$ with root degree ![]() $m\leq d-k$, so by inductively applying Lemma 4, the elements of
$m\leq d-k$, so by inductively applying Lemma 4, the elements of ![]() $\mathcal {R}$ are fields of trees in
$\mathcal {R}$ are fields of trees in ![]() $\mathcal {T}_{d+1}$ whose root degree is
$\mathcal {T}_{d+1}$ whose root degree is ![]() $m+k\leq d$. There is a sequence
$m+k\leq d$. There is a sequence ![]() $\{\zeta _n\}_{n \geq 1} \subseteq \mathcal {R}$ accumulating on
$\{\zeta _n\}_{n \geq 1} \subseteq \mathcal {R}$ accumulating on ![]() $\sigma $ without being equal to
$\sigma $ without being equal to ![]() $\sigma $, which is what we wanted to show.
$\sigma $, which is what we wanted to show.
3.4 The main lemma to carry out the induction: proof of Theorem 6
We are now ready to state the following lemma, which will imply Theorem 6. In this section we will show how Theorem 6 follows from this lemma and the next couple of sections are dedicated to proving Lemma 17.
Lemma 17. Let ![]() $k,d\in \mathbb {Z}_{\geq 2}$ with
$k,d\in \mathbb {Z}_{\geq 2}$ with ![]() $k \leq d$,
$k \leq d$,  $b \in \big (\frac {d-2}{d}, \frac {d-1}{d+1}\big ]\cap \mathbb {Q}$ and
$b \in \big (\frac {d-2}{d}, \frac {d-1}{d+1}\big ]\cap \mathbb {Q}$ and ![]() $\lambda \in \mathbb {S}_{\mathbb {Q}}\setminus \{\pm 1\}$. Suppose there exists a rooted tree in
$\lambda \in \mathbb {S}_{\mathbb {Q}}\setminus \{\pm 1\}$. Suppose there exists a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-k$ that implements a field
$d-k$ that implements a field ![]() $\xi \neq 1$ with the property that
$\xi \neq 1$ with the property that ![]() $|f_k'(\xi )|\geq 1$ and
$|f_k'(\xi )|\geq 1$ and  $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _{\left \lfloor k/2\right \rfloor }},\lambda _{\left \lfloor k/2\right \rfloor }]}$. Then the set of fields implemented by trees in
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _{\left \lfloor k/2\right \rfloor }},\lambda _{\left \lfloor k/2\right \rfloor }]}$. Then the set of fields implemented by trees in ![]() $\mathcal {T}_{d+1}$ is dense in
$\mathcal {T}_{d+1}$ is dense in ![]() $\mathbb {S}$.
$\mathbb {S}$.
Using this lemma, we can prove Theorem 6, which we restate here for convenience.
Theorem 6. Let ![]() $d\geq 2$ be an integer.
$d\geq 2$ be an integer.
(a) Let
 $b \in \big (0, \frac {d-1}{d+1}\big ]$ be a rational. Then
$b \in \big (0, \frac {d-1}{d+1}\big ]$ be a rational. Then  $\mathbb {S}_{\mathbb {Q}}(d,b)=\mathbb {S}_{\mathbb {Q}}\setminus \{\pm 1\}$.
$\mathbb {S}_{\mathbb {Q}}(d,b)=\mathbb {S}_{\mathbb {Q}}\setminus \{\pm 1\}$.(b) Let
 $b \in \big (\frac {d-1}{d+1},1\big )$ be a rational. Then
$b \in \big (\frac {d-1}{d+1},1\big )$ be a rational. Then  $\mathbb {S}_{\mathbb {Q}}(d,b)$ is dense in
$\mathbb {S}_{\mathbb {Q}}(d,b)$ is dense in  $\mathbb {S}\setminus I(\theta _b)$.
$\mathbb {S}\setminus I(\theta _b)$.
Proof. We start with the proof of part (b). Let ![]() $\lambda '\in \mathbb {S}\setminus I(\theta _b)$. By [Reference Peters and Regts42, Corollary 4 and Theorem 5], it follows that there exists
$\lambda '\in \mathbb {S}\setminus I(\theta _b)$. By [Reference Peters and Regts42, Corollary 4 and Theorem 5], it follows that there exists ![]() $\lambda \in \mathbb {S}$ arbitrarily close to
$\lambda \in \mathbb {S}$ arbitrarily close to ![]() $\lambda '$ for which there exists a tree
$\lambda '$ for which there exists a tree ![]() $T\in \mathcal {T}_{d+1}$ such that
$T\in \mathcal {T}_{d+1}$ such that ![]() $Z_T(\lambda ,b)=0$. Choose such a tree T with the minimum number of vertices and let v be a leaf of T, from now on referred to as the root of T. Denote
$Z_T(\lambda ,b)=0$. Choose such a tree T with the minimum number of vertices and let v be a leaf of T, from now on referred to as the root of T. Denote ![]() $T'=T-v$ and let u be the unique neighbour of v in T. Then
$T'=T-v$ and let u be the unique neighbour of v in T. Then ![]() $Z_{T,\mathrm {\texttt {-}} v}(\lambda ,b)\neq 0$. Indeed, if
$Z_{T,\mathrm {\texttt {-}} v}(\lambda ,b)\neq 0$. Indeed, if ![]() $Z_{T,\mathrm {\texttt {-}} v}(\lambda ,b)= 0$, then
$Z_{T,\mathrm {\texttt {-}} v}(\lambda ,b)= 0$, then ![]() $Z_{T,\mathrm {\texttt {+}} v}(\lambda ,b)= 0$. Since
$Z_{T,\mathrm {\texttt {+}} v}(\lambda ,b)= 0$. Since
 $$ \begin{align*}\left (\begin{array}{lr} \lambda &\lambda b \\ b&1 \end{array}\right) \left (\begin{array}{l} Z_{T',\mathrm{\texttt{+}} u}(\lambda,b)\\Z_{T',\mathrm{\texttt{-}} u}(\lambda,b)\end{array}\right) = \left (\begin{array}{l} Z_{T,\mathrm{\texttt{+}} v}(\lambda,b)\\Z_{T,\mathrm{\texttt{-}} v}(\lambda,b)\end{array}\right) \end{align*} $$
$$ \begin{align*}\left (\begin{array}{lr} \lambda &\lambda b \\ b&1 \end{array}\right) \left (\begin{array}{l} Z_{T',\mathrm{\texttt{+}} u}(\lambda,b)\\Z_{T',\mathrm{\texttt{-}} u}(\lambda,b)\end{array}\right) = \left (\begin{array}{l} Z_{T,\mathrm{\texttt{+}} v}(\lambda,b)\\Z_{T,\mathrm{\texttt{-}} v}(\lambda,b)\end{array}\right) \end{align*} $$and since the matrix is invertible (as ![]() $|b|\neq 1$), this would imply
$|b|\neq 1$), this would imply ![]() $Z_{T',+u}(\lambda ,b)=Z_{T',-u}(\lambda ,b)=0$ and hence
$Z_{T',+u}(\lambda ,b)=Z_{T',-u}(\lambda ,b)=0$ and hence ![]() $Z_{T'}(\lambda ,b)=0$, contradicting the minimality of T. Therefore,
$Z_{T'}(\lambda ,b)=0$, contradicting the minimality of T. Therefore, ![]() $R_{T,v}=-1$.
$R_{T,v}=-1$.
Since the map  $ z \mapsto \xi (z) :=\frac {Z_{T,\mathrm {\texttt {+}} v}(z,b)}{Z_{T,\mathrm {\texttt {-}} v}(z,b)}$ is holomorphic near
$ z \mapsto \xi (z) :=\frac {Z_{T,\mathrm {\texttt {+}} v}(z,b)}{Z_{T,\mathrm {\texttt {-}} v}(z,b)}$ is holomorphic near ![]() $z = \lambda $, it follows that there exists
$z = \lambda $, it follows that there exists ![]() $\lambda ''\in \mathbb {S}_{\mathbb {Q}}$ arbitrarily close to
$\lambda ''\in \mathbb {S}_{\mathbb {Q}}$ arbitrarily close to ![]() $\lambda '$ such that
$\lambda '$ such that ![]() $ \xi =\xi (\lambda '')\in \operatorname {\mathrm {Arc}}(\lambda _1(b),\overline {\lambda _1(b)})\setminus \{-1\}$. Therefore, by Lemma 14 and Theorem 12, the orbit
$ \xi =\xi (\lambda '')\in \operatorname {\mathrm {Arc}}(\lambda _1(b),\overline {\lambda _1(b)})\setminus \{-1\}$. Therefore, by Lemma 14 and Theorem 12, the orbit  $\{f^n_{\xi ,1}(1)\}$ is dense in
$\{f^n_{\xi ,1}(1)\}$ is dense in ![]() $\mathbb {S}$. So from Lemma 4, by using paths with the tree T attached to all but one of its vertices at the root v of T, we obtain a collection of trees contained in
$\mathbb {S}$. So from Lemma 4, by using paths with the tree T attached to all but one of its vertices at the root v of T, we obtain a collection of trees contained in ![]() $\mathcal {T}_{d+1}$ whose fields are dense in
$\mathcal {T}_{d+1}$ whose fields are dense in ![]() $\mathbb {S}$.
$\mathbb {S}$.
We next prove part (a) for all ![]() $d\geq 2$ and
$d\geq 2$ and  $b \in (\frac {d-2}{d},\frac {d-1}{d+1}]$. The case
$b \in (\frac {d-2}{d},\frac {d-1}{d+1}]$. The case  $b \in (0,\frac {d-2}{d}]$ follows from this by invoking smaller values for d. Let
$b \in (0,\frac {d-2}{d}]$ follows from this by invoking smaller values for d. Let ![]() $\lambda \in \mathbb {S}_{\mathbb {Q}}\setminus \{\pm 1\}$.
$\lambda \in \mathbb {S}_{\mathbb {Q}}\setminus \{\pm 1\}$.
Let ![]() $k_0 = d$ and
$k_0 = d$ and ![]() $m_0 = 0$, and define the sequences
$m_0 = 0$, and define the sequences ![]() $k_n$ and
$k_n$ and ![]() $m_n$ by
$m_n$ by  $k_{n+1} = \left \lfloor \frac {k_n}{2}\right \rfloor $ and
$k_{n+1} = \left \lfloor \frac {k_n}{2}\right \rfloor $ and ![]() $m_{n+1} = m_n + k_{n+1}$. Inductively we show that
$m_{n+1} = m_n + k_{n+1}$. Inductively we show that ![]() $m_n \leq d - k_n$: we have
$m_n \leq d - k_n$: we have ![]() $m_0 = d - k_0$ and then
$m_0 = d - k_0$ and then
 $$ \begin{align*} m_{n+1} = m_n + k_{n+1} \leq d- k_n + k_{n+1} = d - \big(k_n - \left\lfloor\tfrac{k_n}{2}\right\rfloor\big) \leq d - \left\lfloor\tfrac{k_n}{2}\right\rfloor = d - k_{n+1}. \end{align*} $$
$$ \begin{align*} m_{n+1} = m_n + k_{n+1} \leq d- k_n + k_{n+1} = d - \big(k_n - \left\lfloor\tfrac{k_n}{2}\right\rfloor\big) \leq d - \left\lfloor\tfrac{k_n}{2}\right\rfloor = d - k_{n+1}. \end{align*} $$Clearly, there is an integer N such that ![]() $k_{N+1} = 1$. We claim that for every
$k_{N+1} = 1$. We claim that for every ![]() $n \in \{0, \dots , N\}$ there is a rooted tree in
$n \in \{0, \dots , N\}$ there is a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree
$\mathcal {T}_{d+1}$ with root degree ![]() $m_n$ that implements a field
$m_n$ that implements a field ![]() $\xi _n$ so that
$\xi _n$ so that ![]() $|f'(\xi _n)|>1$ and at least one of the following holds:
$|f'(\xi _n)|>1$ and at least one of the following holds:
1. There is a tree in
 $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most  $m_n$ that implements a field inside
$m_n$ that implements a field inside  $\operatorname {\mathrm {Arc}}{(\lambda _{k_{n+1}},\overline {\lambda _{k_{n+1}}})}\setminus \{-1\}$, or else
$\operatorname {\mathrm {Arc}}{(\lambda _{k_{n+1}},\overline {\lambda _{k_{n+1}}})}\setminus \{-1\}$, or else2. the set of fields implemented by trees in
 $\mathcal {T}_{d+1}$ is dense in
$\mathcal {T}_{d+1}$ is dense in  $\mathbb {S}$.
$\mathbb {S}$.
To show this for ![]() $n = 0$, we consider the tree consisting of a single vertex. This tree implements the field
$n = 0$, we consider the tree consisting of a single vertex. This tree implements the field ![]() $\lambda $ and its root degree is
$\lambda $ and its root degree is ![]() $0$. By equation (2) of Lemma 10 and since
$0$. By equation (2) of Lemma 10 and since  $b\leq \frac {d-1}{d+1}$, we have that
$b\leq \frac {d-1}{d+1}$, we have that ![]() $|f_{d}'(z)|> 1$ for all
$|f_{d}'(z)|> 1$ for all ![]() $z \in \mathbb {S} \setminus \{1\}$ and, in particular, we have
$z \in \mathbb {S} \setminus \{1\}$ and, in particular, we have ![]() $|f_{d}'(\lambda )|> 1$. If
$|f_{d}'(\lambda )|> 1$. If ![]() $\lambda \in \operatorname {\mathrm {Arc}}[\overline {\lambda _{k_1}},\lambda _{k_1}]$, then we apply Lemma 17 to obtain Item (2). If
$\lambda \in \operatorname {\mathrm {Arc}}[\overline {\lambda _{k_1}},\lambda _{k_1}]$, then we apply Lemma 17 to obtain Item (2). If ![]() $\lambda \in \operatorname {\mathrm {Arc}}{(\lambda _{k_{1}},\overline {\lambda _{k_{1}}})}$, then the tree consisting of a single vertex satisfies the conditions of Item (1).
$\lambda \in \operatorname {\mathrm {Arc}}{(\lambda _{k_{1}},\overline {\lambda _{k_{1}}})}$, then the tree consisting of a single vertex satisfies the conditions of Item (1).
Now suppose that we have shown the claim for ![]() $n-1$ for some
$n-1$ for some ![]() $n\geq 1$ and assume that we are in the case of Item (1) (otherwise, we are done); that is, there is a tree in
$n\geq 1$ and assume that we are in the case of Item (1) (otherwise, we are done); that is, there is a tree in ![]() $\mathcal {T}_{d+1}$ with root degree
$\mathcal {T}_{d+1}$ with root degree ![]() $m_{n-1}$ that implements a field
$m_{n-1}$ that implements a field ![]() $\xi $ inside
$\xi $ inside ![]() $\operatorname {\mathrm {Arc}}{(\lambda _{k_{n}},\overline {\lambda _{k_{n}}})}\setminus \{-1\}$. We can apply Lemma 16 to obtain a tree T in
$\operatorname {\mathrm {Arc}}{(\lambda _{k_{n}},\overline {\lambda _{k_{n}}})}\setminus \{-1\}$. We can apply Lemma 16 to obtain a tree T in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $k_n + m_{n-1} = m_n$ that implements a field
$k_n + m_{n-1} = m_n$ that implements a field ![]() $\zeta \neq -1$ such that
$\zeta \neq -1$ such that  $|f_{k_{n}}'(\zeta )|> 1$. If
$|f_{k_{n}}'(\zeta )|> 1$. If ![]() $\zeta \in \operatorname {\mathrm {Arc}}[\overline {\lambda _{k_{n+1}}},\lambda _{k_{n+1}}]$, we can apply Lemma 17 to obtain Item (2). We can apply this lemma because
$\zeta \in \operatorname {\mathrm {Arc}}[\overline {\lambda _{k_{n+1}}},\lambda _{k_{n+1}}]$, we can apply Lemma 17 to obtain Item (2). We can apply this lemma because ![]() $m_n \leq d - k_n$. If
$m_n \leq d - k_n$. If ![]() $\zeta \in \operatorname {\mathrm {Arc}}{(\lambda _{k_{n+1}},\overline {\lambda _{k_{n+1}}})}$, then T itself satisfies the conditions of Item (1), which proves the claim.
$\zeta \in \operatorname {\mathrm {Arc}}{(\lambda _{k_{n+1}},\overline {\lambda _{k_{n+1}}})}$, then T itself satisfies the conditions of Item (1), which proves the claim.
To finish the proof, it remains to consider the case of Item (1), where we can find a tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $m_N < d - 1$ which implements a field
$m_N < d - 1$ which implements a field ![]() $\xi $ inside
$\xi $ inside ![]() $\operatorname {\mathrm {Arc}}{(\lambda _{1},\overline {\lambda _{1}})}\setminus \{-1\}$. We have shown in Lemma 14 that
$\operatorname {\mathrm {Arc}}{(\lambda _{1},\overline {\lambda _{1}})}\setminus \{-1\}$. We have shown in Lemma 14 that ![]() $f_{\xi ,1}$ is conjugate to an irrational rotation and thus the orbit
$f_{\xi ,1}$ is conjugate to an irrational rotation and thus the orbit  $\{f_{\xi ,1}^n(1)\}_{n \geq 1}$ is dense in
$\{f_{\xi ,1}^n(1)\}_{n \geq 1}$ is dense in ![]() $\mathbb {S}$. The elements of this orbit correspond to rooted trees in
$\mathbb {S}$. The elements of this orbit correspond to rooted trees in ![]() $\mathcal {T}_{d+1}$ and, hence, we can conclude Item (2) in this case as well.
$\mathcal {T}_{d+1}$ and, hence, we can conclude Item (2) in this case as well.
Let ![]() $\mathcal {R}$ denote the set of all fields implemented by rooted trees in
$\mathcal {R}$ denote the set of all fields implemented by rooted trees in ![]() $\mathcal {T}_{d+1}$. Let
$\mathcal {T}_{d+1}$. Let ![]() $\zeta \in \mathcal {R}$ and T be a tree in
$\zeta \in \mathcal {R}$ and T be a tree in ![]() $\mathcal {T}_{d+1}$ that implements
$\mathcal {T}_{d+1}$ that implements ![]() $\zeta $. We construct the tree
$\zeta $. We construct the tree ![]() $\tilde {T}$ with root r obtained by attaching r to the root of T with an edge. Then, the root of
$\tilde {T}$ with root r obtained by attaching r to the root of T with an edge. Then, the root of ![]() $\tilde {T}$ has degree 1 and the field implemented by
$\tilde {T}$ has degree 1 and the field implemented by ![]() $\tilde {T}$ is
$\tilde {T}$ is ![]() $f_{\lambda ,1}(\zeta )$. So the set of fields implemented by rooted trees in
$f_{\lambda ,1}(\zeta )$. So the set of fields implemented by rooted trees in ![]() $\mathcal {T}_{d+1}$ whose root degrees are
$\mathcal {T}_{d+1}$ whose root degrees are ![]() $1$ contains
$1$ contains ![]() $f_{\lambda ,1}(\mathcal {R})$. Since
$f_{\lambda ,1}(\mathcal {R})$. Since ![]() $f_{\lambda ,1}(\mathbb {S}) = \mathbb {S}$ and
$f_{\lambda ,1}(\mathbb {S}) = \mathbb {S}$ and ![]() $\mathcal {R}$ is dense in
$\mathcal {R}$ is dense in ![]() $\mathbb {S}$, we conclude that
$\mathbb {S}$, we conclude that ![]() $f_{\lambda ,1}(\mathcal {R})$ is dense in
$f_{\lambda ,1}(\mathcal {R})$ is dense in ![]() $\mathbb {S}$ as well.
$\mathbb {S}$ as well.
Remark 18. We note that our proof of part (b) rests on the existence of zeros for trees proved in [Reference Peters and Regts42], which in turn depends on the chaotic behaviour of the map ![]() $f_{d,\lambda }$. Alternatively, one could also prove part (b) directly from Lemma 15. The same proof also yields a dense set of
$f_{d,\lambda }$. Alternatively, one could also prove part (b) directly from Lemma 15. The same proof also yields a dense set of ![]() $\lambda \in \mathbb {S}_{\mathbb {Q}}$ for which the collection of fields of trees in
$\lambda \in \mathbb {S}_{\mathbb {Q}}$ for which the collection of fields of trees in ![]() $\mathcal {T}_{d+1}$ with root degree
$\mathcal {T}_{d+1}$ with root degree ![]() $1$ is dense in
$1$ is dense in ![]() $\mathbb {S}$ when
$\mathbb {S}$ when  $b\in (0,\frac {d-1}{d+1}$].
$b\in (0,\frac {d-1}{d+1}$].
4 Contracting maps that cover via degree-derivative interplay
In this section, we adapt the contracting/covering maps framework of [Reference Bezáková, Galanis, Goldberg and Štefankovič6] in our setting and show how to apply it using the degree-derivative inteplay alluded to in Subsection 2.3. Subsection 4.1 gives the details of the framework, and Subsection 4.2 gives the main lemmas that exploit this interplay.
4.1 Density on circular arcs via contracting maps that cover
The contracting maps that cover framework is captured by the following lemma on the interval ![]() $[0,1]$, which yields Corollary 20 on circular arcs of the unit circle
$[0,1]$, which yields Corollary 20 on circular arcs of the unit circle ![]() $\mathbb {S}$.
$\mathbb {S}$.
Lemma 19. Let ![]() $f_1, \dots , f_k$ be continuously differentiable maps from the interval
$f_1, \dots , f_k$ be continuously differentiable maps from the interval ![]() $[0,1]$ to itself such that
$[0,1]$ to itself such that ![]() $0 < f_m'(x) < 1$ for each index m and
$0 < f_m'(x) < 1$ for each index m and ![]() $x \in (0,1)$ and such that
$x \in (0,1)$ and such that  $\bigcup _{m=1}^k {f_m \left ( \left [0,1\right ] \right )} = [0,1]$.
$\bigcup _{m=1}^k {f_m \left ( \left [0,1\right ] \right )} = [0,1]$.
Then for any open interval ![]() $J \subseteq [0,1]$, there is a sequence of indices
$J \subseteq [0,1]$, there is a sequence of indices ![]() $m_1, \dots , m_N$ such that
$m_1, \dots , m_N$ such that
Proof. For ![]() $m \in \{1,\dots , k\}$, define the closed interval
$m \in \{1,\dots , k\}$, define the closed interval ![]() $I_m = f_m\left ([0,1]\right ) = [f_m(0),f_m(1)]$ and note that
$I_m = f_m\left ([0,1]\right ) = [f_m(0),f_m(1)]$ and note that ![]() $f_m: [0,1] \to I_m$ is bijective with a differentiable inverse. We define a sequence of intervals in the following way. Let
$f_m: [0,1] \to I_m$ is bijective with a differentiable inverse. We define a sequence of intervals in the following way. Let ![]() $J_0 = J$, and as long as there exists an index m such that
$J_0 = J$, and as long as there exists an index m such that ![]() $J_n \subseteq I_m$, we define
$J_n \subseteq I_m$, we define ![]() $J_{n+1} = f_m^{-1}(J)$. We will show that this cannot be done indefinitely; that is, there will be some interval
$J_{n+1} = f_m^{-1}(J)$. We will show that this cannot be done indefinitely; that is, there will be some interval ![]() $J_n$ such that
$J_n$ such that ![]() $J_n \not \subseteq I_m$ for all m.
$J_n \not \subseteq I_m$ for all m.
For an interval ![]() $I \subseteq [0,1]$, let
$I \subseteq [0,1]$, let ![]() $\ell (I)$ denote the length of the interval and denote
$\ell (I)$ denote the length of the interval and denote ![]() $\ell (J)$ by
$\ell (J)$ by ![]() $\epsilon $. For each index m choose a partition
$\epsilon $. For each index m choose a partition ![]() $I_m = I_{m,L} \cup I_{m,M} \cup I_{m,R}$, where
$I_m = I_{m,L} \cup I_{m,M} \cup I_{m,R}$, where ![]() $I_{m,L}, I_{m,M}, I_{m,R}$ are of the form
$I_{m,L}, I_{m,M}, I_{m,R}$ are of the form ![]() $[f_m(0),a), [a,b], (b, f_m(1)]$, respectively, for a choice of
$[f_m(0),a), [a,b], (b, f_m(1)]$, respectively, for a choice of ![]() $a,b \in \mathrm {int}(I_m)$ such that
$a,b \in \mathrm {int}(I_m)$ such that ![]() $a<b$ and both
$a<b$ and both ![]() $\ell (I_{m,L})$ and
$\ell (I_{m,L})$ and ![]() $\ell (I_{m,R})$ are less than
$\ell (I_{m,R})$ are less than ![]() $\epsilon /4$. We can choose
$\epsilon /4$. We can choose ![]() $C> 1$ such that
$C> 1$ such that  ${f_m^{-1}}'(x)> C$ for all indices m and
${f_m^{-1}}'(x)> C$ for all indices m and ![]() $x \in I_{m,M}$. We will show inductively that for all
$x \in I_{m,M}$. We will show inductively that for all ![]() $n \geq 0$ for which
$n \geq 0$ for which ![]() $J_n$ is defined it is the case that
$J_n$ is defined it is the case that ![]() $\ell (J_{n}) \geq \epsilon \cdot (1+C^{n})/2$. For
$\ell (J_{n}) \geq \epsilon \cdot (1+C^{n})/2$. For ![]() $n = 0$ the statement is true. Suppose that the statement is true for
$n = 0$ the statement is true. Suppose that the statement is true for ![]() $n \geq 0$ for which
$n \geq 0$ for which ![]() $J_{n+1}$ is defined. By definition, there is an index m such that
$J_{n+1}$ is defined. By definition, there is an index m such that ![]() $J_n \subseteq I_m$ and
$J_n \subseteq I_m$ and ![]() $J_{n+1} = f_m^{-1}(J_n)$. We find
$J_{n+1} = f_m^{-1}(J_n)$. We find
 $$ \begin{align*} \ell(J_{n+1}) &= \ell(f_m^{-1}(J_n \cap I_{m,M})) + \ell(f_m^{-1}(J_n \cap I_{m,L})) + \ell(f_m^{-1}(J_n \cap I_{m,R}))\\ &\geq C \cdot \ell(J_n \cap I_{m,M}) + \ell(J_n \cap I_{m,L}) + \ell(J_n \cap I_{m,R})\\ &= C \left(\ell(J_n) - \ell(J_n \cap I_{m,L}) - \ell(J_n \cap I_{m,R})\right) + \ell(J_n \cap I_{m,L}) + \ell(J_n \cap I_{m,R}),\\[-15pt] \end{align*} $$
$$ \begin{align*} \ell(J_{n+1}) &= \ell(f_m^{-1}(J_n \cap I_{m,M})) + \ell(f_m^{-1}(J_n \cap I_{m,L})) + \ell(f_m^{-1}(J_n \cap I_{m,R}))\\ &\geq C \cdot \ell(J_n \cap I_{m,M}) + \ell(J_n \cap I_{m,L}) + \ell(J_n \cap I_{m,R})\\ &= C \left(\ell(J_n) - \ell(J_n \cap I_{m,L}) - \ell(J_n \cap I_{m,R})\right) + \ell(J_n \cap I_{m,L}) + \ell(J_n \cap I_{m,R}),\\[-15pt] \end{align*} $$where we have used that  ${f_m^{-1}}'(x) \geq 1$ for
${f_m^{-1}}'(x) \geq 1$ for ![]() $x \in I_m$. Because
$x \in I_m$. Because ![]() $\ell (J_n \cap I_{m,L}) + \ell (J_n \cap I_{m,R}) \leq \epsilon /2$, this is again at least equal to
$\ell (J_n \cap I_{m,L}) + \ell (J_n \cap I_{m,R}) \leq \epsilon /2$, this is again at least equal to
It follows that there is an index n such that ![]() $J_n$ is not totally contained inside
$J_n$ is not totally contained inside ![]() $I_m$ for any index m. This means that there is an m such that
$I_m$ for any index m. This means that there is an m such that ![]() $J_n$ contains at least one of the endpoints of
$J_n$ contains at least one of the endpoints of ![]() $I_m$. Without loss of generality, we can assume that
$I_m$. Without loss of generality, we can assume that ![]() $J_n$ contains the left endpoint of
$J_n$ contains the left endpoint of ![]() $I_m$. It follows that there is an
$I_m$. It follows that there is an ![]() $a> 0$ such that
$a> 0$ such that ![]() $f_m([0,a]) \subset J_n$ and thus there is a sequence
$f_m([0,a]) \subset J_n$ and thus there is a sequence ![]() $m_1, \dots , m_n$ such that
$m_1, \dots , m_n$ such that ![]() $(f_{m_1} \circ \cdots \circ f_{m_n} \circ f_m)([0,a]) \subset J$. We complete the proof by showing that for at least one of the maps
$(f_{m_1} \circ \cdots \circ f_{m_n} \circ f_m)([0,a]) \subset J$. We complete the proof by showing that for at least one of the maps ![]() $f_i$ there is an index
$f_i$ there is an index ![]() $N_a$ for any
$N_a$ for any ![]() $a> 0$ such that
$a> 0$ such that  $f_i^{N_a}([0,1]) \subset [0,a]$.
$f_i^{N_a}([0,1]) \subset [0,a]$.
Observe that there must be at least one map ![]() $f_i$ such that
$f_i$ such that ![]() $f_i(0) = 0$. We obtain an inclusion of intervals
$f_i(0) = 0$. We obtain an inclusion of intervals  $[0,1] \supset f_i([0,1]) \supset f_i^2([0,1]) \supset \cdots $, where
$[0,1] \supset f_i([0,1]) \supset f_i^2([0,1]) \supset \cdots $, where  $f_i^N([0,1]) = [0, f_i^N(1)]$. This shows that the sequence
$f_i^N([0,1]) = [0, f_i^N(1)]$. This shows that the sequence  $\{f_i^N(1)\}_{N \geq 0}$ is decreasing and thus has a limit L. If
$\{f_i^N(1)\}_{N \geq 0}$ is decreasing and thus has a limit L. If ![]() $L \neq 0$, we would have
$L \neq 0$, we would have ![]() $f_i([0,L]) = [0,L]$, which contradicts the fact that
$f_i([0,L]) = [0,L]$, which contradicts the fact that ![]() $f_i'(x) < 1$ for all
$f_i'(x) < 1$ for all ![]() $x \in (0,L)$, so
$x \in (0,L)$, so ![]() $L = 0$. This concludes the proof.
$L = 0$. This concludes the proof.
Corollary 20. Let ![]() $A \subset \mathbb {S}$ be a closed circular arc and let
$A \subset \mathbb {S}$ be a closed circular arc and let ![]() $f_1, \dots , f_k$ be orientation-preserving continuously differentiable maps from A, such that
$f_1, \dots , f_k$ be orientation-preserving continuously differentiable maps from A, such that  $\bigcup _{m=1}^k {f_m \left (A\right )} = A$ and
$\bigcup _{m=1}^k {f_m \left (A\right )} = A$ and ![]() $0 < |f_m'(x)| < 1$ for each index m and
$0 < |f_m'(x)| < 1$ for each index m and ![]() $x \in A$ not equal to either of the endpoints of A.
$x \in A$ not equal to either of the endpoints of A.
Then for any open circular arc ![]() $J \subseteq A$ there is a sequence of indices
$J \subseteq A$ there is a sequence of indices ![]() $m_1, \dots , m_N$ such that
$m_1, \dots , m_N$ such that
4.2 Exploiting the dependence of derivatives on the degrees
In this section, we show a few key lemmas that demonstrate how we employ the contracting maps that cover idea, by exploiting the dependence of derivatives on the degrees.
Lemma 21. Let ![]() $k \in \mathbb {Z}_{\geq 1}$ and
$k \in \mathbb {Z}_{\geq 1}$ and  $b \in \big [\frac {k}{k+2},1\big )$. Let
$b \in \big [\frac {k}{k+2},1\big )$. Let ![]() $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _{k+1}},\lambda _{k+1}]}$ with
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _{k+1}},\lambda _{k+1}]}$ with ![]() $\xi \neq 1$ be such that
$\xi \neq 1$ be such that ![]() $|f_{2k+1}'(R_k(\xi ))| \geq 1$. Then there is an arc A of
$|f_{2k+1}'(R_k(\xi ))| \geq 1$. Then there is an arc A of ![]() $\mathbb {S}$ such that the orbit of
$\mathbb {S}$ such that the orbit of ![]() $1$ under the action of the semigroup generated by
$1$ under the action of the semigroup generated by ![]() $f_{\xi ,k+1}$ and
$f_{\xi ,k+1}$ and ![]() $f_{\xi ,k}$ is dense in A.
$f_{\xi ,k}$ is dense in A.
Proof. We can assume that ![]() $\xi $ lies in the upper half-plane. Since all maps in this argument use the parameter
$\xi $ lies in the upper half-plane. Since all maps in this argument use the parameter ![]() $\xi $, we will write
$\xi $, we will write ![]() $f_{m}$ instead of
$f_{m}$ instead of ![]() $f_{\xi ,m}$ for all m. Define the arc
$f_{\xi ,m}$ for all m. Define the arc ![]() $A = \operatorname {\mathrm {Arc}}{[R_{k}(\xi ), R_{k+1}(\xi )]}$. Using equation (2), we find that for every m,
$A = \operatorname {\mathrm {Arc}}{[R_{k}(\xi ), R_{k+1}(\xi )]}$. Using equation (2), we find that for every m,
 $$ \begin{align*} |f_m'(R_{k}(\xi))| = \frac{m}{2k + 1} \cdot |f_{2k+1}'(R_{k}(\xi))| \geq \frac{m}{2k + 1}. \end{align*} $$
$$ \begin{align*} |f_m'(R_{k}(\xi))| = \frac{m}{2k + 1} \cdot |f_{2k+1}'(R_{k}(\xi))| \geq \frac{m}{2k + 1}. \end{align*} $$By using the fact that ![]() $R_{k+1}(\xi )$ is either a parabolic or an attracting fixed point of
$R_{k+1}(\xi )$ is either a parabolic or an attracting fixed point of ![]() $f_{k+1}$, we deduce that for all
$f_{k+1}$, we deduce that for all ![]() $z \in A$,
$z \in A$,
where the second inequality is strict when ![]() $z \neq R_{k+1}(\xi )$. It follows that for all
$z \neq R_{k+1}(\xi )$. It follows that for all ![]() $z \in A$ not equal to
$z \in A$ not equal to ![]() $R_{k+1}(\xi )$ we have
$R_{k+1}(\xi )$ we have ![]() $k/(2k+1) \leq |f_{k}'(z)| < 1$ and
$k/(2k+1) \leq |f_{k}'(z)| < 1$ and ![]() $(k+1)/(2k+1) \leq |f_{k+1}'(z)| < 1$. Therefore,
$(k+1)/(2k+1) \leq |f_{k+1}'(z)| < 1$. Therefore,
 $$ \begin{align*} \ell(A)> \ell(f_{k}(A)) > \frac{k}{2k+1}\ell(A) \quad\text{ and }\quad \ell(A) > \ell(f_{k+1}(A)) > \frac{k+1}{2k+1}\ell(A). \end{align*} $$
$$ \begin{align*} \ell(A)> \ell(f_{k}(A)) > \frac{k}{2k+1}\ell(A) \quad\text{ and }\quad \ell(A) > \ell(f_{k+1}(A)) > \frac{k+1}{2k+1}\ell(A). \end{align*} $$From this we deduce that ![]() $\ell (f_{k}(A)) + \ell (f_{k+1}(A))> \ell (A)$. Thus, because
$\ell (f_{k}(A)) + \ell (f_{k+1}(A))> \ell (A)$. Thus, because ![]() $f_{k}(A)$ is of the form
$f_{k}(A)$ is of the form ![]() $\operatorname {\mathrm {Arc}}{[R_{k}(\xi ), a]}$ and
$\operatorname {\mathrm {Arc}}{[R_{k}(\xi ), a]}$ and ![]() $f_{k+1}(A)$ is of the form
$f_{k+1}(A)$ is of the form ![]() $\operatorname {\mathrm {Arc}}{[b, R_{k+1}(\xi )]}$ for some
$\operatorname {\mathrm {Arc}}{[b, R_{k+1}(\xi )]}$ for some ![]() $a,b \in A$, we conclude that
$a,b \in A$, we conclude that ![]() $f_{k}(A) \cup f_{k+1}(A) = A$.
$f_{k}(A) \cup f_{k+1}(A) = A$.
It follows from item (iv) of Lemma 10 that there is some M such that  $f_{k+1}^M(1) \in A$. Let
$f_{k+1}^M(1) \in A$. Let ![]() $J \subseteq A$ be any open arc. According to Corollary 20, there is a sequence of indices
$J \subseteq A$ be any open arc. According to Corollary 20, there is a sequence of indices ![]() $m_1,\dots , m_N\in \{k,k+1\}$ such that
$m_1,\dots , m_N\in \{k,k+1\}$ such that  $\left (f_{m_1} \circ \cdots \circ f_{m_N} \circ f_{k+1}^M\right ){\left (1\right )} \in J$. The fact that J was chosen as an arbitrary open arc in A concludes the proof.
$\left (f_{m_1} \circ \cdots \circ f_{m_N} \circ f_{k+1}^M\right ){\left (1\right )} \in J$. The fact that J was chosen as an arbitrary open arc in A concludes the proof.
Lemma 22. Let ![]() $k \in \mathbb {Z}_{\geq 1}$ and
$k \in \mathbb {Z}_{\geq 1}$ and  $b \in \big [\frac {k-1}{k+1},1\big )$. Let
$b \in \big [\frac {k-1}{k+1},1\big )$. Let ![]() $\xi _1, \xi _2 \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _k},\lambda _k]}$ such that
$\xi _1, \xi _2 \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _k},\lambda _k]}$ such that ![]() $\xi _1, \xi _2$ are distinct and lie in the same half-plane; that is, both in the upper or lower half-plane and such that
$\xi _1, \xi _2$ are distinct and lie in the same half-plane; that is, both in the upper or lower half-plane and such that ![]() $|f_{2k}'(R_k(\xi _i))| \geq 1$ for
$|f_{2k}'(R_k(\xi _i))| \geq 1$ for ![]() $i \in \{1,2\}$. Then there is an arc A of
$i \in \{1,2\}$. Then there is an arc A of ![]() $\mathbb {S}$ such that the orbit of
$\mathbb {S}$ such that the orbit of ![]() $1$ under the action of the semigroup generated by
$1$ under the action of the semigroup generated by ![]() $f_{\xi _1,k}$ and
$f_{\xi _1,k}$ and ![]() $f_{\xi _2,k}$ is dense in A.
$f_{\xi _2,k}$ is dense in A.
Proof. We can assume that ![]() $\xi _1$ and
$\xi _1$ and ![]() $\xi _2$ lie in the upper half-plane and that
$\xi _2$ lie in the upper half-plane and that ![]() $\text {Arg}(\xi _1) < \text {Arg}(\xi _2)$. Let
$\text {Arg}(\xi _1) < \text {Arg}(\xi _2)$. Let ![]() $A = \operatorname {\mathrm {Arc}}{[R_k(\xi _1),R_k(\xi _2)]}$; then for all
$A = \operatorname {\mathrm {Arc}}{[R_k(\xi _1),R_k(\xi _2)]}$; then for all ![]() $z \in A$ we have
$z \in A$ we have
 $$ \begin{align*} \frac{1}{2} \leq \frac{1}{2}\cdot \left|f_{2k}'(R_k(\xi_1))\right| = \left|f_{k}'(R_k(\xi_1))\right| \leq \left|f_{k}'(z)\right| \leq \left|f_{k}'(R_k(\xi_2))\right| \leq 1, \end{align*} $$
$$ \begin{align*} \frac{1}{2} \leq \frac{1}{2}\cdot \left|f_{2k}'(R_k(\xi_1))\right| = \left|f_{k}'(R_k(\xi_1))\right| \leq \left|f_{k}'(z)\right| \leq \left|f_{k}'(R_k(\xi_2))\right| \leq 1, \end{align*} $$where the second to last inequality is strict when ![]() $z \neq R_{k}(\xi _2)$. Therefore, for
$z \neq R_{k}(\xi _2)$. Therefore, for ![]() $i \in \{1,2\}$ we have
$i \in \{1,2\}$ we have
 $$ \begin{align*} \ell(A)> \ell(f_{\xi_i,k}(A)) > \frac{1}{2} \cdot\ell(A), \end{align*} $$
$$ \begin{align*} \ell(A)> \ell(f_{\xi_i,k}(A)) > \frac{1}{2} \cdot\ell(A), \end{align*} $$and from this we deduce that ![]() $\ell (f_{\xi _1,k}(A)) + \ell (f_{\xi _2,k}(A))> \ell (A)$. The rest of the proof proceeds exactly as the proof of Lemma 21.
$\ell (f_{\xi _1,k}(A)) + \ell (f_{\xi _2,k}(A))> \ell (A)$. The rest of the proof proceeds exactly as the proof of Lemma 21.
Lemma 23. Let ![]() $k \geq 5$,
$k \geq 5$,  $b \in \big (\frac {k-1}{k+1},1\big )$ and
$b \in \big (\frac {k-1}{k+1},1\big )$ and ![]() $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _k},\lambda _k]}$ with
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _k},\lambda _k]}$ with ![]() $\xi \neq 1$ such that there is an integer
$\xi \neq 1$ such that there is an integer ![]() $2k \leq p \leq 3k - 5$ for which
$2k \leq p \leq 3k - 5$ for which ![]() $|f_p'(\xi )| \geq 1$. Then at least one of the following two statements holds:
$|f_p'(\xi )| \geq 1$. Then at least one of the following two statements holds:
(i) The orbit of
 $1$ under the action of the semigroup generated by
$1$ under the action of the semigroup generated by  $f_{\xi ,k-2}, f_{\xi ,k-1}$ and
$f_{\xi ,k-2}, f_{\xi ,k-1}$ and  $f_{\xi ,k}$ is dense in an arc of
$f_{\xi ,k}$ is dense in an arc of  $\mathbb {S}$.
$\mathbb {S}$.(ii) We have
 $|f_k'(R_{k}(\xi ))|> 1-\frac {p-k+2}{p} \cdot \frac {p-2k+1}{k}$.
$|f_k'(R_{k}(\xi ))|> 1-\frac {p-k+2}{p} \cdot \frac {p-2k+1}{k}$.
Proof. W.l.o.g., we may assume that ![]() $\xi $ lies in the upper half plane. We write
$\xi $ lies in the upper half plane. We write ![]() $f_{m} = f_{\xi ,m}$ for all indices m. Define the arcs
$f_{m} = f_{\xi ,m}$ for all indices m. Define the arcs ![]() $A_1 = \operatorname {\mathrm {Arc}}{[R_{k-2}(\xi ),R_{k-1}(\xi )]}$ and
$A_1 = \operatorname {\mathrm {Arc}}{[R_{k-2}(\xi ),R_{k-1}(\xi )]}$ and ![]() $A_2 = \operatorname {\mathrm {Arc}}{[R_{k-1}(\xi ),R_{k}(\xi )]}$. Analogous to the proofs of Lemmas 21 and 22, we can use Corollary 20 to show that the orbit of
$A_2 = \operatorname {\mathrm {Arc}}{[R_{k-1}(\xi ),R_{k}(\xi )]}$. Analogous to the proofs of Lemmas 21 and 22, we can use Corollary 20 to show that the orbit of ![]() $1$ under the action of the semigroup generated by
$1$ under the action of the semigroup generated by ![]() $f_{k-2}, f_{k-1}$ and
$f_{k-2}, f_{k-1}$ and ![]() $f_{k}$ is dense in
$f_{k}$ is dense in ![]() $A_1 \cup A_2$ if
$A_1 \cup A_2$ if
We will assume that this is not the case and show that this leads to statement (ii). First, we will show that the left-hand side of equation (8) does cover ![]() $A_1$. For any arc A in the upper half-plane such that
$A_1$. For any arc A in the upper half-plane such that ![]() $\text {Arg}{(x)} \geq \text {Arg}{(\xi )}$ for all
$\text {Arg}{(x)} \geq \text {Arg}{(\xi )}$ for all ![]() $x \in A$ and index m, we have
$x \in A$ and index m, we have
 $$ \begin{align} \ell{\left(f_m(A)\right)}> |f_m'(\xi)| \cdot \ell{\left(A\right)} = \frac{m\cdot |f_p'(\xi)|}{p} \cdot \ell{\left(A\right)} \geq \frac{m}{p} \cdot \ell{\left(A\right)}. \end{align} $$
$$ \begin{align} \ell{\left(f_m(A)\right)}> |f_m'(\xi)| \cdot \ell{\left(A\right)} = \frac{m\cdot |f_p'(\xi)|}{p} \cdot \ell{\left(A\right)} \geq \frac{m}{p} \cdot \ell{\left(A\right)}. \end{align} $$We use this and the fact that ![]() $\ell {\left (A_2\right )} \geq \ell {\left (A_1\right )}$, which follows from item (v) of Lemma 10, to conclude the following:
$\ell {\left (A_2\right )} \geq \ell {\left (A_1\right )}$, which follows from item (v) of Lemma 10, to conclude the following:
 $$ \begin{align*} \ell{\left(f_{k-2}(A_1 \cup A_2)\right)} + \ell{\left(f_{k-1}(A_1)\right)} &\geq \frac{k-2}{p} \ell{\left(A_1 \cup A_2\right)} + \frac{k-1}{p} \ell{\left(A_1\right)} \\ &\geq \frac{2(k-2)}{p} \ell{\left(A_1\right)} + \frac{k-1}{p} \ell{\left(A_1\right)} \\ & = \frac{3k - 5}{p} \ell{\left(A_1\right)} \geq \ell{\left(A_1\right)}. \end{align*} $$
$$ \begin{align*} \ell{\left(f_{k-2}(A_1 \cup A_2)\right)} + \ell{\left(f_{k-1}(A_1)\right)} &\geq \frac{k-2}{p} \ell{\left(A_1 \cup A_2\right)} + \frac{k-1}{p} \ell{\left(A_1\right)} \\ &\geq \frac{2(k-2)}{p} \ell{\left(A_1\right)} + \frac{k-1}{p} \ell{\left(A_1\right)} \\ & = \frac{3k - 5}{p} \ell{\left(A_1\right)} \geq \ell{\left(A_1\right)}. \end{align*} $$Because ![]() $f_{k-2}(A_1 \cup A_2)$ is of the form
$f_{k-2}(A_1 \cup A_2)$ is of the form ![]() $\operatorname {\mathrm {Arc}}{[R_{k-2}(\xi ),a]}$ and
$\operatorname {\mathrm {Arc}}{[R_{k-2}(\xi ),a]}$ and ![]() $f_{k-1}(A_1)$ is of the form
$f_{k-1}(A_1)$ is of the form ![]() $\operatorname {\mathrm {Arc}}{[b,R_{k-1}(\xi )]}$, we have that
$\operatorname {\mathrm {Arc}}{[b,R_{k-1}(\xi )]}$, we have that ![]() $A_1$ is covered by
$A_1$ is covered by ![]() $f_{k-2}(A_1 \cup A_2) \cup f_{k-1}(A_1)$. Our assumption can be formulated as
$f_{k-2}(A_1 \cup A_2) \cup f_{k-1}(A_1)$. Our assumption can be formulated as
Note that
 $$ \begin{align*} \ell{\left(f_{k-1}(A_2)\right)} + \ell{\left(f_{k}(A_1 \cup A_2)\right)} \geq \frac{k-1}{p} \ell{\left(A_2\right)} + \frac{k}{p} \left(\ell{\left(A_1\right)} + \ell{\left(A_2\right)}\right). \end{align*} $$
$$ \begin{align*} \ell{\left(f_{k-1}(A_2)\right)} + \ell{\left(f_{k}(A_1 \cup A_2)\right)} \geq \frac{k-1}{p} \ell{\left(A_2\right)} + \frac{k}{p} \left(\ell{\left(A_1\right)} + \ell{\left(A_2\right)}\right). \end{align*} $$Combining the previous two inequalities, we get
 $$ \begin{align} \ell{\left(A_1\right)} \leq \frac{p-2k+1}{k} \cdot \ell{\left(A_2\right)}. \end{align} $$
$$ \begin{align} \ell{\left(A_1\right)} \leq \frac{p-2k+1}{k} \cdot \ell{\left(A_2\right)}. \end{align} $$Let ![]() $A_0 = \operatorname {\mathrm {Arc}}{[1,R_{k-2}(\xi )]}$. By using the fact that
$A_0 = \operatorname {\mathrm {Arc}}{[1,R_{k-2}(\xi )]}$. By using the fact that ![]() $R_m(\xi )$ is a fixed point of
$R_m(\xi )$ is a fixed point of ![]() $f_m$ and
$f_m$ and ![]() $f_m(1) = \xi $ for every m, we see that
$f_m(1) = \xi $ for every m, we see that ![]() $f_{k-2}(A_0) = \operatorname {\mathrm {Arc}}{[\xi , R_{k-2}(\xi )]}$,
$f_{k-2}(A_0) = \operatorname {\mathrm {Arc}}{[\xi , R_{k-2}(\xi )]}$, ![]() $f_{k-1}(A_0 \cup A_1) = \operatorname {\mathrm {Arc}}{[\xi , R_{k-1}(\xi )]}$ and
$f_{k-1}(A_0 \cup A_1) = \operatorname {\mathrm {Arc}}{[\xi , R_{k-1}(\xi )]}$ and ![]() $f_{k}(A_0 \cup A_1 \cup A_2) = \operatorname {\mathrm {Arc}}{[\xi , R_{k}(\xi )]}$. It follows from the relation between the derivative of different maps given in item (i) of Lemma 10 that for any arc A on which
$f_{k}(A_0 \cup A_1 \cup A_2) = \operatorname {\mathrm {Arc}}{[\xi , R_{k}(\xi )]}$. It follows from the relation between the derivative of different maps given in item (i) of Lemma 10 that for any arc A on which ![]() $f_{m_1}$ and
$f_{m_1}$ and ![]() $f_{m_2}$ are injective we have
$f_{m_2}$ are injective we have
 $$ \begin{align*} \ell{\left(f_{m_1}(A)\right)} = m_1 \cdot \ell{\left(f_{1}(A)\right)} = \frac{m_1}{m_2} \cdot \ell{\left(f_{m_2}(A)\right)}. \end{align*} $$
$$ \begin{align*} \ell{\left(f_{m_1}(A)\right)} = m_1 \cdot \ell{\left(f_{1}(A)\right)} = \frac{m_1}{m_2} \cdot \ell{\left(f_{m_2}(A)\right)}. \end{align*} $$These observations can be used to write ![]() $\ell {\left (A_1\right )}$ and
$\ell {\left (A_1\right )}$ and ![]() $\ell {\left (A_2\right )}$ as follows:
$\ell {\left (A_2\right )}$ as follows:
 $$ \begin{align*} \ell{\left(A_1\right)} &= \ell{\left(f_{k-1}(A_0 \cup A_1)\right)} - \ell{\left(f_{k-2}(A_0)\right)}\\ &= \frac{k-2}{k-1}\ell{\left(f_{k-1}(A_0 \cup A_1)\right)} + \frac{1}{k-1}\ell{\left(f_{k-1}(A_0 \cup A_1)\right)} - \frac{k-2}{k-1}\ell{\left(f_{k-1}(A_0)\right)}\\ &= \frac{k-2}{k-1}\ell{\left(f_{k-1}(A_1)\right)} + \frac{1}{k-1}\ell{\left(f_{k-1}(A_0 \cup A_1)\right)} \end{align*} $$
$$ \begin{align*} \ell{\left(A_1\right)} &= \ell{\left(f_{k-1}(A_0 \cup A_1)\right)} - \ell{\left(f_{k-2}(A_0)\right)}\\ &= \frac{k-2}{k-1}\ell{\left(f_{k-1}(A_0 \cup A_1)\right)} + \frac{1}{k-1}\ell{\left(f_{k-1}(A_0 \cup A_1)\right)} - \frac{k-2}{k-1}\ell{\left(f_{k-1}(A_0)\right)}\\ &= \frac{k-2}{k-1}\ell{\left(f_{k-1}(A_1)\right)} + \frac{1}{k-1}\ell{\left(f_{k-1}(A_0 \cup A_1)\right)} \end{align*} $$and
 $$ \begin{align*} \ell{\left(A_2\right)} = \ell{\left(f_{k}(A_0 \cup A_1 \cup A_2)\right)} - \ell{\left(f_{k-1}(A_0 \cup A_1)\right)} = \ell{\left(f_{k}(A_2)\right)} + \frac{1}{k-1} \cdot \ell{\left(f_{k-1}(A_0 \cup A_1)\right)}. \end{align*} $$
$$ \begin{align*} \ell{\left(A_2\right)} = \ell{\left(f_{k}(A_0 \cup A_1 \cup A_2)\right)} - \ell{\left(f_{k-1}(A_0 \cup A_1)\right)} = \ell{\left(f_{k}(A_2)\right)} + \frac{1}{k-1} \cdot \ell{\left(f_{k-1}(A_0 \cup A_1)\right)}. \end{align*} $$By considering our way of writing ![]() $\ell {\left (A_1\right )}$ and the inequalities given in (9) and (10), we obtain the following inequalities:
$\ell {\left (A_1\right )}$ and the inequalities given in (9) and (10), we obtain the following inequalities:
 $$ \begin{align*} \frac{1}{k-1}\cdot\ell{\left(f_{k-1}(A_0 \cup A_1)\right)} &= \ell{\left(A_1\right)} - \frac{k-2}{k-1}\cdot\ell{\left(f_{k-1}(A_1)\right)}< \ell{\left(A_1\right)} - \frac{k-2}{k-1} \cdot \frac{k-1}{p} \ell{\left(A_1\right)} \\ &= \frac{p-k+2}{p} \cdot \ell{\left(A_1\right)}< \frac{p-k+2}{p} \cdot \frac{p-2k+1}{k} \cdot \ell{\left(A_2\right)}. \end{align*} $$
$$ \begin{align*} \frac{1}{k-1}\cdot\ell{\left(f_{k-1}(A_0 \cup A_1)\right)} &= \ell{\left(A_1\right)} - \frac{k-2}{k-1}\cdot\ell{\left(f_{k-1}(A_1)\right)}< \ell{\left(A_1\right)} - \frac{k-2}{k-1} \cdot \frac{k-1}{p} \ell{\left(A_1\right)} \\ &= \frac{p-k+2}{p} \cdot \ell{\left(A_1\right)}< \frac{p-k+2}{p} \cdot \frac{p-2k+1}{k} \cdot \ell{\left(A_2\right)}. \end{align*} $$It follows from the fact that ![]() $\text {Arg}{(R_{k}(\xi ))} \geq \text {Arg}{(x)}$ for all
$\text {Arg}{(R_{k}(\xi ))} \geq \text {Arg}{(x)}$ for all ![]() $x \in A_2$ that
$x \in A_2$ that ![]() $\ell {\left (f_{k}(A_2)\right )} < |f_k'(R_{k}(\xi ))| \cdot \ell {\left (A_2\right )}$. By using this inequality and the previous inequality, we obtain
$\ell {\left (f_{k}(A_2)\right )} < |f_k'(R_{k}(\xi ))| \cdot \ell {\left (A_2\right )}$. By using this inequality and the previous inequality, we obtain
 $$ \begin{align*} \ell{\left(A_2\right)} &= \ell{\left(f_{k}(A_2)\right)} + \frac{1}{k-1} \cdot \ell{\left(f_{k-1}(A_0 \cup A_1)\right)} \\ &< |f_k'(R_{k}(\xi))| \cdot \ell{\left(A_2\right)} + \frac{p-k+2}{p} \cdot \frac{p-2k+1}{k} \cdot \ell{\left(A_2\right)}. \end{align*} $$
$$ \begin{align*} \ell{\left(A_2\right)} &= \ell{\left(f_{k}(A_2)\right)} + \frac{1}{k-1} \cdot \ell{\left(f_{k-1}(A_0 \cup A_1)\right)} \\ &< |f_k'(R_{k}(\xi))| \cdot \ell{\left(A_2\right)} + \frac{p-k+2}{p} \cdot \frac{p-2k+1}{k} \cdot \ell{\left(A_2\right)}. \end{align*} $$We can cancel ![]() $\ell {\left (A_2\right )}$ and rewrite to obtain
$\ell {\left (A_2\right )}$ and rewrite to obtain
 $$ \begin{align*} |f_k'(R_{k}(\xi))|> 1-\frac{p-k+2}{p} \cdot \frac{p-2k+1}{k}, \end{align*} $$
$$ \begin{align*} |f_k'(R_{k}(\xi))|> 1-\frac{p-k+2}{p} \cdot \frac{p-2k+1}{k}, \end{align*} $$which is what we set out to prove.
Corollary 24. Let m be a positive integer,  $b \in \big (\frac {m-1}{m+1},1\big )$ and
$b \in \big (\frac {m-1}{m+1},1\big )$ and ![]() $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _m},\lambda _m]}$ with
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _m},\lambda _m]}$ with ![]() $\xi \neq 1$ such that either of the following holds:
$\xi \neq 1$ such that either of the following holds:
(a)
 $m \geq 8$ and
$m \geq 8$ and  $|f_{2m}'(\xi )| \geq 1$;
$|f_{2m}'(\xi )| \geq 1$;(b)
 $m \geq 9$ and
$m \geq 9$ and  $|f_{2m+1}'(\xi )| \geq 1$.
$|f_{2m+1}'(\xi )| \geq 1$.
Then the orbit of ![]() $1$ under the action of the semigroup generated by
$1$ under the action of the semigroup generated by ![]() $f_{\xi ,m-3},f_{\xi ,m-2},f_{\xi ,m-1}$ and
$f_{\xi ,m-3},f_{\xi ,m-2},f_{\xi ,m-1}$ and ![]() $f_{\xi ,m}$ is dense in an arc of
$f_{\xi ,m}$ is dense in an arc of ![]() $\mathbb {S}$.
$\mathbb {S}$.
Proof. We will again assume that ![]() $\xi $ lies in the upper half-plane. We apply Lemma 23 with
$\xi $ lies in the upper half-plane. We apply Lemma 23 with ![]() $k = m-1$ and
$k = m-1$ and ![]() $p = 2m$ for item (a) and
$p = 2m$ for item (a) and ![]() $p = 2m + 1$ for item (b). If the first statement of that lemma holds, we see that orbit of
$p = 2m + 1$ for item (b). If the first statement of that lemma holds, we see that orbit of ![]() $1$ under the action of
$1$ under the action of ![]() $f_{m-3},f_{m-2}$ and
$f_{m-3},f_{m-2}$ and ![]() $f_{m-1}$ generates an arc, in which case we are done. If we assume that the second statement holds, we obtain
$f_{m-1}$ generates an arc, in which case we are done. If we assume that the second statement holds, we obtain
 $$ \begin{align*} f_{m-1}'(R_{m-1}(\xi))> 1-\frac{2m-(m-1)+2}{2m} \cdot \frac{2m-2(m-1)+1}{m-1} > \frac{1}{2} \end{align*} $$
$$ \begin{align*} f_{m-1}'(R_{m-1}(\xi))> 1-\frac{2m-(m-1)+2}{2m} \cdot \frac{2m-2(m-1)+1}{m-1} > \frac{1}{2} \end{align*} $$in the case where ![]() $p = 2m$ and
$p = 2m$ and
 $$ \begin{align*} f_{m-1}'(R_{m-1}(\xi))> 1-\frac{2m+1-(m-1)+2}{2m+1} \cdot \frac{2m+1-2(m-1)+1}{m-1} > \frac{1}{2} \end{align*} $$
$$ \begin{align*} f_{m-1}'(R_{m-1}(\xi))> 1-\frac{2m+1-(m-1)+2}{2m+1} \cdot \frac{2m+1-2(m-1)+1}{m-1} > \frac{1}{2} \end{align*} $$in the case where ![]() $p = 2m+1$. It follows that for
$p = 2m+1$. It follows that for ![]() $x \in \operatorname {\mathrm {Arc}}{[R_{k-1}(\xi ),R_{k}(\xi )]}$, we obtain
$x \in \operatorname {\mathrm {Arc}}{[R_{k-1}(\xi ),R_{k}(\xi )]}$, we obtain ![]() $1>|f_{m}'(x)| > |f_{m-1}'(x)| > 1/2$. Therefore, with
$1>|f_{m}'(x)| > |f_{m-1}'(x)| > 1/2$. Therefore, with ![]() $A = \operatorname {\mathrm {Arc}}{[R_{k-1}(\xi ),R_{k}(\xi )]}$, we get
$A = \operatorname {\mathrm {Arc}}{[R_{k-1}(\xi ),R_{k}(\xi )]}$, we get
This, together with Corollary 20, implies that the orbit of ![]() $1$ under the action of the semigroup generated by
$1$ under the action of the semigroup generated by ![]() $f_{m-1}$ and
$f_{m-1}$ and ![]() $f_{m}$ is dense in A.
$f_{m}$ is dense in A.
5 Proof of Lemma 17 for Some Special Cases
The arguments of this section will be used to cover some leftover cases in the proof of Lemma 17 that are not directly covered by the results of the previous section.
5.1 Proof of Lemma 17 for powers of 2
The following lemma will be used in the proof of Lemma 17 for those values of k for which either k or ![]() $k+1$ is a power of 2; see the proof in Section 6 for details.
$k+1$ is a power of 2; see the proof in Section 6 for details.
Lemma 25. Let ![]() $d\geq 2,k\geq 0$ be integers,
$d\geq 2,k\geq 0$ be integers,  $b \in \big (0,\frac {d-1}{d+1}\big ]\cap \mathbb {Q}$,
$b \in \big (0,\frac {d-1}{d+1}\big ]\cap \mathbb {Q}$, ![]() $\lambda \in \mathbb {S}_{\mathbb {Q}}\setminus \{\pm 1\}$ and
$\lambda \in \mathbb {S}_{\mathbb {Q}}\setminus \{\pm 1\}$ and ![]() $\xi \in \Lambda _{2^k}(b)\cap \mathbb {S}_{\mathbb {Q}}$ with
$\xi \in \Lambda _{2^k}(b)\cap \mathbb {S}_{\mathbb {Q}}$ with ![]() $\xi \neq \pm 1$. Suppose there is a tree in
$\xi \neq \pm 1$. Suppose there is a tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-(2^{k+1}-1)$ that implements the field
$d-(2^{k+1}-1)$ that implements the field ![]() $\xi $. Then the set of fields implemented by rooted trees in
$\xi $. Then the set of fields implemented by rooted trees in ![]() $\mathcal {T}_{d+1}$ is dense in
$\mathcal {T}_{d+1}$ is dense in ![]() $\mathbb {S}$.
$\mathbb {S}$.
Proof. We will prove this by induction on k. For ![]() $k=0$, the field
$k=0$, the field ![]() $\xi $ has to lie in
$\xi $ has to lie in ![]() $\operatorname {\mathrm {Arc}}(\lambda _1,\overline {\lambda _1})\setminus \{-1\}$ and the root degree of the tree in
$\operatorname {\mathrm {Arc}}(\lambda _1,\overline {\lambda _1})\setminus \{-1\}$ and the root degree of the tree in ![]() $\mathcal {T}_{d+1}$ implementing
$\mathcal {T}_{d+1}$ implementing ![]() $\xi $ is at most
$\xi $ is at most ![]() $d-1$. From Corollary 13 and Lemma 14, we have that
$d-1$. From Corollary 13 and Lemma 14, we have that ![]() $f_{\xi ,1}$ is conjugate to an irrational rotation and thus the orbit of any initial point
$f_{\xi ,1}$ is conjugate to an irrational rotation and thus the orbit of any initial point ![]() $z_0\in \mathbb {S}$ is dense in
$z_0\in \mathbb {S}$ is dense in ![]() $\mathbb {S}$. By Lemma 4, every element of the set
$\mathbb {S}$. By Lemma 4, every element of the set  $\{f_{\xi ,1}^n(\lambda )\}_{n \geq 1}$ is the field implemented by a tree in
$\{f_{\xi ,1}^n(\lambda )\}_{n \geq 1}$ is the field implemented by a tree in ![]() $\mathcal {T}_{d+1}$ and hence we obtain the theorem for
$\mathcal {T}_{d+1}$ and hence we obtain the theorem for ![]() $k=0$.
$k=0$.
Now suppose that ![]() $k \geq 1$ and that we have proved the statement for
$k \geq 1$ and that we have proved the statement for ![]() $k-1$. If
$k-1$. If ![]() $b < (2^{k-1}-1)/(2^{k-1}+1)$, then we must have
$b < (2^{k-1}-1)/(2^{k-1}+1)$, then we must have ![]() $k>1$, and by Lemma 8 we can immediately apply the induction hypothesis with
$k>1$, and by Lemma 8 we can immediately apply the induction hypothesis with ![]() $\xi =\lambda $ and tree consisting of a single vertex. So, assume that
$\xi =\lambda $ and tree consisting of a single vertex. So, assume that ![]() $b \geq (2^{k-1}-1)/(2^{k-1}+1)$ and observe that the parameter
$b \geq (2^{k-1}-1)/(2^{k-1}+1)$ and observe that the parameter ![]() $\lambda _{2^{k-1}}\in \mathbb {S}$ from Lemma 10 exists. It follows from Lemma 16 that there is
$\lambda _{2^{k-1}}\in \mathbb {S}$ from Lemma 10 exists. It follows from Lemma 16 that there is ![]() $\sigma \in \mathbb {S}$ with
$\sigma \in \mathbb {S}$ with ![]() $|f_{2^k}'(\sigma )|> 1$ and a set
$|f_{2^k}'(\sigma )|> 1$ and a set ![]() $\mathcal {R}= \{\zeta _n\}_{n \geq 1}$ accumulating on
$\mathcal {R}= \{\zeta _n\}_{n \geq 1}$ accumulating on ![]() $\sigma $ such that each
$\sigma $ such that each ![]() $\zeta _n$ is implemented by a tree in
$\zeta _n$ is implemented by a tree in ![]() $\mathcal {T}_{d+1}$ whose root degree is at most
$\mathcal {T}_{d+1}$ whose root degree is at most ![]() $d - (2^{k+1} - 1) + 2^k = d-(2^{k} - 1)$. If
$d - (2^{k+1} - 1) + 2^k = d-(2^{k} - 1)$. If ![]() $\mathcal {R}$ has a nonempty intersection with
$\mathcal {R}$ has a nonempty intersection with ![]() $\operatorname {\mathrm {Arc}}{(\lambda _{2^{k-1}},\overline {\lambda _{2^{k-1}}})}\setminus \{-1\}$, we can apply the induction hypothesis to the tree corresponding to the field in this intersection. Therefore, we assume that the elements of
$\operatorname {\mathrm {Arc}}{(\lambda _{2^{k-1}},\overline {\lambda _{2^{k-1}}})}\setminus \{-1\}$, we can apply the induction hypothesis to the tree corresponding to the field in this intersection. Therefore, we assume that the elements of ![]() $\mathcal {R}$ accumulate on
$\mathcal {R}$ accumulate on ![]() $\sigma $ from inside
$\sigma $ from inside ![]() $\operatorname {\mathrm {Arc}}{[\overline {\lambda _{2^{k-1}}},\lambda _{2^{k-1}}]}$. It follows that we can find two distinct elements
$\operatorname {\mathrm {Arc}}{[\overline {\lambda _{2^{k-1}}},\lambda _{2^{k-1}}]}$. It follows that we can find two distinct elements ![]() $r_1,r_2 \in \mathcal {R}$ such that they both lie in either
$r_1,r_2 \in \mathcal {R}$ such that they both lie in either ![]() $\operatorname {\mathrm {Arc}}{(\overline {\lambda _{2^{k-1}}},1)}$ or
$\operatorname {\mathrm {Arc}}{(\overline {\lambda _{2^{k-1}}},1)}$ or ![]() $\operatorname {\mathrm {Arc}}{(1,\lambda _{2^{k-1}})}$ and such that
$\operatorname {\mathrm {Arc}}{(1,\lambda _{2^{k-1}})}$ and such that ![]() $|f_{2^k}'(r_i)|>1$ for
$|f_{2^k}'(r_i)|>1$ for ![]() $i =1,2$. By Remark 11, we have
$i =1,2$. By Remark 11, we have ![]() $|f_{2^k}'(R_{2^{k-1}}(r_i))|>|f_{2^k}'(r_i)|>1$ and thus we can apply Lemma 22 to conclude that the following set is dense in an arc A of the circle:
$|f_{2^k}'(R_{2^{k-1}}(r_i))|>|f_{2^k}'(r_i)|>1$ and thus we can apply Lemma 22 to conclude that the following set is dense in an arc A of the circle:
 $$ \begin{align*} \mathcal{A} = \left\{ (f_{r_{i_1},2^{k-1}} \circ \cdots \circ f_{r_{i_n},2^{k-1}})(1) : n\in \mathbb{Z}_{\geq 1} \text{ and } i_1, \dots, i_n \in \{1,2\} \right\}. \end{align*} $$
$$ \begin{align*} \mathcal{A} = \left\{ (f_{r_{i_1},2^{k-1}} \circ \cdots \circ f_{r_{i_n},2^{k-1}})(1) : n\in \mathbb{Z}_{\geq 1} \text{ and } i_1, \dots, i_n \in \{1,2\} \right\}. \end{align*} $$Since ![]() $r_1,r_2$ are implemented by trees in
$r_1,r_2$ are implemented by trees in ![]() $\mathcal {T}_{d+1}$ whose root degrees are at most
$\mathcal {T}_{d+1}$ whose root degrees are at most ![]() $d - (2^{k+1} - 1) + 2^k = d-(2^{k} - 1)$, by Lemma 4, every element of
$d - (2^{k+1} - 1) + 2^k = d-(2^{k} - 1)$, by Lemma 4, every element of ![]() $\mathcal {A}$ is implemented by a tree in
$\mathcal {A}$ is implemented by a tree in ![]() $\mathcal {T}_{d+1}$ whose root degree is bounded by
$\mathcal {T}_{d+1}$ whose root degree is bounded by ![]() $d-(2^{k} - 1)+ 2^{k-1} = d - (2^{k-1} -1 ) \leq d$. We have seen that (2) implies that for
$d-(2^{k} - 1)+ 2^{k-1} = d - (2^{k-1} -1 ) \leq d$. We have seen that (2) implies that for ![]() $b \leq (d-1)/(d+1)$ it holds that
$b \leq (d-1)/(d+1)$ it holds that ![]() $|f_d'(z)|> 1$ for all
$|f_d'(z)|> 1$ for all ![]() $z \in \mathbb {S}\setminus \{1\}$. This implies that there is some
$z \in \mathbb {S}\setminus \{1\}$. This implies that there is some ![]() $N \in \mathbb {Z}_{\geq 1}$ such that
$N \in \mathbb {Z}_{\geq 1}$ such that  $f_d^N(A) = \mathbb {S}$. It follows that the set
$f_d^N(A) = \mathbb {S}$. It follows that the set  $\{f_{\lambda ,d}^N(a): a \in \mathcal {A}\}$ is dense in
$\{f_{\lambda ,d}^N(a): a \in \mathcal {A}\}$ is dense in ![]() $\mathbb {S}$, finishing the proof, since every element of this set corresponds to the field of a tree in
$\mathbb {S}$, finishing the proof, since every element of this set corresponds to the field of a tree in ![]() $\mathcal {T}_{d+1}$ (again using Lemma 4).
$\mathcal {T}_{d+1}$ (again using Lemma 4).
5.2 Proof of Lemma 17 for small cases
In this section, we give the main lemma needed to cover certain small cases of Lemma 17. Interestingly, the proof uses a Cantor-style construction, explained in detail in the next subsection.
5.2.1 Near-arithmetic progressions
Let ![]() $\alpha \in (0,1)$ and define the maps from the unit interval to itself given by
$\alpha \in (0,1)$ and define the maps from the unit interval to itself given by ![]() $\phi _0(x) = \alpha x$ and
$\phi _0(x) = \alpha x$ and ![]() $\phi _1(x) = \alpha x + (1-\alpha )$. Let
$\phi _1(x) = \alpha x + (1-\alpha )$. Let ![]() $\Omega = \cup _{n=0}^\infty \{0,1\}^n$ be the set of finite binary sequences. For
$\Omega = \cup _{n=0}^\infty \{0,1\}^n$ be the set of finite binary sequences. For ![]() $\omega \in \Omega $ we let
$\omega \in \Omega $ we let ![]() $|\omega |$ denote the length of
$|\omega |$ denote the length of ![]() $\omega $ and for
$\omega $ and for ![]() $\omega _1, \omega _2 \in \Omega $ we let
$\omega _1, \omega _2 \in \Omega $ we let ![]() $\omega _1 \oplus \omega _2 \in \Omega $ denote the concatenation of the two sequences. For
$\omega _1 \oplus \omega _2 \in \Omega $ denote the concatenation of the two sequences. For ![]() $\omega \in \Omega $ of the form
$\omega \in \Omega $ of the form ![]() $(\omega ^1, \dots ,\omega ^n)$ and two maps
$(\omega ^1, \dots ,\omega ^n)$ and two maps ![]() $f_0, f_1$, we let
$f_0, f_1$, we let ![]() $f_\omega = f_{\omega ^1} \circ \cdots \circ f_{\omega ^n}$ and if
$f_\omega = f_{\omega ^1} \circ \cdots \circ f_{\omega ^n}$ and if ![]() $|\omega | = 0$ we let
$|\omega | = 0$ we let ![]() $f_\omega $ denote the identity map. The properties of the semigroup generated by
$f_\omega $ denote the identity map. The properties of the semigroup generated by ![]() $\phi _0$ and
$\phi _0$ and ![]() $\phi _1$ for certain parameters
$\phi _1$ for certain parameters ![]() $\alpha $ have been studied extensively. For
$\alpha $ have been studied extensively. For  $\alpha \in (0,\frac {1}{2})$, the set
$\alpha \in (0,\frac {1}{2})$, the set
 $$ \begin{align*} \mathcal{C}_\alpha = \bigcap_{n=0}^\infty \bigcup_{\substack{\omega \in \Omega\\|\omega| = n}} \phi_{\omega}([0,1]) \end{align*} $$
$$ \begin{align*} \mathcal{C}_\alpha = \bigcap_{n=0}^\infty \bigcup_{\substack{\omega \in \Omega\\|\omega| = n}} \phi_{\omega}([0,1]) \end{align*} $$is a Cantor set, with ![]() $\mathcal {C}_{1/3}$ being the Cantor ternary set. We will not use the properties of Cantor sets, so we do not define them. First we state some easy-to-prove properties of this semigroup to describe a construction that will help us to prove Lemma 17 for small cases of k.
$\mathcal {C}_{1/3}$ being the Cantor ternary set. We will not use the properties of Cantor sets, so we do not define them. First we state some easy-to-prove properties of this semigroup to describe a construction that will help us to prove Lemma 17 for small cases of k.
Lemma 26. Let ![]() $\omega \in \Omega $ and
$\omega \in \Omega $ and ![]() $\alpha \in (0,1)$. Then
$\alpha \in (0,1)$. Then ![]() $\phi _\omega ([0,1])$ is an interval of length
$\phi _\omega ([0,1])$ is an interval of length ![]() $\alpha ^{|\omega |}$ and, furthermore, the intervals
$\alpha ^{|\omega |}$ and, furthermore, the intervals ![]() $\phi _{\omega \oplus (0)}([0,1])$ and
$\phi _{\omega \oplus (0)}([0,1])$ and ![]() $\phi _{\omega \oplus (1)}([0,1])$ are subintervals of
$\phi _{\omega \oplus (1)}([0,1])$ are subintervals of ![]() $\phi _\omega ([0,1])$ sharing the left and right boundaries, respectively.
$\phi _\omega ([0,1])$ sharing the left and right boundaries, respectively.
Proof. Because the derivative of ![]() $\phi _i$ is constantly equal to
$\phi _i$ is constantly equal to ![]() $\alpha $ for
$\alpha $ for ![]() $i = 1,2$, it follows that the length of
$i = 1,2$, it follows that the length of ![]() $\phi _\omega ([0,1])$ is
$\phi _\omega ([0,1])$ is ![]() $\alpha ^{|\omega |}$. The maps
$\alpha ^{|\omega |}$. The maps ![]() $\phi _i$ are increasing and thus we can write
$\phi _i$ are increasing and thus we can write ![]() $\phi _\omega ([0,1]) = [\phi _\omega (0),\phi _\omega (1)]$ and also
$\phi _\omega ([0,1]) = [\phi _\omega (0),\phi _\omega (1)]$ and also ![]() $\phi _{\omega \oplus (0)}([0,1])= [\phi _{\omega \oplus (0)}(0),\phi _{\omega \oplus (0)}(1)]=[\phi _{\omega }(0),\phi _{\omega \oplus (0)}(1)]$. Therefore, the left boundaries of
$\phi _{\omega \oplus (0)}([0,1])= [\phi _{\omega \oplus (0)}(0),\phi _{\omega \oplus (0)}(1)]=[\phi _{\omega }(0),\phi _{\omega \oplus (0)}(1)]$. Therefore, the left boundaries of ![]() $\phi _\omega ([0,1])$ and
$\phi _\omega ([0,1])$ and ![]() $\phi _{\omega \oplus (0)}([0,1])$ are equal. The length of the latter interval is
$\phi _{\omega \oplus (0)}([0,1])$ are equal. The length of the latter interval is ![]() $\alpha ^{|\omega | + 1}$, which is less than the length of
$\alpha ^{|\omega | + 1}$, which is less than the length of ![]() $\phi _\omega ([0,1])$, and thus
$\phi _\omega ([0,1])$, and thus ![]() $\phi _{\omega \oplus (0)}([0,1])$ is indeed contained in
$\phi _{\omega \oplus (0)}([0,1])$ is indeed contained in ![]() $\phi _\omega ([0,1])$. The stated property of
$\phi _\omega ([0,1])$. The stated property of ![]() $\phi _{\omega \oplus (1)}([0,1])$ follows completely analogously.
$\phi _{\omega \oplus (1)}([0,1])$ follows completely analogously.
For two sets ![]() $A, B \subseteq \mathbb {R}$, we will let
$A, B \subseteq \mathbb {R}$, we will let ![]() $A + B = \{a+b: a \in A, b \in B\}$. A famous property of the Cantor ternary set is that
$A + B = \{a+b: a \in A, b \in B\}$. A famous property of the Cantor ternary set is that ![]() $\mathcal {C}_{1/3} + \mathcal {C}_{1/3} = [0,2]$. More generally, one can show that
$\mathcal {C}_{1/3} + \mathcal {C}_{1/3} = [0,2]$. More generally, one can show that ![]() $\mathcal {C}_\alpha + \mathcal {C}_\alpha = [0,2]$ for all
$\mathcal {C}_\alpha + \mathcal {C}_\alpha = [0,2]$ for all  $\alpha \in [\frac {1}{3},1)$. In [Reference Mendes and Oliveira37], an overview is given of the possible structures of
$\alpha \in [\frac {1}{3},1)$. In [Reference Mendes and Oliveira37], an overview is given of the possible structures of ![]() $\mathcal {C}_{\alpha _1} + \mathcal {C}_{\alpha _2}$ for pairs of
$\mathcal {C}_{\alpha _1} + \mathcal {C}_{\alpha _2}$ for pairs of ![]() $\alpha _1,\alpha _2 \in (0,1)$. Similar methods to those used in [Reference Mendes and Oliveira37] can be used to show the following.
$\alpha _1,\alpha _2 \in (0,1)$. Similar methods to those used in [Reference Mendes and Oliveira37] can be used to show the following.
Lemma 27. Let  $\alpha \in [\frac {1}{3},1)$ and
$\alpha \in [\frac {1}{3},1)$ and ![]() $\epsilon> 0$. Then there are sequences
$\epsilon> 0$. Then there are sequences ![]() $\omega _1, \omega _2, \omega _3 \in \Omega $ such that for all triples
$\omega _1, \omega _2, \omega _3 \in \Omega $ such that for all triples ![]() $p_1, p_2, p_3$ with
$p_1, p_2, p_3$ with ![]() $p_i \in \phi _{\omega _i}([0,1])$,
$p_i \in \phi _{\omega _i}([0,1])$,
 $$ \begin{align} \left| \frac{p_2-p_1}{p_3 - p_2} - 1\right| < \epsilon. \end{align} $$
$$ \begin{align} \left| \frac{p_2-p_1}{p_3 - p_2} - 1\right| < \epsilon. \end{align} $$Proof. First assume that  $\alpha \in [\frac {1}{2},1)$. Then
$\alpha \in [\frac {1}{2},1)$. Then ![]() $\phi _0([0,1])\cup \phi _1([0,1]) = [0,1]$. It follows from Lemma 19 that for any
$\phi _0([0,1])\cup \phi _1([0,1]) = [0,1]$. It follows from Lemma 19 that for any ![]() $\delta> 0$ there are elements
$\delta> 0$ there are elements ![]() $\omega _1,\omega _2$ and
$\omega _1,\omega _2$ and ![]() $\omega _3$ in
$\omega _3$ in ![]() $\Omega $ such that
$\Omega $ such that
By choosing ![]() $\delta $ small enough, we can guarantee the inequality in (11).
$\delta $ small enough, we can guarantee the inequality in (11).
Assume now that  $\alpha \in [\frac {1}{3},\frac {1}{2})$. We will first show that if there are
$\alpha \in [\frac {1}{3},\frac {1}{2})$. We will first show that if there are ![]() $\omega _i \in \Omega $ with
$\omega _i \in \Omega $ with ![]() $|\omega _i| = n$ and
$|\omega _i| = n$ and ![]() $q_i \in \phi _{\omega _i}([0,1])$ for
$q_i \in \phi _{\omega _i}([0,1])$ for ![]() $i = 1,2,3$ such that
$i = 1,2,3$ such that ![]() $q_1 + q_3 = 2q_2$, then there are choices of indices
$q_1 + q_3 = 2q_2$, then there are choices of indices ![]() $k_i \in \{0,1\}$ such that there exist
$k_i \in \{0,1\}$ such that there exist ![]() $\tilde {q_i} \in \phi _{\omega _i \oplus (k_i)}([0,1])$ for which
$\tilde {q_i} \in \phi _{\omega _i \oplus (k_i)}([0,1])$ for which ![]() $\tilde {q_1} + \tilde {q_3} = 2\tilde {q_2}$. Suppose that we are given such
$\tilde {q_1} + \tilde {q_3} = 2\tilde {q_2}$. Suppose that we are given such ![]() $\omega _i$ and
$\omega _i$ and ![]() $q_i$. Let
$q_i$. Let ![]() $I_i = \phi _{\omega _i}([0,1])$ and
$I_i = \phi _{\omega _i}([0,1])$ and  $I_i^{k} = \phi _{\omega _i\oplus (k)}([0,1])$ for
$I_i^{k} = \phi _{\omega _i\oplus (k)}([0,1])$ for ![]() $i = 1,2,3$ and
$i = 1,2,3$ and ![]() $k=0,1$. We will show that
$k=0,1$. We will show that
 $$ \begin{align} I_1 + I_3 = (I_1^0 + I_3^0) \cup (I_1^1 + I_3^0) \cup (I_1^0 + I_3^1). \end{align} $$
$$ \begin{align} I_1 + I_3 = (I_1^0 + I_3^0) \cup (I_1^1 + I_3^0) \cup (I_1^0 + I_3^1). \end{align} $$Let ![]() $a_1$ and
$a_1$ and ![]() $a_3$ be the left boundaries of
$a_3$ be the left boundaries of ![]() $I_1$ and
$I_1$ and ![]() $I_3$, respectively. Because
$I_3$, respectively. Because ![]() $|\omega _1| = |\omega _3| = n$, it follows that
$|\omega _1| = |\omega _3| = n$, it follows that ![]() $I_1 = [a_1, a_1 + \alpha ^n]$ and
$I_1 = [a_1, a_1 + \alpha ^n]$ and ![]() $I_3 = [a_3, a_3 + \alpha ^n]$ and thus
$I_3 = [a_3, a_3 + \alpha ^n]$ and thus ![]() $I_1 + I_3 = [a_1 + a_3, a_1 + a_3 + 2\alpha ^n]$, which we can denote as
$I_1 + I_3 = [a_1 + a_3, a_1 + a_3 + 2\alpha ^n]$, which we can denote as ![]() $a_1 + a_3 + \alpha ^n \cdot [0,2]$. Now
$a_1 + a_3 + \alpha ^n \cdot [0,2]$. Now
 $$\begin{align*} I_1^0 + I_3^0 &= \left(a_1 + \alpha^{n}\cdot [0,\alpha]\right) + \left(a_3 + \alpha^{n}\cdot [0,\alpha]\right) &&= a_1 + a_3 + \alpha^n \cdot [0,2\alpha]\\ I_1^1 + I_3^0 &= \left(a_1 + \alpha^{n}\cdot [1-\alpha,1]\right) + \left(a_3 + \alpha^{n}\cdot [0,\alpha]\right) &&= a_1 + a_3 + \alpha^n \cdot [1-\alpha,1+\alpha]\\ I_1^1 + I_3^1 &= \left(a_1 + \alpha^{n}\cdot [1-\alpha,1]\right) + \left(a_3 + \alpha^{n}\cdot [1-\alpha,1]\right) &&= a_1 + a_3 + \alpha^n \cdot [2-2\alpha,2]. \end{align*}$$
$$\begin{align*} I_1^0 + I_3^0 &= \left(a_1 + \alpha^{n}\cdot [0,\alpha]\right) + \left(a_3 + \alpha^{n}\cdot [0,\alpha]\right) &&= a_1 + a_3 + \alpha^n \cdot [0,2\alpha]\\ I_1^1 + I_3^0 &= \left(a_1 + \alpha^{n}\cdot [1-\alpha,1]\right) + \left(a_3 + \alpha^{n}\cdot [0,\alpha]\right) &&= a_1 + a_3 + \alpha^n \cdot [1-\alpha,1+\alpha]\\ I_1^1 + I_3^1 &= \left(a_1 + \alpha^{n}\cdot [1-\alpha,1]\right) + \left(a_3 + \alpha^{n}\cdot [1-\alpha,1]\right) &&= a_1 + a_3 + \alpha^n \cdot [2-2\alpha,2]. \end{align*}$$Because  $\alpha \in [\frac {1}{3},1)$, it follows that
$\alpha \in [\frac {1}{3},1)$, it follows that
thus showing (12). Because there are ![]() $q_i \in I_i$ such that
$q_i \in I_i$ such that ![]() $q_1 + q_3 = 2 q_2$, we know that
$q_1 + q_3 = 2 q_2$, we know that ![]() $I_1 + I_3$ is not disjoint from
$I_1 + I_3$ is not disjoint from ![]() $2I_2$. These two intervals have the same length and thus at least one of the boundary points of
$2I_2$. These two intervals have the same length and thus at least one of the boundary points of ![]() $2I_2$ lies in
$2I_2$ lies in ![]() $I_1 + I_3$; therefore, there is a
$I_1 + I_3$; therefore, there is a ![]() $k_2 \in \{0,1\}$ such that
$k_2 \in \{0,1\}$ such that  $2I_2^{k_2}$ is not disjoint from
$2I_2^{k_2}$ is not disjoint from ![]() $I_1 + I_3$ because the intervals
$I_1 + I_3$ because the intervals ![]() $I_2^{0}$ and
$I_2^{0}$ and ![]() $I_2^{1}$ contain the respective boundary points of
$I_2^{1}$ contain the respective boundary points of ![]() $I_2$. This means that
$I_2$. This means that  $2I_2^{k_2}$ is not disjoint from
$2I_2^{k_2}$ is not disjoint from  $(I_1^0 + I_3^0) \cup (I_1^1 + I_3^0) \cup (I_1^0 + I_3^1)$ and thus there are also choices of
$(I_1^0 + I_3^0) \cup (I_1^1 + I_3^0) \cup (I_1^0 + I_3^1)$ and thus there are also choices of ![]() $k_1, k_3 \in \{0,1\}$ such that
$k_1, k_3 \in \{0,1\}$ such that  $I_1^{k_1} + I_3^{k_3}$ is not disjoint from
$I_1^{k_1} + I_3^{k_3}$ is not disjoint from  $2I_2^{k_2}$. It follows that there are
$2I_2^{k_2}$. It follows that there are  $\tilde {q_i} \in I_i^{k_i}$ such that
$\tilde {q_i} \in I_i^{k_i}$ such that ![]() $\tilde {q_1} + \tilde {q_3} = 2\tilde {q_2}$.
$\tilde {q_1} + \tilde {q_3} = 2\tilde {q_2}$.
Let ![]() $\omega _1 = (0,0)$,
$\omega _1 = (0,0)$, ![]() $\omega _2 = (0,1)$ and
$\omega _2 = (0,1)$ and ![]() $\omega _3 = (1,0)$. Note that
$\omega _3 = (1,0)$. Note that ![]() $0 \in \phi _{\omega _1}([0,1])$ and
$0 \in \phi _{\omega _1}([0,1])$ and ![]() $1-\alpha \in \phi _{\omega _3}([0,1]) = [1-\alpha , 1-\alpha + \alpha ^2]$. Furthermore, it can be checked, using the fact that
$1-\alpha \in \phi _{\omega _3}([0,1]) = [1-\alpha , 1-\alpha + \alpha ^2]$. Furthermore, it can be checked, using the fact that  $\alpha \in [\frac {1}{3},\frac {1}{2})$, that
$\alpha \in [\frac {1}{3},\frac {1}{2})$, that ![]() $(1-\alpha )/2 \in \phi _{\omega _2}([0,1]) = [\alpha -\alpha ^2,\alpha ]$, and thus there are
$(1-\alpha )/2 \in \phi _{\omega _2}([0,1]) = [\alpha -\alpha ^2,\alpha ]$, and thus there are ![]() $q_i \in \phi _{\omega _i}([0,1])$ such that
$q_i \in \phi _{\omega _i}([0,1])$ such that ![]() $q_1 + q_3 - 2q_2 = 0$. From the previous considerations it follows that there are
$q_1 + q_3 - 2q_2 = 0$. From the previous considerations it follows that there are ![]() $\tilde {\omega }_i \in \Omega $ of arbitrary length such that there are
$\tilde {\omega }_i \in \Omega $ of arbitrary length such that there are ![]() $\tilde {q}_i \in \phi _{\omega _i \oplus \tilde {\omega }_i}([0,1])$ for which
$\tilde {q}_i \in \phi _{\omega _i \oplus \tilde {\omega }_i}([0,1])$ for which ![]() $\tilde {q}_1 + \tilde {q}_3 - 2\tilde {q}_2 = 0$. See Figure 1 for an illustration of the construction described in this proof. By taking the length of
$\tilde {q}_1 + \tilde {q}_3 - 2\tilde {q}_2 = 0$. See Figure 1 for an illustration of the construction described in this proof. By taking the length of ![]() $\tilde {\omega }_i$ large enough, the lengths of the intervals can be made arbitrarily small, and thus we can guarantee that
$\tilde {\omega }_i$ large enough, the lengths of the intervals can be made arbitrarily small, and thus we can guarantee that
 $$ \begin{align*} \left|p_3 - p_2 \right| \cdot \left| \frac{p_2-p_1}{p_3 - p_2} - 1\right| = \left|p_1 + p_3 - 2p_2 \right| < \epsilon \cdot (1 - 2\alpha) \end{align*} $$
$$ \begin{align*} \left|p_3 - p_2 \right| \cdot \left| \frac{p_2-p_1}{p_3 - p_2} - 1\right| = \left|p_1 + p_3 - 2p_2 \right| < \epsilon \cdot (1 - 2\alpha) \end{align*} $$for all triples ![]() $p_i \in \phi _{\omega _i \oplus \tilde {\omega }_i}([0,1])$. Because
$p_i \in \phi _{\omega _i \oplus \tilde {\omega }_i}([0,1])$. Because ![]() $\phi _{\omega _i \oplus \tilde {\omega }_i}([0,1]) \subseteq \phi _{\omega _i}([0,1])$, we conclude that
$\phi _{\omega _i \oplus \tilde {\omega }_i}([0,1]) \subseteq \phi _{\omega _i}([0,1])$, we conclude that ![]() $p_3 - p_2$ is at least
$p_3 - p_2$ is at least ![]() $1 - 2\alpha $. The inequality in (11) follows.
$1 - 2\alpha $. The inequality in (11) follows.

Figure 1 An illustration of the union of ![]() $\phi _\omega ([0,1])$, where
$\phi _\omega ([0,1])$, where ![]() $\omega \in \Omega $ runs over all sequences of length n for
$\omega \in \Omega $ runs over all sequences of length n for ![]() $n = 0,1, \dots , 6$ for
$n = 0,1, \dots , 6$ for ![]() $\alpha = 7/16$. At each level, starting at level 2, three red intervals are highlighted containing elements
$\alpha = 7/16$. At each level, starting at level 2, three red intervals are highlighted containing elements ![]() $q_1, q_2$ and
$q_1, q_2$ and ![]() $q_3$, respectively, such that
$q_3$, respectively, such that ![]() $q_1 + q_3 = 2q_2$.
$q_1 + q_3 = 2q_2$.
Lemma 28. Let  $\alpha \in [\frac {1}{3},1)$,
$\alpha \in [\frac {1}{3},1)$, ![]() $\epsilon> 0$ and
$\epsilon> 0$ and ![]() $f_0,f_1$ differentiable maps from
$f_0,f_1$ differentiable maps from ![]() $[0,1]$ to itself with fixed points
$[0,1]$ to itself with fixed points ![]() $0$ and
$0$ and ![]() $1$, respectively. Then there is a constant
$1$, respectively. Then there is a constant ![]() $\delta> 0$ such that if
$\delta> 0$ such that if ![]() $|f_i'(x) - \alpha | < \delta $ for
$|f_i'(x) - \alpha | < \delta $ for ![]() $i = 0,1$ and all
$i = 0,1$ and all ![]() $x \in [0,1]$, then there are
$x \in [0,1]$, then there are ![]() $\omega _1, \omega _2, \omega _3 \in \Omega $ such that for all triples
$\omega _1, \omega _2, \omega _3 \in \Omega $ such that for all triples ![]() $p_1, p_2, p_3$ with
$p_1, p_2, p_3$ with ![]() $p_i \in f_{\omega _i}([0,1])$ it holds that
$p_i \in f_{\omega _i}([0,1])$ it holds that
 $$ \begin{align} \left| \frac{p_2 - p_1}{p_3 - p_2} - 1\right| < \epsilon. \end{align} $$
$$ \begin{align} \left| \frac{p_2 - p_1}{p_3 - p_2} - 1\right| < \epsilon. \end{align} $$Proof. Suppose that ![]() $|f_i'(x) - \alpha | < \delta $ for
$|f_i'(x) - \alpha | < \delta $ for ![]() $i = 0,1$ and all
$i = 0,1$ and all ![]() $x \in [0,1]$. For any
$x \in [0,1]$. For any ![]() $x \in [0,1]$, we can write
$x \in [0,1]$, we can write
 $$ \begin{align*} f_0(x) = \int_0^x f_0'(t) dt \quad\text{ and }\quad f_1(x) = 1 - \int_x^1 f_1'(t) dt. \end{align*} $$
$$ \begin{align*} f_0(x) = \int_0^x f_0'(t) dt \quad\text{ and }\quad f_1(x) = 1 - \int_x^1 f_1'(t) dt. \end{align*} $$We show inductively that for all ![]() $x \in [0,1]$ and
$x \in [0,1]$ and ![]() $\omega \in \Omega $ we have
$\omega \in \Omega $ we have ![]() $|f_\omega (x) - \phi _\omega (x)| \leq |\omega | \cdot \delta $. When
$|f_\omega (x) - \phi _\omega (x)| \leq |\omega | \cdot \delta $. When ![]() $|\omega | = 0$, the statement is clear, so we suppose that
$|\omega | = 0$, the statement is clear, so we suppose that ![]() $|\omega |> 0$. Assume that the first entry of
$|\omega |> 0$. Assume that the first entry of ![]() $\omega $ is a
$\omega $ is a ![]() $0$, so we write
$0$, so we write ![]() $\omega = (0)\ \oplus \ \omega '$ for some
$\omega = (0)\ \oplus \ \omega '$ for some ![]() $\omega ' \in \Omega $ with
$\omega ' \in \Omega $ with ![]() $|\omega | = |\omega '| + 1$. Let
$|\omega | = |\omega '| + 1$. Let ![]() $x \in [0,1]$; we assume that we have shown that
$x \in [0,1]$; we assume that we have shown that ![]() $|f_{\omega '}(x) - \phi _{\omega '}(x)| < \delta \cdot |\omega '|$. We denote
$|f_{\omega '}(x) - \phi _{\omega '}(x)| < \delta \cdot |\omega '|$. We denote ![]() $f_{\omega '}(x)$ by y and
$f_{\omega '}(x)$ by y and ![]() $\phi _{\omega '}(x)$ by
$\phi _{\omega '}(x)$ by ![]() $y + r$, where
$y + r$, where ![]() $|r| \leq \delta \cdot |\omega '|$. Now
$|r| \leq \delta \cdot |\omega '|$. Now
 $$ \begin{align*} \left|f_\omega(x) - \phi_\omega(x)\right| &= \left|f_0(y) - \phi_0(y + r)\right|= \left|\int_0^y f_0'(t) dt - \alpha \cdot (y+r) \right| = \left|\int_0^y \left(f_0'(t) - \alpha\right) dt - \alpha r \right|\\ &\leq \int_0^y |f_0'(t)-\alpha| dt + \alpha |r| \leq y \delta + \alpha \delta |\omega'|< \delta (|\omega'| + 1) = \delta |\omega|. \end{align*} $$
$$ \begin{align*} \left|f_\omega(x) - \phi_\omega(x)\right| &= \left|f_0(y) - \phi_0(y + r)\right|= \left|\int_0^y f_0'(t) dt - \alpha \cdot (y+r) \right| = \left|\int_0^y \left(f_0'(t) - \alpha\right) dt - \alpha r \right|\\ &\leq \int_0^y |f_0'(t)-\alpha| dt + \alpha |r| \leq y \delta + \alpha \delta |\omega'|< \delta (|\omega'| + 1) = \delta |\omega|. \end{align*} $$If the first entry of ![]() $\omega $ is a
$\omega $ is a ![]() $1$, the calculation is analogous.
$1$, the calculation is analogous.
Let ![]() $\omega _1, \omega _2, \omega _3 \in \Omega $ such that for all triples
$\omega _1, \omega _2, \omega _3 \in \Omega $ such that for all triples ![]() $p_1, p_2, p_3$ with
$p_1, p_2, p_3$ with ![]() $p_i \in \phi _{\omega _i}([0,1])$ it holds that
$p_i \in \phi _{\omega _i}([0,1])$ it holds that  $\big | \tfrac {p_2-p_1}{p_3 - p_2} - 1\big | < \epsilon /2$. These choices of
$\big | \tfrac {p_2-p_1}{p_3 - p_2} - 1\big | < \epsilon /2$. These choices of ![]() $\omega _i$ exist by Lemma 27. For this inequality to hold, it must be the case that
$\omega _i$ exist by Lemma 27. For this inequality to hold, it must be the case that ![]() $\phi _{\omega _2}([0,1]) \cap \phi _{\omega _3}([0,1]) = \emptyset $ and thus, since the map
$\phi _{\omega _2}([0,1]) \cap \phi _{\omega _3}([0,1]) = \emptyset $ and thus, since the map ![]() $(p_1,p_2,p_3) \to (p_2-p_1)/(p_3-p_2)$ is continuous in all points where
$(p_1,p_2,p_3) \to (p_2-p_1)/(p_3-p_2)$ is continuous in all points where ![]() $p_2 \neq p_3$, we can find three open intervals
$p_2 \neq p_3$, we can find three open intervals ![]() $I_1,I_2,I_3$ with
$I_1,I_2,I_3$ with ![]() $\phi _{\omega _i}([0,1]) \subseteq I_i$ such that for all triples
$\phi _{\omega _i}([0,1]) \subseteq I_i$ such that for all triples ![]() $q_i \in I_i$ we have
$q_i \in I_i$ we have
 $$ \begin{align*} \left| \frac{q_2-q_1}{q_3 - q_2} - 1\right| < \epsilon. \end{align*} $$
$$ \begin{align*} \left| \frac{q_2-q_1}{q_3 - q_2} - 1\right| < \epsilon. \end{align*} $$We showed that by making ![]() $\delta $ small enough we obtain bounds on the difference between
$\delta $ small enough we obtain bounds on the difference between ![]() $f_\omega (x)$ and
$f_\omega (x)$ and ![]() $\phi _\omega (x)$ uniformly over all
$\phi _\omega (x)$ uniformly over all ![]() $x \in [0,1]$ and
$x \in [0,1]$ and ![]() $\omega $ of bounded length. Therefore, we can make
$\omega $ of bounded length. Therefore, we can make ![]() $\delta $ sufficiently small such that
$\delta $ sufficiently small such that ![]() $f_{\omega _i}([0,1]) \subset I_i$ for
$f_{\omega _i}([0,1]) \subset I_i$ for ![]() $i \in \{1,2,3\}$, which is enough to conclude the statement of the lemma.
$i \in \{1,2,3\}$, which is enough to conclude the statement of the lemma.
Corollary 29. Let  $\alpha \in [\frac {1}{3},1)$,
$\alpha \in [\frac {1}{3},1)$, ![]() $\epsilon> 0$. There is
$\epsilon> 0$. There is ![]() $\delta>0$ such that the following holds for any closed circular arc
$\delta>0$ such that the following holds for any closed circular arc ![]() $A \subseteq \mathbb {S}^1$ and two maps
$A \subseteq \mathbb {S}^1$ and two maps ![]() $f_0, f_1:A\rightarrow A$ with the respective endpoints of A as fixed points with the property that
$f_0, f_1:A\rightarrow A$ with the respective endpoints of A as fixed points with the property that ![]() $||f_i'(z)|-\alpha | < \delta $ for all
$||f_i'(z)|-\alpha | < \delta $ for all ![]() $z\in A$.
$z\in A$.
There exist ![]() $\omega _1, \omega _2, \omega _3 \in \Omega $ such that for all triples
$\omega _1, \omega _2, \omega _3 \in \Omega $ such that for all triples ![]() $p_i$ with
$p_i$ with ![]() $p_i \in f_{\omega _i}(A)$ we have that
$p_i \in f_{\omega _i}(A)$ we have that ![]() $\operatorname {\mathrm {Arc}}[p_1,p_2]$ and
$\operatorname {\mathrm {Arc}}[p_1,p_2]$ and ![]() $\operatorname {\mathrm {Arc}}[p_2,p_3]$ are subsets of A satisfying
$\operatorname {\mathrm {Arc}}[p_2,p_3]$ are subsets of A satisfying
 $$ \begin{align*} \left|\frac{\ell(\operatorname{\mathrm{Arc}}[p_1,p_2])}{\ell(\operatorname{\mathrm{Arc}}[p_2,p_3])} - 1\right| < \epsilon. \end{align*} $$
$$ \begin{align*} \left|\frac{\ell(\operatorname{\mathrm{Arc}}[p_1,p_2])}{\ell(\operatorname{\mathrm{Arc}}[p_2,p_3])} - 1\right| < \epsilon. \end{align*} $$We are now ready to prove the following lemma.
Lemma 30. Let ![]() $d \in \mathbb {Z}_{\geq 2}$,
$d \in \mathbb {Z}_{\geq 2}$, ![]() $k \in \mathbb {Z}_{\geq 1}$,
$k \in \mathbb {Z}_{\geq 1}$,  $b \in \big [\frac {k-1}{k+1},\frac {d-1}{d+1}\big ]$ with
$b \in \big [\frac {k-1}{k+1},\frac {d-1}{d+1}\big ]$ with ![]() $b \neq 0$ and
$b \neq 0$ and ![]() $\lambda \in \mathbb {S}$. Let
$\lambda \in \mathbb {S}$. Let ![]() $\xi \in \mathbb {S}\setminus \{-1\}$ with
$\xi \in \mathbb {S}\setminus \{-1\}$ with ![]() $|f^{\prime }_{3k}(\xi )|> 1$. Let
$|f^{\prime }_{3k}(\xi )|> 1$. Let ![]() $\{\xi _n\}_{n \geq 1}$ be a sequence in
$\{\xi _n\}_{n \geq 1}$ be a sequence in ![]() $\mathbb {S}$ converging to
$\mathbb {S}$ converging to ![]() $\xi $ and not equal to
$\xi $ and not equal to ![]() $\xi $ such that for all positive integers n there is a rooted tree
$\xi $ such that for all positive integers n there is a rooted tree ![]() $T_n$ in
$T_n$ in ![]() $\mathcal {T}_{d+1}$, with root degree
$\mathcal {T}_{d+1}$, with root degree ![]() $m \leq d-2k$ implementing the field
$m \leq d-2k$ implementing the field ![]() $\xi _n$. Then at least one of the following is true:
$\xi _n$. Then at least one of the following is true:
1. The set of fields implemented by rooted trees in
 $\mathcal {T}_{d+1}$ is dense in
$\mathcal {T}_{d+1}$ is dense in  $\mathbb {S}$.
$\mathbb {S}$.2. Given
 $\epsilon> 0$, there is a rooted tree in
$\epsilon> 0$, there is a rooted tree in  $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most  $m+k$ that implements the field
$m+k$ that implements the field  $r \in \operatorname {\mathrm {Arc}}{(\lambda _k,\overline {\lambda _k})}\setminus \{-1\}$ with
$r \in \operatorname {\mathrm {Arc}}{(\lambda _k,\overline {\lambda _k})}\setminus \{-1\}$ with  $|f_{3k}'(r)|> |f^{\prime }_{3k}(\xi )| - \epsilon $.
$|f_{3k}'(r)|> |f^{\prime }_{3k}(\xi )| - \epsilon $.
Proof. We distinguish the following three cases:
(i)
 $\xi \in \operatorname {\mathrm {Arc}}(\lambda _k,\overline {\lambda _k})$.
$\xi \in \operatorname {\mathrm {Arc}}(\lambda _k,\overline {\lambda _k})$.(ii)
 $\xi \in \operatorname {\mathrm {Arc}}[\overline {\lambda _k},\lambda _k]$ and
$\xi \in \operatorname {\mathrm {Arc}}[\overline {\lambda _k},\lambda _k]$ and  $R_k(\xi ) \in \operatorname {\mathrm {Arc}}(\lambda _k,\overline {\lambda _k})$.
$R_k(\xi ) \in \operatorname {\mathrm {Arc}}(\lambda _k,\overline {\lambda _k})$.(iii)
 $\xi \in \operatorname {\mathrm {Arc}}[\overline {\lambda _k},\lambda _k]$ and
$\xi \in \operatorname {\mathrm {Arc}}[\overline {\lambda _k},\lambda _k]$ and  $R_k(\xi ) \in \operatorname {\mathrm {Arc}}[\overline {\lambda _k},\lambda _k]$.
$R_k(\xi ) \in \operatorname {\mathrm {Arc}}[\overline {\lambda _k},\lambda _k]$.
Suppose first we are in case (i). Then, since ![]() $\xi _n \to \xi $ and thus
$\xi _n \to \xi $ and thus ![]() $f_{3k}'(\xi _n) \to f_{3k}'(\xi )$, given
$f_{3k}'(\xi _n) \to f_{3k}'(\xi )$, given ![]() $\epsilon $, there is an integer n such that
$\epsilon $, there is an integer n such that ![]() $\xi _n \in \operatorname {\mathrm {Arc}}(\lambda _k,\overline {\lambda _k})\setminus \{-1\}$ and
$\xi _n \in \operatorname {\mathrm {Arc}}(\lambda _k,\overline {\lambda _k})\setminus \{-1\}$ and ![]() $|f_{3k}'(\xi _n)|> |f^{\prime }_{3k}(\xi )| - \epsilon $. The rooted tree
$|f_{3k}'(\xi _n)|> |f^{\prime }_{3k}(\xi )| - \epsilon $. The rooted tree ![]() $T_n$ satisfies the requirements of statement (2) of the lemma.
$T_n$ satisfies the requirements of statement (2) of the lemma.
To prove the lemma for cases (ii) and (iii), we define the following set:
 $$ \begin{align*} \mathcal{R} = \left\{f_{\xi_n,k}^N(\xi_n): n,N \geq 1 \right\}. \end{align*} $$
$$ \begin{align*} \mathcal{R} = \left\{f_{\xi_n,k}^N(\xi_n): n,N \geq 1 \right\}. \end{align*} $$By repeatedly applying Lemma 4, we see that every element of ![]() $\mathcal {R}$ corresponds to the field implemented by a rooted tree in
$\mathcal {R}$ corresponds to the field implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ whose root degree is at most
$\mathcal {T}_{d+1}$ whose root degree is at most ![]() $m + k$. The following limits follow from continuity:
$m + k$. The following limits follow from continuity:
 $$ \begin{align*} \lim_{N \to \infty} \lim_{n \to \infty} f_{\xi_n,k}^N(\xi_n) = \lim_{N \to \infty} f_{\xi,k}^N(\xi) = R_k(\xi). \end{align*} $$
$$ \begin{align*} \lim_{N \to \infty} \lim_{n \to \infty} f_{\xi_n,k}^N(\xi_n) = \lim_{N \to \infty} f_{\xi,k}^N(\xi) = R_k(\xi). \end{align*} $$Therefore, ![]() $R_k(\xi )$ is an accumulation of
$R_k(\xi )$ is an accumulation of ![]() $\mathcal {R}$ and, in fact, there is a sequence
$\mathcal {R}$ and, in fact, there is a sequence ![]() $\{\zeta _n\}_{n \geq 1}$ of elements in
$\{\zeta _n\}_{n \geq 1}$ of elements in ![]() $\mathcal {R}$ converging to
$\mathcal {R}$ converging to ![]() $R_k(\xi )$ but not equal to
$R_k(\xi )$ but not equal to ![]() $R_k(\xi )$. If we are in case (ii), by Remark 11 we can take
$R_k(\xi )$. If we are in case (ii), by Remark 11 we can take ![]() $\zeta _n$ sufficiently close to
$\zeta _n$ sufficiently close to ![]() $R_k(\xi )$ so that
$R_k(\xi )$ so that ![]() $\zeta _n \in \operatorname {\mathrm {Arc}}{(\lambda _k,\overline {\lambda _k})}\setminus \{-1\}$. Since
$\zeta _n \in \operatorname {\mathrm {Arc}}{(\lambda _k,\overline {\lambda _k})}\setminus \{-1\}$. Since ![]() $|f_{3k}'(R_k(\xi ))|> |f_{3k}'(\xi )|$ by Remark 11, we can further ensure that
$|f_{3k}'(R_k(\xi ))|> |f_{3k}'(\xi )|$ by Remark 11, we can further ensure that ![]() $|f_{3k}'(\zeta _n)|> |f_{3k}'(\xi )|$. The corresponding tree with field
$|f_{3k}'(\zeta _n)|> |f_{3k}'(\xi )|$. The corresponding tree with field ![]() $\zeta _n$ satisfies the condition of statement (2) of the lemma.
$\zeta _n$ satisfies the condition of statement (2) of the lemma.
Suppose now we are in case (iii) and suppose first that ![]() $R_k(\xi ) \in \{\overline {\lambda _k},\lambda _k\}$. If a subsequence
$R_k(\xi ) \in \{\overline {\lambda _k},\lambda _k\}$. If a subsequence ![]() $(\zeta _n)$ converges to
$(\zeta _n)$ converges to ![]() $R_k(\xi )$ along the arc
$R_k(\xi )$ along the arc ![]() $\operatorname {\mathrm {Arc}}(\lambda _k,\overline {\lambda _k})$, we obtain a
$\operatorname {\mathrm {Arc}}(\lambda _k,\overline {\lambda _k})$, we obtain a ![]() $\zeta _n \in \operatorname {\mathrm {Arc}}(\lambda _k,\overline {\lambda _k})$ and, by the same reasoning as in the previous case, we can conclude that statement (2) of the lemma holds. So we can assume that for large enough n, all
$\zeta _n \in \operatorname {\mathrm {Arc}}(\lambda _k,\overline {\lambda _k})$ and, by the same reasoning as in the previous case, we can conclude that statement (2) of the lemma holds. So we can assume that for large enough n, all ![]() $\zeta _n$ lie in
$\zeta _n$ lie in ![]() $\operatorname {\mathrm {Arc}}(\overline {\lambda _k},\lambda _k)$. In this case, we find that for sufficiently high n the elements
$\operatorname {\mathrm {Arc}}(\overline {\lambda _k},\lambda _k)$. In this case, we find that for sufficiently high n the elements ![]() $\zeta _n$ get arbitrarily close to either
$\zeta _n$ get arbitrarily close to either ![]() $\lambda _k$ or
$\lambda _k$ or ![]() $\overline {\lambda _k}$ and thus
$\overline {\lambda _k}$ and thus ![]() $|f_{k}'(R_k(\zeta _n))|$ gets arbitrarily close to
$|f_{k}'(R_k(\zeta _n))|$ gets arbitrarily close to ![]() $1$. It follows that we can find
$1$. It follows that we can find ![]() $n_1$ and
$n_1$ and ![]() $n_2$ such that
$n_2$ such that ![]() $\zeta _{n_1}$ and
$\zeta _{n_1}$ and ![]() $\zeta _{n_2}$ lie in the same half-plane and such that
$\zeta _{n_2}$ lie in the same half-plane and such that ![]() $|f_{2k}'(R_k(\zeta _{n_i}))|> 1$ for
$|f_{2k}'(R_k(\zeta _{n_i}))|> 1$ for ![]() $i = 1,2$. It follows then from Lemma 22 that, if we let
$i = 1,2$. It follows then from Lemma 22 that, if we let ![]() $g_0 = f_{\zeta _{n_1},k}$ and
$g_0 = f_{\zeta _{n_1},k}$ and ![]() $g_1 = f_{\zeta _{n_2},k}$, the set
$g_1 = f_{\zeta _{n_2},k}$, the set
is dense in an arc ![]() $A \subseteq S$. By applying Lemma 4, we observe that every
$A \subseteq S$. By applying Lemma 4, we observe that every ![]() $r \in \mathcal {R}_1$ corresponds to the field implemented by a rooted tree in
$r \in \mathcal {R}_1$ corresponds to the field implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $m + 2k \leq d$. Because the tree consisting of a single vertex implements the field
$m + 2k \leq d$. Because the tree consisting of a single vertex implements the field ![]() $\lambda $, we can apply Lemma 4 to see that every element in the set
$\lambda $, we can apply Lemma 4 to see that every element in the set
corresponds to the field implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most d. Because b is chosen such that
$\mathcal {T}_{d+1}$ with root degree at most d. Because b is chosen such that ![]() $|f_d'(z)|> 1$ for all
$|f_d'(z)|> 1$ for all ![]() $z \in \mathbb {S}-\{1\}$, we find that
$z \in \mathbb {S}-\{1\}$, we find that  $f_{\lambda ,d}^N(A) = \mathbb {S}$ for a sufficiently large N and thus
$f_{\lambda ,d}^N(A) = \mathbb {S}$ for a sufficiently large N and thus ![]() $\mathcal {R}_2$ is dense in
$\mathcal {R}_2$ is dense in ![]() $\mathbb {S}$, which shows that in this case statement (1) of the lemma holds.
$\mathbb {S}$, which shows that in this case statement (1) of the lemma holds.
Finally, we assume that ![]() $R_{k}(\xi ) \in \operatorname {\mathrm {Arc}}(\overline {\lambda _k},\lambda _k)$. W.l.o.g., assume that
$R_{k}(\xi ) \in \operatorname {\mathrm {Arc}}(\overline {\lambda _k},\lambda _k)$. W.l.o.g., assume that ![]() $\xi $ lies in the upper half-plane. Let
$\xi $ lies in the upper half-plane. Let ![]() $\alpha = |f_k'(R_k(\xi ))|$. It follows from the fact that
$\alpha = |f_k'(R_k(\xi ))|$. It follows from the fact that ![]() $R_k(\xi ) \in \operatorname {\mathrm {Arc}}(\xi , \lambda _k)$ that
$R_k(\xi ) \in \operatorname {\mathrm {Arc}}(\xi , \lambda _k)$ that ![]() $\alpha \in (1/3,1)$. Let
$\alpha \in (1/3,1)$. Let ![]() $\epsilon _1,\epsilon _2>0$ be two reals whose value will be determined later. Let
$\epsilon _1,\epsilon _2>0$ be two reals whose value will be determined later. Let ![]() $\delta $ be the constant obtained from applying Corollary 29 to
$\delta $ be the constant obtained from applying Corollary 29 to ![]() $\alpha $ and
$\alpha $ and ![]() $\epsilon =\epsilon _1$. Now choose
$\epsilon =\epsilon _1$. Now choose ![]() $n_1,n_2$ such that
$n_1,n_2$ such that ![]() $\xi _{n_1},\xi _{n_2}$ have the following properties:
$\xi _{n_1},\xi _{n_2}$ have the following properties:
(a)
 $\xi _{n_1}$ and
$\xi _{n_1}$ and  $\xi _{n_2}$ lie in the upper half-plane,
$\xi _{n_2}$ lie in the upper half-plane,  $\text {Arg}(\xi _{n_1}) < \text {Arg}(\xi _{n_2})$,
$\text {Arg}(\xi _{n_1}) < \text {Arg}(\xi _{n_2})$,  $\operatorname {\mathrm {Arc}}{[R_{k}(\xi _{n_1}), R_{k}(\xi _{n_2})]} \subseteq \operatorname {\mathrm {Arc}}{(1,\lambda _k)}$ and
$\operatorname {\mathrm {Arc}}{[R_{k}(\xi _{n_1}), R_{k}(\xi _{n_2})]} \subseteq \operatorname {\mathrm {Arc}}{(1,\lambda _k)}$ and  $\text {Arg}(R_k(R_k(\xi _{n_1})))> \text {Arg}(R_k(\xi ))$.
$\text {Arg}(R_k(R_k(\xi _{n_1})))> \text {Arg}(R_k(\xi ))$.(b) For all
 $z \in \operatorname {\mathrm {Arc}}{[R_{k}(\xi _{n_1}), R_{k}(\xi _{n_2})]}$ we have
$z \in \operatorname {\mathrm {Arc}}{[R_{k}(\xi _{n_1}), R_{k}(\xi _{n_2})]}$ we have  $||f_k'(z)|-\alpha |<\delta $.
$||f_k'(z)|-\alpha |<\delta $.(c) For all
 $z_1,z_2\in \operatorname {\mathrm {Arc}}{[R_{k}(\xi _{n_1}), R_{k}(\xi _{n_2})]}$ we have
$z_1,z_2\in \operatorname {\mathrm {Arc}}{[R_{k}(\xi _{n_1}), R_{k}(\xi _{n_2})]}$ we have  $||R_k'(z_1)/R_k'(z_2)|-1|<\epsilon _2$.
$||R_k'(z_1)/R_k'(z_2)|-1|<\epsilon _2$.
That it is possible to choose ![]() $n_1, n_2$ such that the first two properties hold follows from the fact that both
$n_1, n_2$ such that the first two properties hold follows from the fact that both ![]() $R_k$ and the derivative of
$R_k$ and the derivative of ![]() $f_k$ are continuous on
$f_k$ are continuous on ![]() $\operatorname {\mathrm {Arc}}{[\overline {\lambda _k},\lambda _k]}$. The existence of
$\operatorname {\mathrm {Arc}}{[\overline {\lambda _k},\lambda _k]}$. The existence of ![]() $n_1,n_2$ satisfying the third property follows from the fact that the derivative of
$n_1,n_2$ satisfying the third property follows from the fact that the derivative of ![]() $z \mapsto R_k(z)$ is continuous and nonzero on
$z \mapsto R_k(z)$ is continuous and nonzero on ![]() $\operatorname {\mathrm {Arc}}{(1,\lambda _k)}$.
$\operatorname {\mathrm {Arc}}{(1,\lambda _k)}$.
Let ![]() $g_0 = f_{\xi _{n_1},k}$ and
$g_0 = f_{\xi _{n_1},k}$ and ![]() $g_1 = f_{\xi _{n_2},k}$. Since
$g_1 = f_{\xi _{n_2},k}$. Since ![]() $\xi _{n_1},\xi _{n_2}$ are implemented by rooted trees in
$\xi _{n_1},\xi _{n_2}$ are implemented by rooted trees in ![]() $\mathcal {T}_{d+1}$ with root degrees at most m, we have by Lemma 4 that, if r is implemented by a rooted tree in
$\mathcal {T}_{d+1}$ with root degrees at most m, we have by Lemma 4 that, if r is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$, then
$\mathcal {T}_{d+1}$, then ![]() $g_i(r)$ is the field implemented by a tree in
$g_i(r)$ is the field implemented by a tree in ![]() $\mathcal {T}_{d+1}$ and root degree
$\mathcal {T}_{d+1}$ and root degree ![]() $m+k\leq d$. Let
$m+k\leq d$. Let ![]() $A = \operatorname {\mathrm {Arc}}{[R_{k}(\xi _{n_1}), R_{k}(\xi _{n_2})]}$ and note that the maps
$A = \operatorname {\mathrm {Arc}}{[R_{k}(\xi _{n_1}), R_{k}(\xi _{n_2})]}$ and note that the maps ![]() $g_0,g_1$ have the respective endpoints of A as fixed points. Furthermore,
$g_0,g_1$ have the respective endpoints of A as fixed points. Furthermore, ![]() $||g_i'(z)|-\alpha | < \delta $ for all
$||g_i'(z)|-\alpha | < \delta $ for all ![]() $z \in A$ and thus it follows from Corollary 29 that there is a triple
$z \in A$ and thus it follows from Corollary 29 that there is a triple ![]() $\omega _1,\omega _2,\omega _3 \in \Omega $ such that for all triples
$\omega _1,\omega _2,\omega _3 \in \Omega $ such that for all triples ![]() $p_i \in g_{\omega _i}(A)$ we have
$p_i \in g_{\omega _i}(A)$ we have ![]() $\text {Arg}(p_1) < \text {Arg}(p_2) < \text {Arg}(p_3)$ and
$\text {Arg}(p_1) < \text {Arg}(p_2) < \text {Arg}(p_3)$ and
 $$ \begin{align*} \left|\frac{\ell(\operatorname{\mathrm{Arc}}[p_1,p_2])}{\ell(\operatorname{\mathrm{Arc}}[p_2,p_3])} - 1\right| < \epsilon_1. \end{align*} $$
$$ \begin{align*} \left|\frac{\ell(\operatorname{\mathrm{Arc}}[p_1,p_2])}{\ell(\operatorname{\mathrm{Arc}}[p_2,p_3])} - 1\right| < \epsilon_1. \end{align*} $$ The orbit of ![]() $\xi _{n_2}$ under iteration of
$\xi _{n_2}$ under iteration of ![]() $g_1$ converges to
$g_1$ converges to ![]() $R_k(\xi _{n_2})$ approaching from an anti-clockwise direction and thus there is some number N such that if we let
$R_k(\xi _{n_2})$ approaching from an anti-clockwise direction and thus there is some number N such that if we let ![]() $\omega _N$ be the constant
$\omega _N$ be the constant ![]() $1$ sequence of length N,
$1$ sequence of length N, ![]() $g_{\omega _N}(\xi _{n_2}) \in A$. For
$g_{\omega _N}(\xi _{n_2}) \in A$. For ![]() $i = 1,2,3$ we define
$i = 1,2,3$ we define ![]() $\zeta _i = g_{\omega _i \oplus \omega _N}(\xi _{n_2})$ and note that each
$\zeta _i = g_{\omega _i \oplus \omega _N}(\xi _{n_2})$ and note that each ![]() $\zeta _i$ is contained in the interval
$\zeta _i$ is contained in the interval ![]() $(\overline {\lambda _k},\lambda _k)$ and is implemented by a rooted tree in
$(\overline {\lambda _k},\lambda _k)$ and is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree
$\mathcal {T}_{d+1}$ with root degree ![]() $m+k$. Furthermore, we have
$m+k$. Furthermore, we have ![]() $\text {Arg}(\zeta _1) < \text {Arg}(\zeta _2) < \text {Arg}(\zeta _3)$ and
$\text {Arg}(\zeta _1) < \text {Arg}(\zeta _2) < \text {Arg}(\zeta _3)$ and
 $$ \begin{align} \left|\frac{\ell(\operatorname{\mathrm{Arc}}[\zeta_1,\zeta_2])}{\ell(\operatorname{\mathrm{Arc}}[\zeta_2,\zeta_3])} - 1\right| < \epsilon_1. \end{align} $$
$$ \begin{align} \left|\frac{\ell(\operatorname{\mathrm{Arc}}[\zeta_1,\zeta_2])}{\ell(\operatorname{\mathrm{Arc}}[\zeta_2,\zeta_3])} - 1\right| < \epsilon_1. \end{align} $$Let ![]() $h_i = f_{\zeta _i,k}$. Analogous to the above, if r is implemented by a rooted tree in
$h_i = f_{\zeta _i,k}$. Analogous to the above, if r is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$, then
$\mathcal {T}_{d+1}$, then ![]() $h_i(r)$ is implemented by a rooted tree in
$h_i(r)$ is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $m+2k\leq d$. Redefine
$m+2k\leq d$. Redefine ![]() $A = \operatorname {\mathrm {Arc}}{[R_k(\zeta _1),R_k(\zeta _3)]}$. We will show that we can choose
$A = \operatorname {\mathrm {Arc}}{[R_k(\zeta _1),R_k(\zeta _3)]}$. We will show that we can choose ![]() $\epsilon _1$ and
$\epsilon _1$ and ![]() $\epsilon _2$ sufficiently small such that
$\epsilon _2$ sufficiently small such that ![]() $A = h_1(A) \cup h_2(A) \cup h_3(A)$. To do this, define
$A = h_1(A) \cup h_2(A) \cup h_3(A)$. To do this, define ![]() $A_1 = \operatorname {\mathrm {Arc}}{[R_k(\zeta _1),R_k(\zeta _2)]}$ and
$A_1 = \operatorname {\mathrm {Arc}}{[R_k(\zeta _1),R_k(\zeta _2)]}$ and ![]() $A_2 = \operatorname {\mathrm {Arc}}{[R_k(\zeta _2),R_k(\zeta _3)]}$. It follows from the mean value theorem that there are
$A_2 = \operatorname {\mathrm {Arc}}{[R_k(\zeta _2),R_k(\zeta _3)]}$. It follows from the mean value theorem that there are ![]() $x_i \in \operatorname {\mathrm {Arc}}{[\zeta _{i},\zeta _{i+1}]}$ such that
$x_i \in \operatorname {\mathrm {Arc}}{[\zeta _{i},\zeta _{i+1}]}$ such that ![]() $\ell (A_i) = |R_k'(x_i)| \cdot \ell (\operatorname {\mathrm {Arc}}{[\zeta _{i},\zeta _{i+1}]})$ for
$\ell (A_i) = |R_k'(x_i)| \cdot \ell (\operatorname {\mathrm {Arc}}{[\zeta _{i},\zeta _{i+1}]})$ for ![]() $i = 1,2$. Because both
$i = 1,2$. Because both ![]() $x_1$ and
$x_1$ and ![]() $x_2$ lie in
$x_2$ lie in ![]() $\operatorname {\mathrm {Arc}}{[R_{k}(\xi _{n_1}), R_{k}(\xi _{n_2})]}$, it follows from property (c) above that we can write
$\operatorname {\mathrm {Arc}}{[R_{k}(\xi _{n_1}), R_{k}(\xi _{n_2})]}$, it follows from property (c) above that we can write ![]() $|R_k'(x_1)/R_k'(x_2)| = 1 + r_2$ for some
$|R_k'(x_1)/R_k'(x_2)| = 1 + r_2$ for some ![]() $r_2 \in \mathbb {R}$ with
$r_2 \in \mathbb {R}$ with ![]() $|r_2| < \epsilon _2$. We use the bound in (14) to obtain the following inequality:
$|r_2| < \epsilon _2$. We use the bound in (14) to obtain the following inequality:
 $$\begin{align*}\left|\frac{\ell(A_1)}{\ell(A_2)}-1\right| &= \left|\frac{|R_k'(x_1)| \cdot \ell(\operatorname{\mathrm{Arc}}{[\zeta_{1},\zeta_{2}]})}{|R_k'(x_2)| \cdot \ell(\operatorname{\mathrm{Arc}}{[\zeta_{2},\zeta_{3}]})}-1\right| = \left|(1+r_2)\frac{\ell(\operatorname{\mathrm{Arc}}{[\zeta_{1},\zeta_{2}]})}{\ell(\operatorname{\mathrm{Arc}}{[\zeta_{2},\zeta_{3}]})}-1\right| \\ &\leq \left|1+r_2\right| \cdot\left|\frac{\ell(\operatorname{\mathrm{Arc}}{[\zeta_{1},\zeta_{2}]})}{\ell(\operatorname{\mathrm{Arc}}{[\zeta_{2},\zeta_{3}]})}-1\right| + |r_2| < \left|1+r_2\right| \cdot \epsilon_1 + |r_2|\\ &\leq \epsilon_1 + \epsilon_2 + \epsilon_1 \cdot \epsilon_2. \end{align*}$$
$$\begin{align*}\left|\frac{\ell(A_1)}{\ell(A_2)}-1\right| &= \left|\frac{|R_k'(x_1)| \cdot \ell(\operatorname{\mathrm{Arc}}{[\zeta_{1},\zeta_{2}]})}{|R_k'(x_2)| \cdot \ell(\operatorname{\mathrm{Arc}}{[\zeta_{2},\zeta_{3}]})}-1\right| = \left|(1+r_2)\frac{\ell(\operatorname{\mathrm{Arc}}{[\zeta_{1},\zeta_{2}]})}{\ell(\operatorname{\mathrm{Arc}}{[\zeta_{2},\zeta_{3}]})}-1\right| \\ &\leq \left|1+r_2\right| \cdot\left|\frac{\ell(\operatorname{\mathrm{Arc}}{[\zeta_{1},\zeta_{2}]})}{\ell(\operatorname{\mathrm{Arc}}{[\zeta_{2},\zeta_{3}]})}-1\right| + |r_2| < \left|1+r_2\right| \cdot \epsilon_1 + |r_2|\\ &\leq \epsilon_1 + \epsilon_2 + \epsilon_1 \cdot \epsilon_2. \end{align*}$$Let ![]() $\epsilon _3 = \epsilon _1 + \epsilon _2 + \epsilon _1 \cdot \epsilon _2$ and note that
$\epsilon _3 = \epsilon _1 + \epsilon _2 + \epsilon _1 \cdot \epsilon _2$ and note that ![]() $\epsilon _3$ can be made arbitrarily small by choosing
$\epsilon _3$ can be made arbitrarily small by choosing ![]() $\epsilon _1$ and
$\epsilon _1$ and ![]() $\epsilon _2$ sufficiently small. It follows that there is some
$\epsilon _2$ sufficiently small. It follows that there is some ![]() $r_3 \in \mathbb {R}$ with
$r_3 \in \mathbb {R}$ with ![]() $|r_3| < \epsilon _3$ such that
$|r_3| < \epsilon _3$ such that ![]() $\ell (A_1) = (1+r_3)\cdot \ell (A_2)$. Because
$\ell (A_1) = (1+r_3)\cdot \ell (A_2)$. Because ![]() $\text {Arg}(R_k(\zeta _1))> \text {Arg}(R_k(R_k(\xi _{n_1}))) > \text {Arg}(R_k(\xi ))$, we find that
$\text {Arg}(R_k(\zeta _1))> \text {Arg}(R_k(R_k(\xi _{n_1}))) > \text {Arg}(R_k(\xi ))$, we find that ![]() $1>|f_k'(z)| > \alpha $ for all
$1>|f_k'(z)| > \alpha $ for all ![]() $z \in A$ and thus
$z \in A$ and thus ![]() $1>|h_i'(z)| > \alpha $ for all
$1>|h_i'(z)| > \alpha $ for all ![]() $z \in A$ and
$z \in A$ and ![]() $i = 1,2,3$. It follows that
$i = 1,2,3$. It follows that
 $$ \begin{align*} \ell(h_1(A_1 \cup A_2)) + \ell(h_2(A_1)) &> \alpha\cdot(\ell(A_1) + \ell(A_2)) + \alpha \cdot \ell(A_1) = \alpha\cdot(2\ell(A_1) + \ell(A_2)) \\ & = \alpha\cdot\Big(2 + \frac{1}{1+r_3}\Big) \ell(A_1) = \alpha \cdot \frac{3+2r_3}{1+r_3} \cdot \ell(A_1) \end{align*} $$
$$ \begin{align*} \ell(h_1(A_1 \cup A_2)) + \ell(h_2(A_1)) &> \alpha\cdot(\ell(A_1) + \ell(A_2)) + \alpha \cdot \ell(A_1) = \alpha\cdot(2\ell(A_1) + \ell(A_2)) \\ & = \alpha\cdot\Big(2 + \frac{1}{1+r_3}\Big) \ell(A_1) = \alpha \cdot \frac{3+2r_3}{1+r_3} \cdot \ell(A_1) \end{align*} $$and
 $$ \begin{align*} \ell(h_2(A_2)) + \ell(h_3(A_1 \cup A_2)) &> \alpha \cdot \ell(A_2) + \alpha\cdot(\ell(A_1) + \ell(A_2)) = \alpha\cdot(\ell(A_1) + 2\ell(A_2)) \\ & = \alpha\cdot\left((1+r_3) + 2\right) \ell(A_2) = \alpha \cdot (3+r_3) \cdot \ell(A_2). \end{align*} $$
$$ \begin{align*} \ell(h_2(A_2)) + \ell(h_3(A_1 \cup A_2)) &> \alpha \cdot \ell(A_2) + \alpha\cdot(\ell(A_1) + \ell(A_2)) = \alpha\cdot(\ell(A_1) + 2\ell(A_2)) \\ & = \alpha\cdot\left((1+r_3) + 2\right) \ell(A_2) = \alpha \cdot (3+r_3) \cdot \ell(A_2). \end{align*} $$Because ![]() $\alpha> 1/3$, we can choose
$\alpha> 1/3$, we can choose ![]() $\epsilon _3$ sufficiently small such that
$\epsilon _3$ sufficiently small such that
Because ![]() $h_1(A_1 \cup A_2)$ and
$h_1(A_1 \cup A_2)$ and ![]() $h_2(A_1)$ share the respective endpoints of
$h_2(A_1)$ share the respective endpoints of ![]() $A_1$, it follows that
$A_1$, it follows that ![]() $A_1 \subseteq h_1(A_1 \cup A_2) \cup h_2(A_1)$. Similarly, we find that
$A_1 \subseteq h_1(A_1 \cup A_2) \cup h_2(A_1)$. Similarly, we find that ![]() $A_2 \subseteq h_3(A_1 \cup A_2) \cup h_2(A_2)$. It follows that
$A_2 \subseteq h_3(A_1 \cup A_2) \cup h_2(A_2)$. It follows that ![]() $A = h_1(A) \cup h_2(A) \cup h_3(A)$. Finally, let
$A = h_1(A) \cup h_2(A) \cup h_3(A)$. Finally, let  $s = h_3^N(1)$, where we have taken N sufficiently large such that
$s = h_3^N(1)$, where we have taken N sufficiently large such that ![]() $s \in A$, and consider
$s \in A$, and consider
 $$ \begin{align*} \mathcal{S} = \left\{(h_{i_1} \circ \cdots \circ h_{i_l})(s): l \in \mathbb{Z}_{\geq 1} \text{ and } i_1,\dots,i_l \in \{1,2,3\}\right\}. \end{align*} $$
$$ \begin{align*} \mathcal{S} = \left\{(h_{i_1} \circ \cdots \circ h_{i_l})(s): l \in \mathbb{Z}_{\geq 1} \text{ and } i_1,\dots,i_l \in \{1,2,3\}\right\}. \end{align*} $$It follows from Corollary 20 that ![]() $\mathcal {S}$ is a dense subset of A. Every
$\mathcal {S}$ is a dense subset of A. Every ![]() $r \in \mathcal {S}$ is implemented by a rooted tree in
$r \in \mathcal {S}$ is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree
$\mathcal {T}_{d+1}$ with root degree ![]() $m+2k \leq d$. Finally, we let
$m+2k \leq d$. Finally, we let
and we find, because ![]() $|f_d'(z)|> 1$ for all
$|f_d'(z)|> 1$ for all ![]() $z \in \mathbb {S}-\{1\}$, that
$z \in \mathbb {S}-\{1\}$, that ![]() $\mathcal {S}_2$ is dense in
$\mathcal {S}_2$ is dense in ![]() $\mathbb {S}$. Every
$\mathbb {S}$. Every ![]() $r \in \mathcal {S}_2$ is implemented by a tree in
$r \in \mathcal {S}_2$ is implemented by a tree in ![]() $\mathcal {T}_{d+1}$. This shows that in this case item (1) of the lemma holds.
$\mathcal {T}_{d+1}$. This shows that in this case item (1) of the lemma holds.
Lemma 31. Suppose ![]() $d \in \mathbb {Z}_{\geq 5}$,
$d \in \mathbb {Z}_{\geq 5}$,  $b \in \big (0, \frac {d-1}{d+1}\big ] \cap \mathbb {Q}$,
$b \in \big (0, \frac {d-1}{d+1}\big ] \cap \mathbb {Q}$, ![]() $\lambda \in \mathbb {S}_{\mathbb {Q}}\setminus \{\pm 1\}$ and
$\lambda \in \mathbb {S}_{\mathbb {Q}}\setminus \{\pm 1\}$ and ![]() $\xi \in \Lambda _3(b)\cap \mathbb {S}_{\mathbb {Q}}$ with
$\xi \in \Lambda _3(b)\cap \mathbb {S}_{\mathbb {Q}}$ with ![]() $\xi \neq \pm 1$.
$\xi \neq \pm 1$.
Suppose there is a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-5$ and field
$d-5$ and field ![]() $\xi $. Then the set of fields implemented by rooted trees in
$\xi $. Then the set of fields implemented by rooted trees in ![]() $\mathcal {T}_{d+1}$ is dense in
$\mathcal {T}_{d+1}$ is dense in ![]() $\mathbb {S}$.
$\mathbb {S}$.
Proof. It follows from Lemma 16 that there is ![]() $\sigma \in \mathbb {S}$ with
$\sigma \in \mathbb {S}$ with ![]() $|f_{3}'(\sigma )|> 1$ together with a sequence
$|f_{3}'(\sigma )|> 1$ together with a sequence ![]() $\{\zeta _n\}_{n \geq 1}$ accumulating on
$\{\zeta _n\}_{n \geq 1}$ accumulating on ![]() $\sigma $ such that every
$\sigma $ such that every ![]() $\zeta _n$ is the field implemented by a tree in
$\zeta _n$ is the field implemented by a tree in ![]() $\mathcal {T}_{d+1}$ whose root degree is bounded by
$\mathcal {T}_{d+1}$ whose root degree is bounded by ![]() $(d-5)+3 = d-2$. We can now apply Lemma 30 with
$(d-5)+3 = d-2$. We can now apply Lemma 30 with ![]() $k = 1$. It follows that either the set of fields implemented by rooted trees in
$k = 1$. It follows that either the set of fields implemented by rooted trees in ![]() $\mathcal {T}_{d+1}$ is dense in
$\mathcal {T}_{d+1}$ is dense in ![]() $\mathbb {S}$ or there is a tree in
$\mathbb {S}$ or there is a tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $(d-2)+1 = d-1$ and field
$(d-2)+1 = d-1$ and field ![]() $\zeta \in \operatorname {\mathrm {Arc}}{(\lambda _1,\overline {\lambda _1})}\setminus \{-1\}$. We conclude from Lemma 14 that
$\zeta \in \operatorname {\mathrm {Arc}}{(\lambda _1,\overline {\lambda _1})}\setminus \{-1\}$. We conclude from Lemma 14 that ![]() $f_{\zeta ,1}$ is conjugate to an irrational rotation and thus the orbit
$f_{\zeta ,1}$ is conjugate to an irrational rotation and thus the orbit  $\{f_{\zeta ,1}^n(1)\}_{n \geq 1}$ is dense in
$\{f_{\zeta ,1}^n(1)\}_{n \geq 1}$ is dense in ![]() $\mathbb {S}$. Every element in this orbit is implemented by a rooted tree in
$\mathbb {S}$. Every element in this orbit is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$, and thus we are done.
$\mathcal {T}_{d+1}$, and thus we are done.
6 Proof of Lemma 17
We are now ready to prove Lemma 17, which we restate here for convenience.
Lemma 17 . Let ![]() $k,d\in \mathbb {Z}_{\geq 2}$ with
$k,d\in \mathbb {Z}_{\geq 2}$ with ![]() $k \leq d$,
$k \leq d$,  $b \in \big (\frac {d-2}{d}, \frac {d-1}{d+1}\big ]\cap \mathbb {Q}$ and
$b \in \big (\frac {d-2}{d}, \frac {d-1}{d+1}\big ]\cap \mathbb {Q}$ and ![]() $\lambda \in \mathbb {S}_{\mathbb {Q}}\setminus \{\pm 1\}$. Suppose there exists a rooted tree in
$\lambda \in \mathbb {S}_{\mathbb {Q}}\setminus \{\pm 1\}$. Suppose there exists a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-k$ that implements a field
$d-k$ that implements a field ![]() $\xi \neq 1$ with the property that
$\xi \neq 1$ with the property that ![]() $|f_k'(\xi )|\geq 1$ and
$|f_k'(\xi )|\geq 1$ and  $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _{\left \lfloor k/2\right \rfloor }},\lambda _{\left \lfloor k/2\right \rfloor }]}$. Then the set of fields implemented by trees in
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _{\left \lfloor k/2\right \rfloor }},\lambda _{\left \lfloor k/2\right \rfloor }]}$. Then the set of fields implemented by trees in ![]() $\mathcal {T}_{d+1}$ is dense in
$\mathcal {T}_{d+1}$ is dense in ![]() $\mathbb {S}$.
$\mathbb {S}$.
Proof. The proof consists of a careful case analysis. We give a seperate argument first for when k is a power of two and for when ![]() $k + 1$ is a power of 2 and then for each value of k within the set
$k + 1$ is a power of 2 and then for each value of k within the set ![]() $\{5,6,9,10,11,12,13,14,17\}$ and, lastly, we prove the statement for all other k.
$\{5,6,9,10,11,12,13,14,17\}$ and, lastly, we prove the statement for all other k.
We remark that in some cases we will show that the set of fields implemented by rooted trees in ![]() $\mathcal {T}_{d+1}$ is dense in an arc A of the circle. Since b is such that
$\mathcal {T}_{d+1}$ is dense in an arc A of the circle. Since b is such that ![]() $|f_d'(z)|>1$ for all
$|f_d'(z)|>1$ for all ![]() $z \in \mathbb {S}\setminus \{1\}$ (see (2) of Lemma 10), it follows that for all arcs A there is an
$z \in \mathbb {S}\setminus \{1\}$ (see (2) of Lemma 10), it follows that for all arcs A there is an ![]() $N\geq 1$ such that
$N\geq 1$ such that  $f_{\lambda ,d}^N(A) = \mathbb {S}$. Density of fields in the whole unit circle therefore follows from density in A.
$f_{\lambda ,d}^N(A) = \mathbb {S}$. Density of fields in the whole unit circle therefore follows from density in A.
First suppose ![]() $k = 2^m$ is a power of 2. In this case,
$k = 2^m$ is a power of 2. In this case, ![]() $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _{2^{m-1}}},\lambda _{2^{m-1}}]}\setminus \{1\}$ is implemented by a rooted tree in
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _{2^{m-1}}},\lambda _{2^{m-1}}]}\setminus \{1\}$ is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-2^m$ and with
$d-2^m$ and with ![]() $|f_{2^m}'(\xi )| \geq 1$. Let
$|f_{2^m}'(\xi )| \geq 1$. Let ![]() $\xi _2 = f_{\xi ,1}(\xi )$. By item (v) of Lemma 10, we have
$\xi _2 = f_{\xi ,1}(\xi )$. By item (v) of Lemma 10, we have ![]() $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _{1}},\lambda _{1}]}\setminus \{1\}$ and hence
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _{1}},\lambda _{1}]}\setminus \{1\}$ and hence ![]() $\xi _2\neq \xi $ by item (iv) of the same lemma. Moreover, by Lemma 4,
$\xi _2\neq \xi $ by item (iv) of the same lemma. Moreover, by Lemma 4, ![]() $\xi _2$ is the field of a rooted tree in
$\xi _2$ is the field of a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-(2^m - 1)$. If
$d-(2^m - 1)$. If ![]() $\xi _2\in \operatorname {\mathrm {Arc}}{(\lambda _{2^{m-1}},\overline {\lambda _{2^{m-1}}})}$, then the desired result follows from Lemma 25. Otherwise,
$\xi _2\in \operatorname {\mathrm {Arc}}{(\lambda _{2^{m-1}},\overline {\lambda _{2^{m-1}}})}$, then the desired result follows from Lemma 25. Otherwise, ![]() $\xi ,\xi _2 \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _{2^{m-1}}},\lambda _{2^{m-1}}]}$ and the result follows from applying Lemma 22 to these two parameters.
$\xi ,\xi _2 \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _{2^{m-1}}},\lambda _{2^{m-1}}]}$ and the result follows from applying Lemma 22 to these two parameters.
Now suppose ![]() $k+1$ is a power of 2, so
$k+1$ is a power of 2, so ![]() $k = 2^{m+1} - 1$ for
$k = 2^{m+1} - 1$ for ![]() $m\geq 1$. In this case,
$m\geq 1$. In this case, ![]() $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _{2^{m}-1}},\lambda _{2^{m}-1}]} \setminus \{1\}$ is implemented by a rooted tree in
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _{2^{m}-1}},\lambda _{2^{m}-1}]} \setminus \{1\}$ is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-(2^{m+1} - 1)$ and with
$d-(2^{m+1} - 1)$ and with ![]() $|f_{2^{m+1} - 1}'(\xi )| \geq 1$. If
$|f_{2^{m+1} - 1}'(\xi )| \geq 1$. If ![]() $\xi \in \operatorname {\mathrm {Arc}}{(\lambda _{2^{m}},\overline {\lambda _{2^{m}}})}$, the result follows from Lemma 25. Otherwise, if
$\xi \in \operatorname {\mathrm {Arc}}{(\lambda _{2^{m}},\overline {\lambda _{2^{m}}})}$, the result follows from Lemma 25. Otherwise, if ![]() $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _{2^m}},\lambda _{2^m}]}$, the result follows from Lemma 21.
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _{2^m}},\lambda _{2^m}]}$, the result follows from Lemma 21.
We now continue with the list of individual cases.
![]() $\mathbf {k = 5:}$ In this case,
$\mathbf {k = 5:}$ In this case, ![]() $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _2},\lambda _2]}\setminus \{1\}$ is the field of a rooted tree with root degree at most
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _2},\lambda _2]}\setminus \{1\}$ is the field of a rooted tree with root degree at most ![]() $d-5$ and with
$d-5$ and with ![]() $|f_5'(\xi )| \geq 1$. If
$|f_5'(\xi )| \geq 1$. If ![]() $\xi \in \operatorname {\mathrm {Arc}}{(\lambda _3,\overline {\lambda _3})}$, the result follows from Lemma 31. Otherwise, if
$\xi \in \operatorname {\mathrm {Arc}}{(\lambda _3,\overline {\lambda _3})}$, the result follows from Lemma 31. Otherwise, if ![]() $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _3},\lambda _3]}$, the result follows from Lemma 21.
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _3},\lambda _3]}$, the result follows from Lemma 21.
![]() $\mathbf {k = 6:}$ In this case,
$\mathbf {k = 6:}$ In this case, ![]() $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _3},\lambda _3]}\setminus \{1\}$ is implemented by a rooted tree in
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _3},\lambda _3]}\setminus \{1\}$ is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-6$ and with
$d-6$ and with ![]() $|f_6'(\xi )| \geq 1$. Let
$|f_6'(\xi )| \geq 1$. Let ![]() $\xi _2 = f_{\xi ,1}(\xi )$, which is the field of a rooted tree in
$\xi _2 = f_{\xi ,1}(\xi )$, which is the field of a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-5$. If
$d-5$. If ![]() $\xi _2\in \operatorname {\mathrm {Arc}}(\lambda _3,\overline {\lambda _3})$, then the result follows from Lemma 31. Otherwise,
$\xi _2\in \operatorname {\mathrm {Arc}}(\lambda _3,\overline {\lambda _3})$, then the result follows from Lemma 31. Otherwise, ![]() $\xi ,\xi _2 \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _{3}},\lambda _{3}]}$ and the result follows from applying Lemma 22 to these two parameters.
$\xi ,\xi _2 \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _{3}},\lambda _{3}]}$ and the result follows from applying Lemma 22 to these two parameters.
![]() $\mathbf {k = 9:}$ In this case,
$\mathbf {k = 9:}$ In this case, ![]() $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _4},\lambda _4]}\setminus \{1\}$ is implemented by a rooted tree in
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _4},\lambda _4]}\setminus \{1\}$ is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-9$ and with
$d-9$ and with ![]() $|f_9'(\xi )| \geq 1$. Consider the orbit
$|f_9'(\xi )| \geq 1$. Consider the orbit  $\{f_{\xi ,1}^n(\xi ): n \geq 1\}$. The elements of this orbit are implemented by trees in
$\{f_{\xi ,1}^n(\xi ): n \geq 1\}$. The elements of this orbit are implemented by trees in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-8$ and they accumulate on
$d-8$ and they accumulate on ![]() $R_1(\xi )$. Note that
$R_1(\xi )$. Note that ![]() $|f_9'(R_1(\xi ))|> 1$. It follows from Lemma 30 that either we obtain the desired density or we obtain a rooted tree with root degree at most
$|f_9'(R_1(\xi ))|> 1$. It follows from Lemma 30 that either we obtain the desired density or we obtain a rooted tree with root degree at most ![]() $(d-8) + 3 = d-5$ that implements a field in
$(d-8) + 3 = d-5$ that implements a field in ![]() $\operatorname {\mathrm {Arc}}{(\lambda _3,\overline {\lambda _3})}$. In this latter case, the result follows from applying Lemma 31 to this tree.
$\operatorname {\mathrm {Arc}}{(\lambda _3,\overline {\lambda _3})}$. In this latter case, the result follows from applying Lemma 31 to this tree.
![]() $\mathbf {k = 10:}$ In this case,
$\mathbf {k = 10:}$ In this case, ![]() $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _5},\lambda _5]}\setminus \{1\}$ is implemented by a rooted tree in
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _5},\lambda _5]}\setminus \{1\}$ is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-10$ and with
$d-10$ and with ![]() $|f_{10}'(\xi )| \geq 1$. Then it follows from Lemma 23 that the orbit of
$|f_{10}'(\xi )| \geq 1$. Then it follows from Lemma 23 that the orbit of ![]() $1$ under the action of the semigroup generated by
$1$ under the action of the semigroup generated by ![]() $f_{\xi ,3},f_{\xi ,4}$ and
$f_{\xi ,3},f_{\xi ,4}$ and ![]() $f_{\xi ,5}$ is dense in an arc of
$f_{\xi ,5}$ is dense in an arc of ![]() $\mathbb {S}$, in which case the result follows. Or we can conclude that
$\mathbb {S}$, in which case the result follows. Or we can conclude that  $|f_5'(R_5(\xi ))|> \frac {43}{50}$. In that case, we consider the orbit
$|f_5'(R_5(\xi ))|> \frac {43}{50}$. In that case, we consider the orbit  $\mathcal {R}=\{f_{\xi ,5}^n(\xi ):n \geq 1\}$. This orbit accumulates on
$\mathcal {R}=\{f_{\xi ,5}^n(\xi ):n \geq 1\}$. This orbit accumulates on ![]() $R_5(\xi )$ and every element is implemented by a rooted tree with root degree at most
$R_5(\xi )$ and every element is implemented by a rooted tree with root degree at most ![]() $d-10+5 = d-5$. If
$d-10+5 = d-5$. If ![]() $R_5(\xi ) \in \operatorname {\mathrm {Arc}}{(\lambda _3,\overline {\lambda _3})}$, then there are also fields
$R_5(\xi ) \in \operatorname {\mathrm {Arc}}{(\lambda _3,\overline {\lambda _3})}$, then there are also fields ![]() $\zeta \in \mathcal {R}$ with
$\zeta \in \mathcal {R}$ with ![]() $\zeta \in \operatorname {\mathrm {Arc}}{(\lambda _3,\overline {\lambda _3})}$. In that case, we can apply Lemma 31 to obtain density of the fields. Otherwise, if
$\zeta \in \operatorname {\mathrm {Arc}}{(\lambda _3,\overline {\lambda _3})}$. In that case, we can apply Lemma 31 to obtain density of the fields. Otherwise, if ![]() $R_5(\xi ) \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _3},\lambda _3]}$, then we can find
$R_5(\xi ) \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _3},\lambda _3]}$, then we can find ![]() $\zeta _1,\zeta _2 \in \mathcal {R}$ such that
$\zeta _1,\zeta _2 \in \mathcal {R}$ such that ![]() $\zeta _1,\zeta _2 \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _3},\lambda _3]}$ are distinct, lie in the same half-plane and
$\zeta _1,\zeta _2 \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _3},\lambda _3]}$ are distinct, lie in the same half-plane and  $|f_5'(\zeta _i)|> \frac {43}{50}$ for
$|f_5'(\zeta _i)|> \frac {43}{50}$ for ![]() $i = 1,2$. It follows that for both fields
$i = 1,2$. It follows that for both fields ![]() $\zeta _i$ we have
$\zeta _i$ we have
 $$ \begin{align*} |f_6'(R_3(\zeta_i))|> |f_6'(\zeta_i)| = \frac{6}{5} \cdot |f_5'(\zeta_i)| > \frac{6}{5} \cdot \frac{43}{50} = \frac{129}{125} > 1. \end{align*} $$
$$ \begin{align*} |f_6'(R_3(\zeta_i))|> |f_6'(\zeta_i)| = \frac{6}{5} \cdot |f_5'(\zeta_i)| > \frac{6}{5} \cdot \frac{43}{50} = \frac{129}{125} > 1. \end{align*} $$Density of the fields now follows from applying Lemma 22 to ![]() $\zeta _1$ and
$\zeta _1$ and ![]() $\zeta _2$.
$\zeta _2$.
![]() $\mathbf {k = 11:}$ In this case,
$\mathbf {k = 11:}$ In this case, ![]() $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _5},\lambda _5]}\setminus \{1\}$ is implemented by a rooted tree in
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _5},\lambda _5]}\setminus \{1\}$ is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-11$ and with
$d-11$ and with ![]() $|f_{11}'(\xi )| \geq 1$. If
$|f_{11}'(\xi )| \geq 1$. If ![]() $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _6},\lambda _6]}$, the result follows from Lemma 21. Otherwise, if
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _6},\lambda _6]}$, the result follows from Lemma 21. Otherwise, if ![]() $\xi \in \operatorname {\mathrm {Arc}}{(\lambda _6,\overline {\lambda _6})}$, we apply Lemma 16 to find a parameter
$\xi \in \operatorname {\mathrm {Arc}}{(\lambda _6,\overline {\lambda _6})}$, we apply Lemma 16 to find a parameter ![]() $\sigma \in \mathbb {S}$ with
$\sigma \in \mathbb {S}$ with ![]() $|f_6'(\sigma )|>1$ together with a sequence of fields
$|f_6'(\sigma )|>1$ together with a sequence of fields ![]() $\{\zeta _n\}_{n \geq 1}$ accumulating on
$\{\zeta _n\}_{n \geq 1}$ accumulating on ![]() $\sigma $ such that every
$\sigma $ such that every ![]() $\zeta _n$ is implemented by a rooted tree in
$\zeta _n$ is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ whose root degree is at most
$\mathcal {T}_{d+1}$ whose root degree is at most ![]() $d-11+6 = d-5$. If there is any
$d-11+6 = d-5$. If there is any ![]() $\zeta _n \in \operatorname {\mathrm {Arc}}{(\lambda _3,\overline {\lambda _3})}$, then density of the fields in the circle follows from Lemma 31. Otherwise, the sequence accumulates on
$\zeta _n \in \operatorname {\mathrm {Arc}}{(\lambda _3,\overline {\lambda _3})}$, then density of the fields in the circle follows from Lemma 31. Otherwise, the sequence accumulates on ![]() $\sigma $ from inside
$\sigma $ from inside ![]() $\operatorname {\mathrm {Arc}}{[\overline {\lambda _3},\lambda _3]}$ and thus we can find
$\operatorname {\mathrm {Arc}}{[\overline {\lambda _3},\lambda _3]}$ and thus we can find ![]() $\zeta _{n_1},\zeta _{n_2} \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _3},\lambda _3]}$ that are distinct, lie in the same half-plane and have the property that
$\zeta _{n_1},\zeta _{n_2} \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _3},\lambda _3]}$ that are distinct, lie in the same half-plane and have the property that ![]() $|f_6'(\zeta _i)|> 1$ for
$|f_6'(\zeta _i)|> 1$ for ![]() $i = 1,2$. The desired density now follows from applying Lemma 22 to
$i = 1,2$. The desired density now follows from applying Lemma 22 to ![]() $\zeta _1$ and
$\zeta _1$ and ![]() $\zeta _2$.
$\zeta _2$.
![]() $\mathbf {k = 12:}$ In this case,
$\mathbf {k = 12:}$ In this case, ![]() $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _6},\lambda _6]}\setminus \{1\}$ is implemented by a rooted tree in
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _6},\lambda _6]}\setminus \{1\}$ is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-12$ and with
$d-12$ and with ![]() $|f_{12}'(\xi )| \geq 1$. This case can be done in a very similar way to the
$|f_{12}'(\xi )| \geq 1$. This case can be done in a very similar way to the ![]() $k=9$ case. Consider the orbit
$k=9$ case. Consider the orbit  $\{f_{\xi ,1}^n(\xi ): n \geq 1\}$. The elements of this orbit are fields of trees in
$\{f_{\xi ,1}^n(\xi ): n \geq 1\}$. The elements of this orbit are fields of trees in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-11$ and they accumulate on
$d-11$ and they accumulate on ![]() $R_1(\xi )$. Note that
$R_1(\xi )$. Note that ![]() $|f_{12}'(R_1(\xi ))|> 1$. It follows from Lemma 30 that either we obtain the desired density or we obtain a rooted tree with root degree at most
$|f_{12}'(R_1(\xi ))|> 1$. It follows from Lemma 30 that either we obtain the desired density or we obtain a rooted tree with root degree at most ![]() $(d-11) + 4 = d-7$ and field in
$(d-11) + 4 = d-7$ and field in ![]() $\operatorname {\mathrm {Arc}}{(\lambda _4,\overline {\lambda _4})}$. In this latter case, the result follows from applying Lemma 25 to this tree.
$\operatorname {\mathrm {Arc}}{(\lambda _4,\overline {\lambda _4})}$. In this latter case, the result follows from applying Lemma 25 to this tree.
![]() $\mathbf {k = 13:}$ In this case,
$\mathbf {k = 13:}$ In this case, ![]() $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _6},\lambda _6]}\setminus \{1\}$ is implemented by a rooted tree in
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _6},\lambda _6]}\setminus \{1\}$ is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-13$ and with
$d-13$ and with ![]() $|f_{13}'(\xi )| \geq 1$. Then it follows from Lemma 23 that the orbit of
$|f_{13}'(\xi )| \geq 1$. Then it follows from Lemma 23 that the orbit of ![]() $1$ under the action of the semigroup generated by
$1$ under the action of the semigroup generated by ![]() $f_{\xi ,4},f_{\xi ,5}$ and
$f_{\xi ,4},f_{\xi ,5}$ and ![]() $f_{\xi ,6}$ is dense in an arc of
$f_{\xi ,6}$ is dense in an arc of ![]() $\mathbb {S}$, in which case the result follows. Or we can conclude that
$\mathbb {S}$, in which case the result follows. Or we can conclude that  $|f_6'(R_6(\xi ))|> \frac {10}{13}$. In that case, we consider the orbit
$|f_6'(R_6(\xi ))|> \frac {10}{13}$. In that case, we consider the orbit  $\mathcal {R}=\{f_{\xi ,6}^n(\xi ):n \geq 1\}$. This orbit accumulates on
$\mathcal {R}=\{f_{\xi ,6}^n(\xi ):n \geq 1\}$. This orbit accumulates on ![]() $R_6(\xi )$ and every element is implemented by a rooted tree in
$R_6(\xi )$ and every element is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-13+6 = d-7$. If
$d-13+6 = d-7$. If ![]() $R_6(\xi ) \in \operatorname {\mathrm {Arc}}{(\lambda _4,\overline {\lambda _4})}$, then there is also a field
$R_6(\xi ) \in \operatorname {\mathrm {Arc}}{(\lambda _4,\overline {\lambda _4})}$, then there is also a field ![]() $\zeta \in \mathcal {R}$ with
$\zeta \in \mathcal {R}$ with ![]() $\zeta \in \operatorname {\mathrm {Arc}}{(\lambda _4,\overline {\lambda _4})}$. In that case, we can apply Lemma 25 to obtain density of the fields. Otherwise, if
$\zeta \in \operatorname {\mathrm {Arc}}{(\lambda _4,\overline {\lambda _4})}$. In that case, we can apply Lemma 25 to obtain density of the fields. Otherwise, if ![]() $R_6(\xi ) \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _4},\lambda _4]}$, then we can find
$R_6(\xi ) \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _4},\lambda _4]}$, then we can find ![]() $\zeta _1,\zeta _2 \in \mathcal {R}$ such that
$\zeta _1,\zeta _2 \in \mathcal {R}$ such that ![]() $\zeta _1,\zeta _2 \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _4},\lambda _4]}$ are distinct, lie in the same half-plane and
$\zeta _1,\zeta _2 \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _4},\lambda _4]}$ are distinct, lie in the same half-plane and  $|f_6'(\zeta _i)|> \frac {10}{13}$ for
$|f_6'(\zeta _i)|> \frac {10}{13}$ for ![]() $i = 1,2$. It follows that for both fields
$i = 1,2$. It follows that for both fields ![]() $\zeta _i$ we have
$\zeta _i$ we have
 $$ \begin{align*} |f_8'(R_4(\zeta_i))|> |f_8'(\zeta_i)| = \frac{8}{6} \cdot |f_6'(\zeta_i)| > \frac{8}{6} \cdot \frac{10}{13} = \frac{40}{39} > 1. \end{align*} $$
$$ \begin{align*} |f_8'(R_4(\zeta_i))|> |f_8'(\zeta_i)| = \frac{8}{6} \cdot |f_6'(\zeta_i)| > \frac{8}{6} \cdot \frac{10}{13} = \frac{40}{39} > 1. \end{align*} $$Density of the fields now follows from applying Lemma 22 to ![]() $\zeta _1$ and
$\zeta _1$ and ![]() $\zeta _2$.
$\zeta _2$.
![]() $\mathbf {k = 14:}$ In this case,
$\mathbf {k = 14:}$ In this case, ![]() $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _7},\lambda _7]}\setminus \{1\}$ is implemented by a rooted tree in
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _7},\lambda _7]}\setminus \{1\}$ is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-14$ and with
$d-14$ and with ![]() $|f_{14}'(\xi )| \geq 1$. Then it follows from Lemma 23 that the orbit of
$|f_{14}'(\xi )| \geq 1$. Then it follows from Lemma 23 that the orbit of ![]() $1$ under the action of the semigroup generated by
$1$ under the action of the semigroup generated by ![]() $f_{\xi ,5},f_{\xi ,6}$ and
$f_{\xi ,5},f_{\xi ,6}$ and ![]() $f_{\xi ,7}$ is dense in an arc of
$f_{\xi ,7}$ is dense in an arc of ![]() $\mathbb {S}$, in which case the result follows. Or we can conclude that
$\mathbb {S}$, in which case the result follows. Or we can conclude that  $|f_7'(R_7(\xi ))|> \frac {89}{98}$. In that case, we consider the orbit
$|f_7'(R_7(\xi ))|> \frac {89}{98}$. In that case, we consider the orbit  $\mathcal {R}=\{f_{\xi ,7}^n(\xi ):n \geq 1\}$. This orbit accumulates on
$\mathcal {R}=\{f_{\xi ,7}^n(\xi ):n \geq 1\}$. This orbit accumulates on ![]() $R_7(\xi )$ and every element is implemented by a rooted tree in
$R_7(\xi )$ and every element is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-14+7 = d-7$. If
$d-14+7 = d-7$. If ![]() $R_7(\xi ) \in \operatorname {\mathrm {Arc}}{(\lambda _4,\overline {\lambda _4})}$, then there is also a field
$R_7(\xi ) \in \operatorname {\mathrm {Arc}}{(\lambda _4,\overline {\lambda _4})}$, then there is also a field ![]() $\zeta \in \mathcal {R}$ with
$\zeta \in \mathcal {R}$ with ![]() $\zeta \in \operatorname {\mathrm {Arc}}{(\lambda _4,\overline {\lambda _4})}$. In that case, we can apply Lemma 25 to obtain density of the fields. Otherwise, if
$\zeta \in \operatorname {\mathrm {Arc}}{(\lambda _4,\overline {\lambda _4})}$. In that case, we can apply Lemma 25 to obtain density of the fields. Otherwise, if ![]() $R_7(\xi ) \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _4},\lambda _4]}$, then we can find
$R_7(\xi ) \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _4},\lambda _4]}$, then we can find ![]() $\zeta _1,\zeta _2 \in \mathcal {R}$ such that
$\zeta _1,\zeta _2 \in \mathcal {R}$ such that ![]() $\zeta _1,\zeta _2 \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _4},\lambda _4]}$ are distinct, lie in the same half-plane and
$\zeta _1,\zeta _2 \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _4},\lambda _4]}$ are distinct, lie in the same half-plane and  $|f_7'(\zeta _i)|> \frac {89}{98}$ for
$|f_7'(\zeta _i)|> \frac {89}{98}$ for ![]() $i = 1,2$. It follows that for both fields
$i = 1,2$. It follows that for both fields ![]() $\zeta _i$ we have
$\zeta _i$ we have
 $$ \begin{align*} |f_8'(R_4(\zeta_i))|> |f_8'(\zeta_i)| = \frac{8}{7} \cdot |f_7'(\zeta_i)| > \frac{8}{7} \cdot \frac{89}{98} = \frac{356}{343} > 1. \end{align*} $$
$$ \begin{align*} |f_8'(R_4(\zeta_i))|> |f_8'(\zeta_i)| = \frac{8}{7} \cdot |f_7'(\zeta_i)| > \frac{8}{7} \cdot \frac{89}{98} = \frac{356}{343} > 1. \end{align*} $$Density of the fields now follows from applying Lemma 22 to ![]() $\zeta _1$ and
$\zeta _1$ and ![]() $\zeta _2$.
$\zeta _2$.
![]() $\mathbf {k = 17:}$ In this case,
$\mathbf {k = 17:}$ In this case, ![]() $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _8},\lambda _8]}\setminus \{1\}$ is implemented by a rooted tree in
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _8},\lambda _8]}\setminus \{1\}$ is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-17$ and with
$d-17$ and with ![]() $|f_{17}'(\xi )| \geq 1$. If
$|f_{17}'(\xi )| \geq 1$. If ![]() $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _9},\lambda _9]}$, the result follows from Lemma 21; therefore, we assume that
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _9},\lambda _9]}$, the result follows from Lemma 21; therefore, we assume that ![]() $\xi \in \operatorname {\mathrm {Arc}}{(\lambda _9, \overline {\lambda _9})}$. We apply Lemma 16 to find a parameter
$\xi \in \operatorname {\mathrm {Arc}}{(\lambda _9, \overline {\lambda _9})}$. We apply Lemma 16 to find a parameter ![]() $\sigma \in \mathbb {S}$ with
$\sigma \in \mathbb {S}$ with ![]() $|f_9'(\sigma )|>1$ together with a sequence of fields
$|f_9'(\sigma )|>1$ together with a sequence of fields ![]() $\{\zeta _n\}_{n \geq 1}$ accumulating on
$\{\zeta _n\}_{n \geq 1}$ accumulating on ![]() $\sigma $ such that every
$\sigma $ such that every ![]() $\zeta _n$ is implemented by a rooted tree in
$\zeta _n$ is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ whose root degree is at most
$\mathcal {T}_{d+1}$ whose root degree is at most ![]() $d-17+9= d-8$. It follows from Lemma 30 that we either obtain the required density of fields or there is a tree in
$d-17+9= d-8$. It follows from Lemma 30 that we either obtain the required density of fields or there is a tree in ![]() $\mathcal {T}_{d+1}$ whose root degree is bounded by
$\mathcal {T}_{d+1}$ whose root degree is bounded by ![]() $d-5$ with field inside
$d-5$ with field inside ![]() $\operatorname {\mathrm {Arc}}{(\lambda _3, \overline {\lambda _3})}$. In the latter case, the result follows from Lemma 31.
$\operatorname {\mathrm {Arc}}{(\lambda _3, \overline {\lambda _3})}$. In the latter case, the result follows from Lemma 31.
Finally, we complete the proof for ![]() $k> 17$. In that case, write
$k> 17$. In that case, write ![]() $k = 2m$ if k is even and
$k = 2m$ if k is even and ![]() $k = 2m+1$ if k is odd. Note that
$k = 2m+1$ if k is odd. Note that ![]() $m \geq 9$. We are then given that
$m \geq 9$. We are then given that ![]() $\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _m},\lambda _m]}\setminus \{1\}$ is implemented by a rooted tree in
$\xi \in \operatorname {\mathrm {Arc}}{[\overline {\lambda _m},\lambda _m]}\setminus \{1\}$ is implemented by a rooted tree in ![]() $\mathcal {T}_{d+1}$ with root degree at most
$\mathcal {T}_{d+1}$ with root degree at most ![]() $d-k$ and with
$d-k$ and with ![]() $|f_{k}'(\xi )| \geq 1$. It follows from Corollary 24 that the orbit of
$|f_{k}'(\xi )| \geq 1$. It follows from Corollary 24 that the orbit of ![]() $1$ under the action of the semigroup generated by
$1$ under the action of the semigroup generated by ![]() $f_{\xi ,m-3},f_{\xi ,m-2},f_{\xi ,m-1}$ and
$f_{\xi ,m-3},f_{\xi ,m-2},f_{\xi ,m-1}$ and ![]() $f_{\xi ,m}$ is dense in an arc of
$f_{\xi ,m}$ is dense in an arc of ![]() $\mathbb {S}$ from which our desired conclusion follows. This finishes the proof of Lemma 17.
$\mathbb {S}$ from which our desired conclusion follows. This finishes the proof of Lemma 17.
7 Fast implementation of fields
In this section, we bootstrap Theorem 6 to obtain fast algorithms for implementing fields which will be important in our reductions. For a number ![]() $\alpha =p/q\in \mathbb {Q}$ with
$\alpha =p/q\in \mathbb {Q}$ with ![]() $\mathrm {gcd}(p,q)=1$, we use size
$\mathrm {gcd}(p,q)=1$, we use size ![]() $(\alpha )$ to denote the total number of bits needed to represent
$(\alpha )$ to denote the total number of bits needed to represent ![]() $p,q$, and we extend this to numbers in
$p,q$, and we extend this to numbers in ![]() $\mathbb {C}_{\mathbb {Q}}$ by adding the sizes of the real and imaginary parts. For
$\mathbb {C}_{\mathbb {Q}}$ by adding the sizes of the real and imaginary parts. For ![]() $\alpha _1,\ldots ,\alpha _t\in \mathbb {C}_{\mathbb {Q}}$, we denote by
$\alpha _1,\ldots ,\alpha _t\in \mathbb {C}_{\mathbb {Q}}$, we denote by ![]() $\mathrm {size}(\alpha _1,\ldots ,\alpha _t)$ the total of the sizes of
$\mathrm {size}(\alpha _1,\ldots ,\alpha _t)$ the total of the sizes of ![]() $\alpha _1,\ldots ,\alpha _t$.
$\alpha _1,\ldots ,\alpha _t$.
Lemma 32. Fix an integer ![]() $\Delta \geq 3$, a rational number
$\Delta \geq 3$, a rational number ![]() $b\in (0,1)$ and
$b\in (0,1)$ and ![]() $\lambda \in \mathbb {S}_{\mathbb {Q}}(\Delta -1,b)$. Then, there is an algorithm, which on input
$\lambda \in \mathbb {S}_{\mathbb {Q}}(\Delta -1,b)$. Then, there is an algorithm, which on input ![]() $\hat {\lambda }\in \mathbb {S}_{\mathbb {Q}}$ and rational
$\hat {\lambda }\in \mathbb {S}_{\mathbb {Q}}$ and rational ![]() $\epsilon>0$, returns in time
$\epsilon>0$, returns in time ![]() $poly(\mathrm {size}(\hat {\lambda },\epsilon )))$ a rooted tree T in
$poly(\mathrm {size}(\hat {\lambda },\epsilon )))$ a rooted tree T in ![]() $\mathcal {T}_\Delta $ with root degree
$\mathcal {T}_\Delta $ with root degree ![]() $1$ that implements a field
$1$ that implements a field ![]() $\lambda '$ such that
$\lambda '$ such that ![]() $|\lambda '-\hat {\lambda }|\leq \epsilon $.
$|\lambda '-\hat {\lambda }|\leq \epsilon $.
Proof of Lemma 32. Let ![]() $d=\Delta -1$. We start by setting up some parameters that will be useful.
$d=\Delta -1$. We start by setting up some parameters that will be useful.
Let ![]() $\lambda _1$ be as in Lemma 10. As
$\lambda _1$ be as in Lemma 10. As ![]() $\tilde {\lambda }$ approaches
$\tilde {\lambda }$ approaches ![]() $\lambda _1$ from inside
$\lambda _1$ from inside ![]() $\operatorname {\mathrm {Arc}}{(1,\lambda _1)}$, we know that
$\operatorname {\mathrm {Arc}}{(1,\lambda _1)}$, we know that ![]() $R_1(\tilde {\lambda })$ approaches
$R_1(\tilde {\lambda })$ approaches ![]() $R_1(\lambda _1)$. Since
$R_1(\lambda _1)$. Since ![]() $|f_1'(R_1(\lambda _1))| = 1$, there must be
$|f_1'(R_1(\lambda _1))| = 1$, there must be ![]() $\tilde {\lambda } \in \operatorname {\mathrm {Arc}}{(1,\lambda _1)}$ such that
$\tilde {\lambda } \in \operatorname {\mathrm {Arc}}{(1,\lambda _1)}$ such that  $|f_1'(R_1(\xi ))| \in (\frac {1}{2},1)$ for all
$|f_1'(R_1(\xi ))| \in (\frac {1}{2},1)$ for all ![]() $\xi \in \operatorname {\mathrm {Arc}}{(\tilde {\lambda },\lambda _1)}$. By Theorem 6, there exist trees
$\xi \in \operatorname {\mathrm {Arc}}{(\tilde {\lambda },\lambda _1)}$. By Theorem 6, there exist trees ![]() $T_1,T_2$ in
$T_1,T_2$ in ![]() $\mathcal {T}_{d+1}$ with root degree
$\mathcal {T}_{d+1}$ with root degree ![]() $1$ and fields
$1$ and fields ![]() $\xi _1,\xi _2 \in \operatorname {\mathrm {Arc}}{(\tilde {\lambda },\lambda _1)} \cap \mathbb {S}_{\mathbb {Q}}$ with
$\xi _1,\xi _2 \in \operatorname {\mathrm {Arc}}{(\tilde {\lambda },\lambda _1)} \cap \mathbb {S}_{\mathbb {Q}}$ with ![]() $\text {Arg}(\xi _1) < \text {Arg}(\xi _2)$. Because the map
$\text {Arg}(\xi _1) < \text {Arg}(\xi _2)$. Because the map ![]() $\xi \mapsto R_1(\xi )$ is orientation preserving with nonzero derivative, we have
$\xi \mapsto R_1(\xi )$ is orientation preserving with nonzero derivative, we have ![]() $\text {Arg}(R_1(\xi _1)) < \text {Arg}(R_1(\xi _2))$. For
$\text {Arg}(R_1(\xi _1)) < \text {Arg}(R_1(\xi _2))$. For ![]() $i\in \{1,2\}$, the fixed point
$i\in \{1,2\}$, the fixed point ![]() $R_1(\xi _i)$ is a solution to the quadratic equation
$R_1(\xi _i)$ is a solution to the quadratic equation ![]() $\xi _i (z+b) = z (b z + 1)$ and hence we can approximate it with any desired rational precision
$\xi _i (z+b) = z (b z + 1)$ and hence we can approximate it with any desired rational precision ![]() $\tau>0$ in time
$\tau>0$ in time ![]() $poly(\mathrm {size}(\tau ))$.
$poly(\mathrm {size}(\tau ))$.
Let ![]() $I = \operatorname {\mathrm {Arc}}(R_1(\xi _1),R_1(\xi _2))$ and note that this arc is contained in the upper half-plane. We will show that the arc I gets mapped onto
$I = \operatorname {\mathrm {Arc}}(R_1(\xi _1),R_1(\xi _2))$ and note that this arc is contained in the upper half-plane. We will show that the arc I gets mapped onto ![]() $\mathbb {S}$ in a fixed number of applications of
$\mathbb {S}$ in a fixed number of applications of ![]() $f_{\lambda ,d}$. The idea of the algorithm is then to find a small enough neighbourhood of a point in I that gets mapped close to the field that we are trying to (approximately) implement. Then we use that we are able to quickly and accurately approach any value inside I using
$f_{\lambda ,d}$. The idea of the algorithm is then to find a small enough neighbourhood of a point in I that gets mapped close to the field that we are trying to (approximately) implement. Then we use that we are able to quickly and accurately approach any value inside I using ![]() $f_{\xi _1,1}$ and
$f_{\xi _1,1}$ and ![]() $f_{\xi _2,1}$. This algorithm is very similar to the proof of Lemma 19.
$f_{\xi _2,1}$. This algorithm is very similar to the proof of Lemma 19.
We now show that I gets mapped onto ![]() $\mathbb {S}$ in a fixed number of applications of
$\mathbb {S}$ in a fixed number of applications of ![]() $f_{\lambda ,d}$. We first consider the case that
$f_{\lambda ,d}$. We first consider the case that  $b\in (0,\frac {d-1}{d+1}]$. Let
$b\in (0,\frac {d-1}{d+1}]$. Let  $C_1 = \lvert f_{\lambda ,d}'(1) \rvert = d\frac {1-b}{1+b}$ and let
$C_1 = \lvert f_{\lambda ,d}'(1) \rvert = d\frac {1-b}{1+b}$ and let  $C_2 = \lvert f_{\lambda ,d}'(-1) \rvert = d\frac {1+b}{1-b}$. Note that
$C_2 = \lvert f_{\lambda ,d}'(-1) \rvert = d\frac {1+b}{1-b}$. Note that ![]() $C_1$ and
$C_1$ and ![]() $C_2$ are both greater than 1 and that for any
$C_2$ are both greater than 1 and that for any ![]() $z \in \mathbb {S}$ the inequality
$z \in \mathbb {S}$ the inequality  $C_1 \leq \lvert f_{\lambda ,d}'(z) \rvert \leq C_2$ holds (cf. item (i) of Lemma 10). This means that for any circular arc J and integer n we get
$C_1 \leq \lvert f_{\lambda ,d}'(z) \rvert \leq C_2$ holds (cf. item (i) of Lemma 10). This means that for any circular arc J and integer n we get
From this, we deduce that  $f_{\lambda ,d}^N(I)=\mathbb {S}$, where
$f_{\lambda ,d}^N(I)=\mathbb {S}$, where  $N = \big \lceil \tfrac {\log (2\pi /\ell (I))}{\log (C_1)} \big \rceil $.
$N = \big \lceil \tfrac {\log (2\pi /\ell (I))}{\log (C_1)} \big \rceil $.
Next, in case  $b\in (\frac {d-1}{d+1},1)$, we recall the conformal metric
$b\in (\frac {d-1}{d+1},1)$, we recall the conformal metric ![]() $\mu $ from the proof of Lemma 15. Let us denote the length of a circular arc J with respect to this metric by
$\mu $ from the proof of Lemma 15. Let us denote the length of a circular arc J with respect to this metric by ![]() $\text {length}(J)$ and denote
$\text {length}(J)$ and denote ![]() $c=\text {length}(\mathbb {S})$. Since there exists a constant
$c=\text {length}(\mathbb {S})$. Since there exists a constant ![]() $\kappa>1$ such that
$\kappa>1$ such that ![]() $f_{d,\lambda }$ is uniformly expanding on
$f_{d,\lambda }$ is uniformly expanding on ![]() $\mathbb {S}$ with a factor
$\mathbb {S}$ with a factor ![]() $\kappa $ with respect to this metric, it follows that
$\kappa $ with respect to this metric, it follows that  $f_{\lambda ,d}^N(I)=\mathbb {S}$, where
$f_{\lambda ,d}^N(I)=\mathbb {S}$, where  $N = \big \lceil \tfrac {\log (c/\text {length}(I))}{\log (\kappa )} \big \rceil $. Note that the right-hand side of (15) is also valid for
$N = \big \lceil \tfrac {\log (c/\text {length}(I))}{\log (\kappa )} \big \rceil $. Note that the right-hand side of (15) is also valid for  $b\in (\frac {d-1}{d+1},1)$ (with
$b\in (\frac {d-1}{d+1},1)$ (with ![]() $C_2$ defined in the same way).
$C_2$ defined in the same way).
Let ![]() $ x_0, \dots , x_m $ be points such that the clockwise arcs between
$ x_0, \dots , x_m $ be points such that the clockwise arcs between ![]() $x_{i-1}$ and
$x_{i-1}$ and ![]() $x_i$ form a partition of I with
$x_i$ form a partition of I with ![]() $x_0=R_1(\xi _1)$,
$x_0=R_1(\xi _1)$, ![]() $x_m = R_1(\xi _2)$ and chosen so that
$x_m = R_1(\xi _2)$ and chosen so that ![]() $x_1,\ldots , x_{m-1}\in \mathbb {S}_{\mathbb {Q}}$ and the length of an arc between two subsequent points is less than
$x_1,\ldots , x_{m-1}\in \mathbb {S}_{\mathbb {Q}}$ and the length of an arc between two subsequent points is less than  $2\pi /C_2^N$. In this way, we ensure that these arcs are not mapped onto the whole circle by N applications of
$2\pi /C_2^N$. In this way, we ensure that these arcs are not mapped onto the whole circle by N applications of ![]() $f_{\lambda ,d}$ and thus each arc is bijectively mapped to an arc on the unit circle by
$f_{\lambda ,d}$ and thus each arc is bijectively mapped to an arc on the unit circle by  $f_{\lambda ,d}^N$.
$f_{\lambda ,d}^N$.
We now describe an algorithm that, on input ![]() $\hat {\lambda } \in \mathbb {S}_{\mathbb {Q}}$ and rational
$\hat {\lambda } \in \mathbb {S}_{\mathbb {Q}}$ and rational ![]() $\epsilon>0$, yields in
$\epsilon>0$, yields in ![]() $poly(\mathrm {size}(\hat {\lambda },\epsilon ))$ a rooted tree
$poly(\mathrm {size}(\hat {\lambda },\epsilon ))$ a rooted tree ![]() $\hat {T}$ in
$\hat {T}$ in ![]() $\mathcal {T}_{d+1}$ with
$\mathcal {T}_{d+1}$ with ![]() $\mathcal {O}(\log (\epsilon ^{-1}))$ vertices whose field has distance at most
$\mathcal {O}(\log (\epsilon ^{-1}))$ vertices whose field has distance at most ![]() $\epsilon $ from
$\epsilon $ from ![]() $\hat {\lambda }$; we will account for the degree of the root later. We assume for convenience that
$\hat {\lambda }$; we will account for the degree of the root later. We assume for convenience that ![]() $\epsilon \ll \ell (I)$.
$\epsilon \ll \ell (I)$.
The first step of the algorithm is to find ![]() $i \in \{1, \dots , m\}$ such that
$i \in \{1, \dots , m\}$ such that  $\hat {\lambda } \in \operatorname {\mathrm {Arc}}{[f_{\lambda ,d}^N(x_{i-1}),f_{\lambda ,d}^N(x_{i})]}$. We know that such an arc must exist because I is mapped surjectively onto
$\hat {\lambda } \in \operatorname {\mathrm {Arc}}{[f_{\lambda ,d}^N(x_{i-1}),f_{\lambda ,d}^N(x_{i})]}$. We know that such an arc must exist because I is mapped surjectively onto ![]() $\mathbb {S}$ by
$\mathbb {S}$ by  $f_{\lambda ,d}^N$ and, since
$f_{\lambda ,d}^N$ and, since  $f_{\lambda ,d}^N(z)$ is a rational function of z with fixed degree, we can find i in time
$f_{\lambda ,d}^N(z)$ is a rational function of z with fixed degree, we can find i in time ![]() $poly(\mathrm {size}(\hat {\lambda }))$. Now we consider the bijective map
$poly(\mathrm {size}(\hat {\lambda }))$. Now we consider the bijective map
 $$ \begin{align*} f_{\lambda,d}^N: \operatorname{\mathrm{Arc}}{[x_{i-1},x_i]} \to \operatorname{\mathrm{Arc}}{[f_{\lambda,d}^N(x_{i-1}),f_{\lambda,d}^N(x_{i})]}. \end{align*} $$
$$ \begin{align*} f_{\lambda,d}^N: \operatorname{\mathrm{Arc}}{[x_{i-1},x_i]} \to \operatorname{\mathrm{Arc}}{[f_{\lambda,d}^N(x_{i-1}),f_{\lambda,d}^N(x_{i})]}. \end{align*} $$Analogously, with  $n = \lceil \log _{3/2}(\ell {(\operatorname {\mathrm {Arc}}{[x_{i-1},x_i]})} \cdot C_2^N / \epsilon ) \rceil $ applications of
$n = \lceil \log _{3/2}(\ell {(\operatorname {\mathrm {Arc}}{[x_{i-1},x_i]})} \cdot C_2^N / \epsilon ) \rceil $ applications of  $f_{\lambda ,d}^N$, we can determine using binary search in time
$f_{\lambda ,d}^N$, we can determine using binary search in time ![]() $poly(\mathrm {size}(\hat {\lambda },\epsilon ))$ an arc
$poly(\mathrm {size}(\hat {\lambda },\epsilon ))$ an arc ![]() $J \subseteq \operatorname {\mathrm {Arc}}{[x_{i-1},x_i]}$ with endpoints in
$J \subseteq \operatorname {\mathrm {Arc}}{[x_{i-1},x_i]}$ with endpoints in ![]() $\mathbb {S}_{\mathbb {Q}}$ such that
$\mathbb {S}_{\mathbb {Q}}$ such that  $\hat {\lambda } \in f_{\lambda ,d}^N(J)$ and whose length satisfies
$\hat {\lambda } \in f_{\lambda ,d}^N(J)$ and whose length satisfies
 $$ \begin{align*} 3^{-n} \cdot \ell(\operatorname{\mathrm{Arc}}{[x_{i-1},x_i]})\leq \ell(J) \leq (2/3)^{n} \cdot \ell(\operatorname{\mathrm{Arc}}{[x_{i-1},x_i]}) \leq \epsilon/ C_2^N. \end{align*} $$
$$ \begin{align*} 3^{-n} \cdot \ell(\operatorname{\mathrm{Arc}}{[x_{i-1},x_i]})\leq \ell(J) \leq (2/3)^{n} \cdot \ell(\operatorname{\mathrm{Arc}}{[x_{i-1},x_i]}) \leq \epsilon/ C_2^N. \end{align*} $$Note that the length of J is bounded below by ![]() $C_3 \cdot \epsilon ^5$, where
$C_3 \cdot \epsilon ^5$, where ![]() $C_3$ is a constant independent of
$C_3$ is a constant independent of ![]() $\hat {\lambda }$ or
$\hat {\lambda }$ or ![]() $\epsilon $. It follows from (15) that
$\epsilon $. It follows from (15) that  $\ell {(f_{\lambda ,d}^N(J))} \leq \epsilon $, which means that the arc J is mapped by
$\ell {(f_{\lambda ,d}^N(J))} \leq \epsilon $, which means that the arc J is mapped by  $f_{\lambda ,d}^N$ to an arc of length at most
$f_{\lambda ,d}^N$ to an arc of length at most ![]() $\epsilon $ that includes
$\epsilon $ that includes ![]() $\hat {\lambda }$. We will next show how to construct in
$\hat {\lambda }$. We will next show how to construct in ![]() $poly(\mathrm {size}(\hat {\lambda },\epsilon ))$ a rooted tree T in
$poly(\mathrm {size}(\hat {\lambda },\epsilon ))$ a rooted tree T in ![]() $\mathcal {T}_{d+1}$ with
$\mathcal {T}_{d+1}$ with ![]() $s=\mathcal {O}(\log (\epsilon ^{-1}))$ vertices that implements a field
$s=\mathcal {O}(\log (\epsilon ^{-1}))$ vertices that implements a field ![]() $w\in J$. Then, using Lemma 4,Footnote 8 we obtain a rooted tree
$w\in J$. Then, using Lemma 4,Footnote 8 we obtain a rooted tree ![]() $\hat {T}$ with
$\hat {T}$ with ![]() $ (d^N-1)/(d-1) +d^N s $ vertices that implements the field
$ (d^N-1)/(d-1) +d^N s $ vertices that implements the field  $\lambda '=f_{\lambda ,d}^N(w)$ with
$\lambda '=f_{\lambda ,d}^N(w)$ with ![]() $|\lambda '-\hat {\lambda }|\leq \epsilon $.
$|\lambda '-\hat {\lambda }|\leq \epsilon $.
To construct T, we first fix some constants. Let ![]() $C_4 = \lvert f_{1}'(R_1(\xi _1)) \rvert $ and
$C_4 = \lvert f_{1}'(R_1(\xi _1)) \rvert $ and ![]() $C_5 = \lvert f_{1}'(R_1(\xi _2)) \rvert $ and note that
$C_5 = \lvert f_{1}'(R_1(\xi _2)) \rvert $ and note that  $C_4, C_5 \in (\frac {1}{2},1)$. We also have
$C_4, C_5 \in (\frac {1}{2},1)$. We also have ![]() $C_4 \leq |f_{1}'(z)| \leq C_5$ for all
$C_4 \leq |f_{1}'(z)| \leq C_5$ for all ![]() $z \in I$. It follows that
$z \in I$. It follows that ![]() $f_{\xi _2,1}(I) = \operatorname {\mathrm {Arc}}{[f_{\xi _2,1}(R_1(\xi _1)),R_1(\xi _2)]}$ is contained in I and its length is strictly bigger than
$f_{\xi _2,1}(I) = \operatorname {\mathrm {Arc}}{[f_{\xi _2,1}(R_1(\xi _1)),R_1(\xi _2)]}$ is contained in I and its length is strictly bigger than ![]() $\ell (I)/2$. Furthermore, it follows that
$\ell (I)/2$. Furthermore, it follows that  $f_{\xi _1,1}^{-1}(\operatorname {\mathrm {Arc}}{[R_1(\xi _1),f_{\xi _2,1}(R_1(\xi _1))]}) = \operatorname {\mathrm {Arc}}{[R_1(\xi _1),f_{\xi _1}^{-1}(f_{\xi _2}(R_1(\xi _1)))]}$ is strictly contained inside I. Let
$f_{\xi _1,1}^{-1}(\operatorname {\mathrm {Arc}}{[R_1(\xi _1),f_{\xi _2,1}(R_1(\xi _1))]}) = \operatorname {\mathrm {Arc}}{[R_1(\xi _1),f_{\xi _1}^{-1}(f_{\xi _2}(R_1(\xi _1)))]}$ is strictly contained inside I. Let ![]() $J_0 = J$, and for
$J_0 = J$, and for ![]() $k\geq 0$, as long as
$k\geq 0$, as long as ![]() $f_{\xi _2,1}(R_1(\xi _1)) \not \in J_k$, define
$f_{\xi _2,1}(R_1(\xi _1)) \not \in J_k$, define
 $$ \begin{align*} J_{k+1} = \begin{cases} f^{-1}_{\xi_1,1}(J_k) & \text{if }J_k \subset \operatorname{\mathrm{Arc}}{[R_1(\xi_1),f_{\xi_2,1}(R_1(\xi_1))]}\\ f^{-1}_{\xi_2,1}(J_k) & \text{if }J_k \subset \operatorname{\mathrm{Arc}}{[f_{\xi_2,1}(R_1(\xi_1))),R_1(\xi_2)]}. \end{cases} \end{align*} $$
$$ \begin{align*} J_{k+1} = \begin{cases} f^{-1}_{\xi_1,1}(J_k) & \text{if }J_k \subset \operatorname{\mathrm{Arc}}{[R_1(\xi_1),f_{\xi_2,1}(R_1(\xi_1))]}\\ f^{-1}_{\xi_2,1}(J_k) & \text{if }J_k \subset \operatorname{\mathrm{Arc}}{[f_{\xi_2,1}(R_1(\xi_1))),R_1(\xi_2)]}. \end{cases} \end{align*} $$We have that ![]() $J_k \subseteq I$ for every k and
$J_k \subseteq I$ for every k and  $\ell (J_k) \geq C_5^{-k} \cdot \ell {(J_0)} \geq C_3 \cdot C_5^{-k} \cdot \epsilon ^5$. Because
$\ell (J_k) \geq C_5^{-k} \cdot \ell {(J_0)} \geq C_3 \cdot C_5^{-k} \cdot \epsilon ^5$. Because ![]() $C_5 < 1$, we deduce that there is
$C_5 < 1$, we deduce that there is ![]() $N_1 \geq 0$ such that
$N_1 \geq 0$ such that ![]() $f_{\xi _2,1}(R_1(\xi _1)) \in J_{N_1}$ where
$f_{\xi _2,1}(R_1(\xi _1)) \in J_{N_1}$ where ![]() $N_1$ is bounded above by
$N_1$ is bounded above by
 $$ \begin{align*} \Big \lceil \tfrac{\log(C_3 \cdot \epsilon^5 / \ell(I))}{\log(C_5)} \Big \rceil = \mathcal{O}(\log(\epsilon^{-1})). \end{align*} $$
$$ \begin{align*} \Big \lceil \tfrac{\log(C_3 \cdot \epsilon^5 / \ell(I))}{\log(C_5)} \Big \rceil = \mathcal{O}(\log(\epsilon^{-1})). \end{align*} $$ Let ![]() $i_1, \dots , i_{N_1}$ be the sequence of indices such that
$i_1, \dots , i_{N_1}$ be the sequence of indices such that ![]() $f_{\xi _{i_k}}(J_{k}) = J_{k-1}$ and note that these can be computed in
$f_{\xi _{i_k}}(J_{k}) = J_{k-1}$ and note that these can be computed in ![]() $poly(\mathrm {size}(\hat {\lambda },\epsilon ))$ time. Let
$poly(\mathrm {size}(\hat {\lambda },\epsilon ))$ time. Let  $K = f_{\xi _2,1}^{-1}(J_{N_1})$. We see that
$K = f_{\xi _2,1}^{-1}(J_{N_1})$. We see that ![]() $R_1(\xi _1) \in K$ and
$R_1(\xi _1) \in K$ and
 $$ \begin{align*} \big(f_{\xi_{i_1},1}\circ\cdots\circ f_{\xi_{i_{N_1}},1} \circ f_{\xi_2,1}\big)(K) = J.\\[-15pt] \end{align*} $$
$$ \begin{align*} \big(f_{\xi_{i_1},1}\circ\cdots\circ f_{\xi_{i_{N_1}},1} \circ f_{\xi_2,1}\big)(K) = J.\\[-15pt] \end{align*} $$Furthermore, because the maps  $f_{\xi _i,1}^{-1}$ are expanding on I, we find
$f_{\xi _i,1}^{-1}$ are expanding on I, we find ![]() $\ell (K) \geq \ell (J) \geq C_3 \cdot \epsilon ^5$. This means that there is an arc of length at least
$\ell (K) \geq \ell (J) \geq C_3 \cdot \epsilon ^5$. This means that there is an arc of length at least  $\frac {1}{2} \cdot C_3\cdot \epsilon ^5$ extending from
$\frac {1}{2} \cdot C_3\cdot \epsilon ^5$ extending from ![]() $R_1(\xi _1)$, going either clockwise or counterclockwise, contained in K. In the case that such a clockwise arc exists – that is,
$R_1(\xi _1)$, going either clockwise or counterclockwise, contained in K. In the case that such a clockwise arc exists – that is,  $\operatorname {\mathrm {Arc}}[R_1(\xi _1)\cdot e^{-i \frac {1}{2}C_3 \epsilon ^5},R_1(\xi _1)]\subseteq K$ – we see that, because
$\operatorname {\mathrm {Arc}}[R_1(\xi _1)\cdot e^{-i \frac {1}{2}C_3 \epsilon ^5},R_1(\xi _1)]\subseteq K$ – we see that, because ![]() $R_1$ is an attracting fixed point of
$R_1$ is an attracting fixed point of ![]() $f_{\xi _1}$, there is some
$f_{\xi _1}$, there is some ![]() $N_2$, specified below, such that
$N_2$, specified below, such that  $f_{\xi _1,1}^{N_2}(\xi _1) \in K$. Using that for integers n we have
$f_{\xi _1,1}^{N_2}(\xi _1) \in K$. Using that for integers n we have
 $$ \begin{align*} \ell(\operatorname{\mathrm{Arc}}{[f_{\xi_1,1}^{n}(\xi_1),R_1(\xi_1)]}) = \ell(f_{\xi_1,1}^{n}(\operatorname{\mathrm{Arc}}{[\xi_1,R_1(\xi_1)]})) \leq C_4^n \cdot \ell(\operatorname{\mathrm{Arc}}{[\xi_1,R_1(\xi_1)])} < C_4^n \cdot 2 \pi,\\[-15pt] \end{align*} $$
$$ \begin{align*} \ell(\operatorname{\mathrm{Arc}}{[f_{\xi_1,1}^{n}(\xi_1),R_1(\xi_1)]}) = \ell(f_{\xi_1,1}^{n}(\operatorname{\mathrm{Arc}}{[\xi_1,R_1(\xi_1)]})) \leq C_4^n \cdot \ell(\operatorname{\mathrm{Arc}}{[\xi_1,R_1(\xi_1)])} < C_4^n \cdot 2 \pi,\\[-15pt] \end{align*} $$we see that it suffices to take  $N_2 = \big \lceil \tfrac {\log (C_3 \cdot \epsilon ^5/(4 \pi ))}{\log (C_4)}\big \rceil = \mathcal {O}(\log (\epsilon ^{-1}))$. In the case that such a clockwise arc does not exist, we find that a counterclockwise arc of length
$N_2 = \big \lceil \tfrac {\log (C_3 \cdot \epsilon ^5/(4 \pi ))}{\log (C_4)}\big \rceil = \mathcal {O}(\log (\epsilon ^{-1}))$. In the case that such a clockwise arc does not exist, we find that a counterclockwise arc of length  $\frac {1}{2} \cdot C_3\cdot \epsilon ^5$ is contained in K. Note that there is some integer
$\frac {1}{2} \cdot C_3\cdot \epsilon ^5$ is contained in K. Note that there is some integer ![]() $N_c$ independent of
$N_c$ independent of ![]() $\hat {\lambda }$ and
$\hat {\lambda }$ and ![]() $\epsilon $ such that
$\epsilon $ such that  $f_{\xi _2,1}^{N_c}(\xi _1) \in I$. The same analysis as above shows that then
$f_{\xi _2,1}^{N_c}(\xi _1) \in I$. The same analysis as above shows that then  $(f_{\xi _1,1}^{N_2} \circ f_{\xi _2,1}^{N_c})(\xi _1) \in K$. We let
$(f_{\xi _1,1}^{N_2} \circ f_{\xi _2,1}^{N_c})(\xi _1) \in K$. We let ![]() $N_3$ be equal to zero if a clockwise arc of sufficient length is contained in K and, otherwise, we let
$N_3$ be equal to zero if a clockwise arc of sufficient length is contained in K and, otherwise, we let ![]() $N_3 = N_c$. We conclude that
$N_3 = N_c$. We conclude that
 $$ \begin{align} \big(f_{\lambda,d}^N \circ f_{\xi_{i_1},1}\circ\cdots\circ f_{\xi_{i_{N_1}},1} \circ f_{\xi_2,1} \circ f_{\xi_1,1}^{N_2} \circ f_{\xi_2,1}^{N_3}\big)(\xi_1)\\[-15pt]\nonumber \end{align} $$
$$ \begin{align} \big(f_{\lambda,d}^N \circ f_{\xi_{i_1},1}\circ\cdots\circ f_{\xi_{i_{N_1}},1} \circ f_{\xi_2,1} \circ f_{\xi_1,1}^{N_2} \circ f_{\xi_2,1}^{N_3}\big)(\xi_1)\\[-15pt]\nonumber \end{align} $$has a distance at most ![]() $\epsilon $ from
$\epsilon $ from ![]() $\hat {\lambda }$. By repeatedly applying the constructions laid out in Lemma 4 (cf. Footnote 8), we conclude that we can construct a tree T in
$\hat {\lambda }$. By repeatedly applying the constructions laid out in Lemma 4 (cf. Footnote 8), we conclude that we can construct a tree T in ![]() $\mathcal {T}_{d+1}$ whose field is given by the value in (16) and with
$\mathcal {T}_{d+1}$ whose field is given by the value in (16) and with ![]() $\mathcal {O}(\log (\epsilon ^{-1}))$ vertices.
$\mathcal {O}(\log (\epsilon ^{-1}))$ vertices.
This finishes the description of the algorithm, modulo that the root of the tree we constructed has degree d. To obtain a rooted tree with root degree 1, we run the algorithm described on input  $f_{\lambda ,1}^{-1}(\hat {\lambda })$ and
$f_{\lambda ,1}^{-1}(\hat {\lambda })$ and  $\epsilon \cdot \frac {d-1}{d+1}$ to obtain a rooted tree with root degree d and field
$\epsilon \cdot \frac {d-1}{d+1}$ to obtain a rooted tree with root degree d and field ![]() $\zeta $ with
$\zeta $ with  $|f_{\lambda ,1}^{-1}(\hat {\lambda })- \zeta | < \epsilon \cdot \frac {d-1}{d+1}$. Attaching one new vertex by an edge to this root yields a rooted tree with root degree
$|f_{\lambda ,1}^{-1}(\hat {\lambda })- \zeta | < \epsilon \cdot \frac {d-1}{d+1}$. Attaching one new vertex by an edge to this root yields a rooted tree with root degree ![]() $1$ and field
$1$ and field ![]() $f_{\lambda ,1}(\zeta )$ which satisfies, using Item i of Lemma 10, that
$f_{\lambda ,1}(\zeta )$ which satisfies, using Item i of Lemma 10, that
 $$ \begin{align*}|\hat{\lambda} - f_{\lambda,1}(\zeta)| \leq |f_{\lambda,1}^{-1}(\hat \lambda)- \zeta| \cdot \max_{z \in S} |f_{\lambda,1}'(z)| < \epsilon \cdot \frac{d-1}{d+1} \cdot \frac{d+1}{d-1} = \epsilon,\\[-15pt] \end{align*} $$
$$ \begin{align*}|\hat{\lambda} - f_{\lambda,1}(\zeta)| \leq |f_{\lambda,1}^{-1}(\hat \lambda)- \zeta| \cdot \max_{z \in S} |f_{\lambda,1}'(z)| < \epsilon \cdot \frac{d-1}{d+1} \cdot \frac{d+1}{d-1} = \epsilon,\\[-15pt] \end{align*} $$as wanted. This finishes the proof of Lemma 32.
8 Reduction
In this section, we prove our inapproximability results. Throughout this section, we use ![]() $\mathcal {G}_\Delta $ to denote the set of all graphs with maximum degree at most
$\mathcal {G}_\Delta $ to denote the set of all graphs with maximum degree at most ![]() $\Delta $. We start in Subsection 8.1 with some preliminaries that will be used in our proofs. Subsection 8.2 gives the main reduction, and we show how to use this in Subsection 8.3 to conclude the proof of Theorem 1.
$\Delta $. We start in Subsection 8.1 with some preliminaries that will be used in our proofs. Subsection 8.2 gives the main reduction, and we show how to use this in Subsection 8.3 to conclude the proof of Theorem 1.
8.1 Preliminaries
We will use the following lemma from [Reference Peters and Regts42].
Lemma 33 [Reference Peters and Regts42]
Let ![]() $\Delta \geq 3$ be an integer and let
$\Delta \geq 3$ be an integer and let ![]() $\lambda \in \mathbb {S}_{\mathbb {Q}}$ with
$\lambda \in \mathbb {S}_{\mathbb {Q}}$ with ![]() $\lambda \neq -1$. Then, there exists
$\lambda \neq -1$. Then, there exists ![]() $\eta =\eta (\Delta ,\lambda )>1$ such that, for all
$\eta =\eta (\Delta ,\lambda )>1$ such that, for all ![]() $b\in (1/\eta ,\eta )$, for all graphs
$b\in (1/\eta ,\eta )$, for all graphs ![]() $G\in \mathcal {G}_\Delta $, it holds that
$G\in \mathcal {G}_\Delta $, it holds that ![]() $Z_G(\lambda ,b)\neq 0$.
$Z_G(\lambda ,b)\neq 0$.
For a graph G and vertices ![]() $u,v$ in G, let
$u,v$ in G, let ![]() $Z_{G,\mathrm {\tt {\pm }} u,\mathrm {\tt {\pm }} v}(\lambda ,b)$ denote the contribution to the partition function when
$Z_{G,\mathrm {\tt {\pm }} u,\mathrm {\tt {\pm }} v}(\lambda ,b)$ denote the contribution to the partition function when ![]() $u,v$ are assigned the spins
$u,v$ are assigned the spins ![]() $\mathrm {\tt {\pm }}$, respectively. For a configuration
$\mathrm {\tt {\pm }}$, respectively. For a configuration ![]() $\sigma $ on G, we use
$\sigma $ on G, we use ![]() $w_{G,\sigma }(\lambda ,b)$ to denote the weight
$w_{G,\sigma }(\lambda ,b)$ to denote the weight ![]() $\lambda ^{|n_{\mathrm {\texttt {+}}}(\sigma )|} b^{\delta (\sigma )}$ of
$\lambda ^{|n_{\mathrm {\texttt {+}}}(\sigma )|} b^{\delta (\sigma )}$ of ![]() $\sigma $. We will use the following observation.
$\sigma $. We will use the following observation.
Lemma 34. Let ![]() $\lambda \in \mathbb {S}$ and
$\lambda \in \mathbb {S}$ and ![]() $b\in \mathbb {R}$. Then, for an arbitrary graph
$b\in \mathbb {R}$. Then, for an arbitrary graph ![]() $G=(V_G,E_G)$ and vertices
$G=(V_G,E_G)$ and vertices ![]() $u,v$ of G, it holds that
$u,v$ of G, it holds that
 $$ \begin{align*}Z_{G,\mathrm{\texttt{+}} u,\mathrm{\texttt{+}} v}(\lambda,b)=\lambda^{|V(G)|}\,\overline{Z_{G,\mathrm{\texttt{-}} u,\mathrm{\texttt{-}} v}(\lambda,b)},\quad Z_{G,\mathrm{\texttt{+}} u,\mathrm{\texttt{-}} v}(\lambda,b)=\lambda^{|V(G)|}\,\overline{Z_{G,\mathrm{\texttt{-}} u,\mathrm{\texttt{+}} v}(\lambda,b)}.\end{align*} $$
$$ \begin{align*}Z_{G,\mathrm{\texttt{+}} u,\mathrm{\texttt{+}} v}(\lambda,b)=\lambda^{|V(G)|}\,\overline{Z_{G,\mathrm{\texttt{-}} u,\mathrm{\texttt{-}} v}(\lambda,b)},\quad Z_{G,\mathrm{\texttt{+}} u,\mathrm{\texttt{-}} v}(\lambda,b)=\lambda^{|V(G)|}\,\overline{Z_{G,\mathrm{\texttt{-}} u,\mathrm{\texttt{+}} v}(\lambda,b)}.\end{align*} $$Proof. For an assignment ![]() $\sigma :V_G\rightarrow \{\mathrm {\texttt {+}},\mathrm {\texttt {-}} \}$, let
$\sigma :V_G\rightarrow \{\mathrm {\texttt {+}},\mathrm {\texttt {-}} \}$, let ![]() $\bar {\sigma }:V_G\rightarrow \{\mathrm {\texttt {+}},\mathrm {\texttt {-}} \}$ be the assignment obtained by interchanging the assignment of
$\bar {\sigma }:V_G\rightarrow \{\mathrm {\texttt {+}},\mathrm {\texttt {-}} \}$ be the assignment obtained by interchanging the assignment of ![]() $\mathrm {\texttt {+}}$’s with
$\mathrm {\texttt {+}}$’s with ![]() $\mathrm {\texttt {-}}$’s. Then
$\mathrm {\texttt {-}}$’s. Then
 $$ \begin{align*}w_{G,\bar{\sigma}}(\lambda,b)=\lambda^{|n_{\mathrm{\texttt{+}}}(\bar{\sigma})|}b^{\delta(\bar{\sigma})}=\lambda^{|V_G|-|n_{\mathrm{\texttt{+}}}(\sigma)|}b^{\delta(\sigma)}=\lambda^{|V(G)|}\overline{w_{G,\sigma}(\lambda,b)}.\end{align*} $$
$$ \begin{align*}w_{G,\bar{\sigma}}(\lambda,b)=\lambda^{|n_{\mathrm{\texttt{+}}}(\bar{\sigma})|}b^{\delta(\bar{\sigma})}=\lambda^{|V_G|-|n_{\mathrm{\texttt{+}}}(\sigma)|}b^{\delta(\sigma)}=\lambda^{|V(G)|}\overline{w_{G,\sigma}(\lambda,b)}.\end{align*} $$The result follows by summing over the relevant ![]() $\sigma $ for each of
$\sigma $ for each of ![]() $Z_{G,\mathrm {\texttt {+}} u,\mathrm {\texttt {+}} v}(\lambda ,b)$ and
$Z_{G,\mathrm {\texttt {+}} u,\mathrm {\texttt {+}} v}(\lambda ,b)$ and ![]() $Z_{G,\mathrm {\texttt {+}} u,\mathrm {\texttt {-}} v}(\lambda ,b)$.
$Z_{G,\mathrm {\texttt {+}} u,\mathrm {\texttt {-}} v}(\lambda ,b)$.
The following lemma will be useful in general for handling rational points on the circle. Ideally, we would like to describe a number on ![]() $\mathbb {S}$ by a rational angle, but this may not correspond to a rational Cartesian point, which would complicate computations. However, rational points are dense on the circle, and we can compute one arbitrarily close to a given angle, as follows.
$\mathbb {S}$ by a rational angle, but this may not correspond to a rational Cartesian point, which would complicate computations. However, rational points are dense on the circle, and we can compute one arbitrarily close to a given angle, as follows.
Lemma 35. Given a rational angle ![]() $\theta \in [0 ,2\pi )$ and
$\theta \in [0 ,2\pi )$ and ![]() $\epsilon \in (0,1)$, there exists a number
$\epsilon \in (0,1)$, there exists a number ![]() $\hat {\theta }$ such that
$\hat {\theta }$ such that ![]() $|\theta - \hat {\theta }|< \epsilon $ and
$|\theta - \hat {\theta }|< \epsilon $ and ![]() $\cos \hat {\theta }, \sin \hat {\theta } \in \mathbb {Q}$ are rational numbers of size at most
$\cos \hat {\theta }, \sin \hat {\theta } \in \mathbb {Q}$ are rational numbers of size at most ![]() $poly(\mathrm {size}(\theta ,\epsilon ))$. Furthermore, we can compute
$poly(\mathrm {size}(\theta ,\epsilon ))$. Furthermore, we can compute ![]() $\cos \hat {\theta }$ and
$\cos \hat {\theta }$ and ![]() $\sin \hat {\theta }$ in time
$\sin \hat {\theta }$ in time ![]() $poly(\mathrm {size}(\theta ,\epsilon ))$.
$poly(\mathrm {size}(\theta ,\epsilon ))$.
Proof. By symmetry, we may assume that ![]() $\theta \in [0, \pi /4]$. Given
$\theta \in [0, \pi /4]$. Given ![]() $\theta $, take a rational approximation r of
$\theta $, take a rational approximation r of ![]() $\tan (\theta / 2)$ such that
$\tan (\theta / 2)$ such that ![]() $|\tan ( \theta / 2) - r| < \epsilon / 2$. We claim that
$|\tan ( \theta / 2) - r| < \epsilon / 2$. We claim that ![]() $\hat {\theta }=2 \arctan (r)$ has the desired properties.
$\hat {\theta }=2 \arctan (r)$ has the desired properties.
Write ![]() $s,c,t$ respectively for
$s,c,t$ respectively for ![]() $\sin \hat {\theta }, \cos \hat {\theta }, \tan \hat {\theta }$. Using the tan double angle formula, we have
$\sin \hat {\theta }, \cos \hat {\theta }, \tan \hat {\theta }$. Using the tan double angle formula, we have ![]() $s/c = t = 2r/(1-r^2)$. We also know that
$s/c = t = 2r/(1-r^2)$. We also know that ![]() $s^2 + c^2 = 1$. Solving these simultaneously gives that
$s^2 + c^2 = 1$. Solving these simultaneously gives that ![]() $s = 2r/(1+r^2)$ and
$s = 2r/(1+r^2)$ and ![]() $c = (1 - r^2)/(1+r^2)$, which are both rational since r is rational.
$c = (1 - r^2)/(1+r^2)$, which are both rational since r is rational.
Also, writing ![]() $f(x) = 2\arctan (x)$ for
$f(x) = 2\arctan (x)$ for ![]() $x \in [0,1]$, note that
$x \in [0,1]$, note that ![]() $f'(x) = 2/(1+x^2) \in [1,2]$ for
$f'(x) = 2/(1+x^2) \in [1,2]$ for ![]() $x \in [0,1]$. Hence,
$x \in [0,1]$. Hence, ![]() $|f(x) - f(y)| \leq 2|x-y|$ for
$|f(x) - f(y)| \leq 2|x-y|$ for ![]() $x,y \in [0,1]$ and so
$x,y \in [0,1]$ and so ![]() $|\theta - \theta '| < \epsilon $.
$|\theta - \theta '| < \epsilon $.
Finally, we can compute r in ![]() $poly(\mathrm {size}(\theta ,\epsilon ))$ using a series expansion of
$poly(\mathrm {size}(\theta ,\epsilon ))$ using a series expansion of ![]() $\tan $ from which we can compute s and c from the formulas above.
$\tan $ from which we can compute s and c from the formulas above.
Finally, we will use the following well-known lemma for continued-fraction approximation.
Lemma 36 [Reference Schrijver43, Corollary 6.3a]
There is a poly-time algorithm which, on input a rational number ![]() $\alpha $ and integer
$\alpha $ and integer ![]() $K\geq 1$, decides whether there exists a rational number
$K\geq 1$, decides whether there exists a rational number ![]() $p/q$ with
$p/q$ with ![]() $1 \leq q \leq K$ and
$1 \leq q \leq K$ and ![]() $|\alpha - (p/q)| < 1/2K^2$ and, if so, finds this (unique) rational number.
$|\alpha - (p/q)| < 1/2K^2$ and, if so, finds this (unique) rational number.
8.2 The reduction
To prove Theorem 1, we will show how to use a poly-time algorithm for ![]() $\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ and
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ and ![]() $\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$ to compute exactly
$\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$ to compute exactly ![]() $Z_G(\lambda ,\hat {b})$ on graphs G of maximum degree 3 for some appropriate value of
$Z_G(\lambda ,\hat {b})$ on graphs G of maximum degree 3 for some appropriate value of ![]() $\hat {b}$ that we next specify.
$\hat {b}$ that we next specify.
Let ![]() $\eta =\eta (3,\lambda )>1$ be as in Lemma 33, so that
$\eta =\eta (3,\lambda )>1$ be as in Lemma 33, so that
For ![]() $k=2,3,\ldots ,$ let
$k=2,3,\ldots ,$ let ![]() $P_k$ be the path with k vertices whose endpoints are labelled
$P_k$ be the path with k vertices whose endpoints are labelled ![]() $u_k,v_k$ and all vertex activities are equal to 1. Then, it is not hard to see that
$u_k,v_k$ and all vertex activities are equal to 1. Then, it is not hard to see that
 $$ \begin{align} \left[\begin{array}{cc} Z_{P_k,\mathrm{\texttt{+}} u_k,\mathrm{\texttt{+}} v_k}(1,b)& Z_{P_k,\mathrm{\texttt{+}} u_k,\mathrm{\texttt{-}} v_k}(1,b) \\ Z_{P_k,\mathrm{\texttt{-}} u_k,\mathrm{\texttt{+}} v_k}(1,b)&Z_{P_k,\mathrm{\texttt{-}} u_k,\mathrm{\texttt{-}} v_k}(1,b)\end{array}\right]=\left[\begin{array}{cc} 1& b \\ b& 1\end{array}\right]^{k-1}. \end{align} $$
$$ \begin{align} \left[\begin{array}{cc} Z_{P_k,\mathrm{\texttt{+}} u_k,\mathrm{\texttt{+}} v_k}(1,b)& Z_{P_k,\mathrm{\texttt{+}} u_k,\mathrm{\texttt{-}} v_k}(1,b) \\ Z_{P_k,\mathrm{\texttt{-}} u_k,\mathrm{\texttt{+}} v_k}(1,b)&Z_{P_k,\mathrm{\texttt{-}} u_k,\mathrm{\texttt{-}} v_k}(1,b)\end{array}\right]=\left[\begin{array}{cc} 1& b \\ b& 1\end{array}\right]^{k-1}. \end{align} $$Clearly, for all k it holds that
 $$ \begin{align} Z_{P_k, +u_k,\mathrm{\texttt{+}} v_k}(1,b)=Z_{P_k,\mathrm{\texttt{-}} u_k,\mathrm{\texttt{-}} v_k}(1,b) \mbox{ and } \frac{Z_{P_k,\mathrm{\texttt{+}} u_k,\mathrm{\texttt{-}} v_k}(1,b)}{Z_{P_k,\mathrm{\texttt{-}} u_k,\mathrm{\texttt{-}} v_k}(1,b)}=\frac{Z_{P_k,\mathrm{\texttt{-}} u_k,\mathrm{\texttt{+}} v_k}(1,b)}{Z_{P_k,\mathrm{\texttt{-}} u_k,\mathrm{\texttt{-}} v_k}(1,b)}=:b_k. \end{align} $$
$$ \begin{align} Z_{P_k, +u_k,\mathrm{\texttt{+}} v_k}(1,b)=Z_{P_k,\mathrm{\texttt{-}} u_k,\mathrm{\texttt{-}} v_k}(1,b) \mbox{ and } \frac{Z_{P_k,\mathrm{\texttt{+}} u_k,\mathrm{\texttt{-}} v_k}(1,b)}{Z_{P_k,\mathrm{\texttt{-}} u_k,\mathrm{\texttt{-}} v_k}(1,b)}=\frac{Z_{P_k,\mathrm{\texttt{-}} u_k,\mathrm{\texttt{+}} v_k}(1,b)}{Z_{P_k,\mathrm{\texttt{-}} u_k,\mathrm{\texttt{-}} v_k}(1,b)}=:b_k. \end{align} $$Moreover, using (18), we have that there exists k such that
By the choice of k and (17), we conclude that
The main step in the reduction is captured by the following lemma.
Lemma 37. Let ![]() $\Delta \geq 3$ be an integer,
$\Delta \geq 3$ be an integer, ![]() $b \in (0,1)$ be a rational and let
$b \in (0,1)$ be a rational and let ![]() $\lambda \in \mathbb {C}_{\mathbb {Q}}(\Delta -1,b)$ Let
$\lambda \in \mathbb {C}_{\mathbb {Q}}(\Delta -1,b)$ Let ![]() $K=1.001$ and
$K=1.001$ and ![]() $\rho =\pi /40$. Assume that a poly-time algorithm exists for either
$\rho =\pi /40$. Assume that a poly-time algorithm exists for either ![]() $\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ or
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ or ![]() $\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$. Then, there exists a poly-time algorithm that on input a graph
$\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$. Then, there exists a poly-time algorithm that on input a graph ![]() $G\in \mathcal {G}_3$ and an edge
$G\in \mathcal {G}_3$ and an edge ![]() $e=\{u,v\}$ of G outputs the value of the ratio
$e=\{u,v\}$ of G outputs the value of the ratio
 $$ \begin{align*}R_{G,e}=\frac{\hat{b}^2 z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+ \hat{b}(z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})+z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}}{\hat{b}^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}+\hat{b}(z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})+z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}}, \text{ where } z_{\mathrm{\tt{\pm}}\mathrm{\tt{\pm}}}:=Z_{G\backslash e,\mathrm{\tt{\pm}} u,\mathrm{\tt{\pm}} v}(\lambda,\hat{b}).\end{align*} $$
$$ \begin{align*}R_{G,e}=\frac{\hat{b}^2 z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+ \hat{b}(z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})+z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}}{\hat{b}^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}+\hat{b}(z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})+z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}}, \text{ where } z_{\mathrm{\tt{\pm}}\mathrm{\tt{\pm}}}:=Z_{G\backslash e,\mathrm{\tt{\pm}} u,\mathrm{\tt{\pm}} v}(\lambda,\hat{b}).\end{align*} $$The algorithm also outputs the value of the ratio  $R_{G,e}'=z_{\mathrm {\texttt {-}}\mathrm {\texttt {-}}}/z_{\mathrm {\texttt {+}}\mathrm {\texttt {+}}}$, provided that
$R_{G,e}'=z_{\mathrm {\texttt {-}}\mathrm {\texttt {-}}}/z_{\mathrm {\texttt {+}}\mathrm {\texttt {+}}}$, provided that ![]() $z_{\mathrm {\texttt {+}}\mathrm {\texttt {+}}}\neq 0$.
$z_{\mathrm {\texttt {+}}\mathrm {\texttt {+}}}\neq 0$.
Remark 38. As will be shown in the proof of Lemma 37, the ratio ![]() $R_{G,e}$ is well-defined for all graphs
$R_{G,e}$ is well-defined for all graphs ![]() $G\in \mathcal {G}_3$ and edges e in G using the zero-free region in Lemma 33 and the choice of
$G\in \mathcal {G}_3$ and edges e in G using the zero-free region in Lemma 33 and the choice of ![]() $\hat {b}$. It is harder to show that
$\hat {b}$. It is harder to show that  $R_{G,e}'$ is well-defined (we cannot use Lemma 33 directly) and hence the need for the assumption that
$R_{G,e}'$ is well-defined (we cannot use Lemma 33 directly) and hence the need for the assumption that ![]() $z_{\mathrm {\texttt {+}}\mathrm {\texttt {+}}}\neq 0$ in Lemma 37.
$z_{\mathrm {\texttt {+}}\mathrm {\texttt {+}}}\neq 0$ in Lemma 37.
Proof. Suppose that ![]() $G=(V,E)$ with
$G=(V,E)$ with ![]() $n=|V|$ and
$n=|V|$ and ![]() $m=|E|$. Let
$m=|E|$. Let
 $$ \begin{align} \begin{aligned} r&=\hat{b}^2 z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+ \hat{b}(z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})+z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}},\quad r'=(\hat{b}^2-1)^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}},\\ t&=\hat{b}^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}+\hat{b}(z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})+z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}},\quad t'=(\hat{b}^2-1)^2z_{\mathrm{\texttt{+}} \mathrm{\texttt{+}}}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} r&=\hat{b}^2 z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+ \hat{b}(z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})+z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}},\quad r'=(\hat{b}^2-1)^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}},\\ t&=\hat{b}^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}+\hat{b}(z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})+z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}},\quad t'=(\hat{b}^2-1)^2z_{\mathrm{\texttt{+}} \mathrm{\texttt{+}}}. \end{aligned} \end{align} $$We first show that ![]() $r,t\neq 0$. Consider the graph
$r,t\neq 0$. Consider the graph ![]() $H=(V_H,E_H)$ obtained from G by subdividing edge e; that is, we remove edge
$H=(V_H,E_H)$ obtained from G by subdividing edge e; that is, we remove edge ![]() $e=\{u,v\}$ and then add a new vertex s which is connected to both
$e=\{u,v\}$ and then add a new vertex s which is connected to both ![]() $u,v$. Note that H is obtained from
$u,v$. Note that H is obtained from ![]() $G\backslash e$ by adding the edges
$G\backslash e$ by adding the edges ![]() $\{s,u\}, \{s,v\}$, so it is not hard to see that
$\{s,u\}, \{s,v\}$, so it is not hard to see that
Note that H is a graph of maximum degree ![]() $\Delta $ and we have
$\Delta $ and we have ![]() $Z_{H}(\lambda ,\hat {b})\neq 0$ from (21). Moreover, from Lemma 34, we have
$Z_{H}(\lambda ,\hat {b})\neq 0$ from (21). Moreover, from Lemma 34, we have ![]() $r=\lambda ^{n} \overline {t}$. Combining these, we obtain that
$r=\lambda ^{n} \overline {t}$. Combining these, we obtain that ![]() $r,t\neq 0$. From assumption, we also have that
$r,t\neq 0$. From assumption, we also have that ![]() $t'\neq 0$.
$t'\neq 0$.
We will show how to compute the ratios ![]() $R_{\mathsf {goal}}=-\frac {r}{t}$ and
$R_{\mathsf {goal}}=-\frac {r}{t}$ and  $R_{\mathsf {goal}}'=-\frac {r'}{t'}$ (note that these are well-defined since
$R_{\mathsf {goal}}'=-\frac {r'}{t'}$ (note that these are well-defined since ![]() $t,t'\neq 0$). By Lemma 34, we have that
$t,t'\neq 0$). By Lemma 34, we have that ![]() $r=\lambda ^{n} \overline {t}$ and
$r=\lambda ^{n} \overline {t}$ and ![]() $r'=\lambda ^{n} \overline {t'}$, so
$r'=\lambda ^{n} \overline {t'}$, so  $R_{\mathsf {goal}},R_{\mathsf {goal}}'\in \mathbb {S}_{\mathbb {Q}}$. In fact, letting
$R_{\mathsf {goal}},R_{\mathsf {goal}}'\in \mathbb {S}_{\mathbb {Q}}$. In fact, letting ![]() $p,p',p'',q$ be integers such that
$p,p',p'',q$ be integers such that ![]() $\hat {b}=p/q$ and
$\hat {b}=p/q$ and ![]() $\lambda =(p'+\mathrm {i} p'')/q$, we have that
$\lambda =(p'+\mathrm {i} p'')/q$, we have that  $R_{\mathsf {goal}},R_{\mathsf {goal}}'\in \mathcal {R}\cap \mathbb {S}_{\mathbb {Q}}$, where
$R_{\mathsf {goal}},R_{\mathsf {goal}}'\in \mathcal {R}\cap \mathbb {S}_{\mathbb {Q}}$, where
 $$ \begin{align*}\mathcal{R}=\Big\{\frac{P+\mathrm{i} Q}{P'+\mathrm{i} Q'}\mid\, P,Q, P',Q'\in \{-M,\ldots,0, \ldots, M\}\Big\}\mbox{ and }M:=2^{n} |p|^{m} (|p'|+|p''|)^{n}q^{m+n}.\end{align*} $$
$$ \begin{align*}\mathcal{R}=\Big\{\frac{P+\mathrm{i} Q}{P'+\mathrm{i} Q'}\mid\, P,Q, P',Q'\in \{-M,\ldots,0, \ldots, M\}\Big\}\mbox{ and }M:=2^{n} |p|^{m} (|p'|+|p''|)^{n}q^{m+n}.\end{align*} $$ Let ![]() $\epsilon =1/(10M)^{16}$. Note that for any two distinct numbers
$\epsilon =1/(10M)^{16}$. Note that for any two distinct numbers ![]() $z,z'\in \mathcal {R}$ it holds that
$z,z'\in \mathcal {R}$ it holds that ![]() $|z-z'|\geq 10\epsilon $, so if we manage to produce
$|z-z'|\geq 10\epsilon $, so if we manage to produce ![]() $\hat {R},\hat {R}'\in \mathbb {S}_{\mathbb {Q}}$ with
$\hat {R},\hat {R}'\in \mathbb {S}_{\mathbb {Q}}$ with ![]() $poly(n)$ size so that
$poly(n)$ size so that ![]() $|R_{\mathsf {goal}}-\hat {R}|\leq \epsilon $ and
$|R_{\mathsf {goal}}-\hat {R}|\leq \epsilon $ and  $|R_{\mathsf {goal}}'-\hat {R}'|\leq \epsilon $, we can in fact compute
$|R_{\mathsf {goal}}'-\hat {R}'|\leq \epsilon $, we can in fact compute ![]() $R_{\mathsf {goal}}$ and
$R_{\mathsf {goal}}$ and  $R_{\mathsf {goal}}'$ in time
$R_{\mathsf {goal}}'$ in time ![]() $poly(n,\mathrm {size}(\epsilon ))=poly(n)$.Footnote 9
$poly(n,\mathrm {size}(\epsilon ))=poly(n)$.Footnote 9
We first focus on how to compute ![]() $\hat {R}\in \mathbb {S}_{\mathbb {Q}}$ so that
$\hat {R}\in \mathbb {S}_{\mathbb {Q}}$ so that ![]() $|R_{\mathsf {goal}}-\hat {R}|\leq \epsilon $. At this point, it will be helpful to represent complex numbers on the unit circle
$|R_{\mathsf {goal}}-\hat {R}|\leq \epsilon $. At this point, it will be helpful to represent complex numbers on the unit circle ![]() $\mathbb {S}$ with their arguments. Let
$\mathbb {S}$ with their arguments. Let ![]() $\theta _{\mathsf {goal}}=\text {Arg}(R_{\mathsf {goal}})$ and
$\theta _{\mathsf {goal}}=\text {Arg}(R_{\mathsf {goal}})$ and ![]() $g(\theta ):=t \mathrm {e}^{\mathrm {i} \theta }+r$. Note that
$g(\theta ):=t \mathrm {e}^{\mathrm {i} \theta }+r$. Note that
 $$ \begin{align} \begin{aligned} |g(\theta)|&=|g(\theta)-g(\theta_{\mathsf{goal}})|=|t||\mathrm{e}^{\mathrm{i} \theta}-\mathrm{e}^{\mathrm{i} \theta_{\mathsf{goal}}}|=2|t|\big| \sin((\theta-\theta_{\mathsf{goal}})/2)\big|, \\ \text{Arg}(g(\theta))&=(\theta-\theta_{\mathsf{goal}})/2+\text{Arg}(t) \mod 2\pi, \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} |g(\theta)|&=|g(\theta)-g(\theta_{\mathsf{goal}})|=|t||\mathrm{e}^{\mathrm{i} \theta}-\mathrm{e}^{\mathrm{i} \theta_{\mathsf{goal}}}|=2|t|\big| \sin((\theta-\theta_{\mathsf{goal}})/2)\big|, \\ \text{Arg}(g(\theta))&=(\theta-\theta_{\mathsf{goal}})/2+\text{Arg}(t) \mod 2\pi, \end{aligned} \end{align} $$the latter provided ![]() $\theta \neq \theta _{\mathsf {goal}}$.
$\theta \neq \theta _{\mathsf {goal}}$.
We will compute in ![]() $poly(n)$ time a rational
$poly(n)$ time a rational ![]() $\hat {\theta }$ such that
$\hat {\theta }$ such that ![]() $|\hat {\theta }-\theta _{\mathsf {goal}}|\leq \epsilon /2$, yielding the desired
$|\hat {\theta }-\theta _{\mathsf {goal}}|\leq \epsilon /2$, yielding the desired ![]() $\hat {R}$ (via Lemma 35).
$\hat {R}$ (via Lemma 35).
Let ![]() $\tau =1/500$ and
$\tau =1/500$ and ![]() $\kappa =\epsilon /10^3$. We will show that a poly-time algorithm for
$\kappa =\epsilon /10^3$. We will show that a poly-time algorithm for ![]() $\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ can be used to compute, for every rational
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ can be used to compute, for every rational ![]() $\theta $, a positive number
$\theta $, a positive number ![]() $\hat {g}_\theta $ in time
$\hat {g}_\theta $ in time ![]() $poly(n,\mathrm {size}(\theta ))$ such that, whenever
$poly(n,\mathrm {size}(\theta ))$ such that, whenever ![]() $|\theta -a|\geq \kappa $ for every
$|\theta -a|\geq \kappa $ for every ![]() $a\in \text {arg}(R_{\mathsf {goal}})$, it holds that
$a\in \text {arg}(R_{\mathsf {goal}})$, it holds that
When ![]() $|\theta - a|\leq \kappa $ for some
$|\theta - a|\leq \kappa $ for some ![]() $a\in \text {arg}(R_{\mathsf {goal}})$, there is no guarantee on the value of
$a\in \text {arg}(R_{\mathsf {goal}})$, there is no guarantee on the value of ![]() $\hat {g}_\theta $. Similarly, we will show that a poly-time algorithm for
$\hat {g}_\theta $. Similarly, we will show that a poly-time algorithm for ![]() $\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$ can be used to compute, for every rational
$\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$ can be used to compute, for every rational ![]() $\theta $, a positive number
$\theta $, a positive number ![]() $\hat {a}_\theta $ in time
$\hat {a}_\theta $ in time ![]() $poly(n,\mathrm {size}(\theta ))$ such that, whenever
$poly(n,\mathrm {size}(\theta ))$ such that, whenever ![]() $|\theta -a|\geq \kappa $ for every
$|\theta -a|\geq \kappa $ for every ![]() $a\in \text {arg}(R_{\mathsf {goal}})$, it holds that
$a\in \text {arg}(R_{\mathsf {goal}})$, it holds that
Using these, we compute the desired ![]() $\hat {\theta }$ via binary search following techniques similar to those in [Reference Goldberg and Guo18, Reference Goldberg and Jerrum20, Reference Bezáková, Galanis, Goldberg and Štefankovič6], though in our case the details are a bit different because we have to work on the unit circle. For the norm, we will utilise that
$\hat {\theta }$ via binary search following techniques similar to those in [Reference Goldberg and Guo18, Reference Goldberg and Jerrum20, Reference Bezáková, Galanis, Goldberg and Štefankovič6], though in our case the details are a bit different because we have to work on the unit circle. For the norm, we will utilise that ![]() $|g(\theta )|$ is increasing in the interval
$|g(\theta )|$ is increasing in the interval ![]() $[\theta _{\mathsf {goal}},\theta _{\mathsf {goal}}+\pi ]$ and decreasing in the interval
$[\theta _{\mathsf {goal}},\theta _{\mathsf {goal}}+\pi ]$ and decreasing in the interval ![]() $[\theta _{\mathsf {goal}}-\pi ,\theta _{\mathsf {goal}}]$, whereas for the argument we will utilise that
$[\theta _{\mathsf {goal}}-\pi ,\theta _{\mathsf {goal}}]$, whereas for the argument we will utilise that ![]() $\text {Arg}(g(\theta ))$ changes abruptly around
$\text {Arg}(g(\theta ))$ changes abruptly around ![]() $\theta _{\mathsf {goal}}$ (roughly by
$\theta _{\mathsf {goal}}$ (roughly by ![]() $\pi $). In particular, we proceed as follows.
$\pi $). In particular, we proceed as follows.
Algorithm for ![]() $\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ (Step 1): We first find an interval of length
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ (Step 1): We first find an interval of length ![]() $<2\pi /3$ with rational endpoints containing
$<2\pi /3$ with rational endpoints containing ![]() $\theta _{\mathsf {goal}}$ in
$\theta _{\mathsf {goal}}$ in ![]() $poly(n)$ time. For
$poly(n)$ time. For ![]() $j = 0, \ldots , 18$, let
$j = 0, \ldots , 18$, let ![]() $\theta _{j} = j/3$,
$\theta _{j} = j/3$, ![]() $g_j = |g(\theta _j)|$ and
$g_j = |g(\theta _j)|$ and ![]() $\hat {g}_j=\hat {g}_{\theta _j}$; note that the
$\hat {g}_j=\hat {g}_{\theta _j}$; note that the ![]() $\hat {g}_j$s can be computed in
$\hat {g}_j$s can be computed in ![]() $poly(n)$ time. For convenience, extend these definitions by setting
$poly(n)$ time. For convenience, extend these definitions by setting ![]() $\theta _{19h+j}=\theta _j+2h \pi $,
$\theta _{19h+j}=\theta _j+2h \pi $, ![]() $g_{19h+j} = g_j$ and
$g_{19h+j} = g_j$ and ![]() $\hat {g}_{19h+j}=\hat {g}_j$ for every integer h and
$\hat {g}_{19h+j}=\hat {g}_j$ for every integer h and ![]() $j = 0, \ldots , 18$. Note that for all j we have that
$j = 0, \ldots , 18$. Note that for all j we have that ![]() $1/3\geq |\theta _{j+1}-\theta _{j}|\geq 1/4>\pi /15$.
$1/3\geq |\theta _{j+1}-\theta _{j}|\geq 1/4>\pi /15$.
Consider an index ![]() $j\in \{0,\ldots ,18\}$ such that
$j\in \{0,\ldots ,18\}$ such that ![]() $\text {arg}(R_{\mathsf {goal}})$ does not intersect with the intervals
$\text {arg}(R_{\mathsf {goal}})$ does not intersect with the intervals ![]() $[\theta _j-\kappa ,\theta _{j+1}+\kappa ]$ and
$[\theta _j-\kappa ,\theta _{j+1}+\kappa ]$ and ![]() $[\theta _j-\pi , \theta _{j+1}-\pi ]$. Then, we have that
$[\theta _j-\pi , \theta _{j+1}-\pi ]$. Then, we have that
We claim that ![]() $g_{j+1} - g_j$ has the same sign as
$g_{j+1} - g_j$ has the same sign as ![]() $\hat {g}_{j+1} - \hat {g}_j$. To see this, assume w.l.o.g.
$\hat {g}_{j+1} - \hat {g}_j$. To see this, assume w.l.o.g. ![]() $g_{j+1} - g_j> 0$ that the other possibility follows in a similar way. Observe that we must have
$g_{j+1} - g_j> 0$ that the other possibility follows in a similar way. Observe that we must have ![]() $\theta _j,\theta _{j+1}\in (\theta _{\mathsf {goal}},\theta _{\mathsf {goal}}+\pi )$, as
$\theta _j,\theta _{j+1}\in (\theta _{\mathsf {goal}},\theta _{\mathsf {goal}}+\pi )$, as ![]() $\theta \mapsto \sin (\theta /2-\theta _{\mathsf {goal}}/2)$ is increasing on
$\theta \mapsto \sin (\theta /2-\theta _{\mathsf {goal}}/2)$ is increasing on ![]() $(\theta _{\mathsf {goal}},\theta _{\mathsf {goal}}+\pi )$, and so
$(\theta _{\mathsf {goal}},\theta _{\mathsf {goal}}+\pi )$, and so
 $$ \begin{align} \begin{aligned} g_{j+1} - g_j &= |g(\theta_{j+1})| - |g(\theta_j)|\geq 2|t|\min_{\phi \in [0, \pi/2 - \pi/30)]} [\sin(\phi + \pi / 30)-\sin\phi] \\ &\geq 2|t|\big[\sin(\pi/2)-\sin (\pi/2-\pi/30)\big] \geq |t|/100. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} g_{j+1} - g_j &= |g(\theta_{j+1})| - |g(\theta_j)|\geq 2|t|\min_{\phi \in [0, \pi/2 - \pi/30)]} [\sin(\phi + \pi / 30)-\sin\phi] \\ &\geq 2|t|\big[\sin(\pi/2)-\sin (\pi/2-\pi/30)\big] \geq |t|/100. \end{aligned} \end{align} $$On the other hand, if ![]() $\hat {g}_{j+1} - \hat {g}_j <0$, from (26) we have
$\hat {g}_{j+1} - \hat {g}_j <0$, from (26) we have ![]() $(1- \tau )g_{j+1} - (1+ \tau )g_j < 0$. This gives
$(1- \tau )g_{j+1} - (1+ \tau )g_j < 0$. This gives ![]() $g_{j+1} - g_j \leq \tau (g_{j+1} + g_j) \leq 2 \tau |t|$, a contradiction to the above.
$g_{j+1} - g_j \leq \tau (g_{j+1} + g_j) \leq 2 \tau |t|$, a contradiction to the above.
Let ![]() $j^*$ be such that
$j^*$ be such that ![]() $\theta _{\mathsf {goal}} \in [\theta _{j^*}, \theta _{j^*+1})$. From (23), the sequence
$\theta _{\mathsf {goal}} \in [\theta _{j^*}, \theta _{j^*+1})$. From (23), the sequence ![]() $g_{j}$ is decreasing until
$g_{j}$ is decreasing until ![]() $j^*$ and increasing after
$j^*$ and increasing after ![]() $j^*+1$. From the claim above, the sequence
$j^*+1$. From the claim above, the sequence ![]() $\hat {g}_j$ must therefore be decreasing for indices j in
$\hat {g}_j$ must therefore be decreasing for indices j in ![]() $[j^*-8,j^*-1]$ and increasing for indices
$[j^*-8,j^*-1]$ and increasing for indices ![]() $[j^*+2,j^*+9]$. Therefore, from the values of
$[j^*+2,j^*+9]$. Therefore, from the values of ![]() $\hat {g}_j$s we can find
$\hat {g}_j$s we can find ![]() $\hat {j}$ so that
$\hat {j}$ so that ![]() $\theta _{\mathsf {goal}}\in [\theta _{\hat {j}-3},\theta _{\hat {j}+3}]$. By enlarging slightly the interval
$\theta _{\mathsf {goal}}\in [\theta _{\hat {j}-3},\theta _{\hat {j}+3}]$. By enlarging slightly the interval ![]() $[\theta _{\hat {j}-3},\theta _{\hat {j}+3}]$, we obtain the desired interval of length
$[\theta _{\hat {j}-3},\theta _{\hat {j}+3}]$, we obtain the desired interval of length ![]() $<2\pi /3$ with rational endpoints.
$<2\pi /3$ with rational endpoints.
Algorithm for ![]() $\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ (Step 2): Given an interval
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ (Step 2): Given an interval ![]() $[\theta _1, \theta _2]$ with rational endpoints containing
$[\theta _1, \theta _2]$ with rational endpoints containing ![]() $\theta _{\mathsf {goal}}$ with
$\theta _{\mathsf {goal}}$ with ![]() $|\theta _1 - \theta _2|=\ell $ and
$|\theta _1 - \theta _2|=\ell $ and ![]() $\ell \in (100\kappa ,2\pi /3)$, we show how to find in
$\ell \in (100\kappa ,2\pi /3)$, we show how to find in ![]() $poly(n,\mathrm {size}(\theta _1,\theta _2))$ time an interval with rational endpoints that is a factor of
$poly(n,\mathrm {size}(\theta _1,\theta _2))$ time an interval with rational endpoints that is a factor of ![]() $1/2$ smaller in length and also contains
$1/2$ smaller in length and also contains ![]() $\theta _{\mathsf {goal}}$. The analysis will be similar to step 1.
$\theta _{\mathsf {goal}}$. The analysis will be similar to step 1.
For ![]() $j = 0, \ldots , 19$ define
$j = 0, \ldots , 19$ define ![]() $\phi _j = \theta _1 + (\theta _2 - \theta _1)j /19$ and let
$\phi _j = \theta _1 + (\theta _2 - \theta _1)j /19$ and let ![]() $g_j = |g(\phi _j)|$ and
$g_j = |g(\phi _j)|$ and ![]() $\hat {g}_j=\hat {g}_{\phi _j}$. Since
$\hat {g}_j=\hat {g}_{\phi _j}$. Since ![]() $\theta _{\mathsf {goal}} \in [\theta _1, \theta _2]$ and
$\theta _{\mathsf {goal}} \in [\theta _1, \theta _2]$ and ![]() $|\theta _1 - \theta _2|=\ell $, for any
$|\theta _1 - \theta _2|=\ell $, for any ![]() $\theta \in [\theta _1, \theta _2]$ we have
$\theta \in [\theta _1, \theta _2]$ we have ![]() $|g(\theta )| \leq 2|t|\sin (\ell /2) \leq \ell |t|$. In particular, we have
$|g(\theta )| \leq 2|t|\sin (\ell /2) \leq \ell |t|$. In particular, we have ![]() $g_j \leq \ell |t|$ for all j.
$g_j \leq \ell |t|$ for all j.
Moreover, for an index j such that ![]() $\theta _{\mathsf {goal}}\notin [\phi _j,\phi _{j+1}]$, we claim that
$\theta _{\mathsf {goal}}\notin [\phi _j,\phi _{j+1}]$, we claim that ![]() $g_{j+1} - g_j$ has the same sign as
$g_{j+1} - g_j$ has the same sign as ![]() $\hat {g}_{j+1} - \hat {g}_j$. To prove the claim, assume
$\hat {g}_{j+1} - \hat {g}_j$. To prove the claim, assume ![]() $g_{j+1} - g_j \geq 0$, so
$g_{j+1} - g_j \geq 0$, so ![]() $\phi _{j+1}, \phi _j \geq \theta _{\mathsf {goal}}$; the other possibility follows in a similar way. The derivative of
$\phi _{j+1}, \phi _j \geq \theta _{\mathsf {goal}}$; the other possibility follows in a similar way. The derivative of ![]() $|g(\theta )|$ in the interval
$|g(\theta )|$ in the interval ![]() $[\theta _{\mathsf {goal}},\theta _{\mathsf {goal}}+\ell ]$ is bounded below by
$[\theta _{\mathsf {goal}},\theta _{\mathsf {goal}}+\ell ]$ is bounded below by ![]() $|t|\cos (\ell /2)\geq |t|/2$, so by the mean value theorem we have that
$|t|\cos (\ell /2)\geq |t|/2$, so by the mean value theorem we have that
 $$ \begin{align*} g_{j+1} - g_j \geq \frac{|t|}{2}(\phi_{j+1} - \phi_{j})\geq |t|\ell/50. \end{align*} $$
$$ \begin{align*} g_{j+1} - g_j \geq \frac{|t|}{2}(\phi_{j+1} - \phi_{j})\geq |t|\ell/50. \end{align*} $$On the other hand, if ![]() $\hat {g}_{j+1} - \hat {g}_j <0$, then, as before, we have
$\hat {g}_{j+1} - \hat {g}_j <0$, then, as before, we have ![]() $(1- \tau )g_{j+1} - (1+ \tau )g_j < 0$, which implies
$(1- \tau )g_{j+1} - (1+ \tau )g_j < 0$, which implies ![]() $g_{j+1} - g_j \leq \tau (g_{j+1} + g_j) \leq 2\tau \ell |t|$, a contradiction to the above. This proves the claim.
$g_{j+1} - g_j \leq \tau (g_{j+1} + g_j) \leq 2\tau \ell |t|$, a contradiction to the above. This proves the claim.
Using the claim, we can conclude just as we did in step 1 and find an index ![]() $\hat {j}$ so that
$\hat {j}$ so that ![]() $\theta _{\mathsf {goal}}\in [\phi _{\hat {j}-3},\phi _{\hat {j}+3}]$, giving the desired interval.
$\theta _{\mathsf {goal}}\in [\phi _{\hat {j}-3},\phi _{\hat {j}+3}]$, giving the desired interval.
Algorithm for ![]() $\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$: Given a rational endpoint
$\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$: Given a rational endpoint ![]() $\theta _1$ and a rational length
$\theta _1$ and a rational length  $\ell \in (100\kappa ,\tfrac {63}{10}]$ such that
$\ell \in (100\kappa ,\tfrac {63}{10}]$ such that ![]() $\theta _{\mathsf {goal}}$ lies in the interval
$\theta _{\mathsf {goal}}$ lies in the interval ![]() $[\theta _1, \theta _2]$ for some
$[\theta _1, \theta _2]$ for some ![]() $\theta _2\leq \theta _1+\ell $, we show how to find in
$\theta _2\leq \theta _1+\ell $, we show how to find in ![]() $poly(n,\mathrm {size}(\theta _1,\ell ))$ time a rational endpoint
$poly(n,\mathrm {size}(\theta _1,\ell ))$ time a rational endpoint ![]() $\theta _1'$ and a rational length
$\theta _1'$ and a rational length ![]() $\ell '$ such that
$\ell '$ such that ![]() $\ell '\leq \ell /4$ and
$\ell '\leq \ell /4$ and ![]() $\theta _{\mathsf {goal}}\in [\theta _1', \theta _2']$ for some
$\theta _{\mathsf {goal}}\in [\theta _1', \theta _2']$ for some ![]() $\theta _2'\leq \theta _1'+\ell '$.
$\theta _2'\leq \theta _1'+\ell '$.
For ![]() $j = 0, \ldots , 25$, define
$j = 0, \ldots , 25$, define ![]() $\phi _j = \theta _1 + \ell j /26$ and let
$\phi _j = \theta _1 + \ell j /26$ and let ![]() $a_j = \text {Arg}(g(\phi _j))$,
$a_j = \text {Arg}(g(\phi _j))$, ![]() $\hat {a}_j=\hat {a}_{\phi _j}$. For convenience, extend these definitions by setting
$\hat {a}_j=\hat {a}_{\phi _j}$. For convenience, extend these definitions by setting ![]() $\phi _{26h+j}=\phi _j$,
$\phi _{26h+j}=\phi _j$, ![]() $a_{26h+j}= a_{j}$ and
$a_{26h+j}= a_{j}$ and ![]() $\hat {a}_{26h+j}= \hat {a}_{j}$ for every integer h and
$\hat {a}_{26h+j}= \hat {a}_{j}$ for every integer h and ![]() $j = 0, \ldots , 25$. For indices
$j = 0, \ldots , 25$. For indices ![]() $j,j'$, let
$j,j'$, let
 $$ \begin{align*}D_{j,j'}=\min\{|a_{j'} - a_j|,2\pi-|a_{j'} - a_j|\}\mbox{ and }\widehat{D}_{j,j'}=\min\{|\hat{a}_{j'} - \hat{a}_j|,2\pi-|\hat{a}_{j'} - \hat{a}_j|\}.\end{align*} $$
$$ \begin{align*}D_{j,j'}=\min\{|a_{j'} - a_j|,2\pi-|a_{j'} - a_j|\}\mbox{ and }\widehat{D}_{j,j'}=\min\{|\hat{a}_{j'} - \hat{a}_j|,2\pi-|\hat{a}_{j'} - \hat{a}_j|\}.\end{align*} $$Consider an index j such that ![]() $\theta _{\mathsf {goal}}\notin [\phi _j-\kappa ,\phi _{j+1}+\kappa ]$. Then, we have that
$\theta _{\mathsf {goal}}\notin [\phi _j-\kappa ,\phi _{j+1}+\kappa ]$. Then, we have that ![]() $D_{j,j+1}=|\phi _{j+1}-\phi _j|/2\leq \pi /10$ and hence
$D_{j,j+1}=|\phi _{j+1}-\phi _j|/2\leq \pi /10$ and hence  $\widehat {D}_{j,j+1}\leq \pi /5$. On the other hand, for an index j such that
$\widehat {D}_{j,j+1}\leq \pi /5$. On the other hand, for an index j such that ![]() $\theta _{\mathsf {goal}}\in [\phi _{j},\phi _{j+1}]$, we have that
$\theta _{\mathsf {goal}}\in [\phi _{j},\phi _{j+1}]$, we have that ![]() $D_{j-1,j+1}=\pi -|\phi _{j+1}-\phi _{j-1}|/2\geq 4\pi /5$ and, similarly,
$D_{j-1,j+1}=\pi -|\phi _{j+1}-\phi _{j-1}|/2\geq 4\pi /5$ and, similarly, ![]() $D_{j,j+2}\geq 4\pi /5$. Therefore, at least one of
$D_{j,j+2}\geq 4\pi /5$. Therefore, at least one of  $\widehat {D}_{j-1,j+1}\geq 3\pi /5$,
$\widehat {D}_{j-1,j+1}\geq 3\pi /5$,  $\widehat {D}_{j,j+2}\geq 3\pi /5$ must hold. Therefore, using the
$\widehat {D}_{j,j+2}\geq 3\pi /5$ must hold. Therefore, using the ![]() $\hat {a}_j$s, we can find an index
$\hat {a}_j$s, we can find an index ![]() $\hat {j}$ so that
$\hat {j}$ so that ![]() $\theta _{\mathsf {goal}}\in [\phi _{\hat {j}-2},\phi _{\hat {j}+2}]$, giving the desired interval.
$\theta _{\mathsf {goal}}\in [\phi _{\hat {j}-2},\phi _{\hat {j}+2}]$, giving the desired interval.
By repeating the above, we conclude that, using a poly-time algorithm for either the problem ![]() $\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ or
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ or ![]() $\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$, we can compute in
$\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$, we can compute in ![]() $poly(n)$ time a rational
$poly(n)$ time a rational ![]() $\hat {\theta }$ such that
$\hat {\theta }$ such that ![]() $|\hat {\theta }-\theta |\leq 400\kappa \leq \epsilon /2$, yielding the desired
$|\hat {\theta }-\theta |\leq 400\kappa \leq \epsilon /2$, yielding the desired ![]() $\hat {R}$ (via Lemma 35). We thus focus on proving that for a rational
$\hat {R}$ (via Lemma 35). We thus focus on proving that for a rational ![]() $\theta $ we can obtain in time
$\theta $ we can obtain in time ![]() $poly(n,\mathrm {size}(\theta ))$ values
$poly(n,\mathrm {size}(\theta ))$ values ![]() $\hat {g}_\theta , \hat {a}_\theta $ satisfying (24) and (25), respectively.
$\hat {g}_\theta , \hat {a}_\theta $ satisfying (24) and (25), respectively.
Let ![]() $\epsilon _2=\kappa \epsilon /10^{5}$,
$\epsilon _2=\kappa \epsilon /10^{5}$,  $\epsilon _1:=\epsilon _2/\big (2^{4n}(2\hat {b})^{2m}\big )$,
$\epsilon _1:=\epsilon _2/\big (2^{4n}(2\hat {b})^{2m}\big )$, ![]() $\epsilon _0=\epsilon _1/(k4^k)$. By Lemmas 32 and 35, for a rational number
$\epsilon _0=\epsilon _1/(k4^k)$. By Lemmas 32 and 35, for a rational number ![]() $\phi $, we can construct in time
$\phi $, we can construct in time ![]() $poly(n,\mathrm {size}(\phi ))$ a rooted tree
$poly(n,\mathrm {size}(\phi ))$ a rooted tree ![]() $T_\phi $ in
$T_\phi $ in ![]() $\mathcal {T}_{\Delta }$ with root
$\mathcal {T}_{\Delta }$ with root ![]() $x_\phi $ that has degree 1 and implements a field
$x_\phi $ that has degree 1 and implements a field ![]() $\lambda _\phi $ such that
$\lambda _\phi $ such that ![]() $|\lambda _\phi -\mathrm {e}^{\mathrm {i} \phi }|\leq \epsilon _0$. For convenience, let
$|\lambda _\phi -\mathrm {e}^{\mathrm {i} \phi }|\leq \epsilon _0$. For convenience, let
 $$ \begin{align} Q_\phi^{\mathrm{\tt{\pm}}}:=Z_{T_\phi,\mathrm{\tt{\pm}} x_\phi}(\lambda,b) \mbox{ and note that } \Big|\frac{Q_\phi^{\mathrm{\texttt{+}}}}{Q_\phi^{\mathrm{\texttt{-}}}}-\mathrm{e}^{\mathrm{i} \phi}\Big|\leq \epsilon_0. \end{align} $$
$$ \begin{align} Q_\phi^{\mathrm{\tt{\pm}}}:=Z_{T_\phi,\mathrm{\tt{\pm}} x_\phi}(\lambda,b) \mbox{ and note that } \Big|\frac{Q_\phi^{\mathrm{\texttt{+}}}}{Q_\phi^{\mathrm{\texttt{-}}}}-\mathrm{e}^{\mathrm{i} \phi}\Big|\leq \epsilon_0. \end{align} $$Let ![]() $T_\theta ,T_{0}$ be the trees obtained for
$T_\theta ,T_{0}$ be the trees obtained for ![]() $\phi =\theta ,0$ and note that that
$\phi =\theta ,0$ and note that that ![]() $T_\theta , T_0$ implement the vertex activities
$T_\theta , T_0$ implement the vertex activities ![]() $\mathrm {e}^{\mathrm {i} \theta }, 1$, respectively (with precision
$\mathrm {e}^{\mathrm {i} \theta }, 1$, respectively (with precision ![]() $\epsilon _0$).
$\epsilon _0$).
Recall that ![]() $P_k$ is the path with k vertices and endpoints
$P_k$ is the path with k vertices and endpoints ![]() $u_k,v_k$, and we denote by
$u_k,v_k$, and we denote by ![]() $V_{P_k}$ the set of its vertices. Let
$V_{P_k}$ the set of its vertices. Let ![]() $P_{k, T_{0}}$ be the tree obtained from
$P_{k, T_{0}}$ be the tree obtained from ![]() $P_k$ by attaching
$P_k$ by attaching ![]() $k-2$ disjoint copies of the graph
$k-2$ disjoint copies of the graph ![]() $T_{0}$ to the internal vertices of the path; that is, for
$T_{0}$ to the internal vertices of the path; that is, for ![]() $i=1,\ldots , k-2$, identify the root
$i=1,\ldots , k-2$, identify the root ![]() $x_{0}$ of the ith copy of
$x_{0}$ of the ith copy of ![]() $T_{0}$ with the ith internal vertex of the path. For convenience, let
$T_{0}$ with the ith internal vertex of the path. For convenience, let
 $$ \begin{align} A_{\mathrm{\tt{\pm}}\mathrm{\tt{\pm}}}:=Z_{P_{k, T_{0}},\mathrm{\tt{\pm}} u_k,\mathrm{\tt{\pm}} v_k}(\lambda,b). \end{align} $$
$$ \begin{align} A_{\mathrm{\tt{\pm}}\mathrm{\tt{\pm}}}:=Z_{P_{k, T_{0}},\mathrm{\tt{\pm}} u_k,\mathrm{\tt{\pm}} v_k}(\lambda,b). \end{align} $$ Recall that ![]() $H=(V_H,E_H)$ denotes the graph obtained by subdividing edge e of G. Let
$H=(V_H,E_H)$ denotes the graph obtained by subdividing edge e of G. Let ![]() $H_\theta \in \mathcal {G}_\Delta $ be the graph obtained from H by replacing every edge
$H_\theta \in \mathcal {G}_\Delta $ be the graph obtained from H by replacing every edge ![]() $\{x,y\}$ of H by a distinct copy of
$\{x,y\}$ of H by a distinct copy of ![]() $P_{k, T_{0}}$ (identifying x with
$P_{k, T_{0}}$ (identifying x with ![]() $u_k$ and y with
$u_k$ and y with ![]() $v_k$) and attaching the tree
$v_k$) and attaching the tree ![]() $T_\theta $ on the vertex s of H (identifying s with the root
$T_\theta $ on the vertex s of H (identifying s with the root ![]() $x_\theta $). Effectively, the construction of
$x_\theta $). Effectively, the construction of ![]() $H_{\theta }$ is so that the Ising model on
$H_{\theta }$ is so that the Ising model on ![]() $H_\theta $ with edge activities equal to b and vertex activities equal to
$H_\theta $ with edge activities equal to b and vertex activities equal to ![]() $\lambda $ corresponds to an Ising model on H with edge activities equal to
$\lambda $ corresponds to an Ising model on H with edge activities equal to ![]() $\hat {b}$ and vertex activities equal to
$\hat {b}$ and vertex activities equal to ![]() $\lambda $ apart from that of vertex s which is set to
$\lambda $ apart from that of vertex s which is set to ![]() $\mathrm {e}^{\mathrm {i} \theta }$. In this latter model, the contribution to the partition function from configurations where s is set to
$\mathrm {e}^{\mathrm {i} \theta }$. In this latter model, the contribution to the partition function from configurations where s is set to ![]() $\mathrm {\texttt {+}}$ is given by t and the contribution to the partition function from configurations where s is set to
$\mathrm {\texttt {+}}$ is given by t and the contribution to the partition function from configurations where s is set to ![]() $\mathrm {\texttt {-}}$ is given by r, where
$\mathrm {\texttt {-}}$ is given by r, where ![]() $t,r$ are as in (22). Based on this, we will soon show that
$t,r$ are as in (22). Based on this, we will soon show that
 $$ \begin{align} \Big|\frac{Z_{H_\theta}(\lambda,b)}{Q^{\mathrm{\texttt{-}}}_\theta(A_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}})^{m+1}}-g(\theta)\Big|\leq \epsilon_2. \end{align} $$
$$ \begin{align} \Big|\frac{Z_{H_\theta}(\lambda,b)}{Q^{\mathrm{\texttt{-}}}_\theta(A_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}})^{m+1}}-g(\theta)\Big|\leq \epsilon_2. \end{align} $$From (30), we obtain the desired approximations ![]() $\hat {g}_{\theta }, \hat {a}_\theta $ that satisfy (24), (25), respectively, as follows. First, observe that
$\hat {g}_{\theta }, \hat {a}_\theta $ that satisfy (24), (25), respectively, as follows. First, observe that ![]() $|g(\theta )|\geq |t|\kappa /2\geq 10\epsilon _2/\tau $ since
$|g(\theta )|\geq |t|\kappa /2\geq 10\epsilon _2/\tau $ since ![]() $|\theta -a|\geq \kappa $ for every
$|\theta -a|\geq \kappa $ for every ![]() $a\in \text {arg}(R_{\mathsf {goal}})$. Second,
$a\in \text {arg}(R_{\mathsf {goal}})$. Second, ![]() $T_\theta $ and
$T_\theta $ and ![]() $P_{k, T_{0}}$ are trees of size
$P_{k, T_{0}}$ are trees of size ![]() $poly(n, \mathrm {size}(\theta ))$, so we can compute
$poly(n, \mathrm {size}(\theta ))$, so we can compute ![]() $Q^{\mathrm {\texttt {-}}}_\theta $ and
$Q^{\mathrm {\texttt {-}}}_\theta $ and ![]() $A_{\mathrm {\texttt {+}}\mathrm {\texttt {+}}}$ in time
$A_{\mathrm {\texttt {+}}\mathrm {\texttt {+}}}$ in time ![]() $poly(n, \mathrm {size}(\theta ))$. Using a poly-time algorithm for
$poly(n, \mathrm {size}(\theta ))$. Using a poly-time algorithm for ![]() $\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$, we can compute
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$, we can compute ![]() $\hat {Z}_{\theta }$ in time
$\hat {Z}_{\theta }$ in time ![]() $poly(n,\mathrm {size}(\theta ))$ which is within a factor of
$poly(n,\mathrm {size}(\theta ))$ which is within a factor of ![]() $1\pm \tau $ from
$1\pm \tau $ from ![]() $|Z_{H_\theta }(\lambda ,b)|$, thus yielding
$|Z_{H_\theta }(\lambda ,b)|$, thus yielding  $\hat {g}_{\theta }=\frac {\hat {Z}_{\theta }}{|Q^{\mathrm {\texttt {-}}}_\theta |\,|A_{\mathrm {\texttt {+}}\mathrm {\texttt {+}}}|^{m+1}}$ that satisfies (24). Similarly, using a poly-time algorithm for
$\hat {g}_{\theta }=\frac {\hat {Z}_{\theta }}{|Q^{\mathrm {\texttt {-}}}_\theta |\,|A_{\mathrm {\texttt {+}}\mathrm {\texttt {+}}}|^{m+1}}$ that satisfies (24). Similarly, using a poly-time algorithm for ![]() $\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$, we can compute
$\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$, we can compute ![]() $\hat {A}_{\theta }$ in time
$\hat {A}_{\theta }$ in time ![]() $poly(n,\mathrm {size}(\theta ))$ which is within distance
$poly(n,\mathrm {size}(\theta ))$ which is within distance ![]() $\rho $ from
$\rho $ from ![]() $\mathrm {Arg}(Z_{H_\theta }(\lambda ,b))$. Noting that the argument
$\mathrm {Arg}(Z_{H_\theta }(\lambda ,b))$. Noting that the argument ![]() $\alpha $ of
$\alpha $ of  $\frac {Z_{H_\theta }(\lambda ,b)}{Q^{\mathrm {\texttt {-}}}_\theta (A_{\mathrm {\texttt {+}}\mathrm {\texttt {+}}})^{m+1}}-g(\theta )$ satisfies
$\frac {Z_{H_\theta }(\lambda ,b)}{Q^{\mathrm {\texttt {-}}}_\theta (A_{\mathrm {\texttt {+}}\mathrm {\texttt {+}}})^{m+1}}-g(\theta )$ satisfies ![]() $\sin (\alpha )\leq \epsilon _2/g(\theta )$, from which it follows that
$\sin (\alpha )\leq \epsilon _2/g(\theta )$, from which it follows that ![]() $\alpha \leq \rho $. Hence,
$\alpha \leq \rho $. Hence,  $\hat {a}_{\theta }=\hat {A}_{\theta }-\text {Arg}(Q^{\mathrm {\texttt {-}}}_\theta )-(m+1)\text {Arg}(A_{\mathrm {\texttt {+}}\mathrm {\texttt {+}}}) (\mathrm {mod}\ 2\pi )$ satisfies (25).
$\hat {a}_{\theta }=\hat {A}_{\theta }-\text {Arg}(Q^{\mathrm {\texttt {-}}}_\theta )-(m+1)\text {Arg}(A_{\mathrm {\texttt {+}}\mathrm {\texttt {+}}}) (\mathrm {mod}\ 2\pi )$ satisfies (25).
It remains to prove (30). We first claim that
 $$ \begin{align} \Big|\frac{A_{\mathrm{\tt{\pm}}\mathrm{\tt{\pm}}}}{(Q^{\mathrm{\texttt{-}}}_{0})^{k-2}}-Z_{P_{k},\mathrm{\tt{\pm}} u_k,\mathrm{\tt{\pm}} v_k}(1,b)\Big|\leq \frac{\epsilon_1}{4}Z_{P_{k},\mathrm{\tt{\pm}} u_k,\mathrm{\tt{\pm}} v_k}(1,b). \end{align} $$
$$ \begin{align} \Big|\frac{A_{\mathrm{\tt{\pm}}\mathrm{\tt{\pm}}}}{(Q^{\mathrm{\texttt{-}}}_{0})^{k-2}}-Z_{P_{k},\mathrm{\tt{\pm}} u_k,\mathrm{\tt{\pm}} v_k}(1,b)\Big|\leq \frac{\epsilon_1}{4}Z_{P_{k},\mathrm{\tt{\pm}} u_k,\mathrm{\tt{\pm}} v_k}(1,b). \end{align} $$Indeed, for a fixed ![]() $\sigma :V_{P_k}\rightarrow \{\mathrm {\texttt {+}},\mathrm {\texttt {-}}\}$, the aggregate contribution to
$\sigma :V_{P_k}\rightarrow \{\mathrm {\texttt {+}},\mathrm {\texttt {-}}\}$, the aggregate contribution to ![]() $Z_{P_{k,T_{0}}}(1,b)$ from configurations on
$Z_{P_{k,T_{0}}}(1,b)$ from configurations on ![]() $P_{k,T_{0}}$ that agree with
$P_{k,T_{0}}$ that agree with ![]() $\sigma $ on
$\sigma $ on ![]() $V_{P_k}$ is
$V_{P_k}$ is  $(Q^{\mathrm {\texttt {+}}}_{0})^{n_{\mathrm {\texttt {+}}}(\sigma )}(Q^{\mathrm {\texttt {-}}}_{0})^{n_{\mathrm {\texttt {-}}}(\sigma )}w_{P_k,\sigma }(1,b)$ where
$(Q^{\mathrm {\texttt {+}}}_{0})^{n_{\mathrm {\texttt {+}}}(\sigma )}(Q^{\mathrm {\texttt {-}}}_{0})^{n_{\mathrm {\texttt {-}}}(\sigma )}w_{P_k,\sigma }(1,b)$ where ![]() $n_{\mathrm {\tt {\pm }}}(\sigma )$ is the number of internal vertices in
$n_{\mathrm {\tt {\pm }}}(\sigma )$ is the number of internal vertices in ![]() $P_k$ that have spin
$P_k$ that have spin ![]() $\mathrm {\tt {\pm }}$ under
$\mathrm {\tt {\pm }}$ under ![]() $\sigma $, so (31) follows from aggregating over the relevant
$\sigma $, so (31) follows from aggregating over the relevant ![]() $\sigma $ and observing thatFootnote 10
$\sigma $ and observing thatFootnote 10  $\big |\frac {(Q^{\mathrm {\texttt {+}}}_{0})^{j}}{(Q^{\mathrm {\texttt {-}}}_{0})^{j}}-1\big |\leq k\epsilon _0$ for all
$\big |\frac {(Q^{\mathrm {\texttt {+}}}_{0})^{j}}{(Q^{\mathrm {\texttt {-}}}_{0})^{j}}-1\big |\leq k\epsilon _0$ for all ![]() $j=0,\ldots ,k$. From (19) and (31), it follows that
$j=0,\ldots ,k$. From (19) and (31), it follows that ![]() $A_{\mathrm {\tt {\pm }},\mathrm {\tt {\pm }}}\neq 0$ and
$A_{\mathrm {\tt {\pm }},\mathrm {\tt {\pm }}}\neq 0$ and
 $$ \begin{align} \Big|\frac{A_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}}}{A_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}}-\hat{b}\Big|\leq \epsilon_1,\quad\Big|\frac{A_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}}{A_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}}-1\Big|\leq \epsilon_1. \end{align} $$
$$ \begin{align} \Big|\frac{A_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}}}{A_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}}-\hat{b}\Big|\leq \epsilon_1,\quad\Big|\frac{A_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}}{A_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}}-1\Big|\leq \epsilon_1. \end{align} $$Now, for ![]() $\sigma : V_H\rightarrow \{\mathrm {\texttt {+}},\mathrm {\texttt {-}}\}$ with
$\sigma : V_H\rightarrow \{\mathrm {\texttt {+}},\mathrm {\texttt {-}}\}$ with ![]() $\sigma (s)=\mathrm {\texttt {+}}$, let
$\sigma (s)=\mathrm {\texttt {+}}$, let ![]() $W^{\mathrm {\texttt {+}}}_\sigma $ be the aggregate weight of configurations on
$W^{\mathrm {\texttt {+}}}_\sigma $ be the aggregate weight of configurations on ![]() $H_\theta $ that agree with
$H_\theta $ that agree with ![]() $\sigma $ on
$\sigma $ on ![]() $V(H)$. Define analogously
$V(H)$. Define analogously ![]() $W^{\mathrm {\texttt {-}}}_\sigma $. Then, we have that
$W^{\mathrm {\texttt {-}}}_\sigma $. Then, we have that
 $$ \begin{align*}W^{\mathrm{\tt{\pm}}}_\sigma=Q^{\mathrm{\tt{\pm}}}_\theta(A_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}})^{m_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}(\sigma)}(A_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}})^{m_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}(\sigma)}(A_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}})^{m_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}(\sigma)},\end{align*} $$
$$ \begin{align*}W^{\mathrm{\tt{\pm}}}_\sigma=Q^{\mathrm{\tt{\pm}}}_\theta(A_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}})^{m_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}(\sigma)}(A_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}})^{m_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}(\sigma)}(A_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}})^{m_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}(\sigma)},\end{align*} $$where ![]() $m_{\mathrm {\texttt {+}}\mathrm {\texttt {+}}}(\sigma ),m_{\mathrm {\texttt {+}}\mathrm {\texttt {-}}}(\sigma ),m_{\mathrm {\texttt {-}}\mathrm {\texttt {-}}}(\sigma )$ denote the number edges of
$m_{\mathrm {\texttt {+}}\mathrm {\texttt {+}}}(\sigma ),m_{\mathrm {\texttt {+}}\mathrm {\texttt {-}}}(\sigma ),m_{\mathrm {\texttt {-}}\mathrm {\texttt {-}}}(\sigma )$ denote the number edges of ![]() $E_H$ whose endpoints are assigned
$E_H$ whose endpoints are assigned ![]() $\mathrm {\texttt {+}}\mathrm {\texttt {+}},\mathrm {\texttt {+}}\mathrm {\texttt {-}},\mathrm {\texttt {-}}\mathrm {\texttt {-}}$, respectively. Since the total number of edges in
$\mathrm {\texttt {+}}\mathrm {\texttt {+}},\mathrm {\texttt {+}}\mathrm {\texttt {-}},\mathrm {\texttt {-}}\mathrm {\texttt {-}}$, respectively. Since the total number of edges in ![]() $E_H$ is
$E_H$ is ![]() $m+1$, we obtain
$m+1$, we obtain
 $$ \begin{align} \bigg|\frac{W^{\mathrm{\texttt{+}}}_\sigma}{Q^{\mathrm{\texttt{-}}}_\theta(A_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}})^{m+1}}-\mathrm{e}^{\mathrm{i} \theta}\, w_{H,\sigma}(\lambda,\hat{b})\bigg|\leq \epsilon_2/10^n, \quad \bigg|\frac{W^{\mathrm{\texttt{-}}}_\sigma}{Q^{\mathrm{\texttt{-}}}_\theta(A_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}})^{m+1}}- w_{H,\sigma}(\lambda,\hat{b})\bigg|\leq \epsilon_2/10^n. \end{align} $$
$$ \begin{align} \bigg|\frac{W^{\mathrm{\texttt{+}}}_\sigma}{Q^{\mathrm{\texttt{-}}}_\theta(A_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}})^{m+1}}-\mathrm{e}^{\mathrm{i} \theta}\, w_{H,\sigma}(\lambda,\hat{b})\bigg|\leq \epsilon_2/10^n, \quad \bigg|\frac{W^{\mathrm{\texttt{-}}}_\sigma}{Q^{\mathrm{\texttt{-}}}_\theta(A_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}})^{m+1}}- w_{H,\sigma}(\lambda,\hat{b})\bigg|\leq \epsilon_2/10^n. \end{align} $$Observe also that the quantities ![]() $t,r$, as defined in (22), are such that
$t,r$, as defined in (22), are such that
 $$ \begin{align*}t=\sum_{\sigma: V_H\rightarrow \{\mathrm{\texttt{+}},\mathrm{\texttt{-}}\}; \sigma(s)=\mathrm{\texttt{+}}}w_{H,\sigma}(\lambda,\hat{b}) \mbox{ and } r=\sum_{\sigma: V_H\rightarrow \{\mathrm{\texttt{+}},\mathrm{\texttt{-}}\}; \sigma(s)=\mathrm{\texttt{-}}}w_{H,\sigma}(\lambda,\hat{b}),\end{align*} $$
$$ \begin{align*}t=\sum_{\sigma: V_H\rightarrow \{\mathrm{\texttt{+}},\mathrm{\texttt{-}}\}; \sigma(s)=\mathrm{\texttt{+}}}w_{H,\sigma}(\lambda,\hat{b}) \mbox{ and } r=\sum_{\sigma: V_H\rightarrow \{\mathrm{\texttt{+}},\mathrm{\texttt{-}}\}; \sigma(s)=\mathrm{\texttt{-}}}w_{H,\sigma}(\lambda,\hat{b}),\end{align*} $$so summing (33) over all ![]() $\sigma $ gives (30). This finishes the proof of (30) and hence completes the computation of
$\sigma $ gives (30). This finishes the proof of (30) and hence completes the computation of ![]() $R_{\mathsf {goal}}$ in
$R_{\mathsf {goal}}$ in ![]() $poly(n)$ time.
$poly(n)$ time.
The computation of  $R_{\mathsf {goal}}'$ is completely analogous, once we establish an analogue of (30). In particular, let
$R_{\mathsf {goal}}'$ is completely analogous, once we establish an analogue of (30). In particular, let ![]() $H'$ be the graph obtained from H by removing vertex s and adding the vertices
$H'$ be the graph obtained from H by removing vertex s and adding the vertices ![]() $u',v',s'$ and the edges
$u',v',s'$ and the edges ![]() $\{u,u'\},\{u',s'\},\{s',v'\},\{v',v\}$; note that
$\{u,u'\},\{u',s'\},\{s',v'\},\{v',v\}$; note that ![]() $H'$ is obtained from G by replacing the edge e by a path with three vertices. We construct
$H'$ is obtained from G by replacing the edge e by a path with three vertices. We construct ![]() $H_\theta '$ from
$H_\theta '$ from ![]() $H'$ as above, with a minor twist: we replace every edge
$H'$ as above, with a minor twist: we replace every edge ![]() $\{x,y\}$ of
$\{x,y\}$ of ![]() $H'$ with a distinct copy of
$H'$ with a distinct copy of ![]() $P_{k, T_{0}}$ (identifying x with
$P_{k, T_{0}}$ (identifying x with ![]() $u_k$ and y with
$u_k$ and y with ![]() $v_k$), we attach the rooted tree
$v_k$), we attach the rooted tree ![]() $T_\theta $ on the vertex
$T_\theta $ on the vertex ![]() $s'$ of
$s'$ of ![]() $H'$ (identifying
$H'$ (identifying ![]() $s'$ with the root
$s'$ with the root ![]() $x_\theta $) and we attach two distinct copies of the rooted tree
$x_\theta $) and we attach two distinct copies of the rooted tree ![]() $T_\pi $ on the vertices
$T_\pi $ on the vertices ![]() $u',v'$ of
$u',v'$ of ![]() $H'$ (identifying
$H'$ (identifying ![]() $u',v'$ with the corresponding roots
$u',v'$ with the corresponding roots ![]() $x_\pi $ in the two copies of
$x_\pi $ in the two copies of ![]() $T_\pi $). Note the use of the tree
$T_\pi $). Note the use of the tree ![]() $T_\pi $ in the construction of
$T_\pi $ in the construction of ![]() $H'$ which, analogousFootnote 11 to (28), implements the field
$H'$ which, analogousFootnote 11 to (28), implements the field ![]() $\mathrm {e}^{\mathrm {i} \pi }=-1$ (with precision
$\mathrm {e}^{\mathrm {i} \pi }=-1$ (with precision ![]() $\epsilon _0$). Effectively, the construction of
$\epsilon _0$). Effectively, the construction of ![]() $H_{\theta }'$ is so that the Ising model on
$H_{\theta }'$ is so that the Ising model on ![]() $H_\theta '$ with edge activities equal to b and vertex activities equal to
$H_\theta '$ with edge activities equal to b and vertex activities equal to ![]() $\lambda $ corresponds to an Ising model on
$\lambda $ corresponds to an Ising model on ![]() $H'$ with edge activities equal to
$H'$ with edge activities equal to ![]() $\hat {b}$ and vertex activities equal to
$\hat {b}$ and vertex activities equal to ![]() $\lambda $ apart from those of
$\lambda $ apart from those of ![]() $u',s',v'$ which are set to
$u',s',v'$ which are set to ![]() $-1,\mathrm {e}^{\mathrm {i} \theta },-1$, respectively. In this latter model, the contribution to the partition function from configurations where
$-1,\mathrm {e}^{\mathrm {i} \theta },-1$, respectively. In this latter model, the contribution to the partition function from configurations where ![]() $s'$ is set to
$s'$ is set to ![]() $\mathrm {\texttt {+}}$ is given by
$\mathrm {\texttt {+}}$ is given by ![]() $t'=(\hat {b}^2-1)^2z_{\mathrm {\texttt {+}}\mathrm {\texttt {+}}}$ and the contribution to the partition function from configurations where
$t'=(\hat {b}^2-1)^2z_{\mathrm {\texttt {+}}\mathrm {\texttt {+}}}$ and the contribution to the partition function from configurations where ![]() $s'$ is set to
$s'$ is set to ![]() $\mathrm {\texttt {-}}$ is given by
$\mathrm {\texttt {-}}$ is given by ![]() $r'=(\hat {b}^2-1)^2z_{\mathrm {\texttt {-}}\mathrm {\texttt {-}}}$. Based on this, we obtain, similar to the above, the following analogue of (30):
$r'=(\hat {b}^2-1)^2z_{\mathrm {\texttt {-}}\mathrm {\texttt {-}}}$. Based on this, we obtain, similar to the above, the following analogue of (30):
 $$ \begin{align} \Big|\frac{Z_{H_\theta'}(\lambda,b)}{Q^{\mathrm{\texttt{-}}}_\theta (Q^{\mathrm{\texttt{-}}}_\pi)^2(A_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}})^{m+2}}-\big(t'\mathrm{e}^{\mathrm{i} \theta}+r'\big)\Big|\leq \epsilon_2. \end{align} $$
$$ \begin{align} \Big|\frac{Z_{H_\theta'}(\lambda,b)}{Q^{\mathrm{\texttt{-}}}_\theta (Q^{\mathrm{\texttt{-}}}_\pi)^2(A_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}})^{m+2}}-\big(t'\mathrm{e}^{\mathrm{i} \theta}+r'\big)\Big|\leq \epsilon_2. \end{align} $$Having (34) at hand, the computation of  $R_{\mathsf {goal}}'$ can be carried out using exactly the same procedure as for
$R_{\mathsf {goal}}'$ can be carried out using exactly the same procedure as for ![]() $R_{\mathsf {goal}}$. This finishes the proof of Lemma 37.
$R_{\mathsf {goal}}$. This finishes the proof of Lemma 37.
8.3 Proof of our main theorem
We are now ready to finish the proof of Theorem 1, which we restate here for convenience.
Theorem 1. Let ![]() $\Delta \geq 3$ be an integer and let
$\Delta \geq 3$ be an integer and let ![]() $K=1.001$ and
$K=1.001$ and ![]() $\rho =\pi /40$.
$\rho =\pi /40$.
(a) Let
 $b \in \big (0,\frac {\Delta -2}{\Delta }\big ]$ be a rational and
$b \in \big (0,\frac {\Delta -2}{\Delta }\big ]$ be a rational and  $\lambda \in \mathbb {S}_{\mathbb {Q}}$ such that
$\lambda \in \mathbb {S}_{\mathbb {Q}}$ such that  $\lambda \neq \pm 1$. Then the problems
$\lambda \neq \pm 1$. Then the problems  $\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ and
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ and  $\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$ are
$\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$ are  $\mathsf {\#P}$-hard.
$\mathsf {\#P}$-hard.(b) Let
 $b\in \big (\frac {\Delta -2}{\Delta },1\big )$ be a rational. Then the collection of complex numbers
$b\in \big (\frac {\Delta -2}{\Delta },1\big )$ be a rational. Then the collection of complex numbers  $\lambda \in \mathbb {S}_{\mathbb {Q}}$ for which
$\lambda \in \mathbb {S}_{\mathbb {Q}}$ for which  $\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ and
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ and  $\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$ are
$\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$ are  $\mathsf {\#P}$-hard is dense in the arc
$\mathsf {\#P}$-hard is dense in the arc  $\mathbb {S}\setminus I(\theta _b)$.
$\mathbb {S}\setminus I(\theta _b)$.
Proof of Theorem 1. Let ![]() $b\in (0,1)$ be a rational number and let
$b\in (0,1)$ be a rational number and let ![]() $\ \lambda \in \mathbb {S}_{\mathbb {Q}}(\Delta -1,b)$. By Theorem 6, it suffices to show that
$\ \lambda \in \mathbb {S}_{\mathbb {Q}}(\Delta -1,b)$. By Theorem 6, it suffices to show that ![]() $\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ and
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ and ![]() $\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$ are
$\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$ are ![]() $\mathsf {\#P}$-hard. To prove the
$\mathsf {\#P}$-hard. To prove the ![]() $\mathsf {\#P}$-hardness for these problems, we will show that, assuming a poly-time algorithm for either
$\mathsf {\#P}$-hardness for these problems, we will show that, assuming a poly-time algorithm for either ![]() $\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ or
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta ,K)$ or ![]() $\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$, on input of a graph
$\#\mathsf {IsingArg}(\lambda ,b,\Delta ,\rho )$, on input of a graph ![]() $G\in \mathcal {G}_3$ we can compute
$G\in \mathcal {G}_3$ we can compute ![]() $Z_{G}(\lambda ,\hat {b})$ in poly-time, which is
$Z_{G}(\lambda ,\hat {b})$ in poly-time, which is ![]() $\mathsf {\#P}$-hard by [Reference Kowalczyk and Cai28, Theorem 1.1]. In fact, it suffices to compute in poly-time, for an arbitrary edge e of G, the ratio
$\mathsf {\#P}$-hard by [Reference Kowalczyk and Cai28, Theorem 1.1]. In fact, it suffices to compute in poly-time, for an arbitrary edge e of G, the ratio  $\frac {Z_{G}(\lambda ,\hat {b})}{Z_{G\backslash e}(\lambda ,\hat {b})}$, since then we can compute
$\frac {Z_{G}(\lambda ,\hat {b})}{Z_{G\backslash e}(\lambda ,\hat {b})}$, since then we can compute ![]() $Z_{G}(\lambda ,\hat {b})$ using a telescoping product over the edges of the graph G.
$Z_{G}(\lambda ,\hat {b})$ using a telescoping product over the edges of the graph G.
So fix an arbitrary edge ![]() $e=\{u,v\}$ of G and let
$e=\{u,v\}$ of G and let ![]() $z_{\mathrm {\tt {\pm }}\mathrm {\tt {\pm }}}:=Z_{G,\mathrm {\tt {\pm }} u,\mathrm {\tt {\pm }} v}(\lambda ,\hat {b})$. The ratio
$z_{\mathrm {\tt {\pm }}\mathrm {\tt {\pm }}}:=Z_{G,\mathrm {\tt {\pm }} u,\mathrm {\tt {\pm }} v}(\lambda ,\hat {b})$. The ratio  $r^*:=\frac {Z_{G}(\lambda ,\hat {b})}{Z_{G\backslash e}(\lambda ,\hat {b})}$ is well-defined since, by the choice of
$r^*:=\frac {Z_{G}(\lambda ,\hat {b})}{Z_{G\backslash e}(\lambda ,\hat {b})}$ is well-defined since, by the choice of ![]() $\hat {b}$, we have
$\hat {b}$, we have  $Z_{G\backslash e}(\lambda ,\hat {b})\neq 0$ (cf. (20) and (21)). Moreover, we can express
$Z_{G\backslash e}(\lambda ,\hat {b})\neq 0$ (cf. (20) and (21)). Moreover, we can express ![]() $r^*$ using the
$r^*$ using the ![]() $z_{\mathrm {\tt {\pm }}\mathrm {\tt {\pm }}}$s as follows:
$z_{\mathrm {\tt {\pm }}\mathrm {\tt {\pm }}}$s as follows:
 $$ \begin{align*}r^*=\frac{z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}+\hat{b}(z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})}{z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}}}.\end{align*} $$
$$ \begin{align*}r^*=\frac{z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}+\hat{b}(z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})}{z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}}}.\end{align*} $$ We will compute ![]() $r^*$ using Lemma 37. Namely, by Lemma 37, we can compute in poly-time the value of the ratio
$r^*$ using Lemma 37. Namely, by Lemma 37, we can compute in poly-time the value of the ratio
 $$ \begin{align} r=R_{G,e}=\frac{A^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+ AB(z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})+B^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}}{A^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}+AC(z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})+C^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}}, \mbox{\, where \, }\begin{array}{l}A:=\hat{b}\\B:=1\\ C:=1\end{array}. \end{align} $$
$$ \begin{align} r=R_{G,e}=\frac{A^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+ AB(z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})+B^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}}{A^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}+AC(z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})+C^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}}, \mbox{\, where \, }\begin{array}{l}A:=\hat{b}\\B:=1\\ C:=1\end{array}. \end{align} $$Let ![]() $G'$ be the graph obtained from
$G'$ be the graph obtained from ![]() $G\setminus e$ by adding two new vertices
$G\setminus e$ by adding two new vertices ![]() $u',v'$ and adding the edges
$u',v'$ and adding the edges ![]() $\{u,u'\},\{u',v'\},\{v',v\}$. We next apply Lemma 37 to the graph
$\{u,u'\},\{u',v'\},\{v',v\}$. We next apply Lemma 37 to the graph ![]() $G'$ with the edge
$G'$ with the edge ![]() $e'=\{u',v'\}$. We first express
$e'=\{u',v'\}$. We first express  $Z_{G'\backslash e',\mathrm {\tt {\pm }} u',\mathrm {\tt {\pm }} v'}(\lambda ,\hat {b})$ in terms of the
$Z_{G'\backslash e',\mathrm {\tt {\pm }} u',\mathrm {\tt {\pm }} v'}(\lambda ,\hat {b})$ in terms of the ![]() $z_{\mathrm {\tt {\pm }}\mathrm {\tt {\pm }}}$s. We have
$z_{\mathrm {\tt {\pm }}\mathrm {\tt {\pm }}}$s. We have
 $$ \begin{align*} Z_{G'\backslash e',\mathrm{\texttt{+}} u',\mathrm{\texttt{+}} v'}(\lambda,\hat{b})&=\lambda^2 \big(z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+\hat{b} (z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})+\hat{b}^2 z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}\big),\\ Z_{G'\backslash e',\mathrm{\texttt{+}} u',\mathrm{\texttt{-}} v'}(\lambda,\hat{b})&= \lambda\big(\hat{b} z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+\hat{b}^2 z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}}+\hat{b} z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}\big),\\ Z_{G'\backslash e',\mathrm{\texttt{-}} u',\mathrm{\texttt{+}} v'}(\lambda,\hat{b})&= \lambda\big(\hat{b} z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+\hat{b}^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+ z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}}+\hat{b} z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}\big),\\ Z_{G'\backslash e',\mathrm{\texttt{-}} u',\mathrm{\texttt{-}} v'}(\lambda,\hat{b})&= \hat{b}^2 z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+\hat{b} (z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})+ z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}. \end{align*} $$
$$ \begin{align*} Z_{G'\backslash e',\mathrm{\texttt{+}} u',\mathrm{\texttt{+}} v'}(\lambda,\hat{b})&=\lambda^2 \big(z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+\hat{b} (z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})+\hat{b}^2 z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}\big),\\ Z_{G'\backslash e',\mathrm{\texttt{+}} u',\mathrm{\texttt{-}} v'}(\lambda,\hat{b})&= \lambda\big(\hat{b} z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+\hat{b}^2 z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}}+\hat{b} z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}\big),\\ Z_{G'\backslash e',\mathrm{\texttt{-}} u',\mathrm{\texttt{+}} v'}(\lambda,\hat{b})&= \lambda\big(\hat{b} z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+\hat{b}^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+ z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}}+\hat{b} z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}\big),\\ Z_{G'\backslash e',\mathrm{\texttt{-}} u',\mathrm{\texttt{-}} v'}(\lambda,\hat{b})&= \hat{b}^2 z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+\hat{b} (z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})+ z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}. \end{align*} $$Then, by Lemma 37, we can compute in poly-time the value of the ratio
 $$ \begin{align} r'=R_{G',e'}=\frac{(A')^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+ A'B'(z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})+(B')^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}}{(A')^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}+A'C'(z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})+(C')^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}}, \mbox{\, where }\begin{array}{l}A':=\hat{b}(\lambda+1)\\B':=1+\hat{b}^2\lambda\\ C':=\hat{b}^2+\lambda\end{array}. \end{align} $$
$$ \begin{align} r'=R_{G',e'}=\frac{(A')^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+ A'B'(z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})+(B')^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}}{(A')^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}+A'C'(z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}})+(C')^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}}, \mbox{\, where }\begin{array}{l}A':=\hat{b}(\lambda+1)\\B':=1+\hat{b}^2\lambda\\ C':=\hat{b}^2+\lambda\end{array}. \end{align} $$ We are now in position to complete the computation of ![]() $r^*$. We first show how to decide in poly-time whether
$r^*$. We first show how to decide in poly-time whether ![]() $z_{\mathrm {\texttt {+}} \mathrm {\texttt {+}}}=0$. We claim that
$z_{\mathrm {\texttt {+}} \mathrm {\texttt {+}}}=0$. We claim that
Indeed, if ![]() $z_{\mathrm {\texttt {+}} \mathrm {\texttt {+}}}=0$, then
$z_{\mathrm {\texttt {+}} \mathrm {\texttt {+}}}=0$, then ![]() $z_{\mathrm {\texttt {-}}\mathrm {\texttt {-}}}=0$ from Lemma 34 and, therefore, from (35), (36) we have that
$z_{\mathrm {\texttt {-}}\mathrm {\texttt {-}}}=0$ from Lemma 34 and, therefore, from (35), (36) we have that ![]() $r=B/C$ and
$r=B/C$ and ![]() $r'=B'/C'$. Conversely, using that
$r'=B'/C'$. Conversely, using that ![]() $A^2\neq B C$ and
$A^2\neq B C$ and ![]() $(A')^2\neq B' C'$, we have that
$(A')^2\neq B' C'$, we have that
which together imply that ![]() $z_{\mathrm {\texttt {+}} \mathrm {\texttt {+}}}=0$.
$z_{\mathrm {\texttt {+}} \mathrm {\texttt {+}}}=0$.
Using (37), we can decide in poly-time whether ![]() $z_{\mathrm {\texttt {+}} \mathrm {\texttt {+}}}=0$. If so, by Lemma 34, we have
$z_{\mathrm {\texttt {+}} \mathrm {\texttt {+}}}=0$. If so, by Lemma 34, we have ![]() $z_{\mathrm {\texttt {-}}\mathrm {\texttt {-}}}=0$ and hence
$z_{\mathrm {\texttt {-}}\mathrm {\texttt {-}}}=0$ and hence ![]() $r^*=\hat {b}$. So, assume
$r^*=\hat {b}$. So, assume ![]() $z_{\mathrm {\texttt {+}} \mathrm {\texttt {+}}}\neq 0$, and hence
$z_{\mathrm {\texttt {+}} \mathrm {\texttt {+}}}\neq 0$, and hence ![]() $z_{\mathrm {\texttt {-}}\mathrm {\texttt {-}}}\neq 0$ in what follows. We claim that
$z_{\mathrm {\texttt {-}}\mathrm {\texttt {-}}}\neq 0$ in what follows. We claim that
 $$ \begin{align} z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}}=0 \Longleftrightarrow r=\frac{A^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+B^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}}{A^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}+C^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}}, r'=\frac{(A')^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+(B')^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}}{(A')^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}+(C')^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}}.\\[-17pt]\nonumber \end{align} $$
$$ \begin{align} z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}}=0 \Longleftrightarrow r=\frac{A^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+B^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}}{A^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}+C^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}}, r'=\frac{(A')^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+(B')^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}}{(A')^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}+(C')^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}}.\\[-17pt]\nonumber \end{align} $$The forward direction is again trivial. For the backward direction, we have
 $$ \begin{align*} r&=\frac{A^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+B^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}}{A^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}+C^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}} \Longrightarrow C z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}=Bz_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}} \mbox{ or }z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}}=0,\\ r'&=\frac{(A')^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+(B')^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}}{(A')^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}+(C')^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}} \Longrightarrow C'z_{\mathrm{\texttt{+}} \mathrm{\texttt{+}}}=B'z_{\mathrm{\texttt{-}} \mathrm{\texttt{-}}} \mbox{ or }z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}}=0.\\[-17pt] \end{align*} $$
$$ \begin{align*} r&=\frac{A^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+B^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}}{A^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}+C^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}} \Longrightarrow C z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}=Bz_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}} \mbox{ or }z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}}=0,\\ r'&=\frac{(A')^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}+(B')^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}}{(A')^2z_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}+(C')^2z_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}} \Longrightarrow C'z_{\mathrm{\texttt{+}} \mathrm{\texttt{+}}}=B'z_{\mathrm{\texttt{-}} \mathrm{\texttt{-}}} \mbox{ or }z_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}+z_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}}=0.\\[-17pt] \end{align*} $$Since ![]() $z_{\mathrm {\texttt {+}} \mathrm {\texttt {+}}},z_{\mathrm {\texttt {-}}\mathrm {\texttt {-}}}\neq 0$, we therefore obtain that
$z_{\mathrm {\texttt {+}} \mathrm {\texttt {+}}},z_{\mathrm {\texttt {-}}\mathrm {\texttt {-}}}\neq 0$, we therefore obtain that ![]() $z_{\mathrm {\texttt {+}}\mathrm {\texttt {-}}}+z_{\mathrm {\texttt {-}}\mathrm {\texttt {+}}}=0$, proving (38).
$z_{\mathrm {\texttt {+}}\mathrm {\texttt {-}}}+z_{\mathrm {\texttt {-}}\mathrm {\texttt {+}}}=0$, proving (38).
Note that we can decide the right-hand side of (38) in poly-time using the value of the ratio ![]() $r''=z_{\mathrm {\texttt {-}}\mathrm {\texttt {-}}}/z_{\mathrm {\texttt {+}}\mathrm {\texttt {+}}}$ from the second part of Lemma 37. If it turns out that
$r''=z_{\mathrm {\texttt {-}}\mathrm {\texttt {-}}}/z_{\mathrm {\texttt {+}}\mathrm {\texttt {+}}}$ from the second part of Lemma 37. If it turns out that ![]() $z_{\mathrm {\texttt {+}}\mathrm {\texttt {-}}}+z_{\mathrm {\texttt {-}}\mathrm {\texttt {+}}}=0$, then
$z_{\mathrm {\texttt {+}}\mathrm {\texttt {-}}}+z_{\mathrm {\texttt {-}}\mathrm {\texttt {+}}}=0$, then ![]() $r^*=1$ and we are done. Otherwise, we can use the values of r and
$r^*=1$ and we are done. Otherwise, we can use the values of r and ![]() $r''$ to compute the ratios
$r''$ to compute the ratios  $\frac {z_{\mathrm {\texttt {+}} \mathrm {\texttt {+}}}}{z_{\mathrm {\texttt {+}}\mathrm {\texttt {-}}}+z_{\mathrm {\texttt {-}}\mathrm {\texttt {+}}}}, \frac {z_{\mathrm {\texttt {-}}\mathrm {\texttt {-}}}}{z_{\mathrm {\texttt {+}}\mathrm {\texttt {-}}}+z_{\mathrm {\texttt {-}}\mathrm {\texttt {+}}}}$, which we can then use to compute
$\frac {z_{\mathrm {\texttt {+}} \mathrm {\texttt {+}}}}{z_{\mathrm {\texttt {+}}\mathrm {\texttt {-}}}+z_{\mathrm {\texttt {-}}\mathrm {\texttt {+}}}}, \frac {z_{\mathrm {\texttt {-}}\mathrm {\texttt {-}}}}{z_{\mathrm {\texttt {+}}\mathrm {\texttt {-}}}+z_{\mathrm {\texttt {-}}\mathrm {\texttt {+}}}}$, which we can then use to compute ![]() $r^*$.
$r^*$.
This completes the computation of the ratio ![]() $r^*$ and therefore the proof of Theorem 1.
$r^*$ and therefore the proof of Theorem 1.
9 Equivalence for  $\lambda =-1$ with Approximately Counting Perfect Matchings
$\lambda =-1$ with Approximately Counting Perfect Matchings
In this section, we show that for ![]() $\lambda =-1$, the problem of approximating the partition of the ferromagnetic Ising model on graphs of maximum degree
$\lambda =-1$, the problem of approximating the partition of the ferromagnetic Ising model on graphs of maximum degree ![]() $\Delta $ is equivalent to the problem
$\Delta $ is equivalent to the problem ![]() $\#\mathsf {PerfectMatchings}$, the problem of approximately counting perfect matchings on general graphs. The proof follows the technique in [Reference Goldberg and Jerrum19], where the case of negative b but
$\#\mathsf {PerfectMatchings}$, the problem of approximately counting perfect matchings on general graphs. The proof follows the technique in [Reference Goldberg and Jerrum19], where the case of negative b but ![]() $\lambda =1$ was considered; here, however, we need to rework the relevant ingredients. The main such ingredient is the following ‘high-temperature’ expansion formula for
$\lambda =1$ was considered; here, however, we need to rework the relevant ingredients. The main such ingredient is the following ‘high-temperature’ expansion formula for ![]() $\lambda =-1$.
$\lambda =-1$.
Lemma 39. Let ![]() $\lambda =-1$ and
$\lambda =-1$ and ![]() $b\neq -1$ be an arbitrary number. Then, for any graph
$b\neq -1$ be an arbitrary number. Then, for any graph ![]() $G=(V,E)$,
$G=(V,E)$,
 $$ \begin{align*}Z_G(\lambda,b)=(-2)^{|V|}\Big(\frac{1+b}{2}\Big)^{|E|}\sum_{S\subseteq E;\, S\, \text{odd } } \Big(\frac{1-b}{1+b}\Big)^{|S|},\\[-17pt]\end{align*} $$
$$ \begin{align*}Z_G(\lambda,b)=(-2)^{|V|}\Big(\frac{1+b}{2}\Big)^{|E|}\sum_{S\subseteq E;\, S\, \text{odd } } \Big(\frac{1-b}{1+b}\Big)^{|S|},\\[-17pt]\end{align*} $$where the sum is over ![]() $S\subseteq E$ such that every vertex
$S\subseteq E$ such that every vertex ![]() $v\in V$ has odd degree in the subgraph
$v\in V$ has odd degree in the subgraph ![]() $(V,S)$.
$(V,S)$.
Proof. Let ![]() $G=(V,E)$ be a graph. For a set
$G=(V,E)$ be a graph. For a set ![]() $S\subseteq E$ and a vertex
$S\subseteq E$ and a vertex ![]() $v\in V$, we let
$v\in V$, we let ![]() $d_v(S)$ denote the degree of v in the subgraph
$d_v(S)$ denote the degree of v in the subgraph ![]() $(V,S)$.
$(V,S)$.
For the purposes of this proof, it will be convenient to view configurations of the Ising model on G as vectors in ![]() $\{\pm 1\}^{V}$. Now, for a configuration
$\{\pm 1\}^{V}$. Now, for a configuration ![]() $\sigma \in \{\pm 1\}^{V}$, we use the notation
$\sigma \in \{\pm 1\}^{V}$, we use the notation ![]() $n_+(\sigma )$ to denote the number of vertices with spin
$n_+(\sigma )$ to denote the number of vertices with spin ![]() $+1$. Observe that
$+1$. Observe that  $n_+(\sigma )=\tfrac {1}{2}\big (|V|+\sum _{v\in V}\sigma _v\big )$ and that for an edge
$n_+(\sigma )=\tfrac {1}{2}\big (|V|+\sum _{v\in V}\sigma _v\big )$ and that for an edge ![]() $e=(u,v)$, we have
$e=(u,v)$, we have  $b^{\mathbf {1}\{\sigma _u\neq \sigma _v\}}=\tfrac {1+b}{2}\big (1+\tfrac {1-b}{1+b}\sigma _u\sigma _v\big )=\rho \big (1+\nu \sigma _u\sigma _v\big )$, where for convenience we set
$b^{\mathbf {1}\{\sigma _u\neq \sigma _v\}}=\tfrac {1+b}{2}\big (1+\tfrac {1-b}{1+b}\sigma _u\sigma _v\big )=\rho \big (1+\nu \sigma _u\sigma _v\big )$, where for convenience we set  $\rho :=\tfrac {1+b}{2}$ and
$\rho :=\tfrac {1+b}{2}$ and  $\nu :=\tfrac {1-b}{1+b}$. So, using that
$\nu :=\tfrac {1-b}{1+b}$. So, using that ![]() $\mathrm {i}^2=-1$,
$\mathrm {i}^2=-1$,
 $$ \begin{align*} Z_G(\lambda,b)&=\rho^{|E|}\sum_{\sigma\in\{\pm 1\}^{V}}\lambda^{n_+(\sigma)}\prod_{e=(u,v)\in E}(1+\nu\sigma_u\sigma_v)=\rho^{|E|}\sum_{\sigma\rightarrow\{\pm 1\}^{V}}\lambda^{n_+(\sigma)}\sum_{S\subseteq E}\nu^{|S|}\prod_{v\in V}(\sigma_v)^{d_v(S)}\\ &=\mathrm{i}^{|V|}\rho^{|E|}\sum_{S\subseteq E}\nu^{|S|}\sum_{\sigma\in\{\pm 1\}^{V}}\prod_{v\in V}\mathrm{i}^{\sigma_v}(\sigma_v)^{d_v(S)}. \end{align*} $$
$$ \begin{align*} Z_G(\lambda,b)&=\rho^{|E|}\sum_{\sigma\in\{\pm 1\}^{V}}\lambda^{n_+(\sigma)}\prod_{e=(u,v)\in E}(1+\nu\sigma_u\sigma_v)=\rho^{|E|}\sum_{\sigma\rightarrow\{\pm 1\}^{V}}\lambda^{n_+(\sigma)}\sum_{S\subseteq E}\nu^{|S|}\prod_{v\in V}(\sigma_v)^{d_v(S)}\\ &=\mathrm{i}^{|V|}\rho^{|E|}\sum_{S\subseteq E}\nu^{|S|}\sum_{\sigma\in\{\pm 1\}^{V}}\prod_{v\in V}\mathrm{i}^{\sigma_v}(\sigma_v)^{d_v(S)}. \end{align*} $$The latter sum is equal to  $\prod _{v\in V}\sum _{\sigma _v\in \{\pm 1\}}\mathrm {i}^{\sigma _v}(\sigma _v)^{d_v(S)}$, which equals
$\prod _{v\in V}\sum _{\sigma _v\in \{\pm 1\}}\mathrm {i}^{\sigma _v}(\sigma _v)^{d_v(S)}$, which equals ![]() $0$ if
$0$ if ![]() $d_v(S)$ is even and
$d_v(S)$ is even and ![]() $2\mathrm {i}$ otherwise. Plugging this in the expression above yields the lemma.
$2\mathrm {i}$ otherwise. Plugging this in the expression above yields the lemma.
Now, we are ready to show the main theorem for this section. For counting problems ![]() $A,B$ we use the notion of
$A,B$ we use the notion of ![]() $\mathsf {AP}$-reductions; see [Reference Dyer, Goldberg, Greenhill and Jerrum13]. Roughly, we have that
$\mathsf {AP}$-reductions; see [Reference Dyer, Goldberg, Greenhill and Jerrum13]. Roughly, we have that ![]() $A\leq _{\mathsf {AP}} B$ if an
$A\leq _{\mathsf {AP}} B$ if an ![]() $\mathsf {FPRAS}$ for B can be converted to an
$\mathsf {FPRAS}$ for B can be converted to an ![]() $\mathsf {FPRAS}$ for A and
$\mathsf {FPRAS}$ for A and ![]() $A\equiv _{\mathsf {AP}} B$ if both
$A\equiv _{\mathsf {AP}} B$ if both ![]() $A\leq _{\mathsf {AP}} B$ and
$A\leq _{\mathsf {AP}} B$ and ![]() $B\leq _{\mathsf {AP}} A$ hold.
$B\leq _{\mathsf {AP}} A$ hold.
Theorem 40. Let ![]() $\lambda =-1$ and
$\lambda =-1$ and ![]() $b\in (0,1)$ be a rational. Then, for any connected graph G, we have
$b\in (0,1)$ be a rational. Then, for any connected graph G, we have ![]() $Z_G(\lambda ,b)>0$ if G has an even number of vertices and
$Z_G(\lambda ,b)>0$ if G has an even number of vertices and ![]() $Z_G(\lambda ,b)=0$ otherwise.
$Z_G(\lambda ,b)=0$ otherwise.
Moreover, for all integers ![]() $\Delta \geq 3$, we have that
$\Delta \geq 3$, we have that ![]() $\#\mathsf {IsingNorm}(\lambda ,b,\Delta )\equiv _{\mathsf {AP}} \#\mathsf {PerfectMatchings}$.
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta )\equiv _{\mathsf {AP}} \#\mathsf {PerfectMatchings}$.
Proof. The statement about the sign of ![]() $Z_G(\lambda ,b)$ follows from Lemma 39 and the fact that every connected graph with an even number of vertices has a spanning subgraph where every vertex has odd degree. We thus focus on proving the
$Z_G(\lambda ,b)$ follows from Lemma 39 and the fact that every connected graph with an even number of vertices has a spanning subgraph where every vertex has odd degree. We thus focus on proving the ![]() $\mathsf {AP}$-equivalence.
$\mathsf {AP}$-equivalence.
![]() $\boldsymbol {\#\mathsf {PerfectMatchings}\leq _{\mathsf {AP}} \#\mathsf {IsingNorm}(\lambda ,b,\Delta )}$. It is well-known that the problem of approximating the number of perfect matchings on general graphs is
$\boldsymbol {\#\mathsf {PerfectMatchings}\leq _{\mathsf {AP}} \#\mathsf {IsingNorm}(\lambda ,b,\Delta )}$. It is well-known that the problem of approximating the number of perfect matchings on general graphs is ![]() $\mathsf {AP}$-equivalent to the same problem on graphs of maximum degree 3; see, for example, [Reference Guo, Liao, Lu and Zhang23, Lemma 28]. So, let
$\mathsf {AP}$-equivalent to the same problem on graphs of maximum degree 3; see, for example, [Reference Guo, Liao, Lu and Zhang23, Lemma 28]. So, let ![]() $G=(V_G,E_G)$ be a graph of maximum degree 3, with
$G=(V_G,E_G)$ be a graph of maximum degree 3, with ![]() $n=|V_G|$ and
$n=|V_G|$ and ![]() $m=|E_G|$, and let
$m=|E_G|$, and let ![]() $\mathcal {M}$ be the set of perfect matchings of G. Since we can check whether a graph has a perfect matching in polynomial time, we may further assume that
$\mathcal {M}$ be the set of perfect matchings of G. Since we can check whether a graph has a perfect matching in polynomial time, we may further assume that ![]() $|\mathcal {M}|>0$ and, in particular, that n is even. Let
$|\mathcal {M}|>0$ and, in particular, that n is even. Let ![]() $\epsilon \in (0,1)$ be the desired relative error that we want to approximate
$\epsilon \in (0,1)$ be the desired relative error that we want to approximate ![]() $|\mathcal {M}|$.
$|\mathcal {M}|$.
Analogous to (18) and (19), for  $k=1+2\lceil \tfrac {m^2+\ln (1/\epsilon )}{-\ln (1-b)}\rceil $, let
$k=1+2\lceil \tfrac {m^2+\ln (1/\epsilon )}{-\ln (1-b)}\rceil $, let ![]() $P_k=(V_k,E_k)$ be the path with k vertices whose endpoints are labelled
$P_k=(V_k,E_k)$ be the path with k vertices whose endpoints are labelled ![]() $u_k,v_k$ and
$u_k,v_k$ and ![]() $P_k^*=(V_k^*,E_k^*)$ be the graph obtained from
$P_k^*=(V_k^*,E_k^*)$ be the graph obtained from ![]() $P_k$ by attaching a vertex
$P_k$ by attaching a vertex ![]() $z_i$ to the ith internal vertex
$z_i$ to the ith internal vertex ![]() $w_i$ of
$w_i$ of ![]() $P_k$, for
$P_k$, for ![]() $i=1,\ldots ,k-2$. Let
$i=1,\ldots ,k-2$. Let ![]() $A_{\mathrm {\tt {\pm }},\mathrm {\tt {\pm }}}:=Z_{P_k^*,\mathrm {\tt {\pm }} u_k,\mathrm {\tt {\pm }} v_k}(\lambda ,b)$. Then, it is not hard to see thatFootnote 12
$A_{\mathrm {\tt {\pm }},\mathrm {\tt {\pm }}}:=Z_{P_k^*,\mathrm {\tt {\pm }} u_k,\mathrm {\tt {\pm }} v_k}(\lambda ,b)$. Then, it is not hard to see thatFootnote 12
 $$ \begin{align*} \left[\begin{array}{cc} A_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}& -A_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}} \\ -A_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}}&A_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}\end{array}\right]=(1-b)^{k-2}\left[\begin{array}{cc} 1& b \\ b& 1\end{array}\right]^{k-1}\\[-17pt] \end{align*} $$
$$ \begin{align*} \left[\begin{array}{cc} A_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}& -A_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}} \\ -A_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}}&A_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}\end{array}\right]=(1-b)^{k-2}\left[\begin{array}{cc} 1& b \\ b& 1\end{array}\right]^{k-1}\\[-17pt] \end{align*} $$and so
 $$ \begin{align*} &A_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}= A_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}=\tfrac{1}{2}\big((1+b)^{k-1}+(1-b)^{k-1}\big)(1-b)^{k-2}, \text{ and } \\ &A_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}= A_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}}=\tfrac{1}{2}\big((1-b)^{k-1}-(1+b)^{k-1}\big)(1-b)^{k-2}.\\[-17pt] \end{align*} $$
$$ \begin{align*} &A_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}= A_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}=\tfrac{1}{2}\big((1+b)^{k-1}+(1-b)^{k-1}\big)(1-b)^{k-2}, \text{ and } \\ &A_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}= A_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}}=\tfrac{1}{2}\big((1-b)^{k-1}-(1+b)^{k-1}\big)(1-b)^{k-2}.\\[-17pt] \end{align*} $$We next set
 $$ \begin{align} b_k:= -\frac{A_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}}{A_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}}=-\frac{A_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}}}{A_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}},\quad \mbox{and observe that}\quad 1-(1-b)^{k-1}<b_k<1.\\[-17pt]\nonumber \end{align} $$
$$ \begin{align} b_k:= -\frac{A_{\mathrm{\texttt{+}}\mathrm{\texttt{-}}}}{A_{\mathrm{\texttt{+}}\mathrm{\texttt{+}}}}=-\frac{A_{\mathrm{\texttt{-}}\mathrm{\texttt{+}}}}{A_{\mathrm{\texttt{-}}\mathrm{\texttt{-}}}},\quad \mbox{and observe that}\quad 1-(1-b)^{k-1}<b_k<1.\\[-17pt]\nonumber \end{align} $$ Let ![]() $H=(V_H,E_H)$ be an instance of
$H=(V_H,E_H)$ be an instance of ![]() $\#\mathsf {IsingNorm}(\lambda ,b,\Delta )$ obtained from G by replacing every edge
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta )$ obtained from G by replacing every edge ![]() $e=(u,v)$ of G with a distinct copy of
$e=(u,v)$ of G with a distinct copy of ![]() $P_k^*$, identifying the endpoints
$P_k^*$, identifying the endpoints ![]() $u,v$ with
$u,v$ with ![]() $u_k,v_k$, respectively. Then, we claim that
$u_k,v_k$, respectively. Then, we claim that
Indeed, for a configuration ![]() $\sigma :V_G\rightarrow \{\mathrm {\texttt {+}},\mathrm {\texttt {-}}\}$, let
$\sigma :V_G\rightarrow \{\mathrm {\texttt {+}},\mathrm {\texttt {-}}\}$, let  $\Omega _{H,\sigma }=\{\sigma ': V_H\rightarrow \{\mathrm {\texttt {+}},\mathrm {\texttt {-}}\}\mid \sigma _{V_G}'=\sigma \}$ be the configurations on H which agree with
$\Omega _{H,\sigma }=\{\sigma ': V_H\rightarrow \{\mathrm {\texttt {+}},\mathrm {\texttt {-}}\}\mid \sigma _{V_G}'=\sigma \}$ be the configurations on H which agree with ![]() $\sigma $ on
$\sigma $ on ![]() $V_G$ and
$V_G$ and ![]() $Z_{H,\sigma }(\lambda ,b)$ be the contribution to
$Z_{H,\sigma }(\lambda ,b)$ be the contribution to ![]() $Z_{H}(\lambda ,b)$ from configurations in
$Z_{H}(\lambda ,b)$ from configurations in ![]() $\Omega _{H,\sigma }$. Then, we have
$\Omega _{H,\sigma }$. Then, we have
 $$ \begin{align*}Z_{H,\sigma}(\lambda,b)=\lambda^{|n_{\mathrm{\texttt{+}}}(\sigma)|}\prod_{e=(u,v)\in E_G}(-1)^{\mathbf{1}_{\sigma_u\neq \sigma_v}}A_{\sigma_u\sigma_v}=(A_{\mathrm{\texttt{+}} \mathrm{\texttt{+}}})^{m} \lambda^{|n_{\mathrm{\texttt{+}}}(\sigma)|} b_k^{\delta(\sigma)},\end{align*} $$
$$ \begin{align*}Z_{H,\sigma}(\lambda,b)=\lambda^{|n_{\mathrm{\texttt{+}}}(\sigma)|}\prod_{e=(u,v)\in E_G}(-1)^{\mathbf{1}_{\sigma_u\neq \sigma_v}}A_{\sigma_u\sigma_v}=(A_{\mathrm{\texttt{+}} \mathrm{\texttt{+}}})^{m} \lambda^{|n_{\mathrm{\texttt{+}}}(\sigma)|} b_k^{\delta(\sigma)},\end{align*} $$proving (40). Note from Lemma 39 we have that
 $$ \begin{align} Z_G(\lambda,b_k)=2^{n}\Big(\frac{1+b_k}{2}\Big)^{m}\sum_{S\subseteq E;\, S\, \text{odd } } \Big(\frac{1-b_k}{1+b_k}\Big)^{|S|}. \end{align} $$
$$ \begin{align} Z_G(\lambda,b_k)=2^{n}\Big(\frac{1+b_k}{2}\Big)^{m}\sum_{S\subseteq E;\, S\, \text{odd } } \Big(\frac{1-b_k}{1+b_k}\Big)^{|S|}. \end{align} $$Perfect matchings in G are in 1-1 correspondence with odd sets ![]() $S\subseteq E$ with
$S\subseteq E$ with ![]() $|S|= n/2$. Moreover, for any other odd set
$|S|= n/2$. Moreover, for any other odd set ![]() $S\subseteq E$ we have
$S\subseteq E$ we have ![]() $|S|>n/2+1$ and hence, using also (40), we obtain
$|S|>n/2+1$ and hence, using also (40), we obtain
 $$ \begin{align*}\bigg|\frac{Z_H(\lambda,b)}{(A_{\mathrm{\texttt{+}} \mathrm{\texttt{+}}})^{m}2^{n}\big(\frac{1+b_k}{2}\big)^{m}\big(\frac{1-b_k}{1+b_k}\big)^{n/2}}-|\mathcal{M}|\bigg|\leq 2^m\Big(\frac{1-b_k}{1+b_k}\Big)\leq \epsilon |\mathcal{M}|.\end{align*} $$
$$ \begin{align*}\bigg|\frac{Z_H(\lambda,b)}{(A_{\mathrm{\texttt{+}} \mathrm{\texttt{+}}})^{m}2^{n}\big(\frac{1+b_k}{2}\big)^{m}\big(\frac{1-b_k}{1+b_k}\big)^{n/2}}-|\mathcal{M}|\bigg|\leq 2^m\Big(\frac{1-b_k}{1+b_k}\Big)\leq \epsilon |\mathcal{M}|.\end{align*} $$Therefore, using an FPRAS for ![]() $\#\mathsf {IsingNorm}(\lambda ,b,\Delta )$, we can approximate
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta )$, we can approximate ![]() $Z_H(\lambda ,b)$ within relative error
$Z_H(\lambda ,b)$ within relative error ![]() $\epsilon $ in time
$\epsilon $ in time ![]() $poly(n,1/\epsilon )$ and therefore compute
$poly(n,1/\epsilon )$ and therefore compute ![]() $|\mathcal {M}|$ within relative error
$|\mathcal {M}|$ within relative error ![]() $\epsilon $, finishing the
$\epsilon $, finishing the ![]() $\mathsf {AP}$-reduction.
$\mathsf {AP}$-reduction.
![]() $\boldsymbol {\#\mathsf {IsingNorm}(\lambda ,b,\Delta )\leq _{\mathsf {AP}}\#\mathsf {PerfectMatchings}}$. We first consider the case
$\boldsymbol {\#\mathsf {IsingNorm}(\lambda ,b,\Delta )\leq _{\mathsf {AP}}\#\mathsf {PerfectMatchings}}$. We first consider the case ![]() $\Delta =3$. Let
$\Delta =3$. Let ![]() $G=(V,E)$ be a graph of maximum degree
$G=(V,E)$ be a graph of maximum degree ![]() $\Delta =3$ that is input to
$\Delta =3$ that is input to ![]() $\#\mathsf {IsingNorm}(\lambda ,b,\Delta )$ and set
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta )$ and set ![]() $n=|V|$,
$n=|V|$, ![]() $m=|E|$. We may assume that n is even, since otherwise we can output 0 for the partition function. By Lemma 39 we have that
$m=|E|$. We may assume that n is even, since otherwise we can output 0 for the partition function. By Lemma 39 we have that
 $$ \begin{align} Z_G(\lambda,b)=2^{n}\Big(\frac{1+b}{2}\Big)^{m}\sum_{S\subseteq E;\, S\, \text{odd } } \Big(\frac{1-b}{1+b}\Big)^{|S|}. \end{align} $$
$$ \begin{align} Z_G(\lambda,b)=2^{n}\Big(\frac{1+b}{2}\Big)^{m}\sum_{S\subseteq E;\, S\, \text{odd } } \Big(\frac{1-b}{1+b}\Big)^{|S|}. \end{align} $$ To formulate this in terms of perfect matchings, we construct a graph ![]() $G'=(V',E')$ as follows, resembling the construction in [Reference Fisher14]. For
$G'=(V',E')$ as follows, resembling the construction in [Reference Fisher14]. For ![]() $v\in V$, let
$v\in V$, let ![]() $d_v$ be the degree of v in G. For a vertex
$d_v$ be the degree of v in G. For a vertex ![]() $v\in V $, if
$v\in V $, if ![]() $d_v=3$, replace v with a triangle of vertices
$d_v=3$, replace v with a triangle of vertices ![]() $T_v=\{v_1,v_2,v_3\}$; otherwise, keep v in
$T_v=\{v_1,v_2,v_3\}$; otherwise, keep v in ![]() $G'$ as well and let for convenience
$G'$ as well and let for convenience ![]() $T_v=\{v\}$. For every edge
$T_v=\{v\}$. For every edge ![]() $(u,v)\in E$, add an edge in
$(u,v)\in E$, add an edge in ![]() $G'$ between a vertex in
$G'$ between a vertex in ![]() $T_u$ and
$T_u$ and ![]() $T_w$ so that
$T_w$ so that ![]() $G'$ has maximum degree 3; note that edges of G that are not incident to degree-3 vertices belong to
$G'$ has maximum degree 3; note that edges of G that are not incident to degree-3 vertices belong to ![]() $G'$ as well. We call internal all edges of
$G'$ as well. We call internal all edges of ![]() $G'$ whose endpoints belong to some
$G'$ whose endpoints belong to some ![]() $T_v$ and external all other edges of
$T_v$ and external all other edges of ![]() $G'$. Note that an edge e of G maps to an external edge
$G'$. Note that an edge e of G maps to an external edge ![]() $\mathrm {ex}(e)$ of
$\mathrm {ex}(e)$ of ![]() $G'$ bijectively under the natural mapping. We use
$G'$ bijectively under the natural mapping. We use ![]() $\mathrm {ex}(G')$ to denote the external edges of
$\mathrm {ex}(G')$ to denote the external edges of ![]() $G'$.
$G'$.
For ![]() $v\in V$, observe that any perfect matching in
$v\in V$, observe that any perfect matching in ![]() $G'$ must contain exactly one external edge incident to a vertex in
$G'$ must contain exactly one external edge incident to a vertex in ![]() $T_v$ if
$T_v$ if ![]() $|T_v|=1$ and two or three edges if
$|T_v|=1$ and two or three edges if ![]() $|T_v|=3$, either one internal and one external or three external, respectively. Based on this, we have that a perfect matching
$|T_v|=3$, either one internal and one external or three external, respectively. Based on this, we have that a perfect matching ![]() $M'$ in
$M'$ in ![]() $G'$ maps bijectively to an odd subset S of G, by adding an edge e of G to S iff
$G'$ maps bijectively to an odd subset S of G, by adding an edge e of G to S iff ![]() $\mathrm {ex}(e)\in M'$. Therefore, with
$\mathrm {ex}(e)\in M'$. Therefore, with ![]() $\mathcal {M}'$ denoting the set of perfect matchings in
$\mathcal {M}'$ denoting the set of perfect matchings in ![]() $G'$, we can rewrite (42) as
$G'$, we can rewrite (42) as
 $$ \begin{align*}Z_G(\lambda,b)=2^{n}\Big(\frac{1+b}{2}\Big)^{m}\sum_{M'\in \mathcal{M}'}\Big(\frac{1-b}{1+b}\Big)^{|M'\cap \mathrm{ex}(G')|}.\end{align*} $$
$$ \begin{align*}Z_G(\lambda,b)=2^{n}\Big(\frac{1+b}{2}\Big)^{m}\sum_{M'\in \mathcal{M}'}\Big(\frac{1-b}{1+b}\Big)^{|M'\cap \mathrm{ex}(G')|}.\end{align*} $$ Let ![]() $n'=|V'|\leq 3n$ and
$n'=|V'|\leq 3n$ and ![]() $m'=|E'|$. Let
$m'=|E'|$. Let ![]() $p,q$ be positive integers with
$p,q$ be positive integers with ![]() $\mathrm {gcd}(p,q)=1$ such that
$\mathrm {gcd}(p,q)=1$ such that  $\frac {p}{q}=\frac {1-b}{1+b}$. Let
$\frac {p}{q}=\frac {1-b}{1+b}$. Let ![]() $G''$ be the multigraph obtained from
$G''$ be the multigraph obtained from ![]() $G'$ by replacing every external edge
$G'$ by replacing every external edge ![]() $e=(u,v)$ with p parallel edges connecting u to a new vertex
$e=(u,v)$ with p parallel edges connecting u to a new vertex ![]() $w_e$, q parallel edges connecting
$w_e$, q parallel edges connecting ![]() $w_e$ to a new vertex
$w_e$ to a new vertex ![]() $z_e$ and an edge between
$z_e$ and an edge between ![]() $z_e$ and v; note that internal edges of
$z_e$ and v; note that internal edges of ![]() $G'$ are left intact. Let
$G'$ are left intact. Let ![]() $\mathcal {M}'$ and
$\mathcal {M}'$ and ![]() $\mathcal {M}''$ be the set of perfect matchings of
$\mathcal {M}''$ be the set of perfect matchings of ![]() $G'$ and
$G'$ and ![]() $G''$ Then, there is a one-to-many correspondence between perfect matchings
$G''$ Then, there is a one-to-many correspondence between perfect matchings ![]() $M'\in \mathcal {M}'$ in
$M'\in \mathcal {M}'$ in ![]() $G'$ and perfect matchings
$G'$ and perfect matchings ![]() $M''\in \mathcal {M}''$, where an internal edge e is matched in
$M''\in \mathcal {M}''$, where an internal edge e is matched in ![]() $M'$ iff e is matched in
$M'$ iff e is matched in ![]() $M''$, while an external edge
$M''$, while an external edge ![]() $e=(u,v)$ is matched in
$e=(u,v)$ is matched in ![]() $M'$ iff
$M'$ iff ![]() $(z_e,v)$ is matched in
$(z_e,v)$ is matched in ![]() $M''$. Note that, for an external edge e and a perfect matching
$M''$. Note that, for an external edge e and a perfect matching ![]() $M''$ of
$M''$ of ![]() $G''$, if
$G''$, if ![]() $(z_e,v)$ belongs to
$(z_e,v)$ belongs to ![]() $M''$, then u must be matched by one of the p parallel edges connecting u to
$M''$, then u must be matched by one of the p parallel edges connecting u to ![]() $w_e$, whereas if
$w_e$, whereas if ![]() $(z_e,v)$ does not belong to
$(z_e,v)$ does not belong to ![]() $M''$,
$M''$, ![]() $w_e$ and
$w_e$ and ![]() $z_e$ must be matched by one of the q parallel edges connecting u to
$z_e$ must be matched by one of the q parallel edges connecting u to ![]() $w_e$. It follows that
$w_e$. It follows that
 $$ \begin{align*}|\mathcal{M}''|=\sum_{M\in \mathcal{M}'}p^{|M\cap \mathrm{ex}(G')|}q^{m-|M\cap \mathrm{ex}(G')|}.\end{align*} $$
$$ \begin{align*}|\mathcal{M}''|=\sum_{M\in \mathcal{M}'}p^{|M\cap \mathrm{ex}(G')|}q^{m-|M\cap \mathrm{ex}(G')|}.\end{align*} $$ Finally, if we let ![]() $G'''$ be the graph obtained from
$G'''$ be the graph obtained from ![]() $G''$ by replacing every edge of
$G''$ by replacing every edge of ![]() $G''$ with a path of length 3, we have that the set of perfect matchings
$G''$ with a path of length 3, we have that the set of perfect matchings ![]() $\mathcal {M}'''$ off
$\mathcal {M}'''$ off ![]() $G'''$ is in 1-1 correspondence with
$G'''$ is in 1-1 correspondence with ![]() $\mathcal {M}''$ and we see that
$\mathcal {M}''$ and we see that  $2^{n}\big (\frac {1+b}{2}\big )^{m}q^{m}|\mathcal {M}'''|$ equals
$2^{n}\big (\frac {1+b}{2}\big )^{m}q^{m}|\mathcal {M}'''|$ equals ![]() $Z_G(\lambda ,b)$, completing the
$Z_G(\lambda ,b)$, completing the ![]() $\mathsf {AP}$-reduction for
$\mathsf {AP}$-reduction for ![]() $\Delta =3$.
$\Delta =3$.
To handle the case ![]() $\Delta \geq 4$, it suffices to show that
$\Delta \geq 4$, it suffices to show that ![]() $\#\mathsf {IsingNorm}(\lambda ,b,\Delta )\leq _{\mathsf {AP}} \#\mathsf {IsingNorm}(\lambda ,b,3)$, since
$\#\mathsf {IsingNorm}(\lambda ,b,\Delta )\leq _{\mathsf {AP}} \#\mathsf {IsingNorm}(\lambda ,b,3)$, since ![]() $\mathsf {AP}$-reductions are transitive; see [Reference Dyer, Goldberg, Greenhill and Jerrum13]. Let
$\mathsf {AP}$-reductions are transitive; see [Reference Dyer, Goldberg, Greenhill and Jerrum13]. Let ![]() $G=(V,E)$ be a graph of maximum degree
$G=(V,E)$ be a graph of maximum degree ![]() $\Delta $ and set
$\Delta $ and set ![]() $n=|V|$. Let
$n=|V|$. Let ![]() $V_{\leq 3}=\{v\in V\mid d_v\leq 3\}$ be the set of vertices in G with degree
$V_{\leq 3}=\{v\in V\mid d_v\leq 3\}$ be the set of vertices in G with degree ![]() $\leq 3$ and
$\leq 3$ and ![]() $V_{>3}$ be the set of the remaining vertices.
$V_{>3}$ be the set of the remaining vertices.
Construct a graph ![]() $G'=(V',E')$ from G by replacing every vertex
$G'=(V',E')$ from G by replacing every vertex ![]() $v\in V$ with
$v\in V$ with ![]() $d_v=t\geq 4$, with a path of
$d_v=t\geq 4$, with a path of ![]() $2t-1$ vertices if t is odd and of
$2t-1$ vertices if t is odd and of ![]() $2t-3$ vertices if t is even. We partition the vertices on the path into two sets
$2t-3$ vertices if t is even. We partition the vertices on the path into two sets ![]() $T_v,T_v'$ according to their parity, so that the endpoints of the path belong to
$T_v,T_v'$ according to their parity, so that the endpoints of the path belong to ![]() $T_v$; note that
$T_v$; note that ![]() $|T_v|=t$ if t is odd, while
$|T_v|=t$ if t is odd, while ![]() $|T_v|=t-1$ if t is even. We keep vertices
$|T_v|=t-1$ if t is even. We keep vertices ![]() $v\in V_{\leq 3}$ in
$v\in V_{\leq 3}$ in ![]() $G'$, and for such vertices, for convenience, we let
$G'$, and for such vertices, for convenience, we let ![]() $T_v=\{v\}$. Then, for every edge
$T_v=\{v\}$. Then, for every edge ![]() $(u,v)\in E$, we add an edge in
$(u,v)\in E$, we add an edge in ![]() $G'$ between a vertex in
$G'$ between a vertex in ![]() $T_u$ and
$T_u$ and ![]() $T_v$ so that, in the end,
$T_v$ so that, in the end, ![]() $G'$ has maximum degree 3 and, further, for vertices
$G'$ has maximum degree 3 and, further, for vertices ![]() $v\in V_{>3}$ with
$v\in V_{>3}$ with ![]() $d_v$ even, exactly one endpoint of the path on
$d_v$ even, exactly one endpoint of the path on ![]() $T_v\cup T_v'$ has degree 3 in
$T_v\cup T_v'$ has degree 3 in ![]() $G'$ (and the other has degree 2). As before, we call an edge in
$G'$ (and the other has degree 2). As before, we call an edge in ![]() $G'$ internal if both of its endpoints lie within a set
$G'$ internal if both of its endpoints lie within a set ![]() $T_v$ for some
$T_v$ for some ![]() $v\in V$ and external otherwise.
$v\in V$ and external otherwise.
The key observation is that the aggregate contribution to ![]() $Z_{G'}(\lambda ,b)$ from configurations on
$Z_{G'}(\lambda ,b)$ from configurations on ![]() $G'$ where, for some
$G'$ where, for some ![]() $v\in V$, the vertices in
$v\in V$, the vertices in ![]() $T_v$ do not get the same spin is zero.Footnote 13 For a configuration
$T_v$ do not get the same spin is zero.Footnote 13 For a configuration ![]() $\sigma $ on G, let
$\sigma $ on G, let ![]() $\Omega _{G',\sigma }$ be the set of configurations on
$\Omega _{G',\sigma }$ be the set of configurations on ![]() $G'$ such that all vertices in
$G'$ such that all vertices in ![]() $T_v$ get the spin
$T_v$ get the spin ![]() $\sigma _v$, and let
$\sigma _v$, and let ![]() $Z_{G',\sigma }(\lambda ,b)$ be their aggregate contribution to
$Z_{G',\sigma }(\lambda ,b)$ be their aggregate contribution to ![]() $Z_{G'}(\lambda ,b)$, so that, from the observation above, we have
$Z_{G'}(\lambda ,b)$, so that, from the observation above, we have
 $$ \begin{align*}Z_{G'}(\lambda,b)=\sum_{\sigma: V\rightarrow\{\mathrm{\texttt{+}},\mathrm{\texttt{-}}\}} Z_{G',\sigma}(\lambda,b).\end{align*} $$
$$ \begin{align*}Z_{G'}(\lambda,b)=\sum_{\sigma: V\rightarrow\{\mathrm{\texttt{+}},\mathrm{\texttt{-}}\}} Z_{G',\sigma}(\lambda,b).\end{align*} $$For a configuration ![]() $\sigma : V\rightarrow \{\mathrm {\texttt {+}},\mathrm {\texttt {-}}\}$, external edges and the external fields on
$\sigma : V\rightarrow \{\mathrm {\texttt {+}},\mathrm {\texttt {-}}\}$, external edges and the external fields on ![]() $V_{\leq 3}$ contribute to
$V_{\leq 3}$ contribute to ![]() $Z_{G',\sigma }(\lambda ,b)$ a factor of
$Z_{G',\sigma }(\lambda ,b)$ a factor of ![]() $\lambda ^{|n_{\mathrm {\texttt {+}}}(\sigma )\cap V_{\leq 3}|}b^{|\delta _G(\sigma )|}$. For
$\lambda ^{|n_{\mathrm {\texttt {+}}}(\sigma )\cap V_{\leq 3}|}b^{|\delta _G(\sigma )|}$. For ![]() $v\in V_{>3}$ with
$v\in V_{>3}$ with ![]() $\sigma _v=\mathrm {\texttt {+}}$, the edges in
$\sigma _v=\mathrm {\texttt {+}}$, the edges in ![]() $T_v\cup T_v'$ and the external fields on
$T_v\cup T_v'$ and the external fields on ![]() $T_v\cup T_v'$ contribute to
$T_v\cup T_v'$ contribute to ![]() $Z_{G',\sigma }(\lambda ,b)$ a factor of
$Z_{G',\sigma }(\lambda ,b)$ a factor of ![]() $-(1-b^2)^{|T_v|}$ and a factor of
$-(1-b^2)^{|T_v|}$ and a factor of ![]() $(1-b^2)^{|T_v|}$ if
$(1-b^2)^{|T_v|}$ if ![]() $\sigma _v=\mathrm {\texttt {-}}$. It follows that
$\sigma _v=\mathrm {\texttt {-}}$. It follows that ![]() $Z_{G',\sigma }(\lambda ,b)=(1-b^2)^{|T|}\lambda ^{|n_{\mathrm {\texttt {+}}}(\sigma )|}w_{G,\sigma }(\lambda ,b)$ where
$Z_{G',\sigma }(\lambda ,b)=(1-b^2)^{|T|}\lambda ^{|n_{\mathrm {\texttt {+}}}(\sigma )|}w_{G,\sigma }(\lambda ,b)$ where ![]() $T=\cup _{v\in V;d_v\geq 4} |T_v|$. It follows that
$T=\cup _{v\in V;d_v\geq 4} |T_v|$. It follows that
therefore completing the ![]() $\mathsf {AP}$-reduction, since by construction
$\mathsf {AP}$-reduction, since by construction ![]() $G'$ is a graph of maximum degree 3.
$G'$ is a graph of maximum degree 3.
This finishes the proof of Theorem 40.
Acknowledgements
We thank an anonymous referee for constructive feedback. PB is supported by the Netherlands Organisation of Scientific Research (NWO): 613.001.851. VP is supported by the Dutch Research Council (NWO) through the Gravitation Programme Networks (024.002.003). GR was (partly) supported by grant VI.Vidi.193.068 from the Dutch Research Council (NWO).
Conflict of interest
None.