Article contents
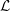 ${\mathcal{L}}$ -INVARIANTS AND LOCAL–GLOBAL COMPATIBILITY FOR THE GROUP
${\mathcal{L}}$ -INVARIANTS AND LOCAL–GLOBAL COMPATIBILITY FOR THE GROUP 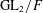 $\text{GL}_{2}/F$
$\text{GL}_{2}/F$
Published online by Cambridge University Press: 10 June 2016
Abstract
Let 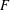 $F$ be a totally real number field,
$F$ be a totally real number field, 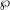 ${\wp}$ a place of
${\wp}$ a place of 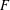 $F$ above
$F$ above 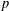 $p$ . Let
$p$ . Let 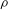 ${\it\rho}$ be a
${\it\rho}$ be a 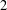 $2$ -dimensional
$2$ -dimensional 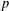 $p$ -adic representation of
$p$ -adic representation of 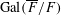 $\text{Gal}(\overline{F}/F)$ which appears in the étale cohomology of quaternion Shimura curves (thus
$\text{Gal}(\overline{F}/F)$ which appears in the étale cohomology of quaternion Shimura curves (thus 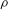 ${\it\rho}$ is associated to Hilbert eigenforms). When the restriction
${\it\rho}$ is associated to Hilbert eigenforms). When the restriction 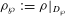 ${\it\rho}_{{\wp}}:={\it\rho}|_{D_{{\wp}}}$ at the decomposition group of
${\it\rho}_{{\wp}}:={\it\rho}|_{D_{{\wp}}}$ at the decomposition group of 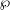 ${\wp}$ is semistable noncrystalline, one can associate to
${\wp}$ is semistable noncrystalline, one can associate to 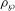 ${\it\rho}_{{\wp}}$ the so-called Fontaine–Mazur
${\it\rho}_{{\wp}}$ the so-called Fontaine–Mazur 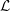 ${\mathcal{L}}$ -invariants, which are however invisible in the classical local Langlands correspondence. In this paper, we prove one can find these
${\mathcal{L}}$ -invariants, which are however invisible in the classical local Langlands correspondence. In this paper, we prove one can find these 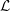 ${\mathcal{L}}$ -invariants in the completed cohomology group of quaternion Shimura curves, which generalizes some of Breuil’s results [Breuil, Astérisque, 331 (2010), 65–115] in the
${\mathcal{L}}$ -invariants in the completed cohomology group of quaternion Shimura curves, which generalizes some of Breuil’s results [Breuil, Astérisque, 331 (2010), 65–115] in the 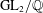 $\text{GL}_{2}/\mathbb{Q}$ -case.
$\text{GL}_{2}/\mathbb{Q}$ -case.
MSC classification
Information
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author 2016
References
- 5
- Cited by


