Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-11T01:41:31.947Z Has data issue: false hasContentIssue false
  • English
  • Français

MIXING FOR PROGRESSIONS IN NONABELIAN GROUPS

Part of: Representation theory of groups Sequences and sets

Published online by Cambridge University Press:  29 August 2013

TERENCE TAO
TERENCE TAO*
Affiliation:
UCLA Department of Mathematics, Los Angeles, CA 90095-1555, USAtao@math.ucla.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the mixing properties of progressions 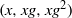$(x, xg, x{g}^{2} )$, 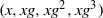$(x, xg, x{g}^{2} , x{g}^{3} )$ of length three and four in a model class of finite nonabelian groups, namely the special linear groups 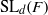${\mathrm{SL} }_{d} (F)$ over a finite field 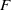$F$, with 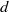$d$ bounded. For length three progressions 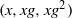$(x, xg, x{g}^{2} )$, we establish a strong mixing property (with an error term that decays polynomially in the order 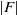$\vert F\vert $ of 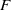$F$), which among other things counts the number of such progressions in any given dense subset 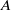$A$ of 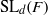${\mathrm{SL} }_{d} (F)$, answering a question of Gowers for this class of groups. For length four progressions 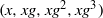$(x, xg, x{g}^{2} , x{g}^{3} )$, we establish a partial result in the 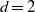$d= 2$ case if the shift 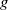$g$ is restricted to be diagonalizable over 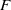$F$, although in this case we do not recover polynomial bounds in the error term. Our methods include the use of the Cauchy–Schwarz inequality, the abelian Fourier transform, the Lang–Weil bound for the number of points in an algebraic variety over a finite field, some algebraic geometry, and (in the case of length four progressions) the multidimensional Szemerédi theorem.

MSC classification

Secondary: 11B30: Arithmetic combinatorics; higher degree uniformity 20D60: Arithmetic and combinatorial problems
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 1 , 2013 , e2
Creative Commons
Creative Common License - CCCreative Common License - BY
The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
Copyright
© The Author(s) 2013.

References

Babai, L., Nikolov, N. and Pyber, L., ‘Product growth and mixing in finite groups’, In Proceedings of the Nineteenth Annual ACM-SIAM Symposium on Discrete Algorithms (ACM, New York, 2008), 248–257.Google Scholar
Bateman, M. and Katz, N. H., ‘New bounds on cap sets’, J. Amer. Math. Soc. 25 (2012), 585–613.Google Scholar
Behrend, F. A., ‘On sets of integers which contain no three terms in arithmetic progression’, Proc. Natl. Acad. Sci. 32 (1946), 331–332.Google Scholar
Bergelson, V. and Tao, T., ‘Multiple recurrence in quasirandom groups’, to appear. arXiv:1211.6372.Google Scholar
Bourgain, J., ‘On triples in arithmetic progression’, Geom. Funct. Anal. 9 (1999), 968–984.Google Scholar
Bourgain, J. and Gamburd, A., ‘Uniform expansion bounds for Cayley graphs of ${\mathrm{SL} }_{2} ({F}_{p} )$ ’, Ann. of Math. (2) 167(2) (2008), 625–642.CrossRefGoogle Scholar
Breuillard, E., Green, B. and Tao, T., ‘Approximate subgroups of linear groups’, Geom. Funct. Anal. 21 (2011), 774–819.CrossRefGoogle Scholar
Furstenberg, H. and Katznelson, Y., ‘An ergodic Szemerédi theorem for commuting transformations’, J. Anal. Math. 34 (1978), 275–291 (1979).Google Scholar
Gowers, W. T., ‘A new proof of Szemerédi’s theorem for progressions of length four’, Geom. Funct. Anal. 8(3) (1998), 529–551.Google Scholar
Gowers, W. T., ‘A new proof of Szemerédi’s theorem’, Geom. Funct. Anal. 11(3) (2001), 465–588.CrossRefGoogle Scholar
Gowers, W. T., ‘Hypergraph regularity and the multidimensional Szemerédi theorem’, Ann. of Math. (2) 166(3) (2007), 897–946.CrossRefGoogle Scholar
Gowers, W. T., ‘Quasirandom groups’, Combin. Probab. Comput. 17(3) (2008), 363–387.Google Scholar
Green, B. and Tao, T., ‘New bounds for Szemerédi’s theorem. II. A new bound for ${r}_{4} (N)$ ’, In Analytic Number Theory (Cambridge University Press, Cambridge, 2009), 180–204.Google Scholar
Helfgott, H. A., ‘Growth and generation in ${\mathrm{SL} }_{2} (\mathbf{Z} / p\mathbf{Z} )$ ’, Ann. of Math. (2) 167(2) (2008), 601–623.CrossRefGoogle Scholar
Humphreys, J., Linear Algebraic Groups, Graduate Texts in Mathematics, 21 (Springer, New York-Heidelberg, 1975).Google Scholar
Landazuri, V. and Seitz, G., ‘On the minimal degrees of projective representations of the finite Chevalley groups’, J. Algebra 32 (1974), 418–443.CrossRefGoogle Scholar
Lang, S. and Weil, A., ‘Number of points of varieties in finite fields’, Amer. J. Math. 76 (1954), 819–827.Google Scholar
Lubotzky, A., ‘Expander graphs in pure and applied mathematics’, Bull. Amer. Math. Soc. (N.S.) 49(1) (2012), 113–162.Google Scholar
Polymath, D. H. J., ‘A new proof of the density Hales–Jewett theorem’, Ann. of Math. (2) 175(3) (2012), 1283–1327.Google Scholar
Pyber, L. and Szabó, E., ‘Growth in finite simple groups of Lie type’, Preprint (2010) arXiv:1001.4556.Google Scholar
Rankin, R. A., ‘Sets of integers containing not more than a given number of terms in arithmetical progression’, Proc. Roy. Soc. Edinburgh Sect. A 65 (1960/1961), 332–344.Google Scholar
Rödl, V. and Schacht, M., ‘Regular partitions of hypergraphs: regularity lemmas’, Combin. Probab. Comput. 16(6) (2007), 833–885.CrossRefGoogle Scholar
Rödl, V. and Skokan, J., ‘Applications of the regularity lemma for uniform hypergraphs’, Random Structures Algorithms 28(2) (2006), 180–194.CrossRefGoogle Scholar
Sanders, T., ‘On Roth’s theorem on progressions’, Ann. of Math. (2) 174(1) (2011), 619–636.CrossRefGoogle Scholar
Schwartz, J., ‘Fast probabilistic algorithms for verification of polynomial identities’, J. ACM 27 (1980), 701–717.Google Scholar
Szemerédi, E., ‘On sets of integers containing no k elements in arithmetic progression’, Acta Arith. 27 (1975), 299–345.Google Scholar
Tao, T., ‘A variant of the hypergraph removal lemma’, J. Combin. Theory Ser. A 113(7) (2006), 1257–1280.Google Scholar
Tao, T., ‘Expanding polynomials over finite fields of large characteristic, and a regularity lemma for definable sets’, Preprint. arXiv:1211.2894.Google Scholar
Tao, T. and Vu, V., Additive Combinatorics (Cambridge University Press, 2006).Google Scholar