Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T17:34:34.366Z Has data issue: false hasContentIssue false
  • English
  • Français

The moduli space of Harnack curves in toric surfaces

Part of: Special varieties Polytopes and polyhedra Curves

Published online by Cambridge University Press:  27 May 2021

Jorge Alberto Olarte Open the ORCID record for Jorge Alberto Olarte [Opens in a new window]
Jorge Alberto Olarte*
Affiliation:
Institut für Mathematik, Technische Universität Berlin, Straße des 17. Juni 135, Berlin, Germany; E-mail: olarte@math.tu-berlin.de

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In 2006, Kenyon and Okounkov Kenyon and Okounkov [12] computed the moduli space of Harnack curves of degree d in ${\mathbb {C}\mathbb {P}}^2$. We generalise their construction to any projective toric surface and show that the moduli space 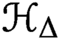${\mathcal {H}_\Delta }$ of Harnack curves with Newton polygon 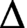$\Delta $ is diffeomorphic to 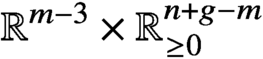${\mathbb {R}}^{m-3}\times {\mathbb {R}}_{\geq 0}^{n+g-m}$, where 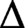$\Delta $ has m edges, g interior lattice points and n boundary lattice points. This solves a conjecture of Crétois and Lang. The main result uses abstract tropical curves to construct a compactification of this moduli space where additional points correspond to collections of curves that can be patchworked together to produce a curve in 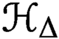${\mathcal {H}_\Delta }$. This compactification has a natural stratification with the same poset as the secondary polytope of 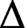$\Delta $.

MSC classification

Primary: 14H50: Plane and space curves
Secondary: 14H10: Families, moduli (algebraic) 14M25: Toric varieties, Newton polyhedra 52B20: Lattice polytopes (including relations with commutative algebra and algebraic geometry)
Type
Algebraic and Complex Geometry
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e43
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Caporaso, L., ‘Algebraic and tropical curves: Comparing their moduli spaces’, in Handbook of Moduli. Vol. I, Advanced Lectures in Mathematics (ALM) vol. 24 (International Press, Somerville, MA, 2013), 119–160.Google Scholar
Cox, D. A., Little, J. B. and Schenck, H. K., Toric Varieties, Graduate Studies in Mathematics vol. 124 (American Mathematical Society, Providence, RI, 2011).Google Scholar
Crétois, R. and Lang, L., ‘The vanishing cycles of curves in toric surfaces I’, Compos. Math. 154(8) (2018), 1659–1697.CrossRefGoogle Scholar
De Loera, J. A., Rambau, J. and Santos, F., Triangulations, Algorithms and Computation in Mathematics vol. 25 (Springer-Verlag, Berlin, 2010).CrossRefGoogle Scholar
Forsberg, M., Passare, M. and Tsikh, A., ‘Laurent determinants and arrangements of hyperplane amoebas’, Adv. Math. 151(1) (2000), 45–70.CrossRefGoogle Scholar
Galashin, P., Karp, S. N. and Lam, T., ‘Regularity theorem for totally nonnegative flag varieties’, Preprint, 2019, arXiv:1904.00527 .Google Scholar
Gelfand, I. M., Kapranov, M. M and Zelevinsky, A. V., Discriminants, Resultants, and Multidimensional Determinants Mathematics: Theory & Applications (Birkhäuser Boston, Inc., Boston, MA, 1994).CrossRefGoogle Scholar
Gordon, W., ‘On the diffeomorphisms of euclidean space’, Amer. Math. Monthly 79(7) (1972), 755–759.CrossRefGoogle Scholar
Harnack, A., ‘Ueber die Vieltheiligkeit der ebenen algebraischen Curven’, Math. Ann. 10(2) (1876), 189–198.CrossRefGoogle Scholar
Itenberg, I. and Viro, O., ‘Patchworking algebraic curves disproves the Ragsdale conjecture’, Math. Intelligencer 18(4) (1996), 19–28.CrossRefGoogle Scholar
Joyce, D., ‘A generalization of manifolds with corners’, Adv. Math. 299 (2016), 760–862.CrossRefGoogle Scholar
Kenyon, R. and Okounkov, A., ‘Planar dimers and Harnack curves’, Duke Math. J. 131(3) (2006), 499–524.CrossRefGoogle Scholar
Kenyon, R., Okounkov, A. and Sheffield, S., ‘Dimers and amoebae’, Ann. of Math. (2) 163(3) (2006), 1019–1056.CrossRefGoogle Scholar
Khovanskii, A. G., ‘Newton polyhedra and the genus of complete intersections’, Funct. Anal. Appl. 12(1) (1978), 38–46.CrossRefGoogle Scholar
Lang, L., ‘A generalization of simple Harnack curves’, Preprint, 2015, arXiv:1504.07256 .Google Scholar
Mikhalkin, G., ‘Real algebraic curves, the moment map and amoebas’, Ann. of Math. (2) 151(1) (2000), 309–326.CrossRefGoogle Scholar
Mikhalkin, G. and Okounkov, A., ‘Geometry of planar log-fronts’, Mosc. Math. J. 7(3) (2007), 507–531, 575.CrossRefGoogle Scholar
Mikhalkin, G. and Rullgård, H., ‘Amoebas of maximal area’, Int. Math. Res. Not. IMRN 2001(9) (2001), 441–451.CrossRefGoogle Scholar
Passare, M. and Risler, J.-J., ‘On the curvature of the real amoeba’, in Proceedings of the Gökova Geometry-Topology Conference 2010 (International Press, Somerville, MA, 2011), 129–134.Google Scholar
Passare, M. and Rullgård, H., ‘Amoebas, Monge-Ampère measures, and triangulations of the Newton polytope’, Duke Math. J. 121(3) (2004), 481–507.CrossRefGoogle Scholar
Ronkin, L. I., Introduction to the Theory of Entire Functions of Several Variables, Translations of Mathematical Monographs vol. 44 (American Mathematical Society, Providence, RI, 1974). Translated from the Russian by Israel Program for Scientific Translations.CrossRefGoogle Scholar
Viro, O., ‘Patchworking real algebraic varieties’, Preprint, 2006, arxiv:0611.382.Google Scholar