Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T16:45:56.622Z Has data issue: false hasContentIssue false
  • English
  • Français

THE MOTIVE OF THE HILBERT CUBE $X^{[3]}$

Part of: Cycles and subschemes

Published online by Cambridge University Press:  27 October 2016

MINGMIN SHEN  and
CHARLES VIAL
MINGMIN SHEN
Affiliation:
KdV Institute for Mathematics, University of Amsterdam, P.O. Box 94248, 1090 GE Amsterdam, Netherlands; m.shen@uva.nl
CHARLES VIAL
Affiliation:
DPMMS, University of Cambridge, Wilberforce Road, Cambridge CB3 0WB, UK; c.vial@dpmms.cam.ac.uk

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

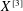The Hilbert scheme 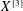$X^{[3]}$ of length-3 subschemes of a smooth projective variety 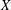$X$ is known to be smooth and projective. We investigate whether the property of having a multiplicative Chow–Künneth decomposition is stable under taking the Hilbert cube. This is achieved by considering an explicit resolution of the rational map 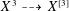$X^{3}{\dashrightarrow}X^{[3]}$. The case of the Hilbert square was taken care of in Shen and Vial [Mem. Amer. Math. Soc.240(1139) (2016), vii+163 pp]. The archetypical examples of varieties endowed with a multiplicative Chow–Künneth decomposition is given by abelian varieties. Recent work seems to suggest that hyperKähler varieties share the same property. Roughly, if a smooth projective variety 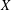$X$ has a multiplicative Chow–Künneth decomposition, then the Chow rings of its powers 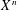$X^{n}$ have a filtration, which is the expected Bloch–Beilinson filtration, that is split.

MSC classification

Primary: 14C05: Parametrization (Chow and Hilbert schemes)
Secondary: 14C25: Algebraic cycles 14C15: (Equivariant) Chow groups and rings; motives
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 4 , 2016 , e30
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2016

References

Beauville, A., ‘Sur l’anneau de Chow d’une variété abélienne’, Math. Ann. 273 (1986), 647–651.CrossRefGoogle Scholar
Beauville, A., ‘On the splitting of the Bloch–Beilinson filtration’, inAlgebraic Cycles and Motives, Vol. 2, London Mathematical Society Lecture Notes, 344 (Cambridge University Press, 2007), 38–53.Google Scholar
Beauville, A. and Voisin, C., ‘On the Chow ring of a K3 surface’, J. Algebraic Geom. 13 (2004), 417–426.Google Scholar
Cheah, J., ‘Cellular decompositions for nested Hilbert schemes of points’, Pacific. J. Math. 183(1) (1998), 39–90.Google Scholar
Fu, L., Tian, Zh. and Vial, Ch., ‘Motivic hyperKähler resolution conjecture for generalized Kummer varieties’, Preprint, 2016, arXiv:1608.04968.Google Scholar
Fulton, W., Intersection Theory, 2nd edn, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics , (Springer, 1998).Google Scholar
Jannsen, U., ‘Motivic sheaves and filtrations on Chow groups’, inMotives (Seattle, WA, 1991), Proceedings of Symposia in Pure Mathematics, 55 (American Mathematical Society, Providence, RI, 1994), 245–302.Google Scholar
Manin, Y., ‘Correspondences, motifs and monoidal transformations’, Mat. Sb. (N.S.) 77 (1968), 475–507.Google Scholar
Murre, J., ‘On the motive of an algebraic surface’, J. Reine Angew. Math. 409 (1990), 190–204.Google Scholar
Murre, J., ‘On a conjectural filtration on the Chow groups of an algebraic variety. I. The general conjectures and some examples’, Indag. Math. (N.S.) 4(2) (1993), 177–188.CrossRefGoogle Scholar
Riess, U., ‘On the Chow ring of birational irreducible symplectic varieties’, Manuscripta Math. 145(3–4) (2014), 473–501.Google Scholar
Shen, M. and Vial, Ch., ‘The Fourier transform for certain hyperKähler fourfolds’, Mem. Amer. Math. Soc. 240(1139) (2016), vii+163 pp.Google Scholar
Vial, Ch., ‘Algebraic cycles and fibrations’, Doc. Math. 18 (2013), 1521–1553.CrossRefGoogle Scholar
Vial, Ch., ‘On the motive of some hyperKähler varieties’, J. Reine Angew. Math. to appear, doi:10.1515/crelle-2015-0008.Google Scholar
Voisin, C., ‘Chow rings and decomposition theorems for families of K3 surfaces and Calabi–Yau hypersurfaces’, Geom. Topol. 16 (2012), 433–473.Google Scholar
Voisin, C., ‘The generalized Hodge and Bloch conjectures are equivalent for general complete intersections’, Ann. Sci. Éc. Norm. Supér. (3) 46 (2013), 449–475.Google Scholar