Article contents
THE MULTI-MARGINAL OPTIMAL PARTIAL TRANSPORT PROBLEM
Published online by Cambridge University Press: 16 September 2015
Abstract
We introduce and study a multi-marginal optimal partial transport problem. Under a natural and sharp condition on the dominating marginals, we establish uniqueness of the optimal plan. Our strategy of proof establishes and exploits a connection with another novel problem, which we call the Monge–Kantorovich partial barycenter problem (with quadratic cost). This latter problem has a natural interpretation as a variant of the factories-and-mines description of optimal transport. We then turn our attention to various analytic properties of these two problems. Of particular interest, we show that monotonicity of the active marginals with respect to the amount 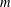 $m$ of mass to be transported can fail, a surprising difference from the two-marginal case.
$m$ of mass to be transported can fail, a surprising difference from the two-marginal case.
MSC classification
Information
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2015
References
- 4
- Cited by


