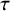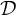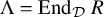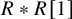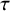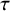1 Introduction
Cluster algebras were introduced by Fomin and Zelevinsky [Reference Fomin and Zelevinsky27] around 2000. The geometric aspect of cluster theory was explored and developed by Fomin, Shapiro and Thurston [Reference Fomin, Shapiro and Thurston25] and Labardini-Fragoso [Reference Labardini-Fragoso40], where they construct a quiver with potential [Reference Derksen, Weyman and Zelevinski23] from any triangulation of a marked surface. However, cluster categories of acyclic quivers were introduced by Buan, Marsh, Reineke, Reiten and Todorov [Reference Buan, Marsh, Reineke, Reiten and Todorov14] in order to categorify cluster algebras, which were generalized later by Amiot [Reference Amiot2] to cluster categories of quivers with potential.
The indecomposable objects in the cluster category from a marked surface without punctures are classified via curves by Brüstle and Zhang [Reference Brüstle and Zhang13], where the Auslander-Reiten translation is realized by the rotation. The dimension of
![]() $\operatorname {Ext}^1$
between certain indecomposable objects is shown by Zhang, Zhou and Zhu [Reference Zhang, Zhou and Zhu53] to equal the intersection number between the corresponding curves, and the middle terms between such extensions are explicitly described by Canakci and Schroll [Reference Canakci and Schroll17] via smoothing. The Calabi-Yau reduction introduced by Iyama and Yoshino [Reference Iyama and Yoshino35] in this case is interpreted via the cutting of the surface by Marsh and Palu [Reference Marsh and Palu44]. For the punctured case (with nonempty boundary), Brüstle and Qiu [Reference Brüstle and Qiu12] realize the Auslander-Reiten translation via the tagged rotation, Qiu and Zhou [Reference Qiu and Zhou49] classify certain indecomposable objects via tagged curves and show the equality between the dimension of
$\operatorname {Ext}^1$
between certain indecomposable objects is shown by Zhang, Zhou and Zhu [Reference Zhang, Zhou and Zhu53] to equal the intersection number between the corresponding curves, and the middle terms between such extensions are explicitly described by Canakci and Schroll [Reference Canakci and Schroll17] via smoothing. The Calabi-Yau reduction introduced by Iyama and Yoshino [Reference Iyama and Yoshino35] in this case is interpreted via the cutting of the surface by Marsh and Palu [Reference Marsh and Palu44]. For the punctured case (with nonempty boundary), Brüstle and Qiu [Reference Brüstle and Qiu12] realize the Auslander-Reiten translation via the tagged rotation, Qiu and Zhou [Reference Qiu and Zhou49] classify certain indecomposable objects via tagged curves and show the equality between the dimension of
![]() $\operatorname {Ext}^1$
and the intersection number, and Amiot and Plamondon [Reference Amiot and Plamondon5] give another approach via group actions and orbifolds.
$\operatorname {Ext}^1$
and the intersection number, and Amiot and Plamondon [Reference Amiot and Plamondon5] give another approach via group actions and orbifolds.
The Jacobian algebra of the quiver with potential associated to a certain triangulation of a marked surface with nonempty boundary is a skew-gentle algebra with some properties (e.g., Gorenstein dimension at most one) [Reference Assem, Brüstle, Charbonneau-Jodoin and Plamondon8, Reference Geiß, Labardini-Fragoso and Schröer30, Reference Qiu and Zhou49]. Skew-gentle algebras were introduced by Geiß and de la Peña [Reference Geiß and de la Peña31], whose indecomposable modules are classified by Bondarenko [Reference Bondarenko10], Crawley-Boevey [Reference Crawley-Boevey19] and Deng [Reference Deng22], and whose morphism spaces are described by Geiß [Reference Geiß29]. In a previous work [Reference He, Zhou and Zhu33], we give a geometric model of the module category of an arbitrary skew-gentle algebra, inspired by the geometric model [Reference Qiu and Zhou49] of cluster categories of punctured marked surfaces and the geometric model of the module categories of gentle algebras given by Baur and Simões [Reference Baur and Coelho Simões9]. There is also some work on geometric models of the derived categories of gentle/skew-gentle algebras; cf., for example, [Reference Haiden, Katzarkov and Kontsevich32, Reference Lekili and Polishchuk43, Reference Opper, Plamondon and Schroll46, Reference Opper45, Reference Amiot, Plamondon and Schroll6, Reference Amiot and Brüstle4, Reference Amiot3, Reference Labardini-Fragoso, Schroll and Valdivieso42].
Adachi, Iyama and Reiten [Reference Adachi, Iyama and Reiten1] introduced
![]() $\tau $
-tilting theory to generalize the cluster structure to arbitrary finite-dimensional algebras via mutation of support
$\tau $
-tilting theory to generalize the cluster structure to arbitrary finite-dimensional algebras via mutation of support
![]() $\tau $
-tilting modules. The support
$\tau $
-tilting modules. The support
![]() $\tau $
-tilting modules have been found to be deeply connected with other contents of representation theory, such as functorially finite torsion classes, 2-term silting objects, cluster tilting objects and immediate t-structures. In contrast to the classical tilting case, where an almost complete tilting module may have exactly one complement, any support
$\tau $
-tilting modules have been found to be deeply connected with other contents of representation theory, such as functorially finite torsion classes, 2-term silting objects, cluster tilting objects and immediate t-structures. In contrast to the classical tilting case, where an almost complete tilting module may have exactly one complement, any support
![]() $\tau $
-tilting module can always be mutated at an arbitrary indecomposable direct summand to obtain a new support
$\tau $
-tilting module can always be mutated at an arbitrary indecomposable direct summand to obtain a new support
![]() $\tau $
-tilting module. The exchange graph
$\tau $
-tilting module. The exchange graph
![]() $\operatorname {EG}(\operatorname {s\tau -tilt} A)$
of support
$\operatorname {EG}(\operatorname {s\tau -tilt} A)$
of support
![]() $\tau $
-tilting modules of a finite-dimensional algebra A has (isoclasses of) basic support
$\tau $
-tilting modules of a finite-dimensional algebra A has (isoclasses of) basic support
![]() $\tau $
-tilting modules over A as vertices and has mutations as edges. One important problem is to count the number of connected components of
$\tau $
-tilting modules over A as vertices and has mutations as edges. One important problem is to count the number of connected components of
![]() $\operatorname {EG}(\operatorname {s\tau -tilt} A)$
.
$\operatorname {EG}(\operatorname {s\tau -tilt} A)$
.
In our previous work [Reference He, Zhou and Zhu33], using a geometric model, we classify support
![]() $\tau $
-tilting modules of skew-gentle algebras via certain dissections of marked surfaces. In the current paper, after establishing a framework for the theory of mutation in two-term subcategories of a 2-Calabi-Yau triangulated category, we generalize the geometric model from skew-gentle algebras to the endomorphism algebras of rigid objects in the cluster categories arising from punctured marked surfaces. One important application is the connectedness of the exchange graph
$\tau $
-tilting modules of skew-gentle algebras via certain dissections of marked surfaces. In the current paper, after establishing a framework for the theory of mutation in two-term subcategories of a 2-Calabi-Yau triangulated category, we generalize the geometric model from skew-gentle algebras to the endomorphism algebras of rigid objects in the cluster categories arising from punctured marked surfaces. One important application is the connectedness of the exchange graph
![]() $\operatorname {EG}(\operatorname {s\tau -tilt} A)$
for A an arbitrary skew-gentle algebra. This generalizes the main result in [Reference Fu, Geng, Liu and Zhou28] where A is a gentle algebra, and one main result in [Reference Qiu and Zhou49] where A is a skew-gentle Jacobian algebra.
$\operatorname {EG}(\operatorname {s\tau -tilt} A)$
for A an arbitrary skew-gentle algebra. This generalizes the main result in [Reference Fu, Geng, Liu and Zhou28] where A is a gentle algebra, and one main result in [Reference Qiu and Zhou49] where A is a skew-gentle Jacobian algebra.
We also note that it is shown in [Reference Asai7] that
![]() $\operatorname {EG}(\operatorname {s\tau -tilt} A)$
has one or two components in the case that A is a complete gentle (or, more generally, special biserial) algebra. See [Reference Breaz, Marcus and Modoi11, Reference Kimura, Koshio, Kozakai, Minamoto and Mizuno38, Reference Zhang and Huang52] for some related results.
$\operatorname {EG}(\operatorname {s\tau -tilt} A)$
has one or two components in the case that A is a complete gentle (or, more generally, special biserial) algebra. See [Reference Breaz, Marcus and Modoi11, Reference Kimura, Koshio, Kozakai, Minamoto and Mizuno38, Reference Zhang and Huang52] for some related results.
The paper is organized as follows. In Section 2, we introduce and investigate mutation in two-term subcategories of a 2-Calabi-Yau triangulated category. In Section 3, we recall basic notions and results on the cluster categories from punctured marked surfaces. In Section 4, we give a geometric model for the endomorphism algebra of a rigid object in the cluster category arising from a punctured marked surface and show that this includes the class of skew-gentle algebras. Moreover, we classify support
![]() $\tau $
-tilting modules via certain dissections. In Section 5, we introduce the notion of flip of dissections and show that it is compatible with the mutation of support
$\tau $
-tilting modules via certain dissections. In Section 5, we introduce the notion of flip of dissections and show that it is compatible with the mutation of support
![]() $\tau $
-tilting modules. As an application, the connectedness of the exchange graph of support
$\tau $
-tilting modules. As an application, the connectedness of the exchange graph of support
![]() $\tau $
-tilting modules over a skew-gentle algebra is obtained.
$\tau $
-tilting modules over a skew-gentle algebra is obtained.
Convention
Throughout this paper, we assume
![]() ${\mathbf {k}}$
to be an algebraically closed field. Any additive category
${\mathbf {k}}$
to be an algebraically closed field. Any additive category
![]() $\mathcal {D}$
in this paper is assumed to be
$\mathcal {D}$
in this paper is assumed to be
-
(1)
 ${\mathbf {k}}$
-linear and Hom-finite (i.e.,
${\mathbf {k}}$
-linear and Hom-finite (i.e.,
 $\operatorname {Hom}_{\mathcal {D}}(X,Y)$
is a finite-dimensional vector space over
$\operatorname {Hom}_{\mathcal {D}}(X,Y)$
is a finite-dimensional vector space over
 ${\mathbf {k}}$
for any pair of objects
${\mathbf {k}}$
for any pair of objects
 $X,Y$
), and
$X,Y$
), and -
(2) Krull-Schmidt (i.e., any object is isomorphic to a finite direct sum of objects whose endomorphism rings are local).
We use
![]() $X\in \mathcal {D}$
to denote that X is an object in
$X\in \mathcal {D}$
to denote that X is an object in
![]() $\mathcal {D}$
. For any
$\mathcal {D}$
. For any
![]() $X\in \mathcal {D}$
, denote by
$X\in \mathcal {D}$
, denote by
-
(1)
 $|X|$
the number of isomorphism classes of indecomposable direct summands of X,
$|X|$
the number of isomorphism classes of indecomposable direct summands of X, -
(2)
 $\operatorname {add} X$
the additive hull of X, that is, the smallest subcategory of
$\operatorname {add} X$
the additive hull of X, that is, the smallest subcategory of
 $\mathcal {D}$
, which contains X and is closed under isomorphisms, finite direct sums and direct summands, and
$\mathcal {D}$
, which contains X and is closed under isomorphisms, finite direct sums and direct summands, and -
(3)
 ${}^\perp X$
and
${}^\perp X$
and
 $X^\perp $
the full subcategories of
$X^\perp $
the full subcategories of
 $\mathcal {D}$
consisting of all objects Y such that
$\mathcal {D}$
consisting of all objects Y such that
 $\operatorname {Hom}_{\mathcal {D}}(Y,X)=0$
and
$\operatorname {Hom}_{\mathcal {D}}(Y,X)=0$
and
 $\operatorname {Hom}_{\mathcal {D}}(X,Y)=0$
, respectively.
$\operatorname {Hom}_{\mathcal {D}}(X,Y)=0$
, respectively.
We call
![]() $X\in \mathcal {D}$
basic if
$X\in \mathcal {D}$
basic if
![]() $|X|$
is the number of indecomposable direct summands of X (i.e., any two distinct indecomposable direct summands of X are not isomorphic). For any object
$|X|$
is the number of indecomposable direct summands of X (i.e., any two distinct indecomposable direct summands of X are not isomorphic). For any object
![]() $X\in \mathcal {D}$
and any direct summand Y of X, we denote by
$X\in \mathcal {D}$
and any direct summand Y of X, we denote by
![]() $X\setminus Y$
the direct summand of X such that
$X\setminus Y$
the direct summand of X such that
![]() $X=Y\,{\oplus}\, (X\setminus Y)$
.
$X=Y\,{\oplus}\, (X\setminus Y)$
.
We call a morphism
![]() $g\in \operatorname {Hom}_{\mathcal {D}}(X,Y)$
right minimal if for any
$g\in \operatorname {Hom}_{\mathcal {D}}(X,Y)$
right minimal if for any
![]() $h\in \operatorname {Hom}_{\mathcal {D}}(X,X)$
such that
$h\in \operatorname {Hom}_{\mathcal {D}}(X,X)$
such that
![]() $g\circ h=g$
, we have that h is an isomorphism. For any subcategory
$g\circ h=g$
, we have that h is an isomorphism. For any subcategory
![]() $\mathcal {T}$
of
$\mathcal {T}$
of
![]() $\mathcal {D}$
, we call
$\mathcal {D}$
, we call
![]() $f\in \operatorname {Hom}_{\mathcal {D}}(X,Y)$
a right
$f\in \operatorname {Hom}_{\mathcal {D}}(X,Y)$
a right
![]() $\mathcal {T}$
-approximation of
$\mathcal {T}$
-approximation of
![]() $Y\in \mathcal {D}$
if
$Y\in \mathcal {D}$
if
![]() $X\in \mathcal {T}$
and
$X\in \mathcal {T}$
and
is exact as functors on
![]() $\mathcal {T}$
. A right
$\mathcal {T}$
. A right
![]() $\mathcal {T}$
-approximation is said to be minimal if it is right minimal. We call
$\mathcal {T}$
-approximation is said to be minimal if it is right minimal. We call
![]() $\mathcal {T}$
a contravariantly finite subcategory of
$\mathcal {T}$
a contravariantly finite subcategory of
![]() $\mathcal {D}$
if any
$\mathcal {D}$
if any
![]() $Y\in \mathcal {D}$
admits a right
$Y\in \mathcal {D}$
admits a right
![]() $\mathcal {T}$
-approximation. The left minimal maps, (minimal) left
$\mathcal {T}$
-approximation. The left minimal maps, (minimal) left
![]() $\mathcal {T}$
-approximations and covariantly finite subcategories are defined dually. A subcategory is said to be functorially finite if it is both covariantly and contravariantly finite.
$\mathcal {T}$
-approximations and covariantly finite subcategories are defined dually. A subcategory is said to be functorially finite if it is both covariantly and contravariantly finite.
When
![]() $\mathcal {D}$
is a triangulated category, for any
$\mathcal {D}$
is a triangulated category, for any
![]() $X,Y\in \mathcal {D}$
, denote by
$X,Y\in \mathcal {D}$
, denote by
![]() $X\ast _{\mathcal {D}} Y$
the full subcategory of
$X\ast _{\mathcal {D}} Y$
the full subcategory of
![]() $\mathcal {D}$
consisting of all
$\mathcal {D}$
consisting of all
![]() $M\in \mathcal {D}$
such that there is a triangle
$M\in \mathcal {D}$
such that there is a triangle
with
![]() $X_M\in \operatorname {add} X$
and
$X_M\in \operatorname {add} X$
and
![]() $Y_M\in \operatorname {add} Y$
. When there is no confusion arising, we simply denote
$Y_M\in \operatorname {add} Y$
. When there is no confusion arising, we simply denote
![]() $X\ast Y=X\ast _{\mathcal {D}} Y$
.
$X\ast Y=X\ast _{\mathcal {D}} Y$
.
2 Categorical interpretation
Throughout this section, let
![]() $\mathcal {D}$
be a triangulated category, and we use
$\mathcal {D}$
be a triangulated category, and we use
![]() $\operatorname {Hom}(X,Y)$
to simply denote
$\operatorname {Hom}(X,Y)$
to simply denote
![]() $\operatorname {Hom}_{\mathcal {D}}(X,Y)$
. We assume that
$\operatorname {Hom}_{\mathcal {D}}(X,Y)$
. We assume that
![]() $\mathcal {D}$
is 2-Calabi-Yau; that is, there exists a bi-functorial isomorphism
$\mathcal {D}$
is 2-Calabi-Yau; that is, there exists a bi-functorial isomorphism
for any
![]() $X,Y\in \mathcal {D}$
, where
$X,Y\in \mathcal {D}$
, where
![]() $D=\operatorname {Hom}_{\mathbf {k}}(-,{\mathbf {k}})$
.
$D=\operatorname {Hom}_{\mathbf {k}}(-,{\mathbf {k}})$
.
Definition 2.1. An object
![]() $R\in \mathcal {D}$
is called
$R\in \mathcal {D}$
is called
-
(1) rigid provided that
 $\operatorname {Hom}(R,R[1])=0$
,
$\operatorname {Hom}(R,R[1])=0$
, -
(2) maximal rigid if it is maximal with respect to the rigid property, that is, R is rigid and for any object
 $N\in \mathcal {D}$
with
$N\in \mathcal {D}$
with
 $N\,{\oplus}\, R$
rigid, we have
$N\,{\oplus}\, R$
rigid, we have
 $N\in \operatorname {add} R$
,
$N\in \operatorname {add} R$
, -
(3) cluster tilting if R is rigid and for any object
 $N\in \mathcal {D}$
with
$N\in \mathcal {D}$
with
 $\operatorname {Hom}(R,N[1])=0$
, we have
$\operatorname {Hom}(R,N[1])=0$
, we have
 $N\in \operatorname {add} R$
.
$N\in \operatorname {add} R$
.
Note that any cluster tilting object is maximal rigid, but the converse is not true in general (cf. [Reference Burban, Iyama, Keller and Reiten16, Reference Koenig and Zhu39]). We also note that the triangulated category
![]() $\mathcal {D}$
may not admit any cluster tilting object (cf. [Reference Buan, Marsh and Vatne15]). If
$\mathcal {D}$
may not admit any cluster tilting object (cf. [Reference Buan, Marsh and Vatne15]). If
![]() $\mathcal {D}$
admits a cluster tilting object, then any maximal rigid object is cluster tilting (see [Reference Zhou and Zhu54]).
$\mathcal {D}$
admits a cluster tilting object, then any maximal rigid object is cluster tilting (see [Reference Zhou and Zhu54]).
For a rigid object
![]() $R\in \mathcal {D}$
, the full subcategory
$R\in \mathcal {D}$
, the full subcategory
![]() $R\ast R[1]$
of
$R\ast R[1]$
of
![]() $\mathcal {D}$
is called the two-term subcategory with respect to R. In this section, we will extend the theory of mutation of cluster tilting objects, or more generally, mutation of maximal objects in
$\mathcal {D}$
is called the two-term subcategory with respect to R. In this section, we will extend the theory of mutation of cluster tilting objects, or more generally, mutation of maximal objects in
![]() $\mathcal {D}$
[Reference Iyama and Yoshino35, Reference Buan, Marsh, Reineke, Reiten and Todorov14, Reference Zhou and Zhu54] to
$\mathcal {D}$
[Reference Iyama and Yoshino35, Reference Buan, Marsh, Reineke, Reiten and Todorov14, Reference Zhou and Zhu54] to
![]() $R\ast R[1]$
.
$R\ast R[1]$
.
By [Reference Iyama and Yoshino35, Proposition 2.1],
![]() $R\ast R[1]$
is closed under taking direct summands. Any object
$R\ast R[1]$
is closed under taking direct summands. Any object
![]() $M\in R\ast R[1]$
admits an R-presentation – that is, a triangle
$M\in R\ast R[1]$
admits an R-presentation – that is, a triangle
with
![]() $R^0_M, R^1_M\in \operatorname {add} R$
. Since R is rigid, we have that
$R^0_M, R^1_M\in \operatorname {add} R$
. Since R is rigid, we have that
![]() $\iota _0$
is a right
$\iota _0$
is a right
![]() $\operatorname {add} R$
-approximation of M and
$\operatorname {add} R$
-approximation of M and
![]() $\iota _1$
is a left
$\iota _1$
is a left
![]() $\operatorname {add} R[1]$
-approximation of M. Moreover, in (2.1),
$\operatorname {add} R[1]$
-approximation of M. Moreover, in (2.1),
![]() $\iota _0$
can be chosen to be right minimal, or equivalently,
$\iota _0$
can be chosen to be right minimal, or equivalently,
![]() $\iota _1$
can be chosen to be left minimal. In such case, we call (2.1) a minimal R-presentation.
$\iota _1$
can be chosen to be left minimal. In such case, we call (2.1) a minimal R-presentation.
Proposition 2.2. If (2.1) is a minimal R-presentation, then
![]() $R^1_M$
and
$R^1_M$
and
![]() $R^0_M$
do not have an indecomposable direct summand in common.
$R^0_M$
do not have an indecomposable direct summand in common.
Proof. The proof of [Reference Dehy and Keller21, Proposition 2.1] also works here.
2.1 Rigid objects in two-term subcategories
Throughout the rest of this section, let R be a basic rigid object in
![]() $\mathcal {D}$
. We introduce the notion of maximal rigid objects with respect to
$\mathcal {D}$
. We introduce the notion of maximal rigid objects with respect to
![]() $R\ast R[1]$
.
$R\ast R[1]$
.
Definition 2.3. An object
![]() $U\in R\ast R[1]$
is called maximal rigid with respect to
$U\in R\ast R[1]$
is called maximal rigid with respect to
![]() $R\ast R[1]$
provided that it is rigid and for any object
$R\ast R[1]$
provided that it is rigid and for any object
![]() $N\in R\ast R[1]$
with
$N\in R\ast R[1]$
with
![]() $N\,{\oplus}\, U$
rigid, we have
$N\,{\oplus}\, U$
rigid, we have
![]() $N\in \operatorname {add} U$
.
$N\in \operatorname {add} U$
.
Denote by
![]() $\operatorname {rigid-}(R\ast R[1])$
the set of (isoclasses of) basic rigid objects in
$\operatorname {rigid-}(R\ast R[1])$
the set of (isoclasses of) basic rigid objects in
![]() $R\ast R[1]$
, and by
$R\ast R[1]$
, and by
![]() $\operatorname {max}\operatorname {rigid-}(R\ast R[1])$
the set of (isoclasses of) basic maximal rigid objects with respect to
$\operatorname {max}\operatorname {rigid-}(R\ast R[1])$
the set of (isoclasses of) basic maximal rigid objects with respect to
![]() $R\ast R[1]$
.
$R\ast R[1]$
.
In the case that R is maximal rigid (resp. cluster tilting), by [Reference Zhou and Zhu54, Corollary 2.5], any rigid object in
![]() $\mathcal {D}$
also belongs to
$\mathcal {D}$
also belongs to
![]() $R\ast R[1]$
. Therefore, the maximal rigid objects with respect to
$R\ast R[1]$
. Therefore, the maximal rigid objects with respect to
![]() $R\ast R[1]$
are exactly the maximal rigid (resp. cluster tilting) objects in
$R\ast R[1]$
are exactly the maximal rigid (resp. cluster tilting) objects in
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
Lemma 2.4. For any
![]() $U\in \operatorname {max}\operatorname {rigid-}(R\ast R[1])$
, we have
$U\in \operatorname {max}\operatorname {rigid-}(R\ast R[1])$
, we have
![]() $R\in \operatorname {rigid-}(U[-1]\ast U)$
. For any triangle
$R\in \operatorname {rigid-}(U[-1]\ast U)$
. For any triangle
the following hold.
-
(1) If
 $\iota _0$
is a right
$\iota _0$
is a right
 $\operatorname {add} U[-1]$
-approximation of R, then
$\operatorname {add} U[-1]$
-approximation of R, then
 $U^1_R\in \operatorname {add} U$
.
$U^1_R\in \operatorname {add} U$
. -
(2) If
 $\iota _1$
is a left
$\iota _1$
is a left
 $\operatorname {add} U$
-approximation of R, then
$\operatorname {add} U$
-approximation of R, then
 $U^0_R\in \operatorname {add} U$
.
$U^0_R\in \operatorname {add} U$
.
Proof. Due to the existence of right
![]() $\operatorname {add} U[-1]$
-approximations of R, the assertion (1) implies
$\operatorname {add} U[-1]$
-approximations of R, the assertion (1) implies
![]() $R\in \operatorname {rigid-}(U[-1]\ast U)$
. Similarly, the assertion (2) implies
$R\in \operatorname {rigid-}(U[-1]\ast U)$
. Similarly, the assertion (2) implies
![]() $R\in \operatorname {rigid-}(U[-1]\ast U)$
, too. So it suffices to show (1) and (2). We only prove (1) since (2) can be proved dually.
$R\in \operatorname {rigid-}(U[-1]\ast U)$
, too. So it suffices to show (1) and (2). We only prove (1) since (2) can be proved dually.
Since
![]() $\iota _0$
is a right
$\iota _0$
is a right
![]() $\operatorname {add} U[-1]$
-approximation, we have
$\operatorname {add} U[-1]$
-approximation, we have
![]() $U^0_R\in \operatorname {add} U$
. Since
$U^0_R\in \operatorname {add} U$
. Since
![]() $U\in R\ast R[1]$
and
$U\in R\ast R[1]$
and
![]() $R\ast R[1]$
is closed under taking direct summands, we have
$R\ast R[1]$
is closed under taking direct summands, we have
![]() $U^0_R\in R\ast R[1]$
. Hence,
$U^0_R\in R\ast R[1]$
. Hence,
![]() $U^1_R\in R\ast U^0_R\subseteq R\ast R[1]$
. Applying
$U^1_R\in R\ast U^0_R\subseteq R\ast R[1]$
. Applying
![]() $\operatorname {Hom}(U[-1],-)$
to the triangle (2.2), we get a long exact sequence in
$\operatorname {Hom}(U[-1],-)$
to the triangle (2.2), we get a long exact sequence in
![]() $\mathcal {D}$
$\mathcal {D}$
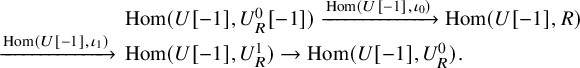 $$\begin{align*}\begin{array}{rl} &\operatorname{Hom}(U[-1],U^0_R[-1])\xrightarrow{\operatorname{Hom}(U[-1],\iota_0)}\operatorname{Hom}(U[-1],R)\\ \xrightarrow{\operatorname{Hom}(U[-1],\iota_1)}&\operatorname{Hom}(U[-1],U^1_R) \to \operatorname{Hom}(U[-1],U^0_R). \end{array}\end{align*}$$
$$\begin{align*}\begin{array}{rl} &\operatorname{Hom}(U[-1],U^0_R[-1])\xrightarrow{\operatorname{Hom}(U[-1],\iota_0)}\operatorname{Hom}(U[-1],R)\\ \xrightarrow{\operatorname{Hom}(U[-1],\iota_1)}&\operatorname{Hom}(U[-1],U^1_R) \to \operatorname{Hom}(U[-1],U^0_R). \end{array}\end{align*}$$
Since U is rigid, the last term
![]() $\operatorname {Hom}(U[-1],U^0_R)=0$
. Since
$\operatorname {Hom}(U[-1],U^0_R)=0$
. Since
![]() $\iota _0$
is a right
$\iota _0$
is a right
![]() $\operatorname {add} U[-1]$
-approximation of R, the morphism
$\operatorname {add} U[-1]$
-approximation of R, the morphism
![]() $\operatorname {Hom}(U[-1],\iota _0)$
is surjective. So
$\operatorname {Hom}(U[-1],\iota _0)$
is surjective. So
![]() $\operatorname {Hom}(U[-1],U^1_R)=0$
, which implies
$\operatorname {Hom}(U[-1],U^1_R)=0$
, which implies
![]() $\operatorname {Hom}(U^1_R,U[1])=0$
by the 2-Calabi-Yau property. In particular,
$\operatorname {Hom}(U^1_R,U[1])=0$
by the 2-Calabi-Yau property. In particular,
![]() $\operatorname {Hom}(U^1_R,U^0_R[1])=0$
.
$\operatorname {Hom}(U^1_R,U^0_R[1])=0$
.
For any
![]() $f\in \operatorname {Hom}(U^1_R,U^1_R[1])$
, consider the following diagram.
$f\in \operatorname {Hom}(U^1_R,U^1_R[1])$
, consider the following diagram.
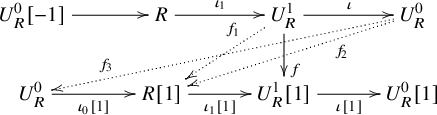
Since
![]() $\iota [1]\circ f\in \operatorname {Hom}(U^1_R,U^0_R[1])=0$
, there exists
$\iota [1]\circ f\in \operatorname {Hom}(U^1_R,U^0_R[1])=0$
, there exists
![]() $f_1\in \operatorname {Hom}(U^1_R,R[1])$
such that
$f_1\in \operatorname {Hom}(U^1_R,R[1])$
such that
![]() $f=\iota _1[1]\circ f_1$
. Since
$f=\iota _1[1]\circ f_1$
. Since
![]() $f_1\circ \iota _1\in \operatorname {Hom}(R,R[1])=0$
, there exists
$f_1\circ \iota _1\in \operatorname {Hom}(R,R[1])=0$
, there exists
![]() $f_2\in \operatorname {Hom}(U^0_R,R[1])$
such that
$f_2\in \operatorname {Hom}(U^0_R,R[1])$
such that
![]() $f_1=f_2\circ \iota $
. Since
$f_1=f_2\circ \iota $
. Since
![]() $\iota _0[1]$
is a right
$\iota _0[1]$
is a right
![]() $\operatorname {add} U$
-approximation of
$\operatorname {add} U$
-approximation of
![]() $R[1]$
, there exists
$R[1]$
, there exists
![]() $f_3\in \operatorname {Hom}(U^0_R,U^0_R)$
such that
$f_3\in \operatorname {Hom}(U^0_R,U^0_R)$
such that
![]() $f_2=(\iota _0[1])f_3$
. Hence, we have
$f_2=(\iota _0[1])f_3$
. Hence, we have
![]() $f=\iota _1[1]\circ \iota _0[1]\circ f_3\circ \iota $
, which is zero since
$f=\iota _1[1]\circ \iota _0[1]\circ f_3\circ \iota $
, which is zero since
![]() $\iota _1[1]\circ \iota _0[1]=0$
. So
$\iota _1[1]\circ \iota _0[1]=0$
. So
![]() $U^1_R$
is rigid, and hence
$U^1_R$
is rigid, and hence
![]() $\operatorname {Hom}((U^1_R\,{\oplus}\, U),(U^1_R\,{\oplus}\, U)[1])=0$
. Since U is maximal rigid with respect to
$\operatorname {Hom}((U^1_R\,{\oplus}\, U),(U^1_R\,{\oplus}\, U)[1])=0$
. Since U is maximal rigid with respect to
![]() $R\ast R[1]$
, we have
$R\ast R[1]$
, we have
![]() $U^1_R\in \operatorname {add} U$
.
$U^1_R\in \operatorname {add} U$
.
We use
![]() $K_0^{\mbox {sp}}(R)$
to denote the split Grothendieck group of
$K_0^{\mbox {sp}}(R)$
to denote the split Grothendieck group of
![]() $\operatorname {add} R$
. For any
$\operatorname {add} R$
. For any
![]() $M\in R\ast R[1]$
, define the index of M with respect to R as the element in
$M\in R\ast R[1]$
, define the index of M with respect to R as the element in
![]() $K_0^{\mbox {sp}}(R)$
$K_0^{\mbox {sp}}(R)$
where
![]() $R^1_M\to R^0_M\to M\to R^1_M[1]$
is an R-presentation of M. We write
$R^1_M\to R^0_M\to M\to R^1_M[1]$
is an R-presentation of M. We write
![]() $R=\,{\oplus}\, ^n_{i=1}R_i$
with
$R=\,{\oplus}\, ^n_{i=1}R_i$
with
![]() $R_i$
indecomposable. Then
$R_i$
indecomposable. Then
![]() $[R_i],1\leq i\leq n$
, form a
$[R_i],1\leq i\leq n$
, form a
![]() $\mathbb {Z}$
-basis of
$\mathbb {Z}$
-basis of
![]() $K_0^{\mbox {sp}}(R)$
. Denote by
$K_0^{\mbox {sp}}(R)$
. Denote by
![]() $[\operatorname {ind}_R M:R_i]$
the coefficient of
$[\operatorname {ind}_R M:R_i]$
the coefficient of
![]() $[R_i]$
in the decomposition of
$[R_i]$
in the decomposition of
![]() $\operatorname {ind}_RM$
with respect to this basis. Then we have
$\operatorname {ind}_RM$
with respect to this basis. Then we have
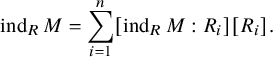 $$ \begin{align*}\operatorname{ind}_RM=\sum_{i=1}^{n}[\operatorname{ind}_RM:R_i][R_i].\end{align*} $$
$$ \begin{align*}\operatorname{ind}_RM=\sum_{i=1}^{n}[\operatorname{ind}_RM:R_i][R_i].\end{align*} $$
Remark 2.5. We refer to [Reference Dehy and Keller21, Section 2.3], [Reference Palu47, Section 2.1] and [Reference Plamondon48, Section 2.5] for a similar definition of the index with respect to cluster tilting objects. Moreover, if R is a direct summand of a cluster tilting object T, then for any object
![]() $M\in \mathcal {D}$
, we have
$M\in \mathcal {D}$
, we have
![]() $M\in R\ast R[1]$
if and only if
$M\in R\ast R[1]$
if and only if
![]() $[\operatorname {ind}_T M:X]=0$
for any indecomposable direct summand X of
$[\operatorname {ind}_T M:X]=0$
for any indecomposable direct summand X of
![]() $T\setminus R$
.
$T\setminus R$
.
Proposition 2.6. Let
![]() $U=\,{\oplus}\, ^m_{i=1}U_i$
be a basic rigid object in
$U=\,{\oplus}\, ^m_{i=1}U_i$
be a basic rigid object in
![]() $R\ast R[1]$
with
$R\ast R[1]$
with
![]() $U_i, 1\leq i\leq m$
, indecomposable. Then the elements
$U_i, 1\leq i\leq m$
, indecomposable. Then the elements
![]() $\operatorname {ind}_RU_i, 1\leq i\leq m$
, are linearly independent in
$\operatorname {ind}_RU_i, 1\leq i\leq m$
, are linearly independent in
![]() $K_0^{\mbox {sp}}(R)$
.
$K_0^{\mbox {sp}}(R)$
.
Proof. The proof of [Reference Dehy and Keller21, Theorem 2.4] also works here.
We have the following criterion of a rigid object in
![]() $R\ast R[1]$
to be maximal rigid with respect to
$R\ast R[1]$
to be maximal rigid with respect to
![]() $R\ast R[1]$
by counting rank.
$R\ast R[1]$
by counting rank.
Proposition 2.7. For any
![]() $U\in \operatorname {rigid-}(R\ast R[1])$
, we have
$U\in \operatorname {rigid-}(R\ast R[1])$
, we have
![]() $|U|\leq |R|$
, where equality holds if and only if
$|U|\leq |R|$
, where equality holds if and only if
![]() $U\in \operatorname {max}\operatorname {rigid-}(R\ast R[1])$
.
$U\in \operatorname {max}\operatorname {rigid-}(R\ast R[1])$
.
Proof. Let
![]() $U=\,{\oplus}\, ^m_{i=1}U_i$
be a basic rigid object in
$U=\,{\oplus}\, ^m_{i=1}U_i$
be a basic rigid object in
![]() $R\ast R[1]$
with
$R\ast R[1]$
with
![]() $U_i,1\leq i\leq m$
, indecomposable. By Proposition 2.6, we have
$U_i,1\leq i\leq m$
, indecomposable. By Proposition 2.6, we have
where
![]() $\operatorname {rank} X$
denotes the rank of a set
$\operatorname {rank} X$
denotes the rank of a set
![]() $X\subseteq K_0^{\mbox {sp}}(R)$
.
$X\subseteq K_0^{\mbox {sp}}(R)$
.
Let U be a maximal rigid object with respect to
![]() $R\ast R[1]$
. On the one hand, U is rigid in
$R\ast R[1]$
. On the one hand, U is rigid in
![]() $R\ast R[1]$
, which implies
$R\ast R[1]$
, which implies
![]() $|U|\leq |R|$
. On the other hand, by Lemma 2.4, we have
$|U|\leq |R|$
. On the other hand, by Lemma 2.4, we have
![]() $R\in \operatorname {rigid-}(U[-1]\ast U)$
, which implies
$R\in \operatorname {rigid-}(U[-1]\ast U)$
, which implies
![]() $|R|\leq |U|$
. Hence, we have
$|R|\leq |U|$
. Hence, we have
![]() $|R|=|U|$
. Conversely, let
$|R|=|U|$
. Conversely, let
![]() $U\in \operatorname {rigid-}(R\ast R[1])$
with
$U\in \operatorname {rigid-}(R\ast R[1])$
with
![]() $|U|=|R|$
. For any
$|U|=|R|$
. For any
![]() $N\in R\ast R[1]$
such that
$N\in R\ast R[1]$
such that
![]() $U\,{\oplus}\, N$
is rigid, we have
$U\,{\oplus}\, N$
is rigid, we have
![]() $|U\,{\oplus}\, N|\leq |R|$
. Then
$|U\,{\oplus}\, N|\leq |R|$
. Then
![]() $|U|=|U\,{\oplus}\, N|$
, which implies
$|U|=|U\,{\oplus}\, N|$
, which implies
![]() $N\in \operatorname {add} U$
. So U is maximal rigid with respect to
$N\in \operatorname {add} U$
. So U is maximal rigid with respect to
![]() $R\ast R[1]$
.
$R\ast R[1]$
.
As a consequence of Lemma 2.4 and Proposition 2.7, we have the following dual relation between two rigid objects.
Corollary 2.8. Let U and R be rigid objects in
![]() $\mathcal {D}$
. Then
$\mathcal {D}$
. Then
![]() $U\in \operatorname {max}\operatorname {rigid-}(R\ast R[1])$
if and only if
$U\in \operatorname {max}\operatorname {rigid-}(R\ast R[1])$
if and only if
![]() $R\in \operatorname {max}\operatorname {rigid-}(U[-1]\ast U)$
.
$R\in \operatorname {max}\operatorname {rigid-}(U[-1]\ast U)$
.
Proof. For any
![]() $U\in \operatorname {max}\operatorname {rigid-}(R\ast R[1])$
, by Lemma 2.4, we have
$U\in \operatorname {max}\operatorname {rigid-}(R\ast R[1])$
, by Lemma 2.4, we have
![]() $R\in \operatorname {rigid-}(U[-1]\ast U)$
, and by Proposition 2.7, we have
$R\in \operatorname {rigid-}(U[-1]\ast U)$
, and by Proposition 2.7, we have
![]() $|U|=|R|$
. Then
$|U|=|R|$
. Then
![]() $|R|=|U[-1]|$
. So by Proposition 2.7 again, we have
$|R|=|U[-1]|$
. So by Proposition 2.7 again, we have
![]() $R\in \operatorname {max}\operatorname {rigid-}(U[-1]\ast U)$
. The opposite implication can be obtained by switching R with
$R\in \operatorname {max}\operatorname {rigid-}(U[-1]\ast U)$
. The opposite implication can be obtained by switching R with
![]() $U[-1]$
.
$U[-1]$
.
The following lemma is useful.
Lemma 2.9. Let U and R be basic rigid objects in
![]() $\mathcal {D}$
. If
$\mathcal {D}$
. If
![]() $R\in \operatorname {max}\operatorname {rigid-}(U[-1]\ast U)$
, then for any indecomposable summand Y of U, we have
$R\in \operatorname {max}\operatorname {rigid-}(U[-1]\ast U)$
, then for any indecomposable summand Y of U, we have
![]() $[\operatorname {ind}_{U[-1]}R:Y[-1]]\neq 0$
.
$[\operatorname {ind}_{U[-1]}R:Y[-1]]\neq 0$
.
Proof. Let
![]() $N=U\setminus Y$
. If
$N=U\setminus Y$
. If
![]() $[\operatorname {ind}_{U[-1]}R:Y[-1]]= 0$
then by the definition of index, R admits an
$[\operatorname {ind}_{U[-1]}R:Y[-1]]= 0$
then by the definition of index, R admits an
![]() $N[-1]$
-presentation. So by Proposition 2.7, we have
$N[-1]$
-presentation. So by Proposition 2.7, we have
![]() $|R|\leq |N|<|U|$
. Since
$|R|\leq |N|<|U|$
. Since
![]() $R\in \operatorname {max}\operatorname {rigid-}(U[-1]\ast U)$
, again by Proposition 2.7, we have
$R\in \operatorname {max}\operatorname {rigid-}(U[-1]\ast U)$
, again by Proposition 2.7, we have
![]() $|R|=|U|$
, a contradiction.
$|R|=|U|$
, a contradiction.
2.2 Mutation in two-term subcategories
By Proposition 2.7, any rigid object in
![]() $R\ast R[1]$
can be completed to a maximal rigid object with respect to
$R\ast R[1]$
can be completed to a maximal rigid object with respect to
![]() $R\ast R[1]$
.
$R\ast R[1]$
.
Definition 2.10. A basic rigid object N in
![]() $R\ast R[1]$
is called almost maximal rigid with respect to
$R\ast R[1]$
is called almost maximal rigid with respect to
![]() $R\ast R[1]$
if
$R\ast R[1]$
if
![]() $|N|=|R|-1$
.
$|N|=|R|-1$
.
Let N be an almost maximal rigid object with respect to
![]() $R\ast R[1]$
. An indecomposable object Y is called a completion of N if
$R\ast R[1]$
. An indecomposable object Y is called a completion of N if
![]() $N\,{\oplus}\, Y$
is maximal rigid with respect to
$N\,{\oplus}\, Y$
is maximal rigid with respect to
![]() $R\ast R[1]$
.
$R\ast R[1]$
.
Lemma 2.11. Let N be an almost maximal rigid object with respect to
![]() $R\ast R[1]$
, and
$R\ast R[1]$
, and
![]() $Y,Y^{\prime }$
be two non-isomorphic completions of N. Then
$Y,Y^{\prime }$
be two non-isomorphic completions of N. Then
Proof. Let
![]() $[\operatorname {ind}_{(Y\,{\oplus}\, N)[-1]}R:Y[-1]]=t$
and
$[\operatorname {ind}_{(Y\,{\oplus}\, N)[-1]}R:Y[-1]]=t$
and
![]() $[\operatorname {ind}_{(Y^{\prime }\,{\oplus}\, N)[-1]}R:Y^{\prime }[-1]]=s.$
Assume conversely
$[\operatorname {ind}_{(Y^{\prime }\,{\oplus}\, N)[-1]}R:Y^{\prime }[-1]]=s.$
Assume conversely
![]() $ts\geq 0$
. By Lemma 2.9, we have
$ts\geq 0$
. By Lemma 2.9, we have
![]() $t\neq 0$
and
$t\neq 0$
and
![]() $s\neq 0$
. So either
$s\neq 0$
. So either
![]() $t<0$
and
$t<0$
and
![]() $s<0$
, or
$s<0$
, or ![]() and
and ![]() . We only make a contradiction for the case
. We only make a contradiction for the case
![]() $t<0$
and
$t<0$
and
![]() $s<0$
since the other case is similar. Let
$s<0$
since the other case is similar. Let
![]() $U=N\,{\oplus}\, Y$
and
$U=N\,{\oplus}\, Y$
and
![]() $U^{\prime }=N\,{\oplus}\, Y^{\prime }$
. Consider the following diagram
$U^{\prime }=N\,{\oplus}\, Y^{\prime }$
. Consider the following diagram
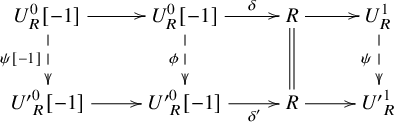
where the first (resp. second) row is a minimal
![]() $U[-1]$
-presentation (resp.
$U[-1]$
-presentation (resp.
![]() $U^{\prime }[-1]$
-presentation) of R. Since
$U^{\prime }[-1]$
-presentation) of R. Since
![]() $t<0$
and
$t<0$
and
![]() $s<0$
, by Proposition 2.2, both
$s<0$
, by Proposition 2.2, both
![]() $U_R^0$
and
$U_R^0$
and
![]() ${U^{\prime }}^0_R$
belong to
${U^{\prime }}^0_R$
belong to
![]() $\operatorname {add} N$
, and Y and
$\operatorname {add} N$
, and Y and
![]() $Y^{\prime }$
are direct summands of
$Y^{\prime }$
are direct summands of
![]() $U^1_R$
and
$U^1_R$
and
![]() ${U^{\prime }}^1_R$
, respectively. So both
${U^{\prime }}^1_R$
, respectively. So both
![]() $\delta $
and
$\delta $
and
![]() $\delta ^{\prime }$
are minimal right
$\delta ^{\prime }$
are minimal right
![]() $\operatorname {add} N[-1]$
-approximations of R. Hence, there exists an isomorphism
$\operatorname {add} N[-1]$
-approximations of R. Hence, there exists an isomorphism
![]() $\phi :U_R^0[-1]\to {U^{\prime }}^0_R[-1]$
such that the middle square of the above diagram commutes. It follows that there exists an isomorphism
$\phi :U_R^0[-1]\to {U^{\prime }}^0_R[-1]$
such that the middle square of the above diagram commutes. It follows that there exists an isomorphism
![]() $\psi :U_R^1\to {U^{\prime }}_R^1$
, and hence,
$\psi :U_R^1\to {U^{\prime }}_R^1$
, and hence,
![]() $Y\cong Y^{\prime }$
, a contradiction.
$Y\cong Y^{\prime }$
, a contradiction.
It follows from Lemma 2.11 that any almost maximal rigid object with respect to
![]() $R\ast R[1]$
has at most two completions. In what follows, we shall prove that the number of completions is exactly two. For this, we need the following notion of left/right mutation of a basic rigid object in
$R\ast R[1]$
has at most two completions. In what follows, we shall prove that the number of completions is exactly two. For this, we need the following notion of left/right mutation of a basic rigid object in
![]() $\mathcal {D}$
at an indecomposable summand, introduced in [Reference Iyama and Yoshino35, Definition 2.5].
$\mathcal {D}$
at an indecomposable summand, introduced in [Reference Iyama and Yoshino35, Definition 2.5].
Definition 2.12. Let
![]() $U=N\,{\oplus}\, Y$
be a basic rigid object in
$U=N\,{\oplus}\, Y$
be a basic rigid object in
![]() $\mathcal {D}$
, with Y an indecomposable direct summand of U. The right mutation
$\mathcal {D}$
, with Y an indecomposable direct summand of U. The right mutation
![]() $\mu ^+_Y(U)=N\,{\oplus}\, Z$
and the left mutation
$\mu ^+_Y(U)=N\,{\oplus}\, Z$
and the left mutation
![]() $\mu ^-_Y(U)=N\,{\oplus}\, W$
of U at Y are defined respectively by the triangles
$\mu ^-_Y(U)=N\,{\oplus}\, W$
of U at Y are defined respectively by the triangles
where
![]() $\alpha _Y$
and
$\alpha _Y$
and
![]() $\beta _Y$
are minimal right and left
$\beta _Y$
are minimal right and left
![]() $\operatorname {add} N$
-approximations of Y, respectively. The triangles (2.4) and (2.5) are called the right and left exchange triangles of U at Y, respectively.
$\operatorname {add} N$
-approximations of Y, respectively. The triangles (2.4) and (2.5) are called the right and left exchange triangles of U at Y, respectively.
In Definition 2.12, both Z and W are indecomposable and not isomorphic to Y, both
![]() $\mu ^+_Y(U)$
and
$\mu ^+_Y(U)$
and
![]() $\mu ^-_Y(U)$
are rigid, and
$\mu ^-_Y(U)$
are rigid, and
![]() $|\mu ^+_Y(U)|=|\mu ^-_Y(U)|=|U|$
; cf. [Reference Marsh and Palu44, Section 2.1]. Hence, by Proposition 2.7, we have the following result.
$|\mu ^+_Y(U)|=|\mu ^-_Y(U)|=|U|$
; cf. [Reference Marsh and Palu44, Section 2.1]. Hence, by Proposition 2.7, we have the following result.
Lemma 2.13. Let U be a basic rigid object in
![]() $\mathcal {D}$
, with Y an indecomposable direct summand of U. If U is a basic maximal rigid object with respect to
$\mathcal {D}$
, with Y an indecomposable direct summand of U. If U is a basic maximal rigid object with respect to
![]() $R\ast R[1]$
, then so is
$R\ast R[1]$
, then so is
![]() $\mu ^\varepsilon _Y(U)$
, provided that it is in
$\mu ^\varepsilon _Y(U)$
, provided that it is in
![]() $R\ast R[1]$
, where
$R\ast R[1]$
, where
![]() $\varepsilon \in \{+,-\}$
.
$\varepsilon \in \{+,-\}$
.
Note that any of
![]() $\mu ^+_Y(U)$
and
$\mu ^+_Y(U)$
and
![]() $\mu ^-_Y(U)$
may not be in
$\mu ^-_Y(U)$
may not be in
![]() $R\ast R[1]$
.
$R\ast R[1]$
.
Proposition 2.14. Let
![]() $U=N\,{\oplus}\, Y\in \operatorname {max}\operatorname {rigid-}(R\ast R[1])$
and Y be an indecomposable summand of U. We use the triangles (2.4) and (2.5). The following are equivalent.
$U=N\,{\oplus}\, Y\in \operatorname {max}\operatorname {rigid-}(R\ast R[1])$
and Y be an indecomposable summand of U. We use the triangles (2.4) and (2.5). The following are equivalent.
-
(1)
 .
. -
(2)
 $\operatorname {Hom}(R,\alpha _Y)$
is surjective.
$\operatorname {Hom}(R,\alpha _Y)$
is surjective. -
(3)
 $\mu ^+_Y(U)\in \operatorname {max}\operatorname {rigid-}(R\ast R[1])$
and
$\mu ^+_Y(U)\in \operatorname {max}\operatorname {rigid-}(R\ast R[1])$
and
 $[\operatorname {ind}_{\mu ^+_Y(U)[-1]}R:Z[-1]]<0$
.
$[\operatorname {ind}_{\mu ^+_Y(U)[-1]}R:Z[-1]]<0$
.
Dually, the following are equivalent.
-
(1’)
 $[\operatorname {ind}_{U[-1]}R:Y[-1]]<0$
.
$[\operatorname {ind}_{U[-1]}R:Y[-1]]<0$
. -
(2’)
 $\operatorname {Hom}(\beta _Y,R[1])$
is surjective.
$\operatorname {Hom}(\beta _Y,R[1])$
is surjective. -
(3’)
 $\mu ^-_Y(U)\in \operatorname {max}\operatorname {rigid-}(R\ast R[1])$
and
$\mu ^-_Y(U)\in \operatorname {max}\operatorname {rigid-}(R\ast R[1])$
and  .
.
Proof. We only prove the equivalences between (1), (2) and (3), since the equivalences between (1’), (2’) and (3’) can be proved dually.
![]() $(1)\Rightarrow (2)$
. Take a minimal
$(1)\Rightarrow (2)$
. Take a minimal
![]() $U[-1]$
-presentation of R:
$U[-1]$
-presentation of R:
Since
![]() $\iota _1$
is a left
$\iota _1$
is a left
![]() $\operatorname {add} U$
-approximation of R, for any morphism
$\operatorname {add} U$
-approximation of R, for any morphism
![]() $g\in \operatorname {Hom}(R,Y)$
, there exists
$g\in \operatorname {Hom}(R,Y)$
, there exists
![]() $h\in \operatorname {Hom}(U^1_R,Y)$
such that
$h\in \operatorname {Hom}(U^1_R,Y)$
such that
![]() $g=h\circ \iota _1$
. Since
$g=h\circ \iota _1$
. Since ![]() , by Proposition 2.2, we have
, by Proposition 2.2, we have
![]() $U^1_R\in \operatorname {add} N$
. Since
$U^1_R\in \operatorname {add} N$
. Since
![]() $\alpha _Y$
is a right
$\alpha _Y$
is a right
![]() $\operatorname {add} N$
-approximation of Y, there exists
$\operatorname {add} N$
-approximation of Y, there exists
![]() $h^{\prime }\in \operatorname {Hom}(U^R_1,N_0)$
such that
$h^{\prime }\in \operatorname {Hom}(U^R_1,N_0)$
such that
![]() $h=\alpha _Y\circ h^{\prime }$
. Then we have
$h=\alpha _Y\circ h^{\prime }$
. Then we have
![]() $g=\alpha _Y\circ h^{\prime }\circ \iota _1$
, which implies
$g=\alpha _Y\circ h^{\prime }\circ \iota _1$
, which implies
![]() $\operatorname {Hom}(R,\alpha _Y)$
is surjective.
$\operatorname {Hom}(R,\alpha _Y)$
is surjective.
![]() $(2)\Rightarrow (3)$
. Let
$(2)\Rightarrow (3)$
. Let
be a minimal R-presentation of Y. Since
![]() $\operatorname {Hom}(R,\alpha _Y)$
is surjective, there exists
$\operatorname {Hom}(R,\alpha _Y)$
is surjective, there exists
![]() $\iota ^{\prime }_0\in \operatorname {Hom}(R^0_Y,N_0)$
such that
$\iota ^{\prime }_0\in \operatorname {Hom}(R^0_Y,N_0)$
such that
![]() $\iota ^0_Y=\alpha _Y\circ \iota ^{\prime }_0$
. So by the octahedral axiom, we have the following commutative diagram of triangles.
$\iota ^0_Y=\alpha _Y\circ \iota ^{\prime }_0$
. So by the octahedral axiom, we have the following commutative diagram of triangles.
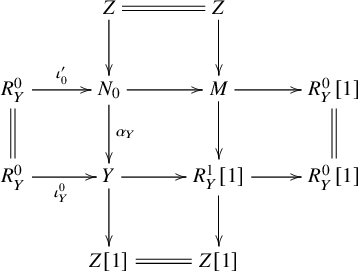
Since
![]() $M\in N_0\ast R^0_Y[1]\subseteq R\ast R[1]$
, we have
$M\in N_0\ast R^0_Y[1]\subseteq R\ast R[1]$
, we have
![]() $Z\in R^1_Y\ast M\subseteq R\ast R[1]$
. Thus, by Lemma 2.13, we have
$Z\in R^1_Y\ast M\subseteq R\ast R[1]$
. Thus, by Lemma 2.13, we have
![]() $\mu ^+_Y(U)=N\,{\oplus}\, Z\in \operatorname {max}\operatorname {rigid-}(R\ast R[1])$
.
$\mu ^+_Y(U)=N\,{\oplus}\, Z\in \operatorname {max}\operatorname {rigid-}(R\ast R[1])$
.
Applying
![]() $\operatorname {Hom}(R,-)$
to the right exchange triangle (2.4), we have the following exact sequence:
$\operatorname {Hom}(R,-)$
to the right exchange triangle (2.4), we have the following exact sequence:
Since
![]() $\operatorname {Hom}(R,\alpha _Y)$
is surjective, we have
$\operatorname {Hom}(R,\alpha _Y)$
is surjective, we have
![]() $\operatorname {Hom}(R,\alpha _N[1])$
is injective. So by the 2-Calabi-Yau property, the morphism
$\operatorname {Hom}(R,\alpha _N[1])$
is injective. So by the 2-Calabi-Yau property, the morphism
![]() $\operatorname {Hom}(\alpha _N,R[1])$
is surjective. Hence, any
$\operatorname {Hom}(\alpha _N,R[1])$
is surjective. Hence, any
![]() $g\in \operatorname {Hom}(Z[-1],R)$
factors through
$g\in \operatorname {Hom}(Z[-1],R)$
factors through
![]() $N_0[-1]$
. So any right
$N_0[-1]$
. So any right
![]() $\operatorname {add} N[-1]$
-approximation of R is also a right
$\operatorname {add} N[-1]$
-approximation of R is also a right
![]() $\operatorname {add}\mu ^+_Y(U)[-1]$
-approximation of R. By Lemma 2.9, it follows that
$\operatorname {add}\mu ^+_Y(U)[-1]$
-approximation of R. By Lemma 2.9, it follows that
![]() $[\operatorname {ind}_{\mu ^+_Y(U)[-1]}R:Z[-1]]<0$
.
$[\operatorname {ind}_{\mu ^+_Y(U)[-1]}R:Z[-1]]<0$
.
![]() $(3)\Rightarrow (1)$
. Since
$(3)\Rightarrow (1)$
. Since
![]() $Z\not \cong Y$
, this implication follows from Lemma 2.11 directly.
$Z\not \cong Y$
, this implication follows from Lemma 2.11 directly.
Now we are ready to show that each almost maximal rigid object with respect to
![]() $R\ast R[1]$
has exactly two completions.
$R\ast R[1]$
has exactly two completions.
Theorem 2.15. Let N be an almost maximal rigid object with respect to
![]() $R\ast R[1]$
. Then there are exactly two complements Y and
$R\ast R[1]$
. Then there are exactly two complements Y and
![]() $Y^{\prime }$
of N. Moreover, we have
$Y^{\prime }$
of N. Moreover, we have
In the case ![]() and
and
![]() $[\operatorname {ind}_{(N\,{\oplus}\, Y^{\prime })[-1]}R:Y^{\prime }[-1]]<0$
, there is a triangle
$[\operatorname {ind}_{(N\,{\oplus}\, Y^{\prime })[-1]}R:Y^{\prime }[-1]]<0$
, there is a triangle
with
![]() $E\in \operatorname {add} N$
, and which under the functor
$E\in \operatorname {add} N$
, and which under the functor
![]() $\operatorname {Hom}(R,-)$
becomes an exact sequence
$\operatorname {Hom}(R,-)$
becomes an exact sequence
Proof. By Proposition 2.7, there is a completion X of N. By Lemma 2.9, we have
![]() $[\operatorname {ind}_{(N\,{\oplus}\, X)[-1]}R:X[-1]]\neq 0$
. If
$[\operatorname {ind}_{(N\,{\oplus}\, X)[-1]}R:X[-1]]\neq 0$
. If ![]() , we take
, we take
![]() $Y=X$
and
$Y=X$
and
![]() $Y^{\prime }=\mu ^+_X(N\,{\oplus}\, X)\setminus N$
. Then by Proposition 2.14, the triangle (2.4) becomes the required one. If
$Y^{\prime }=\mu ^+_X(N\,{\oplus}\, X)\setminus N$
. Then by Proposition 2.14, the triangle (2.4) becomes the required one. If
![]() $[\operatorname {ind}_{(N\,{\oplus}\, X)[-1]}R:X[-1]]<0$
, we take
$[\operatorname {ind}_{(N\,{\oplus}\, X)[-1]}R:X[-1]]<0$
, we take
![]() $Y^{\prime }=X$
and
$Y^{\prime }=X$
and
![]() $Y=\mu ^-_{X}(N\,{\oplus}\, X)\setminus N$
. Then by Proposition 2.14, the triangle (2.5) becomes the required one.
$Y=\mu ^-_{X}(N\,{\oplus}\, X)\setminus N$
. Then by Proposition 2.14, the triangle (2.5) becomes the required one.
An alternative description of Theorem 2.15 is the following mutation version.
Corollary 2.16. Let
![]() $U\in \operatorname {max}\operatorname {rigid-}(R\ast R[1])$
and Y be an indecomposable summand of U. Then there is a unique (up to isomorphism) object
$U\in \operatorname {max}\operatorname {rigid-}(R\ast R[1])$
and Y be an indecomposable summand of U. Then there is a unique (up to isomorphism) object
![]() $\mu _Y(U)$
in
$\mu _Y(U)$
in
![]() $\operatorname {max}\operatorname {rigid-}(R\ast R[1])$
such that
$\operatorname {max}\operatorname {rigid-}(R\ast R[1])$
such that
![]() $\mu _Y(U)$
contains
$\mu _Y(U)$
contains
![]() $U\setminus Y$
as a direct summand and is not isomorphic to U. Moreover,
$U\setminus Y$
as a direct summand and is not isomorphic to U. Moreover,
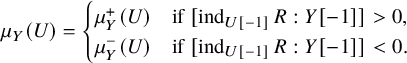
Remark 2.17. By Proposition 2.2, ![]() (resp.
(resp.
![]() $<0$
) if and only if
$<0$
) if and only if ![]() (resp.
(resp.
![]() $<0$
) for some indecomposable direct summand G of R.
$<0$
) for some indecomposable direct summand G of R.
2.3 Compatibility with
 $\tau $
-tilting theory
$\tau $
-tilting theory
In this subsection, we show that the mutation in
![]() $\operatorname {max}\operatorname {rigid-}(R\ast R[1])$
is compatible with the mutation of
$\operatorname {max}\operatorname {rigid-}(R\ast R[1])$
is compatible with the mutation of
![]() $\tau $
-tilting pairs over the endomorphism algebra
$\tau $
-tilting pairs over the endomorphism algebra
![]() $\operatorname {End} R$
.
$\operatorname {End} R$
.
We briefly recall the
![]() $\tau $
-tilting theory from [Reference Adachi, Iyama and Reiten1]. Let
$\tau $
-tilting theory from [Reference Adachi, Iyama and Reiten1]. Let
![]() $\Lambda $
be a finite-dimensional algebra. Denote by
$\Lambda $
be a finite-dimensional algebra. Denote by
![]() $\operatorname {mod}\Lambda $
the category of finitely generated right
$\operatorname {mod}\Lambda $
the category of finitely generated right
![]() $\Lambda $
-modules, and by
$\Lambda $
-modules, and by
![]() $\tau $
the Auslander-Reiten translation in
$\tau $
the Auslander-Reiten translation in
![]() $\operatorname {mod}\Lambda $
. For any
$\operatorname {mod}\Lambda $
. For any
![]() $M\in \operatorname {mod}\Lambda $
, we denote by
$M\in \operatorname {mod}\Lambda $
, we denote by
![]() $\operatorname {Fac}(M)$
the subcategory of
$\operatorname {Fac}(M)$
the subcategory of
![]() $\operatorname {mod}\Lambda $
consisting of factor modules of direct sums of copies of M.
$\operatorname {mod}\Lambda $
consisting of factor modules of direct sums of copies of M.
Definition 2.18. Let
![]() $M,P\in \operatorname {mod}\Lambda $
with P projective.
$M,P\in \operatorname {mod}\Lambda $
with P projective.
-
(1) The module M is called
 $\tau $
-rigid if
$\tau $
-rigid if
 $\operatorname {Hom}_{\Lambda }(M,\tau M)=0$
.
$\operatorname {Hom}_{\Lambda }(M,\tau M)=0$
. -
(2) The pair
 $(M,P)$
is called a
$(M,P)$
is called a
 $\tau $
-rigid pair if M is
$\tau $
-rigid pair if M is
 $\tau $
-rigid and
$\tau $
-rigid and
 $\operatorname {Hom}_{\Lambda }(P,M)=0$
.
$\operatorname {Hom}_{\Lambda }(P,M)=0$
. -
(3) The pair
 $(M,P)$
is called a
$(M,P)$
is called a
 $\tau $
-tilting pair if it is a
$\tau $
-tilting pair if it is a
 $\tau $
-rigid pair and
$\tau $
-rigid pair and
 $|M|+|P|=|\Lambda |$
. In this case, M is called a support
$|M|+|P|=|\Lambda |$
. In this case, M is called a support
 $\tau $
-tilting module.
$\tau $
-tilting module. -
(4) The pair
 $(M,P)$
is called an almost complete
$(M,P)$
is called an almost complete
 $\tau $
-tilting pair if it is a
$\tau $
-tilting pair if it is a
 $\tau $
-rigid pair and
$\tau $
-rigid pair and
 $|M|+|P|=|\Lambda |-1$
. In this case, M is called an almost complete support
$|M|+|P|=|\Lambda |-1$
. In this case, M is called an almost complete support
 $\tau $
-tilting module.
$\tau $
-tilting module.
For any basic support
![]() $\tau $
-tilting module M, there is a unique P (up to isomorphism) such that
$\tau $
-tilting module M, there is a unique P (up to isomorphism) such that
![]() $(M,P)$
is a basic
$(M,P)$
is a basic
![]() $\tau $
-tilting pair. Hence, one can identify basic support
$\tau $
-tilting pair. Hence, one can identify basic support
![]() $\tau $
-tilting modules with basic
$\tau $
-tilting modules with basic
![]() $\tau $
-tilting pairs. There is a partial order on the set of basic support
$\tau $
-tilting pairs. There is a partial order on the set of basic support
![]() $\tau $
-tilting modules, given by
$\tau $
-tilting modules, given by
![]() $M\geq N$
if and only if
$M\geq N$
if and only if
![]() $N\in \operatorname {Fac} M$
.
$N\in \operatorname {Fac} M$
.
Theorem 2.19 [Reference Adachi, Iyama and Reiten1, Theorem 2.18 and Definition-Proposition 2.28]
Any basic almost complete
![]() $\tau $
-tilting pair
$\tau $
-tilting pair
![]() $(N,Q)$
is a direct summand of exactly two non-isomorphic basic
$(N,Q)$
is a direct summand of exactly two non-isomorphic basic
![]() $\tau $
-tilting pairs
$\tau $
-tilting pairs
![]() $(M,P)$
and
$(M,P)$
and
![]() $(M^{\prime },P^{\prime })$
. Moreover, either
$(M^{\prime },P^{\prime })$
. Moreover, either ![]() or
or ![]() .
.
In the setting of Theorem 2.19, suppose ![]() . Then
. Then
![]() $(M,P)$
is called the right mutation of
$(M,P)$
is called the right mutation of
![]() $(M^{\prime },P^{\prime })$
at
$(M^{\prime },P^{\prime })$
at
![]() $(N,Q)$
and denote
$(N,Q)$
and denote
![]() $(M,P)=\mu ^+_{(N,Q)}(M^{\prime },P^{\prime })$
. Dually,
$(M,P)=\mu ^+_{(N,Q)}(M^{\prime },P^{\prime })$
. Dually,
![]() $(M^{\prime },P^{\prime })$
is called the left mutation of
$(M^{\prime },P^{\prime })$
is called the left mutation of
![]() $(M,P)$
at
$(M,P)$
at
![]() $(N,Q)$
and denote
$(N,Q)$
and denote
![]() $(M^{\prime },P^{\prime })=\mu ^-_{(N,Q)}(M,P)$
.
$(M^{\prime },P^{\prime })=\mu ^-_{(N,Q)}(M,P)$
.
Definition 2.20. The exchange graph
![]() $\operatorname {EG}(\operatorname {s\tau -tilt}\Lambda )$
of support
$\operatorname {EG}(\operatorname {s\tau -tilt}\Lambda )$
of support
![]() $\tau $
-tilting modules over
$\tau $
-tilting modules over
![]() $\Lambda $
has basic
$\Lambda $
has basic
![]() $\tau $
-tilting pairs as vertices and has mutations as edges.
$\tau $
-tilting pairs as vertices and has mutations as edges.
Let
![]() $\Lambda _R=\operatorname {End} R$
. The following result establishes a link between
$\Lambda _R=\operatorname {End} R$
. The following result establishes a link between
![]() $R\ast R[1]$
and
$R\ast R[1]$
and
![]() $\operatorname {mod}\Lambda _R$
.
$\operatorname {mod}\Lambda _R$
.
Theorem 2.21 [Reference Iyama and Yoshino35, Proposition 6.2], [Reference Chang, Zhang and Zhu18, Proposition 2.2, Theorem 3.2]
The functor
![]() $\operatorname {Hom}(R,-):\mathcal {D}\to \operatorname {mod}\Lambda _R$
induces an equivalence
$\operatorname {Hom}(R,-):\mathcal {D}\to \operatorname {mod}\Lambda _R$
induces an equivalence
such that for any
![]() $X\in R\ast R[1]$
without nonzero common direct summands with
$X\in R\ast R[1]$
without nonzero common direct summands with
![]() $R[1]$
, we have
$R[1]$
, we have
Moreover, this equivalence induces a bijection
where
![]() $\operatorname {\tau -rigidp}\operatorname {mod}\Lambda _R$
is the set of (isoclasses of) basic
$\operatorname {\tau -rigidp}\operatorname {mod}\Lambda _R$
is the set of (isoclasses of) basic
![]() $\tau $
-rigid pairs in
$\tau $
-rigid pairs in
![]() $\operatorname {mod}\Lambda _R$
,
$\operatorname {mod}\Lambda _R$
,
![]() $X_2\in \operatorname {add} R[1]$
and
$X_2\in \operatorname {add} R[1]$
and
![]() $X_1$
has no nonzero common direct summands with
$X_1$
has no nonzero common direct summands with
![]() $R[1]$
. This bijection restricts to a bijection from
$R[1]$
. This bijection restricts to a bijection from
![]() $\operatorname {max}\operatorname {rigid-}(R\ast R[1])$
to the set of (isoclasses of) basic
$\operatorname {max}\operatorname {rigid-}(R\ast R[1])$
to the set of (isoclasses of) basic
![]() $\tau $
-tilting pairs.
$\tau $
-tilting pairs.
This allows us to apply our results of mutation on
![]() $R\ast R[1]$
to the
$R\ast R[1]$
to the
![]() $\tau $
-tilting theory in
$\tau $
-tilting theory in
![]() $\operatorname {mod}\Lambda _R$
.
$\operatorname {mod}\Lambda _R$
.
Theorem 2.22. For any
![]() $U=N\,{\oplus}\, Y\in \operatorname {max}\operatorname {rigid-}(R\ast R[1])$
with Y an indecomposable summand of U, we have
$U=N\,{\oplus}\, Y\in \operatorname {max}\operatorname {rigid-}(R\ast R[1])$
with Y an indecomposable summand of U, we have
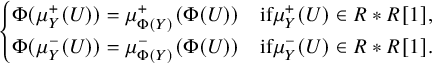 $$\begin{align*}\begin{cases} \Phi(\mu^+_Y(U))=\mu^+_{\Phi(Y)}(\Phi(U))&\text{if} \mu^+_Y(U)\in R\ast R[1],\\ \Phi(\mu^-_Y(U))=\mu^-_{\Phi(Y)}(\Phi(U))&\text{if} \mu^-_Y(U)\in R\ast R[1]. \end{cases}\end{align*}$$
$$\begin{align*}\begin{cases} \Phi(\mu^+_Y(U))=\mu^+_{\Phi(Y)}(\Phi(U))&\text{if} \mu^+_Y(U)\in R\ast R[1],\\ \Phi(\mu^-_Y(U))=\mu^-_{\Phi(Y)}(\Phi(U))&\text{if} \mu^-_Y(U)\in R\ast R[1]. \end{cases}\end{align*}$$
Proof. Let
![]() $Y^{\prime }$
be another completion of N. If
$Y^{\prime }$
be another completion of N. If
![]() $\mu ^+_Y(U)\in R\ast R[1]$
, then it is maximal rigid with respect to
$\mu ^+_Y(U)\in R\ast R[1]$
, then it is maximal rigid with respect to
![]() $R\ast R[1]$
by Lemma 2.13. So by Corollary 2.16, we have
$R\ast R[1]$
by Lemma 2.13. So by Corollary 2.16, we have
![]() $\mu ^+_Y(U)=N\,{\oplus}\, Y^{\prime }$
and
$\mu ^+_Y(U)=N\,{\oplus}\, Y^{\prime }$
and ![]() . Then by Theorem 2.15, there is a triangle
. Then by Theorem 2.15, there is a triangle
with
![]() $E\in \operatorname {add} N$
and such that there is an exact sequence
$E\in \operatorname {add} N$
and such that there is an exact sequence
In particular, we have
![]() $\operatorname {Hom}(R,U)\in \operatorname {Fac}\operatorname {Hom}(R,N)\subseteq \operatorname {Fac}\operatorname {Hom}(R,\mu ^+_Y(U))$
. By definition, we have
$\operatorname {Hom}(R,U)\in \operatorname {Fac}\operatorname {Hom}(R,N)\subseteq \operatorname {Fac}\operatorname {Hom}(R,\mu ^+_Y(U))$
. By definition, we have ![]() , which implies
, which implies
![]() $\Phi (\mu ^+_Y(U))=\mu ^+_{\Phi (Y)}(\Phi (U))$
, as required. The case
$\Phi (\mu ^+_Y(U))=\mu ^+_{\Phi (Y)}(\Phi (U))$
, as required. The case
![]() $\mu ^-_Y(U)\in R\ast R[1]$
can be proved dually.
$\mu ^-_Y(U)\in R\ast R[1]$
can be proved dually.
2.4 Relations with reductions
Let G be a rigid object in
![]() $\mathcal {D}$
. Denote by
$\mathcal {D}$
. Denote by
![]() $\mathcal {D}_G={}^{\perp }G[1]/ {\langle } \operatorname {add} G{\rangle }$
the quotient of the full subcategory
$\mathcal {D}_G={}^{\perp }G[1]/ {\langle } \operatorname {add} G{\rangle }$
the quotient of the full subcategory
![]() ${}^{\perp }G[1]$
by the ideal
${}^{\perp }G[1]$
by the ideal
![]() ${\langle }\operatorname {add} G{\rangle }$
consisting of morphisms that factor through objects in
${\langle }\operatorname {add} G{\rangle }$
consisting of morphisms that factor through objects in
![]() $\operatorname {add} G$
. For any morphism f in
$\operatorname {add} G$
. For any morphism f in
![]() ${}^{\perp }G[1]$
, denote by
${}^{\perp }G[1]$
, denote by
![]() $\bar {f}$
the image of f in the quotient
$\bar {f}$
the image of f in the quotient
![]() $\mathcal {D}_G$
.
$\mathcal {D}_G$
.
Theorem 2.23 [Reference Iyama and Yoshino35, Theorem 4.2]
The category
![]() $\mathcal {D}_G$
is a triangulated category whose suspension functor
$\mathcal {D}_G$
is a triangulated category whose suspension functor
![]() ${\langle }1{\rangle }_G$
and its inverse
${\langle }1{\rangle }_G$
and its inverse
![]() ${\langle }-1{\rangle }_G$
are given by the triangles in
${\langle }-1{\rangle }_G$
are given by the triangles in
![]() $\mathcal {D}$
$\mathcal {D}$
and
respectively, where
![]() $\beta _Y$
(resp.
$\beta _Y$
(resp.
![]() $\alpha _Y$
) is a left (resp. right)
$\alpha _Y$
) is a left (resp. right)
![]() $\operatorname {add} G$
-approximation of Y. The triangles in
$\operatorname {add} G$
-approximation of Y. The triangles in
![]() $\mathcal {D}_G$
are isomorphic to
$\mathcal {D}_G$
are isomorphic to
induced by the following diagram of triangles in
![]() $\mathcal {D}$
:
$\mathcal {D}$
:
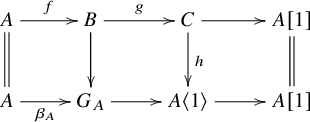
with
![]() $A,B,C\in {}^{\perp }G[1]$
.
$A,B,C\in {}^{\perp }G[1]$
.
We simply denote
![]() ${\langle }1{\rangle }={\langle }1{\rangle }_G$
and
${\langle }1{\rangle }={\langle }1{\rangle }_G$
and
![]() ${\langle }-1{\rangle }={\langle }-1{\rangle }_G$
, if there is no confusion arising.
${\langle }-1{\rangle }={\langle }-1{\rangle }_G$
, if there is no confusion arising.
Remark 2.24. Let
![]() $U=N\,{\oplus}\, Y$
be a rigid object in
$U=N\,{\oplus}\, Y$
be a rigid object in
![]() $\mathcal {D}$
. Comparing triangles 2.4 and 2.5 with Theorem 2.23, we have
$\mathcal {D}$
. Comparing triangles 2.4 and 2.5 with Theorem 2.23, we have
![]() $\mu ^+_Y(U)=N\,{\oplus}\, Y{\langle }-1{\rangle }_N$
and
$\mu ^+_Y(U)=N\,{\oplus}\, Y{\langle }-1{\rangle }_N$
and
![]() $\mu ^-_Y(U)=N\,{\oplus}\, Y{\langle }1{\rangle }_N$
.
$\mu ^-_Y(U)=N\,{\oplus}\, Y{\langle }1{\rangle }_N$
.
Now consider the case that G is a direct summand of R. Denote by
![]() $\operatorname {max}\operatorname {rigid}_G\operatorname {-}(R\ast _{\mathcal {D}} R[1])$
the subset of
$\operatorname {max}\operatorname {rigid}_G\operatorname {-}(R\ast _{\mathcal {D}} R[1])$
the subset of
![]() $\operatorname {max}\operatorname {rigid-}(R\ast _{\mathcal {D}} R[1])$
consisting of those objects that admit G as a direct summand.
$\operatorname {max}\operatorname {rigid-}(R\ast _{\mathcal {D}} R[1])$
consisting of those objects that admit G as a direct summand.
Proposition 2.25. Let G be a direct summand of R. Then there is a bijection
sending U to
![]() $U\setminus G$
. Moreover, for any
$U\setminus G$
. Moreover, for any
![]() $U\in \operatorname {max}\operatorname {rigid}_G\operatorname {-}(R\ast _{\mathcal {D}} R[1])$
and any indecomposable summand Y of
$U\in \operatorname {max}\operatorname {rigid}_G\operatorname {-}(R\ast _{\mathcal {D}} R[1])$
and any indecomposable summand Y of
![]() $U\setminus G$
, we have that
$U\setminus G$
, we have that
![]() $\mu ^{\varepsilon }_Y(U)\in \operatorname {max}\operatorname {rigid-}(R\ast _{\mathcal {D}} R[1])$
if and only if
$\mu ^{\varepsilon }_Y(U)\in \operatorname {max}\operatorname {rigid-}(R\ast _{\mathcal {D}} R[1])$
if and only if
![]() $\mu ^{\varepsilon }_{\Psi (Y)}(\Psi (U))\in \operatorname {max}\operatorname {rigid-}(R\ast _{\mathcal {D}_G} R{\langle }1{\rangle }),$
for any
$\mu ^{\varepsilon }_{\Psi (Y)}(\Psi (U))\in \operatorname {max}\operatorname {rigid-}(R\ast _{\mathcal {D}_G} R{\langle }1{\rangle }),$
for any
![]() $\varepsilon \in \{+,-\}$
, and in this case,
$\varepsilon \in \{+,-\}$
, and in this case,
![]() $\Psi (\mu ^{\varepsilon }_Y(U))=\mu ^{\varepsilon }_{\Psi (Y)}(\Psi (U))$
.
$\Psi (\mu ^{\varepsilon }_Y(U))=\mu ^{\varepsilon }_{\Psi (Y)}(\Psi (U))$
.
Proof. Let
![]() $U=G\,{\oplus}\, X$
be a basic object in
$U=G\,{\oplus}\, X$
be a basic object in
![]() $R\ast R[1]$
. By [Reference Iyama and Yoshino35, Lemma 4.8], U is rigid in
$R\ast R[1]$
. By [Reference Iyama and Yoshino35, Lemma 4.8], U is rigid in
![]() $\mathcal {D}$
if and only if X is rigid in
$\mathcal {D}$
if and only if X is rigid in
![]() ${\mathcal {D}_G}$
. Since an indecomposable object in
${\mathcal {D}_G}$
. Since an indecomposable object in
![]() $R\ast R[1]$
is isomorphic to zero in
$R\ast R[1]$
is isomorphic to zero in
![]() ${\mathcal {D}_G}$
if and only if it is isomorphic to a direct summand of G, we have
${\mathcal {D}_G}$
if and only if it is isomorphic to a direct summand of G, we have
![]() $|U|=|R|$
in
$|U|=|R|$
in
![]() $\mathcal {D}$
if and only if
$\mathcal {D}$
if and only if
![]() $|X|=|R\setminus G|$
in
$|X|=|R\setminus G|$
in
![]() ${\mathcal {D}_G}$
. So by Proposition 2.7, we have that
${\mathcal {D}_G}$
. So by Proposition 2.7, we have that
![]() $U\in \operatorname {max}\operatorname {rigid}_G\operatorname {-}(R\ast _{\mathcal {D}} R[1])$
if and only if
$U\in \operatorname {max}\operatorname {rigid}_G\operatorname {-}(R\ast _{\mathcal {D}} R[1])$
if and only if
![]() $X\in \operatorname {max}\operatorname {rigid-}(R\ast _{\mathcal {D}_G} R{\langle }1{\rangle })$
. Thus, we get the bijection
$X\in \operatorname {max}\operatorname {rigid-}(R\ast _{\mathcal {D}_G} R{\langle }1{\rangle })$
. Thus, we get the bijection
![]() $\Psi $
.
$\Psi $
.
By Theorem 2.23, a minimal U-presentation
of
![]() $R[1]$
in
$R[1]$
in
![]() $\mathcal {D}$
gives rise to a minimal X-presentation
$\mathcal {D}$
gives rise to a minimal X-presentation
of
![]() $R{\langle }1{\rangle }$
in
$R{\langle }1{\rangle }$
in
![]() ${\mathcal {D}_G}$
. So for any indecomposable summand Y of X, we have
${\mathcal {D}_G}$
. So for any indecomposable summand Y of X, we have
Then for any
![]() $\varepsilon \in \{+,-\}$
, by Proposition 2.14, we have
$\varepsilon \in \{+,-\}$
, by Proposition 2.14, we have
![]() $\mu ^{\varepsilon }_Y(U)\in \operatorname {max}\operatorname {rigid}_G\operatorname {-}(R\ast _{\mathcal {D}} R[1])$
if and only if
$\mu ^{\varepsilon }_Y(U)\in \operatorname {max}\operatorname {rigid}_G\operatorname {-}(R\ast _{\mathcal {D}} R[1])$
if and only if
![]() $\mu ^{\varepsilon }_{\Psi (Y)}(\Psi (U))\in \operatorname {max}\operatorname {rigid-}(R\ast _{\mathcal {D}_G} R{\langle }1{\rangle })$
. Then the last assertion follows from [Reference Iyama and Yoshino35, Proposition 4.4 (2)].
$\mu ^{\varepsilon }_{\Psi (Y)}(\Psi (U))\in \operatorname {max}\operatorname {rigid-}(R\ast _{\mathcal {D}_G} R{\langle }1{\rangle })$
. Then the last assertion follows from [Reference Iyama and Yoshino35, Proposition 4.4 (2)].
3 Cluster categories arising from punctured marked surfaces
In this section, we recall the cluster categories arising from punctured marked surfaces.
3.1 Punctured marked surfaces and triangulations
We recall from [Reference Fomin, Shapiro and Thurston25] and [Reference Qiu and Zhou49] some notions about punctured marked surfaces.
A punctured marked surface
![]() $\mathbf {S}$
is a triple
$\mathbf {S}$
is a triple
![]() $(S,\mathbf {M},\mathbf {P})$
, where
$(S,\mathbf {M},\mathbf {P})$
, where
-
○ S is a compact oriented surface with nonempty boundary
 $\partial S$
,
$\partial S$
, -
○
 $\mathbf {M}\subseteq \partial S$
is a finite set of marked points such that each component of
$\mathbf {M}\subseteq \partial S$
is a finite set of marked points such that each component of
 $\partial S$
contains at least one marked point in
$\partial S$
contains at least one marked point in
 $\mathbf {M}$
, and
$\mathbf {M}$
, and -
○
 $\mathbf {P}\subseteq (S\setminus \partial S)$
is a finite set of punctures.
$\mathbf {P}\subseteq (S\setminus \partial S)$
is a finite set of punctures.
Denote
![]() $\mathbf {S}^\circ :=S\setminus (\partial S\cup \mathbf {P})$
the interior of
$\mathbf {S}^\circ :=S\setminus (\partial S\cup \mathbf {P})$
the interior of
![]() $\mathbf {S}$
. The closures of connected components in
$\mathbf {S}$
. The closures of connected components in
![]() $\partial S\setminus \mathbf {M}$
are called boundary segments. Denote by B the set of boundary segments of
$\partial S\setminus \mathbf {M}$
are called boundary segments. Denote by B the set of boundary segments of
![]() $\mathbf {S}$
.
$\mathbf {S}$
.
An arc on S is an immersion
![]() $\gamma :[0,1]\to S$
such that
$\gamma :[0,1]\to S$
such that
-
(1)
 $\gamma (0),\gamma (1)\in \mathbf {M}\cup \mathbf {P}$
,
$\gamma (0),\gamma (1)\in \mathbf {M}\cup \mathbf {P}$
,
 $\gamma (t)\in \mathbf {S}^\circ $
for any
$\gamma (t)\in \mathbf {S}^\circ $
for any
 $t\in (0,1)$
,
$t\in (0,1)$
, -
(2)
 $\gamma $
is neither null-homotopic nor homotopic to a boundary segment, and
$\gamma $
is neither null-homotopic nor homotopic to a boundary segment, and -
(3)
 $\gamma $
has no self-intersections in
$\gamma $
has no self-intersections in
 $\mathbf {S}^\circ $
.
$\mathbf {S}^\circ $
.
Any arc is considered up to homotopy relative to its endpoints.
Definition 3.1 [Reference Fomin, Shapiro and Thurston25, Definition 2.6]
An ideal triangulation of
![]() $\mathbf {S}$
is a maximal collection of arcs on
$\mathbf {S}$
is a maximal collection of arcs on
![]() $\mathbf {S}$
that do not intersect each other in
$\mathbf {S}$
that do not intersect each other in
![]() $\mathbf {S}^\circ $
.
$\mathbf {S}^\circ $
.
Any ideal triangulation divides S into triangles. A triangle is called self-folded if two of its sides coincide, as shown in the left picture of Figure 1, where we use
![]() $\epsilon ^{\prime }$
to denote the folded side of a self-folded triangle whose non-folded side is
$\epsilon ^{\prime }$
to denote the folded side of a self-folded triangle whose non-folded side is
![]() $\epsilon $
. Note that the point p enclosed by
$\epsilon $
. Note that the point p enclosed by
![]() $\epsilon $
is always in
$\epsilon $
is always in
![]() $\mathbf {P}$
.
$\mathbf {P}$
.
Figure 1 From ideal triangulations to tagged triangulations.
Definition 3.2. A partial ideal triangulation
![]() $\mathbf {R}$
is a subset of an ideal triangulation
$\mathbf {R}$
is a subset of an ideal triangulation
![]() $\mathbf {T}$
such that for any self-folded triangle of
$\mathbf {T}$
such that for any self-folded triangle of
![]() $\mathbf {T}$
, if its non-folded side is in
$\mathbf {T}$
, if its non-folded side is in
![]() $\mathbf {R}$
, then so is its folded side.
$\mathbf {R}$
, then so is its folded side.
Definition 3.3 [Reference Fomin, Shapiro and Thurston25, Definition 7.1]
A tagged arc on
![]() $\mathbf {S}$
is an arc
$\mathbf {S}$
is an arc
![]() $\gamma $
that does not cut out a once-punctured monogon by a self-intersection in
$\gamma $
that does not cut out a once-punctured monogon by a self-intersection in
![]() $\mathbf {M}\cup \mathbf {P}$
, and is equipped with a map
$\mathbf {M}\cup \mathbf {P}$
, and is equipped with a map
such that
![]() $\kappa _\gamma (0)=\kappa _\gamma (1)$
if
$\kappa _\gamma (0)=\kappa _\gamma (1)$
if
![]() $\gamma (0)=\gamma (1)\in \mathbf {P}$
. The value
$\gamma (0)=\gamma (1)\in \mathbf {P}$
. The value
![]() $\kappa (t)$
is called the tagging of
$\kappa (t)$
is called the tagging of
![]() $\gamma $
at the end
$\gamma $
at the end
![]() $\gamma (t)$
. Denote by
$\gamma (t)$
. Denote by
![]() $\operatorname {A}^\times (\mathbf {S})$
the set of tagged arcs on
$\operatorname {A}^\times (\mathbf {S})$
the set of tagged arcs on
![]() $\mathbf {S}$
.
$\mathbf {S}$
.
In figures, we use the symbol
![]() $\times $
on one end of a tagged arc
$\times $
on one end of a tagged arc
![]() $\gamma $
to stand for that the value of
$\gamma $
to stand for that the value of
![]() $\kappa _\gamma $
at this end is taken to be
$\kappa _\gamma $
at this end is taken to be
![]() $-1$
.
$-1$
.
Remark 3.4. Each arc
![]() $\gamma $
can be viewed as a tagged arc
$\gamma $
can be viewed as a tagged arc
![]() $\gamma ^\times $
whose underlying arc is
$\gamma ^\times $
whose underlying arc is
![]() $\gamma $
and whose tagging is 1 at each punctured end.
$\gamma $
and whose tagging is 1 at each punctured end.
For an arc
![]() $\epsilon $
which is a loop enclosing a puncture p, although it can not be completed to a tagged arc by adding tagging directly, we still associate a tagged arc
$\epsilon $
which is a loop enclosing a puncture p, although it can not be completed to a tagged arc by adding tagging directly, we still associate a tagged arc
![]() $\epsilon ^\times $
to it, whose underlying arc is
$\epsilon ^\times $
to it, whose underlying arc is
![]() $\epsilon ^{\prime }$
, the unique arc in the interior of the once-puncture monogon enclosed by
$\epsilon ^{\prime }$
, the unique arc in the interior of the once-puncture monogon enclosed by
![]() $\epsilon $
, and whose tagging is
$\epsilon $
, and whose tagging is
![]() $-1$
on the end at p. See Figure 1.
$-1$
on the end at p. See Figure 1.
Definition 3.5 [Reference Qiu and Zhou49, Definition 3.3]
Let
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
be tagged arcs in minimal position.
$\gamma _2$
be tagged arcs in minimal position.
-
(1) Any pair
 $(t_1,t_2)$
with
$(t_1,t_2)$
with
 $0<t_1,t_2< 1$
and
$0<t_1,t_2< 1$
and
 $\gamma _1(t_1)=\gamma _2(t_2)$
is called an interior intersection between
$\gamma _1(t_1)=\gamma _2(t_2)$
is called an interior intersection between
 $\gamma _1$
and
$\gamma _1$
and
 $\gamma _2$
.
$\gamma _2$
. -
(2) A pair
 $(t_1,t_2)$
with
$(t_1,t_2)$
with
 $t_1,t_2\in \{0,1\}$
and
$t_1,t_2\in \{0,1\}$
and
 $\gamma _1(t_1)=\gamma _2(t_2)\in \mathbf {P}$
is called a tagged intersection between
$\gamma _1(t_1)=\gamma _2(t_2)\in \mathbf {P}$
is called a tagged intersection between
 $\gamma _1$
and
$\gamma _1$
and
 $\gamma _2$
if the following conditions hold.
$\gamma _2$
if the following conditions hold.-
(a)
 $\kappa _{\gamma _1}(t_1)\neq \kappa _{\gamma _2}(t_2)$
.
$\kappa _{\gamma _1}(t_1)\neq \kappa _{\gamma _2}(t_2)$
. -
(b) If
 $\gamma _1|_{t_1\to (1-t_1)}\sim \gamma _2|_{t_2\to (1-t_2)}$
, where
$\gamma _1|_{t_1\to (1-t_1)}\sim \gamma _2|_{t_2\to (1-t_2)}$
, where
 $\gamma _i|_{t_i\to (1-t_i)}$
denotes the orientation of
$\gamma _i|_{t_i\to (1-t_i)}$
denotes the orientation of
 $\gamma _i$
from
$\gamma _i$
from
 $t_i$
to
$t_i$
to
 $1-t_i$
, for
$1-t_i$
, for
 $i=1,2$
, then
$i=1,2$
, then
 $\gamma _1(1-t_1)=\gamma _2(1-t_2)\in \mathbf {P}$
and
$\gamma _1(1-t_1)=\gamma _2(1-t_2)\in \mathbf {P}$
and
 $\kappa _{\gamma _1}(1-t_1)\neq \kappa _{\gamma _2}(1-t_2)$
.
$\kappa _{\gamma _1}(1-t_1)\neq \kappa _{\gamma _2}(1-t_2)$
.
-
Denote by
![]() $\cap (\gamma _1,\gamma _2)$
the set of interior intersections and tagged intersections, and by
$\cap (\gamma _1,\gamma _2)$
the set of interior intersections and tagged intersections, and by
![]() $\operatorname {Int}(\gamma _1,\gamma _2)=|\cap (\gamma _1,\gamma _2)|$
the intersection number between the tagged arcs
$\operatorname {Int}(\gamma _1,\gamma _2)=|\cap (\gamma _1,\gamma _2)|$
the intersection number between the tagged arcs
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
.
$\gamma _2$
.
For any two tagged arcs
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
,
$\gamma _2$
,
![]() $\operatorname {Int}(\gamma _1,\gamma _2)=0$
if and only if they are compatible in the sense of [Reference Fomin, Shapiro and Thurston25, Definition 7.4].
$\operatorname {Int}(\gamma _1,\gamma _2)=0$
if and only if they are compatible in the sense of [Reference Fomin, Shapiro and Thurston25, Definition 7.4].
Definition 3.6. A tagged triangulation of
![]() $\mathbf {S}$
[Reference Fomin, Shapiro and Thurston25, Section 7] is a maximal collection
$\mathbf {S}$
[Reference Fomin, Shapiro and Thurston25, Section 7] is a maximal collection
![]() $\mathbf {T}$
of tagged arcs on
$\mathbf {T}$
of tagged arcs on
![]() $\mathbf {S}$
such that
$\mathbf {S}$
such that
![]() $\operatorname {Int}(\gamma _1,\gamma _2)=0$
for any
$\operatorname {Int}(\gamma _1,\gamma _2)=0$
for any
![]() $\gamma _1,\gamma _2\in \mathbf {T}$
. A partial tagged triangulation of
$\gamma _1,\gamma _2\in \mathbf {T}$
. A partial tagged triangulation of
![]() $\mathbf {S}$
is a subset of a tagged triangulation.
$\mathbf {S}$
is a subset of a tagged triangulation.
Let
![]() $\mathbf {R}$
be a partial tagged triangulation of
$\mathbf {R}$
be a partial tagged triangulation of
![]() $\mathbf {S}$
. We denote by
$\mathbf {S}$
. We denote by
![]() $\mathbf {P}_{\mathbf {R}}$
the subset of
$\mathbf {P}_{\mathbf {R}}$
the subset of
![]() $\mathbf {P}$
consisting of punctures p that are endpoints of arcs in
$\mathbf {P}$
consisting of punctures p that are endpoints of arcs in
![]() $\mathbf {R}$
. When
$\mathbf {R}$
. When
![]() $\mathbf {R}=\mathbf {T}$
is a tagged triangulation, we have
$\mathbf {R}=\mathbf {T}$
is a tagged triangulation, we have
![]() $\mathbf {P}_{\mathbf {T}}=\mathbf {P}$
. We define a map
$\mathbf {P}_{\mathbf {T}}=\mathbf {P}$
. We define a map
![]() $\kappa _{\mathbf {R}}:\mathbf {P}_{\mathbf {R}}\to \{-1,0,1\}$
as
$\kappa _{\mathbf {R}}:\mathbf {P}_{\mathbf {R}}\to \{-1,0,1\}$
as
 $$\begin{align*}\kappa_{\mathbf{R}}(p)=\begin{cases} -1& \textit{if any arc in}\ \mathbf{R}\ \textit{incident to p has tagging}\ \text{-1}\ \textit{there},\\ 1& \textit{if any arc in}\ \mathbf{R}\ \textit{incident to p has tagging}\ \text{1}\ \textit{there},\\ 0& \textit{otherwise}. \end{cases} \end{align*}$$
$$\begin{align*}\kappa_{\mathbf{R}}(p)=\begin{cases} -1& \textit{if any arc in}\ \mathbf{R}\ \textit{incident to p has tagging}\ \text{-1}\ \textit{there},\\ 1& \textit{if any arc in}\ \mathbf{R}\ \textit{incident to p has tagging}\ \text{1}\ \textit{there},\\ 0& \textit{otherwise}. \end{cases} \end{align*}$$
Remark 3.7. Using the correspondence
![]() $\gamma \mapsto \gamma ^\times $
given in Remark 3.4, each partial ideal triangulation
$\gamma \mapsto \gamma ^\times $
given in Remark 3.4, each partial ideal triangulation
![]() $\mathbf {R}$
corresponds to a partial tagged triangulation
$\mathbf {R}$
corresponds to a partial tagged triangulation
![]() $\mathbf {R}^\times $
. By identifying
$\mathbf {R}^\times $
. By identifying
![]() $\mathbf {R}$
with
$\mathbf {R}$
with
![]() $\mathbf {R}^\times $
, we regard a partial ideal triangulation
$\mathbf {R}^\times $
, we regard a partial ideal triangulation
![]() $\mathbf {R}$
as a partial tagged triangulation such that
$\mathbf {R}$
as a partial tagged triangulation such that
![]() $\kappa _{\mathbf {R}}(p)\geq 0$
for any
$\kappa _{\mathbf {R}}(p)\geq 0$
for any
![]() $p\in \mathbf {P}_{\mathbf {R}}$
. In particular, we regard each ideal triangulation as a tagged triangulation in such a way.
$p\in \mathbf {P}_{\mathbf {R}}$
. In particular, we regard each ideal triangulation as a tagged triangulation in such a way.
Conversely, we associate a partial ideal triangulation with any partial tagged triangulation as follows.
Construction 3.8. Let
![]() $\mathbf {R}$
be a partial tagged triangulation. We construct a partial ideal triangulation
$\mathbf {R}$
be a partial tagged triangulation. We construct a partial ideal triangulation
![]() $\mathbf {R}^\circ $
by
$\mathbf {R}^\circ $
by
-
(1) for
 $p\in \mathbf {P}_{\mathbf {R}}$
with
$p\in \mathbf {P}_{\mathbf {R}}$
with
 $\kappa _{\mathbf {R}}(p)\neq 0$
, removing the taggings of tagged arcs in
$\kappa _{\mathbf {R}}(p)\neq 0$
, removing the taggings of tagged arcs in
 $\mathbf {R}$
at p, and
$\mathbf {R}$
at p, and -
(2) for
 $p\in \mathbf {P}_{\mathbf {R}}$
with
$p\in \mathbf {P}_{\mathbf {R}}$
with
 $\kappa _{\mathbf {R}}(p)=0$
, replacing the two tagged arcs in
$\kappa _{\mathbf {R}}(p)=0$
, replacing the two tagged arcs in
 $\mathbf {R}$
incident to p by a self-folded triangle enclosing p, as shown in Figure 1 (from right to left).
$\mathbf {R}$
incident to p by a self-folded triangle enclosing p, as shown in Figure 1 (from right to left).
Note that when
![]() $\mathbf {R}=\mathbf {T}$
is a tagged triangulation,
$\mathbf {R}=\mathbf {T}$
is a tagged triangulation,
![]() $\mathbf {T}^\circ $
is an ideal triangulation. For any tagged arc
$\mathbf {T}^\circ $
is an ideal triangulation. For any tagged arc
![]() $\gamma \in \mathbf {R}$
, we denote by
$\gamma \in \mathbf {R}$
, we denote by
![]() $\gamma ^{\circ _{\mathbf {R}}}$
the arc in
$\gamma ^{\circ _{\mathbf {R}}}$
the arc in
![]() $\mathbf {R}^\circ $
corresponding to
$\mathbf {R}^\circ $
corresponding to
![]() $\gamma $
. Usually, we simply denote
$\gamma $
. Usually, we simply denote
![]() $\gamma ^{\circ _{\mathbf {R}}}$
by
$\gamma ^{\circ _{\mathbf {R}}}$
by
![]() $\gamma ^{\circ }$
, when there is no confusion arising.
$\gamma ^{\circ }$
, when there is no confusion arising.
Note that we have
![]() $(\mathbf {R}^\times )^\circ =\mathbf {R}$
for any partial ideal triangulation
$(\mathbf {R}^\times )^\circ =\mathbf {R}$
for any partial ideal triangulation
![]() $\mathbf {R}$
, but
$\mathbf {R}$
, but
![]() $(\mathbf {R}^\circ )^\times \neq \mathbf {R}$
for a partial tagged triangulation
$(\mathbf {R}^\circ )^\times \neq \mathbf {R}$
for a partial tagged triangulation
![]() $\mathbf {R}$
in general, where the only difference is the taggings of arcs at
$\mathbf {R}$
in general, where the only difference is the taggings of arcs at
![]() $p\in \mathbf {P}_{\mathbf {R}}$
with
$p\in \mathbf {P}_{\mathbf {R}}$
with
![]() $\kappa _{\mathbf {R}}(p)<0$
.
$\kappa _{\mathbf {R}}(p)<0$
.
Construction 3.9. Let
![]() $\mathbf {R}$
be a partial tagged triangulation. For any tagged arc
$\mathbf {R}$
be a partial tagged triangulation. For any tagged arc
![]() $\delta $
, we construct a tagged arc
$\delta $
, we construct a tagged arc
![]() $\delta ^{\mathbf {R}}$
, which is obtained from
$\delta ^{\mathbf {R}}$
, which is obtained from
![]() $\delta $
by changing taggings at
$\delta $
by changing taggings at
![]() $p\in \mathbf {P}_{\mathbf {R}}$
with
$p\in \mathbf {P}_{\mathbf {R}}$
with
![]() $\kappa _{\mathbf {R}}(p)<0$
.
$\kappa _{\mathbf {R}}(p)<0$
.
Remark 3.10. For any partial tagged triangulation
![]() $\mathbf {R}$
, there exists a tagged triangulation
$\mathbf {R}$
, there exists a tagged triangulation
![]() $\mathbf {T}$
such that
$\mathbf {T}$
such that
![]() $\mathbf {R}\subset \mathbf {T}$
and
$\mathbf {R}\subset \mathbf {T}$
and
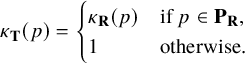 $$ \begin{align*}\kappa_{\mathbf{T}}(p)=\begin{cases} \kappa_{\mathbf{R}}(p)&\text{if}\ p\in\mathbf{P}_{\mathbf{R}},\\ 1&\text{otherwise.}\end{cases}\end{align*} $$
$$ \begin{align*}\kappa_{\mathbf{T}}(p)=\begin{cases} \kappa_{\mathbf{R}}(p)&\text{if}\ p\in\mathbf{P}_{\mathbf{R}},\\ 1&\text{otherwise.}\end{cases}\end{align*} $$
Then we have
![]() $\gamma ^{\circ _{\mathbf {R}}}=\gamma ^{\circ _{\mathbf {T}}}$
for any
$\gamma ^{\circ _{\mathbf {R}}}=\gamma ^{\circ _{\mathbf {T}}}$
for any
![]() $\gamma \in \mathbf {R}$
, and
$\gamma \in \mathbf {R}$
, and
![]() $\delta ^{\mathbf {T}}=\delta ^{\mathbf {R}}$
for any
$\delta ^{\mathbf {T}}=\delta ^{\mathbf {R}}$
for any
![]() $\delta \in \operatorname {A}^\times (\mathbf {S})$
.
$\delta \in \operatorname {A}^\times (\mathbf {S})$
.
3.2 Laminates and shear coordinates
We recall from [Reference Fomin and Thurston26] (cf. also [Reference Reading50, Reference Yurikusa51]) the notion of laminates and their shear coordinates. The elementary laminate
![]() $e(\delta )$
of a tagged arc
$e(\delta )$
of a tagged arc
![]() $\delta \in \operatorname {A}^\times (\mathbf {S})$
is defined as follows.
$\delta \in \operatorname {A}^\times (\mathbf {S})$
is defined as follows.
-
○
 $e(\delta )$
is an arc running along
$e(\delta )$
is an arc running along
 $\delta $
in a small neighbourhood of it;
$\delta $
in a small neighbourhood of it; -
○ If
 $\delta $
has an endpoint m on
$\delta $
has an endpoint m on
 $\partial S$
, then the corresponding endpoint of
$\partial S$
, then the corresponding endpoint of
 $e(\delta )$
is located near m on
$e(\delta )$
is located near m on
 $\partial S$
in the clockwise direction as in the left picture of Figure 2;
$\partial S$
in the clockwise direction as in the left picture of Figure 2;
Figure 2 Elementary laminate.
-
○ If
 $\delta $
has an endpoint at a puncture p, then the corresponding end of
$\delta $
has an endpoint at a puncture p, then the corresponding end of
 $e(\delta )$
is a spiral around p clockwise (resp. anticlockwise) if
$e(\delta )$
is a spiral around p clockwise (resp. anticlockwise) if
 $\kappa _\delta $
takes value
$\kappa _\delta $
takes value
 $1$
(resp.
$1$
(resp.
 $-1$
) at p as in the right picture of Figure 2.
$-1$
) at p as in the right picture of Figure 2.
The co-elementary laminate
![]() $e^{op}(\delta )$
of
$e^{op}(\delta )$
of
![]() $\delta $
is defined in the opposite direction.
$\delta $
is defined in the opposite direction.
Definition 3.11 [Reference Brüstle and Qiu12, Definition 3.4]
The tagged rotation
![]() $\rho (\gamma )$
of a tagged arc
$\rho (\gamma )$
of a tagged arc
![]() $\gamma \in \operatorname {A}^\times (\mathbf {S})$
is obtained from
$\gamma \in \operatorname {A}^\times (\mathbf {S})$
is obtained from
![]() $\gamma $
by moving each endpoint of
$\gamma $
by moving each endpoint of
![]() $\gamma $
that is in
$\gamma $
that is in
![]() $\mathbf {M}$
along the boundary anticlockwise to the next marked point and changing the tagging as
$\mathbf {M}$
along the boundary anticlockwise to the next marked point and changing the tagging as
![]() $\kappa _{\rho (\gamma )}(t)=-\kappa _{\gamma }(t)$
for any t with
$\kappa _{\rho (\gamma )}(t)=-\kappa _{\gamma }(t)$
for any t with
![]() $\gamma (t)\in \mathbf {P}$
.
$\gamma (t)\in \mathbf {P}$
.
Remark 3.12. For any
![]() $\delta \in \operatorname {A}^\times (\mathbf {S})$
, we have
$\delta \in \operatorname {A}^\times (\mathbf {S})$
, we have
![]() $e(\rho (\delta ))=e^{op}(\delta )$
and
$e(\rho (\delta ))=e^{op}(\delta )$
and
![]() $e^{op}(\rho ^{-1}(\delta ))=e(\delta )$
.
$e^{op}(\rho ^{-1}(\delta ))=e(\delta )$
.
Definition 3.13. Let L be the elementary laminate
![]() $e(\delta )$
or the co-elementary laminate
$e(\delta )$
or the co-elementary laminate
![]() $e^{op}(\delta )$
of a tagged arc
$e^{op}(\delta )$
of a tagged arc
![]() $\delta $
. Let
$\delta $
. Let
![]() $\mathbf {R}$
be a partial tagged triangulation. Define
$\mathbf {R}$
be a partial tagged triangulation. Define
![]() $L^{\mathbf {R}}=e(\delta ^{\mathbf {R}})$
for the case
$L^{\mathbf {R}}=e(\delta ^{\mathbf {R}})$
for the case
![]() $L=e(\delta )$
, and
$L=e(\delta )$
, and
![]() $L^{\mathbf {R}}=e^{op}(\delta ^{\mathbf {R}})$
for the case
$L^{\mathbf {R}}=e^{op}(\delta ^{\mathbf {R}})$
for the case
![]() $L=e^{op}(\delta )$
, where
$L=e^{op}(\delta )$
, where
![]() $\delta ^{\mathbf {R}}$
is given in Construction 3.9. We call L shears
$\delta ^{\mathbf {R}}$
is given in Construction 3.9. We call L shears
![]() $\mathbf {R}$
provided that each segment of
$\mathbf {R}$
provided that each segment of
![]() $L^{\mathbf {R}}$
divided by arcs in
$L^{\mathbf {R}}$
divided by arcs in
![]() $\mathbf {R}^\circ $
cuts out an angle between two arcs in
$\mathbf {R}^\circ $
cuts out an angle between two arcs in
![]() $\mathbf {R}^\circ \cup B$
.
$\mathbf {R}^\circ \cup B$
.
Note that when
![]() $\mathbf {R}=\mathbf {T}$
is a tagged triangulation, L always shears
$\mathbf {R}=\mathbf {T}$
is a tagged triangulation, L always shears
![]() $\mathbf {T}$
.
$\mathbf {T}$
.
Let
![]() $|\mathbf {R}|$
be the number of arcs in
$|\mathbf {R}|$
be the number of arcs in
![]() $\mathbf {R}$
. Using the notations in Definition 3.13, if L shears
$\mathbf {R}$
. Using the notations in Definition 3.13, if L shears
![]() $\mathbf {R}$
, the shear coordinate vector
$\mathbf {R}$
, the shear coordinate vector
of L with respect to
![]() $\mathbf {R}$
is defined as follows.
$\mathbf {R}$
is defined as follows.
For the case that
![]() $\mathbf {R}$
is a partial ideal triangulation, let
$\mathbf {R}$
is a partial ideal triangulation, let
![]() $\gamma $
be an arc in
$\gamma $
be an arc in
![]() $\mathbf {R}$
and q an intersection between
$\mathbf {R}$
and q an intersection between
![]() $\gamma $
and L. If
$\gamma $
and L. If
![]() $\gamma $
is not the folded side of a self-folded triangle of
$\gamma $
is not the folded side of a self-folded triangle of
![]() $\mathbf {R}$
, then
$\mathbf {R}$
, then
![]() $\gamma $
is the common edge of the two angles of
$\gamma $
is the common edge of the two angles of
![]() $\mathbf {R}$
that L cuts out consecutively. The contribution
$\mathbf {R}$
that L cuts out consecutively. The contribution
![]() $b_{q,\gamma ,\mathbf {R}}(L)$
of q is defined as shown in Figure 3.
$b_{q,\gamma ,\mathbf {R}}(L)$
of q is defined as shown in Figure 3.
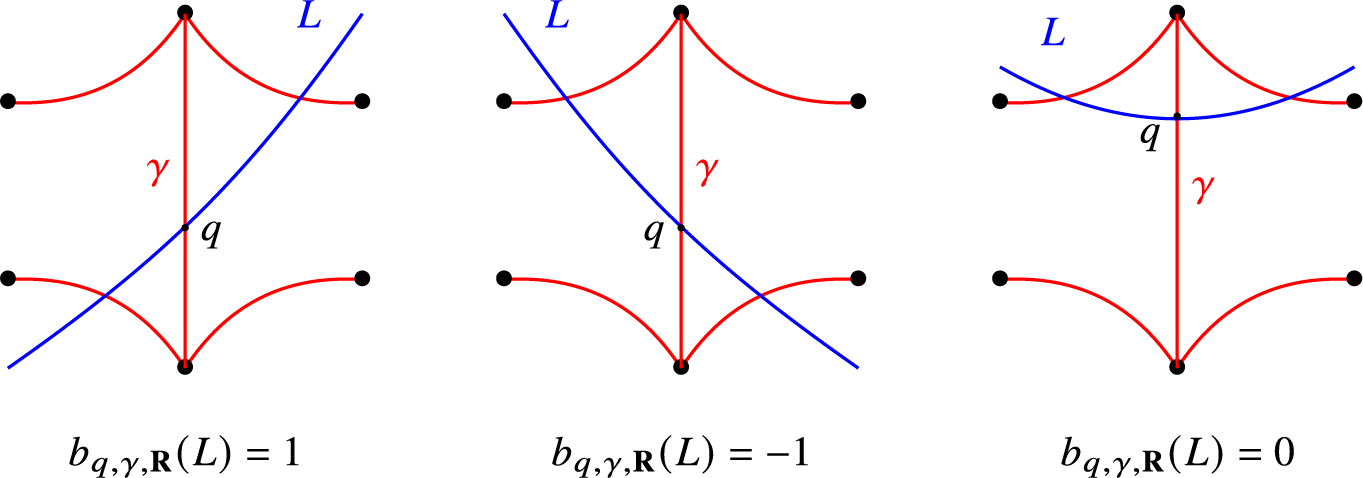
Figure 3 Contribution of an intersection q between L and
![]() $\gamma \in \mathbf {R}$
.
$\gamma \in \mathbf {R}$
.
In this case, define
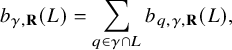 $$ \begin{align*}b_{\gamma,\mathbf{R}}(L)=\sum_{q\in\gamma\cap L} b_{q,\gamma,\mathbf{R}}(L),\end{align*} $$
$$ \begin{align*}b_{\gamma,\mathbf{R}}(L)=\sum_{q\in\gamma\cap L} b_{q,\gamma,\mathbf{R}}(L),\end{align*} $$
where
![]() $\gamma \cap L$
is the set of intersections between
$\gamma \cap L$
is the set of intersections between
![]() $\gamma $
and L. Since only finitely many q contribute nonzero values, the sum is well defined. If
$\gamma $
and L. Since only finitely many q contribute nonzero values, the sum is well defined. If
![]() $\gamma =\epsilon ^{\prime }$
is the folded side of a self-folded triangle of
$\gamma =\epsilon ^{\prime }$
is the folded side of a self-folded triangle of
![]() $\mathbf {R}$
whose non-folded side is
$\mathbf {R}$
whose non-folded side is
![]() $\epsilon $
and whose enclosing puncture is p (cf. the left picture of Figure 1), define
$\epsilon $
and whose enclosing puncture is p (cf. the left picture of Figure 1), define
where
![]() $L^{(p)}$
is obtained from L by changing the directions of its spirals at p if they exist.
$L^{(p)}$
is obtained from L by changing the directions of its spirals at p if they exist.
For the case that
![]() $\mathbf {R}$
is a partial tagged triangulation, for any
$\mathbf {R}$
is a partial tagged triangulation, for any
![]() $\gamma \in \mathbf {R}$
, define
$\gamma \in \mathbf {R}$
, define
where
![]() $\mathbf {R}^\circ $
and
$\mathbf {R}^\circ $
and
![]() $\gamma ^\circ $
are defined in Construction 3.8, and
$\gamma ^\circ $
are defined in Construction 3.8, and
![]() $L^{\mathbf {R}}$
is defined in Definition 3.13. By definition, for any tagged triangulation
$L^{\mathbf {R}}$
is defined in Definition 3.13. By definition, for any tagged triangulation
![]() $\mathbf {T}$
containing
$\mathbf {T}$
containing
![]() $\mathbf {R}$
and for any
$\mathbf {R}$
and for any
![]() $\gamma \in \mathbf {R}$
, we have
$\gamma \in \mathbf {R}$
, we have
Remark 3.14. Let
![]() $\mathbf {R}$
be a partial tagged triangulation of
$\mathbf {R}$
be a partial tagged triangulation of
![]() $\mathbf {S}$
and
$\mathbf {S}$
and
![]() $\gamma \in \mathbf {R}$
. Let
$\gamma \in \mathbf {R}$
. Let
![]() $\delta $
a tagged arc and let
$\delta $
a tagged arc and let
![]() $L=e(\delta )$
or
$L=e(\delta )$
or
![]() $e^{op}(\delta )$
. If there exists an intersection q between
$e^{op}(\delta )$
. If there exists an intersection q between
![]() $\gamma $
and L such that
$\gamma $
and L such that
![]() $b_{q,\gamma ,\mathbf {R}}(L)=1$
(resp.
$b_{q,\gamma ,\mathbf {R}}(L)=1$
(resp.
![]() $-1$
), then for any intersection
$-1$
), then for any intersection
![]() $q^{\prime }$
between
$q^{\prime }$
between
![]() $\gamma $
and L, we have
$\gamma $
and L, we have
![]() $b_{q^{\prime },\gamma ,\mathbf {R}}(L)\geq 0$
(resp.
$b_{q^{\prime },\gamma ,\mathbf {R}}(L)\geq 0$
(resp.
![]() $\leq 0$
). This is because L has no self-intersections.
$\leq 0$
). This is because L has no self-intersections.
3.3 Cluster categories from punctured marked surfaces
A quiver is a 4-tuple
![]() $Q=(Q_0,Q_1,s,t)$
, where
$Q=(Q_0,Q_1,s,t)$
, where
![]() $Q_0$
is a set of vertices,
$Q_0$
is a set of vertices,
![]() $Q_1$
is a set of arrows, and
$Q_1$
is a set of arrows, and
![]() $s,t:Q_1\to Q_0$
are the maps sending an arrow to its start and terminal, respectively. A quiver with potential is a pair
$s,t:Q_1\to Q_0$
are the maps sending an arrow to its start and terminal, respectively. A quiver with potential is a pair
![]() $(Q,W)$
with Q a quiver and W a linear combination of cycles of Q. For more details on quivers with potential, we refer to [Reference Derksen, Weyman and Zelevinski23].
$(Q,W)$
with Q a quiver and W a linear combination of cycles of Q. For more details on quivers with potential, we refer to [Reference Derksen, Weyman and Zelevinski23].
Let
![]() $\mathbf {S}$
be a punctured marked surface. To a tagged triangulation
$\mathbf {S}$
be a punctured marked surface. To a tagged triangulation
![]() $\mathbf {T}$
of
$\mathbf {T}$
of
![]() $\mathbf {S}$
, there is an associated quiver with potential
$\mathbf {S}$
, there is an associated quiver with potential
![]() $(Q^{\mathbf {T}},W^{\mathbf {T}})$
[Reference Fomin, Shapiro and Thurston25, Reference Labardini-Fragoso40, Reference Irelli and Labardini-Fragoso34], where
$(Q^{\mathbf {T}},W^{\mathbf {T}})$
[Reference Fomin, Shapiro and Thurston25, Reference Labardini-Fragoso40, Reference Irelli and Labardini-Fragoso34], where
![]() $Q_0^{\mathbf {T}}$
is in bijection with
$Q_0^{\mathbf {T}}$
is in bijection with
![]() $\mathbf {T}$
. By [Reference Irelli and Labardini-Fragoso34, Theorem 5.7], the Jacobian algebra
$\mathbf {T}$
. By [Reference Irelli and Labardini-Fragoso34, Theorem 5.7], the Jacobian algebra
![]() $\Lambda ^{\mathbf {T}}$
of
$\Lambda ^{\mathbf {T}}$
of
![]() $(Q^{\mathbf {T}},W^{\mathbf {T}})$
is finite-dimensional and is isomorphic to
$(Q^{\mathbf {T}},W^{\mathbf {T}})$
is finite-dimensional and is isomorphic to
where
![]() ${\mathbf {k}} Q^{\mathbf {T}}$
is the path algebra of
${\mathbf {k}} Q^{\mathbf {T}}$
is the path algebra of
![]() $Q^{\mathbf {T}}$
over the field
$Q^{\mathbf {T}}$
over the field
![]() ${\mathbf {k}}$
and
${\mathbf {k}}$
and
![]() ${\langle }\partial W^{\mathbf {T}}{\rangle }$
is the ideal of
${\langle }\partial W^{\mathbf {T}}{\rangle }$
is the ideal of
![]() ${\mathbf {k}} Q^{\mathbf {T}}$
generated by
${\mathbf {k}} Q^{\mathbf {T}}$
generated by
![]() $\partial W^{\mathbf {T}}=\{\partial _a W^{\mathbf {T}}\mid a\in Q^{\mathbf {T}}_1\}$
. Then by [Reference Amiot2], there is a
$\partial W^{\mathbf {T}}=\{\partial _a W^{\mathbf {T}}\mid a\in Q^{\mathbf {T}}_1\}$
. Then by [Reference Amiot2], there is a
![]() ${\mathbf {k}}$
-linear, Hom-finite, Krull-Schmidt, 2-Calabi-Yau triangulated category
${\mathbf {k}}$
-linear, Hom-finite, Krull-Schmidt, 2-Calabi-Yau triangulated category
![]() $\mathcal {C}(Q^{\mathbf {T}},W^{\mathbf {T}})$
, called (generalized) cluster category associated to
$\mathcal {C}(Q^{\mathbf {T}},W^{\mathbf {T}})$
, called (generalized) cluster category associated to
![]() $(Q^{\mathbf {T}},W^{\mathbf {T}})$
, with a cluster tilting object
$(Q^{\mathbf {T}},W^{\mathbf {T}})$
, with a cluster tilting object
![]() $T^{\mathbf {T}}$
such that there is an equivalence of categories
$T^{\mathbf {T}}$
such that there is an equivalence of categories
Moreover, by [Reference Fomin, Shapiro and Thurston25, Reference Labardini-Fragoso40, Reference Irelli and Labardini-Fragoso34, Reference Keller and Yang37], up to equivalence, the category
![]() $\mathcal {C}(Q^{\mathbf {T}},W^{\mathbf {T}})$
does not depend on the choice of the triangulation
$\mathcal {C}(Q^{\mathbf {T}},W^{\mathbf {T}})$
does not depend on the choice of the triangulation
![]() $\mathbf {T}$
. So we can use
$\mathbf {T}$
. So we can use
![]() $\mathcal {C}(\mathbf {S})$
to denote this category.
$\mathcal {C}(\mathbf {S})$
to denote this category.
Theorem 3.15 [Reference Qiu and Zhou49]
There is a bijection
from the set
![]() $\operatorname {A}^\times (\mathbf {S})$
of tagged arcs on
$\operatorname {A}^\times (\mathbf {S})$
of tagged arcs on
![]() $\mathbf {S}$
to the set
$\mathbf {S}$
to the set
![]() $\operatorname {ind}\operatorname {rigid}\mathcal {C}(\mathbf {S})$
of isoclasses of indecomposable rigid objects in
$\operatorname {ind}\operatorname {rigid}\mathcal {C}(\mathbf {S})$
of isoclasses of indecomposable rigid objects in
![]() $\mathcal {C}(\mathbf {S})$
, such that the following hold.
$\mathcal {C}(\mathbf {S})$
, such that the following hold.
-
(1) For any
 $\gamma \in \operatorname {A}^\times {(\mathbf {S})}$
, we have
$\gamma \in \operatorname {A}^\times {(\mathbf {S})}$
, we have  $$ \begin{align*}X(\rho(\gamma))=X(\gamma)[1].\end{align*} $$
$$ \begin{align*}X(\rho(\gamma))=X(\gamma)[1].\end{align*} $$
-
(2) For any tagged arcs
 $\gamma _1,\gamma _2$
, we have
$\gamma _1,\gamma _2$
, we have  $$ \begin{align*}\operatorname{Int}(\gamma_1,\gamma_2)=\dim_{\mathbf{k}}\operatorname{Hom}(X(\gamma_1),X(\gamma_2)[1]).\end{align*} $$
$$ \begin{align*}\operatorname{Int}(\gamma_1,\gamma_2)=\dim_{\mathbf{k}}\operatorname{Hom}(X(\gamma_1),X(\gamma_2)[1]).\end{align*} $$
-
(3) The bijection X induces a bijection
from the set $$ \begin{align*}\begin{array}{rccc} X:&\operatorname{R}^{\times}(\mathbf{S})&\to&\operatorname{rigid-}\mathcal{C}(\mathbf{S})\\ &\mathbf{R}&\mapsto&\bigoplus_{\gamma\in\mathbf{R}}X(\gamma) \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{rccc} X:&\operatorname{R}^{\times}(\mathbf{S})&\to&\operatorname{rigid-}\mathcal{C}(\mathbf{S})\\ &\mathbf{R}&\mapsto&\bigoplus_{\gamma\in\mathbf{R}}X(\gamma) \end{array}\end{align*} $$
 $\operatorname {R}^{\times }(\mathbf {S})$
of partial tagged triangulations of
$\operatorname {R}^{\times }(\mathbf {S})$
of partial tagged triangulations of
 $\mathbf {S}$
to the set
$\mathbf {S}$
to the set
 $\operatorname {rigid-}\mathcal {C}(\mathbf {S})$
of isoclasses of basic rigid objects in
$\operatorname {rigid-}\mathcal {C}(\mathbf {S})$
of isoclasses of basic rigid objects in
 $\mathcal {C}(\mathbf {S})$
, such that
$\mathcal {C}(\mathbf {S})$
, such that
 $\mathbf {R}$
is a tagged triangulation if and only if
$\mathbf {R}$
is a tagged triangulation if and only if
 $X(\mathbf {R})$
is a cluster tilting object.
$X(\mathbf {R})$
is a cluster tilting object.
-
(4) The cluster exchange graph of
 $\mathcal {C}(\mathbf {S})$
(i.e. the graph whose vertices are cluster tilting objects in
$\mathcal {C}(\mathbf {S})$
(i.e. the graph whose vertices are cluster tilting objects in
 $\mathcal {C}(\mathbf {S})$
and whose edges are mutations) is connected.
$\mathcal {C}(\mathbf {S})$
and whose edges are mutations) is connected.
Recall from (2.3) the definition of index
![]() $\operatorname {ind}_TM$
of an object M in
$\operatorname {ind}_TM$
of an object M in
![]() $\mathcal {C}(\mathbf {S})$
with respect to a cluster tilting object T.
$\mathcal {C}(\mathbf {S})$
with respect to a cluster tilting object T.
Proposition 3.16. Let
![]() $\mathbf {T}$
be a tagged triangulation of
$\mathbf {T}$
be a tagged triangulation of
![]() $\mathbf {S}$
. For any tagged arc
$\mathbf {S}$
. For any tagged arc
![]() $\delta $
, we have
$\delta $
, we have
and
Proof. Starting from the quiver
![]() $Q^{\mathbf {T}}$
, there is a cluster algebra
$Q^{\mathbf {T}}$
, there is a cluster algebra
![]() $\mathcal {A}$
[Reference Fomin and Zelevinsky27]. By [Reference Fomin, Shapiro and Thurston25, Theorem 7.11], there is a bijection x from the set
$\mathcal {A}$
[Reference Fomin and Zelevinsky27]. By [Reference Fomin, Shapiro and Thurston25, Theorem 7.11], there is a bijection x from the set
![]() $\operatorname {A}^\times (\mathbf {S})$
of tagged arcs on
$\operatorname {A}^\times (\mathbf {S})$
of tagged arcs on
![]() $\mathbf {S}$
to the set of cluster variables of
$\mathbf {S}$
to the set of cluster variables of
![]() $\mathcal {A}$
, such that x induces a bijection from the set of tagged triangulations to the set of clusters of
$\mathcal {A}$
, such that x induces a bijection from the set of tagged triangulations to the set of clusters of
![]() $\mathcal {A}$
, which sends
$\mathcal {A}$
, which sends
![]() $\mathbf {T}$
to the initial cluster and commutes with flips of tagged triangulations and mutations of clusters.
$\mathbf {T}$
to the initial cluster and commutes with flips of tagged triangulations and mutations of clusters.
For the 2-Calabi-Yau category
![]() $\mathcal {C}(\mathbf {S})$
with cluster tilting object
$\mathcal {C}(\mathbf {S})$
with cluster tilting object
![]() $T^{\mathbf {T}}$
, by [Reference Palu47] and Theorem 3.15 (4), there is a bijection
$T^{\mathbf {T}}$
, by [Reference Palu47] and Theorem 3.15 (4), there is a bijection
![]() $cc$
(called cluster character) from the set of indecomposable objects in
$cc$
(called cluster character) from the set of indecomposable objects in
![]() $\mathcal {C}(\mathbf {S})$
to the set of cluster variables of
$\mathcal {C}(\mathbf {S})$
to the set of cluster variables of
![]() $\mathcal {A}$
, such that
$\mathcal {A}$
, such that
![]() $cc$
induces a bijection from the set of basic cluster tilting objects to the set of reachable clusters of
$cc$
induces a bijection from the set of basic cluster tilting objects to the set of reachable clusters of
![]() $\mathcal {A}$
, which sends
$\mathcal {A}$
, which sends
![]() $T^{\mathbf {T}}$
to the initial cluster and commutes with mutations.
$T^{\mathbf {T}}$
to the initial cluster and commutes with mutations.
Then by Theorem 3.15, we have the following commutative diagram of bijections:
So for any tagged arc
![]() $\delta $
,
$\delta $
,
![]() $x(\delta )=cc(X(\delta ))$
. By [Reference Reading50, Proposition 5.2] (cf. also [Reference Labardini-Fragoso41, Theorem 7.1]), the g-vector of
$x(\delta )=cc(X(\delta ))$
. By [Reference Reading50, Proposition 5.2] (cf. also [Reference Labardini-Fragoso41, Theorem 7.1]), the g-vector of
![]() $x(\delta )$
is
$x(\delta )$
is
![]() $-b_{\mathbf {T}}(e(\delta ))$
. However, by [Reference Plamondon48, Proposition 3.6], the g-vector of
$-b_{\mathbf {T}}(e(\delta ))$
. However, by [Reference Plamondon48, Proposition 3.6], the g-vector of
![]() $cc(X(\delta ))$
is
$cc(X(\delta ))$
is
![]() $\operatorname {ind}_{T^{\mathbf {T}}}X(\delta )$
. Thus, we get (3.2).
$\operatorname {ind}_{T^{\mathbf {T}}}X(\delta )$
. Thus, we get (3.2).
For (3.3), we have
 $$ \begin{align*} \operatorname{ind}_{X(\mathbf{T})[-1]}X(\delta)&{}=\operatorname{ind}_{X(\mathbf{T})}X(\delta)[1]\\&=\operatorname{ind}_{X(\mathbf{T})}X(\rho(\delta)){}\\ &=-b_{\mathbf{T}}(e(\rho(\delta)))\\&=-b_{\mathbf{T}}(e^{op}(\delta)), \end{align*} $$
$$ \begin{align*} \operatorname{ind}_{X(\mathbf{T})[-1]}X(\delta)&{}=\operatorname{ind}_{X(\mathbf{T})}X(\delta)[1]\\&=\operatorname{ind}_{X(\mathbf{T})}X(\rho(\delta)){}\\ &=-b_{\mathbf{T}}(e(\rho(\delta)))\\&=-b_{\mathbf{T}}(e^{op}(\delta)), \end{align*} $$
where the second equality holds by Theorem 3.15 (1), the third one is (3.2), and the last one is due to Remark 3.12.
Corollary 3.17. Let
![]() $\mathbf {T}$
be a tagged triangulation of
$\mathbf {T}$
be a tagged triangulation of
![]() $\mathbf {S}$
and
$\mathbf {S}$
and
![]() $\mathbf {R}\subseteq \mathbf {T}$
. Then for any
$\mathbf {R}\subseteq \mathbf {T}$
. Then for any
![]() $\delta \in \operatorname {A}^\times (\mathbf {S})$
,
$\delta \in \operatorname {A}^\times (\mathbf {S})$
,
![]() $b_{\gamma ,\mathbf {T}}(e(\delta ))=0$
for all
$b_{\gamma ,\mathbf {T}}(e(\delta ))=0$
for all
![]() $\gamma \in \mathbf {T}\setminus \mathbf {R}$
if and only if
$\gamma \in \mathbf {T}\setminus \mathbf {R}$
if and only if
![]() $X(\delta )\in X(\mathbf {R})\ast X(\mathbf {R})[1]$
.
$X(\delta )\in X(\mathbf {R})\ast X(\mathbf {R})[1]$
.
Proof. By Proposition 3.16,
![]() $b_{\gamma ,\mathbf {T}}(e(\delta ))=0$
if and only if
$b_{\gamma ,\mathbf {T}}(e(\delta ))=0$
if and only if
![]() $[\operatorname {ind}_{X(\mathbf {T})}X(\delta ):X(\gamma )]=0$
. Then by Remark 2.5, we get this assertion.
$[\operatorname {ind}_{X(\mathbf {T})}X(\delta ):X(\gamma )]=0$
. Then by Remark 2.5, we get this assertion.
Corollary 3.18. Let
![]() $\mathbf {T}$
be a tagged triangulation of
$\mathbf {T}$
be a tagged triangulation of
![]() $\mathbf {S}$
. Then for any
$\mathbf {S}$
. Then for any
![]() $\gamma ,\delta \in \mathbf {T}$
, we have
$\gamma ,\delta \in \mathbf {T}$
, we have
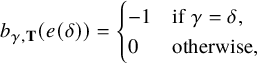 $$ \begin{align*}b_{\gamma,\mathbf{T}}(e(\delta))=\begin{cases} -1&\mathrm{if}\ \gamma=\delta,\\ 0&\mathrm{otherwise,} \end{cases}\end{align*} $$
$$ \begin{align*}b_{\gamma,\mathbf{T}}(e(\delta))=\begin{cases} -1&\mathrm{if}\ \gamma=\delta,\\ 0&\mathrm{otherwise,} \end{cases}\end{align*} $$
and
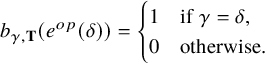 $$ \begin{align*}b_{\gamma,\mathbf{T}}(e^{op}(\delta))=\begin{cases} 1&\mathrm{if}\ \gamma=\delta,\\ 0&\mathrm{otherwise.} \end{cases}\end{align*} $$
$$ \begin{align*}b_{\gamma,\mathbf{T}}(e^{op}(\delta))=\begin{cases} 1&\mathrm{if}\ \gamma=\delta,\\ 0&\mathrm{otherwise.} \end{cases}\end{align*} $$
Proof. By Theorem 3.15 and the definition of index, we have
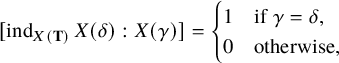 $$ \begin{align*}[\operatorname{ind}_{X(\mathbf{T})}X(\delta):X(\gamma)]=\begin{cases}1&\mathrm{if}\ \gamma=\delta,\\ 0&\mathrm{otherwise,}\end{cases}\end{align*} $$
$$ \begin{align*}[\operatorname{ind}_{X(\mathbf{T})}X(\delta):X(\gamma)]=\begin{cases}1&\mathrm{if}\ \gamma=\delta,\\ 0&\mathrm{otherwise,}\end{cases}\end{align*} $$
and
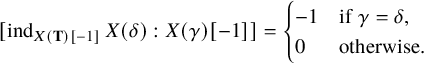 $$ \begin{align*}[\operatorname{ind}_{X(\mathbf{T})[-1]}X(\delta):X(\gamma)[-1]]=\begin{cases}-1&\mathrm{if}\ \gamma=\delta,\\ 0&\mathrm{otherwise.}\end{cases}\end{align*} $$
$$ \begin{align*}[\operatorname{ind}_{X(\mathbf{T})[-1]}X(\delta):X(\gamma)[-1]]=\begin{cases}-1&\mathrm{if}\ \gamma=\delta,\\ 0&\mathrm{otherwise.}\end{cases}\end{align*} $$
Then by Proposition 3.16, the required formulas follow.
4 A geometric model of surface rigid algebras
In this section, we give a geometric model for the module category of the endomorphism algebra of a rigid object in the cluster category of a punctured marked surface. We also show that any skew-gentle algebra is contained in this case.
Definition 4.1. A finite-dimensional algebra over
![]() ${\mathbf {k}}$
is called a surface rigid algebra if it is isomorphic to the endomorphism algebra
${\mathbf {k}}$
is called a surface rigid algebra if it is isomorphic to the endomorphism algebra
![]() $\Lambda _R:=\operatorname {End}_{\mathcal {C}(\mathbf {S})}R$
of a rigid object R in the cluster category
$\Lambda _R:=\operatorname {End}_{\mathcal {C}(\mathbf {S})}R$
of a rigid object R in the cluster category
![]() $\mathcal {C}(\mathbf {S})$
of a punctured marked surface
$\mathcal {C}(\mathbf {S})$
of a punctured marked surface
![]() $\mathbf {S}$
.
$\mathbf {S}$
.
See [Reference David-Roesler and Schiffler20] for an unpunctured version of the above notion.
By Theorem 3.15 (3), each surface rigid algebra can be realized as the endomorphism algebra
![]() $\Lambda _{\mathbf {R}}:=\Lambda _{X(\mathbf {R})}$
of
$\Lambda _{\mathbf {R}}:=\Lambda _{X(\mathbf {R})}$
of
![]() $X(\mathbf {R})$
for a partial tagged triangulation
$X(\mathbf {R})$
for a partial tagged triangulation
![]() $\mathbf {R}$
of a punctured marked surface
$\mathbf {R}$
of a punctured marked surface
![]() $\mathbf {S}=(S,\mathbf {M},\mathbf {P})$
.
$\mathbf {S}=(S,\mathbf {M},\mathbf {P})$
.
4.1 Standard arcs and dissections
For any tagged arc
![]() $\delta \in \operatorname {A}^\times (\mathbf {S})$
whose both endpoints are in
$\delta \in \operatorname {A}^\times (\mathbf {S})$
whose both endpoints are in
![]() $\mathbf {P}$
, the tagged arc
$\mathbf {P}$
, the tagged arc
![]() $\rho (\delta )=\rho ^{-1}(\delta )$
is said to be adjoint to
$\rho (\delta )=\rho ^{-1}(\delta )$
is said to be adjoint to
![]() $\delta $
.
$\delta $
.
For any partial ideal triangulation
![]() $\mathbf {R}$
of
$\mathbf {R}$
of
![]() $\mathbf {S}$
and any curve
$\mathbf {S}$
and any curve
![]() $\delta $
in a minimal position with (the arcs in)
$\delta $
in a minimal position with (the arcs in)
![]() $\mathbf {R}$
, an arc segment of
$\mathbf {R}$
, an arc segment of
![]() $\delta $
(with respect to
$\delta $
(with respect to
![]() $\mathbf {R}$
) is a segment of
$\mathbf {R}$
) is a segment of
![]() $\delta $
between two neighboring intersections between
$\delta $
between two neighboring intersections between
![]() $\delta $
and
$\delta $
and
![]() $\mathbf {R}\cup B$
, where recall that B is the set of boundary segments of S. An arc segment of
$\mathbf {R}\cup B$
, where recall that B is the set of boundary segments of S. An arc segment of
![]() $\delta $
is called an end arc segment if it has an endpoint in
$\delta $
is called an end arc segment if it has an endpoint in
![]() $\mathbf {M}\cup \mathbf {P}$
.
$\mathbf {M}\cup \mathbf {P}$
.
Definition 4.2. Let
![]() $\mathbf {R}$
be a partial ideal triangulation of
$\mathbf {R}$
be a partial ideal triangulation of
![]() $\mathbf {S}$
. A tagged arc
$\mathbf {S}$
. A tagged arc
![]() $\delta \in \operatorname {A}^\times (\mathbf {S})$
is called
$\delta \in \operatorname {A}^\times (\mathbf {S})$
is called
![]() $\mathbf {R}$
-standard if and only if one of the following holds.
$\mathbf {R}$
-standard if and only if one of the following holds.
-
(1)
 $\delta \in \mathbf {R}^\times $
or
$\delta \in \mathbf {R}^\times $
or
 $\delta $
is adjoint to some arc in
$\delta $
is adjoint to some arc in
 $\mathbf {R}^\times $
.
$\mathbf {R}^\times $
. -
(2)
 $\delta $
itself is an arc segment and cuts out an angle
$\delta $
itself is an arc segment and cuts out an angle
 $\theta $
between two arcs in
$\theta $
between two arcs in
 $\mathbf {R}\cup B$
, such that the tagging of
$\mathbf {R}\cup B$
, such that the tagging of
 $\delta $
has the form as shown in the first picture of Figure 4, where the left endpoint of
$\delta $
has the form as shown in the first picture of Figure 4, where the left endpoint of
 $\delta $
is a puncture with tagging
$\delta $
is a puncture with tagging
 $-1$
, and the right endpoint of
$-1$
, and the right endpoint of
 $\delta $
is either a marked point or a puncture with tagging
$\delta $
is either a marked point or a puncture with tagging
 $1$
.
$1$
.
Figure 4 Arc segments of standard tagged arcs.
-
(3)
 $\delta $
is divided by
$\delta $
is divided by
 $\mathbf {R}$
into at least two arc segments, satisfying that each arc segment
$\mathbf {R}$
into at least two arc segments, satisfying that each arc segment
 $\eta $
cuts out an angle
$\eta $
cuts out an angle
 $\theta $
between two arcs in
$\theta $
between two arcs in
 $\mathbf {R}\cup B$
(see the last three pictures of Figure 4), and in case
$\mathbf {R}\cup B$
(see the last three pictures of Figure 4), and in case
 $\eta $
having an endpoint
$\eta $
having an endpoint
 $\mathfrak {q}$
in
$\mathfrak {q}$
in
 $\mathbf {M}\cup \mathbf {P}$
, the edge of
$\mathbf {M}\cup \mathbf {P}$
, the edge of
 $\theta $
with vertex
$\theta $
with vertex
 $\mathfrak {q}$
is the first arc in
$\mathfrak {q}$
is the first arc in
 $\mathbf {R}\cup B$
next to
$\mathbf {R}\cup B$
next to
 $\eta $
in the anticlockwise order around
$\eta $
in the anticlockwise order around
 $\mathfrak {q}$
if
$\mathfrak {q}$
if
 $\mathfrak {q}\in \mathbf {P}$
and the tagging of
$\mathfrak {q}\in \mathbf {P}$
and the tagging of
 $\eta $
at this end is
$\eta $
at this end is
 $-1$
(see the third picture of Figure 4), or in the clockwise order otherwise (see the last picture of Figure 4).
$-1$
(see the third picture of Figure 4), or in the clockwise order otherwise (see the last picture of Figure 4).
Dually, a tagged arc
![]() $\delta \in \operatorname {A}^\times (\mathbf {S})$
is called
$\delta \in \operatorname {A}^\times (\mathbf {S})$
is called
![]() $\mathbf {R}$
-co-standard if and only if one of the following holds.
$\mathbf {R}$
-co-standard if and only if one of the following holds.
-
(1)
 $\delta \in \mathbf {R}^\times $
or
$\delta \in \mathbf {R}^\times $
or
 $\delta $
is adjoint to some arc in
$\delta $
is adjoint to some arc in
 $\mathbf {R}^\times $
.
$\mathbf {R}^\times $
. -
(2)
 $\delta $
itself is an arc segment and cuts out an angle
$\delta $
itself is an arc segment and cuts out an angle
 $\theta $
between two arcs in
$\theta $
between two arcs in
 $\mathbf {R}\cup B$
, such that the tagging of
$\mathbf {R}\cup B$
, such that the tagging of
 $\delta $
has the form as shown in the first picture of Figure 5, where the right endpoint of
$\delta $
has the form as shown in the first picture of Figure 5, where the right endpoint of
 $\delta $
is a puncture with tagging
$\delta $
is a puncture with tagging
 $-1$
, and the left endpoint of
$-1$
, and the left endpoint of
 $\delta $
is either a marked point or a puncture with tagging
$\delta $
is either a marked point or a puncture with tagging
 $1$
.
$1$
.
Figure 5 Arc segments of co-standard tagged arcs.
-
(3)
 $\delta $
is divided by
$\delta $
is divided by
 $\mathbf {R}$
into at least two arc segments, satisfying that each arc segment
$\mathbf {R}$
into at least two arc segments, satisfying that each arc segment
 $\eta $
cuts out an angle
$\eta $
cuts out an angle
 $\theta $
between two arcs in
$\theta $
between two arcs in
 $\mathbf {R}\cup B$
, and in case
$\mathbf {R}\cup B$
, and in case
 $\eta $
having an endpoint
$\eta $
having an endpoint
 $\mathfrak {q}\in \mathbf {M}\cup \mathbf {P}$
, the edge of
$\mathfrak {q}\in \mathbf {M}\cup \mathbf {P}$
, the edge of
 $\theta $
which is incident to the vertex
$\theta $
which is incident to the vertex
 $\mathfrak {q}$
is the first arc in
$\mathfrak {q}$
is the first arc in
 $\mathbf {R}\cup B$
next to
$\mathbf {R}\cup B$
next to
 $\eta $
in the clockwise order around
$\eta $
in the clockwise order around
 $\mathfrak {q}$
if
$\mathfrak {q}$
if
 $\mathfrak {q}\in \mathbf {P}$
and the tagging of
$\mathfrak {q}\in \mathbf {P}$
and the tagging of
 $\eta $
at this end is
$\eta $
at this end is
 $-1$
, or in the anticlockwise order otherwise. See the last three pictures of Figure 5.
$-1$
, or in the anticlockwise order otherwise. See the last three pictures of Figure 5.
Let
![]() $\mathbf {R}$
be a partial tagged triangulation of
$\mathbf {R}$
be a partial tagged triangulation of
![]() $\mathbf {S}$
. A tagged arc
$\mathbf {S}$
. A tagged arc
![]() $\delta \in \operatorname {A}^\times (\mathbf {S})$
is called
$\delta \in \operatorname {A}^\times (\mathbf {S})$
is called
![]() $\mathbf {R}$
-standard (resp.
$\mathbf {R}$
-standard (resp.
![]() $\mathbf {R}$
-co-standard) if
$\mathbf {R}$
-co-standard) if
![]() $\delta ^{\mathbf {R}}$
is
$\delta ^{\mathbf {R}}$
is
![]() $\mathbf {R}^\circ $
-standard (resp.
$\mathbf {R}^\circ $
-standard (resp.
![]() $\mathbf {R}^\circ $
-co-standard). Denote by
$\mathbf {R}^\circ $
-co-standard). Denote by
![]() $\operatorname {A}^\times _{\mathbf {R}\operatorname {-st}}$
(resp.
$\operatorname {A}^\times _{\mathbf {R}\operatorname {-st}}$
(resp.
![]() $\operatorname {A}^\times _{\mathbf {R}\operatorname {-co-st}}$
) the set of
$\operatorname {A}^\times _{\mathbf {R}\operatorname {-co-st}}$
) the set of
![]() $\mathbf {R}$
-standard (resp.
$\mathbf {R}$
-standard (resp.
![]() $\mathbf {R}$
-co-standard) tagged arcs.
$\mathbf {R}$
-co-standard) tagged arcs.
Remark 4.3. In Definition 4.2, since
![]() $\delta $
is a tagged arc, the two edges of
$\delta $
is a tagged arc, the two edges of
![]() $\theta $
are not from the same arc in
$\theta $
are not from the same arc in
![]() $\mathbf {R}$
, unless in the second pictures of Figures 4 and 5, where they may be the different ends of an arc in
$\mathbf {R}$
, unless in the second pictures of Figures 4 and 5, where they may be the different ends of an arc in
![]() $\mathbf {R}$
.
$\mathbf {R}$
.
In the following, we give sufficient and necessary conditions on tagged arcs to be standard/co-standard.
Proposition 4.4. Let
![]() $\mathbf {R}$
be a partial tagged triangulation of
$\mathbf {R}$
be a partial tagged triangulation of
![]() $\mathbf {S}$
and
$\mathbf {S}$
and
![]() $\delta $
a tagged arc. Then the following are equivalent.
$\delta $
a tagged arc. Then the following are equivalent.
-
(1)
 $\delta $
is
$\delta $
is
 $\mathbf {R}$
-standard (resp.
$\mathbf {R}$
-standard (resp.
 $\mathbf {R}$
-co-standard).
$\mathbf {R}$
-co-standard). -
(2)
 $e(\delta )$
(resp.
$e(\delta )$
(resp.
 $e^{op}(\delta )$
) shears
$e^{op}(\delta )$
) shears
 $\mathbf {R}$
(see Definition 3.13).
$\mathbf {R}$
(see Definition 3.13). -
(3) For some/any tagged triangulation
 $\mathbf {T}$
such that
$\mathbf {T}$
such that
 $\mathbf {R}\subset \mathbf {T}$
, we have
$\mathbf {R}\subset \mathbf {T}$
, we have
 $b_{\gamma ,\mathbf {T}}(e(\delta ))=0$
(resp.
$b_{\gamma ,\mathbf {T}}(e(\delta ))=0$
(resp.
 $b_{\gamma ,\mathbf {T}}(e^{op}(\delta ))=0$
) for any
$b_{\gamma ,\mathbf {T}}(e^{op}(\delta ))=0$
) for any
 $\gamma \in \mathbf {T}\setminus \mathbf {R}$
.
$\gamma \in \mathbf {T}\setminus \mathbf {R}$
. -
(4)
 $X(\delta )\in X(\mathbf {R})\ast X(\mathbf {R})[1]$
.
$X(\delta )\in X(\mathbf {R})\ast X(\mathbf {R})[1]$
.
Proof. We only show the equivalences between statements for the
![]() $\mathbf {R}$
-standard case, since the
$\mathbf {R}$
-standard case, since the
![]() $\mathbf {R}$
-co-standard case can be shown dually. By Corollary 3.17, (4) is equivalent to (3). By definition, (1) is equivalent to that
$\mathbf {R}$
-co-standard case can be shown dually. By Corollary 3.17, (4) is equivalent to (3). By definition, (1) is equivalent to that
![]() $\delta ^{\mathbf {R}}$
is
$\delta ^{\mathbf {R}}$
is
![]() $\mathbf {R}^\circ $
-standard, (2) is equivalent to that
$\mathbf {R}^\circ $
-standard, (2) is equivalent to that
![]() $e(\delta ^{\mathbf {R}})$
shears
$e(\delta ^{\mathbf {R}})$
shears
![]() $\mathbf {R}^\circ $
. By Remark 3.10, (3) is equivalent to that for some/any tagged triangulation
$\mathbf {R}^\circ $
. By Remark 3.10, (3) is equivalent to that for some/any tagged triangulation
![]() $\mathbf {T}$
satisfying the condition in Remark 3.10 and
$\mathbf {T}$
satisfying the condition in Remark 3.10 and
![]() $\mathbf {R}\subset \mathbf {T}$
, we have
$\mathbf {R}\subset \mathbf {T}$
, we have
![]() $b_{\gamma ^\circ ,\mathbf {T}^\circ }(e(\delta ^{\mathbf {R}}))=0$
for any
$b_{\gamma ^\circ ,\mathbf {T}^\circ }(e(\delta ^{\mathbf {R}}))=0$
for any
![]() $\gamma \in \mathbf {T}\setminus \mathbf {R}$
. So we may assume that
$\gamma \in \mathbf {T}\setminus \mathbf {R}$
. So we may assume that
![]() $\mathbf {R}$
is a partial ideal triangulation.
$\mathbf {R}$
is a partial ideal triangulation.
‘(1)
![]() $\Rightarrow $
(2)’: We list all the possible cases of arc segments of an
$\Rightarrow $
(2)’: We list all the possible cases of arc segments of an
![]() $\mathbf {R}$
-standard tagged arc
$\mathbf {R}$
-standard tagged arc
![]() $\delta $
and its elementary laminate
$\delta $
and its elementary laminate
![]() $e(\delta )$
in Figure 6, where the pictures in the first row are for
$e(\delta )$
in Figure 6, where the pictures in the first row are for
![]() $\delta \in \mathbf {R}^\times $
and
$\delta \in \mathbf {R}^\times $
and
![]() $\delta ^\circ $
not a side of a self-folded triangle, those in the second row are for
$\delta ^\circ $
not a side of a self-folded triangle, those in the second row are for
![]() $\delta \in \mathbf {R}^\times $
and
$\delta \in \mathbf {R}^\times $
and
![]() $\delta ^\circ $
a side of a self-folded triangle, those in the third row are for
$\delta ^\circ $
a side of a self-folded triangle, those in the third row are for
![]() $\delta $
adjoint to
$\delta $
adjoint to
![]() $\mathbf {R}^\times $
but not in
$\mathbf {R}^\times $
but not in
![]() $\mathbf {R}^\times $
, those in the fourth row are for the arc segments in the first two pictures of Figure 4, and those in the last row are for the arc segments in the last two pictures of Figure 4. In each case, any segment of
$\mathbf {R}^\times $
, those in the fourth row are for the arc segments in the first two pictures of Figure 4, and those in the last row are for the arc segments in the last two pictures of Figure 4. In each case, any segment of
![]() $e(\delta )$
cuts out an angle between two arcs in
$e(\delta )$
cuts out an angle between two arcs in
![]() $\mathbf {R}\cup B$
. Hence, (2) holds.
$\mathbf {R}\cup B$
. Hence, (2) holds.
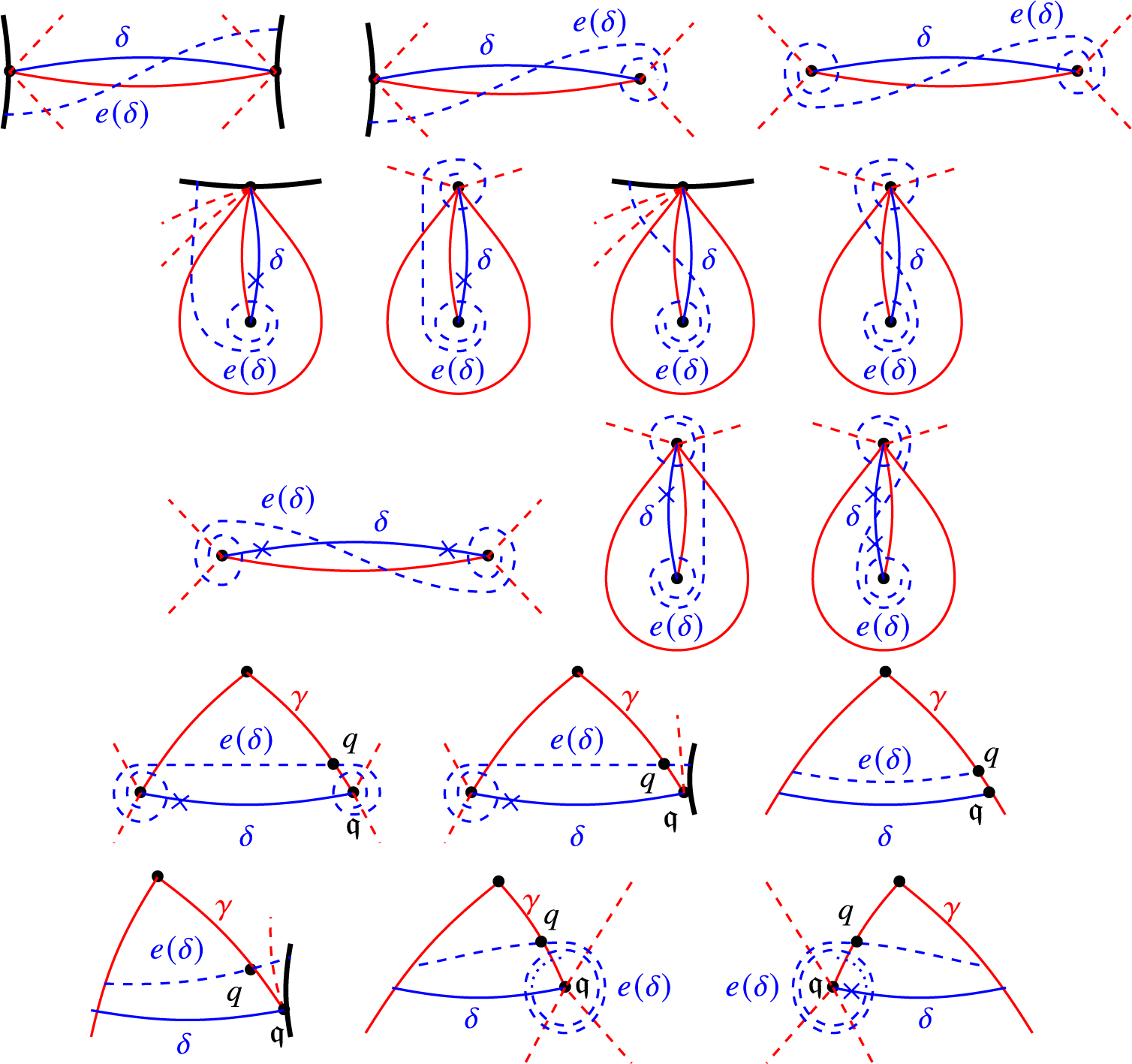
Figure 6 The elementary laminate of a standard tagged arc.
‘(2)
![]() $\Rightarrow $
(3)’: By (2),
$\Rightarrow $
(3)’: By (2),
![]() $e(\delta )$
is divided by
$e(\delta )$
is divided by
![]() $\mathbf {R}$
into segments, each of which cuts out an angle between two arcs in
$\mathbf {R}$
into segments, each of which cuts out an angle between two arcs in
![]() $\mathbf {R}\cup B$
. Let
$\mathbf {R}\cup B$
. Let
![]() $\mathbf {T}$
be an ideal triangulation containing
$\mathbf {T}$
be an ideal triangulation containing
![]() $\mathbf {R}$
,
$\mathbf {R}$
,
![]() $\gamma \in \mathbf {T}\setminus \mathbf {R}$
and q an intersection between
$\gamma \in \mathbf {T}\setminus \mathbf {R}$
and q an intersection between
![]() $\gamma $
and a segment
$\gamma $
and a segment
![]() $\eta $
of
$\eta $
of
![]() $e(\delta )$
. Then
$e(\delta )$
. Then
![]() $\gamma $
divides the angle cut by
$\gamma $
divides the angle cut by
![]() $\eta $
into two parts. Hence,
$\eta $
into two parts. Hence,
![]() $b_{q,\gamma ,\mathbf {T}}(e(\delta ))=0$
(cf. the third picture in Figure 3). Thus, we have
$b_{q,\gamma ,\mathbf {T}}(e(\delta ))=0$
(cf. the third picture in Figure 3). Thus, we have
![]() $b_{\gamma ,\mathbf {T}}(e(\delta ))=0$
.
$b_{\gamma ,\mathbf {T}}(e(\delta ))=0$
.
‘(3)
![]() $\Rightarrow $
(1)’: If
$\Rightarrow $
(1)’: If
![]() $\delta $
has no interior intersections with any arc in
$\delta $
has no interior intersections with any arc in
![]() $\mathbf {R}$
, then we have the following three subcases.
$\mathbf {R}$
, then we have the following three subcases.
-
(i)
 $\operatorname {Int}(\delta ,\gamma ^\times )=0$
for any
$\operatorname {Int}(\delta ,\gamma ^\times )=0$
for any
 $\gamma \in \mathbf {R}$
. Then there is a tagged triangulation
$\gamma \in \mathbf {R}$
. Then there is a tagged triangulation
 $\mathbf {T}_1$
containing
$\mathbf {T}_1$
containing
 $\mathbf {R}^\times $
and
$\mathbf {R}^\times $
and
 $\delta $
. By Corollary 3.18, we have
$\delta $
. By Corollary 3.18, we have
 $b_{\delta ,\mathbf {T}_1}(e(\delta ))=-1$
. Hence by (3), we have
$b_{\delta ,\mathbf {T}_1}(e(\delta ))=-1$
. Hence by (3), we have
 $\delta \in \mathbf {R}^\times $
, which implies
$\delta \in \mathbf {R}^\times $
, which implies
 $\delta $
is
$\delta $
is
 $\mathbf {R}$
-standard.
$\mathbf {R}$
-standard. -
(ii) Exactly one endpoint of
 $\delta $
, say
$\delta $
, say
 $\delta (0)$
, is a tagged intersection with some arc in
$\delta (0)$
, is a tagged intersection with some arc in
 $\mathbf {R}^\times $
. Then
$\mathbf {R}^\times $
. Then
 $\delta (0)\neq \delta (1)$
. If
$\delta (0)\neq \delta (1)$
. If
 $\kappa _\delta (0)=1$
, then there is an arc
$\kappa _\delta (0)=1$
, then there is an arc
 $\epsilon \in \mathbf {R}$
such that
$\epsilon \in \mathbf {R}$
such that
 $\epsilon ^\times (0)=\delta (0)$
and
$\epsilon ^\times (0)=\delta (0)$
and
 $\kappa _{\epsilon ^\times }(0)=-1$
. Then
$\kappa _{\epsilon ^\times }(0)=-1$
. Then
 $\epsilon $
is a loop enclosing
$\epsilon $
is a loop enclosing
 $\delta (0)$
. Note that
$\delta (0)$
. Note that
 $\delta $
has no interior intersections with any arc in
$\delta $
has no interior intersections with any arc in
 $\mathbf {R}$
. So
$\mathbf {R}$
. So
 $\delta $
is in the once-punctured monogon enclosed by
$\delta $
is in the once-punctured monogon enclosed by
 $\epsilon $
. Thus,
$\epsilon $
. Thus,
 $\delta $
is homotopic to
$\delta $
is homotopic to
 $\epsilon $
. Then by the definition of tagged intersections,
$\epsilon $
. Then by the definition of tagged intersections,
 $\delta (1)$
is also a tagged intersection between
$\delta (1)$
is also a tagged intersection between
 $\delta $
and
$\delta $
and
 $\epsilon ^\times $
, a contradiction with the setting of subsection (ii). Hence,
$\epsilon ^\times $
, a contradiction with the setting of subsection (ii). Hence,
 $\kappa _\delta (0)=-1$
. Let
$\kappa _\delta (0)=-1$
. Let
 $\delta _0$
be the tagged arc homotopic to
$\delta _0$
be the tagged arc homotopic to
 $\delta $
and whose tagging at each tagged end is
$\delta $
and whose tagging at each tagged end is
 $1$
. Since
$1$
. Since
 $\delta _0$
has zero (if
$\delta _0$
has zero (if
 $\kappa _\delta (1)=1$
) or two (if
$\kappa _\delta (1)=1$
) or two (if
 $\kappa _\delta (1)=-1$
) tagged intersections with
$\kappa _\delta (1)=-1$
) tagged intersections with
 $\delta $
, there are arcs in
$\delta $
, there are arcs in
 $\mathbf {R}$
which have
$\mathbf {R}$
which have
 $\delta (0)$
as an endpoint and is not homotopic to
$\delta (0)$
as an endpoint and is not homotopic to
 $\delta _0$
. Take
$\delta _0$
. Take
 $\gamma $
to be the first arc among them next to
$\gamma $
to be the first arc among them next to
 $\delta _0$
in the anticlockwise order around
$\delta _0$
in the anticlockwise order around
 $\delta (0)$
. Let
$\delta (0)$
. Let
 $\gamma '$
be the arc or the boundary segment such that
$\gamma '$
be the arc or the boundary segment such that
 $\Delta =\{\gamma ^{\prime },\delta _0,\gamma \}$
is a (possibly self-folded) triangle with the angle from
$\Delta =\{\gamma ^{\prime },\delta _0,\gamma \}$
is a (possibly self-folded) triangle with the angle from
 $\delta _0$
to
$\delta _0$
to
 $\gamma $
in the anticlockwise order as an inner angle. Since
$\gamma $
in the anticlockwise order as an inner angle. Since
 $\delta _0$
has no interior intersections with arcs in
$\delta _0$
has no interior intersections with arcs in
 $\mathbf {R}$
, neither does
$\mathbf {R}$
, neither does
 $\gamma ^{\prime }$
. Let
$\gamma ^{\prime }$
. Let
 $\mathbf {T}_2$
be an ideal triangulation containing
$\mathbf {T}_2$
be an ideal triangulation containing
 $\mathbf {R}$
,
$\mathbf {R}$
,
 $\delta _0$
and
$\delta _0$
and
 $\gamma ^{\prime }$
. If
$\gamma ^{\prime }$
. If
 $\Delta $
is self-folded, since
$\Delta $
is self-folded, since
 $\gamma $
is not homotopic to
$\gamma $
is not homotopic to
 $\delta $
and
$\delta $
and
 $\delta $
is a tagged arc (which implies that
$\delta $
is a tagged arc (which implies that
 $\delta $
is not the non-folded side of a self-fold triangle), we have that
$\delta $
is not the non-folded side of a self-fold triangle), we have that
 $\gamma ^{\prime }$
and
$\gamma ^{\prime }$
and
 $\delta _0$
are folded, and
$\delta _0$
are folded, and
 $\gamma $
is the non-folded side (cf. the last picture in Figure 7). So
$\gamma $
is the non-folded side (cf. the last picture in Figure 7). So
 $\delta (1)$
is a tagged intersection with either
$\delta (1)$
is a tagged intersection with either
 $\gamma ^\times $
(if
$\gamma ^\times $
(if
 $\kappa _\delta (1)=1$
) or
$\kappa _\delta (1)=1$
) or
 ${\gamma ^{\prime }}^\times =\delta _0$
(if
${\gamma ^{\prime }}^\times =\delta _0$
(if
 $\kappa _\delta (1)=-1$
). But since
$\kappa _\delta (1)=-1$
). But since
 $\gamma \in \mathbf {R}$
, by Definition 3.2, we have
$\gamma \in \mathbf {R}$
, by Definition 3.2, we have
 $\gamma ^{\prime }\in \mathbf {R}$
, a contradiction with the setting of subsection (ii). Hence, the triangle
$\gamma ^{\prime }\in \mathbf {R}$
, a contradiction with the setting of subsection (ii). Hence, the triangle
 $\Delta $
is not self-folded. In particular, none of
$\Delta $
is not self-folded. In particular, none of
 $\gamma $
,
$\gamma $
,
 $\delta _0$
and
$\delta _0$
and
 $\gamma ^{\prime }$
is the folded side of a self-folded triangle in
$\gamma ^{\prime }$
is the folded side of a self-folded triangle in
 $\mathbf {T}_2$
.
$\mathbf {T}_2$
.
Figure 7 No interior intersections but one tagged intersection.
-
(a) If
 $\gamma ^{\prime }$
is a boundary segment (see the first picture in Figure 7), by Definition 4.2 (2) (see the first picture in Figure 4),
$\gamma ^{\prime }$
is a boundary segment (see the first picture in Figure 7), by Definition 4.2 (2) (see the first picture in Figure 4),
 $\delta $
is
$\delta $
is
 $\mathbf {R}$
-standard.
$\mathbf {R}$
-standard. -
(b) If
 $\gamma ^{\prime }$
is not a boundary segment and either
$\gamma ^{\prime }$
is not a boundary segment and either
 $\delta (1)\in \mathbf {M}$
or
$\delta (1)\in \mathbf {M}$
or
 $\delta (1)\in \mathbf {P}$
with
$\delta (1)\in \mathbf {P}$
with
 $\kappa _\delta (1)=1$
(see the second and the third pictures in Figure 7), by definition,
$\kappa _\delta (1)=1$
(see the second and the third pictures in Figure 7), by definition,
 $b_{q,\gamma ^{\prime },\mathbf {T}_2}(e(\delta ))\neq 0$
. Then by Remark 3.14, we have
$b_{q,\gamma ^{\prime },\mathbf {T}_2}(e(\delta ))\neq 0$
. Then by Remark 3.14, we have
 $b_{\gamma ^{\prime },\mathbf {T}_2}(e(\delta ))\neq 0$
, which implies
$b_{\gamma ^{\prime },\mathbf {T}_2}(e(\delta ))\neq 0$
, which implies
 $\gamma ^{\prime }\in \mathbf {R}$
by (3). Then by Definition 4.2 (2) (see the first picture in Figure 4),
$\gamma ^{\prime }\in \mathbf {R}$
by (3). Then by Definition 4.2 (2) (see the first picture in Figure 4),
 $\delta $
is
$\delta $
is
 $\mathbf {R}$
-standard.
$\mathbf {R}$
-standard. -
(c) If
 $\delta (1)\in \mathbf {P}$
and
$\delta (1)\in \mathbf {P}$
and
 $\kappa _\delta (1)=-1$
(see the fourth picture in Figure 7), we have
$\kappa _\delta (1)=-1$
(see the fourth picture in Figure 7), we have
 $\delta =\rho (\delta _0)$
. So by Corollary 3.18,
$\delta =\rho (\delta _0)$
. So by Corollary 3.18,
 $b_{\delta _0,\mathbf {T}_2}(e(\delta ))=-1$
. Then by (3),
$b_{\delta _0,\mathbf {T}_2}(e(\delta ))=-1$
. Then by (3),
 $\delta _0\in \mathbf {R}$
, a contradiction with the setting of subsection (ii), since
$\delta _0\in \mathbf {R}$
, a contradiction with the setting of subsection (ii), since
 $\delta (1)$
is a tagged intersection between
$\delta (1)$
is a tagged intersection between
 $\delta $
and
$\delta $
and
 $\delta ^\times _0\in \mathbf {R}^\times $
.
$\delta ^\times _0\in \mathbf {R}^\times $
.
-
-
(iii) Both endpoints of
 $\delta $
are tagged intersections between
$\delta $
are tagged intersections between
 $\delta $
and some arcs in
$\delta $
and some arcs in
 $\mathbf {R}^\times $
. Let
$\mathbf {R}^\times $
. Let
 $\delta _0$
be the underlying arc of
$\delta _0$
be the underlying arc of
 $\delta $
. Note that
$\delta $
. Note that
 $\delta _0$
has no intersections with
$\delta _0$
has no intersections with
 $\mathbf {R}$
. Let
$\mathbf {R}$
. Let
 $\mathbf {T}_3$
be an ideal triangulation containing
$\mathbf {T}_3$
be an ideal triangulation containing
 $\mathbf {R}$
and
$\mathbf {R}$
and
 $\delta _0$
. Then
$\delta _0$
. Then
 $b_{\delta _0,\mathbf {T}_3}(e(\delta ))\neq 0$
by Corollary 3.18, which by (3) implies
$b_{\delta _0,\mathbf {T}_3}(e(\delta ))\neq 0$
by Corollary 3.18, which by (3) implies
 $\delta _0\in \mathbf {R}$
. So
$\delta _0\in \mathbf {R}$
. So
 $\delta $
is adjoint to
$\delta $
is adjoint to
 $\delta ^\times _0\in \mathbf {R}^\times $
and hence is
$\delta ^\times _0\in \mathbf {R}^\times $
and hence is
 $\mathbf {R}$
-standard.
$\mathbf {R}$
-standard.
If
![]() $\delta $
has interior intersections with some arc in
$\delta $
has interior intersections with some arc in
![]() $\mathbf {R}$
, then
$\mathbf {R}$
, then
![]() $\delta $
is divided by
$\delta $
is divided by
![]() $\mathbf {R}$
into at least two arc segments. Let
$\mathbf {R}$
into at least two arc segments. Let
![]() $\gamma $
be the first arc in
$\gamma $
be the first arc in
![]() $\mathbf {T}\cup B$
next to
$\mathbf {T}\cup B$
next to
![]() $\delta $
around
$\delta $
around
![]() $\delta (0)$
in the anticlockwise order if
$\delta (0)$
in the anticlockwise order if
![]() $\kappa _\delta (0)=-1$
or in the clockwise order otherwise. If
$\kappa _\delta (0)=-1$
or in the clockwise order otherwise. If
![]() $\gamma \in \mathbf {T}$
, we have
$\gamma \in \mathbf {T}$
, we have
![]() $b_{\gamma ,\mathbf {T}}(e(\delta ))\neq 0$
as shown in the pictures of the last row in Figure 6. Then by (3), we have
$b_{\gamma ,\mathbf {T}}(e(\delta ))\neq 0$
as shown in the pictures of the last row in Figure 6. Then by (3), we have
![]() $\gamma \in \mathbf {R}$
. So the end arc segment of
$\gamma \in \mathbf {R}$
. So the end arc segment of
![]() $\delta $
is as shown in the last two pictures in Figure 4. For any arc segment
$\delta $
is as shown in the last two pictures in Figure 4. For any arc segment
![]() $\eta $
of
$\eta $
of
![]() $\delta $
between two arcs
$\delta $
between two arcs
![]() $\gamma _1,\gamma _2\in \mathbf {R}$
, let
$\gamma _1,\gamma _2\in \mathbf {R}$
, let
![]() $\gamma ^{\prime }_0=\gamma _1,\gamma ^{\prime }_1,\cdots ,\gamma ^{\prime }_{s-1},\gamma ^{\prime }_s=\gamma _2$
be the arcs in
$\gamma ^{\prime }_0=\gamma _1,\gamma ^{\prime }_1,\cdots ,\gamma ^{\prime }_{s-1},\gamma ^{\prime }_s=\gamma _2$
be the arcs in
![]() $\mathbf {T}$
which
$\mathbf {T}$
which
![]() $\eta $
crosses in order. By (3), we have
$\eta $
crosses in order. By (3), we have
![]() $b_{\gamma ^{\prime }_i,\mathbf {T}}(e(\delta ))=0$
for any
$b_{\gamma ^{\prime }_i,\mathbf {T}}(e(\delta ))=0$
for any
![]() $1\leq i\leq s-1$
. Hence,
$1\leq i\leq s-1$
. Hence,
![]() $\eta $
cuts out an angle bounded by
$\eta $
cuts out an angle bounded by
![]() $\gamma _1$
and
$\gamma _1$
and
![]() $\gamma _2$
(cf. the third picture in Figure 3). So
$\gamma _2$
(cf. the third picture in Figure 3). So
![]() $\delta $
is
$\delta $
is
![]() $\mathbf {R}$
-standard.
$\mathbf {R}$
-standard.
Remark 4.5. Let
![]() $\mathbf {R}$
be a partial ideal triangulation of
$\mathbf {R}$
be a partial ideal triangulation of
![]() $\mathbf {S}$
and
$\mathbf {S}$
and
![]() $\gamma \in \mathbf {R}$
which is not the folded side of a self-folded triangle of
$\gamma \in \mathbf {R}$
which is not the folded side of a self-folded triangle of
![]() $\mathbf {R}$
. Let
$\mathbf {R}$
. Let
![]() $\delta $
be an
$\delta $
be an
![]() $\mathbf {R}$
-standard (resp.
$\mathbf {R}$
-standard (resp.
![]() $\mathbf {R}$
-co-standard) tagged arc which is neither in
$\mathbf {R}$
-co-standard) tagged arc which is neither in
![]() $\mathbf {R}^\times $
nor adjoint to some arc in
$\mathbf {R}^\times $
nor adjoint to some arc in
![]() $\mathbf {R}^\times $
, and let
$\mathbf {R}^\times $
, and let
![]() $L=e(\delta )$
(resp.
$L=e(\delta )$
(resp.
![]() $L=e^{op}(\delta )$
). We denote by
$L=e^{op}(\delta )$
). We denote by
![]() $\gamma \cap \alpha =\{(t_1,t_2) \mid \gamma (t_1)=\alpha (t_2) \}$
the set of intersections between
$\gamma \cap \alpha =\{(t_1,t_2) \mid \gamma (t_1)=\alpha (t_2) \}$
the set of intersections between
![]() $\gamma $
and
$\gamma $
and
![]() $\alpha $
, where
$\alpha $
, where
![]() $\alpha =\delta $
or L. Note that
$\alpha =\delta $
or L. Note that
![]() $\gamma \cap \delta $
contains
$\gamma \cap \delta $
contains
![]() $\cap (\gamma ,\delta )$
(see Definition 3.5) as a subset. There is an injective map
$\cap (\gamma ,\delta )$
(see Definition 3.5) as a subset. There is an injective map
as shown in the last two rows of Figure 6 (for the case
![]() $L=e(\delta )$
). Any intersection
$L=e(\delta )$
). Any intersection
![]() $q\in \gamma \cap L$
which is not in the image of E does not contribute to
$q\in \gamma \cap L$
which is not in the image of E does not contribute to
![]() $b_{\gamma ,\mathbf {R}}(L)$
; that is„
$b_{\gamma ,\mathbf {R}}(L)$
; that is„
![]() $b_{q,\gamma ,\mathbf {R}}(L)=0$
. For any
$b_{q,\gamma ,\mathbf {R}}(L)=0$
. For any
![]() $\mathfrak {q}\in \gamma \cap \delta $
and its corresponding
$\mathfrak {q}\in \gamma \cap \delta $
and its corresponding
![]() $q\in \gamma \cap L$
, we have the following equivalences.
$q\in \gamma \cap L$
, we have the following equivalences.
-
○
 if and only if either
if and only if either
 $\mathfrak {q}\in \mathbf {S}^\circ $
and we are in the situation shown in the first picture of the first row of Figure 8, or
$\mathfrak {q}\in \mathbf {S}^\circ $
and we are in the situation shown in the first picture of the first row of Figure 8, or
 $\mathfrak {q}\in \mathbf {P}$
with tagging
$\mathfrak {q}\in \mathbf {P}$
with tagging
 $-1$
(resp.
$-1$
(resp.
 $\mathfrak {q}\in \mathbf {M}$
or
$\mathfrak {q}\in \mathbf {M}$
or
 $\mathbf {P}$
with tagging
$\mathbf {P}$
with tagging
 $1$
) and
$1$
) and
 $\gamma $
is the first arc in
$\gamma $
is the first arc in
 $\mathbf {R}$
next to
$\mathbf {R}$
next to
 $\delta $
anticlockwise around
$\delta $
anticlockwise around
 $\mathfrak {q}$
(see the first picture of the second (resp. third) row of Figure 8). In each case, we call
$\mathfrak {q}$
(see the first picture of the second (resp. third) row of Figure 8). In each case, we call
 $\mathfrak {q}$
positive.
$\mathfrak {q}$
positive.
Figure 8 Alternative intersections of (co-)standard tagged arcs.
-
○
 $b_{q,\gamma ,\mathbf {R}}(L)<0$
if and only if either
$b_{q,\gamma ,\mathbf {R}}(L)<0$
if and only if either
 $\mathfrak {q}\in \mathbf {S}^\circ $
and we are in the situation shown in the second picture of the first row of Figure 8, or
$\mathfrak {q}\in \mathbf {S}^\circ $
and we are in the situation shown in the second picture of the first row of Figure 8, or
 $\mathfrak {q}\in \mathbf {M}$
or
$\mathfrak {q}\in \mathbf {M}$
or
 $\mathbf {P}$
with tagging
$\mathbf {P}$
with tagging
 $1$
(resp.
$1$
(resp.
 $\mathfrak {q}\in \mathbf {P}$
with tagging
$\mathfrak {q}\in \mathbf {P}$
with tagging
 $-1$
) and
$-1$
) and
 $\gamma $
is the first arc in
$\gamma $
is the first arc in
 $\mathbf {R}$
next to
$\mathbf {R}$
next to
 $\delta $
clockwise around
$\delta $
clockwise around
 $\mathfrak {q}$
(see the second picture of the second (resp. third) row of Figure 8). In each case, we call
$\mathfrak {q}$
(see the second picture of the second (resp. third) row of Figure 8). In each case, we call
 $\mathfrak {q}$
negative.
$\mathfrak {q}$
negative.
Any positive or negative intersection
![]() $\mathfrak {q}\in \gamma \cap \delta $
is called alternative.
$\mathfrak {q}\in \gamma \cap \delta $
is called alternative.
Definition 4.6. Let
![]() $\mathbf {R}$
be a partial tagged triangulation of
$\mathbf {R}$
be a partial tagged triangulation of
![]() $\mathbf {S}$
. An
$\mathbf {S}$
. An
![]() $\mathbf {R}$
-dissection (resp.
$\mathbf {R}$
-dissection (resp.
![]() $\mathbf {R}$
-co-dissection) is a maximal collection
$\mathbf {R}$
-co-dissection) is a maximal collection
![]() $\mathbf {U}$
of
$\mathbf {U}$
of
![]() $\mathbf {R}$
-standard (resp.
$\mathbf {R}$
-standard (resp.
![]() $\mathbf {R}$
-co-standard) arcs such that
$\mathbf {R}$
-co-standard) arcs such that
![]() $\operatorname {Int}(\gamma _1,\gamma _2)=0$
for any
$\operatorname {Int}(\gamma _1,\gamma _2)=0$
for any
![]() $\gamma _1,\gamma _2\in \mathbf {U}$
. We denote by
$\gamma _1,\gamma _2\in \mathbf {U}$
. We denote by
![]() $D(\mathbf {R})$
(resp.
$D(\mathbf {R})$
(resp.
![]() $D^{op}(\mathbf {R})$
) the set of
$D^{op}(\mathbf {R})$
) the set of
![]() $\mathbf {R}$
-dissections (resp.
$\mathbf {R}$
-dissections (resp.
![]() $\mathbf {R}$
-co-dissections).
$\mathbf {R}$
-co-dissections).
By definition, any
![]() $\mathbf {R}$
-dissection is also a partial tagged triangulation of
$\mathbf {R}$
-dissection is also a partial tagged triangulation of
![]() $\mathbf {S}$
.
$\mathbf {S}$
.
Theorem 4.7. Let
![]() $\mathbf {R}$
be a partial tagged triangulation of
$\mathbf {R}$
be a partial tagged triangulation of
![]() $\mathbf {S}$
. The bijection X in Theorem 3.15 restricts to bijections
$\mathbf {S}$
. The bijection X in Theorem 3.15 restricts to bijections
which induce bijections
and
respectively. Moreover, for any
![]() $\delta \in \operatorname {A}^\times _{\mathbf {R}\operatorname {-st}}$
and any
$\delta \in \operatorname {A}^\times _{\mathbf {R}\operatorname {-st}}$
and any
![]() $\gamma \in \mathbf {R}$
, we have
$\gamma \in \mathbf {R}$
, we have
and for any
![]() $\delta ^{\prime }\in \operatorname {A}^\times _{\mathbf {R}\operatorname {-co-st}}$
and any
$\delta ^{\prime }\in \operatorname {A}^\times _{\mathbf {R}\operatorname {-co-st}}$
and any
![]() $\gamma \in \mathbf {R}$
, we have
$\gamma \in \mathbf {R}$
, we have
Proof. By the equivalence between (1) and (4) in Proposition 4.4, we get the required bijections. The last assertion then follows from Proposition 3.16 and the equality (3.1).
One consequence of the above theorem is the rank of a dissection/co-dissection.
Corollary 4.8. Let
![]() $\mathbf {R}$
be a partial tagged triangulation of
$\mathbf {R}$
be a partial tagged triangulation of
![]() $\mathbf {S}$
, and
$\mathbf {S}$
, and
![]() $\mathbf {U}$
a set of
$\mathbf {U}$
a set of
![]() $\mathbf {R}$
-standard (resp.
$\mathbf {R}$
-standard (resp.
![]() $\mathbf {R}$
-co-standard) arcs such that
$\mathbf {R}$
-co-standard) arcs such that
![]() $\operatorname {Int}(\gamma _1,\gamma _2)=0$
for any
$\operatorname {Int}(\gamma _1,\gamma _2)=0$
for any
![]() $\gamma _1,\gamma _2\in \mathbf {U}$
. Then
$\gamma _1,\gamma _2\in \mathbf {U}$
. Then
![]() $\mathbf {U}$
is an
$\mathbf {U}$
is an
![]() $\mathbf {R}$
-dissection (resp.
$\mathbf {R}$
-dissection (resp.
![]() $\mathbf {R}$
-co-dissection) if and only if
$\mathbf {R}$
-co-dissection) if and only if
![]() $|\mathbf {U}|=|\mathbf {R}|$
.
$|\mathbf {U}|=|\mathbf {R}|$
.
The following result tells us that dissection and co-dissection are dual notions.
Corollary 4.9. Let
![]() $\mathbf {R}$
and
$\mathbf {R}$
and
![]() $\mathbf {U}$
be two partial tagged triangulations of
$\mathbf {U}$
be two partial tagged triangulations of
![]() $\mathbf {S}$
. Then
$\mathbf {S}$
. Then
![]() $\mathbf {U}$
is an
$\mathbf {U}$
is an
![]() $\mathbf {R}$
-dissection if and only if
$\mathbf {R}$
-dissection if and only if
![]() $\mathbf {R}$
is a
$\mathbf {R}$
is a
![]() $\mathbf {U}$
-co-dissection.
$\mathbf {U}$
-co-dissection.
Proof. By Theorem 4.7,
![]() $\mathbf {U}\in D(\mathbf {R})$
if and only if
$\mathbf {U}\in D(\mathbf {R})$
if and only if
![]() $X(\mathbf {U})\in \operatorname {max}\operatorname {rigid-}(X(\mathbf {R})\ast X(\mathbf {R})[1])$
, and
$X(\mathbf {U})\in \operatorname {max}\operatorname {rigid-}(X(\mathbf {R})\ast X(\mathbf {R})[1])$
, and
![]() $\mathbf {R}\in D^{op}(\mathbf {U})$
if and only if
$\mathbf {R}\in D^{op}(\mathbf {U})$
if and only if
![]() $X(\mathbf {R})\in \operatorname {max}\operatorname {rigid-}(X(\mathbf {U})[-1]\ast X(\mathbf {U}))$
. So the statement follows by Corollary 2.8.
$X(\mathbf {R})\in \operatorname {max}\operatorname {rigid-}(X(\mathbf {U})[-1]\ast X(\mathbf {U}))$
. So the statement follows by Corollary 2.8.
The following lemma is useful in Section 5.
Lemma 4.10. Let
![]() $\mathbf {R}$
be a partial tagged triangulation of
$\mathbf {R}$
be a partial tagged triangulation of
![]() $\mathbf {S}$
, and
$\mathbf {S}$
, and
![]() $\mathbf {U}$
an
$\mathbf {U}$
an
![]() $\mathbf {R}$
-dissection. Then for any
$\mathbf {R}$
-dissection. Then for any
![]() $l\in \mathbf {U}$
, there exists
$l\in \mathbf {U}$
, there exists
![]() $\gamma \in \mathbf {R}$
such that
$\gamma \in \mathbf {R}$
such that
![]() $b_{l,\mathbf {U}}(e^{op}(\gamma ))\neq 0$
. Moreover, if
$b_{l,\mathbf {U}}(e^{op}(\gamma ))\neq 0$
. Moreover, if ![]() (resp.
(resp.
![]() $<0$
), then for any
$<0$
), then for any
![]() $\gamma ^{\prime }\in \mathbf {R}$
, we have
$\gamma ^{\prime }\in \mathbf {R}$
, we have
![]() $b_{l,\mathbf {U}}(e^{op}(\gamma ^{\prime }))\geq 0$
(resp.
$b_{l,\mathbf {U}}(e^{op}(\gamma ^{\prime }))\geq 0$
(resp.
![]() $\leq 0$
).
$\leq 0$
).
Proof. By Corollary 4.9,
![]() $\mathbf {R}$
is a
$\mathbf {R}$
is a
![]() $\mathbf {U}$
-co-dissection. In particular, any
$\mathbf {U}$
-co-dissection. In particular, any
![]() $\gamma \in \mathbf {R}$
is
$\gamma \in \mathbf {R}$
is
![]() $\mathbf {U}$
-co-standard. Then for any
$\mathbf {U}$
-co-standard. Then for any
![]() $l\in \mathbf {U}$
, by (4.4), we have
$l\in \mathbf {U}$
, by (4.4), we have
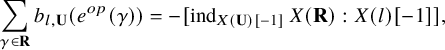 $$ \begin{align*}\sum_{\gamma\in\mathbf{R}}b_{l,\mathbf{U}}(e^{op}(\gamma))=-[\operatorname{ind}_{X(\mathbf{U})[-1]}X(\mathbf{R}):X(l)[-1]],\end{align*} $$
$$ \begin{align*}\sum_{\gamma\in\mathbf{R}}b_{l,\mathbf{U}}(e^{op}(\gamma))=-[\operatorname{ind}_{X(\mathbf{U})[-1]}X(\mathbf{R}):X(l)[-1]],\end{align*} $$
which is not zero by Lemma 2.9. Hence, there exists
![]() $\gamma \in \mathbf {R}$
such that
$\gamma \in \mathbf {R}$
such that
![]() $b_{l,\mathbf {U}}(e^{op}(\gamma ))\neq 0$
. The last assertion then follows by Remark 2.17.
$b_{l,\mathbf {U}}(e^{op}(\gamma ))\neq 0$
. The last assertion then follows by Remark 2.17.
We have the following geometric interpretation of a certain subcategory of the module category of a surface rigid algebra.
Theorem 4.11. Let
![]() $\mathbf {R}$
be a partial tagged triangulation of a punctured marked surface
$\mathbf {R}$
be a partial tagged triangulation of a punctured marked surface
![]() $\mathbf {S}$
, and
$\mathbf {S}$
, and
![]() $\Lambda _{\mathbf {R}}=\operatorname {End}_{\mathcal {C}(\mathbf {S})}X(\mathbf {R})$
the corresponding surface rigid algebra. Then there is a bijection
$\Lambda _{\mathbf {R}}=\operatorname {End}_{\mathcal {C}(\mathbf {S})}X(\mathbf {R})$
the corresponding surface rigid algebra. Then there is a bijection
where
![]() $\operatorname {ind}\operatorname {\tau -rigid}\operatorname {mod}\Lambda _{\mathbf {R}}$
is the set of (isoclasses of) indecomposable
$\operatorname {ind}\operatorname {\tau -rigid}\operatorname {mod}\Lambda _{\mathbf {R}}$
is the set of (isoclasses of) indecomposable
![]() $\tau $
-rigid
$\tau $
-rigid
![]() $\Lambda _{\mathbf {R}}$
-modules, such that for any
$\Lambda _{\mathbf {R}}$
-modules, such that for any
![]() $\gamma _1,\gamma _2\in \operatorname {A}^\times _{\mathbf {R}\operatorname {-st}}\setminus \rho (\mathbf {R})$
, we have
$\gamma _1,\gamma _2\in \operatorname {A}^\times _{\mathbf {R}\operatorname {-st}}\setminus \rho (\mathbf {R})$
, we have
Proof. For any
![]() $\gamma \in \operatorname {A}^\times _{\mathbf {R}\operatorname {-st}}\setminus \rho (\mathbf {R})$
, define
$\gamma \in \operatorname {A}^\times _{\mathbf {R}\operatorname {-st}}\setminus \rho (\mathbf {R})$
, define
![]() $M(\gamma )=\operatorname {Hom}_{\mathcal {C}(\mathbf {S})}(X(\mathbf {R}),X(\gamma ))$
. Then by Theorem 4.7 and Theorem 2.21, M is a bijection from
$M(\gamma )=\operatorname {Hom}_{\mathcal {C}(\mathbf {S})}(X(\mathbf {R}),X(\gamma ))$
. Then by Theorem 4.7 and Theorem 2.21, M is a bijection from
![]() $\operatorname {A}^\times _{\mathbf {R}\operatorname {-st}}\setminus \rho (\mathbf {R})$
to
$\operatorname {A}^\times _{\mathbf {R}\operatorname {-st}}\setminus \rho (\mathbf {R})$
to
![]() $\operatorname {ind} \operatorname {\tau -rigid}\operatorname {mod}\Lambda $
.
$\operatorname {ind} \operatorname {\tau -rigid}\operatorname {mod}\Lambda $
.
Let
![]() $X_i=X(\gamma _i)$
and
$X_i=X(\gamma _i)$
and
![]() $M_i=M(\gamma _i)$
,
$M_i=M(\gamma _i)$
,
![]() $i=1,2$
. Then we have
$i=1,2$
. Then we have
 $$\begin{align*}\begin{aligned} \operatorname{Hom}_{\mathcal{C}(\mathbf{S})}(X_1,X_2[1])&{}=\operatorname{Hom}_{\mathcal{C}(\mathbf{S})/R[1]}(X_1,X_2[1])\,{\oplus}\,[R[1]](X_1,X_2[1])\\ &\cong\operatorname{Hom}_{\mathcal{C}(\mathbf{S})/R[1]}(X_1,X_2[1])\,{\oplus}\, D\operatorname{Hom}_{\mathcal{C}(\mathbf{S})/R[1]}(X_2,X_1[1])\\ &\cong\operatorname{Hom}_{\Lambda_R}(M_1,\tau M_2)\,{\oplus}\, D\operatorname{Hom}_{\Lambda_R}(M_2,\tau M_1), \end{aligned}\end{align*}$$
$$\begin{align*}\begin{aligned} \operatorname{Hom}_{\mathcal{C}(\mathbf{S})}(X_1,X_2[1])&{}=\operatorname{Hom}_{\mathcal{C}(\mathbf{S})/R[1]}(X_1,X_2[1])\,{\oplus}\,[R[1]](X_1,X_2[1])\\ &\cong\operatorname{Hom}_{\mathcal{C}(\mathbf{S})/R[1]}(X_1,X_2[1])\,{\oplus}\, D\operatorname{Hom}_{\mathcal{C}(\mathbf{S})/R[1]}(X_2,X_1[1])\\ &\cong\operatorname{Hom}_{\Lambda_R}(M_1,\tau M_2)\,{\oplus}\, D\operatorname{Hom}_{\Lambda_R}(M_2,\tau M_1), \end{aligned}\end{align*}$$
where the first isomorphism is due to [Reference Chang, Zhang and Zhu18, Lemma 2.3] and the last one is due to Theorem 2.21. By Theorem 3.15, we have
![]() $\operatorname {Int}(\gamma _1,\gamma _2)=\dim _{\mathbf {k}}\operatorname {Hom}_{\mathcal {C}(\mathbf {S})}(X_1,X_2[1])$
. Hence, we get the required formula.
$\operatorname {Int}(\gamma _1,\gamma _2)=\dim _{\mathbf {k}}\operatorname {Hom}_{\mathcal {C}(\mathbf {S})}(X_1,X_2[1])$
. Hence, we get the required formula.
4.2 Skew-gentle algebras as surface rigid algebras
In this subsection, we show that skew-gentle algebras are surface rigid algebras. So the geometric model in Theorem 4.11 is a generalization of a weak version of our previous work [Reference He, Zhou and Zhu33].
Definition 4.12. A triple
![]() $(Q,Sp,I)$
of a quiver Q, a subset
$(Q,Sp,I)$
of a quiver Q, a subset
![]() $Sp\subseteq Q_0$
and a set I of paths of length 2 in Q is called skew-gentle if
$Sp\subseteq Q_0$
and a set I of paths of length 2 in Q is called skew-gentle if
![]() $(Q^{sp},I^{sp})$
satisfies the following conditions, where
$(Q^{sp},I^{sp})$
satisfies the following conditions, where
![]() $Q^{sp}_0=Q_0, Q^{sp}_1=Q_1\cup \{\epsilon _i\mid i\in Sp\}$
with
$Q^{sp}_0=Q_0, Q^{sp}_1=Q_1\cup \{\epsilon _i\mid i\in Sp\}$
with
![]() $\epsilon _i$
a loop at i and
$\epsilon _i$
a loop at i and
![]() $I^{sp}=I\cup \{\epsilon ^2_i\mid i\in Sp\}$
.
$I^{sp}=I\cup \{\epsilon ^2_i\mid i\in Sp\}$
.
-
○ Each vertex in
 $Q^{sp}_0$
is the start of at most two arrows in
$Q^{sp}_0$
is the start of at most two arrows in
 $Q_1^{sp}$
, and is the terminal of at most two arrows in
$Q_1^{sp}$
, and is the terminal of at most two arrows in
 $Q_1^{sp}$
;
$Q_1^{sp}$
; -
○ For each arrow
 $\alpha \in Q^{sp}_1$
, there is at most one arrow
$\alpha \in Q^{sp}_1$
, there is at most one arrow
 $\beta \in Q^{sp}_1$
(resp.
$\beta \in Q^{sp}_1$
(resp.
 $\gamma \in Q^{sp}_1$
) such that
$\gamma \in Q^{sp}_1$
) such that
 $\alpha \beta \in I^{sp}$
(resp.
$\alpha \beta \in I^{sp}$
(resp.
 $\alpha \gamma \notin I^{sp}$
);
$\alpha \gamma \notin I^{sp}$
); -
○ For each arrow
 $\alpha \in Q^{sp}_1$
, there is at most one arrow
$\alpha \in Q^{sp}_1$
, there is at most one arrow
 $\beta \in Q^{sp}_1$
(resp.
$\beta \in Q^{sp}_1$
(resp.
 $\gamma \in Q^{sp}_1$
) such that
$\gamma \in Q^{sp}_1$
) such that
 $\beta \alpha \in I^{sp}$
(resp.
$\beta \alpha \in I^{sp}$
(resp.
 $\gamma \alpha \notin I^{sp}$
).
$\gamma \alpha \notin I^{sp}$
).
A finite-dimensional algebra
![]() $\Lambda $
is said to be skew-gentle if
$\Lambda $
is said to be skew-gentle if
![]() $\Lambda \cong {\mathbf {k}} Q^{sp}/{\langle }I^{sg}{\rangle }$
for some skew-gentle triple
$\Lambda \cong {\mathbf {k}} Q^{sp}/{\langle }I^{sg}{\rangle }$
for some skew-gentle triple
![]() $(Q,Sp,I)$
, where
$(Q,Sp,I)$
, where
![]() ${\langle }I^{sg}{\rangle }$
is the ideal generated by
${\langle }I^{sg}{\rangle }$
is the ideal generated by
![]() $I^{sg}=I\cup \{\epsilon ^2_i-\epsilon _i\mid i\in Sp\}$
.
$I^{sg}=I\cup \{\epsilon ^2_i-\epsilon _i\mid i\in Sp\}$
.
A partial ideal triangulation of
![]() $\mathbf {S}$
is called admissible if each puncture is contained in a self-folded triangle.
$\mathbf {S}$
is called admissible if each puncture is contained in a self-folded triangle.
Definition 4.13 [Reference Baur and Coelho Simões9, Definition 2.1],[Reference He, Zhou and Zhu33, Definition 1.8]
Let
![]() $\mathbf {R}$
be an admissible partial ideal triangulation of
$\mathbf {R}$
be an admissible partial ideal triangulation of
![]() $\mathbf {S}$
. Denote by
$\mathbf {S}$
. Denote by
![]() $\mathbf {R}_0$
the subset of
$\mathbf {R}_0$
the subset of
![]() $\mathbf {R}$
such that
$\mathbf {R}$
such that
![]() $\mathbf {R}\setminus \mathbf {R}_0$
consists of the folded sides of self-folded triangles of
$\mathbf {R}\setminus \mathbf {R}_0$
consists of the folded sides of self-folded triangles of
![]() $\mathbf {R}$
, and by
$\mathbf {R}$
, and by
![]() $\mathbf {R}_1$
the subset of
$\mathbf {R}_1$
the subset of
![]() $\mathbf {R}_0$
consisting of the non-folded sides of self-folded triangles of
$\mathbf {R}_0$
consisting of the non-folded sides of self-folded triangles of
![]() $\mathbf {R}$
. The tiling algebra of
$\mathbf {R}$
. The tiling algebra of
![]() $\mathbf {R}$
is defined to be
$\mathbf {R}$
is defined to be
![]() $\Lambda ^t_{\mathbf {R}}={\mathbf {k}} Q_{\mathbf {R}}/{\langle }I^t_{\mathbf {R}}{\rangle }$
, where the quiver
$\Lambda ^t_{\mathbf {R}}={\mathbf {k}} Q_{\mathbf {R}}/{\langle }I^t_{\mathbf {R}}{\rangle }$
, where the quiver
![]() $Q_{\mathbf {R}}=((Q_{\mathbf {R}})_0,(Q_{\mathbf {R}})_1,s,t)$
and the relation set
$Q_{\mathbf {R}}=((Q_{\mathbf {R}})_0,(Q_{\mathbf {R}})_1,s,t)$
and the relation set
![]() $I^t_{\mathbf {R}}$
are given by the following.
$I^t_{\mathbf {R}}$
are given by the following.
-
○ The vertices in
 $(Q_{\mathbf {R}})_0$
are (indexed by) the arcs in
$(Q_{\mathbf {R}})_0$
are (indexed by) the arcs in
 $\mathbf {R}_0$
.
$\mathbf {R}_0$
. -
○ There is an arrow
 $\alpha \in (Q_{\mathbf {R}})_1$
from i to j whenever the corresponding arcs i and j share an endpoint
$\alpha \in (Q_{\mathbf {R}})_1$
from i to j whenever the corresponding arcs i and j share an endpoint
 $p_{\alpha }\in \mathbf {M}$
such that j follows i anticlockwise immediately in
$p_{\alpha }\in \mathbf {M}$
such that j follows i anticlockwise immediately in
 $\mathbf {R}_0$
. Note that by this construction, each vertex in
$\mathbf {R}_0$
. Note that by this construction, each vertex in
 $(Q_{\mathbf {R}})_0$
admits at most one loop.
$(Q_{\mathbf {R}})_0$
admits at most one loop. -
○ The relation set
 $I^t_{\mathbf {R}}=I^t_{\mathbf {R},1}\cup I^t_{\mathbf {R},2}$
, where
$I^t_{\mathbf {R}}=I^t_{\mathbf {R},1}\cup I^t_{\mathbf {R},2}$
, where-
–
 $I^t_{\mathbf {R},1}$
consists of squares of loops in
$I^t_{\mathbf {R},1}$
consists of squares of loops in
 $(Q_{\mathbf {R}})_1$
, and
$(Q_{\mathbf {R}})_1$
, and -
–
 $I^t_{\mathbf {R},2}$
consisting of all
$I^t_{\mathbf {R},2}$
consisting of all
 $\alpha \beta $
if
$\alpha \beta $
if
 $p_{\beta }\neq p_{\alpha }$
, or the endpoints of the curve (corresponding to)
$p_{\beta }\neq p_{\alpha }$
, or the endpoints of the curve (corresponding to)
 $t(\beta )=s(\alpha )$
coincide and we are in one of the situations in Figure 9.
$t(\beta )=s(\alpha )$
coincide and we are in one of the situations in Figure 9.
Figure 9 Relations in
 $I^t_{\mathbf {R},2}$
, the case
$I^t_{\mathbf {R},2}$
, the case
 $p_\beta =p_\alpha $
and
$p_\beta =p_\alpha $
and
 $s(\alpha )=t(\beta )$
is a loop.
$s(\alpha )=t(\beta )$
is a loop.
-
Let
![]() $I^{s\text {-}t}_{\mathbf {R}}$
be the subset obtained from
$I^{s\text {-}t}_{\mathbf {R}}$
be the subset obtained from
![]() $I^t_{\mathbf {R}}$
by replacing
$I^t_{\mathbf {R}}$
by replacing
![]() $\epsilon ^2$
with
$\epsilon ^2$
with
![]() $\epsilon ^2-\epsilon $
for each loop
$\epsilon ^2-\epsilon $
for each loop
![]() $\epsilon $
at a vertex in
$\epsilon $
at a vertex in
![]() $\mathbf {R}_1$
. The skew-tiling algebra of
$\mathbf {R}_1$
. The skew-tiling algebra of
![]() $\mathbf {R}$
is defined to be
$\mathbf {R}$
is defined to be
![]() $\Lambda ^{s\text {-}t}_{\mathbf {R}}={\mathbf {k}} Q_{\mathbf {R}}/{\langle }I^{s\text {-}t}_{\mathbf {R}}{\rangle }$
.
$\Lambda ^{s\text {-}t}_{\mathbf {R}}={\mathbf {k}} Q_{\mathbf {R}}/{\langle }I^{s\text {-}t}_{\mathbf {R}}{\rangle }$
.
By definition, skew-tiling algebras are obtained from tiling algebras by specializing nilpotent loops at vertices in
![]() $\mathbf {R}_1$
to be idempotents.
$\mathbf {R}_1$
to be idempotents.
Remark 4.14. In the original definition of tiling algebras introduced in [Reference Baur and Coelho Simões9], there are no punctures on the surface. However, after replacing each puncture by a boundary component with a marked point, and replacing each self-folded triangle of
![]() $\mathbf {R}$
by a monogon with the corresponding new boundary component in its interior, our definition coincides with the original one.
$\mathbf {R}$
by a monogon with the corresponding new boundary component in its interior, our definition coincides with the original one.
Theorem 4.15 [Reference Baur and Coelho Simões9, Theorem 1] and [Reference He, Zhou and Zhu33, Corollary 1.12]
A finite-dimensional algebra is a (skew-)gentle algebra if and only if it is a (skew-)tiling algebra.
In the following, we show that the skew-gentle algebras form a special class of surface rigid algebras.
Theorem 4.16. Let
![]() $\mathbf {R}$
be an admissible partial ideal triangulation of
$\mathbf {R}$
be an admissible partial ideal triangulation of
![]() $\mathbf {S}$
and
$\mathbf {S}$
and
![]() $\Lambda _{\mathbf {R}}=\operatorname {End}_{\mathcal {C}(\mathbf {S})}(X(\mathbf {R}))$
the corresponding surface rigid algebra. Then there is an algebra isomorphism
$\Lambda _{\mathbf {R}}=\operatorname {End}_{\mathcal {C}(\mathbf {S})}(X(\mathbf {R}))$
the corresponding surface rigid algebra. Then there is an algebra isomorphism
In particular, skew-gentle algebras are surface rigid algebras.
Proof. Let
![]() $\mathbf {T}$
be an admissible triangulation containing
$\mathbf {T}$
be an admissible triangulation containing
![]() $\mathbf {R}$
. By [Reference Amiot2, Theorem 3.5], there is an algebra isomorphism
$\mathbf {R}$
. By [Reference Amiot2, Theorem 3.5], there is an algebra isomorphism
sending the identity
![]() $\operatorname {id}_{X(\gamma )}$
of
$\operatorname {id}_{X(\gamma )}$
of
![]() $X(\gamma )$
to the idempotent
$X(\gamma )$
to the idempotent
![]() $e^\gamma $
of
$e^\gamma $
of
![]() $\Lambda ^{\mathbf {T}}$
corresponding to
$\Lambda ^{\mathbf {T}}$
corresponding to
![]() $\gamma \in Q_0^{\mathbf {T}}$
, for any
$\gamma \in Q_0^{\mathbf {T}}$
, for any
![]() $\gamma \in \mathbf {T}$
. Let
$\gamma \in \mathbf {T}$
. Let
![]() $e^{\mathbf {R}}=\sum _{\gamma \in \mathbf {R}}e^\gamma \in \Lambda ^{\mathbf {T}}$
and
$e^{\mathbf {R}}=\sum _{\gamma \in \mathbf {R}}e^\gamma \in \Lambda ^{\mathbf {T}}$
and
![]() $e_{\mathbf {R}}=\sum _{\gamma \in \mathbf {R}_0}e_\gamma \in \Lambda ^{s\text {-}t}_{\mathbf {T}}$
, where
$e_{\mathbf {R}}=\sum _{\gamma \in \mathbf {R}_0}e_\gamma \in \Lambda ^{s\text {-}t}_{\mathbf {T}}$
, where
![]() $e_\gamma $
is the idempotent of
$e_\gamma $
is the idempotent of
![]() $\Lambda ^{s\text {-}t}_{\mathbf {T}}$
corresponding to
$\Lambda ^{s\text {-}t}_{\mathbf {T}}$
corresponding to
![]() $\gamma \in \mathbf {R}_0$
. So we have
$\gamma \in \mathbf {R}_0$
. So we have
where the first isomorphism is induced by
![]() $\psi $
, and the last isomorphism is due to [Reference Qiu and Zhou49, Proposition 4.4].
$\psi $
, and the last isomorphism is due to [Reference Qiu and Zhou49, Proposition 4.4].
Let
![]() $\mathbf {S}^t$
be the unpunctured marked surface obtained from
$\mathbf {S}^t$
be the unpunctured marked surface obtained from
![]() $\mathbf {S}$
by replacing each puncture by a boundary component with one marked point. By Remark 4.14,
$\mathbf {S}$
by replacing each puncture by a boundary component with one marked point. By Remark 4.14,
![]() $\Lambda ^t_{\mathbf {T}}$
and
$\Lambda ^t_{\mathbf {T}}$
and
![]() $\Lambda ^t_{\mathbf {R}}$
are exactly tiling algebras defined in [Reference Baur and Coelho Simões9] on
$\Lambda ^t_{\mathbf {R}}$
are exactly tiling algebras defined in [Reference Baur and Coelho Simões9] on
![]() $\mathbf {S}^t$
. So we have
$\mathbf {S}^t$
. So we have
![]() $e_{\mathbf {R}}\Lambda ^t_{\mathbf {T}} e_{\mathbf {R}}\cong \Lambda ^t_{\mathbf {R}}$
by [Reference Baur and Coelho Simões9, Theorem 2.8]. Denote by
$e_{\mathbf {R}}\Lambda ^t_{\mathbf {T}} e_{\mathbf {R}}\cong \Lambda ^t_{\mathbf {R}}$
by [Reference Baur and Coelho Simões9, Theorem 2.8]. Denote by
![]() $\mathbf {T}_1$
the subset of
$\mathbf {T}_1$
the subset of
![]() $\mathbf {T}$
consisting of all non-folded sides of self-folded triangles. Since
$\mathbf {T}$
consisting of all non-folded sides of self-folded triangles. Since
![]() $\mathbf {R}$
is admissible, we have
$\mathbf {R}$
is admissible, we have
![]() $\mathbf {R}_1=\mathbf {T}_1$
. So
$\mathbf {R}_1=\mathbf {T}_1$
. So
![]() $\Lambda ^{s\text {-}t}_{\mathbf {T}}$
and
$\Lambda ^{s\text {-}t}_{\mathbf {T}}$
and
![]() $\Lambda ^{s\text {-}t}_{\mathbf {R}}$
are obtained from
$\Lambda ^{s\text {-}t}_{\mathbf {R}}$
are obtained from
![]() $\Lambda ^t_{\mathbf {T}}$
and
$\Lambda ^t_{\mathbf {T}}$
and
![]() $\Lambda ^t_{\mathbf {R}}$
, respectively, by specializing the same set of nilpotent loops to be idempotents. Hence,
$\Lambda ^t_{\mathbf {R}}$
, respectively, by specializing the same set of nilpotent loops to be idempotents. Hence,
![]() $e_{\mathbf {R}}\Lambda ^{s\text {-}t}_{\mathbf {T}} e_{\mathbf {R}}\cong \Lambda ^{s\text {-}t}_{\mathbf {R}}$
, which implies the isomorphism
$e_{\mathbf {R}}\Lambda ^{s\text {-}t}_{\mathbf {T}} e_{\mathbf {R}}\cong \Lambda ^{s\text {-}t}_{\mathbf {R}}$
, which implies the isomorphism
![]() $\Lambda _{\mathbf {R}}\cong \Lambda ^{s\text {-}t}_{\mathbf {R}}$
.
$\Lambda _{\mathbf {R}}\cong \Lambda ^{s\text {-}t}_{\mathbf {R}}$
.
The last assertion then follows from Theorem 4.15.
5 Connectedness of exchange graphs
Throughout this section, let
![]() $\mathbf {R}$
be a partial tagged triangulation of a punctured marked surface
$\mathbf {R}$
be a partial tagged triangulation of a punctured marked surface
![]() $\mathbf {S}$
and
$\mathbf {S}$
and
![]() $\Lambda _{\mathbf {R}}=\operatorname {End}_{\mathcal {C}(\mathbf {S})}X(\mathbf {R})$
the corresponding surface rigid algebra.
$\Lambda _{\mathbf {R}}=\operatorname {End}_{\mathcal {C}(\mathbf {S})}X(\mathbf {R})$
the corresponding surface rigid algebra.
5.1 Flips of dissections
Recall from Definition 3.3 that
![]() $\operatorname {A}^\times (\mathbf {S})$
denotes the set of tagged arcs on
$\operatorname {A}^\times (\mathbf {S})$
denotes the set of tagged arcs on
![]() $\mathbf {S}$
. For any tagged arc
$\mathbf {S}$
. For any tagged arc
![]() $\eta \in \operatorname {A}^\times (\mathbf {S})$
, let
$\eta \in \operatorname {A}^\times (\mathbf {S})$
, let
and let
![]() $\mathbf {S}/\{\eta \}$
be the punctured marked surface obtained from
$\mathbf {S}/\{\eta \}$
be the punctured marked surface obtained from
![]() $\mathbf {S}$
by cutting along
$\mathbf {S}$
by cutting along
![]() $\eta $
(cf. [Reference Qiu and Zhou49, Section 5.2]). Then there is a natural bijection
$\eta $
(cf. [Reference Qiu and Zhou49, Section 5.2]). Then there is a natural bijection
sending
![]() $\gamma $
to the tagged arc on
$\gamma $
to the tagged arc on
![]() $\mathbf {S}/\{\eta \}$
obtained from
$\mathbf {S}/\{\eta \}$
obtained from
![]() $\gamma $
by forgetting the taggings at each puncture which is an endpoint of
$\gamma $
by forgetting the taggings at each puncture which is an endpoint of
![]() $\eta $
(and hence becomes a marked point on the boundary of
$\eta $
(and hence becomes a marked point on the boundary of
![]() $\mathbf {S}/{\{\eta \}}$
), unless
$\mathbf {S}/{\{\eta \}}$
), unless
![]() $\gamma $
is homotopic to
$\gamma $
is homotopic to
![]() $\eta $
, where
$\eta $
, where
![]() $F_{\{\eta \}}(\gamma )$
is the tagged arc shown in Figure 10. Note that for any
$F_{\{\eta \}}(\gamma )$
is the tagged arc shown in Figure 10. Note that for any
![]() $\gamma _1,\gamma _2\in \operatorname {A}^\times (\mathbf {S})_{\{\eta \}}$
, we have
$\gamma _1,\gamma _2\in \operatorname {A}^\times (\mathbf {S})_{\{\eta \}}$
, we have
![]() $\operatorname {Int}(\gamma _1,\gamma _2)=0$
if and only if
$\operatorname {Int}(\gamma _1,\gamma _2)=0$
if and only if
![]() $\operatorname {Int}(F_{\{\eta \}}(\gamma _1),F_{\{\eta \}}(\gamma _2))=0$
. Therefore,
$\operatorname {Int}(F_{\{\eta \}}(\gamma _1),F_{\{\eta \}}(\gamma _2))=0$
. Therefore,
![]() $F_{\{\eta \}}$
induces a bijection from the set of partial tagged triangulations of
$F_{\{\eta \}}$
induces a bijection from the set of partial tagged triangulations of
![]() $\mathbf {S}$
containing
$\mathbf {S}$
containing
![]() $\eta $
to the set of partial tagged triangulations of
$\eta $
to the set of partial tagged triangulations of
![]() $\mathbf {S}/\{\eta \}$
.
$\mathbf {S}/\{\eta \}$
.
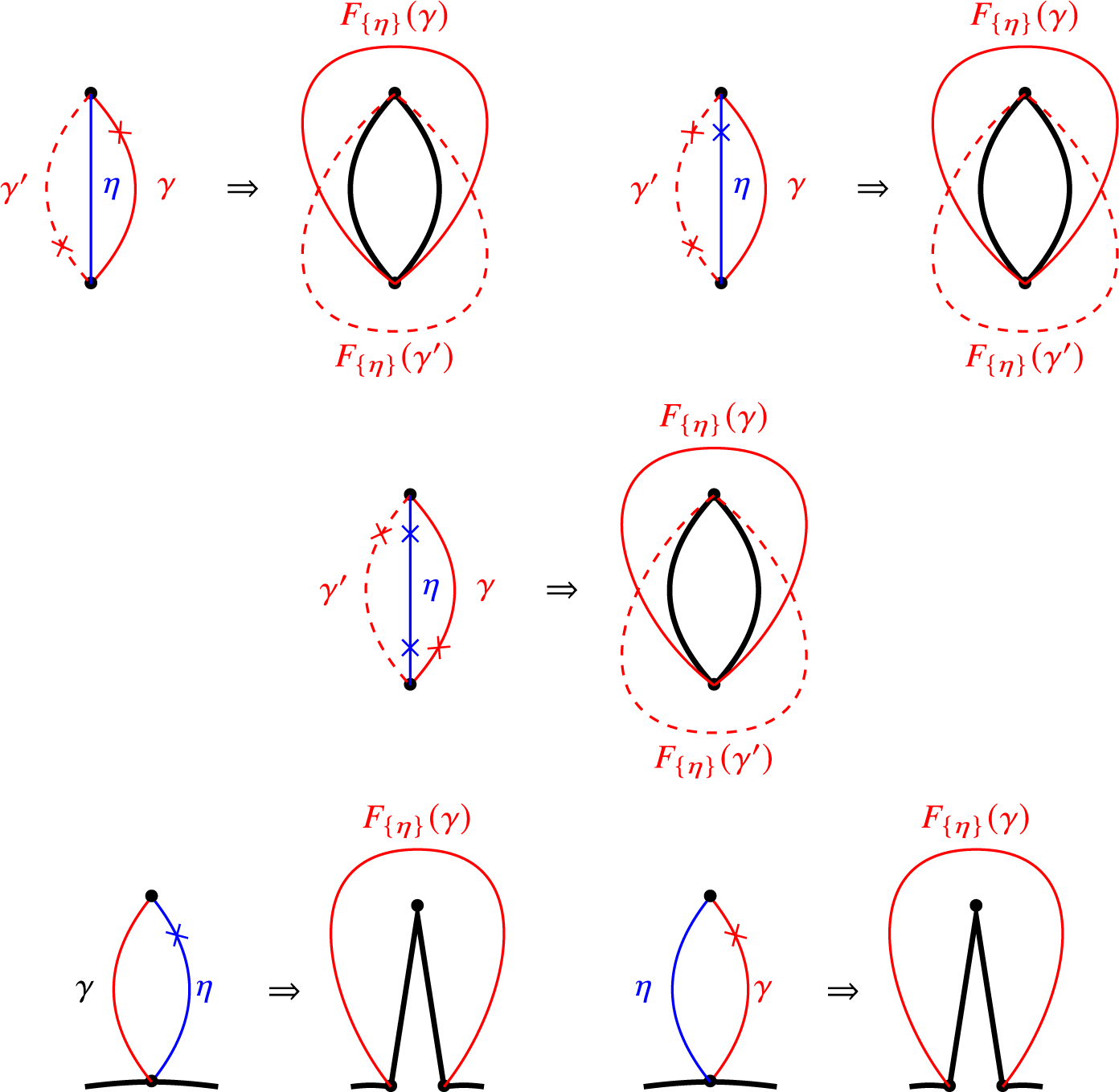
Figure 10 The bijection
![]() $F_{\{\eta \}}$
.
$F_{\{\eta \}}$
.
For any partial tagged triangulation
![]() $\mathbf {N}$
of
$\mathbf {N}$
of
![]() $\mathbf {S}$
, set
$\mathbf {S}$
, set
Assume that we have defined a punctured marked surface
![]() $\mathbf {S}/{\mathbf {N}^{\prime }}$
and a bijection
$\mathbf {S}/{\mathbf {N}^{\prime }}$
and a bijection
![]() $F_{\mathbf {N}^{\prime }}:\operatorname {A}^\times (\mathbf {S})_{\mathbf {N}^{\prime }}\to \operatorname {A}^\times (\mathbf {S}/\mathbf {N}^{\prime })$
for some
$F_{\mathbf {N}^{\prime }}:\operatorname {A}^\times (\mathbf {S})_{\mathbf {N}^{\prime }}\to \operatorname {A}^\times (\mathbf {S}/\mathbf {N}^{\prime })$
for some
![]() $\mathbf {N}^{\prime }\subset \mathbf {N}$
with
$\mathbf {N}^{\prime }\subset \mathbf {N}$
with
![]() $\mathbf {N}=\mathbf {N}^{\prime }\cup \{\eta \}$
. Then
$\mathbf {N}=\mathbf {N}^{\prime }\cup \{\eta \}$
. Then
![]() $F_{\mathbf {N}^{\prime }}$
restricts to a bijection
$F_{\mathbf {N}^{\prime }}$
restricts to a bijection
![]() $F_{\mathbf {N}^{\prime }}|_{\operatorname {A}^\times (\mathbf {S})_{\mathbf {N}}}:\operatorname {A}^\times (\mathbf {S})_{\mathbf {N}}\to \operatorname {A}^\times (\mathbf {S}/\mathbf {N}^{\prime })_{F_{\mathbf {N}^{\prime }}(\eta )}$
. So we can define inductively the punctured marked surface
$F_{\mathbf {N}^{\prime }}|_{\operatorname {A}^\times (\mathbf {S})_{\mathbf {N}}}:\operatorname {A}^\times (\mathbf {S})_{\mathbf {N}}\to \operatorname {A}^\times (\mathbf {S}/\mathbf {N}^{\prime })_{F_{\mathbf {N}^{\prime }}(\eta )}$
. So we can define inductively the punctured marked surface
and the bijection
Recall from Theorem 2.23 that
![]() $\mathcal {C}(\mathbf {S})_{X(\mathbf {N})}={}^\bot X(\mathbf {N})[1]/{\langle }\operatorname {add} X(\mathbf {N}){\rangle }$
is a triangulated category.
$\mathcal {C}(\mathbf {S})_{X(\mathbf {N})}={}^\bot X(\mathbf {N})[1]/{\langle }\operatorname {add} X(\mathbf {N}){\rangle }$
is a triangulated category.
Lemma 5.1. Let
![]() $\mathbf {N}$
be a partial tagged triangulation of
$\mathbf {N}$
be a partial tagged triangulation of
![]() $\mathbf {S}$
. Then there is a triangle equivalence
$\mathbf {S}$
. Then there is a triangle equivalence
such that
holds for any
![]() $\gamma \in \operatorname {A}^\times (\mathbf {S})_{\mathbf {N}}$
, where
$\gamma \in \operatorname {A}^\times (\mathbf {S})_{\mathbf {N}}$
, where
![]() $X_{\mathbf {S}/\mathbf {N}}$
is the bijection in Theorem 3.15 for
$X_{\mathbf {S}/\mathbf {N}}$
is the bijection in Theorem 3.15 for
![]() $\mathbf {S}/\mathbf {N}$
.
$\mathbf {S}/\mathbf {N}$
.
Proof. Let
![]() $\mathbf {T}$
be a tagged triangulation containing
$\mathbf {T}$
be a tagged triangulation containing
![]() $\mathbf {N}$
. Then
$\mathbf {N}$
. Then
![]() $F_{\mathbf {N}}(\mathbf {T}\setminus \mathbf {N})$
is a tagged triangulation of
$F_{\mathbf {N}}(\mathbf {T}\setminus \mathbf {N})$
is a tagged triangulation of
![]() $\mathbf {S}/\mathbf {N}$
and the corresponding quiver with potential
$\mathbf {S}/\mathbf {N}$
and the corresponding quiver with potential
![]() $(Q^{F_{\mathbf {N}}(\mathbf {T}\setminus \mathbf {N})},W^{F_{\mathbf {N}}(\mathbf {T}\setminus \mathbf {N})})$
can be obtained from the quiver with potential
$(Q^{F_{\mathbf {N}}(\mathbf {T}\setminus \mathbf {N})},W^{F_{\mathbf {N}}(\mathbf {T}\setminus \mathbf {N})})$
can be obtained from the quiver with potential
![]() $(Q^{\mathbf {T}},W^{\mathbf {T}})$
by deleting the vertices corresponding to the tagged arcs in
$(Q^{\mathbf {T}},W^{\mathbf {T}})$
by deleting the vertices corresponding to the tagged arcs in
![]() $\mathbf {N}$
and the incident arrows. Then by [Reference Keller36, Theorem 7.4], the canonical projection
$\mathbf {N}$
and the incident arrows. Then by [Reference Keller36, Theorem 7.4], the canonical projection
![]() $\pi :\Lambda ^{\mathbf {T}}\to \Lambda ^{F_{\mathbf {N}}(\mathbf {T}\setminus \mathbf {N})}$
induces the triangle equivalence (5.1) such that (5.2) holds for any
$\pi :\Lambda ^{\mathbf {T}}\to \Lambda ^{F_{\mathbf {N}}(\mathbf {T}\setminus \mathbf {N})}$
induces the triangle equivalence (5.1) such that (5.2) holds for any
![]() $\gamma \in \mathbf {T}\setminus \mathbf {N}$
. Then by Theorem 3.15, (5.2) holds for any
$\gamma \in \mathbf {T}\setminus \mathbf {N}$
. Then by Theorem 3.15, (5.2) holds for any
![]() $\gamma \in \operatorname {A}^\times (\mathbf {S})_{\mathbf {N}}$
.
$\gamma \in \operatorname {A}^\times (\mathbf {S})_{\mathbf {N}}$
.
Recall from Construction 3.8 that for any partial tagged triangulation
![]() $\mathbf {N}$
, there is an associated partial ideal triangulation
$\mathbf {N}$
, there is an associated partial ideal triangulation
![]() $\mathbf {N}^\circ $
. For any
$\mathbf {N}^\circ $
. For any
![]() $l\in \mathbf {N}$
, denote by
$l\in \mathbf {N}$
, denote by
![]() $l^{\circ _{\mathbf {N}}}$
the arc in
$l^{\circ _{\mathbf {N}}}$
the arc in
![]() $\mathbf {N}^\circ $
corresponding to l, which is sometimes simply denoted by
$\mathbf {N}^\circ $
corresponding to l, which is sometimes simply denoted by
![]() $l^\circ $
when there is no confusion arising.
$l^\circ $
when there is no confusion arising.
Remark 5.2. Let
![]() $\mathbf {N}$
be a partial tagged triangulation of
$\mathbf {N}$
be a partial tagged triangulation of
![]() $\mathbf {S}$
. By the construction,
$\mathbf {S}$
. By the construction,
![]() $\mathbf {S}/\mathbf {N}$
is obtained from
$\mathbf {S}/\mathbf {N}$
is obtained from
![]() $\mathbf {S}$
by cutting along arcs in
$\mathbf {S}$
by cutting along arcs in
![]() $\mathbf {N}^\circ $
.
$\mathbf {N}^\circ $
.
Definition 5.3. Let
![]() $\mathbf {N}$
be a partial tagged triangulation of
$\mathbf {N}$
be a partial tagged triangulation of
![]() $\mathbf {S}$
. The tagged rotation with respect to
$\mathbf {S}$
. The tagged rotation with respect to
![]() $\mathbf {N}$
is defined to be the bijection
$\mathbf {N}$
is defined to be the bijection
where
![]() $\rho _{\mathbf {S}/\mathbf {N}}$
is the tagged rotation on
$\rho _{\mathbf {S}/\mathbf {N}}$
is the tagged rotation on
![]() $\mathbf {S}/\mathbf {N}$
.
$\mathbf {S}/\mathbf {N}$
.
To better understand the tagged rotation with respect to a partial tagged triangulation, we introduce the following notion of flip of a partial ideal triangulation.
Definition 5.4. Let
![]() $\mathbf {V}$
be a partial ideal triangulation of
$\mathbf {V}$
be a partial ideal triangulation of
![]() $\mathbf {S}$
and
$\mathbf {S}$
and
![]() $l^\circ \in \mathbf {V}$
not the folded side of a self-folded triangle of
$l^\circ \in \mathbf {V}$
not the folded side of a self-folded triangle of
![]() $\mathbf {V}$
. Recall that B is the set of boundary segments. We denote
$\mathbf {V}$
. Recall that B is the set of boundary segments. We denote
-
○
 $l^\circ _s$
(resp.
$l^\circ _s$
(resp.
 $l^\circ _t$
) the arc in
$l^\circ _t$
) the arc in
 $\mathbf {V}\cup B$
the first arc in
$\mathbf {V}\cup B$
the first arc in
 $(\mathbf {V}\setminus \{l^\circ \})\cup B$
next to
$(\mathbf {V}\setminus \{l^\circ \})\cup B$
next to
 $l^\circ $
around
$l^\circ $
around
 $l^\circ (0)=l^\circ _s(0)$
(resp.
$l^\circ (0)=l^\circ _s(0)$
(resp.
 $l^\circ (1)=l^\circ _t(1)$
) in the clockwise order, and
$l^\circ (1)=l^\circ _t(1)$
) in the clockwise order, and -
○
 $(l^\circ )^s$
(resp.
$(l^\circ )^s$
(resp.
 $(l^\circ )^t$
) the first arc in
$(l^\circ )^t$
) the first arc in
 $(\mathbf {V}\setminus \{l^\circ \})\cup B$
next to
$(\mathbf {V}\setminus \{l^\circ \})\cup B$
next to
 $l^\circ $
around
$l^\circ $
around
 $l^\circ (0)=(l^\circ )^s(0)$
(resp.
$l^\circ (0)=(l^\circ )^s(0)$
(resp.
 $l^\circ (1)=(l^\circ )^t(1)$
) in the anticlockwise order.
$l^\circ (1)=(l^\circ )^t(1)$
) in the anticlockwise order.
See Figures 17 and 18 for these notations. We remark that some of
![]() $l^\circ _s,l^\circ _t,(l^\circ )^s,(l^\circ )^t$
may not exist.
$l^\circ _s,l^\circ _t,(l^\circ )^s,(l^\circ )^t$
may not exist.
The negative (resp. positive) flip
![]() $f^-_{\mathbf {V}}(l^\circ )$
(resp.
$f^-_{\mathbf {V}}(l^\circ )$
(resp.
![]() $f^+_{\mathbf {V}}(l^\circ )$
) of
$f^+_{\mathbf {V}}(l^\circ )$
) of
![]() $l^\circ $
with respect to
$l^\circ $
with respect to
![]() $\mathbf {V}$
is defined to be the arc obtained from
$\mathbf {V}$
is defined to be the arc obtained from
![]() $l^\circ $
by moving
$l^\circ $
by moving
![]() $l^\circ (0)$
along
$l^\circ (0)$
along
![]() $l^\circ _s$
(resp.
$l^\circ _s$
(resp.
![]() $(l^\circ )^s$
), if exists, to
$(l^\circ )^s$
), if exists, to
![]() $l^\circ _s(1)$
(resp.
$l^\circ _s(1)$
(resp.
![]() $(l^\circ )^s(1)$
) and moving
$(l^\circ )^s(1)$
) and moving
![]() $l^\circ (1)$
along
$l^\circ (1)$
along
![]() $l^\circ _t$
(resp.
$l^\circ _t$
(resp.
![]() $(l^\circ )^t$
), if exists, to
$(l^\circ )^t$
), if exists, to
![]() $l^\circ _t(0)$
(resp.
$l^\circ _t(0)$
(resp.
![]() $(l^\circ )^t(0)$
). The positive flip
$(l^\circ )^t(0)$
). The positive flip
![]() $f^+_{l^\circ }(\mathbf {V})$
and the negative flip
$f^+_{l^\circ }(\mathbf {V})$
and the negative flip
![]() $f^-_{l^\circ }(\mathbf {V})$
of
$f^-_{l^\circ }(\mathbf {V})$
of
![]() $\mathbf {V}$
at
$\mathbf {V}$
at
![]() $l^\circ $
are defined, respectively, to be
$l^\circ $
are defined, respectively, to be
We also denote by
![]() $\theta _s$
(resp.
$\theta _s$
(resp.
![]() $\theta ^s$
,
$\theta ^s$
,
![]() $\theta _t$
and
$\theta _t$
and
![]() $\theta ^t$
) the angle between a segment of
$\theta ^t$
) the angle between a segment of
![]() $l^\circ $
near
$l^\circ $
near
![]() $l^\circ (0)$
(resp.
$l^\circ (0)$
(resp.
![]() $l^\circ (0)$
,
$l^\circ (0)$
,
![]() $l^\circ (1)$
and
$l^\circ (1)$
and
![]() $l^\circ (1)$
) and a segment of
$l^\circ (1)$
) and a segment of
![]() $l^\circ _s$
(resp.
$l^\circ _s$
(resp.
![]() $(l^\circ )^s$
,
$(l^\circ )^s$
,
![]() $l^\circ _t$
and
$l^\circ _t$
and
![]() $(l^\circ )^t$
) near
$(l^\circ )^t$
) near
![]() $l^\circ _s(0)$
(resp.
$l^\circ _s(0)$
(resp.
![]() $(l^\circ )^s(0)$
,
$(l^\circ )^s(0)$
,
![]() $l^\circ _t(1)$
and
$l^\circ _t(1)$
and
![]() $(l^\circ )^t(1)$
).
$(l^\circ )^t(1)$
).
Lemma 5.5. Let
![]() $\mathbf {U}=\mathbf {N}\cup \{l\}$
be a partial tagged triangulation of
$\mathbf {U}=\mathbf {N}\cup \{l\}$
be a partial tagged triangulation of
![]() $\mathbf {S}$
such that
$\mathbf {S}$
such that
![]() $l^\circ $
is not the folded side of a self-folded triangle of
$l^\circ $
is not the folded side of a self-folded triangle of
![]() $\mathbf {U}^\circ $
. Then
$\mathbf {U}^\circ $
. Then
![]() $(\mathbf {N}\cup \{\rho ^{-1}_{\mathbf {N}}(l)\})^\circ =f^-_{l^\circ }(\mathbf {U}^\circ )$
and
$(\mathbf {N}\cup \{\rho ^{-1}_{\mathbf {N}}(l)\})^\circ =f^-_{l^\circ }(\mathbf {U}^\circ )$
and
![]() $(\mathbf {N}\cup \{\rho _{\mathbf {N}}(l)\})^\circ =f^+_{l^\circ }(\mathbf {U}^\circ )$
.
$(\mathbf {N}\cup \{\rho _{\mathbf {N}}(l)\})^\circ =f^+_{l^\circ }(\mathbf {U}^\circ )$
.
Proof. We only prove the first equality while the second can be proved similarly. Since
![]() $l^\circ $
is not the folded side of a self-folded triangle of
$l^\circ $
is not the folded side of a self-folded triangle of
![]() $\mathbf {U}^\circ $
, we have
$\mathbf {U}^\circ $
, we have
![]() $\mathbf {U}^\circ =\mathbf {N}^\circ \cup \{l^\circ \}$
and that
$\mathbf {U}^\circ =\mathbf {N}^\circ \cup \{l^\circ \}$
and that
![]() $F_{\mathbf {N}}(l)$
is homotopic to
$F_{\mathbf {N}}(l)$
is homotopic to
![]() $l^\circ $
. By Remark 5.2,
$l^\circ $
. By Remark 5.2,
![]() $\mathbf {S}/\mathbf {N}$
is obtained from
$\mathbf {S}/\mathbf {N}$
is obtained from
![]() $\mathbf {S}$
by cutting the surface along arcs in
$\mathbf {S}$
by cutting the surface along arcs in
![]() $\mathbf {N}^\circ $
. Then
$\mathbf {N}^\circ $
. Then
![]() $l^\circ _s$
and
$l^\circ _s$
and
![]() $l^\circ _t$
(if exist) are the boundary segments of
$l^\circ _t$
(if exist) are the boundary segments of
![]() $\mathbf {S}/\mathbf {N}$
next to
$\mathbf {S}/\mathbf {N}$
next to
![]() $F_{\mathbf {N}}(l)$
around
$F_{\mathbf {N}}(l)$
around
![]() $l^\circ (0)$
and
$l^\circ (0)$
and
![]() $l^\circ (1)$
, respectively, in the clockwise order. Hence, by definition,
$l^\circ (1)$
, respectively, in the clockwise order. Hence, by definition,
![]() $\rho ^{-1}_{\mathbf {S}/\mathbf {N}}(F_{\mathbf {N}}(l))$
is homotopic to
$\rho ^{-1}_{\mathbf {S}/\mathbf {N}}(F_{\mathbf {N}}(l))$
is homotopic to
![]() $f^-_{\mathbf {U}^\circ }(l^\circ )$
.
$f^-_{\mathbf {U}^\circ }(l^\circ )$
.
Denote
![]() $\mathbf {U}^{\prime }=\mathbf {N}\cup \{\rho ^{-1}_{\mathbf {N}}(l)\}$
. If
$\mathbf {U}^{\prime }=\mathbf {N}\cup \{\rho ^{-1}_{\mathbf {N}}(l)\}$
. If
![]() $\rho ^{-1}_{\mathbf {N}}(l)$
is not the folded side of a self-folded triangle of
$\rho ^{-1}_{\mathbf {N}}(l)$
is not the folded side of a self-folded triangle of
![]() ${\mathbf {U}^{\prime }}^\circ $
, then
${\mathbf {U}^{\prime }}^\circ $
, then
If
![]() $\rho ^{-1}_{\mathbf {N}}(l)$
is the folded side of a self-folded triangle
$\rho ^{-1}_{\mathbf {N}}(l)$
is the folded side of a self-folded triangle
![]() $\Delta $
of
$\Delta $
of
![]() $\mathbf {U}^{\prime \circ }$
, then there is
$\mathbf {U}^{\prime \circ }$
, then there is
![]() $h\in \mathbf {N}$
such that
$h\in \mathbf {N}$
such that
![]() $h^{\circ _{\mathbf {U}^{\prime }}}$
is the non-folded side of
$h^{\circ _{\mathbf {U}^{\prime }}}$
is the non-folded side of
![]() $\Delta $
. So
$\Delta $
. So
![]() $h^{\circ _{\mathbf {U}^{\prime }}}$
is homotopic to
$h^{\circ _{\mathbf {U}^{\prime }}}$
is homotopic to
![]() $f^-_{\mathbf {U}^\circ }(l^\circ )$
and
$f^-_{\mathbf {U}^\circ }(l^\circ )$
and
![]() $\rho ^{-1}_{\mathbf {N}}(l)^{\circ _{\mathbf {U}^{\prime }}}$
is homotopic to
$\rho ^{-1}_{\mathbf {N}}(l)^{\circ _{\mathbf {U}^{\prime }}}$
is homotopic to
![]() $h^{\circ _{\mathbf {N}}}=h^{\circ _{\mathbf {U}}}$
. Thus, we also have
$h^{\circ _{\mathbf {N}}}=h^{\circ _{\mathbf {U}}}$
. Thus, we also have
![]() ${\mathbf {U}^{\prime }}^\circ =f^-_{l^\circ }(\mathbf {U}^\circ )$
.
${\mathbf {U}^{\prime }}^\circ =f^-_{l^\circ }(\mathbf {U}^\circ )$
.
By Lemma 4.10, for any l in an
![]() $\mathbf {R}$
-dissection
$\mathbf {R}$
-dissection
![]() $\mathbf {U}$
, either there exists
$\mathbf {U}$
, either there exists
![]() $\gamma \in \mathbf {R}$
such that
$\gamma \in \mathbf {R}$
such that ![]() or there exists
or there exists
![]() $\gamma \in \mathbf {R}$
such that
$\gamma \in \mathbf {R}$
such that
![]() $b_{l,\mathbf {U}}(e^{op}(\gamma ))<0$
, but not both. This ensures the well-definedness of the following notion of flip of dissections.
$b_{l,\mathbf {U}}(e^{op}(\gamma ))<0$
, but not both. This ensures the well-definedness of the following notion of flip of dissections.
Definition 5.6. Let
![]() $\mathbf {U}$
be an
$\mathbf {U}$
be an
![]() $\mathbf {R}$
-dissection. For any
$\mathbf {R}$
-dissection. For any
![]() $l\in \mathbf {U}$
, the flip
$l\in \mathbf {U}$
, the flip
![]() $f^{\mathbf {R}}_l(\mathbf {U})$
of
$f^{\mathbf {R}}_l(\mathbf {U})$
of
![]() $\mathbf {U}$
at l is defined to be
$\mathbf {U}$
at l is defined to be
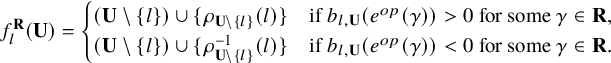
We denote by
![]() $f^{\mathbf {R}}_{\mathbf {U}}(l)$
the tagged arc in
$f^{\mathbf {R}}_{\mathbf {U}}(l)$
the tagged arc in
![]() $f_l^{\mathbf {R}}(\mathbf {U})$
, but not in
$f_l^{\mathbf {R}}(\mathbf {U})$
, but not in
![]() $\mathbf {U}$
.
$\mathbf {U}$
.
We will simply denote
![]() $f_{\mathbf {U}}(l)=f_{\mathbf {U}}^{\mathbf {R}}(l)$
and
$f_{\mathbf {U}}(l)=f_{\mathbf {U}}^{\mathbf {R}}(l)$
and
![]() $f_{l}(\mathbf {U})=f_{l}^{\mathbf {R}}(\mathbf {U})$
when there is no confusion arising. By Lemma 5.5, for any
$f_{l}(\mathbf {U})=f_{l}^{\mathbf {R}}(\mathbf {U})$
when there is no confusion arising. By Lemma 5.5, for any
![]() $l\in \mathbf {U}$
such that
$l\in \mathbf {U}$
such that
![]() $l^\circ $
is not the folded side of a self-folded triangle of
$l^\circ $
is not the folded side of a self-folded triangle of
![]() $\mathbf {U}^\circ $
, we have
$\mathbf {U}^\circ $
, we have
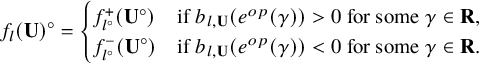
Remark 5.7. In the case that
![]() $\mathbf {R}$
is a tagged triangulation, the
$\mathbf {R}$
is a tagged triangulation, the
![]() $\mathbf {R}$
-dissections are exactly the tagged triangulations of
$\mathbf {R}$
-dissections are exactly the tagged triangulations of
![]() $\mathbf {S}$
, and the flip in Definition 5.6 coincides with the flip of tagged triangulations introduced in [Reference Fomin, Shapiro and Thurston25].
$\mathbf {S}$
, and the flip in Definition 5.6 coincides with the flip of tagged triangulations introduced in [Reference Fomin, Shapiro and Thurston25].
Proposition 5.8. For any
![]() $\mathbf {R}$
-dissection
$\mathbf {R}$
-dissection
![]() $\mathbf {U}$
and any
$\mathbf {U}$
and any
![]() $l\in \mathbf {U}$
, we have that
$l\in \mathbf {U}$
, we have that
![]() $f_l(\mathbf {U})$
is the unique
$f_l(\mathbf {U})$
is the unique
![]() $\mathbf {R}$
-dissection such that
$\mathbf {R}$
-dissection such that
![]() $\mathbf {U}\setminus f_l(\mathbf {U})=\{l\}$
. Moreover, under the bijection (4.1) in Theorem 4.7, the flip of
$\mathbf {U}\setminus f_l(\mathbf {U})=\{l\}$
. Moreover, under the bijection (4.1) in Theorem 4.7, the flip of
![]() $\mathbf {R}$
-dissections is compatible with the mutation of maximal rigid objects with respect to
$\mathbf {R}$
-dissections is compatible with the mutation of maximal rigid objects with respect to
![]() $X(\mathbf {R})\ast X(\mathbf {R})[1]$
.
$X(\mathbf {R})\ast X(\mathbf {R})[1]$
.
Proof. Let
![]() $\mathbf {N}=\mathbf {U}\setminus \{l\}$
. It suffices to show
$\mathbf {N}=\mathbf {U}\setminus \{l\}$
. It suffices to show
![]() $X(f_l(\mathbf {U}))$
is the unique (up to isomorphism) basic maximal rigid object with respect to
$X(f_l(\mathbf {U}))$
is the unique (up to isomorphism) basic maximal rigid object with respect to
![]() $X(\mathbf {R})\ast X(\mathbf {R})[1]$
such that
$X(\mathbf {R})\ast X(\mathbf {R})[1]$
such that
![]() $X(f_l(\mathbf {U}))$
contains
$X(f_l(\mathbf {U}))$
contains
![]() $X(\mathbf {N})$
as a direct summand and is not isomorphic to
$X(\mathbf {N})$
as a direct summand and is not isomorphic to
![]() $X(\mathbf {U})$
. By Corollary 2.16 and Remark 2.17, this is equivalent to showing
$X(\mathbf {U})$
. By Corollary 2.16 and Remark 2.17, this is equivalent to showing
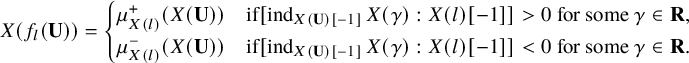
Then by (3.3), it suffices to show
and
By Remark 2.24, this is equivalent to showing that
where
![]() ${\langle }1{\rangle }_{X(\mathbf {N})}$
and
${\langle }1{\rangle }_{X(\mathbf {N})}$
and
![]() ${\langle }-1{\rangle }_{X(\mathbf {N})}$
are the suspension functor of
${\langle }-1{\rangle }_{X(\mathbf {N})}$
are the suspension functor of
![]() $\mathcal {C}(\mathbf {S})_{\mathbf {N}}$
and its inverse, respectively (see Theorem 2.23).
$\mathcal {C}(\mathbf {S})_{\mathbf {N}}$
and its inverse, respectively (see Theorem 2.23).
Using (5.2), we have
Hence,
![]() $X(\rho _{\mathbf {N}}(l))=X(l)\langle 1\rangle _{X(\mathbf {N})}$
. Similarly, we have
$X(\rho _{\mathbf {N}}(l))=X(l)\langle 1\rangle _{X(\mathbf {N})}$
. Similarly, we have
![]() $X(\rho ^{-1}_{\mathbf {N}}(l))=X(l)\langle -1\rangle _{X(\mathbf {N})}$
.
$X(\rho ^{-1}_{\mathbf {N}}(l))=X(l)\langle -1\rangle _{X(\mathbf {N})}$
.
Definition 5.9. The exchange graph
![]() $\operatorname {EG}^\times (\mathbf {R})$
of
$\operatorname {EG}^\times (\mathbf {R})$
of
![]() $\mathbf {R}$
-dissections has
$\mathbf {R}$
-dissections has
![]() $\mathbf {R}$
-dissections as vertices and has flips as edges.
$\mathbf {R}$
-dissections as vertices and has flips as edges.
Lemma 5.10. There is an isomorphism of graphs
![]() $\operatorname {EG}^\times (\mathbf {R})\cong \operatorname {EG}(\operatorname {s\tau -tilt} \Lambda _{\mathbf {R}})$
.
$\operatorname {EG}^\times (\mathbf {R})\cong \operatorname {EG}(\operatorname {s\tau -tilt} \Lambda _{\mathbf {R}})$
.
Proof. By Theorem 2.21 and Theorem 4.7, there is a bijection between support
![]() $\tau $
-tilting A-modules and
$\tau $
-tilting A-modules and
![]() $\mathbf {R}$
-dissections, such that, by Theorem 2.22 and Proposition 5.8, the mutations of support
$\mathbf {R}$
-dissections, such that, by Theorem 2.22 and Proposition 5.8, the mutations of support
![]() $\tau $
-tilting modules are compatible with the flips of
$\tau $
-tilting modules are compatible with the flips of
![]() $\mathbf {R}$
-dissections. Thus, we can get the required isomorphism.
$\mathbf {R}$
-dissections. Thus, we can get the required isomorphism.
Example 5.11. Let
![]() $\mathbf {S}$
be a punctured marked surface with genus zero, two boundary components and one puncture as shown in the left picture of Figure 11, where a partial ideal triangulation
$\mathbf {S}$
be a punctured marked surface with genus zero, two boundary components and one puncture as shown in the left picture of Figure 11, where a partial ideal triangulation
![]() $\mathbf {R}$
consisting of the red arcs
$\mathbf {R}$
consisting of the red arcs
![]() $1,2$
and
$1,2$
and
![]() $3$
is given. Then, by Theorem 4.16, the corresponding surface rigid algebra
$3$
is given. Then, by Theorem 4.16, the corresponding surface rigid algebra
![]() $\Lambda _{\mathbf {R}}$
is isomorphic to the skew-gentle algebra
$\Lambda _{\mathbf {R}}$
is isomorphic to the skew-gentle algebra
![]() ${\mathbf {k}} Q_{\mathbf {R}}/\langle I_{\mathbf {R}}^{s\text {-}t}\rangle $
, where
${\mathbf {k}} Q_{\mathbf {R}}/\langle I_{\mathbf {R}}^{s\text {-}t}\rangle $
, where
![]() $Q_{\mathbf {R}}$
is shown in the right picture of Figure 11 and the relation set
$Q_{\mathbf {R}}$
is shown in the right picture of Figure 11 and the relation set
![]() $I^{s\text {-}t}_{\mathbf {R}}=\{ba,ab,\epsilon ^2-\epsilon \}$
.
$I^{s\text {-}t}_{\mathbf {R}}=\{ba,ab,\epsilon ^2-\epsilon \}$
.
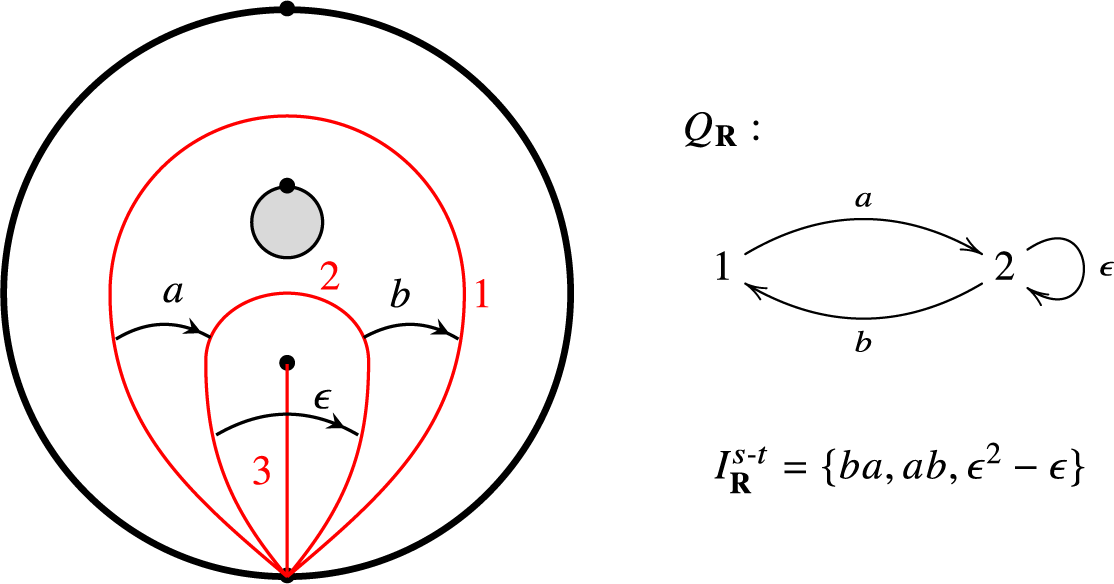
Figure 11 An example of a partial ideal triangulation of a marked surface with the associated surface rigid algebra.
The algebra
![]() ${\mathbf {k}} Q_{\mathbf {R}}/I^{s\text {-}t}_{\mathbf {R}}$
is Morita equivalent to
${\mathbf {k}} Q_{\mathbf {R}}/I^{s\text {-}t}_{\mathbf {R}}$
is Morita equivalent to
![]() $\Lambda ={\mathbf {k}} Q/\langle I\rangle $
, where
$\Lambda ={\mathbf {k}} Q/\langle I\rangle $
, where

For any vertex i of Q, let
![]() $S_i$
,
$S_i$
,
![]() $P_i$
and
$P_i$
and
![]() $I_i$
be the corresponding simple, projective module and injective module, respectively. Let
$I_i$
be the corresponding simple, projective module and injective module, respectively. Let
![]() $M,N$
be the following two representations of Q bounded by I:
$M,N$
be the following two representations of Q bounded by I:
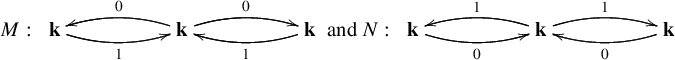
Then the Auslander-Reiten quiver of
![]() $\Lambda $
is as follows:
$\Lambda $
is as follows:
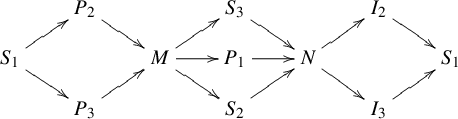
The exchange graph of support
![]() $\tau $
-tilting
$\tau $
-tilting
![]() $\Lambda $
-modules is shown in Figure 12, and the corresponding isomorphic exchange graph of
$\Lambda $
-modules is shown in Figure 12, and the corresponding isomorphic exchange graph of
![]() $\mathbf {R}$
-dissections is shown in Figure 13.
$\mathbf {R}$
-dissections is shown in Figure 13.
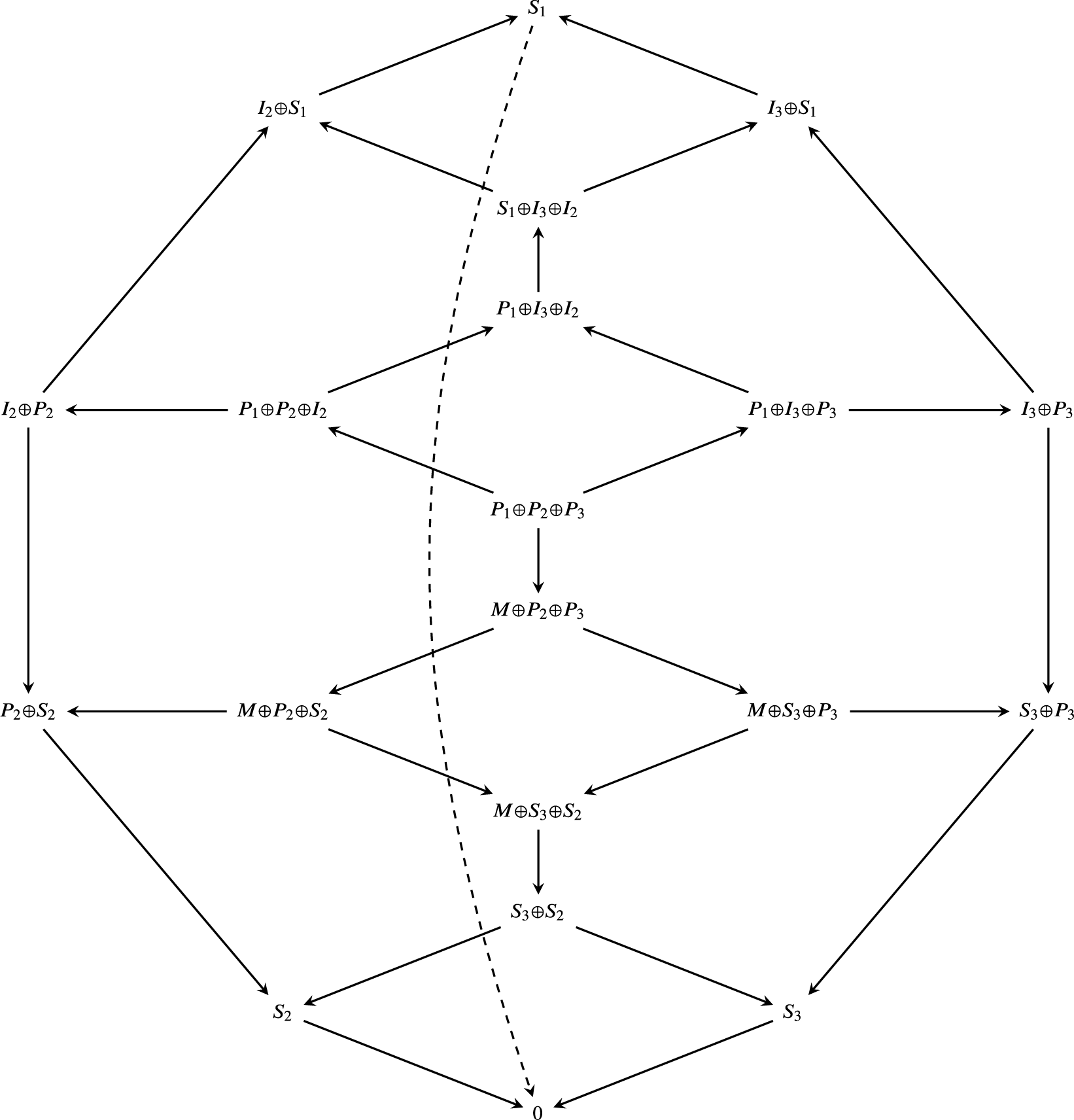
Figure 12 An exchange graph of support
![]() $\tau $
-tilting modules.
$\tau $
-tilting modules.
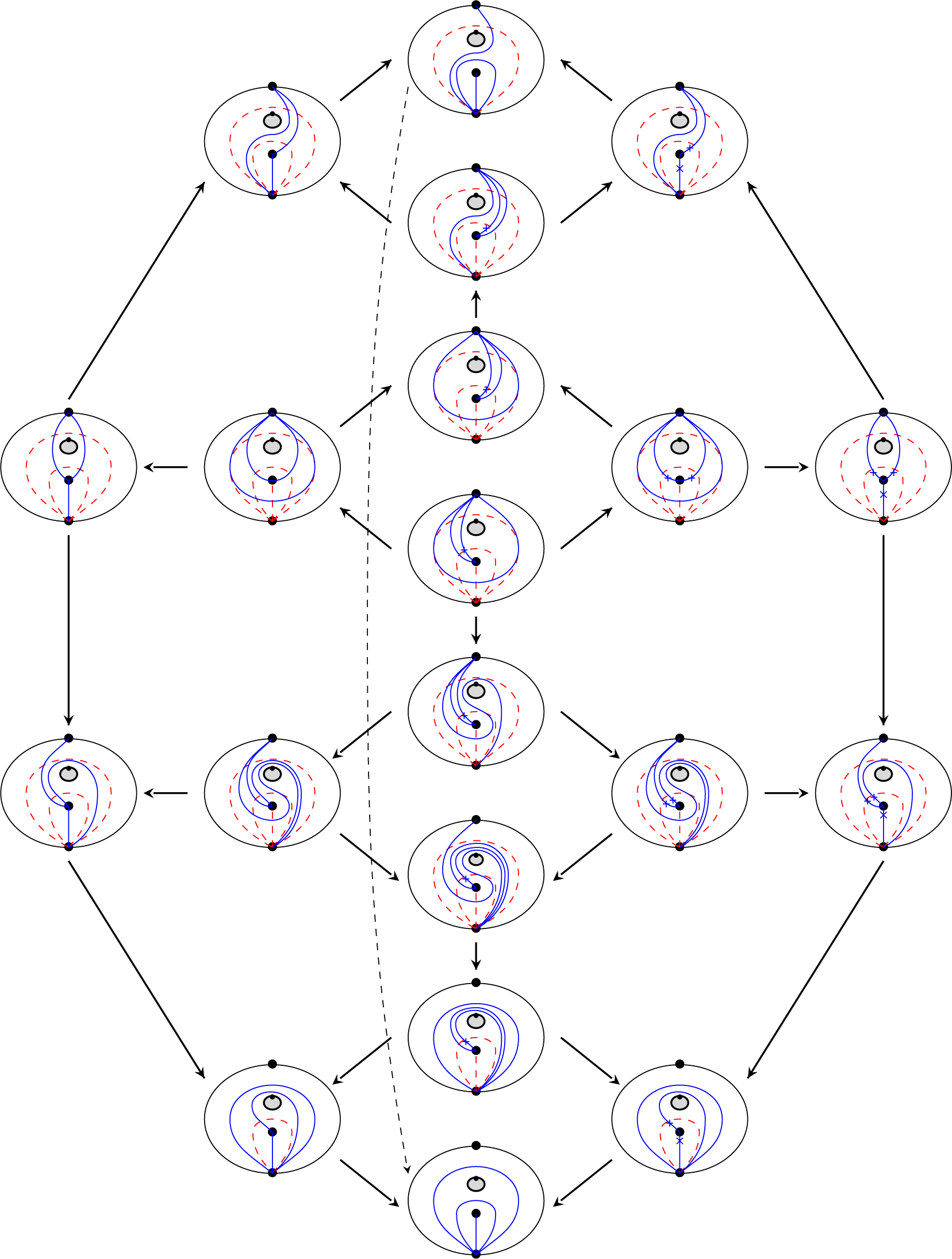
Figure 13 An exchange graph of dissections.
A subset
![]() $\mathbf {R}_1$
of
$\mathbf {R}_1$
of
![]() $\mathbf {R}$
is said to be connected if there is no decomposition
$\mathbf {R}$
is said to be connected if there is no decomposition
![]() $\mathbf {R}_1=\mathbf {R}^{\prime }\cup \mathbf {R}^{\prime \prime }$
such that any arc in
$\mathbf {R}_1=\mathbf {R}^{\prime }\cup \mathbf {R}^{\prime \prime }$
such that any arc in
![]() $\mathbf {R}^{\prime }$
and any arc in
$\mathbf {R}^{\prime }$
and any arc in
![]() $\mathbf {R}^{\prime \prime }$
have no endpoints in common. A connected component of
$\mathbf {R}^{\prime \prime }$
have no endpoints in common. A connected component of
![]() $\mathbf {R}$
is a maximal connected subset of
$\mathbf {R}$
is a maximal connected subset of
![]() $\mathbf {R}$
.
$\mathbf {R}$
.
Definition 5.12. We call
![]() $\mathbf {R}$
is connected to the boundary if each connected component of
$\mathbf {R}$
is connected to the boundary if each connected component of
![]() $\mathbf {R}$
contains at least one arc incident to a marked point in
$\mathbf {R}$
contains at least one arc incident to a marked point in
![]() $\mathbf {M}$
.
$\mathbf {M}$
.
For any
![]() $\eta \in \mathbf {R}$
, we denote by
$\eta \in \mathbf {R}$
, we denote by
![]() $\mathbf {R}/\{\eta \}$
the partial tagged triangulation
$\mathbf {R}/\{\eta \}$
the partial tagged triangulation
![]() $F_{\{\eta \}}(\mathbf {R}\setminus \{\eta \})$
of
$F_{\{\eta \}}(\mathbf {R}\setminus \{\eta \})$
of
![]() $\mathbf {S}/\{\eta \}$
.
$\mathbf {S}/\{\eta \}$
.
Lemma 5.13. If
![]() $\mathbf {R}$
is connected to the boundary, then so does
$\mathbf {R}$
is connected to the boundary, then so does
![]() $\mathbf {R}/\{\eta \}$
.
$\mathbf {R}/\{\eta \}$
.
Proof. Let
![]() $\mathbf {R}=\mathbf {R}^{\prime }\cup \mathbf {R}^{\prime \prime }$
with
$\mathbf {R}=\mathbf {R}^{\prime }\cup \mathbf {R}^{\prime \prime }$
with
![]() $\mathbf {R}^{\prime }$
the connected component of
$\mathbf {R}^{\prime }$
the connected component of
![]() $\mathbf {R}$
containing
$\mathbf {R}$
containing
![]() $\eta $
. Let
$\eta $
. Let
![]() $\mathbf {R}^{\prime }\setminus \{\eta \}=\mathbf {R}_1\cup \cdots \cup \mathbf {R}_s$
with
$\mathbf {R}^{\prime }\setminus \{\eta \}=\mathbf {R}_1\cup \cdots \cup \mathbf {R}_s$
with
![]() $\mathbf {R}_i,1\leq i\leq s$
, connected components of
$\mathbf {R}_i,1\leq i\leq s$
, connected components of
![]() $\mathbf {R}^{\prime }\setminus \{\eta \}$
. Since
$\mathbf {R}^{\prime }\setminus \{\eta \}$
. Since
![]() $\mathbf {R}^{\prime }$
is connected, for each
$\mathbf {R}^{\prime }$
is connected, for each
![]() $1\leq i\leq s$
, there exists
$1\leq i\leq s$
, there exists
![]() $\gamma _i\in \mathbf {R}_i$
having a common endpoint with
$\gamma _i\in \mathbf {R}_i$
having a common endpoint with
![]() $\eta $
. So
$\eta $
. So
![]() $F_{\{\eta \}}(\gamma _i)$
has a marked point as an endpoint. Hence,
$F_{\{\eta \}}(\gamma _i)$
has a marked point as an endpoint. Hence,
![]() $F_{\{\eta \}}(\mathbf {R}\setminus \{\eta \})= F_{\{\eta \}}(\mathbf {R}_1)\cup \cdots \cup F_{\{\eta \}}(\mathbf {R}_s)\cup F_{\{\eta \}}(\mathbf {R}^{\prime \prime })$
is also connected to the boundary.
$F_{\{\eta \}}(\mathbf {R}\setminus \{\eta \})= F_{\{\eta \}}(\mathbf {R}_1)\cup \cdots \cup F_{\{\eta \}}(\mathbf {R}_s)\cup F_{\{\eta \}}(\mathbf {R}^{\prime \prime })$
is also connected to the boundary.
Denote by
![]() $D(\mathbf {R})_{\{\eta \}}$
the subset of
$D(\mathbf {R})_{\{\eta \}}$
the subset of
![]() $D(\mathbf {R})$
consisting of all
$D(\mathbf {R})$
consisting of all
![]() $\mathbf {R}$
-dissections containing
$\mathbf {R}$
-dissections containing
![]() $\eta $
, and
$\eta $
, and
![]() $D(\mathbf {R}/\{\eta \})$
the set of
$D(\mathbf {R}/\{\eta \})$
the set of
![]() $\mathbf {R}/\{\eta \}$
-dissections on
$\mathbf {R}/\{\eta \}$
-dissections on
![]() $\mathbf {S}/\{\eta \}$
.
$\mathbf {S}/\{\eta \}$
.
Lemma 5.14. There is a bijection
such that flips on both sides are compatible.
Proof. The bijection (4.1) in Theorem 4.7 restricts a bijection
such that, by Proposition 5.8, the flip on the left side is compatible with the mutation on the right side. By Proposition 2.25, there is a bijection
such that the mutations on both sides are compatible. The triangle equivalence (5.1) for
![]() $\mathbf {N}=\{\eta \}$
gives rise to a bijection
$\mathbf {N}=\{\eta \}$
gives rise to a bijection
such that the mutations on both sides are compatible, where
![]() $R^{\prime }=X_{\mathbf {S}/\{\eta \}}(\mathbf {R}/\{\eta \})$
. Combining the above three bijections, we get the required one.
$R^{\prime }=X_{\mathbf {S}/\{\eta \}}(\mathbf {R}/\{\eta \})$
. Combining the above three bijections, we get the required one.
The following lemma, which is crucial in the proof of the main result, will be proved in the next subsection.
Lemma 5.15. Let
![]() $\mathbf {R}$
be a partial tagged triangulation on
$\mathbf {R}$
be a partial tagged triangulation on
![]() $\mathbf {S}$
connected to the boundary. Then for any
$\mathbf {S}$
connected to the boundary. Then for any
![]() $\mathbf {R}$
-dissection
$\mathbf {R}$
-dissection
![]() $\mathbf {U}$
, there exists a sequence of flips
$\mathbf {U}$
, there exists a sequence of flips
![]() $f_{l_1},\cdots ,f_{l_k}$
such that
$f_{l_1},\cdots ,f_{l_k}$
such that
![]() $\mathbf {R}\cap f_{l_k}\circ \cdots \circ f_{l_1}(\mathbf {U})\neq \emptyset $
.
$\mathbf {R}\cap f_{l_k}\circ \cdots \circ f_{l_1}(\mathbf {U})\neq \emptyset $
.
The main result in this section is the following connectedness of the graph of
![]() $\mathbf {R}$
-dissections.
$\mathbf {R}$
-dissections.
Theorem 5.16. Let
![]() $\mathbf {R}$
be a partial tagged triangulation on
$\mathbf {R}$
be a partial tagged triangulation on
![]() $\mathbf {S}$
connected to the boundary. Then the exchange graph
$\mathbf {S}$
connected to the boundary. Then the exchange graph
![]() $\operatorname {EG}^\times (\mathbf {R})$
is connected.
$\operatorname {EG}^\times (\mathbf {R})$
is connected.
Proof. We call two
![]() $\mathbf {R}$
-dissections
$\mathbf {R}$
-dissections
![]() $\mathbf {U}$
and
$\mathbf {U}$
and
![]() $\mathbf {U}^{\prime }$
flip-connected to each other if one can be obtained from the other by a sequence of flips. To show that
$\mathbf {U}^{\prime }$
flip-connected to each other if one can be obtained from the other by a sequence of flips. To show that
![]() $\operatorname {EG}^\times (\mathbf {R})$
is connected, it is enough to show the assertion that any
$\operatorname {EG}^\times (\mathbf {R})$
is connected, it is enough to show the assertion that any
![]() $\mathbf {R}$
-dissection
$\mathbf {R}$
-dissection
![]() $\mathbf {U}$
is flip-connected to
$\mathbf {U}$
is flip-connected to
![]() $\mathbf {R}$
. We use the induction on
$\mathbf {R}$
. We use the induction on
![]() $|\mathbf {R}|$
. When
$|\mathbf {R}|$
. When
![]() $|\mathbf {R}|=1$
, the assertions follows directly from Lemma 5.15. Suppose the assertion is true when
$|\mathbf {R}|=1$
, the assertions follows directly from Lemma 5.15. Suppose the assertion is true when
![]() $|\mathbf {R}|\leq n-1$
for some
$|\mathbf {R}|\leq n-1$
for some ![]() , and consider the case when
, and consider the case when
![]() $|\mathbf {R}|=n$
. By Lemma 5.15, there exists some
$|\mathbf {R}|=n$
. By Lemma 5.15, there exists some
![]() $\eta \in \mathbf {R}$
and an
$\eta \in \mathbf {R}$
and an
![]() $\mathbf {R}$
-dissection
$\mathbf {R}$
-dissection
![]() $\mathbf {U}^{\prime }$
such that
$\mathbf {U}^{\prime }$
such that
![]() $\eta \in \mathbf {R}\cap \mathbf {U}^{\prime }$
and
$\eta \in \mathbf {R}\cap \mathbf {U}^{\prime }$
and
![]() $\mathbf {U}^{\prime }$
is flip-connected to
$\mathbf {U}^{\prime }$
is flip-connected to
![]() $\mathbf {U}$
. By Lemma 5.14,
$\mathbf {U}$
. By Lemma 5.14,
![]() $F_{\{\eta \}}(\mathbf {U}^{\prime }\setminus \{\eta \})$
is an
$F_{\{\eta \}}(\mathbf {U}^{\prime }\setminus \{\eta \})$
is an
![]() $\mathbf {R}/\{\eta \}$
-dissection. By Lemma 5.13,
$\mathbf {R}/\{\eta \}$
-dissection. By Lemma 5.13,
![]() $\mathbf {R}/\{\eta \}$
is a partial tagged triangulation of
$\mathbf {R}/\{\eta \}$
is a partial tagged triangulation of
![]() $\mathbf {S}/\{\eta \}$
connected to the boundary. Since
$\mathbf {S}/\{\eta \}$
connected to the boundary. Since
![]() $|\mathbf {R}/\{\eta \}|=n-1$
, using the induction hypothesis,
$|\mathbf {R}/\{\eta \}|=n-1$
, using the induction hypothesis,
![]() $F_{\{\eta \}}(\mathbf {U}^{\prime }\setminus \{\eta \})$
is flip-connected to
$F_{\{\eta \}}(\mathbf {U}^{\prime }\setminus \{\eta \})$
is flip-connected to
![]() $\mathbf {R}/\{\eta \}$
. Hence, by Lemma 5.14 again,
$\mathbf {R}/\{\eta \}$
. Hence, by Lemma 5.14 again,
![]() $\mathbf {U}^{\prime }$
is flip-connected to
$\mathbf {U}^{\prime }$
is flip-connected to
![]() $\mathbf {R}$
. So
$\mathbf {R}$
. So
![]() $\mathbf {U}$
is flip-connected to
$\mathbf {U}$
is flip-connected to
![]() $\mathbf {R}$
.
$\mathbf {R}$
.
Remark 5.17. If
![]() $\mathbf {R}$
is a tagged triangulation, it is automatically connected to the boundary. Hence, Theorem 5.16 generalizes [Reference Fomin, Shapiro and Thurston25, Proposition 7.10].
$\mathbf {R}$
is a tagged triangulation, it is automatically connected to the boundary. Hence, Theorem 5.16 generalizes [Reference Fomin, Shapiro and Thurston25, Proposition 7.10].
We have the following important consequence.
Corollary 5.18. The exchange graph
![]() $\operatorname {EG}(\operatorname {s\tau -tilt} A)$
of support
$\operatorname {EG}(\operatorname {s\tau -tilt} A)$
of support
![]() $\tau $
-tilting modules over any surface rigid algebra A is connected. In particular,
$\tau $
-tilting modules over any surface rigid algebra A is connected. In particular,
![]() $\operatorname {EG}(\operatorname {s\tau -tilt} A)$
is connected for A a skew-gentle algebra.
$\operatorname {EG}(\operatorname {s\tau -tilt} A)$
is connected for A a skew-gentle algebra.
5.2 Proof of Lemma 5.15
This subsection devotes to proving Lemma 5.15. We may assume
![]() $\mathbf {U}\cap \mathbf {R}=\emptyset $
. Recall that by Corollary 4.9,
$\mathbf {U}\cap \mathbf {R}=\emptyset $
. Recall that by Corollary 4.9,
![]() $\mathbf {R}$
is a
$\mathbf {R}$
is a
![]() $\mathbf {U}$
-co-dissection. In particular, any
$\mathbf {U}$
-co-dissection. In particular, any
![]() $\gamma \in \mathbf {R}$
is
$\gamma \in \mathbf {R}$
is
![]() $\mathbf {U}$
-co-standard. So by Proposition 4.4,
$\mathbf {U}$
-co-standard. So by Proposition 4.4,
![]() $e^{op}(\gamma )$
shears
$e^{op}(\gamma )$
shears
![]() $\mathbf {U}$
.
$\mathbf {U}$
.
We first introduce some notions and notations. For any
![]() $\gamma \in \mathbf {R}$
and any
$\gamma \in \mathbf {R}$
and any
![]() $l\in \mathbf {U}$
, denote by
$l\in \mathbf {U}$
, denote by
![]() $\gamma \cap l^\circ \cap \mathbf {S}^\circ $
the subset of
$\gamma \cap l^\circ \cap \mathbf {S}^\circ $
the subset of
![]() $\gamma \cap l^\circ $
consisting of the intersections not in
$\gamma \cap l^\circ $
consisting of the intersections not in
![]() $\mathbf {M}\cup \mathbf {P}$
. We also denote
$\mathbf {M}\cup \mathbf {P}$
. We also denote
 $$ \begin{align*}\operatorname{Int}^\circ(\mathbf{R},l^\circ)=\sum_{\gamma\in\mathbf{R}}|\gamma\cap l^\circ\cap\mathbf{S}^\circ|,\end{align*} $$
$$ \begin{align*}\operatorname{Int}^\circ(\mathbf{R},l^\circ)=\sum_{\gamma\in\mathbf{R}}|\gamma\cap l^\circ\cap\mathbf{S}^\circ|,\end{align*} $$
and
An arc
![]() $l\in \mathbf {U}$
is said to be
$l\in \mathbf {U}$
is said to be
-
○ maximal if
 $\operatorname {Int}^\circ (\mathbf {R},l^\circ )\geq \operatorname {Int}^\circ (\mathbf {R},h^\circ )$
for any
$\operatorname {Int}^\circ (\mathbf {R},l^\circ )\geq \operatorname {Int}^\circ (\mathbf {R},h^\circ )$
for any
 $h\in \mathbf {U}$
;
$h\in \mathbf {U}$
; -
○ double if l is homotopic to another arc in
 $\mathbf {U}$
(i.e.,
$\mathbf {U}$
(i.e.,
 $l^\circ $
is a side of a self-folded triangle of
$l^\circ $
is a side of a self-folded triangle of
 $\mathbf {U}^\circ $
);
$\mathbf {U}^\circ $
); -
○ single if l is not homotopic to any other arc in
 $\mathbf {U}$
.
$\mathbf {U}$
.
For a maximal
![]() $l\in \mathbf {U}$
, we also call
$l\in \mathbf {U}$
, we also call
![]() $l^\circ $
maximal in
$l^\circ $
maximal in
![]() $\mathbf {U}^\circ $
.
$\mathbf {U}^\circ $
.
Denote by
![]() $\mathbf {U}^{non}$
the subset of
$\mathbf {U}^{non}$
the subset of
![]() $\mathbf {U}$
consisting of all arcs l such that
$\mathbf {U}$
consisting of all arcs l such that
![]() $l^\circ $
is not the folded side of a self-folded triangle of
$l^\circ $
is not the folded side of a self-folded triangle of
![]() $\mathbf {U}^\circ $
. By definition, any maximal arc in
$\mathbf {U}^\circ $
. By definition, any maximal arc in
![]() $\mathbf {U}$
is in
$\mathbf {U}$
is in
![]() $\mathbf {U}^{non}$
.
$\mathbf {U}^{non}$
.
Next, we deal with two special cases. Recall that two tagged arcs
![]() $\gamma $
and l are called adjoint to each other if
$\gamma $
and l are called adjoint to each other if
![]() $\gamma (0),\gamma (1)\in \mathbf {P}$
and
$\gamma (0),\gamma (1)\in \mathbf {P}$
and
![]() $l=\rho (\gamma )$
.
$l=\rho (\gamma )$
.
Lemma 5.19. Let
![]() $\gamma $
be a tagged arc in
$\gamma $
be a tagged arc in
![]() $\mathbf {R}$
not adjoint to any arc in
$\mathbf {R}$
not adjoint to any arc in
![]() $\mathbf {U}$
and such that
$\mathbf {U}$
and such that
![]() $\operatorname {Int}^\circ (\gamma ,\mathbf {U}^\circ )=0$
. Then there exists a sequence of flips
$\operatorname {Int}^\circ (\gamma ,\mathbf {U}^\circ )=0$
. Then there exists a sequence of flips
![]() $f_{l_1},\cdots ,f_{l_k}$
such that
$f_{l_1},\cdots ,f_{l_k}$
such that
![]() $\gamma \in f_{l_k}\circ \cdots \circ f_{l_1}(\mathbf {U})$
.
$\gamma \in f_{l_k}\circ \cdots \circ f_{l_1}(\mathbf {U})$
.
Proof. Since
![]() $\operatorname {Int}^\circ (\gamma ,\mathbf {U}^\circ )=0$
, by Definition 4.2 and Remark 4.3, there is
$\operatorname {Int}^\circ (\gamma ,\mathbf {U}^\circ )=0$
, by Definition 4.2 and Remark 4.3, there is
![]() $l\in \mathbf {U}^{non}$
such that
$l\in \mathbf {U}^{non}$
such that
![]() $\gamma ^{\mathbf {U}}$
,
$\gamma ^{\mathbf {U}}$
,
![]() $l_s^\circ $
and
$l_s^\circ $
and
![]() $l^\circ $
form a contractible triangle clockwise, and with a certain orientation of
$l^\circ $
form a contractible triangle clockwise, and with a certain orientation of
![]() $\gamma ^{\mathbf {U}}$
, we have
$\gamma ^{\mathbf {U}}$
, we have
![]() $\gamma ^{\mathbf {U}}(1)=l^\circ (1)$
,
$\gamma ^{\mathbf {U}}(1)=l^\circ (1)$
,
![]() $\kappa _{\gamma ^{\mathbf {U}}}(1)=-1$
,
$\kappa _{\gamma ^{\mathbf {U}}}(1)=-1$
,
![]() $\gamma ^{\mathbf {U}}(0)=l_s^\circ (1)$
and
$\gamma ^{\mathbf {U}}(0)=l_s^\circ (1)$
and
![]() $\kappa _{\gamma ^{\mathbf {U}}}(0)=1$
if
$\kappa _{\gamma ^{\mathbf {U}}}(0)=1$
if
![]() $\gamma ^{\mathbf {U}}(0)\in \mathbf {P}$
; see Figure 14. So by Remark 4.5 (see also Figure 8), we have
$\gamma ^{\mathbf {U}}(0)\in \mathbf {P}$
; see Figure 14. So by Remark 4.5 (see also Figure 8), we have
![]() $b_{l,\mathbf {U}}(e^{op}(\gamma ))<0$
. Hence, by equation (5.3),
$b_{l,\mathbf {U}}(e^{op}(\gamma ))<0$
. Hence, by equation (5.3),
![]() $f_l(\mathbf {U})^\circ =f^-_{l^\circ }(\mathbf {U}^\circ )=\mathbf {U}^\circ \setminus \{l^\circ \}\cup \{f^-_{\mathbf {U}^\circ }(l^\circ )\}$
. Note that
$f_l(\mathbf {U})^\circ =f^-_{l^\circ }(\mathbf {U}^\circ )=\mathbf {U}^\circ \setminus \{l^\circ \}\cup \{f^-_{\mathbf {U}^\circ }(l^\circ )\}$
. Note that
![]() $\gamma ^{\mathbf {U}}(0)\neq \gamma ^{\mathbf {U}}(1)$
since
$\gamma ^{\mathbf {U}}(0)\neq \gamma ^{\mathbf {U}}(1)$
since
![]() $\gamma ^{\mathbf {U}}$
is a tagged arc.
$\gamma ^{\mathbf {U}}$
is a tagged arc.
Figure 14 The case
![]() $\operatorname {Int}^\circ (\gamma ,\mathbf {U}^\circ )=0$
.
$\operatorname {Int}^\circ (\gamma ,\mathbf {U}^\circ )=0$
.
Let
![]() $p=\gamma ^{\mathbf {U}}(1)$
and
$p=\gamma ^{\mathbf {U}}(1)$
and
![]() $\mathbf {U}^\circ (p)$
be the set of arc segments of arcs in
$\mathbf {U}^\circ (p)$
be the set of arc segments of arcs in
![]() $\mathbf {U}^\circ $
that have p as an endpoint. We use the induction on
$\mathbf {U}^\circ $
that have p as an endpoint. We use the induction on
![]() $|\mathbf {U}^\circ (p)|$
.
$|\mathbf {U}^\circ (p)|$
.
If
![]() $|\mathbf {U}^\circ (p)|=1$
, then
$|\mathbf {U}^\circ (p)|=1$
, then
![]() $l^\circ (0)\neq p$
and there is no other
$l^\circ (0)\neq p$
and there is no other
![]() $h^\circ \in \mathbf {U}^\circ $
having p as an endpoint. This implies
$h^\circ \in \mathbf {U}^\circ $
having p as an endpoint. This implies
![]() $\operatorname {Int}(\gamma ,h)=0$
for any
$\operatorname {Int}(\gamma ,h)=0$
for any
![]() $h\in \mathbf {U}\setminus \{l\}$
. Since
$h\in \mathbf {U}\setminus \{l\}$
. Since
![]() $\gamma $
is
$\gamma $
is
![]() $\mathbf {R}$
-standard and
$\mathbf {R}$
-standard and
![]() $\gamma \neq l$
(due to
$\gamma \neq l$
(due to
![]() $\mathbf {R}\cap \mathbf {U}=\emptyset $
), by Proposition 5.8, we have
$\mathbf {R}\cap \mathbf {U}=\emptyset $
), by Proposition 5.8, we have
![]() $f_{\mathbf {U}}(l)=\gamma $
, that is,
$f_{\mathbf {U}}(l)=\gamma $
, that is,
![]() $\gamma \in f_l(\mathbf {U})$
.
$\gamma \in f_l(\mathbf {U})$
.
Suppose the assertion holds for
![]() $|\mathbf {U}^\circ (p)|<m$
with
$|\mathbf {U}^\circ (p)|<m$
with
![]() $k\geq 0$
and consider the case when
$k\geq 0$
and consider the case when
![]() $|\mathbf {U}^\circ (p)|=m$
. We have the following cases.
$|\mathbf {U}^\circ (p)|=m$
. We have the following cases.
-
(1)
 $l^\circ (0)=l^\circ (1)$
, which contains the case that l is double; see the first picture in Figure 15. Then one endpoint of
$l^\circ (0)=l^\circ (1)$
, which contains the case that l is double; see the first picture in Figure 15. Then one endpoint of
 $f_{\mathbf {U}}(l)^\circ $
is
$f_{\mathbf {U}}(l)^\circ $
is
 $\gamma ^{\mathbf {U}}(0)\neq p$
. So
$\gamma ^{\mathbf {U}}(0)\neq p$
. So
 $|f_l(\mathbf {U})^\circ (p)|<m$
, and we are done by the induction hypothesis.
$|f_l(\mathbf {U})^\circ (p)|<m$
, and we are done by the induction hypothesis.
Figure 15 The cases of flip of
 $l^\circ $
for
$l^\circ $
for
 $\operatorname {Int}^\circ (\gamma ,\mathbf {U}^\circ )=0$
.
$\operatorname {Int}^\circ (\gamma ,\mathbf {U}^\circ )=0$
. -
(2)
 $l^\circ (0)\neq l^\circ (1)$
and
$l^\circ (0)\neq l^\circ (1)$
and
 $l^\circ _t(0)\neq l^\circ _t(1)$
; see the second picture of Figure 15. Then
$l^\circ _t(0)\neq l^\circ _t(1)$
; see the second picture of Figure 15. Then
 $f_{\mathbf {U}}(l)^\circ $
has
$f_{\mathbf {U}}(l)^\circ $
has
 $\gamma ^{\mathbf {U}}(0)$
and
$\gamma ^{\mathbf {U}}(0)$
and
 $l^\circ _t(0)$
as the endpoints, both of which are not p. So
$l^\circ _t(0)$
as the endpoints, both of which are not p. So
 $|f_l(\mathbf {U})^\circ (p)|<m$
, and we are done by the induction hypothesis.
$|f_l(\mathbf {U})^\circ (p)|<m$
, and we are done by the induction hypothesis. -
(3)
 $l^\circ (0)\neq l^\circ (1)$
and
$l^\circ (0)\neq l^\circ (1)$
and
 $l_t^\circ (0)=l_t^\circ (1)$
; see the third picture in Figure 15. Then exactly one of the endpoints of
$l_t^\circ (0)=l_t^\circ (1)$
; see the third picture in Figure 15. Then exactly one of the endpoints of
 $f_{\mathbf {U}}(l)^\circ $
is not p. So
$f_{\mathbf {U}}(l)^\circ $
is not p. So
 $|f_l(\mathbf {U})^\circ (p)|=m$
, and we go back to Case (1). Thus, we are done.
$|f_l(\mathbf {U})^\circ (p)|=m$
, and we go back to Case (1). Thus, we are done.
Lemma 5.20. Let
![]() $\gamma $
be a tagged arc in
$\gamma $
be a tagged arc in
![]() $\mathbf {R}$
adjoint to
$\mathbf {R}$
adjoint to
![]() $l\in \mathbf {U}$
. Then l is the unique arc in
$l\in \mathbf {U}$
. Then l is the unique arc in
![]() $\mathbf {U}$
such that
$\mathbf {U}$
such that
![]() $b_{l,\mathbf {U}}(e^{op}(\gamma ))\neq 0$
. Moreover, if
$b_{l,\mathbf {U}}(e^{op}(\gamma ))\neq 0$
. Moreover, if
![]() $\operatorname {Int}^\circ (\mathbf {R},l^\circ )\neq 0$
, then there exists a sequence of flips
$\operatorname {Int}^\circ (\mathbf {R},l^\circ )\neq 0$
, then there exists a sequence of flips
![]() $f_{l_1},\cdots ,f_{l_k}$
such that
$f_{l_1},\cdots ,f_{l_k}$
such that
![]() $\gamma \in f_{l_k}\circ \cdots \circ f_{l_1}(\mathbf {U})$
.
$\gamma \in f_{l_k}\circ \cdots \circ f_{l_1}(\mathbf {U})$
.
Proof. By Remark 3.12,
![]() $e^{op}(\gamma )=e^{op}(\rho ^{-1}(l))=e(l)$
. So for any
$e^{op}(\gamma )=e^{op}(\rho ^{-1}(l))=e(l)$
. So for any
![]() $h\in \mathbf {U}$
,
$h\in \mathbf {U}$
,
![]() $b_{h,\mathbf {U}}(e^{op}(\gamma ))=b_{h,\mathbf {U}}(e(l))$
, which by Corollary 3.18 is nonzero if and only if
$b_{h,\mathbf {U}}(e^{op}(\gamma ))=b_{h,\mathbf {U}}(e(l))$
, which by Corollary 3.18 is nonzero if and only if
![]() $h=l$
. Hence, l is the unique arc in
$h=l$
. Hence, l is the unique arc in
![]() $\mathbf {U}$
such that
$\mathbf {U}$
such that
![]() $b_{l,\mathbf {U}}(e^{op}(\gamma ))\neq 0$
. Indeed, we have
$b_{l,\mathbf {U}}(e^{op}(\gamma ))\neq 0$
. Indeed, we have
![]() $b_{l,\mathbf {U}}(e^{op}(\gamma ))<0$
by Corollary 3.18. Hence, by equation (5.3),
$b_{l,\mathbf {U}}(e^{op}(\gamma ))<0$
by Corollary 3.18. Hence, by equation (5.3),
![]() $f_l(\mathbf {U})^\circ =f^-_{l^\circ }(\mathbf {U}^\circ )=\mathbf {U}^\circ \setminus \{l^\circ \}\cup \{f^-_{\mathbf {U}^\circ }(l^\circ )\}$
.
$f_l(\mathbf {U})^\circ =f^-_{l^\circ }(\mathbf {U}^\circ )=\mathbf {U}^\circ \setminus \{l^\circ \}\cup \{f^-_{\mathbf {U}^\circ }(l^\circ )\}$
.
If
![]() $\operatorname {Int}^\circ (\mathbf {R},l^\circ )\neq 0$
, since l is adjoint to
$\operatorname {Int}^\circ (\mathbf {R},l^\circ )\neq 0$
, since l is adjoint to
![]() $\gamma \in \mathbf {R}$
, there is a self-folded triangle of
$\gamma \in \mathbf {R}$
, there is a self-folded triangle of
![]() $\mathbf {U}^\circ $
such that
$\mathbf {U}^\circ $
such that
![]() $l^\circ $
is its non-folded side. Let
$l^\circ $
is its non-folded side. Let
![]() ${l^{\prime }}^\circ $
be the corresponding folded side. Then
${l^{\prime }}^\circ $
be the corresponding folded side. Then
![]() $\gamma $
is homotopic to
$\gamma $
is homotopic to
![]() ${l^{\prime }}^\circ \in f_l(\mathbf {U})^\circ $
. So
${l^{\prime }}^\circ \in f_l(\mathbf {U})^\circ $
. So
![]() $\operatorname {Int}^\circ (\gamma ,f_l(\mathbf {U})^\circ )=0$
. Since
$\operatorname {Int}^\circ (\gamma ,f_l(\mathbf {U})^\circ )=0$
. Since
![]() $l\notin f_l(\mathbf {U})$
,
$l\notin f_l(\mathbf {U})$
,
![]() $\gamma $
is not adjoint to any arc in
$\gamma $
is not adjoint to any arc in
![]() $f_l(\mathbf {U})$
, the assertion follows by Lemma 5.19.
$f_l(\mathbf {U})$
, the assertion follows by Lemma 5.19.
Lemma 5.21. Let
![]() $\gamma \in \mathbf {R}$
. Suppose
$\gamma \in \mathbf {R}$
. Suppose
![]() $\operatorname {Int}^\circ (\gamma ,\mathbf {U}^\circ )\neq 0$
. Then for any maximal tagged arc
$\operatorname {Int}^\circ (\gamma ,\mathbf {U}^\circ )\neq 0$
. Then for any maximal tagged arc
![]() $l\in \mathbf {U}$
, any alternative intersection between
$l\in \mathbf {U}$
, any alternative intersection between
![]() $l^\circ $
and
$l^\circ $
and
![]() $\gamma $
is interior.
$\gamma $
is interior.
Figure 16 The case
![]() $l^\circ $
has an alternative intersection in
$l^\circ $
has an alternative intersection in
![]() $\mathbf {M}\cup \mathbf {P}$
with some
$\mathbf {M}\cup \mathbf {P}$
with some
![]() $\gamma \in \mathbf {R}$
satisfying
$\gamma \in \mathbf {R}$
satisfying
![]() $\operatorname {Int}^\circ (\gamma ,\mathbf {U}^\circ )\neq 0$
.
$\operatorname {Int}^\circ (\gamma ,\mathbf {U}^\circ )\neq 0$
.
Figure 17 The case that no angle of
![]() $\mathbf {U}^\circ $
is formed by the two ends of
$\mathbf {U}^\circ $
is formed by the two ends of
![]() $l^\circ $
.
$l^\circ $
.
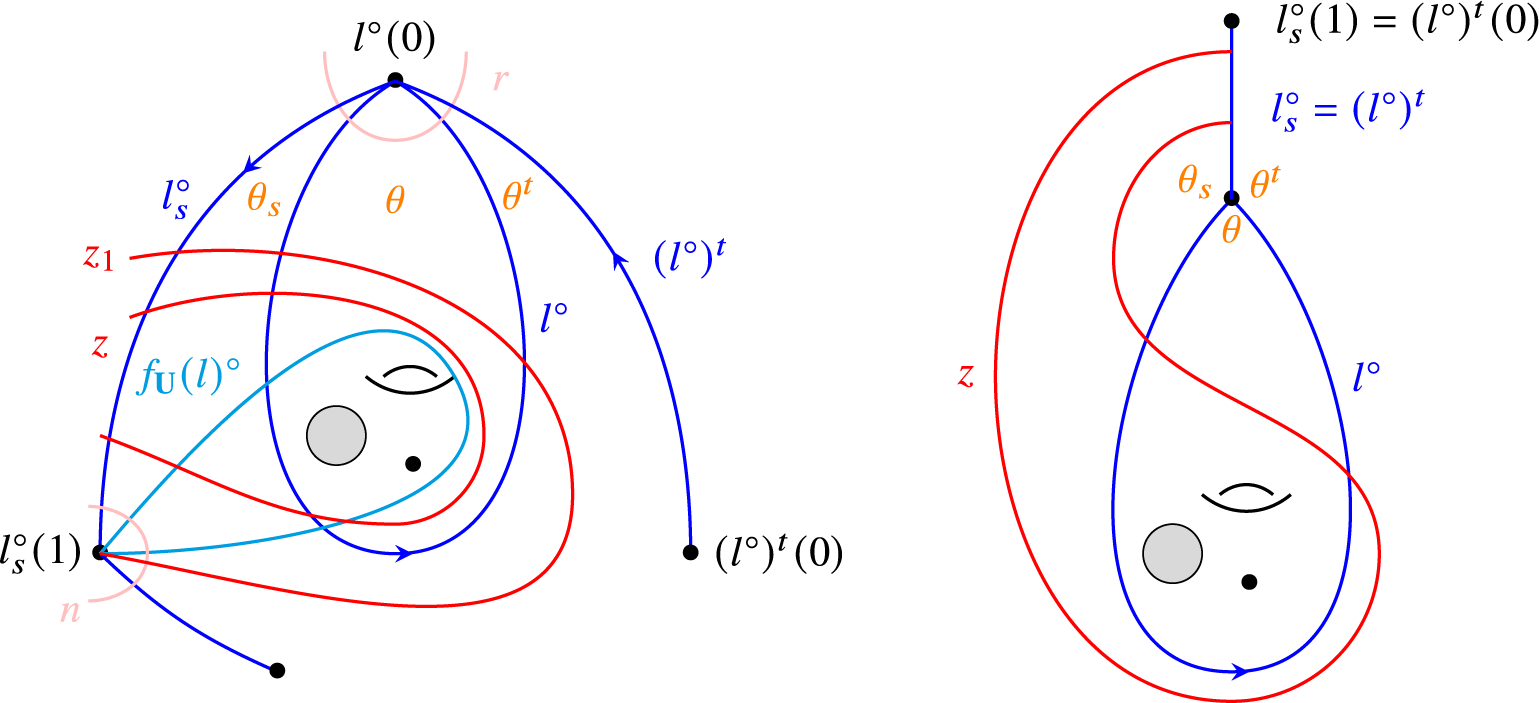
Figure 18 The case that one angle of
![]() $\mathbf {U}^\circ $
is formed by the two ends of
$\mathbf {U}^\circ $
is formed by the two ends of
![]() $l^\circ $
.
$l^\circ $
.
Proof. Suppose conversely that
![]() $l^\circ $
has an alternative intersection
$l^\circ $
has an alternative intersection
![]() $\mathfrak {q}\in \mathbf {M}\cup \mathbf {P}$
with
$\mathfrak {q}\in \mathbf {M}\cup \mathbf {P}$
with
![]() $\gamma $
. Suppose without loss of generality that
$\gamma $
. Suppose without loss of generality that
![]() $\mathfrak {q}$
is negative. Let
$\mathfrak {q}$
is negative. Let
![]() $\eta $
be the end arc segment of
$\eta $
be the end arc segment of
![]() $\gamma ^{\mathbf {U}}$
incident to
$\gamma ^{\mathbf {U}}$
incident to
![]() $\mathfrak {q}$
. Then by Remark 4.5, we are in one of the situations shown in Figure 16. In each case, let m be the number of non-end arc segments of arcs in
$\mathfrak {q}$
. Then by Remark 4.5, we are in one of the situations shown in Figure 16. In each case, let m be the number of non-end arc segments of arcs in
![]() $\mathbf {R}$
cutting out the same angle as
$\mathbf {R}$
cutting out the same angle as
![]() $\eta $
and
$\eta $
and ![]() the number of end arc segments of arcs in
the number of end arc segments of arcs in
![]() $\mathbf {R}$
homotopic to
$\mathbf {R}$
homotopic to
![]() $\eta $
. Then
$\eta $
. Then
![]() $\operatorname {Int}(\mathbf {R},l^\circ )=m$
and either
$\operatorname {Int}(\mathbf {R},l^\circ )=m$
and either
![]() $\operatorname {Int}(\mathbf {R},l^\circ _s)\geq m+n$
(see the left picture of Figure 16) or
$\operatorname {Int}(\mathbf {R},l^\circ _s)\geq m+n$
(see the left picture of Figure 16) or
![]() $\operatorname {Int}(\mathbf {R},(l^\circ )^s)\geq m+n$
(see the right picture of Figure 16), a contradiction to that l is maximal.
$\operatorname {Int}(\mathbf {R},(l^\circ )^s)\geq m+n$
(see the right picture of Figure 16), a contradiction to that l is maximal.
We need the following notions similarly as in [Reference Disarlo and Palier24]. For any arc
![]() $l\in \mathbf {U}$
, we say flipping l is convenient if
$l\in \mathbf {U}$
, we say flipping l is convenient if
![]() $\operatorname {Int}^\circ (\mathbf {R},f_l(\mathbf {U})^\circ )<\operatorname {Int}^\circ (\mathbf {R},\mathbf {U}^\circ )$
, or neutral if
$\operatorname {Int}^\circ (\mathbf {R},f_l(\mathbf {U})^\circ )<\operatorname {Int}^\circ (\mathbf {R},\mathbf {U}^\circ )$
, or neutral if
![]() $\operatorname {Int}^\circ (\mathbf {R},f_l(\mathbf {U})^\circ )=\operatorname {Int}^\circ (\mathbf {R},\mathbf {U}^\circ )$
, where
$\operatorname {Int}^\circ (\mathbf {R},f_l(\mathbf {U})^\circ )=\operatorname {Int}^\circ (\mathbf {R},\mathbf {U}^\circ )$
, where
 $$ \begin{align*}\operatorname{Int}^\circ(\mathbf{R},\mathbf{U}^\circ):=\sum_{l\in\mathbf{U}}\operatorname{Int}^\circ(\mathbf{R},l^\circ)=\sum_{\gamma\in\mathbf{R}}\operatorname{Int}^\circ(\gamma,\mathbf{U}^\circ).\end{align*} $$
$$ \begin{align*}\operatorname{Int}^\circ(\mathbf{R},\mathbf{U}^\circ):=\sum_{l\in\mathbf{U}}\operatorname{Int}^\circ(\mathbf{R},l^\circ)=\sum_{\gamma\in\mathbf{R}}\operatorname{Int}^\circ(\gamma,\mathbf{U}^\circ).\end{align*} $$
In what follows, for any
![]() $\gamma \in \mathbf {R}$
and a positive integer n, an n-arc segment of
$\gamma \in \mathbf {R}$
and a positive integer n, an n-arc segment of
![]() $\gamma $
is a segment of
$\gamma $
is a segment of
![]() $\gamma $
formed by n arc segments.
$\gamma $
formed by n arc segments.
Lemma 5.22. Let l be a maximal arc in
![]() $\mathbf {U}$
such that there is a negative (resp. positive) interior intersection
$\mathbf {U}$
such that there is a negative (resp. positive) interior intersection
![]() $\mathfrak {q}$
between
$\mathfrak {q}$
between
![]() $l^\circ $
and some arc
$l^\circ $
and some arc
![]() $\gamma \in \mathbf {R}$
. Then flipping l is either convenient or neutral. Moreover, if flipping l is neutral, then
$\gamma \in \mathbf {R}$
. Then flipping l is either convenient or neutral. Moreover, if flipping l is neutral, then
-
(1) l is single,
-
(2) each alternative intersection in
 $\mathbf {S}^\circ $
between
$\mathbf {S}^\circ $
between
 $l^\circ $
and an arc in
$l^\circ $
and an arc in
 $\mathbf {R}$
is not an endpoint of an end arc segment of the arc divided by
$\mathbf {R}$
is not an endpoint of an end arc segment of the arc divided by
 $\mathbf {U}^\circ $
, and
$\mathbf {U}^\circ $
, and -
(3) both
 $l^\circ _s$
and
$l^\circ _s$
and
 $l^\circ _t$
(resp. both
$l^\circ _t$
(resp. both
 $(l^\circ )^s$
and
$(l^\circ )^s$
and
 $(l^\circ )^t$
) exist and are maximal if
$(l^\circ )^t$
) exist and are maximal if
 $\mathfrak {q}$
is negative (resp. positive).
$\mathfrak {q}$
is negative (resp. positive).
Proof. We only deal with the case that
![]() $\mathfrak {q}$
is negative since the proof when
$\mathfrak {q}$
is negative since the proof when
![]() $\mathfrak {q}$
is positive is similar. By equation (5.3), l is flip-convenient if
$\mathfrak {q}$
is positive is similar. By equation (5.3), l is flip-convenient if
![]() $\operatorname {Int}^\circ (\mathbf {R},f^-_{\mathbf {U}^\circ }(l^\circ ))<\operatorname {Int}^\circ (\mathbf {R},l^\circ )$
, or flip-neutral if
$\operatorname {Int}^\circ (\mathbf {R},f^-_{\mathbf {U}^\circ }(l^\circ ))<\operatorname {Int}^\circ (\mathbf {R},l^\circ )$
, or flip-neutral if
![]() $\operatorname {Int}^\circ (\mathbf {R},f^-_{\mathbf {U}^\circ }(l^\circ ))=\operatorname {Int}^\circ (\mathbf {R},l^\circ )$
. We may assume that
$\operatorname {Int}^\circ (\mathbf {R},f^-_{\mathbf {U}^\circ }(l^\circ ))=\operatorname {Int}^\circ (\mathbf {R},l^\circ )$
. We may assume that
![]() $f^-_{\mathbf {U}^\circ }(l^\circ )$
is not homotopic to any arc in
$f^-_{\mathbf {U}^\circ }(l^\circ )$
is not homotopic to any arc in
![]() $\mathbf {R}$
, because otherwise,
$\mathbf {R}$
, because otherwise,
![]() $\operatorname {Int}^\circ (\mathbf {R},f^-_{\mathbf {U}^\circ }(l^\circ ))=0<\operatorname {Int}^\circ (\mathbf {R},l^\circ )$
. By Remark 4.5, we are in the situation shown in the second picture of the first row of Figure 8 with replacing
$\operatorname {Int}^\circ (\mathbf {R},f^-_{\mathbf {U}^\circ }(l^\circ ))=0<\operatorname {Int}^\circ (\mathbf {R},l^\circ )$
. By Remark 4.5, we are in the situation shown in the second picture of the first row of Figure 8 with replacing
![]() $\gamma $
by
$\gamma $
by
![]() $l^\circ $
and replacing
$l^\circ $
and replacing
![]() $\delta $
by some arc
$\delta $
by some arc
![]() $\gamma \in \mathbf {R}$
. There are the following cases.
$\gamma \in \mathbf {R}$
. There are the following cases.
-
(a) Suppose that there is no angle of
 $\mathbf {U}^\circ $
formed by
$\mathbf {U}^\circ $
formed by
 $l^\circ $
and itself. In this case, the four angles
$l^\circ $
and itself. In this case, the four angles
 $\theta _s,\theta ^s,\theta _t,\theta ^t$
(which are defined in Definition 5.4) are different. We shall use the following notations; see the first picture in Figure 17, where the label on each arc segment does not represent the arc segment itself, but rather the number of such arc segments.
$\theta _s,\theta ^s,\theta _t,\theta ^t$
(which are defined in Definition 5.4) are different. We shall use the following notations; see the first picture in Figure 17, where the label on each arc segment does not represent the arc segment itself, but rather the number of such arc segments.-
– Let
 $r_1$
(resp.
$r_1$
(resp.
 $r_2$
) be the number of 2-arc segments of arcs in
$r_2$
) be the number of 2-arc segments of arcs in
 $\mathbf {R}$
that cut out the angles
$\mathbf {R}$
that cut out the angles
 $\theta _t$
and
$\theta _t$
and
 $\theta ^t$
(resp.
$\theta ^t$
(resp.
 $\theta _s$
and
$\theta _s$
and
 $\theta ^s$
) and whose arc segment cutting out
$\theta ^s$
) and whose arc segment cutting out
 $\theta _t$
(resp.
$\theta _t$
(resp.
 $\theta _s$
) does not have an endpoint in
$\theta _s$
) does not have an endpoint in
 $\mathbf {M}\cup \mathbf {P}$
.
$\mathbf {M}\cup \mathbf {P}$
. -
– Let
 $d_1$
(resp.
$d_1$
(resp.
 $d_2$
) be the number of 2-arc segments of arcs in
$d_2$
) be the number of 2-arc segments of arcs in
 $\mathbf {R}$
that cut out the angles
$\mathbf {R}$
that cut out the angles
 $\theta _t$
and
$\theta _t$
and
 $\theta ^t$
(resp.
$\theta ^t$
(resp.
 $\theta _s$
and
$\theta _s$
and
 $\theta ^s$
) and whose arc segment cutting out
$\theta ^s$
) and whose arc segment cutting out
 $\theta _t$
(resp.
$\theta _t$
(resp.
 $\theta _s$
) has an endpoint in
$\theta _s$
) has an endpoint in
 $\mathbf {M}\cup \mathbf {P}$
; see the dashed ones in the left picture of Figure 17.
$\mathbf {M}\cup \mathbf {P}$
; see the dashed ones in the left picture of Figure 17. -
– Let
 $n_1$
(resp.
$n_1$
(resp.
 $n_2$
) be the number of arc segments of arcs in
$n_2$
) be the number of arc segments of arcs in
 $\mathbf {R}$
that cross
$\mathbf {R}$
that cross
 $l^\circ _t$
(resp.
$l^\circ _t$
(resp.
 $l^\circ _s$
) and cut out the angle at
$l^\circ _s$
) and cut out the angle at
 $l^\circ _t(0)$
(resp.
$l^\circ _t(0)$
(resp.
 $l^\circ _s(1)$
) clockwise from
$l^\circ _s(1)$
) clockwise from
 $l^\circ _t$
(resp.
$l^\circ _t$
(resp.
 $l^\circ _s$
).
$l^\circ _s$
). -
– Let z be the number of 2-arc segments of arcs in
 $\mathbf {R}$
that cut out the angles
$\mathbf {R}$
that cut out the angles
 $\theta _s$
and
$\theta _s$
and
 $\theta _t$
and are not incident to any point in
$\theta _t$
and are not incident to any point in
 $\mathbf {M}\cup \mathbf {P}$
.
$\mathbf {M}\cup \mathbf {P}$
. -
– Let
 $z_1$
(resp.
$z_1$
(resp.
 $z_2$
) be the number of 2-arc segments of arcs in
$z_2$
) be the number of 2-arc segments of arcs in
 $\mathbf {R}$
that cut out the angles
$\mathbf {R}$
that cut out the angles
 $\theta _s$
and
$\theta _s$
and
 $\theta _t$
and have one endpoint in
$\theta _t$
and have one endpoint in
 $\mathbf {M}\cup \mathbf {P}$
.
$\mathbf {M}\cup \mathbf {P}$
.
Then we have the following.
 $$\begin{align*}\operatorname{Int}^\circ(\mathbf{R},l^\circ)=r_1+r_2+d_1+d_2+z+z_1+z_2,\end{align*}$$
$$\begin{align*}\operatorname{Int}^\circ(\mathbf{R},l^\circ)=r_1+r_2+d_1+d_2+z+z_1+z_2,\end{align*}$$
 $$\begin{align*}\operatorname{Int}^\circ(\mathbf{R},f^-_{\mathbf{U}^\circ}(l^\circ))=n_1+n_2+z,\end{align*}$$
$$\begin{align*}\operatorname{Int}^\circ(\mathbf{R},f^-_{\mathbf{U}^\circ}(l^\circ))=n_1+n_2+z,\end{align*}$$
 $$\begin{align*}\operatorname{Int}^\circ(\mathbf{R},l^\circ_t)=r_1+n_1+z+z_1,\end{align*}$$
There are the following subcases.
$$\begin{align*}\operatorname{Int}^\circ(\mathbf{R},l^\circ_t)=r_1+n_1+z+z_1,\end{align*}$$
There are the following subcases. $$\begin{align*}\operatorname{Int}^\circ(\mathbf{R},l^\circ_s)=r_2+n_2+z+z_2.\end{align*}$$
$$\begin{align*}\operatorname{Int}^\circ(\mathbf{R},l^\circ_s)=r_2+n_2+z+z_2.\end{align*}$$
-
(1) Both
 $d_1$
and
$d_1$
and
 $d_2$
are nonzero. Since arcs in
$d_2$
are nonzero. Since arcs in
 $\mathbf {R}$
do not cross each other in the interior, we have
$\mathbf {R}$
do not cross each other in the interior, we have
 $n_1=n_2=0$
. So
$n_1=n_2=0$
. So 
-
(2) Exactly one of
 $d_1$
and
$d_1$
and
 $d_2$
is not zero. Without loss of generality, suppose
$d_2$
is not zero. Without loss of generality, suppose
 $d_1=0$
and
$d_1=0$
and
 $d_2\neq 0$
. Since arcs in
$d_2\neq 0$
. Since arcs in
 $\mathbf {R}$
do not cross each other in the interior, we have
$\mathbf {R}$
do not cross each other in the interior, we have
 $n_2=z=z_2=0$
, which implies
$n_2=z=z_2=0$
, which implies
 $z_1\neq 0$
by the existence of a negative intersection
$z_1\neq 0$
by the existence of a negative intersection
 $\mathfrak {q}$
. So
$\mathfrak {q}$
. So 
-
(3) Both
 $d_1$
and
$d_1$
and
 $d_2$
are zero. So
$d_2$
are zero. So  $$\begin{align*}\operatorname{Int}^\circ(\mathbf{R},l^\circ)-\operatorname{Int}^\circ(\mathbf{R},f^-_{\mathbf{U}^\circ}(l^\circ))=2\operatorname{Int}^\circ(\mathbf{R},l^\circ)-\operatorname{Int}^\circ(\mathbf{R},l^\circ_s)-\operatorname{Int}^\circ(\mathbf{R},l_t^\circ)\geq0.\end{align*}$$
$$\begin{align*}\operatorname{Int}^\circ(\mathbf{R},l^\circ)-\operatorname{Int}^\circ(\mathbf{R},f^-_{\mathbf{U}^\circ}(l^\circ))=2\operatorname{Int}^\circ(\mathbf{R},l^\circ)-\operatorname{Int}^\circ(\mathbf{R},l^\circ_s)-\operatorname{Int}^\circ(\mathbf{R},l_t^\circ)\geq0.\end{align*}$$
Hence, flipping l is either convenient or neutral. When flipping l is neutral, we have
 $d_1=d_2=0$
and
$d_1=d_2=0$
and
 $\operatorname {Int}^\circ (\mathbf {R},l^\circ )=\operatorname {Int}^\circ (\mathbf {R},l^\circ _s)=\operatorname {Int}^\circ (\mathbf {R},l_t^\circ )$
, which implies that both
$\operatorname {Int}^\circ (\mathbf {R},l^\circ )=\operatorname {Int}^\circ (\mathbf {R},l^\circ _s)=\operatorname {Int}^\circ (\mathbf {R},l_t^\circ )$
, which implies that both
 $l_s$
and
$l_s$
and
 $l_t$
exist and are maximal, and
$l_t$
exist and are maximal, and
 $r_2+z_2=n_1$
and
$r_2+z_2=n_1$
and
 $r_1+z_1=n_2$
. Since at least one of
$r_1+z_1=n_2$
. Since at least one of
 $n_1$
and
$n_1$
and
 $z_2$
(resp.
$z_2$
(resp.
 $n_2$
and
$n_2$
and
 $z_1$
) is zero, we have
$z_1$
) is zero, we have
 $z_1=z_2=0$
,
$z_1=z_2=0$
,
 $r_2=n_1$
and
$r_2=n_1$
and
 $r_1=n_2$
. If in addition, l is double, then with the chosen orientations, we have
$r_1=n_2$
. If in addition, l is double, then with the chosen orientations, we have
 $(l^\circ )^s=l_t^\circ $
(with opposite orientations); see the second picture of Figure 17. Since the arc segment crossing
$(l^\circ )^s=l_t^\circ $
(with opposite orientations); see the second picture of Figure 17. Since the arc segment crossing
 $l_t^\circ $
and cutting out the angle at
$l_t^\circ $
and cutting out the angle at
 $l^\circ _t(0)$
clockwise from
$l^\circ _t(0)$
clockwise from
 $l^\circ _t$
is a loop enclosing the puncture
$l^\circ _t$
is a loop enclosing the puncture
 $l^\circ _t(0)$
, we have
$l^\circ _t(0)$
, we have
 $n_1=0$
. So
$n_1=0$
. So
 $r_2=0$
, which implies
$r_2=0$
, which implies
 $z=0$
. So we have
$z=0$
. So we have
 $z+z_1+z_2=0$
, which contradicts with that
$z+z_1+z_2=0$
, which contradicts with that
 $\mathfrak {q}$
is negative.
$\mathfrak {q}$
is negative. -
-
(b) Otherwise, by Definition 4.2,
 $\gamma $
cuts out an angle
$\gamma $
cuts out an angle
 $\theta $
formed by the different end segments of
$\theta $
formed by the different end segments of
 $l^\circ $
; see the first picture in Figure 18. In this case, we have
$l^\circ $
; see the first picture in Figure 18. In this case, we have
 $l^\circ _s=l^\circ _t$
and
$l^\circ _s=l^\circ _t$
and
 $(l^\circ )^s=(l^\circ )^t$
, both with opposite orientations. The three angles
$(l^\circ )^s=(l^\circ )^t$
, both with opposite orientations. The three angles
 $\theta ,\theta _s$
and
$\theta ,\theta _s$
and
 $\theta ^t$
are different. We shall use the following notations; see the first picture in Figure 18.
$\theta ^t$
are different. We shall use the following notations; see the first picture in Figure 18.-
– Let r be the number of 3-arc segments of arcs in
 $\mathbf {R}$
that cut out the angles
$\mathbf {R}$
that cut out the angles
 $\theta _s$
,
$\theta _s$
,
 $\theta $
and
$\theta $
and
 $\theta ^t$
in order.
$\theta ^t$
in order. -
– Let n be the number of arc segments of arcs in
 $\mathbf {R}$
that cross
$\mathbf {R}$
that cross
 $l^\circ _s$
and cut out the angle at
$l^\circ _s$
and cut out the angle at
 $l^\circ _s(1)$
clockwise from
$l^\circ _s(1)$
clockwise from
 $l^\circ _s$
.
$l^\circ _s$
. -
– Let z be the number of 3-arc segments of arcs in
 $\mathbf {R}$
that cut out the angles
$\mathbf {R}$
that cut out the angles
 $\theta _s$
,
$\theta _s$
,
 $\theta $
and
$\theta $
and
 $\theta _s$
in order and are not incident to any point in
$\theta _s$
in order and are not incident to any point in
 $\mathbf {M}\cup \mathbf {P}$
.
$\mathbf {M}\cup \mathbf {P}$
. -
– Let
 $z_1$
be the number of 3-arc segments of arcs in
$z_1$
be the number of 3-arc segments of arcs in
 $\mathbf {R}$
that cut out the angles
$\mathbf {R}$
that cut out the angles
 $\theta _s$
,
$\theta _s$
,
 $\theta $
and
$\theta $
and
 $\theta _s$
in order and such that
$\theta _s$
in order and such that
 $l^\circ $
is the first or last arc in
$l^\circ $
is the first or last arc in
 $\mathbf {U}$
they cross.
$\mathbf {U}$
they cross.
Then
 $$\begin{align*}\operatorname{Int}^\circ(\mathbf{R},l^\circ)=2r+2z+2z_1,\end{align*}$$
$$\begin{align*}\operatorname{Int}^\circ(\mathbf{R},l^\circ)=2r+2z+2z_1,\end{align*}$$
 $$\begin{align*}\operatorname{Int}^\circ(\mathbf{R},f^-_{\mathbf{U}^\circ}(l^\circ))=2z+2n,\end{align*}$$
So we have
$$\begin{align*}\operatorname{Int}^\circ(\mathbf{R},f^-_{\mathbf{U}^\circ}(l^\circ))=2z+2n,\end{align*}$$
So we have $$\begin{align*}\operatorname{Int}^\circ(\mathbf{R},l^\circ_s)=r+n+2z+z_1.\end{align*}$$
Hence, flipping l is either convenient or neutral. When flipping l is neutral, we have
$$\begin{align*}\operatorname{Int}^\circ(\mathbf{R},l^\circ_s)=r+n+2z+z_1.\end{align*}$$
Hence, flipping l is either convenient or neutral. When flipping l is neutral, we have $$\begin{align*}\begin{array}{rl} &\operatorname{Int}^\circ(\mathbf{R},l^\circ)-\operatorname{Int}^\circ(\mathbf{R},f^-_{\mathbf{U}^\circ}(l^\circ)) \\ =&2r+2z_1-2n\\ =&2(\operatorname{Int}^\circ(\mathbf{R},l^\circ)-\operatorname{Int}^\circ(\mathbf{R},l^\circ_s))\geq0. \end{array}\end{align*}$$
$$\begin{align*}\begin{array}{rl} &\operatorname{Int}^\circ(\mathbf{R},l^\circ)-\operatorname{Int}^\circ(\mathbf{R},f^-_{\mathbf{U}^\circ}(l^\circ)) \\ =&2r+2z_1-2n\\ =&2(\operatorname{Int}^\circ(\mathbf{R},l^\circ)-\operatorname{Int}^\circ(\mathbf{R},l^\circ_s))\geq0. \end{array}\end{align*}$$
 $\operatorname {Int}^\circ (\mathbf {R},l^\circ )=\operatorname {Int}^\circ (\mathbf {R},l^\circ _s)$
, which implies that
$\operatorname {Int}^\circ (\mathbf {R},l^\circ )=\operatorname {Int}^\circ (\mathbf {R},l^\circ _s)$
, which implies that
 $l_s=l_t$
exists and is maximal, and
$l_s=l_t$
exists and is maximal, and
 $r+z_1=n$
. Since at least one of n and
$r+z_1=n$
. Since at least one of n and
 $z_1$
is zero, we have
$z_1$
is zero, we have
 $z_1=0$
and
$z_1=0$
and
 $r=n$
. So
$r=n$
. So
 $z\neq 0$
by the existence of a negative intersection
$z\neq 0$
by the existence of a negative intersection
 $\mathfrak {q}$
. If in addition, l is double, then
$\mathfrak {q}$
. If in addition, l is double, then
 $l^\circ _s=(l^\circ )^t$
(with opposite orientations) be the folded side that is enclosed by
$l^\circ _s=(l^\circ )^t$
(with opposite orientations) be the folded side that is enclosed by
 $l^\circ $
; see the second picture of Figure 18. Then any arc in
$l^\circ $
; see the second picture of Figure 18. Then any arc in
 $\mathbf {R}$
cuts out one of
$\mathbf {R}$
cuts out one of
 $\theta _s$
,
$\theta _s$
,
 $\theta $
and
$\theta $
and
 $\theta ^t$
can only cut out these three angles (by the
$\theta ^t$
can only cut out these three angles (by the
 $\mathbf {U}$
-co-standard property) and hence does not exist. This contradicts
$\mathbf {U}$
-co-standard property) and hence does not exist. This contradicts
 $z\neq 0$
.
$z\neq 0$
.
-
Now we are ready to complete the proof of Lemma 5.15.
We use induction hypothesis on
![]() $\operatorname {Int}^\circ (\mathbf {R},\mathbf {U}^\circ )$
. For the starting case
$\operatorname {Int}^\circ (\mathbf {R},\mathbf {U}^\circ )$
. For the starting case
![]() $\operatorname {Int}^\circ (\mathbf {R},\mathbf {U}^\circ )=0$
, since
$\operatorname {Int}^\circ (\mathbf {R},\mathbf {U}^\circ )=0$
, since
![]() $\mathbf {R}$
is connected to the boundary, there is a tagged arc
$\mathbf {R}$
is connected to the boundary, there is a tagged arc
![]() $\gamma ^{\prime }\in \mathbf {R}$
which has an endpoint in
$\gamma ^{\prime }\in \mathbf {R}$
which has an endpoint in
![]() $\mathbf {M}$
. By definition,
$\mathbf {M}$
. By definition,
![]() $\gamma ^{\prime }$
is not adjoint to any arc in
$\gamma ^{\prime }$
is not adjoint to any arc in
![]() $\mathbf {U}$
. So the assertion holds by Lemma 5.19.
$\mathbf {U}$
. So the assertion holds by Lemma 5.19.
Suppose the assertion holds when
![]() $\operatorname {Int}^\circ (\mathbf {R},\mathbf {U}^\circ )\leq k-1$
for some
$\operatorname {Int}^\circ (\mathbf {R},\mathbf {U}^\circ )\leq k-1$
for some
![]() $k\geq 1$
, and consider the case when
$k\geq 1$
, and consider the case when
![]() $\operatorname {Int}^\circ (\mathbf {R},\mathbf {U}^\circ )=k$
.
$\operatorname {Int}^\circ (\mathbf {R},\mathbf {U}^\circ )=k$
.
Let l be a maximal arc in
![]() $\mathbf {U}$
. Then
$\mathbf {U}$
. Then
![]() $\operatorname {Int}^\circ (\mathbf {R},l^\circ )\neq 0$
. By Lemma 4.10, the set
$\operatorname {Int}^\circ (\mathbf {R},l^\circ )\neq 0$
. By Lemma 4.10, the set
is nonempty. For any
![]() $\gamma \in \mathbf {R}(l)$
, if
$\gamma \in \mathbf {R}(l)$
, if
![]() $\gamma $
is adjoint to
$\gamma $
is adjoint to
![]() $\mathbf {U}$
, then by Lemma 5.20, the assertion follows; if
$\mathbf {U}$
, then by Lemma 5.20, the assertion follows; if
![]() $\gamma $
is not adjoint to
$\gamma $
is not adjoint to
![]() $\mathbf {U}$
and
$\mathbf {U}$
and
![]() $\operatorname {Int}^\circ (\gamma ,\mathbf {U}^\circ )=0$
, then the assertion follows by Lemma 5.19. Hence, we only need to deal with the following case.
$\operatorname {Int}^\circ (\gamma ,\mathbf {U}^\circ )=0$
, then the assertion follows by Lemma 5.19. Hence, we only need to deal with the following case.
-
(*) For any maximal
 $l\in \mathbf {U}$
and any
$l\in \mathbf {U}$
and any
 $\gamma \in \mathbf {R}(l)$
, we have
$\gamma \in \mathbf {R}(l)$
, we have
 $\operatorname {Int}^\circ (\gamma ,\mathbf {U}^\circ )\neq 0$
.
$\operatorname {Int}^\circ (\gamma ,\mathbf {U}^\circ )\neq 0$
.
Note that in this case, each
![]() $\gamma \in \mathbf {R}(l)$
has an alternative intersection with
$\gamma \in \mathbf {R}(l)$
has an alternative intersection with
![]() $l^\circ $
by Remark 4.5 and any such alternative intersection is interior by Lemma 5.21. So by Lemma 5.22, each maximal arc in
$l^\circ $
by Remark 4.5 and any such alternative intersection is interior by Lemma 5.21. So by Lemma 5.22, each maximal arc in
![]() $\mathbf {U}$
is either flip-convenient or flip-neutral. We use the induction on the minimum number m satisfying that there exists
$\mathbf {U}$
is either flip-convenient or flip-neutral. We use the induction on the minimum number m satisfying that there exists
![]() $\gamma \in \mathbf {R}$
which crosses
$\gamma \in \mathbf {R}$
which crosses
![]() $l_1^\circ ,\cdots ,l_m^\circ \in \mathbf {U}^\circ $
in succession, at
$l_1^\circ ,\cdots ,l_m^\circ \in \mathbf {U}^\circ $
in succession, at
![]() $\mathfrak {q}_1,\cdots ,\mathfrak {q}_m$
, respectively, such that
$\mathfrak {q}_1,\cdots ,\mathfrak {q}_m$
, respectively, such that
-
(1)
 $\mathfrak {q}_1,\cdots ,\mathfrak {q}_m$
are interior, with only
$\mathfrak {q}_1,\cdots ,\mathfrak {q}_m$
are interior, with only
 $\mathfrak {q}_m$
is alternative, and
$\mathfrak {q}_m$
is alternative, and -
(2)
 $l_1^\circ ,\cdots ,l_m^\circ $
are maximal in
$l_1^\circ ,\cdots ,l_m^\circ $
are maximal in
 $\mathbf {U}$
, but the previous arc
$\mathbf {U}$
, but the previous arc
 $l_0^\circ $
(if exists) in
$l_0^\circ $
(if exists) in
 $\mathbf {U}^\circ $
that
$\mathbf {U}^\circ $
that
 $\gamma $
crosses before
$\gamma $
crosses before
 $l_1^\circ $
is not.
$l_1^\circ $
is not.
Note that m is well defined because some arc in
![]() $\mathbf {R}$
has an interior alternative intersection with
$\mathbf {R}$
has an interior alternative intersection with
![]() $\widetilde {l}^\circ $
for a maximal arc
$\widetilde {l}^\circ $
for a maximal arc
![]() $\widetilde {l}\in \mathbf {U}$
, and hence, we can track along
$\widetilde {l}\in \mathbf {U}$
, and hence, we can track along
![]() $\gamma $
to get a sequence satisfying the conditions above (although
$\gamma $
to get a sequence satisfying the conditions above (although
![]() $\widetilde {l}$
may be one of
$\widetilde {l}$
may be one of
![]() $l_1,\cdots ,l_m$
); see Figure 19.
$l_1,\cdots ,l_m$
); see Figure 19.
Figure 19 The conditions for the definition of m.
We denote
![]() $l=l_m$
and, without loss of generality, assume that
$l=l_m$
and, without loss of generality, assume that
![]() $\mathfrak {q}_m$
is negative. For the starting case
$\mathfrak {q}_m$
is negative. For the starting case
![]() $m=1$
, if flipping l is neutral, then by Lemma 5.22,
$m=1$
, if flipping l is neutral, then by Lemma 5.22,
![]() $\mathfrak {q}_1$
is not an endpoint of an end arc segment of
$\mathfrak {q}_1$
is not an endpoint of an end arc segment of
![]() $\gamma $
divided by
$\gamma $
divided by
![]() $\mathbf {U}^\circ $
, and both
$\mathbf {U}^\circ $
, and both
![]() $l_s^\circ $
and
$l_s^\circ $
and
![]() $l_t^\circ $
exist and are maximal. However, in this case, either
$l_t^\circ $
exist and are maximal. However, in this case, either
![]() $l_s^\circ $
or
$l_s^\circ $
or
![]() $l_t^\circ $
is
$l_t^\circ $
is
![]() $l_0^\circ $
which is not maximal, a contradiction. So flipping l is convenient, and the assertion holds by the induction hypothesis on
$l_0^\circ $
which is not maximal, a contradiction. So flipping l is convenient, and the assertion holds by the induction hypothesis on
![]() $\operatorname {Int}^\circ (\mathbf {R},\mathbf {U}^\circ )$
.
$\operatorname {Int}^\circ (\mathbf {R},\mathbf {U}^\circ )$
.
Suppose the assertion holds when
![]() $m<k^{\prime }$
for some
$m<k^{\prime }$
for some ![]() and consider the case when
and consider the case when
![]() $m=k^{\prime }$
. Let O be the common endpoint of
$m=k^{\prime }$
. Let O be the common endpoint of
![]() $l_1^\circ ,\cdots ,l_m^\circ $
and fix the orientation of
$l_1^\circ ,\cdots ,l_m^\circ $
and fix the orientation of
![]() $l_m^\circ $
with O as the starting point; see Figure 19. Since if flipping l is convenient then the assertion follows by the induction hypothesis on
$l_m^\circ $
with O as the starting point; see Figure 19. Since if flipping l is convenient then the assertion follows by the induction hypothesis on
![]() $\operatorname {Int}^\circ (\mathbf {R},\mathbf {U}^\circ )$
, in what follows, we assume that flipping l is neutral. By Lemma 5.22, l is single,
$\operatorname {Int}^\circ (\mathbf {R},\mathbf {U}^\circ )$
, in what follows, we assume that flipping l is neutral. By Lemma 5.22, l is single,
![]() $\mathfrak {q}_m$
is not an endpoint of an end arc segment of
$\mathfrak {q}_m$
is not an endpoint of an end arc segment of
![]() $\gamma $
divided by
$\gamma $
divided by
![]() $\mathbf {U}^\circ $
, and both
$\mathbf {U}^\circ $
, and both
![]() $l^\circ _s$
and
$l^\circ _s$
and
![]() $l^\circ _t$
exist and maximal. It follows that the next intersection
$l^\circ _t$
exist and maximal. It follows that the next intersection
![]() $\mathfrak {q}_{m+1}$
of
$\mathfrak {q}_{m+1}$
of
![]() $\gamma $
with
$\gamma $
with
![]() $\mathbf {U}^\circ $
after
$\mathbf {U}^\circ $
after
![]() $\mathfrak {q}_m$
is also interior and with a maximal arc
$\mathfrak {q}_m$
is also interior and with a maximal arc
![]() $l_{m+1}^\circ \in \mathbf {U}^\circ $
. For any
$l_{m+1}^\circ \in \mathbf {U}^\circ $
. For any
![]() $(l^{\prime })^\circ \in \mathbf {U}^\circ $
, let
$(l^{\prime })^\circ \in \mathbf {U}^\circ $
, let
Note that we have
![]() $|\mathfrak {q}((l^{\prime })^\circ )|\leq 2$
, and the equality holds only if
$|\mathfrak {q}((l^{\prime })^\circ )|\leq 2$
, and the equality holds only if
![]() $(l^{\prime })^\circ $
is a loop at O. Depending on
$(l^{\prime })^\circ $
is a loop at O. Depending on
![]() $l^\circ $
being whether
$l^\circ $
being whether
![]() $l^\circ _{m+1}$
,
$l^\circ _{m+1}$
,
![]() $l^\circ _{m-1}$
or not, there are the following three cases.
$l^\circ _{m-1}$
or not, there are the following three cases.
-
(1) Suppose
 $l^\circ =l_{m+1}^\circ $
. Then
$l^\circ =l_{m+1}^\circ $
. Then
 $l^\circ $
cuts out an angle
$l^\circ $
cuts out an angle
 $\theta $
by its two ends,
$\theta $
by its two ends,
 $|\mathfrak {q}(l^\circ )|=1$
and
$|\mathfrak {q}(l^\circ )|=1$
and
 $l^\circ _t=l^\circ _s=l^\circ _{m-1}$
. If
$l^\circ _t=l^\circ _s=l^\circ _{m-1}$
. If
 $|\mathfrak {q}(l^\circ _s)|=2$
, then there is
$|\mathfrak {q}(l^\circ _s)|=2$
, then there is
 $1\leq i\leq m-2$
such that
$1\leq i\leq m-2$
such that
 $l^\circ _{m-1}=l^\circ _i$
; see the first picture in Figure 20. Similarly as in the case (b) in the proof of Lemma 5.22 (cf. the first picture of Figure 18), we denote
$l^\circ _{m-1}=l^\circ _i$
; see the first picture in Figure 20. Similarly as in the case (b) in the proof of Lemma 5.22 (cf. the first picture of Figure 18), we denote
Figure 20 The case
 $l^\circ =l_{m+1}^\circ $
.
$l^\circ =l_{m+1}^\circ $
.-
○ z the number of 3-arc segments of arcs in
 $\mathbf {R}$
that cut out the angle
$\mathbf {R}$
that cut out the angle
 $\theta _s$
,
$\theta _s$
,
 $\theta $
and
$\theta $
and
 $\theta _s$
in order and are not incident to any point in
$\theta _s$
in order and are not incident to any point in
 $\mathbf {M}\cup \mathbf {P}$
;
$\mathbf {M}\cup \mathbf {P}$
; -
○ r the number of 3-arc segments of arcs in
 $\mathbf {R}$
that cut out the angle
$\mathbf {R}$
that cut out the angle
 $\theta ^t, \theta $
and
$\theta ^t, \theta $
and
 $\theta _s$
, and
$\theta _s$
, and -
○ n the number of arc segments of arcs in
 $\mathbf {R}$
that cross
$\mathbf {R}$
that cross
 $l^\circ _s$
and cut out the angle at
$l^\circ _s$
and cut out the angle at
 $l^\circ _s(1)$
clockwise from
$l^\circ _s(1)$
clockwise from
 $l^\circ _s$
.
$l^\circ _s$
.
Since any arcs in
 $\mathbf {R}$
have no intersections with each other, we have
$\mathbf {R}$
have no intersections with each other, we have
 $n\geq r+1$
in this case. So and
$n\geq r+1$
in this case. So and $$\begin{align*}\operatorname{Int}(\mathbf{R},l^\circ)=2z+2r\end{align*}$$
which contradicts with
$$\begin{align*}\operatorname{Int}(\mathbf{R},l^\circ)=2z+2r\end{align*}$$
which contradicts with
 $l^\circ $
is maximal. So
$l^\circ $
is maximal. So
 $|\mathfrak {q}(l_s^\circ )|=1$
in this case, see the second picture in Figure 20. Then after flipping l, the value m decreases. If we are no longer in the case (
$|\mathfrak {q}(l_s^\circ )|=1$
in this case, see the second picture in Figure 20. Then after flipping l, the value m decreases. If we are no longer in the case (
 $\ast $
), then we are already done. If we are still in the case (
$\ast $
), then we are already done. If we are still in the case (
 $\ast $
), then by applying the induction hypothesis on m, we get the assertion.
$\ast $
), then by applying the induction hypothesis on m, we get the assertion.
-
-
(2) Suppose
 $l^\circ =l^\circ _{m-1}$
. Then
$l^\circ =l^\circ _{m-1}$
. Then
 $l^\circ $
cuts out an angle
$l^\circ $
cuts out an angle
 $\theta $
by its two ends and
$\theta $
by its two ends and
 $|\mathfrak {q}(l^\circ )|=2$
. So
$|\mathfrak {q}(l^\circ )|=2$
. So
 $l_t^\circ =l_s^\circ =l_{m+1}^\circ =l_{m-2}^\circ $
. Since flipping l is neutral, by Lemma 5.22,
$l_t^\circ =l_s^\circ =l_{m+1}^\circ =l_{m-2}^\circ $
. Since flipping l is neutral, by Lemma 5.22,
 $l_{m+1}^\circ =l_s^\circ $
is maximal. But
$l_{m+1}^\circ =l_s^\circ $
is maximal. But
 $l^\circ _0$
(if exists) is not maximal, so we have
$l^\circ _0$
(if exists) is not maximal, so we have
 $m-2\geq 1$
. Then
$m-2\geq 1$
. Then
 $|\mathfrak {q}(l_t^\circ )|\geq 1$
. The same argument in the above case
$|\mathfrak {q}(l_t^\circ )|\geq 1$
. The same argument in the above case
 $l^\circ =l^\circ _{m+1}$
can be used in the current case (see Figure 21) to get the required assertion.
$l^\circ =l^\circ _{m+1}$
can be used in the current case (see Figure 21) to get the required assertion.
Figure 21 The case
 $l^\circ =l_{m-1}^\circ $
.
$l^\circ =l_{m-1}^\circ $
.
Figure 22 The case
 $|\mathfrak {q}(l)|=|\mathfrak {q}(l_t)|=2$
.
$|\mathfrak {q}(l)|=|\mathfrak {q}(l_t)|=2$
.
Figure 23 The case
 $|\mathfrak {q}(l)|=2$
,
$|\mathfrak {q}(l)|=2$
,
 $|\mathfrak {q}(l_t)|=1$
.
$|\mathfrak {q}(l_t)|=1$
.
Figure 24 The case
 $|\mathfrak {q}(l^\circ )|=1$
,
$|\mathfrak {q}(l^\circ )|=1$
,
 $|\mathfrak {q}(l_t^\circ )|=1$
.
$|\mathfrak {q}(l_t^\circ )|=1$
. -
(3) Suppose that
 $l^\circ $
is neither
$l^\circ $
is neither
 $l_{m+1}^\circ $
nor
$l_{m+1}^\circ $
nor
 $l_{m-1}^\circ $
. Then
$l_{m-1}^\circ $
. Then
 $l^\circ _t=l^\circ _{m+1}$
,
$l^\circ _t=l^\circ _{m+1}$
,
 $l^\circ _s=l^\circ _{m-1}$
and
$l^\circ _s=l^\circ _{m-1}$
and
 $|\mathfrak {q}(l_t^\circ )|\leq |\mathfrak {q}(l^\circ )|$
. We shall use the notations in case (a) in the proof of Lemma 5.22; that is, we denote
$|\mathfrak {q}(l_t^\circ )|\leq |\mathfrak {q}(l^\circ )|$
. We shall use the notations in case (a) in the proof of Lemma 5.22; that is, we denote-
○
 $r_1$
(resp.
$r_1$
(resp.
 $r_2$
) the number of 2-arc segments of arcs in
$r_2$
) the number of 2-arc segments of arcs in
 $\mathbf {R}$
that cut out the angles
$\mathbf {R}$
that cut out the angles
 $\theta _t$
and
$\theta _t$
and
 $\theta ^t$
(resp.
$\theta ^t$
(resp.
 $\theta _s$
and
$\theta _s$
and
 $\theta ^s$
) and whose arc segment cutting out
$\theta ^s$
) and whose arc segment cutting out
 $\theta _t$
(resp.
$\theta _t$
(resp.
 $\theta _s$
) do not have an endpoint in
$\theta _s$
) do not have an endpoint in
 $\mathbf {M}\cup \mathbf {P}$
;
$\mathbf {M}\cup \mathbf {P}$
; -
○
 $n_1$
(resp.
$n_1$
(resp.
 $n_2$
) the number of arc segments of arcs in
$n_2$
) the number of arc segments of arcs in
 $\mathbf {R}$
that cross
$\mathbf {R}$
that cross
 $l^\circ _t$
(resp.
$l^\circ _t$
(resp.
 $l^\circ _s$
) and cut out the angle at
$l^\circ _s$
) and cut out the angle at
 $l^\circ _t(0)$
(resp.
$l^\circ _t(0)$
(resp.
 $l^\circ _s(1)$
) clockwise from
$l^\circ _s(1)$
) clockwise from
 $l^\circ _t$
(resp.
$l^\circ _t$
(resp.
 $l^\circ _s$
);
$l^\circ _s$
); -
○ z the number of 2-arc segments of arcs in
 $\mathbf {R}$
that cut out the angles
$\mathbf {R}$
that cut out the angles
 $\theta _s$
and
$\theta _s$
and
 $\theta _t$
and are not incident to any point in
$\theta _t$
and are not incident to any point in
 $\mathbf {M}\cup \mathbf {P}$
.
$\mathbf {M}\cup \mathbf {P}$
.
There are the following cases.
-
(a)
 $|\mathfrak {q}(l^\circ )|=2$
, that is, there is
$|\mathfrak {q}(l^\circ )|=2$
, that is, there is
 $1\leq k\leq m-2$
such that
$1\leq k\leq m-2$
such that
 $l^\circ =l_k^\circ $
. If
$l^\circ =l_k^\circ $
. If
 $k=1$
, then
$k=1$
, then
 $l^\circ _0$
exists and is the same as
$l^\circ _0$
exists and is the same as
 $l^\circ _{m+1}$
. Note that
$l^\circ _{m+1}$
. Note that
 $l^\circ _0$
is not maximal but
$l^\circ _0$
is not maximal but
 $l^\circ _{m+1}$
is maximal, a contradiction. So we have
$l^\circ _{m+1}$
is maximal, a contradiction. So we have
 $k\neq 1$
and
$k\neq 1$
and
 $l^\circ _{m+1}=l^\circ _{k-1}$
. Then
$l^\circ _{m+1}=l^\circ _{k-1}$
. Then
 $|\mathfrak {q}(l^\circ _t)|\geq 1$
. If
$|\mathfrak {q}(l^\circ _t)|\geq 1$
. If
 $|\mathfrak {q}(l^\circ _t)|=2$
, then there is
$|\mathfrak {q}(l^\circ _t)|=2$
, then there is
 $1\leq i< m$
,
$1\leq i< m$
,
 $i\neq k-1,k$
, such that
$i\neq k-1,k$
, such that
 $l^\circ _{k-1}=l^\circ _i$
; see the pictures of Figure 22, where the left is for
$l^\circ _{k-1}=l^\circ _i$
; see the pictures of Figure 22, where the left is for
 $1\leq i<k-1$
and the right is for
$1\leq i<k-1$
and the right is for
 $k<i<m$
. Since arcs in
$k<i<m$
. Since arcs in
 $\mathbf {R}$
do not cross each other in the interior, we have
$\mathbf {R}$
do not cross each other in the interior, we have
 $n_1\geq r_2+1$
. Hence, and
$n_1\geq r_2+1$
. Hence, and $$\begin{align*}\operatorname{Int}(\mathbf{R},l^\circ)=r_1+r_2+z,\end{align*}$$
contradicts to
$$\begin{align*}\operatorname{Int}(\mathbf{R},l^\circ)=r_1+r_2+z,\end{align*}$$
contradicts to
 $l^\circ $
is maximal. So in this case, we have
$l^\circ $
is maximal. So in this case, we have
 $|\mathfrak {q}(l^\circ _t)|=1$
(see Figure 23), where the left picture is for
$|\mathfrak {q}(l^\circ _t)|=1$
(see Figure 23), where the left picture is for
 $|\mathfrak {q}(l_{m-1}^\circ )|=1$
and the right one is for
$|\mathfrak {q}(l_{m-1}^\circ )|=1$
and the right one is for
 $|\mathfrak {q}(l_{m-1}^\circ )|=2$
. Then after flipping l, the value m decreases 2 for the left picture and decreases 1 for the right picture. If we are no longer in the case
$|\mathfrak {q}(l_{m-1}^\circ )|=2$
. Then after flipping l, the value m decreases 2 for the left picture and decreases 1 for the right picture. If we are no longer in the case
 $(\ast )$
, then we are already done. If we are still in the case
$(\ast )$
, then we are already done. If we are still in the case
 $(\ast )$
, then applying the induction hypothesis on m, we get the assertion.
$(\ast )$
, then applying the induction hypothesis on m, we get the assertion.
-
(b)
 $|\mathfrak {q}(l^\circ )|=1$
. Then
$|\mathfrak {q}(l^\circ )|=1$
. Then
 $|\mathfrak {q}(l_{m+1}^\circ )|\leq 1$
. If
$|\mathfrak {q}(l_{m+1}^\circ )|\leq 1$
. If
 $|\mathfrak {q}(l_{m+1}^\circ )|=1$
, then there is
$|\mathfrak {q}(l_{m+1}^\circ )|=1$
, then there is
 $1\leq i\leq m-1$
such that
$1\leq i\leq m-1$
such that
 $l_{m+1}^\circ =l_i^\circ $
; see Figure 24. Since arcs in
$l_{m+1}^\circ =l_i^\circ $
; see Figure 24. Since arcs in
 $\mathbf {R}$
do not cross each other in the interior, we have
$\mathbf {R}$
do not cross each other in the interior, we have
 $n_1\geq r_2+1$
. Hence, and
$n_1\geq r_2+1$
. Hence, and $$\begin{align*}\operatorname{Int}(\mathbf{R},l^\circ)=r_1+r_2+z,\end{align*}$$
contradicts to
$$\begin{align*}\operatorname{Int}(\mathbf{R},l^\circ)=r_1+r_2+z,\end{align*}$$
contradicts to
 $l^\circ $
is maximal. So in this case, we have
$l^\circ $
is maximal. So in this case, we have
 $|\mathfrak {q}(l^\circ _{m+1})|=0$
. There are the following two subcases
$|\mathfrak {q}(l^\circ _{m+1})|=0$
. There are the following two subcases
-
(i)
 $|\mathfrak {q}(l^\circ _{m-1})|=1$
; see the first picture in Figure 25. Then after flipping l, the value m decreases
$|\mathfrak {q}(l^\circ _{m-1})|=1$
; see the first picture in Figure 25. Then after flipping l, the value m decreases
 $1$
. If we are no longer in the case
$1$
. If we are no longer in the case
 $(\ast )$
, then we are already done. If we are still in the case
$(\ast )$
, then we are already done. If we are still in the case
 $(\ast )$
, then applying the induction hypothesis on m, we get the assertion.
$(\ast )$
, then applying the induction hypothesis on m, we get the assertion.
Figure 25 The case
 $|\mathfrak {q}(l^\circ )|=1$
,
$|\mathfrak {q}(l^\circ )|=1$
,
 $|\mathfrak {q}(l_{m+1}^\circ )|=0$
.
$|\mathfrak {q}(l_{m+1}^\circ )|=0$
. -
(ii)
 $|\mathfrak {q}(l^\circ _{m-1})|=2$
, that is, there is
$|\mathfrak {q}(l^\circ _{m-1})|=2$
, that is, there is
 $1\leq i< m-1$
such that
$1\leq i< m-1$
such that
 $l_{m-1}^\circ =l_i^\circ $
; see the second picture in Figure 25. Then after flipping l, the value m does not change. If we are no longer in the case
$l_{m-1}^\circ =l_i^\circ $
; see the second picture in Figure 25. Then after flipping l, the value m does not change. If we are no longer in the case
 $(\ast )$
, then we are already done. If we are still in the case
$(\ast )$
, then we are already done. If we are still in the case
 $(\ast )$
, then we go back to cases (2) and (3.a). So we are also done.
$(\ast )$
, then we go back to cases (2) and (3.a). So we are also done.
-
-
Competing interest
None.
Financial Support
This research was supported by National Natural Science Foundation of China (Grants No. 12271279, 12031007, 12371034).