Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T03:17:13.310Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonspecial varieties and generalised Lang–Vojta conjectures

Part of: Arithmetic problems. Diophantine geometry Holomorphic functions of several complex variables Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  10 February 2021

Erwan Rousseau ,
Amos Turchet Open the ORCID record for Amos Turchet [Opens in a new window]  and
Julie Tzu-Yueh Wang
Erwan Rousseau
Affiliation:
Institut Universitaire de France & Aix-Marseille Université, CNRS, Centrale Marseille, I2M, Marseille, France; E-mail: erwan.rousseau@univ-amu.fr Freiburg Institute for Advanced Studies, University of Freiburg, Albertstr. 19, 79104Freiburg, Germany
Amos Turchet
Affiliation:
Dipartimento di Matematica e Fisica, Universitá degli studi Roma 3, L.go S. L. Murialdo 1, 00146Roma, Italy; E-mail: amos.turchet@uniroma3.it
Julie Tzu-Yueh Wang
Affiliation:
Institute of Mathematics, Academia Sinica No. 1, Sec. 4, Roosevelt Road Taipei10617, Taiwan; E-mail: jwang@math.sinica.edu.tw

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We construct a family of fibred threefolds 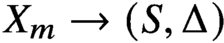$X_m \to (S , \Delta )$ such that 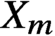$X_m$ has no étale cover that dominates a variety of general type but it dominates the orbifold 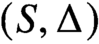$(S,\Delta )$ of general type. Following Campana, the threefolds 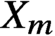$X_m$ are called weakly special but not special. The Weak Specialness Conjecture predicts that a weakly special variety defined over a number field has a potentially dense set of rational points. We prove that if m is big enough, the threefolds 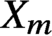$X_m$ present behaviours that contradict the function field and analytic analogue of the Weak Specialness Conjecture. We prove our results by adapting the recent method of Ru and Vojta. We also formulate some generalisations of known conjectures on exceptional loci that fit into Campana’s program and prove some cases over function fields.

Keywords

Campana’s conjecturesFunction fieldsNevanlinna TheoryOrbifoldsHyperbolicity

MSC classification

Primary: 14G40: Arithmetic varieties and schemes; Arakelov theory; heights
Secondary: 11J97: Analogues of methods in Nevanlinna theory (work of Vojta et al.) 14G05: Rational points 32A22: Nevanlinna theory (local); growth estimates; other inequalities
Type
Algebraic and Complex Geometry
Information
Forum of Mathematics, Sigma , Volume 9 , 2021 , e11
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Ascher, K., DeVleming, K. and Turchet, A., ‘Hyperbolicity and uniformity of varieties of log general type’, International Mathematics Research Notices, 2020, published online. https://doi.org/10.1093/imrn/rnaa186CrossRefGoogle Scholar
Autissier, P., ‘Sur la non-densité des points entiers’, Duke Math. J. 158(1) (2011), 13–27.CrossRefGoogle Scholar
Bombieri, E. and Gubler, W., Heights in Diophantine Geometry, New Mathematical Monographs, 4 (Cambridge University Press, Cambridge, 2006).Google Scholar
Bogomolov, F. A., ‘Holomorphic tensors and vector bundles on projective varieties’, Math. USSR Izv. 13 (1979), 499–555.CrossRefGoogle Scholar
Bianco, F. Lo, E. Rousseau and F. Touzet, ‘Symmetries of transversely projective foliations’, Preprint, 2019, arXiv:1901.05656.Google Scholar
Bogomolov, F. and Tschinkel, Y., ‘Special elliptic fibrations’, in The Fano Conference (University of Torino, Turin, Italy, 2004), 223–234.Google Scholar
Campana, F., ‘Orbifolds, special varieties and classification theory’, Ann. Inst. Fourier (Grenoble) 54(3) (2004), 499–630.CrossRefGoogle Scholar
Campana, F., ‘Orbifoldes géométriques spéciales et classification biméromorphe des variétés kählériennes compactes’, J. Inst. Math. Jussieu 10(4) (2011), 809–934.CrossRefGoogle Scholar
X., Chen, ‘On algebraic hyperbolicity of log varieties’, Commun. Contemp. Math. 6(4) (2004), 513–559.Google Scholar
Campana, F. and Păun, M., ‘Variétés faiblement spéciales à courbes entières dégénérées’, Compos. Math. 143(1) (2007), 95–111.CrossRefGoogle Scholar
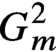Capuano, L. and Turchet, A., ‘Lang–Vojta conjecture over function fields for surfaces dominating ${G}_m^2$’, Preprint, 2019, arXiv:1911.07562.Google Scholar
Corvaja, P. and Zannier, U., ‘On integral points on surfaces’, Ann. of Math. (2) 160(2) (2004), 705–726.CrossRefGoogle Scholar
Corvaja, P. and Zannier, U., ‘Some cases of Vojta’s Conjecture on integral points over function fields’, J. Algebraic Geometry 17 (2008), 195–333.CrossRefGoogle Scholar
Corvaja, P. and Zannier, U., ‘Integral points, divisibility between values of polynomials and entire curves on surfaces’, Adv. Math. 225(2) (2010), 1095–1118.CrossRefGoogle Scholar
Corvaja, P. and Zannier, U., ‘Algebraic hyperbolicity of ramified covers of ${G}_m^2$ (and integral points on affine subsets of ${\mathbb{P}}_2$), J. Differential Geom. 93(3) (2013), 355–377.CrossRefGoogle Scholar
Demailly, J.-P., ‘Algebraic criteria for Kobayashi hyperbolic projective varieties and jet differentials’, in Algebraic geometry—Santa Cruz 1995, Proceedings of Symposia in Pure Mathematics, 62, (American Mathematical Society, Providence, RI, 1997), 285–360.CrossRefGoogle Scholar
Faltings, G., ‘The general case of S. Lang’s conjecture’, in Barsotti Symposium in Algebraic Geometry (Abano Terme, 1991), Perspectives in Mathematics, 15 (Academic Press, San Diego, 1994), 175–182.CrossRefGoogle Scholar
Friedman, R. and Morgan, J. W.. Smooth Four-Manifolds and Complex Surfaces, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), 27 (Springer-Verlag, Berlin, 1994).CrossRefGoogle Scholar
Grauert, H., ‘Mordells Vermutung über rationale Punkte auf algebraischen Kurven und Funktionenkörper’, Publ. Math. Inst. Hautes Études Sci. 25 (1965), 131–149.CrossRefGoogle Scholar
Guo, J. and Wang, J. T.-Y., ‘Asymptotic gcd and divisible sequences for entire functions’, Trans. Amer. Math. Soc. 371(9) (2019), 6241–6256.CrossRefGoogle Scholar
Hussein, S. and Ru, M., ‘A general defect relation and height inequality for divisors in subgeneral position’, Asian J. Math. 22(3) (2018), 477–491.CrossRefGoogle Scholar
Hindry, M. and Silverman, J. H., Diophantine Geometry, Graduate Texts in Mathematics, 201 (Springer-Verlag, New York, 2000). An introduction.CrossRefGoogle Scholar
Harris, J. and Tschinkel, Y., ‘Rational points on quartics’, Duke Math. J. 104(3) (2000), 477–500.Google Scholar
Hassett, B. and Tschinkel, Y., ‘Density of integral points on algebraic varieties’, in Rational Points on Algebraic Varieties, Progress in Mathematics, 199, (Birkhäuser, Basel, 2001), 169–197.CrossRefGoogle Scholar
Javanpeykar, A. and Xie, J., ‘Finiteness properties of pseudo-hyperbolic varieties’, International Mathematics Research Notices, 2020, published online. https://doi.org/10.1093/imrn/rnaa168CrossRefGoogle Scholar
Kawamata, Y., ‘On Bloch’s conjecture’, Invent. Math. 57(1) (1980), 97–100.CrossRefGoogle Scholar
Lang, S., ‘Hyperbolic and Diophantine analysis’, Bull. Amer. Math. Soc. (N.S.) 14(2) (1986), 159–205.CrossRefGoogle Scholar
Lang, S., Number Theory, III – Diophantine Geometry, Encyclopaedia of Mathematical Sciences, 60 (Springer-Verlag, Berlin, 1991).Google Scholar
Lazarsfeld, R., Positivity in Algebraic Geometry. I, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), 48 (Springer-Verlag, Berlin, 2004).Google Scholar
Levin, A.. ‘Generalizations of Siegel’s and Picard’s theorems’, Ann. of Math. (2) 170(2) (2009), 609–655.CrossRefGoogle Scholar
Manin, Ju. I., ‘Proof of an analogue of Mordell’s conjecture for algebraic curves over function fields’, Dokl. Akad. Nauk SSSR 152 (1963), 1061–1063.Google Scholar
McQuillan, M., ‘Diophantine approximations and foliations’, Publ. Math. Inst. Hautes Études Sci. 87 (1998), 121–174.CrossRefGoogle Scholar
Noguchi, J., ‘A higher-dimensional analogue of Mordell’s conjecture over function fields’, Math. Ann. 258(2) (1981/82), 207–212.CrossRefGoogle Scholar
Rousseau, E., ‘Hyperbolicity of geometric orbifolds’, Trans. Amer. Math. Soc. 362(7) (2010), 3799–3826.CrossRefGoogle Scholar
Ru, M., ‘On a general form of the second main theorem’, Trans. Amer. Math. Soc. 349(12) (1997), 5093–5105.CrossRefGoogle Scholar
Ru, M. and Vojta, P., ‘A birational Nevanlinna constant and its consequences’, Am. J. Math. 142(3) (2020), 957–991.CrossRefGoogle Scholar
Turchet, A., ‘Fibered threefolds and Lang-Vojta’s conjecture over function fields’, Trans. Amer. Math. Soc. 369(12) (2017), 8537–8558.CrossRefGoogle Scholar
van Bommel, R., A. Javanpeykar and L. Kamenova, ‘Boundedness in families with applications to arithmetic hyperbolicity’, Preprint, 2019, arXiv:1907.11225.Google Scholar
Vojta, P., ‘Diophantine approximation and Nevanlinna theory’, in Arithmetic Geometry, Lecture Notes in Mathematics, 2009 (Springer, Berlin, 2011), 111–224.Google Scholar
Vojta, P., Diophantine Approximations and Value Distribution Theory, Lecture Notes in Mathematics, 1239 (Springer, Berlin, 1987).CrossRefGoogle Scholar
Vojta, P., ‘On Cartan’s theorem and Cartan’s conjecture’, Amer. J. Math. 119(1) (1997), 1–17.CrossRefGoogle Scholar
Wang, J. T.-Y., ‘An effective Schmidt’s subspace theorem over function fields’, Math. Z. 246(4) (2004), 811–844.CrossRefGoogle Scholar
Yamanoi, K., ‘Holomorphic curves in algebraic varieties of maximal Albanese dimension’, Internat. J. Math. 26(6) (2015), 1541006.CrossRefGoogle Scholar