Article contents
On n-dependent groups and fields II
Published online by Cambridge University Press: 07 May 2021
Abstract
We continue the study of n-dependent groups, fields and related structures, largely motivated by the conjecture that every n-dependent field is dependent. We provide evidence toward this conjecture by showing that every infinite n-dependent valued field of positive characteristic is henselian, obtaining a variant of Shelah’s Henselianity Conjecture in this case and generalizing a recent result of Johnson for dependent fields. Additionally, we prove a result on intersections of type-definable connected components over generic sets of parameters in n-dependent groups, generalizing Shelah’s absoluteness of 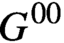 $G^{00}$ in dependent theories and relative absoluteness of
$G^{00}$ in dependent theories and relative absoluteness of 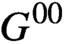 $G^{00}$ in
$G^{00}$ in 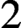 $2$-dependent theories. In an effort to clarify the scope of this conjecture, we provide new examples of strictly
$2$-dependent theories. In an effort to clarify the scope of this conjecture, we provide new examples of strictly 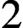 $2$-dependent fields with additional structure, showing that Granger’s examples of non-degenerate bilinear forms over dependent fields are
$2$-dependent fields with additional structure, showing that Granger’s examples of non-degenerate bilinear forms over dependent fields are 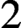 $2$-dependent. Along the way, we obtain some purely model-theoretic results of independent interest: we show that n-dependence is witnessed by formulas with all but one variable singletons; provide a type-counting criterion for
$2$-dependent. Along the way, we obtain some purely model-theoretic results of independent interest: we show that n-dependence is witnessed by formulas with all but one variable singletons; provide a type-counting criterion for 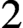 $2$-dependence and use it to deduce
$2$-dependence and use it to deduce 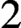 $2$-dependence for compositions of dependent relations with arbitrary binary functions (the Composition Lemma); and show that an expansion of a geometric theory T by a generic predicate is dependent if and only if it is n-dependent for some n, if and only if the algebraic closure in T is disintegrated. An appendix by Martin Bays provides an explicit isomorphism in the Kaplan-Scanlon-Wagner theorem.
$2$-dependence for compositions of dependent relations with arbitrary binary functions (the Composition Lemma); and show that an expansion of a geometric theory T by a generic predicate is dependent if and only if it is n-dependent for some n, if and only if the algebraic closure in T is disintegrated. An appendix by Martin Bays provides an explicit isomorphism in the Kaplan-Scanlon-Wagner theorem.
Information
- Type
- Research Article
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 7
- Cited by


