Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-10T14:04:36.388Z Has data issue: false hasContentIssue false
  • English
  • Français

ON NONUNIQUENESS FOR THE ANISOTROPIC CALDERÓN PROBLEM WITH PARTIAL DATA

Part of: Scattering theory Partial differential equations on manifolds; differential operators Spectral theory and eigenvalue problems

Published online by Cambridge University Press:  28 January 2020

THIERRY DAUDÉ ,
NIKY KAMRAN  and
FRANÇOIS NICOLEAU
THIERRY DAUDÉ
Affiliation:
Département de Mathématiques, UMR CNRS 8088, Université de Cergy-Pontoise, 95302Cergy-Pontoise, France; thierry.daude@u-cergy.fr
NIKY KAMRAN
Affiliation:
Department of Mathematics and Statistics, McGill University, Montreal, QC, H3A 0B9, Canada; nkamran@math.mcgill.ca
FRANÇOIS NICOLEAU
Affiliation:
Laboratoire de Mathématiques Jean Leray, UMR CNRS 6629, 2 Rue de la Houssinière BP 92208, F-44322, Nantes Cedex 03, France; francois.nicoleau@univ-nantes.fr

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that there is nonuniqueness for the Calderón problem with partial data for Riemannian metrics with Hölder continuous coefficients in dimension greater than or equal to three. We provide simple counterexamples in the case of cylindrical Riemannian manifolds with boundary having two ends. The coefficients of these metrics are smooth in the interior of the manifold and are only Hölder continuous of order 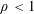$\unicode[STIX]{x1D70C}<1$ at the end where the measurements are made. More precisely, we construct a toroidal ring 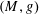$(M,g)$ and we show that there exist in the conformal class of 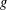$g$ an infinite number of Riemannian metrics 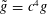$\tilde{g}=c^{4}g$ such that their corresponding partial Dirichlet-to-Neumann maps at one end coincide. The corresponding smooth conformal factors are harmonic with respect to the metric 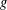$g$ and do not satisfy the unique continuation principle.

MSC classification

Primary: 81U40: Inverse scattering problems 35P25: Scattering theory
Secondary: 58J50: Spectral problems; spectral geometry; scattering theory
Type
Differential Equations
Information
Forum of Mathematics, Sigma , Volume 8 , 2020 , e7
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2020

References

Alessandrini, G., De Hoop, M. V. and Gaburro, R., ‘Uniqueness for the electrostatic inverse boundary value problem with piecewise constant anisotropic conductivities’, Inverse Problems 33(12) (2017), 125013.CrossRefGoogle Scholar
Astala, K., Lassas, M. and Paivarinta, L., ‘Calderón’s inverse problem for anisotropic conductivities in the plane’, Comm. Partial Differential Equations 30 (2005), 207–224.CrossRefGoogle Scholar
Astala, K., Lassas, M. and Päivärinta, L., ‘The borderlines of invisibility and visibility in Calderón’s inverse problem’, Anal. PDE 9(1) (2016), 43–98.CrossRefGoogle Scholar
Astala, K. and Paivarinta, L., ‘Calderón’s inverse conductivity problem in the plane’, Ann. of Math. (2) 163 (2006), 265–299.CrossRefGoogle Scholar
Caro, P. and Rogers, K. M., ‘Global uniqueness for the Calderón problem with Lipschitz conductivities’, Forum Math. Pi 4 (2016), e2, 28 pp.CrossRefGoogle Scholar
Daudé, T., Kamran, N. and Nicoleau, F., ‘Non uniqueness results in the anisotropic Calderón problem with Dirichlet and Neumann data measured on disjoint sets, (2015)’, Ann. Inst. Fourier (Grenoble) 69(1) (2019), 119–170.CrossRefGoogle Scholar
Daudé, T., Kamran, N. and Nicoleau, F., ‘On the hidden mechanism behind non-uniqueness for the anisotropic Calderón problem with data on disjoint sets, (2017)’, Ann. Henri Poincaré 20(3) (2019), 859–887.CrossRefGoogle Scholar
Daudé, T., Kamran, N. and Nicoleau, F., ‘A survey of non-uniqueness results for the anisotropic Calderón problem with disjoint data’, inHarvard CMSA Series in Mathematics, Volume 2: Nonlinear Analysis in Geometry and Applied Mathematics (eds. Collins, T. and Yau, S.-T.) (International Press, Boston, 2018).Google Scholar
Daudé, T., Kamran, N. and Nicoleau, F., ‘The anisotropic Calderón problem for singular metric of warped product type: the borderline between uniqueness and invisibility’, J. Spectr. Theory, to appear, arXiv:1805.05627.Google Scholar
Dos Santos Ferreira, D., Kenig, C. E., Salo, M. and Uhlmann, G., ‘Limiting Carleman weights and anisotropic inverse problems’, Invent. Math. 178(1) (2009), 119–171.CrossRefGoogle Scholar
Dos Santos Ferreira, D., Kurylev, Y., Lassas, M. and Salo, M., ‘The Calderón problem in transversally anisotropic geometries’, J. Eur. Math. Soc. (JEMS) 18(11) (2016), 2579–2626.CrossRefGoogle Scholar
Giannotti, C., ‘A compactly supported solution to a three-dimensional uniformly elliptic equation without zero-order term’, J. Differential Equations 201 (2004), 234–249.CrossRefGoogle Scholar
Gilbarg, D. and Trudinger, N. N., Elliptic Partial Differential Equations of Second Order, Classics in Mathematics (Springer, Berlin, 2001), xiv+517 pp. Reprint of the 1998 edition.Google Scholar
Greenleaf, A., Kurylev, Y., Lassas, M. and Uhlmann, G., ‘Invisibility and inverse problems’, Bull. Amer. Math. Soc. (N.S.) 46(1) (2009), 55–97.CrossRefGoogle Scholar
Greenleaf, A., Lassas, M. and Uhlmann, G., ‘On non-uniqueness for Calderón’s inverse problem’, Math. Res. Lett. 10(5) (2003), 685–693.CrossRefGoogle Scholar
Guillarmou, C. and Sà Barreto, A., ‘Inverse problems for Einstein manifolds’, Inverse Probl. Imaging 3 (2009), 1–15.CrossRefGoogle Scholar
Guillarmou, C. and Tzou, L., ‘Calderón inverse problem with partial data on Riemann surfaces’, Duke Math. J. 158(1) (2011), 83–120.CrossRefGoogle Scholar
Guillarmou, C. and Tzou, L., ‘The Calderón inverse problem in two dimensions’, inInverse Problems and Applications: Inside Out. II, Mathematical Sciences Research Institute Publications, series 60 (Cambridge University Press, Cambridge, 2013), 119–166.Google Scholar
Haberman, B., ‘Uniqueness in Calderón’s problem for conductivities with unbounded gradient’, Comm. Math. Phys. 340(2) (2015), 639–659.CrossRefGoogle Scholar
Haberman, B. and Tataru, D., ‘Uniqueness in Calderón’s problem with Lipschitz conductivities’, Duke Math. J. 162(3) (2013), 496–516.CrossRefGoogle Scholar
Hörmander, L., The Analysis of Linear Partial Differential Operators, III, Grundlehren der matematischen Wissenschaften, 256 (Springer, Berlin, Heidelberg, 1985).Google Scholar
Hörmander, L., ‘Uniqueness theorems for second order elliptic differential equations’, Comm. Partial Differential Equations 8(1) (1983), 21–64.Google Scholar
Imanuvilov, O., Uhlmann, G. and Yamamoto, M., ‘The Calderón problem with partial data in two dimensions’, J. Amer. Math. Soc. 23 (2010), 655–691.CrossRefGoogle Scholar
Imanuvilov, O. Y., Uhlmann, G. and Yamamoto, M., ‘Inverse boundary value problem by measuring Dirichlet data and Neumann data on disjoint sets’, Inverse Problems 27(8) (2011), 085007, 26p.CrossRefGoogle Scholar
Isakov, V., ‘On uniqueness in the inverse conductivity problem with local data’, Inverse Probl. Imaging 1 (2007), 95–105.CrossRefGoogle Scholar
Kang, H. and Yun, K., ‘Boundary determination of conductivities and Riemannian metrics via local Dirichlet-to-Neumann operators’, SIAM J. Math. Anal. 34(3) (2003), 719–735.CrossRefGoogle Scholar
Katchalov, A., Kurylev, Y. and Lassas, M., Inverse boundary spectral problems, Monographs and Surveys in Pure and Applied Mathematics, 123 (Chapman Hall/CRC, 2001).CrossRefGoogle Scholar
Katchalov, A., Kurylev, Y., Lassas, M. and Mandache, N., ‘Equivalence of time-domain inverse problems and boundary spectral problem’, Inverse Problems 20 (2004), 419–436.CrossRefGoogle Scholar
Kenig, C. and Salo, M., ‘The Calderón problem with partial data on manifolds and applications’, Anal. PDE 6(8) (2013), 2003–2048.CrossRefGoogle Scholar
Kenig, C. and Salo, M., ‘Recent progress in the Calderón problem with partial data’, Contemp. Math. 615 (2014), 193–222.CrossRefGoogle Scholar
Kenig, C., Sjöstrand, J. and Uhlmann, G., ‘The Calderón problem with partial data’, Ann. of Math. (2) 165 (2007), 567–591.CrossRefGoogle Scholar
Krupchyk, K. and Uhlmann, G., ‘The Calderón problem with partial data for conductivities with 3/2 derivatives’, Comm. Math. Phys. 348(1) (2016), 185–219.CrossRefGoogle Scholar
Lassas, M., Taylor, G. and Uhlmann, G., ‘The Dirichlet-to-Neumann map for complete Riemannian manifolds with boundary’, Comm. Anal. Geom. 11 (2003), 207–221.CrossRefGoogle Scholar
Lassas, M. and Uhlmann, G., ‘On determining a Riemannian manifold from the Dirichlet-to-Neumann map’, Ann. Sci. Éc. Norm. Supér. (4) 34 (2001), 771–787.CrossRefGoogle Scholar
Lee, J. M., Introduction to Smooth Manifolds, 2nd edn, Graduate Texts in Mathematics (Springer, New York, 2000).Google Scholar
Lee, J. M. and Uhlmann, G., ‘Determining anisotropic real-analytic conductivities by boundary measurements’, Comm. Pure Appl. Math. 42(8) (1989), 1097–1112.CrossRefGoogle Scholar
Lionheart, W. R. B., ‘Conformal uniqueness results in anisotropic electrical impedance imaging’, Inverse Problems 13 (1997), 125–134.CrossRefGoogle Scholar
Mandache, N., ‘On a counterexample concerning unique continuation for elliptic equations in divergence form’, Mat. Fiz. Anal. Geom. 3(3/4) (1996), 308–331.Google Scholar
Miller, K., ‘Non-unique continuation for uniformly parabolic and elliptic equations in self-adjoint divergence form with Hölder continuous coefficients’, Arch. Ration. Mech. Anal. 54(2) (1974), 105–117.CrossRefGoogle Scholar
Pliś, A., ‘On non-uniqueness in Cauchy problem for an elliptic second order differential equation’, Bull. Acad. Pol. Sci. S. Mat. XI(3) (1963), 95–100.Google Scholar
Salo, M., ‘The Calderón problem on Riemannian manifolds’, inInverse Problems and Applications: Inside Out. II, Mathematical Sciences Research Institute Publications, 60 (Cambridge University Press, Cambridge, 2013), 167–247.Google Scholar
Tataru, D., ‘Unique continuation for PDEs’, IMA Vol. Math. Appl. 137 (2003), 239–255.Google Scholar
Taylor, M., Partial Differential Equations. I. Basic Theory, Applied Mathematical Sciences, 115 (Springer, New York, 2011).CrossRefGoogle Scholar
Uhlmann, G., ‘Electrical impedance tomography and Calderón’s problem’, Inverse Problems 25 123011 (2009), 39p.CrossRefGoogle Scholar
Uhlmann, G., ‘Inverse problems: seeing the unseen’, Bull. Math. Sci. 4(2) (2014), 209–279.CrossRefGoogle Scholar