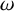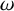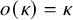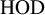1 Introduction
A prominent line of research in set theory is the study of the set theoretic universe V (i.e., model of the axioms of set theory,
![]() $\mathrm {ZFC}$
) by considering canonical inner model
$\mathrm {ZFC}$
) by considering canonical inner model
![]() $M \subseteq V$
with additional strong features, which approximates V. The concept builds on the suggestion that if M is sufficiently ‘close’ to V, then some of the properties of M may lift to V and allow us to derive new consequences about models of set theory.
$M \subseteq V$
with additional strong features, which approximates V. The concept builds on the suggestion that if M is sufficiently ‘close’ to V, then some of the properties of M may lift to V and allow us to derive new consequences about models of set theory.
The prospects of this approach are demonstrated in the theory of Gödel’s constructible universe
![]() $L \subseteq V$
and Jensen’s Covering Theorem ([Reference Devlin and Jensen8]), which asserts that under the anti-large cardinal assumption of the nonexistence of
$L \subseteq V$
and Jensen’s Covering Theorem ([Reference Devlin and Jensen8]), which asserts that under the anti-large cardinal assumption of the nonexistence of
![]() $0^{\#}$
, the covering property holds for
$0^{\#}$
, the covering property holds for
![]() $L \subseteq V$
.Footnote
1
The combination of covering for
$L \subseteq V$
.Footnote
1
The combination of covering for
![]() $L \subseteq V$
, together with the rigid structure of L, has been shown to have many implications both on cardinal arithmetic in V,Footnote
2
as well as on the existence of incompactness phenomena in V such as an Abelian group
$L \subseteq V$
, together with the rigid structure of L, has been shown to have many implications both on cardinal arithmetic in V,Footnote
2
as well as on the existence of incompactness phenomena in V such as an Abelian group
![]() $G \in V$
of size
$G \in V$
of size
![]() $\aleph _{\omega +1}$
that is not free, although every subgroup
$\aleph _{\omega +1}$
that is not free, although every subgroup
![]() $H \triangleleft G$
of smaller cardinality is free.
$H \triangleleft G$
of smaller cardinality is free.
Jensen’s Covering Lemma describes one side of a sharp dichotomy: if
![]() $0^{\#}$
does not exist, then L covers subsets of V successfully. By Silver, if
$0^{\#}$
does not exist, then L covers subsets of V successfully. By Silver, if
![]() $0^{\#}$
does exist, then L fails to approximate even the most basic features of V. For example, in the presence of
$0^{\#}$
does exist, then L fails to approximate even the most basic features of V. For example, in the presence of
![]() $0^{\#}$
, L never computes successor cardinals correctly.
$0^{\#}$
, L never computes successor cardinals correctly.
Jensen’s Covering Lemma can be utilized to obtain a lower bound for the consistency strength of set theoretical statements, which do not necessarily mention large cardinals. However, it is quite restrictive. To be able to obtain various lower bounds, one has to construct canonical models that can accommodate stronger large cardinal axioms. The construction of such inner models is the subject of a prominent program in set theory known as the Inner Model program. For a large cardinal property
![]() $\Phi $
,Footnote
3
one would like to to construct a canonical L-like inner model K that is maximal with respect to inner models that do not satisfy the large cardinal property
$\Phi $
,Footnote
3
one would like to to construct a canonical L-like inner model K that is maximal with respect to inner models that do not satisfy the large cardinal property
![]() $\Phi $
(see Schimmerling-Steel [Reference Schimmerling and Steel32] for the precise statement). This maximality property couples with a covering lemma: assuming there is no inner model of V with the property
$\Phi $
(see Schimmerling-Steel [Reference Schimmerling and Steel32] for the precise statement). This maximality property couples with a covering lemma: assuming there is no inner model of V with the property
![]() $\Phi $
, K approximates the universe V by satisfying a certain covering property. For example, for
$\Phi $
, K approximates the universe V by satisfying a certain covering property. For example, for
![]() $\Phi $
being the existence of
$\Phi $
being the existence of
![]() $0^{\#}$
,
$0^{\#}$
,
![]() $K = L$
.
$K = L$
.
For stronger
![]() $\Phi $
, the existence of such an inner model K would allow us to extend Jensen’s sharp dichotomy. Namely, either the large cardinal property
$\Phi $
, the existence of such an inner model K would allow us to extend Jensen’s sharp dichotomy. Namely, either the large cardinal property
![]() $\Phi $
holds, or V is close to K and therefore inherits various combinatorial properties such as the existence of certain incompactness phenomena.
$\Phi $
holds, or V is close to K and therefore inherits various combinatorial properties such as the existence of certain incompactness phenomena.
Starting in the 1970s, inner models for increasing large cardinal properties
![]() $\Phi $
have been constructed. Starting from the seminal studies of Kunen, Silver and Solovay on a model
$\Phi $
have been constructed. Starting from the seminal studies of Kunen, Silver and Solovay on a model
![]() $L[U]$
with a measurable cardinal ([Reference Kunen18],[Reference Silver35]), extended by Dodd-Jensen ([Reference Dodd and Jensen10]) and Mitchell ([Reference Mitchell23]), to large cardinal properties
$L[U]$
with a measurable cardinal ([Reference Kunen18],[Reference Silver35]), extended by Dodd-Jensen ([Reference Dodd and Jensen10]) and Mitchell ([Reference Mitchell23]), to large cardinal properties
![]() $\Phi $
involving coherent sequences of normal measures and many measurable cardinals. Then, following major developments and the introduction of iteration trees in Martin and Steel ([Reference Martin and Steel20]), Mitchell and Steel ([Reference Mitchell and Steel24]), and Steel ([Reference Steel36]), the theory was extended to the level of Woodin cardinals.
$\Phi $
involving coherent sequences of normal measures and many measurable cardinals. Then, following major developments and the introduction of iteration trees in Martin and Steel ([Reference Martin and Steel20]), Mitchell and Steel ([Reference Mitchell and Steel24]), and Steel ([Reference Steel36]), the theory was extended to the level of Woodin cardinals.
The program took a significant turn after Woodin showed that there cannot be a single maximal inner model, in an absolute sense, past a Woodin cardinal. This has sparked new lines of study, involving forms of the
![]() $K^c$
construction (see Jensen, Schimmerling, Schindler, and Steel [Reference Jensen, Schimmerling, Schindler and Steel17] and Andereta, Neeman and Steel [Reference Andretta, Neeman and Steel2]).
$K^c$
construction (see Jensen, Schimmerling, Schindler, and Steel [Reference Jensen, Schimmerling, Schindler and Steel17] and Andereta, Neeman and Steel [Reference Andretta, Neeman and Steel2]).
Another seminal development was the introduction of The Core Model Induction method, first introduced by Woodin and extensively developed by Steel, Schindler, Sargsyan, Trang and many others ([Reference Schindler and Steel34]). The method establishes new consistency results for stronger large cardinal properties by incorporation ideas from descriptive set theory with various local construction methods. The relevant large cardinal properties are often described in terms of expansions of the Axiom of Determinacy (
![]() $\mathrm {AD}$
) in inner models M of
$\mathrm {AD}$
) in inner models M of
![]() $\mathrm {ZF}$
and can be further translated to inner models of
$\mathrm {ZF}$
and can be further translated to inner models of
![]() $\mathrm {ZFC}$
with large cardinal properties.
$\mathrm {ZFC}$
with large cardinal properties.
First results on fine structural inner models for finite levels of supercompact cardinals were obtained by Neeman and Steel, [Reference Neeman and Steel27] and by Woodin. It is still unknown whether similar constructions could lead to an inner model with a (full) supercompact cardinal, and some recent results of Woodin suggest that major obstructions appear past the level of finite supercompactness [Reference Woodin41]. There are many excellent resources for the introduction of the inner model theory, the inner model program and its development. We refer the reader to [Reference Jensen16, Reference Mitchell22, Reference Neeman26, Reference Sargsyan29, Reference Schimmerling33, Reference Steel37, Reference Zeman43].
The inner model of Hereditarily Ordinal Definable sets (HOD) plays a significant role in many of the recent advancements in the Inner Model program.
Definition 1.1. Let M be a model of set theory. A set
![]() $x \in M$
is hereditarily ordinal definable in M if both x and every set in the transitive closure of x is definable in V using some formula with ordinal parameters. The class of all hereditarily ordinal definable sets in a model M is denoted by
$x \in M$
is hereditarily ordinal definable in M if both x and every set in the transitive closure of x is definable in V using some formula with ordinal parameters. The class of all hereditarily ordinal definable sets in a model M is denoted by
![]() $\operatorname {\mathrm {HOD}}^M\kern-1pt$
.
$\operatorname {\mathrm {HOD}}^M\kern-1pt$
.
We write
![]() $\operatorname {\mathrm {HOD}}$
for
$\operatorname {\mathrm {HOD}}$
for
![]() $\operatorname {\mathrm {HOD}}^V \subseteq V$
.
$\operatorname {\mathrm {HOD}}^V \subseteq V$
.
The class
![]() $\operatorname {\mathrm {HOD}}$
was first introduced by Gödel, and has been extensively studied (for example, see [Reference Myhill and Scott25]). The study of
$\operatorname {\mathrm {HOD}}$
was first introduced by Gödel, and has been extensively studied (for example, see [Reference Myhill and Scott25]). The study of
![]() $\operatorname {\mathrm {HOD}}$
in inner models of strong forms of
$\operatorname {\mathrm {HOD}}$
in inner models of strong forms of
![]() $\mathrm {AD}$
and the associated strategic-extender models plays a critical role in Descriptive Inner Model Theory. See [Reference Sargsyan and Trang30, Reference Sargsyan and Trang31, Reference Steel and Woodin38].
$\mathrm {AD}$
and the associated strategic-extender models plays a critical role in Descriptive Inner Model Theory. See [Reference Sargsyan and Trang30, Reference Sargsyan and Trang31, Reference Steel and Woodin38].
In [Reference Woodin39], Woodin presents a new approach of addressing the inner model problem for all large cardinals. Woodin analyses the possible properties and limitations of some of the current methods, and introduces the seminal notions of a suitable extender model N for a supercompact cardinal
![]() $\delta $
(in V), which in addition to several properties similar to well-known inner models, requires that N captures witnessing
$\delta $
(in V), which in addition to several properties similar to well-known inner models, requires that N captures witnessing
![]() $\delta $
-supercompact measures in V.Footnote
4
In a following work (see [Reference Woodin41]), Woodin presents the ‘V = Ultimate-L’ axiom, to assert (roughly) that
$\delta $
-supercompact measures in V.Footnote
4
In a following work (see [Reference Woodin41]), Woodin presents the ‘V = Ultimate-L’ axiom, to assert (roughly) that
![]() $\Sigma _2$
-definable properties of the universe are satisfied in canonical strategic-extender models of the form
$\Sigma _2$
-definable properties of the universe are satisfied in canonical strategic-extender models of the form
![]() $\operatorname {\mathrm {HOD}}^{L(A,\mathbb {R})} \cap V_{\Theta }$
, for some Universally Baire set
$\operatorname {\mathrm {HOD}}^{L(A,\mathbb {R})} \cap V_{\Theta }$
, for some Universally Baire set
![]() $A \subseteq \mathbb {R}$
.
$A \subseteq \mathbb {R}$
.
Combining the above notions, Woodin has formulated the ‘Ultimate-L’ conjecture, asserting that there exists a suitable extender model
![]() $N \subseteq \operatorname {\mathrm {HOD}}$
which satisfies the axiom ‘V = Ultimate-L’. Following the search for some N, the theory established in [Reference Woodin39] studies the possibility of
$N \subseteq \operatorname {\mathrm {HOD}}$
which satisfies the axiom ‘V = Ultimate-L’. Following the search for some N, the theory established in [Reference Woodin39] studies the possibility of
![]() $\operatorname {\mathrm {HOD}} \subseteq V$
being a suitable extender model, and possible implications. For this, Woodin introduces a new assumption known as the HOD-conjecture (Conjecture 1.3 below) and shows that, remarkably, if the
$\operatorname {\mathrm {HOD}} \subseteq V$
being a suitable extender model, and possible implications. For this, Woodin introduces a new assumption known as the HOD-conjecture (Conjecture 1.3 below) and shows that, remarkably, if the
![]() $\operatorname {\mathrm {HOD}}$
-conjecture is true, then a sufficiently strong large cardinal assumption (e.g., an extendible cardinal) guarantees a version of the covering lemma for
$\operatorname {\mathrm {HOD}}$
-conjecture is true, then a sufficiently strong large cardinal assumption (e.g., an extendible cardinal) guarantees a version of the covering lemma for
![]() $\operatorname {\mathrm {HOD}} \subseteq V$
. However, if the
$\operatorname {\mathrm {HOD}} \subseteq V$
. However, if the
![]() $\operatorname {\mathrm {HOD}}$
-conjecture fails in the presence of sufficiently large cardinals, then
$\operatorname {\mathrm {HOD}}$
-conjecture fails in the presence of sufficiently large cardinals, then
![]() $\operatorname {\mathrm {HOD}}$
is very far from V, just like the smaller inner models. See Theorem 1.5 for an exact formulation.
$\operatorname {\mathrm {HOD}}$
is very far from V, just like the smaller inner models. See Theorem 1.5 for an exact formulation.
We remark that, in general, the inner model
![]() $\operatorname {\mathrm {HOD}}$
of an arbitrary model of
$\operatorname {\mathrm {HOD}}$
of an arbitrary model of
![]() $\mathrm {ZFC}$
can be easily modified by forcing. Nevertheless, it contains every canonical inner model and thus, the
$\mathrm {ZFC}$
can be easily modified by forcing. Nevertheless, it contains every canonical inner model and thus, the
![]() $\operatorname {\mathrm {HOD}}$
-conjecture might be a consequence of the covering theorem for some extremely large canonical inner model [Reference Woodin40]. An appealing aspect of the
$\operatorname {\mathrm {HOD}}$
-conjecture might be a consequence of the covering theorem for some extremely large canonical inner model [Reference Woodin40]. An appealing aspect of the
![]() $\operatorname {\mathrm {HOD}}$
-conjecture is that it is a combinatorial statement about the
$\operatorname {\mathrm {HOD}}$
-conjecture is that it is a combinatorial statement about the
![]() $\operatorname {\mathrm {HOD}}$
and V, and it does not rely on inner model theory. Even without any further development in the inner model program, Woodin established that the
$\operatorname {\mathrm {HOD}}$
and V, and it does not rely on inner model theory. Even without any further development in the inner model program, Woodin established that the
![]() $\operatorname {\mathrm {HOD}}$
-conjecture poses many significant limitations on the consistency of large cardinals in the choice-less context. Moreover, large cardinals beyond choice, if consistent, form a hierarchy of failures of the
$\operatorname {\mathrm {HOD}}$
-conjecture poses many significant limitations on the consistency of large cardinals in the choice-less context. Moreover, large cardinals beyond choice, if consistent, form a hierarchy of failures of the
![]() $\operatorname {\mathrm {HOD}}$
-conjecture [Reference Bagaria, Koellner and Woodin3].
$\operatorname {\mathrm {HOD}}$
-conjecture [Reference Bagaria, Koellner and Woodin3].
The
![]() $\operatorname {\mathrm {HOD}}$
-conjecture centers around the notion of
$\operatorname {\mathrm {HOD}}$
-conjecture centers around the notion of
![]() $\omega $
-strongly measurable cardinals in
$\omega $
-strongly measurable cardinals in
![]() $\operatorname {\mathrm {HOD}}$
. Not much was know about this notion, and previously, Woodin has raised the question ([Reference Woodin41]) of whether more than three
$\operatorname {\mathrm {HOD}}$
. Not much was know about this notion, and previously, Woodin has raised the question ([Reference Woodin41]) of whether more than three
![]() $\omega $
-strongly measurables in
$\omega $
-strongly measurables in
![]() $\operatorname {\mathrm {HOD}}$
can exist. In this work, we study the notion of
$\operatorname {\mathrm {HOD}}$
can exist. In this work, we study the notion of
![]() $\omega $
-strongly measurable cardinals in
$\omega $
-strongly measurable cardinals in
![]() $\operatorname {\mathrm {HOD}}$
, we prove several consistency results concerning this notion and we establish the consistency of a model where all successors of regular cardinal are
$\operatorname {\mathrm {HOD}}$
, we prove several consistency results concerning this notion and we establish the consistency of a model where all successors of regular cardinal are
![]() $\omega $
-strongly measurable in
$\omega $
-strongly measurable in
![]() $\operatorname {\mathrm {HOD}}$
.
$\operatorname {\mathrm {HOD}}$
.
Definition 1.2. Let
![]() $\kappa $
be an uncountable regular cardinal, and let S be a stationary subset of
$\kappa $
be an uncountable regular cardinal, and let S be a stationary subset of
![]() $\kappa $
. We say that
$\kappa $
. We say that
![]() $\kappa $
is strongly measurable in
$\kappa $
is strongly measurable in
![]() $\operatorname {\mathrm {HOD}}$
with respect to S if there exists some
$\operatorname {\mathrm {HOD}}$
with respect to S if there exists some
![]() $\eta < \kappa $
such that
$\eta < \kappa $
such that
![]() $(2^{\eta })^{\operatorname {\mathrm {HOD}}} < \kappa $
and there is no partition
$(2^{\eta })^{\operatorname {\mathrm {HOD}}} < \kappa $
and there is no partition
![]() ${\langle } S_{\alpha } \mid \alpha < \eta {\rangle } \in \operatorname {\mathrm {HOD}}$
of S into sets, all stationary sets in V. We say that
${\langle } S_{\alpha } \mid \alpha < \eta {\rangle } \in \operatorname {\mathrm {HOD}}$
of S into sets, all stationary sets in V. We say that
![]() $\kappa $
is
$\kappa $
is
![]() $\omega $
-strongly measurable in
$\omega $
-strongly measurable in
![]() $\operatorname {\mathrm {HOD}}$
if it is strongly measurable in
$\operatorname {\mathrm {HOD}}$
if it is strongly measurable in
![]() $\operatorname {\mathrm {HOD}}$
with respect to the set
$\operatorname {\mathrm {HOD}}$
with respect to the set
![]() $S = \kappa \cap \operatorname {\mathrm {Cof}}(\omega )$
, and that it is strongly measurable in
$S = \kappa \cap \operatorname {\mathrm {Cof}}(\omega )$
, and that it is strongly measurable in
![]() $\operatorname {\mathrm {HOD}}$
if it is strongly measurable in
$\operatorname {\mathrm {HOD}}$
if it is strongly measurable in
![]() $\operatorname {\mathrm {HOD}}$
with respect to
$\operatorname {\mathrm {HOD}}$
with respect to
![]() $S = \kappa $
.
$S = \kappa $
.
In general, one might replace
![]() $\operatorname {\mathrm {HOD}}$
with any other inner model of V, M, obtaining a meaningful notion of strong measurability in M. Since, in this paper, we will be interested solely in strong measurability in
$\operatorname {\mathrm {HOD}}$
with any other inner model of V, M, obtaining a meaningful notion of strong measurability in M. Since, in this paper, we will be interested solely in strong measurability in
![]() $\operatorname {\mathrm {HOD}}$
, we will occasionally omit the emphasis ‘in
$\operatorname {\mathrm {HOD}}$
, we will occasionally omit the emphasis ‘in
![]() $\operatorname {\mathrm {HOD}}$
’ and say simply that
$\operatorname {\mathrm {HOD}}$
’ and say simply that
![]() $\kappa $
is strongly measurable.
$\kappa $
is strongly measurable.
It is shown in [Reference Woodin39] that if
![]() $\kappa $
is an
$\kappa $
is an
![]() $\omega $
-strongly measurable in
$\omega $
-strongly measurable in
![]() $\operatorname {\mathrm {HOD}}$
, then there are stationary sets
$\operatorname {\mathrm {HOD}}$
, then there are stationary sets
![]() $S \subseteq \kappa \cap \operatorname {\mathrm {Cof}}(\omega )$
for which the restriction of the filter
$S \subseteq \kappa \cap \operatorname {\mathrm {Cof}}(\omega )$
for which the restriction of the filter
![]() $\operatorname {\mathrm {CUB}}_{\kappa } \restriction S$
to
$\operatorname {\mathrm {CUB}}_{\kappa } \restriction S$
to
![]() $\operatorname {\mathrm {HOD}}$
forms a measure on
$\operatorname {\mathrm {HOD}}$
forms a measure on
![]() $\kappa $
in
$\kappa $
in
![]() $\operatorname {\mathrm {HOD}}$
. However, Woodin shows ([Reference Woodin39]) that the existence of a class of regular cardinals which are not
$\operatorname {\mathrm {HOD}}$
. However, Woodin shows ([Reference Woodin39]) that the existence of a class of regular cardinals which are not
![]() $\omega $
-strongly measurable in
$\omega $
-strongly measurable in
![]() $\operatorname {\mathrm {HOD}}$
, together with the existence of a
$\operatorname {\mathrm {HOD}}$
, together with the existence of a
![]() $\operatorname {\mathrm {HOD}}$
-supercompact, implies that
$\operatorname {\mathrm {HOD}}$
-supercompact, implies that
![]() $\operatorname {\mathrm {HOD}}$
satisfies many appealing approximation properties with respect to V. The results promote Woodin’s
$\operatorname {\mathrm {HOD}}$
satisfies many appealing approximation properties with respect to V. The results promote Woodin’s
![]() $\operatorname {\mathrm {HOD}}$
-conjecture.
$\operatorname {\mathrm {HOD}}$
-conjecture.
Conjecture 1.3 (
 $\operatorname {\mathrm {HOD}}$
conjecture, [Reference Woodin39, Definition 191]).
$\operatorname {\mathrm {HOD}}$
conjecture, [Reference Woodin39, Definition 191]).
There is a proper class of regular uncountable cardinals
![]() $\kappa $
which are not
$\kappa $
which are not
![]() $\omega $
-strongly measurable in
$\omega $
-strongly measurable in
![]() $\operatorname {\mathrm {HOD}}$
.
$\operatorname {\mathrm {HOD}}$
.
In light of the
![]() $\operatorname {\mathrm {HOD}}$
-conjecture, it is natural to attempt forming models with as many as possible
$\operatorname {\mathrm {HOD}}$
-conjecture, it is natural to attempt forming models with as many as possible
![]() $\omega $
-strongly measurable cardinals in
$\omega $
-strongly measurable cardinals in
![]() $\operatorname {\mathrm {HOD}}$
. Woodin has established the consistency (relative to large cardinals) of models with up to three
$\operatorname {\mathrm {HOD}}$
. Woodin has established the consistency (relative to large cardinals) of models with up to three
![]() $\omega $
-strongly measurable cardinals (see [Reference Woodin41, Remark 3.43]). The main purpose of this work is to prove that many strongly measurable cardinals can be obtained from a relatively mild large cardinal assumption of hypermeasurability.
$\omega $
-strongly measurable cardinals (see [Reference Woodin41, Remark 3.43]). The main purpose of this work is to prove that many strongly measurable cardinals can be obtained from a relatively mild large cardinal assumption of hypermeasurability.
Theorem 1.4. It is consistent relative to the existence of an inaccessible cardinal
![]() $\theta $
for which
$\theta $
for which
![]() $\{ o(\kappa ) \mid \kappa < \theta \}$
is unbounded in
$\{ o(\kappa ) \mid \kappa < \theta \}$
is unbounded in
![]() $\theta $
, that every successor of a regular cardinal is strongly measurable in
$\theta $
, that every successor of a regular cardinal is strongly measurable in
![]() $\operatorname {\mathrm {HOD}}$
.
$\operatorname {\mathrm {HOD}}$
.
Cummings, Friedman and Golshani ([Reference Cummings, Friedman and Golshani7]) have established the consistency of a model where
![]() $(\alpha ^+)^{\operatorname {\mathrm {HOD}}} < \alpha ^+$
for every infinite cardinal
$(\alpha ^+)^{\operatorname {\mathrm {HOD}}} < \alpha ^+$
for every infinite cardinal
![]() $\alpha $
. In [Reference Gitik and Merimovich15, Theorem 2.2], Gitik and Merimovich prove that it is consistent relative to large cardinals that every regular uncountable cardinal is measurable in
$\alpha $
. In [Reference Gitik and Merimovich15, Theorem 2.2], Gitik and Merimovich prove that it is consistent relative to large cardinals that every regular uncountable cardinal is measurable in
![]() $\operatorname {\mathrm {HOD}}$
. A similar result is obtained using a different technique in [Reference Ben-Neria and Unger5, Theorem 1.4]. Perhaps more related to our work is [Reference Ben-Neria and Unger5, Theorem 1.3], in which a club of cardinals which are measurable in
$\operatorname {\mathrm {HOD}}$
. A similar result is obtained using a different technique in [Reference Ben-Neria and Unger5, Theorem 1.4]. Perhaps more related to our work is [Reference Ben-Neria and Unger5, Theorem 1.3], in which a club of cardinals which are measurable in
![]() $\operatorname {\mathrm {HOD}}$
is obtained from a large cardinal axiom weaker than
$\operatorname {\mathrm {HOD}}$
is obtained from a large cardinal axiom weaker than
![]() $o(\kappa ) = \kappa $
. In those models, there are no
$o(\kappa ) = \kappa $
. In those models, there are no
![]() $\omega $
-strongly measurable successor cardinals.
$\omega $
-strongly measurable successor cardinals.
We note that these results do not apply to models where there is an extendible cardinal. The existence of an extendible cardinal in V derives a sharp dichotomy between
![]() $\operatorname {\mathrm {HOD}}$
being either very close or very far from V, as shown by Woodin’s
$\operatorname {\mathrm {HOD}}$
being either very close or very far from V, as shown by Woodin’s
![]() $\operatorname {\mathrm {HOD}}$
-Dichotomy Theorem ([Reference Woodin39]).
$\operatorname {\mathrm {HOD}}$
-Dichotomy Theorem ([Reference Woodin39]).
Theorem 1.5 (The
 $\operatorname {\mathrm {HOD}}$
-Dichotomy, Woodin, [Reference Woodin, Davis and Rodríguez42]).
$\operatorname {\mathrm {HOD}}$
-Dichotomy, Woodin, [Reference Woodin, Davis and Rodríguez42]).
Let
![]() $\delta $
be an extendible cardinal. Then one of the following holds:
$\delta $
be an extendible cardinal. Then one of the following holds:
-
1. Every cardinal
 $\eta $
above
$\eta $
above
 $\delta $
, which is singular in V, is singular in
$\delta $
, which is singular in V, is singular in
 $\operatorname {\mathrm {HOD}}$
and
$\operatorname {\mathrm {HOD}}$
and
 $(\eta ^+)^{\operatorname {\mathrm {HOD}}} = \eta ^+$
.
$(\eta ^+)^{\operatorname {\mathrm {HOD}}} = \eta ^+$
. -
2. Every regular cardinal above
 $\delta $
is
$\delta $
is
 $\omega $
-strongly measurable in
$\omega $
-strongly measurable in
 $\operatorname {\mathrm {HOD}}$
.
$\operatorname {\mathrm {HOD}}$
.
In the last part of this work, we prove a consistency result regarding strong measurability at successors of singular cardinals. Woodin ([Reference Woodin39]) establishes the consistency of a successor of a singular cardinal
![]() $\lambda $
, which is a
$\lambda $
, which is a
![]() $\omega $
-strongly measurable cardinal in
$\omega $
-strongly measurable cardinal in
![]() $\operatorname {\mathrm {HOD}}$
, from the large cardinal assumption
$\operatorname {\mathrm {HOD}}$
, from the large cardinal assumption
![]() $I_0$
. Here, we prove a weaker consistency result from a weaker large cardinal assumption.
$I_0$
. Here, we prove a weaker consistency result from a weaker large cardinal assumption.
Theorem 1.6. Suppose that
![]() $\kappa < \lambda $
are cardinals,
$\kappa < \lambda $
are cardinals,
![]() $\kappa $
is
$\kappa $
is
![]() $\lambda $
-supercompact and
$\lambda $
-supercompact and
![]() $\lambda $
is measurable. Then, there is a generic extension in which
$\lambda $
is measurable. Then, there is a generic extension in which
![]() $\kappa $
is a singular cardinal of cofinality
$\kappa $
is a singular cardinal of cofinality
![]() $\omega $
, and
$\omega $
, and
![]() $\lambda = \kappa ^+$
is strongly measurable in
$\lambda = \kappa ^+$
is strongly measurable in
![]() $\operatorname {\mathrm {HOD}}$
with respect to S, for some stationary subset
$\operatorname {\mathrm {HOD}}$
with respect to S, for some stationary subset
![]() $S \subseteq \lambda \cap \operatorname {\mathrm {Cof}}(\omega )$
.
$S \subseteq \lambda \cap \operatorname {\mathrm {Cof}}(\omega )$
.
A brief summary of this paper. In section 2
, we review some basic facts about strong measurability which will be central in the proof of the main theorem. In the following sections, we gradually develop the forcing methods used to prove our main results (Theorems 1.4 and 1.6). In section 3
, we show how to obtain a model where
![]() $\omega _1$
is strongly measurable in
$\omega _1$
is strongly measurable in
![]() $\operatorname {\mathrm {HOD}}$
starting with a single measurable cardinal. The case of
$\operatorname {\mathrm {HOD}}$
starting with a single measurable cardinal. The case of
![]() $\kappa = \omega _1$
is different from the general case as it does not require incorporating posets for changing cofinalities. It can also be seen as a warmup for the general case. In section 4
, we further develop the ideas from the previous section and combine them with a suitable iteration for changing cofinalities. As a result, we establish the consistency of a strongly measurable cardinal which is a successor of an arbitrary regular cardinal
$\kappa = \omega _1$
is different from the general case as it does not require incorporating posets for changing cofinalities. It can also be seen as a warmup for the general case. In section 4
, we further develop the ideas from the previous section and combine them with a suitable iteration for changing cofinalities. As a result, we establish the consistency of a strongly measurable cardinal which is a successor of an arbitrary regular cardinal
![]() $\lambda $
, from the large cardinal assumption of
$\lambda $
, from the large cardinal assumption of
![]() $o(\kappa ) = \lambda +1$
. In section 6
, we introduce a method to construct a Prikry-type poset which is equivalent to the forcing from the previous section and has a direct extension order that is
$o(\kappa ) = \lambda +1$
. In section 6
, we introduce a method to construct a Prikry-type poset which is equivalent to the forcing from the previous section and has a direct extension order that is
![]() $\lambda $
-closed. This is utilized in section 5
to form iterations of the single cardinal forcing, thus obtaining models with many strongly measurable cardinals. In section 7
, we prove our theorem concerning successors of singular cardinals. The results of this section do not depend on the other sections past our preliminaries.
$\lambda $
-closed. This is utilized in section 5
to form iterations of the single cardinal forcing, thus obtaining models with many strongly measurable cardinals. In section 7
, we prove our theorem concerning successors of singular cardinals. The results of this section do not depend on the other sections past our preliminaries.
In the appendix, we cite and prove some useful results related to homogeneous forcings and their iterations (including Prikry type forcings), and homogeneous iterations for changing cofinalities.
Our notations are mostly standard. We follow the Jerusalem forcing convention, in which for two conditions
![]() $p,p'$
in a poset
$p,p'$
in a poset
![]() $\mathbb {P}$
, the fact that
$\mathbb {P}$
, the fact that
![]() $p'$
is stronger (more informative) than p is denoted by
$p'$
is stronger (more informative) than p is denoted by
![]() $p' \geq p$
.
$p' \geq p$
.
2 Variations of strong measurability
We start with several observations concerning a natural generalization of the notion of
![]() $\omega $
-strong measurability.
$\omega $
-strong measurability.
Definition 2.1. Let
![]() $S \subseteq \kappa $
,
$S \subseteq \kappa $
,
![]() $S \in \operatorname {\mathrm {HOD}}$
stationary, and let
$S \in \operatorname {\mathrm {HOD}}$
stationary, and let
![]() $\eta $
be a cardinal in
$\eta $
be a cardinal in
![]() $\operatorname {\mathrm {HOD}}$
.
$\operatorname {\mathrm {HOD}}$
.
![]() $\kappa $
is
$\kappa $
is
![]() $(S,<\eta )$
-strongly measurable if there is no partition in
$(S,<\eta )$
-strongly measurable if there is no partition in
![]() $\operatorname {\mathrm {HOD}}$
of S into
$\operatorname {\mathrm {HOD}}$
of S into
![]() $\eta $
many disjoint stationary sets.
$\eta $
many disjoint stationary sets.
![]() $\kappa $
is
$\kappa $
is
![]() $(S,\eta )$
-strongly measurable if it is
$(S,\eta )$
-strongly measurable if it is
![]() $(S, <(\eta ^{+})^{\operatorname {\mathrm {HOD}}})$
-strongly measurable.
$(S, <(\eta ^{+})^{\operatorname {\mathrm {HOD}}})$
-strongly measurable.
Definition 2.2. A cardinal
![]() $\kappa $
is S-strongly measurable if
$\kappa $
is S-strongly measurable if
![]() $S \in \operatorname {\mathrm {HOD}}$
, and
$S \in \operatorname {\mathrm {HOD}}$
, and
![]() $\kappa $
is
$\kappa $
is
![]() $(S, <\eta )$
-strongly measurable for some
$(S, <\eta )$
-strongly measurable for some
![]() $\eta $
such that
$\eta $
such that
![]() $(2^{\eta })^{\operatorname {\mathrm {HOD}}} < \kappa $
. We say that
$(2^{\eta })^{\operatorname {\mathrm {HOD}}} < \kappa $
. We say that
![]() $\kappa $
is strongly measurable if
$\kappa $
is strongly measurable if
![]() $\kappa $
is
$\kappa $
is
![]() $\kappa $
-strongly measurable.
$\kappa $
-strongly measurable.
Therefore, a cardinal
![]() $\kappa $
is
$\kappa $
is
![]() $\omega $
-strongly measurable if it is
$\omega $
-strongly measurable if it is
![]() $(S^{\kappa }_{\omega },\eta )$
-strongly measurable for
$(S^{\kappa }_{\omega },\eta )$
-strongly measurable for
![]() $\eta $
such that
$\eta $
such that
![]() $\left (2^{\eta }\right )^{\operatorname {\mathrm {HOD}}} < \kappa $
. Note that if
$\left (2^{\eta }\right )^{\operatorname {\mathrm {HOD}}} < \kappa $
. Note that if
![]() $S \subseteq T$
are stationary subsets of
$S \subseteq T$
are stationary subsets of
![]() $\kappa $
in
$\kappa $
in
![]() $\operatorname {\mathrm {HOD}}$
and
$\operatorname {\mathrm {HOD}}$
and
![]() $\kappa $
is T-strongly measurable, then it is S-strongly measurable. In particular, every strongly measurable cardinal is
$\kappa $
is T-strongly measurable, then it is S-strongly measurable. In particular, every strongly measurable cardinal is
![]() $\omega $
-strongly measurable.
$\omega $
-strongly measurable.
Theorem 2.3 (Woodin).
Let
![]() $\delta $
be an extendible cardinal. Then the following are equivalent:
$\delta $
be an extendible cardinal. Then the following are equivalent:
-
1. There is a regular cardinal
 $\kappa \geq \delta $
which is not
$\kappa \geq \delta $
which is not
 $\omega $
-strongly measurable.
$\omega $
-strongly measurable. -
2. There is a regular cardinal
 $\kappa \geq \delta $
which is not
$\kappa \geq \delta $
which is not
 $(S, \delta )$
-strongly measurable for some
$(S, \delta )$
-strongly measurable for some
 $S \in \operatorname {\mathrm {HOD}}$
which consists of singular ordinals of cofinality
$S \in \operatorname {\mathrm {HOD}}$
which consists of singular ordinals of cofinality
 $<\delta $
.
$<\delta $
. -
3. The
 $\operatorname {\mathrm {HOD}}$
-conjecture.
$\operatorname {\mathrm {HOD}}$
-conjecture. -
4. There is no regular
 $\omega $
-strongly measurable cardinal above
$\omega $
-strongly measurable cardinal above
 $\delta $
.
$\delta $
.
For the proof, see [Reference Woodin39, Theorems 197, 212, 213]. Without the assumption that the ordinals of S have fixed V-cofinality, the equivalence might fail.
The next result provides a necessary and sufficient condition for a cardinal
![]() $\kappa $
to be
$\kappa $
to be
![]() $\omega $
-strongly measurable in
$\omega $
-strongly measurable in
![]() $\operatorname {\mathrm {HOD}}$
. This observation will guide us in devising the main forcing construction, which will be used to prove theorem 1.4.
$\operatorname {\mathrm {HOD}}$
. This observation will guide us in devising the main forcing construction, which will be used to prove theorem 1.4.
Lemma 2.4. A cardinal
![]() $\kappa $
is strongly measurable with respect to
$\kappa $
is strongly measurable with respect to
![]() $S \in \operatorname {\mathrm {HOD}}$
if and only if
$S \in \operatorname {\mathrm {HOD}}$
if and only if
![]() $\kappa $
is an inaccessible cardinal in
$\kappa $
is an inaccessible cardinal in
![]() $\operatorname {\mathrm {HOD}}$
, and the restriction of the club filter on S to
$\operatorname {\mathrm {HOD}}$
, and the restriction of the club filter on S to
![]() $\operatorname {\mathrm {HOD}}$
is the intersection of
$\operatorname {\mathrm {HOD}}$
is the intersection of
![]() $\eta $
normal measures from
$\eta $
normal measures from
![]() $\operatorname {\mathrm {HOD}}$
,
$\operatorname {\mathrm {HOD}}$
,
![]() ${\langle } U_{\kappa ,i} \mid i < \eta {\rangle } \in \operatorname {\mathrm {HOD}}$
, for some
${\langle } U_{\kappa ,i} \mid i < \eta {\rangle } \in \operatorname {\mathrm {HOD}}$
, for some
![]() $\eta < \kappa $
.
$\eta < \kappa $
.
Proof. For the backwards implication, since
![]() $\kappa $
is inaccessible in
$\kappa $
is inaccessible in
![]() $\operatorname {\mathrm {HOD}}$
and
$\operatorname {\mathrm {HOD}}$
and
![]() $\eta < \kappa $
,
$\eta < \kappa $
,
![]() $\left (2^{\eta }\right )^{\operatorname {\mathrm {HOD}}} < \kappa $
.
$\left (2^{\eta }\right )^{\operatorname {\mathrm {HOD}}} < \kappa $
.
Let
![]() $\langle T_{\alpha } \mid \alpha < (\eta ^+)^{\operatorname {\mathrm {HOD}}}\rangle \in \operatorname {\mathrm {HOD}}$
be a decomposition of S into stationary sets. By the assumption, for each
$\langle T_{\alpha } \mid \alpha < (\eta ^+)^{\operatorname {\mathrm {HOD}}}\rangle \in \operatorname {\mathrm {HOD}}$
be a decomposition of S into stationary sets. By the assumption, for each
![]() $\alpha $
there is a measure
$\alpha $
there is a measure
![]() $U_{\kappa ,i}$
in
$U_{\kappa ,i}$
in
![]() $\operatorname {\mathrm {HOD}}$
such that
$\operatorname {\mathrm {HOD}}$
such that
![]() $T_{\alpha } \in U_{\kappa ,i}$
. Since the sets
$T_{\alpha } \in U_{\kappa ,i}$
. Since the sets
![]() $T_{\alpha }$
are pairwise disjoint, it is impossible for
$T_{\alpha }$
are pairwise disjoint, it is impossible for
![]() $\alpha \neq \beta $
to belong to the same
$\alpha \neq \beta $
to belong to the same
![]() $U_{\kappa ,i}$
. Thus, we obtain an injective function from
$U_{\kappa ,i}$
. Thus, we obtain an injective function from
![]() $(\eta ^+)^{\operatorname {\mathrm {HOD}}}$
to
$(\eta ^+)^{\operatorname {\mathrm {HOD}}}$
to
![]() $\eta $
in
$\eta $
in
![]() $\operatorname {\mathrm {HOD}}$
– a contradiction.
$\operatorname {\mathrm {HOD}}$
– a contradiction.
Let us assume now that
![]() $\kappa $
is strongly measurable with respect to
$\kappa $
is strongly measurable with respect to
![]() $S \in \operatorname {\mathrm {HOD}}$
. In particular,
$S \in \operatorname {\mathrm {HOD}}$
. In particular,
![]() $\kappa $
is inaccessible in
$\kappa $
is inaccessible in
![]() $\operatorname {\mathrm {HOD}}$
. Let
$\operatorname {\mathrm {HOD}}$
. Let
![]() $\mathcal {S} \in \operatorname {\mathrm {HOD}}$
be a maximal collection of pairwise disjoint stationary subsets of S, in
$\mathcal {S} \in \operatorname {\mathrm {HOD}}$
be a maximal collection of pairwise disjoint stationary subsets of S, in
![]() $\operatorname {\mathrm {HOD}}$
, such that for all
$\operatorname {\mathrm {HOD}}$
, such that for all
![]() $T \in \mathcal S$
, the club filter restricted to T is an ultrafilter in
$T \in \mathcal S$
, the club filter restricted to T is an ultrafilter in
![]() $\operatorname {\mathrm {HOD}}$
. Let us denote this ultrafilter by
$\operatorname {\mathrm {HOD}}$
. Let us denote this ultrafilter by
![]() $U_T$
. Since this collection is a partition of S into stationary sets,
$U_T$
. Since this collection is a partition of S into stationary sets,
![]() $|\mathcal S| < \kappa $
.
$|\mathcal S| < \kappa $
.
If
![]() $\bigcap \{U_T \mid T \in \mathcal S\}$
is not the club filter restricted to S in
$\bigcap \{U_T \mid T \in \mathcal S\}$
is not the club filter restricted to S in
![]() $\operatorname {\mathrm {HOD}}$
, then it contains a set
$\operatorname {\mathrm {HOD}}$
, then it contains a set
![]() $S \setminus S'$
, where
$S \setminus S'$
, where
![]() $S' \subseteq S$
stationary,
$S' \subseteq S$
stationary,
![]() $S' \in \operatorname {\mathrm {HOD}}$
. In particular,
$S' \in \operatorname {\mathrm {HOD}}$
. In particular,
![]() $S' \notin U_T$
for all
$S' \notin U_T$
for all
![]() $T \in \mathcal S$
, so
$T \in \mathcal S$
, so
![]() $S' \cap T$
is nonstationary for all
$S' \cap T$
is nonstationary for all
![]() $T \in \mathcal S$
, and
$T \in \mathcal S$
, and
![]() $S" = S' \setminus \bigcup _{T \in \mathcal S} (S' \cap T)$
is a stationary subset of S, disjoint from all members of
$S" = S' \setminus \bigcup _{T \in \mathcal S} (S' \cap T)$
is a stationary subset of S, disjoint from all members of
![]() $\mathcal S$
. Since
$\mathcal S$
. Since
![]() $\kappa $
is strongly measurable with respect to S, it is also strongly measurable with respect to
$\kappa $
is strongly measurable with respect to S, it is also strongly measurable with respect to
![]() $S"$
. Thus, there is some
$S"$
. Thus, there is some
![]() $T' \subseteq S"$
stationary such that the club filter restricted to
$T' \subseteq S"$
stationary such that the club filter restricted to
![]() $T'$
is an ultrafilter. But this contradicts the maximality of
$T'$
is an ultrafilter. But this contradicts the maximality of
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
Corollary 2.5. Let
![]() $\kappa $
be
$\kappa $
be
![]() $(S,{<}\kappa )$
-strongly measurable. Then S is contained in the regular cardinals of
$(S,{<}\kappa )$
-strongly measurable. Then S is contained in the regular cardinals of
![]() $\operatorname {\mathrm {HOD}}$
, up to a nonstationary error.
$\operatorname {\mathrm {HOD}}$
, up to a nonstationary error.
3
 $\omega _1$
is strongly measurable from one measurable cardinal
$\omega _1$
is strongly measurable from one measurable cardinal
In this section, we would like to present a forcing that forces
![]() $\omega _1$
to be strongly measurable. By Lemma 2.4, this means that in
$\omega _1$
to be strongly measurable. By Lemma 2.4, this means that in
![]() $\operatorname {\mathrm {HOD}}$
, the club filter of
$\operatorname {\mathrm {HOD}}$
, the club filter of
![]() $\omega _1$
is an intersection of countably many normal measures. In the case of
$\omega _1$
is an intersection of countably many normal measures. In the case of
![]() $\omega _1$
, we can take a single measure. So, we would like to collapse a measurable cardinal
$\omega _1$
, we can take a single measure. So, we would like to collapse a measurable cardinal
![]() $\kappa $
with a normal measure to be
$\kappa $
with a normal measure to be
![]() $\omega _1$
and then using a Mathias-type forcing, add a club that diagonalizes the normal measure. In order to show that this works, we need to show two things. First, we must show that the iteration is cone homogeneous. This is done in Lemma 3.3. Second, we need to show that it does not collapse
$\omega _1$
and then using a Mathias-type forcing, add a club that diagonalizes the normal measure. In order to show that this works, we need to show two things. First, we must show that the iteration is cone homogeneous. This is done in Lemma 3.3. Second, we need to show that it does not collapse
![]() $\omega _1$
. This amount to showing that the second step of the iteration is
$\omega _1$
. This amount to showing that the second step of the iteration is
![]() $\sigma $
-distributive, which in turn requires us to be able to add a U-generic point to the generic club. See Lemma 3.1 for the precise formulation.
$\sigma $
-distributive, which in turn requires us to be able to add a U-generic point to the generic club. See Lemma 3.1 for the precise formulation.
Let us present the forcing. Suppose that
![]() $\kappa $
is a measurable cardinal in a model V, and U is a normal measure on
$\kappa $
is a measurable cardinal in a model V, and U is a normal measure on
![]() $\kappa $
. Force with Levy collapse poset
$\kappa $
. Force with Levy collapse poset
![]() $\operatorname {\mathrm {Coll}}(\omega ,<\kappa )$
over V. Let H be a V-generic filter.
$\operatorname {\mathrm {Coll}}(\omega ,<\kappa )$
over V. Let H be a V-generic filter.
Working in the generic extension
![]() $V[H]$
, let
$V[H]$
, let
![]() $\mathbb {C}_U$
be the poset consisting of pairs
$\mathbb {C}_U$
be the poset consisting of pairs
![]() $x = {\langle } c, A{\rangle }$
, where
$x = {\langle } c, A{\rangle }$
, where
![]() $c \subseteq \kappa $
is a bounded closed subset of
$c \subseteq \kappa $
is a bounded closed subset of
![]() $\kappa $
and
$\kappa $
and
![]() $A \in U$
. The condition
$A \in U$
. The condition
![]() $x' = {\langle } c',A'{\rangle }$
extends x if
$x' = {\langle } c',A'{\rangle }$
extends x if
![]() $c'$
is an end extension of c,
$c'$
is an end extension of c,
![]() $A' \subseteq A$
, and
$A' \subseteq A$
, and
![]() $c'\setminus c \subseteq A$
.
$c'\setminus c \subseteq A$
.
It is clear that if
![]() $x = {\langle } c,A{\rangle }$
and
$x = {\langle } c,A{\rangle }$
and
![]() $x' = {\langle } c',A'{\rangle }$
are two conditions with the same bounded closed set
$x' = {\langle } c',A'{\rangle }$
are two conditions with the same bounded closed set
![]() $c = c'$
, then
$c = c'$
, then
![]() $x,x'$
are compatible. Since
$x,x'$
are compatible. Since
![]() $\kappa ^{<\kappa } = \kappa $
in
$\kappa ^{<\kappa } = \kappa $
in
![]() $V[H]$
, then
$V[H]$
, then
![]() $\mathbb {C}_U$
satisfies
$\mathbb {C}_U$
satisfies
![]() $\kappa ^+$
-c.c. (which is
$\kappa ^+$
-c.c. (which is
![]() $\aleph _2^{V[H]}$
-c.c.). The forcing
$\aleph _2^{V[H]}$
-c.c.). The forcing
![]() $\mathbb {C}_U$
adds a diagonalizing club to U. It has also been studied in [Reference Rinot28] in the context of well-behaved posets which can introduce square sequences and was found useful in other contexts.
$\mathbb {C}_U$
adds a diagonalizing club to U. It has also been studied in [Reference Rinot28] in the context of well-behaved posets which can introduce square sequences and was found useful in other contexts.
The following lemma is the key ingredient in the proof of the distributivity of
![]() $\mathbb {C}_U$
.
$\mathbb {C}_U$
.
Lemma 3.1. Work in
![]() $V[H]$
and fix some regular cardinal
$V[H]$
and fix some regular cardinal
![]() $\theta> \kappa ^+$
. There exists a stationary set of structures
$\theta> \kappa ^+$
. There exists a stationary set of structures
![]() $M \prec H_{\theta }$
of size
$M \prec H_{\theta }$
of size
![]() $|M| < \kappa $
, with the property that
$|M| < \kappa $
, with the property that
![]() $\sup (M \cap \kappa ) \in A$
for every
$\sup (M \cap \kappa ) \in A$
for every
![]() $A \in U \cap M$
.
$A \in U \cap M$
.
Proof. Fix any
![]() $f\colon H_{\theta }^{<\omega } \to H_{\theta }$
in
$f\colon H_{\theta }^{<\omega } \to H_{\theta }$
in
![]() $V[H]$
. We would like to show that there exists some
$V[H]$
. We would like to show that there exists some
![]() $M \subseteq H_{\theta }$
which is closed under f and satisfies the conditions in the statement of the lemma.
$M \subseteq H_{\theta }$
which is closed under f and satisfies the conditions in the statement of the lemma.
Fix in V a name
![]() for f and let
for f and let
![]() $f' \colon \operatorname {\mathrm {Coll}}(\omega , <\kappa ) \times (H_{\theta }^V)^{<\omega } \to H_{\theta }^V$
be a function that sends
$f' \colon \operatorname {\mathrm {Coll}}(\omega , <\kappa ) \times (H_{\theta }^V)^{<\omega } \to H_{\theta }^V$
be a function that sends
![]() $(p, x) \in \operatorname {\mathrm {Coll}}(\omega ,<\kappa )\times (H_{\theta })^{<\omega }$
to y if
$(p, x) \in \operatorname {\mathrm {Coll}}(\omega ,<\kappa )\times (H_{\theta })^{<\omega }$
to y if
![]() . Note that x is a finite sequence of names.
. Note that x is a finite sequence of names.
By the definition of
![]() $f'$
, if
$f'$
, if
![]() $M' \prec H_{\theta }^V$
is closed under
$M' \prec H_{\theta }^V$
is closed under
![]() $f'$
,
$f'$
,
![]() $M' \cap \kappa \in \kappa $
, and
$M' \cap \kappa \in \kappa $
, and
![]() $\kappa , U \in M'$
, then
$\kappa , U \in M'$
, then
![]() $M' = M \cap H_{\theta }^V$
for some
$M' = M \cap H_{\theta }^V$
for some
![]() $M \subseteq H_{\theta }$
which is closed under f. Indeed, we may take
$M \subseteq H_{\theta }$
which is closed under f. Indeed, we may take
![]() $M = M'[H \cap M]$
. By the chain condition of
$M = M'[H \cap M]$
. By the chain condition of
![]() $\operatorname {\mathrm {Coll}}(\omega ,<\kappa )$
, every name for a ground model object that belongs to
$\operatorname {\mathrm {Coll}}(\omega ,<\kappa )$
, every name for a ground model object that belongs to
![]() $M'$
can be refined to a nice name which is contained in
$M'$
can be refined to a nice name which is contained in
![]() $M'$
.
$M'$
.
Since
![]() $U \subseteq H_{\theta }^V$
, it is therefore sufficient to prove that there exists some
$U \subseteq H_{\theta }^V$
, it is therefore sufficient to prove that there exists some
![]() $M' \subseteq H_{\theta }^V$
which is closed under
$M' \subseteq H_{\theta }^V$
which is closed under
![]() $f'$
and satisfies
$f'$
and satisfies
![]() $|M'| < \kappa $
and
$|M'| < \kappa $
and
![]() $\sup (M' \cap \kappa ) \in A$
for all
$\sup (M' \cap \kappa ) \in A$
for all
![]() $A \in M' \cap U$
.
$A \in M' \cap U$
.
Working in V, take an elementary substructure
![]() $N \prec H_{\theta }^V$
satisfying
$N \prec H_{\theta }^V$
satisfying
![]() $f'[N] \subseteq N$
,
$f'[N] \subseteq N$
,
![]() $N^{<\kappa } \subseteq N$
,
$N^{<\kappa } \subseteq N$
,
![]() $|N| = \kappa $
,
$|N| = \kappa $
,
![]() $\kappa \in N$
. Let
$\kappa \in N$
. Let
![]() $j \colon V \to W \cong \mathrm {Ult}(V,U)$
be the ultrapower embedding induced by U. Consider the structure
$j \colon V \to W \cong \mathrm {Ult}(V,U)$
be the ultrapower embedding induced by U. Consider the structure
![]() $\tilde {M}' = j" N \prec j(H_{\theta }^V)$
.
$\tilde {M}' = j" N \prec j(H_{\theta }^V)$
.
![]() $\tilde {M}' \in W$
is closed under
$\tilde {M}' \in W$
is closed under
![]() $j(f')$
, and
$j(f')$
, and
![]() $\tilde {M}' \cap j(\kappa ) \in j(\kappa )$
. It follows that
$\tilde {M}' \cap j(\kappa ) \in j(\kappa )$
. It follows that
![]() $0_{j(\operatorname {\mathrm {Coll}}(\omega ,<\kappa ))}$
forces
$0_{j(\operatorname {\mathrm {Coll}}(\omega ,<\kappa ))}$
forces
![]() $\tilde {M}'$
to be closed under
$\tilde {M}'$
to be closed under
![]() . Finally, for every
. Finally, for every
![]() $A \in \tilde {M}' \cap j(U)$
,
$A \in \tilde {M}' \cap j(U)$
,
![]() $A = j(\bar {A})$
for some
$A = j(\bar {A})$
for some
![]() $\bar {A}\in U$
and therefore,
$\bar {A}\in U$
and therefore,
![]() $\kappa \in A$
.
$\kappa \in A$
.
So
![]() $\tilde {M}$
satisfies the conclusion of the lemma in W, and it is closed under
$\tilde {M}$
satisfies the conclusion of the lemma in W, and it is closed under
![]() $j(f')$
. By the elementarity of j, there is
$j(f')$
. By the elementarity of j, there is
![]() $M' \in V$
satisfying the conclusion of the lemma and closed under
$M' \in V$
satisfying the conclusion of the lemma and closed under
![]() $f'$
. Thus,
$f'$
. Thus,
![]() $M'[H \cap M'] = M$
satisfies the requirements of the lemma.
$M'[H \cap M'] = M$
satisfies the requirements of the lemma.
Proposition 3.2.
![]() $\mathbb {C}_{U}$
is
$\mathbb {C}_{U}$
is
![]() $\kappa $
-distributive.
$\kappa $
-distributive.
Proof. Since
![]() $\kappa = \aleph _1$
in
$\kappa = \aleph _1$
in
![]() $V[H]$
, we need to check that the intersection of a countable family
$V[H]$
, we need to check that the intersection of a countable family
![]() $\{ D_n \mid n<\omega \}$
of dense open subsets of
$\{ D_n \mid n<\omega \}$
of dense open subsets of
![]() $\mathbb {C}_{U}$
is dense. Pick some regular cardinal
$\mathbb {C}_{U}$
is dense. Pick some regular cardinal
![]() $\theta> \kappa ^+$
such that
$\theta> \kappa ^+$
such that
![]() $\mathbb {C}_U, \{D_n \mid n<\omega \} \in H_{\theta }$
. By lemma 3.1, for every condition
$\mathbb {C}_U, \{D_n \mid n<\omega \} \in H_{\theta }$
. By lemma 3.1, for every condition
![]() $x \in \mathbb {C}_{U}$
, there exists an elementary substructure
$x \in \mathbb {C}_{U}$
, there exists an elementary substructure
![]() $M \prec H_{\theta }$
of size
$M \prec H_{\theta }$
of size
![]() $|M| = \aleph _0$
, with
$|M| = \aleph _0$
, with
![]() $x, \mathbb {P},\mathbb {C}_{U},\{D_n \mid n < \omega \} \in M$
and further satisfies that
$x, \mathbb {P},\mathbb {C}_{U},\{D_n \mid n < \omega \} \in M$
and further satisfies that
![]() $\sup (M \cap \kappa ) \in A$
for every
$\sup (M \cap \kappa ) \in A$
for every
![]() $A \in M \cap \kappa $
. We may also assume that
$A \in M \cap \kappa $
. We may also assume that
![]() $M = M'[H \cap M']$
for
$M = M'[H \cap M']$
for
![]() $M' \in V$
,
$M' \in V$
,
![]() $M' \prec H_{\theta }^V$
.
$M' \prec H_{\theta }^V$
.
Denote
![]() $\sup (M \cap \kappa )$
by
$\sup (M \cap \kappa )$
by
![]() $\alpha $
and pick a cofinal sequence
$\alpha $
and pick a cofinal sequence
![]() ${\langle } \alpha _n \mid n < \omega {\rangle }$
in
${\langle } \alpha _n \mid n < \omega {\rangle }$
in
![]() $\alpha $
. We can construct an increasing sequence of extensions
$\alpha $
. We can construct an increasing sequence of extensions
![]() ${\langle } x_n \mid n<\omega {\rangle } \subseteq M$
of x,
${\langle } x_n \mid n<\omega {\rangle } \subseteq M$
of x,
![]() $x_n = {\langle } c_n,A_n{\rangle }$
such that
$x_n = {\langle } c_n,A_n{\rangle }$
such that
![]() $x_{n+1} \in D_n$
and
$x_{n+1} \in D_n$
and
![]() $\max (c_n) \geq \alpha _n$
for every
$\max (c_n) \geq \alpha _n$
for every
![]() $n<\omega $
. Without loss of generality, we may assume that for every
$n<\omega $
. Without loss of generality, we may assume that for every
![]() $A \in U \cap M$
, there is
$A \in U \cap M$
, there is
![]() $n < \omega $
such that
$n < \omega $
such that
![]() $A_n \subseteq A$
.
$A_n \subseteq A$
.
Since
![]() $x_n = {\langle } c_n,A_n{\rangle } \in M$
, then
$x_n = {\langle } c_n,A_n{\rangle } \in M$
, then
![]() $\alpha \in A_n$
for all
$\alpha \in A_n$
for all
![]() $n < \omega $
. It follows that
$n < \omega $
. It follows that
![]() $x^* = {\langle } \{ \alpha \} \cup (\bigcup _n c_n), \bigcap _n A_n{\rangle }$
is a condition in
$x^* = {\langle } \{ \alpha \} \cup (\bigcup _n c_n), \bigcap _n A_n{\rangle }$
is a condition in
![]() $\mathbb {C}_U$
, which is clearly an upper bound of
$\mathbb {C}_U$
, which is clearly an upper bound of
![]() ${\langle } x_n \mid n < \omega {\rangle }$
.Footnote
5
We conclude that there exists
${\langle } x_n \mid n < \omega {\rangle }$
.Footnote
5
We conclude that there exists
![]() $x^*$
extending our given condition x such that
$x^*$
extending our given condition x such that
![]() $x^* \in \bigcap _n D_n$
.
$x^* \in \bigcap _n D_n$
.
Lemma 3.3.
![]() $\mathbb {C}_{U}$
is cone homogeneous.
$\mathbb {C}_{U}$
is cone homogeneous.
Proof. Let
![]() $x_1 = {\langle } c_1,A_1{\rangle }$
,
$x_1 = {\langle } c_1,A_1{\rangle }$
,
![]() $x_2 = {\langle } c_2,A_2{\rangle }$
be two conditions of
$x_2 = {\langle } c_2,A_2{\rangle }$
be two conditions of
![]() $\mathbb {C}_{U}$
. Take
$\mathbb {C}_{U}$
. Take
![]() $\nu \in A_1 \cap A_2$
above
$\nu \in A_1 \cap A_2$
above
![]() $\max (c_1),\max (c_2)$
and consider the extensions
$\max (c_1),\max (c_2)$
and consider the extensions
![]() $y_1 = {\langle } c_1 \cup \{\nu \}, (A_1 \cap A_2) \setminus (\nu +1){\rangle }$
,
$y_1 = {\langle } c_1 \cup \{\nu \}, (A_1 \cap A_2) \setminus (\nu +1){\rangle }$
,
![]() $y_2 = \langle c_2 \cup \{\nu \}, (A_1 \cap A_2) \setminus (\nu +1){\rangle }$
of
$y_2 = \langle c_2 \cup \{\nu \}, (A_1 \cap A_2) \setminus (\nu +1){\rangle }$
of
![]() $x_1$
Define a cone isomorphism
$x_1$
Define a cone isomorphism
![]() $\sigma \colon \mathbb {C}_U/y_1 \to \mathbb {C}_U/y_2$
by
$\sigma \colon \mathbb {C}_U/y_1 \to \mathbb {C}_U/y_2$
by
![]() $\sigma $
is clearly an order preserving map onto
$\sigma $
is clearly an order preserving map onto
![]() $\mathbb {C}_U/y_1$
and has an order preserving inverse which is given by
$\mathbb {C}_U/y_1$
and has an order preserving inverse which is given by
Theorem 3.4. Suppose
![]() $C \subseteq \mathbb {C}_U$
is a
$C \subseteq \mathbb {C}_U$
is a
![]() $V[H]$
-generic filter. Then, in
$V[H]$
-generic filter. Then, in
![]() $V[H \ast C]$
,
$V[H \ast C]$
,
![]() $\kappa = \aleph _1^{V[H \ast C]}$
is strongly measurable.
$\kappa = \aleph _1^{V[H \ast C]}$
is strongly measurable.
Proof. By Lemma 8.3,
![]() $\operatorname {\mathrm {Coll}}(\omega ,<\kappa ) * \mathbb {C}_U$
is cone homogeneous, and therefore,
$\operatorname {\mathrm {Coll}}(\omega ,<\kappa ) * \mathbb {C}_U$
is cone homogeneous, and therefore,
![]() $\operatorname {\mathrm {HOD}}^{V[H \ast C]} \subseteq V$
. It is clear from the definition of
$\operatorname {\mathrm {HOD}}^{V[H \ast C]} \subseteq V$
. It is clear from the definition of
![]() $\mathbb {C}_U$
that for every subset
$\mathbb {C}_U$
that for every subset
![]() $S \subseteq \kappa $
in V, S is stationary in
$S \subseteq \kappa $
in V, S is stationary in
![]() $V[H \ast C]$
if and only if
$V[H \ast C]$
if and only if
![]() $S \in U$
. It follows that the closed unbounded filter on
$S \in U$
. It follows that the closed unbounded filter on
![]() $\kappa = \aleph _1^{V[H \ast C]}$
in
$\kappa = \aleph _1^{V[H \ast C]}$
in
![]() $V[H \ast C]$
is a
$V[H \ast C]$
is a
![]() $\operatorname {\mathrm {HOD}}$
-ultrafilter. Therefore
$\operatorname {\mathrm {HOD}}$
-ultrafilter. Therefore
![]() $V[H \ast C]\models \kappa $
is strongly measurable.
$V[H \ast C]\models \kappa $
is strongly measurable.
4 Strongly measurable successor of a regular cardinal
In this section, we would like to force a successor of an uncountable regular cardinal,
![]() $\kappa = \lambda ^+$
, to be strongly measurable. There are a few difficulties that arise. First, there is a definable splitting of the ordinals below
$\kappa = \lambda ^+$
, to be strongly measurable. There are a few difficulties that arise. First, there is a definable splitting of the ordinals below
![]() $\kappa $
, according to the cofinalities, so the club filter cannot be an ultrafilter but rather an intersection of a few normal measures. This means that we should fix a collection of normal measures so that their intersection is indented to become the club filter. Moreover, when killing a stationary set which is small with respect to the designated filter, we are forcing a club through the previous regulars, which are now going to change cofinalities to various possibilities. This means that a Levy collapse by itself would not provide all the cofinality changes that we need, and we must use a more complicated method of changing cofinalities in a homogeneous way.
$\kappa $
, according to the cofinalities, so the club filter cannot be an ultrafilter but rather an intersection of a few normal measures. This means that we should fix a collection of normal measures so that their intersection is indented to become the club filter. Moreover, when killing a stationary set which is small with respect to the designated filter, we are forcing a club through the previous regulars, which are now going to change cofinalities to various possibilities. This means that a Levy collapse by itself would not provide all the cofinality changes that we need, and we must use a more complicated method of changing cofinalities in a homogeneous way.
Suppose that
![]() $\lambda < \kappa $
are two cardinals such that
$\lambda < \kappa $
are two cardinals such that
![]() $\lambda $
is regular and
$\lambda $
is regular and
![]() $\kappa $
is measurable with
$\kappa $
is measurable with
![]() $o(\kappa ) = \lambda +1$
. Let
$o(\kappa ) = \lambda +1$
. Let
![]() $\mathcal {U} = {\langle } U_{\alpha ,\tau } \mid \lambda < \alpha \leq \kappa , \tau < o^{\mathcal {U}}(\alpha ){\rangle }$
be a coherent sequence of normal measures with
$\mathcal {U} = {\langle } U_{\alpha ,\tau } \mid \lambda < \alpha \leq \kappa , \tau < o^{\mathcal {U}}(\alpha ){\rangle }$
be a coherent sequence of normal measures with
![]() $o^{\mathcal {U}}(\kappa ) = \lambda + 1$
.
$o^{\mathcal {U}}(\kappa ) = \lambda + 1$
.
Let
![]() $\mathbb {P}^{\mathcal {U}}_{\kappa } = {\langle } \mathbb {P}_{\alpha }, \mathbb {Q}_{\alpha } \mid \alpha < \kappa {\rangle }$
be the homogeneous iteration of subsection 8.2. In the next two sections,
$\mathbb {P}^{\mathcal {U}}_{\kappa } = {\langle } \mathbb {P}_{\alpha }, \mathbb {Q}_{\alpha } \mid \alpha < \kappa {\rangle }$
be the homogeneous iteration of subsection 8.2. In the next two sections,
![]() $\mathbb {P}$
stands for
$\mathbb {P}$
stands for
![]() $\mathbb {P}^{\mathcal {U}}_{\kappa }$
. For the main properties of
$\mathbb {P}^{\mathcal {U}}_{\kappa }$
. For the main properties of
![]() $\mathbb {P}$
, we refer the reader to Fact 8.6. We will explicitly need the following additional property of the iteration.
$\mathbb {P}$
, we refer the reader to Fact 8.6. We will explicitly need the following additional property of the iteration.
Remark 4.1. We note that it follows at once from the definition of
![]() $\mathbb {Q}_{\alpha }$
that every V-set
$\mathbb {Q}_{\alpha }$
that every V-set
![]() $A \in \bigcap _{i<o^{\mathcal {U}}(\alpha )} U_{\alpha ,i}$
contains a tail of the cofinal sequence
$A \in \bigcap _{i<o^{\mathcal {U}}(\alpha )} U_{\alpha ,i}$
contains a tail of the cofinal sequence
![]() $b_{\alpha }$
. This is because every condition
$b_{\alpha }$
. This is because every condition
![]() $q = {\langle } t, T{\rangle } \in \mathbb {Q}_{\alpha }$
has a direct extension
$q = {\langle } t, T{\rangle } \in \mathbb {Q}_{\alpha }$
has a direct extension
![]() $q^A = {\langle } t, T^A{\rangle }$
of q, which satisfies that
$q^A = {\langle } t, T^A{\rangle }$
of q, which satisfies that
![]() $\operatorname {\mathrm {succ}}_T(s) \subseteq A$
for all
$\operatorname {\mathrm {succ}}_T(s) \subseteq A$
for all
![]() $s \in T$
.
$s \in T$
.
Definition 4.2. Let
![]() $G \subseteq \mathbb {P}$
be a V-generic filter, and let
$G \subseteq \mathbb {P}$
be a V-generic filter, and let
![]() $H \subseteq \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
be the Levy collapse generic over
$H \subseteq \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
be the Levy collapse generic over
![]() $V[G]$
. Working in
$V[G]$
. Working in
![]() $V[G \ast H]$
, we consider the filter
$V[G \ast H]$
, we consider the filter
![]() $\mathcal {F}_{\kappa }$
generated by
$\mathcal {F}_{\kappa }$
generated by
![]() $\bigcap _{i \leq \lambda } U_{\kappa ,i}$
,
$\bigcap _{i \leq \lambda } U_{\kappa ,i}$
,
The filter
![]() $\mathcal {F}_{\kappa }$
is going to generate the club filter in
$\mathcal {F}_{\kappa }$
is going to generate the club filter in
![]() $\operatorname {\mathrm {HOD}}$
in the generic extension.
$\operatorname {\mathrm {HOD}}$
in the generic extension.
Lemma 4.3.
![]() $\mathcal {F}_{\kappa }$
is a
$\mathcal {F}_{\kappa }$
is a
![]() $\kappa $
-complete filter in
$\kappa $
-complete filter in
![]() $V[G\ast H]$
.
$V[G\ast H]$
.
Proof. Suppose that
![]() ${\langle } A_{\nu } \mid \nu < \beta {\rangle } \in V[G\ast H]$
is a sequence of
${\langle } A_{\nu } \mid \nu < \beta {\rangle } \in V[G\ast H]$
is a sequence of
![]() $\beta < \kappa $
many sets of
$\beta < \kappa $
many sets of
![]() $\mathcal {F}_{\kappa }$
. We would like to show that
$\mathcal {F}_{\kappa }$
. We would like to show that
![]() $\bigcap _{\nu < \beta } A_{\nu }$
belongs to
$\bigcap _{\nu < \beta } A_{\nu }$
belongs to
![]() $\mathcal {F}_{\kappa }$
. We may assume that
$\mathcal {F}_{\kappa }$
. We may assume that
![]() $A_{\nu } \in \bigcap _{i \leq \lambda } U_{\kappa _i}$
for all
$A_{\nu } \in \bigcap _{i \leq \lambda } U_{\kappa _i}$
for all
![]() $\nu < \beta $
.
$\nu < \beta $
.
In order to prove the claim, we move from
![]() $V[G\ast H]$
to
$V[G\ast H]$
to
![]() $V[G]$
, and then to V. Working in
$V[G]$
, and then to V. Working in
![]() $V[G]$
, let
$V[G]$
, let
![]() be a
be a
![]() $\operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
-name for the V-set in
$\operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
-name for the V-set in
![]() $\bigcap _{i\leq \lambda } U_{\kappa ,i}$
. Since
$\bigcap _{i\leq \lambda } U_{\kappa ,i}$
. Since
![]() $\operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
satisfies
$\operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
satisfies
![]() $\kappa $
-c.c., there exists a family of V-sets
$\kappa $
-c.c., there exists a family of V-sets
![]() $X_{\nu } \subseteq \bigcap _{i\leq \lambda } U_{\kappa ,i}$
,
$X_{\nu } \subseteq \bigcap _{i\leq \lambda } U_{\kappa ,i}$
,
![]() $X_{\nu } \in V[G]$
, of size
$X_{\nu } \in V[G]$
, of size
![]() $<\kappa $
such that
$<\kappa $
such that
![]() . Fix in V a
. Fix in V a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() for each
for each
![]() $X_{\nu }$
.
$X_{\nu }$
.
Let
![]() $p \in G$
be a condition forcing the above. Moving back to V, the fusion lemma for nonstationary support iteration of Prikry type forcings [Reference Ben-Neria and Unger5, Lemma 3.6] guarantees that there exists some
$p \in G$
be a condition forcing the above. Moving back to V, the fusion lemma for nonstationary support iteration of Prikry type forcings [Reference Ben-Neria and Unger5, Lemma 3.6] guarantees that there exists some
![]() $q \in G$
and a sequence of sets
$q \in G$
and a sequence of sets
![]() ${\langle } Y_{\nu } \mid \nu < \beta {\rangle }$
in V, so that for each
${\langle } Y_{\nu } \mid \nu < \beta {\rangle }$
in V, so that for each
![]() $\nu < \beta $
,
$\nu < \beta $
,
![]() $Y_{\nu } \subseteq \bigcap _{i \leq \lambda }U_{\kappa ,i}$
has size
$Y_{\nu } \subseteq \bigcap _{i \leq \lambda }U_{\kappa ,i}$
has size
![]() $|Y_{\nu }| < \kappa $
, and
$|Y_{\nu }| < \kappa $
, and
![]() . For each
. For each
![]() $\nu $
, let
$\nu $
, let
![]() $A^{\prime }_{\nu } = \bigcap Y_{\nu }$
, and
$A^{\prime }_{\nu } = \bigcap Y_{\nu }$
, and
![]() $A' = \bigcap _{\nu < \beta } A^{\prime }_{\nu }$
. Since
$A' = \bigcap _{\nu < \beta } A^{\prime }_{\nu }$
. Since
![]() $U_{\kappa ,i}$
is
$U_{\kappa ,i}$
is
![]() $\kappa $
-complete for all
$\kappa $
-complete for all
![]() $i \leq \lambda $
, we have in
$i \leq \lambda $
, we have in
![]() $V[G\ast H]$
that
$V[G\ast H]$
that
![]() $A' \in \mathcal {F}_{\kappa }$
and
$A' \in \mathcal {F}_{\kappa }$
and
![]() $A' \subseteq \bigcap _{\nu < \beta } A_{\nu }$
.
$A' \subseteq \bigcap _{\nu < \beta } A_{\nu }$
.
To produce a model where
![]() $\kappa $
is
$\kappa $
is
![]() $\omega $
-strongly measurable, we will force over
$\omega $
-strongly measurable, we will force over
![]() $V[G\ast H]$
to add a closed unbounded set
$V[G\ast H]$
to add a closed unbounded set
![]() $C \subseteq \kappa $
which is almost contained in every set
$C \subseteq \kappa $
which is almost contained in every set
![]() $A \in \mathcal {F}_{\kappa }$
.
$A \in \mathcal {F}_{\kappa }$
.
Definition 4.4. Working in a V-generic extension
![]() $V[G\ast H]$
by
$V[G\ast H]$
by
![]() $G\ast H \subseteq \mathbb {P}*\operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
, we define the forcing
$G\ast H \subseteq \mathbb {P}*\operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
, we define the forcing
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
. Conditions
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
. Conditions
![]() $x \in \mathbb {C}_{\mathcal {F}_{\kappa }}$
are pairs
$x \in \mathbb {C}_{\mathcal {F}_{\kappa }}$
are pairs
![]() $x = {\langle } c, A{\rangle }$
where c is a closed and bounded subset of
$x = {\langle } c, A{\rangle }$
where c is a closed and bounded subset of
![]() $\kappa $
and
$\kappa $
and
![]() $A \in \mathcal {F}_{\kappa }$
. A condition
$A \in \mathcal {F}_{\kappa }$
. A condition
![]() $x' = {\langle } c', A'{\rangle } \in \mathbb {C}_{\mathcal {F}_{\kappa }}$
extends x (denoted
$x' = {\langle } c', A'{\rangle } \in \mathbb {C}_{\mathcal {F}_{\kappa }}$
extends x (denoted
![]() $x' \geq x$
) if
$x' \geq x$
) if
-
(i)
 $c' \cap \max (c) = c$
,
$c' \cap \max (c) = c$
, -
(ii)
 $A' \subseteq A$
, and
$A' \subseteq A$
, and -
(iii)
 $c' \setminus c \subseteq A$
.
$c' \setminus c \subseteq A$
.
For conditions
![]() $x = {\langle } c,A{\rangle } \in \mathbb {C}_{\mathcal {F}_{\kappa }}$
, we will frequently denote c and A by
$x = {\langle } c,A{\rangle } \in \mathbb {C}_{\mathcal {F}_{\kappa }}$
, we will frequently denote c and A by
![]() $c^x$
and
$c^x$
and
![]() $A^x$
, respectively. It is clear that if
$A^x$
, respectively. It is clear that if
![]() $R \subseteq \mathbb {C}_{\mathcal {F}_{\kappa }}$
is generic, then the union
$R \subseteq \mathbb {C}_{\mathcal {F}_{\kappa }}$
is generic, then the union
![]() $C = \bigcup \{ c^x \mid x \in R\}$
is a closed and unbounded subset of
$C = \bigcup \{ c^x \mid x \in R\}$
is a closed and unbounded subset of
![]() $\kappa $
which is almost contained in every
$\kappa $
which is almost contained in every
![]() $A \in \mathcal {F}_{\kappa }$
. Since
$A \in \mathcal {F}_{\kappa }$
. Since
![]() $\mathcal {F}_{\kappa }$
is a filter and
$\mathcal {F}_{\kappa }$
is a filter and
![]() $\kappa ^{<\kappa } = \kappa $
, the forcing
$\kappa ^{<\kappa } = \kappa $
, the forcing
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
is
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
is
![]() $\kappa $
-centered and therefore satisfies
$\kappa $
-centered and therefore satisfies
![]() $\kappa ^+$
-chain condition.
$\kappa ^+$
-chain condition.
The following lemma is a parallel of Lemma 3.1. From this lemma we will infer the distributivity of the forcing
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
.
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
.
Lemma 4.5. Working in
![]() $V[G\ast H]$
, for any regular cardinal
$V[G\ast H]$
, for any regular cardinal
![]() $\theta> \kappa ^+$
and
$\theta> \kappa ^+$
and
![]() $\tau \leq \lambda $
, there exists a stationary set of structures
$\tau \leq \lambda $
, there exists a stationary set of structures
![]() $M \prec H_{\theta }$
with
$M \prec H_{\theta }$
with
![]() $\sup (M \cap \kappa ) = \alpha $
which satisfy
$\sup (M \cap \kappa ) = \alpha $
which satisfy
-
(i)
 $M^{<\tau } \subseteq M$
;
$M^{<\tau } \subseteq M$
; -
(ii)
 $o^{\mathcal {U}}(\alpha ) = \tau $
;
$o^{\mathcal {U}}(\alpha ) = \tau $
; -
(iii) For every
 $A \in \mathcal {F}_{\kappa } \cap M$
,
$A \in \mathcal {F}_{\kappa } \cap M$
,
 $\alpha \in A$
and, moreover,
$\alpha \in A$
and, moreover,
 $b_{\alpha } \subseteq ^* A$
(namely
$b_{\alpha } \subseteq ^* A$
(namely
 $b_{\alpha } \setminus A$
is bounded in
$b_{\alpha } \setminus A$
is bounded in
 $\alpha $
).
$\alpha $
).
Proof. Fix a function
![]() $f\colon [H_{\theta }]^{<\omega } \to H_{\theta }$
in
$f\colon [H_{\theta }]^{<\omega } \to H_{\theta }$
in
![]() $V[G\ast H]$
. Back in the ground model V, let
$V[G\ast H]$
. Back in the ground model V, let
![]() be a
be a
![]() $\mathbb {P} * \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
-name for f. Since
$\mathbb {P} * \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
-name for f. Since
![]() $\operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
is
$\operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
is
![]() $\kappa $
-c.c., there exists a
$\kappa $
-c.c., there exists a
![]() $\mathbb {P}$
-name function
$\mathbb {P}$
-name function
![]() such that
such that
![]() is forced to be a member of
is forced to be a member of
![]() for every
for every
![]() $x \in H_{\theta }^V$
.
$x \in H_{\theta }^V$
.
Let us consider our ability to approximate
![]() in V. Let
in V. Let
![]() $N \prec H_{\theta }^V$
be an elementary substructure of size
$N \prec H_{\theta }^V$
be an elementary substructure of size
![]() $\kappa $
with
$\kappa $
with
![]() $N^{<\kappa } \subseteq N$
and
$N^{<\kappa } \subseteq N$
and
![]() .
.
Claim 4.6. Let N be as above and
![]() $p \in \mathbb {P} \cap N$
. Then, there is
$p \in \mathbb {P} \cap N$
. Then, there is
![]() $p^* \leq p$
which is N-generic, namely, for every name for an ordinal
$p^* \leq p$
which is N-generic, namely, for every name for an ordinal
![]() , there is set of ordinals
, there is set of ordinals
![]() $S \in N$
such that
$S \in N$
such that
![]() $S \subseteq N$
and
$S \subseteq N$
and
![]() .
.
Proof. By a standard argument concerning capturing dense open sets in Prikry-type forcings and fat-trees (e.g., see [Reference Gitik13]) for every dense open set D of
![]() $\mathbb {P}$
,
$\mathbb {P}$
,
![]() $p \in \mathbb {P}$
, there exists a direct extension
$p \in \mathbb {P}$
, there exists a direct extension
![]() $p' \geq ^* p$
which reduces capturing D to a dense subset of
$p' \geq ^* p$
which reduces capturing D to a dense subset of
![]() $\mathbb {P}_{\mu }$
for some
$\mathbb {P}_{\mu }$
for some
![]() $\mu < \kappa $
, namely, the set of all
$\mu < \kappa $
, namely, the set of all
![]() $r \in \mathbb {P}_{\mu }$
such that
$r \in \mathbb {P}_{\mu }$
such that
![]() $r^{\smallfrown } p' \restriction [\mu ,\kappa ) \in D$
is dense below
$r^{\smallfrown } p' \restriction [\mu ,\kappa ) \in D$
is dense below
![]() $p' \restriction \mu $
. Moreover, given
$p' \restriction \mu $
. Moreover, given
![]() $\nu < \kappa $
, we can also make the direct extension
$\nu < \kappa $
, we can also make the direct extension
![]() $p'$
to agree with p up to
$p'$
to agree with p up to
![]() $\nu +1$
(i.e.,
$\nu +1$
(i.e.,
![]() $p'\restriction \nu +1 = p\restriction \nu +1$
), in which case
$p'\restriction \nu +1 = p\restriction \nu +1$
), in which case
![]() $\mu> \nu $
.
$\mu> \nu $
.
Given an initial condition
![]() $p \in \mathbb {P}$
, we can list the dense open sets in N,
$p \in \mathbb {P}$
, we can list the dense open sets in N,
![]() ${\langle } D_i \mid i < \kappa {\rangle }$
, and form an increasing sequence of direct extensions of p,
${\langle } D_i \mid i < \kappa {\rangle }$
, and form an increasing sequence of direct extensions of p,
![]() ${\langle } p^i \mid i < \kappa {\rangle }$
, together with a closed unbounded set
${\langle } p^i \mid i < \kappa {\rangle }$
, together with a closed unbounded set
![]() $C^* = {\langle } \nu _i \mid i <\kappa {\rangle }$
such that for every successor ordinal
$C^* = {\langle } \nu _i \mid i <\kappa {\rangle }$
such that for every successor ordinal
![]() $i = i'+1$
,
$i = i'+1$
,
![]() $p^i \in N$
reduces the dense set
$p^i \in N$
reduces the dense set
![]() $D_{i'}$
of
$D_{i'}$
of
![]() $\mathbb {P}$
to a bounded dense set
$\mathbb {P}$
to a bounded dense set
![]() $D_{i'}^{\prime }$
of
$D_{i'}^{\prime }$
of
![]() $\mathbb {P}_{\mu _i}$
for some
$\mathbb {P}_{\mu _i}$
for some
![]() $\nu _i <\mu _i < \kappa $
, and
$\nu _i <\mu _i < \kappa $
, and
![]() $p^i\restriction \nu _i+1 = p^{i'}\restriction \nu _i+1$
. By a standard argument concerning nonstationary support iterations (e.g., see the fusion argument in the proof of [Reference Ben-Neria and Unger5, Lemma 2.2]), the sequence of direct extensions
$p^i\restriction \nu _i+1 = p^{i'}\restriction \nu _i+1$
. By a standard argument concerning nonstationary support iterations (e.g., see the fusion argument in the proof of [Reference Ben-Neria and Unger5, Lemma 2.2]), the sequence of direct extensions
![]() ${\langle } p^i \mid i < \kappa {\rangle }$
has an upper bound
${\langle } p^i \mid i < \kappa {\rangle }$
has an upper bound
![]() $p^* \geq ^* p$
. It follows that for every
$p^* \geq ^* p$
. It follows that for every
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() of an element of
of an element of
![]() $H_{\theta }^V$
, there exists some
$H_{\theta }^V$
, there exists some
![]() $\mu < \kappa $
and a
$\mu < \kappa $
and a
![]() $\mathbb {P}_{\mu }$
-name
$\mathbb {P}_{\mu }$
-name
![]() such that
such that
![]() .
.
In particular, for each such name
![]() ,
,
![]() $p^*$
forces that it can take
$p^*$
forces that it can take
![]() $<\kappa $
many values in
$<\kappa $
many values in
![]() $H_{\theta }^V$
, all of which are in N. This follows from the elementarity of N in
$H_{\theta }^V$
, all of which are in N. This follows from the elementarity of N in
![]() $H_{\theta }$
and the fact
$H_{\theta }$
and the fact
![]() $\kappa +1 \subseteq N$
.
$\kappa +1 \subseteq N$
.
Let
![]() $j_{\tau }\colon V \to M_{\tau }$
be the ultrapower embedding by
$j_{\tau }\colon V \to M_{\tau }$
be the ultrapower embedding by
![]() $U_{\kappa ,\tau }$
and
$U_{\kappa ,\tau }$
and
![]() $M' = j_{\tau }" N \prec j_{\tau }(H_{\theta }^V)$
,
$M' = j_{\tau }" N \prec j_{\tau }(H_{\theta }^V)$
,
![]() $M' \in M_{\tau }$
.
$M' \in M_{\tau }$
.
Claim 4.7.
![]() $j_{\tau }(p^*)$
forces that
$j_{\tau }(p^*)$
forces that
![]() $M'$
is closed under
$M'$
is closed under
![]() .
.
Proof. Indeed, if
![]() $G^* \subseteq j_{\tau }(\mathbb {P})$
is
$G^* \subseteq j_{\tau }(\mathbb {P})$
is
![]() $M_{\tau }$
-generic with
$M_{\tau }$
-generic with
![]() $j_{\tau }(p^*) \in G^*$
, then for each
$j_{\tau }(p^*) \in G^*$
, then for each
![]() $\mu < \kappa $
,
$\mu < \kappa $
,
![]() $G^*_{\mu } = \{ p\restriction \mu \mid p \in G^*\}$
is a V-generic filter for
$G^*_{\mu } = \{ p\restriction \mu \mid p \in G^*\}$
is a V-generic filter for
![]() $\mathbb {P}_{\mu }$
. For every
$\mathbb {P}_{\mu }$
. For every
![]() and
and
![]() ,
,
![]() is the
is the
![]() $G^*$
-generic interpretation of the
$G^*$
-generic interpretation of the
![]() $j_{\tau }(\mathbb {P})$
-name
$j_{\tau }(\mathbb {P})$
-name
![]() . As
. As
![]() $p^*$
forces
$p^*$
forces
![]() for some
for some
![]() which is a
which is a
![]() $\mathbb {P}_{\mu }$
-name for some
$\mathbb {P}_{\mu }$
-name for some
![]() $\mu < \kappa $
, we see that
$\mu < \kappa $
, we see that
![]() $j_{\tau }(p^*)$
forces
$j_{\tau }(p^*)$
forces
![]() , where
, where
![]() is a
is a
![]() $j_{\tau }(\mathbb {P}_{\mu }) = \mathbb {P}_{\mu }$
-name. If
$j_{\tau }(\mathbb {P}_{\mu }) = \mathbb {P}_{\mu }$
-name. If
![]() $q \in G_{\mu }$
and
$q \in G_{\mu }$
and
![]() $z \in N \cap H_{\theta }^V$
are such that
$z \in N \cap H_{\theta }^V$
are such that
![]() , then
, then
![]() . We conclude that
. We conclude that
![]() $F^*(y) = z \in M'$
.
$F^*(y) = z \in M'$
.
We now return to prove the statement of the lemma. It is sufficient to prove that in
![]() $V[G]$
there exists some
$V[G]$
there exists some
![]() $M' \subseteq H_{\theta }^V$
which is closed under F and satisfies requirements (i)–(iii). Let
$M' \subseteq H_{\theta }^V$
which is closed under F and satisfies requirements (i)–(iii). Let
![]() $p \in \mathbb {P}$
be a condition. By a standard density argument, there are
$p \in \mathbb {P}$
be a condition. By a standard density argument, there are
![]() $N \prec H_{\theta }^V$
and
$N \prec H_{\theta }^V$
and
![]() $p^* \in G$
which is N-generic, with
$p^* \in G$
which is N-generic, with
![]() $p^* \geq ^* p$
.Footnote
6
By Claim 4.7,
$p^* \geq ^* p$
.Footnote
6
By Claim 4.7,
![]() $j_{\tau }(p^*)$
forces that
$j_{\tau }(p^*)$
forces that
![]() $M' = j_{\tau }\text {"} N$
is closed under
$M' = j_{\tau }\text {"} N$
is closed under
![]() $j_{\tau }(F)$
. It is now clear that
$j_{\tau }(F)$
. It is now clear that
![]() $M'$
satisfies condition (ii) in the ultrapower, as
$M'$
satisfies condition (ii) in the ultrapower, as
![]() $o^{j_{\tau }(\mathcal {U})}(\kappa ) = \tau $
and
$o^{j_{\tau }(\mathcal {U})}(\kappa ) = \tau $
and
![]() $M' \cap j_{\tau }(\kappa ) = \kappa $
. Condition (i) holds as well, since
$M' \cap j_{\tau }(\kappa ) = \kappa $
. Condition (i) holds as well, since
![]() $j(\mathbb {P}_{\kappa }) / \mathbb {P}_{\kappa }$
does not introduce new
$j(\mathbb {P}_{\kappa }) / \mathbb {P}_{\kappa }$
does not introduce new
![]() ${<}\tau $
-sequences to
${<}\tau $
-sequences to
![]() $j_{\tau } \text {"} N$
. Therefore, it remains to verify that
$j_{\tau } \text {"} N$
. Therefore, it remains to verify that
![]() $j_{\tau }(p^*)$
forces
$j_{\tau }(p^*)$
forces
![]() $M'$
to satisfy condition (iii). For every
$M'$
to satisfy condition (iii). For every
![]() $A \in M' \cap j_{\tau }(\mathcal {F}_{\kappa })$
, there is some
$A \in M' \cap j_{\tau }(\mathcal {F}_{\kappa })$
, there is some
![]() $B \in \mathcal {F}_{\kappa }$
such that
$B \in \mathcal {F}_{\kappa }$
such that
![]() $A = j_{\tau }(B)$
. In particular,
$A = j_{\tau }(B)$
. In particular,
![]() $A \cap \kappa = B \in \mathcal {F}_{\kappa }$
and
$A \cap \kappa = B \in \mathcal {F}_{\kappa }$
and
![]() $\kappa \in A$
. Since
$\kappa \in A$
. Since
![]() $\mathcal {F}_{\kappa } \subseteq \bigcap _{i \leq \tau } U_{\kappa ,i}$
(which is
$\mathcal {F}_{\kappa } \subseteq \bigcap _{i \leq \tau } U_{\kappa ,i}$
(which is
![]() $\mathcal {F}_{\kappa }^{M_{\tau }}$
), it follows form remark 4.1 that for every generic filter
$\mathcal {F}_{\kappa }^{M_{\tau }}$
), it follows form remark 4.1 that for every generic filter
![]() $G^* \subseteq j_{\tau }(\mathbb {P})$
over
$G^* \subseteq j_{\tau }(\mathbb {P})$
over
![]() $M_{\tau }$
, if
$M_{\tau }$
, if
![]() $b_{\kappa }$
is the
$b_{\kappa }$
is the
![]() $G^*$
-induced
$G^*$
-induced
![]() $\mathbb {Q}_{\kappa }^{\tau }$
cofinal generic sequence, then it is almost contained in
$\mathbb {Q}_{\kappa }^{\tau }$
cofinal generic sequence, then it is almost contained in
![]() $B = A \cap \kappa $
.
$B = A \cap \kappa $
.
Proposition 4.8.
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
is
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
is
![]() $\kappa $
-distributive.
$\kappa $
-distributive.
Proof. Since
![]() $\kappa = \lambda ^+$
in
$\kappa = \lambda ^+$
in
![]() $V[G\ast H]$
, we need to check that the intersection of every set
$V[G\ast H]$
, we need to check that the intersection of every set
![]() $\{ D_i \mid i < \lambda \}$
of
$\{ D_i \mid i < \lambda \}$
of
![]() $\lambda $
-many dense open subsets of
$\lambda $
-many dense open subsets of
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
is dense. Pick some regular cardinal
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
is dense. Pick some regular cardinal
![]() $\theta> \kappa ^+$
such that
$\theta> \kappa ^+$
such that
![]() $\mathbb {P}, \mathbb {C}_{\mathcal {F}_{\kappa }}, \{D_i \mid i < \lambda \} \in H_{\theta }$
. By Lemma 4.5, for every condition
$\mathbb {P}, \mathbb {C}_{\mathcal {F}_{\kappa }}, \{D_i \mid i < \lambda \} \in H_{\theta }$
. By Lemma 4.5, for every condition
![]() $x \in \mathbb {C}_{\mathcal {F}}$
, there exists an elementary substructure
$x \in \mathbb {C}_{\mathcal {F}}$
, there exists an elementary substructure
![]() $M \prec H_{\theta }$
of cardinality
$M \prec H_{\theta }$
of cardinality
![]() $< \kappa $
, with
$< \kappa $
, with
![]() $x, \mathbb {P},\mathbb {C}_{\mathcal {F}_{\kappa }},\{D_i \mid i < \lambda \} \in M$
and which further satisfies (i)
$x, \mathbb {P},\mathbb {C}_{\mathcal {F}_{\kappa }},\{D_i \mid i < \lambda \} \in M$
and which further satisfies (i)
![]() $M^{<\lambda } \subseteq M$
; (ii)
$M^{<\lambda } \subseteq M$
; (ii)
![]() $\sup (M \cap \kappa ) = \alpha $
has
$\sup (M \cap \kappa ) = \alpha $
has
![]() $o^{\mathcal {U}}(\alpha ) = \lambda $
; and (iii)
$o^{\mathcal {U}}(\alpha ) = \lambda $
; and (iii)
![]() $\alpha \in A$
and
$\alpha \in A$
and
![]() $b_{\alpha }$
is almost contained in A for every
$b_{\alpha }$
is almost contained in A for every
![]() $A \in \mathcal {F}_{\kappa } \cap M$
.
$A \in \mathcal {F}_{\kappa } \cap M$
.
Let
![]() ${\langle } \alpha _i \mid i < \lambda {\rangle }$
be an increasing enumeration of
${\langle } \alpha _i \mid i < \lambda {\rangle }$
be an increasing enumeration of
![]() $b_{\alpha }$
. We construct by induction an increasing sequence of extensions
$b_{\alpha }$
. We construct by induction an increasing sequence of extensions
![]() ${\langle } x_j \mid j < \lambda {\rangle }$
of x, together with an increasing subsequence
${\langle } x_j \mid j < \lambda {\rangle }$
of x, together with an increasing subsequence
![]() ${\langle } \alpha _{i_j} \mid j < \lambda {\rangle }$
of
${\langle } \alpha _{i_j} \mid j < \lambda {\rangle }$
of
![]() $b_{\alpha }$
such that
$b_{\alpha }$
such that
![]() $x_{j+1} \in D_j$
for every
$x_{j+1} \in D_j$
for every
![]() $j < \lambda $
, and
$j < \lambda $
, and
![]() $\{\alpha \} \cup \{ \alpha _{i_j} \mid j> j^*\} \subseteq A^{x_{j^*}}$
for all
$\{\alpha \} \cup \{ \alpha _{i_j} \mid j> j^*\} \subseteq A^{x_{j^*}}$
for all
![]() $j^* < \lambda $
. For notational simplicity, denote x by
$j^* < \lambda $
. For notational simplicity, denote x by
![]() $x_{-1}$
. Given a condition
$x_{-1}$
. Given a condition
![]() $x_j \in M$
with a suitable
$x_j \in M$
with a suitable
![]() $\alpha _j$
as above, we take
$\alpha _j$
as above, we take
![]() $x_{j+1}\in D_{j+1}$
to be an extension of
$x_{j+1}\in D_{j+1}$
to be an extension of
![]() $x_j$
with
$x_j$
with
![]() $\max (c^{x_{j+1}})> \alpha _{i_j}$
. Since
$\max (c^{x_{j+1}})> \alpha _{i_j}$
. Since
![]() $A^{x_{j+1}} \in M \cap \mathcal {F}_{\kappa }$
, we can use (iii) and get that
$A^{x_{j+1}} \in M \cap \mathcal {F}_{\kappa }$
, we can use (iii) and get that
![]() $\alpha \in A^{x_{j+1}}$
and there exist some
$\alpha \in A^{x_{j+1}}$
and there exist some
![]() $i'> i_j$
such that
$i'> i_j$
such that
![]() $\{ \alpha _i \mid i>i'\} \subseteq A^{x_{j+1}}$
. Take
$\{ \alpha _i \mid i>i'\} \subseteq A^{x_{j+1}}$
. Take
![]() $i_{j+1} < \lambda $
to be the minimal such
$i_{j+1} < \lambda $
to be the minimal such
![]() $i'> i_j$
. It remains to show that the construction goes through at limit stages
$i'> i_j$
. It remains to show that the construction goes through at limit stages
![]() $\delta \leq \lambda $
. Given
$\delta \leq \lambda $
. Given
![]() ${\langle } x_j \mid j < \delta {\rangle }$
, we define
${\langle } x_j \mid j < \delta {\rangle }$
, we define
![]() $i_{\delta } = \sup _{j < \delta } \alpha _{i_j}$
. It is clear from our construction at successor steps that
$i_{\delta } = \sup _{j < \delta } \alpha _{i_j}$
. It is clear from our construction at successor steps that
![]() $\alpha _{i_{\delta }} = \sup _{j < \delta } \max (c^{x_j})$
and
$\alpha _{i_{\delta }} = \sup _{j < \delta } \max (c^{x_j})$
and
![]() $\alpha _{i_{\delta }} \in A^{x_j}$
for every
$\alpha _{i_{\delta }} \in A^{x_j}$
for every
![]() $j < \delta $
. It follows that the condition
$j < \delta $
. It follows that the condition
![]() $x_{\delta } = {\langle } \{ \alpha _{\delta } \} \cup \bigcup _{j < \delta } c^{x_j}, \bigcap _{j<\delta } A^{x_j}{\rangle }$
satisfies the desirable conditions. Moreover, if
$x_{\delta } = {\langle } \{ \alpha _{\delta } \} \cup \bigcup _{j < \delta } c^{x_j}, \bigcap _{j<\delta } A^{x_j}{\rangle }$
satisfies the desirable conditions. Moreover, if
![]() $\delta < \lambda $
, then
$\delta < \lambda $
, then
![]() $x_{\delta } \in M$
since M is closed under
$x_{\delta } \in M$
since M is closed under
![]() $<\lambda $
-sequences.
$<\lambda $
-sequences.
Since the limit construction goes through at stage
![]() $\lambda $
as well (although not producing a condition in M), the limit condition
$\lambda $
as well (although not producing a condition in M), the limit condition
![]() $x_{\lambda }$
is an extension of x and belongs to
$x_{\lambda }$
is an extension of x and belongs to
![]() $\bigcap _{j <\lambda } D_j$
.
$\bigcap _{j <\lambda } D_j$
.
The argument of the proof of lemma 3.3 for
![]() $\mathbb {C}_U$
applies to
$\mathbb {C}_U$
applies to
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
as well.
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
as well.
Lemma 4.9.
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
is cone homogeneous.
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
is cone homogeneous.
Theorem 4.10. In the generic extension by
![]() $\mathbb {P} * \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) * \mathbb {C}_{\mathcal {F}_{\kappa }}$
,
$\mathbb {P} * \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) * \mathbb {C}_{\mathcal {F}_{\kappa }}$
,
![]() $\kappa $
is strongly measurable.
$\kappa $
is strongly measurable.
Proof. Suppose
![]() $G(\mathbb {C}_{\mathcal {F}_{\kappa }}) \subseteq \mathbb {C}_{\mathcal {F}_{\kappa }}$
is a generic filter over
$G(\mathbb {C}_{\mathcal {F}_{\kappa }}) \subseteq \mathbb {C}_{\mathcal {F}_{\kappa }}$
is a generic filter over
![]() $V[G\ast H]$
. We may identify
$V[G\ast H]$
. We may identify
![]() $G(\mathbb {C}_{\mathcal {F}_{\kappa }})$
with its derived generic closed and unbounded set
$G(\mathbb {C}_{\mathcal {F}_{\kappa }})$
with its derived generic closed and unbounded set
By a standard density argument, we have that for every set
![]() $X \subseteq \kappa $
in V, if
$X \subseteq \kappa $
in V, if
![]() $X \notin U_{\kappa ,\tau }$
for all
$X \notin U_{\kappa ,\tau }$
for all
![]() $\tau \leq \lambda $
, then
$\tau \leq \lambda $
, then
![]() $|C \cap X| < \kappa $
.
$|C \cap X| < \kappa $
.
We conclude that for
![]() $X \subseteq \kappa $
in V to be stationary in
$X \subseteq \kappa $
in V to be stationary in
![]() $V[G \ast H \ast C]$
, it must belong to
$V[G \ast H \ast C]$
, it must belong to
![]() $U_{\kappa ,\tau }$
for some
$U_{\kappa ,\tau }$
for some
![]() $\tau \leq \lambda $
. It follows that if
$\tau \leq \lambda $
. It follows that if
![]() ${\langle } S_i \mid i <\eta {\rangle } \subseteq V$
is a partition of
${\langle } S_i \mid i <\eta {\rangle } \subseteq V$
is a partition of
![]() $\kappa $
into disjoint sets which are stationary in
$\kappa $
into disjoint sets which are stationary in
![]() $V[G \ast H \ast C]$
, then
$V[G \ast H \ast C]$
, then
![]() $|\eta | \leq \lambda $
. Moreover, since
$|\eta | \leq \lambda $
. Moreover, since
![]() $\kappa $
is inaccessible in V, we have
$\kappa $
is inaccessible in V, we have
![]() $(2^{\eta })^V < \kappa $
.
$(2^{\eta })^V < \kappa $
.
Finally, we know that each poset
![]() $\mathbb {P}$
,
$\mathbb {P}$
,
![]() $\operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
, and
$\operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
, and
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
is forced in turn to be cone homogeneous and clearly definable using parameters from the ground model. Therefore,
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
is forced in turn to be cone homogeneous and clearly definable using parameters from the ground model. Therefore,
![]() $\mathbb {P}* \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) \ast \mathbb {C}_{\mathcal {F}_{\kappa }}$
is cone homogeneous, and therefore,
$\mathbb {P}* \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) \ast \mathbb {C}_{\mathcal {F}_{\kappa }}$
is cone homogeneous, and therefore,
![]() $\operatorname {\mathrm {HOD}}^{V[G \ast H \ast C]} \subseteq V$
. The claim follows.
$\operatorname {\mathrm {HOD}}^{V[G \ast H \ast C]} \subseteq V$
. The claim follows.
The result in this section is weaker than the result of section 3 since the club filter is not an ultrafilter in
![]() $\operatorname {\mathrm {HOD}}$
. Since the club filter restricted to
$\operatorname {\mathrm {HOD}}$
. Since the club filter restricted to
![]() $S^{\omega _2}_{\omega }$
is an ultrafilter in a model of
$S^{\omega _2}_{\omega }$
is an ultrafilter in a model of
![]() $\mathrm {AD} + V = L(\mathbb {R})$
, one can force with the
$\mathrm {AD} + V = L(\mathbb {R})$
, one can force with the
![]() $\mathbb {P}_{max}$
forcing and obtain a generic extension in which the club filter restricted to
$\mathbb {P}_{max}$
forcing and obtain a generic extension in which the club filter restricted to
![]() $S^{\omega _2}_{\omega }$
is an ultrafilter in
$S^{\omega _2}_{\omega }$
is an ultrafilter in
![]() $\operatorname {\mathrm {HOD}}$
.Footnote
7
$\operatorname {\mathrm {HOD}}$
.Footnote
7
Question 4.11. Is it consistent that the club filter restricted to
![]() $S^{\lambda }_{\omega }$
is an ultrafilter in
$S^{\lambda }_{\omega }$
is an ultrafilter in
![]() $\operatorname {\mathrm {HOD}}$
for a regular cardinal
$\operatorname {\mathrm {HOD}}$
for a regular cardinal
![]() $\lambda> \aleph _2$
?
$\lambda> \aleph _2$
?
By the general behavior of covering arguments, it is possible that the consistency strength of
![]() $\omega _2$
being
$\omega _2$
being
![]() $\omega $
-strongly measurable in
$\omega $
-strongly measurable in
![]() $\operatorname {\mathrm {HOD}}$
might be much lower than the same property for successors of higher regular cardinals, and possibly as low as a single measurable cardinal.
$\operatorname {\mathrm {HOD}}$
might be much lower than the same property for successors of higher regular cardinals, and possibly as low as a single measurable cardinal.
Question 4.12. What is the consistency strength of
![]() $\omega _2$
being
$\omega _2$
being
![]() $\omega $
-strongly measurable in
$\omega $
-strongly measurable in
![]() $\operatorname {\mathrm {HOD}}$
?
$\operatorname {\mathrm {HOD}}$
?
5 Many
 $\omega $
-strongly measurable cardinals
$\omega $
-strongly measurable cardinals
Suppose that
![]() $\mathcal {U}$
is a coherent sequence of normal measures so that
$\mathcal {U}$
is a coherent sequence of normal measures so that
![]() $\lambda < \kappa $
are regular cardinals and
$\lambda < \kappa $
are regular cardinals and
![]() $o^{\mathcal {U}}(\kappa ) = \lambda + 1$
and that the first measure in
$o^{\mathcal {U}}(\kappa ) = \lambda + 1$
and that the first measure in
![]() $\mathcal {U}$
is on a cardinal strictly greater than
$\mathcal {U}$
is on a cardinal strictly greater than
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $\mathbb {P}^{\mathcal {U}}$
be the nonstationary support iteration of Prikry/Magidor forcing from [Reference Ben-Neria and Unger5], and
$\mathbb {P}^{\mathcal {U}}$
be the nonstationary support iteration of Prikry/Magidor forcing from [Reference Ben-Neria and Unger5], and
![]() $\mathbb {C}_{\mathcal {F}^{\mathcal {U}}_{\kappa }}$
be the
$\mathbb {C}_{\mathcal {F}^{\mathcal {U}}_{\kappa }}$
be the
![]() $\mathbb {P}^{\mathcal {U}}* \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
-name of the associated diagonalizing club forcing for the filter
$\mathbb {P}^{\mathcal {U}}* \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
-name of the associated diagonalizing club forcing for the filter
![]() $\mathcal {F}^{\mathcal {U}}_{\kappa } = \bigcap _{\tau \leq \lambda } U_{\kappa ,\lambda }$
on
$\mathcal {F}^{\mathcal {U}}_{\kappa } = \bigcap _{\tau \leq \lambda } U_{\kappa ,\lambda }$
on
![]() $\kappa $
. In the next section, we construct a
$\kappa $
. In the next section, we construct a
![]() $\mathbb {P}^{\mathcal {U}} * \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
-name of a Prikry-type forcing notion
$\mathbb {P}^{\mathcal {U}} * \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
-name of a Prikry-type forcing notion
![]() $\bar {\mathbb {C}}_{\mathcal {F}^{\mathcal {U}}_{\kappa }}$
, which is equivalent to
$\bar {\mathbb {C}}_{\mathcal {F}^{\mathcal {U}}_{\kappa }}$
, which is equivalent to
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
, and its direct extension order is
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
, and its direct extension order is
![]() $\lambda $
-closed. We will use that as a black box in this section.
$\lambda $
-closed. We will use that as a black box in this section.
Definition 5.1. Denote the post
![]() $\mathbb {P}^{\mathcal {U}} * \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) * \bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
by
$\mathbb {P}^{\mathcal {U}} * \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) * \bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
by
![]() $\mathbb {Q}[\mathcal {U}]$
.
$\mathbb {Q}[\mathcal {U}]$
.
We have shown in the previous section that
![]() $\mathbb {Q}[\mathcal {U}]$
is cone homogeneous and equivalent as a forcing notion to the iteration
$\mathbb {Q}[\mathcal {U}]$
is cone homogeneous and equivalent as a forcing notion to the iteration
![]() $\mathbb {P}^{\mathcal {U}} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) \ast \mathbb {C}_{\mathcal {F}_{\kappa }}$
. By theorem 4.10, we conclude that
$\mathbb {P}^{\mathcal {U}} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) \ast \mathbb {C}_{\mathcal {F}_{\kappa }}$
. By theorem 4.10, we conclude that
![]() $\kappa $
is strongly measurable in the generic extension by
$\kappa $
is strongly measurable in the generic extension by
![]() $\mathbb {Q}[\mathcal {U}]$
.
$\mathbb {Q}[\mathcal {U}]$
.
In what follows, we would like to view
![]() $\mathbb {Q}[\mathcal {U}]$
as a Prikry-type forcing whose direct extension order is
$\mathbb {Q}[\mathcal {U}]$
as a Prikry-type forcing whose direct extension order is
![]() $\lambda $
-closed. This is easily possible since
$\lambda $
-closed. This is easily possible since
![]() $\mathbb {Q}[\mathcal {U}]$
is an iteration of three posets, each of which can be seen as a Prikry-forcing whose direct extension order is
$\mathbb {Q}[\mathcal {U}]$
is an iteration of three posets, each of which can be seen as a Prikry-forcing whose direct extension order is
![]() $\lambda $
-closed (for
$\lambda $
-closed (for
![]() $\operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
, we identify the direct extension order with the standard order of the poset).
$\operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
, we identify the direct extension order with the standard order of the poset).
We finally turn to prove our main result.
Proof (Theorem 1.4).
To simplify our arguments, we work over a minimal Mitchell model
![]() $V = L[\mathcal {U}]$
with a coherent sequence of measures
$V = L[\mathcal {U}]$
with a coherent sequence of measures
![]() $\mathcal {U}$
witnessing the assumed large cardinal assumption. Therefore,
$\mathcal {U}$
witnessing the assumed large cardinal assumption. Therefore,
![]() $\theta $
is the least inaccessible cardinal in V for which
$\theta $
is the least inaccessible cardinal in V for which
![]() $\{ o(\kappa ) \mid \kappa < \theta \}$
is unbounded in
$\{ o(\kappa ) \mid \kappa < \theta \}$
is unbounded in
![]() $\theta $
. We note that all normal measures in this model appear on the main sequence
$\theta $
. We note that all normal measures in this model appear on the main sequence
![]() $\mathcal {U}$
, in particular,
$\mathcal {U}$
, in particular,
![]() $o(\kappa ) = o^{\mathcal {U}}(\kappa )$
for all
$o(\kappa ) = o^{\mathcal {U}}(\kappa )$
for all
![]() $\kappa $
. We also record here that by the Mitchell Covering Theorem and the fact
$\kappa $
. We also record here that by the Mitchell Covering Theorem and the fact
![]() $\theta $
is not measurable, there is no generic extension of
$\theta $
is not measurable, there is no generic extension of
![]() $V = L[\mathcal {U}]$
which preserves the cardinals below
$V = L[\mathcal {U}]$
which preserves the cardinals below
![]() $\theta $
and changes the cofinality of
$\theta $
and changes the cofinality of
![]() $\theta $
. Similarly, the Mitchell Covering Theorem guarantees that generic extensions of
$\theta $
. Similarly, the Mitchell Covering Theorem guarantees that generic extensions of
![]() $V = L[\mathcal {U}]$
satisfy the Weak Covering Lemma with respect to V, which implies that successors of singular cardinals cannot be collapsed.
$V = L[\mathcal {U}]$
satisfy the Weak Covering Lemma with respect to V, which implies that successors of singular cardinals cannot be collapsed.
Let
![]() $\langle \kappa _{\alpha } \mid \alpha < \theta \rangle $
be an increasing sequence of cardinals below
$\langle \kappa _{\alpha } \mid \alpha < \theta \rangle $
be an increasing sequence of cardinals below
![]() $\theta $
, which satisfies the following conditions:
$\theta $
, which satisfies the following conditions:
-
1.
 $\kappa _0 = \omega $
,
$\kappa _0 = \omega $
,
 $\kappa _1$
is the least measurable,
$\kappa _1$
is the least measurable, -
2. for a limit ordinal
 $\alpha $
,
$\alpha $
,
 $\kappa _{\alpha } = (\sup _{\beta < \alpha } \kappa _{\beta } )^+$
,
$\kappa _{\alpha } = (\sup _{\beta < \alpha } \kappa _{\beta } )^+$
, -
3. for a successor ordinal
 $\alpha + 1$
, let
$\alpha + 1$
, let
 $\kappa _{\alpha + 1}$
be the least cardinal such that
$\kappa _{\alpha + 1}$
be the least cardinal such that
 $o^{\mathcal {U^{\alpha }}}(\kappa _{\alpha + 1}) = \kappa _{\alpha } + 1$
, for the coherent sequence of measures
$o^{\mathcal {U^{\alpha }}}(\kappa _{\alpha + 1}) = \kappa _{\alpha } + 1$
, for the coherent sequence of measures
 $\mathcal {U}^{\alpha } = \mathcal {U}\restriction _{(\kappa _{\alpha },\kappa _{\alpha +1}]}$
. In particular, the first measure of the sequence
$\mathcal {U}^{\alpha } = \mathcal {U}\restriction _{(\kappa _{\alpha },\kappa _{\alpha +1}]}$
. In particular, the first measure of the sequence
 $\mathcal {U}^{\alpha }$
has critical point
$\mathcal {U}^{\alpha }$
has critical point
 $> \kappa _{\alpha }$
.
$> \kappa _{\alpha }$
.
We define by induction on
![]() $\alpha < \theta $
a Magidor iteration
$\alpha < \theta $
a Magidor iteration
![]() $\mathbb {P} = {\langle } \mathbb {P}_{\alpha }, \mathbb {Q}_{\alpha } \mid \alpha < \theta {\rangle }$
of Prikry type forcings. Our description of the Magidor style iteration follows Gitik’s handbook chapter [Reference Gitik13]. We recall that conditions are sequences of the form
$\mathbb {P} = {\langle } \mathbb {P}_{\alpha }, \mathbb {Q}_{\alpha } \mid \alpha < \theta {\rangle }$
of Prikry type forcings. Our description of the Magidor style iteration follows Gitik’s handbook chapter [Reference Gitik13]. We recall that conditions are sequences of the form
![]() $\langle q_{\alpha } \mid \alpha < \theta \rangle $
where only finitely many coordinates are not a direct extension of the weakest condition
$\langle q_{\alpha } \mid \alpha < \theta \rangle $
where only finitely many coordinates are not a direct extension of the weakest condition
![]() $0_{\mathbb {Q}_{\alpha }}$
. Let
$0_{\mathbb {Q}_{\alpha }}$
. Let
![]() $\mathbb {Q}_{0}$
be
$\mathbb {Q}_{0}$
be
![]() $\operatorname {\mathrm {Coll}}(\omega , <\kappa _1) * \mathbb {C}^*_{\mathcal {F}_{\kappa _1}}$
, where
$\operatorname {\mathrm {Coll}}(\omega , <\kappa _1) * \mathbb {C}^*_{\mathcal {F}_{\kappa _1}}$
, where
![]() $\mathcal {F}_{\kappa _1}$
is the filter generated from the normal measure on
$\mathcal {F}_{\kappa _1}$
is the filter generated from the normal measure on
![]() $\kappa _1$
. For
$\kappa _1$
. For
![]() $\alpha> 0$
, we define
$\alpha> 0$
, we define
![]() $\mathbb {Q}_{\alpha } = \mathbb {Q}[\mathcal {U}^{\alpha }]$
.
$\mathbb {Q}_{\alpha } = \mathbb {Q}[\mathcal {U}^{\alpha }]$
.
The coherent sequence
![]() $\mathcal {U}^{\alpha }$
from
$\mathcal {U}^{\alpha }$
from
![]() $L[\mathcal {U}]$
uniquely extends in a generic extension by
$L[\mathcal {U}]$
uniquely extends in a generic extension by
![]() $\mathbb {P}_{\alpha }$
and can therefore be used to force with
$\mathbb {P}_{\alpha }$
and can therefore be used to force with
![]() $\mathbb {Q}[\mathcal {U}^{\alpha }]$
. This is because as
$\mathbb {Q}[\mathcal {U}^{\alpha }]$
. This is because as
![]() $L[\mathcal {U}]$
satisfies the
$L[\mathcal {U}]$
satisfies the
![]() $\operatorname {\mathrm {GCH}}$
, we have that
$\operatorname {\mathrm {GCH}}$
, we have that
![]() $|\mathbb {P}_{\alpha }| \leq \kappa _{\alpha }$
and all measures of
$|\mathbb {P}_{\alpha }| \leq \kappa _{\alpha }$
and all measures of
![]() $\mathcal {U}^{\alpha }$
are assumed to have critical points strictly above
$\mathcal {U}^{\alpha }$
are assumed to have critical points strictly above
![]() $\kappa _{\alpha }$
. It is clear from our definitions that
$\kappa _{\alpha }$
. It is clear from our definitions that
![]() $\mathbb {Q}_{\alpha }$
satisfies the Prikry Property, that its direct extension order is
$\mathbb {Q}_{\alpha }$
satisfies the Prikry Property, that its direct extension order is
![]() $\kappa _{\alpha }$
-closed and that
$\kappa _{\alpha }$
-closed and that
![]() $\mathbb {Q}_{\alpha }$
is forced to be cone homogeneous.
$\mathbb {Q}_{\alpha }$
is forced to be cone homogeneous.
By the general theory of Magidor iteration of Prikry type posets, the iteration
![]() $\mathbb {P}_{\theta }/ \mathbb {P}_1$
also satisfies the Prikry Property. Moreover, for every
$\mathbb {P}_{\theta }/ \mathbb {P}_1$
also satisfies the Prikry Property. Moreover, for every
![]() $\alpha < \theta $
,
$\alpha < \theta $
,
![]() $\mathbb {P}_{\theta } / \mathbb {P}_{\alpha }$
has the Prikry Property in the generic extension by
$\mathbb {P}_{\theta } / \mathbb {P}_{\alpha }$
has the Prikry Property in the generic extension by
![]() $\mathbb {P}_{\alpha }$
, and its direct extension order is
$\mathbb {P}_{\alpha }$
, and its direct extension order is
![]() $\kappa _{\alpha }$
-closed (see [Reference Gitik13] for details).
$\kappa _{\alpha }$
-closed (see [Reference Gitik13] for details).
Claim 5.2. Every bounded subset of
![]() $\kappa _{\alpha }$
is introduced by
$\kappa _{\alpha }$
is introduced by
![]() $\mathbb {P}_{\alpha }$
. Moreover, in the generic extension by
$\mathbb {P}_{\alpha }$
. Moreover, in the generic extension by
![]() $\mathbb {P}_{\theta }$
,
$\mathbb {P}_{\theta }$
,
![]() $\kappa _{\alpha }$
is a regular cardinal for all
$\kappa _{\alpha }$
is a regular cardinal for all
![]() $\alpha < \theta $
.
$\alpha < \theta $
.
Proof. The first assertion is an immediate consequence of the fact that
![]() $\mathbb {P}_{\theta }/ \mathbb {P}_{\alpha }$
satisfies the Prikry Property and its direct extension order is
$\mathbb {P}_{\theta }/ \mathbb {P}_{\alpha }$
satisfies the Prikry Property and its direct extension order is
![]() $\kappa _{\alpha }$
closed. It follows that, in order to show that all cardinal
$\kappa _{\alpha }$
closed. It follows that, in order to show that all cardinal
![]() $\kappa _{\alpha }$
remain regular in a generic extension by
$\kappa _{\alpha }$
remain regular in a generic extension by
![]() $\mathbb {P}_{\theta }$
, it suffices to show that
$\mathbb {P}_{\theta }$
, it suffices to show that
![]() $\kappa _{\alpha }$
remains regular in the intermediate generic extension by
$\kappa _{\alpha }$
remains regular in the intermediate generic extension by
![]() $\mathbb {P}_{\alpha }$
. We prove the last assertion by induction on
$\mathbb {P}_{\alpha }$
. We prove the last assertion by induction on
![]() $\alpha < \theta $
.
$\alpha < \theta $
.
For a limit ordinal
![]() $\alpha $
, the assertion follows from the fact that the generic extension by
$\alpha $
, the assertion follows from the fact that the generic extension by
![]() $\mathbb {P}_{\alpha }$
satisfies the Weak Covering property with respect to the ground model
$\mathbb {P}_{\alpha }$
satisfies the Weak Covering property with respect to the ground model
![]() $V = L[\mathcal {U}]$
. Indeed,
$V = L[\mathcal {U}]$
. Indeed,
![]() $\kappa _{\alpha } = (\sup _{\beta < \alpha } \kappa _{\beta } )^+$
cannot be collapsed without collapsing a tail of the cardinals
$\kappa _{\alpha } = (\sup _{\beta < \alpha } \kappa _{\beta } )^+$
cannot be collapsed without collapsing a tail of the cardinals
![]() $\kappa _{\beta }$
,
$\kappa _{\beta }$
,
![]() $\beta < \alpha $
, which would contradict our inductive assumption.
$\beta < \alpha $
, which would contradict our inductive assumption.
Suppose now that
![]() $\alpha $
is a successor ordinal. Then the forcing of
$\alpha $
is a successor ordinal. Then the forcing of
![]() $\mathbb {P}_{\alpha }$
naturally breaks into two parts
$\mathbb {P}_{\alpha }$
naturally breaks into two parts
![]() $\mathbb {P}_{\alpha } \cong \mathbb {P}_{\alpha - 1} * \mathbb {Q}_{\alpha -1}$
. The size of
$\mathbb {P}_{\alpha } \cong \mathbb {P}_{\alpha - 1} * \mathbb {Q}_{\alpha -1}$
. The size of
![]() $\mathbb {P}_{\alpha - 1}$
is
$\mathbb {P}_{\alpha - 1}$
is
![]() $\left (2^{\kappa _{\alpha -1}}\right )^V < \kappa _{\alpha }$
and cannot singularize
$\left (2^{\kappa _{\alpha -1}}\right )^V < \kappa _{\alpha }$
and cannot singularize
![]() $\kappa _{\alpha }$
. The second poset
$\kappa _{\alpha }$
. The second poset
![]() $\mathbb {Q}_{\alpha -1}$
does not collapse
$\mathbb {Q}_{\alpha -1}$
does not collapse
![]() $\kappa _{\alpha }$
by Proposition 4.8. Note that, in order to apply the result of Proposition 4.8, we use our inductive hypothesis that
$\kappa _{\alpha }$
by Proposition 4.8. Note that, in order to apply the result of Proposition 4.8, we use our inductive hypothesis that
![]() $\kappa _{\alpha -1}$
remains regular in a generic extension by
$\kappa _{\alpha -1}$
remains regular in a generic extension by
![]() $\mathbb {P}_{\alpha -1}$
.
$\mathbb {P}_{\alpha -1}$
.
Claim 5.3. In the generic extension,
![]() $\theta $
is regular.
$\theta $
is regular.
Proof. This follows from the Mitchell Covering Theorem and the smallness assumption of
![]() $\theta $
, as was mentioned at the beginning of the proof.
$\theta $
, as was mentioned at the beginning of the proof.
Claim 5.4.
![]() $\mathbb {P}$
is cone homogeneous.
$\mathbb {P}$
is cone homogeneous.
Proof. It suffices to verify conditions (i) and (ii) of Lemma 8.5 hold for every
![]() $\alpha < \kappa $
. (i) holds for
$\alpha < \kappa $
. (i) holds for
![]() $\mathbb {Q}_{\alpha } = \mathbb {Q}[\mathcal {U}\restriction _{(\kappa _{\alpha },\kappa _{\alpha +1}]}]$
since
$\mathbb {Q}_{\alpha } = \mathbb {Q}[\mathcal {U}\restriction _{(\kappa _{\alpha },\kappa _{\alpha +1}]}]$
since
![]() $\mathbb {Q}_{\alpha },\leq _{\mathbb {Q}_{\alpha }},\leq ^*_{\mathbb {Q}_{\alpha }}$
are clearly definable in
$\mathbb {Q}_{\alpha },\leq _{\mathbb {Q}_{\alpha }},\leq ^*_{\mathbb {Q}_{\alpha }}$
are clearly definable in
![]() $V = L[\mathcal {U}]$
from
$V = L[\mathcal {U}]$
from
![]() $\mathcal {U}$
,
$\mathcal {U}$
,
![]() $\kappa _{\alpha }$
, and
$\kappa _{\alpha }$
, and
![]() $\kappa _{\alpha +1}$
. The fact
$\kappa _{\alpha +1}$
. The fact
![]() $(\mathbb {Q}_{\alpha },\leq _{\mathbb {Q}_{\alpha }},\leq ^*_{\mathbb {Q}_{\alpha }})$
is an immediate consequence of Lemma 6.12.
$(\mathbb {Q}_{\alpha },\leq _{\mathbb {Q}_{\alpha }},\leq ^*_{\mathbb {Q}_{\alpha }})$
is an immediate consequence of Lemma 6.12.
Let
![]() $G_{\theta } \subseteq \mathbb {P}_{\theta }$
be a generic filter over V. We conclude that
$G_{\theta } \subseteq \mathbb {P}_{\theta }$
be a generic filter over V. We conclude that
![]() $\operatorname {\mathrm {HOD}}^{V[G_{\theta }]} \subseteq V$
.Footnote
8
Moreover, for each
$\operatorname {\mathrm {HOD}}^{V[G_{\theta }]} \subseteq V$
.Footnote
8
Moreover, for each
![]() $\alpha < \kappa $
, the
$\alpha < \kappa $
, the
![]() $\mathbb {Q}[\mathcal {U}^{\alpha }]$
generic filter induced by
$\mathbb {Q}[\mathcal {U}^{\alpha }]$
generic filter induced by
![]() $G_{\theta }$
guarantees that
$G_{\theta }$
guarantees that
![]() $\kappa _{\alpha +1} = (\kappa _{\alpha }^+)^{V[G_{\theta }]}$
and that
$\kappa _{\alpha +1} = (\kappa _{\alpha }^+)^{V[G_{\theta }]}$
and that
![]() $\kappa _{\alpha }$
is strongly measurable in
$\kappa _{\alpha }$
is strongly measurable in
![]() $\operatorname {\mathrm {HOD}}^{V[G_{\theta }]}$
. It follows that all successors of regular cardinals below
$\operatorname {\mathrm {HOD}}^{V[G_{\theta }]}$
. It follows that all successors of regular cardinals below
![]() $\theta $
in
$\theta $
in
![]() $V[G_{\theta }]$
are strongly measurable in
$V[G_{\theta }]$
are strongly measurable in
![]() $\operatorname {\mathrm {HOD}}$
. Since
$\operatorname {\mathrm {HOD}}$
. Since
![]() $\theta $
remains strongly inaccessible in
$\theta $
remains strongly inaccessible in
![]() $V[G_{\theta }]$
and all the relevant witnessing objects clearly belong to
$V[G_{\theta }]$
and all the relevant witnessing objects clearly belong to
![]() $V_{\theta }^{V[G_{\theta }]}$
, we conclude that in
$V_{\theta }^{V[G_{\theta }]}$
, we conclude that in
![]() $V_{\theta }^{V[G_{\theta }]}$
, all successors of regular cardinals are strongly measurable.
$V_{\theta }^{V[G_{\theta }]}$
, all successors of regular cardinals are strongly measurable.
6 Embedding
 $\mathbb {C}_{\mathcal {F}_{\kappa }}$
in suitable Prikry-type forcings
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
in suitable Prikry-type forcings
The method of Section 4 can be iterated finitely many times in order to get finitely many successive
![]() $\omega $
-strongly measurable cardinals. In order to get a global result (or even just infinitely many
$\omega $
-strongly measurable cardinals. In order to get a global result (or even just infinitely many
![]() $\omega $
-strongly measurables), we need to have a preservation of distributivity under iterations.
$\omega $
-strongly measurables), we need to have a preservation of distributivity under iterations.
This is, in general, a difficult task. One way to obtain this is by shifting our goal from preserving distributivity into preserving the Prikry Property. There are several ways to iterate Prikry-type forcings and preserve the Prikry Property as well as the closure properties of the direct extension. Thus, embedding the distributive forcings into a Prikry-type forcing can be used in order to get a suitable distributivity of the iteration. Usually, in order to achieve this, some strong compactness assumption is made that enables one to embed any sufficiently distributive forcing into a Prikry-type forcing. See [Reference Gitik14, Reference Benhamou, Gitik and Hayut6] for some examples for the consistency strength of such constructions.
Our goal is to embed
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
into a Prikry-type forcing without increasing our large cardinal hypothesis from
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
into a Prikry-type forcing without increasing our large cardinal hypothesis from
![]() $o(\kappa )= \lambda +1$
. For this, our approach follows the finer technique, introduced by Gitik in [Reference Gitik12].
$o(\kappa )= \lambda +1$
. For this, our approach follows the finer technique, introduced by Gitik in [Reference Gitik12].
This section is devoted to prove the following technical lemma:
Proposition 6.1. Let us assume that
![]() $\mathcal {U}$
is a coherent measure sequence witnessing
$\mathcal {U}$
is a coherent measure sequence witnessing
![]() $o(\kappa ) = \lambda +1$
. Let
$o(\kappa ) = \lambda +1$
. Let
![]() $\mathbb {P}^{\mathcal {U}}$
be the nonstationary support iteration of Subsection 8.2. Then, in
$\mathbb {P}^{\mathcal {U}}$
be the nonstationary support iteration of Subsection 8.2. Then, in
![]() $\mathbb {P}^{\mathcal {U}} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
, there is a Prikry-type forcing notion
$\mathbb {P}^{\mathcal {U}} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
, there is a Prikry-type forcing notion
![]() $\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
, whose direct extension order is
$\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
, whose direct extension order is
![]() $\lambda $
-closed, and it has a dense subset isomorphic to
$\lambda $
-closed, and it has a dense subset isomorphic to
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
.
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
.
Moreover, both orders
![]() $\leq $
and
$\leq $
and
![]() $\leq ^*$
witness the forcing
$\leq ^*$
witness the forcing
![]() $\mathbb {P}^{\mathcal {U}} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) \ast \bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
to be cone homogeneous.
$\mathbb {P}^{\mathcal {U}} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) \ast \bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
to be cone homogeneous.
The proof of the first part of the proposition is given in Corollary 6.10, and the proof of the second part appears in Lemma 6.12. Let us sketch the main ideas behind the proof of the proposition. In order to construct a Prikry-type forcing that projects onto
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
, we first work in the generic extension in which
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
, we first work in the generic extension in which
![]() $\kappa $
is singularized to be of cofinality
$\kappa $
is singularized to be of cofinality
![]() $\lambda $
. In this model, the Magidor sequence is already a closed unbounded set that diagonalizes the filter
$\lambda $
. In this model, the Magidor sequence is already a closed unbounded set that diagonalizes the filter
![]() $\mathcal {F}_{\kappa }$
, so we can use it as a guide to the generic of
$\mathcal {F}_{\kappa }$
, so we can use it as a guide to the generic of
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
. This means that there is a projection from the generic extension by the singularizing forcing iterated by a
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
. This means that there is a projection from the generic extension by the singularizing forcing iterated by a
![]() $\lambda $
-closed forcing onto
$\lambda $
-closed forcing onto
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
.
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
.
![]() $\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
is obtained by ‘forgetting’ the Magidor sequence and keeping the diagonalizing club. A technical issue that arises when trying to pull up this strategy is that the singularizing forcing must be defined after the cardinals between
$\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
is obtained by ‘forgetting’ the Magidor sequence and keeping the diagonalizing club. A technical issue that arises when trying to pull up this strategy is that the singularizing forcing must be defined after the cardinals between
![]() $\lambda $
and
$\lambda $
and
![]() $\kappa $
were collapsed, and a major part of this section is devoted to developing this forcing.
$\kappa $
were collapsed, and a major part of this section is devoted to developing this forcing.
The rest of this section is organized as follows. In subsection 6.1, we review the basic construction and properties of the tree Prikry-type forcing notions of the form
![]() $\mathbb {Q}^{\tau }_{\kappa }$
,
$\mathbb {Q}^{\tau }_{\kappa }$
,
![]() $\tau \leq o^{\mathcal {U}}(\kappa )$
, which is defined in the generic extension by
$\tau \leq o^{\mathcal {U}}(\kappa )$
, which is defined in the generic extension by
![]() $\mathbb {P}$
. Then, we introduce a filter-based variant
$\mathbb {P}$
. Then, we introduce a filter-based variant
![]() $\mathbb {Q}_{\kappa ,\tau }^*$
to be forced over a generic extension
$\mathbb {Q}_{\kappa ,\tau }^*$
to be forced over a generic extension
![]() $V[G \ast H]$
by
$V[G \ast H]$
by
![]() $\mathbb {P} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
extension
$\mathbb {P} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
extension
![]() $V[G \ast H]$
of V, where
$V[G \ast H]$
of V, where
![]() $\kappa = \lambda ^+$
is no longer measurable.
$\kappa = \lambda ^+$
is no longer measurable.
In subsection 6.2, we use the posets
![]() $\mathbb {Q}_{\kappa ,\tau }^*$
,
$\mathbb {Q}_{\kappa ,\tau }^*$
,
![]() $\tau \leq \lambda $
in order to introduce a forcing equivalent
$\tau \leq \lambda $
in order to introduce a forcing equivalent
![]() $\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
of
$\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
of
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
with a dense Prikry-type subforcing
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
with a dense Prikry-type subforcing
![]() $\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
whose direct extension order is
$\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
whose direct extension order is
![]() $\lambda $
-closed.
$\lambda $
-closed.
This completes the proof of Section 5, as the posets
![]() $\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
can be iterated on different cardinals to construct models with many
$\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
can be iterated on different cardinals to construct models with many
![]() $\omega $
-strongly measurable cardinals.
$\omega $
-strongly measurable cardinals.
6.1 The forcing
 $\mathbb {Q}^*_{\kappa ,\tau }$
$\mathbb {Q}^*_{\kappa ,\tau }$
We turn back to consider our forcing scenario with
![]() $\mathcal {F}_{\kappa }$
over
$\mathcal {F}_{\kappa }$
over
![]() $V[G\ast H]$
, where
$V[G\ast H]$
, where
![]() $G \subseteq \mathbb {P}$
is generic over V, and
$G \subseteq \mathbb {P}$
is generic over V, and
![]() $H \subseteq \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
is generic over
$H \subseteq \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
is generic over
![]() $V[G]$
. Recall that
$V[G]$
. Recall that
![]() $o^{\mathcal {U}}(\kappa ) = \lambda +1$
and that each measure
$o^{\mathcal {U}}(\kappa ) = \lambda +1$
and that each measure
![]() $U_{\kappa ,\tau }$
,
$U_{\kappa ,\tau }$
,
![]() $\tau \leq \lambda $
in V extends in
$\tau \leq \lambda $
in V extends in
![]() $V[G]$
to
$V[G]$
to
![]() $U_{\kappa ,\tau }(t)$
, where t is
$U_{\kappa ,\tau }(t)$
, where t is
![]() $\tau $
-coherent. For each such
$\tau $
-coherent. For each such
![]() $\tau \leq \lambda $
and t, let
$\tau \leq \lambda $
and t, let
![]() $j_{\kappa ,\tau ,t}\colon V[G] \to M_{\kappa ,\tau ,t}$
be the ultrapower embedding of
$j_{\kappa ,\tau ,t}\colon V[G] \to M_{\kappa ,\tau ,t}$
be the ultrapower embedding of
![]() $V[G]$
by
$V[G]$
by
![]() $U_{\kappa ,\tau }(t)$
.
$U_{\kappa ,\tau }(t)$
.
Moving to the further generic extension
![]() $V[G \ast H]$
of
$V[G \ast H]$
of
![]() $V[G]$
,
$V[G]$
,
![]() $\kappa $
is no longer measurable. Let
$\kappa $
is no longer measurable. Let
![]() $F_{\kappa ,\tau }(t)$
denote the filter generated by
$F_{\kappa ,\tau }(t)$
denote the filter generated by
![]() $U_{\kappa ,\tau }(t)$
on
$U_{\kappa ,\tau }(t)$
on
![]() $\mathcal {P}(\kappa )^{V[G]}$
, and let
$\mathcal {P}(\kappa )^{V[G]}$
, and let
![]() $F_{\kappa ,\tau }(t)^+$
denote the poset on
$F_{\kappa ,\tau }(t)^+$
denote the poset on
![]() $\mathcal {P}(\kappa )^{V[G]}$
of
$\mathcal {P}(\kappa )^{V[G]}$
of
![]() $F_{\kappa ,\tau }(t)$
positive sets where a set A is stronger than B if
$F_{\kappa ,\tau }(t)$
positive sets where a set A is stronger than B if
![]() $A \setminus B$
belongs to the dual ideal of
$A \setminus B$
belongs to the dual ideal of
![]() $F_{\kappa ,\tau }(t)$
.
$F_{\kappa ,\tau }(t)$
.
By further forcing with the collapse quotient
over
![]() $V[G \ast H]$
, producing a generic filter
$V[G \ast H]$
, producing a generic filter
![]() $H_{\tau }^* \subseteq \operatorname {\mathrm {Coll}}(\lambda ,<j_{\kappa ,\tau ,t}(\kappa ))$
, with
$H_{\tau }^* \subseteq \operatorname {\mathrm {Coll}}(\lambda ,<j_{\kappa ,\tau ,t}(\kappa ))$
, with
![]() $H_{\tau }^* \restriction \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) = H$
, the elementary embedding
$H_{\tau }^* \restriction \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) = H$
, the elementary embedding
![]() $j_{\kappa ,\tau ,t}$
extends into
$j_{\kappa ,\tau ,t}$
extends into
In turn, the embedding
![]() $j^*_{\kappa ,\tau ,t}$
generates a
$j^*_{\kappa ,\tau ,t}$
generates a
![]() $V[G \ast H]$
ultrafilter
$V[G \ast H]$
ultrafilter
![]() $U_{\kappa ,\tau }(t)^* \subseteq F_{\kappa ,\tau }(t)^+$
, which is an
$U_{\kappa ,\tau }(t)^* \subseteq F_{\kappa ,\tau }(t)^+$
, which is an
![]() $F_{\kappa ,\tau }(t)^+$
-generic ultrafilter over
$F_{\kappa ,\tau }(t)^+$
-generic ultrafilter over
![]() $V[G \ast H]$
, by standard arguments connecting forcing with positive sets and generic ultrapowers.Footnote
9
Since the poset
$V[G \ast H]$
, by standard arguments connecting forcing with positive sets and generic ultrapowers.Footnote
9
Since the poset
![]() $\mathbb {R}_{\tau } = \operatorname {\mathrm {Coll}}(\lambda ,<j_{\kappa ,\tau ,t}(\kappa ))/H$
is
$\mathbb {R}_{\tau } = \operatorname {\mathrm {Coll}}(\lambda ,<j_{\kappa ,\tau ,t}(\kappa ))/H$
is
![]() $\lambda $
-closed in
$\lambda $
-closed in
![]() $V[G \ast H]$
, we have that
$V[G \ast H]$
, we have that
![]() $F_{\kappa ,\tau }(t)^+$
has a
$F_{\kappa ,\tau }(t)^+$
has a
![]() $\lambda $
-closed dense subforcing
$\lambda $
-closed dense subforcing
![]() $D_{\kappa ,\tau ,t}$
. Other examples of applications of Prikry-type forcings generated by ideals can be found in [Reference Ben-Neria4] and [Reference Adolf, Ben-Neria, Schindler and Martin1].
$D_{\kappa ,\tau ,t}$
. Other examples of applications of Prikry-type forcings generated by ideals can be found in [Reference Ben-Neria4] and [Reference Adolf, Ben-Neria, Schindler and Martin1].
It would be useful for our purposes to work with a concrete description of the sets in
![]() $D_{\kappa ,\tau ,t}$
. We proceed to introduce the relevant notions.
$D_{\kappa ,\tau ,t}$
. We proceed to introduce the relevant notions.
Definition 6.2. Let
![]() $G \subseteq \mathbb {P}$
be a generic filter over V. For each cardinal
$G \subseteq \mathbb {P}$
be a generic filter over V. For each cardinal
![]() $\nu < \kappa $
with
$\nu < \kappa $
with
![]() $o^{\mathcal {U}}(\nu )> 0$
, let
$o^{\mathcal {U}}(\nu )> 0$
, let
![]() $b_{\nu }$
be the G-induced generic cofinal sequence in
$b_{\nu }$
be the G-induced generic cofinal sequence in
![]() $\nu $
.
$\nu $
.
-
1. Recall that every finite coherent sequence
 $t = {\langle } \nu _0,\dots , \nu _{k-1}{\rangle } \in [\kappa ]^{<\omega }$
in
$t = {\langle } \nu _0,\dots , \nu _{k-1}{\rangle } \in [\kappa ]^{<\omega }$
in
 $V[G]$
has an assigned closed unbounded set
$V[G]$
has an assigned closed unbounded set
 $b_t = \cup _{i<k} (b_{\nu _i} \cup \{\nu _i\})$
. For a coherent sequence t and a finite set of ordinals
$b_t = \cup _{i<k} (b_{\nu _i} \cup \{\nu _i\})$
. For a coherent sequence t and a finite set of ordinals
 $s \in [\min (t)]^{<\omega }$
, we define
$s \in [\min (t)]^{<\omega }$
, we define
 $\pi ^s(t) = \min (b_t \setminus (\max (s)+1))$
. When
$\pi ^s(t) = \min (b_t \setminus (\max (s)+1))$
. When
 $t = {\langle } \nu {\rangle }$
has a single element, we will often abuse this definition and write
$t = {\langle } \nu {\rangle }$
has a single element, we will often abuse this definition and write
 $\pi ^s(\nu )$
for
$\pi ^s(\nu )$
for
 $\pi ^s({\langle } \nu {\rangle })$
.
$\pi ^s({\langle } \nu {\rangle })$
.For every
 $\eta $
, the function defines a Rudin-Keisler projection from
$\eta $
, the function defines a Rudin-Keisler projection from $$\begin{align*}\pi^s_{\eta}(\nu) = \min( \{ \mu \in b_{\nu} \setminus (\max(s)+1) \mid o^{\mathcal{U}}(\mu) = \eta\})\end{align*}$$
$$\begin{align*}\pi^s_{\eta}(\nu) = \min( \{ \mu \in b_{\nu} \setminus (\max(s)+1) \mid o^{\mathcal{U}}(\mu) = \eta\})\end{align*}$$
 $U_{\kappa ,\tau }(s)$
to
$U_{\kappa ,\tau }(s)$
to
 $U_{\kappa ,\eta }(s)$
, for all
$U_{\kappa ,\eta }(s)$
, for all
 $ \tau> \eta $
. In particular,
$ \tau> \eta $
. In particular,
 $\pi ^s = \pi ^s_0 \colon \kappa \to \kappa $
is a Rudin-Keisler projection of
$\pi ^s = \pi ^s_0 \colon \kappa \to \kappa $
is a Rudin-Keisler projection of
 $U_{\kappa ,\tau }(s)$
to its normal projected measure
$U_{\kappa ,\tau }(s)$
to its normal projected measure
 $U_{\kappa ,0}(s)$
, for every
$U_{\kappa ,0}(s)$
, for every
 $\tau \geq 0$
.
$\tau \geq 0$
.
-
2. Let
 $T \subseteq [\kappa ]^{<\omega }$
be a tree,
$T \subseteq [\kappa ]^{<\omega }$
be a tree,
 $t \in [\kappa ]^{<\omega }$
, and
$t \in [\kappa ]^{<\omega }$
, and
 $Q\colon T \to \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
be a function. We say that Q is
$Q\colon T \to \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
be a function. We say that Q is
 $(T,t)$
-suitable if for every
$(T,t)$
-suitable if for every
 $s \in T$
, we have
$s \in T$
, we have-
•
 $Q(s) \in \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
, and
$Q(s) \in \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
, and -
• for every
 $s' \in T$
that extends s,
$s' \in T$
that extends s,
 $Q(s')\restriction \lambda \times \pi _0^{t {}^{\frown } s}(s') = Q(s)$
.
$Q(s')\restriction \lambda \times \pi _0^{t {}^{\frown } s}(s') = Q(s)$
.
For every
 $s \in T$
, we define
$s \in T$
, we define
 $Q_s$
to be the induced function on
$Q_s$
to be the induced function on
 $T_s = \{ r \in [\kappa ]^{<\omega } \mid s {}^{\frown } r \in T\}$
, given by
$T_s = \{ r \in [\kappa ]^{<\omega } \mid s {}^{\frown } r \in T\}$
, given by  $$\begin{align*}Q_s(r) = Q(s {}^{\frown} r).\end{align*}$$
$$\begin{align*}Q_s(r) = Q(s {}^{\frown} r).\end{align*}$$
-
-
3. Suppose that
 $H \subseteq \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
is generic over
$H \subseteq \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
is generic over
 $V[G]$
,
$V[G]$
,
 $T,Q \in V[G]$
as above, and let
$T,Q \in V[G]$
as above, and let
 $A = \operatorname {\mathrm {succ}}_T(\emptyset )$
. We define in
$A = \operatorname {\mathrm {succ}}_T(\emptyset )$
. We define in
 $V[G][H]$
the set Q-generic restriction of A with respect to H to be the set
$V[G][H]$
the set Q-generic restriction of A with respect to H to be the set  $$\begin{align*}A^H_Q = \{ \nu \in A \mid Q(\nu) \in H\}.\end{align*}$$
$$\begin{align*}A^H_Q = \{ \nu \in A \mid Q(\nu) \in H\}.\end{align*}$$
Let
![]() $G \subseteq \mathbb {P}$
be generic over V and
$G \subseteq \mathbb {P}$
be generic over V and
![]() $H \subseteq \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
be generic over
$H \subseteq \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
be generic over
![]() $V[G]$
. In
$V[G]$
. In
![]() $V[G]$
, for all
$V[G]$
, for all
![]() $\tau \leq \lambda $
and
$\tau \leq \lambda $
and
![]() $t \in [\kappa ]^{<\omega }$
, the function
$t \in [\kappa ]^{<\omega }$
, the function
![]() $\pi ^t = \pi ^t_0$
represents
$\pi ^t = \pi ^t_0$
represents
![]() $\kappa $
in the ultrapower by
$\kappa $
in the ultrapower by
![]() $U_{\kappa ,\tau }(t)$
. It is therefore immediate from our definition of
$U_{\kappa ,\tau }(t)$
. It is therefore immediate from our definition of
![]() $D_{\kappa ,\tau ,t} \subseteq F_{\kappa ,\tau }(t)^+$
that sets in
$D_{\kappa ,\tau ,t} \subseteq F_{\kappa ,\tau }(t)^+$
that sets in
![]() $D_{\kappa ,\tau ,t}$
are of the form
$D_{\kappa ,\tau ,t}$
are of the form
![]() $A^H_{r} = \{ \nu \in A \mid r(\nu ) \in H\}$
where
$A^H_{r} = \{ \nu \in A \mid r(\nu ) \in H\}$
where
![]() $A \in U_{\kappa ,\tau }(t)$
, and
$A \in U_{\kappa ,\tau }(t)$
, and
![]() $r\colon A \to \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
satisfying
$r\colon A \to \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
satisfying
![]() $r(\nu ) \in \operatorname {\mathrm {Coll}}(\lambda ,[\pi ^t(\nu ),\kappa ))$
for all
$r(\nu ) \in \operatorname {\mathrm {Coll}}(\lambda ,[\pi ^t(\nu ),\kappa ))$
for all
![]() $\nu \in A$
.Footnote
10
$\nu \in A$
.Footnote
10
We use these facts to introduce a variant of Gitik’s forcing
![]() $\mathbb {Q}_{\kappa ,\tau }$
in
$\mathbb {Q}_{\kappa ,\tau }$
in
![]() $V[G \ast H]$
. The following poset
$V[G \ast H]$
. The following poset
![]() $\mathbb {Q}^*_{\kappa ,\tau }$
collapses cardinals up to
$\mathbb {Q}^*_{\kappa ,\tau }$
collapses cardinals up to
![]() $\kappa ^+$
to
$\kappa ^+$
to
![]() $\lambda $
and adds a cofinal Magidor sequence
$\lambda $
and adds a cofinal Magidor sequence
![]() $b_{\kappa }$
of length
$b_{\kappa }$
of length
![]() $\omega ^{\tau }$
to
$\omega ^{\tau }$
to
![]() $\kappa $
, which diagonalizes the filter
$\kappa $
, which diagonalizes the filter
![]() $\bigcap _{\tau ' < \tau } U_{\kappa ,\tau '}$
(i.e.,
$\bigcap _{\tau ' < \tau } U_{\kappa ,\tau '}$
(i.e.,
![]() $b_{\kappa }$
is almost contained in each filter set).
$b_{\kappa }$
is almost contained in each filter set).
Definition 6.3. In
![]() $V[G \ast H]$
, the forcing
$V[G \ast H]$
, the forcing
![]() $\mathbb {Q}^*_{\kappa ,\tau }$
consists of all
$\mathbb {Q}^*_{\kappa ,\tau }$
consists of all
![]() $(t, T, Q) \in V[G]$
such that:
$(t, T, Q) \in V[G]$
such that:
-
1. t is a
 $\tau $
-coherent finite sequence of ordinals below
$\tau $
-coherent finite sequence of ordinals below
 $\kappa $
,
$\kappa $
, -
2. T is a tree of
 $\tau $
-coherent finite sequences with stem t,
$\tau $
-coherent finite sequences with stem t, -
3. Q is a
 $(T,t)$
-suitable function,
$(T,t)$
-suitable function, -
4.
 $Q(\emptyset ) \in H$
and
$Q(\emptyset ) \in H$
and -
5. For every
 $s, s' \in T$
, if
$s, s' \in T$
, if
 $b_{t {}^{\frown } s} = b_{t {}^{\frown } s'}$
, then
$b_{t {}^{\frown } s} = b_{t {}^{\frown } s'}$
, then
 $Q(s) = Q(s')$
.
$Q(s) = Q(s')$
.
As in
![]() $\mathbb {Q}_{\kappa ,\tau }$
, we identify two conditions
$\mathbb {Q}_{\kappa ,\tau }$
, we identify two conditions
![]() $(t,T,Q),(t',T,Q) \in \mathbb {Q}_{\kappa ,\tau }^*$
, whenever
$(t,T,Q),(t',T,Q) \in \mathbb {Q}_{\kappa ,\tau }^*$
, whenever
![]() $b_t= b_{t'}$
.
$b_t= b_{t'}$
.
The direct extension ordering of
![]() $\mathbb {Q}^*_{\kappa ,\tau }$
naturally extends the direct extension ordering of
$\mathbb {Q}^*_{\kappa ,\tau }$
naturally extends the direct extension ordering of
![]() $\mathbb {Q}_{\kappa ,\tau }$
. Namely, for two conditions
$\mathbb {Q}_{\kappa ,\tau }$
. Namely, for two conditions
![]() $(t,T,Q)$
,
$(t,T,Q)$
,
![]() $(t^*,T^*,Q^*)$
of
$(t^*,T^*,Q^*)$
of
![]() $\mathbb {Q}^*_{\kappa ,\tau }$
, we have
$\mathbb {Q}^*_{\kappa ,\tau }$
, we have
![]() $(t,T,Q) \leq ^* (t^*,T^*,Q^*)$
if
$(t,T,Q) \leq ^* (t^*,T^*,Q^*)$
if
![]() $(t,T)\leq ^*_{\mathbb {Q}_{\kappa ,\tau }} (t^*,T^*)$
and
$(t,T)\leq ^*_{\mathbb {Q}_{\kappa ,\tau }} (t^*,T^*)$
and
![]() $Q^*(s) \geq Q(s)$
for every
$Q^*(s) \geq Q(s)$
for every
![]() $s \in T^*$
.
$s \in T^*$
.
We observe that the direct extension order
![]() $\leq ^*$
is
$\leq ^*$
is
![]() $\lambda $
-closed in
$\lambda $
-closed in
![]() $V[G\ast H]$
. For this, note that it is immediate from the definition above that the partial order
$V[G\ast H]$
. For this, note that it is immediate from the definition above that the partial order
![]() $\tilde \leq \in V[G]$
, obtained from
$\tilde \leq \in V[G]$
, obtained from
![]() $\leq ^*$
by removing the requirement
$\leq ^*$
by removing the requirement
![]() $Q(\emptyset )\in H$
, belongs to
$Q(\emptyset )\in H$
, belongs to
![]() $V[G]$
and is clearly
$V[G]$
and is clearly
![]() $\lambda $
-closed in both
$\lambda $
-closed in both
![]() $V[G]$
and
$V[G]$
and
![]() $V[G\ast H]$
(note that the two generic extensions agree on sequences of length
$V[G\ast H]$
(note that the two generic extensions agree on sequences of length
![]() $<\lambda $
). Then, as
$<\lambda $
). Then, as
![]() $\leq ^*$
is equivalent to the restriction of
$\leq ^*$
is equivalent to the restriction of
![]() $\tilde {\leq }$
to a
$\tilde {\leq }$
to a
![]() $\lambda $
-closed set (which is essentially H), it remains
$\lambda $
-closed set (which is essentially H), it remains
![]() $\lambda $
-closed in
$\lambda $
-closed in
![]() $V[G\ast H]$
.
$V[G\ast H]$
.
The end-extension ordering of
![]() $\mathbb {Q}^*_{\kappa ,\tau }$
is based on the restriction of the end-extension of
$\mathbb {Q}^*_{\kappa ,\tau }$
is based on the restriction of the end-extension of
![]() $\mathbb {Q}_{\kappa ,\tau }$
to the Q-generic restriction of T with respect to H. Namely, for a condition
$\mathbb {Q}_{\kappa ,\tau }$
to the Q-generic restriction of T with respect to H. Namely, for a condition
![]() $p = (t, T, Q)$
, the only values
$p = (t, T, Q)$
, the only values
![]() $\nu \in \operatorname {\mathrm {succ}}_T(\emptyset )$
which are allowed to be used when taking a one-point extension, are
$\nu \in \operatorname {\mathrm {succ}}_T(\emptyset )$
which are allowed to be used when taking a one-point extension, are
![]() $\nu \in \operatorname {\mathrm {succ}}_T(\emptyset )^H_Q$
.Footnote
11
In this case, the resulting one-point extension is defined to be
$\nu \in \operatorname {\mathrm {succ}}_T(\emptyset )^H_Q$
.Footnote
11
In this case, the resulting one-point extension is defined to be
![]() $p {}^{\frown } {\langle } \nu {\rangle } = (t \cup \{\nu \}, T_{{\langle } \nu {\rangle }}, Q_{{\langle } \nu {\rangle }})$
. In general, for a sequence
$p {}^{\frown } {\langle } \nu {\rangle } = (t \cup \{\nu \}, T_{{\langle } \nu {\rangle }}, Q_{{\langle } \nu {\rangle }})$
. In general, for a sequence
![]() $r = {\langle } \nu _0,\dots , \nu _{k-1} {\rangle } \in T$
, the end extension of p by r, denoted
$r = {\langle } \nu _0,\dots , \nu _{k-1} {\rangle } \in T$
, the end extension of p by r, denoted
![]() $p {}^{\frown } r$
, is the one obtained by taking a sequence of one-point extensions by
$p {}^{\frown } r$
, is the one obtained by taking a sequence of one-point extensions by
![]() $\nu _0,\dots ,\nu _{k-1}$
, in turn.
$\nu _0,\dots ,\nu _{k-1}$
, in turn.
We note that although
![]() $\mathbb {Q}_{\kappa ,\tau }^*$
depends on the collapse generic H, and is fully defined only in
$\mathbb {Q}_{\kappa ,\tau }^*$
depends on the collapse generic H, and is fully defined only in
![]() $V[G\ast H]$
, we still have that
$V[G\ast H]$
, we still have that
![]() $\mathbb {Q}_{\kappa ,\tau }^* \subseteq V[G]$
. Moreover, dropping the requirement
$\mathbb {Q}_{\kappa ,\tau }^* \subseteq V[G]$
. Moreover, dropping the requirement
![]() $Q(\emptyset ) \in H$
in the definition of conditions
$Q(\emptyset ) \in H$
in the definition of conditions
![]() $p =(t,T,Q) \in \mathbb {Q}_{\kappa ,\tau }^*$
allows us to examine conditions
$p =(t,T,Q) \in \mathbb {Q}_{\kappa ,\tau }^*$
allows us to examine conditions
![]() $(t,T,Q)$
and evaluate possible direct extensions and one-point extensions in
$(t,T,Q)$
and evaluate possible direct extensions and one-point extensions in
![]() $V[G]$
. For example, working in
$V[G]$
. For example, working in
![]() $V[G]$
, we can consider possible one-point extensions
$V[G]$
, we can consider possible one-point extensions
![]() $p {}^{\frown } {\langle } \nu {\rangle }$
of a condition
$p {}^{\frown } {\langle } \nu {\rangle }$
of a condition
![]() $p= (t,T,Q)$
by an arbitrary
$p= (t,T,Q)$
by an arbitrary
![]() $\nu \in \operatorname {\mathrm {succ}}_T(\emptyset )$
. Although eventually, in
$\nu \in \operatorname {\mathrm {succ}}_T(\emptyset )$
. Although eventually, in
![]() $V[G\ast H]$
, p will be a valid condition only if
$V[G\ast H]$
, p will be a valid condition only if
![]() $Q(\emptyset ) \in H$
, and
$Q(\emptyset ) \in H$
, and
![]() $p {}^{\frown } {\langle } \nu {\rangle }$
will form valid extensions of p only for a
$p {}^{\frown } {\langle } \nu {\rangle }$
will form valid extensions of p only for a
![]() $D_{\kappa ,\tau ,t}$
-positive set of ordinals
$D_{\kappa ,\tau ,t}$
-positive set of ordinals
![]() $\nu \in \operatorname {\mathrm {succ}}_T(\emptyset )$
, it is still possible to decide certain properties of such extensions on a measure one set of
$\nu \in \operatorname {\mathrm {succ}}_T(\emptyset )$
, it is still possible to decide certain properties of such extensions on a measure one set of
![]() $U_{\kappa ,\tau }(t)$
in
$U_{\kappa ,\tau }(t)$
in
![]() $V[G]$
. This approach of arguing from
$V[G]$
. This approach of arguing from
![]() $V[G]$
about the poset
$V[G]$
about the poset
![]() $\mathbb {Q}_{\kappa ,\tau }^*$
in
$\mathbb {Q}_{\kappa ,\tau }^*$
in
![]() $V[G\ast H]$
plays a significant role in our proof below, showing that
$V[G\ast H]$
plays a significant role in our proof below, showing that
![]() $\mathbb {Q}_{\kappa ,\tau }^*$
satisfies the Prikry Property.
$\mathbb {Q}_{\kappa ,\tau }^*$
satisfies the Prikry Property.
Remark 6.4. The forcing
![]() $\operatorname {\mathrm {Coll}}(\kappa < \lambda ) * \mathbb {Q}^*_{\kappa , \tau }$
is isomorphic to the collection of all
$\operatorname {\mathrm {Coll}}(\kappa < \lambda ) * \mathbb {Q}^*_{\kappa , \tau }$
is isomorphic to the collection of all
![]() $(t, T, Q)$
that satisfy all requirements of Definition 6.3 except the fourth one,
$(t, T, Q)$
that satisfy all requirements of Definition 6.3 except the fourth one,
![]() $Q(\emptyset ) \in H$
. Nevertheless, the decomposition into the collapse part and the singularization part would be more appropriate for our construction, as eventually
$Q(\emptyset ) \in H$
. Nevertheless, the decomposition into the collapse part and the singularization part would be more appropriate for our construction, as eventually
![]() $\mathbb {Q}^*_{\kappa ,\tau }$
is used as merely an auxiliary forcing.
$\mathbb {Q}^*_{\kappa ,\tau }$
is used as merely an auxiliary forcing.
The coherency requirements in Definition 6.3 allow us to obtain a natural amalgamation property, similar to the one satisfied by the
![]() $V[G]$
poset
$V[G]$
poset
![]() $\mathbb {Q}_{\kappa ,\tau }$
.
$\mathbb {Q}_{\kappa ,\tau }$
.
Lemma 6.5. Work in
![]() $V[G]$
. Let
$V[G]$
. Let
![]() $p = (t,T,Q)$
, forced to be a condition in
$p = (t,T,Q)$
, forced to be a condition in
![]() $\mathbb {Q}^*_{\kappa ,\tau }$
by
$\mathbb {Q}^*_{\kappa ,\tau }$
by
![]() $q = Q(\emptyset )$
, and
$q = Q(\emptyset )$
, and
![]() $A = \operatorname {\mathrm {succ}}_T(\emptyset )$
. For each
$A = \operatorname {\mathrm {succ}}_T(\emptyset )$
. For each
![]() $\eta < \tau $
, denote
$\eta < \tau $
, denote
Suppose that there are
![]() $\bar {\eta } < \tau $
, a set
$\bar {\eta } < \tau $
, a set
![]() $A'(\bar {\eta }) \subseteq A(\bar {\eta })$
with
$A'(\bar {\eta }) \subseteq A(\bar {\eta })$
with
![]() $A'(\bar {\eta }) \in U_{\kappa ,\bar {\eta }}(t)$
and a sequence of conditions
$A'(\bar {\eta }) \in U_{\kappa ,\bar {\eta }}(t)$
and a sequence of conditions
![]() ${\langle } (t\cup \{\nu \} , T^{\nu },Q^{\nu }) \mid \nu \in A'(\bar {\eta }) {\rangle }$
, such that
${\langle } (t\cup \{\nu \} , T^{\nu },Q^{\nu }) \mid \nu \in A'(\bar {\eta }) {\rangle }$
, such that
![]() $(t\cup \{\nu \} , T^{\nu },Q^{\nu })$
is a direct extension of
$(t\cup \{\nu \} , T^{\nu },Q^{\nu })$
is a direct extension of
![]() $p {}^{\frown } {\langle } \nu {\rangle }$
for all
$p {}^{\frown } {\langle } \nu {\rangle }$
for all
![]() $\nu \in A'(\bar {\eta })$
. Then, there exists a direct extension
$\nu \in A'(\bar {\eta })$
. Then, there exists a direct extension
![]() $p^* \geq ^* p$
,
$p^* \geq ^* p$
,
![]() $p^* = (t,T^*,Q^*)$
, such that the set
$p^* = (t,T^*,Q^*)$
, such that the set
![]() $\{ (t{}^{\frown } {\langle } \nu {\rangle },T^{\nu },Q^{\nu }) \mid \nu \in A'(\bar {\eta }) \}$
is forced by
$\{ (t{}^{\frown } {\langle } \nu {\rangle },T^{\nu },Q^{\nu }) \mid \nu \in A'(\bar {\eta }) \}$
is forced by
![]() $Q^*(\emptyset )$
to be predense above
$Q^*(\emptyset )$
to be predense above
![]() $p^*$
.
$p^*$
.
Remark 6.6. In the proof of the lemma, we make use of several construction arguments involving trees T associated to conditions
![]() $(t, T)$
in the poset
$(t, T)$
in the poset
![]() $\mathbb {Q}_{\kappa ,\tau }$
from [Reference Gitik11]. We list these arguments and refer the reader to [Reference Gitik11] for proofs.
$\mathbb {Q}_{\kappa ,\tau }$
from [Reference Gitik11]. We list these arguments and refer the reader to [Reference Gitik11] for proofs.
For a finite sequence s, we write
![]() $o(s) = \max (\{o(\nu ) \mid \nu \in s\} )$
.
$o(s) = \max (\{o(\nu ) \mid \nu \in s\} )$
.
-
1. Suppose that
 $(t,T)$
is a condition of
$(t,T)$
is a condition of
 $\mathbb {Q}_{\kappa ,\tau }$
and
$\mathbb {Q}_{\kappa ,\tau }$
and
 $A'(\eta ) \subseteq \operatorname {\mathrm {succ}}_T(\emptyset )$
belongs to
$A'(\eta ) \subseteq \operatorname {\mathrm {succ}}_T(\emptyset )$
belongs to
 $U_{\kappa ,\eta }(t)$
for some
$U_{\kappa ,\eta }(t)$
for some
 $\eta < \tau $
. Then there exists a subtree
$\eta < \tau $
. Then there exists a subtree
 $T'$
of T, so that
$T'$
of T, so that
 $(t,T') \in \mathbb {Q}_{\kappa ,\tau }$
is a direct extension of
$(t,T') \in \mathbb {Q}_{\kappa ,\tau }$
is a direct extension of
 $(t,T)$
, and
$(t,T)$
, and  $$\begin{align*}\{ \nu \in \operatorname{\mathrm{succ}}_{T'}(\emptyset) \mid o(\nu) = \eta\} \subseteq A'(\eta) .\end{align*}$$
$$\begin{align*}\{ \nu \in \operatorname{\mathrm{succ}}_{T'}(\emptyset) \mid o(\nu) = \eta\} \subseteq A'(\eta) .\end{align*}$$
Similarly, for every
 $s \in T$
and
$s \in T$
and
 $A^{\prime }_s(\eta ) \subseteq \operatorname {\mathrm {succ}}_T(s)$
which belongs to
$A^{\prime }_s(\eta ) \subseteq \operatorname {\mathrm {succ}}_T(s)$
which belongs to
 $U_{\kappa ,\eta }(t{}^{\frown } s)$
there is a direct extension
$U_{\kappa ,\eta }(t{}^{\frown } s)$
there is a direct extension
 $(t,T')$
of
$(t,T')$
of
 $(t,T)$
, which only requires shrinking the tree T above s (i.e., shrinking
$(t,T)$
, which only requires shrinking the tree T above s (i.e., shrinking
 $T_s$
) and in particular
$T_s$
) and in particular
 $s\in T'$
, so that
$s\in T'$
, so that
 $\{ \nu \in \operatorname {\mathrm {succ}}_{T'}(s) \mid o(\nu ) = \eta \} \subseteq A^{\prime }_s(\eta )$
.
$\{ \nu \in \operatorname {\mathrm {succ}}_{T'}(s) \mid o(\nu ) = \eta \} \subseteq A^{\prime }_s(\eta )$
.Furthermore, this construction can be naturally combined over different values
 $s \in T$
. Namely, given a family
$s \in T$
. Namely, given a family
 $\{ A^{\prime }_s(\eta ) \mid s \in T \}$
of sets as above we can apply the same procedure, level by level, to the tree T and obtain a subtree
$\{ A^{\prime }_s(\eta ) \mid s \in T \}$
of sets as above we can apply the same procedure, level by level, to the tree T and obtain a subtree
 $T' \subseteq T$
with the property that
$T' \subseteq T$
with the property that
 $(t,T') \in \mathbb {Q}_{\kappa ,\tau }$
and for every
$(t,T') \in \mathbb {Q}_{\kappa ,\tau }$
and for every
 $s \in T'$
,
$s \in T'$
,  $$\begin{align*}\{ \nu \in \operatorname{\mathrm{succ}}_{T'}(s) \mid o(\nu) = \eta\} \subseteq A^{\prime}_s(\eta). \end{align*}$$
$$\begin{align*}\{ \nu \in \operatorname{\mathrm{succ}}_{T'}(s) \mid o(\nu) = \eta\} \subseteq A^{\prime}_s(\eta). \end{align*}$$
-
2. For a condition
 $(t,T)$
,
$(t,T)$
,
 $s \in T$
, and
$s \in T$
, and
 $\eta < \tau $
, there exists a direct extension
$\eta < \tau $
, there exists a direct extension
 $(t,T') \geq ^* (t,T)$
, which only requires shrinking the tree T above s such that for all
$(t,T') \geq ^* (t,T)$
, which only requires shrinking the tree T above s such that for all
 $s' \in T$
which end extends s, if there exists
$s' \in T$
which end extends s, if there exists
 $\nu \in b_{s'}\setminus b_s$
such that
$\nu \in b_{s'}\setminus b_s$
such that
 $o(\nu ) = \eta $
,Footnote
12
then
$o(\nu ) = \eta $
,Footnote
12
then
 $\nu ' = \pi ^{t {}^{\frown } s}_{\eta }(s')$
(the minimal such
$\nu ' = \pi ^{t {}^{\frown } s}_{\eta }(s')$
(the minimal such
 $\nu $
) belongs to
$\nu $
) belongs to
 $\operatorname {\mathrm {succ}}_{T'}(s)$
. Repeating this construction, level by level, produces a direct extension
$\operatorname {\mathrm {succ}}_{T'}(s)$
. Repeating this construction, level by level, produces a direct extension
 $(t,T')$
of
$(t,T')$
of
 $(t,T)$
satisfying that for every
$(t,T)$
satisfying that for every
 $s \in T'$
and
$s \in T'$
and
 $s' \in T'$
which extends s,
$s' \in T'$
which extends s,
 $\nu ' = \pi _{\eta }^{t {}^{\frown } s}(s') \in \operatorname {\mathrm {succ}}_{T'}(s) \cap \{ \nu < \kappa \mid o(\nu ) = \eta \}$
.
$\nu ' = \pi _{\eta }^{t {}^{\frown } s}(s') \in \operatorname {\mathrm {succ}}_{T'}(s) \cap \{ \nu < \kappa \mid o(\nu ) = \eta \}$
.We note that if
 $s \in T'$
satisfies that
$s \in T'$
satisfies that
 $o(\mu ) < \eta $
for all
$o(\mu ) < \eta $
for all
 $\mu \in s$
, then for every
$\mu \in s$
, then for every
 $\mu \in \operatorname {\mathrm {succ}}_{T'}(s)$
with
$\mu \in \operatorname {\mathrm {succ}}_{T'}(s)$
with
 $o(\mu ) \geq \eta $
, we have
$o(\mu ) \geq \eta $
, we have
 $\pi ^{t{}^{\frown } s}_{\eta }(\mu ) = \pi ^t_{\eta }(s {}^{\frown } {\langle }\mu {\rangle })$
, which by our assumption of
$\pi ^{t{}^{\frown } s}_{\eta }(\mu ) = \pi ^t_{\eta }(s {}^{\frown } {\langle }\mu {\rangle })$
, which by our assumption of
 $T'$
(applied to
$T'$
(applied to
 $s' = s {}^{\frown } {\langle } \mu {\rangle }$
), implies that
$s' = s {}^{\frown } {\langle } \mu {\rangle }$
), implies that
 $\pi ^t_{\eta }(s {}^{\frown } {\langle }\mu {\rangle }) \in \operatorname {\mathrm {succ}}_{T'}(\emptyset )$
. It follows that
$\pi ^t_{\eta }(s {}^{\frown } {\langle }\mu {\rangle }) \in \operatorname {\mathrm {succ}}_{T'}(\emptyset )$
. It follows that  $$\begin{align*}\operatorname{\mathrm{succ}}_{T'}(s) \cap \{\nu \mid o(\nu) = \eta\} \subseteq \operatorname{\mathrm{succ}}_{T'}(\emptyset) \cap \{\nu \mid o(\nu) = \eta\}. \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{succ}}_{T'}(s) \cap \{\nu \mid o(\nu) = \eta\} \subseteq \operatorname{\mathrm{succ}}_{T'}(\emptyset) \cap \{\nu \mid o(\nu) = \eta\}. \end{align*}$$
Since the former set belongs to
 $U_{\kappa ,\eta }(t {}^{\frown } s)$
, we conclude that as well.
$U_{\kappa ,\eta }(t {}^{\frown } s)$
, we conclude that as well. $$\begin{align*}\operatorname{\mathrm{succ}}_{T'}(\emptyset) \cap \{\nu \mid o(\nu) = \eta\} \in U_{\kappa,\eta}(t {}^{\frown} s)\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{succ}}_{T'}(\emptyset) \cap \{\nu \mid o(\nu) = \eta\} \in U_{\kappa,\eta}(t {}^{\frown} s)\end{align*}$$
The same consideration applies to any
 $s \in T'$
and
$s \in T'$
and
 $s'\in T'$
which extends s, and for which
$s'\in T'$
which extends s, and for which
 $o(\nu ) < \eta $
for every
$o(\nu ) < \eta $
for every
 $\nu \in s'\setminus s$
, and implies that
$\nu \in s'\setminus s$
, and implies that  $$\begin{align*}\operatorname{\mathrm{succ}}_{T'}(s) \cap \{\nu \mid o(\nu) = \eta\} \in U_{\kappa,\eta}(t {}^{\frown} s').\end{align*}$$
$$\begin{align*}\operatorname{\mathrm{succ}}_{T'}(s) \cap \{\nu \mid o(\nu) = \eta\} \in U_{\kappa,\eta}(t {}^{\frown} s').\end{align*}$$
-
3. Let
 $(t,T')$
be a condition as in the previous clause. There exists a direct extension
$(t,T')$
be a condition as in the previous clause. There exists a direct extension
 $(t,T^*)$
of
$(t,T^*)$
of
 $(t,T')$
such that for every
$(t,T')$
such that for every
 $s' \in T^*$
for which
$s' \in T^*$
for which
 $\nu ' = \pi ^{t}_{\eta }(s') \in b_{s'}\setminus b_t$
is defined, not only that but further, there is some
$\nu ' = \pi ^{t}_{\eta }(s') \in b_{s'}\setminus b_t$
is defined, not only that but further, there is some $$\begin{align*}\nu' \in \operatorname{\mathrm{succ}}_{T^*}(\emptyset) \cap \{\nu \mid o(\nu) = \eta\},\end{align*}$$
$$\begin{align*}\nu' \in \operatorname{\mathrm{succ}}_{T^*}(\emptyset) \cap \{\nu \mid o(\nu) = \eta\},\end{align*}$$
 $s" \in T^*$
which extends
$s" \in T^*$
which extends
 ${\langle } \nu '{\rangle }$
such that
${\langle } \nu '{\rangle }$
such that
 $b_{t {}^{\frown } s"} = b_{t {}^{\frown } s'}$
and
$b_{t {}^{\frown } s"} = b_{t {}^{\frown } s'}$
and
 $T^*_{s'} \subseteq T^*_{s"}$
. We note that it implies that the set is predense above
$T^*_{s'} \subseteq T^*_{s"}$
. We note that it implies that the set is predense above $$\begin{align*}\{ (t \cup \{ \nu \}, T^*_{\langle \nu \rangle}) \mid \nu \in \operatorname{\mathrm{succ}}_{T^*}(\emptyset) , o(\nu) = \eta\}\end{align*}$$
$$\begin{align*}\{ (t \cup \{ \nu \}, T^*_{\langle \nu \rangle}) \mid \nu \in \operatorname{\mathrm{succ}}_{T^*}(\emptyset) , o(\nu) = \eta\}\end{align*}$$
 $(t,T^*)$
.
$(t,T^*)$
.
We turn to the proof of Lemma 6.5.
Proof (Lemma 6.5).
For
![]() $s \in T$
, define
$s \in T$
, define
![]() $o(s) = \max (\{o(\nu ) \mid \nu \in s\})$
, and for a tree
$o(s) = \max (\{o(\nu ) \mid \nu \in s\})$
, and for a tree
![]() $T \subseteq [\kappa ]^{<\omega }$
, and
$T \subseteq [\kappa ]^{<\omega }$
, and
![]() $\eta $
,
$\eta $
,
![]() $T(<\eta ) = \{ s \in T \mid o(s) < \eta \}$
. Let
$T(<\eta ) = \{ s \in T \mid o(s) < \eta \}$
. Let
![]() $p = (t,T,Q)$
,
$p = (t,T,Q)$
,
![]() $A'(\bar {\eta })$
, and
$A'(\bar {\eta })$
, and
![]() ${\langle } (t\cup \{\nu \} , T^{\nu },Q^{\nu }) \mid \nu \in A'(\bar {\eta }) {\rangle }$
, as in the statement of the Lemma. By part (1) of Remark 6.6 above, we may assume (by reducing to a suitable subtree) that
${\langle } (t\cup \{\nu \} , T^{\nu },Q^{\nu }) \mid \nu \in A'(\bar {\eta }) {\rangle }$
, as in the statement of the Lemma. By part (1) of Remark 6.6 above, we may assume (by reducing to a suitable subtree) that
![]() $\operatorname {\mathrm {succ}}_T(\emptyset ) \cap \{ \nu \mid o(\nu ) = \bar {\eta }\} \subseteq A'(\bar {\eta })$
. Furthermore, by part (2) of the remark, we may further assume that
$\operatorname {\mathrm {succ}}_T(\emptyset ) \cap \{ \nu \mid o(\nu ) = \bar {\eta }\} \subseteq A'(\bar {\eta })$
. Furthermore, by part (2) of the remark, we may further assume that
![]() $A'(\bar {\eta }) \in U_{\kappa ,\bar {\eta }}(t {}^{\frown } s)$
for every
$A'(\bar {\eta }) \in U_{\kappa ,\bar {\eta }}(t {}^{\frown } s)$
for every
![]() $s \in T$
with
$s \in T$
with
![]() $o(s) < \bar {\eta }$
.
$o(s) < \bar {\eta }$
.
Recall that for each sequence
![]() $s \in T$
,
$s \in T$
,
![]() $o(s) < \bar {\eta }$
, the function
$o(s) < \bar {\eta }$
, the function
![]() $\pi ^{t {}^{\frown } s}(\nu )$
is a normal projection of
$\pi ^{t {}^{\frown } s}(\nu )$
is a normal projection of
![]() $U_{\kappa ,\bar {\eta }}(t {}^{\frown } s)$
to
$U_{\kappa ,\bar {\eta }}(t {}^{\frown } s)$
to
![]() $U_{\kappa ,0}(t {}^{\frown } s)$
. Since
$U_{\kappa ,0}(t {}^{\frown } s)$
. Since
![]() $Q^{\nu }(\emptyset )\restriction \lambda \times \pi ^{t {}^{\frown } s}(\nu )$
is bounded in
$Q^{\nu }(\emptyset )\restriction \lambda \times \pi ^{t {}^{\frown } s}(\nu )$
is bounded in
![]() $\pi ^{t {}^{\frown } s}(\nu )$
,Footnote
13
we can press down on its value and find a subset
$\pi ^{t {}^{\frown } s}(\nu )$
,Footnote
13
we can press down on its value and find a subset
![]() $A^{\prime }_{s}(\bar {\eta }) \in U_{\kappa ,\bar {\eta }}(t {}^{\frown } s)$
of
$A^{\prime }_{s}(\bar {\eta }) \in U_{\kappa ,\bar {\eta }}(t {}^{\frown } s)$
of
![]() $A'(\bar {\eta })$
and a collapse condition
$A'(\bar {\eta })$
and a collapse condition
![]() $Q'(s)$
such that
$Q'(s)$
such that
![]() $Q^{\nu }(\emptyset )\restriction \pi ^{t {}^{\frown } s}(\nu ) = Q'(s)$
for all
$Q^{\nu }(\emptyset )\restriction \pi ^{t {}^{\frown } s}(\nu ) = Q'(s)$
for all
![]() $\nu \in A^{\prime }_{s}(\bar {\eta })$
.
$\nu \in A^{\prime }_{s}(\bar {\eta })$
.
By applying the construction arguments of Remark 6.6, we may find direct extension
![]() $(t,T')$
of
$(t,T')$
of
![]() $(t,T)$
having both properties from parts (1) and (2) of the remark, where (1) is applied with respect to the sets
$(t,T)$
having both properties from parts (1) and (2) of the remark, where (1) is applied with respect to the sets
![]() $A^{\prime }_s(\bar {\eta })$
,
$A^{\prime }_s(\bar {\eta })$
,
![]() $s \in T'$
,
$s \in T'$
,
![]() $o(s) < \bar {\eta }$
, given by the pressing down process above, by which
$o(s) < \bar {\eta }$
, given by the pressing down process above, by which
![]() $Q'(s)$
is defined. We note that, as mentioned at the end of part (2) of the remark, for every
$Q'(s)$
is defined. We note that, as mentioned at the end of part (2) of the remark, for every
![]() $s' \in T'(<\bar {\eta }) = \{ s \in T' \mid o(s) < \bar {\eta }\}$
which end extends s,
$s' \in T'(<\bar {\eta }) = \{ s \in T' \mid o(s) < \bar {\eta }\}$
which end extends s,
Moreover, since
we conclude that
![]() $A^{\prime }_{s}(\bar {\eta }) \in U_{\kappa ,\bar {\eta }}(s')$
. It follows that
$A^{\prime }_{s}(\bar {\eta }) \in U_{\kappa ,\bar {\eta }}(s')$
. It follows that
![]() $A^{\prime }_s(\bar {\eta }) \cap A^{\prime }_{s'}(\bar {\eta }) \neq \emptyset $
, which in turn, implies that
$A^{\prime }_s(\bar {\eta }) \cap A^{\prime }_{s'}(\bar {\eta }) \neq \emptyset $
, which in turn, implies that
(as witnessed by
![]() $Q^{\nu }(\emptyset )$
for any
$Q^{\nu }(\emptyset )$
for any
![]() $\nu \in A^{\prime }_s(\bar {\eta }) \cap A^{\prime }_{s'}(\bar {\eta })$
).
$\nu \in A^{\prime }_s(\bar {\eta }) \cap A^{\prime }_{s'}(\bar {\eta })$
).
Finally, we form a subtree
![]() $T"$
of
$T"$
of
![]() $T'$
by intersecting
$T'$
by intersecting
![]() $T^{\prime }_{{\langle } \nu {\rangle }}$
with
$T^{\prime }_{{\langle } \nu {\rangle }}$
with
![]() $T^{\nu }$
, for each
$T^{\nu }$
, for each
![]() $\nu \in \operatorname {\mathrm {succ}}_{T'}(\emptyset ) \cap \{\nu \mid o(\nu ) = \bar {\eta }\} \subseteq A'(\bar {\eta })$
. By appealing to part (3) of the previous remark, we can find a direct extension
$\nu \in \operatorname {\mathrm {succ}}_{T'}(\emptyset ) \cap \{\nu \mid o(\nu ) = \bar {\eta }\} \subseteq A'(\bar {\eta })$
. By appealing to part (3) of the previous remark, we can find a direct extension
![]() $(t,T^*)$
of
$(t,T^*)$
of
![]() $(t,T")$
which further satisfies that for every
$(t,T")$
which further satisfies that for every
![]() $s \in T^*$
for which
$s \in T^*$
for which
![]() $\nu _{s} := \pi ^{t}_{\eta }(s) \in b_{s}\setminus b_t$
is defined,
$\nu _{s} := \pi ^{t}_{\eta }(s) \in b_{s}\setminus b_t$
is defined,
![]() $\nu _{s} \in \operatorname {\mathrm {succ}}_{T^*}(\emptyset ) \cap \{\nu \mid o(\nu ) = \eta \}$
, and there exists some
$\nu _{s} \in \operatorname {\mathrm {succ}}_{T^*}(\emptyset ) \cap \{\nu \mid o(\nu ) = \eta \}$
, and there exists some
![]() $s' \in T^*$
which end extends
$s' \in T^*$
which end extends
![]() ${\langle } \nu _s{\rangle }$
, such that
${\langle } \nu _s{\rangle }$
, such that
![]() $b_{t {}^{\frown } s'} = b_{t {}^{\frown } s}$
and
$b_{t {}^{\frown } s'} = b_{t {}^{\frown } s}$
and
![]() $T^*_{s} \subseteq T^*_{s'}$
. Let
$T^*_{s} \subseteq T^*_{s'}$
. Let
![]() $\bar {s} = s'\setminus \nu _s+1$
.
$\bar {s} = s'\setminus \nu _s+1$
.
![]() $Q^{\nu _s}(\bar {s})$
is defined, since
$Q^{\nu _s}(\bar {s})$
is defined, since
![]() $T^*_{{\langle } \nu _{s}{\rangle }} \subseteq T^{\nu _{s}} = \operatorname {\mathrm {dom}}(Q^{\nu _{s}})$
. Moreover, since
$T^*_{{\langle } \nu _{s}{\rangle }} \subseteq T^{\nu _{s}} = \operatorname {\mathrm {dom}}(Q^{\nu _{s}})$
. Moreover, since
![]() $(t\cup \{\nu _s\},T^{\nu _s},Q^{\nu _s})$
is assumed to be a condition in
$(t\cup \{\nu _s\},T^{\nu _s},Q^{\nu _s})$
is assumed to be a condition in
![]() $\mathbb {Q}^*_{\kappa ,\tau }$
, the value
$\mathbb {Q}^*_{\kappa ,\tau }$
, the value
![]() $Q^{\nu _s}(\bar {s})$
does not depend on the choice of a sequence
$Q^{\nu _s}(\bar {s})$
does not depend on the choice of a sequence
![]() $s'$
and its associated subsequence
$s'$
and its associated subsequence
![]() $\bar {s} \in T^{\nu _s}$
satisfying
$\bar {s} \in T^{\nu _s}$
satisfying
![]() $b_{t {}^{\frown }{\langle } \nu _s{\rangle } {}^{\frown } \bar {s}} = b_{t {}^{\frown } s'} = b_{t {}^{\frown } s}$
.
$b_{t {}^{\frown }{\langle } \nu _s{\rangle } {}^{\frown } \bar {s}} = b_{t {}^{\frown } s'} = b_{t {}^{\frown } s}$
.
We turn to define the function
![]() $Q^*$
on
$Q^*$
on
![]() $T^*$
. We follow the convention from the last paragraph, where for
$T^*$
. We follow the convention from the last paragraph, where for
![]() $s \in T^*$
with
$s \in T^*$
with
![]() $o(s) \geq \bar {\eta }$
, we denote
$o(s) \geq \bar {\eta }$
, we denote
![]() $\nu _s = \pi ^t_{\bar {\eta }}(s)$
. We set
$\nu _s = \pi ^t_{\bar {\eta }}(s)$
. We set
 $$\begin{align*}Q^*(s) = \begin{cases} Q^{\nu_s}(\bar{s}) &\mbox{ if } o(s) \geq \bar{\eta}, \bar{s} \in T^{\nu_s} \text{ satisfies } b_{t {}^{\frown} {\langle} \nu_s {\rangle} {}^{\frown} \bar{s}} = b_{t {}^{\frown} s}\\ Q'(s) &\mbox{ if } o(s) < \bar{\eta} \end{cases} \end{align*}$$
$$\begin{align*}Q^*(s) = \begin{cases} Q^{\nu_s}(\bar{s}) &\mbox{ if } o(s) \geq \bar{\eta}, \bar{s} \in T^{\nu_s} \text{ satisfies } b_{t {}^{\frown} {\langle} \nu_s {\rangle} {}^{\frown} \bar{s}} = b_{t {}^{\frown} s}\\ Q'(s) &\mbox{ if } o(s) < \bar{\eta} \end{cases} \end{align*}$$
We claim that
![]() $Q^*(\emptyset )$
forces that
$Q^*(\emptyset )$
forces that
![]() $(t,T^*,Q^*)$
is a condition that extends
$(t,T^*,Q^*)$
is a condition that extends
![]() $(t,T,Q)$
. We show first that
$(t,T,Q)$
. We show first that
![]() $Q^*(\emptyset )$
forces
$Q^*(\emptyset )$
forces
![]() $(t,T^*,Q^*)$
is a condition of
$(t,T^*,Q^*)$
is a condition of
![]() $\mathbb {Q}^*_{\kappa ,\tau }$
, which requires verifying the first three conditions in the definition of the poset. Conditions (i) and (ii) are clearly satisfied as
$\mathbb {Q}^*_{\kappa ,\tau }$
, which requires verifying the first three conditions in the definition of the poset. Conditions (i) and (ii) are clearly satisfied as
![]() $(t,T^*) \in \mathbb {Q}_{\kappa ,\tau }$
. To verify condition (iii), we need to check that for every
$(t,T^*) \in \mathbb {Q}_{\kappa ,\tau }$
. To verify condition (iii), we need to check that for every
![]() $s,s' \in T^*$
, if
$s,s' \in T^*$
, if
![]() $s'$
extends s, then
$s'$
extends s, then
![]() $Q^*(s) = Q^*(s')\restriction \lambda \times \pi ^{t {}^{\frown } s}(s')$
. The verification breaks down to three cases.
$Q^*(s) = Q^*(s')\restriction \lambda \times \pi ^{t {}^{\frown } s}(s')$
. The verification breaks down to three cases.
Case I: If
![]() $o(s),o(s') < \bar {\eta }$
, then
$o(s),o(s') < \bar {\eta }$
, then
![]() $s,s' \in T^*(<\bar {\eta })$
and, as described above, the result is an immediate consequence of the fact that
$s,s' \in T^*(<\bar {\eta })$
and, as described above, the result is an immediate consequence of the fact that
![]() $s' \in T'(<\bar {\eta })$
end extends s.
$s' \in T'(<\bar {\eta })$
end extends s.
Case II: If
![]() $o(s) < \bar {\eta }$
and
$o(s) < \bar {\eta }$
and
![]() $o(s') \geq \bar {\eta }$
, then
$o(s') \geq \bar {\eta }$
, then
![]() $\nu ' = \pi ^{t{}^{\frown } s}_{\bar \eta }(s') \in A^{\prime }_s(\bar {\eta })$
. As
$\nu ' = \pi ^{t{}^{\frown } s}_{\bar \eta }(s') \in A^{\prime }_s(\bar {\eta })$
. As
![]() $\pi ^{t {}^{\frown } s}(s') = \pi ^{t {}^{\frown } s}(\nu ')$
and
$\pi ^{t {}^{\frown } s}(s') = \pi ^{t {}^{\frown } s}(\nu ')$
and
![]() $(t \cup \{\nu '\}, T^{\nu },Q^{\nu }) \in \mathbb {Q}^*_{\kappa ,\tau }$
, it follows that
$(t \cup \{\nu '\}, T^{\nu },Q^{\nu }) \in \mathbb {Q}^*_{\kappa ,\tau }$
, it follows that
 $$\begin{align*}\begin{matrix} Q^*(s')\restriction \lambda \times \pi^{t {}^{\frown} s}(s') = & \\ Q^{\nu'}(\bar{s'}) \restriction \lambda \times \pi^{t {}^{\frown} s}(s') = & \\ Q^{\nu'}(\emptyset) \restriction \lambda \times \pi^{t {}^{\frown} s}(\nu') = & Q'(s) = Q^*(s). \end{matrix}\end{align*}$$
$$\begin{align*}\begin{matrix} Q^*(s')\restriction \lambda \times \pi^{t {}^{\frown} s}(s') = & \\ Q^{\nu'}(\bar{s'}) \restriction \lambda \times \pi^{t {}^{\frown} s}(s') = & \\ Q^{\nu'}(\emptyset) \restriction \lambda \times \pi^{t {}^{\frown} s}(\nu') = & Q'(s) = Q^*(s). \end{matrix}\end{align*}$$
Case III: If
![]() $o(s) \geq \bar {\eta }$
, then there exists some
$o(s) \geq \bar {\eta }$
, then there exists some
![]() $\bar {s} \in T^*_{\nu _{s}} \subseteq T^{\nu _s}$
such that
$\bar {s} \in T^*_{\nu _{s}} \subseteq T^{\nu _s}$
such that
![]() $b_{t {}^{\frown } {\langle } \nu _s {\rangle } {}^{\frown } \bar {s}} = b_{t {}^{\frown } s}$
and
$b_{t {}^{\frown } {\langle } \nu _s {\rangle } {}^{\frown } \bar {s}} = b_{t {}^{\frown } s}$
and
![]() $T^*_s \subseteq T^*_{{\langle } \nu _s {\rangle } {}^{\frown } \bar {s}}$
. In particular,
$T^*_s \subseteq T^*_{{\langle } \nu _s {\rangle } {}^{\frown } \bar {s}}$
. In particular,
![]() $Q^*(s) = Q^*(\bar {s})$
and
$Q^*(s) = Q^*(\bar {s})$
and
![]() $s' \in T^*_{{\langle } \nu _s {\rangle } {}^{\frown } \bar {s}} \subseteq T^{\nu _s}_{\bar {s}}$
. Since
$s' \in T^*_{{\langle } \nu _s {\rangle } {}^{\frown } \bar {s}} \subseteq T^{\nu _s}_{\bar {s}}$
. Since
![]() $Q^{\nu _s}$
is
$Q^{\nu _s}$
is
![]() $(t \cup \{\nu _s\}, T^{\nu _s})$
-coherent, we conclude that
$(t \cup \{\nu _s\}, T^{\nu _s})$
-coherent, we conclude that
This concludes the proof that
![]() $p^* = (t,T^*,Q^*)$
satisfies the property (iii) of the definition of
$p^* = (t,T^*,Q^*)$
satisfies the property (iii) of the definition of
![]() $\mathbb {Q}^*_{\kappa ,\tau }$
, and thus, that
$\mathbb {Q}^*_{\kappa ,\tau }$
, and thus, that
![]() $Q^*(\emptyset ) \in \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
forces it as a condition of
$Q^*(\emptyset ) \in \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
forces it as a condition of
![]() $\mathbb {Q}^*_{\kappa ,\tau }$
. It is immediate from its definition that
$\mathbb {Q}^*_{\kappa ,\tau }$
. It is immediate from its definition that
![]() $p^*$
is a direct extension of p. Finally, our choice of the tree
$p^*$
is a direct extension of p. Finally, our choice of the tree
![]() $T^*$
above, obtained from
$T^*$
above, obtained from
![]() $T'$
using fact (3) from Remark 6.6 above, implies at once that
$T'$
using fact (3) from Remark 6.6 above, implies at once that
![]() $Q^*(\emptyset )$
forces
$Q^*(\emptyset )$
forces
![]() $\{ (t{}^{\frown } {\langle } \nu {\rangle },T^{\nu },Q^{\nu }) \mid \nu \in A'(\bar {\eta }) \}$
to be predense above
$\{ (t{}^{\frown } {\langle } \nu {\rangle },T^{\nu },Q^{\nu }) \mid \nu \in A'(\bar {\eta }) \}$
to be predense above
![]() $p^*$
.
$p^*$
.
Lemma 6.7.
![]() $\mathbb {Q}^*_{\kappa ,\tau }$
satisfies the Prikry Property.
$\mathbb {Q}^*_{\kappa ,\tau }$
satisfies the Prikry Property.
Proof. Suppose otherwise. Working in
![]() $V[G \ast H]$
, let
$V[G \ast H]$
, let
![]() $(t,T,Q)$
,
$(t,T,Q)$
,
![]() $\sigma $
be condition and statement of
$\sigma $
be condition and statement of
![]() $\mathbb {Q}^*_{\kappa ,\tau }$
, respectively, such that no direct extension of
$\mathbb {Q}^*_{\kappa ,\tau }$
, respectively, such that no direct extension of
![]() $(t,T,Q)$
decides
$(t,T,Q)$
decides
![]() $\sigma $
. Back in
$\sigma $
. Back in
![]() $V[G]$
, let
$V[G]$
, let
![]() $q \in H$
be a condition which forces this statement about
$q \in H$
be a condition which forces this statement about
![]() $(t,T,Q)$
and
$(t,T,Q)$
and
![]() $\sigma $
. Since q forces
$\sigma $
. Since q forces
![]() $(t,T,Q)$
to be a condition of
$(t,T,Q)$
to be a condition of
![]() $\mathbb {Q}^*_{\kappa ,\tau }$
, we have that
$\mathbb {Q}^*_{\kappa ,\tau }$
, we have that
![]() $q \geq Q(\emptyset )$
. Therefore, by moving to a direct extension of
$q \geq Q(\emptyset )$
. Therefore, by moving to a direct extension of
![]() $(t,T,Q)$
, we may assume that
$(t,T,Q)$
, we may assume that
![]() $q = Q(\emptyset )$
. For notational simplicity, we make the assumption that
$q = Q(\emptyset )$
. For notational simplicity, we make the assumption that
![]() $t = \emptyset $
. The proof for an arbitrary sequence t is similar.
$t = \emptyset $
. The proof for an arbitrary sequence t is similar.
Let
![]() $A = \operatorname {\mathrm {succ}}_T(\emptyset )$
. We may assume that
$A = \operatorname {\mathrm {succ}}_T(\emptyset )$
. We may assume that
![]() $q\in V_{\mu _0}$
, where
$q\in V_{\mu _0}$
, where
![]() $\mu _0 = \min (\{ \pi _0^{\emptyset }(\nu ) \mid \nu \in A\})$
. For each
$\mu _0 = \min (\{ \pi _0^{\emptyset }(\nu ) \mid \nu \in A\})$
. For each
![]() $\nu \in A$
, we choose a condition
$\nu \in A$
, we choose a condition
![]() $q(\nu ) \in \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
, extending
$q(\nu ) \in \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
, extending
![]() $q \cup Q(\nu )$
, which decides the
$q \cup Q(\nu )$
, which decides the
![]() $\operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
statement of whether there exists a direct extension
$\operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
statement of whether there exists a direct extension
![]() $p^{\nu } = ({\langle } \nu {\rangle },T^{\nu },Q^{\nu })$
of
$p^{\nu } = ({\langle } \nu {\rangle },T^{\nu },Q^{\nu })$
of
![]() $p {}^{\frown } {\langle } \nu {\rangle }$
which decides
$p {}^{\frown } {\langle } \nu {\rangle }$
which decides
![]() $\sigma $
, and if so, whether
$\sigma $
, and if so, whether
![]() $p^{\nu }$
forces
$p^{\nu }$
forces
![]() $\sigma $
or
$\sigma $
or
![]() $\neg \sigma $
. Let
$\neg \sigma $
. Let
![]() $A^0$
be the sets of
$A^0$
be the sets of
![]() $\nu \in A$
for which
$\nu \in A$
for which
![]() $q(\nu )$
forces
$q(\nu )$
forces
![]() $p^{\nu }$
exists, and ‘
$p^{\nu }$
exists, and ‘
![]() $p^{\nu } \Vdash \sigma $
’. Similarly, let
$p^{\nu } \Vdash \sigma $
’. Similarly, let
![]() $A^1 \subseteq A$
consist of
$A^1 \subseteq A$
consist of
![]() $\nu $
such that
$\nu $
such that
![]() $q(\nu )$
forces
$q(\nu )$
forces
![]() $p^{\nu }$
exists, and ‘
$p^{\nu }$
exists, and ‘
![]() $p^{\nu } \Vdash \neg \sigma $
’ and
$p^{\nu } \Vdash \neg \sigma $
’ and
![]() $A^2 = A \setminus (A^0 \uplus A^1)$
. The proof splits now into three main cases:
$A^2 = A \setminus (A^0 \uplus A^1)$
. The proof splits now into three main cases:
Case 0: There exists some
![]() $\bar {\eta } < \tau $
such that
$\bar {\eta } < \tau $
such that
![]() $A^0 \in U_{\kappa ,\bar {\eta }}(\emptyset )$
.
$A^0 \in U_{\kappa ,\bar {\eta }}(\emptyset )$
.
Let
![]() $A'(\bar {\eta }) = A^0 \cap \{ \nu \mid o(\nu ) = \bar {\eta }\}$
. By applying Lemma 6.5 with respect to the family of conditions
$A'(\bar {\eta }) = A^0 \cap \{ \nu \mid o(\nu ) = \bar {\eta }\}$
. By applying Lemma 6.5 with respect to the family of conditions
![]() $\{ p^{\nu } =( {\langle } \nu {\rangle },T^{\nu },Q^{\nu }) \mid \nu \in A'(\bar {\eta }) \}$
, we can find a
$\{ p^{\nu } =( {\langle } \nu {\rangle },T^{\nu },Q^{\nu }) \mid \nu \in A'(\bar {\eta }) \}$
, we can find a
![]() $p^* = (\emptyset ,T^*,Q^*)$
which is forced by
$p^* = (\emptyset ,T^*,Q^*)$
which is forced by
![]() $Q^*(\emptyset )$
to be a direct extension of
$Q^*(\emptyset )$
to be a direct extension of
![]() $(\emptyset ,T,Q)$
, and to have
$(\emptyset ,T,Q)$
, and to have
![]() $\{ p^{\nu } \mid \nu \in A'(\bar {\eta }) \}$
be a predense in
$\{ p^{\nu } \mid \nu \in A'(\bar {\eta }) \}$
be a predense in
![]() $\mathbb {Q}^*_{\kappa ,\tau }/(\emptyset ,T^*,Q^*)$
. It follows that
$\mathbb {Q}^*_{\kappa ,\tau }/(\emptyset ,T^*,Q^*)$
. It follows that
![]() $Q^*(\emptyset ) \geq Q(\emptyset ) = q$
forces
$Q^*(\emptyset ) \geq Q(\emptyset ) = q$
forces
![]() $p^* = (\emptyset ,T^*,Q^*)$
is a direct extension of p which decides
$p^* = (\emptyset ,T^*,Q^*)$
is a direct extension of p which decides
![]() $\sigma $
. This contradicts our assumption.
$\sigma $
. This contradicts our assumption.
Case 1: There exists some
![]() $\bar {\eta } < \tau $
such that
$\bar {\eta } < \tau $
such that
![]() $A^1 \in U_{\kappa ,\bar {\eta }}(\emptyset )$
.
$A^1 \in U_{\kappa ,\bar {\eta }}(\emptyset )$
.
The argument for this case is similar to the previous one and leads to an extension
![]() $q^* \geq q$
in
$q^* \geq q$
in
![]() $\operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
and a direct extension
$\operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
and a direct extension
![]() $\bar {p} \geq ^* p$
, such that
$\bar {p} \geq ^* p$
, such that
![]() $q^*$
forces
$q^*$
forces
![]() $\bar {p} \Vdash _{\mathbb {Q}^*_{\kappa ,\tau }}\neg \sigma $
. Contradiction.
$\bar {p} \Vdash _{\mathbb {Q}^*_{\kappa ,\tau }}\neg \sigma $
. Contradiction.
Case 2:
![]() $A^2 \in \bigcap _{\eta < \tau } U_{\kappa ,\eta }(\emptyset )$
.
$A^2 \in \bigcap _{\eta < \tau } U_{\kappa ,\eta }(\emptyset )$
.
Let
![]() $A^2(0) = A^2 \cap \{ \nu \mid o(\nu ) = 0\}$
, and apply Lemma 6.5 with respect to
$A^2(0) = A^2 \cap \{ \nu \mid o(\nu ) = 0\}$
, and apply Lemma 6.5 with respect to
![]() $A^2(0)$
and
$A^2(0)$
and
![]() $\{ p {}^{\frown } {\langle } \nu {\rangle } \mid \nu \in A^2(0)\}$
to obtain a direct extension
$\{ p {}^{\frown } {\langle } \nu {\rangle } \mid \nu \in A^2(0)\}$
to obtain a direct extension
![]() $p_0^* = (\emptyset , T_0^*,Q_0^*)$
of p, with
$p_0^* = (\emptyset , T_0^*,Q_0^*)$
of p, with
![]() $\{ p{}^{\frown } {\langle }{\nu }{\rangle } \mid \nu \in A^2(0) \}$
being predense in
$\{ p{}^{\frown } {\langle }{\nu }{\rangle } \mid \nu \in A^2(0) \}$
being predense in
![]() $\mathbb {Q}^*_{\kappa ,\tau }/p_0^*$
.
$\mathbb {Q}^*_{\kappa ,\tau }/p_0^*$
.
Denoting
![]() $q_0^* = Q_0^*(\emptyset )$
, we define
$q_0^* = Q_0^*(\emptyset )$
, we define
![]() $\bar {A}^2$
to be the set of all
$\bar {A}^2$
to be the set of all
![]() $\nu \in A^2$
for which
$\nu \in A^2$
for which
![]() $q^*_0$
forces there is no direct extension
$q^*_0$
forces there is no direct extension
![]() $p^{\nu } \geq ^* p' {}^{\frown } \nu $
which decides
$p^{\nu } \geq ^* p' {}^{\frown } \nu $
which decides
![]() $\sigma $
. Note that
$\sigma $
. Note that
![]() $\bar {A}^2$
must belong to
$\bar {A}^2$
must belong to
![]() $\bigcap _{\eta < \tau }U_{\kappa ,\eta }(\emptyset )$
, since otherwise, there would be some
$\bigcap _{\eta < \tau }U_{\kappa ,\eta }(\emptyset )$
, since otherwise, there would be some
![]() $\eta < \tau $
, and a set
$\eta < \tau $
, and a set
![]() $A'(\eta ) \subseteq \bar {A}^2$
consisting of
$A'(\eta ) \subseteq \bar {A}^2$
consisting of
![]() $\nu $
for which some
$\nu $
for which some
![]() $q^*(\nu ) \geq q^*_0$
forces there exists a direct extension of
$q^*(\nu ) \geq q^*_0$
forces there exists a direct extension of
![]() $p^*_0 {}^{\frown } \nu $
which decides
$p^*_0 {}^{\frown } \nu $
which decides
![]() $\sigma $
. This, in turn would allow us to repeat the construction of one of the previous cases 0 and 1, to show that there is
$\sigma $
. This, in turn would allow us to repeat the construction of one of the previous cases 0 and 1, to show that there is
![]() $q^* \geq ^* q^*_0$
which forces some direct extension
$q^* \geq ^* q^*_0$
which forces some direct extension
![]() $p^*$
of
$p^*$
of
![]() $p^*_0$
to force either
$p^*_0$
to force either
![]() $\sigma $
or
$\sigma $
or
![]() $\neg \sigma $
, contradicting the choice of
$\neg \sigma $
, contradicting the choice of
![]() $q^*_0$
.
$q^*_0$
.
Let
![]() $q^1:=q^*_0$
and
$q^1:=q^*_0$
and
![]() $p^1 = ( \emptyset , T^1, Q^1)$
be the direct extension of
$p^1 = ( \emptyset , T^1, Q^1)$
be the direct extension of
![]() $p^*_0$
obtained by shrinking
$p^*_0$
obtained by shrinking
![]() $\operatorname {\mathrm {succ}}_{T^{p_0^*}}(\emptyset )$
to points in
$\operatorname {\mathrm {succ}}_{T^{p_0^*}}(\emptyset )$
to points in
![]() $\bar {A}^2$
. It follows from the construction
$\bar {A}^2$
. It follows from the construction
![]() $q^1$
forces that for all
$q^1$
forces that for all
![]() $\nu \in \operatorname {\mathrm {succ}}_{T^1}(\emptyset )$
,
$\nu \in \operatorname {\mathrm {succ}}_{T^1}(\emptyset )$
,
![]() $p^1 {}^{\frown } {\langle } \nu {\rangle }$
does not have a direct extension in
$p^1 {}^{\frown } {\langle } \nu {\rangle }$
does not have a direct extension in
![]() $\mathbb {Q}^*_{\kappa ,\tau }$
which decides
$\mathbb {Q}^*_{\kappa ,\tau }$
which decides
![]() $\sigma $
.
$\sigma $
.
Next, we move up to the second level of the tree. To each
![]() $\mu \in \operatorname {\mathrm {succ}}_{T^1}(\emptyset )$
, we can repeat the above analysis with respect to
$\mu \in \operatorname {\mathrm {succ}}_{T^1}(\emptyset )$
, we can repeat the above analysis with respect to
![]() $q(\mu ) = q^1 \cup Q^1(\mu )$
and
$q(\mu ) = q^1 \cup Q^1(\mu )$
and
![]() $p^1 {}^{\frown } {\langle }\mu {\rangle } = ( {\langle } \mu {\rangle }, T^1_{{\langle } \mu {\rangle }}, Q^1_{{\langle } \mu {\rangle }})$
. Accordingly, we split
$p^1 {}^{\frown } {\langle }\mu {\rangle } = ( {\langle } \mu {\rangle }, T^1_{{\langle } \mu {\rangle }}, Q^1_{{\langle } \mu {\rangle }})$
. Accordingly, we split
![]() $B = \operatorname {\mathrm {succ}}_{T^1}(\emptyset )$
into three sets,
$B = \operatorname {\mathrm {succ}}_{T^1}(\emptyset )$
into three sets,
![]() $B^0, B^1, B^2$
, based on whether the analysis for
$B^0, B^1, B^2$
, based on whether the analysis for
![]() $q(\mu )$
and
$q(\mu )$
and
![]() $p^1 {}^{\frown } {\langle }\mu {\rangle }$
has produced an extension
$p^1 {}^{\frown } {\langle }\mu {\rangle }$
has produced an extension
![]() $q^*(\mu ) \geq q(\mu )$
which forces some direct extension
$q^*(\mu ) \geq q(\mu )$
which forces some direct extension
![]() $p^{1,\mu } \geq ^* p^1 {}^{\frown } {\langle }\mu {\rangle }$
to decide
$p^{1,\mu } \geq ^* p^1 {}^{\frown } {\langle }\mu {\rangle }$
to decide
![]() $\sigma $
(
$\sigma $
(
![]() $B^0$
and
$B^0$
and
![]() $B^1$
for forcing
$B^1$
for forcing
![]() $\sigma $
and
$\sigma $
and
![]() $\neg \sigma $
, respectively). The argument above shows that if
$\neg \sigma $
, respectively). The argument above shows that if
![]() $B^0$
or
$B^0$
or
![]() $B^1$
belongs to
$B^1$
belongs to
![]() $U_{\kappa ,\eta }(\emptyset )$
for some
$U_{\kappa ,\eta }(\emptyset )$
for some
![]() $\eta < \tau $
, then there exists some
$\eta < \tau $
, then there exists some
![]() $q^* \geq q^1$
which forces that
$q^* \geq q^1$
which forces that
![]() $p^1$
has a direct extension which decides
$p^1$
has a direct extension which decides
![]() $\sigma $
, contradicting our assumptions.
$\sigma $
, contradicting our assumptions.
It follows that
![]() $B^2 \in \bigcap _{\eta < \tau }U_{\kappa ,\eta }(\emptyset )$
, and by repeating the argument from the beginning of Case 2 for each
$B^2 \in \bigcap _{\eta < \tau }U_{\kappa ,\eta }(\emptyset )$
, and by repeating the argument from the beginning of Case 2 for each
![]() $p^1{}^{\frown } {\langle }\mu {\rangle }$
,
$p^1{}^{\frown } {\langle }\mu {\rangle }$
,
![]() $\mu \in B^2$
, we can find for each
$\mu \in B^2$
, we can find for each
![]() $\mu \in B^2$
, conditions
$\mu \in B^2$
, conditions
![]() $q^*(\mu ) \geq q^1(\mu )$
,
$q^*(\mu ) \geq q^1(\mu )$
,
![]() $q^*(\mu ) \in \operatorname {\mathrm {Coll}}(\lambda ,\pi ^{\emptyset }_0(\mu ))$
, and
$q^*(\mu ) \in \operatorname {\mathrm {Coll}}(\lambda ,\pi ^{\emptyset }_0(\mu ))$
, and
![]() $p^*_{\mu } = ( {\langle } \mu {\rangle }, T^*_{\mu }, Q^1_{\mu }) \geq ^* p^1 {}^{\frown } \mu $
, such that
$p^*_{\mu } = ( {\langle } \mu {\rangle }, T^*_{\mu }, Q^1_{\mu }) \geq ^* p^1 {}^{\frown } \mu $
, such that
![]() $q^*(\mu )$
forces there is no direct extension of
$q^*(\mu )$
forces there is no direct extension of
![]() $p^*_{\mu } {}^{\frown } \nu $
which decides
$p^*_{\mu } {}^{\frown } \nu $
which decides
![]() $\sigma $
, for any
$\sigma $
, for any
![]() $\nu \in \operatorname {\mathrm {succ}}_{T^*_{\mu }}(\emptyset )$
. We may assume
$\nu \in \operatorname {\mathrm {succ}}_{T^*_{\mu }}(\emptyset )$
. We may assume
![]() $q^*(\mu ) = Q^1_{\mu }(\emptyset )$
and apply Lemma 6.5 with respect to
$q^*(\mu ) = Q^1_{\mu }(\emptyset )$
and apply Lemma 6.5 with respect to
![]() $B^2(0)$
and
$B^2(0)$
and
![]() $\{ p^*_{\mu } \mid \mu \in B^2(0)\}$
, to conclude, similarly to the above, that there are extensions
$\{ p^*_{\mu } \mid \mu \in B^2(0)\}$
, to conclude, similarly to the above, that there are extensions
![]() $q^2 \geq q^1$
and
$q^2 \geq q^1$
and
![]() $p^2 = (\emptyset ,T^2,Q^2) \geq ^* p^1$
, such that
$p^2 = (\emptyset ,T^2,Q^2) \geq ^* p^1$
, such that
![]() $q^2$
forces that for any pair
$q^2$
forces that for any pair
![]() ${\langle } \nu _0,\nu _1{\rangle } \in T^2$
,
${\langle } \nu _0,\nu _1{\rangle } \in T^2$
,
![]() $p^2_{{\langle } \nu _0,\nu _1 {\rangle }}$
does not have a direct extension which decides
$p^2_{{\langle } \nu _0,\nu _1 {\rangle }}$
does not have a direct extension which decides
![]() $\sigma $
.
$\sigma $
.
The construction is now repeated level by level, for all
![]() $n < \omega $
. This produces sequences of extensions
$n < \omega $
. This produces sequences of extensions
![]() $q = q^0 \leq q^1 \leq \cdots \leq q^n \cdots $
in
$q = q^0 \leq q^1 \leq \cdots \leq q^n \cdots $
in
![]() $\operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
and
$\operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
and
![]() $p = p^0 \leq ^* p^1 \leq ^* \cdots \leq ^* p^n \cdots $
in
$p = p^0 \leq ^* p^1 \leq ^* \cdots \leq ^* p^n \cdots $
in
![]() $\mathbb {Q}^*_{\kappa ,\tau }$
, such that for each
$\mathbb {Q}^*_{\kappa ,\tau }$
, such that for each
![]() $n < \omega $
, writing
$n < \omega $
, writing
![]() $p^n = (\emptyset , T^n,Q^n)$
, we have that
$p^n = (\emptyset , T^n,Q^n)$
, we have that
![]() $q^n$
forces that for all sequences
$q^n$
forces that for all sequences
![]() $s \in T^n$
of length
$s \in T^n$
of length
![]() $|s| \leq n$
,
$|s| \leq n$
,
![]() $p^n {}^{\frown } s$
does not have a direct extension which decides
$p^n {}^{\frown } s$
does not have a direct extension which decides
![]() $\sigma $
. Finally, let
$\sigma $
. Finally, let
![]() $q^{\omega } \in \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
be a union of all
$q^{\omega } \in \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
be a union of all
![]() $q^n$
,
$q^n$
,
![]() $n < \omega $
, and
$n < \omega $
, and
![]() $p^* \in \mathbb {Q}^*_{\kappa ,\tau }$
be a direct extension of
$p^* \in \mathbb {Q}^*_{\kappa ,\tau }$
be a direct extension of
![]() $p^n$
for all
$p^n$
for all
![]() $n < \omega $
. Writing
$n < \omega $
. Writing
![]() $p^* = (\emptyset , T^*,Q^*)$
, it follows from the construction that
$p^* = (\emptyset , T^*,Q^*)$
, it follows from the construction that
![]() $p^{\omega }$
forces that for no
$p^{\omega }$
forces that for no
![]() $s \in T^*$
such that
$s \in T^*$
such that
![]() $p^* {}^{\frown } s$
has a direct extension which decides
$p^* {}^{\frown } s$
has a direct extension which decides
![]() $\sigma $
. This is, of course, absurd.
$\sigma $
. This is, of course, absurd.
We conclude that
![]() $( \mathbb {Q}^*_{\kappa ,\tau },\leq ,\leq ^*)$
is a Prikry-type forcing whose direct extension order
$( \mathbb {Q}^*_{\kappa ,\tau },\leq ,\leq ^*)$
is a Prikry-type forcing whose direct extension order
![]() $\leq ^*$
is
$\leq ^*$
is
![]() $\lambda $
-closed. In particular, it does not add bounded subsets to
$\lambda $
-closed. In particular, it does not add bounded subsets to
![]() $\lambda $
. Moreover, like
$\lambda $
. Moreover, like
![]() $\mathbb {Q}^{\tau }_{\kappa }$
,
$\mathbb {Q}^{\tau }_{\kappa }$
,
![]() $(\mathbb {Q}^*_{\kappa ,\tau },\leq )$
introduces a generic club
$(\mathbb {Q}^*_{\kappa ,\tau },\leq )$
introduces a generic club
![]() $b^{\tau }_{\kappa } \subseteq \kappa $
of order-type
$b^{\tau }_{\kappa } \subseteq \kappa $
of order-type
![]() $\mathop {\mathrm {ot}}(b^{\tau }_{\kappa }) = \omega ^{\tau }$
. Finally, since
$\mathop {\mathrm {ot}}(b^{\tau }_{\kappa }) = \omega ^{\tau }$
. Finally, since
![]() $U_{\kappa ,\tau '} \subseteq F_{\kappa ,\tau '}(t)$
is clearly contained in
$U_{\kappa ,\tau '} \subseteq F_{\kappa ,\tau '}(t)$
is clearly contained in
![]() $D_{\kappa ,\tau ',t}$
for every coherent sequence t, it follows from a standard density argument that if
$D_{\kappa ,\tau ',t}$
for every coherent sequence t, it follows from a standard density argument that if
![]() $b_{\kappa }^{\tau }$
is a
$b_{\kappa }^{\tau }$
is a
![]() $\mathbb {Q}^*_{\kappa ,\tau }$
-generic sequence over
$\mathbb {Q}^*_{\kappa ,\tau }$
-generic sequence over
![]() $V[G\ast H]$
, then for every V-set
$V[G\ast H]$
, then for every V-set
![]() $A \in \mathcal {F}_{\kappa }$
, there exists some
$A \in \mathcal {F}_{\kappa }$
, there exists some
![]() $\beta < \kappa $
such that
$\beta < \kappa $
such that
![]() $b^{\tau }_{\kappa } \setminus \beta \subseteq A$
.
$b^{\tau }_{\kappa } \setminus \beta \subseteq A$
.
6.2 The forcing
 $\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
$\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
Our goal now is to introduce a poset
![]() $\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
which is equivalent to
$\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
which is equivalent to
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
, and further has a dense subforcing
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
, and further has a dense subforcing
![]() $\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
, which is of the Prikry-type, and its direct extension order is
$\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
, which is of the Prikry-type, and its direct extension order is
![]() $\lambda $
-closed. We first introduce the poset
$\lambda $
-closed. We first introduce the poset
![]() $\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
, obtained from
$\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
, obtained from
![]() $\mathbb {Q}^*_{\kappa ,\lambda }$
and
$\mathbb {Q}^*_{\kappa ,\lambda }$
and
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
.
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
.
Recall that
![]() $G \ast H$
is V generic for
$G \ast H$
is V generic for
![]() $\mathbb {P} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
. Working in
$\mathbb {P} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
. Working in
![]() $V[G \ast H]$
, we consider the two-step iterations
$V[G \ast H]$
, we consider the two-step iterations
![]() $\mathbb {Q}^*_{\kappa ,\lambda } \ast \mathbb {C}_{\mathcal {F}_{\kappa }}$
consisting of conditions
$\mathbb {Q}^*_{\kappa ,\lambda } \ast \mathbb {C}_{\mathcal {F}_{\kappa }}$
consisting of conditions
![]() so that
so that
![]() . Note that when forcing with
. Note that when forcing with
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
over a
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
over a
![]() $V[G \ast H]$
-generic extension by
$V[G \ast H]$
-generic extension by
![]() $\mathbb {Q}^*_{\kappa ,\lambda }$
, we require that the bounded closed sets
$\mathbb {Q}^*_{\kappa ,\lambda }$
, we require that the bounded closed sets
![]() $c \subseteq \kappa $
in the conditions
$c \subseteq \kappa $
in the conditions
![]() $x = {\langle } c,A{\rangle } \in \mathbb {C}_{\mathcal {F}_{\kappa }}$
are actually ground model sets, from
$x = {\langle } c,A{\rangle } \in \mathbb {C}_{\mathcal {F}_{\kappa }}$
are actually ground model sets, from
![]() $V[G \ast H]$
. In particular, for every condition
$V[G \ast H]$
. In particular, for every condition
![]() , there exists an extension
, there exists an extension
![]() $q' \geq q$
and a pair
$q' \geq q$
and a pair
![]() $x \in \mathbb {C}_{\mathcal {F}_{\kappa }}$
so that
$x \in \mathbb {C}_{\mathcal {F}_{\kappa }}$
so that
![]() .
.
Let
![]() $b^{\lambda }_{\kappa } \subseteq \kappa $
be a
$b^{\lambda }_{\kappa } \subseteq \kappa $
be a
![]() $\mathbb {Q}^*_{\kappa ,\lambda }$
generic club in
$\mathbb {Q}^*_{\kappa ,\lambda }$
generic club in
![]() $\kappa $
. We know that
$\kappa $
. We know that
![]() $\mathop {\mathrm {ot}}(b^{\lambda }_{\kappa }) = \lambda $
and that
$\mathop {\mathrm {ot}}(b^{\lambda }_{\kappa }) = \lambda $
and that
![]() $b^{\lambda }_{\kappa }$
is almost contained in every set
$b^{\lambda }_{\kappa }$
is almost contained in every set
![]() $A \in \mathcal {F}_{\kappa }$
. Working in a
$A \in \mathcal {F}_{\kappa }$
. Working in a
![]() $\mathbb {Q}_{\kappa ,\lambda }^*$
generic extension
$\mathbb {Q}_{\kappa ,\lambda }^*$
generic extension
![]() $V[G \ast H \ast b^{\lambda }_{\kappa }]$
of
$V[G \ast H \ast b^{\lambda }_{\kappa }]$
of
![]() $V[G \ast H]$
, we see that for every condition
$V[G \ast H]$
, we see that for every condition
![]() $x = {\langle } c, A{\rangle }$
in
$x = {\langle } c, A{\rangle }$
in
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
, there exists some
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
, there exists some
![]() $\beta \in A \setminus (\max c + 1)$
such that
$\beta \in A \setminus (\max c + 1)$
such that
![]() $x' = {\langle } c', A{\rangle }$
, with
$x' = {\langle } c', A{\rangle }$
, with
![]() $c' = c \cup \{\beta \}$
, extends x and satisfies that
$c' = c \cup \{\beta \}$
, extends x and satisfies that
![]() $b^{\lambda }_{\kappa } \setminus (\max c'+1) \subseteq A$
.
$b^{\lambda }_{\kappa } \setminus (\max c'+1) \subseteq A$
.
Definition 6.8 (
 $\mathbb {C}^{\lambda }_{\mathcal {F}_{\kappa }}$
).
$\mathbb {C}^{\lambda }_{\mathcal {F}_{\kappa }}$
).
![]() ${}$
Working in a
${}$
Working in a
![]() $\mathbb {Q}_{\kappa ,\lambda }^*$
generic extension
$\mathbb {Q}_{\kappa ,\lambda }^*$
generic extension
![]() $V[G \ast H \ast b^{\lambda }_{\kappa }]$
of
$V[G \ast H \ast b^{\lambda }_{\kappa }]$
of
![]() $V[G \ast H]$
, let
$V[G \ast H]$
, let
![]() $\mathbb {C}^{\lambda }_{\mathcal {F}_{\kappa }}$
denote the subset of
$\mathbb {C}^{\lambda }_{\mathcal {F}_{\kappa }}$
denote the subset of
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
, consisting of conditions
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
, consisting of conditions
![]() $x' = {\langle } c', A'{\rangle }$
so that
$x' = {\langle } c', A'{\rangle }$
so that
![]() $\max (c') \in b^{\lambda }_{\kappa }$
, and
$\max (c') \in b^{\lambda }_{\kappa }$
, and
![]() $b^{\lambda }_{\kappa } \setminus (\max (c')+1) \subseteq A'$
.
$b^{\lambda }_{\kappa } \setminus (\max (c')+1) \subseteq A'$
.
It follows from the above that
![]() $\mathbb {C}^{\lambda }_{\mathcal {F}_{\kappa }}$
is a dense subset of
$\mathbb {C}^{\lambda }_{\mathcal {F}_{\kappa }}$
is a dense subset of
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
. Since
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
. Since
![]() $b^{\lambda }_{\kappa } \subseteq \kappa $
is closed of order-type
$b^{\lambda }_{\kappa } \subseteq \kappa $
is closed of order-type
![]() $\lambda = \operatorname {\mathrm {cf}}(\kappa )^{V[G \ast H \ast b^{\lambda }_{\kappa }]}$
, and no sequences of ordinals of length
$\lambda = \operatorname {\mathrm {cf}}(\kappa )^{V[G \ast H \ast b^{\lambda }_{\kappa }]}$
, and no sequences of ordinals of length
![]() $<\lambda $
are introduced by
$<\lambda $
are introduced by
![]() $b^{\lambda }_{\kappa }$
, it follows that the restriction of the
$b^{\lambda }_{\kappa }$
, it follows that the restriction of the
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
order to
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
order to
![]() $\mathbb {C}^{\lambda }_{\mathcal {F}_{\kappa }}$
is
$\mathbb {C}^{\lambda }_{\mathcal {F}_{\kappa }}$
is
![]() $\lambda $
-closed.
$\lambda $
-closed.
With this observation, we move back to
![]() $V[G \ast H]$
to define the poset
$V[G \ast H]$
to define the poset
![]() $\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
.
$\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
.
Definition 6.9 (
 $\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
).
$\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
).
![]() ${}$
Let
${}$
Let
![]() $\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
be the two step iteration
$\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
be the two step iteration
![]() $\mathbb {C}^*_{\mathcal {F}_{\kappa }} = \mathbb {Q}^*_{\kappa ,\lambda } \ast \mathbb {C}^{\lambda }_{\mathcal {F}_{\kappa }}$
. We define the direct extension ordering
$\mathbb {C}^*_{\mathcal {F}_{\kappa }} = \mathbb {Q}^*_{\kappa ,\lambda } \ast \mathbb {C}^{\lambda }_{\mathcal {F}_{\kappa }}$
. We define the direct extension ordering
![]() $\leq ^*$
of
$\leq ^*$
of
![]() $\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
to be the extension of the usual direct extension order of
$\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
to be the extension of the usual direct extension order of
![]() $\mathbb {Q}^{\lambda }_{\kappa }$
with the standard order on the second
$\mathbb {Q}^{\lambda }_{\kappa }$
with the standard order on the second
![]() $\mathbb {C}^{\lambda }_{\mathcal {F}_{\kappa }}$
component.
$\mathbb {C}^{\lambda }_{\mathcal {F}_{\kappa }}$
component.
Corollary 6.10.
![]() $\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
is a dense subforcing of
$\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
is a dense subforcing of
![]() $\mathbb {Q}^*_{\kappa ,\lambda } \ast \mathbb {C}_{\mathcal {F}_{\kappa }}$
which satisfies the Prikry Property, and its direct extension order is
$\mathbb {Q}^*_{\kappa ,\lambda } \ast \mathbb {C}_{\mathcal {F}_{\kappa }}$
which satisfies the Prikry Property, and its direct extension order is
![]() $\lambda $
-closed.
$\lambda $
-closed.
Note that for every dense subset D of
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
and a condition
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
and a condition
![]() , there exists a direct extension
, there exists a direct extension
![]() such that
such that
![]() . Similarly, it is clear that the set of conditions
. Similarly, it is clear that the set of conditions
![]() $(q',\check {x'}) \in \mathbb {C}^*_{\mathcal {F}_{\kappa }} $
, for which the second component is a canonical name
$(q',\check {x'}) \in \mathbb {C}^*_{\mathcal {F}_{\kappa }} $
, for which the second component is a canonical name
![]() $\check {x'}$
of a condition
$\check {x'}$
of a condition
![]() $x' \in \mathbb {C}_{\mathcal {F}_{\kappa }}$
, is dense in
$x' \in \mathbb {C}_{\mathcal {F}_{\kappa }}$
, is dense in
![]() $\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
. The map
$\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
. The map
![]() $(q',\check {x'}) \mapsto x'$
defined on this dense set naturally induces a forcing projection
$(q',\check {x'}) \mapsto x'$
defined on this dense set naturally induces a forcing projection
![]() $\pi $
from
$\pi $
from
![]() $\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
to the boolean completion of
$\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
to the boolean completion of
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
. This projection sends a condition of the form
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
. This projection sends a condition of the form
![]() to the join of the collection of all
to the join of the collection of all
![]() $y \in \mathbb {C}_{\mathcal {F}_{\kappa }}$
such that there is some extension of q,
$y \in \mathbb {C}_{\mathcal {F}_{\kappa }}$
such that there is some extension of q,
![]() $q'$
that forces
$q'$
that forces
![]() .
.
Next, we follow Gitik’s machinery from [Reference Gitik13], to form a Prikry-type forcing notion
![]() $\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
which is equivalent to
$\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
which is equivalent to
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
, from
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
, from
![]() $\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
.
$\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
.
Definition 6.11 (
 $\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
).
$\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
).
We define a Prikry-type forcing notion
![]() $(\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }},\leq ',\leq ^*)$
as follows.
$(\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }},\leq ',\leq ^*)$
as follows.
-
•
 $\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}= \mathbb {C}^*_{\mathcal {F}_{\kappa }}$
,
$\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}= \mathbb {C}^*_{\mathcal {F}_{\kappa }}$
, -
• the partial ordering
 $\leq '$
is defined by
$\leq '$
is defined by
 $p' \geq ' p$
if
$p' \geq ' p$
if
 $\pi (p') \geq \pi (p)$
and
$\pi (p') \geq \pi (p)$
and -
•
 $\leq ^*$
is taken to be the same direct extension order of
$\leq ^*$
is taken to be the same direct extension order of
 $\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
$\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
It is immediate from the definition that
![]() $(\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}, \leq ')$
is equivalent as a forcing notion to
$(\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}, \leq ')$
is equivalent as a forcing notion to
![]() $(\mathbb {C}_{\mathcal {F}_{\kappa }},\leq )$
and that the direct extension order
$(\mathbb {C}_{\mathcal {F}_{\kappa }},\leq )$
and that the direct extension order
![]() $\leq ^*$
of
$\leq ^*$
of
![]() $\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
is
$\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
is
![]() $\lambda $
-closed. To show that
$\lambda $
-closed. To show that
![]() $(\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }},\leq ',\leq ^*)$
satisfies the Prikry Property, it suffices to verify that for every statement
$(\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }},\leq ',\leq ^*)$
satisfies the Prikry Property, it suffices to verify that for every statement
![]() $\sigma $
in the forcing language of
$\sigma $
in the forcing language of
![]() $\mathbb {C}_{\mathcal {F}_{\kappa }}$
and every condition
$\mathbb {C}_{\mathcal {F}_{\kappa }}$
and every condition
![]() $p \in \bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
, there is a direct extension
$p \in \bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
, there is a direct extension
![]() $p^* \geq ^* p$
such that
$p^* \geq ^* p$
such that
![]() $\pi (p^*)$
decides
$\pi (p^*)$
decides
![]() $\sigma $
. Indeed, defining
$\sigma $
. Indeed, defining
![]() $D_0 = \{ p' \in \mathbb {C}^*_{\mathcal {F}_{\kappa }} \mid \pi (p') \Vdash \sigma \}$
and
$D_0 = \{ p' \in \mathbb {C}^*_{\mathcal {F}_{\kappa }} \mid \pi (p') \Vdash \sigma \}$
and
![]() $D_1 = \{ p' \in \mathbb {C}^*_{\mathcal {F}_{\kappa }} \mid \pi (p') \Vdash \neg \sigma \}$
, it is clear that
$D_1 = \{ p' \in \mathbb {C}^*_{\mathcal {F}_{\kappa }} \mid \pi (p') \Vdash \neg \sigma \}$
, it is clear that
![]() $D_0 \cup D_1$
is dense in
$D_0 \cup D_1$
is dense in
![]() $\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
and that a generic filter
$\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
and that a generic filter
![]() $G^*$
of
$G^*$
of
![]() $\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
will have a nontrivial intersection with exactly one of the two sets. Let
$\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
will have a nontrivial intersection with exactly one of the two sets. Let
![]() . Then
. Then
![]() $\sigma ^*$
is a statement for the forcing language of
$\sigma ^*$
is a statement for the forcing language of
![]() $\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
. Moreover, it is clear from our construction that for a condition
$\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
. Moreover, it is clear from our construction that for a condition
![]() $p^* \in \mathbb {C}^*_{\mathcal {F}_{\kappa }}$
which decides
$p^* \in \mathbb {C}^*_{\mathcal {F}_{\kappa }}$
which decides
![]() $\sigma ^*$
, we have that
$\sigma ^*$
, we have that
![]() $p^* \Vdash \sigma ^*$
implies that
$p^* \Vdash \sigma ^*$
implies that
![]() $\pi (p^*) \Vdash \sigma $
, and
$\pi (p^*) \Vdash \sigma $
, and
![]() $p^* \Vdash \neg \sigma ^*$
implies that
$p^* \Vdash \neg \sigma ^*$
implies that
![]() $\pi (p^*)\Vdash \sigma $
. Since
$\pi (p^*)\Vdash \sigma $
. Since
![]() $\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
satisfies the Prikry Property, every condition p has a direct extension
$\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
satisfies the Prikry Property, every condition p has a direct extension
![]() $p^* \geq ^* p$
which decides
$p^* \geq ^* p$
which decides
![]() $\sigma ^*$
.
$\sigma ^*$
.
We note that, similarly to
![]() $\mathbb {P} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) \ast \mathbb {C}_{\mathcal {F}_{\kappa }}$
, the forcing
$\mathbb {P} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) \ast \mathbb {C}_{\mathcal {F}_{\kappa }}$
, the forcing
![]() $\mathbb {P} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) \ast \mathbb {C}^*_{\mathcal {F}_{\kappa }}$
is cone homogeneous. In most applications of homogeneity, moving to an equivalent forcing does not change the main properties of its iterations. In order to apply the results from section 8.1 and argue that the iteration
$\mathbb {P} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) \ast \mathbb {C}^*_{\mathcal {F}_{\kappa }}$
is cone homogeneous. In most applications of homogeneity, moving to an equivalent forcing does not change the main properties of its iterations. In order to apply the results from section 8.1 and argue that the iteration
![]() $\mathbb {P} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) \ast \bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
is cone homogeneous, we need to verify that this poset meets the assumptions of Lemma 8.5.
$\mathbb {P} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) \ast \bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
is cone homogeneous, we need to verify that this poset meets the assumptions of Lemma 8.5.
Lemma 6.12. Denote
![]() $\mathbb {P} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) \ast \mathbb {C}^*_{\mathcal {F}_{\kappa }}$
by
$\mathbb {P} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) \ast \mathbb {C}^*_{\mathcal {F}_{\kappa }}$
by
![]() $\mathbb {W}$
, and its regular and direct extension orders by
$\mathbb {W}$
, and its regular and direct extension orders by
![]() $\leq _{\mathbb {W}}$
and
$\leq _{\mathbb {W}}$
and
![]() $\leq ^*_{\mathbb {W}}$
, respectively.
$\leq ^*_{\mathbb {W}}$
, respectively.
For every
![]() $w_0, w_1 \in \mathbb {W}$
there are direct extensions
$w_0, w_1 \in \mathbb {W}$
there are direct extensions
![]() $w_0^*,w_1^*$
of
$w_0^*,w_1^*$
of
![]() $w_0,w_1$
, respectively, and a cone isomorphism
$w_0,w_1$
, respectively, and a cone isomorphism
![]() $\varphi \colon \mathbb {W}/w_0^* \to \mathbb {W}/w_1^*$
which respects the direct extension order
$\varphi \colon \mathbb {W}/w_0^* \to \mathbb {W}/w_1^*$
which respects the direct extension order
![]() $\leq ^*_{\mathbb {W}}$
.
$\leq ^*_{\mathbb {W}}$
.
In particular, the forcing
![]() $\mathbb {P} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )\ast \bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
is cone homogeneous.
$\mathbb {P} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )\ast \bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
is cone homogeneous.
We observe that assuming the coherent sequence
![]() $\mathcal {U}$
(by which
$\mathcal {U}$
(by which
![]() $\mathbb {W} = \mathbb {P} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) \ast \mathbb {C}^*_{\mathcal {F}_{\kappa }}$
is defined) is ordinal definable in V, then the statement of the lemma guarantees that
$\mathbb {W} = \mathbb {P} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) \ast \mathbb {C}^*_{\mathcal {F}_{\kappa }}$
is defined) is ordinal definable in V, then the statement of the lemma guarantees that
![]() $\mathbb {W}$
satisfies the requirements of the iterated poset
$\mathbb {W}$
satisfies the requirements of the iterated poset
![]() $\mathbb {Q}_{\alpha }$
from Lemma 8.5.
$\mathbb {Q}_{\alpha }$
from Lemma 8.5.
Proof. Let us start with the last assertion. Since the identity is a projection from
![]() $\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
to
$\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
to
![]() $\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
, an isomorphism of a cone of elements in
$\bar {\mathbb {C}}_{\mathcal {F}_{\kappa }}$
, an isomorphism of a cone of elements in
![]() $\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
naturally induces an isomorphism of the corresponding cone in
$\mathbb {C}^*_{\mathcal {F}_{\kappa }}$
naturally induces an isomorphism of the corresponding cone in
![]() ${\bar {\mathbb {C}}}_{\mathcal {F}_{\kappa }}$
.
${\bar {\mathbb {C}}}_{\mathcal {F}_{\kappa }}$
.
Let
![]() and
and
![]() , where the conditions
, where the conditions
![]() $q_0 = \langle t_0, T_0, Q_0\rangle $
and
$q_0 = \langle t_0, T_0, Q_0\rangle $
and
![]() $q_1 = \langle t_1, T_1, Q_1\rangle $
belong to
$q_1 = \langle t_1, T_1, Q_1\rangle $
belong to
![]() $\mathbb {Q}^*_{\kappa ,\lambda }$
.
$\mathbb {Q}^*_{\kappa ,\lambda }$
.
By [Reference Ben-Neria and Unger5, Theorem 4.6] applied to the iteration
![]() $\mathbb {P} \ast \mathbb {Q}_{\kappa ,\lambda }$
, there are direct extensions
$\mathbb {P} \ast \mathbb {Q}_{\kappa ,\lambda }$
, there are direct extensions
![]() ${\langle } p_0^*, (t_0,T) {\rangle }$
of
${\langle } p_0^*, (t_0,T) {\rangle }$
of
![]() ${\langle } p_0, (t_0,T_0) {\rangle }$
, and
${\langle } p_0, (t_0,T_0) {\rangle }$
, and
![]() ${\langle } p_1^*, (t_1,T) {\rangle }$
of
${\langle } p_1^*, (t_1,T) {\rangle }$
of
![]() ${\langle } p_1, (t_1,T_1) {\rangle }$
, with a common top tree T, and an isomorphism
${\langle } p_1, (t_1,T_1) {\rangle }$
, with a common top tree T, and an isomorphism
![]() $\psi $
between the cone below
$\psi $
between the cone below
![]() ${\langle } p_0^*, (t_0,T) {\rangle }$
and the cone below
${\langle } p_0^*, (t_0,T) {\rangle }$
and the cone below
![]() ${\langle } p_1^*, (t_1,T) {\rangle }$
. We record here that the map
${\langle } p_1^*, (t_1,T) {\rangle }$
. We record here that the map
![]() $\psi $
constructed in the proof of [Reference Ben-Neria and Unger5, Theorem 4.6] satisfies two additional properties. First, it does not make any changes to the
$\psi $
constructed in the proof of [Reference Ben-Neria and Unger5, Theorem 4.6] satisfies two additional properties. First, it does not make any changes to the
![]() $\mathcal {F}_{\kappa }$
-trees S appearing in conditions
$\mathcal {F}_{\kappa }$
-trees S appearing in conditions
![]() $p {}^{\frown } {\langle } s,S {\rangle } \in \mathbb {P} \ast \mathbb {Q}_{\kappa ,\lambda }$
. Second, it respects the direct extension order of
$p {}^{\frown } {\langle } s,S {\rangle } \in \mathbb {P} \ast \mathbb {Q}_{\kappa ,\lambda }$
. Second, it respects the direct extension order of
![]() $\mathbb {P} \ast \mathbb {Q}_{\kappa ,\lambda }$
.
$\mathbb {P} \ast \mathbb {Q}_{\kappa ,\lambda }$
.
Next, we move to examine the Levy collapse condition and the suitable functions in the conditions from
![]() $\mathbb {W}$
. Since the collapsing forcing
$\mathbb {W}$
. Since the collapsing forcing
![]() $\operatorname {\mathrm {Coll}}(\lambda , <\kappa )$
is evaluated in the generic extension by
$\operatorname {\mathrm {Coll}}(\lambda , <\kappa )$
is evaluated in the generic extension by
![]() $\mathbb {P}$
,
$\mathbb {P}$
,
![]() $\psi $
naturally acts also on the
$\psi $
naturally acts also on the
![]() $\mathbb {P}$
-names
$\mathbb {P}$
-names
![]() $c_0$
and
$c_0$
and
![]() $Q_0$
that appear in
$Q_0$
that appear in
![]() $w_0$
. As usual, we denote the resulting names by
$w_0$
. As usual, we denote the resulting names by
![]() $c_0^{\psi }$
and
$c_0^{\psi }$
and
![]() $Q_0^{\psi }$
. Let
$Q_0^{\psi }$
. Let
![]() $\tau _{\emptyset }$
be a
$\tau _{\emptyset }$
be a
![]() $\mathbb {P}$
-name of an automorphism of the Levy collapse poset which maps an extension
$\mathbb {P}$
-name of an automorphism of the Levy collapse poset which maps an extension
![]() $c_0'$
of
$c_0'$
of
![]() $c_0^{\psi }$
to an extension
$c_0^{\psi }$
to an extension
![]() $c_1^*$
of
$c_1^*$
of
![]() $c_1$
, and define
$c_1$
, and define
![]() $c_0^* = (c_0')^{\psi ^{-1}}$
. Note that since
$c_0^* = (c_0')^{\psi ^{-1}}$
. Note that since
![]() $c_i$
forces
$c_i$
forces
![]() , we may extend
, we may extend
![]() $Q_0(\emptyset ),Q_1(\emptyset )$
to
$Q_0(\emptyset ),Q_1(\emptyset )$
to
![]() $Q_0^*(\emptyset ),Q_1^*(\emptyset )$
so that
$Q_0^*(\emptyset ),Q_1^*(\emptyset )$
so that
![]() $c_i = Q_i^*(\emptyset )$
for
$c_i = Q_i^*(\emptyset )$
for
![]() $i = 0,1$
. Next, for each
$i = 0,1$
. Next, for each
![]() $s \in T$
and
$s \in T$
and
![]() $i = 0,1$
, define
$i = 0,1$
, define
![]() $\operatorname {\mathrm {dom}}_1(Q_i(s)) = \{ \alpha < \kappa \mid Q_i(s)\restriction \lambda \times \{\alpha \} \neq \emptyset \}$
and
$\operatorname {\mathrm {dom}}_1(Q_i(s)) = \{ \alpha < \kappa \mid Q_i(s)\restriction \lambda \times \{\alpha \} \neq \emptyset \}$
and
![]() $\rho ^i_s = \sup (\operatorname {\mathrm {dom}}_1(Q_i(s)))$
. Set
$\rho ^i_s = \sup (\operatorname {\mathrm {dom}}_1(Q_i(s)))$
. Set
![]() $\rho _s = \max (\rho _s^0,\rho _s^1)$
. By moving to a direct extension tree
$\rho _s = \max (\rho _s^0,\rho _s^1)$
. By moving to a direct extension tree
![]() $T^*$
of T, we may assume that for every
$T^*$
of T, we may assume that for every
![]() $s \in T^*$
and
$s \in T^*$
and
![]() $\nu \in \operatorname {\mathrm {succ}}_{T^*}(s)$
,
$\nu \in \operatorname {\mathrm {succ}}_{T^*}(s)$
,
![]() $\pi ^{t {}^{\frown } s}_0(\nu )> \rho _s$
where the projection is computed in both generic extensions. This leaves enough space between the conditions
$\pi ^{t {}^{\frown } s}_0(\nu )> \rho _s$
where the projection is computed in both generic extensions. This leaves enough space between the conditions
![]() $Q_i(s), Q_i(s {}^{\frown } {\langle } \nu {\rangle })$
,
$Q_i(s), Q_i(s {}^{\frown } {\langle } \nu {\rangle })$
,
![]() $i = 0,1$
, to define autormorphisms taking an extension
$i = 0,1$
, to define autormorphisms taking an extension
![]() $Q_0^*(s)$
of
$Q_0^*(s)$
of
![]() $Q_0(s)$
to an extension
$Q_0(s)$
to an extension
![]() $Q_1^*(s)$
of
$Q_1^*(s)$
of
![]() $Q_1(s)$
, without conflicting with
$Q_1(s)$
, without conflicting with
![]() $Q_i(s {}^{\frown } {\langle } \nu {\rangle })$
,
$Q_i(s {}^{\frown } {\langle } \nu {\rangle })$
,
![]() $i = 0,1$
. We can therefore define by induction on the lexicographic order
$i = 0,1$
. We can therefore define by induction on the lexicographic order
![]() $<_{lex}$
on
$<_{lex}$
on
![]() $T^*$
(where two sequences are compared from their top elements down) automorphisms
$T^*$
(where two sequences are compared from their top elements down) automorphisms
![]() $\tau _s$
,
$\tau _s$
,
![]() $s \in T^*$
, of
$s \in T^*$
, of
![]() $\operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
, and collapse extensions
$\operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
, and collapse extensions
![]() $Q_i^*(s) \geq Q_i(s)$
,
$Q_i^*(s) \geq Q_i(s)$
,
![]() $i = 0,1$
, with the following properties. For all
$i = 0,1$
, with the following properties. For all
![]() $s \in T^*$
,
$s \in T^*$
,
-
•
 $\tau _s$
is supported in
$\tau _s$
is supported in
 $\operatorname {\mathrm {Coll}}(\lambda ,<\rho _s)$
,Footnote
14
$\operatorname {\mathrm {Coll}}(\lambda ,<\rho _s)$
,Footnote
14
-
•
 $\tau _s((Q_0^*)^{\psi }(s)) =Q^*_1(s)$
,
$\tau _s((Q_0^*)^{\psi }(s)) =Q^*_1(s)$
, -
• If
 $s' \in T^*_s$
, then
$s' \in T^*_s$
, then
 $\tau _{s'}\restriction \operatorname {\mathrm {Coll}}(\lambda ,<\pi _0^{t {}^{\frown } s}(s)) = \tau _s$
,
$\tau _{s'}\restriction \operatorname {\mathrm {Coll}}(\lambda ,<\pi _0^{t {}^{\frown } s}(s)) = \tau _s$
, -
• If
 $\bar {s} \in T^*$
and
$\bar {s} \in T^*$
and
 $b_{t_0 {}^{\frown } s} = b_{ t_0 {}^{\frown } \bar {s}}$
, then
$b_{t_0 {}^{\frown } s} = b_{ t_0 {}^{\frown } \bar {s}}$
, then
 $\tau _{s} = \tau _{\bar {s}}$
.
$\tau _{s} = \tau _{\bar {s}}$
.
Let
![]() $\bar {\mathbb {W}} = \mathbb {P} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) \ast \mathbb {Q}_{\kappa ,\lambda }^*$
be the initial forcing iteration of
$\bar {\mathbb {W}} = \mathbb {P} \ast \operatorname {\mathrm {Coll}}(\lambda ,<\kappa ) \ast \mathbb {Q}_{\kappa ,\lambda }^*$
be the initial forcing iteration of
Let
![]() $w_0\restriction \bar {\mathbb {W}} = {\langle } p_0, c_0, {\langle } t_0,T_0,Q_0{\rangle } {\rangle }$
and
$w_0\restriction \bar {\mathbb {W}} = {\langle } p_0, c_0, {\langle } t_0,T_0,Q_0{\rangle } {\rangle }$
and
![]() $w_1\restriction \bar {\mathbb {W}} = {\langle } p_1,c_1,{\langle } t_1,T_1,Q_1{\rangle } {\rangle }$
be the restrictions of
$w_1\restriction \bar {\mathbb {W}} = {\langle } p_1,c_1,{\langle } t_1,T_1,Q_1{\rangle } {\rangle }$
be the restrictions of
![]() $w_0,w_1$
to
$w_0,w_1$
to
![]() $\bar {\mathbb {W}}$
, and consider their direct extensions
$\bar {\mathbb {W}}$
, and consider their direct extensions
![]() $\bar {w_o},\bar {w_1}$
in
$\bar {w_o},\bar {w_1}$
in
![]() $\bar {\mathbb {W}}$
, defined by
$\bar {\mathbb {W}}$
, defined by
![]() $\bar {w_i} = {\langle } p^*_0, c^*_0, {\langle } t_0,T^*,Q^*_0{\rangle } {\rangle }$
,
$\bar {w_i} = {\langle } p^*_0, c^*_0, {\langle } t_0,T^*,Q^*_0{\rangle } {\rangle }$
,
![]() $i = 0,1$
.
$i = 0,1$
.
Our choice of cone isomorphism
![]() $\psi $
for
$\psi $
for
![]() $\mathbb {P} \ast \mathbb {Q}_{\kappa ,\lambda }$
, together with the collection of Levy-Collapse automorphisms
$\mathbb {P} \ast \mathbb {Q}_{\kappa ,\lambda }$
, together with the collection of Levy-Collapse automorphisms
![]() $\vec {\tau } = \{\tau _s\}_{s \in T^*}$
, naturally induces a function
$\vec {\tau } = \{\tau _s\}_{s \in T^*}$
, naturally induces a function
![]() $\bar {\varphi }$
on the cone
$\bar {\varphi }$
on the cone
![]() $\bar {\mathbb {W}}/ \bar {w_0}$
, defined as follows. For a condition
$\bar {\mathbb {W}}/ \bar {w_0}$
, defined as follows. For a condition
![]() $\bar {w} = {\langle } p, c,{\langle } s , S, Q{\rangle }{\rangle } $
, we set
$\bar {w} = {\langle } p, c,{\langle } s , S, Q{\rangle }{\rangle } $
, we set
![]() $\bar {\varphi }(\bar {w}) = {\langle } p',c',{\langle } s', S,Q'{\rangle }{\rangle }$
to be:
$\bar {\varphi }(\bar {w}) = {\langle } p',c',{\langle } s', S,Q'{\rangle }{\rangle }$
to be:
We claim that
![]() ${\langle } p',c',{\langle } s',S, Q'{\rangle }{\rangle }$
is a condition in
${\langle } p',c',{\langle } s',S, Q'{\rangle }{\rangle }$
is a condition in
![]() $\bar {\mathbb {W}}$
. First, it is immediate from our choice of
$\bar {\mathbb {W}}$
. First, it is immediate from our choice of
![]() $p,c$
that
$p,c$
that
![]() ${\langle } p',c'{\rangle } \in \mathbb {P} * \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
. It therefore remains to verify that
${\langle } p',c'{\rangle } \in \mathbb {P} * \operatorname {\mathrm {Coll}}(\lambda ,<\kappa )$
. It therefore remains to verify that
![]() ${\langle } s',S,Q'{\rangle }$
is forced by
${\langle } s',S,Q'{\rangle }$
is forced by
![]() ${\langle } p',c'{\rangle }$
to be a condition in
${\langle } p',c'{\rangle }$
to be a condition in
![]() $\mathbb {Q}^*_{\lambda ,<\kappa }$
. The fact that
$\mathbb {Q}^*_{\lambda ,<\kappa }$
. The fact that
![]() ${\langle } s',S,Q'{\rangle }$
satisfies requirements
${\langle } s',S,Q'{\rangle }$
satisfies requirements
![]() $(1)$
and
$(1)$
and
![]() $(2)$
of definition 6.3 is immediate. To verify the coherency requirement
$(2)$
of definition 6.3 is immediate. To verify the coherency requirement
![]() $(3)$
of definition 6.3, we note that
$(3)$
of definition 6.3, we note that
![]() $Q'$
is forced by
$Q'$
is forced by
![]() $p'$
to be
$p'$
to be
![]() $(s, S)$
-suitable. Indeed, it follows from our choice of
$(s, S)$
-suitable. Indeed, it follows from our choice of
![]() $\tau _{s'}$
that its support is bounded below the projection
$\tau _{s'}$
that its support is bounded below the projection
![]() $\pi ^{s {}^{\frown } s'}_0(\nu )$
, for any
$\pi ^{s {}^{\frown } s'}_0(\nu )$
, for any
![]() $\nu \in \operatorname {\mathrm {succ}}_{T^*}(s')$
. Property
$\nu \in \operatorname {\mathrm {succ}}_{T^*}(s')$
. Property
![]() $(4)$
follows from the fact that the statement “
$(4)$
follows from the fact that the statement “
![]() ” is forced by
” is forced by
![]() $p \in \mathbb {P}$
, which implies that
$p \in \mathbb {P}$
, which implies that
![]() is forced by
is forced by
![]() $p'$
. This, combined with definition of
$p'$
. This, combined with definition of
![]() $c'$
and
$c'$
and
![]() $Q'$
, and the fact that the name
$Q'$
, and the fact that the name
![]() is a fixed point of both
is a fixed point of both
![]() $\tau _{\emptyset }$
and
$\tau _{\emptyset }$
and
![]() $\psi $
, guarantees that requirement
$\psi $
, guarantees that requirement
![]() $(4)$
is satisfied. Next,
$(4)$
is satisfied. Next,
![]() $(s',S,Q')$
satisfies requirement
$(s',S,Q')$
satisfies requirement
![]() $(5)$
of definition 6.3 by a similar argument to the previous one, using the fact that
$(5)$
of definition 6.3 by a similar argument to the previous one, using the fact that
![]() $(s, S, Q)$
satisfies property
$(s, S, Q)$
satisfies property
![]() $(5)$
together with the last property listed above for
$(5)$
together with the last property listed above for
![]() $\{\tau _s\}_{s\in T}$
. Having verified that
$\{\tau _s\}_{s\in T}$
. Having verified that
![]() ${\langle } p',c',{\langle } s',S, Q'{\rangle }{\rangle }$
is a condition in
${\langle } p',c',{\langle } s',S, Q'{\rangle }{\rangle }$
is a condition in
![]() $\bar {\mathbb {W}}$
, it is straightforward to check that it extends
$\bar {\mathbb {W}}$
, it is straightforward to check that it extends
![]() $\bar {w_1}$
and thus
$\bar {w_1}$
and thus
![]() $\bar {\varphi }\colon \bar {\mathbb {W}}/\bar {w_0} \to \bar {\mathbb {W}}/\bar {w_1}$
is a well defined function. In order to show that it is cone isomorphism, we need to show that it is order-preserving.
$\bar {\varphi }\colon \bar {\mathbb {W}}/\bar {w_0} \to \bar {\mathbb {W}}/\bar {w_1}$
is a well defined function. In order to show that it is cone isomorphism, we need to show that it is order-preserving.
Let us remark that the automorphism
![]() $\psi $
modifies the values of
$\psi $
modifies the values of
![]() $b_s$
for
$b_s$
for
![]() $s \in T^*$
by changing the value of their initial segments. Since those initial segments do not affect the definition of
$s \in T^*$
by changing the value of their initial segments. Since those initial segments do not affect the definition of
![]() $\tau _{b_s}$
, we will ignore it and write always
$\tau _{b_s}$
, we will ignore it and write always
![]() $b_s$
instead
$b_s$
instead
![]() $b_s^{\psi }$
.
$b_s^{\psi }$
.
Let
![]() $\bar {w}_1 = {\langle } p_1, c_1, {\langle } s_1, S_1, Q_1{\rangle } {\rangle },\, \bar {w}_2 ={\langle } p_2, c_2, {\langle } s_2, S_2, Q_2{\rangle } {\rangle }$
be a pair of conditions in the cone above
$\bar {w}_1 = {\langle } p_1, c_1, {\langle } s_1, S_1, Q_1{\rangle } {\rangle },\, \bar {w}_2 ={\langle } p_2, c_2, {\langle } s_2, S_2, Q_2{\rangle } {\rangle }$
be a pair of conditions in the cone above
![]() $\bar {w}_0$
. We need to show that
$\bar {w}_0$
. We need to show that
![]() $\bar {\varphi }(\bar {w}_1) \leq \bar {\varphi }(\bar {w}_2)$
if and only if
$\bar {\varphi }(\bar {w}_1) \leq \bar {\varphi }(\bar {w}_2)$
if and only if
![]() $\bar {w}_1 \leq \bar {w}_2$
.
$\bar {w}_1 \leq \bar {w}_2$
.
For direct extensions, this is clear, as the tree
![]() $S_1$
does not move under
$S_1$
does not move under
![]() $\bar \varphi $
. Let us assume that
$\bar \varphi $
. Let us assume that
![]() $\bar {w}_2$
is a one-point extension of
$\bar {w}_2$
is a one-point extension of
![]() $\bar {w}_1$
, by the point
$\bar {w}_1$
, by the point
![]() ${\langle }\nu {\rangle }$
. By moving to a dense subset,
${\langle }\nu {\rangle }$
. By moving to a dense subset,
![]() $c_2 \geq c_1, Q_1({\langle } \nu {\rangle })$
and
$c_2 \geq c_1, Q_1({\langle } \nu {\rangle })$
and
![]() $b_{s_2} = b_{s_1 {}^{\frown } {\langle }\nu {\rangle }}$
. Let us apply
$b_{s_2} = b_{s_1 {}^{\frown } {\langle }\nu {\rangle }}$
. Let us apply
![]() $\bar {\varphi }$
on
$\bar {\varphi }$
on
![]() $\bar {w}_1, \bar {w}_2$
. The trees
$\bar {w}_1, \bar {w}_2$
. The trees
![]() $S_1$
and
$S_1$
and
![]() $S_2$
do not move, so we must verify that
$S_2$
do not move, so we must verify that
![]() ${\langle }\nu {\rangle }$
is still a legitimate choice for an one-point extension of
${\langle }\nu {\rangle }$
is still a legitimate choice for an one-point extension of
![]() $\bar \varphi (\bar {w}_1)$
. Indeed,
$\bar \varphi (\bar {w}_1)$
. Indeed,
![]() $\tau _{b_{s_2}}(c_2)$
is (by the definition of
$\tau _{b_{s_2}}(c_2)$
is (by the definition of
![]() $\tau _{b_{s_2}}$
) stronger than
$\tau _{b_{s_2}}$
) stronger than
![]() $\tau _{{\langle } \nu {\rangle }}(Q_1({\langle }\nu {\rangle })$
. Thus, we conclude that
$\tau _{{\langle } \nu {\rangle }}(Q_1({\langle }\nu {\rangle })$
. Thus, we conclude that
![]() $\bar \varphi (\bar w_2)$
is an one-point extension of
$\bar \varphi (\bar w_2)$
is an one-point extension of
![]() $\bar \varphi (\bar w_2)$
by
$\bar \varphi (\bar w_2)$
by
![]() ${\langle }\nu {\rangle }$
. The other direction is the same.
${\langle }\nu {\rangle }$
. The other direction is the same.
Finally, to obtain a desirable cone isomorphism
![]() $\varphi $
for
$\varphi $
for
![]() $\mathbb {W} = \bar {\mathbb {W}} \ast \mathbb {C}^{\lambda }_{\kappa }$
, it remains to extend
$\mathbb {W} = \bar {\mathbb {W}} \ast \mathbb {C}^{\lambda }_{\kappa }$
, it remains to extend
![]() $\bar {\varphi }$
to the final additional components
$\bar {\varphi }$
to the final additional components
of
![]() $\mathbb {C}^{\lambda }_{\mathcal {F}_{\kappa }}$
. The proof Lemma 4.9 shows that there are
$\mathbb {C}^{\lambda }_{\mathcal {F}_{\kappa }}$
. The proof Lemma 4.9 shows that there are
![]() $\bar {\mathbb {W}}$
-names
$\bar {\mathbb {W}}$
-names
of extensions of
respectively, and a name of a cone isomorphism
. Accordingly, we set
and define direct extensions
![]() $w_0^* \geq ^* w_0,w_1^*\geq ^* w_1$
and a map
$w_0^* \geq ^* w_0,w_1^*\geq ^* w_1$
and a map
![]() $\varphi \colon \mathbb {W}/w_0^* \to \mathbb {W}/w_1^*$
by
$\varphi \colon \mathbb {W}/w_0^* \to \mathbb {W}/w_1^*$
by
and
The fact that
![]() $w_0^*,w_1^*,\varphi $
satisfies the result stated in the lemma is an immediate consequence of the fact that
$w_0^*,w_1^*,\varphi $
satisfies the result stated in the lemma is an immediate consequence of the fact that
![]() $\bar {w}_0,\bar {w}_1,\bar {\varphi }$
satisfies similar properties for
$\bar {w}_0,\bar {w}_1,\bar {\varphi }$
satisfies similar properties for
![]() $\bar {\mathbb {W}}$
and our choice of
$\bar {\mathbb {W}}$
and our choice of
![]() $\varphi $
,
$\varphi $
,
.
7 Strong measurability at successors of singulars
Suppose that
![]() $V = \operatorname {\mathrm {HOD}}$
,
$V = \operatorname {\mathrm {HOD}}$
,
![]() $\kappa $
is a supercompact cardinal and
$\kappa $
is a supercompact cardinal and
![]() $\lambda> \kappa $
is a measurable cardinal with a normal measure
$\lambda> \kappa $
is a measurable cardinal with a normal measure
![]() $\mathcal {U}$
. We would like to construct a cone homogeneous poset in V which will collapse
$\mathcal {U}$
. We would like to construct a cone homogeneous poset in V which will collapse
![]() $\lambda $
to be the successor of
$\lambda $
to be the successor of
![]() $\kappa $
, change the cofinality of
$\kappa $
, change the cofinality of
![]() $\kappa $
to
$\kappa $
to
![]() $\omega $
and add a closed unbounded subset of
$\omega $
and add a closed unbounded subset of
![]() $\lambda $
whose restriction to the set of
$\lambda $
whose restriction to the set of
![]() $\{ \alpha < \lambda \mid \alpha \text { is regular in } V\}$
is almost contained in every set
$\{ \alpha < \lambda \mid \alpha \text { is regular in } V\}$
is almost contained in every set
![]() $A \in \mathcal {U}$
.
$A \in \mathcal {U}$
.
It is natural to attempt obtaining this result by starting with an indestructible supercompact cardinal
![]() $\kappa $
, and forcing with a Levy collapse of
$\kappa $
, and forcing with a Levy collapse of
![]() $\lambda $
to
$\lambda $
to
![]() $\kappa ^+$
followed by a Prikry forcing at
$\kappa ^+$
followed by a Prikry forcing at
![]() $\kappa $
and a club forcing at
$\kappa $
and a club forcing at
![]() $\lambda $
. The difficulty with this approach is in its second step, where the choice of the measure on
$\lambda $
. The difficulty with this approach is in its second step, where the choice of the measure on
![]() $\kappa $
depends on the generic filter for the Levy collapse and might lead to a Prikry generic sequence which will introduce to
$\kappa $
depends on the generic filter for the Levy collapse and might lead to a Prikry generic sequence which will introduce to
![]() $\operatorname {\mathrm {HOD}}$
information about the collapse of
$\operatorname {\mathrm {HOD}}$
information about the collapse of
![]() $\lambda $
to
$\lambda $
to
![]() $\kappa ^+$
, and in particular prevent from
$\kappa ^+$
, and in particular prevent from
![]() $\operatorname {\mathrm {HOD}}$
to witness that
$\operatorname {\mathrm {HOD}}$
to witness that
![]() $\lambda $
is a measurable cardinal.
$\lambda $
is a measurable cardinal.
Instead, our approach will be based on recent use of the supercompact extender based forcing, introduced by Merimovich ([Reference Merimovich21]). Given a supercompact cardinal
![]() $\kappa $
, we derive a
$\kappa $
, we derive a
![]() $(\kappa ,\lambda )$
-supercompact extender E from a supercompact embedding
$(\kappa ,\lambda )$
-supercompact extender E from a supercompact embedding
![]() $j\colon V \to M$
for which
$j\colon V \to M$
for which
![]() ${}^{\lambda }M \subseteq M$
. Let
${}^{\lambda }M \subseteq M$
. Let
![]() $\mathbb {P}_{E}$
be the supercompact extender based forcing associated to the extender E of [Reference Merimovich21]. The conditions of
$\mathbb {P}_{E}$
be the supercompact extender based forcing associated to the extender E of [Reference Merimovich21]. The conditions of
![]() $\mathbb {P}_E$
are pairs of the form
$\mathbb {P}_E$
are pairs of the form
![]() $\langle f, T\rangle $
where f is roughly a condition in the Cohen forcing and T is a tree, with large splittings. We denote by
$\langle f, T\rangle $
where f is roughly a condition in the Cohen forcing and T is a tree, with large splittings. We denote by
![]() $\mathbb {P}_E^*$
the Cohen part.
$\mathbb {P}_E^*$
the Cohen part.
The forcing
![]() $\mathbb {P}_E$
preserves
$\mathbb {P}_E$
preserves
![]() $\lambda $
and singularizes all the regular cardinals in the interval
$\lambda $
and singularizes all the regular cardinals in the interval
![]() $[\kappa , \lambda )$
. We will follow the definitions and notations of [Reference Merimovich21]. In [Reference Gitik and Merimovich15], Gitik and Merimovich show that this forcing is weakly homogeneous (and therefore cone homogeneous).
$[\kappa , \lambda )$
. We will follow the definitions and notations of [Reference Merimovich21]. In [Reference Gitik and Merimovich15], Gitik and Merimovich show that this forcing is weakly homogeneous (and therefore cone homogeneous).
Let
![]() $\mathcal U$
be a normal measure on
$\mathcal U$
be a normal measure on
![]() $\lambda $
in the ground model. We would like to force a club to diagonalize
$\lambda $
in the ground model. We would like to force a club to diagonalize
![]() $\mathcal {U}$
relative to the set of V-regular cardinals below
$\mathcal {U}$
relative to the set of V-regular cardinals below
![]() $\lambda $
. Note that the ordinals of uncountable cofinality below
$\lambda $
. Note that the ordinals of uncountable cofinality below
![]() $\lambda $
in the extender based forcing extension are of measure zero in
$\lambda $
in the extender based forcing extension are of measure zero in
![]() $\mathcal {U}$
. Therefore, our club shooting poset has to allow V-singular ordinals as well. Moreover, since the set of previous inaccessible cardinals below
$\mathcal {U}$
. Therefore, our club shooting poset has to allow V-singular ordinals as well. Moreover, since the set of previous inaccessible cardinals below
![]() $\lambda $
does not reflect at its complement, it is impossible for the generic club to avoid ground model singular cardinals of countable cofinality. Thus, we restrict our club forcing poset to diagonalize
$\lambda $
does not reflect at its complement, it is impossible for the generic club to avoid ground model singular cardinals of countable cofinality. Thus, we restrict our club forcing poset to diagonalize
![]() $\mathcal {U}$
only relative to the set of the regular cardinals in V. To make this precise, we denote by
$\mathcal {U}$
only relative to the set of the regular cardinals in V. To make this precise, we denote by
![]() $\operatorname {\mathrm {Sing}}$
the set of all ground model singular cardinals below
$\operatorname {\mathrm {Sing}}$
the set of all ground model singular cardinals below
![]() $\lambda $
and define
$\lambda $
and define
![]() $\bar {\mathcal {U}}= \{ \operatorname {\mathrm {Sing}} \cup A \mid A \in \mathcal {U}\}$
. We force with the poset
$\bar {\mathcal {U}}= \{ \operatorname {\mathrm {Sing}} \cup A \mid A \in \mathcal {U}\}$
. We force with the poset
![]() $\mathbb {C}_{\bar {\mathcal {U}}}$
, consisting of pairs
$\mathbb {C}_{\bar {\mathcal {U}}}$
, consisting of pairs
![]() $(c,B)$
where
$(c,B)$
where
![]() $c \subseteq \lambda $
is a closed bounded set and
$c \subseteq \lambda $
is a closed bounded set and
![]() $B \in \bar {\mathcal {U}}$
. The extension order is as in the previous section.
$B \in \bar {\mathcal {U}}$
. The extension order is as in the previous section.
We start by recalling a fundamental and useful fact, which lies in the heart of the proof of the Prikry Property of
![]() $\mathbb {P}_E$
.
$\mathbb {P}_E$
.
Lemma 7.1. Let M be an elementary submodel of
![]() $H_{\chi }$
for some large
$H_{\chi }$
for some large
![]() $\chi $
such that
$\chi $
such that
![]() $M \cap \lambda = \delta \in \lambda $
is inaccessible cardinal and
$M \cap \lambda = \delta \in \lambda $
is inaccessible cardinal and
![]() $M^{<\delta } \subseteq M$
. Let
$M^{<\delta } \subseteq M$
. Let
![]() $p\in M \cap \mathbb {P}_E$
.
$p\in M \cap \mathbb {P}_E$
.
Then, there is a condition
![]() $f^* \in \mathbb {P}_E^{*}$
which is M-generic (namely, it belongs to every dense open subset of
$f^* \in \mathbb {P}_E^{*}$
which is M-generic (namely, it belongs to every dense open subset of
![]() $\mathbb {P}_E^*$
in M) and
$\mathbb {P}_E^*$
in M) and
![]() $\operatorname {\mathrm {dom}} f^* = M \cap \lambda $
. Moreover, if
$\operatorname {\mathrm {dom}} f^* = M \cap \lambda $
. Moreover, if
![]() $p^* = \langle f^*, T\rangle $
is a condition in
$p^* = \langle f^*, T\rangle $
is a condition in
![]() $\mathbb {P}_E$
, then there is
$\mathbb {P}_E$
, then there is
![]() $T^* \subseteq T$
,
$T^* \subseteq T$
,
![]() $E(f^*)$
-large such that
$E(f^*)$
-large such that
![]() $T^* \subseteq M$
and
$T^* \subseteq M$
and
![]() $D \in M$
is a dense open subset of
$D \in M$
is a dense open subset of
![]() $\mathbb {P}_E$
, then there is a natural number n such that for every
$\mathbb {P}_E$
, then there is a natural number n such that for every
![]() $\langle \nu _0, \dots , \nu _{n-1}\rangle $
in the n-th level of
$\langle \nu _0, \dots , \nu _{n-1}\rangle $
in the n-th level of
![]() $T*$
,
$T*$
,
![]() $p^*_{\langle \nu _0, \dots , \nu _{n-1}\rangle } \in D$
.
$p^*_{\langle \nu _0, \dots , \nu _{n-1}\rangle } \in D$
.
Proof. The first claim follows from the closure of
![]() $\mathbb {P}_E^*$
. Let us focus on the second part.
$\mathbb {P}_E^*$
. Let us focus on the second part.
Let
![]() $f^*$
be as in the lemma. Let
$f^*$
be as in the lemma. Let
![]() $D\in M$
be dense open. For each
$D\in M$
be dense open. For each
![]() $\langle \nu _0, \dots , \nu _{n-1}\rangle \in M$
and for each
$\langle \nu _0, \dots , \nu _{n-1}\rangle \in M$
and for each
![]() $g\in \mathbb {P}_E^* \cap M$
, we can ask whether there is a condition
$g\in \mathbb {P}_E^* \cap M$
, we can ask whether there is a condition
![]() $q \in D$
of the form
$q \in D$
of the form
![]() $\langle h, S\rangle \in D$
such that
$\langle h, S\rangle \in D$
such that
![]() $h \geq ^* g_{\langle \nu _0, \dots , \nu _{n-1}\rangle }$
. The set of conditions that decide this statement is dense open and definable in M, and thus
$h \geq ^* g_{\langle \nu _0, \dots , \nu _{n-1}\rangle }$
. The set of conditions that decide this statement is dense open and definable in M, and thus
![]() $f^*$
decides whether there is such extension or not (for each possible
$f^*$
decides whether there is such extension or not (for each possible
![]() $\langle \nu _0, \dots , \nu _{n-1}\rangle $
). Let
$\langle \nu _0, \dots , \nu _{n-1}\rangle $
). Let
![]() $D_{\vec {\nu }}$
be this set, and let us split it into two parts
$D_{\vec {\nu }}$
be this set, and let us split it into two parts
![]() $D_{\vec {\nu }}^0 \cup D_{\vec \nu }^1$
according to the decision, where conditions in
$D_{\vec {\nu }}^0 \cup D_{\vec \nu }^1$
according to the decision, where conditions in
![]() $D_{\vec \nu }^0$
are direct extensions that enter D after the nondirect extension.
$D_{\vec \nu }^0$
are direct extensions that enter D after the nondirect extension.
Let
![]() $p^* = \langle f^*, T\rangle $
. Since a typical point
$p^* = \langle f^*, T\rangle $
. Since a typical point
![]() $\nu $
in a measure one tree T, associate with the measures
$\nu $
in a measure one tree T, associate with the measures
![]() $E(f^*)$
is a finite sequence of elements contained in M each has size
$E(f^*)$
is a finite sequence of elements contained in M each has size
![]() $|\nu | < \kappa $
, we may assume that
$|\nu | < \kappa $
, we may assume that
![]() $T \subseteq M$
. There is an extension
$T \subseteq M$
. There is an extension
![]() $q \geq p^*$
in D. By the definition of the order of
$q \geq p^*$
in D. By the definition of the order of
![]() $\mathbb {P}_E$
, q is obtained by taking first some Prikry extension and then a direct extension, and therefore the Prikry extension is done using some
$\mathbb {P}_E$
, q is obtained by taking first some Prikry extension and then a direct extension, and therefore the Prikry extension is done using some
![]() $\vec {\nu } \in M$
. Thus, for this specific Prikry extension,
$\vec {\nu } \in M$
. Thus, for this specific Prikry extension,
![]() $f^* \in D_{\vec {\nu }}^0$
. We conclude that already
$f^* \in D_{\vec {\nu }}^0$
. We conclude that already
![]() $p^*_{\vec {\nu }} \in D$
.
$p^*_{\vec {\nu }} \in D$
.
We can now shrink T in order to stabilize the length of the extensions that enter D.
Lemma 7.2.
![]() $\bar {\mathcal {U}}$
extends to a
$\bar {\mathcal {U}}$
extends to a
![]() $\lambda $
-complete filter in the generic extension by
$\lambda $
-complete filter in the generic extension by
![]() $\mathbb {P}_E$
.
$\mathbb {P}_E$
.
Proof. Assume that this is not the case. Since
![]() $\kappa $
is singular, the closure of
$\kappa $
is singular, the closure of
![]() $\bar {\mathcal {U}}$
must drop to some cardinal
$\bar {\mathcal {U}}$
must drop to some cardinal
![]() $\rho < \kappa $
. Let
$\rho < \kappa $
. Let
![]() be a sequence of names of elements in
be a sequence of names of elements in
![]() $\bar {\mathcal {U}}$
which are forced to have non-measure one intersection.
$\bar {\mathcal {U}}$
which are forced to have non-measure one intersection.
Using the strong Prikry Property, we can find a sequence of direct extensions
![]() $p_i$
and natural numbers
$p_i$
and natural numbers
![]() $n_i$
such that any
$n_i$
such that any
![]() $n_i$
-length Prikry extension of
$n_i$
-length Prikry extension of
![]() $p_i$
decides the value of
$p_i$
decides the value of
![]() . Since there are fewer than
. Since there are fewer than
![]() $\lambda $
many such extensions, we can find a set
$\lambda $
many such extensions, we can find a set
![]() $B_i \in \bar {\mathcal {U}}$
such that
$B_i \in \bar {\mathcal {U}}$
such that
![]() . In particular,
. In particular,
![]() , but
, but
![]() $\bigcap B_i \in \bar {\mathcal {U}}$
.
$\bigcap B_i \in \bar {\mathcal {U}}$
.
Lemma 7.3.
![]() $\mathbb {C}_{\bar {\mathcal {U}}}$
is
$\mathbb {C}_{\bar {\mathcal {U}}}$
is
![]() $\lambda $
-distributive in the generic extension by
$\lambda $
-distributive in the generic extension by
![]() $\mathbb {P}_E$
.
$\mathbb {P}_E$
.
Proof. Since
![]() $\kappa $
is singular in the extension by
$\kappa $
is singular in the extension by
![]() $\mathbb {P}_E$
, it is enough to show that the forcing
$\mathbb {P}_E$
, it is enough to show that the forcing
![]() $\mathbb {C}_{\bar {\mathcal {U}}}$
is
$\mathbb {C}_{\bar {\mathcal {U}}}$
is
![]() $\rho $
-distributive for every
$\rho $
-distributive for every
![]() $\rho < \kappa $
.
$\rho < \kappa $
.
We first work in V. Let
![]() be a sequence of
be a sequence of
![]() $\mathbb {P}_E$
-names for dense open subsets of
$\mathbb {P}_E$
-names for dense open subsets of
![]() $\mathbb {C}_{\bar {\mathcal {U}}}$
,
$\mathbb {C}_{\bar {\mathcal {U}}}$
,
![]() $\rho < \kappa $
. Let
$\rho < \kappa $
. Let
![]() $\langle p,q\rangle $
be a condition in
$\langle p,q\rangle $
be a condition in
![]() $\mathbb {P}_E * \mathbb {C}_{\bar {\mathcal {U}}}$
. Let us define an increasing sequence of models
$\mathbb {P}_E * \mathbb {C}_{\bar {\mathcal {U}}}$
. Let us define an increasing sequence of models
![]() $\langle M_i \mid i < \rho \rangle $
such that:
$\langle M_i \mid i < \rho \rangle $
such that:
-
•
 .
. -
•
 $M_i \prec H_{\chi }$
for some large
$M_i \prec H_{\chi }$
for some large
 $\chi $
,
$\chi $
,
 $M_i \cap \lambda = \delta _i \in \lambda $
inaccessible.
$M_i \cap \lambda = \delta _i \in \lambda $
inaccessible. -
•
 $M_{i}^{<\delta _{i}} \subseteq M_{i}$
and
$M_{i}^{<\delta _{i}} \subseteq M_{i}$
and
 $\delta _{i} \in \bigcap \{A \in \mathcal {U} \cap M_{i}\}$
.
$\delta _{i} \in \bigcap \{A \in \mathcal {U} \cap M_{i}\}$
. -
•
 $\langle M_j \mid j < i\rangle \in M_i$
.
$\langle M_j \mid j < i\rangle \in M_i$
.
This chain of models can be easily obtained using the same argument as in Lemma 3.1.
Next, let us pick by induction, for each
![]() $i < \rho $
, an
$i < \rho $
, an
![]() $M_i$
-generic condition
$M_i$
-generic condition
![]() $f^*_i\in \mathbb {P}_E^*$
such that
$f^*_i\in \mathbb {P}_E^*$
such that
![]() $f^*_i \in M_{i+1}$
and
$f^*_i \in M_{i+1}$
and
![]() $f^*_i \subseteq f^*_j$
for
$f^*_i \subseteq f^*_j$
for
![]() $i < j$
. We will define a sequence of names
$i < j$
. We will define a sequence of names
![]() and a sequence of conditions
and a sequence of conditions
![]() $p_i$
such that:
$p_i$
such that:
-
•
 $p_i = \langle f^*_i, T_i\rangle \in M_{i+1}$
,
$p_i = \langle f^*_i, T_i\rangle \in M_{i+1}$
,
 $q_i \in M_i$
.
$q_i \in M_i$
. -
•
 .
. -
• The sequence of conditions
 $p_i$
is
$p_i$
is
 $\leq ^*$
-increasing. Let
$\leq ^*$
-increasing. Let
 $p_{\rho }$
be their limit.
$p_{\rho }$
be their limit. -
•
 $p_{\rho }$
forces that the conditions
$p_{\rho }$
forces that the conditions
 $q_i$
are increasing and they have a limit
$q_i$
are increasing and they have a limit
 $q_{\rho }$
.
$q_{\rho }$
.
In
![]() $M_{i}$
, let
$M_{i}$
, let
![]() $D^{\prime }_i$
be the dense open set in
$D^{\prime }_i$
be the dense open set in
![]() $\mathbb {P}_E$
of all extensions of
$\mathbb {P}_E$
of all extensions of
![]() $p_i$
that force for some condition
$p_i$
that force for some condition
![]() $q = (c^q, B^q) \geq q_i$
to be in
$q = (c^q, B^q) \geq q_i$
to be in
![]() , and decide its maximum and its large set
, and decide its maximum and its large set
![]() $B^q$
from
$B^q$
from
![]() $\bar {\mathcal {U}}$
. By applying Lemma 7.1 inside
$\bar {\mathcal {U}}$
. By applying Lemma 7.1 inside
![]() $M_{i}$
, we conclude that there is an
$M_{i}$
, we conclude that there is an
![]() $E(f^*_i)$
-large tree
$E(f^*_i)$
-large tree
![]() $T_i\subseteq M_i$
and a natural number
$T_i\subseteq M_i$
and a natural number
![]() $n_i$
such that, for the condition
$n_i$
such that, for the condition
![]() $p_{i} = \langle f^*_i, T_i\rangle $
, for every
$p_{i} = \langle f^*_i, T_i\rangle $
, for every
![]() $\vec {\nu } \in Lev_{n_i}(T_i)$
,
$\vec {\nu } \in Lev_{n_i}(T_i)$
,
![]() $(p_i)_{\vec {\nu }}\in D^{\prime }_i$
. In particular, it picks a condition
$(p_i)_{\vec {\nu }}\in D^{\prime }_i$
. In particular, it picks a condition
![]() $q_{i+1, \vec {\nu }} \geq q_i$
from
$q_{i+1, \vec {\nu }} \geq q_i$
from
![]() $\mathbb {C}_{\bar {\mathcal {U}}}$
, which is going to be in
$\mathbb {C}_{\bar {\mathcal {U}}}$
, which is going to be in
![]() $M_{i}$
. Since this condition is in
$M_{i}$
. Since this condition is in
![]() $M_i$
, it is going to be bounded below
$M_i$
, it is going to be bounded below
![]() $\delta _{i}$
, and its large set belongs to
$\delta _{i}$
, and its large set belongs to
![]() $\bar {\mathcal {U}} \cap M_{i}$
.
$\bar {\mathcal {U}} \cap M_{i}$
.
Note that the collection of all n-step extensions of a fixed condition in
![]() $\mathbb {P}_E$
is always a maximal antichain above this condition and thus, we can define
$\mathbb {P}_E$
is always a maximal antichain above this condition and thus, we can define
![]() to be equal to
to be equal to
![]() $q_{i+1, \vec {\nu }}$
above
$q_{i+1, \vec {\nu }}$
above
![]() $(p_i)_{\vec {\nu }}$
, and trivial below any condition which is incompatible with
$(p_i)_{\vec {\nu }}$
, and trivial below any condition which is incompatible with
![]() $p_i$
. Finally, we define
$p_i$
. Finally, we define
![]() to be the extension of
to be the extension of
![]() by the single ordinal
by the single ordinal
![]() $\delta _{i}$
. By the construction, this is indeed an extension, as
$\delta _{i}$
. By the construction, this is indeed an extension, as
![]() $\delta _{i} \in B$
for all
$\delta _{i} \in B$
for all
![]() $B \in \bar {\mathcal {U}} \cap M_{i}$
.
$B \in \bar {\mathcal {U}} \cap M_{i}$
.
At limit steps, we define
![]() to be the limit of previous conditions. This is possible since the filter
to be the limit of previous conditions. This is possible since the filter
![]() $\bar {\mathcal {U}}$
is still
$\bar {\mathcal {U}}$
is still
![]() $\lambda $
-complete and since the maximal element of the closed set in
$\lambda $
-complete and since the maximal element of the closed set in
![]() is forced to be
is forced to be
![]() $\delta _j$
. Therefore, the maximal element of
$\delta _j$
. Therefore, the maximal element of
![]() is
is
![]() $\delta _i$
which is singular strong limit cardinal in the limit case.
$\delta _i$
which is singular strong limit cardinal in the limit case.
Lemma 7.4. Let
![]() $B' \in \mathcal {U}$
. Then,
$B' \in \mathcal {U}$
. Then,
![]() $B'$
is stationary in
$B'$
is stationary in
![]() $\mathbb {P}_E * \mathbb {C}_{\bar {\mathcal {U}}}$
.
$\mathbb {P}_E * \mathbb {C}_{\bar {\mathcal {U}}}$
.
Proof. Let
![]() be a name for a club. We show that every condition
be a name for a club. We show that every condition
![]() $q \in \mathbb {C}_{\bar {\mathcal {U}}}$
has an extension which forces that
$q \in \mathbb {C}_{\bar {\mathcal {U}}}$
has an extension which forces that
![]() . Working in V, let
. Working in V, let
![]() $M \prec H_{\chi }$
, such that
$M \prec H_{\chi }$
, such that
![]() $M \cap \lambda = \delta $
,
$M \cap \lambda = \delta $
,
![]() , and
, and
![]() $\delta \in B'$
is inaccessible. Moreover, let us assume that M is obtained as a union of a chain of models of length
$\delta \in B'$
is inaccessible. Moreover, let us assume that M is obtained as a union of a chain of models of length
![]() $\delta $
,
$\delta $
,
![]() $M_i$
, such that
$M_i$
, such that
![]() $M_i \cap \lambda = \delta _i$
and
$M_i \cap \lambda = \delta _i$
and
![]() $M_{i+1}^{<\delta _{i+1}} \subseteq M_{i+1}$
and
$M_{i+1}^{<\delta _{i+1}} \subseteq M_{i+1}$
and
![]() $\delta _{i+1} \in \bigcap (\mathcal {U} \cap M_{i+1})$
.
$\delta _{i+1} \in \bigcap (\mathcal {U} \cap M_{i+1})$
.
For each i, let
![]() $f^*_i$
be
$f^*_i$
be
![]() $M_i$
-generic for
$M_i$
-generic for
![]() $\mathbb {P}_E^*$
, such that
$\mathbb {P}_E^*$
, such that
![]() $f_i^* \subseteq f_j^*$
for
$f_i^* \subseteq f_j^*$
for
![]() $i < j$
. Let
$i < j$
. Let
![]() $f^* = \bigcup f_i^*$
.
$f^* = \bigcup f_i^*$
.
Let
![]() $G \subseteq \mathbb {P}_E$
be a generic filter that contains a condition
$G \subseteq \mathbb {P}_E$
be a generic filter that contains a condition
![]() $p^* = \langle f^*, A\rangle $
,
$p^* = \langle f^*, A\rangle $
,
![]() $A \subseteq M$
. In
$A \subseteq M$
. In
![]() $V[G]$
,
$V[G]$
,
![]() $\operatorname {\mathrm {cf}} \delta = \omega $
. Let
$\operatorname {\mathrm {cf}} \delta = \omega $
. Let
![]() $\langle \delta _n \mid n < \omega \rangle $
be a cofinal sequence in
$\langle \delta _n \mid n < \omega \rangle $
be a cofinal sequence in
![]() $\delta $
. For each n, for sufficiently large
$\delta $
. For each n, for sufficiently large
![]() $\xi < \delta $
,
$\xi < \delta $
,
![]() $M_{\xi }$
contains the dense set of conditions in
$M_{\xi }$
contains the dense set of conditions in
![]() $\mathbb {P}_E$
that decide on some condition
$\mathbb {P}_E$
that decide on some condition
![]() $q \in \mathbb {C}_{\bar {\mathcal {U}}}$
that forces some ordinal
$q \in \mathbb {C}_{\bar {\mathcal {U}}}$
that forces some ordinal
![]() $\gamma _n \geq \delta _n$
to be in
$\gamma _n \geq \delta _n$
to be in
![]() .
.
Following the same arguments as in the previous lemma, we can define a condition
![]() by going over some maximal antichain. The maximum of the closed set of
by going over some maximal antichain. The maximum of the closed set of
![]() is always
is always
![]() $\delta _{n + 1}$
. Finally, the sequence of conditions
$\delta _{n + 1}$
. Finally, the sequence of conditions
![]() $q_n^G$
has an upper bound, by attaching
$q_n^G$
has an upper bound, by attaching
![]() $\delta $
on top of the union. Let
$\delta $
on top of the union. Let
![]() $q_{\omega }$
be the upper bound. Clearly,
$q_{\omega }$
be the upper bound. Clearly,
![]() $q_{\omega }$
forces
$q_{\omega }$
forces
![]() , as wanted.
, as wanted.
Finally, the following proposition finishes the proof of Theorem 1.6.
Proposition 7.5. Let
![]() $\kappa $
be
$\kappa $
be
![]() $\lambda $
-supercompact, where
$\lambda $
-supercompact, where
![]() $\lambda $
is measurable. Then, there is a generic extension in which
$\lambda $
is measurable. Then, there is a generic extension in which
![]() $\operatorname {\mathrm {cf}} \kappa = \omega $
,
$\operatorname {\mathrm {cf}} \kappa = \omega $
,
![]() $\kappa $
is a cardinal,
$\kappa $
is a cardinal,
![]() $\lambda = \kappa ^+$
and it is
$\lambda = \kappa ^+$
and it is
![]() $((S_{reg}^{\lambda })^V, 1)$
-strongly measurable cardinal.
$((S_{reg}^{\lambda })^V, 1)$
-strongly measurable cardinal.
We can now finish the proof of Theorem 1.6.
Proof of Theorem 1.6.
The iteration
![]() $\mathbb {P}_E * \mathbb {C}_{\bar {\mathcal {U}}}$
is cone homogeneous as an iteration of two cone homogeneous, ordinal definable forcing notions. Since
$\mathbb {P}_E * \mathbb {C}_{\bar {\mathcal {U}}}$
is cone homogeneous as an iteration of two cone homogeneous, ordinal definable forcing notions. Since
![]() $\mathbb {P}_E$
preserves cardinals below
$\mathbb {P}_E$
preserves cardinals below
![]() $\kappa $
and
$\kappa $
and
![]() $\geq \lambda $
and
$\geq \lambda $
and
![]() $\mathbb {C}_{\bar {\mathcal {U}}}$
preserves cardinals, the result follows. The set
$\mathbb {C}_{\bar {\mathcal {U}}}$
preserves cardinals, the result follows. The set
![]() $S_{reg}^{\lambda }$
is stationary by Lemma 7.4.
$S_{reg}^{\lambda }$
is stationary by Lemma 7.4.
The result that we obtain for the successor of a singular cardinal is weaker than the result for a successor of a regular cardinal. The reason is that, in order to get the closed unbounded filter to be sets from the intersection of some ground model normal measures, we will have to obtain a situation in which the regular cardinals between the supercompact cardinal
![]() $\kappa $
and the measurable cardinal
$\kappa $
and the measurable cardinal
![]() $\lambda $
are going to change cofinalities into values which differ from the cofinality of
$\lambda $
are going to change cofinalities into values which differ from the cofinality of
![]() $\kappa $
in the generic extension. This is also the reason that such a method cannot work for getting an
$\kappa $
in the generic extension. This is also the reason that such a method cannot work for getting an
![]() $\omega $
-strongly measurable successor of a singular cardinal of uncountable cofinality.
$\omega $
-strongly measurable successor of a singular cardinal of uncountable cofinality.
We remark that Woodin in [Reference Woodin39], proved that it is consistent relative to the large cardinal axiom
![]() $I_0$
that a successor of a singular cardinal is
$I_0$
that a successor of a singular cardinal is
![]() $\omega $
-strongly measurable.
$\omega $
-strongly measurable.
Question 7.6. Is it consistent that there is an
![]() $\omega $
-strongly measurable cardinal
$\omega $
-strongly measurable cardinal
![]() $\lambda ^+$
, where
$\lambda ^+$
, where
![]() $\operatorname {\mathrm {cf}} \lambda> \omega $
is a limit cardinal?
$\operatorname {\mathrm {cf}} \lambda> \omega $
is a limit cardinal?
Question 7.7. Is it consistent that there is a cardinal
![]() $\lambda ^+$
, where
$\lambda ^+$
, where
![]() $\operatorname {\mathrm {cf}} \lambda> \omega $
is a limit cardinal and
$\operatorname {\mathrm {cf}} \lambda> \omega $
is a limit cardinal and
![]() $(S^{\lambda ^{+}}_{reg})^{\operatorname {\mathrm {HOD}}}$
contains a club in V?
$(S^{\lambda ^{+}}_{reg})^{\operatorname {\mathrm {HOD}}}$
contains a club in V?
8 Appendix - homogeneity
In this section we review some basic facts related to homogeneity and develop some basic tools in order to preserve homogeneity of iterations of Prikry-type forcings.
8.1 Homogeneity and
 $\operatorname {\mathrm {HOD}}$
$\operatorname {\mathrm {HOD}}$
When dealing with
![]() $\operatorname {\mathrm {HOD}}$
, we would like to modify the universe (via forcing) while not adding objects to
$\operatorname {\mathrm {HOD}}$
, we would like to modify the universe (via forcing) while not adding objects to
![]() $\operatorname {\mathrm {HOD}}$
. The main method to obtain this is to force with posets which satisfy a certain weak homogeneity property. The main results of this work will focus on the notion of cone homogeneous posets.
$\operatorname {\mathrm {HOD}}$
. The main method to obtain this is to force with posets which satisfy a certain weak homogeneity property. The main results of this work will focus on the notion of cone homogeneous posets.
Definition 8.1. We say that a poset
![]() $\mathbb {P}$
is cone homogeneous if, for every
$\mathbb {P}$
is cone homogeneous if, for every
![]() $p,q \in \mathbb {P}$
, there are extensions
$p,q \in \mathbb {P}$
, there are extensions
![]() $p^*,q^*$
of
$p^*,q^*$
of
![]() $p,q$
, respectively, and a forcing isomorphism
$p,q$
, respectively, and a forcing isomorphism
![]() $\varphi $
from the cone
$\varphi $
from the cone
![]() $\mathbb {P}/p^*$
(i.e., of conditions extending
$\mathbb {P}/p^*$
(i.e., of conditions extending
![]() $p^*$
) to the cone
$p^*$
) to the cone
![]() $\mathbb {P}/q^*$
.
$\mathbb {P}/q^*$
.
This notion can also be found under different names in the literature concerning weak forms of homogeneity. Our terminology follows Dorbinen and Friedman, [Reference Dobrinen and Friedman9] for the most part. It is easy to see that cone homogeneous posets satisfy most standard properties of homogeneous posets concerning ordinal definability sets. In particular, the following well-known result holds.
Fact 8.2 (Levy, [Reference Lévy19]).
If
![]() $\mathbb {P}$
is cone homogeneous and belongs to
$\mathbb {P}$
is cone homogeneous and belongs to
![]() $\operatorname {\mathrm {HOD}}$
, and
$\operatorname {\mathrm {HOD}}$
, and
![]() $G \subseteq \mathbb {P}$
is generic over V, then
$G \subseteq \mathbb {P}$
is generic over V, then
![]() $\operatorname {\mathrm {HOD}}^{V[G]} \subseteq \operatorname {\mathrm {HOD}}^V$
.
$\operatorname {\mathrm {HOD}}^{V[G]} \subseteq \operatorname {\mathrm {HOD}}^V$
.
If
![]() $\varphi $
is an isomorphism of two cones
$\varphi $
is an isomorphism of two cones
![]() $\mathbb {P} /p_0$
and
$\mathbb {P} /p_0$
and
![]() $\mathbb {P}/p_1$
, and
$\mathbb {P}/p_1$
, and
![]() $\sigma $
is a
$\sigma $
is a
![]() $\mathbb {P} /p_0$
name, then by recursively applying
$\mathbb {P} /p_0$
name, then by recursively applying
![]() $\varphi $
, we obtain a
$\varphi $
, we obtain a
![]() $\mathbb {P} /p_1$
-name, which we denote by
$\mathbb {P} /p_1$
-name, which we denote by
![]() $\sigma ^{\varphi }$
.
$\sigma ^{\varphi }$
.
Let
![]() $\mathbb {P} = \mathbb {P}_{\kappa }$
where
$\mathbb {P} = \mathbb {P}_{\kappa }$
where
![]() ${\langle } \mathbb {P}_{\alpha },\mathbb {Q}_{\alpha } \mid \alpha < \kappa {\rangle }$
is an iteration of cone homogeneous posets
${\langle } \mathbb {P}_{\alpha },\mathbb {Q}_{\alpha } \mid \alpha < \kappa {\rangle }$
is an iteration of cone homogeneous posets
![]() $\mathbb {Q}_{\alpha },$
and moreover, let us assume that all cone automorphisms of
$\mathbb {Q}_{\alpha },$
and moreover, let us assume that all cone automorphisms of
![]() $\mathbb {P}_{\alpha }$
do not modify
$\mathbb {P}_{\alpha }$
do not modify
![]() $\mathbb {Q}_{\alpha }$
as a poset. For simplicity, we may assume that
$\mathbb {Q}_{\alpha }$
as a poset. For simplicity, we may assume that
![]() $\mathbb {Q}_{\alpha }$
and its order are ordinal definable.
$\mathbb {Q}_{\alpha }$
and its order are ordinal definable.
Given two conditions
![]() $\vec {p} = {\langle } p_{\alpha } \mid \alpha < \kappa {\rangle }, \vec {q} = {\langle } q_{\alpha } \mid \alpha < \kappa {\rangle }$
in
$\vec {p} = {\langle } p_{\alpha } \mid \alpha < \kappa {\rangle }, \vec {q} = {\langle } q_{\alpha } \mid \alpha < \kappa {\rangle }$
in
![]() $\mathbb {P}$
, it is natural to try forming extensions
$\mathbb {P}$
, it is natural to try forming extensions
![]() $\vec {p^*} = {\langle } p^*_{\alpha } \mid \alpha < \kappa {\rangle } \geq \vec {p}$
,
$\vec {p^*} = {\langle } p^*_{\alpha } \mid \alpha < \kappa {\rangle } \geq \vec {p}$
,
![]() $\vec {q^*} = {\langle } q^*_{\alpha } \mid \alpha < \kappa {\rangle } \geq \vec {q}$
, and an isomorphism
$\vec {q^*} = {\langle } q^*_{\alpha } \mid \alpha < \kappa {\rangle } \geq \vec {q}$
, and an isomorphism
![]() $\varphi \colon \mathbb {P}/\vec {p^*} \to \mathbb {P}/\vec {q^*}$
as follows.
$\varphi \colon \mathbb {P}/\vec {p^*} \to \mathbb {P}/\vec {q^*}$
as follows.
By induction on
![]() $\beta \leq \kappa $
, we attempt defining extensions
$\beta \leq \kappa $
, we attempt defining extensions
![]() $\vec {p}^{\beta } = {\langle } p^*_{\alpha } \mid \alpha < \beta {\rangle } $
of
$\vec {p}^{\beta } = {\langle } p^*_{\alpha } \mid \alpha < \beta {\rangle } $
of
![]() $\vec {p}\restriction \beta $
, and
$\vec {p}\restriction \beta $
, and
![]() $\vec {q}^{\beta } = {\langle } q^*_{\alpha } \mid \alpha < \beta {\rangle }$
of
$\vec {q}^{\beta } = {\langle } q^*_{\alpha } \mid \alpha < \beta {\rangle }$
of
![]() $\vec {q}\restriction \beta $
, and an isomorphism
$\vec {q}\restriction \beta $
, and an isomorphism
![]() $\varphi _{\beta } \colon \mathbb {P}_{\beta }/\vec {p}^{\beta } \to \mathbb {P}_{\beta }/\vec {q}^{\beta }$
. Our inductive assumptions further include
$\varphi _{\beta } \colon \mathbb {P}_{\beta }/\vec {p}^{\beta } \to \mathbb {P}_{\beta }/\vec {q}^{\beta }$
. Our inductive assumptions further include
![]() $\vec {p}^{\beta _1}\restriction \beta _0 = \vec {p}^{\beta _0}$
,
$\vec {p}^{\beta _1}\restriction \beta _0 = \vec {p}^{\beta _0}$
,
![]() $\vec {q}^{\beta _1}\restriction \beta _0 = \vec {q}^{\beta _0}$
, and
$\vec {q}^{\beta _1}\restriction \beta _0 = \vec {q}^{\beta _0}$
, and
![]() $\varphi _{\beta _1} \restriction \mathbb {P}_{\beta _0}/\vec {p}^{\beta _0} = \varphi _{\beta _0}$
,Footnote
15
for all
$\varphi _{\beta _1} \restriction \mathbb {P}_{\beta _0}/\vec {p}^{\beta _0} = \varphi _{\beta _0}$
,Footnote
15
for all
![]() $\beta _0 < \beta _1$
.
$\beta _0 < \beta _1$
.
For
![]() $\beta =0$
, where
$\beta =0$
, where
![]() $\mathbb {P}_0 = \{ 0_{\mathbb {P}_0}\}$
is a trivial forcing, we take
$\mathbb {P}_0 = \{ 0_{\mathbb {P}_0}\}$
is a trivial forcing, we take
![]() $\varphi _0$
to be the identity. At a successor step, assuming
$\varphi _0$
to be the identity. At a successor step, assuming
![]() $\vec {p}^{\beta },\vec {q}^{\beta }$
and
$\vec {p}^{\beta },\vec {q}^{\beta }$
and
![]() $\varphi _{\beta }$
have been defined, we have that
$\varphi _{\beta }$
have been defined, we have that
![]() $\varphi _{\beta }(\vec {p}^{\beta }) = \vec {q}^{\beta }$
forces that
$\varphi _{\beta }(\vec {p}^{\beta }) = \vec {q}^{\beta }$
forces that
![]() $p_{\beta }^{\varphi _{\beta }}$
and
$p_{\beta }^{\varphi _{\beta }}$
and
![]() $q_{\beta }$
are conditions of the cone homogeneous poset
$q_{\beta }$
are conditions of the cone homogeneous poset
![]() $\mathbb {Q}_{\beta }$
. There are therefore
$\mathbb {Q}_{\beta }$
. There are therefore
![]() $\mathbb {P}_{\beta }$
-names
$\mathbb {P}_{\beta }$
-names
![]() $p^{\prime }_{\beta }$
and
$p^{\prime }_{\beta }$
and
![]() $q^{\prime }_{\beta }$
of extensions of
$q^{\prime }_{\beta }$
of extensions of
![]() $p_{\beta }^{\varphi _{\beta }}$
and
$p_{\beta }^{\varphi _{\beta }}$
and
![]() $q_{\beta }$
, respectively, and a name of a cone isomorphism
$q_{\beta }$
, respectively, and a name of a cone isomorphism
![]() $\psi _{\beta } \colon \mathbb {Q}_{\beta }/p^{\prime }_{\beta } \to \mathbb {Q}_{\beta }/q^{\prime }_{\beta }$
. We stress that we use the maximality principle and do not extend the conditions
$\psi _{\beta } \colon \mathbb {Q}_{\beta }/p^{\prime }_{\beta } \to \mathbb {Q}_{\beta }/q^{\prime }_{\beta }$
. We stress that we use the maximality principle and do not extend the conditions
![]() $\vec {p}^{\beta }$
and
$\vec {p}^{\beta }$
and
![]() $\vec {q}^{\beta }$
in order to determine the values of
$\vec {q}^{\beta }$
in order to determine the values of
![]() $p^{\prime }_{\beta }, q^{\prime }_{\beta }$
and
$p^{\prime }_{\beta }, q^{\prime }_{\beta }$
and
![]() $\psi _{\beta }$
.
$\psi _{\beta }$
.
Let
![]() $p^*_{\beta } = (p^{\prime }_{\beta })^{\varphi _{\beta }}$
and
$p^*_{\beta } = (p^{\prime }_{\beta })^{\varphi _{\beta }}$
and
![]() $q^*_{\beta } = q^{\prime }_{\beta }$
. Clearly,
$q^*_{\beta } = q^{\prime }_{\beta }$
. Clearly,
![]() $\vec {p}^{\beta }$
,
$\vec {p}^{\beta }$
,
![]() $\vec {q}^{\beta }$
force that
$\vec {q}^{\beta }$
force that
![]() $p^*_{\beta },q^*_{\beta }$
extend
$p^*_{\beta },q^*_{\beta }$
extend
![]() $p_{\beta }, q_{\beta }$
, respectively. We set
$p_{\beta }, q_{\beta }$
, respectively. We set
![]() $\vec {p}^{\beta +1} = \vec {p}^{\beta } {}^{\frown } {\langle } p^*_{\beta }{\rangle }$
,
$\vec {p}^{\beta +1} = \vec {p}^{\beta } {}^{\frown } {\langle } p^*_{\beta }{\rangle }$
,
![]() $\vec {q}^{\beta +1} = \vec {q}^{\beta } {}^{\frown } {\langle } q^*_{\beta }{\rangle }$
and define
$\vec {q}^{\beta +1} = \vec {q}^{\beta } {}^{\frown } {\langle } q^*_{\beta }{\rangle }$
and define
![]() $\varphi _{\beta +1}\colon \mathbb {P}_{\beta +1}/\vec {p}^{\beta +1} \to \mathbb {P}_{\beta +1}/\vec {q}^{\beta +1}$
by mapping a condition
$\varphi _{\beta +1}\colon \mathbb {P}_{\beta +1}/\vec {p}^{\beta +1} \to \mathbb {P}_{\beta +1}/\vec {q}^{\beta +1}$
by mapping a condition
![]() $\vec {r} = \vec {r}\restriction \beta {}^{\frown } {\langle } r_{\beta }{\rangle } \in \mathbb {P}_{\beta +1}/\vec {p}^{\beta +1}$
to
$\vec {r} = \vec {r}\restriction \beta {}^{\frown } {\langle } r_{\beta }{\rangle } \in \mathbb {P}_{\beta +1}/\vec {p}^{\beta +1}$
to
It is immediate from our assumption of
![]() $\varphi _{\beta }$
and choice of
$\varphi _{\beta }$
and choice of
![]() $\psi _{\beta }$
that
$\psi _{\beta }$
that
![]() $\varphi _{\beta +1}$
is an isomorphism. Finally, for a limit ordinal
$\varphi _{\beta +1}$
is an isomorphism. Finally, for a limit ordinal
![]() $\delta \leq \kappa $
,
$\delta \leq \kappa $
,
![]() $\vec {p}^{\delta }$
(similarly
$\vec {p}^{\delta }$
(similarly
![]() $\vec {q}^{\delta }$
) is determined by the requirement
$\vec {q}^{\delta }$
) is determined by the requirement
![]() $\vec {p}^{\delta }\restriction \beta = \vec {p}^{\beta }$
for all
$\vec {p}^{\delta }\restriction \beta = \vec {p}^{\beta }$
for all
![]() $\beta < \delta $
(similarly for
$\beta < \delta $
(similarly for
![]() $\vec {q}^{\delta }$
), and
$\vec {q}^{\delta }$
), and
![]() $\varphi _{\delta }$
by the requirement
$\varphi _{\delta }$
by the requirement
![]() $\varphi _{\delta }\restriction \mathbb {P}_{\beta }/\vec {p}^{\beta } = \varphi _{\beta }$
for all
$\varphi _{\delta }\restriction \mathbb {P}_{\beta }/\vec {p}^{\beta } = \varphi _{\beta }$
for all
![]() $\beta < \delta $
. See [Reference Dobrinen and Friedman9] for a more detailed proof for the validity of this construction.
$\beta < \delta $
. See [Reference Dobrinen and Friedman9] for a more detailed proof for the validity of this construction.
We conclude that, for this construction to succeed, the following conditions need to hold for all
![]() $\beta \leq \kappa $
: (i)
$\beta \leq \kappa $
: (i)
![]() $\vec {p}^{\beta },\vec {q}^{\beta }$
are well-defined conditions in
$\vec {p}^{\beta },\vec {q}^{\beta }$
are well-defined conditions in
![]() $\mathbb {P}_{\beta }$
which extend
$\mathbb {P}_{\beta }$
which extend
![]() $\vec {p}\restriction \beta ,\vec {q}\restriction \beta $
, respectively, and (ii)
$\vec {p}\restriction \beta ,\vec {q}\restriction \beta $
, respectively, and (ii)
![]() $\varphi _{\beta }$
is a well-defined cone isomorphism.
$\varphi _{\beta }$
is a well-defined cone isomorphism.
If the construction succeeds throughout all stages
![]() $\beta \leq \kappa $
, then the final conditions
$\beta \leq \kappa $
, then the final conditions
![]() $\vec {p^*} = \vec {p}^{\kappa }$
,
$\vec {p^*} = \vec {p}^{\kappa }$
,
![]() $\vec {q^*} = \vec {q}^{\kappa }$
and cone isomorphism
$\vec {q^*} = \vec {q}^{\kappa }$
and cone isomorphism
![]() $\varphi = \varphi _{\kappa }$
satisfy the required properties. It is easy to see that condition (i) and (ii) may only fail at limit stages
$\varphi = \varphi _{\kappa }$
satisfy the required properties. It is easy to see that condition (i) and (ii) may only fail at limit stages
![]() $\delta \leq \kappa $
, where the precise formation of the iteration (e.g., its support) may prevent
$\delta \leq \kappa $
, where the precise formation of the iteration (e.g., its support) may prevent
![]() $\vec {p}^{\delta }$
from being a condition in
$\vec {p}^{\delta }$
from being a condition in
![]() $\mathbb {P}_{\delta }$
. Similarly, the definition of the limit order
$\mathbb {P}_{\delta }$
. Similarly, the definition of the limit order
![]() $\leq _{\mathbb {P}_{\delta }}$
might prevent the defined map
$\leq _{\mathbb {P}_{\delta }}$
might prevent the defined map
![]() $\varphi _{\delta }$
from being an isomorphism.
$\varphi _{\delta }$
from being an isomorphism.
This problem does not occur for finite iteration.
Lemma 8.3 ([Reference Dobrinen and Friedman9]).
A finite iteration of ordinal definable cone homogeneous forcings is cone homogeneous.
Since our proof of Theorem 1.4 is based on a construction of a Magidor Iteration
![]() $\mathbb {P} = {\langle } \mathbb {P}_{\alpha },\mathbb {Q}_{\alpha } \mid \alpha < \theta {\rangle }$
of Prikry-type forcings
$\mathbb {P} = {\langle } \mathbb {P}_{\alpha },\mathbb {Q}_{\alpha } \mid \alpha < \theta {\rangle }$
of Prikry-type forcings
![]() $(\mathbb {Q}_{\alpha },\leq _{\mathbb {Q}_{\alpha }},\leq ^*_{\mathbb {Q}_{\alpha }})$
, we conclude this section with a description of a specific variant of cone homogeneity for the posets
$(\mathbb {Q}_{\alpha },\leq _{\mathbb {Q}_{\alpha }},\leq ^*_{\mathbb {Q}_{\alpha }})$
, we conclude this section with a description of a specific variant of cone homogeneity for the posets
![]() $\mathbb {Q}_{\alpha }$
, which guarantees that the Magidor iteration
$\mathbb {Q}_{\alpha }$
, which guarantees that the Magidor iteration
![]() $\mathbb {P}$
is cone homogeneous as well.
$\mathbb {P}$
is cone homogeneous as well.
Definition 8.4 (Prikry-type forcing, [Reference Gitik13]).
![]() $\langle \mathbb {P}, \leq , \leq ^*\rangle $
is a Prikry-type forcing if
$\langle \mathbb {P}, \leq , \leq ^*\rangle $
is a Prikry-type forcing if
-
•
 $\leq \supseteq \leq ^*$
are partial orders on
$\leq \supseteq \leq ^*$
are partial orders on
 $\mathbb {P}$
and
$\mathbb {P}$
and -
• (the Prikry Property) for every statement
 $\sigma $
in the forcing language for
$\sigma $
in the forcing language for
 $\langle \mathbb {P}, \leq \rangle $
, and a condition p, there is a condition
$\langle \mathbb {P}, \leq \rangle $
, and a condition p, there is a condition
 $p^*$
,
$p^*$
,
 $p \leq ^* p^*$
such that
$p \leq ^* p^*$
such that
 $p^* \Vdash \sigma $
or
$p^* \Vdash \sigma $
or
 $p^* \Vdash \neg \sigma $
.
$p^* \Vdash \neg \sigma $
.
Conditions in the Magidor iteration
![]() $\mathbb {P} = {\langle } \mathbb {P}_{\alpha },\mathbb {Q}_{\alpha } \mid \alpha < \kappa {\rangle }$
of Prikry-type posets
$\mathbb {P} = {\langle } \mathbb {P}_{\alpha },\mathbb {Q}_{\alpha } \mid \alpha < \kappa {\rangle }$
of Prikry-type posets
![]() ${\langle } \mathbb {Q}_{\alpha }, \leq _{\mathbb {Q}_{\alpha }},\leq ^*_{\mathbb {Q}_{\alpha }}{\rangle }$
are sequences
${\langle } \mathbb {Q}_{\alpha }, \leq _{\mathbb {Q}_{\alpha }},\leq ^*_{\mathbb {Q}_{\alpha }}{\rangle }$
are sequences
![]() $\vec {p} = {\langle } p_{\alpha } \mid \alpha < \kappa {\rangle }$
, which beyond the standard requirement of
$\vec {p} = {\langle } p_{\alpha } \mid \alpha < \kappa {\rangle }$
, which beyond the standard requirement of
![]() $p\restriction \alpha \Vdash p_{\alpha } \in \mathbb {Q}_{\alpha }$
, also satisfy that for all but finitely many ordinals
$p\restriction \alpha \Vdash p_{\alpha } \in \mathbb {Q}_{\alpha }$
, also satisfy that for all but finitely many ordinals
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $\vec {p} \restriction \alpha \Vdash p_{\alpha } \geq ^*_{\mathbb {Q}_{\alpha }} 0_{\mathbb {Q}_{\alpha }}$
. We note that, in particular, the definition allows using full-support conditions, as long as almost all components
$\vec {p} \restriction \alpha \Vdash p_{\alpha } \geq ^*_{\mathbb {Q}_{\alpha }} 0_{\mathbb {Q}_{\alpha }}$
. We note that, in particular, the definition allows using full-support conditions, as long as almost all components
![]() $p_{\alpha }$
are direct extensions of the trivial conditions. Similarly, for the definition of the ordering
$p_{\alpha }$
are direct extensions of the trivial conditions. Similarly, for the definition of the ordering
![]() $\leq _{\mathbb {P}}$
, we have that
$\leq _{\mathbb {P}}$
, we have that
![]() $\vec {p'} \geq \vec {p}$
requires both that
$\vec {p'} \geq \vec {p}$
requires both that
![]() $\vec {p'}\restriction \alpha \Vdash p^{\prime }_{\alpha } \geq _{\mathbb {Q}_{\alpha }} p_{\alpha }$
for all
$\vec {p'}\restriction \alpha \Vdash p^{\prime }_{\alpha } \geq _{\mathbb {Q}_{\alpha }} p_{\alpha }$
for all
![]() $\alpha $
and that for all but finitely many ordinals
$\alpha $
and that for all but finitely many ordinals
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $\vec {p'}\restriction \alpha \Vdash p^{\prime }_{\alpha } \geq ^* p_{\alpha }$
. See [Reference Gitik13] for a comprehensive description of the Magidor iteration style and its main properties.
$\vec {p'}\restriction \alpha \Vdash p^{\prime }_{\alpha } \geq ^* p_{\alpha }$
. See [Reference Gitik13] for a comprehensive description of the Magidor iteration style and its main properties.
Lemma 8.5. Suppose that
![]() $\mathbb {P} = {\langle } \mathbb {P}_{\alpha },\mathbb {Q}_{\alpha } \mid \alpha < \kappa {\rangle }$
is a Magidor iteration of Prikry-type posets
$\mathbb {P} = {\langle } \mathbb {P}_{\alpha },\mathbb {Q}_{\alpha } \mid \alpha < \kappa {\rangle }$
is a Magidor iteration of Prikry-type posets
![]() ${\langle } \mathbb {Q}_{\alpha }, \leq _{\mathbb {Q}_{\alpha }}, \leq ^*_{\mathbb {Q}_{\alpha }}{\rangle }$
so that the following conditions hold for each
${\langle } \mathbb {Q}_{\alpha }, \leq _{\mathbb {Q}_{\alpha }}, \leq ^*_{\mathbb {Q}_{\alpha }}{\rangle }$
so that the following conditions hold for each
![]() $\alpha < \kappa $
:
$\alpha < \kappa $
:
-
(i)
 $\mathbb {Q}_{\alpha }$
,
$\mathbb {Q}_{\alpha }$
,
 $\leq _{\mathbb {Q}_{\alpha }}$
and
$\leq _{\mathbb {Q}_{\alpha }}$
and
 $\leq ^*_{\mathbb {Q}_{\alpha }}$
are ordinal definable in V, and
$\leq ^*_{\mathbb {Q}_{\alpha }}$
are ordinal definable in V, and -
(ii) it is forced by
 $0_{\mathbb {P}_{\alpha }}$
that for every two conditions
$0_{\mathbb {P}_{\alpha }}$
that for every two conditions
 $p,q \in \mathbb {Q}_{\alpha }$
, there are
$p,q \in \mathbb {Q}_{\alpha }$
, there are
 $p^* \geq _{\mathbb {Q}_{\alpha }}^* p$
and
$p^* \geq _{\mathbb {Q}_{\alpha }}^* p$
and
 $q^* \geq ^*_{\mathbb {Q}_{\alpha }} q$
and a cone isomorphism
$q^* \geq ^*_{\mathbb {Q}_{\alpha }} q$
and a cone isomorphism
 $\psi _{\alpha }\colon \mathbb {Q}_{\alpha }/p^* \to \mathbb {Q}_{\alpha }/q^*$
which respects the direct extension order
$\psi _{\alpha }\colon \mathbb {Q}_{\alpha }/p^* \to \mathbb {Q}_{\alpha }/q^*$
which respects the direct extension order
 $\leq ^*_{\mathbb {Q}_{\alpha }}$
.
$\leq ^*_{\mathbb {Q}_{\alpha }}$
.
Then
![]() $\mathbb {P}$
is cone homogeneous.
$\mathbb {P}$
is cone homogeneous.
Proof. Let
![]() $\vec {p},\vec {q} \in \mathbb {P}$
, and let
$\vec {p},\vec {q} \in \mathbb {P}$
, and let
![]() $(\vec {p}^{\beta },\vec {q}^{\beta },\varphi _{\beta } \mid \beta \leq \kappa )$
be the sequence obtained form the procedure described above. It suffices to verify inductively that conditions (i) and (ii) are satisfied by the sequence.
$(\vec {p}^{\beta },\vec {q}^{\beta },\varphi _{\beta } \mid \beta \leq \kappa )$
be the sequence obtained form the procedure described above. It suffices to verify inductively that conditions (i) and (ii) are satisfied by the sequence.
We note that, in the successor step construction of
![]() $p^{\prime }_{\beta }$
,
$p^{\prime }_{\beta }$
,
![]() $p^*_{\beta } = (p^{\prime }_{\beta })^{\varphi _{\beta }^{-1}}$
,
$p^*_{\beta } = (p^{\prime }_{\beta })^{\varphi _{\beta }^{-1}}$
,
![]() $q^*_{\beta } = q^{\prime }_{\beta }$
, and
$q^*_{\beta } = q^{\prime }_{\beta }$
, and
![]() $\psi _{\beta }$
, we may assume that
$\psi _{\beta }$
, we may assume that
![]() $\varphi _{\beta }(\vec {p}^{\beta }) \Vdash p^{\prime }_{\beta } \geq ^*_{\mathbb {Q}_{\beta }} p_{\beta }^{\varphi _{\beta }}$
,
$\varphi _{\beta }(\vec {p}^{\beta }) \Vdash p^{\prime }_{\beta } \geq ^*_{\mathbb {Q}_{\beta }} p_{\beta }^{\varphi _{\beta }}$
,
![]() $\vec {q}^{\beta }\Vdash q^{\prime }_{\beta } \geq ^* q_{\beta }$
, and that
$\vec {q}^{\beta }\Vdash q^{\prime }_{\beta } \geq ^* q_{\beta }$
, and that
![]() $\psi _{\beta }$
is
$\psi _{\beta }$
is
![]() $\leq ^*_{\mathbb {Q}_{\beta }}$
-preserving. Since
$\leq ^*_{\mathbb {Q}_{\beta }}$
-preserving. Since
![]() $\leq ^*_{\mathbb {Q}_{\beta }}$
is ordinal definable in V,
$\leq ^*_{\mathbb {Q}_{\beta }}$
is ordinal definable in V,
![]() $0_{\mathbb {P}_{\beta }} \Vdash \leq ^*_{\mathbb {Q}_{\beta }} = (\leq ^*_{\mathbb {Q}_{\beta }})^{\varphi _{\beta }^{-1}}$
, and therefore by applying the automorphism
$0_{\mathbb {P}_{\beta }} \Vdash \leq ^*_{\mathbb {Q}_{\beta }} = (\leq ^*_{\mathbb {Q}_{\beta }})^{\varphi _{\beta }^{-1}}$
, and therefore by applying the automorphism
![]() $\varphi _{\beta }^{-1}$
we get
$\varphi _{\beta }^{-1}$
we get
![]() $\vec {p}^{\beta } \Vdash p^*_{\beta } \geq ^*_{\mathbb {Q}_{\beta }} p_{\beta }$
, and
$\vec {p}^{\beta } \Vdash p^*_{\beta } \geq ^*_{\mathbb {Q}_{\beta }} p_{\beta }$
, and
![]() $p \mapsto \psi _{\beta }(p^{\varphi _{\beta }})$
is forced by
$p \mapsto \psi _{\beta }(p^{\varphi _{\beta }})$
is forced by
![]() $\vec {p}^{\beta }$
to be
$\vec {p}^{\beta }$
to be
![]() $\leq ^*_{\mathbb {Q}_{\beta }}$
-preserving in the cone below
$\leq ^*_{\mathbb {Q}_{\beta }}$
-preserving in the cone below
![]() $p^*_{\beta }$
. In particular, assuming
$p^*_{\beta }$
. In particular, assuming
![]() $\varphi _{\beta }$
is order preserving and
$\varphi _{\beta }$
is order preserving and
![]() $\vec {r}^{\beta +1} \geq \vec {s}^{\beta +1} \in \mathbb {P}_{\beta +1}/\vec {p}^{\beta +1}$
,
$\vec {r}^{\beta +1} \geq \vec {s}^{\beta +1} \in \mathbb {P}_{\beta +1}/\vec {p}^{\beta +1}$
,
![]() $\vec {r}^{\beta +1} = \vec {r}^{\beta } {}^{\frown } {\langle } r_{\beta }{\rangle }$
,
$\vec {r}^{\beta +1} = \vec {r}^{\beta } {}^{\frown } {\langle } r_{\beta }{\rangle }$
,
![]() $\vec {s}^{\beta +1} = \vec {s}^{\beta } {}^{\frown } {\langle } s_{\beta }{\rangle }$
, we have that if
$\vec {s}^{\beta +1} = \vec {s}^{\beta } {}^{\frown } {\langle } s_{\beta }{\rangle }$
, we have that if
![]() $\vec {r}^{\beta } \Vdash r_{\beta } \geq ^*_{\mathbb {Q}_{\beta }} s_{\beta }$
then
$\vec {r}^{\beta } \Vdash r_{\beta } \geq ^*_{\mathbb {Q}_{\beta }} s_{\beta }$
then
![]() $\varphi _{\beta }(\vec {r}^{\beta }) \Vdash \psi _{\beta }(r_{\beta }^{\varphi _{\beta }}) \geq ^*_{\mathbb {Q}_{\beta }} \psi _{\beta }(r_{\beta }^{\varphi _{\beta }}) = \varphi _{\beta +1}(\vec {s}^{\beta +1})_{\beta }$
. The same conclusion holds for
$\varphi _{\beta }(\vec {r}^{\beta }) \Vdash \psi _{\beta }(r_{\beta }^{\varphi _{\beta }}) \geq ^*_{\mathbb {Q}_{\beta }} \psi _{\beta }(r_{\beta }^{\varphi _{\beta }}) = \varphi _{\beta +1}(\vec {s}^{\beta +1})_{\beta }$
. The same conclusion holds for
![]() $\leq _{\mathbb {Q}_{\beta }}$
which is also ordinal definable in V.
$\leq _{\mathbb {Q}_{\beta }}$
which is also ordinal definable in V.
We conclude that, first,
![]() $p^*_{\beta }, q_{\beta }^*$
are forced to be direct extensions of
$p^*_{\beta }, q_{\beta }^*$
are forced to be direct extensions of
![]() $0_{\mathbb {Q}_{\beta }}$
whenever
$0_{\mathbb {Q}_{\beta }}$
whenever
![]() $p_{\beta },q_{\beta }$
are, which in turn, implies that
$p_{\beta },q_{\beta }$
are, which in turn, implies that
![]() $\vec {p}^{\alpha },\vec {q}^{\alpha }$
are conditions of
$\vec {p}^{\alpha },\vec {q}^{\alpha }$
are conditions of
![]() $\mathbb {P}_{\alpha }$
for all
$\mathbb {P}_{\alpha }$
for all
![]() $\alpha \leq \kappa $
. Hence, (i) is satisfied. Second, for every
$\alpha \leq \kappa $
. Hence, (i) is satisfied. Second, for every
![]() $\vec {r}^{\alpha },\vec {s}^{\alpha } \in \mathbb {P}_{\alpha }/\vec {p}^{\alpha }$
and
$\vec {r}^{\alpha },\vec {s}^{\alpha } \in \mathbb {P}_{\alpha }/\vec {p}^{\alpha }$
and
![]() $\beta < \alpha $
, if
$\beta < \alpha $
, if
![]() $\vec {r}^{\alpha } \restriction \beta \Vdash r_{\beta } \geq ^*_{\mathbb {Q}_{\beta }} s_{\beta }$
, then
$\vec {r}^{\alpha } \restriction \beta \Vdash r_{\beta } \geq ^*_{\mathbb {Q}_{\beta }} s_{\beta }$
, then
![]() $\varphi _{\alpha }(\vec {r}^{\alpha })\restriction \beta \Vdash \varphi _{\alpha }(\vec {r}^{\alpha })_{\beta } \geq ^*_{\mathbb {Q}_{\beta }} \varphi _{\alpha }(\vec {s}^{\alpha })_{\beta }$
, and similarly, when replacing
$\varphi _{\alpha }(\vec {r}^{\alpha })\restriction \beta \Vdash \varphi _{\alpha }(\vec {r}^{\alpha })_{\beta } \geq ^*_{\mathbb {Q}_{\beta }} \varphi _{\alpha }(\vec {s}^{\alpha })_{\beta }$
, and similarly, when replacing
![]() $\leq ^*_{\mathbb {Q}_{\beta }}$
with
$\leq ^*_{\mathbb {Q}_{\beta }}$
with
![]() $\leq _{\mathbb {Q}_{\beta }}$
. It follows at once from this and the definition of the ordering
$\leq _{\mathbb {Q}_{\beta }}$
. It follows at once from this and the definition of the ordering
![]() $\leq _{\mathbb {P}_{\alpha }}$
of the Magidor iteration that
$\leq _{\mathbb {P}_{\alpha }}$
of the Magidor iteration that
![]() $\varphi _{\alpha }$
is a cone isomorphism. Hence, (ii) holds.
$\varphi _{\alpha }$
is a cone isomorphism. Hence, (ii) holds.
8.2 Homogeneous change of cofinalities
Our approach to construct a model with an
![]() $\omega $
-strongly measurable cardinal
$\omega $
-strongly measurable cardinal
![]() $\kappa $
is to force over a ground model satisfying
$\kappa $
is to force over a ground model satisfying
![]() $V = \operatorname {\mathrm {HOD}}$
with a weakly homogeneous poset (i.e., therefore also cone-homogeneous) to form a generic extension
$V = \operatorname {\mathrm {HOD}}$
with a weakly homogeneous poset (i.e., therefore also cone-homogeneous) to form a generic extension
![]() $V[G]$
with a cardinal
$V[G]$
with a cardinal
![]() $\kappa $
, which satisfies the conditions of Lemma 2.4. In light of Lemma 2.5 above, we see that many regular cardinals in V need to change their cofinality in
$\kappa $
, which satisfies the conditions of Lemma 2.4. In light of Lemma 2.5 above, we see that many regular cardinals in V need to change their cofinality in
![]() $V[G]$
. The main challenge in that regard is to change the cofinality of many cardinals with a weakly homogeneous forcing.
$V[G]$
. The main challenge in that regard is to change the cofinality of many cardinals with a weakly homogeneous forcing.
Fortunately, such forcing has been constructed in [Reference Ben-Neria and Unger5], where the theory of nonstationary support iteration of Prikry-type forcings is developed and employed to form a weakly homogeneous variant of the Gitik iteration ([Reference Gitik11]). We note that, as opposed to an Easton-style version of the Gitik iteration, which has a good chain condition (i.e.,
![]() $\kappa $
-c.c. when iterating up to a Mahlo cardinal
$\kappa $
-c.c. when iterating up to a Mahlo cardinal
![]() $\kappa $
), the nonstationary support variant of [Reference Ben-Neria and Unger5] has a weaker, fusion-type property.
$\kappa $
), the nonstationary support variant of [Reference Ben-Neria and Unger5] has a weaker, fusion-type property.
We briefly describe the construction of the nonstationary support iteration
![]() $\mathbb {P}$
of iteration of Prikry-type forcings
$\mathbb {P}$
of iteration of Prikry-type forcings
![]() $\mathbb {Q}_{\alpha }$
from [Reference Ben-Neria and Unger5]. The iteration, which is based on the given coherent sequence of measures
$\mathbb {Q}_{\alpha }$
from [Reference Ben-Neria and Unger5]. The iteration, which is based on the given coherent sequence of measures
![]() ${\langle } U_{\alpha ,\tau }\mid \alpha <\kappa , \tau <o^{\mathcal {U}}(\alpha ){\rangle }$
, is nontrivial at each
${\langle } U_{\alpha ,\tau }\mid \alpha <\kappa , \tau <o^{\mathcal {U}}(\alpha ){\rangle }$
, is nontrivial at each
![]() $\alpha < \kappa $
,
$\alpha < \kappa $
,
![]() $o^{\mathcal {U}}(\alpha )> 0$
. As this
$o^{\mathcal {U}}(\alpha )> 0$
. As this
![]() $\alpha $
, the forcing
$\alpha $
, the forcing
![]() $\mathbb {Q}_{\alpha }$
adds a cofinal closed unbounded set
$\mathbb {Q}_{\alpha }$
adds a cofinal closed unbounded set
![]() $b_{\alpha }$
to
$b_{\alpha }$
to
![]() $\alpha $
of order-type
$\alpha $
of order-type
![]() $\omega ^{o(\alpha )}$
(ordinal exponentiation). More specifically, given a V-generic filter
$\omega ^{o(\alpha )}$
(ordinal exponentiation). More specifically, given a V-generic filter
![]() $G_{\alpha } \subseteq \mathbb {P}_{\alpha }$
, which adds clubs
$G_{\alpha } \subseteq \mathbb {P}_{\alpha }$
, which adds clubs
![]() $b_{\beta }$
, for
$b_{\beta }$
, for
![]() $\beta < \alpha $
,
$\beta < \alpha $
,
![]() $o^{\mathcal {U}}(\beta )> 0$
, one considers finite sequences
$o^{\mathcal {U}}(\beta )> 0$
, one considers finite sequences
![]() $t = {\langle }\nu _0,\dots ,\nu _{k-1}{\rangle }$
with the property that for every
$t = {\langle }\nu _0,\dots ,\nu _{k-1}{\rangle }$
with the property that for every
![]() $i < k-1$
, if
$i < k-1$
, if
![]() $o^{\mathcal {U}}(\nu _i) < o^{\mathcal {U}}(\nu _{i+1})$
then
$o^{\mathcal {U}}(\nu _i) < o^{\mathcal {U}}(\nu _{i+1})$
then
![]() $\nu _i \in b_{\nu _{i+1}}$
and
$\nu _i \in b_{\nu _{i+1}}$
and
![]() $b_{\nu _{i+1}} \cap \nu _i = b_{\nu _i}$
. Such sequences are called coherent (with respect to
$b_{\nu _{i+1}} \cap \nu _i = b_{\nu _i}$
. Such sequences are called coherent (with respect to
![]() $G_{\alpha }$
). If
$G_{\alpha }$
). If
![]() $\rho $
is an ordinal so that
$\rho $
is an ordinal so that
![]() $o(\nu _i) < \rho $
for all
$o(\nu _i) < \rho $
for all
![]() $i < k$
, then we say t is
$i < k$
, then we say t is
![]() $\rho $
-coherent. Otherwise, we denote by
$\rho $
-coherent. Otherwise, we denote by
![]() $t\restriction \rho $
to be the subsequence of
$t\restriction \rho $
to be the subsequence of
![]() $\nu _i \in t$
so that
$\nu _i \in t$
so that
![]() $o(\nu _i) < \rho $
.
$o(\nu _i) < \rho $
.
Working at
![]() $V[G_{\alpha }]$
, one constructs posets
$V[G_{\alpha }]$
, one constructs posets
![]() $\mathbb {Q}_{\alpha ,\tau }$
,
$\mathbb {Q}_{\alpha ,\tau }$
,
![]() $\tau \leq o^{\mathcal {U}}(\alpha )$
and simultaneously shows by induction on
$\tau \leq o^{\mathcal {U}}(\alpha )$
and simultaneously shows by induction on
![]() $\tau \leq o^{\mathcal {U}}(\alpha )$
that, for each
$\tau \leq o^{\mathcal {U}}(\alpha )$
that, for each
![]() $\tau $
-coherent sequence t,
$\tau $
-coherent sequence t,
![]() $U_{\alpha ,\tau } \in \mathcal {U}$
extends to
$U_{\alpha ,\tau } \in \mathcal {U}$
extends to
![]() $U_{\alpha ,\tau }(t)$
. We define
$U_{\alpha ,\tau }(t)$
. We define
![]() $\mathbb {Q}^0_{\alpha }$
to be the trivial poset, and given that the measures
$\mathbb {Q}^0_{\alpha }$
to be the trivial poset, and given that the measures
![]() $U_{\alpha ,\tau '}(t')$
have been defined for every
$U_{\alpha ,\tau '}(t')$
have been defined for every
![]() $\tau ' < \tau $
, and every
$\tau ' < \tau $
, and every
![]() $\tau '$
-coherent sequence
$\tau '$
-coherent sequence
![]() $t'$
, the forcing
$t'$
, the forcing
![]() $\mathbb {Q}^{\tau }_{\alpha }$
consists of pairs
$\mathbb {Q}^{\tau }_{\alpha }$
consists of pairs
![]() $q = {\langle } t, T{\rangle }$
where t is
$q = {\langle } t, T{\rangle }$
where t is
![]() $\tau $
-coherent,
$\tau $
-coherent,
![]() $T \subseteq [\alpha ]^{<\omega }$
is a tree whose stem is
$T \subseteq [\alpha ]^{<\omega }$
is a tree whose stem is
![]() $\emptyset $
and for every
$\emptyset $
and for every
![]() $s \in T$
,
$s \in T$
,
![]() $\operatorname {\mathrm {succ}}_T(s) := \{ \mu < \kappa \mid s {}^{\frown } {\langle } \mu {\rangle } \in T\} \in \bigcap _{\tau ' < \tau } U_{\alpha ,\tau '}( t{}^{\frown } s\restriction \tau ')$
. Direct extensions and end extensions of
$\operatorname {\mathrm {succ}}_T(s) := \{ \mu < \kappa \mid s {}^{\frown } {\langle } \mu {\rangle } \in T\} \in \bigcap _{\tau ' < \tau } U_{\alpha ,\tau '}( t{}^{\frown } s\restriction \tau ')$
. Direct extensions and end extensions of
![]() $\mathbb {Q}_{\alpha }^{\tau }$
are defined as usual.
$\mathbb {Q}_{\alpha }^{\tau }$
are defined as usual.
![]() $\mathbb {Q}_{\alpha }^{\tau }$
is a Prikry-type forcing whose direct extension is
$\mathbb {Q}_{\alpha }^{\tau }$
is a Prikry-type forcing whose direct extension is
![]() $\alpha $
-closed. With
$\alpha $
-closed. With
![]() $\mathbb {Q}_{\alpha ,\tau }$
determined, we consider the V-ultrapower by
$\mathbb {Q}_{\alpha ,\tau }$
determined, we consider the V-ultrapower by
![]() $U_{\alpha ,\tau }$
, by taking
$U_{\alpha ,\tau }$
, by taking
![]() $j_{\alpha ,\tau }\colon V \to M_{\alpha ,\tau } \cong Ult(V,U_{\alpha ,\tau })$
, and define for each
$j_{\alpha ,\tau }\colon V \to M_{\alpha ,\tau } \cong Ult(V,U_{\alpha ,\tau })$
, and define for each
![]() $\tau $
-coherent sequence t a
$\tau $
-coherent sequence t a
![]() $V[G_{\alpha }]$
measure
$V[G_{\alpha }]$
measure
![]() $U_{\alpha ,\tau }(t)$
by
$U_{\alpha ,\tau }(t)$
by
if there exist
![]() $p \in G_{\alpha }$
and a valid tree T such that
$p \in G_{\alpha }$
and a valid tree T such that
Fact 8.6.
-
1. For each
 $\alpha $
such that
$\alpha $
such that
 $o^{\mathcal {U}}(\alpha )> 0$
,
$o^{\mathcal {U}}(\alpha )> 0$
,
 $b_{\alpha }$
is a cofinal sequence at
$b_{\alpha }$
is a cofinal sequence at
 $\alpha $
of order type
$\alpha $
of order type
 $\omega ^{o^{\mathcal {U}}(\alpha )}$
(ordinal exponentiation).
$\omega ^{o^{\mathcal {U}}(\alpha )}$
(ordinal exponentiation). -
2. For each
 $\alpha \leq \kappa $
,
$\alpha \leq \kappa $
,
 $(\mathbb {P}_{\alpha },\leq ,\leq ^*)$
is a Prikry-type forcing.
$(\mathbb {P}_{\alpha },\leq ,\leq ^*)$
is a Prikry-type forcing. -
3. For every
 $\gamma < \alpha \leq \kappa $
, the quotient
$\gamma < \alpha \leq \kappa $
, the quotient
 $(\mathbb {P}_{\alpha }/\mathbb {P}_{\gamma }, \leq ,\leq ^*)$
is a Prikry-type forcing whose direct extension order
$(\mathbb {P}_{\alpha }/\mathbb {P}_{\gamma }, \leq ,\leq ^*)$
is a Prikry-type forcing whose direct extension order
 $\leq ^*$
is
$\leq ^*$
is
 $\gamma $
-closed. In particular, the quotient
$\gamma $
-closed. In particular, the quotient
 $\mathbb {P}_{\alpha }/\mathbb {P}_{\gamma }$
does not add new bounded subsets to
$\mathbb {P}_{\alpha }/\mathbb {P}_{\gamma }$
does not add new bounded subsets to
 $\gamma $
.
$\gamma $
. -
4. For every
 $\gamma < \alpha $
, the iteration
$\gamma < \alpha $
, the iteration
 $\mathbb {P}_{\alpha } / \mathbb {P}_{\gamma +1}$
is weakly homogeneous.
$\mathbb {P}_{\alpha } / \mathbb {P}_{\gamma +1}$
is weakly homogeneous.
Acknowledgements
We are grateful to Sandra Müller and Grigor Sargsyan for valuable conversations concerning the Inner Model Program and the study of
![]() $\operatorname {\mathrm {HOD}}$
. We are also grateful to the anonymous referee, whose suggestions helped us to improve the paper considerably.
$\operatorname {\mathrm {HOD}}$
. We are also grateful to the anonymous referee, whose suggestions helped us to improve the paper considerably.
Conflict of Interest
The authors have no conflict of interest to declare.
Funding statement
The first author was partially supported by the Israel Science Foundation Grant 1832/19. The second author research was partially supported by the Lise Meitner FWF grant 2650-N35 and by the Israel Science Foundation Grant 1967/21.