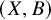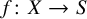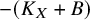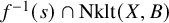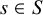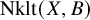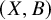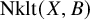1 Introduction
In birational geometry, one of the fundamental and most studied problems is the classification of singularities. The study of singularities can be carried out either from a local viewpoint, that is, considering a germ of a normal singularity
![]() $x \in X$
, or from a global one, considering a normal proper variety Y. More often than not, though, we are led to consider more general frameworks: namely, in the local case, we consider germs of a normal singularity
$x \in X$
, or from a global one, considering a normal proper variety Y. More often than not, though, we are led to consider more general frameworks: namely, in the local case, we consider germs of a normal singularity
![]() $x\in X$
and an effective Weil divisor B with coefficients in
$x\in X$
and an effective Weil divisor B with coefficients in
![]() $[0,1]$
, while in the global one, we consider log pairs
$[0,1]$
, while in the global one, we consider log pairs
![]() $(Y, B)$
(see Section 2.3 for the precise definitions). The importance of this generalization is evident if, for example, one considers the Riemann–Hurwitz formula for a proper finite map, cf. [Reference Kollár and Mori27, Proposition 5.20], or when attempting to extend the adjunction formula to the non-Gorenstein case, cf. [Reference Kollár23, Chapter 16]. From the point of view of the birational classification of algebraic varieties, and in particular, the Minimal Model Program, log canonical singularities are the broader class of interest. Roughly speaking, log canonical singularities can be characterized by the requirement that the pullback of a locally generating top-dimensional differential form may only have poles of order at most one along the exceptional divisors of a log resolution, cf. Section 2.3 for a more precise definition. It has been clear since the 1990s, through the work of Nadel and many others, that the locus of maximal singularities, that is, the set of points that are dominated by exceptional valuations along which poles of order one appear when pulling back a locally generating top-dimensional form, features very important geometrical and cohomological properties that can be used, for example, to construct and lift sections of log divisors from lower-dimensional subvarieties: this type of technique is one of the fundamental tools in the Minimal Model Program and birational geometry, at large. Such locus where the singularities are maximal is called the non-klt locus and, therefore, it is of particular interest to study its structure.
$(Y, B)$
(see Section 2.3 for the precise definitions). The importance of this generalization is evident if, for example, one considers the Riemann–Hurwitz formula for a proper finite map, cf. [Reference Kollár and Mori27, Proposition 5.20], or when attempting to extend the adjunction formula to the non-Gorenstein case, cf. [Reference Kollár23, Chapter 16]. From the point of view of the birational classification of algebraic varieties, and in particular, the Minimal Model Program, log canonical singularities are the broader class of interest. Roughly speaking, log canonical singularities can be characterized by the requirement that the pullback of a locally generating top-dimensional differential form may only have poles of order at most one along the exceptional divisors of a log resolution, cf. Section 2.3 for a more precise definition. It has been clear since the 1990s, through the work of Nadel and many others, that the locus of maximal singularities, that is, the set of points that are dominated by exceptional valuations along which poles of order one appear when pulling back a locally generating top-dimensional form, features very important geometrical and cohomological properties that can be used, for example, to construct and lift sections of log divisors from lower-dimensional subvarieties: this type of technique is one of the fundamental tools in the Minimal Model Program and birational geometry, at large. Such locus where the singularities are maximal is called the non-klt locus and, therefore, it is of particular interest to study its structure.
Connectedness of the non-klt locus
In this work, we prove an optimal and general structure theorem for the non-klt locus of positively curved pairs, which falls in the framework of the following connectedness principle.
Connectedness Principle. Let
![]() $(X,B)$
be a log canonical pair. Let
$(X,B)$
be a log canonical pair. Let
![]() $f \colon X \rightarrow S$
be a contraction. If
$f \colon X \rightarrow S$
be a contraction. If
![]() $-({K_{X}}+ B)$
is f-nef and f-big, then
$-({K_{X}}+ B)$
is f-nef and f-big, then
![]() $\operatorname {\mathrm {Nklt}}(X,B)$
is connected in a neighborhood of any fiber of f.
$\operatorname {\mathrm {Nklt}}(X,B)$
is connected in a neighborhood of any fiber of f.
The original version of the connectedness principle dates back to [Reference Kollár23, Theorem 17.4], which generalized a result of Shokurov, [Reference Shokurov34, 5.7], who proved the principle for antiample log canonical divisors. Many more instances and generalizations of the principle have appeared throughout the years. Despite its simplicity, this statement has many powerful applications: for example, inversion of adjunction (see [Reference Kollár23, Theorem 17.6], [Reference Kawakita21], and [Reference Hacon15] for a more recent and general version) or the fact that log canonical singularities are Du-Bois (see [Reference Kollár and Kovács26]), or yet again, the study of the geometry and boundedness of varieties of Fano-type and complements (see [Reference Birkar5, Reference Hacon and McKernan18, Reference Keel and McKernan22]). Perhaps more surprisingly, the connectedness principle has also been used to study hyperbolicity questions related to the positivity of log pairs and even foliations (see [Reference Spicer and Svaldi35, Reference Svaldi36]). We work with the following setup: we consider log pairs
![]() $(X,B)$
together with a contraction
$(X,B)$
together with a contraction
![]() $f \colon X \rightarrow S$
, such that
$f \colon X \rightarrow S$
, such that
![]() $-({K_{X}} + B) \ f$
-nef. Defining the auxiliary class
$-({K_{X}} + B) \ f$
-nef. Defining the auxiliary class
![]() and considering the Cartier closure
and considering the Cartier closure
![]() $\mathbf {M}$
of
$\mathbf {M}$
of
![]() $\mathbf {M} _X$
, we obtain a generalized pair
$\mathbf {M} _X$
, we obtain a generalized pair
![]() $(X, B, \mathbf {M})$
. This new pair has the advantage of being a Calabi–Yau generalized pair, that is
$(X, B, \mathbf {M})$
. This new pair has the advantage of being a Calabi–Yau generalized pair, that is
![]() $K_X+B+\mathbf {M}_X \sim _{\mathbb {Q}} 0$
, a condition that is maintained when taking a birational contraction of the space X; moreover, passing to the framework of generalized pairs does not alter the non-klt locus. Using these data, we are reduced to studying connectedness properties of the non-klt locus of generalized pairs of Calabi–Yau type. In this framework, we are able to fully and explicitly describe the extent to which failure of the connectedness of
$K_X+B+\mathbf {M}_X \sim _{\mathbb {Q}} 0$
, a condition that is maintained when taking a birational contraction of the space X; moreover, passing to the framework of generalized pairs does not alter the non-klt locus. Using these data, we are reduced to studying connectedness properties of the non-klt locus of generalized pairs of Calabi–Yau type. In this framework, we are able to fully and explicitly describe the extent to which failure of the connectedness of
![]() $f^{-1} (s) \cap \operatorname {\mathrm {Nklt}}(X,B)$
may be realized.
$f^{-1} (s) \cap \operatorname {\mathrm {Nklt}}(X,B)$
may be realized.
Theorem 1.1. Let
![]() $(X,B,\mathbf {M})/S$
be a generalized pair and
$(X,B,\mathbf {M})/S$
be a generalized pair and
![]() $f \colon X \rightarrow S$
be a projective morphism, such that
$f \colon X \rightarrow S$
be a projective morphism, such that
![]() ${K_{X}} + B + \mathbf {M}_X \sim _{\mathbb {Q},f} 0$
. Fix
${K_{X}} + B + \mathbf {M}_X \sim _{\mathbb {Q},f} 0$
. Fix
![]() $s \in S$
, and assume that
$s \in S$
, and assume that
![]() $f^{-1} (s)$
is connected but
$f^{-1} (s)$
is connected but
![]() $f^{-1} (s) \cap \operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})$
is disconnected (as
$f^{-1} (s) \cap \operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})$
is disconnected (as
![]() $k(s)$
-schemes). Then,
$k(s)$
-schemes). Then,
![]() $f^{-1} (s) \cap \operatorname {\mathrm {Nklt}}(X,B,\mathbf {M} )$
has exactly two connected components. Moreover, taking a dlt model
$f^{-1} (s) \cap \operatorname {\mathrm {Nklt}}(X,B,\mathbf {M} )$
has exactly two connected components. Moreover, taking a dlt model
![]() $\overline f \colon (\overline X, \overline B , \mathbf {M}) \rightarrow S$
of
$\overline f \colon (\overline X, \overline B , \mathbf {M}) \rightarrow S$
of
![]() $(X, B, \mathbf {M})$
, then
$(X, B, \mathbf {M})$
, then
-
(1)
 $(\overline X,\overline B,\mathbf {M})/S$
is generalized plt in a neighborhood of
$(\overline X,\overline B,\mathbf {M})/S$
is generalized plt in a neighborhood of
 $\overline {f}^{-1} (s)$
; and
$\overline {f}^{-1} (s)$
; and -
(2) there are an étale morphism
 $(s' \in S') \rightarrow (s \in S)$
and a projective morphism
$(s' \in S') \rightarrow (s \in S)$
and a projective morphism
 $T' \rightarrow S'$
, such that
$T' \rightarrow S'$
, such that
 $k(s)=k(s')$
and
$k(s)=k(s')$
and
 $(\overline X, \overline B,\mathbf {M} ) \times _S S'$
is birational to a standard
$(\overline X, \overline B,\mathbf {M} ) \times _S S'$
is birational to a standard
 ${\mathbb P}^{1}$
-link over
${\mathbb P}^{1}$
-link over
 $T'$
.
$T'$
.
After the completion of this work, we learned that Birkar has also obtained a similar statement to Theorem 1.1 using different techniques, [Reference Birkar4].
In dimension 2, Shokurov proved that Theorem 1.1 for log Calabi–Yau pairs, that is, when
![]() ${K_{X}} + B$
is numerically trivial, [Reference Kollár23, Proposition 12.3.1]; Prokhorov then settled the theorem, in general, for log canonical of dimension 2, [Reference Prokhorov32, Section 3.3]. In the log Calabi–Yau case, a version of the theorem was proven by Fujino in dimension 3, [Reference Fujino11], and later Kollár and Kovács extended it in any dimension, [Reference Kollár and Kovács26]. More recently, Hacon and Han, [Reference Hacon and Han16], proved a weaker version of Theorem 1.1 conditionally to termination of flips or to the dimension of X being at most 4. Our approach is rather different than the most recent results of [Reference Hacon and Han16], and our main insight is the adoption of the language of generalized pairs, cf. Section 2.3, together with the establishment of a canonical bundle formula for these pairs (see Theorem 2.20).
${K_{X}} + B$
is numerically trivial, [Reference Kollár23, Proposition 12.3.1]; Prokhorov then settled the theorem, in general, for log canonical of dimension 2, [Reference Prokhorov32, Section 3.3]. In the log Calabi–Yau case, a version of the theorem was proven by Fujino in dimension 3, [Reference Fujino11], and later Kollár and Kovács extended it in any dimension, [Reference Kollár and Kovács26]. More recently, Hacon and Han, [Reference Hacon and Han16], proved a weaker version of Theorem 1.1 conditionally to termination of flips or to the dimension of X being at most 4. Our approach is rather different than the most recent results of [Reference Hacon and Han16], and our main insight is the adoption of the language of generalized pairs, cf. Section 2.3, together with the establishment of a canonical bundle formula for these pairs (see Theorem 2.20).
The statement of Theorem 1.1 is sharp, in that none of its hypotheses may be weakened. We remark that we do not assume any hypothesis on the singularities of the generalized pair
![]() $(X, B, \mathbf {M})$
. Properties (1)–(2) in the above statement imply that, when
$(X, B, \mathbf {M})$
. Properties (1)–(2) in the above statement imply that, when
![]() $\operatorname {\mathrm {Nklt}}(X,B,\mathbf {M} )$
is disconnected in a neighborhood of
$\operatorname {\mathrm {Nklt}}(X,B,\mathbf {M} )$
is disconnected in a neighborhood of
![]() $f^{-1}(s)$
, then
$f^{-1}(s)$
, then
![]() $(X, B, \mathbf {M})$
is actually generalized log canonical and, étale locally around s, the pair admits exactly two disjoint log canonical centers that coincide with the two connected components of
$(X, B, \mathbf {M})$
is actually generalized log canonical and, étale locally around s, the pair admits exactly two disjoint log canonical centers that coincide with the two connected components of
![]() $\operatorname {\mathrm {Nklt}}(X,B,\mathbf {M} )$
in a neighborhood of
$\operatorname {\mathrm {Nklt}}(X,B,\mathbf {M} )$
in a neighborhood of
![]() $f^{-1}(s)$
. Furthermore, easy examples show that, in order to conclude that properties (1)–(2) hold in the statement of Theorem 1.1, we may be forced to pass to a dlt model of
$f^{-1}(s)$
. Furthermore, easy examples show that, in order to conclude that properties (1)–(2) hold in the statement of Theorem 1.1, we may be forced to pass to a dlt model of
![]() $(X, B, \mathbf {M})$
(see Section 2.4 for the definition and existence of dlt models).
$(X, B, \mathbf {M})$
(see Section 2.4 for the definition and existence of dlt models).
Example 1.2. Let us consider
![]() (while S will be a point in this example and
(while S will be a point in this example and
![]() $M=0$
) with homogeneous coordinates,
$M=0$
) with homogeneous coordinates,
![]() $X_0, X_1, X_2$
, and let
$X_0, X_1, X_2$
, and let
![]() , where
, where
![]() and
and
![]() . Then
. Then
![]() $(\mathbb P^2, B)$
is log canonical, but not dlt,
$(\mathbb P^2, B)$
is log canonical, but not dlt,
![]() $K_{\mathbb P^2} +B \sim _{\mathbb Q} 0$
, and its log canonical centers are the point
$K_{\mathbb P^2} +B \sim _{\mathbb Q} 0$
, and its log canonical centers are the point
![]() $[0:0:1]$
and the line
$[0:0:1]$
and the line
![]() $\{X_2=0\}$
. Hence,
$\{X_2=0\}$
. Hence,
![]() $\operatorname {\mathrm {Nklt}}(X, B)$
is disconnected, but it is not divisorial — which shows that
$\operatorname {\mathrm {Nklt}}(X, B)$
is disconnected, but it is not divisorial — which shows that
![]() $(X, B)$
is not dlt. To obtain a dlt model
$(X, B)$
is not dlt. To obtain a dlt model
![]() $(\overline X, \overline B)$
of
$(\overline X, \overline B)$
of
![]() $(X, B)$
, it suffices to blow up the point
$(X, B)$
, it suffices to blow up the point
![]() $[0:0:1]$
. Thus, in this case,
$[0:0:1]$
. Thus, in this case,
![]() $\overline X=F_1$
and
$\overline X=F_1$
and
![]() $\overline {B} = \{0\} \times \mathbb P^1 + \{\infty \} \times \mathbb P^1 + \frac 2 3 (\mathbb P^1 \times \{0\} + \mathbb P^1 \times \{1\} + \mathbb P^1 \times \{\infty \})$
, which immediately shows how the projection of
$\overline {B} = \{0\} \times \mathbb P^1 + \{\infty \} \times \mathbb P^1 + \frac 2 3 (\mathbb P^1 \times \{0\} + \mathbb P^1 \times \{1\} + \mathbb P^1 \times \{\infty \})$
, which immediately shows how the projection of
![]() $X'$
to the second factor endows the pair
$X'$
to the second factor endows the pair
![]() $(\overline X, \overline B)$
with a
$(\overline X, \overline B)$
with a
![]() $\mathbb {P}^1$
-link structure over
$\mathbb {P}^1$
-link structure over
![]() $\mathbb {P}^1$
.
$\mathbb {P}^1$
.
The notion of standard
![]() ${\mathbb P}^{1}$
-link mentioned in (2) of the above theorem is an adaptation to the framework of generalized pairs of the following fundamental example. It is recalled and defined precisely in the context of generalized pairs in Section 2.6.
${\mathbb P}^{1}$
-link mentioned in (2) of the above theorem is an adaptation to the framework of generalized pairs of the following fundamental example. It is recalled and defined precisely in the context of generalized pairs in Section 2.6.
Example 1.3. Let
![]() $(T,\Delta )$
be a klt pair. Then, the pair
$(T,\Delta )$
be a klt pair. Then, the pair
![]() $({\mathbb P}^{1} \times T,\lbrace 0 \rbrace \times T + \lbrace \infty \rbrace \times T + {\mathbb P}^{1} \times \Delta )$
together with the morphism
$({\mathbb P}^{1} \times T,\lbrace 0 \rbrace \times T + \lbrace \infty \rbrace \times T + {\mathbb P}^{1} \times \Delta )$
together with the morphism
![]() $f \colon {\mathbb P}^{1} \times T \rightarrow T$
is a standard
$f \colon {\mathbb P}^{1} \times T \rightarrow T$
is a standard
![]() ${\mathbb P}^{1}$
-link. Notice that
${\mathbb P}^{1}$
-link. Notice that
![]() $f^{-1} (t) \cap \operatorname {\mathrm {Nklt}}({\mathbb P}^{1} \times T,\lbrace 0 \rbrace \times T + \lbrace \infty \rbrace \times T + {\mathbb P}^{1} \times \Delta )$
has two connected components for every
$f^{-1} (t) \cap \operatorname {\mathrm {Nklt}}({\mathbb P}^{1} \times T,\lbrace 0 \rbrace \times T + \lbrace \infty \rbrace \times T + {\mathbb P}^{1} \times \Delta )$
has two connected components for every
![]() $t \in T$
, each one corresponding to one of the two distinguished sections of f.
$t \in T$
, each one corresponding to one of the two distinguished sections of f.
 $\mathbb {P}^1$
-links
$\mathbb {P}^1$
-links
The content of Theorem 1.1 can be used inductively to study the combinatorics of the log canonical centers of a dlt pair
![]() $(X,B)$
with
$(X,B)$
with
![]() $-({K_{X}} + B) \ f$
-nef for some contraction
$-({K_{X}} + B) \ f$
-nef for some contraction
![]() $f \colon X \rightarrow S$
. More precisely, we obtain the following statement, generalizing the content of [Reference Kollár25, Theorem 4.40].
$f \colon X \rightarrow S$
. More precisely, we obtain the following statement, generalizing the content of [Reference Kollár25, Theorem 4.40].
Theorem 1.4. Let
![]() $(X,B, \mathbf {M})/S$
be a generalized dlt pair and
$(X,B, \mathbf {M})/S$
be a generalized dlt pair and
![]() $f \colon X \rightarrow S$
be a projective morphism, such that
$f \colon X \rightarrow S$
be a projective morphism, such that
![]() ${K_{X}} + B + \mathbf {M} _X \sim _{\mathbb {Q},f} 0$
. Fix
${K_{X}} + B + \mathbf {M} _X \sim _{\mathbb {Q},f} 0$
. Fix
![]() $s \in S$
, such that
$s \in S$
, such that
![]() $f^{-1} (s)$
is connected. Let
$f^{-1} (s)$
is connected. Let
![]() $Z \subset X$
be minimal (with respect to inclusion) among the generalized log canonical centers, such that
$Z \subset X$
be minimal (with respect to inclusion) among the generalized log canonical centers, such that
![]() $s \in f (Z)$
. Let W be a generalized log canonical center, such that
$s \in f (Z)$
. Let W be a generalized log canonical center, such that
![]() $s \in f (W)$
. Then, there exists a generalized log canonical center
$s \in f (W)$
. Then, there exists a generalized log canonical center
![]() $Z_W \subset W$
, such that Z and
$Z_W \subset W$
, such that Z and
![]() $Z_W$
are
$Z_W$
are
![]() ${\mathbb P}^{1}$
-linked and
${\mathbb P}^{1}$
-linked and
![]() $s \in f(Z_W)$
. In particular, all the minimal (with respect to inclusion) generalized log canonical centers
$s \in f(Z_W)$
. In particular, all the minimal (with respect to inclusion) generalized log canonical centers
![]() $Z_i \subset Z$
, such that
$Z_i \subset Z$
, such that
![]() $s \in f (Z_i)$
are
$s \in f (Z_i)$
are
![]() ${\mathbb P}^{1}$
-linked to each other.
${\mathbb P}^{1}$
-linked to each other.
In [Reference Hacon and Han16], Hacon and Han proved a similar statement for log pairs, conditionally to termination of flips or to the condition
![]() $\dim (X) \leq 4$
.
$\dim (X) \leq 4$
.
We illustrate the idea behind Theorem 1.4 with an example.
Example 1.5. Consider the pair
![]() $(X, B)$
, where
$(X, B)$
, where
![]() $X={\mathbb P}^{1} \times {\mathbb P}^{1}$
and
$X={\mathbb P}^{1} \times {\mathbb P}^{1}$
and
![]() is a toric invariant divisor, whose irreducible components are the
is a toric invariant divisor, whose irreducible components are the
![]() $B_i$
. Then, the pair
$B_i$
. Then, the pair
![]() $(X,B)$
is dlt with
$(X,B)$
is dlt with
![]() ${K_{X}} + B \sim 0$
and Theorem 1.4 applies. The minimal log canonical centers of the pair
${K_{X}} + B \sim 0$
and Theorem 1.4 applies. The minimal log canonical centers of the pair
![]() $(X,B)$
are the four toric invariant points given by the intersections of the
$(X,B)$
are the four toric invariant points given by the intersections of the
![]() $B_i$
. For every
$B_i$
. For every
![]() $i= 1, \ldots , 4$
,
$i= 1, \ldots , 4$
,
![]() $(B_i,(B-B_i)|_{D_{i}}) = (B_i, p_{i, 0} + p_{i, 1}) \simeq ({\mathbb P}^{1},\lbrace 0 \rbrace + \lbrace \infty \rbrace )$
. For any i, we say that the points
$(B_i,(B-B_i)|_{D_{i}}) = (B_i, p_{i, 0} + p_{i, 1}) \simeq ({\mathbb P}^{1},\lbrace 0 \rbrace + \lbrace \infty \rbrace )$
. For any i, we say that the points
![]() $p_{i, 0}, p_{i, 1}$
are directly
$p_{i, 0}, p_{i, 1}$
are directly
![]() ${\mathbb P}^{1}$
-linked, as they lie on the same log canonical center. Not all of the
${\mathbb P}^{1}$
-linked, as they lie on the same log canonical center. Not all of the
![]() $p_{i, j}$
,
$p_{i, j}$
,
![]() $i=1, \dots , 4$
,
$i=1, \dots , 4$
,
![]() $j = 0, 1$
are directly
$j = 0, 1$
are directly
![]() ${\mathbb P}^{1}$
-linked, as we can choose a pair of them that do not lie on the same curve
${\mathbb P}^{1}$
-linked, as we can choose a pair of them that do not lie on the same curve
![]() $B_i$
. Nonetheless, the property of being
$B_i$
. Nonetheless, the property of being
![]() ${\mathbb P}^{1}$
-linked is an equivalence relation, and so we can partition the set of four points into the orbits of this equivalence relation. In the case of
${\mathbb P}^{1}$
-linked is an equivalence relation, and so we can partition the set of four points into the orbits of this equivalence relation. In the case of
![]() ${\mathbb P}^{1} \times {\mathbb P}^{1}$
, and more generally for the case of toric pairs, it is immediate to see that the conclusion of Theorem 1.4 holds at once: namely, all
${\mathbb P}^{1} \times {\mathbb P}^{1}$
, and more generally for the case of toric pairs, it is immediate to see that the conclusion of Theorem 1.4 holds at once: namely, all
![]() $p_{i, j}$
are
$p_{i, j}$
are
![]() ${\mathbb P}^{1}$
-linked.
${\mathbb P}^{1}$
-linked.
Dual complex for generalized log Calabi–Yau pairs
The dual complex of singularities
![]() $\mathcal {DMR}(X,B)$
of a log canonical pair
$\mathcal {DMR}(X,B)$
of a log canonical pair
![]() $(X,B)$
is a piecewise-linear (PL) homeomorphism equivalence class of CW-complexes encoding combinatorial information about the strata of
$(X,B)$
is a piecewise-linear (PL) homeomorphism equivalence class of CW-complexes encoding combinatorial information about the strata of
![]() $\operatorname {\mathrm {Nklt}}(X,B)$
. Given a log resolution
$\operatorname {\mathrm {Nklt}}(X,B)$
. Given a log resolution
![]() $\pi \colon Y \rightarrow X$
of
$\pi \colon Y \rightarrow X$
of
![]() $(X,B)$
, it is possible to construct a CW-complex
$(X,B)$
, it is possible to construct a CW-complex
![]() $\mathcal {D}(B_Y^{=1})$
, whose cells are in correspondence with the intersections of the irreducible components of the simple normal crossing variety
$\mathcal {D}(B_Y^{=1})$
, whose cells are in correspondence with the intersections of the irreducible components of the simple normal crossing variety
![]() $B_Y^{=1}$
containing all prime divisors of Y along which
$B_Y^{=1}$
containing all prime divisors of Y along which
![]() $K_X+B$
has poles of order one (see Section 2.7 for a rigorous definition). By work of de Fernex, Kollár, and Xu, [Reference de Fernex, Kollár and Xu8], the PL-homeomorphism type of
$K_X+B$
has poles of order one (see Section 2.7 for a rigorous definition). By work of de Fernex, Kollár, and Xu, [Reference de Fernex, Kollár and Xu8], the PL-homeomorphism type of
![]() $\mathcal {D}(B_Y^{=1})$
is independent of the choice of log resolution
$\mathcal {D}(B_Y^{=1})$
is independent of the choice of log resolution
![]() $\pi \colon Y \rightarrow X$
. In [Reference Kollár and Xu28], Kollár and Xu studied the dual complex of log canonical pairs
$\pi \colon Y \rightarrow X$
. In [Reference Kollár and Xu28], Kollár and Xu studied the dual complex of log canonical pairs
![]() $(X,B)$
with
$(X,B)$
with
![]() ${K_{X}} + B \sim _{\mathbb {Q}} 0$
, proving that the PL-homeomorphism class
${K_{X}} + B \sim _{\mathbb {Q}} 0$
, proving that the PL-homeomorphism class
![]() $\mathcal {DMR}(X,B)$
of the dual complex of
$\mathcal {DMR}(X,B)$
of the dual complex of
![]() $(X, B)$
admits as a representative an equidimensional complex, and it satisfies
$(X, B)$
admits as a representative an equidimensional complex, and it satisfies
Furthermore, they described sufficient conditions for the contractibility of
![]() $\mathcal {DMR}(X,B)$
.
$\mathcal {DMR}(X,B)$
.
In this paper, we study the dual complex and its topological and cohomological features for log canonical pairs
![]() $(X,B)$
with
$(X,B)$
with
![]() $-({K_{X}} + B)$
nef, once again, by translating this problem into the analogous one for log Calabi–Yau generalized pairs with log canonical singularities. Theorems 1.1 and 1.4 provide us with powerful tools to extend the results of [Reference Kollár and Xu28] to this much wider context.
$-({K_{X}} + B)$
nef, once again, by translating this problem into the analogous one for log Calabi–Yau generalized pairs with log canonical singularities. Theorems 1.1 and 1.4 provide us with powerful tools to extend the results of [Reference Kollár and Xu28] to this much wider context.
Theorem 1.6. Let
![]() $(X, B, \mathbf {M})$
be a generalized pair with log canonical singularities. Assume that
$(X, B, \mathbf {M})$
be a generalized pair with log canonical singularities. Assume that
![]() $K_X+B+M \sim _{\mathbb {Q}} 0$
. Then the dual complex
$K_X+B+M \sim _{\mathbb {Q}} 0$
. Then the dual complex
![]() $\mathcal {DMR}(X,B, \mathbf {M} )$
is an equidimensional pseudo-manifold (with boundary). Moreover, exactly one of the following condition holds:
$\mathcal {DMR}(X,B, \mathbf {M} )$
is an equidimensional pseudo-manifold (with boundary). Moreover, exactly one of the following condition holds:
-
1.
 $\mathcal {DMR}(X,B, \mathbf {M} )$
is disconnected, and it only contains two points;
$\mathcal {DMR}(X,B, \mathbf {M} )$
is disconnected, and it only contains two points; -
2.
 $\mathcal {DMR}(X,B, \mathbf {M})$
is connected and collapsible to a point;
$\mathcal {DMR}(X,B, \mathbf {M})$
is connected and collapsible to a point; -
3.
 $\mathcal {DMR}(X,B, \mathbf {M})$
is connected, noncollapsible, and
$\mathcal {DMR}(X,B, \mathbf {M})$
is connected, noncollapsible, and  $$ \begin{align*} H^i(\mathcal{DMR}(X,B, \mathbf{M}), \mathbb Q)=0, \ \text{for} \ 0 < i < \dim \mathcal{DMR}(X,B, \mathbf{M}). \end{align*} $$
$$ \begin{align*} H^i(\mathcal{DMR}(X,B, \mathbf{M}), \mathbb Q)=0, \ \text{for} \ 0 < i < \dim \mathcal{DMR}(X,B, \mathbf{M}). \end{align*} $$
In order to prove Theorem 1.6, we show that the computation of the dual complex of a generalized log canonical pair can be reduced to the classical case of log pairs, in the noncollapsible case. Under this hypothesis, we show that, in general, the PL-homeomorphism class
![]() $\mathcal {DMR}(X,B, \mathbf {M})$
admits as a representative a finite quotient of the dual complex obtained by adjunction to a general fiber of the morphism
$\mathcal {DMR}(X,B, \mathbf {M})$
admits as a representative a finite quotient of the dual complex obtained by adjunction to a general fiber of the morphism
![]() $\tilde {q} \colon \tilde {X} \rightarrow Z$
constructed in Corollary 5.2 — here,
$\tilde {q} \colon \tilde {X} \rightarrow Z$
constructed in Corollary 5.2 — here,
![]() $\tilde X$
is a birational model of X crepant for the generalized pair
$\tilde X$
is a birational model of X crepant for the generalized pair
![]() $(X, B, \mathbf {M})$
. Moreover, using that
$(X, B, \mathbf {M})$
. Moreover, using that
![]() $\mathcal {DMR}(X,B, \mathbf {M})$
is noncollapsible, we show that, upon restricting to the general fiber F of
$\mathcal {DMR}(X,B, \mathbf {M})$
is noncollapsible, we show that, upon restricting to the general fiber F of
![]() $\tilde q$
, the moduli part
$\tilde q$
, the moduli part
![]() $\mathbf {M}$
becomes
$\mathbf {M}$
becomes
![]() $0$
on F and we can invoke the results of [Reference Kollár and Xu28].
$0$
on F and we can invoke the results of [Reference Kollár and Xu28].
Recent work of Nakamura, [Reference Nakamura31], extends the construction of dual complex also to the category of log pairs with singularities worse than log canonical. Nakamura, [Reference Nakamura31, Theorem 1.1], showed that the dual complex of a log pair
![]() $(X, B)$
is collapsible provided that
$(X, B)$
is collapsible provided that
![]() $-({K_{X}} + B)$
is nef and big, without any assumption on the singularities of
$-({K_{X}} + B)$
is nef and big, without any assumption on the singularities of
![]() $(X,B)$
. Using the techniques of [Reference Nakamura31] together with the ideas used in the proof of Theorem 1.6, we obtain the following theorem generalizing Nakamura’s result.
$(X,B)$
. Using the techniques of [Reference Nakamura31] together with the ideas used in the proof of Theorem 1.6, we obtain the following theorem generalizing Nakamura’s result.
Theorem 1.7. Let
![]() $(X, B, \mathbf {M})$
be a generalized pair with singularities worse than log canonical. Assume that
$(X, B, \mathbf {M})$
be a generalized pair with singularities worse than log canonical. Assume that
![]() $K_X+B + \mathbf {M} _X \sim _{\mathbb {Q}} 0$
. Then the dual complex
$K_X+B + \mathbf {M} _X \sim _{\mathbb {Q}} 0$
. Then the dual complex
![]() $\mathcal {DMR}(X,B, \mathbf {M})$
is collapsible.
$\mathcal {DMR}(X,B, \mathbf {M})$
is collapsible.
Strategy of proof.
The proof of Theorem 1.1 consists of several reductions. For simplicity, we sketch them under the assumption that
![]() $(X,B, \mathbf {M})$
is generalized log canonical. The general case is treated similarly but requires some heavy notation. In Section 3, we show that the number of connected components of
$(X,B, \mathbf {M})$
is generalized log canonical. The general case is treated similarly but requires some heavy notation. In Section 3, we show that the number of connected components of
![]() $\operatorname {\mathrm {Nklt}}(X,B, \mathbf {M})$
are preserved under birational morphisms. In particular, this allows us to run certain minimal model programs (MMPs) while preserving the assumptions of the statement. For instance, we can assume that X is
$\operatorname {\mathrm {Nklt}}(X,B, \mathbf {M})$
are preserved under birational morphisms. In particular, this allows us to run certain minimal model programs (MMPs) while preserving the assumptions of the statement. For instance, we can assume that X is
![]() $\mathbb {Q}$
-factorial, and that
$\mathbb {Q}$
-factorial, and that
![]() $(X,B, \mathbf {M})$
is generalized dlt. Thus, we have
$(X,B, \mathbf {M})$
is generalized dlt. Thus, we have
![]() $\operatorname {\mathrm {Nklt}}(X,B, \mathbf {M})=B^{=1}$
.
$\operatorname {\mathrm {Nklt}}(X,B, \mathbf {M})=B^{=1}$
.
Then, the core of the proof consists in showing that some component of
![]() $B^{=1}$
dominates S. This is done in Proposition 6.1. We illustrate the main idea under the assumption that S is a curve, and that
$B^{=1}$
dominates S. This is done in Proposition 6.1. We illustrate the main idea under the assumption that S is a curve, and that
![]() $s \in S$
is a closed point. Assume that no component of
$s \in S$
is a closed point. Assume that no component of
![]() $B^{=1}$
dominates S. Then, we can assume that all the connected components of
$B^{=1}$
dominates S. Then, we can assume that all the connected components of
![]() $B^{=1}$
map to s. For notation’s sake, assume that there are two, denoted by
$B^{=1}$
map to s. For notation’s sake, assume that there are two, denoted by
![]() $\Delta _1$
and
$\Delta _1$
and
![]() $\Delta _2$
. Let
$\Delta _2$
. Let
![]() $\tilde X \rightarrow X$
be a log resolution of
$\tilde X \rightarrow X$
be a log resolution of
![]() $(X,B)$
, and denote by
$(X,B)$
, and denote by
![]() $(\tilde X,B_{\tilde X}, \mathbf {M})$
the trace of
$(\tilde X,B_{\tilde X}, \mathbf {M})$
the trace of
![]() $(X,B, \mathbf {M})$
on
$(X,B, \mathbf {M})$
on
![]() $\tilde X$
(see the line before Definition 2.4 for the definition of trace of a generalized pair). By the results of Section 3,
$\tilde X$
(see the line before Definition 2.4 for the definition of trace of a generalized pair). By the results of Section 3,
![]() $B_{\tilde X}^{=1}$
has two distinct connected components,
$B_{\tilde X}^{=1}$
has two distinct connected components,
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
, each one mapping to the corresponding
$\Gamma _2$
, each one mapping to the corresponding
![]() $\Delta _i$
. Notice that
$\Delta _i$
. Notice that
![]() $\Gamma _1 \cup \Gamma _2 \subset \tilde X _s$
, where
$\Gamma _1 \cup \Gamma _2 \subset \tilde X _s$
, where
![]() $\tilde X _s$
denotes the fiber over s. By our assumption, the fiber
$\tilde X _s$
denotes the fiber over s. By our assumption, the fiber
![]() $\tilde X _s$
contains other irreducible components that connect
$\tilde X _s$
contains other irreducible components that connect
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
. Denote the support of these residual components by E. In order to get a contradiction, we would like to contract E. By ideas similar to ones contained in [Reference Fujino and Gongyo13, proof of Theorem 1.1], we can run a suitable MMP over S that contracts E, while preserving at least one irreducible component of each
$\Gamma _2$
. Denote the support of these residual components by E. In order to get a contradiction, we would like to contract E. By ideas similar to ones contained in [Reference Fujino and Gongyo13, proof of Theorem 1.1], we can run a suitable MMP over S that contracts E, while preserving at least one irreducible component of each
![]() $\Gamma _i$
. Thus, we reach a model
$\Gamma _i$
. Thus, we reach a model
![]() $\overline {X} \rightarrow S$
, where the fiber over s consists of the strict transforms of
$\overline {X} \rightarrow S$
, where the fiber over s consists of the strict transforms of
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $\Gamma _2$
, which are now connected. This contradicts suitable results in Section 3, which guarantee that the MMP we just ran cannot connect different connected components of the non-klt locus.
$\Gamma _2$
, which are now connected. This contradicts suitable results in Section 3, which guarantee that the MMP we just ran cannot connect different connected components of the non-klt locus.
When
![]() $\dim (S) \geq 2$
, this step is more delicate. Indeed, the components
$\dim (S) \geq 2$
, this step is more delicate. Indeed, the components
![]() $D_1$
and
$D_1$
and
![]() $D_2$
can dominate different subvarieties
$D_2$
can dominate different subvarieties
![]() $T_1$
and
$T_1$
and
![]() $T_2$
, each one containing s. To control this phenomenon, we make use of the generalized canonical bundle formula (see Section 2.5). For simplicity, assume that
$T_2$
, each one containing s. To control this phenomenon, we make use of the generalized canonical bundle formula (see Section 2.5). For simplicity, assume that
![]() $X \rightarrow S$
is a contraction. Then, the generalized canonical bundle formula allows us to define a generalized pair
$X \rightarrow S$
is a contraction. Then, the generalized canonical bundle formula allows us to define a generalized pair
![]() $(S,B_S,{\mathbf N})/S$
. In this way, we can regard
$(S,B_S,{\mathbf N})/S$
. In this way, we can regard
![]() $T_1$
and
$T_1$
and
![]() $T_2$
as non-klt centers of
$T_2$
as non-klt centers of
![]() $(S,B_S, {\mathbf N})$
. Then, the results of Section 3 guarantee that a generalized dlt model
$(S,B_S, {\mathbf N})$
. Then, the results of Section 3 guarantee that a generalized dlt model
![]() $\hat S$
of
$\hat S$
of
![]() $(S,B_S, {\mathbf N})$
preserves the connected components of
$(S,B_S, {\mathbf N})$
preserves the connected components of
![]() $\operatorname {\mathrm {Nklt}}(S,B_S, {\mathbf N})$
. To conclude, we show that a similar argument as in the case
$\operatorname {\mathrm {Nklt}}(S,B_S, {\mathbf N})$
. To conclude, we show that a similar argument as in the case
![]() $\dim (S)=1$
works over
$\dim (S)=1$
works over
![]() $\hat S$
. Once it is established that at least one connected component of
$\hat S$
. Once it is established that at least one connected component of
![]() $B^{=1}$
dominates S, we can conclude the proof of Theorem 1.1. Let
$B^{=1}$
dominates S, we can conclude the proof of Theorem 1.1. Let
![]() $D_1,\ldots ,D_k$
be the connected components of
$D_1,\ldots ,D_k$
be the connected components of
![]() $B^{=1}$
. Up to relabelling, we can assume that
$B^{=1}$
. Up to relabelling, we can assume that
![]() $D_1$
dominates S. Then, the divisor
$D_1$
dominates S. Then, the divisor
![]() ${K_{X}} + B^{< 1} +M$
is not pseudo-effective over S. Therefore, we may run a
${K_{X}} + B^{< 1} +M$
is not pseudo-effective over S. Therefore, we may run a
![]() $({K_{X}} + B^{<1} + \mathbf {M} _X)$
-MMP over S, which terminates with a Mori fiber space
$({K_{X}} + B^{<1} + \mathbf {M} _X)$
-MMP over S, which terminates with a Mori fiber space
![]() $g \colon \tilde X \rightarrow Z$
. Denote by
$g \colon \tilde X \rightarrow Z$
. Denote by
![]() $(\tilde X,\tilde B , \mathbf {M})$
the trace of
$(\tilde X,\tilde B , \mathbf {M})$
the trace of
![]() $(X,B, \mathbf {M})$
on
$(X,B, \mathbf {M})$
on
![]() $\tilde X$
. Since this is a
$\tilde X$
. Since this is a
![]() $(-B)^{=1}$
-MMP, it follows from the results in Section 3 that the connected components of
$(-B)^{=1}$
-MMP, it follows from the results in Section 3 that the connected components of
![]() $B^{=1}$
are in one-to-one correspondence with the connected components of
$B^{=1}$
are in one-to-one correspondence with the connected components of
![]() $\tilde B^{=1}$
. Since
$\tilde B^{=1}$
. Since
![]() $\tilde D _1$
is g-ample and
$\tilde D _1$
is g-ample and
![]() $\tilde D_1 \cap \tilde D_i = \emptyset $
for
$\tilde D_1 \cap \tilde D_i = \emptyset $
for
![]() $i \geq 2$
, it follows that g has relative dimension 1 with general fiber
$i \geq 2$
, it follows that g has relative dimension 1 with general fiber
![]() ${\mathbb P}^{1}$
. This forces every
${\mathbb P}^{1}$
. This forces every
![]() $D_i$
to be horizontal over Z. Since
$D_i$
to be horizontal over Z. Since
![]() ${K_{\tilde {X}}} + \tilde B + {\mathbf {M}}_{\tilde {X}} \sim _{\mathbb {Q}} 0/Z$
, it follows that
${K_{\tilde {X}}} + \tilde B + {\mathbf {M}}_{\tilde {X}} \sim _{\mathbb {Q}} 0/Z$
, it follows that
![]() $k =2$
. By direct inspection, we conclude that, when
$k =2$
. By direct inspection, we conclude that, when
![]() $k=2$
,
$k=2$
,
![]() $(\tilde X, \tilde B , \mathbf {M}) \rightarrow Z$
is a standard
$(\tilde X, \tilde B , \mathbf {M}) \rightarrow Z$
is a standard
![]() ${\mathbb P}^{1}$
-link up to an étale base change.
${\mathbb P}^{1}$
-link up to an étale base change.
The proof of Theorem 1.4 follows the proof of [Reference Kollár25, Theorem 4.40], which deals with the case of log Calabi–Yau pairs. The argument is by induction on the dimension and relies on Theorem 1.1 to reduce to the case when
![]() $\operatorname {\mathrm {Nklt}}(X,B, \mathbf {M})$
is connected along the fibers of the morphism.
$\operatorname {\mathrm {Nklt}}(X,B, \mathbf {M})$
is connected along the fibers of the morphism.
We conclude by sketching the proof of Theorem 1.6. Theorem 1.1 gives an explicit description of the case when
![]() $\mathcal {DMR}(X,B, \mathbf {M})$
is not connected. Therefore, we can assume that
$\mathcal {DMR}(X,B, \mathbf {M})$
is not connected. Therefore, we can assume that
![]() $\mathcal {DMR}(X,B, \mathbf {M})$
is connected. Then, as a direct combinatorial consequence of Theorem 1.4, we obtain that the dual complex
$\mathcal {DMR}(X,B, \mathbf {M})$
is connected. Then, as a direct combinatorial consequence of Theorem 1.4, we obtain that the dual complex
![]() $\mathcal {DMR}(X,B,\mathbf {M})$
is equidimensional at each point. In Section 5, we follow the ideas of [Reference Kollár and Xu28] and show that, under certain assumptions, we can construct a morphism
$\mathcal {DMR}(X,B,\mathbf {M})$
is equidimensional at each point. In Section 5, we follow the ideas of [Reference Kollár and Xu28] and show that, under certain assumptions, we can construct a morphism
![]() $f \colon X \rightarrow Z$
, such that
$f \colon X \rightarrow Z$
, such that
![]() $\dim (Z) \geq 1$
and
$\dim (Z) \geq 1$
and
![]() $\mathcal {DMR}(X,B, \mathbf {M}) \simeq \mathcal {DMR}(X_z,B_z, \mathbf {M} |_{X_{z}})/G$
, where
$\mathcal {DMR}(X,B, \mathbf {M}) \simeq \mathcal {DMR}(X_z,B_z, \mathbf {M} |_{X_{z}})/G$
, where
![]() $X_z$
is a general fiber of f and G is a finite group. Then, in this situation, we can argue by induction on the dimension. In the leftover cases, we have that
$X_z$
is a general fiber of f and G is a finite group. Then, in this situation, we can argue by induction on the dimension. In the leftover cases, we have that
![]() $B^{=1}$
fully supports a big and semiample divisor. This condition on
$B^{=1}$
fully supports a big and semiample divisor. This condition on
![]() $\operatorname {\mathrm {Nklt}}(X,B, \mathbf {M})$
allows us to apply a version of Kawamata–Viehweg vanishing for generalized pairs and conclude the proof of Theorem 1.6.
$\operatorname {\mathrm {Nklt}}(X,B, \mathbf {M})$
allows us to apply a version of Kawamata–Viehweg vanishing for generalized pairs and conclude the proof of Theorem 1.6.
2 Preliminaries
In this section, we set our notation and collect some definitions and preliminary results that will be useful in the paper.
2.1 Terminology and conventions
Throughout this paper, we will work over an algebraically closed field of characteristic 0. For anything not explicitly addressed in this subsection, we direct the reader to the terminology and the conventions of [Reference Kollár and Mori27] and [Reference Kollár25].
A contraction is a projective morphism
![]() $f\colon X \rightarrow Z$
of quasiprojective varieties with
$f\colon X \rightarrow Z$
of quasiprojective varieties with
![]() $f_* {\mathcal {O}_{X}} = {\mathcal {O}_{ Z}}$
. If X is normal, then so is Z and the fibers of f are connected. Let
$f_* {\mathcal {O}_{X}} = {\mathcal {O}_{ Z}}$
. If X is normal, then so is Z and the fibers of f are connected. Let
![]() $\mathbb {K}$
denote
$\mathbb {K}$
denote
![]() $\mathbb {Z}$
,
$\mathbb {Z}$
,
![]() $\mathbb {Q}$
, or
$\mathbb {Q}$
, or
![]() $\mathbb {R}$
. We say that D is a
$\mathbb {R}$
. We say that D is a
![]() $\mathbb {K}$
-divisor on a variety X if we can write
$\mathbb {K}$
-divisor on a variety X if we can write
![]() $D = \sum _{i=1}^n d_i P_i$
, where
$D = \sum _{i=1}^n d_i P_i$
, where
![]() $d_i \in \mathbb {K}$
,
$d_i \in \mathbb {K}$
,
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $P_i$
is a prime Weil divisor on X for all
$P_i$
is a prime Weil divisor on X for all
![]() $i=1, \ldots , n$
. We say that D is
$i=1, \ldots , n$
. We say that D is
![]() $\mathbb {K}$
-Cartier if it can be written as a
$\mathbb {K}$
-Cartier if it can be written as a
![]() $\mathbb {K}$
-linear combination of
$\mathbb {K}$
-linear combination of
![]() $\mathbb {Z}$
-divisors that are Cartier. The support of a
$\mathbb {Z}$
-divisors that are Cartier. The support of a
![]() $\mathbb {K}$
-divisor
$\mathbb {K}$
-divisor
![]() $D=\sum _{i=1}^n d_iP_i$
is the union of the prime divisors appearing in the formal sum
$D=\sum _{i=1}^n d_iP_i$
is the union of the prime divisors appearing in the formal sum
![]() $\mathrm {Supp}(D)= \sum _{i=1}^n P_i$
.
$\mathrm {Supp}(D)= \sum _{i=1}^n P_i$
.
In all of the above, if
![]() $\mathbb {K}= \mathbb {Z}$
, we will systematically drop it from the notation.
$\mathbb {K}= \mathbb {Z}$
, we will systematically drop it from the notation.
Given a prime divisor P in the support of D, we will denote by
![]() $\mu _P (D)$
the coefficient of P in D. Given a divisor
$\mu _P (D)$
the coefficient of P in D. Given a divisor
![]() $D = \sum _{i=1}^n \mu _{P_i}(D) P_i$
, we define its round down
$D = \sum _{i=1}^n \mu _{P_i}(D) P_i$
, we define its round down
![]() . The round up
. The round up
![]() $\lceil D \rceil $
of D is defined analogously. The fractional part
$\lceil D \rceil $
of D is defined analogously. The fractional part
![]() $\{D\}$
of D is defined as
$\{D\}$
of D is defined as
![]() . Let
. Let
![]() $D_1 = \sum _{i=1} ^n \mu _{P_i}(D_1) P_i$
and
$D_1 = \sum _{i=1} ^n \mu _{P_i}(D_1) P_i$
and
![]() $D_2= \sum _{i=1} ^n \mu _{P_i}(D_2) P_i$
. We define
$D_2= \sum _{i=1} ^n \mu _{P_i}(D_2) P_i$
. We define
![]() . Similarly, we set
. Similarly, we set
![]() . For a divisor D, we set
. For a divisor D, we set
![]() , where
, where
![]() $0$
denotes the zero divisor. Similarly, we define
$0$
denotes the zero divisor. Similarly, we define
![]() . In particular, we have
. In particular, we have
![]() $D=D^{\geq 0} - D^{\leq 0}$
.
$D=D^{\geq 0} - D^{\leq 0}$
.
Given a divisor
![]() $D = \sum \mu _{P_i}(D) P_i$
on a normal variety X, and a morphism
$D = \sum \mu _{P_i}(D) P_i$
on a normal variety X, and a morphism
![]() $\pi \colon X \to Z$
, we define
$\pi \colon X \to Z$
, we define
2.2 B-divisors
Let
![]() $\mathbb {K}$
denote
$\mathbb {K}$
denote
![]() $\mathbb {Z}$
,
$\mathbb {Z}$
,
![]() $\mathbb {Q}$
, or
$\mathbb {Q}$
, or
![]() $\mathbb {R}$
. Given a normal variety X, a
$\mathbb {R}$
. Given a normal variety X, a
![]() $\mathbb {K}$
-b-divisor
$\mathbb {K}$
-b-divisor
![]() $\mathbf {D}$
is a (possibly infinite) sum of geometric valuations
$\mathbf {D}$
is a (possibly infinite) sum of geometric valuations
![]() $V_i$
of
$V_i$
of
![]() $k(X)$
with coefficients in
$k(X)$
with coefficients in
![]() $\mathbb {K}$
,
$\mathbb {K}$
,
such that for every normal variety
![]() $X'$
birational to X, only a finite number of the
$X'$
birational to X, only a finite number of the
![]() $V_i$
can be realized by divisors on
$V_i$
can be realized by divisors on
![]() $X'$
. The trace
$X'$
. The trace
![]() $\mathbf {D}_{X'}$
of
$\mathbf {D}_{X'}$
of
![]() $\mathbf {D}$
on
$\mathbf {D}$
on
![]() $X'$
is defined as
$X'$
is defined as

where
![]() $c_{X'}(V_i)$
denotes the center of the valuation on
$c_{X'}(V_i)$
denotes the center of the valuation on
![]() $X'$
.
$X'$
.
Given a
![]() $\mathbb {K}$
-b-divisor
$\mathbb {K}$
-b-divisor
![]() $\mathbf {D}$
over X, we say that
$\mathbf {D}$
over X, we say that
![]() $\mathbf {D}$
is a
$\mathbf {D}$
is a
![]() $\mathbb {K}$
-b-Cartier
$\mathbb {K}$
-b-Cartier
![]() $\mathbb {K}$
-b-divisor if there exists a birational model
$\mathbb {K}$
-b-divisor if there exists a birational model
![]() $X'$
of X, such that
$X'$
of X, such that
![]() $\mathbf {D}_{X'}$
is
$\mathbf {D}_{X'}$
is
![]() $\mathbb K$
-Cartier on
$\mathbb K$
-Cartier on
![]() $X'$
and for any model
$X'$
and for any model
![]() $r \colon X" \rightarrow X', \; \mathbf {D}_{X"} = r^{\ast } \mathbf {D}_{X'}$
. When that is the case, we will say that
$r \colon X" \rightarrow X', \; \mathbf {D}_{X"} = r^{\ast } \mathbf {D}_{X'}$
. When that is the case, we will say that
![]() $\mathbf {D}$
descends to
$\mathbf {D}$
descends to
![]() $X'$
and write
$X'$
and write
![]() $\mathbf {D}= \overline {\mathbf {D}_{X'}}$
. We say that
$\mathbf {D}= \overline {\mathbf {D}_{X'}}$
. We say that
![]() $\mathbf {D}$
is b-effective, if
$\mathbf {D}$
is b-effective, if
![]() $\mathbf {D}_{X'}$
is effective for any model
$\mathbf {D}_{X'}$
is effective for any model
![]() $X'$
. We say that
$X'$
. We say that
![]() $\mathbf {D}$
is b-nef, if it is
$\mathbf {D}$
is b-nef, if it is
![]() $\mathbb {K}$
-b-Cartier and, moreover, there exists a model
$\mathbb {K}$
-b-Cartier and, moreover, there exists a model
![]() $X'$
of X, such that
$X'$
of X, such that
![]() $\mathbf {D}= \overline {\mathbf {D}_{X'}}$
and
$\mathbf {D}= \overline {\mathbf {D}_{X'}}$
and
![]() $\mathbf {D}_{X'}$
is nef on
$\mathbf {D}_{X'}$
is nef on
![]() $X'$
. The notion of b-nef b-divisor can be extended analogously to the relative case.
$X'$
. The notion of b-nef b-divisor can be extended analogously to the relative case.
In all of the above, if
![]() $\mathbb {K}= \mathbb {Z}$
, we will systematically drop it from the notation.
$\mathbb {K}= \mathbb {Z}$
, we will systematically drop it from the notation.
Example 2.1. Let X be a normal variety, and denote by
![]() $K_X$
the choice of a divisor in the canonical class. The canonical b-divisor
$K_X$
the choice of a divisor in the canonical class. The canonical b-divisor
![]() $\mathbf {K}$
extending
$\mathbf {K}$
extending
![]() $K_X$
is defined as follows: its trace
$K_X$
is defined as follows: its trace
![]() $\mathbf K_{X}$
on X is
$\mathbf K_{X}$
on X is
![]() $K_X$
, while the trace
$K_X$
, while the trace
![]() $\mathbf K_{X'}$
on a birational model
$\mathbf K_{X'}$
on a birational model
![]() $\pi \colon X' \rightarrow X$
is given by
$\pi \colon X' \rightarrow X$
is given by
![]() ${K_{X'}}$
, where the divisor
${K_{X'}}$
, where the divisor
![]() ${K_{X'}}$
in the canonical class of
${K_{X'}}$
in the canonical class of
![]() $X'$
is chosen so that
$X'$
is chosen so that
![]() $\pi _* {K_{X'}} = {K_{X}}$
. The b-divisor
$\pi _* {K_{X'}} = {K_{X}}$
. The b-divisor
![]() $\mathbf {K}$
is not
$\mathbf {K}$
is not
![]() $\mathbb {Q}$
-b-Cartier, as it follows easily by blowing up a smooth point.
$\mathbb {Q}$
-b-Cartier, as it follows easily by blowing up a smooth point.
Example 2.2. Let
![]() $(X, B)$
be a log subpair. The discrepancy b-divisor
$(X, B)$
be a log subpair. The discrepancy b-divisor
![]() $\mathbf {A}(X,B)$
is defined as follows: on a birational model
$\mathbf {A}(X,B)$
is defined as follows: on a birational model
![]() $\pi \colon X' \rightarrow X$
, its trace
$\pi \colon X' \rightarrow X$
, its trace
![]() $\mathbf {A}(X,B)_{X'}$
is given by the identity
$\mathbf {A}(X,B)_{X'}$
is given by the identity
![]() . Then, the b-divisor
. Then, the b-divisor
![]() $\mathbf {A}^{\ast } (X,B)$
is defined taking its trace
$\mathbf {A}^{\ast } (X,B)$
is defined taking its trace
![]() $\mathbf {A}^{\ast } (X,B)_{X'}$
on
$\mathbf {A}^{\ast } (X,B)_{X'}$
on
![]() $X'$
to be
$X'$
to be
![]() $\sum _{a_i> -1} a_i D_i$
, where
$\sum _{a_i> -1} a_i D_i$
, where
![]() $\mathbf {A}(X,B)_{X'} = \sum _i a_i D_i$
.
$\mathbf {A}(X,B)_{X'} = \sum _i a_i D_i$
.
Given a morphism of normal varieties
![]() $\pi \colon X \to T$
, and a
$\pi \colon X \to T$
, and a
![]() $\mathbb K$
-b-Cartier
$\mathbb K$
-b-Cartier
![]() $\mathbb K$
-b-divisor
$\mathbb K$
-b-divisor
![]() $\mathbf {M}$
(respectively,
$\mathbf {M}$
(respectively,
![]() ${\mathbf N}$
) on X (respectively, T), we will write
${\mathbf N}$
) on X (respectively, T), we will write
![]() $\mathbf {M} \sim _{\mathbb K} \pi ^{\ast } {\mathbf N}$
to indicate that there exists a birational model
$\mathbf {M} \sim _{\mathbb K} \pi ^{\ast } {\mathbf N}$
to indicate that there exists a birational model
![]() $\pi ' \colon X' \rightarrow T'$
of
$\pi ' \colon X' \rightarrow T'$
of
![]() $\pi \colon X \rightarrow T$
, such that
$\pi \colon X \rightarrow T$
, such that
![]() ${\mathbf {M}_{ X'}} \sim _{\mathbb {Q}}(\pi ')^*\mathbf {N}_{T'}$
,
${\mathbf {M}_{ X'}} \sim _{\mathbb {Q}}(\pi ')^*\mathbf {N}_{T'}$
,
![]() $\mathbf {M}= \overline {{\mathbf {M}_{ X'}}}$
, and
$\mathbf {M}= \overline {{\mathbf {M}_{ X'}}}$
, and
![]() $\mathbf {N}=\overline {\mathbf {N}_{T'}}$
.
$\mathbf {N}=\overline {\mathbf {N}_{T'}}$
.
2.3 Generalized pairs and singularities
We recall the definition of generalized pairs, first introduced in [Reference Birkar and Zhang7]. This is a generalization of the classic setting of log pairs.
Definition 2.3. A generalized subpair
![]() $(X,B, \mathbf {M})/Z$
over Z is the datum of:
$(X,B, \mathbf {M})/Z$
over Z is the datum of:
-
• a normal variety
 $X \rightarrow Z$
projective over Z;
$X \rightarrow Z$
projective over Z; -
• an
 $\mathbb R$
-Weil divisor B on X;
$\mathbb R$
-Weil divisor B on X; -
• a b-
 $\mathbb R$
-Cartier b-divisor
$\mathbb R$
-Cartier b-divisor
 $\mathbf {M}$
over X which descends to an
$\mathbf {M}$
over X which descends to an
 $\mathbb R$
-Cartier divisor
$\mathbb R$
-Cartier divisor
 $\mathbf {M}_{X'}$
on some birational model
$\mathbf {M}_{X'}$
on some birational model
 $X' \rightarrow X$
, and
$X' \rightarrow X$
, and
 $\mathbf {M}_{X'}$
is relatively nef over Z.
$\mathbf {M}_{X'}$
is relatively nef over Z.
Moreover, we require that
![]() $K_X +B+ \mathbf {M}_X$
is
$K_X +B+ \mathbf {M}_X$
is
![]() $\mathbb R$
-Cartier. If B is effective, we say that
$\mathbb R$
-Cartier. If B is effective, we say that
![]() $(X,B,\mathbf {M})/Z$
is a generalized pair.
$(X,B,\mathbf {M})/Z$
is a generalized pair.
In the above definition, we can always replace
![]() $X'$
with a higher birational model
$X'$
with a higher birational model
![]() $X"$
and
$X"$
and
![]() $\mathbf {M}_{X'}$
with
$\mathbf {M}_{X'}$
with
![]() $\mathbf {M}_{X"}$
without changing the generalized pair. Whenever
$\mathbf {M}_{X"}$
without changing the generalized pair. Whenever
![]() $\mathbf {M}_{X"}$
descends to
$\mathbf {M}_{X"}$
descends to
![]() $X"$
, then the data of the rational map
$X"$
, then the data of the rational map
![]() $X" \dashrightarrow X$
, B, and
$X" \dashrightarrow X$
, B, and
![]() $\mathbf {M}_{X"}$
encode all the information of the generalized pair.
$\mathbf {M}_{X"}$
encode all the information of the generalized pair.
When the setup is clear, we will denote the generalized subpair
![]() $(X, B, \mathbf {M})/Z$
by
$(X, B, \mathbf {M})/Z$
by
![]() $(X,B+\mathbf {M}_X)/Z$
and we will say that
$(X,B+\mathbf {M}_X)/Z$
and we will say that
![]() $(X,B+\mathbf {M}_X)$
is a generalized pair over Z with datum
$(X,B+\mathbf {M}_X)$
is a generalized pair over Z with datum
![]() $\mathbf {M}$
; for the sake of simplifying the notation, we will often replace
$\mathbf {M}$
; for the sake of simplifying the notation, we will often replace
![]() $\mathbf {M}_X$
by M, and write
$\mathbf {M}_X$
by M, and write
![]() $(X, B+M)$
. When
$(X, B+M)$
. When
![]() $Z = \mathrm {Spec}(\mathbb {C})$
, we will simply write
$Z = \mathrm {Spec}(\mathbb {C})$
, we will simply write
![]() $(X, B, \mathbf {M})$
and
$(X, B, \mathbf {M})$
and
![]() $(X, B +M)$
.
$(X, B +M)$
.
Let
![]() $(X,B, \mathbf {M})/Z$
be a generalized subpair and
$(X,B, \mathbf {M})/Z$
be a generalized subpair and
![]() $\pi \colon Y \rightarrow X$
a projective birational morphism. Then, we may write
$\pi \colon Y \rightarrow X$
a projective birational morphism. Then, we may write
Given a prime divisor E on Y, we define the generalized log discrepancy of E with respect to
![]() $(X,B+M)/Z$
to be
$(X,B+M)/Z$
to be
![]() . In this setup, we call
. In this setup, we call
![]() $(Y,B_Y,\mathbf {M})/Z$
the trace of
$(Y,B_Y,\mathbf {M})/Z$
the trace of
![]() $(X,B,\mathbf {M})/Z$
on Y.
$(X,B,\mathbf {M})/Z$
on Y.
Definition 2.4. Let
![]() $(X,B, \mathbf {M})/Z$
be a generalized subpair. If
$(X,B, \mathbf {M})/Z$
be a generalized subpair. If
![]() $a_E(X,B+M) \geq 0$
for all divisors E over X, we say that
$a_E(X,B+M) \geq 0$
for all divisors E over X, we say that
![]() $(X,B+M)$
is generalized sublog canonical. Similarly, if
$(X,B+M)$
is generalized sublog canonical. Similarly, if
![]() $a_E(X,B+M)> 0$
for all divisors E over X and
$a_E(X,B+M)> 0$
for all divisors E over X and
![]() $\lfloor B \rfloor \leq 0$
, we say that
$\lfloor B \rfloor \leq 0$
, we say that
![]() $(X,B+M)$
is generalized sub-klt. When
$(X,B+M)$
is generalized sub-klt. When
![]() $B \geq 0$
, we say that
$B \geq 0$
, we say that
![]() $(X,B+M)$
is generalized log canonical or generalized klt, respectively.
$(X,B+M)$
is generalized log canonical or generalized klt, respectively.
Remark 2.5. Let
![]() $(X,B, \mathbf {M})/Z$
be a generalized subpair, and let N be an
$(X,B, \mathbf {M})/Z$
be a generalized subpair, and let N be an
![]() $\mathbb R$
-Cartier divisor on X, such that
$\mathbb R$
-Cartier divisor on X, such that
![]() $\mathbf {M}_{X'}+f^{\ast } N$
is nef over Z, where
$\mathbf {M}_{X'}+f^{\ast } N$
is nef over Z, where
![]() $f \colon X' \rightarrow X$
is a birational model of X on which
$f \colon X' \rightarrow X$
is a birational model of X on which
![]() $\mathbf {M}_{X'}$
descends. Then,
$\mathbf {M}_{X'}$
descends. Then,
![]() $(X, B, \mathbf {M}+\overline {N})/Z$
is a generalized subpair with datum
$(X, B, \mathbf {M}+\overline {N})/Z$
is a generalized subpair with datum
![]() $\mathbf {M}+ \bar {N}$
and
$\mathbf {M}+ \bar {N}$
and
![]() $a_E(X,B+M)=a_E(X,B+(M+N))$
for every divisor E over X.
$a_E(X,B+M)=a_E(X,B+(M+N))$
for every divisor E over X.
Example 2.6. Let
![]() $(X,B,\mathbf {M})$
be a generalized subpair. The generalized discrepancy b-divisor
$(X,B,\mathbf {M})$
be a generalized subpair. The generalized discrepancy b-divisor
![]() $\mathbf {A}(X,B,\mathbf {M})$
is defined as follows: on a birational model
$\mathbf {A}(X,B,\mathbf {M})$
is defined as follows: on a birational model
![]() $\pi \colon X' \rightarrow X$
, its trace
$\pi \colon X' \rightarrow X$
, its trace
![]() $\mathbf {A}(X,B,\mathbf {M})_{X'}$
is given by the identity
$\mathbf {A}(X,B,\mathbf {M})_{X'}$
is given by the identity
![]() . Then, the b-divisor
. Then, the b-divisor
![]() $\mathbf {A}^{\ast } (X,B,\mathbf {M})$
is defined taking its trace
$\mathbf {A}^{\ast } (X,B,\mathbf {M})$
is defined taking its trace
![]() $\mathbf {A}^{\ast } (X,B,\mathbf {M})_{X'}$
on
$\mathbf {A}^{\ast } (X,B,\mathbf {M})_{X'}$
on
![]() $X'$
to be
$X'$
to be
![]() , where
, where
![]() $\mathbf {A}(X,B,\mathbf {M})_{X'} = \sum _i a_i D_i$
. Notice that, if
$\mathbf {A}(X,B,\mathbf {M})_{X'} = \sum _i a_i D_i$
. Notice that, if
![]() $\mathbf {M}$
descends to
$\mathbf {M}$
descends to
![]() $X'$
, we have identities of b-divisors
$X'$
, we have identities of b-divisors
![]() $\mathbf {A}(X,B,\mathbf {M})=\mathbf {A}(X',B')$
, and
$\mathbf {A}(X,B,\mathbf {M})=\mathbf {A}(X',B')$
, and
![]() $\mathbf {A}^{\ast } (X,B,\mathbf {M})=\mathbf {A}^{\ast } (X',B')$
, where
$\mathbf {A}^{\ast } (X,B,\mathbf {M})=\mathbf {A}^{\ast } (X',B')$
, where
![]() $B'=-\mathbf {A}(X,B,\mathbf {M})_{X'}$
.
$B'=-\mathbf {A}(X,B,\mathbf {M})_{X'}$
.
Definition 2.7. Let
![]() $(X,B,\mathbf {M})/Z$
be a generalized subpair, and let E be a divisor over X. If
$(X,B,\mathbf {M})/Z$
be a generalized subpair, and let E be a divisor over X. If
![]() $a_E(X,B+M) \leq 0$
, we say that E is a non-klt place for the generalized pair, and
$a_E(X,B+M) \leq 0$
, we say that E is a non-klt place for the generalized pair, and
![]() $c_X(E)\subset X$
is a non-klt center for the generalized pair. The non-klt locus
$c_X(E)\subset X$
is a non-klt center for the generalized pair. The non-klt locus
![]() $\operatorname {\mathrm {Nklt}}(X,B, \mathbf {M})$
is defined as the union of all the non-klt centers of
$\operatorname {\mathrm {Nklt}}(X,B, \mathbf {M})$
is defined as the union of all the non-klt centers of
![]() $(X,B+M)$
. If
$(X,B+M)$
. If
![]() $a_E(X,B+M) = 0$
, we say that E is a generalized log canonical place for
$a_E(X,B+M) = 0$
, we say that E is a generalized log canonical place for
![]() $(X,B+M)$
, and
$(X,B+M)$
, and
![]() $c_X(E)$
is a generalized log canonical center for
$c_X(E)$
is a generalized log canonical center for
![]() $(X,B+M)$
, provided that
$(X,B+M)$
, provided that
![]() $(X, B+M)$
is generalized log canonical in a neighborhood of
$(X, B+M)$
is generalized log canonical in a neighborhood of
![]() $c_X(E)$
.
$c_X(E)$
.
It is possible to extend the classical results on adjunction for log canonical pairs, cf. [Reference Kollár23, Section 16], to the context of generalized pairs.
Let
![]() $(X,B,\mathbf {M})/Z$
be a generalized pair. Let S be an irreducible component of
$(X,B,\mathbf {M})/Z$
be a generalized pair. Let S be an irreducible component of
![]() $\lfloor B \rfloor $
, and denote by
$\lfloor B \rfloor $
, and denote by
![]() $S^{\nu }$
its normalization. Let
$S^{\nu }$
its normalization. Let
![]() $f \colon X' \rightarrow X$
be a log resolution of
$f \colon X' \rightarrow X$
be a log resolution of
![]() $(X,B)$
, where
$(X,B)$
, where
![]() $\mathbf {M}$
descends. Denote by
$\mathbf {M}$
descends. Denote by
![]() $g \colon S' \rightarrow S^{\nu }$
the induced morphism, where
$g \colon S' \rightarrow S^{\nu }$
the induced morphism, where
![]() $S'$
represents the strict transform of S on
$S'$
represents the strict transform of S on
![]() $X'$
. Then, we can write
$X'$
. Then, we can write
Up to replacing
![]() $\mathbf {M}$
in its
$\mathbf {M}$
in its
![]() $\mathbb {K}$
-linear equivalence class, we can assume that
$\mathbb {K}$
-linear equivalence class, we can assume that
![]() $S'$
does not appear in the support of
$S'$
does not appear in the support of
![]() $\mathbf {M}_{X'}$
. Then, we set
$\mathbf {M}_{X'}$
. Then, we set
where
, and
. Define
, and
. By construction, we get
We refer to such operation as generalized divisorial adjunction. By construction, the generalized pair
![]() $(S^{\nu },B_{S^{\nu }},\mathbf {N})$
is a generalized pair over Z. We may write
$(S^{\nu },B_{S^{\nu }},\mathbf {N})$
is a generalized pair over Z. We may write
![]() $\mathbf {M} |_{S^{\nu }}.$
for
$\mathbf {M} |_{S^{\nu }}.$
for
![]() ${\mathbf N}$
to highlight that indeed
${\mathbf N}$
to highlight that indeed
![]() ${\mathbf N}$
comes from the restriction of
${\mathbf N}$
comes from the restriction of
![]() $\mathbf {M}$
to S.
$\mathbf {M}$
to S.
2.4 Generalized dlt pairs and dlt models
In this section, we recall the notion of dlt and plt singularities in the context of generalized pairs, and we prove the existence of dlt models.
Definition 2.8. We say that a generalized pair
![]() $(X,B, \mathbf {M})/Z$
is generalized dlt, if it is generalized log canonical and for the generic point
$(X,B, \mathbf {M})/Z$
is generalized dlt, if it is generalized log canonical and for the generic point
![]() $\eta $
of any generalized log canonical center, the following conditions hold:
$\eta $
of any generalized log canonical center, the following conditions hold:
-
(i)
 $(X,B)$
is log smooth in a neighborhood of
$(X,B)$
is log smooth in a neighborhood of
 $\eta $
; and
$\eta $
; and -
(ii)
 $\mathbf {M} = \overline {{\mathbf {M}_{X}}}$
over a neighborhood of
$\mathbf {M} = \overline {{\mathbf {M}_{X}}}$
over a neighborhood of
 $\eta $
.
$\eta $
.
If, in addition, every connected component of
![]() $\lfloor B \rfloor $
is irreducible, we say that
$\lfloor B \rfloor $
is irreducible, we say that
![]() $(X,B+M)$
is generalized plt.
$(X,B+M)$
is generalized plt.
The following result is a refinement of [Reference Filipazzi10, Theorem 3.2] and proves the existence of generalized dlt models.
Theorem 2.9. Let
![]() $(X,B, \mathbf {M})/Z$
be a generalized pair. Then, there exists a
$(X,B, \mathbf {M})/Z$
be a generalized pair. Then, there exists a
![]() $\mathbb {Q}$
-factorial model
$\mathbb {Q}$
-factorial model
![]() $f^m\colon X^m \rightarrow X$
, such that every
$f^m\colon X^m \rightarrow X$
, such that every
![]() $f^m$
-exceptional divisor has generalized log discrepancy with respect to
$f^m$
-exceptional divisor has generalized log discrepancy with respect to
![]() $(X,B+M)$
at most
$(X,B+M)$
at most
![]() $0$
. Let
$0$
. Let
![]() $E^m$
denote the reduced
$E^m$
denote the reduced
![]() $f^m$
-exceptional divisor. Then the generalized pair
$f^m$
-exceptional divisor. Then the generalized pair
![]() $(X^m,B^m,\mathbf {M})/Z$
is generalized dlt, where
$(X^m,B^m,\mathbf {M})/Z$
is generalized dlt, where
![]() .
.
Proof. Let
![]() $f\colon X' \rightarrow X$
be a log resolution of
$f\colon X' \rightarrow X$
be a log resolution of
![]() $(X,B)$
, where
$(X,B)$
, where
![]() $\mathbf {M}$
descends. For the sake of simplifying notation, we will use
$\mathbf {M}$
descends. For the sake of simplifying notation, we will use
![]() $M'$
to denote
$M'$
to denote
![]() $\mathbf {M}_{X'}$
. By Hironaka’s theorem, we can assume that f is obtained by blowing up loci of codimension at least two, and that there exists an effective f-exceptional divisor
$\mathbf {M}_{X'}$
. By Hironaka’s theorem, we can assume that f is obtained by blowing up loci of codimension at least two, and that there exists an effective f-exceptional divisor
![]() $C'$
, such that
$C'$
, such that
![]() $-C'$
is f-ample. We define
$-C'$
is f-ample. We define
![]() $B'$
via the identity
$B'$
via the identity
In view of this definition, we can decompose
![]() $B'$
as
$B'$
as
![]() $B'=f_*^{-1} \lbrace B \rbrace + E^+ + F' - G'$
, where
$B'=f_*^{-1} \lbrace B \rbrace + E^+ + F' - G'$
, where
-
•
 $E^+$
denotes the (not necessarily f-exceptional) divisors with generalized log discrepancy at most
$E^+$
denotes the (not necessarily f-exceptional) divisors with generalized log discrepancy at most
 $0$
with respect to
$0$
with respect to
 $(X, B, \mathbf {M})$
;
$(X, B, \mathbf {M})$
; -
•
 $F'$
the sum of all f-exceptional divisors with generalized log discrepancy in
$F'$
the sum of all f-exceptional divisors with generalized log discrepancy in
 $(0, 1]$
; and,
$(0, 1]$
; and, -
•
 $G'$
the sum of all f-exceptional divisors with generalized log discrepancy
$G'$
the sum of all f-exceptional divisors with generalized log discrepancy
 $>1$
.
$>1$
.
We define
. Letting H be a sufficiently ample divisor on X, for all
![]() $\epsilon , \nu , \tau \in \mathbb {R}$
,
$\epsilon , \nu , \tau \in \mathbb {R}$
,
and for any
![]() $0< \epsilon \ll \tau $
and
$0< \epsilon \ll \tau $
and
![]() $\epsilon \ll 1$
, both
$\epsilon \ll 1$
, both
![]() $\tau (-C'+f^{\ast } H)+M'$
and
$\tau (-C'+f^{\ast } H)+M'$
and
![]() $\tau (\epsilon E' - C' + f^{\ast } H) + M'$
are ample over X. For any such choice of
$\tau (\epsilon E' - C' + f^{\ast } H) + M'$
are ample over X. For any such choice of
![]() $\epsilon $
and
$\epsilon $
and
![]() $\tau $
, we can choose divisors
$\tau $
, we can choose divisors
![]() $H^{\prime }_{1,\tau } \sim _{\mathbb {R},X} \tau (-C'+f^{\ast } H)+M'$
and
$H^{\prime }_{1,\tau } \sim _{\mathbb {R},X} \tau (-C'+f^{\ast } H)+M'$
and
![]() $H^{\prime }_{2,\tau , \epsilon } \sim _{\mathbb {R},X} \tau (\epsilon E' - C' + f^{\ast } H) + M'$
, such that
$H^{\prime }_{2,\tau , \epsilon } \sim _{\mathbb {R},X} \tau (\epsilon E' - C' + f^{\ast } H) + M'$
, such that
![]() $B'+H^{\prime }_{1,\tau }+H^{\prime }_{2,\tau , \epsilon }$
has simple normal crossing support, and
$B'+H^{\prime }_{1,\tau }+H^{\prime }_{2,\tau , \epsilon }$
has simple normal crossing support, and
![]() $\lfloor H^{\prime }_{1,\tau } \rfloor = \lfloor H^{\prime }_{2,\tau , \epsilon } \rfloor =0$
. Thus, if
$\lfloor H^{\prime }_{1,\tau } \rfloor = \lfloor H^{\prime }_{2,\tau , \epsilon } \rfloor =0$
. Thus, if
![]() $0 < \tau <1 $
and
$0 < \tau <1 $
and
![]() $0 < \nu \ll 1$
, the pair
$0 < \nu \ll 1$
, the pair
is klt. By [Reference Birkar, Cascini, Hacon and McKernan6], we can run a
![]() $(K_{X'} + \Delta ^{\prime }_{\epsilon , \tau , \nu })$
-MMP over X that terminates with a relative
$(K_{X'} + \Delta ^{\prime }_{\epsilon , \tau , \nu })$
-MMP over X that terminates with a relative
![]() $\mathbb {Q}$
-factorial minimal model
$\mathbb {Q}$
-factorial minimal model
By (1),
![]() $f^m_{\epsilon ,\tau ,\nu }$
is also a minimal model over X for the pair
$f^m_{\epsilon ,\tau ,\nu }$
is also a minimal model over X for the pair
As the dlt property is preserved under steps of the MMP [Reference Kollár and Mori27, Corollary 3.44], both
![]() $(X^m_{\epsilon ,\nu , \tau }, \Delta ^m_{\epsilon ,\nu , \tau })$
and
$(X^m_{\epsilon ,\nu , \tau }, \Delta ^m_{\epsilon ,\nu , \tau })$
and
![]() $(X^m_{\epsilon ,\nu , \tau }, \Gamma ^m_{\nu , \tau })$
are dlt pairs, where
$(X^m_{\epsilon ,\nu , \tau }, \Gamma ^m_{\nu , \tau })$
are dlt pairs, where
![]() $\Delta ^m_{\epsilon ,\nu , \tau }$
(respectively,
$\Delta ^m_{\epsilon ,\nu , \tau }$
(respectively,
![]() $\Gamma ^m_{\nu , \tau }$
) is the pushforward of
$\Gamma ^m_{\nu , \tau }$
) is the pushforward of
![]() $\Delta ^{\prime }_{\epsilon ,\nu , \tau }$
(respectively,
$\Delta ^{\prime }_{\epsilon ,\nu , \tau }$
(respectively,
![]() $\Gamma ^{\prime }_{\nu , \tau }$
) on
$\Gamma ^{\prime }_{\nu , \tau }$
) on
![]() $X^m_{\epsilon , \nu , \tau }$
. Hence, the pair
$X^m_{\epsilon , \nu , \tau }$
. Hence, the pair
![]() $(X^m_{\epsilon ,\nu , \tau },B^m_{\epsilon ,\nu , \tau })$
is dlt, where
$(X^m_{\epsilon ,\nu , \tau },B^m_{\epsilon ,\nu , \tau })$
is dlt, where
![]() $B^m_{\epsilon ,\nu , \tau }$
is the pushforward of
$B^m_{\epsilon ,\nu , \tau }$
is the pushforward of
![]() $f^{-1}_* \lbrace B \rbrace +E' +F'$
on
$f^{-1}_* \lbrace B \rbrace +E' +F'$
on
![]() $X^m_{\epsilon ,\nu , \tau }$
.
$X^m_{\epsilon ,\nu , \tau }$
.
To simplify the notation, we will denote by
![]() $A^m$
the strict transform on
$A^m$
the strict transform on
![]() $X_{\epsilon ,\nu , \tau }^m$
of any divisor A on
$X_{\epsilon ,\nu , \tau }^m$
of any divisor A on
![]() $X'$
. In particular, we will denote
$X'$
. In particular, we will denote
![]() $\mathbf {M}_{X^m_{\epsilon , \nu , \tau }}$
by
$\mathbf {M}_{X^m_{\epsilon , \nu , \tau }}$
by
![]() $M^m$
. Then, we define
$M^m$
. Then, we define

The divisor N is
![]() $f^m_{\epsilon ,\nu , \tau }$
-nef, while T is
$f^m_{\epsilon ,\nu , \tau }$
-nef, while T is
![]() $f^m_{\epsilon ,\nu , \tau }$
-trivial, and
$f^m_{\epsilon ,\nu , \tau }$
-trivial, and
so that
![]() $-D$
is
$-D$
is
![]() $f_{\epsilon ,\nu , \tau }^m$
-nef and
$f_{\epsilon ,\nu , \tau }^m$
-nef and
![]() $f_{\epsilon ,\nu , \tau \ast }^m D \geq 0$
. Therefore, by the negativity lemma [Reference Kollár and Mori27, Lemma 3.39], D is effective.
$f_{\epsilon ,\nu , \tau \ast }^m D \geq 0$
. Therefore, by the negativity lemma [Reference Kollár and Mori27, Lemma 3.39], D is effective.
As
![]() $C'$
,
$C'$
,
![]() $E^+-E'$
,
$E^+-E'$
,
![]() $F'$
and
$F'$
and
![]() $G'$
are independent of
$G'$
are independent of
![]() ${\epsilon ,\nu , \tau }$
, if we choose
${\epsilon ,\nu , \tau }$
, if we choose
![]() $0 < \epsilon \ll \tau \ll \nu \ll 1$
, the
$0 < \epsilon \ll \tau \ll \nu \ll 1$
, the
![]() $(K_{X'} + \Delta ^{\prime }_{\epsilon , \nu , \tau })$
-MMP contracts
$(K_{X'} + \Delta ^{\prime }_{\epsilon , \nu , \tau })$
-MMP contracts
![]() $F'$
and
$F'$
and
![]() $G'$
, as
$G'$
, as
Indeed, as the effective divisors
![]() $G'$
,
$G'$
,
![]() $F'$
, and
$F'$
, and
![]() $E^+-E'$
share no prime components,
$E^+-E'$
share no prime components,
![]() $\operatorname {\mathrm {Supp}}(C') \subset \operatorname {\mathrm {Supp}}(E'+F'+G')$
, and
$\operatorname {\mathrm {Supp}}(C') \subset \operatorname {\mathrm {Supp}}(E'+F'+G')$
, and
![]() $\tau \ll \nu $
, for every prime divisor
$\tau \ll \nu $
, for every prime divisor
![]() $P'$
on
$P'$
on
![]() $X' \ \mu _{P'} (G' + \nu F' -\tau C' -(E^+-E'))> 0$
if and only if
$X' \ \mu _{P'} (G' + \nu F' -\tau C' -(E^+-E'))> 0$
if and only if
![]() $\mu _{P'} (G' + \nu F' -(E^+-E'))>0$
. We fix once and for all such a choice of the coefficients
$\mu _{P'} (G' + \nu F' -(E^+-E'))>0$
. We fix once and for all such a choice of the coefficients
![]() $\epsilon , \tau , \nu $
, and we drop the dependence from
$\epsilon , \tau , \nu $
, and we drop the dependence from
![]() ${\epsilon ,\nu , \tau }$
in our notation.
${\epsilon ,\nu , \tau }$
in our notation.
The generalized pair
![]() $(X^m,B^m+M^m)/Z$
is generalized log canonical. In fact,
$(X^m,B^m+M^m)/Z$
is generalized log canonical. In fact,
![]() $f^{\ast } H-C'$
is ample, as H is assumed to be sufficiently ample; picking
$f^{\ast } H-C'$
is ample, as H is assumed to be sufficiently ample; picking
![]() $0 \leq A' \sim _{\mathbb {Q}} \tau (f^{\ast } H - C')$
a general element in its
$0 \leq A' \sim _{\mathbb {Q}} \tau (f^{\ast } H - C')$
a general element in its
![]() $\mathbb {Q}$
-linear equivalence class, so that
$\mathbb {Q}$
-linear equivalence class, so that
![]() $(X',f_*^{-1} \lbrace B \rbrace + E' + (1+\nu )F' + A')$
is dlt by Bertini’s theorem, the generalized pair
$(X',f_*^{-1} \lbrace B \rbrace + E' + (1+\nu )F' + A')$
is dlt by Bertini’s theorem, the generalized pair
![]() $(X',f_*^{-1} \lbrace B \rbrace + E' + (1+\nu )F' + A', \mathbf {M})/Z$
is generalized dlt, and each step in the
$(X',f_*^{-1} \lbrace B \rbrace + E' + (1+\nu )F' + A', \mathbf {M})/Z$
is generalized dlt, and each step in the
![]() $(K_{X'} + \Delta ^{\prime }_{\epsilon , \nu , \tau })$
-MMP leading to
$(K_{X'} + \Delta ^{\prime }_{\epsilon , \nu , \tau })$
-MMP leading to
![]() $X^m$
is a
$X^m$
is a
![]() $({K_{X'}} + f_*^{-1} \lbrace B \rbrace + E' + (1+\nu )F' + A'+M')$
-negative contraction. Therefore, the generalized pair
$({K_{X'}} + f_*^{-1} \lbrace B \rbrace + E' + (1+\nu )F' + A'+M')$
-negative contraction. Therefore, the generalized pair
![]() $(X^m,B^m+A^m,\mathbf {M})/Z$
is generalized log canonical. As
$(X^m,B^m+A^m,\mathbf {M})/Z$
is generalized log canonical. As
![]() $X^m$
is
$X^m$
is
![]() $\mathbb {Q}$
-factorial, then
$\mathbb {Q}$
-factorial, then
![]() $(X^m,B^m, \mathbf {M})/Z$
is generalized log canonical. Thus,
$(X^m,B^m, \mathbf {M})/Z$
is generalized log canonical. Thus,
![]() $(X^m,B^m+M^m)$
has all the claimed properties, besides the fact that it may not be generalized dlt.
$(X^m,B^m+M^m)$
has all the claimed properties, besides the fact that it may not be generalized dlt.
To conclude, it suffices to substitute
![]() $(X^m,B^m+M^m)$
with a generalized dlt model, which exists by [Reference Birkar5, 2.13.(2)] as
$(X^m,B^m+M^m)$
with a generalized dlt model, which exists by [Reference Birkar5, 2.13.(2)] as
![]() $(X^m,B^m+M^m)$
is log canonical. Passing to such model only extracts divisors with generalized log discrepancy
$(X^m,B^m+M^m)$
is log canonical. Passing to such model only extracts divisors with generalized log discrepancy
![]() $0$
with respect to
$0$
with respect to
![]() $(X^m,B^m+M^m)$
. This completes the proof of the theorem.
$(X^m,B^m+M^m)$
. This completes the proof of the theorem.
Definition 2.10. For a generalized pair
![]() $(X, B, \mathbf {M})/Z$
, we call the generalized pair constructed in Theorem 2.9 and denoted by
$(X, B, \mathbf {M})/Z$
, we call the generalized pair constructed in Theorem 2.9 and denoted by
![]() $(X^m,B^m, \mathbf {M})/Z$
a generalized dlt model for
$(X^m,B^m, \mathbf {M})/Z$
a generalized dlt model for
![]() $(X,B+M)$
.
$(X,B+M)$
.
Finally, we include, here, a couple of technical results that will be used in the proof of Theorem 4.2. We first introduce a couple of definitions.
Definition 2.11. Given a generalized pair
![]() $(X,B,\mathbf {M})$
and a closed subset
$(X,B,\mathbf {M})$
and a closed subset
![]() $C \subset X$
, we say that
$C \subset X$
, we say that
![]() $(X,B,\mathbf {M})$
is generalized dlt away from C if
$(X,B,\mathbf {M})$
is generalized dlt away from C if
![]() $(X \setminus C,B,\mathbf {M})$
is generalized dlt. Here, we restrict B to the open subset
$(X \setminus C,B,\mathbf {M})$
is generalized dlt. Here, we restrict B to the open subset
![]() $X \setminus C$
as in [Reference Hartshorne19, Proposition II.6.5]. Similarly, the preimage of
$X \setminus C$
as in [Reference Hartshorne19, Proposition II.6.5]. Similarly, the preimage of
![]() $X \setminus C$
is open in every higher birational model of X. Therefore, we can therefore restrict
$X \setminus C$
is open in every higher birational model of X. Therefore, we can therefore restrict
![]() $\mathbf {M}$
to
$\mathbf {M}$
to
![]() $X \setminus C$
by restricting all its traces to the preimages of
$X \setminus C$
by restricting all its traces to the preimages of
![]() $X \setminus C$
.
$X \setminus C$
.
Definition 2.12. Let F be an effective
![]() $\mathbb {R}$
-divisor on a variety X, and let D be an
$\mathbb {R}$
-divisor on a variety X, and let D be an
![]() $\mathbb R$
-divisor on X. We say that F fully supports D if D is effective, and the support of D coincides with the support of F. Moreover, given a morphism of varieties
$\mathbb R$
-divisor on X. We say that F fully supports D if D is effective, and the support of D coincides with the support of F. Moreover, given a morphism of varieties
![]() $f \colon X \to Z$
, we say that F fully supports an f-ample divisor if F fully supports an effective f-ample
$f \colon X \to Z$
, we say that F fully supports an f-ample divisor if F fully supports an effective f-ample
![]() $\mathbb {R}$
-divisor H.
$\mathbb {R}$
-divisor H.
Lemma 2.13. Let
![]() $(X,B,\mathbf {M})$
be a
$(X,B,\mathbf {M})$
be a
![]() $\mathbb {Q}$
-factorial generalized log canonical pair, and let
$\mathbb {Q}$
-factorial generalized log canonical pair, and let
![]() $q \colon X \rightarrow Z$
be a contraction. Assume that
$q \colon X \rightarrow Z$
be a contraction. Assume that
![]() $B^{=1}$
fully supports a q-ample divisor, and that
$B^{=1}$
fully supports a q-ample divisor, and that
![]() $(X,B,\mathbf {M})$
is generalized dlt away from
$(X,B,\mathbf {M})$
is generalized dlt away from
![]() $B^{=1}$
. Let
$B^{=1}$
. Let
![]() $\pi \colon (X',B',\mathbf {M}) \rightarrow X$
be a generalized dlt model for
$\pi \colon (X',B',\mathbf {M}) \rightarrow X$
be a generalized dlt model for
![]() $(X,B,\mathbf {M})$
. Then,
$(X,B,\mathbf {M})$
. Then,
![]() $(B')^{=1}$
fully supports a
$(B')^{=1}$
fully supports a
![]() $(q \circ \pi )$
-ample divisor.
$(q \circ \pi )$
-ample divisor.
Remark 2.14. In the setup of Lemma 2.13, the condition on the dlt-ness of the pair away from
![]() $B^{=1}$
together with
$B^{=1}$
together with
![]() $\mathbb {Q}$
-factoriality of X guarantees that, when passing to a generalized dlt model of
$\mathbb {Q}$
-factoriality of X guarantees that, when passing to a generalized dlt model of
![]() $(X,B,\mathbf {M})$
, we only extract divisors with center in
$(X,B,\mathbf {M})$
, we only extract divisors with center in
![]() $B^{=1}$
.
$B^{=1}$
.
Proof. Let
![]() $\pi \colon X' \rightarrow X$
be as in the statement. Let H be a q-ample divisor that is fully supported on
$\pi \colon X' \rightarrow X$
be as in the statement. Let H be a q-ample divisor that is fully supported on
![]() $B^{=1}$
. Since X is
$B^{=1}$
. Since X is
![]() $\mathbb {Q}$
-factorial, by [Reference Kollár and Mori27, Lemma 2.62], there is an effective divisor F that is fully supported on the
$\mathbb {Q}$
-factorial, by [Reference Kollár and Mori27, Lemma 2.62], there is an effective divisor F that is fully supported on the
![]() $\pi $
-exceptional divisors, such that
$\pi $
-exceptional divisors, such that
![]() $-F$
is
$-F$
is
![]() $\pi $
-ample. Thus, for
$\pi $
-ample. Thus, for
![]() $0 < \epsilon \ll 1$
,
$0 < \epsilon \ll 1$
,
![]() $\pi ^{\ast } H-\epsilon F$
is ample over Z. By assumption, the
$\pi ^{\ast } H-\epsilon F$
is ample over Z. By assumption, the
![]() $\pi $
-exceptional divisors all have center on
$\pi $
-exceptional divisors all have center on
![]() $\operatorname {\mathrm {Supp}} (H ) = \operatorname {\mathrm {Supp}} (B^{=1})$
. Therefore, if
$\operatorname {\mathrm {Supp}} (H ) = \operatorname {\mathrm {Supp}} (B^{=1})$
. Therefore, if
![]() $\epsilon $
is small enough,
$\epsilon $
is small enough,
![]() $\pi ^{\ast } H-\epsilon F$
is effective. By definition of a dlt model,
$\pi ^{\ast } H-\epsilon F$
is effective. By definition of a dlt model,
![]() $\operatorname {\mathrm {Supp}} \mathrm {Exc}(\pi ) \subset \operatorname {\mathrm {Supp}}((B')^{=1})$
. Thus,
$\operatorname {\mathrm {Supp}} \mathrm {Exc}(\pi ) \subset \operatorname {\mathrm {Supp}}((B')^{=1})$
. Thus,
![]() $\operatorname {\mathrm {Supp}}(\pi ^{\ast } H-\epsilon F) = \operatorname {\mathrm {Supp}} ((B')^{=1})$
, and the claim follows.
$\operatorname {\mathrm {Supp}}(\pi ^{\ast } H-\epsilon F) = \operatorname {\mathrm {Supp}} ((B')^{=1})$
, and the claim follows.
Lemma 2.15. Let
![]() $(X,B,\mathbf {M})/Z$
be a
$(X,B,\mathbf {M})/Z$
be a
![]() $\mathbb {Q}$
-factorial generalized log canonical pair. Assume that for some
$\mathbb {Q}$
-factorial generalized log canonical pair. Assume that for some
![]() $0 < \epsilon \leq 1$
, the generalized pair
$0 < \epsilon \leq 1$
, the generalized pair
![]() $(X,B^{<1} + (1-\epsilon )B^{=1},\mathbf {M})/Z$
is generalized klt. Fix a generalized dlt model
$(X,B^{<1} + (1-\epsilon )B^{=1},\mathbf {M})/Z$
is generalized klt. Fix a generalized dlt model
![]() $(X^m,B^m,\mathbf {M})/Z$
of
$(X^m,B^m,\mathbf {M})/Z$
of
![]() $(X,B,\mathbf {M})/Z$
, and let
$(X,B,\mathbf {M})/Z$
, and let
![]() $\pi \colon X^m \rightarrow X$
denote the corresponding morphism. Then,
$\pi \colon X^m \rightarrow X$
denote the corresponding morphism. Then,
![]() $\operatorname {\mathrm {Supp}}(\pi ^{\ast } (B^{=1}))=\operatorname {\mathrm {Supp}}((B^m)^{=1})$
.
$\operatorname {\mathrm {Supp}}(\pi ^{\ast } (B^{=1}))=\operatorname {\mathrm {Supp}}((B^m)^{=1})$
.
Proof. This follows at once, since
![]() $\pi $
only extracts divisors appearing in
$\pi $
only extracts divisors appearing in
![]() $\operatorname {\mathrm {Supp}}((B^m)^{=1})$
and the condition that
$\operatorname {\mathrm {Supp}}((B^m)^{=1})$
and the condition that
![]() $(X,B^{<1} + (1-\epsilon )B^{=1},\mathbf {M})/Z$
is generalized klt implies that
$(X,B^{<1} + (1-\epsilon )B^{=1},\mathbf {M})/Z$
is generalized klt implies that
![]() $\pi (\mathrm {Exc}(\pi )) \subset B^{=1}$
.
$\pi (\mathrm {Exc}(\pi )) \subset B^{=1}$
.
2.5 Canonical bundle formula
In this section, we recall the statement of the canonical bundle formula for generalized log canonical pairs, and we extend it to the relative setting. We refer the interested reader to [Reference Ambro2, Reference Ambro3, Reference Fujino and Gongyo13] for the notation involved and a more detailed discussion about the topic, in the case of log canonical pairs.
Definition 2.16. Let
![]() $(X, B)$
be a subpair. A contraction
$(X, B)$
be a subpair. A contraction
![]() $f \colon X \rightarrow T$
of quasiprojective varieties is an lc-trivial fibration if
$f \colon X \rightarrow T$
of quasiprojective varieties is an lc-trivial fibration if
-
(i)
 $(X,B)$
is a subpair with coefficients in
$(X,B)$
is a subpair with coefficients in
 $\mathbb {Q}$
that is sublog canonical over the generic point of T;
$\mathbb {Q}$
that is sublog canonical over the generic point of T; -
(ii)
 $\mathrm {rank} f_* {\mathcal {O}_{X}} (\lceil \mathbf {A}^{\ast } (X,B)\rceil )=1$
, where
$\mathrm {rank} f_* {\mathcal {O}_{X}} (\lceil \mathbf {A}^{\ast } (X,B)\rceil )=1$
, where
 $\mathbf {A}^{\ast } (X,B)$
is the b-divisor defined in Example 2.2; and
$\mathbf {A}^{\ast } (X,B)$
is the b-divisor defined in Example 2.2; and -
(iii) there exists a
 $\mathbb {Q}$
-Cartier
$\mathbb {Q}$
-Cartier
 $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
 $L_T$
on T, such that
$L_T$
on T, such that
 ${K_{X}} + B \sim _{\mathbb {Q}} f^{\ast } L_T$
.
${K_{X}} + B \sim _{\mathbb {Q}} f^{\ast } L_T$
.
Condition (ii) above is automatically satisfied if B is effective over the generic point of T.
Given a subpair
![]() $(X,B)$
and an lc-trivial fibration
$(X,B)$
and an lc-trivial fibration
![]() $f \colon X \rightarrow T$
, there exist
$f \colon X \rightarrow T$
, there exist
![]() $\mathbb {Q}$
-b-divisors
$\mathbb {Q}$
-b-divisors
![]() $\mathbf {B}$
and
$\mathbf {B}$
and
![]() $\mathbf {N}$
over T, such that the following linear equivalence relation, known as the canonical bundle formula, holds
$\mathbf {N}$
over T, such that the following linear equivalence relation, known as the canonical bundle formula, holds
The b-divisor
![]() $\mathbf {B}$
is called the boundary part in the canonical bundle formula; it is a canonically defined b-divisor. Furthermore, if B is effective, then so is
$\mathbf {B}$
is called the boundary part in the canonical bundle formula; it is a canonically defined b-divisor. Furthermore, if B is effective, then so is
![]() $\mathbf {B}_T$
. The b-divisor
$\mathbf {B}_T$
. The b-divisor
![]() $\mathbf {N}$
, in turn, is called the moduli part in the canonical bundle formula, and it is, in general, defined only up to
$\mathbf {N}$
, in turn, is called the moduli part in the canonical bundle formula, and it is, in general, defined only up to
![]() $\mathbb {Q}$
-linear equivalence. The linear equivalence (2) holds at the level of b-divisors: namely,
$\mathbb {Q}$
-linear equivalence. The linear equivalence (2) holds at the level of b-divisors: namely,
where
![]() $\mathbf {K}$
denotes the canonical b-divisor. The moduli b-divisor
$\mathbf {K}$
denotes the canonical b-divisor. The moduli b-divisor
![]() $\mathbf {N}$
is expected to detect the variation of the restriction of the pair induced on fibers of the morphism f by restricting B.
$\mathbf {N}$
is expected to detect the variation of the restriction of the pair induced on fibers of the morphism f by restricting B.
Theorem 2.17 [Reference Fujino and Gongyo13, cf. Theorem 3.6].
Let
![]() $(X, B)/S$
be a subpair, and let
$(X, B)/S$
be a subpair, and let
![]() $f \colon (X,B) \rightarrow T$
be an lc-trivial fibration. Let
$f \colon (X,B) \rightarrow T$
be an lc-trivial fibration. Let
![]() $\mathbf {B}$
and
$\mathbf {B}$
and
![]() $\mathbf {N}$
be the boundary and the moduli part of f, respectively. Then,
$\mathbf {N}$
be the boundary and the moduli part of f, respectively. Then,
![]() $\mathbf K + \mathbf B$
and
$\mathbf K + \mathbf B$
and
![]() ${\mathbf N}$
are
${\mathbf N}$
are
![]() $\mathbb {Q}$
-b-Cartier b-divisors. Furthermore,
$\mathbb {Q}$
-b-Cartier b-divisors. Furthermore,
![]() $\mathbf {N}$
is b-nef over S.
$\mathbf {N}$
is b-nef over S.
Remark 2.18. In the setup of Theorem 2.17, let
![]() $T'$
be a model, where the nef part
$T'$
be a model, where the nef part
![]() ${\mathbf N}$
descends in the sense of b-divisors. Then,
${\mathbf N}$
descends in the sense of b-divisors. Then,
![]() ${{\mathbf N}}_{T'}$
is nef over S. In particular,
${{\mathbf N}}_{T'}$
is nef over S. In particular,
![]() $(T, {\mathbf {B}_{ T}}, \mathbf {N})/S$
is a generalized subpair. If
$(T, {\mathbf {B}_{ T}}, \mathbf {N})/S$
is a generalized subpair. If
![]() $B \geq 0$
, then
$B \geq 0$
, then
![]() $(T, {\mathbf {B}_{T}},\mathbf {N})/S$
is a generalized pair.
$(T, {\mathbf {B}_{T}},\mathbf {N})/S$
is a generalized pair.
A generalization of the canonical bundle formula to the category of generalized pairs was introduced in [Reference Filipazzi10, Theorem 1.4], where Theorem 2.17 is extended to the case of generalized subpairs
![]() $(X,B+M)$
endowed with the analog for generalized pairs of an lc-trivial fibration.
$(X,B+M)$
endowed with the analog for generalized pairs of an lc-trivial fibration.
Definition 2.19. Let
![]() $(X,B,\mathbf {M})/Z$
be a generalized subpair. A contraction
$(X,B,\mathbf {M})/Z$
be a generalized subpair. A contraction
![]() $f \colon X \rightarrow T$
of quasiprojective varieties over Z is a generalized lc-trivial fibration if
$f \colon X \rightarrow T$
of quasiprojective varieties over Z is a generalized lc-trivial fibration if
-
(i)
 $(X,B,\mathbf {M})$
is a generalized subpair with coefficients in
$(X,B,\mathbf {M})$
is a generalized subpair with coefficients in
 $\mathbb {Q}$
that is generalized sublog canonical over the generic point of T;
$\mathbb {Q}$
that is generalized sublog canonical over the generic point of T; -
(ii)
 $\mathrm {rank} f_* {\mathcal {O}_{X}} (\lceil \mathbf {A}^{\ast } (X,B,\mathbf {M})\rceil )=1$
, where
$\mathrm {rank} f_* {\mathcal {O}_{X}} (\lceil \mathbf {A}^{\ast } (X,B,\mathbf {M})\rceil )=1$
, where
 $\mathbf {A}^{\ast } (X,B,\mathbf {M})$
is the b-divisor defined in Example 2.6; and
$\mathbf {A}^{\ast } (X,B,\mathbf {M})$
is the b-divisor defined in Example 2.6; and -
(iii) there exists a
 $\mathbb {Q}$
-Cartier divisor
$\mathbb {Q}$
-Cartier divisor
 $L_T$
on T, such that
$L_T$
on T, such that
 ${K_{X}} + B + \mathbf {M}_X \sim _{\mathbb {Q}} f^{\ast } L_T$
.
${K_{X}} + B + \mathbf {M}_X \sim _{\mathbb {Q}} f^{\ast } L_T$
.
As in Definition 2.16, condition (ii) in Definition 2.19 is automatically satisfied if B is effective over the generic point of T.
We are able to adapt the proof of [Reference Filipazzi10, Theorem 1.4] with minor changes to further extend the canonical bundle formula for generalized pairs to the relative setting. Hence, we will work in this broader context and highlight the relevant modifications that need to occur in the proof of [Reference Filipazzi10, Theorem 1.4].
Let
![]() $(X,B,\mathbf {M})/S$
be a generalized subpair over a quasiprojective variety X, and let
$(X,B,\mathbf {M})/S$
be a generalized subpair over a quasiprojective variety X, and let
![]() $f \colon X \rightarrow T$
be a generalized lc-trivial fibration over S. Without loss of generality, we can assume that
$f \colon X \rightarrow T$
be a generalized lc-trivial fibration over S. Without loss of generality, we can assume that
![]() $\dim T> 0$
. Fix a divisor
$\dim T> 0$
. Fix a divisor
![]() $L_T$
on T, such that
$L_T$
on T, such that
![]() ${K_{X}} + B + M \sim _{\mathbb {Q}} f^{\ast } L_T$
. For any prime divisor D on T, let
${K_{X}} + B + M \sim _{\mathbb {Q}} f^{\ast } L_T$
. For any prime divisor D on T, let
![]() $l_D$
be the generalized log canonical threshold of
$l_D$
be the generalized log canonical threshold of
![]() $f^{\ast } D$
with respect to
$f^{\ast } D$
with respect to
![]() $(X,B+M)$
over the generic point of D. Then, we define
$(X,B+M)$
over the generic point of D. Then, we define
where
, so that
Given
![]() $\tilde X$
and
$\tilde X$
and
![]() $\tilde T$
higher birational models of X and T, respectively, fitting in the following commutative diagram of morphisms
$\tilde T$
higher birational models of X and T, respectively, fitting in the following commutative diagram of morphisms

we will denote by
![]() $(\tilde X, \tilde B + \tilde M)$
the trace of the generalized subpair
$(\tilde X, \tilde B + \tilde M)$
the trace of the generalized subpair
![]() $(X,B+M)$
on
$(X,B+M)$
on
![]() $\tilde X$
. Furthermore, we set
$\tilde X$
. Furthermore, we set
. With this piece of data, we can define divisors
![]() $B_{\tilde T}$
and
$B_{\tilde T}$
and
![]() $M_{\tilde T}$
, such that
$M_{\tilde T}$
, such that
![]() $B_{T}= \psi _* B_{\tilde T}$
, and
$B_{T}= \psi _* B_{\tilde T}$
, and
![]() $N_{T}= \psi _* N_{\tilde T}$
. In this way, Weil b-divisors
$N_{T}= \psi _* N_{\tilde T}$
. In this way, Weil b-divisors
![]() $\mathbf {B}$
and
$\mathbf {B}$
and
![]() $\mathbf {N}$
are defined. We write
$\mathbf {N}$
are defined. We write
![]() ${\mathbf {B}_{\tilde {T}}}$
and
${\mathbf {B}_{\tilde {T}}}$
and
![]() ${\mathbf N}_{\tilde {T}}$
for the traces of
${\mathbf N}_{\tilde {T}}$
for the traces of
![]() $\mathbf {B}$
and
$\mathbf {B}$
and
![]() ${\mathbf N}$
on any higher model
${\mathbf N}$
on any higher model
![]() $\tilde {T}$
. When the setup is clear, we shall write
$\tilde {T}$
. When the setup is clear, we shall write
![]() $B_{\tilde T}$
and
$B_{\tilde T}$
and
![]() $N_{\tilde {T}}$
in place of
$N_{\tilde {T}}$
in place of
![]() $\mathbf {B}_{\tilde T}$
and
$\mathbf {B}_{\tilde T}$
and
![]() $\mathbf {N}_{\tilde {T}}$
, respectively. In this setup, we have the following theorem, referred to as generalized canonical bundle formula.
$\mathbf {N}_{\tilde {T}}$
, respectively. In this setup, we have the following theorem, referred to as generalized canonical bundle formula.
Theorem 2.20. Let
![]() $(X,B,\mathbf {M})/S$
be a generalized subpair. Let
$(X,B,\mathbf {M})/S$
be a generalized subpair. Let
![]() $f\colon X \rightarrow T$
be a generalized lc-trivial fibration over S. If B is effective over the generic point of T, then the b-divisor
$f\colon X \rightarrow T$
be a generalized lc-trivial fibration over S. If B is effective over the generic point of T, then the b-divisor
![]() ${\mathbf N}$
is
${\mathbf N}$
is
![]() $\mathbb {Q}$
-b-Cartier and b-nef over S.
$\mathbb {Q}$
-b-Cartier and b-nef over S.
Below, we shall summarize the relevant changes to the proof of [Reference Filipazzi10, Theorem 1.4] in order to drop the assumption on the projectivity of the pairs and on
![]() $S = \operatorname {Spec}(\mathbb {C})$
. We refer to [Reference Filipazzi9] for a detailed proof.
$S = \operatorname {Spec}(\mathbb {C})$
. We refer to [Reference Filipazzi9] for a detailed proof.
Sketch of proof.
Throughout the proof, S will be a quasiprojective variety, with no further assumption. For the reader’s convenience, we subdivide the proof into several steps.
Step 1: In this step, we show that the statement of the theorem holds if we assume that
![]() $\mathbf {M}$
is b-semiample.
$\mathbf {M}$
is b-semiample.
Let
![]() $X'$
be a model where
$X'$
be a model where
![]() $\mathbf {M}$
descends. For brevity, we set
$\mathbf {M}$
descends. For brevity, we set
![]() . Let
. Let
![]() $h \colon X' \rightarrow T$
be the induced morphism. Let
$h \colon X' \rightarrow T$
be the induced morphism. Let
![]() $\mathcal {U} \subset |M'|_{\mathbb {Q}}$
be the set consisting of
$\mathcal {U} \subset |M'|_{\mathbb {Q}}$
be the set consisting of
![]() $\mathbb {Q}$
-divisors
$\mathbb {Q}$
-divisors
![]() $0 \leq \Delta ' \sim _{\mathbb {Q}} M'$
, such that
$0 \leq \Delta ' \sim _{\mathbb {Q}} M'$
, such that
![]() $(X',B'+\Delta ')$
is sublog canonical over the generic point of T. As
$(X',B'+\Delta ')$
is sublog canonical over the generic point of T. As
![]() $M'$
is semiample,
$M'$
is semiample,
![]() $\mathcal {U}$
is nonempty. Given
$\mathcal {U}$
is nonempty. Given
![]() $\Delta ' \in \mathcal {U}$
, we can apply Theorem 2.17 to
$\Delta ' \in \mathcal {U}$
, we can apply Theorem 2.17 to
![]() $(X',B'+\Delta ') \rightarrow T$
, thus obtaining a
$(X',B'+\Delta ') \rightarrow T$
, thus obtaining a
![]() $\mathbb {Q}$
-b-Cartier b-divisor
$\mathbb {Q}$
-b-Cartier b-divisor
![]() ${\mathbf N}^{\Delta '}$
that is b-nef over S. As discussed in [Reference Filipazzi10, Remark 4.8], we have
${\mathbf N}^{\Delta '}$
that is b-nef over S. As discussed in [Reference Filipazzi10, Remark 4.8], we have
We wish to apply weak semistable reduction to argue that
![]() ${\mathbf N}$
is a
${\mathbf N}$
is a
![]() $\mathbb {Q}$
-b-Cartier b-divisor that descends to a model satisfying explicit properties (see the proof of [Reference Filipazzi10, Theorem 4.13]). The proof of the b-nefness of
$\mathbb {Q}$
-b-Cartier b-divisor that descends to a model satisfying explicit properties (see the proof of [Reference Filipazzi10, Theorem 4.13]). The proof of the b-nefness of
![]() ${\mathbf N}$
over S goes then through as explained in the proof of [Reference Filipazzi10, Theorem 4.15]. One first shows that the statement is true if
${\mathbf N}$
over S goes then through as explained in the proof of [Reference Filipazzi10, Theorem 4.15]. One first shows that the statement is true if
![]() $\dim T = 2$
, cf. [Reference Filipazzi10, Remark 4.14]. To conclude, we reduce to the case of dimension
$\dim T = 2$
, cf. [Reference Filipazzi10, Remark 4.14]. To conclude, we reduce to the case of dimension
![]() $2$
by taking general hyperplane cuts on T, cf. the proof of [Reference Filipazzi10, Theorem 4.15].
$2$
by taking general hyperplane cuts on T, cf. the proof of [Reference Filipazzi10, Theorem 4.15].
Step 2: In this step, we show that the theorem holds when
![]() $\mathbf {M}$
is b-semiample over T.
$\mathbf {M}$
is b-semiample over T.
Let
![]() $X'$
and
$X'$
and
![]() $M'$
be the objects constructed in Step 1. Let A be a divisor on T which is ample over S. Since
$M'$
be the objects constructed in Step 1. Let A be a divisor on T which is ample over S. Since
![]() $M'$
is nef over S, and hence over T, and it is semiample over T,
$M'$
is nef over S, and hence over T, and it is semiample over T,
![]() $M'+ \epsilon h^{\ast } A$
is semiample over S for any
$M'+ \epsilon h^{\ast } A$
is semiample over S for any
![]() $\epsilon> 0$
, cf. [Reference Filipazzi10, Proposition 4.7]. Fix
$\epsilon> 0$
, cf. [Reference Filipazzi10, Proposition 4.7]. Fix
![]() $\epsilon> 0$
with
$\epsilon> 0$
with
![]() $\epsilon \in \mathbb {Q}$
. Let H be an ample divisor on S and write
$\epsilon \in \mathbb {Q}$
. Let H be an ample divisor on S and write
![]() $p \colon X' \rightarrow S, \; s\colon T \rightarrow S$
. Hence, for
$p \colon X' \rightarrow S, \; s\colon T \rightarrow S$
. Hence, for
![]() $n=n(\epsilon ) \gg 0, \; M'+\epsilon h^{\ast } A + n p^{\ast } H$
is semiample. We consider the generalized subpairs
$n=n(\epsilon ) \gg 0, \; M'+\epsilon h^{\ast } A + n p^{\ast } H$
is semiample. We consider the generalized subpairs
![]() $(X',B',\mathbf {M} +\epsilon \overline { g^{\ast } A})/S$
and
$(X',B',\mathbf {M} +\epsilon \overline { g^{\ast } A})/S$
and
![]() $(X',B',\mathbf {M} +\epsilon \overline {g^{\ast } A} + n \overline {p^{\ast } H})/S$
. Let
$(X',B',\mathbf {M} +\epsilon \overline {g^{\ast } A} + n \overline {p^{\ast } H})/S$
. Let
![]() $\mathbf {B}^{\epsilon }$
,
$\mathbf {B}^{\epsilon }$
,
![]() ${\mathbf N} ^{\epsilon }$
and
${\mathbf N} ^{\epsilon }$
and
![]() $\mathbf {B}^{\epsilon ,n}$
,
$\mathbf {B}^{\epsilon ,n}$
,
![]() ${\mathbf N} ^{\epsilon ,n}$
be the b-divisors, respectively, induced on T. By Remark 2.5, the generalized discrepancies of
${\mathbf N} ^{\epsilon ,n}$
be the b-divisors, respectively, induced on T. By Remark 2.5, the generalized discrepancies of
![]() $(X,B,\mathbf {M})/S$
,
$(X,B,\mathbf {M})/S$
,
![]() $(X',B',\mathbf {M} +\epsilon \overline {g^{\ast } A})/S$
, and
$(X',B',\mathbf {M} +\epsilon \overline {g^{\ast } A})/S$
, and
![]() $(X',B',\mathbf {M} +\epsilon \overline { g^{\ast } A }+ n \overline {p^{\ast } H})/S$
agree by construction. Thus, we have
$(X',B',\mathbf {M} +\epsilon \overline { g^{\ast } A }+ n \overline {p^{\ast } H})/S$
agree by construction. Thus, we have
Therefore, if for some
![]() $(\epsilon ,n)$
the b-divisor
$(\epsilon ,n)$
the b-divisor
![]() ${\mathbf N} {^{\epsilon ,n}}$
is
${\mathbf N} {^{\epsilon ,n}}$
is
![]() $\mathbb {Q}$
-b-Cartier, then so are
$\mathbb {Q}$
-b-Cartier, then so are
![]() ${\mathbf N}$
and
${\mathbf N}$
and
![]() ${\mathbf N} ^{\epsilon '}$
for any
${\mathbf N} ^{\epsilon '}$
for any
![]() $\epsilon '>0$
and all these b-divisors descend to the same model of T. We can then apply Step 1 to the generalized pair
$\epsilon '>0$
and all these b-divisors descend to the same model of T. We can then apply Step 1 to the generalized pair
![]() $(X',B',\mathbf {M} + \epsilon \overline {g^{\ast } A} + n\overline { p^{\ast } H})/S$
together with the morphism
$(X',B',\mathbf {M} + \epsilon \overline {g^{\ast } A} + n\overline { p^{\ast } H})/S$
together with the morphism
![]() $h \colon X' \rightarrow T$
and obtain
$h \colon X' \rightarrow T$
and obtain
![]() $\mathbb {Q}$
-b-Cartier b-divisor
$\mathbb {Q}$
-b-Cartier b-divisor
![]() ${\mathbf N}^{\epsilon ,n}$
which is b-nef
${\mathbf N}^{\epsilon ,n}$
which is b-nef
![]() $/S$
. Since we have
$/S$
. Since we have
![]() ${\mathbf N}^{\epsilon ,n} = {\mathbf N}^{\epsilon } + n\overline {s^{\ast } H}$
and
${\mathbf N}^{\epsilon ,n} = {\mathbf N}^{\epsilon } + n\overline {s^{\ast } H}$
and
![]() $\overline {s^{\ast } H}$
is trivial over S,
$\overline {s^{\ast } H}$
is trivial over S,
![]() ${\mathbf N} ^{\epsilon }$
is a
${\mathbf N} ^{\epsilon }$
is a
![]() $\mathbb {Q}$
-b-Cartier b-divisor that is b-nef
$\mathbb {Q}$
-b-Cartier b-divisor that is b-nef
![]() $/S$
. We let
$/S$
. We let
![]() $\epsilon>0$
vary and approach 0. Thus, as
$\epsilon>0$
vary and approach 0. Thus, as
![]() ${\mathbf N}$
is a limit of
${\mathbf N}$
is a limit of
![]() $\mathbb {Q}$
-b-Cartier b-divisors that all descend to the same model of T and are all b-nef over S, then
$\mathbb {Q}$
-b-Cartier b-divisors that all descend to the same model of T and are all b-nef over S, then
![]() ${\mathbf N}$
is a
${\mathbf N}$
is a
![]() $\mathbb {Q}$
-b-Cartier b-divisor that is b-nef over S.
$\mathbb {Q}$
-b-Cartier b-divisor that is b-nef over S.
Step 3: In this step, we show that the statement of the theorem holds when X is
![]() $\mathbb {Q}$
-factorial klt,
$\mathbb {Q}$
-factorial klt,
![]() $\rho (X/T)=1$
and
$\rho (X/T)=1$
and
![]() $\mathbf {M}_X$
is relatively ample over T.
$\mathbf {M}_X$
is relatively ample over T.
The proof of this case goes through as in [Reference Filipazzi10, Lemma 5.2] and reduces to Step 2. More precisely, since
![]() $\mathbf {M}$
is b-nef over S and
$\mathbf {M}$
is b-nef over S and
![]() ${\mathbf {M}_{X}}$
is ample over T, we can approximate
${\mathbf {M}_{X}}$
is ample over T, we can approximate
![]() $\mathbf {M}$
with b-divisors that are b-nef over S and b-semiample over T. The fact that X is a
$\mathbf {M}$
with b-divisors that are b-nef over S and b-semiample over T. The fact that X is a
![]() $\mathbb {Q}$
-factorial klt variety allows us to move the difference between
$\mathbb {Q}$
-factorial klt variety allows us to move the difference between
![]() $\mathbf {M}$
and its approximation to the boundary part of a generalized pair. So, we can regard
$\mathbf {M}$
and its approximation to the boundary part of a generalized pair. So, we can regard
![]() $(X,B,\mathbf {M})$
as being approximated by generalized subpairs to which Step 2 can be applied. Since the boundary parts of these approximations can be arranged to have the same support, we can apply the observation in Step 1 about the explicit description of the model where the b-divisors descend. This allows us to conclude, as
$(X,B,\mathbf {M})$
as being approximated by generalized subpairs to which Step 2 can be applied. Since the boundary parts of these approximations can be arranged to have the same support, we can apply the observation in Step 1 about the explicit description of the model where the b-divisors descend. This allows us to conclude, as
![]() $\mathbf {N}$
is realized as a limit of
$\mathbf {N}$
is realized as a limit of
![]() $\mathbb {Q}$
-b-Cartier b-divisors that descend to the same model, and hence it is
$\mathbb {Q}$
-b-Cartier b-divisors that descend to the same model, and hence it is
![]() $\mathbb {Q}$
-b-Cartier itself.
$\mathbb {Q}$
-b-Cartier itself.
Step 4: In this step, we show that the statement of the theorem holds in its full generality.
By Theorem 2.9, we can assume that X is
![]() $\mathbb {Q}$
-factorial and
$\mathbb {Q}$
-factorial and
![]() $(X,B^h)$
is dlt. If
$(X,B^h)$
is dlt. If
![]() $\mathbf {M}_X$
is numerically trivial along the generic fiber of
$\mathbf {M}_X$
is numerically trivial along the generic fiber of
![]() $X \rightarrow T$
, we can reduce to Theorem 2.17. If
$X \rightarrow T$
, we can reduce to Theorem 2.17. If
![]() $\mathbf {M}_X$
is not numerically trivial along the generic fiber of
$\mathbf {M}_X$
is not numerically trivial along the generic fiber of
![]() $X \rightarrow T$
,
$X \rightarrow T$
,
![]() $(X,B^h)$
is not pseudo-effective over T. Thus, we can run a
$(X,B^h)$
is not pseudo-effective over T. Thus, we can run a
![]() $({K_{X}} + B^h)$
-MMP over T with scaling, which terminates with a Mori fiber space
$({K_{X}} + B^h)$
-MMP over T with scaling, which terminates with a Mori fiber space
![]() $X" \rightarrow U$
. Thus, we can apply Step 3 to
$X" \rightarrow U$
. Thus, we can apply Step 3 to
![]() $(X",B",\mathbf {M})/S$
and
$(X",B",\mathbf {M})/S$
and
![]() $X" \rightarrow U$
. By [Reference Filipazzi10, Lemma 5.1], we can then conclude inductively.
$X" \rightarrow U$
. By [Reference Filipazzi10, Lemma 5.1], we can then conclude inductively.
2.6 Standard
 ${\mathbb P}^{1}$
-links and
${\mathbb P}^{1}$
-links and
 $\mathbb P^1$
-linkage
$\mathbb P^1$
-linkage
In this section, we recall the notion of standard
![]() ${\mathbb P}^{1}$
-link and extend it to generalized pairs. The definition of pullback for b-divisors can be found at the end of Section 2.2.
${\mathbb P}^{1}$
-link and extend it to generalized pairs. The definition of pullback for b-divisors can be found at the end of Section 2.2.
Definition 2.21. A generalized pair
![]() $(X,D_1+D_2+\Delta ,\mathbf {M})/S$
endowed with a projective morphism
$(X,D_1+D_2+\Delta ,\mathbf {M})/S$
endowed with a projective morphism
![]() $\pi \colon X \rightarrow T$
over S is a standard
$\pi \colon X \rightarrow T$
over S is a standard
![]() ${\mathbb P}^{1}$
-link if
${\mathbb P}^{1}$
-link if
-
0.
 $D_1$
and
$D_1$
and
 $D_2$
are distinct reduced prime divisors and
$D_2$
are distinct reduced prime divisors and
 $\lfloor \Delta \rfloor =0$
;
$\lfloor \Delta \rfloor =0$
; -
1.
 ${K_{X}} + D_1 + D_2 + \Delta \sim _{\mathbb {Q},\pi } 0$
;
${K_{X}} + D_1 + D_2 + \Delta \sim _{\mathbb {Q},\pi } 0$
; -
2. there exists a
 $\mathbb {Q}$
-b-Cartier
$\mathbb {Q}$
-b-Cartier
 $\mathbb {Q}$
-b-divisor
$\mathbb {Q}$
-b-divisor
 $\mathbf {N}$
on T, such that
$\mathbf {N}$
on T, such that
 $\mathbf {M} \sim _{\mathbb Q} \pi ^* \mathbf {N}$
;
$\mathbf {M} \sim _{\mathbb Q} \pi ^* \mathbf {N}$
; -
3.
 $\pi \vert _{D_i} \colon D_i \rightarrow T$
is an isomorphism for
$\pi \vert _{D_i} \colon D_i \rightarrow T$
is an isomorphism for
 $i=1,2$
;
$i=1,2$
; -
4.
 $(X,D_1+D_2+\Delta ,\mathbf {M})/S$
is generalized plt; and
$(X,D_1+D_2+\Delta ,\mathbf {M})/S$
is generalized plt; and -
5. every reduced fiber of
 $\pi $
is isomorphic to
$\pi $
is isomorphic to
 ${\mathbb P}^{1}$
.
${\mathbb P}^{1}$
.
The following lemma shows that condition (2) in Definition 2.21 is implied by the condition
![]() ${\mathbf {M}_{X}} \sim _{\mathbb Q, T} 0$
. We note, though, that the two conditions are not equivalent, since condition (2) in Definition 2.21 only restricts the behavior of
${\mathbf {M}_{X}} \sim _{\mathbb Q, T} 0$
. We note, though, that the two conditions are not equivalent, since condition (2) in Definition 2.21 only restricts the behavior of
![]() $\mathbf {M}$
along the general fiber of the contraction
$\mathbf {M}$
along the general fiber of the contraction
![]() $\pi $
.
$\pi $
.
Lemma 2.22. Let
![]() $f \colon X \rightarrow T$
be a projective contraction over a base scheme S and
$f \colon X \rightarrow T$
be a projective contraction over a base scheme S and
![]() $\mathbf {M}$
be a
$\mathbf {M}$
be a
![]() $\mathbb Q$
-b-Cartier
$\mathbb Q$
-b-Cartier
![]() $\mathbb Q$
-b-divisor on X that is b-nef over S. If
$\mathbb Q$
-b-divisor on X that is b-nef over S. If
![]() ${\mathbf {M}_{X}} \sim _{\mathbb Q,T} 0$
, then there is a
${\mathbf {M}_{X}} \sim _{\mathbb Q,T} 0$
, then there is a
![]() $\mathbb {Q}$
-b-Cartier b-divisor
$\mathbb {Q}$
-b-Cartier b-divisor
![]() $\mathbf {N}$
on T, such that
$\mathbf {N}$
on T, such that
![]() $\mathbf {M} \sim _{\mathbb Q}f^* {\mathbf N}$
.
$\mathbf {M} \sim _{\mathbb Q}f^* {\mathbf N}$
.
Proof. Let
![]() $X^r \rightarrow X$
be a resolution of X, such that
$X^r \rightarrow X$
be a resolution of X, such that
![]() $\mathbf {M}$
descends to
$\mathbf {M}$
descends to
![]() $X^r$
. Let
$X^r$
. Let
![]() $X^f \rightarrow T^f$
be a flattening of
$X^f \rightarrow T^f$
be a flattening of
![]() $X^r \rightarrow T$
, see [Reference Raynaud and Gruson33, Théorème 5.2.2], and let
$X^r \rightarrow T$
, see [Reference Raynaud and Gruson33, Théorème 5.2.2], and let
![]() $\widetilde {T}$
be a resolution of
$\widetilde {T}$
be a resolution of
![]() $T^f$
. Let
$T^f$
. Let
![]() $\widetilde {X}$
be the normalization of the main component of
$\widetilde {X}$
be the normalization of the main component of
![]() $X^f\times _{T^f}\widetilde {T}$
. This ensures that
$X^f\times _{T^f}\widetilde {T}$
. This ensures that
![]() $\widetilde {X}\to \widetilde {T}$
still has equidimensional fibers. Since
$\widetilde {X}\to \widetilde {T}$
still has equidimensional fibers. Since
![]() ${\mathbf {M}_{X}}$
is torsion along the generic fiber of
${\mathbf {M}_{X}}$
is torsion along the generic fiber of
![]() $X \rightarrow T$
, the same holds true for
$X \rightarrow T$
, the same holds true for
![]() ${\mathbf {M}_{\widetilde {X}}}$
along the generic fiber of
${\mathbf {M}_{\widetilde {X}}}$
along the generic fiber of
![]() $\widetilde {X}\to \widetilde {T}$
by the negativity lemma. Thus, by the proof of [Reference Witaszek37, Lemma 2.18], under our assumptions,Footnote
1
it follows that
$\widetilde {X}\to \widetilde {T}$
by the negativity lemma. Thus, by the proof of [Reference Witaszek37, Lemma 2.18], under our assumptions,Footnote
1
it follows that
![]() ${\mathbf {M}_{{\widetilde {X}}}} \sim _{\mathbb {Q},\widetilde {T}} 0$
. Since
${\mathbf {M}_{{\widetilde {X}}}} \sim _{\mathbb {Q},\widetilde {T}} 0$
. Since
![]() $\mathbf {M}$
is the b-Cartier closure of
$\mathbf {M}$
is the b-Cartier closure of
![]() $\mathbf {M}_{\widetilde {X}}$
, the conclusion of the statement follows at once.
$\mathbf {M}_{\widetilde {X}}$
, the conclusion of the statement follows at once.
Remark 2.23. Conditions (1), (3), and (5) of Definition 2.21 imply that
![]() $\Delta $
is vertical over T. Moreover, up to replacing
$\Delta $
is vertical over T. Moreover, up to replacing
![]() $\mathbf {M}$
with
$\mathbf {M}$
with
![]() $\pi ^*\mathbf {N}$
in its
$\pi ^*\mathbf {N}$
in its
![]() $\mathbb Q$
-linear equivalence class as b-divisor, the composition
$\mathbb Q$
-linear equivalence class as b-divisor, the composition
![]() $\pi \vert _{D_2}^{-1} \circ \pi \vert _{D_1}$
induces an isomorphism of generalized klt pairs
$\pi \vert _{D_2}^{-1} \circ \pi \vert _{D_1}$
induces an isomorphism of generalized klt pairs
Definition 2.24. Let
![]() $(X, B,\mathbf {M})/S$
be generalized dlt. Assume that there is a morphism
$(X, B,\mathbf {M})/S$
be generalized dlt. Assume that there is a morphism
![]() $\pi \colon X \rightarrow T$
over S, such that
$\pi \colon X \rightarrow T$
over S, such that
![]() ${K_{X}} + B + M \sim _{\mathbb {Q},\pi } 0$
. Let
${K_{X}} + B + M \sim _{\mathbb {Q},\pi } 0$
. Let
![]() $Z_1$
,
$Z_1$
,
![]() $Z_2$
be two generalized log canonical centers.
$Z_2$
be two generalized log canonical centers.
-
1. We say that
 $Z_1$
and
$Z_1$
and
 $Z_2$
are directly
$Z_2$
are directly
 ${\mathbb P}^{1}$
-linked if there is a generalized log canonical center W (alternatively,
${\mathbb P}^{1}$
-linked if there is a generalized log canonical center W (alternatively,
 $W=X$
itself) satisfying the following properties:
$W=X$
itself) satisfying the following properties:-
(a)
 $Z_i \subset W$
,
$Z_i \subset W$
,
 $i=1, 2$
;
$i=1, 2$
; -
(b)
 $\pi (W) = \pi (Z_1) = \pi (Z_2)$
; and
$\pi (W) = \pi (Z_1) = \pi (Z_2)$
; and -
(c) over a nonempty open subset of
 $\pi (W)$
, the generalized pair
$\pi (W)$
, the generalized pair
 $(W,B_W+N_W)$
induced by generalized adjunction onto W is birational to a standard
$(W,B_W+N_W)$
induced by generalized adjunction onto W is birational to a standard
 ${\mathbb P}^{1}$
-link, with the
${\mathbb P}^{1}$
-link, with the
 $Z_i$
mapping to the two horizontal sections of the
$Z_i$
mapping to the two horizontal sections of the
 ${\mathbb P}^{1}$
-link structure.
${\mathbb P}^{1}$
-link structure.
-
-
2. We say that
 $Z_1$
and
$Z_1$
and
 $Z_2$
are
$Z_2$
are
 ${\mathbb P}^{1}$
-linked if either
${\mathbb P}^{1}$
-linked if either
 $Z_1=Z_2$
or there exists a sequence of (distinct) generalized log canonical centers
$Z_1=Z_2$
or there exists a sequence of (distinct) generalized log canonical centers
 $Z_1', \ldots , Z_n'$
, such that
$Z_1', \ldots , Z_n'$
, such that
 $Z_1 ' = Z_1$
,
$Z_1 ' = Z_1$
,
 $Z_n ' =Z_2$
, and
$Z_n ' =Z_2$
, and
 $Z_i'$
is directly
$Z_i'$
is directly
 ${\mathbb P}^{1}$
-linked to
${\mathbb P}^{1}$
-linked to
 $Z_{i+1}'$
for
$Z_{i+1}'$
for
 $i=i, \ldots , n-1$
.
$i=i, \ldots , n-1$
.
It is an immediate consequence of the previous definition that every
![]() ${\mathbb P}^{1}$
-linking defines a birational map between
${\mathbb P}^{1}$
-linking defines a birational map between
![]() $(Z_1,B_{Z_1} + N_{Z_{1}})$
and
$(Z_1,B_{Z_1} + N_{Z_{1}})$
and
![]() $(Z_2, B_{Z_{2}} + N_{Z_{2}})$
.
$(Z_2, B_{Z_{2}} + N_{Z_{2}})$
.
Remark 2.25. With the notation and assumptions of Definition 2.24, if Z is a generalized log canonical center, then Z is never directly
![]() $\mathbb {P}^1$
-linked to itself: indeed, as
$\mathbb {P}^1$
-linked to itself: indeed, as
![]() $(X, B+M)$
is generalized dlt, by adjunction, any generalized log canonical center
$(X, B+M)$
is generalized dlt, by adjunction, any generalized log canonical center
![]() $Z_1$
directly
$Z_1$
directly
![]() $\mathbb {P}^1$
-linked to Z must be distinct from Z itself. Therefore, being directly
$\mathbb {P}^1$
-linked to Z must be distinct from Z itself. Therefore, being directly
![]() ${\mathbb P}^{1}$
-linked is not a reflexive relation. Furthermore, considering the log Calabi–Yau surface
${\mathbb P}^{1}$
-linked is not a reflexive relation. Furthermore, considering the log Calabi–Yau surface
![]() $(\mathbb {P}^1\times \mathbb {P}^1, B)$
,
$(\mathbb {P}^1\times \mathbb {P}^1, B)$
,
![]() , it is immediate to see that the relation is not transitive either. The definition of
, it is immediate to see that the relation is not transitive either. The definition of
![]() $\mathbb P^1$
-linkage provides instead an equivalence relation, which is the smallest equivalence relation that includes that of direct
$\mathbb P^1$
-linkage provides instead an equivalence relation, which is the smallest equivalence relation that includes that of direct
![]() $\mathbb P^1$
-linkage.
$\mathbb P^1$
-linkage.
Remark 2.26. A generalized log canonical center
![]() $Z_1$
for a generalized dlt pair
$Z_1$
for a generalized dlt pair
![]() $(X, B+ M)/S$
is minimal, with respect to inclusion, if and only if the generalized pair
$(X, B+ M)/S$
is minimal, with respect to inclusion, if and only if the generalized pair
![]() $(Z_1,B_{Z_1}, \mathbf {N})$
induced by adjunction along
$(Z_1,B_{Z_1}, \mathbf {N})$
induced by adjunction along
![]() $Z_1$
is generalized klt, cf. [Reference Birkar and Zhang7, Definition 4.7]. If
$Z_1$
is generalized klt, cf. [Reference Birkar and Zhang7, Definition 4.7]. If
![]() $(Z_1,B_{Z_1} + N_{Z_1})$
is generalized klt and
$(Z_1,B_{Z_1} + N_{Z_1})$
is generalized klt and
![]() $Z_2$
is
$Z_2$
is
![]() ${\mathbb P}^{1}$
-linked to
${\mathbb P}^{1}$
-linked to
![]() $Z_1$
, then also
$Z_1$
, then also
![]() $(Z_2,B_{Z_2} + N_{Z_2})$
is generalized klt, cf. [Reference Kollár25, Corollary 4.35]. In particular,
$(Z_2,B_{Z_2} + N_{Z_2})$
is generalized klt, cf. [Reference Kollár25, Corollary 4.35]. In particular,
![]() $Z_1$
is a minimal generalized log canonical center if and only if so is
$Z_1$
is a minimal generalized log canonical center if and only if so is
![]() $Z_2$
.
$Z_2$
.
The following example shows that in Definition 2.24.1.(c) the birational map between the generalized log canonical center W and the standard
![]() $\mathbb P^1$
-link may not be a morphism, that is, it may not be defined everywhere.
$\mathbb P^1$
-link may not be a morphism, that is, it may not be defined everywhere.
Example 2.27. We follow the notation of Definition 2.24. Let us take
![]() $X= \mathbb P^1 \times \mathbb P^1=W$
,
$X= \mathbb P^1 \times \mathbb P^1=W$
,
![]() $S= \mathrm {Spec}(k)$
,
$S= \mathrm {Spec}(k)$
,
![]() $T= \mathbb P^1$
, and the projection
$T= \mathbb P^1$
, and the projection
![]() $pr_1 \colon \mathbb P^1 \times \mathbb P^1 \to \mathbb P^1$
onto the first copy as
$pr_1 \colon \mathbb P^1 \times \mathbb P^1 \to \mathbb P^1$
onto the first copy as
![]() $\pi $
. Moreover, set
$\pi $
. Moreover, set
![]() ,
,
![]() $\mathbf {M}=0$
, where
$\mathbf {M}=0$
, where
![]() $H= \mathbb P^1 \times \{ 0 \}=Z_1$
,
$H= \mathbb P^1 \times \{ 0 \}=Z_1$
,
![]() $V= \{ 0 \} \times \mathbb P^1$
, and
$V= \{ 0 \} \times \mathbb P^1$
, and
![]() $C \in \vert \mathcal O_{\mathbb P^1 \times \mathbb P^1}(1, 1)\vert =Z_2$
is a general element. Thus,
$C \in \vert \mathcal O_{\mathbb P^1 \times \mathbb P^1}(1, 1)\vert =Z_2$
is a general element. Thus,
![]() $pr_1(C)=pr_1(H)=pr_1(X)=T$
, and C, H are directly
$pr_1(C)=pr_1(H)=pr_1(X)=T$
, and C, H are directly
![]() $\mathbb P^1$
-linked since they are sections of
$\mathbb P^1$
-linked since they are sections of
![]() $\pi $
. Nonetheless, any birational morphism to a standard
$\pi $
. Nonetheless, any birational morphism to a standard
![]() $\mathbb P^1$
-link cannot be taken to be everywhere defined since C and H intersect in X, whereas in the definition of standard
$\mathbb P^1$
-link cannot be taken to be everywhere defined since C and H intersect in X, whereas in the definition of standard
![]() $\mathbb P^1$
-link, the two sections are disjoint (see (0) in Definition 2.21).
$\mathbb P^1$
-link, the two sections are disjoint (see (0) in Definition 2.21).
2.7 Dual complexes for generalized log canonical pairs.
We recall the notion of dual complex of a simple normal crossing variety.
Definition 2.28. Let E be a simple normal crossing variety defined over a field k with irreducible components
![]() $\lbrace E_i | i \in I \rbrace $
. A stratum F of E is any irreducible component F of
$\lbrace E_i | i \in I \rbrace $
. A stratum F of E is any irreducible component F of
![]() $\cap _{i \in J} E_i$
for some
$\cap _{i \in J} E_i$
for some
![]() $J \subset I$
.
$J \subset I$
.
Given a simple normal crossing variety
![]() $E= \bigcup _{i \in I} E_i$
and a stratum
$E= \bigcup _{i \in I} E_i$
and a stratum
![]() $F \subset \bigcap _{i \in J} E_i$
of E, for any
$F \subset \bigcap _{i \in J} E_i$
of E, for any
![]() $j \in J$
, there is a unique irreducible component
$j \in J$
, there is a unique irreducible component
![]() $F_j$
of
$F_j$
of
![]() $\bigcap _{i \in J \setminus \lbrace j \rbrace } E_i$
that contains F. Using this observation, it is possible to construct a regular
$\bigcap _{i \in J \setminus \lbrace j \rbrace } E_i$
that contains F. Using this observation, it is possible to construct a regular
![]() $\Delta $
-complex, in the sense of [Reference Hatcher20, page 103], that encodes the combinatorial structure of the strata of E.
$\Delta $
-complex, in the sense of [Reference Hatcher20, page 103], that encodes the combinatorial structure of the strata of E.
Definition 2.29. Let E be a simple normal crossing variety defined over a field k with irreducible components
![]() $\lbrace E_i | i \in I \rbrace $
. The dual complex of E, denoted by
$\lbrace E_i | i \in I \rbrace $
. The dual complex of E, denoted by
![]() $\mathcal {D}(E)$
, is a CW-complex, whose vertices are labeled by the irreducible components of E, and for every stratum
$\mathcal {D}(E)$
, is a CW-complex, whose vertices are labeled by the irreducible components of E, and for every stratum
![]() $F \subset \bigcap _{i \in J} E_i$
, we attach a
$F \subset \bigcap _{i \in J} E_i$
, we attach a
![]() $(|J|-1)$
-dimensional cell
$(|J|-1)$
-dimensional cell
![]() $C_F$
by attaching the facet corresponding to the inclusion
$C_F$
by attaching the facet corresponding to the inclusion
![]() $J \setminus \{j\}$
to the cell corresponding to
$J \setminus \{j\}$
to the cell corresponding to
![]() $F_j$
.
$F_j$
.
Let
![]() $(X, B, \mathbf {M})/S$
be a generalized log canonical pair. Consider a log resolution
$(X, B, \mathbf {M})/S$
be a generalized log canonical pair. Consider a log resolution
![]() $f \colon X' \rightarrow X$
of
$f \colon X' \rightarrow X$
of
![]() $(X,B)$
, where
$(X,B)$
, where
![]() $\mathbf {M}$
descends. In particular, the support
$\mathbf {M}$
descends. In particular, the support
![]() $f_{\ast }^{-1}B + \mathrm {Exc}(f)$
is a simple normal crossing divisor, and we can write
$f_{\ast }^{-1}B + \mathrm {Exc}(f)$
is a simple normal crossing divisor, and we can write
Hence, we can define the dual complex
![]() $\mathcal {D}((B')^{=1})$
of the simple normal crossing variety
$\mathcal {D}((B')^{=1})$
of the simple normal crossing variety
![]() $(B')^{=1}$
as in Definition 2.29.
$(B')^{=1}$
as in Definition 2.29.
Definition 2.30. Let
![]() $(X, B, \mathbf {M})/S$
be a generalized log canonical pair, and let
$(X, B, \mathbf {M})/S$
be a generalized log canonical pair, and let
![]() $f \colon X' \rightarrow X$
be a log resolution of
$f \colon X' \rightarrow X$
be a log resolution of
![]() $(X,B)$
, where
$(X,B)$
, where
![]() $\mathbf {M}$
descends. The dual complex
$\mathbf {M}$
descends. The dual complex
![]() $\mathcal {DMR}(X,B, \mathbf {M})$
of
$\mathcal {DMR}(X,B, \mathbf {M})$
of
![]() $(X, B, \mathbf {M})/S$
is the PL-homeomorphism class of the
$(X, B, \mathbf {M})/S$
is the PL-homeomorphism class of the
![]() $\Delta $
-complex
$\Delta $
-complex
![]() $\mathcal {D}((B')^{=1})$
constructed above.
$\mathcal {D}((B')^{=1})$
constructed above.
Let
![]() $g \colon X" \rightarrow X$
be a different log resolution of
$g \colon X" \rightarrow X$
be a different log resolution of
![]() $(X,B)$
, where
$(X,B)$
, where
![]() $\mathbf {M}_{X"}$
descends, and write
$\mathbf {M}_{X"}$
descends, and write
As for
![]() $(B')^{=1}$
, we can define the dual complex
$(B')^{=1}$
, we can define the dual complex
![]() $\mathcal {D}((B")^{=1})$
of
$\mathcal {D}((B")^{=1})$
of
![]() $(B")^{=1}$
. By construction, the subpairs
$(B")^{=1}$
. By construction, the subpairs
![]() $(X',B')$
and
$(X',B')$
and
![]() $(X",B")$
are crepant birational to each other, as we have chosen both log resolutions f and g so that
$(X",B")$
are crepant birational to each other, as we have chosen both log resolutions f and g so that
![]() $\mathbf {M}$
descends to
$\mathbf {M}$
descends to
![]() $X'$
and
$X'$
and
![]() $X"$
. Hence, using the weak factorization theorem for the birational map
$X"$
. Hence, using the weak factorization theorem for the birational map
![]() $X' \dashrightarrow X"$
, it is possible to prove that the complexes
$X' \dashrightarrow X"$
, it is possible to prove that the complexes
![]() $\mathcal {D}((B')^{=1})$
and
$\mathcal {D}((B')^{=1})$
and
![]() $\mathcal {D}((B")^{=1})$
are PL-homeomorphic to each other (see [Reference de Fernex, Kollár and Xu8, Proposition 11] for full details of the argument).
$\mathcal {D}((B")^{=1})$
are PL-homeomorphic to each other (see [Reference de Fernex, Kollár and Xu8, Proposition 11] for full details of the argument).
Remark 2.31. In the setup of Definition 2.30, if we further assume that
![]() $(X,B, \mathbf {M})$
is
$(X,B, \mathbf {M})$
is
![]() $\mathbb {Q}$
-factorial and generalized dlt, then every log canonical place of
$\mathbb {Q}$
-factorial and generalized dlt, then every log canonical place of
![]() $(X,B+M)$
is a log canonical place of
$(X,B+M)$
is a log canonical place of
![]() $(X,B)$
, and vice versa, cf. Definition 2.8. Thus, in this case, we have
$(X,B)$
, and vice versa, cf. Definition 2.8. Thus, in this case, we have
![]() $\mathcal {DMR}(X,B)=\mathcal {DMR}(X,B, \mathbf {M})$
.
$\mathcal {DMR}(X,B)=\mathcal {DMR}(X,B, \mathbf {M})$
.
2.8 Dual complex of nonlog canonical pairs
We extend the definition of dual complex to generalized pairs that are not necessarily generalized log canonical. To this end, we will use dlt models of generalized log pairs, cf. Section 2.4 and the notation defined there.
Definition 2.32. Let
![]() $(X, B, \mathbf {M})/S$
be a generalized pair. Assume that
$(X, B, \mathbf {M})/S$
be a generalized pair. Assume that
![]() $(X, B, \mathbf {M})/S$
is not generalized log canonical. The dual complex
$(X, B, \mathbf {M})/S$
is not generalized log canonical. The dual complex
![]() $\mathcal {DMR}(X,B, \mathbf {M})$
of
$\mathcal {DMR}(X,B, \mathbf {M})$
of
![]() $(X, B, \mathbf {M})/S$
is the simple homotopy equivalence class of the
$(X, B, \mathbf {M})/S$
is the simple homotopy equivalence class of the
![]() $\Delta $
-complex
$\Delta $
-complex
![]() $\mathcal {D}((B^{m})^{=1})$
, where
$\mathcal {D}((B^{m})^{=1})$
, where
![]() $(X^m,B^m,\mathbf {M})$
is a generalized dlt model of
$(X^m,B^m,\mathbf {M})$
is a generalized dlt model of
![]() $(X,B,\mathbf {M})$
.
$(X,B,\mathbf {M})$
.
Let
![]() $(X,B, \mathbf {M})$
be a generalized pair that is not generalized log canonical, we ought to show that Definition 2.32 is independent of the choice of a generalized dlt model of
$(X,B, \mathbf {M})$
be a generalized pair that is not generalized log canonical, we ought to show that Definition 2.32 is independent of the choice of a generalized dlt model of
![]() $(X,B, \mathbf {M})$
, or, equivalently, that the dual complexes of any two generalized dlt models of
$(X,B, \mathbf {M})$
, or, equivalently, that the dual complexes of any two generalized dlt models of
![]() $(X,B, \mathbf {M})$
are simple homotopy equivalent.
$(X,B, \mathbf {M})$
are simple homotopy equivalent.
Remark 2.33. In Definition 2.30, the dual complex of a generalized log canonical pair was defined by considering the PL-homeomorphism class of the dual complex. For singularities that are worse than log canonical, we are bound to use the weaker notion of simple-homotopy equivalence class. Nevertheless, this notion is good enough to discuss the collapsibility of
![]() $\mathcal {DMR}(X,B, \mathbf {M})$
and to compute its cohomology.
$\mathcal {DMR}(X,B, \mathbf {M})$
and to compute its cohomology.
Lemma 2.34. Assume the same notations and assumptions introduced above. Consider two generalized dlt models of
![]() $(X,B,\mathbf {M})$
, denoted by
$(X,B,\mathbf {M})$
, denoted by
![]() $\rho _i \colon (X_i^m,B_i^m, \mathbf {M}) \rightarrow X$
,
$\rho _i \colon (X_i^m,B_i^m, \mathbf {M}) \rightarrow X$
,
![]() $i=1, 2$
. Then
$i=1, 2$
. Then
![]() $\mathcal {D}((B_1^m)^{=1})$
and
$\mathcal {D}((B_1^m)^{=1})$
and
![]() $\mathcal {D}((B_2^m)^{=1})$
are simple homotopy equivalent.
$\mathcal {D}((B_2^m)^{=1})$
are simple homotopy equivalent.
By Remark 2.5, consider the pair
![]() $(X,B, \mathbf {M} + \overline {H})$
, where H is a suitable ample divisor on X,
$(X,B, \mathbf {M} + \overline {H})$
, where H is a suitable ample divisor on X,
![]() $\mathbf {M} + \overline {H}$
is b-nef and b-big. Hence, up to substituting
$\mathbf {M} + \overline {H}$
is b-nef and b-big. Hence, up to substituting
![]() $\mathbf {M}$
with
$\mathbf {M}$
with
![]() $\mathbf {M}+ \overline {H}$
, we can assume that
$\mathbf {M}+ \overline {H}$
, we can assume that
![]() $\mathbf {M}$
is b-nef and b-big. Now, let
$\mathbf {M}$
is b-nef and b-big. Now, let
![]() $\pi \colon X' \rightarrow X$
be a log resolution of
$\pi \colon X' \rightarrow X$
be a log resolution of
![]() $(X,B)$
, where
$(X,B)$
, where
![]() $\mathbf {M}$
descends. We will assume that
$\mathbf {M}$
descends. We will assume that
![]() $\pi $
factors through both
$\pi $
factors through both
![]() $X_1^m$
and
$X_1^m$
and
![]() $X_2^m$
. Let
$X_2^m$
. Let
![]() $\pi _i \colon X' \rightarrow X_i^m$
denote the corresponding morphisms for
$\pi _i \colon X' \rightarrow X_i^m$
denote the corresponding morphisms for
![]() $i=1,2$
.
$i=1,2$
.
Lemma 2.35. With the same notations and assumptions as above, if
![]() $X'$
is a sufficiently high model of X, then there exists an effective
$X'$
is a sufficiently high model of X, then there exists an effective
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $E'$
, such that the following conditions hold:
$E'$
, such that the following conditions hold:
-
1.
 $\operatorname {\mathrm {Supp}}(E') \cup \operatorname {\mathrm {Supp}}(B')$
is simple normal crossing; and
$\operatorname {\mathrm {Supp}}(E') \cup \operatorname {\mathrm {Supp}}(B')$
is simple normal crossing; and -
2. for every sufficiently large positive integer
 $k \gg 1$
, there exists a big and semiample
$k \gg 1$
, there exists a big and semiample
 $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
 $A^{\prime }_k$
, such that
$A^{\prime }_k$
, such that
 $\mathbf {M}_{X'} \sim _{\mathbb {Q}} A^{\prime }_k + E^{\prime }_k$
, where
$\mathbf {M}_{X'} \sim _{\mathbb {Q}} A^{\prime }_k + E^{\prime }_k$
, where
 .
.
Proof. As
![]() $\mathbf {M}_{X'}$
is nef and big, and it descends to the model
$\mathbf {M}_{X'}$
is nef and big, and it descends to the model
![]() $X'$
fixed before the lemma, there exists an effective divisor E, such that
$X'$
fixed before the lemma, there exists an effective divisor E, such that
![]() $\mathbf {M}_{X'} \sim _{\mathbb {Q}} A_k+E_k$
, where
$\mathbf {M}_{X'} \sim _{\mathbb {Q}} A_k+E_k$
, where
![]() $A_k$
is ample for
$A_k$
is ample for
![]() (see [Reference Kollár and Mori27, Proposition 2.61]). As E may not be simple normal crossing, it suffices to replace
(see [Reference Kollár and Mori27, Proposition 2.61]). As E may not be simple normal crossing, it suffices to replace
![]() $X'$
with a log resolution of
$X'$
with a log resolution of
![]() $(X, E)$
and define
$(X, E)$
and define
![]() $A^{\prime }_k$
,
$A^{\prime }_k$
,
![]() $E'$
to be their pullback on the new model.
$E'$
to be their pullback on the new model.
For
![]() $i=1,2$
, we define
$i=1,2$
, we define
![]() $B_i'$
by the log pullback formula
$B_i'$
by the log pullback formula
![]() ${K_{X'}} + B_i'=\pi _i^{\ast } ({K_{X_i^m}} + B_i^m)$
. As
${K_{X'}} + B_i'=\pi _i^{\ast } ({K_{X_i^m}} + B_i^m)$
. As
![]() $E'$
is effective, we may find
$E'$
is effective, we may find
![]() $0 < \epsilon \ll 1$
so that
$0 < \epsilon \ll 1$
so that
![]() $\operatorname {\mathrm {Supp}}( (B_i')^{\geq 1})= \operatorname {\mathrm {Supp}}((B_i' + \epsilon E')^{\geq 1})$
for
$\operatorname {\mathrm {Supp}}( (B_i')^{\geq 1})= \operatorname {\mathrm {Supp}}((B_i' + \epsilon E')^{\geq 1})$
for
![]() $i=1,2$
. Thus, for
$i=1,2$
. Thus, for
![]() $k \gg 1$
, we have
$k \gg 1$
, we have
![]() $\operatorname {\mathrm {Supp}}( (B_i')^{\geq 1})= \operatorname {\mathrm {Supp}}((B_i' + E^{\prime }_k)^{\geq 1})$
for
$\operatorname {\mathrm {Supp}}( (B_i')^{\geq 1})= \operatorname {\mathrm {Supp}}((B_i' + E^{\prime }_k)^{\geq 1})$
for
![]() $i=1,2$
. Let us fix one such value of k and let
$i=1,2$
. Let us fix one such value of k and let
![]() $A^{\prime }_k$
be a generic effective divisor in its
$A^{\prime }_k$
be a generic effective divisor in its
![]() $\mathbb {Q}$
-linear equivalence class. For
$\mathbb {Q}$
-linear equivalence class. For
![]() $i =1, 2$
, we define
$i =1, 2$
, we define
By construction, the following two conditions hold:
-
(i)
 $a_F(X,B+M) \geq a_F(X,B+\Gamma )$
for every divisorial valuation F centered on X; and
$a_F(X,B+M) \geq a_F(X,B+\Gamma )$
for every divisorial valuation F centered on X; and -
(ii) a prime divisor
 $G \subset X'$
satisfies
$G \subset X'$
satisfies
 $a_G(X_i^m,B_i^m+\Gamma _i^m) \leq 0$
if and only if
$a_G(X_i^m,B_i^m+\Gamma _i^m) \leq 0$
if and only if
 $a_G(X^m_i,B^m_i) \leq 0$
.
$a_G(X^m_i,B^m_i) \leq 0$
.
Both properties follow from the fact that
![]() $\mathbf {M}_{X'} \sim _{\mathbb {Q}} A^{\prime }_k + E^{\prime }_k$
and
$\mathbf {M}_{X'} \sim _{\mathbb {Q}} A^{\prime }_k + E^{\prime }_k$
and
![]() $\operatorname {\mathrm {Supp}}( (B_i')^{\geq 1})= \operatorname {\mathrm {Supp}}((B_i' + E^{\prime }_k)^{\geq 1})$
, while
$\operatorname {\mathrm {Supp}}( (B_i')^{\geq 1})= \operatorname {\mathrm {Supp}}((B_i' + E^{\prime }_k)^{\geq 1})$
, while
![]() $A^{\prime }_k$
does not contribute to any singularity by Bertini’s theorem.
$A^{\prime }_k$
does not contribute to any singularity by Bertini’s theorem.
By (i), it follows that
![]() $X_i^m \rightarrow X$
extracts only divisors with nonpositive log discrepancy for
$X_i^m \rightarrow X$
extracts only divisors with nonpositive log discrepancy for
![]() $(X, B+\Gamma )$
. Therefore,
$(X, B+\Gamma )$
. Therefore,
![]() $B_i^m+\Gamma _i^m$
is effective for
$B_i^m+\Gamma _i^m$
is effective for
![]() $i=1,2$
. As
$i=1,2$
. As
![]() $X'$
is a log resolution of all the divisors involved, we can use it as input variety to construct a dlt model by means of a suitable MMP, as in Theorem 2.9. By running a suitable relative MMP over
$X'$
is a log resolution of all the divisors involved, we can use it as input variety to construct a dlt model by means of a suitable MMP, as in Theorem 2.9. By running a suitable relative MMP over
![]() $X_i^m$
, we can obtain a
$X_i^m$
, we can obtain a
![]() $\mathbb {Q}$
-factorial dlt model
$\mathbb {Q}$
-factorial dlt model
![]() $(X_i",B_i"+\Gamma _i")$
of
$(X_i",B_i"+\Gamma _i")$
of
![]() $(X_i^m,B_i^m+\Gamma _i^m)$
.
$(X_i^m,B_i^m+\Gamma _i^m)$
.
Lemma 2.36. With the same notations and assumptions as above,
![]() $\mathcal {D}((B_i^m)^{=1})$
is simple homotopy equivalent to
$\mathcal {D}((B_i^m)^{=1})$
is simple homotopy equivalent to
![]() $\mathcal {D}((B_i"+\Gamma _i")^{=1})$
for
$\mathcal {D}((B_i"+\Gamma _i")^{=1})$
for
![]() $i=1,2$
.
$i=1,2$
.
Proof. Since by construction
![]() $(X_i",B_i"+\Gamma _i")$
is also a dlt model for
$(X_i",B_i"+\Gamma _i")$
is also a dlt model for
![]() $(X,B+\Gamma )$
. Therefore, by [Reference Nakamura31, Proposition 2.14],
$(X,B+\Gamma )$
. Therefore, by [Reference Nakamura31, Proposition 2.14],
![]() $\mathcal {D}((B_1"+\Gamma _1")^{=1})$
and
$\mathcal {D}((B_1"+\Gamma _1")^{=1})$
and
![]() $\mathcal {D}((B_2"+\Gamma _2")^{=1})$
are simple homotopy equivalent to each other, as they compute the dual complex of
$\mathcal {D}((B_2"+\Gamma _2")^{=1})$
are simple homotopy equivalent to each other, as they compute the dual complex of
![]() $(X,B+\Gamma )$
.
$(X,B+\Gamma )$
.
We are now ready to prove the proof that Definition 2.32 depends neither on the choice of the ample divisor H, nor on the choice of the representatives
![]() $A^{\prime }_k, E^{\prime }_k$
that we made in the course of the construction contained in this section.
$A^{\prime }_k, E^{\prime }_k$
that we made in the course of the construction contained in this section.
Proof of Lemma 2.34.
By construction, the exceptional divisors of
![]() $X_i" \rightarrow X_i^m$
appear as divisors on
$X_i" \rightarrow X_i^m$
appear as divisors on
![]() $X'$
. Furthermore, as already observed, a divisor
$X'$
. Furthermore, as already observed, a divisor
![]() $E \subset X'$
satisfies
$E \subset X'$
satisfies
![]() $a_E(X_i^m,B_i^m+\Gamma _i^m) \leq 0$
if and only if
$a_E(X_i^m,B_i^m+\Gamma _i^m) \leq 0$
if and only if
![]() $a_E(X^m_i,B^m_i) \leq 0$
. Therefore,
$a_E(X^m_i,B^m_i) \leq 0$
. Therefore,
![]() $X_i" \rightarrow X_i^m$
only extracts divisors E with
$X_i" \rightarrow X_i^m$
only extracts divisors E with
![]() $a_E(X^m_i,B^m_i) \leq 0$
. Hence, the variety
$a_E(X^m_i,B^m_i) \leq 0$
. Hence, the variety
![]() $X^{\prime \prime }_i$
provides a dlt model for the dlt pair
$X^{\prime \prime }_i$
provides a dlt model for the dlt pair
![]() $(X^m_i,B^m_i)$
. Hence,
$(X^m_i,B^m_i)$
. Hence,
![]() $\mathcal {D}((B_i"+\Gamma _i")^{=1})$
computes
$\mathcal {D}((B_i"+\Gamma _i")^{=1})$
computes
![]() $\mathcal {DMR}(X_i^m,B_i^m)$
. As
$\mathcal {DMR}(X_i^m,B_i^m)$
. As
![]() $(X^m_i,B^m_i)$
is dlt, by [Reference de Fernex, Kollár and Xu8, Proposition 11],
$(X^m_i,B^m_i)$
is dlt, by [Reference de Fernex, Kollár and Xu8, Proposition 11],
![]() $\mathcal {DMR}(X_i^m,B_i^m)$
is a well-defined PL-homeomorphism class. Therefore,
$\mathcal {DMR}(X_i^m,B_i^m)$
is a well-defined PL-homeomorphism class. Therefore,
![]() $\mathcal {D}((B_i^m)^{=1})$
is PL-homeomorphic to
$\mathcal {D}((B_i^m)^{=1})$
is PL-homeomorphic to
![]() $\mathcal {D}((B_i"+\Gamma _i")^{=1})$
for
$\mathcal {D}((B_i"+\Gamma _i")^{=1})$
for
![]() $i=1,2$
. Thus,
$i=1,2$
. Thus,
![]() $\mathcal {D}((B_i^m)^{=1})$
is simple homotopy equivalent to
$\mathcal {D}((B_i^m)^{=1})$
is simple homotopy equivalent to
![]() $\mathcal {D}((B_i"+\Gamma _i")^{=1})$
for
$\mathcal {D}((B_i"+\Gamma _i")^{=1})$
for
![]() $i=1,2$
.
$i=1,2$
.
3 Connectedness for birational maps
In this section, we recall some results explaining how the structure of the non-klt locus of generalized pairs changes under birational maps. The first result is an adaptation to the generalized pair case of [Reference Kollár23, Theorem 17.4]. It provides a partial relative birational version of the connectedness principle for generalized pairs.
Proposition 3.1 (cf. [Reference Birkar5, Lemma 2.14]).
Let
![]() $(X, B, \mathbf {M})/Z$
be a generalized subpair, where
$(X, B, \mathbf {M})/Z$
be a generalized subpair, where
![]() $h \colon X \rightarrow Z$
is a projective contraction of normal varieties. Assume that
$h \colon X \rightarrow Z$
is a projective contraction of normal varieties. Assume that
-
1.
 $h_{\ast } B^{<0}=0$
; and
$h_{\ast } B^{<0}=0$
; and -
2.
 $-(K_X+B+M)$
is h-nef and h-big.
$-(K_X+B+M)$
is h-nef and h-big.
Let
![]() $g \colon W \rightarrow X$
be a log resolution of
$g \colon W \rightarrow X$
be a log resolution of
![]() $(X, B)$
to which
$(X, B)$
to which
![]() $\mathbf {M}$
descends. Let
$\mathbf {M}$
descends. Let
Let
![]() . Then
. Then
![]() $(g \circ h) \vert _{\operatorname {\mathrm {Supp}} (F)} \colon \operatorname {\mathrm {Supp}} (F) \to Z$
has connected fibers.
$(g \circ h) \vert _{\operatorname {\mathrm {Supp}} (F)} \colon \operatorname {\mathrm {Supp}} (F) \to Z$
has connected fibers.
Remark 3.2. The support of F is exactly the non-klt locus of the generalized subpair
![]() $(W, -\sum a_iE_i, \mathbf {M})/Z$
.
$(W, -\sum a_iE_i, \mathbf {M})/Z$
.
Remark 3.3. When h is birational, then it suffices to require that
![]() $-(K_X+B+M)$
is h-nef.
$-(K_X+B+M)$
is h-nef.
Proof. Let
![]() , and let
, and let
![]() . Then,
. Then,
and, by relative Kawamata–Viehweg vanishing,
since
![]() $\mathbf {M}_W -g^{*}(K_X+B+M)$
is s-big and s-nef and
$\mathbf {M}_W -g^{*}(K_X+B+M)$
is s-big and s-nef and
![]() $\{-A \} + \{F\}$
is simple normal crossing. Considering the following exact sequence
$\{-A \} + \{F\}$
is simple normal crossing. Considering the following exact sequence
and applying
![]() $s_*$
, we get that
$s_*$
, we get that
is surjective. As
![]() $\lceil A \rceil $
is s-exceptional, then
$\lceil A \rceil $
is s-exceptional, then
![]() $s_* \mathcal {O}_X(\lceil A \rceil ) \simeq \mathcal {O}_Z$
. Hence,
$s_* \mathcal {O}_X(\lceil A \rceil ) \simeq \mathcal {O}_Z$
. Hence,
![]() $s_* \mathcal {O}_X(\lceil A \rceil )$
is locally principally generated in a neighborhood of z.
$s_* \mathcal {O}_X(\lceil A \rceil )$
is locally principally generated in a neighborhood of z.
Assume by contradiction that
![]() $\operatorname {\mathrm {Supp}} (F)$
is not connected over some point
$\operatorname {\mathrm {Supp}} (F)$
is not connected over some point
![]() $z \in Z$
. Then,
$z \in Z$
. Then,
![]() $\mathcal {O}_{\lfloor F \rfloor }(\lceil A \rceil )$
is not locally principally generated over z, since it contains the pushforward of the sections vanishing on any but one of the components of the
$\mathcal {O}_{\lfloor F \rfloor }(\lceil A \rceil )$
is not locally principally generated over z, since it contains the pushforward of the sections vanishing on any but one of the components of the
![]() $\lfloor F \rfloor $
. On the other hand, the locally principally generated sheaf
$\lfloor F \rfloor $
. On the other hand, the locally principally generated sheaf
![]() $s_* \mathcal {O}_X(\lceil A \rceil ) \simeq \mathcal {O}_Z$
surjects onto
$s_* \mathcal {O}_X(\lceil A \rceil ) \simeq \mathcal {O}_Z$
surjects onto
![]() $\mathcal {O}_{\lfloor F \rfloor }(\lceil A \rceil )$
. This leads to a contradiction.
$\mathcal {O}_{\lfloor F \rfloor }(\lceil A \rceil )$
. This leads to a contradiction.
Remark 3.4. By applying Proposition 3.1 in the case where
![]() $Z=X$
and h is the identity map, we obtain that the number of connected components
$Z=X$
and h is the identity map, we obtain that the number of connected components
![]() $\operatorname {\mathrm {Nklt}}(X, B , \mathbf M)$
is unchanged by passing to a log resolution where
$\operatorname {\mathrm {Nklt}}(X, B , \mathbf M)$
is unchanged by passing to a log resolution where
![]() $\mathbf {M}$
descends.
$\mathbf {M}$
descends.
Lemma 3.5. Let
![]() $(X, B, \mathbf {M})/S$
be a
$(X, B, \mathbf {M})/S$
be a
![]() $\mathbb Q$
-factorial generalized pair, and let
$\mathbb Q$
-factorial generalized pair, and let
![]() $f \colon X \rightarrow Y$
be a proper morphism of algebraic varieties over S. Let
$f \colon X \rightarrow Y$
be a proper morphism of algebraic varieties over S. Let
![]() $\pi \colon X \to X_1$
be a divisorial contraction over Y, that is, we have the following commutative diagram
$\pi \colon X \to X_1$
be a divisorial contraction over Y, that is, we have the following commutative diagram

Assume that
-
•
 $\rho (X/X_1)=1$
;
$\rho (X/X_1)=1$
; -
•
 $K_X+B+M \sim _{\mathbb {R}, f} 0$
;
$K_X+B+M \sim _{\mathbb {R}, f} 0$
; -
•
 $B^{\geq 1}$
is
$B^{\geq 1}$
is
 $\pi $
-ample; and
$\pi $
-ample; and -
•
 $\operatorname {\mathrm {Nklt}}(X, B , \mathbf {M}) \subset \operatorname {\mathrm {Supp}} (B^{\geq 1})$
.
$\operatorname {\mathrm {Nklt}}(X, B , \mathbf {M}) \subset \operatorname {\mathrm {Supp}} (B^{\geq 1})$
.
Then
![]() $\operatorname {\mathrm {Nklt}}(X_1, B_1 , \mathbf {M}) \subset \operatorname {\mathrm {Supp}}(B_1^{\geq 1})$
, where
$\operatorname {\mathrm {Nklt}}(X_1, B_1 , \mathbf {M}) \subset \operatorname {\mathrm {Supp}}(B_1^{\geq 1})$
, where
.
Moreover, for any point
![]() $y \in Y$
, the number of connected components of
$y \in Y$
, the number of connected components of
![]() $\operatorname {\mathrm {Nklt}}(X_{1}, B_1, \mathbf {M}) \cap f_1^{-1}(y)$
is the same as the number of connected components of
$\operatorname {\mathrm {Nklt}}(X_{1}, B_1, \mathbf {M}) \cap f_1^{-1}(y)$
is the same as the number of connected components of
![]() $\operatorname {\mathrm {Nklt}}(X, B, \mathbf {M}) \cap f^{-1}(y)$
.
$\operatorname {\mathrm {Nklt}}(X, B, \mathbf {M}) \cap f^{-1}(y)$
.
Proof. Let E be the divisor contracted by
![]() $\pi $
. As
$\pi $
. As
![]() $K_X+B+M \sim _{\mathbb {R}, f} 0$
,
$K_X+B+M \sim _{\mathbb {R}, f} 0$
,
![]() $\operatorname {\mathrm {Nklt}}(X_1, B_1 , \mathbf {M}) = \pi (\operatorname {\mathrm {Nklt}}(X, B , \mathbf M))$
. If
$\operatorname {\mathrm {Nklt}}(X_1, B_1 , \mathbf {M}) = \pi (\operatorname {\mathrm {Nklt}}(X, B , \mathbf M))$
. If
![]() $E \not \subset \operatorname {\mathrm {Nklt}}(X, B, \mathbf {M})$
, then there is nothing to prove. Instead, if
$E \not \subset \operatorname {\mathrm {Nklt}}(X, B, \mathbf {M})$
, then there is nothing to prove. Instead, if
![]() $E \subset \operatorname {\mathrm {Nklt}}(X, B, \mathbf {M})$
, then
$E \subset \operatorname {\mathrm {Nklt}}(X, B, \mathbf {M})$
, then
![]() $\mu _E (B) \geq 1$
. As E is exceptional for
$\mu _E (B) \geq 1$
. As E is exceptional for
![]() $\pi $
, then
$\pi $
, then
![]() $E \cdot R < 0$
, where R is the extremal ray of
$E \cdot R < 0$
, where R is the extremal ray of
![]() $\overline {NE}(X/Y)$
corresponding to the contraction
$\overline {NE}(X/Y)$
corresponding to the contraction
![]() $\pi $
. As
$\pi $
. As
![]() $B^{\geq 1}$
is
$B^{\geq 1}$
is
![]() $\pi $
-ample, there exists a component G included in the support of
$\pi $
-ample, there exists a component G included in the support of
![]() $B^{\geq 1}$
, such that
$B^{\geq 1}$
, such that
![]() $G \cdot R>0$
. In particular,
$G \cdot R>0$
. In particular,
![]() $\pi _{\ast } G \supset \pi (E)$
, which proves the claim, as
$\pi _{\ast } G \supset \pi (E)$
, which proves the claim, as
![]() $B_1^{\geq 1} = \pi _{\ast } (B^{\geq 1})$
.
$B_1^{\geq 1} = \pi _{\ast } (B^{\geq 1})$
.
To prove the last assertion, it suffices to notice that, since we have
![]() $\operatorname {\mathrm {Nklt}}(X_1, B_1 , \mathbf {M}) = \pi (\operatorname {\mathrm {Nklt}}(X, B , \mathbf M))$
, the number of connected components of
$\operatorname {\mathrm {Nklt}}(X_1, B_1 , \mathbf {M}) = \pi (\operatorname {\mathrm {Nklt}}(X, B , \mathbf M))$
, the number of connected components of
![]() $\operatorname {\mathrm {Nklt}}(X_1, B_1 , \mathbf {M}) \cap f_1^{-1}(y)$
cannot be strictly larger than the number of those of
$\operatorname {\mathrm {Nklt}}(X_1, B_1 , \mathbf {M}) \cap f_1^{-1}(y)$
cannot be strictly larger than the number of those of
![]() $\operatorname {\mathrm {Nklt}}(X, B , \mathbf {M}) \cap f^{-1}(y)$
. If the number of components were to actually decrease, then taking a common resolution
$\operatorname {\mathrm {Nklt}}(X, B , \mathbf {M}) \cap f^{-1}(y)$
. If the number of components were to actually decrease, then taking a common resolution

where
![]() $\mathbf {M}$
descends and applying Proposition 3.1 with
$\mathbf {M}$
descends and applying Proposition 3.1 with
![]() $h=\pi $
,
$h=\pi $
,
![]() $Z=X_1$
,
$Z=X_1$
,
![]() $g=q$
,
$g=q$
,
![]() $p=g \circ h$
, we would obtain a contradiction, since that situation would imply a lack of connectedness of the fibers of
$p=g \circ h$
, we would obtain a contradiction, since that situation would imply a lack of connectedness of the fibers of
![]() $p\vert _{\operatorname {\mathrm {Supp}} F} \colon \operatorname {\mathrm {Supp}} F \to X_1$
, where F is the divisor defined in the statement of Proposition 3.1.
$p\vert _{\operatorname {\mathrm {Supp}} F} \colon \operatorname {\mathrm {Supp}} F \to X_1$
, where F is the divisor defined in the statement of Proposition 3.1.
Lemma 3.6. Let
![]() $(X, B, \mathbf {M})/S$
be a
$(X, B, \mathbf {M})/S$
be a
![]() $\mathbb Q$
-factorial generalized pair, and let
$\mathbb Q$
-factorial generalized pair, and let
![]() $f \colon X \rightarrow Y$
be a proper morphism of algebraic varieties over S. Let
$f \colon X \rightarrow Y$
be a proper morphism of algebraic varieties over S. Let
![]() $\pi \colon X \dashrightarrow X^+$
be a
$\pi \colon X \dashrightarrow X^+$
be a
![]() $(K_X+B+M)$
-flop over Y, that is, we have the following commutative diagram
$(K_X+B+M)$
-flop over Y, that is, we have the following commutative diagram

Assume that
-
•
 $B^{\geq 1}$
is g-ample; and
$B^{\geq 1}$
is g-ample; and -
•
 $\operatorname {\mathrm {Nklt}}(X, B , \mathbf {M}) \subset \operatorname {\mathrm {Supp}}(B^{\geq 1})$
.
$\operatorname {\mathrm {Nklt}}(X, B , \mathbf {M}) \subset \operatorname {\mathrm {Supp}}(B^{\geq 1})$
.
Then
![]() $\operatorname {\mathrm {Nklt}}(X^+, B^+ , \mathbf {M}) \subset \operatorname {\mathrm {Supp}}((B^{+})^{ \geq 1})$
, where
$\operatorname {\mathrm {Nklt}}(X^+, B^+ , \mathbf {M}) \subset \operatorname {\mathrm {Supp}}((B^{+})^{ \geq 1})$
, where
![]() $B^+$
is the strict transform of B.
$B^+$
is the strict transform of B.
Moreover, for any point
![]() $y \in Y$
, the number of connected components of
$y \in Y$
, the number of connected components of
![]() $\operatorname {\mathrm {Nklt}}(X^+, B^+, \mathbf {M}) \cap (f^{+})^{-1}(y)$
is the same as the number of connected components of
$\operatorname {\mathrm {Nklt}}(X^+, B^+, \mathbf {M}) \cap (f^{+})^{-1}(y)$
is the same as the number of connected components of
![]() $\operatorname {\mathrm {Nklt}}(X, B, \mathbf {M}) \cap f^{-1}(y)$
.
$\operatorname {\mathrm {Nklt}}(X, B, \mathbf {M}) \cap f^{-1}(y)$
.
Proof. As l is a flopping contraction, then
where
![]() . This, in turn, implies that
. This, in turn, implies that
and
![]() $l_{\ast } (B^{\geq 1})=l^+_{\ast } (B^{+ \geq 1})$
. As
$l_{\ast } (B^{\geq 1})=l^+_{\ast } (B^{+ \geq 1})$
. As
![]() $B^{\geq 1}$
is l-ample, it follows that
$B^{\geq 1}$
is l-ample, it follows that
![]() $-(B^{+})^{ \geq 1}$
is
$-(B^{+})^{ \geq 1}$
is
![]() $l^+$
-ample. Since
$l^+$
-ample. Since
![]() $-(B^{+})^{ \geq 1}$
is antieffective, it follows that the
$-(B^{+})^{ \geq 1}$
is antieffective, it follows that the
![]() $l^+$
-exceptional locus is contained in
$l^+$
-exceptional locus is contained in
![]() $\operatorname {\mathrm {Supp}}((B^{+})^{ \geq 1})$
. Thus,
$\operatorname {\mathrm {Supp}}((B^{+})^{ \geq 1})$
. Thus,
![]() $\operatorname {\mathrm {Nklt}}(X^+, B^+ , \mathbf {M}) \subset \operatorname {\mathrm {Supp}}((B^{+})^{ \geq 1})$
.
$\operatorname {\mathrm {Nklt}}(X^+, B^+ , \mathbf {M}) \subset \operatorname {\mathrm {Supp}}((B^{+})^{ \geq 1})$
.
To prove the last assertion, it suffices to notice that, since
![]() $\pi $
is a flop over Y and
$\pi $
is a flop over Y and
![]() $l, l^+$
are the associated flopping contractions, then
$l, l^+$
are the associated flopping contractions, then
![]() $l(\operatorname {\mathrm {Nklt}}(X, B , \mathbf {M})) = l^+(\operatorname {\mathrm {Nklt}}(X^+, B^+ , \mathbf M))$
. Taking a resolution of indeterminacies of
$l(\operatorname {\mathrm {Nklt}}(X, B , \mathbf {M})) = l^+(\operatorname {\mathrm {Nklt}}(X^+, B^+ , \mathbf M))$
. Taking a resolution of indeterminacies of
![]() $\pi $
$\pi $

where
![]() $\mathbf {M}$
descends and applying Proposition 3.1 twice, first to
$\mathbf {M}$
descends and applying Proposition 3.1 twice, first to
![]() $h=l$
,
$h=l$
,
![]() $g=q$
, and then to
$g=q$
, and then to
![]() $h=l^+$
,
$h=l^+$
,
![]() $g=p$
, we see that the number of connected components of
$g=p$
, we see that the number of connected components of
![]() $\operatorname {\mathrm {Nklt}}(X^+, B^+, \mathbf {M}) \cap (f^{+})^{-1}(y)$
(respectively,
$\operatorname {\mathrm {Nklt}}(X^+, B^+, \mathbf {M}) \cap (f^{+})^{-1}(y)$
(respectively,
![]() $\operatorname {\mathrm {Nklt}}(X, B, \mathbf {M}) \cap f^{-1}(y)$
) is the same as the number of connected components of
$\operatorname {\mathrm {Nklt}}(X, B, \mathbf {M}) \cap f^{-1}(y)$
) is the same as the number of connected components of
![]() $\operatorname {\mathrm {Nklt}}(Z, B_Z, \mathbf {M}) \cap (f_Z)^{-1}(y)$
, where
$\operatorname {\mathrm {Nklt}}(Z, B_Z, \mathbf {M}) \cap (f_Z)^{-1}(y)$
, where
, as otherwise that situation would imply a lack of connectedness of the fibers of
![]() $(l^+ \circ p)\vert _{\operatorname {\mathrm {Supp}} F} \colon \operatorname {\mathrm {Supp}} F \to Z$
(respectively,
$(l^+ \circ p)\vert _{\operatorname {\mathrm {Supp}} F} \colon \operatorname {\mathrm {Supp}} F \to Z$
(respectively,
![]() $(l \circ p)\vert _{\operatorname {\mathrm {Supp}} F} \colon \operatorname {\mathrm {Supp}} F \to Z$
), where F is the divisor defined in the statement of Proposition 3.1.
$(l \circ p)\vert _{\operatorname {\mathrm {Supp}} F} \colon \operatorname {\mathrm {Supp}} F \to Z$
), where F is the divisor defined in the statement of Proposition 3.1.
Remark 3.7. Let
![]() $(X, B, \mathbf {M})$
be a generalized pair. Let
$(X, B, \mathbf {M})$
be a generalized pair. Let
![]() $(X^m,B^m, \mathbf {M})$
be a generalized pair together with a dlt modification
$(X^m,B^m, \mathbf {M})$
be a generalized pair together with a dlt modification
![]() $f^m \colon X^m \rightarrow X$
of
$f^m \colon X^m \rightarrow X$
of
![]() $(X,B+M)$
, as in Theorem 2.9. Let us denote by
$(X,B+M)$
, as in Theorem 2.9. Let us denote by
![]() $B'$
the unique boundary supported on
$B'$
the unique boundary supported on
![]() $\operatorname {\mathrm {Supp}}(B^m)$
and defined by the identity
$\operatorname {\mathrm {Supp}}(B^m)$
and defined by the identity
Then, every non-klt center of
![]() $(X^m,B'+M^m)$
is contained in
$(X^m,B'+M^m)$
is contained in
![]() $\operatorname {\mathrm {Supp}}((B')^{\geq 1})$
. Assume not, and fix a non-klt center
$\operatorname {\mathrm {Supp}}((B')^{\geq 1})$
. Assume not, and fix a non-klt center
![]() $W \subset X^m$
not contained in
$W \subset X^m$
not contained in
![]() $\operatorname {\mathrm {Supp}}((B')^{\geq 1})$
. Then,
$\operatorname {\mathrm {Supp}}((B')^{\geq 1})$
. Then,
![]() $B'=B^m= (B^m){^{<1}}$
near the generic point of W. Since
$B'=B^m= (B^m){^{<1}}$
near the generic point of W. Since
![]() $(X,B^m+M^m)$
is generalized dlt,
$(X,B^m+M^m)$
is generalized dlt,
![]() $(X,(B^m)^{<1}+M^m)$
is generalized klt. Thus,
$(X,(B^m)^{<1}+M^m)$
is generalized klt. Thus,
![]() $(X^m,B' + M^m)$
is also klt at the generic point of W, which gives a contradiction.
$(X^m,B' + M^m)$
is also klt at the generic point of W, which gives a contradiction.
4 Generalized log Calabi–Yau pairs and their structure
In this section, we collect some technical results related to the structure of generalized log Calabi–Yau pairs which will be useful in the analysis of dual complexes for such class of pairs.
4.1 A Kawamata–Viehweg type result for generalized klt pairs
In this subsection, we prove the following vanishing result of Kawamata–Viehweg type that will be used to show contractibility of certain types of dual complex for generalized log Calabi–Yau pairs.
Theorem 4.1. Let
![]() $(X,B, \mathbf {M})$
be a generalized pair with generalized klt singularities. Let L be a Cartier divisor on X, such that
$(X,B, \mathbf {M})$
be a generalized pair with generalized klt singularities. Let L be a Cartier divisor on X, such that
![]() is nef and big. Then,
is nef and big. Then,
![]() $H^i(X,L)=0$
for
$H^i(X,L)=0$
for
![]() $i> 0$
.
$i> 0$
.
Proof. Let
![]() $\pi \colon X' \rightarrow X$
be a log resolution for
$\pi \colon X' \rightarrow X$
be a log resolution for
![]() $(X,B)$
, where
$(X,B)$
, where
![]() $\mathbf {M}$
descends. Thus, we may write
$\mathbf {M}$
descends. Thus, we may write
where
![]() $E' \geq 0$
,
$E' \geq 0$
,
![]() $F' \geq 0$
,
$F' \geq 0$
,
![]() $E' \wedge F' = 0$
,
$E' \wedge F' = 0$
,
![]() $E'-F'$
is
$E'-F'$
is
![]() $\pi $
-exceptional and
$\pi $
-exceptional and
![]() $\pi _*^{-1} (B) + E' - F'$
has simple normal crossing support. Thus,
$\pi _*^{-1} (B) + E' - F'$
has simple normal crossing support. Thus,
As
![]() $M' + \pi ^{\ast } H$
is nef and big, by Kawamata–Viehweg vanishing [Reference Kollár and Mori27, Theorem 2.64], we have
$M' + \pi ^{\ast } H$
is nef and big, by Kawamata–Viehweg vanishing [Reference Kollár and Mori27, Theorem 2.64], we have
![]() $H^i(X',\pi ^{\ast } L + \lceil F' \rceil )=0$
for
$H^i(X',\pi ^{\ast } L + \lceil F' \rceil )=0$
for
![]() $i>0$
. Similarly, by [Reference Hacon and Kovács17, Theorem 3.45], we have
$i>0$
. Similarly, by [Reference Hacon and Kovács17, Theorem 3.45], we have
![]() $R^i\pi _* {\mathcal {O}_{ X'}} (\pi ^{\ast } L + \lceil F' \rceil )=0$
for
$R^i\pi _* {\mathcal {O}_{ X'}} (\pi ^{\ast } L + \lceil F' \rceil )=0$
for
![]() $i>0$
. Since
$i>0$
. Since
![]() $\lceil F' \rceil $
is
$\lceil F' \rceil $
is
![]() $\pi $
-exceptional, the projection formula implies
$\pi $
-exceptional, the projection formula implies
![]() $\pi _* {\mathcal {O}_{X'}}(\pi ^{\ast } L + \lceil F' \rceil )={\mathcal {O}_{X}} (L)$
. Hence, we conclude that
$\pi _* {\mathcal {O}_{X'}}(\pi ^{\ast } L + \lceil F' \rceil )={\mathcal {O}_{X}} (L)$
. Hence, we conclude that
![]() $H^i(X,L)=0$
for
$H^i(X,L)=0$
for
![]() $i>0$
.
$i>0$
.
4.2 Special birational models
In this subsection, we show how to reduce the problem of studying the dual complex of a generalized log Calabi–Yau pair to the log Fano case. The following result is a generalization of [Reference Kollár and Xu28, Theorem 49].
Theorem 4.2. Let
![]() $(X,B,\mathbf {M})$
be
$(X,B,\mathbf {M})$
be
![]() $\mathbb {Q}$
-factorial generalized dlt pair. Assume that
$\mathbb {Q}$
-factorial generalized dlt pair. Assume that
![]() ${K_{X}} + B + M \sim _{\mathbb {Q}} 0$
. Then, there exist a crepant birational map
${K_{X}} + B + M \sim _{\mathbb {Q}} 0$
. Then, there exist a crepant birational map
![]() $\phi \colon X \dashrightarrow \overline {X}$
, a generalized pair
$\phi \colon X \dashrightarrow \overline {X}$
, a generalized pair
![]() $(\overline {X}, \overline {B}, \mathbf {M})$
, and a morphism
$(\overline {X}, \overline {B}, \mathbf {M})$
, and a morphism
![]() $q \colon \overline {X} \rightarrow Z$
, such that:
$q \colon \overline {X} \rightarrow Z$
, such that:
-
(1)
 $\overline {B}^{\hspace{1pt}=1}$
fully supports a q-ample divisor;
$\overline {B}^{\hspace{1pt}=1}$
fully supports a q-ample divisor; -
(2) every generalized log canonical center of
 $(\overline {X},\overline {B},\mathbf {M})$
dominates Z;
$(\overline {X},\overline {B},\mathbf {M})$
dominates Z; -
(3)
 $\overline {E} \subset \overline {B}^{\hspace{1pt}=1}$
for every
$\overline {E} \subset \overline {B}^{\hspace{1pt}=1}$
for every
 $\phi ^{-1}$
-exceptional divisor
$\phi ^{-1}$
-exceptional divisor
 $\overline {E} \subset \overline {X}$
; and
$\overline {E} \subset \overline {X}$
; and -
(4)
 $\phi ^{-1}$
is an isomorphism over
$\phi ^{-1}$
is an isomorphism over
 $\overline {X} \setminus \overline {B}^{\hspace{1pt}=1}$
.
$\overline {X} \setminus \overline {B}^{\hspace{1pt}=1}$
.
Remark 4.3. Properties (3) and (4) in Theorem 4.2 imply that
![]() $\operatorname {\mathrm {Nklt}}(\overline {X},\overline {B},\mathbf {M})= \overline {B}^{\hspace{1pt}=1}$
, and that
$\operatorname {\mathrm {Nklt}}(\overline {X},\overline {B},\mathbf {M})= \overline {B}^{\hspace{1pt}=1}$
, and that
![]() $\overline {B} \geq 0$
.
$\overline {B} \geq 0$
.
Proof. If
![]() $(X,B, \mathbf {M})$
is generalized klt, then it suffices to take
$(X,B, \mathbf {M})$
is generalized klt, then it suffices to take
![]() $Z=\overline {X}=X$
. Hence, we can assume that
$Z=\overline {X}=X$
. Hence, we can assume that
![]() $\operatorname {\mathrm {Nklt}}(X,B, \mathbf {M}) \neq \emptyset $
.
$\operatorname {\mathrm {Nklt}}(X,B, \mathbf {M}) \neq \emptyset $
.
Step 0. In this step, we reduce to the case when the dual complex is connected.
If
![]() $\operatorname {\mathrm {Nklt}}(X,B, \mathbf {M})$
is disconnected, the statement follows from Theorem 1.1 and its proof. More precisely, as
$\operatorname {\mathrm {Nklt}}(X,B, \mathbf {M})$
is disconnected, the statement follows from Theorem 1.1 and its proof. More precisely, as
![]() $(X,B,\mathbf {M})$
is already
$(X,B,\mathbf {M})$
is already
![]() $\mathbb Q$
-factorial generalized dlt, we may apply the algorithm in the proof of Theorem 1.1 to X: we run a
$\mathbb Q$
-factorial generalized dlt, we may apply the algorithm in the proof of Theorem 1.1 to X: we run a
![]() $(K_X+B^{<1}+{\mathbf {M}_{X}})$
-MMP
$(K_X+B^{<1}+{\mathbf {M}_{X}})$
-MMP
![]() $X \dashrightarrow \overline {X}$
, which will terminate, by construction, with a Mori fiber space
$X \dashrightarrow \overline {X}$
, which will terminate, by construction, with a Mori fiber space
![]() $\overline {X} \rightarrow Z$
, the morphism whose existence is claimed in the statement of 4.2. By Theorem 1.1, items (1)–(2) in the statement of 4.2 hold. By construction,
$\overline {X} \rightarrow Z$
, the morphism whose existence is claimed in the statement of 4.2. By Theorem 1.1, items (1)–(2) in the statement of 4.2 hold. By construction,
![]() $X \dashrightarrow \overline {X}$
is a birational contraction, so item (3) is satisfied. Lastly, this MMP is a
$X \dashrightarrow \overline {X}$
is a birational contraction, so item (3) is satisfied. Lastly, this MMP is a
![]() $(-B^{=1})$
-MMP, and thus by the results in Section 3, also item (4) is satisfied. Therefore, we can assume that
$(-B^{=1})$
-MMP, and thus by the results in Section 3, also item (4) is satisfied. Therefore, we can assume that
![]() $\operatorname {\mathrm {Supp}}(B^{=1})$
is connected and nonempty.
$\operatorname {\mathrm {Supp}}(B^{=1})$
is connected and nonempty.
Step 1. In this step, we construct a birational map
![]() $X \dashrightarrow X'$
and a fibration
$X \dashrightarrow X'$
and a fibration
![]() $X' \rightarrow Z$
satisfying properties (1), (3), and (4) in the statement of the theorem.
$X' \rightarrow Z$
satisfying properties (1), (3), and (4) in the statement of the theorem.
We run a
![]() $({K_{X}} + B^{<1} +M)$
-MMP with scaling of an ample divisor
$({K_{X}} + B^{<1} +M)$
-MMP with scaling of an ample divisor
and we define
![]() , and
, and
![]() . As
. As
![]() ${K_{X}} + B^{<1} + M \sim _{\mathbb {Q}} -B^{=1}$
, each step of the
${K_{X}} + B^{<1} + M \sim _{\mathbb {Q}} -B^{=1}$
, each step of the
![]() $({K_{X}} + B^{<1} +M)$
-MMP in (3) is
$({K_{X}} + B^{<1} +M)$
-MMP in (3) is
![]() $(B^{=1})$
-positive; moreover, this run of the MMP terminates with a Mori fiber space
$(B^{=1})$
-positive; moreover, this run of the MMP terminates with a Mori fiber space
![]() $q \colon X' \rightarrow Z$
and we have an induced generalized pair
$q \colon X' \rightarrow Z$
and we have an induced generalized pair
![]() $(X', B', \mathbf {M})$
,
$(X', B', \mathbf {M})$
,
![]() , such that
, such that
![]() $K_{X'}+B' +\mathbf {M}_{X'} \sim _{\mathbb {Q}} 0$
. As each step of (3) is
$K_{X'}+B' +\mathbf {M}_{X'} \sim _{\mathbb {Q}} 0$
. As each step of (3) is
![]() $(B^{=1})$
-positive, the indeterminacy locus of the inverse map
$(B^{=1})$
-positive, the indeterminacy locus of the inverse map
![]() $\pi _i^{-1} \colon X_{i} \dashrightarrow X_{i-1}$
is contained in
$\pi _i^{-1} \colon X_{i} \dashrightarrow X_{i-1}$
is contained in
![]() $B_i^{=1}$
. This implies that property (4) in the statement of the theorem holds for
$B_i^{=1}$
. This implies that property (4) in the statement of the theorem holds for
![]() $(X', B', \mathbf {M})$
; property (1) is satisfied as q is a Mori fiber space, while (3) holds, by construction, since
$(X', B', \mathbf {M})$
; property (1) is satisfied as q is a Mori fiber space, while (3) holds, by construction, since
![]() $X \dashrightarrow X'$
is a birational contraction.
$X \dashrightarrow X'$
is a birational contraction.
If property (2) holds for
![]() $(X', B', \mathbf {M})$
, then the proof of the theorem is completed. Hence, we shall assume that not all generalized log canonical centers of
$(X', B', \mathbf {M})$
, then the proof of the theorem is completed. Hence, we shall assume that not all generalized log canonical centers of
![]() $(X',B', \mathbf {M})$
dominate Z.
$(X',B', \mathbf {M})$
dominate Z.
Step 2. In this step, assuming property (2) does not hold for
![]() $(X', B', \mathbf {M})$
, we construct a birational map
$(X', B', \mathbf {M})$
, we construct a birational map
![]() $X \dashrightarrow \widetilde {X}$
over Z, a generalized pair
$X \dashrightarrow \widetilde {X}$
over Z, a generalized pair
![]() $(\widetilde X, \widetilde B, \mathbf {M})$
crepant to
$(\widetilde X, \widetilde B, \mathbf {M})$
crepant to
![]() $(X, B, \mathbf {M})$
, and a commutative diagram
$(X, B, \mathbf {M})$
, and a commutative diagram

where
![]() $\widetilde {q}$
is a Mori fibration,
$\widetilde {q}$
is a Mori fibration,
![]() $\widetilde {Z} \rightarrow Z$
is a birational contraction, and all the log canonical centers of
$\widetilde {Z} \rightarrow Z$
is a birational contraction, and all the log canonical centers of
![]() $(\widetilde X, \widetilde B, \mathbf {M})$
that do not dominate Z are fully supported on the pullback of a divisor on
$(\widetilde X, \widetilde B, \mathbf {M})$
that do not dominate Z are fully supported on the pullback of a divisor on
![]() $\widetilde Z$
. Moreover,
$\widetilde Z$
. Moreover,
![]() $(\widetilde X, \widetilde B, \mathbf {M})$
satisfies properties (3), (4), and
$(\widetilde X, \widetilde B, \mathbf {M})$
satisfies properties (3), (4), and
![]() $\widetilde {B}^{\hspace{1pt}=1}$
fully supports an effective divisor that is relatively ample over
$\widetilde {B}^{\hspace{1pt}=1}$
fully supports an effective divisor that is relatively ample over
![]() $\widetilde {Z} \setminus \widetilde {q}(\widetilde {B} {^{=1,v}})$
.
$\widetilde {Z} \setminus \widetilde {q}(\widetilde {B} {^{=1,v}})$
.
By construction,
![]() $(X', B', \mathbf {M})$
is
$(X', B', \mathbf {M})$
is
![]() $\mathbb {Q}$
-factorial and generalized dlt away from
$\mathbb {Q}$
-factorial and generalized dlt away from
![]() $B^{\prime =1}$
. We pass to a generalized dlt model
$B^{\prime =1}$
. We pass to a generalized dlt model
![]() $\psi \colon X" \rightarrow X'$
,
$\psi \colon X" \rightarrow X'$
,
Property (3) holds on
![]() $X"$
by construction. The morphism
$X"$
by construction. The morphism
![]() $\psi $
is an isomorphism over
$\psi $
is an isomorphism over
![]() $X' \setminus B^{\prime =1}$
, hence, property (4) holds on
$X' \setminus B^{\prime =1}$
, hence, property (4) holds on
![]() $X"$
as well. Lemma 2.13 implies that property (1) is also preserved.
$X"$
as well. Lemma 2.13 implies that property (1) is also preserved.
Thus, up to substituting
![]() $X'$
with
$X'$
with
![]() $X"$
, we can assume that
$X"$
, we can assume that
![]() $(X',B', \mathbf {M})$
is
$(X',B', \mathbf {M})$
is
![]() $\mathbb Q$
-factorial and generalized dlt, and that any of its log canonical places is a log canonical place for the pair
$\mathbb Q$
-factorial and generalized dlt, and that any of its log canonical places is a log canonical place for the pair
![]() $(X',B')$
.
$(X',B')$
.
To simplify the notation, we write
![]() .
.
Claim 1. Up to substituting
![]() $(X', B', \mathbf {M)}$
with a crepant birational generalized pair on a higher model of
$(X', B', \mathbf {M)}$
with a crepant birational generalized pair on a higher model of
![]() $X'$
, we can assume that any generalized log canonical center of
$X'$
, we can assume that any generalized log canonical center of
![]() $(X', B', \mathbf {M})$
vertical over Z is contained in
$(X', B', \mathbf {M})$
vertical over Z is contained in
![]() $B^{\prime =1, v}$
and properties (1), (3), and (4) still hold on
$B^{\prime =1, v}$
and properties (1), (3), and (4) still hold on
![]() $X'$
.
$X'$
.
In particular, we can assume that for any
![]() $0 \leq \delta < 1$
, the generalized pair
$0 \leq \delta < 1$
, the generalized pair
![]() $(X',B^{\prime <1} + B^{\prime =1, h} + \delta B^{\prime =1, v} + \overline {M})$
has no vertical log canonical centers.
$(X',B^{\prime <1} + B^{\prime =1, h} + \delta B^{\prime =1, v} + \overline {M})$
has no vertical log canonical centers.
Proof of Claim 1.
Let W be a log canonical center for
![]() $(X',B')$
vertical over Z. If
$(X',B')$
vertical over Z. If
![]() $W \not \subset B^{\prime =1, v}$
, then W is the intersection of components of
$W \not \subset B^{\prime =1, v}$
, then W is the intersection of components of
![]() $B^{\prime =1,h}$
. Let
$B^{\prime =1,h}$
. Let
![]() $\mathcal {C}$
be the subcomplex of
$\mathcal {C}$
be the subcomplex of
![]() $\mathcal {DMR}(X',B^{\prime =1})$
, whose cells correspond to all components of
$\mathcal {DMR}(X',B^{\prime =1})$
, whose cells correspond to all components of
![]() $B^{\prime =1}$
together with the strata of
$B^{\prime =1}$
together with the strata of
![]() $B^{\prime =1,h}$
that dominate Z and all strata of
$B^{\prime =1,h}$
that dominate Z and all strata of
![]() $B^{\prime =1,v}$
. The subcomplex
$B^{\prime =1,v}$
. The subcomplex
![]() $\mathcal {C}$
is closed inside
$\mathcal {C}$
is closed inside
![]() $\mathcal {DMR}(X',B^{\prime =1})$
, as it is closed within each simplex of
$\mathcal {DMR}(X',B^{\prime =1})$
, as it is closed within each simplex of
![]() $\mathcal {DMR}(X',B^{\prime =1})$
: in fact, if a stratum
$\mathcal {DMR}(X',B^{\prime =1})$
: in fact, if a stratum
![]() $W'$
of
$W'$
of
![]() $\mathcal {DMR}(X',B^{\prime =1, h})$
does not dominate Z, the same holds for any stratum
$\mathcal {DMR}(X',B^{\prime =1, h})$
does not dominate Z, the same holds for any stratum
![]() $W" \subset W'$
. Thus, up to substituting
$W" \subset W'$
. Thus, up to substituting
![]() $(X', B')$
with the crepant birational pair constructed by [Reference Kollár and Xu28, Lemma 57], we can assume that
$(X', B')$
with the crepant birational pair constructed by [Reference Kollár and Xu28, Lemma 57], we can assume that
![]() $B^{\prime =1,v}\neq 0$
, and that
$B^{\prime =1,v}\neq 0$
, and that
![]() $(X',B^{\prime <1} + B^{\prime =1,h},\mathbf {M})$
has no vertical log canonical centers. By Lemma 2.13 and [Reference Kollár and Xu28, Lemma 57], this process preserves properties (1), (3), and (4).
$(X',B^{\prime <1} + B^{\prime =1,h},\mathbf {M})$
has no vertical log canonical centers. By Lemma 2.13 and [Reference Kollár and Xu28, Lemma 57], this process preserves properties (1), (3), and (4).
By construction,
![]() $B^{\prime =1}$
fully supports an effective
$B^{\prime =1}$
fully supports an effective
![]() $\mathbb {Q}$
-divisor H ample over Z, hence, for
$\mathbb {Q}$
-divisor H ample over Z, hence, for
![]() $0 < \epsilon \ll 1$
, the support of
$0 < \epsilon \ll 1$
, the support of
![]() $B^{\prime =1} -\epsilon H$
coincides with that of
$B^{\prime =1} -\epsilon H$
coincides with that of
![]() $B^{\prime =1}$
, and, moreover,
$B^{\prime =1}$
, and, moreover,
![]() $\lfloor B^{\prime =1} -\epsilon H \rfloor =0$
, so that
$\lfloor B^{\prime =1} -\epsilon H \rfloor =0$
, so that
and
![]() $(X', B^{\prime <1} + (B^{\prime =1} -\epsilon H)^h + \mathbf {M}_{X'} + \epsilon H)$
is generalized klt over Z.
$(X', B^{\prime <1} + (B^{\prime =1} -\epsilon H)^h + \mathbf {M}_{X'} + \epsilon H)$
is generalized klt over Z.
By [Reference Birkar and Zhang7, Lemma 4.4], we can run a
![]() $({K_{X'}} + B^{\prime <1} + (B^{\prime =1} -\epsilon H)^h + \mathbf {M}_{X'} + \epsilon H)$
-MMP with scaling of an ample divisor over Z, that terminates with a relatively good minimal model/Z
$({K_{X'}} + B^{\prime <1} + (B^{\prime =1} -\epsilon H)^h + \mathbf {M}_{X'} + \epsilon H)$
-MMP with scaling of an ample divisor over Z, that terminates with a relatively good minimal model/Z

We denote by
![]() $\widetilde B, \widetilde F, \widetilde H$
the strict transforms of
$\widetilde B, \widetilde F, \widetilde H$
the strict transforms of
![]() $B', F', H$
on
$B', F', H$
on
![]() $\widetilde X$
. The morphism
$\widetilde X$
. The morphism
![]() $\widetilde Z \rightarrow Z$
is birational, as
$\widetilde Z \rightarrow Z$
is birational, as
![]() $\overline F$
is vertical
$\overline F$
is vertical
![]() $/Z$
. Since the MMP in (5) is positive for
$/Z$
. Since the MMP in (5) is positive for
![]() $F'$
by construction, then
$F'$
by construction, then
![]() $\widetilde F> 0$
and
$\widetilde F> 0$
and
![]() $\widetilde F \sim _{\mathbb {Q}, \widetilde q} 0$
. The map
$\widetilde F \sim _{\mathbb {Q}, \widetilde q} 0$
. The map
![]() $X \dashrightarrow \widetilde X$
satisfies properties (3) and (4) in view of [Reference Kollár and Xu28, Lemma 55] and the fact that
$X \dashrightarrow \widetilde X$
satisfies properties (3) and (4) in view of [Reference Kollár and Xu28, Lemma 55] and the fact that
![]() $\operatorname {\mathrm {Supp}}(F') \subset \operatorname {\mathrm {Supp}}(B^{\prime =1})$
.
$\operatorname {\mathrm {Supp}}(F') \subset \operatorname {\mathrm {Supp}}(B^{\prime =1})$
.
On the other hand, property (1) may no longer hold on
![]() $\widetilde X$
. Nevertheless, the following claim holds.
$\widetilde X$
. Nevertheless, the following claim holds.
Claim 2.
![]() $\widetilde {B}^{\hspace{1pt}=1}$
fully supports an effective divisor that is relatively ample over
$\widetilde {B}^{\hspace{1pt}=1}$
fully supports an effective divisor that is relatively ample over
![]() $\widetilde {Z} \setminus \widetilde {q}(\widetilde {B} {^{=1,v}})$
.
$\widetilde {Z} \setminus \widetilde {q}(\widetilde {B} {^{=1,v}})$
.
Proof of Claim 2.
As we modified
![]() $X'$
by means of an MMP for a divisor supported on
$X'$
by means of an MMP for a divisor supported on
![]() $(B') {^{=1,v}}$
, property (1) still holds true over the complement of
$(B') {^{=1,v}}$
, property (1) still holds true over the complement of
![]() $q((B') {^{=1,v}})$
.
$q((B') {^{=1,v}})$
.
Step 3. In this step, we show that there exist generalized pairs
![]() $(\widetilde Z, B_{\widetilde Z}, \mathbf {M}_{\widetilde Z})$
,
$(\widetilde Z, B_{\widetilde Z}, \mathbf {M}_{\widetilde Z})$
,
![]() $(\widetilde Z, \Delta _{\widetilde Z}, \mathbf {M}_{\widetilde Z})$
on
$(\widetilde Z, \Delta _{\widetilde Z}, \mathbf {M}_{\widetilde Z})$
on
![]() $\widetilde Z$
, such that
$\widetilde Z$
, such that
![]() $K_{\widetilde Z}+ B_{\widetilde Z}+ \mathbf {M}_{\widetilde Z} \sim _{\mathbb {Q}} 0$
and
$K_{\widetilde Z}+ B_{\widetilde Z}+ \mathbf {M}_{\widetilde Z} \sim _{\mathbb {Q}} 0$
and
![]() $-(K_{\widetilde Z}+ \Delta _{\widetilde Z}+ \mathbf {M}_{\widetilde Z})$
is pseudo-effective.
$-(K_{\widetilde Z}+ \Delta _{\widetilde Z}+ \mathbf {M}_{\widetilde Z})$
is pseudo-effective.
The generalized pair
![]() $(\widetilde {X},\widetilde B^{<1} + \widetilde B {^{=1,h}} + \epsilon \widetilde H^v, \mathbf {M})$
has no log canonical centers vertical over
$(\widetilde {X},\widetilde B^{<1} + \widetilde B {^{=1,h}} + \epsilon \widetilde H^v, \mathbf {M})$
has no log canonical centers vertical over
![]() $\widetilde Z$
, and
$\widetilde Z$
, and
by (4). Theorem 2.20 implies the existence of generalized pairs
![]() $(\widetilde Z, B_{\widetilde Z}, \mathbf {M}_{\widetilde Z})$
,
$(\widetilde Z, B_{\widetilde Z}, \mathbf {M}_{\widetilde Z})$
,
![]() $(\widetilde Z, \Delta _{\widetilde Z}, \mathbf {M}_{\widetilde Z})$
, such that
$(\widetilde Z, \Delta _{\widetilde Z}, \mathbf {M}_{\widetilde Z})$
, such that
 $$ \begin{align} \begin{aligned} 0\sim_{\mathbb{Q}} {K_{\widetilde X}} + \widetilde B + \mathbf{M}_{\widetilde X} &\sim_{\mathbb{Q}} \widetilde q ^{\ast} ({K_{\widetilde Z}} + B_{\widetilde Z} + \mathbf{M}_{\widetilde Z}), \\ {K_{\widetilde X}} + \widetilde B^{<1} + \widetilde B {^{=1,h}} + \epsilon \widetilde H^v + \mathbf{M}_{\widetilde X} &\sim_{\mathbb{Q}} \widetilde q^{\ast} ({K_{\widetilde Z}} + \Delta_{\widetilde Z} + \mathbf{M}_{\widetilde Z}). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} 0\sim_{\mathbb{Q}} {K_{\widetilde X}} + \widetilde B + \mathbf{M}_{\widetilde X} &\sim_{\mathbb{Q}} \widetilde q ^{\ast} ({K_{\widetilde Z}} + B_{\widetilde Z} + \mathbf{M}_{\widetilde Z}), \\ {K_{\widetilde X}} + \widetilde B^{<1} + \widetilde B {^{=1,h}} + \epsilon \widetilde H^v + \mathbf{M}_{\widetilde X} &\sim_{\mathbb{Q}} \widetilde q^{\ast} ({K_{\widetilde Z}} + \Delta_{\widetilde Z} + \mathbf{M}_{\widetilde Z}). \end{aligned} \end{align} $$
The two generalized pairs in (6) have the same moduli b-divisor
![]() $\mathbf {M}_{\widetilde {Z}}$
, since
$\mathbf {M}_{\widetilde {Z}}$
, since
along the generic fiber
![]() $\widetilde {X}_{\eta }$
of
$\widetilde {X}_{\eta }$
of
![]() $\widetilde q$
. Furthermore,
$\widetilde q$
. Furthermore,
since
![]() $\widetilde B {^{=1,v}} = \epsilon \widetilde H^v + \widetilde F$
. As no log canonical center of
$\widetilde B {^{=1,v}} = \epsilon \widetilde H^v + \widetilde F$
. As no log canonical center of
![]() $(\widetilde {X},\widetilde B^{<1} + \widetilde B {^{=1,h}} + \epsilon \widetilde H^v, \mathbf {M})$
is vertical over
$(\widetilde {X},\widetilde B^{<1} + \widetilde B {^{=1,h}} + \epsilon \widetilde H^v, \mathbf {M})$
is vertical over
![]() $\widetilde Z$
, the generalized pair
$\widetilde Z$
, the generalized pair
![]() $(\widetilde Z, \Delta _{\widetilde Z} + \mathbf {M}_{\widetilde Z})$
is generalized klt, cf. [Reference Ambro1, proof of Proposition 3.4]. Hence,
$(\widetilde Z, \Delta _{\widetilde Z} + \mathbf {M}_{\widetilde Z})$
is generalized klt, cf. [Reference Ambro1, proof of Proposition 3.4]. Hence,
 $$ \begin{align} \begin{aligned} {K_{\widetilde Z}} + \Delta _{\widetilde{Z}} + \mathbf{M} _{\widetilde{Z}}&\sim_{\mathbb{Q}} \Delta _{\widetilde{Z}} - B _{\widetilde{Z}}, \\ K_{\widetilde X} + \widetilde B^{<1} + \widetilde B^{=1,h} + \epsilon \widetilde H^v + \mathbf{M}_{\widetilde X} &\sim_{\mathbb{Q}} \widetilde{q}^{\ast}(\Delta _{\widetilde{Z}} - B _{\widetilde{Z}}), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} {K_{\widetilde Z}} + \Delta _{\widetilde{Z}} + \mathbf{M} _{\widetilde{Z}}&\sim_{\mathbb{Q}} \Delta _{\widetilde{Z}} - B _{\widetilde{Z}}, \\ K_{\widetilde X} + \widetilde B^{<1} + \widetilde B^{=1,h} + \epsilon \widetilde H^v + \mathbf{M}_{\widetilde X} &\sim_{\mathbb{Q}} \widetilde{q}^{\ast}(\Delta _{\widetilde{Z}} - B _{\widetilde{Z}}), \end{aligned} \end{align} $$
which concludes the proof of this step.
Step 4. In this step, we obtain a birational contraction
![]() $\widetilde {Z} \dashrightarrow \widehat Z$
together with a Mori fiber space
$\widetilde {Z} \dashrightarrow \widehat Z$
together with a Mori fiber space
![]() $\widehat Z \rightarrow W$
. Furthermore, we show that we can lift the birational contraction
$\widehat Z \rightarrow W$
. Furthermore, we show that we can lift the birational contraction
![]() $\widetilde {Z} \dashrightarrow \widehat Z$
to a birational contraction
$\widetilde {Z} \dashrightarrow \widehat Z$
to a birational contraction
![]() $\widetilde X \dashrightarrow \widehat X$
and
$\widetilde X \dashrightarrow \widehat X$
and
![]() $\widehat X$
is endowed with a morphism
$\widehat X$
is endowed with a morphism
![]() $\widehat X \rightarrow \widehat Z$
.
$\widehat X \rightarrow \widehat Z$
.
By construction,
![]() $(\widetilde X,\widetilde B^{<1} + \widetilde B^{=1,h} + \epsilon \widetilde H^v,\mathbf {M})$
satisfies the following properties:
$(\widetilde X,\widetilde B^{<1} + \widetilde B^{=1,h} + \epsilon \widetilde H^v,\mathbf {M})$
satisfies the following properties:
-
(a) it is generalized dlt;
-
(b) all of its log canonical centers dominate
 $\widetilde Z$
; and
$\widetilde Z$
; and -
(c)
 $\widetilde B^{=1,h}$
fully supports a divisor
$\widetilde B^{=1,h}$
fully supports a divisor
 $\widetilde H ^h$
that is ample over
$\widetilde H ^h$
that is ample over
 $\widetilde Z \setminus \operatorname {\mathrm {Supp}}(B _{\widetilde {Z}} - \Delta _{\widetilde {Z}})$
.
$\widetilde Z \setminus \operatorname {\mathrm {Supp}}(B _{\widetilde {Z}} - \Delta _{\widetilde {Z}})$
.
Claim 3. The following properties hold:
-
(d)
 $(\widetilde X,\widetilde B^{<1} + \widetilde B^{=1,h} - \delta \widetilde H ^h + \epsilon \widetilde H^v,\mathbf {M})$
is generalized klt, where
$(\widetilde X,\widetilde B^{<1} + \widetilde B^{=1,h} - \delta \widetilde H ^h + \epsilon \widetilde H^v,\mathbf {M})$
is generalized klt, where
 $0 < \delta \ll 1$
;
$0 < \delta \ll 1$
; -
(e) for a general element
 $\widetilde D \in |\widetilde H ^h/\widetilde Z|_{\mathbb {Q}}$
, the generalized pair
$\widetilde D \in |\widetilde H ^h/\widetilde Z|_{\mathbb {Q}}$
, the generalized pair
 $(\widetilde X,\widetilde B^{<1} + \widetilde B^{=1,h} - \delta \widetilde H ^h + \epsilon \widetilde H^v + \delta \widetilde D,\mathbf {M})$
is generalized klt, and (8)
$(\widetilde X,\widetilde B^{<1} + \widetilde B^{=1,h} - \delta \widetilde H ^h + \epsilon \widetilde H^v + \delta \widetilde D,\mathbf {M})$
is generalized klt, and (8) $$ \begin{align} {K_{\widetilde X}} + \widetilde B^{<1} + (\widetilde B^{=1,h} - \delta \widetilde H ^h) + \epsilon \widetilde H^v + \delta \widetilde D + {\mathbf{M}_{\widetilde X}} \sim_{\mathbb{Q}, \widetilde{Z}} \widetilde{q}^{\ast} (\Delta _{\widetilde{Z}} - B _{\widetilde{Z}}). \end{align} $$
$$ \begin{align} {K_{\widetilde X}} + \widetilde B^{<1} + (\widetilde B^{=1,h} - \delta \widetilde H ^h) + \epsilon \widetilde H^v + \delta \widetilde D + {\mathbf{M}_{\widetilde X}} \sim_{\mathbb{Q}, \widetilde{Z}} \widetilde{q}^{\ast} (\Delta _{\widetilde{Z}} - B _{\widetilde{Z}}). \end{align} $$
Proof of Claim 3.
-
(d) This follows at once from properties (a–b) stated right before Claim 3.
-
(e) As
 $\widetilde H ^h$
is ample over
$\widetilde H ^h$
is ample over
 $\widetilde Z \setminus \operatorname {\mathrm {Supp}}(B _{\widetilde {Z}} - \Delta _{\widetilde {Z}})$
by Claim 2, the relative
$\widetilde Z \setminus \operatorname {\mathrm {Supp}}(B _{\widetilde {Z}} - \Delta _{\widetilde {Z}})$
by Claim 2, the relative
 $\mathbb {Q}$
-linear series
$\mathbb {Q}$
-linear series
 $|\widetilde H ^h/\widetilde Z|_{\mathbb {Q}}$
is free over
$|\widetilde H ^h/\widetilde Z|_{\mathbb {Q}}$
is free over
 $\widetilde Z \setminus \operatorname {\mathrm {Supp}}(B _{\widetilde {Z}} - \Delta _{\widetilde {Z}})$
. In particular, a sufficiently general member
$\widetilde Z \setminus \operatorname {\mathrm {Supp}}(B _{\widetilde {Z}} - \Delta _{\widetilde {Z}})$
. In particular, a sufficiently general member
 $\widetilde {D} \in |\widetilde H ^h/\widetilde Z|_{\mathbb {Q}}$
avoids the generic point of every log canonical center of
$\widetilde {D} \in |\widetilde H ^h/\widetilde Z|_{\mathbb {Q}}$
avoids the generic point of every log canonical center of
 $(\widetilde X,\widetilde B^{<1} + \widetilde B^{=1,h} + \epsilon \widetilde H^v,\mathbf {M})$
, as these all dominate
$(\widetilde X,\widetilde B^{<1} + \widetilde B^{=1,h} + \epsilon \widetilde H^v,\mathbf {M})$
, as these all dominate
 $\widetilde Z$
. The generalized log canonical centers of
$\widetilde Z$
. The generalized log canonical centers of
 $(\widetilde X,\widetilde B^{<1} + \widetilde B^{=1,h} - \delta \widetilde H ^h + \epsilon \widetilde H^v + \delta \widetilde D,\mathbf {M})$
are a subset of the ones of
$(\widetilde X,\widetilde B^{<1} + \widetilde B^{=1,h} - \delta \widetilde H ^h + \epsilon \widetilde H^v + \delta \widetilde D,\mathbf {M})$
are a subset of the ones of
 $(\widetilde X,\widetilde B^{<1} + \widetilde B^{=1,h} + \epsilon \widetilde H^v,\mathbf {M})$
, cf. [Reference Kollár and Mori27, Corollary 2.33]. Thus, as
$(\widetilde X,\widetilde B^{<1} + \widetilde B^{=1,h} + \epsilon \widetilde H^v,\mathbf {M})$
, cf. [Reference Kollár and Mori27, Corollary 2.33]. Thus, as
 $\widetilde D$
avoids the log canonical centers that dominate
$\widetilde D$
avoids the log canonical centers that dominate
 $\widetilde Z$
, the conclusion follows.
$\widetilde Z$
, the conclusion follows.
This concludes the proof.
We run a
![]() $({K_{\widetilde Z}} + \Delta _{\widetilde {Z}} + M _{\widetilde {Z}})$
-MMP with scaling of an ample divisor
$({K_{\widetilde Z}} + \Delta _{\widetilde {Z}} + M _{\widetilde {Z}})$
-MMP with scaling of an ample divisor

that terminates with a Mori fiber space
![]() $r \colon \widehat Z \rightarrow W$
. We define
$r \colon \widehat Z \rightarrow W$
. We define

Claim 4. Let us define
. For any
![]() $0\leq i \leq n$
, there exists a
$0\leq i \leq n$
, there exists a
![]() $\mathbb {Q}$
-factorial generalized log canonical pair
$\mathbb {Q}$
-factorial generalized log canonical pair
![]() $(\widetilde {X}_{i}, \widetilde {B}_i, \mathbf {M})$
with
$(\widetilde {X}_{i}, \widetilde {B}_i, \mathbf {M})$
with
![]() $\widetilde {B}_i \neq 0$
, and morphisms
$\widetilde {B}_i \neq 0$
, and morphisms
![]() $m_i \colon X_i \rightarrow Z_i$
, such that the following diagram commutes
$m_i \colon X_i \rightarrow Z_i$
, such that the following diagram commutes

each
![]() $\widetilde {\pi }_i$
is a birational contraction,
$\widetilde {\pi }_i$
is a birational contraction,
![]() $\widetilde {m}_i$
is a contraction satisfying properties (a–e) in Claim 3. Moreover, for any
$\widetilde {m}_i$
is a contraction satisfying properties (a–e) in Claim 3. Moreover, for any
![]() $0 \leq i \leq n$
,
$0 \leq i \leq n$
,
![]() $\operatorname {\mathrm {Nklt}}(\widetilde {X}_{i}, \widetilde {B}_i, \mathbf {M}) = \operatorname {\mathrm {Supp}}(\widetilde B^{=1}_{i})$
.
$\operatorname {\mathrm {Nklt}}(\widetilde {X}_{i}, \widetilde {B}_i, \mathbf {M}) = \operatorname {\mathrm {Supp}}(\widetilde B^{=1}_{i})$
.
Proof. We use induction on
![]() $i \in \{0, 1, \dots , n\}$
. We define
$i \in \{0, 1, \dots , n\}$
. We define
![]() .
.
For
![]() $i=0$
, there is nothing to prove. Thus, we can assume that the statement of the claim holds up to
$i=0$
, there is nothing to prove. Thus, we can assume that the statement of the claim holds up to
![]() $i-1$
, and we shall prove that it holds for i as well.
$i-1$
, and we shall prove that it holds for i as well.
Hence, it suffices to show that the diagram

can be completed to a diagram

satisfying the conditions in the statement of the claim. If
![]() $\widetilde {\psi }_i \colon \widetilde {Z}_{i-1} \rightarrow \widetilde {Z}_i$
is a divisorial contraction, then for a general choice of
$\widetilde {\psi }_i \colon \widetilde {Z}_{i-1} \rightarrow \widetilde {Z}_i$
is a divisorial contraction, then for a general choice of
![]() $\widetilde {D}_{i-1} \in |\widetilde {H}^h_{i-1}/\widetilde {Z}_{i}|_{\mathbb {Q}}$
, in view of property (e) of Claim 3, the generalized pair
$\widetilde {D}_{i-1} \in |\widetilde {H}^h_{i-1}/\widetilde {Z}_{i}|_{\mathbb {Q}}$
, in view of property (e) of Claim 3, the generalized pair
![]() $(\widetilde {X}_{i-1}, \widetilde B^{<1} _{i-1} + (\widetilde B^{=1,h} _{i-1} -\delta \widetilde H _{i-1}^{h}) + \epsilon \widetilde H^v_{i-1}+\delta \widetilde {D}_{i-1}, \mathbf {M})$
is generalized klt and
$(\widetilde {X}_{i-1}, \widetilde B^{<1} _{i-1} + (\widetilde B^{=1,h} _{i-1} -\delta \widetilde H _{i-1}^{h}) + \epsilon \widetilde H^v_{i-1}+\delta \widetilde {D}_{i-1}, \mathbf {M})$
is generalized klt and
By [Reference Birkar and Zhang7, Lemma 4.4], we can run a
![]() $({K_{\widetilde {X}_{i-1}}}+ \widetilde B^{<1} _{i-1} + (\widetilde B^{=1,h} _{i-1} -\delta \widetilde H _{i-1}^{h}) + \epsilon \widetilde H^v_{i-1}+ \delta \widetilde {D}_{i-1}+ \mathbf {M}_{\widetilde {X}_{i-1}})$
-MMP over
$({K_{\widetilde {X}_{i-1}}}+ \widetilde B^{<1} _{i-1} + (\widetilde B^{=1,h} _{i-1} -\delta \widetilde H _{i-1}^{h}) + \epsilon \widetilde H^v_{i-1}+ \delta \widetilde {D}_{i-1}+ \mathbf {M}_{\widetilde {X}_{i-1}})$
-MMP over
![]() $Z_i$
with scaling of an ample divisor and this terminates, as
$Z_i$
with scaling of an ample divisor and this terminates, as
![]() $\widetilde D _{i-1}$
is big over
$\widetilde D _{i-1}$
is big over
![]() $Z_{i}$
. Thus, we can define
$Z_{i}$
. Thus, we can define
![]() $\widetilde {X}_i$
in (10) to be a good minimal model for this
$\widetilde {X}_i$
in (10) to be a good minimal model for this
![]() $({K_{\widetilde {X}_{i-1}}} + \widetilde B^{<1} _{i-1} + (\widetilde B^{=1,h} _{i-1} -\delta \widetilde H _{i-1}^{h}) + \epsilon \widetilde H^v_{i-1} + \delta \widetilde {D}_{i-1}+ \mathbf {M}_{\widetilde {X}_{i-1}})$
-MMP over
$({K_{\widetilde {X}_{i-1}}} + \widetilde B^{<1} _{i-1} + (\widetilde B^{=1,h} _{i-1} -\delta \widetilde H _{i-1}^{h}) + \epsilon \widetilde H^v_{i-1} + \delta \widetilde {D}_{i-1}+ \mathbf {M}_{\widetilde {X}_{i-1}})$
-MMP over
![]() $\widetilde {Z}_i$
. As
$\widetilde {Z}_i$
. As
![]() $\widetilde F _{i-1} = m^{\ast } _{i-1} (B_{\widetilde {Z}_{i-1}} - \Delta _{\widetilde {Z}_{i-1}})$
, (11) implies that each step of the MMP above is
$\widetilde F _{i-1} = m^{\ast } _{i-1} (B_{\widetilde {Z}_{i-1}} - \Delta _{\widetilde {Z}_{i-1}})$
, (11) implies that each step of the MMP above is
![]() $\widetilde F _{i-1}$
-positive. Hence, the exceptional locus of
$\widetilde F _{i-1}$
-positive. Hence, the exceptional locus of
![]() $\widetilde \pi ^{-1}_{i}$
must be contained in
$\widetilde \pi ^{-1}_{i}$
must be contained in
![]() $\widetilde F_{i}$
, and
$\widetilde F_{i}$
, and
![]() $\widetilde \pi _{i}$
is an isomorphism above
$\widetilde \pi _{i}$
is an isomorphism above
![]() $\operatorname {\mathrm {Supp}}(B_{\widetilde {Z}_i} - \Delta _{\widetilde {Z}_i})$
, so that properties (a–e) also hold for the morphism
$\operatorname {\mathrm {Supp}}(B_{\widetilde {Z}_i} - \Delta _{\widetilde {Z}_i})$
, so that properties (a–e) also hold for the morphism
![]() $m_i$
.
$m_i$
.
Similarly, if
![]() $\widetilde {\psi }_i$
is a flipping contraction
$\widetilde {\psi }_i$
is a flipping contraction

for a general choice of
![]() $\widetilde {D}_{i-1} \in |\widetilde {H}^h_{i-1}/ Z_{i}|_{\mathbb {Q}}$
, the generalized pair
$\widetilde {D}_{i-1} \in |\widetilde {H}^h_{i-1}/ Z_{i}|_{\mathbb {Q}}$
, the generalized pair
![]() $(\widetilde {X}_{i-1}, \widetilde B^{<1} _{i-1} + (\widetilde B^{=1,h} _{i-1} -\delta \widetilde H _{i-1}^{h}) + \epsilon \widetilde H^v_{i-1}+ \delta \widetilde {D}_{i-1}, \mathbf {M})$
is klt and
$(\widetilde {X}_{i-1}, \widetilde B^{<1} _{i-1} + (\widetilde B^{=1,h} _{i-1} -\delta \widetilde H _{i-1}^{h}) + \epsilon \widetilde H^v_{i-1}+ \delta \widetilde {D}_{i-1}, \mathbf {M})$
is klt and
By [Reference Birkar and Zhang7, Lemma 4.4], we can run a
![]() $({K_{\widetilde {X}_{i-1}}} + \widetilde B^{<1} _{i-1} + (\widetilde B^{=1,h} _{i-1} -\delta \widetilde H _{i-1}^{h}) + \epsilon \widetilde H^v_{i-1}+ \delta \widetilde {D}_{i-1}+ \mathbf {M}_{\widetilde {X}_{i-1}})$
-MMP over
$({K_{\widetilde {X}_{i-1}}} + \widetilde B^{<1} _{i-1} + (\widetilde B^{=1,h} _{i-1} -\delta \widetilde H _{i-1}^{h}) + \epsilon \widetilde H^v_{i-1}+ \delta \widetilde {D}_{i-1}+ \mathbf {M}_{\widetilde {X}_{i-1}})$
-MMP over
![]() $Z_i$
with scaling of an ample divisor and this terminates, as
$Z_i$
with scaling of an ample divisor and this terminates, as
![]() $\widetilde D _{i-1}$
is big over
$\widetilde D _{i-1}$
is big over
![]() $Z_{i}$
. Thus, we can define
$Z_{i}$
. Thus, we can define
![]() $\widetilde {X}_i$
in (10) to be a good minimal model for this
$\widetilde {X}_i$
in (10) to be a good minimal model for this
![]() $({K_{\widetilde {X}_{i-1}}} + \widetilde B^{<1} _{i-1} + (\widetilde B^{=1,h} _{i-1} -\delta \widetilde H _{i-1}^{h}) + \epsilon \widetilde H^v_{i-1}+ \delta \widetilde {D}_{i-1}+ \mathbf {M}_{\widetilde {X}_{i-1}})$
-MMP over
$({K_{\widetilde {X}_{i-1}}} + \widetilde B^{<1} _{i-1} + (\widetilde B^{=1,h} _{i-1} -\delta \widetilde H _{i-1}^{h}) + \epsilon \widetilde H^v_{i-1}+ \delta \widetilde {D}_{i-1}+ \mathbf {M}_{\widetilde {X}_{i-1}})$
-MMP over
![]() $Z_i$
, since
$Z_i$
, since
![]() $\widetilde {Z}_i= \mathrm {Proj}_{\mathcal {O}_{Z_i}}(\bigoplus _ {m \geq 0} p_{i\ast }'\mathcal {O}_{Z_i}(m(\Delta _{\widetilde {Z}_i} - B_{\widetilde {Z}_i})))$
and by (12). As
$\widetilde {Z}_i= \mathrm {Proj}_{\mathcal {O}_{Z_i}}(\bigoplus _ {m \geq 0} p_{i\ast }'\mathcal {O}_{Z_i}(m(\Delta _{\widetilde {Z}_i} - B_{\widetilde {Z}_i})))$
and by (12). As
![]() $\widetilde F _{i-1} = m^{\ast } _{i-1} (B_{\widetilde {Z}_{i-1}} - \Delta _{\widetilde {Z}_{i-1}})$
, (12) implies that each step of the MMP above is
$\widetilde F _{i-1} = m^{\ast } _{i-1} (B_{\widetilde {Z}_{i-1}} - \Delta _{\widetilde {Z}_{i-1}})$
, (12) implies that each step of the MMP above is
![]() $\widetilde F _{i-1}$
-positive. Hence, the exceptional locus of
$\widetilde F _{i-1}$
-positive. Hence, the exceptional locus of
![]() $\widetilde \pi ^{-1}_{i}$
must be contained in
$\widetilde \pi ^{-1}_{i}$
must be contained in
![]() $\widetilde F_{i}$
, and
$\widetilde F_{i}$
, and
![]() $\widetilde \pi _{i}$
is an isomorphism above
$\widetilde \pi _{i}$
is an isomorphism above
![]() $\operatorname {\mathrm {Supp}}(B_{\widetilde {Z}_i} - \Delta _{\widetilde {Z}_i})$
, so that properties (a–d) also hold for the morphism
$\operatorname {\mathrm {Supp}}(B_{\widetilde {Z}_i} - \Delta _{\widetilde {Z}_i})$
, so that properties (a–d) also hold for the morphism
![]() $m_i$
.
$m_i$
.
We define divisors
![]() $\widehat F, \widehat H$
to be the strict transforms on
$\widehat F, \widehat H$
to be the strict transforms on
![]() $\widehat X$
of
$\widehat X$
of
![]() $F, H$
, respectively; thus,
$F, H$
, respectively; thus,
![]() $\widehat F = \widehat q ^{\ast } (B_{\widehat Z} - \Delta _{\widehat Z})$
. By construction,
$\widehat F = \widehat q ^{\ast } (B_{\widehat Z} - \Delta _{\widehat Z})$
. By construction,
![]() $\widetilde Z \dashrightarrow \widehat Z$
is an isomorphism outside of
$\widetilde Z \dashrightarrow \widehat Z$
is an isomorphism outside of
![]() $\operatorname {\mathrm {Supp}} (B_{\widehat Z} - \Delta _{\widehat Z})$
; thus, [Reference Kollár and Xu28, Lemma 54]Footnote
2
implies that the rational map
$\operatorname {\mathrm {Supp}} (B_{\widehat Z} - \Delta _{\widehat Z})$
; thus, [Reference Kollár and Xu28, Lemma 54]Footnote
2
implies that the rational map
![]() $\widetilde X \dashrightarrow \widehat X$
is an isomorphism over the complement of
$\widetilde X \dashrightarrow \widehat X$
is an isomorphism over the complement of
![]() $\operatorname {\mathrm {Supp}} (B_{\widehat Z} - \Delta _{\widehat Z})$
. As
$\operatorname {\mathrm {Supp}} (B_{\widehat Z} - \Delta _{\widehat Z})$
. As
![]() $\operatorname {\mathrm {Supp}}(\widehat F) = \operatorname {\mathrm {Supp}} (\widehat B^{=1,v})$
,
$\operatorname {\mathrm {Supp}}(\widehat F) = \operatorname {\mathrm {Supp}} (\widehat B^{=1,v})$
,
![]() $X \dashrightarrow \widehat X$
satisfies properties (3) and (4).
$X \dashrightarrow \widehat X$
satisfies properties (3) and (4).
Step 5. In this step, we modify
![]() $\widehat X$
so that property (1) is achieved for
$\widehat X$
so that property (1) is achieved for
![]() $\widehat X \rightarrow W$
.
$\widehat X \rightarrow W$
.
By construction,
![]() $\widehat B^{=1}$
fully supports a divisor
$\widehat B^{=1}$
fully supports a divisor
![]() $\widehat H$
that is
$\widehat H$
that is
![]() $\widehat q$
-ample over
$\widehat q$
-ample over
![]() $\widehat Z \setminus \operatorname {\mathrm {Supp}} (B_{\widehat Z} - \Delta _{\widehat Z})$
. As r is a
$\widehat Z \setminus \operatorname {\mathrm {Supp}} (B_{\widehat Z} - \Delta _{\widehat Z})$
. As r is a
![]() $(B_{\widehat Z} - \Delta _{\widehat Z})$
-Mori fiber space, then
$(B_{\widehat Z} - \Delta _{\widehat Z})$
-Mori fiber space, then
![]() $\operatorname {\mathrm {Supp}} (B_{\widehat Z} - \Delta _{\widehat Z})$
fully supports an r-ample divisor
$\operatorname {\mathrm {Supp}} (B_{\widehat Z} - \Delta _{\widehat Z})$
fully supports an r-ample divisor
![]() $H_{\widehat Z}$
. Since
$H_{\widehat Z}$
. Since
![]() $\widetilde q^{-1} (\operatorname {\mathrm {Supp}}(B _{\widetilde {Z}} - \Delta _{\widetilde {Z}})) = \operatorname {\mathrm {Supp}}(\widetilde B^{=1,v})$
, by construction of the birational contractions
$\widetilde q^{-1} (\operatorname {\mathrm {Supp}}(B _{\widetilde {Z}} - \Delta _{\widetilde {Z}})) = \operatorname {\mathrm {Supp}}(\widetilde B^{=1,v})$
, by construction of the birational contractions
![]() $\widetilde Z \dashrightarrow \widehat Z$
,
$\widetilde Z \dashrightarrow \widehat Z$
,
![]() $\widetilde X \dashrightarrow \widehat X$
, and
$\widetilde X \dashrightarrow \widehat X$
, and
![]() $\mathbb {Q}$
-factoriality of all varieties involved, it follows that
$\mathbb {Q}$
-factoriality of all varieties involved, it follows that
![]() $\widehat q^{-1} (\operatorname {\mathrm {Supp}} (B_{\widehat Z} - \Delta _{\widehat Z})) = \operatorname {\mathrm {Supp}} (\widehat B^{=1,v})$
. Thus, both
$\widehat q^{-1} (\operatorname {\mathrm {Supp}} (B_{\widehat Z} - \Delta _{\widehat Z})) = \operatorname {\mathrm {Supp}} (\widehat B^{=1,v})$
. Thus, both
![]() $\widehat H$
and
$\widehat H$
and
![]() $\widehat q ^{\ast } H_{\widehat Z}$
are supported on
$\widehat q ^{\ast } H_{\widehat Z}$
are supported on
![]() $\widehat B^{=1}$
. Furthermore, since
$\widehat B^{=1}$
. Furthermore, since
![]() $\widehat H$
is fully supported on
$\widehat H$
is fully supported on
![]() $\widehat B^{=1}$
, it follows that
$\widehat B^{=1}$
, it follows that
![]() $\widehat H + m \widehat q ^{\ast } H_{\widehat Z}$
is fully supported on
$\widehat H + m \widehat q ^{\ast } H_{\widehat Z}$
is fully supported on
![]() $\widehat B^{=1}$
for every
$\widehat B^{=1}$
for every
![]() $m \geq 0$
. Similarly, since
$m \geq 0$
. Similarly, since
![]() $\widehat H ^h$
is fully supported on
$\widehat H ^h$
is fully supported on
![]() $\widehat B^{=1,h}$
and
$\widehat B^{=1,h}$
and
![]() $\widehat q ^{\ast } H_{\widehat Z}$
is fully supported on
$\widehat q ^{\ast } H_{\widehat Z}$
is fully supported on
![]() $\widehat B^{=1,v}$
,
$\widehat B^{=1,v}$
,
![]() $\widehat H ^h + m \widehat q ^{\ast } H_{\widehat Z}$
is fully supported on
$\widehat H ^h + m \widehat q ^{\ast } H_{\widehat Z}$
is fully supported on
![]() $\widehat B^{=1}$
for every
$\widehat B^{=1}$
for every
![]() $m> 0$
.
$m> 0$
.
If
![]() $\widehat H$
or
$\widehat H$
or
![]() $\widehat H ^h$
are
$\widehat H ^h$
are
![]() $\widehat q$
-ample, then
$\widehat q$
-ample, then
![]() $\widehat H + m \widehat q ^{\ast } H_{\widehat Z}$
is
$\widehat H + m \widehat q ^{\ast } H_{\widehat Z}$
is
![]() $r \circ \widehat q$
-ample for
$r \circ \widehat q$
-ample for
![]() $m \gg 0$
, and property (1) holds on
$m \gg 0$
, and property (1) holds on
![]() $\widehat X$
.
$\widehat X$
.
Thus, we can assume that
![]() $\widehat H ^h$
is not
$\widehat H ^h$
is not
![]() $\widehat q$
-ample: we will construct a new birational model of
$\widehat q$
-ample: we will construct a new birational model of
![]() $\widehat {X}$
, where relative ampleness of
$\widehat {X}$
, where relative ampleness of
![]() $\widehat H ^h$
over
$\widehat H ^h$
over
![]() $\widehat {Z}$
is achieved. In Step 4, we showed that there exists an effective
$\widehat {Z}$
is achieved. In Step 4, we showed that there exists an effective
![]() $\widehat {D}\sim _{\mathbb {Q},\widehat {Z}} \widehat {H}^h$
, such that
$\widehat {D}\sim _{\mathbb {Q},\widehat {Z}} \widehat {H}^h$
, such that
-
(f) for
 $0 < \delta \ll 1$
,
$0 < \delta \ll 1$
,
 $(\widehat X, \widehat B^{<1} + (\widehat B^{=1,h} -\delta \widehat {H}^h) + \epsilon \widehat H^v + \delta \widehat {D}, \mathbf {M})$
is generalized klt; and
$(\widehat X, \widehat B^{<1} + (\widehat B^{=1,h} -\delta \widehat {H}^h) + \epsilon \widehat H^v + \delta \widehat {D}, \mathbf {M})$
is generalized klt; and -
(g) by (f) for
 $0< \sigma \ll \delta \ll 1$
, then
$0< \sigma \ll \delta \ll 1$
, then
 $(\widehat X, \widehat B^{<1} + (\widehat B^{=1,h} -\delta \widehat {H}^h) + \epsilon \widehat H^v + \delta \widehat {D}+\sigma \widehat {D}, \mathbf {M})$
is generalized klt; moreover, (13)
$(\widehat X, \widehat B^{<1} + (\widehat B^{=1,h} -\delta \widehat {H}^h) + \epsilon \widehat H^v + \delta \widehat {D}+\sigma \widehat {D}, \mathbf {M})$
is generalized klt; moreover, (13) $$ \begin{align} {K_{\widehat{X}}} + \widehat B^{<1} + (\widehat B^{=1,h} - \delta \widehat H ^h) + \epsilon \widehat H^v + \delta \widehat D +\sigma\widehat{D} + {\mathbf{M}_{\widehat{X}}} \sim_{\mathbb{Q},\widehat{Z}} \sigma \widehat{H}^h, \end{align} $$
$$ \begin{align} {K_{\widehat{X}}} + \widehat B^{<1} + (\widehat B^{=1,h} - \delta \widehat H ^h) + \epsilon \widehat H^v + \delta \widehat D +\sigma\widehat{D} + {\mathbf{M}_{\widehat{X}}} \sim_{\mathbb{Q},\widehat{Z}} \sigma \widehat{H}^h, \end{align} $$
and
 $\widehat {H}^h$
is relatively ample over
$\widehat {H}^h$
is relatively ample over
 $\widehat {Z} \setminus \operatorname {\mathrm {Supp}}(B_{\widehat {Z}} - \Delta _{\widehat {Z}})$
.
$\widehat {Z} \setminus \operatorname {\mathrm {Supp}}(B_{\widehat {Z}} - \Delta _{\widehat {Z}})$
.
By (13) and [Reference Birkar and Zhang7, Lemma 4.4], if we run a relative MMP with scaling of an ample divisor over
![]() $\widehat {Z}$
for
$\widehat {Z}$
for
![]() $(\widehat X, \widehat B^{<1} + (\widehat B^{=1,h} - \delta \widehat H ^h) + \epsilon \widehat H^v + \delta \widehat D +\sigma \widehat {D}, \mathbf {M})$
, this must terminate with a relative good minimal model
$(\widehat X, \widehat B^{<1} + (\widehat B^{=1,h} - \delta \widehat H ^h) + \epsilon \widehat H^v + \delta \widehat D +\sigma \widehat {D}, \mathbf {M})$
, this must terminate with a relative good minimal model
![]() $\check q ' \colon (\check X ', \check B ', \mathbf {M}) \rightarrow \widehat {Z}$
over
$\check q ' \colon (\check X ', \check B ', \mathbf {M}) \rightarrow \widehat {Z}$
over
![]() $\widehat {Z}$
; we denote by
$\widehat {Z}$
; we denote by
![]() $\check q \colon (\check X, \check B,\mathbf {M}) \rightarrow \widehat {Z}$
the corresponding relative ample model. The MMP that we have just described is an isomorphism over
$\check q \colon (\check X, \check B,\mathbf {M}) \rightarrow \widehat {Z}$
the corresponding relative ample model. The MMP that we have just described is an isomorphism over
![]() $\widehat {Z} \setminus \operatorname {\mathrm {Supp}}(B_{\widehat {Z}} - \Delta _{\widehat {Z}})$
. The following properties hold:
$\widehat {Z} \setminus \operatorname {\mathrm {Supp}}(B_{\widehat {Z}} - \Delta _{\widehat {Z}})$
. The following properties hold:
-
•
 $\widehat X \dashrightarrow \check X '$
and
$\widehat X \dashrightarrow \check X '$
and
 $\widehat X \dashrightarrow \check X$
are isomorphisms over
$\widehat X \dashrightarrow \check X$
are isomorphisms over
 $\widehat Z \setminus \operatorname {\mathrm {Supp}} (B_{\widehat Z} - \Delta _{\widehat Z})$
, hence, properties (3) and (4) are preserved;
$\widehat Z \setminus \operatorname {\mathrm {Supp}} (B_{\widehat Z} - \Delta _{\widehat Z})$
, hence, properties (3) and (4) are preserved; -
•
 $(\check X ', \check B ', \mathbf {M})$
and
$(\check X ', \check B ', \mathbf {M})$
and
 $(\check X , \check B , \mathbf {M})$
are generalized log canonical, and the former has
$(\check X , \check B , \mathbf {M})$
are generalized log canonical, and the former has
 $\mathbb {Q}$
-factorial singularities. Furthermore, by step 4, and the fact that
$\mathbb {Q}$
-factorial singularities. Furthermore, by step 4, and the fact that
 $\widehat {X} \dashrightarrow \check {X}'$
is an isomorphism over
$\widehat {X} \dashrightarrow \check {X}'$
is an isomorphism over
 $\widehat {Z} \setminus \operatorname {\mathrm {Supp}}(B_{\widehat {Z}} - \Delta _{\widehat {Z}})$
,
$\widehat {Z} \setminus \operatorname {\mathrm {Supp}}(B_{\widehat {Z}} - \Delta _{\widehat {Z}})$
,
 $(\check X ', \check B ', \mathbf {M})$
is generalized dlt over
$(\check X ', \check B ', \mathbf {M})$
is generalized dlt over
 $\widehat {Z} \setminus \operatorname {\mathrm {Supp}}(B_{\widehat {Z}} - \Delta _{\widehat {Z}})$
;
$\widehat {Z} \setminus \operatorname {\mathrm {Supp}}(B_{\widehat {Z}} - \Delta _{\widehat {Z}})$
; -
•
 $(\check B '){^{=1,h}}$
fully supports a divisor
$(\check B '){^{=1,h}}$
fully supports a divisor
 $(\check H ')^h$
that is relatively big and semiample over
$(\check H ')^h$
that is relatively big and semiample over
 $\widehat {Z}$
, and its pushforward to
$\widehat {Z}$
, and its pushforward to
 $\check X$
, denoted by
$\check X$
, denoted by
 $\check H ^h$
, is relatively ample over
$\check H ^h$
, is relatively ample over
 $\widehat {Z}$
. As r is a
$\widehat {Z}$
. As r is a
 $(\Delta _{\widehat {Z}} - B_{\widehat {Z}})$
-Mori fiber space,
$(\Delta _{\widehat {Z}} - B_{\widehat {Z}})$
-Mori fiber space,
 $\operatorname {\mathrm {Supp}}(B _{\widehat {Z}}-\Delta _{\widehat {Z}})$
fully supports an r-ample divisor
$\operatorname {\mathrm {Supp}}(B _{\widehat {Z}}-\Delta _{\widehat {Z}})$
fully supports an r-ample divisor
 $H _{\widehat {Z}}$
; as
$H _{\widehat {Z}}$
; as
 $\widehat {q}{^{-1}}(\operatorname {\mathrm {Supp}}(B _{\widehat {Z}}-\Delta _{\widehat {Z}}))=\operatorname {\mathrm {Supp}}((\check B '){^{=1,v}})$
, then
$\widehat {q}{^{-1}}(\operatorname {\mathrm {Supp}}(B _{\widehat {Z}}-\Delta _{\widehat {Z}}))=\operatorname {\mathrm {Supp}}((\check B '){^{=1,v}})$
, then
 $(\check B ')^{=1}$
fully supports a divisor that is big and semiample over W, which we denote by
$(\check B ')^{=1}$
fully supports a divisor that is big and semiample over W, which we denote by
 $\check H '$
.
$\check H '$
.Similarly,
 $\check B^{=1}$
fully supports a divisor that is ample over W, which we denote by
$\check B^{=1}$
fully supports a divisor that is ample over W, which we denote by
 $\check H$
. Furthermore, by construction,
$\check H$
. Furthermore, by construction,
 $\check H '$
is relatively ample away from
$\check H '$
is relatively ample away from
 $\operatorname {\mathrm {Nklt}}(\check X ', \check B ', \mathbf {M})$
: namely,
$\operatorname {\mathrm {Nklt}}(\check X ', \check B ', \mathbf {M})$
: namely,
 $\check X ' \dashrightarrow \mathrm {Proj}_W \bigoplus _m (r \circ \check q ') _*({\mathcal {O}_{\check X'}} (m \check H '))=\check X$
is a birational morphism, whose exceptional locus is contained in
$\check X ' \dashrightarrow \mathrm {Proj}_W \bigoplus _m (r \circ \check q ') _*({\mathcal {O}_{\check X'}} (m \check H '))=\check X$
is a birational morphism, whose exceptional locus is contained in
 $\operatorname {\mathrm {Nklt}}(\check X ', \check B ', \mathbf {M})$
.
$\operatorname {\mathrm {Nklt}}(\check X ', \check B ', \mathbf {M})$
.
Claim 5. By construction, we have
![]() $\operatorname {\mathrm {Nklt}}(\check X ', \check B ', \mathbf {M}) = \operatorname {\mathrm {Supp}}((\check B')^{=1})$
. Furthermore, we may take a generalized dlt model
$\operatorname {\mathrm {Nklt}}(\check X ', \check B ', \mathbf {M}) = \operatorname {\mathrm {Supp}}((\check B')^{=1})$
. Furthermore, we may take a generalized dlt model
![]() $(\check X ^m, \check B ^m, \mathbf {M}) \rightarrow (\check X ', \check B ', \mathbf {M})$
, such that properties (3) and (4) are preserved, and
$(\check X ^m, \check B ^m, \mathbf {M}) \rightarrow (\check X ', \check B ', \mathbf {M})$
, such that properties (3) and (4) are preserved, and
![]() $\operatorname {\mathrm {Supp}}((B^m)^{=1})$
fully supports a divisor that is relatively big and semiample over
$\operatorname {\mathrm {Supp}}((B^m)^{=1})$
fully supports a divisor that is relatively big and semiample over
![]() $\widehat Z$
, and that is relatively ample away from
$\widehat Z$
, and that is relatively ample away from
![]() $\operatorname {\mathrm {Nklt}}(\check X ^m, \check B ^m, \mathbf {M})$
.
$\operatorname {\mathrm {Nklt}}(\check X ^m, \check B ^m, \mathbf {M})$
.
Proof. By construction,
![]() $\check X '$
is
$\check X '$
is
![]() $\mathbb {Q}$
-factorial. By property (f),
$\mathbb {Q}$
-factorial. By property (f),
![]() $(\widehat X, \widehat B^{<1} + \widehat B^{=1,h} + \epsilon \widehat H^v + \delta (\widehat {D}-\widehat {H}^h), \mathbf {M})$
is generalized klt and its generalized log canonical divisor is relatively trivial over
$(\widehat X, \widehat B^{<1} + \widehat B^{=1,h} + \epsilon \widehat H^v + \delta (\widehat {D}-\widehat {H}^h), \mathbf {M})$
is generalized klt and its generalized log canonical divisor is relatively trivial over
![]() $\widehat {Z}$
. Thus, it follows that
$\widehat {Z}$
. Thus, it follows that
![]() $(\check X ', (\check B ')^{<1} + (\check B '){^{=1,h}} + \epsilon (\check H ')^v + \delta (\check {D}'-(\check {H}')^h), \mathbf {M})$
is generalized klt. Since
$(\check X ', (\check B ')^{<1} + (\check B '){^{=1,h}} + \epsilon (\check H ')^v + \delta (\check {D}'-(\check {H}')^h), \mathbf {M})$
is generalized klt. Since
![]() $\check X '$
is
$\check X '$
is
![]() $\mathbb {Q}$
-factorial,
$\mathbb {Q}$
-factorial,
![]() $(\check X ', (\check B ')^{<1}, \mathbf {M})$
is generalized klt. Thus, by Lemma 2.15, if we take a generalized dlt model
$(\check X ', (\check B ')^{<1}, \mathbf {M})$
is generalized klt. Thus, by Lemma 2.15, if we take a generalized dlt model
![]() $(\check X ^m, \check B ^m, \mathbf {M})$
of
$(\check X ^m, \check B ^m, \mathbf {M})$
of
![]() $(\check X ', \check B ', \mathbf {M})$
, every divisor extracted has positive coefficient in the pullback of
$(\check X ', \check B ', \mathbf {M})$
, every divisor extracted has positive coefficient in the pullback of
![]() $(\check B ')^{=1}$
. Then, since
$(\check B ')^{=1}$
. Then, since
![]() $\operatorname {\mathrm {Supp}}((\check B')^{=1})$
fully supports a divisor that is relatively big and semiample over
$\operatorname {\mathrm {Supp}}((\check B')^{=1})$
fully supports a divisor that is relatively big and semiample over
![]() $\widehat {Z}$
, and that is relatively ample away from
$\widehat {Z}$
, and that is relatively ample away from
![]() $\operatorname {\mathrm {Nklt}}(\check X ' , \check B ', \mathbf {M})$
, then so does
$\operatorname {\mathrm {Nklt}}(\check X ' , \check B ', \mathbf {M})$
, then so does
![]() $\operatorname {\mathrm {Supp}}((B^m)^{=1})$
. Indeed, every divisor extracted by
$\operatorname {\mathrm {Supp}}((B^m)^{=1})$
. Indeed, every divisor extracted by
![]() $\check X ^m \rightarrow \check X '$
appears with positive coefficient in the pullback of
$\check X ^m \rightarrow \check X '$
appears with positive coefficient in the pullback of
![]() $\check H '$
. Furthermore, passing to the model
$\check H '$
. Furthermore, passing to the model
![]() $\check X ^m$
preserves properties (3) and (4).
$\check X ^m$
preserves properties (3) and (4).
Step 6. Conclusion.
By construction, the generalized pair
![]() $(\check X, \check B,\mathbf {M})$
together with the morphism
$(\check X, \check B,\mathbf {M})$
together with the morphism
![]() $r \circ \check q \colon \check X \rightarrow W$
satisfies the properties (1), (3), and (4). If property
$r \circ \check q \colon \check X \rightarrow W$
satisfies the properties (1), (3), and (4). If property
![]() $(2)$
holds for
$(2)$
holds for
![]() $\check X \rightarrow W$
, then we can stop. Otherwise, we perform the following procedure:
$\check X \rightarrow W$
, then we can stop. Otherwise, we perform the following procedure:
-
(i) we replace
 $(\check X, \check B + \check M)$
with a generalized dlt model
$(\check X, \check B + \check M)$
with a generalized dlt model
 $(\check X ^m, \check B ^m, \mathbf {M})$
as at the end of step 5;
$(\check X ^m, \check B ^m, \mathbf {M})$
as at the end of step 5; -
(ii) we repeat the arguments in steps (2–5) for
 $(\check X ^m, \check B ^m , \mathbf {M})$
and
$(\check X ^m, \check B ^m , \mathbf {M})$
and
 $\check X ^m \rightarrow W$
, thus obtaining a new birational model
$\check X ^m \rightarrow W$
, thus obtaining a new birational model
 $\check X" \rightarrow V$
satisfying properties (1), (3), and (4) with
$\check X" \rightarrow V$
satisfying properties (1), (3), and (4) with
 $\dim V < \dim W$
;
$\dim V < \dim W$
; -
(iii) if property
 $(2)$
holds for
$(2)$
holds for
 $\check X" \rightarrow V$
, then we can stop; otherwise, we restart from (i) with input data
$\check X" \rightarrow V$
, then we can stop; otherwise, we restart from (i) with input data
 $(\check X", \check B" , \mathbf {M})$
and
$(\check X", \check B" , \mathbf {M})$
and
 $\check X" \rightarrow V$
.
$\check X" \rightarrow V$
.
The procedure described in (i)–(iii) must terminate after finitely many iterations, as at each time the dimension of the base of the fibration drops, the final outcome will then satisfy property (2).
To conclude our proof, we need to show that, in the procedure (i–iii) just introduced, whenever in (i), if we take a generalized dlt model of
![]() $(\check X, \check B, \mathbf {M})$
, then this does not constitute an issue with respect to property (1). That is, if we replace
$(\check X, \check B, \mathbf {M})$
, then this does not constitute an issue with respect to property (1). That is, if we replace
![]() $(\check X, \check B, \mathbf {M})$
with a generalized dlt model, property (1) may not hold anymore. On the other hand, we will argue that a suitable weaker version
$(\check X, \check B, \mathbf {M})$
with a generalized dlt model, property (1) may not hold anymore. On the other hand, we will argue that a suitable weaker version
![]() $(1')$
of property (1) still holds, and that this property is enough to run the proof.
$(1')$
of property (1) still holds, and that this property is enough to run the proof.
Let
![]() $(\check X ^m, \check B ^m, \mathbf {M})$
be the generalized dlt model of
$(\check X ^m, \check B ^m, \mathbf {M})$
be the generalized dlt model of
![]() $(\check X , \check B , \mathbf {M})$
introduced in step 5. Recall that the morphism
$(\check X , \check B , \mathbf {M})$
introduced in step 5. Recall that the morphism
![]() $\check X ^m \rightarrow \check X$
preserves (3) and (4) for the rational map
$\check X ^m \rightarrow \check X$
preserves (3) and (4) for the rational map
![]() $X \dashrightarrow \check X ^m$
. Recall that
$X \dashrightarrow \check X ^m$
. Recall that
![]() $(\check B ^m)^{=1}$
fully supports a divisor
$(\check B ^m)^{=1}$
fully supports a divisor
![]() $\check H ^m$
that is big and semiample relatively to W. Furthermore,
$\check H ^m$
that is big and semiample relatively to W. Furthermore,
![]() $\check H ^m$
is relatively ample away from
$\check H ^m$
is relatively ample away from
![]() $\operatorname {\mathrm {Nklt}}(\check X ^m, \check B ^m, \mathbf {M})$
.
$\operatorname {\mathrm {Nklt}}(\check X ^m, \check B ^m, \mathbf {M})$
.
Now, consider the following weaker version of property (1):
-
(1′)
 $(\check B ^m)^{=1}$
fully supports a divisor that is relatively big and semiample over W. Furthermore, this divisor is ample over W away from
$(\check B ^m)^{=1}$
fully supports a divisor that is relatively big and semiample over W. Furthermore, this divisor is ample over W away from
 $\operatorname {\mathrm {Nklt}}(\check X ^m, \check B ^m, \mathbf {M})$
.
$\operatorname {\mathrm {Nklt}}(\check X ^m, \check B ^m, \mathbf {M})$
.
Notice that (
![]() $1'$
) is stable under the extraction of valuations of generalized log discrepancy
$1'$
) is stable under the extraction of valuations of generalized log discrepancy
![]() $0$
for
$0$
for
![]() $(X, B, \mathbf {M})$
. Thus, we are free to replace
$(X, B, \mathbf {M})$
. Thus, we are free to replace
![]() $\check X '$
with a higher generalized dlt model. In particular, (
$\check X '$
with a higher generalized dlt model. In particular, (
![]() $1'$
) is stable under the operations performed in Claim 1. Furthermore, for
$1'$
) is stable under the operations performed in Claim 1. Furthermore, for
![]() $0 < \epsilon \ll 1 \ (\check X ^m, (\check B ^m){^{< 1}} + ((\check B ^m)^{=1} - \epsilon \check H ^m)^{h} + \epsilon \check H ^m,\mathbf {M})$
is generalized klt and satisfies the hypotheses of [Reference Birkar and Zhang7, Lemma 4.4]. In particular, we can repeat Step 2, and produce new birational models
$0 < \epsilon \ll 1 \ (\check X ^m, (\check B ^m){^{< 1}} + ((\check B ^m)^{=1} - \epsilon \check H ^m)^{h} + \epsilon \check H ^m,\mathbf {M})$
is generalized klt and satisfies the hypotheses of [Reference Birkar and Zhang7, Lemma 4.4]. In particular, we can repeat Step 2, and produce new birational models
![]() $\widetilde {X}'$
and
$\widetilde {X}'$
and
![]() $\widetilde {W}$
of
$\widetilde {W}$
of
![]() $\check X '$
and W, respectively. These two models satisfy the conclusions of Step 2, besides that the conclusion of Claim 2 is replaced by its weaker version with property (
$\check X '$
and W, respectively. These two models satisfy the conclusions of Step 2, besides that the conclusion of Claim 2 is replaced by its weaker version with property (
![]() $1'$
).
$1'$
).
Notice that we can reproduce Step 3 with the varieties
![]() $\widetilde {X}'$
and
$\widetilde {X}'$
and
![]() $\widetilde {W}$
with no significant changes.
$\widetilde {W}$
with no significant changes.
Now, we would like to reproduce Step 4. Notice that the key facts for Step 4 to hold are properties (d–e). Indeed, these guarantee that we can apply [Reference Kollár and Xu28, Lemma 54]. By construction, properties (a–b) are still satisfied by
![]() $\widetilde {X}'$
and
$\widetilde {X}'$
and
![]() $\widetilde {W}$
, while (c) does not hold, as (c) is equivalent to the conclusion of Claim 2. On the other hand, since a weaker version of Claim 2 where ampleness is replaced by bigness and semiampleness holds, the corresponding weaker version of (c) holds. Now, notice that this weakening of (c) is sufficient in the proof of Claim 3, as it is enough to be able to apply a Bertini-like argument. In particular, this implies that we can replicate Step 4 with
$\widetilde {W}$
, while (c) does not hold, as (c) is equivalent to the conclusion of Claim 2. On the other hand, since a weaker version of Claim 2 where ampleness is replaced by bigness and semiampleness holds, the corresponding weaker version of (c) holds. Now, notice that this weakening of (c) is sufficient in the proof of Claim 3, as it is enough to be able to apply a Bertini-like argument. In particular, this implies that we can replicate Step 4 with
![]() $\widetilde {X}'$
and
$\widetilde {X}'$
and
![]() $\widetilde {W}$
. Hence, we produce a variety
$\widetilde {W}$
. Hence, we produce a variety
![]() $\check X "$
which is birational to X, and a variety V with
$\check X "$
which is birational to X, and a variety V with
![]() $\dim (V) < \dim (W)$
.
$\dim (V) < \dim (W)$
.
Finally, we can reproduce Step 5 in its entirety. More precisely, Step 5 can be reproduced, replacing property (1) with property (
![]() $1'$
). Then, the conclusions of Step 5 still hold. Therefore, as indicated in (iii) in Step 6, we can iterate this argument until property (2) is satisfied. Since after each iteration the dimension of the base drops, the algorithm has to terminate, and the final outcome will satisfy properties (1–4).
$1'$
). Then, the conclusions of Step 5 still hold. Therefore, as indicated in (iii) in Step 6, we can iterate this argument until property (2) is satisfied. Since after each iteration the dimension of the base drops, the algorithm has to terminate, and the final outcome will satisfy properties (1–4).
The following is a generalization of [Reference Kollár and Xu28, Corollary 58]. We will use the same notation as in Theorem 4.2.
Corollary 4.4. Let
![]() $(X,B,\mathbf {M})$
be a generalized log canonical pair. Assume that
$(X,B,\mathbf {M})$
be a generalized log canonical pair. Assume that
![]() ${K_{X}} + B + \mathbf {M}_X \sim _{\mathbb {Q}} 0$
. Then, there exist a
${K_{X}} + B + \mathbf {M}_X \sim _{\mathbb {Q}} 0$
. Then, there exist a
![]() $\mathbb {Q}$
-factorial, generalized dlt pair
$\mathbb {Q}$
-factorial, generalized dlt pair
![]() $(\tilde X, \tilde B , \mathbf {M})$
which is crepant birational to
$(\tilde X, \tilde B , \mathbf {M})$
which is crepant birational to
![]() $(X, B, \mathbf {M})$
, and crepant birational maps
$(X, B, \mathbf {M})$
, and crepant birational maps
together with a morphism
![]() $\tilde q \colon \tilde X \rightarrow Z$
, such that:
$\tilde q \colon \tilde X \rightarrow Z$
, such that:
-
(1) every generalized log canonical center of
 $(\tilde {X},\tilde {B} + \tilde {M})$
dominates Z;
$(\tilde {X},\tilde {B} + \tilde {M})$
dominates Z; -
(2)
 $\tilde B^{=1} = g^{-1} (\overline {B}^{\hspace{1pt}=1})$
;
$\tilde B^{=1} = g^{-1} (\overline {B}^{\hspace{1pt}=1})$
; -
(3)
 $g^{-1} (\overline {B}^{\hspace{1pt}=1})$
fully supports a
$g^{-1} (\overline {B}^{\hspace{1pt}=1})$
fully supports a
 $\tilde q$
-big and
$\tilde q$
-big and
 $\tilde q$
-semiample divisor;
$\tilde q$
-semiample divisor; -
(4) every prime divisor
 $\tilde E \subset \tilde X$
that does not dominate Z has nonempty intersection with
$\tilde E \subset \tilde X$
that does not dominate Z has nonempty intersection with
 $g^{-1} (\overline {B}^{\hspace{1pt}=1})$
; and
$g^{-1} (\overline {B}^{\hspace{1pt}=1})$
; and -
(5)
 $\psi ^{-1}$
is a crepant birational contraction and
$\psi ^{-1}$
is a crepant birational contraction and
 $\tilde E \subset \tilde B^{=1}$
for every
$\tilde E \subset \tilde B^{=1}$
for every
 $\psi ^{-1}$
-exceptional divisor.
$\psi ^{-1}$
-exceptional divisor.
Proof. Let
![]() $(\hat X, \hat B, \mathbf {M})$
be a generalized dlt model of
$(\hat X, \hat B, \mathbf {M})$
be a generalized dlt model of
![]() $(X,B, \mathbf {M})$
. Let
$(X,B, \mathbf {M})$
. Let
![]() $\overline q \colon (\overline {X}, \overline B , \mathbf {M})\rightarrow Z$
be an outcome of Theorem 4.2 applied to
$\overline q \colon (\overline {X}, \overline B , \mathbf {M})\rightarrow Z$
be an outcome of Theorem 4.2 applied to
![]() $(\hat X, \hat B , \mathbf {M})$
. Write
$(\hat X, \hat B , \mathbf {M})$
. Write
![]() $\phi \colon X \dashrightarrow \overline {X}$
. By construction, every
$\phi \colon X \dashrightarrow \overline {X}$
. By construction, every
![]() $\phi ^{-1}$
-exceptional divisor is contained in
$\phi ^{-1}$
-exceptional divisor is contained in
![]() $\overline {B}^{\hspace{1pt}=1}$
. Let
$\overline {B}^{\hspace{1pt}=1}$
. Let
![]() $(\tilde X, \tilde B , \mathbf {M})$
be a generalized dlt model of
$(\tilde X, \tilde B , \mathbf {M})$
be a generalized dlt model of
![]() $(\overline {X},\overline {B} , \mathbf {M})$
, and set
$(\overline {X},\overline {B} , \mathbf {M})$
, and set
![]() $g \colon \tilde {X} \rightarrow \overline {X}$
. By Theorem 4.2,
$g \colon \tilde {X} \rightarrow \overline {X}$
. By Theorem 4.2,
![]() $(\overline {X}, \overline {B} , \mathbf {M})$
satisfies (1), and so does
$(\overline {X}, \overline {B} , \mathbf {M})$
satisfies (1), and so does
![]() $(\tilde X, \tilde B , \mathbf {M})$
. Since
$(\tilde X, \tilde B , \mathbf {M})$
. Since
![]() $(\tilde X, \tilde B , \mathbf {M})$
is a generalized dlt model of
$(\tilde X, \tilde B , \mathbf {M})$
is a generalized dlt model of
![]() $(\overline {X}, \overline {B} , \mathbf {M})$
, we have
$(\overline {X}, \overline {B} , \mathbf {M})$
, we have
![]() $g^{-1}(\overline {B}^{\hspace{1pt}=1}) \subset \tilde B^{=1}$
. By Remark 4.3, we have the reversed inclusion, and (2) holds. By construction,
$g^{-1}(\overline {B}^{\hspace{1pt}=1}) \subset \tilde B^{=1}$
. By Remark 4.3, we have the reversed inclusion, and (2) holds. By construction,
![]() $\overline {B}^{\hspace{1pt}=1}$
fully supports a
$\overline {B}^{\hspace{1pt}=1}$
fully supports a
![]() $\overline {q}$
-ample divisor. As
$\overline {q}$
-ample divisor. As
![]() $\operatorname {\mathrm {Supp}}(g^{\ast } \overline {B}^{\hspace{1pt}=1})=g^{-1} (\overline {B}^{\hspace{1pt}=1})$
, then (3) holds. Furthermore, any divisor
$\operatorname {\mathrm {Supp}}(g^{\ast } \overline {B}^{\hspace{1pt}=1})=g^{-1} (\overline {B}^{\hspace{1pt}=1})$
, then (3) holds. Furthermore, any divisor
![]() $\tilde E \subset \tilde X$
that does not dominate Z and is not g-exceptional intersects
$\tilde E \subset \tilde X$
that does not dominate Z and is not g-exceptional intersects
![]() $g^{-1} (\overline {B}^{\hspace{1pt}=1})$
, as
$g^{-1} (\overline {B}^{\hspace{1pt}=1})$
, as
![]() $\overline {B}^{\hspace{1pt}=1}$
fully supports a
$\overline {B}^{\hspace{1pt}=1}$
fully supports a
![]() $\overline {q}$
-ample divisor. Then, as every g-exceptional divisor is in
$\overline {q}$
-ample divisor. Then, as every g-exceptional divisor is in
![]() $g^{-1} (\overline {B}^{\hspace{1pt}=1})$
, (4) follows. Finally, by construction, we either used Theorem 4.2 or generalized dlt models to produce new varieties. Hence, (5) holds true.
$g^{-1} (\overline {B}^{\hspace{1pt}=1})$
, (4) follows. Finally, by construction, we either used Theorem 4.2 or generalized dlt models to produce new varieties. Hence, (5) holds true.
Remark 4.5. If
![]() $\dim \tilde X - \dim Z \geq 2$
, then property (4) in the statement of Corollary 4.4 can be further strengthened. In fact, under such assumption, every prime divisor
$\dim \tilde X - \dim Z \geq 2$
, then property (4) in the statement of Corollary 4.4 can be further strengthened. In fact, under such assumption, every prime divisor
![]() $\tilde E \subset \tilde X$
has nonempty intersection with
$\tilde E \subset \tilde X$
has nonempty intersection with
![]() $g^{-1} (\overline {B}^{\hspace{1pt}=1})$
.
$g^{-1} (\overline {B}^{\hspace{1pt}=1})$
.
On the other hand, if
![]() $\dim Z = \dim \tilde X -1$
, this stronger statement could fail. Indeed, to construct an example showing this cannot be achieved, it suffices to fix an elliptic curve E and define
$\dim Z = \dim \tilde X -1$
, this stronger statement could fail. Indeed, to construct an example showing this cannot be achieved, it suffices to fix an elliptic curve E and define
![]() ,
,
![]() ,
,
![]() $M'=\tilde M =0$
, and
$M'=\tilde M =0$
, and
![]() $\tilde B$
to be the union of the two disjoint sections of
$\tilde B$
to be the union of the two disjoint sections of
![]() $\tilde X \rightarrow Z$
. This example is an admissible case of Corollary 4.4, and
$\tilde X \rightarrow Z$
. This example is an admissible case of Corollary 4.4, and
![]() $\tilde B$
has empty intersection with other sections of
$\tilde B$
has empty intersection with other sections of
![]() $\tilde X \rightarrow Z$
.
$\tilde X \rightarrow Z$
.
Theorem 4.2 and Corollary 4.4 make it possible to reduce the study of the dual complex of a generalized pair
![]() $(X,B,\mathbf {M})$
to the study of the dual complex of lower-dimensional pairs via the construction of suitable fibrations on the variety X. The next result furthers this strategy by establishing a comparison between the dual complex of a variety and the dual complex of the generic fiber of a morphism.
$(X,B,\mathbf {M})$
to the study of the dual complex of lower-dimensional pairs via the construction of suitable fibrations on the variety X. The next result furthers this strategy by establishing a comparison between the dual complex of a variety and the dual complex of the generic fiber of a morphism.
Lemma 4.6 [Reference Kollár and Xu28, Lemmata 28–30].
Let
![]() $E = \bigcup _{i \in I} E_i$
be a simple normal crossing variety over a field k.
$E = \bigcup _{i \in I} E_i$
be a simple normal crossing variety over a field k.
-
(1) Let
 $K/k$
be a Galois extension with Galois group G. Then G acts on
$K/k$
be a Galois extension with Galois group G. Then G acts on
 $\mathcal {D}(E_K)$
and
$\mathcal {D}(E_K)$
and
 $\mathcal {D}(E_k)=\mathcal {D}(E_K)/G$
.
$\mathcal {D}(E_k)=\mathcal {D}(E_K)/G$
.
Let
![]() $q \colon E \rightarrow Z$
be a morphism.
$q \colon E \rightarrow Z$
be a morphism.
-
(2) The generic fiber
 $E_{k(Z)}$
is a simple normal crossing variety over the function field
$E_{k(Z)}$
is a simple normal crossing variety over the function field
 $k(Z)$
and
$k(Z)$
and
 $\mathcal {D}(E_{k(Z)})$
is a subcomplex of
$\mathcal {D}(E_{k(Z)})$
is a subcomplex of
 $\mathcal {D}(E)$
. Furthermore, if every stratum dominates Z, then
$\mathcal {D}(E)$
. Furthermore, if every stratum dominates Z, then
 $\mathcal {D}(E_{k(Z)})=\mathcal {D}(E)$
.
$\mathcal {D}(E_{k(Z)})=\mathcal {D}(E)$
. -
(3) Assume that every stratum of E dominates Z. Let
 $z \in Z$
be a general point and
$z \in Z$
be a general point and
 $E_z$
the fiber over z. Then
$E_z$
the fiber over z. Then
 $E_z$
is a simple normal crossing variety and there is a finite group G acting on
$E_z$
is a simple normal crossing variety and there is a finite group G acting on
 $\mathcal {D}(E_z)$
, such that
$\mathcal {D}(E_z)$
, such that
 $\mathcal {D}(E)= \mathcal {D}(E_z)/G$
.
$\mathcal {D}(E)= \mathcal {D}(E_z)/G$
.
5 The dual complex of generalized log Calabi–Yau pairs
In this section, we collect some technical and partial results that will be used to prove our main theorem on the structure of the dual complex for generalized log Calabi–Yau pairs.
5.1 Dual complex and MRC fibration
Firstly, we aim to show that, to study the dual complex of generalized log canonical pairs of log Calabi–Yau type, it suffices to consider the case when the underlying variety is rationally connected.
Proposition 5.1. Let
![]() $(X, B, \mathbf {M})$
be a generalized dlt pair. Assume that
$(X, B, \mathbf {M})$
be a generalized dlt pair. Assume that
![]() ${K_{X}} + B + \mathbf {M}_X \sim _{\mathbb {Q}} 0$
. Let
${K_{X}} + B + \mathbf {M}_X \sim _{\mathbb {Q}} 0$
. Let
![]() $g \colon X \dashrightarrow Z$
be a dominant rational map to a nonuniruled variety Z. Assume that there exists a nonempty open set of the base
$g \colon X \dashrightarrow Z$
be a dominant rational map to a nonuniruled variety Z. Assume that there exists a nonempty open set of the base
![]() $U \subset Z$
, such that the restriction of g to
$U \subset Z$
, such that the restriction of g to
![]() $g^{-1}(U)$
is a morphism with connected fibers over U. Then, every irreducible component D of
$g^{-1}(U)$
is a morphism with connected fibers over U. Then, every irreducible component D of
![]() $B^{=1}$
dominates Z.
$B^{=1}$
dominates Z.
Proof. We follow the strategy of the proof of [Reference Kollár and Xu28, Proposition 19].
Let us assume by contradiction that some component D of
![]() $B^{=1}$
does not dominate Z. Up to replacing Z birationally, we can assume that Z is smooth and projective, and that every prime divisor in X either dominates Z or dominates a prime divisor in Z. In particular, D dominates a prime divisor
$B^{=1}$
does not dominate Z. Up to replacing Z birationally, we can assume that Z is smooth and projective, and that every prime divisor in X either dominates Z or dominates a prime divisor in Z. In particular, D dominates a prime divisor
![]() $P \subset Z$
. Let
$P \subset Z$
. Let
![]() $X"$
be the normalization of the closure of the graph of g, and let
$X"$
be the normalization of the closure of the graph of g, and let
![]() $(X",B"+M")$
denote the log pullback of
$(X",B"+M")$
denote the log pullback of
![]() $(X, B, \mathbf {M})$
on
$(X, B, \mathbf {M})$
on
![]() $X"$
. Under these assumptions, the divisor
$X"$
. Under these assumptions, the divisor
![]() $B"$
may be noneffective. Let
$B"$
may be noneffective. Let
![]() $h \colon X" \rightarrow Z$
and
$h \colon X" \rightarrow Z$
and
![]() $\pi \colon X" \rightarrow X$
denote the induced morphisms. Let
$\pi \colon X" \rightarrow X$
denote the induced morphisms. Let
![]() $C \subset X$
be a sufficiently general complete intersection curve. Thus,
$C \subset X$
be a sufficiently general complete intersection curve. Thus,
![]() $D \cdot C> 0$
, and we may assume that C avoids any prescribed set of codimension at least 2. In particular, we may assume that C avoids the indeterminacy locus of g and the exceptional locus of
$D \cdot C> 0$
, and we may assume that C avoids any prescribed set of codimension at least 2. In particular, we may assume that C avoids the indeterminacy locus of g and the exceptional locus of
![]() $\pi $
, and we may identify C with its strict transform in
$\pi $
, and we may identify C with its strict transform in
![]() $X"$
.
$X"$
.
Claim 1. For every prime divisor
![]() $R \subset Z$
with
$R \subset Z$
with
![]() $R \cap h(C) \neq \emptyset $
,
$R \cap h(C) \neq \emptyset $
,
![]() $\operatorname {\mathrm {Supp}}(h^{\ast } (R))$
contains a prime divisor that is not exceptional for
$\operatorname {\mathrm {Supp}}(h^{\ast } (R))$
contains a prime divisor that is not exceptional for
![]() $X" \rightarrow X$
. In particular,
$X" \rightarrow X$
. In particular,
![]() $\operatorname {\mathrm {Supp}}(h^{\ast } (R))$
contains a divisor that has nonnegative coefficient in
$\operatorname {\mathrm {Supp}}(h^{\ast } (R))$
contains a divisor that has nonnegative coefficient in
![]() $B"$
, and that dominates R.
$B"$
, and that dominates R.
Proof. Fix a prime divisor R so that
![]() $R \cap h(C) \neq \emptyset $
. Since Z is smooth, R is Cartier, so
$R \cap h(C) \neq \emptyset $
. Since Z is smooth, R is Cartier, so
![]() $h^{\ast }(R)$
is well-defined and
$h^{\ast }(R)$
is well-defined and
![]() $\operatorname {\mathrm {Supp}}(h^{\ast } (R))$
is purely divisorial. Since
$\operatorname {\mathrm {Supp}}(h^{\ast } (R))$
is purely divisorial. Since
![]() $R \cap h(C) \neq \emptyset $
, there is a prime divisor,
$R \cap h(C) \neq \emptyset $
, there is a prime divisor,
![]() $O \subset \operatorname {\mathrm {Supp}}(h^{\ast } (R))$
so that
$O \subset \operatorname {\mathrm {Supp}}(h^{\ast } (R))$
so that
![]() $O \cap C \neq \emptyset $
. Since
$O \cap C \neq \emptyset $
. Since
![]() $X" \rightarrow X$
is an isomorphism along C, it is an isomorphism along the generic point of O. In particular, O is the strict transform of a prime divisor on X. Since
$X" \rightarrow X$
is an isomorphism along C, it is an isomorphism along the generic point of O. In particular, O is the strict transform of a prime divisor on X. Since
![]() $B \geq 0$
, it follows that
$B \geq 0$
, it follows that
![]() $B"$
has nonnegative coefficient along O. Finally, by assumption on Z, every prime divisor on X either dominates Z, or it dominates a prime divisor in Z. Thus, O has to dominate R.
$B"$
has nonnegative coefficient along O. Finally, by assumption on Z, every prime divisor on X either dominates Z, or it dominates a prime divisor in Z. Thus, O has to dominate R.
Since
![]() $X"$
and Z are normal and generically h has connected fibers, it follows that h has connected fibers everywhere. By construction, we have
$X"$
and Z are normal and generically h has connected fibers, it follows that h has connected fibers everywhere. By construction, we have
![]() ${K_{X"}} + B" + M" \sim _{\mathbb {Q}} 0$
. Thus, we can apply Theorem 2.20 to h, and induce a generalized subpair
${K_{X"}} + B" + M" \sim _{\mathbb {Q}} 0$
. Thus, we can apply Theorem 2.20 to h, and induce a generalized subpair
![]() $(Z,B_Z,{\mathbf N})$
, such that
$(Z,B_Z,{\mathbf N})$
, such that
Moreover,
![]() ${K_{Z}} \cdot h(C) \geq 0$
, by [Reference Miyaoka and Mori30, Corollary 3] since C is a complete intersection of ample divisors, g is dominant, and Z is not uniruled. In addition, as
${K_{Z}} \cdot h(C) \geq 0$
, by [Reference Miyaoka and Mori30, Corollary 3] since C is a complete intersection of ample divisors, g is dominant, and Z is not uniruled. In addition, as
![]() ${\mathbf N} _Z$
is pseudo-effective,
${\mathbf N} _Z$
is pseudo-effective,
![]() ${\mathbf N} _Z \cdot h(C) \geq 0$
. By the generalized canonical bundle formula, as D dominates P and
${\mathbf N} _Z \cdot h(C) \geq 0$
. By the generalized canonical bundle formula, as D dominates P and
![]() $\mu _D(B)=1$
, then
$\mu _D(B)=1$
, then
![]() $\mu _P (B_Z)> 0$
. Furthermore, if
$\mu _P (B_Z)> 0$
. Furthermore, if
![]() $\mu _Q (B_Z)<0$
for some prime divisor
$\mu _Q (B_Z)<0$
for some prime divisor
![]() $Q \subset Z$
, it follows that for every prime divisor
$Q \subset Z$
, it follows that for every prime divisor
![]() $\Gamma \subset X"$
that dominates Q, we have
$\Gamma \subset X"$
that dominates Q, we have
![]() $\mu _{\Gamma } (B") < 0$
. Thus, Claim 1 implies that
$\mu _{\Gamma } (B") < 0$
. Thus, Claim 1 implies that
![]() $h(C)$
is disjoint from any prime divisor Q with
$h(C)$
is disjoint from any prime divisor Q with
![]() $\mu _Q (B_Z)<0$
. As
$\mu _Q (B_Z)<0$
. As
![]() $D \cdot C> 0$
, then
$D \cdot C> 0$
, then
![]() $P \cdot h(C)>0$
. This implies that
$P \cdot h(C)>0$
. This implies that
which leads to the required contradiction.
Proposition 5.1 allows a first interesting reduction in the study of the dual complex of a generalized pair of log Calabi–Yau type.
Any normal and proper variety X admits a birational contraction, called a maximal rationally chain connected (in short, mrcc) fibration
![]() $g \colon X \dashrightarrow Z$
(see [Reference Kollár24, Theorem IV.5.2] for the details of the construction). Roughly speaking, the mrcc fibration is characterized by the following properties:
$g \colon X \dashrightarrow Z$
(see [Reference Kollár24, Theorem IV.5.2] for the details of the construction). Roughly speaking, the mrcc fibration is characterized by the following properties:
-
• the fibers of g are rationally chain connected; and
-
• almost every rational curve is contained in a fiber of g: namely, for a very general
 $z \in Z$
, any rational curve intersecting
$z \in Z$
, any rational curve intersecting
 $X_z$
is contained in
$X_z$
is contained in
 $X_z$
.
$X_z$
.
The mrcc fibration is uniquely determined up to birational equivalence. By [Reference Kollár24, Theorem IV.4.17], the birational contraction g is a well-defined morphism with connected fibers over a nonempty open set of the base Z. If the variety X is smooth, then the general fiber of g will be rationally connected; in this case, the morphism g is called the maximal rationally connected (mrc) fibration. Work of Hacon and McKernan, [Reference Hacon and McKernan18], shows that the same actually holds in the case of dlt pairs. Therefore, for our purposes, we can always consider the mrc fibration of a dlt model of a generalized log canonical pair.
By work of Graber, Harris, and Starr, cf. [Reference Graber, Harris and Starr14, Corollary 1.4], the base Z of an mrc fibration is not uniruled. Therefore, Proposition 5.1 applies to the mrc fibration of a generalized dlt pair
![]() $(X,B, \mathbf {M})$
with
$(X,B, \mathbf {M})$
with
![]() ${K_{X}} + B + M \sim _{\mathbb {Q}} 0$
. In particular, by Lemma 4.6, we can reduce the study of the dual complex to the case when X is a rationally connected variety.
${K_{X}} + B + M \sim _{\mathbb {Q}} 0$
. In particular, by Lemma 4.6, we can reduce the study of the dual complex to the case when X is a rationally connected variety.
5.2 Reduction to the ample case
Let
![]() $(X, B, \mathbf {M})$
be a generalized log canonical pair. Assume that
$(X, B, \mathbf {M})$
be a generalized log canonical pair. Assume that
![]() ${K_{X}} + B + M \sim _{\mathbb {Q}} 0$
. We are interested in studying
${K_{X}} + B + M \sim _{\mathbb {Q}} 0$
. We are interested in studying
![]() $\mathcal {DMR}(X,B, \mathbf {M})$
. By the results of Section 5.1, we can assume that X is a rationally connected
$\mathcal {DMR}(X,B, \mathbf {M})$
. By the results of Section 5.1, we can assume that X is a rationally connected
![]() $\mathbb {Q}$
-factorial klt variety.
$\mathbb {Q}$
-factorial klt variety.
As
![]() ${K_{X}} + B +M \sim _{\mathbb {Q}} 0$
, we aim to use vanishing theorems, cf. Theorem 4.1, to show that
${K_{X}} + B +M \sim _{\mathbb {Q}} 0$
, we aim to use vanishing theorems, cf. Theorem 4.1, to show that
![]() $H^i(X,{\mathcal {O}_{X}})=0$
, for
$H^i(X,{\mathcal {O}_{X}})=0$
, for
![]() $i> 0$
; the vanishing of the higher cohomology of the structure sheaf is known to imply the vanishing of the cohomology of the dual complex (see [Reference Kollár and Xu28, Section 4]). On the other hand, since we are interested in studying
$i> 0$
; the vanishing of the higher cohomology of the structure sheaf is known to imply the vanishing of the cohomology of the dual complex (see [Reference Kollár and Xu28, Section 4]). On the other hand, since we are interested in studying
![]() $\mathcal {DMR}(X,B, \mathbf {M})$
, we can assume that the generalized pair
$\mathcal {DMR}(X,B, \mathbf {M})$
, we can assume that the generalized pair
![]() $(X,B+M)$
is not generalized klt. In general, the vanishing theorems are not expected to hold for purely log canonical pairs, without imposing some conditions on the positivity of
$(X,B+M)$
is not generalized klt. In general, the vanishing theorems are not expected to hold for purely log canonical pairs, without imposing some conditions on the positivity of
![]() $B+M$
. Nonetheless, in Corollary 4.4, we showed that we can assume that X is endowed with a fibration
$B+M$
. Nonetheless, in Corollary 4.4, we showed that we can assume that X is endowed with a fibration
![]() $X \to Z$
, such that B fully supports an effective divisor which is big and semiample over Z.
$X \to Z$
, such that B fully supports an effective divisor which is big and semiample over Z.
Let
![]() $\eta $
be the generic point of Z. It follows from Lemma 4.6 that
$\eta $
be the generic point of Z. It follows from Lemma 4.6 that
Furthermore, Lemma 4.6 implies the existence of a finite group G, such that
for a general closed point
![]() $z \in Z$
. As we are interested in showing that the identity
$z \in Z$
. As we are interested in showing that the identity
![]() $H^i(\mathcal {DMR}(X,B, \mathbf {M}),\mathbb {Q})=0$
holds, for
$H^i(\mathcal {DMR}(X,B, \mathbf {M}),\mathbb {Q})=0$
holds, for
![]() $i>0$
, it suffices to show that the corresponding identity
$i>0$
, it suffices to show that the corresponding identity
![]() $H^i(\mathcal {DMR}(\tilde X _z, \tilde B _z , \mathbf {M} |_{\tilde {X}_z}),\mathbb {Q})=0$
holds, for
$H^i(\mathcal {DMR}(\tilde X _z, \tilde B _z , \mathbf {M} |_{\tilde {X}_z}),\mathbb {Q})=0$
holds, for
![]() $i>0$
.
$i>0$
.
Therefore, invoking Corollary 4.4, we can assume that
![]() $(X,B+M)$
is
$(X,B+M)$
is
![]() $\mathbb {Q}$
-factorial generalized dlt, and that
$\mathbb {Q}$
-factorial generalized dlt, and that
![]() $B^{=1}$
fully supports a big and semiample effective
$B^{=1}$
fully supports a big and semiample effective
![]() $\mathbb {Q}$
-divisor H with
$\mathbb {Q}$
-divisor H with
![]() $B \geq H$
. Then, the generalized pair
$B \geq H$
. Then, the generalized pair
![]() $(X,B-H,\mathbf {M})$
is generalized klt. Hence,
$(X,B-H,\mathbf {M})$
is generalized klt. Hence,
and
![]() $(X, B-H, \mathbf {M} + \overline {H})$
is generalized klt. Theorem 4.1 then implies that
$(X, B-H, \mathbf {M} + \overline {H})$
is generalized klt. Theorem 4.1 then implies that
5.3 Reduction to the classical case
In this subsection, we show that if the dual complex of a generalized log Calabi–Yau pair
![]() $(X, B, \mathbf {M})$
is not collapsible to a point, then we can reduce the study of
$(X, B, \mathbf {M})$
is not collapsible to a point, then we can reduce the study of
![]() $H^i(\mathcal {DMR}(X,B, \mathbf {M}),\mathbb {Q})$
to the study of the cohomology of the dual complex of a log pair
$H^i(\mathcal {DMR}(X,B, \mathbf {M}),\mathbb {Q})$
to the study of the cohomology of the dual complex of a log pair
![]() $(\tilde X, \tilde B)$
with
$(\tilde X, \tilde B)$
with
![]() $K_{\tilde X}+ \tilde B \sim _{\mathbb {Q}} 0$
; the latter case was studied in detail in [Reference Kollár and Xu28].
$K_{\tilde X}+ \tilde B \sim _{\mathbb {Q}} 0$
; the latter case was studied in detail in [Reference Kollár and Xu28].
We will use the notation introduced in Section 5.2.
Corollary 5.2. Let
![]() $(X, B, \mathbf {M})$
be a generalized log canonical pair. Assume that
$(X, B, \mathbf {M})$
be a generalized log canonical pair. Assume that
![]() ${K_{X}} + B + M \sim _{\mathbb {Q}} 0$
. Let
${K_{X}} + B + M \sim _{\mathbb {Q}} 0$
. Let
![]() $(\tilde X, \tilde B , \mathbf {M})$
be the generalized pair constructed in Corollary 4.4 together with the morphism
$(\tilde X, \tilde B , \mathbf {M})$
be the generalized pair constructed in Corollary 4.4 together with the morphism
![]() $\tilde q \colon \tilde X \rightarrow Z$
, whose existence is claimed in the corollary. Let
$\tilde q \colon \tilde X \rightarrow Z$
, whose existence is claimed in the corollary. Let
![]() $\eta $
be the generic point of Z. Assume that
$\eta $
be the generic point of Z. Assume that
![]() $\mathcal {DMR}(X,B, \mathbf {M})$
is not collapsible to a point. Then,
$\mathcal {DMR}(X,B, \mathbf {M})$
is not collapsible to a point. Then,
![]() $\lfloor \tilde {B}_{\eta } \rfloor = \tilde B _{\eta }$
and
$\lfloor \tilde {B}_{\eta } \rfloor = \tilde B _{\eta }$
and
![]() $\mathbf {M} |_{\tilde {X} _{\eta }} \equiv 0$
.
$\mathbf {M} |_{\tilde {X} _{\eta }} \equiv 0$
.
Proof. Set
![]() . Assume that
. Assume that
![]() $\tilde B^{=1}_{\eta } \not \equiv \tilde B _{\eta } + \tilde M _{\eta }$
. Then,
$\tilde B^{=1}_{\eta } \not \equiv \tilde B _{\eta } + \tilde M _{\eta }$
. Then,
![]() ${K_{\tilde X}} + \tilde B^{=1}$
is not pseudo-effective over Z. Thus, we may run a
${K_{\tilde X}} + \tilde B^{=1}$
is not pseudo-effective over Z. Thus, we may run a
![]() $({K_{\tilde X}} + \tilde B^{=1})$
-MMP with scaling over Z, which terminates with a Fano contraction
$({K_{\tilde X}} + \tilde B^{=1})$
-MMP with scaling over Z, which terminates with a Fano contraction
![]() $p \colon \hat X \rightarrow Y$
. The final model
$p \colon \hat X \rightarrow Y$
. The final model
![]() $(\hat X, \hat B^{=1})$
of this MMP is dlt, where
$(\hat X, \hat B^{=1})$
of this MMP is dlt, where
![]() $\hat B$
is the strict transform of
$\hat B$
is the strict transform of
![]() $\tilde B$
on
$\tilde B$
on
![]() $\hat X$
. As
$\hat X$
. As
![]() $B^{=1}$
fully supports a divisor that is big and semiample over Z, then
$B^{=1}$
fully supports a divisor that is big and semiample over Z, then
![]() $\hat B^{=1}$
dominates Y. Therefore, by [Reference Kollár and Xu28, Proposition 24],
$\hat B^{=1}$
dominates Y. Therefore, by [Reference Kollár and Xu28, Proposition 24],
![]() $\mathcal {DMR}(\hat X, \hat B^{=1})$
is collapsible to a point.
$\mathcal {DMR}(\hat X, \hat B^{=1})$
is collapsible to a point.
Let
![]() $h \colon (\check X,\check B, \mathbf {M}) \rightarrow (\hat X, \hat B, \mathbf {M})$
be a generalized dlt model of
$h \colon (\check X,\check B, \mathbf {M}) \rightarrow (\hat X, \hat B, \mathbf {M})$
be a generalized dlt model of
![]() $(\hat X , \hat B, \mathbf {M})$
. By Corollary 4.4,
$(\hat X , \hat B, \mathbf {M})$
. By Corollary 4.4,
![]() $\check B^{=1}$
fully supports a big and mobile divisor over Z, so that,
$\check B^{=1}$
fully supports a big and mobile divisor over Z, so that,
![]() $\check B^{=1}$
dominates Z, and we have
$\check B^{=1}$
dominates Z, and we have
![]() $\check B^{=1} = h^{-1} (\hat B^{=1})$
, cf [Reference Kollár and Xu28, Section 22]. By [Reference de Fernex, Kollár and Xu8, Theorem 3],
$\check B^{=1} = h^{-1} (\hat B^{=1})$
, cf [Reference Kollár and Xu28, Section 22]. By [Reference de Fernex, Kollár and Xu8, Theorem 3],
![]() $\mathcal {DMR}(\check X,\check B , \mathbf {M})$
collapses to
$\mathcal {DMR}(\check X,\check B , \mathbf {M})$
collapses to
![]() $\mathcal {DMR}(\hat X, \hat B^{=1})$
.
$\mathcal {DMR}(\hat X, \hat B^{=1})$
.
Remark 5.3. Using the result from the previous subsection, Corollary 5.2 implies that the study of the cohomology of the dual complex of generalized log Calabi–Yau pairs reduces to the case of log Calabi–Yau pairs. Indeed, if
![]() $\mathcal {DMR}(X,B, \mathbf {M})$
is collapsible, there is nothing to prove. Otherwise, we can consider the relation
$\mathcal {DMR}(X,B, \mathbf {M})$
is collapsible, there is nothing to prove. Otherwise, we can consider the relation
![]() $\mathcal {DMR}(X,B, \mathbf {M}) \simeq \mathcal {DMR}(\tilde X _z, \tilde B _z , \mathbf {M} |_{\tilde X _z})$
discussed in Section 5.2, where
$\mathcal {DMR}(X,B, \mathbf {M}) \simeq \mathcal {DMR}(\tilde X _z, \tilde B _z , \mathbf {M} |_{\tilde X _z})$
discussed in Section 5.2, where
![]() $\tilde X _z$
denotes a general fiber of the morphism
$\tilde X _z$
denotes a general fiber of the morphism
![]() $X \to Z$
, whose existence is stated in Corollary 4.4. Then, by Corollary 5.2, we have
$X \to Z$
, whose existence is stated in Corollary 4.4. Then, by Corollary 5.2, we have
![]() $\tilde M _z \equiv 0$
. This implies that
$\tilde M _z \equiv 0$
. This implies that
![]() $(\tilde X _z, \tilde B _z , \mathbf {M} |_{\tilde X _z})$
is a pair. Therefore, to study
$(\tilde X _z, \tilde B _z , \mathbf {M} |_{\tilde X _z})$
is a pair. Therefore, to study
![]() $\mathcal {DMR}(\tilde X _z, \tilde B _z , \mathbf M |_{\tilde X _z})$
we can use the results in [Reference Kollár and Xu28].
$\mathcal {DMR}(\tilde X _z, \tilde B _z , \mathbf M |_{\tilde X _z})$
we can use the results in [Reference Kollár and Xu28].
We conclude this section by showing that, in the setup of this work, the dual complex of a generalized pair is equidimensional.
Theorem 5.4. Let
![]() $(X, B, \mathbf {M})$
be a generalized log canonical pair. Assume that
$(X, B, \mathbf {M})$
be a generalized log canonical pair. Assume that
![]() ${K_{X}} + B + M \sim _{\mathbb {Q}} 0$
. Then,
${K_{X}} + B + M \sim _{\mathbb {Q}} 0$
. Then,
![]() $\mathcal {DMR}(X,B, \mathbf {M})$
has the same dimension at every point.
$\mathcal {DMR}(X,B, \mathbf {M})$
has the same dimension at every point.
Proof. Let
![]() $(\overline {X},\overline {B}, \mathbf {M})$
be a generalized dlt model of
$(\overline {X},\overline {B}, \mathbf {M})$
be a generalized dlt model of
![]() $(X,B+M)$
. By Remark 2.31, we have
$(X,B+M)$
. By Remark 2.31, we have
![]() $\mathcal {DMR}(X,B, \mathbf {M})=\mathcal {DMR}(\overline {X},\overline {B})$
. Furthermore, by [Reference Kollár and Mori27, Theorem 2.44], we may compute
$\mathcal {DMR}(X,B, \mathbf {M})=\mathcal {DMR}(\overline {X},\overline {B})$
. Furthermore, by [Reference Kollár and Mori27, Theorem 2.44], we may compute
![]() $\mathcal {DMR}(\overline {X},\overline {B})$
directly by
$\mathcal {DMR}(\overline {X},\overline {B})$
directly by
![]() $\mathcal {D}(\overline {B}^{\hspace{1pt}=1})$
. Theorem 1.4 implies that
$\mathcal {D}(\overline {B}^{\hspace{1pt}=1})$
. Theorem 1.4 implies that
![]() $\mathcal {D}(\overline {B}^{\hspace{1pt}=1})$
gives rise to an equidimensional CW-complex.
$\mathcal {D}(\overline {B}^{\hspace{1pt}=1})$
gives rise to an equidimensional CW-complex.
6 Proof of the theorems
The following proposition will be used in the proof of Theorem 1.1.
Proposition 6.1. Let
![]() $(X,B,\mathbf {M})/S$
be a generalized pair. Assume that X is a generalized dlt model for
$(X,B,\mathbf {M})/S$
be a generalized pair. Assume that X is a generalized dlt model for
![]() $(X,B,\mathbf {M})/S$
. Let
$(X,B,\mathbf {M})/S$
. Let
![]() $f \colon X \rightarrow S$
be a projective morphism, such that
$f \colon X \rightarrow S$
be a projective morphism, such that
![]() ${K_{X}} + B + \mathbf {M}_X \sim _{\mathbb {Q},f} 0$
. Fix
${K_{X}} + B + \mathbf {M}_X \sim _{\mathbb {Q},f} 0$
. Fix
![]() $s \in S$
, and assume that
$s \in S$
, and assume that
![]() $f^{-1} (s)$
is connected, but
$f^{-1} (s)$
is connected, but
![]() $f^{-1} (s) \cap \operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})$
is disconnected (as
$f^{-1} (s) \cap \operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})$
is disconnected (as
![]() $k(s)$
-schemes). Then, a component of
$k(s)$
-schemes). Then, a component of
![]() $B^{\geq 1}$
dominates S.
$B^{\geq 1}$
dominates S.
Proof. We divide the proof into steps, for the reader’s convenience.
Step 0. In this step, we show that it suffices to show that the proposition holds for the contraction in the Stein factorization of f.
By assumption, X is
![]() $\mathbb {Q}$
-factorial and
$\mathbb {Q}$
-factorial and
![]() $(X,B \wedge \operatorname {\mathrm {Supp}}(B),\mathbf {M})/S$
is generalized dlt. Let
$(X,B \wedge \operatorname {\mathrm {Supp}}(B),\mathbf {M})/S$
is generalized dlt. Let
![]() $\phi \colon X \rightarrow Y$
denote the Stein factorization of f and let
$\phi \colon X \rightarrow Y$
denote the Stein factorization of f and let
![]() $\psi \colon Y \rightarrow S$
the induced finite morphism. Since the fiber of f over s is connected, and
$\psi \colon Y \rightarrow S$
the induced finite morphism. Since the fiber of f over s is connected, and
![]() $\phi $
has geometrically connected fibers, there exists a unique point
$\phi $
has geometrically connected fibers, there exists a unique point
![]() $y \in Y$
mapping to
$y \in Y$
mapping to
![]() $s \in S$
. Furthermore, as
$s \in S$
. Furthermore, as
![]() $f^{-1} (s) \cap \operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})$
is disconnected, then so is
$f^{-1} (s) \cap \operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})$
is disconnected, then so is
![]() $\phi ^{-1} (y) \cap \operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})$
; hence, the hypotheses of the statement apply to the morphism
$\phi ^{-1} (y) \cap \operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})$
; hence, the hypotheses of the statement apply to the morphism
![]() $\phi \colon X \rightarrow Y$
as well. Furthermore,
$\phi \colon X \rightarrow Y$
as well. Furthermore,
![]() $B^{\geq 1}$
dominates S if and only if it dominates Y.
$B^{\geq 1}$
dominates S if and only if it dominates Y.
Therefore, up to substituting S (respectively, s, f) with Y (respectively, y,
![]() $\phi $
), from now on, we shall assume that the morphism f satisfies the additional property
$\phi $
), from now on, we shall assume that the morphism f satisfies the additional property
![]() $f_{\ast } {\mathcal {O}_{X}} = {\mathcal {O}_{S}}$
.
$f_{\ast } {\mathcal {O}_{X}} = {\mathcal {O}_{S}}$
.
Step 1. In this step, we make further reductions and explain the strategy of proof.
Remark 3.7 implies that
![]() $\operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})= \mathrm {Supp} B^{\geq 1}$
. Moreover, by [Reference Kollár25, 4.38], passing to an étale neighborhood of
$\operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})= \mathrm {Supp} B^{\geq 1}$
. Moreover, by [Reference Kollár25, 4.38], passing to an étale neighborhood of
![]() $s \in S$
, we may assume that
$s \in S$
, we may assume that
![]() $\mathbf {(\ast )}$
different connected components of
$\mathbf {(\ast )}$
different connected components of
![]() $\operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})\cap f^{-1} (s)$
are contained in different connected components of
$\operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})\cap f^{-1} (s)$
are contained in different connected components of
![]() $\operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})$
.
$\operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})$
.
To prove the proposition, we shall argue by contradiction: namely, we shall assume that no component of
![]() $B^{\geq 1}$
dominates S. Given two distinct connected components
$B^{\geq 1}$
dominates S. Given two distinct connected components
![]() $D_1$
and
$D_1$
and
![]() $D_2$
of
$D_2$
of
![]() $B^{\geq 1}$
intersecting
$B^{\geq 1}$
intersecting
![]() $f^{-1} (y)$
, we will obtain the sought contradiction by using the fact that the components of
$f^{-1} (y)$
, we will obtain the sought contradiction by using the fact that the components of
![]() $B^{\geq 1}$
are vertical over S to show that
$B^{\geq 1}$
are vertical over S to show that
![]() $D_1$
and
$D_1$
and
![]() $D_2$
actually intersect.
$D_2$
actually intersect.
Step 2. In this step, we define a generalized pair
![]() $(S,B_S + M_S)$
on S using the canonical bundle formula. We introduce an auxiliary divisor
$(S,B_S + M_S)$
on S using the canonical bundle formula. We introduce an auxiliary divisor
![]() $\Sigma '$
on a higher model
$\Sigma '$
on a higher model
![]() $S' \to S$
;
$S' \to S$
;
![]() $\Sigma '$
is only needed to treat the case when
$\Sigma '$
is only needed to treat the case when
![]() $(X,B,\mathbf {M})$
is not generalized log canonical.
$(X,B,\mathbf {M})$
is not generalized log canonical.
By [Reference Filipazzi10, Theorem 1.4], there exists
![]() $(S,B_S + M_S)$
, a generalized pair induced by the generalized canonical bundle formula on S. Thus, [Reference Filipazzi10, Proposition 4.16] implies that there is some generalized non-klt center of
$(S,B_S + M_S)$
, a generalized pair induced by the generalized canonical bundle formula on S. Thus, [Reference Filipazzi10, Proposition 4.16] implies that there is some generalized non-klt center of
![]() $(Y, B_S + M_S)$
containing s. Let
$(Y, B_S + M_S)$
containing s. Let
![]() $\alpha \colon S' \rightarrow S$
be a generalized dlt model for
$\alpha \colon S' \rightarrow S$
be a generalized dlt model for
![]() $(S, B_S + M_S)$
, and let
$(S, B_S + M_S)$
, and let
![]() $(S', B_{S'} + M_{S'})$
denote the trace of
$(S', B_{S'} + M_{S'})$
denote the trace of
![]() $(S,B_S+M_S)$
on
$(S,B_S+M_S)$
on
![]() $S'$
. Let
$S'$
. Let
![]() $X'$
be the normalization of the main component of
$X'$
be the normalization of the main component of
![]() $X \times _S S'$
. Let
$X \times _S S'$
. Let
![]() $\beta \colon X' \rightarrow X$
and
$\beta \colon X' \rightarrow X$
and
![]() $g \colon X' \rightarrow S'$
denote the induced morphisms. The assumption that
$g \colon X' \rightarrow S'$
denote the induced morphisms. The assumption that
![]() $\operatorname {\mathrm {Nklt}}(X, B, \mathbf {M})$
does not dominate S implies that
$\operatorname {\mathrm {Nklt}}(X, B, \mathbf {M})$
does not dominate S implies that
![]() $(X',B', \mathbf {M})$
is generalized klt over the generic point of
$(X',B', \mathbf {M})$
is generalized klt over the generic point of
![]() $S'$
, where
$S'$
, where
![]() $(X',B', \mathbf {M})$
is the subpair induced by log pullback on
$(X',B', \mathbf {M})$
is the subpair induced by log pullback on
![]() $X'$
.
$X'$
.
Let us define the divisor
![]() on
on
![]() $S'$
. Then
$S'$
. Then
![]() $\Sigma '$
is the only divisor supported on
$\Sigma '$
is the only divisor supported on
![]() $\operatorname {\mathrm {Supp}} (B_{S'}^{\geq 1})$
, such that
$\operatorname {\mathrm {Supp}} (B_{S'}^{\geq 1})$
, such that
![]() $B_{S'} \wedge \operatorname {\mathrm {Supp}}(B_{S'})$
is the boundary part on
$B_{S'} \wedge \operatorname {\mathrm {Supp}}(B_{S'})$
is the boundary part on
![]() $S'$
for the generalized canonical bundle formula applied to
$S'$
for the generalized canonical bundle formula applied to
![]() $K_X'+B'+g^{\ast }\Sigma '+\mathbf {M}$
. By definition, we have
$K_X'+B'+g^{\ast }\Sigma '+\mathbf {M}$
. By definition, we have
![]() $\Sigma ' \leq 0$
; moreover,
$\Sigma ' \leq 0$
; moreover,
![]() $\Sigma ' = 0$
if
$\Sigma ' = 0$
if
![]() $(X,B,\mathbf {M})/S$
is generalized log canonical. By inversion of adjunction for the generalized canonical bundle formula, cf. [Reference Filipazzi10, Proposition 4.16], for every irreducible component
$(X,B,\mathbf {M})/S$
is generalized log canonical. By inversion of adjunction for the generalized canonical bundle formula, cf. [Reference Filipazzi10, Proposition 4.16], for every irreducible component
![]() $D'$
of
$D'$
of
![]() $\operatorname {\mathrm {Supp}}(B_{S'}^{\geq 1})$
, there is a divisorial valuation
$\operatorname {\mathrm {Supp}}(B_{S'}^{\geq 1})$
, there is a divisorial valuation
![]() $E'$
over
$E'$
over
![]() $X'$
, such that
$X'$
, such that
![]() $a_{E'}(X',B'+g^{\ast }\Sigma ',\mathbf {M}) = 0$
and
$a_{E'}(X',B'+g^{\ast }\Sigma ',\mathbf {M}) = 0$
and
![]() $c_{X'}(E')$
dominates
$c_{X'}(E')$
dominates
![]() $D'$
. Furthermore, the same results imply that the generalized subpair
$D'$
. Furthermore, the same results imply that the generalized subpair
![]() $(X',B'+g^{\ast }\Sigma ', \mathbf {M})$
is generalized sublog canonical.
$(X',B'+g^{\ast }\Sigma ', \mathbf {M})$
is generalized sublog canonical.
Step 3. Let
![]() $\pi \colon X" \rightarrow X'$
be a log resolution of
$\pi \colon X" \rightarrow X'$
be a log resolution of
![]() $(X',\operatorname {\mathrm {Supp}}(B') + g^{\ast }\operatorname {\mathrm {Supp}}(B_{S'}))$
, where
$(X',\operatorname {\mathrm {Supp}}(B') + g^{\ast }\operatorname {\mathrm {Supp}}(B_{S'}))$
, where
![]() $\mathbf {M}$
descends. In this step, we define a divisor
$\mathbf {M}$
descends. In this step, we define a divisor
![]() $F"$
on
$F"$
on
![]() $X"$
, cf. (15), supported on those components of
$X"$
, cf. (15), supported on those components of
![]() $B" +(g \circ \pi )^{\ast }\Sigma '$
of coefficient in
$B" +(g \circ \pi )^{\ast }\Sigma '$
of coefficient in
![]() $ (0, 1)$
, whose image in
$ (0, 1)$
, whose image in
![]() $S'$
is contained in
$S'$
is contained in
![]() $B^{\geq 1}_{S'}$
, and we discuss the properties of
$B^{\geq 1}_{S'}$
, and we discuss the properties of
![]() $F"$
.
$F"$
.
Let
![]() $\pi \colon X" \rightarrow X'$
be a log resolution of
$\pi \colon X" \rightarrow X'$
be a log resolution of
![]() $(X',\operatorname {\mathrm {Supp}}(B') + g^{\ast }\operatorname {\mathrm {Supp}}(B_{S'}))$
, where
$(X',\operatorname {\mathrm {Supp}}(B') + g^{\ast }\operatorname {\mathrm {Supp}}(B_{S'}))$
, where
![]() $\mathbf {M}$
descends, and let
$\mathbf {M}$
descends, and let
![]() $B"$
denote the subboundary induced on
$B"$
denote the subboundary induced on
![]() $X"$
. Up to passing to a higher smooth birational model, we may assume that for every prime component
$X"$
. Up to passing to a higher smooth birational model, we may assume that for every prime component
![]() $D'$
of
$D'$
of
![]() $\operatorname {\mathrm {Supp}}(B_{S'}^{\geq 1})$
, the corresponding divisorial valuation
$\operatorname {\mathrm {Supp}}(B_{S'}^{\geq 1})$
, the corresponding divisorial valuation
![]() $E'$
over
$E'$
over
![]() $X'$
, defined at the end of the previous step, is extracted. In particular, for every prime divisor
$X'$
, defined at the end of the previous step, is extracted. In particular, for every prime divisor
![]() $D' \subset \operatorname {\mathrm {Supp}}(B_{S'}^{\geq 1})$
, there exists always a component of
$D' \subset \operatorname {\mathrm {Supp}}(B_{S'}^{\geq 1})$
, there exists always a component of
![]() $B"+(g\circ \pi )^{\ast }\Sigma '$
of coefficient 1 that dominates
$B"+(g\circ \pi )^{\ast }\Sigma '$
of coefficient 1 that dominates
![]() $D'$
. Let us define
$D'$
. Let us define

In order to reach the sought contradiction, we will show that it is possible to contract
![]() $F"$
by means of suitable runs of the MMP without altering the number of connected components of
$F"$
by means of suitable runs of the MMP without altering the number of connected components of
![]() $\operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})$
around s, in such a way that on the final model,
$\operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})$
around s, in such a way that on the final model,
![]() $\operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})$
is connected around s.
$\operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})$
is connected around s.
As observed at the end of the previous step, by the definition of
![]() $\Sigma '$
and inversion of adjunction for fiber spaces, the generalized subpair
$\Sigma '$
and inversion of adjunction for fiber spaces, the generalized subpair
![]() $(X",B"+(g \circ \pi )^{\ast }\Sigma ',\mathbf {M})$
is generalized sublog canonical. Hence,
$(X",B"+(g \circ \pi )^{\ast }\Sigma ',\mathbf {M})$
is generalized sublog canonical. Hence,
and any prime divisor
![]() $Q" \subset X"$
, such that
$Q" \subset X"$
, such that
![]() $\operatorname {mult}_{Q"} ( B" +(g \circ \pi )^{\ast }\Sigma ' )^{\geq 0}=1$
is mapped into
$\operatorname {mult}_{Q"} ( B" +(g \circ \pi )^{\ast }\Sigma ' )^{\geq 0}=1$
is mapped into
![]() $\operatorname {\mathrm {Supp}}(B_{S'}^{\geq 1})$
. For brevity, we define
$\operatorname {\mathrm {Supp}}(B_{S'}^{\geq 1})$
. For brevity, we define
Fix a rational number
![]() $0 < \epsilon \ll 1$
. Then, as
$0 < \epsilon \ll 1$
. Then, as
![]() $X"$
is a log resolution of
$X"$
is a log resolution of
![]() $(X',\operatorname {\mathrm {Supp}}(B') + g^{\ast }\operatorname {\mathrm {Supp}}(B_{S'}))$
, the pair
$(X',\operatorname {\mathrm {Supp}}(B') + g^{\ast }\operatorname {\mathrm {Supp}}(B_{S'}))$
, the pair
![]() $(X",\Delta " + \epsilon F")$
is dlt, and
$(X",\Delta " + \epsilon F")$
is dlt, and
By construction, the divisor
![]() $G"$
is effective. Moreover, the following claim holds.
$G"$
is effective. Moreover, the following claim holds.
Claim 1. If
![]() $\operatorname {\mathrm {Supp}} G"$
dominates
$\operatorname {\mathrm {Supp}} G"$
dominates
![]() $S'$
, then
$S'$
, then
![]() $G" \not \in \overline {\mathrm {Mov}}(X"/X')$
, where
$G" \not \in \overline {\mathrm {Mov}}(X"/X')$
, where
![]() $\overline {\mathrm {Mov}}(X"/X')$
is the closure of the cone of relatively movable divisors.
$\overline {\mathrm {Mov}}(X"/X')$
is the closure of the cone of relatively movable divisors.
Proof of Claim 1.
Since
![]() $B'$
is effective over the generic point of
$B'$
is effective over the generic point of
![]() $S'$
, as observed in Step 2, and since
$S'$
, as observed in Step 2, and since
![]() $F"$
is vertical over
$F"$
is vertical over
![]() $S'$
, it follows that
$S'$
, it follows that
![]() $\operatorname {\mathrm {Supp}}(G")$
is
$\operatorname {\mathrm {Supp}}(G")$
is
![]() $\pi $
-exceptional over generic point of
$\pi $
-exceptional over generic point of
![]() $S'$
. Let
$S'$
. Let
![]() $U \subset S'$
be a nonempty open subset, such that all the vertical components of
$U \subset S'$
be a nonempty open subset, such that all the vertical components of
![]() $\operatorname {\mathrm {Supp}} G"$
are mapped into
$\operatorname {\mathrm {Supp}} G"$
are mapped into
![]() $S' \setminus U$
. Then, we set
$S' \setminus U$
. Then, we set
![]() and
and
![]() . Also, we let
. Also, we let
![]() $G^{\prime \prime }_U$
be the pullback of
$G^{\prime \prime }_U$
be the pullback of
![]() $G"$
to
$G"$
to
![]() $X^{\prime \prime }_U$
.
$X^{\prime \prime }_U$
.
By definition of relatively movable divisor, if
![]() $G" \in \overline {\mathrm {Mov}}(X"/X')$
, then
$G" \in \overline {\mathrm {Mov}}(X"/X')$
, then
![]() $G^{\prime \prime }_U \in \overline {\mathrm {Mov}}(X^{\prime \prime }_U/X^{\prime }_U)$
. Thus, it suffices to show that
$G^{\prime \prime }_U \in \overline {\mathrm {Mov}}(X^{\prime \prime }_U/X^{\prime }_U)$
. Thus, it suffices to show that
![]() $G^{\prime \prime }_U \not \in \overline {\mathrm {Mov}}(X^{\prime \prime }_U/X^{\prime }_U)$
. By construction,
$G^{\prime \prime }_U \not \in \overline {\mathrm {Mov}}(X^{\prime \prime }_U/X^{\prime }_U)$
. By construction,
![]() $G^{\prime \prime }_U$
is effective and exceptional for
$G^{\prime \prime }_U$
is effective and exceptional for
![]() $X^{\prime \prime }_U \rightarrow X^{\prime }_U$
. Thus,
$X^{\prime \prime }_U \rightarrow X^{\prime }_U$
. Thus,
![]() $G_U"$
is degenerate in the sense of [Reference Lai29, Definition 2.9]. Hence, by [Reference Lai29, Lemma 2.10], it follows that
$G_U"$
is degenerate in the sense of [Reference Lai29, Definition 2.9]. Hence, by [Reference Lai29, Lemma 2.10], it follows that
![]() $G^{\prime \prime }_U \not \in \overline {\mathrm {Mov}}(X^{\prime \prime }_U/X^{\prime }_U)$
.
$G^{\prime \prime }_U \not \in \overline {\mathrm {Mov}}(X^{\prime \prime }_U/X^{\prime }_U)$
.
Step 4. In this step, we run a relative
![]() $({K_{X"}} + \Delta " + \epsilon F" + \mathbf {M}_{X"})$
-MMP over
$({K_{X"}} + \Delta " + \epsilon F" + \mathbf {M}_{X"})$
-MMP over
![]() $X'$
and we show that this MMP contracts those components in
$X'$
and we show that this MMP contracts those components in
![]() $F"$
that dominate
$F"$
that dominate
![]() $S'$
.
$S'$
.
As observed in the proof of Claim 1, any component of
![]() $G"$
that dominates
$G"$
that dominates
![]() $S'$
is
$S'$
is
![]() $\pi $
-exceptional by construction. If such components exist on
$\pi $
-exceptional by construction. If such components exist on
![]() $X"$
, then we observed in Claim 1 that
$X"$
, then we observed in Claim 1 that
![]() ${K_{ X"}} + \Delta " + \epsilon F" + \mathbf {M}_{X"}\not \in \overline {\mathrm {Mov}}(X"/X')$
. To contract those components, we run a
${K_{ X"}} + \Delta " + \epsilon F" + \mathbf {M}_{X"}\not \in \overline {\mathrm {Mov}}(X"/X')$
. To contract those components, we run a
![]() $({K_{X"}} + \Delta " + \epsilon F" + \mathbf {M}_{X"})$
-MMP relative to
$({K_{X"}} + \Delta " + \epsilon F" + \mathbf {M}_{X"})$
-MMP relative to
![]() $X'$
with scaling of an ample divisor. We can run this MMP as the pair is generalized dlt.
$X'$
with scaling of an ample divisor. We can run this MMP as the pair is generalized dlt.
By [Reference Fujino12, Theorem 2.3], whose proof extends to generalized dlt pairs, after finitely many steps, the run of the MMP terminates to yield a model
![]() $X"'$
over which
$X"'$
over which
![]() $({K_{X"'}} + \Delta "' + \epsilon F"' + \mathbf {M}_{X"'})\in \overline {\mathrm {Mov}}(X"'/X')$
. Let
$({K_{X"'}} + \Delta "' + \epsilon F"' + \mathbf {M}_{X"'})\in \overline {\mathrm {Mov}}(X"'/X')$
. Let
![]() $\sigma \colon X"' \rightarrow X'$
and
$\sigma \colon X"' \rightarrow X'$
and
![]() be the induced morphisms, and let
be the induced morphisms, and let
![]() $F"'$
(respectively,
$F"'$
(respectively,
![]() $G"'$
) be the strict transform of
$G"'$
) be the strict transform of
![]() $F"$
(respectively,
$F"$
(respectively,
![]() $G"$
) on
$G"$
) on
![]() $X"'$
. By (16),
$X"'$
. By (16),
![]() $G"' \in \overline {\mathrm {Mov}}(X"/X')$
. Hence, over the generic point of
$G"' \in \overline {\mathrm {Mov}}(X"/X')$
. Hence, over the generic point of
![]() $S'$
,
$S'$
,
![]() $G"$
is supported on divisors that are exceptional for
$G"$
is supported on divisors that are exceptional for
![]() $X" \rightarrow X'$
. By [Reference Lai29, Lemma 2.10], these divisors need to be contracted for
$X" \rightarrow X'$
. By [Reference Lai29, Lemma 2.10], these divisors need to be contracted for
![]() $G"'$
to be a limit of movable divisors relatively to
$G"'$
to be a limit of movable divisors relatively to
![]() $X'$
. Therefore,
$X'$
. Therefore,
![]() $G"'$
is vertical over
$G"'$
is vertical over
![]() $S'$
as desired.
$S'$
as desired.
When
![]() $G"$
does not dominate
$G"$
does not dominate
![]() $S'$
, we do not need to run any MMP, and in the rest of the proof, we have
$S'$
, we do not need to run any MMP, and in the rest of the proof, we have
![]() $X" = X"'$
.
$X" = X"'$
.
Step 5. In this step, we run
![]() $({K_{X"'}} + \Delta "' + \epsilon F"' + \mathbf {M}_{X"'})$
-MMP relative to
$({K_{X"'}} + \Delta "' + \epsilon F"' + \mathbf {M}_{X"'})$
-MMP relative to
![]() $S'$
to contract
$S'$
to contract
![]() $G"'$
.
$G"'$
.
By [Reference Birkar and Zhang7], we can run a
![]() $({K_{X"'}} + \Delta "' + \epsilon F"' + \mathbf {M}_{X"'})$
-MMP over
$({K_{X"'}} + \Delta "' + \epsilon F"' + \mathbf {M}_{X"'})$
-MMP over
![]() $S'$
. We need to show that this MMP terminates. First, we check that it terminates over a big open set of
$S'$
. We need to show that this MMP terminates. First, we check that it terminates over a big open set of
![]() $S'$
. Let
$S'$
. Let
![]() $P"'$
be a prime component of
$P"'$
be a prime component of
![]() $G"'$
.
$G"'$
.
Claim 2. Assume that
![]() $\rho (P"')=D'$
, for a prime divisor
$\rho (P"')=D'$
, for a prime divisor
![]() $D' \subset S'$
. Then
$D' \subset S'$
. Then
![]() $P"'$
is of insufficient fiber type over
$P"'$
is of insufficient fiber type over
![]() $S'$
, cf. [Reference Lai29, Definition 2.9].
$S'$
, cf. [Reference Lai29, Definition 2.9].
Proof of Claim 2.
We first assume that
![]() $D' \subset \operatorname {\mathrm {Supp}} (B_{S'}^{\geq 1})$
. Then, by construction, there is another prime divisor
$D' \subset \operatorname {\mathrm {Supp}} (B_{S'}^{\geq 1})$
. Then, by construction, there is another prime divisor
![]() $Q"' \subset X"'$
not contained in
$Q"' \subset X"'$
not contained in
![]() $\operatorname {\mathrm {Supp}} (G"')$
but mapping to
$\operatorname {\mathrm {Supp}} (G"')$
but mapping to
![]() $D'$
(see the end of Step 2 or, alternatively, the start of Step 3).
$D'$
(see the end of Step 2 or, alternatively, the start of Step 3).
Instead, if
![]() $D' \not \subseteq \operatorname {\mathrm {Supp}}( B_{S'}^{\geq 1})$
, then
$D' \not \subseteq \operatorname {\mathrm {Supp}}( B_{S'}^{\geq 1})$
, then
![]() $D'$
is not
$D'$
is not
![]() $\alpha $
-exceptional, by construction of
$\alpha $
-exceptional, by construction of
![]() $\alpha \colon S' \to S$
, cf. Step 2. Furthermore,
$\alpha \colon S' \to S$
, cf. Step 2. Furthermore,
![]() $B" = B" + (g \circ \pi )^{\ast }\Sigma '$
over the generic point of
$B" = B" + (g \circ \pi )^{\ast }\Sigma '$
over the generic point of
![]() $D'$
. Since our claim can be verified over the generic point of
$D'$
. Since our claim can be verified over the generic point of
![]() $D'$
, we can assume
$D'$
, we can assume
![]() $\Sigma '=0$
in the rest of the proof of this claim. Similarly, as
$\Sigma '=0$
in the rest of the proof of this claim. Similarly, as
![]() $F"$
is mapped into
$F"$
is mapped into
![]() $\operatorname {\mathrm {Supp}}( B_{S'}^{\geq 1})$
, we can assume
$\operatorname {\mathrm {Supp}}( B_{S'}^{\geq 1})$
, we can assume
![]() $F"=0$
for the purpose of this claim. Thus, by these two observations, it follows that
$F"=0$
for the purpose of this claim. Thus, by these two observations, it follows that
![]() $P"'$
is a component of
$P"'$
is a component of
![]() $(B"')^{\leq 0}$
. Now, since
$(B"')^{\leq 0}$
. Now, since
![]() $D'$
is not
$D'$
is not
![]() $\alpha $
-exceptional,
$\alpha $
-exceptional,
![]() $S' \rightarrow S$
is an isomorphism at the generic point of
$S' \rightarrow S$
is an isomorphism at the generic point of
![]() $D'$
. Thus, by definition of
$D'$
. Thus, by definition of
![]() $X'$
,
$X'$
,
![]() $X' \rightarrow X$
is an isomorphism over the generic point of
$X' \rightarrow X$
is an isomorphism over the generic point of
![]() $D'$
. For this reason, as
$D'$
. For this reason, as
![]() $B \geq 0$
, it follows that
$B \geq 0$
, it follows that
![]() $B' \geq 0$
over the generic point of
$B' \geq 0$
over the generic point of
![]() $D'$
. Since
$D'$
. Since
![]() $P"'$
is a component of
$P"'$
is a component of
![]() $(B"')^{\leq 0}$
, it follows that
$(B"')^{\leq 0}$
, it follows that
![]() $P"'$
is exceptional for
$P"'$
is exceptional for
![]() $X"' \rightarrow X'$
. In particular, as
$X"' \rightarrow X'$
. In particular, as
![]() $P"'$
is a component of
$P"'$
is a component of
![]() $\sigma ^*(g^* D')$
, there exists a prime divisor
$\sigma ^*(g^* D')$
, there exists a prime divisor
![]() $Q"' \subset X"'$
that is not
$Q"' \subset X"'$
that is not
![]() $\sigma $
-exceptional, and that dominates
$\sigma $
-exceptional, and that dominates
![]() $D'$
.
$D'$
.
If
![]() $G"'$
has any prime component dominating a prime divisor
$G"'$
has any prime component dominating a prime divisor
![]() $D' \subset S'$
, then by Claim 2 and [Reference Lai29, Lemma 2.10],
$D' \subset S'$
, then by Claim 2 and [Reference Lai29, Lemma 2.10],
![]() $G"' \not \in \overline {\mathrm { Mov}}(X"'/S')$
; thus, by [Reference Fujino12, Theorem 2.3], the
$G"' \not \in \overline {\mathrm { Mov}}(X"'/S')$
; thus, by [Reference Fujino12, Theorem 2.3], the
![]() $({K_{X"'}} + \Delta "' + \epsilon F"' + \mathbf {M}_{X"'})$
-MMP over
$({K_{X"'}} + \Delta "' + \epsilon F"' + \mathbf {M}_{X"'})$
-MMP over
![]() $S'$
with ample scaling terminates at the generic point of
$S'$
with ample scaling terminates at the generic point of
![]() $D'$
and it contracts those components of
$D'$
and it contracts those components of
![]() $G"'$
that are of insufficient fiber type over
$G"'$
that are of insufficient fiber type over
![]() $D'$
. Hence, after finitely many steps of running the
$D'$
. Hence, after finitely many steps of running the
![]() $({K_{X"'}} + \Delta "' + \epsilon F"' + \mathbf {M}_{X"'})$
-MMP relative to
$({K_{X"'}} + \Delta "' + \epsilon F"' + \mathbf {M}_{X"'})$
-MMP relative to
![]() $S'$
, we reach a model
$S'$
, we reach a model
![]() $X"" \to S'$
, such that no component of
$X"" \to S'$
, such that no component of
![]() $G""$
dominates a divisor in
$G""$
dominates a divisor in
![]() $S'$
, where
$S'$
, where
![]() $G""$
is the strict transform of
$G""$
is the strict transform of
![]() $G"'$
on
$G"'$
on
![]() $X""$
. If
$X""$
. If
![]() $G"" = 0$
, we stop. Otherwise, as the image of
$G"" = 0$
, we stop. Otherwise, as the image of
![]() $G"'$
in
$G"'$
in
![]() $S'$
has codimension
$S'$
has codimension
![]() $\geq 2$
, by [Reference Lai29, Lemma 2.10], there is a component
$\geq 2$
, by [Reference Lai29, Lemma 2.10], there is a component
![]() $P"" \subset \operatorname {\mathrm {Supp}}(G"")$
, such that
$P"" \subset \operatorname {\mathrm {Supp}}(G"")$
, such that
![]() $P"" \subset \mathbf {B}_-(G""/S')$
. Therefore,
$P"" \subset \mathbf {B}_-(G""/S')$
. Therefore,
![]() $G""\not \in \overline {\mathrm {Mov}}(X""/S')$
and a further run of the MMP contracts
$G""\not \in \overline {\mathrm {Mov}}(X""/S')$
and a further run of the MMP contracts
![]() $P""$
.
$P""$
.
Step 6. In this step, we list all the properties of the model
![]() $\overline {X}$
that we obtain after contracting the divisors in
$\overline {X}$
that we obtain after contracting the divisors in
![]() $G"'$
and we reach the sought contradiction to conclude the proof.
$G"'$
and we reach the sought contradiction to conclude the proof.
After finitely many steps, we reach a model
![]() $\overline {X}$
with morphism
$\overline {X}$
with morphism
![]() $\tau \colon \overline X \rightarrow S'$
on which
$\tau \colon \overline X \rightarrow S'$
on which
![]() $G""$
has been contracted. In particular, any prime divisor
$G""$
has been contracted. In particular, any prime divisor
![]() $\overline P \subset \overline {X}$
, such that
$\overline P \subset \overline {X}$
, such that
![]() $\tau (\overline {P}) \subset \operatorname {\mathrm {Supp}} ( B_{S'}^{\geq 1})$
satisfies
$\tau (\overline {P}) \subset \operatorname {\mathrm {Supp}} ( B_{S'}^{\geq 1})$
satisfies
![]() $\operatorname {mult}_{\overline {P}} \overline {B} \geq 1$
. Indeed, the components of
$\operatorname {mult}_{\overline {P}} \overline {B} \geq 1$
. Indeed, the components of
![]() $(B" + (g \circ \pi )^{\ast }\Sigma ')^{< 1}$
mapping to
$(B" + (g \circ \pi )^{\ast }\Sigma ')^{< 1}$
mapping to
![]() $\operatorname {\mathrm {Supp}} ( B_{S'}^{\geq 1})$
were supported on
$\operatorname {\mathrm {Supp}} ( B_{S'}^{\geq 1})$
were supported on
![]() $\operatorname {\mathrm {Supp}}((F")^{\geq 0})$
, which is contracted on the model
$\operatorname {\mathrm {Supp}}((F")^{\geq 0})$
, which is contracted on the model
![]() $\overline {X}$
. Furthermore, the fact that
$\overline {X}$
. Furthermore, the fact that
![]() $\Sigma ' \leq 0$
guarantees that if
$\Sigma ' \leq 0$
guarantees that if
![]() $\mu _{Q"}(B")<1$
, then
$\mu _{Q"}(B")<1$
, then
![]() $\mu _{Q"} (B" + (g \circ \pi )^{\ast }\Sigma ')<1$
. Because of this and the fact that the support of
$\mu _{Q"} (B" + (g \circ \pi )^{\ast }\Sigma ')<1$
. Because of this and the fact that the support of
![]() $(B" + (g \circ \pi )^{\ast }\Sigma ')<0$
has been contracted on
$(B" + (g \circ \pi )^{\ast }\Sigma ')<0$
has been contracted on
![]() $\overline X$
, as that was in the support of
$\overline X$
, as that was in the support of
![]() $G"$
, cf. (16), it follows that
$G"$
, cf. (16), it follows that
![]() $\overline {B}\geq 0$
, where
$\overline {B}\geq 0$
, where
![]() $\overline B$
is the strict transform of
$\overline B$
is the strict transform of
![]() $B"$
on
$B"$
on
![]() $\overline {X}$
. By Proposition 3.1 and Remark 3.7, there is a unique connected component
$\overline {X}$
. By Proposition 3.1 and Remark 3.7, there is a unique connected component
![]() $\Omega '$
of
$\Omega '$
of
![]() $\operatorname {\mathrm {Supp}}(B_{S'}^{\geq 1})$
, such that
$\operatorname {\mathrm {Supp}}(B_{S'}^{\geq 1})$
, such that
![]() $y \in \alpha (\Omega ')$
. By construction,
$y \in \alpha (\Omega ')$
. By construction,
![]() $\operatorname {\mathrm {Nklt}}(\overline {X},\overline {B},\mathbf {M})$
is connected over
$\operatorname {\mathrm {Nklt}}(\overline {X},\overline {B},\mathbf {M})$
is connected over
![]() $\Omega '$
, as any prime divisor
$\Omega '$
, as any prime divisor
![]() $\overline P \subset \overline {X}$
, such that
$\overline P \subset \overline {X}$
, such that
![]() $\tau (\overline {P}) \subset \Omega '$
satisfies
$\tau (\overline {P}) \subset \Omega '$
satisfies
![]() $\mu _{\overline {P}} \overline {B} \geq 1$
.
$\mu _{\overline {P}} \overline {B} \geq 1$
.
Let
![]() $\hat X$
be a common resolution of X and
$\hat X$
be a common resolution of X and
![]() $\overline X$
. Then, by Proposition 3.1 applied to
$\overline X$
. Then, by Proposition 3.1 applied to
![]() $\phi \colon \hat X \rightarrow X$
and
$\phi \colon \hat X \rightarrow X$
and
![]() $\overline {\phi } \colon \hat X \rightarrow \overline {X}$
, the connected components of
$\overline {\phi } \colon \hat X \rightarrow \overline {X}$
, the connected components of
![]() $\operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})$
and of
$\operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})$
and of
![]() $\operatorname {\mathrm {Nklt}}(\overline {X},\overline {B}, \mathbf {M})$
are in bijection, as these two generalized pair are crepant to each other; in fact, the connected components of
$\operatorname {\mathrm {Nklt}}(\overline {X},\overline {B}, \mathbf {M})$
are in bijection, as these two generalized pair are crepant to each other; in fact, the connected components of
![]() $\operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})$
and of
$\operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})$
and of
![]() $\operatorname {\mathrm {Nklt}}(\overline {X},\overline {B}, \mathbf {M})$
are in 1 to 1 correspondence with the components of
$\operatorname {\mathrm {Nklt}}(\overline {X},\overline {B}, \mathbf {M})$
are in 1 to 1 correspondence with the components of
![]() $\operatorname {\mathrm {Nklt}}(\hat X, \hat B, \mathbf {M})$
, where
$\operatorname {\mathrm {Nklt}}(\hat X, \hat B, \mathbf {M})$
, where
![]() $(\hat X, \hat B, \mathbf {M})$
denotes the trace of
$(\hat X, \hat B, \mathbf {M})$
denotes the trace of
![]() $(X,B, \mathbf {M})$
on
$(X,B, \mathbf {M})$
on
![]() $\hat X$
. This leads to the sought contradiction. Indeed, as
$\hat X$
. This leads to the sought contradiction. Indeed, as
![]() $\alpha \colon S' \rightarrow S$
has connected fibers,
$\alpha \colon S' \rightarrow S$
has connected fibers,
![]() $\alpha ^{-1}(s) \subset \Omega '$
is connected. As also
$\alpha ^{-1}(s) \subset \Omega '$
is connected. As also
![]() $\tau \colon \overline {X} \rightarrow S'$
has connected fibers, then
$\tau \colon \overline {X} \rightarrow S'$
has connected fibers, then
![]() $\tau ^{-1} (\alpha ^{-1} (s))$
is connected and, by construction,
$\tau ^{-1} (\alpha ^{-1} (s))$
is connected and, by construction,
![]() $\tau ^{-1} (\alpha ^{-1} (s)) \subset \operatorname {\mathrm {Supp}}(\overline {B}^{\geq 1})$
. Applying Proposition 3.1 to
$\tau ^{-1} (\alpha ^{-1} (s)) \subset \operatorname {\mathrm {Supp}}(\overline {B}^{\geq 1})$
. Applying Proposition 3.1 to
![]() $\overline \phi \colon \hat X \rightarrow \overline {X}$
, then
$\overline \phi \colon \hat X \rightarrow \overline {X}$
, then
![]() $\overline {\phi }^{-1} (\tau ^{-1} (\alpha ^{-1} (s))) \cap \operatorname {\mathrm {Nklt}}(\hat X, \hat B ,\mathbf {M})$
is connected. On the other hand, by a similar argument, it follows that
$\overline {\phi }^{-1} (\tau ^{-1} (\alpha ^{-1} (s))) \cap \operatorname {\mathrm {Nklt}}(\hat X, \hat B ,\mathbf {M})$
is connected. On the other hand, by a similar argument, it follows that
![]() $\phi ^{-1} (f^{-1} (s)) \cap \operatorname {\mathrm {Nklt}}(\hat X,\hat B,\mathbf {M})$
is disconnected, since
$\phi ^{-1} (f^{-1} (s)) \cap \operatorname {\mathrm {Nklt}}(\hat X,\hat B,\mathbf {M})$
is disconnected, since
![]() $f^{-1} (s) \cap \operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})$
is disconnected, by Proposition 3.1 applied to
$f^{-1} (s) \cap \operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})$
is disconnected, by Proposition 3.1 applied to
![]() $\phi \colon \hat X \rightarrow X$
.
$\phi \colon \hat X \rightarrow X$
.
Proof of Theorem 1.1.
By Theorem 3.1, we may replace X with a generalized dlt model
![]() $f^m \colon X^m \rightarrow X$
; thus, we can assume that the generalized pair
$f^m \colon X^m \rightarrow X$
; thus, we can assume that the generalized pair
![]() $(X, B \wedge \operatorname {\mathrm {Supp}}(B), \mathbf {M})$
is a
$(X, B \wedge \operatorname {\mathrm {Supp}}(B), \mathbf {M})$
is a
![]() $\mathbb {Q}$
-factorial generalized dlt pair, and that
$\mathbb {Q}$
-factorial generalized dlt pair, and that
![]() $K_X+B+M \sim _{\mathbb {Q},f} 0$
. Remark 3.7 implies that
$K_X+B+M \sim _{\mathbb {Q},f} 0$
. Remark 3.7 implies that
![]() $\operatorname {\mathrm {Nklt}}(X,B , \mathbf {M})= \mathrm {Supp} (B^{\geq 1})$
. Moreover, by [Reference Kollár25, Section 4.38], passing to an étale neighborhood of
$\operatorname {\mathrm {Nklt}}(X,B , \mathbf {M})= \mathrm {Supp} (B^{\geq 1})$
. Moreover, by [Reference Kollár25, Section 4.38], passing to an étale neighborhood of
![]() $s \in S$
, we can assume that
$s \in S$
, we can assume that
![]() $\mathbf {(\ast )}$
different connected components of
$\mathbf {(\ast )}$
different connected components of
![]() $\operatorname {\mathrm {Nklt}}(X,B, \mathbf {M})\cap \pi ^{-1} (s)$
are contained in different connected components of
$\operatorname {\mathrm {Nklt}}(X,B, \mathbf {M})\cap \pi ^{-1} (s)$
are contained in different connected components of
![]() $\operatorname {\mathrm {Nklt}}(X,B, \mathbf {M})$
.
$\operatorname {\mathrm {Nklt}}(X,B, \mathbf {M})$
.
Under these assumptions, we shall show that X is a
![]() $\mathbb {P}^1$
-link over S. Moreover, by Proposition 6.1, we can assume that at least one component of
$\mathbb {P}^1$
-link over S. Moreover, by Proposition 6.1, we can assume that at least one component of
![]() $B^{\geq 1}$
dominates S. Hence,
$B^{\geq 1}$
dominates S. Hence,
![]() ${K_{X}} + B - \epsilon B^{\geq 1} + M$
is not pseudo-effective over S, for any
${K_{X}} + B - \epsilon B^{\geq 1} + M$
is not pseudo-effective over S, for any
![]() $\epsilon>0$
. As in addition
$\epsilon>0$
. As in addition
![]() $(X, B^{<1} + M)$
is generalized klt, we can run a
$(X, B^{<1} + M)$
is generalized klt, we can run a
![]() $(K_X+ B^{<1} +M)$
-MMP over S
$(K_X+ B^{<1} +M)$
-MMP over S

which terminates with a Mori fiber space,
![]() $h\colon X_n \rightarrow Z$
over S, cf. [Reference Birkar and Zhang7, Lemma 4.4]. At each step of the MMP in (17), we define
$h\colon X_n \rightarrow Z$
over S, cf. [Reference Birkar and Zhang7, Lemma 4.4]. At each step of the MMP in (17), we define
![]() and
and
![]() , where
, where
![]() $B_0=B$
; hence,
$B_0=B$
; hence,
![]() $K_{X_k}+B_k+M_k \sim _{\mathbb {Q},f_k} 0$
. Applying Lemmata 3.5 and 3.6 at a given step
$K_{X_k}+B_k+M_k \sim _{\mathbb {Q},f_k} 0$
. Applying Lemmata 3.5 and 3.6 at a given step
![]() $\pi _k$
of (17), the number of connected components of
$\pi _k$
of (17), the number of connected components of
![]() $\operatorname {\mathrm {Nklt}}(X_{k-1}, B_{k-1}, \mathbf {M})$
in a neighborhood of
$\operatorname {\mathrm {Nklt}}(X_{k-1}, B_{k-1}, \mathbf {M})$
in a neighborhood of
![]() $f^{-1}_{k-1}(s')$
,
$f^{-1}_{k-1}(s')$
,
![]() $s' \in S$
, is the same as the number of connected components of
$s' \in S$
, is the same as the number of connected components of
![]() $\operatorname {\mathrm {Nklt}}(X_{k}, B_{k}, \mathbf {M})$
around
$\operatorname {\mathrm {Nklt}}(X_{k}, B_{k}, \mathbf {M})$
around
![]() $f^{-1}_{k}(s')$
. Moreover, while for
$f^{-1}_{k}(s')$
. Moreover, while for
![]() $k>0$
the support of
$k>0$
the support of
![]() $\operatorname {\mathrm {Nklt}}(X_k,B_k, \mathbf {M})$
does not necessarily coincide anymore with
$\operatorname {\mathrm {Nklt}}(X_k,B_k, \mathbf {M})$
does not necessarily coincide anymore with
![]() $B_k^{\geq 1}$
, it still holds that
$B_k^{\geq 1}$
, it still holds that
![]() $\operatorname {\mathrm {Supp}}(B_k^{\geq 1}) \subset \operatorname {\mathrm {Nklt}}(X_k,B_k, \mathbf {M})$
, and every irreducible component of
$\operatorname {\mathrm {Supp}}(B_k^{\geq 1}) \subset \operatorname {\mathrm {Nklt}}(X_k,B_k, \mathbf {M})$
, and every irreducible component of
![]() $\operatorname {\mathrm {Nklt}}(X_k,B_k, \mathbf {M})$
contains at least one component of
$\operatorname {\mathrm {Nklt}}(X_k,B_k, \mathbf {M})$
contains at least one component of
![]() $B_k^{\geq 1}$
, since at each step of this run of the MMP,
$B_k^{\geq 1}$
, since at each step of this run of the MMP,
![]() $B_k^{\geq 1}$
has positive intersection with the contracted extremal ray.
$B_k^{\geq 1}$
has positive intersection with the contracted extremal ray.
Hence, if
![]() $\operatorname {\mathrm {Nklt}}(X, B, \mathbf {M})$
is disconnected in a neighborhood of the fiber
$\operatorname {\mathrm {Nklt}}(X, B, \mathbf {M})$
is disconnected in a neighborhood of the fiber
![]() $f^{-1}(s)$
, then so is
$f^{-1}(s)$
, then so is
![]() $\operatorname {\mathrm {Nklt}}(X_n, B_n, \mathbf {M})$
in a neighborhood of
$\operatorname {\mathrm {Nklt}}(X_n, B_n, \mathbf {M})$
in a neighborhood of
![]() $f_{n}^{-1}(s)$
. As
$f_{n}^{-1}(s)$
. As
![]() $h \colon X_n \rightarrow Z$
is a Mori fiber space and
$h \colon X_n \rightarrow Z$
is a Mori fiber space and
![]() $B_n^{\geq 1}$
is ample over Z, there exists at least one component
$B_n^{\geq 1}$
is ample over Z, there exists at least one component
![]() $\widetilde {D}$
of
$\widetilde {D}$
of
![]() $B_n^{\geq 1}$
ample over Z; thus,
$B_n^{\geq 1}$
ample over Z; thus,
![]() $\widetilde {D}$
dominates both Z and S. Let
$\widetilde {D}$
dominates both Z and S. Let
![]() $D'$
be any other component of
$D'$
be any other component of
![]() $B_n^{\geq 1}$
in a neighborhood of
$B_n^{\geq 1}$
in a neighborhood of
![]() $f_{n}^{-1}(s)$
. As
$f_{n}^{-1}(s)$
. As
![]() $\widetilde D$
is ample over Z, in particular, it is horizontal over Z, hence, as h is a Mori fiber space, then also
$\widetilde D$
is ample over Z, in particular, it is horizontal over Z, hence, as h is a Mori fiber space, then also
![]() $D'$
must be ample over Z, otherwise,
$D'$
must be ample over Z, otherwise,
![]() $D' \supseteq f^{-1}(s)$
and
$D' \supseteq f^{-1}(s)$
and
![]() $D' \cap \widetilde {D} \cap f_n^{-1}(s) \neq \emptyset $
, which would prompt a contradiction. Then,
$D' \cap \widetilde {D} \cap f_n^{-1}(s) \neq \emptyset $
, which would prompt a contradiction. Then,
![]() $D'$
dominates Z and it is h-ample. Hence, we may argue as in [Reference Kollár25, proof of Proposition 4.37]. In particular, all the reduced fibers of h are smooth rational curves, and
$D'$
dominates Z and it is h-ample. Hence, we may argue as in [Reference Kollár25, proof of Proposition 4.37]. In particular, all the reduced fibers of h are smooth rational curves, and
![]() $\tilde D$
and
$\tilde D$
and
![]() $\tilde D '$
are disjoint sections of h. Thus, as
$\tilde D '$
are disjoint sections of h. Thus, as
![]() $(\tilde D +\tilde {D}') \cdot F=2$
for a general fiber F of h, it follows that
$(\tilde D +\tilde {D}') \cdot F=2$
for a general fiber F of h, it follows that
![]() $B_n$
has to have coefficient one along
$B_n$
has to have coefficient one along
![]() $\tilde D$
and
$\tilde D$
and
![]() $\tilde {D}'$
. Furthermore, every other component of
$\tilde {D}'$
. Furthermore, every other component of
![]() $B_n$
is vertical for h. Since we are assuming that
$B_n$
is vertical for h. Since we are assuming that
![]() $\operatorname {\mathrm {Nklt}}(X_n,B_n,\mathbf {M}) \cap f_n^{-1}(s)$
is disconnected, the vertical components of
$\operatorname {\mathrm {Nklt}}(X_n,B_n,\mathbf {M}) \cap f_n^{-1}(s)$
is disconnected, the vertical components of
![]() $B_n^{\geq 1}$
have to be disjoint from
$B_n^{\geq 1}$
have to be disjoint from
![]() $f_n^{-1}(s)$
. Hence, up to shrinking around
$f_n^{-1}(s)$
. Hence, up to shrinking around
![]() $s \in S$
,
$s \in S$
,
![]() $B_n^{\geq 1}=\tilde D +\tilde {D}'$
.
$B_n^{\geq 1}=\tilde D +\tilde {D}'$
.
By construction of
![]() $X \dashrightarrow X_n$
and the fact that
$X \dashrightarrow X_n$
and the fact that
![]() $X_n$
is
$X_n$
is
![]() $\mathbb {Q}$
-factorial, it follows that
$\mathbb {Q}$
-factorial, it follows that
![]() $(X_n,B_n^{<1})$
is a klt pair. Thus, it follows from [Reference Kollár25, Proposition 4.37] and its proof that
$(X_n,B_n^{<1})$
is a klt pair. Thus, it follows from [Reference Kollár25, Proposition 4.37] and its proof that
![]() $(X_n,B_n) \rightarrow Z$
is a standard
$(X_n,B_n) \rightarrow Z$
is a standard
![]() ${\mathbb P}^{1}$
-link. Thus, since
${\mathbb P}^{1}$
-link. Thus, since
![]() ${K_{X_n}} + B_n \sim _{\mathbb {Q},h} 0$
, it follows that
${K_{X_n}} + B_n \sim _{\mathbb {Q},h} 0$
, it follows that
![]() $M_n \sim _{\mathbb {Q},h} 0$
. In particular, conditions (0), (1), (3), and (5) of Definition 2.21 are satisfied. In order to show that also condition (4) in Definition 2.21 is satisfied, it suffices to show that
$M_n \sim _{\mathbb {Q},h} 0$
. In particular, conditions (0), (1), (3), and (5) of Definition 2.21 are satisfied. In order to show that also condition (4) in Definition 2.21 is satisfied, it suffices to show that
![]() $\tilde D$
and
$\tilde D$
and
![]() $\tilde D '$
are the only generalized log canonical centers of
$\tilde D '$
are the only generalized log canonical centers of
![]() $(X_n,B_n,\mathbf {M})$
. Assume by contradiction that it is not the case. Then, as
$(X_n,B_n,\mathbf {M})$
. Assume by contradiction that it is not the case. Then, as
![]() $(X_n,B_n)$
is plt with two log canonical centers, there exists
$(X_n,B_n)$
is plt with two log canonical centers, there exists
![]() $\alpha \in (0,1]$
so that
$\alpha \in (0,1]$
so that
![]() $(X_n,B_n, \alpha \mathbf {M})$
is generalized log canonical and has three or more generalized log canonical centers. What we have shown so far, in particular, implies that the only divisorial components of
$(X_n,B_n, \alpha \mathbf {M})$
is generalized log canonical and has three or more generalized log canonical centers. What we have shown so far, in particular, implies that the only divisorial components of
![]() $\operatorname {\mathrm {Nklt}}(X_n,B_n,\mathbf {M})$
are
$\operatorname {\mathrm {Nklt}}(X_n,B_n,\mathbf {M})$
are
![]() $\tilde D$
and
$\tilde D$
and
![]() $\tilde D '$
. Therefore, since
$\tilde D '$
. Therefore, since
![]() $X_n \rightarrow Z$
has relative dimension 1, it follows that
$X_n \rightarrow Z$
has relative dimension 1, it follows that
![]() $\tilde D$
and
$\tilde D$
and
![]() $\tilde D '$
are the only log canonical centers of
$\tilde D '$
are the only log canonical centers of
![]() $(X_n,B_n, \alpha \mathbf {M})$
that dominate Z. Let
$(X_n,B_n, \alpha \mathbf {M})$
that dominate Z. Let
![]() $\phi \colon X_n' \rightarrow X_n$
be a generalized dlt model for
$\phi \colon X_n' \rightarrow X_n$
be a generalized dlt model for
![]() $(X_n,B_n, \alpha \mathbf {M})$
, and let
$(X_n,B_n, \alpha \mathbf {M})$
, and let
![]() $(X_n',B_n'+\alpha M_n')$
denote its trace on
$(X_n',B_n'+\alpha M_n')$
denote its trace on
![]() $X_n'$
. Since
$X_n'$
. Since
![]() $M_n \sim _{\mathbb {Q},h} 0$
, we have
$M_n \sim _{\mathbb {Q},h} 0$
, we have
![]() ${K_{X_n}} + B_n + \alpha M_n \sim _{\mathbb {Q},h} 0$
. Hence, we have
${K_{X_n}} + B_n + \alpha M_n \sim _{\mathbb {Q},h} 0$
. Hence, we have
![]() ${K_{X_n'}} + B_n' + \alpha M_n' \sim _{\mathbb {Q},Z} 0$
. By construction, we have
${K_{X_n'}} + B_n' + \alpha M_n' \sim _{\mathbb {Q},Z} 0$
. By construction, we have
![]() $B_n' \geq 0$
, as
$B_n' \geq 0$
, as
![]() $\phi $
only extracts divisors with generalized log discrepancy 0. Now, let
$\phi $
only extracts divisors with generalized log discrepancy 0. Now, let
![]() $E'$
be a component of
$E'$
be a component of
![]() $(B_n')^{=1}$
that is not
$(B_n')^{=1}$
that is not
![]() $\tilde D$
nor
$\tilde D$
nor
![]() $\tilde D '$
; such divisor exists by the absurd assumption. Since
$\tilde D '$
; such divisor exists by the absurd assumption. Since
![]() $0 < \alpha \leq 1$
, we have
$0 < \alpha \leq 1$
, we have
![]() $\operatorname {\mathrm {Nklt}}(X_n,B_n,\alpha \mathbf {M}) \subset \operatorname {\mathrm {Nklt}}(X_n,B_n,\mathbf {M})$
. Since
$\operatorname {\mathrm {Nklt}}(X_n,B_n,\alpha \mathbf {M}) \subset \operatorname {\mathrm {Nklt}}(X_n,B_n,\mathbf {M})$
. Since
![]() $\tilde D$
and
$\tilde D$
and
![]() $\tilde D '$
belong to disjoint connected components of
$\tilde D '$
belong to disjoint connected components of
![]() $\operatorname {\mathrm {Nklt}}(X_n,B_n,\mathbf {M})$
, at least one among
$\operatorname {\mathrm {Nklt}}(X_n,B_n,\mathbf {M})$
, at least one among
![]() $\tilde D$
and
$\tilde D$
and
![]() $\tilde D '$
belongs to a connected component of
$\tilde D '$
belongs to a connected component of
![]() $\operatorname {\mathrm {Nklt}}(X^{\prime }_n,B^{\prime }_n,\alpha \mathbf {M})$
that is disjoint from the component containing
$\operatorname {\mathrm {Nklt}}(X^{\prime }_n,B^{\prime }_n,\alpha \mathbf {M})$
that is disjoint from the component containing
![]() $E'$
. Up to swapping the roles, we may assume
$E'$
. Up to swapping the roles, we may assume
![]() $E' \cap \tilde D = \emptyset $
, and that these belong to different connected components of
$E' \cap \tilde D = \emptyset $
, and that these belong to different connected components of
![]() $\operatorname {\mathrm {Nklt}}(X_n',B_n',\alpha \mathbf {M})$
, where we identify
$\operatorname {\mathrm {Nklt}}(X_n',B_n',\alpha \mathbf {M})$
, where we identify
![]() $\tilde D$
with its strict transform on
$\tilde D$
with its strict transform on
![]() $X_n'$
. Thus,
$X_n'$
. Thus,
![]() ${K_{X_n'}} + (B_n'- \tilde D - E')+ \alpha M_n' \sim _{\mathbb {Q},Z} -\tilde D - E'$
is not pseudo-effective over Z, as
${K_{X_n'}} + (B_n'- \tilde D - E')+ \alpha M_n' \sim _{\mathbb {Q},Z} -\tilde D - E'$
is not pseudo-effective over Z, as
![]() $\tilde D$
dominates Z. Then, by [Reference Birkar and Zhang7, Lemma 4.4], we may run a
$\tilde D$
dominates Z. Then, by [Reference Birkar and Zhang7, Lemma 4.4], we may run a
![]() $({K_{X_n'}} + (B_n'- \tilde D - E')+ \alpha M_n')$
-MMP over Z, which terminates with a Mori fiber space
$({K_{X_n'}} + (B_n'- \tilde D - E')+ \alpha M_n')$
-MMP over Z, which terminates with a Mori fiber space
![]() $\hat X _n \rightarrow \hat Z$
over Z. Since
$\hat X _n \rightarrow \hat Z$
over Z. Since
![]() $X_n \rightarrow Z$
has relative dimension 1,
$X_n \rightarrow Z$
has relative dimension 1,
![]() $\hat Z \rightarrow Z$
is birational. Arguing, as in the first part of the proof, we know that distinct connected components of
$\hat Z \rightarrow Z$
is birational. Arguing, as in the first part of the proof, we know that distinct connected components of
![]() $\operatorname {\mathrm {Nklt}}(X^{\prime }_n,B^{\prime }_n,\alpha \mathbf {M})$
have to remain disjoint after the run of the MMP. Therefore, as the MMP is positive for
$\operatorname {\mathrm {Nklt}}(X^{\prime }_n,B^{\prime }_n,\alpha \mathbf {M})$
have to remain disjoint after the run of the MMP. Therefore, as the MMP is positive for
![]() $\tilde D + E'$
and these divisors need to remain disjoint, these two divisors are not contracted by
$\tilde D + E'$
and these divisors need to remain disjoint, these two divisors are not contracted by
![]() $X_n' \dashrightarrow \hat X _n$
. Call
$X_n' \dashrightarrow \hat X _n$
. Call
![]() $\hat D$
and
$\hat D$
and
![]() $\hat E$
the corresponding strict transforms on
$\hat E$
the corresponding strict transforms on
![]() $\hat X$
. Since
$\hat X$
. Since
![]() $\hat X _n \rightarrow \hat Z$
is a Mori fiber space and
$\hat X _n \rightarrow \hat Z$
is a Mori fiber space and
![]() $\hat D$
is relatively big, it is relatively ample. Since
$\hat D$
is relatively big, it is relatively ample. Since
![]() $\hat X _n \rightarrow \hat Z$
has relative dimension 1,
$\hat X _n \rightarrow \hat Z$
has relative dimension 1,
![]() $\hat D$
is horizontal and
$\hat D$
is horizontal and
![]() $\hat D \cap \hat E = \emptyset $
, then
$\hat D \cap \hat E = \emptyset $
, then
![]() $\hat E$
has to be horizontal over
$\hat E$
has to be horizontal over
![]() $\hat Z$
. This is absurd, as its corresponding center on X does not dominate Z.
$\hat Z$
. This is absurd, as its corresponding center on X does not dominate Z.
Finally, Lemma 2.22 implies that condition (2) in Definition 2.21 holds.
Proof of Theorem 1.4.
We follow the proof of [Reference Kollár25, Theorem 4.40] and divide the proof into two steps.
Step 1: In this step, we prove the statement of the theorem over an étale neighborhood
![]() $(s' \in S') \rightarrow (s \in S)$
, such that
$(s' \in S') \rightarrow (s \in S)$
, such that
![]() $k(s) \simeq k(s')$
.
$k(s) \simeq k(s')$
.
We proceed by induction on
![]() $\dim (X)$
and
$\dim (X)$
and
![]() $\dim (Z)$
. If
$\dim (Z)$
. If
![]() $f^{-1} (s) \cap \lfloor B \rfloor $
is disconnected, then, by Theorem 1.1, after an étale base change
$f^{-1} (s) \cap \lfloor B \rfloor $
is disconnected, then, by Theorem 1.1, after an étale base change
![]() $(s' \in S') \rightarrow (s \in S)$
, there are exactly two generalized log canonical centers intersecting the fiber over
$(s' \in S') \rightarrow (s \in S)$
, there are exactly two generalized log canonical centers intersecting the fiber over
![]() $s'$
, and they are
$s'$
, and they are
![]() ${\mathbb P}^{1}$
-linked. Thus, the claim follows.
${\mathbb P}^{1}$
-linked. Thus, the claim follows.
Now, we can assume that
![]() $f^{-1} (s) \cap \lfloor B \rfloor $
is connected. Write
$f^{-1} (s) \cap \lfloor B \rfloor $
is connected. Write
![]() $\lfloor B \rfloor = \sum D_i$
, where each
$\lfloor B \rfloor = \sum D_i$
, where each
![]() $D_i$
is a prime Weil divisor. Then, up to an étale base change that does not change
$D_i$
is a prime Weil divisor. Then, up to an étale base change that does not change
![]() $k(s)$
[Reference Kollár25, Section 4.38], we can assume that each
$k(s)$
[Reference Kollár25, Section 4.38], we can assume that each
![]() $D_i$
has connected fibers over s, and that every generalized log canonical center of
$D_i$
has connected fibers over s, and that every generalized log canonical center of
![]() $(X,B+M)$
intersects
$(X,B+M)$
intersects
![]() $f^{-1} (s)$
. By the connectedness of
$f^{-1} (s)$
. By the connectedness of
![]() $f^{-1} (s) \cap \lfloor B \rfloor $
, up to reordering, we can assume that
$f^{-1} (s) \cap \lfloor B \rfloor $
, up to reordering, we can assume that
![]() $Z \subset D_1$
,
$Z \subset D_1$
,
![]() $W \subset D_r$
, and
$W \subset D_r$
, and
![]() $f^{-1} (s) \cap D_i \cap D_{i+1} \neq \emptyset $
for
$f^{-1} (s) \cap D_i \cap D_{i+1} \neq \emptyset $
for
![]() $i=1,\ldots , r-1$
.
$i=1,\ldots , r-1$
.
By induction on the dimension, we may apply Theorem 1.4 to
![]() $D_1 \rightarrow S$
with Z as minimal generalized log canonical center and
$D_1 \rightarrow S$
with Z as minimal generalized log canonical center and
![]() $D_1 \cap D_2$
as the other center. It follows that there is a generalized log canonical center
$D_1 \cap D_2$
as the other center. It follows that there is a generalized log canonical center
![]() $Z_2 \subset D_1 \cap D_2$
that is
$Z_2 \subset D_1 \cap D_2$
that is
![]() ${\mathbb P}^{1}$
-linked to Z. By Remark 2.26,
${\mathbb P}^{1}$
-linked to Z. By Remark 2.26,
![]() $Z_2$
is also minimal with respect to inclusion among the generalized log canonical centers of
$Z_2$
is also minimal with respect to inclusion among the generalized log canonical centers of
![]() $(X,B+M)$
that intersect
$(X,B+M)$
that intersect
![]() $f^{-1}(s)$
. Let
$f^{-1}(s)$
. Let
![]() $(D_1,B_1 + M_1)$
and
$(D_1,B_1 + M_1)$
and
![]() $(D_2,B_2+M_2)$
denote the generalized pairs induced by generalized adjunction on
$(D_2,B_2+M_2)$
denote the generalized pairs induced by generalized adjunction on
![]() $D_1$
and
$D_1$
and
![]() $D_2$
, respectively. Notice that
$D_2$
, respectively. Notice that
![]() $Z_2$
is a generalized log canonical center of
$Z_2$
is a generalized log canonical center of
![]() $(D_1,B_1+M_1)$
. Then, by the generalized dlt property and generalized adjunction [Reference Birkar5, Section 3.1], it follows that
$(D_1,B_1+M_1)$
. Then, by the generalized dlt property and generalized adjunction [Reference Birkar5, Section 3.1], it follows that
![]() $Z_2$
is a generalized log canonical center also for
$Z_2$
is a generalized log canonical center also for
![]() $(X,B+M)$
and
$(X,B+M)$
and
![]() $(D_2,B_2+M_2)$
. To conclude, we apply this argument inductively to consecutive prime component
$(D_2,B_2+M_2)$
. To conclude, we apply this argument inductively to consecutive prime component
![]() $D_i$
and
$D_i$
and
![]() $D_{i+1}$
, until we have
$D_{i+1}$
, until we have
![]() $i+1 = r$
. This process produces a minimal generalized log canonical center
$i+1 = r$
. This process produces a minimal generalized log canonical center
![]() $Z_r \subset D_r$
that is
$Z_r \subset D_r$
that is
![]() ${\mathbb P}^{1}$
-linked to Z. Since
${\mathbb P}^{1}$
-linked to Z. Since
![]() $Z_r$
may not be contained in W, we apply the inductive hypothesis to the morphism
$Z_r$
may not be contained in W, we apply the inductive hypothesis to the morphism
![]() $D_r \rightarrow S$
with
$D_r \rightarrow S$
with
![]() $Z_r$
and W as the centers involved. This process produced a new generalized log canonical center
$Z_r$
and W as the centers involved. This process produced a new generalized log canonical center
![]() $Z_W \subset W$
with the claimed properties.
$Z_W \subset W$
with the claimed properties.
Step 2: We prove that the étale base change is not necessary.
Let
![]() $g \colon X \rightarrow T$
be the Stein factorization of f, and let
$g \colon X \rightarrow T$
be the Stein factorization of f, and let
![]() $t \in T$
be the unique preimage of s in T. Let
$t \in T$
be the unique preimage of s in T. Let
![]() $Z_1, \ldots , Z_k$
be the minimal log canonical centers with respect to inclusion, such that
$Z_1, \ldots , Z_k$
be the minimal log canonical centers with respect to inclusion, such that
![]() $s \in f(Z_i)$
. Generalized log canonical centers commute with étale base change. Thus, by the previous step, all the
$s \in f(Z_i)$
. Generalized log canonical centers commute with étale base change. Thus, by the previous step, all the
![]() $Z_i$
are
$Z_i$
are
![]() ${\mathbb P}^{1}$
-linked to each other after a suitable base change. Therefore, there is a unique subvariety
${\mathbb P}^{1}$
-linked to each other after a suitable base change. Therefore, there is a unique subvariety
![]() $V \subset T$
, such that
$V \subset T$
, such that
![]() $g(Z_i) = V$
for every i.
$g(Z_i) = V$
for every i.
Let
![]() $v \in T$
be the generic point of V. Since g has connected fibers, we can apply the Step 1 to
$v \in T$
be the generic point of V. Since g has connected fibers, we can apply the Step 1 to
![]() $g \colon (X,B+M) \rightarrow T$
and v. Thus, we get an étale base change
$g \colon (X,B+M) \rightarrow T$
and v. Thus, we get an étale base change
![]() $\pi \colon (v' \in T') \rightarrow (v \in T)$
that induces an isomorphism
$\pi \colon (v' \in T') \rightarrow (v \in T)$
that induces an isomorphism
Thus, each
![]() $Z_i$
is canonically isomorphic to a minimal generalized log canonical center
$Z_i$
is canonically isomorphic to a minimal generalized log canonical center
![]() $Z^{\prime }_i \subset X \times _T T'$
. The centers
$Z^{\prime }_i \subset X \times _T T'$
. The centers
![]() $Z^{\prime }_i$
are
$Z^{\prime }_i$
are
![]() ${\mathbb P}^{1}$
-linked to each other by Step 1. By (18), the
${\mathbb P}^{1}$
-linked to each other by Step 1. By (18), the
![]() ${\mathbb P}^{1}$
-links descend to
${\mathbb P}^{1}$
-links descend to
![]() ${\mathbb P}^{1}$
-links between the
${\mathbb P}^{1}$
-links between the
![]() $Z_i$
.
$Z_i$
.
Proof of Theorem 1.6.
By Theorem 5.4, we know that
![]() $\mathcal {DMR}(X,B, \mathbf {M})$
is equidimensional. If the dual complex is contractible to a point, there is nothing to prove. Otherwise, the observation in Remark 5.3 implies that the result follows from the analogous result for log pairs proved in [Reference Kollár and Xu28].
$\mathcal {DMR}(X,B, \mathbf {M})$
is equidimensional. If the dual complex is contractible to a point, there is nothing to prove. Otherwise, the observation in Remark 5.3 implies that the result follows from the analogous result for log pairs proved in [Reference Kollár and Xu28].
Proof of 1.7.
Without loss of generality, we can assume that X is
![]() $\mathbb {Q}$
-factorial, and that
$\mathbb {Q}$
-factorial, and that
![]() $(X,\Delta ,\mathbf {M})$
is generalized dlt, where
$(X,\Delta ,\mathbf {M})$
is generalized dlt, where
![]() . As
. As
![]() $(X,B,\mathbf {M})$
is not generalized log canonical, then
$(X,B,\mathbf {M})$
is not generalized log canonical, then
![]() $B - \Delta> 0$
and
$B - \Delta> 0$
and
![]() ${K_{X}} + \Delta + \mathbf {M} _X$
is not pseudo-effective. Hence, we can run a
${K_{X}} + \Delta + \mathbf {M} _X$
is not pseudo-effective. Hence, we can run a
![]() $({K_{X}} + \Delta + \mathbf {M} _X)$
-MMP with scaling of an ample divisor H
$({K_{X}} + \Delta + \mathbf {M} _X)$
-MMP with scaling of an ample divisor H
which terminates with a Mori fiber space
![]() $g \colon X_n\rightarrow Z$
. This MMP is also a
$g \colon X_n\rightarrow Z$
. This MMP is also a
![]() $-(B - \Delta )$
-MMP. We shall denote by
$-(B - \Delta )$
-MMP. We shall denote by
![]() $\Gamma _i$
the strict transform on
$\Gamma _i$
the strict transform on
![]() $X_i$
of a divisor
$X_i$
of a divisor
![]() $\Gamma $
on X.
$\Gamma $
on X.
Let
![]() $R_i$
be the extremal ray corresponding to the i-th step
$R_i$
be the extremal ray corresponding to the i-th step
![]() $X_{i-1} \dashrightarrow X_{i}$
of (19). Thus, we have
$X_{i-1} \dashrightarrow X_{i}$
of (19). Thus, we have
![]() $(B_i - \Delta _i) \cdot R_i> 0$
, and there exists a prime component
$(B_i - \Delta _i) \cdot R_i> 0$
, and there exists a prime component
![]() $D_i$
of
$D_i$
of
![]() $\operatorname {\mathrm {Supp}}(B_i^{> 1}) \subset \operatorname {\mathrm {Supp}} (B_i^{\geq 1})$
satisfying
$\operatorname {\mathrm {Supp}}(B_i^{> 1}) \subset \operatorname {\mathrm {Supp}} (B_i^{\geq 1})$
satisfying
![]() $D_i \cdot R_i> 0$
.
$D_i \cdot R_i> 0$
.
Claim. For all i,
![]() $\mathcal {D}(B_i^{\geq 1})$
and
$\mathcal {D}(B_i^{\geq 1})$
and
![]() $\mathcal {D}(B_{i+1}^{\geq 1})$
are simple homotopy equivalent.
$\mathcal {D}(B_{i+1}^{\geq 1})$
are simple homotopy equivalent.
Proof of Claim.
As the MMP in (19) terminates, there exists
![]() $0 < \epsilon \ll 1$
, such that MMP is also a run of the
$0 < \epsilon \ll 1$
, such that MMP is also a run of the
![]() $(K_X+\Delta +(\mathbf {M}_X+\epsilon {H}))$
-MMP. In particular, at each step of (19),
$(K_X+\Delta +(\mathbf {M}_X+\epsilon {H}))$
-MMP. In particular, at each step of (19),
![]() $H_i$
is a big divisor and
$H_i$
is a big divisor and
![]() $\mathbb {B}_+(H_i)$
does not contain any generalized log canonical center of
$\mathbb {B}_+(H_i)$
does not contain any generalized log canonical center of
![]() $(X_i, \Delta _i, \mathbf {M})$
. Since the generalized dlt property is preserved under the steps of the MMP in (19), see Definition 2.32, for all i,
$(X_i, \Delta _i, \mathbf {M})$
. Since the generalized dlt property is preserved under the steps of the MMP in (19), see Definition 2.32, for all i,
![]() $\mathcal {DMR}(X_i,B_i,\mathbf {M}) = \mathcal D (B_i^{\geq 1})$
. Hence, the claim is a direct consequence of Lemma 6.2 and [Reference de Fernex, Kollár and Xu8, Theorem 19], since, as we noted above, there exists a prime component
$\mathcal {DMR}(X_i,B_i,\mathbf {M}) = \mathcal D (B_i^{\geq 1})$
. Hence, the claim is a direct consequence of Lemma 6.2 and [Reference de Fernex, Kollár and Xu8, Theorem 19], since, as we noted above, there exists a prime component
![]() $D_i$
of
$D_i$
of
![]() $\operatorname {\mathrm {Supp}}(\Delta _i)$
, such that
$\operatorname {\mathrm {Supp}}(\Delta _i)$
, such that
![]() $D_i \cdot R_i>0$
.
$D_i \cdot R_i>0$
.
The claim implies that
As
![]() $\mathbf {M}_{X_{n}}$
is pseudo-effective and g is a Mori fiber space, then
$\mathbf {M}_{X_{n}}$
is pseudo-effective and g is a Mori fiber space, then
![]() $-({K_{X_n}} + \Delta _n)$
is g-ample; as
$-({K_{X_n}} + \Delta _n)$
is g-ample; as
![]() $\mathcal D (B_n^{\geq 1})= \mathcal D (\Delta _n^{=1})$
, we can apply [Reference Nakamura31, Lemma 3.1] to conclude that
$\mathcal D (B_n^{\geq 1})= \mathcal D (\Delta _n^{=1})$
, we can apply [Reference Nakamura31, Lemma 3.1] to conclude that
![]() $\mathcal D (\Delta _n^{=1})=\mathcal {DMR}(X,B,\mathbf {M})$
is contractible.
$\mathcal D (\Delta _n^{=1})=\mathcal {DMR}(X,B,\mathbf {M})$
is contractible.
Lemma 6.2. Let
![]() $(X,B,\mathbf {M})$
be a
$(X,B,\mathbf {M})$
be a
![]() $\mathbb {Q}$
-factorial generalized dlt pair. Let H be a big divisor, such that
$\mathbb {Q}$
-factorial generalized dlt pair. Let H be a big divisor, such that
![]() $\mathbb {B}_+(H)$
does not contain any generalized log canonical center of
$\mathbb {B}_+(H)$
does not contain any generalized log canonical center of
![]() $(X,B,\mathbf {M})$
. Then, for any
$(X,B,\mathbf {M})$
. Then, for any
![]() $0<\epsilon \ll 1$
, there exists an effective divisor
$0<\epsilon \ll 1$
, there exists an effective divisor
![]() $\Gamma _{\epsilon }$
, such that
$\Gamma _{\epsilon }$
, such that
![]() $(X,B+\Gamma _{\epsilon })$
is a dlt pair,
$(X,B+\Gamma _{\epsilon })$
is a dlt pair,
and
![]() $\operatorname {\mathrm {Supp}}(B^{=1})=\operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})=\operatorname {\mathrm {Nklt}}(X,B+\Gamma _{\epsilon })$
. Furthermore, the dual complexes of the pair
$\operatorname {\mathrm {Supp}}(B^{=1})=\operatorname {\mathrm {Nklt}}(X,B,\mathbf {M})=\operatorname {\mathrm {Nklt}}(X,B+\Gamma _{\epsilon })$
. Furthermore, the dual complexes of the pair
![]() $(X,B+\Gamma _{\epsilon })$
and of the generalized pair
$(X,B+\Gamma _{\epsilon })$
and of the generalized pair
![]() $(X,B,\mathbf {M})$
agree.
$(X,B,\mathbf {M})$
agree.
Proof. As
![]() $\mathbb {B}_+(H)$
does not contain any generalized log canonical center of
$\mathbb {B}_+(H)$
does not contain any generalized log canonical center of
![]() $(X,B,\mathbf {M})$
, we can write
$(X,B,\mathbf {M})$
, we can write
![]() $H \sim _{\mathbb {Q}} A+E$
, where A is ample and E effective in such a way that for
$H \sim _{\mathbb {Q}} A+E$
, where A is ample and E effective in such a way that for
![]() $0 < \epsilon \ll 1$
,
$0 < \epsilon \ll 1$
,
![]() $(X,B+\epsilon E,\mathbf {M}+\epsilon \overline {A})$
is still generalized dlt, its non-klt locus coincides with that of
$(X,B+\epsilon E,\mathbf {M}+\epsilon \overline {A})$
is still generalized dlt, its non-klt locus coincides with that of
![]() $(X, B, \mathbf {M})$
and its dual complex coincides with that of
$(X, B, \mathbf {M})$
and its dual complex coincides with that of
![]() $(X, B, \mathbf {M})$
. In view of this, thus, it suffices to show that the conclusion of the lemma holds if we substitute H with A. Hence, we shall assume that H is an ample divisor.
$(X, B, \mathbf {M})$
. In view of this, thus, it suffices to show that the conclusion of the lemma holds if we substitute H with A. Hence, we shall assume that H is an ample divisor.
As
![]() $(X,B,\mathbf {M})/\mathbb {C}$
is generalized dlt,
$(X,B,\mathbf {M})/\mathbb {C}$
is generalized dlt,
![]() $\mathbf {M}$
descends to a neighborhood of the generic point of each generalized log canonical center. In particular, there exists a closed subset
$\mathbf {M}$
descends to a neighborhood of the generic point of each generalized log canonical center. In particular, there exists a closed subset
![]() $Z \subset X$
so that
$Z \subset X$
so that
![]() $\mathbf {M}$
descends to
$\mathbf {M}$
descends to
![]() $X \setminus Z$
and no generalized log canonical center is contained in Z. By [Reference Kollár and Mori27, Lemma 2.45], we can find a birational morphism
$X \setminus Z$
and no generalized log canonical center is contained in Z. By [Reference Kollár and Mori27, Lemma 2.45], we can find a birational morphism
![]() $\pi \colon X' \rightarrow X$
from a normal birational model
$\pi \colon X' \rightarrow X$
from a normal birational model
![]() $X'$
so that
$X'$
so that
![]() $\pi $
is an isomorphism over
$\pi $
is an isomorphism over
![]() $X \setminus Z$
and
$X \setminus Z$
and
![]() $\mathbf {M}$
descends to
$\mathbf {M}$
descends to
![]() $X'$
. We write
$X'$
. We write
![]() $(X',B',\mathbf {M})$
for the trace of
$(X',B',\mathbf {M})$
for the trace of
![]() $(X,B,\mathbf {M})$
on
$(X,B,\mathbf {M})$
on
![]() $X'$
.
$X'$
.
As X is
![]() $\mathbb {Q}$
-factorial, we can find an ample divisor
$\mathbb {Q}$
-factorial, we can find an ample divisor
![]() $H'$
on
$H'$
on
![]() $X'$
so that
$X'$
so that
![]() is ample on X and
is ample on X and
![]() $\pi ^{\ast } (H)-H'=F' \geq 0$
is
$\pi ^{\ast } (H)-H'=F' \geq 0$
is
![]() $\pi $
-exceptional.Footnote
3
As
$\pi $
-exceptional.Footnote
3
As
![]() $\pi (\operatorname {\mathrm {Supp}}(F')) \subset Z$
and Z does not contain any generalized log canonical center of
$\pi (\operatorname {\mathrm {Supp}}(F')) \subset Z$
and Z does not contain any generalized log canonical center of
![]() $(X,B,\mathbf {M})$
,
$(X,B,\mathbf {M})$
,
![]() $\operatorname {\mathrm {Supp}}(F')$
does not contain any generalized log canonical center of
$\operatorname {\mathrm {Supp}}(F')$
does not contain any generalized log canonical center of
![]() $(X',B',\mathbf {M})$
. In particular, for
$(X',B',\mathbf {M})$
. In particular, for
![]() $0 < \epsilon \ll 1$
, we have
$0 < \epsilon \ll 1$
, we have
where the first and last equalities come from the fact that
![]() $\mathbf {M}$
descends to
$\mathbf {M}$
descends to
![]() $X'$
. As the equalities in (20) also hold for each generalized log canonical place, then adding
$X'$
. As the equalities in (20) also hold for each generalized log canonical place, then adding
![]() $\epsilon F$
does not introduce new generalized log canonical places and preserves the generalized sublog canonical property, so that
$\epsilon F$
does not introduce new generalized log canonical places and preserves the generalized sublog canonical property, so that
Let us fix
![]() $0 < \epsilon \ll 1$
so that the properties just discussed hold. As
$0 < \epsilon \ll 1$
so that the properties just discussed hold. As
![]() ${\mathbf {M}_{X'}} + \epsilon H'$
is ample, there exists
${\mathbf {M}_{X'}} + \epsilon H'$
is ample, there exists
![]() $\Gamma ^{\prime }_{\epsilon } \sim _{\mathbb {Q}} {\mathbf {M}_{X'}} + \epsilon H'$
, such that
$\Gamma ^{\prime }_{\epsilon } \sim _{\mathbb {Q}} {\mathbf {M}_{X'}} + \epsilon H'$
, such that
![]() $\operatorname {\mathrm {Nklt}}(X',B'+\epsilon F')=\operatorname {\mathrm {Nklt}}(X',B'+\Gamma ^{\prime }_{\epsilon } + \epsilon F')$
, and adding
$\operatorname {\mathrm {Nklt}}(X',B'+\epsilon F')=\operatorname {\mathrm {Nklt}}(X',B'+\Gamma ^{\prime }_{\epsilon } + \epsilon F')$
, and adding
![]() $\Gamma ^{\prime }_{\epsilon }$
does not introduce any new log canonical places. Moreover, by construction,
$\Gamma ^{\prime }_{\epsilon }$
does not introduce any new log canonical places. Moreover, by construction,
 $$ \begin{align*} {K_{X'}} + B' + \Gamma^{\prime}_{\epsilon} + \epsilon F' \sim_{\mathbb{Q}} \pi^{\ast} ({K_{X}} + B + {\mathbf{M}_{X}} + \epsilon H), \ \text{and}\\ \mathcal{D}((B')^{= 1}) = \mathcal{D}((B' +\epsilon F') ^{= 1}) = \mathcal{D}((B' +\Gamma_{\epsilon}'+\epsilon F') ^{= 1}). \end{align*} $$
$$ \begin{align*} {K_{X'}} + B' + \Gamma^{\prime}_{\epsilon} + \epsilon F' \sim_{\mathbb{Q}} \pi^{\ast} ({K_{X}} + B + {\mathbf{M}_{X}} + \epsilon H), \ \text{and}\\ \mathcal{D}((B')^{= 1}) = \mathcal{D}((B' +\epsilon F') ^{= 1}) = \mathcal{D}((B' +\Gamma_{\epsilon}'+\epsilon F') ^{= 1}). \end{align*} $$
Defining
![]() , the pair
, the pair
![]() $(X,B+\Gamma _{\epsilon })$
satisfies the claims of the statement.
$(X,B+\Gamma _{\epsilon })$
satisfies the claims of the statement.
Acknowledgements
The authors wish to thank Tommaso de Fernex, Gabriele Di Cerbo, Christopher Hacon, Mirko Mauri, James McKernan, and Joe Waldron for helpful discussions and encouragements. The authors wish to thank Christopher Hacon and Mirko Mauri also for reading a first draft of this work. We wish to thank the anonymous referee for useful comments and suggestions that helped the authors improve the clarity of this work. Part of this work was completed during a visit of RS to the University of Utah. RS would like to thank the University of Utah for the hospitality and the nice working environment, and Christopher Hacon for funding his visit. SF acknowledges support from a Graduate Research Fellowship awarded by the University of Utah. He was also partially supported by National Science Foundation research grant numbers: DMS-1801851, DMS-195252 and by a grant from the Simons Foundation, Award Number: 256202. RS was partially supported by Churchill College, Cambridge, by the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 842071, and by the Programma per giovani ricercatori “Rita Levi Montalcini”.
Competing interests
The authors have no competing interest to declare.