1 Introduction
Banach spaces and descriptive set theory have a long history of mutual interactions. Explicit use of descriptive set theory to Banach space theory can be traced back at least to the seminal papers of Bourgain ([Reference Bourgain9, Reference Bourgain8]), where it has become apparent that descriptive set theory is an indispensable tool for universality problems. That is a theme that has been investigated by researchers working with Banach spaces ever since (see, e.g., [Reference Argyros and Dodos2, Reference Dodos14] and references therein).
As it eventually turned out, ‘Descriptive set theory of Banach spaces’ is an interesting and rich subject and has received considerable attention in recent years. One of the starting points was the idea of Bossard of coding separable Banach spaces in [Reference Bossard6, Reference Bossard7]. His approach, which can be considered standard, was to choose some universal separable Banach space X, such as ![]() $C(2^{\mathbb {N}})$, and consider the Effros-Borel space
$C(2^{\mathbb {N}})$, and consider the Effros-Borel space ![]() $F(X)$. Recall that this is the set of closed subsets of X equipped with a certain
$F(X)$. Recall that this is the set of closed subsets of X equipped with a certain ![]() $\sigma $-algebra that makes
$\sigma $-algebra that makes ![]() $F(X)$ a standard Borel space: that is, a measurable space that is isomorphic, as a measurable space, to a Polish space equipped with the
$F(X)$ a standard Borel space: that is, a measurable space that is isomorphic, as a measurable space, to a Polish space equipped with the ![]() $\sigma $-algebra of Borel sets. It is then not too difficult to show that the subset
$\sigma $-algebra of Borel sets. It is then not too difficult to show that the subset ![]() $SB(X)\subseteq F(X)$ consisting of all closed linear subspaces is a Borel subset and therefore a standard Borel space itself.
$SB(X)\subseteq F(X)$ consisting of all closed linear subspaces is a Borel subset and therefore a standard Borel space itself.
Although this approach has found numerous significant applications in Banach space theory, its drawback is that there is no canonical or natural (Polish) topology on ![]() $SB(X)$. So although one can ask whether a given class of Banach spaces is Borel or not, the question about the exact complexity of that particular class is meaningless. Let us specify this. Many of the applications may be interpreted as computing co/analytic sets of Banach spaces and deriving consequences from this; this concerns especially various universality results (see, e.g., [Reference Dodos14, Chapter 7] and [Reference Kurka23]). Having a topology allows us to separate two classes of Banach spaces, which are both known to be Borel (we comment more on this issue in the sequel [Reference Cúth, Doležal, Doucha and Kurka13]).
$SB(X)$. So although one can ask whether a given class of Banach spaces is Borel or not, the question about the exact complexity of that particular class is meaningless. Let us specify this. Many of the applications may be interpreted as computing co/analytic sets of Banach spaces and deriving consequences from this; this concerns especially various universality results (see, e.g., [Reference Dodos14, Chapter 7] and [Reference Kurka23]). Having a topology allows us to separate two classes of Banach spaces, which are both known to be Borel (we comment more on this issue in the sequel [Reference Cúth, Doležal, Doucha and Kurka13]).
Moreover, one of the active and ongoing research streams is to find out whether for a particular Banach space its isomorphism class is Borel or not (see, e.g., [Reference Kurka25, Reference Godefroy18] or the survey [Reference Godefroy17] and references therein): spaces with Borel isomorphism classes are rare and can be considered simply definable (up to isomorphism). It is then desirable, for spaces whose classes are Borel, to have a finer description of how simply definable they are (see, e.g., [Reference Godefroy18, Problem 3]).
A recent work [Reference Godefroy and Saint-Raymond19] of Godefroy and Saint-Raymond addresses this general issue of associating a natural topology to the set of codes of Banach spaces. They still work with the space ![]() $SB(X)$, but among the many Polish topologies on
$SB(X)$, but among the many Polish topologies on ![]() $SB(X)$ giving the Effros-Borel structure, they select some particular subclass that is called admissible topologies. Although no particular admissible topology is canonical, the set of requirements put on this class guarantees that the exact Borel complexities vary little.
$SB(X)$ giving the Effros-Borel structure, they select some particular subclass that is called admissible topologies. Although no particular admissible topology is canonical, the set of requirements put on this class guarantees that the exact Borel complexities vary little.
This paper presents an alternative approach by considering a concrete and natural Polish space (and some variants of it) of separable Banach spaces, which is convenient to work with. We have three main reasons and advantages for that in mind. The first one, which was our original motivation, is to further push the programme initiated by Godefroy and Saint-Raymond on computing precise Borel complexities of various classes of Banach spaces. It turns out that in our new space, the computations of Borel complexities are usually as straightforward as they could be, and besides many new results, we are also able to improve several estimates already obtained in [Reference Godefroy and Saint-Raymond19] (see also [Reference Ghawadrah16] for additional results in this direction). Most of these results are contained in the sequel to this paper [Reference Cúth, Doležal, Doucha and Kurka13]. It should also be mentioned that computing exact Borel complexities has been a traditional research topic in analysis and topology of independent interest (see [Reference Kechris21, Chapter 23] for a comprehensive but already outdated list of examples), and among our contributions in that regard, presented in [Reference Cúth, Doležal, Doucha and Kurka13], are new elegant characterizations of the Hilbert space ![]() $\ell _{2}$. Briefly,
$\ell _{2}$. Briefly, ![]() $\ell _{2}$ is the unique (up to isometry) infinite-dimensional separable Banach space with a closed isometry class, and it is the unique (up to isomorphism) infinite-dimensional separable Banach space with an
$\ell _{2}$ is the unique (up to isometry) infinite-dimensional separable Banach space with a closed isometry class, and it is the unique (up to isomorphism) infinite-dimensional separable Banach space with an ![]() $F_{\sigma }$ isomorphism class. Recall that Bossard [Reference Bossard7, Problem 2.9] originally asked whether
$F_{\sigma }$ isomorphism class. Recall that Bossard [Reference Bossard7, Problem 2.9] originally asked whether ![]() $\ell _{2}$ is the unique space with a Borel isomorphism class. Although this is now known to be false, we can show that no other Banach space can have such a simple isomorphism class.
$\ell _{2}$ is the unique space with a Borel isomorphism class. Although this is now known to be false, we can show that no other Banach space can have such a simple isomorphism class.
The remaining two reasons have different origins; one is functional analytic, and the other comes from logic. For the former, the feature of the topology we work with is that basic open sets are essentially definitions of finite-dimensional Banach spaces up to ![]() $\varepsilon $-isomorphism, where
$\varepsilon $-isomorphism, where ![]() $\varepsilon>0$ is arbitrarily small. This connects this topological approach with the local theory of Banach spaces. The basic manifestation of this is that the finite representability of Banach spaces is expressed in elementary topological terms and, for example, leads to a natural reformulation of the Dvoretzky theorem that the infinite-dimensional separable Hilbert space is contained in the closure of the isometry class of every infinite-dimensional separable Banach space (see Corollary 2.11). Further applications to the local theory might be a subject of future research.
$\varepsilon>0$ is arbitrarily small. This connects this topological approach with the local theory of Banach spaces. The basic manifestation of this is that the finite representability of Banach spaces is expressed in elementary topological terms and, for example, leads to a natural reformulation of the Dvoretzky theorem that the infinite-dimensional separable Hilbert space is contained in the closure of the isometry class of every infinite-dimensional separable Banach space (see Corollary 2.11). Further applications to the local theory might be a subject of future research.
Finally, our approach brings closer the two different interactions of logic with Banach space theory that had not interacted significantly: that is, the descriptive set theory of Banach spaces and the continuous model theory of Banach spaces. Continuous model theory, or model theory of metric structures, is a generalization of classical model theory to structures that are inherently metric and has its origins, motivations as well as most of the applications in Banach space theory. We refer the reader to [Reference Ben Yaacov, Berenstein, Henson and Usvyatsov4] for an introduction and more motivation. Our space of Banach spaces is closely related to how countable, respectively separable models are coded in classical, respectively continuous model theory (see, e.g., [Reference Gao15, Section 3.6] for the classical case and [Reference Ben Yaacov, Doucha, Nies and Tsankov5, Section 4] for the metric case). Moreover, the exact Borel complexities that our space allows us to compute are directly related to the López-Escobar theorem from continuous infinitary logic, which connects such complexities with the complexities of formulas that define the corresponding classes (we refer to [Reference Ben Yaacov, Doucha, Nies and Tsankov5, Section 6]). It may also be of interest for future research to investigate the relation, for a given Banach space, between having an isometry class of low Borel complexity and having an axiomatization in continuous first-order logic.
Having motivated our approach, let us now outline some more details and the main results contained in this paper. Informally, the space we introduce is the space of all norms, respectively pseudonorms, on the space of all finitely supported sequences of rational numbers – the unique infinite-dimensional vector space over ![]() $\mathbb {Q}$ with a countable Hamel basis. This is also, in spirit, similar to how (for instance) Vershik topologized the space of all Polish metric spaces ([Reference Vershik26]), or how Grigorchuk topologized the space of all n-generated, respectively finitely generated, groups ([Reference Grigorchuk20]).
$\mathbb {Q}$ with a countable Hamel basis. This is also, in spirit, similar to how (for instance) Vershik topologized the space of all Polish metric spaces ([Reference Vershik26]), or how Grigorchuk topologized the space of all n-generated, respectively finitely generated, groups ([Reference Grigorchuk20]).
This space has already appeared in previous works of the authors in [Reference Cúth, Doucha and Kurka11] and [Reference Cúth, Doucha and Kurka12] as a useful coding of Banach spaces. Here we investigate it further.
Some of the main results of this paper are listed now. The first theorem below presents the main part of the comparison of the space of norms with admissible topologies, whose proof is the core of Section 3, where also all other comparison results are proved.
Theorem A. There is a ![]() $\boldsymbol {\Sigma }_{2}^{0}$-measurable mapping from the space of norms to any admissible topology of Godefroy and Saint-Raymond that associates to each norm a space isometric to the space that the norm defines, and vice versa.
$\boldsymbol {\Sigma }_{2}^{0}$-measurable mapping from the space of norms to any admissible topology of Godefroy and Saint-Raymond that associates to each norm a space isometric to the space that the norm defines, and vice versa.
Therefore, while the exact Borel complexities are more or less independent of our coding or the choice of the admissible topology, some finer topological properties, such as being meager or comeager (this is mentioned below), or the description of the topological closures, are not. We obtain a neat characterization of topological closures in the spaces of norms and pseudonorms in terms of finite representability; we refer the reader to Proposition 2.9.
Then, directly motivated by [Reference Godefroy and Saint-Raymond19, Problem 5.5], we investigate the generic properties in the spaces of norms and in admissible topologies. First we show the genericity of the Gurariĭ space in the space of norms and pseudonorms.
Theorem B. The isometry class of the Gurariĭ space is a dense ![]() $G_{\delta }$-set in the space of norms and pseudonorms: that is, the Gurariĭ space is the generic separable Banach space (see Theorem 4.1).
$G_{\delta }$-set in the space of norms and pseudonorms: that is, the Gurariĭ space is the generic separable Banach space (see Theorem 4.1).
Then we continue with a similar investigation for admissible topologies, and among other things, we show that the Gurariĭ space is not always generic.
Theorem C. For any isometrically universal separable Banach space X, any admissible topology ![]() $\tau $ on
$\tau $ on ![]() $SB(X)$ and any infinite-dimensional Banach spaces Y and Z such that
$SB(X)$ and any infinite-dimensional Banach spaces Y and Z such that ![]() $Y\hookrightarrow Z$ and
$Y\hookrightarrow Z$ and ![]() $Z\not \hookrightarrow Y\oplus F$ for every finite-dimensional space F, there exists a finer admissible topology
$Z\not \hookrightarrow Y\oplus F$ for every finite-dimensional space F, there exists a finer admissible topology ![]() $\tau ^{\prime }\supseteq \tau $ such that the class of Banach spaces isomorphic to Z is nowhere dense in
$\tau ^{\prime }\supseteq \tau $ such that the class of Banach spaces isomorphic to Z is nowhere dense in ![]() $(SB(X),\tau ^{\prime })$. In particular, there exists an admissible topology in which the Gurariĭ space is meager (see Theorem 4.12).
$(SB(X),\tau ^{\prime })$. In particular, there exists an admissible topology in which the Gurariĭ space is meager (see Theorem 4.12).
On the other hand, the isometry class of the Gurariĭ space ![]() $\mathbb {G}$, as a subset of
$\mathbb {G}$, as a subset of ![]() $SB(\mathbb {G})$, is a dense
$SB(\mathbb {G})$, is a dense ![]() $G_{\delta }$-set in the Wijsman topology (see Theorem 4.10).
$G_{\delta }$-set in the Wijsman topology (see Theorem 4.10).
1.1 Notation
Let us conclude the introduction by setting up some notation used throughout the paper.
Throughout the paper, we usually denote the Borel classes of low complexity by the traditional notation such as ![]() $F_{\sigma }$ and
$F_{\sigma }$ and ![]() $G_{\delta }$, or even
$G_{\delta }$, or even ![]() $F_{\sigma \delta }$ (countable intersection of
$F_{\sigma \delta }$ (countable intersection of ![]() $F_{\sigma }$ sets) and
$F_{\sigma }$ sets) and ![]() $G_{\delta \sigma }$ (countable union of
$G_{\delta \sigma }$ (countable union of ![]() $G_{\delta }$-sets). However, whenever it is more convenient or necessary, we use the notation
$G_{\delta }$-sets). However, whenever it is more convenient or necessary, we use the notation ![]() $\boldsymbol {\Sigma }_{\alpha }^{0}$, respectively
$\boldsymbol {\Sigma }_{\alpha }^{0}$, respectively ![]() $\boldsymbol {\Pi }_{\alpha }^{0}$, where
$\boldsymbol {\Pi }_{\alpha }^{0}$, where ![]() $\alpha <\omega _{1}$ (we refer to [Reference Kechris21, Section 11] for this notation). We emphasize that open sets, respectively closed sets, are
$\alpha <\omega _{1}$ (we refer to [Reference Kechris21, Section 11] for this notation). We emphasize that open sets, respectively closed sets, are ![]() $\boldsymbol {\Sigma }^{0}_{1}$, respectively
$\boldsymbol {\Sigma }^{0}_{1}$, respectively ![]() $\boldsymbol {\Pi }^{0}_{1}$, by this notation.
$\boldsymbol {\Pi }^{0}_{1}$, by this notation.
Moreover, given a class ![]() $\boldsymbol {\Gamma }$ of sets in metrizable spaces, we say that
$\boldsymbol {\Gamma }$ of sets in metrizable spaces, we say that ![]() $f:X\to Y$ is
$f:X\to Y$ is ![]() $\boldsymbol {\Gamma }$-measurable if
$\boldsymbol {\Gamma }$-measurable if ![]() $f^{-1}(U)\in \boldsymbol {\Gamma }$ for every open set
$f^{-1}(U)\in \boldsymbol {\Gamma }$ for every open set ![]() $U\subseteq Y$.
$U\subseteq Y$.
Given Banach spaces X and Y, we denote by ![]() $X\equiv Y$ (respectively
$X\equiv Y$ (respectively ![]() $X\simeq Y$) the fact that those two spaces are linearly isometric (respectively isomorphic). We denote by
$X\simeq Y$) the fact that those two spaces are linearly isometric (respectively isomorphic). We denote by ![]() $X\hookrightarrow Y$ the fact that Y contains a subspace isomorphic to X. For
$X\hookrightarrow Y$ the fact that Y contains a subspace isomorphic to X. For ![]() $K\geq 1$, a K-isomorphism
$K\geq 1$, a K-isomorphism ![]() $T:X\to Y$ is a linear map with
$T:X\to Y$ is a linear map with ![]() $K^{-1}\|x\|\leq \|Tx\|\leq K\|x\|$,
$K^{-1}\|x\|\leq \|Tx\|\leq K\|x\|$, ![]() $x\in X$. If
$x\in X$. If ![]() $x_{1},\ldots ,x_{n}$ are linearly independent elements of X and
$x_{1},\ldots ,x_{n}$ are linearly independent elements of X and ![]() $y_{1},\ldots ,y_{n}\in Y$, we write
$y_{1},\ldots ,y_{n}\in Y$, we write  $(Y,y_{1},\ldots ,y_{n}){\stackrel {{K}}{\sim } (X,x_{1},\ldots ,x_{n})}$ if the linear operator
$(Y,y_{1},\ldots ,y_{n}){\stackrel {{K}}{\sim } (X,x_{1},\ldots ,x_{n})}$ if the linear operator ![]() $T:\operatorname {span}\{x_{1},\ldots ,x_{n}\}\to \operatorname {span}\{y_{1},\ldots ,y_{n}\}$ sending
$T:\operatorname {span}\{x_{1},\ldots ,x_{n}\}\to \operatorname {span}\{y_{1},\ldots ,y_{n}\}$ sending ![]() $x_{i}$ to
$x_{i}$ to ![]() $y_{i}$ satisfies
$y_{i}$ satisfies ![]() $\max \{\|T\|,\|T^{-1}\|\}<K$. If X has a canonical basis
$\max \{\|T\|,\|T^{-1}\|\}<K$. If X has a canonical basis ![]() $(x_{1},\ldots ,x_{n})$, which is clear from the context, we just write
$(x_{1},\ldots ,x_{n})$, which is clear from the context, we just write  $(Y,y_{1},\ldots ,y_{n}){\stackrel {K}{\sim } X}$ instead of
$(Y,y_{1},\ldots ,y_{n}){\stackrel {K}{\sim } X}$ instead of  $(Y,y_{1},\ldots ,y_{n}){\stackrel {K}{\sim } (X,x_{1},\ldots ,x_{n})}$. Moreover, if Y is clear from the context, we write
$(Y,y_{1},\ldots ,y_{n}){\stackrel {K}{\sim } (X,x_{1},\ldots ,x_{n})}$. Moreover, if Y is clear from the context, we write  $(y_{1},\ldots ,y_{n}){\stackrel {K}{\sim } X}$ instead of
$(y_{1},\ldots ,y_{n}){\stackrel {K}{\sim } X}$ instead of  $(Y,y_{1},\ldots ,y_{n}){\stackrel {K}{\sim } X}$.
$(Y,y_{1},\ldots ,y_{n}){\stackrel {K}{\sim } X}$.
Throughout the text, ![]() $\ell _{p}^{n}$ denotes the n-dimensional
$\ell _{p}^{n}$ denotes the n-dimensional ![]() $\ell _{p}$-space: that is, the upper index denotes dimension. Finally, in order to avoid any confusion, we emphasize that if we write that a mapping is an ‘isometry’ or an ‘isomorphism’, we do not mean it is surjective if this is not explicitly mentioned.
$\ell _{p}$-space: that is, the upper index denotes dimension. Finally, in order to avoid any confusion, we emphasize that if we write that a mapping is an ‘isometry’ or an ‘isomorphism’, we do not mean it is surjective if this is not explicitly mentioned.
2 The Polish spaces  $\mathcal {P}_{\infty }$ and
$\mathcal {P}_{\infty }$ and  $\mathcal {B}$, and their basic properties
$\mathcal {B}$, and their basic properties
In this section we introduce the main notions of this paper: the Polish spaces of pseudonorms ![]() $\mathcal {P}$ (and
$\mathcal {P}$ (and ![]() $\mathcal {P}_{\infty }$) representing separable (infinite-dimensional) Banach spaces, and we recall the space of norms
$\mathcal {P}_{\infty }$) representing separable (infinite-dimensional) Banach spaces, and we recall the space of norms ![]() $\mathcal {B}$ that has appeared in our previous works [Reference Cúth, Doucha and Kurka11, Reference Cúth, Doucha and Kurka12]. We show some interesting features of these spaces, such as the neat relation between finite representability and topological closures in these spaces; see Proposition 2.9 and its corollaries.
$\mathcal {B}$ that has appeared in our previous works [Reference Cúth, Doucha and Kurka11, Reference Cúth, Doucha and Kurka12]. We show some interesting features of these spaces, such as the neat relation between finite representability and topological closures in these spaces; see Proposition 2.9 and its corollaries.
Let us start with the following idea of coding the class of separable (infinite-dimensional) Banach spaces. It is based on the idea already presented in our previous papers [Reference Cúth, Doucha and Kurka11, Reference Cúth, Doucha and Kurka12], where the space ![]() $\mathcal {B}$ was defined.
$\mathcal {B}$ was defined.
By V, we shall denote the vector space over ![]() $\mathbb {Q}$ of all finitely supported sequences of rational numbers: that is, the unique infinite-dimensional vector space over
$\mathbb {Q}$ of all finitely supported sequences of rational numbers: that is, the unique infinite-dimensional vector space over ![]() $\mathbb {Q}$ with a countable Hamel basis
$\mathbb {Q}$ with a countable Hamel basis ![]() $(e_{n})_{n\in \mathbb {N}}$.
$(e_{n})_{n\in \mathbb {N}}$.
Definition 2.1. Let us denote by ![]() $\mathcal {P}$ the space of all pseudonorms on the vector space V. Since
$\mathcal {P}$ the space of all pseudonorms on the vector space V. Since ![]() $\mathcal {P}$ is a closed subset of
$\mathcal {P}$ is a closed subset of ![]() $\mathbb {R}^{V}$, this gives
$\mathbb {R}^{V}$, this gives ![]() $\mathcal {P}$ the Polish topology inherited from
$\mathcal {P}$ the Polish topology inherited from ![]() $\mathbb {R}^{V}$. The subbasis of this topology is given by sets of the form
$\mathbb {R}^{V}$. The subbasis of this topology is given by sets of the form ![]() $U[v,I]:=\{\mu \in \mathcal {P}:\; \mu (v)\in I\}$, where
$U[v,I]:=\{\mu \in \mathcal {P}:\; \mu (v)\in I\}$, where ![]() $v\in V$ and I is an open interval.
$v\in V$ and I is an open interval.
We often identify ![]() $\mu \in \mathcal {P}$ with its extension to the pseudonorm on the space
$\mu \in \mathcal {P}$ with its extension to the pseudonorm on the space ![]() $c_{00}$: that is, the vector space over
$c_{00}$: that is, the vector space over ![]() $\mathbb {R}$ of all finitely supported sequences of real numbers.
$\mathbb {R}$ of all finitely supported sequences of real numbers.
For every ![]() $\mu \in \mathcal {P}$, we denote by
$\mu \in \mathcal {P}$, we denote by ![]() $X_{\mu }$ the Banach space given as the completion of the quotient space
$X_{\mu }$ the Banach space given as the completion of the quotient space ![]() $X/N$, where
$X/N$, where ![]() $X = (c_{00},\mu )$ and
$X = (c_{00},\mu )$ and ![]() $N = \{x\in c_{00}:\; \mu (x) = 0\}$. In what follows, we often consider V as a subspace of
$N = \{x\in c_{00}:\; \mu (x) = 0\}$. In what follows, we often consider V as a subspace of ![]() $X_{\mu }$: that is, we identify every
$X_{\mu }$: that is, we identify every ![]() $v\in V$ with its equivalence class
$v\in V$ with its equivalence class ![]() $[v]_{N}\in X_{\mu }$.
$[v]_{N}\in X_{\mu }$.
By ![]() $\mathcal {P}_{\infty }$, we denote the set of those
$\mathcal {P}_{\infty }$, we denote the set of those ![]() $\mu \in \mathcal {P}$ for which
$\mu \in \mathcal {P}$ for which ![]() $X_{\mu }$ is infinite-dimensional Banach space. As we did in [Reference Cúth, Doucha and Kurka11, Reference Cúth, Doucha and Kurka12], by
$X_{\mu }$ is infinite-dimensional Banach space. As we did in [Reference Cúth, Doucha and Kurka11, Reference Cúth, Doucha and Kurka12], by ![]() $\mathcal {B}$, we denote the set of those
$\mathcal {B}$, we denote the set of those ![]() $\mu \in \mathcal {P}_{\infty }$ for which the extension of
$\mu \in \mathcal {P}_{\infty }$ for which the extension of ![]() $\mu $ to
$\mu $ to ![]() $c_{00}$ is an actual norm: that is, the vectors
$c_{00}$ is an actual norm: that is, the vectors ![]() $ e_{1}, e_{2}, \dots $ are linearly independent in
$ e_{1}, e_{2}, \dots $ are linearly independent in ![]() $X_{\mu }$.
$X_{\mu }$.
We endow ![]() $\mathcal {P}_{\infty }$ and
$\mathcal {P}_{\infty }$ and ![]() $\mathcal {B}$ with the topologies inherited from
$\mathcal {B}$ with the topologies inherited from ![]() $\mathcal {P}$.
$\mathcal {P}$.
Our first aim is to show that the topologies on ![]() $\mathcal {P}_{\infty }$ and
$\mathcal {P}_{\infty }$ and ![]() $\mathcal {B}$ are Polish (see Corollary 2.5). This can be easily verified directly: here, we obtain it as a corollary of the fact that the relation
$\mathcal {B}$ are Polish (see Corollary 2.5). This can be easily verified directly: here, we obtain it as a corollary of the fact that the relation ![]() ${\stackrel {K}{\sim }}$ defined before is open in
${\stackrel {K}{\sim }}$ defined before is open in ![]() $\mathcal {P}$, a very useful fact that will prove important many times in the paper.
$\mathcal {P}$, a very useful fact that will prove important many times in the paper.
We need the following background first. Given a metric space ![]() $(M,d)$,
$(M,d)$, ![]() $\varepsilon>0$ and
$\varepsilon>0$ and ![]() $N,S\subseteq M$, we say that N is
$N,S\subseteq M$, we say that N is ![]() $\varepsilon $-dense for S if for every
$\varepsilon $-dense for S if for every ![]() $x\in S$ there is
$x\in S$ there is ![]() $y\in N$ with
$y\in N$ with ![]() $d(x,y)<\varepsilon $ (let us emphasize that we do not assume
$d(x,y)<\varepsilon $ (let us emphasize that we do not assume ![]() $N\subseteq S$). For further references, we recall the following well-known approximation lemma; for a proof, see for example [Reference Albiac and Kalton1, Lemma 12.1.11].
$N\subseteq S$). For further references, we recall the following well-known approximation lemma; for a proof, see for example [Reference Albiac and Kalton1, Lemma 12.1.11].
Lemma 2.2. There is a function ![]() $\phi _{1}:[0,1)\to [0,1)$ continuous at zero with
$\phi _{1}:[0,1)\to [0,1)$ continuous at zero with ![]() $\phi _{1}(0)=0$ such that whenever
$\phi _{1}(0)=0$ such that whenever ![]() $T:E\to X$ is a linear operator between Banach spaces,
$T:E\to X$ is a linear operator between Banach spaces, ![]() $\varepsilon \in (0,1)$,
$\varepsilon \in (0,1)$, ![]() $M\subseteq E$ is
$M\subseteq E$ is ![]() $\varepsilon $-dense for
$\varepsilon $-dense for ![]() $S_{E}$ and
$S_{E}$ and
then T is a ![]() $(1+\phi _{1}(\varepsilon ))$-isomorphism between E and
$(1+\phi _{1}(\varepsilon ))$-isomorphism between E and ![]() $T(E)$.
$T(E)$.
The following definition precises the notation ![]() ${\stackrel {K}{\sim }}$ defined in the introduction.
${\stackrel {K}{\sim }}$ defined in the introduction.
Definition 2.3. If ![]() $v_{1},\ldots ,v_{n}\in V$ are given, for
$v_{1},\ldots ,v_{n}\in V$ are given, for ![]() $\mu \in \mathcal {P}$, instead of
$\mu \in \mathcal {P}$, instead of  $(X_{\mu },v_{1},\ldots ,v_{n}){\stackrel {K}{\sim } X}$, we shall write
$(X_{\mu },v_{1},\ldots ,v_{n}){\stackrel {K}{\sim } X}$, we shall write  $(\mu ,v_{1},\ldots ,v_{n}){\stackrel {K}{\sim } X}$.
$(\mu ,v_{1},\ldots ,v_{n}){\stackrel {K}{\sim } X}$.
Lemma 2.4. Let X be a Banach space with ![]() $\{x_{1},\ldots ,x_{n}\}\subseteq X$ linearly independent, and let
$\{x_{1},\ldots ,x_{n}\}\subseteq X$ linearly independent, and let ![]() $v_{1},\ldots ,v_{n}\in V$. Then for any
$v_{1},\ldots ,v_{n}\in V$. Then for any ![]() $K>1$, the set
$K>1$, the set
 $$ \begin{align*} \mathcal{N}((x_{i})_{i},K,(v_{i})_{i})=\{\mu\in \mathcal{P}\colon (\mu,v_{1},\ldots,v_{n}){\stackrel{K}{\sim} (X,x_{1},\ldots,x_{n})} \}\end{align*} $$
$$ \begin{align*} \mathcal{N}((x_{i})_{i},K,(v_{i})_{i})=\{\mu\in \mathcal{P}\colon (\mu,v_{1},\ldots,v_{n}){\stackrel{K}{\sim} (X,x_{1},\ldots,x_{n})} \}\end{align*} $$is open in ![]() $\mathcal {P}$.
$\mathcal {P}$.
In particular, the set of those ![]() $\mu \in \mathcal {P}$ for which the set
$\mu \in \mathcal {P}$ for which the set ![]() $\{v_{1},\ldots ,v_{n}\}$ is linearly independent in
$\{v_{1},\ldots ,v_{n}\}$ is linearly independent in ![]() $X_{\mu }$ is open in
$X_{\mu }$ is open in ![]() $\mathcal {P}$.
$\mathcal {P}$.
Proof. Pick some ![]() $\mu \in \mathcal {N}((x_{i})_{i},K,(v_{i})_{i})$. By definition, the linear map T sending
$\mu \in \mathcal {N}((x_{i})_{i},K,(v_{i})_{i})$. By definition, the linear map T sending ![]() $v_{i}$ to
$v_{i}$ to ![]() $x_{i}\in X$,
$x_{i}\in X$, ![]() $i\leq n$, is a linear isomorphism satisfying
$i\leq n$, is a linear isomorphism satisfying ![]() $\max \{\|T\|,\|T^{-1}\|\}<L$ for some
$\max \{\|T\|,\|T^{-1}\|\}<L$ for some ![]() $L<K$. Let
$L<K$. Let ![]() $\phi _{1}$ be the function provided by Lemma 2.2, and pick
$\phi _{1}$ be the function provided by Lemma 2.2, and pick ![]() $\varepsilon>0$ such that
$\varepsilon>0$ such that ![]() $L(1 + \phi _{1}(2\varepsilon ))<K$. Let
$L(1 + \phi _{1}(2\varepsilon ))<K$. Let ![]() $N\subseteq V$ be a finite
$N\subseteq V$ be a finite ![]() $\varepsilon $-dense set for the sphere of
$\varepsilon $-dense set for the sphere of ![]() $\operatorname {span}\{v_{1},\ldots ,v_{n}\}\subseteq X_{\mu }$ such that
$\operatorname {span}\{v_{1},\ldots ,v_{n}\}\subseteq X_{\mu }$ such that ![]() $\mu (v)\in (1-\varepsilon ,1+\varepsilon )$ for every
$\mu (v)\in (1-\varepsilon ,1+\varepsilon )$ for every ![]() $v\in N$. Then
$v\in N$. Then
is an open neighborhood of ![]() $\mu $, and
$\mu $, and ![]() $U\subseteq \mathcal {N}((x_{i})_{i},K,(v_{i})_{i})$. Indeed, for any
$U\subseteq \mathcal {N}((x_{i})_{i},K,(v_{i})_{i})$. Indeed, for any ![]() $\nu \in U$, we have that
$\nu \in U$, we have that ![]() $id:(\operatorname {span}\{v_{1},\ldots ,v_{n}\},\mu )\to (\operatorname {span}\{v_{1},\ldots ,v_{n}\},\nu )$ is a
$id:(\operatorname {span}\{v_{1},\ldots ,v_{n}\},\mu )\to (\operatorname {span}\{v_{1},\ldots ,v_{n}\},\nu )$ is a ![]() $(1+\phi _{1}(2\varepsilon ))$-isomorphism; hence, the linear map T considered as a map between
$(1+\phi _{1}(2\varepsilon ))$-isomorphism; hence, the linear map T considered as a map between ![]() $(\operatorname {span}\{v_{1},\ldots ,v_{n}\},\nu )$, and
$(\operatorname {span}\{v_{1},\ldots ,v_{n}\},\nu )$, and ![]() $\operatorname {span}\{x_{1},\ldots ,x_{n}\}$ satisfies
$\operatorname {span}\{x_{1},\ldots ,x_{n}\}$ satisfies ![]() $\|T\|<L(1 + \phi _{1}(2\varepsilon ))<K$, and similarly
$\|T\|<L(1 + \phi _{1}(2\varepsilon ))<K$, and similarly ![]() $\|T^{-1}\|<K$; hence,
$\|T^{-1}\|<K$; hence, ![]() $\nu \in \mathcal {N}((x_{i})_{i},K,(v_{i})_{i})$.
$\nu \in \mathcal {N}((x_{i})_{i},K,(v_{i})_{i})$.
The ‘In particular’ part easily follows, because ![]() $v_{1},\ldots ,v_{n}\in V$ are linearly independent if and only if there exists
$v_{1},\ldots ,v_{n}\in V$ are linearly independent if and only if there exists ![]() $K>1$ with
$K>1$ with  $(\mu ,v_{1},\ldots ,v_{n}){\stackrel {K}{\sim } \ell _{1}^{n}}$.
$(\mu ,v_{1},\ldots ,v_{n}){\stackrel {K}{\sim } \ell _{1}^{n}}$.
Corollary 2.5. Both ![]() $\mathcal {P}_{\infty }$ and
$\mathcal {P}_{\infty }$ and ![]() $\mathcal {B}$ are
$\mathcal {B}$ are ![]() $G_{\delta }$-sets in
$G_{\delta }$-sets in ![]() $\mathcal {P}$.
$\mathcal {P}$.
Since we are interested mainly in subsets of ![]() $\mathcal {P}$ closed under isometries, we introduce the following notation.
$\mathcal {P}$ closed under isometries, we introduce the following notation.
Notation 2.6. Let Z be a separable Banach space, and let ![]() $\mathcal {I}$ be a subset of
$\mathcal {I}$ be a subset of ![]() $\mathcal {P}$. We put
$\mathcal {P}$. We put
 $$ \begin{align*} {\langle Z\rangle_{\equiv}^{\mathcal{I}}} :=\{\mu\in\mathcal{I}:\; X_{\mu}\equiv Z\} \quad \text{and} \quad {\langle Z\rangle_{\simeq}^{\mathcal{I}}} :=\{\mu\in\mathcal{I}:\; X_{\mu}\simeq Z\}. \end{align*} $$
$$ \begin{align*} {\langle Z\rangle_{\equiv}^{\mathcal{I}}} :=\{\mu\in\mathcal{I}:\; X_{\mu}\equiv Z\} \quad \text{and} \quad {\langle Z\rangle_{\simeq}^{\mathcal{I}}} :=\{\mu\in\mathcal{I}:\; X_{\mu}\simeq Z\}. \end{align*} $$If ![]() $\mathcal {I}$ is clear from the context, we write
$\mathcal {I}$ is clear from the context, we write ![]() ${\langle Z\rangle _{\equiv }}$ and
${\langle Z\rangle _{\equiv }}$ and ![]() ${\langle Z\rangle _{\simeq }}$ instead of
${\langle Z\rangle _{\simeq }}$ instead of ![]() ${\langle Z\rangle _{\equiv }^{\mathcal {I}}}$ and
${\langle Z\rangle _{\equiv }^{\mathcal {I}}}$ and ![]() ${\langle Z\rangle _{\simeq }^{\mathcal {I}}}$, respectively.
${\langle Z\rangle _{\simeq }^{\mathcal {I}}}$, respectively.
The important feature of the topology of the spaces ![]() $\mathcal {P}$,
$\mathcal {P}$, ![]() $\mathcal {P}_{\infty }$ and
$\mathcal {P}_{\infty }$ and ![]() $\mathcal {B}$ is that basic open neighborhoods are defined using finite data: that is, finitely many vectors. That suggests that the topological properties of the aforementioned spaces should be closely related to the local theory of Banach spaces. This is certainly a point that could be investigated further in future research. Here we just observe how topological closures are related to finite representability; see Proposition 2.9. In order to formulate our results, let us consider the following generalization of the classical notion of finite representability.
$\mathcal {B}$ is that basic open neighborhoods are defined using finite data: that is, finitely many vectors. That suggests that the topological properties of the aforementioned spaces should be closely related to the local theory of Banach spaces. This is certainly a point that could be investigated further in future research. Here we just observe how topological closures are related to finite representability; see Proposition 2.9. In order to formulate our results, let us consider the following generalization of the classical notion of finite representability.
Definition 2.7. Let ![]() $\mathcal {F}\; $ be a family of Banach spaces. We say that a Banach space X is finitely representable in
$\mathcal {F}\; $ be a family of Banach spaces. We say that a Banach space X is finitely representable in ![]() $\mathcal {F}$ if, given any finite-dimensional subspace E of X and any
$\mathcal {F}$ if, given any finite-dimensional subspace E of X and any ![]() $\varepsilon> 0$, there exists a finite-dimensional subspace F of some
$\varepsilon> 0$, there exists a finite-dimensional subspace F of some ![]() $Y\in \mathcal {F}$ that is
$Y\in \mathcal {F}$ that is ![]() $(1+\varepsilon )$-isomorphic to E.
$(1+\varepsilon )$-isomorphic to E.
If the family ![]() $\mathcal {F}$ consists of one Banach space Y only, we say that X is finitely representable in Y rather than in
$\mathcal {F}$ consists of one Banach space Y only, we say that X is finitely representable in Y rather than in ![]() $\{Y\}$.
$\{Y\}$.
If ![]() $\mathcal {F}\subseteq \mathcal {P}$, by saying that X is finitely representable in
$\mathcal {F}\subseteq \mathcal {P}$, by saying that X is finitely representable in ![]() $\mathcal {F}$, we mean it is finitely representable in
$\mathcal {F}$, we mean it is finitely representable in ![]() $\{X_{\mu }:\; \mu \in \mathcal {F}\}$.
$\{X_{\mu }:\; \mu \in \mathcal {F}\}$.
The following is an easy observation that we will use further; the proof follows, for example, immediately from [Reference Albiac and Kalton1, Lemma 12.1.7] in the case that ![]() $\mathcal {F}$ contains one Banach space only. For the more general situation, the proof is analogous.
$\mathcal {F}$ contains one Banach space only. For the more general situation, the proof is analogous.
Lemma 2.8. Let ![]() $\mathcal {F}$ be a family of infinite-dimensional Banach spaces and
$\mathcal {F}$ be a family of infinite-dimensional Banach spaces and ![]() $\mu \in \mathcal {P}_{\infty }$. Let
$\mu \in \mathcal {P}_{\infty }$. Let ![]() $\{k(n)\}_{n=1}^{\infty }$ be a sequence such that
$\{k(n)\}_{n=1}^{\infty }$ be a sequence such that ![]() $\{e_{k(n)}:\; n\in \mathbb {N}\}$ is a linearly independent set in
$\{e_{k(n)}:\; n\in \mathbb {N}\}$ is a linearly independent set in ![]() $X_{\mu }$ and
$X_{\mu }$ and ![]() $\overline {\operatorname {span}}\{e_{k(n)}:\; n\in \mathbb {N}\}=X_{\mu }$. Then
$\overline {\operatorname {span}}\{e_{k(n)}:\; n\in \mathbb {N}\}=X_{\mu }$. Then ![]() $X_{\mu }$ is finitely representable in
$X_{\mu }$ is finitely representable in ![]() $\mathcal {F}$ if and only if for every
$\mathcal {F}$ if and only if for every ![]() $n\in \mathbb {N}$ and
$n\in \mathbb {N}$ and ![]() $\varepsilon>0$, there exists a finite-dimensional subspace F of some
$\varepsilon>0$, there exists a finite-dimensional subspace F of some ![]() $Y\in \mathcal {F}$ that is
$Y\in \mathcal {F}$ that is ![]() $(1+\varepsilon )$-isomorphic to
$(1+\varepsilon )$-isomorphic to ![]() $(\operatorname {span}\{e_{k(1)},\ldots ,e_{k(n)}\},\mu )$.
$(\operatorname {span}\{e_{k(1)},\ldots ,e_{k(n)}\},\mu )$.
Proposition 2.9. Let ![]() $\mathcal {F}\subseteq \mathcal {B}$ be such that
$\mathcal {F}\subseteq \mathcal {B}$ be such that ![]() ${\langle X_{\mu }\rangle _{\equiv }^{\mathcal {B}}}\subseteq \mathcal {F}$ for every
${\langle X_{\mu }\rangle _{\equiv }^{\mathcal {B}}}\subseteq \mathcal {F}$ for every ![]() $\mu \in \mathcal {F}$. Then
$\mu \in \mathcal {F}$. Then
The same holds if we replace ![]() $\mathcal {B}$ with
$\mathcal {B}$ with ![]() $\mathcal {P}_{\infty }$ or
$\mathcal {P}_{\infty }$ or ![]() $\mathcal {P}$.
$\mathcal {P}$.
In particular, if X is a separable infinite-dimensional Banach space, then
 $$ \begin{align*}\{\nu\in\mathcal{B}:\; X_{\nu}\text{ is finitely representable in }X\} = \overline{{\langle X\rangle_{\equiv}^{\mathcal{B}}}}\cap\mathcal{B},\end{align*} $$
$$ \begin{align*}\{\nu\in\mathcal{B}:\; X_{\nu}\text{ is finitely representable in }X\} = \overline{{\langle X\rangle_{\equiv}^{\mathcal{B}}}}\cap\mathcal{B},\end{align*} $$and similarly also if we replace ![]() $\mathcal {B}$ with
$\mathcal {B}$ with ![]() $\mathcal {P}_{\infty }$ or with
$\mathcal {P}_{\infty }$ or with ![]() $\mathcal {P}$.
$\mathcal {P}$.
Proof. ‘![]() $\subseteq $’: Fix
$\subseteq $’: Fix ![]() $\nu \in \mathcal {B}$ such that
$\nu \in \mathcal {B}$ such that ![]() $X_{\nu }$ is finitely representable in
$X_{\nu }$ is finitely representable in ![]() $\mathcal {F}$. Pick
$\mathcal {F}$. Pick ![]() $v_{1},\ldots ,v_{n}\in V$ and
$v_{1},\ldots ,v_{n}\in V$ and ![]() $\varepsilon>0$. We shall show there is
$\varepsilon>0$. We shall show there is ![]() $\mu _{0}\in \mathcal {F}$ with
$\mu _{0}\in \mathcal {F}$ with ![]() $|\mu _{0}(v_{i})-\nu (v_{i})|<\varepsilon $,
$|\mu _{0}(v_{i})-\nu (v_{i})|<\varepsilon $, ![]() $i\leq n$. Let
$i\leq n$. Let ![]() $m\in \mathbb {N}$ be such that
$m\in \mathbb {N}$ be such that ![]() $\{v_{1},\ldots ,v_{n}\}\subseteq \operatorname {span}_{\mathbb {Q}}\{e_{j}:\; j\leq m\}$. Put
$\{v_{1},\ldots ,v_{n}\}\subseteq \operatorname {span}_{\mathbb {Q}}\{e_{j}:\; j\leq m\}$. Put ![]() $C:=\max \{\nu (v_{i}):\; i=1,\ldots ,n\}$ and
$C:=\max \{\nu (v_{i}):\; i=1,\ldots ,n\}$ and ![]() $Z:=\operatorname {span} \{e_{1},\ldots ,e_{m}\}\subseteq X_{\nu }$. Since
$Z:=\operatorname {span} \{e_{1},\ldots ,e_{m}\}\subseteq X_{\nu }$. Since ![]() $X_{\nu }$ is finitely representable in
$X_{\nu }$ is finitely representable in ![]() $\mathcal {F}$, there is
$\mathcal {F}$, there is ![]() $\mu \in \mathcal {F}$ and a
$\mu \in \mathcal {F}$ and a ![]() $(1+\tfrac {\varepsilon }{2C})$-isomorphism
$(1+\tfrac {\varepsilon }{2C})$-isomorphism ![]() $T:Z\to X_{\mu }$. Set
$T:Z\to X_{\mu }$. Set ![]() $x_{i}:=T(e_{i})$,
$x_{i}:=T(e_{i})$, ![]() $i\leq m$, and extend
$i\leq m$, and extend ![]() $x_{1},\ldots ,x_{m}$ to a linearly independent sequence
$x_{1},\ldots ,x_{m}$ to a linearly independent sequence ![]() $(x_{i})_{i=1}^{\infty }$ whose span is dense in
$(x_{i})_{i=1}^{\infty }$ whose span is dense in ![]() $X_{\mu }$. Consider
$X_{\mu }$. Consider ![]() $\mu _{0}\in \mathcal {P}$ given by setting
$\mu _{0}\in \mathcal {P}$ given by setting ![]() $\mu _{0}(\sum _{i\in I} \alpha _{i} e_{i})=\mu (\sum _{i\in I} \alpha _{i} x_{i})$, where
$\mu _{0}(\sum _{i\in I} \alpha _{i} e_{i})=\mu (\sum _{i\in I} \alpha _{i} x_{i})$, where ![]() $I\subseteq \mathbb {N}$ is finite and
$I\subseteq \mathbb {N}$ is finite and ![]() $(\alpha _{i})_{i\in I}\subseteq \mathbb {Q}$. Clearly,
$(\alpha _{i})_{i\in I}\subseteq \mathbb {Q}$. Clearly, ![]() $X_{\mu _{0}}\equiv X_{\mu }$ and
$X_{\mu _{0}}\equiv X_{\mu }$ and ![]() $\mu _{0}\in \mathcal {B}$, so
$\mu _{0}\in \mathcal {B}$, so ![]() $\mu _{0}\in \mathcal {F}$. Finally, for every
$\mu _{0}\in \mathcal {F}$. Finally, for every ![]() $i\leq n$, we have
$i\leq n$, we have  $v_{i} = \sum _{j=1}^{m} \alpha _{j} e_{j}$ for some
$v_{i} = \sum _{j=1}^{m} \alpha _{j} e_{j}$ for some ![]() $(\alpha _{j})\in \mathbb {R}^{m}$, and so we have
$(\alpha _{j})\in \mathbb {R}^{m}$, and so we have
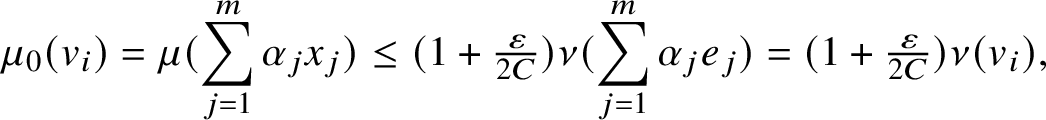 $$ \begin{align*}\mu_{0}(v_{i}) = \mu(\sum_{j=1}^{m} \alpha_{j} x_{j})\leq (1+\tfrac{\varepsilon}{2C})\nu(\sum_{j=1}^{m} \alpha_{j} e_{j}) = (1+\tfrac{\varepsilon}{2C})\nu(v_{i}),\end{align*} $$
$$ \begin{align*}\mu_{0}(v_{i}) = \mu(\sum_{j=1}^{m} \alpha_{j} x_{j})\leq (1+\tfrac{\varepsilon}{2C})\nu(\sum_{j=1}^{m} \alpha_{j} e_{j}) = (1+\tfrac{\varepsilon}{2C})\nu(v_{i}),\end{align*} $$and similarly  $\mu _{0}(v_{i})\geq (1+\tfrac {\varepsilon }{2C})^{-1}\nu (v_{i})\geq (1-\tfrac {\varepsilon }{2C})\nu (v_{i})$. Thus,
$\mu _{0}(v_{i})\geq (1+\tfrac {\varepsilon }{2C})^{-1}\nu (v_{i})\geq (1-\tfrac {\varepsilon }{2C})\nu (v_{i})$. Thus, ![]() $|\mu _{0}(v_{i}) - \nu (v_{i})|\leq \tfrac {\varepsilon }{2}<\varepsilon $ for every
$|\mu _{0}(v_{i}) - \nu (v_{i})|\leq \tfrac {\varepsilon }{2}<\varepsilon $ for every ![]() $i\leq n$.
$i\leq n$.
The case when we replace ![]() $\mathcal {B}$ with
$\mathcal {B}$ with ![]() $\mathcal {P}_{\infty }$ or
$\mathcal {P}_{\infty }$ or ![]() $\mathcal {P}$ is analogous; this time, we do not require
$\mathcal {P}$ is analogous; this time, we do not require ![]() $(x_{i})_{i=1}^{\infty }$ to be linearly independent.
$(x_{i})_{i=1}^{\infty }$ to be linearly independent.
‘![]() $\supseteq $’: Fix
$\supseteq $’: Fix ![]() $\nu \in \overline {\mathcal {F}}\cap \mathcal {B}$. In order to see that
$\nu \in \overline {\mathcal {F}}\cap \mathcal {B}$. In order to see that ![]() $X_{\nu }$ is finitely representable in
$X_{\nu }$ is finitely representable in ![]() $\mathcal {F}$, we will use Lemma 2.8. Pick
$\mathcal {F}$, we will use Lemma 2.8. Pick ![]() $n\in \mathbb {N}$ and
$n\in \mathbb {N}$ and ![]() $\varepsilon>0$. Let
$\varepsilon>0$. Let ![]() $\phi _{1}$ be the function from Lemma 2.2, let
$\phi _{1}$ be the function from Lemma 2.2, let ![]() $\delta>0$ be such that
$\delta>0$ be such that ![]() $\phi _{1}(2\delta )<\varepsilon $ and let
$\phi _{1}(2\delta )<\varepsilon $ and let ![]() $N\subseteq V$ be a finite set that is
$N\subseteq V$ be a finite set that is ![]() $\delta $-dense for the sphere of
$\delta $-dense for the sphere of ![]() $(\operatorname {span}\{e_{1},\ldots ,e_{n}\},\nu )$ and
$(\operatorname {span}\{e_{1},\ldots ,e_{n}\},\nu )$ and ![]() $\nu (v)\in (1-\delta ,1+\delta )$ for every
$\nu (v)\in (1-\delta ,1+\delta )$ for every ![]() $v\in N$. Pick
$v\in N$. Pick ![]() $\mu \in \mathcal {F}$ such that
$\mu \in \mathcal {F}$ such that ![]() $|\mu (v)-\nu (v)|<\delta $,
$|\mu (v)-\nu (v)|<\delta $, ![]() $v\in N$. Then
$v\in N$. Then ![]() $id:(\operatorname {span}\{e_{1},\ldots ,e_{n}\},\nu )\to (\operatorname {span}\{e_{1},\ldots ,e_{n}\},\mu )$ is a
$id:(\operatorname {span}\{e_{1},\ldots ,e_{n}\},\nu )\to (\operatorname {span}\{e_{1},\ldots ,e_{n}\},\mu )$ is a ![]() $(1+\phi _{1}(2\delta ))$-isomorphism. Thus,
$(1+\phi _{1}(2\delta ))$-isomorphism. Thus, ![]() $X_{\nu }$ is finitely representable in
$X_{\nu }$ is finitely representable in ![]() $\mathcal {F}$. The case when we replace
$\mathcal {F}$. The case when we replace ![]() $\mathcal {B}$ with
$\mathcal {B}$ with ![]() $\mathcal {P}_{\infty }$ or
$\mathcal {P}_{\infty }$ or ![]() $\mathcal {P}$ is similar.
$\mathcal {P}$ is similar.
This result has interesting consequences.
Corollary 2.10. Let X be a separable Banach space such that every Banach space is finitely representable in X. Then its isometry class is dense (in ![]() $\mathcal {P}$,
$\mathcal {P}$, ![]() $\mathcal {P}_{\infty }$ and also in
$\mathcal {P}_{\infty }$ and also in ![]() $\mathcal {B}$).
$\mathcal {B}$).
Proof. Follows immediately from Proposition 2.9.
Corollary 2.11. Let X be a separable infinite-dimensional Banach space. Then  ${\langle \ell _{2}\rangle _{\equiv }^{\mathcal {B}}}\subseteq \overline {{\langle \mathcal {B}\rangle _{\equiv }^{X}}}\cap \mathcal {B}$. The same holds if we replace
${\langle \ell _{2}\rangle _{\equiv }^{\mathcal {B}}}\subseteq \overline {{\langle \mathcal {B}\rangle _{\equiv }^{X}}}\cap \mathcal {B}$. The same holds if we replace ![]() $\mathcal {B}$ with
$\mathcal {B}$ with ![]() $\mathcal {P}_{\infty }$ or
$\mathcal {P}_{\infty }$ or ![]() $\mathcal {P}$.
$\mathcal {P}$.
Proof. By the Dvoretzky theorem, ![]() $\ell _{2}$ is finitely representable in every separable infinite-dimensional Banach space (see, e.g., [Reference Albiac and Kalton1, Theorem 13.3.7]). So we are done by applying Proposition 2.9.
$\ell _{2}$ is finitely representable in every separable infinite-dimensional Banach space (see, e.g., [Reference Albiac and Kalton1, Theorem 13.3.7]). So we are done by applying Proposition 2.9.
We conclude this subsection by showing another nice feature of the above topologies on examples. We can show that the natural maps ![]() $K\mapsto C(K)$ and
$K\mapsto C(K)$ and ![]() $\lambda \mapsto L_{p}(\lambda )$, where K is a compact metrizable space, and
$\lambda \mapsto L_{p}(\lambda )$, where K is a compact metrizable space, and ![]() $\lambda $ is a Borel probability measure on a fixed compact metric space, are continuous.
$\lambda $ is a Borel probability measure on a fixed compact metric space, are continuous.
Example 2.12. (a) Let ![]() $\mathcal K([0,1]^{\mathbb {N}})$ denote the space of all compact subsets of the Hilbert cube
$\mathcal K([0,1]^{\mathbb {N}})$ denote the space of all compact subsets of the Hilbert cube ![]() $[0,1]^{\mathbb {N}}$ endowed with the Vietoris topology. Then there exists a continuous mapping
$[0,1]^{\mathbb {N}}$ endowed with the Vietoris topology. Then there exists a continuous mapping ![]() $\rho \colon \mathcal K([0,1]^{\mathbb {N}})\rightarrow \mathcal P$ such that
$\rho \colon \mathcal K([0,1]^{\mathbb {N}})\rightarrow \mathcal P$ such that ![]() $X_{\rho (K)}\equiv C(K)$ for every
$X_{\rho (K)}\equiv C(K)$ for every ![]() $K\in \mathcal K([0,1]^{\mathbb {N}})$.
$K\in \mathcal K([0,1]^{\mathbb {N}})$.
(b) Let L be a compact metric space, let ![]() $p\in [1,\infty )$ be fixed, and let
$p\in [1,\infty )$ be fixed, and let ![]() ${\mathcal Prob}(L)$ denote the space of all Borel probability measures on L endowed with the weak* topology (generated by elements of the Banach space
${\mathcal Prob}(L)$ denote the space of all Borel probability measures on L endowed with the weak* topology (generated by elements of the Banach space ![]() $C(L)$). Then there exists a continuous mapping
$C(L)$). Then there exists a continuous mapping ![]() $\sigma \colon {\mathcal Prob}(L)\rightarrow \mathcal P$ such that
$\sigma \colon {\mathcal Prob}(L)\rightarrow \mathcal P$ such that ![]() $X_{\sigma (\lambda )}\equiv L_{p}(\lambda )$ for every
$X_{\sigma (\lambda )}\equiv L_{p}(\lambda )$ for every ![]() $\lambda \in {\mathcal Prob}(L)$.
$\lambda \in {\mathcal Prob}(L)$.
Proof. (a) Let ![]() $\{f_{i}\colon i\in \mathbb N\}$ be a linearly dense subset of
$\{f_{i}\colon i\in \mathbb N\}$ be a linearly dense subset of ![]() $C([0,1]^{\mathbb {N}})$. For every compact subset K of
$C([0,1]^{\mathbb {N}})$. For every compact subset K of ![]() $[0,1]^{\mathbb {N}}$, we define
$[0,1]^{\mathbb {N}}$, we define ![]() $\rho (K)\in \mathcal P$ by
$\rho (K)\in \mathcal P$ by
 $$ \begin{align*}\rho(K)\left(\sum_{i=1}^{n}r_{i}e_{i}\right)=\sup_{x\in K}\left|\sum_{i=1}^{n}r_{i}f_{i}(x)\right|, \qquad \sum_{i=1}^{n}r_{i}e_{i}\in V.\end{align*} $$
$$ \begin{align*}\rho(K)\left(\sum_{i=1}^{n}r_{i}e_{i}\right)=\sup_{x\in K}\left|\sum_{i=1}^{n}r_{i}f_{i}(x)\right|, \qquad \sum_{i=1}^{n}r_{i}e_{i}\in V.\end{align*} $$It is clear that ![]() $X_{\rho (K)}\equiv C(K)$, so we only need to check the continuity of
$X_{\rho (K)}\equiv C(K)$, so we only need to check the continuity of ![]() $\rho $. It is enough to show that
$\rho $. It is enough to show that ![]() $\rho ^{-1}(U[v,I])$ is an open subset of
$\rho ^{-1}(U[v,I])$ is an open subset of ![]() $\mathcal K([0,1]^{\mathbb {N}})$ for every
$\mathcal K([0,1]^{\mathbb {N}})$ for every ![]() $v\in V$ and every open interval I (recall that
$v\in V$ and every open interval I (recall that ![]() $U[v,I]=\{\mu \in \mathcal P\colon \mu (v)\in I\}$). So let us fix
$U[v,I]=\{\mu \in \mathcal P\colon \mu (v)\in I\}$). So let us fix ![]() $\widetilde K\in \rho ^{-1}(U[v,I])$, and assume that
$\widetilde K\in \rho ^{-1}(U[v,I])$, and assume that ![]() $v=\sum _{i=1}^{n}r_{i}e_{i}$. Fix
$v=\sum _{i=1}^{n}r_{i}e_{i}$. Fix ![]() $x_{0}\in \widetilde K$ such that
$x_{0}\in \widetilde K$ such that
 $$ \begin{align*}\left|\sum_{i=1}^{n}r_{i}f_{i}(x_{0})\right|=\sup_{x\in\widetilde K}\left|\sum_{i=1}^{n}r_{i}f_{i}(x)\right|.\end{align*} $$
$$ \begin{align*}\left|\sum_{i=1}^{n}r_{i}f_{i}(x_{0})\right|=\sup_{x\in\widetilde K}\left|\sum_{i=1}^{n}r_{i}f_{i}(x)\right|.\end{align*} $$Also fix ![]() $\varepsilon>0$ such that both numbers
$\varepsilon>0$ such that both numbers  $\left |\sum _{i=1}^{n}r_{i}f_{i}(x_{0})\right |\pm \varepsilon $ belong to I. Now find open subsets
$\left |\sum _{i=1}^{n}r_{i}f_{i}(x_{0})\right |\pm \varepsilon $ belong to I. Now find open subsets ![]() $U,V$ of
$U,V$ of ![]() $[0,1]^{\mathbb {N}}$ such that
$[0,1]^{\mathbb {N}}$ such that ![]() $x_{0}\in U$ and
$x_{0}\in U$ and ![]() $\widetilde K\subseteq V$ and such that
$\widetilde K\subseteq V$ and such that
 $$ \begin{align*}\inf_{x\in U}\left|\sum_{i=1}^{n}r_{i}f_{i}(x)\right|>\left|\sum_{i=1}^{n}r_{i}f_{i}(x_{0})\right|-\varepsilon\end{align*} $$
$$ \begin{align*}\inf_{x\in U}\left|\sum_{i=1}^{n}r_{i}f_{i}(x)\right|>\left|\sum_{i=1}^{n}r_{i}f_{i}(x_{0})\right|-\varepsilon\end{align*} $$and
 $$ \begin{align*}\sup_{x\in V}\left|\sum_{i=1}^{n}r_{i}f_{i}(x)\right|<\sup_{x\in\widetilde K}\left|\sum_{i=1}^{n}r_{i}f_{i}(x)\right|+\varepsilon.\end{align*} $$
$$ \begin{align*}\sup_{x\in V}\left|\sum_{i=1}^{n}r_{i}f_{i}(x)\right|<\sup_{x\in\widetilde K}\left|\sum_{i=1}^{n}r_{i}f_{i}(x)\right|+\varepsilon.\end{align*} $$Then
is an open neighborhood of ![]() $\widetilde K$ such that
$\widetilde K$ such that ![]() $\rho (\mathcal U)\subseteq U[v,I]$.
$\rho (\mathcal U)\subseteq U[v,I]$.
(b) This is similar to (a) but even easier. Let ![]() $\{g_{i}\colon i\in \mathbb N\}$ be a linearly dense subset of
$\{g_{i}\colon i\in \mathbb N\}$ be a linearly dense subset of ![]() $C(L)$. For every Borel probability measure
$C(L)$. For every Borel probability measure ![]() $\lambda $ on L, we define
$\lambda $ on L, we define ![]() $\sigma (\lambda )\in \mathcal P$ by
$\sigma (\lambda )\in \mathcal P$ by
 $$ \begin{align*}\sigma(\lambda)\left(\sum_{i=1}^{n}r_{i}e_{i}\right)=\left(\int\limits_{L}\left|\sum_{i=1}^{n}r_{i}g_{i}\right|{}^{p}\,d\lambda\right)^{\frac 1p}, \qquad \sum_{i=1}^{n}r_{i}e_{i}\in V.\end{align*} $$
$$ \begin{align*}\sigma(\lambda)\left(\sum_{i=1}^{n}r_{i}e_{i}\right)=\left(\int\limits_{L}\left|\sum_{i=1}^{n}r_{i}g_{i}\right|{}^{p}\,d\lambda\right)^{\frac 1p}, \qquad \sum_{i=1}^{n}r_{i}e_{i}\in V.\end{align*} $$It is clear that ![]() $X_{\sigma (\lambda )}\equiv L_{p}(\lambda )$, so we only need to check the continuity of
$X_{\sigma (\lambda )}\equiv L_{p}(\lambda )$, so we only need to check the continuity of ![]() $\sigma $. It is enough to show that
$\sigma $. It is enough to show that ![]() $\sigma ^{-1}(U[v,I])$ is an open subset of
$\sigma ^{-1}(U[v,I])$ is an open subset of ![]() ${\mathcal Prob}(L)$ for every
${\mathcal Prob}(L)$ for every ![]() $v\in V$ and every open interval I. But this is clear as, for
$v\in V$ and every open interval I. But this is clear as, for ![]() $v=\sum _{i=1}^{n}r_{i}e_{i}$, we have
$v=\sum _{i=1}^{n}r_{i}e_{i}$, we have
 $$ \begin{align*}\sigma^{-1}(U[v,I])=\left\{\lambda\in{\mathcal Prob}(L)\colon\left(\int\limits_{L}\left|\sum_{i=1}^{n}r_{i}g_{i}\right|{}^{p}\,d\lambda\right)^{\frac 1p}\in I\right\}.\\[-52pt]\end{align*} $$
$$ \begin{align*}\sigma^{-1}(U[v,I])=\left\{\lambda\in{\mathcal Prob}(L)\colon\left(\int\limits_{L}\left|\sum_{i=1}^{n}r_{i}g_{i}\right|{}^{p}\,d\lambda\right)^{\frac 1p}\in I\right\}.\\[-52pt]\end{align*} $$Remark 2.13. After the introduction of the spaces ![]() $\mathcal {P}$,
$\mathcal {P}$, ![]() $\mathcal {P}_{\infty }$ and
$\mathcal {P}_{\infty }$ and ![]() $\mathcal {B}$, one faces the question of which of them is ‘the right one’ with which to work. For now, we leave the question undecided. Since we are mainly interested in infinite-dimensional Banach spaces, we prefer to work mainly with
$\mathcal {B}$, one faces the question of which of them is ‘the right one’ with which to work. For now, we leave the question undecided. Since we are mainly interested in infinite-dimensional Banach spaces, we prefer to work mainly with ![]() $\mathcal {P}_{\infty }$ and
$\mathcal {P}_{\infty }$ and ![]() $\mathcal {B}$. On the other hand, it turns out that at least as far as one wants to transfer some computations performed in the space of pseudonorms directly to admissible topologies, the space
$\mathcal {B}$. On the other hand, it turns out that at least as far as one wants to transfer some computations performed in the space of pseudonorms directly to admissible topologies, the space ![]() $\mathcal {P}$ is useful: Theorem 3.3 below shows that whatever we compute in the space
$\mathcal {P}$ is useful: Theorem 3.3 below shows that whatever we compute in the space ![]() $\mathcal {P}$ also holds true in any admissible topology.
$\mathcal {P}$ also holds true in any admissible topology.
Regarding ![]() $\mathcal {P}_{\infty }$ and
$\mathcal {P}_{\infty }$ and ![]() $\mathcal {B}$, in most of the arguments, it makes no difference whether we are working with the former or the latter space. However, there are a few exceptions when it seems to be convenient to work with the assumption that the sequence of vectors
$\mathcal {B}$, in most of the arguments, it makes no difference whether we are working with the former or the latter space. However, there are a few exceptions when it seems to be convenient to work with the assumption that the sequence of vectors ![]() $\langle e_{n}\colon n\in \mathbb {N}\rangle \subseteq V$ is linearly independent, and then it might be more natural to work with
$\langle e_{n}\colon n\in \mathbb {N}\rangle \subseteq V$ is linearly independent, and then it might be more natural to work with ![]() $\mathcal {B}$.
$\mathcal {B}$.
3 Choice of the Polish space of separable Banach spaces
The main outcome of this section is Theorem A (denoted here as Theorem 3.11). We also prove partial converses to this result; see Theorem 3.3 and Proposition 3.6. Let us give some more details.
1. In the first subsection, we recall the coding
 $SB(X)$ (and
$SB(X)$ (and  $SB_{\infty }(X)$) of separable (infinite-dimensional) Banach spaces. We recall the notion of an admissible topology introduced in [Reference Godefroy and Saint-Raymond19], which is a Polish topology corresponding to the Effros-Borel structure of
$SB_{\infty }(X)$) of separable (infinite-dimensional) Banach spaces. We recall the notion of an admissible topology introduced in [Reference Godefroy and Saint-Raymond19], which is a Polish topology corresponding to the Effros-Borel structure of  $SB(X)$. We explore some basic relations between codings
$SB(X)$. We explore some basic relations between codings  $\mathcal {P}$,
$\mathcal {P}$,  $\mathcal {P}_{\infty }$,
$\mathcal {P}_{\infty }$,  $\mathcal {B}$,
$\mathcal {B}$,  $SB(X)$ and
$SB(X)$ and  $SB_{\infty }(X)$. We show there is a continuous reduction from
$SB_{\infty }(X)$. We show there is a continuous reduction from  $SB(X)$ to
$SB(X)$ to  $\mathcal {P}$, a
$\mathcal {P}$, a  $\boldsymbol {\Sigma }_{2}^{0}$-measurable reduction from
$\boldsymbol {\Sigma }_{2}^{0}$-measurable reduction from  $\mathcal {P}_{\infty }$ to
$\mathcal {P}_{\infty }$ to  $\mathcal {B}$, and a
$\mathcal {B}$, and a  $\boldsymbol {\Sigma }_{4}^{0}$-measurable reduction from
$\boldsymbol {\Sigma }_{4}^{0}$-measurable reduction from  $\mathcal {P}$ to
$\mathcal {P}$ to  $SB(X)$; see Theorem 3.3, Proposition 3.6, and Theorem 3.10. Here, by a ‘reduction’, we mean a map
$SB(X)$; see Theorem 3.3, Proposition 3.6, and Theorem 3.10. Here, by a ‘reduction’, we mean a map  $\Phi $ such that a code and its image are both codes of the same (up to isometry) Banach space.
$\Phi $ such that a code and its image are both codes of the same (up to isometry) Banach space.2. The second subsection is devoted to the proof of Theorem 3.11, by which there is a
 $\boldsymbol {\Sigma }_{2}^{0}$-measurable reduction from
$\boldsymbol {\Sigma }_{2}^{0}$-measurable reduction from  $\mathcal {B}$ to
$\mathcal {B}$ to  $SB_{\infty }(X)$. Further, we note that the developed techniques also lead to a
$SB_{\infty }(X)$. Further, we note that the developed techniques also lead to a  $\boldsymbol {\Sigma }_{3}^{0}$-measurable reduction from
$\boldsymbol {\Sigma }_{3}^{0}$-measurable reduction from  $\mathcal {P}$ to
$\mathcal {P}$ to  $SB(X)$, which is an improvement of the result mentioned above.
$SB(X)$, which is an improvement of the result mentioned above.
The importance of the reductions above is that there is not a big difference between Borel ranks when considered in any of the Polish spaces mentioned above.
Let us emphasize that the existence of a Borel reduction from ![]() $\mathcal {B}$ to
$\mathcal {B}$ to ![]() $SB_{\infty }(X)$ has been essentially proved in [Reference Kurka24, Lemma 2.4]. Going through the proof of [Reference Kurka24, Lemma 2.4], one may obtain a reduction that is
$SB_{\infty }(X)$ has been essentially proved in [Reference Kurka24, Lemma 2.4]. Going through the proof of [Reference Kurka24, Lemma 2.4], one may obtain a reduction that is ![]() $\boldsymbol {\Sigma }_{3}^{0}$-measurable; however, the proof does not seem to give a
$\boldsymbol {\Sigma }_{3}^{0}$-measurable; however, the proof does not seem to give a ![]() $\boldsymbol {\Sigma }_{2}^{0}$-measurable reduction (which is the optimal result). In order to obtain this improvement (see Theorem 3.11), we have to develop a whole machinery of new ideas in combination with very technical results, and this is why we devote a whole subsection to the proof.
$\boldsymbol {\Sigma }_{2}^{0}$-measurable reduction (which is the optimal result). In order to obtain this improvement (see Theorem 3.11), we have to develop a whole machinery of new ideas in combination with very technical results, and this is why we devote a whole subsection to the proof.
Since our reductions from ![]() $SB_{\infty }(X)$ to
$SB_{\infty }(X)$ to ![]() $\mathcal {P}_{\infty }$ and from
$\mathcal {P}_{\infty }$ and from ![]() $\mathcal {B}$ to
$\mathcal {B}$ to ![]() $SB_{\infty }(X)$ are optimal, it seems to be a very interesting open problem whether there exists a continuous reduction from
$SB_{\infty }(X)$ are optimal, it seems to be a very interesting open problem whether there exists a continuous reduction from ![]() $\mathcal {P}_{\infty }$ to
$\mathcal {P}_{\infty }$ to ![]() $\mathcal {B}$ or at least a
$\mathcal {B}$ or at least a ![]() $\boldsymbol {\Sigma }_{2}^{0}$-measurable reduction from
$\boldsymbol {\Sigma }_{2}^{0}$-measurable reduction from ![]() $\mathcal {P}_{\infty }$ to
$\mathcal {P}_{\infty }$ to ![]() $SB_{\infty }(X)$; see Question 1 and Question 2.
$SB_{\infty }(X)$; see Question 1 and Question 2.
3.1 Relations between codings  $\mathcal {P}$,
$\mathcal {P}$,  $\mathcal {P}_{\infty }$,
$\mathcal {P}_{\infty }$,  $\mathcal {B}$,
$\mathcal {B}$,  $SB(X)$ and
$SB(X)$ and  $SB_{\infty }(X)$
$SB_{\infty }(X)$
Here we recall the approach to topologizing the class of all separable (infinite-dimensional) Banach spaces by Godefroy and Saint-Raymond from [Reference Godefroy and Saint-Raymond19], which was a partial motivation for our research.
Definition 3.1. Let X be a Polish space, and let us denote by ![]() $\mathcal {F}(X)$ the set of all closed subsets of X. For an open set
$\mathcal {F}(X)$ the set of all closed subsets of X. For an open set ![]() $U\subseteq X$, we put
$U\subseteq X$, we put ![]() $E^{+}(U) = \{F\in \mathcal {F}(X):\; U\cap F\neq \emptyset \}$. Following [Reference Godefroy and Saint-Raymond19], we say that a Polish topology
$E^{+}(U) = \{F\in \mathcal {F}(X):\; U\cap F\neq \emptyset \}$. Following [Reference Godefroy and Saint-Raymond19], we say that a Polish topology ![]() $\tau $ on the set
$\tau $ on the set ![]() $\mathcal {F}(X)$ is admissible if it satisfies the following two conditions:
$\mathcal {F}(X)$ is admissible if it satisfies the following two conditions:
1. For every open subset U of X, the set
 $E^{+}(U)$ is
$E^{+}(U)$ is  $\tau $-open.
$\tau $-open.2. There exists a subbasis of
 $\tau $ such that every set from this subbasis is a countable union of sets of the form
$\tau $ such that every set from this subbasis is a countable union of sets of the form  $E^{+}(U)\setminus E^{+}(V)$, where U and V are open in X.Footnote 1
$E^{+}(U)\setminus E^{+}(V)$, where U and V are open in X.Footnote 1
We note that Godefroy and Saint-Raymond also suggest the following optional condition that is satisfied by many natural admissible topologies.
3. The set
 $\{(x,F)\in X\times \mathcal {F}(X):\; x\in F\}$ is closed in
$\{(x,F)\in X\times \mathcal {F}(X):\; x\in F\}$ is closed in  $X\times \mathcal {F}(X)$.
$X\times \mathcal {F}(X)$.
If X is a separable Banach space, we denote by ![]() $SB(X)\subseteq \mathcal {F}(X)$ the set of closed vector subspaces of X. We denote by
$SB(X)\subseteq \mathcal {F}(X)$ the set of closed vector subspaces of X. We denote by ![]() $SB_{\infty }(X)$ the subset of
$SB_{\infty }(X)$ the subset of ![]() $SB(X)$ consisting of infinite-dimensional spaces. We say that a topology on
$SB(X)$ consisting of infinite-dimensional spaces. We say that a topology on ![]() $SB(X)$ or
$SB(X)$ or ![]() $SB_{\infty }(X)$ is admissible if it is induced by an admissible topology on
$SB_{\infty }(X)$ is admissible if it is induced by an admissible topology on ![]() $\mathcal {F}(X)$. Both
$\mathcal {F}(X)$. Both ![]() $SB(X)$ and
$SB(X)$ and ![]() $SB_{\infty }(X)$ are Polish spaces when endowed with an admissible topology; see Remark 3.2.
$SB_{\infty }(X)$ are Polish spaces when endowed with an admissible topology; see Remark 3.2.
If Z is a separable Banach space, we put, similarly as in Notation 2.6,
It will always be clear from the context whether we work with subsets of ![]() $\mathcal {P}$ or
$\mathcal {P}$ or ![]() $SB(X)$.
$SB(X)$.
Remark 3.2. If X is a separable Banach space and ![]() $\tau $ is an admissible topology on
$\tau $ is an admissible topology on ![]() $\mathcal {F}(X)$, then
$\mathcal {F}(X)$, then ![]() $SB(X)$ is a
$SB(X)$ is a ![]() $G_{\delta }$-subset of
$G_{\delta }$-subset of ![]() $(\mathcal {F}(X),\tau )$ (see [Reference Godefroy and Saint-Raymond19, Section 3]). Moreover, by [Reference Godefroy and Saint-Raymond19, Corollary 4.2],
$(\mathcal {F}(X),\tau )$ (see [Reference Godefroy and Saint-Raymond19, Section 3]). Moreover, by [Reference Godefroy and Saint-Raymond19, Corollary 4.2], ![]() $SB_{\infty }(X)$ is a
$SB_{\infty }(X)$ is a ![]() $G_{\delta }$-subset of
$G_{\delta }$-subset of ![]() $(SB(X),\tau )$. (In fact, [Reference Godefroy and Saint-Raymond19] deals only with the case
$(SB(X),\tau )$. (In fact, [Reference Godefroy and Saint-Raymond19] deals only with the case ![]() $X=C(2^{\omega })$, but the generalization to any separable Banach space is easy.)
$X=C(2^{\omega })$, but the generalization to any separable Banach space is easy.)
A certain connection between codings ![]() $SB(X)$ and
$SB(X)$ and ![]() $\mathcal {P}$ of separable Banach spaces might be deduced already from [Reference Godefroy and Saint-Raymond19].
$\mathcal {P}$ of separable Banach spaces might be deduced already from [Reference Godefroy and Saint-Raymond19].
Theorem 3.3. Let X be an isometrically universal separable Banach space, and let ![]() $\tau $ be an admissible topology on
$\tau $ be an admissible topology on ![]() $SB(X)$. Then there is a continuous mapping
$SB(X)$. Then there is a continuous mapping ![]() $\Phi :(SB(X),\tau )\to \mathcal {P}$ such that for every
$\Phi :(SB(X),\tau )\to \mathcal {P}$ such that for every ![]() $F\in SB(X)$, we have
$F\in SB(X)$, we have ![]() $F\equiv X_{\Phi (F)}$.
$F\equiv X_{\Phi (F)}$.
Proof. By [Reference Godefroy and Saint-Raymond19, Theorem 4.1], there are continuous functions ![]() $(f_{n})_{n\in \mathbb {N}}$ on
$(f_{n})_{n\in \mathbb {N}}$ on ![]() $SB(X)$ with values in X such that for each
$SB(X)$ with values in X such that for each ![]() $F\in SB(X)$, we have
$F\in SB(X)$, we have ![]() $\overline {\{f_{n}(F):\; n\in \mathbb {N}\}} = F$. Consider the mapping
$\overline {\{f_{n}(F):\; n\in \mathbb {N}\}} = F$. Consider the mapping ![]() $\Phi $ given by
$\Phi $ given by  $\Phi (F)(\sum _{n=1}^{k} a_{n} e_{n}):=\|\sum _{n=1}^{k} a_{n}f_{n}(F)\|_{X}$ for every
$\Phi (F)(\sum _{n=1}^{k} a_{n} e_{n}):=\|\sum _{n=1}^{k} a_{n}f_{n}(F)\|_{X}$ for every ![]() $F\in SB(X)$ and
$F\in SB(X)$ and ![]() $a_{1},\ldots ,a_{k}\in \mathbb {Q}$. Then it is easy to see that
$a_{1},\ldots ,a_{k}\in \mathbb {Q}$. Then it is easy to see that ![]() $\Phi $ is the mapping we need.
$\Phi $ is the mapping we need.
The following relation between various codings of Banach spaces as ![]() $SB(X)$ is easy.
$SB(X)$ is easy.
Observation 3.4. Let ![]() $X,Y$ be isometrically universal separable Banach spaces, and let
$X,Y$ be isometrically universal separable Banach spaces, and let ![]() $\tau _{1}$ and
$\tau _{1}$ and ![]() $\tau _{2}$ be admissible topologies on
$\tau _{2}$ be admissible topologies on ![]() $SB(X)$ and
$SB(X)$ and ![]() $SB(Y)$, respectively. Then there is a
$SB(Y)$, respectively. Then there is a ![]() $\boldsymbol {\Sigma }_{2}^{0}$-measurable mapping
$\boldsymbol {\Sigma }_{2}^{0}$-measurable mapping ![]() $f:(SB(X),\tau _{1})\to (SB(Y),\tau _{2})$ such that for every
$f:(SB(X),\tau _{1})\to (SB(Y),\tau _{2})$ such that for every ![]() $F\in SB(X)$, we have
$F\in SB(X)$, we have ![]() $F\equiv f(F)$. Moreover, f can be chosen such that for every open set
$F\equiv f(F)$. Moreover, f can be chosen such that for every open set ![]() $U\subseteq Y$ there is an open set
$U\subseteq Y$ there is an open set ![]() $V\subseteq X$ such that
$V\subseteq X$ such that ![]() $f^{-1}(E^{+}(U)) = E^{+}(V)$.
$f^{-1}(E^{+}(U)) = E^{+}(V)$.
Proof. Let ![]() $j:X\to Y$ be an isometry (not necessarily surjective). Then the mapping f given by
$j:X\to Y$ be an isometry (not necessarily surjective). Then the mapping f given by ![]() $f(F):= j(F)$,
$f(F):= j(F)$, ![]() $F\in SB(X)$, does the job, because
$F\in SB(X)$, does the job, because ![]() $f^{-1}(E^{+}(U)) = E^{+}(j^{-1}(U))$ for every open set
$f^{-1}(E^{+}(U)) = E^{+}(j^{-1}(U))$ for every open set ![]() $U\subseteq Y$.
$U\subseteq Y$.
Let us note the following easy fact, which we record here for a later reference. The proof is easy and so is omitted.
Lemma 3.5. Let X be an isometrically universal separable Banach space, ![]() $\tau $ be an admissible topology on
$\tau $ be an admissible topology on ![]() $SB(X)$, Y be a Polish space,
$SB(X)$, Y be a Polish space, ![]() $f:Y\to SB(X)$ be a mapping and
$f:Y\to SB(X)$ be a mapping and ![]() $n\in \mathbb {N}$,
$n\in \mathbb {N}$, ![]() $n\geq 2$, be such that
$n\geq 2$, be such that ![]() $f^{-1}(E^{+}(U))$ is a
$f^{-1}(E^{+}(U))$ is a ![]() $\boldsymbol {\Delta }_{n}^{0}$ set in Y for every open set
$\boldsymbol {\Delta }_{n}^{0}$ set in Y for every open set ![]() $U\subseteq X$. Then f is
$U\subseteq X$. Then f is ![]() $\boldsymbol {\Sigma }_{n}^{0}$-measurable.
$\boldsymbol {\Sigma }_{n}^{0}$-measurable.
A straightforward idea leads to the following relation between ![]() $\mathcal {P}_{\infty }$ and
$\mathcal {P}_{\infty }$ and ![]() $\mathcal {B}$.
$\mathcal {B}$.
Proposition 3.6. There is a ![]() $\boldsymbol {\Sigma }_{2}^{0}$-measurable mapping
$\boldsymbol {\Sigma }_{2}^{0}$-measurable mapping ![]() $\Phi :\mathcal {P}_{\infty }\to \mathcal {B}$ such that for every
$\Phi :\mathcal {P}_{\infty }\to \mathcal {B}$ such that for every ![]() $\mu \in \mathcal {P}_{\infty }$, we have
$\mu \in \mathcal {P}_{\infty }$, we have ![]() $X_{\mu }\equiv X_{\Phi (\mu )}$.
$X_{\mu }\equiv X_{\Phi (\mu )}$.
Moreover, ![]() $\Phi $ can be chosen such that
$\Phi $ can be chosen such that  $\Phi ^{-1}(U[v,I])\in \boldsymbol{\Delta}_{2}^{0}(\mathcal {P}_{\infty })$ for each
$\Phi ^{-1}(U[v,I])\in \boldsymbol{\Delta}_{2}^{0}(\mathcal {P}_{\infty })$ for each ![]() $v\in V$ and each open interval I.
$v\in V$ and each open interval I.
Proof. For each ![]() $\mu \in \mathcal {P}_{\infty }$, let us inductively define natural numbers
$\mu \in \mathcal {P}_{\infty }$, let us inductively define natural numbers ![]() $(n_{k}(\mu ))_{k\in \mathbb {N}}$ by
$(n_{k}(\mu ))_{k\in \mathbb {N}}$ by
 $$ \begin{align*}\begin{split} n_{1}(\mu) & :=\min\{n\in\mathbb{N}:\; \mu(e_{n})\neq 0\},\\ n_{k+1}(\mu) & :=\min\{n\in\mathbb{N}:\; e_{n_{1}(\mu)},\ldots,e_{n_{k}(\mu)}, e_{n}\text{ are linearly independent}\}. \end{split} \end{align*} $$
$$ \begin{align*}\begin{split} n_{1}(\mu) & :=\min\{n\in\mathbb{N}:\; \mu(e_{n})\neq 0\},\\ n_{k+1}(\mu) & :=\min\{n\in\mathbb{N}:\; e_{n_{1}(\mu)},\ldots,e_{n_{k}(\mu)}, e_{n}\text{ are linearly independent}\}. \end{split} \end{align*} $$Consider the mapping ![]() $\Phi $ given by
$\Phi $ given by  $\Phi (\mu )(\sum _{i=1}^{k} a_{n} e_{n}):=\mu (\sum _{i=1}^{k} a_{i}e_{n_{i}(\mu )})$ for every
$\Phi (\mu )(\sum _{i=1}^{k} a_{n} e_{n}):=\mu (\sum _{i=1}^{k} a_{i}e_{n_{i}(\mu )})$ for every ![]() $\mu \in \mathcal {P}_{\infty }$ and
$\mu \in \mathcal {P}_{\infty }$ and ![]() $a_{1},\ldots ,a_{k}\in \mathbb {Q}$. It is easy to see that
$a_{1},\ldots ,a_{k}\in \mathbb {Q}$. It is easy to see that ![]() $\Phi (\mu )\in \mathcal {B}$ and that
$\Phi (\mu )\in \mathcal {B}$ and that ![]() $X_{\mu }$ is isometric to
$X_{\mu }$ is isometric to ![]() $X_{\Phi (\mu )}$ for each
$X_{\Phi (\mu )}$ for each ![]() $\mu \in \mathcal {P}_{\infty }$.
$\mu \in \mathcal {P}_{\infty }$.
For all natural numbers ![]() $N_{1}<\ldots <N_{k}$, the set
$N_{1}<\ldots <N_{k}$, the set ![]() $\{\mu \in \mathcal {P}_{\infty }:\; n_{1}(\mu )=N_{1},\ldots ,n_{k}(\mu )=N_{k}\}$ is a
$\{\mu \in \mathcal {P}_{\infty }:\; n_{1}(\mu )=N_{1},\ldots ,n_{k}(\mu )=N_{k}\}$ is a ![]() $\boldsymbol{\Delta}_{2}^{0}$ set in
$\boldsymbol{\Delta}_{2}^{0}$ set in ![]() $\mathcal {P}_{\infty }$. Indeed, we may prove it by induction on k because for each
$\mathcal {P}_{\infty }$. Indeed, we may prove it by induction on k because for each ![]() $k\in \mathbb {N}$ and each
$k\in \mathbb {N}$ and each ![]() $\mu \in \mathcal {P}_{\infty }$, we have that
$\mu \in \mathcal {P}_{\infty }$, we have that ![]() $n_{1}(\mu )=N_{1},\ldots ,n_{k+1}(\mu )=N_{k+1}$ iff
$n_{1}(\mu )=N_{1},\ldots ,n_{k+1}(\mu )=N_{k+1}$ iff
 $$ \begin{align*}\begin{split} n_{1}(\mu) & =N_{1}, \ldots, n_{k}(\mu)=N_{k}\quad\&\\ &\forall n=N_{k}+1,\ldots,N_{k+1}-1: e_{N_{1}},\ldots,e_{N_{k}},e_{n}\text{ are linearly dependent}\\ & \&\quad e_{N_{1}},\ldots,e_{N_{k+1}}\text{ are linearly independent}, \end{split}\end{align*} $$
$$ \begin{align*}\begin{split} n_{1}(\mu) & =N_{1}, \ldots, n_{k}(\mu)=N_{k}\quad\&\\ &\forall n=N_{k}+1,\ldots,N_{k+1}-1: e_{N_{1}},\ldots,e_{N_{k}},e_{n}\text{ are linearly dependent}\\ & \&\quad e_{N_{1}},\ldots,e_{N_{k+1}}\text{ are linearly independent}, \end{split}\end{align*} $$which is an intersection of a ![]() $\boldsymbol{\Delta}_{2}^{0}$-condition (by the inductive assumption) with a closed and an open condition (by Lemma 2.4).
$\boldsymbol{\Delta}_{2}^{0}$-condition (by the inductive assumption) with a closed and an open condition (by Lemma 2.4).
Let us pick  $v = \sum _{i=1}^{k} a_{n} e_{n}\in V$ and an open interval I. Then
$v = \sum _{i=1}^{k} a_{n} e_{n}\in V$ and an open interval I. Then
 $$ \begin{align*} \Phi^{-1}(U[v,I]) = \{\mu\in\mathcal{P}_{\infty}:\; \mu(\sum_{i=1}^{k} a_{i}e_{n_{i}(\mu)})\in I\}, \end{align*} $$
$$ \begin{align*} \Phi^{-1}(U[v,I]) = \{\mu\in\mathcal{P}_{\infty}:\; \mu(\sum_{i=1}^{k} a_{i}e_{n_{i}(\mu)})\in I\}, \end{align*} $$which is a ![]() $\boldsymbol {\Delta }_{2}^{0}$ set in
$\boldsymbol {\Delta }_{2}^{0}$ set in ![]() $\mathcal {P}_{\infty }$. Indeed, on one hand we have
$\mathcal {P}_{\infty }$. Indeed, on one hand we have ![]() $\mu \in \Phi ^{-1}(U[v,I])$ iff there are natural numbers
$\mu \in \Phi ^{-1}(U[v,I])$ iff there are natural numbers ![]() $N_{1}<N_{2}<\ldots <N_{k}$ such that
$N_{1}<N_{2}<\ldots <N_{k}$ such that ![]() $n_{1}(\mu )=N_{1},\ldots ,n_{k}(\mu )=N_{k}$ and
$n_{1}(\mu )=N_{1},\ldots ,n_{k}(\mu )=N_{k}$ and  $\mu (\sum _{i=1}^{k} a_{i} e_{N_{i}})\in I$, which witnesses that
$\mu (\sum _{i=1}^{k} a_{i} e_{N_{i}})\in I$, which witnesses that  $\Phi ^{-1}(U[v,I])\in \boldsymbol {\Sigma }_{2}^{0}(\mathcal {P}_{\infty })$ as it is a countable union of
$\Phi ^{-1}(U[v,I])\in \boldsymbol {\Sigma }_{2}^{0}(\mathcal {P}_{\infty })$ as it is a countable union of ![]() $\boldsymbol{\Delta}_{2}^{0}$ sets. On the other hand, we have that
$\boldsymbol{\Delta}_{2}^{0}$ sets. On the other hand, we have that ![]() $\mu \in \Phi ^{-1}(U[v,I])$ iff for each
$\mu \in \Phi ^{-1}(U[v,I])$ iff for each ![]() $l\in \mathbb {N}$, we have that either
$l\in \mathbb {N}$, we have that either ![]() $n_{k}(\mu )> l$ or there are natural numbers
$n_{k}(\mu )> l$ or there are natural numbers ![]() $N_{1}<N_{2}<\ldots <N_{k}\leq l$ such that
$N_{1}<N_{2}<\ldots <N_{k}\leq l$ such that ![]() $n_{1}(\mu )=N_{1},\ldots ,n_{k}(\mu )=N_{k}$ and
$n_{1}(\mu )=N_{1},\ldots ,n_{k}(\mu )=N_{k}$ and  $\mu (\sum _{i=1}^{k} a_{i} e_{N_{i}})\in I$, which witnesses that
$\mu (\sum _{i=1}^{k} a_{i} e_{N_{i}})\in I$, which witnesses that  $\Phi ^{-1}(U[v,I])\in \boldsymbol {\Pi }_{2}^{0}(\mathcal {P}_{\infty })$ as it is a countable intersection of
$\Phi ^{-1}(U[v,I])\in \boldsymbol {\Pi }_{2}^{0}(\mathcal {P}_{\infty })$ as it is a countable intersection of ![]() $\boldsymbol{\Delta}_{2}^{0}$ sets.
$\boldsymbol{\Delta}_{2}^{0}$ sets.
This proves the ‘Moreover’ part, from which it easily follows that ![]() $\Phi $ is
$\Phi $ is ![]() $\boldsymbol {\Sigma }_{2}^{0}$-measurable.
$\boldsymbol {\Sigma }_{2}^{0}$-measurable.
Remark 3.7. For ![]() $d\in \mathbb {N}$, let us consider the sets
$d\in \mathbb {N}$, let us consider the sets ![]() $\mathcal {P}_{d}:=\{\mu \in \mathcal {P}:\; \dim X_{\mu } = d\}$ and
$\mathcal {P}_{d}:=\{\mu \in \mathcal {P}:\; \dim X_{\mu } = d\}$ and
A similar argument as in Proposition 3.6 shows that for every ![]() $d\in \mathbb {N}$, there is a
$d\in \mathbb {N}$, there is a ![]() $\boldsymbol {\Sigma }_{2}^{0}$-measurable mapping
$\boldsymbol {\Sigma }_{2}^{0}$-measurable mapping ![]() $\Phi :\mathcal {P}_{d}\to \mathcal {B}_{d}$ such that for every
$\Phi :\mathcal {P}_{d}\to \mathcal {B}_{d}$ such that for every ![]() $\mu \in \mathcal {P}_{d}$, we have
$\mu \in \mathcal {P}_{d}$, we have ![]() $X_{\mu }\equiv X_{\Phi (\mu )}$.
$X_{\mu }\equiv X_{\Phi (\mu )}$.
Finally, let us consider the reduction from ![]() $\mathcal {P}$ to
$\mathcal {P}$ to ![]() $SB(X)$. An optimal result would be to have a
$SB(X)$. An optimal result would be to have a ![]() $\boldsymbol {\Sigma }_{2}^{0}$-reduction. This is because, as was already observed in [Reference Godefroy and Saint-Raymond19], the identity map between two admissible topologies is only
$\boldsymbol {\Sigma }_{2}^{0}$-reduction. This is because, as was already observed in [Reference Godefroy and Saint-Raymond19], the identity map between two admissible topologies is only ![]() $\boldsymbol{\Sigma}^{0}_{2}$-measurable in general. Using the ideas of the proof of [Reference Kurka24, Lemma 2.4], we obtain Theorem 3.10. This result is improved in the next subsection (see Theorem 3.14), but since some steps remain the same, let us give a sketch of the argument (we will be a bit sketchy at the places that will be modified later).
$\boldsymbol{\Sigma}^{0}_{2}$-measurable in general. Using the ideas of the proof of [Reference Kurka24, Lemma 2.4], we obtain Theorem 3.10. This result is improved in the next subsection (see Theorem 3.14), but since some steps remain the same, let us give a sketch of the argument (we will be a bit sketchy at the places that will be modified later).
Lemma 3.8. Let ![]() $n\in \mathbb {N}$, X be an isometrically universal separable Banach space and
$n\in \mathbb {N}$, X be an isometrically universal separable Banach space and ![]() $\tau $ be an admissible topology on
$\tau $ be an admissible topology on ![]() $SB(X)$. Let there exist
$SB(X)$. Let there exist ![]() $\boldsymbol {\Sigma }_{n}^{0}$-measurable mappings
$\boldsymbol {\Sigma }_{n}^{0}$-measurable mappings ![]() $\chi _{k} : \mathcal {B} \to X$,
$\chi _{k} : \mathcal {B} \to X$, ![]() $k\in \mathbb {N}$, such that
$k\in \mathbb {N}$, such that ![]() $X_{\mu }\equiv \overline {\operatorname {span}}\{\chi _{k}(\mu ):\; k\in \mathbb {N}\}$ for every
$X_{\mu }\equiv \overline {\operatorname {span}}\{\chi _{k}(\mu ):\; k\in \mathbb {N}\}$ for every ![]() $\mu \in \mathcal {B}$.
$\mu \in \mathcal {B}$.
Then there exists a  $\boldsymbol {\Sigma }_{n+1}^{0}$-measurable mapping
$\boldsymbol {\Sigma }_{n+1}^{0}$-measurable mapping ![]() $\Phi :\mathcal {B}\to (SB(X),\tau )$ such that for every
$\Phi :\mathcal {B}\to (SB(X),\tau )$ such that for every ![]() $\mu \in \mathcal {B}$, we have
$\mu \in \mathcal {B}$, we have ![]() $X_{\mu }\equiv \Phi (\mu )$.
$X_{\mu }\equiv \Phi (\mu )$.
Proof. Consider the mapping ![]() $\Phi :\mathcal {B}\to (SB(X),\tau )$ defined as
$\Phi :\mathcal {B}\to (SB(X),\tau )$ defined as
We have ![]() $X_{\nu }\equiv \Phi (\nu )$. For every open set
$X_{\nu }\equiv \Phi (\nu )$. For every open set ![]() $U\subseteq X$, using the
$U\subseteq X$, using the ![]() $\boldsymbol {\Sigma }_{n}^{0}$-measurability of
$\boldsymbol {\Sigma }_{n}^{0}$-measurability of ![]() $\chi _{k}$’s, it is easy to see that
$\chi _{k}$’s, it is easy to see that ![]() $\Phi ^{-1}(E^{+}(U))$ is a
$\Phi ^{-1}(E^{+}(U))$ is a ![]() $\boldsymbol {\Sigma }_{n}^{0}$-set in
$\boldsymbol {\Sigma }_{n}^{0}$-set in ![]() $\mathcal {B}$. Thus, by Lemma 3.5, the mapping
$\mathcal {B}$. Thus, by Lemma 3.5, the mapping ![]() $\Phi $ is
$\Phi $ is  $\boldsymbol {\Sigma }_{n+1}^{0}$-measurable.
$\boldsymbol {\Sigma }_{n+1}^{0}$-measurable.
Remark 3.9. Similarly as in Remark 3.7, an analogous approach leads to a similar statement valid for any ![]() $\mathcal {B}_{d}$,
$\mathcal {B}_{d}$, ![]() $d\in \mathbb {N}$, instead of
$d\in \mathbb {N}$, instead of ![]() $\mathcal {B}$.
$\mathcal {B}$.
Theorem 3.10. Let X be an isometrically universal separable Banach space, and let ![]() $\tau $ be an admissible topology on
$\tau $ be an admissible topology on ![]() $SB(X)$. Then there is a
$SB(X)$. Then there is a ![]() $\boldsymbol {\Sigma }_{4}^{0}$-measurable mapping
$\boldsymbol {\Sigma }_{4}^{0}$-measurable mapping ![]() $\Phi :\mathcal {P}\to (SB(X),\tau )$ such that for every
$\Phi :\mathcal {P}\to (SB(X),\tau )$ such that for every ![]() $\mu \in \mathcal {P}$, we have
$\mu \in \mathcal {P}$, we have ![]() $X_{\mu }\equiv \Phi (\mu )$.
$X_{\mu }\equiv \Phi (\mu )$.
Sketch of the proof.
By Remark 3.7, it suffices to find, for every ![]() $d\in \mathbb {N}\cup \{\infty \}$, a
$d\in \mathbb {N}\cup \{\infty \}$, a ![]() $\boldsymbol {\Sigma }_{3}^{0}$-measurable reduction from
$\boldsymbol {\Sigma }_{3}^{0}$-measurable reduction from ![]() $\mathcal {B}_{d}$ to
$\mathcal {B}_{d}$ to ![]() $SB(X)$, where
$SB(X)$, where ![]() $\mathcal {B}_{\infty } = \mathcal {B}$. This is done for every
$\mathcal {B}_{\infty } = \mathcal {B}$. This is done for every ![]() $d\in \mathbb {N}\cup \{\infty \}$ in a similar way. Let us concentrate further only on the case of
$d\in \mathbb {N}\cup \{\infty \}$ in a similar way. Let us concentrate further only on the case of ![]() $d=\infty $; the other cases are similar. From the proof of [Reference Kurka24, Lemma 2.4], it follows that there are Borel measurable mappings
$d=\infty $; the other cases are similar. From the proof of [Reference Kurka24, Lemma 2.4], it follows that there are Borel measurable mappings ![]() $\chi _{k} : \mathcal {B} \to X$,
$\chi _{k} : \mathcal {B} \to X$, ![]() $k\in \mathbb {N}$, such that
$k\in \mathbb {N}$, such that ![]() $X_{\mu }\equiv \overline {\operatorname {span}} \{\chi _{k}(\mu ):\; k\in \mathbb {N}\}$ for every
$X_{\mu }\equiv \overline {\operatorname {span}} \{\chi _{k}(\mu ):\; k\in \mathbb {N}\}$ for every ![]() $\mu \in \mathcal {B}$. A careful inspection of the proof actually shows that the mappings
$\mu \in \mathcal {B}$. A careful inspection of the proof actually shows that the mappings ![]() $\chi _{k}$ are
$\chi _{k}$ are ![]() $\boldsymbol {\Sigma }_{2}^{0}$-measurable (since this part is improved in the next subsection [see Proposition 3.12], we do not give any more details here). Thus, an application of Lemma 3.8 finishes the proof.
$\boldsymbol {\Sigma }_{2}^{0}$-measurable (since this part is improved in the next subsection [see Proposition 3.12], we do not give any more details here). Thus, an application of Lemma 3.8 finishes the proof.
3.2 An optimal reduction from  $\mathcal B$ to
$\mathcal B$ to  $SB(X)$
$SB(X)$
The last subsection is devoted to the proof of the following result. The rest of the paper does not depend on it.
Theorem 3.11. Let X be an isometrically universal separable Banach space, and let ![]() $\tau $ be an admissible topology on
$\tau $ be an admissible topology on ![]() $SB(X)$. Then there is a
$SB(X)$. Then there is a ![]() $\boldsymbol {\Sigma }_{2}^{0}$-measurable mapping
$\boldsymbol {\Sigma }_{2}^{0}$-measurable mapping ![]() $\Phi :\mathcal {B}\to (SB(X),\tau )$ such that for every
$\Phi :\mathcal {B}\to (SB(X),\tau )$ such that for every ![]() $\mu \in \mathcal {B}$, we have
$\mu \in \mathcal {B}$, we have ![]() $X_{\mu }\equiv \Phi (\mu )$.
$X_{\mu }\equiv \Phi (\mu )$.
The main ingredient of the proof is the following.
Proposition 3.12. For any isometrically universal separable Banach space ![]() $ X $, there exist continuous mappings
$ X $, there exist continuous mappings ![]() $ \chi _{k} : \mathcal {B} \to X, k \in \mathbb {N}, $ such that
$ \chi _{k} : \mathcal {B} \to X, k \in \mathbb {N}, $ such that
 $$ \begin{align*} \Big\Vert \sum_{k=1}^{n} a_{k} \chi_{k}(\nu) \Big\Vert = \nu \Big( \sum_{k=1}^{n} a_{k} e_{k} \Big) \end{align*} $$
$$ \begin{align*} \Big\Vert \sum_{k=1}^{n} a_{k} \chi_{k}(\nu) \Big\Vert = \nu \Big( \sum_{k=1}^{n} a_{k} e_{k} \Big) \end{align*} $$for every ![]() $ \sum _{k=1}^{n} a_{k} e_{k} \in c_{00} $ and every
$ \sum _{k=1}^{n} a_{k} e_{k} \in c_{00} $ and every ![]() $ \nu \in \mathcal {B} $.
$ \nu \in \mathcal {B} $.
Remark 3.13. Similarly as in Remark 3.7, we may easily obtain a variant of Proposition 3.12 for ![]() $\mathcal {B}_{d}$,
$\mathcal {B}_{d}$, ![]() $d\in \mathbb {N}$. Indeed, let
$d\in \mathbb {N}$. Indeed, let ![]() $d\in \mathbb {N}$ be given. For
$d\in \mathbb {N}$ be given. For ![]() $\nu \in \mathcal {B}_{d}$, let us define
$\nu \in \mathcal {B}_{d}$, let us define ![]() $\widetilde {\nu }\in \mathcal {B}$ by
$\widetilde {\nu }\in \mathcal {B}$ by
 $$ \begin{align*}\widetilde{\nu} \Big( \sum_{i=1}^{\infty} a_{i}e_{i} \Big) :=\nu \Big( \sum_{i=1}^{d} a_{i}e_{i} \Big) + \sum_{i=d+1}^{\infty} |a_{i}|,\quad \sum_{i=1}^{\infty} a_{i}e_{i}\in c_{00}.\end{align*} $$
$$ \begin{align*}\widetilde{\nu} \Big( \sum_{i=1}^{\infty} a_{i}e_{i} \Big) :=\nu \Big( \sum_{i=1}^{d} a_{i}e_{i} \Big) + \sum_{i=d+1}^{\infty} |a_{i}|,\quad \sum_{i=1}^{\infty} a_{i}e_{i}\in c_{00}.\end{align*} $$If ![]() $ \chi _{k}$,
$ \chi _{k}$, ![]() $k\in \mathbb {N},$ are as in Proposition 3.12, then we may consider mappings
$k\in \mathbb {N},$ are as in Proposition 3.12, then we may consider mappings ![]() $ \widetilde {\chi }_{k}:\mathcal {B}_{d}\to X$,
$ \widetilde {\chi }_{k}:\mathcal {B}_{d}\to X$, ![]() $k\leq d,$ defined by
$k\leq d,$ defined by ![]() $\widetilde {\chi }_{k}(\nu ) = \chi _{k}(\widetilde {\nu }) $,
$\widetilde {\chi }_{k}(\nu ) = \chi _{k}(\widetilde {\nu }) $, ![]() $ \nu \in \mathcal {B}_{d} $.
$ \nu \in \mathcal {B}_{d} $.
We postpone the proof of Proposition 3.12 to the very end of this subsection.
Similarly as above, we obtain also the following.
Theorem 3.14. Let X be an isometrically universal separable Banach space, and let ![]() $\tau $ be an admissible topology on
$\tau $ be an admissible topology on ![]() $SB(X)$. Then there is a
$SB(X)$. Then there is a ![]() $\boldsymbol {\Sigma }_{3}^{0}$-measurable mapping
$\boldsymbol {\Sigma }_{3}^{0}$-measurable mapping ![]() $\Phi :\mathcal {P}\to (SB(X),\tau )$ such that for every
$\Phi :\mathcal {P}\to (SB(X),\tau )$ such that for every ![]() $\mu \in \mathcal {P}$, we have
$\mu \in \mathcal {P}$, we have ![]() $X_{\mu }\equiv \Phi (\mu )$.
$X_{\mu }\equiv \Phi (\mu )$.
Proof. This is similar to the proof of Theorem 3.10; the only modification is that we use Proposition 3.12 and Remark 3.13 instead of the reference to the proof of [Reference Kurka24, Lemma 2.4].
The aim of the remainder of this subsection is now to prove Proposition 3.12. Its proof is based on two auxiliary results, namely Proposition 3.15 and Lemma 3.18; the first of them is a reformulation of our task. Although we will use only the implication ![]() $ (2^{\prime }) \Rightarrow (1) $ for the set of norms with
$ (2^{\prime }) \Rightarrow (1) $ for the set of norms with ![]() $ \nu (e_{k}) = 1 $, we prove a bit more and keep the formulation for a general set of (pseudo)norms. The implication
$ \nu (e_{k}) = 1 $, we prove a bit more and keep the formulation for a general set of (pseudo)norms. The implication ![]() $ (1) \Rightarrow (2) $, which is not obligatory for us, is a simple application of the Hahn-Banach theorem, and we think it is appropriate to include the proof.
$ (1) \Rightarrow (2) $, which is not obligatory for us, is a simple application of the Hahn-Banach theorem, and we think it is appropriate to include the proof.
In fact, we do not know if the conditions hold for the set of all pseudonorms (or, equivalently, for the set of pseudonorms with ![]() $ \nu (e_{k}) \leq 1 $). So, it is open if Proposition 3.12 holds not only for
$ \nu (e_{k}) \leq 1 $). So, it is open if Proposition 3.12 holds not only for ![]() $ \mathcal {B} $, but even for
$ \mathcal {B} $, but even for ![]() $ \mathcal {P} $.
$ \mathcal {P} $.
Proposition 3.15. For each ![]() $ \mathcal {A} \subseteq \mathcal {P} $, the following conditions are equivalent:
$ \mathcal {A} \subseteq \mathcal {P} $, the following conditions are equivalent:
(1) There are a separable Banach space ![]() $ U $ and continuous mappings
$ U $ and continuous mappings ![]() $ \chi _{k} : \mathcal {A} \to U, k \in \mathbb {N}, $ such that
$ \chi _{k} : \mathcal {A} \to U, k \in \mathbb {N}, $ such that
 $$ \begin{align*} \Big\Vert \sum_{k=1}^{n} a_{k} \chi_{k}(\nu) \Big\Vert = \nu \Big( \sum_{k=1}^{n} a_{k} e_{k} \Big) \end{align*} $$
$$ \begin{align*} \Big\Vert \sum_{k=1}^{n} a_{k} \chi_{k}(\nu) \Big\Vert = \nu \Big( \sum_{k=1}^{n} a_{k} e_{k} \Big) \end{align*} $$for every ![]() $ \sum _{k=1}^{n} a_{k} e_{k} \in c_{00} $ and every
$ \sum _{k=1}^{n} a_{k} e_{k} \in c_{00} $ and every ![]() $ \nu \in \mathcal {A} $.
$ \nu \in \mathcal {A} $.
(2) There are continuous functions ![]() $ \alpha _{k} : \mathcal {A}^{2} \to [0, \infty ), k \in \mathbb {N}, $ such that
$ \alpha _{k} : \mathcal {A}^{2} \to [0, \infty ), k \in \mathbb {N}, $ such that
for every ![]() $ \nu $ and
$ \nu $ and ![]() $ k $, and the following property is satisfied: If
$ k $, and the following property is satisfied: If ![]() $ \nu \in \mathcal {A} $ and
$ \nu \in \mathcal {A} $ and ![]() $ z^{*} \in (c_{00})^{\#} $ satisfy
$ z^{*} \in (c_{00})^{\#} $ satisfy ![]() $ |z^{*}(x)| \leq \nu (x) $ for every
$ |z^{*}(x)| \leq \nu (x) $ for every ![]() $ x \in c_{00} $, then there is a mapping
$ x \in c_{00} $, then there is a mapping ![]() $ \Gamma : \mathcal {A} \to (c_{00})^{\#} $ such that
$ \Gamma : \mathcal {A} \to (c_{00})^{\#} $ such that ![]() $ \Gamma (\nu ) = z^{*} $,
$ \Gamma (\nu ) = z^{*} $, ![]() $ |\Gamma (\mu )(x)| \leq \mu (x) $ for every
$ |\Gamma (\mu )(x)| \leq \mu (x) $ for every ![]() $ \mu \in \mathcal {A} $ and
$ \mu \in \mathcal {A} $ and ![]() $ x \in c_{00} $, and
$ x \in c_{00} $, and
for every ![]() $ \mu , \lambda \in \mathcal {A} $ and every
$ \mu , \lambda \in \mathcal {A} $ and every ![]() $ k $.
$ k $.
Moreover, if ![]() $ \mathcal {A} $ consists only of pseudonorms
$ \mathcal {A} $ consists only of pseudonorms ![]() $ \nu $ with
$ \nu $ with ![]() $ \nu (e_{k}) \leq 1 $ for every
$ \nu (e_{k}) \leq 1 $ for every ![]() $ k $, then these conditions are equivalent with:
$ k $, then these conditions are equivalent with:
(2’) For every ![]() $ \eta \in [0, 1) $, there are continuous functions
$ \eta \in [0, 1) $, there are continuous functions ![]() $ \beta _{k} : \mathcal {A}^{2} \to [0, \infty ), k \in \mathbb {N}, $ such that
$ \beta _{k} : \mathcal {A}^{2} \to [0, \infty ), k \in \mathbb {N}, $ such that
for every ![]() $ \nu $ and
$ \nu $ and ![]() $ k $, and the following property is satisfied: If
$ k $, and the following property is satisfied: If ![]() $ \nu \in \mathcal {A} $ and
$ \nu \in \mathcal {A} $ and ![]() $ z^{*} \in (c_{00})^{\#} $ satisfy
$ z^{*} \in (c_{00})^{\#} $ satisfy ![]() $ |z^{*}(x)| \leq \nu (x) $ for every
$ |z^{*}(x)| \leq \nu (x) $ for every ![]() $ x \in c_{00} $, then there is a mapping
$ x \in c_{00} $, then there is a mapping ![]() $ \Gamma : \mathcal {A} \to (c_{00})^{\#} $ such that
$ \Gamma : \mathcal {A} \to (c_{00})^{\#} $ such that ![]() $ \Gamma (\nu ) = \eta \cdot z^{*} $,
$ \Gamma (\nu ) = \eta \cdot z^{*} $, ![]() $ |\Gamma (\mu )(x)| \leq \mu (x) $ for every
$ |\Gamma (\mu )(x)| \leq \mu (x) $ for every ![]() $ \mu \in \mathcal {A} $ and
$ \mu \in \mathcal {A} $ and ![]() $ x \in c_{00} $, and
$ x \in c_{00} $, and
for every ![]() $ \mu , \lambda \in \mathcal {A} $ and every
$ \mu , \lambda \in \mathcal {A} $ and every ![]() $ k $.
$ k $.
Remark 3.16. The conditions (1) and (2) from Proposition 3.15 are also equivalent to the following one:
(3) There are continuous functions ![]() $ \alpha _{k} : \mathcal {A}^{2} \to [0, \infty ), k \in \mathbb {N}, $ such that
$ \alpha _{k} : \mathcal {A}^{2} \to [0, \infty ), k \in \mathbb {N}, $ such that
for every ![]() $\nu $ and
$\nu $ and ![]() $ k $ and
$ k $ and
 $$ \begin{align*}\sum_{\mu, \lambda, k} |a_{\mu, \lambda, k}| \alpha_{k}(\mu, \lambda) \geq \nu \Big( \sum_{\lambda, k} (a_{\nu, \lambda, k} - a_{\lambda, \nu, k}) e_{k} \Big) - \sum_{\mu \neq \nu} \mu \Big( \sum_{\lambda, k} (a_{\mu, \lambda, k} - a_{\lambda, \mu, k}) e_{k} \Big)\end{align*} $$
$$ \begin{align*}\sum_{\mu, \lambda, k} |a_{\mu, \lambda, k}| \alpha_{k}(\mu, \lambda) \geq \nu \Big( \sum_{\lambda, k} (a_{\nu, \lambda, k} - a_{\lambda, \nu, k}) e_{k} \Big) - \sum_{\mu \neq \nu} \mu \Big( \sum_{\lambda, k} (a_{\mu, \lambda, k} - a_{\lambda, \mu, k}) e_{k} \Big)\end{align*} $$for every ![]() $ \nu \in \mathcal {A} $ and every system
$ \nu \in \mathcal {A} $ and every system ![]() $ (a_{\mu , \lambda , k})_{\mu , \lambda \in \mathcal {A}, k \in \mathbb {N}} $ of real numbers with finite support.
$ (a_{\mu , \lambda , k})_{\mu , \lambda \in \mathcal {A}, k \in \mathbb {N}} $ of real numbers with finite support.
The proof is similar to the proof of ![]() $(1)\Leftrightarrow (2)$ below (for
$(1)\Leftrightarrow (2)$ below (for ![]() $(1)\Rightarrow (3)$, the choice of
$(1)\Rightarrow (3)$, the choice of ![]() $\alpha _k$’s is the same as in the proof of
$\alpha _k$’s is the same as in the proof of ![]() $(1)\Rightarrow (2)$; for
$(1)\Rightarrow (2)$; for ![]() $(3)\Rightarrow (1)$, the construction of the space U is the same as in
$(3)\Rightarrow (1)$, the construction of the space U is the same as in ![]() $(2)\Rightarrow (1)$). We omit the full proof because the details are technical, and we do not use condition
$(2)\Rightarrow (1)$). We omit the full proof because the details are technical, and we do not use condition ![]() $(3)$ any further. Let us note that even though we tried to find an application of condition
$(3)$ any further. Let us note that even though we tried to find an application of condition ![]() $(3)$, we did not find it, and this is basically why we had to develop conditions
$(3)$, we did not find it, and this is basically why we had to develop conditions ![]() $(2)$ and
$(2)$ and ![]() $(2')$.
$(2')$.
Proof of Proposition 3.15.
(1) ![]() $ \Rightarrow $ (2): Given such
$ \Rightarrow $ (2): Given such ![]() $ U $ and
$ U $ and ![]() $ \chi _{k} : \mathcal {A} \to U, k \in \mathbb {N} $, we put
$ \chi _{k} : \mathcal {A} \to U, k \in \mathbb {N} $, we put
Denote by ![]() $ I_{\mu } : (c_{00}, \mu ) \to U $ the isometry given by
$ I_{\mu } : (c_{00}, \mu ) \to U $ the isometry given by ![]() $ e_{k} \mapsto \chi _{k}(\mu ) $. Let
$ e_{k} \mapsto \chi _{k}(\mu ) $. Let ![]() $ \nu \in \mathcal {A} $ and
$ \nu \in \mathcal {A} $ and ![]() $ z^{*} \in (c_{00})^{\#} $ satisfying
$ z^{*} \in (c_{00})^{\#} $ satisfying ![]() $ |z^{*}(x)| \leq \nu (x) $ be given. For
$ |z^{*}(x)| \leq \nu (x) $ be given. For ![]() $ x, y \in c_{00} $ with
$ x, y \in c_{00} $ with ![]() $ I_{\nu }x = I_{\nu }y $, we have
$ I_{\nu }x = I_{\nu }y $, we have ![]() $ |z^{*}(y - x)| \leq \nu (y - x) = \Vert I_{\nu }(y - x) \Vert = 0 $, and so
$ |z^{*}(y - x)| \leq \nu (y - x) = \Vert I_{\nu }(y - x) \Vert = 0 $, and so ![]() $ z^{*}(x) = z^{*}(y) $. Thus, the formula
$ z^{*}(x) = z^{*}(y) $. Thus, the formula
defines a functional on ![]() $ I_{\nu }(c_{00}) $ such that
$ I_{\nu }(c_{00}) $ such that ![]() $ |u^{*}(I_{\nu }x)| = |z^{*}(x)| \leq \nu (x) = \Vert I_{\nu }x \Vert $. By the Hahn-Banach theorem, we can extend
$ |u^{*}(I_{\nu }x)| = |z^{*}(x)| \leq \nu (x) = \Vert I_{\nu }x \Vert $. By the Hahn-Banach theorem, we can extend ![]() $ u^{*} $ to the whole
$ u^{*} $ to the whole ![]() $ U $ in the way that
$ U $ in the way that
For every ![]() $ \mu \in \mathcal {A} $, let us put
$ \mu \in \mathcal {A} $, let us put
We obtain ![]() $ |\Gamma (\mu )(x)| = |u^{*}(I_{\mu }x)| \leq \Vert I_{\mu }x \Vert = \mu (x) $ and
$ |\Gamma (\mu )(x)| = |u^{*}(I_{\mu }x)| \leq \Vert I_{\mu }x \Vert = \mu (x) $ and  $ |\Gamma (\mu )(e_{k}) - \Gamma (\lambda )(e_{k})| = |u^{*}(I_{\mu }e_{k}) - u^{*}(I_{\lambda }e_{k})| = |u^{*}(\chi _{k}(\mu ) - \chi _{k}(\lambda ))| \leq \Vert \chi _{k}(\mu ) - \chi _{k}(\lambda ) \Vert = \alpha _{k}(\mu , \lambda ) $ for
$ |\Gamma (\mu )(e_{k}) - \Gamma (\lambda )(e_{k})| = |u^{*}(I_{\mu }e_{k}) - u^{*}(I_{\lambda }e_{k})| = |u^{*}(\chi _{k}(\mu ) - \chi _{k}(\lambda ))| \leq \Vert \chi _{k}(\mu ) - \chi _{k}(\lambda ) \Vert = \alpha _{k}(\mu , \lambda ) $ for ![]() $ \mu , \lambda \in \mathcal {A} $ and
$ \mu , \lambda \in \mathcal {A} $ and ![]() $ k \in \mathbb {N} $.
$ k \in \mathbb {N} $.
(2) ![]() $ \Rightarrow $ (1): Given such
$ \Rightarrow $ (1): Given such ![]() $ \alpha _{k} : \mathcal {A}^{2} \to [0, \infty ), k \in \mathbb {N} $, we define a subset of
$ \alpha _{k} : \mathcal {A}^{2} \to [0, \infty ), k \in \mathbb {N} $, we define a subset of ![]() $ c_{00}(\mathcal {A} \times \mathbb {N}) $ by
$ c_{00}(\mathcal {A} \times \mathbb {N}) $ by
 $$ \begin{align*} \Omega = \mathrm{co} \bigg( \bigcup_{\mu} \Big\{ \sum_{k} a_{k} e_{\mu, k} : \mu \Big( \sum_{k} a_{k} e_{k} \Big) \leq 1 \Big\} \cup \bigcup_{\mu, \lambda, k} \big\{ c \cdot (e_{\mu, k} - e_{\lambda, k}) : |c| \cdot \alpha_{k}(\mu, \lambda) \leq 1 \big\} \bigg), \end{align*} $$
$$ \begin{align*} \Omega = \mathrm{co} \bigg( \bigcup_{\mu} \Big\{ \sum_{k} a_{k} e_{\mu, k} : \mu \Big( \sum_{k} a_{k} e_{k} \Big) \leq 1 \Big\} \cup \bigcup_{\mu, \lambda, k} \big\{ c \cdot (e_{\mu, k} - e_{\lambda, k}) : |c| \cdot \alpha_{k}(\mu, \lambda) \leq 1 \big\} \bigg), \end{align*} $$and denote the corresponding Minkowski functional by ![]() $ \varrho $. Let
$ \varrho $. Let ![]() $ U $ be the completion of the quotient space
$ U $ be the completion of the quotient space ![]() $ X/N $, where
$ X/N $, where ![]() $ X = (c_{00}(\mathcal {A} \times \mathbb {N}), \varrho ) $ and
$ X = (c_{00}(\mathcal {A} \times \mathbb {N}), \varrho ) $ and ![]() $ N = \{ x \in c_{00}(\mathcal {A} \times \mathbb {N}) : \rho (x) = 0 \} $. In what follows, we identify every
$ N = \{ x \in c_{00}(\mathcal {A} \times \mathbb {N}) : \rho (x) = 0 \} $. In what follows, we identify every ![]() $ x \in c_{00}(\mathcal {A} \times \mathbb {N}) $ with its equivalence class
$ x \in c_{00}(\mathcal {A} \times \mathbb {N}) $ with its equivalence class ![]() $ [x]_{N} \in U $. Let us define
$ [x]_{N} \in U $. Let us define
As ![]() $ c \cdot (e_{\mu , k} - e_{\lambda , k}) \in \Omega $ whenever
$ c \cdot (e_{\mu , k} - e_{\lambda , k}) \in \Omega $ whenever ![]() $ |c| \cdot \alpha _{k}(\mu , \lambda ) \leq 1 $, we obtain
$ |c| \cdot \alpha _{k}(\mu , \lambda ) \leq 1 $, we obtain ![]() $ \varrho (e_{\mu , k} - e_{\lambda , k}) \leq \alpha _{k}(\mu , \lambda ) $: that is,
$ \varrho (e_{\mu , k} - e_{\lambda , k}) \leq \alpha _{k}(\mu , \lambda ) $: that is, ![]() $ \varrho (\chi _{k}(\mu ) - \chi _{k}(\lambda )) \leq \alpha _{k}(\mu , \lambda ) $. For a fixed
$ \varrho (\chi _{k}(\mu ) - \chi _{k}(\lambda )) \leq \alpha _{k}(\mu , \lambda ) $. For a fixed ![]() $ \mu $, we have
$ \mu $, we have ![]() $ \alpha _{k}(\mu , \lambda ) \to \alpha _{k}(\mu , \mu ) = 0 $ as
$ \alpha _{k}(\mu , \lambda ) \to \alpha _{k}(\mu , \mu ) = 0 $ as ![]() $ \lambda \to \mu $, and consequently
$ \lambda \to \mu $, and consequently ![]() $ \varrho (\chi _{k}(\mu ) - \chi _{k}(\lambda )) \to 0 $ as
$ \varrho (\chi _{k}(\mu ) - \chi _{k}(\lambda )) \to 0 $ as ![]() $ \lambda \to \mu $. Therefore,
$ \lambda \to \mu $. Therefore, ![]() $ \chi _{k} $ is continuous on
$ \chi _{k} $ is continuous on ![]() $ \mathcal {A} $. It follows that the image of
$ \mathcal {A} $. It follows that the image of ![]() $ \chi _{k} $ is separable. As these images contain all basic vectors
$ \chi _{k} $ is separable. As these images contain all basic vectors ![]() $ e_{\nu , k} $, the space
$ e_{\nu , k} $, the space ![]() $ U $ is separable.
$ U $ is separable.
We need to show that
for fixed ![]() $ \nu \in \mathcal {A} $,
$ \nu \in \mathcal {A} $, ![]() $ x = \sum _{k \in \mathbb {N}} a_{k} e_{k} \in c_{00} $ and its image
$ x = \sum _{k \in \mathbb {N}} a_{k} e_{k} \in c_{00} $ and its image ![]() $ \overline {x} = \sum _{k \in \mathbb {N}} a_{k} e_{\nu , k} $. The inequality
$ \overline {x} = \sum _{k \in \mathbb {N}} a_{k} e_{\nu , k} $. The inequality ![]() $ \nu (x) \geq \varrho (\overline {x}) $ follows immediately from the definition of
$ \nu (x) \geq \varrho (\overline {x}) $ follows immediately from the definition of ![]() $ \Omega $ (for any
$ \Omega $ (for any ![]() $ c \geq \nu (x) $ with
$ c \geq \nu (x) $ with ![]() $ c> 0 $, we have
$ c> 0 $, we have  $ \nu (\frac {1}{c}x) \leq 1 $, and so
$ \nu (\frac {1}{c}x) \leq 1 $, and so  $ \frac {1}{c}\overline {x} \in \Omega $, hence
$ \frac {1}{c}\overline {x} \in \Omega $, hence  $ \varrho (\frac {1}{c}\overline {x}) \leq 1 $ and
$ \varrho (\frac {1}{c}\overline {x}) \leq 1 $ and ![]() $ \varrho (\overline {x}) \leq c $). Let us show the opposite inequality
$ \varrho (\overline {x}) \leq c $). Let us show the opposite inequality ![]() $ \nu (x) \leq \varrho (\overline {x}) $. Using the Hahn-Banach theorem, we can pick
$ \nu (x) \leq \varrho (\overline {x}) $. Using the Hahn-Banach theorem, we can pick ![]() $ z^{*} \in (c_{00})^{\#} $ satisfying
$ z^{*} \in (c_{00})^{\#} $ satisfying ![]() $ z^{*}(x) = \nu (x) $ and
$ z^{*}(x) = \nu (x) $ and ![]() $ |z^{*}(y)| \leq \nu (y) $ for every
$ |z^{*}(y)| \leq \nu (y) $ for every ![]() $ y \in c_{00} $. Let
$ y \in c_{00} $. Let ![]() $ \Gamma : \mathcal {A} \to (c_{00})^{\#} $ be the mapping provided for
$ \Gamma : \mathcal {A} \to (c_{00})^{\#} $ be the mapping provided for ![]() $ \nu $ and
$ \nu $ and ![]() $ z^{*} $, and let
$ z^{*} $, and let ![]() $ u^{*} \in (c_{00}(\mathcal {A} \times \mathbb {N}))^{\#} $ be given by
$ u^{*} \in (c_{00}(\mathcal {A} \times \mathbb {N}))^{\#} $ be given by
Then ![]() $ u^{*}(\overline {x}) = u^{*}(\sum _{k} a_{k} e_{\nu , k}) = \sum _{k} a_{k} u^{*}(e_{\nu , k}) = \sum _{k} a_{k} \Gamma (\nu )(e_{k}) = \Gamma (\nu )(\sum _{k} a_{k} e_{k}) = z^{*}(x) = \nu (x) $. It is sufficient to show that
$ u^{*}(\overline {x}) = u^{*}(\sum _{k} a_{k} e_{\nu , k}) = \sum _{k} a_{k} u^{*}(e_{\nu , k}) = \sum _{k} a_{k} \Gamma (\nu )(e_{k}) = \Gamma (\nu )(\sum _{k} a_{k} e_{k}) = z^{*}(x) = \nu (x) $. It is sufficient to show that ![]() $ u^{*} \leq 1 $ on
$ u^{*} \leq 1 $ on ![]() $ \Omega $ (equivalently
$ \Omega $ (equivalently ![]() $ |u^{*}(y)| \leq \varrho (y) $ for every
$ |u^{*}(y)| \leq \varrho (y) $ for every ![]() $ y \in c_{00}(\mathcal {A} \times \mathbb {N}) $), since it follows that
$ y \in c_{00}(\mathcal {A} \times \mathbb {N}) $), since it follows that ![]() $ \nu (x) = u^{*}(\overline {x}) \leq \varrho (\overline {x}) $.
$ \nu (x) = u^{*}(\overline {x}) \leq \varrho (\overline {x}) $.
To show that ![]() $ u^{*} \leq 1 $ on
$ u^{*} \leq 1 $ on ![]() $ \Omega $, we need to check that
$ \Omega $, we need to check that
 $$ \begin{align*} \mu \Big( \sum_{k} b_{k} e_{k} \Big) \leq 1 \quad \Rightarrow \quad u^{*} \Big( \sum_{k} b_{k} e_{\mu, k} \Big) \leq 1 \end{align*} $$
$$ \begin{align*} \mu \Big( \sum_{k} b_{k} e_{k} \Big) \leq 1 \quad \Rightarrow \quad u^{*} \Big( \sum_{k} b_{k} e_{\mu, k} \Big) \leq 1 \end{align*} $$and
Concerning the first implication, we compute ![]() $ u^{*}(\sum _{k} b_{k} e_{\mu , k}) = \sum _{k} b_{k} u^{*}(e_{\mu , k}) = \sum _{k} b_{k} \Gamma (\mu )(e_{k}) = \Gamma (\mu )(\sum _{k} b_{k} e_{k}) \leq \mu (\sum _{k} b_{k} e_{k}) \leq 1 $. Concerning the second implication, we compute
$ u^{*}(\sum _{k} b_{k} e_{\mu , k}) = \sum _{k} b_{k} u^{*}(e_{\mu , k}) = \sum _{k} b_{k} \Gamma (\mu )(e_{k}) = \Gamma (\mu )(\sum _{k} b_{k} e_{k}) \leq \mu (\sum _{k} b_{k} e_{k}) \leq 1 $. Concerning the second implication, we compute ![]() $ u^{*}(c \cdot (e_{\mu , k} - e_{\lambda , k})) = c u^{*}(e_{\mu , k}) - c u^{*}(e_{\lambda , k}) = c \Gamma (\mu )(e_{k}) - c \Gamma (\lambda )(e_{k}) \leq |c| \alpha _{k}(\mu , \lambda ) \leq 1 $.
$ u^{*}(c \cdot (e_{\mu , k} - e_{\lambda , k})) = c u^{*}(e_{\mu , k}) - c u^{*}(e_{\lambda , k}) = c \Gamma (\mu )(e_{k}) - c \Gamma (\lambda )(e_{k}) \leq |c| \alpha _{k}(\mu , \lambda ) \leq 1 $.
(2) ![]() $ \Rightarrow $ (2’): The choice
$ \Rightarrow $ (2’): The choice ![]() $ \beta _{k} = \alpha _{k} $ works. Indeed, if
$ \beta _{k} = \alpha _{k} $ works. Indeed, if ![]() $ \Gamma $ is provided by (2), we can take
$ \Gamma $ is provided by (2), we can take ![]() $ \eta \cdot \Gamma $.
$ \eta \cdot \Gamma $.
(2’) ![]() $ \Rightarrow $ (2): For every
$ \Rightarrow $ (2): For every ![]() $ n \in \mathbb {N} $, let
$ n \in \mathbb {N} $, let  $ \beta _{k}^{n} : \mathcal {A}^{2} \to [0, \infty ), k \in \mathbb {N}, $ be provided by (2’) for
$ \beta _{k}^{n} : \mathcal {A}^{2} \to [0, \infty ), k \in \mathbb {N}, $ be provided by (2’) for ![]() $ \eta = (1 - 2^{-n}) $. We can assume that each
$ \eta = (1 - 2^{-n}) $. We can assume that each ![]() $ \beta _{k}^{n} $ is a pseudometric. Indeed, instead of
$ \beta _{k}^{n} $ is a pseudometric. Indeed, instead of ![]() $ \beta _{k}^{n} $, we can take the maximal minorizing pseudometric
$ \beta _{k}^{n} $, we can take the maximal minorizing pseudometric ![]() $ \widetilde {\beta }^{n}_{k} $ (in such a case,
$ \widetilde {\beta }^{n}_{k} $ (in such a case, ![]() $ \widetilde {\beta }^{n}_{k} $ is continuous, and since the function
$ \widetilde {\beta }^{n}_{k} $ is continuous, and since the function ![]() $ (\mu , \lambda ) \mapsto |\Gamma (\mu )(e_{k}) - \Gamma (\lambda )(e_{k})| $ is a pseudometric, if it minorizes
$ (\mu , \lambda ) \mapsto |\Gamma (\mu )(e_{k}) - \Gamma (\lambda )(e_{k})| $ is a pseudometric, if it minorizes ![]() $ \beta _{k}^{n} $, then it minorizes
$ \beta _{k}^{n} $, then it minorizes ![]() $ \widetilde {\beta }^{n}_{k} $ as well). Moreover, we can assume that
$ \widetilde {\beta }^{n}_{k} $ as well). Moreover, we can assume that ![]() $ \beta _{1}^{1} $ is a metric (it is possible to add a compatible metric on
$ \beta _{1}^{1} $ is a metric (it is possible to add a compatible metric on ![]() $ \mathcal {A} $ to
$ \mathcal {A} $ to ![]() $ \beta _{1}^{1} $).
$ \beta _{1}^{1} $).
Let us define
 $$ \begin{align*} \alpha(\mu, \lambda) = \max_{n, k} \min \{ \beta_{k}^{n}(\mu, \lambda), 2^{- \max\{n, k\}} \}, \quad \mu, \lambda \in \mathcal{A}. \end{align*} $$
$$ \begin{align*} \alpha(\mu, \lambda) = \max_{n, k} \min \{ \beta_{k}^{n}(\mu, \lambda), 2^{- \max\{n, k\}} \}, \quad \mu, \lambda \in \mathcal{A}. \end{align*} $$It is easy to check that ![]() $ \alpha $ is continuous. Due to our additional assumptions,
$ \alpha $ is continuous. Due to our additional assumptions, ![]() $ \alpha $ is a metric on
$ \alpha $ is a metric on ![]() $ \mathcal {A} $. We want to show that there are some constants
$ \mathcal {A} $. We want to show that there are some constants ![]() $ c_{k} $ such that the choice
$ c_{k} $ such that the choice ![]() $ \alpha _{k} = c_{k} \cdot \alpha $ works.
$ \alpha _{k} = c_{k} \cdot \alpha $ works.
Let ![]() $ \nu \in \mathcal {A} $ and
$ \nu \in \mathcal {A} $ and ![]() $ z^{*} \in (c_{00})^{\#} $ satisfy
$ z^{*} \in (c_{00})^{\#} $ satisfy ![]() $ |z^{*}(x)| \leq \nu (x) $ for every
$ |z^{*}(x)| \leq \nu (x) $ for every ![]() $ x \in c_{00} $. For every
$ x \in c_{00} $. For every ![]() $ n \in \mathbb {N} $, there is a mapping
$ n \in \mathbb {N} $, there is a mapping ![]() $ \Gamma ^{n} : \mathcal {A} \to (c_{00})^{\#} $ such that
$ \Gamma ^{n} : \mathcal {A} \to (c_{00})^{\#} $ such that
and, if we denote
then
for every ![]() $ \mu , \lambda \in \mathcal {A} $ and every
$ \mu , \lambda \in \mathcal {A} $ and every ![]() $ k $. Let us note that
$ k $. Let us note that
as ![]() $ |\gamma _{k}^{n}(\mu )| = |\Gamma ^{n}(\mu )(e_{k})| \leq \mu (e_{k}) \leq 1 $ by the assumption on
$ |\gamma _{k}^{n}(\mu )| = |\Gamma ^{n}(\mu )(e_{k})| \leq \mu (e_{k}) \leq 1 $ by the assumption on ![]() $ \mathcal {A} $.
$ \mathcal {A} $.
Now, we define the desired mapping ![]() $ \Gamma $. For practical purposes, we first define
$ \Gamma $. For practical purposes, we first define
For every ![]() $ n \in \mathbb {Z} $, let
$ n \in \mathbb {Z} $, let ![]() $ f_{n} $ denote the piecewise linear function supported by
$ f_{n} $ denote the piecewise linear function supported by ![]() $ [2^{-n-3}, 2^{-n-1}] $, which is linear on
$ [2^{-n-3}, 2^{-n-1}] $, which is linear on ![]() $ [2^{-n-3}, 2^{-n-2}] $ and
$ [2^{-n-3}, 2^{-n-2}] $ and ![]() $ [2^{-n-2}, 2^{-n-1}] $, and for which
$ [2^{-n-2}, 2^{-n-1}] $, and for which ![]() $ f_{n}(2^{-n-2}) = 1 $. In this way, we have
$ f_{n}(2^{-n-2}) = 1 $. In this way, we have ![]() $ \sum _{n \in \mathbb {Z}} f_{n} = 1 $ on
$ \sum _{n \in \mathbb {Z}} f_{n} = 1 $ on ![]() $ (0, \infty ) $. We define
$ (0, \infty ) $. We define
and
 $$ \begin{align*} \gamma_{k}(\mu) = \sum_{n \in \mathbb{Z}} f_{n}(\alpha(\mu, \nu)) \gamma_{k}^{n}(\mu), \quad \mu \neq \nu. \end{align*} $$
$$ \begin{align*} \gamma_{k}(\mu) = \sum_{n \in \mathbb{Z}} f_{n}(\alpha(\mu, \nu)) \gamma_{k}^{n}(\mu), \quad \mu \neq \nu. \end{align*} $$Finally, we put ![]() $ \Gamma (\mu )(e_{k}) = \gamma _{k}(\mu ) $, so
$ \Gamma (\mu )(e_{k}) = \gamma _{k}(\mu ) $, so ![]() $ \Gamma (\nu ) = z^{*} $ and
$ \Gamma (\nu ) = z^{*} $ and ![]() $ \Gamma (\mu ) = \sum _{n \in \mathbb {N}} f_{n}(\alpha (\mu , \nu )) \Gamma ^{n}(\mu ) $ for
$ \Gamma (\mu ) = \sum _{n \in \mathbb {N}} f_{n}(\alpha (\mu , \nu )) \Gamma ^{n}(\mu ) $ for ![]() $ \mu \neq \nu $. In both cases
$ \mu \neq \nu $. In both cases ![]() $ \mu = \nu $ and
$ \mu = \nu $ and ![]() $ \mu \neq \nu $, it follows that
$ \mu \neq \nu $, it follows that ![]() $ |\Gamma (\mu )(x)| \leq \mu (x) $ for every
$ |\Gamma (\mu )(x)| \leq \mu (x) $ for every ![]() $ x \in c_{00} $. It remains to prove the inequality
$ x \in c_{00} $. It remains to prove the inequality
for some suitable constants ![]() $ c_{k} $.
$ c_{k} $.
Let us show that the implication
 $$ \begin{align} \alpha(\mu, \lambda) < 2^{-n} \quad \Rightarrow \quad |\gamma_{k}^{n}(\mu) - \gamma_{k}^{n}(\lambda)| \leq 2^{k+1} \alpha(\mu, \lambda) \end{align} $$
$$ \begin{align} \alpha(\mu, \lambda) < 2^{-n} \quad \Rightarrow \quad |\gamma_{k}^{n}(\mu) - \gamma_{k}^{n}(\lambda)| \leq 2^{k+1} \alpha(\mu, \lambda) \end{align} $$holds. Clearly, we can suppose that ![]() $ n \geq 1 $. If
$ n \geq 1 $. If ![]() $ \alpha (\mu , \lambda ) \geq 2^{-k} $, then
$ \alpha (\mu , \lambda ) \geq 2^{-k} $, then  $ 2^{k+1} \alpha (\mu , \lambda ) \geq 2 \geq |\gamma _{k}^{n}(\mu ) - \gamma _{k}^{n}(\lambda )| $. So, let us assume that
$ 2^{k+1} \alpha (\mu , \lambda ) \geq 2 \geq |\gamma _{k}^{n}(\mu ) - \gamma _{k}^{n}(\lambda )| $. So, let us assume that ![]() $ \alpha (\mu , \lambda ) < 2^{-k} $. Since
$ \alpha (\mu , \lambda ) < 2^{-k} $. Since  $ \min \{ \beta _{k}^{n}(\mu , \lambda ), 2^{- \max \{n, k\}} \} \leq \alpha (\mu , \lambda ) < 2^{- \max \{n, k\}} $, we have
$ \min \{ \beta _{k}^{n}(\mu , \lambda ), 2^{- \max \{n, k\}} \} \leq \alpha (\mu , \lambda ) < 2^{- \max \{n, k\}} $, we have  $ \min \{ \beta _{k}^{n}(\mu , \lambda ), 2^{- \max \{n, k\}} \} = \beta _{k}^{n}(\mu , \lambda ) $, and so
$ \min \{ \beta _{k}^{n}(\mu , \lambda ), 2^{- \max \{n, k\}} \} = \beta _{k}^{n}(\mu , \lambda ) $, and so  $ |\gamma _{k}^{n}(\mu ) - \gamma _{k}^{n}(\lambda )| \leq \beta _{k}^{n}(\mu , \lambda ) = \min \{ \beta _{k}^{n}(\mu , \lambda ), 2^{- \max \{n, k\}} \} \leq \alpha (\mu , \lambda ) \leq 2^{k+1} \alpha (\mu , \lambda ) $.
$ |\gamma _{k}^{n}(\mu ) - \gamma _{k}^{n}(\lambda )| \leq \beta _{k}^{n}(\mu , \lambda ) = \min \{ \beta _{k}^{n}(\mu , \lambda ), 2^{- \max \{n, k\}} \} \leq \alpha (\mu , \lambda ) \leq 2^{k+1} \alpha (\mu , \lambda ) $.
Next, we show that
 $$ \begin{align} 2^{-n-4} \leq \alpha(\mu, \nu) < 2^{-n} \quad \Rightarrow \quad |\gamma_{k}^{n}(\mu) - \gamma_{k}(\nu)| \leq (2^{k+1} + 16) \alpha(\mu, \nu). \end{align} $$
$$ \begin{align} 2^{-n-4} \leq \alpha(\mu, \nu) < 2^{-n} \quad \Rightarrow \quad |\gamma_{k}^{n}(\mu) - \gamma_{k}(\nu)| \leq (2^{k+1} + 16) \alpha(\mu, \nu). \end{align} $$If ![]() $ n \geq 1 $, then
$ n \geq 1 $, then ![]() $ \gamma _{k}(\nu ) - \gamma _{k}^{n}(\nu ) = z^{*}(e_{k}) - (1 - 2^{-n}) z^{*}(e_{k}) = 2^{-n} z^{*}(e_{k}) $. If
$ \gamma _{k}(\nu ) - \gamma _{k}^{n}(\nu ) = z^{*}(e_{k}) - (1 - 2^{-n}) z^{*}(e_{k}) = 2^{-n} z^{*}(e_{k}) $. If ![]() $ n \leq 0 $, then
$ n \leq 0 $, then ![]() $ \gamma _{k}(\nu ) - \gamma _{k}^{n}(\nu ) = z^{*}(e_{k}) $. In both cases,
$ \gamma _{k}(\nu ) - \gamma _{k}^{n}(\nu ) = z^{*}(e_{k}) $. In both cases,  $ |\gamma _{k}(\nu ) - \gamma _{k}^{n}(\nu )| \leq 2^{-n} |z^{*}(e_{k})| \leq 2^{-n} \nu (e_{k}) \leq 2^{-n} \leq 2^{4} \alpha (\mu , \nu ) $. Using formula (3.1), we can compute
$ |\gamma _{k}(\nu ) - \gamma _{k}^{n}(\nu )| \leq 2^{-n} |z^{*}(e_{k})| \leq 2^{-n} \nu (e_{k}) \leq 2^{-n} \leq 2^{4} \alpha (\mu , \nu ) $. Using formula (3.1), we can compute
 $$ \begin{align*} |\gamma_{k}^{n}(\mu) - \gamma_{k}(\nu)| \leq |\gamma_{k}^{n}(\mu) - \gamma_{k}^{n}(\nu)| + |\gamma_{k}^{n}(\nu) - \gamma_{k}(\nu)| \leq (2^{k+1} + 2^{4}) \alpha(\mu, \nu). \end{align*} $$
$$ \begin{align*} |\gamma_{k}^{n}(\mu) - \gamma_{k}(\nu)| \leq |\gamma_{k}^{n}(\mu) - \gamma_{k}^{n}(\nu)| + |\gamma_{k}^{n}(\nu) - \gamma_{k}(\nu)| \leq (2^{k+1} + 2^{4}) \alpha(\mu, \nu). \end{align*} $$Further, it follows from formula (3.2) that
Indeed, since ![]() $ f_{n} $ is supported by
$ f_{n} $ is supported by ![]() $ [2^{-n-3}, 2^{-n-1}] $, we always have
$ [2^{-n-3}, 2^{-n-1}] $, we always have
 $$ \begin{align*} f_{n}(\alpha(\mu, \nu)) |\gamma_{k}^{n}(\mu) - \gamma_{k}(\nu)| \leq f_{n}(\alpha(\mu, \nu)) (2^{k+1} + 16) \alpha(\mu, \nu), \end{align*} $$
$$ \begin{align*} f_{n}(\alpha(\mu, \nu)) |\gamma_{k}^{n}(\mu) - \gamma_{k}(\nu)| \leq f_{n}(\alpha(\mu, \nu)) (2^{k+1} + 16) \alpha(\mu, \nu), \end{align*} $$and it is sufficient to use that ![]() $ \gamma _{k}(\mu ) - \gamma _{k}(\nu ) = \sum _{n \in \mathbb {Z}} f_{n}(\alpha (\mu , \nu )) (\gamma _{k}^{n}(\mu ) - \gamma _{k}(\nu )) $ for
$ \gamma _{k}(\mu ) - \gamma _{k}(\nu ) = \sum _{n \in \mathbb {Z}} f_{n}(\alpha (\mu , \nu )) (\gamma _{k}^{n}(\mu ) - \gamma _{k}(\nu )) $ for ![]() $ \mu \neq \nu $.
$ \mu \neq \nu $.
Now, we are going to investigate the value ![]() $ |\gamma _{k}(\mu ) - \gamma _{k}(\lambda )| $. First, we have
$ |\gamma _{k}(\mu ) - \gamma _{k}(\lambda )| $. First, we have
Indeed, as ![]() $ \alpha (\mu , \lambda ) \geq \alpha (\lambda , \nu ) - \alpha (\mu , \nu ) \geq 2 \alpha (\mu , \nu ) - \alpha (\mu , \nu ) = \alpha (\mu , \nu ) $, we can apply inequality (3.3) and write
$ \alpha (\mu , \lambda ) \geq \alpha (\lambda , \nu ) - \alpha (\mu , \nu ) \geq 2 \alpha (\mu , \nu ) - \alpha (\mu , \nu ) = \alpha (\mu , \nu ) $, we can apply inequality (3.3) and write
 $$ \begin{align*} |\gamma_{k}(\mu) - \gamma_{k}(\lambda)| & \leq |\gamma_{k}(\mu) - \gamma_{k}(\nu)| + |\gamma_{k}(\lambda) - \gamma_{k}(\nu)| \\ & \leq (2^{k+1} + 16) (\alpha(\mu, \nu) + \alpha(\lambda, \nu)) \\ & = (2^{k+1} + 16) (\alpha(\lambda, \nu) - \alpha(\mu, \nu) + 2 \alpha(\mu, \nu)) \\ & \leq (2^{k+1} + 16)(1 + 2) \alpha(\mu, \lambda). \end{align*} $$
$$ \begin{align*} |\gamma_{k}(\mu) - \gamma_{k}(\lambda)| & \leq |\gamma_{k}(\mu) - \gamma_{k}(\nu)| + |\gamma_{k}(\lambda) - \gamma_{k}(\nu)| \\ & \leq (2^{k+1} + 16) (\alpha(\mu, \nu) + \alpha(\lambda, \nu)) \\ & = (2^{k+1} + 16) (\alpha(\lambda, \nu) - \alpha(\mu, \nu) + 2 \alpha(\mu, \nu)) \\ & \leq (2^{k+1} + 16)(1 + 2) \alpha(\mu, \lambda). \end{align*} $$Now, we prove the last but most challenging implication:
Let us compute
 $$ \begin{align*} & \gamma_{k}(\mu) - \gamma_{k}(\lambda) = \sum_{n \in \mathbb{Z}} \big[ f_{n}(\alpha(\mu, \nu)) \gamma_{k}^{n}(\mu) - f_{n}(\alpha(\lambda, \nu)) \gamma_{k}^{n}(\lambda) \big] \\ & = \sum_{n \in \mathbb{Z}} \big[ f_{n}(\alpha(\mu, \nu)) \gamma_{k}^{n}(\mu) - f_{n}(\alpha(\lambda, \nu)) \gamma_{k}^{n}(\mu) + f_{n}(\alpha(\lambda, \nu)) \gamma_{k}^{n}(\mu) - f_{n}(\alpha(\lambda, \nu)) \gamma_{k}^{n}(\lambda) \big] \\ & = \sum_{n \in \mathbb{Z}} [f_{n}(\alpha(\mu, \nu)) - f_{n}(\alpha(\lambda, \nu))] \gamma_{k}^{n}(\mu) + \sum_{n \in \mathbb{Z}} f_{n}(\alpha(\lambda, \nu)) [\gamma_{k}^{n}(\mu) - \gamma_{k}^{n}(\lambda)] \\ & = \sum_{n \in \mathbb{Z}} [f_{n}(\alpha(\mu, \nu)) - f_{n}(\alpha(\lambda, \nu))] (\gamma_{k}^{n}(\mu) - \gamma_{k}(\nu)) + \sum_{n \in \mathbb{Z}} f_{n}(\alpha(\lambda, \nu)) [\gamma_{k}^{n}(\mu) - \gamma_{k}^{n}(\lambda)]. \end{align*} $$
$$ \begin{align*} & \gamma_{k}(\mu) - \gamma_{k}(\lambda) = \sum_{n \in \mathbb{Z}} \big[ f_{n}(\alpha(\mu, \nu)) \gamma_{k}^{n}(\mu) - f_{n}(\alpha(\lambda, \nu)) \gamma_{k}^{n}(\lambda) \big] \\ & = \sum_{n \in \mathbb{Z}} \big[ f_{n}(\alpha(\mu, \nu)) \gamma_{k}^{n}(\mu) - f_{n}(\alpha(\lambda, \nu)) \gamma_{k}^{n}(\mu) + f_{n}(\alpha(\lambda, \nu)) \gamma_{k}^{n}(\mu) - f_{n}(\alpha(\lambda, \nu)) \gamma_{k}^{n}(\lambda) \big] \\ & = \sum_{n \in \mathbb{Z}} [f_{n}(\alpha(\mu, \nu)) - f_{n}(\alpha(\lambda, \nu))] \gamma_{k}^{n}(\mu) + \sum_{n \in \mathbb{Z}} f_{n}(\alpha(\lambda, \nu)) [\gamma_{k}^{n}(\mu) - \gamma_{k}^{n}(\lambda)] \\ & = \sum_{n \in \mathbb{Z}} [f_{n}(\alpha(\mu, \nu)) - f_{n}(\alpha(\lambda, \nu))] (\gamma_{k}^{n}(\mu) - \gamma_{k}(\nu)) + \sum_{n \in \mathbb{Z}} f_{n}(\alpha(\lambda, \nu)) [\gamma_{k}^{n}(\mu) - \gamma_{k}^{n}(\lambda)]. \end{align*} $$Hence, ![]() $ |\gamma _{k}(\mu ) - \gamma _{k}(\lambda )| $ is less than or equal to
$ |\gamma _{k}(\mu ) - \gamma _{k}(\lambda )| $ is less than or equal to
 $$ \begin{align*} \sum_{n \in \mathbb{Z}} |f_{n}(\alpha(\mu, \nu)) - f_{n}(\alpha(\lambda, \nu))| |\gamma_{k}^{n}(\mu) - \gamma_{k}(\nu)| + \sum_{n \in \mathbb{Z}} f_{n}(\alpha(\lambda, \nu)) |\gamma_{k}^{n}(\mu) - \gamma_{k}^{n}(\lambda)|. \end{align*} $$
$$ \begin{align*} \sum_{n \in \mathbb{Z}} |f_{n}(\alpha(\mu, \nu)) - f_{n}(\alpha(\lambda, \nu))| |\gamma_{k}^{n}(\mu) - \gamma_{k}(\nu)| + \sum_{n \in \mathbb{Z}} f_{n}(\alpha(\lambda, \nu)) |\gamma_{k}^{n}(\mu) - \gamma_{k}^{n}(\lambda)|. \end{align*} $$Let us notice that
•
 $ f_{n}(\alpha (\mu , \nu )) \neq 0 $ iff
$ f_{n}(\alpha (\mu , \nu )) \neq 0 $ iff  $ 2^{-n-3} < \alpha (\mu , \nu ) < 2^{-n-1} $,
$ 2^{-n-3} < \alpha (\mu , \nu ) < 2^{-n-1} $,•
 $ f_{n}(\alpha (\lambda , \nu )) \neq 0 $ iff
$ f_{n}(\alpha (\lambda , \nu )) \neq 0 $ iff  $ 2^{-n-3} < \alpha (\lambda , \nu ) < 2^{-n-1} $, and
$ 2^{-n-3} < \alpha (\lambda , \nu ) < 2^{-n-1} $, and  $ 2^{-n-4} < \alpha (\mu , \nu ) < 2^{-n-1} $ in this case,
$ 2^{-n-4} < \alpha (\mu , \nu ) < 2^{-n-1} $ in this case,• the function
 $ f_{n} $ is Lipschitz with the constant
$ f_{n} $ is Lipschitz with the constant  $ 2^{n+3} $.
$ 2^{n+3} $.
So, if ![]() $ f_{n}(\alpha (\mu , \nu )) \neq 0 $ or
$ f_{n}(\alpha (\mu , \nu )) \neq 0 $ or ![]() $ f_{n}(\alpha (\lambda , \nu )) \neq 0 $, then
$ f_{n}(\alpha (\lambda , \nu )) \neq 0 $, then ![]() $ 2^{-n-4} < \alpha (\mu , \nu ) < 2^{-n-1} $, and formula (3.2) can be applied. We obtain for the first sum that
$ 2^{-n-4} < \alpha (\mu , \nu ) < 2^{-n-1} $, and formula (3.2) can be applied. We obtain for the first sum that
 $$ \begin{align*} \sum_{n \in \mathbb{Z}} |f_{n}(\alpha(\mu, \nu)) & - f_{n}(\alpha(\lambda, \nu))| |\gamma_{k}^{n}(\mu) - \gamma_{k}(\nu)| \\ & \leq \sum_{2^{-n-4} < \alpha(\mu, \nu) < 2^{-n-1}} 2^{n+3} |\alpha(\mu, \nu) - \alpha(\lambda, \nu)| (2^{k+1} + 16) \alpha(\mu, \nu) \\ & \leq \sum_{2^{-n-4} < \alpha(\mu, \nu) < 2^{-n-1}} 2^{n+3} \alpha(\mu, \lambda) (2^{k+1} + 16) 2^{-n-1} \\ & \leq 3 \cdot 2^{2} (2^{k+1} + 16) \alpha(\mu, \lambda). \end{align*} $$
$$ \begin{align*} \sum_{n \in \mathbb{Z}} |f_{n}(\alpha(\mu, \nu)) & - f_{n}(\alpha(\lambda, \nu))| |\gamma_{k}^{n}(\mu) - \gamma_{k}(\nu)| \\ & \leq \sum_{2^{-n-4} < \alpha(\mu, \nu) < 2^{-n-1}} 2^{n+3} |\alpha(\mu, \nu) - \alpha(\lambda, \nu)| (2^{k+1} + 16) \alpha(\mu, \nu) \\ & \leq \sum_{2^{-n-4} < \alpha(\mu, \nu) < 2^{-n-1}} 2^{n+3} \alpha(\mu, \lambda) (2^{k+1} + 16) 2^{-n-1} \\ & \leq 3 \cdot 2^{2} (2^{k+1} + 16) \alpha(\mu, \lambda). \end{align*} $$ Concerning the second sum, we notice that if ![]() $ f_{n}(\alpha (\lambda , \nu )) \neq 0 $, then
$ f_{n}(\alpha (\lambda , \nu )) \neq 0 $, then ![]() $ \alpha (\lambda , \nu ) < 2^{-n-1} $, and so
$ \alpha (\lambda , \nu ) < 2^{-n-1} $, and so ![]() $ \alpha (\mu , \lambda ) \leq \alpha (\mu , \nu ) + \alpha (\lambda , \nu ) \leq 2\alpha (\lambda , \nu ) < 2^{-n} $. Applying formula (3.1), we obtain
$ \alpha (\mu , \lambda ) \leq \alpha (\mu , \nu ) + \alpha (\lambda , \nu ) \leq 2\alpha (\lambda , \nu ) < 2^{-n} $. Applying formula (3.1), we obtain
 $$ \begin{align*} \sum_{n \in \mathbb{Z}} f_{n}(\alpha(\lambda, \nu)) |\gamma_{k}^{n}(\mu) - \gamma_{k}^{n}(\lambda)| \leq \sum_{n \in \mathbb{Z}} f_{n}(\alpha(\lambda, \nu)) 2^{k+1} \alpha(\mu, \lambda) = 2^{k+1} \alpha(\mu, \lambda), \end{align*} $$
$$ \begin{align*} \sum_{n \in \mathbb{Z}} f_{n}(\alpha(\lambda, \nu)) |\gamma_{k}^{n}(\mu) - \gamma_{k}^{n}(\lambda)| \leq \sum_{n \in \mathbb{Z}} f_{n}(\alpha(\lambda, \nu)) 2^{k+1} \alpha(\mu, \lambda) = 2^{k+1} \alpha(\mu, \lambda), \end{align*} $$and formula (3.5) follows.
Finally, we finish the proof with the observation that formulas (3.4) and (3.5) provide
We can suppose that ![]() $ \alpha (\mu , \nu ) \leq \alpha (\lambda , \nu ) $. If
$ \alpha (\mu , \nu ) \leq \alpha (\lambda , \nu ) $. If ![]() $ \alpha (\lambda , \nu ) \geq 2 \alpha (\mu , \nu ) $, we use formula (3.4), and if
$ \alpha (\lambda , \nu ) \geq 2 \alpha (\mu , \nu ) $, we use formula (3.4), and if ![]() $ \alpha (\lambda , \nu ) < 2 \alpha (\mu , \nu ) $, we use formula (3.5).
$ \alpha (\lambda , \nu ) < 2 \alpha (\mu , \nu ) $, we use formula (3.5).
Definition 3.17. Let ![]() $ \mathcal {B}_{(1)} $ denote the set of all norms
$ \mathcal {B}_{(1)} $ denote the set of all norms ![]() $ \nu \in \mathcal {B} $ such that
$ \nu \in \mathcal {B} $ such that ![]() $ \nu (e_{k}) = 1 $ for each
$ \nu (e_{k}) = 1 $ for each ![]() $ k \in \mathbb {N} $.
$ k \in \mathbb {N} $.
Now we introduce the second auxiliary result for proving Proposition 3.12.
Lemma 3.18. Condition (2’) from Proposition 3.15 is valid for ![]() $ \mathcal {A} = \mathcal {B}_{(1)} $.
$ \mathcal {A} = \mathcal {B}_{(1)} $.
The proof of the lemma is organized according to the order of quantifiers in condition (2’). This is perhaps not the most natural order for reading, and the reader may skip the first paragraph of the proof, in which the functions ![]() $ \beta _{k} $ are introduced in a somewhat incomprehensible way, and come back later. The next part, in which functions
$ \beta _{k} $ are introduced in a somewhat incomprehensible way, and come back later. The next part, in which functions ![]() $ \gamma _{k} $ (the coordinates of
$ \gamma _{k} $ (the coordinates of ![]() $ \Gamma $) are constructed, is natural in some sense. In a recursive procedure, functionals are extended to a space with dimension
$ \Gamma $) are constructed, is natural in some sense. In a recursive procedure, functionals are extended to a space with dimension ![]() $ 1 $ bigger, so there are similarities with the proof of the Hanh-Banach theorem. In our situation, the upper bound by the corresponding norm is a bit relaxed in each step (see formula (3.7)), which is allowed since we prove the relaxed condition (2’). This is needed later for having a control over the difference
$ 1 $ bigger, so there are similarities with the proof of the Hanh-Banach theorem. In our situation, the upper bound by the corresponding norm is a bit relaxed in each step (see formula (3.7)), which is allowed since we prove the relaxed condition (2’). This is needed later for having a control over the difference ![]() $ |\gamma _{k}(\mu ) - \gamma _{k}(\lambda )| $.
$ |\gamma _{k}(\mu ) - \gamma _{k}(\lambda )| $.
Proof. Let ![]() $ \eta \in [0, 1) $ be given. We fix numbers
$ \eta \in [0, 1) $ be given. We fix numbers ![]() $ \kappa _{k} < 1 $ such that
$ \kappa _{k} < 1 $ such that ![]() $ \eta \leq \kappa _{1} < \kappa _{2} < \kappa _{3} < \dots $. For every
$ \eta \leq \kappa _{1} < \kappa _{2} < \kappa _{3} < \dots $. For every ![]() $ \mu , \lambda \in \mathcal {B}_{(1)} $, we define recursively
$ \mu , \lambda \in \mathcal {B}_{(1)} $, we define recursively
and
 $$ \begin{align*} \beta_{k+1}(\mu, \lambda) = \sup \bigg\{ & \Big| \mu \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) - \lambda \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) \Big| + \sum_{i=1}^{k} |a_{i}| \beta_{i}(\mu, \lambda) : \\ & a_{1}, \dots, a_{k} \in \mathbb{R}, \; \min \Big\{ \mu \Big( \sum_{i=1}^{k} a_{i} e_{i} \Big), \lambda \Big( \sum_{i=1}^{k} a_{i} e_{i} \Big) \Big\} < \frac{2\kappa_{k+1}}{\kappa_{k+1} - \kappa_{k}} \bigg\}. \end{align*} $$
$$ \begin{align*} \beta_{k+1}(\mu, \lambda) = \sup \bigg\{ & \Big| \mu \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) - \lambda \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) \Big| + \sum_{i=1}^{k} |a_{i}| \beta_{i}(\mu, \lambda) : \\ & a_{1}, \dots, a_{k} \in \mathbb{R}, \; \min \Big\{ \mu \Big( \sum_{i=1}^{k} a_{i} e_{i} \Big), \lambda \Big( \sum_{i=1}^{k} a_{i} e_{i} \Big) \Big\} < \frac{2\kappa_{k+1}}{\kappa_{k+1} - \kappa_{k}} \bigg\}. \end{align*} $$Clearly, ![]() $ \beta _{k}(\nu , \nu ) = 0 $ for every
$ \beta _{k}(\nu , \nu ) = 0 $ for every ![]() $ \nu \in \mathcal {B}_{(1)} $. Let us sketch a proof of continuity of the functions
$ \nu \in \mathcal {B}_{(1)} $. Let us sketch a proof of continuity of the functions ![]() $ \beta _{k} $. The function
$ \beta _{k} $. The function ![]() $ \beta _{1} = 0 $ is obviously continuous. Assuming that
$ \beta _{1} = 0 $ is obviously continuous. Assuming that ![]() $ \beta _{i} $ is continuous for every
$ \beta _{i} $ is continuous for every ![]() $ i \leq k $, we consider for
$ i \leq k $, we consider for ![]() $ \delta> 0 $ the set
$ \delta> 0 $ the set
 $$ \begin{align*} \mathcal{U}_{\delta}^{k+1}(\mu) = \bigg\{ \mu^{\prime} \in \mathcal{B}_{(1)} : \Big( \forall x \in \mathrm{span} \{ e_{1}, \dots, e_{k+1} \} \setminus \{ 0 \} : (1 + \delta)^{-1} < \frac{\mu^{\prime}(x)}{\mu(x)} < 1 + \delta \Big) \bigg\}. \end{align*} $$
$$ \begin{align*} \mathcal{U}_{\delta}^{k+1}(\mu) = \bigg\{ \mu^{\prime} \in \mathcal{B}_{(1)} : \Big( \forall x \in \mathrm{span} \{ e_{1}, \dots, e_{k+1} \} \setminus \{ 0 \} : (1 + \delta)^{-1} < \frac{\mu^{\prime}(x)}{\mu(x)} < 1 + \delta \Big) \bigg\}. \end{align*} $$Using Lemma 2.2, it is easy to see that  $ \mathcal {U}_{\delta }^{k+1}(\mu ) $ is an open neighborhood of
$ \mathcal {U}_{\delta }^{k+1}(\mu ) $ is an open neighborhood of ![]() $ \mu $ in
$ \mu $ in ![]() $ \mathcal {B}_{(1)} $. Given
$ \mathcal {B}_{(1)} $. Given ![]() $ \varepsilon> 0 $, we can find
$ \varepsilon> 0 $, we can find ![]() $ \delta> 0 $ such that
$ \delta> 0 $ such that ![]() $ |\beta _{k+1}(\mu ^{\prime }, \lambda ^{\prime }) - \beta _{k+1}(\mu , \lambda )| < \varepsilon $ for every
$ |\beta _{k+1}(\mu ^{\prime }, \lambda ^{\prime }) - \beta _{k+1}(\mu , \lambda )| < \varepsilon $ for every  $ (\mu ^{\prime }, \lambda ^{\prime }) \in \mathcal {U}_{\delta }^{k+1}(\mu ) \times \mathcal {U}_{\delta }^{k+1}(\lambda ) $. The details are left to the reader.
$ (\mu ^{\prime }, \lambda ^{\prime }) \in \mathcal {U}_{\delta }^{k+1}(\mu ) \times \mathcal {U}_{\delta }^{k+1}(\lambda ) $. The details are left to the reader.
Let us prove that the functions ![]() $ \beta _{k} $ work. Given
$ \beta _{k} $ work. Given ![]() $ \nu \in \mathcal {B}_{(1)} $ and
$ \nu \in \mathcal {B}_{(1)} $ and ![]() $ z^{*} \in (c_{00})^{\#} $ satisfying
$ z^{*} \in (c_{00})^{\#} $ satisfying ![]() $ |z^{*}(x)| \leq \nu (x) $ for every
$ |z^{*}(x)| \leq \nu (x) $ for every ![]() $ x \in c_{00} $, we define first
$ x \in c_{00} $, we define first
Recursively, we define for every ![]() $ k \in \mathbb {N} $ functions
$ k \in \mathbb {N} $ functions
 $$ \begin{align*} u_{k+1}(\mu) = \sup_{a_{1}, \dots, a_{k}} \Big[ - \kappa_{k+1} \mu \Big( - e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) + \sum_{i=1}^{k} a_{i} \gamma_{i}(\mu) \Big], \end{align*} $$
$$ \begin{align*} u_{k+1}(\mu) = \sup_{a_{1}, \dots, a_{k}} \Big[ - \kappa_{k+1} \mu \Big( - e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) + \sum_{i=1}^{k} a_{i} \gamma_{i}(\mu) \Big], \end{align*} $$ $$ \begin{align*} v_{k+1}(\mu) = \inf_{a_{1}, \dots, a_{k}} \Big[ \kappa_{k+1} \mu \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) - \sum_{i=1}^{k} a_{i} \gamma_{i}(\mu) \Big] \end{align*} $$
$$ \begin{align*} v_{k+1}(\mu) = \inf_{a_{1}, \dots, a_{k}} \Big[ \kappa_{k+1} \mu \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) - \sum_{i=1}^{k} a_{i} \gamma_{i}(\mu) \Big] \end{align*} $$and
where numbers ![]() $ p_{k+1} \geq 0, q_{k+1} \geq 0 $ with
$ p_{k+1} \geq 0, q_{k+1} \geq 0 $ with ![]() $ p_{k+1} + q_{k+1} = 1 $ are chosen in the way that
$ p_{k+1} + q_{k+1} = 1 $ are chosen in the way that
Let us check that it is possible to choose such numbers. Note first that ![]() $ \gamma _{1}(\nu ) = \eta \cdot z^{*}(e_{1}) $. Assuming that the functions
$ \gamma _{1}(\nu ) = \eta \cdot z^{*}(e_{1}) $. Assuming that the functions ![]() $ \gamma _{i} $ are already defined and satisfy
$ \gamma _{i} $ are already defined and satisfy ![]() $ \gamma _{i}(\nu ) = \eta \cdot z^{*}(e_{i}) $ for
$ \gamma _{i}(\nu ) = \eta \cdot z^{*}(e_{i}) $ for ![]() $ i \leq k $, we notice that, for every
$ i \leq k $, we notice that, for every ![]() $ a_{1}, \dots , a_{k} \in \mathbb {R} $,
$ a_{1}, \dots , a_{k} \in \mathbb {R} $,
 $$ \begin{align*} \pm \eta \cdot z^{*}(e_{k+1}) + \sum_{i=1}^{k} a_{i} \gamma_{i}(\nu) = \eta \cdot z^{*} \Big( \pm e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) \leq \kappa_{k+1} \nu \Big( \pm e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big), \end{align*} $$
$$ \begin{align*} \pm \eta \cdot z^{*}(e_{k+1}) + \sum_{i=1}^{k} a_{i} \gamma_{i}(\nu) = \eta \cdot z^{*} \Big( \pm e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) \leq \kappa_{k+1} \nu \Big( \pm e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big), \end{align*} $$and consequently
 $$ \begin{align*} \eta \cdot z^{*}(e_{k+1}) \geq - \kappa_{k+1} \nu \Big( - e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) + \sum_{i=1}^{k} a_{i} \gamma_{i}(\nu), \end{align*} $$
$$ \begin{align*} \eta \cdot z^{*}(e_{k+1}) \geq - \kappa_{k+1} \nu \Big( - e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) + \sum_{i=1}^{k} a_{i} \gamma_{i}(\nu), \end{align*} $$ $$ \begin{align*} \eta \cdot z^{*}(e_{k+1}) \leq \kappa_{k+1} \nu \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) - \sum_{i=1}^{k} a_{i} \gamma_{i}(\nu). \end{align*} $$
$$ \begin{align*} \eta \cdot z^{*}(e_{k+1}) \leq \kappa_{k+1} \nu \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) - \sum_{i=1}^{k} a_{i} \gamma_{i}(\nu). \end{align*} $$This gives
and it follows that suitable ![]() $ p_{k+1} $ and
$ p_{k+1} $ and ![]() $ q_{k+1} $ do exist.
$ q_{k+1} $ do exist.
Let us prove that
 $$ \begin{align} \sum_{i=1}^{k} a_{i} \gamma_{i}(\mu) \leq \kappa_{k} \mu \Big( \sum_{i=1}^{k} a_{i} e_{i} \Big) \end{align} $$
$$ \begin{align} \sum_{i=1}^{k} a_{i} \gamma_{i}(\mu) \leq \kappa_{k} \mu \Big( \sum_{i=1}^{k} a_{i} e_{i} \Big) \end{align} $$for every ![]() $ \mu \in \mathcal {B}_{(1)} $,
$ \mu \in \mathcal {B}_{(1)} $, ![]() $ k \in \mathbb {N} $ and
$ k \in \mathbb {N} $ and ![]() $ a_{1}, \dots , a_{k} \in \mathbb {R} $. For
$ a_{1}, \dots , a_{k} \in \mathbb {R} $. For ![]() $ k = 1 $, we just write
$ k = 1 $, we just write ![]() $ a_{1} \gamma _{1}(\mu ) = a_{1} \eta \cdot z^{*}(e_{1}) \leq |a_{1}| \kappa _{1} \nu (e_{1}) = |a_{1}| \kappa _{1} = |a_{1}| \kappa _{1} \mu (e_{1}) = \kappa _{1} \mu (a_{1} e_{1}) $. Assume that inequality (3.7) is valid for
$ a_{1} \gamma _{1}(\mu ) = a_{1} \eta \cdot z^{*}(e_{1}) \leq |a_{1}| \kappa _{1} \nu (e_{1}) = |a_{1}| \kappa _{1} = |a_{1}| \kappa _{1} \mu (e_{1}) = \kappa _{1} \mu (a_{1} e_{1}) $. Assume that inequality (3.7) is valid for ![]() $ k $. We show first that
$ k $. We show first that
Clearly, it is sufficient to show just that ![]() $ u_{k+1}(\mu ) \leq v_{k+1}(\mu ) $. Given
$ u_{k+1}(\mu ) \leq v_{k+1}(\mu ) $. Given ![]() $ b_{1}, \dots , b_{k} $ and
$ b_{1}, \dots , b_{k} $ and ![]() $ c_{1}, \dots , c_{k} $, we need to check that
$ c_{1}, \dots , c_{k} $, we need to check that
 $$ \begin{align*} - \kappa_{k+1} \mu \Big( - e_{k+1} + \sum_{i=1}^{k} b_{i} e_{i} \Big) + \sum_{i=1}^{k} b_{i} \gamma_{i}(\mu) \leq \kappa_{k+1} \mu \Big( e_{k+1} + \sum_{i=1}^{k} c_{i} e_{i} \Big) - \sum_{i=1}^{k} c_{i} \gamma_{i}(\mu). \end{align*} $$
$$ \begin{align*} - \kappa_{k+1} \mu \Big( - e_{k+1} + \sum_{i=1}^{k} b_{i} e_{i} \Big) + \sum_{i=1}^{k} b_{i} \gamma_{i}(\mu) \leq \kappa_{k+1} \mu \Big( e_{k+1} + \sum_{i=1}^{k} c_{i} e_{i} \Big) - \sum_{i=1}^{k} c_{i} \gamma_{i}(\mu). \end{align*} $$But this is easy, as
 $$ \begin{align*} \sum_{i=1}^{k} b_{i} \gamma_{i}(\mu) + \sum_{i=1}^{k} c_{i} \gamma_{i}(\mu) & = \sum_{i=1}^{k} (b_{i} + c_{i}) \gamma_{i}(\mu) \leq \kappa_{k} \mu \Big( \sum_{i=1}^{k} (b_{i} +c_{i}) e_{i} \Big) \\ & \leq \kappa_{k+1} \Big[ \mu \Big( - e_{k+1} + \sum_{i=1}^{k} b_{i} e_{i} \Big) + \mu \Big( e_{k+1} + \sum_{i=1}^{k} c_{i} e_{i} \Big) \Big]. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{k} b_{i} \gamma_{i}(\mu) + \sum_{i=1}^{k} c_{i} \gamma_{i}(\mu) & = \sum_{i=1}^{k} (b_{i} + c_{i}) \gamma_{i}(\mu) \leq \kappa_{k} \mu \Big( \sum_{i=1}^{k} (b_{i} +c_{i}) e_{i} \Big) \\ & \leq \kappa_{k+1} \Big[ \mu \Big( - e_{k+1} + \sum_{i=1}^{k} b_{i} e_{i} \Big) + \mu \Big( e_{k+1} + \sum_{i=1}^{k} c_{i} e_{i} \Big) \Big]. \end{align*} $$Now, let us verify inequality (3.7) for ![]() $ k + 1 $. We can suppose that
$ k + 1 $. We can suppose that ![]() $ a_{k+1} = \pm 1 $. For
$ a_{k+1} = \pm 1 $. For ![]() $ a_{k+1} = 1 $, it is enough to use
$ a_{k+1} = 1 $, it is enough to use
 $$ \begin{align*} \gamma_{k+1}(\mu) \leq v_{k+1}(\mu) \leq \kappa_{k+1} \mu \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) - \sum_{i=1}^{k} a_{i} \gamma_{i}(\mu), \end{align*} $$
$$ \begin{align*} \gamma_{k+1}(\mu) \leq v_{k+1}(\mu) \leq \kappa_{k+1} \mu \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) - \sum_{i=1}^{k} a_{i} \gamma_{i}(\mu), \end{align*} $$and for ![]() $ a_{k+1} = -1 $, it is enough to use
$ a_{k+1} = -1 $, it is enough to use
 $$ \begin{align*} \gamma_{k+1}(\mu) \geq u_{k+1}(\mu) \geq - \kappa_{k+1} \mu \Big( - e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) + \sum_{i=1}^{k} a_{i} \gamma_{i}(\mu). \end{align*} $$
$$ \begin{align*} \gamma_{k+1}(\mu) \geq u_{k+1}(\mu) \geq - \kappa_{k+1} \mu \Big( - e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) + \sum_{i=1}^{k} a_{i} \gamma_{i}(\mu). \end{align*} $$Next, let us prove that
for every ![]() $ \mu , \lambda \in \mathcal {B}_{(1)} $ and
$ \mu , \lambda \in \mathcal {B}_{(1)} $ and ![]() $ k \in \mathbb {N} $. This is clear for
$ k \in \mathbb {N} $. This is clear for ![]() $ k = 1 $, as
$ k = 1 $, as ![]() $ \gamma _{1} $ is constant. Assume that inequality (3.8) is valid for
$ \gamma _{1} $ is constant. Assume that inequality (3.8) is valid for ![]() $ i \leq k $. To prove it for
$ i \leq k $. To prove it for ![]() $ k + 1 $, it is sufficient to show the inequalities
$ k + 1 $, it is sufficient to show the inequalities
We consider only the function ![]() $ v_{k+1} $, since the inequality for
$ v_{k+1} $, since the inequality for ![]() $ u_{k+1} $ can be shown in the same way. Let us note first that, in the definition of
$ u_{k+1} $ can be shown in the same way. Let us note first that, in the definition of ![]() $ v_{k+1}(\mu ) $, it is possible to take the infimum only over
$ v_{k+1}(\mu ) $, it is possible to take the infimum only over ![]() $ k $-tuples with
$ k $-tuples with
 $$ \begin{align*} \mu \Big( \sum_{i=1}^{k} a_{i} e_{i} \Big) < \frac{2\kappa_{k+1}}{\kappa_{k+1} - \kappa_{k}}. \end{align*} $$
$$ \begin{align*} \mu \Big( \sum_{i=1}^{k} a_{i} e_{i} \Big) < \frac{2\kappa_{k+1}}{\kappa_{k+1} - \kappa_{k}}. \end{align*} $$Indeed, for ![]() $ a_{1}, \dots , a_{k} $ that do not satisfy this condition, using inequality(3.7), we obtain
$ a_{1}, \dots , a_{k} $ that do not satisfy this condition, using inequality(3.7), we obtain
 $$ \begin{align*} \kappa_{k+1} \mu \Big( e_{k+1} + & \sum_{i=1}^{k} a_{i} e_{i} \Big) - \sum_{i=1}^{k} a_{i} \gamma_{i}(\mu) \\ & \geq \kappa_{k+1} \mu \Big( \sum_{i=1}^{k} a_{i} e_{i} \Big) - \kappa_{k+1} \mu(e_{k+1}) - \kappa_{k} \mu \Big( \sum_{i=1}^{k} a_{i} e_{i} \Big) \\ & = (\kappa_{k+1} - \kappa_{k}) \mu \Big( \sum_{i=1}^{k} a_{i} e_{i} \Big) - \kappa_{k+1} \\ & \geq 2 \kappa_{k+1} - \kappa_{k+1} = \kappa_{k+1} = \kappa_{k+1} \mu \Big( e_{k+1} + \sum_{i=1}^{k} 0 \cdot e_{i} \Big) - \sum_{i=1}^{k} 0 \cdot \gamma_{i}(\mu). \end{align*} $$
$$ \begin{align*} \kappa_{k+1} \mu \Big( e_{k+1} + & \sum_{i=1}^{k} a_{i} e_{i} \Big) - \sum_{i=1}^{k} a_{i} \gamma_{i}(\mu) \\ & \geq \kappa_{k+1} \mu \Big( \sum_{i=1}^{k} a_{i} e_{i} \Big) - \kappa_{k+1} \mu(e_{k+1}) - \kappa_{k} \mu \Big( \sum_{i=1}^{k} a_{i} e_{i} \Big) \\ & = (\kappa_{k+1} - \kappa_{k}) \mu \Big( \sum_{i=1}^{k} a_{i} e_{i} \Big) - \kappa_{k+1} \\ & \geq 2 \kappa_{k+1} - \kappa_{k+1} = \kappa_{k+1} = \kappa_{k+1} \mu \Big( e_{k+1} + \sum_{i=1}^{k} 0 \cdot e_{i} \Big) - \sum_{i=1}^{k} 0 \cdot \gamma_{i}(\mu). \end{align*} $$Now, inequality (3.8) is provided by the following computation, in which every sup/inf is meant over ![]() $ k $-tuples with
$ k $-tuples with  $ \mu \Big ( \sum _{i=1}^{k} a_{i} e_{i} \Big ) < \frac {2\kappa _{k+1}}{\kappa _{k+1} - \kappa _{k}} $ or
$ \mu \Big ( \sum _{i=1}^{k} a_{i} e_{i} \Big ) < \frac {2\kappa _{k+1}}{\kappa _{k+1} - \kappa _{k}} $ or  $ \lambda \Big ( \sum _{i=1}^{k} a_{i} e_{i} \Big ) < \frac {2\kappa _{k+1}}{\kappa _{k+1} - \kappa _{k}} $:
$ \lambda \Big ( \sum _{i=1}^{k} a_{i} e_{i} \Big ) < \frac {2\kappa _{k+1}}{\kappa _{k+1} - \kappa _{k}} $:
 $$ \begin{align*} & |v_{k+1}(\mu) - v_{k+1}(\lambda)| \\ & = \bigg| \inf \Big[ \kappa_{k+1} \mu \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) - \sum_{i=1}^{k} a_{i} \gamma_{i}(\mu) \Big] \\ & \hspace{4cm} - \inf \Big[ \kappa_{k+1} \lambda \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) - \sum_{i=1}^{k} a_{i} \gamma_{i}(\lambda) \Big] \bigg| \\ & \leq \sup \bigg| \Big[ \kappa_{k+1} \mu \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) - \sum_{i=1}^{k} a_{i} \gamma_{i}(\mu) \Big] \\ & \hspace{4cm} - \Big[ \kappa_{k+1} \lambda \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) - \sum_{i=1}^{k} a_{i} \gamma_{i}(\lambda) \Big] \bigg| \\ & = \sup \bigg| \kappa_{k+1} \Big[ \mu \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) - \lambda \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) \Big] - \sum_{i=1}^{k} a_{i} \big( \gamma_{i}(\mu) - \gamma_{i}(\lambda) \big) \bigg| \\ & \leq \sup \bigg[ \Big| \mu \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) - \lambda \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) \Big| + \sum_{i=1}^{k} |a_{i}| \beta_{i}(\mu, \lambda) \bigg] = \beta_{k+1}(\mu, \lambda). \end{align*} $$
$$ \begin{align*} & |v_{k+1}(\mu) - v_{k+1}(\lambda)| \\ & = \bigg| \inf \Big[ \kappa_{k+1} \mu \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) - \sum_{i=1}^{k} a_{i} \gamma_{i}(\mu) \Big] \\ & \hspace{4cm} - \inf \Big[ \kappa_{k+1} \lambda \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) - \sum_{i=1}^{k} a_{i} \gamma_{i}(\lambda) \Big] \bigg| \\ & \leq \sup \bigg| \Big[ \kappa_{k+1} \mu \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) - \sum_{i=1}^{k} a_{i} \gamma_{i}(\mu) \Big] \\ & \hspace{4cm} - \Big[ \kappa_{k+1} \lambda \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) - \sum_{i=1}^{k} a_{i} \gamma_{i}(\lambda) \Big] \bigg| \\ & = \sup \bigg| \kappa_{k+1} \Big[ \mu \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) - \lambda \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) \Big] - \sum_{i=1}^{k} a_{i} \big( \gamma_{i}(\mu) - \gamma_{i}(\lambda) \big) \bigg| \\ & \leq \sup \bigg[ \Big| \mu \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) - \lambda \Big( e_{k+1} + \sum_{i=1}^{k} a_{i} e_{i} \Big) \Big| + \sum_{i=1}^{k} |a_{i}| \beta_{i}(\mu, \lambda) \bigg] = \beta_{k+1}(\mu, \lambda). \end{align*} $$ Finally, as usual, we put ![]() $ \Gamma (\mu )(e_{k}) = \gamma _{k}(\mu ) $. The required properties of
$ \Gamma (\mu )(e_{k}) = \gamma _{k}(\mu ) $. The required properties of ![]() $ \Gamma $ follow now from inequalities (3.6), (3.7) and (3.8). Thus, the functions
$ \Gamma $ follow now from inequalities (3.6), (3.7) and (3.8). Thus, the functions ![]() $ \beta _{k} $ work, and the proof of the lemma is completed.
$ \beta _{k} $ work, and the proof of the lemma is completed.
Proof of Proposition 3.12.
Let ![]() $ X $ be an isometrically universal separable Banach space. By Lemma 3.18, the condition (2’) from Proposition 3.15 is valid for
$ X $ be an isometrically universal separable Banach space. By Lemma 3.18, the condition (2’) from Proposition 3.15 is valid for ![]() $ \mathcal {A} = \mathcal {B}_{(1)} $. Hence, the condition (1) from this proposition is valid for
$ \mathcal {A} = \mathcal {B}_{(1)} $. Hence, the condition (1) from this proposition is valid for ![]() $ \mathcal {A} = \mathcal {B}_{(1)} $ as well. There are a separable Banach space
$ \mathcal {A} = \mathcal {B}_{(1)} $ as well. There are a separable Banach space ![]() $ U $ and continuous mappings
$ U $ and continuous mappings ![]() $ \chi _{k} : \mathcal {B}_{(1)} \to U, k \in \mathbb {N}, $ such that
$ \chi _{k} : \mathcal {B}_{(1)} \to U, k \in \mathbb {N}, $ such that
 $$ \begin{align*} \Big\Vert \sum_{k=1}^{n} a_{k} \chi_{k}(\nu) \Big\Vert = \nu \Big( \sum_{k=1}^{n} a_{k} e_{k} \Big) \end{align*} $$
$$ \begin{align*} \Big\Vert \sum_{k=1}^{n} a_{k} \chi_{k}(\nu) \Big\Vert = \nu \Big( \sum_{k=1}^{n} a_{k} e_{k} \Big) \end{align*} $$for every ![]() $ \sum _{k=1}^{n} a_{k} e_{k} \in c_{00} $ and every
$ \sum _{k=1}^{n} a_{k} e_{k} \in c_{00} $ and every ![]() $ \nu \in \mathcal {B}_{(1)} $. Since
$ \nu \in \mathcal {B}_{(1)} $. Since ![]() $ X $ contains an isometric copy of
$ X $ contains an isometric copy of ![]() $ U $, we can suppose that
$ U $, we can suppose that ![]() $ U \subseteq X $.
$ U \subseteq X $.
Let us consider the continuous mapping ![]() $ \Psi : \mathcal {B} \to \mathcal {B}_{(1)} $ given by
$ \Psi : \mathcal {B} \to \mathcal {B}_{(1)} $ given by
 $$ \begin{align*} \Psi(\mu) \Big( \sum_{k=1}^{n} a_{k} e_{k} \Big) = \mu \Big( \sum_{k=1}^{n} \frac{a_{k}}{\mu(e_{k})} e_{k} \Big). \end{align*} $$
$$ \begin{align*} \Psi(\mu) \Big( \sum_{k=1}^{n} a_{k} e_{k} \Big) = \mu \Big( \sum_{k=1}^{n} \frac{a_{k}}{\mu(e_{k})} e_{k} \Big). \end{align*} $$If we define
for each ![]() $ k \in \mathbb {N} $, then we get
$ k \in \mathbb {N} $, then we get
 $$ \begin{align*} \Big\Vert \sum_{k=1}^{n} b_{k} \widetilde{\chi}_{k}(\mu) \Big\Vert = \Big\Vert \sum_{k=1}^{n} b_{k} \mu(e_{k}) \chi_{k}(\Psi(\mu)) \Big\Vert = \Psi(\mu) \Big( \sum_{k=1}^{n} b_{k} \mu(e_{k}) e_{k} \Big) = \mu \Big( \sum_{k=1}^{n} b_{k} e_{k} \Big) \end{align*} $$
$$ \begin{align*} \Big\Vert \sum_{k=1}^{n} b_{k} \widetilde{\chi}_{k}(\mu) \Big\Vert = \Big\Vert \sum_{k=1}^{n} b_{k} \mu(e_{k}) \chi_{k}(\Psi(\mu)) \Big\Vert = \Psi(\mu) \Big( \sum_{k=1}^{n} b_{k} \mu(e_{k}) e_{k} \Big) = \mu \Big( \sum_{k=1}^{n} b_{k} e_{k} \Big) \end{align*} $$for every ![]() $ \sum _{k=1}^{n} b_{k} e_{k} \in c_{00} $ and every
$ \sum _{k=1}^{n} b_{k} e_{k} \in c_{00} $ and every ![]() $ \mu \in \mathcal {B} $.
$ \mu \in \mathcal {B} $.
To summarize, we obtained an optimal reduction from ![]() $\mathcal {B}$ to
$\mathcal {B}$ to ![]() $SB_{\infty }(X)$ and from
$SB_{\infty }(X)$ and from ![]() $SB_{\infty }(X)$ to
$SB_{\infty }(X)$ to ![]() $\mathcal {P}_{\infty }$. However, our reduction from
$\mathcal {P}_{\infty }$. However, our reduction from ![]() $\mathcal {P}_{\infty }$ to
$\mathcal {P}_{\infty }$ to ![]() $\mathcal {B}$ seems not to be optimal, so one is tempted to ask the following.
$\mathcal {B}$ seems not to be optimal, so one is tempted to ask the following.
Question 1. Does there exist a continuous mapping ![]() $\Phi :\mathcal {P}_{\infty }\to \mathcal {B}$ such that for every
$\Phi :\mathcal {P}_{\infty }\to \mathcal {B}$ such that for every ![]() $\mu \in \mathcal {P}_{\infty }$, we have
$\mu \in \mathcal {P}_{\infty }$, we have ![]() $X_{\mu }\equiv X_{\Phi (\mu )}$?
$X_{\mu }\equiv X_{\Phi (\mu )}$?
Note that a positive answer to Question 1 would imply a positive answer to Question 2 and that a sufficient condition for a positive solution of Question 2 is provided by Proposition 3.15.
Question 2. Let X be an isometrically universal separable Banach space, and let ![]() $\tau $ be an admissible topology on
$\tau $ be an admissible topology on ![]() $SB(X)$. Does there exist a
$SB(X)$. Does there exist a ![]() $\boldsymbol {\Sigma }_{2}^{0}$-measurable mapping
$\boldsymbol {\Sigma }_{2}^{0}$-measurable mapping ![]() $\Phi :\mathcal {P}_{\infty } \to (SB(X),\tau )$ such that for every
$\Phi :\mathcal {P}_{\infty } \to (SB(X),\tau )$ such that for every ![]() $\mu \in \mathcal {P}_{\infty }$, we have
$\mu \in \mathcal {P}_{\infty }$, we have ![]() $X_{\mu }\equiv \Phi (\mu )$?
$X_{\mu }\equiv \Phi (\mu )$?
4 Generic properties
As soon as one has a Polish space, or more generally a Baire space, of some objects, it is natural and often useful to find properties (of these objects) that are generic; that is, the corresponding subset of the space is comeager. In the case of the spaces ![]() $\mathcal {P}$,
$\mathcal {P}$, ![]() $\mathcal {P}_{\infty }$ and
$\mathcal {P}_{\infty }$ and ![]() $\mathcal {B}$, we resolve this problem completely; see Theorem 4.1, which is a more precise description of the content of Theorem B.
$\mathcal {B}$, we resolve this problem completely; see Theorem 4.1, which is a more precise description of the content of Theorem B.
In the case of the spaces ![]() $SB(X)$ with an admissible topology, this is the content of Problem 5.5 from [Reference Godefroy and Saint-Raymond19]. We show that in that case, the situation is more complicated. In particular, we confirm the suspicion of Godefroy and Saint-Raymond that being meager in
$SB(X)$ with an admissible topology, this is the content of Problem 5.5 from [Reference Godefroy and Saint-Raymond19]. We show that in that case, the situation is more complicated. In particular, we confirm the suspicion of Godefroy and Saint-Raymond that being meager in ![]() $SB(X)$ is not independent of the chosen admissible topology; see Theorem 4.10 and Theorem 4.12, which together imply Theorem C.
$SB(X)$ is not independent of the chosen admissible topology; see Theorem 4.10 and Theorem 4.12, which together imply Theorem C.
4.1 Generic objects in  $\mathcal {P}$
$\mathcal {P}$
The main result of this subsection is Theorem 4.1 below. Although it may not appear surprising to a specialist in Fraïssé theory, as the Gurariĭ space is the Fraïssé limit of finite-dimensional Banach spaces (see, e.g., [Reference Ben Yaacov3, Theorem 4.3]), its proof is far more involved than analogous results for countable Fraïssé limits. Also, the result has several applications in estimating the complexities of isometry and isomorphism classes of other Banach spaces; see [Reference Cúth, Doležal, Doucha and Kurka13], where this issue is addressed.
Theorem 4.1. Let ![]() $\mathbb {G}$ be the Gurariĭ space. Then the isometry class
$\mathbb {G}$ be the Gurariĭ space. Then the isometry class ![]() ${\langle {\mathbb {G}}\rangle _{\equiv }^{\mathcal I}}$ is a dense
${\langle {\mathbb {G}}\rangle _{\equiv }^{\mathcal I}}$ is a dense ![]() $G_{\delta }$-set in
$G_{\delta }$-set in ![]() $\mathcal {I}$ for any
$\mathcal {I}$ for any ![]() $\mathcal {I}\in \{\mathcal {P},\mathcal {P}_{\infty },\mathcal {B}\}$.
$\mathcal {I}\in \{\mathcal {P},\mathcal {P}_{\infty },\mathcal {B}\}$.
Let us recall what the Gurariĭ space is. One of the characterizations of the Gurariĭ space is the following; for more details, we refer the interested reader to, for example, [Reference Cabello Sánchez, Garbulińska-Wegrzyn and Kubiś10] (the characterization below is provided by [Reference Cabello Sánchez, Garbulińska-Wegrzyn and Kubiś10, Lemma 2.2]).
Definition 4.2. The Gurariĭ space is the unique (up to isometry) separable Banach space such that for every ![]() $\varepsilon> 0$ and every isometric embedding
$\varepsilon> 0$ and every isometric embedding ![]() $g:A\to B$, where B is a finite-dimensional Banach space and A is a subspace of
$g:A\to B$, where B is a finite-dimensional Banach space and A is a subspace of ![]() $\mathbb {G}$, there is a
$\mathbb {G}$, there is a ![]() $(1+\varepsilon )$-isomorphism
$(1+\varepsilon )$-isomorphism ![]() $f:B\to \mathbb {G}$ such that
$f:B\to \mathbb {G}$ such that ![]() $\|f\circ g - id_{A}\|\leq \varepsilon $.
$\|f\circ g - id_{A}\|\leq \varepsilon $.
In the remainder of this subsection, we prove Theorem 4.1. Let us start with the most technical part, namely that ![]() ${\langle {\mathbb {G}}\rangle _{\equiv }^{\mathcal {P}_{\infty }}}$ is a
${\langle {\mathbb {G}}\rangle _{\equiv }^{\mathcal {P}_{\infty }}}$ is a ![]() $G_{\delta }$-set in
$G_{\delta }$-set in ![]() $\mathcal {P}_{\infty }$.
$\mathcal {P}_{\infty }$.
We need two technical lemmas first.
1. Given a basis
 $\mathfrak {b}_{E} = \{e_{1},\ldots ,e_{n}\}$ of a finite-dimensional Banach space E, there are
$\mathfrak {b}_{E} = \{e_{1},\ldots ,e_{n}\}$ of a finite-dimensional Banach space E, there are  $C>0$ and a function
$C>0$ and a function  $\phi _{2}^{\mathfrak {b}_{E}}:[0,C)\to [0,\infty )$ continuous at zero with
$\phi _{2}^{\mathfrak {b}_{E}}:[0,C)\to [0,\infty )$ continuous at zero with  $\phi _{2}^{\mathfrak {b}_{E}}(0)=0$ such that whenever X is a Banach space with
$\phi _{2}^{\mathfrak {b}_{E}}(0)=0$ such that whenever X is a Banach space with  $E\subseteq X$ and
$E\subseteq X$ and  $\{x_{i}:\; i\leq n\}\subseteq X$ are such that
$\{x_{i}:\; i\leq n\}\subseteq X$ are such that  $\|x_{i}-e_{i}\|<\varepsilon $,
$\|x_{i}-e_{i}\|<\varepsilon $,  $i\leq n$, for some
$i\leq n$, for some  $\varepsilon <C$, then the linear operator
$\varepsilon <C$, then the linear operator  $T:E\to X$ given by
$T:E\to X$ given by  $T(e_{i}):=x_{i}$ is a
$T(e_{i}):=x_{i}$ is a  $(1+\phi _{2}^{\mathfrak {b}_{E}}(\varepsilon ))$-isomorphism and
$(1+\phi _{2}^{\mathfrak {b}_{E}}(\varepsilon ))$-isomorphism and  $\|T-Id_{E}\|\leq \phi _{2}^{\mathfrak {b}_{E}}(\varepsilon )$.
$\|T-Id_{E}\|\leq \phi _{2}^{\mathfrak {b}_{E}}(\varepsilon )$.2. Let
 $\varepsilon \in (0,1)$,
$\varepsilon \in (0,1)$,  $T:X\to Y$ be a surjective
$T:X\to Y$ be a surjective  $(1+\varepsilon )$-isomorphism between Banach spaces X and Y, and N be
$(1+\varepsilon )$-isomorphism between Banach spaces X and Y, and N be  $\varepsilon $-dense for
$\varepsilon $-dense for  $S_{X}$. Then
$S_{X}$. Then  $T(N)$ is
$T(N)$ is  $3\varepsilon $-dense for
$3\varepsilon $-dense for  $S_{Y}$.
$S_{Y}$.
Proof. 1: Pick ![]() $C>0$ such that
$C>0$ such that ![]() $C\sum _{i=1}^{n}|\lambda _{i}|\leq \|\sum _{i=1}^{n} \lambda _{i} e_{i}\|$ for every
$C\sum _{i=1}^{n}|\lambda _{i}|\leq \|\sum _{i=1}^{n} \lambda _{i} e_{i}\|$ for every ![]() $(\lambda _{i})_{i=1}^{n}\in \mathbb {R}^{n}$. Then for any
$(\lambda _{i})_{i=1}^{n}\in \mathbb {R}^{n}$. Then for any ![]() $x = \sum _{i=1}^{n} \lambda _{i} e_{i}$, we have
$x = \sum _{i=1}^{n} \lambda _{i} e_{i}$, we have
 $$ \begin{align*}\|Tx - x\|\leq \sum_{i=1}^{n} |\lambda_{i}| \|x_{i}-e_{i}\| < \frac{\varepsilon}{C} \|x\|.\end{align*} $$
$$ \begin{align*}\|Tx - x\|\leq \sum_{i=1}^{n} |\lambda_{i}| \|x_{i}-e_{i}\| < \frac{\varepsilon}{C} \|x\|.\end{align*} $$Thus, ![]() $\|T-Id_{E}\|<\frac {\varepsilon }{C}$,
$\|T-Id_{E}\|<\frac {\varepsilon }{C}$, ![]() $\|T\|\leq 1+\frac {\varepsilon }{C}$ and
$\|T\|\leq 1+\frac {\varepsilon }{C}$ and  $\|Tx\|\geq (1-\frac {\varepsilon }{C})\|x\|= (1+\frac {\varepsilon }{C-\varepsilon })^{-1}\|x\|$. Thus, we may put
$\|Tx\|\geq (1-\frac {\varepsilon }{C})\|x\|= (1+\frac {\varepsilon }{C-\varepsilon })^{-1}\|x\|$. Thus, we may put  $\phi _{2}^{\mathfrak {b}_{E}}(\varepsilon ):=\frac {\varepsilon }{C-\varepsilon }$ for
$\phi _{2}^{\mathfrak {b}_{E}}(\varepsilon ):=\frac {\varepsilon }{C-\varepsilon }$ for ![]() $\varepsilon \in [0,C)$.
$\varepsilon \in [0,C)$.
2: Let ![]() $\varepsilon>0$,
$\varepsilon>0$, ![]() $T:X\to Y$ and N be as in the assumptions. Then for every
$T:X\to Y$ and N be as in the assumptions. Then for every ![]() $y\in S_{Y}$, there is
$y\in S_{Y}$, there is ![]() $x\in N$ with
$x\in N$ with  $\|x-\frac {T^{-1}(y)}{\|T^{-1}(y)\|}\|<\varepsilon $. Thus, we have
$\|x-\frac {T^{-1}(y)}{\|T^{-1}(y)\|}\|<\varepsilon $. Thus, we have
 $$ \begin{align*}\begin{split} \|y - Tx\|&\leq \Big\|y - \frac{y}{\|T^{-1}(y)\|}\Big\| + \|T\|\cdot\Big\|x-\frac{T^{-1}(y)}{\|T^{-1}(y)\|}\Big\|\\ & < \Big|1 - \frac{1}{\|T^{-1}y\|}\Big| + (1+\varepsilon)\varepsilon\leq \varepsilon + 2\varepsilon = 3\varepsilon. \end{split}\\[-46pt]\end{align*} $$
$$ \begin{align*}\begin{split} \|y - Tx\|&\leq \Big\|y - \frac{y}{\|T^{-1}(y)\|}\Big\| + \|T\|\cdot\Big\|x-\frac{T^{-1}(y)}{\|T^{-1}(y)\|}\Big\|\\ & < \Big|1 - \frac{1}{\|T^{-1}y\|}\Big| + (1+\varepsilon)\varepsilon\leq \varepsilon + 2\varepsilon = 3\varepsilon. \end{split}\\[-46pt]\end{align*} $$Lemma 4.4. For every ![]() $\mu \in \mathcal {P}$, finite set
$\mu \in \mathcal {P}$, finite set ![]() $A\subseteq V$ and
$A\subseteq V$ and ![]() $\varepsilon>0$, there exists
$\varepsilon>0$, there exists ![]() $\nu \in \mathcal {B}$ with
$\nu \in \mathcal {B}$ with ![]() $|\mu (x)-\nu (x)|<\varepsilon $ and
$|\mu (x)-\nu (x)|<\varepsilon $ and ![]() $\nu (x)\in \mathbb {Q}$ for every
$\nu (x)\in \mathbb {Q}$ for every ![]() $x\in A$.
$x\in A$.
Proof. It suffices to define such a norm ![]() $\nu $ on
$\nu $ on ![]() $\operatorname {span} A$ since then we can easily find some extension to the whole V. We assume that
$\operatorname {span} A$ since then we can easily find some extension to the whole V. We assume that ![]() $0\notin A$, and moreover, we can assume that no two elements of A lie in the same one-dimensional subspace: that is, are scalar multiples of each other. Indeed, otherwise we would find a subset
$0\notin A$, and moreover, we can assume that no two elements of A lie in the same one-dimensional subspace: that is, are scalar multiples of each other. Indeed, otherwise we would find a subset ![]() $A^{\prime }\subseteq A$ where no elements are scalar multiples of each other and every element of A is a scalar multiple, necessarily rational scalar multiple, of some element from
$A^{\prime }\subseteq A$ where no elements are scalar multiples of each other and every element of A is a scalar multiple, necessarily rational scalar multiple, of some element from ![]() $A^{\prime }$. Then proving the fact for
$A^{\prime }$. Then proving the fact for ![]() $A^{\prime }$ for sufficiently small
$A^{\prime }$ for sufficiently small ![]() $\delta $ automatically proves it for A and
$\delta $ automatically proves it for A and ![]() $\varepsilon $.
$\varepsilon $.
We enumerate A as ![]() $\{a_{1},\ldots ,a_{n}\}$ and so that the first k elements
$\{a_{1},\ldots ,a_{n}\}$ and so that the first k elements ![]() $a_{1},\ldots ,a_{k}$, for some
$a_{1},\ldots ,a_{k}$, for some ![]() $k\leq n$, are linearly independent and form a basis of
$k\leq n$, are linearly independent and form a basis of ![]() $\operatorname {span} A$.
$\operatorname {span} A$.
Claim. By perturbing ![]() $\mu $ on A by an arbitrarily small
$\mu $ on A by an arbitrarily small ![]() $\delta>0$, we can without loss of generality assume that for every
$\delta>0$, we can without loss of generality assume that for every ![]() $i\leq n$,
$i\leq n$, ![]() $\mu (a_{i})< K_{i}:=\inf \{\sum _{j\in J}\mu (\alpha _{j} a_{j})\colon i\notin J\subseteq \{1,\ldots ,n\}, a_{i}=\sum _{j\in J} \alpha _{j} a_{j}\}$.
$\mu (a_{i})< K_{i}:=\inf \{\sum _{j\in J}\mu (\alpha _{j} a_{j})\colon i\notin J\subseteq \{1,\ldots ,n\}, a_{i}=\sum _{j\in J} \alpha _{j} a_{j}\}$.
Suppose the claim is proved. Then for every ![]() $i\leq n$, we set
$i\leq n$, we set ![]() $\nu ^{\prime }(a_{i})$ to be an arbitrary positive rational number in the interval
$\nu ^{\prime }(a_{i})$ to be an arbitrary positive rational number in the interval ![]() $\left [\mu (a_{i}),\min \{K_{i},\mu (a_{i})+\varepsilon \}\right )$. From the assumption it is now clear that for all
$\left [\mu (a_{i}),\min \{K_{i},\mu (a_{i})+\varepsilon \}\right )$. From the assumption it is now clear that for all ![]() $i\leq n$, we have
$i\leq n$, we have
 $$ \begin{align*}\nu^{\prime}(a_{i})\leq \inf\{\sum_{j=1}^{n} |\alpha_{j}|\nu^{\prime}(a_{j})\colon a_{i}=\sum_{j=1}^{n} \alpha_{j} a_{j}\}.\end{align*} $$
$$ \begin{align*}\nu^{\prime}(a_{i})\leq \inf\{\sum_{j=1}^{n} |\alpha_{j}|\nu^{\prime}(a_{j})\colon a_{i}=\sum_{j=1}^{n} \alpha_{j} a_{j}\}.\end{align*} $$We extend ![]() $\nu ^{\prime }$ to a norm
$\nu ^{\prime }$ to a norm ![]() $\nu $ on
$\nu $ on ![]() $\operatorname {span} A$ by the formula
$\operatorname {span} A$ by the formula
 $$ \begin{align*}\nu(v):=\inf\{\sum_{i=1}^{n} |\alpha_{i}| \nu^{\prime}(a_{i})\colon v=\sum_{i=1}^{n} \alpha_{i} a_{i}\},\end{align*} $$
$$ \begin{align*}\nu(v):=\inf\{\sum_{i=1}^{n} |\alpha_{i}| \nu^{\prime}(a_{i})\colon v=\sum_{i=1}^{n} \alpha_{i} a_{i}\},\end{align*} $$for ![]() $v\in \operatorname {span} A$. From the previous assumption, it follows that
$v\in \operatorname {span} A$. From the previous assumption, it follows that ![]() $\nu (a_{i})=\nu ^{\prime }(a_{i})$ for all
$\nu (a_{i})=\nu ^{\prime }(a_{i})$ for all ![]() $i\leq n$. Moreover,
$i\leq n$. Moreover, ![]() $\nu $ is indeed a norm since
$\nu $ is indeed a norm since ![]() $\nu (a_{i})>0$ for all
$\nu (a_{i})>0$ for all ![]() $i\leq n$, and the infimum in the definition of
$i\leq n$, and the infimum in the definition of ![]() $\nu $ is, by compactness, always attained.
$\nu $ is, by compactness, always attained.
It remains to prove the claim. Let ![]() $\|\cdot \|_{2}$ be the
$\|\cdot \|_{2}$ be the ![]() $\ell _{2}$ norm on
$\ell _{2}$ norm on ![]() $\operatorname {span} A$ with
$\operatorname {span} A$ with ![]() $a_{1},\ldots ,a_{k}$ the orthonormal basis. For each
$a_{1},\ldots ,a_{k}$ the orthonormal basis. For each ![]() $m\in \mathbb {N}$, set
$m\in \mathbb {N}$, set  $\mu _{m}:=\mu +\frac {\|\cdot \|_{2}}{m}$. Clearly
$\mu _{m}:=\mu +\frac {\|\cdot \|_{2}}{m}$. Clearly ![]() $\mu _{m}\to \mu $, so it suffices to show that each
$\mu _{m}\to \mu $, so it suffices to show that each ![]() $\mu _{m}$ satisfies the condition from the claim. Suppose that for some
$\mu _{m}$ satisfies the condition from the claim. Suppose that for some ![]() $m\in \mathbb {N}$ and
$m\in \mathbb {N}$ and ![]() $i\leq n$, we have
$i\leq n$, we have
 $$ \begin{align*}\mu_{m}(a_{i})=\inf\{\sum_{j\in J}\mu_{m}(\alpha_{j} a_{j})\colon i\notin J\subseteq \{1,\ldots,n\}, a_{i}=\sum_{j\in J} \alpha_{j} a_{j}\}.\end{align*} $$
$$ \begin{align*}\mu_{m}(a_{i})=\inf\{\sum_{j\in J}\mu_{m}(\alpha_{j} a_{j})\colon i\notin J\subseteq \{1,\ldots,n\}, a_{i}=\sum_{j\in J} \alpha_{j} a_{j}\}.\end{align*} $$By compactness, the infimum is attained: that is, there exists ![]() $(\alpha _{j})_{j\leq n}$, with
$(\alpha _{j})_{j\leq n}$, with ![]() $\alpha _{i}=0$,
$\alpha _{i}=0$, ![]() $a_{i}=\sum _{j\leq n} \alpha _{j} a_{j}$ and
$a_{i}=\sum _{j\leq n} \alpha _{j} a_{j}$ and ![]() $\mu _{m}(a_{i})=\sum _{j\leq n} \mu _{m}(\alpha _{j} a_{j})$. Indeed, if the infimum is approximated by a sequence
$\mu _{m}(a_{i})=\sum _{j\leq n} \mu _{m}(\alpha _{j} a_{j})$. Indeed, if the infimum is approximated by a sequence  $(\alpha ^{l}_{1},\ldots ,\alpha ^{l}_{n})_{l\in \mathbb {N}}\subseteq \mathbb {R}^{n}$, then since each coordinate is bounded (because up to finitely many ls, we have
$(\alpha ^{l}_{1},\ldots ,\alpha ^{l}_{n})_{l\in \mathbb {N}}\subseteq \mathbb {R}^{n}$, then since each coordinate is bounded (because up to finitely many ls, we have  $\sum _{j=1}^{n} \mu _{m}(\alpha _{j}^{l} a_{j})\leq 2 \mu _{m}(a_{i})$), we may pass to a convergent subsequence and attain the infimum at the limit. The
$\sum _{j=1}^{n} \mu _{m}(\alpha _{j}^{l} a_{j})\leq 2 \mu _{m}(a_{i})$), we may pass to a convergent subsequence and attain the infimum at the limit. The ![]() $\ell _{2}$ norm
$\ell _{2}$ norm ![]() $\|\cdot \|_{2}$ is strictly convex, so
$\|\cdot \|_{2}$ is strictly convex, so ![]() $\|a_{i}\|_{2}{<}\sum _{j\leq n} \|\alpha _{j} a_{j}\|_{2}$, while
$\|a_{i}\|_{2}{<}\sum _{j\leq n} \|\alpha _{j} a_{j}\|_{2}$, while ![]() $\mu $ by triangle inequality satisfies
$\mu $ by triangle inequality satisfies ![]() $\mu (a_{i})\leq \sum _{j\leq n} \mu (\alpha _{j} a_{j})$. Since
$\mu (a_{i})\leq \sum _{j\leq n} \mu (\alpha _{j} a_{j})$. Since ![]() $\mu _{m}$ is the sum of
$\mu _{m}$ is the sum of ![]() $\mu $ and a positive multiple of the
$\mu $ and a positive multiple of the ![]() $\ell _{2}$ norm, we must have
$\ell _{2}$ norm, we must have ![]() $\mu _{m}(a_{i})<\sum _{j\leq n} \mu _{m}(\alpha _{j} a_{j})$, a contradiction.
$\mu _{m}(a_{i})<\sum _{j\leq n} \mu _{m}(\alpha _{j} a_{j})$, a contradiction.
Notation 4.5. For a finite set ![]() $A\subseteq V$ and
$A\subseteq V$ and ![]() $P,P^{\prime }$ partial functions on V (i.e., functions whose domains are subsets of V) with
$P,P^{\prime }$ partial functions on V (i.e., functions whose domains are subsets of V) with ![]() $A\subseteq \operatorname {dom}(P),\operatorname {dom}(P^{\prime })$, we put
$A\subseteq \operatorname {dom}(P),\operatorname {dom}(P^{\prime })$, we put ![]() $d_{A}(P,P^{\prime }):=\max _{a\in A} |P(a) - P^{\prime }(a)|$.
$d_{A}(P,P^{\prime }):=\max _{a\in A} |P(a) - P^{\prime }(a)|$.
Let T be the countable set of tuples ![]() $(n,n^{\prime },P,P^{\prime },g)$ such that:
$(n,n^{\prime },P,P^{\prime },g)$ such that:
1.
 $n,n^{\prime }\in \mathbb N$;
$n,n^{\prime }\in \mathbb N$;2.
 $P\in \mathbb {Q}^{\operatorname {dom}(P)}$,
$P\in \mathbb {Q}^{\operatorname {dom}(P)}$,  $P^{\prime }\in \mathbb {Q}^{\operatorname {dom}(P^{\prime })}$, where
$P^{\prime }\in \mathbb {Q}^{\operatorname {dom}(P^{\prime })}$, where  $\operatorname {dom}(P)$ and
$\operatorname {dom}(P)$ and  $\operatorname {dom}(P^{\prime })$ are finite subsets of V;
$\operatorname {dom}(P^{\prime })$ are finite subsets of V;3. there exists
 $\nu \in \mathcal {B}$ such that
$\nu \in \mathcal {B}$ such that  $P^{\prime } = \nu |_{\operatorname {dom}(P^{\prime })}$;
$P^{\prime } = \nu |_{\operatorname {dom}(P^{\prime })}$;4.
 $g:\operatorname {dom}(P)\to \operatorname {dom}(P^{\prime })$ is a one-to-one mapping;
$g:\operatorname {dom}(P)\to \operatorname {dom}(P^{\prime })$ is a one-to-one mapping;5.
 $P=P^{\prime }\circ g$;
$P=P^{\prime }\circ g$;6. whenever
 $\mu ^{\prime }\in \mathcal {P}$,
$\mu ^{\prime }\in \mathcal {P}$,  $\nu ^{\prime }\in \mathcal {B}$ are such that
$\nu ^{\prime }\in \mathcal {B}$ are such that  $P^{\prime }\subseteq \nu ^{\prime }$,
$P^{\prime }\subseteq \nu ^{\prime }$,  $d_{\operatorname {dom}(P)}(P,\mu ^{\prime })<\tfrac {1}{n}$ and
$d_{\operatorname {dom}(P)}(P,\mu ^{\prime })<\tfrac {1}{n}$ and  $\mu ^{\prime }$ restricted to
$\mu ^{\prime }$ restricted to  $\operatorname {span}(\operatorname {dom}(P))\subseteq c_{00}$ is a norm, then there exists
$\operatorname {span}(\operatorname {dom}(P))\subseteq c_{00}$ is a norm, then there exists  $T_{g}:(\operatorname {span}(\operatorname {dom}(P)),\mu ^{\prime })\to (\operatorname {span}(\operatorname {dom}(P^{\prime })),\nu ^{\prime })$ that is a
$T_{g}:(\operatorname {span}(\operatorname {dom}(P)),\mu ^{\prime })\to (\operatorname {span}(\operatorname {dom}(P^{\prime })),\nu ^{\prime })$ that is a  $(1+\tfrac {1}{n^{\prime }})$-isomorphism and
$(1+\tfrac {1}{n^{\prime }})$-isomorphism and  $T_{g}\supseteq g$.
$T_{g}\supseteq g$.
For ![]() $(n,n^{\prime },P,P^{\prime },g)\in T$, we let
$(n,n^{\prime },P,P^{\prime },g)\in T$, we let ![]() $G(n,n^{\prime },P,P^{\prime },g)$ be the set of
$G(n,n^{\prime },P,P^{\prime },g)$ be the set of ![]() $\mu \in \mathcal {P}_{\infty }$ such that
$\mu \in \mathcal {P}_{\infty }$ such that
• whenever
 $d_{\operatorname {dom}(P)}(P,\mu )<\tfrac {1}{n}$ and
$d_{\operatorname {dom}(P)}(P,\mu )<\tfrac {1}{n}$ and  $\mu $ restricted to
$\mu $ restricted to  $\operatorname {span} (\operatorname {dom}(P))\subseteq c_{00}$ is a norm, there is a
$\operatorname {span} (\operatorname {dom}(P))\subseteq c_{00}$ is a norm, there is a  $\mathbb {Q}$-linear mapping
$\mathbb {Q}$-linear mapping  $\Phi :V\cap \operatorname {span} (\operatorname {dom}(P^{\prime }))\to V$ such that
$\Phi :V\cap \operatorname {span} (\operatorname {dom}(P^{\prime }))\to V$ such that  $\mu (\Phi (gx)-x) < \tfrac {2}{n^{\prime }}\mu (x)$ for every
$\mu (\Phi (gx)-x) < \tfrac {2}{n^{\prime }}\mu (x)$ for every  $x\in \operatorname {dom}(P)$ and
$x\in \operatorname {dom}(P)$ and  $|P^{\prime }(x) - \mu (\Phi (x))|<\tfrac {1}{n^{\prime }}P^{\prime }(x)$ for every
$|P^{\prime }(x) - \mu (\Phi (x))|<\tfrac {1}{n^{\prime }}P^{\prime }(x)$ for every  $x\in \operatorname {dom}(P^{\prime })$.
$x\in \operatorname {dom}(P^{\prime })$.
Proposition 4.6. Let ![]() $\mu \in \mathcal {P}_{\infty }$. Then
$\mu \in \mathcal {P}_{\infty }$. Then ![]() $X_{\mu }$ is isometric to the Gurariĭ space if and only if
$X_{\mu }$ is isometric to the Gurariĭ space if and only if ![]() $\mu \in G(n,n^{\prime },P,P^{\prime },g)$ for every
$\mu \in G(n,n^{\prime },P,P^{\prime },g)$ for every ![]() $(n,n^{\prime },P,P^{\prime },g)\in T$.
$(n,n^{\prime },P,P^{\prime },g)\in T$.
Proof. In order to prove the first implication, let ![]() $\mu \in \mathcal {P}_{\infty }$ be such that
$\mu \in \mathcal {P}_{\infty }$ be such that ![]() $X_{\mu }$ is isometric to the Gurariĭ space, and let
$X_{\mu }$ is isometric to the Gurariĭ space, and let ![]() $(n,n^{\prime },P,P^{\prime },g)\in T$ be such that
$(n,n^{\prime },P,P^{\prime },g)\in T$ be such that  $d_{\operatorname {dom}(P)}(P,\mu ) < \tfrac {1}{n}$ and
$d_{\operatorname {dom}(P)}(P,\mu ) < \tfrac {1}{n}$ and ![]() $\mu $ restricted to
$\mu $ restricted to ![]() $\operatorname {span} (\operatorname {dom}(P))\subseteq c_{00}$ is a norm. Consider the finite-dimensional space
$\operatorname {span} (\operatorname {dom}(P))\subseteq c_{00}$ is a norm. Consider the finite-dimensional space ![]() $A:=(\operatorname {span}(\operatorname {dom}(P)),\mu )$. Let
$A:=(\operatorname {span}(\operatorname {dom}(P)),\mu )$. Let ![]() $\nu \in \mathcal {B}$ be as in 3. Put
$\nu \in \mathcal {B}$ be as in 3. Put ![]() $B = (\operatorname {span}(\operatorname {dom} P^{\prime }),\nu )$, and pick a basis
$B = (\operatorname {span}(\operatorname {dom} P^{\prime }),\nu )$, and pick a basis ![]() $\mathfrak {b}\subseteq V$ of B. By 6, there exists
$\mathfrak {b}\subseteq V$ of B. By 6, there exists ![]() $T_{g}:A\to B$, which is a
$T_{g}:A\to B$, which is a  $(1+\tfrac {1}{n^{\prime }})$-isomorphism and
$(1+\tfrac {1}{n^{\prime }})$-isomorphism and ![]() $T_{g}\supseteq g$. By [Reference Kubiś and Solecki22, Lemma 2.2], there is a
$T_{g}\supseteq g$. By [Reference Kubiś and Solecki22, Lemma 2.2], there is a  $(1+\tfrac {1}{3n^{\prime }})$-isomorphism
$(1+\tfrac {1}{3n^{\prime }})$-isomorphism ![]() $S:B\to X_{\mu }$ such that
$S:B\to X_{\mu }$ such that  $\|ST_{g}-Id_{A}\|<\tfrac {1}{n^{\prime }}$. By Lemma 4.31, we may for every
$\|ST_{g}-Id_{A}\|<\tfrac {1}{n^{\prime }}$. By Lemma 4.31, we may for every ![]() $b\in \mathfrak {b}$ find
$b\in \mathfrak {b}$ find ![]() $x_{b}\in V$ such that the linear mapping
$x_{b}\in V$ such that the linear mapping ![]() $Q:S(B)\to X_{\mu }$ given by
$Q:S(B)\to X_{\mu }$ given by ![]() $Q(S(b)) = x_{b}$,
$Q(S(b)) = x_{b}$, ![]() $b\in \mathfrak {b}$, is a
$b\in \mathfrak {b}$, is a  $(1+\tfrac {1}{3n^{\prime }})$-isomorphism with
$(1+\tfrac {1}{3n^{\prime }})$-isomorphism with  $\|Q-Id\|<\tfrac {1}{3n^{\prime }}$. Consider
$\|Q-Id\|<\tfrac {1}{3n^{\prime }}$. Consider ![]() $\Phi = QS|_{V\cap \operatorname {span}(\operatorname {dom} P^{\prime })}$. This is indeed a
$\Phi = QS|_{V\cap \operatorname {span}(\operatorname {dom} P^{\prime })}$. This is indeed a ![]() $\mathbb {Q}$-linear map and since
$\mathbb {Q}$-linear map and since ![]() $QS$ is a
$QS$ is a  $(1+\tfrac {1}{3n^{\prime }})^{2}$-isomorphism and
$(1+\tfrac {1}{3n^{\prime }})^{2}$-isomorphism and  $(1+\tfrac {1}{3n^{\prime }})^{2}<1+\tfrac {1}{n^{\prime }}$, we have
$(1+\tfrac {1}{3n^{\prime }})^{2}<1+\tfrac {1}{n^{\prime }}$, we have  $|\mu (\Phi (x)) - \nu (x)|<\tfrac {1}{n^{\prime }}\nu (x)$ for
$|\mu (\Phi (x)) - \nu (x)|<\tfrac {1}{n^{\prime }}\nu (x)$ for ![]() $x\in \operatorname {dom}(P^{\prime })$. Moreover, for every
$x\in \operatorname {dom}(P^{\prime })$. Moreover, for every ![]() $x\in \operatorname {dom}(P)$, we have
$x\in \operatorname {dom}(P)$, we have
 $$ \begin{align*}\begin{split} \mu(\Phi(gx) - x) & = \mu(QST_{g}x - x)\leq \mu(QST_{g}x - ST_{g}x) + \mu(ST_{g}x - x)\\ & < \tfrac{1}{3n^{\prime}}\|ST_{g}\|\mu(x) + \tfrac{1}{n^{\prime}}\mu(x) \leq \tfrac{2}{n^{\prime}}\mu(x). \end{split}\end{align*} $$
$$ \begin{align*}\begin{split} \mu(\Phi(gx) - x) & = \mu(QST_{g}x - x)\leq \mu(QST_{g}x - ST_{g}x) + \mu(ST_{g}x - x)\\ & < \tfrac{1}{3n^{\prime}}\|ST_{g}\|\mu(x) + \tfrac{1}{n^{\prime}}\mu(x) \leq \tfrac{2}{n^{\prime}}\mu(x). \end{split}\end{align*} $$This shows that ![]() $\mu \in G(n,n^{\prime },P,P^{\prime },g)$.
$\mu \in G(n,n^{\prime },P,P^{\prime },g)$.
In order to prove the second implication, let ![]() $\mu \in \mathcal {P}_{\infty }$ be such that
$\mu \in \mathcal {P}_{\infty }$ be such that ![]() $\mu \in G(n,n^{\prime },P,P^{\prime },g)$ whenever
$\mu \in G(n,n^{\prime },P,P^{\prime },g)$ whenever ![]() $(n,n^{\prime },P,P^{\prime },g)\in T$. In what follows for
$(n,n^{\prime },P,P^{\prime },g)\in T$. In what follows for ![]() $x\in c_{00}$, we denote by
$x\in c_{00}$, we denote by ![]() $[x]{\in} X_{\mu }$ the equivalence class corresponding to x. Pick a finite-dimensional space
$[x]{\in} X_{\mu }$ the equivalence class corresponding to x. Pick a finite-dimensional space ![]() $A\subseteq X_{\mu }$ and an isometry
$A\subseteq X_{\mu }$ and an isometry ![]() $G:A\to B$, where B is a finite-dimensional Banach space; we may without loss of generality assume
$G:A\to B$, where B is a finite-dimensional Banach space; we may without loss of generality assume ![]() $B \subseteq X_{\mu _{B}}$ for some
$B \subseteq X_{\mu _{B}}$ for some ![]() $\mu _{B}\in \mathcal {B}$. Let
$\mu _{B}\in \mathcal {B}$. Let ![]() $\mathfrak {b}_{A}:=\{a_{1},\ldots ,a_{j}\}$ be a normalized basis of A, and extend
$\mathfrak {b}_{A}:=\{a_{1},\ldots ,a_{j}\}$ be a normalized basis of A, and extend ![]() $G(\mathfrak {b}_{A}) = \{G(a_{1}),\ldots ,G(a_{j})\}$ to a normalized basis
$G(\mathfrak {b}_{A}) = \{G(a_{1}),\ldots ,G(a_{j})\}$ to a normalized basis ![]() $\mathfrak {b}_{B} = \{b_{1},\ldots ,b_{k}\}$ of B. Fix
$\mathfrak {b}_{B} = \{b_{1},\ldots ,b_{k}\}$ of B. Fix ![]() $\eta> 0$. It suffices to find a
$\eta> 0$. It suffices to find a ![]() $(1+\eta )$-isomorphism
$(1+\eta )$-isomorphism ![]() $\Psi :B\to X_{\mu }$ with
$\Psi :B\to X_{\mu }$ with ![]() $\|\Psi G - I_{A}\|\leq \eta $. Consider the functions
$\|\Psi G - I_{A}\|\leq \eta $. Consider the functions ![]() $\phi _{1}$ and
$\phi _{1}$ and  $\phi _{2}^{\mathfrak {b}_{A}}$ from Lemma 2.2 and Lemma 4.31. Pick
$\phi _{2}^{\mathfrak {b}_{A}}$ from Lemma 2.2 and Lemma 4.31. Pick ![]() $\delta \in (0,1)$ such that
$\delta \in (0,1)$ such that  $\max \{\phi _{1}(t),\phi _{2}^{\mathfrak {b}_{A}}(t)\}<\eta $ whenever
$\max \{\phi _{1}(t),\phi _{2}^{\mathfrak {b}_{A}}(t)\}<\eta $ whenever ![]() $t<\delta $ and
$t<\delta $ and  $\varepsilon \in (0,\tfrac {1}{20})$ such that
$\varepsilon \in (0,\tfrac {1}{20})$ such that  $\phi _{1}(5\varepsilon )<\tfrac {1}{20}$ and
$\phi _{1}(5\varepsilon )<\tfrac {1}{20}$ and ![]() $\varepsilon + 72\max \{\varepsilon ,\phi _{1}(5\varepsilon )\}<\delta $.
$\varepsilon + 72\max \{\varepsilon ,\phi _{1}(5\varepsilon )\}<\delta $.
Claim 1. There are finite sets ![]() $M,N\subseteq V$ such that
$M,N\subseteq V$ such that ![]() $\mu $ restricted to
$\mu $ restricted to ![]() $\operatorname {span} N\subseteq c_{00}$ is a norm and surjective
$\operatorname {span} N\subseteq c_{00}$ is a norm and surjective ![]() $(1+\varepsilon )$-isomorphisms
$(1+\varepsilon )$-isomorphisms ![]() $T_{A}:A\to (\operatorname {span} N,\mu )$,
$T_{A}:A\to (\operatorname {span} N,\mu )$, ![]() $T_{B}:B\to (\operatorname {span} M,\mu _{B})$ such that:
$T_{B}:B\to (\operatorname {span} M,\mu _{B})$ such that:
• N and M are
 $\varepsilon $-dense sets for
$\varepsilon $-dense sets for  $S_{T_{A}(A)}$ and
$S_{T_{A}(A)}$ and  $S_{T_{B}(B)}$, respectively;
$S_{T_{B}(B)}$, respectively;• we have
 $\|[T_{A}a_{i}]-a_{i}\|_{X_{\mu }}<\varepsilon $ for every
$\|[T_{A}a_{i}]-a_{i}\|_{X_{\mu }}<\varepsilon $ for every  $a_{i}\in \mathfrak {b}_{A}$ and
$a_{i}\in \mathfrak {b}_{A}$ and  $\|(T_{A})^{-1}x-[x]\|_{X_{\mu }}<\varepsilon $,
$\|(T_{A})^{-1}x-[x]\|_{X_{\mu }}<\varepsilon $,  $|\mu (x)-1|<\varepsilon $ for every
$|\mu (x)-1|<\varepsilon $ for every  $x\in N$;
$x\in N$;•
 $(T_{B})^{-1}(M)$ is
$(T_{B})^{-1}(M)$ is  $\tfrac {\varepsilon }{3}$-dense for
$\tfrac {\varepsilon }{3}$-dense for  $S_{B}$ and
$S_{B}$ and  $\max \{|\mu _{B}((T_{B})^{-1}x) - 1|, |\mu _{B}(x) - 1|\}<\tfrac {\varepsilon }{2}$ for every
$\max \{|\mu _{B}((T_{B})^{-1}x) - 1|, |\mu _{B}(x) - 1|\}<\tfrac {\varepsilon }{2}$ for every  $x\in M$;
$x\in M$;•
 $\big (T_{B}G(T_{A})^{-1}\big )(N)\subseteq M$.
$\big (T_{B}G(T_{A})^{-1}\big )(N)\subseteq M$.
Proof of Claim 1.
By Lemma 4.31, we may pick ![]() $\{f_{1},\ldots ,f_{n}\}\subseteq V$ such that the linear operator
$\{f_{1},\ldots ,f_{n}\}\subseteq V$ such that the linear operator ![]() $T_{A}:A\to X_{\mu }$ given by
$T_{A}:A\to X_{\mu }$ given by ![]() $T_{A}(a_{i})=[f_{i}]$,
$T_{A}(a_{i})=[f_{i}]$, ![]() $i\leq j$, is a
$i\leq j$, is a ![]() $(1+\frac {\varepsilon }{6})$-isomorphism and
$(1+\frac {\varepsilon }{6})$-isomorphism and ![]() $\|[T_{A}x]-x\|_{X_{\mu }}{<}\tfrac {\varepsilon }{6}\|x\|_{X_{\mu }}$,
$\|[T_{A}x]-x\|_{X_{\mu }}{<}\tfrac {\varepsilon }{6}\|x\|_{X_{\mu }}$, ![]() $x\in A$. This implies that
$x\in A$. This implies that ![]() $\mu $ restricted to
$\mu $ restricted to ![]() $\operatorname {span} \{f_{1},\ldots ,f_{j}\}$ is a norm, and since
$\operatorname {span} \{f_{1},\ldots ,f_{j}\}$ is a norm, and since ![]() $T_{A}(A)$ is isometric to
$T_{A}(A)$ is isometric to ![]() $(\operatorname {span}\{f_{1},\ldots ,f_{n}\},\mu )$, we consider
$(\operatorname {span}\{f_{1},\ldots ,f_{n}\},\mu )$, we consider ![]() $T_{A}$ a
$T_{A}$ a ![]() $(1+\frac {\varepsilon }{6})$-isomorphism between A and
$(1+\frac {\varepsilon }{6})$-isomorphism between A and ![]() $(\operatorname {span}\{f_{1},\ldots ,f_{n}\},\mu )$. Now, pick
$(\operatorname {span}\{f_{1},\ldots ,f_{n}\},\mu )$. Now, pick ![]() $N^{\prime }\subseteq A$ a finite
$N^{\prime }\subseteq A$ a finite ![]() $\tfrac {\varepsilon }{6}$-dense set for
$\tfrac {\varepsilon }{6}$-dense set for ![]() $S_{A}$ consisting of rational linear combinations of points from
$S_{A}$ consisting of rational linear combinations of points from ![]() $\mathfrak {b}_{A}$ with
$\mathfrak {b}_{A}$ with ![]() $\mathfrak {b}_{A}\subseteq N^{\prime }$ such that
$\mathfrak {b}_{A}\subseteq N^{\prime }$ such that ![]() $|\|x\|_{X_{\mu }}-1|<\tfrac {\varepsilon }{6}$ for every
$|\|x\|_{X_{\mu }}-1|<\tfrac {\varepsilon }{6}$ for every ![]() $x\in N^{\prime }$. Then
$x\in N^{\prime }$. Then ![]() $\|[T_{A}x]-x\|_{X_{\mu }}<\tfrac {\varepsilon }{6}\|x\|_{X_{\mu }}<\tfrac {\varepsilon }{6}(1+\tfrac {\varepsilon }{6})<\tfrac {\varepsilon }{5}$ for every
$\|[T_{A}x]-x\|_{X_{\mu }}<\tfrac {\varepsilon }{6}\|x\|_{X_{\mu }}<\tfrac {\varepsilon }{6}(1+\tfrac {\varepsilon }{6})<\tfrac {\varepsilon }{5}$ for every ![]() $x\in N^{\prime }$. Put
$x\in N^{\prime }$. Put ![]() $N:=T_{A}(N^{\prime })\subseteq V$. Then we easily obtain
$N:=T_{A}(N^{\prime })\subseteq V$. Then we easily obtain ![]() $|\mu (x)-1|<\tfrac {\varepsilon }{2}$ for every
$|\mu (x)-1|<\tfrac {\varepsilon }{2}$ for every ![]() $x\in N$ and, by Lemma 4.32, N is
$x\in N$ and, by Lemma 4.32, N is ![]() $\tfrac {\varepsilon }{2}$-dense in
$\tfrac {\varepsilon }{2}$-dense in ![]() $S_{T_{A}(A)}$. Similarly as above, we may pick
$S_{T_{A}(A)}$. Similarly as above, we may pick ![]() $\{g_{1},\ldots ,g_{k}\}\subseteq V$ such that the linear operator
$\{g_{1},\ldots ,g_{k}\}\subseteq V$ such that the linear operator ![]() $T_{B}:B\to X_{\mu _{B}}$ given by
$T_{B}:B\to X_{\mu _{B}}$ given by ![]() $T_{B}(b_{i})=g_{i}$,
$T_{B}(b_{i})=g_{i}$, ![]() $i\leq k$, is a
$i\leq k$, is a ![]() $(1+\frac {\varepsilon }{6})$-isomorphism, and we find
$(1+\frac {\varepsilon }{6})$-isomorphism, and we find ![]() $M^{\prime }\subseteq B$ a finite
$M^{\prime }\subseteq B$ a finite ![]() $\tfrac {\varepsilon }{6}$-dense set for
$\tfrac {\varepsilon }{6}$-dense set for ![]() $S_{B}$ consisting of rational linear combinations of points from
$S_{B}$ consisting of rational linear combinations of points from ![]() $\mathfrak {b}_{B}$ with
$\mathfrak {b}_{B}$ with ![]() $M^{\prime }\supseteq \{G(x):\; x\in N^{\prime }\}\cup \mathfrak {b}_{B}$ and
$M^{\prime }\supseteq \{G(x):\; x\in N^{\prime }\}\cup \mathfrak {b}_{B}$ and ![]() $|\mu _{B}(x) - 1|<\tfrac {\varepsilon }{6}$ for
$|\mu _{B}(x) - 1|<\tfrac {\varepsilon }{6}$ for ![]() $x\in M^{\prime }$. Put
$x\in M^{\prime }$. Put ![]() $M:=T_{B}(M^{\prime })$; then similarly as above,
$M:=T_{B}(M^{\prime })$; then similarly as above, ![]() $|\mu _{B}(x)-1|<\tfrac {\varepsilon }{2}$ for every
$|\mu _{B}(x)-1|<\tfrac {\varepsilon }{2}$ for every ![]() $x\in M$ and M is
$x\in M$ and M is ![]() $\tfrac {\varepsilon }{2}$-dense in
$\tfrac {\varepsilon }{2}$-dense in ![]() $S_{T_{B}(B)}$. Finally, we obviously have
$S_{T_{B}(B)}$. Finally, we obviously have ![]() $\big (T_{B}G(T_{A})^{-1}\big )(N) = T_{B}(G(N^{\prime }))\subseteq T_{B}(M^{\prime }) = M$.
$\big (T_{B}G(T_{A})^{-1}\big )(N) = T_{B}(G(N^{\prime }))\subseteq T_{B}(M^{\prime }) = M$.
By Lemma 4.4, there is ![]() $\nu \in \mathcal {B}$ having rational values on M with
$\nu \in \mathcal {B}$ having rational values on M with  $d_{M}(\nu ,\mu _{B}\circ (T_{B})^{-1})<\tfrac {\varepsilon }{2}$. Put
$d_{M}(\nu ,\mu _{B}\circ (T_{B})^{-1})<\tfrac {\varepsilon }{2}$. Put ![]() $P^{\prime } = \nu |_{M}$, consider the one-to-one map
$P^{\prime } = \nu |_{M}$, consider the one-to-one map ![]() $g:N\to M$ given by
$g:N\to M$ given by ![]() $g:=T_{B}G(T_{A})^{-1}|_{N}$ and put
$g:=T_{B}G(T_{A})^{-1}|_{N}$ and put ![]() $P = P^{\prime }\circ g$. Let
$P = P^{\prime }\circ g$. Let ![]() $n\in \mathbb N$ be the integer part of
$n\in \mathbb N$ be the integer part of ![]() $\tfrac {2}{3\varepsilon }$ and
$\tfrac {2}{3\varepsilon }$ and ![]() $n^{\prime }\in \mathbb N$ be the integer part of
$n^{\prime }\in \mathbb N$ be the integer part of  $\frac {1}{9\max \{\varepsilon ,\phi _{1}(5\varepsilon )\}}$. Easy computations show that
$\frac {1}{9\max \{\varepsilon ,\phi _{1}(5\varepsilon )\}}$. Easy computations show that  $\tfrac {3}{2}\varepsilon \leq \frac {1}{n}<2\varepsilon $ and
$\tfrac {3}{2}\varepsilon \leq \frac {1}{n}<2\varepsilon $ and  $9\max \{\varepsilon ,\phi _{1}(5\varepsilon )\}\leq \tfrac {1}{n^{\prime }} < 18\max \{\varepsilon ,\phi _{1}(5\varepsilon )\}$ (in the last inequality, we are using that
$9\max \{\varepsilon ,\phi _{1}(5\varepsilon )\}\leq \tfrac {1}{n^{\prime }} < 18\max \{\varepsilon ,\phi _{1}(5\varepsilon )\}$ (in the last inequality, we are using that  $\max \{\varepsilon ,\phi _{1}(5\varepsilon )\}<\tfrac {1}{20}$).
$\max \{\varepsilon ,\phi _{1}(5\varepsilon )\}<\tfrac {1}{20}$).
Note that for every ![]() $x\in M$, we have
$x\in M$, we have
 $$ \begin{align} \max\{|\nu(T_{B}x)-1|,|\nu(x)-1|\}\leq \tfrac{\varepsilon}{2} + \max\{|\mu_{B}(x)-1|,|\mu_{B}((T_{B})^{-1}x)-1|\} < \varepsilon. \end{align} $$
$$ \begin{align} \max\{|\nu(T_{B}x)-1|,|\nu(x)-1|\}\leq \tfrac{\varepsilon}{2} + \max\{|\mu_{B}(x)-1|,|\mu_{B}((T_{B})^{-1}x)-1|\} < \varepsilon. \end{align} $$Claim 2. We have ![]() $(n,n^{\prime },P,P^{\prime },g)\in T$ and
$(n,n^{\prime },P,P^{\prime },g)\in T$ and  $d_{N}(P,\mu )<\tfrac {1}{n}$.
$d_{N}(P,\mu )<\tfrac {1}{n}$.
Proof of Claim 2.
In order to see that  $d_{N}(P,\mu )<\tfrac {1}{n}$, pick
$d_{N}(P,\mu )<\tfrac {1}{n}$, pick ![]() $x\in N$. Then
$x\in N$. Then
 $$ \begin{align*}\begin{split} |P(x) - \mu(x)| \leq \tfrac{\varepsilon}{2} + |\mu_{B}(G(T_{A})^{-1}(x)) - \mu(x)| = \tfrac{\varepsilon}{2} + |\|(T_{A})^{-1}(x)\|_{X_{\mu}} - \|[x]\|_{X_{\mu}}| < \tfrac{3}{2}\varepsilon. \end{split}\end{align*} $$
$$ \begin{align*}\begin{split} |P(x) - \mu(x)| \leq \tfrac{\varepsilon}{2} + |\mu_{B}(G(T_{A})^{-1}(x)) - \mu(x)| = \tfrac{\varepsilon}{2} + |\|(T_{A})^{-1}(x)\|_{X_{\mu}} - \|[x]\|_{X_{\mu}}| < \tfrac{3}{2}\varepsilon. \end{split}\end{align*} $$In order to see that ![]() $(n,n^{\prime },P,P^{\prime },g)\in T$, let us verify condition 6. Let
$(n,n^{\prime },P,P^{\prime },g)\in T$, let us verify condition 6. Let ![]() $\mu ^{\prime }\in \mathcal {P}$,
$\mu ^{\prime }\in \mathcal {P}$, ![]() $\nu ^{\prime }\in \mathcal B$ be such that
$\nu ^{\prime }\in \mathcal B$ be such that ![]() $P^{\prime }\subseteq \nu ^{\prime }$,
$P^{\prime }\subseteq \nu ^{\prime }$,  $d_{N}(P,\mu ^{\prime })<\tfrac {1}{n} < 2\varepsilon $ and
$d_{N}(P,\mu ^{\prime })<\tfrac {1}{n} < 2\varepsilon $ and ![]() $\mu ^{\prime }$ restricted to
$\mu ^{\prime }$ restricted to ![]() $\operatorname {span} N\subseteq c_{00}$ is a norm. Note that
$\operatorname {span} N\subseteq c_{00}$ is a norm. Note that ![]() $|\mu ^{\prime }(x)-1|<5\varepsilon $ for every
$|\mu ^{\prime }(x)-1|<5\varepsilon $ for every ![]() $x\in N$, and so, since N is
$x\in N$, and so, since N is ![]() $\varepsilon $-dense for the sphere of
$\varepsilon $-dense for the sphere of ![]() $T_{A}(A) = (\operatorname {span} N,\mu )$, the mapping
$T_{A}(A) = (\operatorname {span} N,\mu )$, the mapping ![]() $id:(\operatorname {span} N,\mu )\to (\operatorname {span} N,\mu ^{\prime })$ is a
$id:(\operatorname {span} N,\mu )\to (\operatorname {span} N,\mu ^{\prime })$ is a ![]() $(1+\phi _{1}(5\varepsilon ))$-isomorphism. Further,
$(1+\phi _{1}(5\varepsilon ))$-isomorphism. Further, ![]() $|\nu ^{\prime }(x)-1|=|\nu (x)-1|<\varepsilon $ for every
$|\nu ^{\prime }(x)-1|=|\nu (x)-1|<\varepsilon $ for every ![]() $x\in M$, and so the mapping
$x\in M$, and so the mapping ![]() $id:(\operatorname {span} M,\mu _{B})\to (\operatorname {span} M,\nu ^{\prime })$ is a
$id:(\operatorname {span} M,\mu _{B})\to (\operatorname {span} M,\nu ^{\prime })$ is a ![]() $(1+\phi _{1}(5\varepsilon ))$-isomorphism as well. Finally, since
$(1+\phi _{1}(5\varepsilon ))$-isomorphism as well. Finally, since ![]() $T_{B}G(T_{A})^{-1}$ is a
$T_{B}G(T_{A})^{-1}$ is a ![]() $(1+\varepsilon )^{2}$-isomorphism between
$(1+\varepsilon )^{2}$-isomorphism between ![]() $(\operatorname {span} N,\mu )$ and
$(\operatorname {span} N,\mu )$ and ![]() $(\operatorname {span} g(N),\mu _{B})$ and
$(\operatorname {span} g(N),\mu _{B})$ and
 $$ \begin{align*} (1+\phi_{1}(5\varepsilon))^{2}(1+\varepsilon)^{2} \leq (1+3\phi_{1}(5\varepsilon))(1+3\varepsilon)\leq 1 + 9\max\{\varepsilon,\phi_{1}(5\varepsilon)\}\leq 1+\tfrac{1}{n^{\prime}}, \end{align*} $$
$$ \begin{align*} (1+\phi_{1}(5\varepsilon))^{2}(1+\varepsilon)^{2} \leq (1+3\phi_{1}(5\varepsilon))(1+3\varepsilon)\leq 1 + 9\max\{\varepsilon,\phi_{1}(5\varepsilon)\}\leq 1+\tfrac{1}{n^{\prime}}, \end{align*} $$we have that ![]() $T_{g}:=id\circ T_{B}\circ G\circ (T_{A})^{-1}\circ id:(\operatorname {span} N,\mu ^{\prime })\to (\operatorname {span} M,\nu ^{\prime })$ is a
$T_{g}:=id\circ T_{B}\circ G\circ (T_{A})^{-1}\circ id:(\operatorname {span} N,\mu ^{\prime })\to (\operatorname {span} M,\nu ^{\prime })$ is a  $(1+\tfrac {1}{n^{\prime }})$-isomorphism.
$(1+\tfrac {1}{n^{\prime }})$-isomorphism.
Since ![]() $\mu \in G(n,n^{\prime },P,P^{\prime },g)$, there is a
$\mu \in G(n,n^{\prime },P,P^{\prime },g)$, there is a ![]() $\mathbb {Q}$-linear mapping
$\mathbb {Q}$-linear mapping ![]() $\Phi :V\cap (\operatorname {span} M,\nu )\to V$ such that
$\Phi :V\cap (\operatorname {span} M,\nu )\to V$ such that  $\mu (\Phi (gx)-x) < \tfrac {2}{n^{\prime }}\mu (x)$ for every
$\mu (\Phi (gx)-x) < \tfrac {2}{n^{\prime }}\mu (x)$ for every ![]() $x\in N$ and
$x\in N$ and  $|\nu (x) - \mu (\Phi (x))|<\tfrac {1}{n^{\prime }}\nu (x)$ for every
$|\nu (x) - \mu (\Phi (x))|<\tfrac {1}{n^{\prime }}\nu (x)$ for every ![]() $x\in M$. It is easy to see that
$x\in M$. It is easy to see that ![]() $\Phi $ extends to a bounded linear operator
$\Phi $ extends to a bounded linear operator ![]() $\Phi ^{\prime }:(\operatorname {span} M,\nu )\to X_{\mu }$. Finally, consider
$\Phi ^{\prime }:(\operatorname {span} M,\nu )\to X_{\mu }$. Finally, consider ![]() $\Psi :=\Phi ^{\prime }\circ T_{B}:B\to X_{\mu }$.
$\Psi :=\Phi ^{\prime }\circ T_{B}:B\to X_{\mu }$.
For every ![]() $x\in M$, we have
$x\in M$, we have
 $$ \begin{align*}|\mu(\Phi(x)) - 1| \leq |\mu(\Phi(x)) - \nu(x)| + |\nu(x) - 1| \stackrel{(4.1)}{\leq} \tfrac{1}{n^{\prime}}\nu(x) + \varepsilon \stackrel{(4.1)}{\leq} \tfrac{1}{n^{\prime}}(1+\varepsilon) + \varepsilon< \delta;\end{align*} $$
$$ \begin{align*}|\mu(\Phi(x)) - 1| \leq |\mu(\Phi(x)) - \nu(x)| + |\nu(x) - 1| \stackrel{(4.1)}{\leq} \tfrac{1}{n^{\prime}}\nu(x) + \varepsilon \stackrel{(4.1)}{\leq} \tfrac{1}{n^{\prime}}(1+\varepsilon) + \varepsilon< \delta;\end{align*} $$thus, ![]() $|\|\Psi (x)\|_{X_{\mu }} - 1| < \delta $ for every
$|\|\Psi (x)\|_{X_{\mu }} - 1| < \delta $ for every ![]() $x\in (T_{B})^{-1}(M)$ and so
$x\in (T_{B})^{-1}(M)$ and so ![]() $\Psi $ is a
$\Psi $ is a ![]() $(1+\eta )$-isomorphism.
$(1+\eta )$-isomorphism.
Further, we have
 $$ \begin{align*}\begin{split} \|\Psi G(a_{i}) - a_{i}\|_{X_{\mu}} & \leq \|\Phi(g(T_{A} a_{i})) - [T_{A} a_{i}]\|_{X_{\mu}} + \|[T_{A} a_{i}] - a_{i}\|_{X_{\mu}}\\ & < \tfrac{2}{n^{\prime}}(1+\varepsilon)+\varepsilon\le\tfrac{4}{n^{\prime}}+\varepsilon<\delta; \end{split}\end{align*} $$
$$ \begin{align*}\begin{split} \|\Psi G(a_{i}) - a_{i}\|_{X_{\mu}} & \leq \|\Phi(g(T_{A} a_{i})) - [T_{A} a_{i}]\|_{X_{\mu}} + \|[T_{A} a_{i}] - a_{i}\|_{X_{\mu}}\\ & < \tfrac{2}{n^{\prime}}(1+\varepsilon)+\varepsilon\le\tfrac{4}{n^{\prime}}+\varepsilon<\delta; \end{split}\end{align*} $$hence, by Lemma 4.31, we have  $\|\Phi ^{\prime } T_{B} G - I_{A}\|\leq \phi _{2}^{\mathfrak {b}_{A}}(\tfrac {2}{n^{\prime }}(1+\varepsilon )+\varepsilon ) < \eta $.
$\|\Phi ^{\prime } T_{B} G - I_{A}\|\leq \phi _{2}^{\mathfrak {b}_{A}}(\tfrac {2}{n^{\prime }}(1+\varepsilon )+\varepsilon ) < \eta $.
Theorem 4.7. Let ![]() $\mathbb {G}$ be the Gurariĭ space. Then the isometry class
$\mathbb {G}$ be the Gurariĭ space. Then the isometry class ![]() ${\langle \mathbb {G}\rangle _{\equiv }^{\mathcal {P}_{\infty }}}$ is a
${\langle \mathbb {G}\rangle _{\equiv }^{\mathcal {P}_{\infty }}}$ is a ![]() $G_{\delta }$-set in
$G_{\delta }$-set in ![]() $\mathcal {P}_{\infty }$.
$\mathcal {P}_{\infty }$.
Proof. By Proposition 4.6, we have for the countable set T defined before Proposition 4.6 that
 $$ \begin{align*}{\langle \mathbb{G}\rangle_{\equiv}^{\mathcal{P}_{\infty}}} = \bigcap_{(n,n^{\prime},P,P^{\prime},g)\in T} G(n,n^{\prime},P,P^{\prime},g),\end{align*} $$
$$ \begin{align*}{\langle \mathbb{G}\rangle_{\equiv}^{\mathcal{P}_{\infty}}} = \bigcap_{(n,n^{\prime},P,P^{\prime},g)\in T} G(n,n^{\prime},P,P^{\prime},g),\end{align*} $$where ![]() $G(n,n^{\prime },P,P^{\prime },g)$ is the union of a closed and an open set in
$G(n,n^{\prime },P,P^{\prime },g)$ is the union of a closed and an open set in ![]() $\mathcal {P}_{\infty }$ (here we use the observation that the set
$\mathcal {P}_{\infty }$ (here we use the observation that the set ![]() $\{\mu \in \mathcal {P}_\infty \colon \mu \text { restricted to } \operatorname {span}(\operatorname {dom} P)\subseteq c_{00} \text { is a norm}\}$ is open due to Lemma 2.4); thus it is the countable intersection of
$\{\mu \in \mathcal {P}_\infty \colon \mu \text { restricted to } \operatorname {span}(\operatorname {dom} P)\subseteq c_{00} \text { is a norm}\}$ is open due to Lemma 2.4); thus it is the countable intersection of ![]() $G_{\delta }$-sets.
$G_{\delta }$-sets.
Proof of Theorem 4.1.
Let us recall that ![]() $\mathcal {P}_{\infty }$ and
$\mathcal {P}_{\infty }$ and ![]() $\mathcal {B}$ are
$\mathcal {B}$ are ![]() $G_{\delta }$-sets in
$G_{\delta }$-sets in ![]() $\mathcal {P}$; see Corollary 2.5. Thus, since we have
$\mathcal {P}$; see Corollary 2.5. Thus, since we have ![]() ${\langle \mathbb {G}\rangle _{\equiv }^{\mathcal {B}}} = {\langle \mathbb {G}\rangle _{\equiv }^{\mathcal {P}_{\infty }}}\cap \mathcal {B}$, it follows from Proposition 4.6 that
${\langle \mathbb {G}\rangle _{\equiv }^{\mathcal {B}}} = {\langle \mathbb {G}\rangle _{\equiv }^{\mathcal {P}_{\infty }}}\cap \mathcal {B}$, it follows from Proposition 4.6 that ![]() ${\langle \mathbb {G}\rangle _{\equiv }^{\mathcal I}}$ is a
${\langle \mathbb {G}\rangle _{\equiv }^{\mathcal I}}$ is a ![]() $G_{\delta }$-set in any
$G_{\delta }$-set in any ![]() $\mathcal {I}\in \{\mathcal {P},\mathcal {P}_{\infty },\mathcal {B}\}$.
$\mathcal {I}\in \{\mathcal {P},\mathcal {P}_{\infty },\mathcal {B}\}$.
By Corollary 2.10, we also have that ![]() ${\langle \mathbb {G}\rangle _{\equiv }^{\mathcal I}}$ is dense in
${\langle \mathbb {G}\rangle _{\equiv }^{\mathcal I}}$ is dense in ![]() $\mathcal I$ for every
$\mathcal I$ for every ![]() $\mathcal {I}\in \{\mathcal {P},\mathcal {P}_{\infty },\mathcal {B}\}$.
$\mathcal {I}\in \{\mathcal {P},\mathcal {P}_{\infty },\mathcal {B}\}$.
4.2 Generic objects in  $SB(X)$
$SB(X)$
In this subsection, we address Problem 5.5 from [Reference Godefroy and Saint-Raymond19], which suggests investigating generic properties of admissible topologies. We have both positive and negative results. The positive result is Theorem 4.10, which shows that the isometry class of the Gurariĭ space, as a subset of ![]() $SB(\mathbb {G})$, is a dense
$SB(\mathbb {G})$, is a dense ![]() $G_{\delta }$-set in the Wijsman topology. The negative results are Propositions 4.11 and 4.13 and Theorem 4.12.
$G_{\delta }$-set in the Wijsman topology. The negative results are Propositions 4.11 and 4.13 and Theorem 4.12.
Definition 4.8. Given a closed set H in X, we denote by ![]() $E^{-}(H)$ the set
$E^{-}(H)$ the set ![]() $SB(X)\setminus E^{+}(X\setminus H)$: that is,
$SB(X)\setminus E^{+}(X\setminus H)$: that is, ![]() $E^{-}(H) = \{F\in SB(X):\; F\subseteq H\}$. Obviously, this is a closed set in any admissible topology on
$E^{-}(H) = \{F\in SB(X):\; F\subseteq H\}$. Obviously, this is a closed set in any admissible topology on ![]() $SB(X)$.
$SB(X)$.
Definition 4.9. Let X be an isometrically universal separable Banach space. By ![]() $\tau _{W}$, we denote the restriction of the Wijsman topology from
$\tau _{W}$, we denote the restriction of the Wijsman topology from ![]() $\mathcal {F}(X)$ to
$\mathcal {F}(X)$ to ![]() $SB(X)$: that is, the minimal topology on
$SB(X)$: that is, the minimal topology on ![]() $SB(X)$ such that the mappings
$SB(X)$ such that the mappings ![]() $SB(X)\ni F\mapsto \operatorname {dist}_{X}(x,F)$ are continuous for every
$SB(X)\ni F\mapsto \operatorname {dist}_{X}(x,F)$ are continuous for every ![]() $x\in X$. Note that
$x\in X$. Note that ![]() $\tau _{W}$ is admissible; see [Reference Godefroy and Saint-Raymond19, Section 2].
$\tau _{W}$ is admissible; see [Reference Godefroy and Saint-Raymond19, Section 2].
Theorem 4.10. The isometry class ![]() ${\langle \mathbb {G}\rangle _{\equiv }}$ is a dense
${\langle \mathbb {G}\rangle _{\equiv }}$ is a dense ![]() $G_{\delta }$-set in
$G_{\delta }$-set in ![]() $(SB(\mathbb {G}),\tau _{W})$.
$(SB(\mathbb {G}),\tau _{W})$.
Proof. The isometry class ![]() ${\langle \mathbb {G}\rangle _{\equiv }}$ is a
${\langle \mathbb {G}\rangle _{\equiv }}$ is a ![]() $G_{\delta }$-set in
$G_{\delta }$-set in ![]() $(SB(\mathbb {G}),\tau _{W})$ since it is a
$(SB(\mathbb {G}),\tau _{W})$ since it is a ![]() $G_{\delta }$-set in
$G_{\delta }$-set in ![]() $\mathcal {P}$ (by Theorem 4.1) and there is a continuous reduction from
$\mathcal {P}$ (by Theorem 4.1) and there is a continuous reduction from ![]() $(SB(\mathbb {G}),\tau _{W})$ to
$(SB(\mathbb {G}),\tau _{W})$ to ![]() $\mathcal {P}$ by Theorem 3.3. So we must show that it is dense.
$\mathcal {P}$ by Theorem 3.3. So we must show that it is dense.
Choose a basic open set N in ![]() $\tau _{W}$ that is given by some closed subspace
$\tau _{W}$ that is given by some closed subspace ![]() $X\subseteq \mathbb {G}$, finitely many points
$X\subseteq \mathbb {G}$, finitely many points ![]() $x_{1},\ldots ,x_{n}\in \mathbb {G}$ and
$x_{1},\ldots ,x_{n}\in \mathbb {G}$ and ![]() $\varepsilon>0$ so that
$\varepsilon>0$ so that
Let us find a space G isometric to ![]() $\mathbb {G}$ such that
$\mathbb {G}$ such that ![]() $G\in N$. Let Y be
$G\in N$. Let Y be ![]() $\operatorname {span} \{X\cup \{x_{i}\colon i\leq n\}\}$. Since X embeds into both Y and
$\operatorname {span} \{X\cup \{x_{i}\colon i\leq n\}\}$. Since X embeds into both Y and ![]() $\mathbb {G}$, we can consider the push-out of that diagram: that is, the amalgamated sum of Y and
$\mathbb {G}$, we can consider the push-out of that diagram: that is, the amalgamated sum of Y and ![]() $\mathbb {G}$ along the common subspace X. Recall this is nothing but the quotient
$\mathbb {G}$ along the common subspace X. Recall this is nothing but the quotient ![]() $(\mathbb {G}\oplus _{1} Y)/Z$, where
$(\mathbb {G}\oplus _{1} Y)/Z$, where ![]() $Z=\{(z,-z)\colon z\in X\}$. Denote this space by
$Z=\{(z,-z)\colon z\in X\}$. Denote this space by ![]() $G^{\prime }$, and notice that
$G^{\prime }$, and notice that ![]() $\mathbb G$ is naturally embedded into
$\mathbb G$ is naturally embedded into ![]() $G^{\prime }$. It is straightforward to verify that for each
$G^{\prime }$. It is straightforward to verify that for each ![]() $i\leq n$,
$i\leq n$, ![]() $\operatorname {dist}_{G^{\prime }}(x_{i},\mathbb {G})=\operatorname {dist}_{\mathbb {G}} (x_{i},X)$. Since
$\operatorname {dist}_{G^{\prime }}(x_{i},\mathbb {G})=\operatorname {dist}_{\mathbb {G}} (x_{i},X)$. Since ![]() $\mathbb {G}$ is universal, there is a linear isometric embedding
$\mathbb {G}$ is universal, there is a linear isometric embedding ![]() $\iota : G^{\prime }\hookrightarrow \mathbb {G}$. As there is a linear isometry
$\iota : G^{\prime }\hookrightarrow \mathbb {G}$. As there is a linear isometry ![]() $\phi :\iota [\operatorname {span}\{x_{i}\colon i\leq n\}]\rightarrow \operatorname {span}\{x_{i}\colon i\leq n\}$, by [Reference Kubiś and Solecki22, Theorem 1.1], there is a bijective linear isometry
$\phi :\iota [\operatorname {span}\{x_{i}\colon i\leq n\}]\rightarrow \operatorname {span}\{x_{i}\colon i\leq n\}$, by [Reference Kubiś and Solecki22, Theorem 1.1], there is a bijective linear isometry ![]() $\Phi :\mathbb {G}\rightarrow \mathbb {G}$ such that
$\Phi :\mathbb {G}\rightarrow \mathbb {G}$ such that ![]() $\|\Phi \circ \iota (x_{i})-x_{i}\|<\varepsilon $ for each
$\|\Phi \circ \iota (x_{i})-x_{i}\|<\varepsilon $ for each ![]() $i\leq n$. By the triangle inequality, it follows that
$i\leq n$. By the triangle inequality, it follows that ![]() $G:=\Phi \circ \iota [\mathbb {G}\subseteq G^{\prime }]$ satisfies for each
$G:=\Phi \circ \iota [\mathbb {G}\subseteq G^{\prime }]$ satisfies for each ![]() $i\leq n$,
$i\leq n$, ![]() $|\operatorname {dist}_{\mathbb {G}}(x_{i},G)-\operatorname {dist}_{\mathbb {G}}(x_{i},X)|<\varepsilon $, so it is the desired space isometric to
$|\operatorname {dist}_{\mathbb {G}}(x_{i},G)-\operatorname {dist}_{\mathbb {G}}(x_{i},X)|<\varepsilon $, so it is the desired space isometric to ![]() $\mathbb {G}$ lying in the open set N.
$\mathbb {G}$ lying in the open set N.
The rest of the section is devoted to negative results. They show that the definition of an admissible topology allows a lot of flexibility by which one can alter which properties should be meager or not.
Proposition 4.11. Let X be an isometrically universal separable Banach space, and let ![]() $\tau $ be an admissible topology on
$\tau $ be an admissible topology on ![]() $SB(X)$. Then there exists an admissible topology
$SB(X)$. Then there exists an admissible topology ![]() $\tau ^{\prime }\supseteq \tau $ on
$\tau ^{\prime }\supseteq \tau $ on ![]() $SB(X)$ such that the set
$SB(X)$ such that the set ![]() ${\langle \mathbb {G}\rangle _{\simeq }}$ is nowhere dense in
${\langle \mathbb {G}\rangle _{\simeq }}$ is nowhere dense in ![]() $(SB_{\infty }(X),\tau ^{\prime })$.
$(SB_{\infty }(X),\tau ^{\prime })$.
Proof. By the definition of an admissible topology, we may pick ![]() $(U_{n})_{n\in \mathbb N}$, a basis of the topology
$(U_{n})_{n\in \mathbb N}$, a basis of the topology ![]() $\tau $, such that for every
$\tau $, such that for every ![]() $n\in \mathbb N$, there are nonempty open sets
$n\in \mathbb N$, there are nonempty open sets ![]() $V_{k}^{n}$,
$V_{k}^{n}$, ![]() $k=1,\ldots ,N_{n}$, and
$k=1,\ldots ,N_{n}$, and ![]() $W_{n}$ in X such that the set
$W_{n}$ in X such that the set ![]() $U_{n}^{\prime }$ defined by
$U_{n}^{\prime }$ defined by
 $$ \begin{align*} U_{n}^{\prime} = \bigcap_{k=1}^{N_{n}} E^{+}(V_{k}^{n})\setminus E^{+}(W_{n}) \end{align*} $$
$$ \begin{align*} U_{n}^{\prime} = \bigcap_{k=1}^{N_{n}} E^{+}(V_{k}^{n})\setminus E^{+}(W_{n}) \end{align*} $$is a nonempty subset of ![]() $U_{n}$.
$U_{n}$.
We claim that for every ![]() $n\in \mathbb N$, there is
$n\in \mathbb N$, there is ![]() $F_{n}\in U_{n}^{\prime }$ such that
$F_{n}\in U_{n}^{\prime }$ such that ![]() $\mathbb {G}\not \hookrightarrow F_{n}$. Indeed, pick an arbitrary
$\mathbb {G}\not \hookrightarrow F_{n}$. Indeed, pick an arbitrary ![]() $Z\in U_{n}^{\prime }$. We may without loss of generality assume there is
$Z\in U_{n}^{\prime }$. We may without loss of generality assume there is ![]() $H_{0}\subseteq Z$ with
$H_{0}\subseteq Z$ with ![]() $H_{0}\simeq \mathbb {G}$, and since
$H_{0}\simeq \mathbb {G}$, and since ![]() $\mathbb {G}$ is isometrically universal, there is
$\mathbb {G}$ is isometrically universal, there is ![]() $H_{1}\subseteq H_{0}$ with
$H_{1}\subseteq H_{0}$ with ![]() $H_{1}\simeq \ell _{2}$. Now, pick points
$H_{1}\simeq \ell _{2}$. Now, pick points ![]() $v_{k}\in Z\cap V_{k}^{n}$,
$v_{k}\in Z\cap V_{k}^{n}$, ![]() $k=1,\ldots ,N_{n}$. Then we put
$k=1,\ldots ,N_{n}$. Then we put ![]() $F_{n}:= \overline {\operatorname {span}} \{v_{1},\ldots ,v_{N_{n}},u:\; u\in H_{1}\}$. Since
$F_{n}:= \overline {\operatorname {span}} \{v_{1},\ldots ,v_{N_{n}},u:\; u\in H_{1}\}$. Since ![]() $F_{n}$ is a subset of Z, we have
$F_{n}$ is a subset of Z, we have ![]() $F_{n}\notin E^{+}(W_{n})$, and since it contains the points
$F_{n}\notin E^{+}(W_{n})$, and since it contains the points ![]() $v_{1},\ldots ,v_{N_{n}}$, we have
$v_{1},\ldots ,v_{N_{n}}$, we have ![]() $F_{n}\in U_{n}^{\prime }$. Moreover, it is a space isomorphic to
$F_{n}\in U_{n}^{\prime }$. Moreover, it is a space isomorphic to ![]() $\ell _{2}$, and so
$\ell _{2}$, and so ![]() $\mathbb {G}\not \hookrightarrow F_{n}$.
$\mathbb {G}\not \hookrightarrow F_{n}$.
Thus, for every ![]() $n\in \mathbb N$, there is a closed subspace
$n\in \mathbb N$, there is a closed subspace ![]() $F_{n}$ of X such that
$F_{n}$ of X such that ![]() $U_{n}\cap E^{-}(F_{n})$ is a nonempty set disjoint from
$U_{n}\cap E^{-}(F_{n})$ is a nonempty set disjoint from ![]() ${\langle \mathbb {G}\rangle _{\simeq }}$.
${\langle \mathbb {G}\rangle _{\simeq }}$.
It is a classical fact (see, e.g., [Reference Kechris21, Lemma 13.2 and Lemma 13.3]) that the topology ![]() $\tau ^{\prime }$ generated by
$\tau ^{\prime }$ generated by ![]() $\tau \cup \{E^{-}(F_{n}):\; n\in \mathbb N\}$ is Polish. It is easy to check it is admissible. Moreover, for every
$\tau \cup \{E^{-}(F_{n}):\; n\in \mathbb N\}$ is Polish. It is easy to check it is admissible. Moreover, for every ![]() $n\in \mathbb N$, we have that
$n\in \mathbb N$, we have that ![]() $U_{n}\cap E^{-}(F_{n})$ is a nonempty
$U_{n}\cap E^{-}(F_{n})$ is a nonempty ![]() $\tau ^{\prime }$-open set in
$\tau ^{\prime }$-open set in ![]() $U_{n}$ disjoint from
$U_{n}$ disjoint from ![]() ${\langle \mathbb {G}\rangle _{\simeq }}$. It follows that nonempty sets of the form
${\langle \mathbb {G}\rangle _{\simeq }}$. It follows that nonempty sets of the form ![]() $U_{n}\cap \bigcap _{m\in I}E^{-}(F_{m})$, for finite
$U_{n}\cap \bigcap _{m\in I}E^{-}(F_{m})$, for finite ![]() $I\subseteq \mathbb {N}$, give us a
$I\subseteq \mathbb {N}$, give us a ![]() $\pi $-basis of
$\pi $-basis of ![]() $\tau ^{\prime }$. Since obviously each element of the form
$\tau ^{\prime }$. Since obviously each element of the form ![]() $U_{n}\cap \bigcap _{m\in I} E^{-}(F_{m})$ is disjoint from
$U_{n}\cap \bigcap _{m\in I} E^{-}(F_{m})$ is disjoint from ![]() ${\langle \mathbb {G}\rangle _{\simeq }}$, the set
${\langle \mathbb {G}\rangle _{\simeq }}$, the set ![]() ${\langle \mathbb {G}\rangle _{\simeq }}$ is
${\langle \mathbb {G}\rangle _{\simeq }}$ is ![]() $\tau ^{\prime }$-nowhere dense.
$\tau ^{\prime }$-nowhere dense.
Actually, one may observe that the same proof gives the following more general result, where the pair ![]() $(\mathbb {G},\ell _{2})$ is replaced by a more general pair of Banach spaces.
$(\mathbb {G},\ell _{2})$ is replaced by a more general pair of Banach spaces.
Theorem 4.12. Let X be an isometrically universal separable Banach space, and let ![]() $\tau $ be an admissible topology on
$\tau $ be an admissible topology on ![]() $SB(X)$. Let Y and Z be infinite-dimensional Banach spaces such that
$SB(X)$. Let Y and Z be infinite-dimensional Banach spaces such that ![]() $Y\hookrightarrow Z$ and
$Y\hookrightarrow Z$ and ![]() $Z\not \hookrightarrow Y\oplus F$ for every finite-dimensional space F.
$Z\not \hookrightarrow Y\oplus F$ for every finite-dimensional space F.
Then there exists an admissible topology ![]() $\tau ^{\prime }\supseteq \tau $ on
$\tau ^{\prime }\supseteq \tau $ on ![]() $SB(X)$ such that the set
$SB(X)$ such that the set ![]() ${\langle Z\rangle _{\simeq }}$ is nowhere dense in
${\langle Z\rangle _{\simeq }}$ is nowhere dense in ![]() $(SB_{\infty }(X),\tau ^{\prime })$.
$(SB_{\infty }(X),\tau ^{\prime })$.
It is even possible to find an admissible topology ![]() $\tau $ such that
$\tau $ such that ![]() ${\langle \ell _{2}\rangle _{\equiv }}$ is not a meager set in
${\langle \ell _{2}\rangle _{\equiv }}$ is not a meager set in ![]() $(SB_{\infty }(X),\tau )$, which is an immediate consequence of the following more general observation (property
$(SB_{\infty }(X),\tau )$, which is an immediate consequence of the following more general observation (property ![]() $(P)$ below would be ‘X is isometric to
$(P)$ below would be ‘X is isometric to ![]() $\ell _{2}$’).
$\ell _{2}$’).
Proposition 4.13. Let X be an isometrically universal separable Banach space and ![]() $\tau $ be an admissible topology on
$\tau $ be an admissible topology on ![]() $SB_{\infty }(X)$. Let
$SB_{\infty }(X)$. Let ![]() $(P)$ be a non-void property (i.e., there are spaces with such a property) of infinite-dimensional Banach spaces closed under taking subspaces. Then there is an admissible topology
$(P)$ be a non-void property (i.e., there are spaces with such a property) of infinite-dimensional Banach spaces closed under taking subspaces. Then there is an admissible topology ![]() $\tau ^{\prime }\supseteq \tau $ such that the set
$\tau ^{\prime }\supseteq \tau $ such that the set ![]() $\{Y\in SB_{\infty }(X)\colon Y\text { has }(P)\}$ has non-empty interior in
$\{Y\in SB_{\infty }(X)\colon Y\text { has }(P)\}$ has non-empty interior in ![]() $(SB_{\infty }(X),\tau ^{\prime })$.
$(SB_{\infty }(X),\tau ^{\prime })$.
Proof. Pick ![]() $F\in SB_{\infty }(X)$ with
$F\in SB_{\infty }(X)$ with ![]() $(P)$. Using again the classical fact (see, e.g., [Reference Kechris21, Lemma 13.2]) that the topology
$(P)$. Using again the classical fact (see, e.g., [Reference Kechris21, Lemma 13.2]) that the topology ![]() $\tau ^{\prime }$ generated by
$\tau ^{\prime }$ generated by ![]() $\tau \cup \{E^{-}(F)\}$ is Polish, it is easy to check it is admissible. Then the
$\tau \cup \{E^{-}(F)\}$ is Polish, it is easy to check it is admissible. Then the ![]() $\tau ^{\prime }$-open set
$\tau ^{\prime }$-open set ![]() $E^{-}(F)$ is a subset of
$E^{-}(F)$ is a subset of ![]() $\{Y\in SB_{\infty }(X)\colon Y\text { has }(P)\}$.
$\{Y\in SB_{\infty }(X)\colon Y\text { has }(P)\}$.
Conflicts of Interest
None
Funding statement
M. Cúth was supported by Charles University Research program No. UNCE/SCI/023 and by the Czech Science Foundation, project no. GAČR 17-00941S. Research of M. Doležal was supported by the GAČR project 17-27844S and RVO: 67985840. M. Doucha was supported by the GAČR project 19-05271Y and RVO: 67985840. O. Kurka was supported by the Czech Science Foundation, project no. GAČR 17-00941S and RVO: 67985840.















